Chương 5: Thanh Chịu Xoắn Thuần Túy | Môn Sức bền vật liệu - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58970315 09-Aug-22
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI
KHOA XÂY DỰNG DÂN DỤNG VÀ CÔNG NGHIỆP
www: xaydung.huce.edu.vn
Sức bền Vật liệu
Bộ môn Sức bền Vật liệu – Khoa Xây dựng Dân dụng và Công nghiệp
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI 1
CHƯƠNG 5: THANH CHỊU XOẮN THUẦN TÚY 5.1. Kh
áiniệm -Cách xác định mômen xoắn nội lực
5.2 . Ứng suất trên mặt cắt ngang của thanh tròn chịu xoắn 5.3. Bi
ến dạng của thanh tròn chịu xoắn 5.4. Đi
ều kiện bền, ba bài toán cơ bản 5.5 . Bài toánsiêutĩnh
5.6 *. Điều kiện cứng của thanh tròn chịu xoắn
5.7 *. Thế năng biến dạng đàn hồi của thanh tròn chịu xoắn 2 lOMoAR cPSD| 58970315 09-Aug-22
5.1. Khái niệm - Cách xác định mômen xoắn nội lực
5.1.1 . Khái niệm
Thanh chịu xoắn thuần túy là thanh mà khi chịu lực, trên
mặt cắt ngang chỉ tồn tại duy nhất một thành phần ứng lực
là mô men xoắn M . z
Ngoạilựcgâyxoắn:mômenxoắntập
trung,mômenxoắnphânbố,ngẫulực trongmặtcắtngang 3 lOMoAR cPSD| 58970315 09-Aug-22
5.1. Khái niệm - Cách xác định mômen xoắn nội lực
5.1 . Khái niệm - Cách xác định mômen xoắn nội lực Ví dụ : 4 V í dụ : 5 lOMoAR cPSD| 58970315 09-Aug-22
5.1. Khái niệm - Cách xác định mômen xoắn nội lực
5.1 . Khái niệm - Cách xác định mômen xoắn nội lực Ví dụ: M B M A 6 7 lOMoAR cPSD| 58970315 09-Aug-22
5.1. Khái niệm - Cách xác định mômen xoắn nội lực
5.2. Ứng suất trên mặt cắt ngang thanh tròn chịu xoắn
Thí nghiệm: Trước khi tiến hành thí
nghiệm, vẽ lên bề mặt thanh
- Những đường thẳng // với trục thanh
- Các đường tròn chu tuyến
→ tạo thành lưới ô vuông
- Bán kính của mặt cắt ngang tại 2 đầu thanh Quan sát: M
- Những đường thẳng // với trục
thanh bị xoắn, nghiêng góc γ so với phương ban đầu
- Các đường tròn vẫn phẳng và
vuông góc với trục thanh . Khoảng
cách giữa các đường tròn hầu như M không thau đổi
- Các bán kính vẫn thẳng, độ dài không đổi. 8 lOMoAR cPSD| 58970315 09-Aug-22
5.2. Ứng suất trên mặt cắt ngang thanh tròn chịu xoắn
Các giả thiết (về tính chất biến dạng):
Giả thiết 1: Giả thuyết mặt cắt ngang phẳng Bernoulli.
Mặt cắt ngang trước và sau biến dạng phẳng và thẳng
góc với trục thanh, chỉ thực hiện chuyển động xoay
quanh trục. Khoảng các giữa các mặt cắt là không đổi. Jacob Bernoulli
Giả thiết 2: Giả thuyết về các bán kính (1654-1705)
Các bán kính của thanh trước và sau biến dạng vẫn
thẳng và có độ dài không đổi.
Chú ý: Vật liệu làm việc tuân theo định luật Hooke Robert Hooke (1635 -1703)
5.2 . Ứng suất trên mặt cắt ngang thanh tròn chịu xoắn
Ứng suất trên mặt cắt ngang
• Giả thuyết 1 → ε = 0 → σ = 0 z z M
• Giả thuyết 2 → ε = ε = 0 → σ = σ = 0 x y x y
→ Trên mặt cắt ngang chỉ có ứng suất tiếp, phương vuông góc bán kính
và chiều phù hợp với chiều của mô men xoắn nội lực.
M - mô men xoắn trên mặt cắt đang xét z
I - mô men quán tính độc cực của tiết diện p
r – tọa độ điểm tính ứng suất ✓ Hình tròn đặc: ✓ Hình tròn rỗng: 10 lOMoAR cPSD| 58970315 09-Aug-22 9 lOMoAR cPSD| 58970315 09-Aug-22
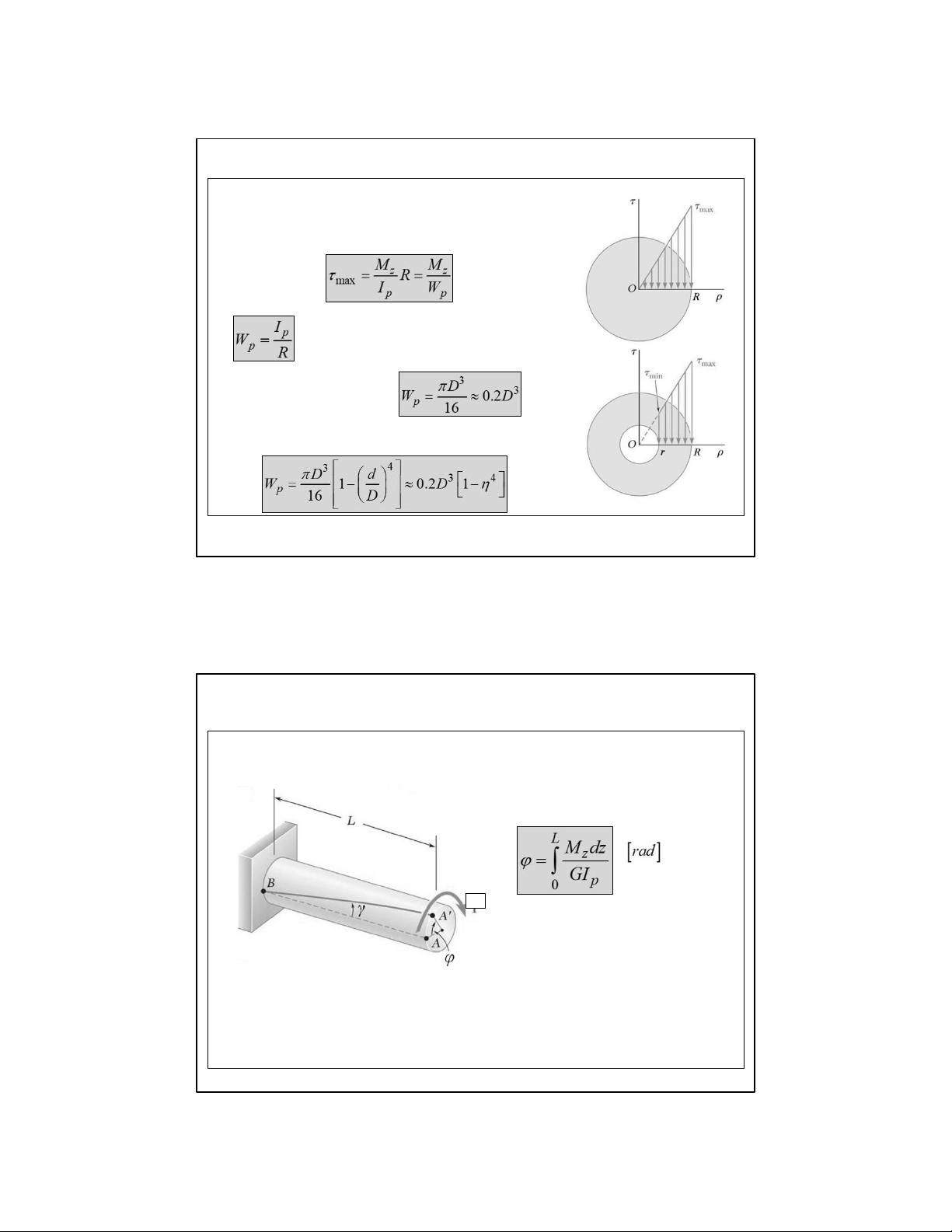
5.2. Ứng suất trên mặt cắt ngang thanh tròn chịu xoắn
Phân bố ứng suất trên mặt cắt ngang
Ứng suất tiếp lớn nhất tại các điểm nằm trên chu vi đường tròn
: Mô men chống xoắn của mặt cắt ngang Tiết diện tròn: Hình vành khăn: 11
5.3 . Biến dạng của thanh tròn chịu xoắn
Góc xoay giữa 2 mặt cắt cách nhau L: M
G – Mô đun đàn hồi trượt
I – Mô men quán tính độc cực p
GI – Độ cứng chống xoắn của tiết diện thanh p 12 lOMoAR cPSD| 58970315 09-Aug-22
5.3. Biến dạng của thanh tròn chịu xoắn • Nếu : M
• Nếu thanh gồm nhiều đoạn, G trên mỗi đoạn n I pn M G L 1 Ip1 n M L 1 13 lOMoAR cPSD| 58970315 09-Aug-22
5.3. Biến dạng của thanh tròn chịu xoắn 15
5.4 . Điều kiện bền – Ba bài toán cơ bản ❖ Điềukiệnbền:
: t 0 được xác định từ thí nghiệm : Theo thuyết bền 3 : Theo thuyết bền 4 16 lOMoAR cPSD| 58970315 09-Aug-22
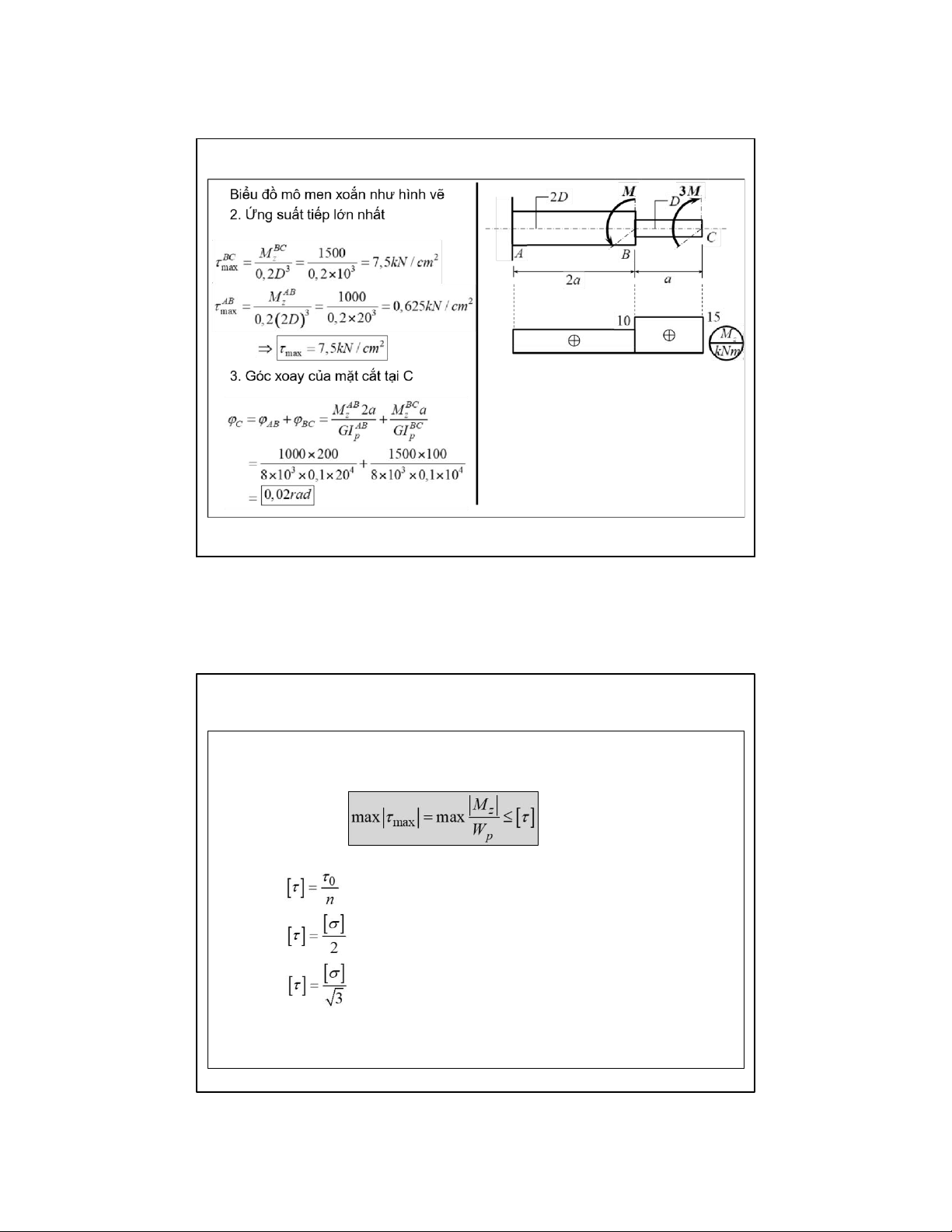
5.4. Điều kiện bền – Ba bài toán cơ bản
❖ Ba dạng bài toán cơ bản:
✓ Kiểm tra điều kiện bền:
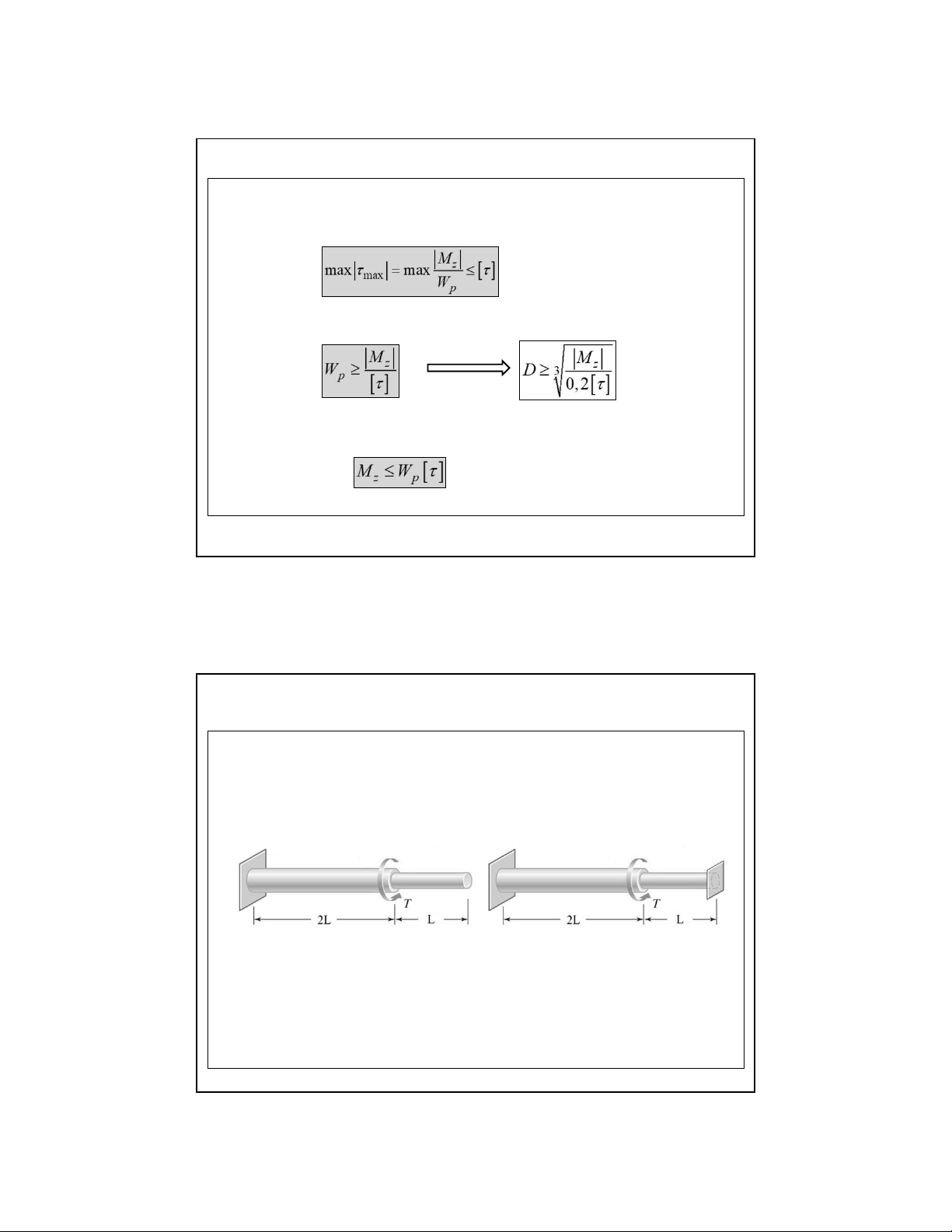
✓ Xác định kích thước tiết diện theo điều kiện
✓ Xác định giá trị tải trọng cho phép theo điều kiện bền 17 5.5 . Bài toán siêu tĩnh
❖ Bài toán siêu tĩnh: phương trình cân bằng tĩnh học là
không đủ để xác định phản lực hay các thành phần ứng lực trong hệ.
❖ Số ẩn > Số phương trình
→ Viết phương trình bổ trợ
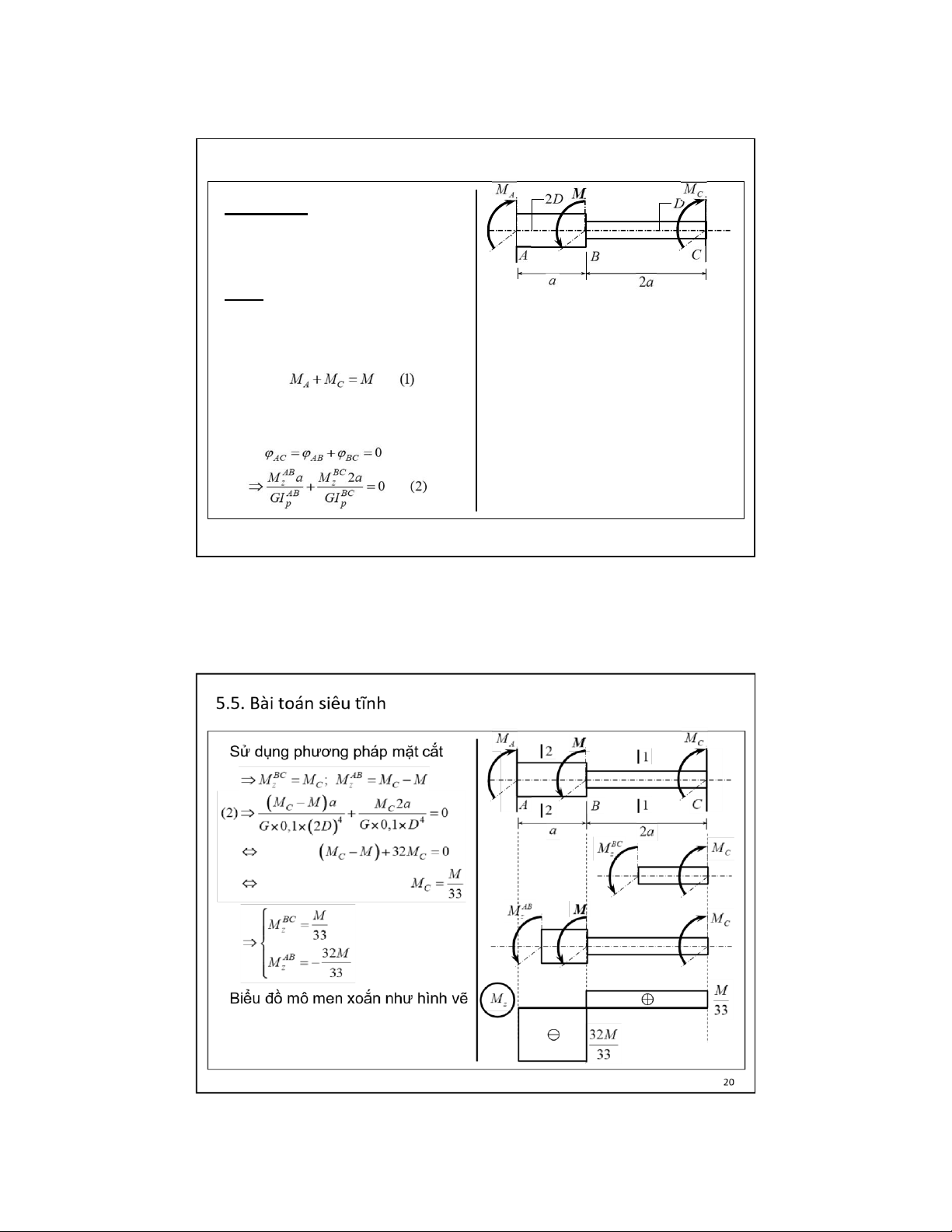
→ thường sử dụng phương trình biến dạng 18 lOMoAR cPSD| 58970315 09-Aug-22 5.5. Bài toán siêu tĩnh Ví dụ 5.2:
Thanh tiết diện tròn thay đổi chịu
lực như hình vẽ. Vẽ biểu đồ mô men xoắn. Giải:
1. Giả thiết phản lực tại A và C
như hình vẽ. Phương trình cân bằng: → Bài toán siêu tĩnh . P
2 hương trình biến dạng : 19 lOMoAR cPSD| 58970315 09-Aug-22 SỨC BỀN VẬT LIỆU lOMoAR cPSD| 58970315 09-Aug-22 Thank you for your attention
BM Sức bền Vật liệu – Đại học Xây dựng Hà Nội lOMoAR cPSD| 58970315 09-Aug-22 21