








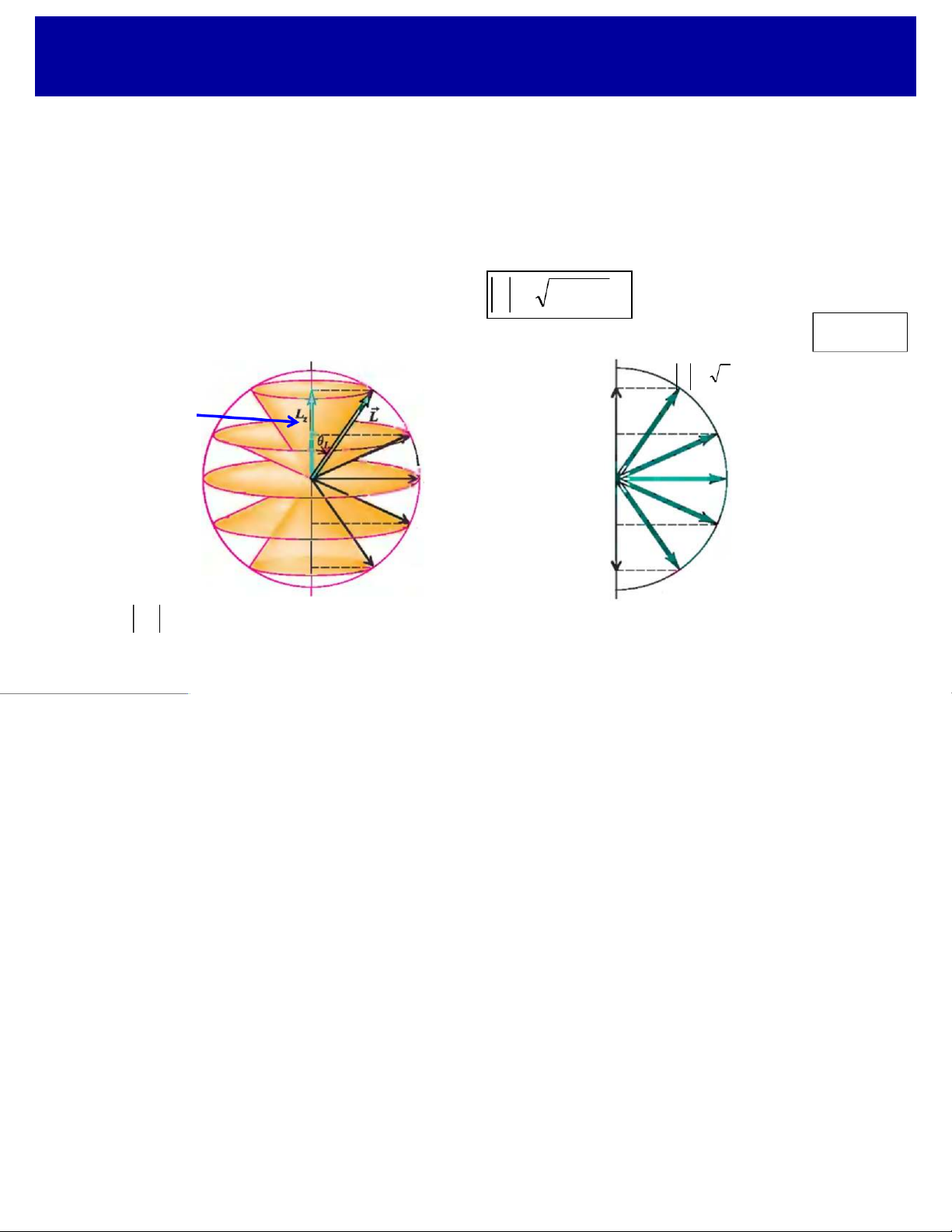




Preview text:
( ) 25.1. Nguyên tử Hidro
25.1.1. Phương trình Schrodinger và nghiệm (thừa nhận) cho electron trong nguyên tử H
25.1.2. Các kết luận về nguyên tử H (năng lượng, trạng thái, xác suất tìm thấy electron).
25.2. Nguyên tử kim loại kiềm (biểu thức năng lượng, các dãy vạch quang phổ)
25.3. Mômen động lượng quỹ đạo và mômen từ quỹ đạo của electron. Hiệu ứng Zeeman 25.4. Spin của electron
25.4.1. Sự tồn tại spin electron
25.4.2. Cấu trúc tế vi của các mức năng lượng
25.4.3. Quy tắc lựa chọn và cấu tạo bội của vạch quang phổ
25.5. Nguyên lý Pauli và nguyên tắc sắp xếp các electron theo các
trạng thái. Bảng tuần hoàn (giới thiệu và giải thích).z 1 1. Nguyên tử hydro
a. Phương trình Schrödinger và nghiệm
§Hàm sóng y và năng lượng của electron trong nguyên tử
hydro là nghiệm của phương trình Schrödinger.
§Thế năng tương tác giữa hạt nhân và electron: z 2 =-Ze U e- 4pe r 0 0 q £ r £ ¥
§Phương trình Schrödinger có dạng: r p/2 £ q £ -p/2 2 m æ Ze ö p+ Dy (y ) 2 , x ,y z + + e ç ÷ W =,x,y z 0 j y 2 ( ) ! è ø 4pe 0£ j £ 2p 0r
melà khối lượng electron; Z = 1 với hydro x
Do U phụ thuộc r nên bài toán có tính đối xứng cầu
à Chuyển hệ tọa độ Descartes sang tọa độ cầu: ì x =r sin cqojs ï= í y r sinq sjin ï=z r cos î q 1. Nguyên tử hydro
Phương trình Schrödinger trong hệ tọa độ cầu: 2 2 1 1¶ ¶æ ö ¶ æ ¶ ö ¶ æ ö 2 y 1 y y Ze2 + sinq y + + ç ÷ ç ÷ e m r ç ÷ W+ = 0 2 2 2 2 2 2 r r ¶ ¶ r èr ø sin ¶ s qi è nq q r ¶ ø ¶ q j ! è ø pe4 r0
Giải phương trình trên bằng phương pháp phân li biến số, nghiệm
của phương trình như sau: ØHàm sóng y (r , ,q j ) = R r Y nl lm . ( ) , q j ( ) trong đó:
Rnl(r)là hàm xuyên tâm, chỉ phụ thuộc vào độ lớn của r.
Ylm(q,j ) là hàm cầu, phụ thuộc vào các góc q và j . Với = 1, 2 n
, 3, 4,… : số lượng tử chính
l= 0, 1, 2, 3,…n- 1 : số lượng tử quĩ đạo (orbital)
m= 0, ±1, ±2,… ±l: số lượng tử từ 4 1 m e Rh ØNăng lượng: e Wn =-=- 2 n n2(4) 2 2 2 pe ! 0 4 m e e 15 1
với R là hằng số Rydberg R 3, 29.10 s- = =4p (4p ) 23 e ! 0 1. Nguyên tử hydro
§Dạng cụ thể của một số hàm Rnl(r)và Yl,m( q,j ).
Hàm xuyên tâm Rn,l Hàm cầu Ylm 1. Nguyên tử hydro Wn(eV) b. Các kết luận
Kế luận 1: Sự lượng tử hoá năng lượng Năng lượng của electron: Trạng thái kích
qWnchỉ phụ thuộc vào số nguyên n thích
nên năng lượng biến thiên gián đoạn
è năng lượng bị lượng tử hóa. qNăng lượng Wnluôn âm. Khi n ®¥ thì Wn ® 0.
mức W1(n = 1): mức K (lớp K),
mức W2(n = 2): mức L (lớp L), Trạng thái
mức W3(n = 3): mức M (lớp M),… cơ
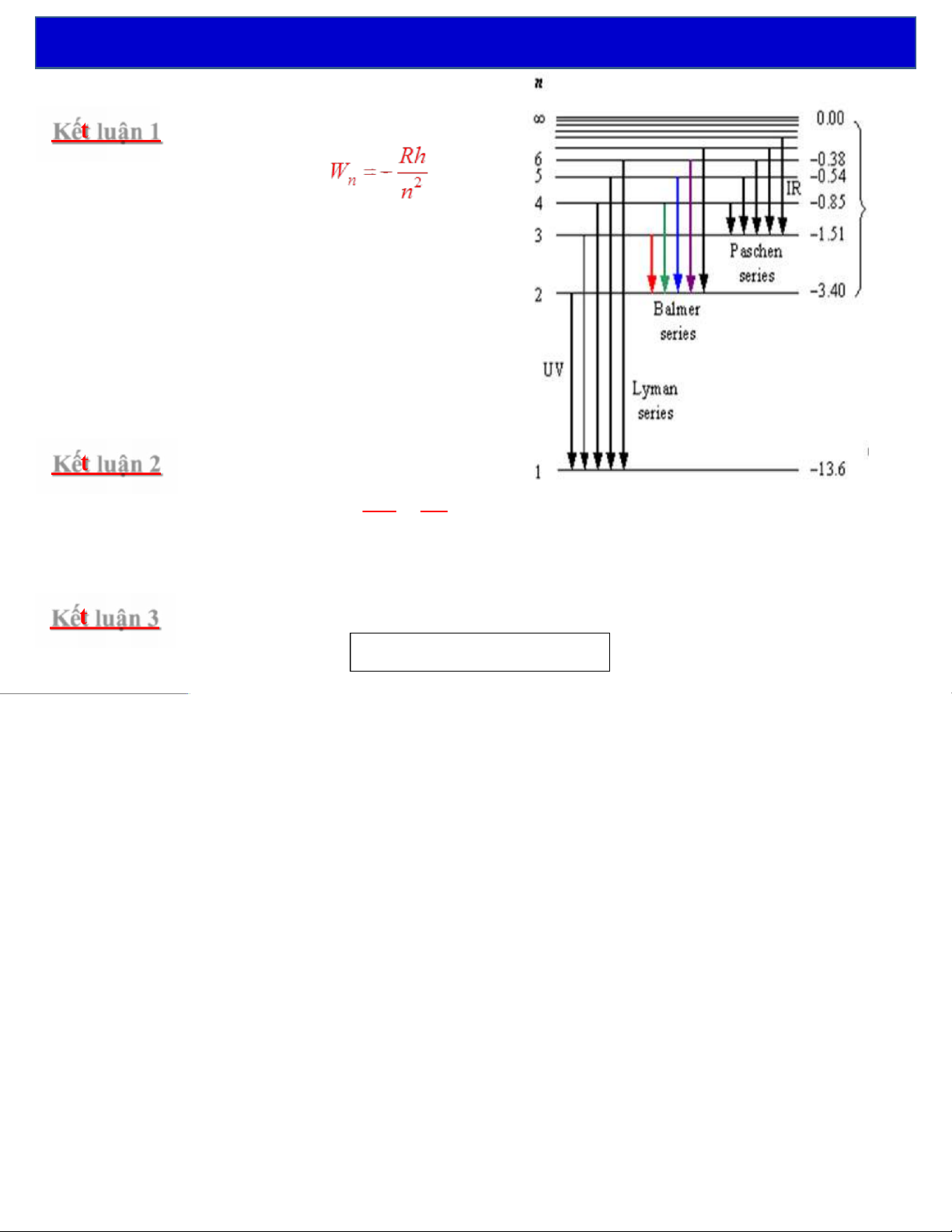
Kế luận 2: Cấu tạo vạch của quang phổ bản æ 1ö 1 W- W =n h Þ=-v R n n ' ç ÷ 2 2 è ø n'n
Dãy Paschen: n’ = 3, n = 4, 5, 6…
Dãy Lyman: n’ = 1, n = 2, 3, 4…
Dãy Brackett: n’ = 4, n = 5, 6, 7…
Dãy Balmer: n’ = 2, n = 3, 4, 5…
Dãy Pfund: n‘ = 5, n = 6, 7, 8…
Kế luận 3: Năng lượng ion hóa là năng lượng cần thiết để e-bứt ra khỏi nguyên tử. =-= i Wh 1 W¥ W 13, 6 eV 1. Nguyên tử hydro
Kế luận 4: Sự suy biến mức năng lượng
Trạng thái lượng tử của e-trong nguyên tử hydro được mô tả bởi hàm sóng: y r,q ,j =q jR r .Y , nlm ( ) nl lm ( ) ( )
F Hàm trạng thái phụ thuộc số lượng tử n, l, m
à chỉ 1 trong 3 số lượng tử
thay đổi à có một trạng thái khác. Với xác định thì: n l= 0, 1, 2, 3,… – n 1 (có n giá trị của l)
và m= 0, ±1, ±2,… ±l(có 2l+1 giá trị của m)
hay với mỗi mức năng lượng Wn, số trạng thái (hàm sóng) khác nhau có được là: n - 1 å + 1 ( 2n - n (2l+ ) 1 = + 1 + 3 .. + . (2n - ) 1 = ) 1 = 2 n è mức W bị n suy biến bội n2 l=0 2
(một mức năng lượng có nhiều trạng thái gọi là sự suy biến NL)
F Trạng thái của e-được ký hiệu là s,p,d,f… tùy vào giá trị của l. n1 2 3 4 l0 0 1012 … 23 Lớp 1s 2s2p3s3 3 p d … 4d 4f m0 0 -1 0 +1 0 -1 0 +1 -2 -1 0 +1 +2 … … … … 1. Nguyên tử hydro
Kế luận 5: Xác suất tìm electron
F Xác suất tìm thấy vi hạt trong thể tích bất kỳ: 2 Y n,l,=m dV 1 ò 2 2 V t Mật Y độ=xác R n suất: 2 l m Y n l ,l ,m , , t Phần tử thể tích: dV =r2dr sin q dqdj 2 2 2 2 Þ Y ò n l = n l ,sm ,in dVl m òR r dr , òY q q d j d , V
xác suất tìm thấy hạt tại vị xác suất tìm thấy hạt
trí cách hạt nhân khoảng r. theo các góc q ,j .
vXác suất tìm electron theo bán kính r:
Ví dụ: Ở trạng thái cơ bản: = 1 thì n l = 0: 3/2 r - æ ö 32r Z - a 0 æ ö R1,02 =ç ÷ e à mật độ xác suất: 2 2 1 w= R r .r= ç 4÷ e .r 1,0 1,0 ( ) 2 a0 è a0 ø è a0 ø 2r d1 w ræ ö - æ ö 1,0 a 0 Þ=-= 4ç ÷ e .2r ç 1 ÷ 0 Hạt nhân dr a è ø a 0 0 è ø w1,0 ìï r 0= è í= = r(a ) o 10 ïî r a 0 0,53.10 m - 1. Nguyên tử hydro + Xét trạng thái = 2 thì n l = 0, 1: + Xét trạng thái = 3 thì n l = 0, 1, 2: w w 3,2 w 2,0 3,0 w3,1 2 w ,1 r( oa) r(ao) 1. Nguyên tử hydro
vXác suất tìm electron theo góc q, j :
Hàm mật độ xác suất phân bố theo góc: 2 w lm lm (q ,j )=q Y j ( ,q ) sin
Ví dụ: Ở trạng thái cơ bản: = 1, n l = 0, m= 0 à trạng thái 1s 2 1 Y = 1s 0,0 4p
Xác suất không phụ thuộc góc
à phân bố xác suất có tính đối xứng cầu l =0; m = 0 2svà 2p l =0; m = 0 l =1; m = -1 l =1; m = 0 l =1; m = 1
2. Nguyên tử kim loại kiềm qĐặc điểm
ØCấu trúc điện tử: chỉ có một điện tử ở lớp ngoài cùng - điện tử hoá trị.
ØPhần còn lại gọi là lõi nguyên tử (hạt nhân và các điện tử Hydro (H) khác).
ØTương tác giữa điện tử hoá trị và phần lõi nguyên tử rất yếu
ØTính chất hoá học, quang học của các nguyên tử kim loại Lithium (Li)
kiềm về cơ bản giống với nguyên tử H.
qNăng lượng của electron hoá trị trong kim loại kiềm
ØNăng lượng liên kết giữa electron hoá trị và hạt nhân (giống Natri (Na)
với năng lượng của electron hoá trị của nguyên tử H).
ØNăng lượng liên kết giữa electron hoá trị và các electron khác trong nguyên tử. 4 m e Rh e 1 E Potassium(K) =! - = - , n ln 2 2 2 l 32 lp e n 0 ( 2 +D ) ( +D )2
với Dllà số bổ chính Rydberg, phụ thuộc vào số lượng tử quỹ đạo l
2. Nguyên tử kim loại kiềm
ØBảng giá trị của số bổ chính Dl Z Nguyên tố DsDpDdDf 3Li 0,412 0,041 0,002 0,000 11 Na 1,373 0,883 0,010 0,001 19 K2,230 1,776 0,146 0,007 37 Rb 3,195 2,711 1,233 0,012 55 Cs 4,131 3,649 2,448 0,022
ØKý hiệu các mức năng lượng nX l= 0 àX = S l= 1 àX = P l= 2 àX = D l= 3 àX = F ... n l Trạng thái Mức năng lượng Lớp 1 0 1s 1S K 2 0 2s 2S L 1 2p 2P 3 0 3s 3S M 1 3p 3P 2 3d 3D
2. Nguyên tử kim loại kiềm
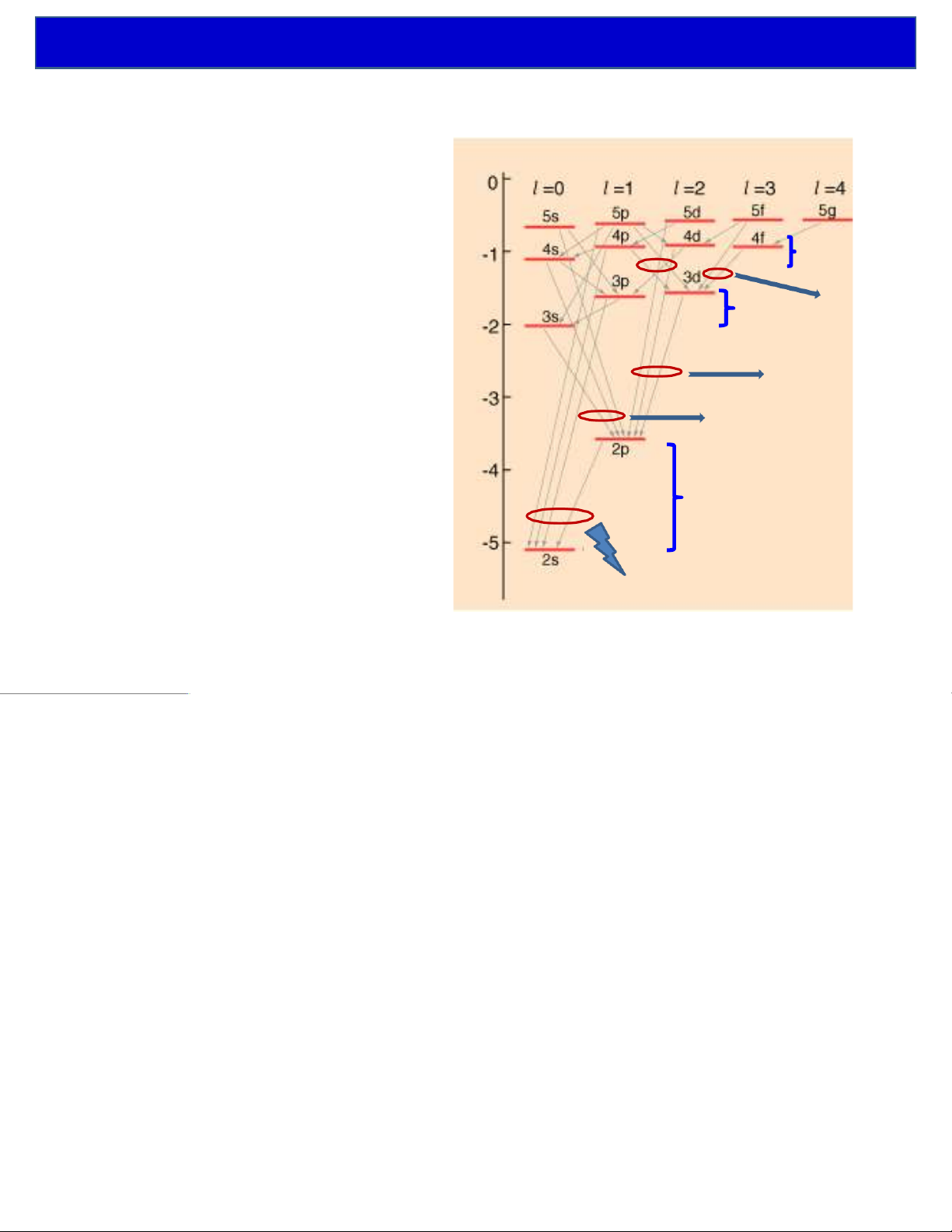
qQuang phổ của nguyên tử kim loại kiềm
Fe-chuyển từ mức cao hơn về
mức thấp hơn Þphát ra photon có năng lượng E = hn.
FSự chuyển mức tuân theo (n= 4) n = 3D-nF quy tắc lựa chọn: Dl=±1 (n= 3) Dãy
Ví dụ: Li, có 3e-: 2e-chiếm mức cơ bản
1S, 1e-hóa trị chưa bị kích thích n = 2P -nD Dãy phụ I
chiếm mức 2S(mức thấp nhất- n = 2P -nS mức cơ bản). Dãy phụ II Năng lượng (eV)
Từ các mức cao hơn chuyển về: t2S: là nP(n³2): Dãy chính n = 2S-nP (n= 2) t2P: là nS(n³3): Dãy phụ II nD(n³3): Dãy phụ I Dãy chính
t3D:là nF(n³4):Dãy cơ bản nP(n³4): h n = 3D-nP
Quang phổ vạch của nguyên tử Li
9.3. Mômen động lượng quỹ đạo và mômen từ quỹ đạo của electron. Hiệu ứng Zeeman
qMô men động lượng quỹ đạo
Electron chuyển động quanh hạt nhân àcó mô men động lượng quỹ đạo.
Do electron chuyển động không có quỹ đạo, nên:
ØVectơ mô men động lượng không có hướng xác định.
ØGiá trị của mô men động lượng của electron lại là một đại lượng xác định
và nó nhận các giá trị gián đoạn: " L =l l ( + ) 1 !
ØHình chiếu lên phương zcủa mô men động lượng Lzbị lượng tử hóa: Lz= m! z z "L = !6 Các vị trí L = 2 ! z có thể của mô men L = ! m = 1 + z động lượng L = 0 z m = 0 L = - ! z m = - 1 L = - 2 ! z m = - 2 FÞchỉ Lz L < zcó
L thể được xác định, còn phương (hay vị trí) của Lkhông
thể xác định chính xác ÞLxvà Lycũng không thể xác định được chính xác.
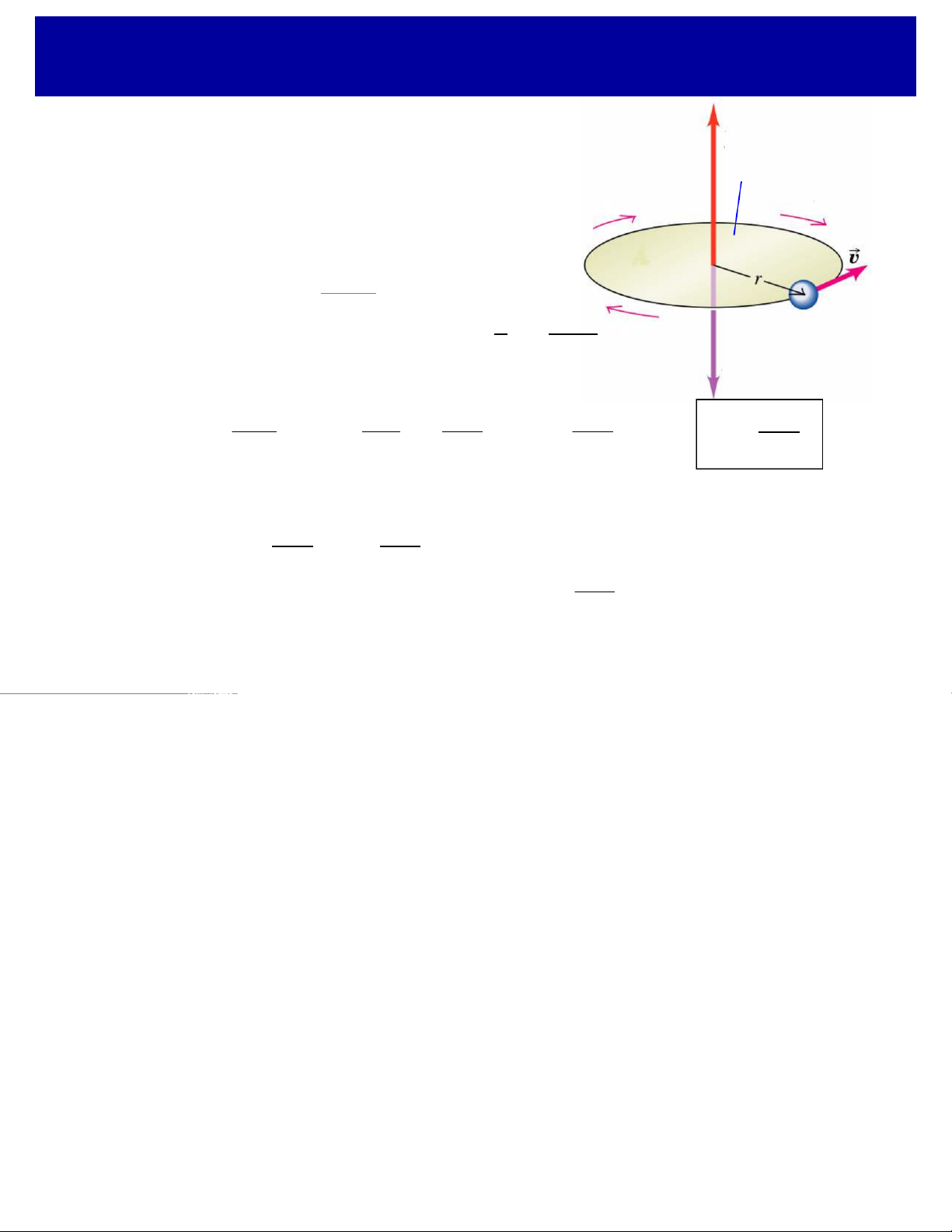
3. Mômen động lượng quỹ đạo và mômen từ quỹ đạo của electron. Hiệu ứng Zeeman !L qMô men từ quỹ đạo !
FMô men từ của dòng điện kín: = !. µ I S S: diện tích mặt kín ii
FChuyển động của e-quanh hạt nhân
(giả sử tròn) với vận tốc vÞchu kỳ quay
của e-trên quỹ đạo: 2p r t = n e v e .
Chuyển động của e-Ûdòng điện: i= - = - t 2.p r. !
có mô men từ là mô men từ quỹ đạo của e-: µ e v . e ! ! = µ . v e r e e i 2L S= - p .r = - = - m µ= - L e r v = - h ay 2p .r 2 2m m 2 e 2me e
FHình chiếu của mô men động lượng quỹ đạo của e-bị lượng tử hóa
àhình chiếu của mô men từ quỹ đạo cũng bị lượng tử hóa: e e µ =z h - ay L = ! z - m µ z = - m B µ m 2 2m e e = ! = e víi µ1 . 3 , 9 0 . 10 - » - 24 . 2 23 2 B m A m A 2me
t µBđược coi là đơn vị cơ sở của mô men từ e-Þgọi là Magneton Bohr 21
3. Mômen động lượng quỹ đạo và mômen từ quỹ đạo của electron. Hiệu ứng Zeeman qHiệu ứng Zeeman
FHiện tượng tách vạch quang phổ nguyên tử thành nhiều vạch sít nhau khi
nguyên tử phát sáng đặt trong từ trường.
FXét nguyên tử đặt trong từ trường có phương z Chuyển mức ! ! D W= - B µ B = 0 B ¹ 0
tNăng lượng W’ của e-khi đặt trong từ trường: W’ = W+m µBB
Wlà năng lượng của e-khi không có từ trường
tKhi chuyển từ trạng thái có năng lượng cao W’2sang trạng thái có năng
lượng thấp W’1, e-phát bức xạ có tần số: W' - W' W - W 2 1 ( m - m µBB D m 2 1 2 n ) '= 1 = + = v+ µ B h h h h B
nlà tần số của vạch quang phổ khi không có từ trường
tQuy tắc lựa chọn khi tách phổ: Dm= 0, ±1 Tần số n’ µ µ B B n = ' n - B n' = n n ' =n + B h h Dm= -1 Dm= 0 Dm= 1
3. Mômen động lượng quỹ đạo và mômen từ quỹ đạo của electron. Hiệu ứng Zeeman qHiệu ứng Zeeman m m m l= 0
tVạch quang phổ (khi không có từ trường) bị tách thành 3 vạch (khi có từ
trường) trong đó vach giữa (Dm= 0) trùng với vạch cũ.
tĐộ rộng giữa 2 mức năng lượng kế tiếp ở mọi trạng thái tương ứng giá trị của µB. 23 4. Spin của electron
qHiệu ứng Zeemann “bất thường”
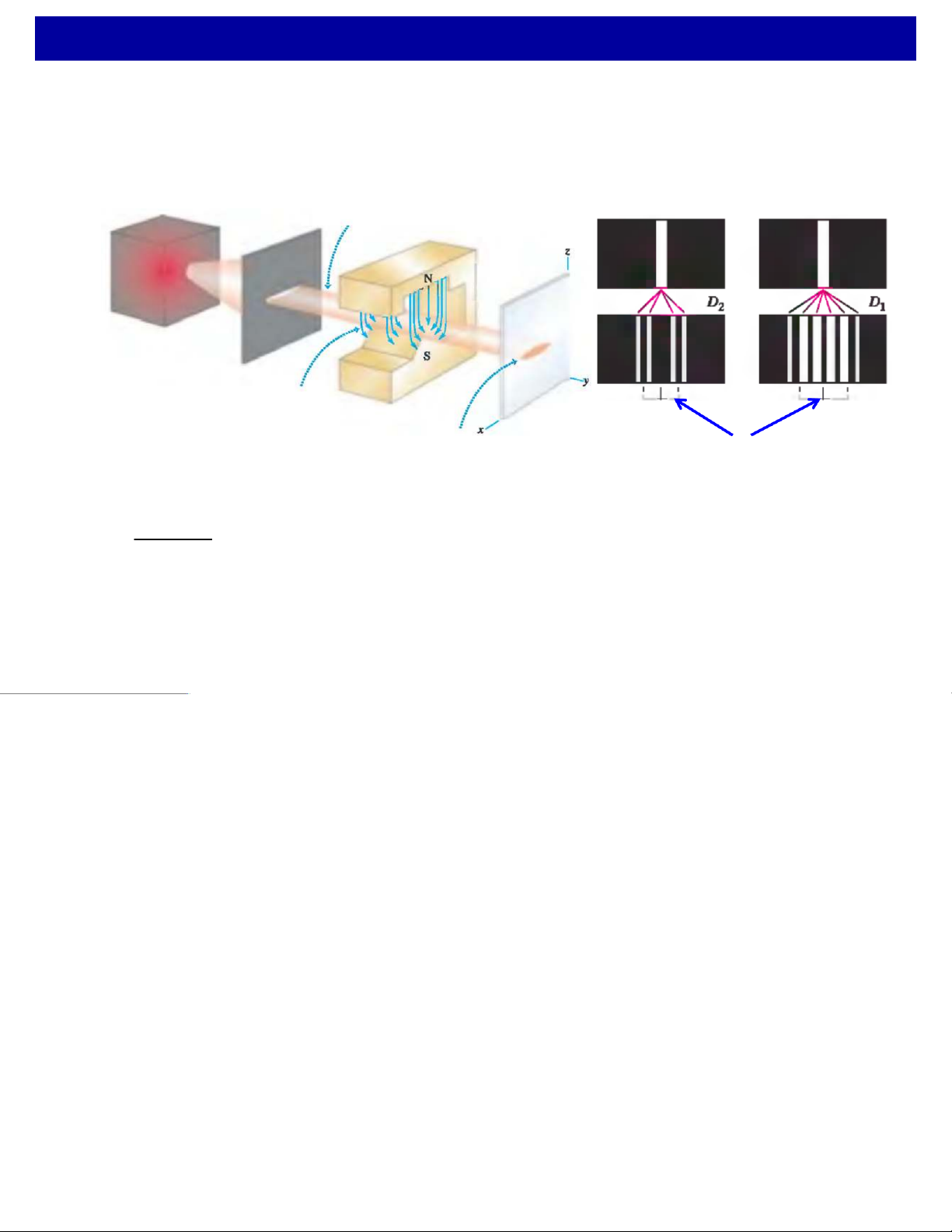
FThực nghiệm Stern-Gerlach:
Vạch phổ thực tế của Natri Chùm e-// trục y Nguồn tạo e- Từ trường không đồng đều Nam Màn châm Quang quan phổ
Vị trí và số vạch lẽ ra thu được với sát
hiệu ứng Zeemann “thường”
tCho chùm e-đi qua một từ trường không đồng đều.
FKết quả: quang phổ được quan sát chính xác có nhiều hơn số vạch đã đề
cập trong hiệu ứng Zeemann “thường” ècấu trúc bội của vạch quang phổ.
tSố vạch thay vì lẻ (2n+ 1) Þthực tế là chẵn (2j+ 1) với j= 1/2, 3/2, 5/2,..
Ûcó 1/2 số lượng tử quỹ đạo Þnguyên nhân? 24 4. Spin của electron
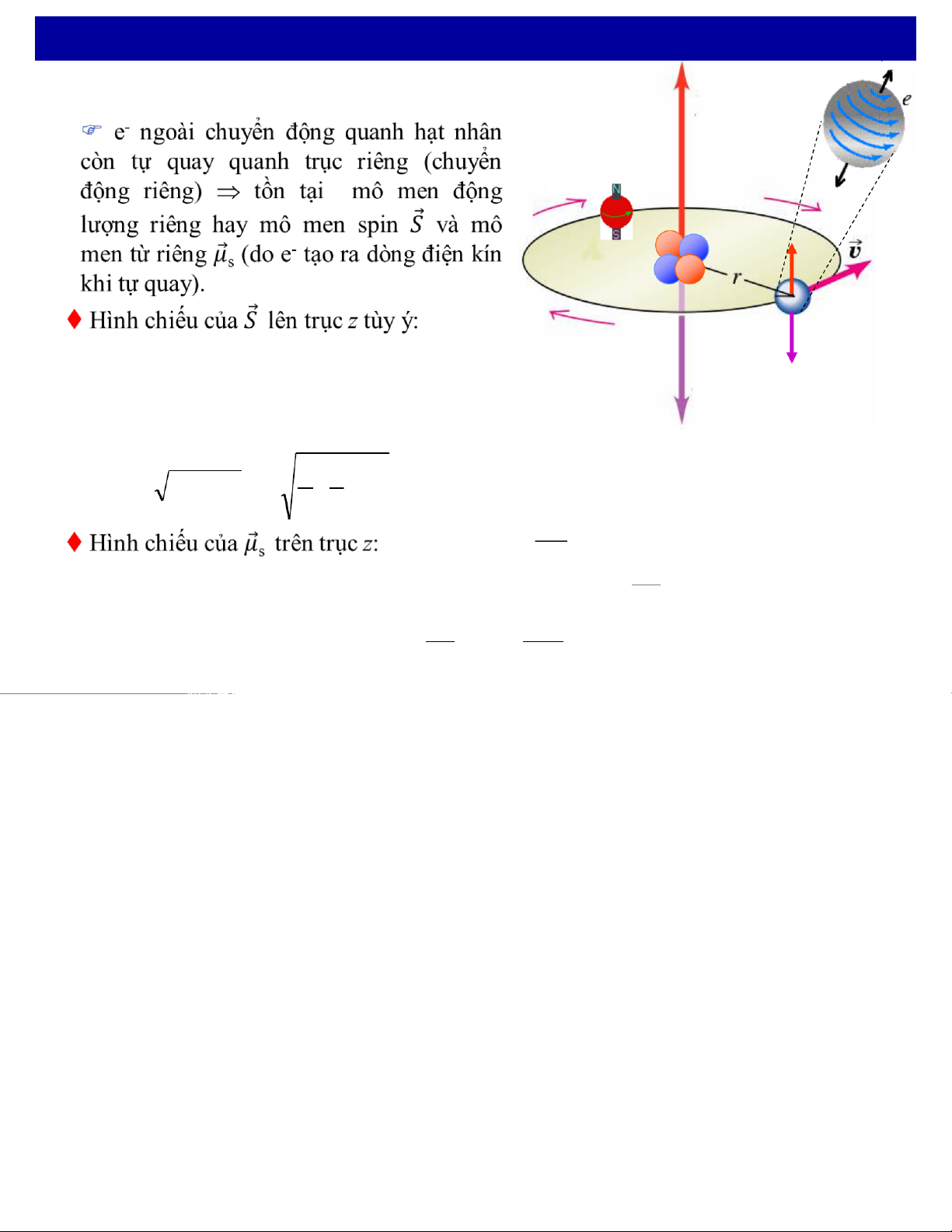
FMột số kết quả thực nghiệm do sự tồn tại của spin của electron: 25 4. Spin của electron ! s l qKhái niệm spin !µ i i s + ! s + i ! S =z m s! µs
ms=±1/2 là số lượng tử hình chiếu spin !µ
tCơ học lượng tử tính được giá trị của mô men spin: = 1 + = 1 æ+ 1 ö S s(s ! ) 1 ÷ ç !
với s= 1/2 là số lượng tử spin (gọi tắt là spin) 2 è2 ø e! = µ " =µ " sz 2 B m= e ! !-
tLiên hệ giữa mô men spin và mô men từ riêng: µ S s me
Chiếu biểu thức lên trục z =: e e" µ- 2 = S != ! z µB sm me e 4. Spin của electron
qTrạng thái và năng lượng của e-trong nguyên tử ! ! ! !
FMô men động lượng toàn phần của e-: J = L+ S l i
tGiá trị của mô men toàn phần: J = j j ( + ) 1 ! ! s 1
t Số lượng tử mô men toàn phần: j = l ± 2 i vTrạng thái của e-
Do có mô men spin nên trạng thái của e-còn phụ thuộc thêm số lượng tử ms,
đặc trưng cho định hướng của spin.
Trạng thái của electron trong nguyên tử được xác định bởi 4 số lượng tử: n, l, m, ms. vNăng lượng của e- FCác tương tác
üTương tác giữa mô men từ riêng và mô men từ quỹ đạo của mỗi e-
üTương tác giữa các mô men từ riêng của các electron trong nguyên tử.
èKhi tính đến spin, năng lượng của e-có thêm phần năng lượng phụ, phụ
thuộc vào định hướng của spin.
Năng lượng toàn phần của electron trong nguyên tử phụ thuộc vào 27
3 số lượng tử : n, l, j.




