Chương 3 - Tóm tắt lý thuyết và bài tập về điện môi môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Chương3-Điệnmôi Họckỳ2024.1
Lưuý:Tàiliệuchỉsửdụngvớimụcđíchôntập,sửdụngvàomụcđíchkhác,CLBkhôngchịutrách nhiệm. I Formôntậpchương3 II Tómtắtlýthuyết 1.Vectorphâncựcđiệnmôi:  P=ε0χ E=ε0(ε−1)  E
2.Vectorđiệncảmtrongđiệnmôi:  D=ε0 E+P
3.Mậtđộđiệnmặtliênkết: σ′lk=Pn=ε0(ε−1)En
4.Mậtđộnănglượngđiệntrường: we=1 2ε0εE2=1 2DE
5.NănglượngđiệntrườngtrongV: W=1 2ˆ ε0εE2dV V 1
CLB Hỗ Trợ Học Tập
III Câu hỏi trắc nghiệm lý thuyết Câu 1
Trên bề mặt vật dẫn, điện trường tại mọi điểm vuông góc với bề mặt, điều này dẫn tới:
A. Điện tích phân bố đều tại mọi điểm trên bề mặt.
B. Điện trường tại mọi điểm trên bề mặt là như nhau.
C. Điện thế tại mọi điểm trên bề mặt là như nhau.
D. Lực điện sẽ thực hiện công khác không khi di chuyển điện tích trên bề mặt. Câu 2
Xét một quả cầu kim loại cô lập, tích điện. Nhúng quả cầu vào trong một chất lỏng điện môi có
hằng số điện môi ϵ. Ta có:
A. Điện thế quả cầu không thay đổi.
B. Điện thế quả cầu giảm.
C. Điện thế quả cầu tăng.
D. Điện tích quả cầu giảm. Câu 3
Khi xảy ra sự phân cực điện môi đối với khối chất điện môi không đồng chất thì:
A. Tất cả các phân tử chất điện môi đều không trở thành một lưỡng cực điện.
B. Tổng mômen lưỡng cực điện phân tử trong toàn bộ khối chất điện môi luôn bằng không.
C. Có sự xuất hiện điện tích trên bề mặt và bên trong khối chất điện môi.
D. Chỉ có sự xuất hiện điện tích trên bề mặt khối điện môi. Câu 4
Khi đặt một thanh điện môi vào trong một điện trường đều, có đường sức song song với thanh thì
một trong hai đầu thanh xuất hiện: A. Điện tích dương. B. Các ion dương.
C. Điện tích của các phân tử. D. (A) và (C) đúng. 2
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu5
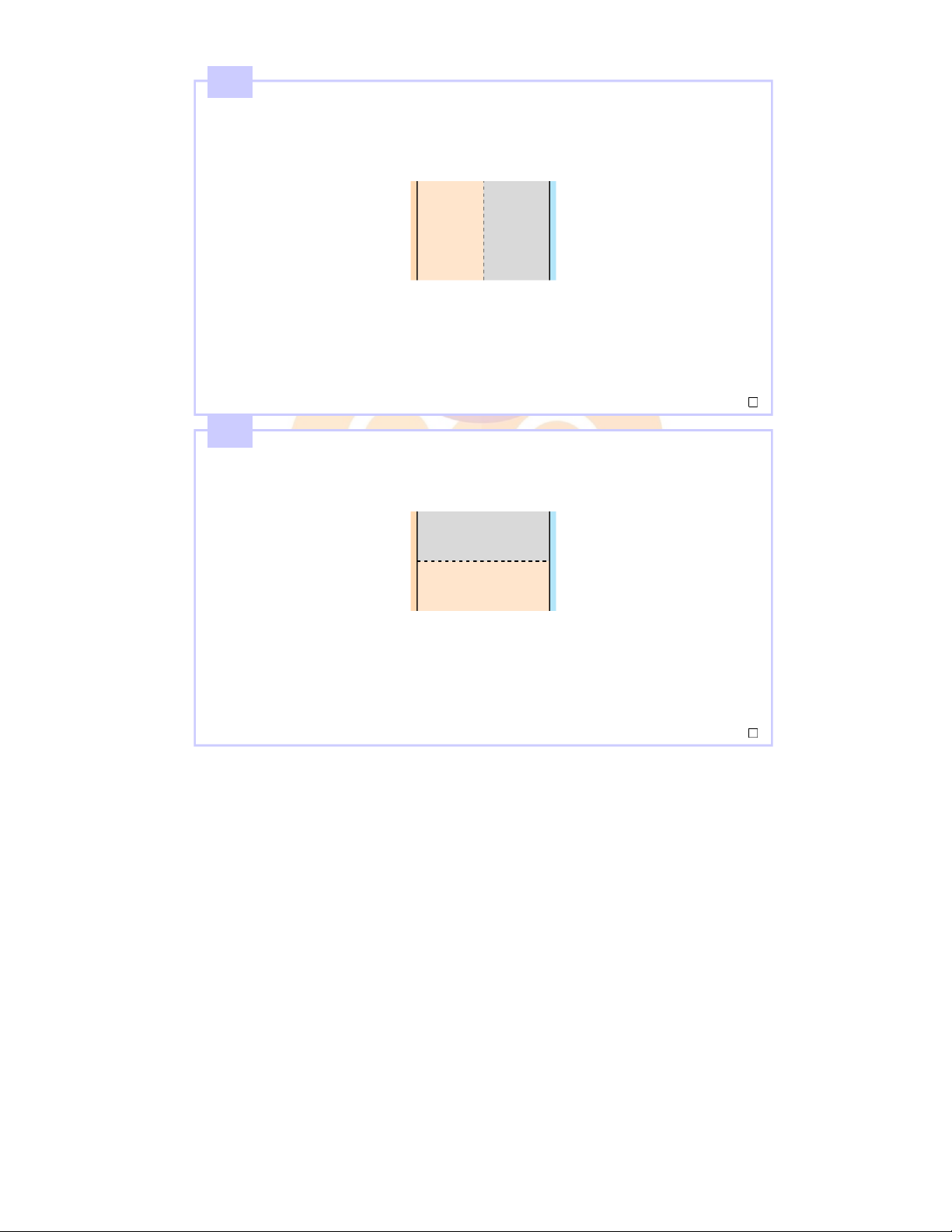
Mộttụđiệnphẳngđượclắpđầybởihaiđiệnmôinhưhìnhvẽ.Sosánhđộlớncủavectơcườngđộ
điệntrườngtronghaiđiệnmôitacó: ε1ε2 A.E1=E2 B.ε1E1=ε2E2 C.ε1E2=ε2E1 D.(ε1−1)E2= (ε2−1)E1 Câu6
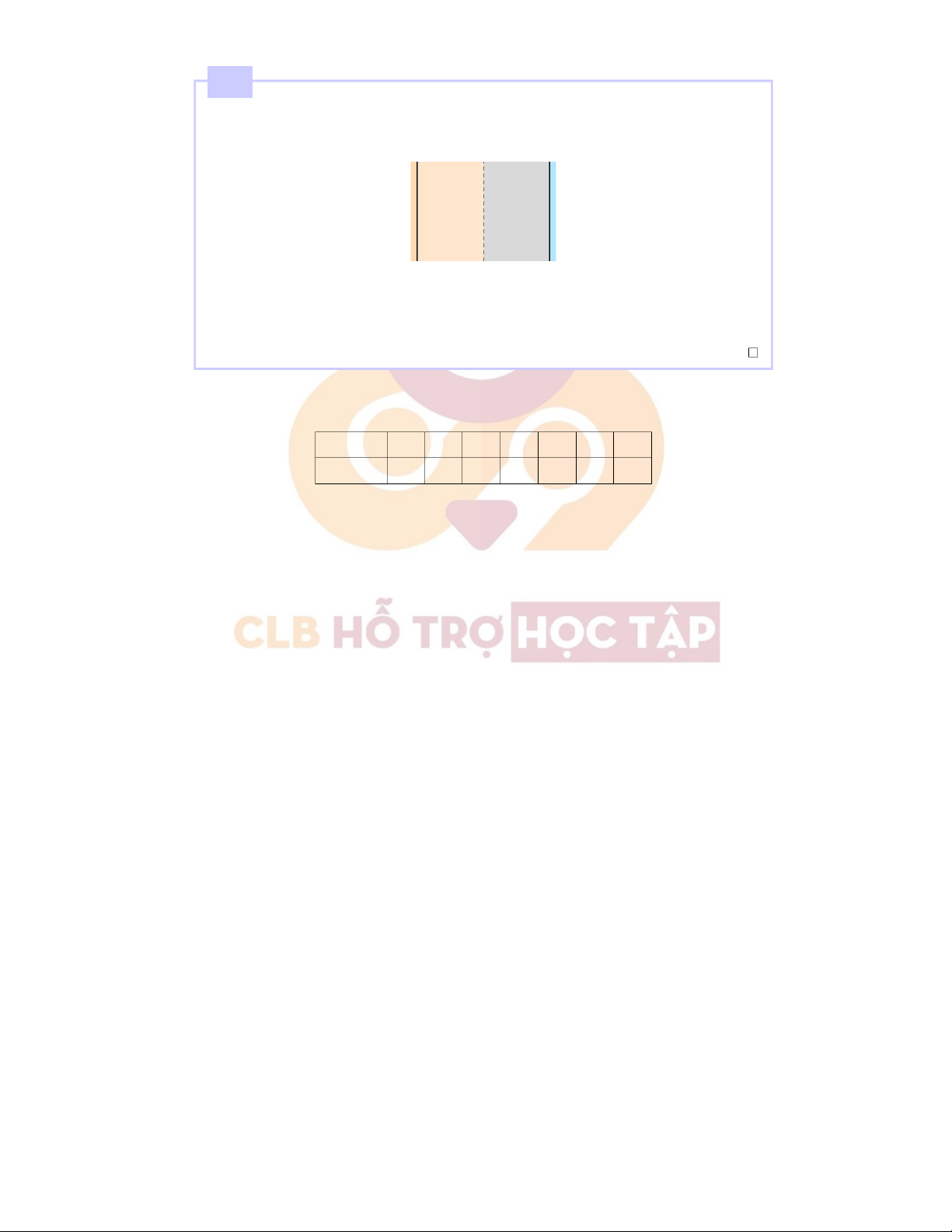
Mộttụđiệnphẳngđượclắpđầybởihaiđiệnmôinhưhìnhvẽ.Sosánhđộlớncủavectơcảmứng
điệntronghaiđiệnmôitacó: ε1 ε2 A.D1=D2 B.ε1D1=ε2D2 C.ε1D2=ε2D1 D.(ε1−1)D2= (ε2−1)D1 3
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập Câu7
Mộttụđiệnphẳngđượclắpđầybởihaiđiệnmôinhưhìnhvẽ.Sosánhnănglượngđiệntrườngtrong haiđiệnmôitacó: ε1ε2 A.U1=U2 B.ε1U1=ε2U2 C.ε1U2=ε2U1 D.(ε1−1)U2= (ε2−1)U1 Đápán Câu1234567 Đápán CBCABCB 4
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
IV Câuhỏitựluậnlýthuyết Câu1
Sựphâncựcđiệnmôilàgì?Giảithíchhiệntượngphâncựcđiệnmôi.Địnhnghĩavàcôngthức
tínhđộlớncủavéctơphâncựcđiệnmôi.Trìnhbàyvềmốiliênhệgiữavéctơphâncựcđiện
môivàmậtđộđiệnmặtcủacácđiệntíchliênkết.Nêucôngthứctínhcườngđộđiệntrường
vàđiệncảmtrongđiệnmôi. [Lờigiải]
1.Sựphâncựcđiệnmôilàgì?
-Hiệntượngtrênthanhđiệnmôiđặttrongđiệntrườngcóxuấthiệnđiệntíchđượcgọilàhiệntượng phâncựcđiệnmôi.
-Trênthanhđiệnmôi,điệntíchxuấthiệnởđâusẽđịnhxứtạiđó,khôngdịchchuyểntựdođượcnên
đượcgọilàđiệntíchliênkết.CácđiệntíchliênkếtsinhrađiệntrườngphụE′.
-Điệntrườngtổnghợptrongđiệnmôi:  E= E0+E′
2.Giảithíchhiệntượngphâncựcđiệnmôi
a)Điệnmôicấutạotừphântửkhôngphâncực: -Khi E0= 0 :  pei= 0
-Khi E0= 0 : cácphântửbịphâncựcthànhcáclưỡngcựcđiệncó  pe=αε0 E
•Mômenđiệncủacácphântửđềuhướngtheochiềuđiệntrường;
•Trênmặtgiớihạncủakhốiđiệnmôixuấthiệncácđiệntíchliênkếttráidấu.
b)Điệnmôicấutạotừphântửphâncực: -Khi E0= 0 : 
pei= 0.Nhưngdochuyểnđộngnhiệtnên  pei= 0 P -Khi E0= 0: •
pexoaytheochiềuđiệntrườngngoài  E0;
•Dochuyểnđộngnhiệt 
petungrahaiphíasovớiphươngcủađiệntrườngngoài; •Tronglòngđiệnmôi: qi= 0; P
•Trênmặtgiớihạn:xuấthiệncácđiệntíchtráidấu.
3.Véctơphâncựcđiệnmôi 5
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
-Giảsửtrongthểtích∆Vcủakhốiđiệnmôiđồngchấtcónphântử.
-Véctơphâncựcđiệnmôilàmộtđạilượngđobằngtổngcácmômen lưỡngcựcđiệncủacácphântử
cótrongmộtđơnvịthểtíchcủakhốiđiệnmôi. n X  Pei  P i=1 e= ∆V
a)Điệnmôicóphântửkhôngphâncực
-Khiđặttrongđiệntrườngđều,mọiphântửđiệnmôiđềucócùngvéctơ  pe  Pe=n  pe ∆V=n0 pe
n0=n ∆Vlàmậtđộphântử
-Gọi Elàvéctơcườngđộđiệntrườngtổnghợptrongđiệnmôi  Pe=n0 pe=n0ε0α E=ε0χe E
χe=n0αlàđộcảmđiệnmôi,khôngthứnguyên,khôngphụthuộcvàoE
b)Điệnmôicóphântửphâncực
-Nếuđiệntrườngngoàiyếu,đãchứngminhđược: 2 
Pe=ε0χe Evớiχe=n0pe3ε0kT
k= 1,38.10−23J/K, T :nhiệtđộtuyệtđốicủakhốiđiệnmôi
-Nếuđiệntrườngngoàimạnh,Tthấp:
Pekhôngtỷlệbậcnhấtvới  Enữa.Nếutăng  Etớimộtgiátrị
đủlớn,tấtcảcácmômenđiệnđềusongsongvới 
E.Hiệntượngphâncựcđiệnmôiđãđạttrạngtháibão hòa. c)Điệnmôitinhthể  Pe=ε0χe EĐơnvị:C/m2
4.Liênhệgiữavéctơphâncựcđiệnmôivớimậtđộđiệnmặtcủacácđiệntíchliênkết
-Táchratrongđiệnmôimộtkhốitrụxiêncó:
•Đườngsinhsongsong  E(tứclàsongsong  Pe,cóchiềudàiL;
•Haiđáysongsong,mỗiđáycódiệntích∆S;
•+σ′,−σ′làmậtđộđiệnmặttrênmỗiđáy; •
n làpháptuyếnngoàicủađáymangđiệntíchdương; 6
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
•Cóthểcoitoànbộkhốitrụnhưmộtlưỡngcựcđiệntạorabởicácđiệntíchliênkết−σ′∆Svà
+σ′∆StrênhaiđáycáchnhaumộtđoạnL.Mômenđiệncủanócóđộlớnσ′∆SL. n | X  pei| P ∆V=σ′∆SL ∆SL cos α=σ′ e=|P i=1 e|= cos α →σ′=Pecos α=Pen
-Kếtluận:Mậtđộđiệnmặtσ′củacácđiệntíchliênkếtxuấthiệntrênmặtgiớihạncủakhốiđiện
môicótrịsốbằnghìnhchiếucủavéctơphâncựcđiệnmôitrênpháptuyếncủamặtgiớihạnđó. -ĐơnvịPe:C/m2
5.Côngthứctínhcườngđộđiệntrườngvàđiệncảmtrongđiệnmôi
a)Cườngđộđiệntrường
•Giảsửcómộtđiệntrườngđều 
E0giữahaimặtphẳngmangđiệnđềubằngnhautráidấu
•Chấtđiệnmôilấpđầykhoảngkhônggiangiữahaimặtphẳng
•Khốiđiệnmôibịphâncực
•Trênmặtđiệnmôixuấthiệncácđiệntíchliênkết+σ′,−σ′
•Cácđiệntíchliênkếtnàygâyrađiệntrườngphụ  E′
Điệntrườngtổnghợptrongđiệnmôi:  E= E0+E′
VìE0ngượcchiều E′nêntacóE=E0−E′  E′=σ′   ε0   σ′=Pen=ε0χeEn=ε0χeE ⇒E′=σ′ =χeE ε0 E=E0−E′=E0−χeE⇒E=E0 =E0 1 + χe ε
ε= 1 + χegọilàhằngsốđiệnmôicủamôitrường
Cườngđộđiệntrườngtrongđiệnmôigiảmđiεlầnsovớicườngđộđiệntrườngtrongchânkhông
b)Điệncảmtrongđiện   D=ε0ε  E  ε= 1 + χe
⇒D=ε0(1 + χe)E=ε0 E+ε0χeE=ε0 E+Pe 7
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập V Bàitập Bàitập1
Mộttụđiệnphẳngcóchứađiệnmôi(ε= 5),khoảngcáchgiữa2bảnlàd= 0,4cm,hiệuđiệnthế giữa2bảnlàU= 1000V.Tính:
a)Cườngđộđiệntrườngtrongchấtđiệnmôi.
b)Mậtđộđiệnmặttrênhaibảntụđiện.
c)Mậtđộđiệnmặttrênchấtđiệnmôi. [Lờigiải]
a) Cườngđộđiệntrườngtrongchấtđiệnmôilà: E=U d=1000 0,4.10−2= 2,5.105(V /m) b) TacócôngthứcE=σ
ε0ε,vìvậymậtđộđiệnmặttrên2bảntụđiệnlà:
σ=ε0εE = 5.8,86.10−12.2,5.105= 110,75.10−7(C/m2)
c) Mậtđộđiệnmặttrênchấtđiệnmôilà:
σ′= (ε−1)ε0E= (5 −1).8,86.10−12.2,5.105= 8,86.10−6(C/m2) Bàitập2
Giữa2bảncủa1tụđiệnphẳng,cómộtbảnthủytinh(ε= 6).Diệntíchmỗibảntụđiệnbằng
150 cm2.Cácbảntụđiệnhútnhauvớimộtlựcbằng6.10−3N.Tínhmậtđộđiệntíchliênkếttrên mặtthủytinh. [Lờigiải]
Gọilựctươngtácgiữa2bảntụđiệnlàF.Tathấycôngdịchchuyển2bảntụđiệnsátlạinhaucótrịsố
bằngnănglượngcủatụđiện,nêntacó: F d =Q2 2C=σ2S22.d εε0S ⇒σ= 2εε0F r S 8
HỗtrợSinhviênBáchKhoa CLBHỗTrợHọcTập
Mặtkhác,tacó σ=εε0E  σ′= (ε−1)ε0E ⇒σ 2εε0F ′=ε−1 εσ=ε−1 ε.r S ⇒σ 2.6.8,86.10−12.6.10−3 ′=5 6.s 0,015 ≈5,43.10−6(C/m2) 9