





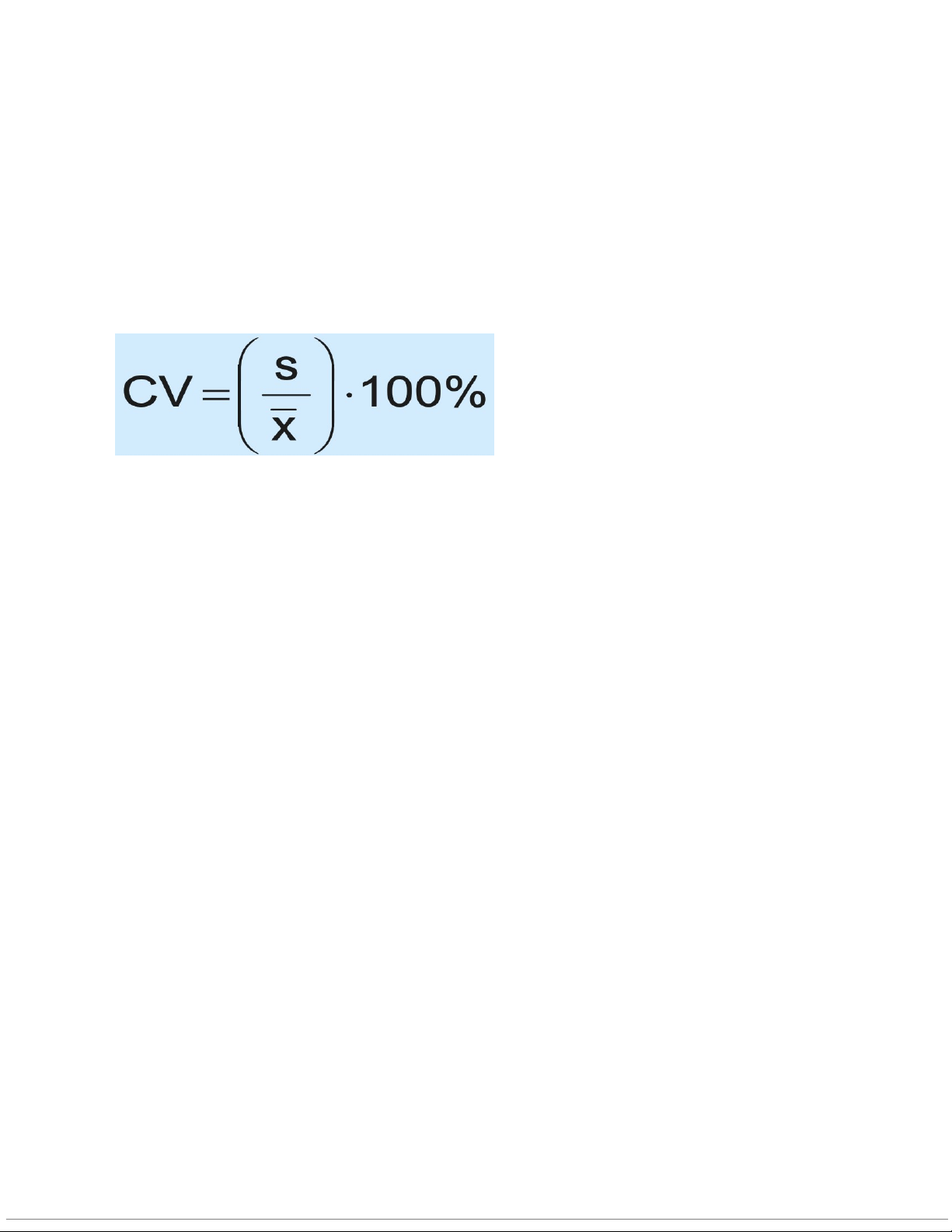

Preview text:
Chương 4: Các mức thống kê mô tả
1. Số tuyệt đối và số tương đối trong thông kê 1.1. Số tuyệt đối 1.1.1. Khái niệm
- Số tuyệt đối trong thống kê là mức độ biểu hiện quy mô, khối lượng của hiện
tượng kinh tế xã hội trong điều kiện thời gian và địa điểm cụ thể.
- Biểu hiện quy mô: Nói lên quy mô của hiện tượng
- Biểu hiện khối lượng: là trị số của một tiêu thức 1.2. Số tương đối 1.2.1. Khái niệm
- Số tương đối trong thống kê biểu hiện quan hệ so sánh giữa hai mức độ nào đó
của hiện tượng nghiên cứu
- Quan hệ so sánh là sự khác biệt cơ bản giữa số tuyệt đối và số tương đối trong thống kê
- Hai mức độ của hiện tượng nghiên cứu có thể là: Hai mức độ cùng loại hoặc khác loại Tác dụng
- Được dùng trong phân tích thống kê, giúp nêu lên kết cấu, quan hê so sánh, trình
độ phát triển, trình độ phổ biến
- Dùng số tương đối để biểu hiện tình hình thực tế trong trường hợp cần giữ bí mật số tuyệt đối.
- Có tác dụng trong công tác lập và kiểm tra tình hình thực hiện kế hoạch
1.2.2. Các loại số tương đối
Số tương đối động thái:
- Khái niệm: Biểu hiện sự biến động về mức độ của hiện tượng nghiên cứu qua
một thời gian nào đó. Là kết quả so sánh 2 mức độ cùng loại nhưng khác nhau về thời gian. - Công thức: t = (lần,%) y1 y2
- Tác dụng: Xác định xu hướng biến đổi và tốc độ phát triển của hiện tượng qua
thời gian hay là biểu hiện xu hướng của hiện tượng
Số tương đối kế hoạch:
Số tương đối nhiệm vụ kế hoạch:
- Khái niệm: Là tỷ lệ so sánh giữa mức độ của 1 chỉ tiêu cần đạt tới và mức độ thực tế ở kỳ gốc (lần,%) - Công thức: = yk Kn y0
- Tác dụng: Dùng để lập kế hoạch
Số tương đối thực hiện kế hoạch:
- Khái niệm: Là tỷ lệ so sánh giữa mức thực hiện trong kỳ với mức kế hoạch của 1 chỉ tiêu nào đó (lần,%) - Công thức: : = y1 Kt yk
- Đặc điểm: Tổng các số tương đối kết cấu của tất cả các bộ phận là 1 hoặc 100%.
Số tương đối không gian:
- Là kết quả so sánh giữa 2 mức độ cùng loại nhưng khác nhau về không gian hoặc
so sánh giữa các bộ phận trong 1 tổng thể.
- So sánh giữa 2 mức độ cùng loại nhưng khác nhau về không gian
- So sánh giữa hai bộ phận trong 1 tổng thể: 2 không gian khác nhau cùng tồn tại trong 1 tổng thể.
Số tương đối cường độ:
- Nói lên trình độ phổ biến của hiện tượng trong điều kiện lịch sử nhất định, là kết
quả so sánh 2 mức độ khác loại nhưng có mối liên hệ với nhau.
- Số tương đối cường độ có đơn vị kép.
1.3. Điều kiện vận dụng:
- Khi sử dụng số tương đối và tuyệt đối phải xét đến đặc điểm của hiện tượng
nghiên cứu để rút ra kết luận cho đúng
- Phải vận dụng kết hợp số tương đối và số tuyệt đối vì:
+ Các số tương đối được tính ra từ số tuyệt đối.
+ Ý nghĩa của số tương đối còn phụ thuộc vào trị số tuyệt đối mà nó phản ánh.
2. Các mức độ điển hình của hiện tượng 2.1. Số bình quân - Số bình quân cộng:
+ Số bình quân cộng giản đơn:
+ Số bình quân cộng gia quyền:
- Số bình quân nhân: chỉ dùng để tính tốc độ phát triển bình quân
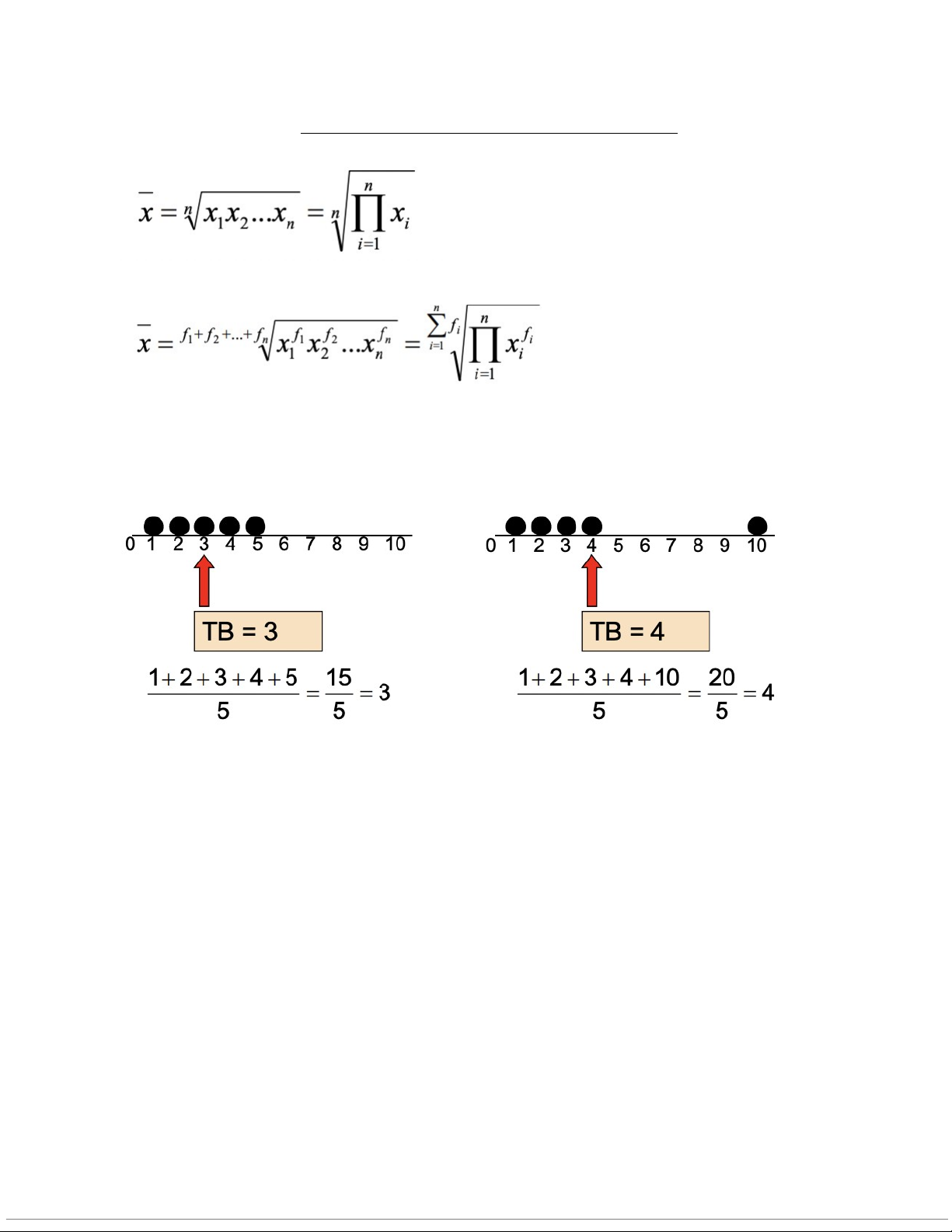
+ Số bình quân nhân giản đơn:
+ Số bình quân nhân gia quyền:
Đặc điểm số trung bình:
- Tham số thông dụng nhất để đo độ tập trung
- Tất cả các lượng biến đều tham gia trong công thức tính
- Bị ảnh hưởng bởi các giá trị ngoại biên (extreme values hoặc outliers)
- Tất cả các bộ dữ liệu được áp dụng thang đo khoảng và tỷ lệ đều tính được số trung bình.
- Số trung bình là duy nhất cho 1 bộ dữ liệu.
- Không tính đại lượng trung bình cho các dữ liệu định danh
- Cân nhắc khi tính đại lượng trung bình cho dữ liệu áp dụng thang đo thứ bậc.
- Chỉ tính được trên dữ liệu định lượng. 2.2. Mố (Mod)t: Khái niệm:
Là biểu hiển của 1 tiêu thức được gặp nhiều nhất trong một tổng thể hay trong 1 dãy số phân phối
Mốt là tham số điển hình dùng cho dữ liệu định tính (do không tính được số trung bình và trung vị). Cách tính mốt:
TH1: Áp dụng cho dãy số không có khoảng cách tôt
- Mốt là lượng biến xi có tần số fi lớn nhất
TH2: Áp dụng cho dãy số có khoảng cách tổ bằng nhau
- Mốt được tính theo 2 bước
+ Bước 1: Xác định tổ có Mốt - là tổ có tần số lớn nhất.
+ Bước 2: Tính trị số gần đúng của Mốt:
TH3: Áp dụng cho dãy số có khoảng cách tổ không bằng nhau
- Trường hợp dãy số không có khoảng cách tổ không bằng nhau: việc xác định Mốt
phải căn cứ vào mật độ phân phối.
Vì các khoảng cách tổ khác nhau nên tổ chứa Mốt sẽ là tổ có mi max. Cần phải
thêm cột vào bảng tính để xác định tổ chứa Mốt và tìm δ1,δ2 theo mM0 … Công thức
tính tương tự như ở trên. 2.3. Trung vị (Me):
Khái niệm: Trung vị là lượng biến của đơn vị đứng ở vị trí chính giữa trong dãy
số lượng biến, chia dãy số thành hai phần bằng nhau Cách tính trung vị:
- Trường hợp dãy số không có khoảng cách tổ: Me là lượng biến của đơn vị đứng ở vị trí giữa.
+ Nếu số đơn vị của tổng thể là số lẻ (2m+1), Me là lượng biến của đơn vị thứ m+1
+ Nếu số đơn vị của tổng thể là số chẵn (2m), Me là trung bình cộng lượng
biến của đơn vị thứ m và m+1
- Trường hợp dãy số có khoảng cách tổ: Trung vị được tính theo 2 bước
+ Bước 1: Xác định tổ có trung vị, là tổ chứa lượng biến của đơn vị đứng ở vị trí giữa .
+ Bước 2: Tính trị số gần đúng của Me:
3. Các tham số đo độ biến thiên của tiêu thức
3.1. Khoảng biến thiên (Range)
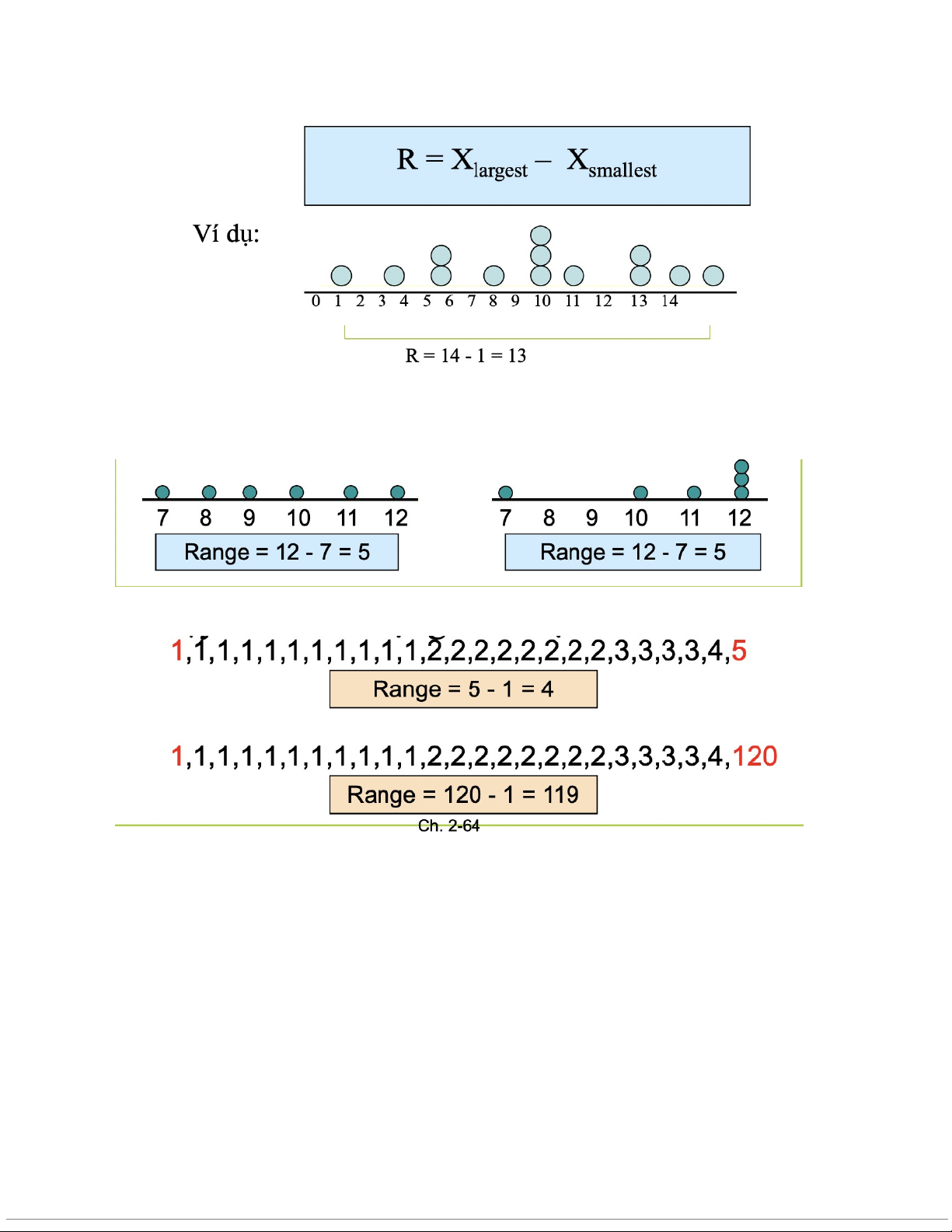
- Là tham số đo độ biến thiên đơn giản nhất
- Là chênh lệch giữa giá trị lớn nhất và bé nhất:
Nhược điểm của khoảng biến thiên
- Không tính đến sự phân bố của dữ liệu
- Nhạy cảm với lượng biến đột xuất Khoảng tứ phân vị:
- Loại trừ ảnh hưởng của các lượng biến đột xuất
- Loại trừ các giá trị quan sát cao và thấp, tính khoảng biến thiên của 50% quan sat ở giữa bộ dữ liệu.
Khoảng tứ phân vị = 33rdquartile−1stquartile IQR = Q3−Q1 Tứ phân vị:
- Phân vị chia bộ dữ liệu đã được sắp xếp thành 4 phần sao cho mỗi phần có số
lượng giá trị quan sát như nhau.
+ Tứ phân vị thứ 1, Q1, là giá trị mà có 25% các quan sát nhỏ hơn giá trị này và
75% các quan sát có giá trị lớn hơn
+ Q2 là giá trị trung vị (50% nhỏ hơn, 50% lớn hơn)
+ Chỉ có 25% các quan sát lớn hơn tứ phân vị thứ 3.
Công thức tính tứ phân vị:
Tìm giá trị tứ phân vị: là giá trị ở vị trí tương ứng theo công thức sau trong dãy số liệu đã sắp xếp: 3.3. Phương sai:
- Trung bình của tổng bình phương độ lệch của các giá trị quan sát với giá trị trung bình Phương sai mẫu:
- Trung bình (xấp xỉ) của tổng bình phương độ lệch giữa các giá trị quan sát và trung bình mẫu: - Phương sai mẫu:
3.4. Độ lệch tiêu chuẩn:
- Tham số đo độ phân tán thông dụng nhất
- Thể hiện biến thiên xoay xung quanh giá trị trung bình.
- Có cùng đơn vị tính với dữ liệu gốc
- Độ lệch tiêu chuẩn của tổng thể:
Độ lệch tiêu chuẩn của mẫu:
- Tham số đo độ phân tán thông dụng nhất
- Thể hiện biến thiên xoay xung quanh giá trị trung bình.
- Có cùng đơn vị tính với dữ liệu gốc
- Độ lệch tiêu chuẩn của mẫu:
Ưu điểm của phương sai và độ lệch chuẩn:
- Tất cả các giá trị trong bộ dữ liệu đều tham gia vào việc tính toán
- Các giá trị cách xa giá trị trung bình có thêm trọng số (bằng cách bình phương khoảng cách)
3.5. Hệ số biến thiên (Coefficient of Variation)
- Đo lường độ phân tán tương đối.
- Luôn có đơn vị tính là phần trăm (%).
- Thể hiện độ phân tán tương đối so với giá trị trung bình.
- Có thể được dùng để so sánh hai hoặc nhiều bộ dữ liệu có đơn vị tính khác nhau.




