Chương 5 - Cảm Ứng Điện Từ môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

CHƯƠNG 5 –
CẢM ỨNG ĐIỆN TỪ
1. Hiện tượng cảmứng điện từ
2. Hiện tượng tựcảm
3. Năng lượng từtrường 1
1. Hiện tượng cảmứng điện từ
Thí nghiệm Faraday r S r S v v S N N r r B' B' rN v II
Michael Faraday (1791-1867) r v N r N v S S r r B' B' II 2
1. Hiện tượng cảmứng điện từ
Thí nghiệm Faraday r r v
B thay đổi r B
Michael Faraday (1791-1867)
Tăng dần r I I B' 3
1. Hiện tượng cảmứng điện từ
Thí nghiệm Faraday
)Dòng cảmứng xuất hiện trong mạch
kín là kết quảcủa quá trình biếnđổi từ thông qua mạch ó. đ
)Dòng cảmứng chỉtồn tại trong thời
gian từthông gửi qua mạch thay đổi.
)Cường độ dòng cảmứng tỉlệthuận
với tốcđộ biếnđổi của từthông.
Michael Faraday (1791-1867)
)Chiều dòng cảmứng phụthuộc vào
từthông gửi qua mạch tăng hay giảm. 4
1. Hiện tượng cảmứng điện từ Định luật Lenz
)Nội dung: Dòng cảmứng có chiều
sao cho từtrường do nó sinh ra ch ng ố
lại sựbiến thiên của từthông sinh ra nó. )Áp dụng:
ªKhi cực Bắc (N) tiến vào vòng dây Heinrich Lenz
⇒từthông Φmdo từtrường B của nam (1804-1865)
châm gửi qua cuộn dây có chiều từtrên r S
xuống và tăng dần⇒xuất hiện dòng v N
cảmứng IC⇒tạo ra B’ cảmứng ngược r B’ S B
chiều B ⇔từthông Φ’ v mcủa B’ ch ng ố lại sựtăng c a ủ Φ N
m⇒xác định chiềuIc. B’ B
ªRút thanh nam ra khỏi vòng dây ⇒ IC
hiện tượng ngược lại. 5 IC
1. Hiện tượng cảmứng điện từ
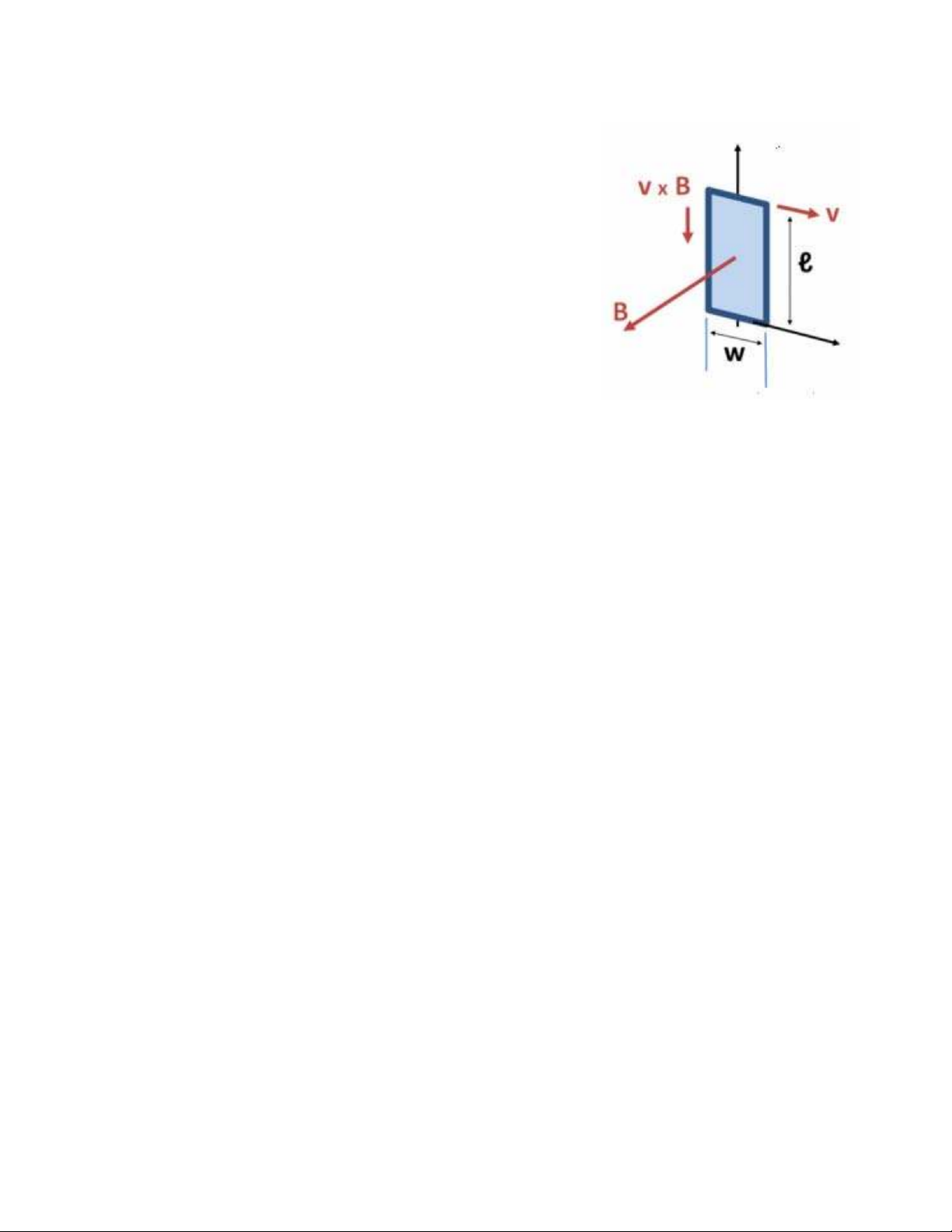
Sứcđiệnđộng cảmứng )Định luật cơ ả b n của hiện tượng cảmứng i đ ện từ
ªVòng dây dẫn kín di chuyển trong B
ªBiến thiên từthông gửi qua vòng
dây trong thời gian dt:d Φm⇒dòng
cảmứng Ic⇔xuất hiện một ngu n ồ
điện cảmứng hay s.đ.đcảmứng Ec.
ªCông của từlựcđể di chuyển vòng dây: dA = Ic. d Φm
ªTheo đ/l Lenz: từlực tác dụng lên Icngăn cản sựdi chuyển
của vòng dây (là nguyên nhân sinh ra Ic) ⇒công cản:
dA’ = - dA = - Ic d . Φm 6
1. Hiện tượng cảmứng điện từ
Sứcđiệnđộng cảmứng
)Định luật cơbản của hiện tượng cảmứng điện từ
ªTheo đ/l bảo toàn năng lượng: dA’ chuyển thành NL củaIc dΦ dA’ = -I m c d
. Φm= Ec.Ic.dt (NL củaIc)d ⇒ t E = − C
ªSứcđiệnđộng cảmứng trong một mạch kín bất kỳbằng vềtrị
sốnhưng khác dấu với tốcđộ thay đổi của t thông ừ qua mạch.
)Định nghĩađơn vịtừthông
ªNếu từthông gửi qua diện tích mạch kín giảm từgiá trị Φmvề0: m m = − d 0 mΦ − Φ Φ E = − =
⇒ Φm= Ec. Δt C dt t Δ Δt
ªVới Δt = 1 s, Ec= 1 V ⇒ Φm= 1 (V) . 1 (s) = 1 Webe (Wb)
ªWebe là từthông gây ra trong một vòng dây dẫn bao quanh
nó một sứcđiệnđộng cảm ng ứ
bằng 1 V khi từthông đó gi m ả
đều xuống giá trị0 trong thời gian 1 s 7
1. Hiện tượng cảmứng điện từ
Máy phát điện xoay chiều ωr r )Khung dây ( I Nvòng dây) C n
diện tích S quay trong từ α r O r trường đều ( ) v B = const ới vận B tốc góc ω .
ªVịtrí ban đầu của khung Chổi than tương ứng góc α giữa pháp r r
tuyến mặt phẳng khung n và B Cổgóp
ªSau khoảng thời gian t⇒ ~
vịtrí khung ứng với góc: ϕ = ωt + α
)Từthông gửi qua khung sau khoảng thời gian t:
Φm= N.B.S.cos ϕ = N.B.S.cos(ωt+α) 8
1. Hiện tượng cảmứng điện từ
Máy phát điện xoay chiều
Vịtrí khung dây trong từtrường B )Khi khung quay đều trong
từtrường ⇒xuất hiện 1 s. . đ đ Φ
cảmứng xoay chiều hình sin
m ,Ec, E = NB.S.ωB.Sω . t Φm C = NB.S.cos ωt theo đ/l Lenz: dΦm N.B.S . .s E i = n −t = C ω ()ω +α dt
ªĐặt Ecmax = N.B.S.ω ⇒E = E . (ωt sin + α) C cmax
ªChu kỳ= chu kỳquay của khung: ω2π T= E NBSω )Dòng cảmứng sin = ωtICc= R R = Ic I = I = 0.sin ω NBSω t c Đặt: Imax 0 R 9
1. Hiện tượng cảmứng điện từ
Dòng xoáy (dòng Foucault/ eddy current)
)Dòng cảmứng (có dạng xoáy) xuất hiện
trên bềmặt vật dẫn khi đặt trong từtrường: E IC = F R )Hệquả:
ªXuất hiện từtrường riêng
Léon Foucault (1819-1868)
của dòng cảmứng IF Từtrường
ªDòng cảmứng xuất hiện Cuộn dây cuộn dây
trên bềmặt vật dẫn sẽbịtiêu
tán dưới dạng nhiệt⇒tiêu hao Từtrường
năng lượng vô ích ⇒giảm dòng xoáy Dòng xoáy
hiệu suất thiết bị(đặc biệt với các động cơ). Vật dẫn 10
1. Hiện tượng cảmứng điện từ
Dòng xoáy (dòng Foucault/ eddy current)
)Do có từtrường của dòng cảmứng xuất hiện trên bềmặt vật
dẫn⇒ứng dụng trong các thiết bịdò tìm kim loại. Báo ng độ Dòng cảm Dòng tạo ứng do từ từtrường trường dòng xoáy Dòng xoáy Cuộn phát Cuộn thu Dòng xoáy Cửa an ninh (security gate)
Thiết bịdò mìn (mine detector) 11
2. Hiện tượng tựcảm
Hiện tượng )Mạch điện: + ống dây có lõi sắt + Điện kế(G)
ªNgắt mạch ⇒từthông qua cuộn dây giảm từ Φ G m→0:
Xuất hiện dòng cảmứng Ic
ngược chiểu dòng ban đầu ( /l đ K
Lenz) ⇒kim của G lệch theo chiều ngược lại.
ªSau khoảng thời gian t⇒kim G trởvề0
ªĐóng mạch ⇒quá trình ngược lại.
ªDòng tựcảm: dòng điện sinh ra trong một mạch i đ ện khi từ
thông gửi qua mạch bởi dòng điện c a
ủ mạch đó thay đổi. 12
2. Hiện tượng tựcảm
S.đ.đtực m ả dm Φ )Theo đ/l Lenz: E = − tc dt Φ ∼ B m Do: Φ ∼ I = L.I B ∼ I m
)Đ/v mạch đứng yên và giữnguyên hình dạng: = ( −) tc = − d LI dI E L (L: Hệsốtựcảm) dt dt
ªTrong mạch điệnđứng yên và không thay đổi hình dạng,
sứcđiệnđộng tựcảm luôn bằng t c
ố độ biến thiên cường độ
dòng điện trong m ch. ạ 13
2. Hiện tượng tựcảm Hệs t ố ực m ả
)Định nghĩađơn vịđo hệsốtựcảm (L) ªĐơ 1Wb Wb
n vị: Henry (H), = A1H = 1 1A N vòng
ªH là hệsốtựcảm của 1 m ch ạ
kín, khi có dòng điện cường độ 1 A
chạy qua mạch đó thì sinh ra trong l S
chân không, từthông bằng 1 Wb.
)Trường hợpống dây có lõi sắt: Φ N.B.S μμ n2 S . .I μμ n2 S . L 0 0 = = = = I I I.l l
ªDo μ lõi sắt lớn⇒đơn vịHlớn⇒thực tếchỉdùng đơn vị
mH = 10-3 H, hoặc 1μH = 10-6 H 14
2. Hiện tượng tựcảm
Hiệuứng bềm t ặ
)Khi cho dòng điện cao tần chạy
qua 1 dây dẫn⇒dòng tựcảm chỉ r B
xuất hiệnởbềmặt dây dẫn
ªTần sốf= 103Hz ⇒dòng tự
cảm chạy trong lớp vật liệu bềmặt ~ 2 mm
ªTần sốf= 105Hz ⇒dòng tựcảm chỉchạy trong lớp ậ v t liệu bềmặt ~ 0,2 mm )Ứng ụ d ng trong công ệ ngh :
ªDùng dây dẫn rỗng để tải dòng cao tần
ªKỹthuật tôi bềmặt hợp kim bằng dòng cao tần 15
3. Năng lượng từtrường
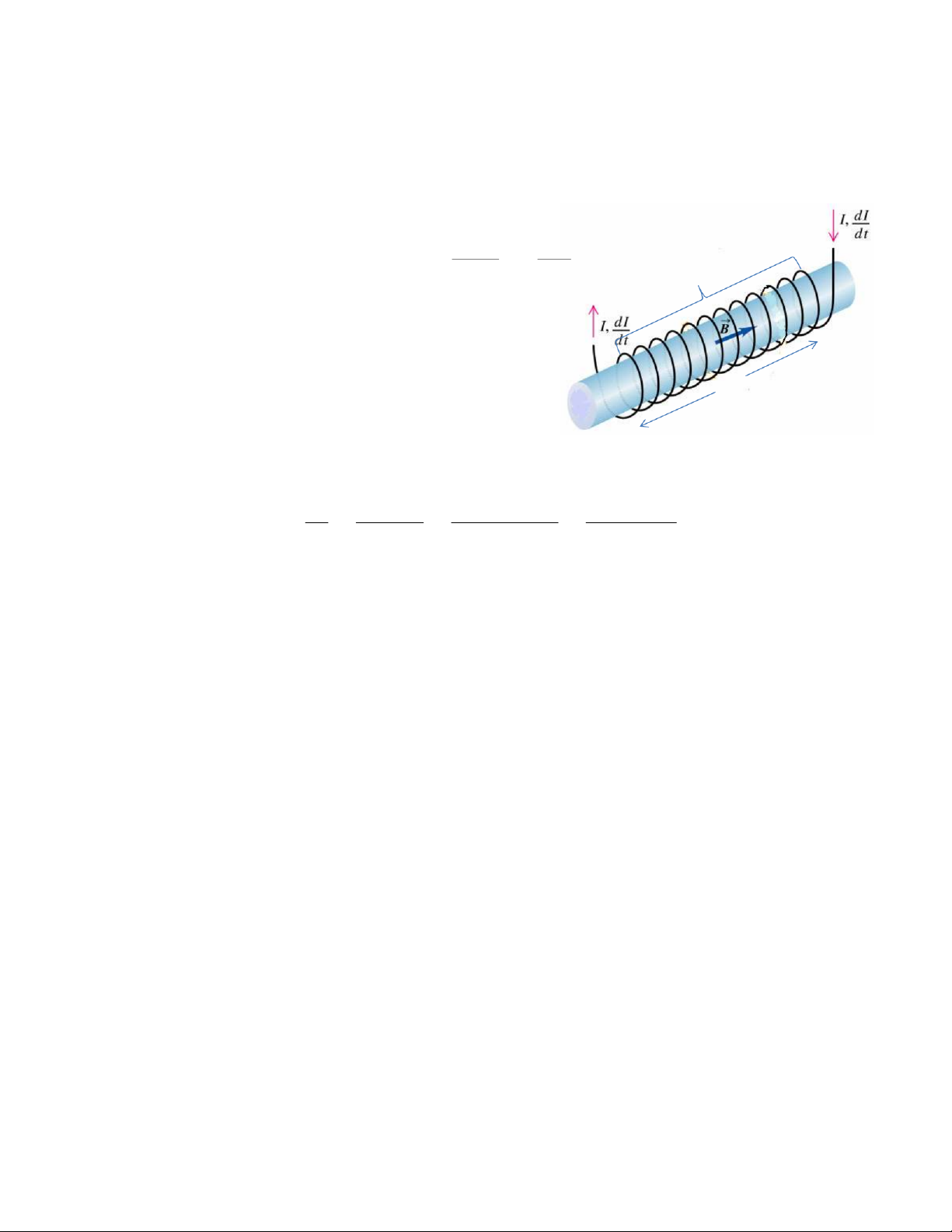
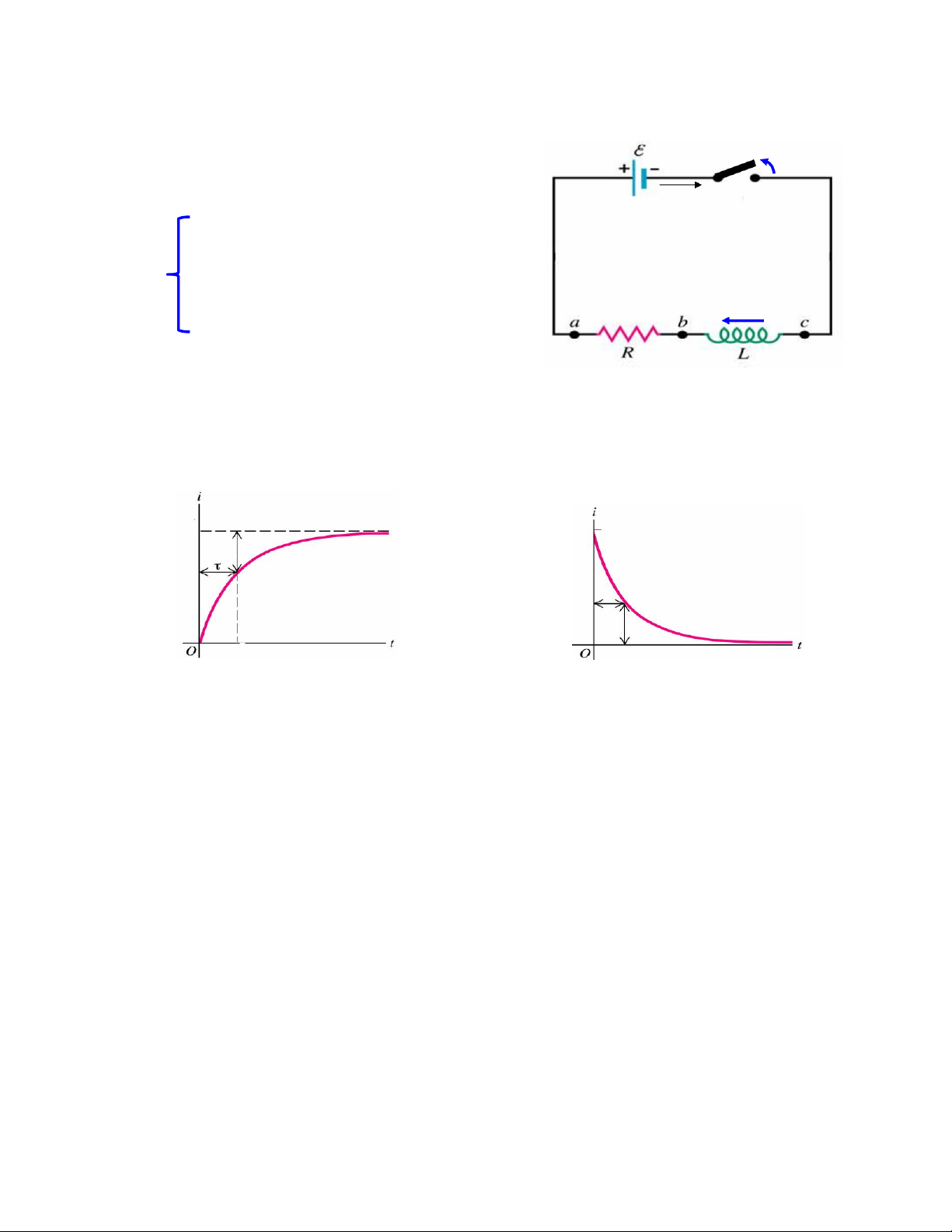
Năng lượng từtrường của mộtống dây )Mạch điện có khóa K: K i0
+ Sứcđiệnđộng E, dòng i0
+ Ống dây hệsốtựcảmL + Điện trởR itc
ªKhi đóng mạch ⇒i ↑ ⇒B
ªKhi ngắt mạch ⇒i ↓ ⇒B
& Φmgửi qua L ↑ ⇒itc ngược
& Φmgửi qua L ↓ ⇒itc cùng
chiềui0⇒i = i0- itc ⇒NL
chiềui0⇒i = i0+ itc ⇒NL
nguồn (~ i02) > NL mạch (~ i2).
nguồn (~ i02) < NL mạch (~ i2). i0i0 16
3. Năng lượng từtrường
Năng lượng từtrường của mộtống dây
)Áp dụng đ/l Ohm trong quá trình
hình thành dòng điệni: E + Etc =R.i di
Hay: E = R.i + L dt ªNhân 2 vếvớiidt:
E idt =R.i2dt + L.i.di
NL nguồnNL nhiệtNL từtrường
ªNL từtrường khi thiết lập dòng i
đ ện trong ống dây: dW = L.i.di i I 1 ∫ = ⇒ ∫ = = 2 W = dW L.i.di L.I 2 0 i=0 17
3. Năng lượng từtrường
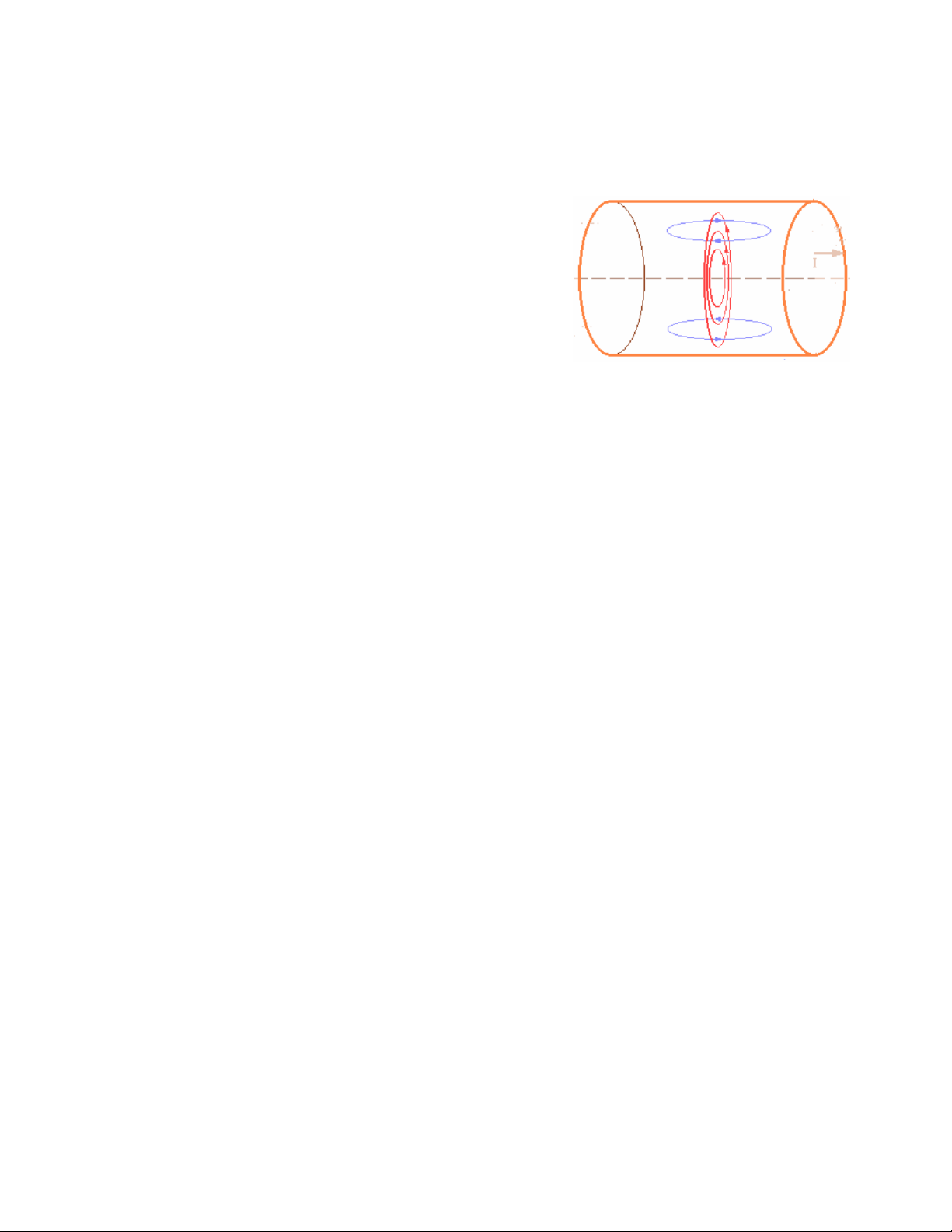
Mậtđộ năng lượng từtrường l
)Trong ống dây có thểtích: V = l.S
ªMậtđộ NL từtrường trong ống dây: 2 1 ⎛ n S ⎞ 2 1 2 μμ I L.I 0 ⎜⎜ ⎟⎟ W 2 l 2 ⎝ ⎠ w = = = m V l.S l.S 2 1 n 2 = μμ I 2 0 2 1 B 2 l
w=(trong ống dây: B= const) n mμμ 2 B 0 0= μμ I l
ªÁp dụng cho mọi từtrường bất kỳ 18
3. Năng lượng từtrường
Năng lượng từtrường không gian
)Chia không gian từtrường thành những thểtích vô
cùng nhỏdV sao cho B = const trong mỗidV.
ªNăng lượng từtrường trong mỗi thểtích dV: 1 B2 m dW m= w dV = dV 2 μμ0
ªNăng lượng từtrường trong cảkhông gian: 1dVB2 = Wm
∫d =Wm ∫ 2 μμ V V0 Wm 1BHdV H = ∫ = B 2 μμ V 0 19