Chương 5 - Đa Cộng Tuyến | Môn Kinh tế lượng - Học viện Chính sách và Phát triển

lOMoAR cPSD| 59452058 lOMoAR cPSD| 59452058
5.1. Bản chất của đa cộng tuyến
Chương 5. ĐA CỘNG TUYẾN lOMoAR cPSD| 59452058 lOMoAR cPSD| 59452058
5.1. Bản chất của đa cộng tuyến Đa cộng tuyến là gì ?
Đa cộng tuyến có nghĩa là sự tồn tại mối quan hệ tuyến
tính “hoàn hảo” hoặc “gần hoàn hảo” giữa một số hoặc
tất cả các biến giải thích trong một mô hình hồi quy. lOMoAR cPSD| 59452058
5.1. Bản chất của đa cộng tuyến
Xét mô hình hồi quy tuyến tính k-1 biến độc lập: Y = 1 + 2X2 + 3X3 + … + kXk + U (1)
● Nếu tồn tại các số thực 2, 3, …, k sao cho: 2X2 + 3X3 + …… + kXk = 0 với i (i = 2, 3,…,k)
không đồng thời bằng không thì mô
hình (1) xảy ra hiện tượng đa cộng tuyến hoàn hảo.
VD: Y = 1 + 2X2 + 3X3 + 4X4 +U (*) Mà có: 5X2 -X3 -7X4 = 0 lOMoAR cPSD| 59452058
5.1. Bản chất của đa cộng tuyến
Mô hình (*) bị đa cộng tuyến hoàn hảo.
● Nếu tồn tại các số thực 2, 3, …, k sao cho: 2X2 + 3X3 + …… + kXk + V = 0
với V là sai số ngẫu nhiên thì mô hình (1) bị hiện tượng đa cộng
tuyến gần hoàn hảo (đa cộng tuyến cao).
Nói cách khác là một biến giải thích nào đó có tương quan với
một hoặc một số biến giải thích khác thì mô hình bị đa cộng tuyến cao. lOMoAR cPSD| 59452058 Vídụ X2 10 15 18 24 30 X3 50 75 90 120 150 X4 52 75 97 129 152
X3 = 5X2, vì vậy mô hình: Y = β1 + β2 X2 +β3 X3 + U bị hiện tượng đa cộng tuyến hoàn hảo.
X2 và X4 có tương quan với nhau nên mô hình: lOMoAR cPSD| 59452058
5.1. Bản chất của đa cộng tuyến
Y = β1 + β2 X2 +β3 X4 + U bị đa cộng tuyến gần hoàn hảo (đa cộng tuyến cao). lOMoAR cPSD| 59452058
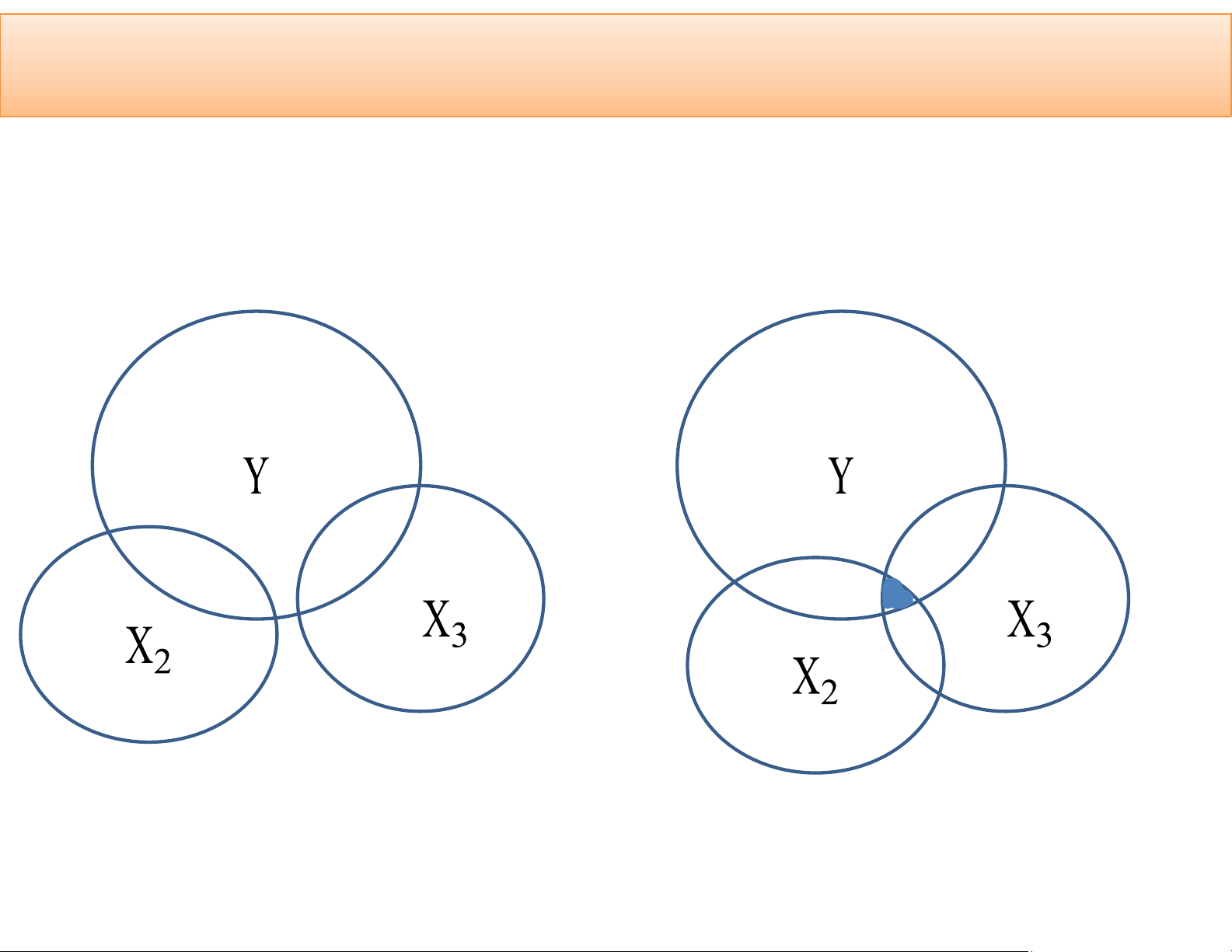
5.1. Bản chất của đa cộng tuyến Không có đa cộng tuyến Đa cộng tuyến thấp lOMoAR cPSD| 59452058
Hình 5.1: Biểu đồ Venn mô tả hiện tượng đa cộng tuyến
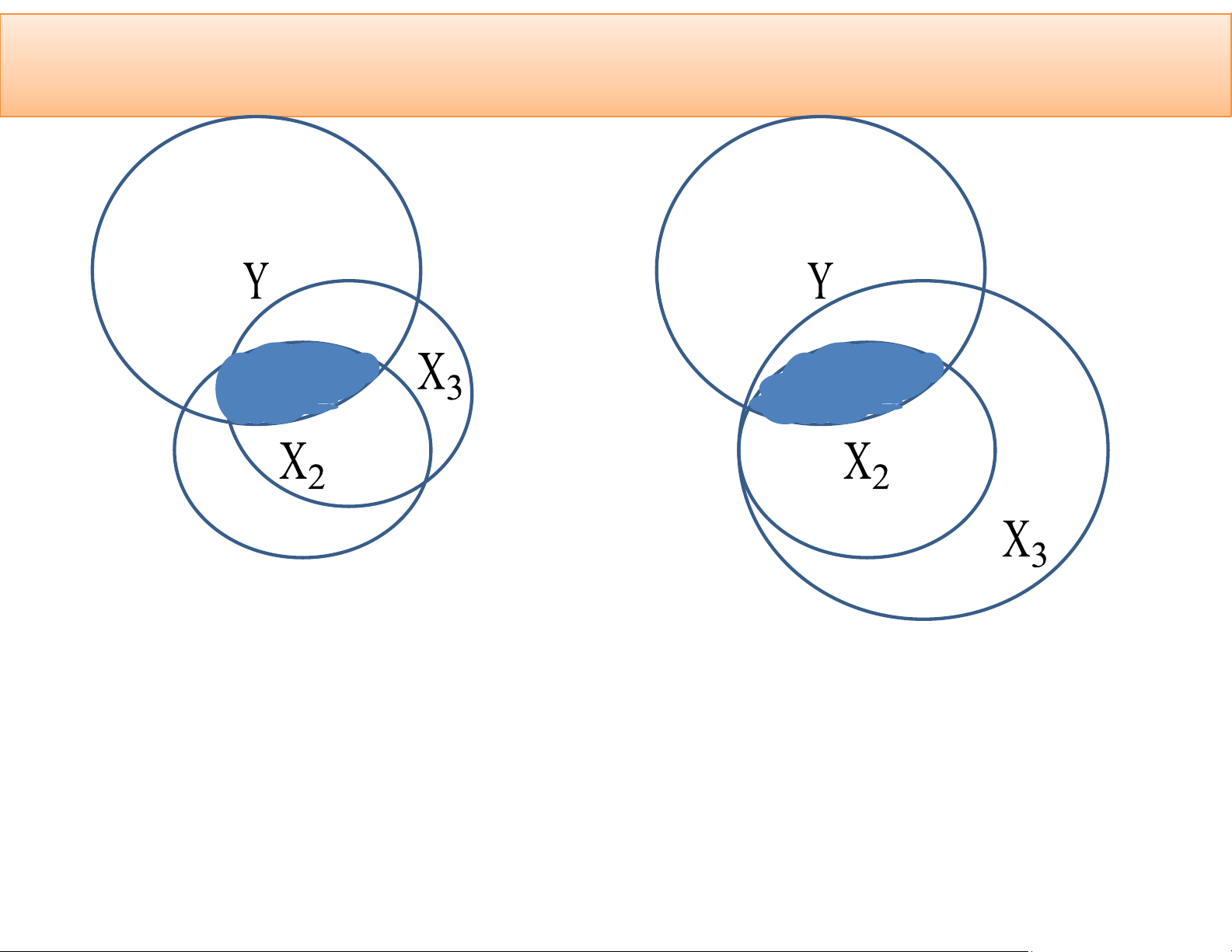
5.1. Bản chất của đa cộng tuyến Đa cộng tuyến cao Đa cộng tuyến hoàn hảo lOMoAR cPSD| 59452058
Hình 5.2: Biểu đồ Venn mô tả hiện tượng đa cộng tuyến lOMoAR cPSD| 59452058
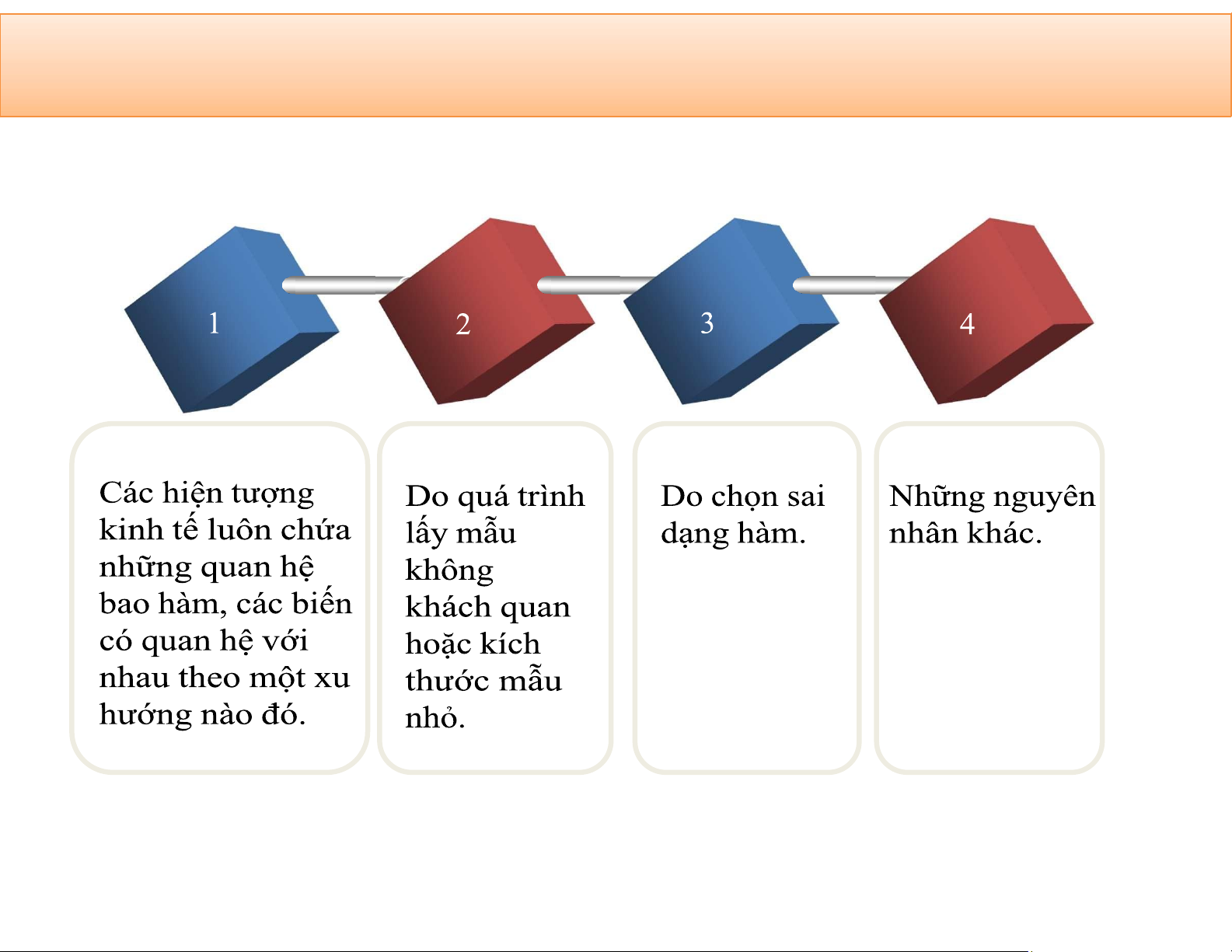
5.2. Nguyên nhân của hiện tượng đa cộng tuyến lOMoAR cPSD| 59452058 lOMoAR cPSD| 59452058
5.3. Hậu quả của đa cộng tuyến
5.3.1. Trường hợp có đa cộng tuyến hoàn hảo
5.3.2. Trường hợp có đa cộng tuyến gần hoàn hảo lOMoAR cPSD| 59452058
5.3.1.Trường hợp có đa cộng tuyến hoàn hảo Xét SRM: Yi ˆ1ˆ 2X2i ˆ3X3i ei ˆ 2 y xi 2i 2 x32i 2 y x i 3i x x2 2i 3i x 2i x3i x x2i 3i lOMoAR cPSD| 59452058
5.3.2.Trường hợp có đa cộng tuyến gần hoàn hảo ˆ y x 3 y xi3i 2 x22i 2 i 2i x x2 2i 3i x x x 2i x3i 2i 3i •
Giả sử X3i= .X2i trong đó 0, thay vào ta có: ˆ 2 y xi2i 2 x22i y xi 2i 2 x22i lOMoAR cPSD| 59452058 x 22i 2x22i 2 x22i
5.3.1.Trường hợp có đa cộng tuyến hoàn hảo Nhận xét: •
Các hệ số ước lượng không xác định: chúng ta không tách
rời tác động của từng biến Xi lên Y do không thể giả định X2
thay đổi trong khi X3 không đổi. lOMoAR cPSD| 59452058
5.3.2.Trường hợp có đa cộng tuyến gần hoàn hảo •
Trong trường hợp đa cộng tuyến hoàn hảo, phương sai và
sai số chuẩn của 2 và 3 là vô hạn. •
Xét mô hình hồi quy 3 biến dưới dạng sau: Yi = 1 + 2 X2i + 3 X3i + ui
Giả định x3i = x2i + vi với 0 và
vi là sai số ngẫu nhiên.
Trong trường hợp này, các hệ số hồi quy 2 và 3 vẫn có thể
ước lượng được bằng OLS, chẳng hạn: lOMoAR cPSD| 59452058 ˆ2 yxi 2i 2 x22i vi2 yxi 2i yvi i 2 x22i x 22i 2x22i vi2 2 x22i lOMoAR cPSD| 59452058
5.3.2.Trường hợp có đa cộng tuyến gần hoàn hảo
● Phương sai của các ước lượng OLS lớn: Var( ˆ ) 2 , Var( ˆ3) 2 2 2 x 2i 1 r23 x3i 1 r23 2 2 2
● Khoảng tin cậy của các hệ số hồi quy riêng rộng: