Chương 5: Điều Tra Chọn Mẫu - Xác Suất và Phân Phối Xác Suất môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

2/22/2021 Chương 5 ĐIỀU TRA CHỌN MẪU Nội dung I II III IV XÁC SUẤT VÀ NHỮNG VẤN ĐỀ ƯỚC LƯỢNG KIỂM ĐỊNH GIẢ QUY LUẬT CHUNG VỀ ĐIỀU KẾT QUẢ ĐIỀU THUYẾT PHÂN PHỐI TRA CHỌN MẪU TRA CHỌN THỐNG KÊ XÁC SUẤT MẪU 1
Xác suất và quy luật phân phối xác suất •Biếnngẫunhiê
• Quy luật phân phối xác suất của biến ngẫu nhiên
Biến ngẫu nhiên (Random Variables)
• Biến ngẫu nhiên là biến nhận một trong các giá trị có thể có của nó tuỳ
thuộc vào sự tác động của các nhân tố ngẫu nhiên trong một phép thử.
• Biến ngẫu nhiên là biến mà các giá trị không được xác định trước qua mỗi
lần thực nghiệm (phép thử) (experiment)
• Biến ngẫu nhiên thường được ký hiệu bằng chữ in hoa X, Y, Z…; các giá
trị của nó được ký hiệu bằng chữ thường x, y, z…
• Biến ngẫu nhiên liên tục (discrete random variable)
• Biến ngẫu nhiên rời rạc (continuous random variable) 2 Xác suất (Probability)
• Xác suất của một biến cố là một con số đặc trưng khả năng khách quan
xuất hiện biến cố đó khi thực hiện phép thử
Quy luật phân phối xác suất của biến ngẫu
nhiên (Probability Distribution)
Quy luật phân phối xác suất của biến ngẫu nhiên là sự tương ứng giữa
giá trị có thể có của nó và xác suất tương ứng với giá trị đó. 0 3 2/22/2021
Quy luật phân phối xác suất của biến ngẫu nhiên
Các phương pháp được sử dụng phổ biến để mô tả quy luật phân phối
xác suất của biến ngẫu nhiên gồm:
• Bảng phân phối xác suất (áp dụng cho biến ngẫu nhiên rời rạc)
• Hàm phân phối xác suất (áp dụng cho cả hai loại biến ngẫu nhiên rời rạc và liên tục)
• Hàm mật độ xác suất (áp dụng cho biến ngẫu nhiên liên tục)
Bảng phân phối xác suất (Probability table)
• Giả sử biến ngẫu nhiên rời rạc X nhận các giá trị x1,x2,..., xnvới các xác
suất tương ứng pi = p (X = xi), i=1÷n, bảng phân phối xác suất của biến ngẫu nhiên X là: Xx 1x2…x n Pp 1p2…p n Lưu ý: 0 ≤ pi≤ 1 𝑝 =1
𝑝 𝐴 < 𝑋 < 𝐵 = 𝑃 𝑋 = 𝑥 = 𝑝 4 2/22/2021
Hàm phân phối xác suất (Probability function)
• Hàm phân phối (phân bố) xác suất của biến ngẫu nhiên X, ký hiệu là F(x),
là xác suất để biến ngẫu nhiên X nhận giá trị nhỏ hơn x, với x là một số thực bất kỳ. F(x) = P (X < x)
• Nếu X là biến ngẫu nhiên rời rạc, hàm phân phối xác suất của X là: 𝐹 𝑥 = 𝑝 Hàm phân phối xác suất
•F(x)luônnhậngiátrịongđoạn[0,1]:≤F(x)≤1
• Nếu a là giá trị nhỏ nhất có thể có của X và b là giá trị lớn nhất có thể có
của X thì: F (x) = 0 với x ≤ a; F (x) = 1 với x > b
• F(x) là hàm không giảm, tức với x2>x 1:F(x 2)≥F(x 1)
• Hàm phân phối xác suất của một biến ngẫu nhiên liên tục bên trái.
Hàm F(x) cho biết tỷ lệ phần trăm giá trị của X nằm về bên trái của số thực x. 5 2/22/2021
Hàm mật độ xác suất (Probability density function)
• Hàm mật độ xác suất của biến ngẫu nhiên liên tục X, ký hiệu là f(x) là đạo hàm bậc nhất
của hàm phân bố xác suất của biến ngẫu nhiên đó. f(x) = F’(x)
• Hàm f(x) luôn không âm: f(x) ≥ 0
• Xác suất để biến ngẫu nhiên liên tục X nhận giá trị trong khoảng (a,b) bằng tích phân xác
định của hàm mật độ phân phối trong khoảng đó: 𝑃 𝑎 < 𝑋 < 𝑏 = ∫𝑓 𝑥 𝑑𝑥
• Hàm phân bố xác suất F(x) của biến ngẫu nhiên liên tục X bằng tích phân suy rộng của
hàm mật độ xác suất trong khoảng (-∞,x): 𝐹(𝑥)=∫𝑓 𝑥 𝑑𝑥
• Tích phân suy rộng trong khoảng (-∞,+ ∞) của hàm mật độ xác suất bằng 1: ∫𝑓 𝑥 𝑑𝑥 =1
Hàm mật độ xác suất của biến ngẫu nhiên X tại mỗi điểm cho biết mức độ tập trung
xác suất tại điểm đó.
Các tham số đặc trưng của biến ngẫu nhiên
• Kỳ vọng toán (Expected value, mean) của biến ngẫu nhiên X là một số, ký hiệu là E(X).
• Với biến ngẫu nhiên rời rạc: 𝐸 𝑋 = 𝑥 𝑝
• Với biến ngẫu nhiên liên tục với hàm mật độ xác suất f(x): 𝐸 𝑋 = 𝑥𝑓 𝑥 𝑑𝑥 6 2/22/2021
Các tham số đặc trưng của biến ngẫu nhiên
• Phương sai (Variance) của biến ngẫu nhiên X, ký hiệu là V(X) là kỳ vọng
toán của bình phương sai lệch của biến ngẫu nhiên so với kỳ vọng toán của nó.
𝑉 𝑋 = 𝐸[𝑋 − 𝐸 𝑋 ] = 𝐸 𝑋 −[𝐸 𝑋 ]
• Với biến ngẫu nhiên rời rạc: 𝑉 𝑋 = ∑[𝑥 − 𝐸 = 𝑋 ∑𝑥] 𝑝 −[𝐸 𝑋 ]
• Với biến ngẫu nhiên liên tục: 𝑉 𝑋 = ∫[𝑥 − 𝐸 =∫ 𝑋 𝑥 ]𝑓 𝑓 𝑥 𝑥 𝑑 𝑑 𝑥 𝑥 − [𝐸 𝑋 ]
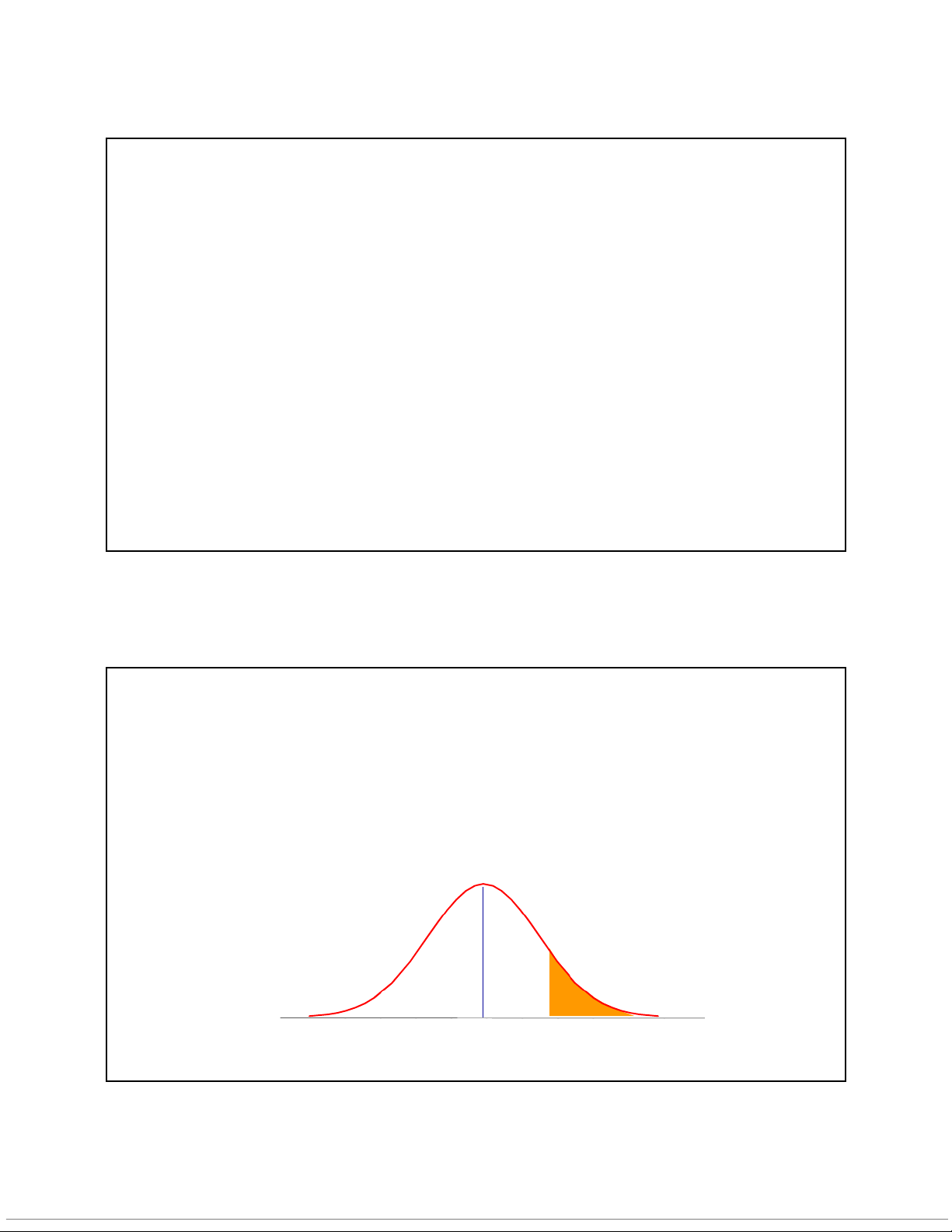
Giá trị tới hạn (Critical value)
•Giátrịớhạnmức𝛼của biến ngẫu nhiên liên tục X, ký hiệu là 𝑥 ,làgiátrị
của X thỏa mãn điều kiện: 𝑃(𝑋 > 𝑥 )=𝛼
•Giátrịớihạn𝑥 là giá trị sao cho diện tích giới hạn bởi trục hoành,
đường cong hàm mật độ xác suất và đường thẳng x= 𝑥 bằng 𝛼 f(x) 𝛼 𝑥 x 7 2/22/2021
Quy luật phân phối không – một A(p) (Bernoulli Distribution)
• Biến ngẫu nhiên rời rạc X nhận một trong hai giá trị có thể có là 0 hoặc 1
với các xác suất tương ứng được cho bởi công thức:
P(X=x) = pxq1−x trong đó 0

→ được gọi là có phân phối theo quy luật 0-1 với tham số p, ký hiệu X ~ A(p)
•E(X)=0xq+1xp=p 𝐸 𝑋 = 𝑝 •VX=𝐸 𝑋 − 𝐸 𝑋
= 𝑝 − 𝑝 = 𝑝 1−𝑝 = 𝑝𝑞
Áp dụng với các biến định tính chỉ có hai thuộc tính/phạm trù
Quy luật phân phối nhị thức B(n,p)
(Binomial Probability Distribution)
• Biến ngẫu nhiên rời rạc X được gọi là có phân phối theo quy luật nhị thức
với các tham số là n và p, ký hiệu X ~ B (n,p), nếu X nhận một trong các
giá trị 0, 1, 2, ... , n với xác suất tương ứng cho bởi công thức Bernoulli: 𝑃 = 𝐶 𝑝 𝑞 với x = 0, 1, 2, …, n •E(X)=np •V(X)=npq 8 2/22/2021
Quy luật phân phối nhị thức B(n,p)
Quy luật nhị thức theo tỷ lệ
• Tần suất xuất hiện biến cố A trong n phép thử độc lập: f = X / n
• Tần suất f vẫn phân phối theo quy luật nhị thức với các tham số n, p. •𝐸 𝑓 = 𝐸 = 𝐸 𝑋 = = 𝑝 •𝑉 𝑓 = 𝑉 = 𝑉 𝑋 = =
Quy luật phân phối chuẩn (Normal Probability Distribution)
• Biến ngẫu nhiên liên tục X nhận các giá trị trong khoảng (-∞,+∞) gọi là
tuân theo quy luật phân phối chuẩn với các tham số 𝜇và 𝜎 ,nếuhàmmật
độ xác suất của nó là: 𝑓 𝑥 = 1 𝑒 ( ) 𝜎 2𝜋
• Hàm phân phối xác suất là: 𝐹 𝑥 = 1 𝑒 ( ) 𝑑𝑥 𝜎 2𝜋 9 2/22/2021
Quy luật phân phối chuẩn
•KhiX~N(𝜇, 𝜎 ), ta có: E(X) = 𝜇V(X) = 𝜎
• Đường cong mật độ có dạng hình chuông, đối xứng qua đường x = μ và nhận Ox
làm tiệm cận ngang. Đỉnh của hàm mật độ đạt tại:
m𝑎𝑥𝑓 𝑥 = 𝑓 𝜇 = 1 f(x) 𝜎 2𝜋 1 𝜎 2𝜋 𝜎 0µ x
Quy luật phân phối chuẩn hóa (Standard
Normal Probability Distribution)
•BiếnngẫunhiêliêntụcUnhậncágiátrịongkhoảng(-∞,+∞)gọilà
tuân theo quy luật phân phối chuẩn hóa nếu hàm mật độ xác suất của nó, 𝜑(u) là: 𝜑 𝑢 = 1𝑒 2𝜋
• Hàm phân phối xác suất của biến ngẫu nhiên chuẩn hóa U được ký hiệu là Φ(u). Φ 𝑢 = ∫𝑒 𝑑𝑢 10 2/22/2021
Quy luật phân phối chuẩn hóa • Khi U ~ N(0;1), ta có: E(U)=0 V(U)=1
• Đường cong biểu diễn mật độ của U đối xứng qua trục tung và nhận trục
hoành làm tiệm cận ngang, đỉnh đạt tại: m𝑎𝑥𝜑 𝑢 = 𝜑 0= 1 𝜑 𝑢 2𝜋 0 u
Quy luật phân phối chuẩn hóa
• Giá trị tới hạn chuẩn mức 𝛼,kýhiệulà𝑢 là giá trị của biến ngẫu nhiên U có
phân phối chuẩn hóa thỏa mãn: P (U> 𝑢 )= 𝛼,với0≤𝛼 ≤1
• Các giá trị của 𝑢 được tính sẵn thành bảng. 𝜑 𝑢𝑢𝜑 • Tính chất: 𝑢 =−𝑢
• Một số giá trị cơ bản:
•u 0,025 =1,96 P(U>1,96)=0,25
•u 0,05 =1,645 P(U>1,645)=0,5
•u 0,95 =-1,645 P(U>-1,645)=0,95 𝑢 0 𝑢 𝑢 11 2/22/2021
Quy luật phân phối chuẩn hóa
• Với biến ngẫu nhiên có phân phối chuẩn X ~ N (𝜇, 𝜎 ), có thể thông qua phép
biến đổi thích hợp để đưa về trường hợp biến ngẫu nhiên chuẩn hóa. 𝑍 = 𝑥 − 𝜇 𝜎
• Khi đó, ta có biến ngẫu nhiên chuẩn hóa Z ~ N(0;1). •KhiXnhậgi átr ịtr ongkhoản(a, b)hì : =1 𝑒 ( ) 𝑏 − 𝜇 𝜎−Φ 𝑎 − 𝜇
𝑃 𝑎 < 𝑋 < 𝑏 = 𝑓 𝑥𝑑𝑥 =Φ 𝑑𝑥 𝜎 2𝜋 𝜎 VớiΦ 𝑢 = ∫ 𝑒 𝑑𝑍 Φ − 𝑢 = - Φ 𝑢
Với mọi u>5: Φ 𝑢 ≈ Φ 5 = 0,5 Φ 𝑢 = 0,5 + Φ 𝑢
Quy tắc hai xích ma và ba xích ma
• Trong một số trường hợp phải tính xác suất để biến ngẫu nhiên X phân phối
chuẩn nhận giá trị sai lệch so với kỳ vọng toán của nó, tức: 𝑋 − 𝜇 < 𝜀
hay 𝜇−ε<𝑋 < 𝜇 +ε • Do đó, ta có:
𝑃 𝑋 − 𝜇 < 𝜀 = 𝑃 𝜇 −ε<𝑋 < 𝜇 +ε =2Φ (𝜀 𝜎)
• Quy tắc hai xích ma và ba xích ma
𝑃 𝑋 − 𝜇 <2𝜎 = 𝑃 𝜇 −2𝜎 < 𝑋 < 𝜇 +2𝜎=2Φ 2=0 , 9 5 4 4
𝑃 𝑋 − 𝜇 <3𝜎 = 𝑃 𝜇 −3𝜎 < 𝑋 < 𝜇 + 3𝜎 =2Φ 3=0 , 9 7 2 12 2/22/2021
Quy tắc hai xích ma và ba xích ma 99.72% 95.44% 68.26% x m–3 sm –1 s m m+ 1s m+ 3s m–2 s m+ 2 s
Tra bảng giá trị tới hạn phân phối chuẩn hóa
z.00 .01 .02 .03 .04 .05 .06 .07 .08 .09 .. . . . . . . . . .
1.5 .9332 .9345 .9357 .9370 .9382 .9394 .9406 .9418 .9429 .9441
1.6 .9452 .9463 .9474 .9484 .9495 .9505 .9515 .9525 .9535 .9545
1.7 .9554 .9564 .9573 .9582 .9591 .9599 .9608 .9616 .9625 .9633
1.8 .9641 .9649 .9656 .9664 .9671 .9678 .9686 .9693 .9699 .9706
1.9 .9713 .9719 .9726 .9732 .9738 .9744 .9750 .9756 .9761 .9767 ...........
Với 𝛼=0,05, phần diện tích phía trái còn lại là 1-0,05=0,95; giá trị tới hạn tương ứng là 1,645 13 2/22/2021
Quy luật phân phối t Student
•BiếnngẫunhiêliêntụcTgọilàphânphốitheoquiluậtStudentvớinbậc
tự do nếu hàm mật độ xác xuất của nó được xác định như sau: 𝑓 𝑡 = ( ) )1+ ∀𝑡 (
Trong đó: Γ(x) là hàm Gamma. •Khiđó: E(T)=0 V(T)=
Quy luật phân phối t Student
• Giá trị tới hạn Studen, ký hiệu là 𝑡
( )là giá trị của biến ngẫu nhiên T phân
phối theo qui luật Student với n bậc tự do, thỏa mãn: 𝑃(𝑇 > 𝑡 ( ))=𝛼 𝑓 𝑡
• Tính chất: 𝑡 ( ) =−𝑡 ( )
Khi số bậc tự do tăng lên, phân phối
Student hội tụ nhanh về phân phối chuẩn hóa.
→ Nếu n khá lớn (n>30) có thể dùng
phân phối chuẩn hóa thay thế cho phân phối Student 0 𝑡 𝑡( ) 𝑡( 𝑡 ( ) 𝑡 ( 14 2/22/2021 Quy luật phân phối Fisher
• Biến ngẫu nhiên liên tục F gọi là phân phối theo quy luật Fisher với n1và
n2bậc tự do nếu hàm mật độ xác suất của nó được xác định là: i ớ 𝑓 𝑥 = 0v 𝐶𝑥 với x > 0 (𝑛 + 𝑛 . 𝑥)
𝑉ớ𝑖: 𝐶 = Γ𝑛 + 𝑛 2. 𝑛 . 𝑛 Γ𝑛 2.Γ 𝑛 2 𝑛 2𝑛 (𝑛 + 𝑛 − 2) 𝐸 𝐹 = 𝑉 𝐹 = 𝑛 − 2 𝑛 (𝑛 − 2) (𝑛 − 4) Quy luật phân phối Fisher
• Giá trị tới hạn Fisher, ký hiệu là 𝑓 ( ,
)là giá trị của biến ngẫu nhiên F
phân phối theo qui luật Fisher với n1và n2bậc tự do, thỏa mãn: 𝑃(𝐹 > 𝑓 ( , ))=𝛼
• Tính chất: 𝑓 ( , )= ( , ) f(x) 𝛼 x 𝑓( , ) 15 2/22/2021
Những vấn đề chung về điều tra chọn mẫu
Một số khái niệm liên quan
Ưu, nhược điểm của điều tra chọn mẫu
Trường hợp vận dụng điều tra chọn mẫu Các cách chọn mẫu •Phânphốimẫu
•Địnhlýgiớhạntrungtâm
Một số khái niệm liên quan
Điều tra chọn mẫu là loại hình điều tra không toàn bộ, trong đó người ta
chỉ chọn ra một số đơn vị đủ lớn thuộc đối tượng nghiên cứu để tiến hành điều tra thực tế.
→Các đơn vị này được chọn theo những quy tắc nhất định để đảm bảo tính
đại biểu và kết quả của ĐTCM được dùng để suy rộng cho toàn bộ hiện tượng. 16 2/22/2021
Một số khái niệm liên quan
Tổng thể chung là tổng thể bao gồm toàn bộ các đơn vị thuộc đối tượng điều tra.
Tổng thể mẫu là tổng thể bao gồm một số đơn vị nhất định được chọn ra
từ tổng thể chung để tiến hành điều tra thực tế.
Suy rộng (ước lượng): từ các mức độ tính toán được trên các đơn vị điều
tra (tổng thể mẫu) suy ra các tham số tương ứng của toàn bộ hiện tượng (tổng thể chung).
• Suy rộng số bình quân theo một tiêu thức.
• Suy rộng tỷ lệ theo một tiêu thức.
Một số khái niệm liên quan Chỉ tiêu Tổng thể chung Tổng thể mẫu Quy mô N n Số bình quân µ 𝑥
Tỷ lệ theo một tiêu thức p f Phương sai 𝜎 𝑆 p(1-p) f(1-f) 17 2/22/2021
Ưu, nhược điểm của điều tra chọn mẫu Ưu điểm
Tiết kiệm (chi phí, nhân lực)
Có thể mở rộng nội dung điều tra
Tài liệu thu được trên mẫu có độ chính xác cao
Nhanh gọn, đảm bảo tính kịp thời Nhược điểm
Không cho biết thông tin đầy đủ về tổng thể
Không tránh khỏi sai số khi suy rộng
Kết quả điều tra không thể tiến hành phân tổ theo mọi phạm vi nghiên cứu
Sai số trong điều tra chọn mẫu
• Sai số do đăng ký, ghi chép • Sai số chọn mẫu
• Vi phạm nguyên tắc chọn mẫu ngẫu nhiên
• Số lượng đơn vị mẫu không đủ lớn
• Kết cấu tổng thể mẫu khác với kết cấu tổng thể chung 18 2/22/2021
Trường hợp vận dụng của điều tra chọn mẫu
• Thay thế cho điều tra toàn bộ
•Kếthợpvớiđiềutraoànbộ
• Kiểm định giả thuyết thống kê
Các phương pháp chọn mẫu
Chọn ngẫu nhiên (chọn xác suất): là kỹ thuật chọn mẫu mà mỗi đơn vị
trong tổng thể có một xác suất được chọn đã biết và khác 0.
Các phương pháp chọn mẫu ngẫu nhiên
•Chọnngẫunhiêgiảnđơn •Chọnhệthống • Chọn phân tầng • Chọn phân cụm •Chọnnhiềugiađoạn 19 2/22/2021
Các phương pháp chọn mẫu
Chọn phi ngẫu nhiên (chọn phi xác suất): là kỹ thuật chọn mẫu mà các đơn vị
của mẫu được chọn dựa trên những đánh giá cá nhân hoặc sự thuận tiện.
→ Xác suất được chọn của mỗi đơn vị trong tổng thể là không biết.
Các phương pháp chọn mẫu phi ngẫu nhiên •Chọnthuậni ê • Chọn theo chủ đích • Chọn theo hạn ngạch
• Chọn kiểu quả cầu tuyết Lưu ý
• Các mẫu ngẫu nhiên là các mẫu được chọn có sử dụng các nguyên lý xác suất
• Nó cho phép xác định phân phối mẫu của một thống kê mẫu
• Có thể xác định xác suất của bất kỳ sai số chọn mẫu nào và thực hiện suy
luận cho các đặc trưng của tổng thể 20