Chương 5: Ước Lượng Khoảng Tin Cậy trong Thống Kê Ứng Dụng. Môn Thống kê ứng dụng | Đại học Văn Hiến.

lOMoAR cPSD| 58968769 15/10/2023 Môn học
THỐNG KÊ ỨNG DỤNG Giảng viên HOÀNG SƠN TÙNG
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn
Chương 5 ƯỚC LƯỢNG KHOẢNG TIN CẬY .
(Confidence Interval Estimation) lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn NỘI DUNG CHƯƠNG
ƯỚC LƯỢNG KHOẢNG CHO TỈ LỆ P
ƯỚC LƯỢNG KHOẢNG CHO TRUNG BÌNH 𝝁
TÌM CHỈ TIÊU CHO ƯỚC LƯỢNG TỶ LỆ P
TÌM CHỈ TIÊU CHO ƯỚC LƯỢNG TRUNG BÌNH 𝝁
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn
1. Ước lượng khoảng tin cậy cho tỷ lệ p lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn Đặt vấn đề
• Tổng thể chia làm 2 loại phần tử. Tỉ lệ phần tử có tính chất A là P chưa biết.
• Căn cứ vào mẫu gồm n phần tử quan sát độc lập mà đưa ra chỉ tiêu
(𝑝1, 𝑝2) để ước lượng P thỏa
P[𝑝1 ≤ 𝑝 ≤ 𝑝2] = 1 – α
• Giá trị 1 – α gọi là độ tin cậy của ước lượng và được cho trước.
• α có giá trị nhỏ, 1%, 2%, … 5%
• Từ mẫu điều tra, tính • Trong đó:
m = số phần tử có tính chất A trong mẫu điều tra n = tổng mẫu
• Từ độ tin cậy 1- α cho trước, tra bảng tìm ra giá trị 𝑡𝛼 tương ứng
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Quy tắc thực hành
Khoảng ước lượng P nằm trong khoảng 𝑓 𝑝 𝑚 ( 1 − 𝑓 𝑚 ) 1 = 𝑓 𝑚 − 𝑡 𝛼 𝑛 𝑓 𝑝 𝑚 ( 1 − 𝑓 𝑚 ) 2 = 𝑓 𝑚 + 𝑡 𝛼 𝑛 (1)
Một số giá trị 𝑡𝛼 tương ứng với 𝛼 lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn α
0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 𝐭𝛂
2.58 2.33 2.17 2.06 1.96 1.88 1.82 1.75 1.65
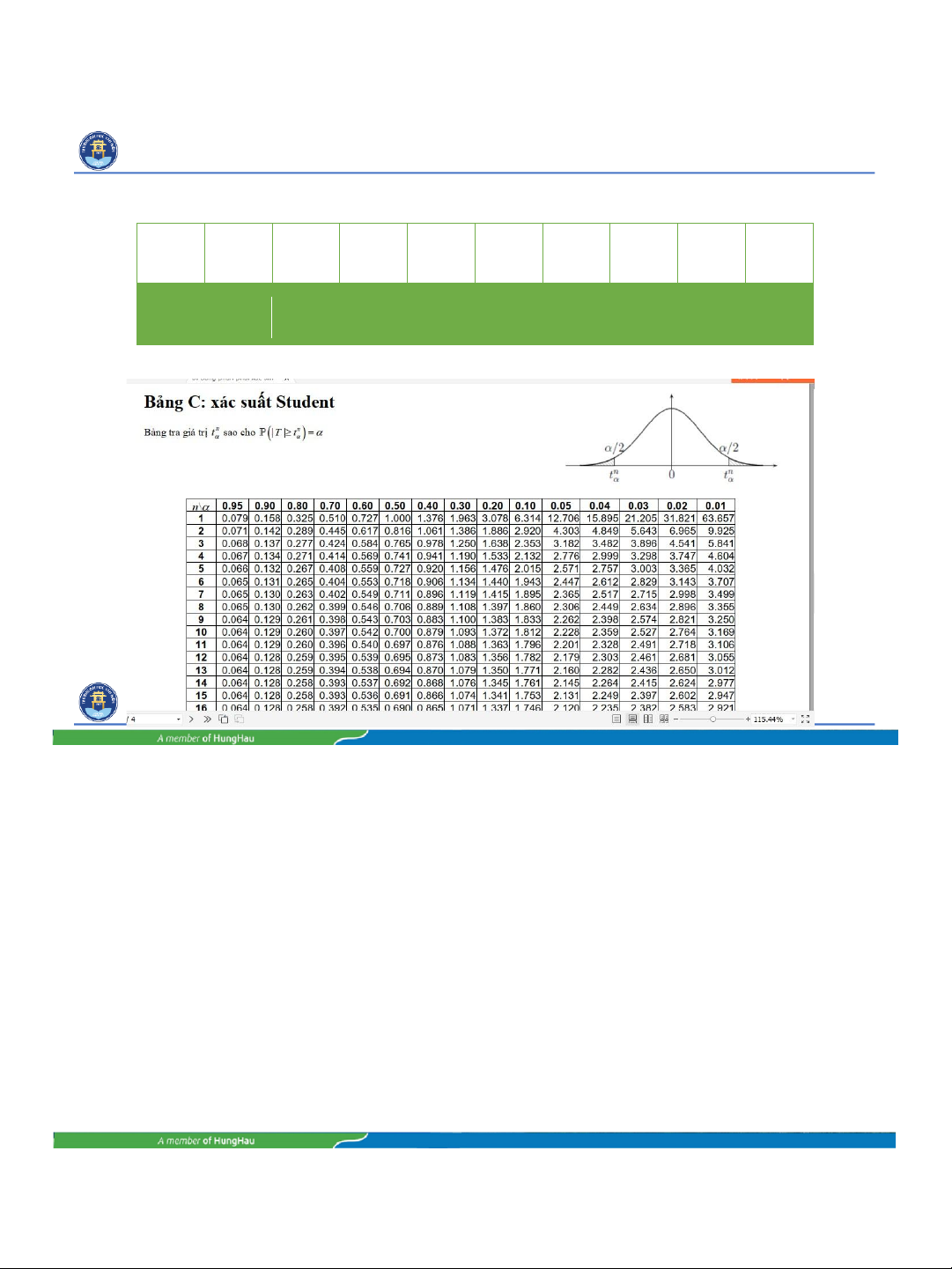
Sử dụng bảng xác suất Student để xác định giá trị 𝒕𝜶
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu
Điều tra 100 sản phẩm của nhà máy sản xuất, người ta phát hiện có 15
sản phẩm không đạt yêu cầu về chất lượng.
Hãy ước lượng tỉ lệ sản phẩm không đạt tiêu chuẩn chất lượng của nhà
máy với độ tin cậy đạt mức 90% lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu Giải:
Đây là bài toán ước lượng khoảng cho tỉ lệ P Ta có:
Khoảng ước lượng là : 0 .15 1 − 0 .15 𝑝 1 = 0 .15 − 1 .65 100 = 0 .091 0 .15 1 − 0 .15 𝑝 2 = 0 .15 + 1 .65 100 = 0 .209
Kết luận: Vậy với độ tin cậy 90%, thì tỉ lệ sản phẩm không đạt yêu cầu
của nhà máy vào khoảng từ 9,1% đến 20,9%.
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn
2. Ước lượng khoảng tin cậy
cho giá trị trung bình 𝝁 lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn Đặt vấn đề
• Tổng thể có trung bình μ chưa biết.
• Căn cứ vào mẫu gồm n quan sát độc lập để đưa ra hai số 𝜇1, 𝜇2 sao cho
P[𝜇1 ≤ 𝜇 ≤ 𝜇2] = 1-α
• Với 1-α đã cho biết trước.
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Quy tắc thực hành
1. TH1: n ≥ 30, 𝝈𝟐 đã biết. Khi đó,
Đã biết độ chính xác 1 − 𝛼 sẽ xác định được 𝑡𝛼 qua tra bảng
➔Tính 𝜇1, 𝜇2 theo công thức lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn 𝜎 2
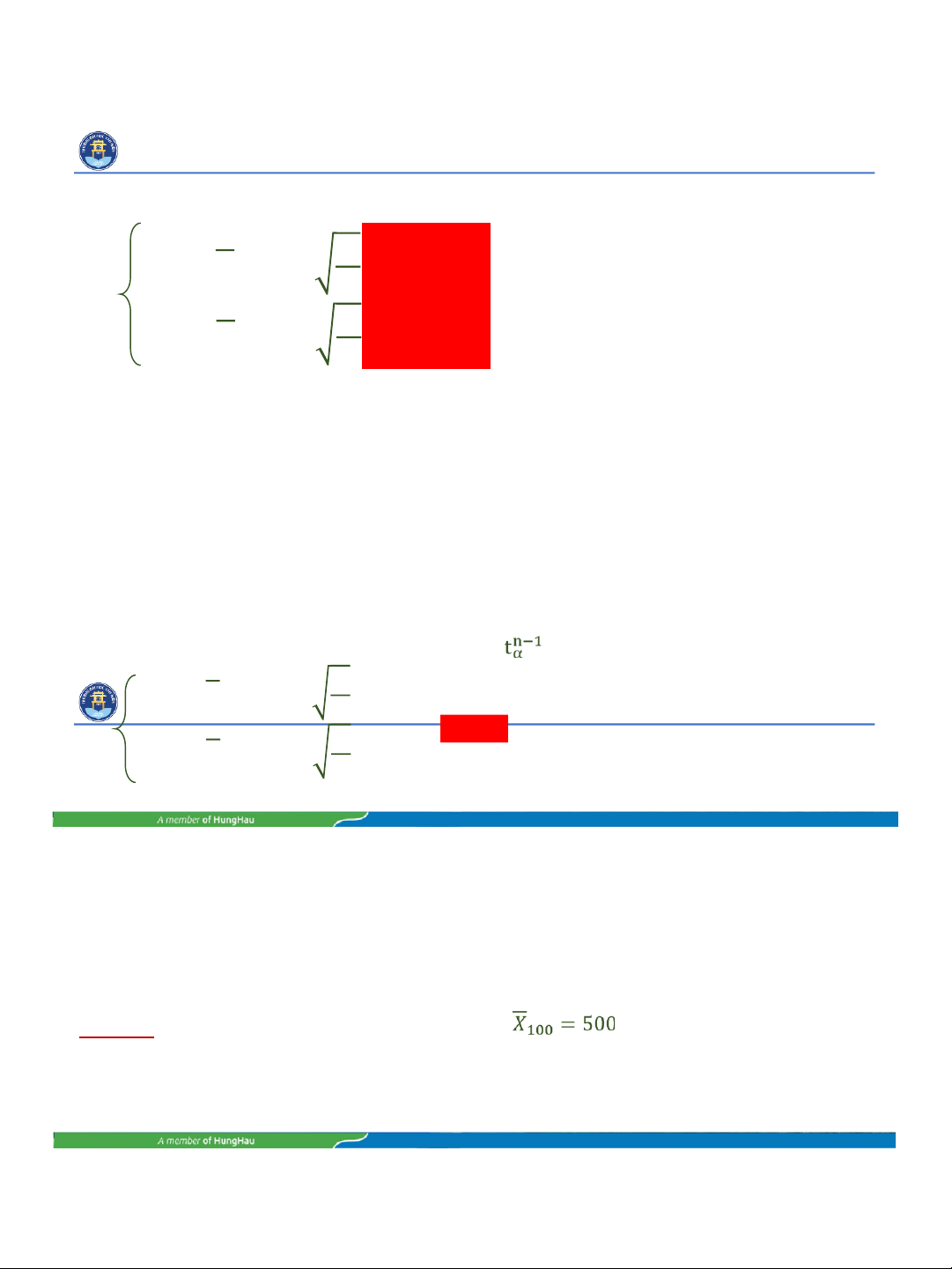
𝜇 1 = 𝑋 𝑛 − 𝑡 𝛼 𝑛 𝜎 2
𝜇 2 = 𝑋 𝑛 + 𝑡 𝛼 𝑛 (2) Quy tắc thực hành
2. TH2: n ≥ 30, 𝛔𝟐 chưa biết
Khi đó, ta thay 𝜎2 bằng 𝑆2 mà đề bài cho trong công thức (2)
3. TH3: n < 30, X chuẩn, 𝛔𝟐 đã biết
Khi đó, tính 𝜇1, 𝜇2 theo công thức như trong TH1
4. TH4: n < 30, X chuẩn 𝛔𝟐 chưa biết
Tra bảng C để xác định tnα−1, sao cho thỏa: P[|tn- 1| ≤ tnα−1] = 1-α
Thay σ2 = S2 đề bài cho và thay tn bằng
ở công thức (2), ta được: μ n − 1 S 2 1 = X n − t α n (3) μ n − 1 S 2 2 = X n + t α n
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu
Bài 1: Cân thử 100 sản phẩm, tính được gram, 𝜎2 = 40.
Giả sử trọng lượng của sản phẩm có phân phối chuẩn, hãy ước lượng
trọng lượng trung bình μ với độ tin cậy 95%. lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn
Giải: n = 100 >30, 𝜎2 đã biết nên đây là bài toán dạng TH1.
Ta có: 1- α = 0.95 → α = 0.05 → 𝑡0.05 = 1.96
Thay vào các công thức dạng 1, ta được kết quả 𝜇1 = 498.76 gram 𝜇2 = 501.24 gram
Kết luận: 95% sản phẩm được sản xuất ra có trọng lượng nằm trong
khoảng 498.76g đến 501.24g Bài tập mẫu
Bài 2: Sau khi thu hoạch 1 loại trái cây, người ta cân thử 100 trái và ghi
nhận kết quả như sau: 𝑋100 = 41g, 𝑆2 = 251,51g2.
Giả sử khối lượng của loại trái cân này có phân phối chuẩn, hãy ước lượng
khối lượng trung bình của sản phẩm với độ tin cậy 92%. Giải:
•n = 100 > 30, 𝜎2 chưa biết, 𝑆2 cho trước ➔ đây là dạng TH 2
•1 - α = 0.92 → α = 0.08 → 𝑡0.08 = 1.75
•Sử dụng công thức dạng 2, ta được kết quả 𝜇1 = 38.22 gram 𝜇2 = 43.78 gram
Kết luận: 92% lượng trái cây sau khi thu hoạch sẽ có trọng lượng nằm
trong khoảng từ 38.22g đến 43.78g
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu
Bài 3: Cân thử 15 gói bột do một nhà máy đóng bao bì sản xuất ra, người ta tính được gram, S2 = 0.144.
Giả thiết trong lượng các gói bột là đại lượng ngẫu nhiên X có phân phối
chuẩn. Hãy ước lượng trọng lượng trung bình μ với độ tin cậy 95%.
Giải: Ta có: n = 15 <30, X phân phối chuẩn, 𝜎2 chưa biết. Đây là bài toán dạng 4 với α = 5%.
• Tra bảng C, ta có 𝑡014.05 = 2.145
• Sử dụng công thức (5.2.2), ta tính được 𝜇1= 39.59 gram 𝜇2 = 40.01 gram
Kết luận: có 95% gói bột được sản xuất ra có khối lượng trong khoảng 39.59g đến 40.01g
3. Tìm chỉ tiêu cho bài toán
ước lượng tỷ lệ
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Đặt vấn đề
Tổng thể có tỉ lệ P chưa biết, ta ước lượng bằng 𝑓𝑛 lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn
• Nếu |p - 𝑓𝑛|≤ ε thì ta gọi ε là độ chính xác của ước lượng • Nếu
P[|p - 𝑓𝑛|≤ ε] = 1- α thì 1- α là độ tin cậy của ước lượng • n là cỡ mẫu. Đặt vấn đề •
Độ tin cậy, độ chính xác và cỡ mẫu là ba chỉ tiêu chính của bài toán ước lượng. •
Cứ biết 2 trong số 3 chỉ tiêu trên, ta sẽ tìm được chỉ tiêu còn lại dựa vào công thức: 𝑓 𝑛 ( 1 − 𝑓 𝑛 ) 𝜀 = 𝑡 𝛼 𝑛 (4)
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Quy tắc thực hành
Dạng 1: Biết độ tin cậy 1- α, cỡ mẫu n, tìm ε f n ( 1 − f n ) ε = t α n (4a)
Dạng 2: Biết ε, biết mẫu cỡ n (fn), tìm được 1- α •
Từ công thức (4), ta có: lOMoAR cPSD| 58968769 15/10/2023
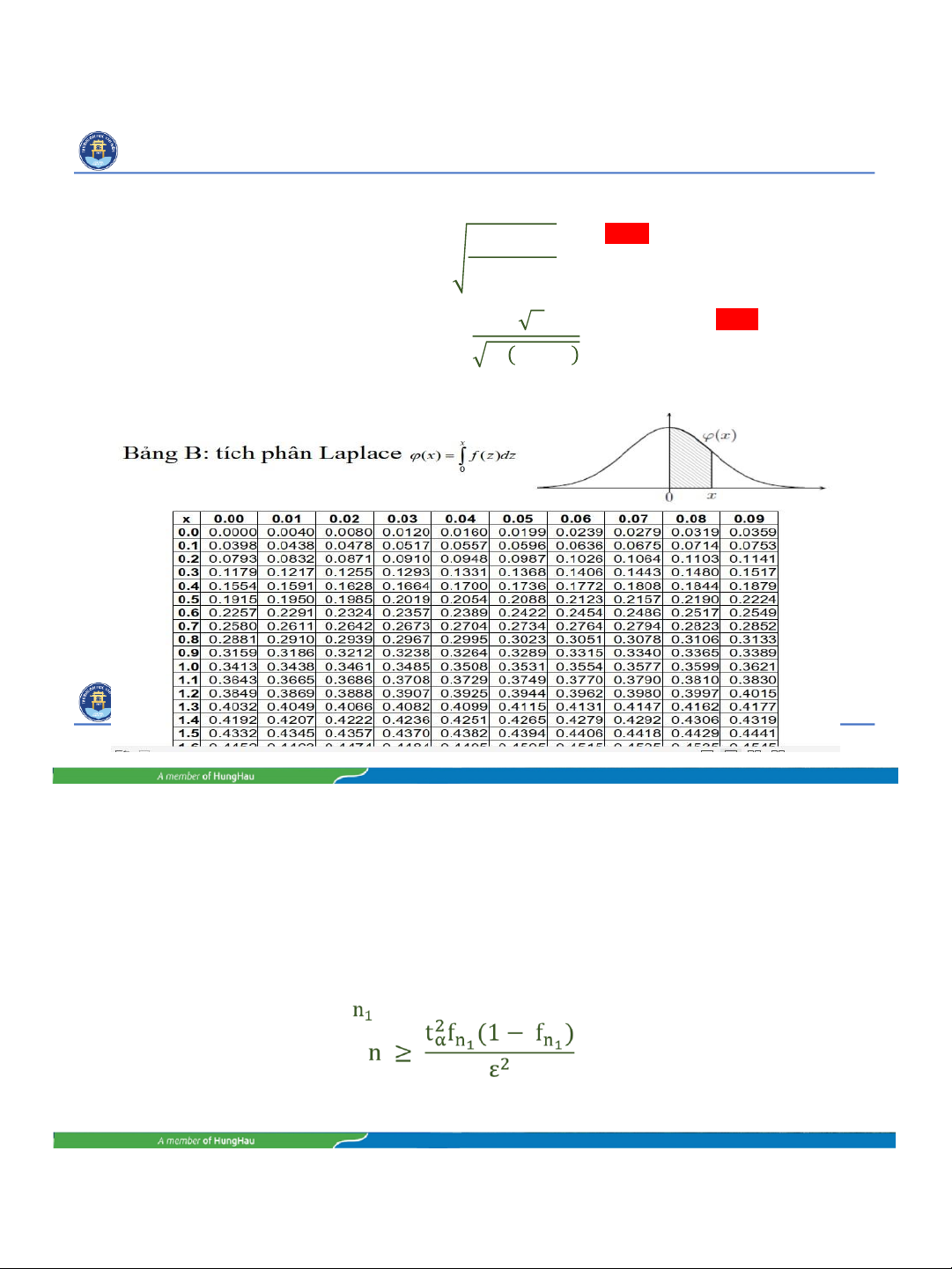
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn (4b) n t α = ε f n ( 1 − f n ) (4c) 𝜀 𝑛 1 − 𝛼 = 2 𝜑 ( ) Sử dụng bảng 𝑓 𝑛 1 − 𝑓 𝑛 tích phân Laplace
để xác định 𝒕𝜶
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Quy tắc thực hành
Dạng 3: Biết 1- α, biết ε, tìm n
• TH1: có điều tra sơ bộ lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn (5a)
Cần điều tra thêm 𝑛2 = 𝑛 − 𝑛1 (nếu n > 𝑛1)
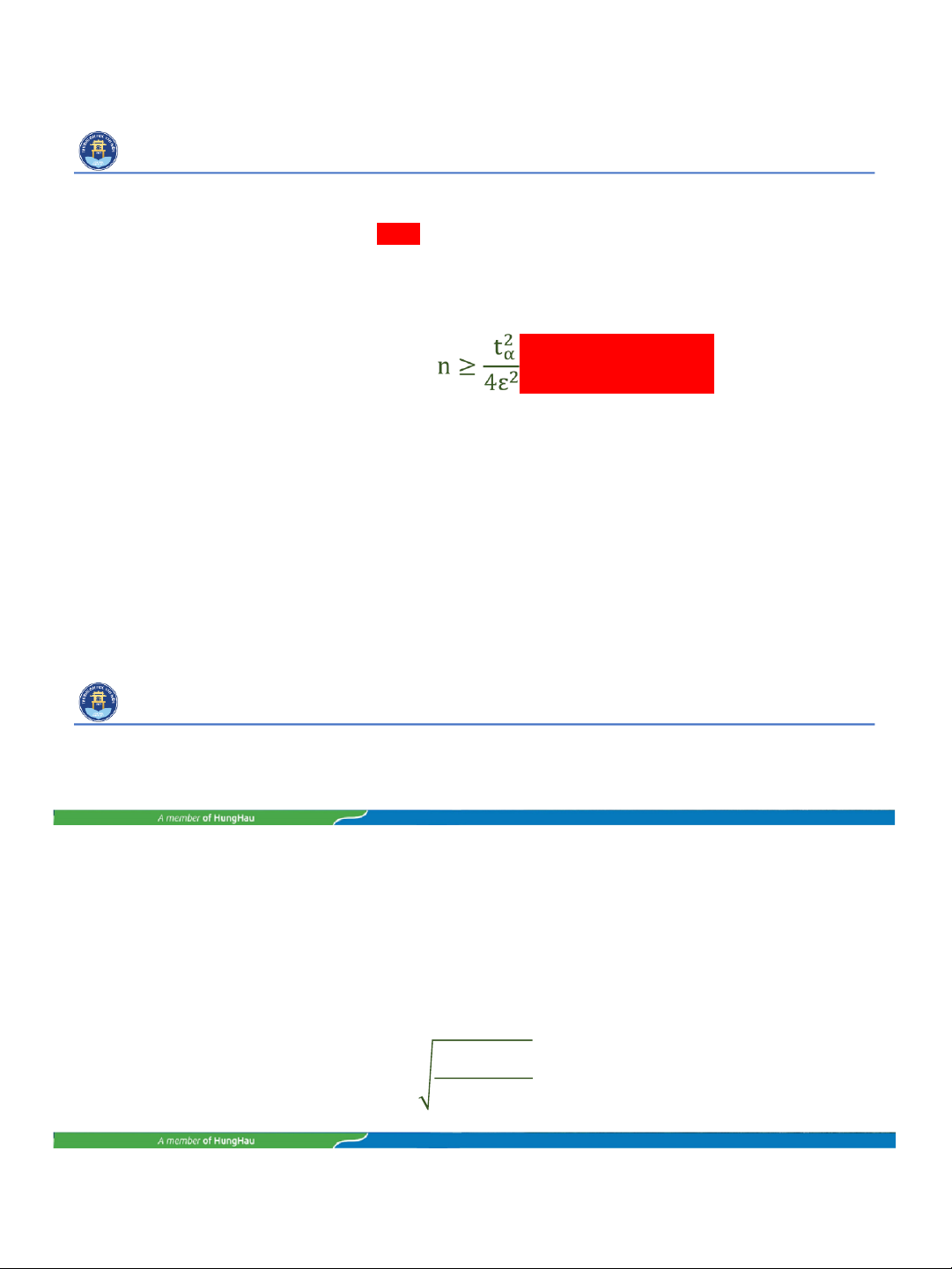
• TH2: chưa có điều tra sơ bộ (5b) Bài tập mẫu
Điều tra 100 sp của nhà máy X, thấy có 15 sản phẩm loại 2.
1.Muốn ước lượng tỉ lệ sản phẩm loại 2 của nhà máy với độ tin cậy 90%
thì phải đảm bảo độ chính xác là bao nhiêu?
2.Muốn ước lượng sản phẩm loại 2 với độ chính xác 4% thì độ tin cậy là bao nhiêu?
3.Muốn ước lượng sản phẩm loại 2 với độ tin cậy 92% và độ chính xác
3,8% thì cần kiểm tra thêm bao nhiêu sản phẩm nữa
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh
www.vhu.edu.vn Bài tập mẫu
1. Đây là bài toán tìm độ chính xác khi biết độ tin cậy và cỡ mẫu.
Thay số vào công thức (4a), ta có: 0 .15 ∗ 0 .85 ε = 1 ,65 ∗ 100 = 0 .0589 lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn
Kết luận: Muốn ước lượng tỉ lệ sp loại 2 của nhà máy với độ tin cậy 90%
thì phải đảm bảo độ chính xác là ε = 5.89% Bài tập mẫu
2. Đây là bài toán tìm độ tin cậy
Thay số vào công thức (4c), ta có: 0.04 ∗ 100 1 − 𝛼 = 2 ∗ 𝜑 0.15 ∗ 0.85 = 2 ∗ 𝜑 1.12 = 2 ∗ 0.3686 = 0.7372
Kết luận: Muốn ước lượng sản phẩm loại 2 với độ chính xác 4% thì độ tin cậy là 73,72%
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu
3. Đây là bài toán tìm cỡ mẫu
Ta có mẫu sơ bộ 𝑛1 = 100, 𝑓𝑛1 = 0.15
Thay vào công thức (5a), ta có: lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn
Kết luận: Muốn ước lượng tỉ lệ sp loại 2 của nhà máy với độ tin cậy 92%
và độ chính xác 3.8% thì ta cần điều tra tối thiểu 271 sp, tức là phải điều tra thêm 171 sp nữa.
4. Tìm chỉ tiêu cho bài toán ước lượng trung bình
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Đặt vấn đề
Tổng thể có trung bình μ chưa biết, ta ước lượng bằng . Trong biểu thức 𝑃 𝑋𝑛 − 𝜇 ≤ 𝜀 = 1 − 𝛼 (6a)
ε là độ chính xác, 1 – α là độ tin cậy và n là cỡ mẫu. •Với n ≥ 30, ta có nên 𝜎
𝑃 𝑋𝑛 − 𝜇 ≤ 𝑡𝛼 𝑛 = 1 − 𝛼 (6b) Đặt vấn đề
Từ (6a) và (6b) ta được lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn (6)
Công thức (6) phản ảnh mối liên hệ giữa 3 chỉ tiêu ε, n và 1- α. Nếu σ đã
biết thì cứ biết 2 trong 3 chỉ tiêu nói trên ra sẽ xác định được chỉ tiêu còn
lại. Nếu σ chưa biết thì ta có thể tính số gần bằng tương đương.
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Quy tắc thực hành
TH1: Tìm độ chính xác ε khi biết cỡ mẫu n (tính được S) và biết 1- α (xác định được 𝑡𝛼).
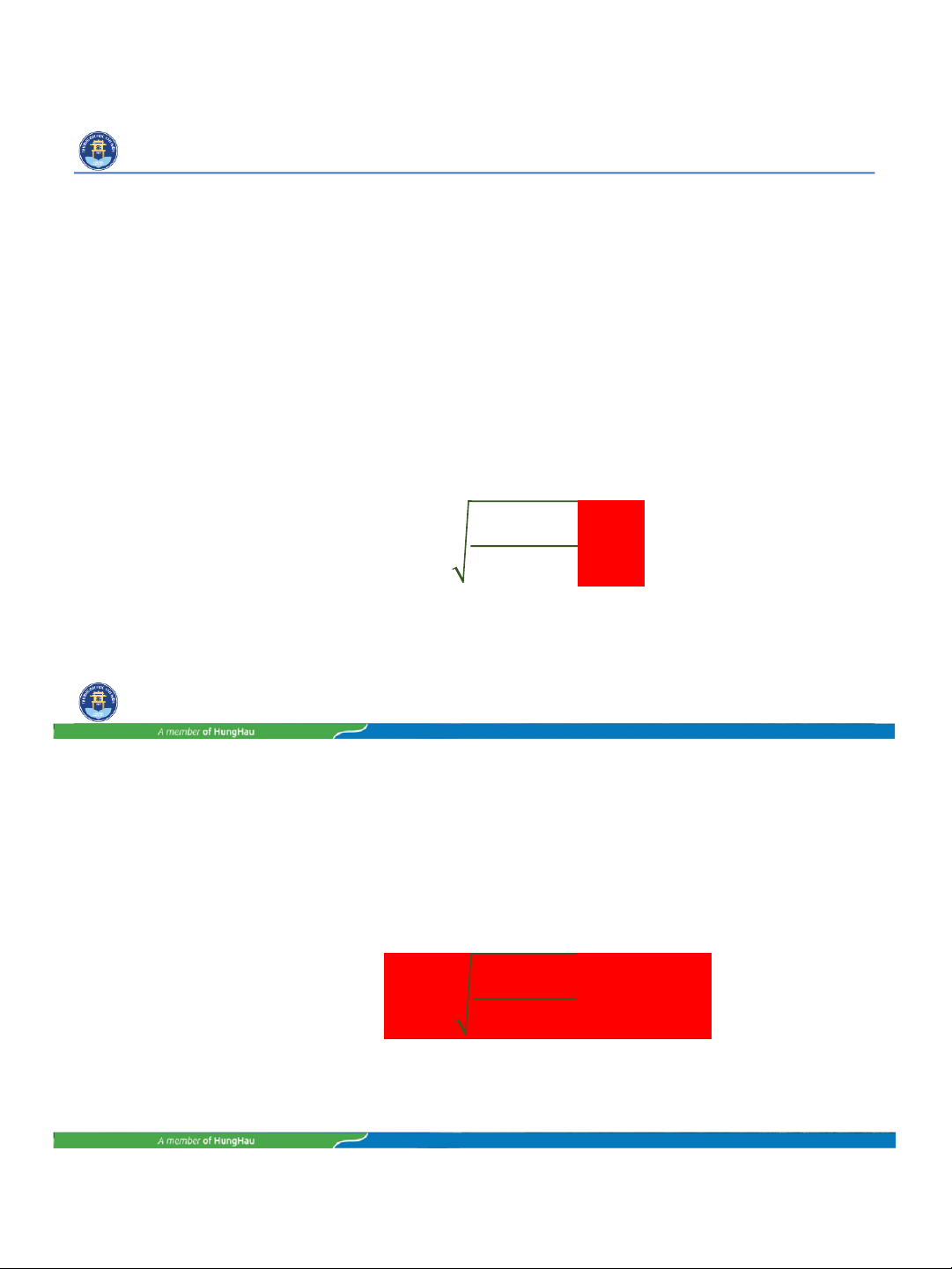
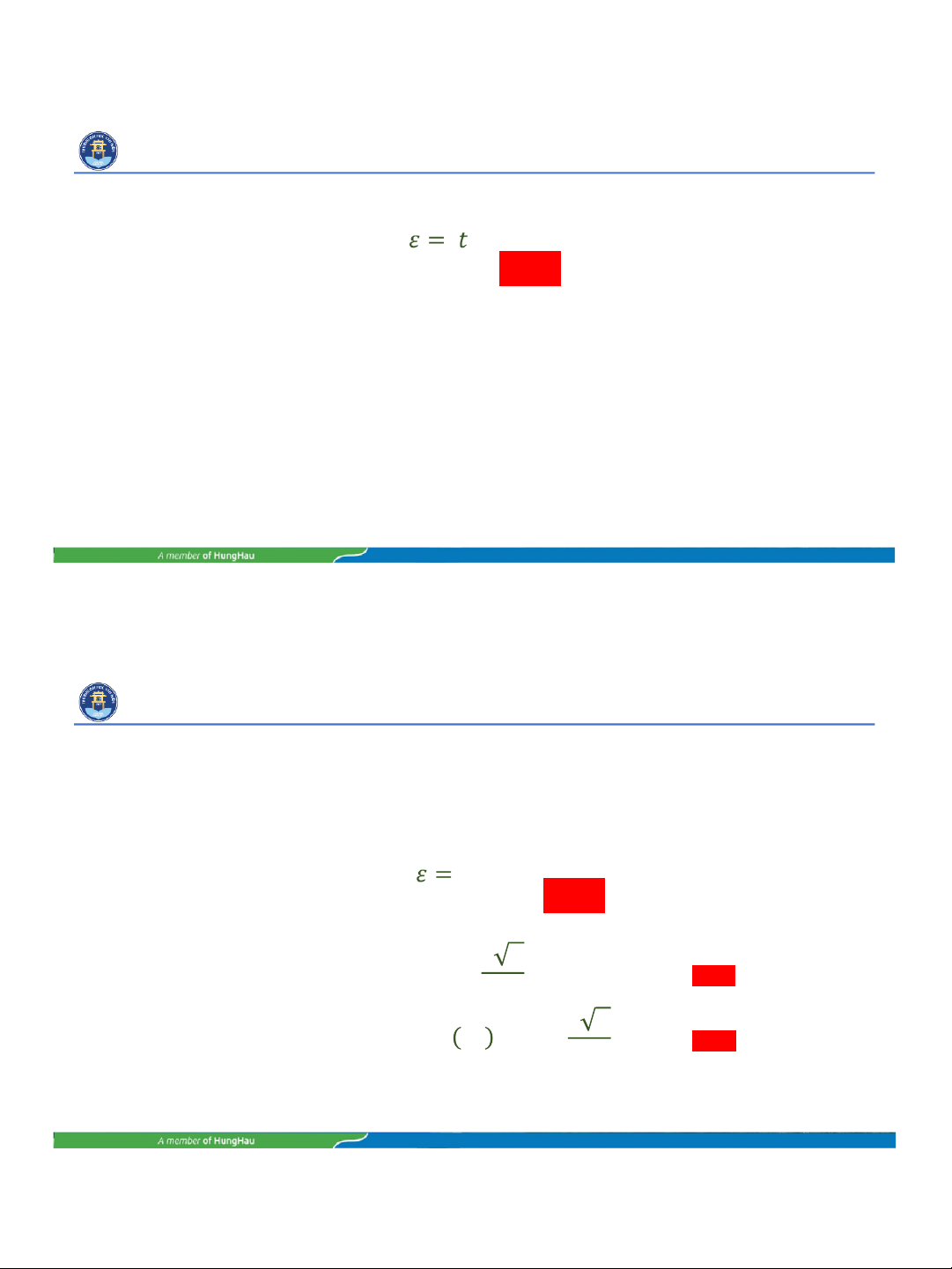
Khi đó, thay vào công thức (6), ta được: (7)
TH2: Tìm độ tin cậy 1 − 𝛼. Biết cỡ mẫu n, biết ε, ta tính được 𝑡𝛼 như sau: 𝜀 𝑛 𝑡 𝛼 = (8 a ) 𝑠 𝜀 𝑛
1 − 𝛼 = 2 𝜑 𝑡 𝛼 = 2 𝜑 ( ) (8 b ) 𝑠 lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn Quy tắc thực hành
TH3: Xác định cỡ mẫu n Từ công thức (6), ta có
Giả sử đã điều tra sơ bộ với cỡ mẫu là 𝑛1 và tính được , khi đó (9)
Ta cần điều tra thêm 𝑛2 = 𝑛 − 𝑛1 (nếu n > 𝑛1)
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh
www.vhu.edu.vn Bài tập mẫu
Kiểm tra 100 sp xuất xưởng của nhà máy chế tạo, người ta xác định được: . 1.
Để ước lượng khối lượng trung bình các sp khác với độ tin cậy 90%
thì độ chính xác là bao nhiêu? 2.
Để ước lượng khối lượng trung bình các sp với độ chính xác 2.8g thì
độ tin cậy là bao nhiêu? 3.
Muốn ước lượng khối lượng trung bình với độ tin cậy 92% và độ
chính xác 3g thì cần điều tra thêm bao nhiêu sp nữa? lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu
1. Đây là bài toán tìm độ chính xác
Thay số vào công thức (7), ta có: 𝜀 = 1 .65 ∗ 251 . 51 62 100 = 2 .
Kết luận: Vậy độ chính xác đảm bảo là 2.62g. Nói cách khác, 90% các
sản phẩm khác sẽ có khối lượng nằm trong khoảng [38.38g – 43. 62g]
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu
2. Đây là bài toán tìm độ tin cậy
Thay số vào CT (8a) và (8b), ta được 2 .8 ∗ 100 𝑡 𝛼 = = 1 .76 251 .51
1 − 𝛼 = 2 ∗ 𝜑 1 .76 = 0 .921 6
Kết luận: Vậy với độ chính xác 2.8g thì có 92,16% các sản phẩm có khối
lượng nằm trong khoảng [38.2 g – 43.8g] lOMoAR cPSD| 58968769 15/10/2023
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568 Thành nhân trước thành danh www.vhu.edu.vn Bài tập mẫu
3. Đây là bài toán tìm cỡ mẫu Cỡ mẫu sơ bộ
thay vào công thức (9), ta được
Kết luận: Như vậy cần phải điều tra tối thiểu 86 sản phẩm để thỏa điều kiện yêu cầu.
Do 𝑛 1 > 𝑛2 nên không cần điều tra thêm
TRƯỜNG ĐẠI HỌC VĂN HIẾN HOTLINE: 18001568
Thành nhân trước thành danh www.vhu.edu.vn HẾT CHƯƠNG 5