Chương 5: Ước Lượng và Kiểm Định Giả Thuyết Thống Kê môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

Bài 5 ƯỚC LƯỢNG VÀ
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ 1 Nội dung I II III ƯỚC KIỂM ĐỊNH ỨNG DỤNG LƯỢNG GIẢ THUYẾT SPSS THỐNG KÊ THỐNG KÊ 2 1 Ước lượng thống kê Một số khái niệm
Khoảng tin cậy cho trung bình tổng thể
Khoảng tin cậy cho tỷ lệ tổng thể Xác định quy mô mẫu 3 Một số khái niệm
Khi tổng thể có dạng phân phối xác suất được xác định nhưng chưa biết giá
trị của các tham số, cần ước lượng chúng dựa trên thông tin từ mẫu.
• Ký hiệu tham số của tổng thể là 𝜃.
Có hai phương pháp ước lượng
•Ước lượng điểm: ước lượng qua một giá trị, bằng cách sử dụng ngay
thống kê tính được từ mẫu
•Ước lượng khoảng: ước lượng qua một khoảng giá trị 4 2 Một số khái niệm
Ước lượng khoảng thường gắn với khoảng tin cậy.
Ước lượng bằng khoảng tin cậy là việc đưa ra một khoảng giá trị của tham
số tổng thể dựa trên thống kê từ mẫu tương ứng với một xác suất nhất định.
• Xác suất đó không bao giờ đạt 100% 5 Một số khái niệm Khoảng tin cậy (Confidence interval) Thống kê mẫu (Statistics)
Giới hạn tin cậy dưới (Lower Confidence Limit) Giới hạn tin cậy trên (Upper Confidence Limit)
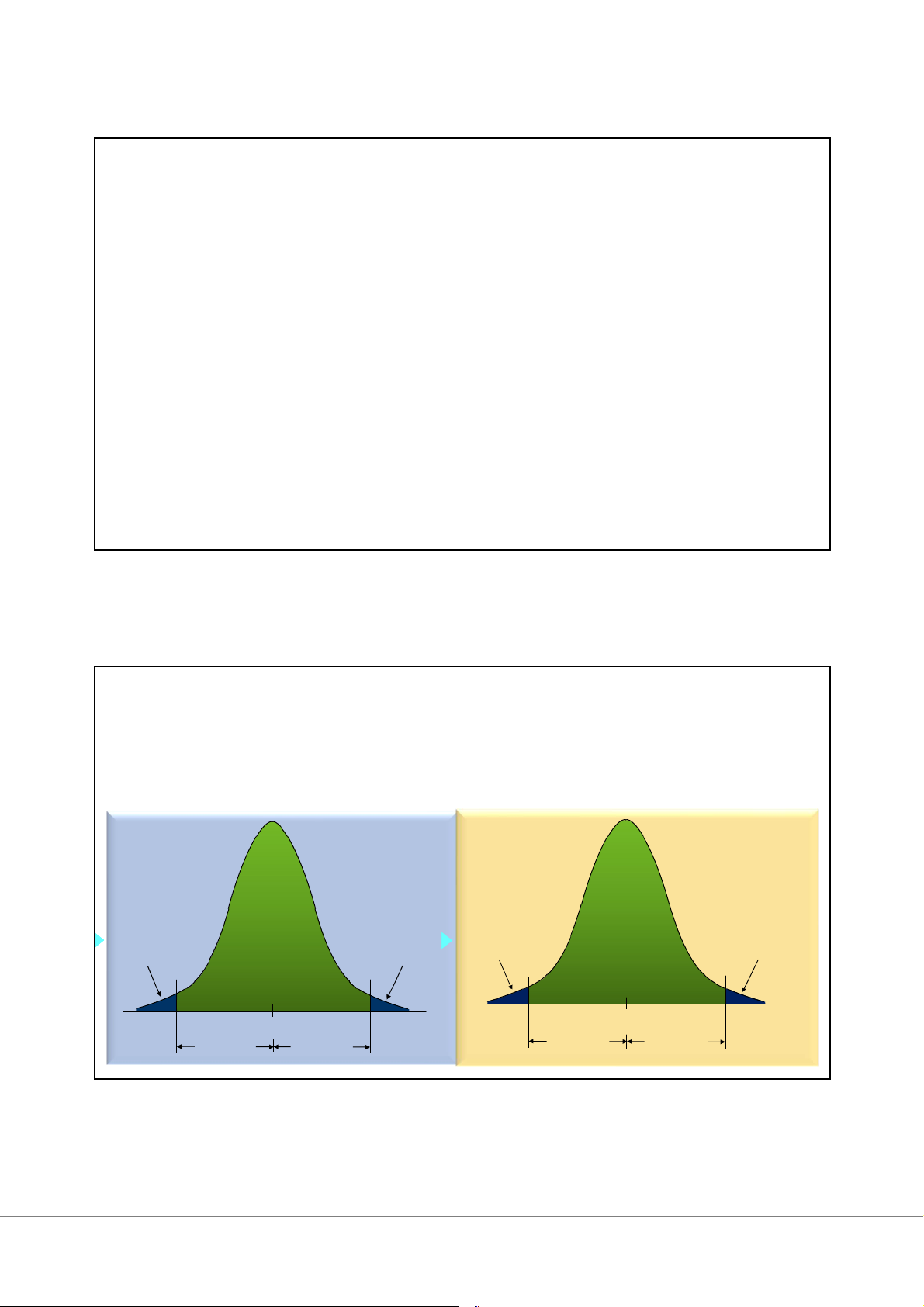
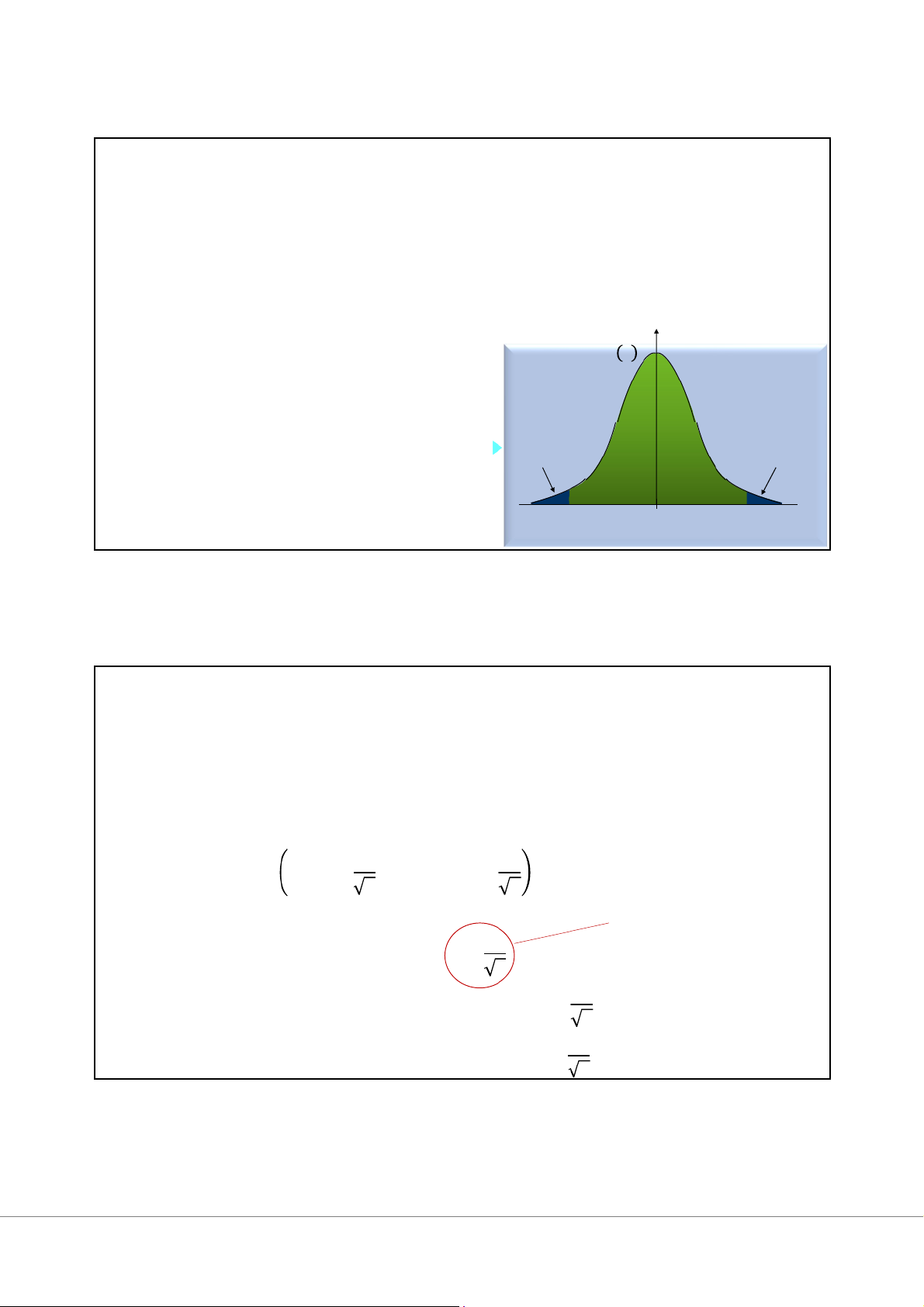
Xác suất để tham số của tổng thể rơi vào trong khoảng tin cậy gọi là độ tin
cậy (level of confidence), là 100(1-α)%.
P(L < 𝜃 < U) = 100(1-α)%
α là xác suất để tham số của tổng thể không rơi vào trong khoảng tin cậy. •Ví dụ: 10%, 5%, 1%... 6 3 Một số khái niệm
Công thức ước lượng khoảng tin cậy:
Tham số của tổng thể ∈[Thống kê mẫu ± Phạm vi sai số chọn mẫu] 𝛉 = 𝛉′ ± 𝛆 7 Một số khái niệm Phân phối mẫu Phân phối mẫu của 𝑥 𝑥 của f      Xac suât /2  Xac suât /2  /2  /2  (1 -   (1 -   𝑥 𝑓  p 𝜀 𝜀 𝜀  𝜀 𝜀   𝜀  8 4
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, đã biết phương sai của tổng thể (𝛔2)
Theo định lý giới hạn trung tâm, nếu X~N μ, σ thì X 󰆽~N μ, 
Khi đó , Z =    ~N 0,1  9
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, đã biết phương sai của tổng thể (𝛔2)
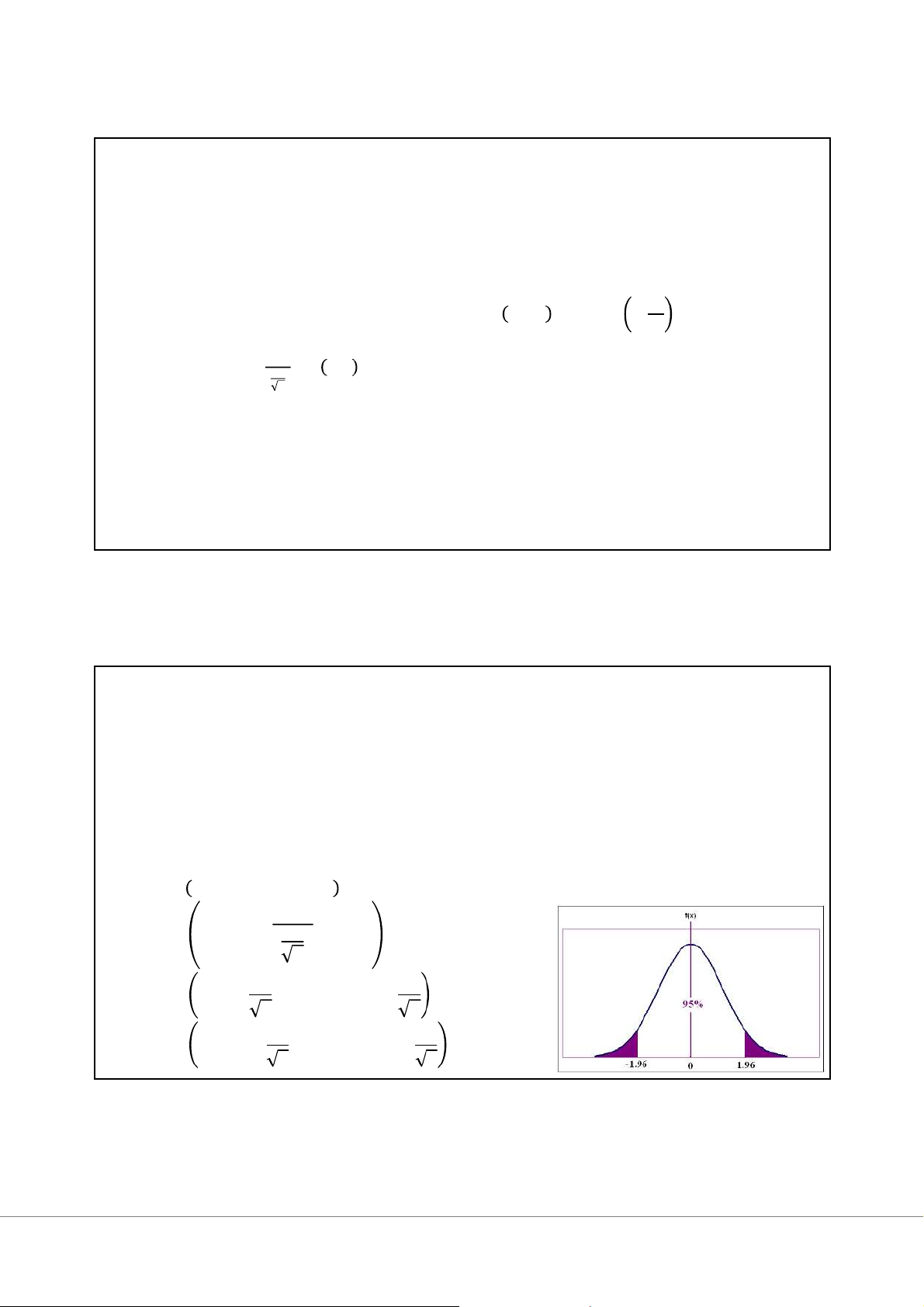
Với một phân phối chuẩn hóa, 95% diện tích dưới đường cong phân phối
nằm trong khoảng từ -1.96 đến + 1.96 P
−1.96 < Z < 1.96 = 0.95 P−1.96 < x − μ σ < 1.96 = 0.95 n
P −1.96 σn< x − μ < 1.96 σn= 0.95 σ σ P x − 1.96 < μ < x + 1.96 = 0.95 n n 10 5
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, đã biết phương sai của tổng thể (𝛔2)
P x − 1.96 σn< μ < x + 1.96 σn= 0.95
Đây được gọi là khoảng tin cậy 95% đối xứng cho trung bình tổng thể μ.
Có thể thay đổi khoảng tin cậy trên bằng cách thay đổi giá trị 1.96
• Sử dụng giá trị 1.645 để có khoảng tin cậy 90%
• Sử dụng giá trị 2.575 để có khoảng tin cậy 99% 11
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, đã biết phương sai của tổng thể (𝛔2)
Ý nghĩa của khoảng tin cậy 95% đối xứng cho trung bình tổng thể:
•x phân phổi chuẩn quanh trung bình thực μ ab
• Mỗi mẫu cụ thể có một KTC cụ thể
• 95% KTC này sẽ chứa μ và 5 % sẽ không chứa μ 12 6
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, đã biết phương sai của tổng thể (𝛔2)
Khoảng tin cậy 100(1-α)% hai phía (đối xứng) của μ là: σ σ Px − z/ n< μ < x + z/ n= 100(1 − α)% • Hoặc có thể viết: σ Phạm vi sai số x ± z/ chọn mẫu (𝜺𝒙) n σ
Giới hạn tin cậy dưới: x − z/ n σ
Giới hạn tin cậy trên: x + z/ n 13
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, đã biết phương sai của tổng thể (𝛔2)
Khoảng tin cậy 100(1-α)% bị chặn trên của μ (tối đa):
−< μ < x + z.σ n
Khoảng tin cậy 100(1-α)% bị chặn dưới của μ (tối thiểu):
x − z. < μ <  14 7
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, chưa biết phương sai của tổng thể (𝛔2)
Sử dụng độ lệch chuẩn của mẫu S thay cho độ lệch chuẩn của tổng thể σ chưa biết. Khi đó  
 không có phân phối chuẩn hóa mà tuân theo quy luật phân phối 
t-Student với n-1 bậc tự do. Giá trị của thống kê t là: t = x− μ s/ n 15 Phân phối t-Student
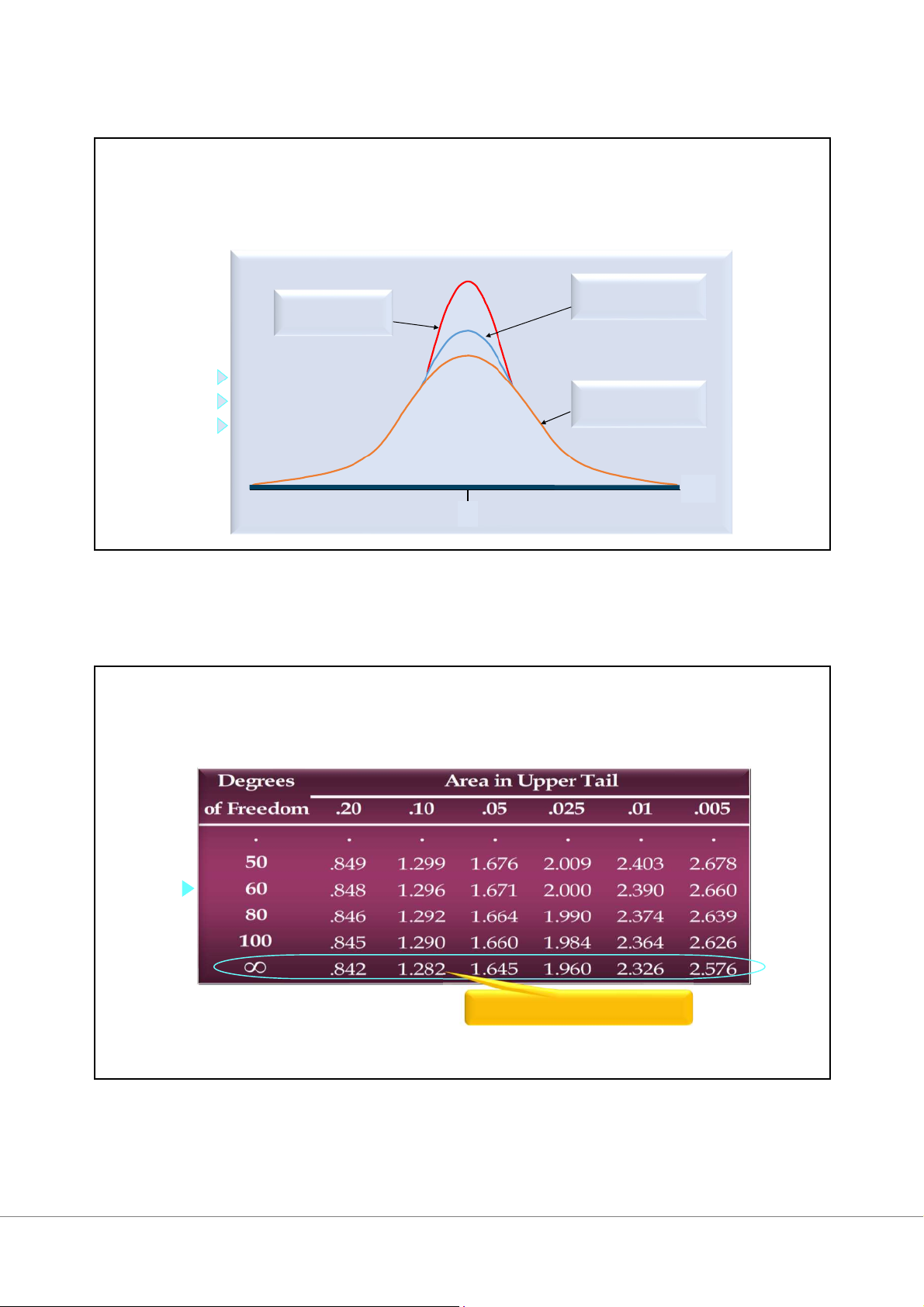
Phân phối Student là một họ các phân phối xác suất tương tự nhau: đối xứng
quanh 0, có dạng hình chuông (giống phân phối chuẩn), nhưng có phương sai lớn hơn phân phối chuẩn.
Một giá trị của phân phối t cụ thể phụ thuộc vào một tham số gọi là bậc tự do.
• Bậc tự do là số lượng phần thông tin độc lập trong tính toán độ lệch chuẩn S.
Một phân phối t có bậc tự do lớn hơn thì có độ biến thiên nhỏ hơn.
Khi bậc tự do tăng lên, phân phối Student sẽ tiệm cận dần phân phối chuẩn hóa.
Trong thực nghiệm, nếu có bậc tự do > 100, giá trị z của phân phối chuẩn hóa sẽ
xấp xỉ giá trị t của phân phối Student.
Lưu ý: Khi số bậc tư do là không hoàn toàn chính xác như trong bảng t, sử dụng
bậc tự do nào ở gần nhất. 16 8 Phân phối t-Student Phân phối t với Phân phối 20 bậc tự do chuẩn hóa Phân phối t với 10 bậc tự do z t , 0 17 Phân phối t-Student Standard normal z values 18 9 Phân phối t-Student
Giá trị tới hạn Student, ký hiệu là t()là giá trị của biến ngẫu nhiên T phân
phối theo qui luật Student với n bậc tự do, thỏa mãn: P(T > t()) = α P𝑡 Tính chất: t () = −t ()   () ( 𝑡 𝑡  𝑡() ( 𝑡     𝑡 19
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, chưa biết phương sai của tổng thể (𝛔2)
Khoảng tin cậy 100(1-α)% hai phía (đối xứng) của μ là: s s Px − t/ n< μ < x + t/ n= 100(1 − α)% • Hoặc có thể viết: Phạm vi sai số s x ± t chọn mẫu (𝜺𝒙) / n s
Giới hạn tin cậy dưới: x − t/ n s
Giới hạn tin cậy trên: x + t/ n 20 10
Khoảng tin cậy cho trung bình tổng thể
Tổng thể phân phối chuẩn, chưa biết phương sai của tổng thể (𝛔2)
Khoảng tin cậy 100(1-α)% bị chặn trên của μ (tối đa):
−< μ < x + t.s n
Khoảng tin cậy 100(1-α)% bị chặn dưới của μ (tối thiểu):
x − t. < μ <  21
Khoảng tin cậy cho trung bình tổng thể
Tổng thể không phân phối chuẩn
Nếu mẫu lớn, có thể dùng xấp xỉ phân phối chuẩn. Theo định lý giới hạn trung
tâm, nếu n > 30 thì: Z = 󰆽  xấp xỉ phân phối N 0,1  → μ ∈ (x ± z   )  Nếu chưa biết
𝛔 thì thay bởi S. Để xấp xỉ phân phối chuẩn – chuẩn hóa, cỡ
mẫu cần lớn hơn, thường lấy n > 40: Z = 󰆽  xấp xỉ phân phối N 0,1  → μ ∈ (x ± z   )   22 11
Khoảng tin cậy cho tỷ lệ tổng thể
Xét mẫu ngẫu nhiên kích thước n và tỷ lệ mẫu là f.
Phân phối mẫu của f xấp xỉ chuẩn nếu nf > 5 và n(1 – f) > 5.
• Giá trị kỳ vọng hay trung bình của tỷ lệ mẫu là tỷ lệ của tổng thể: E(f) = p
• Độ lệch chuẩn của tỷ lệ mẫu (sai số bình quân chọn mẫu): σ=()  Hay: f~N(p,  )
Áp dụng định lý giới hạn trung tâm trong xây dựng KTC cho tỷ lệ tổng thể. Khi mẫu lớn: f − p 𝑍 = ~N(0,1) f(1 − f)/n 23
Khoảng tin cậy cho tỷ lệ tổng thể
Khoảng tin cậy 100(1-α)% hai phía (đối xứng) của p là: f (1 − f) f (1 − f) Pf − z/ n< p < f + z/ n= 100(1 − α)% Phạm vi sai số • Hoặc có thể viết: chọn mẫu (𝜺𝒇) f ± z/.f (1 − f) n
Giới hạn tin cậy dưới: f − z/.f (1 − f) n f (1 − f)
Giới hạn tin cậy trên: f + z/ . n 24 12
Khoảng tin cậy cho tỷ lệ tổng thể
Khoảng tin cậy 100(1-α)% bị chặn trên của p (tối đa): p < f + z.f (1 − f) n
Khoảng tin cậy 100(1-α)% bị chặn dưới của p (tối thiểu): f − z.f 1 − f n< p 25 Lưu ý
Các công thức ước lượng trên đều áp dụng cho tổng thể vô hạn.
Với trường hợp tổng thể hữu hạn, cần nhân thêm vào công thức tính phạm vi
sai số chọn mẫu một hệ số hiệu chỉnh tổng thể hữu hạn là: FPC = (N − n)/(N − 1) 26 13 Ví dụ 1
Một mẫu gồm 20 nhân viên được tiến hành điều tra nhằm thu thập thông tin
liên quan đến một chương trình đào tạo. Người ta tính được thời gian trung
bình để hoàn tất chương trình của 20 nhân viên này là 51,5 ngày với độ
lệch chuẩn là 6,84 ngày. Hãy ước lượng thời gian trung bình để hoàn tất
chương trình với độ tin cậy 95%. Giả sử thời gian hoàn tất trung bình là biến
ngẫu nhiên phân phối chuẩn. 27 Ví dụ 1
Trường hợp ước lượng số trung bình, chưa biết phương sai của TT.
• n=20; 𝑥 = 51,5; 𝑆 =6,84
• Tra bảng t-Student với mức ý nghĩa 0,05 và 19 bậc tự do, t0,025;19=2,093.
• Công thức ước lượng: 51,5 ± 2,093. ,  hay 51,5 ± 3,2
• Kết luận: Với mẫu đã cho, khoảng tin cậy 95% cho thời gian trung bình để
hoàn tất chương trình là: 48,3 ≤ μ ≤ 54,7 (ngày) 28 14 Ví dụ 2
• PSI là một tô chức chuyên thực hiện thăm dò dư luận trong các cuộc bầu cử
ở New York. Các khảo sát được thưc hiện bằng phương pháp phỏng vấn
qua điện thoại, tại đó, PSI sẽ hỏi các cử tri đã đăng ký xem họ sẽ bỏ phiếu
cho ứng cử viên nào nếu cuộc bầu cử được tô chức vào ngày hôm đó.
• Trong chiến dịch bầu cử hiện tại, PSI phát hiện ra rằng có 220 cử tri đã đăng
ký, trong số 500 người đã liên lạc, bày tỏ sư ủng hộ cho ứng cử viên A. PSI
muốn xây dựng khoảng tin cậy 95% cho tỷ lệ cử tri đã đăng ký ủng hộ cho ứng cử viên A. 29 Ví dụ 2
Trường hơp ước lương tỷ lê của TT
• Trong đó n = 500, f= 220/500 = 0,44
• Tra bảng Z với mức ý nghĩa 0,05, Z/ = Z, =1,96
• Khoảng tin cậy 95% cho tỷ lê cử tri ủng hô cho ứng cử viên A f ± Z/.f (1 − f)
n= 0.44 ± 1.96 0.44(1 − 0.44) 500 = 0.44 ± 0.0435
Với mẫu đã cho, PSI tự tin 95% rằng tỷ lệ cử tri ủng hộ cho ứng cử viên A
trong tổng thê là từ 39,65% đến 48,35%. 30 15 Xác định quy mô mẫu Yêu cầu: • Sai số nhỏ nhất • Chi phí thấp nhất
→ Sử dụng định lý giới hạn trung tâm để xác định cỡ mẫu cần thiết khi biết
phương sai của tổng thể. 31 Xác định quy mô mẫu
Ví dụ: Giả sử độ lệch chuẩn của tổng thể là 5. Nếu muốn ước lượng trung
bình của tổng thể sao cho chênh lệch so với trung bình mẫu nằm trong phạm
vi là 3 với độ tin cậy 99%.
• Bước 1: thiết lập phương trình. Px − μ < 3 = 0.99
• Bước 2: chuẩn hóa. P  <   = 0.99   P Z <  = 0.99  P Z < = 0.99 32 16 Xác định quy mô mẫu
• Bước 3: tra bảng z tìm giá trị tới hạn. PZ < 2.575 = 0.99 • Bước 4: tính n. 3n 5= 2.575 n = (2.575 ∗ 5)/3 n = 18.42 ≈ 19
Lưu ý: Cỡ mẫu luôn làm tròn lên. 33 Xác định quy mô mẫu Tổng thể Tổng thể vô hạn Tổng thể hữu hạn Ước lượng n = z/σ n = N. z/. σ Trung bình ε
(N − 1). ε+ z/. σ  n = z/. p(1 − p) n = N. z/. p(1 − p) Tỷ lệ ε
N − 1 . ε+ z/. p(1 − p) 34 17 Xác định quy mô mẫu
Các nhân tố ảnh hưởng tới quy mô mẫu điều tra
• Độ tin cậy của ước lượng (z)
• Phương sai (độ đồng đều) của tổng thể (2)
• Phạm vi sai số chọn mẫu/sai số chọn mẫu cho phép (εhoặc ε) 35 Lưu ý
Trong trường hợp chưa biết phương sai của tổng thể, sử dụng một trong các cách sau:
• Lấy phương sai (2) lớn nhất trong các lần điều tra trước (nếu có). Trong
trường hợp ước lượng tỷ lê, chọn tỷ lệ (p) gần 0,5 nhất.
• Lấy phương sai hoặc tỷ lệ của các cuộc điều tra có tính chất tương tự (nếu có).
• Điều tra thí điểm để xác định phương sai.
• Ước lượng độ lệch chuẩn dựa vào khoảng biến thiên hoặc chọn p=0,5. R x − x σ ≈ = 6 6 36 18 Ví dụ 3
Giả sử PSI muốn tỷ lê mẫu chênh lệch ±3% so với tỷ lê của tổng thê với đô tin
cậy 99%. Vậy quy mô mẫu cần điều tra trong trường hơp này là bao nhiêu?
• Với đô tin cậy 99% → α = 0,01→ z/ = z0,005 = 2,575
• Tỷ lê cử tri ủng hô ứng viên A trong cuộc điều tra trước là 0,44. Vậy p=0,44
• Sai sô chọn mẫu cho phép ε=0,03
• Cỡ mẫu cần điều tra: n = (z/)p(1 ε=− p) (2,575)(0,44)(0,56) (0,03)≅ 1817 37
Kiểm định giả thuyết thống kê
Một số khái niệm liên quan Các loại kiểm định
Các bước tiến hành kiểm định giả thuyết thống kê
Kiểm định giả thuyết về trung bình tổng thể
Kiểm định giả thuyết về tỷ lệ tổng thể 38 19
Một số khái niệm liên quan Giả thuyết thống kê
Kiểm định giả thuyết thống kê
Cặp giả thuyết thống kê
Sai lầm và mức ý nghĩa trong kiểm định
Tiêu chuẩn kiểm định Miền bác bỏ Giá trị tới hạn 39 Giả thuyết thống kê
Giả thuyết thống kê (Hypothesis) là phát biểu về một vấn đề nào đó của
tổng thể cần phải kiểm chứng.
Kiểm định giả thuyết thống kê (Hypothesis Test) là một quy trình dựa trên
bằng chứng từ mẫu để xác định xem giả thuyết thống kê đưa ra có hợp lý không.
• Kiểm định tham số: kiểm định về các tham số của tổng thể như trung bình,
tỷ lệ, phương sai, bằng cách sử dụng phân phối xác suất liên quan trực
tiếp đến các tham số đó.
• Kiểm định phi tham số: kiểm định về phân phối xác suất, các quy luật lý thuyết. 40 20