Chương 6, 7, 8 - Ghi chú và công thức Phân tích hồi quy môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

Chương 6
PHÂN TÍCH HỒI QUY VÀ TƯƠNG QUAN 1. Những vấn đề chung:
1.1. Mối liên hệ giữa các hiện tượng KT – XH Liên hệ hàm số: Định nghĩa:
Là mối liên hệ hoàn toàn chặt chẽ. Khi hiện tượng này thay đổi có tác động quyết định
làm thay đổi hiện tượng liên quan theo một tỷ lệ xác định.
Liên hệ hàm số được biểu diễn dưới dạng: y = f(x) Đặc điểm:
Không những được biểu hiện ở tổng thể (số lớn) mà còn được biểu hiện rõ trên từng đơn vị cá biệt. Ví dụ:
Trong toán học: cho hàm số y = a2 Liên hệ tương quan Định nghĩa:
Là mối liên hệ không hoàn toàn chặt chẽ. Cụ thể: sự thay đổi của hiện tượng này có thể
làm hiện tượng liên quan thay đổi theo nhưng không có ảnh hưởng hoàn toàn quyết định. Đặc điểm:
Không ảnh hưởng rõ trên từng đơn vị cá biệt mà phải qua nghiên cứu số lớn các đơn vị. - Ví dụ:
Mối liên hệ giữa tuổi nghề và NSLĐ.
1.2. Phương pháp phân tích Hồi quy và tương quan
Là phương pháp toán học được vận dụng trong thống kê để biểu diễn và đánh giá mối
liên hệ tương quan giữa các hiện tượng Nhiệm vụ:
Xây dựng phương trình hồi quy biểu diễn mối liên hệ tương quan giữa các hiện tượng (4 bước)
Giải thích sự tồn tại thực tế và bản chất của mối liên hệ Thăm dò mối liên hệ
Lập phương trình hồi quy
Tính toán các tham số và giải thích ý nghĩa
Đánh giá trình độ chặt chẽ của mối liên hệ tương quan và sự phù hợp của mô hình hồi quy
2. Phân tích Hồi quy tuyến tính đơn 2.1:
•Xây dựng phương trình Hồi quy -Ví dụ: -
Có tài liệu về chi phí quảng cáo và doanh thu bán hàng của một doanh nghiệp như sau
-STT -CP Quảng cáo -Doanh Thu -(triệu đồng) -(triệu đồng) - 1 - 2 - 810 - 2 - 4 - 820 - 3 - 7 - 840 - 4 - 9 - 850 - 5 - 10 - 870
-Tổng-32 -4190
-Yêu cầu: Lập phương trình hồi quy tuyến tính biểu diễn mối liên hệ của chi phí
quảng cáo tới doanh thu bán hàng
Giải thích sự tồn tại thực tế và bản chất của mối liên hệ Thăm dò mối liên hệ
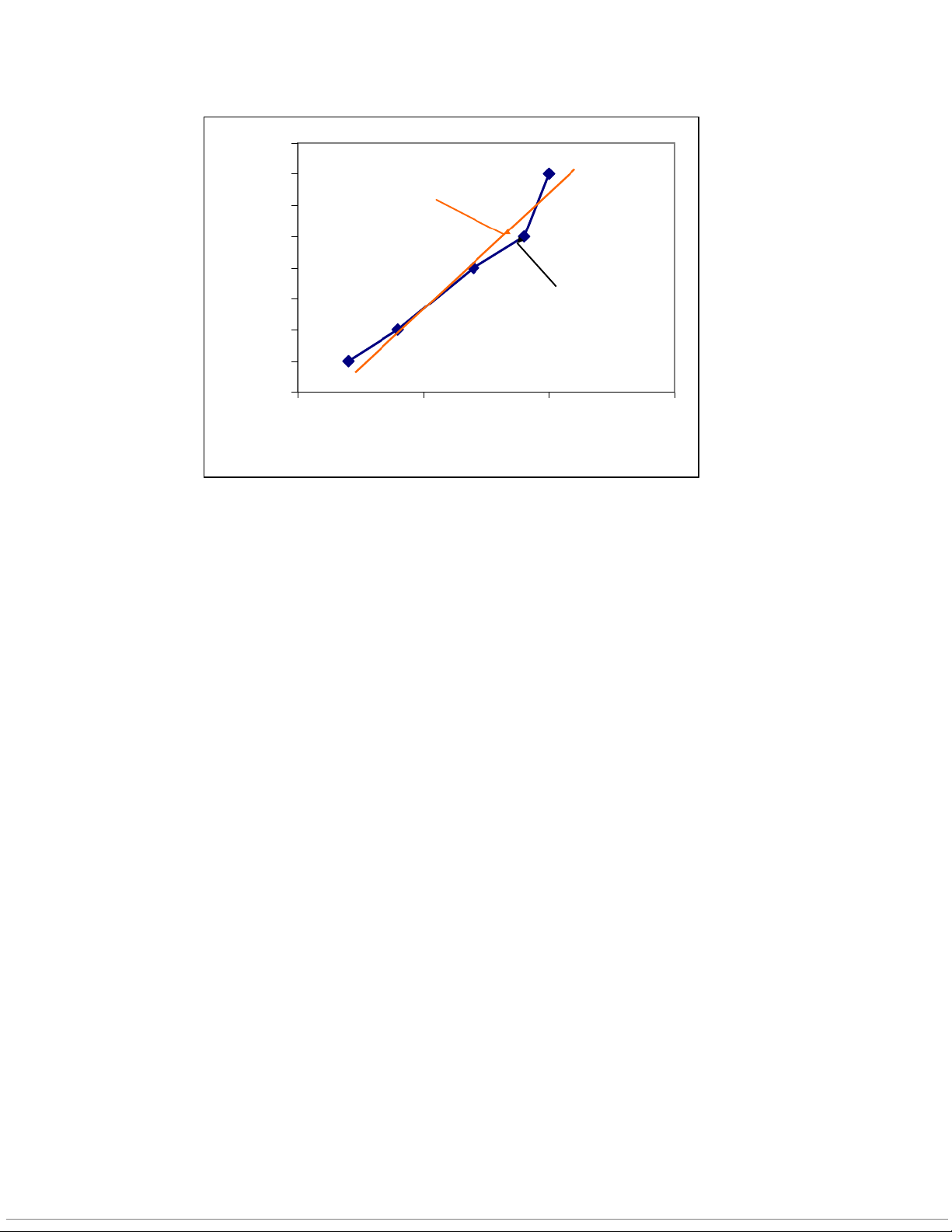
-Đường hồi quy thực tế: là đường gấp khúc được xây dựng trên cơ sở dữ liệu thực tế
-Đường hồi quy lý thuyết: là đường điều chỉnh (bù trừ) các chênh lệch ngẫu nhiên để
phản ánh mối liên hệ cơ bản của hiện tượng
-Phương trình hồi quy: là phương trình xác định vị trí của đường hồi quy lý thuyết 880 870 Đường hồi quy 860 lý thuyết 850 840 830 Đường hồi quy Doanh Thu thực nghiệm 820 810 800 0 5 1015 CP Quảng cáo
Phương trình hồi quy tổng thể
 Yi=β0+β1xi+εi
Yi : Biến phụ thuộc Biến kết quả Biến được giải thích Biến nội sinh β0: Tham số tự do Hệ số chặn
β1: Hệ số hồi quy Hệ số góc
xi : Biến độc lập Biến nguyên nhân Biến giải thích Biến ngoại sinh
εi : phần dư (chênh lệch giữa giá trị thực tế và giá trị lý thuyết)
Phương trình hồi quy tổng thể Ý nghĩa của các tham số o
β0 phản ánh ảnh hưởng của các tiêu thức nguyên nhân khác (ngoài tiêu thức X) tới tiêu thức kết quả Y o
β1 phản ánh ảnh hưởng trực tiếp của tiêu thức nguyên nhân X tới tiêu thức kết quả Y. Cụ
thể: khi X tăng thêm 1 đơn vị thì Y sẽ thay đổi bình quân β1 đơn vị
β1 > 0  X và Y có mối liên hệ thuận (cùng chiều)
β1 < 0  X và Y có mối liên hệ nghịch (ngược chiều)
Phương trình hồi quy mẫu
Với mẫu ngẫu nhiên kích thước n, phương trình hồi quy mẫu xác định vị trí của đường hồi quy lý thuyết sau:
^yi=b0+b1xi
b0 Ước lượng của β0
b1 Ước lượng của β1
Các giả thiết của OLS
1. Mô hình được ước lượng trên cơ sở mẫu ngẫu nhiên
2. Kỳ vọng toán của sai số bằng 0
3. Sai số tuân theo quy luật phân phối chuẩn
4. Phương sai của sai số bằng nhau (Sai số không đổi)
5. Không có tương quan giữa các phần dư (không có hiện tượng tự tương quan)
6. Giữa các biến độc lập không có tương quan tuyến tính hoàn hảo (đa cộng tuyến) – Đối với hồi quy bội
7. Ước lượng tham số b0 và b1
Phương pháp bình phương nhỏ nhất (OLS - Ordinary least squares):
S=∑ (yi− ^yx )2→min
S=∑ (yi−b0−b1x )2→min •Ước lượng tham số •Kiểm định tham số
3. Phân tích Hồi quy tuyến tính bội