Chương 6 - Phân tích Hồi quy và Tương quan trong Kinh tế học môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

Chương 6
PHÂN TÍCH HỒI QUI TƯƠNG QUAN Nội dung I II III MỘT SỐ VẤN HỒI QUI TƯƠNG HỒI QUI ĐỀ CHUNG VỀ QUAN TUYẾN TƯƠNG QUAN PHÂN TÍCH HỒI TÍNH ĐƠN BỘI QUI TƯƠNG QUAN 1 10/10/2020
Một số vấn đề chung về phân tích HQTQ
• Một số khái niệm liên quan
• Trình tự tiến hành phân tích HQTQ
Một số khái niệm liên quan
Hồi qui tương quan là phương pháp phân tích dựa trên mối liên hệ phụ
thuộc của một biến phụ thuộc (biến kết quả) vào một hay nhiều biến độc lập (biến nguyên nhân). Ví dụ:
Chiều cao và tuổi của một người
Thu nhập và chi tiêu của hộ gia đình
Số giờ tự học và điểm số
Mối liên hệ phụ thuộc này được xây dựng bằng một phương trình hồi qui
có thể là tuyến tính hay phi tuyến. 2 10/10/2020
Một số khái niệm liên quan
Liên hệ hàm số: là mối liên hệ hoàn toàn chặt chẽ, sự thay đổi của hiện
tượng này có tác dụng quyết định đến sự thay đổi của hiện tượng liên quan theo một tỷ lệ xác định. Có dạng y=f(x)
không những được biểu hiện ở tổng thể mà còn được biểu hiện
trên từng đơn vị cá biệt.
Liên hệ tương quan: là mối liên hệ không hoàn toàn chặt chẽ. Sự thay đổi
của hiện tượng này có thể làm hiện tượng liên quan thay đổi theo nhưng không
có ảnh hưởng hoàn toàn quyết định.
không được biểu hiện trên từng đơn vị cá biệt mà phải thông qua
hiện tượng số lớn (là tổng thể).
Một số khái niệm liên quan
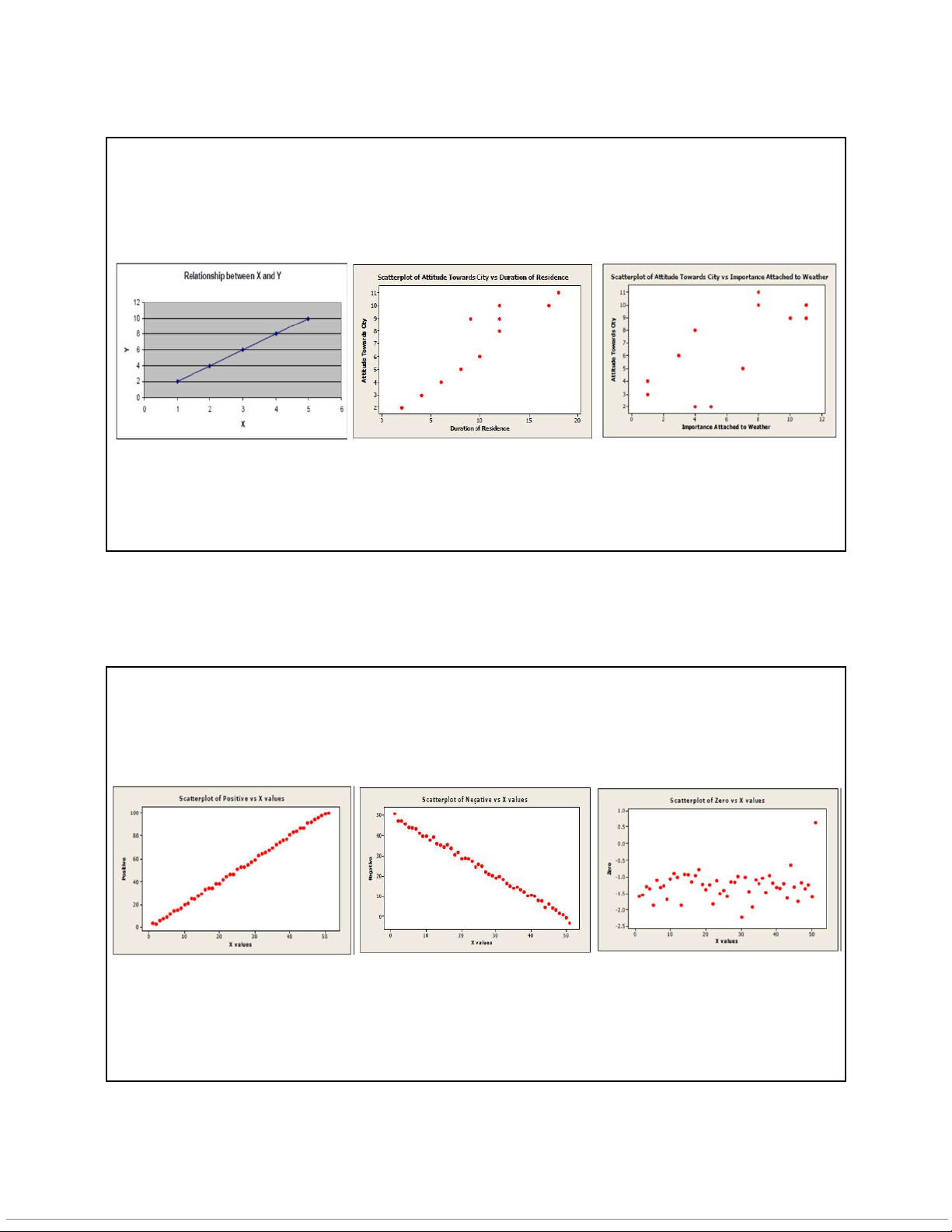
Để tìm ra mối liên hệ giữa hai biến X và Y, có thể vẽ đồ thị phân tán (Scatterplot)
X được gọi là biến độc lập (biến nguyên nhân)
Y được gọi là biến phụ thuộc (biến kết quả)
→ Scatterplot có thể cho biết cường độ và chiều hướng của mối liên hệ
tuyến tính giữa hai biến. 3 10/10/2020
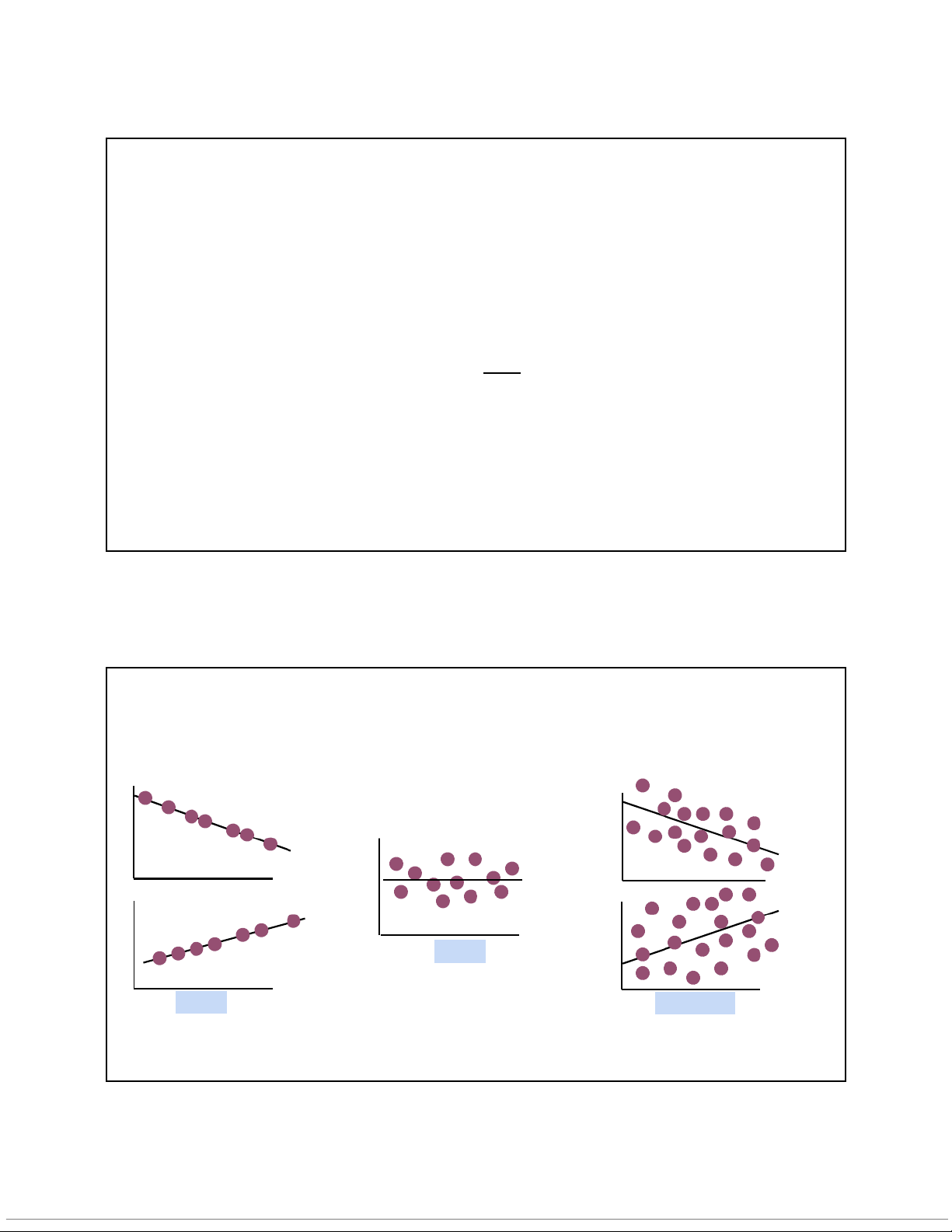
Một số khái niệm liên quan Tương quan hoàn hảo Tương quan một phần Tương quan một phần
(liên hệ hàm số). Mỗi một
(liên hệ tuyến tính chặt chẽ)
(liên hệ tuyến tính kém chặt chẽ)
giá trị của X đưa lại một giá trị của Y.
Một số khái niệm liên quan Tương quan thuận chiều Tương quan ngược chiều
Không có mối liên hệ tương
(dương), khi X tăng thì Y tăng
(âm), khi X tăng thì Y giảm
quan. Khi X thay đổi, Y không và ngược lại. thay đổi. 4 10/10/2020
Trình tự tiến hành phân tích HQTQ
Bước 1: Phân tích bản chất mối liên hê
Bước 2: Xây dựng mô hình
Bước 3: Ước lượng mô hình
Bước 4: Đánh giá mô hình
Hồi qui tương quan tuyến tính đơn
• Xây dựng mô hình hồi qui
• Ước lượng mô hình hồi qui
• Đánh giá cường độ của mối liên hệ, sự phù hợp của mô hình
• Kiểm định các hệ số của mô hình hồi qui 5 10/10/2020
Xây dựng mô hình hồi qui
Mối quan hệ giữa X và Y được mô tả bằng một hàm tuyến tính.
Sự thay đổi của Y được giả định là do sự thay đổi của X gây ra.
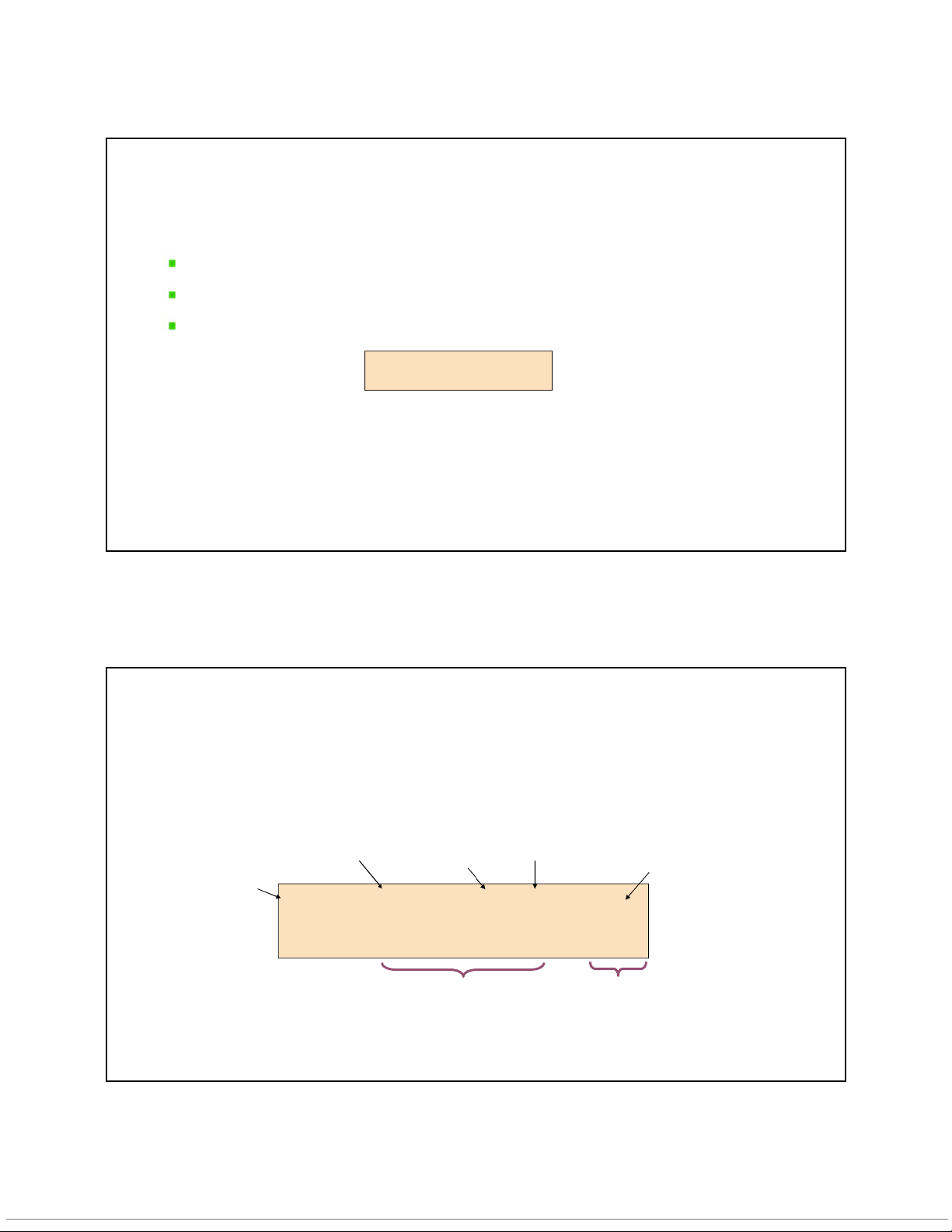
Mô hình hồi qui tuyến tính tổng thể chung:   Y  β β x i ε 0 1 i i Trong đó:
0và 1là các hệ số của mô hình tổng thể chung
là sai số ngẫu nhiên (random error).
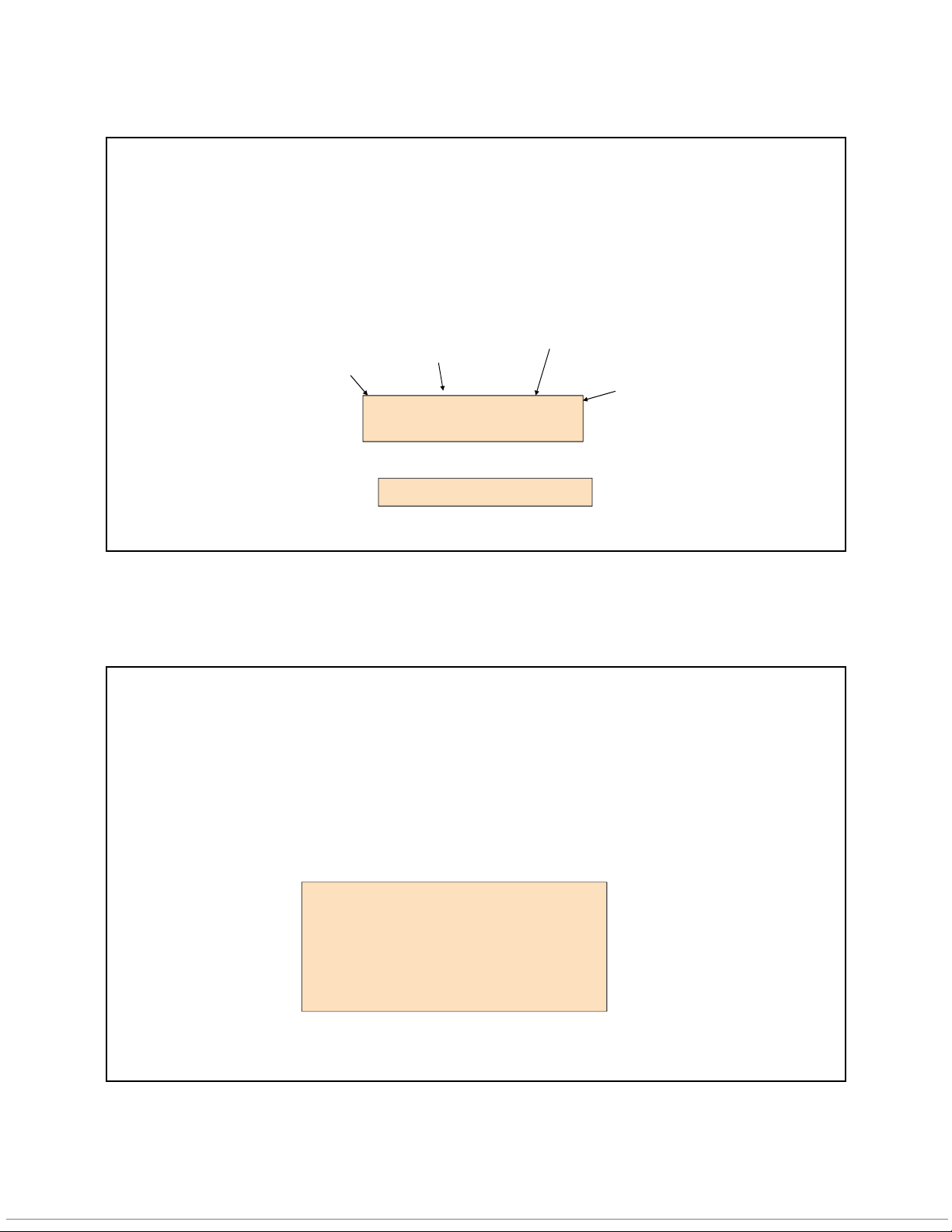
Xây dựng mô hình hồi qui Hệ số hồi Sai số Hệ số tự do Biến độc lập qui tổng ngẫu tổng thể thể nhiên Biến phụ thuộc Y β β X i ε 0  1 i  i Thành phần tuyến tính Thành phần sai số ngẫu nhiên 6 10/10/2020
Xây dựng mô hình hồi qui Y Y β β X i ε 0  1 i  i Giá trị quan sát của Y cho Xi Hệ số hồi qui = β1 εi Giá trị dự đoán Sai số ngẫu nhiên cho của Y cho Xi giá trị Xi Hệ số tự do = β0 Xi X
Ước lượng mô hình hồi qui
Một mẫu gồm có n quan sát
xilà giá trị của biến độc lập thứ i.
yilà giá trị của biến phụ thuộc thứ i.
𝑥 là giá trị trung bình của biến độc lập.
𝑦 là giá trị trung bình của biến phụ thuộc. 7 10/10/2020
Ước lượng mô hình hồi qui
• Phương trình hồi qui tuyến tính mẫu đưa ra một ước lượng cho đường hồi qui tổng thể. Giá trị ước Ước lượng của Ước lượng của lượng (hay lý hệ số tự do hệ số hồi qui thuyết) của y cho quan sát i Giá trị của x cho quan sát i  y  b bˆ i x 0 1 i
Sai số ngẫu nhiên cá nhân eicó trung bình bằng 0  e  y - y y - (b bi x i i i 0 1 (i ˆ ) )
Ước lượng mô hình hồi qui
•Phương pháp bình phương nhỏ nhất (OLS): Xác định giá trị nhỏ nhất
của bình phương chênh lệch giữa giá trị thực tế và giá trị từ phương trình
hồi qui lý thuyết (phần dư ei). 2 min SSE  min e  i 2  min (y yˆ )  i i 2  min [y  (b  b x )]  i 0 1 i 8 10/10/2020
Ước lượng mô hình hồi qui
Các giả thiết của phương pháp bình phương nhỏ nhất (OLS):
• Giả thiết 1: Mô hình được ước lượng trên cơ sở mẫu ngẫu nhiên
• Giả thiết 2: Kỳ vọng toán của sai số bằng không
• Giả thiết 3: Sai số tuân theo quy luật phân bố chuẩn
• Giả thiết 4: Phương sai của sai số bằng nhau (không đổi)
• Giả thiết 5: Không có tương quan giữa các phần dư (không có tự tương quan)
• Giả thiết 6: Giữa các biến độc lập không có tương quan tuyến tính hoàn
hảo (đa cộng tuyến) - Đối với hồi quy bội.
Ước lượng mô hình hồi qui
• Từ OLS suy ra hệ phương trình chuẩn xác định các hệ số b0và b1: y = nbo+ b1x xy = box + b1x2 • Hay:  0  b 1 y b x Trong đó: 𝑥 =   ∑
 𝑦 = ∑ 𝑥𝑦 = ∑
= 𝑥− 𝑥=∑𝑥 −∑𝑥   𝜎 𝑛 𝑛
• Đường hồi qui luôn đi qua trung bình của x, y. 9 10/10/2020
Ước lượng mô hình hồi qui
Giải thích ý nghĩa của các hệ số
b0là hệ số tự do (hệ số chặn) cho biết giá trị của y khi x bằng 0 (nếu
trong tổng thể x có nhận giá trị 0). Hoặc coi đó là ảnh hưởng trung bình
của tất cả biến nguyên nhân khác ngoài biến x tới biến kết quả y.
b1là hệ số hồi qui (hệ số góc) cho biết ảnh hưởng trực tiếp của biến
nguyên nhân x tới biến kết quả y. Cụ thể, khi x thay đổi 1 đơn vị thì y thay
đổi trung bình b1đơn vị. Ngoài ra, nó còn cho biết chiều hướng của mối liên hệ giữa x và y.
Đánh giá cường độ của mối liên hệ, sự phù hợp của mô hình • Hệ số xác định • Hệ số tương quan
• Sai số chuẩn của mô hình (ước lượng) 10 10/10/2020 Hệ số xác định
Tổng biến thiên (variation) được chia thành hai phần: SST  S S R  S SE
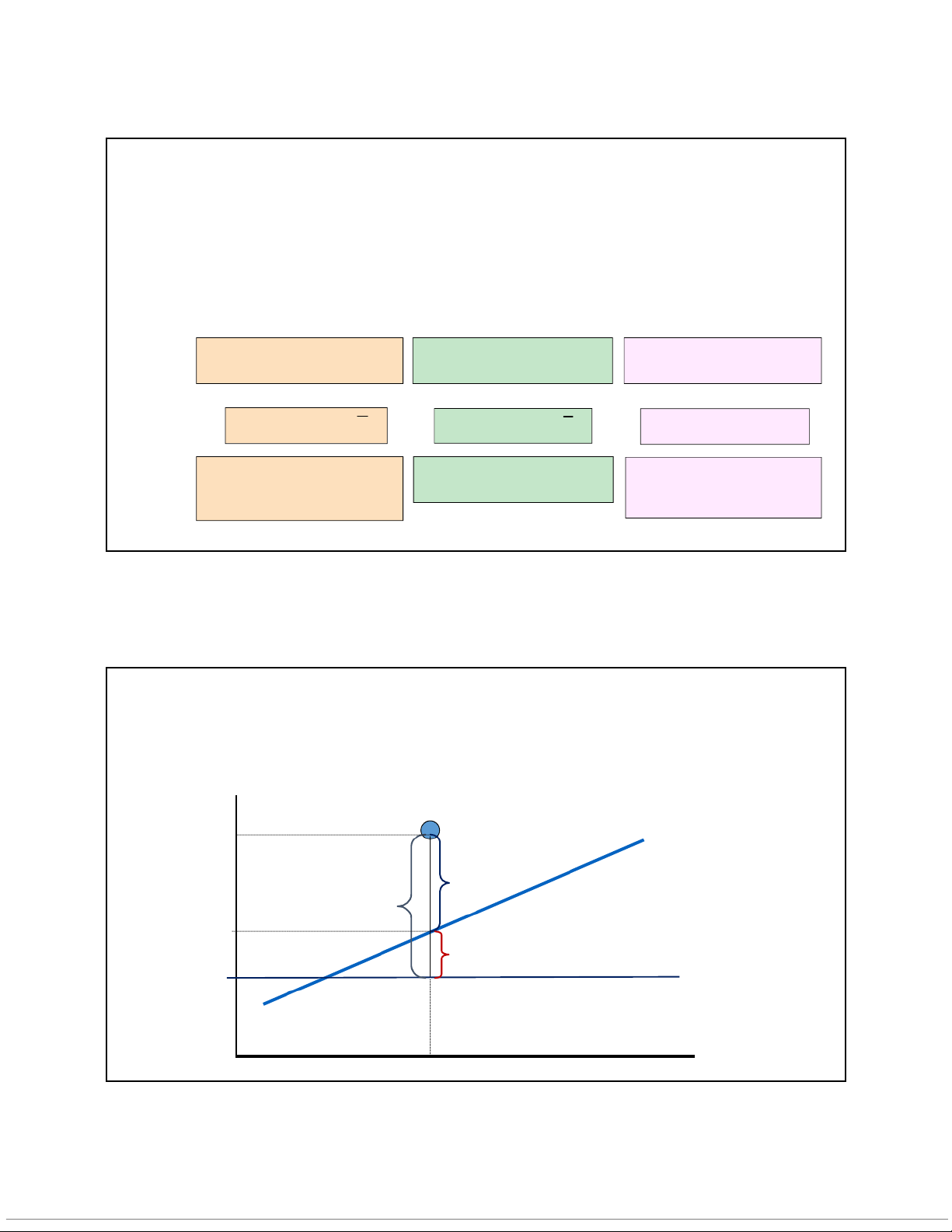
Biến thiên của biến phụ thuộc Biến thiên của hồi qui Biến thiên của phần dư (Total Sum of Squares) (Regression Sum of Squares) (Error Sum of Squares) SST  2 (y  i  ) y SSR ˆ  2  (y i) y SSE  ˆ (  2 y i y  ) i
Đo lường sự biến thiên của Sự hệbitế u n yếth n iê tí nhdo g im ữ ố a ix q vuàan y
Sự biến thiên do các nhân
các giá trị yiquanh giá trị
tố khác ngoài mối quan hệ trung bình 𝑦 của nó tuyến tính giữa x và y Hệ số xác định Y yi   𝑦 = 𝑏+ 𝑏𝑥
𝑺𝑺𝑻 = (𝒚𝒊− 𝒚)𝟐
𝑺𝑺𝑬 = (𝒚𝒊− 𝒚)𝟐   𝑦 
𝑺𝑺𝑹 = (𝒚𝒊− 𝒚)𝟐  𝑦 XiX 11 10/10/2020 Hệ số xác định
Hệ số xác định là tỷ lệ (lần, %) thay đổi của biến phụ thuộc
được giải thích bởi sự thay đổi của biến độc lập, ký hiệu là R2. • Công thức: 𝑅=𝑆𝑆𝑅 𝑆𝑆𝑇
• Tính chất: 0 ≤ R2≤ 1 (100%) Hệ số xác định Y Y Y X X Y Y X r2= 0
Không có mối liên hệ tuyến tính X
giữa X và Y. Giá trị của Y không 0 < r2< 1 X r2= 1 phụ thuộc vào X.
Liên hệ tuyến tính hoàn hảo giữa X
Liên hệ tuyến tính yếu giữa X và Y:
và Y: 100% sự thay đổi của Y được
Một phần sự thay đổi của Y được
giải thích bởi sự thay đổi của X.
giải thích bởi sự thay đổi của X. 12 10/10/2020 Hệ số tương quan
Hệ số tương quan là số tương đối dùng để đánh giá chiều hướng và
cường độ của mối liên hệ tương quan tuyến tính.
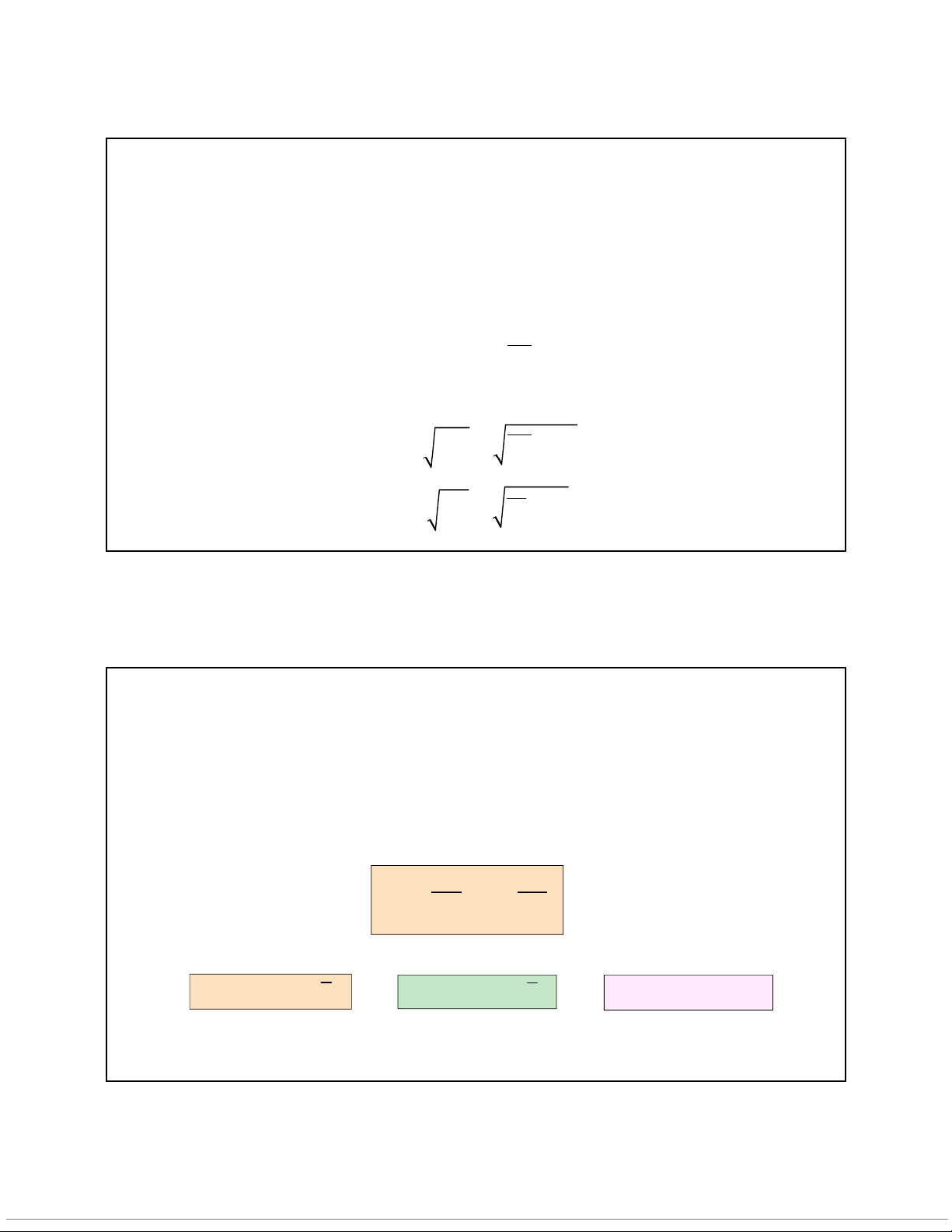
Công thức: 𝑅 =  𝑅 =. 
.= 𝑏 Tính chất: • -1 ≤ R ≤ 1
• R = ±1: giữa x và y có mối liên hệ hàm số
• R=0: giữa x và y không có mối liên hệ tương quan tuyến tính
• R>0: liên hệ thuận; R<0: liên hệ nghịch
• R→±1: mối liên hệ giữa x và y càng chặt chẽ Sai số mô hình
• Trung bình bình phương sai số (MSE) cho biết ước lượng của phương sai sai số
mô hình tổng thể (б2), còn được ký hiệu là se2 s= MSE = SSE n − 2
• Sai số chuẩn của ước lượng (Se) đo lường biến thiên của các giá trị thực tế y
xung quanh đường hồi qui. s=MSE 
Sai số càng lớn, biến thiên càng nhiều, đường hồi qui càng xa các điểm thực
tế. Đây là cơ sở để xác định đường hồi qui phù hợp nhất. Y Y small s XX large s e e 13 10/10/2020
Kiểm định các hệ số của mô hình hồi qui
• Kiểm định ý nghĩa của hệ số hồi qui
• Kiểm định ý nghĩa của hệ số tương quan
• Kiểm định ý nghĩa của mô hình
Kiểm định ý nghĩa của hệ số hồi qui
Liệu có tồn tại mối liên hệ giữa X và Y trong tổng thể không?
• Bước 1: Cặp giả thuyết cần kiểm định.
H0: β1=0 (X không có mối liên hệ với Y)
H1: β1≠0 (X có mối liên hệ với Y)
• Bước 2: Xác định mức ý nghĩa α (với 1-α là hệ số tin cậy).
• Bước 3: Tiêu chuẩn kiểm định t có phân phối Student, bậc tự do n-2
𝑡 = =Với 𝑆𝑒=(sai số chuẩn của hệ số hồi qui) ∑()
• Bước 4: Xác định miền bác bỏ và kết luận.
|t| > tα/2;n-2 : bác bỏ H0và ngược lại. 14 10/10/2020
Khoảng tin cậy của hệ số hồi qui
• Khoảng tin cậy hai phía: 𝑏− 𝑡 ⁄
. 𝑆𝑒< 𝛽< 𝑏+ 𝑡  ⁄ . 𝑆𝑒
• Khoảng tin cậy phía phải:
𝑏− 𝑡. 𝑆𝑒< 𝛽< +∞
• Khoảng tin cậy phía trái:
−∞ < 𝛽< 𝑏+ 𝑡 . 𝑆𝑒
Kiểm định ý nghĩa của hệ số tương quan
Liệu giữa X và Y thực sự có mối liên hệ tương quan tuyến tính?
• Bước 1: Phát biểu giả thiết không
H0: ρ=0 (không có mối liên hệ tương quan tuyến tính giữa X và Y)
• Bước 2: Xác định mức ý nghĩa α
• Bước 3: Tiêu chuẩn kiểm định t có phân phối Student với bậc tự do n-2 𝑡 = 𝑟  1 − 𝑟 𝑛 − 2 15 10/10/2020
Kiểm định ý nghĩa của hệ số tương quan
• Bước 4: Tùy thuộc dạng của giả thuyết đối mà xây dựng miền bác bỏ.
- H1: ρ>0 (có mối liên hệ tương quan tuyến tính dương giữa x và y)
→ t > tα,n-2: bác bỏ H0.
- H1: ρ<0 (có mối liên hệ tương quan tuyến tính âm giữa x và y)
→ |t| > tα,n-2 : bác bỏ H0.
- H1: ρ≠0 (có mối liên hệ tương quan tuyến tính giữa x và y)
→ |t| > tα/2,n-2 : bác bỏ H0.
Kiểm định ý nghĩa của mô hình
Liệu mô hình hồi qui có phù hợp không?
• Bước 1: Cặp giả thuyết cần kiểm định
H0: β1=0 (hoặc R2=0) (mô hình không phù hợp)
H1: β1≠0 (hoặc R2≠0) (mô hình là phù hợp)
• Bước 2: Xác định mức ý nghĩa α
• Bước 3: Tiêu chuẩn kiểm định F có phân phối Fisher với bậc tự do là k=1 và n-k-1=n-2 𝑀𝑆𝐸 =𝑆𝑆𝑅
𝐹 = 𝑀𝑆𝑅 𝑛 𝑘−2 =𝑅(𝑛 − 2) 𝑆𝑆𝐸 1 − 𝑅
• Bước 4: Xác định miền bác bỏ và kết luận.
• F> 𝐹 1, 𝑛 − 2 : bác bỏ H0và ngược lại. 16 10/10/2020 Hồi qui tương quan bội • Mô hình hồi qui bội
• Kiểm định mô hình hồi qui bội Mô hình hồi qui bội
Mục tiêu: Khám phá mối liên hệ tuyến tính giữa 1 biến
phụ thuộc (Y) và 2 hoặc nhiều hơn các biến độc lập (Xj)
Phương trình hồi qui bội tổng thể với k biến độc lập: Hệ số tự do Các hệ số hồi Sai số ngẫu tổng thể qui tổng thể nhiên 1 2 2 Y k k
β β X β X  β  X ε 17 10/10/2020 Mô hình hồi qui bội
Các hệ số của mô hình hồi qui được ước lượng trên cơ sở dữ liệu thu thập từ mẫu Giá trị ước lượng Ước lượng (hay lý thuyết) của của hệ số
Ước lượng của các hệ y cho quan sát i tự do số hồi qui x b x
bˆ i x 0  1 1i  2 2i    k ki
Có thể sử dụng máy tính để tính toán các ước lượng này và một
số đo lường khác trong phân tích hồi qui tương quan bội. Mô hình hồi qui bội
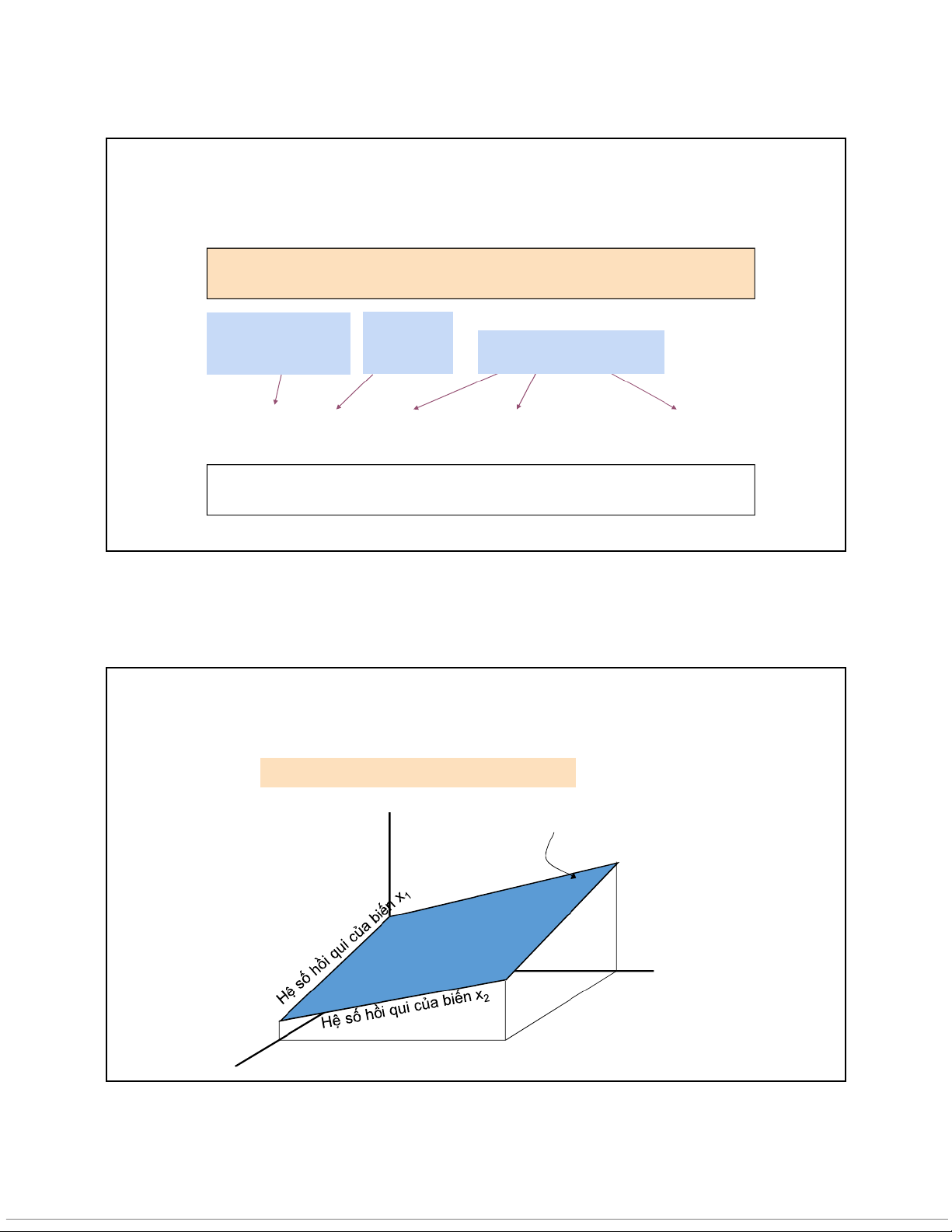
Mô hình hồi qui với 2 biến độc lập y   y b b xˆ 0 b x 1 1 2 2 x2 x1 18 10/10/2020 Mô hình hồi qui bội
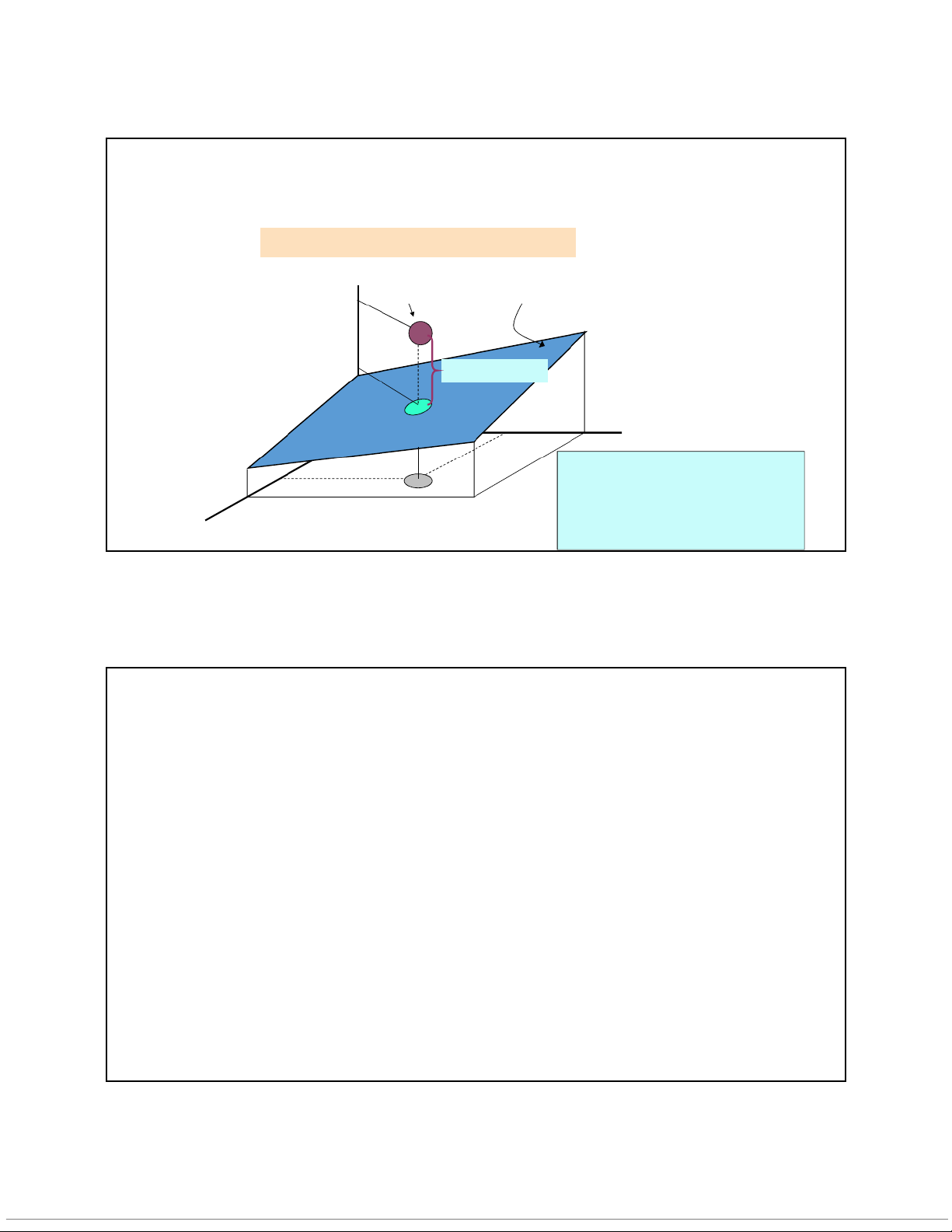
Mô hình hồi qui với 2 biến độc lập y y Q  uan s yát m  ẫ b u b xˆ b i 0 x 1 1 2 2 𝑦 
𝑒= (𝑦− 𝑦 ) x2i x2
Hàm hồi qui tốt nhất, 𝑦 , được x1i
xác định bằng phương pháp bình
phương nhỏ nhất (OLS): tối thiểu x1
hóa tổng bình phương chênh lệch, ei2=min Mô hình hồi qui bội
Ý nghĩa của các hệ số trong mô hình hồi qui bội
•Hệ số tự do b0:cho biết ảnh hưởng của tất cả các biến nguyên nhân
khác không có trong mô hình hồi qui đến biến kết quả.
•Hệ số hồi qui bj:cho biết ảnh hưởng của biến nguyên nhân xjtới biến kết
quả y khi các nguyên nhân khác trong mô hình là không đổi, cụ thể, khi xj
tăng thêm 1 đơn vị thì y sẽ thay đổi trung bình là bjđơn vị. Giá trị của bjcó
thể là âm hoặc dương tùy thuộc vào mối liên hệ giữa xjvà y. 19 10/10/2020 Mô hình hồi qui bội
Hệ số hồi qui chuẩn hóa: dùng để xác định vai trò tác động của các biến
độc lập tới biến phụ thuộc trong mô hình hồi qui.
𝐵𝑒𝑡𝑎= 𝑏𝜎 𝜎 Trong đó: 𝜎  =𝜎 =𝑥− 𝑥  𝜎    =
𝜎 = 𝑦 − 𝑦 Mô hình hồi qui bội
Hệ số xác định: dùng để xác định phần trăm thay đổi của biến phụ thuộc
y được giải thích bởi tất cả các biến độc lập xjtrong mô hình. R=SSR SST = 1 − SSE SST SST  2 (y i  ) y  SSR ˆ 2  y ( i) y SSE  ˆ (  2 y i y  ) i 20