Chương 6 Phân tích tương quan và hồi quy môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh tế Quốc dân

CHƯƠNG 6
PHÂN TÍCH TƯƠNG QUAN VÀ HỒI QUY 1 NỘI DUNG CHÍNH 1. NHỮNG VẤN ĐỀ CHUNG 2. PHÂN TÍCH TƯƠNG QUAN 3. PHÂN TÍCH HỒI QUY 2 1 2025-05-25
1. NHỮNG VẤN ĐỀ CHUNG (1)
1.1. Mối liên hệ giữa các hiện tượng KT – XH Liên hệ hàm số Liên hệ tương quan X Y Y 3
1. NHỮNG VẤN ĐỀ CHUNG (2) Liên hệ hàm số Liên hệ tương quan - Định nghĩa: - Định nghĩa:
Là mối liên hệ hoàn toàn chặt chẽ. Khi hiện Là mối liên hệ không hoàn toàn chặt chẽ.
tượng này thay đổi có tác động quyết định
Cụ thể: sự thay đổi của hiện tượng này có
làm thay đổi hiện tượng liên quan theo một thể làm hiện tượng liên quan thay đổi theo tỷ lệ xác định.
nhưng không có ảnh hưởng hoàn toàn quyết định.
Liên hệ hàm số được biểu diễn dưới dạng: y = f(x) - Đặc điểm: - Đặc điểm:
Không những được biểu hiện ở tổng thể (số Không ảnh hưởng rõ trên từng đơn vị cá
lớn) mà còn được biểu hiện rõ trên từng đơn biệt mà phải qua nghiên cứu số lớn các đơn vị cá biệt. vị. - Ví dụ: - Ví dụ:
Trong toán học: cho hàm số y = a2
Mối liên hệ giữa tuổi nghề và NSLĐ. 4 2 2025-05-25
1. NHỮNG VẤN ĐỀ CHUNG (3)
1.2. Phương pháp phân tích Hồi quy và tương quan
Là phương pháp toán học được vận dụng trong thống kê để biểu diễn và
đánh giá mối liên hệ tương quan giữa các hiện tượng Nhiệm vụ:
Xây dựng phương trình hồi quy biểu diễn mối liên hệ tương quan giữa
các hiện tượng (4 bước)
Giải thích sự tồn tại thực tế và bản chất của mối liên hệ Thăm dò mối liên hệ
Lập phương trình hồi quy
Tính toán các tham số và giải thích ý nghĩa
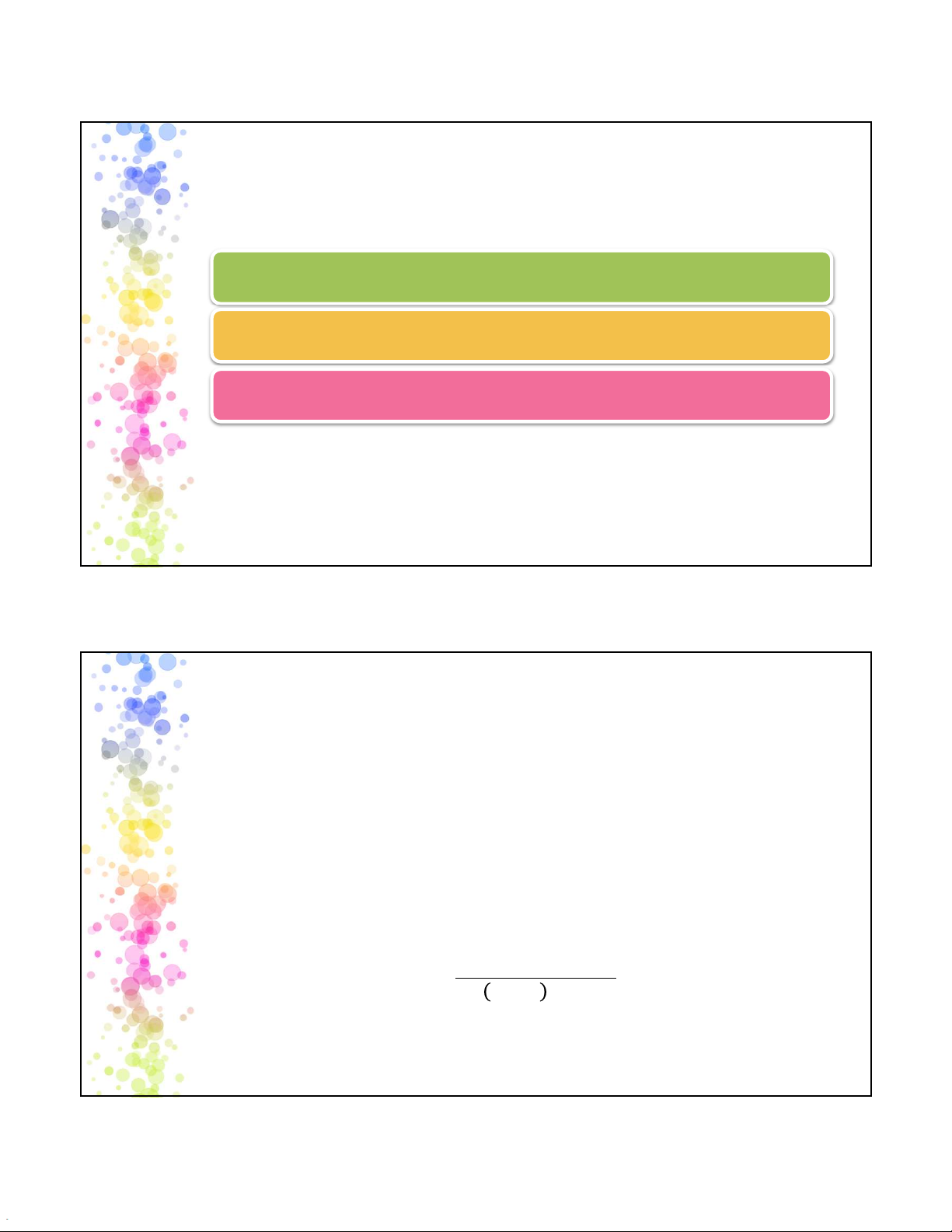
Đánh giá trình độ chặt chẽ của mối liên hệ tương quan và sự phù hợp của mô hình hồi quy 5 Các dạng liên hệ Liên hệ tuyến tính
Liên hệ phi tuyến tính 6 3 2025-05-25 NỘI DUNG CHÍNH 1. NHỮNG VẤN ĐỀ CHUNG 2. PHÂN TÍCH TƯƠNG QUAN 3. PHÂN TÍCH HỒI QUY 7 2. Phân tích tương quan
Phân tích tương quan gồm các kỹ thuật đo lường mối liên hệ giữa hai biến
Hệ số tương quan đo lường mức độ chặt chẽ của mối
liên hệ tương quan tuyến tính giữa hai biến
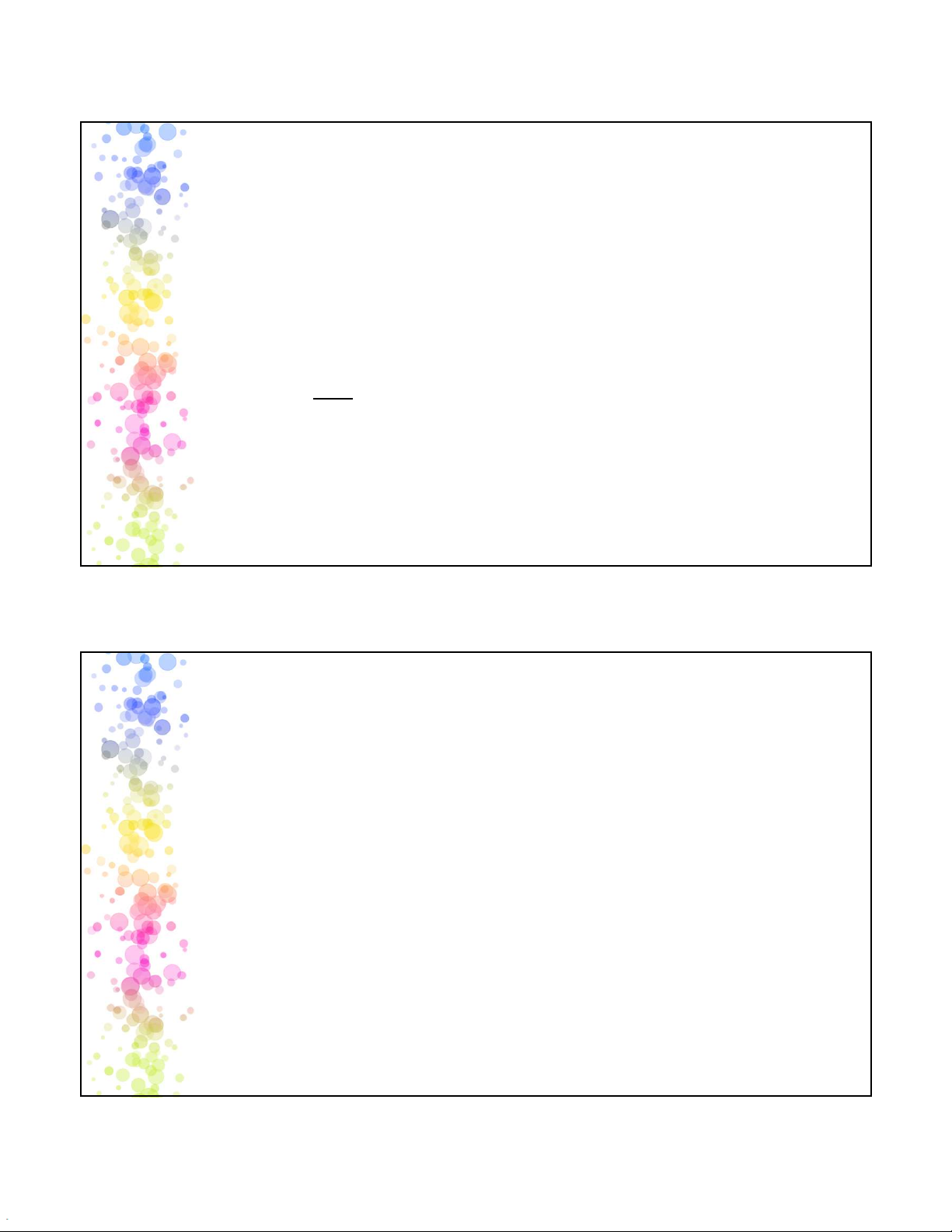
Công thức tính 𝑟 = ∑(𝑥− 𝑥)(𝑦− 𝑦) 𝑛 − 1 𝑆𝑆 8 4 2025-05-25 Phân tích tương quan Tác dụng
- Xác định chiều hướng của mối liên hệ
- Đánh giá mức độ chặt chẽ của liên hệ tương quan tuyến tính 9
Tính chất của hệ số tương quan Không có mối liên hệ Liên hệ hàm số Liên hệ hàm số tuyến tính -1 0 +1 10 5 2025-05-25
Kiểm định hệ số tương quan Cặp giả thuyết 󰇫 𝐻: 𝑟 = 0 𝐻: 𝑟 ≠ 0 𝑇 = 𝑟 Tiêu chuẩn kiểm định 1 − 𝑟 𝑛 − 2
Nếu H0đúng, thống kê T sẽ tuân theo quy luật phân phối student với bậc tự do (n-2)
Với mức ý nghĩa α, Miền bác bỏ giả thuyết H 
0khi 𝑇  > 𝑡 ⁄ 11 3. PHÂN TÍCH HỒI QUY
3.1. Phân tích hồi quy đơn
3.2. Phân tích hồi quy bội 12 6 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy Ví dụ:
Có tài liệu về chi phí quảng cáo và doanh thu bán hàng của một doanh nghiệp như sau CP Quảng cáo Doanh Thu STT (triệu đồng) (triệu đồng) 1 2 810 2 4 820 3 7 840 4 9 850 5 10 870 Tổng 32 4190
Yêu cầu: Lập phương trình hồi quy tuyến tính biểu diễn mối liên hệ
của chi phí quảng cáo tới doanh thu bán hàng. 13
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy
Giải thích sự tồn tại thực tế và bản chất của mối liên hệ Thăm dò mối liên hệ 880
oĐường hồi quy thực tế: là đường 870
gấp khúc được xây dựng trên cơ sở Đường hồi quy 860 lý thuyết dữ liệu thực tế 850
oĐường hồi quy lý thuyết: là đường 840
điều chỉnh (bù trừ) các chênh lệch 830 Đường hồi quy
ngẫu nhiên để phản ánh mối liên hệ Doanh Thu 820 thực nghiệm
cơ bản của hiện tượng 810
oPhương trình hồi quy: là phương 800
trình xác định vị trí của đường hồi 0 5 10 15 quy lý thuyết CP Quảng cáo 14 7 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy
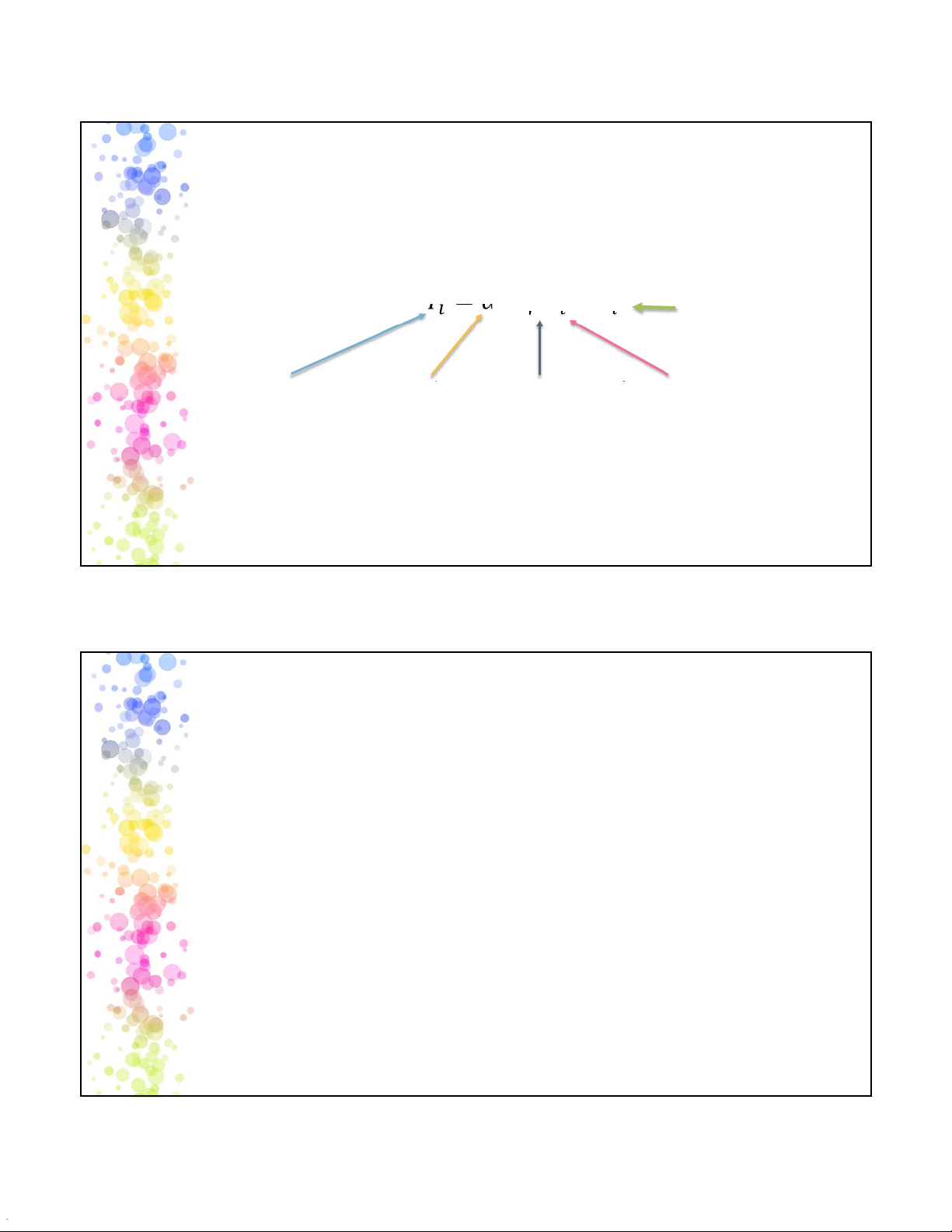
Phương trình hồi quy tổng thể 𝑌 Phần dư (chênh lệch
= 𝛼 + 𝛽𝑥+ 𝜀
giữa giá trị thực tế và giá trị lý thuyết) Biến phụ thuộc Tham số tự do Hệ số hồi quy Biến độc lập Biến kết quả Hệ số chặn Hệ số góc Biến nguyên nhân Biến được giải thích Biến giải thích Biến nội sinh Biến ngoại sinh 15
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy
Phương trình hồi quy tổng thể Ý nghĩa của các tham số
oα phản ánh ảnh hưởng của các tiêu thức nguyên nhân khác (ngoài tiêu
thức X) tới tiêu thức kết quả Y
o𝛽phản ánh ảnh hưởng trực tiếp của tiêu thức nguyên nhân X tới tiêu
thức kết quả Y. Cụ thể: khi X tăng thêm 1 đơn vị thì Y sẽ thay đổi bình quân 𝛽 đơn vị
𝛽> 0 X và Y có mối liên hệ thuận (cùng chiều)
𝛽 < 0 X và Y có mối liên hệ nghịch (ngược chiều) 16 8 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy
Phương trình hồi quy mẫu
Với mẫu ngẫu nhiên kích thước n, phương trình hồi quy mẫu xác định vị
trí của đường hồi quy lý thuyết sau:
𝑦 = 𝑎 + 𝑏𝑥
Ước lượng tham số 𝛼Ước lượng tham số 𝛽 17
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy
Ước lượng tham số a và b
Phương pháp bình phương nhỏ nhất (OLS - Ordinary least squares):
𝑆 =  𝑦𝑖 − 𝑦𝑥2 → 𝑚𝑖𝑛
𝑆 =  𝑦𝑖 − 𝑎 − 𝑏𝑥 2 → 𝑚𝑖𝑛
avà bphải thỏa mãn hệ phương trình 𝜕𝑆
𝜕𝑎 =2 𝑦  − 𝑎 − 𝑏𝑥 −1 = 0 = 0 𝑦
𝑖 = 𝑛𝑎 + 𝑏 𝑥 𝑖  𝜕𝑆 𝜕𝑏 =2 𝑦 𝑖
 − 𝑎 − 𝑏𝑥 −𝑥
𝑥 𝑖𝑦𝑖 = 𝑎 𝑥 𝑖 + 𝑏 𝑥
𝑏 = 𝑥𝑦 − 𝑥𝑦 𝜎 Hoặc 𝑎 = 𝑦 − 𝑏𝑥 18 9 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy Các giả thiết của OLS
1. Mô hình được ước lượng trên cơ sở mẫu ngẫu nhiên
2. Kỳ vọng toán của sai số bằng 0
3. Sai số tuân theo quy luật phân phối chuẩn
4. Phương sai của sai số bằng nhau (không đổi)
5. Không có tương quan giữa các phần dư (không có hiện tượng tự tương quan)
6. Giữa các biến độc lập không có tương quan tuyến tính hoàn
hảo (đa cộng tuyến) – Đối với hồi quy bội 19
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy Ví dụ x y i i Chi phí Doanh Thu STT Quảng cáo xiyi xi2 yi2 (triệu đồng) (triệu đồng) 1 2 810 1620 4 656100 2 4 820 3280 16 672400 3 7 840 5880 49 705600 4 9 850 7650 81 722500 5 10 870 8700 100 756900 Tổng 32 4190 27130 250 3513500 20 10 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Xây dựng phương trình hồi quy
𝑥 = ∑ 𝑥𝑛=32 5= 6.4
Phương trình hồi quy tuyến tính biểu 𝑦 = ∑𝑦𝑛
diễn mối liên hệ giữa CPQC và doanh  =41905= 838 thu có dạng
𝑥𝑦 = ∑𝑥𝑛𝑦=271305= 5426 𝑦𝑥=793.54+6.947xi =∑𝑥  𝜎 𝑛− 𝑥  =250 5− 6,4  = 9,04
𝑏 = 𝑥𝑦 − 𝑥𝑦 =5426 − 6.4 × 838 9.04 = 6.947 𝜎
𝑎 = 𝑦 − 𝑏1𝑥 = 838 – 6.947 x 6.4 = 793.54 21
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Kiểm định ý nghĩa của hệ số hồi quy Giả thuyết: H : : 0  = 0 và H1  ≠ 0
Tiêu chuẩn kiểm định: 𝑇 = () Trong đó: 𝑠𝑒 𝑏 = 𝜎 ∑𝑥− 𝑥   
Trong đó: 𝜎= =∑  
Nếu H đúng thì Thống kê T sẽ tuân theo quy luật phân phối Student 0 với (n-2) bậc tự do
Với mức ý nghĩa α, Miền bác bỏ giả thuyết H khi 𝑇  0  > 𝑡  ⁄ 22 11 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Ước lượng hệ số hồi quy Hai phía 𝑏 − 𝑡/  
𝑠𝑒(𝑏) ≤ 𝛽 ≤ 𝑏+ 𝑡/𝑠𝑒(𝑏) Phía phải
𝑏 − 𝑡𝑠𝑒 𝑏 ≤ 𝛽 ≤ +∞ Phía trái
−∞ ≤ 𝛽 ≤ 𝑏 + 𝑡𝑠𝑒(𝑏) 23
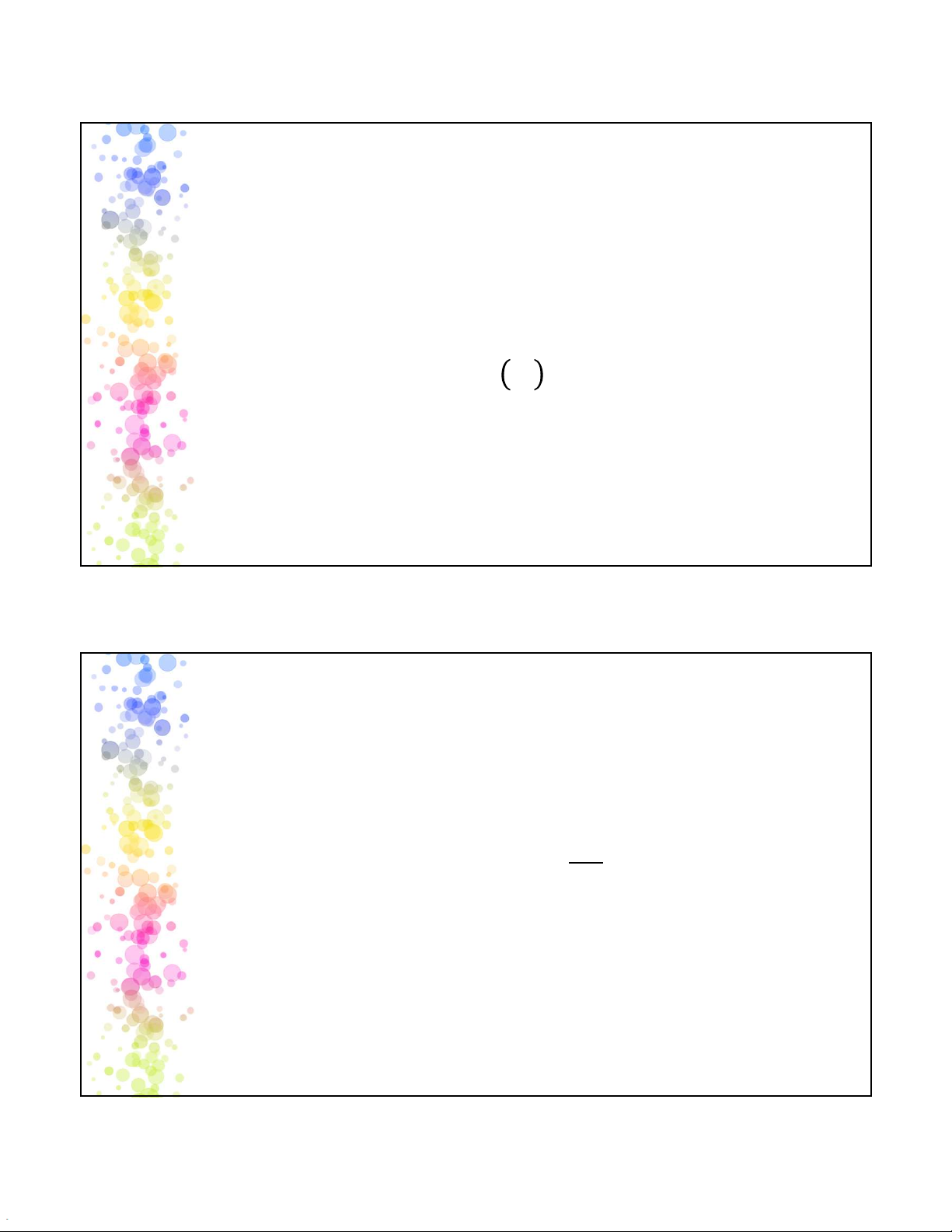
Ước lượng khoảng tin cậy cho biến phụ thuộc ()
Khoảng tin cậy giá trị trung bình
𝑦 ± 𝑡/ 𝑆  +    ∑   ()
Khoảng tin cậy giá trị cá biệt
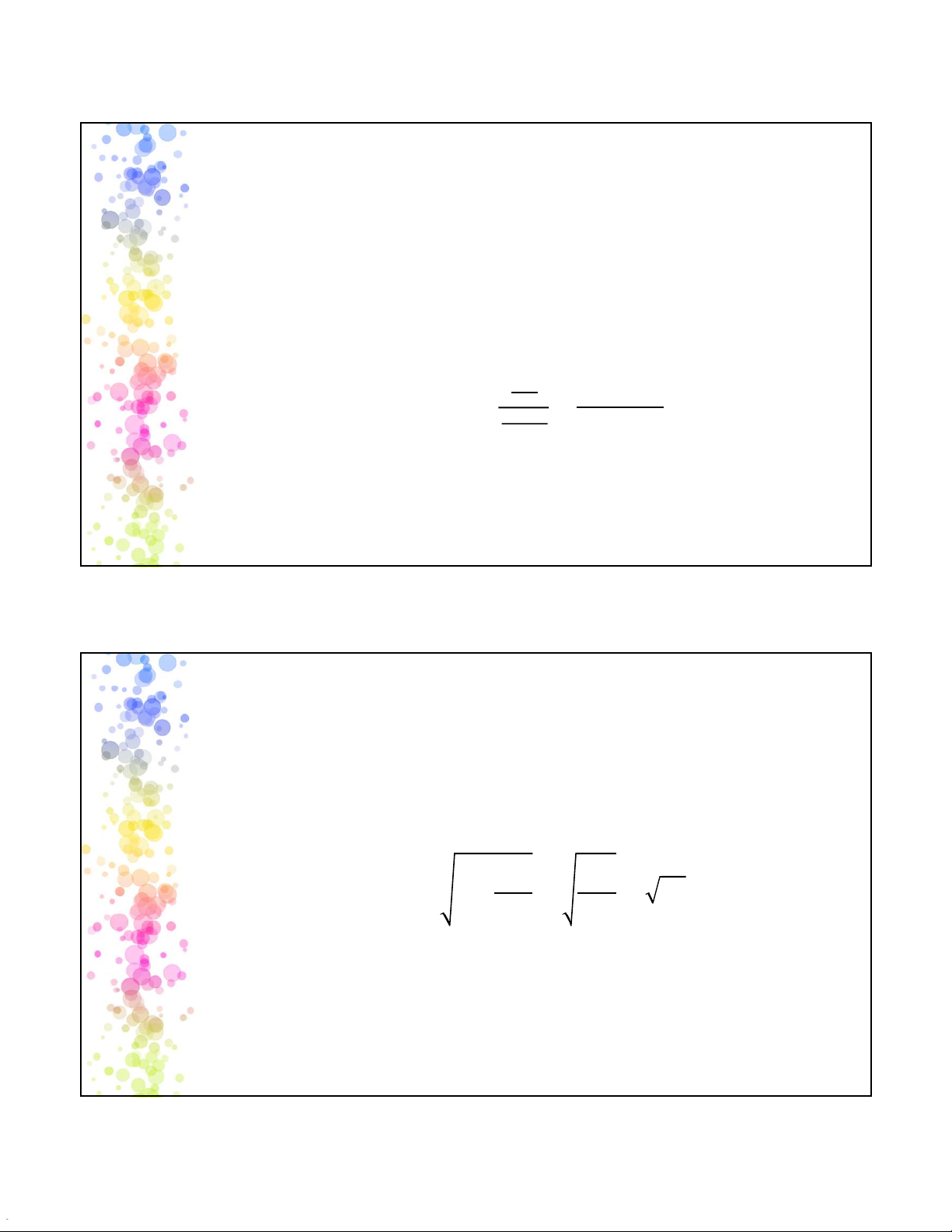
𝑦 ± 𝑡/ 𝑆 1 +  +    ∑   Trong đó
𝑆 = 𝑆𝐸 = ∑() 
Sai số chuẩn của ước lượng 24 12 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Đánh giá sự phù hợp của phương trình hồi quy Hệ số xác định (R2) Yi Y
SSE =∑𝒀 𝒊 −𝒀𝒊𝟐
SST =∑𝒀 𝒊 −𝒀 𝟐 SSR =∑𝒀−𝒀 𝟐 𝒀 X Xi 25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Đánh giá sự phù hợp của phương trình hồi quy
Tổng biến thiên của biến phụ thuộc: SST =∑𝒀𝒊−𝒀 𝟐
Tổng biến thiên được giải thích bởi mô hình hồi quy: SSR =∑𝒀−𝒀𝟐
Tổng biến thiên được giải thích bởi phần dư: SSE =∑𝒀𝒊−𝒀 𝒊𝟐 SST = SSR + SSE Hệ số xác định:
𝑅= = 1 −  
Phản ánh % thay đổi của biến phụ thuộc được giải thích bởi mô hình hồi quy 26 13 2025-05-25
3.1. PHÂN TÍCH HỒI QUY TUYẾN TÍNH ĐƠN
Đánh giá sự phù hợp của phương trình hồi quy
Kiểm định ý nghĩa của mô hình hồi quy
Cặp giả thuyết 󰇫𝐻0: 𝑀 𝐻 ô1: ℎì 𝑀𝑛ôℎ ℎ𝑘ìℎ 𝑛 ô ℎ 𝑛𝑐𝑔 ó 𝑐 ý ó𝑛 ý 𝑔 𝑛 ℎĩ𝑔 𝑎 ℎĩ𝑎 󰇫𝐻0: 𝑅 = 0 𝐻1: 𝑅 ≠ 0 () Tiêu chuẩn kiểm định: 𝐹 =   =() 
Nếu H0 đúng, Thống kê F sẽ tuân theo quy luật phân phối Fisher với bậc tự do (1, n-2)
Với mức ý nghĩa , Miền bác bỏ giả thuyết H khi F > F 0 ,(1, n-2) 27 3. PHÂN TÍCH HỒI QUY
3.1. Phân tích hồi quy đơn
3.2. Phân tích hồi quy bội 28 14 2025-05-25
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Xây dựng phương trình hồi quy
Phương trình hồi quy tổng thể
𝑌= 𝛼 + 𝛽𝑥 + 𝛽𝑥 + ⋯ + 𝛽𝑥 + 𝜀
𝛼- Tham số tự do (hệ số chặn)
𝛽 (𝑗 = 1, 𝑘) – Hệ số hồi quy riêng
𝛽phản ánh ảnh hưởng thuần của nguyên nhân x tới kết j
quả y (khi các yếu tố khác không đổi). Cụ thể: khi x j tăng
thêm 1 đơn vị thì y thay đổi trung bình 𝛽 đơn vị. 29
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Xây dựng phương trình hồi quy
Phương trình hồi quy mẫu
Với mẫu ngẫu nhiên kích thước n, phương trình hồi quy
mẫu sau: 𝑦= 𝑎 + 𝑏𝑥 + 𝑏𝑥 + ⋯ + 𝑏𝑥
a: ước lượng của tham số 𝛼
𝑏: ước lượng của tham số 𝛽 30 15 2025-05-25
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Xây dựng phương trình hồi quy
Kiểm định hệ số hồi quy Giả thuyết: H0: j = 0 và H1: j ≠ 0
Tiêu chuẩn kiểm định: 𝑇 =   ()
Nếu H 0 đúng thì Thống kê T sẽ tuân theo quy luật phân
phối Student với (n-k-1) bậc tự do
Với k là số biến độc lập trong mô hình 31
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Xây dựng phương trình hồi quy
Kiểm định hệ số hồi quy
Miền bác bỏ giả thuyết H0 (W )  - Kiểm định 2 phía:
𝑇 > 𝑡 ,() - Kiểm định phía phải:
𝑇 > 𝑡,() - Kiểm định phía trái:
𝑇 < −𝑡,() 32 16 2025-05-25
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Xây dựng phương trình hồi quy
Ước lượng hệ số hồi quy Hai phía
𝑏− 𝑡/𝑠𝑒(𝑏) ≤ 𝛽≤ 𝑏+ 𝑡/𝑠𝑒(𝑏) Phía phải
𝑏− 𝑡𝑠𝑒 𝑏≤ 𝛽≤ +∞ Phía trái
−∞ ≤ 𝛽≤ 𝑏+ 𝑡 𝑠𝑒(𝑏) 33
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Xây dựng phương trình hồi quy
Hệ số hồi quy chuẩn hóa = 𝑏𝜎 𝐵𝑒𝑡𝑎  𝜎
Phản ánh vai trò của từng biến độc lập tới biến phụ thuộc 34 17 2025-05-25
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Đánh giá sự phù hợp của phương trình hồi quy Hệ số xác định R 2
Tổng biến thiên của biến phụ thuộc: SST =∑𝒀𝒊−𝒀 𝟐
Tổng biến thiên được giải thích bởi mô hình hồi quy: SSR =∑𝒀−𝒀𝟐
Tổng biến thiên được giải thích bởi phần dư: SSE =∑𝒀𝒊−𝒀 𝒊𝟐 SST = SSR + SSE
Hệ số xác định: 𝑅 =  = 1 −   
Phản ánh % thay đổi của biến phụ thuộc được giải thích bởi mô hình hồi quy 35
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Đánh giá sự phù hợp của phương trình hồi quy
Hệ số xác định điều chỉnh 𝑹𝒂𝒅 𝟐 𝒋
= 1 − 𝑆𝑆𝐸 𝑛 − 1 = 1 − (1 − 𝑅 𝑅 )(𝑛 − 1)  𝑛 − 𝑘 − 1 𝑆𝑆𝑇 𝑛 − 𝑘 − 1
Dùng để so sánh, đánh giá sự phù hợp của mô hình khi số lượng biến
trong mô hình hồi quy khác nhau Khi k > 1 thì 𝑅   ≤ 𝑅≤ 1
k càng lớn 𝑅càng nhỏ so với R 2  𝑅 
 có thể âm, khi đó quy ước 𝑅 = 0 36 18 2025-05-25
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Đánh giá sự phù hợp của phương trình hồi quy
Kiểm định ý nghĩa của mô hình hồi quy Cặp giả thuyết 󰇫𝐻0: 𝑅 = 0 𝐻1: 𝑅 ≠ 0  𝐻: 𝑀ô 𝑀 ô ℎì ℎ 𝑛ℎ 𝑛 𝑘ℎ 𝑐óô 𝑛 ý 𝑔 𝑛 𝑐 𝑔 ó ℎĩ ý
𝑎 𝑛𝑔ℎĩ𝑎  𝐻: 𝛽 = 𝛽 = … . = ⋯ 𝛽 = 0 𝐻
𝐻 : 𝑇ồ𝑛 𝑡ạ𝑖 í𝑡 𝑛ℎấ𝑡 𝛽 ≠ 0  () Tiêu chuẩn kiểm định: 𝐹 = 
 = () 
Nếu H0đúng, Thống kê F sẽ tuân theo quy luật phân phối Fisher với bậc tự do (k, n-k-1)
Với mức ý nghĩa , Miền bác bỏ giả thuyết H0khi F > F ,(k, n-k-1) 37
3.2. PHÂN TÍCH HỒI QUY TUYẾN TÍNH BỘI
Đánh giá sự phù hợp của phương trình hồi quy
Hệ số tương quan chung Công thức 𝑅 = 1 − 𝑆𝑆𝐸
𝑆𝑆𝑇 =𝑆𝑆𝑅𝑆𝑆𝑇 = 𝑅 38 19 2025-05-25
Các dạng bài tập của chương
Xây dựng phương trình hồi quy (b0, b1)
Kiểm định và ước lượng các hệ số hồi quy
Tính toán R 2và kiểm định sự phù hợp của mô hình hồi quy
Đánh giá trình độ chặt chẽ của mối liên hệ (R) 39
Ứng dụng SPSS trong phân tích HQ
Analyze > Regression > Linear…
Đưa biến phụ thuộc sang Dependent
Đưa các biến độc lập sang Independent(s) 40 20