Chương 7: Định Lý Ampère môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

CHƯƠNG 7: ĐỊNH LÝ AMPÈRE 1
7.1. LƯU SỐ CỦA TỪ TRƯỜNG CỦA MỘT SỢI DÂY 7. 2 . ĐỊNH LÝ AMPÈRE
7. 3 . ÁP DỤNG ĐỊNH LÝ AMPÈRE
7. 4 . ĐIỀU KIỆN BIÊN CỦA TỪ TRƯỜNG
BÀI TẬP: AD4 p.151, BT: 6, 9 (p.155)
7. 1 . L Ư U S Ố C Ủ A T Ừ T R Ư Ờ N G C Ủ A M Ộ T S Ợ I D Â Y V Ô 2 H ẠN
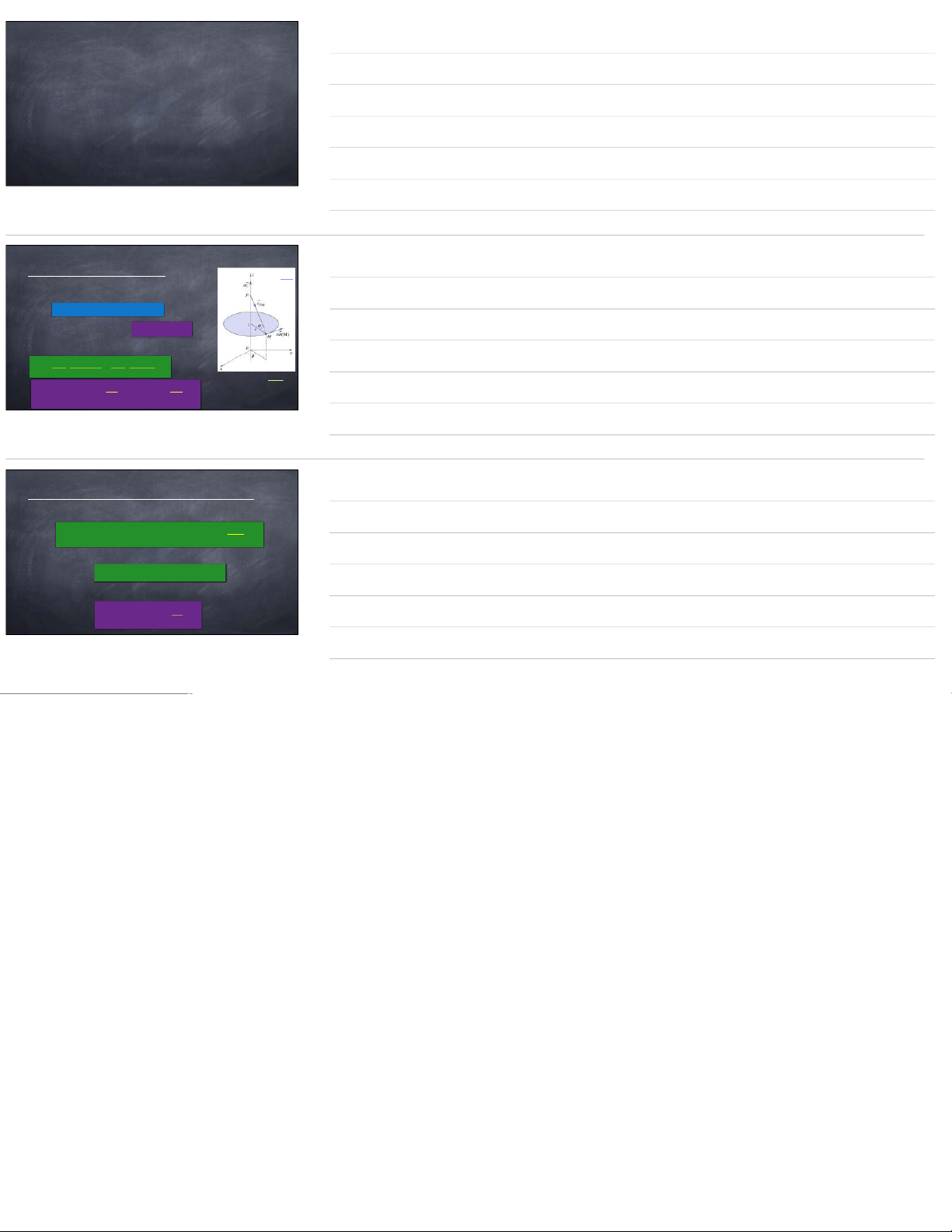
1. Từ trường của một sợi dây vô hạn ≡(Oz) PM =r
• Phân bố đối xứng phẳng qua mọi mặt phẳng chứa cosα trục (O v z) à trục ( là O
z t)rục đx của sợi dây: B(M) = Bθ(r,θ,z) . eθ=Bθ(r,z) . eθ(1)
• Phân bố bất biến đối với phép B(M) = Bθ(r) . eθ(2)
tịnh tiến dọc theo trục :(Oz) •Phần tử gây d ra C từ =I .tr d ường P tại M: B=μ0.I4π.d C∧P e M P 2 M =μ0.I 4π.cosα.dα d r. e OP = (z+r.tanα) . e θ(3) z P=I.r.dz d C=I.d cos2α. ez μ0I eθ.cosα.dα=μ0I ⇒ B(M) = ∫d B=∫π/2 4πr. 2πr. eθ(4) −π/2 cả sợi dây
7. 1 . L Ư U S Ố C Ủ A T Ừ T R Ư Ờ N G C Ủ A M Ộ T S Ợ I D Â Y V Ô 3 H ẠN
2.Lưu số nguyên tố của từ trường của một sợi dây vô hạn
•Từ trường gây bởi sợi dây vô hạn: B≡ eθ=μ0.I
B(M) = B(r,θ,z) = B(r,θ) = B(r) . 2πr. eθ
•Trong tọa độ trụ, dịch chuyển nguyên tố của 1 điểm xác định M bởi: d M=dr . er+r.dθ. eθ+dz . ez
•Lưu số nguyên tố của từ trường của sợi dây vô hạn bằng: M=μ0.I dC = B.d 2π.dθ
7. 1 . L Ư U S Ố C Ủ A T Ừ T R Ư Ờ N G C Ủ A M Ộ T S Ợ I D Â Y V Ô 4 H ẠN
3. Lưu số của trường trên một đường cong kín quấn lấy dây
Lưu số của từ trường trên đường cong ∮Γ dθ= 2π
kín quấn lấy một sợi dây điện cường Γ
độ I theo chiều thuận này được xác định bởi: CΓ=∮Γ B.d M=μ0.I
•Nếu quấn lấy dây theo chiều nghịch: Γ
Đường cong kín Γ quấn lấy CΓ=−μ0.I
một sợi dây theo chiều thuận
7. 1 . L Ư U S Ố C Ủ A T Ừ T R Ư Ờ N G C Ủ A M Ộ T S Ợ I D Â Y V Ô 5 H ẠN
4. Lưu số của trường trên một đường cong kín không quấn lấy dây
Nếu đường cong kín không quấn lấy Γ ∮Γ dθ= 0
sợi dây thẳng dài có dòng điện I chạy
qua, lưu số của từ trường trên đường
cong kín này được xác định bởi: CΓ=∮Γ B.d M= 0 Đường cong kín Γ không quấn lấy sợi dây
7. 1 . L Ư U S Ố C Ủ A T Ừ T R Ư Ờ N G C Ủ A M Ộ T S Ợ I D Â Y V Ô 6 H ẠN
5. Quan hệ với dòng điện đi qua đường cong kín
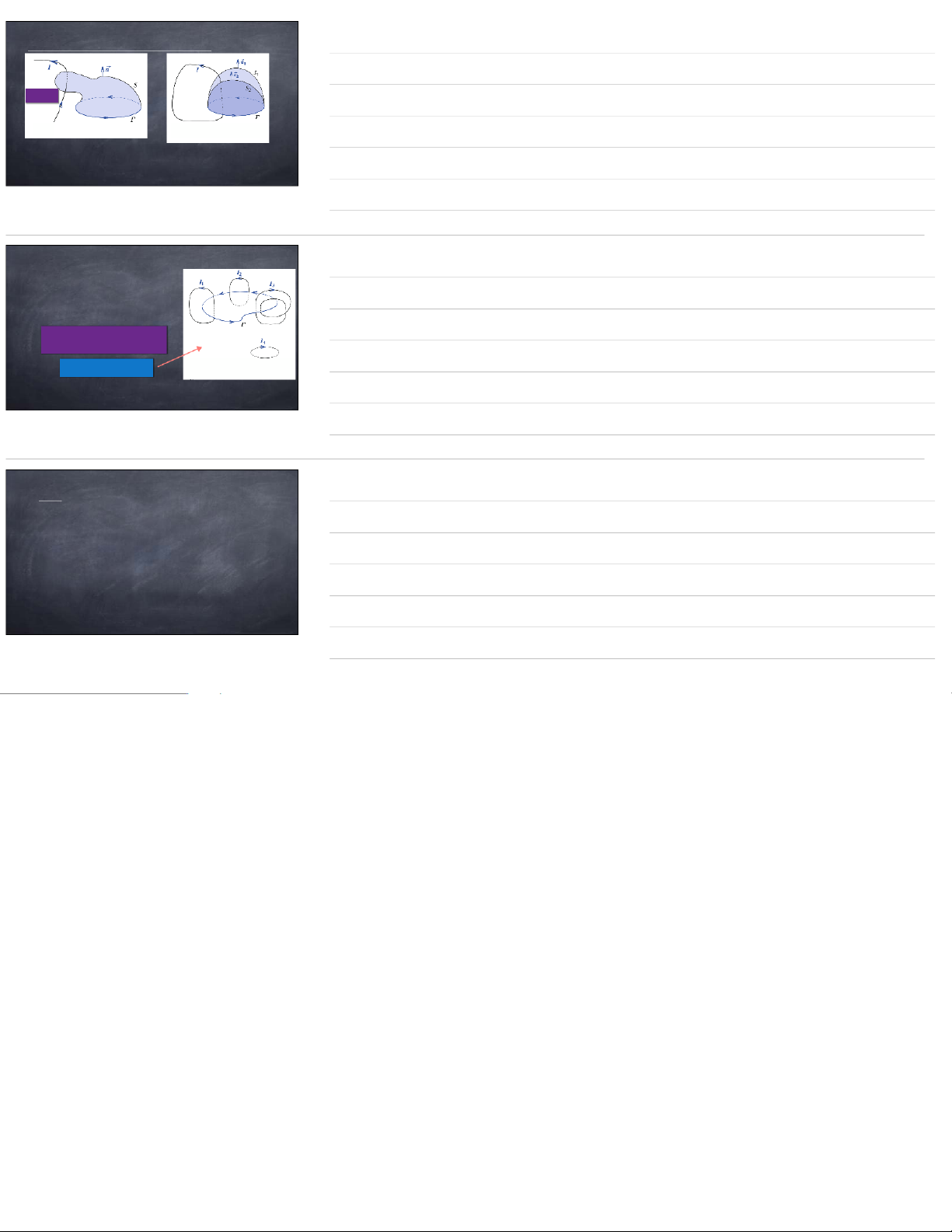
Dòng I đi qua mặt S tựa trên đường
Dòng I không đi qua mặt S
cong kín Γ theo chiều của n được
tựa trên đường cong kín Γ
định hướng bởi chiều của Γ CΓ=μ0.I CΓ= 0
7. 1 . L Ư U S Ố C Ủ A T Ừ T R Ư Ờ N G C Ủ A M Ộ T S Ợ I D Â Y V Ô 7 H ẠN
5. Quan hệ với dòng điện đi qua đường cong kín CΓ= 0 Dòng qua mặt tựa trên Γhai lần
Dòng qua hai mặt tựa trên Γ
➡Ở chế độ không phụ thuộc
thời gian, thông lượng của j là như nhau qua v S à 1 S2
7.2 . Đ Ị N H L Ý A M P È R E 8
Lưu số của trường từ tĩnh tạo ra B
bởi một tập hợp dòng trên một đường cong kín
Γ bằng tổng các dòng bị quấn bởi Γ nhân với μ:0 CΓ=∮Γ B.d M=μ0.∑I bị quấn
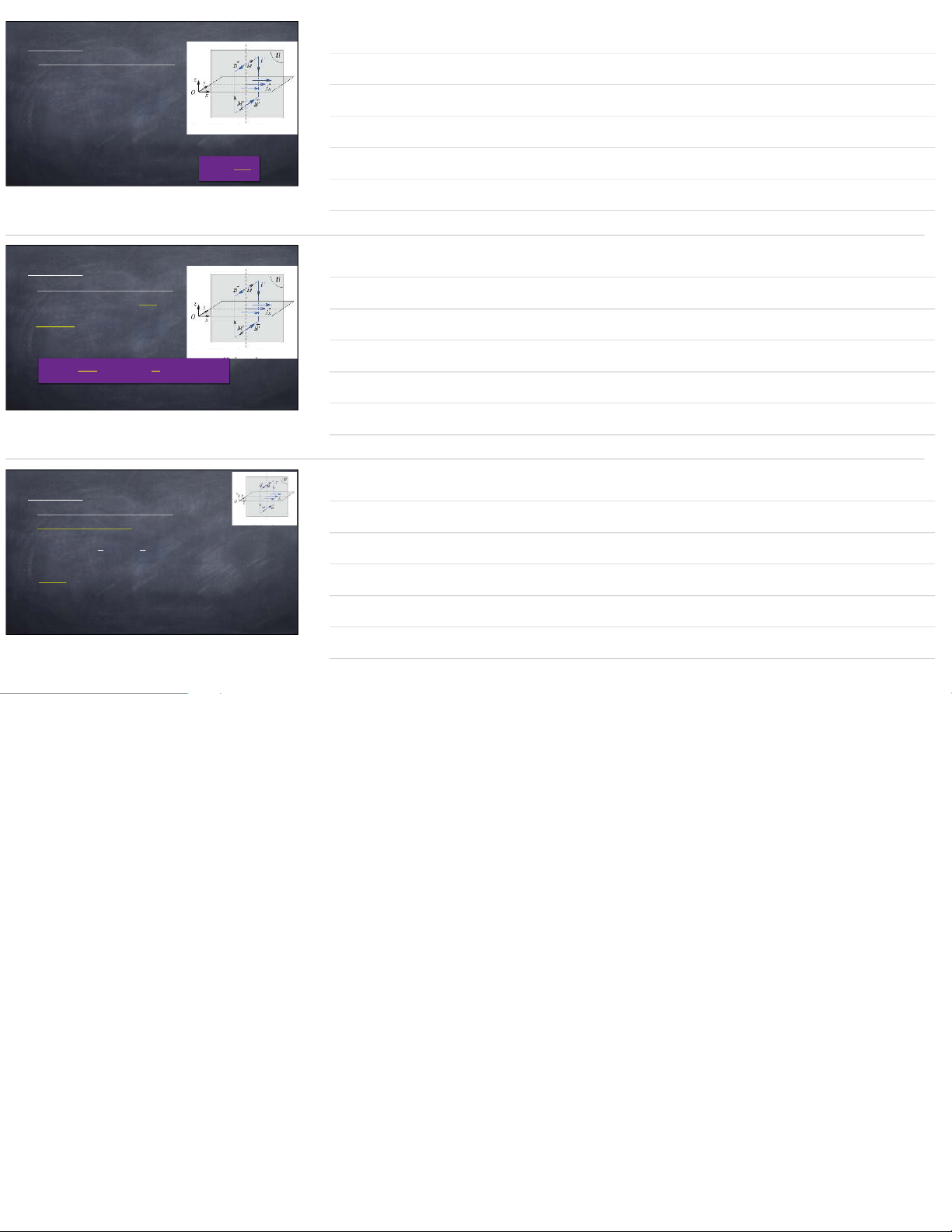
Lưu số của B trên đường cong kín Γ CΓ=μ0.(I1−I2+ 2I3)
chỉ phụ thuộc vào I1,I2 và I3
➡Lưu số không phụ thuộc gì vào I4
7.2 . Đ Ị N H L Ý A M P È R E 9 ✴Lưu ý
➡Định lý Ampère chỉ tuyệt đối có giá trị đối với trường từ tĩnh
➡Định lý Ampère không còn chính xác trong các trường hợp:
•Đường dòng bị đứt đoạn, gây ra sự tích tụ điện tích
•Các trường hợp ngoại lai: đường cong kín gặp m Γ ột mạch
hình sợi, hay 1 đường cong kín mà ta không thể tìm thấy
một cách đơn giản một mặt tựa trên nó
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 10 1. Nguyên tắc tính toán
Định lý Ampère cho phép xác định nhanh từ trường đối với các
phân bố dòng có tính đối xứng cao.
Sau khi xác định được hình dạng của trường nhờ các nhận xét
về tính đối xứng, sự áp dụng định lý cho một đường cong kín có
dạng hình học phù hợp với các tính đối xứng của bài toán cho
phép ta xác định biên độ của trường
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 11 2.Các bước thực hiện
(1) Nhận xét về tính đối xứng
(2) Chọn đường cong kín AMPÈRE
(3) Áp dụng định lý AMPÈRE
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 12 2.Các bước thực hiện
(1) Nhận xét về tính đối xứng
Nhờ vào các tính đối xứng của phân bố, ta phân tích để có được hình dạng của trường
•Sử dụng các mặt phẳng đối xứng hoặc phản đối xứng để xác định hướng của trường.
•Sử dụng tính bất biến với phép quay hoặc phép tịnh tiến để giảm
bớt sự phụ thuộc của thành phần của trường đối với các tọa độ
(tất nhiên, ta cần lựa chọn hệ tọa độ thích hợp với tính đối xứng của bài toán).
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 13 2.Các bước thực hiện
(1) Nhận xét về tính đối xứng
➡hình dạng của trường
(2) Chọn đường cong kín AMPÈRE
Chọn đường cong kín AMPÈRE thích hợp. Hình dạng đã lý luận
để thu được cho trường sẽ quyết định việc lựa chọn một đường
cong kín AMPÈRE cho phép tính lưu số của từ trường và các
dòng bị quấn một cách đơn giản.
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 14 2.Các bước thực hiện
(1) Nhận xét về tính đối xứng
➡hình dạng của trường
(2) Chọn đường cong kín AMPÈRE
➡Tính lưu số của từ trường
(3) Áp dụng định lý AMPÈRE được đơn giản
Áp dụng định lý AMPÈRE để hoàn thành sự xác định từ trường.
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 15 3.Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn
Bài toán 1: Xác định từ trường tạo bởi
một lớp dòng vô hạn, trùng với mặt phẳng với (xOy), jS=jS. ex Lời giải:
(1) Nhận xét về tính đối xứng Lớp phẳng vô hạn B(x,y,z)dxp(xOz) B= =B(x,y,z) . e =B(z) . y tt(Ox,Oy) (B′(−z)dxp(xOy) ey(1) =−B(z))( * )
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 16 3. Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn
(2) Chọn đường cong kín AMPÈRE CΓ=∮Γ
B.d M=B(z) . L+B(−z) . (−L) (*) = 2L.B(z) ( * * ) ∑I=−jS.L(***) Lớp phẳng vô hạn bị quấn (B′(−z)dxp(xOy) =−B(z))( * )
(3) Áp dụng định lý AMPÈRE ⟹B(z) = −μ C (**),(***) 0.jS Γ=∮Γ B.d M=μ0.∑I bị quấn 2(2)
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 17 3. Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn e ( ) = −μ B=B(z) . y(1) B z 0.jS 2(2)
Kết luận 1: Trường tạo bởi một lớp dòng
vô hạn, trùng với mặt phẳng (x v O ớ y)i, jS=jS. ex Lớp phẳng vô hạn B(1),(2) =−μ0.jS ey=μ0 2.sign(z) . 2.sign(z) . ( jS∧ ez)(3)
➡Từ trường có sự bất liên tục μ0. j Skh ∧ i đ e i z qua lớp phẳng
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 18 3. Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn Bài toán 2 (AD3 - p.149): Lớp phẳng vô hạn
1) Xác định trường tạo bởi một lớp phẳng vô hạn nằm giữa các mặt z= + e phẳng v z à= −e mật độ kh 2, ối đều j=j. ex 2
2) Hãy tìm lại trường hợp trước đây coi là giới hạn của trường hợp này? Lời giải:
(1) Nhận xét về tính đối xứng B= B(x,y,z) = B(z) . ey(1) (B′(−z) = −B(z))( * )
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 19 3. Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn Bài toán 2 (AD3 - p.149): Lớp phẳng vô hạn Lời giải: 1) Xác định B
(1) Nhận xét về tính đối xứng B= B(x,y,z) = B(z) . ey(1)
(2) Chọn đường cong kín AMPÈRE (B′(−z) = −B(z))( * ) C ( ) . L+B(−z) . (−L) Γ=∮Γ B.d M=B z (*) = 2L.B(z) ( * * ) −2.j.z.L si 0 < z∑I= 2 ( * * * ) −j.e.L si z >e bị quấn 2
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 20 3. Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn Bài toán 2 (AD3 - p.149): Lớp phẳng vô hạn Lời giải: 1) Xác định B
(1) Nhận xét về tính đối xứng B= B(x,y,z) = B(z) . ey(1)
(2) Chọn đường cong kín AMPÈRE −2.j.z.L si 0 < z2 CΓ= 2L.B(z) ( * * ) ∑I= (***) bị quấn −j.e.L si z >e
(3) Áp dụng định lý AMPÈRE 2 CΓ=∮Γ B.d M=μ0.∑I bị quấn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 21 3. Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn Bài toán 2 (AD3 - p.149): Lớp phẳng vô hạn 1) Xác định B
−2.j.z.L si 0 < zB= B(x,y,z) = B(z) . ey(1) ∑I= 2 ( * * * ) C −j.e.L si z >e Γ= 2L.B(z) ( * * ) bị quấn 2
CΓ=∮Γ B.d M=μ0.∑I(2) bị quấn −μ0.j.z. eysi 0≤|z|≤e
(1), (2), ( * * ), ( * * * ) ⟹ 2 B= (3) −μ0.j.e 2.sign(z) . eysi |z|≥e 2
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 22 3. Áp dụng tính:
A. Từ trường gây bởi lớp phẳng vô hạn Bài toán 2 (AD3 - p.149): Kết luận 2: e −μ ysi 0≤|z|≤e 0.j.z. 1) Xác định B 2 B= (2) −μ0.j.e e 2.sign(z) . ysi |z|≥e 2
2) Tìm lại trường hợp mặt phẳng vô hạn có jS=jS. ex Mặt phẳng vô hạn: (2) B=−μ e ⇒ 0.jS 2.sign(z) . y=μ0 2.sign(z) . ( jS∧ e e→0 z) ⇒jS=j.e
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 23 3. Áp dụng tính:
B. Từ trường của phân bố có tính đối xứng trục: hình xuyến
Bài toán: Xác định trường tạo bởi N
vòng dây quấn trên một hình xuyến và
có dòng cường độ I chạy qua?
Hình xuyến có tiết diện bất kỳ
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 24 3. Áp dụng tính:
B. Từ trường của phân bố có tính đối xứng trục: hình xuyến
Bài toán: Xác định trường tạo bởi N
vòng dây quấn trên một hình xuyến và
có dòng cường độ I chạy qua? Lời giải:
(1) Nhận xét về tính đối xứng
B= B(r,θ,z)dxp(Π)=B(r,θ,z) . eθ
Mặt phẳng đối xứng của phân Pdxp(Oxy) bố dòng =B(r,z) . eθ(1)
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 25 3. Áp dụng tính:
B. Từ trường của phân bố có tính đối xứng trục: hình xuyến Bài toán: Lời giải:
(1) Nhận xét về tính đối xứng B=B(r,z) . eθ(1)
(2) Chọn đường cong kín AMPÈRE: (O;r) CΓ=∮Γ B.d M(1)= 2πr.B(r,z) ( * )
Chọn đường cong kín AMPÈRE ∑I={N.I si Γ≡Γ1 ( * * ) bị quấn 0si Γ≡Γ2
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 26 3. Áp dụng tính:
B. Từ trường của phân bố có tính đối xứng trục: hình xuyến Bài toán: Lời giải:
(1) Nhận xét về tính đối xứng B=B(r,z) . eθ(1)
(2) Chọn đường cong kín AMPÈRE: (O;r) CΓ=∮Γ B.d M(1)= 2πr.B(r,z) ( * )
Chọn đường cong kín AMPÈRE
(3) Áp dụng định lý AMPÈRE ∑I={N.I si Γ≡Γ1 ( * * ) bị quấn 0si Γ≡Γ2 CΓ=∮Γ B.d M=μ0.∑I bị quấn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 27 3. Áp dụng tính:
B. Từ trường của phân bố có tính đối xứng trục: hình xuyến Bài toán: Kết luận
Từ trường gây bởi N vòng dây quấn trên một
hình xuyến và có dòng cường độ I chạy qua: Bint =μ0.N.I
đối với các điểm nằm 2πr. eθ B= trong hình xuyến Bext = 0
đối với trường bên ngoài hình xuyến
Chọn đường cong kín AMPÈRE
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 28 3. Áp dụng tính:
C. Từ trường của phân bố dòng song song có dạng hình trụ
Bài toán 1: Xác định từ trường tạo bởi hình
trụ vô hạn có trục là trục c(ó O ti z ế ),t diện
tròn bán kính R, có một dòng cường độ tổng
hợp I chạy song song với trục ( v Oớ z i) ,mật độ khối đều j=j. ez
Lời giải: (1) Nhận xét về tính đối xứng B= B(r,θ,z)dxp(Π) =B(r,θ,z) . eθ tt(Oz) =B(r) . eθ(1) Hình trụ vô hạn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 29 3. Áp dụng tính:
C. Từ trường của phân bố dòng song song có dạng hình trụ Bài toán 1: Lời giải:
(1) Nhận xét về tính đối xứng B=B(r) . eθ(1) B
(2) Chọn đường cong kín AMPÈRE: (O;r) O CΓ=∮Γ B.d M(1)= 2πr.B(r) ( * ) Γ ∑I=j.πr2=I.r2 R2si 0 < r( * * ) j=I bị quấn j.πR2=I si r >R πR2
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 30 3. Áp dụng tính:
C. Từ trường của phân bố dòng song song có dạng hình trụ Bài toán 1: Lời giải: B=B(r) . eθ(1) CΓ=∮Γ B.d M(1)= 2πr.B(r) ( * ) B ∑I=j.πr O 2=I.r2 R2si 0 < r( * * ) bị quấn Γ j.πR2=I si r >R
(3) Áp dụng định lý AMPÈRE j=I CΓ=∮Γ πR2 B.d M=μ0.∑I(2) bị quấn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 31 3. Áp dụng tính: B O Γ
C. Từ trường của phân bố dòng song song có dạng hình trụ Bài toán 1: Lời giải: j=I πR2 B=B(r) . eθ(1) CΓ=∮Γ B.d M(1)= 2πr.B(r) ( * ) ∑I=j.πr2=I.r2 CΓ=∮Γ B.d M=μ0.∑I(2) R2si 0 < rbị quấn ( * * ) bị quấn j.πR2=I si r >R Bint =(μ0.j.r 2). eθ=(μ0.I.r2πR2). eθsi r ≤R (1),(2),(**),(***) ⟹ B= (3)
− Bext =(μ0.j.R2 2r). eθ=(μ0.I2πr). eθsi r ≥R
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 32 3. Áp dụng tính:
C. Từ trường của phân bố dòng song song có dạng hình trụ
Hình trụ vô hạn có mật độ dòng đều j=j .gây r e a z từ trường Bint =(μ0.j.r 2). eθ=(μ0.I.r2πR2). eθsi r ≤R B=
Bext =(μ0.j.R2 2r). eθ=(μ0.I2πr). eθsi r ≥R Sự biến thiên của B(r)
➡Trường của phân bố khối hữu hạn này là liên tục tại r = R
➡Ở bên ngoài hình trụ, trường đồng nhất với trường tạo ra bởi 1 sợi dây
thẳng vô hạn đặt theo trục (Oz) và có cường độ dòng điện I chạy qua
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 33 3. Áp dụng tính:
C. Từ trường của phân bố dòng song song có dạng hình trụ
Bài toán 2 - AD4 (p.151): Một lỗ hổng hình trụ, trục
có tiết diện tròn bán kính (Oz′),
R’, đã được khoét ra ở trong một hình trụ dẫn trục (Oz b
), án kính R. Ở bên ngoài lỗ
hổng, trụ dẫn có một dòng điện không đổi
mật độ dòng đều chạjy = jq . ua.ez
Hãy xác định từ trường tại mọi điểm của lỗ?
Hình trụ vô hạn được khoét ra ở trong
một hình trụ dẫn vô hạn trục (Oz)
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 34 3. Áp dụng tính:
D. Từ trường của phân bố dòng hình vành có dạng hình trụ:
ống dây thẳng dài vô hạn
Bài toán: Xác định trường tại một điểm ở
bên trong một ống dây “vô hạn” có tiết diện
tròn, có dòng điện I chạy qua và có n vòng
dây trên một đơn vị dài? Biết từ trường
trên trục của ống dây là Baxe =μ0.n.I. ez Ống dây vô hạn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 35 3. Áp dụng tính:
D. Từ trường của phân bố dòng hình vành có dạng hình trụ:
ống dây thẳng dài vô hạn
(1) Nhận xét về tính đối xứng
B= B(r,θ,z)dxp(Π)=B(r,θ,z) . ez tt(Oz) =B(r) . ez(1)
(2) Chọn đường cong kín AMPÈRE: • ở Γ b 1 ê ≡ n A 1tr Bo1n Cg 1 ố D1ng dây Baxe =μ0.n.I. ez CΓ1=∮Γ1
B.d M=A1B1.Baxe −A1B1.B(r) ( * ) Ống dây vô hạn ∑I=−jS.L( * * ) bị quấn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 36 3. Áp dụng tính:
D. Từ trường của phân bố dòng hình vành có dạng hình trụ:
ống dây thẳng dài vô hạn B=B(r) . eθ(1)
(2) Chọn đường cong kín AMPÈRE: • ở b Γ1ê ≡n At1ro B n 1 g C1 ố D n 1 g dây CΓ1=∮Γ1
B.d M=A1B1.Baxe −A1B1.B(r) (2) ∑I= 0 (3) bị quấn Baxe =μ0.n.I. ez • đi Γ q 2 u ≡ a A 2bở B2 i C2D2 vòng dây n.A2B2 Ống dây vô hạn CΓ2=∮Γ2
B.d M=A2B2.Baxe −A2B2.B(r) (4) ∑I=n.A2B2.I(5) bị quấn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 37 3. Áp dụng tính:
D. Từ trường của phân bố dòng hình vành có dạng hình trụ:
ống dây thẳng dài vô hạn B=B(r) . eθ(1)
CΓ=∮Γ1 B.d M=A1B1.Baxe −A1B1.B(r) (2) ∑I= 0 (3) bị quấn
CΓ=∮Γ2 B.d M=A2B2.Baxe −A2B2.B(r) (4) Baxe =μ0.n.I. ez ∑I=n.A2B2.I(5) bị quấn Ống dây vô hạn
(3) Áp dụng định lý AMPÈRE CΓ=∮Γ B.d M=μ0.∑I(6) bị quấn
3.3. ÁP DỤNG ĐỊNH LÝ AMPÈRE 38 3. Áp dụng tính:
D. Từ trường của phân bố dòng hình vành có dạng hình trụ:
ống dây thẳng dài vô hạn Kết luận:
• Từ trường ở bên trong ống dây vô hạn Bint = Baxe =μ0.n.I. ez(7)
• Từ trường ở bên ngoài ống dây vô hạn Bext = 0 (8) Ống dây vô hạn ➡Ống dây vô hạn 1 hì
⇔ nh xuyến có bán kính trung bình và tha →y ∞ n=N 2πr
3.4. ĐIỀU KIỆN BIÊN CỦA TỪ TRƯỜNG 39
1. Sự liên tục của thành phần pháp tuyến của từ trường
Các thành phần pháp tuyến của từ trường
là liên tục khi đi qua một lớp dòng ngăn cách hai môi trường: B2⊥= B1⊥
➡Xem chứng minh tại trang 126 - sách Điện từ học 1
3.4. ĐIỀU KIỆN BIÊN CỦA TỪ TRƯỜNG 40
2.Sự gián đoạn của thành phần tiếp tuyến của từ trường
Khi đi qua một lớp có một dòng trên bề mặt
chạy qua, mật độ thành phần tiếp tuyến của
từ trường chịu một sự bất liên tục (gián đoạn) hữu hạn: B2// − B1// =μ0. jS∧ n12
với n12 là véc tơ đơn vị trực giao với mặt, hướng từ môi trường s ( a 1)ng môi trường (2)
➡Xem chứng minh tại trang 146 - sách Điện từ học 1 41 42