Chương 7: Kiểm Định Phi Tham Số trong Phân Tích Hồi Quy môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

HỒI QUY VÀ TƯƠNG QUAN
à các PP toán học thường được vận dụng để nghiên
ứu các quan hệ thống kê. Phân tích tương quan Phân tích hồi qui giữa các biến
Ước lượng (dự báo) giá trị Mục đích
Đo cường độ mối quan hệ
của các biến trên cơ sở giá
đối xứng (ryx = rxy )Biến phụ thuộc là ĐLNN
trị cho trước của các biến khác ỹ thuật
Các biến là ĐLNN và có tính Biến độc lập là xác định Không có tính đối xứng 1 PHÂN TÍCH HỒI QUY
ghiên cứu mối quan hệ giữa một biến gọi là biến phụ
huộc (biến được giải thích (Y)) với một hoặc một số
iến khác được gọi là biến độc lập (biến giải thích (X))
Các nội dung cơ bản của phân tích hồi qui
1. Xác định mức độ thay đổi của Y tương ứng với sự thay đổi của X
2. Kiểm định bản chất của sự phụ thuộc
3. Ước lượng (dự báo) giá trị biến Y tương ứng với giá trị đã biết của X 2
HÀM HỒI QUI TỔNG THỂ (PRF)
Là hàm hồi qui phản ánh mối quan hệ thực tế
giữa các biến trên phạm vi tổng thể nghiên cứu.
Ví dụ có một tổng thể gồm 30 HGĐ, thu thập dữ
liệu về chi tiêu TD (Y) và thu nhập (X) trong một ngày, kết quả như sau: X50 70 90 110 130 150 170 190 35 41 45 71 91 99 113 133 40 49 56 90 100 115 131 145 Y 45 63 85 94 102 131 146 147 67 88 107 149 76 151 HÀM HỒI QUI TỔNG THỂ
Với một cột của bảng chính là phân phối xác suất
của chi tiêu với thu nhập cho trước (P(Y/Xi) 50 70 90 110 130 150 170 190 1/3 1/4 1/5 1/3 1/4 1/3 1/3 1/5 1/3 1/4 1/5 1/3 1/4 1/3 1/3 1/5 Y/Xi) 1/3 1/4 1/5 1/3 1/4 1/3 1/3 1/5 1/4 1/5 1/4 1/5 1/5 1/5 Y/Xi) 40 55 70 85 100 115 130 145 HÀM HỒI QUI TỔNG THỂ
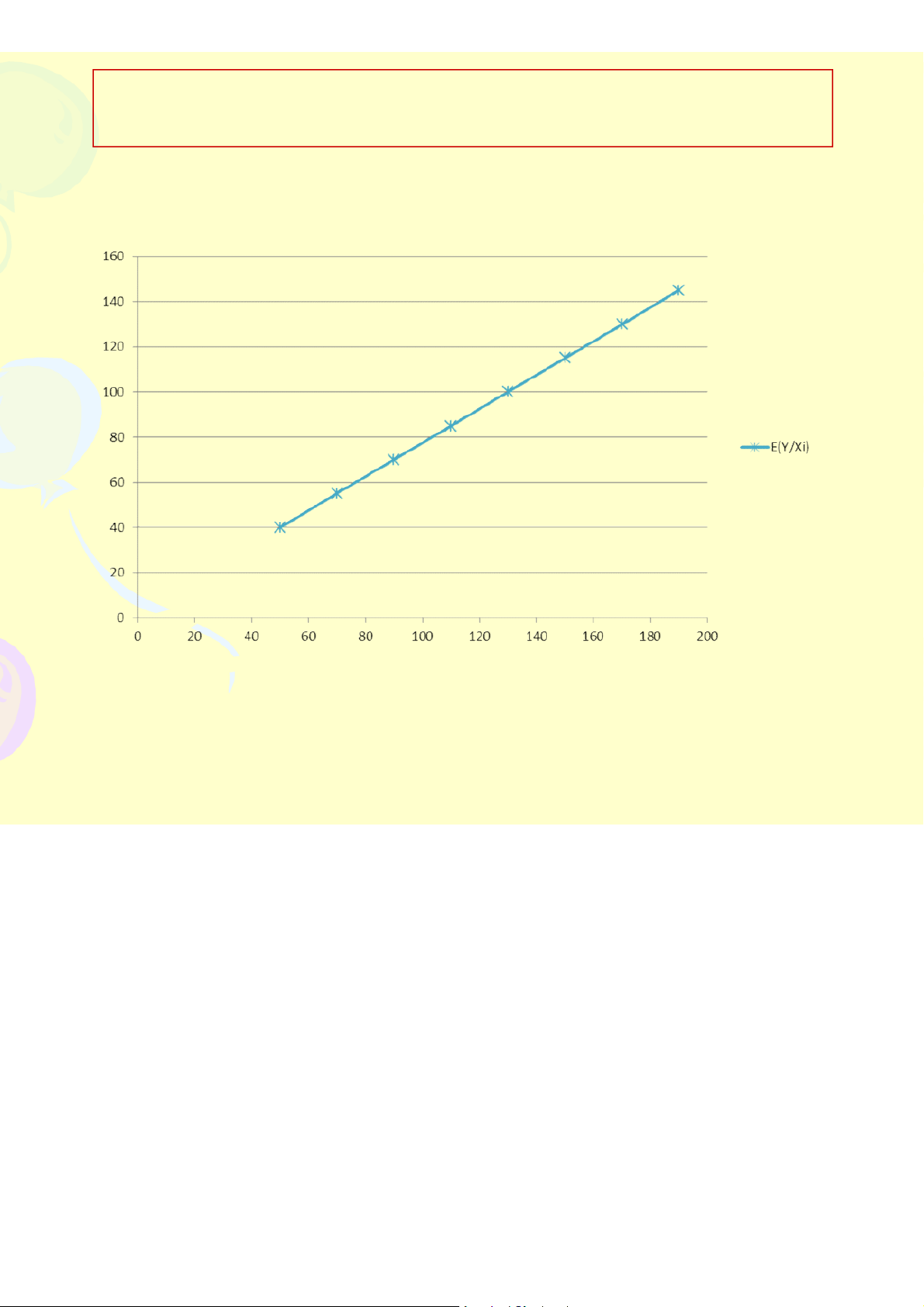
E(Y/Xi) là hàm theo Xi, được mô tả: E(Y/Xi) = f(Xi)
E(Y/Xi) = f(Xi): được gọi là hàm hồi qui tổng thể.
(Cho biết giá trị trung bình của Y thay đổi như thế nào theo X)
Dạng hàm f(Xi)chưa biết, có thể tuyến tính hay phi tuyến
7.1.1. Mô hình tuyến tính (linear)
Giả sử f(Xi) là hàm tuyến tính, ta có: E(Y| X) X   i 1 2 i
β1, β2: Các tham số của hàm hồi qui
β1:hệ số chặn (tham số tự do, không phụ thuộc bất kỳ biến nào)
β2:hệ số góc (phản ánh mức độ ảnh hưởng của biến
X đối với biến Y) (Khi X tăng lên 1 đơn vị thì giá trị
trung bình của Y tăng β2đơn vị) 6
7.1.1. Mô hình tuyến tính (linear)
Vì E(Y/Xi) là giá trị trung bình của Y với X đã biết
nên giá trị cá biệt Yixoay quanh E(Y/Xi).
Kí hiệu: ui= Yi - E(Y/Xi), ta có: Yi = E(Y/Xi)+ ui Hay: Y   X  u i 1 2 i i Trong đó:
Yi: các giá trị cá biệt (giá trị ngẫu nhiên của Y)
ui: nhiễu (sai lệch ngẫu nhiên) (+,-) (phản ánh ảnh
hưởng của các yếu tố ngoài mô hình (yếu tố ngẫu
nhiên) đối với sự biến động của Y 7 HÀM HỒI QUI TỔNG THỂ
Với dữ liệu ở bảng trên, sai số ngẫu nhiên được xác định như sau: X 50 70 90 110 130 150 170 190 -5 -14 -25 -14 -9 -16 -17 -12 0 -6 -14 5 0 0 1 0 5 8 15 9 2 16 16 2 12 18 7 4 6 6 ui/Xi)00000000
E(ui/Xi) =0 (trung bình ảnh hưởng của các yếu tố ngẫu nhi biến phụ thuộc bằng 0) HÀM HỒI QUI MẪU (SRF)
Là hàm hồi qui được xây dựng trên cơ sở dữ liệu
mẫu. Tương ứng với hàm hồi qui tổng thể, hàm hồi qui mẫu có dạng: ˆi X 1 2 i X i e 1 2 i i Trong đó: Y ˆ
: Ước lượng của E(Y|Xi) i ˆ 1  ˆ 2 ,
: Ước lượng của β1, β2 ei: Ước lượng của ui
7.1.1. Mô hình tuyến tính (linear)
Xác định các hệ số hàm hồi quy mẫu:
Giả sử có n cặp quan sát (Xi,Yi): Xi3 5 1 4 2 … 6 Yi0,6 1,0 0,2 1,4 0,8 … 1,8
Phương pháp bình phương bé nhất thường được sử n n 2 dụng, sao cho: (  Y Yˆ ˆ ˆ )2) Y (  (   X  Min i i i 1 2 i i1  i 1 Lấy đạo hàm riêng theo  ˆ 1
ˆ,  2 để tìm cực tiểu, ta được công thức: ˆ XY  X Y   ˆ   ˆ và 1  Y 2 X (  2) 2 2 X  X 10
7.1.1. Mô hình tuyến tính (linear)
Xác định các hệ số hàm hồi quy mẫu:
Ví dụ: Có dữ liệu về quy mô hộ Xivà chi cho thực phẩm Yicủa 6 hộ. Hộ XiYiXiYiXi2 13 0,6 1,8 9,0 ˆ XY  X Y  25 1,0 5,0 25,0 (  2) 2 2 X  X 31 0,2 0,2 1,0 44 1,4 5,6 16,0 1 , 4 7 5 , 3 * 9 , 0 7 52 0,8 1,6 4,0  , 0 269 151 , 7 5 , 3 2 66 1,8 10,8 36,0 TB 3,5 0,97 4,17 15,17 ˆ ˆ  1  2 9 , 0 7 , 0 269 * 5 , 3 0 , 0 27 Hà , m hồiY q , uy 0 027 mẫ u: 0 ˆi X 269  i 11
7.1.1. Mô hình tuyến tính (linear)
Các giả thiết của mô hình
(1) Không xét đến tính ngẫu nhiên của biến độc lập trong mô hình.
(2) Đường hồi quy tổng thể đi qua trung bình của biến
phụ thuộc tại tất cả các Xi: E(Ui|Xi)=0
(3) Phương sai của các yếu tố nhiễu Ui bằng nhau tại các Xikhác nhau.
(4) Không có tương quan giữa các yếu tố nhiễu Uitại các Xikhác nhau.
(5) Không có tương quan giữa các yếu tố nhiễu Uivà các Xi.
(6) Yếu tố nhiễu có phân phối chuẩn 12 Hệ số xác định
Để xem xét mức độ phù hợp của mô hình với dữ
liệu quan sát, sử dụng hệ số xác định 2 (r ) Ta có: n n n 2 2 2 ˆ ˆ (Y Y  )  (Y Y  ) (Y Y)  i  i i i i1 i 1 i 1 TSS = ESS + RSS
SS (Total Sum of Square): phản ánh toàn bộ biến động của
ến phụ thuộc do ảnh hưởng của tất cả các nguyên nhân
SS (Explained Sum of Square): phản ánh biến động của
ến phụ thuộc được giải thích bởi mô hình (do biến độc lập ong mô hình gây ra)
SS (Residual Sum of Square): phản ánh biến động của biến
hụ thuộc chưa được giải thích bởi mô hình (do các yếu tố gẫu nhiên gây ra) ESS RSS
Hệ số xác định: 2r 2 Hay: r 1  13 TSS TSS Hệ số xác định ESS Công thức: 2 r  TSS Ý nghĩa:
Hệ số xác định đo độ phù hợp của SRF. Nó cho biết mô hình
ã giải thích được bao nhiêu % biến động của biến phụ
huộc là do ảnh hưởng bởi biến độc lập trong MH. ính chất: 0 ≤ r2≤ 1
r2= 1 : Đường hồi quy mẫu phù hợp hoàn hảo
r2= 0 : Giữa X và Y không có mối quan hệ
r2càng gần 1 hàm hồi quy mẫu càng phù hợp 14 Ví dụ: Xét dữ liệu Hộ XiYiyi2 Y ˆ2 yˆ i i 13 0,6 0,83 0,13 0,02 Trong đó: 25 1,0 1,37 0,00 0,16  i y ˆ i ˆ Y Y 31 0,2 0,30 0,59 0,45 44 1,4 1,10 0,19 0,02  i y  i Y Y 52 0,8 0,56 0,03 0,16 66 1,8 1,64 0,69 0,45 Tổng 21 5,8 5,8 1,63 1,26 TB 3,5 0,97 0,97 0,27 0,21 n2 ˆy  i ESS 1, 26 Hệ số xác định: 2i 1 r 0,  77     n2 TSS 1, 63 y  i 15 i 1 
iểm định sự phù hợp của mô hình hồi qu
tổng thể (kiểm định t) + Giả thuyết: Ho: β2= 0 H1: β2≠ 0 ˆ  2 ˆ 2 t   với: Se ˆ ( ) 2 n
+ Tiêu chuẩn kiểm định: Se ˆ ( ) 2 n x2i Trong đó: 2 i1 e  i 2 i 1 i i x  i X X    ˆ   n  2 + Tra bảng Tn-2, α/2 + So sánh, kết luận:
| t | >= Tn-2, α/2 : Bác bỏ Ho, mô hình phù hợp.
| t | < Tn-2, α/2 : Chưa đủ cơ sở bác bỏ Ho. 16 Ví dụ: Xét dữ liệu Hộ XiYixi2 Y ˆ2 e i i Trong đó: 13 0,6 0,83 0,25 0,05  i x  i X X 25 1,0 1,37 2,25 0,14 ˆ 31 0,2 0,30 6,25 0,01 e Y i Y i i   44 1,4 1,10 0,25 0,09 n2 52 0,8 0,56 2,25 0,06 e0,37  i 66 1,8 1,64 6,25 0,03 2i 1 ˆ      0 ổng 21 5,8 5,8 17,5 0,37 n  2 6 2 TB 3,5 0,97 0,97 2,92 - ˆ2  0 , 0 9 ˆ   Se( 2  ) 0 , 0 73 n 2 175 , xi 17 i 1 
7.1.1. Mô hình tuyến tính (linear) + Giả thuyết: Ho: β2= 0 H1: β2≠ 0 ˆ  0,269 + Tiêu chuẩn kiểm  định:  2 t  , 3 68 ˆ Se( ) 0,073 2
+ Tra bảng: Tn-2, α/2 = T4;0,025= 2,77
+ So sánh: | t |>Tn-2, α/2 : Bác bỏ Ho, mô hình phù hợ 18
iểm định sự phù hợp của mô hình hồi qu
tổng thể (kiểm định F) + Giả thuyết: Ho: r2= 0 H1: r2≠ 0 ESS
+ Tiêu chuẩn kiểm định: 1 F  RSS n  2 + Tra bảng F1,n-2, α + So sánh, kết luận:
F >= F1,n-2, α : Bác bỏ Ho, mô hình phù hợp.
F < F1,n-2, α : Chưa đủ cơ sở bác bỏ Ho. 19 dụ: Xét dữ liệu Hộ XiYi Y ˆ2 yˆ 2 e Trong đó: i i i 13 0,6 0,83 0,02 0,05  i y ˆ i ˆ Y Y 25 1,0 1,37 0,16 0,14 ˆ 31 0,2 0,30 0,45 0,01 e Y i Y i i   44 1,4 1,10 0,02 0,09 n , 1 ˆ 26 52 0,8 0,56 0,16 0,06 ESS   y2  i i1 66 1,8 1,64 0,45 0,03 n ổng 21 5,8 5,8 1,26 0,37 RSS   e 2i 0,3 TB 3,5 0,97 0,97 0,21 - i 1 ESS , 1 26 1 F   13,6 RSS 0,37 n  2 6  2 20