






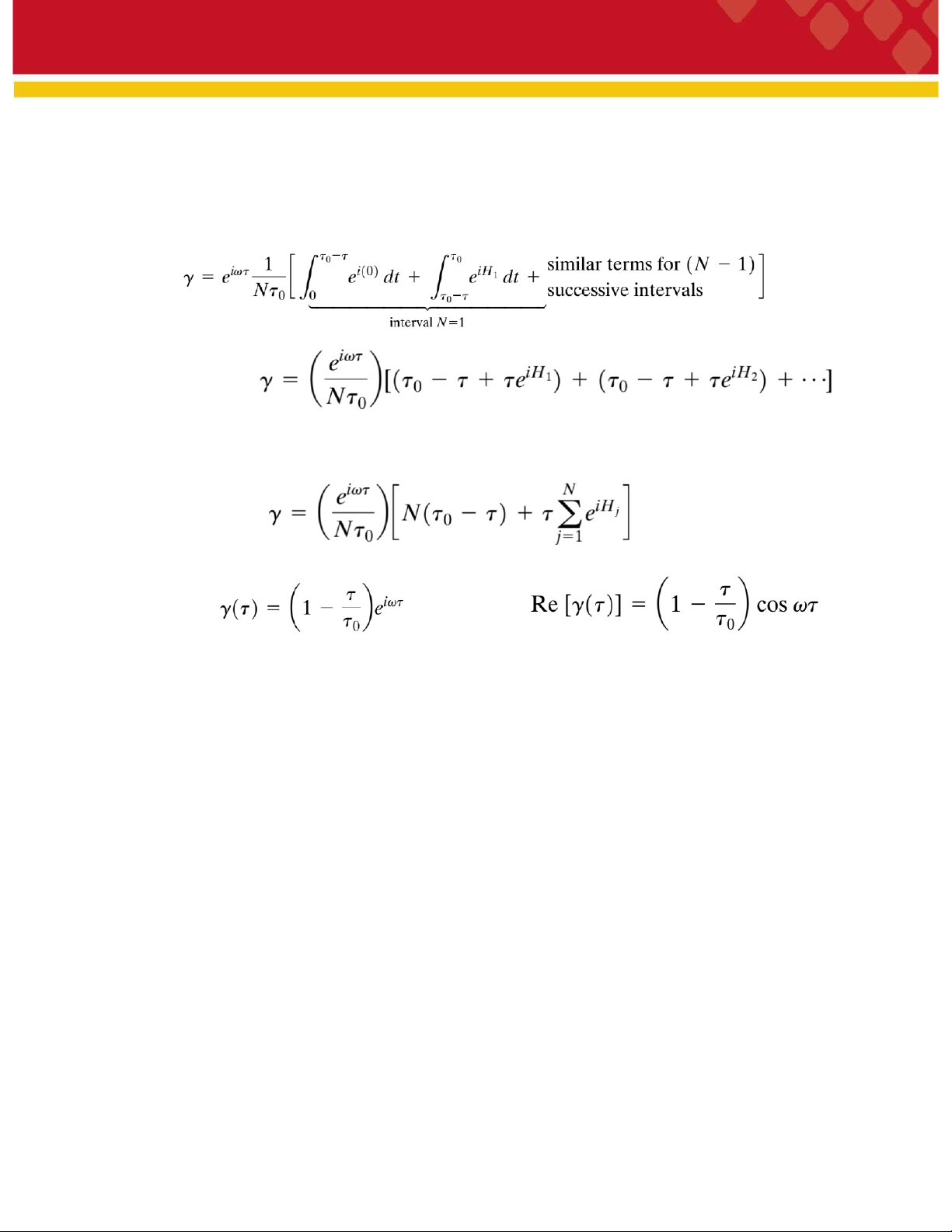




Preview text:
7.1. Phân tích Fourier và sóng điều hòa hữu hạn
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên
7.3. Tính kết hợp không gian
7.1. Phân tích Fourier và sóng điều hòa hữu hạn
- Khi một số sóng điều hòa có tần số bằng nhau, có
thể có pha và biên độ khác nhau tổ hợp với nhau thì
sóng tổ hợp cũng là sóng điều hòa cùng tần số với các sóng thành phần.
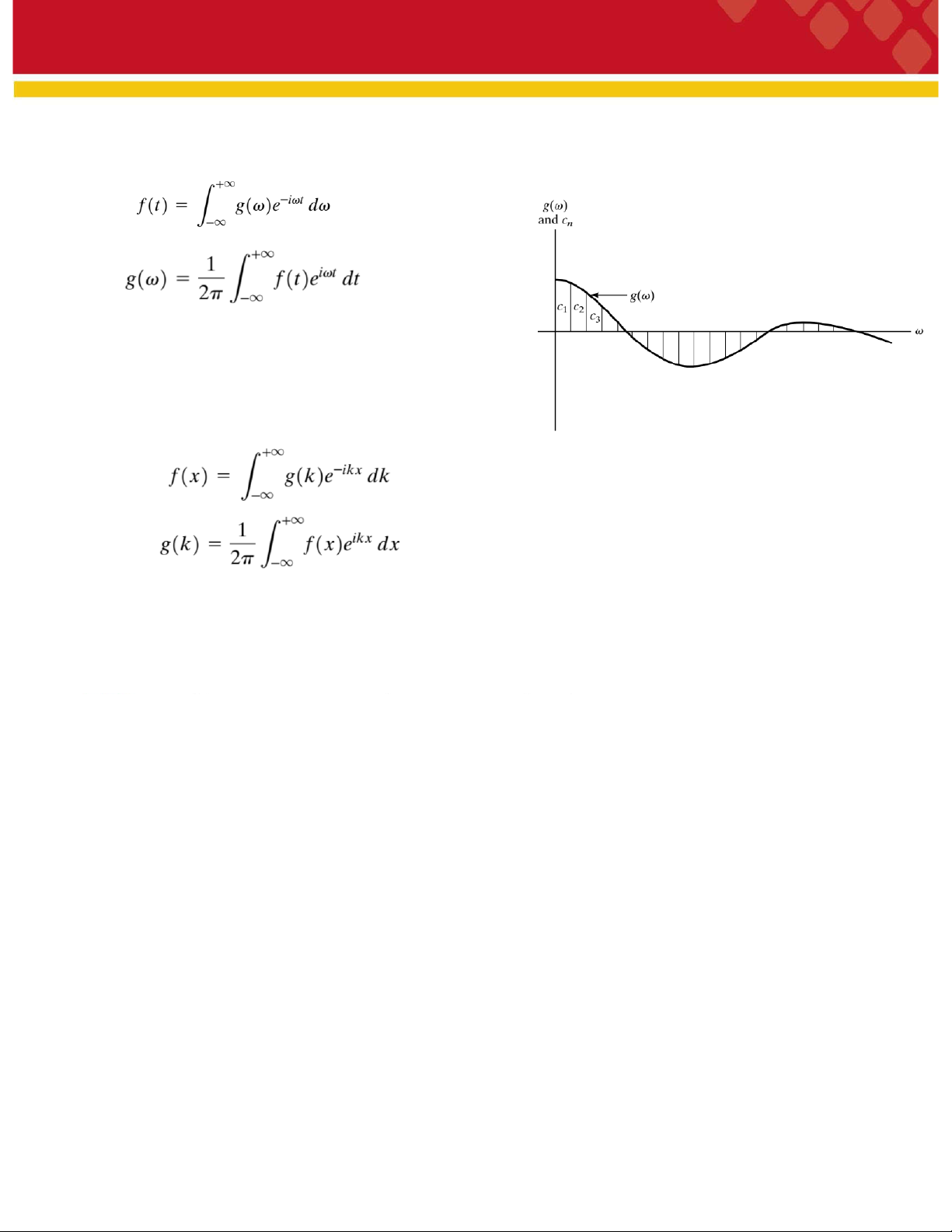
- Nếu các sóng thành phần không cùng tần số thì sóng
tổ hợp là tuần hoàn nhưng không điều hòa, giả sử có
một sóng tùy ý như hình. Quá trình phân tách một
dạng sóng nhất định thành các sóng điều hòa gọi là phân tích Fourier.
- Để phân tách một dạng dạng sóng thành các sóng điều hòa, ta sử dụng nguyên lý Dirichlet:
+ Giả sử f(t) là hàm hữu hạn tuần hoàn với chu kỳ T, với một số hữu hạn các cực đại, cực tiểu hoặc các
điểm gián đoạn trong một chu kỳ, ta có chuỗi Fourier sẽ hội tụ về f(t) tại mọi điểm trong đó f(t) liên tục và
về điểm trung bình của các giới hạn bên phải và bên trái tại mỗi điểm trong đó f(t) không liên tục.
+ Trong đó m là các số nguyên, amvà bmlà biên độ của các sóng điều hòa thành phần, tần số là mω
+ Nếu nhân cả hai vế của phương trình với dt và tích phân trong một chu kỳ T ta có:
Chương 7: Tính kết hợp của sóng
7.1. Phân tích Fourier và sóng điều hòa hữu hạn
- Nếu nhân cả hai vế của phương trình với cosnωt.dt với n là một số nguyên thì tích phân trong một chu
kỳ T ta tìm được hệ số an:
- Nếu nhân cả hai vế của phương trình với sinnωt.dt với n là một số nguyên thì tích phân trong một chu
kỳ T ta tìm được hệ số bn:
Như vậy một khi hàm f(t) được xác định thì các hệ số a0, an, bncó thể tính được và sự khai triển hoàn tất.
Chương 7: Tính kết hợp của sóng
7.1. Phân tích Fourier và sóng điều hòa hữu hạn
- Giả sử có sóng xung vuông như hình, hàm f(t) có dạng:
- Vì f(t)= f(-t) nên f(t) là hàm chẵn do đó hệ số bn= 0 do hàm sin là hàm lẻ, ta có
- Vậy ta có thể khai triển chuỗi:
- Thành dạng tường minh hơn:
- Sử dụng công thức Euler Trong đó:
Chương 7: Tính kết hợp của sóng
7.1. Phân tích Fourier và sóng điều hòa hữu hạn
Trong trường hợp hàm không có chu kỳ, ta có thể xem chu kỳ T tiến tới vô cực, khi đó có thể mở rông khai triển:
Khi hàm sóng được biễu diễn bằng hàm không gian f(x) với
chu kỳ L , khai triển Fourier khi đó cũng có công thức tương
tự bằng cách thay biến số x cho t, chu kỳ T bằng chu kỳ L, tần
số thời gian ω= 2π/T thay bằng tần số không gian k= 2π/L
Chương 7: Tính kết hợp của sóng
7.1. Phân tích Fourier và sóng điều hòa hữu hạn
Đoạn sóng điều hòa hữu hạn
Phổ của một sóng hình sin vô hạn thực chất là một thành phần trong phân tích Fourier tương ứng với tần
số thực tế của sóng. Sóng hình sin vô hạn không có điểm đầu và kết thúc như vậy là đơn giản nhất về
phương diện toán học tuy nhiên trong thực tế sóng chỉ xuất hiện trong một khoảng thời gian nào đó (đoạn
sóng). Phân tích Fourier của đoạn sóng như vậy có thể xem là không có chu kỳ, không liên tục và như
vậy sẽ khá phức tạp. Sử dụng phép biến đổi Fourier có thể bổ sung cho tính liên tục của đoạn sóng. Để
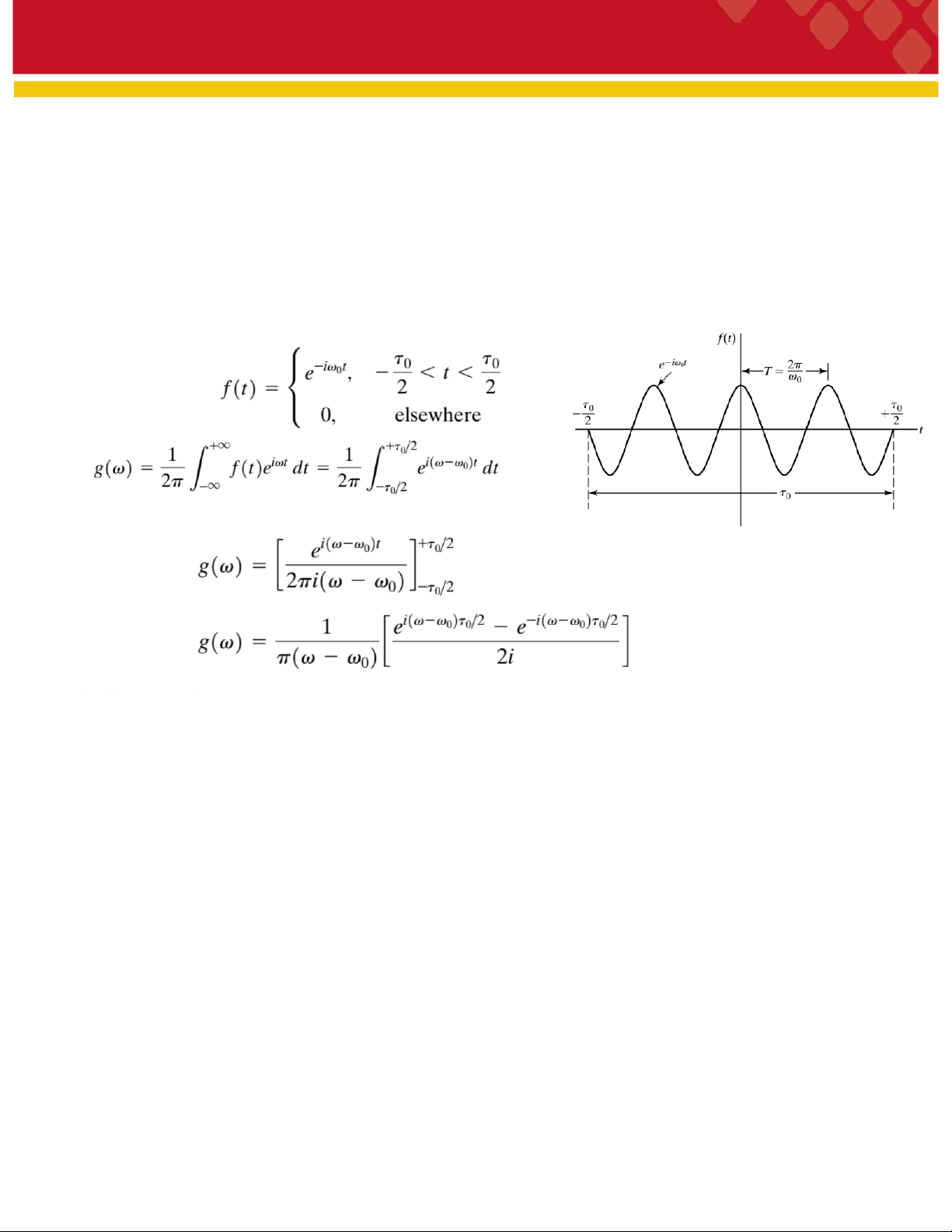
đơn giản ta xem đoạn sóng là đối xứng như hình. Chuỗi sóng có thời gian tồn tại τovà tần số ωo, có thể được biểu diễn bằng Tích phân ta có:
Chương 7: Tính kết hợp của sóng
7.1. Phân tích Fourier và sóng điều hòa hữu hạn
Đoạn sóng điều hòa hữu hạn Sử dụng công thức Euler Đặt: Ta có:
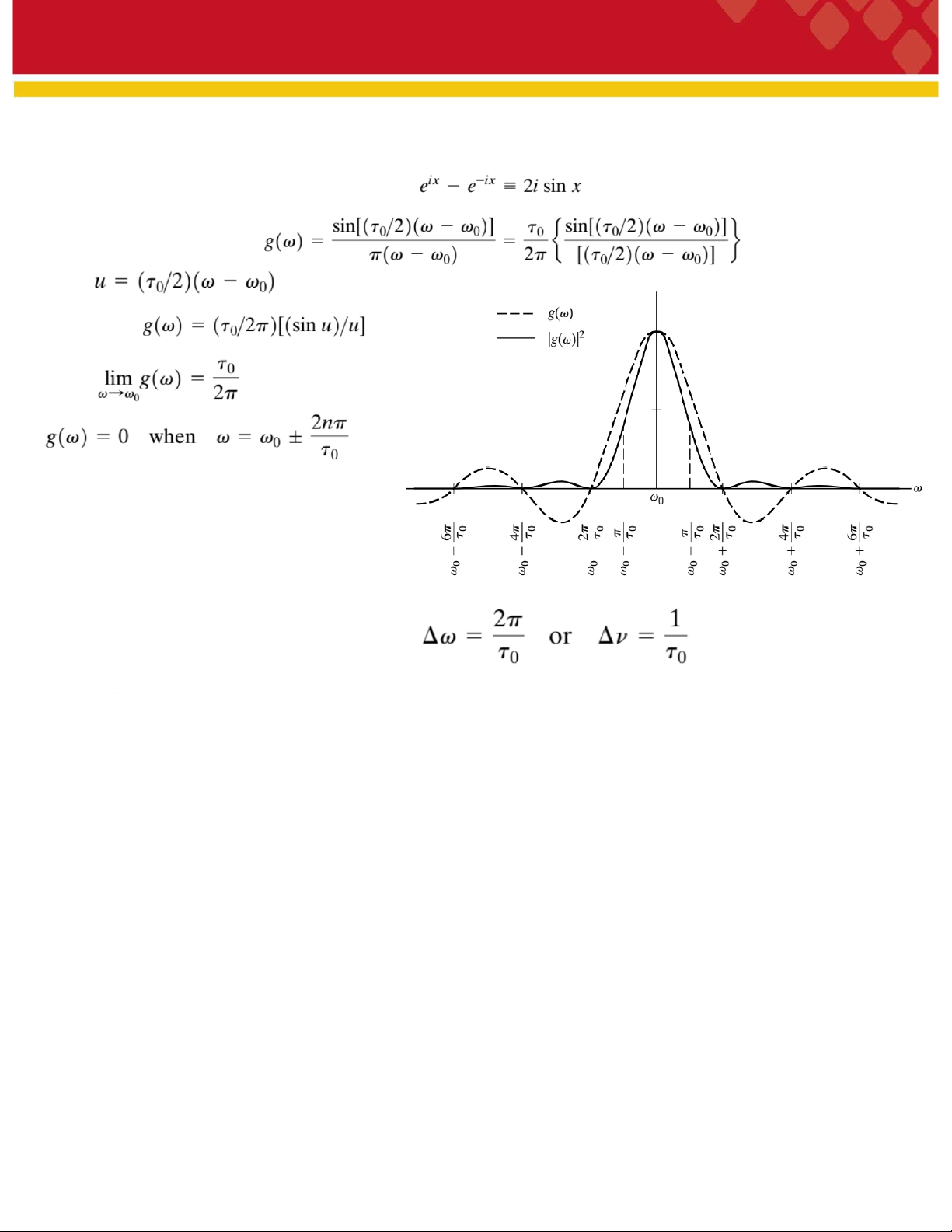
|g(ω)|2 là cường độ sóng
Dạng của hàm g(ω) phụ thuộc vào độ dài
đoạn sóng τ0như Hình bên (τocàng nhỏ thì
cực đại trung tâm càng rộng và ngược lại).
Ta lấy khoảng bán độ rộng 2π/τ0để đặc
trưng cho khoảng tác dụng của đoạn sóng.
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên
Trong thực tế, ta không thể có nguồn đơn sắc tuyết đối. Do sự phát xạ ngẫu nhiên, ta chỉ được
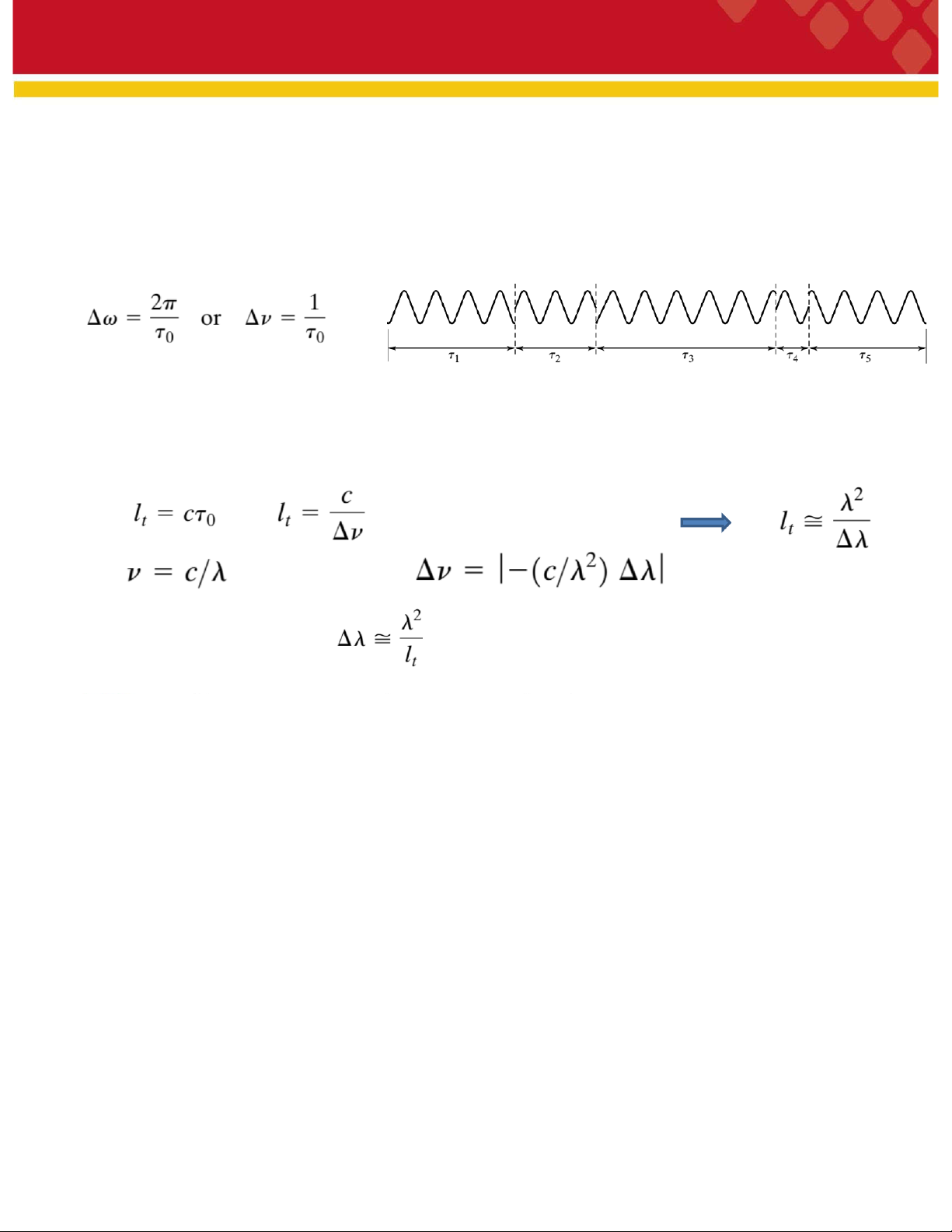
một chuỗi các đoạn sóng đơn sắc nối tiếp nhau với độ lệch pha một cách ngẫu nhiên như hình.
Các đoạn sóng đơn sắc trong những khoảng thời gian τikhác nhau, giá trị trung bình τ0(thời
gian kết hợp) của chúng có thể đặc trưng cho một nguồn cho trước về tính kết hợp từ việc phân tích phương trình:
Độ rộng tự nhiên của phổ tỷ lệ nghịch với thời gian kết hợp τ0. Thời gian kết hợp càng dài,
nguồn càng đơn sắc. Khoảng kết hợp ltcủa đoạn sóng khi đó có thể được xem là khoảng kết hợp của xung: Ta có Đạo hàm ta được
Độ rộng phổ tự nhiên là
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên
Ánh sáng trắng nhìn thấy có phổ từ khoảng, 400 – 700nm có Δλ ~ 300nm, bước sóng trung
bình là 550nm Khi đó ta có khoảng kết hợp
Nguồn sáng trắng như vậy khó tạo ra sự giao thoa do khoảng kết hợp ngắn Các nguồn quang
phổ vạch, laser có phổ hẹp cho khoảng kết hợp lớn hơn. Chẳng hạn vạch xanh 546 nm của hơi
Hg có bề rộng phổ Δλ ~ 0,025 nm cho khoảng kết hợp khoang 1,2cm. Laser CO2thông thường
có Δλ ~ 10-5 nm cho ta khoảng kết hợp cỡ 11km.
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên Kết hợp một phần
- Khi hiệu số pha của các nguồn không đổi ta có các nguồn đó là
kết hợp. Trong thực tế điều kiện hiệu số pha này chỉ đáp ứng được
một phần, khi đó các nguồn này được gọi là kết hợp một phần.
Giả sử ta có hai nguồn S1và S2như hình vẽ cùng xuất phát từ
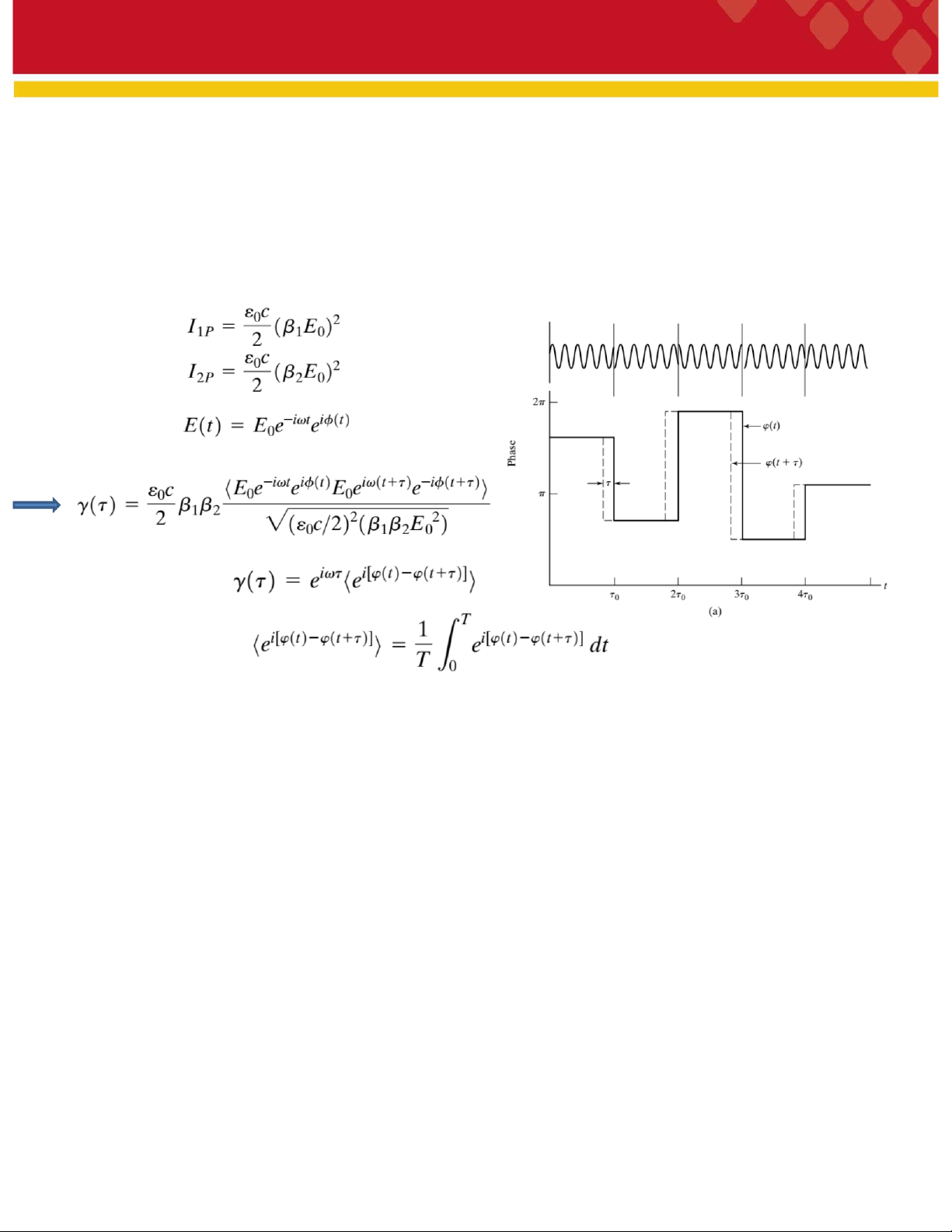
nguồn S nhưng đi theo các quãng đường khác nhau và gặp và giao thoa tại P. - Hàm sóng tại nguồn S: Trong đó
Hàm ɸ (t) liên quan đến tính đơn sắc của nguồn
- Hàm sóng tại P của hai nguồn là:
Trong đó: β1, β2 là các hệ số do sự phân chia thành hai nguồn, do sự thay đổi biên độ phản
xạ truyền qua khi lan truyền từ các nguồn tới P. T1, T2là thời gian truyền theo quang lộ 1 và 2.
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên Kết hợp một phần
- Mật độ công suất bức xạ tại P
Như trong mục trước đây, I1p và I2p là mật độ công suất bức xạ của hai sóng S1và S2, thành
phần còn lại do giao thoa, thành phần giao thoa có thể làm tăng hay giảm cường độ sóng
tổng hợp tùy theo sự tương quan pha giữa 2 sóng . Để đặc trưng cho mối quan hệ đó ta đưa
vào hàm tương quan được xác
- Độ lớn của của mật độ công suất bức xạ tại P phụ thuộc vào hàm tương quan. Ta có
hàm tương quan chuẩn hóa:
- Mật độ công suất bức xạ tại P viết theo hàm tương quan chuẩn hóa.
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên Kết hợp một phần
- Hàm tương quan chuẩn hóa γ(τ) đóng vai trò quan trong trong tính giao thoa, là hàm của vị
trí (P) và τ. Ta dự đoán khi τ > τ0(thời gian kết hợp) sự giao thoa sẽ giảm. Giả sử ta có một
đoàn sóng như hình, đoàn sóng gồm các đoạn sóng điều hòa với các khoảng τ0có pha không liên tục. Ta có - Rút gọn ta được: - Với:
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên Kết hợp một phần
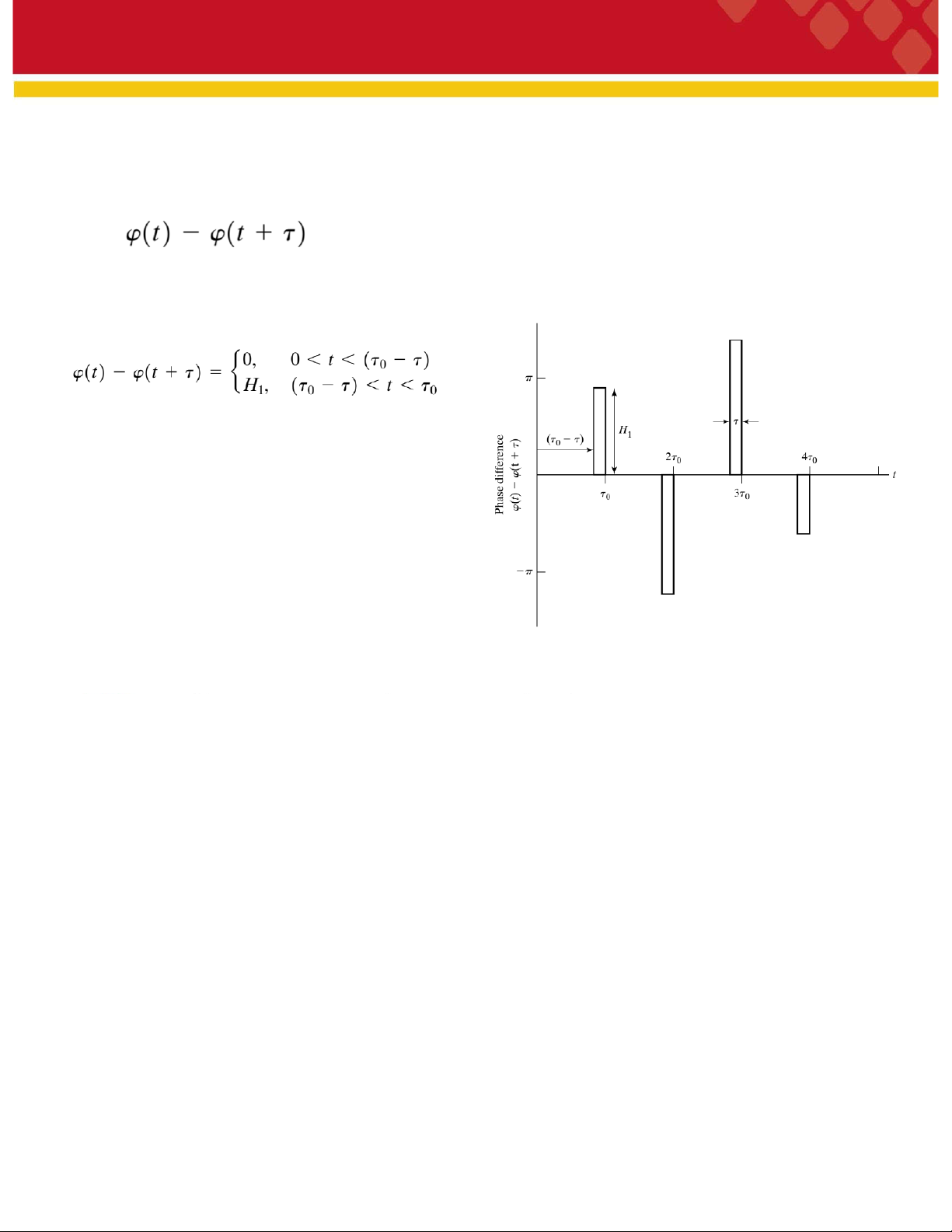
Trong đó T là khoảng thời gian đủ dài. Hàm số
trong số mũ được minh họa trong hình và được coi là một chuỗi
các xung hình chữ nhật cách đều nhau với cường độ ngẫu nhiên giữa -2π và + 2π.
Trong đoạn đầu tiên τ0, hàm xung có thể được thể hiện bằng biểu thức:
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên
Trong những đoạn sóng tiếp theo, biểu thức có dạng tương tự nhau ngọại trừ giá trị H1. Hàm
tương quan với một số lượng lớn các đoạn N là: Lấy tích phân ta có:
Kết hợp các số hạng đầu tiên của mỗi đoạn và tính tổng phần còn lại ta được:
Nếu số N đủ lớn, do Hjlà ngẫu nhiên nên tổng của các eiHj = 0 khi đó ta có Hàm tương quan.
Hàm tương quan có giá trị cực đại bằng 1 khi τ = 0 và cực tiểu bằng 0 khi τ = τ0
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên
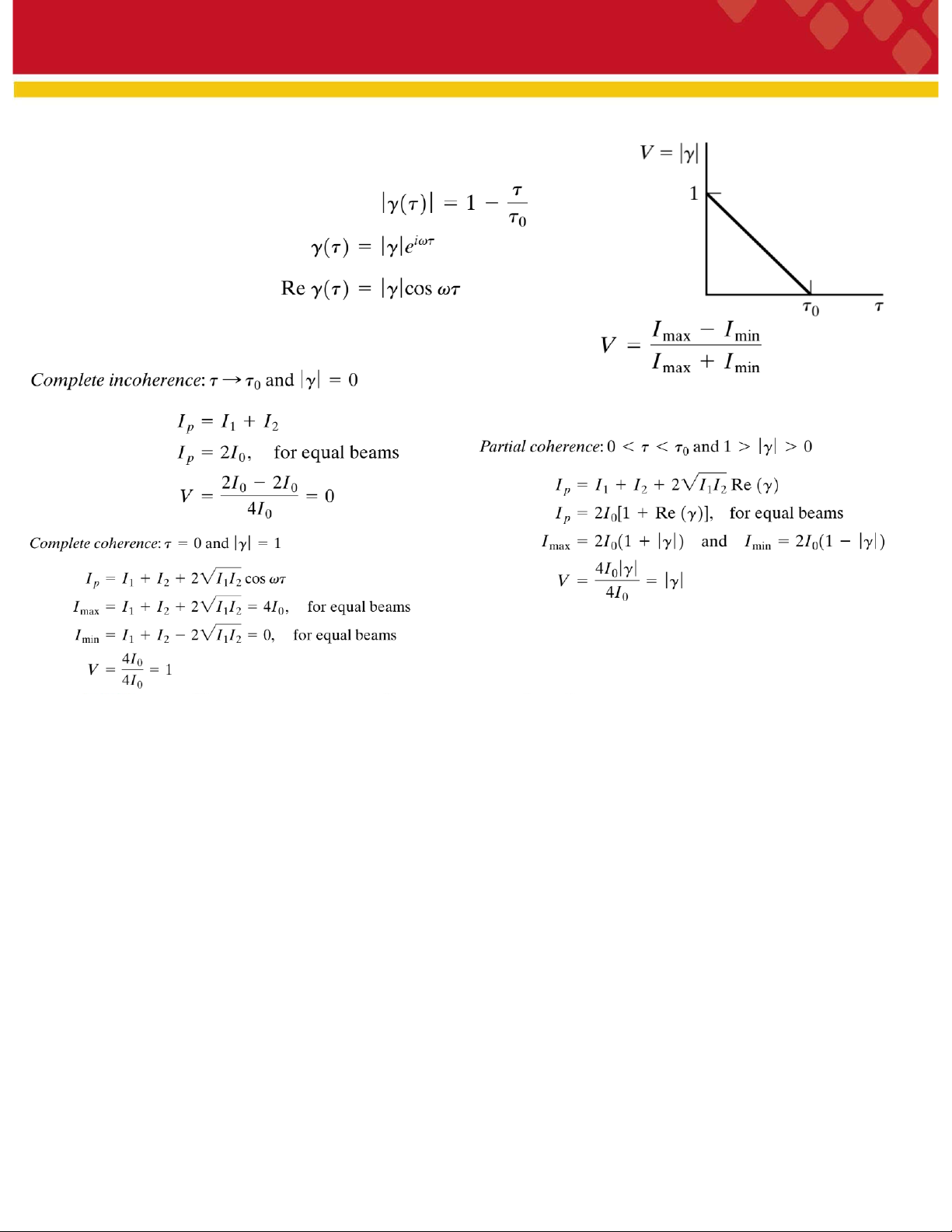
Độ lớn của hàm tương quan là
Liên quan đến độ sáng hay độ tương phản của vân giao thoa
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên
Chương 7: Tính kết hợp của sóng
7.2. Kết hợp thời gian và độ rộng phổ tự nhiên
Chương 7: Tính kết hợp của sóng 7.3. Kết hợp không gian
- Trong phần trên ta khảo sát sự kết hợp thời gian liên quan đến sự tương quan pha giữa các
điểm khác biệt về mặt thời gian của cùng một nguồn bức xạ dọc theo phương lan truyền của nó.
Do vậy, sự kết hợp thời gian còn được gọi là kết hợp dọc. Tính kết hợp thời gian liên quan
đến bước sóng của nguồn, hay nói cách khác vào bản chất của nguồn phát.
- Ngoài ra tính kết hợp còn bị ảnh hưởng của kích thước nguồn,
do sự khác biệt về vị trí trên nguồn phát kéo theo đến sự tương
quan pha. Tính kết hợp liên quan đến vị trí như vậy được
gọi là kết hợp không gian, hay là kết hợp ngang.
- Để hiểu sâu hơn về kết hợp ngang ta phân tích hiện tượng
giao thoa của các khe hẹp trên mặt truyền sóng (hai khe
Young, Michelson, cách tử). Sự kết hợp không gian của các
nguồn thứ cấp A và B được đảm bảo khi nguồn sơ cấp S là
nguồn điểm. Hình ảnh nhiễu xạ quan sát được tại P1xét về
phương diện kết hợp không gian hay thời gian đều liên quan
đến quang lộ SAP1và SBP1.
Kết hợp thời gian liên quan đến hiệu quang lộ:
Nếu Δ << lt(khoảng kết hợp), ta có hình ảnh rõ nét giao thoa tại P1.
Nếu Δ ≥ lt, hình ảnh giao thoa kém hoặc không xuất hiện.
Chương 7: Tính kết hợp của sóng 7.3. Kết hợp không gian
Trên thực tế, nguồn S không phải là nguồn điểm, mà là một
nguồn rộng, như vậy các sóng thứ cấp xuất phát từ A và B do
nhiều nguồn điểm sơ cấp từ S tạo ra. Đối với một nguồn thông
thường (không phải laser) ánh sáng từ các điểm khác nhau (trên
cả dải sóng) kết hợp ít hoặc không kết hợp. Khi đó, sự kết hợp
không gian của ánh sáng từ các khe hẹp phụ thuộc vào sự gần
đúng nguồn điểm của nguồn sơ cấp về cả kích thước và đặc trưng kết hợp.
Khảo sát 2 nguồn điểm có cùng bước sóng λđặt cách nhau một
khoảng s và được quan sát tại P (cách hai nguồn khoảng r,góc
trông là θ) như Hình vẽ. Khoảng có độ kết hợp không gian cao ls thỏa mãn điều kiện:
Từ khoảng kết hợp không gian lsvà khoảng kết hợp ltcó thể kết luận là trong trường sóng
của một nguồn thực sẽ tồn tại một vùng không gian mà tại đó ánh sáng là kết hợp. Vùng
này có khoảng kết hợp không gian là lsvà khoảng kết hợp thời gian ltvà chiếm thể tích ls 2 lt
xung quanh điểm quan sát P. Hiện tượng giao thoa sẽ quan sát được trong miền thể tích này.
Chương 7: Tính kết hợp của sóng 7.3. Kết hợp không gian
Độ rộng kết hợp không gian
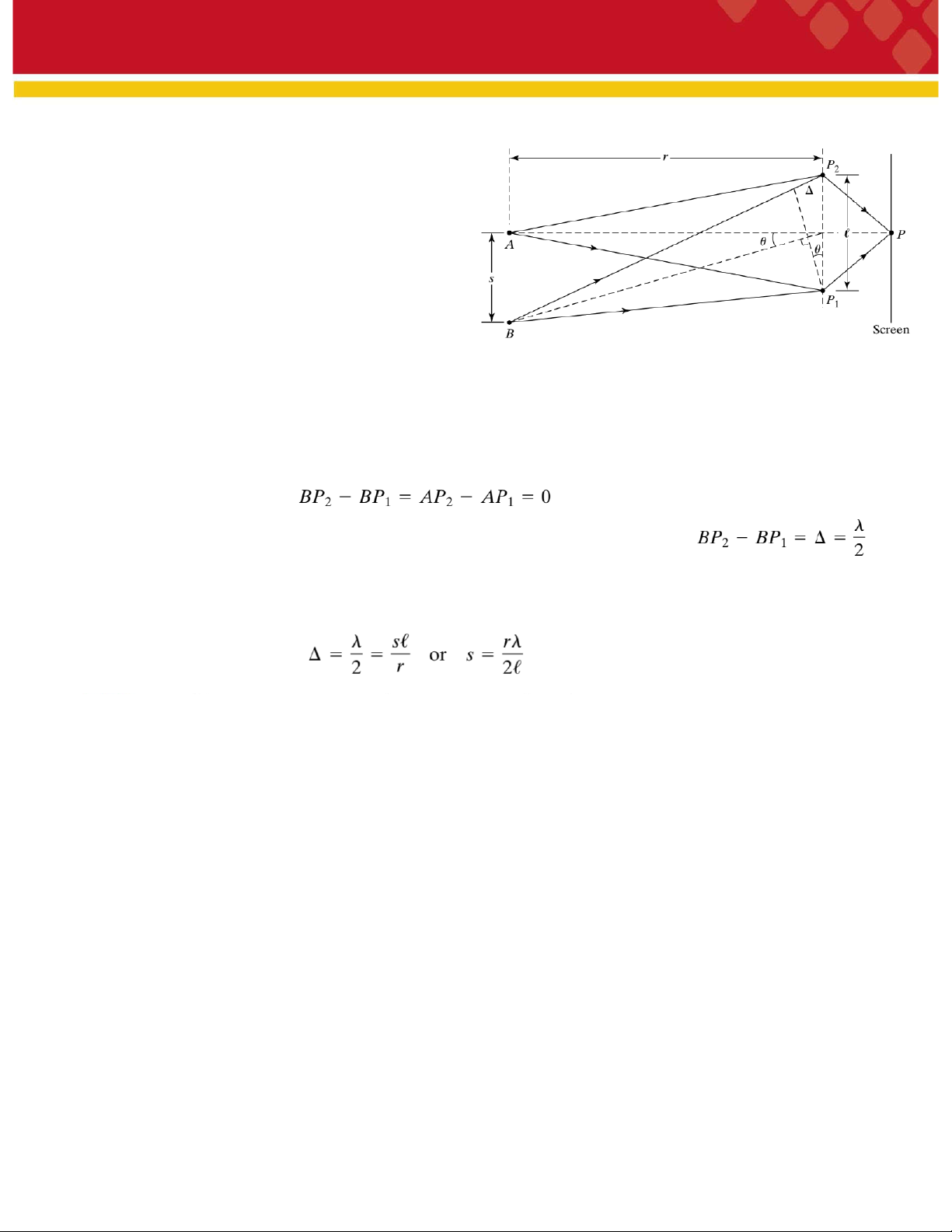
Xét sự kết hợp không gian tại điểm P1và P2(~hai
khe) trong trường sóng của nguồn chuẩn kết hơp có
kích thước lớn được đặc trưng bằng hai điểm biên
nguồn là A và B (Hình vẽ bên).
Giả thiết từ P1và P2sóng thứ cấp lan truyền đến P,
khi đó mỗi nguồn điểm A và B đều tạo ra hình ảnh
giao thoa riêng trên P. Nếu hai hệ giao thoa này
trùng nhau ta thu được hình giao thoa rõ nét (kết hợp cao).
Khi hai hệ giao thoa lệch nhau hình giao thoa tổ hợp khó quan sát hoặc biến mất (không kết hợp).
Giả sử hai điểm A và B là trùng nhau (s = 0) và để đơn giản nằm trên đường trung trực của P1 và P2
sự giao thoa trên màn tương tự như giao thoa của hai khe Young và cực đại tại điểm P đặt tại trung
tâm thỏa mãn điều kiện:
Giả sử điểm B dịch xuống một khoảng s thì hình ảnh giao thoa mở dần đến khi
Tại đó hệ giao thoa do điểm B tạo ra sẽ có cực tiểu tại P Tổng hợp hai hệ giao
thoa (A và B) tại P sẽ biến mất. Từ Hình vẽ bên ta có và θ ~ s/r từ đó suy ra:




