Chương 8: Hồi quy và tương quan trong thống kê ứng dụng môn Thống kê ứng dụng | Trường Đại học Bách Khoa Hà Nội

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI VIỆN KINH TẾ VÀ QUẢN LÝ
EM3230 THỐNG KÊ ỨNG DỤNG TRONG KINH DOANH CHƯƠNG 8
HỒI QUY VÀ TƯƠNG QUAN Nội dung chính
8.1 Làm quen với hồi quy (bài giảng video)
8.2 Mô hình hồi quy tuyến tính đơn biến (bài giảng video)
8.3 Tương quan tuyến tính
8.4 Tương quan giữa các biến định tính
8.5 Hồi quy tuyến tính đa biến (bài giảng video)
8.6 Hồi quy với biến định tính (bài giảng video) 8.7 Hồi quy phi tuyến
8.8 Thực hành phân tích dữ liệu bằng hồi quy tuyến tính với Excel/SPSS
Mục tiêu của chương
Sau khi học xong chương này, người học sẽ:
▪ Nói được phạm vi ứng dụng của phương pháp phân tích hồi quy và tương quan
▪ Biết cách thực hiện một phân tích hồi quy dựa trên dữ liệu mẫu
▪ Nói được những điều kiện và giả định cần thiết khi phân tích hồi quy
▪ Biết được cách tính và ý nghĩa của hệ số tương quan Pearson và hệ số tương quan hạng Spearman
▪ Hiểu và áp dụng được phần mềm Excel/ SPSS cho hồi qui tuyến tính
8.1 Làm quen với hồi quy
8.1 Làm quen với hồi quy
▪ Các sự vật hiện tượng luôn tồn tại trong mối liên hệ tác động qua lại lẫn nhau.
▪ Có những mối liên hệ chặt chẽ, ảnh hưởng quyết định lẫn nhau ▪ Có những mối liên
hệ mang tính ngẫu nhiên, không chặt chẽ.
▪ Nhu cầu quản lý cần thiết phải lượng hóa được mối quan hệ giữa các hiện tượng đó với nhau.
▪ Tương quan giúp đưa ra con số lượng hóa mối liên hệ
▪ Hồi quy giúp đưa ra các mô hình, hàm số về những mối liên hệ đó.
8.1 Làm quen với hồi quy
8.1.1 Khái niệm hồi quy
▪ Regression, Regression to mediority: quy các điểm DL quan sát về một đường lý
thuyết đã biết phương trình để dễ dàng tính toán/ dự báo (nội suy hay ngoại suy)
▪ Phân tích hồi quy là nghiên cứu thống kê về mối liên hệ giữa một hoặc nhiều biến
đầu vào (biến độc lập) và một biến đầu ra (biến phụ thuộc) dưới dạng phương trình
nhằm ước lượng/ dự đoán giá trị trung bình của biến phụ thuộc. ▪ Ví dụ:
▪ Marketing: Doanh số = f(Sản phẩm, Giá bán, Kênh phân phối, Xúc tiến)
▪ Chất lượng SP = f(NVL, thiết bị, con người, quy trình, môi trường)
▪ Động lực làm việc = f(Thù lao, đặc điểm công việc, môi trường làm việc)
8.1 Làm quen với hồi quy
8.1.2 Phân biệt liên hệ thống kê và liên hệ hàm số ▪
Liên hệ hàm số: là liên hệ hết sức chặt chẽ, sự thay đổi của hiện tượng
này hoàn toàn quyết định sự thay đổi của hiện tượng có liên quan theo một tỷ lệ chặt chẽ. ▪ Y= f(x) : 1 X → có 1!Y ▪
Ví dụ mối liên hệ giữa định mức NVL cho 1 sản phẩm với tổng chi phí về
nguyên vật liệu cho kỳ phân tích. ▪
Liên hệ tương quan/ liên hệ thống kê (đối tượng nghiên cứu của phân tích hồi quy):
là liên hệ không hoàn toàn chặt chẽ, sự thay đổi của nhân tố này không chắc đã gây
ra sự thay đổi tương ứng của nhân tố kia. 1 X có thể có nhiều Y
8.1 Làm quen với hồi quy
8.1.3 Một số quy ước về ký hiệu và tên gọi
✓ Hồi quy đơn biến (1 biến độc lập) và hồi quy đa biến/ hồi quy bội (nhiều biến độc lập) Y=b0+b1.X1+b2.X2+…+ bk.Xk+e
✓ Y thường được ký hiệu cho biến phụ thuộc/ biến được giải thích ✓ X1, X2, ..
Xk là các biến độc lập ✓ Ký tự t hoặc i biểu thị lần quan sát thứ t hoặc giá trị
thứ i của các biến ✓ Xki: giá trị quan sát thứ i của biến Xk ✓ b0, b1,b2, …,
bk các hệ số của phương trình hồi quy ✓ e: sai số/ phần dư
8.1 Làm quen với hồi quy
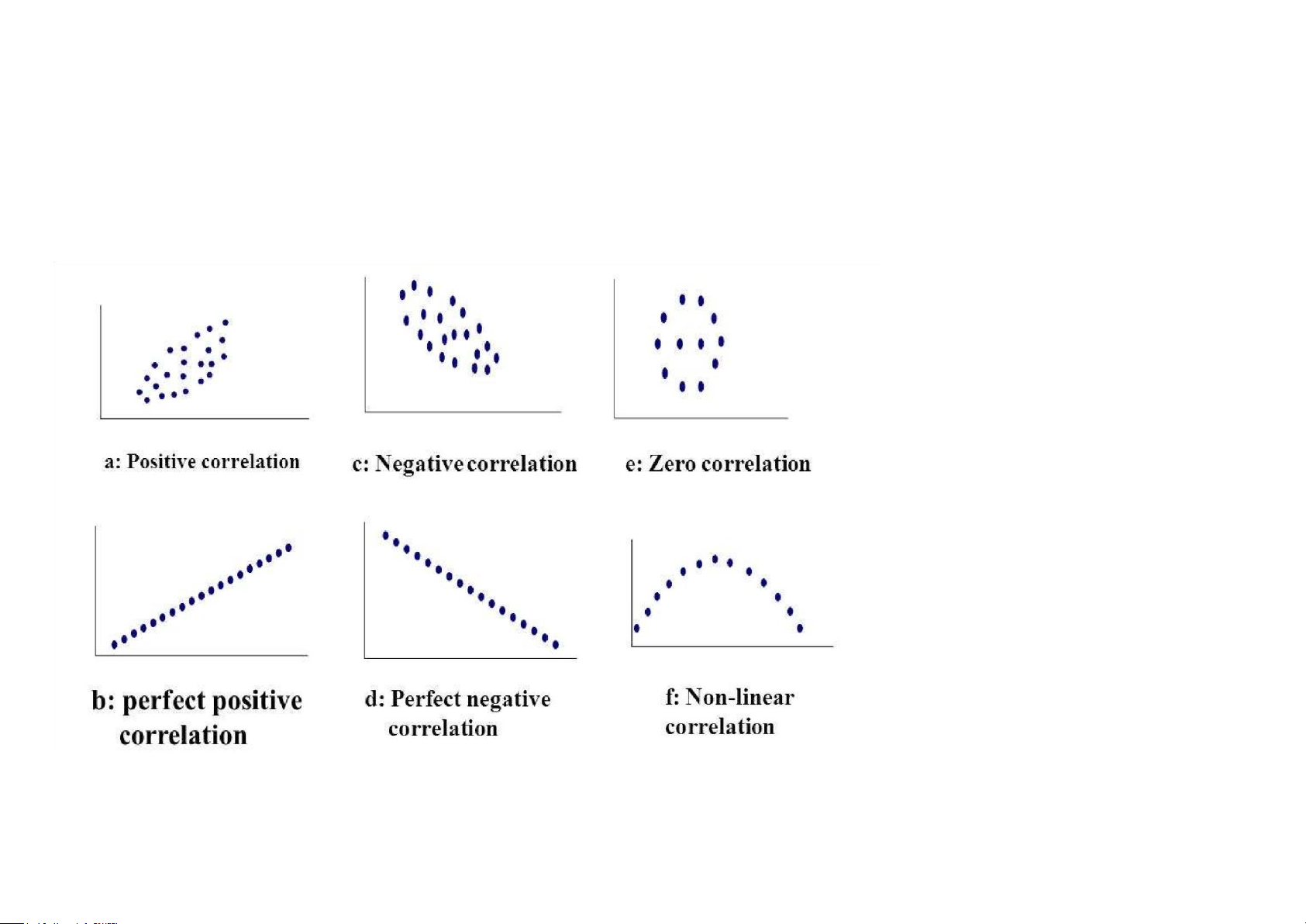
8.1.4 Các dạng liên hệ giữa hai biến X và Y
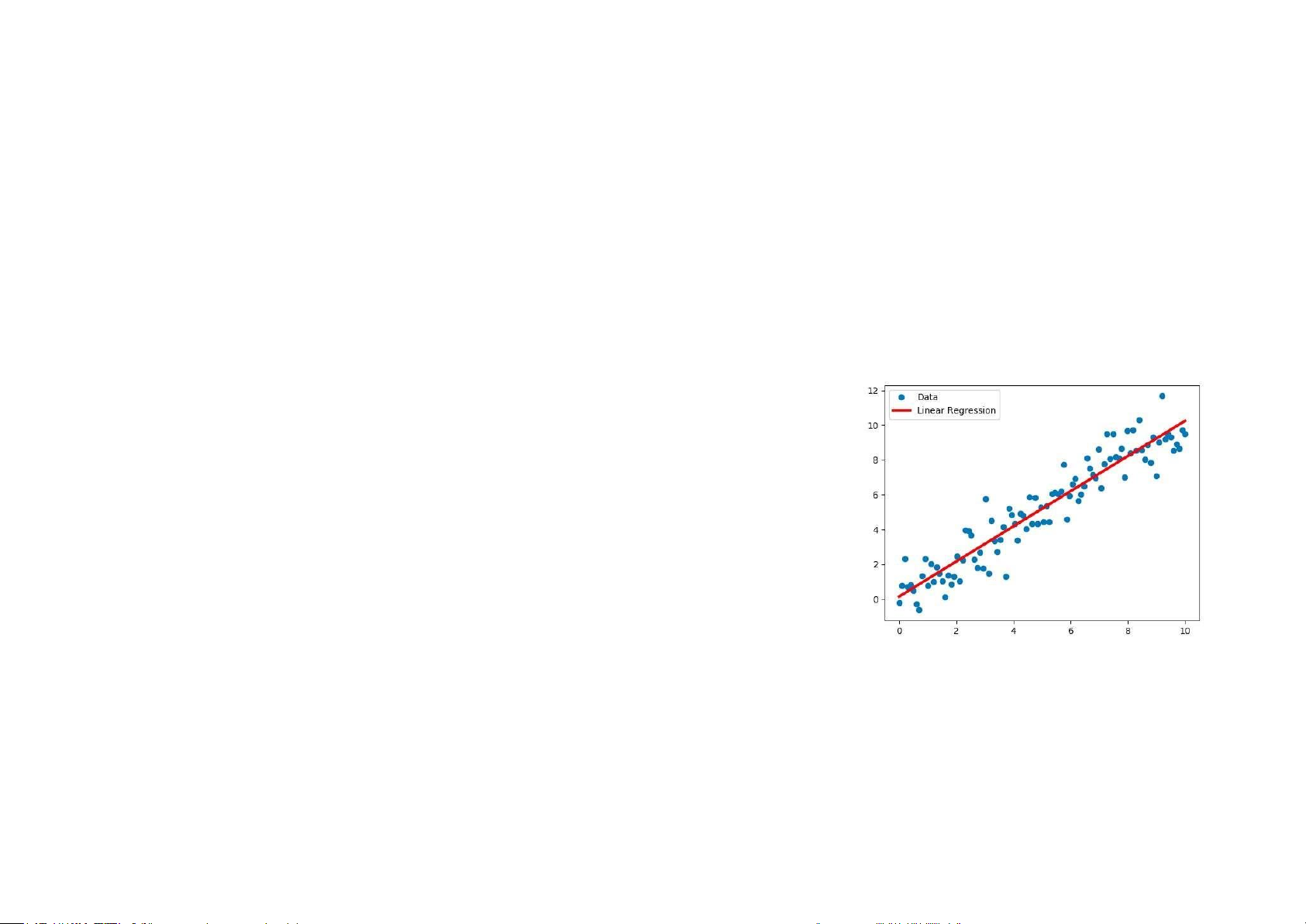
Đồ thị rải điểm – scatter plot -
cách tốt nhất để bắt đầu
quan sát mối liên hệ
Phát hiện hướng (direction),
dạng (form), độ chặt
( strength), đặc điểm bất
thường (unusual features) b: Perfect positive correlation
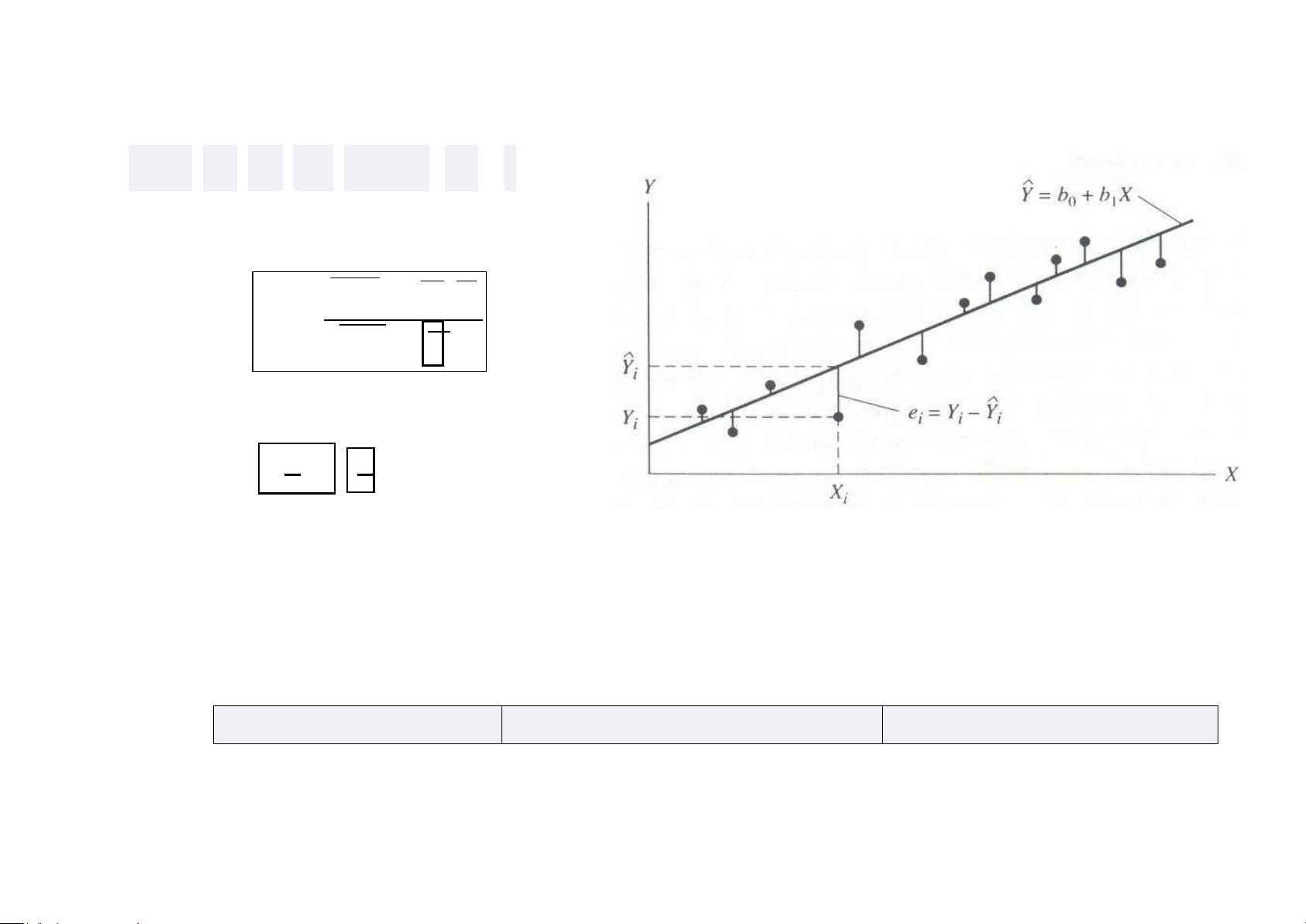
8.2 Mô hình hồi quy tuyến tính đơn 8.2.1 Giới thiệu
▪ Nghiên cứu mối quan hệ giữa biến X và biến Y
▪ Đường lý thuyết E(Y|Xi)=b0+b1Xi
▪ Mối liên hệ thực tế Yi=b0+b1Xi +ei
▪ b0: hệ số chặn, hệ số tung độ gốc ▪ b1: hệ số góc
▪ ei: sai số, thành phần ngẫu nhiên, yếu tố nhiễu
▪ E(Y|Xi): giá trị do đường lý thuyết tạo ra giá trị trung bình/ kỳ vọng của các giá trị Yi khi X= Xi ▪ ei=Yi - E(Y|Xi)
8.2 Mô hình hồi quy tuyến tính đơn
Quy trình thực hiện phân tích hồi quy tuyến tính đơn dựa trên dữ liệu mẫu
▪ Cho biến X = {x1, x2, x3, …, xn} và biến Y = (y1, y2, y3, …, yn)
▪ Bước 1: Dự đoán quan hệ
▪ X và Y có liên hệ tuyến tính không? Biểu đồ scatter plot
▪ X có thể là nguyên nhân sự biến động của Y không? Phân tích lý thuyết ▪ Bước 2: Xác định quan hệ
▪ Xây dựng đường thẳng lý thuyết tốt nhất trên nguyên tắc cực tiểu hóa tổng bình phương của các
phần dư. OLS- ordinary least square
𝒀!𝒊 = b0 + b1Xi 𝑌!! giá trị ước lượng cho các giá trị của Y ở quan sát thứ i
▪ Bước 3: Kiểm định tính có ý nghĩa của hàm hồi quy
▪ Bước 4: Kiểm định mức độ đáp ứng các giả định của hàm hồi quy
8.2 Mô hình hồi quy tuyến tính đơn
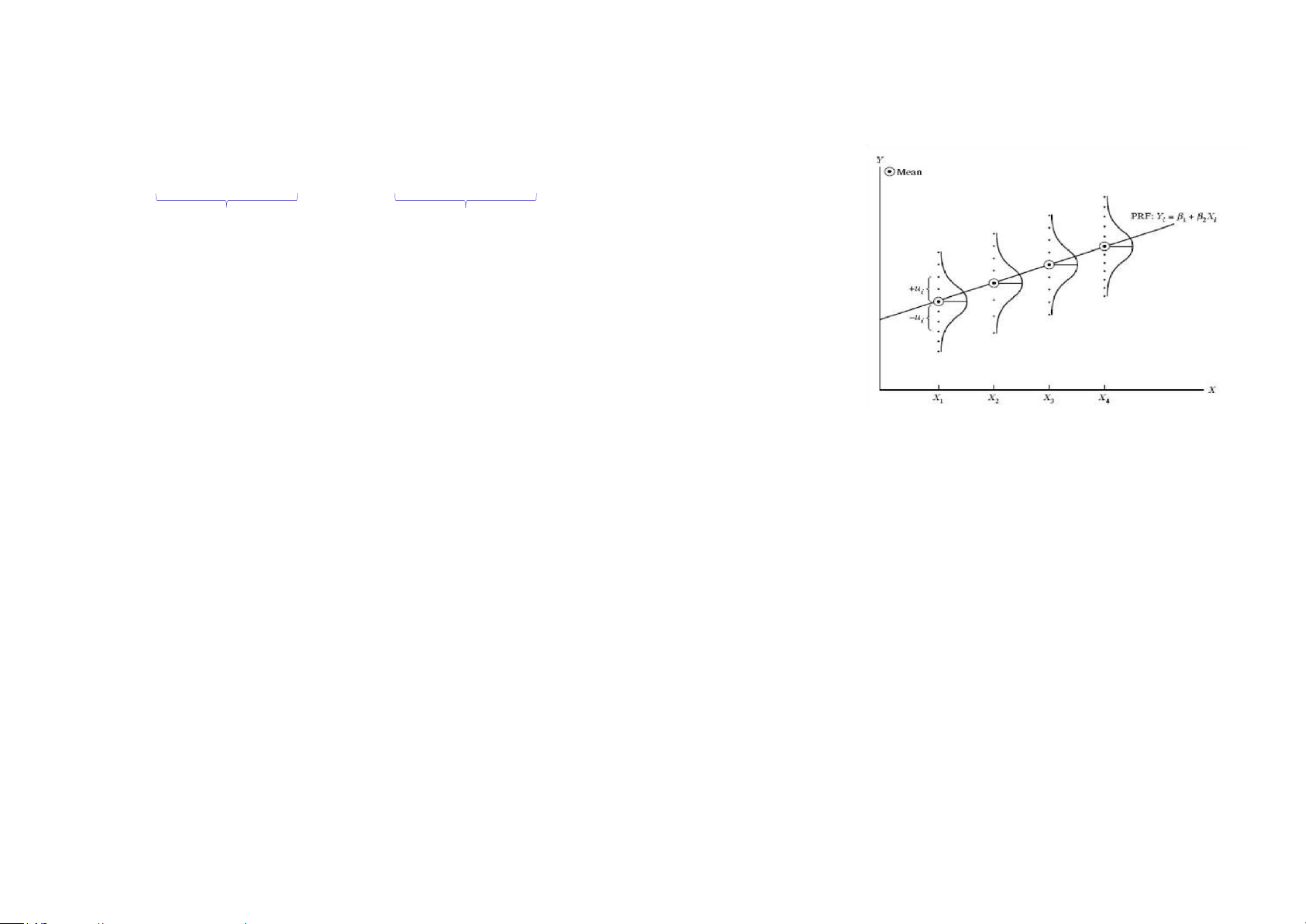
8.2.2 Các giả định liên quan đến yếu tố nhiễu
▪ Tại mỗi giá trị Xi, Yi nhận nhiều giá trị khác nhau→ cũng có nhiều ei
▪ Các ei tại mỗi Xi tạo thành một phân phối bình thường.
Giả định 1: Phương sai các ei tại mỗi Xi là như nhau
Giả định 2: Không có sự tương quan giữa các nhiễu hay các ei độc lập với nhau Yi = b0 + b1Xi + ei Thành phần tuyến tính Thành phần ngẫu nhiên
8.2 Mô hình hồi quy tuyến tính đơn e i e i
Nguyên nhân dẫn đến sự tồn tại của yếu tố nhiễu
▪ Nhà nghiên cứu không biết hết các yếu tố ảnh hưởng đến biến phụ thuộc Y.
Hoặc nếu biết cũng không thể có số liệu cho mọi yếu tố
▪ Không thể đưa tất cả yếu tố vào mô hình vì làm mô hình phức tạp ▪ Sai số đo
lường trong khi thu thập số liệu
▪ Bỏ sót biến giải thích
▪ Dạng mô hình hồi quy không phù hợp
8.2 Mô hình hồi quy tuyến tính đơn
8.2.3 Ý nghĩa và cách xác định các hệ số hồi quy
▪ b0: hệ số chặn, hệ số tung độ gốc: giá trị trung bình của Y khi X=0, có thể coi là ảnh
hưởng trung bình của các yếu tố khác mà không có mặt trong mô hình
▪ b1: hệ số góc, đo lường sự thay đổi trung bình của biến phụ thuộc Y khi X thay đổi 1
đơn vị. Ví dụ khi b1 =12 có nghĩa là khi X tăng lên 1 đơn vị thì ta có thể kỳ vọng trung
bình Y sẽ tăng lên lên 12 đơn vị. Khi b1 = -12, có nghĩa là khi X tăng lên 1 đơn vị thì
trung bình Y sẽ giảm 12 đơn vị.
8.2 Mô hình hồi quy tuyến tính đơn
Cách xác định các hệ số hồi quy ▪ Phương pháp: Tìm b 2
0 và b1 sao cho tổng bình phương các phần dư åei nhỏ
nhất, với giá trị phần dư được tính bằng:
e y yi = i - ˆi =yi -(b bxo + 1 i ) ▪ Ta có : XY XY- .
b1 = (X2 -X2) b0 =y-b1.x
8.2 Mô hình hồi quy tuyến tính đơn
▪ Ví dụ: Số liệu về doanh thu và chi phí quảng cáo của một công ty: Năm Doanh thu (tỷ VNĐ) CP quảng cáo (tỷ VNĐ) 2002 60 2,3 2003 62 2,8 2004 68 2,7 2005 76 3 2006 65 3,2 2007 74 3,6 2008 78 4 2009 88 4,2 2010 70 3,8 2011 66 3,5 2012 56 3 2013 86 4,5 2014 92 4,7 2015 95 4,8 2016 100 5,2 Tổng 1136,0 55,3
8.2 Mô hình hồi quy tuyến tính đơn
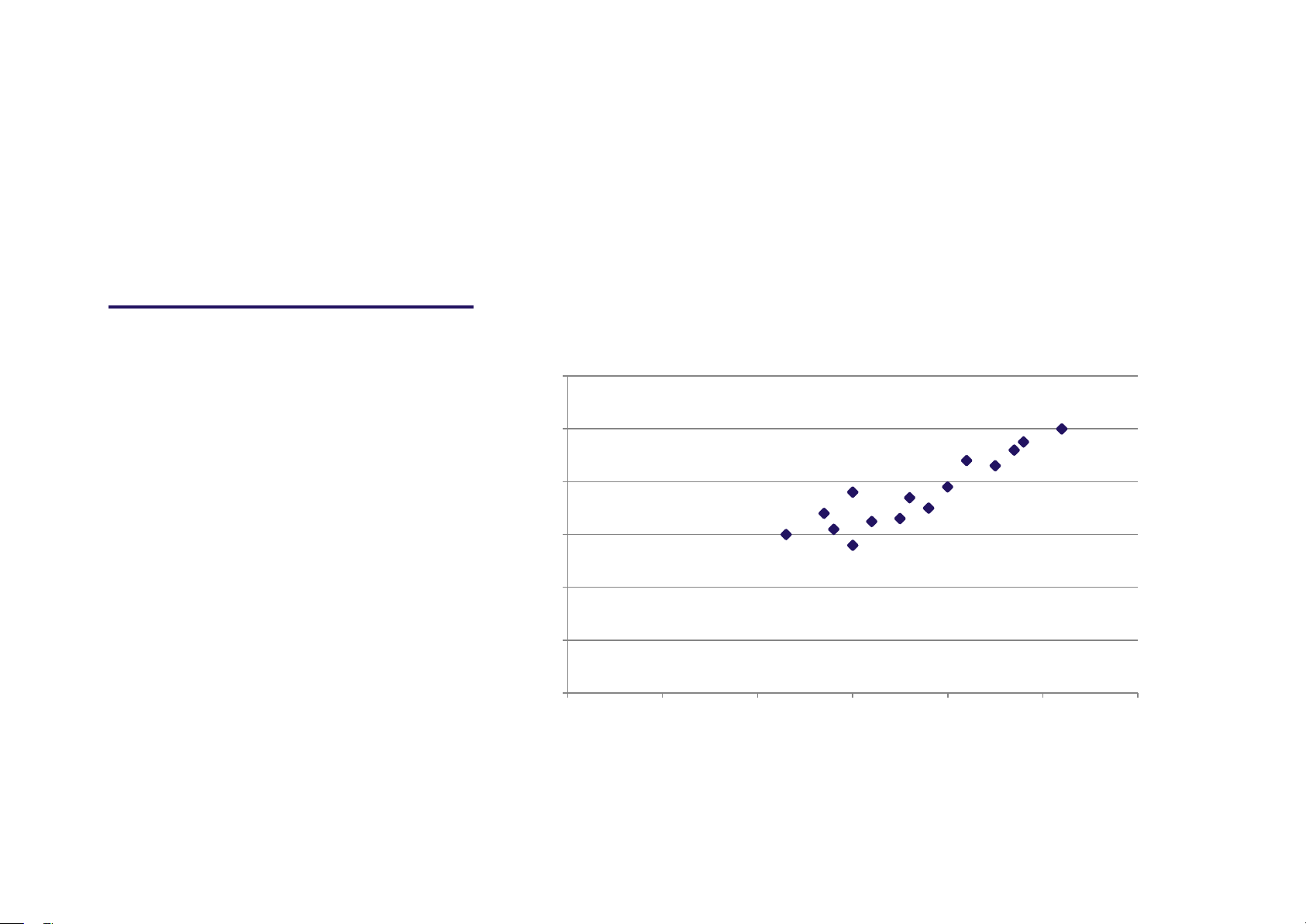
▪ Bước 1: Dự đoán quan hệ 120
❖ Biểuđồrảiđiểm 100 80 60 40 20 0 0 1 2 3 4 5 6
→ giữa DT và CP là mối quan hệ tương đối chặt chẽ ❖ Theo lý thuyết QTKD,
chi phí quảng cáo có sự tác động lên doanh thu bán hàng
8.2 Mô hình hồi quy tuyến tính đơn