Chương I: Điện Trường Tĩnh môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

CHƯƠNG I: ĐIỆN TRƯỜNG TĨNH 1 ¤1. ĐỊNH LUẬT COULOMB ¤2. ĐIỆN TRƯỜNG
I. Kh‡i niệm điện trường
II. VŽctơ cường độ điện trường
III. Nguy•n lý chồng chất điện trường
IV. M™men lưỡng cực điện
V. Đường sức điện trường
¤3. ĐỊNH LÝ OSTROGRADSKI-GAUSS (O-G)
I. Điện cảm. Điện th™ng
II.Định lý Ostrogradski-Gauss vˆ ứng dụng (dạng t’ch ph‰n, kh™ng chứng minh) ¤4. ĐIỆN THẾ
I. T’nh chất thế của điện trường tĩnh. Lưu số của vŽctơ cường độ điện trường
II. Thế năng tương t‡c điện
III. Điện thế vˆ hiệu điện thế
IV. Mặt đẳng thế (những t’nh chất)
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG VË ĐIỆN THẾ 2
Lect. 1 - Electric Charges and Forces - Coulomb's Law - Polarization QUY ƯỚC 3 Nhiễm điện dương Nhiễm điện ‰m Da thœ Thanh nhựa (cao su) Thanh thủy tinh Mảnh lụa
¤0. NHẮC LẠI KHçI NIỆM ĐÌ HỌC 4 Thực
Điện t’ch của một hệ c™ lập nghiệm lu™n được bảo toˆn Benjamin Franklin (1706-1790) (American) Định luật bảo toˆn điện t’ch
¤0. NHẮC LẠI KHçI NIỆM ĐÌ HỌC 5
Điện t’ch tr•n 1 vật mang điện bất kỳ Thực
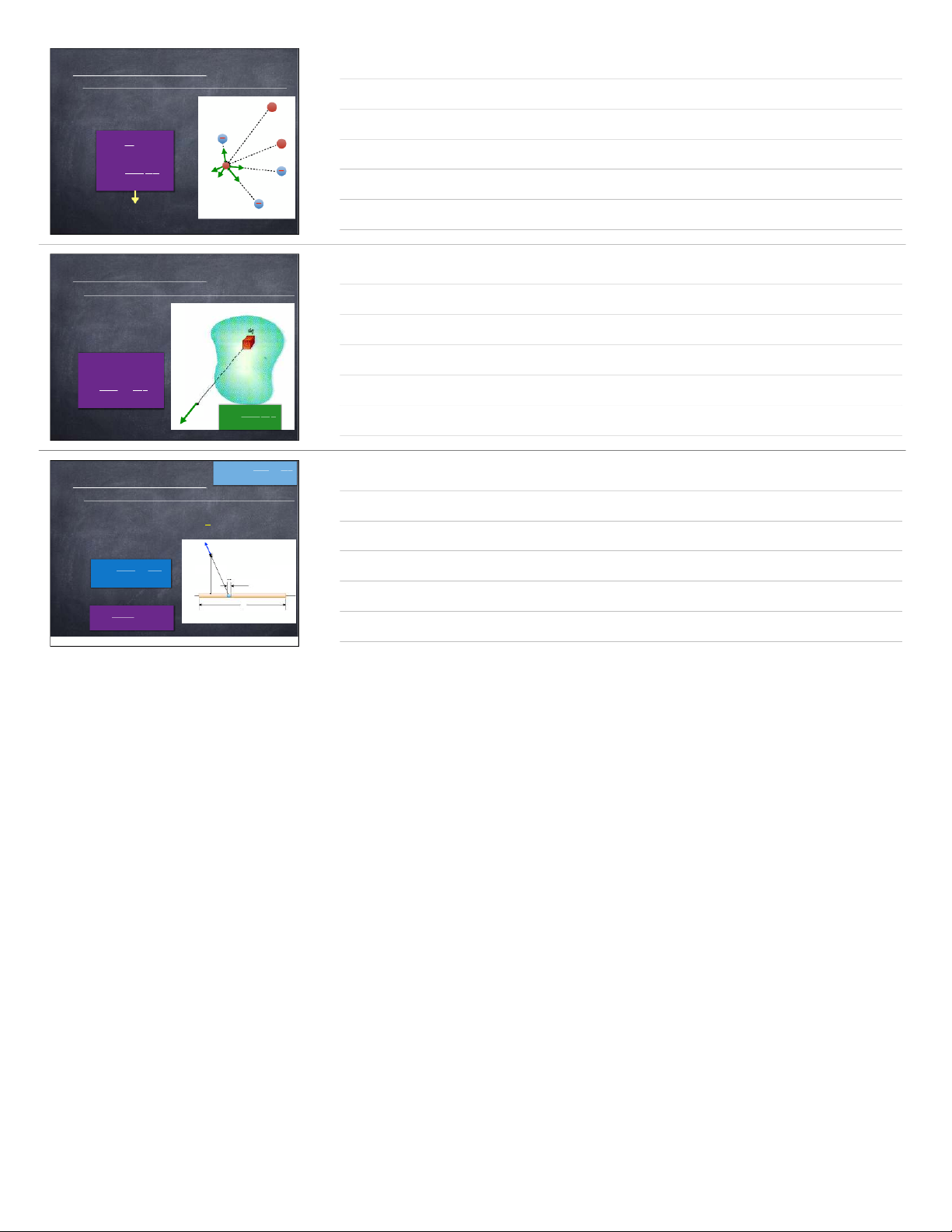
lu™n gi‡n đoạn (bị lượng tử h—a) nghiệm q=n.e;n∈Z,e= 1,6.10−19 C Robert A. Millikan (1868-1953) (American)
Điện t’ch vˆ khối lượng của Electron, Proton vˆ Neutron e= 1,6.10−19 C Điện t’ch nguy•n tố ¤1. ĐỊNH LUẬT COULOMB 6 I. Điện t’ch điểm II. Định luật Coulomb Điểm treo D‰y treo Charles-Augustin de Coulomb (1736-1806) (French) CoulombÕs torsion balance (C‰n xoắn) ¤1. ĐỊNH LUẬT COULOMB 7 II. Định luật Coulomb
1. Định luật Coulomb trong ch‰n kh™ng F12 + q2 r F12 =F21 =k.∣q1.q2∣ F21 r2, k=1 ≈9.109N.m2/C2 4πϵ , 0 q1 ϵ0= 8,86.10−12 C2/N.m2 , ¤1. ĐỊNH LUẬT COULOMB 8 II. Định luật Coulomb ϵ F12 +
2. Định luật Coulomb trong c‡c m™i trường q2 r F F21 12 =F21 =k .∣q1.q2∣ F12 ϵ r2,− q + 1 F12 =k .q1.q2 r r 12 2. r12 q2 ϵ r =1 .q1.q2 r12 r 4πϵ 2. 0ϵ r, F F12 21 + − F q 21 =k .q1.q2 r21 1 r r21 ϵ 2. r q2 =1 .q1.q2 r21 r 4πϵ 2. 0ϵ r. F21 − q1 ¤1. ĐỊNH LUẬT COULOMB 9
III. Nguy•n lý chồng chất lực +q2 r12 − r2 q1 + F= F1+ F2+ . . . + Fn F1 r3 q3 r1 n = ∑ Fi F3 + ri i=1 q0 Fi qi Fn rn F2 qn ¤1. ĐỊNH LUẬT COULOMB 10
III. Nguy•n lý chồng chất lực q< 0 F=∫d F toˆn bộ vật r d F + q0 F=1 q0.dq r d 4πϵ0ϵ r2 r ¤1. ĐỊNH LUẬT COULOMB 11
III. Nguy•n lý chồng chất lực ϵ R2 q2 + F + + 12 + F21 R1 r F12 =F21 =k .∣q1.q2∣ ϵ r2 q1 =1 .∣q1.q2∣ 4πϵ0ϵ r2 ¤2. ĐIỆN TRƯỜNG 12 Lực tương t‡c Khi chỉ c— một đ ện
g ữa hai đ ện t’ch đ m được
t’ch th“ kh™ng gian xung
tru ền đi như thế nˆo? C— ự tham
? quanhđện t’chđ— c— bị bến
gia c a m™i t ường xung quanh đổi g“ kh™ng? kh™ng? Thuyết t‡c dụng xa Thuyết t‡c dụng ần Thực nghiệm ¥ ¥ ¤2. ĐIỆN TRƯỜNG 13
I. Kh‡i niệm điện trường
Kh‡i n ệm đ ện trường Thuyết t‡c dụng ần ¥ ¤2. ĐIỆN TRƯỜNG 14
II. VŽctơ cường độ điện trường M + 1. Định nghĩa F q0 E F E= q0 ¥Đơn vị: V™n tr•n mŽt (Vm)
Fundamentals of Physics, D. Halliday, Wiley, 2013 ¤2. ĐIỆN TRƯỜNG 15
II. VŽctơ cường độ điện trường
2. Cường độ điện trường g‰y bởi một điện t’ch điểm O r E=1 q r M q E 4πϵ0ϵ r2 r
(đœng cho cả trường hợp q> v 0 ˆ q ) < 0 ¤2. ĐIỆN TRƯỜNG 16
III. Nguy•n lý chồng chất điện trường
1. VŽctơ cường độ điện trường g‰y bởi một hệ điện t’ch điểm +q2 n n r Fi q 2 1 + E= ∑ = ∑ Ei E1 q0 r3 q3 i=1 i=1 r1 n E3 + ri 1 qi ri = ∑ , q0 Ei 4πϵ r2 r i=1 0ϵ i i qi E2 En rn qn
Nguy•n lý chồng chất điện trường ¤2. ĐIỆN TRƯỜNG 17
III. Nguy•n lý chồng chất điện trường
2. VŽctơ cường độ điện trường g‰y bởi một vật mang điện bất kỳ q> 0 E=∫d E toˆn bộ vật r =1 r 4πϵ0ϵ∫dq r2 r toˆn bộ vật d E M E=1 dq r d 4πϵ0ϵ r2 r ¤2. ĐIỆN TRƯỜNG =1 r 18 E=∫d E 4πϵ0ϵ∫dq r2 r
III. Nguy•n lý chồng chất điện trường toˆn bộ vật toˆn bộ vật
2. VŽctơ cường độ điện trường g‰y bởi một vật mang điện bất kỳ
¥ Vật mang điện t’ch q lˆ một d‰y t’ch điện c— độ dˆi , c— ℓ
mật độ điện dˆi x‡c định bởi: λ≡q λ ℓ dE M EM=1 4πϵ r dq =λdx 0ϵ∫λdx r3 r a dx (ℓ) ¥ Sợi d‰y dˆi v™ hạn ℓ EM=λ 2πϵ0ϵa=
Fundamentals of Physics, D. Halliday, Wiley, 2013 ¤2. ĐIỆN TRƯỜNG =1 r 19 E=∫d E 4πϵ0ϵ∫dq r2 r
III. Nguy•n lý chồng chất điện trường toˆn bộ vật toˆn bộ vật
2. VŽctơ cường độ điện trường g‰y bởi một vật mang điện bất kỳ
➡Cường độ điện trường g‰y bởi v˜ng tr˜n: EM ‣Tại M: EM=1 Q.h 4πϵ0ϵ (R2+h2)3/2 M =1 λRh h 2ϵ0ϵ (R2+h2)3/2 Q O R ‣Tại O ( h ) = 0 E0= 0 ¤2. ĐIỆN TRƯỜNG =1 r 20 E=∫d E 4πϵ0ϵ∫dq r2 r
III. Nguy•n lý chồng chất điện trường toˆn bộ vật toˆn bộ vật
2. VŽctơ cường độ điện trường g‰y bởi một vật mang điện bất kỳ σ≡q S EM=1 4πϵ0ϵ∫σdS r3 r (S) dq =σdS
¥Đĩa tr˜n mang điện bk R: EM=σ 2ϵ0ϵ(1−h R2+h2) r x M O
¥ Mặt phẳng rộng v™ hạn: h dx EM=
Fundamentals of Physics, D. Halliday, Wiley, 2013 ¤2. ĐIỆN TRƯỜNG =1 r 21 E=∫d E 4πϵ0ϵ∫dq r2 r
III. Nguy•n lý chồng chất điện trường toˆn bộ vật toˆn bộ vật
2. VŽctơ cường độ điện trường g‰y bởi một vật mang điện bất kỳ ρ≡q V
➡Cường độ điện trường g‰y bởi vật tại M: EM=1 4πϵ0ϵ∫ρdV r3 r (V)
¥ Quả cầu mang điện b‡n k’nh R: R EM=q 4πϵ r M 0ϵr2= O ρ ¤2. ĐIỆN TRƯỜNG 22 A pe B l +
IV. M™men lưỡng cực điện (lcđ) −q +q
2. VŽctơ cường độ điện trường g‰y bởi lưỡng cực điện E2 VŽctơ m™men E lưỡng cực điện M M pe=q E l 1 r E2 EN E1 A B E E O 1 N E2 + N r −q l +q r N
¥XŽt trường hợp r >> l: EM=−1 pe EN=1 2 pe 4πϵ0ϵ r3 4πϵ0ϵ r3 pe=q.
l: đặc trưng cho t’nh chất điện của lưỡng cực điện ¤2. ĐIỆN TRƯỜNG 23
V. Đường sức điện trường 1. Định nghĩa E M E= 2. Quy ước const
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 24
I. Điện cảm. Điện th™ng ϵ= 2
1. Điện cảm (vŽctơ cảm ứng điện) D ¥Định nghĩa: q D=ϵ + 0ϵ E r
➡Điện cảm g‰y bởi điện t’ch điểm q: D E=1 q r D=ϵ0ϵ 4π r2 r
Phổ đường cảm ứng điện
¥Đơn vị: Coulomb tr•n mŽt vu™ng (C/m2)
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 25
I. Điện cảm. Điện th™ng
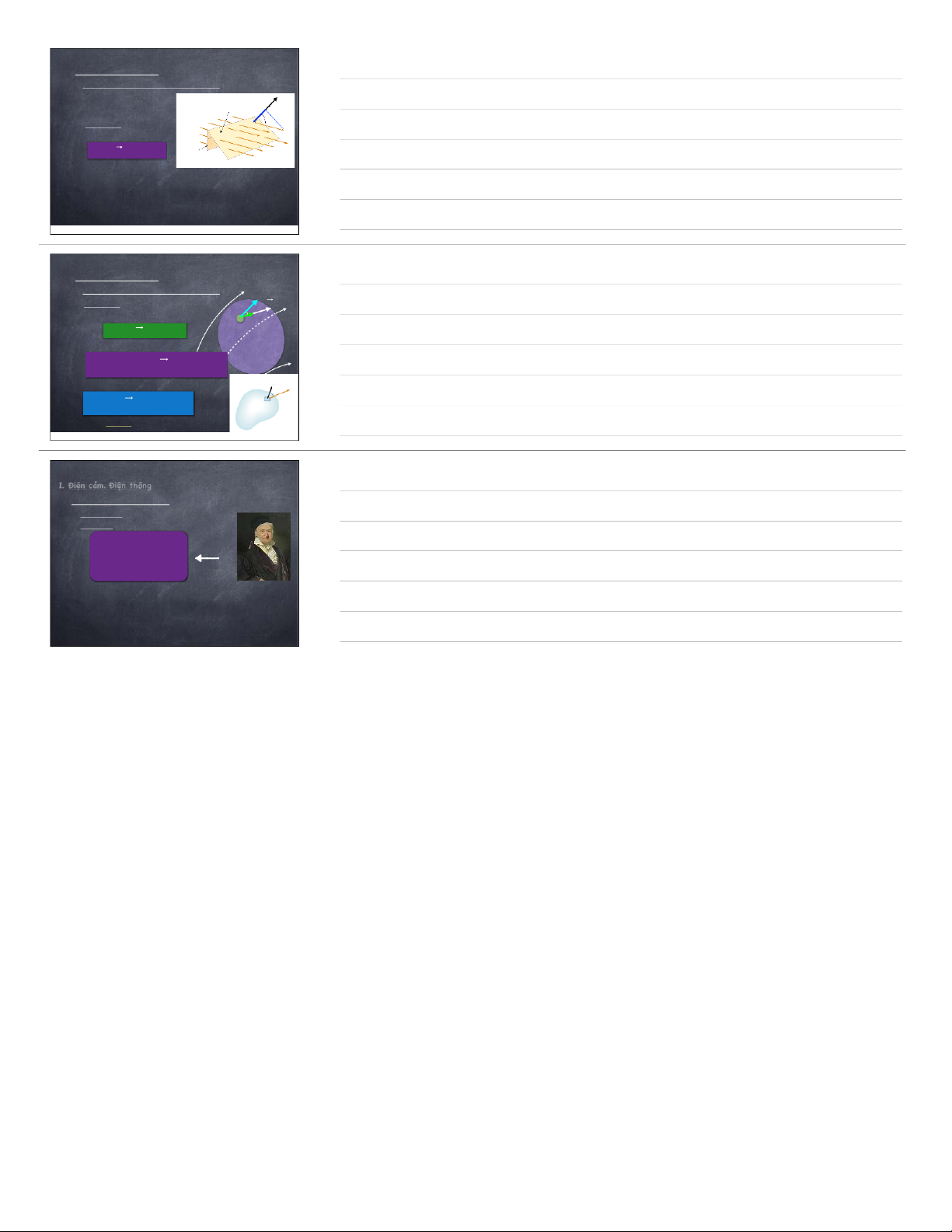
2. Điện th™ng (Th™ng lượng cảm ứng điện)
✴XŽt một diện t’ch S đặt Dn=D.cosα S (S)
trong điện trường đều D D n α ¥Định nghĩa: Điện th™ng D α Φe= D.S=D.S.cosα Sn=S.cosα
Fundamentals of Physics, D. Halliday, Wiley, 2013
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 26
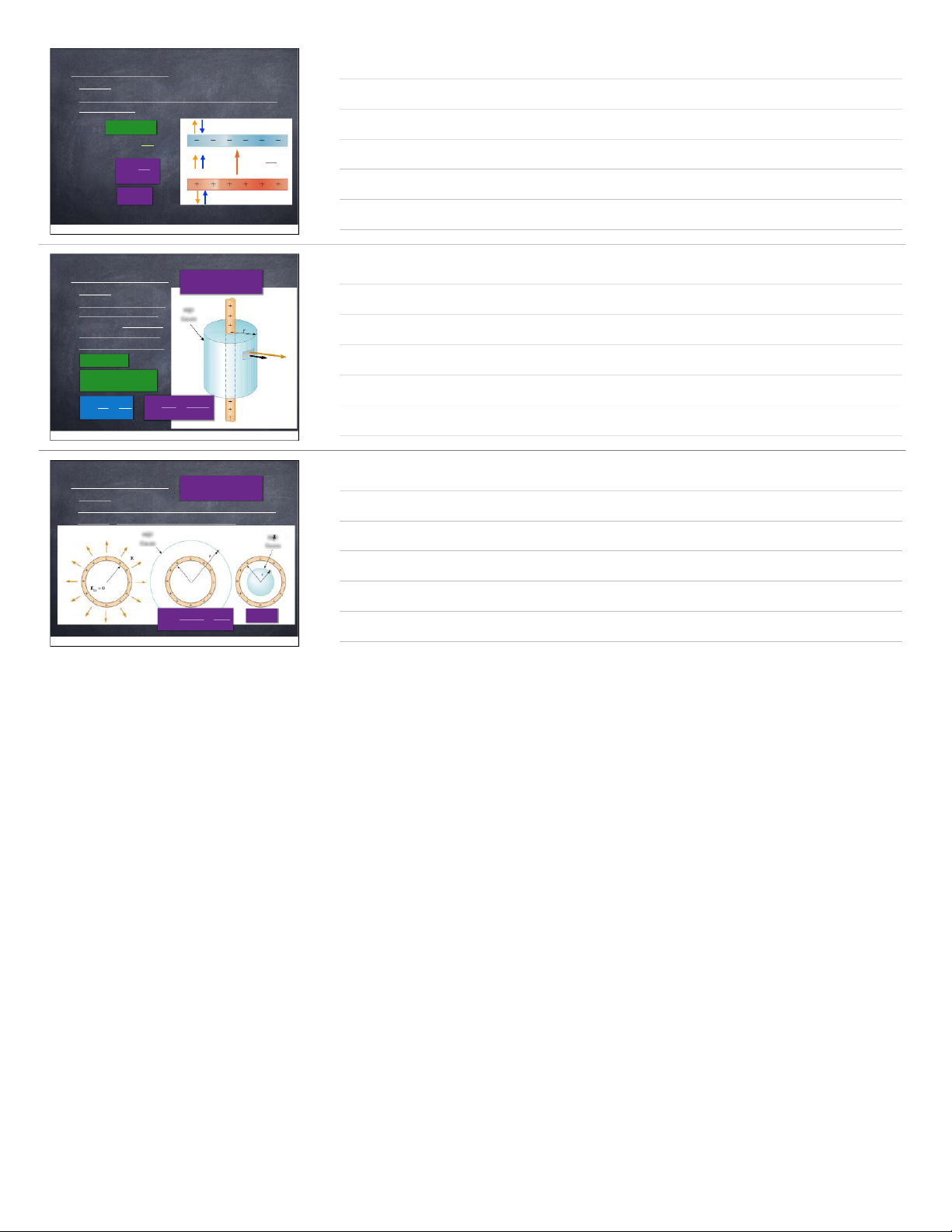
I. Điện cảm. Điện th™ng
2. Điện th™ng (Th™ng lượng cảm ứng điện) D= const ¥Định nghĩa: dS D dS α n dΦe= D.dS =D.S.cosα (S) Φe=∫(S) dΦe=∫(S) D.dS =∫(S) D.dS .cosα d S D α Φe=∮(S) D.dS =∮(S) D.dS .cosα ¥Quy ước: dcủ
S a mặt k’n lu™n hướng ra ph’a ngoˆi
Fundamentals of Physics, D. Halliday, Wiley, 2013
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 27
II. Định lý O-G vˆ ứng dụng 1. Định lý O-G 2. Ứng dụng Định lý O-G (GaussÕs Law) Carl Friedrich Gauss (1777-1855) (German)
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 28
II. Định lý O-G vˆ ứng dụng 1. Định lý O-G Φ
Mặt k’n (S) được gọi e=∮(S) D.d S=∑ qi i lˆ mặt Gauss ¥ Dạng vi ph‰n: divD=ρ Phương tr“nh Poisson
➡Định lý O-G cho ta mối li•n hệ ch’nh x‡c
giữa điện trường vˆ nguy•n nh‰n sinh ra n—
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 29
II. Định lý O-G vˆ ứng dụng 2. Ứng dụng
C‡c bước t“m D, E tại một điểm bằng định lý O-G:
1. Chọn mặt Gauss (S) c— t’nh đối xứng th’ch hợp đi qua điểm cần t“m D, E,
2. AD định lý O-G cho mặt Gauss đ‹ chọn: Φe=∮(S) D.d S=∑ qi(1) i
3. Dựa vˆo t’nh đối xứng của mặt Gauss, lý luận để t“m được:
Φe=∮(S) D.d S(2) vˆ ∑ qi(3) i
4. Thay (2) & (3) vˆo (1) ⇒ D ⇒ tại đ E iểm cần t“m.
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 30
II. Định lý O-G vˆ ứng dụng Φe=∮(S) D.d S=∑ qi 2. Ứng dụng i
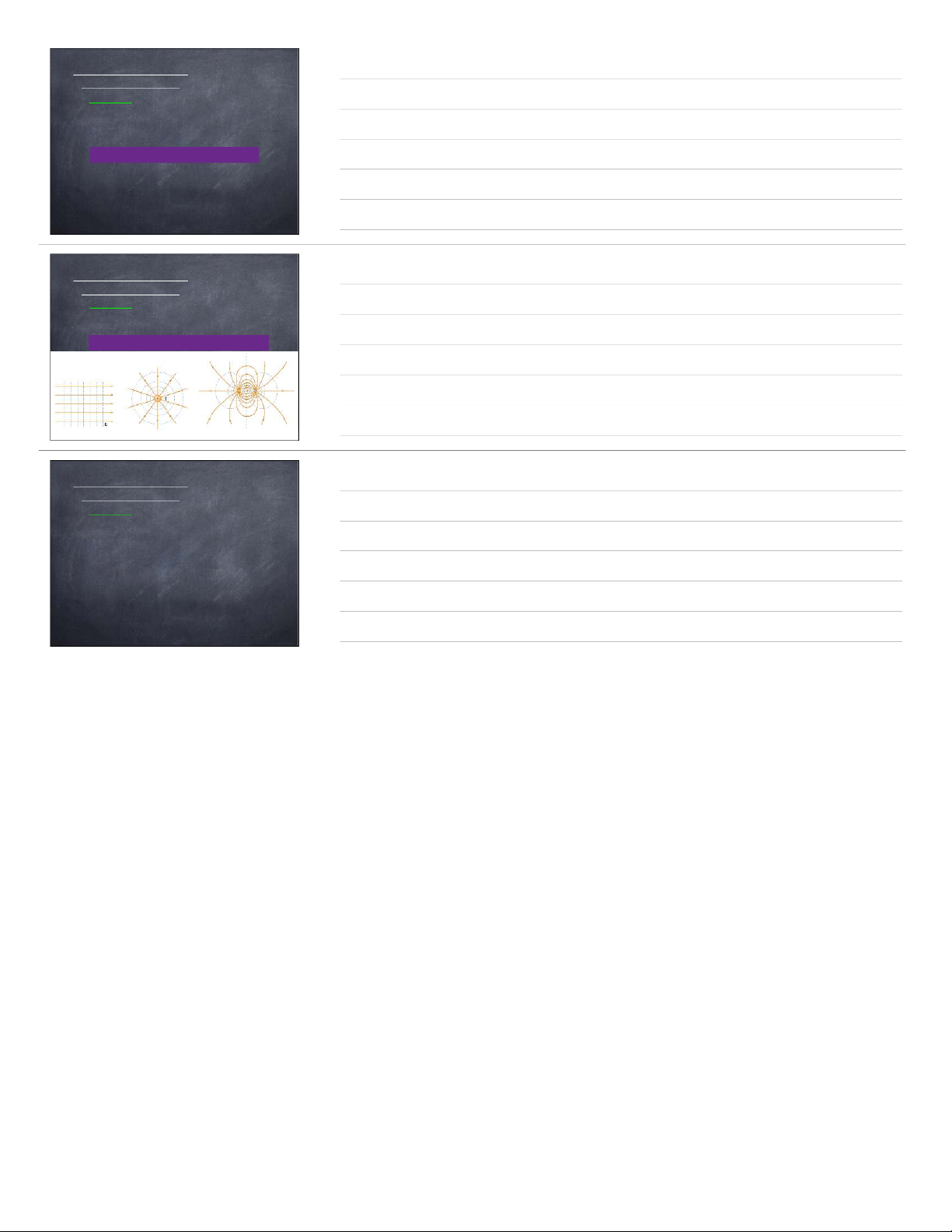
a. T’nh cường độ điện trường g‰y bởi một mặt phẳng mang điện t’ch đều σ ⇒D=σ ⇒E=σ Φe=Φe1+Φe2= 2DS ∑ qi=σ.S 2 2ϵ0ϵ i Mặt S D Gauss σ
College Physics, R.A. Serway, Wiley, 2013
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 31
II. Định lý O-G vˆ ứng dụng 2. Ứng dụng
b. T’nh cường độ điện trường g‰y bởi hai mặt phẳng mang điện t’ch đều tr‡i dấu E= E1+ E2 E1 E2 Eout = 0 E1=E2=σ (2) 2ϵ0ϵ Ein =σ Ein =σ E1 E2 ϵ0ϵ ϵ0ϵ (1) Eout = 0 E1 E2 Eout = 0
College Physics, R.A. Serway, Wiley, 2013
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 32
II. Định lý O-G vˆ ứng dụng Φe=∮(S) D.d S=∑ qi 2. Ứng dụng i
c. T’nh cường độ điện trường Mặt σ
g‰y bởi một mặt trụ dˆi Gauss
(b‡n k’nh R) v™ hạn mang
điện đều với mật độ điện mặt (
σ mật độ điện dˆi ) λ M D ℓ Φe=D.2πr.ℓ d S ∑ qi=σ.2πR.ℓ=λ.ℓ i ⇒D=σR r=λ ⇒E=σR ϵ0ϵr=λ 2πr 2πϵ0ϵr
Fundamentals of Physics, D. Halliday, Wiley, 2013
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 33
II. Định lý O-G vˆ ứng dụng Φe=∮(S) D.d S=∑ qi 2. Ứng dụng i
d. T’nh cường độ điện trường g‰y bởi một mặt cầu (O, R) mang
điện t’ch Q ph‰n bố đều (c— mật độ điện mặt ) σ Mặt M t Gauss Gauss M RR N O OO EM=Q 4πϵ0ϵr2=σR2 EN= 0 ϵ0ϵr2
Fundamentals of Physics, D. Halliday, Wiley, 2013
¤3. ĐỊNH LÝ OSTROGRADSKI - GAUSS (O-G) 34
II. Định lý O-G vˆ ứng dụng 2. Ứng dụng
e. T’nh cường độ điện trường g‰y bởi một quả cầu điện m™i đặc
(O, R) t’ch điện đều Q (mật độ điện khối ) ρ EN=Qr4πϵ0ϵR3=ρ 3ϵ0ϵr M R Mặt N O Gauss O EM=Q 4πϵ0ϵr2=ρR3 1 Mặt R 3ϵ0ϵ r2 Gauss
Fundamentals of Physics, D. Halliday, Wiley, 2013 ¤4. ĐIỆN THẾ 35
I. T’nh chất thế của điện trường tĩnh. Lưu số cuả vŽctơ
cường độ điện trường
1. C™ng của lực tĩnh điện. T’nh chất thế của điện trường tĩnh (M) E s=q F dA =q 0.q 0. E.d 4πϵ0ϵ.r2.dr P (+q0) αd H s
¥ C™ng của lực tĩnh điện trong chuyển rM r (N) dời của q0 từ M N: → r+dr A q0.q rN MN =∫N dA =∫rN 4πϵ0ϵ.r3.dr M rM (+q) O ¤4. ĐIỆN THẾ 36
I. T’nh chất thế của điện trường tĩnh. Lưu số cuả vŽctơ
cường độ điện trường
1. C™ng của lực tĩnh điện. T’nh chất thế của điện trường tĩnh (M) E AMN =q0.q −q0.q F 4πϵ P 0ϵ.rM 4πϵ0ϵ.rN (+q α 0) H d s rM r (N) r+dr rN (+q) O ¤4. ĐIỆN THẾ 37
I. T’nh chất thế của điện trường tĩnh. Lưu số cuả vŽctơ
cường độ điện trường
2. Lưu số của vŽctơ cường độ điện trường E A s=q0.q −q0.q MN =∫N q0. E.d (M) ≡ (N) M 4πϵ0ϵ.rM 4πϵ0ϵ.rN E ➡Nếu r (+q0) M = rN: AMN = 0 d s rM≡rN r (C) ⇒∮(C) E.d s= 0 (+q) O ¤4. ĐIỆN THẾ 38
II. Thế năng tương t‡c điện AMN =∫N q0. E.d s=WtM−WtN M ⇔AMN =WtM−WtN=q0.q −q0.q 4πϵ0ϵ.rM 4πϵ0ϵ.rN ⇒AMN =(q0.q +C)−(q0.q +C) 4πϵ0ϵ.rM 4πϵ0ϵ.rN ¤4. ĐIỆN THẾ 39
II. Thế năng tương t‡c điện WtM=q0.q 4πϵ0ϵ.r+C, (C=const)
Thế năng tương t‡c điện ¤4. ĐIỆN THẾ 40
II. Thế năng tương t‡c điện WtM=q0.q 4πϵ0ϵ.r+C, (C=const) ¥ Quy ước: WtM(r→ ∞) = q0.q 4πϵ0ϵ.∞+C= 0 ⇒C= 0 ⇒WtM=q0.q 4πϵ0ϵr ¤4. ĐIỆN THẾ 41
II. Thế năng tương t‡c điện q0.qi WtM=∑ 4πϵ0ϵ.ri i q0.dq WtM=∫(V) 4πϵ0ϵ.r WtM=∫∞ q0. E.d s =A(M→∞) M ¤4. ĐIỆN THẾ 42
III. Điện thế vˆ hiệu điện thế 1. Định nghĩa WtM=q0.q q0.qi 4πϵ0ϵrWtM=∑ WtM=∫∞ q 4πϵ 0. E.d s i 0ϵ.ri M WtM =A ➡ (M→∞) Tỉ số V M
= được gọi lˆ điện thế của điện q0 q0
trường tại điểm M đang xŽt. WtM =A(M→∞) VM= (1) q0 q0 ¥ Quy ước: Wt∞(M≡ ∞) = 0 ⇒V∞= 0 ¤4. ĐIỆN THẾ VM=A(M→∞) WtM 43 = (1)
III. Điện thế vˆ hiệu điện thế q0 q0 1. Định nghĩa O WtM=A(M→∞)=q0.q +q 4πϵ0ϵr r M + q0 VM (1) ⟹VM=A(M→∞) =q + q2 q0 4πϵ0ϵ.r q1 r2 q0.qi + WtM=A(M→∞)=∑ r3 q3 r1 4πϵ i 0ϵ.ri + ri M q0 VM rn qi (1) ⟹VM=A(M→∞) qi qn =∑ q0 4πϵ0ϵ.ri i ¤4. ĐIỆN THẾ VM=A(M→∞) WtM 44 = (1)
III. Điện thế vˆ hiệu điện thế q0 q0 1. Định nghĩa q0.dq WtM=A(M→∞)=∫(V) 4πϵ0ϵ.r r q q0 + (1) ⟹VM=A(M→∞) dq =∫(V) VM q0 4πϵ0ϵ.r M WtM=A(M→∞)=∫∞ q0. E.d s M (1) ⟹VM=A(M→∞) =∫∞ E.d s q0 M ¤4. ĐIỆN THẾ VM=A(M→∞) WtM 45 = (1)
III. Điện thế vˆ hiệu điện thế q0 q0 1. Định nghĩa VM=A(M→∞) dq =∫(V) r q q0 4πϵ0ϵ.r q0 + VM M VM=A(M→∞) =∫∞ E.d s q0 M ¥ Quy ước:
Đ ện t ế a Tr‡i Đất bằng kh™ng
➡Khi m t ật được i đ t th“ đ ện thế a n— bằng kh™ng. ¤4. ĐIỆN THẾ 46
III. Điện thế vˆ hiệu điện thế 1. Định nghĩa
ÒHiệu điện thế UMN giữa hai điểm M vˆ N trong điện trường:Ó WtM−WtN =AMN UMN =VM−VN= q0 q0 AMN =q0.UMN =q0(VM−VN) AMN =∫N F.d s=∫N q0. E.d s M M ¤4. ĐIỆN THẾ 47
III. Điện thế vˆ hiệu điện thế 2. Ý nghĩa WtM =A(M→∞) VM= (1) q0 q0
ÒHiệu điện thế UMN giữa hai điểm M vˆ N trong điện trường:Ó U W MN =VM−VN=AMN tM−WtN = q0 q0 ¥Nếu q0 = +1C ⇒UMN =VM−VN=AMN ¤4. ĐIỆN THẾ 48
IV. Mặt đẳng thế (c‡c t’nh chất) 1. Định nghĩa V(x,y,z)=const ẳng thế
College Physics, A. Giambattista et al., McGraw-Hill, 2010 ¤4. ĐIỆN THẾ 49
IV. Mặt đẳng thế (c‡c t’nh chất)
2. T’nh chất của mặt đẳng thế ¥ T’nh chất 1:
AMN =q0.UMN =q0(VM−VN)= 0 (do VM=VN) ¤4. ĐIỆN THẾ 50
IV. Mặt đẳng thế (c‡c t’nh chất)
2. T’nh chất của mặt đẳng thế ¥ T’nh chất 2: dA =q0. E.d s= 0 ⇒ E.d s= 0 ⇒( E,d s)= 900
Fundamentals of Physics, D. Halliday, Wiley, 2013 ¤4. ĐIỆN THẾ 51
IV. Mặt đẳng thế (c‡c t’nh chất)
2. T’nh chất của mặt đẳng thế ¥ T’nh chất 3:
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 52 VË ĐIỆN THẾ
I. Hệ thức li•n hệ giữa cường độ điện trường vˆ điện thế
¥ XŽt hai điểm M vˆ N ở rất gần nhau (V+dV) trong điện trường, MN =d s. (VN>VM) ¥Đặt VM = V, VN = V + dV. (V) N
Giả sử: VN>VM⇒dV > 0 d s M ⊕dA = F.d s=q0. E.d s(1)
⊕dA =q0(VM−VN)=q0[V−(V+dV)]=−q0.dV (2)
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 53 VË ĐIỆN THẾ
I. Hệ thức li•n hệ giữa cường độ điện trường vˆ điện thế ⊕dA =q0. E.d s(1) (V+dV) ⊕dA =−q0.dV (2) (VN>VM) (1),(2) ⟹dA =q0. E.d s=−q0.dV (V) N d ⇒dV =− E.d s s ¥ Do: dV > 0 ⇒ E.d s< 0 α E (VN>VM⇒dV =VN−VM> 0) M
⇒E.ds .cosα< 0 ⇒cosα< 0
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 54 VË ĐIỆN THẾ
I. Hệ thức li•n hệ giữa cường độ điện trường vˆ điện thế ⇒Es.ds =−dV hay Es=−dV E.d s=−dV (Es=E.cosα) ds ⇒Ex=−∂V ∂x;Ey=−∂V ∂y;Ez=−∂V ds lˆ bất kỳ ∂z ⇒ E=Ex. i+Ey. j+Ez.
k=−(∂V ∂x. i+∂V∂y. j+∂V∂z. k) ⇒ E=− grad V =− ∇V ➡Dạng vi ph‰n:
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 55 VË ĐIỆN THẾ
I. Hệ thức li•n hệ giữa cường độ điện trường vˆ điện thế E.d s=−dV (V ⇒E N>VM) s.ds =−dV (V+dV) ⇒Es=−dV (Es=E.cosα) ds (V) N ⇒En=E=−dV d s dn E dnP α M En Es
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 56 VË ĐIỆN THẾ
I. Hệ thức li•n hệ giữa cường độ điện trường vˆ điện thế E (V s=−dV N>VM) ds =E.cosα≤E (V+dV) ⇒dVds ≤dV (V) N dn d s E dnP α M En Es
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 57 VË ĐIỆN THẾ II. Ứng dụng E.d r=−dV ( * )
1. T’nh hiệu điện thế giữa hai mặt phẳng v™ hạn song song ¥Ta c—: U12 =V1−V2=−∫(2) dV (*) =∫(2) E.d r=∫(2) E.dr (1) (1) (1) E=Ein =const =σ.d ⇒U=E.∫(2) dr =E.d (2) (1) ϵ E 0ϵ out = 0 −σ E Ein =σ V2 d d r ϵ0ϵ V1 +σ (1) Eout = 0
College Physics, R.A. Serway, Wiley, 2013
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 58 VË ĐIỆN THẾ II. Ứng dụng E.d r=−dV ( * )
2. T’nh hiệu điện thế giữa hai điểm trong điện trường của một
mặt cầu mang điện đều E=Q
¥T’nh hiệu điện thế giữa hai điểm (1) vˆ (2) Q++ + + 4πϵ0ϵr2 + R
b•n ngoˆi mặt cầu t’ch điện đều với điện + + (1) (2) + O +
t’ch Q > 0, c‡ch mặt cầu những khoảng + + + + lần lượt lˆ r + + r1r2 1, r? 2 + U12 =Q4πϵ −1 0ϵ(1 E≡E r in = 0 Q + + + r 2)(1) 1 + + + R +
¥T’nh hiệu điện thế giữa hai điểm (1) vˆ (2) (1) (2) + +
b•n trong mặt cầu t’ch điện đều với điện O + r1 +
t’ch Q > 0, c‡ch mặt cầu những khoảng lần r2 + + lượt lˆ r1,r 2? U12 = 0 (2) + + +
¤5. HỆ THỨC LIæN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG 59 VË ĐIỆN THẾ II. Ứng dụng
3. T’nh hiệu điện thế giữa hai điểm trong điện trường của một mặt
trụ thẳng dˆi v™ hạn mang điện đều (mật độ điện mặt ) σ
¥T’nh hiệu điện thế giữa hai điểm (1) vˆ r1 r2
(2) b•n ngoˆi mặt trụ t’ch điện đều với + + R mật độ điện mặt ? B σ iết hệ đặt trong + +
m™i trường c— hằng số điện m™i ϵ. + (1) (2) + + U12 =σR ϵ0ϵ.ln r2 (1) + + E=σR r1 +σ ϵ0ϵr
BËI TẬP CHƯƠNG I: ĐIỆN TRƯỜNG TĨNH 60
1-5, 1-9, 1-11, 1-12, 1-13, 1-17, 1-18, 1-19, 1-22,
1-24, 1-26, 1-29, 1-32, 1-33, 1-34, 1-35, 1-38, 1-39.
S‡ch BT VLĐC tập II - Lương Duy•n B“nh