Chương I: Động học các phản ứng đơn giản và phức tạp | Tài liệu môn Hóa lý 2 | Đại học Bách khoa hà nội

Chương I: Động học các phản ứng đơn giản và phức tạp. Tài liệu trắc nghiệm môn Phân tích bằng công cụ giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

12 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Hóa lý 2 (CH3061)

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

7 trang 1 tháng trước

Tác giả:

Profile Lê Na
Chương I : ĐỘNG HỌC CÁC PHẢN ỨNG ĐƠN GIẢN VÀ PHỨC TẠP
1, Khi nim v tc đ phn ng:
VD: Xét phản ứng
aA bB dD eE+ → +
Vn tc chung ca phản ứng:
1 [ ] 1 [ ] 1 [D] 1 [ ]
chung
d A d B d d E
v
a dt b dt d dt e dt
= − = − = + = +
(1)
T đ ta c th suy lun đưc vn tc theo tng cht ca phản ứng như sau:
[A] [ ]
. ; .
[ ] [E]
. ; .
A chung B chung
D chung E chung
d d B
v a v v b v
dt dt
d D d
v d v v e v
dt dt
= = − = = −
= = + = = +
chung
v
ta c th xc đnh đưc t biu thc tc dng khi lưng
[ ] [ ]
xy
chung
v k A B=
(2)
T (1) và (2):
1 [ ] 1 [ ] 1 [D] 1 [ ]
[ ] [ ]
xy
chung
d A d B d d E
v k A B
a dt b dt d dt e dt
= − = − = + = + =
Trong đ: k: là hằng s tc độ phản ứng chỉ phụ thuộc vào nhiệt độ, x,y là bc đi với
cht A,B; x+y là bc ca phản ứng, x và y có th bằng hoặc khác hệ s tỉ lưng (a, b)
2, Bậc và phân tử s của phn ng
- Bc ca phản ứng: là tổng cc lũy tha nồng độ ca các cht tham gia phản ứng
trong phương trình biu diễn sự phụ thuộc ca tc độ phản ứng vào nồng độ cht
pư.
- Phân tử s là hệ s tỉ lưng trong phản ứng hóa học.
- Phân tử s bao giờ cũng là một s nguyên, dương, bc ca phản ứng có th là
nguyên hoặc phân s, dương, âm hoặc bằng 0.
3, Phn ng đơn gin (pư sơ cấp)
Trong phản ứng đơn giản bc phản ứng và phân tử s bằng nhau. VD:
Br
2
→ 2Br v = k .[Br
2
], bc 1
I
2
+ H
2
→ 2HI v = k.[I
2
].[H
2
], bc 2
2NO + O
2
→ 2NO
2
v = k.[NO]
2
.[O
2
]
4, Đng học các phn ng đơn gin
4.1 Phản ứng bc 1: Xét phản ứng:
1
0
A sp
ta
t t a x
→
=
=−
Theo đnh nghĩa tc độ phản ứng, đnh lut tác dụng khi lưng có:
Tại t = 0 thì x = 0 thay vào ta có:
lnaC=
ln ln( ) . ln ln ln( ) .a C a x k t a a a x k t= − = − + − − =
ln .
a
kt
ax
=
−
(3) Phương trình động học phản ứng bc 1, dạng tích phân
[]
.[A]
dA
vk
dt
= − =
Phương trình động học phản ứng bc 1, dạng vi phân
• Thời gian bán hy t
1/2
: là khoảng thời gian mà s phân tử giảm đi một nửa.
Tại t = t
1/2
thì x = a/2 thay vào (3) ta có:
1/2
ln . ln2 .
/2
a
k t k t
aa
= =
−
1/2
ln2
t
k
=
(4) Thời gian bán hy ca phản ứng bc 1.
Nhn xét:
- t
1/2
ca phản ứng bc 1 chỉ phụ thuộc vào h/s tc độ phản ứng k, không phụ thuộc
vào nồng độ cht tham gia phản ứng.
- Đơn v ca hằng s k: s
-1
4.2 Phản ứng bc 2
a, Xét TH1: nồng độ đầu ca 2 cht tham gia phản ứng bằng nhau a = b:
1
0
A B sp
t a a
t t a x a x
+→
=
= − −
Theo đ/n:
2
[ ] ( )
[ ][ ] ( )
d A d a x
v k A B v k a x
dt dt
−
= − = = − = −
Bc 2, dạng vi phân
Giải pt vi phân:
11
.kt
a x a
−=
−
bc 2, dạng tích phân.
Thời gian bán hy:
1/2
1
.
t
ka
=
, t
1/2
phụ thuộc vào nồng độ đầu.
Đơn v ca hằng s k: L.mol
-1
s
-1
b, trường hp a ≠ b
1
0
A B sp
t a b
t t a x b x
+→
=
= − −
Dạng vi phân:
()
( )( )
d a x
v k a x b x
dt
−
= − = − −
Dạng tích phân:
1 ( )
ln
( ) ( )
b a x
k
t a b a b x
−
=
−−
4.3 Bc 3 và bc n
Chỉ xét trường hp nồng độ đầu các cht tham gia bằng nhau
Bc 3
Bc n
Dạng vi phân
3
()
dx
v k a x
dt
= = −
()
n
dx
v k a x
dt
= = −
Dạng tích phân
22
1 1 1
2
()
k
t
a x a

=−

−

11
1 1 1
( 1)
()
nn
k
nt
a x a
−−

=−

−
−

t
1/2
1/2
2
3
2.
t
ka
=
1
1/2
1
21
( 1) .
n
n
t
n k a
−
−
−
=
−
5. Cc phương php xc định bậc phn ng
5.1 Phương php thử
PP: Xc đnh nồng độ ca các cht tham gia sau mỗi khoảng thời gian khác nhau. Thay
vào phương trình động học bc 1, 2, 3,… đ tính hằng s k. Phương trình nào cho cc gi
tr k gần nhau nht thì là bc ca phản ứng.
VD. Khi tiến hành phản ứng phân hy acetone:
CH
3
COCH
3
→ C
2
H
4
+ CO + H
2
Áp suất tổng cng biến đổi như sau:
t (phút)
0
6,5
13
19,9
P
tổng
(N.m
-2
)
41589,5
54386,6
65050,4
74914,6
Hãy xc đnh bc phản ứng và tính hằng s tc độ ca phản ứng.
Giải:
Các cht ở th khí, áp sut riêng phần tỉ lệ với nồng độ (do V, T = const)
Gọi P
0
là áp sut ban đầu ca CH
3
COCH
3
, x là lưng CH
3
COCH
3
giảm sau thời gian t
1
.
3 3 2 4 2
0
10
0tP
CH COCH C
t
H CO H
t P x x x x
=
=−
→ + +
Giả sử là bc 1. Biu thức :
0
0
1
ln
P
k
t P x
=
−
(*)
Ta có: t = 0 thì P
0
= P
tổng
= 41589,5 (N.m
-2
)
Tại
0
1 0 0
32
2
PP
t t P P x x P x x
−
= = − + = + =
Suy ra:
1
00
00
3
22
t
P P P P
P P x P

−−
= − = − =
Thay vào (*) có:
0
0
2
1
ln
3
P
k
t P P
=
−
. Thay vào, tính k
1,2,3
suy ra k
tb
= 0.0256 (s
-1
)
5.2 Phương php đồ th
Bc 1
Bc 2
Bc 3
ln ( )c f t=
1
()ft
c
=
2
1
()ft
c
=
Trong đ c là nồng độ cht tham gia tại các thời đim khc nhau. Đồ th nào cho dạng
đường thẳng thì chính hàm đ tương ứng với bc ca phản ứng, và t đ suy ra hằng s
tc độ phản ứng là k = tanα.
5.3 Phương php cô lp
PP: Thay đổi nồng độ 1 cht tham gia và giữ nguyên tt cả các cht tham gia còn lại, t
đ đo tc độ phản ứng đ suy ra bc tng cht tham gia, cui cùng là bc ca cả phản ứng
Mô hình:
[ ] [ ] [ ]
x y z
v k A B C=
Giữ
[B],[C] const=
1
2
11
22
.[ ] [ ] [ ]
.[ ] [ ] [ ]
x y z
t
x y z
t
t t v k A B C
t t v k A B C
= =
= =
1
2
1
2
[]
[]
x
t
t
A
v
vA


=


, t đ tính đưc x
Làm tương tự với cht B và C đ tìm y, z t đ bc phản ứng : x + y + z.
6. Sự ph thuc của hằng s tc đ phn ng vào nhit đ. Năng lưng hoạt hóa
6.1 Quy tắc Van’t hoff:
Đi với phản ứng đồng th trong khoảng nhiệt độ không lớn, Van’t Hoff đưa ra quy tắc
rằng khi tăng nhiệt độ lên 10 độ thì tc độ phản ứng tăng t 2 đến 4 lần.
10T
T
k
k
+
=
Trong đó γ là hệ s nhiệt độ ca hằng s tc độ phản ứng. Tổng quát:
21
2
1
10
TT
T
T
k
k
−
=
γ thường t 2 đến 4.
Quy tắc van’t Hoff không áp dụng cho phản ứng d th và sinh hóa, do phản ứng d th
tăng rt chm theo nhiệt độ và ngưc lại, phản ứng sinh hóa tăng rt nhanh theo nhiệt độ.
6.2 Phương trình Arrhenius
- Đnh nghĩa NLHH E: là năng lưng ti thiu cần cung cp cho các tiu phân đ phản
ứng có th xảy ra.
- Phương trình Arrhenius:
Dạng vi phân:
2
ln
a
E
dk
dT RT
=
dạng tích phân:
.
a
E
RT
k Ae
−
=
Có
12
12
. , .
aa
EE
RT RT
TT
k Ae k Ae
−−
==
, giả sử E
a
là hằng s trong khoảng nhiệt độ T
1
– T
2
ta có:
11
12
22
11
12
11
ln
a
E
TT
R T T
a
TT
kk
E
e
k k R T T

−
−



−
= = −


Trong đó: E
a
là năng lưng hoạt hóa ca phản ứng (J/mol)
A là hằng s Arrhenius chỉ phụ thuộc vào bản cht ca phản ứng
R là hằng s khí lý tưởng 8,314 (J/molK)
k là hằng s tc độ phản ứng
T là nhiệt độ
o
K
6.3 Ý nghĩa của năng lượng hoạt hóa:
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

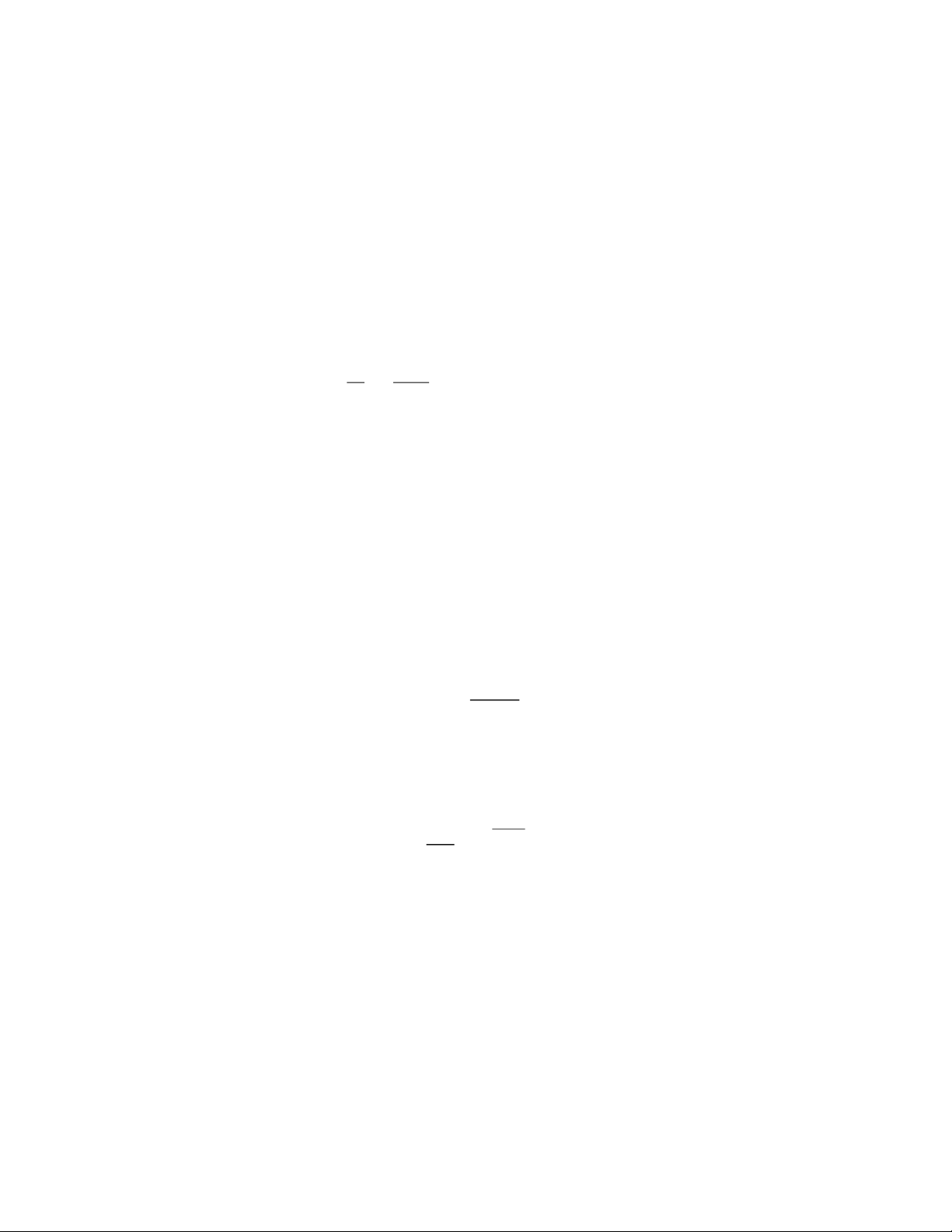
Preview text:

Chương I : ĐỘNG HỌC CÁC PHẢN ỨNG ĐƠN GIẢN VÀ PHỨC TẠP
1, Khái niệm về tốc độ phản ứng: VD: Xét phản ứng
aA+ bB → dD +eE 1 d[A] 1 d[B] 1 d[D] 1 d[E]
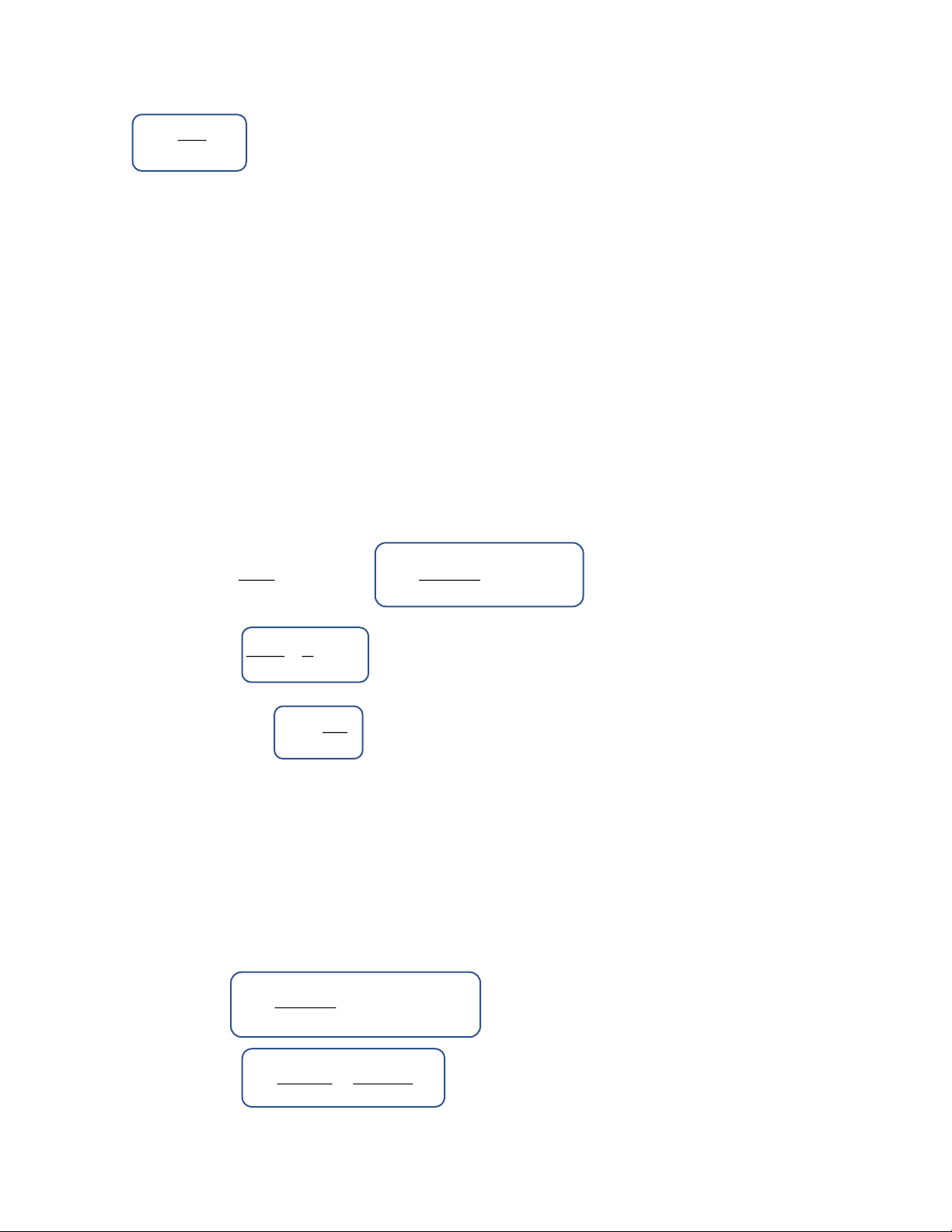
Vận tốc chung của phản ứng: v = − = − = + = + chung a dt b dt d dt e dt (1)
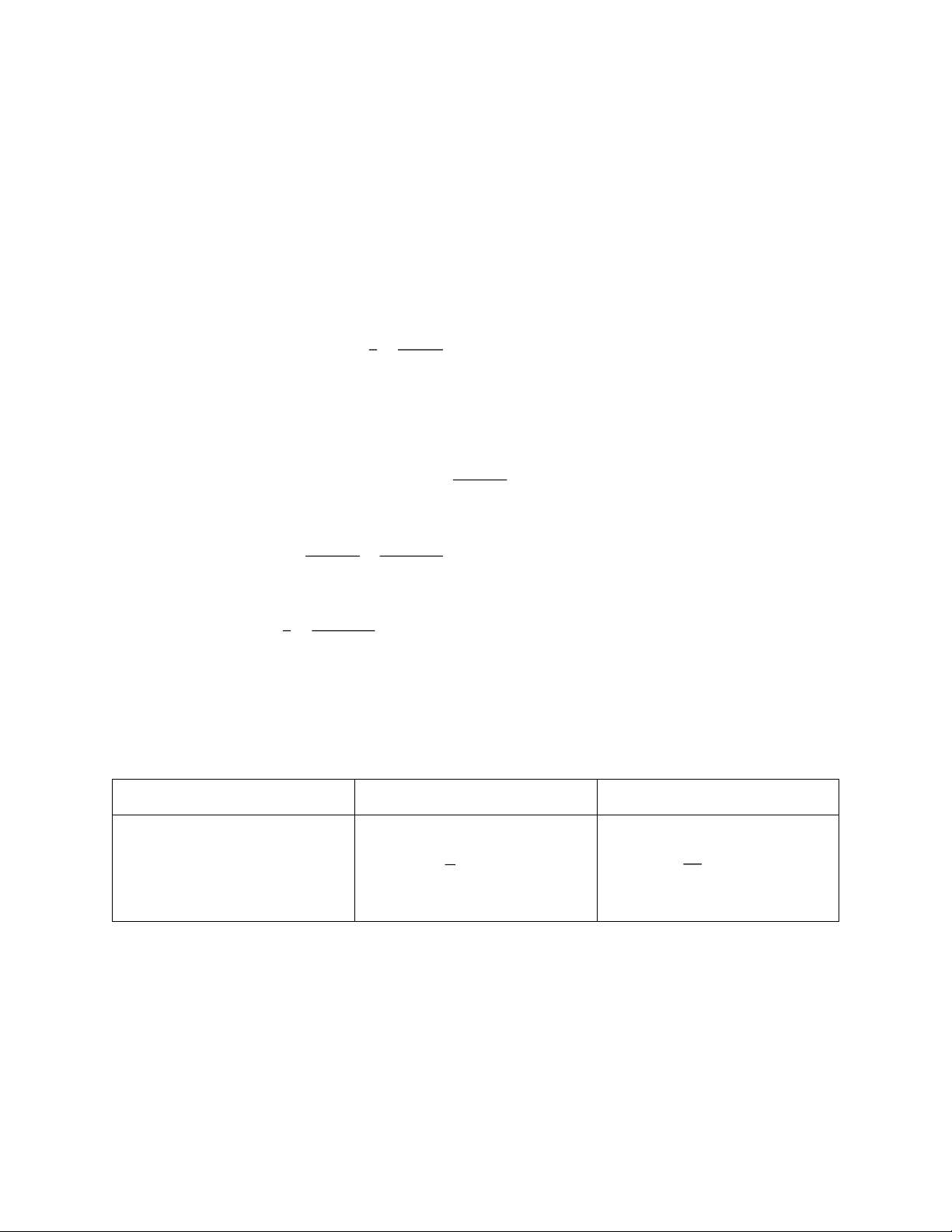
Từ đó ta có thể suy luận được vận tốc theo từng chất của phản ứng như sau: d[A] d[B] v = = − . a v ;v = = − . b v A chung B chung dt dt d[D] d[E] v = = +d.v ;v = = + . e v D chung E chung dt dt v x y v = k A B
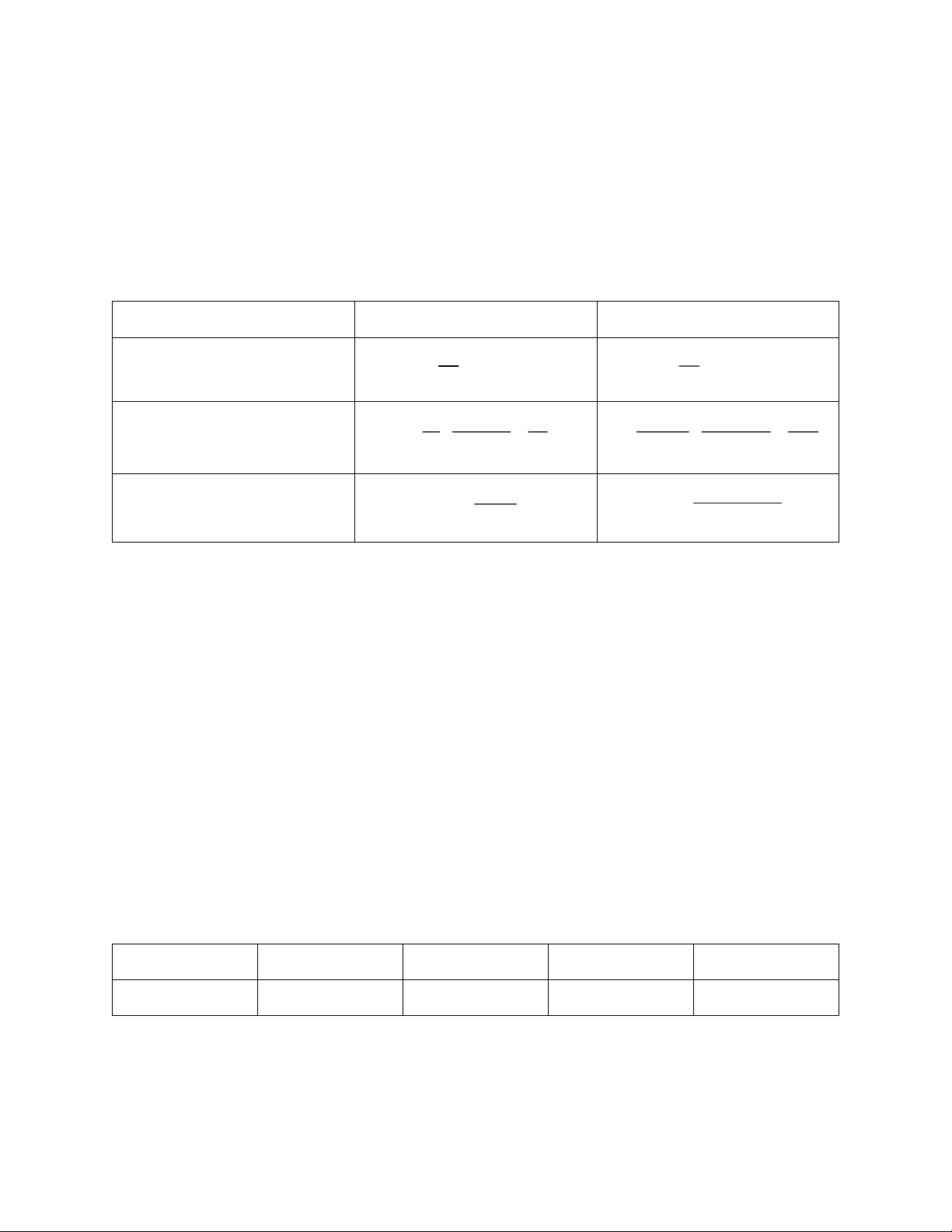
chung ta có thể xác định được từ biểu thức tác dụng khối lượng [ ] [ ] chung (2) 1 d[A] 1 d[B] 1 d[D] 1 d[E] Từ (1) và (2): v = − = − = + = +
= k[A]x[B]y chung a dt b dt d dt e dt
Trong đó: k: là hằng số tốc độ phản ứng chỉ phụ thuộc vào nhiệt độ, x,y là bậc đối với
chất A,B; x+y là bậc của phản ứng, x và y có thể bằng hoặc khác hệ số tỉ lượng (a, b)
2, Bậc và phân tử số của phản ứng
- Bậc của phản ứng: là tổng các lũy thừa nồng độ của các chất tham gia phản ứng
trong phương trình biểu diễn sự phụ thuộc của tốc độ phản ứng vào nồng độ chất pư.
- Phân tử số là hệ số tỉ lượng trong phản ứng hóa học.
- Phân tử số bao giờ cũng là một số nguyên, dương, bậc của phản ứng có thể là
nguyên hoặc phân số, dương, âm hoặc bằng 0.
3, Phản ứng đơn giản (pư sơ cấp)
Trong phản ứng đơn giản bậc phản ứng và phân tử số bằng nhau. VD:
Br2 → 2Br v = k .[Br2], bậc 1
I2 + H2 → 2HI v = k.[I2].[H2], bậc 2
2NO + O2 → 2NO2 v = k.[NO]2.[O2]
4, Động học các phản ứng đơn giản
4.1 Phản ứng bậc 1: Xét phản ứng: A → sp t = 0 a
t = t a − x 1
Theo định nghĩa tốc độ phản ứng, định luật tác dụng khối lượng có: d[A]
d(a − x) v = − = k.[A]  −
= k(a − x) dt dt
d(a − x) 
= −k.dt  ln(a − x) = −k.t + C a − x
Tại t = 0 thì x = 0 thay vào ta có: ln a = C
ln a = C  ln(a − x) = −k.t + ln a  ln a − ln(a − x) = k.t
 ln a = k.t a − x
(3) Phương trình động học phản ứng bậc 1, dạng tích phân d[A] v = − = k.[A] dt
Phương trình động học phản ứng bậc 1, dạng vi phân
• Thời gian bán hủy t1/2 : là khoảng thời gian mà số phân tử giảm đi một nửa. a Tại t = t  ln
= k.t  ln 2 = k.t
1/2 thì x = a/2 thay vào (3) ta có: 1/2 a − a / 2 ln2  t = 1/2 k (4)
Thời gian bán hủy của phản ứng bậc 1. Nhận xét:
- t1/2 của phản ứng bậc 1 chỉ phụ thuộc vào h/s tốc độ phản ứng k, không phụ thuộc
vào nồng độ chất tham gia phản ứng.
- Đơn vị của hằng số k: s-1 4.2 Phản ứng bậc 2
a, Xét TH1: nồng độ đầu của 2 chất tham gia phản ứng bằng nhau a = b:
A + B → sp t = 0 a a
t = t a − x a − x 1 d[A]
d(a − x) Theo đ/n: 2 v = −
= k[A][B]  v = −
= k(a − x) dt dt Bậc 2, dạng vi phân 1 1 Giải pt vi phân: − = k.t a − x a bậc 2, dạng tích phân. 1
Thời gian bán hủy: t = 1/2 k.a
, t1/2 phụ thuộc vào nồng độ đầu.
Đơn vị của hằng số k: L.mol-1s-1 b, trường hợp a ≠ b
A + B → sp t = 0 a b
t = t a − x b − x 1
d(a − x)
Dạng vi phân: v = −
= k(a − x)(b − x) dt 1 ( b a − x) Dạng tích phân: k = ln t(a − b) ( a b − x) 4.3 Bậc 3 và bậc n
Chỉ xét trường hợp nồng độ đầu các chất tham gia bằng nhau Bậc 3 Bậc n dx dx Dạng vi phân 3 v =
= k(a − x) v = = k a − x dt ( )n dt 1  1 1  1  1 1  Dạng tích phân k = −  k = − 2 2 2t    (a x) a  −  1 − 1
(n −1)t  (a − x)n n a −  3 n 1 2 − −1 t t = t = 1/2 1/2 2 2k.a 1/2 n 1
(n −1)k.a −
5. Các phương pháp xác định bậc phản ứng 5.1 Phương pháp thử
PP: Xác định nồng độ của các chất tham gia sau mỗi khoảng thời gian khác nhau. Thay
vào phương trình động học bậc 1, 2, 3,… để tính hằng số k. Phương trình nào cho các giá
trị k gần nhau nhất thì là bậc của phản ứng.
VD. Khi tiến hành phản ứng phân hủy acetone: CH3COCH3 → C2H4 + CO + H2
Áp suất tổng cộng biến đổi như sau: t (phút) 0 6,5 13 19,9 Ptổng (N.m-2) 41589,5 54386,6 65050,4 74914,6
Hãy xác định bậc phản ứng và tính hằng số tốc độ của phản ứng. Giải:
Các chất ở thể khí, áp suất riêng phần tỉ lệ với nồng độ (do V, T = const)
Gọi P0 là áp suất ban đầu của CH3COCH3, x là lượng CH3COCH3 giảm sau thời gian t1.
CH COCH → C H + CO + H 3 3 2 4 2 t = 0 P0 t = t P − x x x x 1 0 1 P
Giả sử là bậc 1. Biểu thức : 0 k = ln t P (*) − x 0
Ta có: t = 0 thì P0 = Ptổng = 41589,5 (N.m-2) P − P Tại 0
t = t P = P − x + 3x = P + 2x x  = 1  0 0 2 P − P 3P − P Suy ra: 0 0
P = P − x = P   − = 1 t 0 0 2 2 1 2P Thay vào (*) có: 0 k = ln t 3P . Thay vào, tính k − P
1,2,3 suy ra ktb = 0.0256 (s-1) 0 
5.2 Phương pháp đồ thị Bậc 1 Bậc 2 Bậc 3
ln c = f (t) 1 1 = f (t) = f (t) c 2 c
Trong đó c là nồng độ chất tham gia tại các thời điểm khác nhau. Đồ thị nào cho dạng
đường thẳng thì chính hàm đó tương ứng với bậc của phản ứng, và từ đó suy ra hằng số
tốc độ phản ứng là k = tanα.
5.3 Phương pháp cô lập
PP: Thay đổi nồng độ 1 chất tham gia và giữ nguyên tất cả các chất tham gia còn lại, từ
đó đo tốc độ phản ứng để suy ra bậc từng chất tham gia, cuối cùng là bậc của cả phản ứng
Mô hình: = [ ]x[ ]y[ ]z v k A B C Giữ [B],[C] = const
t = t v = k.[ ] x
A [B]y[C]z v  [A] x 1 1  1 t  1 1 t = 
 , từ đó tính được x
t = t v = k.[ ] x
A [B]y[C]z v  [A]  2 2  2 t   2 t  2
Làm tương tự với chất B và C để tìm y, z từ đó bậc phản ứng : x + y + z.
6. Sự phụ thuộc của hằng số tốc độ phản ứng vào nhiệt độ. Năng lượng hoạt hóa
6.1 Quy tắc Van’t hoff:
Đối với phản ứng đồng thể trong khoảng nhiệt độ không lớn, Van’t Hoff đưa ra quy tắc
rằng khi tăng nhiệt độ lên 10 độ thì tốc độ phản ứng tăng từ 2 đến 4 lần. kT 10  + = k T
Trong đó γ là hệ số nhiệt độ của hằng số tốc độ phản ứng. Tổng quát: T −T 2 1 k 2T 10 =  k 1 T
γ thường từ 2 đến 4.
Quy tắc van’t Hoff không áp dụng cho phản ứng dị thể và sinh hóa, do phản ứng dị thể
tăng rất chậm theo nhiệt độ và ngược lại, phản ứng sinh hóa tăng rất nhanh theo nhiệt độ.
6.2 Phương trình Arrhenius
- Định nghĩa NLHH E: là năng lượng tối thiểu cần cung cấp cho các tiểu phân để phản ứng có thể xảy ra. - Phương trình Arrhenius: − d ln k E a E Dạng vi phân: a =  dạng tích phân: = . RT k A e 2 dT RT − − a E a E Có R 1 T R 2 k = . A e , k = . T A e
, giả sử Ea là hằng số trong khoảng nhiệt độ T1 – T2 ta có: 1 T 2 T −  1 1  a E k  −  k −   T R T T T E 1 1 1  1 2  1 = e  ln a =  −  k k R T T   2 T 2 T 1 2
Trong đó: Ea là năng lượng hoạt hóa của phản ứng (J/mol)
A là hằng số Arrhenius chỉ phụ thuộc vào bản chất của phản ứng
R là hằng số khí lý tưởng 8,314 (J/molK)
k là hằng số tốc độ phản ứng T là nhiệt độ oK
6.3 Ý nghĩa của năng lượng hoạt hóa: