





Preview text:
Chương II: CÁC QUY TẮC CÂN BẰNG PHA
I. MỘT SỐ KHÁI NIỆM CƠ BẢN
vPha: là tập hợp tất cả các phần đồng thể trong hệ, có thành
phần và thuộc tính hóa học giống nhau và phân biệt với các
phần đồng thể khác bởi bề mặt phân cách
vHợp phần (r): Là các chất hợp thành hệ, mỗi hợp phần đều
có thể tách khỏi hệ và tồn tại độc lập ngoài hệ. Số hợp phần là
tổng số các hợp phần cấu tạo nên hệ.
v Số cấu tử (k): là số hợp phần tối thiểu để tạo thành hệ.
vBậc tự do (c): là số các thông số nhiệt động độc lập (tối
thiểu) để xác định trạng thái của hệ khi cân bằng
Bậc tự do = tổng số các thông số nhiệt động của hệ.
Một hệ được xác định bởi các thông số trang thái bao gồm:
+ Các thông số thành phần nồng độ của tất cả các cấu tử
trong các pha của hệ
+ Các thông số ngoài (T, P).
c = S(thông số trạng thái) - S(phương trình liên hệ)
II. CÁC ĐIỀU KIỆN CÂN BẰNG PHA
Xét hệ gồm k cấu tử (1,2,…k) và tồn tại trong f pha (a,b,…f).
Chúng nằm cân bằng với nhau chỉ khi thỏa mãn:
- Cân bằng nhiệt: nhiệt độ các pha bằng nhau Ta = Tb = … = Tf
- Cân bằng cơ: áp suất tác dụng lên tất cả các pha phải bằng nhau: Pa = Pb = … = Pf
- Cân bằng hóa học: thế hóa của các cấu tử trong các pha phải bằng nhau: μ a b f 1 = μ1 = … = μ1 μ a b f 2 = μ2 = … = μ2 … μ a b f k = μk = … = μk
III. QUY TẮC PHA GIBBS
Biểu thức toán học c = c(f, k, n) được gọi là quy tắc pha Gibbs
c: bậc tự do f: số pha k: số cấu tử
n: số thông số ngoài
vThiết lập quy tắc pha:
vPhương trình: c = k-f+2 vMột số ví dụ:
VD1: Xét hệ nước lỏng nguyên chất gồm 1 cấu tử và 1 pha
VD2: Xét hệ nước lỏng nằm cân bằng với hơi nước
VD3: Hệ gồm 3 pha nước lỏng, hơi, rắn cân bằng với nhau
IV. GIẢN ĐỒ PHA VÀ CÁC QUY TẮC CỦA GIẢN ĐỒ PHA
1. Giản đồ pha, cách biểu diễn các thông số nhiệt động
Đối với thông số T, P, V: Biểu diễn thường trên trục số.
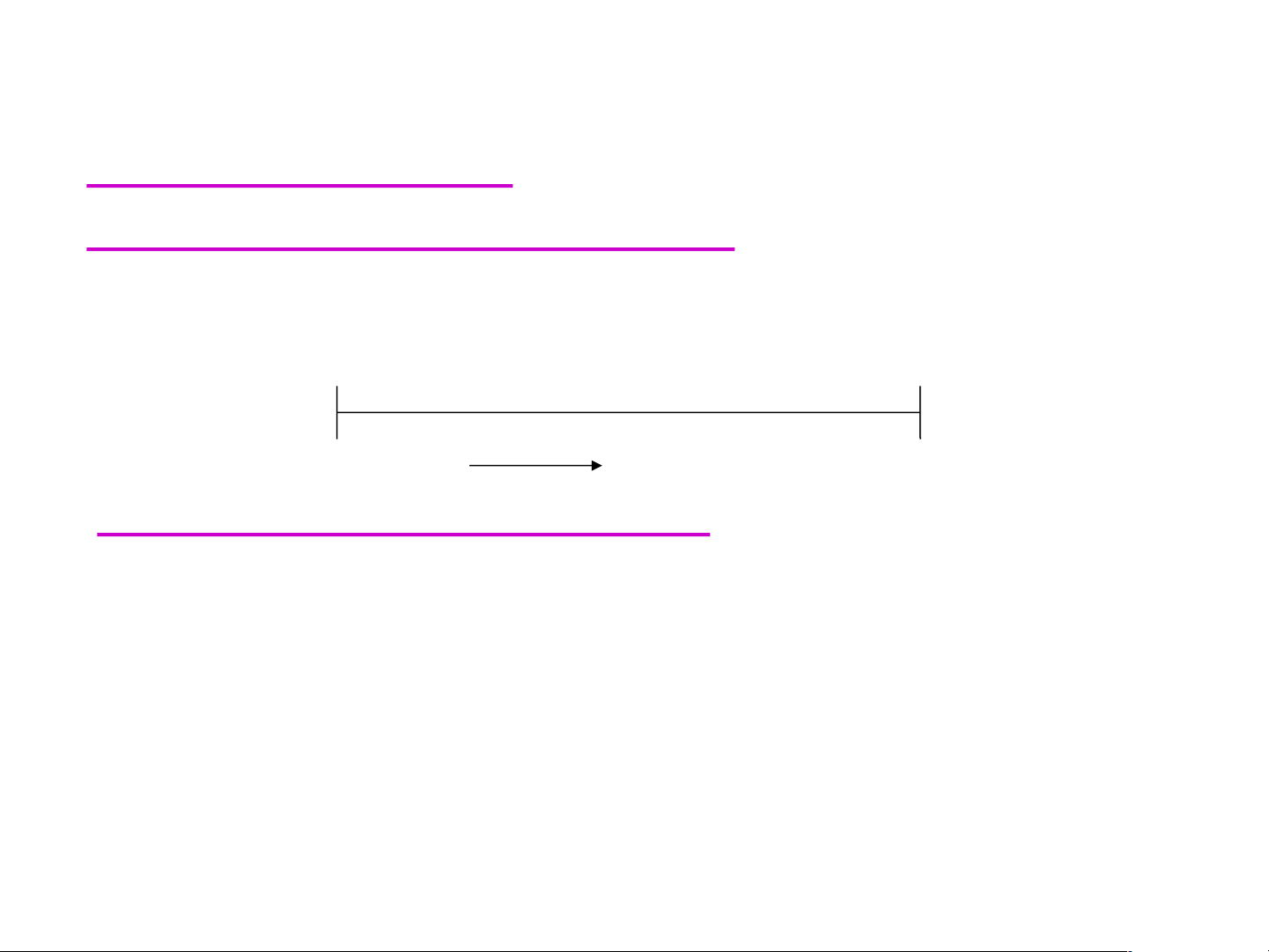
Biểu diễn thành phần hệ hai cấu tử: Thành phần cấu tử
thường dùng là nồng độ phần mol xi hoặc phần trăm khối lượng yi % A B xB 0 1
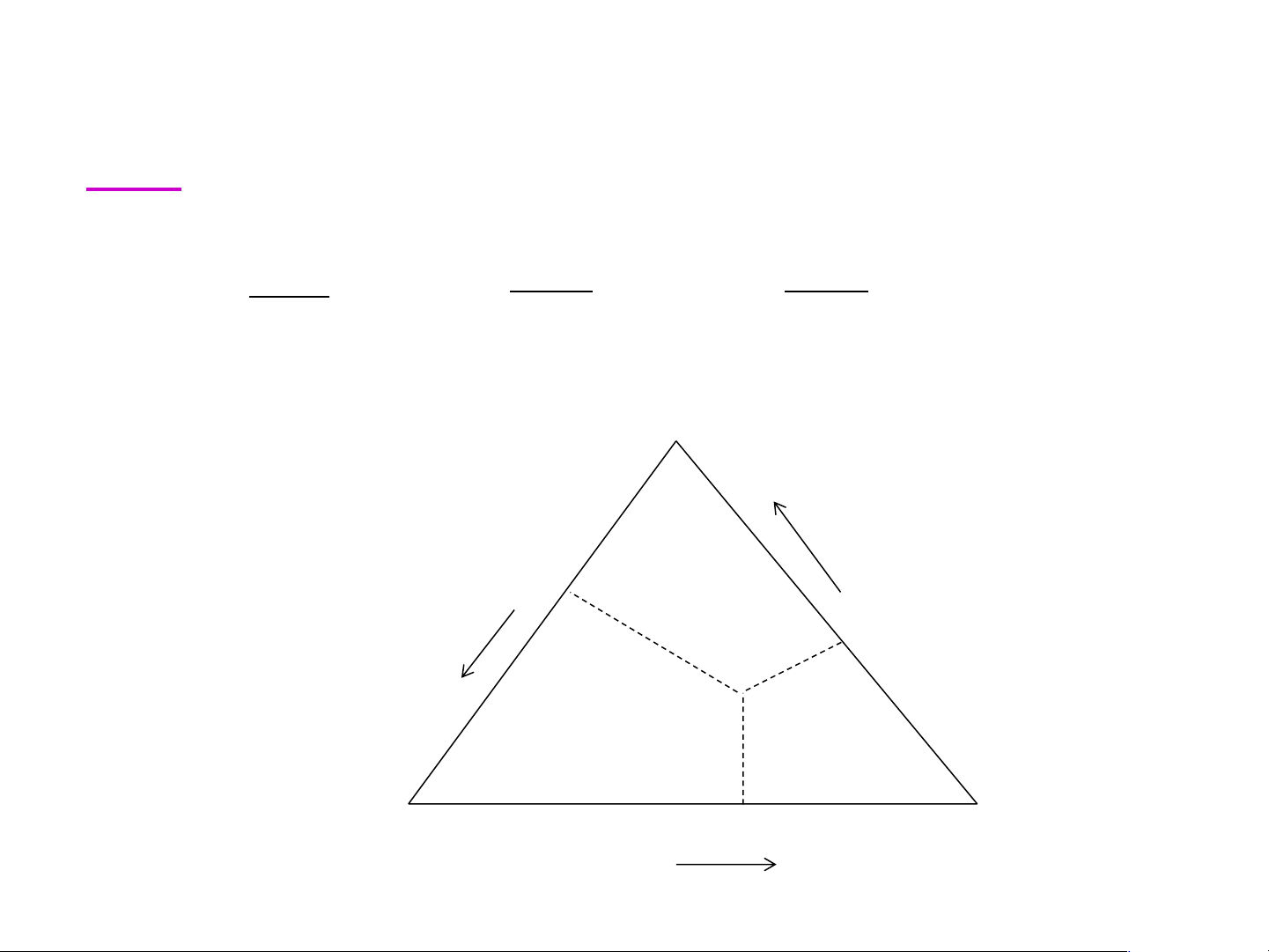
Biểu diễn thành phần hệ 3 cấu tử: biểu diễn trên 1 tam giác:
- Ba đỉnh của tam giác: thành phần của 3 cấu tử nguyên chất A, B, C.
-Ba cạnh tam giác: hệ 2 cấu tử tương ứng A – B, B – C, C – A
-Mỗi điểm trong tam giác biểu diễn một hệ ba cấu tử.
Thành phần mỗi cấu tử được xác định bằng tỉ lệ giữa
đoạn thẳng hạ vuông góc từ điểm biểu diễn xuống cạnh
tương ứng so với đường cao h.
IV. GIẢN ĐỒ PHA VÀ CÁC QUY TẮC CỦA GIẢN ĐỒ PHA
1. Giản đồ pha, cách biểu diễn các thông số nhiệt động
Ví dụ: Hệ D được biểu diễn trên hình gồm: DA' DB' DC' x = x = x = A h B h C h 1 A C’ B’ D 1 1 A’ C B xC
IV. GIẢN ĐỒ PHA VÀ CÁC QUY TẮC CỦA GIẢN ĐỒ PHA
1. Giản đồ pha, cách biểu diễn các thông số nhiệt động
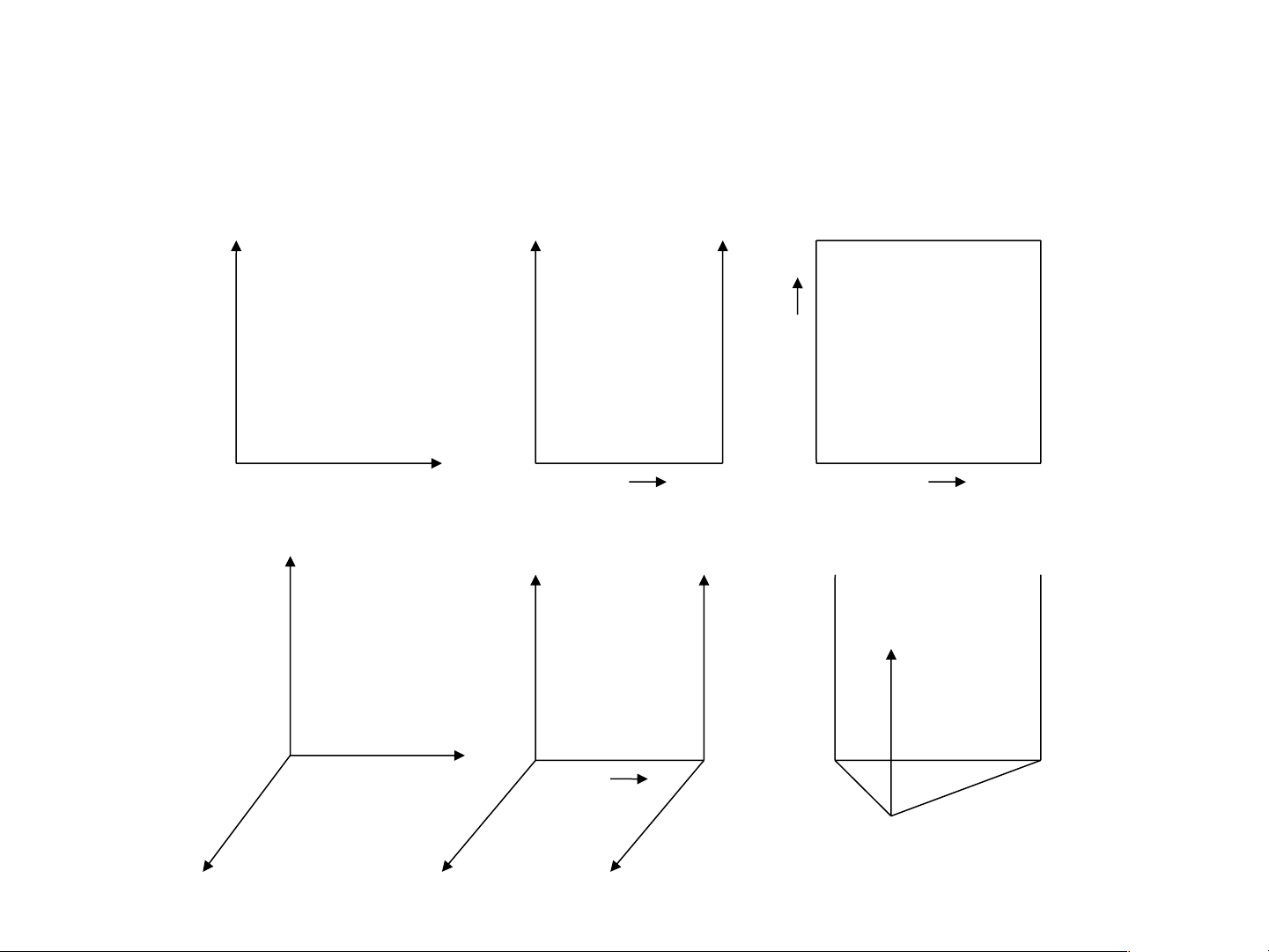
Ghép các tọa độ lại sẽ được các loại giản đồ khác nhau. P T T xhB T A A xB P T T T T B A A xB B V P P
IV. GIẢN ĐỒ PHA VÀ CÁC QUY TẮC CỦA GIẢN ĐỒ PHA
2. Các quy tắc của giản đồ pha
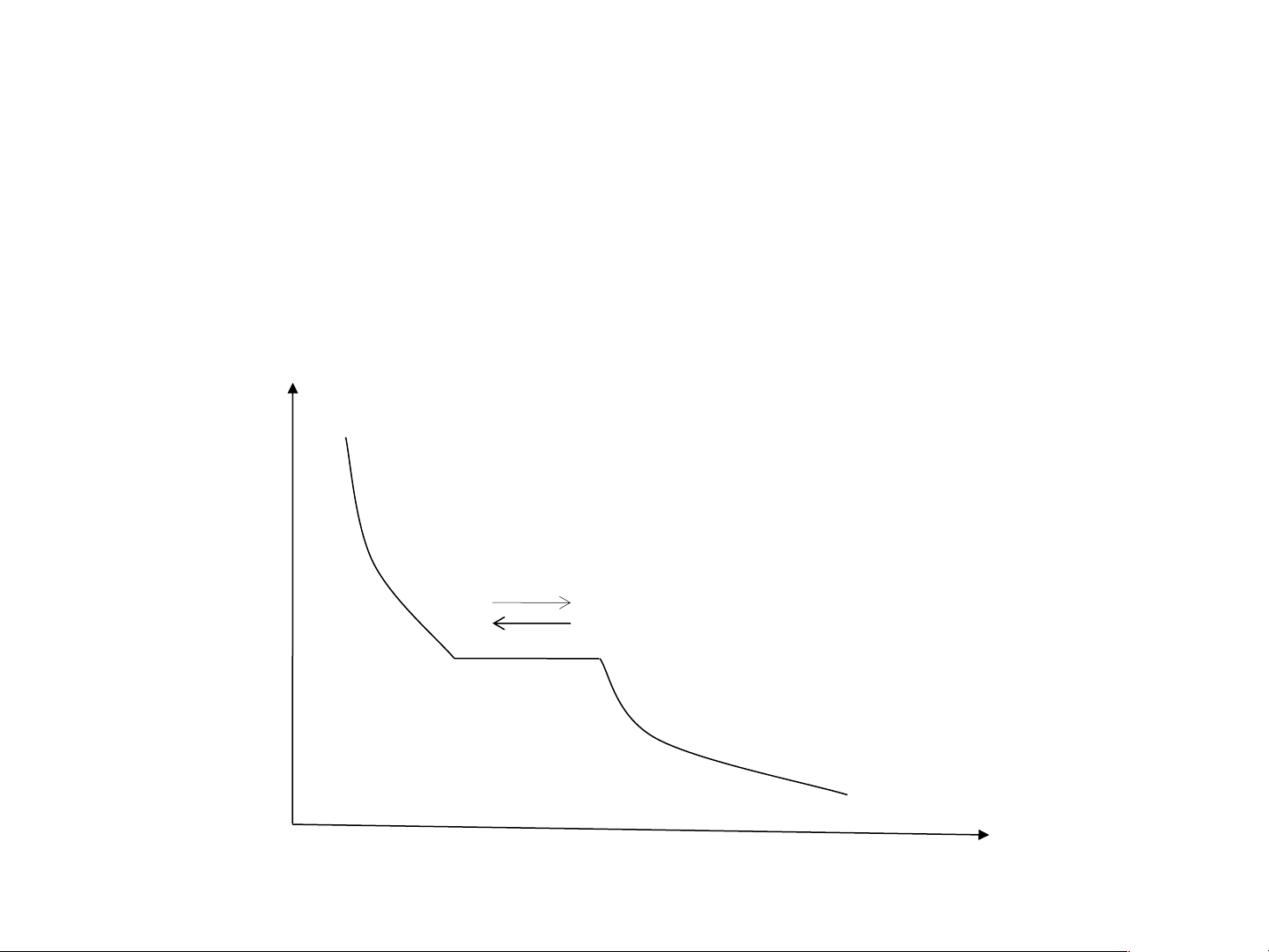
a. Quy tắc liên tục: Các đường hoặc mặt trên giản đồ pha
biểu diễn sự phụ thuộc giữa các thông số nhiệt động của
hệ sẽ liên tục nếu trong hệ không xảy ra sự biến đổi chất,
sự thay đổi số pha hoặc dạng pha. P lỏng lỏng hơi (1) (2) hơi V
IV. GIẢN ĐỒ PHA VÀ CÁC QUY TẮC CỦA GIẢN ĐỒ PHA
2. Các quy tắc của giản đồ pha
b. Quy tắc đường thẳng liên hợp:
Trong điều kiện T, P = const, nếu 1 hệ được phân thành 2
hệ con thì điểm biểu diễn của 3 hệ này nằm trên một
đường thẳng gọi là đường thẳng liên hợp. Hệ H = hệ H1 + hệ H2
Hệ H, H1, H2 gọi là 3 hệ liên hợp
IV. GIẢN ĐỒ PHA VÀ CÁC QUY TẮC CỦA GIẢN ĐỒ PHA
2. Các quy tắc của giản đồ pha
c. Quy tắc đòn bẩy:
Xét 3 hệ liên hợp H, H1, H2, gồm 2 cấu tử A, B
Hệ H biểu diễn bởi điểm H (thành phần cấu tử B là x)
Hệ H1 và H2 biểu diễn bởi điểm H1 và H2 (thành phần cấu tử B là x1 và x2)
Nội dung: trộn g1 đơn vị khối lượng H1 với g2 đơn vị khối
lượng H2, chúng tạo hệ H, lúc đó ta có tỉ lệ: g HH 1 2 = g HH 2 1




