Chương III Tích phân hàm một biến - Giải tích | Trường đại học Bách Khoa, Đại học Đà Nẵng
Chương III Tích phân hàm một biến - Giải tích | Trường đại học Bách Khoa, Đại học Đà Nẵng được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!tài
Môn: Giải tích 1(GT 1) 40 tài liệu
Trường: Trường Đại học Bách khoa, Đại học Đà Nẵng 410 tài liệu
Tác giả:
Preview text:
CHƯƠNG III : TÍCH PHÂN HÀM MỘT BIẾN
BÀI I : TÍCH PHÂN BẤT ĐỊNH (TPBĐ)
I) Nguyên hàm :
1) Định nghĩa : Cho hám y = f(x) xác định trong (a,b) . Nếu tồn tại
hàm F(x) sao cho F’(x) =f(x) , x ( , a ) b ta nói F(x) là m t ộ nguyên hàm c a
ủ f(x) trong (a,b).Chẳng hạn :
F(x) = sinx là nguyên hàm c
ủa f(x) = cosx trên R ( vì (sinx)’ = cosx )
F(x) = 2x là nguyên hàm c a ủ f(x) = x trên R 2
2) Các định lý về nguyên hàm:
a) Định lý 1: Nếu f(x) liên tục trên [a,b] thì tồn tại nguyên hàm trên đó .
b) Định lý 2: Cho F(x) là một nguyên hàm của f(x) trên [a,b] thì
F(x) + C cũng là một nguyên hàm của f(x) trên [a,b]
Nếu G(x) cũng là một nguyên hàm của f(x) thì G(x)=F(x)+C
II) Tích phân bất định ( TPBĐ ) :
1) Định nghĩa : Cho F(x) là một nguyên hàm của f(x) trên [a,b] thì
biểu thức F(x) + C được gọi là TPBĐ của f(x) trên [a,b] . Ký hiệu
f (x)dx F(x) C 2 x
*I cos xdx sin x c , xdx c 2
2) Các tính chất TPBĐ : Cho F(x) là nguyên hàm của f(x) thì :
a) Tính chất 1: [ f ( )xd ]x' f (x) ; d[ f ( ) x d ]
x f (x)dx
b) Tính chất 2 : d[F(x)] F '(x)dx f (x)dx F( )x c
c) Tính chất 3 : kf (x)dx k f (x)dx , k , R k 0
d) Tính chất 4 : [ f (x) g( )x]dx f (x)dx g(x)dx
e) Tính chât 5 : TPBĐ không phụ thuộc vào biến lấy tích phân.
3) Công thức TPBĐ một số p : hám sơ cấ
a) kdx kxC,C R ,k 0 b) 1 x dx dx 1 , 1 ln ; ; dx x dx c x c c 2 x c 2 1 x x x x c) x a x x
e dx e c ; s a dx
c ,0 a 1 ln a
d) sin xdx cosx ,c cosxdx sinx ,c tan xdx ln cosx ,c cot xdx ln sin x c
e) dx tan ; dx x c
cotx c 2 2 cos x sin x f) dx dx x
arcsin x c ; arcsin c 2 2 2 1 x a x a g) dx dx 1 arctan ; arctan x x c c 2 2 2 1 x a x a a h) dx 1 a x dx 1 x a ln c , ln c 2 2 2 2 a x 2a a x x a 2a x a i) dx 2
ln x x b c 2 x b j) 2 x 2 b 2 x bdx x b
ln x x b c 2 2 Các ví dụ : dx dx x 3 5 (5
)dx 5x dx 3 5 2 3 2 2 2 1) x 5 x 3 x ( 5) x 3 5x 1 x 5 2 3. ln
5ln x x 3 c ln5 2 5 x 5 2) 2 2 2 1 3x (1 x ) 2x dx dx 1 dx dx 2
2arc tan x c 2 2 2 2 2 2 x (1 x ) x (1 x ) x 1 x x 3) 1 cos2 x x sin 2 2 sin x xdx dx c 2 2 4
4)Các phương pháp tính TPBĐ :
4.1) phương pháp đổi biến :
a) Đổi biến x (t) : Cho y = f(x) liên tục đối với biến x và x (t) là hàm
khả vi đơn điệu đối với biến t , thì dx '(t)dt f ( )xdx f[(t)] '(t)dt Ví dụ 1) 2 I
1 x dx . x sin t t arcsin ; x t [
, ] dx cos tdt 2 2 2 2 1 cos 2t t sin 2t
arcsin x sin 2(arcsin x) I
1sin t cos tdt cos tdt dt c c 2 2 4 2 4 dx dt I
. x tan t, t ( , ) t arctan x và dx 2) 2 2 2 x 1 x 2 2 cos t costdt d (sint ) 1 1 I c c 2 2 sin t sin t sin t sin(arctan x)
b)Đổi biến u=u(x) : Cho u=u(x) là hàm khả vi liên tục đối với x
sao cho f(x)dx =g[u(x)]u’(x)dx=g(u)du f (x)dx g(u)du Ví dụ : 1) I= xdx 2 du 2
.u x 3 du 2xdx I
u c x 3 c 2 x 3 2 u 2) I= tan x tan dx e dx dx dx x tan x tan (e 3) 3 e d (tan x) 3 x e 3tan x c 2 2 2 2 cos x cos x cos x cos x
3) I = 1ln x dx x ln x Đặt u = 2 dx 2
1 ln x u 1 ln x 2udu
và ln x u 1 x 2 1 ln x 2 u udu u du 1 1 u 1 1 ln x 1 dx 2 2 (1
)du 2(u ln
) c 2 1 ln x ln c 2 2 2 x ln x u 1 u 1 u 1 2 u 1 1 ln x 1 4) I= 3x x 2 e (e ) x e dx dx 2 x x 2 e 1 (e ) 1 Đăt u = x x
e du e dx 3 x 2 e u 1 dx du (1
)du u arctan x
u c e arctan x e c 2 x 2 2 e 1 u 1 u 1
4.2) phương pháp tích phân từng phần : Cho 2 hàm u =u(x) ,
v =v(x) khả vi , liên tục đối với x .Ta có (uv)’=u’v+v’u (u ) v 'dx . v u ' dx .
u v ' dx uv vdu udv udv uv vdu Ví d : ụ
1)I = xcos xdx . u x du dx,dv cosxdx v sin x I xsin x sin xdx xsin x cosxc 2)I = arctan x dx 2 x Đặt u = arctanx dx dx 1 arctan x dx arctan x 1 x du , dv
v I ( )dx 2 2 2 2 1 x x x x ( x 1 x ) x x 1 x I = 2 arctan x dx d(1 x ) arctanx 1 arctan x x 2
ln x ln(1 x ) c ln c 2 2 x x 2(1 x ) x 2 x 1 x
5) TPBĐ một số hàm sơ cấp: 5.1) Hàm hữu tỷ : a) dx 1 dx 1 I
ln ax b c , a 0 , b) 1 ( ax b)
c ,a 0và 1 ax b a (ax b) a(1 ) Ví d : ụ 1) dx 1 dx 1 I
ln 3x 5 c , 2) I c 4 3 3x 5 3 (2x 5) 6(2x 5) c) dx I 2
ax bx c
Phân tích tam thức bậc 2 thành bình phương đủ và áp dụng các công thức TPBĐ : 2 2 2 2 b c b 2 c b b 2 4 ( ) [( ) ] [( ) ac b ax bx c a x x a x a x ] 2 2 a a 2a a 4a 2a 4a 1 d( x ) Ví d 3) ụ dx 2 2x 1 2 I arctan c 2 x x 1 1 2 3 2 3 3 ( x ) ( ) 2 2 A (2 ) ( Ab ax b B ) d) Ax B 2a 2a I dx dx 2 2
ax bx c
ax bx c I = 2 A
d (ax bx c) Ab dx A 2 ( ) ln ( Ab ) dx B ax bx c B 2 2 2 2a
ax bx c 2a
ax bx c 2a 2a
ax bx c 1 (2x2)6 Ví dụ 4) 2 x 5
1 d( x 2 x 5 ) d( x 1 ) 2 I dx dx 6 2 2 2 2 x 2x 5 x 2x 5 2 x 2x 5 ( x1) 4 1 1 x 1 1 x 1 2 2 I
ln x 2x 5 6. arctan
c ln x 2x 5 3arctan c 2 2 2 2 2 1 5) (2x 2) 4 2 x 3
1 d( x 2 x 3) d( x 1 ) 2 I dx dx 4 2 2 2 2 x 2x 3 x 2x 3 2 x 2x 3 (x 1) 4 1 2 1 x 1 2 1 2 x 1 I
ln x 2x 3 4. ln
c ln x 2x 3 ln c 2 2.2 x 1 2 2 x 3 5.2) Hàm vô tỷ : a) [ ,n I f x (x)]dx Đặt ( ) n n t
x t (x) x (
t) dx '(t)dt I f [ ( t),t] ' (t)dt Ví dụ : 1) dx I 3 1 x 1 Đặt 2 2 3t dt t 11 3 3 3 2 t x 1 t x 1 x t 1
dx 3t dt I 3 dt 1 t t 1 dt 3 3 2 3 2 3
I 3 (t 1) dt 3
(t 1) 3ln t 1 c ( x1 1) 3ln x1 1 c t 1 2 2 2) 1 x I dx x 2 x Đặt t= 2 x 2 x 2t 4t t x dx dt 2 2 2 2 x 2 x t 1 (t 1) 2dt 2 tan 2arctan x I arc t c c 2 t 1 2 x b) dx Ax B I và I dx
( cách làm tương tự TP hữu tỷ ) 2 2
ax bx c
ax bx c 1 Ví dụ 3) (2 x 2) 7 2 x 6
1 d (x 2x 10) d (x 1) 2 I dx dx 7 2 2 2 2 2 x 2x 10 x 2x 10 x 2x 10 (x 1) 9 2 2 I
x 2x 10 7 ln (x 1) (x 1) 9 c 1 (2 2x) 1 4) 2 xdx
1 d (3 2x x ) d (x 1) 2 I dx 2 2 2 2 3 2x x 3 2x x 2 3 2x x 4 (x 1) x 1 2
I 3 2x x arcsin c 2 5.3) Hàm lượng giác:
a) I = f (sin ,xcosx)dx
* Phương pháp chung : Áp dụng công thức lượng giác , đặt: 2 2 x dt 2t 1t 2t 1t 2dt t tan
x 2arctan t dx 2 vàsin x ,cos x I ( , ) 2 2 2 2 2 2 2 1 t 1 t 1 t
1 t 1 t 1 t Ví dụ 1) I = dx x 2t 2dt dt 2 2
. t tan sin x ,dx I 2 c c 2 2 2 1 sin x 2 1t 1t (t 1) t 1 tan x 1 2
*Các trường hợp đặc biệt:
- Nếu f(sinx,cosx) là hàm lẽ đối với cosx thì đặt t = cosx
- ------------------------------------------ sinx--------- t = sinx
- ------------------------------chẳn------ cosx ---------t = tanx
- ------------------------------------------ sinx --------- t = cotx Ví dụ 2) 3 4 2 4
I cos x sin xdx (1 sin x) sin x cos xdx Đặt 5 7 5 7 t t sin x sin 2 4 x
t sin x dt cos xdx I (1 t )t dt c c 5 7 5 7 3) dx 1 dx 2 2 (1 tan ) dx I x 6 4 2 2 cos x cos x cos x cos x Đặt 3 5 3 5 dx 2 4 2 t t 2sin x sin tan (1 2 ) sin x t x dt I t t dt t c x c 2 cos x 3 5 3 5
b) I sinaxsinbxdx ,I sinaxcosbxdx ,I cosaxcosbxdx
Áp dụng công thức lượng giác phân tích tích thành tổng Ví dụ 4) sin8x sin 2x cos8x cos2x
I sin 5x cos 3xdx dx c 2 16 4 c) sinn , cosn I xdx I xdx
* Nếu n lẽ thì áp dụng các trường hợp đặc biệt ở trên
* Nếu n chẳn thì áp dụng công thức hạ bậc trong lượng giác Ví dụ 5) 2 1 cos 2x 1 1 cos 2 4 2 x I cos xdx (
) dx ( cos2x )dx 2 4 2 4 x sin 2x 1 cos4x x sin 2x x sin 4x x sin 2x sin 4x I dx c c 4 4 4 4 4 8 2 4 8 6) 5 4 2 2
I sin xdx sin x sin xdx (1 cos x) sin xdx Đặt 3 5 3 5 2t t 2cos x cos 2 2 x
t cos x dt sin xdx I (1 t ) dt t
c cos x c 3 5 3 5
Chú thích : Một số hàm sau không có nguyên hàm dưới dạng sơ cấp : sinx cos x x 2 2 2 e x 1 ,
,sin x ,cosx ,e , , x x ln x x
BÀI II) TÍCH PHÂN XÁC ĐỊNH :
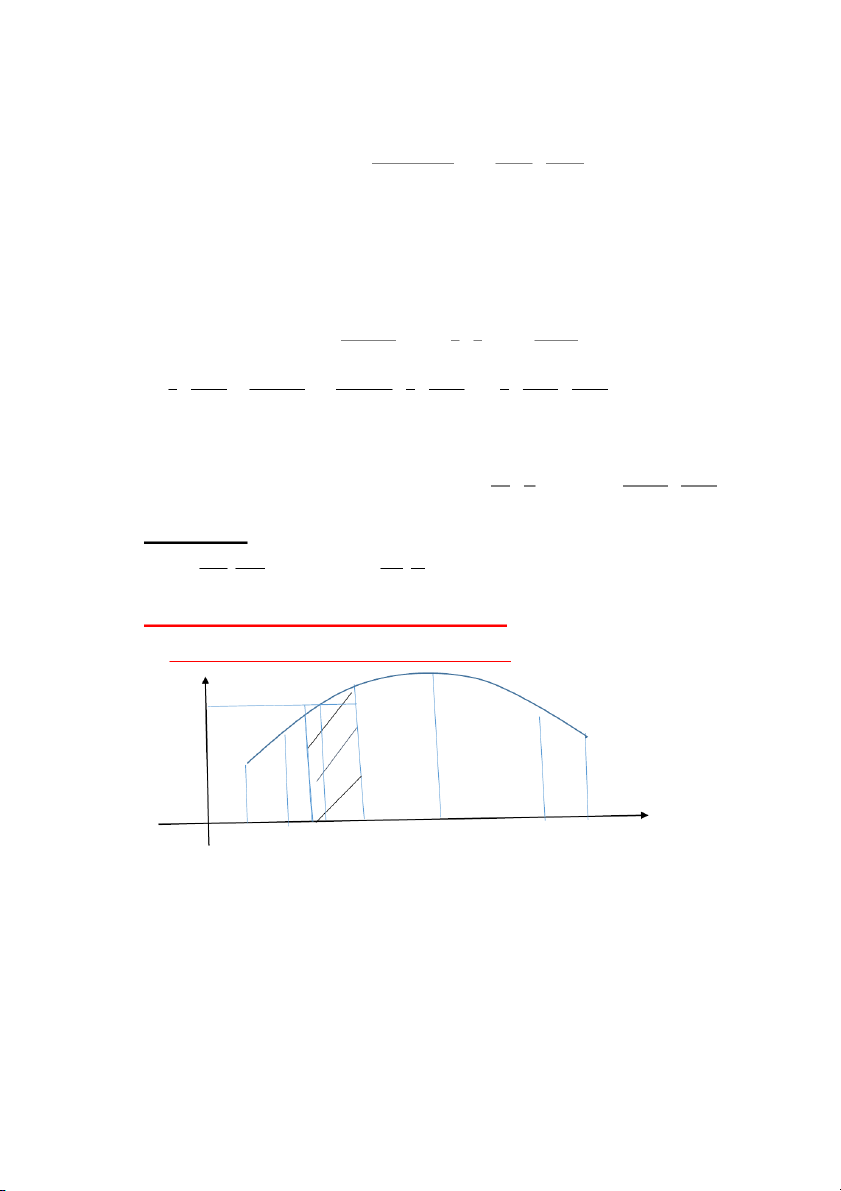
I ) Bài toán tính diện tích hình thang cong y f( ) Y=f(x) i A B O a= x x 0 x x x b i 1 i i n
Cho hinh thang cong AabB được giới hạn bởi đường y = f(x)>0 liên t c ụ
trên [a,b], đường x = a , x = b , tr c ụ ox T
. ính diện tích S c a ủ nó
Chia hình thang cong thành nhiều hình nh b
ỏ ởi các điểm chia trên [a,b]
như sau : a x x x .......... x x ........ . Trên mỗi đoạn 0 1 2 x b i 1 i n
[x , x ] chon ,i 1 , n ,Và x
x x .Khi x
khá bé thì diện tích hình thang cong i 1 i i i i i 1 i
tương ứng trong đoạn đó ấp xĩ vớ x
i diện tích hình chữ nhật có 2 cạnh là n n x
và f ( ) . Vây S f ( )x .Hay S lim f ( )x . i i i i i i 1 n i i1
II)Định nghĩa tích phân xác định(TPXĐ):
Cho hàm y = f(x) xác định trên [a,b] , Chia [a,b] bởi các điểm chia như
trên và cách chọn tương tự bài toán tính diện tích ở trên . Gọi n I f x là t ng t ổ ích phân c a
ủ y = f(x) trêm [a,b] . Khi cho n ( i) i i 1
n sao cho x khá bé , nếu t ng t ổ
ích phân trên tiến tới m t ộ giá trị xác i
định I không phụ thuộc vào cách chia [a,b] và cách chọn điểm trên , ta
gọi giới hạn đó là TPXĐ của y = f(x) trên [a,b] . Ký hiệu :
I= b f (x)dx lim I (maxx 0 ) n i n a Các chú thích : a ) a b a
f (x)dx 0 , ) b
f (x)dx f ( ) x dx a a b
III) Ý nghĩa hình học : Diện tích hình thang cong trong bài toán tính
diện tích ở trên là S = b f( )xdx . a
IV) Định lý điều kiện khả tích : Nếu y = f(x) liên tục trên [a,b] thì
tồn tại TPXĐ ( khả tích ) trên đó .
V) Các tính chất của TPXĐ : 1) b b b b b
kf (x)dx k f (x)dx , và
[ f (x) g(x)]dx f (x)dx g(x)dx a a a a a 2) Nếu b c b
c [a, b] thì f ( ) x dx
f (x)dx f (x)dx a a c 3) Nếu b b
f (x) g( ) x x [ , a ] b thì
f (x)dx g(x)dx a a 4) Nếu b
m f (x) M x
[a,b]thì m(b a) f (x)dx M (b a) a VI) Các định lý :
1) Định lý giá trị trung bình : Nếu f(x) liên tục trên [a,b] thì b c
[a,b] saocho f (x)dx f (c)(b a) a
2) Định lý đạo hàm theo cận trên : Nếu f(x) liên tục trên [a,b] thì hàm x
(x) f (t )dt là m t ộ nguyên hàm c a ủ f(x) trêm [a,b] a x (x)
a)[ f (t )dt]' f (x) , b)[
f (t )dt ]' f [ ( x)]'(x) Hê quả : a a ( ) x c)[
f (t )dt]' f [ (x)] '(x) f [ (x)] '(x) ( ) x 1 Ví dụ :1. Tìm x 2 1 1 2 1 1 2 [ cos t dt]' cos ( )'cos(sin ) x (sin ) x ' cos cos . x cos(sin ) x 2 2 2 sin x x x x x x x 3 3 cost dt [ cost dt]' 2) 0 0 0 3 lim ( ) lim limcos x 1 x 0 x 0 x 0 x 0 x' 3) nh l Đị
ý NIUTON-LEPNIT: Nêú f(x) liên t c ụ trên [a,b] có nguyên
hàm là F(x) trên đó thì :
b f (x)dx F( )b F( ) a F( ) x ] b a a Tha Ví d : ụ 2 3 x 8 2 1 x dx ] 0 3 3 0
VII) Các phương pháp TPXĐ : Tương tự như TPBĐ nhưng chú ý khi
đổi biến phải đổi cận tích phân và thay các giá đó vào nguyên hàm đã xác định. Các ví d : ụ 1) 9 3 2 3 x 1 2 t 1 23 I dx , t
x x t dx 2tdt I
2tdt (2t 2)dt x 1 t 1 3 4 2 2 3 e 4 2) dx , 1 ln dx du I u x du I 2 x 1 ln x x 1 1 u 3) 3 2 2 2 2 1 x dx udu u du 1 2 2 2 I
dx , u 1 x x u 1 I (1 )du 2 2 2 x x u 1 u 1 u 1 1 2 2 1 u 1 2 1 1 1 2 1 I [u ln ] 2 ln 2 ln 2 2 u 1 2 3 2 2 1 4) /3 xdx . ; dx I u x du dx dv
v cot x 2 2 sin x sin /4 x /3 /3 /3 3 3
I [x cot I [ x cot ] x
cot xdx [ xcot x ln sin x ] ln /4 /4 9 4 2 /4 2 2 5) e 1 e 1 dx 2 xdx e 1 I
ln(1 x)dx . u ln(1 x) du
,dv dx v x I [x ln(1 x)] 1 1x x 1 1 0 2 e 1 1 e 1 2 1 e 1 2
I [ xln(1 ) x ] (1
)dx [xln(1 )
x x ln(1 ) x ] e 1 0 0 1 0 x a *Chú thích a 2 f ( ) x dx khi f ( ) x chan
f (x)dx 0 a 0
Khi f (x) le
BÀI III) TÍCH PHÂN SUY RỘNG (TPSR) : I)Tích phân suy r ng c ộ ó cận vô cùng :
1) Định nghĩa 1 : Cho hàm y = f(x) xác định trên [ ,a ) , khả tích trên
[a,b] , với mọi b > a . Khi đó TPSR : b
f (x)dx lim
f (x )dx (1) b a a
Nếu giới hạn trên tồn tại hữu hạn ta nói TPSR hội tụ , nếu giới hạn bằng vô cùng hoặc không t n t
ồ ại ta nói TPSR phân kỳ
2) Định nghĩa 2: Cho hàm s
ố y = f(x) xác định trên ( , ] b , khả tích trên
[a,b] , với mọi a < b . Khi đó TPSR : b b
f (x)dx lim
f (x )dx (2) a a
3) Định nghĩa 3 : Cho hàm s
ố y = f(x) xác định trên R , khả tích trên
[a,b] với mọi a,b có a < b . Khi đó TPSR c
f (x)dx
f (x)dx
f (x)dx , c R (3) c
Ví dụ : Tính các TPSR sau : 1) b dx dx 1 b 1 I lim lim[ ] 2 2 1 (x 1) b
(x 1) b 1 x 2 1 1 2) 1 1 dx dx 1 I lim
lim[ln x 3 ] x 3 x 3 a a a a 3) b b x x 2 I e dx lim e dx , t
x x t dx 2tdt I lim 2 t te dt b b 0 0 0 b t t t t 1
u t du d ,
t dv e dt v e
I lim 2[ t
e e ] 2 lim ( 1 ) 2 b b b b e e 4) dx I , 0 x a Nếu b 1 lim dx I
lim[ln x ]b a b b x a khi b 1 Nếu 1 x b 1
1 I lim x dx lim[ ] 1 a a b b a 1 Kết luận dx hôi t khi ụ
1và phân kỳ khi 1 x a
II) Tích phân của hàm không bị chặn trong khoảng lấy tích phân :
1) Định nghĩa 4 : Cho hàm y = f(x) xác định trên [a,b) và lim f ( )x . xb0 Khi đó TPSR b b f ( ) x dx lim
f (x)dx (4) 00 a a
2) Định nghĩa 5 ; Cho hàm y = f(x) xác định trên (a,b] và lim f( )x . xa 0 Khi đó TPSR b b f ( ) x dx lim f ( ) x dx (5) 00 a a
3) Định nghĩa 6 : Cho y = f(x) xác định trên [a ,c)U(c,b] vàlim f (x) . x c Khi đó TPSR b c b f ( ) x dx f ( ) x dx
f (x)dx (6) . c a c
Ví dụ : Tính các TPSR sau : a) 1 1 dx dx 1 1 I lim lim [ ] 2 2 00 0 0 x x x 0 0 b) e e dx d (ln x) I lim
lim [ln ln x ]e 1 00 0 0 x ln x ln x 1 1 c) b b dx I lim
(x a) dx , 0 0 0 ( x ) a a a Khi b dx 1 I lim
lim [ln x a ]b 0 0 0 0 a x a a khi 1 Khi 1 (x a) b 1 1 I lim [ ] a (b a) 0 0 1 khi 1 1 Kết luận b b dx dx và 0
hội tụ khi 1 và phân kỳ khi 1 (x a) (b x) a a III) Các tiêu chuẩn h i ộ t phâ ụ n kỳ c a
ủ TPSR : các tiêu chuẩn này được
minh họa bằng TPSR có cận trên vô cùng( tương tự cho các TPSR khác)
1) Tiêu chuẩn 1 : Cho 2 hàm f(x) , g(x) > 0 xác định trên [a,) khả
tích trên [a,b] với mọi b > a sao cho f(x) > g(x) > 0 trên đó ; a) Nếu
g(x)dx phân ky
f (x)dx phân ky a a b) Nếu f ( ) x dx hôi tu ( g ) x dx hôi tu a a
2) Tiêu chuẩn 2 : Cho 2 hàm f(x) , g(x) > 0 , x [ , a ) , Khả tich trên
[a,b] với mọi b > a . G i ọ k = f (x) lim
x g( x) Nếu 0 thì
f (x )dx và g (x )dx cùng hội t ho ụ ặc cùng phân kỳ. a a
Nếu k = 0 thì f(x) < g(x) ( áp dụng tiêu chuẩn 1)
Nêu k = f ( )x g(x) ( áp d ng t ụ iêu chuẩn 1 ) Ví dụ : Xét sự h i ộ t , phâ ụ n kỳ của các TPSR sau : 1) ln(1 ) x dx ln(1 ) x ln 2 I ,x 1 0 2 3 2 3 2 1 x x 3 x Ta có ln2 ln2 dx dx ỳ ậy I cũng phân kỳ 2 phân k v 2/3 x 1 3 1 x 2 2 2) x x 1 e e e 1 2 I
dx ,x 1 x 1 2 3 3 3 x x x ex 1 Ta có 1 1 dx dx ộ ụ ậy I cũng hộ ụ 3 h i t , v i t 3 1 ex e 1 x 3) 2 2 2x x 2x x 1 I dx . f ( ) x 0 và g( ) x 0 3 3 3 4x 3 4x x 1 Ta có 2 3 f ( ) x 2x x 1 k lim lim Mà ( ) dx g x dx
phân kỳ , vậy I cũng 3
x g (x ) x 3 4x 4 x 1 1 phân kỳ. 4) arctan x arctan x 1 I
dx , f (x ) 0,g (x ) 0, x [1,) 3 3 3 4 3 4 1 1 x 1 x x 4 f ( ) x x 3 k lim lim(arctan x ) , Mà ( ) dx g x dx
hội tụ , Vậy I cũng hội 4 4/3
x g(x) x 1 x 2 x 1 1 tụ. x x f (x)
0,x[0,1), lim f (x) , 1 5) x 1 x
(1 x )(1 x)(1 x) x I dx . 4 2 1 0 4 0 1 x 1 g (x ) 0, x
[0,1), lim g (x) x1 0 1 x 1 1 f (x) x 1 dx k lim lim
.Mà g(x)dx hội tụ , Vây I cũng 1/2 x 1 0 x 1 0 2 g (x)
(1 x )(1 x) 2 (1 x) 0 0 hội tụ . 6)I= 1 2 x dx 2 5 3 0 (1 x ) Ta có f(x) = 2 2 x x 0, x [0,1), lim f ( ) x 2 5 5 5 3 3 1 0 (1 x )
(1 x ) (1 x ) x g(x) = 1 1 0, x
[0,1) và lim g( ) x 5/3 5 3 1 0 (1 x) (1 x) x 2 f ( ) x x 1 dx k lim lim . Mà 1 1
g(x)dx phân kỳ , Vậy I cũng x 1 0 x 1 0 3 5 3 5 g (x) (1 5/3 x) 2 (1 x) 0 0 phân kỳ. BÀI IV) ỨNG D ỤNG TPXĐ :
I) Tính diện tích hình phẳng :
1) Diện tích hình thang cong : Theo bài toán tính diện tích thì
diện tích là S = b f( )x dx y y=f(x) a
2) Diện tích hình :phẳng bất kỳ
Cho hình phẳng giới hạn o a b x
đường y = f(x) , y = g(x) x = a , x = b y y=f(x)
là S = b f (x) g(x)dx O a b x y=g(x) a
3)Nếu hình phẳng được giới hạn bởi đường cong có phương trình tham
số : x x(t)
, t thì S y(t).x '(t)dt
y y (t ) 4)Nếu hình ph t
ẳng đươc cho trong hệ ọa độ cực :Đường cong có Phương trình 2 () , r r f
thì S d . 2
Ví dụ : 1) Tính diện tích hình phẳng được giới hạn b ng ởi các đườ 2 1 , x x y y
. Hoành độ giao điểm x = -1 ,x= 1 2 y y 2 1 x 2 2 1 y 0 x 2 1 x Diện tích S = 1 2 3 1 x x 1 1 2 (
)dx 2[arctan x ] y 2 0 1 x 2 6 2 3 0
2)Tính diện tích một nhịp Xycloit có phương trình :
x a(t sint )
,a 0,0 t 2 x '(t ) a (1 cost ) 0 x y
a(1 cost ) Diện tích S = 2 2 2 2 2 2 4 ( ) '( ) (1 cos ) 2 sin t y t x t dt a t dt a dt( BT) y 2 0 0 0 3)Tính diện tích hình x Diện tích S = 2 2 2 1 1 2 2 2 2 4 r d
4a (1 cos) d 2a sin d ( BT ) 2 2 2 0 00 0
II) Tính thể tích vật thể : y
1) Vât thể bất kỳ : Cho vật thể được giới hạn S(x)
2 mặt x = a , x = b . Cắt vật thể bởi mặt phẳng a 0 b x
góc với ox có hoành độ x , g i ọ S(x) là diện tích c a ủ
thiết diện thì thể tích vật thể là S=b S(x)dx a
2) Vật thể tròn xoay quanh ox: Cho hình thang cong giới hạn bởi
y = f(x) > 0 ,x = a , x = b , tr c
ụ ox quay quanh ox ta được vật thể tròn
xoay có thể tich S = b 2
f (x)dx y y=f(x) a a o b x
3) Vật thể tròn xoay quanh oy :Cho hình phẳng giới hạn bởi x = g(y) ,y = c , y = d , tr c ụ oy quay quanh oy y x=g(y)
Ta được vật thể tròn xoay có thể tích S = d 2
g (y)dy o x c
Ví dụ : Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi đường
y = ex , x = 0 , x = 1 , y = 0 quay quanh ox y S=1 2 x e x 2 1 2 (e ) dx [ ] (e 1 ) o 1 x 0 2 2 0
III) Tính độ dài đường cong :
1) Độ dài đường cong y =f(x) với b 2
a x b là S 1 y ' dx a
2) Độ dài đường cong có phương trinh tham số :
x x (t ) 2 2 ,
t là S
x ' (t ) y ' (t )dt
y y (t )
3) Độ dài đường cong trong hệ tọa độ cực có phương trình 2 2
r f () , là S
r r ' d
Ví dụ : 1)Độ dài đường y = 2x ,0 x 2 là 2 2 2 x 1 2 2 2 2 2 S 1 y ' dx 1 x dx [
1 x ln x x 1 ] (BT) 0 2 2 0 0
2)Độ dài đường Axtroit 3 2
x a cos t 2 2
,0 t 2 là S
x ' (t ) y ' (t )dt 6a ( BT) 3
y a sin t 0 BÀI TẬP 1) Tính các TPBĐ sau ; a) 2 sin 2xdx 3 3 2 tan , ) , ) 5 , ) dx , ) dx xdx b c x x dx d e 2 4 cos 2 x x 4 x x 1 x f) x cosx arc tan x x 2 xdx dx , g) dx , ) h
sin(ln x)dx , k) dx , l) 2 2 2 2 sin x x x x 1 x 3x 2 2) Tính các TPXĐ sau : 16 3 2 l n2 ln5 x x 3 dx 1 x e e x x 1 2 2 a) , b) dx ,c) 1e dx ,d ) dx ,e) dx 2 x 2 x 9 x x e 3 2 x 3 x 2 0 1 0 0 2 /4 /2 /4 3 /2 x sin 5 xdx x 2 2 3 f )
tan xdx , g) e cos xdx , ) h k) x 1 x dx ,l) cos x cos xdx 3 cos x 0 0 0 0 /2 0 khi f ( ) x le Chú thích a f (x) a dx
2 f (x)dx khi f (x) chan a 0 3) Tính các TPSR sau : e 0 1/ x 1 dx dx ln ) , ) ) x , ) dx ) e a b c dx d e dx f ) x ln xdx 3 2 2 x x ln x x 2 x x 1 1 x 1 x 2 1 1 0 2 2 2 1 3 ) dx , ) x ) xdx , ) dx g h dx k l 2 2 2 (x 2)(x 1) 1 0 4 x 0 1 x 2 4x x 3 4) Xét sự h i ộ tụ , phân kỳ c a ủ : 2 2 1 1 2 x 3 ln(1 x ) x x 2 a) dx b) dx c) x xe dx d ) dx e) dx 3 sin x 2 x 1 x e 1 1 2 0 0 0 1 x 5 ln x x x ln ) ) ) x f dx g dx h dx 3 5 x 5 7 2 x 2e 1 1 1 1 x 1 x 1