

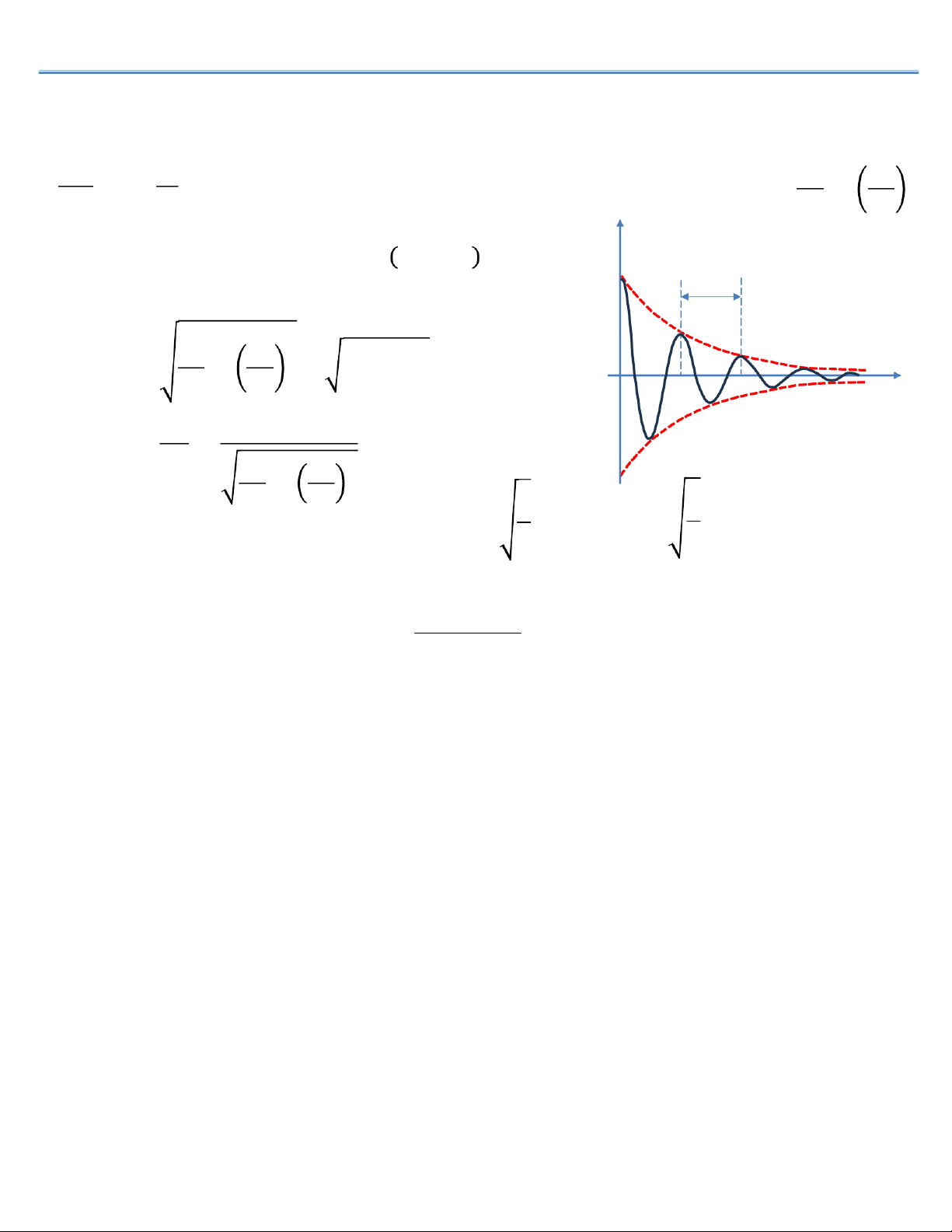



Preview text:
CHƯƠNG IX
DAO ĐỘNG ĐIỆN TỪ
9.1. Dao động điện từ tự do trong mạch RLC U0
9.1.1. Dao động điện từ điều hòa
a. Chuyển đổi năng lượng điện từ trong mạch LC
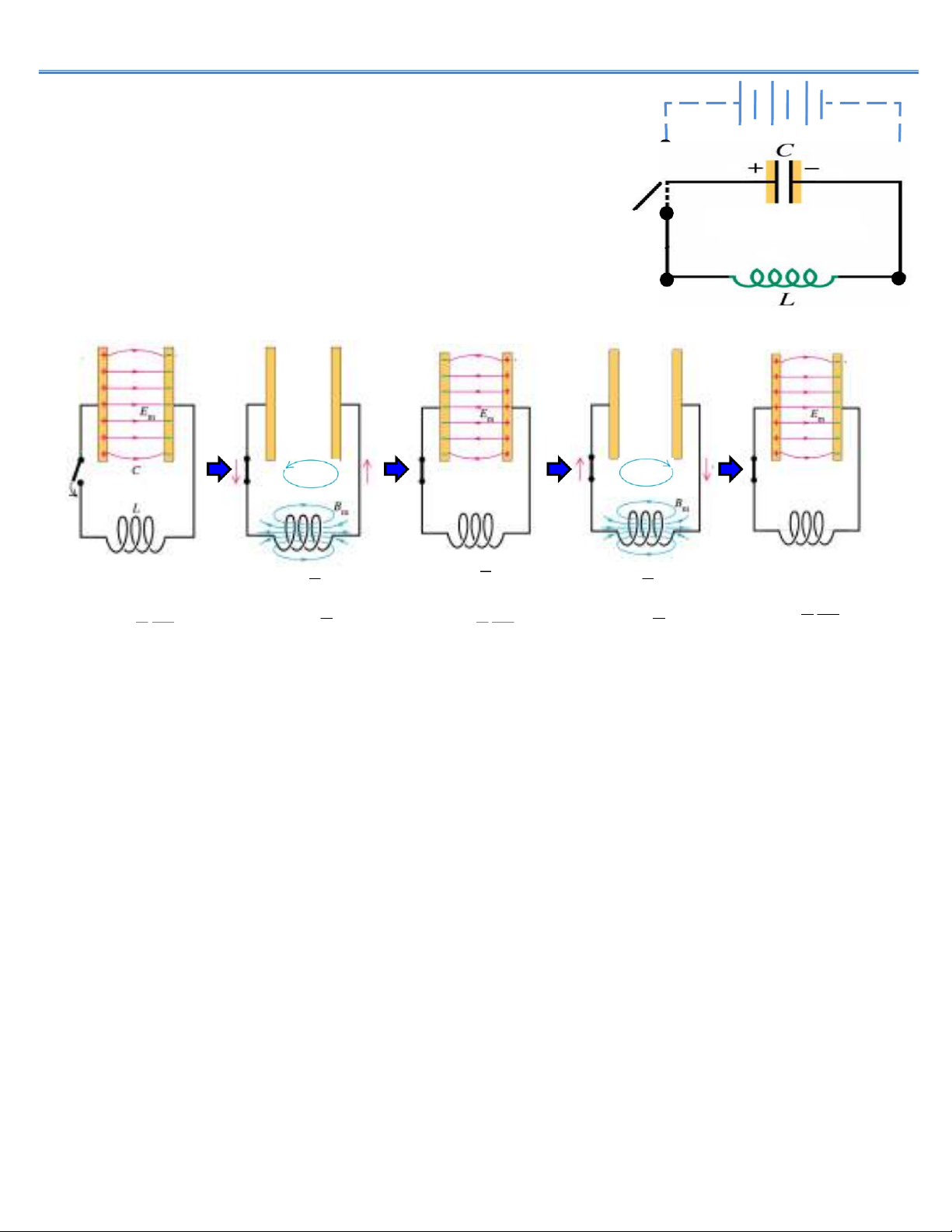
F Mạch điện dao động LC:
Cuộn dây L và tụ điện C; 1
¨ Nạp điện cho tụ C: q 0 = CU0 để cung cấp năng lượng. K
Cườngđộdòngđiệntrongmạchvàđiệntíchcủatụcódạng
hìnhsin vớibiênđộkhông đổi.Vìvậy,daođộng điệntừ 2
trongmạchđượcgọilàdaođộngđiệntừđiềuhòa.
¨ Daođộngđiệntừđiềuhòachỉdomạchdaođộngquyết
định,khôngcósựtham giacủacácyếutốbênngoài.Vì vậy
daođộngđiện từtrongmạchđượcgọilàdaođộngriêng +q0-q0 " " " = ! " ! "= ! = ! " = ! " = ! ! ! ! ! # " ! #$= (!" # " ! #$= (!" # " # " " ! " ! #$ $ = #$ = = ! ! #$%&'! " ! ! #$%&'! " ! !
¨ Tạo ra dao động điện từ điều hòa nếu như ko có mất mát năng lượng
9.1. Dao động điện từ tự do trong mạch RLC
9.1.1. Dao động điện từ điều hòa
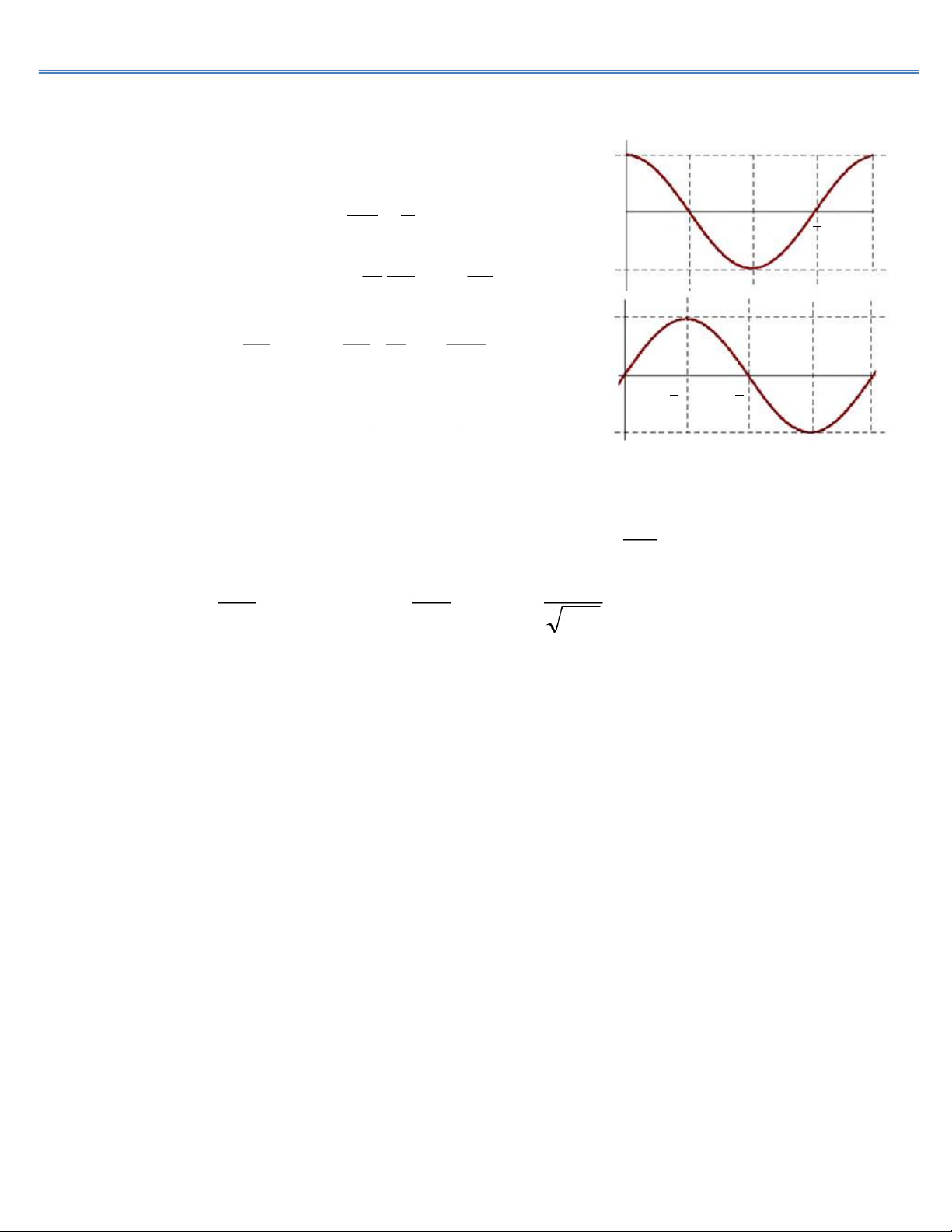
b. Phương trình dao động điện từ điều hòa + q0 W q(t)
F NL toàn phần của mạch dao động bảo toàn: $ ⇔ + )= " w $ t ®
W = We + Wm = const C' !"#$%" # ! " " " ! ! ! T $( $ ! ! ! %!% !# - q0
¨ Đạo hàm theo thời gian: + $# = ! C !" !" I(t) ' Imax ⇒ !# !# # ! # % " & = + ' C # " $ $ = ! !" !" % !" wt ® " " " ! ! ! T " ! ! ! $ ! %
¨ Phương trình dao động: + ! = $ " # ! " Imax $% "#
¨ Nghiệm: q = q0cos(
w0 .t + j) Þ I = dq/dt=
w0 q0sin( w0 .t + j) & % ¨ Thay − nghiệm vào (2 + ), có: + ! +ω !=" "#$( ! ω !)φ " "#$ (ω! ) φ ! #$ & ! & ! ! ⇒ ω % = = % "#$ ω ω
là tần số dao động !" % !" % !" riêng mạch LC.
9.1. Dao động điện từ tự do trong mạch RLC
9.1.1 . Dao động điện từ điều hòa Dao động cơ Dao động điện CL " " " ) ! " ! F = Nă ! ng lượn+g: * = () &' ! = "!#$%+ *= C' !"#$% ! ! ! ( ! " $ ! # # F $ ! "
Phương trình dao động: + ! = ! " + ! = ! $% " # $% "#
F Dạng dao động: x (t)= x0.cos(
w0.t + j)q(t) = q0cos(
w0 .t + j)
F Tương quan giữa các đại lượng: = $ # # ⇔ " x " " #$ ⇔ # " "!" "
Û q; k Û 1/C; m Û L; v Û I; ω ! ! ! # #$ ⇔ ! $!" " " ! ! !
9.1. Dao động điện từ tự do trong mạch RLC
9.1.2. Dao động điện từ tắt dần
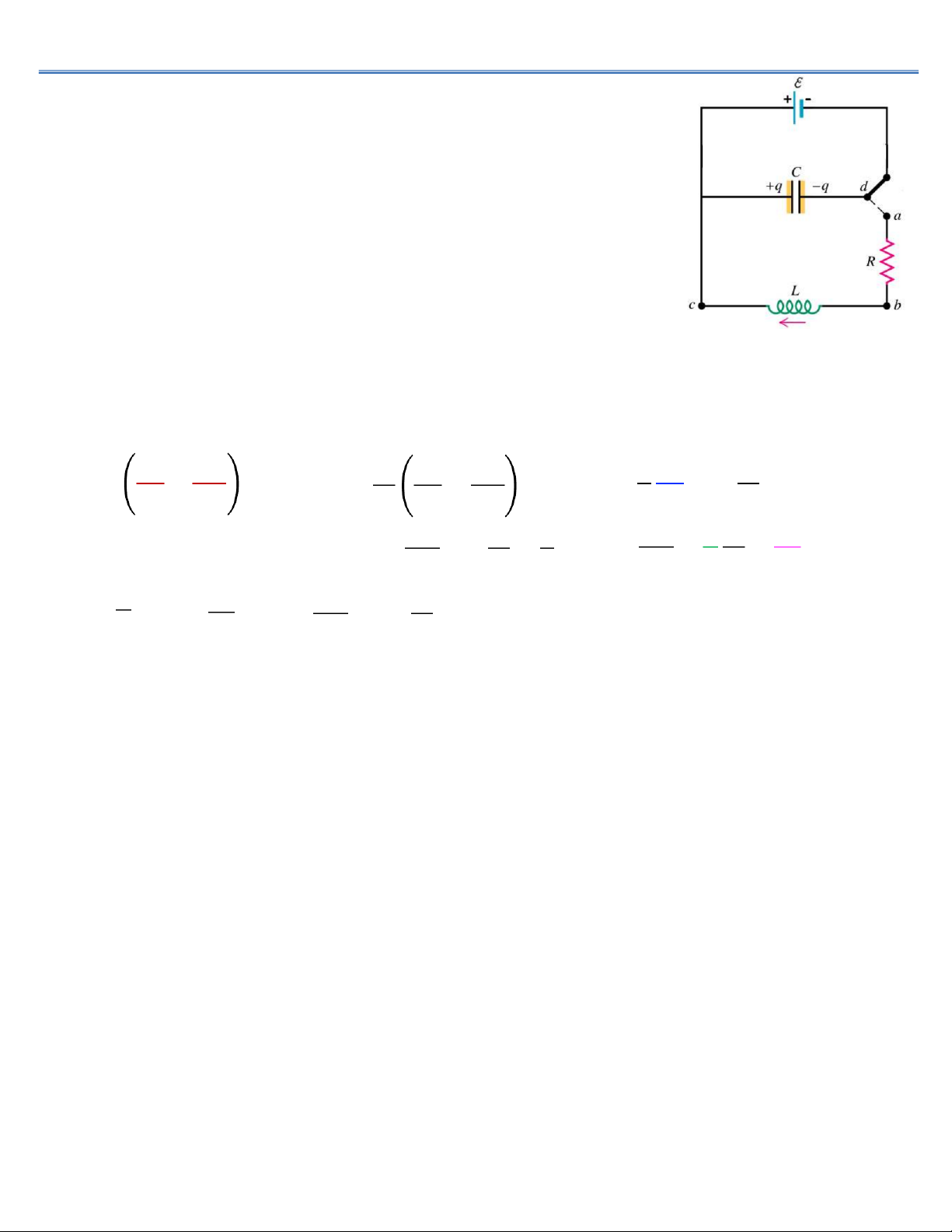
a. Dao động trong mạch RLC F Mạch điện:
¨ Gồm cuộn dây 𝐿, tụ điện 𝐶 được tích điện và điện trở 𝑅;
¨ Trong mạch có thêm điện trở 𝑅 nên năng lượng của mạch
dao động giảm dần
è 𝐼 và 𝑞 không còn dạng hình sin, biên độ giảm dần theo t;
Þ Dao động điện từ trong mạch được gọi là dao động điện từ tắt dần.
F Trong thời gian dt, năng lượng của mạch giảm đi một lượng –dW do chuyển hoá thành nhiệt: − 𝑊 = 2𝑑𝑡 − 𝑞! 2C+LI! ↔𝑑 𝑞! 2C+LI!2=−𝑅𝐼2↔q 𝑑q dt+LIdI 2= 2𝑑𝑡 dt=−𝑅𝐼2(∗) dt C
F Đạo hàm 2 vế (*) và biến đổi:
Ld!I dt!+ R𝑑Idt+I C=0 ↔d!Idt!+R 𝑑I dt+1 LCI=0 L F Đặt: RL=2𝛽;1 !:d!I dt!+2𝛽𝑑I LC=𝜔
!I=0 (4) (4) là phương trình vi phân " dt+𝜔"
của dao động điện từ tắt dần
9.1. Dao động điện từ tự do trong mạch RLC
9.1.2. Dao động điện từ tắt dần
b. Phương trình dao động mạch RLC và điều kiện để có dao động điện từ d!I dt!+2𝛽𝑑I Khi𝜔 ! ">𝛽↔1 LC>R
dt+𝜔 !I=0 (4) (4) là phương trình vi phân "
của dao động điện từ tắt dần 2L I(t)
nghiệm của (4) là : I=I"e#$%cos 𝜔t+𝜑 (5) Ioe- T biên I độ 𝐼 0
"𝑒#$& giảm theo quy luật hàm mũ 𝜷t với𝜔= 1 LC−R ! =𝜔" !−𝛽!(6) 2L t T=2𝜋𝜔=2𝜋 !(7) 𝜷t 1 LC−R –I0 -Ioe- 2L
Mạch chỉ có dao động khi: 𝜔">𝛽↔R<2 L C;R"=2 L
Đặt⇒RR" là điện trở tới hạn; Nếu𝑅 ≥𝑅"trong mạch không có dao động 𝛿 =ln 𝐼"𝑒#$&
¨ Tỉ số giữa 2 biên độ kế tiếp
𝐼"𝑒#$(&())=𝛽T gọi là giảm lượng loga.
R càng lớn thì dao động tắt càng sớm
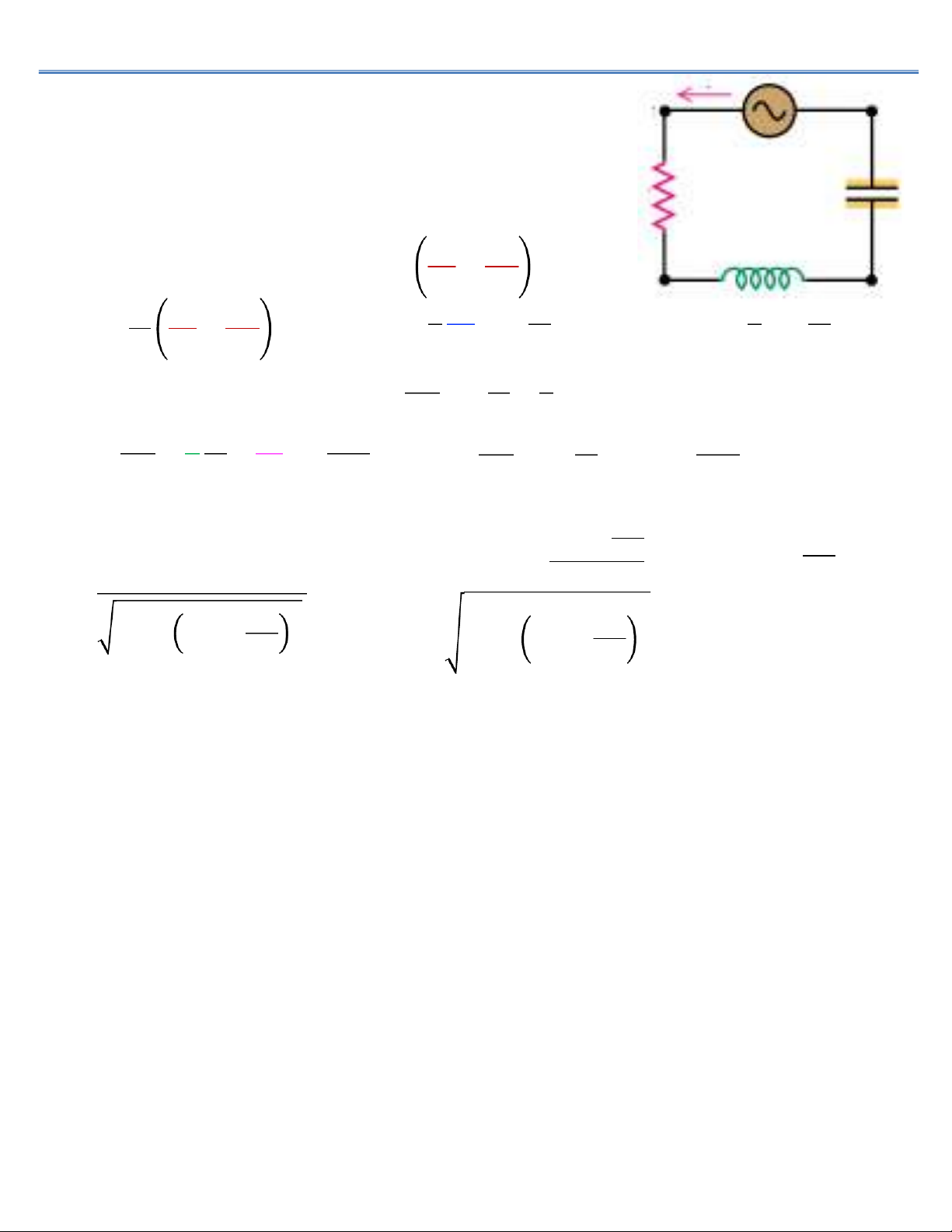
9.2. Dao động điện từ cưỡng bức I
F Nguồn 𝓔(𝑡) duy trì dao động điện từ trong mạch 𝓔(𝑡) = 𝑜sinW𝑡
F Trong thời gian dt, nguồn cung cấp năng lượng 𝓔𝐼𝑑𝑡 E(t) -q
Phần năng lượng này bằng độ tăng năng lượng điện từ dW RC
của mạch và năng lượng tỏa ra do hiệu ứng Joule-Lenz +q ↔ 𝑡 =𝑑 𝑞! 2C+LI! L
𝓔𝐼𝑑𝑡 =𝑑𝑊+𝐼2𝑅𝑑𝑡 2+𝐼2𝑅𝑑𝑡 ↔𝓔𝐼= 𝑑 𝑞!
2C+LI!2+𝐼2𝑅↔𝓔𝑜↔𝓔 sin 𝐼 W= 𝑡 q=q 𝑑q dt+LIdI C+ LdI dt+𝑅𝐼2 dt+ 𝑅I(∗) dt C
F Đạo hàm 2 vế (*) và biến đổi: Ld!I dt!+ R𝑑Idt+I C=W𝓔𝑜cosW𝑡 ↔d!I dt!+R 𝑑I
dt+1 LCI=W𝓔𝑜LcosW𝑡↔d!I dt!+2𝛽𝑑I !I=W𝓔𝑜 dt+𝜔 Lcos L " W𝑡(9)
(9) là phương trình vi phân của dao động điện từ cưỡng bức, có nghiệm cotanF= −WL− 1 𝐼 =𝐼 R(12)Z 0cos(W𝑡 + F) (10) +=1 WC WC(14) 𝐼0=𝓔𝑜 !(11) R!+WL− 1 Z= R ! !+WL− 1 Z,=𝐿W(15) WC (13) WC
9.2. Dao động điện từ cưỡng bức
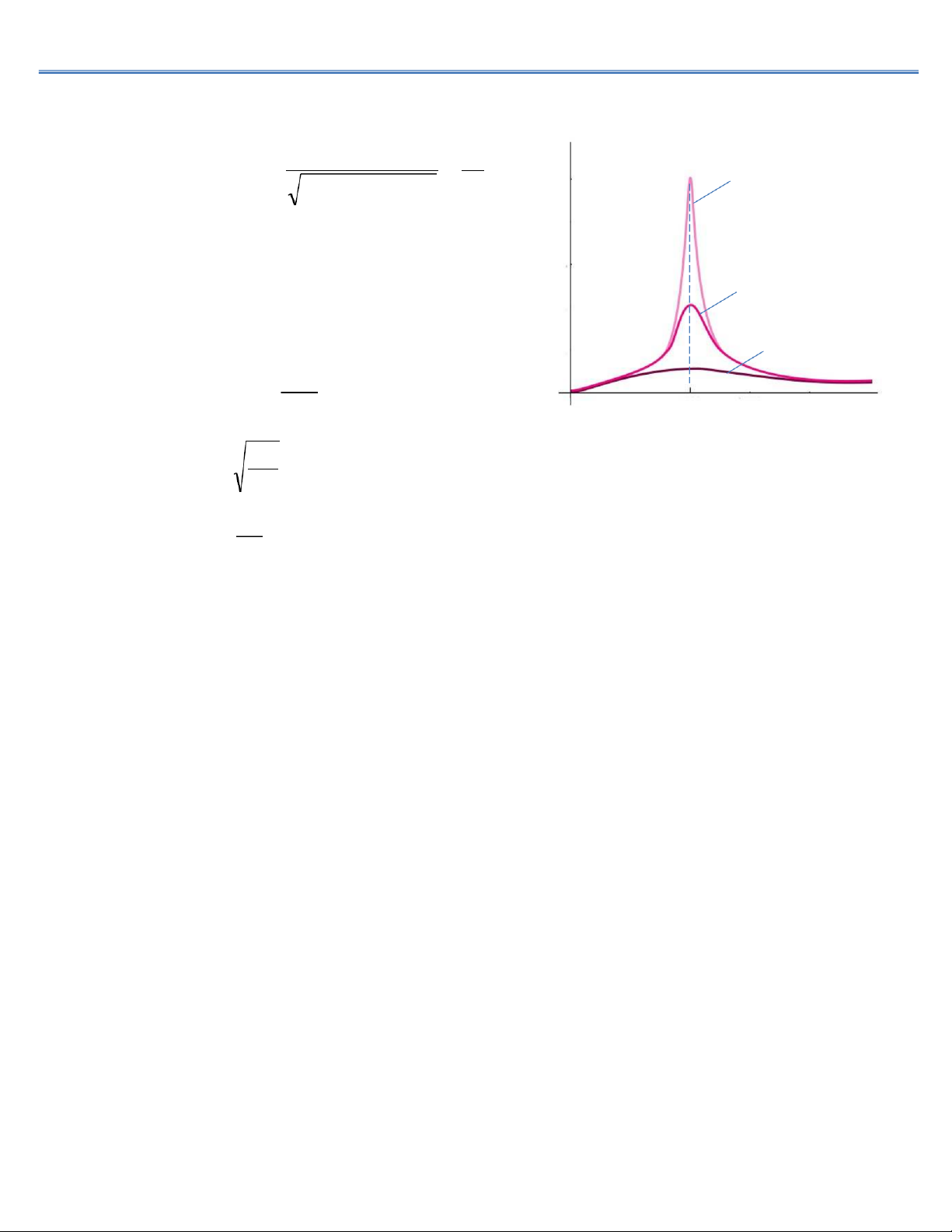
c. Cộng hưởng điện từ mạch RLC I0
R3 > R2 > R 1 E E F Nhận thấy # ! ! ! = = R1 " " + (! ) " ! − ! % $
¨ Biên độ dòng cưỡng bức phụ thuộc nguồn điện kích thích. R2
¨ Khi 𝓔0 và R cố định Þ I0 max khi: R3 % = # " # #$ ! ! = −#"# = Ω" " ! − ! Ω 0 w W 0 (rad/s) " Khi đó: Ω ω = = ! #
tần số riêng của mạch (LC): Cộng hưởng dao đ ! ộng !" E Và: "!!"#$ = ! CHƯƠNG X
SÓNG ĐIỆN TỪ
10.1. Sự tạo thành sóng điện từ
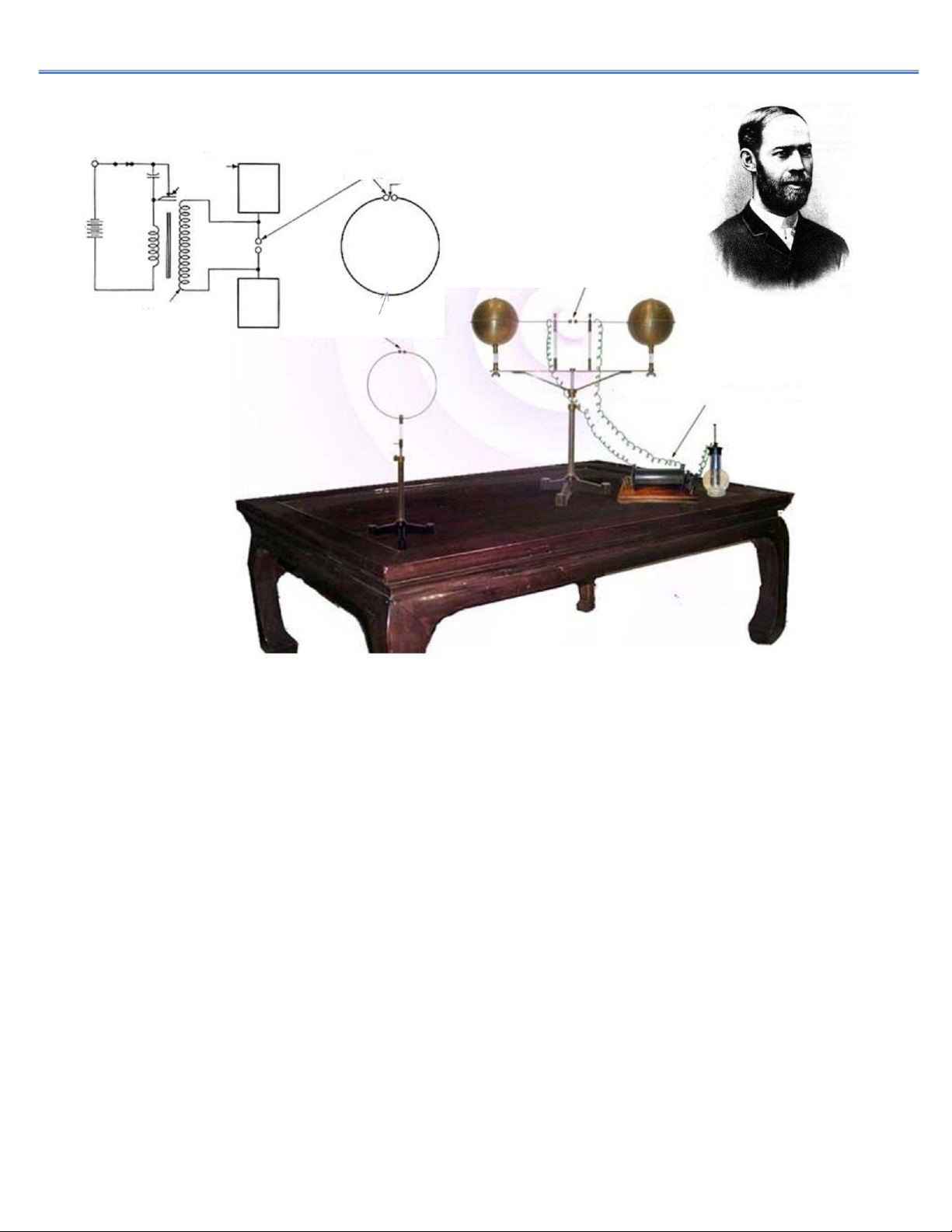
Thí nghiệm Hertz về sự hình thành sóng điện từ Quả cầu tạo
tia lửa điện Khe không khí Quả cầu tạo tia lửa điện Cuộn dây
Heinrich Rudolf Hertz Dụng cụ thu sóng cảm ứng (1857 – 1894)
Sóng điện từ: sự lan truyền Cuộn dây cảm ứng
của điện-từ trường biến thiên trong không gian
10.1. Sự tạo thành sóng điện từ ❖
Thí nghiệm Hertz về sự hình thành sóng điện từ
◆Điều chỉnh UABvà khoảng cách AB sao cho để có
Sóng điện từ
hiện tượng phóng điện giữa AB.
àGiữa AB đã xuất hiện một điện trường biến
thiên theo thời gian (xoay chiều).
◆Nếu dùng các dụng cụ phát hiện sẽ thấy tại mọi
điểm M trong không gian đều có 𝑬, 𝑯biến thiên theo thời gian.
Thí nghiệm chứng tỏ: điện từ trường biến thiên đã
được truyền đi trong không gian.
❖ Giải thích. Theo Maxwell:
Điện trường biến thiên
◆Nếu tại O có một điện trường 𝑬biến thiên 𝑬 𝑬′ 𝑬” 𝑬
àsẽ sinh ra từ trường, tại các điểm M, M’, M”… 𝐎 𝐌 𝐌′𝐌′′
xuất hiện các từ trường 𝑯, 𝑯′, 𝑯”… biến thiên. 𝑯 𝑯′ 𝑯”
◆Các từ trường này lại tiếp tục sinh ra điện trường 𝑬, 𝑬′, 𝑬”… biến thiên theo thời
gian tại các điểm M, M’, M”…
Như vậy, các cặp 𝑬, 𝑯đã được truyền đến mọi điểm trong không gian. Quá trình
truyền đó tạo thành sóng điện từ.
Định nghĩa: Sóng điện từ là trường điện từ biến thiên truyền đi trong không gian.
10.2. Các tính chất của sóng điện từ
a. Hệ phương trình Maxwell của sóng điện từ
✹ Hệ phương trình Maxwell của trường điện từ 𝐫𝐨𝐭𝐄 = −𝝏𝐁 𝝏𝐭; 𝒓𝒐𝒕𝐇= 𝑱+𝝏𝐃
𝝏𝐭;𝒅𝒊𝒗𝐃=𝝆;𝐝𝐢𝐯𝑩=𝟎;
✹ Nếu môi trường đồng chất đẳng hướng thì:
𝐃=𝜺𝜺𝟎𝐄;𝐁=𝝁𝝁𝟎𝐇; 𝑱=𝝈𝑬
✹ Sóng điện từ là điện từ trường biến thiên và nếu chỉ xét sóng điện từ tự do, nghĩa
là sóng truyền trong môi trường không dẫn (không có dòng điện) và không có điện tích. Do đó: 𝑱=𝟎; 𝝆=𝟎
✹ Hệ phương trình Maxwell áp dụng cho sóng điện từ 𝐫𝐨𝐭𝐄 = −𝝏𝐁
𝝏𝐭;𝒓𝒐𝒕𝐇= 𝝏𝐃 𝝏𝐭;𝐝𝐢𝐯𝐃= 𝟎; 𝐝𝐢𝐯𝑩=𝟎;
𝐃=𝜺𝜺𝟎𝐄;𝐁=𝝁𝝁𝟎𝐇;
a. Các tính chất tổng quát của sóng điện từ
✽ Tồn tại trong môi trường chất và trong chân không
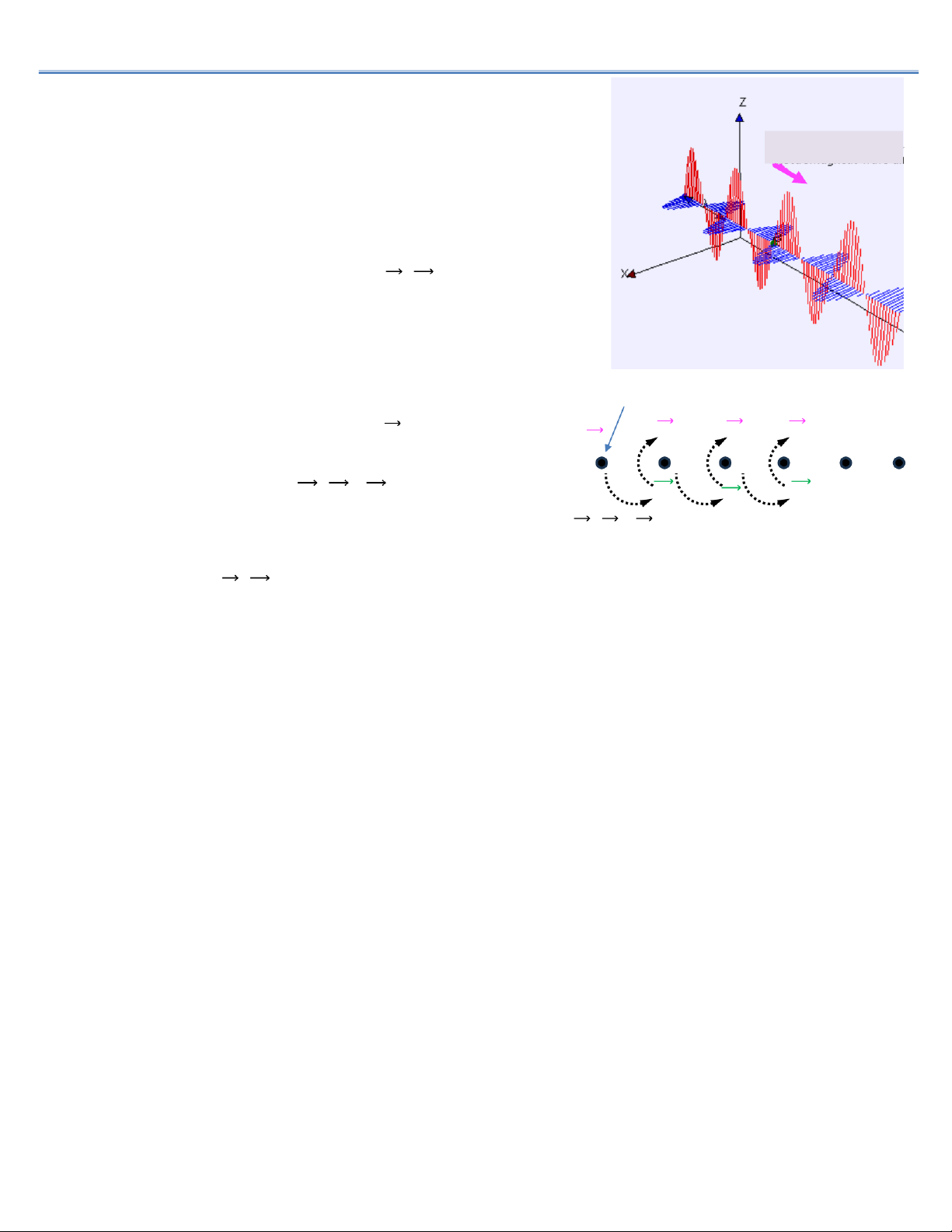
✽ Là sóng ngang, có 𝐄,𝐇 vuông góc nhau và với phương truyền sóng.
✽ Vận tốc truyền sóng điện từ trong môi trường đồng chất đẳng hướng: 𝒗= 𝒄 𝜺𝝁
n= 𝜺𝝁: chiết suất tuyệt đối của môi trường
𝜺: hằng số điện môi; 𝝁: độ từ thẩm của môi trường.
Chân không 𝜺= 𝟏; 𝝁=𝟏: 𝒗=𝒄
Thực nghiệm chứng tỏ n≥ 1nên 𝒗≤ 𝒄: Vận tốc truyền sóng điện từ trong chân
không là lớn nhất.
10.3. Phương trình sóng điện từ phẳng đơn sắc
✽ Đặc điểm của sóng điện từ phẳng, đơn sắc
•Các mặt đầu sóng là những mặt phẳng song song, nghĩa là phương truyền sóng là
những đường thẳng song song, nguồn sóng coi như ở rất xa.
•Các vec tơ 𝐄, 𝐇có phương không đổi và trị số của chúng là hàm sin đối với thời gian.
•Có một tần số 𝛚xác định, tức là chu kỳ T = 𝟐𝛑/𝛚xác định
Có bước sóng 𝝀 = 𝐯𝐓xác định trong môi trường đồng chất.
✽ Tính chất của sóng điện từ phẳng, đơn sắc:
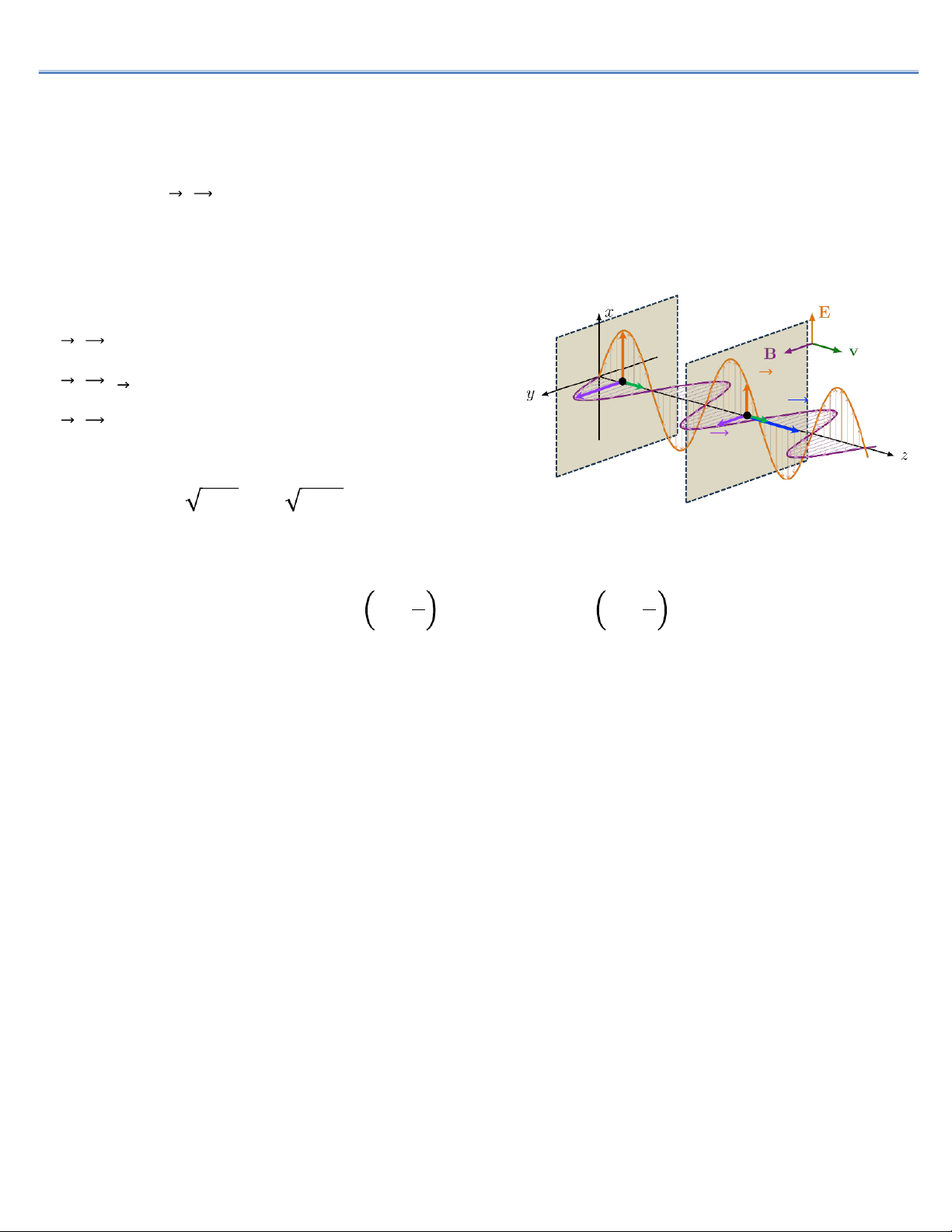
•𝐄, 𝐇luôn vuông góc với nhau, O
•𝐄, 𝐇, 𝐯theo thứ tự lập thành tam diện thuận. 𝐄 P 𝓟
•𝐄, 𝐇luôn dao động cùng pha, có trị số tỷ lệ 𝐇 M với nhau: 𝜺𝜺𝟎E= 𝝁𝝁𝟎H;
✽ Phương trình sóng điện từ phẳng, đơn sắc:
Giả sử tại O: E.=E/cos𝝎t;H.=H/cos𝝎t;
Tại M có toạ độ x: E=E/cos𝝎 t− x v;H = H/cos𝝎 t− x v;
10.5. Năng lượng và năng thông sóng điện từ
a. Năng lượng sóng điện từ
✽ Năng lượng của sóng điện từ là năng lượng của trường điện từ trong khoảng không gian có sóng điện từ ✽ 𝝎=𝝎1+𝝎2=𝟏 𝟐𝜺𝜺𝟎E𝟐+𝟏
Mật độ năng lượng trường điện từ: 𝟐𝝁𝝁𝟎H𝟐
✽ Đối với sóng điện từ phẳng, đơn sắc: 𝜺𝜺𝟎E= 𝝁𝝁𝟎H
⇒𝜺𝜺𝟎E𝟐=𝝁𝝁𝟎H𝟐
➪ Mật độ năng lượng sóng điện từ:
𝝎=𝜺𝜺𝟎E𝟐=𝝁𝝁𝟎H𝟐
𝝎= 𝜺𝜺𝟎E𝝁𝝁𝟎H
b. Năng thông sóng điện từ
✽ Là đại lượng đặc trưng cho sự truyền năng lượng sóng điện từ.
F Khái niệm: Năng thông sóng điện từ bằng năng lượng sóng truyền qua một diện
tích nào đó trong một đơn vị thời gian.
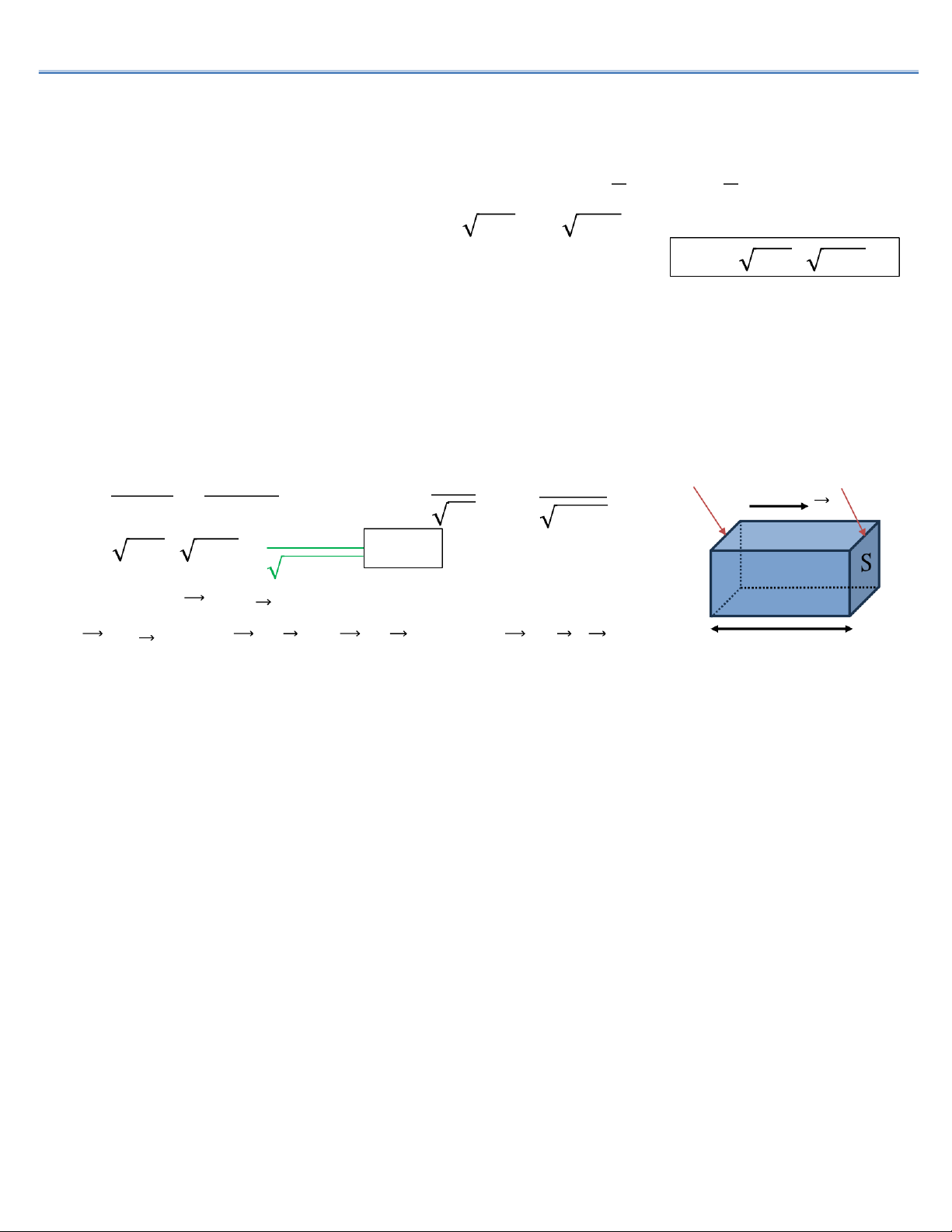
F Mật độ năng thông sóng của điện từ bằng năng thông sóng điện từ qua một đơn vị diện tích: Mặt sóng Mặt sóng 𝓟=𝝎.𝜟𝐕
𝑺.𝜟𝐭 =𝝎𝑺𝒗𝜟𝐭 𝒗= 𝒄𝜺𝝁;𝐜= 𝟏 thời điểm t thời điểm t+ Dt 𝑺.𝜟𝐭 =𝝎𝒗 với 𝜺𝟎𝝁𝟎 𝒗
𝓟= 𝜺𝜺𝟎E𝝁𝝁𝟎H.𝟏 =𝐄𝐇 = 𝟑.𝟏𝟎𝟖m/s 𝜺𝜺𝟎𝝁𝝁𝟎
Dạng véc tơ: 𝓟=𝝎𝒗: véc tơ Umov-Poynting
Vì𝓟 ↑↑𝒗nên𝓟⊥Evà𝓟⊥H.Suy ra: 𝓟=E×H
ℓ=𝒗𝜟𝒕=𝒗. 𝟏=𝒗
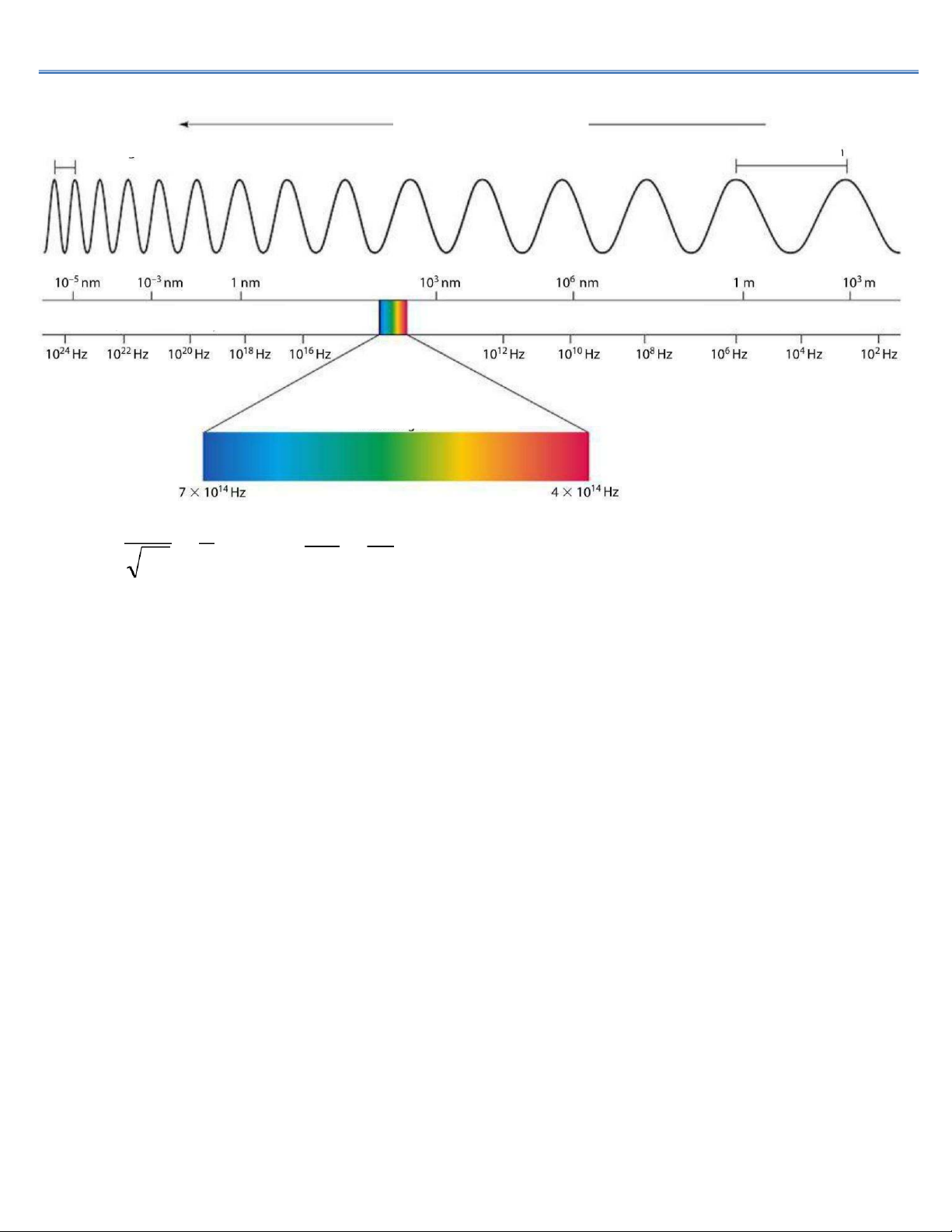
10.6. Thang sóng điện từ
Năng lượng tăng Sóng ngắn Sóng dài Gamma X Cực tím Hồng ngoại Vi ba Vô tuyến
Tần số cao
Tần số thấp
Ánh sáng khả kiến " " # #!" λ == Þ λ = =
(l0 bước sóng điện từ trong chân không) εµ ! ! !
Các sóng điện từ đơn sắc được phân loại theo độ lớn của tần số hoặc bước sóng
trong chân không. Bảng ghi tên các loại sóng điện từ ứng với những bước sóng từ
lớn đến nhỏ gọi là thang sóng điện từ.




