Chuyên Đề Các Phép Biển Đổi Biểu Thức Chứa Căn Ôn Thi Vào 10 Giải Chi Tiết
Đưa thừa số ra ngoài dấu căn. Đưa thừa số vào trong dấu căn. Khử mẫu ở biểu thức chứa căn. Cho a là số không âm, số b, c là số dương. Khẳng định nào sau đây sai? Cho a là số không âm, số b là số dương Kết quả rút gọn biểu thức. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Tài liệu ôn thi vào 10 môn Toán 124 tài liệu
Môn: Môn Toán 1.4 K tài liệu
Tác giả:
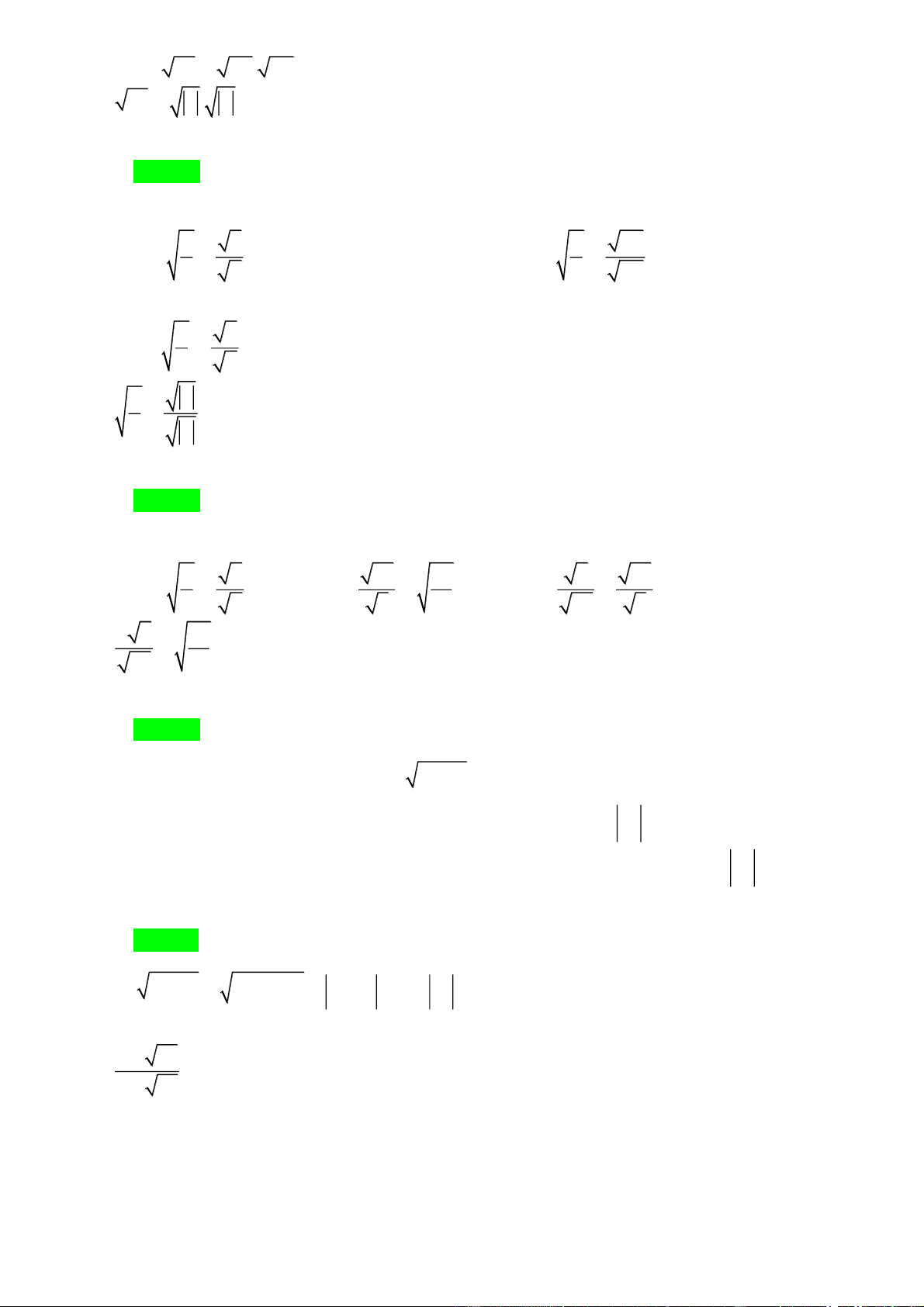
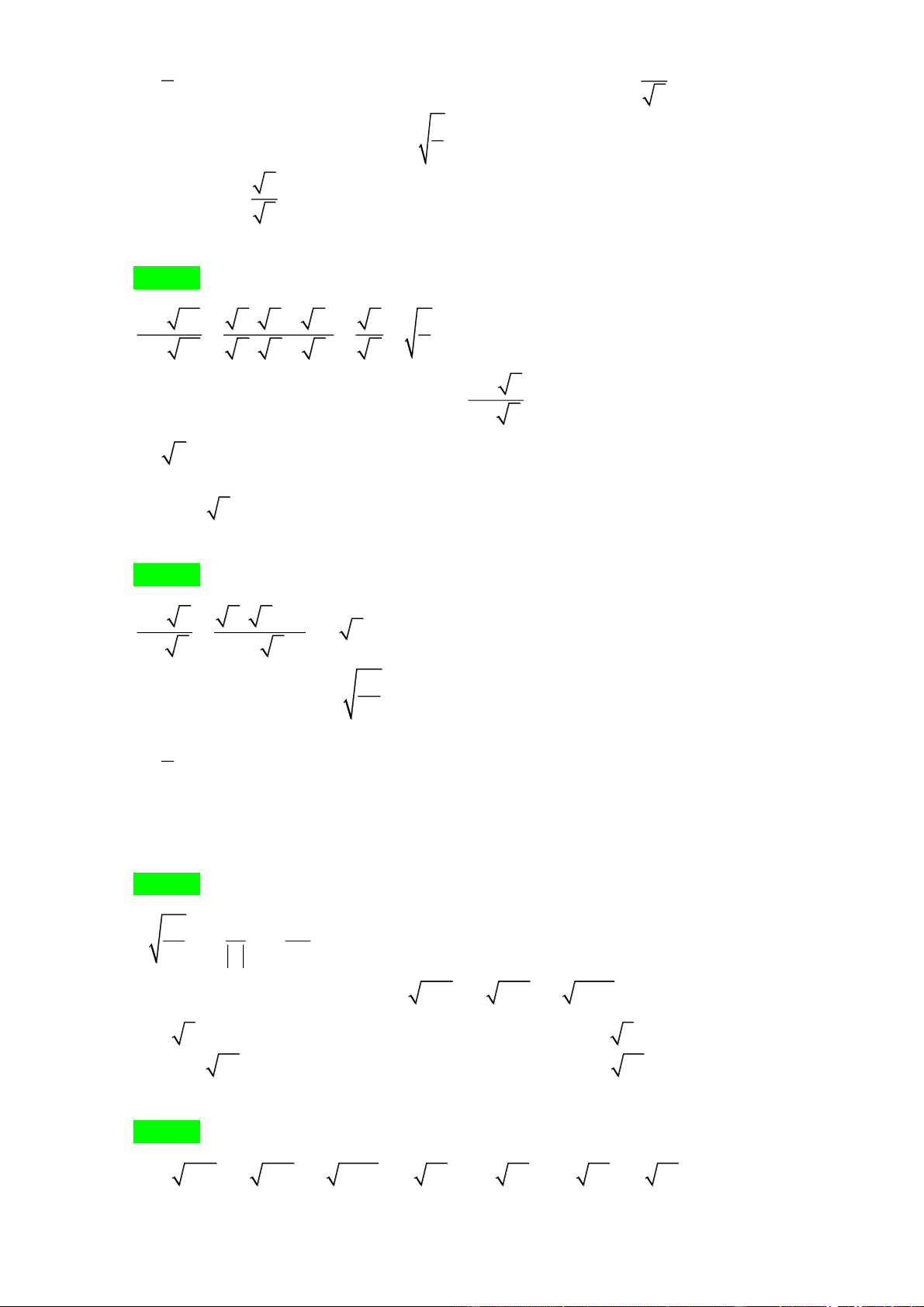
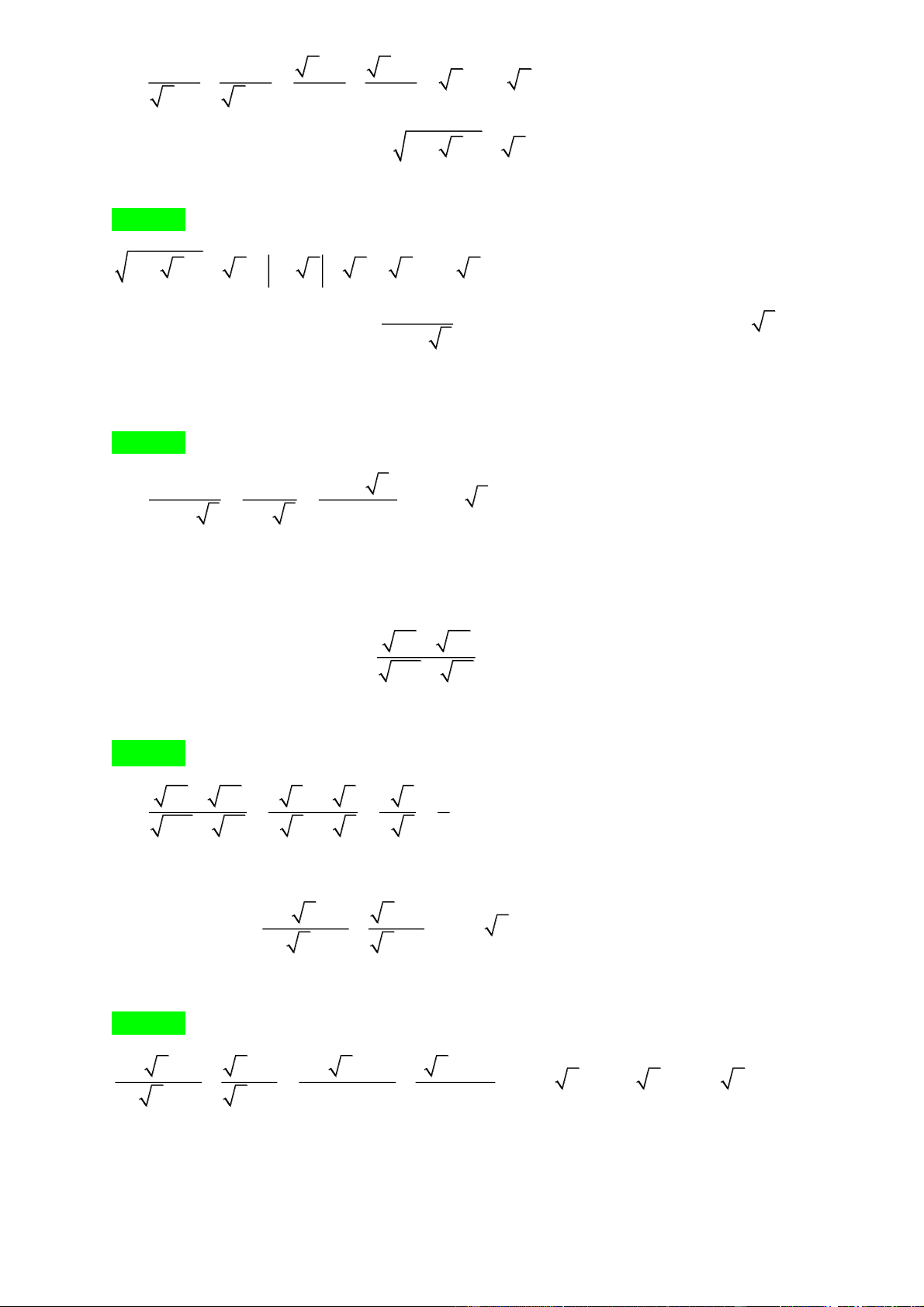
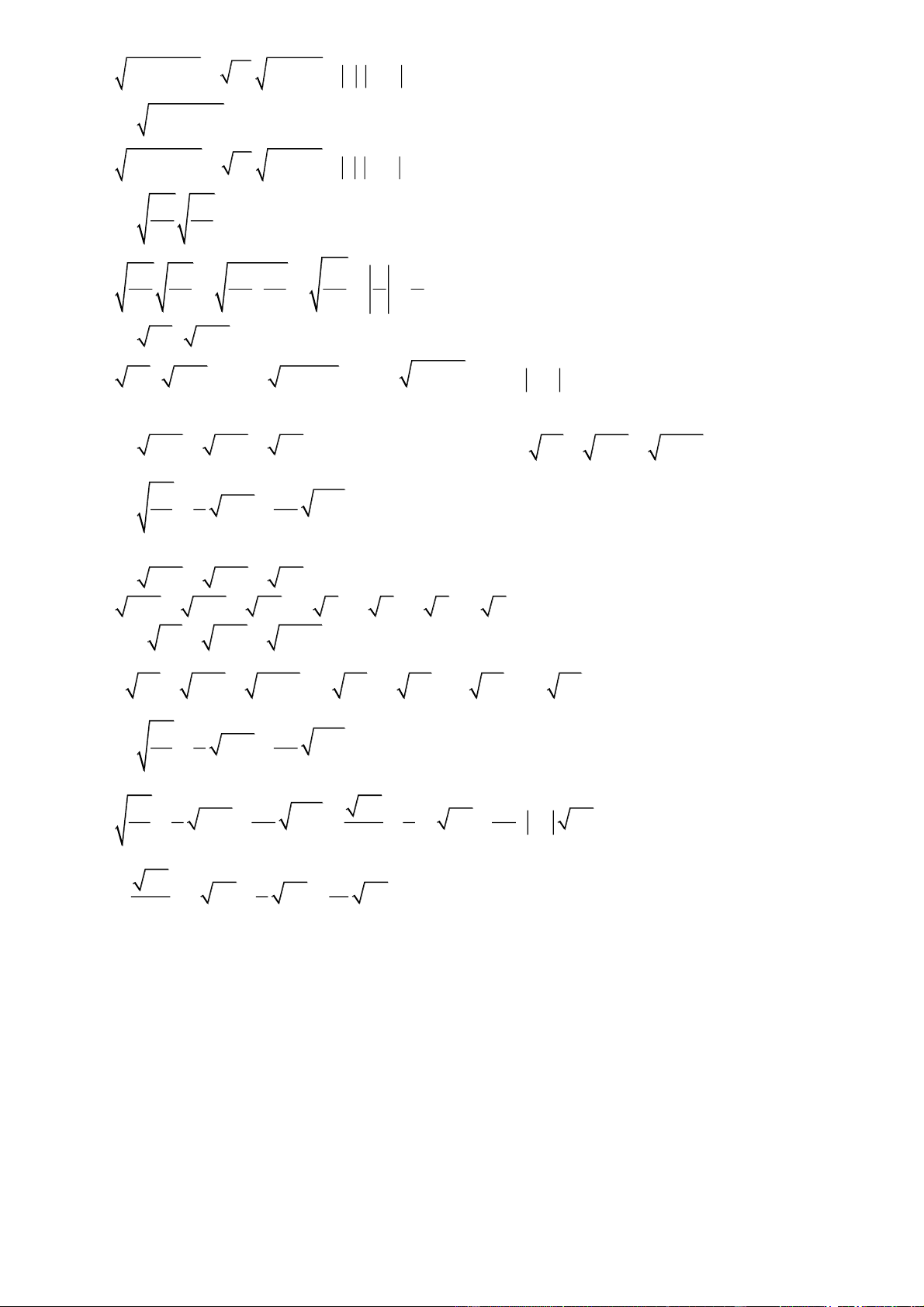
Preview text:
CHUYÊN ĐỀ 3: CÁC PHÉP BIỂN ĐỔI BIỂU THỨC CHỨA CĂN
A. KIẾN THỨC CẦN NHỚ
1. Với A 0, B 0 thì: . A B .
A B và ngược lại . A B . A B
Đặc biệt, khi A 0, ta có: 2 2 A
A A. A A
2. Với A 0, B 0 thì và ngược lại A A B B B B
3. Đưa thừa số ra ngoài dấu căn : 2 A B A
B B 0 .
4. Đưa thừa số vào trong dấu căn: 2 . A B
A B (với A 0; B 0 ) 2 .
A B A .B ( với A 0; B 0 )
5. Khử mẫu ở biểu thức chứa căn: A AB 1
AB (với AB 0; B 0 ) 2 B B B
6. Trục căn thức ở mẫu: M A B M M A M A 0;
A 0;B 0; A B A A A B A B B. BÀI TẬP
DẠNG 1: RÚT GỌN BIỂU THỨC
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN
Câu 1. [NB] Cho a, b R và a;b 0 . Trong các khẳng định sau, khẳng định nào đúng?
A. a. b ab . a a B. . b b C. a b a b .
D. Cả A, B, C đều đúng. Lời giải Chọn A
Câu 2. [NB] Tìm câu trả lời sai:
A.. ab a. b với mọi a, b . B. ab a. b với mọi a, b 0 . Trang 1 C. ab
a. b với mọi a, b 0 . D. ab
a . b với mọi a, b 0 . Lời giải Chọn A
Câu 3. [NB] Chọn câu trả lời sai: a a a a A.. với a, b 0 . B. với a, b 0 . b b b b a a C.
với a 0;b 0 . D. b b a a với a 0;b 0 . b b Lời giải Chọn A
Câu 4. [NB] Cho a là số không âm, số b, c là số dương. Khẳng định nào sau đây sai? a a ab ab a ab A.. . B. . C. . D. b b c c bc c b a ab . bc c Lời giải Chọn C
Câu 5. [TH] Kết quả của phép tính 4 6 9a b là: 2 3 A. 2 3 3a b . B. 3a b . 2 3 C. 2 3 9a b . D. 9a b . Lời giải Chọn B 4 6 2 3 2 2 3 2 3
9a b (3a b ) 3a b 3a b
Câu 6. [TH] Cho a là số không âm, số b là số dương Kết quả rút gọn biểu thức a ab là: b ab Trang 2 a a A. . B. . b b a C. . b b D. . a Lời giải Chọn C a ab a ( a b) a a b ab b( b a ) b b a a
Câu 7. [TH] Kết quả rút gọn của biểu thức với a 0,a 1 là: 1 a A. a . B. a . C. a . D. a . Lời giải Chọn D a a a ( a 1) a 1 a 1 a 1
Câu 8. [TH] Khi x < 0 thì x bằng: 2 x 1 A. . B. x . x C. 1 . D. 1 . Lời giải Chọn D 1 1 1 x x. x. 1 (Vì x 0) 2 x x x
Câu 9. [TH] Rút gọn biểu thức C = 20a + 4 45a - 2 125a với a ≥ 0 ta được: A. 4 5a . B. - 4 5a . C. 4 5a . D. - 4 5a . Lời giải Chọn C
C = 20a + 4 45a - 2 125a = 2 5a + 4.3 5a - 2.5 5a = 4 5a Trang 3 3 a
Câu 10. [TH] Rút gọn biểu thức
với a 0, kết quả là: a A. a . B. a . C. a . D. 2 a . Lời giải Chọn C 3 3 a a 2
a a a (Vì a 0) a a 2 y x
Câu 11. [VD] Rút gọn biểu thức
, với x > 0; y < 0 ta được: 4 x y 1 1 A. . B. - . y y C. y . D. - y . Lời giải Chọn A 2 y x y x y x 1 = . = . = ( Vì x > 0; y < 0 ) 4 2 2 x y x y x y y 2 4 2xy a b
Câu 12. [VD] Cho các số thực dương a, b, x, y khác 0 và A . 2 2 ab 4x y
Khẳng định nào sau đây đúng? A. A a . B. A xy . C. A b . D. A ab . Lời giải Chọn C 2 2 4 2 2 ab 2 2xy a b 2xy (ab ) 2xy 2xy ab A . . . b 2 2 2 ab 4x y ab (2xy) ab 2xy ab 2xy 4 x
Câu 13. [VD] Rút gọn biểu thức 2 M (b 3) với b 3 ta được: 2 b 6b 9 A. (3 b)x . B. 2 (b 3)x . C. (b 3)x . D. 2 (3 b)x . Lời giải Chọn D Trang 4 2 4 2 2 2 x 2 x 2 x M (b 3) (b 3) (b 3) . 2 b 6b 9 b 3 b 3 2 2 x 2 (b 3) . x (3 b) ) 3 (Vì b 3 b
Câu 14. [VDC] Cho biểu thức A = 4 + 4 +
4 + ...... ( có vô hạn số 4 ). Giá trị
của biểu thức A là 1 - 17 1 + 17 - 1 + 17 A. . B. - . C. . D. 2 2 2 1 + 17 . 2 Lời giải Chọn D
Đặt x = 4 + 4 + 4 + ...... + 4 . Ta có: x > 0 . Khi đó: 2 x = 4 + 4 + 4 + 4 + 4 + .... + 4 2 Þ x = 4 + x 2
Û x - x - 4 = 0. D = (- )2
1 - 4.1.(- 4)= 17 > 0 Þ Phương trình có hai nghiệm phân biệt: 1 ± 17 x = . 1 2 1 + 17
Vì x > 0 suy ra x = . 2
2. TRẮC NGHIỆM ĐÚNG SAI
Trong mỗi ý a), b), c), d) ở mỗi câu, em chọn đúng hoặc sai
Câu 1. Cho hai biểu thức: A 4 2 3 4 2 3; B 18 8 2 18 8 2.
a) Giá trị biểu thức A là 2.
b) Giá trị biểu thức B là 8. c) AB 16 3. d) A 2B 10. Lời giải a) S b) Đ c) Đ d) S 2 2
A 4 2 3 4 2 3 ( 3 1) ( 3 1) 3 1 3 1 2 3 nên a sai. Trang 5 2 2
B 18 8 2 18 8 2 (4 2) (4 2) 4 2 4 2 8 nên b đúng
AB 2 3.8 16 3 nên c đúng
A 2B 2 3 8 nên d sai
Câu 1. Cho hai biểu thức: A 4 2 3 4 2 3; B 18 8 2 18 8 2.
a) Giá trị biểu thức A là 2.
b) Giá trị biểu thức B là 8. c) AB 16 3. d) A 2B 10.
Câu 2. Cho các số: 2 5;3 6;5 2; 4 3 .
a) Số nhỏ nhất là 2 5 .
b) Số lớn nhất là 5 2 .
c) Sắp xếp theo thứ tự tăng dần là: 2 5;3 6;5 2; 4 3 .
d) Sắp xếp theo thứ tự giảm dần là: 4 3;5 2;3 6; 2 5 . Lời giải a) Đ b) S c) S d) S Ta có: 2 5 = 20;3 6 = 54;5 2 = 50;4 3 = 48
Số nhỏ nhất là 2 5 nên a đúng
Số lớn nhất là 3 6 nên b sai
Sắp xếp theo thứ tự tăng dần là 2 5; 4 3;5 2;3 6 nên c sai
Sắp xếp the thứ tự giảm dần là 3 6; 5 2; 4 3; 2 5 nên d sai
Câu 3. Cho biểu thức A x 2 4 x .
a) Điều kiện xác định của biểu thức A là x £ 4 .
b) Giá trị lớn nhất của A là 4 . Trang 6
c) Giá trị nhỏ nhất của A là 6 .
d) Giá trị của biểu thức A khi x = 3 là 5 + 1. Lời giải a) S b) S c) Đ d) Đ
Điều kiện xác định của A là - 2 £ x £ 4 nên a Sai 2
A 6 2 (x 2)(4 x);2 (x 2)(4 x) 6 ; do đó 2
A 12 . Vậy GTLN của A là 2 3 khi x = 2 nên b sai 2
A 6 2 (x 2)(4 x) 6 , do đó GTNN của A là 6 khi x = - 2; x = 4(TM) nên c Đúng Khi x = 3 thì A = 5 + 1 nên d đúng
Câu 4. Cho biểu thức 2
A 16 8x x x 4 .
a) Điều kiện xác định của biểu thức A là x ³ 0 .
b) Kết quả rút gọn biểu thức A khi x ³ 4 là - 8 .
c) Kết quả rút gọn biểu thức A khi x £ 4 là - 2x - 8 . .
d) Giá trị của biểu thức A khi x = 2 là - 4 . Lời giải a) S b) Đ c) S d) Đ 2 2
A 16 8x x x 4 (x 4) x 4 x 4 x 4
Điều kiện xác định của A là mọi x nên a sai
x ³ 4Þ A = x - 4- x - 4 = - ( ) 8 nên b đúng
x £ 4Þ A = 4- x - x - 4 = - 2x nên c sai
x = 2 thì A = - 4 nên d đúng.
3. TRẮC NGHIỆM TRẢ LỜI NGẮN 1 1
Câu 1. [NB] Giá trị biểu thức E bằng: 2 1 2 1 Lời giải
Đáp án: E 2 Trang 7 1 1 2 1 2 1 E
2 1 2 1 2 2 1 2 1 2 1 2 1
Câu 2. [NB] Giá trị của biểu thức 2
(1 2) 2 có kết quả bằng: Lời giải
Đáp án: 1 2
(1 2) 2 1 2 2 2 1 2 1 45
Câu 3. [TH] Cho biểu thức P
, đưa P về biểu thức có dạng a b 3. Khi 10 5 3 đó a.b bằng: Lời giải Đáp án: 162 45 9 9(2 3) P 18 9 3 10 5 3 2 3 4 3 Do đó: a 18; b 9. Vậy: a.b 18.9 162. 45 20
Câu 4. [TH] Cho biểu thức A
. Khi đó, giá trị biểu thức 3A bằng: 180 80 Lời giải Đáp án: 7,5 45 20 3 5 2 5 5 5 5 A . 180 80 6 5 4 5 2 5 2 Do đó: 3A 7,5 7(2 2 1) 2 2 Câu 5. [VD] Cho
a b 2 . Khi đó, giá trị của a b bằng: 2 2 1 2 2 Lời giải Đáp án: 8 2 2 7(2 2 1) 2 2 7(2 2 1) ( 2 2)
9 4 2 3 2 2 6 2 2 2 2 1 2 2 8 1 2 4 Do đó: a 6; b 2.
Vậy: a b 6 2 8. Trang 8 x 1
Câu 6. [VDC] Gọi M là giá trị nhỏ nhất của
và N là giá trị lớn nhất cuả x 4
x 5 .Khi đó 2M N bằng: x 2 Lời giải
Đáp án: 2M N 3 x 1 3 1 x 4 x 4
Với x 0 x 4 4 3 3 3 3 3 1 1 x 4 4 x 4 4 x 4 4 1 Do đó: M 4 x 5 3 1 x 2 x 2
Với x 0 x 2 2 3 3 3 5 1 x 2 2 x 2 2 5 Do đó: N 2 1 5 Vậy: 2M N 2. 3 4 2
PHẦN II. BÀI TẬP TỰ LUẬN Phương pháp giải:
☑️ Vận dụng các phép biến đổi để làm bài toán rút gọn
☑️ Vận dụng kĩ năng sử dụng hằng đẳng thức để hỗ trợ bài toán rút gọn
☑️ Vận dụng phá ngoặc biểu thức chứa dấu GTTĐ BÀI TẬP MẪU
Ví dụ 1 [NB]: Rút gọn biểu thức sau: 4 1) 0,09. 64 2) 2 . 7 2 3) 12,1.360 4) 45.80 5) 7. 63 6) 10. 40 7) 2,7 5 1,5 8) 2,5 30 48 Trang 9 Lời giải
1) 0,09. 64 0,09. 64 0,03.8 0, 24 2) 4 2 4 2 2 2 . 7 2 . 7 2 .7 28
3) 12,1.360 121.36 121. 36 11.6 66 4) 2 2
45.80 9.16.5 9. 16. 5 3.4.5 60 5) 2 2
7. 63 7 .9 7 . 9 7.3 21 6) 10. 40 10.40 400 20 7) 2 2
2, 7 5 1,5 9.0,3.5.5.0,3 9. 5 . 0,3 3.5.0,3 4,5
8) 2,5 30 48 2,5.30.48 75.48 25.3.16.3 25. 16. 9 60
Ví dụ 2 [TH]: Rút gọn biểu thức sau: 1) 2 2 13 12 2) 2 2
146,5 109,5 27.256 3) 3) 2 3 2 3 Lời giải 1) 2 2
13 12 (13 12).(13 12) 25. 1 5 2 2 146,5 109,5 27.256
(146,5 109,5)(146,5 109,5) 27.256) 2) 3)
256.37 256.27 256.64 256. 64 16.8 128
3) 2 3 2 3 2 32 3 4 3 1
Ví dụ 3 [TH]: Rút gọn các biểu thức sau: 2 2 165 124 1) 2) 164 6 14 2 3 28 3) 36 12 5 : 6 4)
M 20 300 15 675 5 75: 15 3 2 3 2 2 5) A 2 3 6) 3 2 1 2 8 12 5 27 B 18 48 30 162 Lời giải 2 2 165 124 (165 124)(165 124) 289.41 289 17 1) 164 164 41.4 4 2 Trang 10 2 3 7 6 14 2 2) 2 3 28 2 3 7 2 3) 2 36 12 5 : 6 6. 6 2 5 : 6 6 2 5 6 1 6 1 6 1
4) M 20 300 15 675 5 75 : 15 20.10 3 15.15 3 5.5 3: 15
200 3 225 3 25 3: 15 0 2 2 2 1 3 2 3 2 2 3 3 6 5) A 2 3 2 3 3 2 1 3 2 1 3 3 2
2 3 2 2 2 3 3 2 3 2 4 2 3 3 2 2 6 2 8 12 5 27 2.2 2 2 3 5 3 3 6) B 18 48 30 162 3 2 4 3 30 9 2
Ví dụ 4 [VD]: Tính giá trị các biểu thức sau:
1) A 8 2 15 6 2 5
2) B 12 2 32 9 4 2
3) C 4 7 4 7 2 4)
D 5 21 5 21 Lời giải 2 2
1) A 8 2 15 6 2 5 5 3 5 1
5 3 5 1 5 3 5 1 3 1
2) B 12 2 32 9 4 2 8 2.4 2 4 8 2. 2 1 2 2 2 2 2 2 2 1 2 2 2 2 2 1
2 2 2 2 2 1 4 2 1
3) C 4 7 4 7 2
2C 8 2 7 8 2 7 2
2 2 2C 7 1 7 1 2 2C 7 1 7 1 2 2C 7 1 7 1 2 2C 0 C 0 Trang 11
4) D 5 21 5 21
2D 10 2 21 10 2 21
2 2 2D 7 3 7 3 2D 7 3 7 3
2D 7 3 7 3 2D 7 3 7 3 2D 2 3 D 6
Ví dụ 5 [VD]: Rút gọn các biểu thức sau: 3 1) 2 ab với a 0, b 0 2) 2a a 2 2 4 a b a với a 2 2 x 3a 3) x 5 với x 5 4) a b với 0 a b 2 x 25 2 2 b a Lời giải 3 1) 2 ab với a 0, b 0 2 4 a b 2 3 2 3 2 3 2 3 ab ab ab ab 3 2 4 a b 2 ab 2 2 2 ab ab 2) 2a a 2 a với a 2 2
2a 2 2a a 2 a 2 a 22a a 2 a 2 x 3) x 5 với x 5 2 x 25 x 2 x x 5 x 5 x(x 5)(x 5) 2 x 25 (x 5)(x 5) 3a 4) a b với 0 a b . 2 2 b a 3a 2 3a a b a b 3a(a b)(b a) 2 2 b a (b a)(b a)
✔️BÀI TẬP TỰ LUYỆN
Bài 1. [NB] Rút gọn biểu thức sau: 1) 0,04. 225 2) 6 2 ( 3 ) .5 3) 14, 4.490 4) 32.162 Hướng dẫn Trang 12
1) 0,04. 225 0,04. 225 0, 2.15 3 2) 6 2 ( 3 ) .5 3 2 3 2 3 .5 3 .5 135
3) 14, 4.490 144.49 144. 49 12.7 84
4) 32.162 64.81 64. 81 8.9 72
Bài 2. [TH] Rút gọn các biểu thức sau: 1) 200 - 32 - 72
2) 2 48 4 300 72 3 8 1 1 1 3) 48 5 2 75 5 1 4) 2 3 125 180 7 245 3 3 5 Hướng dẫn
1) 200- 32- 72=10 2-4 2 6 2=0
2) 2 48 4 300 72 3 8 2.4 3 4.10 3 6 2 3.2 2
8 3 40 3 6 2 6 2 48 3 1 1 16 4 3) 48 5 2 75 5 1 4 3 5 3 3 3 3 4 2 2 3 4 3 3 5. 3 3 3 3 1 2 5 4) 2
3 125 180 7 245 3.5 5 6 5 7.7 5 5 5 2 2 88 5 5 15 5 6 5 49 5 5 5
Bài 3. [VD] Rút gọn các biểu thức sau: 1) 2 4 a 3 với a 3 2) 2 9 b 2 với b 2 3) 2 2 a a 1 với a 0 2x 3x 4) 2 2 b b 1 với b 0 5) với x 0 6) 3 8
5x 45x 3x với x 0 . Hướng dẫn 1) 2 4 a 3 với a 3 2 a 2 4 a 3 = 4. 3
2. a 3 2(a 3) 2) 2 9 b 2 với b 2 2 b 2 9 b 2 9. 2
3. b 2 3(2 ) b 3) 2 2 a a 1 với a 0 Trang 13
2 a a 2 2 2 2 a a 1 . 1
a . a 1 a(a 1) a a 4) 2 2 b b 1 với b 0
2 b b 2 2 2 2 b b 1 . 1
b . b 1 ( b 1 )
b b b 2x 3x 5) với x 0 3 8 2 2x 3x 2x 3x x x x 3 8 3 8 4 2 2
6) 5x 45x 3x với x 0 . 2
5x 45x 3x 5x.45x 3x
225x 3x 15x 3x 15x 3x 12x
Bài 4 [VD] Rút gọn các biểu thức sau:
1) 25x 36x 4x với x 0
2) 7 5y 20y 500y với y 0 x 1 1 3 3) 32x 8x với x 0 32 2 4x Hướng dẫn
1) 25x 36x 4x với x 0
25x 36x 4x 5 x 6 x 2 x 9 x
2) 7 5y 20y 500y với y 0
7 5y 20y 500y 7 5y 2 5y 10 5y 5 5y x 1 1 3 3) 32x 8x với x 0 32 2 4x x 1 1 3 2x 1 1 32x 8x 4 2x 2x 2x 32 2 4x 8 2 4x 2x 1 13 2 2x 2x 2x 8 2 8 Trang 14
DẠNG 2: BÀI TOÁN CHỨNG MINH
PHẦN I. BÀI TẬP TRẮC NGHIỆM
1. TRẮC NGHIỆM CHỌN ĐÁP ÁN
Câu 1. [NB] Kết quả của phép tính 2,5 14, 4 là: A. 36. B. 6 . C. 18 . D. 9 Lời giải Chọn B
2,5 14, 4 2,5.14, 4 25.144.0,01 5.12.0,1 6
Câu 2. [NB] Kết quả của phép tính 0,1. 0, 4 là: A. 0, 2 . B. 0 ,2 . 4 C. . D. 100 4 100 Lời giải Chọn B
0,1. 0,4 0,04 0 ,2
Câu 3. [NB] Kết quả của phép tính 16,9. 250 là: A.. 0, 45 . B. 4,5 . C. 65 D. 9 . Lời giải Chọn C
16,9. 250 169.25 13.5 65
Câu 4. [NB] Kết quả của phép tính 4,9. 30. 75 là: A.. 1, 05 . B. 10, 5 . C. 1050 . D. 105 . Lời giải Chọn D
4,9. 30. 75 4,9.30.75 49.225 7.15 105
Câu 5. [TH] Kết quả của phép tính 10 6 là: 2 5 12 Trang 15 A. 2 . B. 3 . 2 C. . 2 3 2 D. . 2 Lời giải Chọn C 10 6 2( 5 3) 2 2 5 12 2( 5 3) 2
Câu 6. [TH] Trục căn thức ở mẫu của biểu thức 1 1 ta có kết quả: 3 5 5 7 7 3 A. . B. 7 3 . 2 7 3 C. 7 3 . D. . 2 Lời giải Chọn D 1 1 5 3 7 5 7 3 3 5 5 7 2 2 2 a
Câu 7. [TH] Kết quả trục căn thức của biểu thức với a 0;a 1 là: 1 a a 1 a a 1 a A. . B. . C. 1 a 1 a a 1 a a 1 a . D. . 1 a 1 a Lời giải Chọn D a a(1 a ) 1 a 1 a 1
Câu 8. [TH] Với x y 0 thì biểu thức 2x .x y2 2 y được rút gọn là: x A. x 2 . B. x 2 . C. x 2 . D. 2x . Trang 16 Lời giải Chọn A 1 2x .x y2 1 2x(x y) 2 2. x . x y 2x y x y x y x
Câu 9. [TH] Giá trị của biểu thức 2 2 9a
b 4 4b khi a 2 và b 3
A. 62 3.
B. 62 3 . C. 32 3 . D. 32 3. Lời giải Chọn A 2 2 2 2 9a b
4 4b 9a . (b 2) 3a . b 2 6 3 2 75
Câu 10. [VD] Kết quả rút gọn với x 5 là: 48x 52 5 5x 5 A. . B. . 4x 5 4 5 75 C. . D. . 45 x 48x 5 Lời giải Chọn C 75 25 5 48x 52 2 16(x 5) 4(5 x)
Câu 11. [VD] Rút gọn biểu thức: x 2 x 1 với x 0 , kết quả là: A. x 1 . B. x 1 . C. x 1. D. x 1. Lời giải Chọn D x 2 x 2 x 1 1
x 1 x 1 Trang 17 Câu 12. [VDC] Rút gọn biểu thức 1 1 1 1 P là: 2 3 3 4 4 5 2n 2n 1
A. P 1 2n 1 . B. P 2n 1 2 .
C. P 2 2n 1. D. P 2 1 2n 1. Lời giải Chọn C 1 1 1 1 P 2 3 3 4 4 5 2n 2n 1 2 3 3 4 4 5 2n 2n 1 ... 1 1 1 1
2 3 3 4 4 5 ... 2n 2n 1 2 2n 1
2. TRẮC NGHIỆM ĐÚNG SAI
Trong mỗi ý a), b), c), d) ở mỗi câu, em chọn đúng hoặc sai
Câu 1. Cho phương trình: 2 2x + x - 6 = x + 2 .
a) Điều kiện của phương trình là x ³ 2 .
b) Bình phương 2 vế của phương trình ta được là 2 x - 3x - 10 = 0 .
c) Phương trình có 2 nghiệm .
d) Tổng bình phương các nghiệm của phương trình bằng 20 . Lời giải a) S b) Đ c) Đ d) S
Điều kiện xác định của PT là x ³ - 2 nên A sai
Bình phương 2 vế ta được: 2 2
2x + x - 6 = x + 4x + 4 do đó 2 x - 3x - 10 = 0 nên b đúng 2
x - 3x - 10 = 0 nên PT có nghiệm x = 5; x = - 2(TM) do đó PT có 2 nghiệm nên c đúng
Tổng bình phương của 2 nghiệm là 2 2 5 + (- 2) = 29 nên d sai
Câu 2. Cho phương trình: 2 x + 2x + 4 = x + 2
ha) Điều kiện của phương trình là x ³ - 2 . Trang 18
b) Bình phương 2 vế của phương trình ta được là 2 x + 3x + 1= 0 .
c) Phương trình có 2 nghiệm phân biệt.
d) Các nghiệm của phương trinh đều là số nguyên. Lời giải a) Đ b) S c) S d) S
Điều kiện xác định của PT là x ³ - 2 nên A đúng
Bình phương 2 vế ta được: 2 x + 2x + 4 = x + 2 do đó 2 x + x + 2 = 0 nên b sai 2
x + x + 2 = 0 nên PT vô nghiệm nên c, d sai
Câu 3. Tốc độ của một chiếc thuyền và độ dài đường sóng nước để lại sau đuôi của nó
được cho bởi công thức V 6 x 4 . Trong đó x(m) là độ dài đường sóng nước để lại
sau đuôi thuyền, V(m/s) là vận tốc thuyền.
a) Khi độ dài đường sóng nước là 12 m thi vận tốc của thuyền là 24 m / s .
b) Khi độ dài đường sóng nước là 21m thi vận tốc của thuyền là 28 m / s .
c) Khi vận tốc của thuyền là 30 m / s thì độ dài đường sóng nước là 21m .
d) Khi vận tốc của thuyền càng lớn thì độ dài đường sóng nước càng dài. Lời giải a) Đ b) S c) Đ d) Đ
Khi x 12 V 6 12 4 24 nên a đúng
Khi x 21V 6 21 4 30 nên b sai
Khi V 30 30 6 x 4 x 21 nên c đúng
Khi V càng lớn thì x càng càng dài nên d đúng 2 3 6 8 4
Câu 4. Cho biểu thức C 2 3 4
a)Kết quả rút gọn biểu thức P là 2 2 1.
b) C có dạng a b 2 thì tổng a b là 2 .
c) C có dạng a b 2 thì hiệu 2 2 a b là 0 .
d) Kết quả so sánh biểu thức C với 3 là C 3. Lời giải a) S b) Đ c) Đ d) Đ Trang 19 2 3 6 8 4
2 3 4 4 6 8 C 2 1 2 3 4 2 3 4
C 2 1 nên a sai
C 2 1 do đó a b 1 a b 2 nên b đúng C 2 1 do đó 2 2
a b 1 a b 0 nên c đúng
C 2 1 do đó C 3 nên d đúng
3. TRẮC NGHIỆM TRẢ LỜI NGẮN 10
Câu 1. [NB] Giá trị biểu thức 2 T ( 5 2) bằng: 2 Lời giải
Đáp án: 2 10 2 T ( 5 2)
5 2 5 5 2 5 2 2 3 5 60
Câu 2. [NB] Giá trị của biểu thức A có kết quả bằng: 5 3 15 Lời giải Đáp án: 0 3 5 60 15 15 2 15 A 0 5 3 15 5 3 15
Câu 3. [TH] Cho biểu thức 6 6 6 6 M Giá trị của 2M là: 1 6 6 Lời giải Đáp án: 1 6 6 1 6 6 6 6 6( 6 1) M 6 6 1 1 1 6 6 1 6 6
Câu 4. [TH] Kết quả rút gọn biểu thức: 2 là: (2 3 5) 37 20 3 Lời giải Đáp án: 10 2 2 (2 3 5) 37 20 3 2 3 5 5 2 3
5 2 3 5 2 3 10 Trang 20