


































































































































Preview text:
CHÖÔNG 1: COÂNG THÖÙC LÖÔÏNG GIAÙC I. Ñònh nghóa
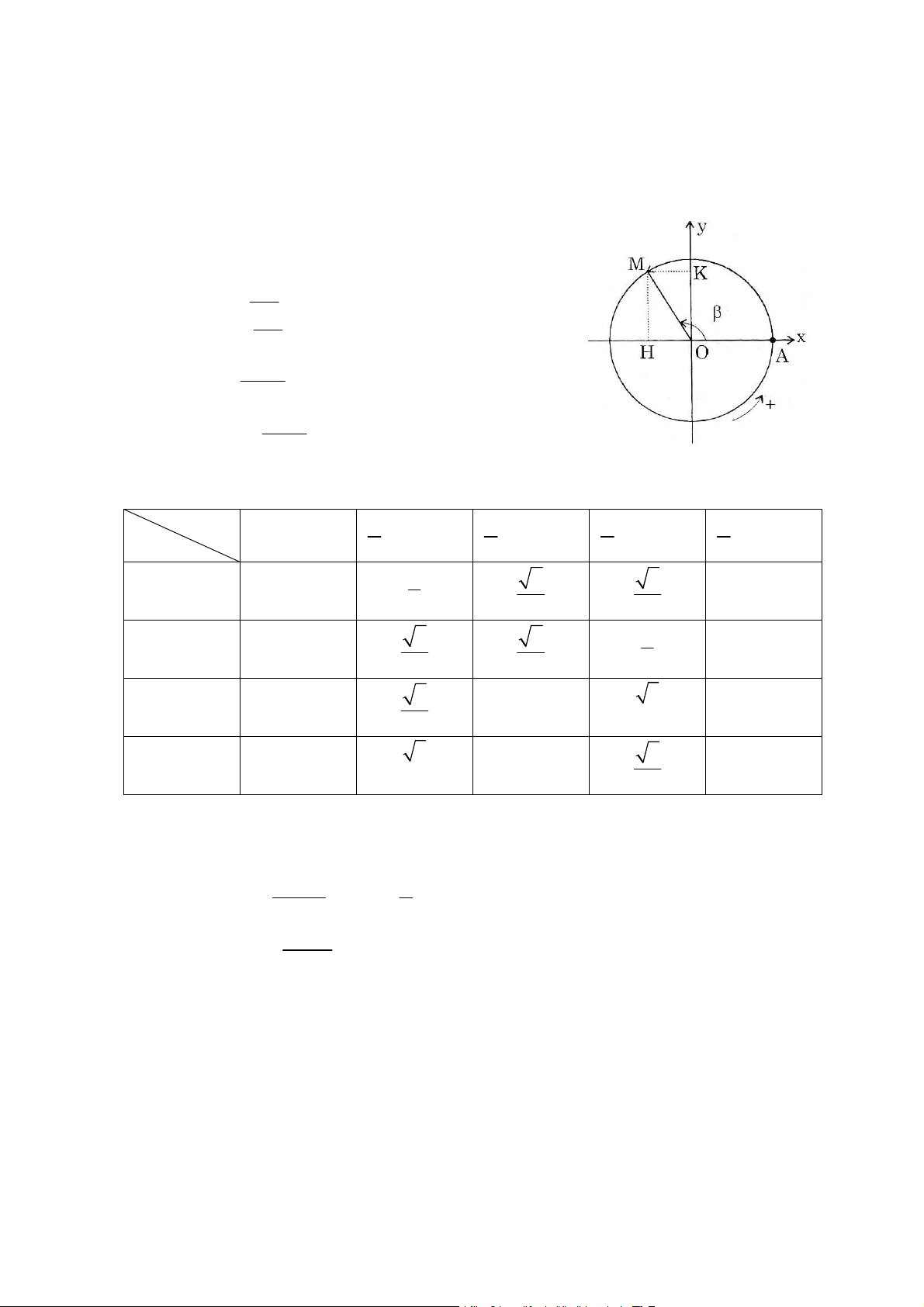
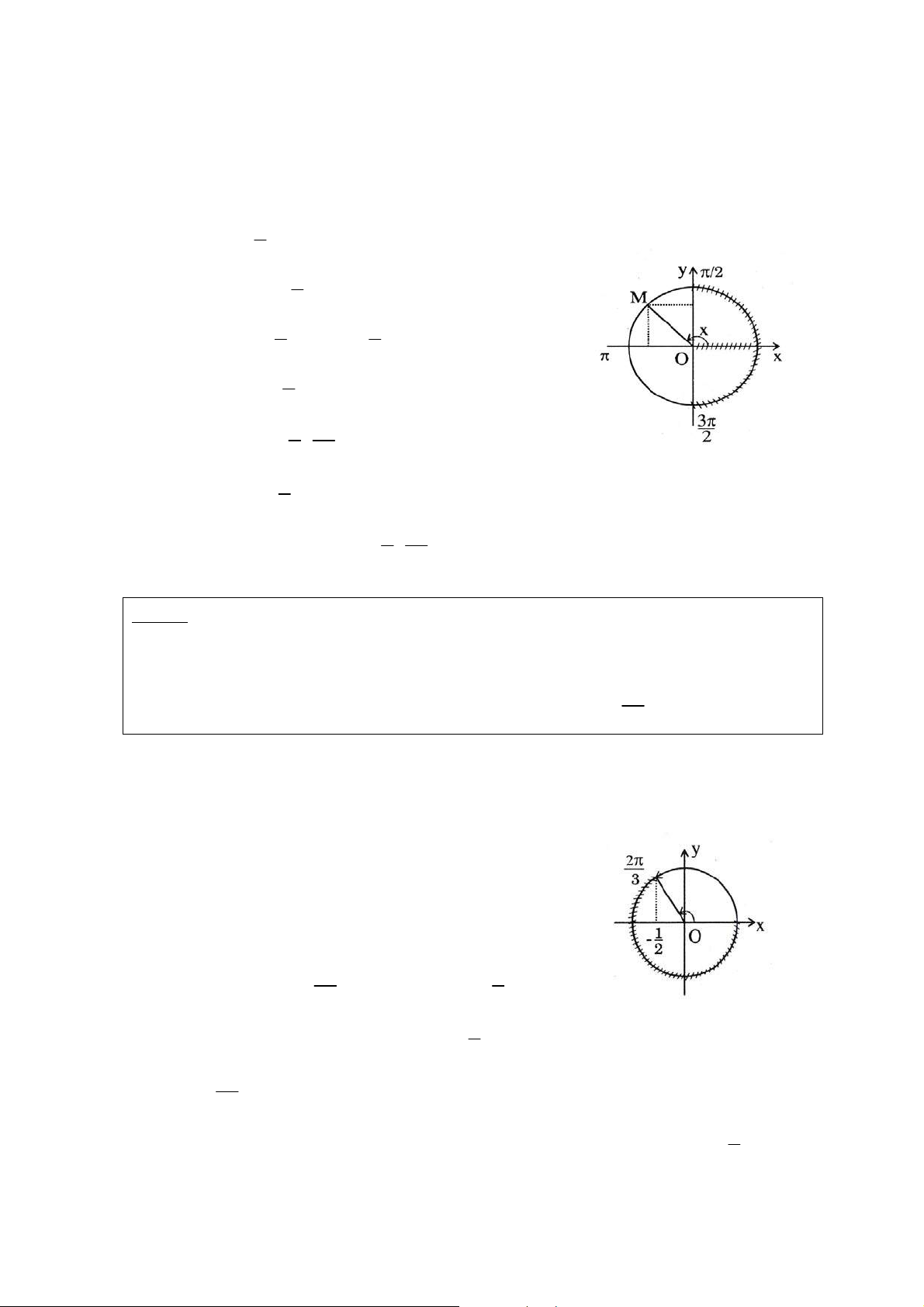
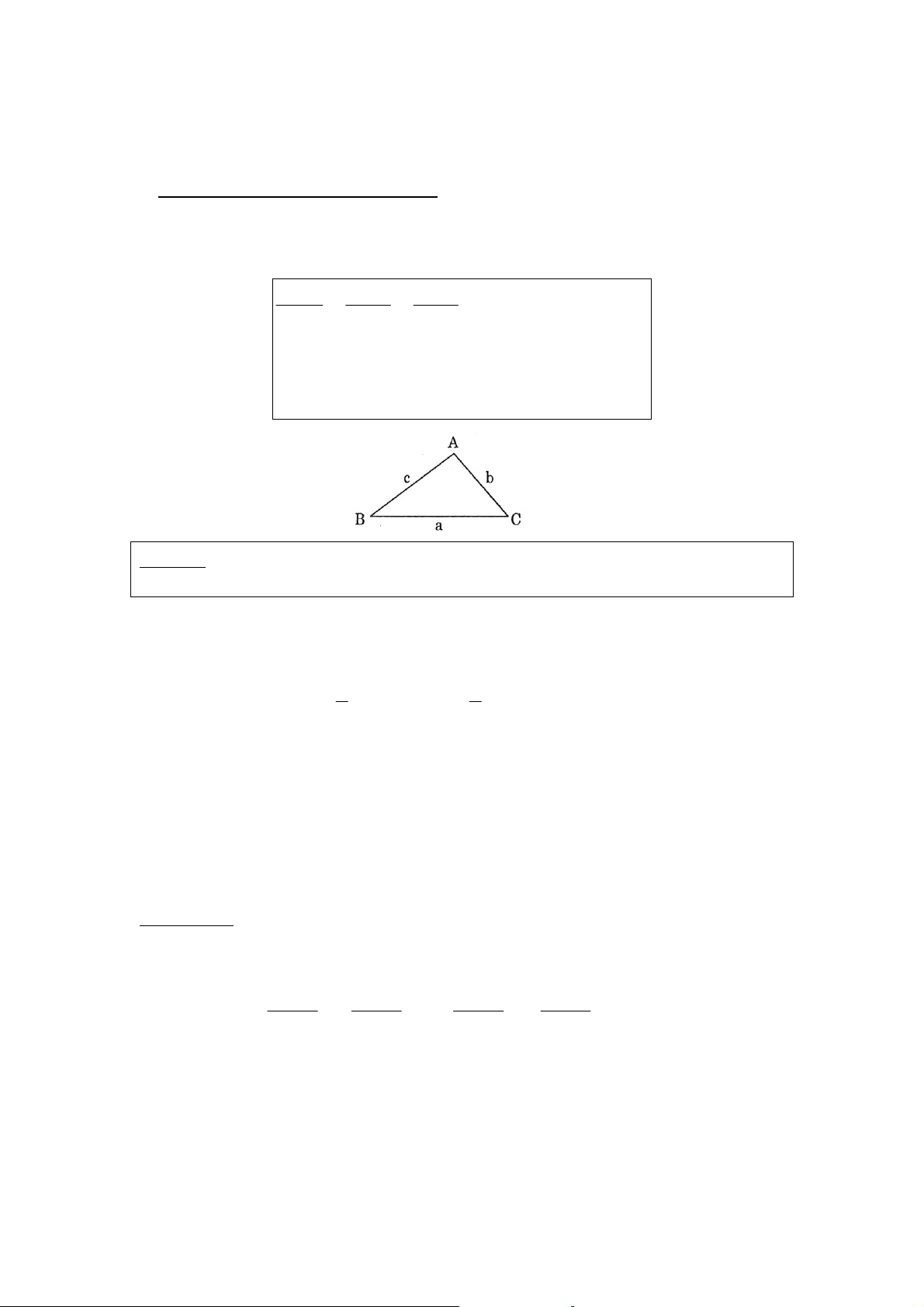
Treân maët phaúng Oxy cho ñöôøng troøn löôïng giaùc taâm O baùn kính R=1 vaø ñieåm M
treân ñöôøng troøn löôïng giaùc maø sñ AM = β vôùi 0 ≤ β ≤ 2π Ñaët α = β + k2 , π k ∈ Z Ta ñònh nghóa: sinα = OK cosα = OH sin tg α α = vôùi cosα ≠ 0 cosα cos cot g α α = vôùi sin α ≠ 0 sinα
II. Baûng giaù trò löôïng giaùc cuûa moät soá cung (hay goùc) ñaëc bieät Goùc α ( o 0 0 ) π ( o 30 ) π ( o 45 ) π ( o 60 ) π ( o 90 ) Giaù trò 6 4 3 2 sinα 0 1 2 3 1 2 2 2 cosα 1 3 2 1 0 2 2 2 tgα 0 3 1 3 || 3 cot gα || 3 1 3 0 3
III. Heä thöùc cô baûn 2 2 sin α + cos α = 1 2 1 1 π + tg α = vôùi α ≠ + kπ(k ∈ Z) 2 cos α 2 2 1 t + cot g = vôùi α ≠ kπ(k ∈ Z) 2 sin α
IV. Cung lieân keát (Caùch nhôù: cos ñoái, sin buø, tang sai π ; phuï cheùo) a. Ñoái nhau: α vaø −α sin(−α) = −sinα cos(−α) = cosα tg(−α) = −tg(α) cot g(−α) = −cotg(α)
b. Buø nhau: α vaø π − α sin(π − α) = sinα cos(π − α) = −cosα tg(π − α) = −tgα cot g(π − α) = −cotgα
c. Sai nhau π : α vaø π + α sin(π + α) = −sinα cos(π + α) = −cosα tg(π + α) = tgα cot g(π + α) = cotgα π d. Phuï nhau: α vaø − α 2 sin⎛ π ⎞ − α = cosα ⎜ 2 ⎟ ⎝ ⎠ cos⎛ π ⎞ − α = sinα ⎜ 2 ⎟ ⎝ ⎠ tg⎛ π ⎞ − α = cot gα ⎜ 2 ⎟ ⎝ ⎠ cot g⎛ π ⎞ − α = tgα ⎜ 2 ⎟ ⎝ ⎠ π π e.Sai nhau : α vaø + α 2 2 sin⎛ π ⎞ + α = cosα ⎜ 2 ⎟ ⎝ ⎠ cos⎛ π ⎞ + α = −sinα ⎜ 2 ⎟ ⎝ ⎠ tg⎛ π ⎞ + α = − cot gα ⎜ 2 ⎟ ⎝ ⎠ cot g⎛ π ⎞ + α = −tgα ⎜ 2 ⎟ ⎝ ⎠ f. sin(x + kπ) = (− )k 1 sin x,k ∈ Z cos(x + kπ) = (− )k 1 cosx,k ∈ Z tg(x + kπ) = tgx,k ∈ Z cot g(x + kπ) = cot gx
V. Coâng thöùc coäng
sin(a ± b) = sinacosb ± sin bcosa
cos(a ± b) = cosacosb ∓ sinasin b ( ± ) tga ± tgb tg a b = 1∓ tgatgb
VI. Coâng thöùc nhaân ñoâi sin2a = 2sinacosa cos2a = 2 cos a − 2 sin a = 1− 2 2sin a = 2 2cos a −1 2tga tg2a = 1− 2 tg a 2 cot g a −1 cot g2a = 2cotga
VII. Coâng thöùc nhaân ba: 3 sin3a = 3sina − 4sin a 3 cos3a = 4cos a − 3cosa
VIII. Coâng thöùc haï baäc: 2 1 sin a = (1− cos2a) 2 2 1 cos a = (1+ cos2a) 2 2 1− cos2a tg a = 1+cos2a
IX. Coâng thöùc chia ñoâi a
Ñaët t = tg (vôùi a ≠ π + k2π ) 2 2t sina = 2 1+ t 2 1− t cosa = 2 1+ t 2t tga = 2 1− t
X. Coâng thöùc bieán ñoåi toång thaønh tích a + b a − b cosa + cosb = 2cos cos 2 2 a + b a − b cosa − cosb = 2 − sin sin 2 2 a + b a − b sina + sin b = 2cos sin 2 2 a + b a − b sina − sin b = 2cos sin 2 2 sin(a ± b) tga ± tgb = cosacosb sin(b ± a) cot ga ± cot gb = sina.sinb
XI. Coâng thöùc bieån ñoåi tích thaønh toång 1 cosa.cosb = ⎡cos ⎣ (a + b) + cos(a − b)⎤ 2 ⎦ 1 sina.sin b − = ⎡cos ⎣ (a + b) − cos(a − b) 2 ⎦⎤ 1 sina.cosb = ⎡sin ⎣ (a + b) + sin(a − b)⎤ 2 ⎦ 4 4 sin a + cos a −1 2 Baøi 1: Chöùng minh = 6 6 sin a + cos a −1 3 Ta coù: + − = ( + )2 4 4 2 2 2 2 2 sin a cos a 1
sin a cos a − 2sin acos a −1 = −2sin acos2 a Vaø: 6 6 sin a + cos a −1 = ( 2 2 sin a + cos a)( 4 2 2 4
sin a − sin acos a + cos a) −1 4 4 2 2
= sin a + cos a − sin acos a −1 = ( 2 2 1− 2sin acos a) 2 2 − sin acos a −1 2 2 = 3s − in acos a 4 4 2 2 sin a + cos a −1 2 − sin acos a 2 Do ñoù: = = 6 6 2 2 sin a + cos a −1 3 − sin acos a 3 1+ cosx ⎡ (1− cosx)2 ⎤
Baøi 2: Ruùt goïn bieåu thöùc A = = 1 ⎢ + ⎥ 2 sin x ⎢ sin x ⎣ ⎥⎦ 1 π
Tính giaù trò A neáu cosx = − vaø < x < π 2 2 2 2
1+ cosx ⎛ sin x +1− 2cosx + cos x ⎞ Ta coù: A = ⎜ 2 sin x sin x ⎟ ⎝ ⎠ 1+ cosx 2(1− cosx) ⇔ A = . 2 sinx sin x 2( 2 1− cos x) 2 2sin x 2 ⇔ A = = = (vôùi sin x ≠ 0) 3 3 sin x sin x sin x Ta coù: 2 2 1 3 sin x = 1− cos x = 1− = 4 4 π
Do: < x < π neân sin x > 0 2 3 Vaäy sin x = 2 2 4 4 3 Do ñoù A = = = sin x 3 3
Baøi 3: Chöùng minh caùc bieåu thöùc sau ñaây khoâng phuï thuoäc x: a. A = 4 − 4 2 2 2
2cos x sin x + sin xcos x + 3sin x 2 cot gx +1 b. B = + tgx −1 cot gx −1 a. Ta coù: 4 4 2 2
A = 2cos x − sin x + sin xcos x + 3sin2 x
⇔ A = 2cos x − (1− cos x)2 4 2 + ( 2 1− cos x) 2 cos x + 3( 2 1− cos x) 4 ⇔ A = 2cos x − ( 2 4 1− 2cos x + cos x) 2 4
+ cos x − cos x + 3 − 3cos2 x
⇔ A = 2 (khoâng phuï thuoäc x)
b. Vôùi ñieàu kieän sin x.cosx ≠ 0,tgx ≠ 1 2 cot gx +1 Ta coù: B = + tgx −1 cot gx −1 1 +1 2 tgx 2 B 1+ tgx ⇔ = + = + tgx −1 1 tgx −1 1− tgx −1 tgx 2 − (1− tgx) 1− tgx ⇔ B = =
= −1 (khoâng phuï thuoäc vaøo x) tgx −1 tgx −1 Baøi 4: Chöùng minh 1+ cosa ⎡ (1− cosa)2 ⎤ 2 2 cos b − sin c 2 2 1 ⎢ − ⎥ +
− cot g bcot g c = cot ga −1 2 2 2 2sina ⎢ sin a ⎥ sin bsin c ⎣ ⎦ Ta coù: 2 2 cos b − sin c * 2 2 − cot g b.cot g c 2 2 sin b.sin c 2 cotg b 1 2 2 = − − cot g bcot g c 2 2 sin c sin b 2 = ( 2 + )−( 2 + ) 2 2 cot g b 1 cot g c
1 cot g b − cot g bcot g c = −1 (1) 1+ cosa ⎡ (1− cosa)2 ⎤ * 1 ⎢ − ⎥ 2 2sina ⎢ sin a ⎥ ⎣ ⎦ 1+ cosa ⎡ (1− cosa)2 ⎤ = 1 ⎢ − ⎥ 2 2sina ⎢ 1− cos a ⎥ ⎣ ⎦ 1+ cosa ⎡ 1− cosa 1 ⎤ = − 2sina ⎢⎣ 1 cosa⎥ + ⎦ 1+ cosa 2cosa = . = cot ga (2) 2sina 1+ cosa
Laáy (1) + (2) ta ñöôïc ñieàu phaûi chöùng minh xong. Baøi 5: Cho AB Δ
C tuøy yù vôùi ba goùc ñeàu laø nhoïn.
Tìm giaù trò nhoû nhaát cuûa P = tgA.tgB.tgC Ta coù: A + B = π − C Neân: tg(A + B) = −tgC tgA + tgB ⇔ = −tgC 1− tgA.tgB
⇔ tgA + tgB = −tgC + tgA.tgB.tgC
Vaäy: P = tgA.tgB.tgC = tgA + tgB+ tgC
AÙp duïng baát ñaúng thöùc Cauchy cho ba soá döông tgA,tgB,tgC ta ñöôïc 3
tgA + tgB+ tgC ≥ 3 tgA.tgB.tgC 3 ⇔ P ≥ 3 P 3 2 ⇔ P ≥ 3 ⇔ P ≥ 3 3 ⎧tgA = tgB = tgC ⎪ π Daáu “=” xaûy ra ⇔ ⎨ π ⇔ A = B = C = 0 < A,B,C < ⎪ 3 ⎩ 2 π
Do ñoù: MinP = 3 3 ⇔ A = B = C = 3
Baøi 6 : Tìm giaù trò lôùn nhaát vaø nhoû nhaát cuûa a/ 8 4 y = 2sin x + cos 2x b/ 4 y = sin x − cos x 4 a/ Ta coù : ⎛ 1 − cos 2x ⎞ 4 y = 2 + cos 2x ⎜ 2 ⎟ ⎝ ⎠
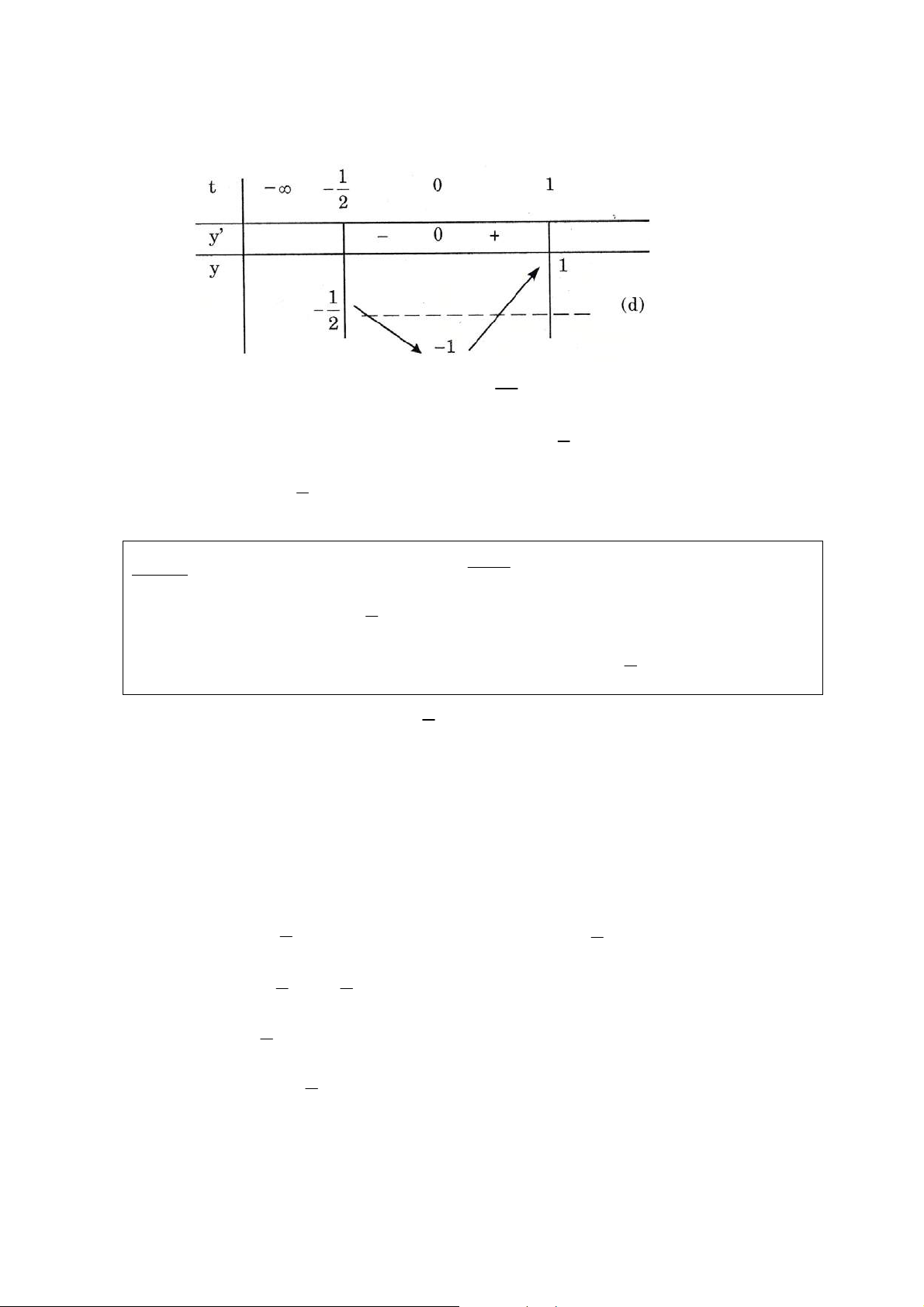
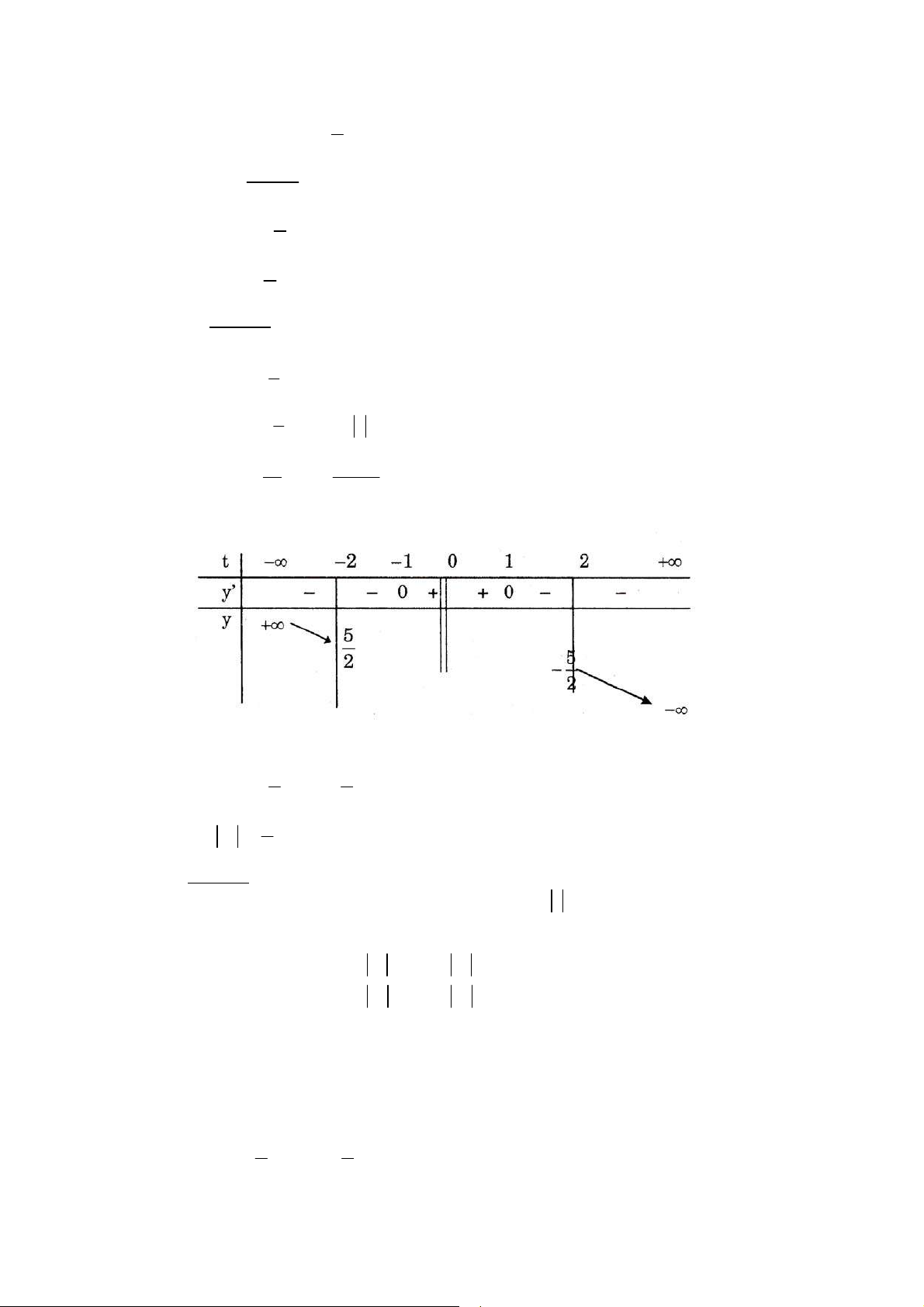
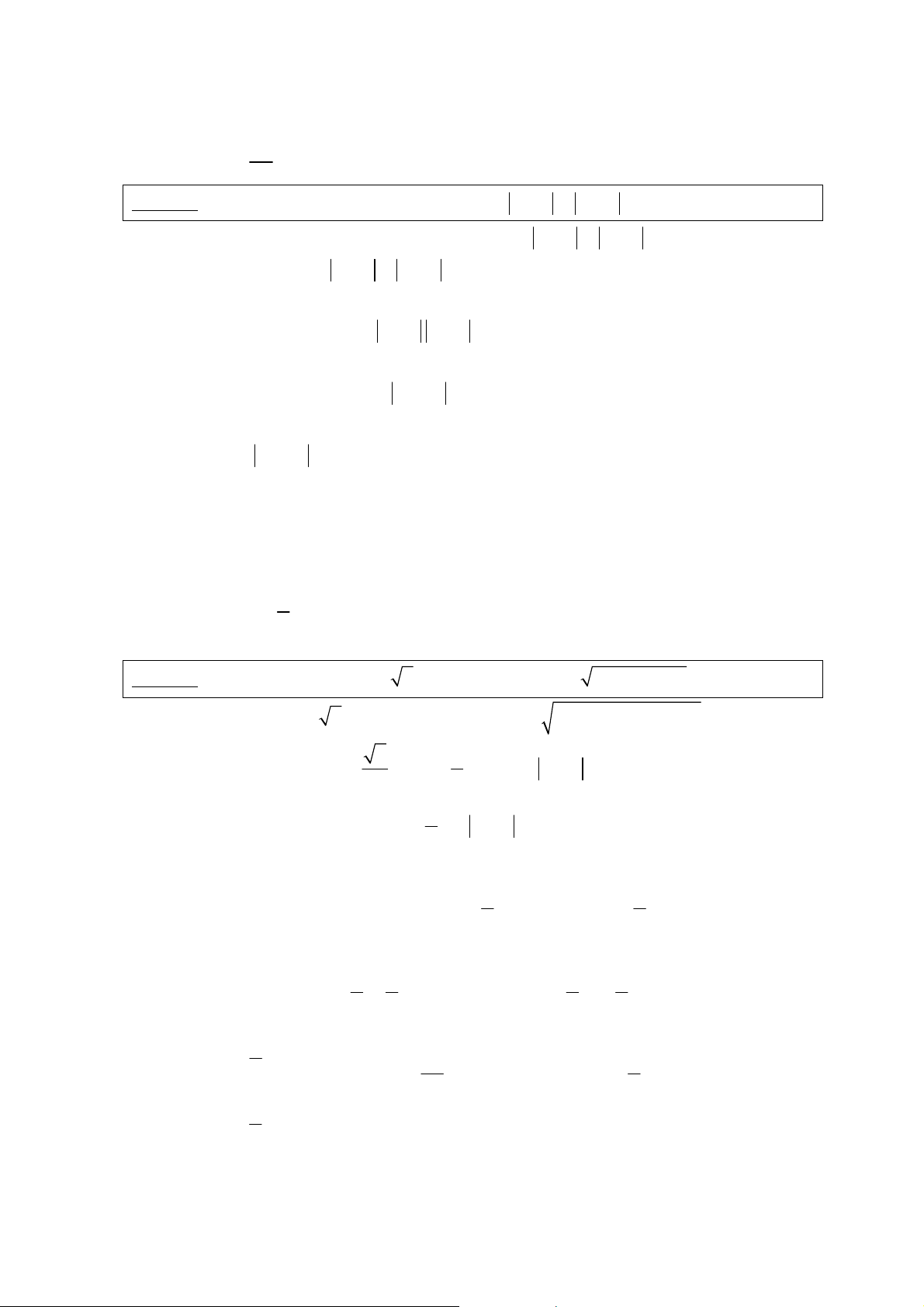
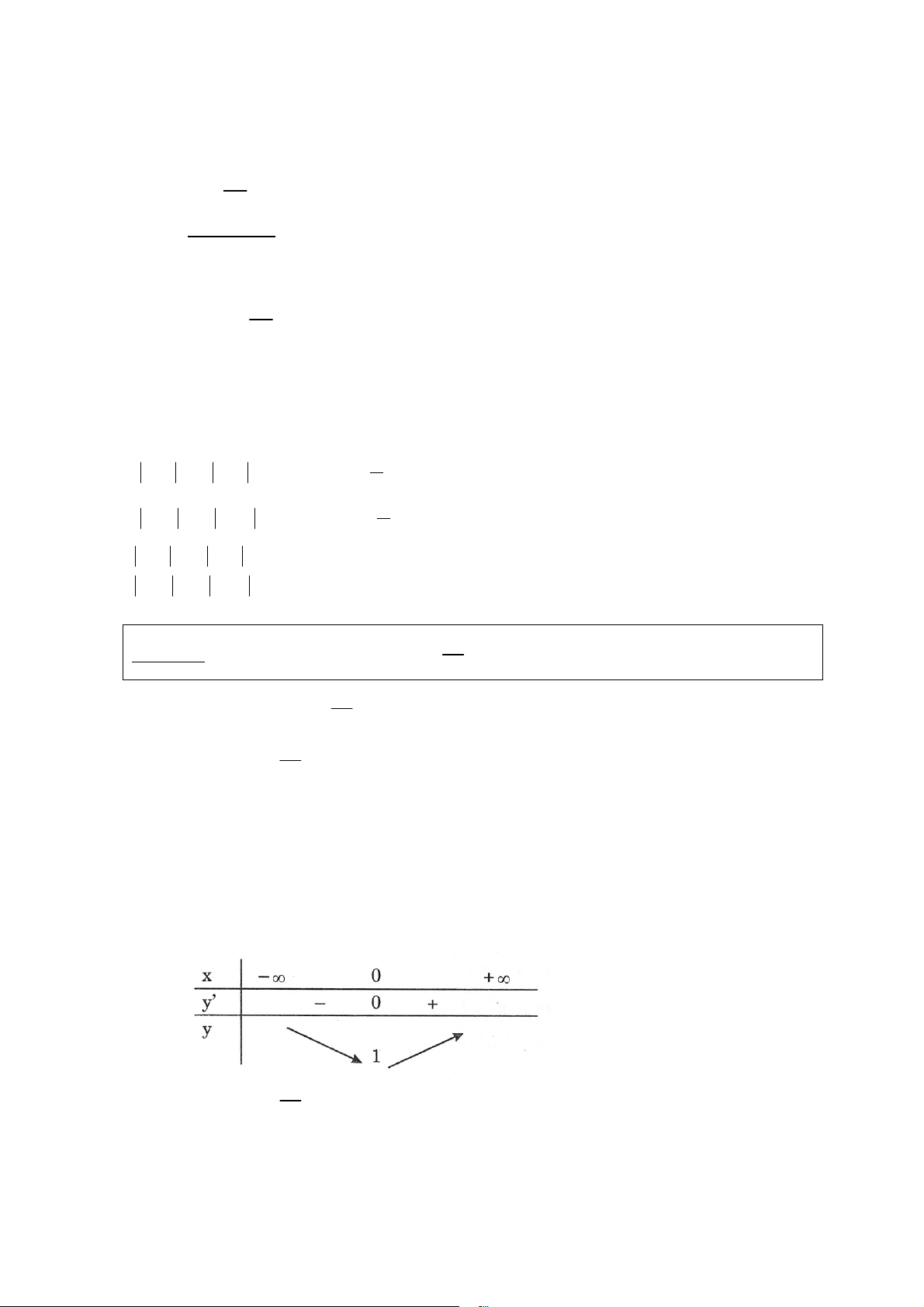
Ñaët t = cos 2x vôùi −1 ≤ t ≤ 1 thì 1 y = (1 − t)4 4 + t 8 1 => y ' = − (1 − t)3 3 + 4t 2 Ta coù : y ' = 0 Ù ( − )3 3 1 t = 8t ⇔ 1 − t = 2t 1 ⇔ t = 3 ⎛ 1 ⎞ 1 Ta coù y(1) = 1; y(-1) = 3; y = ⎜ 3⎟ ⎝ ⎠ 27 1
Do ñoù : Max y = 3 vaø Miny = x∈ x ∈ 27
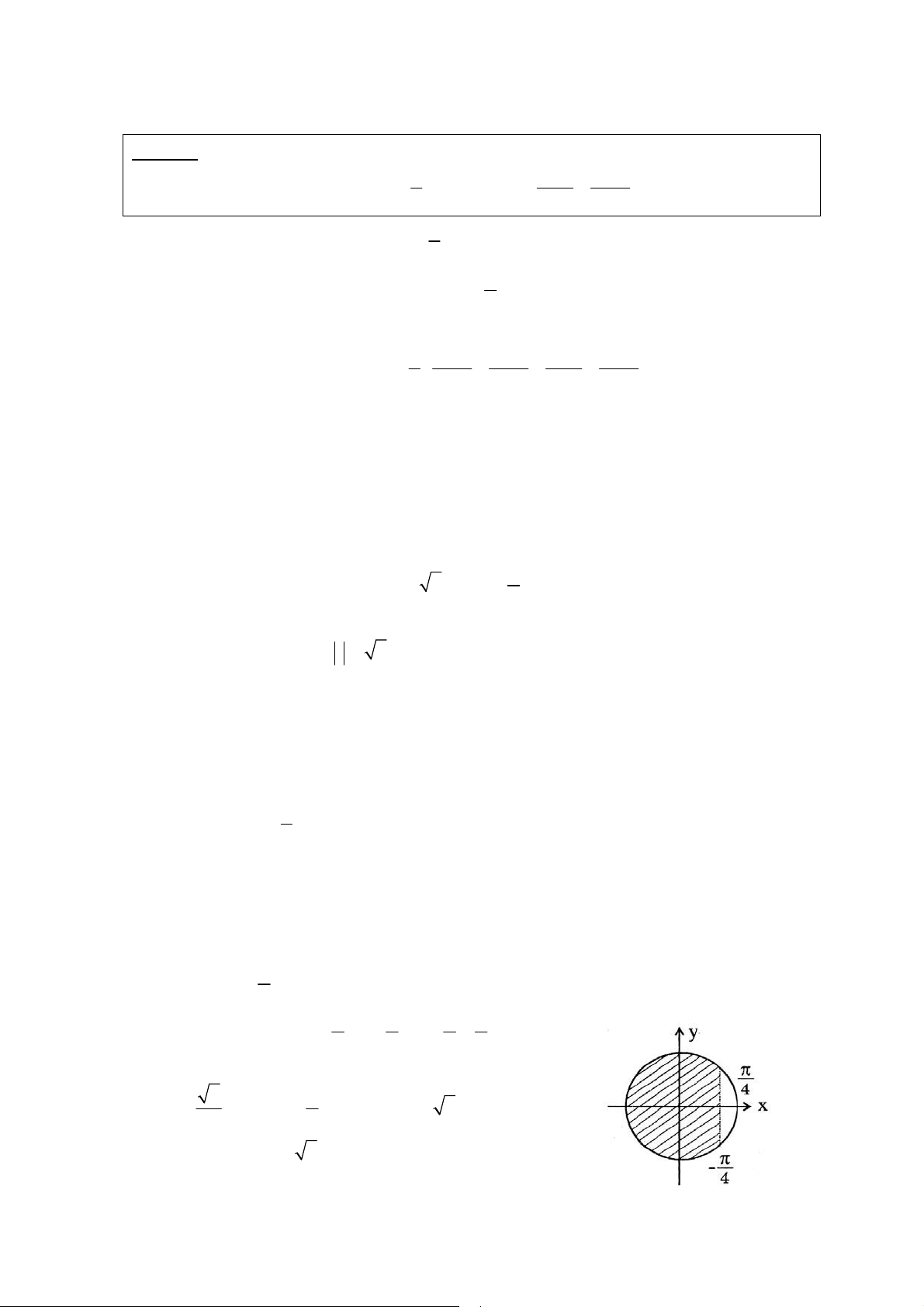
b/ Do ñieàu kieän : sin x ≥ 0 vaø cos x ≥ 0 neân mieàn xaùc ñònh ⎡ π ⎤ D = k π 2 , + k π ⎢ 2 ⎥ vôùi k ∈ ⎣ 2 ⎦
Ñaët t = cos x vôùi 0 ≤ t ≤ 1 thì 4 2 2 t = cos x = 1 − sin x Neân 4 sin x = 1 − t Vaäy 8 4
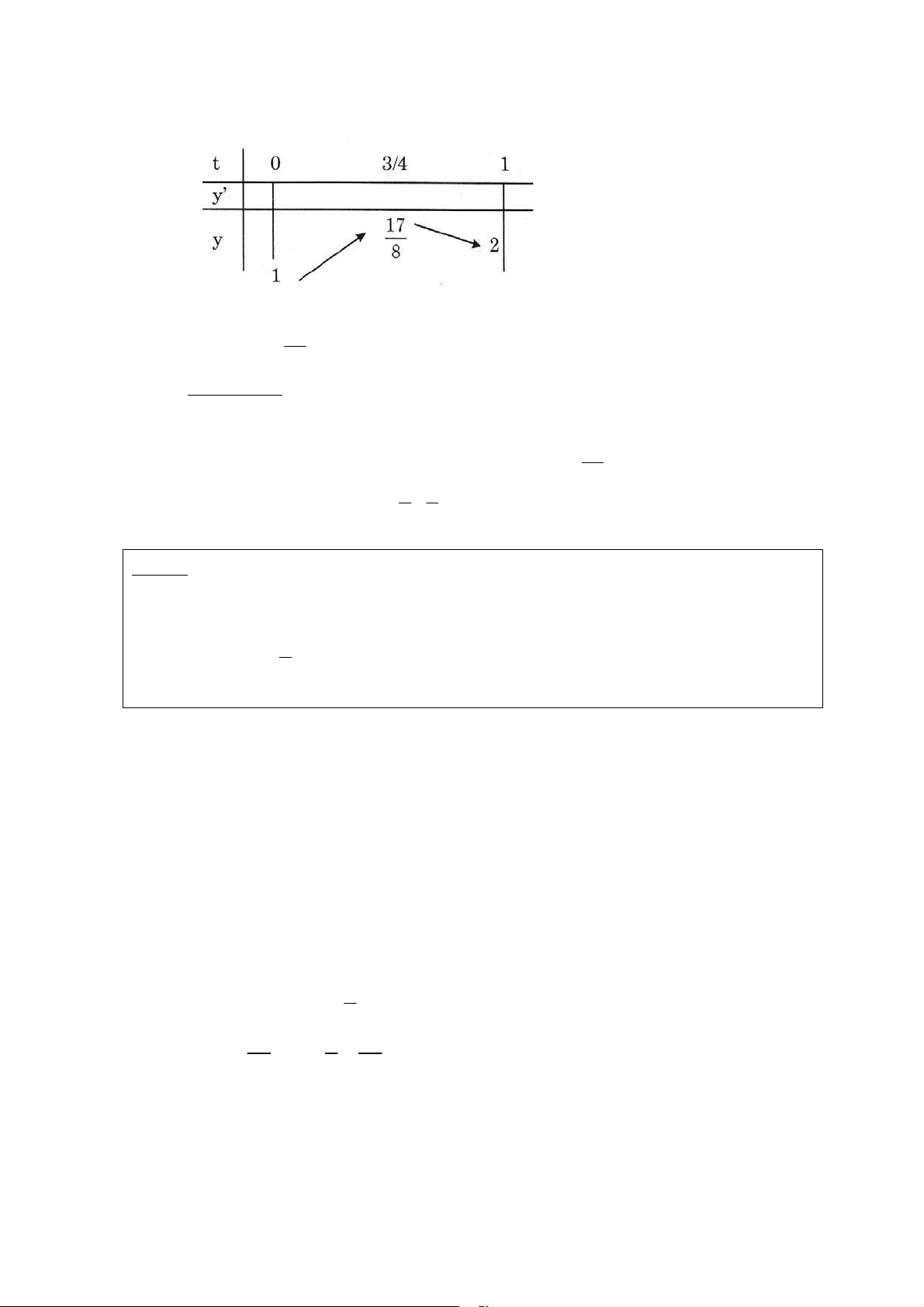
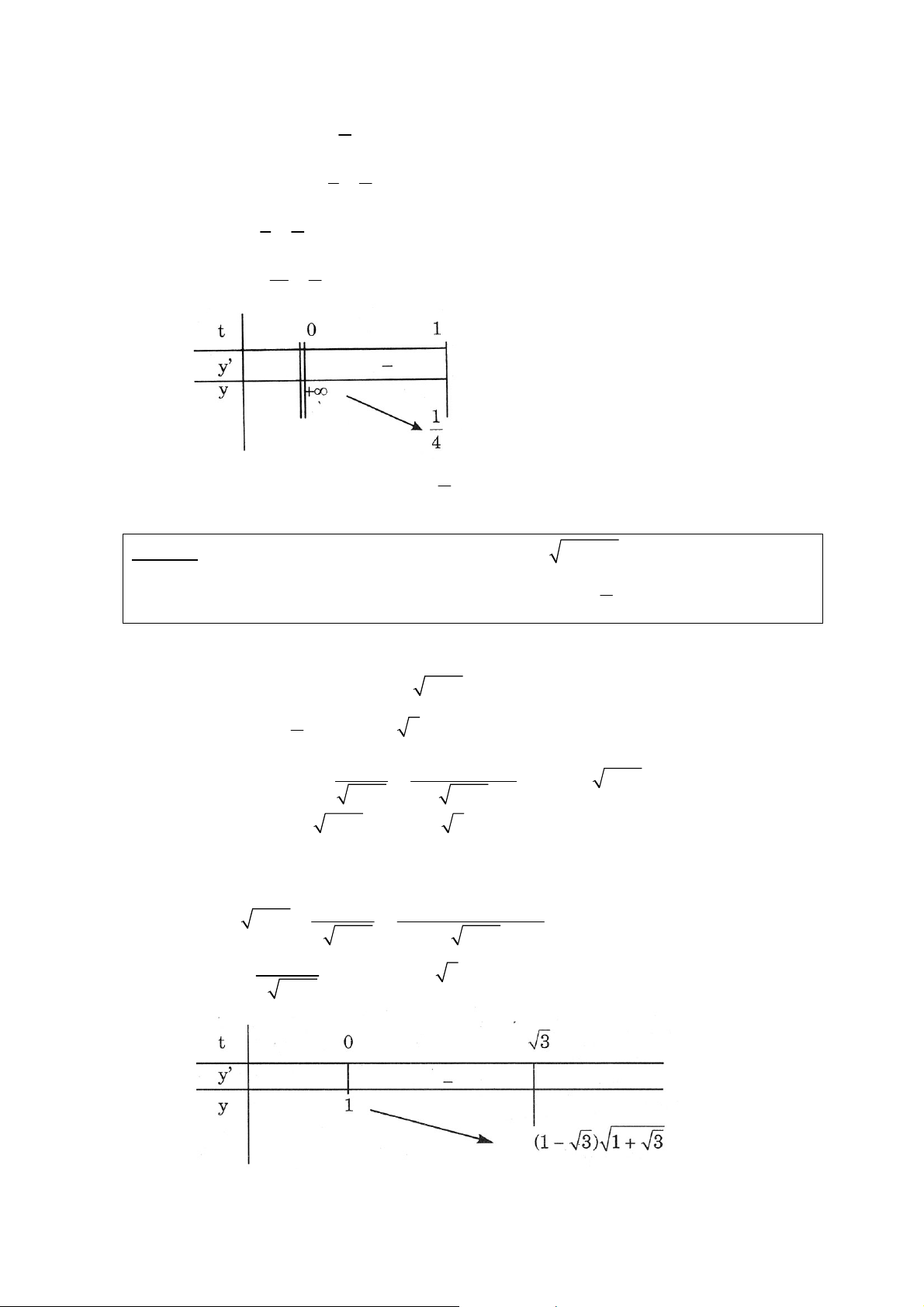
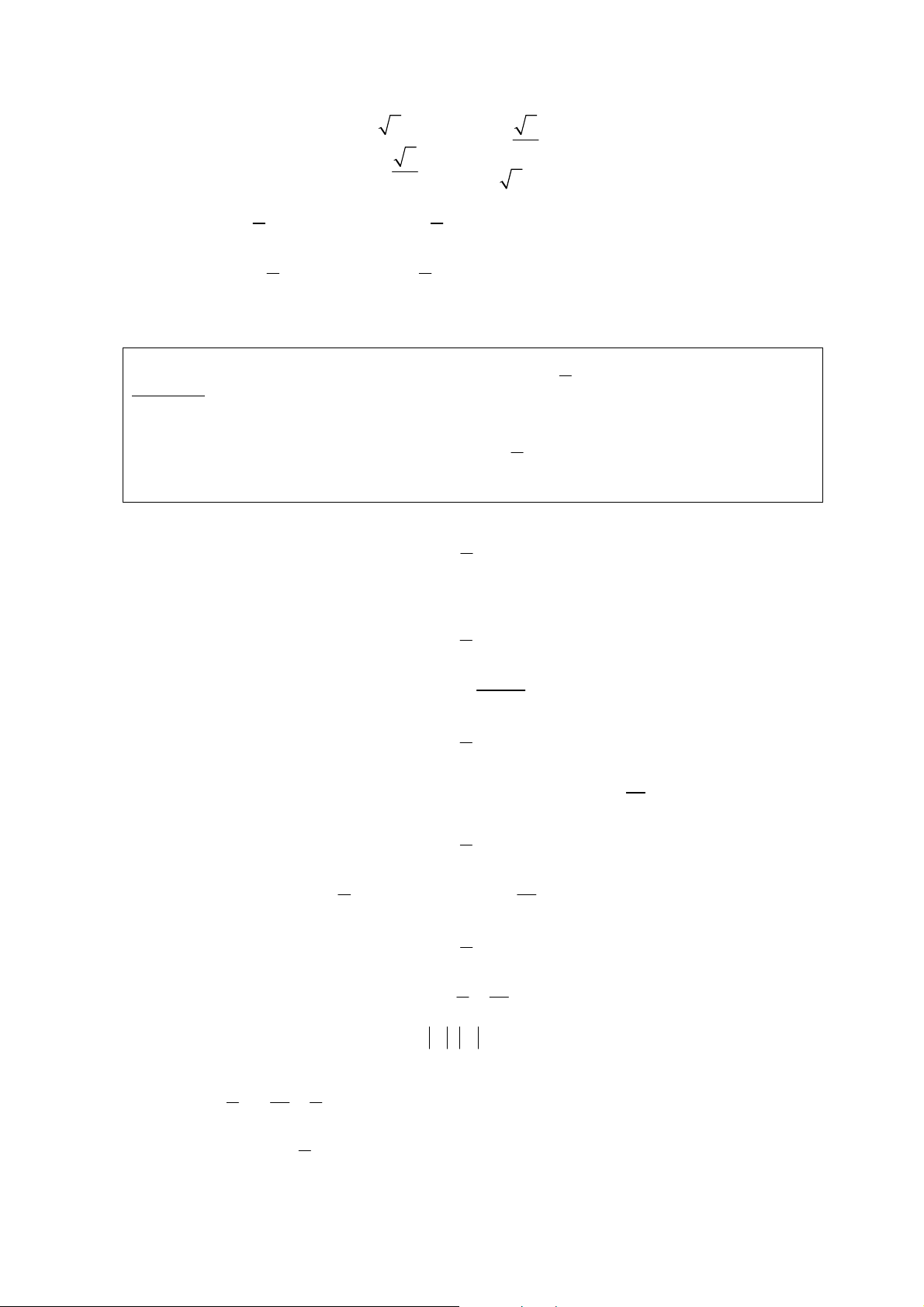
y = 1 − t − t treân D' = [0, ] 1 − 3 t Thì y ' = − 1 < 0 ∀t ∈ [0; ) 1 2. (1 − t )7 4 8
Neân y giaûm treân [ 0, 1 ]. Vaäy : max y = y (0) = 1, min y = y (1) = −1 ∈ x D ∈ x D
Baøi 7: Cho haøm soá 4 4
y = sin x + cos x − 2msin x cos x
Tìm giaù trò m ñeå y xaùc ñònh vôùi moïi x Xeùt 4 4
f (x) = sin x + cos x − 2m sin x cos x ( ) = ( + )2 2 2 2 f x
sin x cos x − m sin 2x − 2sin x cos2 x f (x) 1 2 = 1 − sin 2x − m sin 2x 2
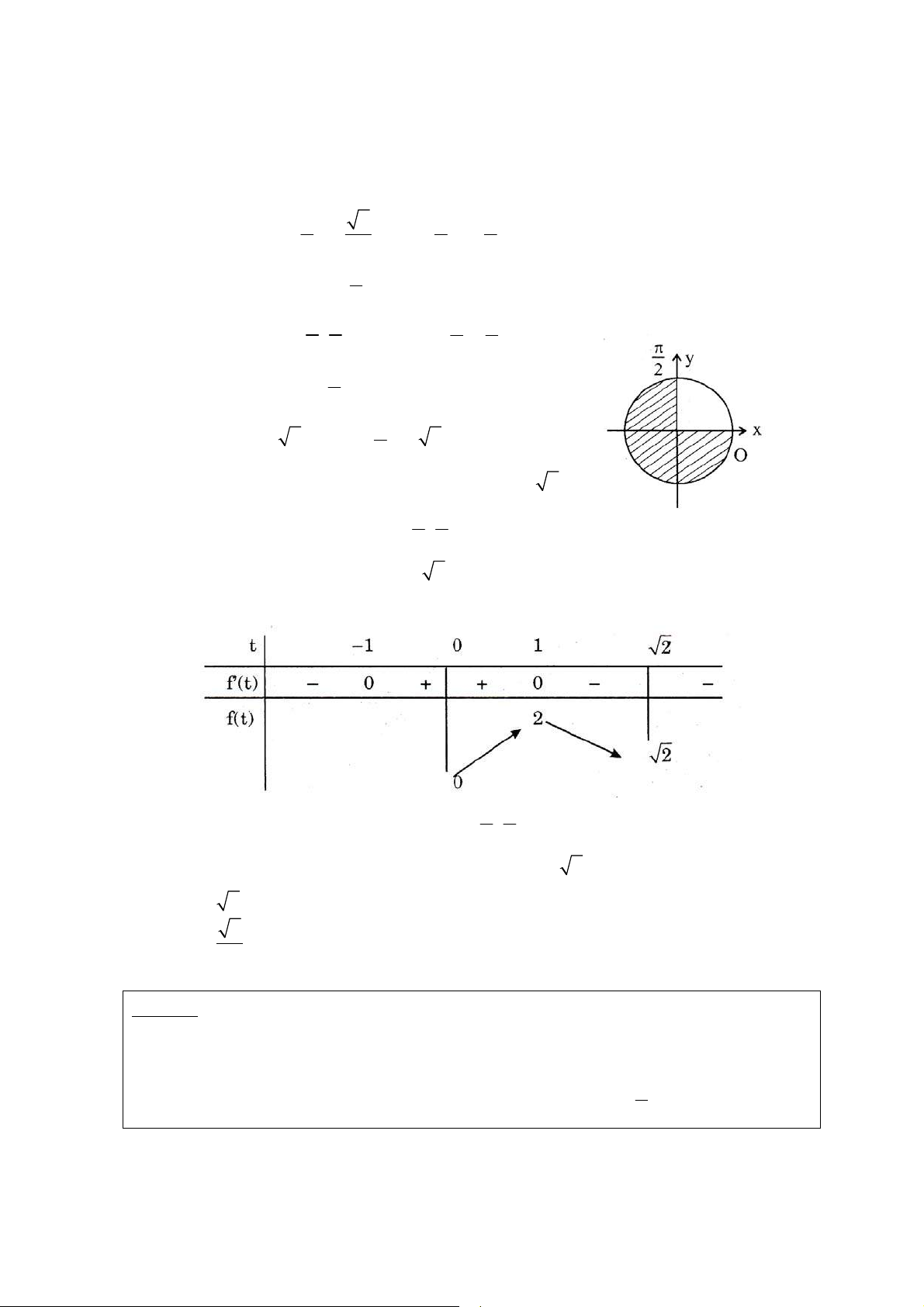
Ñaët : t = sin 2x vôùi t ∈ [ 1 − , ] 1 y xaùc ñònh x ∀ ⇔ f (x) ≥ 0 x ∀ ∈ R 1 ⇔ 2 1 − t − mt ≥ 0 t ∀ ∈ [−1, ] 1 2 ⇔ ( ) 2 g t = t + 2mt − 2 ≤ 0 t ∀ ∈ [ 1 − , ] 1 Do 2
Δ ' = m + 2 > 0 ∀m neân g(t) coù 2 nghieäm phaân bieät t1, t2 Luùc ñoù t t1 t2 g(t) + 0 - 0
Do ñoù : yeâu caàu baøi toaùn ⇔ t ≤ 1 − < 1 ≤ t 1 2 1g ⎧⎪ (−1) ≤ 0 ⎧ 2m − − 1 ≤ 0 ⇔ ⎨ ⇔ ⎨ 1g ⎪⎩ (1) ≤ 0 ⎩2m − 1 ≤ 0 ⎧ 1 m − ≥ ⎪ 1 1 ⇔ ⎪ 2 ⎨ ⇔ − ≤ m ≤ 1 ⎪m 2 2 ≤ ⎪⎩ 2 Caùch khaùc : g (t) 2 = t + 2mt − 2 ≤ 0 t ∀ ∈ [ 1 − , ] 1
⇔ max g(t)≤0⇔ max{g(− ) 1 , g(1 } ) ≤ 0 t [ ∈ − , 1 1 ] ⎧ 1 m − ≥ ⎪⎪ ⇔ 2 max{−2m − ) 1 ,− 2m +1 } ) ≤ 0 ⇔ ⎨ 1 ⎪m ≤ ⎪⎩ 2 ⇔ − 1 ≤ 1 m ≤ 2 2 π 3π 5π 7 3
Baøi 8 : Chöùng minh 4 4 4 4 A sin sin sin sin π = + + + = 16 16 16 16 2 Ta coù : 7 sin π sin ⎛ π π ⎞ = − = cos π 16 ⎜ 2 16⎟ ⎝ ⎠ 16 π 5 ⎛ π π 5 ⎞ sin π 3 = cos − = ⎜ ⎟ cos 16 ⎝ 2 16 ⎠ 16 Maët khaùc : α + α = ( α + α)2 4 4 2 2 2 sin cos sin cos − 2sin α cos2 α 2 2 = 1 − 2sin α cos α 1 2 = 1 − sin 2α 2 π 7π 3 5 Do ñoù : 4 4 4 π 4 A sin sin sin sin π = + + + 16 16 16 16 ⎛ 4 π 4 π ⎞ ⎛ 4 3π 4 3π = sin + cos + sin + cos ⎞ ⎜ 16 16 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 16 16 ⎠ ⎛ 1 2 π ⎞ ⎛ 1 2 = 1 − sin + 1 − sin 3π ⎞ ⎜ 2 8 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 2 8 ⎠ 1 ⎛ 2 π 2 3 2 sin sin π ⎞ = − + 2 ⎜ 8 8 ⎟ ⎝ ⎠ 1 ⎛ 2 π 2 2 sin cos π ⎞ ⎛ 3 = − + π π do sin = cos ⎞ 2 ⎜ 8 8 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 8 8 ⎠ 1 3 = 2 − = 2 2
Baøi 9 : Chöùng minh : o o o o
16sin10 .sin 30 .sin 50 .sin 70 = 1 o Ta coù : A cos10 1 A = =
(16sin10ocos10o)sin30o.sin50o.sin70o o cos10 cos10o 1 ⎛ 1 ⇔ = ( o ) ⎞ o o A 8 sin 20 cos 40 . cos 20 o cos10 ⎜ 2⎟ ⎝ ⎠ 1 ⇔ = ( 0 o o A 4 sin 20 cos 20 .cos 40 o ) cos10 1 ⇔ A = ( o 2 sin 40 ) o cos 40 o cos10 o 1 cos10 ⇔ o A = sin 80 = = 1 o o cos10 cos10 A B B C C A
Baøi 10 : Cho ΔABC . Chöùng minh : tg tg + tg tg + tg tg = 1 2 2 2 2 2 2 A + B π C Ta coù : = − 2 2 2 A + B C Vaäy : tg = cot g 2 2 A B tg + tg 2 2 1 ⇔ A B = C 1 − tg .tg tg 2 2 2 B ⇔ ⎡ A B⎤ C A tg + tg tg = 1 − tg tg ⎢ 2 2 ⎥ ⎣ ⎦ 2 2 2 A C B C A B ⇔ tg tg + tg tg + tg tg = 1 2 2 2 2 2 2
Baøi 11 : Chöùng minh : π π π π 8 + 4tg + 2tg + tg = cot g (*) 8 16 32 32 Ta coù : (*) π π π π ⇔ 8 = cot g − tg − 2tg − 4tg 32 32 16 8 2 2 cos a sin a cos a − sin a Maø : cot ga − tga = − = sin a cos a sin a cos a cos 2a = = 2 cot g2a 1 sin2a 2 Do ñoù : (*) ⎡ π π ⎤ π π ⇔ cot g − tg − 2tg − 4tg = 8 ⎢ 32 32⎥ ⎣ ⎦ 16 8 ⎡ π π ⎤ π ⇔ 2cot g − 2tg − 4tg = 8 ⎢ 16 16⎥ ⎣ ⎦ 8 π π ⇔ 4 cot g − 4tg = 8 8 8 π
⇔ 8cot g = 8 (hieån nhieân ñuùng) 4
Baøi :12 : Chöùng minh : a/ 2 2 ⎛ 2π ⎞ 2 ⎛ 2 cos x + cos + x + cos π − x⎞ 3 = ⎜ 3 ⎟ ⎜ 3 ⎟ ⎝ ⎠ ⎝ ⎠ 2 1 1 1 1 b/ + + + = cot gx − cot g16x sin 2x sin 4x sin 8x sin16x a/ Ta coù : 2 2 ⎛ 2π ⎞ 2 ⎛ 2 cos x + cos + x + cos π − x⎞ ⎜ 3 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 3 ⎠ 1 = ( + ) 1 ⎡ ⎛ 4π ⎞⎤ 1 ⎡ ⎛ 4 1 cos 2x + 1 + cos 2x + + 1 + cos π − 2x⎞⎤ 2 2 ⎢ ⎜ ⎣ ⎝ 3 ⎟⎥ ⎠⎦ 2 ⎢ ⎜ ⎣ ⎝ 3 ⎟⎥ ⎠⎦ 3 1 ⎡ ⎛ 4π ⎞ ⎛ 4π ⎞⎤ = + cos 2x + cos 2x + + cos − 2x 2 2 ⎢ ⎜ ⎟ ⎣ 3 ⎟ ⎜ 3 ⎥ ⎝ ⎠ ⎝ ⎠⎦ 3 1 ⎡ 4 cos 2x 2cos 2x cos π⎤ = + + 2 2 ⎢ 3 ⎥ ⎣ ⎦ 3 1 ⎡ ⎛ 1 = + cos 2x + 2cos 2x ⎞⎤ − 2 2 ⎢ ⎜ ⎣ 2 ⎟⎥ ⎝ ⎠⎦ 3 = 2
cosa cos b sin b cosa − sin a cos b
b/ Ta coù : cot ga − cot gb = − = sin a sin b sin a sin b sin (b − a) = sinasinb sin (2x − x) Do ñoù : 1 cot gx − cot g2x = = (1) sin x sin 2x sin 2x sin (4x − 2x) 1 cot g2x − cot g4x = = (2) sin 2x sin 4x sin 4x sin (8x − 4x) 1 cot g4x − cot g8x = = (3) sin 4x sin 8x sin 8x sin (16x − 8x) 1 cot g8x − cot g16x = = (4) sin16x sin 8x sin16x
Laáy (1) + (2) + (3) + (4) ta ñöôïc 1 1 1 1 cot gx − cot g16x = + + + sin 2x sin 4x sin 8x sin16x
Baøi 13 : Chöùng minh : 3 0 + 2 0 8sin 18 8sin 18 = 1 Ta coù: sin180 = cos720 ⇔ sin180 = 2cos2360 - 1
⇔ sin180 = 2(1 – 2sin2180)2 – 1
⇔ sin180 = 2(1 – 4sin2180+4sin4180)-1
⇔ 8sin4180 – 8sin2180 – sin180 + 1 = 0 (1 )
⇔ (sin180 – 1)(8sin3180 + 8sin2180 – 1) = 0
⇔ 8sin3180 + 8sin2180 – 1 = 0 (do 0 < sin180 < 1) Caùch khaùc :
Chia 2 veá cuûa (1) cho ( sin180 – 1 ) ta coù
( 1 ) ⇔ 8sin2180 ( sin180 + 1 ) – 1 = 0
Baøi 14 : Chöùng minh : a/ 4 4 1 sin x + cos x = (3 + cos4x) 41 b/ sin 6x + cos6x = (5 + 3cos4x) 8 c/ 8 8 1 sin x + cos x = (35 + 28cos4x + cos8x) 64 a/ Ta coù: + = ( + )2 4 4 2 2 2 sin x cos x sin x cos x − 2sin x cos2 x 2 2 = 1 − sin 2x 4 1 = 1 − (1 − cos4x) 4 3 1 = + cos 4x 4 4 b/ Ta coù : sin6x + cos6x = ( 2 2 + )( 4 2 2 4
sin x cos x sin x − sin x cos x + cos x) = ( 4 4 sin x + cos x) 1 2 − sin 2x 4 ⎛ 3 1 ⎞ 1 = + cos 4x − ⎜ ⎟
(1 − cos4x) ( do keát quaû caâu a ) ⎝ 4 4 ⎠ 8 3 5 = cos 4x + 8 8 c/ Ta coù : + = ( + )2 8 8 4 4 − 4 sin x cos x sin x cos x 2sin x cos4 x 1 2 = (3 + cos4x)2 − 4 sin 2x 16 16 2 1 ( 2 ) 1 ⎡1 9 6cos 4x cos 4x (1 cos4x)⎤ = + + − − ⎢ ⎥ 16 8 ⎣2 ⎦ 9 3 1 = + + ( + ) 1 cos4x 1 cos8x − ( 2 1 − 2cos4x + cos 4x) 16 8 32 32 9 3 1 1 1 = + cos4x + cos8x + cos4x − (1 + cos8x) 16 8 32 16 64 35 7 1 = + cos4x + cos8x 64 16 64
Baøi 15 : Chöùng minh : 3 3
sin 3x.sin x + cos3x.cos x = cos3 2x Caùch 1: Ta coù : s 3 3 3
in 3x.sin x + cos3x.cos x = cos 2x = ( 3 − ) 3 + ( 3 − ) 3 3sin x 4 sin x sin x 4 cos x 3cos x cos x 4 6 6
= 3sin x − 4 sin x + 4 cos x − 3cos4 x = ( 4 4 − ) − ( 6 6 3 sin x cos x 4 sin x − cos x) = ( 2 2 − )( 2 2 3 sin x cos x sin x + cos x) − ( 2 2 − )( 4 2 2 4
4 sin x cos x sin x + sin x cos x + cos x) 2 2 = −3cos 2x + 4 cos 2x 1 ⎡ − sin x cos x⎤ ⎣ ⎦ ⎛ 1 2 3cos 2x 4 cos 2x 1 sin 2x⎞ = − + − ⎜ 4 ⎟ ⎝ ⎠ ⎡ ⎛ 1 2 = cos 2x 3 − + 4 1 − sin 2x⎞⎤ ⎢ ⎜ ⎣ 4 ⎟⎥ ⎝ ⎠⎦ = ( 2 cos 2x 1 − sin 2x) 3 = cos 2x Caùch 2 : Ta coù : si 3 3 n 3x.sin x + cos3x.cos x ⎛ 3sin x − sin 3x ⎞ ⎛ 3cos x + cos 3x = sin 3x + cos 3x ⎞ ⎜ 4 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 4 ⎠ 3 = ( + ) 1 sin 3x sin x cos3x cos x + ( 2 2 cos 3x − sin 3x) 4 4 3 = ( − ) 1 cos 3x x + cos6x 4 4 1 = (3cos2x + cos3.2x) 4 1 = (3cos2x + 3
4 cos 2x − 3cos2x) ( boû doøng naøy cuõng ñöôïc) 4 3 = cos 2x
Baøi 16 : Chöùng minh : o o o o o 3 + 1
cos12 + cos18 − 4 cos15 .cos 21 cos 24 = − 2 Ta coù : o o o + − ( o cos12 cos18 4 cos15 cos 21 cos 24o ) o o o = − ( o 2cos15 cos 3 2cos15 cos 45 + cos 3o ) o o o o o o
= 2cos15 cos3 − 2cos15 cos45 − 2cos15 cos3 o o = 2c − os15 cos45 = − ( o o cos 60 + cos 30 ) 3 + 1 = − 2 Baøi 17 : Tính 2 o 2 o
P = sin 50 + sin 70 − cos50 cos70o 1 1 1 Ta coù : P = (1 − o cos100 ) + (1 − o cos140 ) − ( o cos120 + cos20o ) 2 2 2 1 ( o o ) 1 ⎛ 1 P 1 cos100 cos140 cos 20o ⎞ = − + − − + 2 2 ⎜ 2 ⎟ ⎝ ⎠ = − ( o o ) 1 1 P 1 cos120 cos20 + − cos20o 4 2 5 1 o 1 o 5 P = + cos20 − cos20 = 4 2 2 4
Baøi 18 : Chöùng minh : o o o o 8 3 tg30 + tg40 + tg50 + tg60 = cos 20o 3 sin (a + b)
AÙp duïng : tga + tgb = cosacosb Ta coù : ( o o + ) + ( o o tg50 tg40 tg30 + tg60 ) o o sin 90 sin 90 = + o o o cos50 cos 40 cos 30 cos60o 1 1 = + o o sin 40 cos 40 1 o cos 30 2 2 2 = + o o sin 80 cos30 ⎛ 1 1 2 ⎞ = + ⎜ o o cos10 cos 30 ⎟ ⎝ ⎠ o o ⎛ cos30 + cos10 ⎞ = 2⎜ o o cos10 cos 30 ⎟ ⎝ ⎠ p o cos 20 cos10 = 4 o o cos10 cos 30 8 3 o = cos 20 3
Baøi 19 : Cho ΔABC , Chöùng minh : A B C a/
sin A + sin B + sin C = 4 cos cos cos 2 2 2 A B C b/
socA + cosB + cosC = 1 + 4sin sin sin 2 2 2 c/
sin 2A + sin 2B + sin 2C = 4 sin A sin B sin C d/ 2 2 2 cos A + cos B + cos C = 2 − cos A cosBcosC e/ tgA + tgB + tgC = tgA.tgB.tgC f/
cot gA.cot gB + cot gB.cot gC + cot gC.cot gA = 1 A B C A B C g/ cot g + cot g + cot g = cot g .cot g .cot g 2 2 2 2 2 2 A + B A − B
a/ Ta coù : sin A + sin B + sin C = 2sin cos + sin (A + B) 2 2 A + B ⎛ A − B A + B 2sin cos cos ⎞ = + 2 ⎜ 2 2 ⎟ ⎝ ⎠ C A B ⎛ A + B π C ⎞ = 4 cos cos cos do = ⎜ − ⎟ 2 2 2 ⎝ 2 2 2 ⎠ A + B A − B
b/ Ta coù : cos A + cosB + cosC = 2cos cos − cos(A + B) 2 2 A + B A − B ⎛ 2 A + B 2cos cos 2cos − 1⎞ = − 2 2 ⎜ 2 ⎟ ⎝ ⎠ A + B ⎡ A − B A + B 2cos cos cos ⎤ = − + 1 2 ⎢ 2 2 ⎥ ⎣ ⎦ A + B A ⎛ B 4 cos sin sin ⎞ = − − + 1 2 2 ⎜ 2 ⎟ ⎝ ⎠ C A B = 4sin sin sin + 1 2 2 2
c/ sin 2A sin 2B + sin 2C = 2sin (A + B)cos(A − B) + 2sinCcosC
= 2sin C cos(A − B) + 2sin C cosC
= 2sin C[cos(A − B) − cos(A + B) ] = −4sin Csin A sin( − B) = 4 sin C sin A sin B 2 2 2 d/ cos A + cos B + cos C 1 = 1 + (cos2A + cos2B) 2 + cos C 2 = + ( + ) ( − ) 2 1 cos A B cos A B + cos C
= 1 − cosC ⎡cos(A − B) − cosC⎤ ⎣ ⎦ do (cos(A + B) = − cosC)
= 1 − cosC ⎡cos(A − B) + cos(A + B)⎤ ⎣ ⎦ = 1 − 2 cos C.cos A.cos B
e/ Do a + b = π − C neân ta coù tg (A + B) = −tgC tgA + tgB ⇔ = −tgC 1 − tgAtgB
⇔ tgA + tgB = −tgC + tgAtgBtgC
⇔ tgA + tgB + tgC = tgAtgBtgC
f/ Ta coù : cotg(A+B) = - cotgC 1 − tgAtgB ⇔ = − cot gC tgA + tgB −
⇔ cot gA cot gB 1 = − cot gC (nhaân töû vaø maãu cho cotgA.cotgB) cot gB + cot gA
⇔ cot gA cot gB − 1 = − cot gCcot gB − cot gA cot gC
⇔ cot gA cot gB + cot gBcot gC + cot gA cot gC = 1 A + B C g/ Ta coù : tg = cot g 2 2 A B tg + tg 2 2 C ⇔ = cot g A B 2 1 − tg tg 2 2 A B cot g + cot g 2 2 C B ⇔ = cot g A B
(nhaân töû vaø maãu cho cotg A .cotg ) 2 cot g .cot g − 1 2 2 2 2 A B A B C C ⇔ cot g + cot g = cot g cot g cot g − cot g 2 2 2 2 2 2 A B C A B C ⇔ cot g + cot g + cot g = cot g .cot g .cot g 2 2 2 2 2 2
Baøi 20 : Cho ΔABC . Chöùng minh :
cos2A + cos2B + cos 2C + 4cosAcosBcosC + 1 = 0
Ta coù : (cos2A + cos2B) + (cos2C + 1)
= 2 cos (A + B)cos(A - B) + 2cos2C = - 2cosCcos(A - B) + 2cos2C
= - 2cosC[cos(A – B) + cos(A + B)] = - 4cosAcosBcosC
Do ñoù : cos2A + cos2B + cos2C + 1 + 4cosAcosBcosC = 0
Baøi 21 : Cho ΔABC . Chöùng minh : 3A 3B 3C
cos3A + cos3B + cos3C = 1 - 4sin sin sin 2 2 2
Ta coù : (cos3A + cos3B) + cos3C 3 3 2 3C
= 2cos (A + B) cos (A − B) + 1 − 2sin 2 2 2 3 3 3C
Maø : A + B = π − C neân (A + B) = π − 2 2 2 => 3 ( ) ⎛ 3 cos A B cos π 3C ⎞ + = − 2 ⎜ 2 ⎟ ⎝ 2 ⎠ ⎛ π 3C cos ⎞ = − − ⎜ 2 2 ⎟ ⎝ ⎠ 3C = − sin 2
Do ñoù : cos3A + cos3B + cos3C 3C 3(A − B) 2 3C = 2s − in cos − 2sin + 1 2 2 2 3C ⎡ 3(A − B) 3C⎤ = 2 − sin ⎢cos + sin ⎥ + 1 2 2 2 ⎣ ⎦ 3C ⎡ 3(A − B) 3 ⎤ = 2s − in cos − cos (A + B) + ⎢ ⎥ 1 2 2 2 ⎣ ⎦ 3C 3A −3B = 4 sin sin sin( ) + 1 2 2 2 3C 3A 3B = 4 − sin sin sin + 1 2 2 2
Baøi 22 : A, B, C laø ba goùc cuûa moät tam giaùc. Chöùng minh : sin A + sin B − sin C A B C = tg tg cot g cos A + cosB − cosC + 1 2 2 2 A + B A − B C C 2sin cos − 2sin cos
Ta coù : sin A + sin B − sin C 2 2 2 2 = cos A + cos B − cosC + 1 A + B A − B 2 C 2cos cos + 2sin 2 2 2 C ⎡ A − B C⎤ A − B A 2cos cos − sin ⎢ ⎥ cos − cos + B 2 ⎣ 2 2 ⎦ C 2 2 = = cot g . C ⎡ A − B C⎤ 2 A − B A + B 2sin cos + sin cos + cos 2 ⎢ 2 2 ⎥ ⎣ ⎦ 2 2 A ⎛ B 2sin .sin ⎞ − − C 2 ⎜ ⎝ 2 ⎟ cot g . ⎠ = 2 A B 2cos .cos 2 2 C A B = cot g .tg .tg 2 2 2
Baøi 23 : Cho ΔABC . Chöùng minh : A B C B C A C A B sin cos cos + sin cos cos + sin cos cos 2 2 2 2 2 2 2 2 2 A B C A B B C A C = sin sin sin + tg tg + tg tg + tg tg (*) 2 2 2 2 2 2 2 2 2 A + B π C Ta coù : = − vaäy ⎛ A B ⎞ C tg + = cot g 2 2 2 ⎜ 2 2 ⎟ ⎝ ⎠ 2 A B tg + tg 2 2 1 ⇔ A B = C 1 − tg tg tg 2 2 2 B ⇔ ⎡ A B⎤ C A tg + tg tg = 1 − tg tg ⎢ 2 2 ⎥ ⎣ ⎦ 2 2 2 A C B C A B ⇔ tg tg + tg tg + tg tg = 1(1) 2 2 2 2 2 2 A B C B C A C A B
Do ñoù : (*) Ù sin cos cos + sin cos cos + sin cos cos 2 2 2 2 2 2 2 2 2 A B C = sin sin sin + 1 (do (1)) 2 2 2 ⇔ A ⎡ B C B C⎤ A ⎡ B C C B sin cos cos − sin sin + cos sin cos + sin cos ⎤ = 1 2 ⎢ 2 2 2 2⎥ 2 ⎢ ⎣ ⎦ ⎣ 2 2 2 2⎥⎦ A B + C A B + C ⇔ sin cos + cos sin = 1 2 2 2 2 A + B + C ⇔ sin = 1 π
⇔ sin = 1 ( hieån nhieân ñuùng) 2 2 A B C 3 + cos A + cosB + cosC
Baøi 24 : Chöùng minh : tg + tg + tg = (*) 2 2 2 sin A + sin B + sin C Ta coù : A + B A − B ⎡ 2 C cos A cos B cosC 3 2cos cos 1 2sin ⎤ + + + = + − + 3 2 2 ⎢ 2 ⎥ ⎣ ⎦ C A − B 2 = 2sin cos + 4 − 2sin C 2 2 2 C ⎡ A − B C 2sin cos sin ⎤ = − + 4 2 ⎢ 2 2 ⎥ ⎣ ⎦ C ⎡ A − B A + B 2sin cos cos ⎤ = − + 4 2 ⎢ 2 2 ⎥ ⎣ ⎦ C A B = 4 sin sin .sin + 4 (1) 2 2 2 A + B A − B sin A + sin B + sin C = 2sin cos + sin C 2 2 C A − B C = 2cos cos + 2sin cos C 2 2 2 2 C ⎡ A − B A + B 2cos cos cos ⎤ = + 2 ⎢ 2 2 ⎥ ⎣ ⎦ C A B = 4 cos cos cos (2) 2 2 2 Töø (1) vaø (2) ta coù : A B C A B C sin sin sin sin sin sin + 1 (*) ⇔ 2 2 2 2 2 2 A + B + C = A B C cos cos cos cos cos cos 2 2 2 2 2 2 ⇔ A ⎡ B C⎤ B ⎡ A C⎤ C ⎡ A B sin cos cos + sin cos cos + sin cos cos ⎤ 2 ⎢ 2 2 ⎥ 2 ⎢ 2 2 ⎥ 2 ⎢ ⎣ ⎦ ⎣ ⎦ ⎣ 2 2 ⎥⎦ A B C = sin sin sin + 1 2 2 2 ⇔ A ⎡ B C B C⎤ A ⎡ B C C B sin cos cos − sin sin + cos sin cos + sin cos ⎤ = 1 2 ⎢ 2 2 2 2 ⎥ 2 ⎢ ⎣ ⎦ ⎣ 2 2 2 2 ⎥⎦ A B + C A B + C ⇔ sin .cos + cos sin = 1 2 2 2 2 ⎡ A + B + C ⇔sin ⎤ = 1 ⎢ 2 ⎥ ⎣ ⎦ π
⇔ sin = 1 ( hieån nhieân ñuùng) 2 A B C sin sin sin
Baøi 25 : Cho ΔABC . Chöùng minh: 2 2 2 + + = 2 B C C A A B cos cos cos cos cos cos 2 2 2 2 2 2 Caùch 1 : A B A A B B sin sin sin cos + sin cos 2 2 2 2 2 2 Ta coù : B C + C A = A B C cos cos cos cos cos cos cos 2 2 2 2 2 2 2 A + B A sin cos − B 1 sin A + sin B 2 2 = = 2 A B C A B C cos cos cos cos cos cos 2 2 2 2 2 2 C A − B ⎛ A − B ⎞ cos .cos cos⎜ ⎟ 2 2 ⎝ 2 ⎠ = = A B C A cos .cos .cos cos cos B 2 2 2 2 2 ⎛ A − B ⎞ C A − B A cos⎜ ⎟ sin cos + cos + B Do ñoù : Veá traùi ⎝ 2 ⎠ 2 2 2 = A B + A B = A B cos cos cos cos cos cos 2 2 2 2 2 2 A B 2cos cos 2 2 = = 2 A B cos cos 2 2 Caùch 2 : B + C A + C A + B cos cos cos Ta coù veá traùi 2 2 = B C + C A + 2 A B cos cos cos cos cos cos 2 2 2 2 2 2 B C B C A C A C cos cos − sin sin cos cos − sin sin 2 2 2 2 2 2 2 = B C + 2 C A cos cos cos cos 2 2 2 2 A B A cos cos B − sin sin 2 2 2 + 2 A B cos cos 2 2 ⎡ B C A C A B 3 tg tg tg tg tg tg ⎤ = − + + ⎢ 2 2 2 2 2 2 ⎥ ⎣ ⎦ A B B C A B Maø : tg tg + tg tg + tg tg = 1 2 2 2 2 2 2
(ñaõ chöùng minh taïi baøi 10 )
Do ñoù : Veá traùi = 3 – 1 = 2 A B C
Baøi 26 : Cho ΔABC . Coù cot g ,cot g ,cot g theo töù töï taïo caáp soá coäng. 2 2 2 A C Chöùng minh cot g .cot g = 3 2 2 A B C
Ta coù : cot g ,cot g ,cot g laø caáp soá coäng 2 2 2 A C B ⇔ cot g + cot g = 2cot g 2 2 2 A + C B sin 2cos ⇔ 2 = 2 A C B sin sin sin 2 2 2 B cos ⇔ 2 2 cos B2 A C = B sin sin sin 2 2 2 1 2 B ⇔ = (do 0> 0 ) A C A + sin sin cos C 2 2 2 2 A C A C cos cos − sin sin A C ⇔ 2 2 2 2 = 2 cot g cot g = 3 A C ⇔ sin .sin 2 2 2 2
Baøi 27 : Cho ΔABC . Chöùng minh : 1 1 1 1 ⎡ A B C A B C tg tg tg cot g cot g cot g ⎤ + + = + + + + + sin A sin B sin C 2 ⎢ 2 2 2 2 2 2 ⎥ ⎣ ⎦ A B C A B C Ta coù : cot g + cot g + cot g = cot g .cot g .cot g 2 2 2 2 2 2
(Xem chöùng minh baøi 19g ) sin α cosα 2
Maët khaùc : tgα + cot gα = + = cosα sin α sin 2α Do ñoù : 1 ⎡ A B C A B C tg tg tg cotg cotg cotg ⎤ + + + + + 2 ⎢ 2 2 2 2 2 2 ⎥ ⎣ ⎦ 1 ⎡ A B C⎤ 1 ⎡ A B C = tg + tg + tg + cotg + cotg + cotg ⎤ 2 ⎢ 2 2 2 ⎥ 2 ⎢ 2 2 2 ⎥ ⎣ ⎦ ⎣ ⎦ 1 ⎡ A A ⎤ 1 ⎡ B B⎤ 1 ⎡ C C = tg + cot g + tg + cot g + tg + cot g ⎤ 2 ⎢ 2 2 ⎥ 2 ⎢ 2 2 ⎥ 2 ⎢ 2 2 ⎥ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ 1 1 1 = + + sin A sin B sin C BAØI TAÄP 1. Chöùng minh : π 2π 1 a/ cos − cos = 5 5 2 o o cos15 + sin15 b/ = 3 o o cos15 − sin15 2π 4π 6 1 c/ cos cos cos π + + = − 7 7 7 2 3 3 3
d/ sin 2x sin 6x + cos 2x.cos6x = cos 4x e/ o o o o tg20 .tg40 .tg60 .tg80 = 3 f/ π 2π 5π π 8 3 tg π + tg + tg + tg = cos 6 9 18 3 3 9 π 2π 3π 4π 5π 6π 7 1 g/ cos .cos .cos .cos .cos .cos .cos π = 7 15 15 15 15 15 15 15 2
h/ tgx.tg ⎡π x⎤ .tg ⎡π x⎤ − + = tg3x ⎢ 3 ⎥ ⎢ 3 ⎥ ⎣ ⎦ ⎣ ⎦ k/ o o o o tg20 + tg40 + 3tg20 .tg40 = 3 e/ o o o 3 sin 20 .sin 40 .sin 80 = 8 m/ o o o o tg5 .tg55 .tg65 .tg75 = 1 sin ⎧ x = 2sin (x + y)
2. Chöùng minh raèng neáu ⎪⎨⎪x y (2k 1)π + ≠ + (k ∈ z) ⎩ 2 thì sin y
tg(x + y) = cos y − 2
3. Cho ΔABC coù 3 goùc ñeàu nhoïn vaø A ≥ B ≥ C
a/ Chöùng minh : tgA + tgB + tgC = tgA.tgB.tgC
b/ Ñaët tgA.tgB = p; tgA.tgC = q
Chöùng minh (p-1)(q-1) ≥ 4
4. Chöùng minh caùc bieåu thöùc khoâng phuï thuoäc x : a/ 4 = ( 2 + ) 4 + ( 2 + ) 2 2 A sin x 1 sin x
cos x 1 cos x + 5sin x cos x + 1 b/ = ( 8 8 − ) + ( 6 6 B 3 sin x cos x 4 cos x − 2sin x) + 6sin4 x c/ 2 = ( − ) 2
C cos x a + sin (x − b) − 2cos(x − a)sin(x − b)sin(a − b)
5. Cho ΔABC , chöùng minh : cosC cosB a/ cot gB + = cot gC + sin Bcos A sin Ccos A C b/ 3 3 3 A B C 3A 3B 3
sin A + sin B + sin C = 3cos cos cos + cos cos cos 2 2 2 2 2 2 A B − C B A − C
c/ sin A + sin B + sin C = cos .cos + cos .cos 2 2 2 2 C A + cos .cos − B 2 2
d/ cotgAcotgB + cotgBcotgC + cotgCcotgA = 1 e/ 2 2 2
cos A + cos B + cos C = 1 − 2cos A cosBcosC
f/ sin3Asin(B- C)+ sin3Bsin(C- A)+ sin3Csin(A- B) = 0
6. Tìm giaù trò nhoû nhaát cuûa : 1 1 a/ y π = + vôùi 0 < x < sin x cos x 2 9 b/ π y = 4x +
+ sin x vôùi 0 < x < ∞ x c/ 2 y = 2sin x + 4 sin x cos x + 5
7. Tìm giaù trò lôùn nhaát cuûa :
a/ y = sin x cos x + cos x sin x b/ y = sinx + 3sin2x c/ 2 y = cos x + 2 − cos x
Chöông 2 : PHÖÔNG TRÌNH LÖÔÏNG GIAÙC CÔ BAÛN ⎡u = v + k π 2
sin u = sin v ⇔ ⎢⎣u = π − v + k π2
cosu = cos v ⇔ u = ±v + k2π ⎧ π ⎪u ≠ + π k tgu = tgv ⇔ ⎨ 2 (k,k ' ∈ Z) ⎪⎩u = v + k'π ⎧u ≠ kπ
cot gu = cot gv ⇔ ⎨⎩u = v + k'π Ñaëc bieät : sin u π = 0 ⇔ u = kπ cos u = 0 ⇔ u = + π k 2 sin u 1 u π = ⇔ =
+ k2π(k ∈ Z) cosu = 1 ⇔ u = k2π (k ∈ Z) 2 sin u 1 u π = − ⇔ = − + k2π cosu = 1 − ⇔ u = π + k2π 2
Chuù yù : sin u ≠ 0 ⇔ cosu ≠ 1 ± cosu ≠ 0 ⇔ sin u ≠ 1 ±
Baøi 28 : (Ñeà thi tuyeån sinh Ñaïi hoïc khoái D, naêm 2002)
Tìm x ∈ [0,14] nghieäm ñuùng phöông trình
cos 3x − 4 cos 2x + 3cos x − 4 = 0(*) Ta coù (*) : ⇔ ( 3 − ) − ( 2 4 cos x 3cos x
4 2 cos x − 1) + 3cos x − 4 = 0 ⇔ 3 2 4 cos x − 8cos x = 0 ⇔ 2 4 cos x (cos x − 2) = 0
⇔ cos x = 0 hay cos x = 2(loaïi vì cos x ≤ 1) π ⇔ x = + kπ(k ∈ Z) 2 Ta coù : x [0,14] 0 π ∈ ⇔ ≤ + kπ ≤ 14 2 π π 1 14 1
⇔ − ≤ kπ ≤ 14 − ⇔ 0, − 5 = − ≤ k ≤ − ≈ 3,9 2 2 2 π 2 Maø k ⎧π π π π ∈ Z neân k ∈ {0,1,2 } ,3 . Do ñoù : 3 5 7 x , , , ⎫ ∈ ⎨ 2 2 2 2 ⎬ ⎩ ⎭
Baøi 29 : (Ñeà thi tuyeån sinh Ñaïi hoïc khoái D, naêm 2004) Giaûi phöông trình :
(2cos x − 1)(2sin x + cos x) = sin 2x − sin x(*)
Ta coù (*) ⇔ (2cos x − 1)(2sin x + cos x) = sin x (2cos x − 1)
⇔ (2cos x − 1) ⎡⎣(2sin x + cos x) − sin x⎤ 0 ⎦ =
⇔ (2cos x − 1)(sin x + cos x) = 0 1
⇔ cos x = ∨ sin x = − cos x 2 π ⎛ π ⇔ cos x cos tgx 1 tg ⎞ = ∨ = − = − 3 ⎜ 4 ⎟ ⎝ ⎠ π π ⇔ x = ± + k π 2 ∨ x = − + π k , (k ∈ Z) 3 4
Baøi 30 : Giaûi phöông trình cos x + cos2x + cos3x + cos4x = 0(*)
Ta coù (*) ⇔ (cos x + cos4x) + (cos2x + cos3x) = 0 5x 3x 5x x ⇔ 2cos .cos + 2cos .cos = 0 2 2 2 2 ⇔ 5x ⎛ 3x x 2cos cos cos ⎞ + = 0 2 ⎜ 2 2 ⎟ ⎝ ⎠ 5x x ⇔ 4 cos cos x cos = 0 2 2 5x x ⇔ cos = 0 ∨ cos x = 0 ∨ cos = 0 2 2 5x x ⇔ π π π = + π k ∨ x = + π k ∨ = + π k 2 2 2 2 2 π π 2k π ⇔ x = + ∨ x = + π k ∨ x = π + π 2 , (k ∈ Z) 5 5 2
Baøi 31: Giaûi phöông trình 2 2 2 2
sin x + sin 3x = cos 2x + cos 4x (*) 1 1 1 1
Ta coù (*) ⇔ (1 − cos2x) + (1 − cos6x) = (1 + cos4x) + (1 + cos8x) 2 2 2 2
⇔ − (cos 2x + cos 6x) = cos 4x + cos 8x ⇔ 2
− cos4x cos2x = 2cos6x cos2x
⇔ 2 cos 2x (cos 6x + cos 4x) = 0 ⇔ 4 cos 2x cos5x cos x = 0
⇔ cos 2x = 0 ∨ cos5x = 0 ∨ cos x = 0 ⇔ π π π 2x = + π k ∨ 5x + π k ∨ x = + π k , k ∈ ] 2 2 2 k k ⇔ π π π π π x = + ∨ x = + ∨ x = + π k , k ∈ ] 4 2 10 5 2
Baøi 32 : Cho phöông trình 2 2 ⎛ π x ⎞ 7
sin x.cos 4x − sin 2x = 4 sin − − ⎜ ⎟ (*) ⎝ 4 2 ⎠ 2
Tìm caùc nghieäm cuûa phöông trình thoûa: x − 1 < 3 Ta coù : (*) 1 ⎡ ⎛ π ⎞⎤ 7
⇔ sin x.cos 4x − (1 − cos4x) = 2 1 − cos − x − 2 ⎢ ⎜ ⎣ 2 ⎟⎥ ⎝ ⎠⎦ 2 1 1 3
⇔ sin x cos 4x − + cos 4x = − − 2sin x 2 2 2 1
⇔ sin x cos 4x + cos 4x + 1 + 2sin x = 0 21 1 ⇔ ⎛ ⎞ ⎛ ⎞ cos 4x sin x + + 2 sin x + = ⎜ ⎟ ⎜ ⎟ 0 ⎝ 2 ⎠ ⎝ 2 ⎠ ⇔ ( )⎛ 1 cos 4x 2 sin x ⎞ + + = 0 ⎜ 2 ⎟ ⎝ ⎠ ⎡cos 4x = 2 − (loaïi) ⎡ π x = − + k π ⎢ 2 ⇔ ⎢ 6 ⎢ 1 ⎢ sin x = − = sin ⎛ π − ⎞ ⇔ 7π ⎢ ⎣ 2 ⎜ 6⎟ ⎢ ⎝ ⎠ x = + 2hπ ⎢⎣ 6 Ta coù : x − 1 < 3 ⇔ 3
− < x − 1 < 3 ⇔ −2 < x < 4 Vaäy : 2 π − < − + k2π < 4 6 π π 1 1 2 1
⇔ − 2 < 2kπ < 4 + ⇔ − < k < + 6 6 12 π π 12 Do k π
∈ Z neân k = 0. Vaäy x = − 6 7π −2 < + h π 2 < 4 6 7 7 1 7 2 7 ⇔ π π −2 − < h π 2 < 4 − ⇔ − − < h < − 6 6 π 12 π 12 7π 7 ⇒ h = 0 ⇒ x = .Toùm laïi −π π x = hay x = 6 6 6 1 Caùch khaùc : k −π sin x = − ⇔ x = − ( 1) + π k , k ∈ ] 2 6 2 1 4 Vaäy : k −π − k − −2 < (−1) + π k < 4 ⇔ < − ( 1) + k < 6 π 6 π 7
⇔ k=0 vaø k = 1. Töông öùng vôùi −π π x = hay x = 6 6
Baøi 33 : Giaûi phöông trình 3 3 3
sin x cos 3x + cos x sin 3x = sin 4x (*) Ta coù : (*)⇔ 3 ( 3 − ) 3 + ( 3 − ) 3 sin x 4 cos x 3cos x cos x 3sin x 4 sin x = sin 4x ⇔ 3 3 3 3 3 3 3
4sin x cos x − 3sin x cos x + 3sin x cos x − 4sin x cos x = sin 4x ⇔ ( 2 2 − ) 3
3sin x cos x cos x sin x = sin 4x 3 ⇔ 3 sin 2x cos 2x = sin 4x 2 3 ⇔ 3 sin 4x = sin 4x 4 ⇔ 3 3sin 4x − 4sin 4x = 0 ⇔ sin12x = 0 kπ ⇔ 12x = kπ ⇔ x = (k ∈ Z) 12
Baøi 34 : (Ñeà thi tuyeån sinh Ñaïi hoïc khoái B, naêm 2002) Giaûi phöông trình : 2 2 2 2
sin 3x − cos 4x = sin 5x − cos 6a (*) Ta coù : (*)⇔ 1 ( − ) 1 − ( + ) 1 = ( − ) 1 1 cos 6x 1 cos 8x 1 cos10x − (1 + cos12x) 2 2 2 2
⇔ cos 6x + cos 8x = cos10x + cos12x
⇔ 2cos7x cos x = 2cos11x cos x
⇔ 2 cos x (cos7x − cos11x) = 0
⇔ cos x = 0 ∨ cos7x = cos11x ⇔ π x = + π k ∨ 7x = ±11x + k π 2 2 k k ⇔ π π π x = + π k ∨ x = − ∨ x = , k ∈ ] 2 2 9
Baøi 35 : Giaûi phöông trình
(sin x + sin 3x) + sin 2x = (cos x + cos3x) + cos2x
⇔ 2sin 2x cos x + sin 2x = 2cos 2x cos x + cos 2x
⇔ sin 2x (2 cos x + 1) = cos 2x (2 cos x + 1)
⇔ (2cos x + 1)(sin 2x − cos 2x) = 0 1 2π ⇔ cos x = − = cos ∨ sin 2x = cos 2x 2 3 2π π ⇔ x = ± + k2π ∨ tg2x = 1 = tg 3 4 π 2 π π ⇔ x = ± + k π 2 ∨ x = + k , (k ∈ Z) 3 8 2
Baøi 36: Giaûi phöông trình + 2 + = + 3
cos10x 2 cos 4x 6 cos 3x.cos x cos x 8 cos x. cos 3x (*) Ta coù : (*)⇔ + ( + ) = + ( 3 cos10x 1 cos 8x
cos x 2cos x 4 cos 3x − 3cos 3x)
⇔ (cos10x + cos8x) + 1 = cos x + 2cos x.cos 9x
⇔ 2cos 9x cos x + 1 = cos x + 2cos x.cos 9x ⇔ cos x = 1 ⇔ x = k2π (k ∈ Z)
Baøi 37 : Giaûi phöông trình 3 3 2
4 sin x + 3cos x − 3sin x − sin x cos x = 0(*) Ta coù : (*) ⇔ ( 2 ) ( 2 sin x 4 sin x 3 cos x sin x 3cos2 − − − x) = 0 ⇔ ( 2 − ) − ⎡ 2 sin x 4 sin x 3
cos x sin x − 3 (1 − sin2 x)⎤ = ⎣ ⎦ 0 ⇔ ( 2
4 sin x − 3)(sin x − cos x) = 0
⇔ ⎡2(1 − cos 2x) − 3⎤ ⎣ ⎦ (sin x − cos x) = 0 ⎡ 1 2 cos 2x = − = cos π ⇔ ⎢ 2 3 ⎢ ⎣sin x = cos x ⎡ π ⎡ 2 2x π = ± + k2π x = ± + kπ ⎢ ⇔ ⎢ 3 ⇔ 3 (k ∈ Z) ⎢ ⎢ π ⎣tgx = 1 ⎢x = + kπ ⎢⎣ 4
Baøi 38 : (Ñeà thi tuyeån sinh Ñaïi hoïc khoái B naêm 2005) Giaûi phöông trình :
sin x + cos x + 1 + sin 2x + cos 2x = 0(*) Ta coù : (*) ⇔ 2
sin x + cos x + 2sin x cos x + 2cos x = 0
⇔ sin x + cos x + 2 cos x (sin x + cos x) = 0
⇔ (sin x + cos x)(1 + 2cos x) = 0 ⎡sin x = − cos x ⇔ ⎢ 1 2 cos 2x cos π ⎢ = − = ⎣ 2 3 ⎡tgx = 1 − ⇔ ⎢ 2 x π ⎢ = ± + k π 2 ⎣ 3 ⎡x π = − + kπ ⎢ ⇔ 4 ⎢ (k ∈ Z) 2 x π ⎢ = ± + k2π ⎢⎣ 3
Baøi 39 : Giaûi phöông trình ( + )( + − ) 2
2sin x 1 3cos 4x 2sin x 4 + 4 cos x = 3(*) Ta coù : (*) ⇔ ( + )( + − ) + ( 2 2sin x 1 3cos 4x 2sin x 4 4 1 − sin x) − 3 = 0
⇔ (2sin x + 1)(3cos 4x + 2sin x − 4) + (1 + 2sin x)(1 − 2sin x) = 0
⇔ (2sin x + 1) ⎡3cos4x + 2sin x − 4 + ⎣ (1 − 2sin x)⎤ 0 ⎦ =
⇔ 3(cos 4x − 1)(2sin x + 1) = 0 ⎛ π ⇔ 1 cos 4x 1 sin x sin ⎞ = ∨ = − = − 2 ⎜ 6⎟ ⎝ ⎠ 7 ⇔ π π 4x = π k2 ∨ x = − + k π 2 ∨ x = + k2π 6 6 π k π 7π ⇔ x = ∨ x = − + k π 2 ∨ x = + k π 2 , (k ∈ Z) 2 6 6
Baøi 40: Giaûi phöông trình 6 + 6 = ( 8 + 8 sin x cos x 2 sin x cos x) (*) Ta coù : (*) ⇔ 6 8 6 8
sin x − 2sin x + cos x − 2cos x = 0 ⇔ 6 ( 2 − ) 6 − ( 2 sin x 1 2sin x cos x 2cos x − 1) = 0 ⇔ 6 − 6 sin x cos 2x cos x.cos 2x = 0 ⇔ ( 6 6 cos 2x sin x − cos x) = 0 ⇔ 6 6 cos2x = 0 ∨ sin x = cos x ⇔ 6 cos2x = 0 ∨ tg x = 1 π
⇔ 2x = (2k + 1) ∨ tgx = ±1 2 π π
⇔ x = (2k + 1) ∨ x = ± + kπ 4 4 π kπ ⇔ x = + ,k ∈] 4 2
Baøi 41 : Giaûi phöông trình 1 cos x.cos 2x.cos 4x.cos 8x = (*) 16
Ta thaáy x = kπ khoâng laø nghieäm cuûa (*) vì luùc ñoù cos x = 1 ± ,cos2x = cos4x = cos8x = 1 1 (*) thaønh : 1 ± = voâ nghieäm 16
Nhaân 2 veá cuûa (*) cho 16sin x ≠ 0 ta ñöôïc
(*)⇔ (16sin x cos x) cos2x.cos4x.cos8x = sin x vaø sin x ≠ 0
⇔ (8sin 2x cos 2x) cos 4x.cos 8x = sin x vaø sin x ≠ 0
⇔ (4 sin 4x cos 4x) cos 8x = sin x vaø sin x ≠ 0
⇔ 2sin 8x cos 8x = sin x vaø sin x ≠ 0
⇔ sin16x = sin x vaø sin x ≠ 0 π k2 π π k ⇔ x = ∨ x = + , (k ∈ Z) 15 17 17 Do : x = π
h khoâng laø nghieäm neân k ≠ 15m vaø 2k + 1 ≠ 17n (n, m ∈ Z)
Baøi 42: Giaûi phöông trình ⎛ π 3 ⎞ 8cos ⎜ x + ⎟ = cos 3x (*) ⎝ 3 ⎠ π π Ñaët t = x + ⇔ x = t − 3 3
Thì cos 3x = cos (3t − π) = cos (π − 3t) = − cos 3t Vaäy (*) thaønh 3 8 cos t = − cos 3t ⇔ 3 3 8 cos t = 4 − cos t + 3 cos t ⇔ 3 12 cos t − 3cos t = 0 ⇔ ( 2 3 cos t 4 cos t − 1) = 0 ⇔ 3 cos t ⎡2 ⎣ (1 + cos 2t) − 1⎤ 0 ⎦ = ⇔ cos t (2 cos 2t + 1) = 0 1 2π
⇔ cos t = 0 ∨ cos 2t = − = cos 2 3 2 ⇔ t (2k 1) π π = + ∨ 2t = ± + k2π 2 3 π π ⇔ t = + π k ∨ t = ± + π k 2 3 π Maø x = t − 3 2 Vaäy (*) π π ⇔ x = + k π 2 ∨ x = π k ∨ x = + π k , (vôùik ∈ Z) 6 3 Ghi chuù :
Khi giaûi caùc phöông trình löôïng giaùc coù chöùa tgu, cotgu, coù aån ôû maãu, hay
chöùa caên baäc chaün... ta phaûi ñaët ñieàu kieän ñeå phöông trình xaùc ñònh. Ta seõ
duøng caùc caùch sau ñaây ñeå kieåm tra ñieàu kieän xem coù nhaän nghieäm hay khoâng.
+ Thay caùc giaù trò x tìm ñöôïc vaøo ñieàu kieän thöû laïi xem coù thoûa
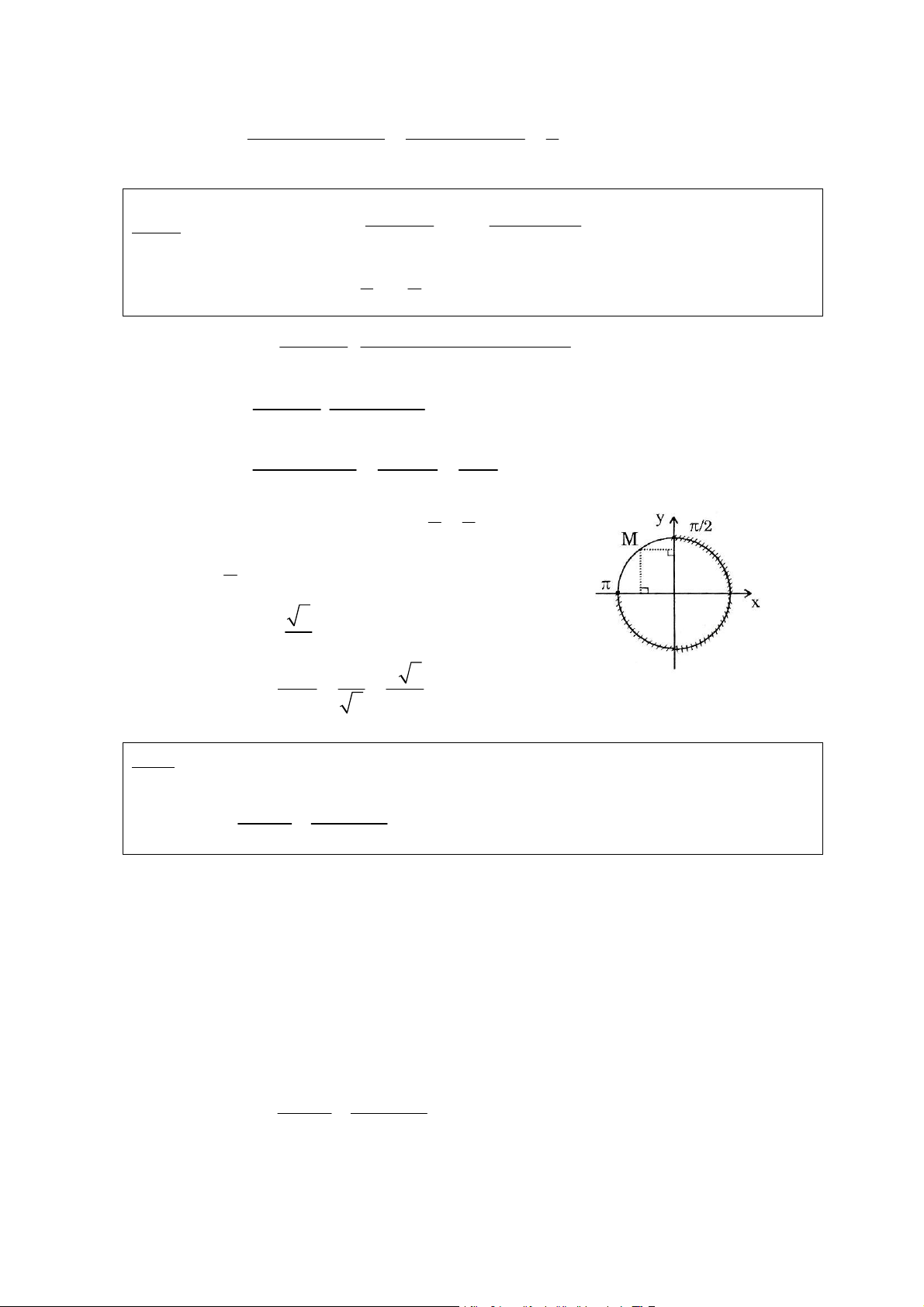
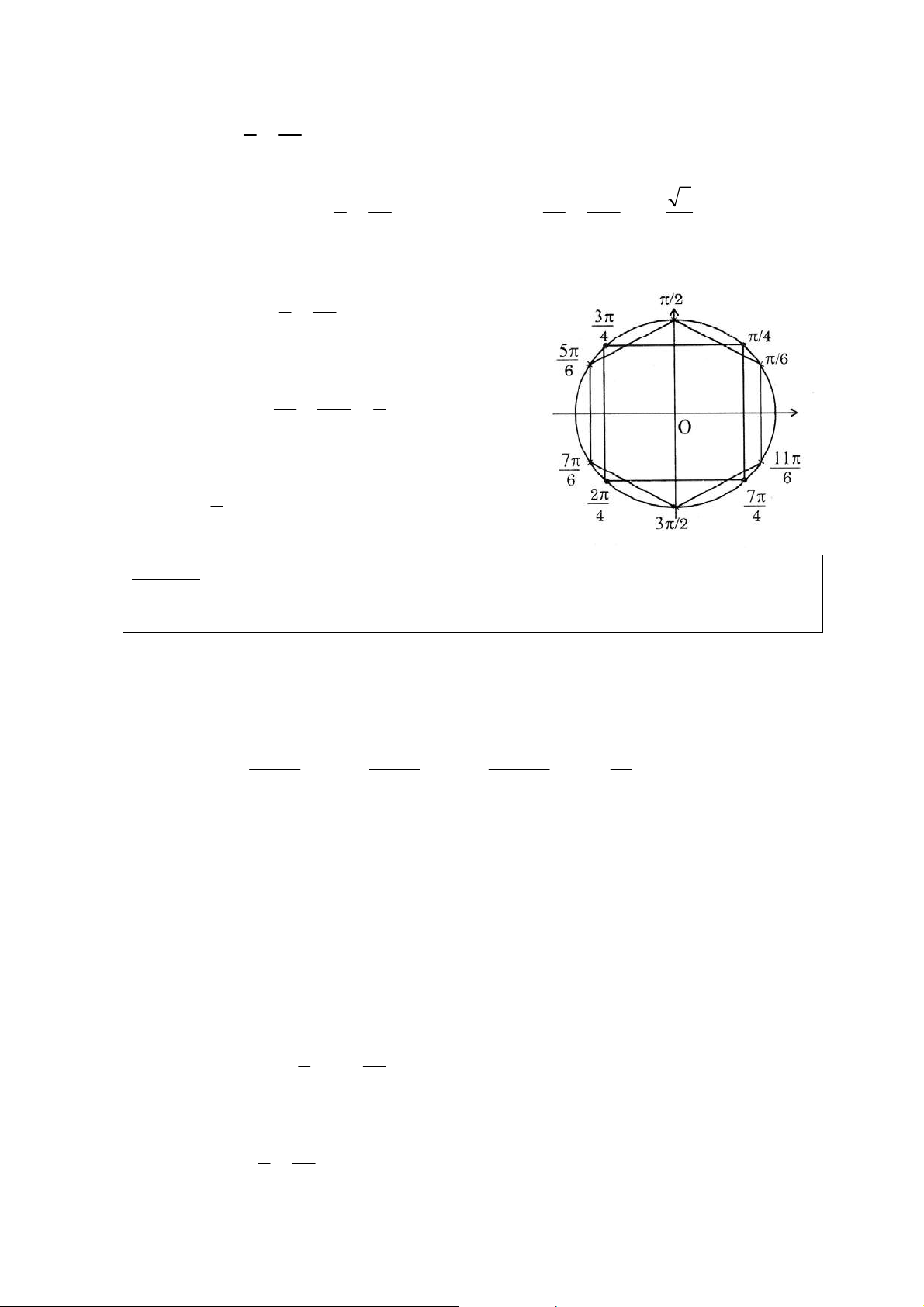
Hoaëc + Bieåu dieãn caùc ngoïn cung ñieàu kieän vaø caùc ngoïn cung tìm ñöôïc treân cuøng
moät ñöôøng troøn löôïng giaùc. Ta seõ loaïi boû ngoïn cung cuûa nghieäm khi coù
truøng vôùi ngoïn cung cuûa ñieàu kieän.
Hoaëc + So vôi caùc ñieàu kieän trong quaù trình giaûi phöông trình.
Baøi 43 : Giaûi phöông trình 2 tg x − tgx.tg3x = 2 (*) ⎧cos x ≠ 0 π π h Ñieàu kieän ⎨ ⇔ cos3x ≠ 0 ⇔ x ≠ + 3
⎩cos 3x = 4 cos x − 3 cos x ≠ 0 6 3
Luùc ñoù ta coù (*) ⇔ tgx (tgx − tg3x) = 2 sin x ⎛ sin x sin 3x ⇔ ⎞ − = 2 cos x ⎜ cos x cos 3x ⎟ ⎝ ⎠ ⇔ ( − ) 2
sin x sin x cos 3x cos x sin 3x = 2 cos x cos 3x ⇔ (− ) 2 sin x sin 2x = 2 cos x.cos 3x ⇔ 2 2 2s
− in x cos x = 2 cos x cos 3x ⇔ 2
− sin x = cos x cos 3x (do cos x ≠ 0 ) 1 1
⇔ − (1 − cos 2x) = (cos 4x + cos 2x) 2 2 ⇔ cos 4x = 1 − ⇔ 4x = π + k2π π kπ ⇔ x = + (k ∈ Z) 4 2 so vôùi ñieàu kieän π kπ Caùch 1 : Khi x ⎛ 3π 3kπ ⎞ 2 = + thì cos 3x = cos + = ± ≠ 0 ⎜ ⎟ (nhaän) 4 2 ⎝ 4 2 ⎠ 2
Caùch 2 : Bieåu dieãn caùc ngoïn cung ñieàu kieän vaø ngoïn cung nghieäm ta thaáy
khoâng coù ngoïn cung naøo truøng nhau. Do ñoù : π kπ (*) ⇔ x = + 4 2
Löu yù caùch 2 raát maát thôøi gian Caùch 3 : 3 3k Neáu π π π 3x = + = + π h 4 2 2 Thì 3 + 6k = 2 + 4h ⇔1 = 4h − 6k 1
⇔ = 2h − 3k (voâ lyù vì k, h ∈ Z) 2
Baøi 44: Giaûi phöông trình 2 2 2 11 tg x + cot g x + cot g 2x = (*) 3 ⎧cos x ≠ 0 Ñieàu kieän si ⎪
⎨ n x ≠ 0 ⇔ sin 2x ≠ 0 si ⎪ n 2x ≠ 0 ⎩ Do ñoù : (*) ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 1 11 ⇔ 1 1 1⎞ − + − + − = ⎜ 2 ⎟ ⎜ 2 ⎟ ⎜ 2 cos x sin x sin 2x ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ 3 1 1 1 20 ⇔ + + = 2 2 2 2 cos x sin x 4 sin x cos x 3 2 2 4 sin x + 4 cos x + 1 20 ⇔ = 2 2 4 sin x cos x 3 5 20 ⇔ = 2 sin 2x 3 ⇔ 2 3
sin 2x = (nhaän do sin2x ≠ 0 ) 4 1 3 ⇔ (1 − cos 4x) = 2 4 1 2π ⇔ cos 4x = − = cos 2 3 2π ⇔ 4x = ± + k2π 3 π kπ ⇔ x = ± + (k ∈ Z) 6 2 2
Chuù yù : Coù theå deã daøng chöùng minh : tgx + cot gx = sin2x ⎛ 1 ⎞ 11
Vaäy (*)⇔ (tgx + cot gx)2 − 2 + − 1 = ⎜ 2 sin x ⎟ ⎝ ⎠ 3 5 20 ⇔ = 2 sin 2x 3
Baøi 45 : (Ñeà thi tuyeån sinh Ñaïi hoïc khoái D, naêm 2003) Giaûi phöông trình 2 ⎛ x π ⎞ 2 2 x sin − tg x − cos = 0 ⎜ ⎟ (*) ⎝ 2 4 ⎠ 2
Ñieàu kieän : cos x ≠ 0 ⇔ sin x ≠ 1 ± luùc ñoù : 2 (*) 1 ⎡ ⎛ π ⎞⎤ sin x 1 ⇔ 1 − cos x − − 1 + cos x = 0 ⎢ ⎜ ⎟⎥ 2 [ ] 2 ⎣ ⎝ 2 ⎠⎦ cos x 2 (1 − sin x)( 2 1 − cos x) ⇔ − 1 + cos x = 0 2 ( ) 1 − sin x 2 1 − cos x ⇔ − (1 + cos x) = 0 1 + sin x ⎡ − ⇔ ( ) 1 cos x 1 cos x 1⎤ + − = 0 ⎢⎣1 sin x ⎥ + ⎦
⇔ (1 + cos x)(− cos x − sin x) = 0 ⎡cos x = 1 − (nhaändo cos x ≠ 0) ⇔ ⎢ ⎣tgx = 1 − ⎡x = π + k π 2 ⇔ ⎢ π ⎢x = − + π k ⎣ 4
Baøi 46 : Giaûi phöông trình ( + ) 2
sin 2x cot gx tg2x = 4 cos x (*) ⎧cos x ≠ ±1 si ⎧ n x ≠ 0 sin ⎧ x ≠ 0 Ñieàu kieän : ⎪ ⎨ ⇔ ⎨ ⇔ ⎨ 2 ⎩cos 2x ≠ 0 2 ⎩2cos x − 1 ≠ 0 ⎪cos x ≠ ± ⎩ 2 cos x sin 2x Ta coù : cot gx + tg2x = + sin x cos 2x cos2x cos x + sin 2x sin x = sin x cos 2x cos x = sin x cos 2x Luùc ñoù : (*) ⎛ cos x ⎞ ⇔ 2 sin x cos x = ⎜ ⎟ 2 4 cos x ⎝ sin x cos 2x ⎠ 2 2cos x ⇔ 2 = 4 cos x (Dosin x ≠ 0) cos 2x ⎡ ⎛ 2 ⎞ ⎡cos x = 0
⎢cos x = 0 ⎜ Nhaän do cos x ≠ vaø ≠ ±1⎟ ⎜ ⎟ ⇔ ⎢ 2 1 ⇔ ⎢ ⎝ ⎠ ⎢ = 2 ⎢ ⎣cos 2x 1 π
⎢cos 2x = = cos , (nhaän do sin x ≠ 0) ⎣ 2 3 ⎡ π x = + π ⎢ k ⇔ ⎢ 2 (k ∈ Z) π ⎢x = ± + π k ⎢⎣ 6
Baøi 47 : Giaûi phöông trình: 2 2
cot g x − tg x = 16(1 + cos4x) cos 2x 2 2 cos x sin x Ta coù : 2 2 cot g x − tg x = − 2 2 sin x cos x 4 4 cos x − sin x 4 cos2x = = 2 2 2 sin x cos x sin 2x si ⎧ n 2x ≠ 0 Ñieàu kieän : ⎨ ⇔ sin 4x ≠ 0 ⎩cos 2x ≠ 0 4 Luùc ñoù (*) ⇔ = 16 1 + cos 4x 2 ( ) sin 2x ⇔ 1 = 4 (1 + cos 4x) 2 sin 2x
⇔ 1 = 2 (1 + cos 4x) (1 − cos 4x) ⇔ 1 = 2 (1 − 2 cos 4x) = 2 2 sin 4x 1 ⇔ 2
sin 4x = (nhaän do sin 4x ≠ 0) 2 1 1 ⇔ (1 − cos 8x) = 2 2 π π k ⇔ cos 8x = 0 ⇔ x = + , k ∈ ] 16 8
Baøi 48: Giaûi phöông trình: 4 4 7 sin x cos x
cot g ⎛ x π ⎞ cot g ⎛ π x⎞ + = + − ⎜ ⎟ ⎜ ⎟ (*) 8 ⎝ 3 ⎠ ⎝ 6 ⎠ sin ⎧ ⎛ x π⎞ 0 s ⎧ in⎛x π⎞ + ≠ + ≠ 0 ⎪ ⎜ ⎪ ⎝ 3 ⎟ ⎪ ⎜ ⎠ ⎪ ⎝ 3 ⎟ Ñieàu kieän ⎠ ⎛ 2 ⎨ ⎨ sin 2x π ⎞ ⇔ ⇔ + ≠ 0 ⎜ ⎪ ⎛ π ⎞ ⎪ ⎛ π ⎞ ⎝ 3 ⎟ sin − x ≠ 0 cos x + ≠ 0 ⎠ ⎜ ⎩ 6 ⎟ ⎜ ⎩ 3 ⎟ ⎪ ⎪ ⎝ ⎠ ⎝ ⎠ 1 3 ⇔ − sin 2x + cos2x ≠ 0 2 2 ⇔ tg2x ≠ 3 1
Ta coù: sin x + cos x = (sin x + cos x)2 4 4 2 2 2 2 2
− 2sin x.cos x = 1 − sin 2x 2
Vaø: cot g ⎛ x π ⎞.cot g ⎛ π x⎞ cot g ⎛ x π ⎞.tg ⎛ π x⎞ + − = + + = 1 ⎜ 3 ⎟ ⎜ 6 ⎟ ⎜ 3 ⎟ ⎜ 3 ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ 1 7 Luùc ñoù: (*) 2 ⇔ 1 − sin 2x = 2 8 1 1 ⇔ − (1 − cos4x) = − 4 8 1 ⇔ cos 4x = 2 π π kπ ⇔ 4x = ± + π k2 ⇔ x = ± + 3 12 2 (nhaän do 3 tg2x = ± ≠ 3 ) 3 1
Baøi 49: Giaûi phöông trình 2tgx + cot g2x = 2sin 2x + (*) sin 2x ⎧cos 2x ≠ 0 Ñieàu kieän: ⎨
⇔ sin 2x ≠ 0 ⇔ cos 2x ≠ ±1 sin ⎩ 2x ≠ 0 2sin x cos 2x 1 Luùc ñoù: (*) ⇔ + = 2sin 2x + cos x sin 2x sin 2x ⇔ 2 4 sin x + cos 2x = 2 2 sin 2x + 1 ⇔ 2 4 sin x + (1 − 2 2 sin x) = 2 2 8 sin x cos x + 1 ⇔ 2 2 sin x (1 − 2 4 cos x) = 0 ⇔ 2
2 sin x ⎡1 − 2 (1 + cos 2x)⎤ = ⎣ ⎦ 0
⎡sin x = 0 (loaïi do sin 2x ≠ 0 ⇒ sin x ≠ 0) ⎢ ⇔ 1 π ⎢ 2 cos 2x = − = cos (nhaän do cos 2x ≠ ±1) ⎢⎣ 2 3 π 2 ⇔ 2x = ± + k π 2 (k ∈ Z) 3 π ⇔ x = ± + π k , k ∈ ] 3 3(sin x + tgx)
Baøi 51: Giaûi phöông trình: − 2(1 + cos x) = 0(*) tgx − sin x sin x
Ñieàu kieän : tgx − sin x ≠ 0 ⇔ − sin x ≠ 0 cos x si ⎧ n x ≠ 0 sin x (1 − cos x) ⇔
≠ 0 ⇔ ⎪⎨cos x ≠ 0 ⇔ sin 2x ≠ 0 cos x ⎪cos x ≠ 1 ⎩ 3(sin x + tgx).cot gx Luùc ñoù (*)⇔ ( − ) − 2(1 + cos x) = 0 tgx sin x .cot gx 3(cos x + 1) ⇔ ( − ) − 2(1 + cos x) = 0 1 cos x 3 ⇔
− 2 = 0 (do sin x ≠ 0 neân cos x + 1 ≠ 0) 1 − cos x ⇔ 1 + 2cos x = 0 1
⇔ cos x = − (nhaän so vôùi ñieàu kieän) 2 2 ⇔ π x = ± + k π 2 , k∈ ] 3
Baøi 52 : Giaûi phöông trình (1 − cos x)2 + (1 + cos x)2 2 1 2 − = + + 4 (1 − sin x) tg x sin x (1 sin x) tg x(*) 2 ⎧cos x ≠ 0 Ñieàu kieän : ⇔ cos x ≠ 0 si ⎨ ⎩ n x ≠ 1 2( 2 1 + cos x) 3 2 Luùc ñoù (*) sin x 1 sin x ⇔ − = + + 4 (1 − sin x) 1 sin x 2 ( ) 2 1 − sin x 2 1 − sin x ⇔ ( 2 + )( + ) 3 − = ( + )( 2 1 cos x 1 sin x 2sin x 1 sin x 1 − sin x) + 2sin2 x ⇔ ( + )( 2 + ) = ( + ) 2 2 1 sinx 1 cos x
1 sin x cos x + 2sin x (1 + sin x) 1 ⎡ + sin x = 0 ⇔ ⎢ 2 2 1 ⎣ + cos x = cos x + 2sin2 x
⎡sin x = −1 ( loaïi do cos x ≠ 0 ) ⇔ ⇔ cos2x = 0 ⎢ ⎣1 = 1 − cos 2x π ⇔ 2x = + kπ 2 π π ⇔ x = + k (nhaän do cosx ≠ 0) 4 2
Baøi 53 : Giaûi phöông trình cos 3x.tg5x = sin 7x (*)
Ñieàu kieän cos5x ≠ 0 sin5x Luùc ñoù : (*) ⇔ cos3x. = sin7x cos5x
⇔ sin 5x.cos 3x = sin7x.cos5x 1 1
⇔ [sin 8x + sin 2x] = [sin12x + sin 2x] 2 2 ⇔ sin 8x = sin12x
⇔ 12x = 8x + k2π ∨ 12x = π − 8x + k2π π k π kπ ⇔ x = ∨ x = + 2 20 10
So laïi vôùi ñieàu kieän kπ 5k x thì cos5x cos π kπ = = = cos (loaïi neáu k leû) 2 2 2 π π k ⎛ π π k ⎞ x = + thì cos 5x = cos + ≠ ⎜ ⎟ 0 nhaän 20 10 ⎝ 4 2 ⎠ k Do ñoù : (*)⇔ π π x = π h ∨ x = + , vôùi k, h ∈] 20 10
Baøi 54 : Giaûi phöông trình 4 4 sin x + cos x 1 = (tgx + cot g2x) (*) sin 2x 2 Ñieàu kieän : sin 2x ≠ 0 Ta coù : + = ( + )2 4 4 2 2 2 sin x cos x sin x cos x − 2sin x cos2 x 1 2 = 1 − sin 2x 2 sin x cos 2x tgx + cot g2x = + cos x sin 2x sin 2x sin x + cos x cos2x = cos x sin 2x cos(2x − x) 1 = = cos x sin 2x sin 2x 1 1 − 2 sin 2x 2 1 Do ñoù : (*) ⇔ = sin 2x 2 sin 2x 1 1 ⇔ 1 − 2 sin 2x = 2 2 ⇔ 2
sin 2x = 1 (nhaän do sin 2x ≠ 0) ⇔ 2 cos 2x = 0 π ⇔ 2x = + π k , k ∈ ] 2 π π k ⇔ x = + , k ∈ ] 4 2
Baøi 55 : Giaûi phöông trình 2 2 2 2
tg x.cot g 2x.cot g3x = tg x − cot g 2x + cot g3x (*)
Ñieàu kieän : cos x ≠ 0∧ sin 2x ≠ 0∧ sin 3x ≠ 0
⇔ sin 2x ≠ 0∧ sin 3x ≠ 0 ⇔ ( 2 2 − ) = 2 − 2 Luùc ñoù (*) cotg3x tg x cot g 2x 1 tg x cot g 2x
⎡⎛ 1 − cos 2x ⎞ ⎛ 1 + cos 4x ⎞ ⎤ 1 − cos 2x 1 + cos 4x ⇔ cot g3x − 1 = ⎢⎜ ⎟ ⎜ ⎟ ⎥ −
⎣⎝ 1 + cos 2x ⎠ ⎝ 1 − cos 4x ⎠ ⎦ 1 + cos 2x 1 − cos 4x
⇔ cot g3x ⎡(1 − cos2x)(1 + cos4x) − (1 + cos2x)(1 − ⎣ cos 4x)⎤⎦
= (1 − cos2x)(1 − cos4x) − (1 + cos4x)(1 + cos2x)
⇔ cot g3x[2cos4x − 2cos2x] = −2(cos4x + cos2x) cos 3x ⇔
[−4sin3xsin x] = −4cos3xcosx sin 3x
⇔ cos 3x sin x = cos 3x cos x (do sin3x ≠ 0)
⇔ cos 3x = 0∨ sin x = cos x π ⇔ 3x = + π k ∨ tgx = 1 2 π π k π ⇔ x = + ∨ x = + π l (k,l ∈ Z) 6 3 4
So vôùi ñieàu kieän: sin 2x.sin 3x ≠ 0 k * Khi π π x 2k = + thì ⎛ π π ⎞ ⎛ π ⎞ sin + .sin + π k ≠ 0 6 3 ⎜ ⎟ ⎜ ⎟ ⎝ 3 3 ⎠ ⎝ 2 ⎠ ⎛ 1 + 2k ⎞ ⇔ sin π ⎜ ⎟ ≠ 0 ⎝ 3 ⎠
Luoân ñuùng ∀ k thoûa 2k + 1 ≠ 3m (m ∈ Z) * Khi π x 3 2 = + lπ thì ⎛ π ⎞ ⎛ π ⎞ sin + π 2l sin + 3 π l = ± ≠ 0 4 ⎜ ⎟ ⎜ ⎟ ⎝ 2 ⎠ ⎝ 4 ⎠ 2 luoân ñuùng ⎡ π π k x = +
, k ∈ Z ∧ 2k ≠ 3m −1 ( m∈ ⎢ ] ) Do ñoù: (*) ⇔ ⎢ 6 3 π ⎢x = + π l , l∈ ⎢ ] ⎣ 4 Caùch khaùc: (*) ⇔ cotg3x ( 2 2 tg x cot g 2x − 1) = 2 tg x − 2 cot g 2x 2 tg x − 2 2 2 cot g 2x tg 2x.tg x − 1 ⇔ cot g3x = = 2 2 tg x cot g 2x − 2 1 tg x − 2 tg 2x
(1 + tg2x.tgx ) (1 − tg2x.tgx )
⇔ cot g3x = (tg2x − tgx)(tg2x + tgx)
⇔ cot g3x = cot gx.cotg3x ⇔ cos 3x = 0 ∨ sin x = cos x BAØI TAÄP 1.
Tìm caùc nghieäm treân ⎛ π ⎞ π ⎜ ,3 ⎝ 3 ⎟ cuûa phöông trình: ⎠ ⎛ 5π ⎞ ⎛ 7π ⎞ sin 2x + − 3cos x − = 1 + ⎜ ⎟ ⎜ ⎟ 2sin x ⎝ 2 ⎠ ⎝ 2 ⎠ 2.
Tìm caùc nghieäm x treân ⎛ π ⎞
⎜ 0, ⎟ cuûa phöông trình ⎝ 2 ⎠ 2 − 2 sin 4x cos 6x = sin (10, π 5 + 10x) 3.
Giaûi caùc phöông trình sau: a/ 3 3 + = ( 5 5 sin x cos x 2 sin x + cos x) sin x + sin 2x + sin 3x b/ = 3 cos x + cos2x + cos3x c/ 2 1 + cos x tg x = 1− sinx d/
tg2x − tg3x − tg5x = tg2x.tg3x.tg5x 4 e/ 2 cos x = cos x 3 f/ ⎛ π ⎞ 1 1 2 2 sin x + = + ⎜ 4 ⎟ ⎝ ⎠ sin x cos x 2 i/ 2tgx + cot g2x = 3 + sin2x2 h/ 3tg3x + cot g2x = 2tgx + sin4x k/ 2 2 2 sin x + sin 2x + sin 3x = 2 sin 2x l/ + 2cos x = 0 1 + sin x m/ 2 25 − 4x (3sin 2 x π + 8sin x π ) = 0 sin x.cot g5x n/ = 1 cos9x 2 o/ 3tg6x − = 2tg2x − cot g4x sin 8x p/ ( 2 2sin 3x 1 − 4 sin x) = 1 q/ 2 1 + cos x tg x = 1− sinx r/ 3 3 2
cos x cos 3x + sin x sin 3x = 4 s/ 4⎛ x ⎞ 4 ⎛ x sin + cos ⎞ 5 = ⎜ 3 ⎟ ⎜ 3 ⎟ ⎝ ⎠ ⎝ ⎠ 8 t/ 3 3 2
cos x − 4 sin x − 3cos x sin x + sin x = 0 x x u/ 4 4 sin + cos = 1 − 2sin x 2 2 v/
sin ⎛3x π ⎞ sin 2x.sin ⎛ − = x π + ⎞ ⎜ 4 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 4 ⎠ ( 2 2 − sin x sin 3x 4 ) w/ tg x + 1 = 4 cos x y/ 2 ⎛ x
tgx cos x cos x sin x 1 tg tgx⎞ + − = + ⎜ 2 ⎟ ⎝ ⎠ 4. Cho phöông trình: ( − )( + + ) 2
2sin x 1 2cos 2x 2sin x m = 3 − 4 cos x (1)
a/ Giaûi phöông trình khi m = 1
b/ Tìm m ñeå (1) coù ñuùng 2 nghieäm treân [0, π] ( ÑS: m = 0 ∨ m < 1 − ∨ m > 3 ) 5. Cho phöông trình: 5 5 2
4 cos x sin x − 4 sin x.cos x = sin 4x + m (1) Bieát raèng
x = π laø moät nghieäm cuûa (1). Haõy giaûi phöông trình trong tröôøng hôïp ñoù. CHÖÔNG III.
PHÖÔNG TRÌNH BAÄC HAI VÔÙI CAÙC HAØM SOÁ LÖÔÏNG GIAÙC 2 a sin u + b sin u + c = 0 (a ≠ 0) 2 a cos u + b cos u + c = 0 (a ≠ 0) 2 atg u + btgu = c = 0 (a ≠ 0) 2 a cot g u + b cot gu + c = 0 (a ≠ 0) Caùch giaûi: Ñaët :
t = sin u hay t = cos u vôùi t ≤ 1 t π = tgu (ñieàu kieän u ≠ + kπ ) 2
t = cot gu (ñieàu kieän u ≠ kπ )
Caùc phöông trình treân thaønh: 2 at + bt + c = 0
Giaûi phöông trình tìm ñöôïc t, so vôùi ñieàu kieän ñeå nhaän nghieäm t.
Töø ñoù giaûi phöông trình löôïng giaùc cô baûn tìm ñöôïc u.
Baøi 56: (Ñeà thi tuyeån sinh Ñaïi hoïc khoái A, naêm 2002)
Tìm caùc nghieäm treân (0,2π) cuûa phöông trình ⎛ cos 3x + sin 3x 5 sin x ⎞ + = 3 + cos 2x ⎜ ⎟ (*) ⎝ 1 + 2sin 2x ⎠ 1
Ñieàu kieän: sin 2x ≠ − 2 Ta coù: + = ( 3 − ) + ( 3 sin 3x cos 3x 3sin x 4 sin x 4 cos x − 3cos x)
= −3(cos x − sin x) + 4 ( 3 3 cos x − sin x)
= (cos x − sin x) ⎡−3 + 4 ⎣ ( 2 2
cos x + cos x sin x + sin x)⎤⎦
= (cos x − sin x)(1 + 2sin 2x) Luùc ñoù: (*) ⇔ ⎡ + ( − )⎤ = + ⎣ ⎦ ( 2 5 sin x cos x sin x 3 2cos x − 1) ⎛ 1 do sin 2x ⎞ ≠ − ⎜ 2 ⎟ ⎝ ⎠ 2 ⇔ 2cos x − 5cos x + 2 = 0 ⎡ 1 cos x = ⎢ ⇔ 2 ⎢ ⎢cos x = 2 ⎣ (loaïi) x π ⇔ = ± + k π 2 (nhaän do 3 1 sin 2x = ± ≠ − ) 3 2 2 π 5 Do π
x ∈ (0,2π) neân x = ∨ x = 3 3
Baøi 57: (Ñeà thi tuyeån sinh Ñaïi hoïc khoái A, naêm 2005) Giaûi phöông trình: 2 2
cos 3x.cos 2x − cos x = 0(*) 1 + cos 6x 1 + cos 2x Ta coù: (*) ⇔ .cos 2x − = 0 2 2
⇔ cos6x.cos2x − 1 = 0 (**) Caùch 1: (**) ⇔ ( 3
4 cos 2x − 3cos 2x)cos2x − 1 = 0 4 2
⇔ 4 cos 2x − 3cos 2x − 1 = 0 2 ⎡cos 2x = 1 ⎢ ⇔ ⎢ 2 1 cos 2x = − (voâ nghieäm) ⎢⎣ 4 ⇔ sin 2x = 0 k 2x k x π ⇔ = π ⇔ = (k ∈ Z) 2 1
Caùch 2: (**) ⇔ (cos8x + cos4x) − 1 = 0 2 ⇔ cos 8x + cos 4x − 2 = 0 2
⇔ 2cos 4x + cos 4x − 3 = 0 ⎡cos 4x = 1 ⎢ ⇔ 3 ⎢cos4x = − (loaïi) ⎣ 2 k 4x k2 x π ⇔ = π ⇔ = (k ∈ Z) 2
Caùch 3: phöông trình löôïng giaùc khoâng maãu möïc: ⎡cos 6x = cos 2x = 1
(**) ⇔ ⎢⎣cos6x = cos2x = 1−
Caùch 4: cos 8x + cos 4x − 2 = 0 ⇔ cos 8x + cos 4x = 2
⇔ cos 8x = cos 4x =1 ⇔ cos 4x = 1
Baøi 58: (Ñeà thi tuyeån sinh Ñaïi hoïc khoái D, naêm 2005) Giaûi phöông trình: 4 4 ⎛ π ⎞ ⎛ π ⎞ 3 cos x + sin x + cos x − sin 3x − − = 0 ⎜ 4 ⎟ ⎜ 4 ⎟ ⎝ ⎠ ⎝ ⎠ 2 Ta coù: (*) ⇔ ( + )2 2 2 2 2 1 ⎡ ⎛ π ⎞ ⎤ 3 sin x cos x − 2sin x cos x + sin 4x − + sin 2x − = 0 2 ⎢ ⎜ ⎣ 2 ⎟ ⎥ ⎝ ⎠ ⎦ 2 1 2 1 ⇔ − + [− + ] 3 1 sin 2x cos 4x sin 2x − = 0 2 2 2 1 2 1 ⇔ − − ( 2 − ) 1 1 sin 2x 1 2sin 2x + sin 2x − = 0 2 2 2 2 2 ⇔ sin 2x + sin 2x − 2 = 0 ⎡sin 2x = 1 ⇔ ⎢ sin 2x = 2 − ⎣ (loaïi) π ⇔ 2x = + k π 2 , k ∈ ] 2 π ⇔ x = + π k , k ∈ ] 4
Baøi 59: (Ñeà thi tuyeån sinh Ñaïi hoïc khoái B, naêm 2004) Giaûi phöông trình: − = ( − ) 2 5 sin x 2 3 1 sinx tg x (*)
Ñieàu kieän: cos x ≠ 0 ⇔ sin x ≠ 1 ± 2 sin x
Khi ñoù: (*) ⇔ 5sin x − 2 = 3(1 − sin x) 2 cos x 2 ⇔ − = ( − ) sin x 5sin x 2 3 1 sin x 2 1 − sin x 2 3sin x ⇔ 5sin x − 2 = 1 + sinx 2 ⇔ 2sin x + 3sin x − 2 = 0 ⎡ 1 sin x = (nhaändosin x ≠ 1 ± ) ⎢ ⇔ 2 ⎢ ⎢sin x = 2 − ⎣ (voâ nghieäm) π 5 x k2 x π ⇔ = + π ∨ = + k2π(k ∈ Z) 6 6 1 1
Baøi 60: Giaûi phöông trình: 2sin 3x − = 2cos 3x + (*) sin x cos x Ñieàu kieän: sin 2x ≠ 0 Luùc ñoù: (*) ⇔ ( − ) 1 1 2 sin 3x cos3x = + sin x cos x ⇔ ⎡ ( + ) − ( 3 3 + ) 1 1 2 3 sin x cos x 4 sin x cos x ⎤ = + ⎣ ⎦ sin x cos x ⇔ ( + ) ⎡ − ( 2 2 − + ) sinx + cosx
2 sin x cos x 3 4 sin x sin x cos x cos x ⎤ = ⎣ ⎦ sin x cos x ( ) ⎡ 1 sin x cos x 2 8sin x cos x ⎤ ⇔ + − + − = 0 ⎢ sin x cos x ⎥ ⎣ ⎦ ( ) ⎡ 2 sin x cos x 4 sin 2x 2⎤ ⇔ + − − = 0 ⎢ sin 2x ⎥ ⎣ ⎦ ⎡tgx = 1 ⎡sin x + cos x = 0 − ⎢ ⇔ ⎢ ⇔ 1
− nhaän so vôùi ñieàu kieän 2 ( )
⎣4 sin 2x − 2sin 2x − 2 = 0 ⎢sin 2x = 1 ∨ sin 2x = ⎣ 2 π π π 7π ⇔ x = − + π k ∨ 2x = + π k2 ∨ 2x = − + π k2 ∨ 2x = + π k2 , k ∈ ] 4 2 6 6 π π 7π ⇔ x = ± + π k ∨ x = − + π k ∨ x = + π k , k ∈ ] 4 12 12 ( + ) − 2 cos x 2 sin x 3 2 2 cos x − 1
Baøi 61: Giaûi phöông trình: = 1 (*) 1 + sin 2x Ñieàu kieän: sin 2x 1 x π ≠ − ⇔ ≠ − + mπ 4 Luùc ñoù: (*) 2
⇔ 2sin x cos x + 3 2 cos x − 2 cos x − 1 = 1 + sin 2x 2
⇔ 2cos x − 3 2 cos x + 2 = 0 2 ⇔ cos x = hay cos x = 2 (voâ nghieäm) 2 ⎡x π = + k2π ⎢ 4 ⇔ ⎢ x π
⎢ = − + k '2π(loaïi do ñieàu kieän) ⎢⎣ 4 x π ⇔ = + k π 2 4
Baøi 62: Giaûi phöông trình: x 3x x 3x 1 cos x.cos .cos − sin x sin sin = (*) 2 2 2 2 2 1 1 1
Ta coù: (*) ⇔ cos x (cos2x + cos x) + sin x(cos2x − cos x) = 2 2 2 2
⇔ cos x.cos 2x + cos x + sin x cos 2x − sin x cos x = 1 ⇔ ( + ) 2
cos 2x cos x sin x = 1 − cos x + sin x cos x
⇔ cos 2x (cos x + sin x) = sin x (sin x + cos x)
⇔ (cos x + sin x)(cos 2x − sin x) = 0(* *) ⇔ ( + )( 2
cos x sin x 1 − 2sin x − sin x) = 0 ⎡cos x = − sin x ⇔ ⎢ 2 ⎣2sin x + sin x − 1 = 0 ⎡ π ⎡ x = − + kπ ⎢ ⎢tgx = 1 − 4 ⎢ ⎢ π ⇔ sin x = 1 ⎢ ⎢ − ⇔ x = − + k2π (k ∈ Z) ⎢ ⎢ 2 1 ⎢ ⎢sin x = π 5π ⎣ 2 ⎢x = + k2π ∨ x = + k2π ⎢⎣ 6 6 Caùch khaùc: (**) tgx 1 cos2x sin x cos⎛ π x⎞ ⇔ = − ∨ = = − ⎜ 2 ⎟ ⎝ ⎠
Baøi 63: Giaûi phöông trình: 3
4 cos x + 3 2 sin 2x = 8cos x (*) Ta coù: (*) 3
⇔ 4 cos x + 6 2 sin x cos x − 8 cos x = 0 ⇔ ( 2
cos x 2cos x + 3 2 sin x − 4) = 0 ⇔ ⎡ ⎣ ( 2
cos x 2 1 − sin x) + 3 2 sin x − 4⎤ 0 ⎦ = 2
⇔ cos x = 0 ∨ 2sin x − 3 2 sin x + 2 = 0 ⎡cos x = 0 ⎢ 2 ⎢ ⇔ sin x = ⎢ 2 ⎢ ⎢sin x = 2 ⎣ (voâ nghieäm) π 2 x k sin x sin π ⇔ = + π ∨ = = 2 2 4 π π 3 x k x k2 x π ⇔ = + π ∨ = + π ∨ = + k2π (k ∈ Z) 2 4 4
Baøi 64: Giaûi phöông trình:
cos⎛2x π ⎞ cos⎛2x π ⎞ + + − + 4 sin x = 2 + 2 ⎜ ⎟ ⎜ ⎟ (1 − sin x)(*) ⎝ 4 ⎠ ⎝ 4 ⎠ (*) 2cos 2x.cos π ⇔
+ 4 sin x = 2 + 2 (1 − sin x) 4 ⇔ 2 ( 2
1 − 2sin x) + (4 + 2)sin x − 2 − 2 = 0 2
⇔ 2 2 sin x − (4 + 2)sin x + 2 = 0 ⎡sin x = 2 (loaïi) ⇔ 2
2 sin x − (2 2 + 1)sin x + 2 = 0 ⎢ ⇔ ⎢ 1 sin x = ⎢⎣ 2 π π 5 ⇔ x = + k π 2 hay x = + k π 2 , k ∈ ] 6 6
Baøi 65: Giaûi phöông trình : 2 + 2
3 cot g x 2 2 sin x = (2 + 3 2) cos x (*)
Ñieàu kieän: sin x ≠ 0 ⇔ cos x ≠ 1 ± Chia hai veá (*) cho 2 sin x ta ñöôïc: 2 cos x cos x (*) ⇔ 3 + 2 2 = 2 + 3 2 vaø sin x ≠ 0 4 ( ) 2 sin x sin x Ñaët cos x t =
ta ñöôïc phöông trình: 2 sin x 2 3t − (2 + 3 2)t + 2 2 = 0 2 ⇔ t = 2 ∨ t = 3 2 * Vôùi t cos x 2 = ta coù: = 3 2 sin x 3 ⇔ 3cos x = 2( 2 1 − cos x) 2 ⇔ 2cos x + 3cos x − 2 = 0 ⎡cos x = 2 − (loaïi) ⎢ ⇔ 1
⎢cos x = (nhaän do cosx ≠ 1 ± ) ⎢⎣ 2 x π ⇔ = ± + k2π (k ∈ Z) 3 * Vôùi t cos x = 2 ta coù: = 2 2 sin x ⇔ cos x = 2 (1 − 2 cos x) ⇔ 2 2 cos x + cos x − 2 = 0 ⎡cos x = − 2 (loaïi) ⎢ ⇔ ⎢ 2 cos x = (nhaän do cos x ≠ ± ⎢ 1) ⎣ 2 π ⇔ x = ± + k π 2 , k∈] 4 2 2
Baøi 66: Giaûi phöông trình: 4 sin 2x + 6 sin x − 9 − 3 cos 2x = 0 (*) cos x Ñieàu kieän: cos x ≠ 0 Luùc ñoù: (*) 2 2
⇔ 4 sin 2x + 6sin x − 9 − 3cos 2x = 0 ⇔ 4 ( 2
1 − cos 2x) + 3(1 − cos2x) − 9 − 3cos2x = 0 2 ⇔ 4 cos 2x + 6cos 2x + 2 = 0 1
⇔ cos 2x = −1 ∨ cos 2x = − 2 2 2 1 ⇔ 2cos x − 1 = 1 − ∨ 2cos x − 1 = − 2
⎡cos x = 0(loaïi doñieàu kieän) ⎢ ⇔ ⎢ 1
cos x = ± (nhaän do cos x ≠ 0) ⎢⎣ 2 π 2 x k2 x π ⇔ = ± + π ∨ = ± + k2π (k ∈ Z) 3 3 Baøi 67: Cho ( ) 1 2 f x = sin x + sin 3x + sin 5x 3 5
Giaûi phöông trình: f '(x) = 0 Ta coù: f '(x) = 0
⇔ cos x + cos 3x + 2cos5x = 0
⇔ (cos x + cos5x) + (cos3x + cos5x) = 0
⇔ 2cos 3x cos 2x + 2cos 4x cos x = 0 ⇔ ( 3 4 cos x − 3cos x)cos2x + ( 2 2cos 2x − 1)cos x = 0 ⇔ ⎡ 2 2
⎣(4 cos x − 3) cos 2x + 2 cos 2x − 1⎤⎦ cos x = 0
⎡⎡2(1 + cos 2x) − 3⎤ cos 2x + 2 2 cos 2x − 1 = ⎣ ⎦ 0 ⇔ ⎢⎢⎣cosx = 0 ⎡ 2 4 cos 2x − cos 2x − 1 = 0 ⇔ ⎢⎣cosx = 0 1 ± 17 ⇔ cos 2x = ∨ cos x = 0 8 1 + 17 1 − 17 ⇔ cos 2x = = cos α ∨ cos 2x = = cosβ ∨ cos x = 0 8 8 x α k x β k x π ⇔ = ± + π ∨ = ± + π ∨ = + kπ (k ∈ Z) 2 2 2 17
Baøi 68: Giaûi phöông trình: 8 8 2 sin x + cos x = cos 2x (*) 16 Ta coù:
sin x + cos x = (sin x + cos x)2 8 8 4 4 4 4 − 2sin x cos x ⎡ = ⎢(sin x + cos x) 2 2 2 2 2 2 ⎤ 1 4 − 2sin x cos x − sin 2x ⎥ ⎣ ⎦ 8 2 ⎛ 1 2 ⎞ 1 4 = 1 − sin 2x − sin 2x ⎜ 2 ⎟ ⎝ ⎠ 8 2 1 4 = 1 − sin 2x + sin 2x 8 Do ñoù: (*) ⎛ 2 1 4 ⎞
⇔ 16 1 − sin 2x + sin 2x = 17 (1 − ⎜ ⎟ sin2 2x) ⎝ 8 ⎠ ⇔ 4 2 sin 2x + 2 sin 2x − 1 = 0 ⎡ 2 sin 2x = −1(loaïi) ⎢ 1 1 ⇔ ⇔ (1 − cos 4x 1 ) ⎢ = 2 sin 2x = 2 2 ⎢⎣ 2 cos 4x 0 x (2k 1) π ⇔ = ⇔ = + , (k ∈ Z) 8 5x x
Baøi 69: Giaûi phöông trình: 3 sin = 5cos x.sin (*) 2 2 x
Nhaän xeùt thaáy: cos = 0 ⇔ x = π + k2π ⇔ cos x = −1 2 Thay vaøo (*) ta ñöôïc: ⎛ π 5 ⎞ ⎛ sin π + 5 π k = − 5.sin + π⎞ ⎜ ⎟ ⎜ k ⎟, khoâng thoûa k ∀ ⎝ 2 ⎠ ⎝ 2 ⎠ x
Do cos khoâng laø nghieäm cuûa (*) neân: 2 ( ) 5x x x x * x ⇔ sin .cos = 2 5 cos x.sin cos vaø cos ≠ 0 2 2 2 2 2 1 x ⇔ (sin 3x + sin 2x) 5 3 = cos x.sin x vaø cos ≠ 0 2 2 2 3 3 x
⇔ 3sin x − 4 sin x + 2sin x cos x = 5cos x.sin x vaø cos ≠ 0 2 ⎧ x ⎪cos ≠ 0 ⇔ ⎨ 2 ⎪ 2 3
⎩3 − 4 sin x + 2cos x = 5cos x ∨ sin x = 0 ⎧ x cos ≠ 0 ⎪⎪ 2 ⇔ ⎨⎪ 3 2 x
5cos x − 4 cos x − 2cos x + 1 = 0 ∨ sin = 0 ⎪⎩ 2 ⎧cos x ≠ 1 − ⎪ ⇔ (⎨ − ⎪ )( 2 + − ) x
cos x 1 5cos x cos x 1 = 0 ∨ sin = 0 ⎩ 2 ⎧cos x ≠ −1 ⎪⎡⎪⎢cosx = ⎪ 1 ⎪⎢ ⇔ ⎨⎢ −1 + 21 cos x = = cos α ⎪⎢ ⎪ 10 ⎢ ⎪⎢ −1 − 21 cos x = = cos β ⎪⎢ ⎩⎣ 10
⇔ x = k2π hay x = ±α + k π 2 hay x = ±β + k π 2 , (k ∈ Z)
Baøi 70: Giaûi phöông trình: ( + ) 2
sin 2x cot gx tg2x = 4 cos x (*)
Ñieàu kieän: cos2x ≠ 0 vaø sin x ≠ 0 ⇔ cos2x ≠ 0 ∧ cos2x ≠ 1 cos x sin 2x Ta coù: cot gx + tg2x = + sin x cos 2x cos 2x cos x + sin 2x sin x = sin x cos 2x cos x = sinxcos2x Luùc ñoù: (*) ⎛ cos x ⎞ 2 ⇔ 2sin x.cos x = 4 cos x ⎜ sin x cos 2x ⎟ ⎝ ⎠ 2 cos x ⇔ = 2 2 cos x cos 2x
⇔ (cos 2x + 1) = 2 cos 2x (cos 2x + 1)
⇔ (cos 2x + 1) = 0 hay 1 = 2 cos 2x 1
⇔ cos 2x = −1 ∨ cos 2x = (nhaän do cos 2x ≠ 0 vaø cos 2x ≠ 1) 2 π ⇔ 2x = π + k π 2 ∨ 2x = ± + k π 2 , k∈] 3 π π ⇔ x = + π k ∨ x = ± + π k , k∈] 2 6
Baøi 71: Giaûi phöông trình: 2 6x 8x 2cos +1 = 3cos (*) 5 5 Ta coù : (*) ⎛ 12x ⎞ ⎛ 2 4x ⎞ ⇔ 1+ cos +1 = ⎜ ⎟ 3⎜2cos −1⎟ ⎝ 5 ⎠ ⎝ 5 ⎠ 3 4x 4x ⎛ 2 4x ⎞ ⇔ 2 + 4 cos − 3cos = 3⎜2cos −1⎟ 5 5 ⎝ 5 ⎠ 4
Ñaët t = cos x(ñieàu kieän t ≤ ) 1 5 Ta coù phöông trình : 3 2 4t − 3t + 2 = 6t − 3 3 2 ⇔ 4t − 6t − 3t + 5 = 0 ⇔ (t − ) 1 ( 2 4t − 2t − 5) = 0 1− 21 1+ 21 ⇔ t = 1∨ t = ∨ t = (loïai) 4 4 Vaäy 4x 4x • cos = 1 ⇔ = 2kπ 5 5 5kπ ⇔ x = (k∈Z) 2 4x 1− 21 • cos =
= cosα (vôùi 0 < α < 2π) 5 4 4x ⇔ = ±α + A2π 5 5α A5 x π ⇔ = ± + ,(A ∈ Z) 4 2
Baøi 72 : Giaûi phöông trình 3 tg ⎛ x π ⎞ − = tgx −1 ⎜ ⎟ (*) ⎝ 4 ⎠ Ñaët t x π x π = − ⇔ = + t 4 4 (*) thaønh : 3 ⎛ π ⎞ 1+ tgt tg t = tg + t −1 =
−1 vôùi cost ≠ 0 ∧ tgt ≠ 1 ⎜ ⎝ 4 ⎟ ⎠ 1− tgt ⇔ 3 2tgt tg t = 1−tgt 3 4 ⇔ tg t − tg t = 2tgt ⇔ tgt ( 3 2 tg t − tg t + 2) = 0 ⇔ tgt (tgt + ) 1 ( 2 tg t − 2tgt + 2) = 0
⇔ tgt = 0 ∨ tgt = −1(nhaän so ñieàu kieän) t k t π ⇔ = π ∨ = − + k , π k∈] 4 Vaäy (*) x π ⇔ = + kπ hay x = k , π k ∈] 4 4 4 sin 2x + cos 2x
Baøi 73 : Giaûi phöông trình 4 = cos 4x (*) tg⎛ π x⎞ tg⎛ π x⎞ − + ⎜ 4 ⎟ ⎜ 4 ⎟ ⎝ ⎠ ⎝ ⎠ Ñieàu kieän sin ⎧ ⎛ π x⎞cos⎛ π x⎞ 0 s ⎧ in⎛ π 2x⎞ − − ≠ − ≠ 0 ⎪ ⎜ ⎪ ⎝ 4 ⎟ ⎜ ⎠ ⎝ 4 ⎟ ⎪ ⎜ ⎠ ⎪ ⎝ 2 ⎟ ⎠ ⎨ ⇔ ⎨ sin ⎪ ⎛ π x⎞cos⎛ π x⎞ 0 s ⎪ + + ≠ in⎛ π + 2x⎞ ≠ 0 ⎜ ⎩ 4 ⎟ ⎜ 4 ⎟ ⎜ ⎩ 2 ⎟ ⎪ ⎪ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
⇔ cos2x ≠ 0 ⇔ sin2x ≠ ±1 Do : ⎛ π ⎞ ⎛ π ⎞ 1− tgx 1+ tgx tg − x tg + x = . = 1 ⎜ ⎝ 4 ⎟ ⎜ ⎠ ⎝ 4 ⎟ ⎠ 1+ tgx 1− tgx Khi cos2x ≠ 0 thì : (*) 4 4 4 ⇔ sin 2x + cos 2x = cos 4x 2 2 4
⇔ 1− 2sin 2x cos 2x = cos 4x 1 2 4 ⇔ 1− sin 4x = cos 4x 2 1 ⇔ 1− ( 2 1− cos 4x) 4 = cos 4x 2 4 2
⇔ 2 cos 4x − cos 4x −1 = 0 2 ⎡cos 4x = 1 ⎢ 2 ⇔ 1 ⇔ 1− sin 4x = 1 2
⎢cos 4x = − (voâ nghieäm) ⎢⎣ 2 ⇔ sin 4x = 0 ⇔ 2sin 2x cos2x = 0 ⇔ sin 2x = 0(do cos2x ≠ 0) π ⇔ 2x = k , π k∈] ⇔ x = k , k∈] 2 1 2
Baøi 74 :Giaûi phöông trình: 48− − 1+ cot g2x cot gx = 0(*) 4 2 ( ) cos x sin x Ñieàu kieän : sin 2x ≠ 0 Ta coù : cos2x cosx 1+ cot g2x cot gx = 1+ . sin 2x sin x sin 2xsin x + cos2x cosx = sin xsin 2x cosx 1 = = do cosx ≠ 0 2 2 ( ) 2sin x cosx 2sin x 1 1 Luùc ñoù (*) ⇔ 48− − = 0 4 4 cos x sin x 4 4 1 1 sin x + cos x ⇔ 48 = + = 4 4 4 4 cos x sin x sin x cos x 4 4 4 4
⇔ 48sin x cos x = sin x + cos x 4 2 2
⇔ 3sin 2x = 1− 2sin x cos x 4 1 2 ⇔ 3sin 2x + sin 2x −1 = 0 2 ⎡ 2 2 sin x = − ⎢ (loïai) 3 ⇔ ⎢⎢ 2 1 sin x = (nhaän do ≠ 0) ⎢⎣ 2 1 ⇔ ( − ) 1 1 cos4x = 2 2 ⇔ cos4x = 0 4x π ⇔ = + kπ 2 π k x π ⇔ = + (k∈Z) 8 4
Baøi 75 : Giaûi phöông trình 8 8 + = ( 10 10 + ) 5
sin x cos x 2 sin x cos x + cos2x(*) 4 Ta coù : (*) ⇔ ( 8 10 − )+( 8 10 − ) 5 sin x 2sin x cos x 2cos x = cos2x 4 8 ⇔ ( 2 − ) 8 − ( 2 − + ) 5 sin x 1 2sin x cos x 1 2cos x = cos2x 4 8 8 5
⇔ sin x.cos2x − cos x cos2x = cos2x 4 ⇔ 4 cos2x( 8 8 sin x − cos x) = 5cos2x ⇔ cos2x = 0 hay 4( 8 8 sin x − cos x) = 5 ⇔ cos2x = 0 hay 4( 4 4 sin x − cos x)( 4 4 sin x + cos x) = 5 ⎛ 1 2 cos2x 0 hay 4 1 sin 2x⎞ ⇔ = − = 5 ⎜ 2 ⎟ ⎝ ⎠ 2
⇔ cos2x = 0 hay − 2sin 2x =1(Voâ nghieäm ) 2x π ⇔ = + k , π k∈] 2 π k x π ⇔ = + ,k∈] 4 2
Caùch khaùc: Ta coù ( 8 8
4 sin x − cos x) = 5 voâ nghieäm Vì ( 8 8
sin x − cos x) ≤ 1,∀x neân ( 8 8
4 sin x − cos x) ≤ 4< 5, x ∀
Ghi chuù : Khi gaëp phöông trình löôïng giaùc daïng R(tgx, cotgx, sin2x, cos2x, tg2x)
vôùi R haøm höõu tyû thì ñaët t = tgx 2 2t 2t 1 − t Luùc ñoù tg2x = ,sin 2x = ,cos 2x = 2 2 1 − t 1 + t 1 + t2
Baøi 76 : (Ñeå thi tuyeån sinh Ñaïi hoïc khoái A, naêm 2003) Giaûi phöông trình cos 2x 1 cot gx − 1 = + 2 sin x − sin 2x (*) 1 + tgx 2
Ñieàu kieän : sin 2x ≠ 0 vaø tgx ≠ 1 −
Ñaët t = tgx thì (*) thaønh : 2 1 − t 2 2 ⎡ + − ⎤ 1 1 t 1 1 t 1 2t − 1 = + 1 − − . ⎢ 2 ⎥ 2 t 1 + t 2 ⎣ 1 + t ⎦ 2 1 + t 2 1 − t 1 − t 1 2t t ⇔ = + . − do t ≠ −1 2 2 2 ( ) t 1 + t 2 1 + t 1 + t 1 − t t − 2t + 1 (1 − t)2 2 ⇔ = = 2 2 t 1 + t 1 + t
⇔ (1 − t)(1 + t ) = (1 − t)2 2 t 1 ⎡ − t = 0 ⎡t = 1 (nhaän do t ≠ 1 − ) ⇔ ⎢ ⇔ ⎢ 2 1 + t = ⎣ (1 − t) 2 t ⎢2t − t + 1 = 0 ⎣ (voâ nghieäm) Vaäy (*) π ⇔ tgx = 1 ⇔ x =
+ kπ (nhaän do sin 2x = 1 ≠ 0) 4
Baøi 77 : Giaûi phöông trình: sin 2x + 2tgx = 3 (*) Ñieàu kieän : cos x ≠ 0
Ñaët t = tgx thì (*) thaønh : 2t + 2t = 3 2 1 + t ⇔ 2t + (2t − 3) (1 + 2 t ) = 0 ⇔ 3 2t − 2 3t + 4t − 3 = 0 ⇔ (t − 1) ( 2 2t − t + 3) = 0 ⎡t = 1 ⇔ ⎢ 2 2t − t + 3 = ⎣ 0 (voâ nghieäm) π Vaäy (*) ⇔ tgx = 1 ⇔ x = + π k (k ∈ Z) 4
Baøi 78 : Giaûi phöông trình 2 cot gx − tgx + 4sin 2x = (*) sin 2x Ñieàu kieän : sin 2x ≠ 0 2t Ñaët t = tgx thì : sin 2x = do sin 2x ≠ 0 neân t ≠ 0 2 1 + t 2 1 8t 1 + t 1 (*) thaønh : − t + = = + t 2 t 1 + t t t 8t ⇔ = 2t 1 + 2 t 4 ⇔ = 1 do t 0 2 ( ≠ ) 1 + t ⇔ 2
t = 3 ⇔ t = ± 3 (nhaän do t ≠ 0) ⎛ π ⎞ Vaäy (*) ⇔ tgx = tg ± ⎜ ⎟ ⎝ 3 ⎠ π ⇔ x = ± + π k , k∈ ] 3
Baøi 79 : Giaûi phöông trình
(1 − tgx)(1 + sin 2x) = 1 + tgx(*) Ñieàu kieän : cos x ≠ 0
Ñaët = tgx thì (*) thaønh : ( )⎛ 2t 1 t 1 ⎞ − + = 1 + t ⎜ 2 ⎝ 1 t ⎟ + ⎠ 2 ( + ⇔ 1 − t) (t 1) = 1 + t 2 1 + t ⎡t = −1 ⎡t = −1 ⎢ ⇔ (1 − t)(1 + t) ⇔ ⎢ 2 2 ⎢ = 1 1 ⎣ − t = 1 + t 2 ⎢⎣ 1 + t ⇔ t = 1 − ∨ t = 0 ⎡tgx = −1 Do ñoù (*) π ⇔ ⇔ x = − + π k hay x = π k , k ∈ ⎢ ] ⎣tgx = 0 4
Baøi 80 : Cho phöông trình cos 2x − (2m + 1)cos x + m + 1 = 0(*) 3
a/ Giaûi phöông trình khi m = 2
b/ Tìm m ñeå (*) coù nghieäm treân ⎛ π 3 , π ⎞ ⎜ 2 2 ⎟ ⎝ ⎠ Ta coù (*) 2
2 cos x − (2m + 1) cos x + m = 0 ⎧t = cos x ([t] ≤ ⎪ 1) ⇔ ⎨⎪ 2 2t − ⎩ (2m + 1) t + m = 0 ⎧t = cos x ([t] ≤ 1) ⎪ ⇔ ⎨ 1 ⎪t = ∨ t = m ⎩ 2 3 a/ Khi m = , phöông trình thaønh 2 1 3 cos x = ∨ cos x = (loaïi) 2 2 π ⇔ x = ± + k π 2 (k ∈ Z) 3 b/ ⎛ π π 3 ⎞ Khi x ∈ , thì cos x = t ∈ [− ⎜ ⎟ 1, 0) ⎝ 2 2 ⎠ 1 Do t = ∉ [−1, ] 0 neân 2 (*) ⎛ π π 3 ⎞ coù nghieäm treân , ⇔ m ∈ ⎡− ⎜ ⎟ ⎣ 1, 0) ⎝ 2 2 ⎠
Baøi 81 : Cho phöông trình ( + )( − ) 2
cos x 1 cos 2x m cos x = m sin x (*) a/ Giaûi (*) khi m= -2
b/ Tìm m sao cho (*) coù ñuùng hai nghieäm treân ⎡ 2 0, π⎤ ⎢ 3 ⎥ ⎣ ⎦ Ta coù (*) ⇔ (cos x + 1)( 2 2cos x − 1 − m cos x) = m( 2 1 − cos x) ⇔ (cos x + 1) 2
⎡2cos x − 1 − m cos x − m (1 − cos x)⎤ = 0 ⎣ ⎦ ⇔ (cos x + 1)( 2 2cos x − 1 − m) = 0
a/ Khi m = -2 thì (*) thaønh : ( + ) ( 2 cos x 1 2 cos x + 1) = 0 ⇔ cosx = -1 ⇔ x = π + k π 2 (k ∈ Z) ⎡ 2π⎤ ⎡ 1 b / Khi x ∈ 0, thì cos x = t ∈ ⎤ ⎢ ⎥ ⎢− ,1 ⎣ 3 ⎦ ⎣ 2 ⎥⎦
Nhaän xeùt raèng vôùi moãi t treân ⎡ 1 ,1⎤ − ⎢
ta chæ tìm ñöôïc duy nhaát moät x treân 2 ⎥ ⎣ ⎦ ⎡ 2 0, π⎤ ⎢ 3 ⎥ ⎣ ⎦ Yeâu caàu baøi toaùn 2 ⎡ 1
⇔ 2t − 1 − m = 0 coù ñuùng hai nghieäm treân ,1⎤ − ⎢ 2 ⎥ ⎣ ⎦ Xeùt 2 y = 2t − 1(P) vaø y = m (d) Ta coù y’ = 4t
Vaäy (*) coù ñuùng hai nghieäm treân ⎡ 2 0, π⎤ ⎢ 3 ⎥ ⎣ ⎦
⇔ (d) caét (P) taïi hai ñieåm phaân bieät treân ⎡ 1 ,1⎤ − ⎢ 2 ⎥ ⎣ ⎦ 1 ⇔ 1 − < m ≤ 2
Baøi 82 : Cho phöông trình ( − ) 2 2 1 a tg x − + 1 + 3a = 0(1) cos x 1 a/ Giaûi (1) khi a = 2
b/ Tìm a ñeå (1) coù nhieàu hôn moät nghieäm treân ⎛0, π ⎞ ⎜ 2 ⎟ ⎝ ⎠ Ñieàu kieän : cos x 0 x π ≠ ⇔ ≠ + kπ 2 (1) ⇔ (1 − a) 2 sin x − 2cos x + (1 + 3a) 2 cos x = 0 ⇔ (1 − a)( 2
1 − cos x) − 2cos x + (1 + 3a) 2 cos x = 0 2
⇔ 4a cos x − 2cos x + 1 − a = 0 ⇔ a ( 2
4 cos x − 1) − (2cos x − 1) = 0 ⇔ (2cos x − 1) ⎡a ⎣ (2 cos x + 1) − 1⎤ = 0 ⎦ 1
a/ Khi a = thì (1) thaønh : ( )⎛ 1 2cos x 1 cos x ⎞ − − = 0 2 ⎜ 2 ⎟ ⎝ ⎠ 1 cos x cos π ⇔ = = (nhaändocos x ≠ 0) 2 3 x π ⇔ = ± + k2π (k ∈ Z) 3 b/ Khi x ⎛ ∈ 0, π ⎞ ⎜ ⎟ thì cos x = t ∈ (0,1) ⎝ 2 ⎠ ⎡ 1 cos x = t = ∈ (0,1) Ta coù : (1) ⎢ ⇔ 2 ⎢ ⎢2a cos x = 1 − a ⎣ (2) ⎧ ⎪a ≠ 0 ⎪ Yeâu caàu baøi toaùn ⎧1⎫ ⎪ 1 − a
⇔ (2) coù nghieäm treân (0,1) \ ⎨ ⎬ ⇔ ⎨0 < < 1 ⎩2⎭ 2a ⎪ ⎪1 − a 1 ≠ ⎪⎩ 2a 2 ⎧a ≠ 0 ⎧ ⎪1 − a ⎪0 < a < 1 ⎧1 ⎪ > 0 ⎪ < a < 1 2a 1 ⎪ ⎪ ⎪ ⎪3 ⇔ ⎨ ⇔ ⎨a < 0 ∨ a > ⇔ 1 3a 3 ⎨ − 1 ⎪ < 0 ⎪ ⎪a ≠ ⎪ 2a ⎪ 1 ⎪⎩ 2 ⎩ ( ) a ≠ ⎪2 1 a 2a ⎪ − ≠ ⎩ 2
Caùch khaùc : daët u = 1 , ñieàu kieän u ≥1; pt thaønh cos x ( − ) 2 − − + + = ⇔ ( − ) 2 1 a ( u 1 ) 2u 1 3a 0 1 a u − 2u + 4a = 0
⇔ ( u − 2) [ (1 − a)u − 2a ] = 0
Baøi 83 : Cho phöông trình : cos 4x + 6sin x cos x = m (1) a/ Giaûi (1) khi m = 1
b/ Tìm m ñeå (1) coù hai nghieäm phaân bieät treân ⎡0, π⎤ ⎢ 4⎥ ⎣ ⎦ Ta coù : (1) ⇔ − 2 1 2sin 2x + 3sin 2x = m ⎧t = sin 2x ⎪ ( t ≤ 1) ⇔ ⎨ 2 ⎪2t − 3t + m − 1 = 0 ⎩ (2) a/ Khi m = 1 thì (1) thaønh ⎧⎪t = sin 2x( t ≤ 1) ⎧t = sin 2x ( t ≤ 1) ⎪ ⎨ ⇔ ⎨ 2 3 ⎪⎩2t − 3t = 0 ⎪t = 0 ∨ t = (loaïi) ⎩ 2 k sin 2x 0 x π ⇔ = ⇔ = 2 b/ Khi ⎡ π⎤ x ∈ 0, thì sin 2x = t ∈ [0, ] ⎢ ⎥ 1 ⎣ 4 ⎦
Nhaän thaáy raèng moãi t tìm ñöôïc treân [0, ]
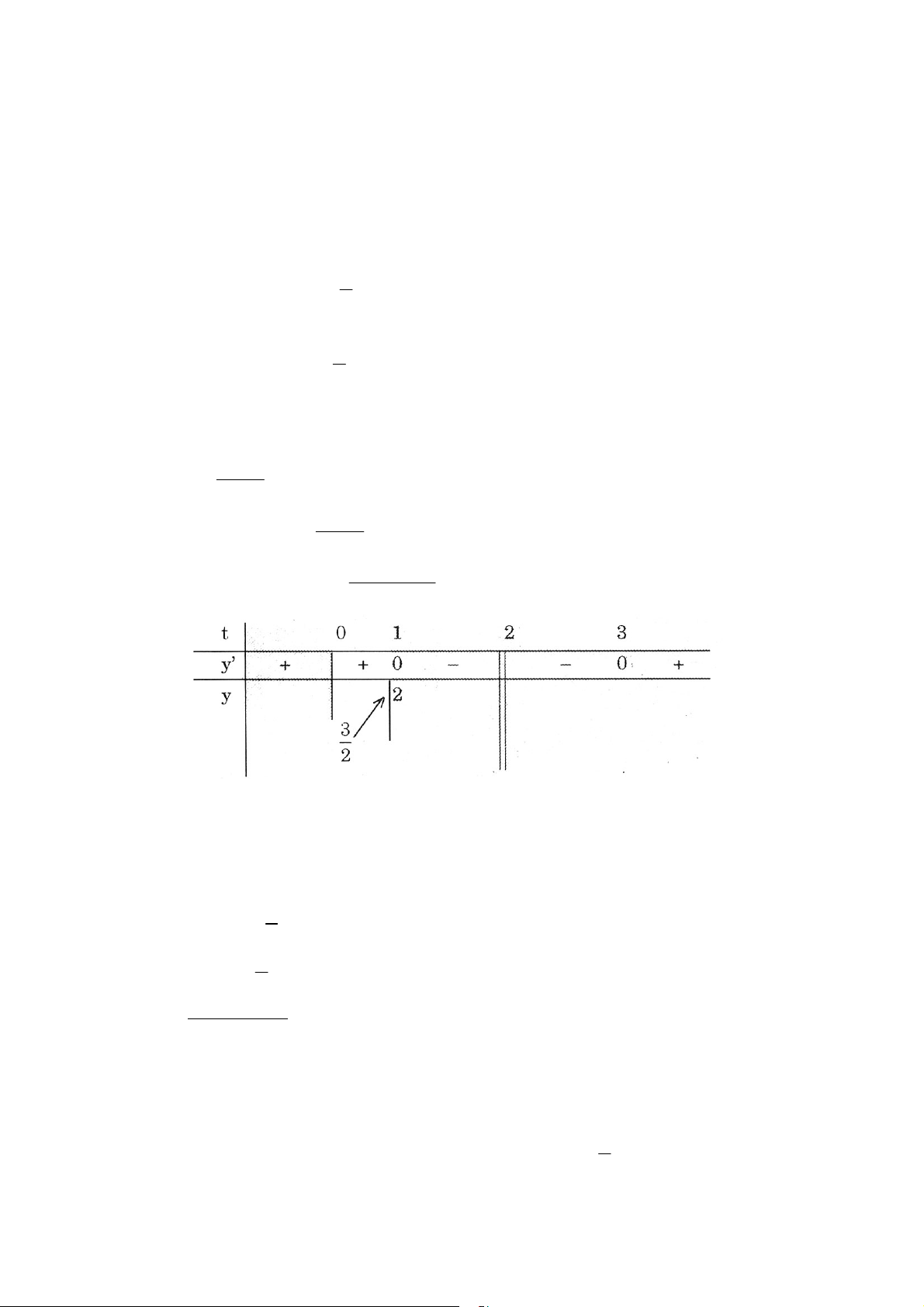
1 ta chæ tìm ñöôïc duy nhaát moät x ⎡0, π⎤ ∈ ⎢ 4⎥ ⎣ ⎦ Ta coù : (2) ⇔ 2 2t − + 3t + 1 = m Xeùt 2 y = −2t + 3t + 1 treân[0, ] 1 Thì y ' = 4 − t + 3
Yeâu caàu baøi toaùn ⇔ (d) y = m caét taïi hai ñieåm phaân bieät treân [0, ] 1 17 ⇔ 2 ≤ m < 8 Caùch khaùc :ñaët = 2 f (x)
2t − 3t + m − 1. Vì a = 2 > 0, neân ta coù ⎧Δ =17 − 8m > 0
⎪ f (0)=m− ≥ ⎪ 1 0 17
Yeâu caàu baøi toaùn ⇔ ⎪⎨ f ( )
1 = m − 2 ≥ 0 ⇔ 2 ≤ m < ⎪ 8 S ⎪ ≤ = 3 0 ≤ ⎪ 1 ⎩ 2 4
Baøi 84 : Cho phöông trình 5 5 2
4 cos x.sin x − 4 sin x cos x = sin 4x + m (1)
a/ Bieát raèng x = π laø nghieäm cuûa (1). Haõy giaûi (1) trong tröôøng hôïp ñoù. b/ Cho bieát x π
= − laø moät nghieäm cuûa (1). Haõy tìm taát caû nghieäm cuûa (1) thoûa 8 4 2 x − 3x + 2 < 0 (1) ⇔ 4 sin x cos x ( 4 4 cos x − sin x) 2 = sin 4x + m ⇔ 2sin 2x ( 2 2 cos x − sin x)( 2 2 cos x + sin x) 2 = sin 4x + m 2
⇔ 2sin 2x.cos 2x = sin 4x + m 2 ⇔ sin 4x − sin 4x + m = 0 (1)
a/ x = π laø nghieäm cuûa (1) 2
⇒sin 4π − sin 4π + m = 0 ⇒ m = 0
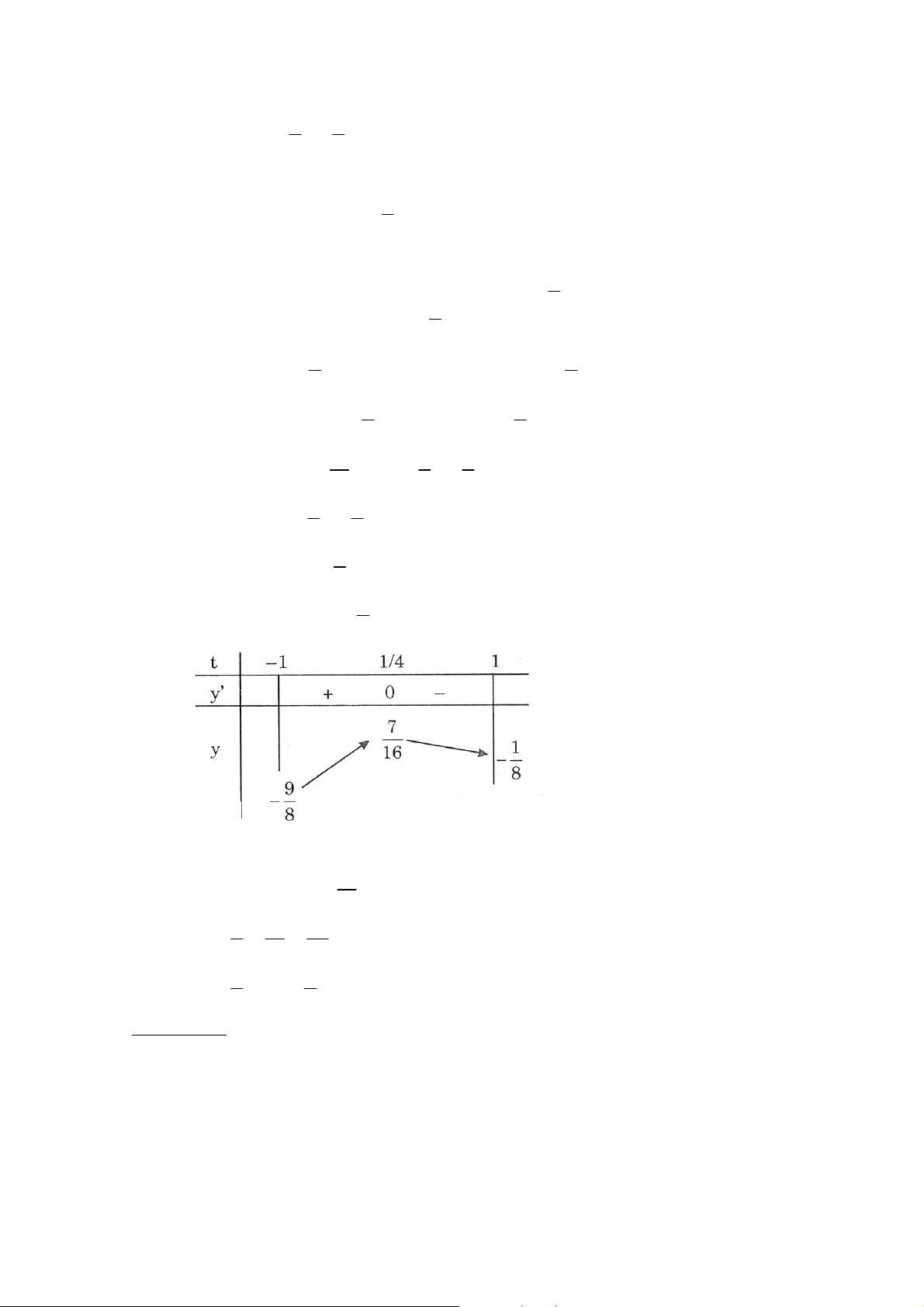
Luùc ñoù (1) ⇔ sin 4x (1 − sin 4x) = 0 ⇔ sin 4x = 0 ∨ sin 4x = 1 π ⇔ 4x = π k ∨ 4x = + k π 2 2 π k π π k ⇔ x = ∨ x = + (k ∈ Z) 4 8 2 2 2 ⎧⎪t = x ≥ 0 ⎧t = x ≥ 0 b/ 4 2 x − 3x + 2 < 0 ⇔ ⎨ ⇔ ⎨ 2 ⎪⎩t − 3t + 2 < 0 1 ⎩ < t < 2 2
⇔1 < x < 2 ⇔ 1 < x < 2
⇔ − 2 < x < −1 ∨ 1 < x < 2 (*) π ⎛ π ⎞ x = − thì sin 4x = sin − = − ⎜ ⎟ 1 8 ⎝ 2 ⎠ x π
= − laø nghieäm cuûa (1) ⇒ 1 + 1 + m = 0 8 ⇒ m = 2 − Luùc ñoù (1) thaønh : 2 sin 4x − sin 4x − 2 = 0
⎧⎪t = sin 4x(vôùi t ≤ 1) ⇔ ⎨ 2 ⎪⎩t − t − 2 = 0 ⎧t = sin 4x ⎪ (vôùi t ≤ 1) ⇔ ⎨⎪t = 1−∨ t = 2 ⎩ (loaïi) ⇔ sin 4x = 1 − 4x π ⇔ = − + k2π 2 π k x π ⇔ = − + 8 2
Keát hôïp vôùi ñieàu kieän (*) suy ra k = 1 π π 3 Vaäy (1) coù nghieäm x π = − + = thoûa 4 2 x − 3x + 2 < 0 8 2 8
Baøi 85 : Tìm a ñeå hai phöông trình sau töông ñöông
2cos x.cos2x = 1 + cos 2x + cos 3x (1) 2
4 cos x − cos 3x = a cos x + (4 − a)(1 + cos2x) (2)
Ta coù : (1) ⇔ cos 3x + cos x = 1 + cos 2x + cos 3x ⇔ cos x = 1 + ( 2 2cos x − 1) ⇔ cos x (1 − 2cos x) = 0 1 ⇔ cos x = 0 ∨ cos x = 2 Ta coù : (2) ⇔ 2 4 cos x − ( 3
4 cos x − 3 cos x) = a cos x + (4 − a) 2cos2 x ⇔ 3 4 cos x + (4 − 2a) 2 cos x (a − 3) cos x = 0 ⎡cos x = 0 ⇔ ⎢⎢ 2 4 cos x + ⎣
2 (2 − a) cos x + a − 3 = 0 ⎛ 1 ⎞ ⇔ cos x = 0 hay cos x − [2cos x + 3 − a] = ⎜ ⎟ 0 ⎝ 2 ⎠ 1 a − 3
⇔ cos x = 0 ∨ cos x = ∨ cos x = 2 2
Vaäy yeâu caàu baøi toaùn ⎡a − 3 = 0 ⎢ 2 ⎢ ⎡a = 3 a − 3 1 ⎢ ⎢ ⇔ = ⇔ a = 4 ⎢ 2 2 ⎢ ⎢ ⎢a < 1 ∨ a > 5 a 3 a − 3 ⎣ − ⎢ < −1 ∨ > 1 ⎢⎣ 2 2
Baøi 86 : Cho phöông trình : cos4x = cos23x + asin2x (*)
a/ Giaûi phöông trì nh khi a = 1
b/ Tìm a ñeå (*) coù nghieäm treân ⎛0, π ⎞ ⎜ 12⎟ ⎝ ⎠ 1 a
Ta coù : (*) ⇔ cos4x = (1 + cos6x) + (1 − cos2x) 2 2 ⇔ 2( 2 2cos 2x − 1) 3
= 1 + 4 cos 2x − 3cos 2x + a (1 − cos2x) ⎧t = cos 2x ( t ≤ 1) ⎪ ⇔ ⎨⎪2⎩( 2 2t − 1) 3 = 1 + 4t − 3t + a (1 − t) ⎧t = cos 2x ⎪ ( t ≤ 1) ⇔ ⎨ 3 2 ⎪ 4t − + 4t + 3t − 3 = a ⎩ (1 − t) 1 ⎧ = cos 2x ( t ≤ 1) ⎪ ⇔ (⎨⎪t −1) ⎩ ( 2 −4t + 3) = a (1 − t) (* *)
a/ Khi a = 1 thì (*) thaønh : ⎧t = cos2x ( t ≤ 1) ⎧ ⎪ ⎪t = cos 2x ( t ≤ 1) ⎨ ⇔ ( ⎨ ⎪ t − 1) ⎩ ( 2 4 − t + 4) = 0 ⎪⎩t = 1 ± ⇔ = ± ⇔ 2 cos 2x 1 cos 2x = 1 π k ⇔ sin 2x = 0 ⇔ 2x = π k ⇔ x = , (k ∈ Z) 2 ⎛ π ⎞ ⎛ π ⎞ ⎛ ⎞ b/ Ta coù : 3 x ∈ 0, ⇔ 2x ∈ 0, .Vaäy cos 2x = t ∈ ⎜ ⎟ ⎜ ⎟ ⎜ ,1 12 6 ⎜ 2 ⎟⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ Vaäy (**) ⇔ (t-1) (− 2 4t + 3) = a (1 − t) ⇔ 2 4t − 3 = a (do t ≠ 1) ⎛ ⎞ Xeùt 2 = − ( ) 3 y 4t 3 P treân ⎜ ,1 2 ⎟ ⎜ ⎟ ⎝ ⎠ ⎛ 3 ⎞ ⇒ y ' = 8t > 0 t ∀ ∈ ⎜ ,1 2 ⎟ ⎜ ⎟ ⎝ ⎠
Do ñoù (*) coù nghieäm treân ⎛ π ⎞ 3 0, ⇔ ⎜ ⎟ (d) : y = a caét (P) ⎛ ⎞ treân ⎜ ,1 ⎟ ⎜ ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ ⎛ 3 ⎞ ⇔ y ⎜ ⎟ < a < y (1) ⎜ 2 ⎟ ⎝ ⎠ ⇔ 0 < a < 1 BAØI TAÄP 1.
Giaûi caùc phöông trình sau : a/ sin4x = tgx b/ 4 4 ⎛ π ⎞ 4 ⎛ π ⎞ 9 sin x + sin x x + + sin x − ⎜ = 4 ⎟ ⎜ 4 ⎟ ⎝ ⎠ ⎝ ⎠ 8 c/ tgx + cot gx = 4 ( − ) 2
sin x 3 2 2cos x − 2sin x − 1 d/ = 1 1 − sin 2x e/ 4 4 cos x + 3 2 sin 2x = 8cos x 1 1 2 f/ + = cos x sin 2x sin 4x g/ sin 2x 2 sin ⎛ x π ⎞ + − = 1 ⎜ 4 ⎟ ⎝ ⎠ h/
2 (2sin x 1) 4(sin x 1) cos⎛2x π ⎞ sin ⎛2x π ⎞ − = − − + − + ⎜ 4 ⎟ ⎜ 4 ⎟ ⎝ ⎠ ⎝ ⎠ 4x k/ 2 cos = cos x 3 x l/ tg .cos x + sin 2x = 0 2 m/ 1 + 3tgx = 2sin 2x n/ cot gx = tgx + 2tg2x p/ 2 3x 4x 2 cos + 1 = 3 cos 5 5 q/ 2 3cos 4x − 2cos 3x = 1 r/ 2 3x 2cos + 1 = 3cos 2x 2 x s/ cos x + tg = 1 2 t/ 2 3tg2x − 4tg3x = tg 3x.tg2x u/ 2 3
cos x.cos 4x + cos2x.cos 3x + cos 4x = 2 v/ 2 2 2 2 3
cos x + cos 2x + cos 3x + cos 4x = 2 w/ sin 4x = tgx 13 x/ 6 6 2 cos x + sin x = cos 2x 8 y/ ⎛3π x ⎞ 1 ⎛ π 3x sin − = sin + ⎞ ⎜ 10 2 ⎟ 2 ⎜ ⎟ ⎝ ⎠ ⎝ 10 2 ⎠ 2. 6 6
sin x + cos x = a sin 2x ( 1 )
a/ Giaûi phöông trình khi a = 1. 1
b/ Tìm a ñeå (1) coù nghieäm (ÑS : a ≥ ) 4 3. Cho phöông trình 6 6 cos x + sin x = 2mtg2x (1) 2 2 cos x − sin x
a/ Giaûi phöông trình khi m = 18 1
b/ Tìm m sao cho (1) coù nghieäm (ÑS : m ≥ ) 8 4. Tìm m ñeå phöông trình
sin 4x = mtgx coù nghieäm x ≠ kπ ⎛ 1 ÑS : m 4⎞ − < < ⎜ 2 ⎟ ⎝ ⎠ 5. Tìm m ñeå phöông trình :
cos3x − cos2x + m cos x − 1 = 0
coù ñuùng 7 nghieäm treân ⎛ π ,2 ⎞ − π ⎜ ⎟ (ÑS :1 < m < 3) ⎝ 2 ⎠ 6. Tìm m ñeå phöông trình : ( 4 4 + ) − ( 6 6 + ) 2 4 sin x cos x
4 sin x cos x − sin 4x = m coù nghieäm ⎛ 1 ÑS : m 1⎞ − ≤ ≤ ⎜ 8 ⎟ ⎝ ⎠ 7. Cho phöông trình : 2 2 2
6sin x − sin x = m cos 2x (1)
a/ Giaûi phöông trình khi m = 3
b/ Tìm m ñeå (1) coù nghieäm (ÑS :m ≥ 0) 8. Tìm m ñeå phöông trình : 4 m (2m + 1) 2 sin x + cos 4x + sin 4x − sin x = 0 4 4
coù hai nghieäm phaân bieät treân ⎛ π , π ⎞ ⎜ 4 2⎟ ⎝ ⎠ ⎛ 1 ÑS :2 5 4 m ⎞ − < < ⎜ 2 ⎟ ⎝ ⎠ 9. Tìm m ñeå phöông trình : 6 6 + = ( 4 4
sin x cos x m sin x + cos x) coù nghieäm ⎛ 1 ÑS : m 1⎞ ≤ ≤ ⎜ 2 ⎟ ⎝ ⎠ 10. Cho phöông trình : 2 2 cos 4x = cos 3x + a sin x
Tìm a ñeå phöông trình coù nghieäm x ⎛0, π ⎞ ∈ ⎜ 2 ⎟ ⎝ ⎠ (ÑS :0 < a < 1) CHÖÔNG IV
PHÖÔNG TRÌNH BAÄC NHAÁT THEO SIN VAØ COSIN
( PHÖÔNG TRÌNH COÅ ÑIEÅN )
a sin u + b cos u = c (*).(a, b ∈ R \ 0 )
Caùch 1 : Chia 2 veá phöông trình cho 2 + 2 a b ≠ 0 Ñaët a b cos α = vaø sin α = vôùi α ∈ [0,2π] 2 2 2 2 a + b a + b ( ) c
Thì * ⇔ sin u cos α + cos u sin α = 2 2 a + b ⇔ ( + α) c sin u = 2 2 a + b Caùch 2 :
Neáu u = π + k2π laø nghieäm cuûa (*) thì :
a sin π + bcos π = c ⇔ −b = c Neáu u ≠ π + k π 2 u
ñaët t = tg thì (*) thaønh : 2 2 2t 1 − t a + b = c 2 2 1 + t 1 + t ⇔ ( + ) 2
b c t − 2at + c − b = 0 (1)(vôùi b + c ≠ 0) Phöông trình coù nghieäm 2
⇔ Δ ' = a − (c + b)(c − b) ≥ 0 2 2 2 2 2 2
⇔ a ≥ c − b ⇔ a + b ≥ c u
Giaûi phöông trình (1) tìm ñöôïc t. Töø t = tg ta tìm ñöôïc u. 2 Baøi 87 : Tìm ⎛ 2π 6 x ∈ , π ⎞ ⎜
⎟ thoûa phöông trình : cos7x − 3 sin 7x = − 2 (*) ⎝ 5 7 ⎠
Chia hai veá cuûa (*) cho 2 ta ñöôïc : ( ) 1 3 2 * ⇔ cos 7x − sin 7x = − 2 2 2 π π 2
⇔ − sin cos 7x + cos sin 7x = 6 6 2 ⎛ π ⎞ π ⇔ sin 7x − = ⎜ ⎟ sin ⎝ 6 ⎠ 4 π π π π 3 ⇔ 7x − = + k π 2 hay 7x − = + h2π , (k, h ∈ Z) 6 4 6 4 π 5 k π 2 1 π 1 h π 2 ⇔ x = + hay x = + , k , h ∈ ] 84 7 84 7 Do ⎛ 2π 6 x ∈ , π ⎞ ⎜ ⎟ neân ta phaûi coù : ⎝ 5 7 ⎠ π 2 π 5 k π 2 π 6 π 2 1 π 1 h π 2 π 6 < + < hay < + < ( k, h ∈ ] ) 5 84 7 7 5 84 7 7 2 5 k2 6 2 11 h2 6 ⇔ < + < hay < + < ( k, h ∈ ] ) 5 84 7 7 5 84 7 7 Suy ra k = 2, h = 1, 2 5π 4π 53 11π 2π 35 Vaäy x = + = π ∨ x = + = π 84 7 84 84 7 84 11π 4π 59 ∨ x = + = π 84 7 84
Baøi 88 : Giaûi phöông trình 3
3sin 3x − 3 cos 9x = 1 + 4 sin 3x (*) Ta coù : ( ) ⇔ ( 3 *
3sin 3x − 4 sin 3x) − 3 cos9x = 1 ⇔ sin 9x − 3 cos9x = 1 1 3 1 ⇔ sin 9x − cos 9x = 2 2 2 ⎛ π ⎞ 1 ⇔ sin 9x − = = sin π ⎜ 3 ⎟ ⎝ ⎠ 2 6 π π π π 5 ⇔ 9x − = + k π 2 hay 9x − = + k π 2 , k ∈ ] 3 6 3 6 π π k2 7π π k2 ⇔ x = + hay x = + , k ∈ ] 18 9 54 9
Baøi 89 : Giaûi phöông trình ⎛ 1 tgx sin 2x cos 2x 2 2cos x ⎞ − − + − = 0 ⎜ ⎟ (*) ⎝ cos x ⎠ Ñieàu kieän : cos x ≠ 0 Luùc ñoù : ( ) sin x 2 * ⇔
− sin 2x − cos 2x + 4 cos x − = 0 cos x cos x 2
⇔ sin x − sin 2x cos x − cos x cos 2x + 4 cos x − 2 = 0 ⇔ ( 2
sin x 1 − 2 cos x) − cos x cos2x + 2cos2x = 0
⇔ − sin x cos2x − cos x cos2x + 2cos2x = 0
⇔ c os 2x = 0 hay − sin x − cos x + 2 = 0
⎡cos 2x = 0 (nhaän do cos2x = 2
2 cos x − 1 = 0 thì cos x ≠ 0 ) ⎢ ⇔ ⎢sinx + cosx = 2 ( 2 voâ nghieäm vì 1 + 2 1 < 2 ⎢⎣ 2 ) 2x (2k 1) π ⇔ = + , k ∈ ] 2 π π k ⇔ x = + , k ∈ ] 4 2
Baøi 90 : Giaûi phöông trình 3 1 8sin x = + (*) cos x sin x Ñieàu kieän : sin 2x ≠ 0 Luùc ñoù (*) 2
⇔ 8sin x cos x = 3 sin x + cos x
⇔ 4 (1 − cos 2x) cos x = 3 sin x + cos x
⇔ −4 cos 2x cos x = 3 sin x − 3 cos x
⇔ −2 (cos 3x + cos x) = 3 sin x − 3cos x 3 1 ⇔ cos 3x = − sin x + cosx 2 2 ⎛ π ⎞ ⇔ cos 3x = cos x + ⎜ ⎟ ⎝ 3 ⎠ π π ⇔ 3x = x + + k π 2 ∨ 3x = −x − + k2π 3 3 π π π k ⇔ x = + π k ∨ x = − + , k ∈ ] 6 12 2
Nhaän so vôùiñieàu kieän sin 2x ≠ 0 Caùch khaùc : (*) 2
⇔ 8sin x cos x = 3 sin x + cos x
( hieån nhieân cosx = 0 hay sinx = 0 khoâng laø nghieäm cuûa pt naøy ) ⇔ − 2
8(1 cos x) cos x = 3 sin x + cos x ⇔ − 3
8 cos x 8 cos x = 3 sin x + cos x ⇔ − 3
6 cos x 8 cos x = 3 sin x − cos x ⇔ 3 1 3
4 cos x − 3 cos x = cos x − sin x 2 2 ⎛ π ⎞ ⇔ cos 3x = cos x + ⎜ ⎟ ⎝ 3 ⎠ π π ⇔ 3x = x + + k π 2 ∨ 3x = −x − + k2π 3 3 π π π k ⇔ x = + π k ∨ x = − + , k ∈ ] 6 12 2
Baøi 91 : Giaûi phöông trình
9sin x + 6 cos x − 3sin 2x + cos 2x = 8(*) Ta coù : (*) ⇔ + − + ( 2 9sin x 6 cos x 6sin x cos x 1 − 2sin x) = 8 ⇔ − − 2
6 cos x 6 sin x cos x 2 sin x + 9 sin x − 7 = 0
6 cos x (1 sin x) 2(sin x 1) ⎛ 7 ⎞ ⇔ − − − sin x − ⎜ ⎟ = 0 ⎝ 2 ⎠ ⎛ 7 ⎞
⇔ 1 − sin x = 0 hay 6 cos x + 2 sin x − = ⎜ ⎟ 0 ⎝ 2 ⎠ ⎡sin x = 1 ⇔ ⎢⎢6cosx + 2sin x = 2 2 2 ⎣
7 (voâ nghieäm do 6 + 2 < 7 ) π ⇔ x = + k π 2 , k ∈ ] 2
Baøi 92 : Giaûi phöông trình: sin 2x + 2cos 2x = 1 + sin x − 4 cos x (*) Ta coù : (*) ⇔ + ( 2
2sin x cos x 2 2cos x − 1) = 1 + sin x − 4cos x ⇔ 2 sin x cos x − sin x + 2 4 cos x + 4 cos x − 3 = 0 ⎛ 1 ⎞ ⎛ 1 ⎞ ⎛ 3 ⎞ ⇔ 2 sin x cos x − + 4 cos x − cos x + = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ 0 ⎝ 2 ⎠ ⎝ 2 ⎠ ⎝ 2 ⎠ 1 ⇔ cos x −
= 0 hay 2 sin x + 4 cos x + 6 = 0 ( 2 voâ nghieäm do 2 + 2 4 < 2 6 ) 2 π ⇔ x = ± + k π 2 3
Baøi 93 : Giaûi phöông trình
2sin 2x − cos 2x = 7 sin x + 2 cos x − 4 (*) Ta coù : (*) ⇔ − ( 2 4 sin x cos x
1 − 2sin x) = 7sin x + 2cos x − 4 ⇔ 2 cos x (2 sin x − 1) + 2 2 sin x − 7 sin x + 3 = 0 2 cos x (2sin x 1) ⎛ 1 ⎞ ⇔ − + 2 sin x − (sin x − ⎜ ⎟ 3) ⎝ 2 ⎠
⇔ 2 cos x (2 sin x − 1) + (2 sin x − 1) (sin x − 3) = 0
⇔ 2 sin x − 1 = 0 hay 2 cos x + sin x − 3 = 0 ( 2 voâ nghieäm vì 1 + 2 2 < 2 3 ) π π 5 ⇔ x = + k π 2 ∨ x = + k π 2 , k ∈ ] 6 6
Baøi 94 : Giaûi phöông trình
sin 2x − cos 2x = 3sin x + cos x − 2(*) Ta coù (*) ⇔ − ( 2 2sin x cos x
1 − 2sin x) = 3sin x + cos x − 2 ⇔ ( − ) + 2 cos x 2 sin x 1 2 sin x − 3sin x + 1 = 0
⇔ cos x (2sin x − 1) + (sin x − 1) (2 sin x − 1) = 0
⇔ 2 sin x − 1 = 0 hay cos x + sin x − 1 = 0 1 ⎛ π ⎞ ⇔ sin x = hay 2 cos x x − ⎜ ⎟ = 1 2 ⎝ 4 ⎠ π π 5 π π ⇔ x = + π k2 ∨ x = + π k2 hay x − = ± + π k2 , k ∈ ] 6 6 4 4 π π 5 π ⇔ x = + π k2 ∨ x = + π k2 hay x = + π k2 ∨ x = π k2 , k ∈ ] 6 6 2
Baøi 95 : Giaûi phöông trình ( )2 sin 2x 3 cos 2x 5 cos⎛2x π ⎞ + − = − ⎜ ⎟ (*) ⎝ 6 ⎠
Ñaët t = sin 2x + 3 cos2x , Điều kiện − a2 + b2 = − ≤ t ≤ = a2 + b2 2 2 ⎛ ⎞ Thì 1 3 t 2⎜ sin 2x cos2x⎟ 2cos⎛2x π ⎞ = + = ⎜ − 2 2 ⎟ ⎜ ⎝ ⎠ ⎝ 6 ⎟⎠ Vaäy (*) thaønh: 2 t 5 t − 5 = ⇔ 2 2t − t − 10 = 0 ⇔ t = ( loaïi ) ∨ t = −2 2 2 Do ñoù (*) ⎛ π ⎞ ⇔ cos 2x − = 1 − ⎜ 6 ⎟ ⎝ ⎠ π 7π ⇔ 2x − = π + k π 2 ⇔ x = + kπ 6 12
Baøi 96 : Giaûi phöông trình 3 2cos x + cos2x + sin x = 0(*) Ta coù (*) 3 2
⇔ 2cos x + 2cos x −1+ sin x = 0 2 ⇔ 2 cos x(cosx + ) 1 −1+ sin x = 0 ⇔ 2( 2
1− sin x)(1+ cosx) − (1− sinx) = 0
⇔ 1− sin x = 0 hay 2(1+ sin x)(1+ cosx) −1 = 0
⇔ 1− sin x = 0 hay 1+ 2sin x cosx + 2(sin x + cosx) = 0 2
⇔ 1− sin x = 0 hay (sin x + cosx ) + 2(sin x + cosx) = 0 ⇔ = + = + + = ( 2 2 2
sin x 1 haysin x cos x 0 hay sin x cosx 2 0 voâ nghieäm do: 1 + 1 < 2 ) π π ⇔ sin x = 1 hay tgx = 1
− ⇔ x = + k2π hay x = − + k2 , π k ∈ ] 2 4 1− cos2x
Baøi 97 : Giaûi phöông trình 1+ cot g2x = * 2 ( ) sin 2x
Ñieàu kieän : sin2x ≠ 0 ⇔ cos2x ≠ 1 ± Ta coù (*) 1− cos2x 1 ⇔ 1+ cot g2x = = 2 1− cos 2x 1+ cos2x 1 ⇔ cot g2x = −1 1+ cos2x cos2x − cos2x ⇔ = sin 2x 1+ cos2x
⎡cos2x = 0(nhaän do ≠ ± ) 1 ⎢ ⇔ 1 − ⎢ 1 = ⎢⎣sin2x 1+ cos2x
⇔ cos2x = 0 ∨1+ cos2x = −sin 2x
⇔ cos2x = 0 ∨ sin 2x + cos2x = −1 ⎛ π ⎞ 1 cos2x 0 sin 2x sin⎛ π ⎞ ⇔ = ∨ + = − = − ⎜ 4 ⎟ 2 ⎜ 4 ⎟ ⎝ ⎠ ⎝ ⎠ π π π π 5 2x k 2x k2 2x π ⇔ = + π ∨ + = − + π ∨ + = + k2 , π k ∈ ] 2 4 4 4 4 π k x π x π ⇔ = +
∨ == − + kπ ∨ 2x = π + k2π(loaïi), k ∈ ] 4 2 4 π k x π ⇔ = + , k ∈ ] 4 2
Baøi 98 : Giaûi phöông trình ( 4 4
4 sin x + cos x) + 3sin4x = 2(*) Ta coù : (*) ⎡( )2 2 2 2 2 4 sin x cos x 2sin x cos x⎤ ⇔ + − + 3 sin 4x = 2 ⎢⎣ ⎥⎦ ⎡ 1 2 ⎤ ⇔ 4 1− sin 2x + 3 sin 4x = ⎢ ⎥ 2 ⎣ 2 ⎦ ⇔ cos4x + 3 sin 4x = −1 1 3 1 ⇔ cos4x + sin 4x = − 2 2 2 ⎛ π ⎞ 2π ⇔ cos 4x − = ⎜ ⎟ cos ⎝ 3 ⎠ 3 π 2π ⇔ 4x − = ± + k2π 3 3 4x k2 hay 4x π ⇔ = π + π = − + k2π,k ∈ ] 3 x π k π hay x π k π ⇔ = + = − + ,k ∈ ] 4 2 12 2 Caùch khaùc : (*) ⇔ ( 2 2 1− sin 2x) + 3sin4x = 0 2
⇔ 2 cos 2x + 2 3 sin 2x cos2x = 0
⇔ cos2x = 0 ∨ cos2x + 3 sin 2x = 0
⇔ cos2x = 0 ∨ cot g2x = − 3 2x π k 2x π ⇔ = + π ∨ = − + k , π k ∈ ] 2 6 π kπ π k x x π ⇔ = + ∨ = − + , k ∈ ] 4 2 12 2
Baøi 99 : Giaûi phöông trình 3 3 1 1+ sin 2x + cos 2x = sin 4x(*) 2 Ta coù (*) ⇔ + ( + )( − ) 1
1 sin 2x cos2x 1 sin2x cos2x = sin 4x 2 1 ( )⎛ 1 1 sin 4x sin 2x cos2x 1 sin 4x⎞ ⇔ − + + − = 0 2 ⎜ 2 ⎟ ⎝ ⎠ 1
⇔ 1− sin 4x = 0 hay 1+ sin 2x + cos2x = 0 2 ⎡sin 4x = 2(loaïi) ⇔ ⎢⎣sin2x+cos2x = −1 ⇔ 2 sin(2x π + ) = 1 − 4 sin⎛2x π ⎞ ⇔ + = sin( π − ) ⎜ 4 ⎟ ⎝ ⎠ 4 ⎡2x π π + = − + k2π ⎢ 4 4 ⇔ ⎢ (k ∈ Z) π 5 2x π ⎢ + = + k2π ⎢⎣ 4 4 x π k x π ⇔ = − + π ∨ = + k , π k∈ ] 4 2
Baøi 100 : Giaûi phöông trình
tgx − 3cot gx = 4(sinx + 3 cosx)(*) sin ⎧ x ≠ 0 Ñieàu kieän ⎨ ⇔ sin 2x ≠ 0 ⎩cosx ≠ 0 sin x cosx Luùc ñoù : (*) ⇔ − 3 = 4(sinx + 3 cosx) cosx sin x 2 2
⇔ sin x − 3cos x = 4sin x cosx(sinx + 3 cosx)
⇔ (sinx + 3 cosx)(sinx − 3 cosx −2sin2x) = 0 ⎡sin x = − 3 cosx ⎢ ⇔ ⎢1 3 sin x − cosx = sin 2x ⎢⎣2 2 ⎡tgx 3 tg⎛ π ⎞ = − = − ⎢ ⎜ ⎝ 3 ⎟⎠ ⇔ ⎢⎢sin⎛x π⎞ − = ⎢ sin 2x ⎜ ⎣ 3 ⎟ ⎝ ⎠ x π k x π 2x k2 x π ⇔ = − + π∨ − = + π ∨ − = π − 2x + k2 , π k ∈ Z 3 3 3 π π 4π k2 x k x k2 x π ⇔ = − + π ∨ = − − π ∨ = + ,k∈ ] 3 3 9 3 π 4π k2 x k x π ⇔ = − + π ∨ = + (nhaän do sin2x ≠ 0) 3 9 3
Baøi 101 : Giaûi phöông trình 3 3
sin x + cos x = sin x − cosx(*) Ta coù : (*) 3 3
⇔ sin x −sin x + cos x + cosx = 0 ⇔ sin x( 2 sin x − ) 3 1 + cos x + cosx = 0 2 3
⇔ −sin x cos x + cos x + cosx = 0 2
⇔ cosx = 0 hay − sin x cosx + cos x + 1 = 0 ⎡cosx = 0 ⇔ ⎢−sin2x + cos2x = 3 − ⎣ (voâ nghieäm do 1+1< 9) x (2k ) 1 π ⇔ = + , k ∈ Z 2
Baøi 102 : Giaûi phöông trình 4 4 ⎛ π ⎞ 1 cos x + sin x + = ⎜ ⎟ (*) ⎝ 4 ⎠ 4 2 1 1 ⎡ ⎛ π ⎞⎤ 1
Ta coù : (*) ⇔ (1+ cos2x)2 + 1− cos 2x + = 4 4 ⎢ ⎜ ⎣ 2 ⎟⎥ ⎝ ⎠⎦ 4 ⇔ ( + )2 + ( + )2 1 cos2x 1 sin 2x = 1 ⇔ cos2x + sin 2x = −1 ⎛ π ⎞ 1 3 ⇔ cos 2x − = − = cos π ⎜ 4 ⎟ ⎝ ⎠ 2 4 π 3 2x π ⇔ − = ± + k2π 4 4 x π k x π ⇔ = + π ∨ = − + k , π k ∈ Z 2 4
Baøi 103 : Giaûi phöông trình 3 3
4sin x.cos3x + 4cos x.sin3x + 3 3 cos4x = 3(*) Ta coù : (*) ⇔ 3 ( 3 − )+ 3 ( − 3 4sin x 4cos x 3cosx
4cos x 3sin x 4sin x) + 3 3 cos4x = 3 ⇔ − 3 12sin x cosx + 3 12sin x cos x + 3 3 cos4x = 3 ⇔ 4sin x cosx(− 2 sin x + 2 cos x) + 3 cos4x =1
⇔ 2sin 2x.cos2x + 3 cos4x = 1 sin π3 ⇔ sin 4x + cos4x = 1 cos π3 sin 4x.cos π sin π π ⇔ + cos4x = cos 3 3 3 sin⎛ 4x π ⎞ ⇔ + = sin π ⎜ 3 ⎟ ⎝ ⎠ 6 π π π 5 4x k2 4x π ⇔ + = + π ∨ + = + k2 , π k ∈ ] 3 6 3 6 π kπ π k x x π ⇔ = − + ∨ = + , k ∈ ] 24 2 8 2
Baøi 104 : Cho phöông trình : 2 2
2sin x − sin x cosx − cos x = m (*)
a/ Tìm m sao cho phöông trình coù nghieäm
b/ Giaûi phöông trình khi m = -1 1 1
Ta coù : (*) ⇔ (1− cos2x) − sin2x − (1+ cos2x) = m 2 2 ⇔ sin2x + 3cos2x = 2 − m +1 2 a/ (*) coù nghieäm 2 2 ⇔ a + b ≥ c ⇔ 1+ 9 ≥ (1− 2m)2 2 ⇔ 4m − 4m − 9 ≤ 0 1− 10 1+ 10 ⇔ ≤ m ≤ 2 2
b/ Khi m = -1 ta ñöôïc phöông trình sin 2x + 3cos2x = 3 ( ) 1 Neáu x (2k ) π • = +1 thì sin2x = 0 vaø cos2x = 1
− neân phöông trình (1) khoâng 2 thoûa. Neáux (2k ) π • ≠ +1 thì cosx ≠ 0,ñaët t = tgx 2 2t 3( 2 1− t ) (1) thaønh + = 3 2 2 1+ t 1+ t ⇔ 2t + 3( 2 1− t ) = 3( 2t +1) 2 ⇔ 6t − 2t = 0 ⇔ t = 0 ∨ t = 3
Vaäy (1) ⇔ tgx = 0 hay tgx =3 = tgϕ ⇔ x = kπ hay x = ϕ + k , π k ∈ ] ⎛ 3 5 4sin π x⎞ + − ⎜ ⎟
Baøi 105 : Cho phöông trình ⎝ 2 ⎠ 6tgα = * 2 ( ) sin x 1+ tg α a/ Giaûi phöông trình khi π α = − 4 b/ Tìm
α ñeå phöông trình (*) coù nghieäm Ta coù : ⎛ 3 sin π x⎞ sin⎛ π x⎞ − = − − = − cosx ⎜ 2 ⎟ ⎜ 2 ⎟ ⎝ ⎠ ⎝ ⎠ 6tgα 6sin α 2 =
.cos α = 3sin2α vôùi cosα ≠ 0 2 1+ tg α cosα 5− 4cosx Vaäy : (*) ⇔
= 3sin 2α (ñieàu kieän sin x ≠ 0 vaø cosα ≠ 0) sin x ⇔ 3sin2αsin x + 4cosx = 5 a/ Khi π
α = − ta ñöôïc phöông trình 4 −3sin x + 4 cos x = 5( )
1 ( Hieån nhieân sin x = 0 khoâng laø nghieäm cuûa (1)) 3 4 ⇔ − sin x + cosx = 1 5 53 4
Ñaët cosϕ = − vaø sin ϕ = vôùi 0 < ϕ < 2π 5 5 Ta coù pt (1) thaønh : sin(ϕ + x) = 1 x π ⇔ ϕ + = + k2π 2 x π ⇔ = −ϕ + + k2π 2 b/ (**) coù nghieäm ⇔ ( α)2 3sin 2 +16 ≥ 25 vaø cosα ≠ 0 2
⇔ sin 2α ≥ 1 vaø cosα ≠ 0 2 ⇔ sin 2α = 1 ⇔ cos2α = 0 π kπ ⇔ α = + ,k ∈ ] 4 2 BAØI TAÄP 1.
Giaûi caùc phöông trình sau : a/
2 2 (sin x + cosx)cosx = 3+ cos2x b/ (2cosx − ) 1 (sin x + cosx) = 1 c/ 2 cos2x = 6 (cosx −sin x) d/ 3sin x = 3 − 3 cosx e/ 2 cos3x + 3 sin x + cosx = 0 f/
cosx + 3 sin x = sin 2x + cosx + sin x 3 g/ cosx + 3 sin x = cosx+ 3sinx+1 h/ sin x + cosx = cos2x k/ 3
4sin x −1 = 3sin x − 3 cos3x 6 i / 3cosx + 4sin x + = 6 3cosx + 4sin x +1 j/
cos7x cos5x − 3 sin 2x = 1− sin 7xsin 5x m/ ( 4 4 4 cos x + sin x) + 3sin4x = 2 p/ 2 2 cos x − 3 sin 2x = 1+ sin x q/
4sin 2x − 3cos2x = 3(4sin x − ) 1 2 r/ tgx − sin2x − cos2x = 4 − cosx + cosx ( ) 2 ⎛ x 2 3 cosx 2sin π ⎞ − − − ⎜ ⎟ s/ ⎝ 2 4 ⎠ =1 2cosx −1 2.
Cho phöông trình cosx + msinx = 2 (1)
a/ Giaûi phöông trình m = 3
b/ Tìm caùc giaù trò m ñeå (1) coù nghieäm (ÑS : m ≥ 3 ) 3. Cho phöông trình : msin x − 2 m cosx − 2 = ( )1 m − 2cosx m − 2sin x
a/ Giaûi phöông trình (1) khi m = 1 b/ Khi
m ≠ 0 vaø m ≠ 2 thì (1) coù bao nhieâu nghieäm treân [20π,30π]? (ÑS : 10 nghieäm) 4. Cho phöông trình 2sin x + cosx +1 = a ( )1 sin x − 2 cosx + 3 1 a/ Giaûi (1)khi a = 3
b/ Tìm a ñeå (1) coù nghieäm CHÖÔNGV.
PHÖÔNG TRÌNH ÑOÁI XÖÙNG THEO SINX, COSX
a (sin x + cos x) + bsin x cos x = c (1) Caùch giaûi
Ñaët t = sin x + cos x vôùi ñieàu kieän t ≤ 2 Thì t 2 sin ⎛ x π ⎞ 2 cos⎛ x π ⎞ = + = − ⎜ 4 ⎟ ⎜ 4 ⎟ ⎝ ⎠ ⎝ ⎠ Ta coù : 2
t = 1 + 2sin x cos x neân (1) thaønh b at + ( 2 t − 1) = c 22 ⇔ bt + 2at − b − 2c = 0
Giaûi (2) tìm ñöôïc t, roài so vôùi ñieàu kieän t ≤ 2 giaûi phöông trình ⎛ π ⎞ 2 sin x + = ⎜ ⎟ t ta tìm ñöôïc x ⎝ 4 ⎠
Baøi 106 : Giaûi phöông trình 2 3 sin x + sin x + cos x = 0(*) (*) ⇔ ( + ) + ( 2 sin x 1 sin x cos x 1 − sin x) = 0
⇔ (1 + sin x) = 0 hay sin x + cos x (1 − sin x) = 0 ⎡sin x = 1 − (1)
⇔ ⎢⎢sinx + cosx − sinxcosx = 0 ⎣ (2) (1) x π • ⇔ = − + k2π (k ∈ Z) 2
Xeùt (2) : ñaët t sin x cos x 2 cos⎛ x π ⎞ • = + = − ⎜ 4 ⎟ ⎝ ⎠ 2
ñieàu kieän t ≤ 2 thì t = 1 + 2sin x cos x 2 Vaäy (2) thaønh t − 1 t − = 0 2 2 ⇔ t − 2t − 1 = 0 ⎡t = 1 − 2 ⇔ ⎢⎢t = 1+ 2 ⎣ (loaïi) Do ñoù ( 2 ) ⎛ π ⇔ 2 cos x ⎞ − = 1 − 2 ⎜ 4 ⎟ ⎝ ⎠ ⎛ π ⎞ 2 ⇔ cos x − =
− 1 = cos ϕ vôùi 0 < ϕ < π ⎜ ⎟ 2 ⎝ 4 ⎠ 2 π 2 ⇔ x − = ±ϕ + h π 2 , h ∈ ] , vôùi cos ϕ = − 1 4 2 π 2 ⇔ x = ± ϕ + h π 2 , h ∈ ], vôùi cos ϕ = − 1 4 2
Baøi 107 : Giaûi phöông trình 3 3 3
−1 + sin x + cos x = sin 2x (*) 2 ( ) ⇔ − + ( + )( − ) 3 * 1
sin x cos x 1 sin x cos x = sin 2x 2 Ñaët t sin x cos x 2 sin ⎛ x π ⎞ = + = + ⎜ 4 ⎟ ⎝ ⎠ Vôùi ñieàu kieän t ≤ 2 Thì 2 t = 1 + 2sin x cos x 2 ⎛ − ⎞ Vaäy (*) thaønh : t 1 3 −1 + t ⎜1 − ⎟ = ⎜ ⎟ ( 2t −1) 2 2 ⎝ ⎠ ⇔ −2 + t ( 2 3 − t ) = 3( 2 t − 1) 3 2 ⇔ t + 3t − 3t − 1 = 0 ⇔ (t − 1)( 2 t + 4t + 1) = 0 ⇔ t = 1 ∨ t = 2
− + 3 ∨ t = −2 − 3 (loaïi) vôùi t = 1 thì ⎛ π ⎞ 1 sin x + = = sin π ⎜ 4 ⎟ ⎝ ⎠ 2 4 π π π π 3 ⇔ x + = = k π 2 ∨ x + = + k π 2 , k ∈ ] 4 4 4 4 π ⇔ x = k π 2 ∨ x = + k π 2 , k ∈ ] 2 vôùi ⎛ π ⎞ 3 − 2 t = 3 − 2 thì sin x + = = ⎜ ⎟ sin ϕ ⎝ 4 ⎠ 2 π π 3 − 2 ⇔ x + = ϕ + m π 2 ∨ x + = π − ϕ + m π 2 , m ∈ ], vôùi = sin ϕ 4 4 2 π π 3 3 − 2 ⇔ x = ϕ − + m π 2 ∨ x = − ϕ + m π 2 , m ∈ ], vôùi = sin ϕ 4 4 2
Baøi 108 :Giaûi phöông trình 2 (sin x + cos x) = tgx + cot gx (*) si ⎧ n x ≠ 0 Ñieàu kieän ⎨ ⇔ sin 2x ≠ 0 ⎩cos x ≠ 0 Luùc ñoù (*) ⇔ ( + ) sin x cos x 2 sin x cos x = + cos x sin x 2 2 ⇔ ( + ) sin x + cos x 1 2 sin x cos x = = sin x cos x sin x cos x Ñaët t sin x cos x 2 sin ⎛ x π ⎞ = + = + ⎜ 4 ⎟ ⎝ ⎠ Thì 2 = + ≤ 2 t 1 2 sin x cos x vôùi t 2 vaø t ≠ 1 2 (*) thaønh 2t = 2 t − 1 3 ⇔ 2t − 2t − 2 = 0
(Hieån nhieân t = ±1 khoâng laø nghieäm) ⇔ (t − 2)( 2 2t + 2t + 2) = 0 ⎡t = 2 ⇔ ⎢ 2 ⎢t + 2t + 1 = 0 ⎣ (voâ nghieäm)
Vaäy (*) ⇔ 2 sin ⎛ x π ⎞ + = 2 ⎜ 4 ⎟ ⎝ ⎠ ⎛ π ⎞ ⇔ sin x + = ⎜ ⎟ 1 ⎝ 4 ⎠ π π ⇔ x + = + k π 2 , k ∈ ] 4 2 π ⇔ x = + k π 2 , k ∈ ] 4
Baøi 109 : Giaûi phöông trình 3(cot gx − cos x) − 5(tgx − sin x) = 2(*)
Vôùi ñieàu kieän sin 2x ≠ 0 , nhaân 2 veá phöông trình cho sinxcosx ≠ 0 thì : ( ) ⇔ 2 ( − ) − 2 * 3 cos x 1 sin x
5 sin x (1 − cos x) = 2sin x cos x ⇔ 2 ( − ) − 2 3 cos x 1 sin x
5 sin x (1 − cos x) = 5sin x cos x − 3sin x cos x
⇔ 3 cos x ⎡cos x (1 − sin x) + sin x⎤ − 5 sin x ⎡ ⎣ ⎦
⎣sin x (1 − cos x) + cos x⎤ = 0 ⎦
⇔ 3 cos x (cos x − sin x cos x + sin x) − 5 sin x (sin x − sin x cos x + cos x) = 0
⎡sin x + cos x − sin x cos x = 0 (1) ⇔ ⎢⎢3cosx − 5sinx = ⎣ 0 (2)
( Ghi chuù: A.B + A.C = A.D ⇔ A = 0 hay B + C = D )
Giaûi (1) Ñaët t sin x cos x 2 sin ⎛ x π ⎞ = + = + ⎜ 4 ⎟ ⎝ ⎠ Thì 2
t = 1 + 2sin x cos x vôùi ñieàu kieän : t ≤ 2 vaø t ≠ ±1 2 (1) thaønh : t − 1 2 t − = 0 ⇔ t − 2t − 1 = 0 2
⎡t = 1 + 2 (loaïi do t ≤ 2) ⇔ ⎢⎢t = 1− 2 ⎣
(nhaän so vôùi ñieàu kieän) Vaäy ⎛ π ⎞ 1 − 2 sin x + = = sin α ⎜ ⎟ (0 < α < 2π) ⎝ 4 ⎠ 2 ⎡ π ⎡ π x + = α + k π 2 x = α − + k π ⎢ ⎢ 2 ⇔ ⎢ 4 ⇔ ⎢ 4 π π ⎢ ⎢ 3 x + = π − α + k π 2 , k ∈ ] x = − α + k π 2 , k ∈ ⎢ ] ⎣ 4 ⎢⎣ 4 ( ) 3 2 ⇔ tgx = = tgβ ⇔ x = β + π
h , h ∈ ] (vôùi 0 < β < π) 5
Baøi 110 : Giaûi phöông trình 3 1+ sin x 3 ( ) 2 ⎛ π x 3tg x tgx 8cos ⎞ − + = − * 2 ⎜ ⎟ ( ) cos x ⎝ 4 2 ⎠
Ñieàu kieän : cosx ≠ 0 ⇔ sin x ≠ 1 ± Luùc ñoù : (*) ⇔ ( 2 − )+ ( + )( 2
tgx 3tg x 1 3 1 sin x 1+ tg x) = 4 1 ⎡ + cos⎛ π −x⎞⎤ ⎢ ⎜ ⎣ 2 ⎟⎥ ⎝ ⎠⎦ = 4(1+ sinx) ⇔ tgx( 2 3tg x − ) 1 + (1+ sin x) ⎡3 ⎣ ( 2 1+ tg x) − 4⎤ = 0 ⎦ ⇔ ( 2 3tg x − ) 1 (tgx +1+ sin x) = 0 ⇔ ( 2 3tg x − )
1 (sin x + cosx + sin x cosx) = 0 2 ⎡3tg x = 1 ( ) 1
⇔ ⎢⎢sinx+cosx+sinxcosx = 0 ⎣ (2) 2 1 3 (1) tg x tgx x π • ⇔ = ⇔ = ± ⇔ = ± + kπ 3 3 6 Giaûi (2) ñaët t sin x cosx 2 sin⎛ x π ⎞ • = + = ⎜ + 4 ⎟ ⎝ ⎠
Vôùi ñieàu kieän t ≤ 2 vaø t ≠ ±1 Thì 2t = 1+ 2sin x cosx 2 (2) thaønh : t −1 2 t + = 0 ⇔ t + 2t −1 = 0 2 ⎡t = 1
− − 2 (loaïi doñieàu kieän t ≤ 2) ⇔ ⎢⎢t = 1−+ 2 ⎣
(nhaän so vôùi ñieàu kieän) Vaäy ⎛ π ⎞ 2 −1 sin x + = = sin ⎜ ϕ 4 ⎟ ⎝ ⎠ 2 ⎡x π k2 ,k ⎡ + = ϕ + π ∈ ] x π = ϕ − + k2 , π k ∈ ⎢ ] 4 ⎢ 4 ⇔ ⎢ ⇔ ⎢ π 3 x k2 ,k ] x π ⎢ ⎢ + = π − ϕ + π ∈ = − ϕ + k2π,k ∈ ⎢ ] ⎣ 4 ⎢⎣ 4
Baøi 111 : Giaûi phöông trình 3 − = 3
2sin x sin x 2cos x − cosx + cos2x(*) ( ) ⇔ ( 3 3 − )−( − ) 2 2 * 2 sin x cos x
sin x cosx + sin x − cos x = 0
⇔ sin x − cosx = 0 hay 2(1+ sin x cosx) −1+ (sin x + cosx) = 0 ⎡sin x − cosx = 0( ) 1 ⇔ ⎢⎢sinx+cosx+sin2x+1= 0 ⎣ (2) •( ) 1 ⇔ tgx = 1 x π ⇔ = + k , π k ∈ ] 4 xeùt (2) ñaët t sin x cosx 2 cosx⎛ x π ⎞ • = + = ⎜ − 4 ⎟ ⎝ ⎠
Vôùi ñieàu kieän : t ≤ 2 2 t = 1+ sin 2x ( ) + ( 2 Vaäy 2 thaønh t t − ) 1 +1 = 0 ⇔ t (t + ) 1 = 0 ⇔ t = 0 ∨ t = 1 − Khi t = 0 thì cos⎛ x π ⎞ − = 0 ⎜ 4 ⎟ ⎝ ⎠ x π (2k ) 1 π ⇔ − = + ,k ∈ ] 4 2 3 x π ⇔ = + k , π k ∈ ] 4 Khi ⎛ π ⎞ 1 3 t = −1 thì cos x − = − = cos π ⎜ 4 ⎟ ⎝ ⎠ 2 4 π 3 x π ⇔ − = ± + k2 , π k ∈ ] 4 4 x k2 hay x π ⇔ = π + π = − + k2 , π k ∈ ] 2
Baøi 112 : Giaûi phöông trình 2 3 4 2 3 4
sin x + sin x + sin x + sin x = cosx + cos x + cos x + cos x(*) Ta coù : (*) ⇔ ( − ) + ( 2 2 − )+( 3 3 − )+( 4 4 sin x cosx sin x cos x sin x cos x sin x − cos x) = 0
⇔ (sin x − cosx) = 0 hay 1+ (sin x + cosx)+ (1+ sin x.cosx) + (sin x + cosx) = 0 ⎡sin x − cosx = 0( ) 1
⇔ ⎢⎢2⎣(sinx+cosx)+sinxcosx+2 = 0(2) Ta coù : (1) ⇔ tgx = 1 x π ⇔ = + k , π k ∈ ] 4
Xeùt (2) : ñaët t sin x cosx 2 cos⎛ x π ⎞ = + = − ⎜ 4 ⎟ ⎝ ⎠ Vôùi ñieàu kieän t ≤ 2 Thì 2t = 1+ 2sin x cosx 2 (2) thaønh t −1 2t + + 2 = 0 2 2 ⇔ t + 4t + 3 = 0
⇔ t = −1∨ t = −3(loaïi) khi t = -1 thì ⎛ π ⎞ 1 3 cos x − = − = cos π ⎜ 4 ⎟ ⎝ ⎠ 2 4 ⎡ π 3 x π − = + k2 , π k ∈ ⎢ ] 4 4 ⇔ ⎢ π 3 x π ⎢ − = − + k2 ,πk ∈ ⎢ ] ⎣ 4 4 ⎡x = π + k2 , π k ∈ ] ⎢ ⇔ x π ⎢ = − + k2 , π k ∈ ] ⎣ 2
Baøi 113 : Giaûi phöông trình 2 ( − 3 ) + 3 tg x 1 sin x cos x −1 = 0(*)
Ñieàu kieän : cosx ≠ 0 ⇔ sin x ≠ 1 ± 2 Luùc ñoù (*) sin x ⇔ ( 3 1− sin x) 3 + cos x −1 = 0 2 cos x ⇔ ( 2 1− cos x)( 3 1− sin x) − ( 3 1− cos x)( 2 1− sin x) = 0 ⇔ (1− cosx)(1− sin x)= 0 hay (1+ cosx)( 2 1+ sin x + sin x) − ( 2 1+ cosx + cos x)(1+ sinx) = 0
⎡cosx = 1(nhaän do ñieàu kieän) ⎢
⇔ ⎢sin x = 1(loaïido ñieàu kieän) ⎢ 2 2 2 2
⎢sin x + sin x cosx − cos x − sin x cos x = 0 ⎣ ⎡cosx = 1 ⇔ ⎢ 2 2 sin x − cos x + sin x cosx ⎣ (sinx − cosx) = 0 ⎡cosx = 1
⇔ ⎢⎣sinx−cosx=0 hay sinx+cosx+sinxcosx = 0 ⎡cosx = 1∨ tgx = 1
⇔ ⎢⎣sinx+cosx+sinxcosx = 0 ⎡x = k2 , π k ∈ ] ⎢ ⇔ x π ⎢ = + k , π k ∈ ] ⎢ 4
⎢sin x + cosx + sin xcosx = 0 ⎣
xeùt pt sin x + cosx + sin x cosx = 0 ñaët t sin x cosx 2 cosx⎛ x π ⎞ = + = −
(ñieàu kieän t ≤ 2 vaø t ≠ ± ⎜ ⎟ )1 ⎝ 4 ⎠ 2 ⇒ t = 1+ 2sin x cos x 2 Ta ñöôïc phöông trình t −1 2 t + = 0 ⇔ t + 2t −1 = 0 2 ⎡t = 1 − − 2 (loaïi) ⇔ ⎢⎢t= −1+ 2 ⎣ (nhaän so vôùi ñk) Vaäy ⎛ π ⎞ 2 −1 cos x − = = cosϕ ⎜ 4 ⎟ ⎝ ⎠ 2 x π k2 ,k ] x π ⇔ − = ±ϕ + π ∈ ⇔ = ± ϕ + k2 , π k ∈ ] 4 4
Baøi 114 : Cho phöông trình m(sinx + cosx + ) 1 =1+ sin2x(*)
Tìm m ñeå phöông trình coù nghieäm thuoäc ñoaïn ⎡0, π⎤ ⎢ 2⎥ ⎣ ⎦ Ñaët t sin x cosx 2 sin⎛ = + = x π − ⎞ ⎜ ⎟ , ñieàu kieän t ≤ 2 ⎝ 4 ⎠ Thì 2t = 1+ sin 2x Vaäy (*) thaønh : ( + ) 2 m t 1 = t Neáu π π π 3 0 x thì x π ≤ ≤ ≤ + ≤ 2 4 4 4 Do ñoù 2 sin⎛ x π ⎞ ≤ + ≤ 1 2 ⎜ 4 ⎟ ⎝ ⎠ ⇔ 1≤ t ≤ 2 ta coù ( + ) 2 m t 1 = t 2 t ⇔ m =
(do t = -1 khoâng laø nghieäm cuûa phöông trình) t +1 2 Xeùt t y = treân 1 ⎡ , 2⎤ t 1 ⎣ ⎦ + 2 Thì t + 2t y' = > 0 t ∀ ∈ 1 ⎡ , 2⎤ (t )2 1 ⎣ ⎦ + Vaäy y taêng treân 1, ⎡ 2⎤ ⎣ ⎦
Vaäy (*) coù nghieäm treân 1, ⎡ π⎤ ⇔ y ⎢ ⎥ ( ) 1 ≤ m ≤ y( 2) ⎣ 2 ⎦ 1 ⇔ ≤ m ≤ 2( 2 − ) 1 2
Baøi 115 : Cho phöông trình 3 3 cos x + sin x = msin x cosx(*)
a/ Giaûi phöông trình khi m = 2
b/ Tìm m ñeå (*) coù nghieäm
Ta coù : (*) ⇔ (cosx + sinx)(1− sinxcosx) = msinxcosx Ñaët t sin x cosx 2 cosx⎛ x π ⎞ = + = − ⎜ 4 ⎟ ⎝ ⎠
Vôùi ñieàu kieän ( t ≤ 2) Thì 2t = 1+ 2sin x cosx 2 2 ⎛ t −1⎞ ⎛ t −1⎞ Vaäy (*) thaønh t ⎜1− ⎟ = m 2 ⎜ ⎟ ⎝ ⎠ ⎝ 2 ⎠ ⇔ ( 2 − ) = ( 2 t 3 t m t − ) 1
a/ Khi m = 2 ta coù phöông trình ( 2 − ) = ( 2 t 3 t 2 t − ) 1 3 2 ⇔ t + 2t − 3t − 2 = 0 ⇔ (t − 2)( 2t + 2 2t + ) 1 = 0
⇔ t = 2 hay t = − 2 + 1 hay t = − 2 −1(loaïi) Vaäy cosx⎛ x π ⎞ • − = 1 ⇔ x π − = k2 , π k ∈ ] ⇔ x π = + k2 , π k ⎜ ∈ ] 4 ⎟ ⎝ ⎠ 4 4 ⎛ π ⎞ 1− 2 • cos x − = = cosα ⎜ 4 ⎟ ⎝ ⎠ 2 x π k2 ,k ] x π ⇔ − = ±α + π ∈ ⇔ = ± α + k2 , π k ∈ ] 4 4 b/ Xeùt phöông trình ( 2 − ) = ( 2 t 3 t k t − ) 1 (**)
Do t = ±1 khoâng laø nghieäm cuûa (**) neân 3 ( ) 3t − t ** ⇔ m = 2t −1 3 Xeùt 3t − t y = C treân ⎡− 2, 2⎤ \ ±1 2 ( ) { } t 1 ⎣ ⎦ − 4 Ta coù −t − 3 y' = < 0 t ∀ = ±1 (t − )2 2 1 suy ra y giaûm treân( 1 − ,1 ) vaø
lim y = + ∞ , lim y = − ∞ + − x→ −1 x→ 1
Do ñoù treân(−1,1 )⊂ ⎡− 2, 2⎤ \ {± } 1 ⎣ ⎦ ta coù 3 (d) y = m caét (C) 3t − t y = vôùi m ∀ ∈ R 2 t −1
Vaäy (*) coù nghieäm ∀m ∈ R
Baøi 116 : Cho phöông trình ( ) 1 ⎛ 1 1 m sin x cosx 1 tgx cot gx ⎞ + + + + + + = 0 ⎜ ⎟ (*) 2 ⎝ sin x cosx ⎠ a/ Giaûi phöông trình khi 1 m = 2
b/ Tìm m ñeå (*) coù nghieäm treân ⎛ 0, π ⎞ ⎜ 2 ⎟ ⎝ ⎠
Vôùi ñieàu kieän sin2x ≠ 0 ta coù (*) ( ) 1 ⎛ sin x cosx 1 1 m sin x cosx 1 ⎞ ⇔ + + + + + + = 0
2 ⎜ cosx sin x sin x cosx ⎟ ⎝ ⎠
⇔ m sin 2x(sin x + cosx) + sin2x + (1+ cosx + sin x) = 0
⇔ m sin 2x(sin x + cosx) + sin2x +1+ cosx + sin x = 0
⇔ m sin 2x(sin x + cosx) + (sin x + cosx)2 + sin x + cosx = 0 ⎡sin x + cosx = 0( ) 1
⇔ ⎢⎢msin2x+sinx+cosx+1= 0 ⎣ (2) Xeùt (2) ñaët t sin x cosx 2 cos⎛ x π ⎞ = + = − ⎜ 4 ⎟ ⎝ ⎠ Thì 2t = 1+ sin2x
Do sin2x ≠ 0 neân t ≤ 2 vaø t = ±1 ⎡t = 0 Vaäy (*) thaønh : ⎢m ⎢⎣ ( 2t − ) 1 + t +1 = 0
⎡t = 0 (nhaän so ñieàu kieän) ⇔ ⎢⎢m ⎣ (t − ) 1 +1 = 0 ( do t ≠ 1 − ) a/ Khi 1 m = thì ta ñöôïc : 2 ⎡t = 0 ⎢ ⎢t = − 1 ⎣ (loaïi do ñieàu kieän) Vaäy sinx + cosx = 0 ⇔ tgx = 1 − x π ⇔ = − + k , π k ∈ ] 4 b/ Ta coù : 0 x π π x π π
< < ⇔ − < − < 2 4 4 4 Luùc ñoù 2 cos⎛x π⎞ < − ≤ 1 ⇒ 1 < t ≤ 2 2 ⎜ 4 ⎟ ⎝ ⎠ Do t = 0 ∉(1, 2⎤⎦
Neân ta xeùt phöông trình : m(t − ) 1 +1 = 0(**) (**) ⇔ mt = m −1 1 ⇔ t = 1−
(do m = 0 thì (**) voâ nghieäm) m
Do ñoù : yeâu caàu baøi toaùn 1 ⇔ 1 < 1− ≤ 2 m ⎧ 1 − > 0 ⎧m < 0 ⎪⎪ m ⎪ ⇔ ⎨ ⇔ ⎨ 1 1 m ≤ = − 2 −1 1 ⎪ 2 ⎪ − ≤ ⎩ 1− 2 ⎪⎩ m ⇔ m ≤ − 2 −1 Baøi 117 : Cho ( ) = 2 f x
cos 2x + 2(sinx + cosx)3 − 3sin2x + m
a/ Giaûi phöông trình f(x) = 0 khi m = -3
b/ Tính theo m giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa f(x) Tìm m cho ⎡⎣ ( ) 2 f x ⎤ ≤ 36 x ∀ ∈ R ⎦ Ñaët t sin x cosx 2 cos⎛ x π ⎞ = + = − ⎜ ⎟ (ñieàu kieän t ≤ 2 ) ⎝ 4 ⎠ Thì 2t = 1+ sin2x Vaø = − = − ( − )2 2 2 2 4
cos 2x 1 sin 2x 1 t 1 = −t + 2t2 Vaäy ( ) ( ) 4 2 3 = − + + − ( 2 f x thaønh g t t 2t 2t 3 t − ) 1 + m a/ Khi m = -3 thì g(t) = 0 2 ⇔ − ( 2 t t − 2t + ) 1 = 0 ⇔ t = 0 ∨ t = 1
vaäy khi m = -3 thì f(x) = 0 ⎛ π ⎞ ⎛ π ⎞ 1 ⇔ cos x − = 0 hay cos x − = ⎜ 4 ⎟ ⎜ 4 ⎟ ⎝ ⎠ ⎝ ⎠ 2 x π (2k ) 1 π hay x π π ⇔ − = + − = ± + k2 , π k∈ ] 4 2 4 4 3 x π π ⇔ =
+ kπ hay x = + k2π ∨ x = k2 , π k ∈ ] 4 2 b/ Ta coù ( ) 3 2 = − + − = − ( 2 g' t 4t 6t 2t 2t 2t − 3t + ) 1 ⎧g'(t) = 0 Vaäy ⎪ 1 ⎨ ⇔ t = 0 ∨ t = 1∨ t = t ∈ ⎡− 2, 2⎤ 2 ⎪⎩ ⎣ ⎦ Ta coù : ( ) = + = ( ) ⎛ 1 ⎞ 47 g 0 3 m g 1 , g = + m ⎜ 2 ⎟ ⎝ ⎠ 16
g( 2) = 4 2 −3+ m, g( 2) = m −3− 4 2
Vaäy : Maxf (x) = Max g(t) = m + 3 t∈⎡− 2, 2 x ⎤ ∈ \ ⎣ ⎦
Minf (x) = Min g(t) = m − 3 − 4 2 t∈⎡− 2, 2 x∈ R ⎤ ⎣ ⎦ Do ñoù : ⎡⎣ ( ) 2 f x ⎤ ≤ 36, x ∀ ∈ R ⇔ −6 ≤ f ⎦ (x) ≤ 6, x ∀ ∈ R ⎧Max f (x) ≤ 6 ⎪ R ⇔ ⎨Minf ⎪ (x) ≥ − 6 ⎩ R ⎧m + 3 ≤ 6 ⎪
⇔ ⎨⎪⎩m−3−4 2 ≥ −6 ⇔ 4 2 − 3 ≤ m ≤ 3
Caùch khaùc : Ta coù ( ) = − ( − + ) + + = − ⎡⎣ ( − ) 2 2 2 g t t t 2t 1 3 m t t 1 ⎤ + 3+ m ⎦ Ñaët 2 u = t − t Khi ⎡ 1
t ∈ − 2, 2 thì u∈ − ,2 + 2⎤ ⎡ ⎤ = ⎣ ⎦ ⎢ D ⎣ 4 ⎥⎦ Vaäy ( ) = ( ) 2 g t h u = −u + 3+ m
Max f (x) = Max g(t) = Max h(u) = m + 3 R t∈⎡− 2 , 2 ⎤ u ∈ D ⎣ ⎦
Min f (x) = Min g(t) = Min h(u)=m − 3 −4 2 R t∈⎡− 2 , 2 ⎤ ⎣ ⎦ u ∈ D
Chuù yù 1 : Phöông trình giaû ñoái xöùng
a(sinx − cosx) + b(sinxcosx) = 0 ñaët t = sinx – cosx thì t 2 sin⎛ x π ⎞ 2 cos⎛ = − = − x π ⎞ ⎜ + 4 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 4 ⎠ vôùi ñieàu kieän 2
t ≤ 2 thì t = 1− 2sin x cosx
Baøi 118 : Giaûi phöông trình 2sin x + cot gx = 2sin 2x + 1(*)
Ñieàu kieän : sin x ≠ 0 ⇔ cos x = 1 ± Luùc ñoù (*) cos x ⇔ 2sin x + = 4 sin x cos x + 1 sin x ⇔ 2 2 sin x + cos x = 2 4 sin x cos x + sin x ⇔ 2 2 sin x − sin x − cos x ( 2 4 sin x − 1) = 0
⇔ sin x (2 sin x − 1) − cos x (2 sin x − 1) (2 sin x + 1) = 0
⇔ 2 sin x − 1 = 0 hay sin x − cos x (2sin x + 1) = 0 ⎡2 sin x − 1 = 0 (1)
⇔ ⎢⎢sinx − cosx − sin2x = ⎣ 0 (2) 1
• Ta coù (1) ⇔ sin x = (nhaän do sin x ≠ 0) 2 π π 5 ⇔ x = + k π 2 ∨ x = + k π 2 , k ∈ ] 6 6 Xeùt (2) ⎛ π ⎞ •
Ñaët t = sin x − cos x = 2 sin ⎜ x − ⎟ ⎝ 4 ⎠
Vôùi ñieàu kieän t ≤ 2 vaø t ≠ ± 1 Thì 2 t = 1 − sin x 2 Vaäy (2) thaønh : − ( 2 t 1 − t ) = 0 2 ⇔ t + t − 1 = 0 −1 + 5 −1 − 5 ⇔ t = ∨ t = (loaïi) 2 2 Do ñoù : ⎛ π ⎞ 1 − + 5 2 sin x − = ⎜ ⎟
(nhaän do t ≤ 2 vaø t ≠ ±1) ⎝ 4 ⎠ 2 ⎛ π ⎞ 5 − 1 ⇔ sin x − = = ⎜ ⎟ sin ϕ ⎝ 4 ⎠ 2 2 ⎡ π x − = ϕ + k π 2 , k ∈ ⎢ ] ⇔ ⎢ 4 π ⎢x − = π − ϕ + k π 2 , k ∈ ⎢ ] ⎣ 4 ⎡ π x = ϕ + + k π 2 , k ∈ ⎢ ] ⇔ ⎢ 4 π ⎢ 5 x = − ϕ + k π 2 , k ∈ ⎢ ] ⎣ 4
Baøi 119 : Giaûi phöông trình
cos2x + 5 = 2(2 − cos x)(sin x − cos x)(*) Ta coù : ( ) ⇔ ( 2 2 *
cos x − sin x) + 5 = 2(2 − cos x)(sin x − cos x) ⇔ (sin x − cos x) ⎡2
⎣ (2 − cos x) + (sin x + cos x)⎤ − 5 0 ⎦ =
⇔ (sin x − cos x)[sin x − cos x + 4] − 5 = 0 Ñaët t sin x cos x 2 sin ⎛ x π ⎞ = − = − ⎜ 4 ⎟ ⎝ ⎠ Vôùi ñieàu kieän t ≤ 2
(*) thaønh : t (t + 4) − 5 = 0 2 ⇔ t + 4t − 5 = 0 ⇔ t = 1 ∨ t = −5(loaïi) Vaäy (*) ⎛ π ⎞ 1 π ⇔ sin x − = = sin ⎜ 4 ⎟ ⎝ ⎠ 2 4 π π π π 3 ⇔ x − = + k π 2 ∨ x − = + k π 2 , k ∈ ] 4 4 4 4 π ⇔ x = + k π 2 ∨ x = π + k π 2 , k ∈ ] 2
Baøi 120 : Giaûi phöông trình 3 3 cos x + sin x = cos 2x (*) Ta coù (*) ⇔ ( + )( − ) 2 2
cos x sin x 1 sin x cos x = cos x − sin x
⇔ cos x + sin x = 0 hay 1 − sin x cos x = cosx − sin x ⎡sin x + cos x = 0 (1)
⇔ ⎢⎢sin x − cosx − sin xcosx +1 = ⎣ 0 (2) Ta coù : (1) ⇔ tgx = 1 − π ⇔ x = − + π k , k ∈ ] 4 Xeùt (2) ñaët t sin x cos x 2 sin ⎛ x π ⎞ = − = − ⎜ 4 ⎟ ⎝ ⎠ Vôùi ñieàu kieän t ≤ 2 Thì 2 t = 1 − 2sin x cos x 2 (2) thaønh 1 − t 2 t − + 1 = 0 ⇔ t + 2t + 1 = 0 2 ⇔ t = 1 − vaäy (2) ⎛ π ⎞ 1 ⎛ π ⇔ sin x − = − = sin − ⎞ ⎜ 4 ⎟ 2 ⎜ ⎟ ⎝ ⎠ ⎝ 4 ⎠ ⎡ π π x − = − + k π 2 , k ∈ ] ⎡x = k π 2 , k ∈ ⎢ ] 4 4 ⎢ ⇔ ⎢ ⇔ π π π 5 ⎢ 3 ⎢ x = + k π 2 , k ∈ x − = + k π 2 , k ∈ ] ] ⎣ ⎢⎣ 2 4 4
Baøi 121 : Cho phöông trình 3 3 cos x − sin x = m (1)
a/ Giaûi phöông trình (1) khi m = 1 baèng caùch ñaët aån phuï t = cos x − sin x
b/ Tìm m sao cho (1) coù ñuùng hai nghieäm x ⎡ π , π⎤ ∈ − ⎢ 4 4⎥ ⎣ ⎦
Ta coù (1) ⇔ (cos x − sin x)(1 + sin x cos x) = m Ñaët t cos x sin x 2 cos⎛ x π ⎞ = − = + ⎜ 4 ⎟ ⎝ ⎠ Vôùi ñieàu kieän t ≤ 2 Thì 2 t = 1 − 2sin x cos x 2 ⎛ − ⎞ Vaäy (1) thaønh : 1 t t ⎜1 + ⎟ = m ⎜ 2 ⎟ ⎝ ⎠ ⇔ ( 2 t 3 − t ) = 2m (2)
a/ Khi m = 1 thì (2) thaønh 3 t − 3t + 2 = 0 ⇔ ( − )( 2 t 1 t + t − 2) = 0 ⇔ t = 1 ∨ t = −2(loaïi) Vaäy ⎛ π ⎞ 2 π π cos x + = ⇔ x + = ± + k π 2 , k ∈ ⎜ ⎟ ] ⎝ 4 ⎠ 2 4 4 π ⇔ x = k π 2 ∨ x = − + k π 2 , k ∈ ] 2 b/ Neáu x ⎡ π , π⎤ ∈ − ⎢ thì 0 ≤ x π π + ≤ 4 4⎥ ⎣ ⎦ 4 2 neân 0 cos⎛ x π ⎞ ≤ + ≤ 1 ⎜ 4 ⎟ ⎝ ⎠ 0 t 2 cos⎛ x π ⎞ ⇔ ≤ = + ≤ 2 ⎜ 4 ⎟ ⎝ ⎠
nhaän xeùt raèng vôùi moãi t tìm ñöôïc treân ⎡0, 2⎤ ⎣ ⎦
ta tìm duy nhaát moät x ⎡ π , π⎤ ∈ − ⎢ 4 4⎥ ⎣ ⎦ xeùt ( ) 3
f t = −t + 3t treân ⎡0, 2⎤ ⎣ ⎦ ⇒ ( ) 2 f ' t = 3 − t + 3
vaäy (1) coù ñuùng hai nghieäm x ⎡ π , π⎤ ∈ − ⎢ 4 4⎥ ⎣ ⎦ ⇔ ( ) = ( ) 3
d y 2m caét C y = −t + 3t treân ⎡0, 2⎤ ⎣
⎦ taïi 2 ñieåm phaân bieät ⇔ 2 ≤ 2m < 2 2 ⇔ ≤ m < 1 2
Baøi 122 : Cho phöông trình 2 2
2cos2x + sin x cos x + sin x cos x = m(sin x + cos x)(*)
a/ Giaûi phöông trình khi m = 2
b/ Tìm m ñeå phöông trình (*) coù ít nhaát moät nghieäm treân ⎡0, π⎤ ⎢ 2⎥ ⎣ ⎦ Ta coù : ( ) ⇔ ( 2 2 *
2 cos x − sin x) + sin x cos x(sin x + cos x) = m(sin x + cos x)
⇔ cos x + sin x = 0 (1) hay 2(cos x − sin x) + sin x cos x = m ( 2) Ñaët t cos x sin x 2 cos⎛ = − = x π + ⎞ ⎜ ⎟ (ñieàu kieän t ≤ 2 ) ⎝ 4 ⎠ Thì 2 t = 1 − 2sin x cos x
Ta coù : (1) ⇔ sin x = − cos x π
⇔ tgx = −1 ⇔ x = − + π k , k ∈ ] 4 2 Ta coù : (2) thaønh 1 − t 2t + = m 2 2 ⇔ −t + 4t + 1 = 2m(* *)
a/ Khi m = 2 thì (**) thaønh 2 t − 4t + 3 = 0 ⇔ t = 1 ∨ t = 3 (loaïi) vaäy ⎛ π ⎞ 2 π π cos x + = ⇔ x + = ± + k π 2 , k ∈ ⎜ ⎟ ] ⎝ 4 ⎠ 2 4 4 π ⇔ x = k π 2 ∨ x = − + π k , k ∈ ] 2 Do ñoù : (*) π π ⇔ x = − + π k ∨ x = k π 2 ∨ x = − + k π 2 , k ∈ ] 4 2 b/ Ta coù ⎡ π⎤ π ⎡ π 3 x π ∈ 0, ⇔ x + ∈ ⎤ ⎢ ⎥ ⎢ , ⎣ 2⎦ 4 ⎣4 ⎥ 4 ⎦ vaäy 2 ⎛ π ⎞ 2 − ≤ cos x + ≤ 2 ⎜ 4 ⎟ ⎝ ⎠ 2 ⇒ 1 − ≤ t ≤ 1 Do nghieäm π ⎡ π⎤ x = − + π k ∉ 0, , ∀ k ∈ ⎢ ⎥ ] 4 ⎣ 2⎦
Neân yeâu caàu baøi toaùn ⇔ (* *)coù nghieäm treân [ 1, − ] 1 Xeùt 2 y = −t + 4t + 1 thì y ' = 2 − t + 4 > 0 t ∀ ∈ [ 1 − , ] 1 ⇒ y taêng treân [ 1 − , ] 1
Do ñoù : yeâu caàu baøi toaùn
⇔ −4 = y (−1) ≤ 2m ≤ y (1) = 4 ⇔ −2 ≤ m ≤ 2
* Chuù yù 2 : Phöông trình löôïng giaùc daïng ( ± ) + ( 2 2 a tgx cot gx b tg x + cot g x) = 0 ta ñaët 2 2 2
t = tgx ± cot gx thì t = tg x + cot g x ± 2 khi 2 t = tgx + cot gx = thì t ≥ 2 (do sin 2x ≤ 1) sin 2x
Baøi 123 : Giaûi phöông trình 2 2
3tg x + 4tgx + 4 cot gx + 3cot g x + 2 = 0(*) Ñaët 2 t = tgx + cot gx = sin2x Vôùi ñieàu kieän t ≥ 2 Thì 2 2 2 t = tg x + cot g x + 2 (*) thaønh : ( 2 3 t − 2) + 4t + 2 = 0 2 ⇔ 3t + 4t − 4 = 0 ⎡ 2 t = ⎢ (loaïi do ñieàu kieän) ⇔ 3 ⎢ ⎣t = −2 Ta coù : 2 t = −2 ⇔ = −2 ⇔ sin 2x = −1 2sin x π ⇔ 2x = − + k π 2 , k ∈ ] 2 π ⇔ x = − + π k , k ∈ ] 4
Baøi 124 : Giaûi phöông trình 2 3 2 3
tgx + tg x + tg x + cotgx + cotg x + cotg x = 6(*) Ta coù (*) ⇔ ( + ) + ( 2 + 2 ) + ( 3 + 3 tgx cot gx tg x cot g x tg x cot g x) = 6
⇔ (tgx + cot gx) + (tgx + cot gx)2 − 2 + (tgx + cot gx)( 2 2 tg x + cot g x − 1) = 6
⇔ (tgx + cot gx) + (tgx + cot gx)2 + (tgx + cot gx) ⎡(tgx + cot gx)2 − 3⎤ = 8 ⎣ ⎦ Ñaët 2 t = tgx + cot gx = (ñieàu kieän t ≥ 2) sin 2x Vaäy (*) thaønh : 2 + + ( 2 t t t t − 3) = 8 3 2 ⇔ t + t − 2t − 8 = 0 ⎡t = 2 ⇔ (t − 2)( 2 t + 3t + 4) = 0 ⇔ ⎢ 2 t + 3t + 4 = 0 ⎣ (voâ nghieäm) ⇔ t = 2 Vaäy 2 = 2 ⇔ sin 2x = 1 sin 2x π ⇔ 2x = + k π 2 , k ∈ ] 2 π ⇔ x = + π k , k ∈ ] 4
Baøi 125 : Giaûi phöông trình 2 + 2
2tg x + 5tgx + 5 cot gx + 4 = 0 * 2 ( ) sin x Caùch 1 : (*) ⇔ ( 2 + ) 2
2 1 cot g x + 2tg x + 5(tgx + cot gx) + 4 = 0 ⇔ 2 ( 2 tg x + 2
cot g x) + 5(tgx + cot gx) + 6 = 0
⇔ 2 ⎡(tgx + cot gx)2 − 2⎤ + 5(tgx + cot gx) + ⎣ ⎦ 6 = 0 Ñaët 2 t = tgx + cot gx = , vôùi t ≥ 2 sin 2x
Ta ñöôïc phöông trình : 2 2t + 5t + 2 = 0 1
⇔ t = −2 ∨ t = − (loaïi ) 2 Vaäy (*) 2 ⇔ = −2 ⇔ sin 2x = −1 sin 2x π ⇔ 2x = − + k π 2 , k ∈ ] 2 π ⇔ x = − + π k , k ∈ ] 4
Caùch 2 : Ñaët u = tgx (vôùi ñieàu kieän u ≠ 0) Vaäy (*) thaønh : 2 2 5 2 + + 2u + 5u + + 4 = 0 2 u u ⇔ 2 + 4 2u + 3 5u + 5u + 2 6u = 0 ⇔ (u + 1) ( 3 2u + 2 3u + 3u + 2) = 0 ⇔ (u + 1)2 ( 2 2u + u + 2) = 0 ⎡u = −1(nhaän) ⇔ ⎢⎢ 2 2u + u + 2 = ⎣ 0 (voâ nghieäm) Vaäy (*) ⇔ tgx = -1 π ⇔ x = − + π k , k ∈ ] 4
Baøi 126 : Cho phöông trình 1 2
+ cot g x + m tgx + cot gx + 2 = 0 (1) 2 ( ) cos x a/ Giaûi phöông trình khi 5 m = 2
b/ Tìm m ñeå phöông trình coù nghieäm Ta coù : (1) 2 2
⇔ tg x + cot g x + m(tgx + cot gx) + 3 = 0 Ñaët 2 t = tgx + cot gx = (ñieàu kieän t ≥ 2) sin 2x 2 2 2 ⇒ t = tg x + cot g x + 2 Vaäy (1) thaønh : 2 t + mt + 1 = 0 (2) a/ Khi 5
m = ta ñöôïc phöông trình 2 2t + 5t + 2 = 0 2 1
⇔ t = −2 ∨ t = − (loaïi) 2 Do ñoù 2 = −2 ⇔ sin 2x = −1 sin 2x π ⇔ 2x = − + k π 2 , k ∈ ] 2 π ⇔ x = − + π k , k ∈ ] 4 b/ Caùch 1 : Ta coù : (2) 2 ⇔ mt = −1 − t 1
⇔ m = − − t (do t = 0 khoâng laø nghieäm cuûa (2)) t Xeùt 1 y = − − t vôùi t ≥ 2 t 2 Thì 1 1 y ' 1 − t = − = 2 2 t t Ta coù : y ' = 0 ⇔ t = ±1
Do ñoù (1) coù nghieäm ⇔ (d) caét (C) treân (− , ∞ − ] 2 U[2,+∞) 5 5 ⇔ m ≤ − ∨ m ≥ 2 2 5 ⇔ m ≥ 2
Caùch 2 : Yeâu caàu baøi toaùn ⇔ ( ) 2
f t = t + mt + 1= 0 coù nghieäm t thoûa t ≥ 2
Nhaän xeùt raèng do P = 1 neân neáu f(t) coù hai nghieäm t , t vôùi t ≤ t 1 2 ( 1 2 ) vaø ⎧ t ≤ 1 ⎧ t ≥ 1
coù nghieäm thì ta coù ⎪ 1 ⎪ ⎨ ∨ ⎨ 1 ⎪ t ≥ ⎩ 1 t 1 2 ⎪ ≤ ⎩ 2 Do ñoù :
Yeâu caàu baøi toaùn ⇔ t ≤ −2 < t < 2 ∨ −2 < t < 2 ≤ t 1 1 1 2
⎧⎪1f (−2) ≤ 0 ⎧⎪1f (2) ≤ 0
⎧−2m + 5 ≤ 0 ⎧−2m + 5 > 0 ⇔ ⎨⎪⎩1f (2) ∨ ⎨ > 0 ⎪⎩1f (−2) ⇔ ⎨ ∨ ⎨ > 0 ⎩2m + 5 > 0 ⎩2m + 5 ≤ 0 5 5 ⇔ m ≥ ∨ m ≤ − 2 2 BAØI TAÄP 1. Giaûi caùc phöông trình : a/ 3 3 1 + cos x − sin x = sin x b/ 3 2
cos x + cos x + 2sin x − 2 = 0 c/
cos2x + 5 = 2(2 − cos x)(sin x − cos x) d/ cot gx − tgx = sin x + cos x e/ 3 3
sin x − cos x = sin x − cos x f/ 1 + tgx = sin x + cos x g/ sin 2x 2 sin ⎛ x π ⎞ + − = 1 ⎜ 4 ⎟ ⎝ ⎠ k/
sin 2x − 12(sin x − cos x) + 12 = 0 l/ sin x + cos x = 1 sin 2x + 1 3 m/ 1 − cos 2x 1 − cos x = 3 1 + cos 2x 1 − sin x n/
5(sin x + cos x) + sin 3x − cos3x = 2 2 (2 + sin 2x) o/
1 + sin x + cos x + sin 2x + 2cos2x = 0 p/ 2 2
sin x cos x − cos 2x + sin x = cos x sin x + cos x r/
cos2x + 5 = 2(2 − cos x)(sin x − cos x) s/ 2 3 cos x + sin x + cos x = 0 t/ 3
4 sin x − 1 = 3sin x − 3 cos 3x 2.
Cho phöông trình sin 2x (sin x + cos x) = m(1)
a/ Chöùng minh neáu m > 2 thì (1) voâ nghieäm
b/ Giaûi phöông trình khi m = 2 3.
Cho phöông trình sin 2x + 4 (cos x − sin x) = m
a/ Giaûi phöông trình khi m = 4
b/ Tìm m ñeå phöông trình coù nghieäm 4.
Cho phöông trình : sin x cos x − m(sin x + cos x) + 1 = 0
a/ Giaûi phöông trình khi m = 2
b/ Tìm m ñeå phöông trình coù nghieäm (ÑS : m ≥ 1) 5. Cho phöông trình 3 2 + 3tg x = m tgx + cot gx = 1 2 ( ) sin x
Tìm m ñeå phöông trình coù nghieäm (ÑS : m ≥ 4) CHÖÔNG VI.
PHÖÔNG TRÌNH ÑAÚNG CAÁP 2 2
a sin u + bsin u cosu + c cos u = d Caùch giaûi : Tìm nghieäm u π • =
+ kπ(luùc ñoù cosu = 0 vaø sin u = 1 ± ) 2 2
• Chia hai veá phöông trình cho cos u ≠ 0 ta ñöôïc phöông trình : 2 + + = ( 2 atg u btgu c d 1 + tg u)
Ñaët t = tgu ta coù phöông trình : ( − ) 2 a d t + bt + c − d = 0
Giaûi phöông trình tìm ñöôïc t = tgu
Baøi 127 : Giaûi phöông trình 2 2
cos x − 3 sin 2x = 1 + sin x (*)
Vì cosx = 0 khoâng laø nghieäm neân Chia hai veá cuûa (*) cho 2 cos ≠ 0 ta ñöôïc ( ) ⇔ − = ( 2 + ) 2 * 1 2 3tgx 1 tg x + tg x
Ñaët t = tgx ta coù phöông trình : 2 2t + 2 3t = 0 ⇔ t = 0 ∨ t = − 3 Vaäy ( π
*) ⇔ tgx = 0 hay tgx = − 3 ⇔ x = π k hay x = − + π k , k ∈ ] 3
Baøi 128 : Giaûi phöông trình 3 3 2
cos x − 4 sin x − 3cos x sin x + sin x = 0(*) π • Khi x =
+ kπ thì cos x = 0 vaø sin x = 1 ± 2 thì (*) voâ nghieäm
• Do cos x = 0 khoâng laø nghieäm neân chia hai veá cuûa (*) cho cos3x ta coù (*) 3 2 ⇔ − − + ( 2
1 4tg x 3tg x tgx 1 + tg x) = 0 ⇔ 3 3tg x + 2 3tg x − tgx − 1 = 0 ⇔ (tgx + 1) ( 2 3tg x − 1) = 0 3 ⇔ tgx = −1 ∨ tgx = ± 3 π π ⇔ x = − + π k ∨ x = ± + π k , k ∈ ] 4 6
Baøi 129 : Giaûi phöông trình 4 2 2 4
3cos x − 4 sin x cos x + sin x = 0(*)
Do cosx = 0 khoâng laø nghieäm neân chia hai veá cuûa (*) cho 4 cos x ≠ 0 Ta coù : (*) 2 4 ⇔ 3 − 4tg x + tg x = 0 ⇔ 2 = ∨ 2 tg x 1 tg x = 3 ⎛ π ⎞ ⎛ π ⇔ tgx = ±1 = tg ± ∨ tgx = tg ± ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ 4 ⎠ ⎝ 3 ⎠ π π ⇔ x = ± + π k ∨ x = ± + π k , k ∈ ] 4 3
Baøi 130 : Giaûi phöông trình sin 2x + 2tgx = 3(*) Chia hai veá cuûa (*) cho 2 cos x ≠ 0 ta ñöôïc 2sin x cos x 2tgx 3 (*) ⇔ + = 2 2 cos x cos x cos2 x ⇔ + ( 2 + ) = ( 2 2tgx 2tgx 1 tg x 3 1 + tg x) ⎧t = tgx ⇔ ⎨ 3 2 ⎩2t − 3t + 4t − 3 = 0 ⎧t = ⎪ tgx ⇔ (⎨t −1)( 2 2t − t + ⎪⎩ 3) = 0 ⇔ tgx = 1 π ⇔ x = + π k , k ∈ ] 4
Baøi 131 : Giaûi phöông trình 3
sin x sin 2x + sin 3x = 6 cos x (*) ( ) 2 3
* ⇔ 2sin x cos x + 3sin x − 4 sin x = 6 cos3 x
• Khi cos x = 0 ( sin x = ± 1 ) thì (*) voâ nghieäm
• Chia hai veá phöông trình (*) cho 3 cos x ≠ 0 ta ñöôïc 2 3 ( 2sin x 3sin x 1 sin x *) ⇔ + . − 4 = 6 2 2 cos x cos x cos x cos3 x ⇔ 2 2tg x + 3tgx (1 + 2 tg x) − 3 4tg x = 6 ⇔ 3 tg x − 2 2tg x − 3tgx + 6 = 0 ⇔ (tgx − 2) ( 2 tg x − 3) = 0 ⇔ tgx = 2 = α tg ∨ tgx = ± 3 π ⇔ x = α + π k ∨ x = ± + π k , k ∈ ] ( vôùi t α g = 2) 3
Baøi 132 : (Ñeà thi tuyeån sinh Ñaïi hoïc khoái A, naêm 2003) Giaûi phöông trình cos 2x 2 1 cot gx − 1 = + sin x − sin 2x (*) 1 + tgx 2
Ñieàu kieän sin 2x ≠ 0 vaø tgx ≠ 1 − cos 2x cos x − sin x ( 2 2 2 2 cos x cos x − sin x) Ta coù : = = 1 + tgx sin x cos x + sin x 1 + cosx
= cos x (cos x − sin x) (do tgx = −1 neân, sin x + cos x ≠ 0) cos x 1 Do ñoù : (*) ⇔ − 1 = ( 2 cos x − sin x cos x) 2 + sin x − sin 2x sin x 2 cos x − sin x ⇔ = 1 − sin 2x sin x
⇔ (cos x − sin x) = sin x (cos x − sin x)2
⇔ cos x − sin x = 0 hay 1 = sin x (cos x − sin x) (**)
⎡tgx = 1(nhaän so vôùi tgx ≠ −1) ⎢ ⇔ ⎢ 1 sin x = − 2 tg x do cos x 0 2 ( ≠ ) ⎢⎣cos x cos x ⎡ π x = + π k , k ∈ ⎢ ] ⇔ ⎢ 4 ⎢ 2 2tg x − tgx + 1 = ⎣ 0 (voâ nghieäm) π ⇔ x = + π
k , k ∈ ] (nhaän do sin 2x ≠ 0) 4
Löu yù : coù theå laøm caùch khaùc ( ) 1 1
* * ⇔ 1 − sin 2x + (1 − cos2x) =0 2 2 ⇔ 3 = sin 2x + cos 2x ⎛ π ⎞ ⇔ 3 = 2 sin 2x + ⎜ ⎟ : voâ nghieäm ⎝ 4 ⎠
Baøi 133 : Giaûi phöông trình sin 3x + cos 3x + 2 cos x = 0(*) ( ) ⇔ ( 3 − ) + ( 3 * 3sin x 4 sin x
4 cos x − 3cos x) + 2cos x = 0 3 3
⇔ 3sin x − 4 sin x + 4 cos x − cos x = 0
Vì cosx = 0 khoâng laø nghieäm neân chia hai veá phöông trình cho 3 cos x ≠ 0 ta ñöôïc ( ) ⇔ ( 2 + ) 3 − + − ( 2 * 3tgx 1 tg x 4tg x 4 1 + tg x) = 0 ⇔ − 3 tg x − 2 tg x + 3tgx + 3 = 0 ⎧t = tgx
⇔ ⎨⎩ 3t + 2t − 3t − 3 = 0 ⎧t = ⎪ tgx ⇔ (⎨t +1)( 2t − 3) = ⎪⎩ 0 ⇔ tgx = −1 ∨ tgx = ± 3 π π ⇔ x = − + π k ∨ x = ± + π k , k ∈ ] 4 3
Baøi 134 : Giaûi phöông trình 3 5sin 4x.cos x 6sin x − 2cos x = (*) 2cos2x Ñieàu kieän : 2 2
cos2x ≠ 0 ⇔ cos x − sin x ≠ 0 ⇔ tgx ≠ 1 ± ⎧ 3 10sin 2x cos 2x cos x ⎪6sin x − 2cos x = Ta coù : (*) ⇔ ⎨ 2cos 2x ⎪⎩cos2x ≠ 0 3
⎧6sin x − 2cos x = 5sin 2x cos x ⇔ ⎨⎩tgx ≠ ±1 3 2
⎧⎪6sin x − 2cos x = 10sin x cos x (* *) ⇔ ⎨ ⎪⎩tgx ≠ 1 ±
Do cosx = 0 khoâng laø nghieäm cuûa (**), chia hai veá phöông trình (**) cho 3 cos x ta ñöôïc ⎧ 6tgx ( ⎪ − = * *) 2 10tgx 2 ⇔ ⎨cos x ⎪⎩tgx ≠ 1 ± ⎧t = tgx vôùi t ≠ ±1 ⎪ ⇔ ⎨6t ⎪⎩ ( 2 1 + t ) − 2 = 10t ⎧t = tgx vôùi t ≠ ±1 ⎧t = tgx vôùi t ≠ ±1 ⇔ ⎨ ⇔ 3 ⎨ ⎩3t − 2t − 1 = 0 ⎩(t − 2 1) (3t + 3t + 1) = 0 ⎧t = tgx vôùi t ≠ ±1 ⇔ ⎨ : voâ nghieäm ⎩t = 1
Baøi 135 : Giaûi phöông trình 3
sin x − 4 sin x + cos x = 0(*)
• Vì cosx = 0 khoâng laø nghieäm neân chia hai veá phöông trình cho cos3x thì ( ) ⇔ ( 2 + ) 3 2 *
tgx 1 tg x − 4tg x + 1 + tg x = 0 ⎧t = tgx ⇔ ⎨⎩− 3 3t + 2 t + t + 1 = 0 ⎧t = ⎪ tgx ⇔ (⎨t −1)( 2 3t + 2t + 1) = ⎪⎩ 0 ⇔ tgx = 1 π ⇔ x = + π k , k ∈ ] 4
Baøi 136 : Giaûi phöông trình 2 2
tgx sin x − 2sin x = 3(cos 2x + sin x cos x)(*)
Chia hai veá cuûa phöông trình (*) cho cos2x 3( 2 2 cos x − sin x + sin x cos x 3 2 ) (*) ⇔ tg x − 2tg x = 2 cos x ⇔ 3 − 2 = ( − 2 tg x 2tg x 3 1 tg x + tgx) ⇔ 3 tg x + 2 tg x − 3tgx − 3 = 0 ⎧t = tgx
⇔ ⎨⎩ 3t + 2t − 3t − 3 = 0 ⎧t = ⎪ tgx ⇔ (⎨t +1)( 2t − 3) = ⎪⎩ 0 ⇔ tgx = −1 ∨ tgx = ± 3 π π ⇔ x = − + π k ∨ x = ± + π k , k ∈ ] 4 3
Baøi 137 : Cho phöông trình ( − ) 3 + ( − ) + ( − ) 2
4 6m sin x 3 2m 1 sin x 2 m 2 sin x cos x − (4m − 3) cos x = 0(*)
a/ Giaûi phöông trình khi m = 2
b/ Tìm m ñeå phöông trình (*) coù duy nhaát moät nghieäm treân ⎡0, π⎤ ⎢ 4⎥ ⎣ ⎦ Khi x π = + π k thì cosx = 0 vaø sin x = 1 ± neân 2
(*) thaønh : ± (4 − 6m) ± 3(2m − 1) = 0 ⇔ 1 = 0 voâ nghieäm chia hai veà (*) cho 3 cos x ≠ 0 thì ( ) ⇔ ( − ) 3 + ( − ) ( 2 + ) + ( − ) 2 * 4 6m tg x 3 2m 1 tgx 1 tg x
2 m 2 tg x − (4m − 3)(1 + tg2x) = 0 ⎧t = tgx ⎪ ⇔ ⎨ 3 2
⎪t − 2m + 1 t + 3 2m − 1 t − 4m + 3 = 0 * * ⎩ ) ( ) ( ) ( ⎧t = tgx ⎪ ⇔ (⎨t −1 ⎪ ) ⎩ ( 2t − 2mt + 4m − 3) = 0 ⎧t = tgx
a/ Khi m = 2 thì (*) thaønh ⎪(⎨t −1 ⎪ ) ⎩ ( 2t − 4t + 5) = 0 π ⇔ tgx = 1 ⇔ x = + π k , k ∈ ] 4 b/ Ta coù : x ⎡ ∈ 0, π⎤ ⎢ tgx = t ∈ 0,1 ⎣ 4 ⎦⎥ thì [ ] Xeùt phöông trình : 2 t − 2mt + 4m − 3 = 0(2) 2 ⇔ t − 3 = 2m (t − 2) 2 t − 3 ⇔
= 2m (do t = 2 khoâng laø nghieäm) t − 2 2 t − 3 Ñaët y = f (t) = (C) vaø (d) y = 2m t − 2 2 Ta coù : ( ) t − 4t y ' f t + 3 = = (t − 2)2
Do (**) luoân coù nghieäm t = 1 ∈ [0, ]
1 treân yeâu caàu baøi toaùn
⎡(d) y = 2m khoâng coù ñieåm chung vôùi (C)
⇔ ⎢⎢⎣(d)caét(C)taïi1ñieåmduynhaátt = 1 3 ⇔ 2m < ∨ 2m ≥ 2 2 3 ⇔ m < ∨ m ≥ 1 4 Caùch khaùc : Y C B T ⇔ f(t) = 2
t − 2mt + 4m − 3 = 0(2) voâ nghieäm treân [ , 0 1 ) . ⎧Δ ≥ 0 ⎪af (0) ≥ ⎪ 0 Ta coù (2) coù nghieäm [ ⎪ ∈ 0, ] 1 ⇔ f ( ) 0 . f ( )
1 ≤ 0 hay ⎨af ( ) 1 ≥ 0 ⎪ S ⎪0 ≤ ≤ ⎪ 1 ⎩ 2
⎧m2 − 4m + 3≥ 0 ⎪ ⎪4m − 3 > ⇔ 0 3 ( 4m − ) 3 (2m − ) 2 ≤ 0 hay ⎨ ⇔ ≤ m ≤1 2m − 2 > ⎪ 0 4 ⎪⎩0≤m≤1
Do ñoù (2) voâ nghieäm treân [ 3 0,1 ) ⇔ m <
hay m >1 hay f ( ) 1 = 0 4 3 ⇔ m < ∨ m ≥ 1 4 BAØI TAÄP
1. Giaûi caùc phöông trình sau : a/ 3 2
cos x + sin x − 3sin x cos x = 0 b/ 2
sin x (tgx + 1) = 3sin x (cos x − sin x) + 3 c/ 2 2cos x + cos2x + sin x = 0 3 1 − cos x d/ 2 tg x = 3 1 − sin x e/ 3 2 2 3
sin x − 5sin x cos x − 3sin x cos x + 3cos x = 0 f/ 3 2
cos x + sin x − 3sin x cos x = 0 g/ 1 + tgx = 2 2 sin x h/ 3 3
sin x + cos x = sin x − cos x k/ 2 2
3tg x + 4tgx + 4 cot gx + 3cot g x + 2 = 0 m/ 3 1 2 ( + sin x) 2 π x tg 3 x − tgx + − 8 cos ( − ) = 0 cos2 x 4 2 sin x + cos x n/ = 1 sin 2x 2. Cho phöông trình : 2 + ( − ) − ( + ) 2 sin x 2 m 1 sin x cos x m 1 cos x = m
a/ Tìm m ñeå phöông trình coù nghieäm
b/ Giaûi phöông trình khi m = -2 (ÑS : m ∈ [−2, ] 1 ) CHÖÔNG VII
PHÖÔNG TRÌNH LÖÔÏNG GIAÙC CHÖÙA CAÊN VAØ PHÖÔNG
TRÌNH LÖÔÏNG GIAÙC CHÖÙA GIAÙ TRÒ TUYEÄT ÑOÁI
A) PHÖÔNG TRÌNH LÖÔÏNG GIAÙC CHÖÙA CAÊN Caùch giaûi :
AÙp duïng caùc coâng thöùc ⎧A ≥ 0 ⎧B ≥ 0 A = B ⇔ ⎨ ⇔ ⎩A = B ⎨ ⎩A = B ⎧B ≥ 0 A = B ⇔ ⎨ 2 ⎩A = B
Ghi chuù : Do theo phöông trình chænh lyù ñaõ boû phaàn baát phöông trình löôïng
giaùc neân ta xöû lyù ñieàu kieän B ≥ 0 baèng phöông phaùp thöû laïi vaø chuùng toâi boû
caùc baøi toaùn quaù phöùc taïp.
Baøi 138 : Giaûi phöông trình 5cos x − cos 2x + 2sin x = 0(*) (*) ⇔ 5cos x − cos2x = 2 − sin x si ⎧ n x ≤ 0 ⇔ ⎨ 2 5 ⎩ cos x − cos 2x = 4 sin x si ⎧ n x ≤ 0 ⎪ ⇔ 5c ⎨ osx − ⎪⎩ ( 2 2cos x − 1) = 4( 2 1 − cos x) si ⎧ n x ≤ 0 ⇔ ⎨ 2 ⎩2cos x + 5cos x − 3 = 0 si ⎧ n x ≤ 0 ⎪ ⇔ ⎨ 1 cos x = ∨ cos x = −3 ⎪ (loaïi) ⎩ 2 ⎧sin x ≤ 0 ⎪ ⇔ ⎨ π x = ± + k π 2 , k ∈ ⎪ ] ⎩ 3 π ⇔ x = − + k π 2 , k ∈ ] 3
Baøi 139 : Giaûi phöông trình 3 3 3 3
sin x + cos x + sin x cot gx + cos xtgx = 2sin 2x Ñieàu kieän : ⎧cos x ≠ 0 ⎪ sin ⎧ 2x ≠ 0 si ⎨ n x ≠ 0 ⇔ ⎨ ⇔ sin 2x > 0 sin ⎪ ⎩ 2x ≥ 0 sin 2x ≥ 0 ⎩ Luùc ñoù : ( ) 3 3 2 2
* ⇔ sin x + cos x + sin x cos x + cos x sin x = 2sin 2x 2 ⇔ ( + ) 2
sin x sin x cos x + cos x (cos x + sin x) = 2sin 2x ⇔ ( + )( 2 2
sin x cos x sin x + cos x) = 2sin 2x sin ⎧ x + cos x ≥ 0 ⎪ ⇔ (⎨⎪sinx + cosx ⎩ )2 = 2sin2x ⎧ ⎛ π ⎞ ⎧ ⎛ π ⎪ 2 sin x + ≥ 0 si ⎜ ⎟ ⎪ n x ⎞ + ≥ 0 ⇔ ⎨ ⎝ 4 ⎜ ⎠ ⇔ ⎨ ⎝ 4 ⎟⎠ 1
⎪⎩ + sin2x = 2sin2x ⎪sin2x = 1 ⎩ (nhaän do sin2x > 0) ⎧ ⎛ π ⎞ ⎧ ⎛ π ⎞ sin x + ≥ 0 sin x + ≥ ⎪ ⎜ ⎟ ⎪ ⎜ ⎟ 0 ⎪ ⎝ 4 ⎠ ⎪ ⎝ 4 ⎠ ⇔ ⎨ ⇔ ⎨ ⎪ π ⎪ π π 5 x = + π k , k ∈ ] x = + m π 2 ∨ x = + m π 2 (loaïi) , m ∈ ⎪ ] ⎩ 4 ⎪⎩ 4 4 π ⇔ x = + m π 2 , m ∈ ] 4
Baøi 140 : Giaûi phöông trình 2 ⎛ π ⎞
1 + 8 sin 2x.cos 2x = 2 sin ⎜3x + ⎟ (*) ⎝ 4 ⎠ sin ⎧ ⎛3x π⎞ + ≥ 0 ⎪ ⎜ ⎪ ⎝ 4 ⎟ Ta coù : (*) ⎠ ⇔ ⎨⎪ 2 2
1 + 8sin 2x cos 2x = 4 sin ⎛3x π ⎞ ⎜ + ⎩ 4 ⎟ ⎪ ⎝ ⎠ ⎧ ⎛ π ⎞ sin 3x + ≥ ⎪ ⎜ ⎟ 0 ⎪ ⎝ 4 ⎠
⇔ ⎨⎪1+4sin2x(1+cos4x) ⎡ π ⎤ = 2 1 − cos( 6x + ) ⎪ ⎢ ⎥ ⎩ ⎣ 2 ⎦ si ⎧ n⎛3x π⎞ + ≥ 0 ⎪ ⎜ ⎨ 4 ⎟ ⇔ ⎝ ⎠ 1 ⎪ + 4sin2x + 2 ⎩
(sin6x − sin2x) = 2(1 + sin6x) ⎧ ⎛ π ⎞ ⎧ ⎛ π ⎞ sin 3x + ≥ 0 sin 3x + ≥ ⎪ ⎜ ⎟ ⎪ ⎜ ⎟ 0 ⎪ ⎝ 4 ⎠ ⎪ ⎝ 4 ⎠ ⇔ ⎨ ⇔ ⎨ ⎪ 1 ⎪ π π 5 sin 2x = x = + π k ∨ x = + π k , k ∈ ⎪ ] ⎩ 2 ⎪⎩ 12 12
So laïi vôùi ñieàu kieän sin ⎛3x π ⎞ + ≥ 0 ⎜ 4 ⎟ ⎝ ⎠ Khi x π • = + kπ thì 12
sin ⎛3x π ⎞ sin ⎛ π 3k ⎞ + = + π = cos k ⎜ π 4 ⎟ ⎜ 2 ⎟ ⎝ ⎠ ⎝ ⎠
⎡1 , (neáu k chaün) (nhaän)
= ⎢⎢−⎣1,(neáu k leû)(loaïi) π 5 • Khi x = + π k thì 12 ⎛ π ⎞ ⎛ π 3 ⎞ ⎛ π sin 3x + = sin + 3 π k = sin − + π⎞ ⎜ ⎟ ⎜ ⎟ ⎜ k ⎟ ⎝ 4 ⎠ ⎝ 2 ⎠ ⎝ 2 ⎠
⎡−1, neáu k chaün (loaïi)
= ⎢⎢⎣1, neáu k leû (nhaän) 5 Do ñoù (*) π π ⇔ x = + m π 2 ∨ x = + (2m + 1) π, m ∈ ] 12 12
Baøi 141 : Giaûi phöông trình 1 − sin 2x + 1 + sin 2x = 4 cos x (*) sin x
Luùc ñoù : (*) ⇔ 1 − sin 2x + 1 + sin 2x = 2sin 2x
( hieån nhieân sinx = 0 khoâng laø nghieäm , vì sinx =0 thì VT = 2, VP = 0 ) ⎧ 2 2
⎪2 + 2 1 − sin 2x = 4 sin 2x ⇔ ⎨si ⎪⎩ n 2x ≥ 0 ⎧ 2 2
⎪ 1 − sin 2x = 2sin 2x − 1 ⇔ ⎨ sin ⎪⎩ 2x ≥ 0 2 4 2 1
⎧ − sin 2x = 4 sin 2x − 4 sin 2x + 1 ⎪ ⎪ 2 1 ⇔ sin ⎨ 2x ≥ 2 ⎪sin ⎪ 2x ≥ 0 ⎩ 2 ⎧ ( 2 sin 2x 4 sin 2x − 3) = 0 ⎪ ⇔ ⎨ 1 sin ⎪ 2x ≥ ⎩ 2 ⎧ 3 − 3 ⎪sin 2x = ∨ sin 2x = ⎪ ⇔ 2 2 ⎨ ⎪ 2 sin 2x ≥ ⎪⎩ 2 3 ⇔ sin 2x = 2 π π 2 ⇔ 2x = + k π 2 ∨ 2x = + k π 2 , k ∈ ] 3 3 π π ⇔ x = + π k ∨ x = + π k , k ∈ ] 6 3
Chuù yù : Coù theå ñöa veà phöông trình chöùa giaù trò tuyeät ñoái ( ) ⎧sin x ≠ ⎪ 0
* ⇔ ⎨⎪cosx − sin x + cosx + sin x = ⎩ 2 sin 2x
⇔ cos x − sin x + cos x + sin x = 2 sin 2x
Baøi 142 : Giaûi phöông trình sin x + 3 cos x + sin x + 3 cos x = 2 (*) sin π Ñaët 3 t = sin x + 3 cos x = sin x + cos x cos π3 1 t
sin ⎛ x π ⎞ 2sin ⎛ x π ⎞ ⇔ = + = + ⎜ π ⎝ 3 ⎟ ⎜ ⎠ ⎝ 3 ⎟ cos ⎠ 3 (*) thaønh t + t = 2 ⇔ t = 2 − t ⎧2 − t ≥ 0 ⎧t ≤ 2 ⇔ ⎨ ⇔ 2 ⎨ ⎩t = 4 − 4t + t ⎩ 2 t − 5t + 4 = 0 ⎧t ≤ 2 ⇔ ⎨ ⇔ t = 1 ⎩t = 1 ∨ t = 4 Do ñoù (*) ⎛ π ⎞ 1 π π π π 5 ⇔ sin x + = ⇔ x + = + k π 2 hay x + = + k π 2 , k ∈ ⎜ ⎟ ] ⎝ 3 ⎠ 2 3 6 3 6 π π ⇔ x = − + k π 2 ∨ x = + k π 2 , k ∈ ] 6 2
Baøi 143 : Giaûi phöông trình
3 tgx + 1 (sin x + 2 cos x) = 5(sin x + 3cos x) (*)
Chia hai veá cuûa (*) cho cos x ≠ 0 ta ñöôïc
(*) ⇔ 3 tgx + 1 (tgx + 2) = 5(tgx + 3)
Ñaët u = tgx + 1 vôùi u ≥ 0 Thì 2 u − 1 = t x g (*) thaønh ( 2 + ) = ( 2 3u u 1 5 u + 2) 3 2 ⇔ 3u − 5u + 3u − 10 = 0 ⇔ ( − )( 2 u 2 3u + u + 5) = 0 2
⇔ u = 2 ∨ 3u + u + 5 = 0(voâ nghieäm) Do ñoù (*) ⇔ tgx + 1 = 2 ⇔ tgx + 1 = 4 tgx 3 tg ⎛ vôùi π π ⎞ ⇔ = = α − < α < ⎜ ⇔ =α + π ∈] 2 2 ⎟ x k , k ⎝ ⎠ 1
Baøi 144 : Giaûi phöông trình ( 1 − cos x + cos x)cos2x = sin4x(*) 2
(*) ⇔ ( 1 − cosx + cosx)cos2x = sin2xcos2x ⎧cos x ≥ 0 ⇔ ⎨
hay 1 − cos x + cos x = sin 2x ⎩cos 2x = 0 ⎧ ⎧cos x ≥ 0 cos x ≥ 0 ⎪ ⎪ ⇔ ⎨ π hay ⎨sin 2x ≥ 0 2x = + π k , k ∈ ⎪ ] ⎪ ⎩ 2 1 + 2 (1 − cos x)cosx = 2 ⎩ sin 2x ⎧ ⎧cos x ≥ 0 cos x ≥ 0 ⎪ ⎪ ⇔ ⎨ π π hay ⎨sin 2x ≥ 0 x = + k , k ∈ ⎪ ] ⎪ ⎩ 4 2 1 + 2 (1 − cos x)cosx = 2 sin 2x ( VT ≥ 1 ≥ ⎩ VP ) ⎧cos x ≥ 0 ⎧cos x ≥ 0 ⎪ ⎪ ⎪sin 2x ≥ 0 ⇔ ⎨ π π 5 hay ⎨ x = ± + π h hay x = ± + π h , h ∈ ] 2 sin 2x = ⎪ ⎪ 1 ⎩ 4 4 ⎪⎩(1− cos x ) cos x = 0 π ⇔ x = ± + hπ, h ∈ ] 4 ⎧sin 2x = 1 ⎧sin 2x = 1 hay ⎨ hay ⎨
⎩cos x = 0 ( ⇒ sin 2x = 0 )
⎩cos x = 1 ( ⇒ sin x = 0 ⇒ sin 2x = 0 ) π ⇔ x = ± + π h , h ∈ ] 4
Baøi 145 : Giaûi phöông trình 3 ( + ) 3
sin x 1 cot gx + cos x (1 + tgx) = 2 sin x cos x (*) ( ) 3 ⎛ sin x + cos x ⎞ 3 ⎛ cos x + sin x * sin x cos x ⎞ ⇔ + = 2 sin x cos ⎜ x sin x ⎟ ⎜ cos x ⎟ ⎝ ⎠ ⎝ ⎠ ⇔ ( + )( 2 2
sin x cos x sin x + cos x) = 2 sin x cos x si ⎧ n x + cos x ≥ 0 ⇔ 1 ⎨ ⎩ + sin 2x = 2sin 2x ⎧ ⎛ π ⎞ sin x + ≥ ⎪ ⎜ ⎟ 0 ⎧sin x + cos x ≥ 0 ⎪ ⎝ 4 ⎠ ⇔ ⎨ ⇔ ⎨ ⎩sin 2x = 1 ⎪ π x = + π k , k ∈ ⎪ ] ⎩ 4 ⎧ ⎛ π ⎞ sin x + ≥ ⎪ ⎜ ⎟ 0 ⎪ ⎝ 4 ⎠ ⇔ ⎨⎪ π π x + = + π k , k ∈ ⎪ ] ⎩ 4 2 ⎧ ⎛ π ⎞ sin x + ≥ ⎪ ⎜ ⎟ 0 ⎪ ⎝ 4 ⎠ ⇔ ⎨⎪ π π π π 3 x + = + h π 2 hay x + = + h π 2 , h ∈ ⎪ ] ⎩ 4 2 4 2 π ⇔ x = + h π 2 , h ∈ ] 4
Baøi 146 : Giaûi phöông trình cos 2x + 1 + sin 2x = 2 sin x + cos x (*)
Ñieàu kieän cos 2x 0 vaø sin ⎛ x π ⎞ ≥ + ≥ 0 ⎜ 4 ⎟ ⎝ ⎠ Luùc ñoù : ( ) 2 2
* ⇔ cos x − sin x + (cos x + sin x)2 = 2 cos x + sin x 2 2
⇔ cos x − sin x + (cos x + sin x)2 + 2 cos 2x (cos x + sin x)2 = 4 (sin x + cos x)
⇔ cos x (cos x + sin x) + (sin x + cos x) cos2x = 2(sin x + cos x) ⎡sin x + cos x = 0 ⇔ ⎢⎣cosx + cos2x = 2 ⎡tgx = 1 − ⇔ ⎢ ⎢ cos 2x = 2 − cos x ⎣ (* *) ⎡tgx = 1 − ⇔ ⎢ 2
⎣cos 2x = 4 − 4 cos x + cos x 2 ⇔ tgx = 1
− ∨ cos x + 4 cos x − 5 = 0
⇔ tgx = −1 ∨ cos x = 1 ∨ cos x = −5(loaïi) π ⇔ x = − + π k ∨ x = k π 2 , k ∈ ] 4 Thöû laïi : π ⎛ π ⎞ • x = − + π k thì cos 2x = cos − = ⎜ ⎟ 0(nhaän) 4 ⎝ 2 ⎠ Vaø sin ⎛ x π ⎞ + = sin kπ = 0 ⎜ ⎟ (nhaän) ⎝ 4 ⎠
• x = k2π thì cos 2x = 1 (nhaän) vaø cos⎛ x π ⎞ + = cos π > 0 ⎜ ⎟ (nhaän) ⎝ 4 ⎠ 4 Do ñoù (*) π ⇔ x = − + π k ∨ x = k π 2 , k ∈ ] 4
Chuù yù : Taïi (**) coù theå duøng phöông trình löôïng giaùc khoâng möïc ( ) ⎧⎪cos x + cos2x = 2 * * ⇔ ⎨ si ⎪⎩ n x + cos x ≥ 0 ⎧cos x = 1 ⎪ 2
⇔ ⎨cos2x = 2cos x − 1 = 1 si ⎪ n x + cos x ≥ 0 ⎩ ⎧cos x = 1 ⇔ ⎨ ⇔ x = 2 π k , k ∈ ] ⎩sin x + cos x ≥ 0 Caùch khaùc ( ) 2 2
* ⇔ cos x − sin x + (cos x + sin x)2 = 2 cos x + sin x ⇔ + − + ( + )2 (cos x sin x).(cos x sin x ) cos x sin x = 2 cos x + sin x ⎧cos x + sin x > ⎪ 0 ⇔ cos x + sin x = 0 hay ⎨
cos x − sin x + (cos x + sin x) = ⎪⎩ 2 ⎧cos x + sin x > ⎪ 0
⇔ tgx = − 1 hay ⎨⎪⎩2cosx + 2 cos2x = 4 ⎧cos x + sin x > ⎪ 0
⇔ tgx = − 1 hay ⎨⎪⎩cosx + cos2x = 2 π ⎧cos x = 1 ⇔ x = − + π k , k ∈ ] hay ⎨ 4 ⎩cos 2x =1 π ⇔ x = − + π k hay x = 2 π k , k ∈ ] 4
( nhaän xeùt: khi cosx =1 thì sinx = 0 vaø sinx + cosx = 1 > 0 ) BAØI TAÄP 1. Giaûi phöông trình : a/ 1 + sin x + cos x = 0 4x 2 cos − cos x b/ 3 = 0 2 1 − tg x
c/ sin x + 3 cos x = 2 + cos 2x + 3 sin 2x d/ 2
sin x − 2sin x + 2 = 2sin x − 1 e/ 3tgx 2 3sin x = − 3 2 sin x − 1 2 4 sin 2x + cos 2x − 1 f/ = 0 sin cos x g/ 2
8 cos 4x cos 2x + 1 − cos 3x + 1 = 0 h/ 2
sin x + sin x + sin x + cos x = 1 k/ 2
5 − 3sin x − 4 cos x = 1 − 2 cos x l/ 2 cos 2x = cos x 1 + tgx 2. Cho phöông trình :
1 + sin x + 1 − sin x = m cos x (1)
a/ Giaûi phöông trình khi m = 2
b/ Giaûi vaø bieän luaän theo m phöông trình (1)
3. Cho f(x) = 3cos62x + sin42x + cos4x – m
a/ Giaûi phöông trình f(x) = 0 khi m = 0 b/ Cho ( ) 2 2
g x = 2cos 2x 3cos 2x + 1 . Tìm taát caû caùc giaù trò m ñeå phöông
trình f(x) = g(x) coù nghieäm. (ÑS : 1 ≤ m ≤ 0)
4. Tìm m ñeå phöông trình sau coù nghieäm 1 + 2cos x + 1 + 2sin x = m (ÑS: 1+ 3 ≤ m ≤ 2 1+ 2)
B) PHÖÔNG TRÌNH LÖÔÏNG GIAÙC CHÖÙA CAÙC TRÒ TUYEÄT ÑOÁI
Caùch giaûi : 1/ Môû giaù trò tuyeät ñoái baèng ñònh nghóa 2/ AÙp duïng • A = B ⇔ A = ±B ⎧B ≥ 0 ⎧B ≥ 0 ⎧A ≥ 0 ⎧A < 0 • A = B ⇔ ⎨ ⇔ ⎨ ⇔ 2 ⎨ ∨ ⎨ ⎩A = ±B ⎩ 2 A = B ⎩A = B ⎩A = −B
Baøi 147 : Giaûi phöông trình cos 3x = 1 − 3 sin 3x (*) ⎧ ( ) 1 ⎪ − 3 sin 3x ≥ 0 * ⇔ ⎨ 2 2
⎪⎩cos 3x = 1 − 2 3 sin 3x + 3sin 3x ⎧ 1 sin 3x ≤ ⎪ ⇔ ⎨ 3 ⎪ ⎩1 − 2 sin 3x = 1 − 2 3 sin 3x + 2 3sin 3x ⎧ 1 sin 3x ≤ ⎪ ⇔ ⎨ 3 ⎪ ⎩ 2 4 sin 3x − 2 3 sin 3x = 0 ⎧ 1 sin 3x ≤ ⎪⎪ 3 ⇔ ⎨⎪ 3 sin 3x = 0 ∨ sin 3x = ⎪⎩ 2 ⇔ sin 3x = 0 π k ⇔ x = , k ∈ ] 3
Baøi 148 : Giaûi phöông trình 3sin x + 2 cos x − 2 = 0(*) (*) ⇔ 2 cos x = 2 − 3sin x ⎧2 − 3sin x ≥ 0 ⇔ ⎨ 2 2
⎩4 cos x = 4 − 12sin x + 9sin x ⎧ 2 sin x ≤ ⎪ ⇔ ⎨ 3 ⎪4 (1 − 2 sin x) = 4 − 12sin x + 2 ⎩ 9 sin x ⎧ 2 ⎪sin x ≤ ⇔ ⎨ 3 ⎪⎩ 2 13sin x − 12 sin x = 0 ⎧ 2 sin x ≤ ⎪⎪ ⇔ 3 ⎨ ⎪ 12 sin x = 0 ∨ sin x = ⎪⎩ 13 ⇔ sin x = 0 ⇔ x = π k , k ∈ ]
Baøi 149 : Giaûi phöông trình sin x cos x + sin x + cos x = 1(*) Ñaët t sin x cos x 2 sin ⎛ x π ⎞ = + = + ⎜ 4 ⎟ ⎝ ⎠
Vôùi ñieàu kieän : 0 ≤ t ≤ 2 Thì 2 t = 1 + 2sin x cos x 2 t − 1 Do ñoù (*) thaønh : + t = 1 2 2 ⇔ t + 2t − 3 = 0 ⇔ t = 1 ∨ t = 3 − (loaïi) Vaäy (*) ⇔ 2 1 = 1 + 2sin x cos x ⇔ sin 2x = 0 π k ⇔ x = , k ∈ ] 2
Baøi 150 : Giaûi phöông trình sin x − cos x + 2sin 2x = 1(*)
Ñaët t = sin x − cos x (ñieàu kieän0 ≤ t ≤ 2) Thì 2 t = 1 − sin 2x ( ) + ( 2 * thaønh: t 2 1 − t ) = 1 2 ⇔ 2t − t − 1 = 0 1
⇔ t = 1 ∨ t = − (loaïi doñieàu kieän) 2 khi t = 1 thì 2 1 = 1 − sin 2x ⇔ sin 2x = 0 π k ⇔ x = , k ∈ ] 2
Baøi 151 : Giaûi phuông trình 4 4
sin x − cos x = sin x + cos x (*) ( ) ⇔ ( 2 2 + )( 2 2 *
sin x cos x sin x − cos x) = sin x + cos x ⇔ − cos 2x = sin x + cos x ⎧− cos 2x ≥ 0 ⎪ ⇔ ⎨ 2 ⎪cos 2x = 1 + 2 sin x cos x ⎩ ⎧cos 2x ≤ 0 ⎪ ⇔ ⎨ 2 1 ⎪ − sin 2x = 1 + sin 2x ⎩ ⎧cos 2x ≤ 0 ⎪ ⇔ ⎨ 2 ⎪ sin 2x = − sin 2x ⎩ ⎧cos 2x ≤ 0 ⇔ si ⎨ ⎩ n 2x = 0 ⎧cos 2x ≤ 0 ⇔ ⎨ ⇔ cos 2x = 1 − 2 ⎩cos 2x = 1 π ⇔ x = + π k , k ∈ ] 2
Baøi 152 : Giaûi phöông trình 2
3 sin 2x − 2cos x = 2 2 + 2cos 2x (*) Ta coù : ( ) 2 ⇔ − = + ( 2 *
2 3 sin x cos x 2cos x 2 2 2 2cos x − 1) ⎛ 3 1 ⎞ ⇔ cos x ⎜ sin x − cos x⎟ = cos x ⎜ 2 2 ⎟ ⎝ ⎠ cos x.sin ⎛ x π ⎞ ⇔ − = cos x ⎜ 6 ⎟ ⎝ ⎠ ⎧cos x > 0 ⎧cos x < 0 cos x 0 ⎪ ⎪ ⇔ = ∨ ⎨ ⎛ π ⎞ ∨ sin x 1 s ⎨ in⎛x π⎞ − = − = 1 ⎪ ⎜ − ⎩ ⎝ 6 ⎟ ⎪ ⎜ ⎠ ⎩ ⎝ 6 ⎟⎠ ⎧cos x > 0 ⎧cos x < 0 ⎪ ⎪ ⇔ cos x = 0 ∨ ⎨ π π ∨ ⎨ π π x − = + k π 2 , k ∈ ] x − = − + k π 2 , k ∈ ⎪ ⎪ ] ⎩ 6 2 ⎩ 6 2 ⎧cos x > 0 ⎧cos x < 0 π ⎪ ⎪ ⇔ x = + π k , k ∈ ] ∨ ⎨ π 2 ∨ ⎨ π 2 x = + k π 2 , k ∈ ] x = − + k π 2 , k ∈ ⎪ ⎪ ] ⎩ 3 ⎩ 3 π ⇔ x = + π k , k ∈ ] 2
Baøi 153 : Tìm caùc nghieäm treân (0,2π) cuûa phöông trình :
sin 3x − sin x = sin2x + cos2x(*) 1 − cos 2x Ta coù : ( ) 2cos 2x sin x * 2 cos⎛2x π ⎞ ⇔ = − 2 sin x ⎜ 4 ⎟ ⎝ ⎠
Ñieàu kieän : sin x ≠ 0 ⇔ x ≠ kπ
• Khi x ∈ (0, π) thìsin x > 0neân : (*) 2 cos 2x 2 cos⎛2x π ⎞ ⇔ = ⎜ − 4 ⎟ ⎝ ⎠ ⎛ π ⎞ ⇔ 2x = ± 2x − + k π 2 , k ∈ ⎜ ⎟ ] ⎝ 4 ⎠ π ⇔ 4x = + π k2 , k ∈ ] 4 π π k ⇔ x = + , k ∈ ] 16 2 (0, ) π π 9 Do x ∈ π neân x = hay x = 16 16 Khi x ∈ ( ,
π 2π) thì sinx < 0 neân : (*) ⎛ π ⎞ ⇔ − cos 2x = cos 2x − ⎜ ⎟ ⎝ 4 ⎠ cos ( 2x) ⎛ π ⎞ ⇔ π − = cos 2x − ⎜ ⎟ ⎝ 4 ⎠ π ⇔ 2x − = ± (π − 2x) + k π 2 , k ∈ ] 4 π 5 ⇔ 4x = + π k2 , k ∈ ] 4 5π π k ⇔ x = + , k ∈ ] 16 2 21 29 Do π π x ∈ ( , π 2π) neân x = ∨ x = • 16 16 Baøi 154 Cho phöông trình : 6 6 sin x + cos x = a sin 2x (*) Tìm a sao cho
phöông trình coù nghieäm. Ta coù : 6 sin x + 6 cos x = ( 2 sin x + 2 cos x) ( 4 sin x − 2 2 sin x cos x + 4 cos x) = (sin x + cos x)2 2 2 − 2 2 3sin x cos x 3 = 1 − 2 sin 2x 4
Ñaët t = sin 2x ñieàu kieän 0 ≤ t ≤ 1 3 thì (*) thaønh : 1 − 2 t = at (* *) 4 1 3
⇔ − t = a (do t = 0 thì (**) voâ nghieäm) t 4 1 3
Xeùt y = − t treân D = (0, ] 1 t 4 1 3 thì y ' = − − < 0 2 t 4 1
Do ñoù : (*) coù nghieäm ⇔ a ≥ • 4 Baøi 155 Cho phöông trình = 2 cos 2x m cos x 1 + tgx (*) Tìm m ñeå phöông
trình coù nghieäm treân ⎡0, π⎤ ⎢ 3⎥ ⎣ ⎦ Ñaët t = tgx thì Vaäy : (*) thaønh: 2
1 − t = m 1 + t (* *) (chia 2 veá cho 2 cos ≠ 0 ) Khi 0 x π ≤ ≤ thì t ∈ ⎡0, 3⎤ 3 ⎣ ⎦ 2 1 − t (1 − t)(1 + t) Vaäy (**) ⇔ m = = = (1 − t) 1 + t 1 + t 1 + t
Xeùt y = (1 − t) 1 + t treân ⎡0, 3⎤ ⎣ ⎦ Ta coù (1 − t) −2 (1 + t) + (1 − t) y ' = − 1 + t + = 2 1 + t 2 1 + t −3t − 1 ⇔ y ' = < 0 ∀t ∈ ⎡0, 3⎤ ⎣ ⎦ 2 1 + t
Do ñoù : (*) coù nghieäm treân ⎡0, π⎤ ⎢
⇔ (1 − 3) 1 + 3 ≤ m ≤ 1 • 3⎥ ⎣ ⎦ BAØI TAÄP
1. Giaûi caùc phöông trình
a/ sin x − cox = 1 − 4 sin 2x b/ 4 sin x + 3 cos x = 3 1 c/ tgx = cot gx + cosx 2 1 1 1 ⎛ 1 + 3cos x ⎞ d/ 2 + − = − 2 ⎜ 2 sin x 1 cos x 1 cos x sin x ⎟ − + ⎝ ⎠ 1 e/ cot gx = tgx + sinx f/ 2cos x − sin x = 1 1 + cos x + 1 − cos x g/ = 4 sin x cos x 1 − cos 2x ⎛ 1 h/ 2 cos x ⎞ = − sin x ⎜ 2 ⎟ ⎝ ⎠ 3 3 m/ cos 2x sin x + cos x + 1 + sin 2x = 2 n/ cos x + sin 3x = 0 1 r/ cot gx = tgx + sinx
s/ cos x + 2sin 2x − cos 3x = 1 + 2sin x − cos 2x 2 tg x 1 o/ t = gx + 1 + tgx − 1 tgx − 1
p/ sin x − cos x + sin x + cos x = 2
2. sin x + cos x + a sin 2x = 1
Tìm tham soá a döông sao cho phöông trình coù nghieäm
3. Cho phöông trình: sin x − cos x + 4 sin 2x = m
a/ Giaûi phöông trình khi m = 0 65
b/ Tìm m ñeå phöông trình coù nghieäm (ÑS 2 − 4 ≤ m ≤ ) 16 CHÖÔNG VIII
PHÖÔNG TRÌNH LÖÔÏNG GIAÙC KHOÂNG MAÃU MÖÏC
Tröôøng hôïp 1: TOÅNG HAI SOÁ KHOÂNG AÂM
AÙp duïng Neáu ⎧A ≥ 0 ∧ B ≥ 0 ⎨ thì A = B = 0 ⎩A + B = 0 Baøi 156 Giaûi phöông trình: 2 2
4 cos x + 3tg x − 4 3 cos x + 2 3tgx + 4 = 0 (*) Ta coù: 2 2
(*) ⇔ (2cos x − 3) + ( 3tgx + 1) = 0 ⎧ 3 ⎪cos x = ⎪ ⇔ 2 ⎨ ⎪ 1 tgx = − ⎪⎩ 3 ⎧ π x = ± + k π 2 , k ∈ ⎪⎪ 6 ⇔ ⎨⎪ 1 tgx = − ⎪⎩ 3 π ⇔ x = − + k π 2 , k ∈ 6 Baøi 157 Giaûi phöông trình: 2
8cos 4x.cos 2x + 1 − cos 3x + 1 = 0 (*)
Ta coù: (*) ⇔ 4 cos 4x (1 + cos 4x) + 1 + 1 − cos 3x = 0 ⇔ ( 2
4 cos 4x + 4 cos 4x + 1) + 1 − cos 3x = 0
⇔ (2 cos 4x + 1)2 + 1 − cos 3x = 0 ⎧ 1 ⎧ 1 ⎪cos 4x = − ⎪cos 4x = − ⇔ ⎨ 2 ⇔ ⎨ 2 ⎪⎩cos3x = 1 ⎪⎩3x = k π 2 , k ∈ ⎧ 1 cos 4x = − ⎪⎪ ⇔ 2 ⎨ π ⎪ k2 x =
, k ∈ (coù 3 ñaàu ngoïn cung) ⎪⎩ 3 ⎧ 1 cos 4x = − ⎪⎪ ⇔ 2 ⎨ π 2 π ⎪ 2 x = − π +m2 hay x = m π 2 hay x = + m π 2 , m ∈ ⎪⎩ 3 3 π 2 ⇔ x = ± + m π 2 , m ∈ 3
(ta nhaän k = ±1 vaø loaïi k = 0 ) Baøi 158 Giaûi phöông trình: 2 2 sin 3x sin x + ( 3 3
cos 3x sin x + sin 3x cos x) = sin xsin2 3x (*) 3sin 4x Ta coù: 3 3 cos3x.sin 3x + sin 3x.cos x = ( 3 4 cos x − 3 cos x) 3 sin x + (3sin x − 3 4 sin x) 3 cos x = − 3 3 cos x sin x + 3 3sin x cos x = 3sin x cos x ( 2 cos x − sin2 x) 3 3 = sin 2x.cos 2x = sin 4x 2 4 ( ) 1 Vaäy: * ⇔ 2 sin x + 2 sin 3x = 2 sin x sin 3x vaø sin 4x ≠ 0 4 ⎛ 1 2 ⎞2 1 1 ⇔ sin 3x − sin x − 4 sin 3x + 2 sin 3x = ⎜ ⎟ 0 vaø sin 4x ≠ 0 ⎝ 2 ⎠ 4 4 ⎛ 1 2 ⎞2 1 ⇔ sin 3x − sin x + 2 sin 3x (1 − 2 sin 3x) = ⎜ ⎟ 0 vaø sin 4x ≠ 0 ⎝ 2 ⎠ 4 ⎛ 1 2 ⎞2 1 ⇔ sin 3x − sin x + 2 sin 6x = ⎜ ⎟ 0 vaø sin 4x ≠ 0 ⎝ 2 ⎠ 16 ⎧sin 4x ≠ 0 ⎪⎪1 ⇔ ⎨ 2 sin 3x = sin x ⎪2 ⎪sin 3x = 0 ∨ cos 3x = ⎩ 0 ⎧sin 4x ≠ 0 ⎧sin 4x ≠ 0 ⎪ ⎪ ⎪1 ⇔ ⎨sin 3x = 0 ∨ ⎨ = sin x ⎪ ⎪2 sin x = ⎩ 0 (VN) ⎪sin 3x = ± ⎩ 1 ⎧sin 4x ≠ 0 ⎪⎪ 1 ⇔ ⎨sin x = ⎪ 2 ⎪⎩3sin x − 3 4 sin x = ±1 ⎧sin 4x ≠ 0 ⎪ ⇔ ⎨ 1 sin x = ⎪⎩ 2 ⎧sin 4x ≠ 0 ⎪ ⇔ ⎨ π π 5 x = + k π 2 ∨ + k π 2 , k ∈ ⎪⎩ 6 6 π π 5 ⇔ x = + k π 2 ∨ x = + k π 2 , k ∈ 6 6 Tröôøng hôïp 2
Phöông phaùp ñoái laäp Neáu ⎧A ≤ M ≤ B ⎨ thì A = B = M ⎩A = B Baøi 159 Giaûi phöông trình: 4 − 4
sin x cos x = sin x + cos x (*) Ta coù: (*) ⇔ 2 − 2 sin x cos x = sin x + cos x ⇔ − cos 2x = sin x + cos x ⎧cos 2x ≤ ⎪ 0 ⇔ ⎨⎪ 2 cos 2x = 1 + ⎩ 2 sin x cos x ⎧cos 2x ≤ ⎪ 0 ⎧cos 2x ≤ 0 ⇔ ⎨ ⇔ 2 ⎨ ⎪− sin 2x = ⎩ 2 sin 2x ⎩sin 2x = 0 (cos 2x = ± 1 ) ⇔ cos 2x = −1 π ⇔ x = + π k , k ∈ 2 Caùch khaùc Ta coù 4 s − 4 ≤ 4 in x cos x
sin x ≤ sin x ≤ sin x + cos x ⎧cos x = 0 Do ñoù ⎪ (*) π ⇔ ⎨ ⇔ cos x = 0 ⇔ x = + π k , k ∈ ⎪ 4 sin x = ⎩ sin x 2 Baøi 160: Giaûi phöông trình: ( − )2
cos 2x cos 4x = 6 + 2sin 3x (*) Ta coù: (*) 2 2
⇔ 4 sin 3x.sin x = 6 + 2sin 3x • Do: 2 sin 3x ≤ 1 vaø 2 sin x ≤ 1 neân 2 2 4sin 3x sin x ≤ 4 • Do
sin 3x ≥ −1 neân 6 + 2sin 3x ≥ 4 Vaäy 2 2
4sin 3x sin x ≤ 4 ≤ 6 + 2sin 3x
Daáu = cuûa phöông trình (*) ñuùng khi vaø chæ khi ⎧ 2 sin 3x = 1 ⎪ ⎧ 2 sin x 1 2 = ⎨sin x = 1 ⇔ ⎨ ⎪ ⎩sin 3x = −1 sin 3x = − ⎩ 1 ⎧ π ⎪x = ± + k π 2 , k ∈ π ⇔ ⎨ 2 ⇔ x = + k2 , π k ∈ ⎪ 2 ⎩sin 3x = −1 3 3 cos x − sin x Baøi 161 Giaûi phöông trình: = 2cos 2x (*) sin x + cos x
Ñieàu kieän: sin x ≥ 0 ∧ cos x ≥ 0 Ta coù: (*) ⇔ ( − )( + ) = ( 2 2 cos x sin x 1 sin x cos x
2 cos x − sin x)( sin x + cos x) ⎡cos x − sin x = 0 (1)
⇔ ⎢⎢1 + sin xcosx = 2(cosx + sinx) ⎣ ( sinx + cosx) (2) Ta coù: π i (1) ⇔ tgx = 1 ⇔ x = + π k , k ∈ 4 i Xeùt (2) Ta coù: khi sin x ≥ 0 thì ≥ ≥ 2 sin x sin x sin x Töông töï ≥ ≥ 2 cos x cos x cos x Vaäy
sin x + cos x ≥ 1 vaø sin x + cos x ≥ 1
Suy ra veá phaûi cuûa (2) thì ≥ 2 1 3
Maø veá traùi cuûa (2): 1 + sin 2x ≤ 2 2 Do ñoù (2) voâ nghieäm Vaäy: (*) π ⇔ x = + π k , k ∈ 4 Baøi 162:
Giaûi phöông trình: 3 − cos x − cos x + 1 = 2(*) Ta coù: (*)
⇔ 3 − cos x = 2 + cos x + 1
⇔ 3 − cos x = 5 + cos x + 4 cos x + 1
⇔ −2(cos x + 1) = 4 cos x + 1 Ta coù: −2(cos x + 1) ≤ 0∀x maø 4 cos x + 1 ≥ 0 x ∀
Do ñoù daáu = cuûa (*) xaûy ra ⇔ cos x = 1 − ⇔ x = π + k π 2 , k ∈ Baøi 163: Giaûi phöông trình: 2 + − = ( 2 cos 3x 2 cos 3x 2 1 + sin 2x)(*)
Do baát ñaúng thöùc Bunhiacoápski: 2 2 2 2 AX + BY ≤ A + B . X + Y neân: 2 2 + − ≤ + ( 2 1cos 3x 1 2 cos 3x 2. cos 3x 2 − cos 3x) = 2 Daáu = xaûy ra 2 ⇔ cos 3x = 2 − cos 3x ⎧cos 3x ≥ 0 ⇔ ⎨ 2 2 ⎩cos 3x = 2 − cos 3x ⎧cos 3x ≥ 0 ⇔ ⎨ ⇔ cos 3x = 1 ⎩cos 3x = 1 ± Maët khaùc: ( 2 2 1 + sin 2x) ≥ 2 daáu = xaûy ra ⇔ sin 2x = 0 Vaäy: 2 + − ≤ ≤ ( 2 cos 3x 2 cos 3x 2 2 1 + sin 2x) daáu = cuûa (*) chæ xaûy ra khi: cos 3x = 1 ∧ sin 2x = 0 ⎧cos 3x = 1 ⎪ ⇔ ⎨ π k x = , k ∈ ⎪ ( coù 4 ñaàu ngoïn cung ) ⎩ 2 ⇔ x = 2 π m , m ∈ Baøi 164: Giaûi phöông trình: 2 2 5 tg x cotg x 2sin ⎛ x π ⎞ + = + (*) ⎜ 4 ⎟ ⎝ ⎠ Ñieàu kieän: sin 2x ≠ 0 •
Do baát ñaúng thöùc Cauchy: 2 2 tg x + cotg x ≥ 2
daáu = xaûy ra khi tgx = cotgx • Maët khaùc: sin ⎛ x π ⎞ + ≤ 1 ⎜ 4 ⎟ ⎝ ⎠ neân 5 2sin ⎛ x π ⎞ + ≤ 2 ⎜ 4 ⎟ ⎝ ⎠
daáu = xaûy ra khi sin ⎛ x π ⎞ + = 1 ⎜ 4 ⎟ ⎝ ⎠ Do ñoù: 2 2 5
tg x cotg x 2 2sin ⎛ x π ⎞ + ≥ ≥ + ⎜ 4 ⎟ ⎝ ⎠ ⎧tgx = cotgx Daáu = cuûa (*) xaûy ra ⎪ ⇔ si ⎨ n⎛x π ⎞ + = 1 ⎪ ⎜ ⎩ ⎝ 4 ⎟⎠ ⎧ 2 tg x = 1 ⎪ ⇔ ⎨ π x = + k π 2 , k ∈ ⎪⎩ 4 π ⇔ x = + k π 2 , k ∈ 4
Tröôøng hôïp 3: AÙp duïng: Neáu ⎧A ≤ M vaø B ≤ M ⎧A = M ⎨ thì ⎩A B M N ⎨ + = + ⎩B = N ⎧sin u =1
sin u + sin v = 2 ⇔ ⎨⎩sinv=1 ⎧sin u = 1
sin u − sin v = 2 ⇔ ⎨⎩sinv=−1 ⎧sin u = −1
sin u + sin v = − 2 ⇔ ⎨⎩sinv=−1
Töông töï cho caùc tröôøng hôïp sau
sin u ± cos v = ± 2 ; cos u ± cos v = ± 2 3x Baøi 165:
Giaûi phöông trình: cos 2x + cos − 2 = 0(*) 4 Ta coù: ( ) 3x * ⇔ cos 2x + cos = 2 4 3x Do cos 2x ≤ 1 vaø cos ≤ 1 4
neân daáu = cuûa (*) chæ xaûy ra ⎧cos 2x = 1 ⎧x = π k , k ∈ ⎪ ⎪ ⇔ ⎨ 3x ⇔ ⎨ π 8h ⇔ x = 8 π m , m ∈ cos = 1 x = , h ∈ ⎪ ⎪ ⎩ 4 ⎩ 3 π 8h 8h Do : π k = ⇔ k = 3 3
ñeå k nguyeân ta choïn h = 3m (m ∈ Ζ) ( thì k = 8m ) Caùch khaùc ⎧cos 2x = 1 ⎧x = π k , k ∈ ⎪ ⎪ ⎨ 3x ⇔ ⎨ 3 π k ⇔ x = 8 π m , m ∈ cos = 1 cos = ⎪ ⎪ 1 ⎩ 4 ⎩ 4 Baøi 166: Giaûi phöông trình:
cos 2x + cos 4x + cos 6x = cos x.cos 2x.cos 3x + 2(*) 2 cos 2x + cos 4x + cos 6x
= 2cos 3x cos x + 2cos 3x − 1
= 2cos 3x (cos x + cos3x) − 1 = 4 cos 3x.cos 2x.cos x − 1 1
Vaäy: cos 3x.cos 2x.cos x = (cos2x + 6cos4x + cos6x + 1) 4 Do ñoù: ( ) 1 9
* ⇔ cos 2x + cos 4x + cos 6x = (cos2x + cos 4x + cos6x) + 4 4 3 9 ⇔ (cos 2x + cos 4x + cos 6x) = 4 4
⇔ cos 2x + cos 4x + cos 6x = 3 ⎧cos 2x = 1 ⎧2x = k π 2 , k ∈ (1) ⎪ ⎪
⇔ ⎨cos 4x = 1 ⇔ ⎨cos 4x = 1 (2) ⎪ ⎪ cos 6x = 1 cos 6x = ⎩ ⎩ 1 (3) ⇔ 2x = k π 2 , k ∈ ⇔ x = π k , k ∈
( Theá (1) vaøo (2) vaø (3) ta thaáy hieån nhieân thoûa)
Baøi 167: Giaûi phöông trình:
cos 2x − 3 sin 2x − 3 sin x − cos x + 4 = 0(*) Ta coù: ( ) ⎛ 1 3 ⎞ ⎛ 3 1 ⎞ * ⇔ 2 = ⎜− cos2x + sin 2x⎟ + ⎜ sin x + ⎜ ⎟ ⎜ cos x⎟⎟ ⎝ 2 2 ⎠ ⎝ 2 2 ⎠ ⎛ π ⎞ ⎛ π ⇔ 2 = sin 2x − + sin x + ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ 6 ⎠ ⎝ 6 ⎠ ⎧ ⎛ π ⎞ ⎧ π π sin 2x − = ⎪ ⎜ ⎟ 1 2x − = + k π 2 , k ∈ 6 ⎪ ⎪ ⎝ ⎠ ⎪ ⇔ 6 2 ⎨ ⇔ ⎨ ⎪ ⎛ π ⎞ π π ⎪ sin x + = 1 x + = + h π 2 , h ∈ ⎜ ⎟ ⎪ 6 ⎪ ⎩ ⎝ ⎠ ⎩ 6 2 ⎧ π x = + π k , k ∈ ⎪⎪ 3 π ⇔ ⎨ ⇔ x = + π h , h ∈ π ⎪ 3 x = + h π 2 , h ∈ ⎪⎩ 3 Caùch khaùc ⎧ ⎛ π ⎞ ⎧ ⎛ π ⎞ sin 2x − = ⎪ ⎜ ⎟ 1 sin 2x − = ⎪ ⎜ ⎟ 1 ⎪ ⎝ 6 ⎠ ⎪ ⎝ 6 ⎠ ( *) ⇔ ⎨ ⇔ ⎨ ⎪ ⎛ π ⎞ ⎪ π π sin x + = ⎜ ⎟ 1 x + = + h π 2 , h ∈ ⎪ 6 ⎪ ⎩ ⎝ ⎠ ⎩ 6 2 ⎧ ⎛ π ⎞ sin 2x − = ⎪ ⎜ ⎟ 1 ⎪ ⎝ 6 ⎠ π ⇔ ⎨ ⇔ x = + h , π h ∈ ⎪ π 3 x = + h π 2 , h ∈ ⎪⎩ 3 Baøi 168:
Giaûi phöông trình: 4 cos x − 2 cos 2x − cos 4x = 1(*) Ta coù: ( ) ⇔ − ( 2 − ) − ( − 2 * 4 cos x 2 2cos x 1 1 2sin 2x) = 1 ⇔ 4cosx − 2 4 cos x + 2 2 8 sin x cos x = 0
⇔ cos x = 0 hay 1 − cos x + 2 2 sin x cos x = 0 ⇔ = + ( 2
cos x 0 hay 1 cos x 2 sin x − 1) = 0
⇔ cos x = 0 hay 1 − cos x cos 2x = 0 ( * *) 1
⇔ cos x = 0 hay 1 − (cos 3x + cos x) = 0 2
⇔ cos x = 0 ∨ cos 3x + cos x = 2 ⎧cos 3x = 1
⇔ cos x = 0 ∨ ⎨⎩cosx = 1 ⎧cos x = 1 ⇔ cos x = 0 ⇔ ⎨⎩ 3 4 cos x − 3 cos x = 1 ⇔ cos x = 0 ∨ cos x = 1 π ⇔ x = + π k ∨ x = k π 2 , k ∈ 2 Caùch khaùc
( * *) ⇔ cos x = 0 hay cos x cos 2x = 1 ⎧cos x = 1 ⎧cos x = − 1 ⇔ cos x = 0 ∨ ⎨ ∨ ⎨
⎩cos 2x = 1 ⎩cos 2x = − 1 π ⎧x = k π 2 , k ∈ ⎧x = π + k π 2 , k ∈ ( loaïi ) ⇔ x = + π k , k ∈ ∨ ⎨ ∨ ⎨ 2 ⎩cos 2x = 1 ⎩cos 2x = − 1 π ⇔ x = + π k ∨ x = k π 2 , k ∈ 2 Baøi 169: Giaûi phöông trình: 1 tg2x + tg3x + = 0(*) sin x cos 2x cos 3x
Ñieàu kieän: sin 2x cos2x cos3x ≠ 0 Luùc ñoù: ( ) sin 2x sin 3x 1 * ⇔ + + = 0
cos 2x cos 3x sin x.cos 2x.cos 3x
⇔ sin 2x sin x cos 3x + sin 3x sin x.cos 2x + 1 = 0
⇔ sin x (sin 2x cos3x + sin 3x cos2x) + 1 = 0 ⇔ sin x.sin 5x = −1 1
⇔ − (cos6x − cos4x) = −1 2 ⇔ cos 6x − cos 4x = 2 ⎧t = cos 2x ⎧t = cos 2x ⎧cos 6x = 1 ⎪ 3 ⎪ ⇔ ⎨ ⇔ ⎨4t − 3t = 1 ⇔ ⎨ 3 4t − 3t = 1 ⎩cos 4x = −1 ⎪ 2 ⎪ 2t − 1 = −1 t = ⎩ ⎩ 0 Do ñoù: (*) voâ nghieäm. Caùch khaùc ⎧sin x =1 ⎧sin x = − 1
⇔ sin x.sin 5x = −1 ⇔ ⎨ hay ⎨ ⎩sin 5x = −1 ⎩sin 5x = 1 ⎧ π ⎧ π ⎪x = + k π 2 , k ∈ ⎪x = − + k π 2 , k ∈ ⇔ ⎨ 2 hay ⎨ 2 ⎪⎩sin5x = −1 ⎪⎩sin 5x = 1 ⇔ x∈∅ Baøi 170: Giaûi phöông trình: 2 2
cos 3x.cos 2x − cos x = 0(*) 1 1
Ta coù: (*) ⇔ (1 + cos6x) cos2x − (1 + cos2x) = 0 2 2 ⇔ cos 6x cos 2x = 1 1 ⇔ (cos 8x + cos 4x) = 1 2 ⇔ cos 8x + cos 4x = 2 ⎧cos 8x = 1 ⇔ ⎨⎩cos4x = 1 ⎧ 2 2 cos 4x − 1 = 1 ⇔ ⎨⎩cos4x = 1 ⎧ 2 cos 4x = 1 ⇔ ⎨⎩cos4x = 1 ⇔ cos 4x = 1 ⇔ 4x = π k2 , k ∈ π k ⇔ x = , k ∈ 2 Caùch khaùc ⇔ cos 6x cos 2x = 1 ⎧cos 2x = 1 ⎧cos 2x = −1 ⇔ ⎨ hay ⎨ ⎩cos 6x = 1 ⎩cos 6x = −1 ⎧2x = k π 2 , k∈ ⎧2x = π + k π 2 , k∈ ⇔ ⎨ hay ⎨ ⎩cos 6x = 1 ⎩cos 6x = −1 π k x = , k ∈ 2 Caùch khaùc ⎧cos 8x = 1 ⎧cos 8x = 1 ⎨ ⇔ ⎨ ⎩cos 4x = 1 ⎩4x = k π 2 , k ∈ π k ⇔ x = , k ∈ 2
Tröôøng hôïp 4:
DUØNG KHAÛO SAÙT HAØM SOÁ
y = ax laø haøm giaûm khi 0< a <1. Do ñoù ta coù π sin m x < sin n x ⇔ n > , m x
∀ ≠ + kπ , k∈ 2 π cos m x < co s n x ⇔ n > , m x
∀ ≠ + kπ , k∈ 2 sin m x ≤ sin n x ⇔ n ≥ , m x ∀ cos m x ≤ co s n x ⇔ n ≥ , m x ∀ 2 x Baøi 171: Giaûi phöông trình: 1 − = cos x (*) 2 2 x Ta coù: (*) ⇔ 1 = + cos x 2 2 x Xeùt y = + cos x treân R 2 Ta coù: y ' = x − sin x vaø y ' = 1 − cos x ≥ 0 x ∀ ∈ R
Do ñoù y’(x) laø haøm ñoàng bieán treân R Vaäy x
∀ ∈ (0,∞) : x > 0 neân y '(x) > y '(0) = 0 x
∀ ∈ (−∞,0) : x < 0 neân y '(x) < y '(0) = 0 Do ñoù: 2 x Vaäy : y = + cos x ≥ 1 x ∀ ∈ R 2
Daáu = cuûa (*) chæ xaûy ra taïi x = 0 Do ñoù (*) ⇔ x = 0 •
Baøi 172: Giaûi phöông trình
sin4 x + sin6 x = sin8 x + sin10 x (*) Ta coù 4 8 2
⎧⎪sin x ≥sin x vaø daáu=xaûy ra khi vaø chæ khi sin x = 1hay sinx = 0 ⎨ 6 10 2
⎪⎩ sin x ≥ sin x vaø daáu=xaûy ra khi vaø chæ khi sin x = 1 hay sinx = 0 ⇔ sin2x = 1 ∨ sinx = 0 π ⇔ x = ± + k π 2 ∨ x = k π 2 , k ∈ 2 Caùch khaùc
(*) ⇔ sin4 x = hay + sin2 x =sin4 x + sin6 0 1 x ⇔ sin x = hay sin2 0 x =1 BAØI TAÄP
Giaûi caùc phöông trình sau 1. lg ( 2 sin x) − 1 + 3 sin x = 0 ⎛ π ⎞ 2.
sin 4x − cos 4x = 1 + 4 2 sin x − ⎜ ⎟ ⎝ 4 ⎠ 2 1 3. sin x + 2 sin 3x = 2 sin x.sin 3x 4 4. πsin x = cos x 5.
2 cos x + 2 sin10x = 3 2 + 2 cos 28x.sin x 6.
(cos 4x − cos 2x)2 = 5 + sin 3x 7.
sin x + cos x = 2 (2 − sin 3x) 8.
sin 3x (cos 2x − 2sin 3x) + cos 3x (1 + sin 2x − 2 cos 3x) = 0 9. tgx + tg2x = − sin 3x cos 2x 10. 2 log (cot gx) = log cos x a 2 ( ) sin x ⎡ π⎤ 11. 2 = cos x vôùi x ∈ ⎢0, ⎥ ⎣ 2⎦ 13 12. cos x + 14 sin x = 1 13.
cos 2x − cos 6x + 4 (sin 2x + 1) = 0 14.
sin x + cos x = 2 (2 − cos 3x) 3 15. sin x + 3 cos x = 2 − 4 sin x 2 16.
cos x − 4 cos x − 2x sin x + 2 x + 3 = 0 sin x 17. 2 + sin x = 2 sin x + cos x 2 18. 3 cot g x + 2
4 cos x − 2 3 cot gx − 4 cos x + 2 = 0 CHÖÔNG IX
HEÄ PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
I. GIAÛI HEÄ BAÈNG PHEÙP THEÁ ⎧2cos x − 1 = 0 (1) Baøi 173:
Giaûi heä phöông trình: ⎪⎨ 3 si ⎪ n 2x = (2) ⎩ 2 Ta coù: ( ) 1 1 ⇔ cos x = 2 x π ⇔ = ± + k2π (k ∈ Z) 3 Vôùi x π =
+ k2π thay vaøo (2), ta ñöôïc 3 ⎛ 2π ⎞ 3 sin 2x = sin + k4π = ⎜ 3 ⎟ ⎝ ⎠ 2 Vôùi x π = − + k π 2 thay vaøo (2), ta ñöôïc 3 ⎛ 2π ⎞ 3 sin 2x 3 = sin − + k4π = − ≠ ⎜ (loaïi) 3 ⎟ ⎝ ⎠ 2 2 Do ñoù nghieäm c π
ủa heä laø: x = + k2 , π k ∈ 3 si ⎧ n x + sin y = 1 Baøi 174:
Giaûi heä phöông trình: ⎪⎨x + y π = ⎪⎩ 3 Caùch 1: ⎧ x + y x − y 2sin .cos = 1 ⎪ Heä ñaõ cho ⎪ 2 2 ⇔ ⎨x y π ⎪ + = ⎪⎩ 3 ⎧ π x − y ⎧ x − y 2.sin .cos = 1 cos = ⎪ ⎪ 1 ⎪ 6 2 ⎪ ⇔ 2 ⎨ ⇔ ⎨ π π ⎪ ⎪ x + y = x + y = ⎪⎩ 3 ⎪⎩ 3 ⎧ x − y ⎧ π = k2π
⎧x − y = 4kπ ⎪ x = + k π ⎪ 2 ⎪ 2 ⎪ ⇔ ⎪ ⎨ ⇔ ⎨ π 6 ⇔ ⎨ (k ∈Z ) π x + y = ⎪ ⎪ π x + y = ⎩ ⎪ 3 y = − k π ⎪ 2 ⎩ 3 ⎪⎩ 6 Caùch 2: Heä ñaõ cho ⎧ π ⎧ π y = − x y = − ⎪ ⎪ x ⎪ 3 ⎪ 3 ⇔ ⎨ ⇔ ⎨ ⎛ π ⎞ 3 1 sin ⎪ x + sin − x = 1 ⎪ ⎜ ⎟ cos x + sin x = 1 ⎪⎩ ⎝ 3 ⎠ ⎪⎩ 2 2 ⎧ π ⎧ π y = − x y = − ⎪ x 3 ⎪ ⎪ ⎪ 3 ⇔ ⎨ ⇔ ⎨ ⎛ π ⎞ π π sin ⎪ + x = 1 ⎪ ⎜ ⎟ + x = + k2π ⎪⎩ ⎝ 3 ⎠ ⎪⎩3 2 ⎧ π x = + k2π ⎪⎪ 6 ⇔ ⎨ k ∈ π ⎪y = − k2π ⎪⎩ 6 sin ⎧⎪ x + sin y = 2 (1)
Baøi 175: Giaûi heä phöông trình: ⎨⎪cosx + cosy = 2 (2) ⎩ Caùch 1: ⎧ x + y x − y 2sin cos = 2 (1) ⎪ Heä ñaõ cho ⎪ 2 2 ⇔ ⎨ x + y x − y ⎪2cos cos = 2 (2) ⎪⎩ 2 2
Laáy (1) chia cho (2) ta ñöôïc: ⎛ x + y ⎞ x − y tg = ⎜ ⎟ 1 ( do cos
= 0 khoâng laø nghieäm cuûa (1) vaø (2) ) ⎝ 2 ⎠ 2 x + y π ⇔ = + kπ 2 4 π π
⇔ x + y = + k2π ⇔ y = − x + k2π 2 2
thay vaøo (1) ta ñöôïc: sin x sin ⎛ π x k2 ⎞ + − + π = 2 ⎜ 2 ⎟ ⎝ ⎠ ⇔ sin x + cos x = 2 ⎛ π ⎞ ⇔ 2 cos x − = 2 ⎜ ⎟ ⎝ 4 ⎠ π ⇔ x − = h2 , π h ∈ 4 ⎧ π x = + h2 , π h∈ ⎪ Do ñoù: heä ñaõ cho ⎪ 4 ⇔ ⎨ π
⎪ y = + (k − h)2 ,πk,h∈ ⎪⎩ 4 ⎧A = B ⎧A + C = B + D Caùch 2: Ta coù ⎨ ⇔ C ⎩ D ⎨ = ⎩A − C = B − D Heä ñaõ cho (
⎧ sin x − cos x) + (sin y − cos y) = ⎪ 0 ⇔ (⎨⎪sinx + ⎩
cos x) + (sin y − cos y) = 2 2 ⎧ ⎛ π ⎞ ⎛ π ⎞ 2 sin x − + 2 sin y − = ⎪ ⎜ ⎟ ⎜ ⎟ 0 ⎪ ⎝ 4 ⎠ ⎝ 4 ⎠ ⇔ ⎨⎪ ⎛ π ⎞ ⎛ π ⎞ 2 sin x + + 2 sin y + = ⎜ ⎟ ⎜ ⎟ 2 2 ⎪⎩ ⎝ 4 ⎠ ⎝ 4 ⎠ ⎧ ⎛ π ⎞ ⎛ π ⎞ sin x − + sin y − = 0 ⎪ ⎜ ⎟ ⎜ ⎟ ⎧ ⎛ π ⎞ ⎛ π ⎞ ⎝ 4 ⎠ ⎝ 4 ⎠ sin x − + sin y − = 0 ⎪ ⎪ ⎜ ⎟ ⎜ ⎟ ⎪ ⎝ 4 ⎠ ⎝ 4 ⎠ ⎪ ⎛ π ⎞ ⇔ ⎨ ⇔ sin ⎨ x + = 1 ⎜ ⎟ ⎪ ⎛ π ⎞ ⎛ π ⎞ ⎪ ⎝ 4 ⎠ sin x + + sin y + = 2 ⎜ ⎟ ⎜ ⎟ ⎪⎩ ⎝ 4 ⎠ ⎝ 4 ⎪ ⎠ ⎛ π ⎞ sin ⎪ y + = 1 ⎜ ⎟ ⎩ ⎝ 4 ⎠ ⎧ π π x + = + k2π ⎪ 4 2 ⎪ ⎪ π π
⇔ ⎨y + = + h2π 4 2 ⎪ ⎪ ⎛ π ⎞ ⎛ π ⎞ sin x − + sin y − = 0 ⎪ ⎜ ⎟ ⎜ ⎟ ⎩ ⎝ 4 ⎠ ⎝ 4 ⎠ ⎧ π x = + k2π ⎪⎪ ⇔ 4 ⎨ π ⎪y = + h π 2 , h, k ∈ Z ⎪⎩ 4 ⎧tgx − tgy − tgxtgy = 1 (1) Baøi 176:
Giaûi heä phöông trình: ⎪⎨⎪⎩cos2y + 3cos2x = −1 (2)
Ta coù: tgx − tgy = 1 + tgxtgy ⎧⎪ ( − ) 1 ⎧ + tgxtgy = 0 tg x y = 1 ⎪ ⇔ ⎨ ∨ ⎨tgx − tgy = 0 1 ⎪⎩ + tgxtgy ≠ 0 ⎪ 2 1 ⎩ + tg x = 0 (VN) x y π π ⇔ − = + kπ (k ∈ Z), vôùi x, y ≠ + kπ 4 2 x y π π ⇔ = + + kπ, vôùi x, y ≠ + kπ 4 2
Thay vaøo (2) ta ñöôïc: cos 2y 3 cos⎛2y π k2 ⎞ + + + π = −1 ⎜ 2 ⎟ ⎝ ⎠
⇔ cos 2y − 3 sin2y = −1 3 1 1 ⎛ π ⎞ ⇔ 1 s in2 y − cos 2 y = ⇔ sin 2y − ⎜ ⎟ = 2 2 2 ⎝ 6 ⎠ 2 π π π 5π
⇔ 2y − = + h2π hay 2y − =
+ h2π (h ∈ Z ) 6 6 6 6 π π ⇔ y = + h , π h ∈ hay y = + h , π h ∈ (loïai) 6 2 Do ñoù: ⎧ 5π x = + (k + h)π ⎪ Heä ñaõ cho ⎪ 6 ⇔ ⎨
(h,k ∈ Z ) π ⎪y = + hπ ⎪⎩ 6 3
⎧⎪cos x − cos x + sin y = 0 (1) Baøi 177:
Giaûi heä phöông trình ⎨ 3 si
⎪⎩ n x − sin y + cos x = 0 (2) Laáy (1) + (2) ta ñöôïc: 3 3 sin x + cos x = 0 3 3 ⇔ sin x = − cos x 3 ⇔ tg x = 1 − ⇔ tgx = 1 − x π ⇔ = − + kπ (k ∈ Z) 4 Thay vaøo (1) ta ñöôïc: 3 = − = ( 2
sin y cos x cos x cos x 1 − cos x) = 2 1 cos x.sin x = sin 2x sin x 2 1 ⎛ π ⎞ ⎛ π = sin − sin − + ⎞ ⎜ ⎟ ⎜ kπ 2 ⎟ ⎝ 2 ⎠ ⎝ 4 ⎠ 1 ⎛ π ⎞ = − sin − + π ⎜ k ⎟ 2 ⎝ 4 ⎠ ⎧ 2 ⎪ (neáu k chaün) ⎪ = 4 ⎨ ⎪ 2 − ⎪ (neáu k leû) ⎩ 4 Ñaët 2 sin α = (vôùi 0 < α < 2π ) 4 ⎧ π ⎧ π x = − + 2 π m , m ∈ x = − + (2m + 1) π, m ∈ ⎪ ⎪ 4 4 Vaäy nghieäm heä ⎪ ⎪ ⎨ ∨ ⎨ ⎡y = α + h π 2 , h ∈ ⎡y = −α + 2 π h , h ∈ ⎪ ⎪ ⎢ ⎢ ⎪⎩⎣y = π − α + h π 2 , h ∈ ⎪⎩⎣y = π + α + h π 2 , h ∈
II. GIAÛI HEÄ BAÈNG PHÖÔNG PHAÙP COÄNG ⎧ 1 sin ⎪ x.cos y = − (1) Baøi 178:
Giaûi heä phöông trình: ⎨ 2 ⎪tgx.cotgy = 1 ⎩ (2)
Ñieàu kieän: cos x.sin y ≠ 0 ⎧1 ⎡ ⎪ ⎣ ( + ) + ( − ) 1 sin x y sin x y ⎤ = ⎦ −
Caùch 1: Heä ñaõ cho ⎪2 2 ⇔ ⎨sin x.cosy ⎪ − 1 = 0 ⎪⎩cos x.sin y
⎧⎪sin (x + y) + sin (x − y) = −1
⇔ ⎨⎪⎩sinxcosy −sinycosx = 0
⎧⎪sin(x + y) + sin(x − y) = 1 − ⇔ ⎨⎪⎩sin(x − y) = 0 ⎧⎪sin (x + y) = −1 ⇔ ⎨⎪⎩sin(x − y) = 0 ⎧ π ⎪x + y = − + k π 2 , k ∈ ⇔ ⎨ 2 ⎪⎩x − y = hπ, h ∈ ⎧ π
x = − + (2k + h) π , k, h ∈ ⎪⎪ ⇔ 4 2 ⎨ π y (2k h) π ⎪ = − + − , k, h ∈ ⎪⎩ 4 2 (nhaän do sin y cos x ≠ 0) Caùch 2: ( ) sin x cos y 2 ⇔
= 1 ⇔ sin x cos y = cos x sin y cos x sin y ⎧ 1
sin x cos y = − (3) ⎪ Theá ( ) 1 vaøo (2) ⎪ 2 ta ñöôïc: ⎨ 1
⎪cos xsin y = − (4) ⎪⎩ 2 si ⎧ n ⎪ (x + y) = 1 − (3) + (4) ⇔ ⎨si ⎪ n ⎩ (x − y) = 0 (3) − (4) ⎧ π
⎪x + y = − + k2 , π k ∈ ⇔ ⎨ 2
⎪⎩x − y = h ,πh∈ ⎧ π π x = − + (2k + h) ⎪ ⎪ 4 2 ⇔ ⎨
(h,k ∈ Z ) π π
⎪ y = − + (2k − h) ⎪⎩ 4 2
III. GIAÛI HEÄ BAÈNG AÅN PHUÏ Baøi 179: Giaûi heä phöông trình: ⎧ 2 3 tgx ⎪ + tgy = ( ) 1 ⎪ 3 ⎨ ⎪ 2 − 3 cotgx + cotgy = (2) ⎪⎩ 3 Ñaët X = tgx, Y = tgy ⎧ 2 3 ⎧ 2 3 ⎪X + Y = ⎪X + Y = Heä ñaõ cho thaønh: ⎪ 3 ⎪ 3 ⎨ ⇔ ⎨ ⎪ 1 1 2 3 ⎪ Y + X 2 3 + = − = − ⎪ X Y 3 ⎪ ⎩ ⎩ YX 3 ⎧ 2 3 ⎧ 2 3 ⎪X + Y = ⎪X + Y = ⎪ 3 ⇔ ⎨ 3 ⇔ ⎨ ⎪ ⎪ 2 2 3 ⎩XY = 1 − X − X − 1 = 0 ⎪⎩ 3 ⎧X = 3 ⎧ 3 ⎪ ⎪X = − ⇔ ⎨ ∨ ⎨ 3 3 ⎪Y = − ⎪ ⎩ 3 ⎩Y = 3 Do ñoù: ⎧tgx = 3 ⎧ 3 ⎪ ⎪tgx = − Heä ñaõ cho : ⇔ ⎨ ∨ ⎨ 3 3 ⎪tgy = − ⎪ ⎩ 3 ⎩tgy = 3 ⎧ π ⎧ π x = + k , π k ∈ x = − + k , π k ∈ ⎪ ⎪ ⎪ 3 ⎪ 6 ⇔ ⎨ ∨ ⎨ π π ⎪y h , ⎪ = − + π h ∈ y = + h , π h∈ ⎪⎩ 6 ⎪⎩ 3 ⎧ 1 si ⎪ n x + sin y = Baøi 180: Cho heä phöông trình: ⎨ 2 ⎪⎩cos2x + cos2y = m 1
a/ Giaûi heä phöông trình khi m = − 2
b/ Tìm m ñeå heä coù nghieäm. ⎧ 1 sin x + sin y = Heä ñaõ cho ⎪ ⇔ 2 ⎨( 2 ⎪ 1 − 2sin x ⎩ ) + ( 2 1 − 2sin y) = m ⎧ 1 sin x + sin y = ⎪⎪ ⇔ 2 ⎨ 2 2 2 − ⎪ m sin x + sin y = ⎪⎩ 2 ⎧ 1 sin x + sin y = ⎪⎪ ⇔ 2 ⎨(⎪ m
sin x + sin y)2 − 2sin x sin y = 1 − ⎪⎩ 2 ⎧ 1 sin x + sin y = ⎪⎪ ⇔ 2 ⎨ ⎪1 m − 2sin x sin y = 1 − ⎪⎩4 2 ⎧ 1 sin x + sin y = ⎪⎪ ⇔ 2 ⎨ ⎪ 3 m sin x sin y = − + ⎪⎩ 8 4
Ñaët X = sin x, Y = sin y vôùi X , Y ≤ 1
thì X, Y laø nghieäm cuûa heä phöông trình 2 1 m 3 t − t + − = 0 (*) 2 4 8 1
a/ Khi m = − thì(*) thaønh : 2 2 1 1 t − t − = 0 2 2 ⇔ 2 2t − t − 1 = 0 1 ⇔ t = 1 ∨ t = − 2 si ⎧ n x = 1 ⎧ 1 ⎪ si ⎪ n x = − Vaäy heä ñaõ cho ⇔ ⎨ 1 ∨ ⎨ 2 sin y = − ⎪⎩ 2 si ⎪⎩ n y = 1 ⎧ π ⎧ h π x = + k2 , π k ∈ x = −(−1) + h , π h∈ ⎪ ⎪ ⎪ 2 ⎪ 6 ⇔ ⎨ ∨ ⎨ h π π ⎪y ( 1) h , ⎪ = − − + π h∈ y = + k2 , π k ∈ ⎪⎩ 6 ⎪⎩ 2 m 1 3 b/ Ta coù : (*) 2 ⇔ = −t + t + 4 2 8 Xeùt 2 1 3
y = −t + t + (C) treân D = [−1, ] 1 2 8 1 thì: y ' = 2 − t + 2 1 y ' = 0 ⇔ t = 4
Heä ñaõ cho coù nghieäm ⇔ (*) coù 2 nghieäm treân[-1, ] 1 ⇔ ( ) m d y =
caét (C) taïi 2 ñieåm hoặ treân -1,1 4 c tiếp xúc [ ] 1 m 7 ⇔ − ≤ ≤ 8 4 16 1 7 ⇔ − ≤ m ≤ 2 4 Caùch khaùc 2
ycbt ⇔ f (t) = 8t − 4t − 3 + 2m = 0 coù 2 nghieäm t1 , t2 thoûa ⇔ 1
− ≤ t ≤t ≤1 1 2 / ⎧Δ = 28 −16m ≥ 0
⎪af (1) =1+ 2m ≥ 0 ⎪⎪ ⇔ 1 7 ⎨af ( 1
− ) = 9 + 2m ≥ 0 ⇔ − ≤ m ≤ ⎪ 2 4 S 1 ⎪ 1 − ≤ = ≤ 1 ⎪⎩ 2 4 2 sin ⎧⎪ x + mtgy = m Baøi 181: Cho heä phöông trình: ⎨ 2 ⎪⎩tg y + msin x = m a/ Giaûi heä khi m = -4 b/
Vôùi giaù trò naøo cuûa m thì heä coù nghieäm.
Ñaët X = sin x vôùi X ≤ 1 Y = tgy 2 ⎧X + mY = m ⎪ (1) Heä thaønh: ⎨ 2 ⎪Y + mX = m ⎩ (2)
Laáy (1) – (2) ta ñöôïc: 2 2 X − Y + m (Y − X) = 0
⇔ (X − Y)(X + Y − m) = 0 ⇔ X = Y ∨ Y = m − X ⎧X = Y
⎧Y = m − X Heä thaønh ⎪ ⎨ hay ⎨ 2 2
⎩X + mX = m ⎪X + ⎩
m (m − X ) = m ⎧X = Y ⎪ ⎧Y = m − X ⎪ ⇔ ⎨ ∨ 2 ⎪X + mX − m = 0 ⎩ (*) ⎨ 2 2 ⎪X − mX + m − m = 0 ⎩ (* *)
a/Khi m = -4 ta ñöôïc heä ⎧X = Y ⎧Y = 4 − − X ⎪ ⎨ ∨ 2 ⎨ 2
⎩X − 4X + 4 = 0 ⎪X + 4X + 20 = 0 ⎩ (voâ nghieäm) ⎧⎪X = 2(loaïido X ≤ 1) ⇔ ⎨⎪⎩Y = 2
Vaäy heä ñaõ cho voâ nghieäm khi m = 4. b/ Ta coù (*) 2
⇔ X + mX − m = 0 vôùi X ≤ 1 2 ⇔ X = m (1 − X) 2 X ⇔
= m (do m khoâng laø nghieäm cuûa *) 1 − X 2 2 Xeùt X = [− ) −X + 2X Z treân 1,1 ⇒ Z' = ; 1 − X (1 − X)2 Z' = 0 ⇔ X = 0 ∨ X = 2 ⎧⎪X = Y ( X ≤ 1) Do ñoù heä ⎨ coù nghieäm ⇔ m ≥ 0 2 ⎪⎩X + mX − m = 0 Xeùt (**): 2 2 X − mX + m − m = 0 Ta coù 2 Δ = − ( 2 − ) 2 m 4 m m = −3m + 4m 4 Δ ≥ 0 ⇔ 0 ≤ m ≤ 3
Keát luaän: i Khi m ≥ 0 thì (I) coù nghieäm neân heä ñaõ cho coù nghieäm
i Khi m < 0 thì (I) voâ nghieäm maø (**) cuøng voâ nghieäm
(do Δ < 0) neân heä ñaõ cho voâ nghieäm
Do ñoù: Heä coù nghieäm ⇔ m ≥ 0 Caùch khaùc Heä coù nghieäm ⇔ = 2 f (X) X + mX − m = 0 (*)hay = 2 − + 2 g(X) X
mX m − m = 0 (**) coù nghieäm treân [-1,1] 2
⎧Δ = m + 4m ≥ 0 1 ⎪af (1) ≥ 0 ⎪ ⇔ ⎪ f ( 1
− ) f (1) ≤ 0 hay ⎨af ( 1 − ) ≥ 0 ⎪ S − m ⎪−1≤ = ≤ 1 ⎪⎩ 2 2 2
⎧Δ = −3m + 4m ≥ 0 2 ⎪ 2
⎪ag(−1) = m +1 ≥ 0 hay ⎪ g( 1
− )g(1) ≤ 0 hay 2
⎨ag( 1)=(m −1) ≥ 0 ⎪ ⎪ S m 1 − ≤ = ≤ 1 ⎪⎩ 2 2 2
⎧Δ = m + 4m ≥ 0 1 4 ⇔ ⎪
1 − 2m ≤ 0 hay 1 ⎨ − 2m ≥ 0 hay m = 1 hay 0 ≤ m ≤ ⎪ 3 −2≤ m ≤ 2 ⎩ ⇔ m ≥ 0
IV. HEÄ KHOÂNG MAÃU MÖÏC ⎧ ⎛ π ⎞ tgx + ⎪ cotgx = 2sin ⎜ y + ⎟ (1) 4 Baøi 182:
Giaûi heä phöông trình: ⎪ ⎝ ⎠ ⎨ ⎪ ⎛ π ⎞
tgy + cotgy = 2sin ⎜ x - ⎟ (2) ⎪⎩ ⎝ 4 ⎠ Caùch 1: 2 2 sinα cos α sin α + cos α 2 Ta coù: tgα + cotgα= + = = cosα sin α sin α cosα sin 2α ⎧ 1 ⎛ π ⎞ = sin y + ⎪ ⎜ ⎟ (1) sin 2x 4 Vaäy heä ñaõ cho ⎪ ⎝ ⎠ ⇔ ⎨⎪ 1 ⎛ π ⎞ = sin x − ⎜ ⎟ (2) ⎪⎩ sin 2y ⎝ 4 ⎠ ⎧ ⎛ π ⎞ 1 = sin 2x sin y + ⎪ ⎜ ⎟ (1) 4 ⎪ ⎝ ⇔ ⎠ ⎨ ⎪ ⎛ π ⎞ 1 = sin 2y.sin x − ⎜ ⎟ (2) ⎪⎩ ⎝ 4 ⎠ ⎧sin 2x = 1 ⎧sin 2x = 1 − Ta coù: (1) ⎪ ⎪ ⇔ ⎨ ⎛ π ⎞ ∨ ⎨ ⎛ π ⎞ sin y + = 1 sin y + = − ⎪ ⎜ ⎟ ⎪ ⎜ ⎟ 1 ⎩ ⎝ 4 ⎠ ⎩ ⎝ 4 ⎠ ⎧ π ⎧ π x = + π k , k ∈ x = − + π k , k ∈ ⎪ ⎪ ⎪ 4 ⎪ ⇔ 4 ⎨ ∨ ⎨ π π ⎪ ⎪ 3 y = + h π 2 , h ∈ y = − + h π 2 , h ∈ ⎪⎩ 4 ⎪⎩ 4 ⎧ π x = + π k , k ∈ ⎪ Thay ⎪ 4 ⎨ vaøo (2) ta ñöôïc π ⎪y = + h π 2 , h ∈ ⎪⎩ 4 sin 2y.sin ⎛ x π ⎞ − = sin π .sin kπ = 0 ≠ 1 ⎜ (loaïi) 4 ⎟ ⎝ ⎠ 2 ⎧ −π x = + π k , k ∈ ⎪ Thay ⎪ 4 ⎨ vaøo (2) ta ñöôïc π ⎪ 3 y = − + h π 2 , h ∈ ⎪⎩ 4 ⎛ π ⎞ ⎛ π 3 ⎞ ⎛ π sin 2y.sin x − = sin − sin − + π⎞ ⎜ ⎟ ⎜ ⎟ ⎜ k ⎟ ⎝ 4 ⎠ ⎝ 2 ⎠ ⎝ 2 ⎠ ⎛ π ⎞ ⎧1 ( neáu k leû) = sin − + π k = ⎜ ⎟ ⎨ ⎝ 2 ⎠ ⎩−1 ( neáu k chaün) Do ñoù heä coù nghieäm ⎧ π x = − + (2m + 1) π ⎪⎪ 4 ⎨ (m, h ∈ Z) • π ⎪ 3 y = − + h π 2 ⎪⎩ 4 Caùch 2:
Do baát ñaúng thöùc Cauchy tgx + cotgx ≥ 2 1
daáu = xaûy ra ⇔ tgx = cotgx ⇔ tgx= tgx ⇔ tgx = 1 ± Do ñoù: tgx+cotgx 2 2sin ⎛ y π ⎞ ≥ ≥ + ⎜ 4 ⎟ ⎝ ⎠
Daáu = taïi (1) chæ xaûy ra khi ⎧tgx = 1 ⎧tgx = −1 ⎪ ⎪ ⇔ ⎨ ⎛ π ⎞ ∨ ⎨ ⎛ π ⎞ sin y + = 1 sin y + = − ⎪ ⎜ ⎟ ⎪ ⎜ ⎟ 1 ⎩ ⎝ 4 ⎠ ⎩ ⎝ 4 ⎠ ⎧ π ⎧ π x = + π k , k ∈ x = − + π k , k ∈ ⎪ ⎪ ⎪ 4 ⎪ ⇔ 4 ⎨ (I) ∨ ⎨ (II) π π ⎪ ⎪ 3 y = + h π 2 , h ∈ y = − + h π 2 , h ∈ ⎪⎩ 4 ⎪⎩ 4 thay (I) vaøo (2): ⎛ π ⎞ tgy + cotgy=2sin ⎜x - ⎟ ⎝ 4 ⎠
ta thaáy 2 = 2sin kπ = 0 khoâng thoûa thay (II) vaøo (2) ta thaáy ⎛ π ⎞ 2 = 2 sin − + k π ⎜ ⎟ ⎝ 2 ⎠ chæ thoûa khi k leû ⎧ π x = − + (2m + 1) π ⎪ Vaäy: heä ñaõ cho ⎪ ⇔ 4 ⎨ , m, h ∈ π ⎪ 3 y = − + 2 π h ⎪⎩ 4 Baøi 183: Cho heä phöông trình: ⎧x − y = m (1) ⎪ ⎨ ⎪2 ⎩ (cos 2x + cos 2y) 2 − 1 − 4 cos m = 0 (2) Tìm m ñeå heä
phöông trình coù nghieäm. ⎧x − y = m Heä ñaõ cho ⎪ ⇔ ⎨⎪4cos ⎩ (x + y)cos(x − y) 2 = 1 + 4 cos m ⎧x − y = ⎪ m ⇔ ⎨⎪− 2
⎩ 4 cos (x + y) cos m + 4 cos m + 1 = 0 ⎧x − y = ⎪ m ⇔ ⎨ ⎪[2 cos m − 2 2 ⎩
cos (x + y)] + 1 − cos (x + y) = 0 ⎧x − y = ⎪ m ⇔ ⎨⎪[2cosm − 2 2 ⎩ cos (x + y)] + sin (x + y) = 0 ⎧x − y = m ⎪ ⇔ ⎨cos (x + y) = 2 cos m ⎪sin(x + y) = ⎩ 0 ⎧x − y = m ⎪ ⇔ ⎨x + y = π k , k ∈ ⎪cos π (k ) = ⎩ 2 cos m 2 Do ñoù heä coù nghieäm π π ⇔ m = ± + h π 2 ∨ m = ± + h π 2 , h ∈ 3 3 BAØI TAÄP
1. Giaûi caùc heä phöông trình sau: sin ⎧ x + sin y = 2 ⎧tgx + tgy + tgxtgy = 1 a/ ⎨ f / 2 2 ⎨ sin ⎩ x + sin y = 2 ⎩3sin 2y − 2 = cos 4x ⎧ 1 ⎧ sin x sin y = − 3 ⎪ ⎪sin x − sin 2y = ⎪ 2 ⎪ ⎨ ⎨ 2 b / g / ⎪ 1 ⎪ = 1 cos x cos y cos x + cos 2y = ⎪⎩ 2 ⎪⎩ 2 ⎧cos(x + y) = 2cos(x − y) ⎧⎪ 2 cos x = 1 + cos y c / h / ⎪ ⎨ ⎨ 3 ⎪⎩ 2 sin x = sin y ⎪cos x.cos y = ⎩ 4 ⎧ 1 sin ⎪ x cos y = sin ⎧ x = 7 cos y d / ⎨ 4 k / 5s ⎨ ⎪ ⎩ in y = cos x − 6 ⎩3tgx = tgy 2 ⎧tgx + tgy = 1 s ⎧⎪ in x = cos x cos y e / l / ⎪ ⎨ ⎨ x y 2 ⎪⎩cos x = sin x sin y tg + tg = 2 ⎪⎩ 2 2 ⎧cos x cos y = m + 1
2.Cho heä phöông trình: ⎨ 2 si ⎩ n x sin y = 4m + 2m 1 a/ Giaûi heä khi m = − 4
b/ Tìm m ñeå heä coù nghieäm ⎛ 3 1 ⎞ ÑS − ≤ m ≤ − ⎜ hay m=0⎟ ⎝ 4 4 ⎠
3. Tìm a ñeå heä sau ñaây coù nghieäm duy nhaát: ⎧⎪ 2 y + 2 tg x = 1 ⎨ ⎪y + 1 = 2 ax + a + ⎩ sin x (ÑS a= 2)
4. Tìm m ñeå caùc heä sau ñaây coù nghieäm. 3 2 ⎧⎪cos x = m cos y sin ⎧ x cos y = m a / ⎨ b / ⎨ 3 sin ⎪⎩ x = m cos y sin ⎩ y cos x = m ( ⎛ 1- 5 1 + 5 ⎞ ÑS 1 ≤ m ≤ 2) ⎜ÑS ≤ m ≤ ⎟ ⎜ ⎟ ⎝ 2 2 ⎠ CHÖÔNG X:
HEÄ THÖÙC LÖÔÏNG TRONG TAM GIAÙC
I. ÑÒNH LYÙ HAØM SIN VAØ COSIN Cho A
Δ BC coù a, b, c laàn löôït laø ba caïnh ñoái dieän cuûa m m l A, B, C, R laø
baùn kính ñöôøng troøn ngoaïi tieáp A Δ BC , S laø dieän tích A Δ BC thì a b c = = = 2R sin A sin B sin C 2 a = 2 b + 2 c − 2bc cos A = 2 b + 2 c − 4S.cotgA 2 b = 2 a + 2 c − 2ac cos B = 2 a + 2 c − 4S.cotgB 2 c = 2 a + 2 b − 2ab cos C = 2 a + 2 b − 4S.cotgC Baøi 184 Cho A Δ BC . Chöùng minh: 2 2 A = 2B ⇔ a = b + bc Ta coù: a2 2 2 2 2 2 2
= b + bc ⇔ 4R sin A = 4R sin B + 4R sin B.sin C ⇔ 2 − 2 sin A sin B = sin B sin C 1 1
⇔ (1 − cos 2A) − (1 − cos 2B) = sin B sin C 2 2
⇔ cos 2B − cos 2A = 2 sin B sin C
⇔ −2 sin (B + A) sin (B − A) = 2sin B sin C
⇔ sin (B + A) sin (A − B) = sin B sin C
⇔ sin (A − B) = sin B (do sin (A + B) = sin C > 0)
⇔ A − B = B ∨ A − B = π − B (loaïi) ⇔ A = 2B Caùch khaùc: 2 − 2 sin A sin B = sin B sin C
⇔ (s in A − sin B) (s in A + sin B) = sin B sin C A + B A − B A + B A − B ⇔ 2 cos sin .2 sin co s = sin B sin C 2 2 2 2
⇔ sin (B + A) sin (A − B) = sin B sin C
⇔ sin (A − B) = sin B (do sin (A + B) = sin C > 0)
⇔ A − B = B ∨ A − B = π − B (loaïi) ⇔ A = 2B sin (A − B) 2 2 a − b Baøi 185: Cho A Δ BC . Chöùng minh: = 2 sin C c 2 2 2 2 2 2 a b 4R sin A 4R sin B Ta coù − − = 2 2 2 c 4R sin C1 1 2 2
(1 − cos 2A) − (1 − cos 2B) sin A − sin B = = 2 2 2 2 sin C sin C cos 2B − cos 2A −2 sin (A + B) sin (B − A) = = 2 2 2 sin C 2 sin C
sin (A + B) .sin (A − B) sin (A − B) = = 2 sin C sin C (do sin(A + B) = sinC > 0) A B 1 Baøi 186: Cho A Δ BC bieát raèng tg ⋅ tg = ⋅ 2 2 3 Chöùng minh a + b = 2c A B 1 A B A B Ta coù : tg ⋅ tg = ⇔ 3sin sin = cos cos 2 2 3 2 2 2 2 ⎛ A B do cos 0,cos 0⎞ > > ⎜ 2 2 ⎟ ⎝ ⎠ A B A B A B ⇔ 2sin sin = cos cos − sin sin 2 2 2 2 2 2 ⎡ A + B A − B⎤ A + B ⇔ − cos − cos = cos ⎢ 2 2 ⎥ ⎣ ⎦ 2 A − B A + B ⇔ cos = 2cos (*) 2 2 Maët khaùc: a + b = 2R (sin A + sin B) A + B A − B = 4R sin cos 2 2 A + B A + B = 8R sin cos (do (*)) 2 2 = 4R sin (A + B) = 4R sin C = 2c Caùch khaùc: a + b = 2c
⇔ 2R (sin A + sin B) = 4R sin C A + B A − B C C ⇔ 2 sin cos = 4 sin cos 2 2 2 2 A − B C A + B ⎛ A + B C ⎞ ⇔ cos = 2 sin = 2 cos do sin = ⎜ cos ⎟ 2 2 2 ⎝ 2 2 ⎠ A B A B A B A B ⇔ cos cos + sin sin = 2 cos cos − 2 sin sin 2 2 2 2 2 2 2 2 A B A B ⇔ 3sin sin = cos cos 2 2 2 2 A B 1 ⇔ tg ⋅ tg = 2 2 3 Baøi 187: Cho A
Δ BC , chöùng minh neáu cotgA,cotgB,cotgC taïo moät caáp soá coäng thì 2 2 2
a , b ,c cuõng laø caáp soá coäng.
Ta coù: cot gA, cot gB, cot gC laø caáp soá coäng ⇔ cot gA + cot gC = 2 cot gB (*) Caùch 1: + Ta coù:(*) sin (A C) 2cosB 2 ⇔ = ⇔ sin B = 2sin A sin C cos B sin A sin C sin B 2
⇔ sin B = − ⎡cos(A + C) − cos(A − C)⎤ ⎡− cos(A + C)⎤ ⎣ ⎦ ⎣ ⎦ 2 2
⇔ sin B = cos (A + C) − cos(A − C) cos(A + C) 2 2 1
⇔ sin B = cos B − [cos2A + cos2C] 2 2 ⇔ = ( 2 − ) 1 sin B 1 sin B − ⎡⎣( 2 1 − 2sin A) + ( 2 1 − 2sin C)⎤ 2 ⎦ 2 2 2 ⇔ 2sin B = sin A + sin C 2 2 2 2b a c ⇔ = + 2 2 2 4R 4R 4R 2 2 2 ⇔ 2b = a + c 2 2 2
⇔ a , b ,c laø caâùp soá coäng • Caùch 2: 2 Ta coù: a = 2 b + 2 c − 2ab cos A 2 2 2 ⎛ 1 ⎞
⇔ a = b + c − 4 ⎜ bc sin A⎟.cotgA ⎝ 2 ⎠ ⇔ 2 a = 2 b + 2 c − 4S cot gA 2 b + 2 c − 2 a Do ñoù cotgA = 4S 2 a + 2 c − 2 2 b a + 2 b − 2 c Töông töï cotgB = , cotgC = 4S 4S 2 2 2 2 2 2 2 2 2 ( ) b + c − a a + b − c a + c − b Do ñoù: * ⇔ + = 2 ⋅ 4S 4S 4S ⇔ 2 2b = 2 a + 2 c Baøi 188: Cho A Δ BC coù 2 2 sin B + sin C = 2sin2 A Chöùng minh n 0 BAC ≤ 60 . 2 2 2 Ta coù: sin B + sin C = 2sin A 2 2 2 b c 2a ⇔ + = 2 2 2 4R 4R 4R 2 2 2 ⇔ b + c = 2a (*)
Do ñònh lyù haøm cosin neân ta coù 2 2 2 a = b + c − 2bc cos A b c a 2 ( 2 b + 2 c ) − 2 b − + − 2 2 2 2 c ⇔ cos A = = ( do (*)) 2bc 4bc 2 b + 2 c 2bc 1 = ≥ = (do Cauchy) 4bc 4bc 2 n Vaïây : BAC ≤ 0 60 . Caùch khaùc: ñònh lyù haøm cosin cho 2 = 2 + 2 − ⇒ 2 + 2 = 2 a b c 2bc cos A b c a + 2bc cos A Do ñoù (*) ⇔ a2 + 2bc cos A = a2 2 a2 b2 + c2 ⇔ 1 cos A = = ≥ ( do Cauchy) 2bc 4bc 2 Baøi 189: Cho A
Δ BC . Chöùng minh : ( 2 2 2 R a + b + c ) cotgA+cotgB+cotgC = abc 2 b + 2 c − 2 a Ta coù: cotgA = 4S 2 a + 2 c − 2 2 b a + 2 b − 2 c Töông töï: cot gB = , cot gC = 4S 4S 2 a + 2 b + 2 2 c a + 2 b + c2
Do ñoù cot gA + cot gB + cot gC = = 4S abc 4 4R 2 a + 2 b + 2 c = R abc Baøi 190: Cho A
Δ BC coù 3 goùc A, B, C taïo thaønh moät caáp soá nhaân coù coâng
boäi q = 2. Giaû söû A < B < C. 1 1 1 Chöùng minh: = + a b c
Do A, B, C laø caáp soá nhaân coù q = 2 neân B = 2A, C = 2B = 4A π 2π 4 Maø A B C neân A ,B ,C π + + = π = = = 7 7 7 Caùch 1: 1 1 1 1 Ta coù: + = + b c 2R sin B 2R sin C ⎛ ⎞ 1 ⎜ 1 1 ⎟ = ⎜ + ⎟ 2R π 2 4π ⎜ sin sin ⎟ ⎜ ⎟ ⎝ 7 7 ⎠ 4π π 2 sin + sin 1 = 7 7 2R π 2 4π sin sin 7 7 π 3 π 2 sin .cos 1 7 7 ⎛ 4π π 3 ⎞ = ⋅ do sin = ⎜ sin ⎟ 2R 2π π 3 ⎝ 7 7 ⎠ sin .sin 7 7 π cos 1 7 1 = ⋅ = R π π 2R sin A 2 sin .cos 7 7 1 = a Caùch 2: 1 1 1 1 1 1 = + ⇔ = + a b c sin A sin B sin C 1 1 1 sin 4A + sin 2A ⇔ = + = sin A sin 2A sin 4A sin 2A sin 4A 1 2 sin 3A.cos A 2 cos A 2 cos A ⇔ = = = sin A sin 2A sin 4A sin 2A 2 sin A cos A π 3 4π do : sin 3A = sin = sin = sin 4A • 7 7 Baøi 191: Tính caùc goùc cuûa A Δ BC neáu sin A sin B sin C = = 1 3 2 a b c Do ñònh lyù haøm sin: = = = 2R sin A sin B sin C sin A sin B sin C neân : = = (*) 1 3 2 a b c ⇔ = = 2R 2R 3 4R b c ⎧⎪b = a 3 ⇔ a = = ⇔ ⎨ 3 2 ⎪⎩c = 2a Ta coù: c = 4a = (a 3)2 2 2 + a2 2 2 2 ⇔ c = b + a Vaïây A Δ BC vuoâng taïiC
Thay sin C = 1 vaøo(*) ta ñöôïc sin A sin B 1 = = 1 3 2 ⎧ 1 sin A = ⎪⎪ 2 ⇔ ⎨⎪ 3 sin B = ⎪⎩ 2 0 ⎧⎪A = 30 ⇔ ⎨ 0 ⎪⎩B = 60 Ghi chuù: Trong tam giaùc ABC ta coù
a = b ⇔ A = B ⇔ sin A = sin B ⇔ cos A = cos B
II. ÑÒNH LYÙ VEÀ ÑÖÔØNG TRUNG TUYEÁN
Cho UABC coù trung tuyeán AM thì: 2 2 2 2 BC AB + AC = 2AM + 2 2 a hay : 2 2 2 c + b = 2m + a 2
Baøi 192: Cho UABC coù AM trung tuyeán, n
AMB = α , AC = b, AB = c, S laø
dieän tích UABC. Vôùi 0 < α < 0 90 2 2 b − c a/ Chöùng minh: cotgα = 4S b/ Giaû söû 0
α = 45 , chöùng minh: cotgC – cotgB = 2 HM MB − BH a/ UAHM vuoâng ⇒ cotgα = = AH AH a BH ⇒ cotgα = − (1) 2AH AH b − c ( 2 2 2 2 a c 2ac cos B) c2 + − − Maët khaùc: = 4S 2AH.a Ñaët BC = a 2 2 b − c a c cos B a BH ⇒ = − = − (2) 4S 2AH AH 2AH AH 2 2 b − c
Töø (1) vaø (2) ta ñöôïc : cotg α = 4S Caùch khaùc:
Goïi S1, S2 laàn löôït laø dieän tích tam giaùc ABH vaø ACH
Aùp duïng ñònh lyù haøm cos trong tam giaùc ABH vaø ACH ta coù: 2 + 2 − 2 AM BM c cotg α = (3) 4S1 2 + 2 − 2 AM CM b − cotg α = (4) 4S2 Laáy (3) – (4) ta coù : 2 − 2 b c cotg α = ( vì S ) 4S 1=S2 = S 2 HC HB HC − HB b/Ta coù: cotgC – cotgB = − = AH AH AH (MH + MC) − (MB − MH) = AH 2MH = = 2 cotg α = 0 2 cotg 45 = 2 AH Caùch khaùc:
Aùp duïng ñònh lyù haøm cos trong tam giaùc ABM vaø ACM ta coù: 2 BM + 2 c − AM2 cotg B = (5) 4S1 2 CM + 2 b − AM2 cotg C = (6) 4S2 Laáy (6) – (5) ta coù : 2 − 2 b c cotg C − cot gB = = 2 cot gα =2 ( vì S vaø caâu a ) 2S 1=S2 = S 2 Baøi 193 Cho
UABC coù trung tuyeán phaùt xuaát töø B vaø C laø m , m thoûa b c c mb =
≠ 1 . Chöùng minh: 2cotgA = cotgB + cotgC b mc 2 2 Ta coù: c mb = 2 2 b mc 1 ⎛ 2 2 2 b ⎞ a c 2 ⎜ + − ⎟ c 2 ⎝ 2 ⎠ ⇔ = 2 b 1 ⎛ 2 2 2 c ⎞ b + a − ⎜ ⎟ 2 ⎝ 2 ⎠ 4 4 c b ⇔ 2 2 b c + 2 2 a c − = 2 2 a b + 2 2 b c − 2 2 1 ⇔ 2 2 a c − 2 2 a b = ( 4 c − 4 b ) 2 1 ⇔ 2 a ( 2 c − 2 b ) = ( 2 c − 2 b ) ( 2 c + 2 b ) 2 2 2 2 2a c b (1) ⎛ c ⎞ ⇔ = + do ≠ ⎜ 1⎟ ⎝ b ⎠ Thay 2 + 2 = 2 b c
a + 2bc cos A vaøo (1), ta coù (1) thaønh a2 = 2bc cos A 2 2 2 a 4R sin A ⇔ cos A = = 2bc 2 (2R sin B) (2R sin C) cos A sin A sin (B + C) ⇔ 2 = = sin A sin B sin C sin B sin C sinBcosC+ sinCcosB ⇔ 2 cotgA = = cotgC+ cotgB sin B sin C
Baøi 194: Chöùng minh neáu UABC coù trung tuyeán AA’ vuoâng goùc vôùi trung
tuyeán BB’ thì cotgC = 2 (cotgA + cotgB)
UGAB vuoâng taïi G coù GC’ trung tuyeán neân AB = 2GC’ 2 Vaäy AB = C ′ C 3 2 2 ⇔ 9c = 4mc 2 ⎛ ⎞ 2 2 2 c ⇔ 9c = 2⎜ b + a − 2 ⎟ ⎝ ⎠ 2 2 2 ⇔ 5c = a + b 2 2
⇔ 5c = c + 2ab cosC(do ñònh lyù haøm cos) 2 ⇔ 2c = ab cosC
⇔ 2(2R sin C)2 = (2R sin A)(2R sin B) cosC ⇔ 2 2 sin C = sin A sin B cos C 2 sin C cos C ⇔ = sin A sin B sin C 2 sin (A + B) ⇔ = cotgC sin A sin B 2 (sin A cos B + sin B cos A) ⇔ = cotgC sin A sin B ⇔ 2 (cotg B + cotgA) = cotgC
III. DIEÄN TÍCH TAM GIAÙC Goïi S: dieän tích UABC
R: baùn kính ñöôøng troøn ngoaïi tieáp UABC
r: baùn kính ñöôøng troøn noäi tieáp UABC p: nöûa chu vi cuûa UABC thì 1 1 1 S = a.h = b.h = c.h a b c 2 2 2 1 1 1
S = absin C = ac sin B = bc sin A 2 2 2 abc S = 4R S = pr
S = p (p − a)(p − b)(p − c) 2S Baøi 195: Cho
UABC chöùng minh: sin 2A + sin 2B + sin 2C = 2 R Ta coù: sin2A+ (sin2B + sin2C)
= sin2A + 2sin(B + C).cos(B - C) = 2sinAcosA + 2sinAcos(B - C) = 2sinA[cosA + cos(B - C)]
= 2sinA[- cos(B + C) + cos(B - C)] = 2sinA.[2sinB.sinC] a b c 1 abc = 4. . . 1 4RS 2S = = = 3 2R 2R 2R 2 R 3 2 2 R R Baøi 196 Cho UABC. Chöùng minh : 1 S = Dieän tích (UABC) = ( 2 2 a sin 2B + b sin 2A) 4 Ta coù : (Δ ) 1 S = dt ABC = absin C 2 1 = ab sin (A + B) 2 1 = ab[sin A cos B + sinB cos A] 2 1 ⎡⎛ a ⎞ ⎛ b ⎞ ⎤ = ab sin B cos B + ⎢⎜ ⎟
⎜ sin A ⎟ cos A⎥ (do ñl haøm sin) 2 ⎣⎝ b ⎠ ⎝ a ⎠ ⎦ 1 = ⎡ 2 2
a sin B cos B+ b sin A cos A⎤ ⎣ ⎦ 2 1 = ( 2 a sin 2B + 2 b sin 2A) 4 Baøi 197: Cho A
Δ BC coù troïng taâm G vaø n n n GAB = α,GBC = , β GCA = γ. ( 2 2 2 3 a + b + c )
Chöùng minh: cotgα + cotgβ +cotgγ = 4S
Goïi M laø trung ñieåm BC, veõ MH ⊥ AB AH AMH Δ ⊥⇒ cos α = AM BH 2BH BH Δ M ⊥⇒ cos B = = MB a Ta coù: AB = HA + HB a ⇔ c = AM cos α + cos B 2 1 ⎛ a cos c cos B⎞ ⇔ α = − ⎜ ⎟ (1) AM ⎝ 2 ⎠
Maët khaùc do aùp duïng ñònh lyù haøm sin vaøo ΔAMB ta coù : MB AM 1 a = ⇔ sin α = MBsin B = sin B (2) sin α sin B AM 2AM
Laáy (1) chia cho (2) ta ñöôïc : a c − cos B 2 2c − a cos B cot α g = = a b sin B a. 2 2R R (4c − 2a cos B) R ( 2 4c − 2ac cos B) = = ab abc 2 3c + 2 b − 2 2 a 3c + 2 b − 2 a = = abc 4S R Chöùng minh töông töï : 2 2 3a + c − b2 cotgβ = 4S 2 2 3b + a − c2 cotgγ = 4S Do ñoù: co α tg + co β tg + co γ tg 2 3c + 2 b − 2 2 a 3a + 2 c − 2 2 b 3b + 2 a − c2 = + + 4S 4S 4S 3( 2 a + 2 b + 2 c ) = 4S 3
Caùch khaùc : Ta coù 2 2 2 m + m + m = ( 2 2 2 a + b + c (*) a b c ) 4 2 2 a c + 2 m − 2 4c + 2 4m − 2 a a α = 4 cotg = a (a) 4S 8S ΔABM 2 2 2 2 2 2 4a + 4m − b 4b + 4m − c Töông töï b c cotgβ = (b),cotgγ = (c) 8S 8S
Coäng (a), (b), (c) vaø keát hôïp (*) ta coù: ( 2 + 2 + 2 3 a b c ) cotg α + cotg β + cotg γ = 4S
IV. BAÙN KÍNH ÑÖÔØNG TROØN
Goïi R baùn kính ñöôøng troøn ngoaïi tieáp A Δ BC
vaø r baùn kính ñöôøng troøn noäi tieáp A Δ BC thì a abc R = = 2 sin A 4S S r = p A B C r = (p − a) tg = (p − b) tg = (p − c) tg 2 2 2
Baøi 198: Goïi I laø taâm ñöôøng troøn noäi tieáp A Δ BC . Chöùng minh: A B C a/ r = 4R sin sin sin 2 2 2 2 b/ IA.IB.IC = 4Rr B BH a/ Ta coù : IB Δ H ⊥⇒ cotg = 2 IH B ⇒ BH = rcotg 2 C Töông töï HC = r cotg 2 Maø : BH + CH = BC neân ⎛ B C ⎞ r cotg + cotg = ⎜ ⎟ a ⎝ 2 2 ⎠ ⎛ B + C ⎞ r sin ⎜ ⎟ ⎝ 2 ⎠ ⇔ = a B C sin sin 2 2 A B C ⇔ r cos = (2R sin A) sin sin 2 2 2 A A A B C ⇔ r cos = 4R sin cos sin sin 2 2 2 2 2 A B C A ⇔ r = 4R sin sin sin . (do cos >0) 2 2 2 2 Α IK r b/ Ta coù : Δ ⊥ ΑΚΙ ⇒ sin = ⇒ IA = 2 IA A sin 2 r r Töông töï IB = ; IC = B sin C sin 2 2 3 r Do ñoù : IA.IB.IC = A B C sin sin sin 2 2 2 3 r 2 = = 4Rr (do keát quaû caâu a) r 4R Baøi 199: Cho A
Δ BC coù ñöôøng troøn noäi tieáp tieáp xuùc caùc caïnh A Δ BC taïi A’, B’, C’. A
Δ 'B'C' coù caùc caïnh laø a’, b’, c’ vaø dieän tích S’. Chöùng minh: a' b ' C ⎛ A B ⎞ a/ + = 2 sin sin + ⎜ sin ⎟ a b 2 ⎝ 2 2 ⎠ S' A B C b/ = 2 sin sin sin S 2 2 2 1 1 1 a/ Ta coù : n n
C'A 'B' = C'IB' = (π − A) = (B + C) 2 2 2
AÙp duïng ñònh lyù hình sin vaøo A Δ 'B'C'
a ' = 2r (r: baùn kính ñöôøng troøn noäi tieáp A Δ BC ) sin A ' m B + C ⇒ a ' = 2r sin A ' = 2r sin (1) 2 A
Δ BC coù : a = BC = BA '+ A 'C B C ⇒ a = r cot g + r cot g 2 2 B + C sin 2 ⇒ a = r (2) B C sin sin 2 2 a′ B C Laáy (1) ta ñöôïc = 2sin sin (2) a 2 2 b' A C Töông töï = 2sin .sin b 2 2 Vaäy a ' b' C ⎛ A B 2sin sin sin ⎞ + = + . a b 2 ⎜ 2 2 ⎟ ⎝ ⎠ 1 1 1 b/ Ta coù: n
A 'C'B' = .B'IA ' = (π − C) = (A + B) 2 2 2 A + B C Vaäy sin C' = sin = cos 2 2 1 S' (Δ ) a ' b'sin C' dt A 'B'C' Ta coù: 2 = = S dt (ΔABC) 1 absinC 2
S ' ⎛ a '⎞ ⎛ b '⎞ sin C ' ⇒ = ⎜ ⎟ ⎜ ⎟ S ⎝ a ⎠ ⎝ b ⎠ sin C C cos B 2 C A ⋅ 2 = 4 sin sin sin 2 2 2 C C 2 sin cos 2 2 B C A = 2 sin ⋅ sin ⋅ sin 2 2 2 Baøi 200: Cho A
Δ BC coù troïng taâm G vaø taâm ñöôøng troøn noäi tieáp I. Bieát GI
vuoâng goùc vôùi ñöôøng phaân giaùc trong cuûa n BCA . Chöùng minh: a + b + c 2ab = 3 a + b
Veõ GH ⊥ AC,GK ⊥ BC,ID ⊥ AC
IG caét AC taïi L vaø caét BC taïi N
Ta coù: Dt(ΔCLN) = 2Dt(ΔLIC) =ID.LC = r.LC (1) Maët khaùc: Dt( C Δ LN) = Dt( GL Δ C) + Dt( G Δ CN) 1 = (GH.LC + GK.CN) (2) 2 Do ΔCLN caân neân LC = CN
Töø (1) vaø (2) ta ñöôïc: 1 rLC = LC(GH + GK) 2 ⇔ 2r = GH + GK
Goïi h , h laø hai ñöôøng cao A
Δ BC phaùt xuaát töø A, B a b Ta coù: GK MG 1 GH 1 = = vaø = h MA 3 h 3 a b 1 Do ñoù: 2r = (h + h (3) a b ) 3 1 1 Maø: S = Dt ( A Δ BC) = pr = a.h = b.h a b 2 2 2pr 2pr Do ñoù: h = vaø h = a a b b Töø (3) ta coù: 2 ⎛ 1 1 2r pr ⎞ = + 3 ⎜ a b⎟ ⎝ ⎠ 1 ⎛ a + b ⎞ ⇔ 1 = p ⎜ ⎟ 3 ⎝ ab ⎠ a + b + c a + b ⇔ 3 = ⋅ 2 ab 2ab a + b + c ⇔ = a + b 3 BAØI TAÄP 1. Cho A
Δ BC coù ba caïnh laø a, b, c. R vaø r laàn löôït laø baùn kính ñöøông troøn
ngoaïi tieáp vaø noäi tieáp A Δ BC . Chöùng minh: C A B a/
(a − b)cotg + (b − c)cotg + (c − a)cotg = 0 2 2 2 r b/ 1 + = cos A + cos B + cosC R A B C c/ Neáu
cotg ,cotg ,cotg laø caáp soá coäng thì a, b, c cuõng laø caáp soá 2 2 2 coäng.
d/ Dieän tích ΔABC = R r (sin A + sin B + sin C) e/ Neáu : 4 4 a = b + c4 thì A
Δ BC coù 3 goùc nhoïn vaø 2 2sin A = tgB.tgC 8 2. Neáu dieän tích ( A
Δ BC) = (c + a -b)(c + b -a) thì tgC = 15 3. Cho A
Δ BC coù ba goùc nhoïn. Goïi A’, B’, C’ laø chaân caùc ñöôøng cao veõ töø
A, B, C. Goïi S, R, r laàn löôït laø dieän tích, baùn kính ñöôøng troøn ngoaïi tieáp, noäi tieáp A
Δ BC. Goïi S’, R’, r’ laàn löôït laø dieän tích, baùn kính
ñöôøng troøn ngoaïi tieáp, noäi tieáp cuûa A Δ 'B'C' . Chöùng minh: a/ S’ = 2ScosA.cosB.cosC R b/ R ' = 2 c/ r’ = 2RcosA.cosB.cosC 4. A
Δ BC coù ba caïnh a, b, c taïo moät caáp soá coäng. Vôùi a < b < c Chöùng minh : a/ ac = 6Rr A − C B b/ cos = 2sin 2 2 c/ Coâng sai 3r ⎛ C A d tg tg ⎞ = − 2 ⎜ 2 2 ⎟ ⎝ ⎠ 5. Cho A
Δ BC coù ba goùc A, B, C theo thöù töï taïo 1 caáp soá nhaân coù coâng boäi q = 2. Chöùng minh: 1 1 1 a/ = + a b c b/ 2 2 2 5 cos A + cos B + cos C = 4 CHÖÔNG XI:
NHAÄN DAÏNG TAM GIAÙC
I. TÍNH CAÙC GOÙC CUÛA TAM GIAÙC
Baøi 201: Tính caùc goùc cuûa ΔABC neáu : ( + ) + ( + ) + ( + ) 3 sin B C sin C A cos A B = ( *) 2 Do A + B + C = π Neân: ( ) 3
* ⇔ sin A + sin B − cosC = 2 A + B A − B ⎛ 2 C ⎞ 3 ⇔ 2 sin cos − ⎜2 cos − 1⎟ = 2 2 ⎝ 2 ⎠ 2 C A − B C 1 ⇔ 2 cos cos − 2 2 cos = 2 2 2 2 2 C C A − B ⇔ 4 cos − 4 cos cos + 1 = 0 2 2 2 ⎛ C A − B ⎞2 2 A − B ⇔ 2 cos − cos + 1 − ⎜ ⎟ cos = 0 ⎝ 2 2 ⎠ 2 ⎛ C A − B ⎞2 2 A − B ⇔ 2 cos − cos + sin = ⎜ ⎟ 0 ⎝ 2 2 ⎠ 2 ⎧ C A − B 2 cos = ⎪ cos ⎪ ⇔ 2 2 ⎨ A − ⎪ B sin = 0 ⎪⎩ 2 ⎧ C 2 cos = cos 0 = 1 ⎧C π ⎪⎪ ⎪ = ⇔ 2 ⎨ ⇔ 2 3 A ⎨ − ⎪ B ⎪ = 0 ⎩A = B ⎪⎩ 2 ⎧ π A = B = ⎪⎪ ⇔ 6 ⎨ π ⎪ 2 C = ⎪⎩ 3 Baøi 202:
Tính caùc goùc cuûa ΔABC bieát: + ( + ) 5 cos2A 3 cos2B cos2C + = 0 (*) 2 5 Ta coù: (*) 2 ⇔ 2cos A − 1 + 2 3 ⎡cos ⎣ (B + C)cos(B − C)⎤ + = 0 ⎦ 2 ⇔ 2
4 cos A − 4 3 cos A.cos (B − C) + 3 = 0 2
⇔ ⎡2 cos A − 3 cos (B − C)⎤ + 3 − 2 3 cos (B − C) ⎣ ⎦ = 0 2
⇔ ⎡2 cos A − 3 cos (B − C)⎤ + 2 3sin (B − C) = ⎣ ⎦ 0 ⎧sin (B − C) = 0 ⎧B − C = 0 ⎪ ⎪ ⇔ ⎨ ⇔ 3 3 ⎪cos A = cos (B − C) ⎨ ⎪cos A = ⎩ 2 ⎩ 2 ⎧⎪A = 0 30 ⇔ ⎨⎪⎩B = C = 0 75
Baøi 203: Chöùng minh ΔABC coù 0 C = 120 neáu : A B C sin A + sin B + sin C − 2sin ⋅ sin = 2sin (*) 2 2 2 Ta coù A + B A − B C C A B C (*) ⇔ 2sin cos + 2sin cos = 2sin sin + 2sin 2 2 2 2 2 2 2 C A − B C C A + B A B ⇔ 2 cos cos + 2sin cos = 2 cos + 2sin sin 2 2 2 2 2 2 2 C ⎛ A − B C ⎞ A B ⇔ cos cos + sin = cos ⋅ cos 2 ⎜ 2 2 ⎟ ⎝ ⎠ 2 2 C ⎡ A − B A + B⎤ A B ⇔ cos cos + cos = cos cos 2 ⎢ 2 2 ⎥ ⎣ ⎦ 2 2 C A B A B ⇔ 2 cos cos cos = cos cos 2 2 2 2 2 C 1 A B A B π ⇔ cos = (do cos > 0 vaø cos > 0 vì 0 < ; < ) 2 2 2 2 2 2 2 ⇔ = 0 C 120
Baøi 204: Tính caùc goùc cuûa ΔΑΒC bieát soá ño 3 goùc taïo caáp soá coäng vaø 3 + 3 sin A + sin B + sin C = 2
Khoâng laøm maát tính chaát toång quaùt cuûa baøi toaùn giaû söû A < B < C Ta coù:
A, B, C taïo 1 caáp soá coäng neân A + C = 2B Maø A π + B + C = π neân B = 3 Luùc ñoù: 3 + 3 sin A + sin B + sin C = 2 π 3 + 3 ⇔ sin A + sin + sin C = 3 2 3 ⇔ sin A + sin C = 2 A + C A − C 3 ⇔ 2sin cos = 2 2 2 B A − C 3 ⇔ 2cos cos = 2 2 2 ⎛ 3 ⎞ A − C 3 ⇔ 2.⎜ ⎟ cos = ⎜ 2 ⎟ 2 2 ⎝ ⎠ C − A 3 cos cos π ⇔ = = 2 2 6
Do C > A neân ΔΑΒC coù: ⎧C − A π ⎧ π = C = ⎪ ⎪ ⎪ 2 6 ⎪ 2 ⎪ π 2 ⎪ π ⎨C + A = ⇔ ⎨A = ⎪ 3 ⎪ 6 ⎪ π ⎪ π B = B = ⎪ ⎪ ⎩ 3 ⎩ 3
Baøi 205: Tính caùc goùc cuûa ΔABC neáu ⎧ 2 + 2 ≤ ⎪ 2 b c a (1) ⎨ ⎪sin A + sin B + sin C = 1 + ⎩ 2 (2) 2 2 2
AÙp duïng ñònh lyù haøm cosin: b + c − a cos A = 2bc 2 2 2 Do (1): b + c ≤ a neân cos A ≤ 0 π π A Do ñoù: π ≤ A < π ⇔ ≤ < 2 4 2 2 Vaäy A π 2 cos ≤ cos = (∗) 2 4 2 B + C B − C
Maët khaùc: sin A + sin B + sin C = sin A + 2sin cos 2 2 A B − C = sin A + 2cos cos 2 2 ⎛ 2 ⎞ B C ≤ 1 + 2 ⎛ ⎞ ⎜ ⎟ ⋅ 1 ⎜ ⎜do (*) − vaø cos ≤ 1 2 ⎟ ⎟ ⎝ ⎠ ⎝ 2 ⎠
Maø sin A + sin B + sin C = 1 + 2 do (2) ⎧ ⎪sin A = 1 ⎧ π ⎪ A = ⎪
Daáu “=” taïi (2) xaûy ra ⎪ A 2 ⇔ ⎪ 2 ⎨cos = ⇔ ⎨ ⎪ 2 2 π ⎪B = C = ⎪ B − C cos ⎪ = ⎩ 4 ⎪ 1 ⎩ 2
Baøi 206: (Ñeà thi tuyeån sinh Ñaïi hoïc khoái A, naêm 2004) Cho
ΔABC khoâng tuø thoûa ñieàu kieän
cos2A + 2 2 cosB + 2 2 cosC = 3 (*) Tính ba goùc cuûa ΔABC
* Caùch 1: Ñaët M = cos 2A + 2 2 cos B + 2 2 cosC − 3 Ta coù: M = 2 B + C B − C 2cos A + 4 2 cos cos − 4 2 2 − ⇔ M = 2 A B C 2cos A + 4 2 sin cos − 4 2 2 A B - C Do sin > 0 vaø cos ≤ 1 2 2 Neân 2 A M ≤ 2cos A + 4 2 sin − 4 2 Maët khaùc: π
ΔABC khoâng tuø neân 0 < A ≤ 2 ⇒ 0 ≤ cos A ≤ 1 ⇒ 2 cos A ≤ cos A A Do ñoù: M ≤ 2cos A + 4 2 sin − 4 2 ⎛ 2 A ⎞ A ⇔ M ≤ 1 − 2sin + 4 2 sin − 4 ⎜ 2 ⎟ ⎝ ⎠ 2 2 A A ⇔ M ≤ 4 − sin + 4 2 sin − 2 2 2 2 ⎛ A M 2 2 sin 1⎞ ⇔ ≤ − − ≤ 0 ⎜ 2 ⎟ ⎝ ⎠
Do giaû thieát (*) ta coù M=0 ⎧ 2 ⎪cos A = cos A ⎪ 0 ⎪ B − C ⎧⎪A = 90 Vaäy: ⎨cos = 1 ⇔ ⎨ 0 2 ⎪ ⎪⎩B = C = 45 ⎪ A 1 sin = ⎪⎩ 2 2
* Caùch 2: (*) ⇔ cos2A + 2 2 cosB + 2 2 cosC − 3 = 0 2 B + C B − C ⇔ cos A + 2 2 cos cos − 2 = 0 2 2 ⇔ ( 2 − ) A B − C
cos A cos A + cos A + 2 2 sin cos − 2 = 0 2 2 ⇔ ( − ) ⎛ 2 A ⎞ A B − C cos A cos A 1 + 1 − 2sin + 2 2 sin cos − 2 = 0 ⎜ 2 ⎟ ⎝ ⎠ 2 2 2 ⇔ ( − ) ⎛ A B − C ⎞ ⎛ 2 B − C cos A cos A 1 − 2 sin − cos − 1 − cos ⎞ = 0 ⎜ 2 2 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 2 ⎠ 2 C ⇔ ( − ) ⎛ A B − C ⎞ 2 B cos A cos A 1 − 2 sin − cos − sin − ⎜ = 0 (*) 2 2 ⎟ ⎝ ⎠ 2
Do ΔABC khoâng tuø neân cos A ≥ 0 vaø cos A − 1 < 0
Vaäy veá traùi cuûa (*) luoân ≤ 0 ⎧ ⎪cos A = 0 ⎪ Daáu “=” xaûy ra ⎪ A B − C ⇔ ⎨ 2 sin = cos 2 2 ⎪ ⎪ B − C sin = 0 ⎪⎩ 2 ⎧⎪A = 0 90 ⇔ ⎨⎪⎩B = C = 0 45
Baøi 207: Chöùng minh ΔABC coù ít nhaát 1 goùc 600 khi vaø chæ khi sin A + sin B + sin C = 3 (*) cos A + cosB + cosC Ta coù:
(*) ⇔ (sin A − 3 cos A) + (sinB − 3 cosB) + (sinC − 3 cosC) = 0
sin ⎛ A π ⎞ sin ⎛B π ⎞ sin ⎛C π ⎞ ⇔ − + − + − = 0 ⎜ 3 ⎟ ⎜ 3 ⎟ ⎜ 3 ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎛ A + B π ⎞ A − B 2sin cos sin ⎛C π ⎞ ⇔ − + − = 0 ⎜ 2 3 ⎟ 2 ⎜ 3 ⎟ ⎝ ⎠ ⎝ ⎠ ⎡⎛ π C ⎞ π⎤ A − B ⎛ C π ⎞ ⎛ C 2sin cos 2sin cos π ⎞ ⇔ − − + − − = 0 ⎢⎜ ⎣ 2 2 ⎟ 3⎥ ⎝ ⎠ ⎦ 2 ⎜ ⎝ 2 6 ⎟ ⎜ ⎠ ⎝ 2 6 ⎟⎠ ⎛ C π ⎞ ⎡ A − B ⎛ C ⇔ 2sin − − cos + cos π ⎞⎤ − = 0 ⎜ 2 6⎟ ⎢⎣ 2 ⎜ 2 6⎟⎥ ⎝ ⎠ ⎝ ⎠⎦ ⎛ C π ⎞ A − B ⎛ C π ⎞ ⎛ π A + B ⇔ sin − = 0 ∨ cos = cos − = cos − ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ 2 6 ⎠ 2 ⎝ 2 6 ⎠ ⎝ 3 2 ⎠ C π A − B π A + B −A + B π A + B ⇔ = ∨ = − ∨ = − 2 6 2 3 2 2 3 2 π π π ⇔ C = ∨ A = ∨ B = 3 3 3
Baøi 208: Cho ΔABC vaø V = cos2A + cos2B + cos2C – 1. Chöùng minh:
a/ Neáu V = 0 thì ΔABC coù moät goùc vuoâng
b/ Neáu V < 0 thì ΔABC coù ba goùc nhoïn
c/ Neáu V > 0 thì ΔABC coù moät goùc tuø 1 1
Ta coù: V = (1 + cos2A) + (1 + cos2B) 2 + cos − 1 2 2 1 ⇔ V = (cos2A + cos2B) 2 + cos C 2
⇔ V = cos(A + B).cos(A − B) 2 + cos C ⇔ V = − cosC.cos(A − B) 2 + cos C
⇔ V = − cosC ⎡cos(A − B) + cos(A + B)⎤ ⎣ ⎦ ⇔ V = −2cosC cos A cos B Do ñoù: a /
V = 0 ⇔ cos A = 0 ∨ cos B = 0 ∨ cos C = 0
⇔ ΔABC ⊥ taïi A hay ΔABC ⊥ taïi B hay ΔABC ⊥ taïi C b /
V < 0 ⇔ cos A.cos B.cos C > 0
⇔ ΔABC coù ba goùc nhoïn
( vì trong 1 tam giaùc khoâng theå coù nhieàu hôn 1 goùc tuø neân
khoâng coù tröôøng hôïp coù 2 cos cuøng aâm ) c /
V > 0 ⇔ cos A.cos B.cos C < 0
⇔ cos A < 0 ∨ cos B < 0 ∨ cos C < 0 ⇔ ΔABC coù 1 goùc tuø. II. TAM GIAÙC VUOÂNG B a c Baøi 209: Cho ΔABC coù + cotg = 2 b Chöùng minh ΔABC vuoâng B a + c Ta coù: cotg = 2 b B
cos 2 2Rsin A + 2RsinC sin A + sinC ⇔ = = B 2R sin B sin B sin 2B A + C A − cos 2 sin .cos C ⇔ 2 = 2 2 B B sin 2 sin .cos B 2 2 2 2 B B A − C B ⇔ cos = cos .cos (do sin > 0) 2 2 2 2 B A − C B ⇔ cos = cos (do cos > 0) 2 2 2 B A − C B C − A ⇔ = ∨ = 2 2 2 2 ⇔ A = B + C ∨ C = A + B π π ⇔ A = ∨ C = 2 2
⇔ ΔABC vuoâng taïi A hay ΔABC vuoâng taïi C Baøi 210: Chöùng minh ΔABC vuoâng taïi A neáu b c a + = cosB cosC sin Bsin C b c a Ta coù: + = cosB cosC sin Bsin C 2R sin B 2R sin C 2R sin A ⇔ + = cos B cosC sin Bsin C sin B cosC + sin C cos B sin A ⇔ = cos B.cosC sin Bsin C sin (B + C) sin A ⇔ = cos B.cosC sin Bsin C
⇔ cos B cosC = sin Bsin C (do sin A > 0)
⇔ cos B.cos C − sin B.sin C = 0 ⇔ cos (B + C) = 0 π ⇔ B + C = 2 ⇔ ΔABC vuoâng taïi A Baøi 211: Cho ΔABC coù: A B C A B C 1 cos ⋅ cos ⋅ cos − sin ⋅ sin ⋅ sin = (*) 2 2 2 2 2 2 2 Chöùng minh ΔABC vuoâng Ta coù: A B C 1 A B C (*) ⇔ cos cos cos = + sin sin sin 2 2 2 2 2 2 2 1 ⎡ A + B A − B⎤ C 1 1 ⎡ A + B A − B C ⇔ cos + cos cos = − cos − ⎤ ⎢ ⎥ ⎢ cos sin 2 ⎣ 2 2 ⎦ 2 2 2 ⎣ ⎥ 2 2 ⎦ 2 ⎡ C A − B⎤ C ⎡ C A − B⎤ C ⇔ sin + cos cos = 1 − sin − ⎢ ⎥ ⎢ cos ⎥ sin ⎣ 2 2 ⎦ 2 ⎣ 2 2 ⎦ 2 C C A − B C 2 C C 2 C A − B C ⇔ sin cos + cos cos = 1 − sin + cos = 1 − sin + cos sin 2 2 2 2 2 2 2 2 2 C C A − B C 2 C A − B C ⇔ sin cos + cos cos = cos + cos sin 2 2 2 2 2 2 2 C ⎡ C C⎤ A − B ⎡ C C⎤ ⇔ cos sin − cos = cos sin − ⎢ ⎥ ⎢ cos ⎥ 2 ⎣ 2 2 ⎦ 2 ⎣ 2 2 ⎦ ⎡ C C⎤ ⎡ C A − B⎤ ⇔ sin − cos cos − cos = ⎢ ⎥ ⎢ ⎥ 0 ⎣ 2 2 ⎦ ⎣ 2 2 ⎦ C C C A − B ⇔ sin = cos ∨ cos = cos 2 2 2 2 C C A − B C B − A ⇔ tg = 1 ∨ = ∨ = 2 2 2 2 2 C π ⇔ = ∨ A = B + C ∨ B = A + C 2 4 π π π ⇔ C = ∨ A = ∨ B = 2 2 2 Baøi 212: Chöùng minh ΔABC vuoâng neáu:
3(cos B + 2sin C) + 4(sin B + 2cosC) = 15
Do baát ñaúng thöùc Bunhiacoápki ta coù: 2 2
3cos B + 4 sin B ≤ 9 + 16 cos B + sin B = 15 vaø 2 2
6sin C + 8cosC ≤ 36 + 64 sin C + cos C = 10 neân:
3(cos B + 2sin C) + 4(sin B + 2cosC) ≤ 15 ⎧cos B sin B ⎧ 4 = tgB = ⎪ ⎪ Daáu “=” xaûy ra ⎪ 3 4 ⎪ ⇔ 3 ⎨ ⇔ sin C cosC ⎨ 4 ⎪ ⎪ = cotgC= ⎪⎩ 6 8 ⎪⎩ 3 ⇔ tgB = cotgC π ⇔ B + C = 2 ⇔ ΔABC vuoâng taïi A. Baøi 213: Cho
ΔABC coù: sin 2A + sin 2B = 4 sin A.sin B Chöùng minh ΔABC vuoâng.
Ta coù: sin 2A + sin 2B = 4 sin A.sin B
⇔ 2 sin(A + B) cos(A − B) = −2[cos(A + B) − cos(A − B)]
⇔ cos(A + B) = [1 − sin(A + B)] cos(A − B)
⇔ − cos C = [1 − sin C] cos(A − B) ⇔ − + = − 2
cos C(1 sin C) (1 sin C).cos(A − B) ⇔ − + = 2
cos C(1 sin C) cos C.cos(A − B)
⇔ cos C = 0 hay − (1 + sin C) = cos C.cos(A − B) (*) ⇔ cos C = 0
( Do sin C > 0 neân −(1 + sin C) < −1 Maø cosC.cos(A − B) ≥ 1
− .Vaäy (*) voâ nghieäm.)
Do ñoù ΔABC vuoâng taïi C III. TAM GIAÙC CAÂN C
Baøi 214:Chöùng minh neáu ΔABC coù tgA + tgB = 2cotg 2 thì laø tam giaùc caân. C Ta coù: tgA + tgB = 2cotg 2 C 2cos sin(A + B) 2 ⇔ = cos A.cos B C sin 2C 2cos sin C 2 ⇔ = cos A.cos B C sin 2 C C C 2sin cos 2cos 2 2 ⇔ = 2 cos A cos B C sin 2 ⇔ 2 C ⎛ C sin cos A.cos B do cos 0⎞ = > 2 ⎜ 2 ⎟ ⎝ ⎠ 1 1
⇔ (1 − cosC) = ⎡cos(A + B) + cos(A − B)⎤ ⎣ ⎦ 2 2
⇔ 1 − cosC = − cosC + cos(A − B) ⇔ cos(A − B) = 1 ⇔ A = B ⇔ ΔABC caân taïi C. Baøi 215: Chöùng minh ΔABC caân neáu: A 3 B B 3 sin .cos A = sin .cos 2 2 2 2 A B B A Ta coù: 3 3 sin .cos = sin .cos 2 2 2 2 ⎛ A ⎞ ⎛ B sin sin ⎞ ⎜ 2 ⎟ 1 ⎜ 2 ⎟ 1 ⇔ ⎜ A ⎟ = ⎜ ⎟ 2 A B 2 B ⎜ cos ⎟ cos ⎜ cos ⎟ cos ⎝ 2 ⎠ 2 ⎝ 2 ⎠ 2 A B (do cos > 0 vaø cos > 0 ) 2 2 A ⎛ 2 A ⎞ B ⎛ 2 B tg 1 tg tg 1 tg ⎞ ⇔ + = + 2 ⎜ 2 ⎟ 2 ⎜ 2 ⎟ ⎝ ⎠ ⎝ ⎠ 3 A 3 B A B ⇔ tg − tg + tg − tg = 0 2 2 2 2 ⎛ A B ⎞ ⎡ 2 A 2 B A B tg tg 1 tg tg tg .tg ⎤ ⇔ − + + + = 0 (*) ⎜ 2 2 ⎟ ⎢ 2 2 2 2 ⎥ ⎝ ⎠ ⎣ ⎦ A B A B A B ⇔ tg = tg ( vì 2 2 1 + tg + tg + tg tg > 0 ) 2 2 2 2 2 2 ⇔ A = B ⇔ ΔABC caân taïi C Baøi 216: Chöùng minh ΔABC caân neáu: 2 2 cos A + cos B 1 = ( 2 2 cotg A + cotg B (*) 2 2 ) sin A + sin B 2 Ta coù: 2 2 (*) cos A + cos B 1 ⎛ 1 1 − 2⎞ ⇔ = + 2 2 ⎜ 2 2 sin A sin B 2 sin A sin B ⎟ + ⎝ ⎠ 2 2 cos A + cos B 1 ⎛ 1 1 1 ⎞ ⇔ + = + 2 2 ⎜ 2 2 sin A sin B 2 sin A sin B ⎟ + ⎝ ⎠ 2 1 ⎛ 1 1 ⎞ ⇔ = + 2 2 ⎜ 2 2 ⎟ sin A + sin B 2 ⎝ sin A sin B ⎠ ⇔ = ( + )2 2 2 2 2 4 sin A sin B sin A sin B ⇔ = ( 2 2 0 sin A − sin B) ⇔ sin A = sin B Vaäy ΔABC caân taïi C Baøi 217: Chöùng minh ΔABC caân neáu: C a + b = tg (atgA + btgB) (*) 2 C
Ta coù: a + b = tg (atgA + btgB) 2 C
⇔ (a + b) cotg = atgA + btgB 2 ⎡ C⎤ ⎡ C ⇔ a tgA − cotg + b tgB − ⎤ ⎢ ⎥ ⎢ cotg = 0 ⎣ 2 ⎦ ⎣ 2 ⎥⎦ ⎡ A + B⎤ ⎡ A + B ⇔ a tgA − tg + b tgB − ⎤ ⎢ ⎥ ⎢ tg = 0 ⎣ 2 ⎦ ⎣ ⎥ 2 ⎦ A − B B − A a sin b sin ⇔ 2 + 2 = 0 A + B A + B cos A.cos cos B.cos 2 2 A − B a b ⇔ sin = 0 hay − = 0 2 cos A cos B 2R sin A 2R sin B ⇔ A = B hay = cos A cos B
⇔ A = B hay tgA = tgB ⇔ ΔABC caân taïi C
IV. NHAÄN DAÏNG TAM GIAÙC Baøi 218: Cho
ΔABC thoûa: a cos B − b cos A = a sin A − bsin B (*) Chöùng minh ΔABC vuoâng hay caân
Do ñònh lyù haøm sin: a = 2R sin A, b = 2R sin B Neân (*) ⇔ − = ( 2 2
2R sin A cos B 2R sin B cos A 2R sin A − sin B) 2 2
⇔ sin A cos B − sin B cos A = sin A − sin B ⇔ ( − ) 1 = ( − ) 1 sin A B 1 cos 2A − (1 − cos2B) 2 2 ⇔ ( − ) 1 sin A B = [cos2B − cos2A] 2
⇔ sin (A − B) = − ⎡sin (A + B)sin (B − A)⎤ ⎣ ⎦ ⇔ sin (A − B) 1 ⎡ − sin ⎣ (A + B)⎤ = 0 ⎦
⇔ sin (A − B) = 0 ∨ sin (A + B) = 1 A B A B π ⇔ = ∨ + = 2
vaäy ΔABC vuoâng hay caân taïi C Caùch khaùc − = 2 − 2
sin A cos B sin B cos A sin A sin B
⇔ sin (A − B) = ( sin A + sin B) ( sin A − sin B) sin (A B) A + B A − B A + B A − B ⇔ − = ( 2 sin cos ) (2 cos sin ) 2 2 2 2
⇔ sin (A − B) = sin (A + B) sin (A − B)
⇔ sin (A − B) = 0 ∨ sin (A + B) = 1 π ⇔ A = B ∨ A + B = 2
Baøi 219 ΔABC laø tam giaùc gì neáu ( 2 2 + ) ( − ) = ( 2 2 a b sin A B a − b )sin(A + B) (*) Ta coù: (*) ⇔ ( 2 2 2 2 + ) ( − ) 2 = ( 2 2 4R sin A 4R sin B sin A B 4R sin A − sin B)sin(A + B) 2 ⇔ ⎡⎣ ( − ) − ( + ) 2 sin A sin A B sin A B ⎤ + sin B ⎡sin ⎦ ⎣ (A − B) + sin(A + B)⎤ = 0 ⎦ 2 ⇔ (− ) 2
2sin A cos A sin B + 2sin Bsin A cos B = 0
⇔ − sin A cos A + sin B cos B = 0 (do sin A > 0 vaø sin B > 0 ) ⇔ sin 2A = sin 2B
⇔ 2A = 2B ∨ 2A = π − 2B A B A B π ⇔ = ∨ + = 2
Vaäy ΔABC caân taïi C hay ΔABC vuoâng taïi C. Baøi 220:
ΔABC laø tam giaùc gì neáu: 2 2
⎧a sin 2B + b sin 2A = 4ab cos A sin B (1) sin ⎨ ⎩ 2A + sin 2B = 4 sin A sin B (2) Ta coù: (1) 2 2 2 2 2 2
⇔ 4R sin A sin 2B + 4R sin Bsin 2A = 16R sin A sin Bcos A 2 2 2
⇔ sin A sin 2B + sin Bsin 2A = 4 sin A sin B cos A 2 2
⇔ 2sin A sin B cos B + 2sin A cos A sin B = 4 sin A sin2 B cos A
⇔ sin A cos B + sin B cos A = 2sin B cos A (do sin A > 0,sin B > 0)
⇔ sin A cos B − sin B cos A = 0 ⇔ sin (A − B) = 0 ⇔ A = B Thay vaøo (2) ta ñöôïc 2 sin 2A = 2sin A 2 ⇔ 2sin A cos A = 2sin A
⇔ cos A = sin A (dosin A > 0) ⇔ tgA = 1 A π ⇔ = 4
Do ñoù ΔABC vuoâng caân taïi C V. TAM GIAÙC ÑEÀU Baøi 221: Chöùng minh ΔABC ñeàu neáu: bc 3 = R ⎡2 ⎣ (b + c) − a⎤ (*) ⎦
Ta coù:(*) ⇔ (2R sin B)(2R sin C) 3 = R ⎡2(2R sin B + 2R sinC) − 2R sin A⎤ ⎣ ⎦
⇔ 2 3 sin B sin C = 2(sin B + sin C) − sin (B + C)
⇔ 2 3 sin B sin C = 2 (sin B + sin C) − sin B cos C − sin C cos B ⎡ 1 3 ⎤ ⎡ 1 3 ⎤ ⇔ 2 sin B ⎢1 − cos C −
sin C⎥ + 2sin C ⎢1 − cos B − sin B⎥ = 0 ⎣ 2 2 ⎦ ⎣ 2 2 ⎦ ⎡ ⎛ π ⎞⎤ ⎡ ⎛ π ⎞⎤ ⇔ sin B 1 − cos C − + sin C 1 − cos B − = ⎢ ⎜ ⎟⎥ ⎢ ⎜ ⎟⎥ 0 (1) ⎣ ⎝ 3 ⎠⎦ ⎣ ⎝ 3 ⎠⎦ Do sin B ⎛ π > 0 vaø 1 cos C ⎞ − − ≥ 0 ⎜ 3 ⎟ ⎝ ⎠ sin C ⎛ π > 0 vaø 1 cos B ⎞ − − ≥ 0 ⎜ 3 ⎟ ⎝ ⎠
Neân veá traùi cuûa (1) luoân ≥ 0 ⎧cos⎛C π⎞ − = 1 ⎪ ⎜ ⎪ ⎝ 3 ⎟ Do ñoù, (1) ⎠ ⇔ ⎨⎪cos⎛B π⎞ − = 1 ⎜ ⎩ 3 ⎟ ⎪ ⎝ ⎠ C B π ⇔ = = ⇔ ΔABC ñeàu. 3 ⎧ 3 sin Bsin C = (1) ⎪ Baøi 222: Chöùng minh ΔABC ñeàu neáu ⎪ 4 ⎨ 3 3 3 ⎪ 2 a − b − c a = (2) ⎪⎩ a − b − c Ta coù: (2) 3 2 2 3 3
⇔ a − a b − a c = a − b − c3 2 ⇔ ( + ) 3 a b c = b + c3 2 ⇔ a (b + c) = (b + c)( 2 b − bc + c2 ) 2 2 2 ⇔ a = b − bc + c 2 2 2 2
⇔ b + c − 2bc cos A = b + c − c b (do ñl haøm cosin) ⇔ 2bc cos A = bc 1 π ⇔ cos A = ⇔ A = 2 3
Ta coù: (1) ⇔ 4 sin B sin C = 3
⇔ 2 ⎡cos (B − C) − cos (B + C)⎤ ⎣ ⎦ = 3
⇔ 2 ⎡⎣cos(B − C) + cos A⎤ = ⎦ 3 2 cos (B C) ⎛ 1 ⎞ ⎛ π ⎞ ⇔ − + 2 = 3 do (1) ta coù A = ⎜ ⎟ ⎜ ⎟ ⎝ 2 ⎠ ⎝ 3 ⎠
⇔ cos (B − C) = 1 ⇔ B = C
Vaäy töø (1), (2) ta coù ΔABC ñeàu Baøi 223: Chöùng minh ΔABC ñeàu neáu:
sin A + sin B + sin C = sin 2A + sin 2B + sin 2C Ta coù:
sin 2A + sin 2B = 2sin (A + B) cos(A − B)
= 2sin C cos(A − B) ≤ 2sin C (1)
Daáu “=” xaûy ra khi: cos(A − B) = 1 Töông töï: sin 2A + sin 2C ≤ 2sin B (2)
Daáu “=” xaûy ra khi: cos(A − C) = 1 Töông töï: sin 2B + sin 2C ≤ 2sin A (3)
Daáu “=” xaûy ra khi: cos(B − C) = 1
Töø (1) (2) (3) ta coù: 2(sin2A + sin2B + sin2 ) C ≤ 2(sinC + sinB + sinA) ⎧cos(A − B) = 1 ⎪
Daáu “=” xaûy ra ⇔ ⎨cos(A − C) = 1 ⇔ A = B = C ⎪cos(B − C) = ⎩ 1 ⇔ ΔABC ñeàu Baøi 224: Cho ΔABC coù: 1 1 1 1 + + = (*) 2 2 2 sin 2A sin 2B sin C 2cos A cosBcosC Chöùng minh ΔABC ñeàu Ta coù: (*) ⇔ 2 2 + 2 2 + 2 2
sin 2B.sin 2C sin 2A sin 2C sin 2Asin 2B sin 2A.sin 2B.sin 2C = ⋅ (sin 2A sin 2Bsin 2C) 2cos A cos B cosC
= 4 sin A sin Bsin C(sin 2A sin 2Bsin 2C)
Maø: 4 sin A sin B sin C = 2 ⎡cos (A − B) − cos (A + B)⎤ ⎣ ⎦ sin (A + B)
= 2 ⎡cos (A − B) + cos C⎤ ⎣ ⎦ sin C
= 2 sin C cos C + 2 cos (A − B) sin (A + B) = sin 2C + sin 2A + sin 2B
Do ñoù,vôùi ñieàu kieän ΔABC khoâng vuoâng ta coù (*) 2 2 2 2 2 2
⇔ sin 2Bsin 2C + sin 2A sin 2C + sin 2A sin 2B
= sin 2A.sin 2B.sin 2C (sin 2A + sin 2B + sin 2C) = 2 sin 2A sin 2B sin 2C + 2 sin 2B sin 2A sin 2C + 2 sin 2C sin 2A sin 2B 1 1
⇔ (sin 2B sin 2A − sin 2B sin 2C)2 + (sin 2A sin 2B − sin 2A sin 2C)2 2 2 1
+ (sin 2Csin 2A − sin 2Csin 2B)2 = 0 2 s
⎧ in 2B sin 2A = sin 2B sin 2C si ⎪
⇔ ⎨ n 2A sin 2B = sin 2A sin 2C si ⎪ n 2A sin 2C = sin2Csin2B ⎩ ⎧sin 2A = sin 2B ⇔ ⎨ ⇔ A = B = C ⇔ ABC ñeàu ⎩sin 2B = sin 2C
Baøi 225: Chöùng minh ΔABC ñeàu neáu: a cos A + b cosB + c cosC 2p = (*) a sin B + bsin C + c sin A 9R
Ta coù: a cos A + b cos B + c cosC
= 2R sin A cos A + 2R sin B cos B + 2R sin C cosC = R (sin 2A + sin 2B + sin 2C) = R ⎡2sin ⎣
(A + B)cos(A − B) + 2sinCcosC⎤⎦ = 2R sin C ⎡cos ⎣
(A − B) − cos(A + B)⎤ = 4RsinCsin A sinB ⎦
Caùch 1: a sin B + b sin C + c sin A
= 2R (sin A sin B + sin Bsin C + sin Csin A) 3 2 2 2
≥ 2R sin A sin Bsin C (do bñt Cauchy) a cos A + b cosB + c cosC 2 Do ñoù veá traùi : 3 ≤ sin A sin Bsin C (1) a sin B + bsin C + c sin A 3 2p a b c 2 Maø veá phaûi: + + = = (sin A + sin B + sin C) 9R 9R 9 2 3 ≥ sin A sin Bsin C (2) 3 Töø (1) vaø (2) ta coù
( * ) ⇔ sin A = sin B = sin C ⇔ ΔABC ñeàu 4R sin A sin Bsin C a + b + c
Caùch 2: Ta coù: (*) ⇔ = a sin B + bsin C + c sin A 9R ⎛ a ⎞ ⎛ b ⎞ ⎛ c 4R ⎞ ⎜ ⎝ 2R ⎟ ⎜ ⎠ ⎝ 2R ⎟ ⎜ ⎠ ⎝ 2R ⎟⎠ a + b + c ⇔ = ⎛ b ⎞ ⎛ c ⎞ ca 9R a + ⎟ b + ⎜ 2R ⎜ 2R ⎟ ⎝ ⎠ ⎝ ⎠ 2R
⇔ 9abc = (a + b + c)(ab + bc + ca)
Do baát ñaúng thöùc Cauchy ta coù 3 a + b + c ≥ abc 3 2 2 2 ab + bc + ca ≥ a b c
Do ñoù: (a + b + c)(ab + bc + ca) ≥ 9abc
Daáu = xaûy ra ⇔ a = b = c ⇔ ΔABC ñeàu.
Baøi 226: Chöùng minh ΔABC ñeàu neáu A B C cot gA + cot gB + cot gC = tg + tg + tg (*) 2 2 2 sin (A + B) Ta coù: sin C cot gA + cot gB = = sin A sin B sin A sin B sin C ≥ (do bñt Cauchy) 2 ⎛ sin A + sin B ⎞ ⎜ 2 ⎟ ⎝ ⎠ C C C 2sin cos 2sin 2 2 2 = = 2 A + B 2 A − B C 2 A sin .cos cos cos − B 2 2 2 2 C ≥ 2tg (1) 2 B
Töông töï: cot gA + cot gC ≥ 2tg (2) 2 A cot gB + cot gC ≥ 2tg (3) 2 Töø (1) (2) (3) ta coù ( ) ⎛ A B C 2 cot gA cot gB cot gC 2 tg tg tg ⎞ + + ≥ + + ⎜ 2 2 2 ⎟ ⎝ ⎠
Do ñoù daáu “=” taïi (*) xaûy ra ⎧ A − B A − C B − C ⎪cos = cos = cos = 1 ⇔ ⎨ 2 2 2 ⎪⎩sin A = sin B = sin C ⇔ A = B = C ⇔ A Δ BC ñeàu. BAØI TAÄP 1.
Tính caùc goùc cuûa ΔABC bieát: 3 π 2 a/ cos A π
= sin B + sin C − (ÑS: B = C = , A = ) 2 6 3 b/ π
sin 6A + sin 6B + sin 6C = 0 (ÑS: A = B = C = ) 3 c/ sin 5A + sin 5B + sin 5C = 0 2.
Tính goùc C cuûa ΔABC bieát: a/ (1 + cot gA)(1 + cot gB) = 2 ⎧A,B nhoïn b/ ⎪ ⎨ 2 2 9 si ⎪⎩ n A + sin B = sin C ⎧ 2 + 2 + 2 cos A cos B cos C < 1 3.
Cho ΔABC coù: ⎨⎩sin5A + sin5B + sin5C = 0 Chöùng minh
Δ coù ít nhaát moät goùc 36 0. 4. Bieát 2 2 2
sin A + sin B + sin C = m. Chöùng minh a/ m = 2 thì ΔABC vuoâng b/ m > 2 thì ΔABC nhoïn c/ m < 2 thì ΔABC tuø. 5.
Chöùng minh ΔABC vuoâng neáu: b + c a/ cosB + cosC = a b c a b/ + = cosB cosC sin BsinC c/
sin A + sin B + sin C = 1 − cos A + cos B + cosC (b − c)2 2 1 ⎡ − cos ⎣ (B − C)⎤ d/ ⎦ = 2 b 1 − cos 2B 6.
Chöùng minh ΔABC caân neáu: a/ 1 + cos B 2a + c = 2 2 sin B a − c sin A sin B sin C A B b/ + + = cot g .cot g sin A + sin B − sin C 2 2 c/ 2 tgA + 2tgB = tgA.tg B d/ ⎛ C ⎞ ⎛ C a cot g − tgA = b tgB − cot g ⎞ ⎜ 2 ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ 2 ⎠ e/ ( − ) C B p b cot g = ptg 2 2 C f/ a + b = tg (atgA + btgB) 2 7. ΔABC laø Δ gì neáu: a/ + = ( + ) A + B atgB btgA a b tg 2 b/ c = c cos 2B + b sin 2B c/ sin 3A + sin 3B + sin 3C = 0 d/
4S = (a + b − c)(a + c − b) 8.
Chöùng minh ΔABC ñeàu neáu a/
2(a cos A + bcosB + c cosC) = a + b + c b/ = 2 ( 3 + 3 + 3 3S 2R sin A sin B sin C) c/
sin A + sin B + sin C = 4 sin A sin B sin C 9R d/ m + m + m =
vôùi m , m , m laø 3 ñöôøng trung tuyeán a b c 2 a b c




