Chuyên đề đường thẳng song song và đường thẳng cắt nhau

Tài liệu gồm 25 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề đường thẳng song song và đường thẳng cắt nhau. Mời bạn đọc đón xem.

148 74 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Đường tròn

Môn: Toán 9

Thông tin:

25 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
A.KIẾN THỨC CẦN NHỚ
1.Hệsốgóccủađườngthẳng

yaxba0
:
a.Đườngthẳng
yaxb
cóhaihệsốlàavàbtrongđóhệsốađượcgọilàhệsốgóccủađườngthẳng.
b.Gọialàgóctạo bởiđườngthẳng

yaxba0
vớitiaOx.Cáchxácđịnhgócnàynhưsau:trước
tiên,taxácđịnhgiaođiểmAcủađườngthẳngvớitiaOx,gócalàgóctạobởitiaAx,vàphầnphíatrên
củađườngthẳng.
c.
Biểuthứcliênhệgiữaavàα: tan a 
Vậynếubiếthệsốgócatacóthểsuyrasốđocủagócαvàngượclại.
Dođó,agọilàhệsổgóccủađườngth
ẳng(hệsốchobiếtgócα).
Nếu
a0 0 90

Nếu
a 0 90 180
d.CácđườngthẳngcócùnghệsốgócthìtạovớitrụcOxcácgócbằngnhau.
2.Đườngthẳngsongsongvàđườngthẳngcắtnhau:
Chohaiđườngthẳng(d):
yaxb
và(dʹ):
ya'xb'
(
aa' 0

a.Haiđườngthẳngsongsong

aa'
dPd'
bb'

b.Haiđườngthẳngtrùngnhau

aa'
dd'
bb'

c.Haiđườngthẳngcắtnhau
+(d)cắt(d’)
aa'

+

dd'aa'1
B.CÁC DẠNG MINH HỌA
Dạng
1: Xét vị trí tương đối của hai đường thẳng
Phương pháp giải: Cho hai đường thẳng: d: y = ax + b với
a0
và d’: y = a’x + b’ với
a' 0
khi đó ta
có:
1. d và d’ song song
aa'
bb'
2. d và d’ trùng nhau
aa'
bb'
3. d và d’ cắt nhau
aa'
. Đặc biệt d và d’ vuông góc với nhau
a.a ' 1
Bài 1: Cho hai đường thẳng
d
và
d'
xác định bởi

yaxa0
và

ya'xa'0
. Chứng minh rằng
điều kiện để các đường thẳng
d
và
d'
vuông góc với nhau là
aa' 1
.
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 2: Hãy chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các
đường thẳng sau:
a)
y3x1;
b)
y2x
; c)
y0,3x;
d)
 y0,3x1;
; e)
x y3 3
; g)
 yx3.
Bài 3: Cho các đường thẳng:
Tìm các giá trị của để:
a)
1
d cắt
2
d b)
1
d song song
2
d
c)
1
d vuông góc
2
d d)
1
d trùng
2
d .
Bài 4: Cho đường thẳng

 ym2xm1d
a) Tìm giá trị của
m
để đường thẳng

d
đi qua góc tọa độ.
b) Tìm giá trị của
m
để đường thẳng

d
cắt trục hoành tại điểm có tung độ bằng
32
.
c) Tìm giá trị của
m
để đường thẳng

d
song song với đường thẳng

y223x2.
Bài 5: Cho ba đường thẳng:

2
12 3
d:y x 2,d:y 2x 1,d:y (m 1)x m.
a) Xác định tọa độ giao điểm của
1
d và
2
d.
b) Tìm các giá trị của tham số m để:
i)
2
d và
3
d song song với nhau.
ii)
1
d và
3
d trùng nhau.
iii)
12
d,d và
3
d đồng quy
Dạng 2: Xác định phương trình đường thẳng
Phương pháp giải: Để xác định phương trình đường thẳng, ta thường làm như sau:
Bước 1: Gọi d: y = ax + b là phương trình đường thẳng cần tìm (a,b là hằng số).
Bước 2: Từ giả thiết của đề bài, tìm được a,b từ đó đi đến kết luận.
Bài 6: Viết phương trình đường thẳng biết
a)
cắt trục tung tại
điểm có tung độ bằng và đi qua điểm

13A; .
b)
song song với đường thẳng và cắt trục hoành tại điểm có hoành độ bằng 5.
c) vuông góc với đường thẳng và cắt đường thẳng tại điểm có tung độ bằng 5.
Bài 7: Trên mặt phẳng
Oxy
cho hai điểm

A1; 1
và

B1;7
. Xác định hàm số biết đồ thị của nó là
đường thẳng

d
đi qua hai điểm
A
và
B
.
Bài 8: Chứng tỏ ba điểm sau thẳng hàng
a)
 




1
A1;3;B ;2;C2;3
2
b)





1
H1;1;I 1;5;K ;3
3
Bài 9: Tìm tập hợp điểm
I
và
K
nằm trên mặt phẳng tọa độ sau đây
a)




m12m1
I;
23
b)




23mm7
K;
53
Bài 10: Trong mặt phẳng
Oxy
cho đường thẳng

2
(d):y x 2
3
a. Vẽ

d
. Viết phương trình đường thẳng qua

A3 ; 2
và song song với

d
.
b. Tìm tọa độ điểm
B
trên trục tung sao cho tam giác
AOB
vuông tại
A
.

12
:21 23;: 1 .dy m x m d y m xm
m
d
d 5
d
28
y
x
d
3
y
x 21
y
x
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 11: Trong mặt phẳng
Oxy
cho

A1;2
và

B3;4.
Tìm trên trục hoành điểm
M
sao cho
MA MB
đạt giá trị nhỏ nhất
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
HƯỚNG DẪN
Dạng
1: Xét vị trí tương đối của hai đường thẳng
Bài 1.
h
o hai đ
ư
ờng thẳng
d
và
d'
xác định bởi
yaxa0
và

a' x a' 0
. Chứng minh rằng điều kiện để các đường thẳng
d
à
d'
vuông góc với nhau là
aa' 1
.
iải:
a
thấy khi
dd'
thì một trong hai đường thẳng
d
và
d'
, có một
ư
ờng (giả sử là
d
) nằm trong góc vuông phần tư I và III, đường kia
à
d'
) nằm trong góc vuông phần tư thứ II và IV, khi đó
0,a' 0
.
Qua điểm

H1;0
, kẻ đường thẳng vuông góc với Ox, cắt
d
và
d'
theo thứ tự tại A và B, ta có
 HA a a; HB a' a
.
Chú ý rằng
H
nằm giữa
A
và
B
nên điều kiện để tam giác
OAB
vuông tại
O
là:


2
HA.HB OH a a' 1 aa' 1
.
Bài 2. Hãy chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường
thẳng sau:
a)
y3x1;
b)
y2x
; c)
y0,3x;
d)
 y0,3x1;
; e)
x
y3 3
; g)
 yx3.
Giải: a và e; b và g; c và d.
Bài 3. Cho các đường thẳng:
Tìm các giá trị của để:
a)
1
d cắt
2
d b)
1
d song song
2
d
c)
1
d vuông góc
2
d d)
1
d trùng
2
d .
Giải:
a)
1
d cắt
2
d
21 1mm
b)
1
d song song
2
d

21 1
2
23
mm
m
mm



c)
1
d vuông góc
2
d

21 1 1mm
0m
hoặc
1
2
m
d)
1
d trùng
2
d

21 1
23
mm
mm



.
Bài 4. Cho đường thẳng

 ym2xm1d
a) Tìm giá trị của
m
để đường thẳng

d
đi qua góc tọa độ.
b) Tìm giá trị của
m
để đường thẳng

d
cắt trục hoành tại điểm có tung độ bằng
32
.
c) Tìm giá trị của
m
để đường thẳng

d
song song với đường thẳng

y223x2.
Giải:
a) Đường thẳng

d
đi qua gốc tọa độ
O
khi
m10
hay
m1
. Khi đó hàm số là
yx

12
:21 23;: 1 .dy m x m d y m xm
m
2m 
m
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b) Ta có
m13 2
hay
m4 2
.
c) Ta có
 m2 223
và
m1 2
 m221
và
m1
 m221
Khi đó hàm số

y223x222
Bài 5. Cho ba đường thẳng:

2
12 3
d:y x 2,d:y 2x 1,d:y (m 1)x m.
a) Xác định tọa độ giao điểm của
1
d và
2
d.
b) Tìm các giá trị của tham số m để:
i)
2
d và
3
d song song với nhau.
ii)
1
d và
3
d trùng nhau.
iii)
12
d,d và
3
d đồng quy.
Giải:
a) Xét phương trình hoành độ giao điểm của
1
d và
2
d :
 x22x1
x1 y3
Vậy tọa độ giao điểm của
1
d và
2
d là
I(1;3)
.
b) i)
2
d và
3
d song song với nhau


2
m12
m1
.
ii)
1
d và
3
d trùng nhau.


2
m12
m1
iii) Ta có: tọa độ giao điểm của
1
d
và
2
d
là
I(1;3)
.
Để
12
d,d và
3
d đồng quy thì
3
Id



2
3m1.1m
m2
m1
.
Dạng 2: Xác định phương trình đường thẳng
Bài 6. Viết phương trình đường thẳng biết:
a)
cắt trục tung tại điểm có tung độ bằng và đi qua điểm

13A; .
b)
song song với đường thẳng và cắt trục hoành tại điểm có hoành độ bằng 5.
c) vuông góc với đường thẳng và cắt đường thẳng tại điểm có tung độ bằng 5.
Giải: Phương trình đường thẳng
d
có dạng:
d:y ax b
a)
cắt trục tung tại điểm có tung độ bằng
b5
Ta có:

 A1;3 d 3 a.1 5 a 8
⇒
d:y 8x 5
.
b)
song song với đường thẳng
a2
.
cắt trục hoành tại điểm có hoành độ bằng 5
 02.5bb10
 y2x10
.
c) vuông góc với đường thẳng
a1
.
cắt đường thẳng tại điểm có tung độ bằng 5 ⟹Tọa độ điểm đó:

A2;5
Ta có:
 51.2bb7
d:y x 7
.
Bài 7. Trên mặt phẳng
Oxy
cho hai điểm

A1; 1
và

B1;7
. Xác định hàm số biết đồ thị của nó là
đường thẳng

d
đi qua hai điểm
A
và
B
.
Giải:
Giả sử đường thẳng

d
đi qua hai điểm
A
và
B
có dạng:
yaxb
1m 
1m
d
d 5
d
28
y
x
d
3
y
x 21
y
x
d 5
d
28
y
x
d
d
3
y
x
d
21
y
x
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vì

A1; 1 d
ta có
 11.ab b a1
Vì

 B1;7 d
ta có
 71.abba7
Suy ra
 a1a7 a 3
Thay
a3
vào
 ba1
ta được
b4
Vậy hàm số
y3x4
có đồ thị là đường thẳng

d
đi qua hai điểm
A
và
B
.
Bài 8. Chứng tỏ ba điểm sau thẳng hàng
a)
 




1
A1;3;B ;2;C2;3
2
b)





1
H1;1;I 1;5;K ;3
3
Giải :
a) Đường thẳng

d
đi qua hai điểm
A
và
B
có dạng:
yaxb

d:y 2x 1

Cd:y 2x1 3 2.21 3 3
( đẳng thức đúng).
b) Đường thẳng

d
đi qua hai điểm
H
và
I
có dạng:
y3x2
Bài 9. Tìm tập hợp điểm
I
và
K
nằm trên mặt phẳng tọa độ sau đây:
a)




m12m1
I;
23
b)




23mm7
K;
53
Giải:
a) Giả sử

I
II
I
m1
x
2
Ix;y
2m 1
y
3
Khử
m
từ hệ điều kiện trên ta được 
II
4x 3y 3 0
Từ đó suy ra
I
nằm trên đường thẳng

4
yx1
3
.
b) Tương tự,
K
nằm trên đường thẳng

523
yx
99
.
Bài 10. Trong mặt phẳng
Oxy
cho đường thẳng

2
(d):y x 2
3
a. Vẽ

d
. Viết phương trình đường thẳng qua

A3 ; 2
và song song với

d
.
b. Tìm tọa độ điểm
B
trên trục tung sao cho tam giác
AOB
vuông tại
A
.
Giải:
X 0
Y -2
Đồ thị hàm số là dường thẳng đi qua 2 điểm

0; 2 ; 3; 0
Phương trình đường thẳng (∆) đi qua A(3; 2) và song song với

d
là
(∆):
2
yx
3
.
b. Kẻ AH
Oy.
OAB
vuông tại A
2
AH OH .HB
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com

2
AH 9
HB
OH 2
Vậy



13
B0:
2
.
Bài 11. Trong mặt phẳng
Oxy
cho

A1;2
và

B3;4.
Tìm trên trục hoành điểm
M
sao cho
MA MB
đạt giá trị nhỏ nhất.
Giải:
Xét bài toán: “Cho đường thẳng

d
và 2 điểm A, B cùng nửa mặt phẳng bờ

d
, tìm trên

d
điểm M sao
cho
MA MB
đạt giá trị nhỏ nhất”
Dựng
A’
là hình chiếu của
A
trên

d
nên M là giao điểm của
A’ B
với

d
.
Áp dụng: Dựng A’ là hình chiếu của A trên Ox nên A’(–1; 2).
Suy ra M là giao điểm của
A’ B
với Ox. Phương trình (
A’ B
) có dạng
yaxb
với a = 3 và b = 5 (thay
tọa độ điểm A’, B vào phương trình)

A’ B : y 3 x – 5
Cho

5
y0 x
3
Vậy



0
5
M;0
3
thì
MA MB
đạt giá trị nhỏ nhất.
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
cắt nhau khi
A.
aa¹
¢
. B.
aa
bb
ì
ï
¹¢
ï
í
ï
¹¢
ï
î
. C.
aa
bb
ì
ï
=¢
ï
í
ï
¹¢
ï
î
. D.
aa
bb
¹¢
=¢
ì
ï
ï
í
ï
ï
î
.
Câu 2. Hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
trùng nhau khi
A.
aa¹
¢
. B.
aa
bb
ì
ï
¹¢
ï
í
ï
¹¢
ï
î
. C.
aa
bb
ì
ï
=¢
ï
í
ï
¹¢
ï
î
. D.
aa
bb
=¢
=¢
ì
ï
ï
í
ï
ï
î
.
Câu 3. Hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
có
aa¹
¢
và
bb¹¢
. Khi đó:
A.
//dd
¢
. B.
ddº
¢
. C.
d
cắt
d
¢
. D.
dd^
¢
.
Câu 4. Hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
có
aa¹
¢
. Khi đó
A.
//dd
¢
. B.
ddº
¢
. C.
d
cắt
d
¢
. D.
dd^
¢
.
Câu 5. Cho hai đường thẳng
:3dy x=+
và
:2dy x
¢
=-
khi đó:
A.
//dd
¢
. B.
ddº
¢
. C.
d
cắt
d
¢
. D.
dd^
¢
.
Câu 6. Cho hai đường thẳng
1
:1
2
dy x=- + và
1
:2
2
dy x=- +
¢
. Khi đó:
A.
//dd
¢
. B.
ddº
¢
. C.
d
cắt
d
¢
. D.
dd^
¢
.
Câu 7. Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng
:(2)dy m x m=+-
và
:221dy x m
¢
=- - +
. Với giá trị nào của
m
thì
d
cắt
d
¢
?
A.
2m ¹-
. B.
4m ¹-
. C.
{}
2; 4m ¹--
. D.
{}
2; 4m ¹-
.
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 8. Cho hai đồ thị hàm số bậc nhất là hai đường thẳng
:(32)2dy mx=- -
và
:4 2dy x m
¢
=-+
.
Với giá trị nào của
m
thì
d
cắt
d
¢
?
A.
31
;
22
m
ìü
ïï
ïï
¹
íý
ïï
ïï
îþ
. B.
3
2
m ¹ . C.
31
;
22
m
ìü
ïï
ïï
¹-
íý
ïï
ïï
îþ
. D.
1
2
m ¹ .
Câu 9. Cho hai đồ thị hàm số bậc nhất là hai đường thẳng
:(32)2dy mx=- -
và
:4 2dy x m
¢
=-+
.
Với giá trị nào của
m
thì
//dd
¢
?
A.
2
m
=-
. B.
4
m
=-
. C.
2
m
=
. D.
{}
2; 4m ¹-
.
Câu 10. Cho hàm số bậc nhất
(2 2) 3ymxm=-+-
tìm
m
để hàm số có đồ
thị song song với đường thẳng
33yxm=-
.
A.
2
5
m =- . B.
2
5
m = . C.
5
2
m = . D.
5
2
m =- .
Câu 11. Cho hai đồ thị hàm số bậc nhất là hai đường thẳng
:(2)dy m x m=+-
và
:221dy x m
¢
=- - +
. Với giá trị nào của
m
thì
ddº
¢
?
A.
2
m =-
. B.
4
m =-
. C.
2
m =
. D. Không có
m
thỏa mãn.
Câu 12. Cho hai đường thẳng
:(1)
2
m
dy mx=- + và
:1dy x=- +
¢
. Với giá
trị nào của
m
thì
ddº
¢
?
A.
2
m =-
. B.
4
m =-
. C.
2
m =
. D. Không có
m
thỏa mãn..
Câu 13. Cho hàm số
(5)4
ym x=--
. Tìm
m
để hàm số nhận giá trị là 5
khi
3
x =
.
A.
6
m =
. B.
7m =
. C.
8
m =
. D.
3
m =-
.
Câu 14. Cho hàm số
732
ymxm=-+
. Tìm
m
để hàm số nhận giá trị là
11
khi
1
x =
.
A.
9
4
m = . B.
4
9
m = . C.
9
m
=
. D.
9
4
m =- .
Câu 15. Viết phương trình đường thẳng
d
biết
d
cắt trục tung tại điểm có tung độ bằng
2
-
và cắt trục hoành
tại điểm có hoành độ
1
.
A.
22
yx=+
. B.
22
yx=- -
. C.
32
yx=-
. D.
22
yx=-
.
Câu 16. . Viết phương trình đường thẳng
d
biết
d
cắt trục tung tại điểm có tung độ bằng
3
và cắt trục hoành
tại điểm có hoành độ
4-
A.
3
3
4
yx=- + . B.
3
3
4
yx=+. C.
3
3
4
yx=- - . D.
3
3
4
yx=-.
Câu 17. Viết phương trình đường thẳng
d
biết
d
song song với đường thẳng
:31dy x=+
¢
và đi qua
điểm
(2;2)
M -
.
A.
28
yx=+
. B.
38
yx=+
. C.
38
yx=-
. D.
3
yx=
.
Câu 18. Viết phương trình đường thẳng
d
biết
d
vuông góc với đường thẳng
1
:3
2
dy x=- +
¢
và đi qua
điểm
(2; 1)
M -
A.
25
yx=+
. B.
4
yx=- +
. C.
25
yx=-
. D.
1
2
yx=- .
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 19. Viết phương trình đường thẳng
d
biết
d
vuông góc với đường thẳng
1
:3
3
dy x
¢
=+ và cắt đường
thẳng
21
yx=+
tại điểm có tung độ bằng 5.
A.
311
yx=- +
. B.
34
yx=- +
. C.
3
yx=-
. D.
311
yx=+
.
Câu 20. Viết phương trình đường thẳng
d
biết
d
vuông góc với đường thẳng
41
yx=+
và cắt đường thẳng
1
yx=-
tại điểm có tung độ bằng
3
.
A.
1
4
4
yx=- - . B.
1
4
4
yx=- + . C.
1
2
4
yx=- + . D.
1
4
yx=- .
Câu 21. Viết phương trình đường thẳng
d
biết
d
song song với đường thẳng
21
yx=- +
và cắt trục hoành
tại điểm có hoành độ bằng
3
.
A.
26
yx=- +
. B.
36
yx=- +
. C.
24
yx=- -
. D.
21
yx=- +
.
Câu 22. Viết phương trình đường thẳng
d
biết
d
song song với đường thẳng
53
yx=- -
và cắt trục hoành
tại điểm có hoành độ bằng 5
A.
1
25
5
yx=-. B.
525
yx=+
. C.
525
yx=- +
. D.
525
yx=- -
.
Câu 23. Viết phương trình đường thẳng
d
biết
d
đi qua hai điểm
(1; 2); ( 2; 0)
AB-
.
A.
24
33
yx=- - . B.
24
33
yx=- + . C.
24
33
yx=-. D.
24
33
yx=+.
Câu 24. Viết phương trình đường thẳng
d
biết
d
đi qua hai điểm
(3; 3); ( 1; 4)
AB-
.
A.
115
44
yx=-. B.
115
44
yx=- + . C.
115
44
yx=- - . D.
115
44
yx=+.
Câu 25. Tìm điểm
M
cố định mà đường thẳng
()33
ymxm=-+
đi qua với mọi
m
.
A.
1
;3
3
M
æö
÷
ç
÷
ç
÷
ç
÷
ç
èø
. B.
1
;3
3
M
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
. C.
1
;3
3
M
æö
÷
ç
÷
--
ç
÷
ç
÷
ç
èø
. D.
1
;3
3
M
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
.
Câu 26. Cho tam giác
ABC
có đường thẳng
1
:1
3
BC y x=- + và
(1; 2)
A
. Viết phương trình đường cao
AH
của tam giác
ABC
A.
2
3
3
yx=-
. B.
2
3x
3
y =+
. C.
3x 2
y =+
. D. Đáp án khác.
Câu 27. Cho đường thẳng
2
(22)4ym m x=-++
. Tìm
m
để
d
cắt
Ox
tại
A
và
Oy
tại
B
sao cho diện tích tam giác
AOB
lớn nhất.
A.
1
m =
. B. 0m = . C.
1
m =-
. D.
2
m =
.
Câu 28. Điểm cố định mà đường thẳng
1
:3(0)
31
k
dy x k k
+
=++³
-
luôn đi qua là:
A.
()
13;31M --
. B.
()
3; 3M
. C.
()
3; 3 1M -
. D. Cả A, B, C đều sai.
Câu 29. Cho đường thẳng
:(21)1
dy m x=+-
tìm
m
để
d
cắt 2 trục tọa độ tạo thành tam giác có diện tích
1
.
2
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
0m =
. B.
1
m =
. C.
1
m =-
. D. Cả A và C đều đúng.
Câu 30. Biết đường thẳng
:4
dy mx=+
cắt
Ox
tại
A
, và cắt
Oy
tại
B
sao cho diện tích tam giác
OAB
bằng 6. Khi đó giá trị của
m
bằng
A.
4
3
m = . B.
4
3
m < . C.
4
3
m > . D.
4
3
m = .
Câu 31. Cho đường thẳng
:1
dy mx m=+-
. Tìm
m
để
d
cắt
Ox
tại
A
và cắt
Oy
tại
B
sao cho tam
giác
AOB
là tam giác vuông cân
A.
1m <
. B.
1
m
=
. C.
1m >
. D.
1
m
=
hoặc
1
m
=-
.
HƯỚNG DẪN
Câu 1. Đáp án A.
Cho hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
d
cắt
d
¢
aa¹
¢
.
Câu 2. Đáp án D.
Cho hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
d
trùng
d
¢
aa
bb
=¢
=¢
ì
ï
ï
í
ï
ï
î
Câu 3. Đáp án A.
Cho hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
+) //
aa
dd
bb
ì
ï
=¢
ï
í
¹¢
¢
ï
ï
î
+)
d
cắt
d
¢
aa¹
¢
+)
aa
dd
bb
ì
ï
=¢
ï
º¢
í
ï
=¢
ï
î
+)
.1dd aa
¢¢
^ =-
Câu 4. Đáp án C.
Cho hai đường thẳng
:(0)dy ax ba=+ ¹
và :(0)dy ax ba=+
¢¢
¹
¢¢
d
cắt
d
¢
aa¹
¢
.
Câu 5. Đáp án C.
Ta thấy
:3
dy x=+
có
1
a =
và
:2dy x
¢
=-
có
2a
¢
=-
(1 2)aa¹ ¹-
¢
2a
¢
=-
nên
d
cắt
d
¢
Câu 6. Đáp án A.
Ta thấy
1
:1
2
dy x=- + có
1
;1
2
ab=- =
và
1
:2
2
dy x=- +
¢
có
1
;2
2
ab-
¢
==
11
22
2()1
aa
bb
ì
æö
ï
÷
ï
ç
÷
=¢- =-
ï
ç
÷
ï
ç
÷
ç
í
èø
ï
ï
¹¢ ¹
ï
ï
î
nên
//dd
¢
.
Câu 7. Đáp án C.
+) Ta thấy
:(2)
dy m x m=+-
có
2am=+
và
:221dy x m
¢
=- - +
có
2a
¢
=-
+) Để
:(2)
dy m x m=+-
là hàm số bậc nhất thì
20 2mm+¹ ¹-
11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+) Để
d
cắt
d
¢
aa¹
¢
22 4mm+¹-¹-
Vậy
{}
2; 4m ¹--
.
Câu 8. Đáp án A.
Ta thấy
:(32)2
dy mx=- -
có
32
am
=-
và
:4 2dy x m
¢
=-+
có
4a
¢
=
Để
:(32)2
dy mx=- -
là hàm số bậc nhất thì
3
32 0
2
mm-¹¹
Để
d
cắt
d
¢
1
32 4 2 1
2
aa m m m¹ - ¹ ¹ ¹
¢
Vậy
31
;
22
m
ìü
ïï
ïï
¹
íý
ïï
ïï
îþ
Câu 9. Đáp án B.
Ta thấy
:(32)2
dy mx=- -
có
20 2am m=+¹¹-
và
:4 2dy x m
¢
=-+
có
20a
¢
=- ¹
Để
//dd
¢
22 4
4( )
21 1
aa m m
mTM
bb m m m
ìì ì
ïï ï
=¢ + =- =-
ïï ï
 =-
íí í
ïï ï
¹¢ - ¹- + ¹
ïï ï
îî î
.
Câu 10. Đáp án C.
Hàm số
(2 2) 3
ymxm=-+-
là hàm số bậc nhất khi
220 1mm-¹ ¹
Để
//dd
¢
5
223
2
33 3
4
m
m
mm
m
ì
ï
ï
=
ì
ï
ï
-=
ï
ï
ï

íí
ïï
-¹-
ïï
î
¹
ï
ï
ï
î
5
()
2
mTM=
Vậy
5
2
m =
.
Câu 11. Đáp án D.
+) Ta thấy
:(2)
dy m x m=+-
có
2am=+
:221dy x m
¢
=- - +
có
2a
¢
=-
+) Điều kiện để
:(2)
dy m x m=+-
là hàm số bậc nhất
20 2mm+¹ ¹-
+) Để
ddº
¢
aa
bb
ì
ï
=¢
ï
í
ï
=¢
ï
î
22
21
m
mm
ì
ï
+=-
ï
í
ï
-=- +
ï
î
4
1
m
m
ì
ï
=-
ï
í
ï
=
ï
î
(vô lý)
Vậy không có giá trị nào của
m
để
ddº
¢
Câu 12. Đáp án C.
Ta thấy :(1)
2
m
dy mx=- + có
1;
2
m
amb=- =
và
:1dy x=- +
¢
có
1; 1ab=-
¢
=
Điều kiện để
:(1)
2
m
dy mx=- +
là hàm số bậc nhất
10 1mm-¹ ¹
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Để
ddº
¢
aa
bb
ì
ï
=¢
ï
í
ï
=¢
ï
î
11
2
2
2
1
2
()
m
m
mtm
m
m
ì
ï
-=-
ì
ï
ï
=
ï
ï
ï
=
íí
ïï
=
=
ïï
î
ï
ï
î
Vậy
2
m
=
Câu 13. Đáp án C.
Thay
3; 5
xy==
vào hàm số
(5)4
ym x=--
ta được
(5).345(5).39 53 8
mmmm--=-=-==
Vậy
8
m =
.
Câu 14. Đáp án A.
Thay
1; 1 1
xy==
vào hàm số
732
ymxm=-+
ta được
9
11 7 .1 3 2 4 9 .
4
mm m m=-+==
Vậy
9
.
4
m =
Câu 15. Đáp án D.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
Vì
d
cắt trục tung tại tại điểm có tung độ bằng
2
-
và cắt trục hoành tại điểm có hoành độ
1
nên
d
đi qua
hai điểm
(0; 2); (1; 0)
AB-
Thay tọa độ điểm
A
vào phương trình đường thẳng
d
ta được
.0 2 2ab b+=-=-
Thay tọa độ điểm
B
và
2
b
=-
vào phương trình đường thẳng
d
ta được
.1 2 0 2aa-= =
Vậy phương trình đường thẳng cần tìm là
22
yx=-
Câu 16. Đáp án B.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
Vì
d
cắt trục tung tại tại điểm có tung độ bằng
3
và cắt trục hoành tại điểm có hoành độ
4-
nên
d
đi qua
hai điểm
(0;3); ( 4;0)
AB-
Thay tọa độ điểm
A
vào phương trình đường thẳng
d
ta được
.0 3 3ab b+= =
Thay tọa độ điểm
B
vào phương trình đường thẳng
d
ta được
3
.( 4) 3 0 .
4
aa-+==
Vậy phương trình đường thẳng cần tìm là
3
3
4
yx=+
.
Câu 17. Đáp án B.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
Vì
//dd
¢
nên
3
:3
1
a
dy x b
b
ì
ï
ï
í
ï
ï
=
î
=
+
¹
Thay tọa độ điểm
M
vào phương trình đường thẳng
d
ta
được
3.( 2) 2 8
bb-+==
( thỏa mãn)
Vậy phương trình đường thẳng
:38
dy x=+
.
Câu 18. Đáp án C.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vì
dd^
¢
nên
1
.12
2
aa
æö
÷
ç
÷
-=-=
ç
÷
ç
÷
ç
èø
(TM)
:2
dy x b=+
Thay tọa độ điểm
M
vào phương trình đường thẳng
d
ta được
2.2 1 5bb+=-=-
Vậy phương trình đường thẳng
:25
dy x=-
Câu 19. Đáp án A.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
Vì
dd^
¢
nên
1
.1 3:3
3
aadyxb=- =- =- +
Gọi điểm
(;5)
Mx
là giao điểm của đường thẳng
d
và đường thẳng
21
yx=+
Khi đó
2152 4 2 (2;5)
xxxM+= = =
Thay tọa độ điểm
M
vào phương trình đường thẳng
d
ta được
3.2 5 11bb-+==
Vậy phương trình đường thẳng
:311
dy x=- +
Câu 20. Đáp án B.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
Vì
dd^
¢
nên
11
.4 1 :
44
aadyxb=- =- =- +
Gọi điểm
(;3)
Mx
là giao điểm của đường thẳng
d
và đường thẳng
1
yx=-
Khi đó
13 4 (4;3)
xxM-= =
Thay tọa độ điểm
M
vào phương trình đường thẳng
1
:
4
dy x b=- +
ta được
1
.4 3 4
4
bb-+==
Vậy phương trình đường thẳng
1
:4
4
dy x=- +
.
Câu 21. Đáp án A.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
Vì
d
song song với đường thẳng
21
yx=- +
nên
2; 1 2
ab yxb=- ¹ =- +
Giao điểm của đường thẳng
d
với trục hoành có tọa độ
(3; 0)
Thay
3; 0
xy==
vào phương trình đường thẳng
d
ta được
2.3 0 6( ) 2 6bbTMyx-+== =-+
Vậy
:26
dy x=- +
Câu 22. Đáp án C.
Gọi phương trình đường thẳng
d
cần tìm là
(0)yaxba=+ ¹
Vì
d
song song với đường thẳng
53
yx=- -
nên
5; 3 : 5
ab dyxb=- ¹- =- +
Giao điểm của đường thẳng
d
với trục hoành có tọa độ
(5; 0)
Thay
5; 0xy==
vào phương trình đường thẳng
d
ta
được
5.5 0 25( ) 5 25bbTMyx-+== =-+
Vậy
:525
dy x=- +
.
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 23. Đáp án .
Gọi phương trình đường thẳng cần tìm là
yaxb=+
Thay tọa độ điểm
A
vào phương trình đường thẳng
d
ta được
2ab+=
2ba=-
Thay tọa độ điểm
B
vào phương trình đường thẳng
d
ta được
202ab b a-+==
Suy ra
2
22
3
aaa=- =
(TM)
24 2 4
2.
33 3 3
byx= = = +
Vậy
24
:
33
dy x=+
.
Câu 24. Đáp án B.
Gọi phương trình đường thẳng cần tìm là
(0)yaxba=+ ¹
Thay tọa độ điểm
A
vào phương trình đường thẳng
d
ta được
33ab+=
33ba=-
Thay tọa độ điểm
B
vào phương trình đường thẳng
d
ta được
1. 4ab-+=
4ba=+
Suy ra
21
22 334 4 1
34
aaa aaa a=- = - =+ =- =-
115 1 15
44
44 4 4
ba yx
æö
-
÷
ç
÷
=+=+- = = +
ç
÷
ç
÷
ç
èø
Vậy
115
:
44
dy x=- +
.
Câu 25. Đáp án B.
Gọi
(;)
Mxy
là điểm cố định cần tìm khi đó
3(3)mx m y-+=
đúng với mọi
m
330
mx m y---=
đúng với mọi
m
(3 1) 3 0
mx y-+--=
đúng với mọi
m
1
310
1
;3
3
30
3
3
x
x
M
y
y
ì
ï
ì
ï
æö
ï
-=
=
ï
ï
÷
ï
ç
÷
-
ç
íí
÷
ç
÷
ïï
ç
-- =
èø
ïï
=-
î
ï
ï
î
Vậy điểm
1
;3
3
M
æö
÷
ç
÷
-
ç
÷
ç
÷
ç
èø
là điểm cố định cần tìm.
Câu 26. Đáp án D.
Giả sử
:ax
AH y b=+
Vì
AH
là đường cao của tam giác
ABC
nên
AH
vuông góc với
BC
nên:
1
.13
3
aa
-
=- =
Mặt khác
AH
đi qua
(1; 2)
A
nên ta có:
3.1 2 1bb+= =-
Vậy
:31
AH y x=-
Câu 27. Đáp án A.
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
{}
{}
2
22
2
04(0;4)|4|4
Ox
0( 2 2) 40
44
;0
22 22
4
22
BB
AA
A
dOy B
xyBOB
dA
ymmx
xA
mm mm
OA
mm
Ç=
= = = =
Ç=
= - + +=
æö
--
÷
ç
÷
=
ç
÷
ç
÷
ç
-+ -+
èø
-
=
-+
22
114 8
. .4.
22
22(1)1
AOB
SOAOB
mm m
D
-
== =
-+ -+
Ta có
2
(1)11mm"-+³
Do đó
2
88
8
1
(1)1
AOB
S
m
D
=£=
-+
Dấu “=” xảy ra khi
10 1mm-= =
Hay tam giác
OAB
có diện tích lớn nhất là
8
khi
1.
m
=
Câu 28. Đáp án A.
Gọi
00
(;)Mx y
là điểm cố định mà d luôn đi qua.
00
;()Mx y d kÎ"
00
1
3
31
k
yxkk
+
= + + "
-
00 00
33330kx x k k y y k++--+-+="
()
0
00
310
13 330
x
xy
+-=
+- +
ì
ï
ï
í
-=
ï
ï
ï
ï
î
0
0
()()
13
1313 330
x
y
ì
ï
=-
ï
ï
í
ï
-+- +-=
ï
ï
î
()
()()
0
0
2
0
0
0
0
13
13
13 4230
13 13 0
13
13
x
x
y
y
x
y
ì
ì
ï
ï
=-
ï
=-
ï
ï
ï
ï

íí
ïï
-+-=
-+-=
ïï
ïï
î
ï
î
ì
ï
=-
ï
ï
í
ï
=- +
ï
ï
î
()
13;31M- -
là điểm cố định mà
d
luôn đi qua.
Câu 29. Đáp án D.
{}
{}
01
(0; 1) | 1 | 1
Ox 0
11
(2 1) 1 0
21 2
11
;0
21 21
BB
A
A
dOy B x y
BOB
dAy
mx x m
m
AOA
mm
Ç= ==-
-=-=
Ç= =
æö
-
÷
ç
÷
+-== ¹
ç
÷
ç
÷
ç
+
èø
æö
÷
ç
÷
=
ç
÷
ç
÷
ç
++
èø
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
11111
..1. 211
222212
||
0
1
()
AOB
SOAOB m
m
m
tmdk
m
D
== =+=
+
é
=
ê
ê
=-
ê
ë
Câu 30. Đáp án A.
{}
{}
04
(0; 4) | 4 | 4
Ox
4
040 (0)
44
;0
BB
AA A
dOy B
xy
BOB
dA
ymx xm
m
AOA
mm
Ç=
= =
==
Ç=
-
= += = ¹
æö
-
÷
ç
÷
=
ç
÷
ç
÷
ç
èø
11444
.6.4.6|| .
22 33
AOB
SOAOB mm
m
D
=====
Câu 31. Đáp án D.
{}
{}
01
(0; 1) | 1 |
Ox
1
010(0)
11
;0
BB
AA A
dOy B
xym
Bm OB m
dA
m
ymxm x m
m
mm
AOA
mm
Ç=
= = -
-=-
Ç=
-
= + -= = ¹
æö
--
÷
ç
÷
=
ç
÷
ç
÷
ç
èø
Tam giác OAB vuông cân tại O
é
-
ê
-=
-
ê
=-
ê
-
ê
-=
ê
=
ë
1
1
1
1
1
|
1
|
m
m
m
m
OA OB m
m
m
m
m
2
2
1
1
1
1
1
11
()
(0
0
)
m
m
m
m
m
m
m
é
é
=
=
ê
ê
ê
ê
æö
=
-
÷
ê
ç
ê
÷
--=
ç
=
ê
÷
ç
ê
÷
ç
èø
ë
ê
ë
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
D.PHIẾU BÀI TỰ LUYỆN
Bài 1. Cho hai đường thẳng:

1
d: 2ymx

2
d: 2 3 2ymx
Với giá trị nào của m thì:
a)

1
d
song song với

2
d
.
b)

1
d
trùng với

2
d
.
c)

1
d
vuông góc với

2
d
.
Bài 2. Cho hai đường thẳng :

1
d: 1 5ym x

2
d: 2 1 4ymxm
.
Xác định m để hai đường thẳng:
a) Cắt nhau.
b) Song song với nhau.
c) Vuông góc với nhau.
Bài 3. Cho 2 đường thẳng

22ym x d


2
21'ym mx d
a) Hai đường thẳng (d) và (d’) có thể trùng nhau không?
b) Tìm các giá trị của m để (d) và (d’) song song với nhau.
Bài 4. Tìm giá trị của k để ba đường thẳng:

1
23dyx

2
32dyx

3
5dykxk
Đồng quy trong mặt phẳng tọa độ.
Bài 5. Cho hai đường thẳng:

62ym x
và

34 5ymm x
a) Chứng minh rằng khi
2m 
thì hai đường thẳng đã cho song song với nhau;
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho song song với nhau.
Bài 6. Cho hai đường thẳng:

13ym x
và

21 4ymx
a) Chứng minh rằng khi
1
2
m 
thì hai đường thẳng đã cho vuông góc với nhau
b) tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau.
Bài 7. Xác định hàm số
yaxb
trong mỗi trường hợp sau:
a) Khi
3a
, đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
3
.
b) Khi
5a 
, đồ thị hàm số đi qua điểm

A2;3
;
c) Đồ thị hàm số đi qua hai điểm

M1;3
và

N2;6
d) Đồ thị hàm số song song với đường thẳng
7yx
và đi qua điểm

1; 7 7 .
Bài 8. Cho đường thẳng:

4dyx
a) Viết phương trình đường thẳng

1
d
song song với đường thẳng (d) và có tung độ gốc bằng 10.
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b) Viết phương trình đường thẳng (d
2
) vuông góc với đường thẳng (d) và cắt trục Ox tại điểm có hoành độ
bằng
8
.
c) Viết phương trình đường thẳng (d
3
) song song với đường thẳng (d) cắt trục Ox tại A, cắt trục Oy tại B và
diện tích tam giác AOB bằng 8.
Bài 9. Cho hàm số

2ym xn
(1).
a) Tìm m và n để đồ thị hàm số cắt Ox tại A; Oy tại B sao cho
AB
3xx.
b) Viết phương trình đường cao OH của tam giác OAB.
Bài 10. Cho đường thẳng

12 dya x a
a) Tìm a để đường thẳng (d) cắt trục tung tại điểm có tung độ là
1
2
.
b) Tìm a để đường thẳng (d) vuông góc với đường thẳng
1
2
yx
.
c) Chứng minh rằng các đường thẳng (d) luôn đi qua một điểm cố định với mọi giá trị của a.
Bài 11.
a) Viết phương trình đường thẳng đi qua hai điểm:
2
A;2
3



và

B3;1
b) Viết phương trình đường trung trực của đoạn AB.
Bài 12. Tìm các giá trị của m để đồ thị hàm số
3ymx
tiếp xúc với đường tròn có tâm trùng với gốc
tọa độ và có bán kính bằng 2.
Bài 13. Trong mặt phẳng tọa độ cho

E2 1;3 2mm
a) Tìm tập hợp các điểm E.
b) Tìm m để OE nhỏ nhất.
HƯỚNG DẪN
Bài 1: Cho hai đường thẳng:

1
d: 2ymx

2
d: 2 3 2ymx
Với giá trị nào của m thì:
a)

1
d
song song với

2
d
.
b)

1
d
trùng với

2
d
.
c)

1
d
vuông góc với

2
d
.
Giải
a)

1
d: 2ymx m
song song với

2
d: 2 3 2ymx
23 3
3
22 1
mm m
m
mm






b)

1
d
trùng với

2
d
23 3
22 1
mm m
mm






(không thỏa mãn).
Suy ra: Hai đường thẳng này không thể trùng nhau.
c)

1
d
vuông góc với

2
d
tương đương với:
19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com


2
.2 3 1
2310
12 1 0
1
1
2
mm
mm
mm
m
m



Bài 2: Cho hai đường thẳng :

1
d: 1 5ym x

2
d: 2 1 4ymxm
.
Xác định m để hai đường thẳng:
a) Cắt nhau.
b) Song song với nhau.
c) Vuông góc với nhau.
Giải
a)
22 1 1mmm
b)
22 1mm
và
54 1mm
và
91mm
c)

2
22 1 1 2 5 30mm mm

12 3 0
1
3
2
mm
m
m


Bài 3: Cho 2 đường thẳng

22ym x d


2
21'ym mx d
a) Hai đường thẳng (d) và (d’) có thể trùng nhau không?
b) Tìm các giá trị của m để (d) và (d’) song song với nhau.
Giải
a) Hai đường thẳng (d) và (d’) có tung độ gốc lần lượt là
2b
và
'1b 
. Rõ rang
'bb
(
21
) nên hai
đường thẳng (d) và (d’) không thể trùng nhau được:
b) Hai đường thẳng (d) và (d’) song song với nhau khi và chỉ khi:

22
22 20
10 1
120
20 2
mmmmm
mm
mm
mm
 






Vậy với
1m
hoặc
2m 
thì hai đường thẳng (d) và (d’) song song với nhau.
Bài 4: Tìm giá trị của k để ba đường thẳng:

1
23dyx

2
32dyx

3
5dykxk
Đồng quy trong mặt phẳng tọa độ.
Giải
20.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Hai đường thẳng (d
1
) và (d
2
) có hệ số của x khác nhau

23
nên chúng cắt nhau tại điểm M trong mặt
phẳng tọa độ. Khi đó tọa độ của điểm M phải thỏa mãn đồng thời hai phương trình:
23yx
và
32yx
Suy ra:
2332 5 5 1xx x x
2 3 231yx 
Tọa độ của điểm M là:

1;1M
.
Để ba đường thẳng đồng quy thì điểm

1; 1M
thuộc đường thẳng (d
3
) suy ra
3k
.
Bài 5: Cho hai đường thẳng:

62ym x
và

34 5ymm x
a) Chứng minh rằng khi
2m 
thì hai đường thẳng đã cho song song với nhau;
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho song song với nhau.
Giải
a) Khi
2m 
hai đường thẳng có cùng hệ số góc là 4 nên chúng song song với nhau.
b) Hai đường thẳng

62ym x
và

34 5ymm x
song song với nhau khi và chỉ khi:


22
6343360 20
1
120
2
mmm mm mm
m
mm
m
  


Bài 6: Cho hai đường thẳng:

13ym x
và

21 4ymx
a) Chứng minh rằng khi
1
2
m 
thì hai đường thẳng đã cho vuông góc với nhau
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau.
Giải
a) Khi
1
2
m 
hai đường thẳng

13ym x
và

21 4ymx
có hệ số góc lần lượt là
1
2
a
,
'2a 
, khi đó

1
'.2 1
2
aa 
. Vậy hai đường thẳng vuông góc với nhau.
b) Hai đường thẳng

13ym x
và đường thẳng

21 4ymx
vuông góc với nhau khi và chỉ khi:

2
12 1 1 2 0 2 1 0
0
1
1
210
2
mm mm mm
m
m
m
m




Bài 7:
Xác định hàm số
yaxb
trong mỗi trường hợp sau:
a) Khi
3a , đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3 .
b) Khi
5a 
, đồ thị hàm số đi qua điểm

A2;3
;
c) Đồ thị hàm số đi qua hai điểm

M1;3
và

N2;6
d) Đồ thị hàm số song song với đường thẳng
7yx
và đi qua điểm

1; 7 7 .
21.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Giải
a) Khi
3a ta có hàm số
3yxb
. Đồ thị hàm số
3yxb
cắt trục tung tại hai điểm có tung độ
bằng
3
nên
3b 
, ta được hàm số
33yx
.
b) Khi
5a 
, ta có hàm số
5yxb
.
Đồ thị hàm số
5yxb
đi qua điểm

A2;3;;
nên:

352 7bb 
Hàm số phải tìm là
57yx
c) Đồ thị hàm số
yaxb
đi qua điểm

M1;3
và điểm

N2;6
, ta có:

3.1
6.2
ab
ab


Suy ra
1, 4ab
, ta được hàm số
4yx
d) Đồ thị hàm số
yaxb
song song với đường thẳng
7yx
nên
7a
. Ta có hàm số
7yxb
Đồ thị hàm số
7yxb
lại đi qua điểm

;7 7a
Nên:
77 71 6bb
Hàm số phải tìm là:
76yx
Bài 8: Cho đường thẳng:

4dyx
a) Viết phương trình đường thẳng

1
d
song song với đường thẳng (d) và có tung độ gốc bằng 10.
b) Viết phương trình đường thẳng (d
2
) vuông góc với đường thẳng (d) và cắt trục Ox tại điểm có hoành độ
bằng
8
.
c) Viết phương trình đường thẳng (d
3
) song song với đường thẳng (d) cắt trục Ox tại A, cắt trục Oy tại B và
diện tích tam giác AOB bằng 8.
Giải
a)
410yx
b) Đường thẳng (d
2
) có dạng
yaxb
Đường thẳng này vuông góc với đường
thẳng (d) nên:
.1aa
, suy ra
1
4
a 
,
ta có hàm số
1
4
yxb
. Đường
thẳng này cắt trục hoành tại điểm có
hoành độ bằng
8
, ta có
2b 
.
Hàm số phải tìm là:
1
2
4
yx
c) Đường thẳng (d
3
) song song với đường
thẳng (d) nên có dạng
4yxb
. Đường
thẳng này cắt trục hoành ở điểm A, cắt trục
tung ở điểm B, ta có:
0y
thì
4
b
x 
, tọa
độ của điểm A là
A;0
4
b



,
0x
thì
yb
, tọa độ của điểm
B
là

B0;b
22.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
tam giác AOB vuông ở O nên:
2
AOB
11
OA.OB .
2248
bb
Sb

Suy ra
2
8
8
b
do đó
2
64b
nên
8b 
Có hai hàm số thỏa mãn yêu cầu đề bài là:
48yx
và
48yx
.
Bài 9: Cho hàm số

2ym xn
(1).
a) Tìm m và n để đồ thị hàm số cắt Ox tại A; Oy tại B sao cho
AB
3xx.
b) Viết phương trình đường cao OH của tam giác OAB.
Giải
a) Đường thẳng (1) cắt Ox tại A sao cho

A
3A3;0x 
.
Đường thẳng (1) cắt Oy tại B sao cho

B
3B0;3y 
.
Thay tọa độ điểm A; B vào (1) ta được:


23 0
1
3
20 3
mn
m
n
mn



Vậy
1; 3mn
ta được hàm số
3yx
b) Phương trình đường cao OH đi qua

O0;0
nên hàm
số có dạng:
yax
.
Mặt khác, OH vuông góc với đường thẳng
3yx
nên:

11 1aa
.
Vậy phương trình đường cao OH là:
yx
.
Bài 10: Cho đường thẳng

12 dya x a
a) Tìm a để đường thẳng (d) cắt trục tung tại điểm có tung độ là
1
2
.
b) Tìm a để đường thẳng (d) vuông góc với đường thẳng
1
2
yx
.
c) Chứng minh rằng các đường thẳng (d) luôn đi qua một điểm cố định với mọi giá trị của a.
Giải
a)
15
2
22
aa

.
b)

1
1. 1 1
2
aa
.
c) Viết

12yax x
dưới dạng:

12 0*ax x y 
.
Phương trình (*) nghiệm đúng với mọi
10 1
201
xx
a
xy y






.
Vậy điểm cố định là

A1;1
.
Bài 11:
23.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Viết phương trình đường thẳng đi qua hai điểm:
2
A;2
3



và

B3;1
b) Viết phương trình đường trung trực của đoạn AB.
Giải
a) Đường thẳng
yaxb
đi qua A và B nên:
2
2
3
3
34
4
13
ab
a
yx
b
ab






b) M là trung điểm của AB nên M có tọa độ là:
2
3
21 533
3
;;
22 62










Đường trung trực của AB có dạng:
yaxb
vuông góc với đường thẳng

34 . 3 1
33
33
yxa
ayxb
 

Đường thẳng này đi qua M, nên:
3353 3
.
236 2
bb
Vậy phương trình đường trung trực của AB là:
32
33
yx
Bài 12: Tìm các giá trị của m để đồ thị hàm số
3ymx
tiếp xúc với đường tròn có tâm trùng với gốc tọa
độ và có bán kính bằng 2.
Giải
Đường thẳng
3ymx
tiếp xúc với

O;2
OH = 2
và
OH AB
.
Xét tam giác vuông OAB có:

2
22 2
111111
OA=3
OH OA OB 4 9 OB

65
5
OB
Suy ra: Tìm được hai điểm B và B’ thuộc x’x sao cho:
65
OB=
5
Nếu
65 65
;0 . 3 0
55
Bm





55
3
52
myx
Nếu
65 65 5
B' ;0 . 3 0
55 2
mm





24.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
5
3
2
yx
Vậy:
5
2
m 
.
Bài 13: Trong mặt phẳng tọa độ cho

E2 1;3 2mm
a) Tìm tập hợp các điểm E.
b) Tìm m để OE nhỏ nhất.
Giải
a)

E2 1;3 2 2 1mm xm
32ym
Từ:
21xm
suy ra:
1
2
x
m
Thay vào
32ym
Ta được:
1
3. 2
2
x
y

37
22
yx
Vậy tập hợp các điểm E là đường thẳng có phương trình là:
37
22
yx
.
b) Cách 1: Tìm tọa độ A; B (xem hình vẽ)
OE
nhỏ nhất
OE AB
.
Xét tam giác vuông OAB, có OE là đường cao.
22
222 2
111 1 1 1 7
13
77
23
OE
OE OA OB OE

 
 
 
Mặt khác,

22
OE= 2 1 3 2mm

4
2
49 4
13 8 5 13 4 0
13 13
mm m m

Vậy:
4
13
m
thì E có tọa độ là
21 14
;
13 13



để OE
nhỏ nhất
7
13
.
Cách 2: Phương trình đường thẳng OE:
yax
vì
OE AB
nên:
32
.1
23
aa 
.
Suy ra, phương trình đường thẳng OE là:
2
3
yx
.
Do E là giao điểm của hai đường thẳng
37
22
yx
và
2
3
yx
nên hoành độ của E thỏa mãn phương
trình:
37 2 21
22 3 13
xxx

Thay
21
13
x 
vào
21xm
, ta được:
4
13
m
.
25.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Khi đó, tọa độ của E là:
21 21
;
13 13



.
Vậy
4
13
m
thì OE
nhỏ nhất
7
13
.
-------------------------Toán Học Sơ Đồ-------------------------
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHUYÊN ĐỀ ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
A.KIẾN THỨC CẦN NHỚ
1. Hệ số góc của đường thẳng y  ax  b a  0 :
a. Đường thẳng y  ax  b có hai hệ số là a và b trong đó hệ số a được gọi là hệ số góc của đường thẳng.
b. Gọi a là góc tạo bởi đường thẳng y  ax  b a  0 với tia Ox. Cách xác định góc này như sau: trước
tiên, ta xác định giao điểm A của đường thẳng với tia Ox, góc a là góc tạo bởi tia Ax, và phần phía trên của đường thẳng.
c. Biểu thức liên hệ giữa a và α : tan  a
Vậy nếu biết hệ số góc a ta có thể suy ra số đo của góc α và ngược lại.
Do đó, a gọi là hệ sổ góc của đường thẳng (hệ số cho biết góc α).
Nếu a  0  0    90
Nếu a  0  90    180
d. Các đường thẳng có cùng hệ số góc thì tạo với trục Ox các góc bằng nhau.
2. Đường thẳng song song và đường thẳng cắt nhau:
Cho hai đường thẳng (d): y  ax  b và (dʹ): y  a'x  b ' ( aa'  0
a. Hai đường thẳng song song     a  a' d P d'   b  b'
b. Hai đường thẳng trùng nhau
     a  a' d d '   b  b'
c. Hai đường thẳng cắt nhau
+ (d) cắt (d’)  a  a'
+ d  d '  aa'  1 B.CÁC DẠNG MINH HỌA
Dạng 1: Xét vị trí tương đối của hai đường thẳng
Phương pháp giải: Cho hai đường thẳng: d: y = ax + b với a  0 và d’: y = a’x + b’ vớia'  0 khi đó ta có:  
1. d và d’ song song a a '   b  b '
2. d và d’ trùng nhau  a  a '    b  b '
3. d và d’ cắt nhau  a  a ' . Đặc biệt d và d’ vuông góc với nhau  a.a '  1
Bài 1: Cho hai đường thẳng d và d ' xác định bởi y axa 0 và y a' xa' 0 . Chứng minh rằng
điều kiện để các đường thẳng d và d' vuông góc với nhau là aa'  1 .
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 2: Hãy chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường thẳng sau:
a) y 3x 1;
b) y 2 x ;
c) y  0,3x;
d) y  0,3x 1; ; e)
y 3 3x ;
g) y  x 3.
Bài 3: Cho các đường thẳng: d : y  2m  1 x  2m  3 ; d : y m  1 x  . m 1     2   Tìm các giá trị của m để: a) d cắt d
b) d song song d 1 2 1 2
c) d vuông góc d d) d trùng d . 1 2 1 2
Bài 4: Cho đường thẳng y  m 2x  m   1 d
a) Tìm giá trị của m để đường thẳng d  đi qua góc tọa độ.
b) Tìm giá trị của m để đường thẳng d  cắt trục hoành tại điểm có tung độ bằng 3 2 .
c) Tìm giá trị của m để đường thẳng d  song song với đường thẳng y  2 2 3x 2 .
Bài 5: Cho ba đường thẳng: d : y x 2, d : y 2x 1, d : y 2
( m 1 )x m. 1 2 3
a) Xác định tọa độ giao điểm của d và d . 1 2
b) Tìm các giá trị của tham số m để:
i) d và d song song với nhau. 2 3
ii) d và d trùng nhau. 1 3
iii) d , d và d đồng quy 1 2 3
Dạng 2: Xác định phương trình đường thẳng
Phương pháp giải: Để xác định phương trình đường thẳng, ta thường làm như sau:
Bước 1: Gọi d: y = ax + b là phương trình đường thẳng cần tìm (a,b là hằng số).
Bước 2: Từ giả thiết của đề bài, tìm được a,b từ đó đi đến kết luận.
Bài 6: Viết phương trình đường thẳng d biết
a) d cắt trục tung tại điểm có tung độ bằng 5  và
đi qua điểm A1; 3.
b) d song song với đường thẳng y  2x  8 và cắt trục hoành tại điểm có hoành độ bằng 5.
c) d vuông góc với đường thẳng y x  3 và cắt đường thẳng
y  2x  1 tại điểm có tung độ bằng 5.
Bài 7: Trên mặt phẳng Oxy cho hai điểm A1;1 và B1;7 . Xác định hàm số biết đồ thị của nó là
đường thẳng d  đi qua hai điểm A và B .
Bài 8: Chứng tỏ ba điểm sau thẳng hàng  11
a) A1;3;B ;2 ;C 2;   3 b)
H 1;1;I 1; 5  
  ; K ;  3  2   3
Bài 9: Tìm tập hợp điểm I và K nằm trên mặt phẳng tọa độ sau đây
m 1 2m 1
2 3m m 7  a) I ;  b) K ;   2 3   5 3 2
Bài 10: Trong mặt phẳng Oxy cho đường thẳng ( d ) : y x 2 3
a. Vẽ d  . Viết phương trình đường thẳng qua A3 ; 2 và song song với d  .
b. Tìm tọa độ điểm B trên trục tung sao cho tam giác AOB vuông tại A .
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 11: Trong mặt phẳng Oxy cho A1; 2 và B3; 4. Tìm trên trục hoành điểm M sao cho MAMB
đạt giá trị nhỏ nhất
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com HƯỚNG DẪN
Dạng 1: Xét vị trí tương đối của hai đường thẳng Bài 1.
ho hai đường thẳng d và d' xác định bởi y ax a 0 và
a' xa' 0 . Chứng minh rằng điều kiện để các đường thẳng d
à d' vuông góc với nhau là aa'  1 . iải:
a thấy khi d d ' thì một trong hai đường thẳng d và d ' , có một
ường (giả sử là d ) nằm trong góc vuông phần tư I và III, đường kia
là d ' ) nằm trong góc vuông phần tư thứ II và IV, khi đó
0 , a' 0 .
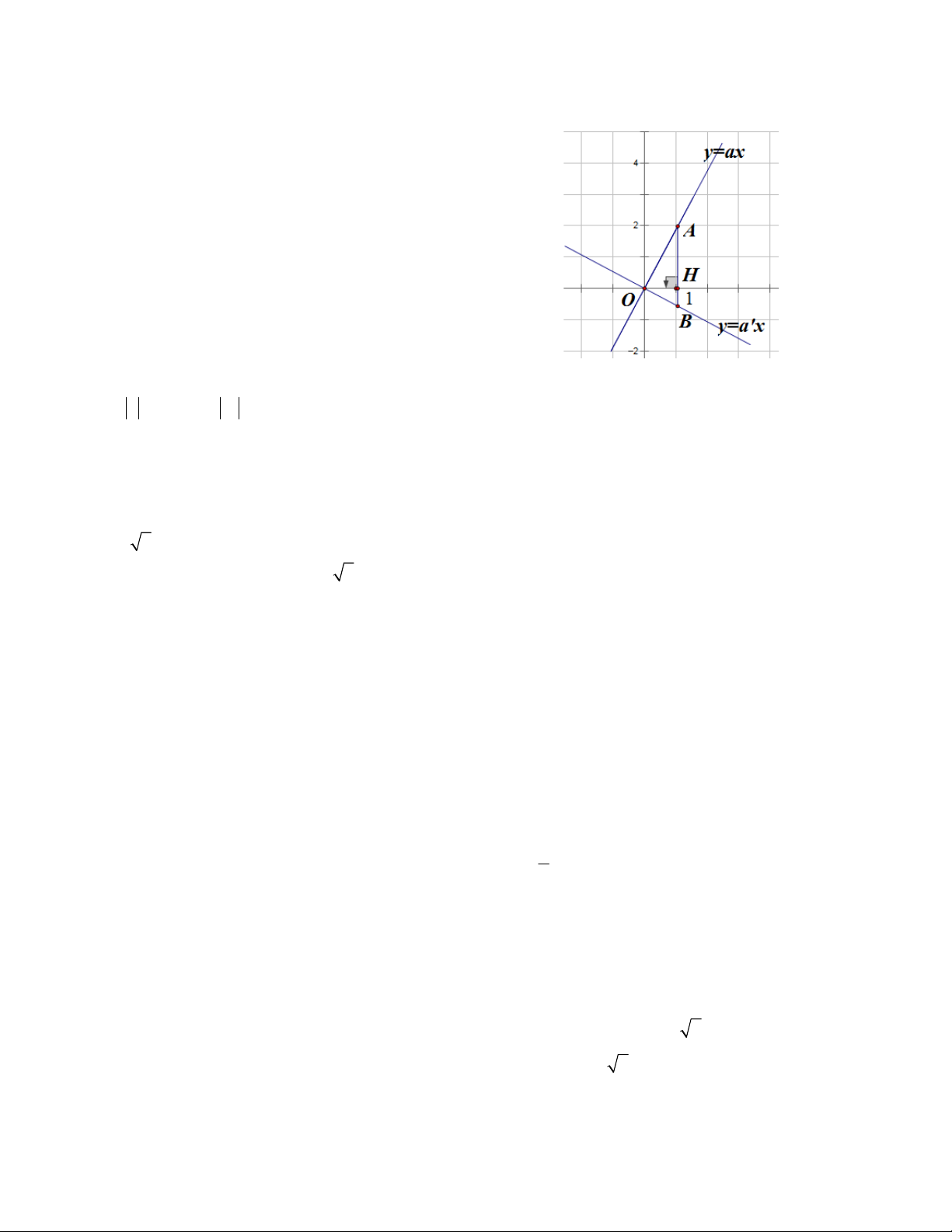
Qua điểm H 1;0 , kẻ đường thẳng vuông góc với Ox, cắt d và d' theo thứ tự tại A và B, ta có
HA a a; HB a'  a .
Chú ý rằng H nằm giữa A và B nên điều kiện để tam giác OAB vuông tại O là:  2
HA.HB OH a a'   1 aa'  1.
Bài 2. Hãy chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường thẳng sau:
a) y 3x 1;
b) y 2 x ;
c) y  0,3x;
d) y  0,3x 1; ; e)
y 3 3x ;
g) y  x 3.
Giải: a và e; b và g; c và d.
Bài 3. Cho các đường thẳng:
d : y  2m  1 x  2m  3 ; d : y m  1 x  . m 1     2   Tìm các giá trị của m để: a) d cắt d
b) d song song d 1 2 1 2
c) d vuông góc d d) d trùng d . 1 2 1 2 Giải:
a) d cắt d  2m 1  m 1   1 2 m  2
2m 1  m 1 
b) d song song d    m  2 1 2 
 2m  3  m 1
c) d vuông góc d  2m   1 m   1  1
  m  0 hoặc m 1 2 2
2m 1  m 1 
d) d trùng d    m . 1 2 
 2m  3  m
Bài 4. Cho đường thẳng y  m 2x  m   1 d
a) Tìm giá trị của m để đường thẳng d  đi qua góc tọa độ.
b) Tìm giá trị của m để đường thẳng d  cắt trục hoành tại điểm có tung độ bằng 3 2 .
c) Tìm giá trị của m để đường thẳng d  song song với đường thẳng y  2 2 3x 2 . Giải:
a) Đường thẳng d  đi qua gốc tọa độ O khi m 1 0 hay m 1. Khi đó hàm số là y x
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
b) Ta có m 1 3 2 hay m 4 2 .
c) Ta có m 2 2 2 3 và m 1  2
m 2 2 1 và m  1 m 2 2 1
Khi đó hàm số y  2 2 3x 2 2 2
Bài 5. Cho ba đường thẳng: d : y x 2, d : y 2x 1, d : y 2
( m 1 )x m. 1 2 3
a) Xác định tọa độ giao điểm của d và d . 1 2
b) Tìm các giá trị của tham số m để:
i) d và d song song với nhau. 2 3
ii) d và d trùng nhau. 1 3
iii) d , d và d đồng quy. 1 2 3 Giải:
a) Xét phương trình hoành độ giao điểm của d và d : x 2 2x 1x 1 y 3 1 2
Vậy tọa độ giao điểm của d và d là I( 1;3 ) . 1 22
m 1 2
b) i) d và d song song với nhau     2 3 m  1. m 12
m 1 2
ii) d và d trùng nhau.    m  1 1 3m 1
iii) Ta có: tọa độ giao điểm của d và d là I( 1;3 ) . 1 2    2 3
m 1.1m
Để d , d và d đồng quy thì I d  
m  2 . 1 2 3 3 m 1
Dạng 2: Xác định phương trình đường thẳng
Bài 6. Viết phương trình đường thẳng d biết:
a) d cắt trục tung tại điểm có tung độ bằng 5  và
đi qua điểm A1; 3.
b) d song song với đường thẳng y  2x  8 và cắt trục hoành tại điểm có hoành độ bằng 5.
c) d vuông góc với đường thẳng y x  3 và cắt đường thẳng
y  2x  1 tại điểm có tung độ bằng 5.
Giải: Phương trình đường thẳng d có dạng: d : y ax b
a) d cắt trục tung tại điểm có tung độ bằng 5
b  5
Ta có: A1;3d 3 a.15 a 8 ⇒ d : y 8x 5 .
b) d song song với đường thẳng
y  2x  8  a  2 .
dcắt trục hoành tại điểm có hoành độ bằng 5  0  2.5 b b 10 y  2x 10 .
c) d vuông góc với đường thẳng y x  3 a  1.
dcắt đường thẳng
y  2x  1 tại điểm có tung độ bằng 5 ⟹Tọa độ điểm đó: A2;5
Ta có: 5  1.2 b b 7 d : y  x 7 .
Bài 7. Trên mặt phẳng Oxy cho hai điểm A1;1 và B1;7 . Xác định hàm số biết đồ thị của nó là
đường thẳng d  đi qua hai điểm A và B . Giải:
Giả sử đường thẳng d  đi qua hai điểm A và B có dạng: y ax b
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Vì A1; 
1 d  ta có 1 1.a b b  a 1
Vì B 1;7d  ta có 7  1.a b b a 7
Suy ra a 1 a 7 a 3
Thay a 3 vào b  a 1 ta được b  4
Vậy hàm số y 3x 4 có đồ thị là đường thẳng d  đi qua hai điểm A và B .
Bài 8. Chứng tỏ ba điểm sau thẳng hàng  11
a) A1;3;B ;2 ;C 2;   3 b)
H 1;1;I 1; 5  
  ; K ;  3  2   3  Giải :
a) Đường thẳng d  đi qua hai điểm A và B có dạng: y ax b
 d : y  2x 1
C d : y  2x 1  3  2.2 1  3  3 ( đẳng thức đúng).
b) Đường thẳng d  đi qua hai điểm H và I có dạng: y 3x 2
Bài 9. Tìm tập hợp điểm I và K nằm trên mặt phẳng tọa độ sau đây:
m 1 2m 1
2 3m m 7  a) I ;  b) K ;   2 3   5 3  Giải:  m x 1  I a) Giả sử  2 I x ; y I I    2m  y 1  I 3
Khử m từ hệ điều kiện trên ta được 4x 3y 3 0 I I 4
Từ đó suy ra I nằm trên đường thẳng y x 1 . 35 23
b) Tương tự, K nằm trên đường thẳng y x  . 9 9 2
Bài 10. Trong mặt phẳng Oxy cho đường thẳng ( d ) : y x 2 3
a. Vẽ d  . Viết phương trình đường thẳng qua A3 ; 2 và song song với d  .
b. Tìm tọa độ điểm B trên trục tung sao cho tam giác AOB vuông tại A . Giải: X 0 Y -2
Đồ thị hàm số là dường thẳng đi qua 2 điểm 0;2;3; 0
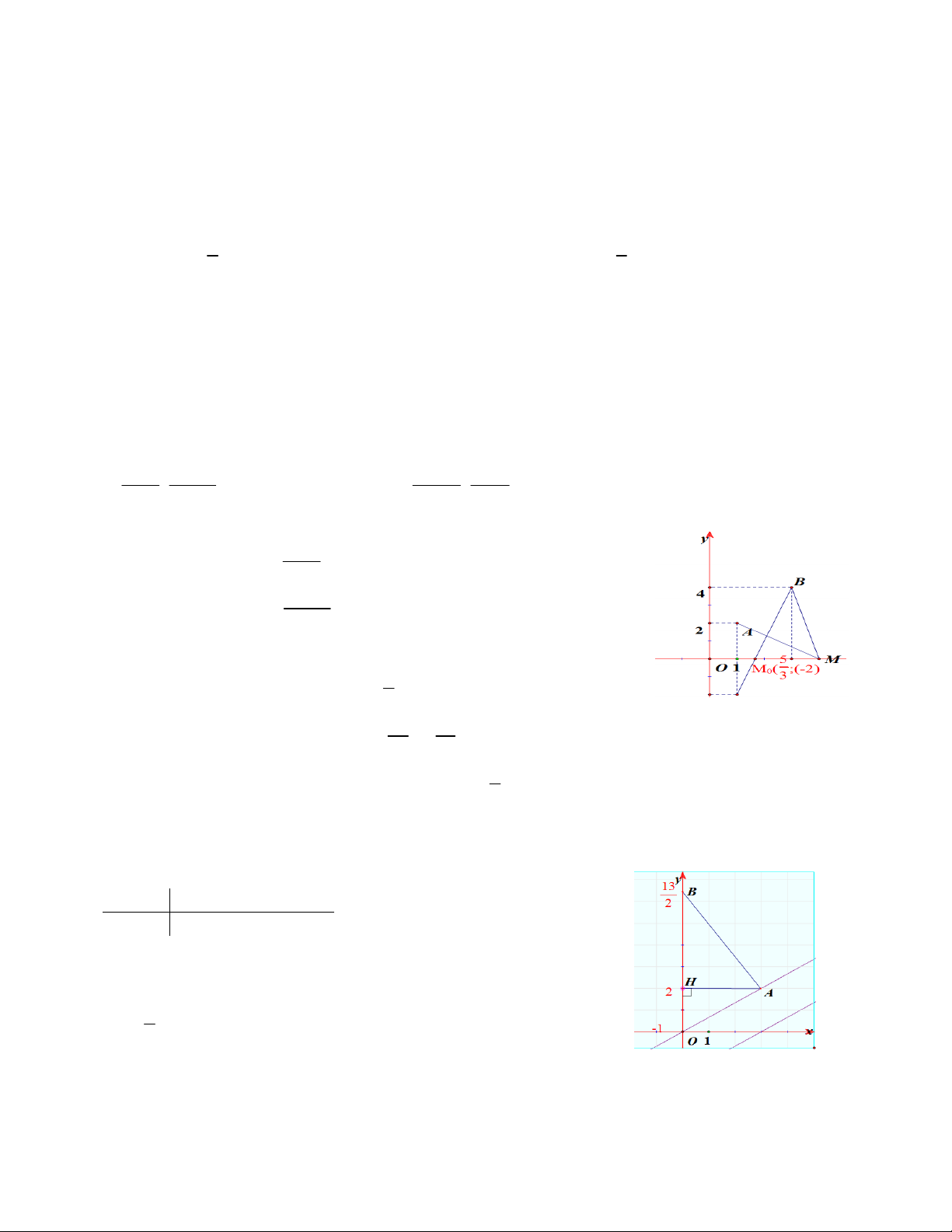
Phương trình đường thẳng (∆) đi qua A(3; 2) và song song với d  là (∆):  2 y x . 3 b. Kẻ AH  Oy.
OAB vuông tại A  2 AH OH .HB
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2   AH 913 HB Vậy B 0 :  . OH 22
Bài 11. Trong mặt phẳng Oxy cho A1; 2 và B3; 4. Tìm trên trục hoành điểm M sao cho MAMB
đạt giá trị nhỏ nhất. Giải:
Xét bài toán: “Cho đường thẳng d  và 2 điểm A, B cùng nửa mặt phẳng bờ d  , tìm trên d  điểm M sao
cho MAMB đạt giá trị nhỏ nhất”
Dựng A’ là hình chiếu của A trên d  nên M là giao điểm của A’B với d  .
Áp dụng: Dựng A’ là hình chiếu của A trên Ox nên A’(–1; 2).
Suy ra M là giao điểm của A’B với Ox. Phương trình ( A’B ) có dạng yaxb với a = 3 và b = 5 (thay
tọa độ điểm A’, B vào phương trình)
  A’B: y3x – 5 Cho    5 y 0 x 35  Vậy M ;0 thì MA 0  
MB đạt giá trị nhỏ nhất.  3
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1. Hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0) cắt nhau khi a ìï ¹ a¢ a ìï = a¢ a ìï ¹ a¢
A. a ¹ a¢ . B. ïí . C. ïí . D. ïí . b ï ¹ b¢ ï ï ¹ ¢ ï = ¢ î b b ïî b b ïî
Câu 2. Hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0) trùng nhau khi a ìï ¹ a¢ a ìï = a¢ a ìï = a¢
A. a ¹ a¢ . B. ïí . C. ïí . D. ïí . b ï ¹ b¢ ï ï ¹ ¢ ï = ¢ î b b ïî b b ïî
Câu 3. Hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0) có a ¹ a¢ và b ¹ b¢ . Khi đó:
A. d / /d¢ . B. d º d¢ .
C. d cắt d¢ .
D. d ^ d¢ .
Câu 4. Hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0) có a ¹ a¢ . Khi đó
A. d / /d¢ . B. d º d¢ .
C. d cắt d¢ .
D. d ^ d¢ .
Câu 5. Cho hai đường thẳng d : y = x + 3 và d¢ : y = 2 - x khi đó:
A. d / /d¢ . B. d º d¢ .
C. d cắt d¢ .
D. d ^ d¢ . 1 1
Câu 6. Cho hai đường thẳng d : y = - x + 1 và d ¢ : y = - x + 2 . Khi đó: 2 2
A. d / /d¢ . B. d º d¢ .
C. d cắt d¢ .
D. d ^ d¢ .
Câu 7. Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng
d : y = (m + 2)x - m và d¢ : y = 2
- x - 2m + 1. Với giá trị nào của m thì d cắt d¢ ?
A. m ¹ -2 . B. m ¹ -4 .
C. m ¹ {-2;-4} . D. m ¹ {2;- } 4 .
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Câu 8. Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d : y = (3 - 2m)x - 2 và d¢ : y = 4x - m + 2 .
Với giá trị nào của m thì d cắt d¢ ? ìï3 1üï 3 ìï 3 1üï 1 A. m ï ; ï ¹ í ý. B. m ¹ . C. m ïí ; ï ¹ - . D. m ¹ . ï ý 2 2ï ïî ïþ 2 ï 2 2ï ïî ïþ 2
Câu 9. Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d : y = (3 - 2m)x - 2 và d¢ : y = 4x - m + 2 .
Với giá trị nào của m thì d / /d¢ ?
A. m = -2 . B. m = -4 . C. m = 2 .
D. m ¹ {2;-4} .
Câu 10. Cho hàm số bậc nhất y = (2m - 2)x + m - 3 tìm m để hàm số có đồ
thị song song với đường thẳng y = 3x - 3m . 2 2 5 5 A. m = - . B. m = . C. m = . D. m = - . 5 5 2 2
Câu 11. Cho hai đồ thị hàm số bậc nhất là hai đường thẳng
d : y = (m + 2)x - m và d¢ : y = 2
- x - 2m + 1. Với giá trị nào của m thì d º d¢ ?
A. m = -2 . B. m = -4 . C. m = 2 .
D. Không có m thỏa mãn. m
Câu 12. Cho hai đường thẳng d : y = (1 - m)x +
và d¢ : y = x - + 1 . Với giá 2
trị nào của m thì d º d¢ ?
A. m = -2 . B. m = -4 . C. m = 2 .
D. Không có m thỏa mãn..
Câu 13. Cho hàm số y = (m - 5)x - 4 . Tìm m để hàm số nhận giá trị là 5 khix = 3 .
A. m = 6 . B. m = 7 . C. m = 8 . D. m = -3 .
Câu 14. Cho hàm số y = 7mx - 3m + 2 . Tìm m để hàm số nhận giá trị là 11 khix = 1 . 9 4 9 A. m = . B. m = . C. m = 9 . D. m = - . 4 9 4
Câu 15. Viết phương trình đường thẳng d biết d cắt trục tung tại điểm có tung độ bằng -2 và cắt trục hoành
tại điểm có hoành độ 1 .
A. y = 2x + 2 . B. y = -2x - 2 .
C. y = 3x - 2 .
D. y = 2x - 2 .
Câu 16. . Viết phương trình đường thẳng d biết d cắt trục tung tại điểm có tung độ bằng 3 và cắt trục hoành
tại điểm có hoành độ -4 3 3 3 3
A. y = - x + 3 .
B. y = x + 3 .
C. y = - x - 3 .
D. y = x - 3 . 4 4 4 4
Câu 17. Viết phương trình đường thẳng d biết d song song với đường thẳng  d¢ : y = 3x + 1 và đi qua điểmM(-2;2) .
A. y = 2x + 8 . B. y = 3x + 8 .
C. y = 3x - 8 .
D. y = 3x . 1
Câu 18. Viết phương trình đường thẳng d biết d vuông góc với đường thẳng d ¢ : y = - x + 3 và đi qua 2 điểm M(2;-1) 1
A. y = 2x + 5 . B. y = x - + 4 .
C. y = 2x - 5 .
D. y = - x . 2
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1
Câu 19. Viết phương trình đường thẳng d biết d vuông góc với đường thẳng d ¢ : y = x + 3 và cắt đường 3
thẳng y = 2x + 1 tại điểm có tung độ bằng 5 .
A. y = -3x + 11.
B. y = -3x + 4 . C. y = -3x .
D. y = 3x + 11 .
Câu 20. Viết phương trình đường thẳng d biết d vuông góc với đường thẳng y = 4x + 1 và cắt đường thẳng
y = x - 1 tại điểm có tung độ bằng 3 . 1 1 1 1
A. y = - x - 4 .
B. y = - x + 4 .
C. y = - x + 2 .
D. y = - x . 4 4 4 4
Câu 21. Viết phương trình đường thẳng d biết d song song với đường thẳng y = -2x + 1 và cắt trục hoành
tại điểm có hoành độ bằng 3 .
A. y = -2x + 6 . B. y = -3x + 6 . C. y = -2x - 4 .
D. y = -2x + 1.
Câu 22. Viết phương trình đường thẳng d biết d song song với đường thẳng y = -5x - 3 và cắt trục hoành
tại điểm có hoành độ bằng 5 1
A. y = x - 25 . B. y = 5x + 25 . C. y = -5x + 25 .
D. y = -5x - 25 . 5
Câu 23. Viết phương trình đường thẳng d biết d đi qua hai điểm (1
A ;2);B(-2; 0) . 2 4 2 4 2 4 2 4
A. y = - x - .
B. y = - x + .
C. y = x - .
D. y = x + . 3 3 3 3 3 3 3 3
Câu 24. Viết phương trình đường thẳng d biết d đi qua hai điểm (3
A ; 3);B(-1; 4). 1 15 1 15 1 15 1 15
A. y = x - .
B. y = - x + .
C. y = - x -
. D. y = x + . 4 4 4 4 4 4 4 4
Câu 25. Tìm điểm M cố định mà đường thẳng y = 3mx - (m + )
3 đi qua với mọi m . æ1 ö æ1 ö æ 1 ö æ 1 ö A. M çç ;3÷÷ ç ÷ ç ÷ ç ÷ ç . B. M ç ; 3 - ÷ . C. M - ç ; 3 - ÷ . D. M - ç ;3÷. çè3 ÷÷ø çè3 ÷÷ø çè 3 ÷÷ø çè 3 ÷÷ø 1
Câu 26. Cho tam giác ABC có đường thẳng BC : y = - x + 1 và (1
A ;2) . Viết phương trình đường cao 3
AH của tam giác ABC 2 2
A. y = 3x - . B. y = 3x + . C. y = 3x + 2 . D. Đáp án khác. 3 3
Câu 27. Cho đường thẳng 2
y = (m - 2m + 2)x + 4 . Tìm m để d cắt Ox tại
A và Oy tại B sao cho diện tích tam giác AOB lớn nhất.
A. m = 1. B. m = 0 . C. m = -1 . D. m = 2 . k + 1
Câu 28. Điểm cố định mà đường thẳng d : y =
x + k + 3(k ³ 0) luôn đi qua là: 3 - 1
A. M (1- 3; 3 - )
1 . B. M ( 3; 3) . C. M ( 3; 3 - ) 1 .
D. Cả A, B, C đều sai.
Câu 29. Cho đường thẳngd : y = (2m + 1)x - 1 tìm m để d cắt 2 trục tọa độ tạo thành tam giác có diện tích 1 . 2
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
A. m = 0 . B. m = 1. C. m = -1 .
D. Cả A và C đều đúng.
Câu 30. Biết đường thẳng d : y = mx + 4 cắt Ox tại A , và cắt Oy tại B sao cho diện tích tam giác OAB
bằng 6. Khi đó giá trị của m bằng 4 4 4 4 A. m =  . B. m < . C. m > . D. m = . 3 3 3 3
Câu 31. Cho đường thẳng d : y = mx + m - 1 . Tìm m để d cắt Ox tại A và cắt Oy tại B sao cho tam
giácAOB là tam giác vuông cân
A. m < 1 . B. m = 1. C. m > 1 .
D. m = 1 hoặc m = -1 . HƯỚNG DẪN Câu 1. Đáp án A.
Cho hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0)
d cắt d¢  a ¹ a¢ . Câu 2. Đáp án D. a ìï = a¢
Cho hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0) d trùng d¢ ï  í b ï = b¢ ïî Câu 3. Đáp án A.
Cho hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0) a ìï = a¢ +) d / /d ï ¢  í b ï ¹ b¢ ïî
+) d cắt d¢  a ¹ a¢ a ìï = a¢ d d ï
º ¢  íbï = b¢ +) ïî
+) d ^ d ¢  a.a¢ = 1 - Câu 4. Đáp án C.
Cho hai đường thẳng d : y = ax + b (a ¹ 0) và d ¢ : y = a x
¢ + b¢ (a¢ ¹ 0)
d cắt d¢  a ¹ a¢ . Câu 5. Đáp án C.
Ta thấy d : y = x + 3 có a = 1 và d¢ : y = 2 - x có a¢ = 2 -  a ¹ a (1 ¢ ¹ 2 - ) a¢ = 2
- nên d cắt d¢ Câu 6. Đáp án A. 1 1 1 a = - ;b = 1 1 a¢ = - ;b = 2
Ta thấy d : y = - x + 1 có 2
và d ¢ : y = - x + 2 có 2 2 2 ìï æ 1 1ö a ïï = a ç ÷ ¢ - ç = - ÷ ï ç  í è 2 2÷÷ø
ïbïï ¹b (¢1 ¹ 2) ïî
nên d / /d¢ . Câu 7. Đáp án C.
+) Ta thấy d : y = (m + 2)x - m có a = m + 2 và d¢ : y = 2
- x - 2m + 1 có a¢ = 2 -
+) Để d : y = (m + 2)x - m là hàm số bậc nhất thì m + 2 ¹ 0  m ¹ 2 -
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
+) Để d cắt d¢  a ¹ a¢  m + 2 ¹ 2 -  m ¹ 4 - m ¹ {-2;- } 4 Vậy . Câu 8. Đáp án A.
Ta thấy d : y = (3 - 2m)x - 2 có a = 3 - 2m và d¢ : y = 4x - m + 2 có a¢ = 4 3
3 - 2m ¹ 0  m ¹
Để d : y = (3 - 2m)x - 2 là hàm số bậc nhất thì 2 1
a ¹ a¢  3 - 2m ¹ 4  2m ¹ 1  m ¹
Để d cắt d¢ 2 ìï3 1üï Vậy m ï ; ï ¹ í ý ï2 2ï ïî ïþ Câu 9. Đáp án B.
Ta thấy d : y = (3 - 2m)x - 2 có a = m + 2 ¹ 0  m ¹ 2 -
và d¢ : y = 4x - m + 2 có a¢ = 2 - ¹ 0 a ìï = a¢ m ìï + 2 = -2 m ìï = -4 ï ï ï  í  í  í  m = -4(TM ) b ï ¹ b¢ ï m - ¹ -2m + 1 m ï ¹ 1 Để d / /d¢ ïî ïî ïî . Câu 10. Đáp án C.
Hàm số y = (2m - 2)x + m - 3 là hàm số bậc nhất khi 2m - 2 ¹ 0  m ¹ 1 ìï 5 ï 2 ìï - 2 = 3 m m ï = ï ï 2  í  í m ï - 3 ¹ -3m ï 3 ïî 5 m
ïï ¹  m = (TM) Để d / /d¢ ïî 4 2 5 m = Vậy 2 . Câu 11. Đáp án D.
+) Ta thấy d : y = (m + 2)x - m có a = m + 2 d¢ : y = 2
- x - 2m + 1 có a¢ = 2 -
+) Điều kiện để d : y = (m + 2)x - m là hàm số bậc nhất m + 2 ¹ 0  m ¹ 2 - +) Để a ìï = a¢ m ìï + 2 = -2 m ìï = -4 d º d¢ ï  í ï  í ï  í (vô lý) b ï = b¢ ï ï- = - + ï = î m 2m 1 ïî m 1 ïî
Vậy không có giá trị nào của m để d º d¢ Câu 12. Đáp án C. m m
a = 1 - m;b = ¢
Ta thấy d : y = (1 - m)x + có
2 và d¢ : y = x - + 1 có a = 1 - ;b = 1 2 m
d : y = (1 - m)x + Điều kiện để
2 là hàm số bậc nhất 1- m ¹ 0  m ¹ 1
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 ìï - m = -1 ï ìï a ìï = a¢ m = 2 ï ï ï   í  í  m = 2(tm) í m ïï = ï b ï = b¢ 1 m = 2 ï ï î Để d º d¢ ïî ïî 2 Vậy m = 2 Câu 13. Đáp án C.
Thay x = 3;y = 5 vào hàm số y = (m - 5)x - 4 ta được
(m - 5).3 - 4 = 5  (m - 5).3 = 9  m - 5 = 3  m = 8 Vậy m = 8 . Câu 14. Đáp án A. 9
11 = 7m.1 - 3m + 2  4m = 9  m = .
Thay x = 1;y = 11 vào hàm số y = 7mx - 3m + 2 ta được 4 9 m = . Vậy 4 Câu 15. Đáp án D.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là
Vì d cắt trục tung tại tại điểm có tung độ bằng -2 và cắt trục hoành tại điểm có hoành độ 1 nên d đi qua hai điểm (0 A ;-2);B(1; 0)
Thay tọa độ điểm A vào phương trình đường thẳng d ta được a.0 + b = 2 -  b = 2 -
Thay tọa độ điểm B và b = -2 vào phương trình đường thẳng d ta được a.1 - 2 = 0  a = 2
Vậy phương trình đường thẳng cần tìm là y = 2x - 2 Câu 16. Đáp án B.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là
Vì d cắt trục tung tại tại điểm có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ -4 nên d đi qua hai điểm (
A 0; 3);B(-4; 0)
Thay tọa độ điểm A vào phương trình đường thẳng d ta được a.0 + b = 3  b = 3 Thay tọa độ điểm B 3
a.(-4) + 3 = 0  a = .
vào phương trình đường thẳng d ta được 4 3 y = x + 3
Vậy phương trình đường thẳng cần tìm là 4 . Câu 17. Đáp án B.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là a ìï = 3 ïí
d : y = 3x + b b ï ¹ 1
Vì d / /d¢ nên ïî
Thay tọa độ điểm M vào phương trình đường thẳng d ta
được 3.(-2) + b = 2  b = 8 ( thỏa mãn)
Vậy phương trình đường thẳng d : y = 3x + 8 . Câu 18. Đáp án C.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com æ 1ö a.ç ÷ - ç ÷ = 1 -  a = 2 çè 2÷÷
Vì d ^ d¢ nên ø
(TM) d : y = 2x + b
Thay tọa độ điểm M vào phương trình đường thẳng d ta được 2.2 + b = 1 -  b = 5 -
Vậy phương trình đường thẳng d : y = 2x - 5 Câu 19. Đáp án A.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là 1 a. = 1 -  a = 3
-  d : y = -3x + b
Vì d ^ d¢ nên 3
Gọi điểm M(x;5) là giao điểm của đường thẳng d và đường thẳng y = 2x + 1
Khi đó 2x + 1 = 5  2x = 4  x = 2  M(2;5)
Thay tọa độ điểm M vào phương trình đường thẳng d ta được 3.
- 2 +b = 5  b = 11
Vậy phương trình đường thẳng d : y = -3x + 11 Câu 20. Đáp án B.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là 1 1
a.4 = -1  a = -  d : y = - x + b
Vì d ^ d¢ nên 4 4
Gọi điểm M(x; 3) là giao điểm của đường thẳng d và đường thẳng y = x - 1
Khi đó x - 1 = 3  x = 4  M(4; 3) 1 1
d : y = - x + b
- .4 + b = 3  b = 4
Thay tọa độ điểm M vào phương trình đường thẳng 4 ta được 4 1
d : y = - x + 4
Vậy phương trình đường thẳng 4 . Câu 21. Đáp án A.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là
Vì d song song với đường thẳng y = -2x + 1 nên a = -2;b ¹ 1  y = -2x + b
Giao điểm của đường thẳng d với trục hoành có tọa độ (3; 0)
Thay x = 3;y = 0 vào phương trình đường thẳng d ta được 2.
- 3 +b = 0  b = 6(TM)  y = 2 - x + 6
Vậy d : y = -2x + 6 Câu 22. Đáp án C.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng d cần tìm là
Vì d song song với đường thẳng y = -5x - 3 nên a = -5;b ¹ -3  d : y = -5x + b
Giao điểm của đường thẳng d với trục hoành có tọa độ (5; 0)
Thay x = 5;y = 0 vào phương trình đường thẳng d ta 5.
- 5 +b = 0  b = 25(TM)  y = 5 - x + 25 được
Vậy d : y = -5x + 25 .
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Câu 23. Đáp án . y = ax +b
Gọi phương trình đường thẳng cần tìm là
Thay tọa độ điểm A vào phương trình đường thẳng d ta được a + b = 2  b = 2 -a
Thay tọa độ điểm B vào phương trình đường thẳng d ta được 2
- a +b = 0  b = 2a 2 2 4 2 4
2a = 2 - a a =  b = 2. =  y = x + Suy ra 3 (TM) 3 3 3 3 2 4
d : y = x + Vậy 3 3 . Câu 24. Đáp án B.
y = ax + b (a ¹ 0)
Gọi phương trình đường thẳng cần tìm là
Thay tọa độ điểm A vào phương trình đường thẳng d ta được 3a + b = 3  b = 3 - 3a
Thay tọa độ điểm B vào phương trình đường thẳng d ta được 1.
- a +b = 4  b = 4 +a 2 1
2a = 2 - a a = 3 - 3a = 4 + a  4a = -1  a = - Suy ra 3 4 æ 1ö ç ÷ 15 1 - 15
b = 4 + a = 4 + - ç ÷ =  y = x + çè 4÷÷ø 4 4 4 1 15
d : y = - x + Vậy 4 4 . Câu 25. Đáp án B.
3mx - (m + 3) = y
Gọi M(x;y) là điểm cố định cần tìm khi đó đúng với mọi m
 3mx - m - 3 - y = 0 đúng với mọi m m(3x -1) + -3 - y = 0 đúng với mọi m ìï ì 1 3 ï x - 1 = 0 ï x ï æ ï = 1 ö ï ç ÷  í  í 3  M ç ;-3÷ ï-3 - y = 0 ï ç ïî ï è3 ÷ y = -3 ÷ø ïî æ1 ö
Vậy điểm M çç ; 3÷ - ÷ ç
là điểm cố định cần tìm. çè3 ÷÷ø Câu 26. Đáp án D.
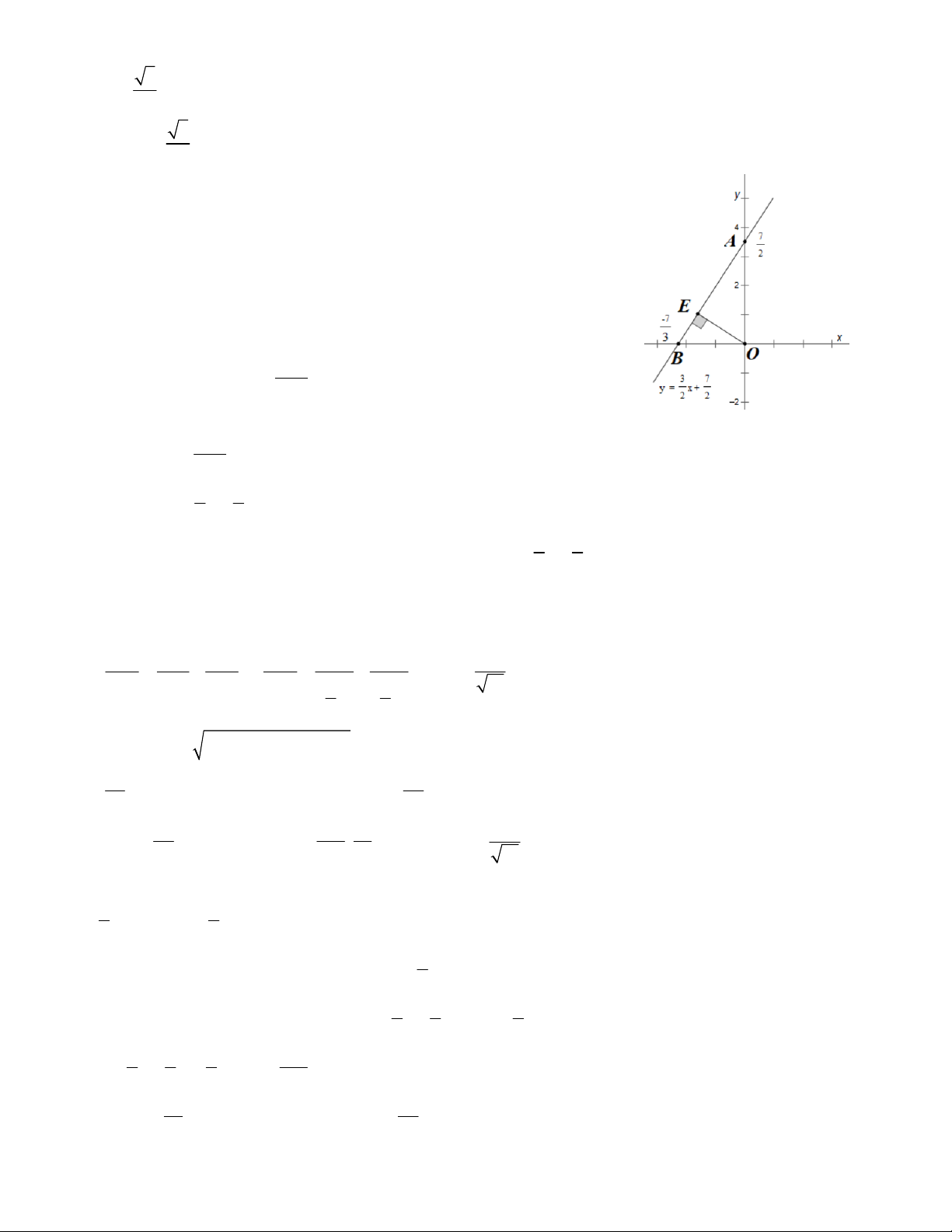
Giả sử AH : y = ax + b -1 a. = -1  a = 3
Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC nên: 3
Mặt khác AH đi qua (1
A ;2) nên ta có: 3.1 +b = 2  b = 1 -
Vậy AH : y = 3x - 1 Câu 27. Đáp án A.
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
d ÇOy = {B}
x = 0  y = 4  B(0;4)  OB | = 4 |= 4 B B d Ç Ox = { } A 2
y = 0  (m - 2m + 2)x + 4 = 0 A A 4 æ 4 ö - -  x =  Açç ; 0÷÷ A 2 ç 2 ÷ m - 2m + 2
çèm - 2m + 2 ÷ø -4  OA = 2 m - 2m + 2 1 1 4 - 8 S = O . AOB = .4. = AOB D 2 2 2 2 m - 2m + 2 (m - 1) + 1 2 (m - 1) + 1 ³ 1 "m Ta có 8 8 S = £ = 8 AOB D 2 Do đó (m - 1) + 1 1
Dấu “=” xảy ra khi m - 1 = 0  m = 1
Hay tam giác OAB có diện tích lớn nhất là 8 khi m = 1. Câu 28. Đáp án A. M(x ;y ) Gọi 0
0 là điểm cố định mà d luôn đi qua. k + 1
M(x ;y ) Î d "k y =
x + k + 3 "k 0 0 0 0 3 - 1 x ìïï + 3 -1 = 0
kx + x + 3k - k - 3 + 3 - 3y + y = 0 "k 0  íï 0 0 0 0 x
ï + 1 - 3 y + 3 - 3 = 0 ï 0 ( ) 0 ïî ì ì x ïï = 1- 3 x ïï = 1- 3 0 0 ï ï  í  í 2 x ìïï = 1- 3 (ï1- 3 ï ) + - = ï ï y 4 2 3 0 ï 1 - 3 y + 1 - 3 = 0 0 ï ( î ï ) 0 ( ) 0  í ïî (
ïï 1- 3) + (1- 3)y + 3 - 3 = 0 ìï 0 ïî x ï = 1 - 3 ï 0  íyïï = -1+ 3 0 ïî  M (1- 3; 3 - )
1 là điểm cố định mà d luôn đi qua. Câu 29. Đáp án D.
d ÇOy = {B}  x = 0  y = -1 B B
B(0;-1)  OB | = -1 |= 1 d Ç Ox = { } A y = 0 A 1 æ 1ö -
 (2m + 1)x - 1 = 0  x = m ç ÷ ç ¹ ÷ A 2m + 1 çè 2 ÷÷ø æ 1 ö ç ÷ 1  Aç ; 0÷  OA = çè2m + 1 ÷÷ø 2m + 1
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 1 1 1 1 S = O . AOB =  .1. = |  2m + 1 |= 1 AOB D 2 2 2 2m + 1 2 m é = 0 ê  (tmdk) m ê = -1 êë Câu 30. Đáp án A.
d ÇOy = {B} x = 0  y = 4 B B
B(0; 4)  OB | = 4 |= 4 d Ç Ox = { } A -4
y = 0  mx + 4 = 0  x = (m ¹ 0) A A A m æ 4 ö - ç ÷ 4  Aç ; 0÷  OA = çè m ÷÷ø m 1 1 4 4 4 S = O . AOB = 6  .4. = 6 |  m |=  m =  . AOB D 2 2 m 3 3 Câu 31. Đáp án D.
d ÇOy = {B}
x = 0  y = m - 1 B B
B(0;m - 1)  OB | = m - 1 | d Ç Ox = { } A 1 - m
y = 0  mx + m - 1 = 0  x = (m ¹ 0) A A A m æ1 m ö - ç ÷ 1 - mAç ; 0÷  OA = çè m ÷÷ø m
Tam giác OAB vuông cân tại O é 1 - ê m m - 1 = 1 - m ê  = | - 1 = |  ê m OA OB m m ê m - 1 m - 1 = ê ë m é 2 m = 1 m é = 1 ê ê ê  æ ö  ê 2 ê 1  m = 1 ç ÷ m - 1 m - 1) 1 ( ) ( ç - ÷ = 0 ê ê ç ÷ = 0 ç ê è m ÷ ê ø ë ë m
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
D.PHIẾU BÀI TỰ LUYỆN Bài 1.
Cho hai đường thẳng: d : y m x  2 1   
d : y  2m  3 x  2 2   
Với giá trị nào của m thì:
a) d song song với d . 2  1  b) d trùng với d . 2  1 
c) d vuông góc với d . 2  1  Bài 2.
Cho hai đường thẳng : d : y m 1 x  5 1   
d : y  2m 1 x m  4 . 2   
Xác định m để hai đường thẳng: a) Cắt nhau. b) Song song với nhau. c) Vuông góc với nhau. Bài 3.
Cho 2 đường thẳng y  m  2 x  2 d y   2
m  2mx 1 d '
a) Hai đường thẳng (d) và (d’) có thể trùng nhau không?
b) Tìm các giá trị của m để (d) và (d’) song song với nhau. Bài 4.
Tìm giá trị của k để ba đường thẳng: y  2  x  3d 1 
y  3x  2 d 2 
y kx k  5 d 3 
Đồng quy trong mặt phẳng tọa độ. Bài 5. Cho hai đường thẳng:
y  m  6 x  2 và y m3m  4 x  5
a) Chứng minh rằng khi m  2
 thì hai đường thẳng đã cho song song với nhau;
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho song song với nhau. Bài 6. Cho hai đường thẳng:
y  m  
1 x  3 và y  2m   1 x  4 1
a) Chứng minh rằng khi m   thì hai đường thẳng đã cho vuông góc với nhau 2
b) tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau. Bài 7.
Xác định hàm số y ax b trong mỗi trường hợp sau:
a) Khi a  3 , đồ thị hàm số cắt trục tung tại điểm có tung độ bằng  3 . b) Khi a  5
 , đồ thị hàm số đi qua điểm A 2  ;3 ;
c) Đồ thị hàm số đi qua hai điểm M 1;3 và N 2  ;6
d) Đồ thị hàm số song song với đường thẳng y  7x và đi qua điểm 1;7  7  . Bài 8.
Cho đường thẳng: y  4x d
a) Viết phương trình đường thẳng d song song với đường thẳng (d) và có tung độ gốc bằng 10. 1 
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
b) Viết phương trình đường thẳng (d2) vuông góc với đường thẳng (d) và cắt trục Ox tại điểm có hoành độ bằng 8 .
c) Viết phương trình đường thẳng (d3) song song với đường thẳng (d) cắt trục Ox tại A, cắt trục Oy tại B và
diện tích tam giác AOB bằng 8. Bài 9.
Cho hàm số y  m  2 x n (1).
a) Tìm m và n để đồ thị hàm số cắt Ox tại A; Oy tại B sao cho x x  3 . A B
b) Viết phương trình đường cao OH của tam giác OAB.
Bài 10. Cho đường thẳng y  a  
1 x  2  a d 1
a) Tìm a để đường thẳng (d) cắt trục tung tại điểm có tung độ là . 2 1
b) Tìm a để đường thẳng (d) vuông góc với đường thẳng y x . 2
c) Chứng minh rằng các đường thẳng (d) luôn đi qua một điểm cố định với mọi giá trị của a. Bài 11.  2 
a) Viết phương trình đường thẳng đi qua hai điểm: A ; 2   và B 3;  1  3 
b) Viết phương trình đường trung trực của đoạn AB.
Bài 12. Tìm các giá trị của m để đồ thị hàm số y mx  3 tiếp xúc với đường tròn có tâm trùng với gốc
tọa độ và có bán kính bằng 2.
Bài 13. Trong mặt phẳng tọa độ cho E 2m 1;3m  2
a) Tìm tập hợp các điểm E.
b) Tìm m để OE nhỏ nhất. HƯỚNG DẪN
Bài 1: Cho hai đường thẳng: d : y m x  2 1   
d : y  2m  3 x  2 2   
Với giá trị nào của m thì:
a) d song song với d . 2  1  b) d trùng với d . 2  1 
c) d vuông góc với d . 2  1  Giải
a) d : y mx  2m song song với d : y  2m  3 x  2 2    1 
m  2m  3 m  3      m  3 2m  2 m  1
m  2m  3 m  3
b) d trùng với d    (không thỏa mãn). 2  1   2m  2 m 1
Suy ra: Hai đường thẳng này không thể trùng nhau.
c) d vuông góc với d tương đương với: 2  1 
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  .
m 2m  3  1  2
 2m  3m 1  0  m   1 2m    1 0 m 1   1 m   2
Bài 2: Cho hai đường thẳng : d : y m 1 x  5 1   
d : y  2m 1 x m  4 . 2   
Xác định m để hai đường thẳng: a) Cắt nhau. b) Song song với nhau. c) Vuông góc với nhau. Giải
a) m  2  2m 1  m  1
b) m  2  2m 1 và 5  m  4  m  1 và m  9  m  1
c) m   m   2 2 2 1  1
  2m  5m  3  0  m   1 2m  3  0 m  1    3  m   2
Bài 3: Cho 2 đường thẳng y  m  2 x  2 d y   2
m  2mx 1 d '
a) Hai đường thẳng (d) và (d’) có thể trùng nhau không?
b) Tìm các giá trị của m để (d) và (d’) song song với nhau. Giải
a) Hai đường thẳng (d) và (d’) có tung độ gốc lần lượt là b  2 và b '  1
 . Rõ rang b b ' ( 2  1) nên hai
đường thẳng (d) và (d’) không thể trùng nhau được:
b) Hai đường thẳng (d) và (d’) song song với nhau khi và chỉ khi: 2 2
m  2  m  2m m m  2  0       
m  m   m 1 0 m 1 1 2  0    m 2 0    m  2 
Vậy với m  1 hoặc m  2
 thì hai đường thẳng (d) và (d’) song song với nhau.
Bài 4: Tìm giá trị của k để ba đường thẳng: y  2  x  3d 1 
y  3x  2 d 2 
y kx k  5 d 3 
Đồng quy trong mặt phẳng tọa độ. Giải
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Hai đường thẳng (d1) và (d2) có hệ số của x khác nhau 2  3
  nên chúng cắt nhau tại điểm M trong mặt
phẳng tọa độ. Khi đó tọa độ của điểm M phải thỏa mãn đồng thời hai phương trình: y  2
x  3 và y  3x  2 Suy ra: 2
x  3  3x  2  5  x  5   x 1 y  2  x  3  2   3 1
Tọa độ của điểm M là: M 1;  1 .
Để ba đường thẳng đồng quy thì điểm M 1; 
1 thuộc đường thẳng (d3) suy ra k  3.
Bài 5: Cho hai đường thẳng:
y  m  6 x  2 và y m3m  4 x  5
a) Chứng minh rằng khi m  2
 thì hai đường thẳng đã cho song song với nhau;
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho song song với nhau. Giải a) Khi m  2
 hai đường thẳng có cùng hệ số góc là 4 nên chúng song song với nhau.
b) Hai đường thẳng y  m  6 x  2 và y m3m  4 x  5 song song với nhau khi và chỉ khi:
m   mm   2 2 6 3
4  3m  3m  6  0  m m  2  0    
m  m   m 1 1
2  0  m  2
Bài 6: Cho hai đường thẳng:
y  m  
1 x  3 và y  2m   1 x  4 1
a) Chứng minh rằng khi m   thì hai đường thẳng đã cho vuông góc với nhau 2
b) Tìm tất cả các giá trị của m để hai đường thẳng đã cho vuông góc với nhau. Giải 1 1
a) Khi m   hai đường thẳng y  m  
1 x  3 và y  2m  
1 x  4 có hệ số góc lần lượt là a  , 2 2 1 a '  2
 , khi đó aa '  . 2    1
 . Vậy hai đường thẳng vuông góc với nhau. 2
b) Hai đường thẳng y  m  
1 x  3 và đường thẳng y  2m  
1 x  4 vuông góc với nhau khi và chỉ khi:
m   m   2 1 2 1  1
  2m m  0  m2m   1  0 m  0 m  1     1 2m 1  0 m    2 Bài 7:
Xác định hàm số y ax b trong mỗi trường hợp sau:
a) Khi a  3 , đồ thị hàm số cắt trục tung tại điểm có tung độ bằng  3 . b) Khi a  5
 , đồ thị hàm số đi qua điểm A 2  ;3 ;
c) Đồ thị hàm số đi qua hai điểm M 1;3 và N 2  ;6
d) Đồ thị hàm số song song với đường thẳng y  7x và đi qua điểm 1;7  7  .
20. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Giải
a) Khi a  3 ta có hàm số y  3x b . Đồ thị hàm số y  3x b cắt trục tung tại hai điểm có tung độ
bằng  3 nên b   3 , ta được hàm số y  3x  3 . b) Khi a  5
 , ta có hàm số y  5  x b .
Đồ thị hàm số y  5
x b đi qua điểm A 2  ;3;; nên: 3  5   2
   b b  7 
Hàm số phải tìm là y  5  x  7
c) Đồ thị hàm số y ax b đi qua điểm M 1;3 và điểm N  2  ;6, ta có: 3  . a 1 b 6  .
a 2  b Suy ra a  1,
b  4 , ta được hàm số y  x  4
d) Đồ thị hàm số y ax b song song với đường thẳng y  7x nên a  7 . Ta có hàm số y  7x b
Đồ thị hàm số y  7x b lại đi qua điểm a;7  7 
Nên: 7  7  7 1 b b  6
Hàm số phải tìm là: y  7x  6
Bài 8: Cho đường thẳng: y  4x d
a) Viết phương trình đường thẳng d song song với đường thẳng (d) và có tung độ gốc bằng 10. 1 
b) Viết phương trình đường thẳng (d2) vuông góc với đường thẳng (d) và cắt trục Ox tại điểm có hoành độ bằng 8 .
c) Viết phương trình đường thẳng (d3) song song với đường thẳng (d) cắt trục Ox tại A, cắt trục Oy tại B và
diện tích tam giác AOB bằng 8. Giải
a) y  4x 10
b) Đường thẳng (d2) có dạng y ax b
Đường thẳng này vuông góc với đường 1 thẳng (d) nên: . a a  1
 , suy ra a   , 4 1
ta có hàm số y   x b . Đường 4
thẳng này cắt trục hoành tại điểm có
hoành độ bằng 8 , ta có b  2  . 1
Hàm số phải tìm là: y x  2 4
c) Đường thẳng (d3) song song với đường
thẳng (d) nên có dạng y  4x b . Đường
thẳng này cắt trục hoành ở điểm A, cắt trục b
tung ở điểm B, ta có: y  0 thì x   , tọa 4  b
độ của điểm A là A  ;0 
 , x  0 thì y b , tọa độ của điểm B là B0;b  4 
21. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
tam giác AOB vuông ở O nên: 2 1 1 bb S  OA.OB  .b  AOB 2 2 4 8 2 b Suy ra 8  do đó 2
b  64 nên b  8  8
Có hai hàm số thỏa mãn yêu cầu đề bài là: y  4x  8 và y  4x 8 .
Bài 9: Cho hàm số y  m  2 x n (1).
a) Tìm m và n để đồ thị hàm số cắt Ox tại A; Oy tại B sao cho x x  3 . A B
b) Viết phương trình đường cao OH của tam giác OAB. Giải
a) Đường thẳng (1) cắt Ox tại A sao cho x  3  A 3;0 . A  
Đường thẳng (1) cắt Oy tại B sao cho y  3  B 0;3 . B  
Thay tọa độ điểm A; B vào (1) ta được:   m  2 
3 n  0 m 1      m  2 
0 n  3 n  3
Vậy m 1;n  3 ta được hàm số y  x  3
b) Phương trình đường cao OH đi qua O0;0 nên hàm
số có dạng: y ax .
Mặt khác, OH vuông góc với đường thẳng y  x  3 nên: a   1  1   a 1.
Vậy phương trình đường cao OH là: y x .
Bài 10: Cho đường thẳng y  a  
1 x  2  a d 1
a) Tìm a để đường thẳng (d) cắt trục tung tại điểm có tung độ là . 2 1
b) Tìm a để đường thẳng (d) vuông góc với đường thẳng y x . 2
c) Chứng minh rằng các đường thẳng (d) luôn đi qua một điểm cố định với mọi giá trị của a. Giải 1  5 a) 2  a   a  . 2 2 b) a   1 1 .  1   a  1  . 2
c) Viết y a x  
1  2  x dưới dạng: a x  
1  2  x y  0   * . x 1  0 x  1
Phương trình (*) nghiệm đúng với mọi a     .
2  x y  0  y 1
Vậy điểm cố định là A 1;  1 . Bài 11:
22. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  2 
a) Viết phương trình đường thẳng đi qua hai điểm: A ; 2   và B 3;  1  3 
b) Viết phương trình đường trung trực của đoạn AB. Giải
a) Đường thẳng y ax b đi qua A và B nên:  2 2  a b  a   3  3  
y   3x  4 b    4 1   3a b
b) M là trung điểm của AB nên M có tọa độ là:  2   3  3 2 1  5 3 3   ;    ;  2 2  6 2         
y   3x  4  . a  3  1 
Đường trung trực của AB có dạng: y ax b vuông góc với đường thẳng 3 3  a   y x b 3 3 3 3 5 3 3
Đường thẳng này đi qua M, nên:  .  b b  2 3 6 2 3 2
Vậy phương trình đường trung trực của AB là: y x  3 3
Bài 12: Tìm các giá trị của m để đồ thị hàm số y mx  3 tiếp xúc với đường tròn có tâm trùng với gốc tọa
độ và có bán kính bằng 2. Giải
Đường thẳng y mx  3 tiếp xúc với O;2  OH = 2 và OH  AB .
Xét tam giác vuông OAB có: 2 1 1 1 1 1 1      OA=3 2 2 2   OH OA OB 4 9 OB 6 5  OB  5 6 5
Suy ra: Tìm được hai điểm B và B’ thuộc x’x sao cho: OB= 5  6 5  6 5 Nếu B  ;0  . m  3  0  5  5   5 5  m    y   x  3 5 2  6 5   6 5  5 Nếu B'  ;0  . m  
  3  0  m   5   5  2    
23. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 5  y x  3 2 5 Vậy: m   . 2
Bài 13: Trong mặt phẳng tọa độ cho E 2m 1;3m  2
a) Tìm tập hợp các điểm E.
b) Tìm m để OE nhỏ nhất. Giải
a) E 2m 1;3m  2  x  2m 1 y  3m  2 x 1
Từ: x  2m 1 suy ra: m  2
Thay vào y  3m  2 x 1 Ta được: y  3.  2 2 3 7
y x  2 2 3 7
Vậy tập hợp các điểm E là đường thẳng có phương trình là: y x  . 2 2
b) Cách 1: Tìm tọa độ A; B (xem hình vẽ)
OEnhỏ nhất  OE  AB .
Xét tam giác vuông OAB, có OE là đường cao. 1 1 1 1 1 1 7        OE  2 2 2 2 2 2 OE OA OB OE  7   7  13      2   3  Mặt khác,
m  2  m  2 OE= 2 1 3 2 49  
13m  8m  5  13m  44 4 2  0  m 13 13 4   21  14  7 Vậy: m  thì E có tọa độ là ;   để OEnhỏ nhất  . 13  13 13  13
Cách 2: Phương trình đường thẳng OE: y ax vì OE  AB nên: 3 2 . a  1   a   . 2 3 2
Suy ra, phương trình đường thẳng OE là: y   x . 3 3 7 2
Do E là giao điểm của hai đường thẳng y x  và y   x nên hoành độ của E thỏa mãn phương 2 2 3 3 7 2 2  1
trình: x    x x  2 2 3 13 21 4  Thay x  
vào x  2m 1, ta được: m  . 13 13
24. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  21  21
Khi đó, tọa độ của E là: ;   .  13 13  4  7 Vậy m  thì OEnhỏ nhất  . 13 13
-------------------------Toán Học Sơ Đồ-------------------------
25. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com