Chuyên đề giá trị lớn nhất và nhỏ nhất của hàm số thông hiểu (có lời giải chi tiết)

Chuyên đề giá trị lớn nhất và nhỏ nhất của hàm số thông hiểu có lời giải chi tiết. Tài liệu được biên soạn dưới dạng file PDF bao gồm 24 trang tổng hợp các kiến thức tổng hợp giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!

57 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile Mỹ Duyên
Trang 1
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ
thị, bảng biến thiên
Giá trị lớn nhất của hàm số
( )
fx
trên đoạn
;ab
Hàm số
( )
fx
liên tục trên đoạn
;ab
và
( )
0, ;
ii
f x x a b
=
. Khi đó giá trị lớn
nhất của hàm số
( )
fx
là
( ) ( ) ( )
max , ,
i
M f a f b f x=
Giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
;ab
Hàm số
( )
fx
liên tục trên đoạn
;ab
và
( )
0, ;
ii
f x x a b
=
. Khi đó giá trị nhỏ
nhất của hàm số
( )
fx
là
( ) ( ) ( )
,,
i
m Min f a f b f x=
Hàm số
đồng biến trên đoạn
;ab
thì
( ) ( )
( ) ( )
;;
;
a b a b
Max f x f b Min f x f a==
Hàm số
nghịch biến trên đoạn
;ab
thì
( ) ( )
( ) ( )
;;
;
a b a b
Max f x f a Min f x f b==
Câu 1. (ĐỀ THI TN THPT 2022) Giá trị lớn nhất của hàm số
( )
32
3 9 10= − − +f x x x x
trên
đoạn
2;2−
bằng
A.
12−
. B. 10 . C. 15 . D.
1−
.
Lời giải
Chọn C
Xét hàm số
( )
32
3 9 10= − − +f x x x x
trên đoạn
2;2−
( )
2
3 6 9. = − −
f x x x
( )
2
1 2;2
0 3 6 9 0
3 2;2
= − −
= − − =
= −
x
f x x x
x
Ta có:
( ) ( ) ( )
2 8; 1 15; 2 12− = − = = −f f f
.
Vậy giá trị lớn nhất của hàm số
( )
32
3 9 10= − − +f x x x x
trên đoạn
2;2−
bằng 15 .
Câu 2. (ĐỀ THI TN THPT 2021) Trên đoạn
[0;3]
, hàm số
3
3y x x= − +
đại giá trị lớn
nhất tại điểm
A.
0x =
. B.
3x =
. C.
1x =
. D.
2x =
.
Lời giải
Chọn C
Tập xác định: .
2
33yx = − +
2
1 (0;3)
0 3 3 0
1 (0;3)
x
yx
x
=
= − + =
= −
Ta có
(0) 0; (1) 2; (3) 18y y y= = = −
.
Vậy
[0;3]
max (1) 2yy==
.
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Chuyên đề 5
Trang 2
Câu 3. (Đề Tham Khảo 2019) Cho hàm số
( )
y f x=
liên tục trên đoạn
1;3−
và có đồ
thị như hình vẽ bên. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm
số đã cho trên đoạn
1;3−
. Giá trị của
Mm−
bằng
A.
1
B.
4
C.
5
D.
0
Lời giải
Chọn C
Dựa và đồ thị suy ra
( ) ( )
3 3; 2 2M f m f= = = = −
Vậy
5Mm−=
Câu 4. (Đề Minh Họa 2017) Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng
biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng
1
.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng
−1
.
C. Hàm số đạt cực đại tại
x = 0
và đạt cực tiểu tại
x = 1
.
D. Hàm số có đúng một cực trị.
Lời giải
Chọn C
Đáp án A sai vì hàm số có
2
điểm cực trị.
Đáp án B sai vì hàm số có giá trị cực tiểu
y =−1
khi
x = 0
.
Đáp án C sai vì hàm số không có GTLN và GTNN trên .
Đáp án D đúng vì hàm số đạt cực đại tại
x = 0
và đạt cực tiểu tại
x = 1
.
Câu 5. Cho hàm số
liên tục trên đoạn
1;1−
và có đồ thị như hình vẽ.
Trang 3
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
1;1−
. Giá trị của
Mm−
bằng
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Từ đồ thị ta thấy
1, 0Mm==
nên
1Mm−=
.
Câu 6. Cho hàm số
liên tục trên
3;2−
và có bảng biến thiên như sau. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
y f x=
trên đoạn
1;2−
. Tính
Mm+
.
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Trên đoạn
1;2−
ta có giá trị lớn nhất
3M =
khi
1x =−
và giá trị nhỏ nhất
0m =
khi
0x =
.
Khi đó
3 0 3Mm+ = + =
.
Câu 7. (Chuyên Lương Thế Vinh Đồng Nai 2019) Cho hàm số
( )
y f x=
xác định và
liên tục trên có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất
m
và giá trị lớn
nhất
M
của hàm số
trên đoạn
2;2−
.
A.
5; 1mM= − = −
. B.
2; 2mM= − =
. C.
1; 0mM= − =
. D.
5; 0mM= − =
.
Lời giải
Nhìn vào đồ thị ta thấy:
( )
2;2
max 1M f x
−
= = −
khi
1x =−
hoặc
2x =
.
( )
2;2
min 5m f x
−
= = −
khi
2x =−
hoặc
1x =
.
Câu 8. (THPT Ba Đình 2019) Xét hàm số với có bảng biến thiên
như sau:
()y f x=
1;5x−
Trang 4
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn
B. Hàm số đã cho đạt GTNN tại và trên đoạn
C. Hàm số đã cho đạt GTNN tại và đạt GTLN tại trên đoạn
D. Hàm số đã cho đạt GTNN tại trên đoạn
Lời giải
A. Đúng. Vì
5
lim
x
y
−
→
= +
nên hàm số không có GTLN trên đoạn .
B. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn .
C. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn và .
D. Sai. Hàm số đã cho chỉ đạt GTNN tại trên đoạn .
Câu 9. (Chuyên Lê Thánh Tông 2019) Cho hàm số
( )
y f x=
liên tục trên , có bảng
biến thiên như hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị lớn nhất bằng
2
và giá trị nhỏ nhất bằng
3−
.
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng
( ) ( )
; 1 , 2;− − +
.
Lời giải
Dựa vào BBT ta thấy hàm số không có GTLN, GTNN.
Câu 10. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Cho hàm số
()=y f x
liên tục và có
bảng biến thiên trên đoạn
1;3−
như hình vẽ bên. Khẳng định nào sau đây đúng?
A.
1;3
max ( ) (0)f x f
−
=
. B.
( ) ( )
1;3
max 3
−
=f x f
. C.
( ) ( )
1;3
max 2
−
=f x f
. D.
( ) ( )
1;3
max 1
−
=−f x f
.
1;5−
1x =−
2x =
1;5−
1x =−
5x =
1;5−
0x =
1;5−
1;5−
2x =
1;5−
2x =
1;5−
5
lim
x
y
→
= +
2x =
1;5−
Trang 5
Lời giải
Nhìn vào bảng biến thiên ta thấy
( ) ( )
1;3
max 0 .f x f
−
=
Câu 11. (VTED 2019) Cho hàm số
( )
fx
liên tục trên
1;5−
và có đồ thị trên đoạn
1;5−
như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
( )
fx
trên đoạn
1;5−
bằng
A.
1−
B.
4
C.
1
D.
2
Lời giải
Từ đồ thị ta thấy:
( )
( )
1;5
1;5
max 3
1.
min 2
M f x
Mn
n f x
−
−
==
+ =
= = −
Câu 12. (THPT Yên Mỹ Hưng Yên 2019) Cho hàm số
( )
y f x=
xác định, liên tục trên
5
1,
2

−


và có đồ thị là đường cong như hình vẽ.
Giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
( )
fx
trên
5
1,
2

−


là:
A.
4, 1Mm==
B.
= = −4, 1Mm
C.
7
,1
2
Mm= = −
D.
7
,1
2
Mm==
Lời giải
Chọn B
Trang 6
Dựa vào đồ thị
= = −4, 1Mm
.
Câu 13. (THPT Nghĩa Hưng Nam Định 2019) Cho hàm số
( )
y f x=
có đồ thị như hình
vẽ. Giá trị lớn nhất của hàm số
( )
fx
trên đoạn
0;2
là:
A.
( )
0;2
2Max f x =
. B.
( )
0;2
2Max f x =
.
C.
( )
0;2
4Max f x =
. D.
( )
0;2
0Max f x =
.
Lời giải
Chọn C
Dựa vào đồ thị ta thấy trên đoạn
0;2
hàm số
( )
fx
có giá trị lớn nhất bằng
4
khi
2x =
Suy ra
( )
0;2
4Max f x =
Câu 14. (Sở Bắc Giang 2019) Cho hàm số
()y f x=
liên tục trên đoạn
1;3−
và có đồ thị
như hình vẽ bên. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm
số đã cho trên đoạn
1;3−
. Giá trị của
Mm+
là
A.
2
B.
6−
C.
5−
D.
2−
Lời giải
Dựa vào đồ thị ta thấy GTLN của hàm số trên đoạn
1;3−
là
2M =
đạt được tại
1x =−
và GTNN của hàm số số trên đoạn
1;3−
là
4m =−
đạt được tại
2x =
2 ( 4) 2Mm + = + − = −
Câu 15. (Sở Hà Nội 2019) Cho hàm số
( )
y f x=
có bảng biến thiên trên
)
5;7−
như sau
Trang 7
Mệnh đề nào dưới đây đúng?
A.
)
( )
5;7
Min 6fx
−
=
. B.
)
( )
5;7
Min 2fx
−
=
. C.
)
( )
-5;7
Max 9fx=
. D.
)
( )
5;7
Max 6fx
−
=
.
Lời giải
Dựa vào bảng biến thiên trên
)
5;7−
, ta có:
)
( ) ( )
5;7
Min 1 2f x f
−
==
.
Câu 16. Cho hàm số
( )
fx
liên tục trên đoạn
0;3
và có đồ thị như hình vẽ bên. Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên
0;3
. Giá trị
của
Mm+
bằng?
A.
5
. B.
3
. C.
2
. D.
1
.
Lời giải
Dựa vào hình vẽ ta có:
3M =
,
2m =−
nên
1Mm+=
.
Câu 17. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số
( )
y f x=
liên tục trên đoạn
[ ]
2;6-
và có đồ thị như hình vẽ bên dưới.
Trang 8
Gọi
M
và
m
lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
[ ]
2;6-
. Giá trị của
Mm-
bằng
A.
9
. B.
8−
. C.
9−
. D.
8
.
Lời giải
Từ đồ thị suy ra
( )
45fx−
2;6 ;x −
( ) ( )
1 4; 4 5ff= − =
5
4
M
m
=
=−
9Mm − =
.
Câu 18. (VTED 2019) Cho hàm số
( )
y f x=
liên tục và có đồ thị trên đoạn
2;4−
như
hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số
( )
y f x=
trên đoạn
2;4−
bằng
A.
5
B.
3
C.
0
D.
2−
Lời giải
Chọn B
Dựa vào đồ thị hàm số ta có
( )
2;4
4
x
m Min f x
−
= = −
,
( )
2;4
7
x
M Max f x
−
==
Khi đó
3Mm+=
Câu 19. (THPT Ngô Sĩ Liên Bắc Giang 2019) Cho hàm số
( )
y f x=
có bảng xét dấu đạo
hàm như sau:
Mệnh đề nào sau đây đúng
A.
(
( ) ( )
1;1
max 0f x f
−
=
B.
( )
( ) ( )
0;
max 1f x f
+
=
C.
( )
( ) ( )
;1
min 1f x f
− −
=−
D.
( )
( ) ( )
1;
min 0f x f
− +
=
Lời giải
Chọn B
Trang 9
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn
Bước 1: Hàm số đã cho
xác định và liên tục trên đoạn


ab;.
Tìm các điểm
n
x x x
12
, ,...,
trên khoảng
( )
ab;
, tại đó
( )
=fx 0
hoặc
( )
fx
không xác định.
Bước 2: Tính
( ) ( ) ( ) ( ) ( )
n
f a f x f x f x f b
12
, , ,..., , .
Bước 3: Khi đó:
( ) ( ) ( ) ( ) ( ) ( )
n
ab
max f x max f x f x f x f a f b
12
,
, ,..., , , .


=
( ) ( ) ( ) ( ) ( ) ( )


=
n
ab
min f x min f x f x f x f a f b
12
,
, ,.. ., , , .
Câu 1. (Đề Minh Họa 2020 Lần 1) Giá trị lớn nhất của hàm số
42
( ) 12 1f x x x= − + +
trên đoạn
1;2−
bằng:
A.
1
. B.
37
. C.
33
. D.
12
.
Lời giải
Chọn C
42
( ) 12 1f x x x= − + +
liên tục trên
1;2−
và
32
0
'( ) 4 24 0 6 ( )
6 ( )
x
f x x x x L
xL
=
= − + = =
=−
Ta có:
( 1) 12; (2) 33; (0) 1f f f− = = =
Vậy, giá trị lớn nhất của hàm số
42
( ) 12 1f x x x= − + +
trên đoạn
1;2−
bằng 33 tại
2x =
Câu 2. (Đề Tham Khảo 2020 Lần 2) Giá trị nhỏ nhất của hàm số
( )
42
10 2f x x x= − +
trên đoạn
1;2−
bằng
A.
2
. B.
23−
. C.
22−
. D.
7−
.
Lời giải
Chọn C
Hàm số đã cho liên tục trên đoạn
1;2−
.
Ta có:
( ) ( )
3
0
4 20 , 0
5
x
f x x x f x
x
=

= − =
=
.
Xét hàm số trên đoạn
1;2−
có:
( ) ( ) ( )
1 7; 0 2; 2 22f f f− = − = = −
.
Vậy
( )
1;2
min 22
x
fx
−
=−
.
Trang 10
Câu 3. (Mã 101 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
( )
3
24f x x x=−
trên đoạn
2;19
bằng
A.
32 2
. B.
40−
. C.
32 2−
. D.
45−
.
Lời giải
Chọn C.
Ta có
( )
2
2 2 2;19
3 24 0 .
2 2 2;19
x
f x x
x
=
= − =
= −
( )
3
2 2 24.2 40f = − = −
;
( ) ( )
3
2 2 2 2 24.2 2 32 2f = − = −
;
( )
3
19 19 24.19 6403f = − =
.
Vậy giá trị nhỏ nhất của hàm số
( )
3
24f x x x=−
trên đoạn
2;19
bằng
32 2−
.
Câu 4. (Mã 102 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số trên đoạn
bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Trên đoạn , ta có: .
Ta có: . Vậy .
Câu 5. (Mã 103 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
3
( ) 30f x x x=−
trên đoạn
2;19
bằng
A.
20 10.
B.
63.−
C.
20 10.−
D.
52.−
Lời giải
Chọn C
Ta có
( ) ( )
( )
( )
22
10
3 30 0 3 30 0
10
xn
f x x f x x
xl
=

= − = − =
=−
.
Khi đó
( )
2 52f =−
;
( )
10 20 10f =−
và
( )
19 6289f =
.
Vậy
( )
( )
2;19
min 10 20 10
x
f x f
= = −
.
Câu 6. (Mã 104 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số
( )
3
33f x x x=−
trên đoạn
2;19
bằng
A.
72−
. B.
22 11−
. C.
58−
. D.
22 11
.
Lời giải
Chọn B
Ta có
( )
2
11 2;19
3 33 0
11 2;19
x
f x x
x
=
= − =
= −
.
( )
3
21f x x x=−
2;19
36−
14 7−
14 7
34−
2;19
2
7 2;19
3 21 0
7 2;19
x
y x y
x
= −

= − =
=
( )
( )
( )
2 34; 7 14 7; 19 6460y y y= − = − =
14 7m =−
Trang 11
Khi đó ta có
( )
2 58f =−
,
( )
11 22 11f =−
,
( )
19 6232f =
. Vậy
( )
min
11 22 11ff= = −
.
Câu 7. (Mã 101 – 2020 Lần 2) Giá trị nhỏ nhất của hàm số
( )
42
10 4f x x x= − −
trên
0;9
bằng
A.
28−
. B.
4−
. C.
13−
. D.
29−
.
Lời giải
Chọn D
Hàm số
( )
y f x=
liên tục trên
0;9
.
Có
( )
3
4 20f x x x
=−
,
( )
0
05
5 0;9
x
f x x
x
=
= =
= −
Ta có
( )
04f =−
,
( )
5 29f =−
,
( )
9 5747f =
Do đó
( )
( )
0;9
min 5 29f x f= = −
.
Câu 8. (Mã 102 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
( )
42
12 4= − −f x x x
trên
đoạn
0;9
bằng
A.
39−
. B.
40−
. C.
36−
. D.
4−
.
Lời giải
Chọn B
Ta có:
( )
3
4 24f x x x
=−
;
( )
0
0
6
x
fx
x
=
=
=
Tính được:
( )
04=−f
;
( )
9 5585=f
và
( )
6 40=−f
.
Suy ra
( )
0;9
min 40=−fx
.
Câu 9. (Mã 103 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
( )
42
10 2f x x x= − −
trên
đoạn
0;9
bằng
A.
2−
. B.
11−
. C.
26−
. D.
27−
.
Lời giải
Chọn D
Ta có
( )
3
' 4 20f x x x=−
( )
'0fx=
3
4 20 0xx − =
( )
( )
( )
0 0;9
5 0;9
5 0;9
x
x
x
=
=
= −
( )
02f =−
;
( )
5 27f =−
;
( )
9 5749f =
.
Vậy
( )
0;9
min 27fx=−
.
Trang 12
Câu 10. (Mã 104 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số
( )
42
12 1f x x x= − −
trên đoạn
0;9
bằng
A.
28−
. B.
1−
. C.
36−
. D.
37−
.
Lời giải
Chọn D
Ta có
( )
3
4 24f x x x
=−
.
( )
3
0 0;9
0 4 24 0 6 0;9
6 0;9
x
f x x x x
x
=
= − = =
= −
.
( )
01f =−
,
( )
6 37f =−
,
( )
9 5588f =
Câu 11. (Mã 102 - 2019) Giá trị nhỏ nhất của hàm số
( )
3
32f x x x= − +
trên đoạn
3;3−
bằng
A.
0
. B.
16−
. C.
20
. D.
4
.
Lời giải
Chọn B
Cách 1:Mode 7
( )
3
32f x x x= − +
.
Start -3
end3step 1
Chọn B
Cách 2:
( )
2
33f x x
=−
.
( )
0 1 3;3f x x
= = −
.
( )
3 16f − = −
;
( )
14f −=
;
( )
10f =
;
( )
3 20f =
.
Giá trị nhỏ nhất là
16−
.
Câu 12. (Mã 110 2017) Tìm giá trị lớn nhất
M
của hàm số
42
23y x x= − +
trên đoạn
0; 3


.
A.
6M =
B.
1M =
C.
9M =
D.
Lời giải
Chọn A
Ta có:
( )
32
4 4 4 1y x x x x
= − = −
0y
=
( )
2
4 1 0xx−=
0
1
1( )
x
x
xl
=
=
=−
Ta có :
( )
03y =
;
( )
12y =
;
( )
36y =
Vậy giá trị lớn nhất của hàm số
42
23y x x= − +
trên đoạn
0; 3


là
( )
36My==
Câu 13. (Đề Minh Họa 2017) Tìm giá trị nhỏ nhất của hàm số
2
3
1
+
=
−
x
y
x
trên đoạn
2;4
.
Trang 13
A.
2;4
min 3=−y
B.
2;4
19
min
3
=y
C.
2;4
min 6=y
D.
2;4
min 2=−y
Lời giải
Chọn C
Tập xác định:
\1=D
Hàm số
2
3
1
+
=
−
x
y
x
xác định và liên tục trên đoạn
2;4
Ta có
( )
2
2
2
23
; 0 2 3 0 3
1
−−

= = − − = =
−
xx
y y x x x
x
hoặc
1=−x
(loại)
Suy ra
( ) ( ) ( )
19
2 7; 3 6; 4
3
= = =y y y
. Vậy
2;4
min 6=y
tại
3=x
.
Câu 14. (Mã 103 - 2019) Giá trị lớn nhất của hàm số
( )
3
3f x x x=−
trên đoạn
[ 3;3]−
bằng
A.
2−
. B.
18
. C.
2
. D.
18−
.
Lời giải
Chọn B
Ta có
2
3 3 0 1y x x
= − = =
( ) ( ) ( ) ( )
3 18; 1 2; 1 2; 3 18f f f f− = − − = = − =
.
Câu 15. (Mã 104 2018) Giá trị lớn nhất của hàm số
42
13y x x= − +
trên đoạn
[ 1;2]−
bằng
A.
85
B.
51
4
C.
13
D.
25
Lời giải
Chọn D
( )
42
13y f x x x= = − +
3
' 4 2y x x=−
3
0 [ 1;2]
1
4 2 0 [ 1;2]
2
1
[ 1;2]
2
x
x x x
x
= −
− = = − −
= −
1 51 1 51
( 1) 13; (2) 25; (0) 13; ;
44
22
f f f f f
− = = = − = =
Giá trị lớn nhất của hàm số
42
13y x x= − +
trên đoạn
[ 1;2]−
bằng
25.
Câu 16. (Mã 104 2017) Tìm giá trị nhỏ nhất
m
của hàm số
2
2
yx
x
=+
trên đoạn
1
;2
2



.
A.
5m =
B.
3m =
C.
17
4
m =
D.
10m =
Lời giải
Chọn B
Trang 14
Đặt
( )
2
2
y f x x
x
= = +
.
Ta có
3
22
2 2 2
2
x
yx
xx
−
= − =
,
1
0 1 ;2
2
yx

= =


.
Khi đó
( ) ( )
1 17
1 3, , 2 5
24
f f f

= = =


.
Vậy
( ) ( )
1
;2
2
min 1 3m f x f



= = =
.
Câu 17. (Chuyên Bắc Ninh 2018) Tìm tập giá trị của hàm số
19y x x= − + −
A.
1; 9T =
. B.
2 2; 4T

=

. C.
( )
1; 9T =
. D.
0; 2 2T

=

.
Lời giải
Tập xác định:
1; 9D =
11
0 9 1
2 1 2 9
y x x
xx
= − = − = −
−−
1
5
91
x
x
xx
=
−=−
.
( ) ( )
1 9 2 2ff==
;
( )
54f =
Vậy tập giá trị là
2 2; 4T

=

.
Câu 18. (Mã 123 2017) Tìm giá trị nhỏ nhất
m
của hàm số
= − + −
32
7 11 2y x x x
trên
đoạn
[0 ; 2]
.
A.
= 3m
B.
= 0m
C.
=−2m
D.
= 11m
Lời giải
Chọn C
Xét hàm số trên đoạn
[0 ; 2]
. Ta có
= − +
2
3 14 11y x x
suy ra
= =01yx
Tính
( ) ( ) ( )
= − = =0 2; 1 3, 2 0f f f
. Suy ra
( ) ( )


= = − =
0;2
min 0 2f x f m
.
Câu 19. (Mã 101 2018) Giá trị lớn nhất của hàm số
42
49y x x= − +
trên đoạn
2;3−
bằng
A.
201
B.
2
C.
9
D.
54
Lời giải
Chọn D
3
48
=−y x x
;
0
0
2
=
=
=
x
y
x
.
Ta có
( )
29y −=
;
( )
3 54y =
;
( )
09y =
;
( )
25y =
.
Vậy
2;3
max 54y
−
=
.
Câu 20. (Đề Tham Khảo 2018) Giá trị lớn nhất của hàm số
( )
42
45f x x x= − +
trêm đoạn
2;3−
bằng
A.
122
B.
50
C.
5
D.
1
Lời giải
Chọn B
Trang 15
3
0
'( ) 4 8 0 2;3
2
=
= − = −
=
x
f x x x
x
;
( )
( )
( ) ( )
0 5; 2 1; 2 5; 3 50f f f f= = − = =
Vậy
2;3
50Max y
−
=
Câu 21. (Mã 105 2017) Tìm giá trị nhỏ nhất
m
của hàm số
= − +
42
13y x x
trên đoạn
−

2;3
.
A.
= 13m
B.
=
51
4
m
C.
=
51
2
m
D.
=
49
4
m
Lời giải
Chọn B
=−
3
42y x x
;
= −

=
= −

0 2;3
0
1
2;3
2
x
y
x
;
Tính
( )
−=2 25y
,
( )
=3 85y
,
( )
=0 13y
,

= =


1 51
12,75
4
2
y
;
Kết luận: giá trị nhỏ nhất
m
của hàm số là
=
51
4
m
.
Câu 22. (Mã 104 2019) Giá trị nhỏ nhất của hàm số
( )
3
3=−f x x x
trên đoạn
3;3−
bằng
A.
18.−
B.
2.−
C.
2.
D.
18.
Lời giải
Chọn A
Ta có
( )
2
1
3 3 0 .
1
=
== − =
=−
x
f x x
x
Mà
( ) ( ) ( ) ( )
3 18; 1 2; 1 2; 3 18.− = − − = = − =f f f f
Vậy giá trị nhỏ nhất của hàm số
( )
3
3=−f x x x
trên đoạn
3;3−
bằng
18.−
Câu 23. (Mã 103 2018) Giá trị nhỏ nhất của hàm số
32
3y x x=+
trên đoạn
4; 1−−
bằng
A.
16−
B.
0
C.
4
D.
4−
Lời giải
Chọn A
Ta có
2
36y x x
=+
;
2
4; 1
0
0 3 6 0
4; 1
2
x
y x x
x
− −
=
= + =
− −
=−
.
Khi đó
( )
4 16y − = −
;
( )
24y −=
;
( )
12y −=
.
Nên
4; 1
min 16y
−−
=−
.
Câu 24. (Mã 102 2018) Giá trị nhỏ nhất của hàm số
32
27y x x x= + −
trên đoạn
0;4
bằng
A.
259−
B.
68
C.
0
D.
4−
Lời giải
Chọn D
Trang 16
TXĐ
D.=
Hàm số liên tục trên đoạn
0;4
.
Ta có
2
3 4 7y x x
= + −
0y
=
1 0 4
7
04
3
x;
x;
=
= −
( ) ( ) ( )
0 0; 1 4; 4 68y y y= = − =
.
Vậy
0;4
min 4y =−
.
Câu 25. (Mã 101 - 2019) Giá trị lớn nhất của hàm số
( )
3
32f x x x= − +
trên đoạn
3;3−
là
A.
4
. B.
16−
. C.
20
. D.
0
.
Lời giải
Chọn C
( )
3
32f x x x= − +
tập xác định .
( )
2
' 0 3 3 0 1 3;3f x x x= − = = −
.
( ) ( ) ( ) ( )
1 0; 1 4; 3 20; 3 16f f f f= − = = − = −
.
Từ đó suy ra
( )
3;3
max (3) 20f x f
−
==
.
Câu 26. (SGD Nam Định) Giá trị nhỏ nhất của hàm số
2
2
yx
x
=+
trên đoạn
2;3
bằng
A.
15
2
. B.
5
. C.
29
3
. D.
3
.
Lời giải
Chọn B
+ Ta có hàm số
2
2
()y f x x
x
= = +
xác định và liên tục trên
2;3
.
+
2
2
' '( ) 2y f x x
x
= = −
;
'( ) 0 1 2;3f x x= =
mà
(2) 5f =
,
29
(3)
3
f =
.
+ Vậy
2;3
min 5y =
tại
2x =
.
Câu 27. (Sở Quảng Trị 2019) Tìm giá trị lớn nhất
M
của hàm số
31
3
x
y
x
−
=
−
trên đoạn
0;2
A.
1
3
M =
. B.
1
3
M =−
. C.
5M =
. D.
5M =−
Lời giải
Chọn A
Trên đoạn
0;2
ta luôn có
( )
( )
2
8
0 0;2
3
yx
x
= −
−
( đạo hàm vô nghiệm trên
(0; 2))
Trang 17
Vì
( ) ( )
1
0 , 2 5
3
yy= =−
nên
0;2
1
max
3
My==
.
Câu 28. (Sở Nam Định-2019) Giá trị lớn nhất của hàm số
2
4yx=−
là
A. 2. B. 0. C. 4. D. 1.
Lời giải
Chọn A
• Tập xác định:
2;2D =−
• Ta có:
2
'
4
x
y
x
−
=
−
( )
0 0 2;2yx
= = −
• Ta có:
( ) ( )
( )
2;2
2 2 0
max 2
02
yy
y
y
−
− = =
=
=
.
Câu 29. (Chuyên Bắc Ninh 2018) Tìm giá trị nhỏ nhất của hàm số
2
sin 4sin 5y x x= − −
.
A.
20−
. B.
8−
. C.
9−
. D.
0
.
Lời giải
Đặt
sin , 1;1t x t= −
. Xét
2
( ) 4 5f t t t= − −
,
1;1t−
.
( ) 2 4 0 2 1;1f t t t
= − = = −
.
( ) ( )
1 8, 1 0ff= − − =
.
Ta thấy
( ) ( )
1;1
min 1 8f t f
−
= = −
. Vậy giá trị nhỏ nhất của hàm số là
8−
.
Câu 30. (THPT Hoa Lư A 2018) Gọi
m
,
M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất
của hàm số
( )
1
1
2
f x x x= − +
trên đoạn
0;3
. Tính tổng
23S m M=+
.
A.
7
2
S =−
. B.
3
2
S =−
. C.
3−
. D.
4S =
.
Lời giải
Ta có:
( )
1 1 1 1
2
2 1 2 1
x
fx
xx
+−
= − =
++
, cho
( )
0 1 1 0 0;3f x x x
= + = =
.
Khi đó:
( )
01f =−
,
( )
1
3
2
f =−
nên
1m =−
và
1
2
M =−
.
Vậy
7
23
2
S m M= + = −
.
Câu 31. (Chuyên ĐHSPHN - 2018) Tìm giá trị lớn nhất của hàm số
( )
sin cosf x x x=+2
trên
;0
là
A.
9
8
. B.
5
4
. C.
2
. D.
1
.
Lời giải
( )
sin cosf x x x=+2
sin sinxx= + −
2
12
Đặt
sin xt=
( )
t01
( )
f t t t= − + +
2
21
,
( )
f t t
= − +41
Trang 18
( )
ft
= 0
t=
1
4
( )
f =01
,
( )
f =10
,
f

=


19
48
Vậy
( )
;
max fx=
01
9
8
.
Câu 32. (THPT Hà Huy Tập - 2018) Giá trị lớn nhất của hàm số
3
4
2cos os
3
y x c x=−
trên
0;
.
A.
0;
2
ax
3
my
=
. B.
0;
10
ax
3
my
=
. C.
0;
22
ax
3
my
=
. D.
0;
ax 0my
=
.
Lời giải
Đặt:
costx=
1;1t −
3
4
2
3
y t t = −
.
2
' 2 4yt=−
'0y =
1
1;1
2
1
1;1
2
x
x
−
= −
= −
.
Tính:
( )
2
1
3
y
−
−=
,
1 2 2
3
2
y
−−

=


,
1 2 2
3
2
y

=


,
( )
2
1
3
y =
.
Vậy:
0;
22
ax
3
my
=
.
Câu 33. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3sin 2
sin 1
x
y
x
+
=
+
trên đoạn
0;
2



. Khi đó giá trị của
22
Mm+
là
A.
31
2
. B.
11
2
. C.
41
4
. D.
61
4
.
Lời giải
Chọn C
Đặt
sintx=
,
0;1t
.
Xét hàm
( )
32
1
t
ft
t
+
=
+
liên tục trên đoạn
0;1
có
( )
( )
2
1
0, 0;1
1
f t t
t
=
+
.
Suy ra hàm số đồng biến trên
0;1
.
0;1
5
Max ( ) (1)
2
M f t f = = =
và
0;1
Min ( ) (0) 2m f t f= = =
.
Khi đó
2
2 2 2
5 41
2
24
Mm

+ = + =


.
Câu 34. (THPT Can Lộc - Hà Tĩnh - 2018) Cho hàm số
2
sin 1
sin sin 1
x
y
xx
+
=
++
. Gọi
M
là
giá trị lớn nhất và
m
là giá trị nhỏ nhất của hàm số đã cho. Chọn mệnh đề đúng.
Trang 19
A.
3
2
Mm=+
. B.
3
2
Mm=
. C.
1Mm=+
. D.
2
3
Mm=+
.
Lời giải
Đặt
sin xt=
,
( )
11t−
ta được
2
1
1
t
y
tt
+
=
++
.
Xét hàm số
2
1
1
t
y
tt
+
=
++
trên đoạn
1;1−
ta có
( )
2
2
2
2
1
tt
y
tt
−−
=
++
.
Giải phương trình
0y
=
2
20tt − − =
0 ( / )
2 ( )
t t m
t loai
=
=−
.
Vì
( )
10y −=
;
( )
01y =
;
( )
2
1
3
y =
nên
( )
1;1
max 0 1yy
−
==
1M=
;
( )
1;1
min 1 0yy
−
= − =
0m=
.
Vậy
1Mm=+
.
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng
(a;b)
Bước 1: Tính đạo hàm
fx()
.
Bước 2: Tìm tất cả các nghiệm
i
x a b( ; )
của phương trình
fx( ) 0
=
và tất cả các điểm
i
ab( ; )
làm cho
fx()
không xác định.
Bước 3. Tính
+
→
=
xa
A f xlim ( )
,
−
→
=
xb
B f xlim ( )
,
i
fx()
,
i
f()
.
Bước 4. So sánh các giá trị tính được và kết luận
ab
M f x
( ; )
max ( )=
,
ab
m f x
( ; )
min ( )=
.
Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ
nhất).
Câu 1. (Đề Tham Khảo 2017) Tính giá trị nhỏ nhất của hàm số
2
4
3yx
x
=+
trên khoảng
( )
0;+
.
A.
( )
0;
33
min
5
y
+
=
B.
( )
3
0;
min 2 9y
+
=
C.
( )
3
0;
min 3 9y
+
=
D.
( )
0;
min 7y
+
=
Lời giải
Chọn C
Cách 1:
3
3
2 2 2
4 3 3 4 3 3 4
3 3 . . 3 9
2 2 2 2
x x x x
yx
x x x
= + = + + =
Dấu
""=
xảy ra khi
3
2
3 4 8
23
x
x
x
= =
.
Vậy
( )
3
0;
min 3 9y
+
=
Cách 2:
Trang 20
Xét hàm số
2
4
3yx
x
=+
trên khoảng
( )
0;+
Ta có
23
48
3 ' 3y x y
xx
= + = −
Cho
3
3
3
8 8 8
' 0 3
33
y x x
x
= = = =
( )
3
3
0;
8
min 3 9
3
yy
+

= =



Câu 2. Gọi
m
là giá trị nhỏ nhất của hàm số
4
1
1
yx
x
= − +
−
trên khoảng
( )
1; +
. Tìm
m
?
A.
5m =
. B.
4m =
. C.
2m =
. D.
3m =
.
Lời giải
Chọn B
Tập xác định
\1DR=
.
( )
2
2
1
23
,0
3
1
x
xx
yy
x
x
=−
−−

= =
=
−
.
Bảng biến thiên:
( )
1;
min 4my
+
= =
khi
3x =
Câu 3. (THPT Minh Châu Hưng Yên 2019) Giá trị nhỏ nhất của hàm số
1
5yx
x
= − +
trên khoảng
( )
0;+
bằng bao nhiêu?
A.
0
B.
1−
C.
3−
D.
2−
Lời giải
Chọn C
Áp dụng bất đẳng thức Cô – si ta có:
11
5 2 . 5 3y x x
xx
= + − − = −
Dấu bằng xảy ra khi
2
1
11x x x
x
= = =
(vì
0x
).
x
0
+
3
8
3
'y
y
3
39
0
−
+
Trang 21
Vậy
( )
0;
min 3y
+
=−
Câu 4. (Chuyên Lương Thế Vinh Đồng Nai 2019) Gọi
m
là giá trị nhở nhất của hàm số
trên khoảng
( )
0;+
. Tìm
m
A.
4m =
. B.
2m =
. C.
1m =
. D.
3m =
.
Lời giải
( )
2
4
'1
' 0 2; 2 0; .
y
x
y x x
=−
= = = +
Bảng biến thiên:
Suy ra giá trị nhỏ nhất của hàm số bằng
2) 4( 4.ym= =
Câu 5. (Chuyên Bắc Giang 2019) Giá trị nhỏ nhất của hàm số
1
()f x x
x
=+
trên nửa
khoảng
)
2;+
là:
A.
2
B.
5
2
C.
0
D.
7
2
Lời giải
Chọn B
Áp dụng bất đẳng thức Cô-si, ta được:
1 3 1 3.2 1 5
( ) 2 .
4 4 4 4 2
x x x
f x x
x x x
= + = + + + =
.
Dấu bằng xảy ra khi
2x =
.
Câu 6. Gọi
m
là giá trị nhỏ nhất của hàm số
4
yx
x
=+
trên khoảng
( )
0;+
. Tìm
m
.
A.
3m =
. B.
4m =
. C.
2m =
. D.
1m =
.
Lời giải
Chọn B
Cách 1:
Hàm số
4
yx
x
=+
liên tục và xác định trên
( )
0;+
.
Ta có
( )
( )
2
22
2 0;
44
' 1 ' 0
2 0;
x
x
yy
xx
x
= +
−
= − = =
= − +
.
Bảng biến thiên
Trang 22
Vậy giá trị nhỏ nhất là
4m =
khi
2.x =
Cách 2:
Với
( )
4
0; ; 0.xx
x
+
Áp dụng bất đẳng thức Cô si ta có:
44
2 . 4.xx
xx
+ =
Dấu bằng xảy ra khi và chỉ khi
0
2.
4
x
x
x
x
=
=
Vậy
4m =
khi
2.x =
Câu 7. Giá trị nhỏ nhất của hàm số
43yx= − +
trên tập xác định của nó là
A.
2 3.+
B.
2 3.
C.
0.
D.
3.
Lời giải
Chọn D
Tập xác định của hàm số là:
(
;4 .D = −
Ta có
1
' 0,
24
y x D
x
−
=
−
Bảng biến thiên
Từ bảng biến thiên suy ra
(
;4
min 3y
−
=
khi
4x =
.Vậy chọn
D
.
Câu 8. Với giá trị nào của
x
thì hàm số
2
1
yx
x
=+
đạt giá trị nhỏ nhất trên khoảng
( )
0;+
?
A.
3
3
4
. B.
1
2
. C.
1
. D.
3
1
2
.
Lời giải
Chọn D
TXD:
\0D = ¡
.
2
1
'2yx
x
=−
,
3
1
' 0 .
2
yx= =
3
+
∞
x
y'
y
∞
4
Trang 23
Dựa vào BBT thì
3
1
2
x =
hàm số đạt giá trị nhỏ nhất trên
( )
0;+
.
Câu 9. Giá trị nhỏ nhất của hàm số
( )
2
2
12yx
x
= + − +
trên khoảng
( )
0; +
A. không tồn tại. B.
3−
. C.
12−+
. D.
0
.
Lời giải
Chọn B
Hàm số xác định và liên tục trên khoảng
( )
0; .+
2
22
22
1.
x
y
xx
−
= − =
2
0.
2
x
y
x
=
=
=−
Bảng biến thiên:
Vậy
( )
( )
0;
min 2 3.yf
+
= = −
Câu 10. Cho hàm số
( )
2
1
2
x
fx
x
-
=
-
với
x
thuộc
( ]
3
; 1 1;
2
D
éù
êú
= - ¥ - È
êú
ëû
. Mệnh đề nào
dưới đây đúng?
A.
( ) ( )
max 0;min 5
D
D
f x f x= = -
. B.
( )
max 0
D
fx=
; không tồn tại
.
C.
( ) ( )
max 0;min 1
D
D
f x f x= = -
. D.
( )
min 0
D
fx=
; không tồn tại
( )
max
D
fx
.
Lời giải
Chọn A
Hàm số xác định và liên tục trên
( ]
3
; 1 1;
2
D
éù
êú
= - ¥ - È
êú
ëû
.
( )
( )
2
2
21
'
21
x
fx
xx
-+
=
--
;
( )
1
'0
2
f x x D= Û = Ï
Trang 24
Vậy
( ) ( )
max 0;min 5
D
D
f x f x= = -
.
Câu 11. (Cụm liên trường Hải Phòng 2019) Mệnh đề nào sau đây là đúng về hàm số
2
1
5
x
y
x
+
=
+
trên tập xác định của nó.
A. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
B. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất.
C. Hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.
Lời giải
Chọn D
Tập xác định:
D=
.
( )
( ) ( )
2
22
2
2
2 2 2 2
2
51
55
25
'
5
5 5 5 5
x
xx
x x x x
x
y
x
x x x x
+ - +
+ - - -
+
= = =
+
+ + + +
.
( )
22
5
' 0 0 5 0 5
55
x
y x x
xx
-
= Û = Û - = Û =
++
.
Bảng biến thiên:
Từ bảng biến thiên có
( )
30
max 5
5
yy==
khi
5x =
.
Hàm số
2
1
5
x
y
x
+
=
+
không có giá trị nhỏ nhất.
Vậy hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Chuyên đề 5
GIÁ TRỊ LỚN NHẤT - GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
Dạng 1. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số thông qua đồ
thị, bảng biến thiên
 Giá trị lớn nhất của hàm số f (x) trên đoạn a;b
Hàm số f (x) liên tục trên đoạn a;b và f (x ) = 0, x a;b . Khi đó giá trị lớn i i
nhất của hàm số f (x) là M = max f (a), f (b), f (xi )
 Giá trị nhỏ nhất của hàm số f (x) trên đoạn a;b
Hàm số f (x) liên tục trên đoạn a;b và f (x ) = 0, x a;b . Khi đó giá trị nhỏ i i
nhất của hàm số f (x) là m = Minf (a), f (b), f (xi )
 Hàm số y = f (x) đồng biến trên đoạn a;b thì
Max f ( x) = f (b); Min f ( x) = f (a) a;b a;b
 Hàm số y = f (x) nghịch biến trên đoạn a;b thì
Max f ( x) = f (a); Min f ( x) = f (b) a;b a;bCâu 1.
(ĐỀ THI TN THPT 2022) Giá trị lớn nhất của hàm số f (x) 3 2
= x −3x −9x +10 trên đoạn  2 − ;2 bằng A. 12 − . B. 10 . C. 15 . D. 1 − . Lời giải Chọn C
Xét hàm số f ( x) 3 2
= x −3x −9x +10 trên đoạn  2 − ;2  f (x) 2
= 3x − 6x −9. f ( x) x = 1 −  2 − ;2 2  
= 0  3x − 6x − 9 = 0   x = 3  −2;2 Ta có: f ( 2 − ) = 8; f (− ) 1 =15; f (2) = 1 − 2 .
Vậy giá trị lớn nhất của hàm số f ( x) 3 2
= x −3x −9x +10 trên đoạn  2 − ;2 bằng 15 . Câu 2.
(ĐỀ THI TN THPT 2021) Trên đoạn [0;3] , hàm số 3
y = −x + 3x đại giá trị lớn nhất tại điểm A. x = 0 . B. x = 3. C. x = 1 . D. x = 2 . Lời giải Chọn C Tập xác định: . 2 y = 3 − x + 3 x =1(0;3) 2 y = 0  3 − x + 3 = 0   x = 1 − (0;3)
Ta có y(0) = 0; y(1) = 2; y(3) = 1 − 8. Vậy max y = y(1) = 2 . [0;3] Trang 1 Câu 3.
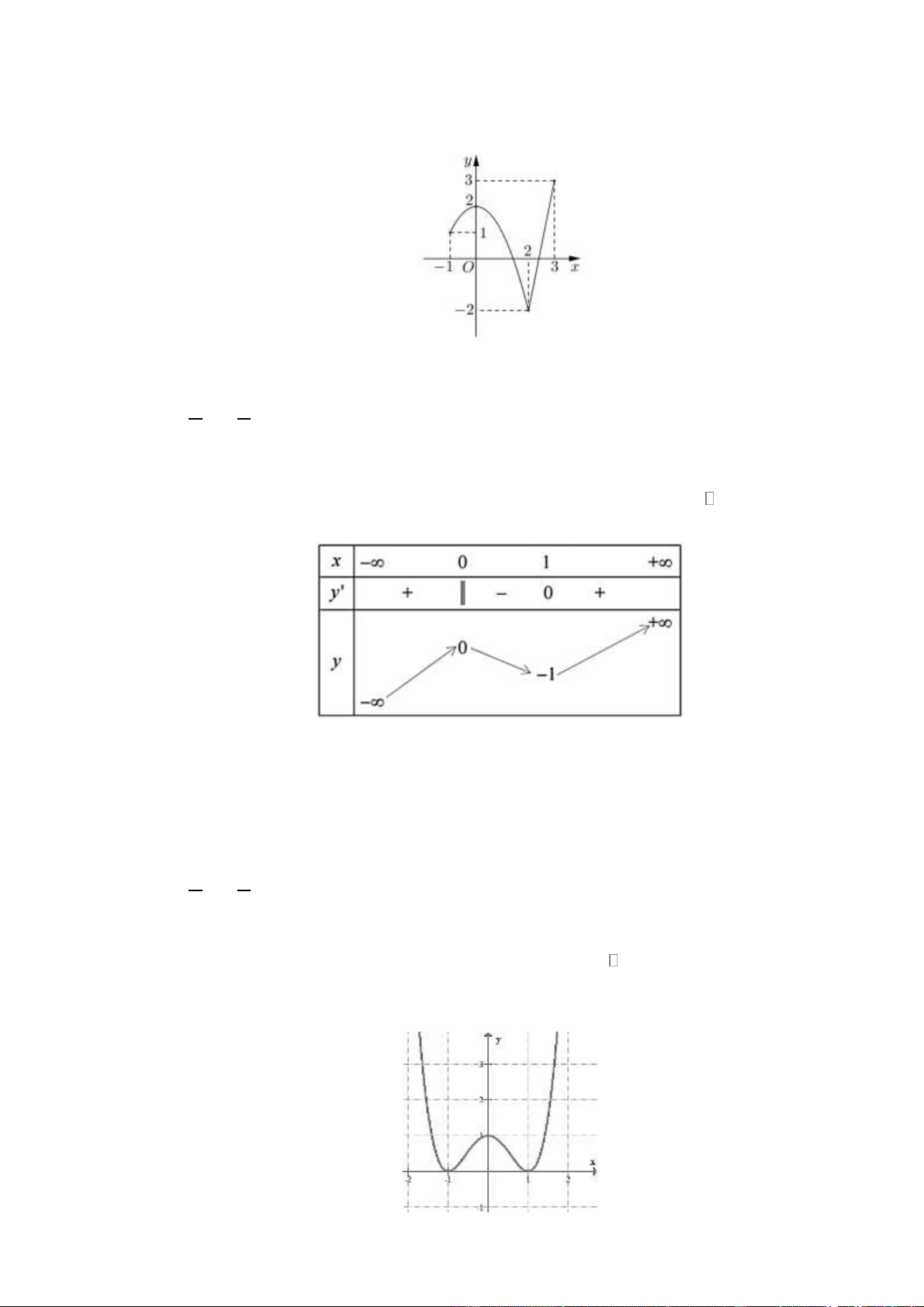
(Đề Tham Khảo 2019) Cho hàm số y = f ( x) liên tục trên đoạn  1 − ;  3 và có đồ
thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm
số đã cho trên đoạn  1 − ; 
3 . Giá trị của M − m bằng A. 1 B. 4 C. 5 D. 0 Lời giải Chọn C
Dựa và đồ thị suy ra M = f ( )
3 = 3; m = f (2) = 2 −
Vậy M − m = 5 Câu 4.
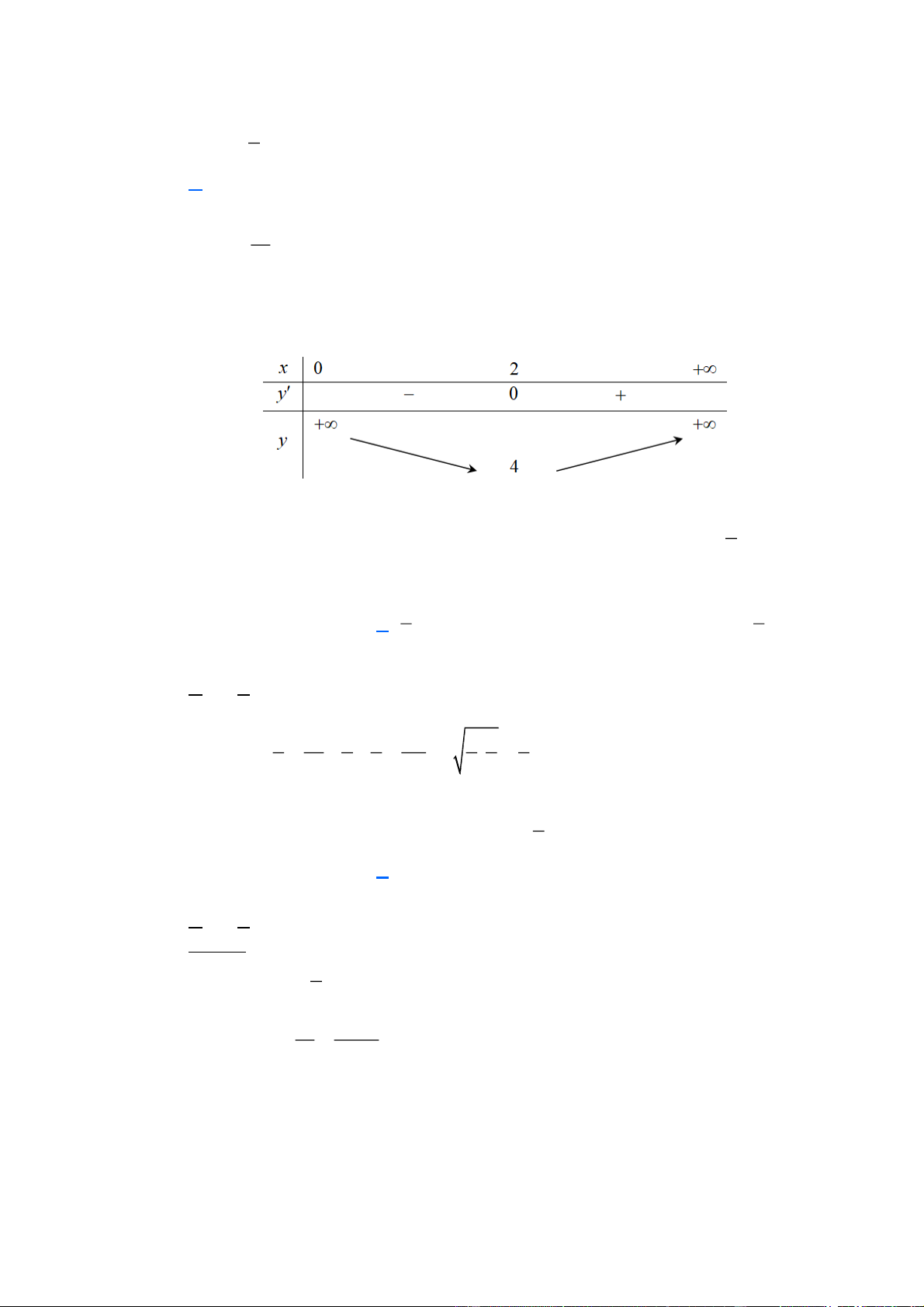
(Đề Minh Họa 2017) Cho hàm số y = f ( x) xác định, liên tục trên và có bảng biến thiên:
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị cực tiểu bằng 1 .
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng −1 .
C. Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 .
D. Hàm số có đúng một cực trị. Lời giải Chọn C
Đáp án A sai vì hàm số có 2 điểm cực trị.
Đáp án B sai vì hàm số có giá trị cực tiểu y = −1 khi x = 0 .
Đáp án C sai vì hàm số không có GTLN và GTNN trên .
Đáp án D đúng vì hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1 . Câu 5.
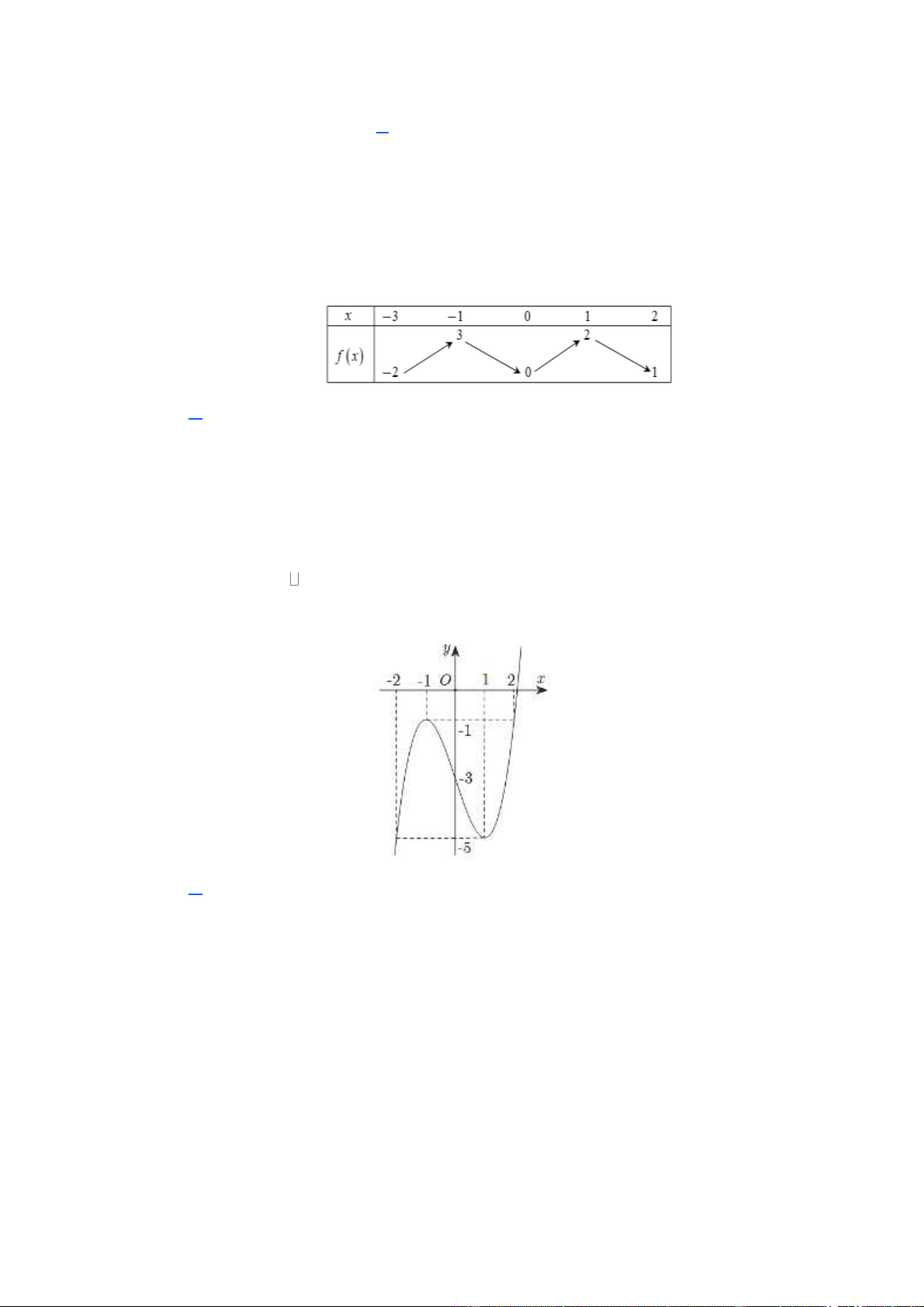
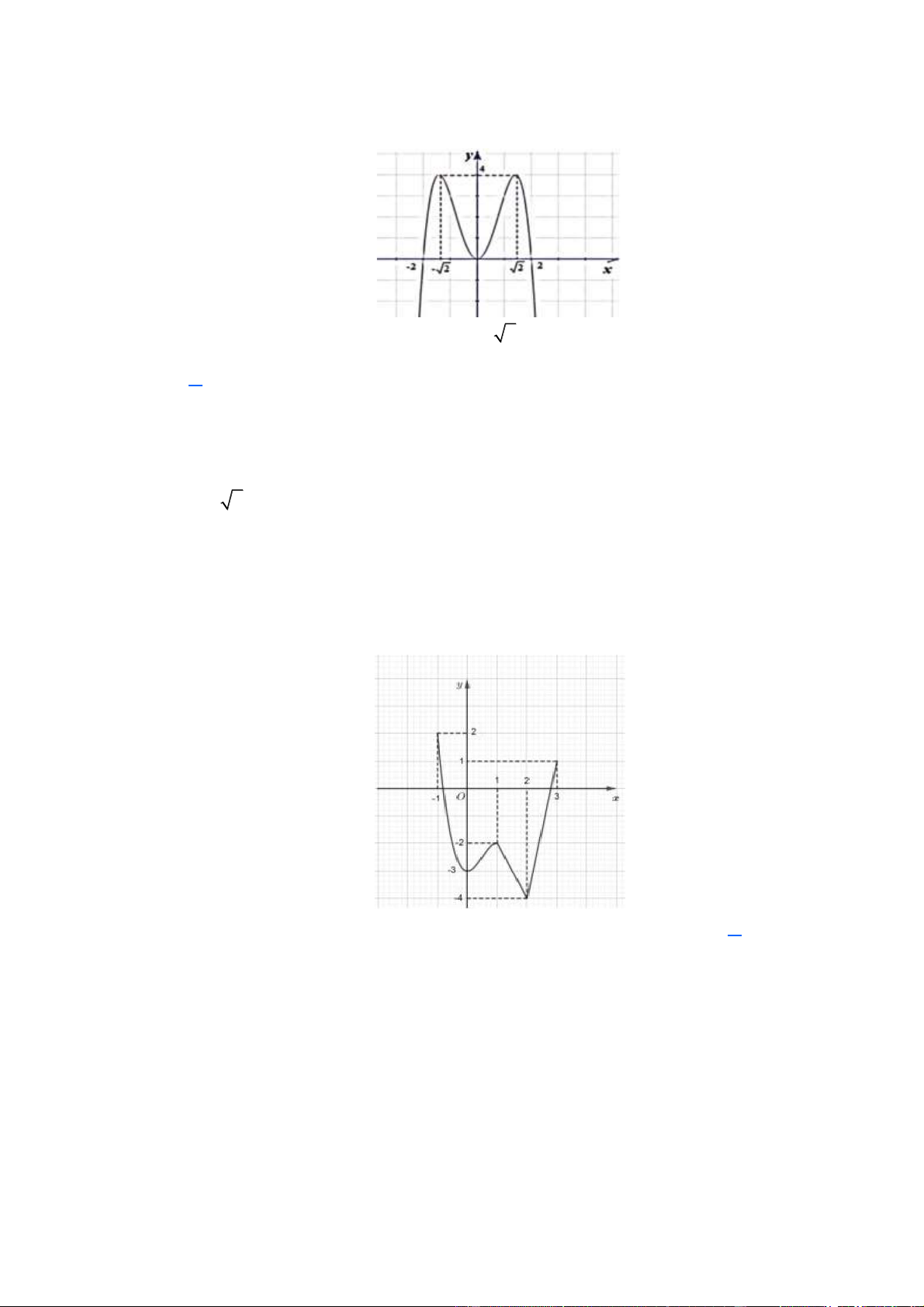
Cho hàm số y = f ( x) liên tục trên đoạn  1 − ; 
1 và có đồ thị như hình vẽ. Trang 2
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn  1 − ; 
1 . Giá trị của M − m bằng A. 0 . B. 1. C. 2 . D. 3 . Lời giải
Từ đồ thị ta thấy M =1,m = 0 nên M − m =1. Câu 6.
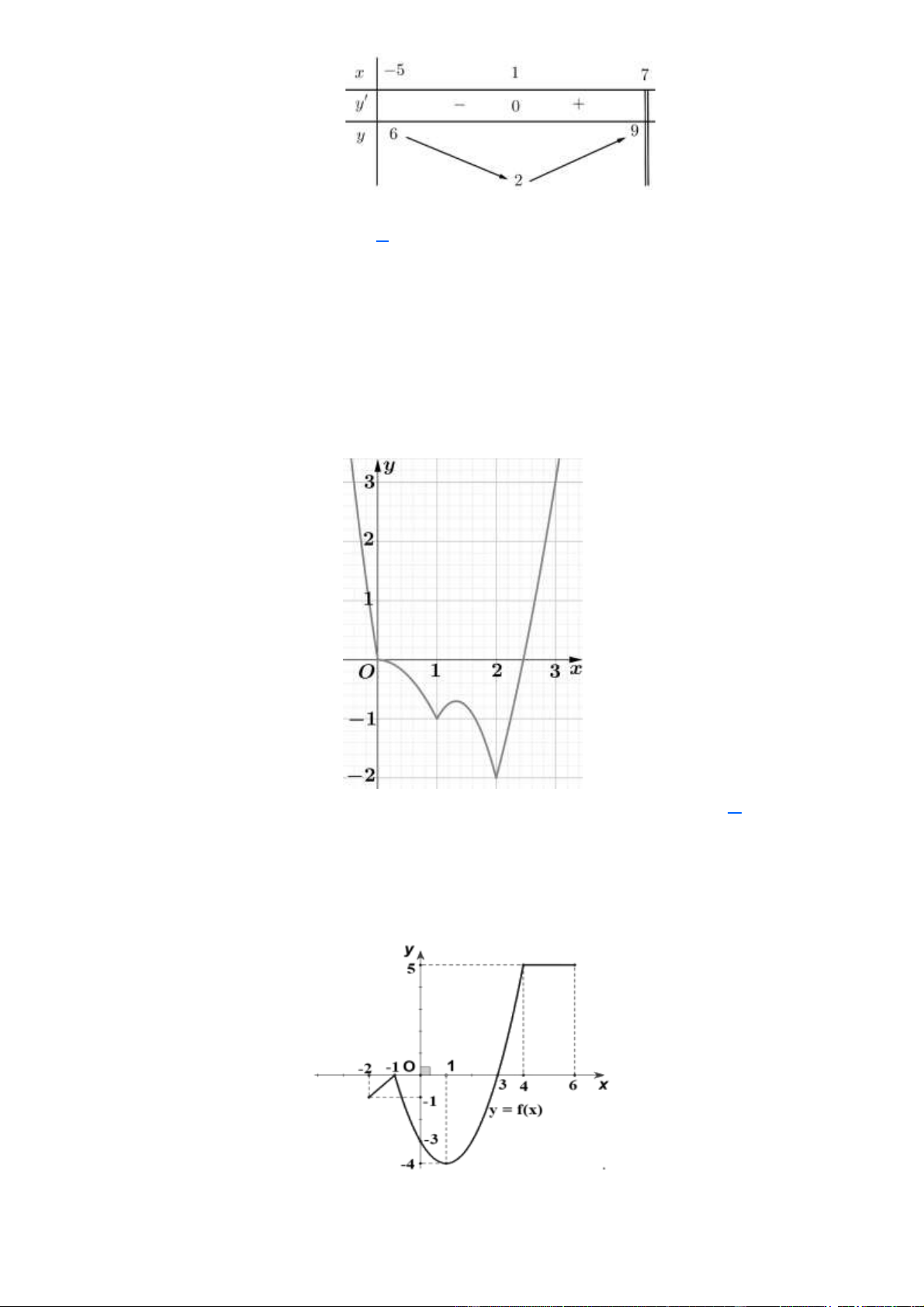
Cho hàm số y = f ( x) liên tục trên  3
− ;2 và có bảng biến thiên như sau. Gọi
M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f ( x) trên đoạn  1 − ; 
2 . Tính M + m . A. 3 . B. 2 . C. 1. D. 4 . Lời giải Trên đoạn  1 − ; 
2 ta có giá trị lớn nhất M = 3 khi x = 1
− và giá trị nhỏ nhất m = 0 khi x = 0 .
Khi đó M + m = 3+ 0 = 3. Câu 7.
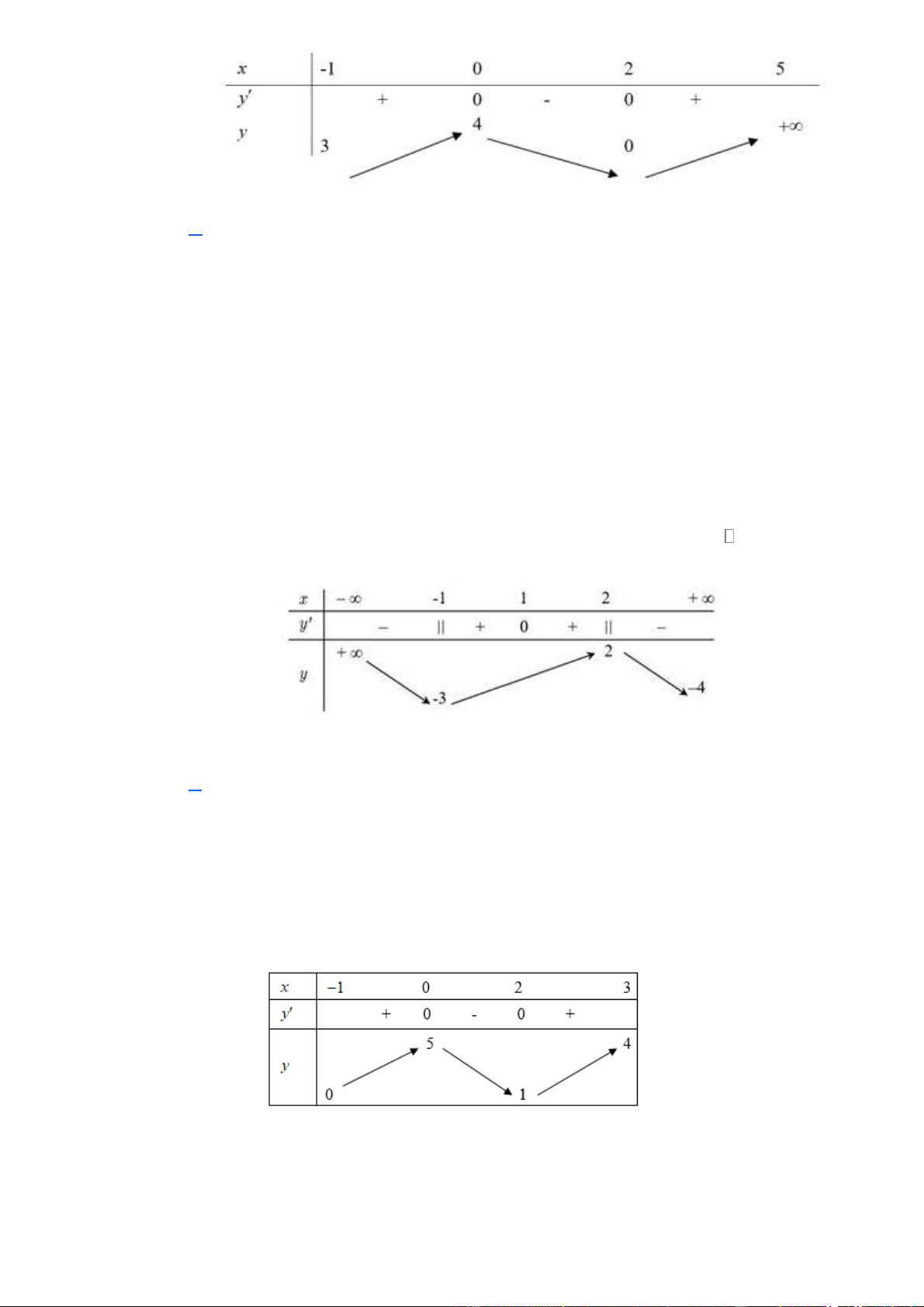
(Chuyên Lương Thế Vinh Đồng Nai 2019) Cho hàm số y = f ( x) xác định và liên tục trên
có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn
nhất M của hàm số y = f ( x) trên đoạn  2 − ;  2 . A. m = 5 − ;M = 1 − . B. m = 2 − ;M = 2. C. m = 1 − ;M = 0. D. m = 5 − ;M = 0 . Lời giải
Nhìn vào đồ thị ta thấy:
M = max f ( x) = 1 − khi x = 1 − hoặc x = 2 .  2 − ;2
m = min f ( x) = 5 − khi x = 2
− hoặc x =1.  2 − ;2 Câu 8.
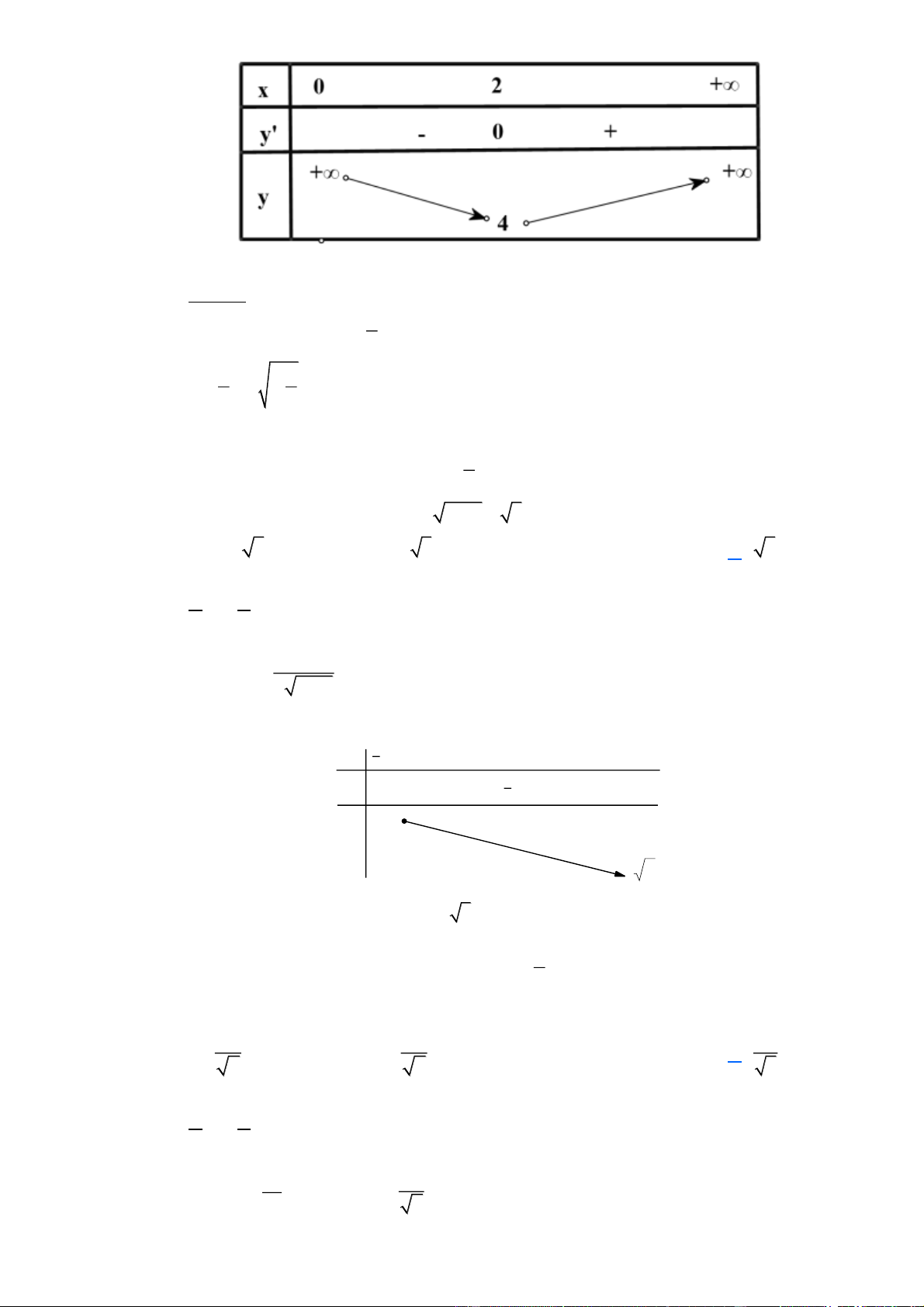
(THPT Ba Đình 2019) Xét hàm số y = f (x) với x  1 − ;  5 có bảng biến thiên như sau: Trang 3
Khẳng định nào sau đây là đúng
A. Hàm số đã cho không tồn taị GTLN trên đoạn 1 − ;  5
B. Hàm số đã cho đạt GTNN tại x = 1
− và x = 2 trên đoạn 1 − ;  5
C. Hàm số đã cho đạt GTNN tại x = 1
− và đạt GTLN tại x = 5trên đoạn  1 − ;  5
D. Hàm số đã cho đạt GTNN tại x = 0 trên đoạn 1 − ;  5 Lời giải
A. Đúng. Vì lim y = + nên hàm số không có GTLN trên đoạn  1 − ;  5 . − x→5
B. Sai. Hàm số đã cho chỉ đạt GTNN tại x = 2 trên đoạn 1 − ;  5 .
C. Sai. Hàm số đã cho chỉ đạt GTNN tại x = 2 trên đoạn 1 − ;  5 và lim y = + . x→5
D. Sai. Hàm số đã cho chỉ đạt GTNN tại x = 2 trên đoạn 1 − ;  5 . Câu 9.
(Chuyên Lê Thánh Tông 2019) Cho hàm số y = f ( x) liên tục trên , có bảng biến thiên như hình sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A. Hàm số có hai điểm cực trị.
B. Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng −3 .
C. Đồ thị hàm số có đúng một đường tiệm cận.
D. Hàm số nghịch biến trên mỗi khoảng (− ;  − ) 1 , (2;+) . Lời giải
Dựa vào BBT ta thấy hàm số không có GTLN, GTNN.
Câu 10. (Chuyên Nguyễn Tất Thành Yên Bái 2019) Cho hàm số y = f ( ) x liên tục và có
bảng biến thiên trên đoạn  1 − ; 
3 như hình vẽ bên. Khẳng định nào sau đây đúng?
A. max f (x) = f (0) .
B. max f ( x) = f (3) . C. max f ( x) = f (2) . D.  1 − ;  3  1 − ;  3  1 − ;  3
max f ( x) = f (− ) 1 .  1 −  ;3 Trang 4 Lời giải
Nhìn vào bảng biến thiên ta thấy max f (x) = f (0).  1 − ;  3
Câu 11. (VTED 2019) Cho hàm số f ( x) liên tục trên  1 − ; 
5 và có đồ thị trên đoạn  1 − ; 
5 như hình vẽ bên dưới. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f ( x) trên đoạn  1 − ;  5 bằng A. 1 − B. 4 C. 1 D. 2 Lời giải
M = max f (x) = 3   1 − ;  Từ đồ thị ta thấy: 5   + = n = f ( x) M n 1. min = 2 −   1−;5
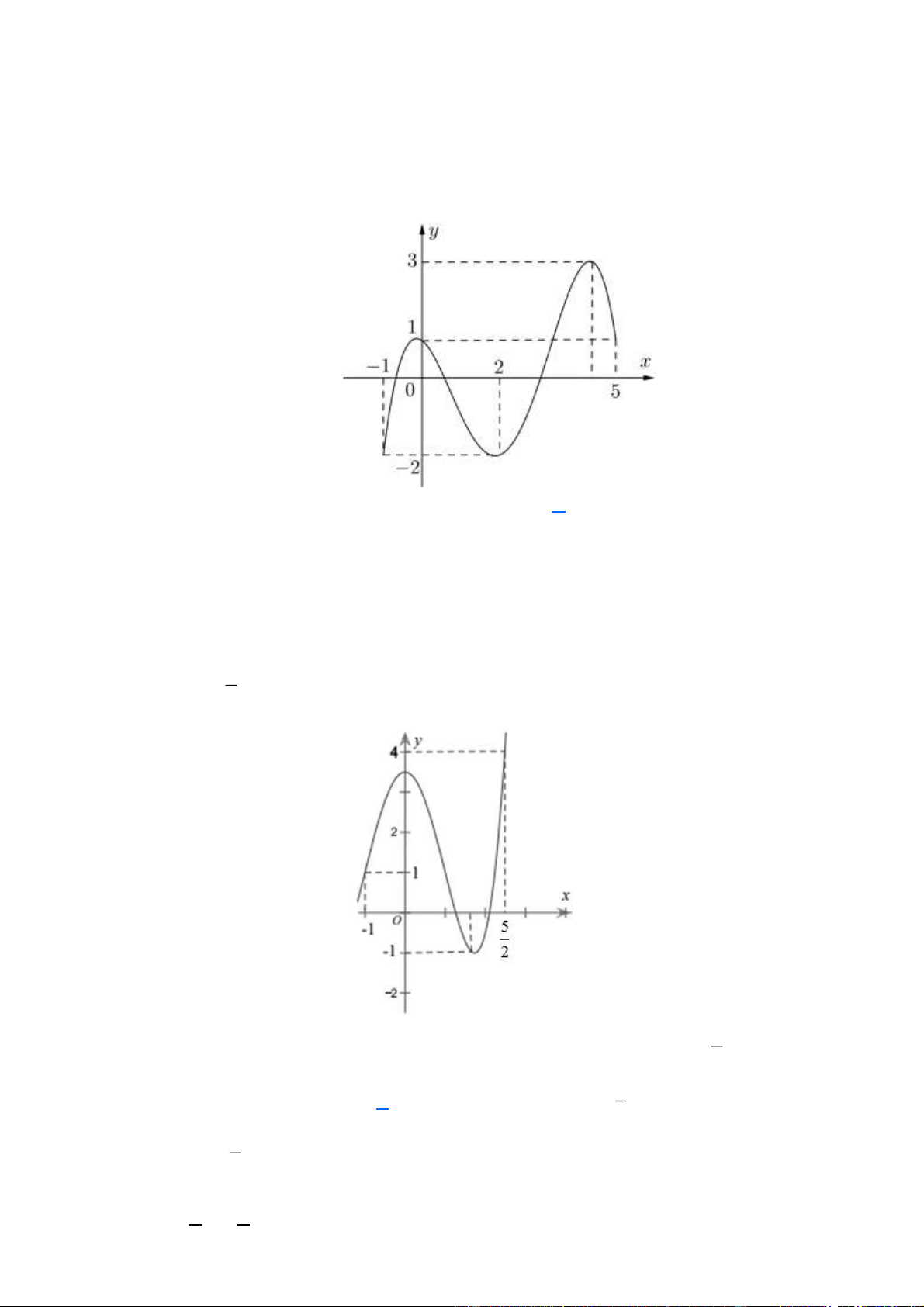
Câu 12. (THPT Yên Mỹ Hưng Yên 2019) Cho hàm số y = f ( x) xác định, liên tục trên  5  1 − , 
 và có đồ thị là đường cong như hình vẽ.  2   5 
Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f (x) trên 1 − ,   là:  2  7
A. M = 4, m =1
B. M = 4,m = −1 C. M = , m = 1 − D. 2 7 M = , m = 1 2 Lời giải Chọn B Trang 5
Dựa vào đồ thị M = 4, m= −1.
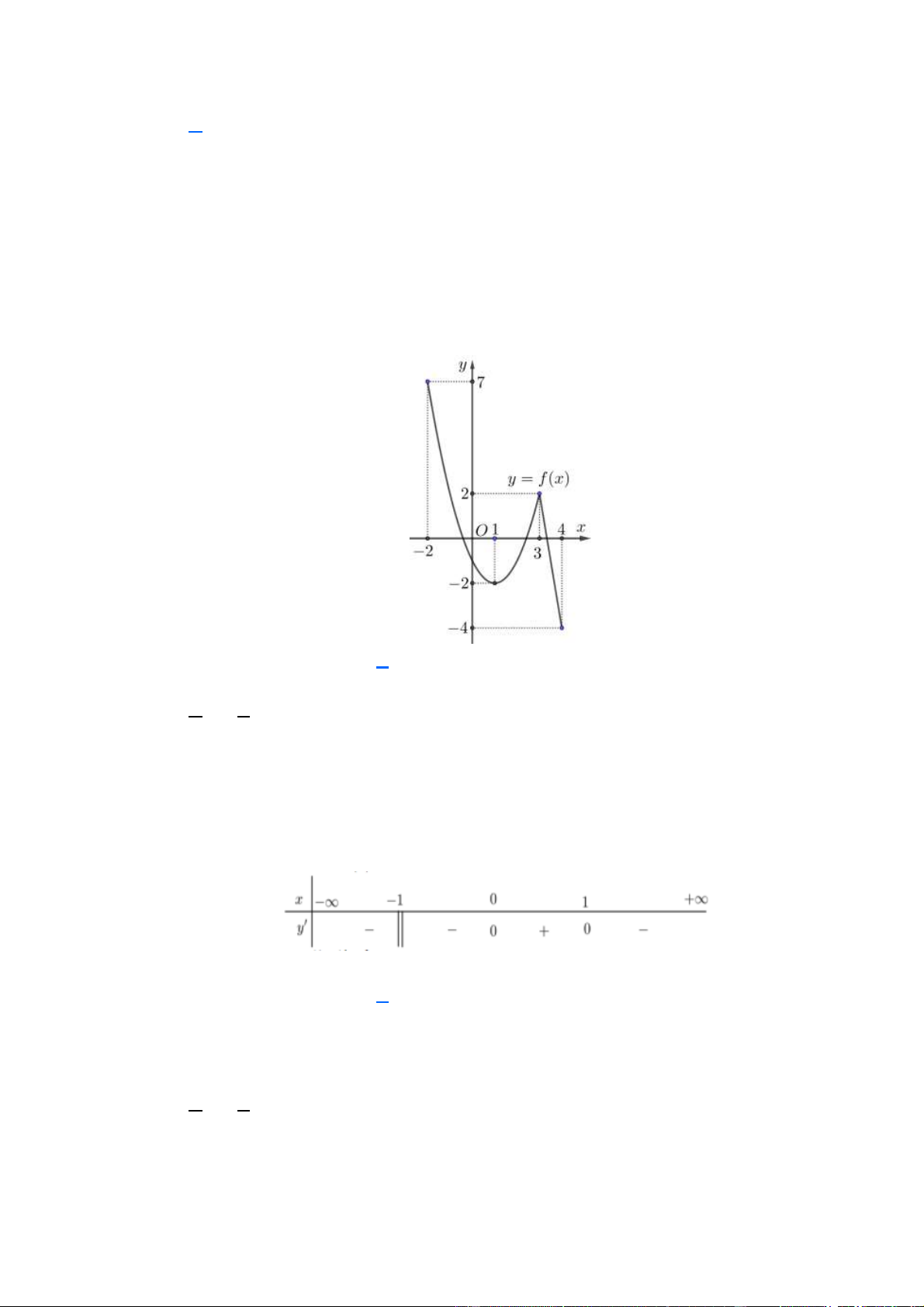
Câu 13. (THPT Nghĩa Hưng Nam Định 2019) Cho hàm số y = f ( x) có đồ thị như hình
vẽ. Giá trị lớn nhất của hàm số f ( x) trên đoạn 0;2 là:
A. Max f ( x) = 2 .
B. Max f ( x) = 2 . 0;2 0;2
C. Max f ( x) = 4 .
D. Max f ( x) = 0 . 0;2 0;2 Lời giải Chọn C
Dựa vào đồ thị ta thấy trên đoạn 0;2 hàm số f (x) có giá trị lớn nhất bằng 4 khi x = 2
Suy ra Max f ( x) = 4 0;2
Câu 14. (Sở Bắc Giang 2019) Cho hàm số y = f ( )
x liên tục trên đoạn  1 − ;  3 và có đồ thị
như hình vẽ bên. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm
số đã cho trên đoạn  1 − ; 
3 . Giá trị của M + m là A. 2 B. −6 C. −5 D. 2 − Lời giải
Dựa vào đồ thị ta thấy GTLN của hàm số trên đoạn  1 − ; 
3 là M = 2 đạt được tại x = 1
− và GTNN của hàm số số trên đoạn  1 − ;  3 là m = 4
− đạt được tại x = 2
M + m = 2+( 4 − ) = 2 −
Câu 15. (Sở Hà Nội 2019) Cho hàm số y = f ( x) có bảng biến thiên trên  5 − ;7) như sau Trang 6
Mệnh đề nào dưới đây đúng?
A. Min f ( x) = 6 .
B. Min f ( x) = 2 .
C. Max f ( x) = 9 . D.  5 − ;7)  5 − ;7) -5;7)
Max f ( x) = 6 .  5 − ;7) Lời giải
Dựa vào bảng biến thiên trên  5
− ;7) , ta có: Min f (x) = f ( ) 1 = 2 .  5 − ;7)
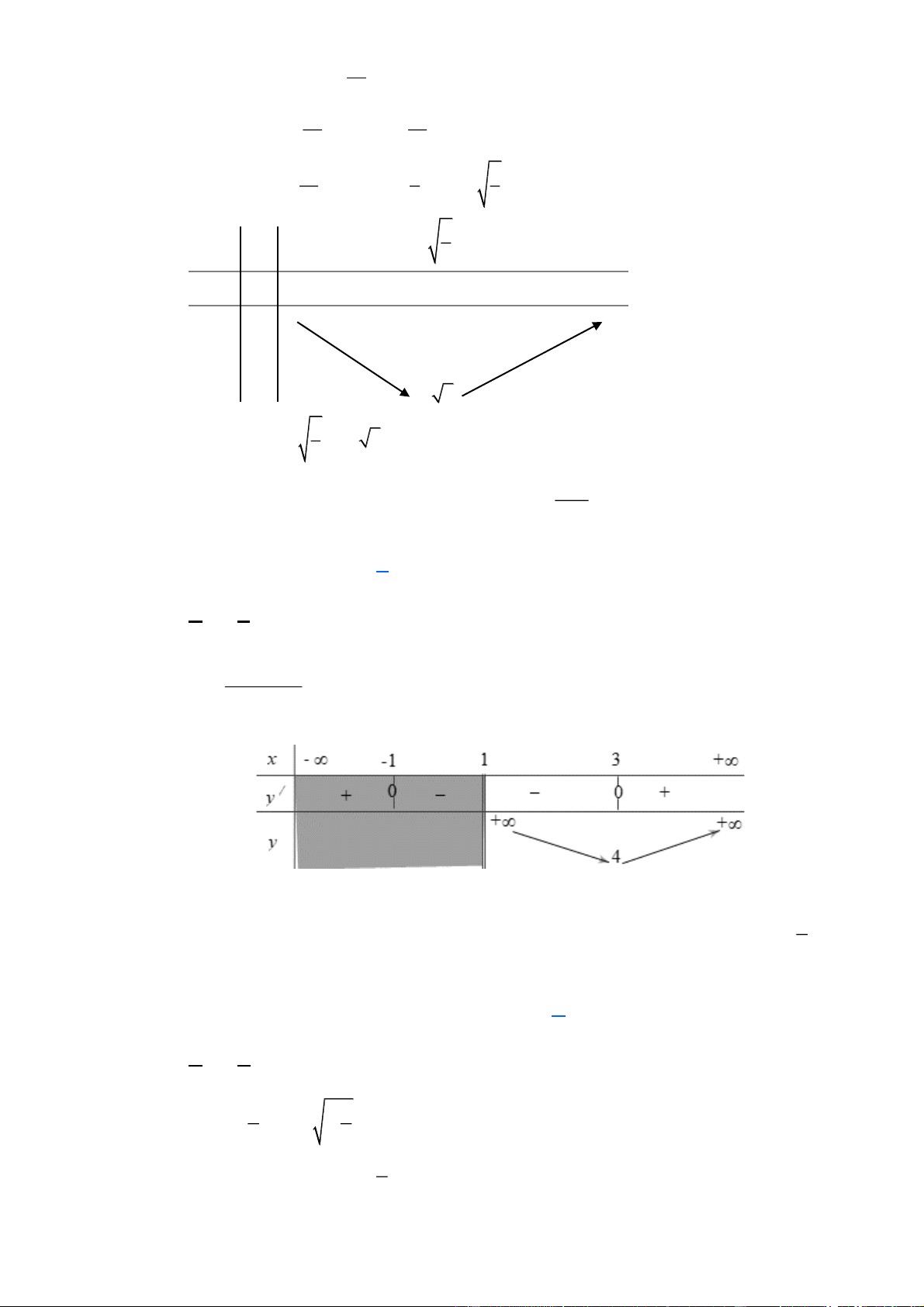
Câu 16. Cho hàm số f ( x) liên tục trên đoạn 0; 
3 và có đồ thị như hình vẽ bên. Gọi M
và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên 0;  3 . Giá trị
của M + m bằng? A. 5 . B. 3 . C. 2 . D. 1. Lời giải
Dựa vào hình vẽ ta có: M = 3 , m = 2
− nên M + m =1.
Câu 17. (Chuyên Lê Quý Đôn Điện Biên 2019) Cho hàm số y = f ( x) liên tục trên đoạn
[- 2;6] và có đồ thị như hình vẽ bên dưới. Trang 7
Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
[- 2;6]. Giá trị của M - m bằng A. 9 . B. −8 . C. −9 . D. 8 . Lời giải Từ đồ thị suy ra 4
−  f (x)  5 x   2 − ;  6 ; f ( ) 1 = 4 − ; f (4) = 5 M = 5  
M − m = 9 . m = −4
Câu 18. (VTED 2019) Cho hàm số y = f ( x) liên tục và có đồ thị trên đoạn  2 − ;4 như
hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f ( x) trên đoạn  2 − ;4 bằng A. 5 B. 3 C. 0 D. 2 − Lời giải Chọn B
Dựa vào đồ thị hàm số ta có
m = Min f ( x) = 4
− , M = Max f (x) = 7 x   2 − ;4 x   2 − ;4
Khi đó M + m = 3
Câu 19. (THPT Ngô Sĩ Liên Bắc Giang 2019) Cho hàm số y = f ( x) có bảng xét dấu đạo hàm như sau:
Mệnh đề nào sau đây đúng
A. max f ( x) = f (0)
B. max f ( x) = f ( ) 1
C. min f ( x) = f (− ) 1 D. ( 1 −  ;1 (0;+) (−;− )1
min f ( x) = f (0) ( 1; − +) Lời giải Chọn B Trang 8
Dạng 2. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên đoạn
Bước 1: Hàm số đã cho y = f (x ) xác định và liên tục trên đoạn a;b  .
Tìm các điểm x ,x ,..., x trên khoảng (a;b) , tại đó f (x ) = 0 hoặc f (x ) không xác định. 1 2 n
Bước 2: Tính f (a ), f (x ), f (x ),..., f (x , f b . 1 2 n ) ( )
Bước 3: Khi đó:
max f (x ) = max  
f (x ),f (x ),...,f (x ,f a ,f b . 1 2 n ) ( ) ( ) a b ,  
min f (x ) = min f x , f x ,..., f x , f a , f b .  1 2 a b ,   ( ) ( ) ( n ) ( ) ( )   Câu 1.
(Đề Minh Họa 2020 Lần 1) Giá trị lớn nhất của hàm số 4 2
f (x) = −x +12x +1 trên đoạn  1 − ;  2 bằng: A. 1. B. 37 . C. 33 . D. 12 . Lời giải Chọn C 4 2
f (x) = −x +12x +1 liên tục trên  1 − ;  2 và x = 0  3 2 f '(x) = 4
− x + 24x = 0  x = 6 (L)  x = − 6 (L)  Ta có: f ( 1
− ) =12; f (2) = 33; f (0) =1
Vậy, giá trị lớn nhất của hàm số 4 2
f (x) = −x +12x +1 trên đoạn  1 − ;  2 bằng 33 tại x = 2 Câu 2.
(Đề Tham Khảo 2020 Lần 2) Giá trị nhỏ nhất của hàm số f ( x) 4 2 = x −10x + 2 trên đoạn  1 − ;  2 bằng A. 2 . B. 23 − . C. 22 − . D. −7 . Lời giải Chọn C
Hàm số đã cho liên tục trên đoạn  1 − ;  2 . x = 0
Ta có: f ( x) 3
= 4x − 20x, f (x) = 0   . x =  5
Xét hàm số trên đoạn  1 − ;  2 có: f (− ) 1 = 7
− ; f (0) = 2; f (2) = 2 − 2.
Vậy min f ( x) = 2 − 2 . x   1 − ;2 Trang 9 Câu 3.
(Mã 101 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số f ( x) 3
= x − 24x trên đoạn 2;1  9 bằng A. 32 2 . B. 40 − . C. 3 − 2 2 . D. 45 − . Lời giải Chọn C.
x = 2 2 2;19 Ta có f ( x) 2 = 3x − 24 = 0   x = −    . 2 2 2;19 f ( ) 3 2 = 2 − 24.2 = 4 − 0 ; f ( )=( )3 2 2 2 2 − 24.2 2 = 3 − 2 2 ; f ( ) 3
19 =19 − 24.19 = 6403 .
Vậy giá trị nhỏ nhất của hàm số f ( x) 3
= x − 24x trên đoạn 2;1  9 bằng 3 − 2 2 . Câu 4.
(Mã 102 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số f ( x) 3
= x − 21x trên đoạn 2;1 9 bằng A. 36 − . B. 14 − 7 . C. 14 7 . D. 34 − . Lời giải Chọn B x = − 7  2;19 2   Trên đoạn 2;1 
9 , ta có: y = 3x − 21  y = 0   .  x = 7   2;19 Ta có: y (2) = 3 − 4; y( 7) = 1
− 4 7; y(19) = 6460 . Vậy m = 14 − 7 . Câu 5.
(Mã 103 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số 3
f (x) = x − 30x trên đoạn 2;1  9 bằng A. 20 10. B. 63. − C. −20 10. D. 52. − Lời giải Chọn C x = 10 (n) Ta có f ( x) 2
= 3x − 30  f (x) 2
= 0  3x − 30 = 0   . x = − 10  (l) Khi đó f (2) = 5 − 2 ; f ( 10) = 2
− 0 10 và f (19) = 6289.
Vậy min f (x) = f = − .  ( 10) 20 10 x 2;1  9 Câu 6.
(Mã 104 - 2020 Lần 1) Giá trị nhỏ nhất của hàm số f ( x) 3
= x −33x trên đoạn 2;1  9 bằng A. 72 − . B. 2 − 2 11. C. 58 − . D. 22 11 . Lời giải Chọn B x = 112;19 Ta có f ( x) 2 = 3x − 33 = 0   . x = − 11  2;19 Trang 10
Khi đó ta có f (2) = 5 − 8, f ( 11) = 2
− 2 11, f (19) = 6232. Vậy f = f 11 = 2 − 2 11 . min ( ) Câu 7.
(Mã 101 – 2020 Lần 2) Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x −10x − 4 trên 0;  9 bằng A. 28 − . B. 4 − . C. −13. D. 29 − . Lời giải Chọn D
Hàm số y = f (x) liên tục trên 0;  9 . x = 0  Có f ( x) 3
= 4x − 20x , f (x) = 0  x = 5 x = − 5  0;9 Ta có f (0) = 4 − , f ( 5) = 2 − 9 , f (9) = 5747
Do đó min f ( x) = f 5 = 2 − 9 . 0;9 ( )   Câu 8.
(Mã 102 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x −12x − 4 trên đoạn 0;9 bằng A. 39 − . B. 40 − . C. 36 − . D. 4 − . Lời giải Chọn B x =
Ta có: f ( x) 3
= 4x − 24x ; f (x) 0 = 0   x =  6
Tính được: f (0) = 4
− ; f (9) = 5585 và f ( 6) = 4 − 0 .
Suy ra min f ( x) = 4 − 0. 0;9 Câu 9.
(Mã 103 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x −10x − 2 trên đoạn 0;9 bằng A. 2 − . B. 11 − . C. 26 − . D. 27 − . Lời giải Chọn D Ta có f ( x) 3 ' = 4x − 20x x = 0(0;9)  f '( x) = 0 3
 4x − 20x = 0  x = 5 (0;9)  x = − 5   (0;9) f (0) = 2 − ; f ( 5) = 2 − 7 ; f (9) = 5749 .
Vậy min f ( x) = 2 − 7. 0;9 Trang 11
Câu 10. (Mã 104 - 2020 Lần 2) Giá trị nhỏ nhất của hàm số f ( x) 4 2
= x −12x −1 trên đoạn 0;9 bằng A. 28 − . B. 1 − . C. 36 − . D. 37 − . Lời giải Chọn D Ta có f ( x) 3 = 4x − 24x . x = 00;9  f ( x) 3
= 0  4x − 24x = 0  x = 6 0;9 .  x = − 6   0;9 f (0) = 1 − , f ( 6) = 3 − 7 , f (9) = 5588
Câu 11. (Mã 102 - 2019) Giá trị nhỏ nhất của hàm số f ( x) 3
= x −3x + 2 trên đoạn  3 − ;  3 bằng A. 0 . B. 16 − . C. 20 . D. 4 . Lời giải Chọn B
Cách 1:Mode 7 f ( x) 3 = x −3x + 2 . Start -3 end3step 1  Chọn B
Cách 2: f ( x) 2
= 3x −3. f (x) = 0  x = 1   3 − ;  3 . f (− ) 3 = 1 − 6 ; f (− ) 1 = 4; f ( ) 1 = 0; f (3) = 20 .
 Giá trị nhỏ nhất là 16 − .
Câu 12. (Mã 110 2017) Tìm giá trị lớn nhất M của hàm số 4 2
y = x − 2x + 3 trên đoạn 0; 3   .
A. M = 6 B. M =1
C. M = 9 D. M = 8 3 Lời giải Chọn A Ta có: 3
y = x − x = x ( 2 4 4 4 x − ) 1  x = 0 
y = 0  x ( 2 4 x − ) 1 = 0  x = 1  x = 1 − (l) 
Ta có : y (0) = 3 ; y ( ) 1 = 2 ; y ( 3) = 6
Vậy giá trị lớn nhất của hàm số 4 2
y = x − 2x + 3 trên đoạn 0; 3   là M = y ( 3) = 6 2 x + 3
Câu 13. (Đề Minh Họa 2017) Tìm giá trị nhỏ nhất của hàm số y =
trên đoạn 2;4 . x −1 Trang 12 19 A. min y = 3 − B. min y =
C. min y = 6 D. 2;  4 2;4 3 2;4 min y= 2 − 2; 4 Lời giải Chọn C
Tập xác định: D = \  1 2 x + 3 Hàm số y =
xác định và liên tục trên đoạn 2;4 x −1 2 x − 2x − 3 Ta có 2 y = y =
x − x − =  x = hoặc x = − ( 1 (loại) x − ) ; 0 2 3 0 3 2 1 Suy ra y ( ) = y ( ) = y ( ) 19 2 7; 3 6; 4 =
. Vậy min y= 6 tại x = 3. 3 2; 4
Câu 14. (Mã 103 - 2019) Giá trị lớn nhất của hàm số f ( x) 3
= x −3x trên đoạn [ −3;3] bằng A. 2 − . B. 18 . C. 2 . D. 18 − . Lời giải Chọn B Ta có 2
y = 3x − 3 = 0  x = 1  f (− ) 3 = 1 − 8; f (− ) 1 = 2; f ( ) 1 = 2 − ; f ( ) 3 = 18 .
Câu 15. (Mã 104 2018) Giá trị lớn nhất của hàm số 4 2
y = x − x +13 trên đoạn [ 1 − ;2] bằng 51 A. 85 B. C. 13 D. 25 4 Lời giải Chọn D
y = f ( x) 4 2
= x − x +13 3
y ' = 4x − 2x  x = 0[ −1;2]   1 3
4x − 2x = 0  x = − [ −1;2]  2   1 x = [ −1;2]  2  1  51  1  51 f ( 1
− ) =13; f (2) = 25; f (0) =13; f − = ; f =      2  4  2  4
Giá trị lớn nhất của hàm số 4 2
y = x − x +13 trên đoạn [ 1 − ;2] bằng 25. 2 1 
Câu 16. (Mã 104 2017) Tìm giá trị nhỏ nhất m của hàm số 2 y = x + trên đoạn ; 2   . x  2  17
A. m = 5
B. m = 3 C. m = D. m = 10 4 Lời giải Chọn B Trang 13
Đặt y = f (x) 2 2 = x + . x 3 2 2x − 2 1 
Ta có y = 2x − =
, y = 0  x = 1 ;2 . 2 2   x x 2    Khi đó f ( ) 1 17 1 = 3, f = , f   (2) = 5.  2  4
Vậy m = min f ( x) = f ( ) 1 = 3 . 1  ;2    2 
Câu 17. (Chuyên Bắc Ninh 2018) Tìm tập giá trị của hàm số y =
x −1 + 9 − x
A. T = 1; 9.
B. T = 2 2; 4   . C. T = (1; 9) . D. T = 0; 2 2    . Lời giải
Tập xác định: D = 1;  9 1 1 x 1 y = −
= 0  9 − x = x −1    x = 5 . 2 x −1 2 9 − x 9
 − x = x −1 f ( )
1 = f (9) = 2 2 ; f (5) = 4
Vậy tập giá trị là T = 2 2; 4   .
Câu 18. (Mã 123 2017) Tìm giá trị nhỏ nhất m của hàm số y = 3 x − 2
7x + 11x − 2 trên đoạn [0 ; 2].
A. m = 3
B. m = 0
C. m = −2 D. m = 11 Lời giải Chọn C
Xét hàm số trên đoạn [0 ; 2]. Ta có  y = 2
3x −14x +11 suy ra  y = 0  x = 1
Tính f (0) = −2; f (1) = 3, f (2) = 0 . Suy ra min f (x) = f (0) = −2 = m. 0;2  
Câu 19. (Mã 101 2018) Giá trị lớn nhất của hàm số 4 2
y = x − 4x + 9 trên đoạn  2 − ;  3 bằng A. 201 B. 2 C. 9 D. 54 Lời giải Chọn D x = 0 3
y = 4x − 8x ; y = 0   . x =  2 Ta có y ( 2 − ) = 9 ; y( )
3 = 54 ; y (0) = 9 ; y ( 2) = 5 .
Vậy max y = 54 .  2 − ;  3
Câu 20. (Đề Tham Khảo 2018) Giá trị lớn nhất của hàm số f ( x) 4 2
= x − 4x +5 trêm đoạn  2 − ;  3 bằng A. 122 B. 50 C. 5 D. 1 Lời giải Chọn B Trang 14x = 0 3
f '(x) = 4x − 8x = 0   −2;  3 ; x =  2
f (0) = 5; f ( 2) =1; f ( 2
− ) = 5; f (3) = 50
Vậy Max y = 50  2 −  ;3
Câu 21. (Mã 105 2017) Tìm giá trị nhỏ nhất m của hàm số y = 4 x − 2 x + 13 trên đoạn −2;3   .
A. m = 13
B. m = 51
C. m = 51 D. m = 49 4 2 4 Lời giải Chọn B x = 0−2;3     y = 3
4x − 2x ; y = 0   ;
x =  1  −2;3     2  1  51
Tính y (−2) = 25 , y (3) = 85 , y (0) = 13 , y  = =   12,75 ;  2  4
Kết luận: giá trị nhỏ nhất m của hàm số là m = 51 . 4
Câu 22. (Mã 104 2019) Giá trị nhỏ nhất của hàm số f ( x) 3
= x −3x trên đoạn  3 − ;  3 bằng A. 18. − B. 2. − C. 2. D. 18. Lời giải Chọn A x = 1 Ta có f ( x) 2 == 3x − 3 = 0  .   x = 1 − Mà f (− ) 3 = 1 − 8; f (− ) 1 = 2; f ( ) 1 = 2 − ; f ( ) 3 =18.
Vậy giá trị nhỏ nhất của hàm số f (x) 3
= x −3x trên đoạn  3 − ;  3 bằng 18. −
Câu 23. (Mã 103 2018) Giá trị nhỏ nhất của hàm số 3 2
y = x + 3x trên đoạn  4 − ;−  1 bằng A. 16 − B. 0 C. 4 D. 4 − Lời giải Chọn A x = 0  4 − ;−1 2   Ta có 2
y = 3x + 6x ; y = 0  3x + 6x = 0   . x = 2 −  4 − ;−  1 Khi đó y( 4 − ) = 1 − 6; y( 2 − ) = 4; y(− ) 1 = 2 . Nên min y = 1 − 6 .  4 − ;−  1
Câu 24. (Mã 102 2018) Giá trị nhỏ nhất của hàm số 3 2
y = x + 2x − 7x trên đoạn 0;4 bằng A. 259 − B. 68 C. 0 D. 4 − Lời giải Chọn D Trang 15 TXĐ D = .
Hàm số liên tục trên đoạn 0;4 . Ta có 2
y = 3x + 4x − 7
x =10;4  y = 0  7 
x = − 0;4  3 y (0) = 0; y( ) 1 = 4 − ; y(4) = 68. Vậy min y = 4 − . 0;4
Câu 25. (Mã 101 - 2019) Giá trị lớn nhất của hàm số f ( x) 3
= x −3x + 2 trên đoạn  3 − ;  3 là A. 4 . B. 16 − . C. 20 . D. 0 . Lời giải Chọn C f ( x) 3
= x −3x + 2 tập xác định . f ( x) 2 '
= 0  3x −3 = 0  x = 1   3 − ;  3 . f ( ) 1 = 0; f (− ) 1 = 4; f ( ) 3 = 20; f (− ) 3 = 1 − 6.
Từ đó suy ra max f ( x) = f (3) = 20 .  3 − ;  3 2
Câu 26. (SGD Nam Định) Giá trị nhỏ nhất của hàm số 2 y = x + trên đoạn 2;  3 bằng x 15 29 A. . B. 5 . C. . D. 3 . 2 3 Lời giải Chọn B + Ta có hàm số 2 2
y = f (x) = x +
xác định và liên tục trên 2;  3 . x 2 29
+ y ' = f '(x) = 2x −
; f '(x) = 0  x =12; 
3 mà f (2) = 5, f (3) = . 2 x 3
+ Vậy min y = 5 tại x = 2 . 2;  3 3x −1
Câu 27. (Sở Quảng Trị 2019) Tìm giá trị lớn nhất M của hàm số y = x − trên đoạn 3 0;  2 1 1 A. M = . B. M = − . C. M = 5 . D. 3 3 M = 5 − Lời giải Chọn A Trên đoạn  8 0; 
2 ta luôn có y = −
0  x 0;2 ( đạo hàm vô nghiệm trên 2 ( ) (x −3) (0; 2)) Trang 16 1 1
Vì y (0) = , y (2) = − 5 nên M = max y = . 3 0;2 3
Câu 28. (Sở Nam Định-2019) Giá trị lớn nhất của hàm số 2 y = 4 − x là A. 2. B. 0. C. 4. D. 1. Lời giải Chọn A
• Tập xác định: D =  2 − ;  2 − • Ta có: x y ' =
y = 0  x = 0( 2 − ;2) 2 4 − xy  ( 2 − ) = y(2) = 0 • Ta có:  .  (  y = y 0) max 2  2 − ;2 = 2
Câu 29. (Chuyên Bắc Ninh 2018) Tìm giá trị nhỏ nhất của hàm số 2
y = sin x − 4sin x − 5 . A. 20 − . B. −8 . C. −9 . D. 0 . Lời giải Đặt t = sin , x t  1 − ;  1 . Xét 2
f (t) = t − 4t − 5 , t  1 − ;  1 . f (
t) = 2t − 4 = 0  t = 2 1 − ;  1 . f ( ) 1 = 8 − , f (− ) 1 = 0 .
Ta thấy min f (t) = f ( ) 1 = 8
− . Vậy giá trị nhỏ nhất của hàm số là −8 .  1 − ;  1
Câu 30. (THPT Hoa Lư A 2018) Gọi m , M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất
của hàm số f ( x) 1
= x − x +1 trên đoạn 0; 
3 . Tính tổng S = 2m + 3M . 2 7 3 A. S = − . B. S = − . C. −3 . D. S = 4 . 2 2 Lời giải x + − Ta có: f ( x) 1 1 1 1 = − = , cho 2 2 x +1 2 x +1
f ( x) = 0  x +1 = 1  x = 00;  3 . Khi đó: 1 f (0) = 1 − , f ( ) 1 3 = − nên m = 1 − và M = − . 2 2 Vậy 7
S = 2m + 3M = − . 2
Câu 31. (Chuyên ĐHSPHN - 2018) Tìm giá trị lớn nhất của hàm số f ( x) = sin x + cos 2x trên  ; 0   là 9 5 A. . B. . C. 2 . D. 1 . 8 4 Lời giải
f ( x) = sin x + cos 2x = sin x + − sin2 1 2 x
Đặt sin x = t (0  t  ) 1
f (t) = − t2 2
+ t +1, f (t) = −4t +1 Trang 17
f (t) = 0  t = 1 4  1  9 f (0) = 1, f ( ) 1 = 0 , f =    4  8 Vậy 9 max f ( x) = . 0; 1 8 4
Câu 32. (THPT Hà Huy Tập - 2018) Giá trị lớn nhất của hàm số 3 y = 2 cos x − o c s x 3 trên 0; . 2 10 2 2 A. ax m y = . B. ax m y = . C. ax m y = . D. 0;  3 0; 3 0; 3 a m x y = 0 . 0; Lời giải Đặt: 4
t = cos x t  1 − ;  1 3
y = 2t − t . 3  1 − x = −1;  1  2 2
y ' = 2 − 4t y ' = 0   .  1 x = −1;  1  2 −  1 −  2 − 2  1  2 2 Tính: y (− ) 2 1 = , y =   , y =   , y ( ) 2 1 = . 3  2  3  2  3 3 2 2 Vậy: ax m y = . 0; 3 3sin x + 2
Câu 33. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin x + 1    trên đoạn 0; 
 . Khi đó giá trị của 2 2
M + m là  2  31 11 41 61 A. . B. . C. . D. . 2 2 4 4 Lời giải Chọn C
Đặt t = sin x, t 0;  1 . t + 1 Xét hàm f (t ) 3 2 =
0;1 có f (t ) =  0,t  0;1 . 2   t + liên tục trên đoạn   1 (t + ) 1
Suy ra hàm số đồng biến trên 0  ;1 . 5
M = Max f (t) = f (1) = và m = Min f (t) = f (0) = 2 . 0; 1 2 0; 1 2   Khi đó 5 41 2 2 2 M + m = + 2 =   .  2  4 sin x +1
Câu 34. (THPT Can Lộc - Hà Tĩnh - 2018) Cho hàm số y = . Gọi M là 2 sin x + sin x +1
giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số đã cho. Chọn mệnh đề đúng. Trang 18 3 3
A. M = m + . B. M = m .
C. M = m +1. D. 2 2 2
M = m + . 3 Lời giải + Đặt t 1 sin x = t , ( 1 −  t  ) 1 ta được y = . 2 t + t +1 + 2 − − Xét hàm số t 1 t 2t y = trên đoạn  1 − ;  1 ta có y = . 2 t + t +1 (t +t + )2 2 1 t = t m
Giải phương trình y = 0 2  t − − 2t = 0 ( / ) 0   . t = 2 − (loai) Vì y (− )
1 = 0 ; y (0) =1; y ( ) 2 1 = nên 3
max y = y (0) = 1  M =1; min y = y (− ) 1 = 0  m = 0 .  1 − ;  1  1 − ;  1 Vậy M = m +1.
Dạng 3. Xác định giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên khoảng (a;b)
Bước 1: Tính đạo hàm f x ( ) .
Bước 2: Tìm tất cả các nghiệm x a
( ;b) của phương trình f x
( ) = 0 và tất cả các điểm i   a
( ;b) làm cho f x ( ) không xác định. i
Bước 3. Tính A = lim f x
( ) , B = lim f (x) , f (x ) , f ( ) . + − i i x →a x →b
Bước 4. So sánh các giá trị tính được và kết luận M = max f (x) , m = min f (x) . (a b ; ) (a b ; )
Nếu giá trị lớn nhất (nhỏ nhất) là A hoặc B thì ta kết luận không có giá trị lớn nhất (nhỏ nhất). 4 Câu 1.
(Đề Tham Khảo 2017) Tính giá trị nhỏ nhất của hàm số y = 3x + trên khoảng 2 x (0;+). 33 A. min y = B. 3 min y = 2 9 C. 3 min y = 3 9 D. (0;+) 5 (0;+) (0;+) min y = 7 (0;+) Lời giải Chọn C Cách 1: 4 3x 3x 4 3x 3x 4 3 3 y = 3x + = + +  3 . . = 3 9 2 2 2 x 2 2 x 2 2 x Dấu 3x 4 8 " = " xảy ra khi 3 =  x = . 2 2 x 3 Vậy 3 min y = 3 9 (0;+) Cách 2: Trang 19 Xét hàm số 4 y = 3x + trên khoảng (0;+) 2 x 4 8 Ta có y = 3x +  y ' = 3− 2 3 x x 8 8 8 Cho 3 3 y ' = 0 
= 3  x =  x = 3 x 3 3 8 x 0 3 + 3 y ' − 0 + y 3 3 9  8  3 3
 min y = y   = 3 9 (   0;+) 3   4 Câu 2.
Gọi m là giá trị nhỏ nhất của hàm số y = x −1+
trên khoảng (1;+) . Tìm m x −1 ? A. m = 5 .
B. m = 4 .
C. m = 2 .
D. m = 3 . Lời giải Chọn B
Tập xác định D = R \   1 . 2 x − 2x − 3 x = 1 − y =  =  (  . x − ) , y 0 2 1 x = 3 Bảng biến thiên:
m = min y = 4 khi x = 3 (1;+) 1 Câu 3.
(THPT Minh Châu Hưng Yên 2019) Giá trị nhỏ nhất của hàm số y = x − 5 + x
trên khoảng (0; +) bằng bao nhiêu? A. 0 B. 1 − C. −3 D. 2 − Lời giải Chọn C
Áp dụng bất đẳng thức Cô – si ta có: 1 1 y = x + − 5  2 . x − 5 = 3 − x x 1 Dấu bằng xảy ra khi 2 x =
x =1  x =1 (vì x  0 ). x Trang 20 Vậy min y = 3 − (0;+) Câu 4.
(Chuyên Lương Thế Vinh Đồng Nai 2019) Gọi m là giá trị nhở nhất của hàm số 4 y = x +
trên khoảng (0;+). Tìm m x A. m = 4 . B. m = 2 . C. m = 1. D. m = 3 . Lời giải 4 y ' = 1− 2 x
y ' = 0  x = 2
 ; x = 2(0;+). Bảng biến thiên:
Suy ra giá trị nhỏ nhất của hàm số bằng y 2 ( ) = 4  m = 4. 1 Câu 5.
(Chuyên Bắc Giang 2019) Giá trị nhỏ nhất của hàm số f (x) = x + trên nửa x khoảng 2;+) là: 5 7 A. 2 B. C. 0 D. 2 2 Lời giải Chọn B
Áp dụng bất đẳng thức Cô-si, ta được: 1 3x x 1 3.2 x 1 5
f (x) = x + = + +  + 2 . = . x 4 4 x 4 4 x 2
Dấu bằng xảy ra khi x = 2 . 4 Câu 6.
Gọi m là giá trị nhỏ nhất của hàm số y = x +
trên khoảng (0;+) . Tìm m . x A. m = 3 . B. m = 4 . C. m = 2 . D. m = 1. Lời giải Chọn B Cách 1: 4
Hàm số y = x +
liên tục và xác định trên (0;+) . x 2 − x = 2 x (0; 4 4 +) Ta có y ' = 1− =  y ' = 0   . 2 2 x xx = 2 −   (0;+) Bảng biến thiên Trang 21
Vậy giá trị nhỏ nhất là m = 4 khi x = 2. Cách 2: Với x ( + ) 4 0;  ; x
 0. Áp dụng bất đẳng thức Cô si ta có: x 4 4 x +  2 . x = 4. x xx  0 
Dấu bằng xảy ra khi và chỉ khi 
4  x = 2. Vậy m = 4 khi x = 2. x =  x Câu 7.
Giá trị nhỏ nhất của hàm số y =
4 − x + 3 trên tập xác định của nó là A. 2 + 3. B. 2 3. C. 0. D. 3. Lời giải Chọn D
Tập xác định của hàm số là: D = (− ;  4. −1 Ta có y ' =  0, x   D 2 4 − x Bảng biến thiên x ∞ 4 y' + ∞ y 3
Từ bảng biến thiên suy ra min y = 3 khi x = 4 .Vậy chọn D . (−;4 1 Câu 8.
Với giá trị nào của x thì hàm số 2 y = x +
đạt giá trị nhỏ nhất trên khoảng x (0;+)? 3 1 1 A. . B. . C. 1. D. . 3 4 2 3 2 Lời giải Chọn D TXD: D = ¡ \   0 . 1 1 y ' = 2x −
, y ' = 0  x = . 2 x 3 2 Trang 22 1 Dựa vào BBT thì x =
hàm số đạt giá trị nhỏ nhất trên (0;+) . 3 2 Câu 9.
Giá trị nhỏ nhất của hàm số y = x + − ( + )2 2 1 2 trên khoảng (0;+) x A. không tồn tại. B. −3 . C. 1 − + 2 . D. 0 . Lời giải Chọn B
Hàm số xác định và liên tục trên khoảng (0;+). 2 2 x − 2 y = 1− = . 2 2 x xx = 2 y = 0   . x = − 2 Bảng biến thiên: Vậy min y = f 2 = 3 − . 0;+ ( ) ( ) 2 x - 1 é 3ù
Câu 10. Cho hàm số f (x)=
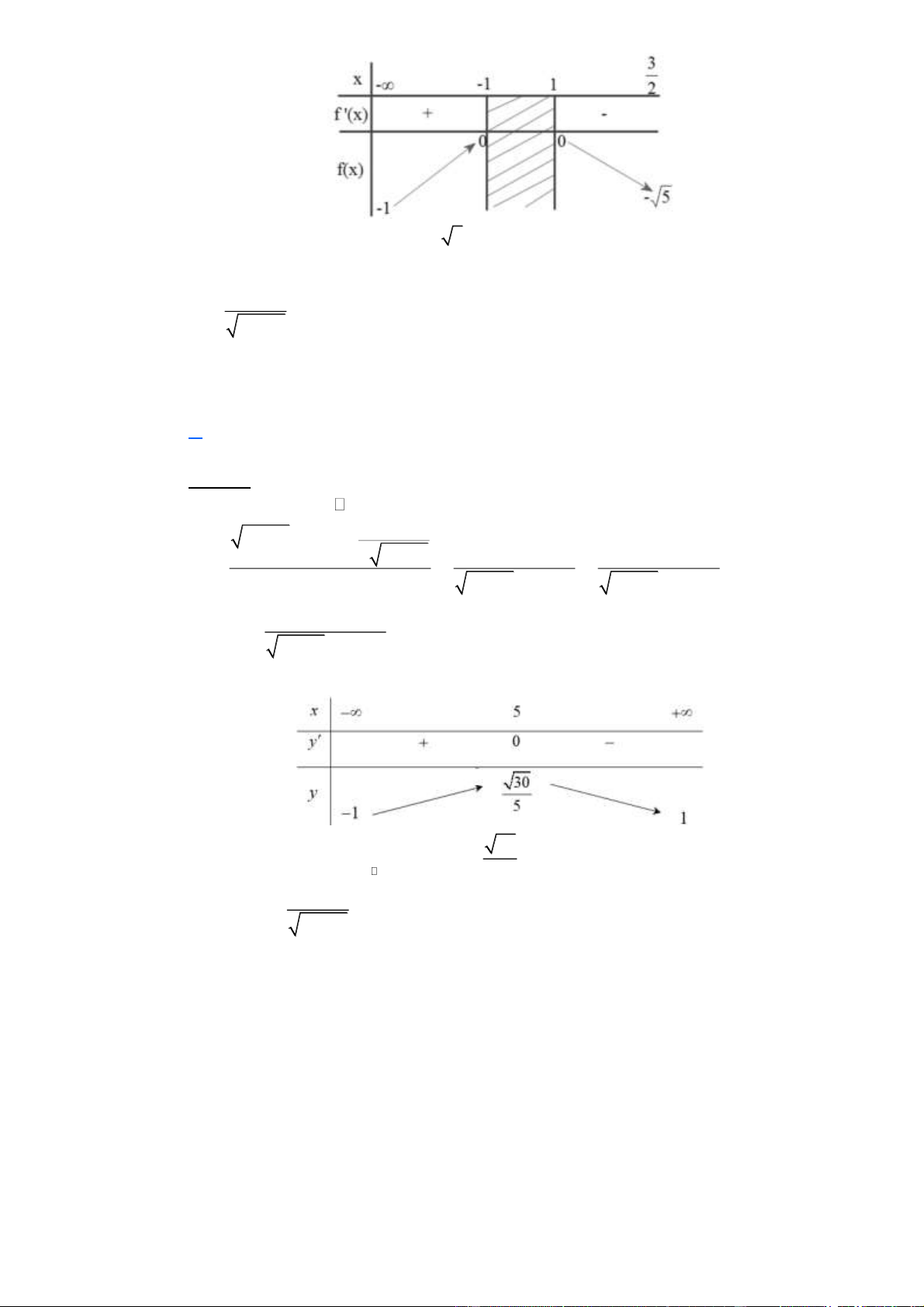
với x thuộc D = (- ¥ ;- ] 1 È 1 ê; ú. Mệnh đề nào x - 2 ê 2ú ë û dưới đây đúng?
A. max f (x)= 0; min f (x)= - 5 .
B. max f (x)= 0 ; không tồn tại D D D
min f (x). D
C. max f (x)= 0;min f (x)= - 1.
D. min f (x)= 0 ; không tồn tại D D D
max f (x). D Lời giải Chọn A é 3ù
Hàm số xác định và liên tục trên D = (- ¥ ;- ] 1 È 1 ê; ú. ê 2ú ë û - 2x + 1 1 f '(x)=
; f '(x)= 0 Û x = Ï D (x- )2 2 2 x - 1 2 Trang 23
Vậy max f (x)= 0;min f (x)= - 5 . D D
Câu 11. (Cụm liên trường Hải Phòng 2019) Mệnh đề nào sau đây là đúng về hàm số x + 1 y =
trên tập xác định của nó. 2 x + 5
A. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
B. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất.
C. Hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất. Lời giải Chọn D
Tập xác định: D = . 2x 2 x + 5 - (x + ) 1 2 2 2 2 x + 5
x + 5- x - x 5- x y ' = = = . 2 2 x + 5 x + 5 ( 2 x + ) 2 5 x + 5 ( 2 x + ) 5 5- x y ' = 0 Û
= 0 Û 5- x = 0 Û x = 5 . 2 x + 5 ( 2 x + ) 5 Bảng biến thiên: Từ bảng biến thiên có 30 max y = y( ) 5 = khi x = 5 . 5 Hàm số x + 1 y =
không có giá trị nhỏ nhất. 2 x + 5
Vậy hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất. Trang 24