






















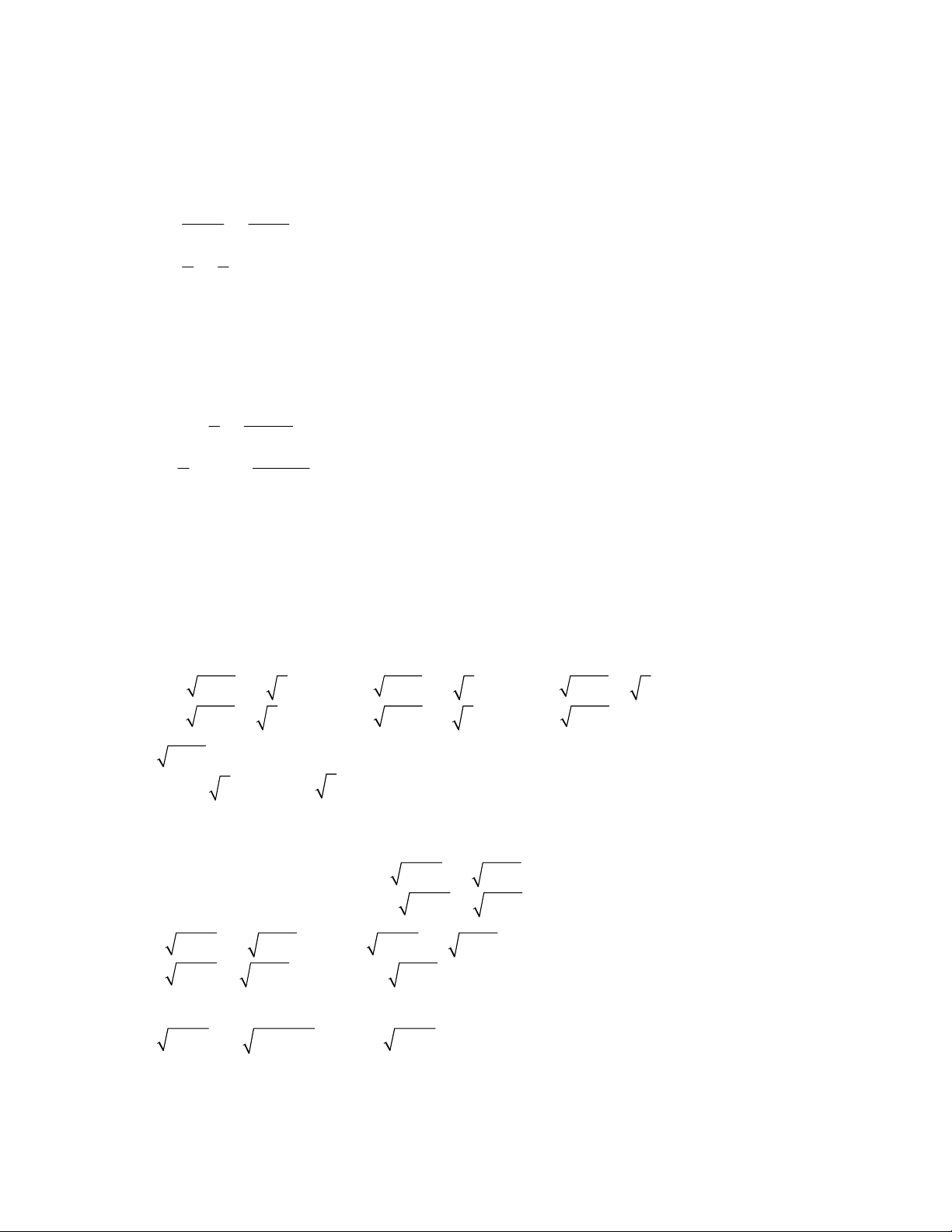
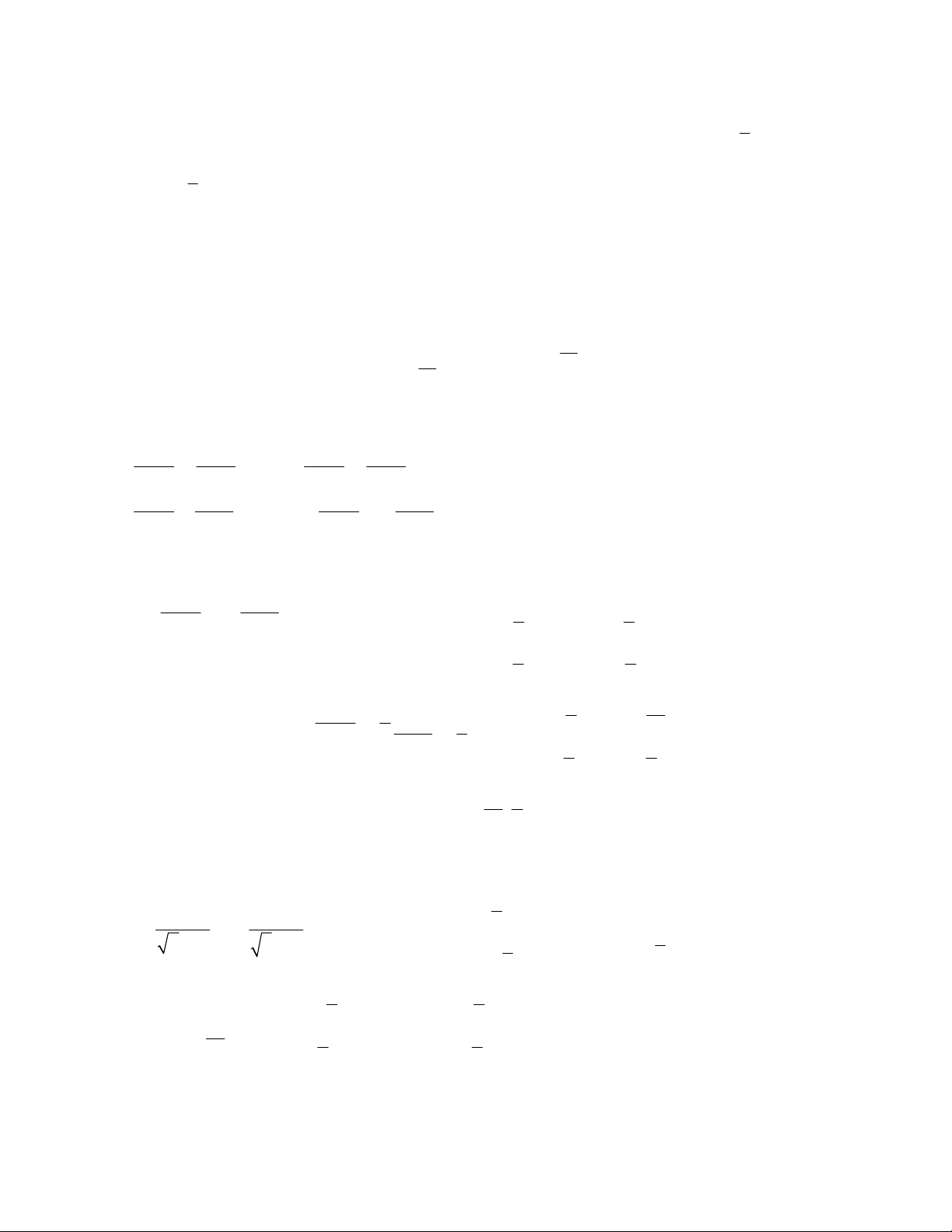

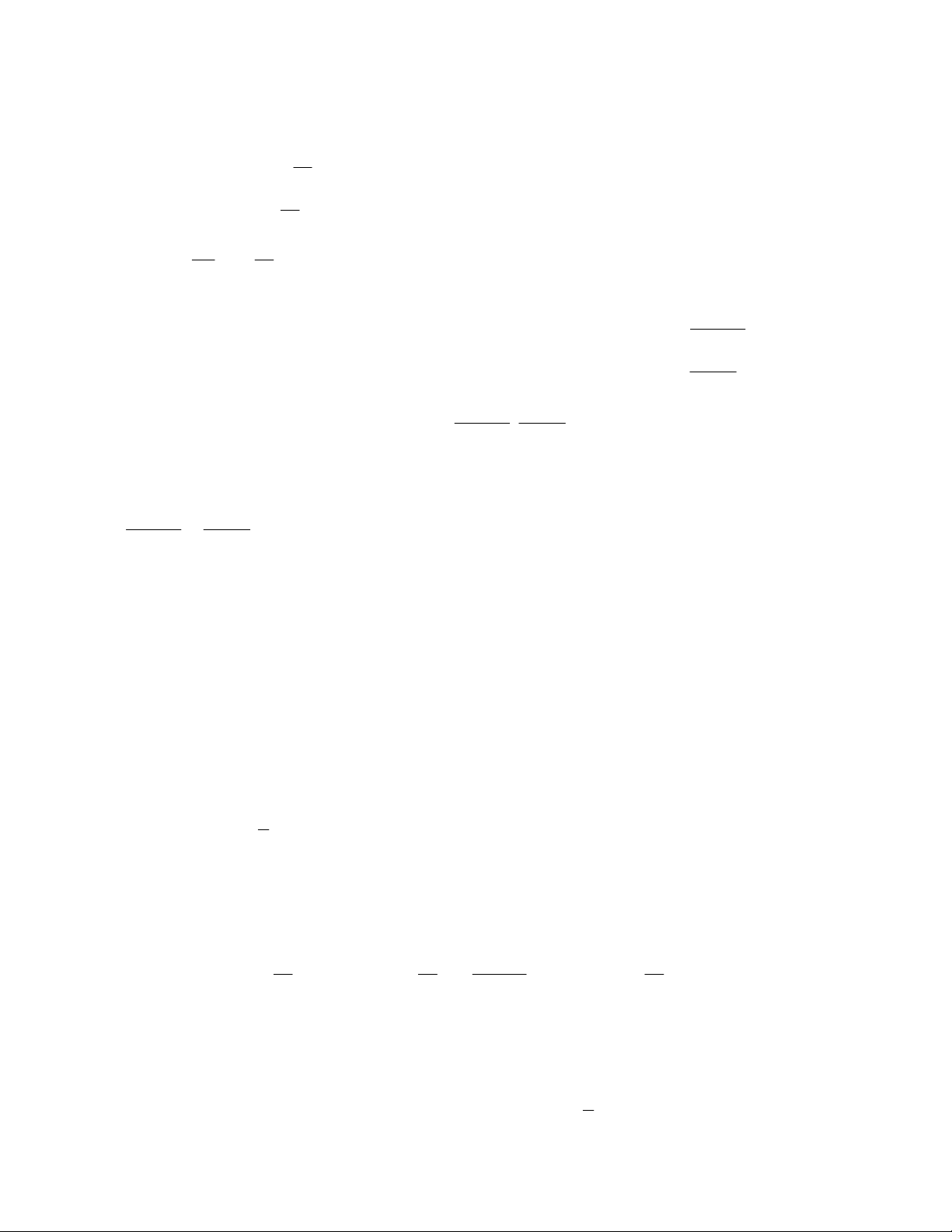


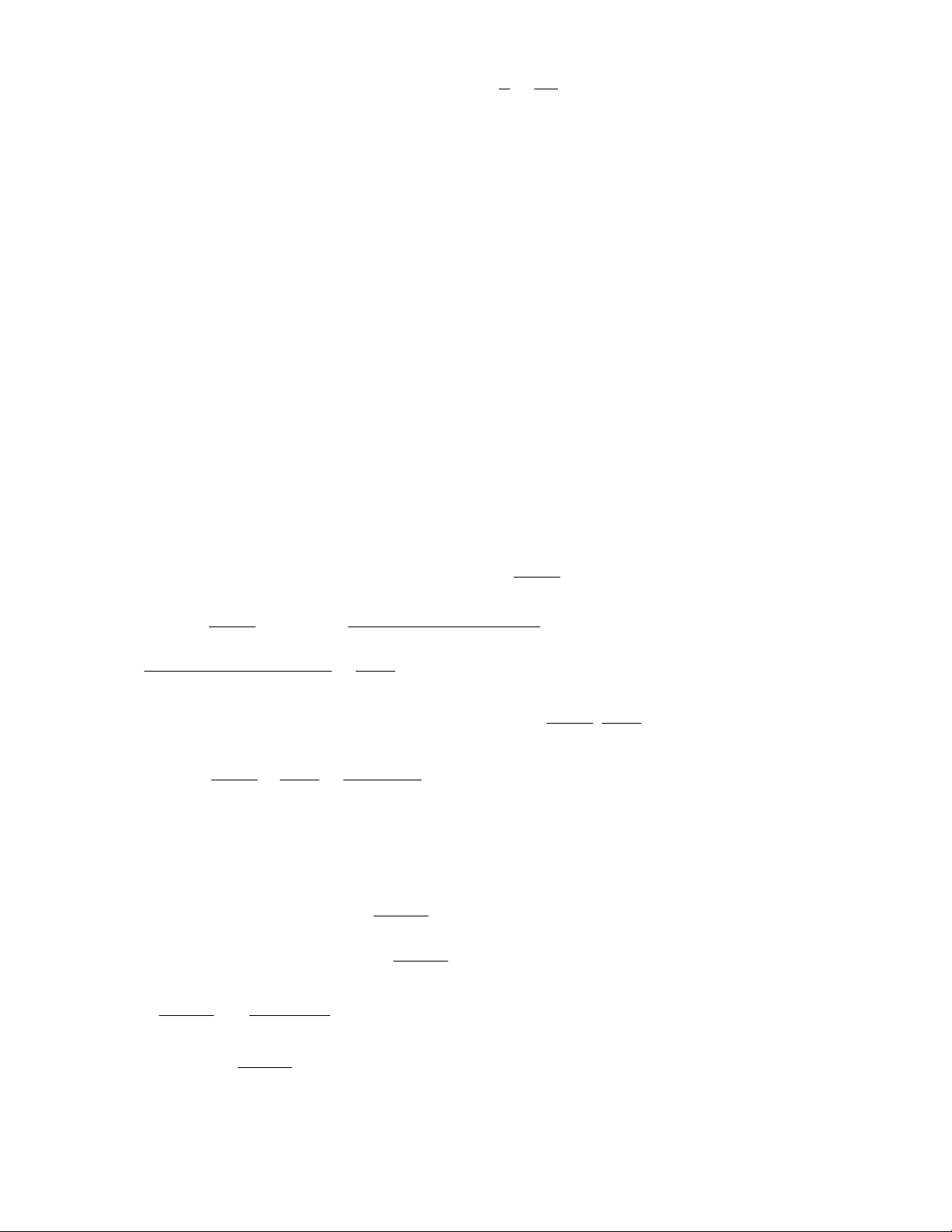


Preview text:
CHUYÊN ĐỀ GIẢI HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
PHẦN I. TRỌNG TÂM CẦN ĐẠT
A. KIẾN THỨC TRỌNG TÂM
a x b y c 1 1 1 1
Giải hệ phương trình bậc nhất hai ẩn: I
a x b y c 2 2 2 2
a. Phương pháp thế:
Bước 1: Từ một phương trình của hệ, ta biểu thị ẩn x theo y (hoặc y theo x).
Bước 2: Thế biểu thức tìm được của x (hoặc của y) vào phương trình còn lại để được phương
trình bậc nhất một ẩn. Giải phương trình bậc nhất vừa tìm được.
Bước 3: Thay giá trị vừa tìm được của ẩn vào biểu thức tìm được trong bước thứ nhất để tìm
giá trị của ẩn còn lại.
b. Phương pháp cộng đại số:
Bước 1: Chọn ẩn muốn khử, thường là x (hoặc y). Bước 2: -
Xem xét hệ số của ẩn muốn khử. -
Khi các hệ số của cùng một ẩn đối nhau thì ta cộng vế theo vế của hệ. -
Khi các hệ số của cùng một ẩn bằng nhau thì ta trừ về theo vế của hệ. -
Nếu các hệ số đó không bằng nhau thì ta nhân các vế của hai phương trình với số thích
hợp (nếu cần) sao cho các hệ số của x (hoặc y) trong hai phương trình của hệ là bằng nhau hoặc
đối nhau (đồng nhất hệ số). Rồi thực hiện các bước ở trên. -
Ta được một phương trình mới, trong đó ẩn muốn khử có hệ số bằng 0.
Bước 3: Giải hệ phương trình gồm một phương trình mới (một ẩn) và một phương trình đã cho. Ta suy ra nghiệm của hệ
* Đối với một số bài toán ta có thể kết hợp phương pháp đặt ẩn phụ để biến đổi hệ phương trình
đã cho thành hệ phương trình đơn giản hơn với ẩn mới.
Sau khi tìm được nghiệm của hệ phương trình mới, ta có thể tìm nghiệm của hệ phương trình ban đầu.
* Sử dụng máy tính CASIO/VINACAL:
Nhấn Mode, chọn mục EQN, chọn số tương ứng với mục: anX+bnY=cn
a x b y c 1 1 1 1
Nếu hệ phương trình theo đúng thứ tự
a x b y c 2 2 2 2
Ta nhập số liệu tương ứng: Hàng thứ nhất: a ; b ;
c và hàng thứ hai: a ; b ; c 1 1 1 2 2 2
Nhấn =; = ta sẽ có kết quả nghiệm của hệ phương trình.
Các em có thể sử dụng máy tính casio để tính ra nghiệm đúng. B. CÁC DẠNG TOÁN
Dạng 1. Giải hệ phương trình bằng phương pháp thế
Ví dụ minh họa 1: Giải các hệ phương trình sau bằng phương pháp thế:
x 2y 1 3
x y 2x y 9 a. b.
2x 5y 7 2
x y x y 1 Hướng dẫn giải:
a. Biến đổi hệ phương trình đã cho thành các hệ phương trình tương đương:
x 2y 1
x 2y 1
x 2y 1 HTP:
2x 5y 7 2 2y 1 5y 7 9y 2 7
x 2y 1
x 2. 1 1 x 1 9y 9 y 1 y 1
Vậy, hệ phương trình đã cho có nghiệm là 1; 1 . 3
x y 2x y 9 b. Hệ phương trình 2
x y x y 1
Cách 1: Thu gọn vế trái của mỗi phương trình trong hệ, biến đổi hệ phương trình đã cho thành các
hệ phương trình tương đương. 3
x y 2x y 9 3
x 3y 2x 2y 9 HPT: 2
x y x y 1
2x 2y x y 1 3
x 3y 2x 2y 9
x 5y 9
x 5y 9
2x 2y x y 1 3
x y 1 3
5y 9 y 1 x 5 y 9 x 1 14 y 28 y 2
Vậy, hệ phương trình đã cho có một nghiệm 1 ;2 .
Cách 2: Sử dụng phương pháp đặt ẩn phụ: đặt u x ;
y v x y , ta có hệ phương trình: 3
x y 2x y 9 3
u 2v 9 2
x y x y 1
2u v 1 3
u 22u 1 9 7u 7 u 1
v 2u 1
v 2u 1 v 3 u 1 x y 1
2 y 3 2 2y 4 x 1 Với
, ta có hệ phương trình v 3
x y 3
x y 3 x y 3 y 2
Vậy, hệ phương trình đã cho có một nghiệm 1 ;2 .
Dạng 2. Giải hệ phương trình bằng phương pháp cộng đại số
Ví dụ minh họa 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
x 2y 1 3
x y 2x y 9 a. b.
2x 5y 7 2
x y x y 1 Hướng dẫn giải:
a. Biến đổi hệ phương trình đã cho thành các hệ phương trình tương đương:
x 2y 1
2x 4y 2 HPT:
(pt 1 được nhân 2 vế cho 2)
2x 5y 7
2x 5y 7
Lấy pt 1 trừ pt 2 vế theo vế, và giữ lại một phương trình:
0x 9y 9 HPT
2x 4y 2
Tìm được giá trị một ẩn, ta thay vào phương trình kia để tìm nghiệm còn lại. y 1 y 1 x 1 HPT 2x 4 1 2 2x 2 y 1
Vậy, hệ phương trình đã cho có nghiệm là 1; 1 . 3
x y 2x y 9 b. Hê phương trình 2
x y x y 1
Cách 1: Thu gọn vế trái của mỗi phương trình trong hệ, biến đổi hệ phương trình đã cho thành các
hệ phương trình tương đương. 3
x y 2x y 9 3
x 3y 2x 2y 9 HPT: 2
x y x y 1
2x 2y x y 1 3
x 3y 2x 2y 9
x 5y 9
x 5y 9
2x 2y x y 1 3
x y 1 1
5x 5y 5
x 5y 9 14 x 14 x 1 15
x 5y 5
x 5y 9 y 2
Vậy, hệ phương trình đã cho có một nghiệm 1 ;2 .
Cách 2: Sử dụng phương pháp đặt ẩn phụ: đặt u x y; v x y , ta có hệ phương trình: 3
x y 2x y 9 3
u 2v 9 2
x y x y 1
2u v 1 3
u 2v 9
7u 0.v 7 u 1
4u 2v 2
2u v 1 v 3 u 1 x y 1 2x 2 x 1 Với
, ta có hệ phương trình v 3 x y 3 x y 1 y 2
Vậy, hệ phương trình đã cho có một nghiệm 1 ;2 .
Dạng 3. Sử dụng phương pháp đặt ẩn phụ
Ví dụ minh họa 3: Bằng cách đặt ẩn phụ, hãy giải hệ phương trình sau: 5 1 10
x 1 y 1 1 3 18
x 1 y 1 Hướng dẫn giải: x 1 0 x 1
Điều kiện để hệ phương trình xác định là: y 1 0 y 1 1 1 Đặt u ;v
, ta có hệ phương trình: x 1 y 1 5 1 10
x 1 y 1
5u v 10 1 3
u 3v 18 18
x 1 y 1
Giải hệ phương trình bằng phương pháp thế: Từ phương trình 5
u v 10, ta có: v 5u 10
Thế vào phương trình u 3v 1 8 , ta được: u 3v 1
8 u 35u 10 1 8 16u 30 18 16u 48 u 3 Thay u 3
vào phương trình v 5u 10, ta được v 5. 3 10 5 u 3 Vậy
, nên ta có hệ phương trình: v 5 1 3 1 3 x 1 x 1 1 3 x 3 1 1 5 y 1 1 5 y 5 5 y 1 2 x 3 x 2 3 5 y 4 4 y 5 2 4
Vậy, hệ phương trình đã cho một nghiệm ; . 3 5
Dạng 4. Một số bài toán liên quan
Ví dụ minh họa 4: Xác định phương trình đường thẳng y ax b biết nó đi qua hai điểm A 1 ;6 và B2; 3 . Hướng dẫn giải:
Đường thẳng y ax b đi qua điểm A 1
;6 , nên ta có 6 a
1 b a b 6 1
Đường thẳng y ax b đi qua điểm B 2; 3 , nên ta có 3 .
a 2 b 2a b 3 2
Vì a, b phải là nghiệm đúng của cả hai phương trình (1) và (2) nên a, b là nghiệm của hệ phương trình:
a b 6 3 a 9 a 3
2a b 3
2a b 3 b 3
Vậy, phương trình đường thẳng cần tìm là: y 3x 3 .
mx 2y 1
Ví dụ minh họa 5: Cho hệ phương trình:
mx my m 1
Giải hệ phương trình khi: a) m 3 ; b) m 2 ; c) m 0 . Hướng dẫn giải:
mx 2y 1 Cho hệ phương trình
mx my m 1
3x 2y 1
3x 2y 1
a. Khi m 3 , ta có hệ phương trình:
3x 3y 31
3x 3y 2 1 y 1 x 3 3 x 1 y 1
Vậy, khi m 3 , hệ phương trình đã cho có nghiệm x y 1 ; ;1 3
2x 2y 1
b. Khi m 2 , ta có hệ phương trình:
2x 2y 1
Hệ phương trình có vô số nghiệm. Công thức nghiệm tổng quát của hệ phương trình là: x y 2 x 1 hoặc 2 y 1 y x 2 2
0x 2y 1 1
c. Khi m 0 , ta có hệ phương trình:
0x 0y 0 1 2
Trong hệ phương trình này, ta thấy phương trình thứ (1) có nghiệm, còn phương trình thứ (2) vô
nghiệm, nên hệ phương trình vô nghiệm.
Vậy khi m 0 , hệ phương trình đã cho vô nghiệm.
SƠ ĐỒ TƯ DUY PHƯƠNG PHÁP GIẢI HỆ PHƯƠNG TRÌNH
Bước 1: Chọn PT dễ nhất (thường là pt có hệ số đơn giản) Rút
ẩn: biểu diễn ẩn này theo ẩn kia (1) Rồi thay vào phương
trình còn lại được (2) Giải hệ bằng Phương pháp thế
Bước 2: Giải phương trình (2) 1 ẩn, ta thay ẩn này vào
phương trình (1) để tìm ẩn còn lại Kết luận nghiệm. HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Bước 1: Xác định ẩn muốn khử (x hoặc y?...)
a x b y c 1 1 1
a x b y c 2 2 2
Bước 2: Đồng nhất hệ số Xem xét hệ số đứng trước ẩn
muốn khử ở hai phương trình (không quan tâm dấu ) Nhân
2 vế của mỗi phương trình cho số thích hợp sao cho hệ số đứng Giải hệ bằng
trước ẩn muốn khử bằng nhau (không quan tâm dấu). Phương pháp cộng đại số
Bước 3: Cộng vế theo vế nếu hệ số của ẩn muốn khử ở hai
phương trình trái dấu, và trừ vế theo vế nếu hệ số của ẩn
muốn khử ở hai phương trình cùng dấu.
Bước 4: Giải phương trình 1 ẩn, suy ra ẩn còn lại và kết luận.
PHẦN II.BÀI TẬP TỰ LUYỆN
Bài 1. Giải các hệ phương trình sau đây bằng phương pháp thế:
x 2y 6
x 3y 5 a. b.
2x y 4
2x y 8
x y 10 3
x y 5 c. d. x y 8 5
x 2y 14
Bài 2. Giải các hệ phương trình sau đây bằng phương pháp thế: y x y 1 1
x y 1 a. 5 2 10 2 b. y x y 1 3
x 2y 10 2 5 5 x y 0
x y 20 2 3 c. d. 4 9 x x x y 8 8
y 4 x 8
Bài 3. Giải các hệ phương trình sau đây bằng phương pháp thế:
x 2 2y 3
x y 3 0 a. b.
2x y 1 6
x 3 2y 1 3
2x 5y 1
2x 5y 2 c. d.
x 5y 2
x 5y 2
Bài 4. Giải các hệ phương trình sau: 3 5
x3y 35 5 3 1 x y 3 a. b.
4x y 4 2 5 x 3 1 y 1
Bài 5. Giải các hệ phương trình sau:
4x 3y 5
x y 1 3
x 7 6x y 1 0 a. b. 2x 4 2y 1 1 4 x
1 2 x 2y 7 0 3
x by 5
Bài 6. Xác định các giá trị của a, b để hệ phương trình:
ax by 12 a. Có nghiệm 1;2 b. Có nghiệm 2; 2
Bài 7. Giải các phương trình sau đây bằng phương pháp đặt ẩn phụ: 1 1 1 7 5 1 x y 3
x 1 y 2 a. b. 1 1 1 1 1 1 x y 12
x 1 y 2 12 4 1 5 2 1 8
x 2y x 2y
x y 3 x y 1 c. d. 20 3 3 1 1 3
x 2y x 2y
x y 3 x y 1 3
x 2y a
Bài 8. Cho hệ phương trình: 15
x 10y 5
a. Có vô số nghiệm với a 1
b. Vô nghiệm với a 1
Bài 9. Giải các phương trình sau đây bằng phương pháp cộng đại số: 5
x y 10
4x 3y 1 0 a. b.
x 3y 1 8
2x 5y 8 1 6 27 1 1 x y x y 2 c. 2 5 10 3 4 d. 9 15 2 x y x y 18 2 2 5
Bài 10. Giải các phương trình sau đây bằng phương pháp cộng đại số: 15
x 8y 46 5
x 3y 19 a. b. 3 4
2x 9y 31 x y 5 5
5x 4y 20 3
x 4y 10 c. d. 1 1 6
x 8y 1 7 x y 1 4 5
Bài 11. Giải các phương trình sau đây bằng phương pháp cộng đại số: 5
x 2y 3x y 99
2x 3y 21 a. b.
x 3y 7x 17 7
x 4 3 x y 1 14 2 x 1 5 y 1 8 4 x 1 23y 1 5 0 c. d. 3 x 1 2 y 1 1 8 x 1 53y 1 9
Bài 12. Giải hệ phương trình sau đây bằng phương pháp cộng đại số: 3 1 x y 3 x 3 1 y 1
Bài 13. Xác định các hệ số a, b để đồ thị hàm số y ax b đi qua hai điểm M và N trong mỗi trường hợp sau:
a. M 1;3 và N 2; 2 b. M 1
; 3 và N 2; 3
c. M 0;0 và N 3;3 d. M 1
;4 và N 4; 1
Bài 14. Xác định giá trị của các hệ số m, n sao cho:
2x my n a. Hệ phương trình
có nghiệm là x 2; y 5 ?
mx ny 5
x y m b. Hệ phương trình
có nghiệm là x 1; y 2 ? 3
x 2y n 1
Bài 15. Giải các hệ phương trình sau bằng phương pháp đặt ẩn phụ: 10 1 27 32 1 7
x 1 y 2
2x y x 3y a. b. 25 3 45 48 2 1
x 1 y 2
2x y x 3y
2 x 6 3 y 1 5
4 x y 3 x y 8 c*. d*. 5
x 6 4 y 1 1 3
x y 5 x y 6
Bài 16*. Giải các hệ phương trình sau: 3
x y z 1
x 3y 2z 8
a. 2x y 2z 5 b.
2x y z 6
x 2y 3z 0
3x y z 6 HƯỚNG DẪN GIẢI
Bài 1. Giải các hệ phương trình sau bằng phương pháp thế:
x 2y 6
x 2y 6
a. Biến đổi hệ phương trình
2x y 4 2
2y 6 y 4 16 14 x 2. 6 x
x 2y 6
x 2y 6 3 3
4y 12 y 4 3 y 16 16 16 y y 3 3 14 16
Vậy, nghiệm của hệ phương trình là ; . 3 3
x 3y 5
x 3y 5
b. Biến đổi hệ phương trình
2x y 8 2
3y 5 y 8 18 29 x 3. 5 x
x 3y 5
x 3y 5 5 5
6y 10 y 8 5 y 1 8 18 18 y y 5 5 29 18
Vậy, nghiệm của hệ phương trình là ; . 5 5
x y 10 x y 10
c. Biến đổi hệ phương trình x y 8 y 10 y 8 x y 10 x y 10 x 1 10 x 9 2y 10 8 2y 2 y 1 y 1
Vậy, nghiệm của hệ phương trình là 9; 1 .
3x y 5
y 3x 5
d. Biến đổi hệ phương trình
5x 2y 14 5 x 2 3x 5 14 24 24 x 3 5 3 5 x y x y x 11 11 5
x 6x 10 14 11 x 24 24 17 y 3. 5 y 11 11 24 17
Vậy, nghiệm của hệ phương trình là ; . 11 11
Bài 2. Giải các hệ phương trình sau bằng phương pháp thế: 1 1 y x 1 x y 1 2
a. Biến đổi hệ phương trình 2 1 3
x 2y 10 3
x 2 x 1 10 2 1 1 x 4
y x 1
y x 1 x 4 2 2 1 y .4 1 y 1 3x x 2 10 2x 8 2
Vậy, nghiệm của hệ phương trình là 4; 1 y x y 1 2y 5 5 2 10
x y 1
b. Biến đổi hệ phương trình y x y 1 5 y 2
x y 2 2 5 5 5 1 y x
2y 5x 5y 1 5x 7y 1 7 7 5
y 2x 2y 2 2
x 3y 2 5 1 2 x 3 x 2 7 7 5 1 5 1 y x y x x 11 7 7 7 7 15 3 1 11 y 8 2 x x 2 x 7 7 7 7
Vậy, nghiệm của hệ phương trình là 11;8 .
c. Hệ phương trình đã cho có điều kiện là: x 8; y 4 x y 0 2 3 3
x 2y 0
Khi đó, biến đổi hệ phương trình 4 9 4
x 8 9 y 4
y 4 x 8 2 3
x 2y 0 3
x 2y 0 x y
x y 3 4 8 9 4
4x 32 9y 36
4x 9y 4 2 8 2 x y x x y 3 19 3 2 12
4x 9y 4 4. y 9y 4 y 3 19 8 12
Vậy, nghiệm của hệ phương trình là ; . 19 19
x y 20
x y 20
d. Biến đổi hệ phương trình x x x y 8
x x 8y x 8 8
x y 20
x y 20
x y 20 8
x x 8y x
6x 8y 0 6
y 20 8y 0
x y 20 x 80 2 y 120 y 60
Vậy, nghiệm của hệ phương trình là 80;60.
Bài 3. Giải các hệ phương trình sau bằng phương pháp thế:
x 2 2y 3
x 2 2y 3
a. Biến đổi hệ phương trình
2x y 1 6 2
2 2y 3 y 1 6 1 2 6 x 2 2. 3
x 2 2y 3
x 2 2y 3 5
4y 6 y 1 6 5y 1 2 6 1 2 6 y 5 1 2 6 2 2 4 12 5 3 x 2 2. 3 x 5 5 1 2 6 1 2 6 y y 5 5 2 2 3 3 x 5 1 2 6 y 5 2 2 3 3 1 2 6
Vậy, nghiệm của hệ phương trình là ; . 5 5
x 3y 0 x 3y
b. Biến đổi hệ phương trình
3x 2y 1 3 3
3y 2y 1 3 1 3 3 3 x 3. x x 3y 5 5
3y 3y 1 3 1 3 1 3 y y 5 5 3 3 1 3
Vậy, nghiệm của hệ phương trình là ; . 5 5
2x 5y 1 x 5y 2
c. Biến đổi hệ phương trình
x 5y 2
2x 5y 1
x 5y 2
x 5y 2
2x 5y 1 2
5y 2 5y 1
x 5y 2
x 5y 2
2 5y 2 5y 1 5 2 1 y 1 1 x 5 x 1 5 2 1 2 1 1 y y 5 5 2 1 2 1
Vậy, nghiệm của hệ phương trình là 1; . 5
2x 5y 2 2
5y2 5y 2
d. Biến đổi hệ phương trình
x 5y 2
x 5y 2 2 y y 2 5 1 2 2 1 2 5 y 5 2
x 5y 2 x 5 2 x 0 5 2
Vậy, nghiệm của hệ phương trình là 0; . 5
Bài 4. Giải các hệ phương trình sau: 3 5
x3y 35 5
a. Biến đổi hệ phương trình
4x y 4 2 5 3 5
x3 4x42 5 35 5 y 4 x 4 2 5 15 5
x 15 5 x 1 y 2 5 y 4x 4 2 5
Vậy, nghiệm của hệ phương trình là 1; 2 5. 3
1x y 3 y 3 1x 3
b. Biến đổi hệ phương trình x 3 1 y 1 x 3 1 3 1 x 3 1 y 3 1x 3 y 3 1x 3 x
3 1 3 1x 3 1 3 1 3x 4 3 y 4 3 4 3 4 3 3 3 1 3 y 3 3 3 4 3 4 3 x x 3 3 1 y 3 4 3 1
. Vậy, nghiệm của hệ phương trình là ; . 4 3 3 3 x 3
Bài 5. Giải các hệ phương trình sau:
4x 3y 5
x y 1
a. Biến đổi hệ phương trình 2x 4 2y 1 1
4x 3y 5
x y 1 4x 3y 5x 5y 1 2x 4 2y 1 1
2x 8y 4 1 3 9
x 8y 1 9 4 y 8y 1 9
x 8y 1 2 3
2x 8y 3 x 4y 3 2 x 4 y 2 27 27 29 36y 8y 1 28y 1 y 2 2 56 3 3 29 3 x 4y x 4y x 4. 2 2 56 2 29 y 56 4 29
. Vậy, nghiệm của hệ phương trình là: ; 4 7 56 x 7 3
x 7 6x y 1 0
b. Biến đổi hệ phương trình 4 x
1 2 x 2y 7 0
3x 21 6x 6y 6 0 3
x 6y 27
4x 4 2x 4y 14 0
6x 4y 1 0
x 2y 9
x 2y 9
x 2y 9
6x 4y 10 6
2y 9 4y 10 8 y 44 x 2 11
11 . Vậy, nghiệm của hệ phương trình là: 2; . y 2 2
3x by 5
Bài 6. Hệ phương trình:
ax by 12 b b a. Có nghiệm 3.1 .2 5 3 2 5 1; 2 .1 a .2 b 12
a b 12 3 2b 5 2b 2 b 1 b 1
a b 12 a b 12 a 1 12 a 11
Vậy, hệ số a 11;b 1. 3. 2 . b 2 5 6 2b 5 b. Có nghiệm 2; 2 . a 2 . b 2 12 2
a 2b 12 11 11 2 11 b b b 2 2
a b 6 11 1 a 6 a 2 2 1 11
Vậy, hệ số a ;b . 2 2 Bài 7. 1 1
a. Điều kiện x 0; y 0 . Đặt ẩn phụ: ; a b x y 1 1 1 1 1 1 a b b b x y 3
Khi đó, hệ phương trình 3 12 3 1 1 1 1 1 a b a b x y 12 12 12 1 1 1 1 1 2b 2b b b 3 12 4 8 8 1 1 1 1 5 a b a b a a 12 12 8 12 24 1 1 1 b 24 8 y 8 x Với 5 5 1 5 a y 8 24 x 24 24
Vậy, nghiệm của hệ phương trình là: ;8 . 5 1 1
b. Điều kiện: x 1; y 2 . Đặt ẩn phụ: ; a b x 1 y 2 7 5 1
7a 5b 1
x 1 y 2
khi đó, hệ phương trình 1 1 1 1 a b 12
x 1 y 2 12 1 5 5
7a 5b 1 7 b 5b 1 12b b 12 12 144 1 a b 1 1 17 12 a b a b a 12 12 144 5 1 5 144 144 b y 2 y 2 144 y 2 144 Với 5 5 17 1 17 144 144 a x 1 x 1 144 x 1 144 17 17 134 y 5 (thỏa điều kiện) 161 x 17 161 134
Vậy, nghiệm của hệ phương trình là: ; . 17 5 1 1
c. Điều kiện: x 2 y . Đặt ẩn phụ: ; a b x 2 y x 2y 4 1 1
x 2y x 2y
4a b 1
khi đó, hệ phương trình 20 3
20a 3b 1 1
x 2y x 2y 1 4 1 4 1 a b a b a 8 20a 3 4a 1 1 32 a 4 1 b 2 1 1 1 a x 3 8 x 2y 8
x 2y 8 Với 5 (thỏa điều kiện) 1 1 1
x 2y 2 y b 2 2 x 2y 2 x 3
Kết luận, vậy hệ phương trình có nghiệm là 5 y 2 x y 3 1 1 d. Điều kiện: . Đặt ẩn phụ: ; a b x y 1 x y 3 x y 1 5 2 14 8 a
x y 3 x y 1 5
a 2b 8
Khi đó, hệ phương trình 11 3 1 3
a b 3 9 3 b
x y 3 x y 1 11 14 1 14 11 53 a
x y 3 x y 11
x y 3 11 Với 14 14 9 1 9 11 19 b x y 1 x y 11
x y 1 11 9 9 211 x 252 743 y 252 211 x
Vậy, nghiệm của hệ phương trình là: 252 743 y 252 3
x 2y a
Bài 8. Cho hệ phương trình: 15
x 10y 5 3
x 2y 1 3
x 2y 1
a. Với a 1, ta có: 15
x 10y 5 3
x 2y 1
Hệ phương trình với a 1 là hệ gồm hai phương trình giống nhau (hai đường thẳng trùng nhau) nên chúng có vô số nghiệm. x
Nghiệm tổng quát của hệ phương trình là: 3 1 y x 2 2
Cách 2: Ta có thể nhìn nhanh số nghiệm của hệ phương trình khi lập tỉ số các hệ số của hai đường thẳng: 3 2 1 Vì:
nên hệ phương trình có vô số nghiệm. 15 10 5 3
x 2y a
b. Với a 1. Ta có hệ phương trình: 15
x 10y 5 3 2 a Vì a 1 nên
. Do đó, hệ phương trình vô nghiệm. 15 10 5
Bài 9. Giải các hệ phương trình sau bằng phương pháp cộng đại số: 5
x y 10 1
5x 3y 30
a. Biến đổi hệ phương trình
x 3y 1 8
x 3y 1 8 16 x 48 x 3
x 3y 1 8 y 5
Vậy, nghiệm của hệ phương trình là 3; 5 .
4x 3y 1 0
4x 3y 1 0
b. Biến đổi hệ phương trình
2x 5y 8
4x 10y 16 13 y 26 y 2
2x 5y 8 x 1
Vậy, nghiệm của hệ phương trình là 1 ;2 . 1 6 27 x y 5
x 12y 27
c. Biến đổi hệ phương trình 2 5 10 9 15
2x 9y 1 5 x y 2 2 5
x 12y 27 1
0x 24y 54
2x 9y 15 10
x 45y 75 21 y 2 1 y 1
2x 9y 1 5 x 3
Vậy, nghiệm của hệ phương trình là 3; 1 . 1 1 4 x y 2 x y 8
d. Biến đổi hệ phương trình 3 4 3 2 2 x y 18 x y 18 5 5 26 x 26 x 15 15 x 15 2 2 .15 y 18 y 12 x y 18 5 5
Vậy, nghiệm của hệ phương trình là 15;12 .
Bài 10. Giải các hệ phương trình sau bằng phương pháp cộng đại số: 5
x 3y 19 10
x 6y 38
a. Biến đổi hệ phương trình:
2x 9y 31 10
x 45y 155 39 y 117 y 3 x 2 5
x 3y 19 5 x 9 19 y 3
Vậy, nghiệm của hệ phương trình là 2;3. 15
x 8y 46 15
x 8y 46
b. Biến đổi hệ phương trình: 3 4 x y 5
x 3y 4 5 5 15
x 8y 46 1 7 y 34 y 2 x 2 15
x 9y 12 5
x 3y 4 5 x 6 4 y 2
Vậy, nghiệm của hệ phương trình là 2;2 . 3
x 4y 10 3 4 10 a b c c. Hệ phương trình
có tỉ lệ giữa các hệ số là: dạng 6
x 8y 1 7 6 8 17
a b c
nên hệ phương trình vô nghiệm.
5x 4y 20 5 4 20 a b c d. Hệ phương trình 1 1
có tỉ lệ giữa các hệ số là: dạng x y 1 1 1 1
a b c 4 5 4 5
nên hệ phương trình có vô số nghiệm. x y
Với nghiệm tổng quát của hệ phương trình là: 5 hoặc 4 y x 5 x y 4 4 5
Bài 11. Giải các hệ phương trình sau bằng phương pháp cộng đại số: 5
x 2y 3x y 99
a. Biến đổi hệ phương trình
x 3y 7x 17 5
x 10y 3x 3y 99
2x 13y 99
6x 3y 17
6x 3y 17 70 19 y x
6x 39y 297 36 y 280 9 18
6x 3y 17
6x 3y 17 70 70 6x 3 17 y 9 9 19 70
Vậy, nghiệm của hệ phương trình là: ; 18 9
2x 3y 21
b. Biến đổi hệ phương trình 7
x 4 3 x y 1 14
2x 3y 21
2x 3y 21
7x 28 3x 3y 3 14 10
x 3y 45 8 x 24 x 3 x 3 3
y 21 2x 3 y 21 6 y 5
Vậy, nghiệm của hệ phương trình là: 3;5 2 x 1 5 y 1 8
c. Biến đổi hệ phương trình 3 x 1 2 y 1 1
2x 2 5y 5 8
2x 5y 11 3
x 3 2y 2 1 3
x 2y 0
6x 15y 33 1 1y 3 3
6x 4y 0 3
x 2y 0 y 3 x 2 3 x 2y y 3
Vậy, nghiệm của hệ phương trình là: 2; 3
* (Những bài toán khá đơn giản như thế này chúng ta không nên đặt ẩn phụ, bởi sẽ tạo ra nhiều
bước thực hiện để hoàn thành bài toán. Cách tốt nhất là khai triển, rồi làm gọn hệ phương trình đã
cho. Sau đó giải theo phương pháp thầy đã nêu.) 4 x 1 23y 1 5 0
d. Biến đổi hệ phương trình 8 x 1 53y 1 9
4x 4 6y 2 5 0
4x 6y 1 8
x 8 15y 5 9 8
x 15y 4 8
x 12y 2 3 y 2 8
x 15y 4
4x 6y 1 2 3 y x 3 4 2 2 4x 6. 1 y 3 3 3 2
Vậy, nghiệm của hệ phương trình là: ; 4 3
Bài 12. Giải hệ phương trình sau bằng phương pháp cộng đại số: 3 1 x y 3
Biến đổi phương trình x 3 1 y 1 3 1 x y 3 3 1x y 3 3 1 x 3 1 3 1 y 3 1 3
1x2y 31 1 3y 1 y 3
3 1 x y 3 3 1x y 3 1 1 y y 3 3 1 y 3 3 x 3 3 1 x 3 1 1 y 3 3 13 3 1 3 3 1 4 3 x 3 3 1 3 3 1 3 4 3 1
Vậy, nghiệm của hệ phương trình là: ; 3 3
Bài 13. Xác định các hệ số a, b để đồ thị hàm số y ax b đi qua hai điểm M và N trong mỗi trường hợp sau:
a. Hàm số y ax b đi qua hai điểm M 1;3 và N 2; 2 :
Điểm M 1;3 thuộc đồ thị hàm số nên ta có phương trình: 3 a b 1 Điểm N 2;
2 thuộc đồ thị hàm số nên ta có phương trình: 2 2
a b 2 1 a 3 a b
Suy ra: a, b là nghiệm của hệ phương trình 3 2 2 a b 8 b 3 1 8
Vậy, a và b . 3 3
b. Hàm số y ax b đi qua hai điểm M 1;
3 và N 2; 3 : Điểm M 1
; 3 thuộc đồ thị hàm số nên ta có phương trình: 3 a b 1
Điểm N 2; 3 thuộc đồ thị hàm số nên ta có phương trình: 3 2a b 2
3 a b a 0
Suy ra: a, b là nghiệm của hệ phương trình
3 2a b b 3 a 0 Vậy, . b 3
c. Hàm số y ax b đi qua hai điểm M 0;0 và N 3;3 :
Điểm M 0;0 thuộc đồ thị hàm số nên ta có phương trình: b 0 1
Điểm N 3;3 thuộc đồ thị hàm số nên ta có phương trình: 3 3a b 2 b 0 a 1
Suy ra: a, b là nghiệm của hệ phương trình 3 3a b b 0 a 1 Vậy, . b 0
d. Hàm số y ax b đi qua hai điểm M 1; 4
và N 4; 1 : Điểm M 1; 4
thuộc đồ thị hàm số nên ta có phương trình: 4 a b 1 Điểm N 4;
1 thuộc đồ thị hàm số nên ta có phương trình: 1
4a b 2
4 a b a 1
Suy ra: a, b là nghiệm của hệ phương trình 1 4a b b 3 a 1 Vậy, . b 3
Bài 14. Xác định giá trị của các hệ số m, n sao cho:
2x my n a. Hệ phương trình
có nghiệm là x 2; y 5
mx ny 5
Thay giá trị x 2; y 5 vào hệ phương trình, ta có hệ: 5 m
4 5m n 5
m n 4 9
2m 5n 5
2m 5n 5 11 n 9 5 11
Vậy, với m và n
thì hệ phương trình đã cho có nghiệm x 2; y 5 . 9 9
x y m b. Hệ phương trình
có nghiệm là x 1; y 2 . 3
x 2y n 1
Thay giá trị x 1; y 2 vào hệ phương trình, ta có hệ:
x y m 1 2 m m 1 3
x 2y n 1 3 4 n 1 n 6 Vậy với m 1
và n 6 thì hệ phương trình đã cho có nghiệm x 1; y 2 .
Bài 15. Giải các hệ phương trình sau bằng phương pháp đặt ẩn phụ: 10 1 1
x 1 y 2 a. Hệ phương trình
có điều kiện x 1; y 2 25 3 2
x 1 y 2
Với x thỏa điểu kiện. 1 1
Đặt ẩn phụ: a ;b
, ta có hệ phương trình mới: x 1 y 2 10 1 1
x 1 y 2 10 a b 1 25 3
25a 3b 2 2
x 1 y 2 1 30
a 3b 3 5 a 1 a 5
25a 3b 2 10 a b 1 b 1 1 1 1 a x 1 5 Từ kết quả 5 , suy ra: 1 b 1 1 y 2 x 1 5 x 6 (thỏa điều kiện) y 2 1 y 3
Vậy, nghiệm của hệ phương trình là 6; 3 . 27 32 7
2x y x 3y
2x y 0 b. Hệ phương trình có điều kiện 45 48 x 3y 0 1
2x y x 3y
Với x thỏa điều kiện. 1 1
Đặt ẩn phụ: a ;b
, ta có hệ phương trình mới: 2x y x 3y 27 32 1 7 a
2x y x 3y
27a 32b 7 9 45 48
45a 48b 1 1 1 b
2x y x 3y 8 1 1 1 a 2x y 9 Từ kết quả 9 , suy ra: 1 1 1 b 8 x 3y 8
2x y 9 x 5 (thỏa điều kiện)
x 3y 8 y 1
Vậy, nghiệm của hệ phương trình là 5; 1 .
2 x 6 3 y 1 5 c*.
. Đặt a x 6 ;b y 1 5
x 6 4 y 1 1
2 x 6 3 y 1 5
2a 3b 5 a 1
Ta có hệ phương trình: 5
x 6 4 y 1 1 5
a 4b 1 b 1 x 6 1 1 y 1 1 x 6 1 2 a 1 x 6 1 y 1 1 Với , suy ra: b 1 y 1 1 x 6 1 3 y 1 1 x 6 1 4 y 1 1 x x Giải 6 1 7 1 y 1 1 y 0 x x Giải 6 1 5 2 y 1 1 y 2 x x Giải 6 1 7 3 y 1 1 y 2 x x Giải 6 1 5 4 y 1 1 y 0
Vậy, hệ phương trình có các nghiệm là: 7;0;5; 2 ;7; 2 ;5;0 .
4 x y 3 x y 8 d*.
. Đặt a x y ;b x y 3
x y 5 x y 6
4 x y 3 x y 8
4a 3b 8 a 2
Ta có hệ phương trình: 3
x y 5 x y 6 3
a 5b 6 b 0
x y 2 1 a 2
x y 2
x y 0 Với , suy ra b 0 x y 0 x y 2 2
x y 0 x y x Giải 2 1 1 x y 0 y 1
x y x Giải 2 1 2 x y 0 y 1
Vậy, hệ phương trình có các nghiệm là: 1; 1 1 ; 1 .
Bài 16*. Giải các hệ phương trình sau: 3
x y z 1
z 3x y 1
a. 2x y 2z 5 2x y 23x y 1 5
x 2y 3z 0 x 2y 3
3x y 1 0
z 3x y 1
z 3x y 1
z 3x y 1
2x y 6x 2y 2 5 8
x y 7 4 y 4
x 2y 9x 3y 3 0 8x 5y 3 8 x y 7
z 3x y 1
z 3x y 1 z 1 y 1 y 1 y 1 8 x 1 7 x 1 x 1
Vậy, nghiệm của hệ phương trình là: 1; 1 ; 1
x 3y 2z 8
x 3y 2 3
x y 6 8
b. 2x y z 6 2x y 3
x y 6 6 3 x y z 6 z 3
x y 6
x 3y 2 3
x y 6 8
x 3y 6x 2y 12 8
2x y 3
x y 6 6 2x y 3x y 6 6 z 3
x y 6 z 3
x y 6 5
x y 4 y 4 x 0 x 0 z 3x y 6 z 10
Vậy, nghiệm của hệ phương trình là: 0; 4 ;10 .
PHẦN III.TRẮC NGHIỆM CỦNG CỐ PHẢN XẠ HƯỚNG DẪN
I. Giải hệ phương trình bằng phương pháp thế Câu 1. Đáp án B. x ìï - y = 5 x ìï = y + 5 x ìï = y + 5 Ta có ïí ïí ï í 3 ï x + 2y = 18 ï ï + + = ï + + = î 3.(y 5) 2y 18 3y 15 2y 18 ïî îï ìï 3 ìï 28 ï ï ìï = + 5 y ï = x x y ï = ï ï 5 ï 5 í í í 5 ï y = 3 ï 3 ï 3 ïî x ïï = 5 + y ïï = ïî 5 ï ï ïî 5 æ28 3ö ç ÷ 84
Vậy hệ phương trình có nghiệm duy nhất (x;y) = ç ; ÷ x.y = ç çè 5 5÷÷ø 25 Câu 2. Đáp án D. x ìï - y = 3 x ìï = y + 3 x ìï = y + 3 x ìï = 10 Ta có ï ï ï ï í í 3 ï í í x - 4y = 2 3
ï (y + 3) - 4y = 2 y ï = 7 y ï = 7 îï ïî ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (10;7) Do đó 2 2 x y = 10 .7 = 700 Câu 3. Đáp án D. ìï 8 + 7y ï ìï ì + ï 2 ìï - 7 = 8 x x y ï = ï 8 7y 8 + 7y x ïï x ï = ï ï = Ta có ï ï 2 í í ï í í 10 ï x + 3y = 21 æ ï 8 7y ö + 2 2 ï ï ï î 10. ï ç ÷ ç ÷ + 3y = 21 ï ï + + = ï ç 40 35y 3y 21 38y = -19 ï çè 2 ÷÷ø ïî ïî ïî ìï 8 + 7y ìï 1 x ïï y ï = ï = - ï 2 ï 2 í í ï 1 ï 9 y ïï x ï = - ï = ïî 2 ï ï ïî 4 æ9 1ö ç ÷ 7
Vậy hệ phương trình có nghiệm duy nhất (x;y) = ç ;- ÷ x + y = ç çè4 2÷÷ø 4 Câu 4. Đáp án C. ìï 11 ìï 11 ï ï 7 ìï - 3 = 5 7 ìï - 3 2 ( - 4 ) = 5 x ï = x x y x x ï = Ta có ï ï ï 19 ï 19 í í í í 4 ï x + y = 2 y ï = 2 - 4x ï 11 ï 6 ïî ïî y ïï = 2 - 4. y ïï = - ïî 19 ï ï ïî 19 æ11 6 ö ç ÷ 5
Vậy hệ phương trình có nghiệm duy nhất (x;y) = ç ;- ÷ x + y = ç çè19 19÷÷ø 19 Câu 5. Đáp án A. ìï ì x - 2y = 12 ï ì x = 12 + 2y ïx = 12 + 2y Ta có ï ï ï í í í ï2x + 3y = 3 ï (
2 12 + 2y) + 3y = 3 ï ïî ï ï7y = - î î 21 ìï ì y = -3 ï ï ïx = 6 í í . ïx = 12 + - 2.( ) 3 ï ï y = - î ïî 3
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (6; 3 - ) Câu 6. Đáp án A. ìï ì 3 ï ï ï 15 ìï ì 3x - 2y = 12 ï ì x = 3 - 2y ïx = 3 - 2y ïy = - ïx = Ta có ï ï ï ï 8 ï í í í í í 4 ïx + 2y = 3 ï (
3 3 - 2y) - 2y = 12 ï-8y = 3 ï 3 ï ïî ïî ïî ï ï 3 ïx = 3 + ïy = - ï 4 ï ïî ïî 8 æ15 3ö
Vậy hệ phương trình có nghiệm duy nhất (x;y) ç = ç ; ÷ - ÷ ç . çè 4 8÷÷ø Câu 7. Đáp án D. ì ì ï ï ì - ï x - 2y = 3 ïx = - 2y - 3 ïïx = - 2y - 3 Ta có ï ï ï í í ï 2x + 2y = - 6 ï 2 2y 3 2y 6 ï (- - ) í ï ï + = - ï-
ï 2y - 6 + 2y = - î 6 ïî ïî x ìïï = - 2y - 3 y ìï Î ï ï í í . ï- ï 6 = - 6 x ï = - 2y - 3 ï ïî ïî
Vậy hệ phương trình có vô số nghiệm. Câu 8. Đáp án A. Ta ì ì x ïï 2 -y 3 = 1 ï (ïï 2 -y 3 ï ) 2 -y 3 =1 có í í x ïï y 3 2 x ï + = ï = 2 - y 3 ïî ïî ìï ì 2 ï y ( 6 3) 1 y ï - + = ï ï ï ( 6 + 3) = 1 í í x ïï 2 y 3 x ï = - ï = 2 - y 3 ïî ïî ìïï 6 - 3 { 6 - 3 ï = = 2 - 3 y y x y ï = í 3 3 ïx ï = 1 ïïî æç 6 - 3ö÷
Vậy hệ phương trình đã cho có nghiệm duy nhất (x;y) = 1 ç ; ÷ ç ÷. ç 3 ÷÷ è ø Câu 9. Đáp án A. (
ìï x + 1)(y -1) = xy -1 xy
ìï - x + y -1 = xy -1 ìï x - + y = 0 Ta có ï ï ï í í í (
ï x - 3)(y - 3) = xy - 3 xy ï
- 3x - 3y + 9 = xy - 3 ï-3x - 3y = -12 ïî ïî ïî x ìï = y x ìï = y x ìï = y x ìï = 2 ï ï ï ï í í í í ï-3y - 3y = 1 - 2 ï-6y = -12 y ï = 2 y ï = 2 ïî ïî ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (2; ) 2 Câu 10. Đáp án D. ( ìï x + ) 1 (y - ) 3 = (x - ) 1 (y + ) 3 x
ìï y - 3x + y - 3 = xy + 3x - y - 3 Ta có ïí ï í ( ï x - ) 3 (y + ) 1 = (x + ) 1 (y - 3) x
ï y + x - 3y - 3 = xy - 3x + y - 3 îï îï 6 ìï x - 2y = 0 x ìï = y x ìï = y x ìï = y x ìï = 0 ï ï ï ï ï í í í í í 4 ï x - 4y = 0 6 ï y - 2y = 0 4 ï y = 0 y ï = 0 y ï = 0 ïî ïî ïî ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (0;0). Câu 11. Đáp án B. ìï 3 ï 2.1 ìï + .(-2) = -1 ìï-2 = -3 b b b ï =
Thay x = 1;y = -2 vào hệ ta được ï ï ï 2 í í í ï .1 b - 2a.(-2) = 1 b ï + 4a = 1 ï3 ïî ïî ïï + 4a = 1 ïïî2 ìï 3 b ïï = ï 13 ï 2 í a -b = - ï 1 8 a ïï = - ïïî 8 13 Vậy a -b = - . 8 Câu 12. Đáp án A. 2 ìï + ( b - ) 2 = 4 -
Thay x = 1;y = -2 vào hệ ta được ïí b ï -a(-2) = -5 ïî
Ta coi đây là một hệ phương trình bậc nhất hai ẩn là a và b và giải hệ phương trình này 2 ìï + ( b -2) = -4 ìï-2b = -6 b ìï = 3 b ìï = 3 ï ï ï ï í í í í b ï -a(-2) = -5 b ï + 2a = -5 3 ï + 2.a = -5 a ï = -4 ïî ïî ïî ïî
Suy ra a + b = -4 + 3 = -1. Câu 13. Đáp án A.
+) Thay tọa độ điểm I vào phương trình d ta được 1
m.(-2) - 2(3n + 2).3 = 6 -2m - 18n = 18 m + 9n = 9 -
+) Thay tọa độ điểm I vào phương trình d ta được 2 (3m - 1).( 2 - ) + 2n.3 = 56 6
- m + 2 + 6n = 56 m - n = 9 - Suy ra hệ phương trình ìï ì m + 9n = -9 ï ì m = -9 + n ï ì m = -9 + n ïn = 0 ï ï ï ï í í í í m.n = 0 . ïm - n = -9
ï-9 + n + 9n = -9 ï10n = 0 ïm = - ïî ïî ïî ïî 9 Vậy m.n = 0 . Câu 14. Đáp án C.
+) Thay tọa độ điểm I vào phương trình d ta được 1 m.( 5
- ) - 2(3n + 2).2 = 18 5
- m - 12n - 8 = 18 5m + 12n = 26 -
+) Thay tọa độ điểm I vào phương trình d ta được 2
(3m - 1).(-5) + 2n.2 = -37 -15m + 5 + 4n = -37 15m - 4n = 42 ìï ì 15m - 42 ì 5 ï m + 12n = -26 ï 5 ï + 12 = -26 ï n m n ï = Suy ra hệ phương trình ï ï ï 4 í í 15m - 42 í 15 ï m - 4n = 42 ï n ï î ï = ï 15m - 42 ï 5 ï ïî ï m + 12. = -26 4 ïïî 4 ìï 15m - 42 ìï 15m - 42 n ïï = n ï ì ï ï = m ï = 2 ï í ï 4 í 4 ï ï ín ï = -3 5 ï m + 3 1 ( 5m - 42) = -26 5 ï 0m - 126 = -26 ï ï ï ï î î î
Vậy m = 2;n = 3 - . Câu 15. Đáp án D.
Thay tọa độ điểm M vào phương trình đường thẳng ta được 3a + b = -5
Thay tọa độ điểm N vào phương trình đường thẳng ta được a + b = 2 ìï -7 ï ìï + = 2 ìï = 2 ì - ï = 2 a a b b a b -a ï =
Từ đó ta có hệ phương trình ï ï ï ï 2 í í í í 3 ï a + b = -5 3 ï a + 2 -a = -5 2 ï a = -7 ï 11 ïî ïî ïî b ïï = ïïî 2 -7 11 Vậy a = ;b = . 2 2 Câu 16. Đáp án A. 1
Điều kiện: x ¹ 2;y ¹ 2 1 1 a ìï +b = 2 a ìï = 2 -b Đặt = a;
= b khi đó ta có hệ phương trình ïí ï í x - 2 2y - 1 2 ï a - 3b = 1 2 ï 2 ( -b) - 3b 1 ï = î îï ìï 3 ìï ì 7 ì a ï = 2 -b ï = - ï a ïï = 2 ï 2 - a a b ï = ï ï ï 5 ï 5 í í 3 í í ï-5b = -3 ï b ï î ï = ï 3 ï 3 ï ï ïî 5 b ï = b ï = ïïî 5 îïï 5 ìï 1 7 ìï 19 ïï = ï ï 7 ìï -14 = 5 x x ï =
Trả lại biến ta được ïx - 2 5 ï ï 7 í í (Thỏa mãn điều kiện) 1 3 í ï 6 ï y - 3 = 5 ï 4 ï = ï ï î y ïï = ï2y - 1 5 ï ïî ïî 3 æ19 4ö
Vậy hệ phương trình có nghiệm duy nhất (x;y) ç = ç ; ÷÷ ç . çè 7 3÷÷ø Câu 17. Đáp án C.
Điều kiện: x ¹ -1;y ¹ -1 ìï 2x y ìï x y ïï 3 2 ï + = ï . + = 3 ïï + + ï Ta có x 1 y 1 ï x + 1 y + 1 í í ï x 3y ï x y ïï 1 ï + = - ï + 3. = -1 ïx + 1 y + 1 ïx + 1 y + 1 ïî ïî x y Đặt = a;
= b khi đó ta có hệ phương trình x + 1 y + 1 2 ìï a +b = 3 b ìï = 3 - 2a b ìï = 3 - 2a b ìï = 3 - 2a ï ï ï ï í í í í a ï + 3b = -1 a ï + 3 3 ( - 2a) = -1 a ï + 9 - 6a = -1 ï-5a = -10 ïî ïî ïî ïî a ìï = 2 a ìï = 2 ï ï í í b ï = 3 - 2.2 b ï = -1 ïî ïî ìï x ïï = 2 ì x ìï = -2 ï x ï = 2x + 2 ï
Thay trở lại cách đặt ta được ïx + 1 ï ï í í í
1 (Thỏa mãn điều kiện) ï y y ï = y - - 1 ï ï = -1 ï y ï î ï = - ï ï î 2 y + 1 ïî æ 1ö
Vậy hệ phương trình có nghiệm duy nhất (x;y) ç = - ç 2; ÷ - ÷ ç . çè 2÷÷ø Câu 18. Đáp án C.
Ta sử dụng: Đa thức P(x) chia hết cho đa thức x -a khi và chỉ khi P(a) = 0
Áp dụng mệnh đề trên với a = -1 , rồi với a = 3 , ta có 3 2
P(-1) = m(-1) + (m - 2).(-1) - (3n - 5).(-1) - 4n = n - - 7 3 2
P(3) = m.3 + (m - 2).3 - (3n - 5).3 - 4n = 36m - 13n - 3
Theo giả thiết, P(x) chia hết cho x + 1 nên P( 1 - ) = 0 tức là n - - 7 = 0
Tương tự, vì P(x) chia hết cho x - 3 nên P(3) = 0 tức là 36m - 13n - 3 = 0 ìï ì n ìï = -7 n - - 7 = 0 n ï = -7 ï
Vậy ta phải giải hệ phương trình ï ï ï í í í ï m - n - = ï m - ( 22 36 13 3 0 36 13. -7) - 3 = 0 ïî ï m ï î ï = - ïî 9 22
Trả lời: Vậy m = - ;n = -7 . 9 Câu 19. Đáp án D.
Ta sử dụng: Đa thức Q(x) chia hết cho đa thức x -a khi và chỉ khi Q(a) = 0
Áp dụng mệnh đề đã cho với a = 2 , rồi với a = 3 - , ta có 3 2
Q(2) = (3m - 1)2 - (2n - 5)2 - n.2 - 9m - 72
= 24m - 8 - 8n + 20 - 2n - 9m - 72 = 15m - 10n - 60 3 2
Q(-3) = (3m - 1)(-3) - (2n - 5)(-3) - n.(-3) - 9m - 72
= -81m + 27 - 18n + 45 + 3n - 9m - 72 = -90m - 15n
Theo giả thiết, Q(x)chia hết cho x - 2 nên Q(2) = 0 tức là 15m - 10n - 60 = 0 (1)
Tương tự, vì Q(x)chia hết cho x + 3 nên Q( 3 - ) = 0 tức là 90
- m - 15n = 0 (2)
Từ (1) và (2) ta có hệ phương trình ìï 4 ï 15 ìï - 10 - 60 = 0 ìï = -6 m m n n m ï = ï ï ï 5 í í í ï-90m - 15n = 0 1
ï 5m - 10(-6m) = 60 ï 24 ïî ïî n ïï = - ïïî 5 4 24
Trả lời: Vậy m = ;n = - . 5 5 Câu 20. Đáp án A. ìï 2 5 5 ì ï ï 1 1 5 ï + = ïï + = ï 2. 5. ï Ta có ï2x + y x + 2y 6 ï + + í 2x y x 2y 6 ï í 3 4 3 ï ï 1 1 3 ï - = - 3. ïï - 4. = - ï2x + y x + 2y 5 ïî ï 2x + y x + 2y 5 ïî ìï 5 ï 1 1 2 ï a + 5b = Đặt = a;
= b ta được hệ phương trình ï 6 í 2x + y x + 2y ï 3 3 ïï a - 4b = - ïïî 5 Câu 21. Đáp án D. ìï 2 6 ì ï ï2 1 1 ï + = 3 ï ï ï . + 6. = 3 ï3x - 9y ï ï x + y ï3 x - 3y ï x + y Ta có í ï í 4 9 ï ï 1 1 ï - = 1 4. ïï - 9. = 1 ïx - 3y ï x + y ï ïî x - 3y ï x + y ïî ìï2 1 1 ïï a + 6b = 3 Đặt = a;
= b ta được hệ phương trình ïí3 x - 3y x + y 4 ïï a - 9b = 1 ïî Câu 22. Đáp án B.
Điều kiện: x ¹ 0;y ¹ 0 1 1 Đặt
= a; = b khi đó ta có hệ phương trình x y a ìï -b = 1 a ìï = 1 +b a ìï = 1 +b ï ï ï í í í 3 ï a + 4b = 5 ï (
3 1 + b) + 4b = 5 7 ï b = 2 ïî ïî ïî ìï 2 ìï 9 b ïï a ï = ï = ï 7 ï 7 í í ï 2 ï 2 a ïï 1 b ï = + ï = ïî 7 ï ï ïî 7 ìï1 9 ìï 7 ïï = a ïï = ï
Trả lại biến ta được x 7 ï 9 í (Thỏa mãn điều kiện) 1 2 í ï ï 7 ï = ï b ïï = ïy 7 ï ïî î 2 7 7
Khi đó 9x + 2y = 9. + 2. = 14 9 2 Câu 23. Đáp án B. ìï15x 7 x ìï ï ï x x ï - = 9 15. ï - 7. = 9 ï ï ï y y ï ï ï y y Ta có í í ï 4x 9 x ï ï ï x x ï + = 5 4 ï . + 9. = 5 ï ï ï y y ï y y ïî ïî x x 15 ìï a - 7b = 9 Đặt = a;
= b ta được hệ phương trình ïí y y 4 ï a + 9b = 5 ïî Câu 24. Đáp án B. Ta có 3
ìï (y - 5) + 2(x - 3) = 0 ìï ì ï
3y - 15 + 2x - 6 = 0 2 ï x + 3y = 21 í ï ï í ï í ( 7 x - ) 4 + ( 3 x + y - ) 1 - 14 = 0 ï ï - + + - - = ï + = î 7x 28 3x 3y 3 14 0 10x 3y 45 ïî îï 3 ìï y = 21- 2x x ìï = 3 x ìï = 3 ï ï í í ï í 8 ï x = 24 3 ï y = 15 y ï = 5 ïî ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (3; ) 5 2 2 2 2
x + y = 3 + 5 = 34 . Câu 25. Đáp án D. ìï ( 2 x + y) + ( 3 x - y) = 4 2
ìï x + 2y + 3x - 3y = 4 5 ìï x - y = 4 Ta có ï ï í í ï í (
ï x + y) + 2(x - y) = 5 x
ï + y + 2x - 2y = 5 3 ï x - y = 5 ïî ïî îï 5 ìï x - y = 4 y ìï = 3x - 5 y ìï = 3x - 5 ï ï í ï í í y ï = 3x - 5 5 ï x - 3 ( x - 5) = 4 5
ï x - 3x + 5 = 4 ïî ïî ïî ìï 1 ìï ì 1 ï 1 ï x ïï = - x ï x ï = - ï = - ï ï 2 ï 2 í 2 í í ï ï -1 ï 13 y ï = 3x - 5 ï y ï ïî ï = 3. - 5 y ïï = - ïî 2 ï ï ïî 2 æ 1 13ö
Vậy hệ phương trình có nghiệm duy nhất (x;y) ç = - ç ; ÷ - ÷ x > y ç
và x - y = 6 . çè 2 2 ÷÷ø
II. Giải hệ phương trình bằng phương pháp cộng đại số Câu 1. Đáp án A. 8 ìï x + 7y = 16 8 ìï x + 7y = 16 8 ìï x + 7y = 16 Ta có ï ï ï í í í 8 ï x - 3y = -24 8
ï x + 7y - (8x - 3y) = 16 - (-24) 1 ï 0y = 40 ïî ïî ïî ì y ìï = 4 y ï = 4 ï ï ï æ 3 ö í í ç ÷
3 . Vậy hệ phương trình có nghiệm duy nhất (x;y) = - ç ; 4÷. 8 ï x + 7.4 = 16 ç ÷ ï x ï ç ÷ î ï = - è 2 ø ïî 2 Câu 2. Đáp án D.
Ta giải hệ phương trình bằng cách nhân hai vế của phương trình thứ hai với 2 rồi trừ từng vế của hai phương trình: ìï ì 4x + 3y = 6 ï ì 4x + 3y = 6 ï ì 4x + 3y = 6 ï ì 4x + 3 - ( 2) = 6 ïx = ï ï ï ï ï 3 í í í í í . ï2x + y = 4 ï4x + 2y = 8 ïy = -2 ïy = -2 ïy = - ïî ïî ïî ïî ïî 2
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (3;-2) . Câu 3. Đáp án B. 2 ìï x - 3y = 1 2 ìï x - 3y = 1 2 ìï x - 3y = 1 x ìï = 2 Ta có ï ï ï ï í í í í 4 ï x + y = 9 1 ï 2x + 3y = 27 1 ï 4x = 28 y ï = 1 ïî ïî ïî ïî
Vậy hệ đã cho có nghiệm duy nhất (x;y) = (2;1) x - y = 2 - 1 = 1 Câu 4. Đáp án D. ì ì ï x ìï ï x ï - = ï 2 - y 3 = 1 ï 2 y 3 1 x ìï - = ï 2 - y 3 = 1 ï ï x 2 y 3 1 ï í í ï ï í í 1 x ïï y 3 2 x ï + = ï 2 + y 6 = 2 (ï 6 + 3 ï )y =1 yï = ïî ïî ï ïî ïïî 6 + 3 ìïï 6 - 3 ì y ï ï = ï 6 - 3 ïï 3 y ï = í í 3 . ïï 6 3 ï - x ï = 1 x ï 2 - 3. = 1 ï ïïî 3 ïî æç 6 - 3ö÷
Vậy hệ đã cho có nghiệm duy nhất (x;y) = 1 ç ; ÷ ç
÷ x + 3 3y = 1 + 3 2 - 3 = 3 2 - 2 . ç 3 ÷÷ è ø Câu 5. Đáp án C.
Nhân hai vế của phương trình thứ nhất với 2 rồi cộng từng vế của hai phương trình 5 ìïï x 3 y 2 2 5 ìïï x 6 y 2 4 6 ìï + = + = ï x 6 = 6 ï ï ï í í í x ïï 6 y 2 2 x ïï 6 y 2 2 x ï - = - = ï 6 - y 2 = 2 ïî ïî ïî ìï 1 ìï x ï ì ï = ï 1 ì ï ï 1 ï 6 ï x ïï = x ï = ï 6 x ï = ï ï í í 6 ï ï 6 í ï 6 í 1 ï ï ï ï ï ï 2 ï . 6 y 2 2 1 ï - = ï - y 2 = 2 ï y ï 2 = -1 y ï = - 6 ïî ïî ïî ïïî 2 æç 6 2 ö÷
Vậy hệ phương trình có nghiệm duy nhất (x;y) = ç ; ÷ - ç ÷ ç 6 2 ÷÷ è ø 6 æç 2ö÷ 3 6
6x + 3 3y = 6. + 3 3.ç ÷ - ç ÷ = 6 - 6 = - . 6 ç 2 ÷÷ 2 2 è ø Câu 6. Đáp án A.
ĐK: x ³ 0;y ³ 0
Nhân hai vế của phương trình thứ nhất với 5 rồi trừ từng vế của hai phương trình: 0 ìï ìï ì ï , 3 x 0, 5 y 3 1 ìï + =
ï ,5 x + 2,5 y = 15 ï ï ï 4, ï 5 y = 13,5 ï y = 3 í í ï ï í í 1
ïï ,5 x 2 y 1,5 1 ï - =
ï ,5 x - 2 y = 1,5 ï ï ï ï - = ï - = î ïî 1,5 x 2 y 1,5 1, 5 x 2.3 1, 5 ïî ïî y ìï = 9 y ìï = 9 y ìï = 9 ï ï ï í í í (thỏa mãn) 1 ï ,5 x = 7,5 ï x = 5 x ï = 25 ï ï ï ïî ïî î
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (25;9) xy = 25.9 = 225 . Câu 7. Đáp án B.
ĐK: x ³ 0;y ³ 0 4 ìï ìï ì ï x 3 y 4 4 ìï - = ï x - 3 y = 4 5 ï y = 0 ïï y = 0 y ìï = 0 Ta có ï ï í í ï ï ï í í í (tm). 2 ïï x y 2 4 ï + = ï x + 2 y = 4 ï ï ï + = ï = x ï = 1 ïî ïî 2 x y 2 2 x 2 ï ïî ïî î
Vậy hệ phương trình có 1 nghiệm duy nhất (x;y) = (1;0) x.y = 0 . Câu 8. Đáp án C. ĐK: x ¹ 0 ìï2 ìï4 ïï y 3 ïï 2y 6 ìï 1 ìï + = + = 1 ï ï x ï ï ï x ï = ï ï = Ta có x x ï í í í 2 í 2 (TM) ï1 ï1 ï ï
ïï - 2y = 4ïï -2y = 4 2 ï x + y = 3 y ï = -1 ï ï ï î ï ïîx ïîx î æ1 ö ç ÷ x 1
Vậy hệ phương trình có 1 nghiệm duy nhất (x;y) = ç ;-1÷ = - ç . çè2 ÷÷ø y 2 Câu 9. Đáp án C. 5
ìï (x + 2y) - 3(x - y) = 99 5
ìï x + 10y - 3x + 3y = 99 2
ìï x + 13y = 99 Ta có ï ï í í ïí x
ï - 3y = 7x - 4y - 17 x
ï - 3y - 7x + 4y = -17 - ï 6x + y = -17 ïî ïî ïî 6
ìï x + 39y = 297
ìï-6x + y = -17 y ìï = 7 ï ï ï í í í ï-6x + y = -17 4 ï 0y = 280 x ï = 4 ïî ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (4;7). Câu 10. Đáp án D. Ta 2
ìï (x + y) - 3(x - y) = 4 2
ìï x + 2y - 3x + 3y = 4 ìï x - + 5y = 4 0 ìï = 1 có ïí ï ï ï í í í (VL) x
ï + 4y = 2x - y + 5 ï ï + - + = ï- + = ï- + = î x 4y 2x y 5 x 5y 5 x 5y 5 ïî ïî ïî
Vậy hệ phương trình vô nghiệm. Câu 11. Đáp án D. ìïx + y x - y ïï = 3
ìï x + 3y = 5x - 5y 2 ìï x = 8y x ìï = 4y Ta có ï 5 3 í ï ï ï í í ï í x y ï x ï = 2y + 4 x ï = 2y + 4 x ï = 2y + 4 ï = + 1 ïî ïî îï ïïî4 2 x ìï = 4y y ìï = 2 ï ï í í 2 ï y - 4 = 0 x ï = 8 ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (2; 8) x > 0;y > 0 . Câu 12. Đáp án A. ìï y 2x - 3 x ïï + = 2
ìï x + y = 2x - 3 y ìï = -3 x ìï = 31 Ta có ï 2 2 í ï ï ï í í ï í x 25 - 9y ï 4
ï x + 24y = 25 - 9y 4 ï x + 33y = 25 y ï = -3 ï + 3y = îï ïî îï ïïî2 8
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (31;-3)
x > 0;y < 0 . Câu 13. Đáp án B. ( ìï x - 3) 2 ( y + 5) = 2 ( x + 7)(y - 1) 7 ìï x -13y = 8 42
ìï x - 78y = 48 Ta có ïí ï ï í ï í 4 ( x + 1)(3y - ) 6 = (6x - ) 1 (2y + ) 3 ï ï- + = ï- + = î 42x 5y 3 42x 5y 3 ïî ïî Câu 14. Đáp án C.
Điều kiện: x ³ 1;y ³ 0 3 ìï ìï ì
ï x - 1 + 2 y = 13 3 ï x 1 2 y 13 2 ï - + = ï x - 1 - y = 4 Ta có ïí ï ï í í 2
ïï x -1 - y = 4 ï ï ï ï - - = ï - = î 4 x 1 2 y 8 7 x 1 21 ïî ïî ìïï x -1 = 3 x ìï -1 = 9 x ìï = 10 ï ï ï í í í (thỏa mãn) 3.3 ïï + 2 y = 13 2 ï y = 4 y ï = 4 ï ï ïî ïî î
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (10; 4) . Nên x - y = 10 - 4 = 6 . Câu 15. Đáp án B.
ìïï x + 3 -2 y +1 = 2
Điều kiện: x ³ -3;y ³ 1 - Ta có ïí 2
ïï x + 3 + y +1 = 4 ïî 2
ìïï x 3 4 y 1 4 ìï + - + =
ï x + 3 - 2 y + 1 = 2 ï ï í í 2 ïï x 3 y 1 4 ï + + + = - ï 5 y + 1 = 0 ïî ïî ìïy = - ì 1 ïy = -1 ìï ì y = -1 ïy = - ï ï ï ï 1 ï í í í í (tm). ï x + 3 - 2. - ( 1) + 1 = 2 ï x + 3 = 2 ïx + 3 = 4 ïx = ï ï ï 1 ïî ïî î ïî
Vậy hệ phương trình có nghiệm duy nhất (x;y) = (1; 1 - ).
Nên x + y = 1 + (-1) = 0 . Câu 16. Đáp án A.
Thay x = 3;y = -4 vào hệ phương trình ta được ìï 2 ìï a.3 + ( b -4) = -1 6 ìï a - 4b = -1 1
ìï 2a - 8b = -2 ì b = 1 ï ï ï 17 ï b = 17 ï ï ï í í í í . ï í .3 b -a.(-4) = 5 4 ï a + 3b = 5 1 ï 2a + 9b = 15 1 ï ï + = ï î ïî ïî 4a 3b 5 ï a î ï = ïî 2 1
Vậya = ;b = 1 . 2 Câu 17. Đáp án D.
Thay x = 2;y = -3 vào hệ phương trình ta được 4 ìï a.2 + 2 . b (-3) = -3 8 ìï a - 6b = -3 5 ìï a = 5 ï ï ï í í í 3 ï .2 b + a(-3) = 8 ï-3a + 6b = 8 ï-3a + 6b = 8 ïî ïî ïî ìï ì a ìï = 1 a = 1 a ï = 1 ï ï ï ï 11 í í í
11 . Vậy a = 1;b = . ï-3.1 + 6b = 8 6 ï b = 11 ïî ï b ï î ï = 6 îï 6 Câu 18. Đáp án C.
ĐK: x ¹ 2;y ¹ 1 ìï 1 1 ìï 1 1 ïï 2 ï + = ï + = 2 ïïx - 2 y + 1 ïïx - 2 y + 1 í í ï 2 3 ï 1 1 ïï 1 2 ï - = ï . - 3. = 1 ïx - 2 y - 1 ï x - 2 y - 1 ïî ïî u ìï + v = 2 2 ìï u + 2v = 4 5 ìï v = 3 ï ï ï í í í 2 ï u - 3v = 1 2 ï u - 3v = 1 u ï + v = 2 ïî ïî ïî 1 1 Đặt = u;
= v (u;v ¹ 0) ta có hệ ìï 3 ìï 3 ï ï x - 2 y - 1 v ï = v ï = ï 5 ï 5 í í (TM ) ï 3 ï 7 u ïï 2 u ï + = ï = ïî 5 ï ï ïî 5 ìï 5 ìï ì 19 ï 1 7 ï x ïï - 2 ï ï = 1 3 = x ï =
Thay lại cách đặt ta được ï ï 7 ï 7 íx - 2 5 = í í (TM ) ï y - 1 5 ï 5 ï 8 ïï y ï ïî ï 1 y ï - = ï = ïî 3 ï ï ïî 3 æ19 8ö
Vậy hệ phương trình có nghiệm duy nhất (x;y) ç = ç ; ÷÷ ç çè 7 3÷÷ø Câu 19. Đáp án D.
Điều kiện: x ³ 0;x ¹ 7;y ³ 0 ìï 5 7 ïï a - 4b = 21 ìï a -12b = 5 1 1 ï Đặt = a; = b ta được ï 3 ï í í 1 x - 7 y + 6 ï 1 ï 20 ïï a +12b = 2 5 ï a + 3b = 2 ï ï î 6 ïî 6 ìï 1 ìï ì 1 21 ï a - 12b = 5 ï a ïï = a ïï = ï ï 3 ï 3 í 41 í í 41 ïï a = ï 1 ï 1 ï 21. ï ïî ï - 12b = 5 ï 3 b ï = ïî 3 ï ï ïî 6 ìï 1 1 ïï = ì ï ï ì ï x - 7 3 ï x - 7 = 3 x ï = 100 Trả lại biến ta có ï ï í í í (TM ) . ï 1 1 ï ï = ï y + 6 = 6 y ï = 0 ï ï ïî î ïï y + 6 6 ïî
Vậy hệ phương trình có nghiệm (x;y) = (100; 0). Câu 20. Đáp án C. ìïx + 1 y ïï - = x + y + 1 Ta có ï 4 2 í ïx - 2 y - 1 ïï + = x + y - 1 ïïî 2 3 ìï ìï ì 1
x + 1 - 2y = 4x + 4y + 4 3 ï x + 6y = -3 ï ï y ïï = - ï í í í 2 3
ï x - 6 + 2y - 2 = 6x + 6y - 6 3 ï x + 4y = -2 ïî ïî x ïï = 0 ïî 1
Thay x = 0;y = - vào phương trình (m + 2)x + 7my = m - 225 ta được 2 æ 1ö ç ÷ 9 (m + 2).0 + 7m - ç
÷ = m - 225 m = 225 m = 50 ç . çè 2÷÷ø 2 Câu 21. Đáp án A. ìï2x + 1 y + 1 4x - 2y + 2 ïï - = Ta có ï 3 4 5 í ï2x - 3 y - 4 ïï - = -2x + 2y - 2 ïïî 4 3 40
ìï x + 20 -15y -15 = 48x - 24y + 24 8
ìï x - 9y = -19 ï ï í í 6
ï x - 9 - 4y + 16 = -24x + 24y - 24 3
ï 0x - 28y = -31 ïî ïî ìï ì 11 120 ï x - 135y = -285 ï x ïï = ï í í 2 120 ï x - 112y = -124 ïî y ïï = 7 ïî 11 Thay x =
;y = 7 vào phương trình 6mx - 5y = 2m - 66 ta được 2 11 6m.
- 5.7 = 2m - 66 31m = -31 m = -1 . 2 Câu 22. Đáp án B.
Đường thẳng y = ax + b đi qua điểm ( A 4 - ; 2 - ) 4 - a + b = 2 - (1)
Đường thẳng y = ax + b đi qua điểm B(2;1) 2a + b = 1 (2) ìï 1 ìï ì - + = - ï a ï ìï - = - ï = 1 4a b 2 6a 3 ï ï ï a ï ï ï = Từ (1) và (2) ta có hệ 2 ï í í í í 2 2 ï a + b = 1 2 ï a + b = 1 ï 1 ï ïî ïî 2. ïï + b = 1 b ï = 0 ï ïïî 2 î 1
Vậy a = ;b = 0 . 2
III. Hệ phương trình bậc nhất hai ẩn chứa tham số Câu 1. Đáp án B. ìï ì 2.1 + . b 3 = a ï ì a - 3b = 2 ï3a - 9b = 6
Thay x = 1;y = 3 vào hệ ta có: ï ï ï í í í ï .1 b + a.3 = 5 ï3a + b = 5 ï3a + b = ïî ïî ïî 5 ìïï 1 ìï10b = -1 ïb = - ï ï í í 10 . ï3a + b = 5 ï ïî ï 17 ïa = ïïî 10 -1 17 Vậy a = ;b =
thì hệ phương trình có nghiệm x = 1,y = 3 10(a + b) = 16 10 10 Câu 2. Đáp án A. ìï 5m + ï 9 ìï ì
x + 2y = m + 3 ï ì
2x + 4y = 2m + 6
ïx + 2y = m + 3 ïx = Ta có ï ï ï ï í í í í 7
ï2x - 3y = m
ï2x - 3y = m ï7y = m + 6 ï m + ïî ïî ïî ï 6 ïy = ïïî 7 æ5m 9 m 6ö + +
Hệ phương trình có nghiệm duy nhất (x;y) ç = ç ; ÷÷ ç çè 7 7 ÷÷ø
Lại có x + y = -3 hay 5m + 9 m + 6 +
= -3 5m + 9 + m + 6 = -21 6m = -36 m = -6 7 7
Vậy với m = -6 thì hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x + y = -3 . Câu 3. Đáp án C. ìï ì
2x + y = 5m - 1 ï ì
y = 5m - 1 - 2x ï ì
y = 5m - 1 - 2x ïx = 2m Ta có ï ï ï ï í í í í ïx - 2y = 2 ïx - 2 5
( m - 1 - 2x) = 2 ï5x = 10m ïy = m - ïî ïî ïî ïî 1 Thay vào 2 2
x - 2y = -2 ta có 2 x - 2 2y = -2 2 2m - 2(m - 2 ( ) 1) = -2 ém = 0 2 ê
2m + 4m = 0 ê . m = - êë 2 Vậy m Î {-2; } 0 . Câu 4. Đáp án B. ìï 7 2
ïï x + 3y = -m 4
ìï x + 6y = 7 - 2m 7 ìï y = 7 - 7m Ta có ï ï ï í 2 í í ï 4
ï x - y = 5m 4 ï x - y = 5 4 ï - = 5 m x y m ï ï î ïî ïî y ìï = 1- m y ìï = 1- m ï ï í í 4 ï x - 1 ( - m) = 5m x ï = 4m + 14 ïî ïî 2 25 æ ö 25 4m 1 25 2 2 + Thay vào 2 2 x + y = ta có ç ÷ x + y = ç ÷ + (1 - 2 m) = 16 ç ÷ 16 ç 4 ÷ è ø 16 2 m + m + + 2 16 8 1
16m - 32m + 16 = 25 2
32m - 24m - 8 = 0 2 4m - 3m - 1 = 0 ém = ê 1 2
4m - 4m + m - 1 = 0 (4m + 1)(m - 1) = 0 êê 1 m = - êë 4 1 Mà m >
m = 1 thỏa mãn. Vậy m = 1. 2 Câu 5. Đáp án D. x ìï + y = 2
Thay m = 2 vào hệ ta được ïí 2 ï x + y = 3 ïî x ìï + y = 2 x ìï + y = 2 x ìï = 1 Khi đó ï ï ï í í í 2 ï x + y = 3 x ï = 1 y ï = 1 ïî ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (1;1) khi m = 2 . Câu 6. Đáp án A.
Thay m = 1 vào hệ phương trình đã cho ta được: x ìï -y = 2 2 ìï x - 2y = 4 3 ìï x = 9 x ìï = 3 ï ï ï ï í í í í x ï + 2y = 5 x ï + 2y = 5 x ï + 2y = 5 y ï = 1 ïî ïî ïî ïî
Vậy hệ phương trình có nghiệm duy nhất (3;1) khi m = 1. Câu 7. Đáp án A.
Từ (m - 1)x + y = 2 thế vào phương trình còn lại ta được phương trình:
mx + 2 - (m - 1)x = m + 1 x = m - 1 suy ra 2
y = 2 - (m - 1) với mọi m
Vậy hệ phương trình luôn có nghiệm duy nhất x y = (m - - m - 2 ( ; ) 1;2 ( 1) )
x + y = m - + - m - 2 = - 2 2 2( 1) 2 ( 1) m + 4m - 1 2
= 3 - (m - 2) £ 3 với mọi m . Câu 8. Đáp án B.
Từ phương trình (1 ) x - my = m x = m + my thế vào phương trình (2) ta được phương trình: 1 m 2 2 2 2 - 2
m(m + my) + y = 1 m + m y + y = 1 (m + 1)y = 1 - m y = 1 + 2 m 2 1 - m 2m (vì 2
1 + m > 0;"m )suy ra x = m + m. = với mọi m 2 2 1 + m 1 + m æ 2 2m 1 m ö -
Vậy hệ phương trình luôn có nghiệm duy nhất (x;y) ç = ç ; ÷÷ ç ÷ 2 2
çè1 + m 1 + m ÷ø 2 2 2m 1 - m m + 2m - 1 x - y = - = 2 2 2 1 + m 1 + m 1 + m Câu 9. Đáp án B. ìï ì
(m - 2)x - 3y = -5 ï(m - ) 2 3
( - my) - 3y = -5 Ta có ï ï í í ïx + my = 3 ïx = - ïî ïî 3 y m ìï 2 ì
3m - m y - 6 + 2my - 3y = -5
ï(m2 - 2m + 3)y = 3m - ï ï 1 1 ( ) í í . ïx = 3 - my ïx = 3 - ï my 2 ( ) ï ï î î Ta có: 2 2
m - 2m + 3 = (m - 1) + 2 > 0 "m nên PT (1) có nghiệm duy nhất "m Hay hệ
phương trình có nghiệm duy nhất "m 3m - 1 9 - 5m Từ (1) ta có:y =
thay vào (2) ta có x = 2 m - 2m + 3 2 m - 2m + 3 æ 9 5m 3m 1 ö - - Vậy (x;y) ç = ç ; ÷÷ ç 2 2 ÷
çèm - 2m + 3 m - 2m + 3÷ø Câu 10. Đáp án D.
ìïmx -y = 2m + 1 Ta có ïí ï2x + my = 1 - ïî m ìï ì
y = mx - 2m - 1
ïy = mx - 2m - ï ï 1 í í
ï2x + m(mx - 2m - ) 1 = 1 - m ï2x + 2 m x - 2 2m - m = 1 - ïî ïî m ì 2 2 (
ï m + 2)x = 2m + ( 1 ) 1 ï í y ï = mx - 2m - ( 1 2) ïî Ta có: 2
m + 2 > 0;"m nên PT (1) có nghiệm duy nhất "m Hệ phương trình có nghiệm duy nhất "m 2 2m + 1 2 2 2m + 1 m - - 3m - 2 Từ (1) ta có:x =
thay vào (2) ta có y = m. - 2m - 1 = 2 m + 2 2 2 m + 2 m + 2 æ 2 2 2m 1 m 3m 2ö + - - - Vậy (x;y) ç = ç ; ÷÷ ç ÷ . 2 2 çè m + 2 m + 2 ÷ø Câu 11. Đáp án A. 3
ìï x + y = 2m + 9 x ìï = m + 2 Ta có ïí ï 2 í
A = xy + x - 1 = 8 - (m - 1) A = 8 khi x ï + y = 5 ï ï = - max î y 3 m ïî m = 1. Câu 12. Đáp án B. x
ìï + my = m + 1 (1) Xét hệ ïí mx ï + y = 2m (2) ïî
Từ (2) y = 2m - mx thay vào (1) ta được 2 2
x + m(2m - mx) = m + 1 2m - m x + x = m + 1 2 2 2 2
(1 - m )x = -2m + m + 1 (m - 1)x = 2m - m - 1 (3)
Hệ phương trình đã cho có nghiệm duy nhất ( ) 3 có nghiệm duy nhất 2
m - 1 ¹ 0 m ¹ 1 ìï 2m + 1 x ïï = ï
Khi đó hệ đã cho có nghiệm duy nhất m + 1 í ï m y ïï = ïïî m + 1 ìï2m + 1 ìï -1 ï ìï ³ ï 2 ï ³ ï ³ 0 x 2 ï ï + ï Ta có m 1 m + 1 x í í í
m + 1 < 0 m < -1 y ï ³ 1 ï m ï -1 ïî ïï ³ 1 ïï ³ 0 ïïîm + 1 ïïîm + 1 Kết hợp với ( )
* ta được giá trị m cần tìm là m < -1. Câu 13. Đáp án C.
Ta xét 2 trường hợp: ì x ìï = -2 2 ï x = -4 ï
+ Nếu a = 0 , hệ có dạng: ï ï í í
5 . Vậy hệ có nghiệm duy nhất. ï-3y = 5 ï y ï î ï = - ïî 3 2 a
+ Nếu a ¹ 0 , hệ có nghiệm duy nhất khi và chỉ khi: 2 ¹
a ¹ -6 (luôn đúng, vì 2 a ³ 0 a -3 với mọi a )
Do đó, với a ¹ 0 , hệ luôn có nghiệm duy nhất.
Tóm lại hệ phương trình đã cho có nghiệm duy nhất với mọi a . Câu 14. Đáp án B. ìï ì
mx + y = 2m ï ì
y = 2m - mx ïy = 2m - ï ï ï mx í í í
ïx + my = m + 1 ïx + m 2
( m - mx) = m + 1 ïx + 2 2m - 2 m x = m + îï ïî ïî 1 ìïy = 2m - ï mx í . ï 2 x(m - ) 1 = 2 2m - m - ïî 1 Với 2 2
m - 1 = 0 m = 1 m = 1
Nếu m = 1 ta được 0x = 0 (đúng với "x ) ⇒ hệ phương trình có vô số nghiệm Nếu m = 1
- ta được 0x = 2 (vô lí) ⇒⇒ hệ phương trình vô nghiệm.
Vậy m = 1 thì hệ đã cho vô số nghiệm. Câu 15. Đáp án A.
Từ PT (1) ta có: y = (a + 1)x - (a + ) 1 ( )
* thế vào PT (2) ta được: x (a 1) (éa 1)x (a 1)ù + - + - + = 2 êë úû 2 2 2 2
x + (a - 1)x - (a - 1) = 2 a x = a + 1 3 ( ) 2 a + 1
Với a ¹ 0 , phương trình (3) có nghiệm duy nhất x = . Thay vào ( ) * ta có: 2 a 2 2 2 a + 1
(a + 1)(a + 1) -a (a + 1) y = (a + 1) - (a + 1) = 2 2 a a 3 2 3 2
a + a + a + 1 - a -a a + 1 = = 2 2 a a æ 2 a 1 a 1ö + +
Suy ra hệ phương trình đã cho có nghiệm duy nhất(x;y) ç = ç ; ÷÷ ç ÷ 2 2 çè a a ÷ø 2 2 a + 1 a + 1 a + a + 2 x + y = + = 2 2 2 a a a Câu 16. Đáp án C. ì 2 ï ì 2
mx - y = m y ï = mx - m ï ï í í 3 2 3 2
ï x + my = m - + 2m + 2 2
ï x + m(mx - m ) = m - + 2m + 2 ï ï ïî ïî ìï 2m + 2 ï ì 2 x y ï = mx - m ï = 2 ï ï ï ï m + 2 í í 2 x
ï (m + 2) = 2m + 2 ï 2m + 2 2 ïïî y ïï = m. - m 2 ïïî m + 2 2m + 2 - 4 m + 2m x = y = 2
(vì m + 2 > 0; "m ) 2 m + 2 2 m + 2 4 m + 2 Suy ra x - y = . 2 m + 2 Câu 17. Đáp án D.
Từ PT (1) ta có: y = (a + 1)x - (a + 1) ( )
* thế vào PT (2) ta được x (a 1) (éa 1)x (a 1)ù + - + - + = 2 êë úû 2 2 2 2
x + (a - 1)x - (a - 1) = 2 a x = a + 1 (3) 2 a + 1
Với a ¹ 0 , phương trình (3) có nghiệm duy nhất x = . Thay vào ( ) * ta có: 2 a 2 2 2 a + 1
(a + 1)(a + 1) -a (a + 1) y = (a + 1) - (a + 1) = 2 2 a a 3 2 3 2
a + a + a + 1 - a -a a + 1 = = 2 2 a a æ 2 a 1 a 1ö + +
Suy ra hệ phương trình đã cho có nghiệm duy nhất(x;y) ç = ç ; ÷÷ ç ÷ 2 2 çè a a ÷ø ì 2 a ï + 1 ï x ìï Î ï Î ï ï 2
Hệ phương trình có nghiệm nguyên: ï a í í (a Î ) y ï Î a ï + 1 ïî ïï Î 2 ïïî a 2 a + 1 1 1
Điều kiện cần: x = = 1 + Î Î mà 2 a > 0 2
a = 1 a = 1 (TM a ¹ 0 2 2 a a 2 a )
Điều kiện đủ: a = 1
- y = 0 Î (nhận); a = 1 y = 2 Î (nhận) Vậy a = 1
hệ phương trình đã cho có nghiệm nguyên. Câu 18. Đáp án C. x ìï + y = 2 Ta có ïí
x + mx = 2 + m x(m + )
1 = m + 2 Nếu m = -1 0.x = 1 (vô lí) mx ï - y = m ïî m + 2 1
Nếu m ¹ -1 x = = 1 + m + 1 m + 1
Để hệ phương trình đã cho có nghiệm nguyên duy nhất x nguyên m = 0;m = 2 - x ìï = 2 Với m 0 ï = í (thỏa mãn) y ï = 0 ïî x ìï = 0 Với m 2 ï = - í (thỏa mãn) y ï = 2 ïî Câu 19. Đáp án A. ìï ì x + 2y = 2 ï ì x = 2 - 2y ïx = 2 - 2y Ta có ï ï ï í í í
ïmx - y = m
ïm(2 - 2y) - y = m ï 2 ( m + 1)y = ïî ïî ïî m 1
Để hệ phương trình có nghiệm duy nhất thì m ¹ - 2 m m 2m + 2 Suy ra y = x = 2 - 2. x = 2m + 1 2m + 1 2m + 1 ìï 2m + 2 x ïï = ï
Vậy hệ có nghiệm duy nhất 2m + 1 í ï m y ïï = ïïî 2m + 1 ìï 2m + 2 ìï 1 ì x ï ï ì ï > ï = > 1 ï > ï x 1 0 ì 1 ï ï ï 2 ï m + 1 > 0 ï + ï m ïï > - Để ï 2m + 1 í í 2m 1 ï í í í 2 m > 0 y ï > 0 ï m ï ï ï > ï î m m 0 y ïï = > 0 ïï > 0 ïî m ï > 0 ï ï ïî 2m + 1 ïïî2m + 1 î 1
Kết hợp điều kiện m ¹ - ta có m > 0 . 2 Câu 20. Đáp án D. mx ìï - y = 2m y ìï = mx - 2m y ìï = mx - 2m Ta có ï ï ï í í í 4
ï x - my = m + 6 2 2 ï ï - - = + ï î 4x m(mx 2m) m 6
x(m - 4) = 2m - m - 6 ïî ïî
Hệ phương trình có nghiệm duy nhất khi 2
m - 4 ¹ 0 m ¹ {2;- } 2 2 2m - m - 6 (2m + 3)(m - 2) 2m + 3 2m + 3 m - Khi đó x = = = y = m. - 2m = 2 m - 4 (m - 2)(m + 2) m + 2 m + 2 m + 2 ìï 2m + 3 ìï 1 ìï 2 x ïï x ïï 2 2 ï = = - ï x = 4 - ï m + 2 ï m + 2 ï m + 2 í í í 2x + y = 3 ï m - ï 2 ï 2 y ïï y ïï 1 y ï = = - + ï = -1 + ïïî m + 2 ïïî m + 2 ïïî m + 2
Vậy hệ thức không phụ thuộc vào m là 2x + y = 3. Câu 21. Đáp án D. ìï ì x + my = 1 ï ì x = 1 - my ï ì x = 1 - my ïx = 1 - ï ï ï ï my í í í 2 í
ïmx - y = -m ïm 1
( - my) - y = -m
ïm - m y - y = -m ï 2 y(m + 1) = ïî ïî ï ï î î 2m 2 2m 2m 1 m 2 - 2
Do m + 1 ³ 1 > 0 y =
x = 1 - my = 1 - = 2 m + 2 1 m + 2 1 m + 1 Xét 2 4m (1 m ) 4m 1 2m m m 2m 1 (1 m ) 2 - 2 2 2 + - 2 + 4 4 + 2 + + 2 2 2 x + y = + = = = = 1 (1 + 2 2 m ) (1 + 2 2 m ) (1 + 2 2 m ) (1 + 2 2 m ) (1 + 2 2 m ) Vậy 2 2
x + y = 1 không phụ thuộc vào giá trị của m . Câu 22. Đáp án C. ìï ì
mx - y = 2m ï ì
y = mx - 2m
ïy = mx - 2m Ta có ï ï ï í í í
ï4x - my = m + 6
ï4x - m(mx - 2m) = m + 6 ï 2 x(m - 4) = 2 2m - m - ïî ïî ïî 6
Hệ phương trình có nghiệm duy nhất khi 2
m - 4 ¹ 0 m ¹ {-2; } 2 2 2m - m - 6 (2m + 3)(m - 2) 2m + 3 2m + 3 Khi đó x = = = y = m. - 2m 2 m - 4 (m - 2)(m + 2) m + 2 m + 2 ìï 2m + 3 x ïï = ï Thay m + 2 í
vào phương trình 6x - 2y = 13 ta được: ï m - y ïï = ïïî m + 2 2m + 3 -m 14m + 18 6. - 2. = 13
= 13 14m + 18 = 13m + 26 m = 8(TM). m + 2 m + 2 m + 2
Vậy m = 8 là giá trị cần tìm. Câu 23. Đáp án A. x
ìï + (m + 1)y = 1 Từ hệ phương trình ïí . 4 ï x - y = -2 ïî ìï 1 ï 4 ìï - = -2 8 ìï - 2 = -4 1 ìï 0 = 1 x x y x y x ï = Ta có hệ ï ï ï ï 10 í í í í 2 ï x + 2y = 5 2 ï x + 2y = 5 2 ï x + 2y = 5 ï 1 ïî ïî ïî y ïï = ïïî 25 1 12 Thay x = vào y =
phương trình x + (m + 1)y = 1 10 5 1 12 5 Ta được + (m + 1).
= 1 1 + 24(m + 1) = 10 24m = -15 m = - . 10 5 8




