Chuyên đề hàm số lượng giác Toán 11 Kết Nối Tri Thức Với Cuộc Sống

Tài liệu gồm 55 trang, được biên soạn bởi thầy giáo Lê Bá Bảo, trình bày lý thuyết, một số dạng toán thường gặp và bài tập trắc nghiệm chuyên đề hàm số lượng giác trong chương trình môn Toán 11 Kết Nối Tri Thức Với Cuộc Sống (KNTTVCS).

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

55 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
HÀM SỐ LƯỢNG GIÁC
TOÁN 11
KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 1
Page: CLB GIÁO VIÊN TRẺ TP HUẾ
PHIẾU HỌC TẬP SỐ 01_TrNg 2021
M«n:
To¸n 11
Chuyªn ®Ò:
HÀM SỐ LƯỢNG GIÁC
Líp To¸n thÇy L£ B¸ B¶O
Tr-êng THPT §Æng Huy Trø S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch
, TP HuÕ
Trung t©m KM 10 H-¬ng Trµ
, HuÕ.
A- LÝ THUYẾT
Giới thiệu tổng quan về các hàm số lượng giác:
cos : 1 sin 1, 1 1x x x
cos
tan cot
: sin 2 sin 2 cos
: tan cot
x x k x x k x
x D x k x x k x


* Các giá trị đặc biệt:
k
2.
4. cos 5. cos 6. cos
tan 8. tan 9
1. sin 0 sin 1 2 3. sin 1 2
22
0 1 2 1 2
2
7. 0 1
4
x x k x x k x x k
x x k x x k x x k
x x k x x k


. tan
cot 11. cot 12. cot
1
4
10. 0 1 1
2 4 4
x x k
x x k x x k x x k
1. Hàm số y = sin x:
* TXĐ:
.D
* Tập giá trị:
: 1 sin 1xx
.
* Hàm số y = sin x là hàm số lẻ. * Tuần hoàn với chu kỳ:
2T
.
Đồ thị:
-
π
π
y
x
-
π
2
π
2
-1
1
O
2. Hàm số y = cos x:
* TXĐ:
.D
* Tập giá trị:
cos: 1 1xx
.
* Hàm số y = cos x là hàm số chẵn. * Tuần hoàn với chu kỳ:
2T
.
Đồ thị:
π
2
-
π
2
x
y
π
-
π
-1
1
O
1
O
cotang
tang
sin
cos
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 2
3. Hàm số y = tan x:
* TXĐ:
\,
2
D k k



* Tập giá trị:
: tanx D x
.
* Hàm số y = tan x là hàm số lẻ. * Tuần hoàn với chu kỳ:
T
.
Đồ thị:
x
y
-
3
π
2
3
π
2
-
π
2
π
2
O
3. Hàm số y = cot x:
* TXĐ:
\,D k k
* Tập giá trị:
co:tx D x
.
* Hàm số y = cot x là hàm số lẻ. * Tuần hoàn với chu kỳ:
T
.
Đồ thị:
x
y
π
2
-
π
π
O
B. MỘT SỐ DẠNG TOÁN THƯỜNG GẶP
Dạng 1: TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ
I. MỘT SỐ KẾT QUẢ
1) Hàm số
Px
y
Qx
xác định khi chỉ khi
cã nghÜa
cã nghÜa.
0
Px
Qx
Qx
2) Hàm số
y P x
xác định khi chỉ khi
cã nghÜa
.
0
Px
Px
3) Hàm số
tany u x
xác định khi chỉ khi
cã nghÜa
.
,
2
ux
u x k k
4) Hàm số
coty u x
xác định khi chỉ khi
cã nghÜa
.
,
ux
u x k k

Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 3
II. BÀI TẬP TỰ LUẬN
Câu 1: Tìm tập xác định của các hàm số sau:
a)
tan .
2
32
4
yx




b)
cot .
3
44
6
yx




c)
sin
.
sin
21
41
x
y
x
d)
22
tan
.
sin cos
x
y
xx
Lời giải:
a) Hàm số xác định khi chỉ khi
cos 20
4
x




, , , .
33
22
4 2 4 8 2
k
x k k x k k x k
Vậy tập xác định của hàm số là
\ , .
3
82
k
Dk




b) Hàm số xác định khi chỉ khi
sin 40
6
x




, , , .44
6 6 24 4
k
x k k x k k x k
Vậy tập xác định của hàm số là
\ , .
24 4
k
Dk




c) Hàm số xác định khi chỉ khi
sin41x
, , .
k
x k k x k42
2 8 2
Vậy tập xác định của hàm số là
\ , .




k
Dk
82
d) Hàm số xác định khi chỉ khi
cos
sin cos
22
0
0
x
xx

cos
, ; .
cos
0
22
20
2
2 4 2
x k x k
x
km
xm
x m x









Vậy tập xác định của hàm số là
\ , , , .
2 4 2
m
D k k m



Câu 2: Tìm tập xác định của các hàm số sau:
a)
tan cot .23y x x
b)
tan
.
sin
2
1
x
y
x
Lời giải:
a) Hàm số xác định khi chỉ khi
sin
sin , ,
cos
0
2 0 2
0
2
x
k
x x k k x k
x
.
Vậy tập xác định của hàm số là
\ , .
2
k
Dk



b) Hàm số xác định khi chỉ khi
sin
cos ,
cos
1
0
0
2
x
x x k k
x

Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 4
Vậy tập xác định của hàm số là
\ , .
2
D k k



Câu 3: Tìm tập xác định của các hàm số sau:
a)
sin .16yx
b)
cos .31yx
c)
cos 2
.
sin 2
x
y
x
d)
sin2 4
.
1 sin3
x
y
x
Lời giải:
a) Hàm số xác định khi chỉ khi
sin sin xx1 6 0 6 1
(đúng với mọi
x
).
Vậy tập xác định của hàm số là
.D
b) Hàm số xác định khi chỉ khi
cos ;
cos cos cos
3 1 1
3 1 0 3 1 3 1
x
x x x


2
3 2 , , .
3
k
x k k x k
Vậy tập xác định của hàm số là
,.
2
3
k
Dk



c) Hàm số xác định khi chỉ khi
cos 2
0
sin 2
sin 2 0,
x
x
xx
(*)
Ta có:
cos 2 0
:
sin 2 0
x
x
x



nên
cos 2
0, .
sin 2
x
x
x
Vậy tập xác định của hàm số là
.D 
d) Hàm số xác định khi chỉ khi
sin2 4
0
1 sin3
1 sin3 0
x
x
x

(*)
Ta có:
sin2 4 0
:
1 sin3 0
x
x
x



nên (*)
x x x k k1 sin3 0 sin3 1 3 2 ,
2

k
xk
2
,
63
Vậy tập xác định của hàm số là
\ , .
2
63
k
Dk




III. BÀI TẬP TỰ LUYỆN
Câu 4: Tìm tập xác định của các hàm số sau:
2) cos 3) 4) cos
6) 7) 8)
cos cos cos
cos
1
1) sin3 sin
31
7 cot sin 2
5) cot 2
2 4 1 1
9) 1
xx
y x y y x y
x
xx
y y x y y
x x x
yx





2
10) 11) 12)
cos
2
32
tan cot
cos cos3
sin
y y y x x
xx
xx
IV. TRẮC NGHIỆM: TẬP XÁC ĐỊNH CỦA HÀM SỐ
Câu 1. Tìm tập xác định của hàm số
sin2 .yx
A.
2;2 .D



B.
1;1 .D



C.
.D
D.
\.Dk
Câu 2. Xét bốn mệnh đề sau:
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 5
(1): Hàm số
sinyx
có tập xác định là
.
(2): Hàm số
cosyx
có tập xác định là
.
(3): Hàm số
tanyx
có tập xác định là
\.k
(4): Hàm số
cotyx
có tập xác định là
\.
2
k



Tìm số phát biểu đúng.
A.
1.
B.
2.
C.
3.
D.
4.
Câu 3. Tìm tập xác định của hàm số
2cot sin 3 .y x x
A.
\.
2
D k k



B.
\.D k k
C.
.D
D.
\.
2
k
Dk



Câu 4. Tìm tập xác định của hàm số
2
tan .
3
yx




A.
2
\.
3
D k k



B.
\.
2
D k k



C.
\.
6
D k k



D.
\.D k k
Câu 5. Tìm tập xác định của hàm số
tan cot .y x x
A.
\.
2
D k k



B.
\.
2
D k k



C.
.D
D.
\.
42
D k k




Câu 6. Tìm tập xác định của hàm số
cot
.
sin 1
x
y
x
A.
\ 2 .
2
D k k



B.
\.
2
D k k



C.
\ 2 ; .
2
D k k k




D.
\.
22
D k k




Câu 7. Tìm tập xác định của hàm số
2017
2016tan 2 .yx
A.
\.
2
D k k



B.
\.
2
D k k



C.
.D
D.
\.
42
D k k




Câu 8. Tìm tập xác định của hàm số
22
1
.
sin cos
y
xx
A.
\.
2
D k k



B.
\.
2
D k k



Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 6
C.
.D
D.
\.
42
D k k




Câu 9. Tìm tập xác định của hàm số
1
.
sin3 sin
y
xx
A.
\.
2
D k k



B.
\.
2
D k k



C.
.D
D.
\.
42
D k k




Câu 10. Tìm tập xác định của hàm số
1
.
sin 3 cos
y
xx
A.
\.
3
D k k



B.
\.
6
D k k



C.
.D
D.
\ 2 .
3
D k k



Câu 11. Tìm tập xác định của hàm số
tan
.
sin 1
x
y
x
A.
\ 2 .
2
D k k



B.
\.
2
D k k



C.
\.
2
D k k



D.
\.
42
D k k




Câu 12. Tập xác định của hàm số
2 cos
sin3
x
y
x
là
A.
\.
3
k
Dk



B.
\.D k k
C.
\.
4
k
Dk



D.
\.
2
k
Dk



Câu 13. Tập xác định của hàm số
sin 1yx
là
A.
.D 
B.
.D
C.
2.
2
D k k


D.
\ 2 .
2
D k k



Câu 14. Tập xác định của hàm số
1
2sin 5
y
x
là
A.
.D 
B.
.D
C.
2.
2
D k k


D.
\ 2 .
2
D k k



Câu 15. Tìm tập xác định của hàm số
2 sin
.
1 cos
x
y
x
A.
\.D k k
B.
\ 2 .D k k
C.
\.
2
D k k



D.
\.
2
D k k



Câu 16. Hàm số nào sau đây có tập xác định là
?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 7
A.
sin .yx
B.
tan2 .yx
C.
cos2 .yx
D.
2
cot 1 .yx
Câu 17. Hàm số nào sau đây có tập xác định là
?
A.
2cos .yx
B.
2
tan2
.
sin 1
x
y
x
C.
1
cos .y
x
D.
sin2 3
.
cos4 5
x
y
x
Câu 18. Tập xác định
D
của hàm số
1
tan
4
y
x



là
A.
3
\ , .
4
D k k



B.
\ , .
2
D k k



C.
\ , .
42
D k k




D.
\ , .
4
D k k



Câu 19. Tập xác định
D
của hàm số
2
3tan 5
1 sin
x
y
x
là
A.
\ 2 , .
2
D k k



B.
\ , .
2
D k k



C.
\ , .D k k
D.
.D
Câu 20. Tìm tập xác định
D
của hàm số
tan cos .
2
yx



A.
\ , .D k k
B.
\ 2 1 , .D k k
C.
.D
D.
\ 2 , .D k k
Câu 21. Tìm tập xác định
D
của hàm số
cot cos .
2
yx



A.
\ , .D k k
B.
\ 2 1 , .D k k
C.
.D
D.
\ , .
2
D k k



Câu 22. Tìm
m
để hàm số
2 sin2
cos 1
x
y
mx
xác định trên toàn trục số.
A.
1 1.m
B.
1 1.m
C.
0.m
D.
0 1.m
Câu 23. Cho hàm số
2 3sin .y m x
Có bao nhiêu giá trị nguyên của tham số
m
thuộc
0;2022
để
hàm số xác định trên ?
A.
2018.
B.
2019.
C.
2020.
D.
2021.
Câu 24. Tìm tập hợp tất cả các giá trị
m
để hàm số
1
sin2
y
xm
có tập xác định là
.
A.
1;1 .


B.
; 1 1; . 
C.
1;1 .
D.
; 1 1; .

 

Câu 25. Tìm tập hợp tất cả các giá trị
m
để hàm số
2
cos 4y x m
có tập xác định là
.
A.
1;1 .


B.
;0 .
C.
; 1 .

D.
;0 .

V. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: TẬP XÁC ĐỊNH CỦA HÀM SỐ
Câu 1. Tìm tập xác định của hàm số
sin2 .yx
A.
2;2 .D



B.
1;1 .D



C.
.D
D.
\.Dk
Lời giải:
Chú ý phân biệt giữa tập giá trị và tập xác định của hàm số.
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 8
Chọn đáp án C.
Câu 2. Xét bốn mệnh đề sau:
(1): Hàm số
sinyx
có tập xác định là
.
(2): Hàm số
cosyx
có tập xác định là
.
(3): Hàm số
tanyx
có tập xác định là
\.k
(4): Hàm số
cotyx
có tập xác định là
\.
2
k



Tìm số phát biểu đúng.
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Hàm số
tanyx
có tập xác định là
\.
2
kk




Vậy (3) sai.
Hàm số
cotyx
có tập xác định là
\.kk
Vậy (4) sai.
Chọn đáp án B.
Câu 3. Tìm tập xác định của hàm số
2cot sin3 .y x x
A.
\.
2
D k k



B.
\.D k k
C.
.D
D.
\.
2
k
Dk



Lời giải:
Hàm số xác định khi chỉ khi
sin 0 , .x x k k
Vậy tập xác định của hàm số là
\.D k k
Chọn đáp án B.
Câu 4. Tìm tập xác định của hàm số
2
tan .
3
yx




A.
2
\.
3
D k k



B.
\.
2
D k k



C.
\.
6
D k k



D.
\.D k k
Lời giải:
Hàm số xác định khi chỉ khi
22
cos 0 , ,
3 3 2 6
x x k k x k k



Vậy tập xác định của hàm số là
\.
6
D k k



Chọn đáp án C.
Câu 5. Tìm tập xác định của hàm số
tan cot .y x x
A.
\.
2
D k k



B.
\.
2
D k k



Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 9
C.
.D
D.
\.
42
D k k




Lời giải:
Hàm số xác định khi chỉ khi
sin 0
sin2 0 2 , , .
cos 0
2
x
k
x x k k x k
x
Vậy tập xác định của hàm số là
\.
2
D k k



Chọn đáp án B.
Câu 6. Tìm tập xác định của hàm số
cot
.
sin 1
x
y
x
A.
\ 2 .
2
D k k



B.
\.
2
D k k



C.
\ 2 ; .
2
D k k k




D.
\.
22
D k k




Lời giải:
Hàm số xác định khi chỉ khi
sin 0
,.
sin 1 2
2
x x k
k
x x k
Vậy tập xác định của hàm số là
\ 2 ; .
2
D k k k




Chọn đáp án C.
Câu 7. Tìm tập xác định của hàm số
2017
2016tan 2 .yx
A.
\.
2
D k k



B.
\.
2
D k k



C.
.D
D.
\.
42
D k k




Lời giải:
Hàm số xác định khi chỉ khi
cos2 0 2 , , .
2 4 2
k
x x k k x k
Vậy tập xác định của hàm số là
\.
42
D k k




Chọn đáp án B.
Câu 8. Tìm tập xác định của hàm số
22
1
.
sin cos
y
xx
A.
\.
2
D k k



B.
\.
2
D k k



C.
.D
D.
\.
42
D k k




Lời giải:
Ta có:
22
11
.
cos2
sin cos
y
x
xx

Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 10
Hàm số xác định khi chỉ khi
cos2 0 2 , , .
2 4 2
k
x x k k x k
Vậy tập xác định của hàm số là
\.
42
D k k




Chọn đáp án D.
Câu 9. Tìm tập xác định của hàm số
1
.
sin3 sin
y
xx
A.
\.
2
D k k



B.
\.
2
D k k



C.
.D
D.
\.
42
D k k




Lời giải:
Ta có:
11
.
sin3 sin 2sin2 cos
y
x x x x

Hàm số xác định khi chỉ khi
sin2 0
sin2 0 2 , , .
cos 0
2
x
k
x x k k x k
x
Vậy tập xác định của hàm số là
\.
2
D k k



Chọn đáp án B.
Câu 10. Tìm tập xác định của hàm số
1
.
sin 3 cos
y
xx
A.
\.
3
D k k



B.
\.
6
D k k



C.
.D
D.
\ 2 .
3
D k k



Lời giải:
Hàm số xác định khi chỉ khi
sin 3 cos 0xx
sin 3 cos tan 3 , .
3
x x x x k k
Vậy tập xác định của hàm số là
\.
3
D k k



Chọn đáp án A.
Câu 11. Tìm tập xác định của hàm số
tan
.
sin 1
x
y
x
A.
\ 2 .
2
D k k



B.
\.
2
D k k



C.
\.
2
D k k



D.
\.
42
D k k




Lời giải:
Hàm số xác định khi chỉ khi
cos 0
cos 0 , .
sin 1
2
x
x x k k
x
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 11
Vậy tập xác định của hàm số là
\.
2
D k k



Chọn đáp án C.
Câu 12. Tập xác định của hàm số
2 cos
sin3
x
y
x
là
A.
\.
3
k
Dk



B.
\.D k k
C.
\.
4
k
Dk



D.
\.
2
k
Dk



Lời giải:
Hàm số xác định khi chỉ khi

2 cos 0
(*)
sin3 0
x
x
Ta có
: 1 cos 1 1 cos 2 3.x x x
Lúc đó, (*)
sin3 0 3 , , .
3
k
x x k k x k
Vậy tập xác định của hàm số là
\.
3
k
Dk



Chọn đáp án A.
Câu 13. Tập xác định của hàm số
sin 1yx
là
A.
.D 
B.
.D
C.
2.
2
D k k


D.
\ 2 .
2
D k k



Lời giải:
Hàm số xác định khi chỉ khi
sin 1 0 sin 1 (*)xx
Ta có
: 1 sin 1.xx
Lúc đó, (*)
sin 1 2 , .
2
x x k k
Vậy tập xác định của hàm số là
2.
2
D k k


Chọn đáp án C.
Câu 14. Tập xác định của hàm số
1
2sin 5
y
x
là
A.
.D 
B.
.D
C.
2.
2
D k k


D.
\ 2 .
2
D k k



Lời giải:
Hàm số xác định khi chỉ khi
5
2sin 5 0 sin (*)
2
xx
Ta có
: 1 sin 1.xx
Lúc đó, (*) vô nghiệm.
Vậy tập xác định của hàm số là
.D 
Chọn đáp án A.
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 12
Câu 15. Tìm tập xác định của hàm số
2 sin
.
1 cos
x
y
x
A.
\.D k k
B.
\ 2 .D k k
C.
\.
2
D k k



D.
\.
2
D k k



Lời giải:
Hàm số xác định khi chỉ khi
2 sin
0
(*)
1 cos
1 cos 0
x
x
x

Ta có
1 sin 1 1 sin 2 3
:.
1 cos 1 1 cos 0
xx
x
xx


Lúc đó, (*)
1 cos 0 cos 1 2 , .x x x k k
Vậy tập xác định của hàm số là
\ 2 .D k k
Chọn đáp án B.
Câu 16. Hàm số nào sau đây có tập xác định là
?
A.
sin .yx
B.
tan2 .yx
C.
cos2 .yx
D.
2
cot 1 .yx
Câu 17. Hàm số nào sau đây có tập xác định là
?
A.
2cos .yx
B.
2
tan2
.
sin 1
x
y
x
C.
1
cos .y
x
D.
sin2 3
.
cos4 5
x
y
x
Lời giải:
Xét hàm số
sin2 3
.
cos4 5
x
y
x
Ta có
1 sin2 1 2 sin2 3 4
sin2 3
: 0.
1 cos4 1 4 cos4 5 6
cos4 5
xx
x
x
xx
x


Vậy hàm số
sin2 3
cos4 5
x
y
x
có tập xác định là
.
Chọn đáp án D.
Câu 18. Tập xác định
D
của hàm số
1
tan
4
y
x



là
A.
3
\ , .
4
D k k



B.
\ , .
2
D k k



C.
\ , .
42
D k k




D.
\ , .
4
D k k



Lời giải:
Hàm số xác định khi thỏa mãn đồng thời các điều kiện sau:
tan
4
x



xác định
cos 0.
4
x



1
tan 0 sin 0.
44
xx

2
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 13
Từ
1
và
2,
suy ra hàm số xác định
sin cos 0 sin2 0
4 4 4
x x x
2.
4 4 2
x k x k k



Câu 19. Tập xác định
D
của hàm số
2
3tan 5
1 sin
x
y
x
là
A.
\ 2 , .
2
D k k



B.
\ , .
2
D k k



C.
\ , .D k k
D.
.D
Lời giải:
Hàm số xác định khi thỏa mãn đồng thời các điều kiện sau:
22
1 sin 0 sin 1.xx
1
tanx
xác định
cos 0.x
2
Từ
1
và
2,
suy ra hàm số xác định
cos 0 .
2
x x k k
Câu 20. Tìm tập xác định
D
của hàm số
tan cos .
2
yx



A.
\ , .D k k
B.
\ 2 1 , .D k k
C.
.D
D.
\ 2 , .D k k
Lời giải:
Hàm số xác định khi và chỉ khi
cos , cos 1 2 ,
22
x k k x k k

øng víi
øng víi
cos 1 0
2,
,.
2,
cos 1 1
xk
x k k
x k k
x k k
xk





Chọn đáp án A.
Câu 21. Tìm tập xác định
D
của hàm số
cot cos .
2
yx



A.
\ , .D k k
B.
\ 2 1 , .D k k
C.
.D
D.
\ , .
2
D k k



Lời giải:
Hàm số xác định khi và chỉ khi
cos , cos 2 ,
2
x k k x k k
cos 0 0 , .
2
x k x k k
øng víi
Chọn đáp án D.
Câu 22. Tìm
m
để hàm số
2 sin2
cos 1
x
y
mx
xác định trên toàn trục số.
A.
1 1.m
B.
1 1.m
C.
0.m
D.
0 1.m
Lời giải:
Hàm số xác định trên khi và chỉ khi
cos 1 0,mx
.x
1
Khi
0m
thì
1
luôn đúng nên nhận giá trị
0.m
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 14
Khi
0m
thì
cos 1mx
có tập giá trị là đoạn
1; 1 .mm


Do đó để
1
đúng khi và chỉ
khi
0
1 0 1 0 1.
m
m m m

Khi
0m
thì
cos 1mx
có tập giá trị là đoạn
1; 1mm



Do đó để
1
đúng khi và chỉ
khi
0
1 0 1 1 0.
m
m m m

Kết hợp ba trường hợp ta được:
1 1.m
Câu 23. Cho hàm số
2 3sin .y m x
Có bao nhiêu giá trị nguyên của tham số
m
thuộc
0;2022
để
hàm số xác định trên ?
A.
2018.
B.
2019.
C.
2020.
D.
2021.
Lời giải:
Hàm số xác định trên khi và chỉ khi
2 3sin 0,mx
x
3
2 3sin , 2 max 3sin 2 3
2
m x x m x m m
0;2022
2;3;4;...;2021 .
m
m
m

Câu 24. Tìm tập hợp tất cả các giá trị
m
để hàm số
1
sin2
y
xm
có tập xác định là
.
A.
1;1 .


B.
; 1 1; . 
C.
1;1 .
D.
; 1 1; .

 

Lời giải:
Yêu cầu bài toán
:sin2 1;1
sin2 0 sin2 1;1
xx
x m m x m





; 1 1; .m  
Chọn đáp án B.
Câu 25. Tìm tập hợp tất cả các giá trị
m
để hàm số
2
cos 4y x m
có tập xác định là
.
A.
1;1 .


B.
;0 .
C.
; 1 .

D.
;0 .

Lời giải:
Yêu cầu bài toán
2
:cos 4 0;1
2 2 2
cos 4 0 cos 4 mincos 4 0.
xx
x m m x m x



;0 .m

Chọn đáp án D.
Dạng 2: TÌM GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
I. MỘT SỐ KẾT QUẢ
1)
2 1 *
: 1 sin 1, 1 sin 1, .
n
x x x n
2 1 *
: 1 cos 1, 1 cos 1, .
n
x x x n
2)
2*
: 0 sin 1, 0 sin 1, .
n
x x x n
2*
: 0 cos 1, 0 cos 1, .
n
x x x n
II. BÀI TẬP TỰ LUẬN
Câu 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a)
sin , ; .
3
0
4
y x x




b)
cos , ; .2 2 5 0
6
y x x



Lời giải:
a) Sử dụng đường tròn lượng giác:
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 15
x
y
4
_
3
π
0
2
π
1
O
Ta có:
; : sin .
3
0 0 1
4
xx



Vậy
3
0;
4
max 1
x
y



đạt được khi
3
sin 1 0; ;
24
xx




3
0;
4
min 0
x
y



đạt được khi
3
sin 0 0 0; .
4
xx



b) Ta có:
; ; .0 2 0
63
xx

Sử dụng đường tròn lượng giác:
x
y
1
_
2
3
_
π
1
1
O
Ta có:
; ; : cos
1
0 2 0 2 1
6 3 2
x x x

cos cos .1 2 2 2 6 2 2 5 7xx
Vậy
0;
6
max 7
x
y



đạt được khi
cos2 1 0 0; ;
6
xx



0;
6
min 6
x
y



đạt được khi
1
cos2 0; .
2 6 6
xx




Câu 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a)
sin .2 4 5yx
b)
cos .3 2 2yx
Lời giải:
a) Ta có:
: sin sin sin1 4 1 2 2 4 2 3 2 4 5 7x x x x
.
Vậy
max 7y
đạt được khi
sin4 1 4 2 , , ;
2 8 2
k
x x k k x k
min 3y
đạt được khi
sin4 1 4 2 , , .
2 8 2
k
x x k k x k
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 16
b) Ta có:
: cos cos cos1 2 1 2 2 2 2 1 3 2 2 5x x x x
Vậy
max 5y
đạt được khi
x x k k x k kcos2 1 2 2 , , ;
2
min 1y
đạt được khi
x x k k x k kcos2 1 2 2 , , .
Câu 3: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a)
sin .3 3 2yx
b)
cos .
2
5 2 4yx
Lời giải:
a) Ta có:
: sin sin sin0 3 1 0 3 3 3 2 3 3 2 5x x x x
.
Vậy
max 5y
đạt được khi

k
x x k k x k
x
k
x x k k x k
2
sin3 1 3 2 , ,
2 6 3
sin3 1 ;
2
sin3 1 3 2 , ,
2 6 3
hoặc
sin3 1 cos3 0 3 , , ;
2 6 3
k
x x x k k x k
min 2y
đạt được khi
sin3 0 sin3 0 3 , , .
3
k
x x x k k x k
b) Ta có:
: cos cos
22
0 2 1 0 5 2 5x x x
cos cos .
22
4 5 2 4 9 2 5 2 4 3xx
Vậy
max 3y
đạt được khi
2
cos2 1 2 2 , ,
cos 2 1 ;
cos2 1 2 2 , ,
2
x x k k x k k
x
x x k k x k k

hoặc
2
cos 2 1 sin2 0 2 , , ;
2
k
x x x k k x k
min 2y
đạt được khi
2
cos 2 0 cos2 0 2 , , .
2 4 2
k
x x x k k x k
Câu 4: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a)
sin cos .
44
y x x
b)
cos cos .
2
3
y x x



Lời giải:
a) Ta có:
cos
sin cos sin . cos .
4 4 2
1 1 1 4 3 1
1 2 1 4
2 2 2 4 4
x
y x x x x
Ta có:
: cos cos cos .
1 1 1 1 1 3
1 4 1 4 4 1
4 4 4 2 4 4
x x x x
Vậy
max 1y
đạt được khi
cos4 1 4 2 , , ;
2
k
x x k k x k
1
min
2
y
đạt được khi
cos4 1 4 2 , , .
42
k
x x k k x k


b) Ta có:
cos cos cos cos cos .
2
2
3 3 3 3
y x x x x
Ta có:
: cos .11
3
xx



Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 17
Vậy
max 1y
đạt được khi
cos 1 2 , 2 , ;
3 3 3
x x k k x k k



min 1y 
đạt được khi
4
cos 1 2 , 2 , .
3 3 3
x x k k x k k



Câu 5: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a)
sin sin .
2
23y x x
b)
cos cos , ; .20
2
y x x x



Lời giải:
a) Xét hàm số
sin sin .
2
23y x x
Đặt
sin 1;1 .tx


Ta có:
, ; .
2
2 3 1 1g t t t t
Bảng biến thiên:
t

1
1

gt

6
2

Dựa vào BBT, suy ra:
1;1
max max 6
t
y g t



đạt được khi
sin 1 2 , ;
2
x x k k
1;1
min min 2
t
y g t



đạt được khi
sin 1 2 , .
2
x x k k
b) Xét hàm số
cos cos cos cos .
2
2 2 1y x x x x
Đặt
cos ; 0; cos 0;1 .
2
t x x x





Ta có:
, ; .
2
2 1 0 1g t t t t
Bảng biến thiên:
t

1
4
0
1

gt

9
8
2
1

Dựa vào BBT, suy ra:
0;1
0;
2
max max 2
t
y g t





đạt được khi
cos 1 0 0; ;
2
xx



0;1
0;
2
min min 1
t
y g t




đạt được khi
cos 0 0; .
22
xx




Câu 6: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 18
a)
sin cos .32y x x
b)
sin sin .
2
2 3 2 1y x x
Lời giải:
Chú ý kết quả:
sin cos sin
22
a x b x a b x
, , , ,sin .
22
b
ab
ab
a) Ta có:
sin ; .2 2 0 4
3
y x y



Vậy
max 4y
đạt được khi
sin 1 2 , 2 , ;
3 3 2 6
x x k k x k k



min 0y
đạt được khi
5
sin 1 2 , 2 , .
3 3 2 6
x x k k x k k



b) Ta có:
sin sin sin cos sin ; .
2
2 3 2 1 3 2 2 2 2 2 2 0 4
6
y x x x x x y



Vậy
max 4y
đạt được khi
sin 2 1 2 2 , , ;
6 6 2 3
x x k k x k k



min 0y
đạt được khi
sin 2 1 2 2 , , .
6 6 2 6
x x k k x k k



III. BÀI TẬP TỰ LUYỆN
Câu 7: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
2
2
22
cos
cos 2) cos 3) 4) cos2
5) 6) cos cos 7) cos cos2 8) cos
22
2
14
1) 2 4 3 8sin . 2sin
3
3 2 sin 2 5 2sin .
3
x
y x y x x y y x x
y x y x x y x x y x x



Câu 8: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
22
4
2) cos
3) cos cos 4) cos cos
cos
2 2 2
22
4
1) sin 4sin 2 sin 0
3sin 5 8sin 2 2sin 4 8sin 1
5) sin
y x x y a x b x a b
y x x x x y x x x x
y x x

6
6) cos
6
siny x x
IV. TRẮC NGHIỆM: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT HÀM SỐ
Câu 1. Hàm số nào sau đây có tập giá trị là
?
A.
sin .yx
B.
tan2 .yx
C.
cos2 cot2 .y x x
D.
sin .y x x
Câu 2. Hàm số nào sau đây có tập giá trị là trên tập xác định của nó?
A.
sin .yx
B.
tan2 .yx
C.
cos2 .yx
D.
1
.
sin
y
x
Câu 3. Tìm tập giá trị
T
của hàm số
sin2 .yx
A.
2;2 .T



B.
1;1 .T



C.
.T
D.
1;1 .T 
Câu 4. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
3
.
2
C.
6.
D.
2.
Câu 5. Tìm tập giá trị
T
của hàm số
2cos .yx
A.
2;2 .T



B.
1;1 .T



C.
.T
D.
1;1 .T 
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 19
Câu 6. Xét bốn mệnh đề sau:
(1): Trên
,
hàm số
cosyx
có tập giá trị là
1;1 .


(2): Trên
0; ,
2



hàm số
cosyx
có tập giá trị là
0;1 .


(3): Trên
3
0; ,
4



hàm số
cosyx
có tập giá trị là
2
0; .
2




(4): Trên
0;
2


hàm số
cosyx
có tập giá trị là
0;1 .
Tìm số phát biểu đúng.
A.
1.
B.
2.
C.
3.
D.
4.
Câu 7. Tìm tập giá trị
T
của hàm số
2cos2 .yx
A.
2;2 .T



B.
1;1 .T



C.
.T
D.
4;4 .T



Câu 8. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
6.
D.
2.
Câu 9. Tìm tập giá trị
T
của hàm số
2sin 1.yx
A.
2;2 .T



B.
1;3 .T



C.
.T
D.
3;3 .T



Câu 10. Tìm tập giá trị
T
của hàm số
4cos 3.yx
A.
1;1 .T



B.
7;1 .T



C.
.T
D.
4;4 .T



Câu 11. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1 sin 3.yx
Khẳng định nào dưới đây đúng?
A.
3 2, 2.Mm
B.
3 2, 3.Mm
C.
3 2, 2.Mm
D.
2 3, 3.Mm
Câu 12. Tìm tập giá trị
T
của hàm số
1 2sin2 .yx
A.
1;3 .T



B.
3;4 .T



C.
.T
D.
3;3 .T



Câu 13. Tìm tập giá trị
T
của hàm số
2
2sin 1.yx
A.
2;2 .T



B.
1;3 .T



C.
.T
D.


1;3 .T
Câu 14. Tìm tập giá trị
T
của hàm số
2
4cos 2 3.yx
A.
3;7 .T


B.
0;7 .T


C.
.T
D.
0;3 .T


Câu 15. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
6.
D.
2.
Câu 16. Tìm tập giá trị
T
của hàm số
2
5sin 4.yx
A.
4;9 .T


B.
1;3 .T



C.
0;2 .T


D.
2;3 .T


Câu 17. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin cos 1y x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
3.
D.
5.
Câu 18. Tìm tập giá trị
T
của hàm số
2
7sin 2 9.yx
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 20
A.
3;4 .T


B.
3; 37 .T


C.
.T
D.
2;3 .T


Câu 19. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2sin2 1yx
trên
.
Tính giá trị
..Mm
A.
3.
B.
3.
C.
6.
D.
1.
Câu 20. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2cos 3yx
trên
.
Tính giá trị
..Mm
A.
3.
B.
5.
C.
6.
D.
1.
Câu 21. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2cos 3yx
trên
0; .
3



Tính giá trị
..Mm
A.
3.
B.
5.
C.
6.
D.
20.
Câu 22. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
44
sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
3
.
2
C.
8.
D.
2.
Câu 23. Tìm tập giá trị
T
của hàm số
1 2 sin2 .yx
A.


1;3 .T
B.
1;3 .T



C.
.T
D.
3;3 .T



Câu 24. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin cos 3y x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
6.
D.
5.
Câu 25. Xét bốn mệnh đề sau:
(1): Trên
,
sinyx
có tập giá trị là
1;1 .


(2): Trên


0; ,
2
sinyx
có tập giá trị là
1;1 .


(3): Trên
0; ,
2



sinyx
có tập giá trị là
0;1 .


(4): Trên
0; ,
2


sinyx
có tập giá trị là
0;1 .
Có bao nhiêu mệnh đề đúng?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 26. Giá trị lớn nhất của hàm số
2
2sin 3sin 5
2
x
yx
bằng
A.
5 1.
B.
0.
C.
10 4.
D.
13 5.
Câu 27. Để tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số
sin cosy x x
, một
học sinh giải theo các bước sau:
Bước 1: Tập xác định:
.D
Bước 2: Ta có:
1 sin 1
: 2 sin cos 2.
1 cos 1
x
x x x
x
Bước 3: Vậy GTLN của hàm số bằng
2,
GTNN của hàm số bằng
2.
Bài giải của bạn đó đã đúng chưa? Và nếu sai, thì sai bắt đầu từ bước nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 21
A. Bài giải đúng. B. Sai từ bước 1.
C. Sai từ bước 2. D. Sai từ bước 3.
Câu 28. Hàm số
2022
3 5sinyx
có giá trị lớn nhất là
M
và giá trị nhỏ nhất là
.m
Giá trị của
Mm
bằng
A.
2022
2.
B.
4044
2.
C.
2022 4044
2 1 2 .
D.
6066
2.
Câu 29. Hàm số
5 4sin2 cos2y x x
có tất cả bao nhiêu giá trị nguyên?
A.
3.
B.
4.
C.
5.
D.
6.
Câu 30. Hàm số
sin sin
3
y x x



có tất cả bao nhiêu giá trị nguyên?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 31. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu
h
(mét) của mực nước
trong kênh được tính tại thời điểm
t
(giờ) trong một ngày bởi công thức
3cos 12.
84
t
h




Mực nước của con kênh cao nhất khi
A.
13t
(giờ). B.
14t
(giờ). C.
15t
(giờ). D.
16t
(giờ).
V. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT HÀM SỐ
Câu 1. Hàm số nào sau đây có tập giá trị là
?
A.
sin .yx
B.
tan2 .yx
C.
cos2 cot2 .y x x
D.
sin .y x x
Câu 2. Hàm số nào sau đây có tập giá trị là trên tập xác định của nó?
A.
sin .yx
B.
tan2 .yx
C.
cos2 .yx
D.
1
.
sin
y
x
Câu 3. Tìm tập giá trị
T
của hàm số
sin2 .yx
A.
2;2 .T



B.
1;1 .T



C.
.T
D.
1;1 .T 
Câu 4. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
3
.
2
C.
6.
D.
2.
Lời giải:
Ta có:
sin cos 2 sin .
4
y x x x



Ta có:
: sin sin .1 1 2 2 2
44
x x x

Suy ra
max 2y
đạt được khi
sin 1 2 , 2 , ;
4 4 2 4
x x k k x k k



min 2y 
đạt được khi
3
sin 1 2 , 2 , .
4 4 2 4
x x k k x k k



Vậy
2; 2 0.M m M m
Chọn đáp án A.
Câu 5. Tìm tập giá trị
T
của hàm số
2cos .yx
A.
2;2 .T



B.
1;1 .T



C.
.T
D.
1;1 .T 
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 22
Lời giải:
Ta có:
: cos cos .1 1 2 2 2x x x
Vậy
max 2y
đạt được khi
cos 1 2 , ;x x k k
min 2y 
đạt được khi

cos 1 2 , .x x k k
Vậy tập giá trị của hàm số là
2;2 .T



Chọn đáp án A.
Câu 6. Xét bốn mệnh đề sau:
(1): Trên
,
hàm số
cosyx
có tập giá trị là
1;1 .


(2): Trên
0; ,
2



hàm số
cosyx
có tập giá trị là
0;1 .


(3): Trên
3
0; ,
4



hàm số
cosyx
có tập giá trị là
2
0; .
2




(4): Trên
0;
2


hàm số
cosyx
có tập giá trị là
0;1 .
Tìm số phát biểu đúng.
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Các mệnh đề (1), (2) và (4) đúng.
Trên
3
0; ,
4



hàm số
cosyx
có tập giá trị là




2
;1 .
2
Vậy (3) sai.
Chọn đáp án C.
Câu 7. Tìm tập giá trị
T
của hàm số
2cos2 .yx
A.
2;2 .T



B.
1;1 .T



C.
.T
D.
4;4 .T



Lời giải:
Ta có:
: cos cos .1 2 1 2 2 2 2x x x
Suy ra
max 2y
đạt được khi
cos2 1 , ;x x k k
min 2y 
đạt được khi
cos2 1 , .
2
x x k k
Vậy tập giá trị của hàm số là
2;2 .T



Chọn đáp án A.
Câu 8. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
6.
D.
2.
Lời giải:
Ta có:
sin cos 2 sin .
4
y x x x



Ta có:
: sin sin .0 1 0 2 2
44
x x x

Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 23
Suy ra
max 2y
đạt được khi
sin 1 cos 0
44
xx

, , ;
4 2 4
x k k x k k
min 0y
đạt được khi



sin 0 , , .
4 4 4
x x k k x k k
Vậy
2; 0 2.M m M m
Chọn đáp án B.
Câu 9. Tìm tập giá trị
T
của hàm số
2sin 1.yx
A.
2;2 .T



B.
1;3 .T



C.
.T
D.
3;3 .T



Lời giải:
Ta có:
: sin sin sin .1 1 2 2 2 1 2 1 3x x x x
Suy ra
max 3y
đạt được khi
sin 1 2 , ;
2
x x k k
min 1y 
đạt được khi
sin 1 2 , .
2
x x k k
Vậy tập giá trị của hàm số là
1;3 .T



Chọn đáp án B.
Câu 10. Tìm tập giá trị
T
của hàm số
4cos 3.yx
A.
1;1 .T



B.
7;1 .T



C.
.T
D.
4;4 .T



Lời giải:
Ta có:
: cos cos cos .1 1 4 4 4 7 4 3 1x x x x
Do đó:
max 1y
đạt được khi
cos 1 2 , ;x x k k
min 7y 
đạt được khi
cos 1 2 , .x x k k

Vậy tập giá trị của hàm số là
7;1 .T



Chọn đáp án B.
Câu 11. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1 sin 3.yx
Khẳng định nào dưới đây đúng?
A.
3 2, 2.Mm
B.
3 2, 3.Mm
C.
3 2, 2.Mm
D.
2 3, 3.Mm
Lời giải:
Ta có:
: sin sin sin1 1 0 1 2 0 1 2x x x x
sin .3 1 3 2 3x
Suy ra
max 2 3y 
đạt được khi
sin 1 2 , ;
2
x x k k
min 3y 
đạt được khi
sin 1 2 , .
2
x x k k
Vậy
2 3; 3.Mm
Chọn đáp án D.
Câu 12. Tìm tập giá trị
T
của hàm số
1 2sin2 .yx
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 24
A.
1;3 .T



B.
3;4 .T



C.
.T
D.
3;3 .T



Lời giải:
Ta có:
: sin sin sin .1 2 1 2 2 2 2 1 1 2 2 3x x x x
Do đó:
max 3y
đạt được khi
sin2 1 , ;
4
x x k k
min 1y 
đạt được khi
sin2 1 , .
4
x x k k
Vậy tập giá trị của hàm số là
1;3 .T



Chọn đáp án A.
Câu 13. Tìm tập giá trị
T
của hàm số
2
2sin 1.yx
A.
2;2 .T



B.
1;3 .T



C.
.T
D.


1;3 .T
Lời giải:
Ta có:
: sin sin sin .
2 2 2
0 1 0 2 2 1 2 1 3x x x x
Do đó:
max 3y
đạt được khi
2
sin 1 cos 0 , ;
2
x x x k k
min 1y
đạt được khi
sin 0 , .x x k k
Vậy tập giá trị của hàm số là


1;3 .T
Chọn đáp án D.
Câu 14. Tìm tập giá trị
T
của hàm số
2
4cos 2 3.yx
A.
3;7 .T


B.
0;7 .T


C.
.T
D.
0;3 .T


Lời giải:
Ta có:
: cos cos cos .
2 2 2
0 2 1 0 4 2 4 3 4 2 3 7x x x x
Suy ra
max 7y
đạt được khi
2
cos 2 1 sin2 0 , ;
2
k
x x x k
min 3y
đạt được khi

cos2 0 , .
42
k
x x k
Vậy tập giá trị của hàm số là
3;7 .T


Chọn đáp án A.
Câu 15. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
6.
D.
2.
Lời giải:
Ta có:
3 sin cos 2 sin .
6
y x x x



Ta có:
: sin sin .0 1 0 2 2
66
x x x

Suy ra
max 2y
đạt được khi
sin 1 cos 0
66
xx

, , ;
6 2 3
x k k x k k
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 25
min 0y
đạt được khi
sin 0 , , .
6 6 6
x x k k x k k



Vậy
2; 0 2.M m M m
Chọn đáp án D.
Câu 16. Tìm tập giá trị
T
của hàm số
2
5sin 4.yx
A.
4;9 .T


B.
1;3 .T



C.
0;2 .T


D.
2;3 .T


Lời giải:
Ta có:
: sin sin sin .
2 2 2
0 1 4 5 4 9 2 5 4 3x x x x
Suy ra
max 3y
đạt được khi
2
sin 1 cos 0 , ;
2
x x x k k
min 2y
đạt được khi
sin 0 , .x x k k
Vậy tập giá trị của hàm số là
2;3 .T


Chọn đáp án D.
Câu 17. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin cos 1y x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
3.
D.
5.
Lời giải:
Ta có:
3 sin cos 1 2sin 1 .
6
y x x x



Ta có:
: sin sin sin1 1 1 2 1 3 0 2 1 3
6 6 6
x x x x
Suy ra
max 3y
đạt được khi
sin 1
6
x




2 , 2 , ;
6 2 3
x k k x k k
min 0y
đạt được khi
2
1
sin , .
3
62
2
xk
xk
xk





Vậy
3; 0 3.M m M m
Chọn đáp án C.
Câu 18. Tìm tập giá trị
T
của hàm số
2
7sin 2 9.yx
A.
3;4 .T


B.
3; 37 .T


C.
.T
D.
2;3 .T


Lời giải:
Ta có:
: sin sin sin .
2 2 2
0 2 1 9 7 2 9 16 3 7 2 9 4x x x x
Suy ra
max 4y
đạt được khi
2
sin 2 1 cos2 0 2 , , ;
2 4 2
k
x x x k k x k
min 3y
đạt được khi
sin2 0 , .
2
k
x x k
Vậy tập giá trị của hàm số là
3;4 .T


Chọn đáp án A.
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 26
Câu 19. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2sin2 1yx
trên
.
Tính giá trị
..Mm
A.
3.
B.
3.
C.
6.
D.
1.
Lời giải:
Ta có:
: sin sin sin .1 2 1 2 2 2 2 1 2 2 1 3x x x x
Suy ra
max 3y
đạt được khi
sin2 1 2 2 , , ;
24
x x k k x k k

min 1y 
đạt được khi
sin2 1 2 2 , , .
24
x x k k x k k

Vậy
1; 3 . 3.m M M m
Chọn đáp án A.
Câu 20. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2cos 3yx
trên
.
Tính giá trị
..Mm
A.
3.
B.
5.
C.
6.
D.
1.
Lời giải:
Ta có:
: cos cos cos .1 1 2 2 2 1 2 3 5x x x x
Suy ra
max 5y
đạt được khi
cos 1 2 , ;x x k k
min 1y
đạt được khi
cos 1 2 , .x x k k

Vậy
1; 5 . 5.m M M m
Chọn đáp án B.
Câu 21. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2cos 3yx
trên
0; .
3



Tính giá trị
..Mm
A.
3.
B.
5.
C.
6.
D.
20.
Lời giải:
Ta có:
; : cos cos cos .
1
0 1 1 2 2 4 2 3 5
32
x x x x



Suy ra



0;
3
max 5y
đạt được khi



cos 1 0 0; ;
3
xx



0;
3
min 4y
đạt được khi
1
cos 0; .
2 3 3
xx




Vậy
4; 5 . 20.m M M m
Chọn đáp án D.
Câu 22. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
44
sin cosy x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
3
.
2
C.
8.
D.
2.
Lời giải:
Ta có:
4 4 2
1
sin cos 1 sin 2 .
2
y x x x
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 27
Ta có:
: sin sin sin .
2 2 2
1 1 1 1
0 2 1 0 2 1 2 1
2 2 2 2
x x x x
Suy ra
max 1y
đạt được khi
sin2 0 , ;
2
k
x x k
1
min
2
y
đạt được khi
2
sin 2 1 cos2 0 , .
42
k
x x x k

Vậy
13
; 1 .
22
m M M m
Chọn đáp án B.
Câu 23. Tìm tập giá trị
T
của hàm số
1 2 sin2 .yx
A.


1;3 .T
B.
1;3 .T



C.
.T
D.
3;3 .T



Lời giải:
Ta có:
: sin sin sin . 0 2 1 0 2 2 2 1 1 2 2 3x x x x
Vậy
max 3y
đạt được khi
sin2 1 cos2 0 , ;
42
k
x x x k

min 1y
đạt được khi
sin2 0 , .
2
k
x x k
Vậy tập giá trị của hàm số là


1;3 .T
Chọn đáp án A.
Câu 24. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin cos 3y x x
trên
.
Tính giá trị
.Mm
A.
0.
B.
2.
C.
6.
D.
5.
Lời giải:
Ta có:
3 sin cos 3 2sin 3 .
6
y x x x



Ta có:
: sin sin sin1 1 1 2 3 5 1 2 3 5
6 6 6
x x x x
.
Suy ra
max 5y
đạt được khi
sin 1
6
x




2 , 2 , ;
6 2 3
x k k x k k
min 1y
đạt được khi
2
sin 1 2 , 2 , .
6 6 2 3
x x k k x k k



Vậy
1; 5 6.m M M m
Chọn đáp án C.
Câu 25. Xét bốn mệnh đề sau:
(1): Trên
,
sinyx
có tập giá trị là
1;1 .


(2): Trên


0; ,
2
sinyx
có tập giá trị là
1;1 .


(3): Trên
0; ,
2



sinyx
có tập giá trị là
0;1 .


Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 28
(4): Trên
0; ,
2


sinyx
có tập giá trị là
0;1 .
Có bao nhiêu mệnh đề đúng?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Các mệnh đề (1), (3) đúng.
Trên


0; ,
2
sinyx
có tập giá trị là
0;1 .
Vậy (2) sai.
Trên
0; ,
2


sinyx
có tập giá trị là
0;1 .
Vậy (4) sai.
Chọn đáp án B.
Câu 26. Giá trị lớn nhất của hàm số
2
2sin 3sin 5
2
x
yx
bằng
A.
5 1.
B.
0.
C.
10 4.
D.
13 5.
Lời giải:
Ta có:
2
1 cos
2sin 3sin 5 2 3sin 5 3sin cos 4 10 sin 4
22
xx
y x x x x x
, với số
thực
thỏa mãn
31
cos , sin .
10 10

Ta có:
: sin sin1 1 10 10 10x x x

sin .10 4 10 4 10 4x
Vậy
max 10 4y 
đạt được khi
sin ;
1x
min 10 4y
đạt được khi
sin .
1x
Chọn đáp án C.
Câu 27. Để tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số
sin cosy x x
, một
học sinh giải theo các bước sau:
Bước 1: Tập xác định:
.D
Bước 2: Ta có:
1 sin 1
: 2 sin cos 2.
1 cos 1
x
x x x
x
Bước 3: Vậy GTLN của hàm số bằng
2,
GTNN của hàm số bằng
2.
Bài giải của bạn đó đã đúng chưa? Và nếu sai, thì sai bắt đầu từ bước nào?
A. Bài giải đúng. B. Sai từ bước 1.
C. Sai từ bước 2. D. Sai từ bước 3.
Lời giải:
Bài giải sai từ bước 3 vì không tồn tại
x
thỏa mãn
sin cos 2xx
,
sin cos 2xx
, do các
hệ
sin 1
cos 1
x
x
và
sin 1
cos 1
x
x


vô nghiệm.
Lời giải đúng:
Ta có:
sin cos 2 sin .
4
y x x x



Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 29
Ta có:
: sin sin .1 1 2 2 2
44
x x x

Vậy
max 2y
đạt được khi
sin 1 2 , 2 , ;
4 4 2 4
x x k k x k k



min 2y 
đạt được khi
3
sin 1 2 , 2 , .
4 4 2 4
x x k k x k k



Chọn đáp án D.
Câu 28. Hàm số
2022
3 5sinyx
có giá trị lớn nhất là
M
và giá trị nhỏ nhất là
.m
Giá trị của
Mm
bằng
A.
2022
2.
B.
4044
2.
C.
2022 4044
2 1 2 .
D.
6066
2.
Lời giải:
Ta có
1 sin 1 5 5sin 5xx 
hay
5 5sin 5x
2022
2022
2 3 5sin 8 0 3 5sin 8 .xx 
Vậy
0m
và
2022 6066
8 2 .M 
Câu 29. Hàm số
5 4sin2 cos2y x x
có tất cả bao nhiêu giá trị nguyên?
A.
3.
B.
4.
C.
5.
D.
6.
Lời giải:
Viết lại
5 4sin 2 cos2 5 2sin4 .y x x x
Mà
1 sin4 1 2 2sin4 2 3 5 2sin4 7.x x x  
Vậy
3 7 3;4;5;6;7
y
yy

nên
y
có
5
giá trị nguyên.
Câu 30. Hàm số
sin sin
3
y x x



có tất cả bao nhiêu giá trị nguyên?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Ta có:
sin sin 2cos sin cos .
3 6 6 6
x x x x
Ta có
1 cos 1
6
x



nên
1 1 1;0;1 .
y
yy

Câu 31. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu
h
(mét) của mực nước
trong kênh được tính tại thời điểm
t
(giờ) trong một ngày bởi công thức
3cos 12.
84
t
h




Mực nước của con kênh cao nhất khi
A.
13t
(giờ). B.
14t
(giờ). C.
15t
(giờ). D.
16t
(giờ).
Lời giải:
Mực nước của con kênh cao nhất khi
h
lớn nhất
cos 1 2 16 2
8 4 8 4
tt
k t k



với
1
0 24 * ,
8
t k k
+ Với
1 14kt
(giờ)
+ Với
2k
t
không thỏa mãn điều kiện
*
Vậy mực nước của con kênh cao nhất khi
14t
(giờ).
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 30
Dạng 3: XÉT TÍNH CHẴN LẺ CỦA HÀM SỐ
I. MỘT SỐ KẾT QUẢ
Để xét tính chẵn lẻ của hàm số
,y f x
ta thực hiện theo các bước sau:
Bước 1: Tìm TXĐ
D
của hàm số và chỉ rõ:
.x D x D
Bước 2:
lµ hµm ch½n trªn .
lµ hµm lÎ trªn
:
.
f x f x y f x D
xD
f x f x y f x D

Các kết quả cần lưu ý:
1) Đồ thị hàm số chẵn nhận trục
Oy
làm trục đối xứng;
Đồ thị hàm số lẻ nhận gốc tọa độ
O
làm tâm đối xứng.
2) Hàm số
sin ; tan ; coty x y x y x
là hàm lẻ trên tập xác định của nó;
Hàm số
cosyx
là hàm chẵn trên tập xác định của nó.
II. BÀI TẬP TỰ LUẬN
Câu 1: Xét tính chẵn – lẻ của các hàm số sau:
a)
sin tan .23y x x
b)
cos
.
2
2 2 5
1
x
y
x
c)
3
sin 2 tan .
2
y x x




Lời giải:
a) TXĐ:
\ , .
2
D k k



+) Ta có:
.x D x D
+) Ta có:
: 2sin 3tan 2sin 3tan 2sin 3tan .x D y x x x x x x x y x
Vậy hàm số lẻ trên
.D
b) TXĐ:
.D
+) Ta có:
.x D x D
+) Ta có:
22
2cos 2 5
2cos2 5
:.
1
1
x
x
x D y x y x
x
x


Vậy hàm số chẵn trên
.D
c) TXĐ:
\ , .
2
D k k



Biến đổi:
3
sin 2 tan sin 2 tan sin 2 tan cos2 tan .
2 2 2
y x x x x x x x x
+) Ta có:
.x D x D
+) Ta có:
x D y x x x x x y x: cos 2 tan cos2 tan .
Vậy hàm số lẻ trên
.D
Câu 2: Xét tính chẵn – lẻ của các hàm số sau:
a)
sin .cos .
2021
4y x x x
b)
sin .1 1 4y x x x
c)
sin
.
cos42
xx
y
x
d)
tan
.
4
42
1
xx
y
xx

Lời giải:
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 31
a) TXĐ:
.D
+) Ta có:
.x D x D
+) Ta có:
2021 2021
: sin .cos 4 sin .cos4 .x D y x x x x x x x y x
Vậy hàm số chẵn trên
.D
b) TXĐ:
.D
+) Ta có:
.x D x D
+) Ta có:
: 1 1 sin 4 1 1 sin4 .x D y x x x x x x x y x
Vậy hàm số chẵn trên
.D
c) TXĐ:
D .
+) Ta có:
.x D x D
+) Ta có:

xx
xx
x D y x y x
x
x
sin
sin
:.
4 cos2
4 cos 2
Vậy hàm số lẻ trên
.D
d) TXĐ:
\ , .
2
D k k



+) Ta có:
.x D x D
+) Ta có:

x x x x
x D y x y x
xx
xx
44
4 2 4 2
tan tan
:.
1
1
Vậy hàm số chẵn trên
.D
III. BÀI TẬP TỰ LUYỆN
Câu 3: Xác định tính chẵn, lẻ của các hàm số:
cos2
cos3 3) 4) 5)
cos2
cos
6) 7) cos 8) cos2
cos
10)
3
3
2000
sin
1) sin3
1
sin2 1 9) sin
1
x x x
y x x y x x y y
xx
x
y x x y x y y x x
x
x
y
11) 12)
cos
2 2010
sin 2010
sin2
sin tan
x
y y x x
x x x

IV. TRẮC NGHIỆM: TÍNH CHẴN LẺ CỦA HÀM SỐ
Câu 1. Khẳng định nào dưới đây đúng?
A. Hàm số
tanyx
là hàm số chẵn. B. Hàm số
sinyx
làm hàm số chẵn.
C. Hàm số
cosyx
là hàm số chẵn. D. Hàm số
cotyx
là hàm số chẵn.
Câu 2. Hàm số nào sau đây là hàm số chẵn?
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 3. Hàm số nào sau đây là hàm số lẻ?
A.
sin .yx
B.
cos .yx
C.
1.y
D.
42
.y x x
Câu 4. Hàm số nào sau đây là hàm số chẵn?
A.
sin .y x x
B.
cos .y x x
C.
tan .yx
D.
cot .yx
Câu 5. Hàm số nào sau đây là hàm số lẻ?
A.
sin .y x x
B.
cos .y x x
C.
tan .y x x
D.
cot .y x x
Câu 6. Hàm số nào sau đây là hàm số chẵn trên
?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 32
A.
2
2.y x x
B.
sin x
y
x
C.
2
sin .yx
D.
tan2 .y x x
Câu 7. Hàm số nào sau đây là hàm số chẵn trên
?
A.
cos 2.yx
B.
3
sin x
y
x
C.
sin2 .yx
D.
4
2017.y x x
Câu 8. Hàm số nào sau đây là hàm số lẻ trên
?
A.
sin4 .y x x
B.
cos
.
x
y
x
C.
3
tan .yx
D.
sin .y x x
Câu 9. Hàm số nào sau đây là hàm số lẻ trên
?
A.
2
tan sin .y x x
B.
cos .y x x
C.
3
tan .yx
D.
2 sin 4 .y x x
Câu 10. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó?
A.
cos 2.yx
B.
5
sin
.
x
y
x
C.
sin2 .yx
D.
3
2017.y x x
Câu 11. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó?
A.
cos 2.yx
B.
5
2
sin
.
x
y
x
C.
tan4 sin 2 .y x x
D.
1.yx
Câu 12. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó?
A.
tan .y x x
B.
63
cot .y x x
C.
2
sin 3 .yx
D.
2017.y
Câu 13. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó?
A.
2
sin
.
sin 1
x
y
x
B.
3
tan
.
x
y
x
C.
tan4 sin 2 .y x x
D.
.yx
Câu 14. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó?
A.
4
sin
.
x
y
x
B.
5
sin
.
x
y
x
C.
sin2 .y x x
D.
3
2017.y x x
Câu 15. Có bao nhiêu hàm số trong các hàm số
2
sin2 ; cos ; tan ; 1y x y x x y x x y
là hàm chẵn
trên
?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 16. Có bao nhiêu hàm số trong các hàm số
2
sin2 ; cos ; tan ; 1y x y x x y x x y
là hàm chẵn
trên tập xác định của nó?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 17. Có bao nhiêu hàm số trong các hàm số
3
sin2 ; cos ; tan ; 1y x y x x y x x y
là hàm lẻ trên
?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 18. Xét bốn mệnh đề sau:
(1): Trên
,
sin2yx
có tập giá trị là
1;1 .


(2): Trên
0; ,
2



sinyx
có tập giá trị là
1;1 .


(3): Trên
,
siny x x
là hàm chẵn.
(4): Trên
,
2
siny x x
là hàm lẻ.
Tìm số phát biểu đúng.
A.
1.
B.
2.
C.
3.
D.
4.
Câu 19. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 33
A.
2
2 3cos .y x x
B.
5
5sin .
2
yx




C.
2
cot 1 tan 2 .y x x
D.
2 tan 2 .yx
IV. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: TÍNH CHẴN LẺ CỦA HÀM SỐ
Câu 1. Khẳng định nào dưới đây đúng?
A. Hàm số
tanyx
là hàm số chẵn. B. Hàm số
sinyx
làm hàm số chẵn.
C. Hàm số
cosyx
là hàm số chẵn. D. Hàm số
cotyx
là hàm số chẵn.
Câu 2. Hàm số nào sau đây là hàm số chẵn?
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 3. Hàm số nào sau đây là hàm số lẻ?
A.
sin .yx
B.
cos .yx
C.
1.y
D.
42
.y x x
Câu 4. Hàm số nào sau đây là hàm số chẵn?
A.
sin .y x x
B.
cos .y x x
C.
tan .yx
D.
cot .yx
Lời giải:
Xét hàm số
sin .y x x
Tập xác định:
.D
+)
.x D x D
+)
: sin sin .x D y x x x x x y x
Vậy hàm số
siny x x
là hàm số chẵn trên
.
Chọn đáp án A.
Câu 5. Hàm số nào sau đây là hàm số lẻ?
A.
sin .y x x
B.
cos .y x x
C.
tan .y x x
D.
cot .y x x
Lời giải:
Xét hàm số
cos .y x x
Tập xác định:
.D
+)
.x D x D
+)
: cos cos .x D y x x x x x y x
Vậy hàm số
cosy x x
là hàm số lẻ trên
.
Chọn đáp án B.
Câu 6. Hàm số nào sau đây là hàm số chẵn trên
?
A.
2
2.y x x
B.
sin x
y
x
C.
2
sin .yx
D.
tan2 .y x x
Lời giải:
Xét hàm số
2
sin .yx
Tập xác định:
.D
+)
.x D x D
+)
22
: sin sin .x D y x x x y x
Vậy hàm số
2
sinyx
là hàm số chẵn trên
.
Lưu ý: Hàm số
sin x
y
x
; tan2y x x
là hàm số chẵn trên tập xác định
D
của nó với
.D
Chọn đáp án C.
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 34
Câu 7. Hàm số nào sau đây là hàm số chẵn trên
?
A.
cos 2.yx
B.
3
sin x
y
x
C.
sin2 .yx
D.
4
2017.y x x
Lời giải:
Xét hàm số
4
2017.y x x
Tập xác định:
.D
+)
.x D x D
+)
4
4
: 2017 2017 .x D y x x x x x y x
Vậy hàm số
4
2017y x x
là hàm số chẵn trên
.
Lưu ý:
Hàm số
cos 2yx
có tập xác định
.
Hàm số
3
sin x
y
x
là hàm số chẵn trên tập xác định
\ 0 .
Chọn đáp án D.
Câu 8. Hàm số nào sau đây là hàm số lẻ trên
?
A.
sin4 .y x x
B.
cos
.
x
y
x
C.
3
tan .yx
D.
sin .y x x
Lời giải:
Xét hàm số
sin .y x x
Tập xác định:
.D
+)
.x D x D
+)
: sin sin .x D y x x x x x y x
Vậy hàm số
siny x x
là hàm số lẻ trên
.
Lưu ý:
Hàm số
3
cos
; tan
x
y y x
x

là hàm số lẻ trên tập xác định
D
của nó với
.D
Chọn đáp án D.
Câu 9. Hàm số nào sau đây là hàm số lẻ trên
?
A.
2
tan sin .y x x
B.
cos .y x x
C.
3
tan .yx
D.
2 sin 4 .y x x
Lời giải:
Xét hàm số
cos .y x x
Tập xác định:
.D
+)
.x D x D
+)
: cos cos .x D y x x x x x y x
Vậy hàm số
cosy x x
là hàm số lẻ trên
.
Lưu ý:
Hàm số
23
tan sin ; tany x x y x
là hàm số lẻ trên tập xác định
D
của nó với
.D
Chọn đáp án B.
Câu 10. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó?
A.
cos 2.yx
B.
5
sin
.
x
y
x
C.
sin2 .yx
D.
3
2017.y x x
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 35
Lời giải:
Xét hàm số
5
sin
.
x
y
x
Tập xác định:
\ 0 .D
+)
.x D x D
+)
5
5
sin
sin
:.
x
x
x D y x y x
x
x
Vậy hàm số
5
sin x
y
x
là hàm số chẵn trên
.D
Chọn đáp án B.
Câu 11. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó?
A.
cos 2.yx
B.
5
2
sin
.
x
y
x
C.
tan4 sin 2 .y x x
D.
1.yx
Lời giải:
Xét hàm số
tan4 sin 2 .y x x
Tập xác định:
\.
84
k
Dk




+)
.x D x D
+)
: tan 4 sin 2 tan4 sin2 .x D y x x x x x y x
Vậy hàm số
tan4 sin 2y x x
là hàm số chẵn trên
.D
Chọn đáp án C.
Câu 12. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó?
A.
tan .y x x
B.
63
cot .y x x
C.
2
sin 3 .yx
D.
2017.y
Lời giải:
Xét hàm số
63
cot .y x x
Tập xác định:
\.D k k
+)
.x D x D
+)
6
3 6 3
: cot cot .x D y x x x x x y x
Vậy hàm số
63
coty x x
là hàm số lẻ trên
.D
Chọn đáp án B.
Câu 13. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó?
A.
2
sin
.
sin 1
x
y
x
B.
3
tan
.
x
y
x
C.
tan4 sin 2 .y x x
D.
.yx
Lời giải:
Xét hàm số
2
sin
.
sin 1
x
y
x
Tập xác định:
.D
+)
.x D x D
+)
22
sin
sin
:.
sin 1 sin 1
x
x
x D y x y x
xx
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 36
Vậy hàm số
2
sin
sin 1
x
y
x
là hàm số lẻ trên
.D
Chọn đáp án A.
Câu 14. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó?
A.
4
sin
.
x
y
x
B.
5
sin
.
x
y
x
C.
sin2 .y x x
D.
3
2017.y x x
Lời giải:
Xét hàm số
5
sin
.
x
y
x
Tập xác định:
\ 0 .D
+)
.x D x D
+)
5
5
sin
sin
:.
x
x
x D y x y x
x
x
Vậy hàm số
5
sin x
y
x
là hàm số chẵn trên
.D
Chọn đáp án B.
Câu 15. Có bao nhiêu hàm số trong các hàm số
2
sin2 ; cos ; tan ; 1y x y x x y x x y
là hàm chẵn
trên
?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Hàm số
1y
là hàm chẵn trên
.
Lưu ý: Hàm số
2
tany x x
là hàm chẵn trên
\.
2
D k k



Chọn đáp án A.
Câu 16. Có bao nhiêu hàm số trong các hàm số
2
sin2 ; cos ; tan ; 1y x y x x y x x y
là hàm chẵn
trên tập xác định của nó?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Hàm số
2
1; tany y x x
là hàm chẵn trên tập xác định của nó
Chọn đáp án B.
Câu 17. Có bao nhiêu hàm số trong các hàm số
3
sin2 ; cos ; tan ; 1y x y x x y x x y
là hàm lẻ trên
?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Hàm số
sin2 ; cosy x y x x
là hàm lẻ trên
.
Lưu ý: Hàm số
3
tany x x
là hàm lẻ trên
\.
2
D k k



Chọn đáp án B.
Câu 18. Xét bốn mệnh đề sau:
(1): Trên
,
sin2yx
có tập giá trị là
1;1 .


Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 37
(2): Trên
0; ,
2



sinyx
có tập giá trị là
1;1 .


(3): Trên
,
siny x x
là hàm chẵn.
(4): Trên
,
2
siny x x
là hàm lẻ.
Tìm số phát biểu đúng.
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải:
Các mệnh đề (1), (3) và (4) là các mệnh đề đúng.
Trên
0; ,
2



sinyx
có tập giá trị là
0;1 .


Vậy (2) sai.
Chọn đáp án C.
Câu 19. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A.
2
2 3cos .y x x
B.
5
5sin .
2
yx




C.
2
cot 1 tan 2 .y x x
D.
2 tan 2 .yx
Lời giải:
Xét hàm số
5
5sin 5sin 2 5cos
22
y x x x

là hàm số chẵn trên
.
Chọn đáp án B.
Dạng 4: XÁC ĐỊNH TÍNH TUẦN HOÀN CỦA CÁC HÀM SỐ LƯỢNG GIÁC
I. MỘT SỐ KẾT QUẢ
1. Chứng minh hàm số
()y f x
tuần hoàn
Xét hàm số
()y f x
, tập xác định D, ta dự đoán có số thực dương
0
T
sao cho:
vµ (1)
(2)
00
0
:
()
x D x T D x T D
f x T f x

2. Chứng minh
0
T
là chu kỳ của hàm số (nghĩa là
0
T
dương nhỏ nhất thoả mãn hệ (1) và (2)). Thực
hiện bằng phản chứng.
Bước 1: Giả sử có số
T
sao cho
0
0 TT
thoả mãn các tính chất (1) và (2):
: ( ) ...x D f x T f x
Mâu thuẫn với giả thiết
0
0 TT
.
Bước 2: Mâu thuẫn này chứng tỏ
0
T
là số dương nhỏ nhất thoả mãn (2).
Kết luận: Vậy
0
T
là chu kỳ của hàm số
()y f x
.
3. Xét tính tuần hoàn các các hàm số lượng giác, ta sử dụng một số kết quả:
a) Hàm số
tuÇn hoµn víi chu kú 2sin , cosy x y x

.
b) Hàm số
tuÇn hoµn víi chu kú tan , coty x y x

.
Mở rộng:
c) Hàm số
( tuÇn hoµn víi chu kú
2
sin , cos 0)y ax b y ax b a
a
.
d) Hàm số
( tuÇn hoµn víi chu kú tan , cot 0)y ax b y ax b a
a
.
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 38
Định lý: Cho cặp hàm số
( ), ( )f x g x
tuần hoàn trên tập M có các chu kỳ lần lượt là
vµ ab
víi
a
b
. Khi
đó, các hàm số:
( ) ( ) ( ), ( ) ( ) ( )F x f x g x G x f x g x
cũng tuần hoàn trên M.
Hệ quả:
Hàm số
( ) ( ) ( )F x mf x ng x
tuần hoàn với chu kỳ T là “bội chung nhỏ nhất” của
µ a v b
.
II. BÀI TẬP TỰ LUẬN
Câu 4: Tìm chu kì của các hàm số sau:
a)
sin .22yx
b)
tan .4 6 3yx
Lời giải:
a) Hàm số
sin22yx
tuần hoàn với chu kì
2
.
2
T

b) Hàm số
tan4 6 3yx
tuần hoàn với chu kì
.
6
T
Câu 5: Tìm chu kì của các hàm số sau:
a)
2sin 3 .
4
yx




b)
sin .
2
42yx
c)
sin .cos .4 3 3y x x
Lời giải:
a) Hàm số




yx2sin 3
4
tuần hoàn với chu kì
2
.
3
T
b) Ta có:
cos
sin . cos .
2
14
4 2 4 2 2 4
2
x
y x x
Vậy hàm số
sin
2
42yx
tuần hoàn với chu kì
2
.
42
T


c) Ta có:
sin .cos sin .4 3 3 2 6y x x x
Vậy hàm số
sin .cos4 3 3y x x
tuần hoàn với chu kì
2
.
63
T


Câu 6: Tìm chu kì của các hàm số sau:
a)
sin2 cos4 .y x x
b)
sin tan .
3
x
yx
Lời giải:
a) Hàm số
sin2yx
tuần hoàn với chu kì
1
2
.
2
T

Hàm số
cos4yx
tuần hoàn với chu kì
2
2
.
42
T


Vậy hàm số
sin2 cos4y x x
tuần hoàn với chu kỳ
.
b) Hàm số
sinyx
tuần hoàn với chu kì
1
2.T
Hàm số
tan
3
x
y
tuần hoàn với chu kì
2
3.
1
3
T

Vậy hàm số
sin tan
3
x
yx
tuần hoàn với chu kỳ
6.
III. BÀI TẬP TỰ LUYỆN
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 39
Câu 7: Tìm chu kỳ của các hàm số sau:
2) cos 5 3) 4) cos
5) cos 6) cos 7) cos 8)
2
1) 2sin tan 2
4 3 4
sin sin 4sin
24
9)
y x y x y x y x
x
y y x x y x x y x
y



.
1
sinx
IV. TRẮC NGHIỆM: TÍNH TUẦN HOÀN CỦA HÀM SỐ - SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA
HÀM SỐ
Câu 1. Hàm số nào sau đây là hàm số tuần hoàn?
A.
2
.yx
B.
sin .yx
C.
sin .y x x
D.
.yx
Câu 2. Hàm số nào sau đây là hàm số tuần hoàn với chu kì
2?
A.
sin2 .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 3. Hàm số nào sau đây là hàm số tuần hoàn với chu kì
?
A.
sin .yx
B.
cos .yx
C.
tan2 .yx
D.
cot .yx
Câu 4. Hàm số nào sau đây là hàm số tuần hoàn với chu kì
?
A.
sin2 .yx
B.
cos .yx
C.
tan2 .yx
D.
cot2 .yx
Câu 5. Hàm số nào sau đây không tuần hoàn với chu kì
?
A.
sin2 .yx
B.
sin .yx
C.
tan .yx
D.
cot .yx
Câu 6. Hàm số
2sin4 3yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
.
2
Câu 7. Hàm số
1 5cos2yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
.
2
Câu 8. Hàm số
2
2sin 7yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
4.
D.
.
2
Câu 9. Hàm số
4sin cos 5y x x
tuần hoàn với chu kì là
A.
2.
B.
.
C.
4.
D.
.
2
Câu 10. Hàm số
sin sin2y x x
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
.
2
Câu 11. Hàm số
sin tan
3
x
yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
6.
Câu 12. Cho hàm số
sin , ; ;y f x a bx c a b c
có đồ thị như hình vẽ. Chu kỳ
T
của hàm số là
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 40
A.
.
6
T
B.
.T
C.
2.T
D.
4.T
Câu 13. Cho hàm số
sin , ; ;y f x a bx c a b c
có đồ thị như hình vẽ. Chu kỳ
T
của hàm số là
A.
3
.
2
T
B.
2.T
C.
3.T
D.
6.T
Câu 14. Hàm số
sinyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
0; .
2



B.
;.
2



C.
0; .
D.
3
;.
2



Câu 15. Hàm số
sinyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
3
;.
2



B.
;.
2



C.
35
;.
22




D.
3
;.
22




Câu 16. Hàm số
cosyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
0; .
2



B.
;.
2



C.
0; .
D.
3
;.
2



Câu 17. Hàm số
cosyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.




;.
2
B.
;.
2



C.
35
;.
22




D.
3
;.
22




Câu 18. Hàm số
sinyx
đồng biến trên khoảng nào dưới đây?
A.
;.
2



B.
5
;3 .
2



C.
3
;.
2




D.
5
; 2 .
2




Câu 19. Hàm số
cosyx
nghịch biến trên khoảng nào sau đây?
A.
3
;.
22




B.
11
; 5 .
2




C.
11
;7 .
2



D.
19
;10 .
2



Câu 20. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 41
-
π
π
y
x
-
π
2
π
2
-1
1
O
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 21. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
π
2
-
π
2
x
y
π
-
π
-1
1
O
1
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 22. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
x
y
-
3
π
2
3
π
2
-
π
2
π
2
O
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 23. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
x
y
π
2
-
π
π
O
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 24. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 42
-
π π
y
x
-
π
2
π
2
-1
1
O
A.
cos .yx
B.
cos2 .yx
C.
sin .yx
D.
sin2 .yx
Câu 25. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
-
π
4
π
4
π
2
-
π
2
x
y
π
-
π
-1
1
O
A.
cos .yx
B.
cos2 .yx
C.
sin .yx
D.
sin2 .yx
Câu 26. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
3
π
2
π
x
y
π
-1
1
O
A.
cos .yx
B.
cos .
2
x
y
C.
sin .yx
D.
sin .
2
x
y
Câu 27. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 43
π
y
x
2
π
3
π
-1
1
O
A.
cos .yx
B.
cos .
2
x
y
C.
sin .yx
D.
sin .
2
x
y
Câu 28. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
π
2
-
π
2
x
y
π
-
π
1
O
A.
sin .yx
B.
cos .yx
C.
sin .yx
D.
cos .yx
Câu 29. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
-
π
π
y
x
-
π
2
π
2
1
O
A.
sin .yx
B.
cos .yx
C.
sin .yx
D.
cos .yx
Câu 30. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 44
π
2
-
π
2
x
y
π
-
π
-1
1
O
A.
sin .yx
B.
sin .yx
C.
sin .yx
D.
sin2 .yx
Câu 31. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
-
π
π
y
x
-
π
2
π
2
-1
1
O
A.
cos .yx
B.
cos .yx
C.
cos .yx
D.
cos2 .yx
Câu 32. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
-
π
π
y
x
-
π
2
π
2
-1
1
O
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
;0 .
B. Hàm số nghịch biến trên
;.
22




C. Hàm số đồng biến trên
0; .
D. Hàm số đồng biến trên
;.
22




Câu 33. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
-
π
π
y
x
-
π
2
π
2
-1
1
O
Khẳng định nào sau đây sai?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 45
A.
;
max 1.
x
y



B.
;
min 1.
x
y




C. Hàm số đồng biến trên
0; .
D. Hàm số đồng biến trên
;.
22




Câu 34. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
π
2
-
π
2
x
y
π
-
π
-1
1
O
1
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
;.

B. Hàm số nghịch biến trên
;.
22




C. Hàm số đồng biến trên
0; .
D. Hàm số đồng biến trên
;0 .
Câu 35. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
π
2
-
π
2
x
y
π
-
π
-1
1
O
1
Khẳng định nào sau đây sai?
A.
;
max 1.
x
y



B.
;
min 1.
x
y



C. Hàm số nghịch biến trên
0; .
D. Hàm số đồng biến trên
;0 .
V. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: TÍNH TUẦN HOÀN CỦA HÀM SỐ - SỰ BIẾN THIÊN
VÀ ĐỒ THỊ CỦA HÀM SỐ
Câu 1. Hàm số nào sau đây là hàm số tuần hoàn?
A.
2
.yx
B.
sin .yx
C.
sin .y x x
D.
.yx
Câu 2. Hàm số nào sau đây là hàm số tuần hoàn với chu kì
2?
A.
sin2 .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 3. Hàm số nào sau đây là hàm số tuần hoàn với chu kì
?
A.
sin .yx
B.
cos .yx
C.
tan2 .yx
D.
cot .yx
Câu 4. Hàm số nào sau đây là hàm số tuần hoàn với chu kì
?
A.
sin2 .yx
B.
cos .yx
C.
tan2 .yx
D.
cot2 .yx
Câu 5. Hàm số nào sau đây không tuần hoàn với chu kì
?
A.
sin2 .yx
B.
sin .yx
C.
tan .yx
D.
cot .yx
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 46
Câu 6. Hàm số
2sin4 3yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
.
2
Lời giải:
Hàm số
2sin4 3yx
tuần hoàn với chu kì
2
.
42

Chọn đáp án D.
Câu 7. Hàm số
1 5cos2yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
.
2
Lời giải:
Hàm số
1 5cos2yx
tuần hoàn với chu kì
2
.
2
Chọn đáp án B.
Câu 8. Hàm số
2
2sin 7yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
4.
D.
.
2
Lời giải:
Hàm số
2
2sin 7 1 cos2 7 8 cos2y x x x
tuần hoàn với chu kì
2
.
2
Chọn đáp án B.
Câu 9. Hàm số
4sin cos 5y x x
tuần hoàn với chu kì là
A.
2.
B.
.
C.
4.
D.
.
2
Lời giải:
Hàm số
4sin cos 5 2sin2 5y x x x
tuần hoàn với chu kì
2
.
2
Chọn đáp án B.
Câu 10. Hàm số
sin sin2y x x
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
.
2
Lời giải:
Hàm số
sinyx
tuần hoàn với chu kì
1
2.T
Hàm số
sin2yx
tuần hoàn với chu kì
2
.T
Vậy hàm số
sin sin2y x x
tuần hoàn với chu kì
2.T
Chọn đáp án A.
Câu 11. Hàm số
sin tan
3
x
yx
tuần hoàn với chu kì là
A.
2.
B.
.
C.
8.
D.
6.
Lời giải:
Hàm số
sinyx
tuần hoàn với chu kì
1
2.T
Hàm số
tan
3
x
y
tuần hoàn với chu kì
2
3.T
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 47
Vậy hàm số
sin tan
3
x
yx
tuần hoàn với chu kì
6.T
Chọn đáp án D.
Câu 12. Cho hàm số
sin , ; ;y f x a bx c a b c
có đồ thị như hình vẽ. Chu kỳ
T
của hàm số là
A.
.
6
T
B.
.T
C.
2.T
D.
4.T
Câu 13. Cho hàm số
sin , ; ;y f x a bx c a b c
có đồ thị như hình vẽ. Chu kỳ
T
của hàm số là
A.
3
.
2
T
B.
2.T
C.
3.T
D.
6.T
Câu 14. Hàm số
sinyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
0; .
2



B.
;.
2



C.
0; .
D.
3
;.
2



Câu 15. Hàm số
sinyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
3
;.
2



B.
;.
2



C.
35
;.
22




D.
3
;.
22




Câu 16. Hàm số
cosyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.
0; .
2



B.
;.
2



C.
0; .
D.
3
;.
2



Câu 17. Hàm số
cosyx
đồng biến trên khoảng nào trong các khoảng dưới đây?
A.




;.
2
B.
;.
2



C.
35
;.
22




D.
3
;.
22




Câu 18. Hàm số
sinyx
đồng biến trên khoảng nào dưới đây?
A.
;.
2



B.
5
;3 .
2



C.
3
;.
2




D.
5
; 2 .
2




Câu 19. Hàm số
cosyx
nghịch biến trên khoảng nào sau đây?
A.
3
;.
22




B.
11
; 5 .
2




C.
11
;7 .
2



D.
19
;10 .
2



Câu 20. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 48
-
π
π
y
x
-
π
2
π
2
-1
1
O
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Lời giải:
Hàm số qua các điểm
0;0 ; ;1 .
2



Chọn đáp án A.
Câu 21. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
π
2
-
π
2
x
y
π
-
π
-1
1
O
1
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Lời giải:
Hàm số qua các điểm
0;1 ; ;0 .
2



Hoặc quan sát nhanh đồ thị đã cho là đồ thị của hàm
chẵn.
Chọn đáp án B.
Câu 22. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
x
y
-
3
π
2
3
π
2
-
π
2
π
2
O
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Lời giải:
Hàm số qua các điểm
0;0
và đồng biến trên
;.
22




Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 49
Hoặc đánh giá hàm số không xác định tại các điểm
,.
2
x k k
Chọn đáp án C.
Câu 23. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
x
y
π
2
-
π
π
O
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Lời giải:
Hàm số qua các điểm
;0
2



và nghịch biến trên
0; .
Hoặc đánh giá hàm số không xác định tại các điểm
,.x k k

Chọn đáp án D.
Câu 24. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
-
π π
y
x
-
π
2
π
2
-1
1
O
A.
cos .yx
B.
cos2 .yx
C.
sin .yx
D.
sin2 .yx
Lời giải:
Hàm số qua các điểm
0;1 ; ; 1 .
2



Chọn đáp án B.
Câu 25. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 50
-
π
4
π
4
π
2
-
π
2
x
y
π
-
π
-1
1
O
A.
cos .yx
B.
cos2 .yx
C.
sin .yx
D.
sin2 .yx
Lời giải:
Hàm số qua các điểm
0;0 ; ;1 .
4



Chọn đáp án D.
Câu 26. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
3
π
2
π
x
y
π
-1
1
O
A.
cos .yx
B.
cos .
2
x
y
C.
sin .yx
D.
sin .
2
x
y
Lời giải:
Hàm số qua các điểm
0;1 ; ;0 .
Chọn đáp án B.
Câu 27. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
π
y
x
2
π
3
π
-1
1
O
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 51
A.
cos .yx
B.
cos .
2
x
y
C.
sin .yx
D.
sin .
2
x
y
Lời giải:
Hàm số qua các điểm
0;0 ; ;1 .
Chọn đáp án D.
Câu 28. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
π
2
-
π
2
x
y
π
-
π
1
O
A.
sin .yx
B.
cos .yx
C.
sin .yx
D.
cos .yx
Lời giải:
Hàm số qua các điểm
0;0 ; ;1 .
2



Chọn đáp án C.
Câu 29. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
-
π
π
y
x
-
π
2
π
2
1
O
A.
sin .yx
B.
cos .yx
C.
sin .yx
D.
cos .yx
Lời giải:
Hàm số qua các điểm
0;1 ; ;1 .
Chọn đáp án D.
Câu 30. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 52
π
2
-
π
2
x
y
π
-
π
-1
1
O
A.
sin .yx
B.
sin .yx
C.
sin .yx
D.
sin2 .yx
Lời giải:
Hàm số qua các điểm
0;0 ; ; 1 .
2



Chọn đáp án B.
Câu 31. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số
nào?
-
π
π
y
x
-
π
2
π
2
-1
1
O
A.
cos .yx
B.
cos .yx
C.
cos .yx
D.
cos2 .yx
Lời giải:
Hàm số qua các điểm
0; 1 ; ;0 ; ;1 .
2



Chọn đáp án B.
Câu 32. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
-
π
π
y
x
-
π
2
π
2
-1
1
O
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
;0 .
B. Hàm số nghịch biến trên
;.
22




C. Hàm số đồng biến trên
0; .
D. Hàm số đồng biến trên
;.
22




Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 53
Lời giải:
Trên
;,
22




đồ thị hàm số là đường đi lên (từ trái sang phải) nên hàm số đồng biến trên
;.
22




Chọn đáp án D.
Câu 33. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
-
π
π
y
x
-
π
2
π
2
-1
1
O
Khẳng định nào sau đây sai?
A.
;
max 1.
x
y



B.
;
min 1.
x
y




C. Hàm số đồng biến trên
0; .
D. Hàm số đồng biến trên
;.
22




Lời giải:
Trên
0; ,
2



đồ thị hàm số là đường đi lên (từ trái sang phải) nên hàm số đồng biến trên
0; .
2



Trên
;,
2



đồ thị hàm số là đường đi xuống (từ trái sang phải) nên hàm số nghịch biến
trên
;.
2



Vậy C sai.
Chọn đáp án C.
Câu 34. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
π
2
-
π
2
x
y
π
-
π
-1
1
O
1
Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên
;.

B. Hàm số nghịch biến trên
;.
22




C. Hàm số đồng biến trên
0; .
D. Hàm số đồng biến trên
;0 .
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 54
Lời giải:
Trên
;0 ,
đồ thị hàm số là đường đi lên (từ trái sang phải) nên hàm số đồng biến trên
;0 .
Chọn đáp án D.
Câu 35. Cho hàm số
y f x
có đồ thị là hình vẽ dưới đây:
π
2
-
π
2
x
y
π
-
π
-1
1
O
1
Khẳng định nào sau đây sai?
A.
;
max 1.
x
y



B.
;
min 1.
x
y



C. Hàm số nghịch biến trên
0; .
D. Hàm số đồng biến trên
;0 .
Lời giải:
Trên
;,

hàm số không tồn tại giá trị nhỏ nhất. Vậy B sai.
Chọn đáp án B.
| 1/55
| | Tải xuống

Có thể bạn quan tâm:

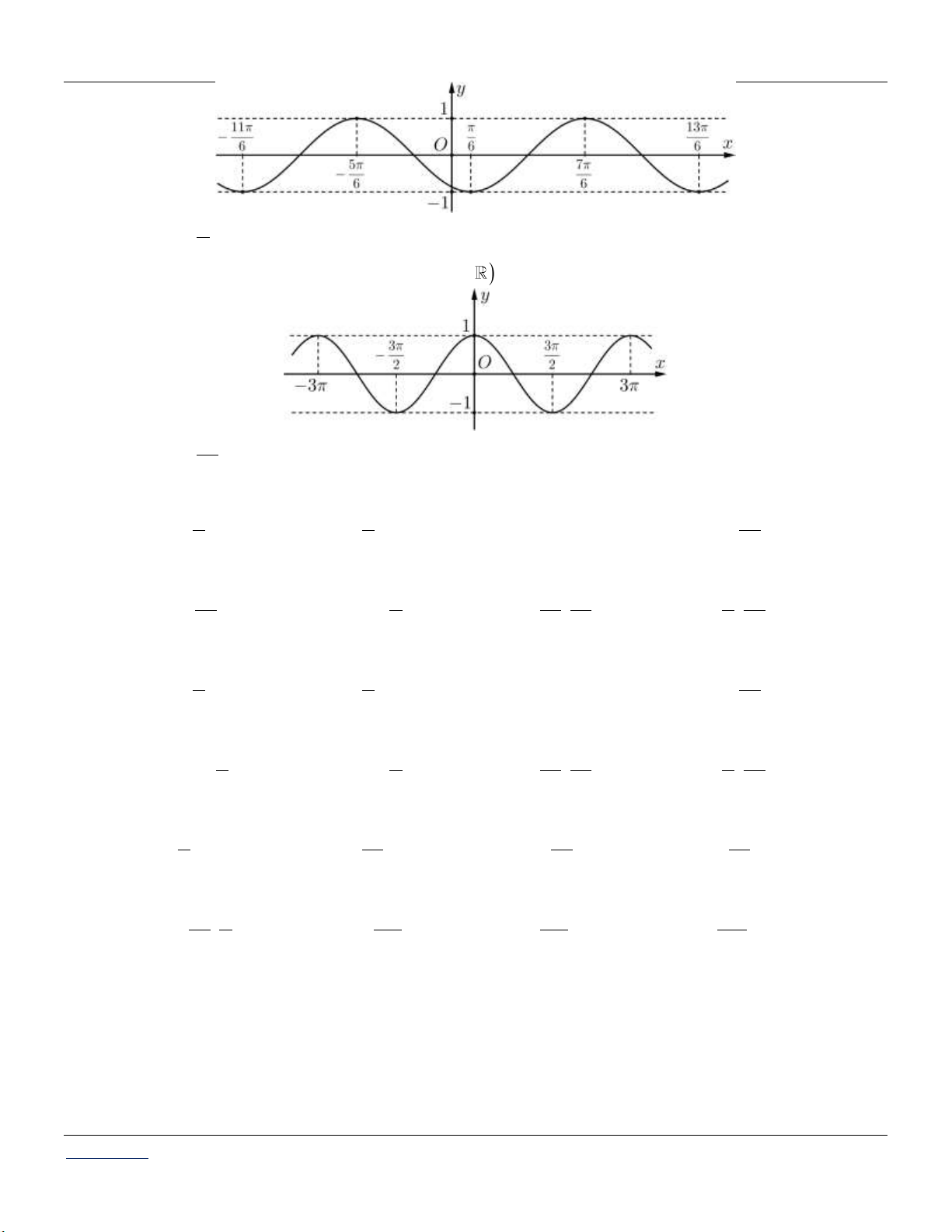
Preview text:

LÊ BÁ BẢO
TRƯỜNG THPT ĐẶNG HUY TRỨ - ADMIN CLB GIÁO VIÊN TRẺ TP HUẾ TOÁN 11
KẾT NỐI TRI THỨC VỚI CUỘC SỐNG HÀM SỐ LƯỢNG GIÁC
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Page: CLB GIÁO VIÊN TRẺ TP HUẾ CHUY£N §Ò TR¾C NGHIÖM M«n: To¸n 11 Chuyªn ®Ò:
HÀM SỐ LƯỢNG GIÁC
PHIẾU HỌC TẬP SỐ 01_TrNg 2021 Líp To¸n thÇy L£ B¸ B¶O Tr-êng THPT §Æng Huy Trø
S§T: 0935.785.115 Facebook: Lª B¸ B¶o
116/04 NguyÔn Lé Tr¹ch, TP HuÕ
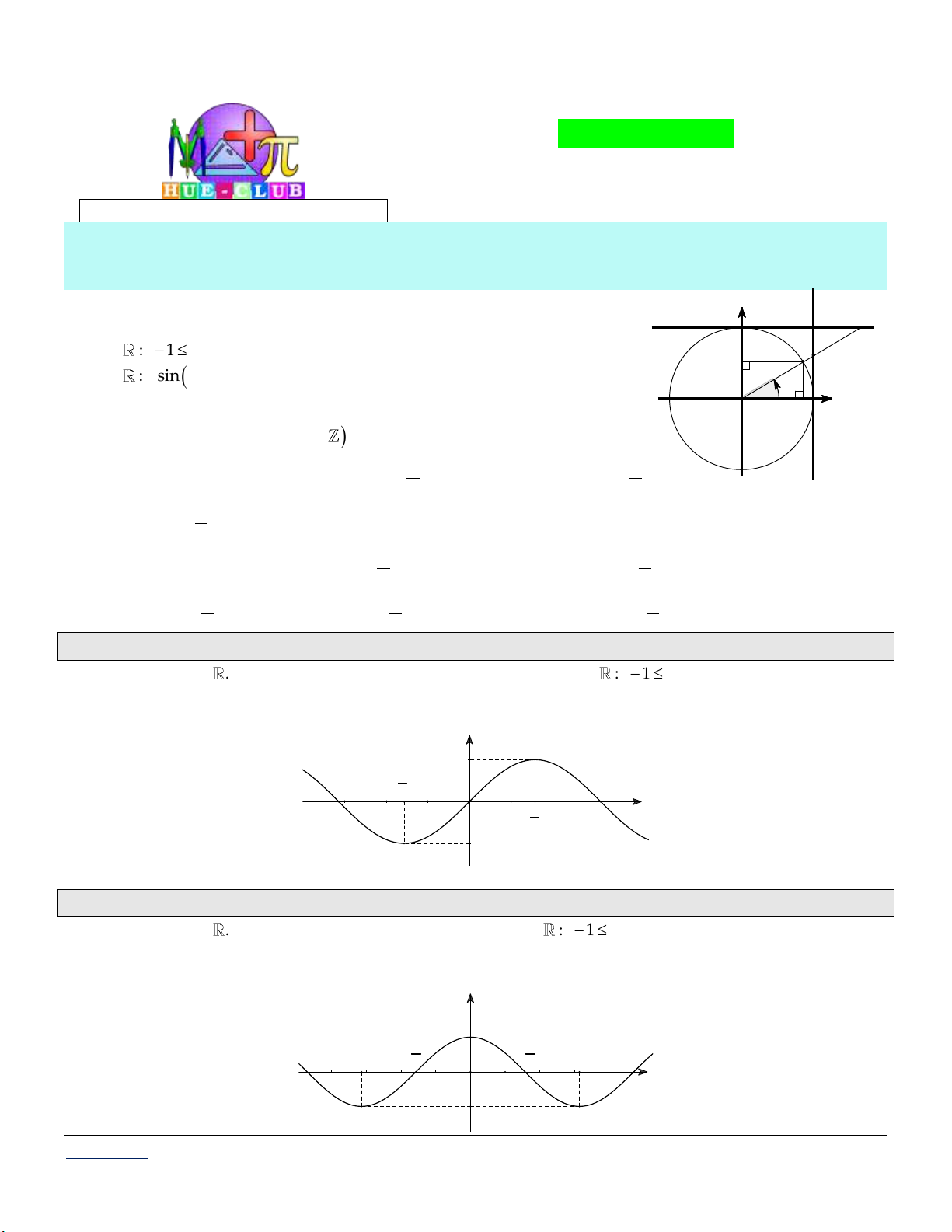
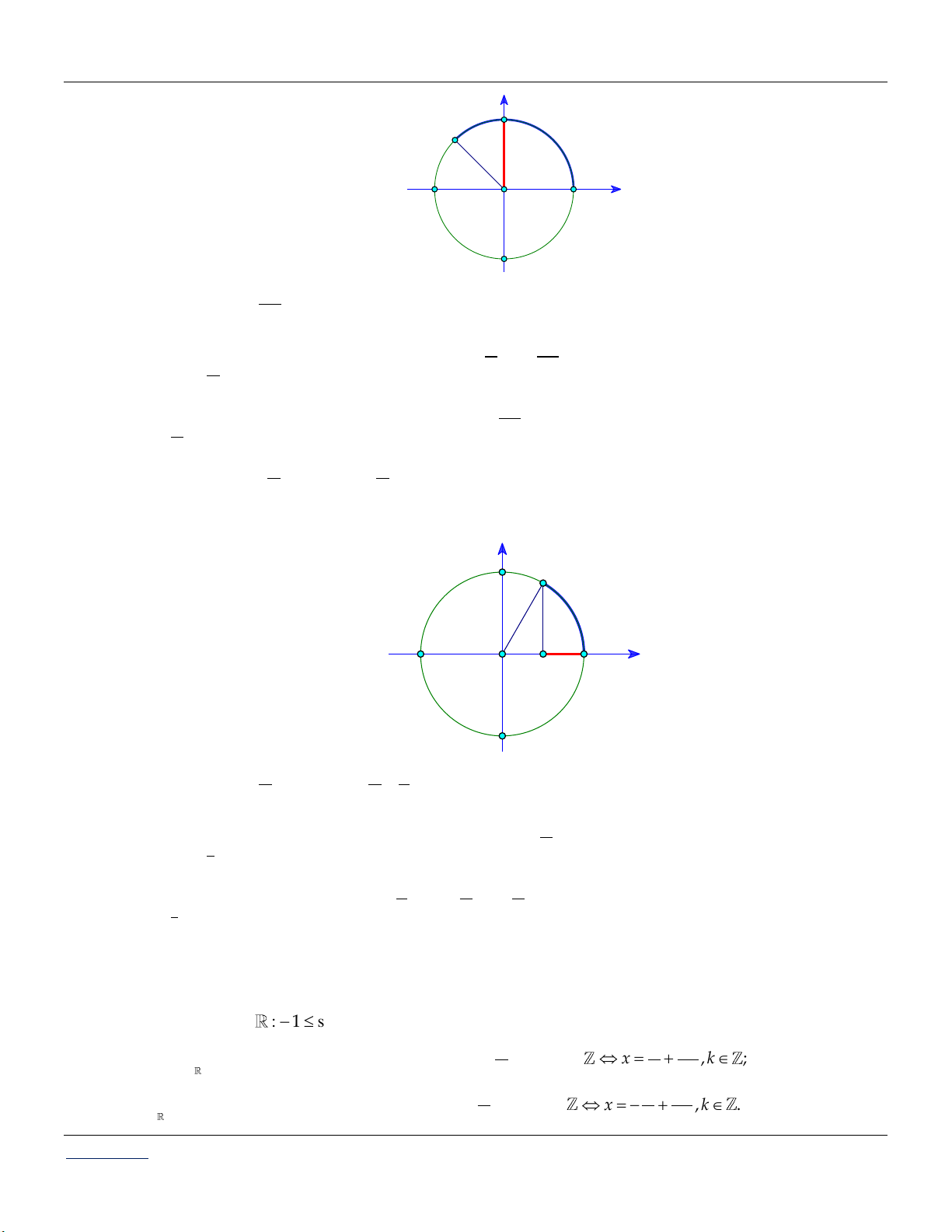
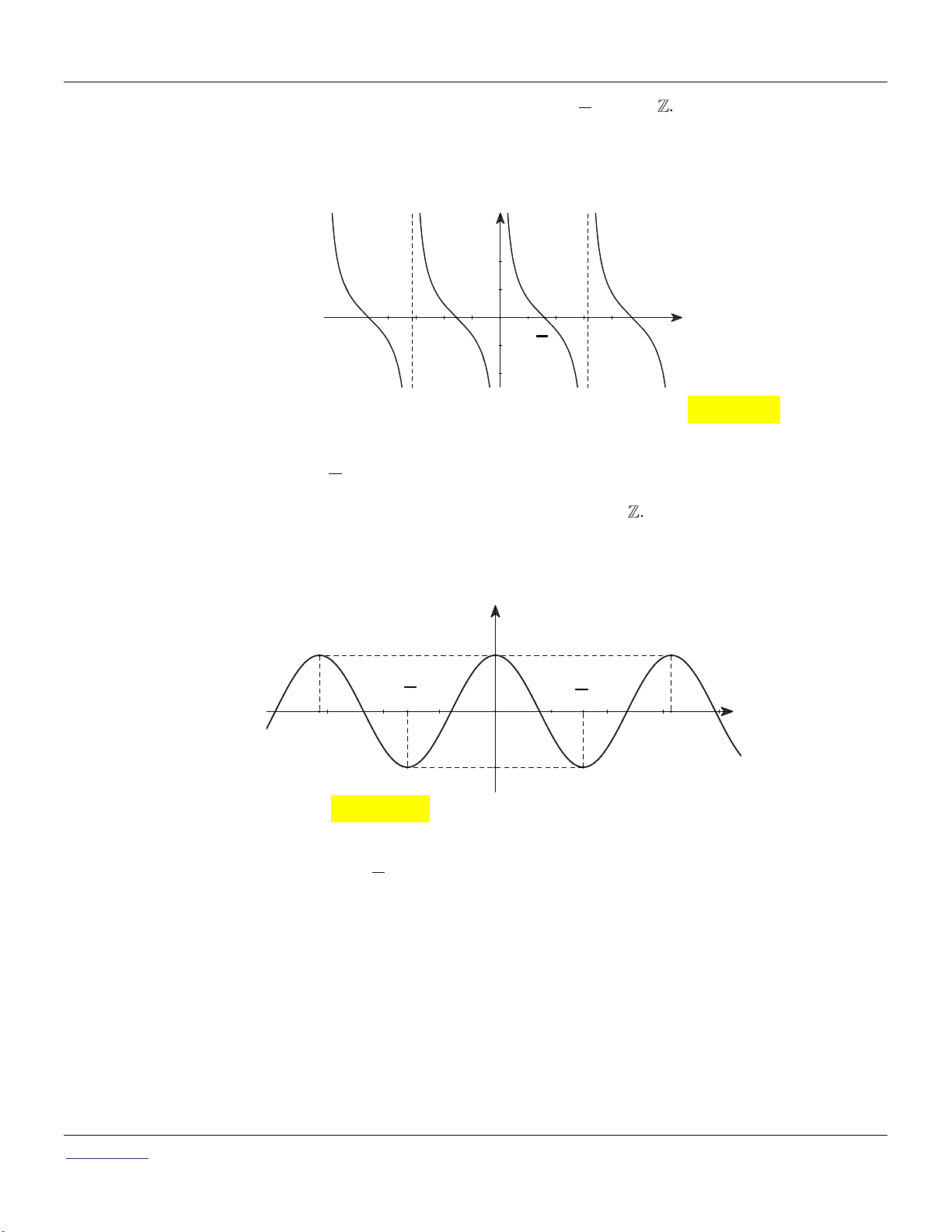
Trung t©m KM 10 H-¬ng Trµ, HuÕ. A- LÝ THUYẾT tang sin cotang
Giới thiệu tổng quan về các hàm số lượng giác: x
  :  1  sin x  1,  1  cosx  1 x
  : sinx k2   sinx cosx k2   cosx O  x
 D : tanx k   tanx cotx k   cot x cos
* Các giá trị đặc biệt: k    
1. sin x  0  x k 2. sin x  1
  x    k2 3. sin x  1  x   k2 2 2 
4. cosx  0  x
k 5. cosx  1  x k2 6. cosx  1
  x    k2 2   ta
7. nx  0  x k 8. tanx  1  x
k 9. tanx  1
  x    k 4 4   
10. cotx  0  x
k 11. cotx  1  x   k 12. cotx  1  x    k 2 4 4 1. Hàm số y = sin x: * TXĐ: D  . * Tập giá trị: x
  :  1  sin x  1 .
* Hàm số y = sin x là hàm số lẻ.
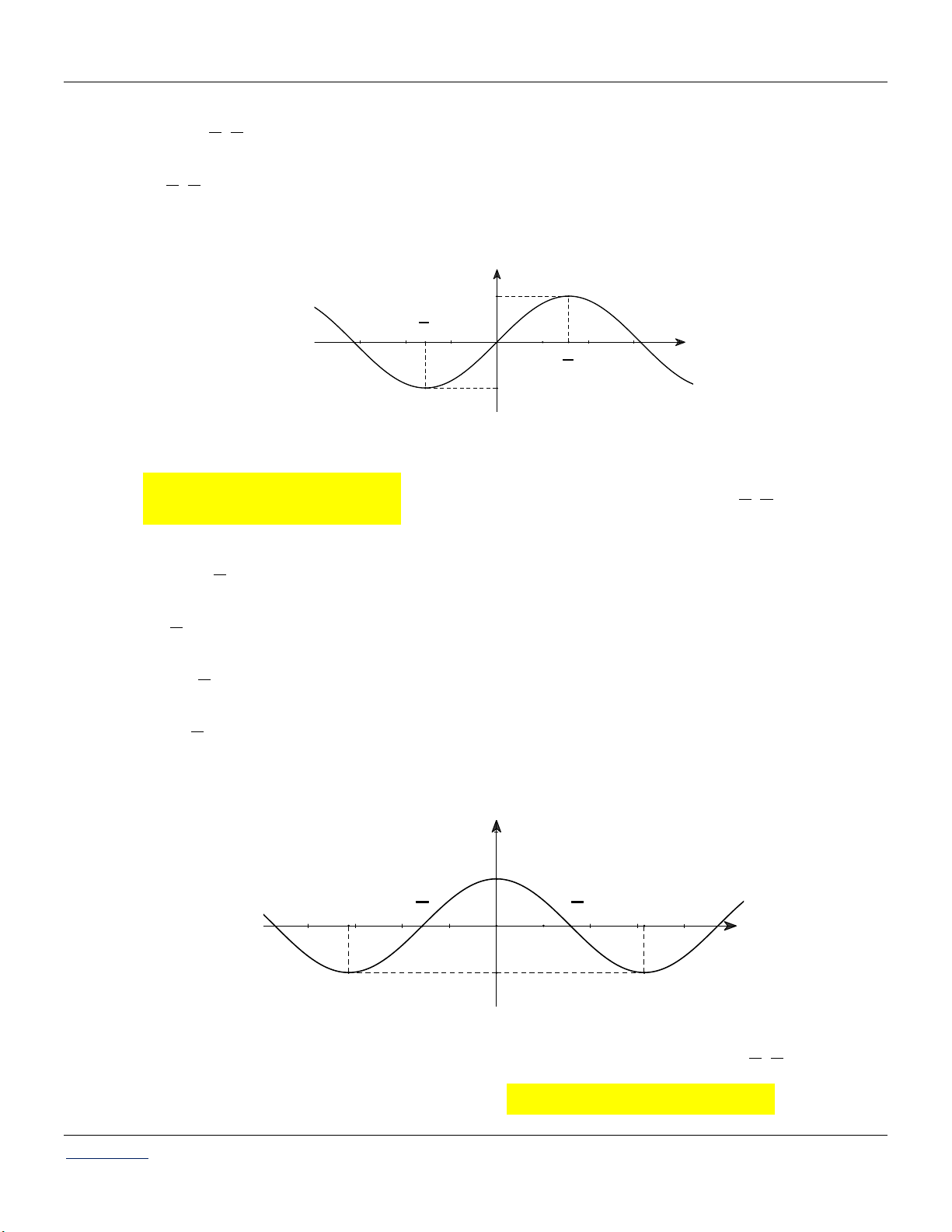
* Tuần hoàn với chu kỳ: T  2 . Đồ thị: y 1 π - 2 π x -π O π 2 -1
2. Hàm số y = cos x: * TXĐ: D  . * Tập giá trị: x
  :  1  cosx  1 .
* Hàm số y = cos x là hàm số chẵn. * Tuần hoàn với chu kỳ: T  2 . Đồ thị: y 1 π π - -π 2 2 π O x 1 -1
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 1
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
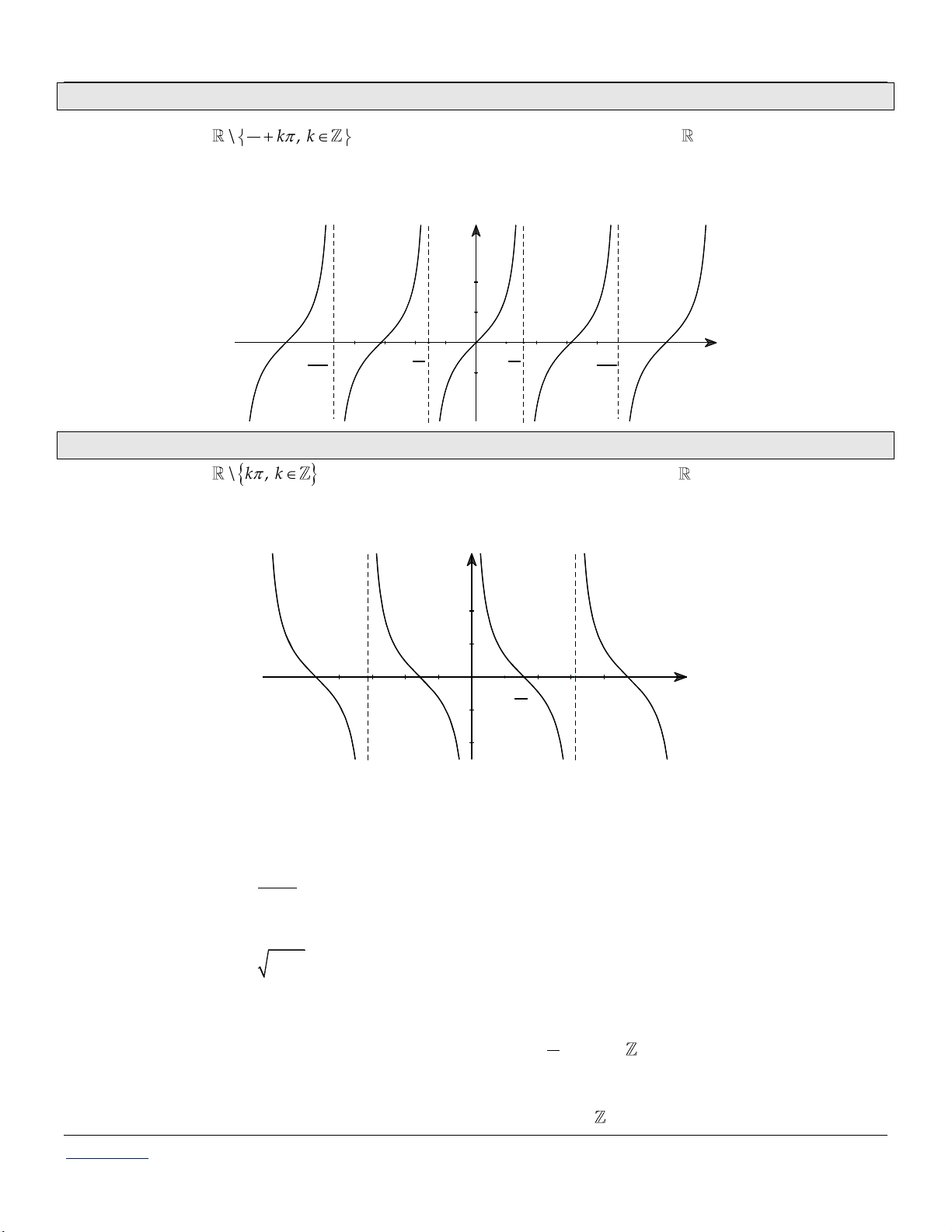
3. Hàm số y = tan x:  
* TXĐ: D  \  k , k   * Tập giá trị: x
  D : tan x .  2 
* Hàm số y = tan x là hàm số lẻ.
* Tuần hoàn với chu kỳ: T   . Đồ thị: y O x 3π π π 3π - - 2 2 2 2
3. Hàm số y = cot x: * TXĐ: D  
\ k , k   * Tập giá trị: x
  D : co t x .
* Hàm số y = cot x là hàm số lẻ.
* Tuần hoàn với chu kỳ: T   . Đồ thị: y O x -π π π 2
B. MỘT SỐ DẠNG TOÁN THƯỜNG GẶP Dạng 1:
TÌM TẬP XÁC ĐỊNH CỦA HÀM SỐ
I. MỘT SỐ KẾT QUẢ
Px cã nghÜa P x  1) Hàm số y
xác định khi chỉ khi Q
 x cã nghÜa. Qx Q  x   0
Px cã nghÜa
2) Hàm số y Px xác định khi chỉ khi  P  x .   0 u  xcã nghÜa 
3) Hàm số y  tanux xác định khi chỉ khi   u  x .   k ,k   2 u
 xcã nghÜa
4) Hàm số y  cot ux xác định khi chỉ khi  ux .  k ,k  
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 2
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 II. BÀI TẬP TỰ LUẬN Câu 1:
Tìm tập xác định của các hàm số sau:       a) y  tan2 3  2x  .  b) y  cot3 4  4x  .   4   6  sin 2x  1 tan x c) y  . d) y  . sin 4x  1 2 2 sin x  cos x Lời giải:   
a) Hàm số xác định khi chỉ khi cos 2x     0  4    3 3 k
 2x    k,k   2x
k,k   x   , k  . 4 2 4 8 2 3 k 
Vậy tập xác định của hàm số là D  \   , k  .  8 2    
b) Hàm số xác định khi chỉ khi sin 4x     0  6     k
 4x   k ,k   4x   k,k   x   , k  . 6 6 24 4   k 
Vậy tập xác định của hàm số là D  \   , k  . 24 4 
c) Hàm số xác định khi chỉ khi sin 4x  1     4    k x k2 , k   x   , k  . 2 8 2   k
Vậy tập xác định của hàm số là D  \   , k  .  8 2  cos x  0
d) Hàm số xác định khi chỉ khi  s
 in2 x  cos2 x  0     x   kx   k cos x  0    2  2      
,k;m  . cos2x  0   m 2x m    x    2  4 2   m 
Vậy tập xác định của hàm số là D  \   k ,  , k,m  .  2 4 2  Câu 2:
Tìm tập xác định của các hàm số sau: 2 tan x
a) y  2 tan x  3cot . x b) y  . sin x  1 Lời giải: s  in x  0 k
a) Hàm số xác định khi chỉ khi 
 sin 2x  0  2x k,k   x  , k  . cos x  0 2 k 
Vậy tập xác định của hàm số là D  \  , k  .  2  s  in x  1  
b) Hàm số xác định khi chỉ khi 
 cos x  0  x   k ,k  cos x  0 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 3
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11  
Vậy tập xác định của hàm số là D
\   k , k  .  2  Câu 3:
Tìm tập xác định của các hàm số sau:
a) y  1  sin 6x.
b) y  cos 3x  . 1 cos x  2 sin 2x  4 c) y  . d) y  . sin x  2 1  sin 3x Lời giải:
a) Hàm số xác định khi chỉ khi 1  sin 6x  0  sin 6x  1 (đúng với mọi x  ).
Vậy tập xác định của hàm số là D  . cos 3x    ; 1 
b) Hàm số xác định khi chỉ khi cos x    cos 1 3 1 0
3x  1  cos3x  1 k2
 3x k2 ,k   x  , k  . 3 k2 
Vậy tập xác định của hàm số là D   , k  .  3  cos x  2   0
c) Hàm số xác định khi chỉ khi  sin x  2 (*)
sin x  2  0, x    cosx  2  0 cos x  2 Ta có: x   : nên  0, x   . sin x  2   0 sin x  2
Vậy tập xác định của hàm số là D  .  sin 2x  4   0
d) Hàm số xác định khi chỉ khi  1  sin 3x (*) 1   sin3x   0 sin2x  4  0  Ta có: x   :
nên (*)  1  sin 3x  0  sin 3x  1  3x   k  2 , k  1  sin 3x   0 2  k   2 x   , k  6 3  k2 
Vậy tập xác định của hàm số là D  \   , k  .  6 3 
III. BÀI TẬP TỰ LUYỆN Câu 4:
Tìm tập xác định của các hàm số sau: x x  1
1) y  sin 3x 2) y  cos 3) y  sin x 4) y  cos 3 x  1 7    cot x sin x  2 5) y
6) y  cot 2x  7) y  8) y    2cosx  4  cosx  1 cosx  1 3 2
9) y  cosx  1 10) y  11) y
12) y  tan x  cot x 2 2 sin x  cos x cos x  cos 3x
IV. TRẮC NGHIỆM: TẬP XÁC ĐỊNH CỦA HÀM SỐ Câu 1.
Tìm tập xác định của hàm số y  sin 2 . x A. D   2  ;2.   B. D   1  ;1.   C. D  . D. D   \ k. Câu 2. Xét bốn mệnh đề sau:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 4
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
(1): Hàm số y  sin x có tập xác định là .
(2): Hàm số y  cos x có tập xác định là .
(3): Hàm số y  tan x có tập xác định là  \ k .   
(4): Hàm số y  cot x có tập xác định là \k .  2 
Tìm số phát biểu đúng. A. 1. B. 2. C. 3. D. 4. Câu 3.
Tìm tập xác định của hàm số y  2cot x  sin 3 . x  
A. D  \  kk  . B. D  
\ kk  .  2  k  C. D  . D. D  \ k  .  2   2  Câu 4.
Tìm tập xác định của hàm số y  tan x   .  3   2    A. D  \
kk  .
B. D  \  kk  .  3   2    
C. D  \  kk  . D. D  
\ kk  .  6  Câu 5.
Tìm tập xác định của hàm số y  tan x  cot . x     
A. D  \  kk  . B. D  \k k  .  2   2     C. D  .
D. D  \  k k  .  4 2  cot x Câu 6.
Tìm tập xác định của hàm số y  . sin x  1     
A. D  \  k2 k  . B. D  \k k  .  2   2      
C. D  \  k2 ; kk  .
D. D  \  k k  .  2   2 2  Câu 7.
Tìm tập xác định của hàm số 2017 y  2016 tan 2 . x     
A. D  \  kk  . B. D  \k k  .  2   2     C. D  .
D. D  \  k k  .  4 2  1 Câu 8.
Tìm tập xác định của hàm số y  . 2 2 sin x  cos x     
A. D  \  kk  . B. D  \k k  .  2   2 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 5
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11    C. D  .
D. D  \  k k  .  4 2  1 Câu 9.
Tìm tập xác định của hàm số y  . sin 3x  sin x     
A. D  \  kk  . B. D  \k k  .  2   2     C. D  .
D. D  \  k k  .  4 2  1
Câu 10. Tìm tập xác định của hàm số y  .
sin x  3 cos x    
A. D  \  kk  .
B. D  \  kk  .  3   6    C. D  .
D. D  \  k2 k  .  3  tan x
Câu 11. Tìm tập xác định của hàm số y  . sin x  1     
A. D  \  k2 k  . B. D  \k k  .  2   2      
C. D  \  kk  .
D. D  \  k k  .  2   4 2  2  cos x
Câu 12. Tập xác định của hàm số y  là sin 3xk  k  k  A. D  \
k  . B. D  
\ kk  . C. D  \
k  . D. D  \ k  .  3   4   2 
Câu 13. Tập xác định của hàm số y  sin x  1 là A. D  . B. D  .    
C. D    k2 k  .
D. D  \  k2 k  .  2   2  1
Câu 14. Tập xác định của hàm số y  là 2 sin x  5 A. D  . B. D  .    
C. D    k2 k  .
D. D  \  k2 k  .  2   2  2  sin x
Câu 15. Tìm tập xác định của hàm số y  . 1  cos x A. D  
\ kk  . B. D  
\ k2 k  .     
C. D  \  kk  . D. D  \k k  .  2   2 
Câu 16. Hàm số nào sau đây có tập xác định là ?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 6
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 A. y  sin x. B. y  tan 2 . x C. y  cos 2 . x D. y   2 cot x  1.
Câu 17. Hàm số nào sau đây có tập xác định là ? tan 2x 1 sin 2x  3
A. y  2cos x. B. y  . C. y  cos . D. y  . 2 sin x  1 x cos 4x  5 1
Câu 18. Tập xác định D của hàm số y  là    tan x     4  3    A. D  \
k , k  .
B. D  \  k , k  .  4   2      
C. D  \  k , k  .
D. D  \  k , k  .  4 2   4  3 tan x  5
Câu 19. Tập xác định D của hàm số y  là 2 1  sin x    
A. D  \  k2 ,k  .
B. D  \  k ,k  .  2   2  C. D  
\ k , k  . D. D  .   
Câu 20. Tìm tập xác định D của hàm số y  tan cos x.  2  A. D  
\ k , k  . B. D  \ 
 2k 1, k . C. D  . D. D  
\ k2 , k  .   
Câu 21. Tìm tập xác định D của hàm số y  cot  cos x.  2    A. D  
\ k , k  . B. D  \ 
 2k 1, k . C. D  .
D. D  \  k , k  .  2  2  sin 2x
Câu 22. Tìm m để hàm số y
xác định trên toàn trục số. mcos x  1
A. 1  m  1. B. 1  m  1. C. m  0. D. 0  m  1.
Câu 23. Cho hàm số y  2m  3sin x. Có bao nhiêu giá trị nguyên của tham số m thuộc 0; 2022 để hàm số xác định trên ? A. 2018. B. 2019. C. 2020. D. 2021. 1
Câu 24. Tìm tập hợp tất cả các giá trị m để hàm số y  có tập xác định là . sin 2x m A. 1;1.   B. ; 1
  1;. C. 1;1. D. ; 1    1  ;   .
Câu 25. Tìm tập hợp tất cả các giá trị m để hàm số 2
y  cos 4x m có tập xác định là . A. 1;1.   B. ;0. C. ; 1.  D. ;0. 
V. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: TẬP XÁC ĐỊNH CỦA HÀM SỐ Câu 1.
Tìm tập xác định của hàm số y  sin 2 . x A. D   2  ;2.   B. D   1  ;1.   C. D  . D. D   \ k. Lời giải:
Chú ý phân biệt giữa tập giá trị và tập xác định của hàm số.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 7
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Chọn đáp án C. Câu 2. Xét bốn mệnh đề sau:
(1): Hàm số y  sin x có tập xác định là .
(2): Hàm số y  cos x có tập xác định là .
(3): Hàm số y  tan x có tập xác định là  \ k .   
(4): Hàm số y  cot x có tập xác định là \k .  2 
Tìm số phát biểu đúng. A. 1. B. 2. C. 3. D. 4. Lời giải:  
Hàm số y  tan x có tập xác định là \  kk  . Vậy (3) sai.  2 
Hàm số y  cot x có tập xác định là 
\ kk  . Vậy (4) sai.
Chọn đáp án B. Câu 3.
Tìm tập xác định của hàm số y  2cot x  sin 3 . x  
A. D  \  kk  . B. D  
\ kk  .  2  k  C. D  . D. D  \ k  .  2  Lời giải:
Hàm số xác định khi chỉ khi sin x  0  x k ,k  .
Vậy tập xác định của hàm số là D  
\ kk  .
Chọn đáp án B.  2  Câu 4.
Tìm tập xác định của hàm số y  tan x   .  3   2    A. D  \
kk  .
B. D  \  kk  .  3   2    
C. D  \  kk  . D. D  
\ kk  .  6  Lời giải:  2  2  
Hàm số xác định khi chỉ khi cos x   0  x
  k ,k   x    k ,k    3  3 2 6   
Vậy tập xác định của hàm số là D  \  kk  .  6 
Chọn đáp án C. Câu 5.
Tìm tập xác định của hàm số y  tan x  cot . x     
A. D  \  kk  . B. D  \k k  .  2   2 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 8
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11    C. D  .
D. D  \  k k  .  4 2  Lời giải: sin x  0 k
Hàm số xác định khi chỉ khi 
 sin2x  0  2x k ,k  x  , k  . cos x   0 2   
Vậy tập xác định của hàm số là D  \k k  .  2 
Chọn đáp án B. cot x Câu 6.
Tìm tập xác định của hàm số y  . sin x  1     
A. D  \  k2 k  . B. D  \k k  .  2   2      
C. D  \  k2 ; kk  .
D. D  \  k k  .  2   2 2  Lời giải:
sin x  0  x k 
Hàm số xác định khi chỉ khi   , k  .
sin x  1  x    k2  2  
Vậy tập xác định của hàm số là D  \  k2 ; kk  .  2 
Chọn đáp án C. Câu 7.
Tìm tập xác định của hàm số 2017 y  2016 tan 2 . x     
A. D  \  kk  . B. D  \k k  .  2   2     C. D  .
D. D  \  k k  .  4 2  Lời giải:   k
Hàm số xác định khi chỉ khi cos 2x  0  2x
k ,k   x   ,k  . 2 4 2   
Vậy tập xác định của hàm số là D  \  k k  .  4 2 
Chọn đáp án B. 1 Câu 8.
Tìm tập xác định của hàm số y  . 2 2 sin x  cos x     
A. D  \  kk  . B. D  \k k  .  2   2     C. D  .
D. D  \  k k  .  4 2  Lời giải: 1 1 Ta có: y   . 2 2 sin x  cos x cos2x
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 9
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11   k
Hàm số xác định khi chỉ khi cos 2x  0  2x
k ,k   x   ,k  . 2 4 2   
Vậy tập xác định của hàm số là D  \  k k  .  4 2 
Chọn đáp án D. 1 Câu 9.
Tìm tập xác định của hàm số y  . sin 3x  sin x     
A. D  \  kk  . B. D  \k k  .  2   2     C. D  .
D. D  \  k k  .  4 2  Lời giải: 1 1 Ta có: y   . sin 3x  sin x 2sin 2x cos x sin2x  0 k
Hàm số xác định khi chỉ khi 
 sin2x  0  2x k ,k   x  , k  . cos x   0 2   
Vậy tập xác định của hàm số là D  \k k  .  2 
Chọn đáp án B. 1
Câu 10. Tìm tập xác định của hàm số y  .
sin x  3 cos x    
A. D  \  kk  .
B. D  \  kk  .  3   6    C. D  .
D. D  \  k2 k  .  3  Lời giải:
Hàm số xác định khi chỉ khi sin x  3 cos x  0 
 sin x  3 cos x  tan x  3  x   k ,k  . 3  
Vậy tập xác định của hàm số là D  \  kk  .  3 
Chọn đáp án A. tan x
Câu 11. Tìm tập xác định của hàm số y  . sin x  1     
A. D  \  k2 k  . B. D  \k k  .  2   2      
C. D  \  kk  .
D. D  \  k k  .  2   4 2  Lời giải: cosx  0 
Hàm số xác định khi chỉ khi 
 cosx  0  x   k ,k  . sin x   1 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 10
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11  
Vậy tập xác định của hàm số là D  \  kk  .  2 
Chọn đáp án C. 2  cos x
Câu 12. Tập xác định của hàm số y  là sin 3xk  k  k  A. D  \
k  . B. D  
\ kk  . C. D  \
k  . D. D  \ k  .  3   4   2  Lời giải: 2  cos x  0
Hàm số xác định khi chỉ khi  sin 3x  (*)  0 Ta có x
  :  1  cos x  1  1  cos x  2  3. k
Lúc đó, (*)  sin 3x  0  3x k ,k   x  , k  . 3 k 
Vậy tập xác định của hàm số là D  \ k  .  3 
Chọn đáp án A.
Câu 13. Tập xác định của hàm số y  sin x  1 là A. D  . B. D  .    
C. D    k2 k  .
D. D  \  k2 k  .  2   2  Lời giải:
Hàm số xác định khi chỉ khi sin x  1  0  sin x  1 (*) Ta có x
  :  1  sin x  1. 
Lúc đó, (*)  sin x  1  x
k2 ,k  . 2  
Vậy tập xác định của hàm số là D    k2 k  .  2 
Chọn đáp án C. 1
Câu 14. Tập xác định của hàm số y  là 2 sin x  5 A. D  . B. D  .    
C. D    k2 k  .
D. D  \  k2 k  .  2   2  Lời giải: 5
Hàm số xác định khi chỉ khi 2sin x  5  0  sin x  (*) 2 Ta có x
  :  1  sin x  1. Lúc đó, (*) vô nghiệm.
Vậy tập xác định của hàm số là D  .
Chọn đáp án A.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 11
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 2  sin x
Câu 15. Tìm tập xác định của hàm số y  . 1  cos x A. D  
\ kk  . B. D  
\ k2 k  .     
C. D  \  kk  . D. D  \k k  .  2   2  Lời giải: 2  sin x   0
Hàm số xác định khi chỉ khi 1  cos x (*) 1   cosx   0  1   sin x  1 1
  sin x  2  3 Ta có x   :    . 1   cosx  1 1  cos x    0
Lúc đó, (*)  1  cos x  0  cos x  1  x k2 , k  .
Vậy tập xác định của hàm số là D  
\ k2 k  .
Chọn đáp án B.
Câu 16. Hàm số nào sau đây có tập xác định là ? A. y  sin x. B. y  tan 2 . x C. y  cos 2 . x D. y   2 cot x  1.
Câu 17. Hàm số nào sau đây có tập xác định là ? tan 2x 1 sin 2x  3
A. y  2cos x. B. y  . C. y  cos . D. y  . 2 sin x  1 x cos 4x  5 Lời giải: sin 2x  3 Xét hàm số y  . cos 4x  5  1   sin2x  1
2  sin2x  3  4 sin 2x  3 Ta có x   :      0. 1   cos4x  1
4  cos 4x  5  6 cos 4x    5 sin 2x  3 Vậy hàm số y  có tập xác định là . cos 4x  5
Chọn đáp án D. 1
Câu 18. Tập xác định D của hàm số y  là    tan x     4  3    A. D  \
k , k  .
B. D  \  k , k  .  4   2      
C. D  \  k , k  .
D. D  \  k , k  .  4 2   4  Lời giải:
Hàm số xác định khi thỏa mãn đồng thời các điều kiện sau:        tan x  
 xác định  cos x     0. 1  4   4         tan x   0  sin x       0. 2  4   4 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 12
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11         
Từ 1 và 2 , suy ra hàm số xác định  sin x  cos x   0  sin2 x         0  4   4   4        2 x
k  x   k k   .  4  4 2 3 tan x  5
Câu 19. Tập xác định D của hàm số y  là 2 1  sin x    
A. D  \  k2 ,k  .
B. D  \  k ,k  .  2   2  C. D  
\ k , k  . D. D  . Lời giải:
Hàm số xác định khi thỏa mãn đồng thời các điều kiện sau:  2 2
1  sin x  0  sin x  1. 1
 tan x xác định  cos x  0. 2 
Từ 1 và 2 , suy ra hàm số xác định  cos x  0  x
k k . 2   
Câu 20. Tìm tập xác định D của hàm số y  tan cos x.  2  A. D  
\ k , k  . B. D  \ 
 2k 1, k . C. D  . D. D  
\ k2 , k  . Lời giải:  
Hàm số xác định khi và chỉ khi cos x
k ,k   cos x  1 2k,k  2 2
cosx  1 øng víi k  0
x k2 ,k     
x kk  cos x  1    , . øng víi k    1
x    k2 ,k
Chọn đáp án A.   
Câu 21. Tìm tập xác định D của hàm số y  cot  cos x.  2    A. D  
\ k , k  . B. D  \ 
 2k 1, k . C. D  .
D. D  \  k , k  .  2  Lời giải:
Hàm số xác định khi và chỉ khi cos x k ,k   cos x  2k,k  2 
 cosx  0 øng ví k i  0  x
k ,k  . 2
Chọn đáp án D. 2  sin 2x
Câu 22. Tìm m để hàm số y
xác định trên toàn trục số. mcos x  1
A. 1  m  1. B. 1  m  1. C. m  0. D. 0  m  1. Lời giải:
Hàm số xác định trên
khi và chỉ khi mcos x  1  0, x  . 1
Khi m  0 thì 1 luôn đúng nên nhận giá trị m  0.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 13
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Khi m  0 thì mcos x  1 có tập giá trị là đoạn m  1;m  1. 
 Do đó để 1 đúng khi và chỉ khi m0
m  1  0  m  1 0  m  1.
Khi m  0 thì mcos x  1 có tập giá trị là đoạn m  1;m  1 
 Do đó để 1 đúng khi và chỉ khi m0
m  1  0  m  1  1  m  0.
Kết hợp ba trường hợp ta được: 1  m  1.
Câu 23. Cho hàm số y  2m  3sin x. Có bao nhiêu giá trị nguyên của tham số m thuộc 0; 2022 để hàm số xác định trên ? A. 2018. B. 2019. C. 2020. D. 2021. Lời giải:
Hàm số xác định trên
khi và chỉ khi 2m  3sin x  0 , x  3
 2m  3sin x, x
   2m  max3sin 
x  2m  3  m  2 m
m 2;3;4;...;2021 . m 0 ; 2022     1
Câu 24. Tìm tập hợp tất cả các giá trị m để hàm số y  có tập xác định là . sin 2x m A. 1;1.   B. ; 1
  1;. C. 1;1. D. ; 1    1  ;   . Lời giải:     Yêu cầu bài toán x :sin 2x 1;1
 sin 2x m  0  m  sin 2x  
m  1  ;1    m; 1   1;.
Chọn đáp án B.
Câu 25. Tìm tập hợp tất cả các giá trị m để hàm số 2
y  cos 4x m có tập xác định là . A. 1;1.   B. ;0. C. ; 1.  D. ;0.  Lời giải: 2     Yêu cầu bài toán 2 2 x :cos 4x 0;1   2
 cos 4x m  0  m  cos 4x 
m  mincos 4x  0.  m;0. 
Chọn đáp án D.
Dạng 2:
TÌM GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ I. MỘT SỐ KẾT QUẢ 1) 2n1 * x
  :  1  sin x  1,  1  sin x  1,n . 2n1 * x
  :  1  cos x  1,  1  cos x  1,n . 2) 2n * x
  : 0  sin x  1, 0  sin x  1, n . 2n * x
  : 0  cos x  1, 0  cos x  1, n . II. BÀI TẬP TỰ LUẬN Câu 1:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:  3     a) y  sin , x x  ; 0 .  
b) y  2cos 2x  , 5 x  ; 0 .    4   6  Lời giải:
a) Sử dụng đường tròn lượng giác:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 14
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 _ 3π 4 0 x O 2π  3  Ta có: x   ; 0 :0  sin x  . 1    4    3 
Vậy max y  1 đạt được khi sin x  1  x   0; ;    3  x 2  4 0;    4   3 
min y  0 đạt được khi sin x  0  x  0  0; .    3  x0;   4   4        b) Ta có: x  ; 0  2x ; 0 .      6   3 
Sử dụng đường tròn lượng giác: y _π 1 3 x O 1 1 _ 2       1 Ta có: x   ; 0  2x ; 0 :  cos2x  1    
 1  2cos2x  2  6  2cos2x  5  7.  6   3  2   
Vậy max y  7 đạt được khi cos 2x  1  x  0  0; ;      x  6 0;    6  1    
min y  6 đạt được khi cos 2x   x   0; .      x0;  2 6  6   6  Câu 2:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y  2sin 4x  5.
b) y  3  2 cos 2 . x Lời giải: a) Ta có: x
  :  1  sin 4x  1  2
  2sin 4x  2  3  2sin 4x  5  7 .   k
Vậy max y  7 đạt được khi sin 4x  1  4x
k2 ,k   x   ,k  ; 2 8 2   k
min y  3 đạt được khi sin 4x  1
  4x    k2 ,k   x    , k  . 2 8 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 15
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 b) Ta có: x
  :  1  cos2x  1  2  2  cos2x  2
  1  3  2cos2x  5 
Vậy max y  5 đạt được khi cos 2x  1  2x    k
2 , k   x    k , k  ; 2
min y  1 đạt được khi cos 2x  1  2x k  2 , k   x   k , k  . Câu 3:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y  3 sin 3x  2. b) y  cos2 5 2x  4. Lời giải: a) Ta có: x
  : 0  sin 3x  1  0  3 sin 3x  3  2  3 sin 3x  2  5 .
Vậy max y  5 đạt được khi    k  2
sin 3x  1  3x   k
2 , k   x   , k   x    2 6 3 sin 3 1 ;    k  2
sin 3x  1  3x    k
2 , k   x    , k   2 6 3   k
hoặc sin 3x  1  cos 3x  0  3x
k ,k   x   , k  ; 2 6 3 k
min y  2 đạt được khi sin 3x  0  sin 3x  0  3x k , k   x  , k  . 3 b) Ta có: x
  :  cos2 x    cos2 0 2 1 0 5 2x  5
  cos2 x     cos2 4 5 2 4 9 2 5 2x  4  3.
cos2x  1  2x k2 ,k   x k ,k  Vậy 
max y  3 đạt được khi 2 cos 2x  1   ;  cos 2x  1
  2x    k2 ,k   x   k ,k   2 khoặc 2
cos 2x  1  sin 2x  0  2x k , k   x  , k  ; 2   k
min y  2 đạt được khi 2
cos 2x  0  cos 2x  0  2x
k ,k   x   ,k  . 2 4 2 Câu 4:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:  2  a)  sin4  cos4 y x . x
b) y  cos x  cos x  .   3  Lời giải: 1 1 1  cos 4x 3 1
a) Ta có: y  sin4 x  cos4 x  1  sin2 2x  1  .   cos4 . x 2 2 2 4 4 1 1 1 1 1 3 Ta có: x
  :  1  cos4x  1    cos4x    cos4x   . 1 4 4 4 2 4 4 k
Vậy max y  1 đạt được khi cos 4x  1  4x k2 ,k   x  , k  ; 2 1  k min y
đạt được khi cos 4x  1
  4x    k2 ,k  x   , k  . 2 4 2  2        
b) Ta có: y  cos x  cos x    2cos x  cos  cos   x  .   3   3  3  3     Ta có: x
  :  1  cosx   .  1  3 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 16
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11     
Vậy max y  1 đạt được khi cos x
 1  x   k2 ,k   x   k2 ,k    ;  3  3 3     4 min y  1
 đạt được khi cos x   1
  x     k2 ,k   x   k2 ,k    .  3  3 3 Câu 5:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:   
a) y  sin2 x  2sin x  . 3
b) y  cos 2x  cos , x x  ; 0 .    2  Lời giải:
a) Xét hàm số y  sin2 x  2sin x  . 3
Đặt t  sin x  1;1 .   Ta có: gt 2
t  2t  , 3 t  ; 1  1 . Bảng biến thiên: t  1  1    g t 6 2 Dựa vào BBT, suy ra: 
max y  max g t  6 đạt được khi sin x  1
  x    k2 ,k  ; t 1  ;1   2 
min y  min g t  2 đạt được khi sin x  1  x
k2 ,k  . t 1  ;1   2
b) Xét hàm số y  cos x  cos x  cos2 2 2
x  cos x  . 1   
Đặt t  cos x; x 0;  cosx0;1 .      2  Ta có: gt 2
 2t t  , 1 t  ; 0  1 . Bảng biến thiên: t  1  0 1  4   g t 2 1  9  8 Dựa vào BBT, suy ra:   
max y  max g t  2 đạt được khi cos x  1  x  0 0; ;      t0;1 0;    2     2     
min y  min g t  1
 đạt được khi cosx  0  x   0; .      t0;1 0;     2  2   2  Câu 6:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 17
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
a) y  sin x  3 cos x  . 2 b) y  sin2 2
x  3 sin 2x  . 1 Lời giải: b Chú ý kết quả: sin  cos 2 2 a x b
x a b sin x    ,, , a b  ,sin  . 2 2 a b   
a) Ta có: y  2sin x   2  y     ;04.  3       
Vậy max y  4 đạt được khi sin x
 1  x    k2 ,k   x   k2 ,k    ;  3  3 2 6      5
min y  0 đạt được khi sin x   1
  x     k2 ,k  x    k2 ,k   .  3  3 2 6    b) Ta có: y  sin2 2
x  3 sin 2x  1  3 sin 2x  cos 2x  2  2sin 2x   2  y     ;04.  6       
Vậy max y  4 đạt được khi sin 2x
 1  2x    k2 ,k  x   k ,k    ;  6  6 2 3      
min y  0 đạt được khi sin 2x   1
  2x     k2 ,k   x    k ,k    .  6  6 2 6
III. BÀI TẬP TỰ LUYỆN Câu 7:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: 2 1  4cos 2 x 2
1) y  2  4cosx 2) y  3  8 sin x c . os x 3) y  4) 2
y  2 sin x  cos2x 3    2 2 2
5) y  3  2 sin x 6) y  cosx  cos x
7) y  cos x  2cos2x 8) y  5    2 sin x c . os x  3  Câu 8:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau: 1) 2
y  sin x  4 sin x  2 2) y asin x  c b osx  2 2
a b  0 2 2 2 2
3) y  3sin x  c 5 os x  8 sin c
x osx  2 4) y  2 sin x  4cos x  8 sin c x osx  1 4 4
5) y  sin x  cos x 6 6
6) y  sin x  cos x
IV. TRẮC NGHIỆM: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT HÀM SỐ Câu 1.
Hàm số nào sau đây có tập giá trị là ? A. y  sin x. B. y  tan 2 . x
C. y  cos 2x  cot 2 .
x D. y x  sin . x Câu 2.
Hàm số nào sau đây có tập giá trị là
trên tập xác định của nó? 1 A. y  sin x. B. y  tan 2 . x C. y  cos 2 . x D. y  . sin x Câu 3.
Tìm tập giá trị T của hàm số y  sin 2 . x A. T   2  ;2.   B. T   1  ;1.   C. T  . D. T   1  ;1. Câu 4.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin x  cos x trên .
Tính giá trị M  . m 3 A. 0. B. . C. 6. D. 2. 2 Câu 5.
Tìm tập giá trị T của hàm số y  2cos . x A. T   2  ;2.   B. T   1  ;1.   C. T  . D. T   1  ;1.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 18
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Câu 6. Xét bốn mệnh đề sau:
(1): Trên , hàm số y  cos x có tập giá trị là 1;1.      (2): Trên 0; , 
 hàm số y  cos x có tập giá trị là 0;1.    2   3   2  (3): Trên 0; , 
 hàm số y  cos x có tập giá trị là 0; .  4   2      (4): Trên 0; 
 hàm số y  cos x có tập giá trị là 0;1.   2 
Tìm số phát biểu đúng. A. 1. B. 2. C. 3. D. 4. Câu 7.
Tìm tập giá trị T của hàm số y  2 cos 2 . x A. T   2  ;2.   B. T   1  ;1.   C. T  . D. T   4  ;4.   Câu 8.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin x  cos x trên .
Tính giá trị M  . m A. 0. B. 2. C. 6. D. 2. Câu 9.
Tìm tập giá trị T của hàm số y  2 sin x  1. A. T   2  ;2.   B. T   1  ;3.   C. T  . D. T   3;  3.  
Câu 10. Tìm tập giá trị T của hàm số y  4 cos x  3. A. T   1  ;1.   B. T   7  ;1.   C. T  . D. T   4  ;4.  
Câu 11. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  1  sin x  3.
Khẳng định nào dưới đây đúng?
A. M  3  2 , m   2. B. M  3  2 , m  3. C. M  3  2 , m  2. D. M  2  3, m  3. 
Câu 12. Tìm tập giá trị T của hàm số y  1  2 sin 2 . x A. T   1  ;3.   B. T   3;  4.   C. T  . D. T   3;  3.  
Câu 13. Tìm tập giá trị T của hàm số 2
y  2 sin x  1. A. T   2  ;2.   B. T   1  ;3.   C. T  . D. T  1; 3  .
Câu 14. Tìm tập giá trị T của hàm số 2
y  4 cos 2x  3. A. T  3;7.   B. T  0;7.   C. T  . D. T  0; 3.  
Câu 15. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
3 sin x  cos x trên
. Tính giá trị M  . m A. 0. B. 2. C. 6. D. 2.
Câu 16. Tìm tập giá trị T của hàm số 2
y  5sin x  4. A. T  4; 9.   B. T   1  ;3.   C. T  0; 2.   D. T  2; 3.  
Câu 17. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  3 sin x  cos x  1 trên
. Tính giá trị M  . m A. 0. B. 2. C. 3. D. 5.
Câu 18. Tìm tập giá trị T của hàm số 2
y  7 sin 2x  9.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 19
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 A. T  3; 4.   B. T  3; 37 .   C. T  . D. T  2; 3.  
Câu 19. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 sin 2x  1 trên . Tính giá trị M. . m A. 3. B. 3. C. 6. D. 1.
Câu 20. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 cos x  3 trên . Tính giá trị M. . m A. 3. B. 5. C. 6. D. 1.   
Câu 21. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 cos x  3 trên 0; .    3  Tính giá trị M. . m A. 3. B. 5. C. 6. D. 20.
Câu 22. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 4
y  sin x  cos x trên .
Tính giá trị M  . m 3 A. 0. B. . C. 8. D. 2. 2
Câu 23. Tìm tập giá trị T của hàm số y  1  2 sin 2x . A. T  1; 3  . B. T   1  ;3.   C. T  . D. T   3;  3.  
Câu 24. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  3 sin x  cos x  3
trên . Tính giá trị M  . m A. 0. B. 2. C. 6. D. 5.
Câu 25. Xét bốn mệnh đề sau:
(1): Trên , y  sin x có tập giá trị là 1;1.     
(2): Trên 0;  , y  sin x có tập giá trị là 1;1.    2     (3): Trên 0; , 
y  sin x có tập giá trị là 0;1.    2     (4): Trên 0; 
 , y  sin x có tập giá trị là 0;1.   2 
Có bao nhiêu mệnh đề đúng? A. 1. B. 2. C. 3. D. 4. x
Câu 26. Giá trị lớn nhất của hàm số 2 y  2 sin
 3sin x  5 bằng 2 A. 5  1. B. 0. C. 10  4. D. 13  5.
Câu 27. Để tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số y  sin x  cos x , một
học sinh giải theo các bước sau:
Bước 1: Tập xác định: D  .  1   sin x  1
Bước 2: Ta có: x   :   2
  sin x  cosx  2. 1   cosx   1
Bước 3: Vậy GTLN của hàm số bằng 2, GTNN của hàm số bằng 2.
Bài giải của bạn đó đã đúng chưa? Và nếu sai, thì sai bắt đầu từ bước nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 20
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Câu 28. Hàm số y    x2022 3 5sin
có giá trị lớn nhất là M và giá trị nhỏ nhất là .
m Giá trị của M m bằng A. 2022 2 . B. 4044 2 . C. 2022  4044 2 1  2 . D. 6066 2 .
Câu 29. Hàm số y  5  4 sin 2xcos 2x có tất cả bao nhiêu giá trị nguyên? A. 3. B. 4. C. 5. D. 6.   
Câu 30. Hàm số y  sin x   
 sin x có tất cả bao nhiêu giá trị nguyên?  3  A. 1. B. 2. C. 3. D. 4.
Câu 31. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước
trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức  t   h  3cos   
 12. Mực nước của con kênh cao nhất khi  8 4  A. t  13 (giờ). B. t  14 (giờ). C. t  15 (giờ). D. t  16 (giờ).
V. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT HÀM SỐ Câu 1.
Hàm số nào sau đây có tập giá trị là ? A. y  sin x. B. y  tan 2 . x
C. y  cos 2x  cot 2 .
x D. y x  sin . x Câu 2.
Hàm số nào sau đây có tập giá trị là
trên tập xác định của nó? 1 A. y  sin x. B. y  tan 2 . x C. y  cos 2 . x D. y  . sin x Câu 3.
Tìm tập giá trị T của hàm số y  sin 2 . x A. T   2  ;2.   B. T   1  ;1.   C. T  . D. T   1  ;1. Câu 4.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin x  cos x trên .
Tính giá trị M  . m 3 A. 0. B. . C. 6. D. 2. 2 Lời giải:   
Ta có: y  sin x  cos x  2 sin x   .  4        Ta có: x
  :  1  sin x
 1   2  2 sin x       2.  4   4       
Suy ra max y  2 đạt được khi sin x
 1  x    k2 ,k   x   k2 ,k    ;  4  4 2 4      3
min y   2 đạt được khi sin x   1
  x     k2 ,k  x    k2 ,k   .  4  4 2 4
Vậy M  2; m   2  M m  0.
Chọn đáp án A. Câu 5.
Tìm tập giá trị T của hàm số y  2cos . x A. T   2  ;2.   B. T   1  ;1.   C. T  . D. T   1  ;1.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 21
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Lời giải: Ta có: x
  :  1  cos x  1  2  2cos x  2.
Vậy max y  2 đạt được khi cos x  1  x k2 ,k  ; min y  2
 đạt được khi cos x  1  x    k  2 , k  .
Vậy tập giá trị của hàm số là T   2  ;2.  
Chọn đáp án A. Câu 6. Xét bốn mệnh đề sau:
(1): Trên , hàm số y  cos x có tập giá trị là 1;1.      (2): Trên 0; , 
 hàm số y  cos x có tập giá trị là 0;1.    2   3   2  (3): Trên 0; , 
 hàm số y  cos x có tập giá trị là 0; .  4   2      (4): Trên 0; 
 hàm số y  cos x có tập giá trị là 0;1.   2 
Tìm số phát biểu đúng. A. 1. B. 2. C. 3. D. 4. Lời giải:
Các mệnh đề (1), (2) và (4) đúng.  3    2 Trên 0; , 
 hàm số y  cos x có tập giá trị là  ;  1 . Vậy (3) sai.  4   2 
Chọn đáp án C. Câu 7.
Tìm tập giá trị T của hàm số y  2 cos 2 . x A. T   2  ;2.   B. T   1  ;1.   C. T  . D. T   4  ;4.   Lời giải: Ta có: x
  :  1  cos2x  1  2  2cos2x  2.
Suy ra max y  2 đạt được khi cos 2x  1  x k , k  ;  min y  2
 đạt được khi cos2x  1  x    k ,k  . 2
Vậy tập giá trị của hàm số là T   2  ;2.  
Chọn đáp án A. Câu 8.
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  sin x  cos x trên .
Tính giá trị M  . m A. 0. B. 2. C. 6. D. 2. Lời giải:   
Ta có: y  sin x  cos x  2 sin x    .  4        Ta có: x
  : 0  sin x
 1  0  2 sin x       2.  4   4 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 22
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11      
Suy ra max y  2 đạt được khi sin x   1  cos x       0  4   4    
x    k ,k   x   k ,k  ; 4 2 4     
min y  0 đạt được khi sin x   0  x   
k , k   x     k ,k    .  4  4 4
Vậy M  2; m  0  M m  2.
Chọn đáp án B. Câu 9.
Tìm tập giá trị T của hàm số y  2 sin x  1. A. T   2  ;2.   B. T   1  ;3.   C. T  . D. T   3;  3.   Lời giải: Ta có: x
  :  1  sin x  1  2  2sin x  2  1  2sin x  1  . 3 
Suy ra max y  3 đạt được khi sin x  1  x
k2 ,k  ; 2  min y  1
 đạt được khi sin x  1
  x    k2 ,k  . 2
Vậy tập giá trị của hàm số là T   1  ;3.  
Chọn đáp án B.
Câu 10. Tìm tập giá trị T của hàm số y  4 cos x  3. A. T   1  ;1.   B. T   7  ;1.   C. T  . D. T   4  ;4.   Lời giải: Ta có: x
  :  1  cos x  1  4  4cos x  4  7  4cos x  3  1.
Do đó: max y  1 đạt được khi cos x  1  x k2 ,k  ; min y  7
 đạt được khi cos x  1
  x    k2 ,k  .
Vậy tập giá trị của hàm số là T   7  ;1.  
Chọn đáp án B.
Câu 11. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  1  sin x  3.
Khẳng định nào dưới đây đúng?
A. M  3  2 , m   2. B. M  3  2 , m  3. C. M  3  2 , m  2. D. M  2  3, m  3.  Lời giải: Ta có: x
  :  1  sin x  1  0  sin x  1  2  0  sin x  1  2  3
  sin x  1  3  2  . 3 
Suy ra max y  2  3 đạt được khi sin x  1  x
k2 ,k  ; 2  min y  3
 đạt được khi sin x  1
  x    k2 ,k  . 2
Vậy M  2  3; m  3.
Chọn đáp án D.
Câu 12. Tìm tập giá trị T của hàm số y  1  2 sin 2 . x
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 23
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 A. T   1  ;3.   B. T   3;  4.   C. T  . D. T   3;  3.   Lời giải: Ta có: x
  :  1  sin 2x  1  2  2  sin 2x  2   1
  1 2sin 2x  3. 
Do đó: max y  3 đạt được khi sin 2x  1  x     k ,k  ; 4  min y  1
 đạt được khi sin2x  1  x    k , k  . 4
Vậy tập giá trị của hàm số là T   1  ;3.  
Chọn đáp án A.
Câu 13. Tìm tập giá trị T của hàm số 2
y  2 sin x  1. A. T   2  ;2.   B. T   1  ;3.   C. T  . D. T  1; 3  . Lời giải: Ta có: x
  :  sin2 x    sin2 x    sin2 0 1 0 2 2 1 2 x  1  . 3 
Do đó: max y  3 đạt được khi 2
sin x  1  cos x  0  x
k ,k  ; 2
min y  1 đạt được khi sin x  0  x k , k  .
Vậy tập giá trị của hàm số là T  1; 3  .
Chọn đáp án D.
Câu 14. Tìm tập giá trị T của hàm số 2
y  4 cos 2x  3. A. T  3;7.   B. T  0;7.   C. T  . D. T  0; 3.   Lời giải: Ta có: x
  :  cos2 x    cos2 x    cos2 0 2 1 0 4 2 4 3 4 2x  3  7.  k
Suy ra max y  7 đạt được khi 2
cos 2x  1  sin 2x  0  x  , k  ; 2   k
min y  3 đạt được khi cos 2x  0  x   , k  . 4 2
Vậy tập giá trị của hàm số là T  3;7.  
Chọn đáp án A.
Câu 15. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
3 sin x  cos x trên
. Tính giá trị M  . m A. 0. B. 2. C. 6. D. 2. Lời giải:   
Ta có: y  3 sin x  cos x  2 sin x    .  6        Ta có: x
  : 0  sinx  
 1  0  2 sin x   .  2  6   6       
Suy ra max y  2 đạt được khi sin x   1  cos x       0  6   6    
x    k ,k   x   k ,k  ; 6 2 3
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 24
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11     
min y  0 đạt được khi sin x
 0  x   k ,k   x    k ,k    .  6  6 6
Vậy M  2; m  0  M m  2.
Chọn đáp án D.
Câu 16. Tìm tập giá trị T của hàm số 2
y  5sin x  4. A. T  4; 9.   B. T   1  ;3.   C. T  0; 2.   D. T  2; 3.   Lời giải: Ta có: x
  :  sin2 x    sin2 x     sin2 0 1 4 5 4 9 2 5 x  4  . 3 
Suy ra max y  3 đạt được khi 2
sin x  1  cos x  0  x
k ,k  ; 2
min y  2 đạt được khi sin x  0  x   k , k  .
Vậy tập giá trị của hàm số là T  2; 3.  
Chọn đáp án D.
Câu 17. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  3 sin x  cos x  1 trên
. Tính giá trị M  . m A. 0. B. 2. C. 3. D. 5. Lời giải:   
Ta có: y  3 sin x  cos x  1  2sin x     1 .  6           Ta có: x
  :  1  sin x   1  1   2sin x
 1  3  0  2sin x   1        3  6   6   6       
Suy ra max y  3 đạt được khi sin x   
 1  x    k2 ,k   x   k2 ,k  ;  6  6 2 3      1 x    k2 
min y  0 đạt được khi sin x     3 , k    . 6 2   
x    k2
Vậy M  3; m  0  M m  3.
Chọn đáp án C.
Câu 18. Tìm tập giá trị T của hàm số 2
y  7 sin 2x  9. A. T  3; 4.   B. T  3; 37 .   C. T  . D. T  2; 3.   Lời giải: Ta có: x
  :  sin2 x    sin2 x     sin2 0 2 1 9 7 2 9 16 3 7 2x  9  . 4   k
Suy ra max y  4 đạt được khi 2
sin 2x  1  cos 2x  0  2x
k ,k   x   , k  ; 2 4 2 k
min y  3 đạt được khi sin 2x  0  x  , k  . 2
Vậy tập giá trị của hàm số là T  3; 4.  
Chọn đáp án A.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 25
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Câu 19. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 sin 2x  1 trên . Tính giá trị M. . m A. 3. B. 3. C. 6. D. 1. Lời giải: Ta có: x
  :  1  sin 2x  1  2  2sin 2x  2  1  2sin 2x  1  3.  
Suy ra max y  3 đạt được khi sin 2x  1  2x
k2 ,k   x   k ,k  ; 2 4   min y  1
 đạt được khi sin2x  1
  2x    k2 ,k   x    k ,k  . 2 4
Vậy m  1; M  3  M.m  3.
Chọn đáp án A.
Câu 20. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 cos x  3 trên . Tính giá trị M. . m A. 3. B. 5. C. 6. D. 1. Lời giải: Ta có: x
  :  1  cos x  1  2  2cos x  2  1  2cos x  3  5.
Suy ra max y  5 đạt được khi cos x  1  x k2 , k  ;
min y  1 đạt được khi cos x  1
  x    k2 ,k  .
Vậy m  1; M  5  M.m  5.
Chọn đáp án B.   
Câu 21. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 cos x  3 trên 0; .    3  Tính giá trị M. . m A. 3. B. 5. C. 6. D. 20. Lời giải:    1 Ta có: x   ; 0 :
 cos x  1  1  2cosx  2  4  2cosx  3  5.    3  2   
Suy ra max y  5 đạt được khi cos x  1  x  0 0; ;    3 0;     3  1    
min y  4 đạt được khi cos x   x   0; .      0;  2 3  3   3 
Vậy m  4; M  5  M.m  20.
Chọn đáp án D.
Câu 22. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 4
y  sin x  cos x trên .
Tính giá trị M  . m 3 A. 0. B. . C. 8. D. 2. 2 Lời giải: 1 Ta có: 4 4 2
y  sin x  cos x  1  sin 2 . x 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 26
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 1 1 1 1 Ta có: x
  : 0  sin2 2x  1  0   sin2 2x     1 sin2 2x  . 1 2 2 2 2 k
Suy ra max y  1 đạt được khi sin 2x  0  x  , k  ; 2 1  k min y  đạt được khi 2
sin 2x  1  cos 2x  0  x   , k  . 2 4 2 1 3
Vậy m  ; M  1  M m  . 2 2
Chọn đáp án B.
Câu 23. Tìm tập giá trị T của hàm số y  1  2 sin 2x . A. T  1; 3  . B. T   1  ;3.   C. T  . D. T   3;  3.   Lời giải:
Ta có: x
: 0  sin 2x  1  0  2 sin 2x  2  1  1  2 sin 2x  3.  k
Vậy max y  3 đạt được khi sin 2x  1  cos 2x  0  x   , k  ; 4 2 k
min y  1 đạt được khi sin 2x  0  x  , k  . 2
Vậy tập giá trị của hàm số là T  1; 3  .
Chọn đáp án A.
Câu 24. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  3 sin x  cos x  3
trên . Tính giá trị M  . m A. 0. B. 2. C. 6. D. 5. Lời giải:   
Ta có: y  3 sin x  cos x  3  2sin x     3 .  6           Ta có: x
  : 1  sin x
 1  1  2sin x
 3  5  1  2sin x   3        5 .  6   6   6       
Suy ra max y  5 đạt được khi sin x   
 1  x    k2 ,k   x   k2 ,k  ;  6  6 2 3      2
min y  1 đạt được khi sin x   1
  x     k2 ,k  x    k2 ,k   .  6  6 2 3
Vậy m  1; M  5  M m  6.
Chọn đáp án C.
Câu 25. Xét bốn mệnh đề sau:
(1): Trên , y  sin x có tập giá trị là 1;1.     
(2): Trên 0;  , y  sin x có tập giá trị là 1;1.    2     (3): Trên 0; , 
y  sin x có tập giá trị là 0;1.    2 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 27
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11    (4): Trên 0; 
 , y  sin x có tập giá trị là 0;1.   2 
Có bao nhiêu mệnh đề đúng? A. 1. B. 2. C. 3. D. 4. Lời giải:
Các mệnh đề (1), (3) đúng.   
Trên 0;  , y  sin x có tập giá trị là 0;  1 . Vậy (2) sai.  2     Trên 0; 
 , y  sin x có tập giá trị là 0;1  . Vậy (4) sai.  2 
Chọn đáp án B. x
Câu 26. Giá trị lớn nhất của hàm số 2 y  2 sin
 3sin x  5 bằng 2 A. 5  1. B. 0. C. 10  4. D. 13  5. Lời giải: x 1  cos x Ta có: y  2 2sin  3sin x  5  2
 3sin x  5  3sin x  cos x  4  10 sinx    4 , với số 2 2 3 1
thực  thỏa mãn cos  , sin   . 10 10 Ta có: x
  :  1  sinx    1   10  10 sinx    10
  10  4  10 sinx    4  10  4.
Vậy max y  10  4 đạt được khi sin x     ; 1
min y   10  4 đạt được khi sin x     1.
Chọn đáp án C.
Câu 27. Để tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số y  sin x  cos x , một
học sinh giải theo các bước sau:
Bước 1: Tập xác định: D  .  1   sin x  1
Bước 2: Ta có: x   :   2
  sin x  cosx  2. 1   cosx   1
Bước 3: Vậy GTLN của hàm số bằng 2, GTNN của hàm số bằng 2.
Bài giải của bạn đó đã đúng chưa? Và nếu sai, thì sai bắt đầu từ bước nào? A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3. Lời giải:
Bài giải sai từ bước 3 vì không tồn tại x
thỏa mãn sin x  cos x  2 , sin x  cos x  2 , do các sinx  1 sin x  1  hệ  và  vô nghiệm. cos x   1 cos x  1   Lời giải đúng:   
Ta có: y  sin x  cos x  2 sin x   .  4 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 28
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11       Ta có: x
  :  1  sin x
 1   2  2 sin x       2.  4   4       
Vậy max y  2 đạt được khi sin x
 1  x    k2 ,k   x   k2 ,k    ;  4  4 2 4      3
min y   2 đạt được khi sin x   1
  x     k2 ,k  x    k2 ,k   .  4  4 2 4
Chọn đáp án D.
Câu 28. Hàm số y    x2022 3 5sin
có giá trị lớn nhất là M và giá trị nhỏ nhất là .
m Giá trị của M m bằng A. 2022 2 . B. 4044 2 . C. 2022  4044 2 1  2 . D. 6066 2 . Lời giải: Ta có 1
  sin x  1 5  5  sin x  5
 hay 5  5sin x  5     x        x2022 2022 2 3 5sin 8 0 3 5sin  8 . Vậy m  0 và 2022 6066 M  8  2 .
Câu 29. Hàm số y  5  4 sin 2xcos 2x có tất cả bao nhiêu giá trị nguyên? A. 3. B. 4. C. 5. D. 6. Lời giải:
Viết lại y  5  4 sin 2x cos 2x  5  2 sin 4 . x Mà 1
  sin 4x  1  2
  2sin 4x  2 
3  5  2sin 4x  7. Vậy 3 7 y y    
y3;4;5;6;7 nên y có 5 giá trị nguyên.   
Câu 30. Hàm số y  sin x   
 sin x có tất cả bao nhiêu giá trị nguyên?  3  A. 1. B. 2. C. 3. D. 4. Lời giải:           Ta có: sin x
 sin x  2cos x  sin  cos x       .  3   6  6  6     Ta có 1   cos x     1 nên 1 1 y y       y 1  ;0;  1 .  6 
Câu 31. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước
trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức  t   h  3cos   
 12. Mực nước của con kênh cao nhất khi  8 4  A. t  13 (giờ). B. t  14 (giờ). C. t  15 (giờ). D. t  16 (giờ). Lời giải:
Mực nước của con kênh cao nhất khi h lớn nhất  t   t   cos   1 
  k2  t  16k    2 với  t    1 0
24 *  k  , k   8 4  8 4 8 + Với k 1 t 14 (giờ) + Với k 2
t không thỏa mãn điều kiện *
Vậy mực nước của con kênh cao nhất khi t  14 (giờ).
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 29
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Dạng 3:
XÉT TÍNH CHẴN LẺ CỦA HÀM SỐ I. MỘT SỐ KẾT QUẢ
Để xét tính chẵn lẻ của hàm số y f x , ta thực hiện theo các bước sau:
Bước 1: Tìm TXĐ D của hàm số và chỉ rõ: x
  D  x . D
f x  f x y f x lµ hµm ch½n trªn . D Bước 2: x   D :   f
 x   f x  y f x lµ hµm lÎ trªn . D
Các kết quả cần lưu ý:
1) Đồ thị hàm số chẵn nhận trục Oy làm trục đối xứng;
Đồ thị hàm số lẻ nhận gốc tọa độ O làm tâm đối xứng.
2) Hàm số y  sin x; y  tan x; y  cot x là hàm lẻ trên tập xác định của nó;
Hàm số y  cos x là hàm chẵn trên tập xác định của nó. II. BÀI TẬP TỰ LUẬN Câu 1:
Xét tính chẵn – lẻ của các hàm số sau: 2cos 2x  5
a) y  2sin x  3 tan . x b) y  . 2 1  x  3  c) y  sin   2x tan . x  2  Lời giải:  
a) TXĐ: D  \  k ,k  .  2  +) Ta có: x
  D  x . D +) Ta có: x
  D :yx  2sinx  3tanx  2
 sin x  3tan x  2sin x  3tan x  yx. Vậy hàm số lẻ trên . D b) TXĐ: D  . +) Ta có: x
  D  x . D 2 cos 2
x  5 2cos2x  5 +) Ta có: x
  D :yx      y x . 2 2      1 1  x x Vậy hàm số chẵn trên . D  
c) TXĐ: D  \  k ,k  .  2   3       
Biến đổi: y  sin
 2x tan x  sin    2x tan x  sin
 2x tanx         cos 2x tan . x  2   2   2  +) Ta có: x
  D  x . D
+) Ta có: x D :yx  cos2xtanx  cos2xtan x  yx. Vậy hàm số lẻ trên . D Câu 2:
Xét tính chẵn – lẻ của các hàm số sau:
a) y xsin2021 . x cos 4 . x
b) y   x  1  x  1 sin 4 . x x  sin x x  tan4 x c) y  . d) y  . 4  cos 2x 4 2 x x  1 Lời giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 30
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 a) TXĐ: D  . +) Ta có: x
  D  x . D +) Ta có: x
  D yx  x 2021 x  x 2021 : sin .cos 4  xsin .
x cos 4x y x. Vậy hàm số chẵn trên . D b) TXĐ: D  . +) Ta có: x
  D  x . D +) Ta có: x
  D :yx   x 1  x  1 sin 4
x   x  1  x 1 sin4x yx. Vậy hàm số chẵn trên . D c) TXĐ: D  . +) Ta có: x
  D  x . D
x  sin x x  sin x
+) Ta có: xD :yx      y x .
4  cos2x       4  cos 2x Vậy hàm số lẻ trên . D  
d) TXĐ: D  \  k ,k  .  2  +) Ta có: x
  D  x . D x  4 tan x x  4 tan x
+) Ta có: x D :y x      y . 4 2 4 2 x
x x  x x  1 1 Vậy hàm số chẵn trên . D
III. BÀI TẬP TỰ LUYỆN Câu 3:
Xác định tính chẵn, lẻ của các hàm số: 3 x  sin x cos2x 1) y  c x os3x 3) 3
y x sin 3x 4) y  5) y  cos2x x 1  cosx
6) y x  sin 2x 7) y  1  cosx 8) y  9) 2000 y  sin
x  cos2x 1  cosx x2 2010 sin x  2010 10) y  11) y
12) y x sin 2x sin x  tan x cosx
IV. TRẮC NGHIỆM: TÍNH CHẴN LẺ CỦA HÀM SỐ Câu 1.
Khẳng định nào dưới đây đúng?
A. Hàm số y  tan x là hàm số chẵn.
B. Hàm số y  sin x làm hàm số chẵn.
C. Hàm số y  cos x là hàm số chẵn.
D. Hàm số y  cot x là hàm số chẵn. Câu 2.
Hàm số nào sau đây là hàm số chẵn? A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x Câu 3.
Hàm số nào sau đây là hàm số lẻ? A. y  sin . x B. y  cos . x C. y  1. D. 4 2
y x x . Câu 4.
Hàm số nào sau đây là hàm số chẵn? A. y x sin . x B. y x cos . x C. y  tan . x D. y  cot . x Câu 5.
Hàm số nào sau đây là hàm số lẻ? A. y x sin . x B. y x cos . x C. y x tan . x
D. y x cot . x Câu 6.
Hàm số nào sau đây là hàm số chẵn trên ?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 31
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 sin x A. 2 y  2x  . x B. y  C. 2 y  sin . x
D. y x tan 2 . x x Câu 7.
Hàm số nào sau đây là hàm số chẵn trên ? 3 sin x
A. y  cos x  2. B. y  C. y  sin 2 . x D. 4
y x x  2017. x Câu 8.
Hàm số nào sau đây là hàm số lẻ trên ? cos x
A. y x sin 4 . x B. y  . C. 3 y  tan . x
D. y x sin . x x Câu 9.
Hàm số nào sau đây là hàm số lẻ trên ? A. 2
y  tan x sin . x B. y x cos . x C. 3 y  tan . x
D. y  2x sin 4 . x
Câu 10. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó? 5 sin x
A. y  cos x  2. B. y  . C. y  sin 2 . x D. 3
y x x  2017. x
Câu 11. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó? 5 sin x
A. y  cos x  2. B. y  .
C. y  tan 4x sin 2 . x
D. y x  1. 2 x
Câu 12. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó? A. y x tan . x B. 6 3 y x cot . x C. 2 y  sin 3 . x D. y  2017.
Câu 13. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó? sin x tan x A. y  . B. y  .
C. y  tan 4x sin 2 . x D. y x . 2 sin x  1 3 x
Câu 14. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó? 4 sin x 5 sin x A. y  . B. y  .
C. y x sin 2 . x D. 3
y x x  2017. x x
Câu 15. Có bao nhiêu hàm số trong các hàm số y
x y x x 2 sin 2 ;
cos ; y x tan x; y  1 là hàm chẵn trên ? A. 1. B. 2. C. 3. D. 4.
Câu 16. Có bao nhiêu hàm số trong các hàm số y
x y x x 2 sin 2 ;
cos ; y x tan x; y  1 là hàm chẵn
trên tập xác định của nó? A. 1. B. 2. C. 3. D. 4.
Câu 17. Có bao nhiêu hàm số trong các hàm số y
x y x x 3 sin 2 ;
cos ; y x tan x; y  1 là hàm lẻ trên ? A. 1. B. 2. C. 3. D. 4.
Câu 18. Xét bốn mệnh đề sau:
(1): Trên , y  sin 2x có tập giá trị là 1;1.      (2): Trên 0; , 
y  sin x có tập giá trị là 1;1.    2 
(3): Trên , y x sin x là hàm chẵn. (4): Trên , 2
y x sin x là hàm lẻ.
Tìm số phát biểu đúng. A. 1. B. 2. C. 3. D. 4.
Câu 19. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 32
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11  5  A. 2
y  2x  3cos x .
B. y  5sin x   .  2  C. 2
y  cot x  1  tanx  2. D. y  2  tan 2 . x
IV. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: TÍNH CHẴN LẺ CỦA HÀM SỐ Câu 1.
Khẳng định nào dưới đây đúng?
A. Hàm số y  tan x là hàm số chẵn.
B. Hàm số y  sin x làm hàm số chẵn.
C. Hàm số y  cos x là hàm số chẵn.
D. Hàm số y  cot x là hàm số chẵn. Câu 2.
Hàm số nào sau đây là hàm số chẵn? A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x Câu 3.
Hàm số nào sau đây là hàm số lẻ? A. y  sin . x B. y  cos . x C. y  1. D. 4 2
y x x . Câu 4.
Hàm số nào sau đây là hàm số chẵn? A. y x sin . x B. y x cos . x C. y  tan . x D. y  cot . x Lời giải:
Xét hàm số y x sin . x
Tập xác định: D  . +) x
  D  x . D +) x
  D : yx  xsinx  xsin x yx.
Vậy hàm số y x sin x là hàm số chẵn trên .
Chọn đáp án A. Câu 5.
Hàm số nào sau đây là hàm số lẻ? A. y x sin . x B. y x cos . x C. y x tan . x
D. y x cot . x Lời giải:
Xét hàm số y x cos . x
Tập xác định: D  . +) x
  D  x . D +) x
  D : yx  xcosx  xcosx  yx.
Vậy hàm số y x cos x là hàm số lẻ trên .
Chọn đáp án B. Câu 6.
Hàm số nào sau đây là hàm số chẵn trên ? sin x A. 2 y  2x  . x B. y  C. 2 y  sin . x
D. y x tan 2 . x x Lời giải: Xét hàm số 2 y  sin . x
Tập xác định: D  . +) x
  D  x . D +) x
  D yx 2  x 2 : sin
 sin x yx. Vậy hàm số 2
y  sin x là hàm số chẵn trên . sin x
Lưu ý: Hàm số y
; y x tan 2x là hàm số chẵn trên tập xác định D của nó với D  . x
Chọn đáp án C.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 33
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Câu 7.
Hàm số nào sau đây là hàm số chẵn trên ? 3 sin x
A. y  cos x  2. B. y  C. y  sin 2 . x D. 4
y x x  2017. x Lời giải: Xét hàm số 4
y x x  2017.
Tập xác định: D  . +) x
  D  x . D 4 +) x
  D yx  x  x 4 :
 2017  x x  2017  yx. Vậy hàm số 4
y x x  2017 là hàm số chẵn trên . Lưu ý:
Hàm số y  cos x  2 có tập xác định .  3 sin x Hàm số y
là hàm số chẵn trên tập xác định  \  0 . x
Chọn đáp án D. Câu 8.
Hàm số nào sau đây là hàm số lẻ trên ? cos x
A. y x sin 4 . x B. y  . C. 3 y  tan . x
D. y x sin . x x Lời giải:
Xét hàm số y x sin . x
Tập xác định: D  . +) x
  D  x . D +) x
  D : yx  x sinx   x sin x  yx.
Vậy hàm số y x sin x là hàm số lẻ trên . Lưu ý: cos x Hàm số 3 y
; y  tan x là hàm số lẻ trên tập xác định D của nó với D  . x
Chọn đáp án D. Câu 9.
Hàm số nào sau đây là hàm số lẻ trên ? A. 2
y  tan x sin . x B. y x cos . x C. 3 y  tan . x
D. y  2x sin 4 . x Lời giải:
Xét hàm số y x cos . x
Tập xác định: D  . +) x
  D  x . D +) x
  D : yx  xcosx  xcosx  yx.
Vậy hàm số y x cos x là hàm số lẻ trên . Lưu ý: Hàm số 2 3
y  tan x sin x; y  tan x là hàm số lẻ trên tập xác định D của nó với D  .
Chọn đáp án B.
Câu 10. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó? 5 sin x
A. y  cos x  2. B. y  . C. y  sin 2 . x D. 3
y x x  2017. x
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 34
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Lời giải: 5 sin x Xét hàm số y  . x
Tập xác định: D   \  0 . +) x
  D  x . D 5 5 sin x sin x +) x
  D : yx       xyx. x 5 sin x Vậy hàm số y  là hàm số chẵn trên . D x
Chọn đáp án B.
Câu 11. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó? 5 sin x
A. y  cos x  2. B. y  .
C. y  tan 4x sin 2 . x
D. y x  1. 2 x Lời giải:
Xét hàm số y  tan 4x sin 2 . x  k 
Tập xác định: D  \  k  .  8 4  +) x
  D  x . D +) x
  D : yx  tan 4  xsin 2
x  tan4xsin2x yx.
Vậy hàm số y  tan 4x sin 2x là hàm số chẵn trên . D
Chọn đáp án C.
Câu 12. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó? A. y x tan . x B. 6 3 y x cot . x C. 2 y  sin 3 . x D. y  2017. Lời giải: Xét hàm số 6 3 y x cot . x
Tập xác định: D  
\ kk  . +) x
  D  x . D 6 +) x
  D yx  x 3 x 6 3 : cot
 x cot x  yx. Vậy hàm số 6 3
y x cot x là hàm số lẻ trên . D
Chọn đáp án B.
Câu 13. Hàm số nào sau đây là hàm số lẻ trên tập xác định của nó? sin x tan x A. y  . B. y  .
C. y  tan 4x sin 2 . x D. y x . 2 sin x  1 3 x Lời giải: sin x Xét hàm số y  . 2 sin x  1
Tập xác định: D  . +) x
  D  x . D sin x sin x +) x
 D : yx       y x . 2 sin x 2    1 sin x  1
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 35
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 sin x Vậy hàm số y  là hàm số lẻ trên . D 2 sin x  1
Chọn đáp án A.
Câu 14. Hàm số nào sau đây là hàm số chẵn trên tập xác định của nó? 4 sin x 5 sin x A. y  . B. y  .
C. y x sin 2 . x D. 3
y x x  2017. x x Lời giải: 5 sin x Xét hàm số y  . x
Tập xác định: D   \  0 . +) x
  D  x . D 5 5 sin x sin x +) x
  D : yx       xyx. x 5 sin x Vậy hàm số y  là hàm số chẵn trên . D x
Chọn đáp án B.
Câu 15. Có bao nhiêu hàm số trong các hàm số y
x y x x 2 sin 2 ;
cos ; y x tan x; y  1 là hàm chẵn trên ? A. 1. B. 2. C. 3. D. 4. Lời giải:
Hàm số y  1 là hàm chẵn trên .  
Lưu ý: Hàm số 2
y x tan x là hàm chẵn trên D  \  kk    .  2 
Chọn đáp án A.
Câu 16. Có bao nhiêu hàm số trong các hàm số y
x y x x 2 sin 2 ;
cos ; y x tan x; y  1 là hàm chẵn
trên tập xác định của nó? A. 1. B. 2. C. 3. D. 4. Lời giải: Hàm số 2
y  1; y x tan x là hàm chẵn trên tập xác định của nó
Chọn đáp án B.
Câu 17. Có bao nhiêu hàm số trong các hàm số y
x y x x 3 sin 2 ;
cos ; y x tan x; y  1 là hàm lẻ trên ? A. 1. B. 2. C. 3. D. 4. Lời giải:
Hàm số y  sin 2x; y x cos x là hàm lẻ trên .  
Lưu ý: Hàm số 3
y x tan x là hàm lẻ trên D  \  kk    .  2 
Chọn đáp án B.
Câu 18. Xét bốn mệnh đề sau:
(1): Trên , y  sin 2x có tập giá trị là 1;1.  
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 36
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11    (2): Trên 0; , 
y  sin x có tập giá trị là 1;1.    2 
(3): Trên , y x sin x là hàm chẵn. (4): Trên , 2
y x sin x là hàm lẻ.
Tìm số phát biểu đúng. A. 1. B. 2. C. 3. D. 4. Lời giải:
Các mệnh đề (1), (3) và (4) là các mệnh đề đúng.    Trên 0; , 
y  sin x có tập giá trị là 0;1.   Vậy (2) sai.  2 
Chọn đáp án C.
Câu 19. Trong các hàm số sau đây, hàm số nào là hàm số chẵn?  5  A. 2
y  2x  3cos x .
B. y  5sin x   .  2  C. 2
y  cot x  1  tanx  2. D. y  2  tan 2 . x Lời giải:  5    
Xét hàm số y  5sin x
 5sin x   2    
 5cos x là hàm số chẵn trên .  2   2 
Chọn đáp án B.
Dạng 4: XÁC ĐỊNH TÍNH TUẦN HOÀN CỦA CÁC HÀM SỐ LƯỢNG GIÁC I. MỘT SỐ KẾT QUẢ
1. Chứng minh hàm số y f (x) tuần hoàn
Xét hàm số y f (x) , tập xác định D, ta dự đoán có số thực dương T sao cho: 0  x
  D : x T D vµ x T   D (1) 0 0  f
 x T   f (x) 0  (2)
2. Chứng minh T là chu kỳ của hàm số (nghĩa là T dương nhỏ nhất thoả mãn hệ (1) và (2)). Thực 0 0
hiện bằng phản chứng.
Bước 1: Giả sử có số T sao cho 0  T T thoả mãn các tính chất (1) và (2): 0 x
  D : f x T  f (x)  ... Mâu thuẫn với giả thiết 0  T T . 0
Bước 2: Mâu thuẫn này chứng tỏ T là số dương nhỏ nhất thoả mãn (2). 0
Kết luận: Vậy T là chu kỳ của hàm số y f (x) . 0
3. Xét tính tuần hoàn các các hàm số lượng giác, ta sử dụng một số kết quả:
a) Hàm số y  sin x, y  cos x tuÇn hoµn víi chu kú 2 .
b) Hàm số y  tan x, y  cot x tuÇn hoµn víi chu kú  . Mở rộng: 2
c) Hàm số y  sinax b, y  cosax b (a  0) tuÇn hoµn víi chu kú . a
d) Hàm số y  tanax b, y  cotax b (a  0) tuÇn hoµn víi chu kú . a
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 37
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 a
Định lý: Cho cặp hàm số f (x), g(x) tuần hoàn trên tập M có các chu kỳ lần lượt là a vµ b víi  . Khi b
đó, các hàm số: F(x)  f (x)  g(x), G(x)  f (x)g(x) cũng tuần hoàn trên M. Hệ quả:
Hàm số F(x)  mf (x)  ng(x) tuần hoàn với chu kỳ T là “bội chung nhỏ nhất” của a µ v b . II. BÀI TẬP TỰ LUẬN Câu 4:
Tìm chu kì của các hàm số sau:
a) y  sin 2x  2.
b) y  4 tan 6x  3. Lời giải: 2
a) Hàm số y  sin 2x  2 tuần hoàn với chu kì T   . 2
b) Hàm số y  4 tan 6x  3 tuần hoàn với chu kì T  . 6 Câu 5:
Tìm chu kì của các hàm số sau:    a) y  2sin   3x . b) y  sin2 4 2 . x  4  c) y  4sin 3 . x cos 3 . x Lời giải:    2 a) Hàm số y  2sin  
3x  tuần hoàn với chu kì T  .  4  3  cos x b) Ta có: y  sin2 1 4 4 2x  . 4  2  2cos4 . x 2 2 
Vậy hàm số y  sin2 4
2x tuần hoàn với chu kì T   . 4 2
c) Ta có: y  4sin 3 .
x cos 3x  2sin 6 . x 2 
Vậy hàm số y  4sin 3 .
x cos 3x tuần hoàn với chu kì T   . 6 3 Câu 6:
Tìm chu kì của các hàm số sau: x
a) y  sin 2x  cos 4 . x
b) y  sin x  tan . 3 Lời giải: 2
a) Hàm số y  sin 2x tuần hoàn với chu kì T   . 1 2 2 
Hàm số y  cos 4x tuần hoàn với chu kì T   . 2 4 2
Vậy hàm số y  sin 2x  cos 4x tuần hoàn với chu kỳ  .
b) Hàm số y  sin x tuần hoàn với chu kì T  2 . 1 x
Hàm số y  tan tuần hoàn với chu kì T   3. 3 2 13 x
Vậy hàm số y  sin x  tan tuần hoàn với chu kỳ 6 . 3
III. BÀI TẬP TỰ LUYỆN
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 38
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Câu 7:
Tìm chu kỳ của các hàm số sau:         
1) y  2 sin  x  2) 
y  cos x   5 3) 
y  tan x  4)  y  cos2x  4   3   4   x   5) y  cos 
6) y  sin x  cosx 7) y  sin c x osx 8) 2 y    4 sin x  2 4  1 9) y  . sin x
IV. TRẮC NGHIỆM: TÍNH TUẦN HOÀN CỦA HÀM SỐ - SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM SỐ Câu 1.
Hàm số nào sau đây là hàm số tuần hoàn? A. 2 y x . B. y  sin . x
C. y  sin x  . x D. y x. Câu 2.
Hàm số nào sau đây là hàm số tuần hoàn với chu kì 2 ? A. y  sin 2 . x B. y  cos . x C. y  tan . x D. y  cot . x Câu 3.
Hàm số nào sau đây là hàm số tuần hoàn với chu kì  ? A. y  sin x. B. y  cos . x C. y  tan 2 . x D. y  cot . x Câu 4.
Hàm số nào sau đây là hàm số tuần hoàn với chu kì  ? A. y  sin 2 . x B. y  cos . x C. y  tan 2 . x D. y  cot 2 . x Câu 5.
Hàm số nào sau đây không tuần hoàn với chu kì  ? A. y  sin 2 . x B. y  sin . x C. y  tan . x D. y  cot . x Câu 6.
Hàm số y  2 sin 4x  3 tuần hoàn với chu kì là  A. 2 . B.  . C. 8 . D. . 2 Câu 7.
Hàm số y  1  5cos 2x tuần hoàn với chu kì là  A. 2 . B.  . C. 8 . D. . 2 Câu 8. Hàm số 2
y  2 sin x  7 tuần hoàn với chu kì là  A. 2 . B.  . C. 4 . D. . 2 Câu 9.
Hàm số y  4sin x cos x  5 tuần hoàn với chu kì là  A. 2 . B.  . C. 4 . D. . 2
Câu 10. Hàm số y  sin x  sin 2x tuần hoàn với chu kì là  A. 2 . B.  . C. 8 . D. . 2 x
Câu 11. Hàm số y  sin x  tan tuần hoàn với chu kì là 3 A. 2 . B.  . C. 8 . D. 6 .
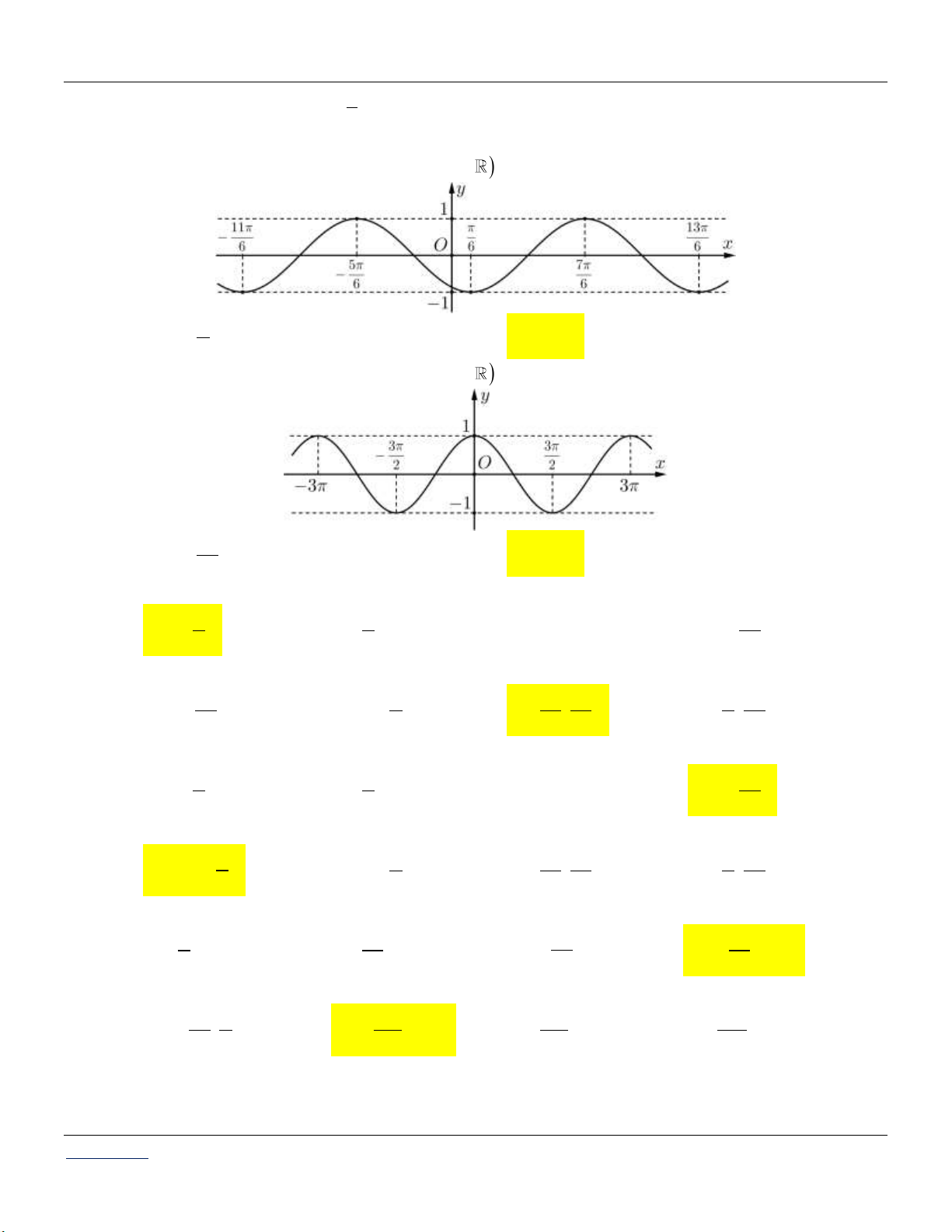
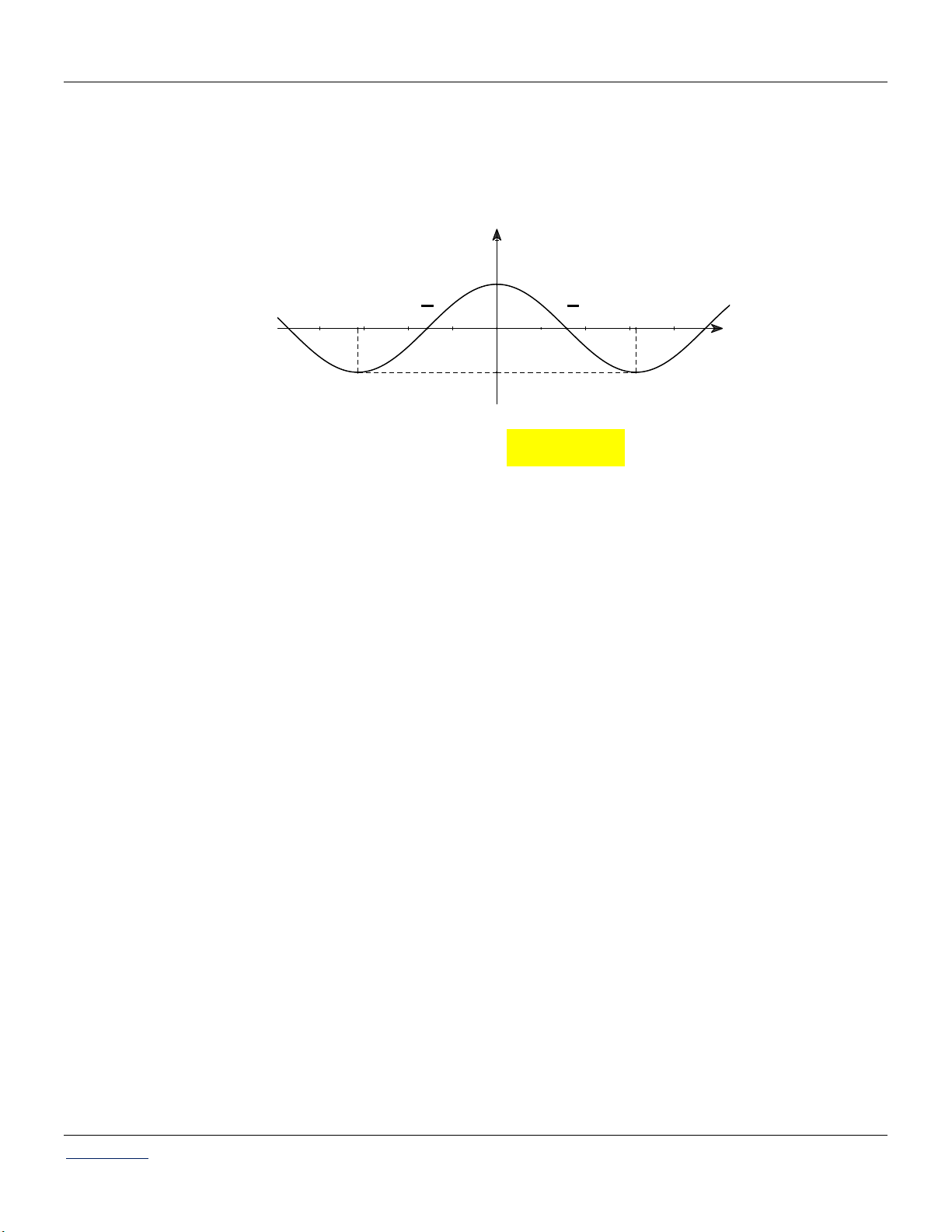
Câu 12. Cho hàm số y f x  asinbx c ,a;b;c   có đồ thị như hình vẽ. Chu kỳ T của hàm số là
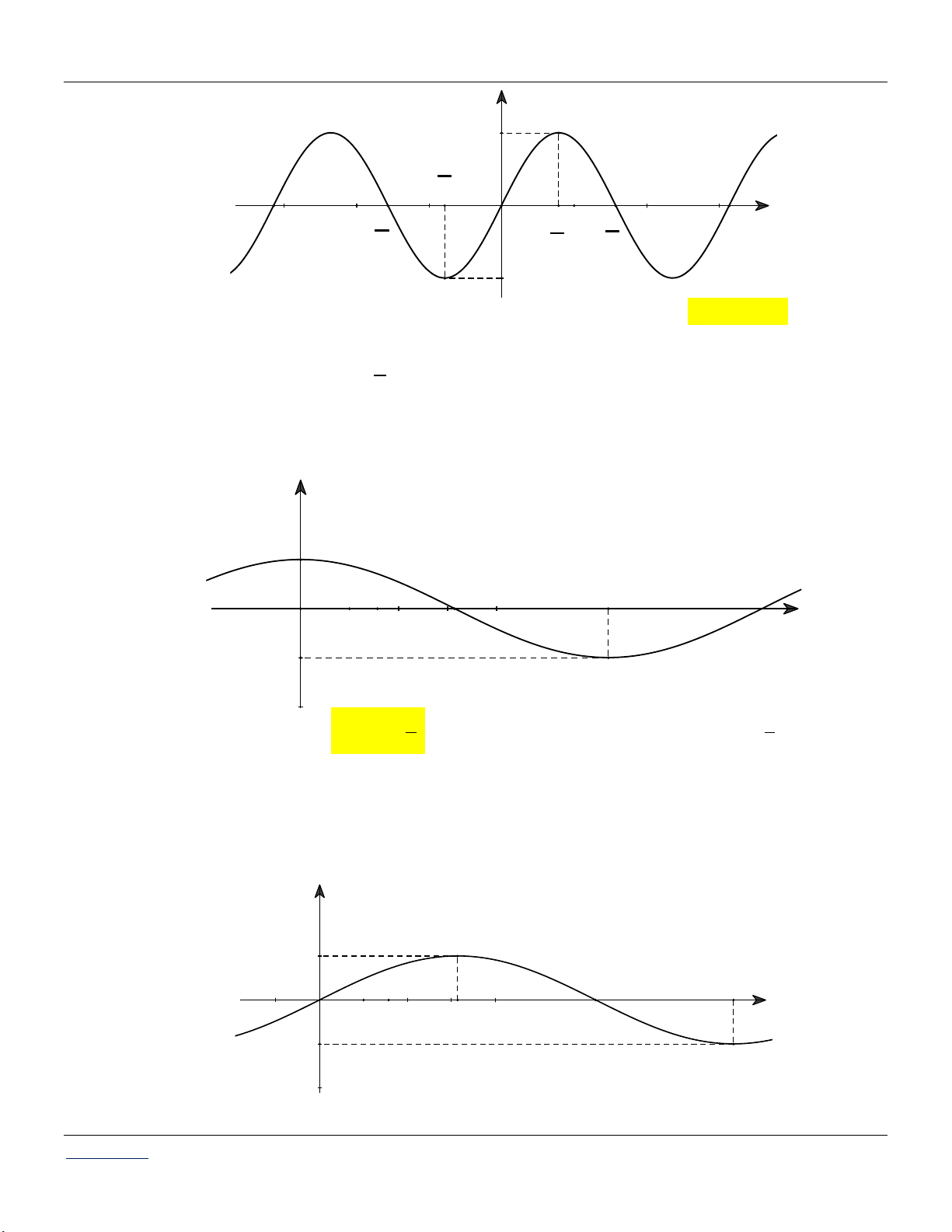
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 39
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11  A. T  . B. T   . C. T  2 . D. T  4 . 6
Câu 13. Cho hàm số y f x  asinbx c ,a;b;c   có đồ thị như hình vẽ. Chu kỳ T của hàm số là 3 A. T  . B. T  2 . C. T  3 . D. T  6 . 2
Câu 14. Hàm số y  sin x đồng biến trên khoảng nào trong các khoảng dưới đây?        3  A. 0; . B.  ; . C. 0; . D.   ; .  2   2   2 
Câu 15. Hàm số y  sin x đồng biến trên khoảng nào trong các khoảng dưới đây?  3      3 5    3  A.   ; . B.    ; . C.  ; . D.  ; .  2   2   2 2   2 2 
Câu 16. Hàm số y  cos x đồng biến trên khoảng nào trong các khoảng dưới đây?        3  A. 0; . B.  ; . C. 0; . D.   ; .  2   2   2 
Câu 17. Hàm số y  cos x đồng biến trên khoảng nào trong các khoảng dưới đây?        3 5    3  A.   ;  . B.    ; . C.  ; . D.  ; .  2   2   2 2   2 2 
Câu 18. Hàm số y  sin x đồng biến trên khoảng nào dưới đây?     5   3   5  A.  ; . B.  ; 3 . C.  ;    . D.   ; 2   .  2   2   2   2 
Câu 19. Hàm số y  cos x nghịch biến trên khoảng nào sau đây?  3    11   11   19  A.   ; . B.   ; 5   . C.  ;7 . D.  ;10 .  2 2   2   2   2 
Câu 20. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 40
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 π - 2 π x -π O π 2 -1 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x
Câu 21. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 π π - -π 2 2 π O x 1 -1 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x
Câu 22. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y O x 3π π π 3π - - 2 2 2 2 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x
Câu 23. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y O x -π π π 2 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x
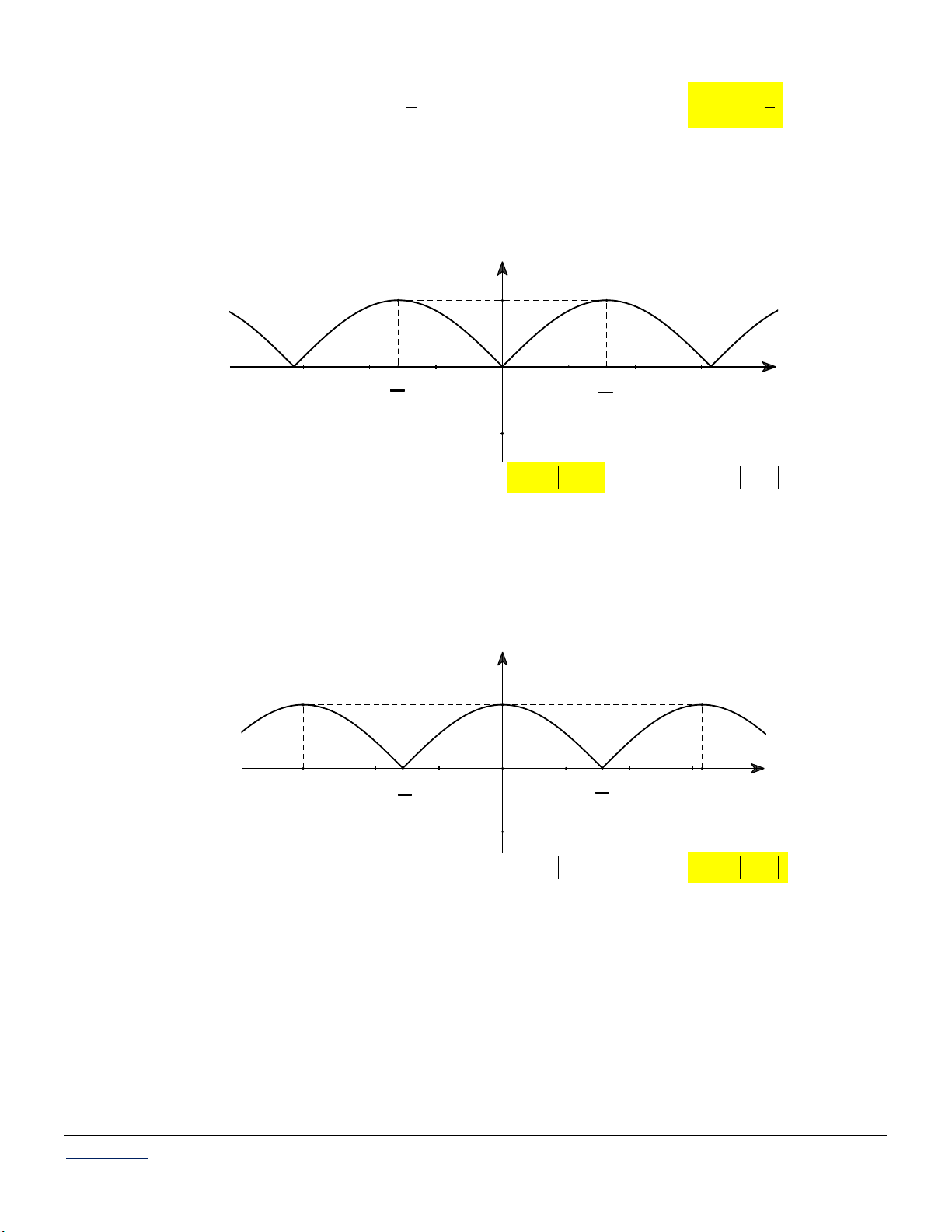
Câu 24. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 41
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 π π - x 2 2 -π O π -1 A. y  cos . x B. y  cos 2 . x C. y  sin . x D. y  sin 2 . x
Câu 25. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 π - -π 4 x π O π π π - 2 4 2 -1 A. y  cos . x B. y  cos 2 . x C. y  sin . x D. y  sin 2 . x
Câu 26. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 π 2π 3π O x -1 x x A. y  cos . x B. y  cos . C. y  sin . x D. y  sin . 2 2
Câu 27. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 42
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 2π x O 3π π -1 x x A. y  cos . x B. y  cos . C. y  sin . x D. y  sin . 2 2
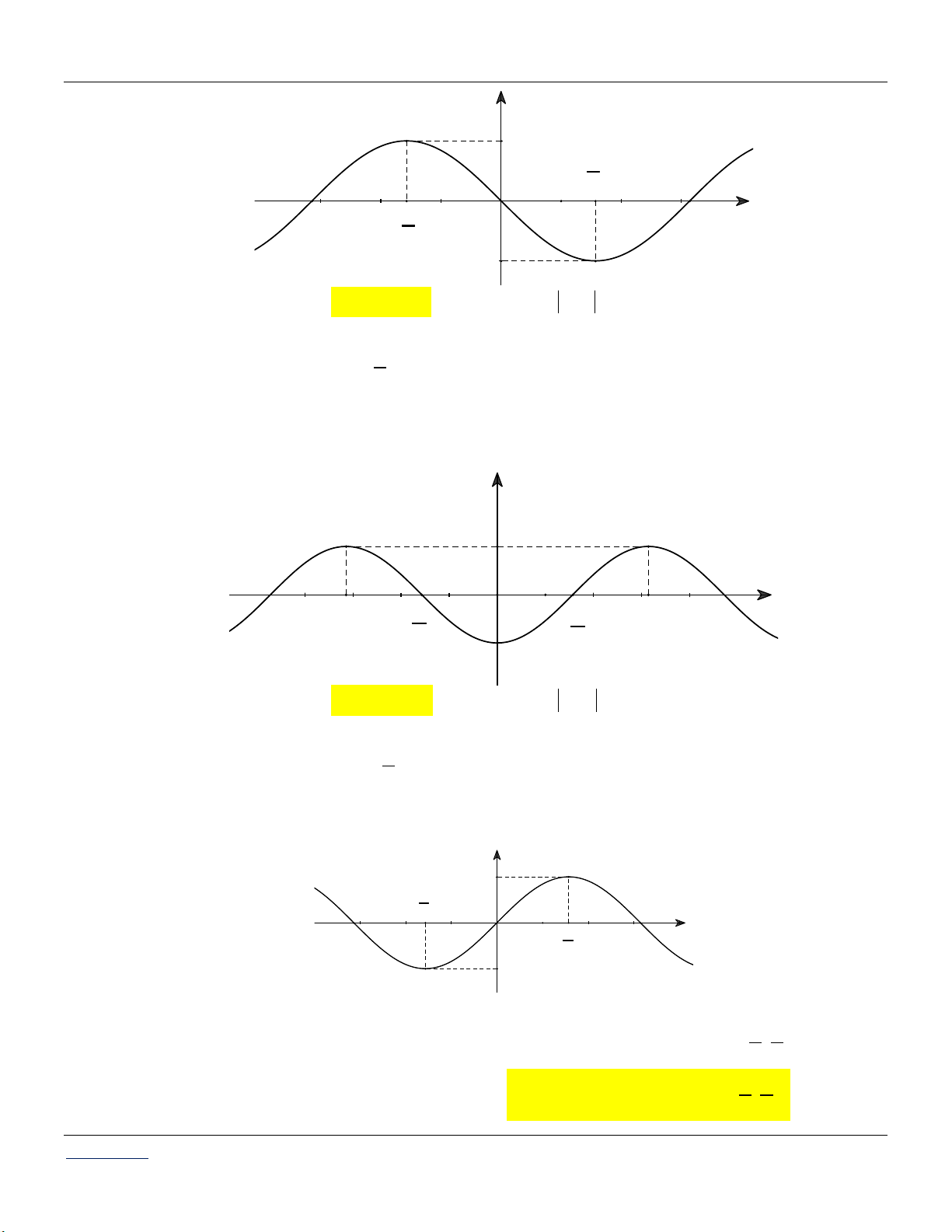
Câu 28. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 x -π π π π - O 2 2 A. y  sin . x B. y  cos . x
C. y  sin x .
D. y  cos x .
Câu 29. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 -π π π π O x - 2 2 A. y  sin . x B. y  cos . x
C. y  sin x .
D. y  cos x .
Câu 30. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 43
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 π -π 2 π O π x - 2 -1 A. y  sin . x B. y  sin . x
C. y  sin x . D. y  sin 2 . x
Câu 31. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 x -π π O π π - 2 2 -1 A. y  cos . x B. y  cos . x
C. y  cos x . D. y  cos 2 . x
Câu 32. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π - 2 π x -π O π 2 -1
Khẳng định nào sau đây đúng?    
A. Hàm số đồng biến trên    ;0.
B. Hàm số nghịch biến trên   ; .  2 2     
C. Hàm số đồng biến trên 0; .
D. Hàm số đồng biến trên   ; .  2 2 
Câu 33. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π - 2 π x -π O π 2 -1
Khẳng định nào sau đây sai?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 44
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 A. max y  1. B. min y  1  . x ;    x ;       
C. Hàm số đồng biến trên 0; .
D. Hàm số đồng biến trên   ; .  2 2 
Câu 34. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π π - -π 2 2 π O x 1 -1
Khẳng định nào sau đây đúng?    
A. Hàm số đồng biến trên    ; .
B. Hàm số nghịch biến trên   ; .  2 2 
C. Hàm số đồng biến trên 0; .
D. Hàm số đồng biến trên    ;0.
Câu 35. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π π - -π 2 2 π O x 1 -1
Khẳng định nào sau đây sai? A. max y  1. B. min y  1  . x ;    x    ; 
C. Hàm số nghịch biến trên 0; .
D. Hàm số đồng biến trên    ;0.
V. LỜI GIẢI CHI TIẾT TRẮC NGHIỆM: TÍNH TUẦN HOÀN CỦA HÀM SỐ - SỰ BIẾN THIÊN
VÀ ĐỒ THỊ CỦA HÀM SỐ Câu 1.
Hàm số nào sau đây là hàm số tuần hoàn? A. 2 y x . B. y  sin . x
C. y  sin x  . x D. y x. Câu 2.
Hàm số nào sau đây là hàm số tuần hoàn với chu kì 2 ? A. y  sin 2 . x B. y  cos . x C. y  tan . x D. y  cot . x Câu 3.
Hàm số nào sau đây là hàm số tuần hoàn với chu kì  ? A. y  sin x. B. y  cos . x C. y  tan 2 . x D. y  cot . x Câu 4.
Hàm số nào sau đây là hàm số tuần hoàn với chu kì  ? A. y  sin 2 . x B. y  cos . x C. y  tan 2 . x D. y  cot 2 . x Câu 5.
Hàm số nào sau đây không tuần hoàn với chu kì  ? A. y  sin 2 . x B. y  sin . x C. y  tan . x D. y  cot . x
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 45
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Câu 6.
Hàm số y  2 sin 4x  3 tuần hoàn với chu kì là  A. 2 . B.  . C. 8 . D. . 2 Lời giải: 2 
Hàm số y  2 sin 4x  3 tuần hoàn với chu kì  . 4 2
Chọn đáp án D. Câu 7.
Hàm số y  1  5cos 2x tuần hoàn với chu kì là  A. 2 . B.  . C. 8 . D. . 2 Lời giải: 2
Hàm số y  1  5cos 2x tuần hoàn với chu kì   . 2
Chọn đáp án B. Câu 8. Hàm số 2
y  2 sin x  7 tuần hoàn với chu kì là  A. 2 . B.  . C. 4 . D. . 2 Lời giải: 2 Hàm số 2
y  2 sin x  7  1  cos 2x  7  8  cos 2x tuần hoàn với chu kì   . 2
Chọn đáp án B. Câu 9.
Hàm số y  4sin x cos x  5 tuần hoàn với chu kì là  A. 2 . B.  . C. 4 . D. . 2 Lời giải: 2
Hàm số y  4sin xcos x  5  2sin 2x  5 tuần hoàn với chu kì   . 2
Chọn đáp án B.
Câu 10. Hàm số y  sin x  sin 2x tuần hoàn với chu kì là  A. 2 . B.  . C. 8 . D. . 2 Lời giải:
Hàm số y  sin x tuần hoàn với chu kì T  2 . 1
Hàm số y  sin 2x tuần hoàn với chu kì T   . 2
Vậy hàm số y  sin x  sin 2x tuần hoàn với chu kì T  2 .
Chọn đáp án A. x
Câu 11. Hàm số y  sin x  tan tuần hoàn với chu kì là 3 A. 2 . B.  . C. 8 . D. 6 . Lời giải:
Hàm số y  sin x tuần hoàn với chu kì T  2 . 1 x
Hàm số y  tan tuần hoàn với chu kì T  3 . 3 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 46
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 x
Vậy hàm số y  sin x  tan tuần hoàn với chu kì T  6 . 3
Chọn đáp án D.
Câu 12. Cho hàm số y f x  asinbx c ,a;b;c   có đồ thị như hình vẽ. Chu kỳ T của hàm số là  A. T  . B. T   . C. T  2 . D. T  4 . 6
Câu 13. Cho hàm số y f x  asinbx c ,a;b;c   có đồ thị như hình vẽ. Chu kỳ T của hàm số là 3 A. T  . B. T  2 . C. T  3 . D. T  6 . 2
Câu 14. Hàm số y  sin x đồng biến trên khoảng nào trong các khoảng dưới đây?        3  A. 0; . B.  ; . C. 0; . D.   ; .  2   2   2 
Câu 15. Hàm số y  sin x đồng biến trên khoảng nào trong các khoảng dưới đây?  3      3 5    3  A.   ; . B.    ; . C.  ; . D.  ; .  2   2   2 2   2 2 
Câu 16. Hàm số y  cos x đồng biến trên khoảng nào trong các khoảng dưới đây?        3  A. 0; . B.  ; . C. 0; . D.   ; .  2   2   2 
Câu 17. Hàm số y  cos x đồng biến trên khoảng nào trong các khoảng dưới đây?        3 5    3  A.   ;  . B.    ; . C.  ; . D.  ; .  2   2   2 2   2 2 
Câu 18. Hàm số y  sin x đồng biến trên khoảng nào dưới đây?     5   3   5  A.  ; . B.  ; 3 . C.  ;    . D.   ; 2   .  2   2   2   2 
Câu 19. Hàm số y  cos x nghịch biến trên khoảng nào sau đây?  3    11   11   19  A.   ; . B.   ; 5   . C.  ;7 . D.  ;10 .  2 2   2   2   2 
Câu 20. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 47
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 π - 2 π x -π O π 2 -1 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x Lời giải:   
Hàm số qua các điểm 0;0; ;1.  2 
Chọn đáp án A.
Câu 21. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 π π - -π 2 2 π O x 1 -1 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x Lời giải:   
Hàm số qua các điểm 0; 
1 ; ;0. Hoặc quan sát nhanh đồ thị đã cho là đồ thị của hàm  2  chẵn.
Chọn đáp án B.
Câu 22. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y O x 3π π π 3π - - 2 2 2 2 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x Lời giải:    
Hàm số qua các điểm 0;0 và đồng biến trên   ; .  2 2 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 48
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11
Hoặc đánh giá hàm số không xác định tại các điểm x
k ,k  . 2
Chọn đáp án C.
Câu 23. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y O x -π π π 2 A. y  sin . x B. y  cos . x C. y  tan . x D. y  cot . x Lời giải:   
Hàm số qua các điểm  ;0 và nghịch biến trên 0; .  2 
Hoặc đánh giá hàm số không xác định tại các điểm x k , k  .
Chọn đáp án D.
Câu 24. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 π π - x 2 2 -π O π -1 A. y  cos . x B. y  cos 2 . x C. y  sin . x D. y  sin 2 . x Lời giải:   
Hàm số qua các điểm 0;  1 ; ; 1   .  2 
Chọn đáp án B.
Câu 25. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 49
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 π - -π 4 x π O π π π - 2 4 2 -1 A. y  cos . x B. y  cos 2 . x C. y  sin . x D. y  sin 2 . x Lời giải:   
Hàm số qua các điểm 0;0; ;1.  4 
Chọn đáp án D.
Câu 26. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 π 2π 3π O x -1 x x A. y  cos . x B. y  cos . C. y  sin . x D. y  sin . 2 2 Lời giải:
Hàm số qua các điểm 0;1; ;0.
Chọn đáp án B.
Câu 27. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 2π x O 3π π -1
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 50
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 x x A. y  cos . x B. y  cos . C. y  sin . x D. y  sin . 2 2 Lời giải:
Hàm số qua các điểm 0;0; ;  1 .
Chọn đáp án D.
Câu 28. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 x -π π π π - O 2 2 A. y  sin . x B. y  cos . x
C. y  sin x .
D. y  cos x . Lời giải:   
Hàm số qua các điểm 0;0;   ;1.  2 
Chọn đáp án C.
Câu 29. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 -π π π π O x - 2 2 A. y  sin . x B. y  cos . x
C. y  sin x .
D. y  cos x . Lời giải:
Hàm số qua các điểm 0;1;   ;  1 .
Chọn đáp án D.
Câu 30. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 51
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 y 1 π -π 2 π O π x - 2 -1 A. y  sin . x B. y  sin . x
C. y  sin x . D. y  sin 2 . x Lời giải:   
Hàm số qua các điểm 0;0; ; 1   .  2 
Chọn đáp án B.
Câu 31. Đường cong trong hình là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 1 x -π π O π π - 2 2 -1 A. y  cos . x B. y  cos . x
C. y  cos x . D. y  cos 2 . x Lời giải:   
Hàm số qua các điểm 0;  1 ; ;0; ;  1 .  2 
Chọn đáp án B.
Câu 32. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π - 2 π x -π O π 2 -1
Khẳng định nào sau đây đúng?    
A. Hàm số đồng biến trên    ;0.
B. Hàm số nghịch biến trên   ; .  2 2     
C. Hàm số đồng biến trên 0; .
D. Hàm số đồng biến trên   ; .  2 2 
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 52
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Lời giải:     Trên  
;  , đồ thị hàm số là đường đi lên (từ trái sang phải) nên hàm số đồng biến trên  2 2        ; .  2 2 
Chọn đáp án D.
Câu 33. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π - 2 π x -π O π 2 -1
Khẳng định nào sau đây sai? A. max y  1. B. min y  1  . x ;    x ;       
C. Hàm số đồng biến trên 0; .
D. Hàm số đồng biến trên   ; .  2 2  Lời giải:   
Trên 0;  , đồ thị hàm số là đường đi lên (từ trái sang phải) nên hàm số đồng biến trên  2     0; .  2    
Trên  ;  , đồ thị hàm số là đường đi xuống (từ trái sang phải) nên hàm số nghịch biến  2    
trên  ; . Vậy C sai.  2 
Chọn đáp án C.
Câu 34. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π π - -π 2 2 π O x 1 -1
Khẳng định nào sau đây đúng?    
A. Hàm số đồng biến trên    ; .
B. Hàm số nghịch biến trên   ; .  2 2 
C. Hàm số đồng biến trên 0; .
D. Hàm số đồng biến trên    ;0.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 53
Chuyên đề HÀM SỐ LƯỢNG GIÁC Toán 11 Lời giải: Trên  
 ;0, đồ thị hàm số là đường đi lên (từ trái sang phải) nên hàm số đồng biến trên    ;0.
Chọn đáp án D.
Câu 35. Cho hàm số y f x có đồ thị là hình vẽ dưới đây: y 1 π π - -π 2 2 π O x 1 -1
Khẳng định nào sau đây sai? A. max y  1. B. min y  1  . x ;    x    ; 
C. Hàm số nghịch biến trên 0; .
D. Hàm số đồng biến trên    ;0. Lời giải: Trên  
 ; , hàm số không tồn tại giá trị nhỏ nhất. Vậy B sai.
Chọn đáp án B.
Giáo viên: LÊ BÁ BẢO...0935.785.115... Trường THPT Đặng Huy Trứ CLB Giáo viên trẻ TP Huế 54