











































Preview text:
HAØM SOÁ LÖÔÏNG GIAÙC VAØ CHUÛ ÑEÀ
PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
Tác giả: Huỳnh Đức Khánh SĐT: 0975120189
Facebook: https://www.facebook.com/duckhanh0205 Baøi 01
HAØM SOÁ LÖÔÏNG GIAÙC I ĐỊNH NGHĨA – 1) Hàm số sin
Quy tắc đặt tương ứng với mỗi số thực x với số thực sin x sin x : ℝ → ℝ
x ֏ y = sin x
được gọi là hàm số sin, kí hiệu là y = sin x.
Tập xác định của hàm số sin là . ℝ 2) Hàm số côsin
Quy tắc đặt tương ứng với mỗi số thực x với số thực cos x cos x : ℝ → ℝ
x ֏ y = cos x
được gọi là hàm số sin, kí hiệu là y = cos x.
Tập xác định của hàm số cô sin là . ℝ 3) Hàm số tang
Hàm số tang là hàm số được xác định bởi công thức sin x y =
(cos x ≠ 0), kí hiệu cos x là y = tan x.
Tập xác định của hàm số π
y = tan x là D = ℝ \ + k , π k ∈ ℤ . 2 4) Hàm số côtang
Hàm số côtang là hàm số được xác định bởi công thức cos x y = (sin x ≠ 0), kí sin x
hiệu là y = cot x.
Tập xác định của hàm số y = cot x là D ℝ \{k , π = k ∈ ℤ}.
II TÍNH TUẦN HO=N V= CHU KÌ CỦA H=M SỐ LƯỢNG GIÁC – 1) Định nghĩa
Hàm số y = f (x) có tập xác định D được gọi là hàm số tuần hoàn, nếu tồn tại
một số T ≠ 0 sao cho với mọi x ∈ D ta có: ● x T
− ∈ D và x +T ∈ D. ●
f (x +T ) = f (x) .
Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.
Người ta chứng minh được rằng hàm số y = sin x tuần hoàn với chu kì T 2π = ; hàm
số y = cos x tuần hoàn với chu kì T 2π =
; hàm số y = tan x tuần hoàn với chu kì T π =
; hàm số y = cot x tuần hoàn với chu kì T . π = 2) Chú ý 2π
● Hàm số y = sin (ax + b) tuần hoàn với chu kì T = . 0 a 2π
● Hàm số y = cos(ax + b) tuần hoàn với chu kì T = . 0 a π
● Hàm số y = tan (ax + b) tuần hoàn với chu kì T = . 0 a π
● Hàm số y = cot (ax + b) tuần hoàn với chu kì T = . 0 a
● Hàm số y = f
x tuần hoàn với chu kì T và hàm số y = f
x tuần hoàn với chu 2 ( ) 1 ( ) 1
kì T thì hàm số y = f x ± f x tuần hoàn với chu kì T là bội chung nhỏ nhất của 1 ( ) 2 ( ) 2 0 T và T . 1 2
III SỰ BIẾN THIÊN V= ĐỒ THỊ CỦA H=M SỐ LƯỢNG GIÁC –
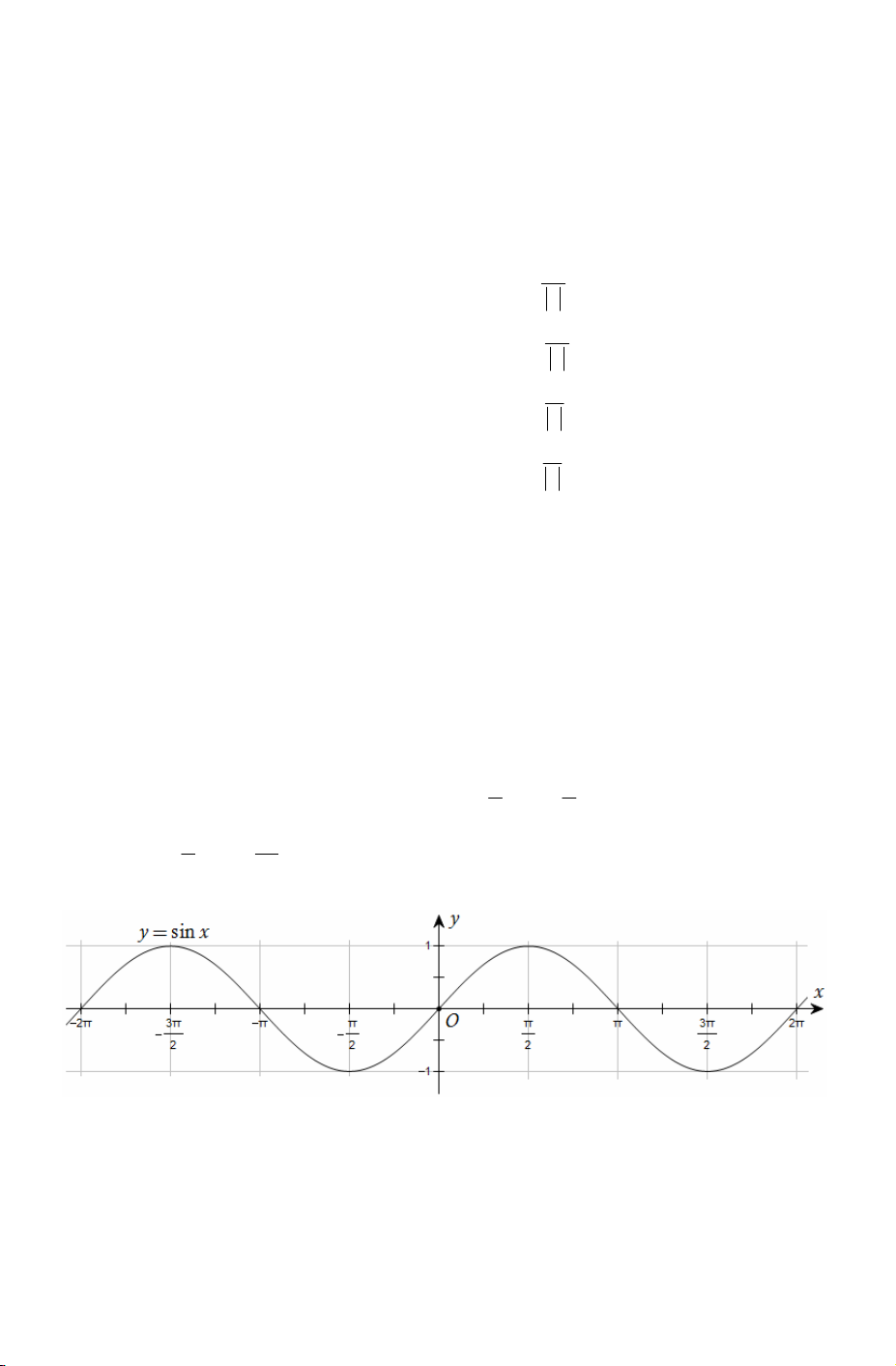
1) Hàm số y = sin x ●
Tập xác định D = ℝ , có nghĩa xác định với mọi x ∈ ℝ; ●
Tập giá trị T = [−1; ]
1 , có nghĩa −1 ≤ sin x ≤ 1; ●
Là hàm số tuần hoàn với chu kì 2 ,
π có nghĩa sin (x k2π +
) = sin x với k ∈ ℤ . π π ●
Hàm số đồng biến trên mỗi khoảng −
+ k2π; + k2π và nghịch biến trên 2 2 mỗi khoảng π 3π + k2 π;
+ k2π , k ∈ ℤ . 2 2 ●
Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng.
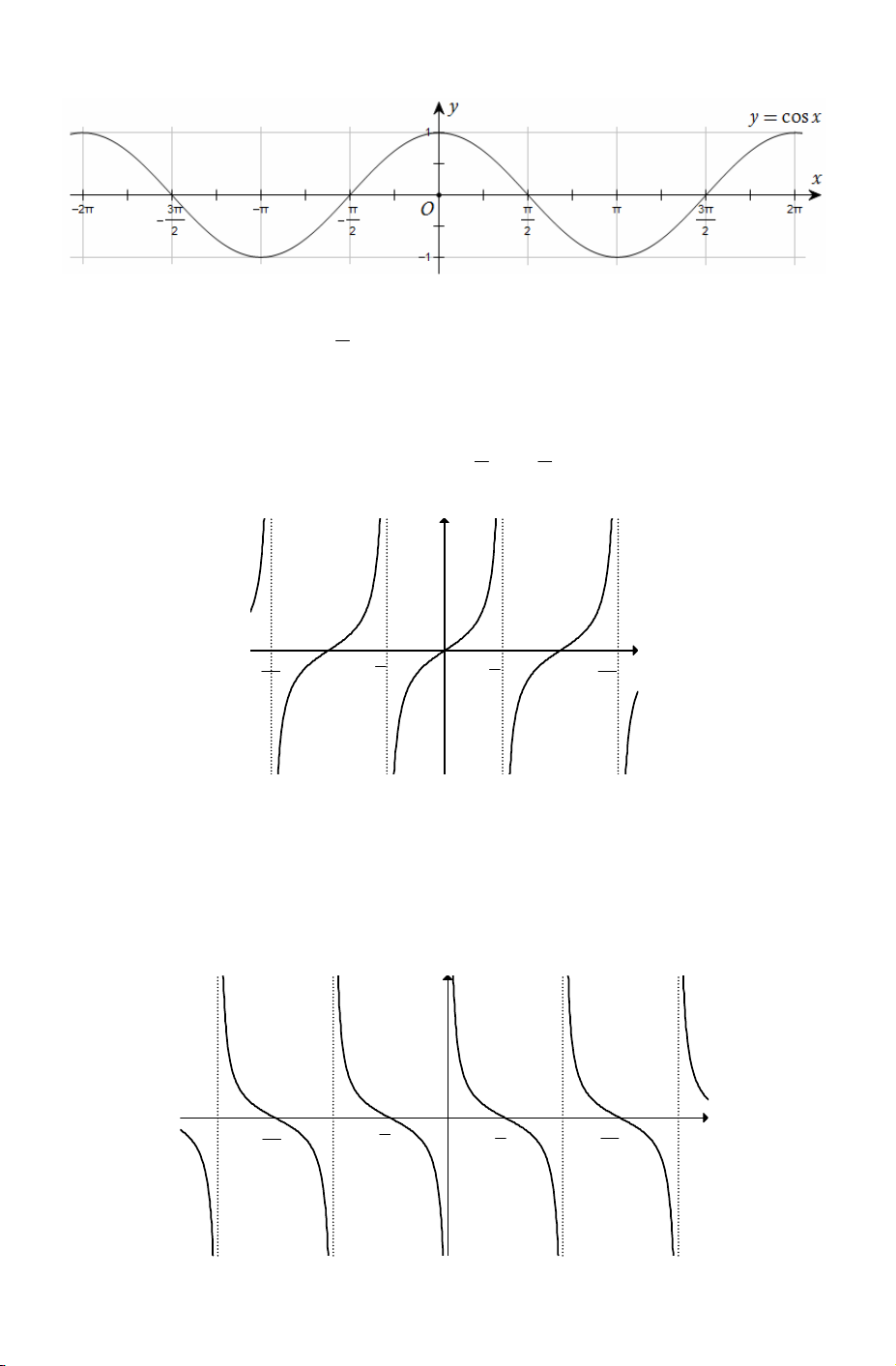
2) Hàm số y = cos x ●
Tập xác định D = ℝ , có nghĩa xác định với mọi x ∈ ℝ; ●
Tập giá trị T = [−1; ]
1 , có nghĩa −1 ≤ cos x ≤ 1; ●
Là hàm số tuần hoàn với chu kì 2 ,
π có nghĩa cos (x k2π +
) = cos x với k ∈ ℤ . ●
Hàm số đồng biến trên mỗi khoảng ( π k2π;k2π − +
) và nghịch biến trên mỗi
khoảng (k2π;π k2π + ) , k ∈ ℤ . ●
Là hàm số chẵn nên đồ thị nhận trục tung làm trục đối xứng.
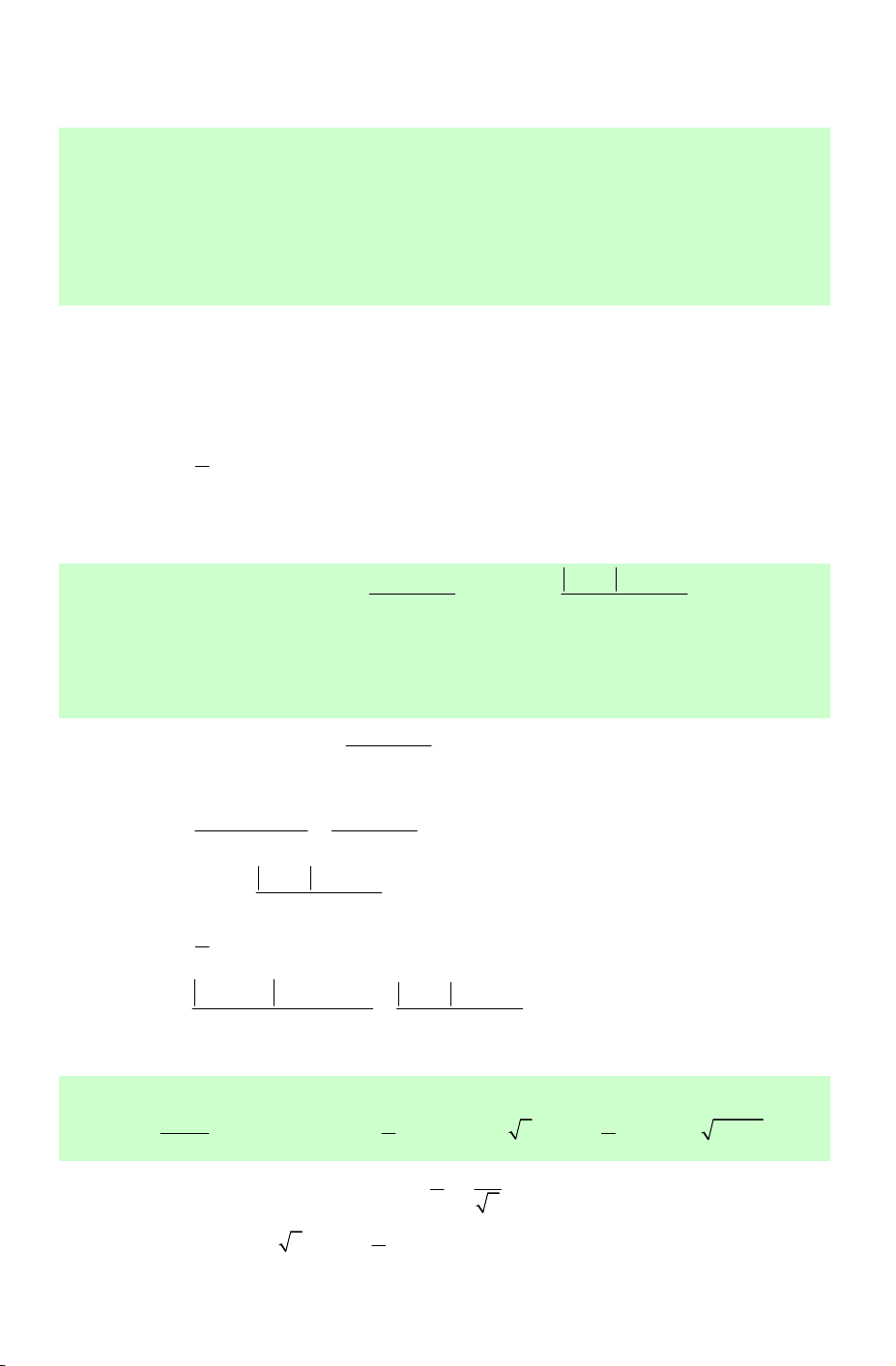
3) Hàm số y = tan x π ●
Tập xác định D = ℝ \ + k , π k ∈ ℤ ; 2 ●
Tập giá trị T = ℝ; ●
Là hàm số tuần hoàn với chu kì , π có nghĩa tan(x kπ +
) = tan x với k ∈ ℤ . π π ●
Hàm số đồng biến trên mỗi khoảng −
+ kπ; + kπ, k ∈ ; ℤ 2 2 ●
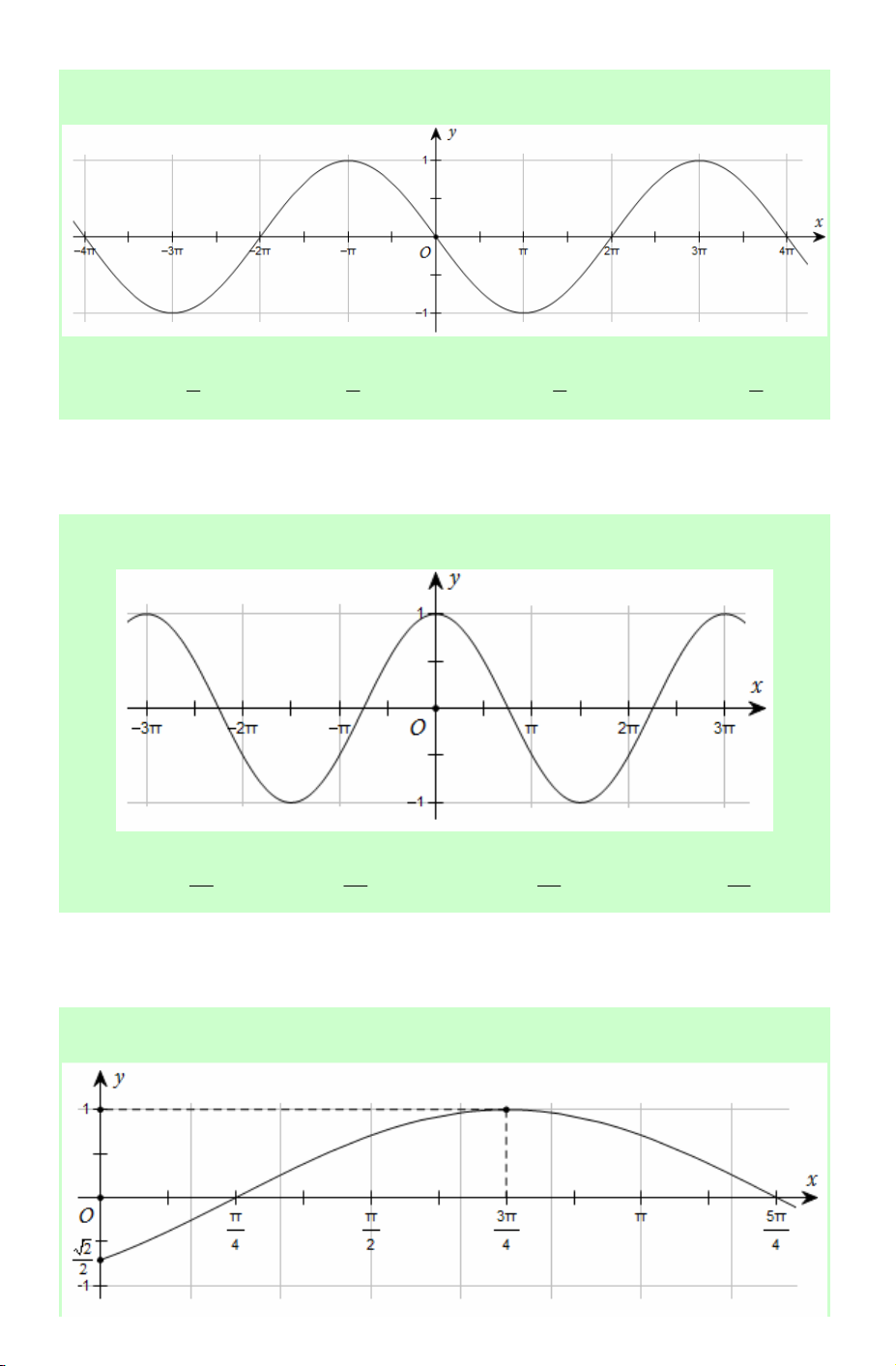
Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng. y x π π 3π − − π O π 3π − 2 2 2 2
4) Hàm số y = cot x ● Tập xác định D ℝ \ {k , π = k ∈ ℤ}; ●
Tập giá trị T = ℝ; ●
Là hàm số tuần hoàn với chu kì , π có nghĩa tan(x kπ +
) = tan x với k ∈ ℤ . ●
Hàm số đồng biến trên mỗi khoảng (kπ;π kπ + ), k ∈ ; ℤ ●
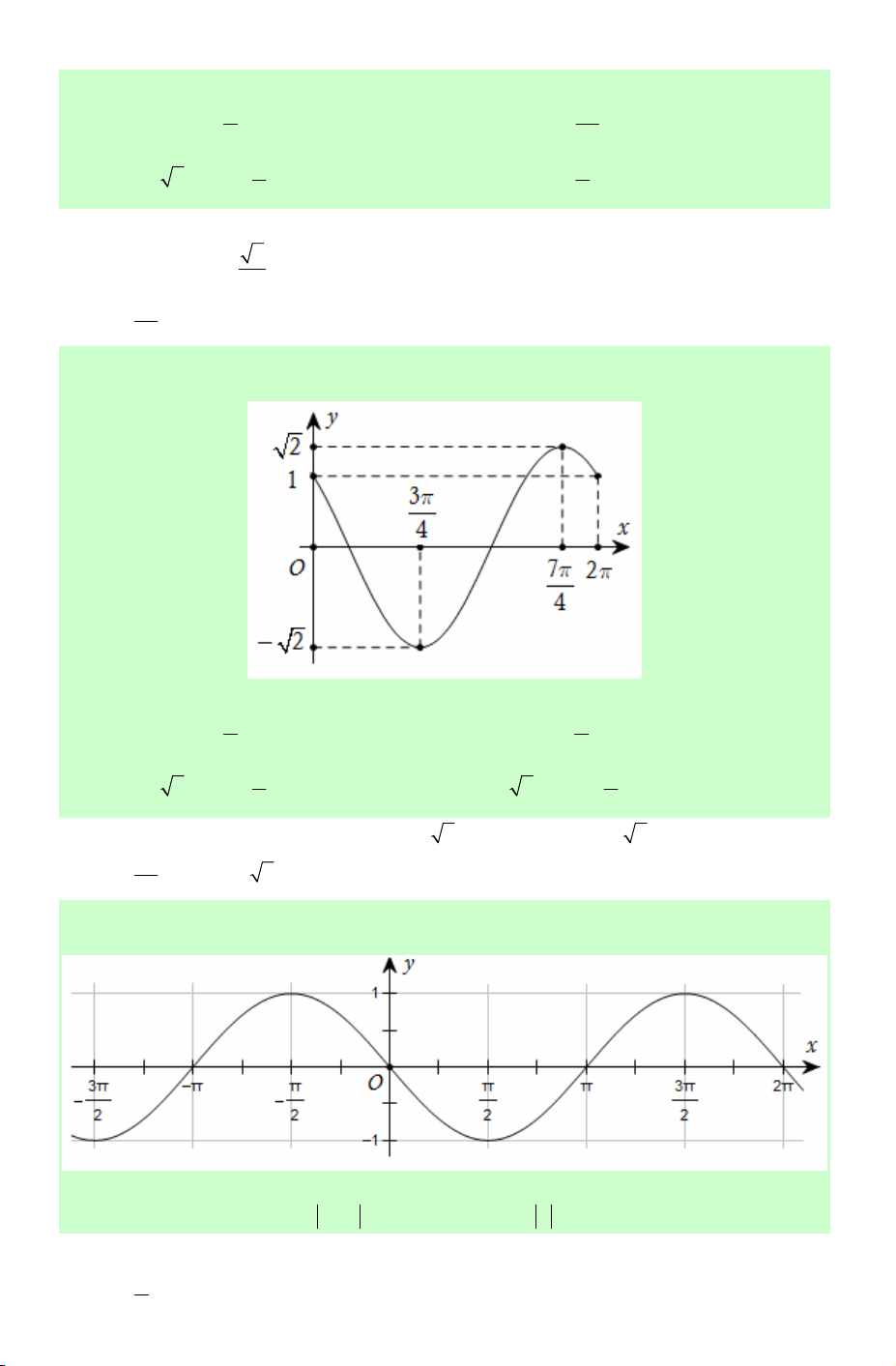
Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng. y π π − 2π − 3π − π O π 3π 2π x − 2 2 2 2
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. TẬP XÁC ĐỊNH
Câu 1. Tìm tập xác định D của hàm số 2017 y = . sin x A. D = . ℝ B. D = ℝ \{0}. C. π D ℝ \ {k , π = k ∈ ℤ}.
D. D = ℝ \ + k , π k ∈ ℤ . 2
Lời giải. Hàm số xác định khi và chỉ khi sin x 0 x k , π ≠ ⇔ ≠ k ∈ . ℤ Vật tập xác định D ℝ \ {k , π =
k ∈ ℤ}. Chọn C.
Câu 2. Tìm tập xác định − x D của hàm số 1 sin y = . cos x −1 A. π D = . ℝ
B. D = ℝ \ + k , π k ∈ ℤ . 2 C. D ℝ \{k , π = k ∈ ℤ}. D. D ℝ \{k2 , π = k ∈ ℤ}.
Lời giải. Hàm số xác định khi và chỉ khi cos x 1 0 cos x 1 x k2 , π − ≠ ⇔ ≠ ⇔ ≠ k ∈ . ℤ Vậy tập xác định D ℝ \ {k2 , π =
k ∈ ℤ}. Chọn D.
Câu 3. Tìm tập xác định D của hàm số 1 y = . π sin x − 2 A. π D ℝ \k , k = ∈ Z . B. D ℝ \{k , π = k ∈ Z}. 2 C. π D ℝ \ ( 1 2k) , k = + ∈ Z . D. D ℝ \ ( { 1 2k) , π = + k ∈ } Z . 2
Lời giải. Hàm số xác định π π π sin ⇔ x
− ≠ 0 ⇔ x −
≠ kπ ⇔ x ≠ + k , π k ∈ . ℤ 2 2 2 Vậy tập xác định π D = ℝ \ + k , π k ∈ ℤ . Chọn C. 2
Câu 4. Tìm tập xác định D của hàm số 1 y = . sin x − cos x A. π D = . ℝ B. D = ℝ \ − + k , π k ∈ ℤ . 4 C. π π D = ℝ \ + k2 , π k ∈ ℤ .
D. D = ℝ \ + k , π k ∈ ℤ . 4 4
Lời giải. Hàm số xác định π sin x cos x 0 tan x 1 x k , π ⇔ − ≠ ⇔ ≠ ⇔ ≠ + k ∈ . ℤ 4 Vậy tập xác định π D = ℝ \ + k , π k ∈ ℤ . Chọn D. 4 Câu 5. Hàm số 1 1
y = tan x + cot x + +
không xác định trong khoảng nào trong sin x cos x các khoảng sau đây? A. π π k2 π;
+ k2π với k ∈ . π + k π + k với k ∈ . ℤ B. 3 2 ; 2π ℤ 2 2 C. π + k2
π; π + k 2π với k ∈ . π k2π;2π k2 với k ∈ . ℤ D. ( π + + ) ℤ 2 Lời giải. s in x ≠ 0 Hàm số xác định kπ ⇔
⇔ sin 2x ≠ 0 ⇔ 2x ≠ kπ ⇔ x ≠ , k ∈ . ℤ c os x ≠ 0 2 Ta chọn 3π π k = 3 → x ≠
nhưng điểm 3 thuộc khoảng (π k2π;2π k2π + + ) . 2 2
Vậy hàm số không xác định trong khoảng (π k2π;2π k2π + + ) . Chọn D.
Câu 6. Tìm tập xác định π D của hàm số y cot = 2x − + sin 2x. 4 A. π D = ℝ \ + k , π k ∈ ℤ . B. D = . ∅ 4 C. π π D ℝ \ k , k = + ∈ ℤ . D. D = . ℝ 8 2
Lời giải. Hàm số xác định π π π kπ sin2x
− ≠ 0 ⇔ 2x − ≠ kπ ⇔ x ≠ + , k ∈ . ℤ 4 4 8 2 Vậy tập xác định π π D ℝ \ k , k = + ∈ ℤ . Chọn C. 8 2
Câu 7. Tìm tập xác định x π D của hàm số 2 y = 3 tan − . 2 4 A. 3π π D = ℝ \ + k2 , π k ∈ ℤ.
B. D = ℝ \ + k2 , π k ∈ ℤ . 2 2 C. 3π π D = ℝ \ + k , π k ∈ ℤ.
D. D = ℝ \ + k , π k ∈ ℤ . 2 2
Lời giải. Hàm số xác định x π x π π 3 2 π ⇔ cos − ≠ 0 ⇔ − ≠ + kπ ⇔ x ≠ + k2 , π k ∈ . ℤ 2 4 2 4 2 2 Vậy tập xác định 3π D = ℝ \ + k2 ,
π k ∈ ℤ. Chọn A. 2 Câu 8. Hàm số cos 2x y =
không xác định trong khoảng nào trong các khoảng sau 1+ tan x đây? A. π 3π π π + k2 π;
+ k2π với k ∈ . − + k π + k với k ∈ . ℤ B. 2 ; 2π ℤ 2 4 2 2 C. 3π 3π π + k2 π;
+ k2π với k ∈ . π + k π + k với k ∈ . ℤ D. 3 2 ; 2π ℤ 4 2 2
Lời giải. Hàm số xác định khi và chỉ khi 1+ tan x ≠ 0 và tan x xác định π
x ≠ − + kπ tan x ≠ −1 4 ⇔ ⇔ , k ∈ . ℤ c os x ≠ 0 π
x ≠ + kπ 2 π x ≠ − Ta chọn 4 π π π k 0 = →
nhưng điểm − thuộc khoảng − + k2 π; + k2π. π 4 2 2 x ≠ 2
Vậy hàm số không xác định trong khoảng π π − + k2 π;
+ k2π . Chọn B. 2 2
Câu 9. Tìm tập xác định 3 tan x −5 D của hàm số y = . 2 1− sin x A. π π D = ℝ \ + k2 , π k ∈ ℤ .
B. D = ℝ \ + k , π k ∈ ℤ . 2 2
C. D ℝ \{π k , π = + k ∈ ℤ}. D. D = . ℝ
Lời giải. Hàm số xác định khi và chỉ khi 2
1− sin x ≠ 0 và tan x xác định 2 s in x ≠ 1 π ⇔
⇔ cos x ≠ 0 ⇔ x ≠ + k , π k ∈ . ℤ c os x ≠ 0 2 Vậy tập xác định π D = ℝ \ + k , π k ∈ ℤ . Chọn B. 2
Câu 10. Tìm tập xác định D của hàm số y = sin x + 2. A. D = . ℝ B. D = [−2;+ ) ∞ . C. D [0;2π = ]. D. D = . ∅
Lời giải. Ta có −1≤ sin x ≤1
→1 ≤ sin x + 2 ≤ 3, ∀x ∈ . ℝ
Do đó luôn tồn tại căn bậc hai của sin x + 2 với mọi x ∈ . ℝ Vậy tập xác định D = . ℝ Chọn A.
Câu 11. Tìm tập xác định D của hàm số y = sin x −2. A. D = . ℝ B. ℝ \{k , π k ∈ ℤ}. C. D =[−1; ] 1 . D. D = . ∅
Lời giải. Ta có −1≤ sin x ≤1
→−3 ≤ sin x − 2 ≤ −1, ∀x ∈ . ℝ
Do đó không tồn tại căn bậc hai của sin x −2. Vậy tập xác định D = . ∅ Chọn D.
Câu 12. Tìm tập xác định D của hàm số 1 y = . 1− sin x A. π D ℝ \ {k , π = k ∈ ℤ}.
B. D = ℝ \ + k , π k ∈ ℤ . 2 C. π D = ℝ \ + k2 , π k ∈ ℤ . D. D = . ∅ 2
Lời giải. Hàm số xác định khi và chỉ khi 1−sin x > 0 ⇔ sin x <1. (*) Mà π
−1 ≤ sin x ≤ 1 nên (*) sin x 1 x k2 , π ⇔ ≠ ⇔ ≠ + k ∈ . ℤ 2 Vậy tập xác định π D = ℝ \ + k2 , π k ∈ ℤ . Chọn C. 2
Câu 13. Tìm tập xác định D của hàm số y = 1−sin 2x − 1+ sin 2x. A. D = . ∅ B. D = . ℝ C. π 5π π π D = + k2π;
+ k2π , k ∈ . ℤ D. 5 13 D = + k2π;
+ k2π , k ∈ . ℤ 6 6 6 6 Lời giải. 1 + sin 2x ≥ 0 Ta có 1 sin 2x 1 − ≤ ≤ ⇒ , ∀x ∈ . ℝ 1 − sin 2x ≥ 0 Vậy tập xác định D = . ℝ Chọn B.
Câu 14. Tìm tập xác định π D của hàm số 2 y 5 2 cot x sin x cot = + − + + x. 2 A. kπ π D ℝ \ , k = ∈ ℤ . B. D = ℝ \ − + k , π k ∈ ℤ . 2 2 C. D = . ℝ D. D ℝ \{k , π = k ∈ ℤ}.
Lời giải. Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời 2 π
5 + 2 cot x − sin x ≥ 0 , cot + x xác định và cot x xác định. 2 2 2 cot x ≥ 0 Ta có 2
→ 5 + 2 cot x −sin x ≥ 0, ∀x ∈ . ℝ −1 ≤ sin x ≤1 →5− sin x ≥ 0 π π π π
cot + x xác định sin ⇔ + x ≠ 0 ⇔
+ x ≠ kπ ⇔ x ≠ − + k , π k ∈ . ℤ 2 2 2 2 cot x xác định sin x 0 x k , π ⇔ ≠ ⇔ ≠ k ∈ . ℤ π
Do đó hàm số xác định x ≠ − + kπ kπ ⇔ 2 ⇔ x ≠ , k ∈ . ℤ 2 x ≠ kπ Vậy tập xác định kπ D ℝ \ , k = ∈ ℤ . Chọn A. 2
Câu 15. Tìm tập xác định π D của hàm số y tan = cos x . 2 A. π π D = ℝ \ + k , π k ∈ ℤ .
B. D = ℝ \ + k2 , π k ∈ ℤ . 2 2 C. D = ℝ . D. D ℝ \{k , π = k ∈ ℤ} .
Lời giải. Hàm số xác định khi và chỉ khi π π .cos x kπ ≠ +
⇔ cos x ≠ 1+ 2k . (*) 2 2 Do k ∈ ℤ nên (*) cos x 1 sin x 0 x k , π ⇔ ≠ ± ⇔ ≠ ⇔ ≠ k ∈ . ℤ Vậy tập xác định D ℝ \ {k , π =
k ∈ ℤ}. Chọn D.
Vấn đề 2. TÍNH CHẴN LẺ
Câu 16. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin x.
B. y = cos x.
C. y = tan x.
D. y = cot x.
Lời giải. Nhắc lại kiến thức cơ bản:
Hàm số y = sin x là hàm số lẻ.
Hàm số y = cos x là hàm số chẵn.
Hàm số y = tan x là hàm số lẻ.
Hàm số y = cot x là hàm số lẻ.
Vậy B là đáp án đúng. Chọn B.
Câu 17. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = − sin x.
B. y = cos x −sin x. C. 2
y = cos x + sin x.
D. y = cos x sin x.
Lời giải. Tất các các hàm số đều có TXĐ: D = ℝ . Do đó ∀x ∈ D ⇒ −x ∈ D.
Bây giờ ta kiểm tra f (−x) = f (x) hoặc f (−x)= − f (x).
Với y = f (x)= − sin x . Ta có f (−x)= − sin(−x)= sin x = −(−sin x)
→ f (−x) = − f (x) . Suy ra hàm số y = − sin x là hàm số lẻ.
Với y = f (x) = cos x −sin x. Ta có f (−x)= cos(−x)−sin(−x)= cos x + sin x
→ f (−x) ≠ {− f (x), f (x)} . Suy ra hàm số y = cos x −sin x không chẵn không lẻ.
Với y = f (x) 2
= cos x + sin x . Ta có f (− x) = (− x) 2 cos + sin (− x) = (−x)+ (− x) 2 = x +[− x ]2 2 cos sin cos sin = cos x + sin x
→ f (−x) = f (x) . Suy ra hàm số 2
y = cos x + sin x là hàm số chẵn. Chọn C.
Với y = f (x) = cos x sin x. Ta có f (−x)= cos(−x).sin(−x)= −cos x sin x
→ f (−x) = − f (x) . Suy ra hàm số y = cos x sin x là hàm số lẻ.
Câu 18. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. x y = sin 2x.
B. y = x cos x.
C. y = cos x.cot x. D. tan y = . sin x Lời giải.
Xét hàm số y = f (x)= sin 2x.
TXĐ: D = ℝ . Do đó ∀x ∈ D ⇒ −x ∈ D.
Ta có f (−x)= sin(−2x)= −sin 2x = − f (x)
→ f (x ) là hàm số lẻ.
Xét hàm số y = f (x)= x cos x.
TXĐ: D = ℝ . Do đó ∀x ∈ D ⇒ −x ∈ D.
Ta có f (−x)= (−x).cos(−x) = −x cos x = − f (x)
→ f (x ) là hàm số lẻ.
Xét hàm số y = f (x)= cos x cot x. TXĐ: D ℝ \{kπ =
(k ∈ ℤ)}. Do đó ∀x ∈ D ⇒ −x ∈ D.
Ta có f (−x)= cos(−x).cot(−x)= −cos x cot x = − f (x)
→ f (x ) là hàm số lẻ. Xét hàm số tan x
y = f (x) = . sin x TXĐ: π D ℝ \k (k ℤ) = ∈
. Do đó ∀x ∈ D ⇒ −x ∈ D. 2 tan Ta có (− x) −tan x tan x f (−x ) = = = = f (x )
→ f (x ) là hàm số chẵn. Chọn D. sin(− x ) −sin x sin x
Câu 19. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. x y = sin x . B. 2
y = x sin x. C. y = .
D. y = x + sin x. cos x
Lời giải. Ta kiểm tra được A là hàm số chẵn, các đáp án B, C, D là hàm số lẻ. Chọn A.
Câu 20. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung? A. π
y = sin x cos 2x. B. 3 y sin x.cos = x − . 2 C. tan x y = . D. 3
y = cos x sin x. 2 tan x +1
Lời giải. Ta dễ dàng kiểm tra được A, C, D là các hàm số lẻ nên có đồ thị đối xứng
qua gốc tọa độ O . Xét đáp án B, ta có π y f (x) 3 3 4 sin x.cos = = x
− = sin x.sin x = sin x . Kiểm tra được 2
đây là hàm số chẵn nên có đồ thị đối xứng qua trục tung. Chọn B.
Câu 21. Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2
y = cos x + sin x.
B. y = sin x + cos x.
C. y = −cos x.
D. y = sin x.cos3x.
Lời giải. Ta kiểm tra được đáp án A và C là các hàm số chẵn. Đáp án B là hàm số
không chẵn, không lẻ. Đáp án D là hàm số lẻ. Chọn D.
Câu 22. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ? A. x + y = cot 4x. B. sin 1 y = . C. 2 y = tan x.
D. y = cot x . cos x
Lời giải. Ta kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ. Chọn A.
Đáp án B là hàm số không chẵn, không lẻ. Đáp án C và D là các hàm số chẵn.
Câu 23. Trong các hàm số sau, hàm số nào là hàm số lẻ? A. π x x y sin =
− x. B. 2 y = sin x. C. cot y = . D. tan y = . 2 cos x sin x
Lời giải. Viết lại đáp án A là π y sin =
− x = cos x. 2
Ta kiểm tra được đáp án A, B và D là các hàm số chẵn. Đáp án C là hàm số lẻ. Chọn C.
Câu 24. Trong các hàm số sau, hàm số nào là hàm số lẻ? A. 2
y = 1− sin x. B. 2
y = cot x .sin x. C. 2
y = x tan 2x − cot x.
D. y =1+ cot x + tan x .
Lời giải. Ta kiểm tra được đáp án A, B và D là các hàm số chẵn. Đáp án C là hàm số lẻ. Chọn C.
Câu 25. Cho hàm số f (x)= sin 2x và g(x) 2
= tan x. Chọn mệnh đề đúng
A. f (x) là hàm số chẵn, g(x) là hàm số lẻ.
B. f (x) là hàm số lẻ, g(x) là hàm số chẵn.
C. f (x) là hàm số chẵn, g(x) là hàm số chẵn.
D. f (x) và g(x) đều là hàm số lẻ.
Lời giải. Xét hàm số f (x)= sin 2x.
TXĐ: D = ℝ . Do đó ∀x ∈ D ⇒ −x ∈ D.
Ta có f (−x)= sin(−2x)= −sin 2x = − f (x)
→ f (x ) là hàm số lẻ.
Xét hàm số g(x) 2 = tan x. TXĐ: π
D = ℝ \ + kπ (k ∈ ℤ). Do đó ∀x ∈ D ⇒ −x ∈ D. 2
Ta có g(−x)= (−x) 2 = (− x )2 2 tan tan
= tan x = g (x) là hàm số chẵn. → f (x ) Chọn B. Câu 26.
sin 2x − cos 3x Cho hai hàm số cos 2x f (x) = và g (x)= . Mệnh đề nào 2 1+ sin 3x 2 2 + tan x sau đây là đúng?
A. f (x) lẻ và g(x) chẵn.
B. f (x) và g(x) chẵn.
C. f (x) chẵn, g(x) lẻ.
D. f (x) và g(x) lẻ.
Lời giải. Xét hàm số cos 2x f (x) = . 2 1+ sin 3x
TXĐ: D = ℝ . Do đó ∀x ∈ D ⇒ −x ∈ D. cos −2 Ta có ( x ) cos 2x f (−x ) = = = f x
→ f (x ) là hàm số chẵn. 2 2 ( ) 1+ sin (−3x ) 1+ sin 3x
sin 2x − cos 3x
Xét hàm số g(x) = . 2 2 + tan x TXĐ: π
D = ℝ \ + kπ (k ∈ ℤ) . Do đó ∀x ∈ D ⇒ −x ∈ D. 2
sin(−2x ) −cos(−3x ) sin 2x − cos 3 Ta có x g (−x ) = = = g (x )
→ g (x) là hàm số chẵn. 2 2 + tan (−x ) 2 2 + tan x
Vậy f (x) và g(x) chẵn. Chọn B.
Câu 27. Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ? A. 1 π π y = . B. y sin = x + . C. y 2 cos = x − .
D. y = sin 2x . 3 sin x 4 4
Lời giải. Viết lại đáp án B là π 1 y sin = x + =
(sin x + cos x). 4 2 Viết lại đáp án C là π y 2 cos = x
− = sin x + cos x. 4
Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ. Chọn A.
Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ. Xét đáp án D. Hàm số xác định π
⇔ sin 2x ≥ 0 ⇔ 2x ∈ [k2π;π + k2π] ⇔ x ∈ kπ; + kπ 2 π
→ D = kπ; + kπ (k ∈ ℤ). 2 Chọn π π x = ∈ D nhưng −x = −
∉ D. Vậy y = sin 2x không chẵn, không lẻ. 4 4
Câu 28. Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số y = sin x đối xứng qua gốc tọa độ . O
B. Đồ thị hàm số y = cos x đối xứng qua trục Oy.
C. Đồ thị hàm số y = tan x đối xứng qua trục Oy.
D. Đồ thị hàm số y = tan x đối xứng qua gốc tọa độ . O
Lời giải. Ta kiểm tra được hàm số y = sin x là hàm số chẵn nên có đồ thị đối xứng
qua trục Oy . Do đó đáp án A sai. Chọn A.
Câu 29. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. π π π y 2 cos = x + + sin(
π − 2x ).
B. y = sin x − + sin x + . 2 4 4 C. π y 2 sin = x + − sin x.
D. y = sin x + cos x. 4
Lời giải. Viết lại đáp án A là π y 2 cos = x
+ + sin(π − 2x ) = −2 sin x + sin 2x. 2 Viết lại đáp án B là π π π y sinx sin = − + x + = 2 sin x.cos = 2 sin x. 4 4 4 Viết lại đáp án C là π y 2 sin = x
+ − sin x = sin x + cos x − sin x = cos x. 4
Ta kiểm tra được đáp án A và B là các hàm số lẻ. Đáp án C là hàm số chẵn. Chọn C. Xét đáp án D. s in x ≥ 0 Hàm số xác định π ⇔
→ D = k2π; + k2π (k ∈ ℤ). c os x ≥ 0 2 Chọn π π x = ∈ D nhưng −x = −
∉ D. Vậy y = sin x + cos x không chẵn, không lẻ. 4 4
Câu 30. Trong các hàm số sau, hàm số nào là hàm số lẻ ? A. 4 π π y x cos = + x − . B. 2017 y x cos = + x − . 3 2 C. 2018
y = 2015 + cos x + sin x. D. 2017 2018 y = tan x + sin x.
Lời giải. Viết lại đáp án B là 2017 π 2017 y x cos = + x
− = y = x + sin x. 2
Ta kiểm tra được đáp án A và D không chẵn, không lẻ. Đáp án B là hàm số lẻ. Đáp án
C là hàm số chẵn. Chọn B.
Vấn đề 3. TÍNH TUẦN HO=N
Câu 31. Mệnh đề nào sau đây là sai?
A. Hàm số y = sin x tuần hoàn với chu kì 2 . π
B. Hàm số y = cos x tuần hoàn với chu kì 2 . π
C. Hàm số y = tan x tuần hoàn với chu kì 2 . π
D. Hàm số y = cot x tuần hoàn với chu kì . π
Lời giải. Chọn C. Vì hàm số y = tan x tuần hoàn với chu kì . π
Câu 32. Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn? A. x y = sin x
B. y = x + sin x
C. y = x cos x. D sin y = . x
Lời giải. Chọn A.
Hàm số y = x + sin x không tuần hoàn. Thật vậy: Tập xác định D = ℝ .
Giả sử f (x +T )= f (x), ∀x ∈ D
⇔ (x +T )+ sin(x +T ) = x + sin x, ∀x ∈ D
⇔ T + sin(x +T ) = sin x, x ∀ ∈ D . (*) T
+ sin x = sin 0 = 0 Cho x = 0 và x π = , ta được T
+ sin(π +T ) = sin π = 0 2T sinT sin (π → + +
+T ) = 0 ⇔ T = 0 . Điều này trái với định nghĩa là T > 0 .
Vậy hàm số y = x + sin x không phải là hàm số tuần hoàn.
Tương tự chứng minh cho các hàm số y = x cos x và sin x y = không tuần hoàn. x
Câu 33. Trong các hàm số sau đây, hàm số nào không tuần hoàn?
A. y = cos x.
B. y = cos 2x. C. 2
y = x cos x . D. 1 y = . sin 2x
Lời giải. Chọn C. Câu 34. Tìm chu kì π
T của hàm số y sin 5 = x − . 4 A. 2π π π π T = . B. 5 T = . C. T = . D. T = . 5 2 2 8
Lời giải. Hàm số π
y = sin(ax + b) tuần hoàn với chu kì 2 T = . a Áp dụng: Hàm số π π y sin 5 = x
− tuần hoàn với chu kì 2 T = . Chọn A. 4 5 Câu 35. Tìm chu kì x
T của hàm số y cos = + 2016 . 2 A. T 4 . π = B. T 2 . π = C. T 2 . π = − D. T . π =
Lời giải. Hàm số π
y = cos(ax + b) tuần hoàn với chu kì 2 T = . a Áp dụng: Hàm số x y cos =
+ 2016 tuần hoàn với chu kì T 4 . π = Chọn A. 2 Câu 36. Tìm chu kì 1
T của hàm số y sin(100πx 50π = − + ). 2 A. 1 π T = . B. 1 T = . C. T = . D. 2 T 200π = . 50 100 50
Lời giải. Hàm số 1 π y sin(100πx 50π = − + ) tuần hoàn với chu kì 2 1 T = = . 2 100π 50 Chọn A. Câu 37. Tìm chu kì x
T của hàm số y = cos 2x + sin . 2 A. π T 4 . π = B. T . π = C. T 2 . π = D. T = . 2
Lời giải. Hàm số 2π
y = cos 2x tuần hoàn với chu kì T . π = = 1 2 Hàm số x 2π y = sin
tuần hoàn với chu kì T 4 . π = = 2 2 1 2 Suy ra hàm số x y = cos 2x + sin
tuần hoàn với chu kì T 4 . π = Chọn A. 2
Nhận xét. T là bội chung nhỏ nhất của T và T . 1 2
Câu 38. Tìm chu kì T của hàm số y = cos3x + cos5x. A. T . π = B. T 3 . π = C. T 2 . π = D. T 5 . π =
Lời giải. Hàm số 2π
y = cos 3x tuần hoàn với chu kì T = . 1 3 Hàm số 2π
y = cos 5x tuần hoàn với chu kì T = . 2 5
Suy ra hàm số y = cos3x + cos5x tuần hoàn với chu kì T 2 . π = Chọn C. Câu 39. Tìm chu kì x
T của hàm số y 3 cos(2x ) 1 2 sin = + − −3. 2 A. T 2 . π = B. T 4π = C. T 6π = D. T . π =
Lời giải. Hàm số 2π y = 3 cos(2x + )
1 tuần hoàn với chu kì T . π = = 1 2 Hàm số x 2π y 2 sin = − −3 .
tuần hoàn với chu kì T 4 . π = = 2 2 1 2 Suy ra hàm số x y 3 cos(2x ) 1 2 sin = + −
−3 tuần hoàn với chu kì T 4 . π = Chọn B. 2 Câu 40. Tìm chu kì π π
T của hàm số y sin2x 2 cos 3 = + + x − . 3 4 A. T 2 . π = B. T . π = C. T 3 . π = D. T 4 . π =
Lời giải. Hàm số π 2π y sin = 2x
+ tuần hoàn với chu kì T . π = = 3 1 2 Hàm số π 2π y 2 cos 3 = x
− tuần hoàn với chu kì T = . 4 2 3 Suy ra hàm số π π y sin2x 2 cos 3 = + + x
− tuần hoàn với chu kì T 2 . π = Chọn A. 3 4
Câu 41. Tìm chu kì T của hàm số y tan 3π = x. A. π π T = . B. 4 T = . C. 2 T = . D. 1 T = . 3 3 3 3
Lời giải. Hàm số π
y = tan (ax + b) tuần hoàn với chu kì T = . a Áp dụng: Hàm số y tan 3π =
x tuần hoàn với chu kì 1 T = . Chọn D. 3
Câu 42. Tìm chu kì T của hàm số y = tan 3x + cot x. A. π T 4 . π = B. T . π = C. T 3 . π = D. T = . 3
Lời giải. Hàm số π
y = cot (ax + b) tuần hoàn với chu kì T = . a Áp dụng: Hàm số π
y = tan 3x tuần hoàn với chu kì T = . 1 3
Hàm số y = cot x tuần hoàn với chu kì T . π = 2
Suy ra hàm số y = tan 3x + cot x tuần hoàn với chu kì T . π = Chọn B.
Nhận xét. T là bội chung nhỏ nhất của T và T . 1 2 Câu 43. Tìm chu kì x
T của hàm số y = cot + sin 2x. 3 A. π T 4 . π = B. T . π = C. T 3 . π = D. T = . 3
Lời giải. Hàm số x y = cot
tuần hoàn với chu kì T 3 . π = 3 1
Hàm số y = sin 2x tuần hoàn với chu kì T . π = 2 Suy ra hàm số x y = cot
+ sin 2x tuần hoàn với chu kì T 3 . π = Chọn C. 3 Câu 44. Tìm chu kì x π
T của hàm số y sin tan = − 2x + . 2 4 A. T 4 . π = B. T . π = C. T 3 . π = D. T 2 . π =
Lời giải. Hàm số x y = sin
tuần hoàn với chu kì T 4 . π = 2 1 Hàm số π π y tan = − 2x
+ tuần hoàn với chu kì T = . 4 2 2 Suy ra hàm số x π y sin tan = − 2x
+ tuần hoàn với chu kì T 4 . π = Chọn A. 2 4
Câu 45. Tìm chu kì T của hàm số 2
y = 2 cos x + 2017. A. T 3 . π = B. T 2 . π = C. T . π = D. T 4 . π = Lời giải. Ta có 2
y = 2 cos x + 2017 = cos 2x + 2018.
Suy ra hàm số tuần hoàn với chu kì T . π = Chọn C.
Câu 46. Tìm chu kì T của hàm số 2 2
y = 2 sin x + 3 cos 3x. A. π T . π = B. T 2 . π = C. T 3 . π = D. T = . 3 Lời giải. Ta có 1− cos 2x 1+ cos 6x 1 y = 2. + 3.
= (3cos 6x −2 cos 2x + ) 5 . 2 2 2 Hàm số 2π π
y = 3 cos 6x tuần hoàn với chu kì T = = . 1 6 3
Hàm số y = −2 cos 2x tuần hoàn với chu kì T . π = 2
Suy ra hàm số đã cho tuần hoàn với chu kì T . π = Chọn A.
Câu 47. Tìm chu kì T của hàm số 2
y = tan 3x − cos 2x. A. π π T . π = B. T = . C. T = . D. T 2 . π = 3 2 Lời giải. Ta có 1+ cos 4x 1 y = tan 3x −
= (2 tan 3x − cos 4x − ) 1 . 2 2 Hàm số π
y = 2 tan 3x tuần hoàn với chu kì T = . 1 3 Hàm số 2π π
y = −cos 4x tuần hoàn với chu kì T = = . 2 4 2
Suy ra hàm số đã cho tuần hoàn với chu kì T . π = Chọn C.
Câu 48. Hàm số nào sau đây có chu kì khác π ? A. π π y sin = − 2x. B. y cos 2 = x + . 3 4
C. y = tan(−2x + ) 1 .
D. y = cos x sin x.
Lời giải. Chọn C. Vì π π
y = tan (−2x + ) 1 có chu kì T = = . −2 2 Nhận xét. Hàm số 1
y = cos x sin x =
sin 2x có chu kỳ là . π 2
Câu 49. Hàm số nào sau đây có chu kì khác 2π ? A. x x x 3 y = cos x. B. y = sin cos . C. 2
y = sin (x + 2). D. 2 y cos = +1 . 2 2 2
Lời giải. Hàm số 1 3 y = cos x =
(cos3x +3cos x) có chu kì là 2 . π 4 Hàm số x x 1 y = sin cos =
sin x có chu kì là 2 . π 2 2 2 Hàm số 1 1 2
y = sin (x + 2) = − cos(2x + 4) có chu kì là . π Chọn C. 2 2 Hàm số x 1 1 2 y cos = +1 =
+ cos(x + 2) có chu kì là 2 . π 2 2 2
Câu 50. Hai hàm số nào sau đây có chu kì khác nhau? A. x
y = cos x và y = cot .
B. y = sin x và y = tan 2x. 2 C. x x y = sin và y = cos .
D. y = tan 2x và y = cot 2x. 2 2
Lời giải. Hai hàm số x
y = cos x và y = cot có cùng chu kì là 2 . π 2 Hai hàm số π
y = sin x có chu kì là 2π , hàm số y = tan 2x có chu kì là . Chọn B. 2 Hai hàm số x x y = sin
và y = cos có cùng chu kì là 4 . π 2 2 Hai hàm số π
y = tan 2x và y = cot 2x có cùng chu kì là . 2
Vấn đề 4. TÍNH ĐƠN ĐIỆU
Câu 51. Cho hàm số y = sin x . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng π π ; π
, nghịch biến trên khoảng 3 π; . 2 2
B. Hàm số đồng biến trên khoảng 3π π π π − ;
− , nghịch biến trên khoảng − ; . 2 2 2 2
C. Hàm số đồng biến trên khoảng π π 0;
, nghịch biến trên khoảng − ;0 . 2 2
D. Hàm số đồng biến trên khoảng π π π π − ;
, nghịch biến trên khoảng 3 ; . 2 2 2 2
Lời giải. Ta có thể hiểu thế này ' Hàm số y = sin x đồng biến khi góc x thuộc gốc
phần tư thứ IV và thứ I; nghịch biến khi góc x thuộc gốc phần tư thứ II và thứ III ' . Chọn D. Câu 52. Với 31π 33π x ∈ ;
, mệnh đề nào sau đây là đúng? 4 4
A. Hàm số y = cot x nghịch biến.
B. Hàm số y = tan x nghịch biến.
C. Hàm số y = sin x đồng biến.
D. Hàm số y = cos x nghịch biến.
Lời giải. Ta có 31π 33π π π ; = − + 8 π;
+ 8π thuộc gốc phần tư thứ I và II. Chọn C. 4 4 4 4 Câu 53. Với π x ∈ 0;
, mệnh đề nào sau đây là đúng? 4
A. Cả hai hàm số y = −sin 2x và y = −1+ cos 2x đều nghịch biến.
B. Cả hai hàm số y = −sin 2x và y = −1+ cos 2x đều đồng biến.
C. Hàm số y = −sin 2x nghịch biến, hàm số y = −1+ cos 2x đồng biến.
D. Hàm số y = −sin 2x đồng biến, hàm số y = −1+ cos 2x nghịch biến. Lời giải. Ta có π π x 0; 2x ∈ → ∈ 0;
thuộc góc phần tư thứ I. Do đó 4 2
y = sin 2x đồng biến
→ y = −sin 2x nghịch biến.
y = cos 2x nghịch biến
→ y = −1+ cos 2x nghịch biến. Chọn A.
Câu 54. Hàm số y = sin 2x đồng biến trên khoảng nào trong các khoảng sau? A. π π π π 0; . B. ; . C. 3 π; . D. 3 ;2 . π π 4 2 2 2
Lời giải. Xét A. Ta có π π x 0; 2x ∈ → ∈ 0;
thuộc gốc phần tư thứ I nên hàm số 4 2
y = sin 2x đồng biến trên khoảng này. Chọn A.
Câu 55. Trong các hàm số sau, hàm số nào đồng biến trên khoảng π π − ; ? 3 6 A. π π y tan = 2x + . B. y cot = 2x + . 6 6 C. π π y sin = 2x + . D. y cos = 2x + . 6 6 Lời giải. Với π π 2π π π π π x ; 2x ; 2x ∈ − → ∈ − → + ∈ − ;
thuộc góc phần tư thứ 3 6 3 3 6 2 2
IV và thứ nhất nên hàm số π π π y sin = 2x
+ đồng biến trên khoảng − ; . Chọn C. 6 3 6
Vấn đề 5. ĐỒ THỊ CỦA H=M SỐ LƯỢNG GIÁC
Câu 56. Đồ thị hàm số π y cos = x
− được suy từ đồ thị (C ) của hàm số y = cos x 2 bằng cách: A. Tịnh tiến π
(C ) qua trái một đoạn có độ dài là . 2 B. Tịnh tiến π
(C ) qua phải một đoạn có độ dài là . 2 C. Tịnh tiến π
(C ) lên trên một đoạn có độ dài là . 2 D. Tịnh tiến π
(C ) xuống dưới một đoạn có độ dài là . 2
Lời giải. Nhắc lại lý thuyết
Cho (C) là đồ thị của hàm số y = f (x) và p > 0 , ta có:
+ Tịnh tiến (C) lên trên p đơn vị thì được đồ thị của hàm số y = f (x)+ p .
+ Tịnh tiến (C) xuống dưới p đơn vị thì được đồ thị của hàm số y = f (x)− p .
+ Tịnh tiến (C) sang trái p đơn vị thì được đồ thị của hàm số y = f (x + p).
+ Tịnh tiến (C) sang phải p đơn vị thì được đồ thị của hàm số y = f (x − p) . Vậy đồ thị hàm số π y cos = x
− được suy từ đồ thị hàm số y = cos x bằng cách tịnh 2
tiến sang phải π đơn vị. Chọn B. 2
Câu 57. Đồ thị hàm số y = sin x được suy từ đồ thị (C) của hàm số y = cos x bằng cách: A. Tịnh tiến π
(C ) qua trái một đoạn có độ dài là . 2 B. Tịnh tiến π
(C ) qua phải một đoạn có độ dài là . 2 C. Tịnh tiến π
(C ) lên trên một đoạn có độ dài là . 2 D. Tịnh tiến π
(C ) xuống dưới một đoạn có độ dài là . 2 Lời giải. Ta có π π y sin x cos x cos = = − = x − . Chọn B. 2 2
Câu 58. Đồ thị hàm số y = sin x được suy từ đồ thị (C) của hàm số y = cos x +1 bằng cách: A. Tịnh tiến π
(C ) qua trái một đoạn có độ dài là và lên trên 1 đơn vị. 2 B. Tịnh tiến π
(C ) qua phải một đoạn có độ dài là và lên trên 1 đơn vị. 2 C. Tịnh tiến π
(C ) qua trái một đoạn có độ dài là và xuống dưới 1 đơn vị. 2 D. Tịnh tiến π
(C ) qua phải một đoạn có độ dài là và xuống dưới 1 đơn vị. 2 Lời giải. Ta có π π y sin x cos x cos = = − = x − . 2 2 Tịnh tiến đồ thị π
y = cos x +1 sang phải
đơn vị ta được đồ thị hàm số 2 π y cos = x − +1. 2
Tiếp theo tịnh tiến đồ thị π y cos = x
− +1 xuống dưới 1 đơn vị ta được đồ thị hàm 2 số π y cos = x − . Chọn D. 2
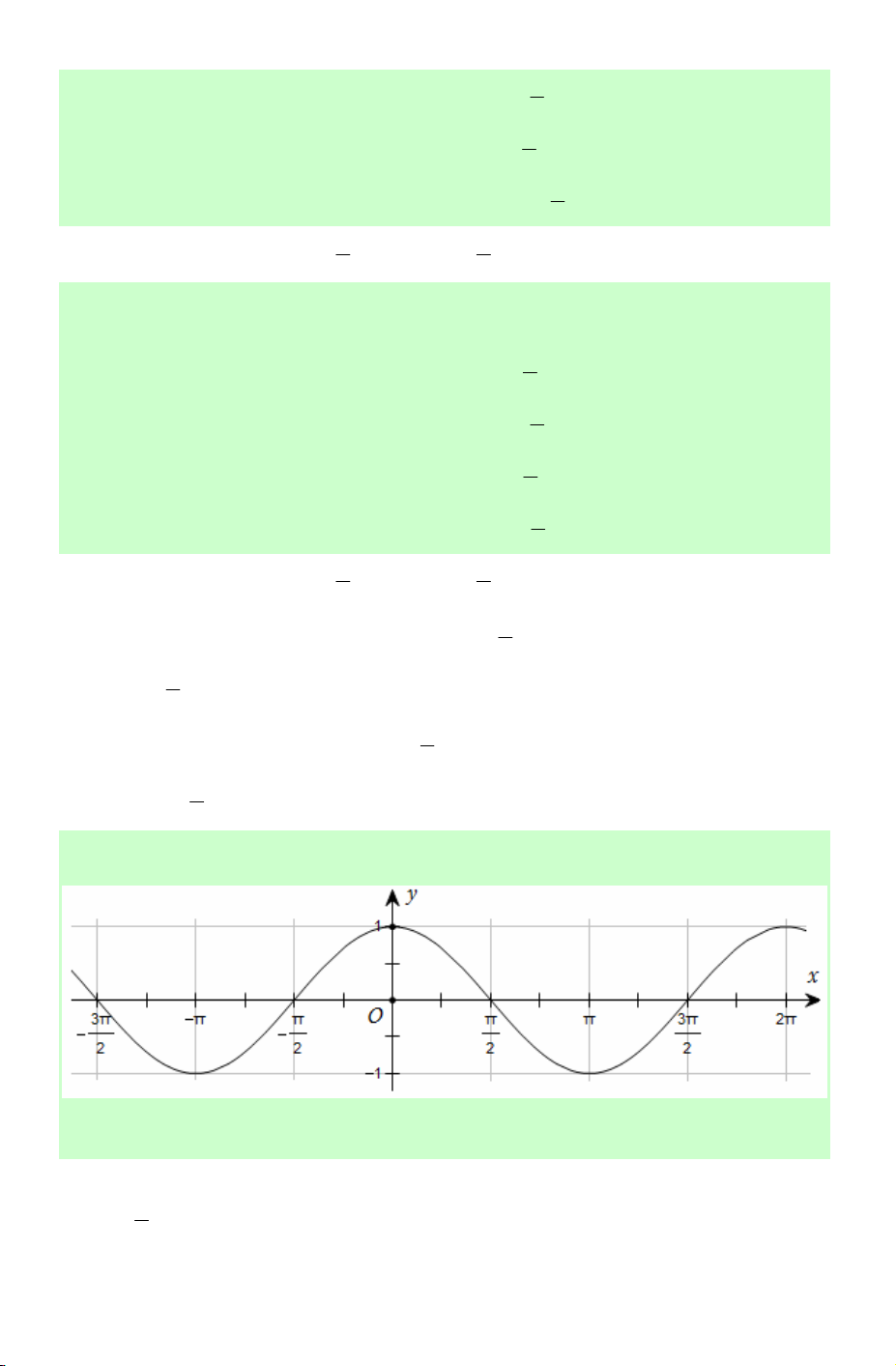
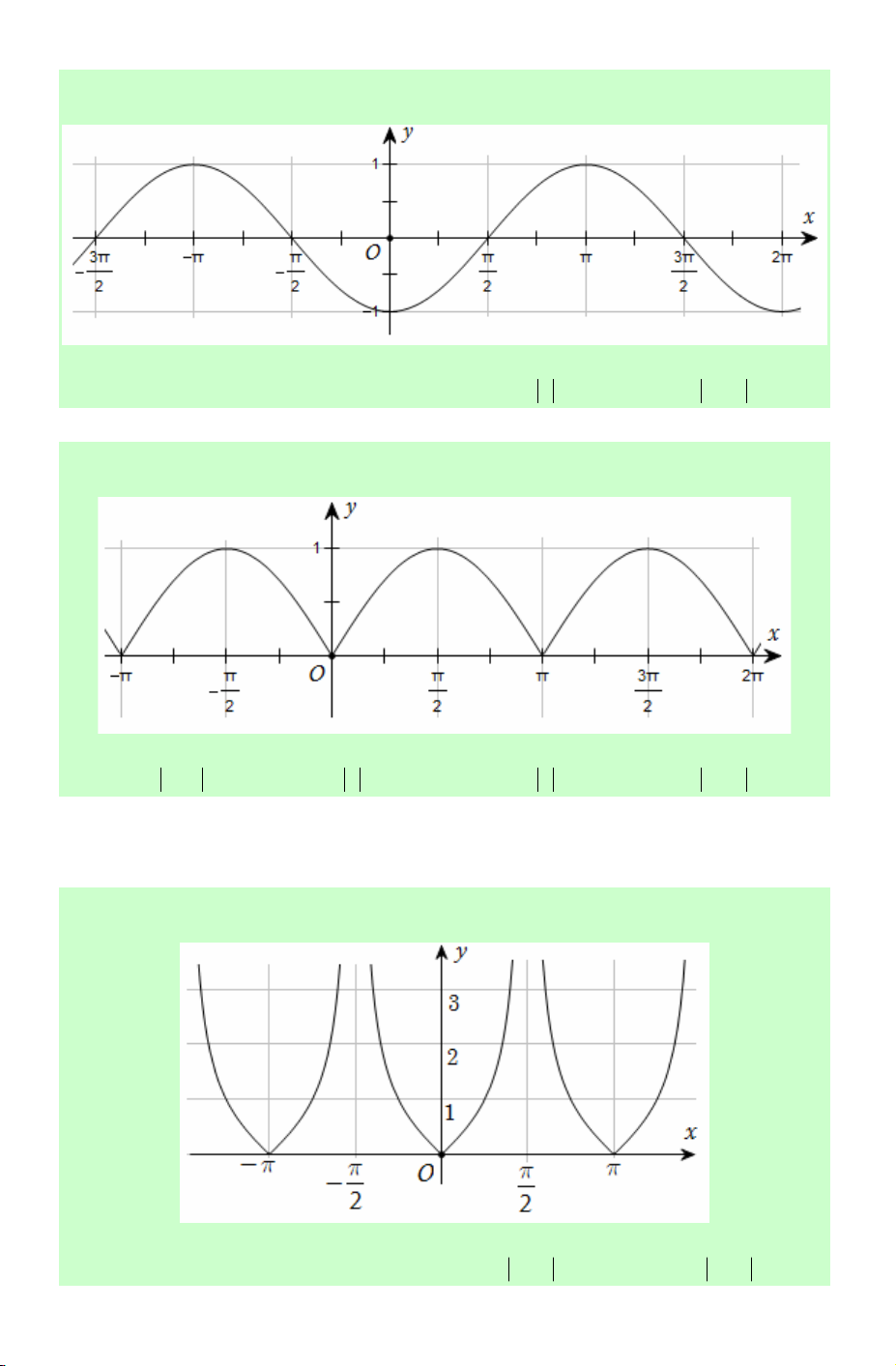
Câu 59. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = 1+ sin 2x. B. y = cos x.
C. y = −sin x.
D. y = −cos x.
Lời giải. Ta thấy tại x = 0 thì y =1. Do đó loại đáp án C và D. Tại π x =
thì y = 0 . Do đó chỉ có đáp án B thỏa mãn. Chọn B. 2
Câu 60. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào? A. x x x x y = sin . B. y = cos . C. y = −cos . D. y sin = − . 2 2 4 2
Lời giải. Ta thấy:
Tại x = 0 thì y = 0 . Do đó loại B và C. Tại x π =
thì y = −1. Thay vào hai đáp án còn lại chỉ có D thỏa. Chọn D.
Câu 61. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào? A. 2x x x x y = cos . B. 2 y = sin . C. 3 y = cos . D. 3 y = sin . 3 3 2 2
Lời giải. Ta thấy:
Tại x = 0 thì y =1. Do đó ta loại đáp án B và D. Tại x 3π =
thì y =1. Thay vào hai đáp án A và C thì chit có A thỏa mãn. Chọn A.
Câu 62. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào? A. π π y sin = x − . B. 3 y cos = x + . 4 4 C. π π y 2 sin = x + . D. y cos = x − . 4 4
Lời giải. Ta thấy hàm số có GTLN bằng 1 và GTNN bằng −1 . Do đó loại đáp án C. Tại x = 0 thì 2 y = − . Do đó loại đáp án D. 2 Tại 3π x =
thì y =1. Thay vào hai đáp án còn lại chỉ có A thỏa mãn. Chọn A. 4
Câu 63. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào? A. π π y sin = x − . B. y cos = x − . 4 4 C. π π y 2 sin = x + . D. y 2 cos = x + . 4 4
Lời giải. Ta thấy hàm số có GTLN bằng 2 và GTNN bằng − 2 . Do đó lại A và B. Tại 3π x =
thì y = − 2 . Thay vào hai đáp án C và D thỉ chỉ có D thỏa mãn. Chọn D. 4
Câu 64. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = sin x.
B. y = sin x .
C. y = sin x .
D. y = −sin x.
Lời giải. Ta thấy tại x = 0 thì y = 0 . Cả 4 đáp án đều thỏa. Tại π x =
thì y = −1. Do đó chỉ có đáp án D thỏa mãn. Chọn D. 2
Câu 65. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = cos x.
B. y = −cos x
C. y = cos x .
D. y = cos x .
Lời giải. Ta thấy tại x = 0 thì y = −1. Do đó chỉ có đáp án B thỏa mãn. Chọn B.
Câu 66. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = sin x .
B. y = sin x .
C. y = cos x .
D. y = cos x .
Lời giải. Ta thấy hàm số có GTNN bằng 0 . Do đó chỉ có A hoặc D thỏa mãn.
Ta thấy tại x = 0 thì y = 0 . Thay vào hai đáp án A và D chỉ có duy nhất A thỏa mãn. Chọn A.
Câu 67. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = tan x.
B. y = cot x.
C. y = tan x .
D. y = cot x .
Lời giải. Ta thấy hàm số có GTNN bằng 0 . Do đó ta loại đáp án A và B.
Hàm số xác định tại x π = và tại x π =
thì y = 0 . Do đó chỉ có C thỏa mãn. Chọn C.
Câu 68. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào? A. π π y sin = x − −1. B. y 2sin = x − . 2 2 C. π π y sin = − x − −1. D. y sin = x + +1. 2 2
Lời giải. Ta thấy hàm số có GTLN bằng 0 , GTNN bằng −2. Do đó ta loại đán án B vì π y 2 sin = x − ∈ [−2;2]. 2
Tại x = 0 thì y = −2 . Thử vào các đáp án còn lại chỉ có A thỏa mãn. Chọn A.
Câu 69. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = 1+ sin x . B. y = sin x .
C. y = 1+ cos x .
D. y = 1+ sin x .
Lời giải. Ta có y = 1+ cos x ≥1 và y = 1+ sin x ≥1 nên loại C và D.
Ta thấy tại x = 0 thì y =1. Thay vào hai đáp án A và B thì chỉ có A thỏa. Chọn A.
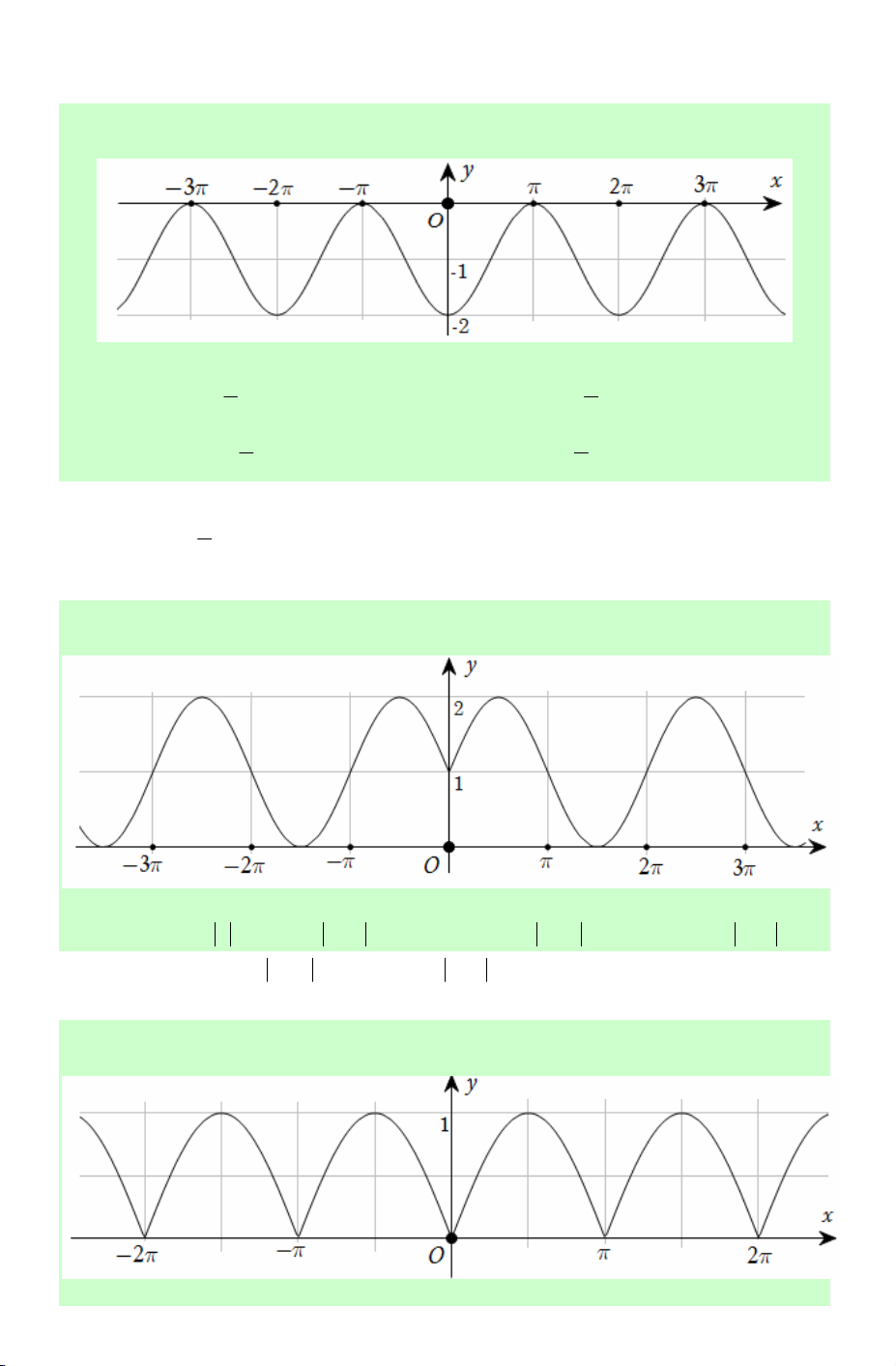
Câu 70. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C, D.
Hỏi hàm số đó là hàm số nào?
A. y = 1+ sin x . B. y = sin x .
C. y = 1+ cos x .
D. y = 1+ sin x .
Lời giải. Ta có y = 1+ cos x ≥1 và y = 1+ sin x ≥1 nên loại C và D. Ta thấy tại x π =
thì y = 0 . Thay vào hai đáp án A và B thì chỉ có B thỏa. Chọn B.
Vấn đề 6. GIÁ TRỊ LỚN NHẤT GIÁ TRỊ NHỎ NHẤT –
Câu 71. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 3sin x −2.
A. M = 1, m = −5.
B. M = 3, m = 1.
C. M = 2, m = −2.
D. M = 0, m = −2.
Lời giải. Ta có −1≤ sin x ≤1
→−3 ≤ 3sin x ≤ 3
→−5 ≤ 3 sin x − 2 ≤ 1 M = 1 5 y 1 →− ≤ ≤ → . Chọn A. m = −5
Câu 72. Tìm tập giá trị T của hàm số y = 3cos 2x +5. A. T = [−1; ] 1 . B. T = [−1;1 ] 1 . C. T = [2;8]. D. T = [5;8].
Lời giải. Ta có −1≤ cos 2x ≤1
→−3 ≤ 3cos 2x ≤ 3
→ 2 ≤ 3 cos 2x + 5 ≤ 8
→ 2 ≤ y ≤ 8
→T = [2;8]. Chọn C.
Câu 73. Tìm tập giá trị T của hàm số y = 5−3sin x. A. T = [−1; ] 1 . B. T = [−3;3]. C. T = [2;8]. D. T = [5;8].
Lời giải. Ta có −1≤ sin x ≤1
→1 ≥ −sin x ≥ −1
→3 ≥ −3sin x ≥ −3
→8 ≥ 5−3 sin x ≥ 2
→ 2 ≤ y ≤ 8 T → = [2;8]. Chọn C. Câu 74. Cho hàm số π y 2 sin = − x
+ + 2 . Mệnh đề nào sau đây là đúng? 3
A. y ≥−4, ∀x ∈ . ℝ
B. y ≥ 4, ∀x ∈ . ℝ
C. y ≥ 0, ∀x ∈ . ℝ
D. y ≥ 2, ∀x ∈ . ℝ Lời giải. Ta có π π 1 sin x 1 2 2 sin − ≤ + ≤ → ≥ − x + ≥ −2 3 3 π 4 2 sin → ≥ − x + + 2 ≥ 0
→ 4 ≥ y ≥ 0 . Chọn C. 3
Câu 75. Hàm số y = 5+ 4 sin 2x cos 2x có tất cả bao nhiêu giá trị nguyên? A. 3. B. 4. C. 5. D. 6.
Lời giải. Ta có y = 5 + 4 sin 2x cos 2x = 5 + 2 sin 4x .
Mà −1 ≤ sin 4x ≤1
→−2 ≤ 2 sin 4x ≤ 2
→ 3 ≤ 5 + 2 sin 4x ≤ 7 3 7 y y ∈ → ≤ ≤
ℤ→ y ∈ {3;4;5;6;7} nên y có 5 giá trị nguyên. Chọn C.
Câu 76. Tìm giá trị nhỏ nhất m của hàm số y = − 2 sin(2016x +2017) .
A. m = −2016 2. B. m = − 2. C. m = −1.
D. m = −2017 2.
Lời giải. Ta có −1≤ sin(2016x +2017)≤1
→ 2 ≥ − 2 sin(2016x + 2017) ≥ − 2.
Do đó giá trị nhỏ nhất của hàm số là − 2. Chọn B.
Câu 77. Tìm giá trị nhỏ nhất m của hàm số 1 y = . cos x +1 A. 1 m = . B. 1 m = .
C. m = 1.
D. m = 2. 2 2
Lời giải. Ta có −1 ≤ cos x ≤1 . Ta có 1
nhỏ nhất khi và chỉ chi cos x lớn nhất ⇔ cos x = 1 . cos x +1 Khi 1 1 cos x = 1 → y = = . Chọn A. cos x +1 2
Câu 78. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = sin x + cos x . Tính P = M − . m
A. P = 4.
B. P = 2 2.
C. P = 2. D. P = 2. Lời giải. Ta có π y sin x cos x 2 sin = + = x + . 4 Mà π π 1 sin x 1 2 2 sin − ≤ + ≤ →− ≤ x + ≤ 2 4 4 M = 2 →
→ P = M − m = 2 2. Chọn B. m = − 2
Câu 79. Tập giá trị T của hàm số y = sin 2017x −cos 2017x.
A. T = [−2;2].
B. T = [−4034;4034]. C. T 2; 2 = − . D. T = 0; 2 . Lời giải. Ta có π y sin 2017x cos 2017x 2 sin = − = 2017x − . 4 Mà π π 1 sin 2017x 1 2 2 sin − ≤ − ≤ →− ≤ 2017x − ≤ 2 4 4 2 y 2 T 2; 2 →− ≤ ≤ → = − . Chọn C. Câu 80. Hàm số π y sin = x
+ − sin x có tất cả bao nhiêu giá trị nguyên? 3 A. 1. B. 2. C. 3. D. 4.
Lời giải. Áp dụng công thức a + b a − b
sin a − sin b = 2 cos sin , ta có 2 2 π π π π sinx sin x 2 cosx sin cos + − = + = x + . 3 6 6 6 Ta có π −1 ≤ cos + ≤1 →−1 ≤ ≤1 y x y ∈ ℤ→ y ∈ {−1;0; } 1 . Chọn C. 6 Câu 81. Hàm số 4 4
y = sin x − cos x đạt giá trị nhỏ nhất tại x = x . Mệnh đề nào sau 0 đây là đúng? A. x k2 , π = k ∈ . ℤ B. x k , π = k ∈ . ℤ 0 0 C. π x π k2 , π = + k ∈ . ℤ D. x k , π = + k ∈ . ℤ 0 0 2 Lời giải. Ta có 4 4 y = x − x = ( 2 2 x + x )( 2 2 sin cos sin cos
sin x − cos x ) = −cos 2x.
Mà −1 ≤ cos 2x ≤1
→−1 ≥ −cos 2x ≥ 1 →−1 ≥ y ≥ 1 .
Do đó giá trị nhỏ nhất của hàm số là −1 . Đẳng thức xảy ra cos 2x 1 2x k2π x kπ ⇔ = ⇔ = ⇔ =
(k ∈ ℤ). Chọn B.
Câu 82. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = 1−2 cos3x .
A. M = 3, m = −1.
B. M = 1, m = −1.
C. M = 2, m = −2.
D. M = 0, m = −2.
Lời giải. Ta có −1≤ cos3x ≤1
→ 0 ≤ cos 3x ≤1
→ 0 ≥ −2 cos 3x ≥ −2 M = 1 1 1 2 cos 3x 1 1 y 1 → ≥ − ≥ − → ≥ ≥ − → . Chọn B. m = −1
Câu 83. Tìm giá trị lớn nhất π M của hàm số 2 y 4 sin x 2 sin = + 2x + . 4 A. M = 2. B. M = 2 −1. C. M = 2 +1. D. M = 2 + 2. Lời giải. Ta có π 1−cos 2x 2
y = 4 sin x + 2 sin2x + = 4
+ sin 2x + cos 2x 4 2 π sin 2x cos 2x 2 2 sin = − + = 2x − + 2. 4 Mà π π 1 sin 2x 1 2 2 2 sin − ≤ − ≤ →− + ≤ 2x − + 2 ≤ 2 + 2 . 4 4
Vậy giá trị lớn nhất của hàm số là 2 + 2. Chọn D.
Câu 84. Tìm tập giá trị T của hàm số 6 6
y = sin x + cos x. A. T = [0;2]. B. 1 T = ;1 . C. 1 T = ;1 . D. 1 T = 0; . 2 4 4
Lời giải. Ta có y = x + x = ( x + x )2 6 6 2 2 2 2 − x x ( 2 2 sin cos sin cos 3 sin cos sin x + cos x ) 3 3 1− cos 4x 5 3 2 2 2
= 1−3sin x cos x = 1− sin 2x = 1− . = + cos 4x. 4 4 2 8 8 Mà 1 5 3 1
−1 ≤ cos 4x ≤ 1 →
≤ + cos 4x ≤1 →
≤ y ≤1. Chọn C. 4 8 8 4 Câu 85. Cho hàm số 4 4
y = cos x + sin x . Mệnh đề nào sau đây là đúng?
A. y ≤ 2, ∀x ∈ .
ℝ B. y ≤1, ∀x ∈ . ℝ
C. y ≤ 2, ∀x ∈ . ℝ D. 2 y ≤ , x ∀ ∈ . ℝ 2
Lời giải. Ta có y = cos x + sin x = (sin x + cos x)2 1 4 4 2 2 2 2 2
− 2 sin x cos x = 1− sin 2x 2 1 1− cos 4x 3 1 = 1− . = + cos 4x. 2 2 4 4 Mà 1 3 1 1
−1 ≤ cos 4x ≤1 → ≤ + cos 4x ≤1
→ ≤ y ≤1 . Chọn B. 2 4 4 2 Câu 86. Hàm số 2
y = 1+ 2 cos x đạt giá trị nhỏ nhất tại x = x . Mệnh đề nào sau đây 0 là đúng? A. π x π k2 , π = + k ∈ . ℤ B. x k , π = + k ∈ . ℤ 0 0 2 C. x k2 , π = k ∈ . ℤ D. x k , π = k ∈ . ℤ 0 0 Lời giải. Ta có 2 2
−1 ≤ cos x ≤1
→ 0 ≤ cos x ≤1
→1 ≤1+ 2 cos x ≤ 3.
Do đó giá trị nhỏ nhất của hàm số bằng 1. Dấu π ' = '' xảy ra cos x 0 x k . π ⇔ = ⇔ = + Chọn B. 2
Câu 87. Tìm giá trị lớn nhất M và nhỏ nhất m của hàm số 2 2
y = sin x + 2 cos x.
A. M = 3, m = 0. B. M = 2, m = 0.
C. M = 2, m = 1.
D. M = 3, m = 1. Lời giải. Ta có 2 2 y = x + x = ( 2 2 x + x ) 2 2 sin 2 cos sin cos
+ cos x = 1+ cos x M = 2 Do 2 2 1 cos x 1 0 cos x 1 1 1 cos x 2 − ≤ ≤ → ≤ ≤ → ≤ + ≤ → . Chọn C. m = 1
Câu 88. Tìm giá trị lớn nhất 2
M của hàm số y = . 2 1+ tan x A. 1 M = . B. 2 M = . C. M = 1. D. M = 2. 2 3 Lời giải. Ta có 2 2 2 y = = = 2 cos x . 2 1+ tan x 1 2 cos x Do 2
0 ≤ cos x ≤ 1
→ 0 ≤ y ≤ 2
→ M = 2. Chọn D.
Câu 89. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = 8 sin x + 3cos 2x . Tính 2
P = 2M − m . A. P = 1. B. P = 2. C. P =112. D. P =130. Lời giải. Ta có 2 2 y = x + x = x + ( 2 − x ) 2 8 sin 3 cos 2 8 sin 3 1 2 sin = 2 sin x + 3. Mà 2 2
−1 ≤ sin x ≤1
→ 0 ≤ sin x ≤ 1
→3 ≤ 2 sin x + 3 ≤ 5 M = 5 2 3 y 5 → ≤ ≤ →
→ P = 2M −m = 1. Chọn A. m = 3
Câu 90. Tìm giá trị nhỏ nhất m của hàm số 2
y = 2 sin x + 3 sin 2x . A. m = 2− 3. B. m = −1. C. m = 1. D. m = − 3. Lời giải. Ta có 2
y = 2 sin x + 3 sin 2x = 1− cos 2x + 3 sin 2x 3 1
= 3 sin 2x −cos 2x +1 = 2
sin 2x − cos 2x+1 2 2 π π π 2sin 2x cos sin cos 2x 1 2 sin = − + = 2x − +1. 6 6 6 Mà π π 1 sin 2x 1 1 1 2 sin − ≤ − ≤ →− ≤ + 2x − ≤ 3 →−1 ≤ y ≤ 3. 6 6
Do đó giá trị nhỏ nhất của hàm số là −1. Chọn B.
Câu 91. Tìm tập giá trị T của hàm số y =12 sin x −5cos x. A. T = [−1; ] 1 . B. T = [−7;7].
C. T = [−13;13].
D. T = [−17;17]. Lời giải. Ta có 12 5 y 12 sin x 5 cos x 13 = − = sin x − cos x . 13 13 Đặt 12 5 cos α sin α = → =
. Khi đó y 13(sin x cosα sin α cos x) 13sin(x α = − = − ) 13 13
→−13 ≤ y ≤13 T → = [−13;13]. Chọn C.
Câu 92. Tìm giá trị lớn nhất M của hàm số y = 4 sin 2x −3cos 2x. A. M = 3. B. M = 1. C. M = 5. D. M = 4. Lời giải. Ta có 4 3 y 4 sin 2x 3 cos 2x 5 = − = sin 2x − cos 2x . 5 5 Đặt 4 3 cos α sin α = → = . Khi đó y 5(cos α sin 2x sin α cos 2x ) 5 sin (2x α = − = − ) 5 5
→−5 ≤ y ≤ 5
→ M = 5. Chọn C.
Câu 93. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y = sin x − 4 sin x + 5 . Tính 2
P = M − 2m .
A. P = 1.
B. P = 7.
C. P = 8.
D. P = 2.
Lời giải. Ta có y = x − x + = ( x − )2 2 sin 4 sin 5 sin 2 +1. Do − ≤ x ≤ →− ≤ x − ≤ − → ≤ ( x − )2 1 sin 1 3 sin 2 1 1 sin 2 ≤ 9 M = 10 2 (sin x 2)2 2 1 10 → ≤ − + ≤ →
P = M − 2m = 2. Chọn D. m = 2 Câu 94. Hàm số 2
y = cos x − cos x có tất cả bao nhiêu giá trị nguyên? A. 1. B. 2. C. 3. D. 4. 2 Lời giải. Ta có 1 1 2 y cos x cos x = − = cos x − − . 2 4 2 Mà 3 1 1 1 9 1 cos x 1 cos x 0 − ≤ ≤ →− ≤ − ≤ → ≤ cos x − ≤ 2 2 2 2 4 2 1 1 1 1 →− ≤ cos − − ≤ 2 →− ≤ ≤ 2 y x y ∈
ℤ→ y ∈ {0;1;2} nên có 3 giá trị thỏa 4 2 4 4 mãn. Chọn C. Câu 95. Hàm số 2
y = cos x + 2 sin x + 2 đạt giá trị nhỏ nhất tại x . Mệnh đề nào sau 0 đây là đúng? A. π π x k2 , π = + k ∈ . ℤ B. x k2 , π = − + k ∈ . ℤ 0 2 0 2 C. x π k2 , π = + k ∈ . ℤ D. x k2 , π = k ∈ . ℤ 0 0 Lời giải. Ta có 2 2
y = cos x + 2 sin x + 2 = 1− sin x + 2 sin x + 2 = − x + x + = −( x − )2 2 sin 2 sin 3 sin 1 + 4. Mà − ≤ x ≤ →− ≤ x − ≤ → ≤ ( x − )2 1 sin 1 2 sin 1 0 0 sin 1 ≤ 4 → ≥ −( x − )2 ≥ − → ≥ −( x − )2 0 sin 1 4 4 sin 1 + 4 ≥ 0 .
Suy ra giá trị nhỏ nhất của hàm số bằng 0 . Dấu π ' = '' xảy ra sin x 1 x k2π ⇔ = − ⇔ = − +
(k ∈ ℤ). Chọn B. 2
Câu 96. Tìm giá trị lớn nhất M và nhất m của hàm số 4 2
y = sin x − 2 cos x +1
A. M = 2, m = −2.
B. M = 1, m = 0.
C. M = 4, m = −1.
D. M = 2, m = −1.
Lời giải. Ta có y = x − x + = x − ( − x )+ = ( x + )2 4 2 4 2 2 sin 2 cos 1 sin 2 1 sin 1 sin 1 − 2. Do ≤ x ≤ → ≤ x + ≤ → ≤ ( x + )2 2 2 2 0 sin 1 1 sin 1 2 1 sin 1 ≤ 4 M = 2 1 (sin x )2 2 1 2 2 →− ≤ + − ≤ → . Chọn D. m = −1
Câu 97. Tìm giá trị nhỏ nhất m của hàm số 4
y = 4 sin x − cos 4x .
A. m = −3.
B. m = −1.
C. m = 3.
D. m = −5. 2 Lời giải. Ta có 1−cos 2x 4
y = 4 sin x − cos 4x = 4. −( 2 2 cos 2x − ) 1 2 = − x − x + = −( x + )2 2 cos 2 2 cos 2 2 cos 2 1 + 3 ≤ 3. Mà − ≤ x ≤ → ≤ x + ≤ → ≤ ( x + )2 1 cos 2 1 0 cos 2 1 2 0 cos 2 1 ≤ 4 →− ≤ −( x + )2 1 cos 2 1 + 3 ≤ 3
→ m = −1. Chọn B.
Câu 98. Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số 2
y = 7 −3 cos x .
A. M = 10, m = 2.
B. M = 7, m = 2.
C. M = 10, m = 7.
D. M = 0, m = 1. Lời giải. Ta có 2
−1 ≤ cos x ≤1 → 0 ≤ cos x ≤1 2 2
→ 4 ≤ 7 −3 cos x ≤ 7
→ 2 ≤ 7 −3 cos x ≤ 7 . Chọn B.
Câu 99. Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm π
2017 được cho bởi một hàm số y = 4 sin
(t −60) +10 với t ∈ ℤ và 0 < t ≤ 365 . Vào 178
ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
A. 28 tháng 5. B. 29 tháng 5. C. 30 tháng 5. D. 31 tháng 5. Lời giải. Vì π π sin
(t −60) ≤1 → y = 4 sin
(t −60) +10 ≤14. 178 178
Ngày có ánh sáng mặt trời nhiều nhất π ⇔ y = 14 ⇔ sin (t −60) = 1 178 π π (t 60) k2π ⇔ − = +
⇔ t = 149 + 356k. 178 2 Do 149 54 0 365 0 149 356 365 k t k k ∈ < ≤ → < + ≤ ⇔ − < ≤ ℤ→ k = 0 . 356 89 Với k = 0
→ t = 149 rơi vào ngày 29 tháng 5 (vì ta đã biết tháng 1 và 3 có 31 ngày,
tháng 4 có 30 ngày, riêng đối với năm 2017 thì không phải năm nhuận nên tháng 2 có
28 ngày hoặc dựa vào dữ kiện 0 < t ≤ 365 thì ta biết năm này tháng 2 chỉ có 28 ngày). Chọn B.
Câu 100. Hằng ngày mực nước của con kênh lên xuống theo thủy triều. Độ sâu h
(mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức πt π h = 3 cos
+ +12. Mực nước của kênh cao nhất khi: 8 4
A. t = 13 (giờ). B. t = 14 (giờ).
C. t = 15 (giờ).
D. t = 16 (giờ).
Lời giải. Mực nước của kênh cao nhất khi h lớn nhất πt π πt π ⇔ cos + = 1 ⇔ +
= k2π với 0 < t ≤ 24 và k ∈ . ℤ 8 4 8 4
Lần lượt thay các đáp án, ta được đáp án B thỏa mãn. Chọn B. Vì với πt π t 14 2π = → ⇔ + =
(đúng với k = 1 ∈ ℤ ) 8 4 Baøi 02
PHÖÔNG TRÌNH LÖÔÏNG GIAÙC CÔ BAÛN
1) Phương trình sin x = a
Trường hợp a >1
→ phương trình vô nghiệm, vì −1 ≤ sin x ≤ 1 với mọi x .
Trường hợp a ≤1
→ phương trình có nghiệm, cụ thể: ▪ 1 2 3 a 0 ; ; ; ; 1 ∈ ± ± ± ± . Khi đó 2 2 2 x α = + k2π
sin x = a ⇔ sin x = sin α ⇔ , k ∈ ℤ . x π α = − + k2π x = a + k π ▪ 1 2 3 a 0 ; ; ; ; 1 ∉ ± ± ± ± . Khi đó arcsin 2
sin x = a ⇔ , k ∈ ℤ . 2 2 2 x π
= − arcsin a + k2π
2) Phương trình cos x = a
Trường hợp a >1
→ phương trình vô nghiệm, vì −1 ≤ cos x ≤ 1 với mọi x .
Trường hợp a ≤1
→ phương trình có nghiệm, cụ thể: ▪ 1 2 3 a 0 ; ; ; ; 1 ∈ ± ± ± ± . Khi đó 2 2 2 x α = + k2π
cos x = a ⇔ cos x = cos α ⇔ , k ∈ ℤ . x α = − + k2π x = a + k π ▪ 1 2 3 a 0 ; ; ; ; 1 ∉ ± ± ± ± . Khi đó arc cos 2
cos x = a ⇔ , k ∈ ℤ . 2 2 2
x = −arc cos a + k2π
3) Phương trình tan x = a Điều kiện: π x kπ ≠ + (k ∈ ℤ). 2 ● 1 a 0 ; ; 1; 3 ∈ ± ± ±
. Khi đó tan x = a ⇔ tan x tan α ⇔ x α k , π = = + k ∈ ℤ . 3 ● 1 a 0 ; ; 1; 3 ∉ ± ± ± . Khi đó tan x a x arctan a k , π = ⇔ = + k ∈ ℤ . 3
4) Phương trình cot x = a Điều kiện: x π kπ ≠ + (k ∈ ℤ). ● 1 a 0 ; ; 1; 3 ∈ ± ± ±
. Khi đó cot x = a cot x cot α x α = k , π ⇔ = ⇔ + k ∈ ℤ . 3 ● 1 a 0 ; ; 1; 3 ∉ ± ± ± . Khi đó cot x a x arccot a k , π = ⇔ = + k ∈ ℤ . 3
CÂU HỎI TRẮC NGHIỆM
Câu 1. Giải phương trình 2x π sin − = 0 . 3 3 A. 2π k3π x kπ = (k ∈ ℤ). B. x = + (k ∈ ℤ). 3 2 C. π π k3π x kπ = + (k ∈ ℤ). D. x = + (k ∈ ℤ). 3 2 2
Lời giải. Phương trình 2x π 2x π sin − = 0 ⇔ − = kπ 3 3 3 3 2x π π k3π kπ ⇔ = + ⇔ x = +
(k ∈ ℤ). Chọn D. 3 3 2 2
Câu 2. Số nghiệm của phương trình sin( 3 0 2x − 40 ) = với 0 0
−180 ≤ x ≤ 180 là? 2 A. 2. B. 4. C. 6. D. 7.
Lời giải. Phương trình sin( 3 0 2x − 40 ) = ⇔ sin( 0 2x − 40 ) 0 = sin 60 2 0 0 0 0 0 0 0 2x 40 60 k360 2x 100 k360 − = + = + x = 50 + 1 k 80 ⇔ ⇔ ⇔ . 0 0 0 0 0 0 0 0
2x − 40 = 180 − 60 + k360
2x = 160 + k360 x = 80 + 1 k 80 Xét nghiệm 0 0 x = 50 + 1 k 80 . Vì 0 0 0 0 0 0
−180 ≤ x ≤ 180 →−180 ≤ 50 + 1 k 80 ≤ 180 0 23 13
k = −1 → x = −130 k k ∈ℤ ⇔ − ≤ ≤ → . 0 18 18
k = 0 → x = 50 Xét nghiệm 0 0 x = 80 + 1 k 80 . Vì 0 0 0 0 0 0
−180 ≤ x ≤ 180 →−180 ≤ 80 + 1 k 80 ≤ 180 0 13 5
k = −1 → x = −100 k k ∈ℤ ⇔ − ≤ ≤ → . 0 9 9
k = 0 → x = 80
Vậy có tất cả 4 nghiệm thỏa mãn bài toán. Chọn B.
Cách 2 (CASIO). Ta có 0 0 0 0
−180 ≤ x ≤ 180
→−360 ≤ 2x ≤ 360 .
Chuyển máy về chế độ DEG, dùng chức năng TABLE nhập hàm 3
f (X ) = sin(2X − 40)−
với các thiết lập Start = −360, End = 360, Step = 40 . Quan 2
sát bảng giá trị của f (X ) ta suy ra phương trình đã cho có 4 nghiệm.
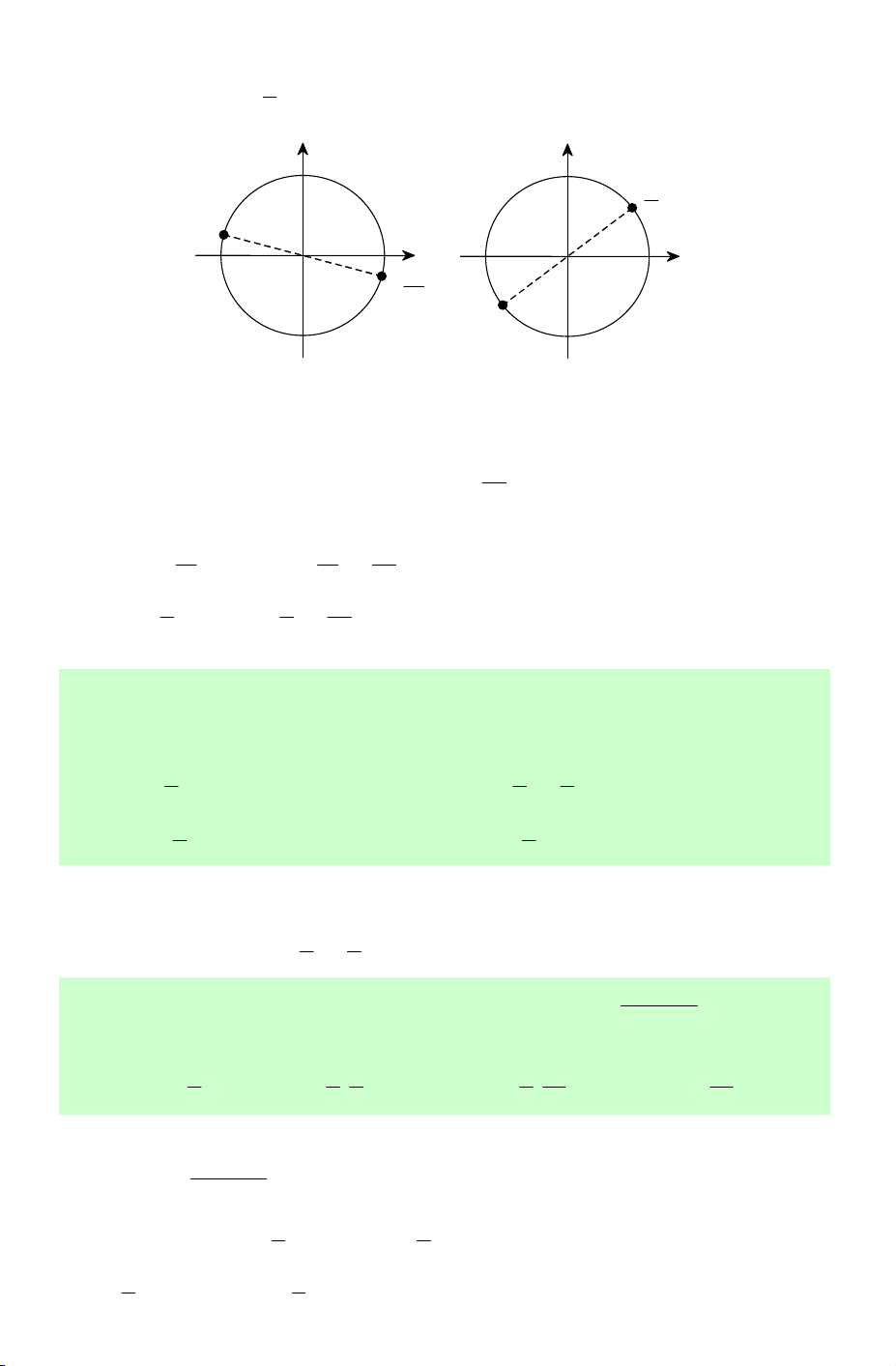
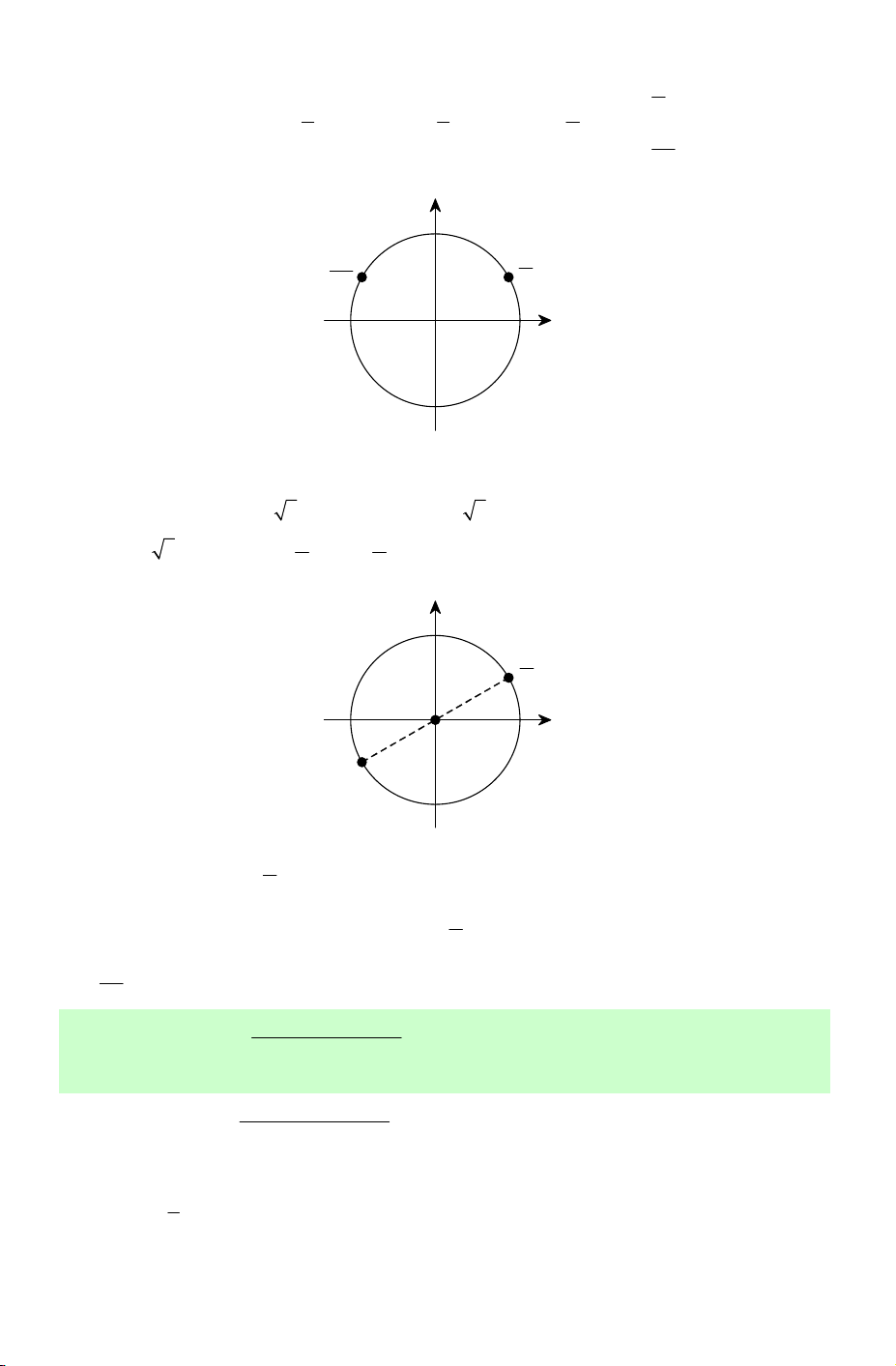
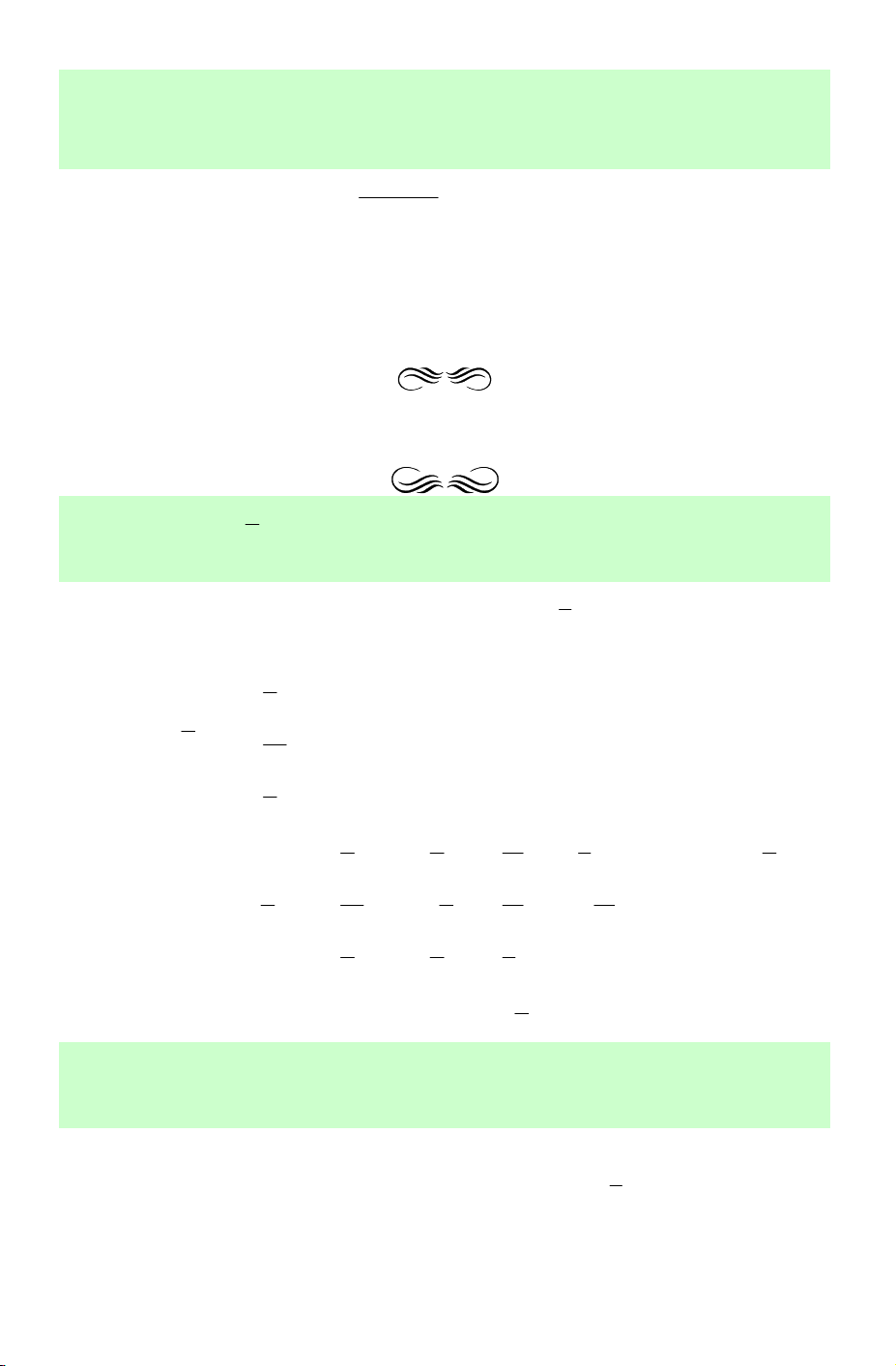
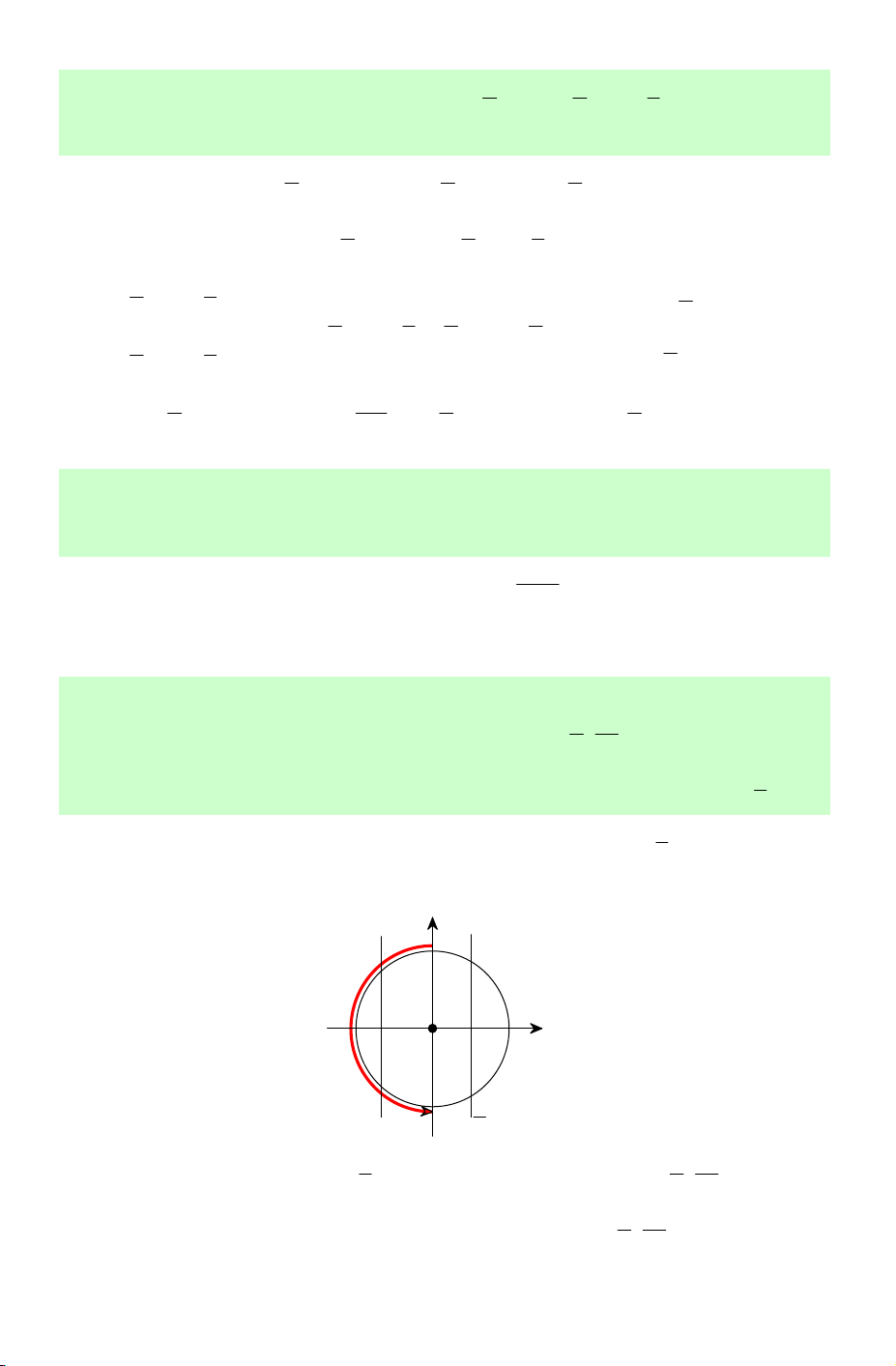
Câu 3. Số vị trí biểu diễn các nghiệm của phương trình π 1 sin2x + = trên đường 3 2 tròn lượng giác là? A. 1. B. 2. C. 4. D. 6. Lời giải. π π π 2x + = + k2π x = − + kπ Phương trình π π 3 6 12 sin ⇔ 2x + = sin ⇔ ⇔ (k ∈ ℤ). 3 6 π π π 2x π + = − + k2π x = + kπ 3 6 4 Biểu diễn nghiệm π x kπ = − +
trên đường tròn lượng giác ta được 2 vị trí (hình 1). 12 Biểu diễn nghiệm π x kπ = +
trên đường tròn lượng giác ta được 2 vị trí (hình 2). 4 sin sin π 4 cos O cos O π − 12 Hình 1 Hình 2
Vậy có tất cả 4 vị trí biểu diễn các nghiệm các nghiệm của phương trình. Chọn C.
Cách trắc nghiệm. Ta đưa về dạng 2π x α = + k
→ số vị trí biểu diễn trên đường n
tròn lượng giác là n . Xét π π 2π x kπ = − + ⇔ x = − + k
→ có 2 vị trí biểu diễn. 12 12 2 Xét π π 2π x kπ = + ⇔ x = + k
→ có 2 vị trí biểu diễn. 4 4 2
Nhận xét. Cách trắc nghiệm tuy nhanh nhưng cẩn thận các vị trí có thể trùng nhau.
Câu 4. Với những giá trị nào của x thì giá trị của các hàm số y = sin 3x và y = sin x bằng nhau?
x = k2π x = kπ A. B. π (k ∈ ℤ). π π (k ∈ ℤ).
x = + k2π x = + k 4 4 2 C. π π x = k (k ∈ ℤ).
D. x = k (k ∈ ℤ). 4 2
Lời giải. Xét phương trình hoành độ giao điểm: sin 3x = sin x x = kπ
3x = x + k2π ⇔ ⇔ Chọn B. π π (k ∈ ℤ). 3x π
= − x + k2π x = + k 4 2 Câu 5. Gọi x
x là nghiệm dương nhỏ nhất của phương trình 2 cos 2 = 0 . Mệnh đề 0 1− sin 2x nào sau đây là đúng? A. π π π π 3π 3π x ∈ 0; .
B. x ∈ ; . C. x ∈ ; . D. x ∈ ;π . 0 4 0 4 2 0 0 2 4 4
Lời giải. Điều kiện: 1−sin 2x ≠ 0 ⇔ sin 2x ≠ 1. sin 2x = 1 loaïi 2 2 2 cos 2x ( ) Phương trình
sin 2 x +cos 2 x 1 0 cos 2x 0 = = ⇔ = → 1 sin 2x − sin 2x = − ( 1 thoûa maõn) π π sin 2x 1 2x k2π x kπ ⇔ = − ⇔ = − + ⇔ = − + (k ∈ ℤ). 2 4 Cho π 1 kπ − + > 0 → k > . 4 4
Do đó nghiệm dương nhỏ nhất ứng với 3π 3π k = 1 → x = ∈
;π . Chọn D. 4 4
Câu 6. Hỏi trên đoạn [−2017;2017], phương trình (sin x + )
1 (sin x − 2) = 0 có tất cả bao nhiêu nghiệm? A. 4034. B. 4035. C. 641. D. 642. sin x = −1
Lời giải. Phương trình π ⇔
⇔ sin x = −1 ⇔ x = − + k2π (k ∈ ℤ). sin x = 2 (vo nghiem) 2 π π −2017 + 2017 + Theo giả thiết π 2 2
−2017 ≤ − + k2π ≤ 2017 ⇔ ≤ k ≤ 2 2π 2π xap xi 320,765 321,265 k k ∈ →− ≤ ≤
ℤ→ k ∈ {−320;−319;...;32 } 1 .
Vậy có tất cả 642 giá trị nguyên của k tương úng với có 642 nghiệm thỏa mãn yêu
cầu bài toán. Chọn D.
Câu 7. Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình π 3 sin 3 x − = bằng: 4 2 A. π . B. π π π − . C. . D. − . 9 6 6 9 π π 3x − = + k2π Lời giải. Ta có π 3 π π 4 3 sin 3 x sin 3 − = ⇔ x − = sin ⇔ 4 2 4 3 π π 3x π − = − + k2π 4 3 7π 7π k2π 3x = + k2π x = + 12 36 3 ⇔ ⇔ (k ∈ ℤ). 11π 11π k2π 3x = + k2π x = + 12 36 3 7 7π
x > 0 ⇔ k > − ⇒ k = 0 → x = min TH1. Với 7π k2π Cho 24 36 x = + → . 36 3 7 17π
x < 0 ⇔ k < − ⇒ k = 1 − → x = − max 24 36 11 11π
x > 0 ⇔ k > − ⇒ k = 0 → x = min TH2. Với 11π k2π Cho 24 36 x = + → . 36 3 11 13π
x < 0 ⇔ k < − ⇒ k = 1 − → x = − max 24 36
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là 13π x = − và nghiệm dương nhỏ 36 nhất là 7π π π π x =
. Khi đó tổng hai nghiệm này bằng 13 7 − + = − .Chọn B. 36 36 36 6 Câu 8. Gọi 3
x là nghiệm âm lớn nhất của phương trình cos( 0 5x − 45 ) = . Mệnh đề 0 2 nào sau đây là đúng? A. x ∈( 0 0 −30 ;0 . B. x ∈( 0 0 −45 ;−30 . 0 ) 0 ) C. x ∈( 0 0 −60 ;−45 . D. x ∈( 0 0 −90 ;−60 . 0 ) 0 ) 0 0 0 Lời giải. Ta có 3
5x − 45 = 30 + k360 cos( 0 5x 45 ) cos( 0 5x 45 ) 0 cos 30 − = ⇔ − = ⇔ 0 0 0 2
5x − 45 = −30 + k360 0 0 0 0 5x 75 k360 = + x = 15 + k72 ⇔ ⇔ (k ∈ ℤ). 0 0 0 0
5x = 15 + k360 x = 3 + k72 TH1. Với 5 0 0 0
x = 15 + k72 < 0 ⇔ k < − ⇒ k = 1 − → x = −57 . max 24 TH2. Với 1 0 0 0
x = 3 + k72 < 0 ⇔ k < − ⇒ k = 1 − ⇒ x = −69 . max 24
So sánh hai nghiệm ta được nghiệm âm lớn nhất của phương trình là 0 x = −57 . Chọn C.
Câu 9. Hỏi trên đoạn π
− ;2π , phương trình 13 cos x = có bao nhiêu nghiệm? 2 14 A. 2 . B. 3 . C. 4 . D. 5 .
Lời giải. Phương trình 13 13 cos x x arccos k2π = ⇔ = ± + (k ∈ ℤ). 14 14 Với 13 π π x arccos k2π = + . Vì 13
x ∈ − ;2π →− ≤ arccos
+ k2π ≤ 2π 14 2 2 14 k∈ 13 CASIO
→−0,3105 ≤ k ≤ 0, 9394 ℤ→ k = 0 → x = arccos . xapxi 14 Với 13 π π x arccos k2 . π = − + Vì 13
x ∈ − ;2π →− ≤ −arccos
+ k2π ≤ 2π 14 2 2 14 ℤ k∈ 13 13 CASIO
→−0,1894 ≤ k ≤ 1,0605 → k ∈ 0;1 → x ∈ − arccos ;− arccos + k2π. xapxi { } 14 14
Vậy có tất cả 3 nghiệm thỏa mãn. Chọn B.
Cách 2 (CASIO). Dùng chức năng TABLE nhập hàm 13
f (X ) = cos X − với các thiết 14 lập π π Start , End 2 , π = − = Step =
. Ta thấy f (X ) đổi dấu 3 lần nên có 3 nghiệm. 2 7
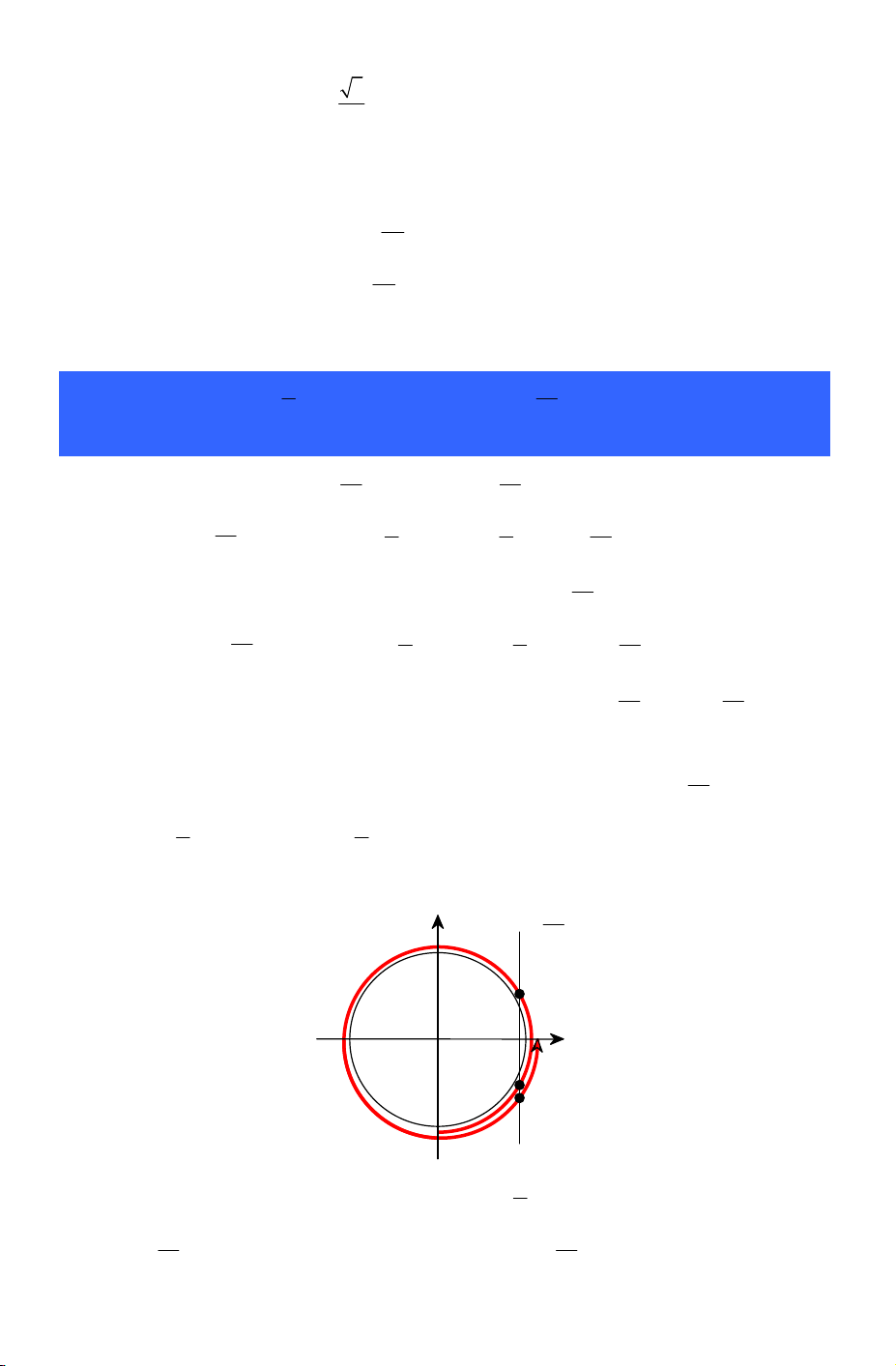
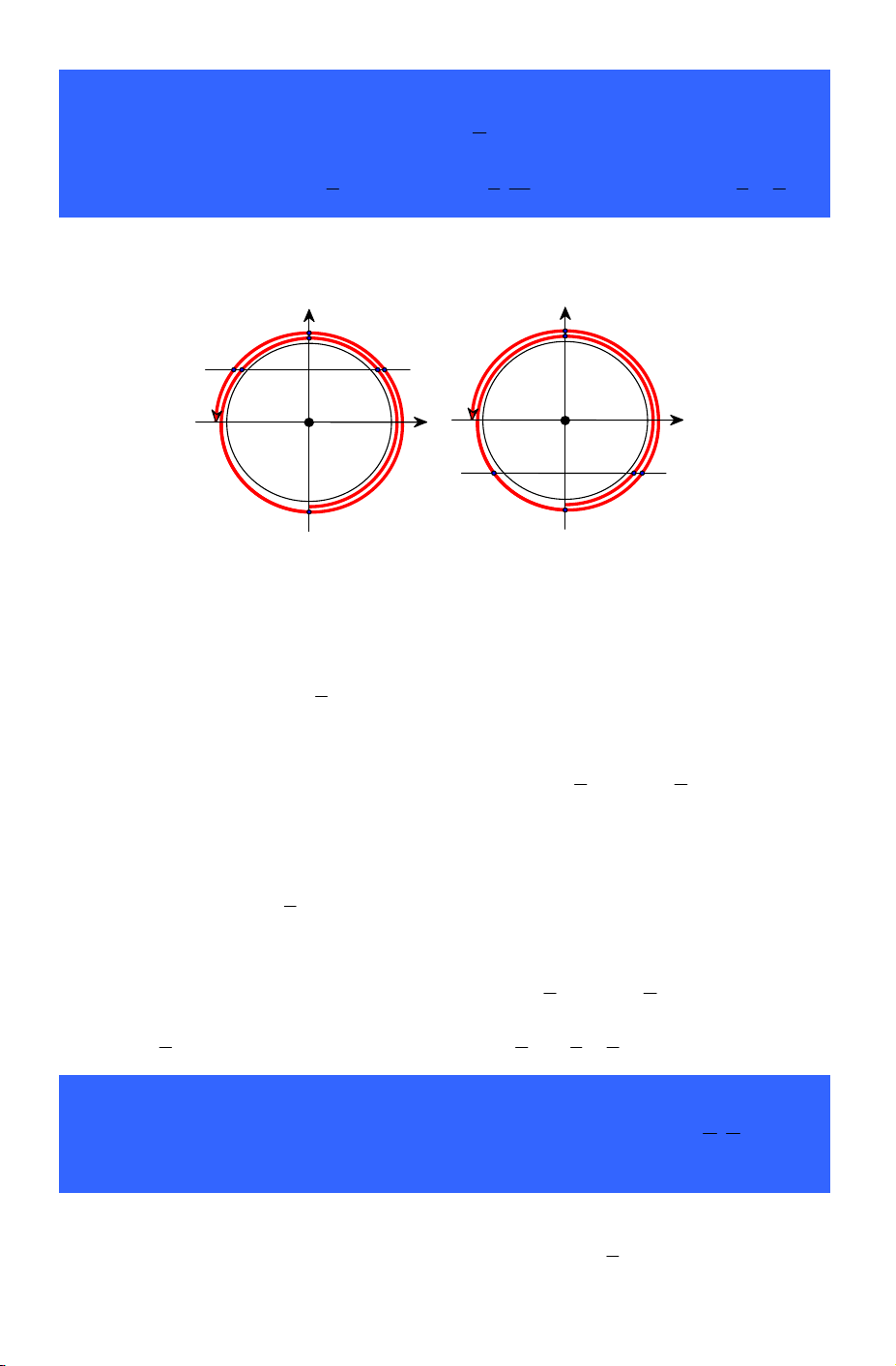
Cách 3. Dùng đường tròn lượng giác sin 13 x = 14 cos O
Vẽ đường tròn lượng giác và biểu diễn cung từ π −
đến 2π . Tiếp theo ta kẻ đường 2 thẳng 13 x =
. Nhìn hình vẽ ta thấy đường thẳng 13 x =
cắt cung lượng giác vừa vẽ 14 14 tại 3 điểm. Câu 10. Gọi x
X là tập nghiệm của phương trình 0
cos +15 = sin x. Mệnh đề nào 2 sau đây là đúng? A. 0 290 ∈ X . B. 0 20 ∈ X. C. 0 220 ∈ X . D. 0 240 ∈ X . Lời giải. Ta có x x 0 0 + = x ⇔ + = ( 0 cos 15 sin cos 15 cos 90 − x ) 2 2 x 0 0 0
+15 = 90 − x + k360 0 0 x = 50 + k240 2 ⇔ ⇔ (k ∈ ℤ). 0 x 0 ( 0 = − x ) 0 x 210 k720 15 90 k360 + = − − + 2 Nhận thấy 0
290 ∈ X (do ứng với k = 1 của nghiệm 0 0
x = 50 + k240 ). Chọn A.
Câu 11. Tính tổng T các nghiệm của phương trình sin 2x −cos x = 0 trên [0;2π]. A. π T 3 . π = B. 5 T = . C. T 2 . π = D. T . π = 2 Lời giải. Ta có π sin 2x cos x 0 sin 2x cos x sin 2x sin − = ⇔ = ⇔ =
− x 2 π π k2π 2x =
− x + k2π x = + 2 6 3 ⇔ ⇔ . π π 2x π = − − x + k2π x = + k2π 2 2 π k2π 1 11 0 ≤ + ≤ 2π − ≤ k ≤ ⇒ k ∈ {0;1;2} Vì 6 3 4 4 x [0;2π ∈ ], suy ra ⇔ . π 1 3 0 ≤
+ k2π ≤ 2π − ≤ k ≤ ⇒ k ∈ {0} 2 4 4
Từ đó suy ra các nghiệm của phương trình trên đoạn π π π π [0;2π] là 5 3 ; ; ; T 3 . π → = 6 6 2 2 Chọn A.
Câu 12. Trên khoảng π π ;2 π
, phương trình cos −2x = sin x có bao nhiêu nghiệm? 2 6 A. 3 . B. 4 . C. 5 . D. 2. Lời giải. Ta có π π π cos 2x sin x cos 2x cos − = ⇔ − = − x 6 6 2 π π π − 2x =
− x + k2π
x = − − k2π 6 2 3 ⇔ ⇔ (k ∈ ℤ). π π 2π k2π − 2x
= − − x+ k2π x = − 6 2 9 3 π π 7 5 < − − k2 ∈ℤ π < 2 k π − ≤ k < − → k = −1 Vì π 2 3 6 12 x ∈ ;2 π , suy ra ⇔ . 2 π 2π k2π 8 5 < − < 2 k∈ℤ π − ≤ k < − → k = {−2;− } 1 2 9 3 3 12
Vậy phương trình đã cho có π
3 nghiệm trên khoảng ;2 π . Chọn A. 2
Câu 13. Tổng các nghiệm của phương trình ( 0
tan 2x −15 ) = 1 trên khoảng ( 0 0 −90 ;90 ) bằng: A. 0 0 . B. 0 −30 . C. 0 30 . D. 0 −60 . Lời giải. Ta có ( 0 x − ) 0 0 0 0 0 tan 2 15
= 1 ⇔ 2x −15 = 45 + 1
k 80 ⇔ x = 30 + k90 (k ∈ ℤ). Do x ∈ ( 4 2 0 0 −90 ;90 ) 0 0 0 0
→−90 < 30 + k90 < 90 ⇔ − < k < 3 3 0
k = −1 → x = −60 k∈ℤ 0 0 0 →
→−60 + 30 = −30 . Chọn B. 0
k = 0 → x = 30
Câu 14. Giải phương trình cot(3x − ) 1 = − 3. A. 1 5π π 1 π π x = + + k (k ∈ ℤ). B. x = + + k (k ∈ ℤ). 3 18 3 3 18 3 C. 5π π 1 π x = + k (k ∈ ℤ). D. x kπ = − + (k ∈ ℤ). 18 3 3 6 Lời giải. Ta có π cot (3x − )
1 = − 3 ⇔ cot (3x − ) 1 = cot − 6 π 1 π π k 1 5π
⇔ 3x −1 = − + k = π ⇔ x = − + k (k ∈ ℤ) 1 → x = + . Chọn A. 6 3 18 3 3 18
Câu 15. Với những giá trị nào của π
x thì giá trị của các hàm số y tan = − x và 4
y = tan 2x bằng nhau? A. π π π π x = + k (k ∈ ℤ). B. x = + k (k ∈ ℤ). 4 2 12 3 C. π π π m + x k π = + (k ∈ ℤ). D. 3 1 x = + k k ≠ ; k, m ∈ ℤ . 12 12 3 2 π π
x ≠ − −mπ Lời giải. cos − x ≠ 0 Điều kiện: 4 π π 4 ⇔ ⇔ x ≠ + m . π π 4 2 c os2x ≠ 0 x ≠ +m 4 2
Xét phương trình hoành độ giao điểm: π tan 2x tan = − x 4 π π π 2x x kπ ⇔ = − + ⇔ x = + k (k ∈ ℤ). 4 12 3
Đối chiếu điều kiện, ta cần có π π π π 3m +1 + k ≠ + m ⇔ k ≠
(k, m ∈ ℤ). 12 3 4 2 2
Vậy phương trình có nghiệm π π 3m +1 x k = + k ≠ ; k, m ∈ ℤ . Chọn D. 12 3 2
Câu 16. Số nghiệm của phương trình 3π π tan x = tan trên khoảng ;2 π là? 11 4 A. 1 B. 2. C. 3. D. 4. Lời giải. Ta có 3π 3π tan x tan x kπ = ⇔ = + (k ∈ ℤ). 11 11 Do π π 3π CASIO ∈ ;2 ∈ ℤ π π → < +
< 2π →−0,027 < <1,72 k x k k
→ k ∈ 0;1 . Chọn B. xap xi { } 4 4 11
Câu 17. Tổng các nghiệm của phương trình tan 5x −tan x = 0 trên nửa khoảng [0;π) bằng: A. π π π . B. 3 . C. 2π . D. 5 . 2 2 Lời giải. Ta có kπ tan 5x tan x 0 tan 5x tan x 5x x kπ − = ⇔ = ⇔ = + ⇔ x = (k ∈ ℤ). 4 Vì kπ x [0; k∈ℤ π ∈ ) , suy ra 0 π ≤ <
⇔ 0 ≤ k < 4 → k = {0;1;2; } 3 . 4
Suy ra các nghiệm của phương trình trên π π π [ 0;π) là 3 0 ; ; ; . 4 2 4 Suy ra π π 3π 3π 0 + + + = . Chọn B. 4 2 4 2
Câu 18. Giải phương trình tan 3x.cot 2x = 1. A. π π π x = k (k ∈ ℤ).
B. x = − + k (k ∈ ℤ). 2 4 2 C. x kπ = (k ∈ ℤ). D. Vô nghiệm. π π x ≠ + k
Lời giải. Điều kiện: c os 3x ≠ 0 6 3 ⇔ (k ∈ ℤ). s in 2x ≠ 0 π x ≠ k 2 Phương trình 1 tan 3x tan 3x tan 2x 3x 2x kπ x kπ ⇔ = ⇔ = ⇔ = + ⇔ = (k ∈ ℤ). cot 2x
Đối chiếu điều kiện, ta thấy nghiệm π x kπ =
không thỏa mãn x ≠ k . 2
Vậy phương trình đã cho vô nghiệm. Chọn D. Câu 19. Cho π π tanx
+ −1 = 0 . Tính sin2x − . 2 6 A. π 1 π sin2x − = − . B. 3 sin2x − = . 6 2 6 2 C. π 3 π sin2x − = − . D. 1 sin 2x − = . 6 2 6 2
Lời giải. Phương trình π π tanx 1 0 tan + − = ⇔ x + = 1 2 2 π π π x kπ x kπ ⇔ + = + ⇔ = − + (k ∈ ℤ). 2 4 4 Suy ra π π 2π 2x k2π 2x k2π = − + → − = − + (k ∈ ℤ). 2 6 3 Do đó π 2π 2π 3 sin2x − = sin− + k2 π = sin − = − . Chọn C. 6 3 3 2
Câu 20. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình tan x = 1 ? A. 2 sin x = . B. 2 cos x = .
C. cot x =1 . D. 2 cot x = 1 . 2 2 Lời giải. Ta có π tan x 1 x kπ = ⇔ = + (k ∈ ℤ). 4 Xét đáp án C, ta có π cot x 1 x kπ = ⇔ = +
(k ∈ ℤ). Chọn C. 4
Cách 2. Ta có đẳng thức 1 cot x =
. Kết hợp với giả thiết tan x = 1 , ta được tan x
cot x = 1 . Vậy hai phương trình tan x = 1 và cot x = 1 là tương đương.
Câu 21. Giải phương trình cos 2x tan x = 0. π A. π x = + kπ x = k (k ∈ ℤ). B. 2 (k ∈ ℤ). 2 x = kπ π π
C. x = + k π 4 2 (k ∈ ℤ). D. x kπ = + (k ∈ ℤ). 2 x = kπ
Lời giải. Điều kiện: π cos x 0 x kπ ≠ ⇔ ≠ + (k ∈ ℤ). 2 Phương trình cos 2x = 0
cos 2x tan x = 0 ⇔ tan x = 0 π π π 2x = + k thoûa maõn π x = + k ( ) ⇔ 2 ⇔ 4 2
(k ∈ ℤ). Chọn C. x = k thoûa maõn π x = kπ( )
Câu 22. Tìm tất các các giá trị thực của tham số m để phương trình sin x = m có nghiệm.
A. m ≤1.
B. m ≥ −1.
C. −1≤ m ≤1.
D. m ≤ −1.
Lời giải. Với mọi x ∈ ℝ, ta luôn có −1≤ sin x ≤1 .
Do đó, phương trình sin x = m có nghiệm khi và chỉ khi −1 ≤ m ≤1. Chọn C.
Câu 23. Tìm tất các các giá trị thực của tham số m để phương trình cos x −m = 0 vô nghiệm. A. m ∈(− ; ∞ − ) 1 ∪(1;+∞).
B. m ∈(1;+∞). C. m ∈[−1; ] 1 . D. m ∈(− ; ∞ − ) 1 .
Lời giải. Áp dụng điều kiện có nghiệm của phương trình cos x = a .
Phương trình có nghiệm khi a ≤1.
Phương trình vô nghiệm khi a >1.
Phương trình cos x −m = 0 ⇔ cos x = . m Do đó, phương trình m < −
cos x = m vô nghiệm 1 ⇔ m > 1 ⇔ . Chọn A. m > 1
Câu 24. Có bao nhiêu giá trị nguyên của tham số m để phương trình cos x = m +1 có nghiệm? A. 1. B. 2. C. 3. D. Vô số.
Lời giải. Áp dụng điều kiện có nghiệm của phương trình cos x = a .
Phương trình có nghiệm khi a ≤1.
Phương trình vô nghiệm khi a >1.
Do đó, phương trình cos x = m +1 có nghiệm khi và chỉ khi m +1 ≤1 1 1 1 2 0 m m m ∈ ⇔ − ≤ + ≤ ⇔ − ≤ ≤
ℤ→ m ∈ {−2;−1;0}. Chọn C.
Câu 25. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình π cos2x
− −m = 2 có nghiệm. Tính tổng T của các phần tử trong S. 3
A. T = 6.
B. T = 3.
C. T = −2.
D. T = −6.
Lời giải. Phương trình π π cos2x m 2 cos − − = ⇔ 2x − = m + 2. 3 3
Phương trình có nghiệm ⇔ 1
− ≤ m + 2 ≤1 ⇔ −3 ≤ m ≤ 1 − m∈
ℤ→S = {−3;−2;− } 1 →T = (− ) 3 +(−2)+(− ) 1 = −6. Chọn D. Baøi 03
MOÄT SOÁ PHÖÔNG TRÌNH LÖÔÏNG GIAÙC THÖÔØNG GAËP
1) Phương trình bậc nhất đối với một hàm số lượng giác
Định nghĩa. Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng at + b = 0
trong đó a, b là các hằng số (a ≠ 0) và t là một hàm số lượng giác.
Cách giải. Chuyển vế rồi chia hai vế phương trình cho a , ta đưa về phương
trình lượng giác cơ bản.
2) Phương trình bậc nhất đối với sin x và cos x
Định nghĩa. Phương trình bậc nhất đối với sin x và cos x là phương trình có dạng
a sin x + b cos x = c
Cách giải. Điều kiện để phương trình có nghiệm: 2 2 2
a + b ≥ c .
Chia hai vế phương trình cho 2 2
a + b , ta đựợc a b c sin x + cos x = . 2 2 2 2 2 2 a + b a + b a + b 2 2 Do a b a b + nên đặt cos α sin . = 1 α = → = 2 2 2 2 a +b a +b 2 2 2 2 a + b a + b
Khi đó phương trình trở thành c c cos α sin x sin α cos x sin(x α + = ⇔ + ) = . 2 2 2 2 a + b a + b
3) Phương trình bậc hai đối với một hàm số lượng giác
Định nghĩa. Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng 2
at + bt + c = 0 trong đó a, ,
b c là các hằng số (a ≠ 0) và t là một hàm số lượng giác.
Cách giải. Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu
có) rồi giải phương trình theo ẩn phụ này. Cuối cùng, ta đưa về việc giải các phương
trình lượng giác cơ bản.
4) Phương trình bậc hai đối với sin x và cos x
Định nghĩa. Phương trình bậc hai đối với sin x và cos x là phương trình có dạng 2 2
a sin x + b sin x cos x + c cos x = 0 Cách giải.
● Kiểm tra cos x = 0 có là nghiệm của phương trình.
● Khi cos x ≠ 0 , chia hai vế phương trình cho 2
cos x ta thu được phương trình 2
a tan x + b tan x + c = 0.
Đây là phương trình bậc hai đối với tan x mà ta đã biết cách giải.
Đặc biệt. Phương trình dạng 2 2
a sin x + b sin x cos x + c cos x = d ta làm như sau: Phương trình 2 2
⇔ a sin x + b sin x cos x + c cos x = d.1 2 2
⇔ a sin x + b sin x cos x + c cos x = d ( 2 2 sin x + cos x ) ⇔ (a − d ) 2
sin x + b sin x cos x +(c − d ) 2 cos x = 0.
5) Phương trình chứa sin x ± cos x và sin x.cos x
Định nghĩa. Phương trình chứa sin x ± cos x và sin x.cos x
a (sin x ± cos x )+ b sin x cos x + c = 0
Cách giải. Đặt t = sin x ± cos x (điều kiện − 2 ≤ t ≤ 2 )
Biểu diễn sin x.cos x theo t ta được phương trình cơ bản.
CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. PHƯƠNG TRÌNH BẬC NHẤT
ĐỐI VỚI MỘT H@M SỐ LƯỢNG GIÁC
Câu 1. Gọi S là tập nghiệm của phương trình 2 cos x − 3 = 0 . Khẳng định nào sau đây là đúng? A. 5π π π π ∈ S.
B. 11 ∈ S.
C. 13 ∉ S. D. 13 − ∉ S. 6 6 6 6 π x = + k2π Lời giải. Ta có π 6
2 cos x − 3 = 0 ⇔ cos x = cos ⇔ (k ∈ ℤ). 6 π
x = − + k2π 6 Nhận thấy với nghiệm π k 11 1 π x = − + k2 = π → x =
∈ S. Chọn B. 6 6 Câu 2. Hỏi 7π x =
là một nghiệm của phương trình nào sau đây? 3
A. 2 sin x − 3 = 0.
B. 2sin x + 3 = 0.
C. 2cos x − 3 = 0.
D. 2cos x + 3 = 0. 7π 3 s in x = sin = Lời giải. Với 7π 2 sin x − 3 = 0 x = , suy ra 3 2 ⇔ . Chọn A. 3 7 π 1 2 cos x −1 = 0 c os x cos = = 3 2 Cách 2. Thử 7π x =
lần lượt vào từng phương trình. 3
Câu 3. Tìm nghiệm dương nhỏ nhất của phương trình π 2 sin 4x − −1 = 0. 3 A. π π π π x = . B. 7 x = .
C. x = . D. x = . 4 24 8 12 Lời giải. Ta có π π 1 π π 2 sin 4x 1 0 sin4x sin − − = ⇔ − = ⇔ 4x − = sin 3 3 2 3 6 π π π π kπ 4x − = + k2π 4x = + k2π x = + 3 6 2 8 2 ⇔ ⇔ ⇔ (k ∈ ℤ). π π 7π 7π kπ 4x π − = − + k2π 4x = + k2π x = + 3 6 6 24 2 TH1. Với π kπ π kπ 1 Cho>0 π x = + → +
> 0 ⇔ k > − → k = 0 ⇒ x = . min 8 2 8 2 4 8 TH2. Với 7π kπ > 7π kπ 7 7 Cho 0 π x = + → + > 0 ⇔ k > − → k = 0 ⇒ x = . min 24 2 24 2 12 24
So sánh hai nghiệm ta được π x =
là nghiệm dương nhỏ nhất. Chọn C. 8
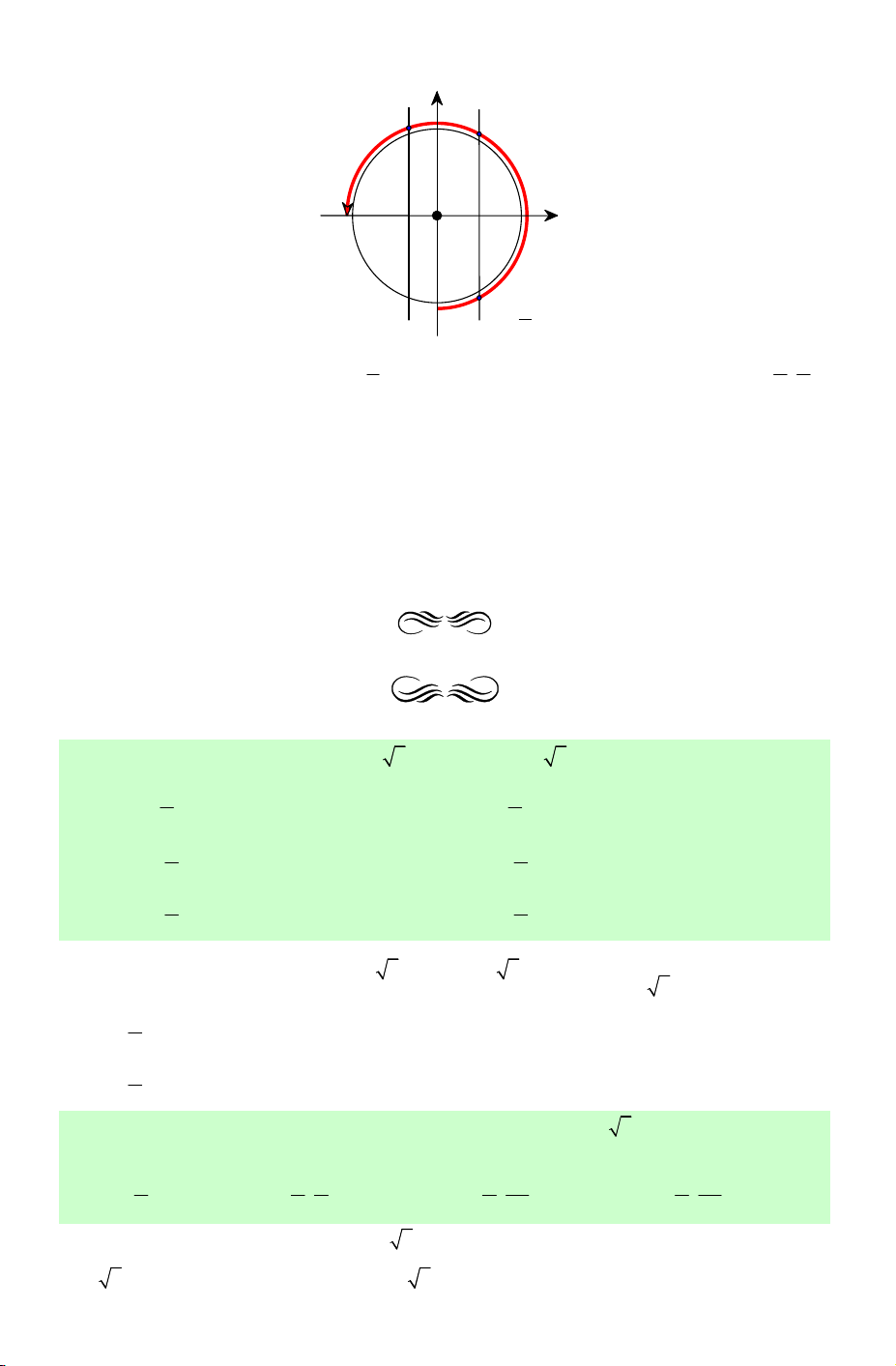
Câu 4. Số vị trí biểu diễn các nghiệm của phương trình π tan 2x − + 3 = 0 trên 3
đường tròn lượng giác là? A. 4 . B. 3 . C. 2 . D. 1. Lời giải. Ta có π π π π tan2x
− + 3 = 0 ⇔ tan2x
− = − 3 ⇔ tan2x − = tan − 3 3 3 3 π π kπ 2x kπ 2x kπ ⇔ − = − + ⇔ = ⇔ x = (k ∈ ℤ). 3 3 2 sin B C A cos O D
Quá dễ để nhận ra có 4 vị trí biểu diễn nghiệm của phương trình đã cho trên đường
tròn lượng giác là A, B, C, D. Chọn A.
Cách trắc nghiệm. Ta có kπ 2π x = = k
→ có 4 vị trí biểu diễn. 2 4
Câu 5. Hỏi trên đoạn [0;2018π] , phương trình 3 cot x −3 = 0 có bao nhiêu nghiệm? A. 6339. B. 6340. C. 2017. D. 2018. Lời giải. Ta có π π cot x 3 cot x cot x kπ = ⇔ = ⇔ = + (k ∈ ℤ). 6 6 Theo giả thiết, ta có π 1 xap xi 0 kπ 2018π ≤ + ≤
→− ≤ k ≤ 2017,833 6 6 3 k∈
ℤ → k ∈ {0;1;...;2017} . Vậy có tất cả 2018 giá trị nguyên của k tương ứng với có
2018 nghiệm thỏa mãn yêu cầu bài toán. Chọn D.
Câu 6. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 2 cos x = 1 ? A. 2 sin x = .
B. 2sin x + 2 = 0. C. tan x = 1. D. 2 tan x = 1. 2 Lời giải. Ta có 1 1 2 2
2 cos x = 1 ⇔ cos x = . Mà 2 2 2
sin x + cos x = 1 → sin x = . 2 2 2 Do đó sin x 2 tan x = = 1 . Vậy 2 2
2 cos x = 1 ⇔ tan x = 1. Chọn D. 2 cos x
Câu 7. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình 2 tan x = 3 ? A. 1 cos x = − . B. 2 4 cos x = 1. C. 1 cot x = . D. 1 cot x = − . 2 3 3 2 Lời giải. Ta có sin x 2 2 2 tan x = 3 ⇔
= 3 ⇔ sin x = 3 cos x 2 cos x 2 2 2
⇔ 1− cos x = 3 cos x ⇔ 4 cos x = 1. Vậy 2 2
tan x = 3 ⇔ 4 cos x = 1 . Chọn B.
Câu 8. Giải phương trình 2 4 sin x = 3 . π π x = + k2π x = + k2π A. 3 3 , (k ∈ ℤ). B. , (k ∈ ℤ). π 2π
x = − + k2π x = + k2π 3 3 π kπ k π C. x = + x = 3
3 (k, ℓ ∈ ℤ). D.
3 (k, ℓ ∈ ℤ). k ≠ 3 ℓ k ≠ 3 ℓ Lời giải. Ta có 3 3 2 2
4 sin x = 3 ⇔ sin x = ⇔ sin x = ± . 4 2 π x = + k2π Với 3 π 3 sin x = ⇔ sin x = sin ⇔ (k ∈ ℤ). 2 3 2π x = + k2π 3 π
x = − + k2π Với 3 π 3 sin x = − ⇔ sin x = sin − ⇔ (k ∈ ℤ). 2 3 4π x = + k2π 3
Nhận thấy chưa có đáp án nào phù hợp. Ta biểu diễn các nghiệm trên đường tròn lượng giác (hình vẽ). sin π 2π 3 3 cos B A O π 2π − − 3 3
Nếu tính luôn hai điểm A, B thì có tất cả 6 điểm cách đều nhau nên ta gộp được 6
điểm này thành một họ nghiệm, đó là π x = k . 3 π x = k kπ
Suy ra nghiệm của phương trình 3 x = ⇔
3 (k, ℓ ∈ ℤ). Chọn D. π k ≠ l π k ≠ 3 ℓ 3
Câu 9. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 2
3 sin x = cos x ? A. 1 3 sin x = . B. 3 cos x = . C. 2 sin x = . D. 2 cot x = 3. 2 2 4 Lời giải. Ta có 2 2
3 sin x = cos x . Chi hai vế phương trình cho 2 sin x, ta được 2 cot x = 3 . Chọn D. Câu 10. Với 3 x thuộc (0; ) 1 , hỏi phương trình 2 cos (6πx) = có bao nhiêu nghiệm? 4 A. 8. B. 10. C. 11. D. 12.
Lời giải. Phương trình 3 3 2 cos (6πx ) cos(6π = ⇔ x ) = ± . 4 2 Với 3 π π cos 6πx cos 6πx cos 6πx k2π = ⇔ = ⇔ = ± + . 2 6 6 1 k 1 35 x = + ∈ (0; ) 1 k − < k ∈ < ℤ→ k = {0;1;2} 36 3 12 12 ⇔ ⇔ → có 6 nghiệm. 1 k 1 37 x = − + ∈ (0; ) 1 k < k ∈ < ℤ→ k = {1;2; } 3 36 3 12 12 Với 3 5π 5π cos 6πx cos 6πx cos 6πx k2π = − ⇔ = ⇔ = ± + . 2 6 6 5 k 5 31 x = + ∈ (0; ) 1 k − < k ∈ < ℤ → k = {0;1;2} 36 3 12 12 ⇔ ⇔ → có 6 nghiệm. 5 k 5 41 x = − + ∈ (0; ) 1 k < k ∈ < ℤ → k = {1;2; } 3 36 3 12 12
Vậy phương trình đã cho có 12 nghiệm. Chọn D.
Câu 11. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình
3 cos x + m −1 = 0 có nghiệm? A. 1. B. 2. C. 3. D. Vô số. Lời giải. Ta có 1− m
3 cos x + m −1 = 0 ⇔ cos x = . 3 Phương trình có nghiệm 1− m ⇔ −1 ≤
≤ 1 ⇔ 1− 3 ≤ m ≤ 1+ 3 m∈ ℤ →m ∈ {0;1;2}. 3
Vậy có tất cả 3 giá trị nguyên của tham số m . Chọn C.
Câu 12. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2108;2018] để
phương trình m cos x +1 = 0 có nghiệm? A. 2018. B. 2019. C. 4036. D. 4038. Lời giải. Ta có 1
m cos x +1 = 0 ⇔ cos x = − . m Phương trình có nghiệm 1 ⇔ −1 ≤ − ≤1 ⇔ m ≥1 m∈ ℤ
→ m ∈ {1;2;3;...;201 } 8 . m [ ∈ −2018;2018] m
Vậy có tất cả 2018 giá trị nguyên của tham số m . Chọn A.
Câu13. Tìm giá trị thực của tham số m để phương trình (m −2)sin 2x = m +1 nhận π x = làm nghiệm. 12 2( 3 + ) 1
A. m ≠ 2. B. m = .
C. m = −4.
D. m = −1. 3 − 2 Lời giải. Vì π x =
là một nghiệm của phương trình (m −2)sin 2x = m +1 nên ta có: 12 2π m − 2 (m −2).sin = m +1 ⇔
= m +1 ⇔ m −2 = 2m + 2 ⇔ m = −4 . 12 2
Vậy m = −4 là giá trị cần tìm. Chọn C.
Câu 14. Tìm tất cả các giá trị của tham số m để phương trình (m + )
1 sin x + 2 − m = 0 có nghiệm.
A. m ≤ −1. B. 1 m ≥ . C. 1
−1 < m ≤ .
D. m > −1. 2 2
Lời giải. Phương trình m − 2 (m + )
1 sin x + 2 − m = 0 ⇔ (m + )
1 sin x = m − 2 ⇔ sin x = . m +1
Để phương trình có nghiệm m − 2 ⇔ 1 − ≤ ≤1 m +1 m − 2 2m −1 1 0 ≤1+ ≥ 0 m ≥ m +1 m +1 2 1 ⇔ ⇔ ⇔ ⇔ m ≥
là giá trị cần tìm. Chọn B. m − 2 3 m < 1 − 2 −1 ≤ 0 − ≤ 0 m 1 m 1 m + + > 1 −
Câu 15. Tìm tất cả các giá trị của tham số m để phương trình (m −2)sin 2x = m +1 vô nghiệm. A. 1 1
m ∈ ;2 . B. m ∈ − ; ∞ ∪(2;+∞). 2 2 C. 1 m ∈ ;2 ∪(2;+ ) ∞ . D. 1 m ∈ ; +∞ . 2 2
Lời giải. TH1. Với m = 2 , phương trình (m −2)sin 2x = m +1 ⇔ 0 = 3 : vô lý.
Suy ra m = 2 thì phương trình đã cho vô nghiệm. TH2. Với m +1
m ≠ 2 , phương trình (m −2)sin 2x = m +1 ⇔ sin 2x = . m − 2 m +1 > 1 m > 2 Để phương trình m +1 ( ) m − 2 ∗ vô nghiệm ⇔ ∉ [ 1 − ; ] 1 ⇔ ⇔ 1 . m − 2 m +1 < m < 2 < 1 − 2 m −2
Kết hợp hai trường hợp, ta được 1 m >
là giá trị cần tìm. Chọn D. 2
Vấn đề 2. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI sin x và cos x
Câu 16. Gọi S là tập nghiệm của phương trình cos 2x −sin 2x = 1. Khẳng định nào sau đây là đúng? A. π π π π ∈ S. B. ∈ S. C. 3 ∈ S. D. 5 ∈ S. 4 2 4 4
Lời giải. Phương trình π π 1 2 cos2x 1 cos ⇔ + = ⇔ 2x + = 4 4 2 π π 2x + = + k2π x = kπ π π 4 4 ⇔ cos2x + = cos ⇔ ⇔ ℤ π , k ∈ . 4 4 π π x = − + kπ 2x + = − + k2π 4 4 4 Xét nghiệm π π x kπ = − +
, với k = 1 ta được 3 x = . Chọn C. 4 4
Câu 17. Số nghiệm của phương trình π
sin 2x + 3 cos 2x = 3 trên khoảng 0; là? 2 A. 1. B. 2. C. 3. D. 4.
Lời giải. Phương trình 1 3 3 π 3 sin 2x cos 2x sin ⇔ + = ⇔ 2x + = 2 2 2 3 2 π π 2x + = + k2π x = kπ π π 3 3 ⇔ sin2x + = sin ⇔ ⇔ ℤ π , k ∈ . 3 3 π π x = + kπ 2x π + = − + k2π 6 3 3 π 1 0 ∈ℤ π < < ⇔ 0 k k < k <
→ không có giá trị k thỏa mãn. 2 2 π π 1 1 π 0 k < + k ∈ℤ π < ⇔ − < k <
→ k = 0 → x = . Chọn A. 6 2 6 3 6
Câu 18. Tính tổng T các nghiệm của phương trình 2 2
cos x − sin 2x = 2 + sin x trên khoảng (0;2π). A. 7π π π π T = . B. 21 T = . C. 11 T = . D. 3 T = . 8 8 4 4
Lời giải. Phương trình 2 2
⇔ cos x − sin x − sin 2x = 2 ⇔ cos 2x − sin 2x = 2 π π π cos ⇔ 2x + = 1 ⇔ 2x +
= k2π ⇔ x = − + kπ (k ∈ ℤ). 4 4 8 7π k = 1 → x = Do π 1 17 ℤ k∈ 8
0 < x < 2π
→ 0 < − + kπ < 2π ⇔ < k < → 8 8 8 15π k = 2 → x = 8 7π 15π 11 T . π → = + = Chọn C. 8 8 4
Câu 19. Tìm nghiệm dương nhỏ nhất x của 3
3 sin 3x − 3 cos 9x = 1+ 4 sin 3x. 0 A. π π π π x = . B. x = . C. x = . D. x = . 0 2 0 18 0 24 0 54
Lời giải. Phương trình 3
⇔ 3 sin 3x − 4 sin 3x − 3 cos 9x = 1 ⇔ sin 9x − 3 cos 9x = 1 1 3 1 π 1 sin 9x cos 9x sin ⇔ − = ⇔ 9x − = 2 2 2 3 2 π π π k2π 9x − = + k2π x = + π π 3 6 18 9 sin ⇔ 9x − = sin ⇔ ⇔ 3 6 π π 7π k2π 9x π − = − + k2π x = + 3 6 54 9 π k2π 1 π + > 0 k ⇔ k ∈ > − ℤ → k = 0 → x = min Cho>0 18 9 4 18 → . 7π k2π 7 k∈ℤ 7π + > 0 ⇔ k > − → k = 0 → x = min 54 9 12 54
So sánh hai nghiệm ta được nghiệm dương nhỏ nhất là π x = . Chọn B. 18
Cách trắc nghiệm. Thử từng nghiệm của đáp án vào phương trình và so sánh
nghiệm nào thỏa mãn phương trình đồng thời là nhỏ nhất thì ta chọn.
Câu 20. Số nghiệm của phương trình π
sin 5x + 3 cos 5x = 2 sin 7x trên khoảng 0; 2 là? A. 2. B. 1. C. 3. D. 4.
Lời giải. Phương trình 1 3 π sin 5x cos 5x sin 7x sin 5 ⇔ + = ⇔ x + = sin 7x 2 2 3 π π
7x = 5x + + k2π x = + kπ π 3 6 ⇔ sin 7x = sin 5 x + ⇔ ⇔ (k ∈ ℤ). 3 π π kπ 7x π = − 5x + + k2π x = + 3 18 6 π π 1 1 π 0 k < + k ∈ℤ π < ⇔ − < k <
→ k = 0 → x = . 6 2 6 3 6 π k = 0 → x = 18 π π π 1 8 ℤ k∈ 2π 0 < + k < ⇔ − < k <
→ k = 1 → x = . 18 6 2 3 3 9 7π k = 2 → x = 18
Vậy có 4 nghiệm thỏa mãn. Chọn D.
Câu 21. Giải phương trình π π 3 cosx sin + + x
− = 2 sin 2x. 2 2 5π 7π x = + k2π x = + k2π A. 6 6 , k ∈ . ℤ B. , k ∈ . ℤ π 2π π 2π x = + k x = − + k 18 3 18 3 5π π 2π x = + k2π x = + k C. 6 18 3 , k ∈ . ℤ D. , k ∈ . ℤ 7π π 2π x = + k2π x = − + k 6 18 3 Lời giải. Ta có π π cosx
+ = −sin x và sinx
− = −cos x . 2 2
Do đó phương trình ⇔ − 3 sin x −cos x = 2 sin 2x ⇔ 3 sin x + cos x = −2 sin 2x 3 1 π π sin x cos x sin 2x sin x sin 2x sin ⇔ + = − ⇔ + = − ⇔ x + = sin(−2x ) 2 2 6 6 π π 2π x +
= −2x + k2π x = − + k 6 18 3 ⇔ ⇔ (k ∈ ℤ). π 5π x π +
= + 2x + k2π x = − − k2π 6 6 Xét nghiệm 5π k=− −k 7 1 ' π x = −
− k2π → x = + k ' 2π . k∈ℤ, k ' 6 ∈ℤ 6
Vậy phương trình có nghiệm π 2π 7π x k , x k ' 2π = − + = +
(k, k ' ∈ ℤ). Chọn B. 18 3 6
Câu 22. Gọi x là nghiệm âm lớn nhất của sin 9x + 3 cos7x = sin7x + 3 cos 9x . 0
Mệnh đề nào sau đây là đúng? A. π π π π π π π x ∈ − ;0 .
B. x ∈ − ;− . C. x ∈ − ; − . D. x ∈ − ; − . 0 12 0 6 12 0 0 3 6 2 3
Lời giải. Phương trình ⇔ sin 9x − 3 cos 9x = sin7x − 3 cos7x π π 9x −
= 7x − + k2π x = kπ π π 3 3 ⇔ sin9x − = sin 7 x − ⇔ ⇔ 5 π kπ 3 3 π π x = + 9x π − = − 7x − + k2π 48 8 3 3 k ∈ℤ
π < 0 ⇔ k < 0 k → k = −1 → x π = − max Cho<0 → So sánh hai nghiệm ta π π π . 5 k 5 + < 0 k ⇔ k ∈ < − ℤ→ k = −1 → x = − max 48 8 6 48
được nghiệm âm lớn nhất của phương trình là π π x = − ∈ − ;0 . Chọn A. 48 12
Câu 23. Biến đổi phương trình cos3x −sin x = 3(cos x −sin3x) về dạng π π
sin (ax + b) = sin(cx + d ) với b , d thuộc khoảng − ;
. Tính b + d . 2 2 A. π π π π b + d = .
B. b + d = .
C. b + d = − .
D. b + d = . 12 4 3 2
Lời giải. Phương trình ⇔ 3 sin 3x + cos3x = sin x + 3 cos x 3 1 1 3 π π sin 3x cos 3x sin x cos x sin 3 x sin ⇔ + = + ⇔ + = x + . 2 2 2 2 6 3 Suy ra π π π b + d = + = . Chọn D. 6 3 2
Câu 24. Giải phương trình cos x − 3 sin x = 0. 1 sin x − 2 A. π π x k , π = + k ∈ . ℤ B. x k2 , π = + k ∈ . ℤ 6 6 C. 7π π x k2 , π = + k ∈ . ℤ D. 7 x k , π = + k ∈ . ℤ 6 6 π
x ≠ +k2π
Lời giải. Điều kiện 1 1 π 6 sin x − ≠ 0 ⇔ sin x ≠ ⇔ sin x ≠ sin ⇔ (k ∈ ℤ). 2 2 6 5π x ≠ + k2π 6 sin π 5π 6 6 cos O Hình 1
Điều kiện bài toán tương đương với bỏ đi vị trí hai điểm trên đường tròn lượng giác (Hình 1).
Phương trình ⇔ cos x − 3 sin x = 0 ⇔ cos x = 3 sin x π π cot x 3 cot x cot x lπ ⇔ = ⇔ = ⇔ = + (l ∈ ℤ). 6 6 sin π 6 O cos Hình 2 Biểu diễn nghiệm π x lπ = +
trên đường tròn lượng giác ta được 2 vị trí như Hình 2. 6
Đối chiếu điều kiện, ta loại nghiệm π x k2π = +
. Do đó phương trình có nghiệm 6 7π x 2lπ = +
(l ∈ ℤ). Chọn C. 6 Câu 25. Hàm số
2 sin 2x + cos 2x y =
có tất cả bao nhiêu giá trị nguyên?
sin 2x − cos 2x + 3 A. 1. B. 2. C. 3. D. 4. Lời giải. Ta có
2 sin 2x + cos 2x y =
⇔ (y −2)sin 2x −(y + ) 1 cos 2x = −3 . y
sin 2x − cos 2x + 3
Điều kiện để phương trình có nghiệm ⇔ (y − )2 +(y + )2 ≥(− y)2 2 2 1 3
⇔ 7 y + 2 y −5 ≤ 0 5 1 y y ∈ ⇔ − ≤ ≤
ℤ → y ∈ {−1;0} nên có 2 giá trị nguyên. Chọn B. 7
Câu 26. Gọi x là nghiệm dương nhỏ nhất của cos 2x + 3 sin 2x + 3 sin x −cos x = 2. 0
Mệnh đề nào sau đây là đúng? A. π π π π π π π x ∈ 0; .
B. x ∈ ; . C. x ∈ ; . D. x ∈ ; . 0 12 0 12 6 0 0 6 3 3 2
Lời giải. Phương trình 1 3 3 1 ⇔ cos 2x + sin 2x +
sin x − cos x = 1 2 2 2 2 π π sin 2x sin ⇔ + + x − = 1 . 6 6 Đặt π π π π π t = x − → x = t + → 2x = 2t + → 2x + = 2t + . 6 6 3 6 2 Phương trình trở thành π sin ⇔ 2t
+ + sin t = 1 ⇔ cos 2t + sin t = 1 2 2
⇔ 2 sin t − sin t = 0 ⇔ sin t (2 sin t − ) 1 = 0. π 1 π sin = 0 ∈ℤ π π ⇔ = → = + > 0 k t t k x k
⇔ k > − → k = 0 → x = . min 6 6 6 π π 1 π t = + k2 ∈ℤ π → x = + k2π > 0 k
⇔ k > − → k = 0 → x = . min 1 6 3 6 3 sin t = ⇔ 2 5π 1 t = + k2 ∈ℤ π → x π = + k2π > 0 k
⇔ k > − → k = 0 → x = . π min 6 2
Suy ra nghiệm dương nhỏ nhất của phương trình là π π π x = ∈ ; . Chọn B. 6 12 6
Câu 27. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10;10] để phương trình π π sinx 3 cos − − x
− = 2m vô nghiệm. 3 3 A. 21. B. 20. C. 18. D. 9.
Lời giải. Phương trình vô nghiệm ⇔ +(− )2 m < −1 1 3 < (2m)2 2 2
⇔ 4m − 4 > 0 ⇔ m >1 m∈
ℤ →m ∈ {−10;−9;−8;...;−2;2;...;8;9;10}
→ có 18 giá trị. Chọn C. m [ ∈ −10;10]
Câu 28. Tìm tất cả các giá trị thực của tham số m để phương trình x + x = ( 2 cos sin 2 m + ) 1 vô nghiệm. A. m ∈(− ; ∞ − ) 1 ∪(1;+∞). B. m ∈[−1; ] 1 . C. m ∈(− ; ∞ +∞) D. m ∈(− ; ∞ 0)∪(0;+∞).
Lời giải. Phương trình vô nghiệm (m ) 2 2 2 2 1 1 2 1 ⇔ + < + 4 2 2
⇔ m + m > ⇔ m ( 2 m + ) 2 2 0
2 > 0 ⇔ m > 0 ⇔ m ≠ 0. Chọn D.
Câu 29. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10;10] để phương trình (m + )
1 sin x − m cos x = 1− m có nghiệm. A. 21. B. 20. C. 18. D. 11.
Lời giải. Phương trình có nghiệm m ≥ 0 ⇔ (m + )2
1 + m ≥ (1− m)2 2 2
⇔ m + 4m ≥ 0 ⇔ m ≤ −4 m∈
ℤ →m ∈ {−10;−9;−8;...;−4;0;1;2;...;8;9;10}
→ có 18 giá trị. Chọn C. m [ ∈ −10;10]
Câu 30. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2018;2018] để
phương trình (m + ) 2
1 sin x − sin 2x + cos 2x = 0 có nghiệm. A. 4037. B. 4036. C. 2019. D. 2020.
Lời giải. Phương trình 1− cos 2x ⇔ (m + ) 1
−sin 2x + cos 2x = 0 2
⇔ −2 sin 2x +(1−m)cos 2x = m − −1.
Phương trình có nghiệm ⇔ (− )2 +( −m)2 ≥( m − − )2 2 1 1
⇔ 4m ≤ 4 ⇔ m ≤1 m∈ ℤ
→ m ∈ {−2018;−2017;...;0; } 1
→ có 2020 giá trị. Chọn D. m [ ∈ −2018;2018]
Vấn đề 3. PHƯƠNG TRÌNH BẬC HAI
ĐỐI VỚI MỘT H@M SỐ LƯỢNG GIÁC
Câu 31. Hỏi trên π 0; , phương trình 2
2 sin x −3sin x +1 = 0 có bao nhiêu nghiệm? 2 A. 1. B. 2. C. 3. D. 4. 1
Lời giải. Phương trình sin x = 2
2 sin x −3 sin x +1 = 0 ⇔ 2 sin x = 1 π x = + k2π 6 π sin x = sin 5π ⇔ 6 ⇔ x =
+ k2π (k ∈ ℤ). 6 sin x = 1 π x = + k2π 2 π π 1 1 π 0 ≤ + k2 k∈ℤ π < − < k <
→ k = 0 → x = 6 2 12 6 6 Theo giả thiết π 5π π 5 1 0 ≤ x < ⇔ 0 ≤ + k2 k∈ℤ π < ⇔ − < k < − → k ∈ ∅ . 2 6 2 12 12 π π 1 ℤ 0 ≤ + k2 ∈ π < − < k < 0 k → k ∈ ∅ 2 2 4
Vậy phương trình có duy nhất một nghiệm trên π 0; . Chọn A. 2
Câu 32. Số vị trí biểu diễn các nghiệm của phương trình 2
2 cos x + 5cos x + 3 = 0 trên
đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4. cos x = −1
Lời giải. Phương trình 2
⇔ 2 cos x + 5 cos x + 3 = 0 ⇔ 3 cos x = − (loaïi) 2 cos x 1 x π k2π ⇔ = − ⇔ = + (k ∈ ℤ).
Suy ra có duy nhất 1 vị trí biểu diễn nghiệm của phương trình trên đường tròn lượng giác. Chọn A.
Câu 33. Cho phương trình 2
cot 3x −3cot 3x + 2 = 0. Đặt t = cot x , ta được phương trình nào sau đây? A. 2
t − 3t + 2 = 0. B. 2
3t − 9t + 2 = 0. C. 2
t − 9t + 2 = 0. D. 2
t − 6t + 2 = 0. Lời giải. Chọn A.
Câu 34. Số nghiệm của phương trình 2
4 sin 2x − 2(1+ 2)sin 2x + 2 = 0 trên (0;π) là? A. 3. B. 4. C. 2. D. 1. 2 sin 2x =
Lời giải. Phương trình 2 x − ( + ) 2 4 sin 2 2 1
2 sin 2x + 2 = 0 ⇔ . 1 sin 2x = 2 π π (0; π π ) 2x = + k2π x = + kπ → x = 2 π 4 8 8 sin 2x = = sin ⇔ ⇔ . 2 4 3π 3π (0; π π ) 3 2x = + k2π x = + kπ → x = 4 8 8 π π (0; π π ) 2x = + k2π x = + kπ → x = 1 π 6 12 12 sin 2x = = sin ⇔ ⇔ . 2 6 5π 5π (0; π π ) 5 2x = + k2π x = + kπ → x = 6 12 12
Vậy có tất cả 4 nghiệm thỏa mãn. Chọn B.
Câu 35. Số nghiệm của phương trình 2
sin 2x −cos 2x +1 = 0 trên đoạn [ π;4π − ] là? A. 2. B. 4. C. 6. D. 8.
Lời giải. Phương trình 2 2
sin 2x − cos 2x +1 = 0 ⇔ −cos 2x − cos 2x + 2 = 0 cos 2x = 1 ⇔
⇔ cos 2x = 1 ⇔ 2x = k2π ⇔ x = k , π k ∈ . ℤ
cos 2x = −2(loaïi) Do ∈[ ∈ℤ π − ;4π] π π →− ≤ ≤ 4π ⇔ 1 − ≤ ≤ 4 k x k k
→ k ∈ {−1;0;1;2;3;4}.
Vậy phương trình có 6 nghiệm thỏa mãn. Chọn C. Câu 36. Tính tổng x x
T tất cả các nghiệm của phương trình 2 2 sin −3cos = 0 trên 4 4 đoạn [0;8π]. A. T = 0. B. T 8 . π = C. T 16 . π = D. T 4 . π =
Lời giải. Phương trình x x x x 2 2 2 sin 3 cos 0 2 1 − = ⇔ −cos −3cos = 0 4 4 4 4 x 1 cos = x x 4 2 x 1 x 2 π ⇔ −2 cos −3 cos + 2 = 0 ⇔ ⇔ cos = ⇔ cos = cos 4 4 x 4 2 4 3 cos = −2(loaïi) 4 x π 4π x [ ∈ 0;8 π π ] 4 = + k2π x =
+ k8π → x = 4 3 3 3 4π 20π ⇔ ⇔ → T = + = 8 . π Chọn B. x π 4π x [ ∈ 0;8 π π ] 20 3 3 = − + k2π x = −
+ k8π → x = 4 3 3 3
Câu 37. Số nghiệm của phương trình 1 − 3 −1 cot x − 3 +1 = 0 trên (0;π) là? 2 ( ) ( ) sin x A. 1. B. 2. C. 3. D. 4.
Lời giải. Điều kiện: sin x 0 x kπ ≠ ⇔ ≠ (k ∈ ℤ). Phương trình ⇔ ( 2 + x )−( − ) x −( + ) 2 1 cot 3 1 cot 3
1 = 0 ⇔ cot x −( 3 − ) 1 cot x − 3 = 0 π π x ( ∈ 0; π π ) 3 cot x = cot −
x = − + kπ → x = (thoûa maõn) cot x = 1 − 4 4 4 ⇔ ⇔ ⇔ . cot x = 3 π x ( ∈ 0; π π π ) cot x = cot x =
+ kπ → x = (thoûa maõn) 6 6 6
Vậy phương trình đã cho có 2 nghiệm thỏa mãn. Chọn B.
Câu 38. Tính tổng T tất cả các nghiệm của phương trình 2cos 2x + 2cos x − 2 = 0
trên đoạn [0;3π] . A. 17π T = . B. T 2 . π = C. T 4 . π = D. T 6 . π = 4
Lời giải. Phương trình x + x − = ⇔ ( 2 2 cos 2 2 cos 2 0 2 2 cos x − ) 1 + 2 cos x − 2 = 0 2 cos x = 2 2 2
⇔ 4 cos x + 2 cos x − 2 − 2 = 0 ⇔ ⇔ cos x = 2 2 +1 cos x = − (loaïi) 2 π x [ ∈ 0;3 π π π ] 9 x =
+ k2π → x = ; x = 4 4 4 π 9π 7π 17π ⇔ →T = + + = . Chọn A. π x [ ∈ 0;3 π π ] 7 4 4 4 4
x = − + k2π → x = 4 4
Câu 39. Số vị trí biểu diễn các nghiệm của phương trình cos 2x +3sin x + 4 = 0 trên
đường tròn lượng giác là? A. 1. B. 2. C. 3. D. 4.
Lời giải. Phương trình ⇔ ( 2 − x ) 2 1 2 sin
+ 3 sin x + 4 = 0 ⇔ −2 sin x + 3 sin x + 5 = 0 sin x = −1 π ⇔ 5
⇔ sin x = −1 ⇔ x = − + k2π (k ∈ ℤ). sin x = (loaïi) 2 2
Suy ra có duy nhất 1 vị trí đường tròn lượng giác biểu diễn nghiệm. Chọn A.
Câu 40. Cho phương trình x x cos x + cos
+1 = 0 . Nếu đặt t = cos , ta được phương 2 2 trình nào sau đây? A. 2 2t + t = 0. B. 2
−2t + t +1 = 0. C. 2
2t + t −1 = 0. D. 2 −2t + t = 0. Lời giải. Ta có x 2 cos x = 2 cos −1. 2 Do đó phương trình x x x x 2 2 ⇔ 2 cos
−1+ cos +1 = 0 ⇔ 2 cos + cos = 0. 2 2 2 2 Đặt x t = cos
, phương trình trở thành 2
2t + t = 0. Chọn A. 2
Câu 41. Số nghiệm của phương trình π π 5 cos 2x 4 cos + + − x = thuộc [0;2π] là? 3 6 2 A. 1. B. 2. C. 3. D. 4. Lời giải. Ta có π 2 π 2 π cos 2x 1 2 sin x 1 2 cos + = − + = − − x . 3 3 6 Do đó phương trình π π 3 2 2 cos x 4 cos ⇔ − − + − x− = 0 6 6 2 π 1 cos − x π =
x = − + k2π 6 2 π 1 π π 6 ⇔
⇔ cos − x = ⇔ − x = ± + k2π ⇔ , k ∈ ℤ . π 3 6 2 6 3 π cos − x = (loaïi) x = + k2π 6 2 2 Ta có π x [ ∈ 0;2 π π π π ] 11 x = − + k2 x∈ 0;2π π → x = ; [ ] x =
+ k2π → x = . 6 6 2 2
Vậy có hai nghiệm thỏa mãn. Chọn B.
Câu 42. Tìm tất cả các giá trị thực của tham số m để phương trình tan x + m cot x = 8 có nghiệm.
A. m >16.
B. m <16.
C. m ≥16.
D. m ≤16.
Lời giải. Phương trình m 2
tan x + m cot x = 8 ⇔ tan x +
= 8 ⇔ tan x −8 tan x + m = 0 . tan x
Để phương trình đã cho có nghiệm khi và chỉ khi ∆′ = (− )2
4 − m ≥ 0 ⇔ m ≤ 16 . Chọn D.
Câu 43. Tìm tất cả các giá trị thực của tham số m để phương trình π π
cos 2x −(2m + )
1 cos x + m +1 = 0 có nghiệm trên khoảng 3 ; . 2 2
A. −1≤ m ≤ 0 . B. −1≤ m < 0 .
C. −1< m < 0 . D. 1 −1 ≤ m < . 2 1
Lời giải. Phương trình cos x = 2
⇔ 2 cos x −(2m + )
1 cos x + m = 0 ⇔ 2 . cos x = m sin cos O 1 m 2 Nhận thấy phương trình 1 π π cos x =
không có nghiệm trên khoảng 3 ; (Hình vẽ). 2 2 2 Do đó yêu cầu bài toán π π
⇔ cos x = m có nghiệm thuộc khoảng 3 ;
⇔ −1 ≤ m < 0 . 2 2 Chọn B.
Câu 44. Biết rằng khi m = m thì phương trình 2 x −( m + ) 2 2 sin 5
1 sin x + 2m + 2m = 0 0 có đúng π
5 nghiệm phân biệt thuộc khoảng − ;3 π
. Mệnh đề nào sau đây là đúng? 2 A. 3 7 3 2 m = −3. B. 1 m = . C. m ∈ ; . D. m ∈ − ; − . 2 0 5 10 0 5 5
Lời giải. Đặt t = sin x (−1≤ t ≤ ) 1 . Phương trình trở thành 2 t −( m + ) 2 2 5
1 + 2m + 2m = 0. (*) sin sin t 2 cos cos O O t 2 Hình 1 Hình 2
Yêu cầu bài toán tương đương với:
TH1: Phương trình (*) có một nghiệm t = −1 (có một nghiệm x ) và một nghiệm 1
0 < t < 1 (có bốn nghiệm x ) (Hình 1). 2 Do c 2 t = −1 → t = − = m − −m . 1 2 a m = −3
→ t = −6 ∉ 0;1 loaïi 2 ( )( )
Thay t = −1 vào phương trình (*), ta được . 1 1 1 m = − → t = ∈ 0;1 thoûa 2 ( )( ) 2 4
TH2: Phương trình (*) có một nghiệm t =1 (có hai nghiệm x ) và một nghiệm 1
−1 < t ≤ 0 (có ba nghiệm x ) (Hình 2). 2 Do c 2 t = 1 → t = = m + m . 1 2 a m = 1
→ t = 2 ∉ −1;0 loaïi 2 ( ]( )
Thay t =1 vào phương trình (*), ta được . 1 1 3 m = → t = ∉ −1;0 loaïi 2 ( ]( ) 2 4 Vậy 1
m = − thỏa mãn yêu cầu bài toán. Do 1 3 2 m = − ∈ − ; − . Chọn D. 2 2 5 5
Câu 45. Tìm tất cả các giá trị thực của tham số m để phương trình 2 π π
2 cos 3x +(3−2m)cos 3x + m −2 = 0 có đúng 3 nghiệm thuộc khoảng − ; . 6 3
A. −1≤ m ≤1.
B. 1< m ≤ 2.
C. 1≤ m ≤ 2.
D. 1≤ m < 2.
Lời giải. Đặt t = cos x (−1≤ t ≤ )
1 . Phương trình trở thành 2
2t +(3−2m)t + m −2 = 0. 1 Ta có t = ∆ = ( m − )2 2
5 . Suy ra phương trình có hai nghiệm 1 2 . t = m −2 2 sin cos O t 1 2 t = 1 2
Ta thấy ứng với một nghiệm 1 π π t =
thì cho ta hai nghiệm x thuộc khoảng − ; . 1 2 6 3
Do đó yêu cầu bài toán −1 < t ≤ 0 ⇔ −1< m −2 ≤ 0 ⇔ 1< m ≤ 2. Chọn B. 2
Cách 2. Yêu cầu bài toán tương đươn với phương trình 2
2t +(3−2m)t + m −2 = 0 có P ≤ 0
hai nghiệm t , t thỏa mãn 1 t 0 t 1 − < ≤ < < ⇔ . a f 1 > 0 . 2 1 ( ) 1 2 .af (− ) 1 > 0
Vấn đề 4. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI sin x và cos x
Câu 46. Giải phương trình 2 x −( + ) 2 sin 3
1 sin x cos x + 3 cos x = 0. A. π π x k2π = + (k ∈ ℤ). B. x kπ = + (k ∈ ℤ). 3 4 π π x = + k2π x = + kπ C. 3 3 (k ∈ ℤ). D. (k ∈ ℤ). π π x = + k2π x = + kπ 4 4 tan x = 1
Lời giải. Phương trình 2 ⇔ tan x −( 3 + ) 1 tan x + 3 = 0 ⇔ tan x = 3 π x = + kπ 4 ⇔
(k ∈ ℤ). Chọn D. π x = + kπ 3
Câu 47. Gọi S là tập nghiệm của phương trình 2 2
2 sin x + 3 3 sin x cos x − cos x = 2 .
Khẳng định nào sau đây là đúng? A. π π π π π π π ; π ⊂ S.
B. ; ⊂ S. C. 5 ; ⊂ S. D. 5 ; ⊂ S. 3 6 2 4 12 2 6
Lời giải. Phương trình 2 2 ⇔ x + x x − x = ( 2 2 2 sin 3 3 sin cos cos
2 sin x + cos x ) 2
⇔ 3 3 sin x cos x −3 cos x = 0 ⇔ 3 cos x ( 3 sin x −cos x) = 0. π π x = ⇔ x = + k = π (k ∈ ℤ) k 0 cos 0 → x = . 2 2
3 sin x −cos x = 0 ⇔ 3 sin x = cos x 1 π π π ⇔ tan x = ⇔ tan x = tan ⇔ x = + k = π (k ∈ ℤ) k 0 → x = . 3 6 6 6
Vậy tập nghiệm của phương trình chứa các nghiệm π và π . Chọn B. 6 2
Câu 48. Trong các phương trình sau, phương trình nào tương đương với phương trình 2 x −( + ) 2 sin 3
1 sin x cos x + 3 cos x = 3 . A. π sin x = 0 . B. sinx + = 1 . 2 C. 3 +1 ( cos x − ) 1 tan x − = 0 . D. 2 .
(tan x +2+ 3)(cos x − ) 1 = 0 1− 3
Lời giải. Phương trình 2 ⇔ x −( + ) 2 x x + x = ( 2 2 sin 3 1 sin cos 3 cos
3 sin x + cos x ) ( ) 2 1 3 sin x ( 3 ) 1 sin x cos x 0 sin x (1 3 )sin x ( 3 ) 1 cos x ⇔ − − + = ⇔ − − + = 0. 2 2
sin x = 0 ⇔ cos x = 1 ⇔ cos x −1 = 0.
(1− 3)sin x −( 3 + )
1 cos x = 0 ⇔ (1− 3)sin x = ( 3 + ) 1 cos x 3 +1 ⇔ tan x =
⇔ tan x = −2 − 3 ⇔ tan x + 2 + 3 = 0. 1− 3
Vậy phương trình đã cho tương đương với ( x + + )( 2 tan 2 3 cos x − ) 1 = 0 . Chọn D.
Câu 49. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình 2
sin x + 3 sin x cos x = 1 ? A. π π x ( 2 cos cot x − ) 3 = 0 . B. sinx + . tanx + −2 − 3 = 0 . 2 4 C. 2 π cos x + −1. . D. (sin x − ) 1 (cot x − 3) = 0 . (tan x − 3)= 0 2
Lời giải. Phương trình 2 2 2
⇔ sin x + 3 sin x cos x = sin x + cos x 2
⇔ 3 sin x cos x − cos x = 0 ⇔ cos x ( 3 sin x −cos x) = 0. π cos x 0 sin = ⇔ x + = 0. 2 1
3 sin x − cos x = 0 ⇔ tan x = . 3 π 1 + +1 tan x tan Ta có π 4 3 π tan x 2 3 tan + = = = + ⇔ x + − 2 − 3 = 0. 4 π 1 4 1− tan x.tan 1− .1 4 3
Vậy phương trình đã cho tương đương với π π sinx + . tanx
+ −2 − 3 = 0 .Chọn B. 2 4
Câu 50. Cho phương trình 2
cos x −3 sin x cos x +1 = 0 . Mệnh đề nào sau đây là sai? A. x kπ =
không là nghiệm của phương trình.
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x −3 tan x + 2 = 0 .
C. Nếu chia 2 vế của phương trình cho 2
sin x thì ta được phương trình 2
2 cot x + 3cot x +1 = 0 .
D. Phương trình đã cho tương đương với cos 2x −3sin 2x +3 = 0 . = Lời giải. sin x 0 s in x = 0
Với x = k π → ⇔
. Thay vào phương trình ta thấy 2 c os x = ±1 c os x = 1
thỏa mãn. Vậy A đúng. Phương trình 2 2 2
⇔ cos x −3 sin x cos x + sin x + cos x = 0 2 2 2
⇔ sin x − 3sin x cos x + 2 cos x = 0 ⇔ tan x −3 tan x + 2 = 0 . Vậy B đúng. Phương trình 2 2 2
⇔ cos x −3 sin x cos x + sin x + cos x = 0 2 2 2
⇔ 2 cos x − 3sin x cos x + sin x = 0 ⇔ 2 cot x −3 cot x +1 = 0 . Vậy C sai. Chọn C. Phương trình 1+ cos 2x sin 2x ⇔ −3
+1 = 0 ⇔ cos 2x −3 sin 2x + 3 = 0. Vậy D đúng. 2 2
Câu 51. Số vị trí biểu diễn các nghiệm phương trình 2 2
sin x − 4 sin x cos x + 4 cos x = 5
trên đường tròn lượng giác là? A. 4 . B. 3 . C. 2 . D. 1.
Lời giải. Phương trình 2 2 ⇔ x − x x + x = ( 2 2 sin 4 sin cos 4 cos
5 sin x + cos x ) ⇔ − x − x x − x = ⇔ ( x + x )2 2 2 4 sin 4 sin cos cos 0 2 sin cos
= 0 ⇔ 2 sin x + cos x = 0 1 ⇔ tan x = −
→ có 2 vị trí biểu diễn nghiệm trên đường tròn lượng gác. Chọn C. 2
Câu 52. Số nghiệm của phương trình 2 2
cos x −3 sin x cos x + 2 sin x = 0 trên ( 2π;2π − ) ? A. 2 . B. 4 . C. 6 . D. 8 . π tan x = 1 x = + kπ
Lời giải. Phương trình 2 4
⇔ 1−3 tan x + 2 tan x = 0 ⇔ 1 ⇔ . tan x = 1 x = arctan 2 + kπ 2 Vì π 9 7 ∈ (−2 ∈ℤ π; 2π) →−2π π < + < 2 k x k π → − < k <
→ k ∈ {−2;−1;0; } 1 . 4 4 4 Vì 1 x ( 2π;2π) 2π arctan kπ 2π ∈ − →− < + < 2 CASIO 28,565 24,565 k k ∈ →− < < −
ℤ → k ∈ −28;−27;−26;−25 . xapxi { }
Vậy có tất cả 8 nghiệm. Chọn D.
Câu 53. Nghiệm dương nhỏ nhất của phương trình 2 2
4 sin x + 3 3 sin 2x − 2 cos x = 4 là: A. π . B. π . C. π . D. π . 12 6 4 3
Lời giải. Phương trình 2 2 ⇔ x + x − x = ( 2 2 4 sin 3 3 sin 2 2 cos
4 sin x + cos x ) cos x = 0 2
⇔ 3 3 sin 2x −6 cos x = 0 ⇔ 6 cos x ( 3 sin x −cos x) = 0 ⇔ 1 tan x = 3 π π 1 π x = + k ∈ℤ π + kπ > 0 k
⇔ k > − → k = 0 → x = min 2 Cho>0 2 2 2 ⇔ → . π π 1 π x = + k ∈ℤ π + kπ > 0 k
⇔ k > − → k = 0 → x = min 6 6 6 6
So sánh hai nghiệm ta được π x =
là nghiệm dương nhỏ nhất. Chọn B. 6
Câu 54. Cho phương trình ( − ) 2 x + x +( + ) 2 2 1 sin sin 2 2
1 cos x − 2 = 0 . Trong các
mệnh đề sau, mệnh đề nào sai? A. 7π x =
là một nghiệm của phương trình. 8
B. Nếu chia hai vế của phương trình cho 2
cos x thì ta được phương trình 2
tan x − 2 tan x −1 = 0 .
C. Nếu chia hai vế của phương trình cho 2
sin x thì ta được phương trình 2
cot x + 2 cot x −1 = 0 .
D. Phương trình đã cho tương đương với cos 2x −sin 2x = 1.
Lời giải. Chọn D.
Câu 55. Giải phương trình 2 x +( − ) x x +( − ) 2 2 sin 1 3 sin cos 1 3 cos x = 1. A. π π π π − . B. − . C. 2 − . D. − . 6 4 3 12
Lời giải. Phương trình 2 ⇔ x +( − ) x x +( − ) 2 2 2 2 sin 1 3 sin cos 1
3 cos x = sin x + cos x 2 ⇔ x +( − ) 2 sin 1
3 sin x cos x − 3 cos x = 0 π tan = −1 x = − + k x π 2 4 ⇔ tan x +(1− 3) a t n x − 3 = 0 ⇔ ⇔ tan x = 3 π x = + kπ 3 π 1 π − + k ∈ℤ π < 0 k ⇔ k < → k = 0 → x = − max Cho<0 4 4 4 → . π 1 k ℤ 2π + k ∈
π < 0 ⇔ k < − → k = −1 → x = − max 3 3 3
So sánh hai nghiệm ta được π x = −
là nghiệm âm lớn nhất. Chọn B. 4
Câu 56. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10;10] để phương trình 2 x +(m − ) 2 11sin
2 sin 2x + 3 cos x = 2 có nghiệm? A. 16. B. 21. C. 15. D. 6.
Lời giải. Phương trình 2 ⇔ x +(m − ) 2 9 sin
2 sin 2x + cos x = 0 1− cos 2x 1+ cos 2x ⇔ 9.
+(m −2)sin 2x +
= 0 ⇔ (m −2)sin 2x − 4 cos 2x = −5. 2 2 Phương trình có nghiệm m ≥ ⇔ (m − )2 + ≥ ⇔ (m − )2 5 2 16 25 2 ≥ 9 ⇔ m ≤ −1 m∈
ℤ →m ∈ {−10;−9;...;−1;5;6;...;10}
→ có 16 giá trị nguyên. Chọn A. m [ ∈ −10;10]
Câu 57. Có bao nhiêu giá trị nguyên của tham số m thuộc để phương trình 2 x − (m − ) x x −(m − ) 2 sin 2 1 sin cos
1 cos x = m có nghiệm? A. 2. B. 1. C. 0. D. Vô số.
Lời giải. Phương trình ⇔ ( −m) 2 x − (m − ) x x −( m − ) 2 1 sin 2 1 sin cos 2 1 cos x = 0 1− cos 2x 1+ cos 2x ⇔ (1−m). −(m − )
1 sin 2x −(2m − ) 1 . = 0 2 2 ⇔ 2(m − )
1 sin 2x + m cos 2x = 2 −3 . m
Phương trình có nghiệm (m − )2 + m ≥( − m)2 2 2 4 1 2 3
⇔ 4m − 4m ≤ 0 ⇔ 0 ≤ m ≤1 m∈ ℤ →m ∈ {0; } 1
→ có 2 giá trị nguyên. Chọn A.
Câu 58. Tìm điều kiện để phương trình 2 2
a sin x + a sin x cos x + b cos x = 0 với a ≠ 0 có nghiệm. A. b b a ≥ 4b .
B. a ≤ −4b . C. 4 ≤1 . D. 4 ≤1. a a
Lời giải. Phương trình 2
a tan x + a tan x + b = 0 . Phương trình có nghiệm 2
⇔ ∆ = a − 4ab ≥ 0 ⇔ a(a − 4b)≥ 0 4b − a 4b
⇔ a(4b −a) ≤ 0 ⇔ ≤ 0 ⇔ ≤1. Chọn C. a a
Câu 59. Tìm tất cả các giá trị của tham số m để phương trình 2
2 sin x + m sin 2x = 2m vô nghiệm. A. 4 0 ≤ m ≤ . B. m < 0 , 4 m > . C. 4 0 < m < . D. 4 m < − , m > 0 . 3 3 3 3
Lời giải. Phương trình 1− cos 2x ⇔ 2.
+ m sin 2x = 2m ⇔ m sin 2x −cos 2x = 2m −1. 2 m < 0 Phương trình vô nghiệm
⇔ m +1 < (2m − )2 2 2 1
⇔ 3m − 4m > 0 ⇔ 4 . Chọn B. m > 3
Câu 60. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−3;3] để phương trình ( 2 m + ) 2
2 cos x − 2m sin 2x +1 = 0 có nghiệm. A. 3 . B. 7 . C. 6 . D. 4 .
Lời giải. Phương trình ⇔ ( 1+ cos 2x 2 m + 2).
−2m sin 2x +1 = 0 2 ⇔ m x −( 2 m + ) 2 4 sin 2
2 cos 2x = m + 4 .
Phương trình có nghiệm ⇔ m +(m + )2 ≥(m + )2 2 2 2 2 2 16 2 4
⇔ 12m ≥12 ⇔ m ≥ 1 ⇔ m ≥1 m∈ ℤ
→ m ∈ {−3;−2;−1;1;2; } 3
→ có 6 giá trị nguyên. Chọn C. m [ ∈ −3;3]
Vấn đề 5. PHƯƠNG TRÌNH CHỨA sin x ± cos x và sin x cos x.
Câu 61. Giải phương trình sin x cos x + 2(sin x + cos x)= 2 . π π
A. x = + kπ x = + k π 2 , k ∈ . ℤ B. 2 2 , k ∈ . ℤ x = kπ
x = k2π π π
C. x = − + k2π x = − + kπ 2 , k ∈ . ℤ D. 2 , k ∈ . ℤ
x = k2π x = kπ Lời giải. Đặt π π t sin x cos x 2 sin = + = x + . Vì sin x + ∈ [ 1 − ; ] 1 ⇒ t ∈ − 2; 2 . 4 4 2 Ta có t −1
t = (sin x + cos x )2 2 2 2
= sin x + cos x + 2 sin x cos x ⇒ sin x cos x = . 2 2 t − = 1
Khi đó, phương trình đã cho trở thành t 1 2 2t 2 t 4t 5 0 + = ⇔ + − = ⇔ . 2 t = −5(loaïi) Với π π π t = 1 , ta được 1 sin x cos x 1 sinx sin + = ⇔ + = ⇔ x + = sin . 4 2 4 4 π π x + = + k2π
x = k2π 4 4 ⇔ ⇔ ℤ . Chọn B. π , k ∈ π π
x = + k2π x π + = − + k2π 2 4 4
Câu 62. Cho phương trình 3 2 (sin x +cos x)+2sin 2x + 4 = 0 . Đặt t = sin x +cos x , ta
được phương trình nào dưới đây? A. 2
2t + 3 2 t + 2 = 0. B. 2
4t + 3 2 t + 4 = 0. C. 2
2t + 3 2 t − 2 = 0. D. 2
4t + 3 2 t − 4 = 0. Lời giải. Đặt 2
t = sin x + cos x
→ sin 2x = t −1.
Phương trình đã cho trở thành t + ( 2 t − ) 2 3 2 2
1 + 4 = 0 ⇔ 2t + 3 2 t + 2 = 0. Chọn A.
Câu 63. Cho phương trình 5sin 2x + sin x + cos x + 6 = 0 . Trong các phương trình sau,
phương trình nào tương đương với phương trình đã cho? A. π 2 π sin x + = . B. 3 cosx − = . 4 2 4 2
C. tan x = 1. D. 2 1+ tan x = 0. Lời giải. Đặt π t sin x cos x 2 sin = + = x
+ . Điều kiện − 2 ≤ t ≤ 2. 4 Ta có t = ( x + x )2 2 2 2 2 sin cos
= sin x + cos x + 2.sin x.cos x ⇒ sin 2x = t −1.
Khi đó, phương trình đã cho trở thành ( 2t − ) 2 5
1 + t + 6 = 0 ⇔ 5t + t +1 = 0 : vô nghiệm.
Nhận thấy trong các đáp án A, B, C, D thì phương trình ở đáp án D vô nghiệm.
Vậy phương trình đã cho tương đương với phương trình 2
1+ tan x = 0. Chọn D.
Câu 64. Nghiệm âm lớn nhất của phương trình 1
sin x + cos x = 1− sin 2x là: 2 A. π π − . B. . π − C. 3 − . D. 2 . π − 2 2 Lời giải. Đặt π t sin x cos x 2 sin = + = x
+ . Điều kiện − 2 ≤ t ≤ 2. 4 Ta có t = ( x + x )2 2 2 2 2 sin cos
= sin x + cos x + 2 sin x cos x ⇒ sin 2x = t −1. 2 t − = 1
Phương trình đã cho trở thành t 1 2 t 1 t 2t 3 0 = − ⇔ + − = ⇔ . 2 t = −3(loaïi) Với π π π π t = 1 , ta được 1 2 sin x 1 sinx sin + = ⇔ + = ⇔ x + = sin 4 4 2 4 4 π π x + = + k2π
x = k2π 4 4 ⇔ ⇔ ℤ . π , k ∈ π π
x = + k2π x π + = − + k2π 2 4 4 TH1. Với = 2 ∈ℤ π < 0 ⇔ < 0 k x k k → k = 1 − → x = −2 . π max TH2. Với π 1 k∈ℤ 3π x =
+ k2π < 0 ⇔ k < − → k = 1 − → x = − . max 2 4 2
Vậy nghiệm âm lớn nhất của phương trình là 3π x = − . Chọn C. 2 Câu 65. Cho π
x thỏa mãn phương trình sin 2x + sin x − cos x = 1 . Tính sinx − . 4 A. π π π π sin x
− = 0 hoặc sinx
− = 1 . B. sinx
− = 0 hoặc 2 sin x − = . 4 4 4 4 2 C. π 2 π π sinx − = − . D. sinx
− = 0 hoặc 2 sinx − = − . 4 2 4 4 2 Lời giải. Đặt π t sin x cos x 2 sin = − = x
− . Điều kiện − 2 ≤ t ≤ 2. 4 Ta có t = ( x − x )2 2 2 2 2 sin cos
= sin x + cos x − 2 sin x cos x ⇒ sin 2x = 1−t .
Phương trình đã cho trở thành t = 0 2 2
1− t + t = 1 ⇔ t − t = 0 ⇔ . t = 1 Với π π t = 1 , ta được 1 2 sin x 1 sin − = ⇔ x − = . 4 4 2 Với π π
t = 0 , ta được 2 sin x 0 sin − = ⇔ x − = 0. 4 4 Chọn B.
Câu 66. Từ phương trình π
5 sin 2x −16(sin x −cos x )+16 = 0 , ta tìm được sinx + có 4 giá trị bằng: A. 2 . B. 2 − . C. 1. D. 2 ± . 2 2 2 Lời giải. Đặt π t sin x cos x 2 sin = − = x
− . Điều kiện − 2 ≤ t ≤ 2. 4 Ta có t = ( x − x )2 2 2 2 2 sin cos
= sin x + cos x − 2.sin x cos x ⇒ sin 2x = 1− t . t = 1
Phương trình đã cho trở thành 5( 2
1− t )−16t +16 = 0 ⇔ 21 . t = − (loaïi) 5
Với t = 1 ⇒ sin x −cos x = 1. ( ) ∗ Mặt khác ( x + x )2 +( x − x )2 sin cos sin cos = 2 , kết hợp với ( ) ∗ suy ra π ( x x )2 2 sin cos 1 2 sin x cos x 1 sin + + = ⇔ + = ± ⇔ x + = ± . Chọn D. 4 2 Câu 67. Cho π
x thỏa mãn 6(sin x −cos x)+ sin x cos x + 6 = 0 . Tính cosx + . 4 A. π π cosx + = −1. B. cosx + = 1. 4 4 C. π 1 π cosx + = . D. 1 cosx + = − . 4 2 4 2 Lời giải. Đặt π t sin x cos x 2 sin = − = x
− . Điều kiện − 2 ≤ t ≤ 2. 4 2 Ta có 1− t
t = (sin x − cos x)2 2 2 2
= sin x + cos x −2 sin x cos x ⇒ sin x cos x = . 2 2 t − = 1 −
Phương trình đã cho trở thành 1 t 6t 6 0 + + = ⇔ 2 t = 13(loaïi) π π 1 π 1 2 sin x 1 sin x sin ⇒ − = − ⇔ − = − ⇔ − x = 4 4 2 4 2 π π 1 π 1 ⇒ cos − − x = ⇔ cosx + = . Chọn C. 2 4 2 4 2
Câu 68. Từ phương trình (1+ 3)(cos x +sin x)−2sin x cos x − 3 −1= 0 , nếu ta đặt
t = cos x + sin x thì giá trị của t nhận được là:
A. t = 1 hoặc t = 2 .
B. t = 1 hoặc t = 3 . C. t = 1 . D. t = 3 . 2 Lời giải. Đặt − = x − x (− ≤ t ≤ ) 1 t t sin cos 2 2
→ sin x cos x = . 2
Phương trình trở thành ( + )t −( 2 1 3 t − ) 1 − 3 −1 = 0 t = 1 2 t (1 3)t 3 0 ⇔ − + + = ⇔
⇔ t = 1. Chọn C. t = 3 (loaïi)
Câu 69. Nếu (1+ 5)(sin x −cos x)+sin2x −1− 5 = 0 thì sin x bằng bao nhiêu? A. 2 sin x = . B. 2 sin x = hoặc 2 sin x = − . 2 2 2
C. sin x = −1 hoặc sin x = 0 .
D. sin x = 0 hoặc sin x = 1 . 2 Lời giải. Đặt − = x − x (− ≤ t ≤ ) 1 t t sin cos 2 2
→ sin x cos x = . 2
Phương trình trở thành ( + ) 2 1
5 t +1− t −1− 5 = 0 t = 1 2 t (1 5)t 5 0 ⇔ − + + = ⇔ t = 5 (loaïi)
⇒ sin x − cos x = 1 ⇔ cos x = sin x −1 . Mặt khác sin x = 0
sin x + cos x = 1 ⇒ sin x +(sin x − )2 2 2 2 1 = 1 ⇔ . Chọn D. sin x = 1 Câu 70. Nếu π
(1+ sin x)(1+ cos x) = 2 thì cosx
− bằng bao nhiêu? 4 A. −1. B. 1. C. 2 . D. 2 − . 2 2
Lời giải. Ta có (1+sin x)(1+cos x)= 2 ⇔ 1+sin x +cos x +sin x.cos x = 2
⇔ sin x + cos x + sin x.cos x = 1 ⇔ 2(sin x + cos x)+ 2.sin x.cos x = 2. ( ) ∗ 2 Đặt − t = x + x (− ≤ t ≤ ) t 1 sin cos 2 2
→ sin x cos x = . 2 t = 1 Khi đó ( ) ∗ trở thành 2 2 2t t 1 2 t 2t 3 0 + − = ⇔ + − = ⇔ t = −3 (loaïi)
⇒ sin x + cos x = 1 . Ta có π π π 2 2 cosx − = cos x cos + sin x sin =
(cos x + sin x) = . Chọn C. 4 4 4 2 2
Câu 71. Cho x thỏa mãn 2sin 2x −3 6 sin x + cos x +8 = 0 . Tính sin 2x. A. 1
sin 2x = − . B. 2 sin 2x = − . C. 1 sin 2x = . D. 2 sin 2x = . 2 2 2 2 Lời giải. Đặt π π t sin x cos x 2 sin = + = x + . Vì sin x + ∈ [ 1 − ; ] 1 ⇒ t ∈ 0; 2 . 4 4 Ta có t = ( x + x )2 2 2 2 2 sin cos
= sin x + cos x + 2 sin x cos x ⇒ sin 2x = t −1. 6 t
Phương trình đã cho trở thành = 2( 2 t ) 1 3 6 t 8 0 − − + = ⇔ 2 t = 6 (loaïi) 1 2
sin 2x = t −1 = . Chọn C. 2
Câu 72. Hỏi trên đoạn [0;2018π] , phương trình sin x −cos x + 4 sin 2x =1 có bao nhiêu nghiệm? A. 4037. B. 4036. C. 2018. D. 2019. Lời giải. Đặt π π t sin x cos x 2 sin = − = x − . Vì sin x − ∈ [ 1 − ; ] 1 ⇒ t ∈ 0; 2 . 4 4 Ta có t = ( x − x )2 2 2 2 2 sin cos
= sin x + cos x − 2 sin x cos x ⇒ sin 2x = 1−t . t = 1
Phương trình đã cho trở thành t + 4( 2 1− t ) = 1 ⇔ 3 . t = − (loaïi) 4 Với kπ
t = 1 , ta được sin 2x 0 2x kπ = ⇔ = ⇔ x = , k ∈ ℤ . 2 Theo giả thiết kπ x [0;2018π] 0 2018π ∈ → ≤ ≤ ⇔ 0 ≤ k ≤ 4046 2 k∈
ℤ → k ∈ {0;1;2;3;...;4036}
→ có 4037 giá trị của k nê có 4037 nghiệm. Chọn A.
Câu 73. Từ phương trình 2 (sin x +cos x)= tan x +cot x , ta tìm được cos x có giá trị bằng: A. 1. B. 2 − . C. 2 . D. 1 − . 2 2
Lời giải. Điều kiện s in x ≠ 0 ⇔ sin 2x ≠ 0 . c os x ≠ 0 Ta có sin x cos x
2 (sin x + cos x ) = tan x + cot x ⇔ 2 (sin x + cos x ) = + cos x sin x 2 2 sin x + cos x
⇔ 2 (sin x + cos x) =
⇔ 2 sin x cos x. 2 (sin x + cos x) = 2. sin x cos x 2 Đặt − t = x + x (− ≤ t ≤ ) t 1 sin cos 2 2
→ sin x cos x = . 2
Phương trình trở thành ⇔ t ( 2 t − ) 3 2
1 = 2 ⇔ t − t − 2 = 0 ⇔ t = 2
⇒ sin x + cos x = 2 ⇔ sin x = 2 − cos x. Mà x + x = ⇒ x +( − x )2 2 2 2 2 sin cos 1 cos 2 cos
= 1 ⇔ 2 cos x − 2 2 cos x +1 = 0 ⇔ ( x − )2 1 2 cos 1 = 0 ⇔ cos x = . Chọn C. 2
Câu 74. Từ phương trình 3 3 3 π
1+ sin x + cos x =
sin 2x , ta tìm được cosx + có giá trị 2 4 bằng: A. 1. B. 2 − . C. 2 . D. 2 ± . 2 2 2
Lời giải. Phương trình 3
⇔ 1+(sin x + cos x )(1− sin x cos x) = sin 2x 2
⇔ 2 +(sin x + cos x)(2 −sin 2x) = 3sin 2x. 2 Đặt − t = x + x (− ≤ t ≤ ) t 1 sin cos 2 2
→ sin x cos x = . 2
Phương trình trở thành + t ( 2 − t + ) = ( 2 2 2 1 3 t − ) 1 t = 1 − 3 2 t 3t 3t 5 0 ⇔ + − − = ⇔ . t = 1 − ± 6 (loaïi) Với π t = −1 , ta được 1 sin x cos x 1 sin + = − ⇔ x + = − . 4 2 Mà π π π 1 π 2 2 2 2 sin x cos x 1 cos x cos + + + = → + = ⇔ x + = ± . Chọn D. 4 4 4 2 4 2
Câu 75. Có bao nhiêu giá trị nguyên của tham số m để phương trình
sin x cos x − sin x − cos x + m = 0 có nghiệm? A. 1. B. 2. C. 3. D. 4. 2 Lời giải. Đặt − t = x + x (− ≤ t ≤ ) t 1 sin cos 2 2
→ sin x cos x = . 2 2
Phương trình trở thành t −1−t + m = 0 ⇔ −2m = t −2t −1 ⇔ (t − )2 2 1 = −2m + 2 . 2 Do − ≤ t ≤ →− − ≤ t − ≤ − → ≤ (t − )2 2 2 2 1 1 2 1 0 1 ≤ 3 + 2 2 .
Vậy để phương trình có nghiệm 1+ 2 2
⇔ 0 ≤ −2m + 2 ≤ 3 + 2 2 ⇔ − ≤ m ≤ 1 2 m∈ ℤ →m ∈ {−1;0; } 1 . Chọn C.




