Chuyên đề hàm số lượng giác và phương trình lượng giác – Nguyễn Bảo Vương

Chuyên đề hàm số lượng giác và phương trình lượng giác 2018 của thầy Nguyễn Bảo Vương gồm 58 trang, với tóm tắt lý thuyết, phân dạng, phương pháp giải

Môn:

Toán 11 3.3 K tài liệu

Thông tin:
59 trang 1 năm trước
Tác giả:
K
Kim Oanh
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Chuyên đề hàm số lượng giác và phương trình lượng giác – Nguyễn Bảo Vương

Chuyên đề hàm số lượng giác và phương trình lượng giác 2018 của thầy Nguyễn Bảo Vương gồm 58 trang, với tóm tắt lý thuyết, phân dạng, phương pháp giải

62 31 lượt tải Tải xuống

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT) 134 tài liệu

Môn: Toán 11 3.3 K tài liệu

Thông tin:

59 trang 1 năm trước

Tác giả:

Profile Kim Oanh
Ch¬ng i.
hµm sè lîng
gi¸c vµ
ph¬ng tr×nh
lîng gi¸c
.
NguyÔn b¶o v¬ng
TµI LIÖU Cã §¸P ¸N Vµ Hdg
Năm học: 2017-2018
C¸c em häc sinh theo dâi facebook:
https://www.facebook.com/phong.baovuong
®Ó nhËn ®îc nhiÒu tµi liÖu hay h¬n.
Gi¸o viªn muèn
mua file word
liªn hÖ
0946798489
®Ó biÕt thªm chi tiÕt.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
1
BµI 1.
HµM Sè Lîng gi¸c
a. kiÕn thøc cÇn nhí.
Hàm số sin:
siny x
Tính chất:
•Tập xác định
.
•Tập giá trị:
1;1
,có nghĩa là
.
•Hàm số tuần hoàn với chu kì
2
, có nghĩa
sin 2 sinx k x
với
k
.
•Hàm số đồng biến trên mỗi khoảng
2 ; 2
2 2
k k
và nghịch biến trên mỗi
khoảng
3
2 ; 2
2 2
k k
,
k
.
•
siny x
là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng (Hình 1).
Hình 1.
•Một số giá trị đặc biệt:
sin 0 ,( )x x k k
sin 1 2 ,( )
2
x x k k
sin 1 2 ,( )
2
x x k k
Hàm số côsin:
cosy x
Tính chất:
•Tập xác định
.
•Tập giá trị:
1;1
,có nghĩa là
1 cos 1,x x
.
•Hàm số tuần hoàn với chu kì
2
, có nghĩa
cos 2 cosx k x
với
k
.
•Hàm số đồng biến trên mỗi khoảng
2 ; 2
k k
và nghịch biến trên mỗi khoảng
2 ; 2
k k
,
k
.
•
cosy x
là hàm số chẵn, đồ thị hàm số nhận Oy làm trục đối xứng (Hình 2).
O
x
y
-
3π
2
-
π
2
3π
2
π
2
-1
1
3π2π
π
-3π
-π
-2π
f
x
( ) = sin
x
( )
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
2
Hình 2.
•Một số giá trị đặc biệt:
cos 0 ,( )
2
x x k k
cos 1 2 ,( )x x k k
.
cos 1 2 ,( )x x k k
.
Hàm số tang:
sin
tan
cos
x
y x
x
Tính chất:
•Tập xác định:
\
2
k k
•Tâp giá trị là
.
•Hàm số tuần hoàn với chu kì
, có nghĩa
tan tan ,( )
x k x k
.
•Hàm số đồng biến trên mỗi khoảng
; ,
2 2
k k k
.
•
tany x
là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng và nhận
mỗi đường thẳng
,
2
x k k
làm đường tiệm cận.(Hình 3)
Hình 3.
•Một số giá trị đặc biệt :
tan 0 ,x x k k
1
-1
O
y
x
-
3π
2
-
π
2
3π
2
π
2
3π
2π
π-π
-2π
-3π
f
x
( ) = cos
x
( )
-
3π
2
-
π
2
3π
2
π
2
2π
-π
π
-2π
O
y
x
f
x
( )
= tan
x
( )
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
3
tan 1 ,
4
x x k k
.
tan 1 ,
4
x x k k
.
Hàm số cotang:
cos
cot
sin
x
y x
x
.
Tính chất:
•Tập xác định:
\ k k
.
•Tập giá trị:
.
•Hàm số tuần hoàn với chu kì
, có nghĩa
cot cot ,( )
x k x k
.
•Hàm số nghịch biến trên mỗi khoảng
; ,k k k
.
•
coty x
là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng và nhận
mỗi đường thẳng
,x k k
làm đường tiệm cận (Hình 4).
Hình 4
•Một số giá trị đặc biệt :
cot 0 ,
2
x x k k
.
cot 1 ,
4
x x k k
.
cot 1 ,
4
x x k k
.
ii. c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.
Daïng toaùn 1: Tìm taäp xaùc ñònh cuûa haøm soá.

Phương pháp giải:
Khi tìm tập xác định của hàm số, ta cần chú ý:
• Các hàm số
sin , cosy x y x
xác định trên
.
3π
2
π
2
-
π
2
-
3π
2
2π
π
-π
-2π
f(x)=cotan(x)
O
y
x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
4
• Hàm số
P x
y
Q x
xác định khi
0.
Q x
Từ đó suy ra:
- Hàm số
tany x
xác định khi
cos 0.x
- Hàm số
coty x
xác định khi
sin 0.x
• Hàm số
y f x
xác định khi
0.
f x
Ví dụ 1. Tìm tập xác định
D
của hàm số
2
sin 2
sin .cos
x
y
x x
A.
\ , .
2
k
D k
B.
\ , .
2
D k k
C.
\ 2 , .
2
D k k
D.
\ , .
D k k
Ví dụ 2. Tìm tập xác định của hàm số
2 cos 3
sin 1
x
y
x
.
A.
\ , .
2
D k k
B.
\ 2 , .
2
D k k
C.
.D
D.
\ 2 , .
2
D k k
Áp dụng làm các bài tập sau:
Câu 1. Hàm số
cos
2 sin 3
x
y
x
có tập xác định là:
A.
\ 2 , .
3
k k
B.
\ , .
6
k k
C.
5
\ 2 , 2 , .
6 6
k k k
D.
2
\ 2 , 2 , .
3 3
k k k
Câu 2. Hàm số
tan
2 4
x
y
có tập xác định là:
A.
\ 2 , .
2
k k
B.
\ , .
2
k k
C.
3
\ 2 , .
2
k k
D.
.
Câu 3. Tập xác định của hàm số
cot 2 2
3
y x
là:
A.
\ , .
6
k k
B.
\ 2 , .
6
k k
C.
5
\ , .
12 2
k
k
C.
\ , .
6 2
k
k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
5
Câu 4. Hàm số
1 cos
1 sin
x
y
x
có tập xác định là:
A.
\ , .
k k
B.
\ , .
2
k k
C.
\ 2 , .
2
k k
D.
\ , .
2
k
k
Câu 5. Cho hàm số
sin
1 tan
x
y
x
và
.k
Khoảng nào dưới đây không nằm trong tập xác
định của hàm số?
A.
2 ; 2 .
2 2
k k
B.
3
2 ; 2 .
2
k k
C.
3 3
2 ; 2 .
4 2
k k
D.
3
2 ; 2 .
2 4
k k
Câu 6. Hàm số
cos 1
3 sin
x
y
x
có tập xác định là:
A.
.
B.
\ 2 , .
k k
C.
2 , .
k k
D.
.
Đáp án: 1D 2C 3D 4C 5A 6C
Daïng toaùn 2: Xaùc ñònh tính chaün, leû cuûa haøm soá.

Phương pháp giải:
Khi xác định tính chẵn, lẻ của hàm số
y f x
ta thực hiện các bước sau:
Bước 1. Tìm tập xác định
D
của hàm số.
• Nếu
D
không là tập đối xứng, nghĩa là
x D
sao cho
x D
thì ta kết luận ngay hàm số
y f x
không, chẵn, không lẻ.
• Nếu
D
là tập đối xứng ta thực hiện bước 2.
Bước 2.
• Nếu
f x f x
với mọi
x D
thì hàm số
y f x
là hàm số chẵn.
• Nếu
f x f x
với mọi
x D
thì hàm số
y f x
là hàm số lẻ.
• Nếu
x D
mà
f x f x
hoặc
f x f x
thì hàm số
y f x
là hàm số không
chẵn (không lẻ).
Chú ý: Khi xác định tính chẵn, lẻ của hàm số lượng giác ta cần lưu ý:
•
,sin sin .x x x
•
, cos cos .x x x
•
\ , , tan tan .
2
x k k x x
•
\ , , cot cot .x k k x x
Ví dụ 3. Hàm số nào sau đây không phải là hàm số lẻ?
A.
sin .y x
B.
cos .y x
C.
tan .y x
D.
cot .y x
Ví dụ 4. Hàm số
sin . cosy x x
là:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
6
A. Hàm số không có tính chẵn, lẻ. B. Hàm chẵn.
C. Hàm có giá trị lớn nhất bằng 1. D. Hàm lẻ.
Áp dụng làm các bài tập sau:
Câu 7. Hàm số
sin .cos 2y x x
là:
A. Hàm chẵn. B. Hàm không có tính chẵn, lẻ.
C. Hàm không có tính tuần hoàn. D. Hàm lẻ.
Câu 8. Hàm số
3
tan 3
sin
x
y
x
thỏa mãn tính chất nào sau đây?
A. Hàm chẵn. B. Hàm không có tính chẵn , lẻ.
C. Xác định trên
.
D. Hàm lẻ.
Câu 9. Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
sin .y x
B.
2
sin .cos .y x x
C.
tan
.
cos
x
y
x
D.
cos
.
sin
x
y
x
Câu 10. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
2
tan 2
.
tan 1
x
y
x
B.
sin .cos 2 .y x x
C.
cos sin .y x x
D.
3
cos sin .y x x
Câu 11. Trong các hàm số sau, hàm số nào không là hàm chẵn và cũng không là hàm lẻ?
A.
1
tan .
sin
y x
x
B.
2 sin .
4
y x
C.
sin tan .y x x
D.
4 4
sin cos .y x x
Đáp án 7D 8A 9C 10C 11B
Daïng toaùn 3: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá.

Phương pháp giải:
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số lượng giác, ta biến đổi hàm số đã cho
về dạng
siny a b t
hoặc
cos .y a b t
Và sử dụng kết quả:
1 sin 1, 1 cos 1.t t
Ví dụ 5. Hàm số
2 sin cos cos 2y x x x
có giá trị lớn nhất là:
A.
3.
B.
2 2.
C.
2.
D.
2.
Ví dụ 6. Hàm số
2
sin cos cos2y x x x
có giá trị nhỏ nhất là:
A.
1.
B.
1 2.
C.
0.
D.
1 2.
Áp dụng làm các bài tập sau:
Câu 12. Hàm số
2
sin cos cos2y x x x
có giá trị lớn nhất là:
A.
1 2.
B.
3.
C.
5.
D.
2.
Câu 13. Hàm số
3 sin cosy x x
có giá trị nhỏ nhất là:
A.
1 3.
B.
3.
C.
2.
D.
1 3.
Câu 14. Cho hàm số
cos 1
cos 2
x
y
x
. Mệnh đề nào trong số các mệnh đề sau là sai?
A. Tập xác định của hàm số là
.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
7
B. Hàm số có giá trị lớn nhất bằng
0.
C. Hàm số có giá trị nhỏ nhất bằng
2.
D. Hàm số tuần hoàn với chu kì
2.T
Câu 15. Hàm số nào sau đây có giá trị lớn nhất bằng
2.
A.
tan cot .y x x
B.
2 tan .y x
C.
2 cos sin .y x x
D.
sin 2 .
4
y x
Câu 16. Giá trị nhỏ nhất của hàm số
2 2
3 4 sin cosy x x
là:
A.
1.
B.
2.
C.
1.
D.
3.
Đáp án 12A 13C 14D 15C 16B
Daïng toaùn 4: Tìm chu kì cuûa haøm soá löôïng giaùc.

Phương pháp giải:
Khi tìm chu kì của hàm số lượng giác ta cần lưu ý rằng:
• Hàm số
sin , cosy x y x
có chu kì
2 .T
• Hàm số
tan , coty x y x
có chu kì
.T
• Hàm số
sin , cos , 0
y ax b y ax b a
có chu kì
2
.
T
a
• Hàm số
tan , tan , 0
y ax b y ax b a
có chu kì
.
T
a
• Nếu hàm số
1
f
có chu kì là
1
T
,
2
f
có chu kì là
2
T
thì hàm số
1 2
f f f
có chu kì
T
với
T
là
số nhỏ nhất sao cho
*
1 2
: , .
T kT lT k l
Ví dụ 7. Hàm số
2
2 cos 1y x
là hàm tuần hoàn với chu kì:
A.
.T
B.
2 .T
C.
2
.T
D.
.
2
T
Ví dụ 8. Hàm số
sin cos
2 3
x
y x
là hàm tuần hoàn với chu kì:
A.
.T
B.
2 .T
C.
3 .T
D.
6 .T
Áp dụng làm các bài tập sau:
Câu 17. Hàm số
1 cos 2y x
có chu kì là:
A.
2 .T
B.
2 .T
C.
.T
D.
.T
Câu 18. Hai hàm số nào sau đây có chu kì khác nhau?
A.
cos
2
x
và
sin .
2
x
B.
sin x
và
tan .x
C.
cos x
và
cot .
2
x
D.
tan 2x
và
cot2 .x
Câu 19. Chu kì của hàm số
2 sin 2 3 cos 2
3 4
y x x
là:
A.
2 .T
B.
.T
C.
.
2
T
D.
4 .T
Câu 20. Chu kì hàm số
sin 2 2 cos 3y x x
là:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
8
A.
2 .T
B.
.T
C.
2
.
3
T
D.
.
3
T
Đáp án
17C 18B 19B 20A
Daïng toaùn 5: Xaùc ñònh haøm soá coù ñoà thò cho tröôùc.

Phương pháp giải:
Khi xác định hàm số lượng giác có đồ thị cho trước, ta cần chú ý đến các yếu tố sau:
• Các điểm đặc biệt mà đồ thị đi qua;
• Xác định chu kì của đồ thị hàm số thông qua đồ thị.
Ví dụ 9. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây:
A.
sin .
2
x
y
B.
cos .
2
x
y
C.
cos .
4
x
y
D.
sin .
2
x
y
Ví dụ 10. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây:
A.
sin .
2
x
y
B.
sin .y x
C.
cos .
2
x
y
D.
cos .y x
Áp dụng làm các bài tập sau:
Câu 21. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây:
A.
sin 2 .y x
B.
sin 3 .y x
C.
cos .y x
D.
cos 2 .y x
Câu 22. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
9
A.
tan 2 .y x
B.
cot 3 .y x
C.
tan .
2
x
y
D.
cot2 .y x
Đáp án 21A 22A
Ph¬ng ph¸p sö dông casio ®Ó gi¶I quyÕt d¹ng to¸n t×m tËp x¸c ®Þnh.
Bước 1. Chọn đơn vị sử dụng
Bước 2. Nhập biểu thức vào máy tính
Bước 3. Thử các giá trị tường minh.
Ví dụ 11. Cho hàm số
1
.
2 cos 1
y
x
Tập xác định của hàm số là:
A.
\ 2 , .
6
D k k
B.
\ 2 , .
4
D k k
C.
\ 2 , .
3
D k k
D.
\ , .
2
D k k
Sử dụng máy tính CASIO fx – 570MS, bằng cách thực hiện theo thứ tự:
• Chọn đơn vị là radial ta ấn: wwww2
• Nhập biểu thức
2 cos 1x
ta ấn: 2kQ[)p1
• Ta lần lượt thử với các giá trị
, ,
6 4 3
x x x
qr…
Dễ thấy
3
x
thì kết quả máy tính bằng
0
. Nên chọn C.
Ngoài ra, phương pháp này có thể áp dụng cho các bài toán phương trình lượng giác, vấn
đề này sẽ nói sau.
iii. bµi tËp tr¾c nghiÖm tù luyÖn (cã ®¸p ¸n).
Câu 1.
Tập xác định của hàm số
1 siny x
là:
A.
1;1 .D
B.
0;1D
C.
.D
D.
1;1 .D
Câu 2.
Tập xác định của hàm số
2
1 cosy x
là:
A.
1;1 .D
B.
0;1 .D
C.
.D
D.
\ 1 .D
Câu 3.
Tập xác định của hàm số
tan coty x x
là:
A.
| , .
2
x x k k
B.
| , .
2
x x k k
C.
| , .x x k k
D.
| 2 , .x x k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
10
Câu 4.
Tập xác định của hàm số
2
1
cot
cos
y x
x
là:
A.
| , .
2
x x k k
B.
| , .
3
x x k k
C.
| , .
5
k
x x k
D.
| , .
7
k
x x k
Câu 5.
Tập xác định của hàm số
1 cosy x
là:
A.
1;1 .
D
B.
.D
C.
1;1 .
D
D.
.D
Câu 6.
Trong các hàm số sau đây, hàm số nào là hàm số lẻ?
A.
2
cos sin .y x x
B.
sin cos .y x x
C.
cos .y x
D.
sin .cos 3 .y x x
Câu 7.
Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A.
sin .y x
B.
sin cos .y x x
C.
2
cos sin .y x x
D.
sin .cos .y x x
Câu 8.
Giá trị lớn nhất của hàm số
y
là:
A.
2 2
.
4
B.
4
8.
C.
2.
D.
1.
Câu 9.
Giá trị bé nhất của hàm số
y
là:
A.
2
.
11
B.
0.
C.
1
.
2
D.
1.
Câu 10.
Giá trị lớn nhất của hàm số
cos siny x x
là:
A.
2 2
.
4
B.
4
8.
C.
2.
D.
1.
Câu 11.
Giá trị lớn nhất của hàm số sau đây bằng bao nhiêu
sin cos .y x x
A.
2.
B.
2.
C.
1.
D.
0.
Câu 12.
Hàm số nào sau đây đồng biến trên khoảng
0; ?
A.
sin .y x
B.
cos .y x
C.
tan .y x
D.
2
.y x
Câu 13.
Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
A.
2 3 sin .y x x
B.
sin cos .y x x x
C.
2
sin .y x
D.
2
sin .y x x
Câu 14.
Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
A.
2
cos .y x x
B.
2
cos .y x
C.
2 2
cos .y x x
D.
2
.y x
Câu 15.
Chu kì của hàm số
2
siny x
là:
A.
.T
B.
2 .T
C.
2
.T
D.
4 .T
Câu 16.
Chu kì của hàm số
sin 2 cos 3 .y x x
là:
A.
.T
B.
3 .T
C.
.
6
T
D.
2 .T
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
11
Câu 17.
Chu kì của hàm số
cot cot cot .
2 3
x x
f x x
là:
A.
.T
B.
2 .T
C.
3 .T
D.
6 .T
Câu 18.
Chu kì của hàm số
cos tan .
x
y x
là:
A.
.T
B.
2.T
C.
2
.T
D. Không có chu kì.
Câu 19.
Tập giá trị của hàm số
2
sin 2 sin 5y x x
là:
A.
4;8 .
T
B.
0;1 .
T
C.
3;5 .
T
D.
.T
Câu 20.
Tập giá trị của hàm số
2
cos cos 1y x x
là:
A.
3; 3 .
T
B.
3
;3 .
4
T
C.
1;4 .
T
D.
.T
Câu 21.
Cho hàm số
sin 2 2 cos 3f x x x
. Chu kì tuần hoàn của hàm số bằng:
A.
2
.
3
T
B.
.T
C.
2 .T
D.
4 .T
Câu 22.
Giá trị lớn nhất của biểu thức
4 4
sin cosx x
là:
A.
0.
B.
1.
C.
2.
D.
1
.
2
Câu 23.
Giá trị nhỏ nhất của hàm số
cos 2 4 cosy x x
là:
A.
5.
B.
3.
C.
0.
D.
1.
Câu 24.
Tập giá trị của hàm số
2 sin 2 3y x
là:
A.
0;1 .
T
B.
2; 3 .
T
C.
2; 3 .
T
D.
1;5 .
T
Câu 25.
Cho hàm số
2 tan 3 tan
2 3
x x
f x
. Chu kì tuần hoàn của hàm số là:
A.
12 .T
B.
6 .T
C.
3 .T
D.
.T
Câu 26.
Giá trị bé nhất của biểu thức
2
cos sinx x
bằng:
A.
2.
B.
3
.
2
C.
1.
D.
0.
Câu 27.
Giá trị lớn nhất của biểu thức
2
cos sinx x
bằng:
A.
2.
B.
0.
C.
5
.
4
D.
1.
Câu 28.
Tập giá trị của hàm số
1 2 sin 3y x
là:
A.
1;1 .
T
B.
0;1 .
T
C.
1;0 .
T
D.
1;3 .
T
Đáp án.
1C
2C
3B
4A
5B
6D
7C
8C
9A
10B
11B
12D
13C
14B
15A
16D
17C
18D
19A
20B
21C
22B
23B
24D
25B
26C
27C
28A
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
12
BµI 2. PH¦¥NG TR×NH Lîng gi¸c c¬ b¶n
I. kiÕn thøc cÇn nhí.
Phương trình
sin 1x a
•
1a
: Phương trình
1
vô nghiệm.
•
1a
: Gọi
là một cung sao cho
sin .a
Khi đó
1 sin sinx
và
1
có các
nghiệm
2 ,
.
2 ,
x k k
x k k
Chú ý:
- Khi
2 2
và
sin a
thì ta viết
arcsin .a
- Phương trình
sin sinx
có các nghiệm:
360 ,
.
180 360 ,
x k k
x k k
- Trong một công thức nghiệm của phương trình lượng giác, không được đồng thời
dùng hai đơn vị độ và radian.
Phương trình
cos 2x a
•
1a
: Phương trình
2
vô nghiệm.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
13
•
1
a
: Gọi
là một cung sao cho
sin .a
Khi đó
2 cos cos
x
và
2
có các
nghiệm
2 ,
.
2 ,
x k k
x k k
Chú ý:
- Khi
0
và
cos a
thì ta viết
arccos .a
- Phương trình
cos cosx
có các nghiệm:
360 ,
.
360 ,
x k k
x k k
Phương trình
tan 3
x a
• `Phương trình
3
xác định khi
, .
2
x k k
•
a
, tồn tại cung
sao cho
tan a
, Khi đó
3 tan tan
x
và
3
có nghiệm
, .
x k k
Chú ý:
- Khi
2 2
và
tan a
thì ta viết
arctan .a
- Phương trình
tan tanx
có các nghiệm:
180 , .x k k
Phương trình
cot 4
x a
• `Phương trình
4
xác định khi
, .x k k
•
a
, tồn tại cung
sao cho
tan a
, Khi đó
4 cot cot
x
và
4
có nghiệm
, .
x k k
Chú ý:
- Khi
và
cot a
thì ta viết
arccot .a
- Phương trình
cot cotx
có các nghiệm:
180 , .x k k
Ph¬ng ph¸p casio ®Ó gi¶I to¸n tr¾c nghiÖm ph¬ng tr×nh lîng gi¸c
Với mục đích là kiểm tra nghiệm của phương trình lượng giác.
Dạng 1. Nghiệm phương trình lượng giác
sin;cos;tan;cot 0
F
. Để kiểm tra nghiệm
ta dùng chức năng tính bảng giá trị (Table).
Khi làm việc với hàm lượng giác, máy tính phải đưa về chế độ RAD ® : Shift >Mode>4.
Phương pháp:
Nhập hàm, chuyển tất cả phương trình về 1 vế trái, vế phải luôn bằng 0.
Nhận xét trước các phương án để chọn khoảng xét:
+ Nếu các nghiệm đều dương thì chọn khoảng xét là
0;2
.
+ Nếu có nghiệm âm thì chọn
;
.
+ Chọn 1 vòng đường tròn lượng giác là để xét
2
k
hay
k
hay
2
k
.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
14
Xét các giá trị nghiệm chọn bước nhảy thích hợp. Sau khi có bảng, thì nếu cột
0
F X X
là nghiệm.
Ví dụ: giải phương trình
sin 3 sin cos 3 cosx x x x
có nghiệm là:
A.
2 ;
2 4
k k
B.
;
2 4
k k
C.
;
2 8 2
k k
D.
;
8
k k
k
.
Ấn mode 7. Nhập hàm
sin 3 sin cos 3 cosX X X X
Start?: 0
End?
2
Step:
8
Nhìn vào cột F(X) nhanh chóng chọn đáp án
8 2
k
và
2
là nghiệm chọn C.
II. Mét sè vÝ dô.
Ví dụ 1. Phương trình
sin cosx x
có số nghiệm thuộc đoạn
0;
là:
A.
1.
B.
4.
C.
5.
D.
2.
Ví dụ 2. Phương trình
sin2 1x
có nghiệm là:
A.
4 , .
2
x k k
B.
, .
2
x k k
C.
2 , .
4
x k k
D.
, .
4
x k k
Ví dụ 3. Phương trình
2
sin 1
3
x
có nghiệm là:
A.
2 , .
2
x k k
B.
3
2 , .
2
x k k
C.
3
3 , .
2
x k k
D.
, .x k k
Ví dụ 4. Phương trình
2 cos 3 0x
có tập nghiệm trong khoảng
0;2
:
A.
11
; .
6 6
B.
2 4
; .
3 3
C.
5
; .
3 3
D.
5 7
; .
6 6
Ví dụ 5. Phương trình
sin cos 2 1
x
có nghiệm là:
A.
, .x k k
B.
2 , .x k k
C.
, .
2
x k k
D.
, .
6
x k k
IIi. Bµi tËp tr¾c nghiÖm (cã ®¸p ¸n).
Câu 29.
Phương trình
cos 1
2
x
có nghiệm là:
A.
2 4 , .x k k
B.
2 , .x k k
C.
2 , .x k k
D.
2 , .x k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
15
Câu 30.
Phương trình
2
cos 3 1x
có nghiệm là:
A.
, .x k k
B.
, .
2
k
x k
C.
, .
3
k
x k
D.
, .
4
k
x k
Câu 31.
Phương trình
tan 0
4
x
có nghiệm là:
A.
, .
4
x k k
B.
3
, .
4
x k k
C.
, .x k k
D.
2 , .x k k
Câu 32.
Phương trình
cot 0
4
x
có nghiệm là:
A.
, .
4
x k k
B.
, .
4
x k k
C.
2 , .
4
x k k
D.
2 , .
4
x k k
Câu 33.
Trong
0;
, phương trình
2
sin 1 cosx x
có tập nghiệm là:
A.
.
2
B.
3
; .
2 2
C.
0; .
D.
0; ; .
2
Câu 34.
Trong
0;2
, phương trình
cos2 sin 0x x
có tập nghiệm là:
A.
7 11
; .
6 6
B.
7 11
; ; .
2 6 6
C.
5 7
; .
6 6
D.
7 5
; ; .
6 6 6
Câu 35.
Trong
0;2
, phương trình
sin 2 sin 0x x
có số nghiệm là:
A.
1.
B.
2.
C.
3.
D.
4.
Câu 36.
Phương trình
sin 3 cos 1x x
có số nghiệm thuộc
0; 3
là:
A.
2.
B.
3.
C.
4.
D.
6.
Câu 37.
Số nghiệm của phương trình
2 cos 1
3
x
thuộc
0;2
là:
A.
0.
B.
2.
C.
1.
D.
3.
Câu 38.
Số nghiệm của phương trình
sin 1
4
x
thuộc
0; 3
là:
A.
1.
B.
0.
C.
2.
D.
3.
Câu 39.
Trong các phương trình sau, phương trình nào có nghiệm?
A.
3 sin 2.x
B.
1 1
cos 4 .
4 2
x
C.
2 sin 3 cos 1.x x
D.
2
cot cot 5 0.x x
Câu 40.
Trong các phương trình sau, phương trình nào vô nghiệm?
A.
sin2 cos2 1.x x
B.
sin2 cos 0.x x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
16
C.
2
sin .
5
x
D.
sin 3 cos 0.x x
Câu 41.
Tập nghiệm của phương trình
3 tan 3
4
x
trong khoảng
0;2
là:
A.
2
.
3
B.
3
.
2
C.
2
; .
3 3
D.
3
; .
2 2
Câu 42.
Tập nghiệm của phương trình
2
cos cos 2 0x x
trong khoảng
0;2
là:
A.
0; .
B.
0; .
2
C.
3
; .
2 2
D.
3
0; .
2
Câu 43.
Phương trình
cos sin 1
x
có nghiệm là:
A.
, .x k k
B.
2 , .x k k
C.
, .
2
x k k
D.
, .
4
x k k
Câu 44.
Phương trình
cos cos 3 1
x
có nghiệm là:
A.
, .
8 4
x k k
B.
, .
4 2
x k k
C.
, .
6 3
x k k
D.
, .
2
x k k
Câu 45.
Phương trình
sin 1
tan 1
x
x
có tập nghiệm là:
A.
, .
2
k k
B.
2 , .
2
k k
C.
.
D.
2 , .
2
k k
Câu 46.
Phương trình
sin 2 2 cos sin 1
0
tan 3
x x x
x
có tập nghiệm là:
A.
2 , .
3
k k
B.
2 , .
3
k k
C.
2 , 2 , .
3 2
k k k
D.
2 , .
2
k k
Câu 47.
Phương trình
sin 3 cos2 sin 0x x x
có tập nghiệm trong
0;
là:
A.
3
; .
4 4
B.
.
4
C.
3
.
4
D.
3
; ; .
6 4 4
Câu 48.
Phương trình
2
cos 2 2 cos 1 0x x
có tập nghiệm là:
A.
, .
4
k k
B.
, .
4 2
k k
C.
2 , .
4
k k
D.
, .
k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
17
Câu 49.
Phương trình
2 cos 3 0
2
x
có nghiệm là:
A.
5
4 , .
3
x k k
B.
5
2 , .
6
x k k
C.
5
4 , .
6
x k k
D.
5
, .
3
x k k
Câu 50.
Phương trình
3 tan 3 0x
có nghiệm là:
A.
, .
3
x k k
B.
2 , .
3
x k k
C.
, .
6
x k k
D.
, .
3
x k k
Câu 51.
Mệnh đề nào sau đây sai?
A.
sin 1 2 , .
2
x x k k
B.
sin 0 , .x x k k
C.
sin 0 2 , .x x k k
D.
sin 1 2 , .
2
x x k k
Câu 52.
Nghiệm của phương trình
sin 2 cos 3 0
x x
là:
A.
, .
2
6
x k
k
x k
B.
, .
6
x k
k
x k
C.
2
, .
2
3
x k
k
x k
D.
2 , .
6
x k k
Câu 53.
Nghiệm của phương trình
2
cos cos 0x x
thuộc
0;
là:
A.
.
2
x
B.
0.x
C.
.x
D.
.
2
x
Câu 54.
Phương trình
cos2 0x
có nghiệm là:
A.
2
6
, .
5
2
6
x k
k
x k
B.
, .
4 2
x k k
C.
2
2 , .
3
x k k
D.
, .
4
x k k
Câu 55.
Phương trình
2
sin 3
2
x
có nghiệm là:
A.
, .
4
k
x k
B.
, .x k k
C.
2 2
; , .
12 3 4 3
k k
x x k
D.
, .
6 2
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
18
Câu 56.
Nghiệm phương trình
1
cos 0
2
x
là:
A.
2 , .
6
x k k
B.
5
, .
6
x k k
C.
2
2 , .
3
x k k
D.
2 , .
3
x k k
Câu 57.
Nghiệm phương trình
tan 1 0x
là:
A.
, .
2
x k k
B.
, .
4
x k k
C.
, .
4
x k k
D.
3
2 , .
4
x k k
Câu 58.
Nghiệm phương trình
3 tan 3 0x
là:
A.
2 , .
3
x k k
B.
, .
6
x k k
C.
, .
6
x k k
D.
, .
3
x k k
Câu 59.
Nghiệm phương trình
1
cot2
3
x
là:
A.
, .
4
x k k
B.
, .x k k
C.
2 2
; , .
12 3 4 3
k k
x x k
D.
, .
6 2
k
x k
Câu 60.
Nghiệm phương trình
19
sin 9
18
x
là:
A.
, .
4
x k k
B.
, .x k k
C.
, .
6 2
k
x k
D. Vô nghiệm.
Câu 61.
Phương trình
tan 4 0x
có nghiệm là:
A.
, .
4
x k k
B.
, .x k k
C.
2 2
; , .
12 3 4 3
k k
x x k
D.
, .
6 2
k
x k
Câu 62.
Phương trình
3
sin 4 1
2
x
có nghiệm là:
A.
1 1
; , .
4 12 2 4 6 2
k k
x x k
B.
2 ; 2 , .
2
x k x k k
C.
1
, .
24 12
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
19
D.
165 115
180 ; 180 , .
2 2
x k x k k
Câu 63.
Phương trình
2
cos 2 30
2
x
có nghiệm là:
A.
1 1
; , .
4 12 2 4 6 2
k k
x x k
B.
2 ; 2 , .
2
x k x k k
C.
1
, .
24 12
k
x k
D.
165 115
180 ; 180 , .
2 2
x k x k k
Câu 64.
Các giá trị nào sau đây là nghiệm của phương trình
1
sin
2
x
?
A.
2 , .
3
x k k
B.
, .
6
x k k
C.
5
2 , .
6
x k k
D.
2 , .
6
x k k
Câu 65.
Nghiệm của phương trình
3
sin
2
x
là:
A.
, .
3
x n n
B.
1
1 , .
3
n
x n n
C.
1 , .
4
n
x n n
D.
1 , .
3
n
x n n
Câu 66.
Nghiệm của phương trình
2
sin
2
x
là:
A.
1
1 , .
4
n
x n n
B.
, .
8
x k k
C.
1 , .
4
n
x n n
D.
2
.
2
x
Câu 67.
Nghiệm của phương trình
1
cos
2
x
là:
A.
, .
6
x k k
B.
2 , .
6
x k k
C.
, .
3
x k k
D.
2
2 , .
3
x k k
Câu 68.
Nghiệm của phương trình
3
cos
2
x
là:
A.
, .
6
x k k
B.
2 , .
6
x k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
20
C.
5
, .
6
x k k
D.
5
2 , .
6
x k k
Câu 69.
Phương trình
tan 1x
có nghiệm là:
A.
5
2 ; 2 , .
6 6
x k x k k
B.
, .
4 2
k
x k
C.
, .
4
x k k
D.
, .
6
x k k
Câu 70.
Phương trình
cot 3x
có nghiệm là:
A.
5
2 ; 2 , .
6 6
x k x k k
B.
, .
4 2
k
x k
C.
, .
4
x k k
D.
, .
6
x k k
Câu 71.
Phương trình
2
3
sin 3
4
x
có nghiệm là:
A.
, .
6 2
k
x k
B.
1
, .
10 5
k
x k
C.
x k
D.
, .
12 4
k
x k
Câu 72.
Phương trình
2
tan 2 3x
có nghiệm là:
A.
, .
6 2
k
x k
B.
1
, .
10 5
k
x k
C.
x k
D.
, .
12 4
k
x k
Câu 73.
Phương trình
2
1
cot 4
3
x
có nghiệm là:
A.
, .
6 2
k
x k
B.
1
, .
10 5
k
x k
C.
x k
D.
, .
12 4
k
x k
Câu 74.
Cho hàm số
1
.
2 cos 1
y
x
Tập xác định của hàm số là:
A.
\ 2 , .
6
D k k
B.
\ 2 , .
4
D k k
C.
\ 2 , .
3
D k k
D.
\ , .
2
D k k
Câu 75.
Số nghiệm của phương trình
cos 0
2 4
x
thuộc đoạn
2 ; 4
là:
A.
1.
B.
2.
C.
3
. D.
4.
Câu 76.
Phương trình
cos sinx x
có số nghiệm thuộc đoạn
;
là:
A.
2.
B.
4.
C.
5
. D.
6.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
21
Câu 77.
Số nghiệm của phương trình
sin 1
4
x
thuộc đoạn
;2
là:
A.
1.
B.
2.
C.
3
. D.
0.
Câu 78.
Giải phương trình
2 2
sin 2 cos ( )
4
x x
A.
4
, .
2 3
x k
k
k
x
B.
2
4
, .
12 3
x k
k
k
x
C.
4
, .
12 3
x k
k
k
x
D.
4
, .
12 3
x k
k
k
x
ĐÁP ÁN
1A 2C 3A 4B 5D 6B 7D 8B 9B 10C
11C 12C 13A 14A 15A 16C 17C 18A 19A 20B
21A 22D 23C 24A 25A 26B 27C 28C 29B 30B
31D 32D 33A 34A 35D 36C 37B 38C 39D 40D
41C 42D 43C 44A 45D 46C 47A 48A 49D 50D
BµI 3.
MéT Sè PH¦¥NG TR×NH Lîng gi¸c thêng gÆp
i. kiÕn thøc cÇn nhí.
Tài liệu chỉ nhắc đến các dạng toán thường gặp.
ii.c¸c d¹ng to¸n thêng gÆp vµ ph¬ng ph¸p gi¶i.
Daïng toaùn 1: Phöông trình baäc nhaát ñoái vôùi sinx vaø cosx
sin cos 0a x b x c
.

Phương pháp giải:
2 2
2 2
2 2 2
2 2
2
2 2 2 2 2 2
cos
2 2
sin
sin cos sin cos
sin
chia ve
a b
a
DK
a b
b
a b c
a b
a b c
a x b x c x x
a b a b a b
c
x Dap An
a b
Ví dụ 1. Giải phương trình:
Hướng dẫn: Chia hai vế cho
2.
Ví dụ 2. Giải phương trình:
5 sin2 12cos2 13x x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
22
Hướng dẫn: Chia hai vế cho
13.
Ví dụ 3. Giải phương trình:
3 sin 2 cos 2 2 cos 1.x x x
Hướng dẫn:
2
sin2 2 sin cos , cos2 2 cos 1.x x x x x
Ví dụ 4. Giải phương trình:
3 2
2 sin sin .
4 4 2
x x
Hướng dẫn:
sin cos
sin .
4
2
x x
x
Ví dụ 5. Giải phương trình:
2 cos 3 sin cos cos 3 sin 1.x x x x x
Hướng dẫn:
2
2 cos 3 sin cos 2 cos 3 sin 2 .x x x x x
Ví dụ 6. Giải phương trình:
sin 8 cos 6 3 sin 6 cos 8x x x x
Hướng dẫn:
sin 8 3 cos 8 3 sin 6 cos 6 .x x x x
Áp dụng làm các bài tập sau:
Câu 1. Tập nghiệm của phương trình:
sin 3 cos 2x x
là:
A.
5
, .
6
k k
B.
5
2 , .
6
k k
C.
, .
2
k k
D.
2 , .
6
k k
Câu 2. Phương trình
2 sin 1 2 cos 3 1a x a x a
có nghiệm khi:
A.
2
.
1
2
a
a
B.
1
.
2
2
a
a
C.
1
2.
2
a
D.
1
2 .
2
a
Câu 3. Nghiệm của phương trình
sin cos 1x x
là:
A.
2 , .x k k
B.
2 , .
4
x k k
C.
2
, .
2
2
x k
k
x k
D.
2
4
, .
2
4
x k
k
x k
Câu 4. Phương trình
3 sin 3 cos 3 1x x
tương đương với phương trình nào sau đây?
A.
1
sin 3 .
6 2
x
B.
sin 3 .
6 6
x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
23
C.
1
sin 3 .
6 2
x
D.
1
sin 3 .
6 2
x
Câu 5. Điều kiện để phương trình
3 sin cos 5x m x
vô nghiệm là:
A.
4
.
4
m
m
B.
4.m
C.
4.m
D.
4 4.m
Câu 6. Tổng các nghiệm của phương trình
cos 2 sin 2 1x x
trong khoảng
0;2
là:
A.
7
.
4
B.
14
.
4
C.
15
.
8
D.
13
.
4
Câu 7. Nghiệm của phương trình
2 sin cos 1 3 cos 2x x x
là:
A.
2
3
4 2
x k
k
x k
B.
3
, .
4
9 3
x k
k
x k
C.
2
3
2 2
x k
k
x k
D.
3
, .
2
9 3
x k
k
x k
Câu 8. Tổng các nghiệm của phương trình
cos 2 3 sin 2 1x x
trong khoảng
0;
là:
A.
0.
B.
.
C.
2 .
D.
2
.
3
Câu 9. Phương trình
2 sin cos 1
sin 2 cos 3
x x
m
x x
có nghiệm khi:
A.
2
.
1
2
m
m
B.
1
2 .
2
m
C.
1
2.
2
m
D.
1
2.
2
m
Câu 10. Phương trình
2 sin 2 cos 2 1
m x m x m
có nghiệm khi:
A.
4
.
0
m
m
B.
0
.
4
m
m
C.
4 0.m
D.
0 4.m
Câu 11. Giải phương trình
3 sin cos 1 0.x x
A.
, .
3
x k
k
x k
B.
, .
2 2
3
x k
k
x k
C.
2
, .
4
2
3
x k
k
x k
D.
, .
2
3
x k
k
x k
Câu 12. Giải phương trình
3 sin 2 cos 2 2.x x
A.
7
24
, .
24
x k
k
x k
B.
7
2
24
, .
2
24
x k
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
24
C.
7
24 2
, .
24 2
k
x
k
k
x
D.
5
24
, .
24
x k
k
x k
Câu 13. Giải phương trình
sin 3 3 cos 3 2 cos 5x x x
A.
5
48 5
, .
5
12
k
x
k
x k
B.
5
48 4
, .
5
2
12
k
x
k
x k
C.
5
48 4
, .
5
12 2
k
x
k
x k
D.
5
48 4
, .
5
12
k
x
k
x k
Câu 14. Giải phương trình
3 sin 2 cos 7 sin 7 cos 2x x x x
A.
2
10 5
, .
7 2
54 9
k
x
k
x k
B.
3
10 5
, .
7
54 3
k
x
k
x k
C.
10 5
, .
7 2
54 9
k
x
k
x k
D.
2
10 5
, .
7 2
54 9
k
x
k
x k
Câu 15. Giải phương trình
4 4
4 sin cos 3 sin 4 2.
x x x
A.
4 7
, .
12 7
k
x
k
x k
B.
4 5
, .
12 5
k
x
k
x k
C.
4 3
, .
12 3
k
x
k
x k
D.
4 2
, .
12 2
k
x
k
x k
Câu 16. Tìm tất cả các giá trị của tham số
m
để phương trình
2 sin 3 cos 2x m x m
có
nghiệm.
A.
2 2.m
B.
1 1.m
C.
2.m
D.
2 .m
Câu 17. Tìm tất cả các giá trị của tham số
m
để phương trình
2
sin sin2 1x m x
có
nghiệm.
A.
0.m
B.
1.m
C.
2.m
D.
.m
Câu 18. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
3sin 4 cos 5y x x
.
A.
min 0, max 12.y y
B.
min 0, max 10.y y
C.
min 0, max 5.y y
D.
min 2, max 5.y y
Câu 19. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
sin 2 cos 1
sin cos 2
x x
y
x x
.
A.
min 2,max 1.y y
B.
min 1, max 1.y y
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
25
C.
min 1, max 2.y y
D.
min 2, max 2.y y
Đ/a
1B 2C 3C 4C 5D 6B 7A 8D 9C 10A
11C
12A 13D 14D 15D 16D 17D 18B 19A
Daïng toaùn 2: Phöông trình baäc hai ñoái vôùi moät haøm soá löôïng giaùc.

Phương pháp giải:
2
sin sin 0 0
a u b u c a
. Đặt
sint u
,điều kiện
1 1t
.
2
cos cos 0 0
a u b u c a
. Đặt
cost u
,điều kiện
1 1t
.
2
tan tan 0 0
a u b u c a
. Đặt
tant u
, điều kiện
cos 0u
.
2
cot cot 0 0
a u b u c a
. Đặt
cott u
,điều kiện
sin 0u
.
Ví dụ 7. Giải phương trình sau:
2
2cos 3 cos 1 0x x
Hướng dẫn:
cost x
Ví dụ 8. Giải phương trình sau:
2
4 sin 4 sin 3 0x x
.
Hướng dẫn:
sin .t x
Ví dụ 9. Giải phương trình sau:
2
tan 3 1 tan 3 0
x x
.
Hướng dẫn:
tan .x t
Ví dụ 10. Giải phương trình sau:
2
cot 4 cot 3 0x x
.
Hướng dẫn:
cot .x t
Ví dụ 11. Giải phương trình sau:
3 2
sin 3 sin 2 sin 0x x x
.
Hướng dẫn:
sin .t x
Ví dụ 12. Giải phương trình sau:
3
tan cot
2
x x
.
Hướng dẫn:
1
cot . tan
tan
x t x
x
Áp dụng làm các bài tập sau:
Câu 20. Nghiệm của phương trình
2
2cos 3 sin 3 0x x
thuộc
0;
2
là:
A.
.
3
x
B.
.
4
x
C.
.
6
x
D.
5
.
6
x
Câu 21. Tổng các nghiệm của phương trình
2
3
sin 2 3 cos 2 2 0
4 4
x x
trong
khoảng
0;2
là:
A.
7
.
8
B.
3
.
8
C.
.x
D.
7
.
4
x
Câu 22. Nghiệm bé nhất của phương trình
2
2 sin 5 sin 3 0x x
thuộc
0;2
là:
A.
1.
B.
2.
C.
3.
D.
4.
Câu 23. Số nghiệm của phương trình
2
cos2 sin 2 cos 1 0x x x
thuộc
0; 4
là:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
26
A.
1.
B.
2.
C.
4.
D.
6.
Câu 24. Nghiệm của phương trình
2
2sin 5sin 3 0x x
là:
A.
2 , .
2
x k k
B.
, .
2
x k k
C.
, .
2
x k k
D.
2 , .x k k
Câu 25. Phương trình
cos2 2 cos 11 0x x
có tập nghiệm là:
A.
2 , .
k k
B.
, .
k k
C.
2 , .
2
k k
D.
.
Câu 26. Giải phương trình
2
2 sin 5 sin 3 0.x x
A.
, .
2
x k k
B.
, .
2 2
x k k
C.
3 , .
2
x k k
D.
2 , .
2
x k k
Câu 27. Giải phương trình
cos 2 5 sin 3 0.x x
A.
6
, .
7
6
x k
k
x k
B.
3
6
, .
7
3
6
x k
k
x k
C.
4
6
, .
7
4
6
x k
k
x k
D.
2
6
, .
7
2
6
x k
k
x k
Câu 28. Giải phương trình
2
cos2 3 cos 4 cos .
2
x
x x
A.
2
, .
3
x k k
B.
2 2
, .
3 3
x k k
C.
2
4 , .
3
x k k
D.
2
2 , .
3
x k k
Hướng dẫn: Đưa về cùng cung
x
.
Câu 29. Giải phương trình
cos 3 cos2 cos 1 0.x x x
A.
, .x k k
B.
2 2
, .
3 3
x k k
C.
2
2 , .
3
x k k
D.
2 2
,
.
3 3
,
x k k
x k k
Hướng dẫn: Đưa về cùng cung
x
.
Câu 30. Giải phương trình
2
1
3 cot 1 0.
sin
x
x
A.
4 2
, .
arccot 2
2
x k
k
k
x
B.
4 3
, .
arccot 2
3
x k
k
k
x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
27
C.
, .
4
arccot 2
x k
k
x k
D.
, .
4
arccot 2
x k
k
x k
Hướng dẫn:
2
2
1
1 cot .
sin
x
x
Câu 31. Giải phương trình
2
1 5 sin 2 cos 0.x
A.
2
6
, .
5
2
6
x k
k
x k
B.
2
6
, .
2
6
x k
k
x k
C.
2
3
, .
2
2
3
x k
k
x k
D.
2
3
, .
2
3
x k
k
x k
Câu 32. Giải phương trình sau
2
1
1 3 tan 1 3 0.
cos
x
x
A.
3
, .
3
x k
k
x k
B.
2
3
, .
2
4
x k
k
x k
C.
3
, .
4
x k
k
x k
D.
4
, .
3
4
x k
k
x k
Hướng dẫn:
2
2
1
1 tan .
cos
x
x
Câu 33. Giải phương trình
2
2
1 1
cos 2 cos 2 0.
cos
cos
x x
x
x
A.
2 , .x k k
B.
2 , .
2
x k k
C.
, .
2
x k k
D.
2 , .x k k
Hướng dẫn:
2
2
2
1 1
cos 2 cos
cos
cos
x x
x
x
Câu 34. Giải phương trình
1 tan 1 sin 2 1 tan .x x x
A.
2
, .
2
4
x k
k
x k
B.
2
, .
2
4
x k
k
x k
C.
2
, .
2
2
x k
k
x k
D.
, .
2
4
x k
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
28
Hướng dẫn: Đặt
2
2
tan sin 2
1
t
t x x
t
Câu 35. Giải phương trình
2
cos2 cos 2 tan 1 2.
x x x
A.
2
, .
2
3
x k
k
x k
B.
2
, .
2
3
x k
k
x k
C.
, .
2
3
x k
k
x k
D.
2
, .
2
3
x k
k
x k
Hướng dẫn:
sin
tan
cos
x
x
x
Câu 36. Giải phương trình
2
tan tan tan3 2.x x x
A.
, .
4 2
k
x k
B.
, .
3
x k k
C.
, .
4 2
k
x k
D.
2 , .
4
x k k
Hướng dẫn:
sin
tan
cos
x
x
x
Câu 37. Giải phương trình
2 2
2 2
1 1
sin sin
sin sin
x x
x x
A.
2 , .x k k
B.
2 , .x k k
C.
2 , .
2
x k k
D.
2 , .
2
x k k
Hướng dẫn: Đặt
sint x
Câu 38. Giải phương trình
1
2 tan cot 2 sin 2
sin 2
x x x
x
A.
6
, .
4 2
x k
k
x k
B.
3
, .
4 2
x k
k
x k
C.
2
3
, .
4
x k
k
x k
D.
2
3
, .
2
x k
k
x k
Hướng dẫn:
sin cos
tan , cot
cos sin
x x
x x
x x
Câu 39. Giải phương trình
4 4
11
sin cos sin 2
8
x x x
A.
6
, .
5
6
x k
k
x k
B.
12
, .
5
12
x k
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
29
C.
2
12
, .
5
2
12
x k
k
x k
D.
2
6
, .
5
2
6
x k
k
x k
Hướng dẫn:
4 4 2
1
sin cos 1 sin 2
2
x x x
Câu 40. Giải phương trình
5 5 4
4 sin cos 4 cos sin sin 4x x x x x
A.
, .
2
2
x k
k
x k
B.
, .
2
2
x k
k
x k
C.
4
, .
8 2
k
x
k
k
x
D.
4
, .
4 2
k
x
k
k
x
Hướng dẫn:
5 5 2 2 2 2
4 sin cos 4 cos sin 4 sin cos sin cos sin cosx x x x x x x x x x
Câu 41. Giải phương trình
cos 2 cos 2 4 sin 2 2 1 sin
4 4
x x x x
A.
2
6
, .
2
6
x k
k
x k
B.
2
3
, .
2
2
3
x k
k
x k
C.
2
6
, .
5
2
6
x k
k
x k
D.
2
3
, .
2
3
x k
k
x k
Hướng dẫn:
cos 2 cos 2 2 cos2 cos
4 4 4
x x x
Đáp án
20C
21D
22A
23B
24A
25D
26A 27A 28D 29D 30C 31A
32C 33C 34D 35B 36C 37D
38A 39B 40C 41C
Daïng toaùn 3: Phöông trình thuaàn nhaát ( ñaúng caáp) ñoái vôùi sin vaø cos
2 2
sin sin cos cos 1
a x b x x c x d
.

Phương pháp giải:
2 2
sin sin cos cos 1
a x b x x c x d
Cách giải.Xét 2 trường hợp :
Trường hợp 1 :Xét
cos 0 sin 1x x
.Thay vào (1) xem thoả hay không thoả.Kết luận
Trường hợp 2:Xét
cos 0.x
Chia hai vế của (1) cho
2
cos x
,rồi đưa về phương trình bậc hai
theo
tan x
,giải bình thường.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
30
2
1 tan tan 0.a d x b x c d
Sơ đồ tư duy:
Ví dụ 13. Giải phương trình:
2 2
3 sin 6 sin cos 3 2 3 cos 3x x x x
.
Hướng dẫn: Chia hai vế cho
2
cos .x
Ví dụ 14. Giải phương trình:
2 2
2 sin 3 3 sin cos cos 4x x x
.
Hướng dẫn: Chia hai vế cho
2
cos .x
Ví dụ 15. Giải phương trình:
2 2
1
sin sin 2 2 cos
2
x x x
.
Hướng dẫn: Chia hai vế cho
2
cos .x
Ví dụ 16. Giải phương trình:
4 2 2 4
3 cos 4 sin cos sin 0x x x x
.
Hướng dẫn: Chia hai vế cho
4
cos .x
Ví dụ 17. Giải phương trình:
2
2
sin sin sin 2 cos 3 1 sin 1 sinx x x x x x
.
Hướng dẫn:
2
1 sin 1 sin sin 2 cos 3 1 sin 1 sinx x x x x x
Áp dụng làm các bài tập sau:
Câu 42. Tập nghiệm của phương trình:
2 2
3 sin 2 3 sin cos 3 cos 0x x x x
là:
A.
, , .
6 3
k k k
B.
2 , 2 , .
6 3
k k k
C.
, .
6
k k
D.
5
.
6
x
Câu 43. Phương trình
2 2
3 sin sin2 4 cos 0x m x x
có nghiệm khi:
A.
4.m
B.
4.m
C.
4.m
D.
.m
Câu 44. Nghiệm của phương trình
2
sin sin cos 1x x x
là:
A.
4
, .
2
x k
k
x k
B.
4
, .
2
x k
k
x k
C.
2
4
, .
2
2
x k
k
x k
D.
2
4
, .
2
2
x k
k
x k
Câu 45. Nghiệm của phương trình
2 2
cos 3 sin 2 1 sinx x x
là:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
31
A.
2
3
x k
k
x k
B.
, .
3
x k
k
x k
C.
2
, .
3
x k
k
x k
D.
, .
3
x k
k
x k
Câu 46. Số nghiệm của phương trình
2 2
sin 2 sin cos 3cos 3x x x x
thuộc khoảng
0;2
là:
A.
1.
B.
2.
C.
3.
D.
4.
Câu 47. Nghiệm của phương trình:
3 2 2 2
sin 3 cos 3 sin cos sin cos 0x x x x x x
là:
A.
4
, .
3
x k
k
x k
B.
4
, .
3
x k
k
x k
C.
4
, .
3
x k
k
x k
D.
2
4
, .
2
3
x k
k
x k
Câu 48. Giải phương trình
2 2
2 cos 6 sin cos 6sin 1x x x x
A.
2
4
, .
1
arctan 2
5
x k
k
x k
B.
2
4
, .
1
arctan
5
x k
k
x k
C.
4
, .
1
arctan
5 2
x k
k
k
x
D.
4
, .
1
arctan
5
x k
k
x k
Câu 49. Giải phương trình
3 2 2
4 sin 3 cos 3 sin sin cos 0x x x x x
A.
2
4
, .
2
3
x k
k
x k
B.
4 2
, .
3 2
k
x
k
k
x
C.
4 3
, .
3 3
k
x
k
k
x
D.
4
, .
3
x k
k
x k
Hướng dẫn: Chia 2 vế cho
3
cos x
Câu 50. Giải phương trình
3
2cos sin 3x x
A.
arctan 2 2
, .
2
4
x k
k
x k
B.
arctan 2
2
, .
4 2
k
x
k
k
x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
32
C.
arctan 2
3
, .
4 3
k
x
k
k
x
D.
arctan 2
, .
4
x k
k
x k
Hướng dẫn:
3
sin 3 3sin 4 sinx x x
Câu 51. Giải phương trình
2 2
2 sin 3 sin cos 3 cos 2x x x x
A.
2
2
, .
1
arctan
3
x k
k
x k
B.
1
arctan
3
, .
2
x k
k
x k
C.
1
arctan , .
3
x k k
D.
, .
1
arctan 2
3
x k
k
x k
Câu 52. Giải phương trình
sin2 2 tan 3x x
A.
, .
3
x k
k
x k
B.
2
, .
4
x k
k
x k
C.
, .
4
x k k
D.
, .
4
x k
k
x k
Hướng dẫn: Chia hai vế cho
2
cos x
Câu 53. Giải phương trình sau
2 2
2 sin 3 3 sin cos 3 1 cos 1
x x x x
A.
; , .
4 6
x k x k k
B.
2 ; , .
4 6
x k x k k
C.
; , .
4 2
x k x k k
D.
; , .
2 6
x k x k k
Câu 54. Giải phương trình
2 2
2 sin sin cos 3 cos 0x x x x
A.
3
2 ; arctan , .
2 2
x k x k k
B.
; arctan 3 , .
4
x k x k k
C.
3
; arctan , .
4 2
x k x k k
D.
; arctan 3 2 , .
x k x k k
Câu 55. Giải phương trình
2 2
2 cos 6 3 sin cos 4 sin 4x x x x
A.
; , .
2 6
x k x k k
B.
2 ; , .
2 6
x k x k k
C.
2 ; , .
2 6
x k x k k
D.
; , .
2 6
x k x k k
Câu 56. Giải phương trình
2 2
cos 3 sin 2 1 sinx x x
A.
; , .
3
x k x k k
B.
2 ; , .
2 3
x k x k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
33
C.
; , .
3
x k x k k
D.
, .
3
x k k
Câu 57. Giải phương trình
3 3 2
cos 4 sin 3 cos sin sin 0x x x x x
A.
; , .
4 3
x k x k k
B.
; , .
4 6
x k x k k
C.
; , .
3
x k x k k
D.
; , .
4 6
x k x k k
Câu 58. Giải phương trình
2 2
3 sin 4 sin cos 5 cos 2.x x x x
A.
; arctan 3 , .
4
x k x k k
B.
; arctan 3 , .
4
x k x k k
C.
3
; arctan , .
4 2
x k x k k
D.
; arctan 3 2 , .
x k x k k
Câu 59. Giải phương trình
2 2
1
sin sin 2 2 cos .
2
x x x
A.
; arctan 3 , .
4
x k x k k
B.
; arctan 5 , .
4
x k x k k
C.
5
; arctan , .
4 2
x k x k k
D.
; arctan 5 2 , .x k x k k
Câu 60. Giải phương trình
4 2 2 4
3 cos 4 sin cos sin 0x x x x
A.
; , .
4 3
x k x k k
B.
; 2 , .
4 4
x k x k k
C.
; , .
4 3
x k x k k
D.
, .
3
x k k
Câu 61. Giải phương trình
2
sin sin 2 sin 3 6 cosx x x x
A.
; , .
3
x k x k k
B.
; arctan2 2 , .
3
x k x k k
C.
; , .
4 3
x k x k k
D.
; arctan 2 , .
3
x k x k k
Câu 62. Giải phương trình
2
cos2 1
cot 1 sin sin 2
1 tan 2
x
x x x
x
A.
; , .
4
x k x k k
B.
; 2 , .
3 4
x k x k k
C.
, .
4
x k k
D.
, .
4
x k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
34
Câu 63. Giải phương trình
sin 3 cos 3 2 cos 0x x x
A.
; , .
4
x k x k k
B.
; 2 , .
3 4
x k x k k
C.
; , .
3 4
x k x k k
D.
; , .
4 3
x k x k k
Câu 64. Giải phương trình
3
sin 4 sin cos 0x x x
A.
, .
4
x k k
B.
2 ; , .
4 3
x k x k k
C.
; , .
4
x k x k k
D.
, .
4
x k k
Câu 65. Giải phương trình
2 2
tan sin 2 sin 3 cos 2 sin cosx x x x x x
A.
; , .
4
x k x k k
B.
; , .
3 4
x k x k k
C.
; , .
3 4
x k x k k
D.
; 2 , .
3 4
x k x k k
Câu 66. Giải phương trình
3 2
cos sin 3 sin cos 0x x x x
A.
, arctan 2 , .
4
x k x k k
B.
, .
4
x k k
C.
1
, arctan , .
4 2
x k x k k
D.
, .
4
x k k
Câu 67. Giải phương trình
2
sin tan 1 3 sin cos sin 3
x x x x x
A.
; , .
4 3
x k x k k
B.
; , .
4
x k x k k
C.
; , .
4 3
x k x k k
D.
2 ; , .
4 3
x k x k k
Đáp án 42A 43D 44A 45D 46C 47A
48D 49D 50D 51B 52C 53A
54C 55A 56A 57D 58A 59B
60C 61D 62C 63D 64A 65B
66C 67A
Daïng toaùn 4: Phöông trình ñoái xöùng
sin cos sin cos 0 1
a x x b x x c
.

Phương pháp giải:
sin cos sin cos 0 1
a x x b x x c
Cách giải.Đặt :
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
35
2
1
sin cos sin cos 2 2
2
t
t x x x x t
2
1
sin cos sin cos 2 2
2
t
t x x x x t
2
1
cos sin sin cos 2 2
2
t
t x x x x t
Thay vào (1) rồi giải phuong trình bậc 2 theo t.
Sơ đồ tư duy:
Ví dụ 18. Giải phương trình
sin cos sin cos 1 0.x x x x
Hướng dẫn:
2
1
sin cos sin cos 2 2
2
t
t x x x x t
Ví dụ 19. Giải phương trình
tan 1 2 2 sinx x
.
Hướng dẫn:
sin
tan
cos
x
x
x
Ví dụ 20. Giải phương trình
2 sin2 3 3 sin cos 5 0x x x
.
Hướng dẫn:
2
1
sin cos sin cos 2 2
2
t
t x x x x t
Ví dụ 21. Giải phương trình
2 sin 2 3 6 sin cos 8 0.x x x
Hướng dẫn: Đặt
sin cost x x
( Đk :
0 2t
)
2 2
(sin cos )t x x
2
sin2 1x t
Ví dụ 22. Giải phương trình
sin2 2 sin 1.
4
x x
Hướng dẫn:
sin 2 (sin cos ) 1x x x
Daïng toaùn 5: Phöông trình ñoái xöùng.
2 2
tan cot tan cot 0 1a x x b x x c
.

Ví dụ 23. Giải phương trình lượng giác
2 tan 5 tan 2 cot 5 cot 8 0x x x x
.
Hướng dẫn:
2 2
1 tan cot 5 tan cot 8 0.x x x x
Ví dụ 24. Giải phương trình lượng giác
2 2
3 tan 8 cot 8 tan 3 cot 2 3x x x x
.
Hướng dẫn:
2 2
1 3 tan cot 8 tan cot 2 3 0.x x x x
Áp dụng làm các bài tập sau:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
36
Câu 68. Giải phương trình
sin 2 4 sin cos 4.
x x x
A.
, .
2
x k
k
x k
B.
2
2 3
, .
2
3
x k
k
x k
C.
1
2 2
, .
1
2
x k
k
x k
C.
2
, .
2
2
x k
k
x k
Câu 69. Giải phương trình
sin2 2 sin 1.
4
x x
A.
; ; 2 , .
4 2
x k x k x k k
B.
1 1 1
; ; , .
4 2 2 2 2
x k x k x k k
C.
2 2
; ; 2 , .
4 3 2 3
x k x k x k k
D.
; 2 ; 2 , .
4 2
x k x k x k k
Câu 70. Giải phương trình
cos sin 2 sin 2 1
x x x
A.
, .x k k
B.
1
, .
2
x k k
C.
2 , .x k k
D.
, .
2
x k k
Câu 71. Giải phương trình
cos sin 3 sin 2 1
x x x
A.
, .x k k
B.
1
, .
2
x k k
C.
2 , .x k k
D.
, .
2
x k k
Câu 72. Giải phương trình
2 sin cos 3 sin 2 2
x x x
A.
2 ; 2 , .
2
x k x k k
B.
; , .
2
x k x k k
C.
2 ; 2 , .x k x k k
D.
; 2 , .
3
x k x k k
Câu 73. Giải phương trình
3 3
3
1 sin 2 cos 2 sin 4
2
x x x
A.
; 2 , .
4 2
x k x k k
B.
; , .
4 2
x k x k k
C.
2 ; 2 , .x k x k k
D.
; 2 , .
3
x k x k k
Hướng dẫn: Dùng hằng đẳng thức
3 3 2 2
a b a b a ab b
phân tích
3 3
sin 2 cos 2x x
và chuyển
sin 4 2 sin 2 cos 2 .x x x
Câu 74. Giải phương trình
6 sin cos sin cos 6 0
x x x x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
37
A.
, 2 , .
2
x k x k k
B.
2 , 2 , .
2
x k x k k
C.
3
2 , 2 , .
2
x k x k k
D.
2 , 2 , .
3
x k x k k
Câu 75. Giải phương trình
cos 2 5 2 2 cos sin cosx x x x
A.
, 2 , .
2
x k x k k
B.
2 , 2 , .
2
x k x k k
C.
3
2 , 2 , .
2
x k x k k
D.
2 , 2 , .
2
x k x k k
Hướng dẫn:
2 2
cos 2 cos sin cos sin cos sinx x x x x x x
Câu 76. Giải phương trình
3
sin cos 2 sin 2 1 sin cos 2
x x x x x
A.
, 2 , .
4
x k x k k
B.
2 , .
4
x k k
C.
2 , 2 , .
4
x k x k k
D.
2 , , .
2
x k x k k
Hướng dẫn:
2
sin 2 1 sin cos , sin cosx x x t x x
Câu 77. Giải phương trình
3 3 2 2
tan cot 3 tan cot 3 tan cot 10 0
x x x x x x
A.
1 1
, arctan , .
8 2 2 2 2
k k
x x k
B.
2 , 2 , .
8 4
x k x k k
C.
7
, , .
4 8
x k x k k
D.
, 2 , .
2
x k x k k
Hướng dẫn:
2 2 2
3
3 3 3
tan cot 2
tan cot ,
tan cot tan cot 3 tan cot tan cot 3
x x t
t x x
x x x x x x x x t t
Câu 78. Giải phương trình

3 cos 4 sin cos 2
x x x
A.
, 2 , .
8 2 4
k
x x k k
B.
2 , 2 , .
8 4
x k x k k
C.
7
, , .
4 8
x k x k k
D.
2 , 2 , .
2
x k x k k
Câu 79. Giải phương trình
2
2
3
3 cot 4 tan cot 1 0
cos
x x x
x
A.
, .
4
x k k
B.
2 , .
4
x k k
C.
7
, .
12
x k k
D.
, .
2
x k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
38
Câu 80. Giải phương trình
2
2
2
2 tan 5 tan cot 4 0
sin
x x x
x
A.
, .
12
x k k
B.
2 , .
4
x k k
C.
, .
4
x k k
D.
2 , .
2
x k k
Câu 81. Giải phương trình
4 4
1 sin cos
cos
sin
x x
x
x
A.
2 ; , .
2 4
x k x k k
B.
2 , .
4
x k k
C.
, .
4
x k k
D.
; , .
2 4
x k x k k
Câu 82. Giải phương trình
3
2 cos cos2 sin 0x x x
A.
2 ; , .
2 4
x k x k k
B.
; , .
2 4
x k x k k
C.
, .
4
x k k
D.
2 , .
2
x k k
Câu 83. Giải phương trình
tan 3 cot 4 sin 3 cosx x x x
A.
4 2
; , .
3 9 3
k
x k x k
B.
; , .
3 4
x k x k k
C.
2 ; , .
3 4
x k x k k
D.
2
; , .
3 9 3
k
x k x k
Câu 84. Giải phương trình
3 3
sin cos sin cosx x x x
A.
2 , .
3
x k k
B.
, .
3
x k k
C.
, .
4
x k k
D.
, .
2
x k k
Câu 85. Giải phương trình
2 cos 1 sin cos 1
x x x
A.
2
2 ; , .
6 3
k
x k x k
B.
2 ; , .
3
x k x k k
C.
; , .
4
x k x k k
D.
; , .
2
x k x k k
Câu 86. Giải phương trình
2 cos2 6 cos sinx x x
A.
2
2 ; , .
12 6 3
k
x k x k
B.
2 ; , .
12 3
x k x k k
C.
5
2 ; 2 , .
12 12
x k x k k
D.
2 ; , .
6 2
x k x k k
Đáp án 68D 69D 70B 71B 72A 73B 74C 75D 76B
77A 78D 79A 80C 81D 82A 83A 84D 85A
86C
`
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
39
ÔN TẬP CHƯƠNG I.
PhÇn 1. Hµm sè lîng gi¸c.
Câu 1.
Tìm tập xác định của hàm số
1 sin 2
.
cos 3 1
x
y
x
A.
2
\ , .
3
k
D k
B.
\ , .
6
k
D k
C.
\ , .
3
k
D k
D.
\ , .
2
k
D k
Câu 2.
Tìm tập xác định của hàm số
1 cos 3
1 sin 4
x
y
x
A.
\ , .
8 2
k
D k
B.
3
\ , .
8 2
k
D k
C.
\ , .
4 2
k
D k
D.
\ , .
6 2
k
D k
Câu 3.
Tìm tập xác định của hàm số
tan 2
3 sin 2 cos 2
x
y
x x
A.
\ , ; , .
4 2 12 2
k t
D k t
B.
\ , ; , .
3 2 5 2
k t
D k t
C.
\ , ; , .
4 2 3 2
k t
D k t
D.
\ , ; , .
3 2 12 2
k t
D k t
Câu 4.
Tìm tập xác định của hàm số sau
tan 2
3
y x
A.
\ , .
3 2
k
D k
B.
\ , .
4 2
k
D k
C.
\ , .
12 2
k
D k
D.
\ , .
8 2
k
D k
Câu 5.
Tìm tập xác định của hàm số sau
tan 3 .cot5y x x
A.
\ , ; , .
6 3 5
k n
D k n
B.
\ , ; , .
5 3 5
k n
D k n
C.
\ , ; , .
6 4 5
k n
D k n
D.
\ , ; , .
4 3 5
k n
D k n
Câu 6.
Tìm tập xác định của hàm số sau
tan .cot
4 3
y x x
A.
3
\ , ; .
4 3
D k k k
B.
3
\ , ; .
4 5
D k k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
40
C.
\ , ; .
4 3
D k k k
D.
3
\ , ; .
5 6
D k k k
Câu 7.
Hàm số
sinf x x
tuần hoàn với chu kì:
A.
2 .T
B.
.T
C.
.
2
T
D.
.
4
T
Câu 8.
Hàm số
tan 2f x x
tuần hoàn với chu kì:
A.
.
2
T
B.
2 .T
C.
.T
D.
.
4
T
Câu 9.
Hàm số
sin 2 sinf x x x
tuần hoàn với chu kì:
A.
2 .T
B.
.
2
T
C.
.T
D.
.
4
T
Câu 10.
Hàm số
tan . tan 3f x x x
tuần hoàn với chu kì:
A.
.T
B.
2 .T
C.
.
4
T
D.
.
2
T
Câu 11.
Hàm số
sin 3 2 cos 2f x x x
tuần hoàn với chu kì:
A.
2 .T
B.
.
2
T
C.
.T
D.
.
4
T
Câu 12.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 3 sin 3y x
A.
min 2;max 5.y y
B.
min 1;max 4.y y
C.
min 1; max 5.y y
D.
min 5;max 5.y y
Câu 13.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
1 4 sin 2y x
A.
min 2;max 1.y y
B.
min 3;max 5.y y
C.
min 5;max 1.y y
D.
min 3;max 1.y y
Câu 14.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 sin 3y x
A.
min 1;max 5.y y
B.
min 5;max 2 5.y y
C.
min 2;max 5.y y
D.
min 5; max 3.y y
Câu 15.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3 2 2 sin 4y x
A.
min 3 2 2; max 3 2 3.y y
B.
min 2 2 2;max 3 2 3.y y
C.
min 3 2 2;max 3 2 3.y y
D.
min 3 2 2; max 3 3 3.y y
Câu 16.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 cos sin 4y x x
A.
min 2; max 4.y y
B.
min 2; max 6.y y
C.
min 4;max 6.y y
D.
min 2; max 8.y y
Câu 17.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
1 2 cos 1y x
A.
min 1 3; max 1.y y
B.
min 1 3; max 3.y y
C.
min 1 3; max 2.y y
D.
min 1 3;max 0.y y
Câu 18.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3 2 cos 3y x
A.
min 1; max 2.y y
B.
min 1;max 3.y y
C.
min 2; max 3.y y
D.
min 1;max 3.y y
Câu 19.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1 2 sin 2y x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
41
A.
min 2; max 1 3.y y
B.
min 2;max 2 3.y y
C.
min 1;max 1 3.y y
D.
min 1; max 2.y y
Câu 20.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
4
1 2 sin
y
x
A.
4
min ;max 4.
3
y y
B.
4
min ;max 3.
3
y y
C.
4
min ;max 2.
3
y y
D.
1
min ; max 4.
2
y y
Câu 21.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 2
2 sin cos 2y x x
A.
3
min ;max 4.
4
y y
B.
min 2; max 3.y y
C.
min 2; max 4.y y
D.
3
min ;max 3.
4
y y
Câu 22.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 sin 4 cos 1y x x
A.
min 6; max 4.y y
B.
min 6;max 5.y y
C.
min 3; max 4.y y
D.
min 6;max 6.y y
Câu 23.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 2
2 sin 3 sin 2 4 cosy x x x
A.
min 3 2 1; max 3 2 1.y y
B.
min 3 2 1; max 3 2 1.y y
C.
min 3 2;max 3 2 1.y y
D.
min 3 2 2;max 3 2 1.y y
Câu 24.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 2
sin 3 sin 2 3 cosy x x x
A.
min 2 10;max 2 10.y y
B.
min 2 5;max 2 5.y y
C.
min 2 2; max 2 2.y y
D.
min 2 7; max 2 7.y y
Câu 25.
Khi
x
thay đổi trong nửa khoảng
;
3 3
thì
cosy x
lấy mọi giá trị thuộc:
A.
1
;1 .
2
B.
1 1
; .
2 2
C.
1 1
; .
2 2
D.
1
1; .
2
Câu 26.
Khi
x
thay đổi trong khoảng
5 7
;
4 4
thì
siny x
lấy mọi giá trị thuộc:
A.
2
;1 .
2
B.
2
1; .
2
C.
2
;0 .
2
D.
1;1 .
Câu 27.
Tập giá trị của hàm số
4 cos 2 3 sin 2 6y x x
là:
A.
3;10 .
B.
6;10 .
C.
1;13 .
D.
1;11 .
Câu 28.
Trong các mệnh đề sau, mệnh đề nào sai?
A.
2 siny x
là hàm số lẻ. B.
tan siny x x
là hàm số lẻ.
C.
tan cosy x x
là hàm số lẻ. D.
siny x x
là hàm số lẻ.
Câu 29.
Trong các mệnh đề sau, mệnh đề nào sai?
A. Tổng của hai hàm số chẵn là một hàm số chẵn.
B. Tích của hai hàm số lẻ là một hàm số chẵn.
C. Tổng của hai hàm lẻ là một hàm số lẻ.
D. Tổng của hai hàm số chẵn là một hàm số lẻ.
Câu 30.
Hàm số
siny x
nghịch biến trên khoảng:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
42
A.
19
;10 .
2
B.
11
;5 .
2
C.
15
7 ; .
2
D.
3 5
; .
2 2
Câu 31.
Hàm số
cosy x
nghịch biến trên khoảng:
A.
19
;10 .
2
B.
11
;6 .
2
C.
15
7 ; .
2
D.
5
;6 .
2
Câu 32.
Cho hàm số
sin .cos 3y x x
. Chọn mệnh đề đúng?
A.
y
là hàm số chẵn. B.
y
là hàm số lẻ.
C.
y
là hàm số không chẵn, không lẻ. D.
y
là hàm số vừa chẵn, vừa lẻ.
Câu 33.
Cho hàm số
2 1 *
cos ,
n
y f x x n
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 34.
Cho hàm số
2
siny f x x
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 35.
Cho hàm số
2
sin cosy f x x x
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 36.
Cho hàm số
2
2 tan
1 tan
x
y f x
x
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 37.
Cho hàm số
cos siny f x x x
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 38.
Cho hàm số
2
2
tan 3 cos
2
x x
y f x
x
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 39.
Cho hàm số
tan cosy f x x x
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 40.
Cho hàm số
2
sin 2 3 cos
cos 3
x x
y f x
x
. Hàm số
f x
là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 41.
Hình vẽ dưới đây là đồ thị của hàm số nào?
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
43
A.
tan 2 .y x
B.
tan .y x
C.
2 tan .y x
D.
cot .y x
Câu 42.
Hình vẽ dưới đây là đồ thị của hàm số nào?
A.
tan 2 .y x
B.
2
1 2 cos .y x
C.
2 tan .y x
D.
cot .y x
Câu 43.
Hình vẽ dưới đây là đồ thị của hàm số nào?
A.
cos 2 .y x
B.
tan .y x
C.
sin 2 .y x
D.
cos .y x
Câu 44.
Hình vẽ dưới đây là đồ thị của hàm số nào?
A.
cos 2 .y x
B.
tan .y x
C.
sin 2 .y x
D.
2 cos .y x
Câu 45.
Đồ thị hàm số
siny x
trên đoạn
0;2
là:
A.
B.
C. D.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
44
Câu 46.
Đồ thị hàm số
siny x
trên đoạn
0;2
là:
A.
B.
C.
D.
ĐÁP ÁN.
1A 2A 3A 4C 5A 6A 7A 8A 9A 10A
11A 12C 13D 14A 15A 16B 17D 18B 19A 20A
21D 22A 23B 24A 25A 26B 27D 28C 29D 30C
31D 32B 33D 34D 35D 36B 37C 38D 39C 40D
41A 42B 43C 44D 45B 46C
Hướng dẫn giải:
Câu 16.
3 1
2 cos sin 4 2 sin 4.
2 2 3
y x x x
Câu 21. Đặt
2
2 2
1 3
sin , 0 1 cos2 1 2 4 2 1 2
2 4
t x t x t y t t t
Câu 22.
5 sin 1y x
Câu 23.
1 cos2 3 sin 2 2 1 cos2
3 sin 2 3 cos 2 1 3 2 sin 2 1
4
y x x x
x x x
Câu 24.
3 1 cos2
1 cos 2
3 sin 2 3 sin 2 cos 2 2
2 2
x
x
y x x x
PhÇn 2. Ph¬ng tr×nh lîng gi¸c c¬ b¶n.
Câu 1.
Trong các mệnh đề sau, mệnh đề nào sai?
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
45
A.
sin 1 2 , .
2
x x k k
B.
sin 0 , .x x k k
C.
sin 0 2 , .x x k k
D.
sin 1 2 , .
2
x x k k
Câu 2.
Giải phương trình:
1
sin .
2
x
A.
2
6
, .
5
2
6
x k
k
x k
B.
6
, .
6
x k
k
x k
C.
, .
6
x k k
D.
3
, .
3
x k
k
x k
Câu 3.
Giải phương trình
2
sin 0.
3 3
x
A.
x k
B.
, .x k k
C.
, .
2
x k k
D.
2
, .
2 3
k
x k
Câu 4.
Giải phương trình
1 2 cos2 0.x
A.
, .
3
x k k
B.
2 , .
3
x h k
C.
, .
3
x k k
D.
, .
3
x k k
Câu 5.
Giải phương trình
cos 3 cos .
15
x
A.
x k k
B.
2
, .
45 3
k
x k
C.
2
, .
45 3
k
x k
D.
2
, .
45 3
k
x k
Câu 6.
Giải phương trình
3
sin2 .
2
x
A.
6
, .
2
3
x k
k
x k
B.
6
, .
6
x k
k
x k
C.
, .
6
x k k
D.
3
, .
3
x k
k
x k
Câu 7.
Giải phương trình
2 cos 3 0.
2
x
A.
5
2 , .
3
x k k
B.
5
2 , .
6
x k k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
46
C.
5
4 , .
6
x k k
D.
5
4 , .
3
x k k
Câu 8.
Giải phương trình
sin cos .x x
A.
8 2
, .
4
k
x
k
x k
B.
, .
8
x k k
C.
, .
4
x k k
D.
2
4
, .
8
x k
k
x k
Câu 9.
Giải phương trình lượng giác:
3 tan 3 0.x
A.
, .
3
x k k
B.
2 , .
3
x k k
C.
, .
6
x k k
D.
, .
3
x k k
Câu 10.
Giải phương trình:
2
tan 3.x
A.
, .
6
x k k
B.
, .
3
x k k
C. Vô nghiệm. D.
, .
6
x k k
Câu 11.
Giải phương trình
cos 2 60 cos 30 .
x x
A.
90 360 , .x k k
B.
10 120 , .x k k
C.
90 360
, .
10 120
x k
k
x k
D.
2
2
, .
2
18 3
x k
k
x k
Câu 12.
Hàm số
tan 3y x
và
tan 2
3
y x
có giá trị bằng nhau khi:
A.
, .
15
x k k
B.
2 , .
15
x k k
C.
, .
15 5
x k k
D.
, .
15 2
x k k
Câu 13.
Giải phương trình
2 2
sin 2 cos 2 cos 3x x x
A.
2
, .
7
2
x k
k
x k
B.
2
, .
7 7
2
x k
k
x k
C.
2 , .
7
x k k
D.
2 , .x k k
Câu 14.
Giải phương trình
6 sin 4 5 sin 8 0.x x
A.
4
, .
1 3
arccos
4 5 2
k
x
k
k
x
B.
4
, .
1 3
arccos
3 5 2
k
x
k
k
x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
47
C.
1
4
, .
1 3
arccos
4 5 2
k
x
k
k
x
D.
4
, .
1 3
arccos
4 5 2
k
x
k
k
x
Câu 15.
Nghiệm của phương trình
sin 2 cos 3 0
x x
là:
A.
, .
2
6
x k
k
x k
B.
, .
6
x k
k
x k
C.
2
, .
2
3
x k
k
x k
D.
2 , .
6
x k k
Câu 16.
Phương trình
sin .cos .cos 2 0x x x
có nghiệm là:
A.
, .
16
x k k
B.
, .
2
x k k
C.
, .
4
x k k
D.
, .
8
x k k
Câu 17.
Giải phương trình
cot2 .sin 3 0.x x
A.
4 2
2
, .
3
3
x k
x k k
x k
B.
4 2
, .
2
3
x k
k
x k
C.
4 2
, .
3
x k
k
x k
D.
4 2
, .
3
x k
k
x k
Câu 18.
Giải phương trình
cot .cot2 1.x x
A.
, .
6 3
x k k
B.
, .
3 3
x k k
C.
, .
6
x k k
D.
, .
3
x k k
Câu 19.
Giải phương trình
tan 3 tan 4x x
.
A.
, .
2
x k k
B.
2 , .x k k
C.
2 , .x k k
D.
, .x k k
Câu 20.
Giải phương trình
sin
0
1 cos
x
x
có nghiệm.
A.
, .x k k
B.
2 1 , .
x k k
C.
2 , .x k k
D.
2 1 , .
2
x k k
Câu 21.
Giải phương trình
cos 3 sin
0
1
sin
2
x x
x
.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
48
A.
2 , .
6
x k k
B. Vô nghiệm.
C.
, .
6
x k k
D.
7
2 , .
6
x k k
Câu 22.
Giải phương trình
2
3 tan 1 sin 1 0
x x
có nghiệm là:
A.
2 , .
3
x k k
B.
2 , .
6
x k k
C.
, .
6
x k k
D.
, .
3
x k k
Câu 23.
Phương trình
cos 2 cos 2
3 3
x x
có nghiệm dương nhỏ nhất là:
A.
3
.
2
x
B.
.x
C.
2 .x
D.
.
2
x
Câu 24.
Nghiệm dương nhỏ nhất của phương trình
3
cot 1
2
x
là:
A.
3
.
4
x
B.
7
.
4
x
C.
.
4
x
D.
.
2
x
Câu 25.
Giải phương trình
2 2
3 3
x
.
A.
, .
2
x k k
B.
2
, .
2 3
x k k
C.
2 , .
2
x k k
D.
2 , .
3
x k k
Câu 26.
Giải phương trình
cot cos 1 1
4
x
.
A.
2 , .
2
x k k
B.
, .
2 2
x k k
C.
, .
2 3
x k k
D.
, .
2
x k k
Câu 27.
Phương trình
sin cosx x
có nghiệm thuộc đoạn
;
là:
A.
2.
B.
4.
C.
5.
D.
6.
Câu 28.
Phương trình
cos 4
tan 2
cos2
x
x
x
có số nghiệm thuộc khoảng
0;
2
là:
A.
2.
B.
3.
C.
4.
D.
5.
Câu 29.
Giải phương trình
2 sin 2 1x
với điều kiện
cos 0.x
A.
12
, .
5
2
12
x k
k
x k
B.
12
, .
5
2
12
x k
k
x k
C.
12
, .
5
2
12
x k
k
x k
D.
12
, .
5
2
12
x k
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
49
Câu 30.
Giải phương trình
3 cot2 3x
với điều kiện
cos 0.x
A.
2
6
2
x k
k
x k
B.
2
6
2
x k
k
x k
C.
2
6
, .
2
3
x k
k
x k
D.
2
6
2
x k
k
x k
Câu 31.
Giải phương trình
2 sin 3
0
cos
x
x
.
A.
2
3
, .
2
2
3
x k
k
x k
B.
2
3
2
2
x k
k
x k
C.
2
3
, .
2
2
3
x k
k
x k
D.
2
6
2
x k
k
x k
Câu 32.
Giải phương trình
2 cos 2
0.
2 sin 1
x
x
A.
3
, .
4
x k k
B.
3
2 , .
4
x k k
C.
3
, .
4
x k k
D.
2 , .
4
x k k
Câu 33.
Phương trình
cos 0x m
vô nghiệm khi và chỉ khi:
A.
1
.
1
m
m
B.
1.m
C.
1 1.m
D.
1.m
Câu 34.
Phương trình
1
sin 2
2
x
có bao nhiêu nghiệm thỏa
0 .x
A.
1.
B.
3.
C.
2.
D.
4.
Câu 35.
Phương trình
1
sin
2
x
có nghiệm thỏa
2 2
x
là:
A.
.
6
x
B.
.
6
x
C.
.
3
x
D.
.
3
x
Câu 36.
Số nghiệm của phương trình
sin 1
4
x
với
3x
là:
A.
1.
B.
0.
C.
2.
D.
3.
Câu 37.
Nghiệm của phương trình lượng giác:
2
cos cos 0x x
thỏa điều kiện
0 x
là:
A.
.
2
x
B.
0.x
C.
.x
D.
.
4
x
Câu 38.
Số nghiệm của phương trình
2 cos 1
3
x
với
0 2x
là:
A.
0.
B.
2.
C.
1.
D.
3.
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
50
Câu 39.
Giải phương trình
2
sin 2 15 ,
2
x
với
120 90 .x
A.
30 ; 75 ; 105 .x x x
B.
30 ; 105 .x x
C.
60 ; 90 ; 105 .x x x
D.
30 ; 75 ; 45 .x x x
Câu 40.
Phương trình
sin sin 0
4 4
x x
có tổng các nghiệm thuộc khoảng
0; 4
bằng:
A.
10 .
B.
9 .
C.
6 .
D.
2 .
ĐÁP ÁN:
1C 2A 3D 4A 5B 6A 7D 8C 9D 10B
11C 12C 13B 14D 15A 16C 17A 18A 19D 20C
21C 22B 23D 24D 25C 26D 27A 28A 29A 30A
31A 32B 33A 34C 35B 36A 37A 38B 39A 40C
PhÇn 3.Mét sè ph¬ng tr×nh lîng gi¸c thêng gÆp.
Câu 1.
Giải phương trình
2
2 sin 3 sin 1 0.x x
A.
2
2
, .
6
5
6
x k
x k k
x k
B.
2
2
2
, .
6 3
5 2
6 3
x k
x k k
x k
C.
2
2
1
, .
6 2
5 1
6 2
x k
x k k
x k
D.
2
2
2 , .
6
5
2
6
x k
x k k
x k
Câu 2.
Giải phương trình
2 cos2 3 sin 1 0.x x
A.
2
1
arcsin , .
4
1
arcsin
4
x k
x k k
x k
B.
1
2 2
1 1
arcsin , .
4 2
1 1
arcsin
4 2
x k
x k k
x k
C.
2
2 3
2
, .
6 3
5 2
6 3
x k
x k k
x k
D.
2
2
1
arcsin 2 , .
4
1
arcsin 2
4
x k
x k k
x k
Câu 3.
Giải phương trình
cos2 cos 1 0.x x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
51
A.
2
2 , , .
2 3
x k x k k
B.
2
, , .
2 3
x k x k k
C.
2 7
3 , , .
2 3 2
x k x k k
D.
2
, 2 , .
2 3
x k x k k
Câu 4.
Giải phương trình
2 2
6 sin 2sin 2 5.x x
A.
2
, .
4 3
x k k
B.
, .
4 3
x k k
C.
, .
4 4
x k k
D.
, .
4 2
x k k
Câu 5.
Giải phương trình
4 4
2 sin 2 cos 2 sin 2 1.x x x
A.
2 , .
4
x k k
B.
2
, .
4 3
x k k
C.
, .
4 2
x k k
D.
, .
4
x k k
Câu 6.
Giải phương trình
4 4
5 1 cos 2 sin cos .x x x
A.
2
, .
3
x k k
B.
x k
C.
2
2 , .
3
x k k
D.
2 , .
3
x k k
Câu 7.
Giải phương trình
3 tan cot 3 1 0.x x
A.
4
, .
6 2
x k
k
x k
B.
2
4
, .
2
6
x k
k
x k
C.
3
4
, .
3
6
x k
k
x k
D.
4
, .
6
x k
k
x k
Câu 8.
Giải phương trình
2
3 cos 4 sin 2 cos2 2 0.x x x
A.
2
, .
6
arccos 2
7
x k
k
x k
B.
2
2
, .
6
arccos 2
7
x k
k
x k
C.
3
, .
6
arccos 2
7
x k
k
x k
D.
2
, .
6
arccos
7
x k
k
x k
Câu 9.
Giải phương trình
4 cos cos2 1 0.x x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
52
A.
2
3
, .
1 5
arccos 2
8
x k
k
x k
B.
2
3
, .
1 5
arccos 2
8
x k
k
x k
C.
2
3
, .
1 5
arccos 2
8
x k
k
x k
D.
2
3
, .
1 5
arccos 2
8
x k
k
x k
Câu 10.
Giải phương trình
2
3
2 tan 3 .
cos
x
x
A.
2 , .x k k
B.
, .x k k
C.
2
.
3
x k
D.
.
3
x k
Câu 11.
Giải phương trình
2
4
9 13 cos 0.
1 tan
x
x
A.
2 , .x k k
B.
, .x k k
C.
, .
2
x k k
D.
2
, .
3
x k k
Câu 12.
Giải phương trình
5 7
sin 2 3 cos 1 2 sin
2 2
x x x
.
A.
2
2 , .
6
5
6
x k
x k k
x k
B.
2
, .
6
5
2
6
x k
x k k
x k
C.
2 , .
6
5
2
6
x k
x k k
x k
D.
2
2 , .
6
5
2
6
x k
x k k
x k
Câu 13.
Giải phương trình
2
cos 3 sin cos 1 0.x x x
A.
2
, .
2
3
x k
k
x k
B.
2
, .
3 2
x k
k
x k
C.
3
, .
3 3
x k
k
x k
D.
, .
3
x k
k
x k
Câu 14.
Giải phương trình
2 2
cos 3 sin 2 1 sin .x x x
A.
, .
3
x k
k
x k
B.
2
x k
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
53
C.
2
, .
3
x k
k
x k
D.
, .
2
3
x k
k
x k
Câu 15.
Giải phương trình
2
cos 2 sin .cos
3.
2 cos sin 1
x x x
x x
A.
5
, .
18 3
x k k
B.
2
, .
18 3
x k k
C.
, .
18
x k k
D.
5 5
, .
18 3
x k k
Câu 16.
Giải phương trình
2 2
cos sin .cos 2 sin 1 0.x x x x
A.
2
, .
1
arctan 2
3
x k
k
x k
B.
3
, .
1
arctan
3 3
x k
k
x k
C.
2
, .
1
arctan
3 2
x k
k
x k
D.
, .
1
arctan
3
x k
k
x k
Câu 17.
Giải phương trình
2
cos 4 cos 3 .x x
A.
2
, .
3
12 2
x k
k
x k
B.
, .
3
12 2
x k
k
x k
C.
2
, .
12 2
x k
k
x k
D.
, .
12 2
x k
k
x k
Câu 18.
Giải phương trình
2
2 tan
5.
1 tan
x
x
A.
1 26
arctan 2 , .
5
x k k
B.
1 26
arctan , .
5 2
x k k
C.
1 26
arctan , .
5
x k k
D.
1 26
arctan , .
5
x k k
Câu 19.
Giải phương trình
sin cos 1.x x
A.
2
4
2
x k
k
x k
B.
4
, .
4
x k
k
x k
C.
2
, .
2
2
x k
k
x k
D.
2
2
x k
k
x k
Câu 20.
Phương trình
sin cos 1x x
chỉ có các nghiệm là:
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
54
A.
2
4
2
x k
k
x k
B.
4
, .
4
x k
k
x k
C.
2
, .
2
4
x k
k
x k
D.
2 1
2
x k
k
x k
Câu 21.
Giải phương trình
sin 2 12 sin cos 12 0.
x x x
A.
, 2 , .
2
x k x k k
B.
2
2 , , .
2 3
x k x k k
C.
2
, , .
2 3 3
x k x k k
D.
2 , 2 , .
2
x k x k k
Câu 22.
Giải phương trình
1 tan 2 2 sin .x x
A.
, .
4
x k k
B.
2 , .
4
x k k
C.
2
, .
4 3
x k k
D.
, .
4 3
x k k
Câu 23.
Giải phương trình
cos sin 2 sin 2 1.
x x x
A.
, .
2
k
x k
B.
, .x k k
C.
, .
2
x k k
D.
, .
4
k
x k
Câu 24.
Giải phương trình
3 3
cos sin cos2 .x x x
A.
2 , , , .
4 2
x k x k x k k
B.
2
, , , .
4 3 2
x k x k x k k
C.
1 2
, , 2 , .
4 3 2 3
x k x k x k k
D.
, 2 , 2 , .
4 2
x k x k x k k
Câu 25.
Giải phương trình
3 3
cos sin 2 sin2 sin cos .x x x x x
A.
, .
2
k
x k
B.
, .x k k
C.
, .
2
x k k
D.
, .
4
k
x k
Câu 26.
Giải phương trình
tan cot 2 sin 2 cos 2 .x x x x
A.
4 3
, .
8 3
x k
k
x k
B.
4
, .
8
x k
k
x k
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
55
C.
4
, .
8 2
x k
k
x k
D.
4 2
, .
8 2
x k
k
x k
Câu 27.
Giải phương trình
3 3 5 5
cos sin 2 cos sin .x x x x
A.
2 , .
4
x k k
B.
, .
4
x k k
C.
, .
4 3
x k k
D.
, .
4 2
x k k
Câu 28.
Giải phương trình
2
sin 3 tan cos 4 sin cos .x x x x x
A.
2 , arctan 1 2 2 , .
4
x k x k k
B.
, arctan 1 2 , .
4 2 2
x k x k k
C.
2 2
, arctan 1 2 , .
4 3 3
x k x k k
D.
, arctan 1 2 , .
4
x k x k k
Câu 29.
Giải phương trình
8 8 2
16 sin cos 17 cos 2 .x x x
A.
, .
8 4
x k k
B.
7
, .
8 4
x k k
C.
9
, .
8 4
x k k
D.
5
, .
8 4
x k k
Câu 30.
Giải phương trình
4 6
cos cos2 2 sin 0.x x x
A.
2 , .x k k
B.
, .
2
x k k
C.
2
, .
3
x k k
D.
, .x k k
Câu 31.
Giải phương trình
3
sin cos sin 2 3 cos 3 2 cos 4 sin .x x x x x x
A.
2
6
2
x k
k
x k
B.
2
6
, .
2
42
x k
k
x k
C.
6
, .
2
42 7
x k
k
x k
D.
2
6
x k
k
x k
Câu 32.
Giải phương trình
2 2 2 2
sin 3 cos 4 sin 5 cos 6 .x x x x
A.
2
, .
9
x k
k
k
x
B.
2
, .
2
9
x k
k
k
x
C.
2
, .
9
k
x
k
k
x
D.
2
, .
9 9
x k
k
k
x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
56
Câu 33.
Phương trình
3 sin 1 cos 2
x m x m
(với
m
là tham số) có nghiệm khi:
A.
1.m
B.
1.m
C.
1.m
D.
1.m
Câu 34.
Phương trình
sin 3cos 2m x x m
có nghiệm khi:
A.
3.
m
B.
3.
m
C.
3.
m
D.
3.
m
Câu 35.
Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số
A.
min 2 5; max 2 5.y y
B.
min 2 7; max 2 7.y y
C.
min 2 3; max 2 3.y y
D.
min 2 10; max 2 10.y y
Câu 36.
Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số
4 sin 3 3 cos 3 1.y x x
A.
min 3;max 6.y y
B.
min 4;max 6.y y
C.
min 4;max 4.y y
D.
min 2;max 6.y y
Câu 37.
Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số
sin 2 2 cos 2 3
.
2 sin 2 cos2 4
x x
y
x x
A.
2
min ; max 2.
11
y y
B.
2
min ;max 3.
11
y y
C.
2
min ; max 4.
11
y y
D.
2
min ;max 2.
11
y y
Câu 38.
Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số
2
2 sin 3 4 sin 3 cos 3 1
.
sin 6 4 cos 6 10
x x x
y
x x
A.
11 9 7 11 9 7
min ; max .
83 83
y y
B.
22 9 7 22 9 7
min ;max .
11 11
y y
C.
33 9 7 33 9 7
min ;max .
83 83
y y
D.
22 9 7 22 9 7
min ; max .
83 83
y y
Câu 39.
Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số
2
2
sin 2 3 sin 4
.
2 cos 2 sin 4 2
x x
y
x x
A.
5 2 22 5 2 22
min ;max .
7 7
y y
B.
5 2 22 5 2 22
min ;max .
7 7
y y
C.
5 97 5 97
min ; max .
8 8
y y
D.
7 97 7 97
min ; max .
8 8
y y
Câu 40.
Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số
2
3 3 sin 4 cos 4 3 sin 4 cos 1.
y x x x x
A.
1
min ;max 96.
3
y y
B.
1
min ; max 6.
3
y y
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
57
C.
1
min ; max 96.
3
y y
D.
min 2; max 6.y y
ĐÁP ÁN:
1D 2D 3D 4D 5D 6C 7D 8A 9B 10A
11A 12C 13D 14B 15B 16D 17D 18D 19C 20D
21D 22C 23A 24D 25A 26D 27B 28D 29A 30D
31A 32C 33B 34C 35D 36B 37D 38D 39B 40C
Hướng dẫn giải:
Câu 2. Dùng công thức nhân đôi
2
cos 2 1 2 sinx x
Câu 3. Dùng công thức nhân đôi
2
cos 2 2 cos 1.x x
Câu 4. Dùng công thức hạ bậc
2
1 cos 2
sin
2
x
x
và
2 2
sin 2 1 cos 2 .x x
Câu 5. Áp dụng
2
4 4 2 2 2 2
2 .a b a b a b
Câu 6. Áp dụng
4 4 2 2 2 2
.a b a b a b
Câu 7.
1
cot .
tan
x
x
Câu 8.
2 2 2
cos 4 2 cos 2 1,sin 2 1 cos 2 .x x x x
Câu 9.
2
cos 2 2 cos 1x x
Câu 10.
2
2
1
tan 1
cos
x
x
Câu 11.
2
2
1
tan 1
cos
x
x
Câu 12.
2
sin 2 cos 2 , cos2 1 2 sin .
2
x x x x
Câu 13.
2 2
cos 1 sin .x x
Câu 14.
2 2
cos sin cos 2x x x
Câu 15.
2
2 cos 1 cos2 , 2 sin cos sin 2 .x x x x x
Câu 16.
sin 3 sin cosx x x
Câu 17.
3 2
2 cos 4 1 cos 6 4 cos 2 4 cos 2 3 cos2 3 0.x x x x x
Câu 23.
2
sin cos 2 cos sin 2 1
4
t x x x x t
Câu 24.
sin cos 1 sin cos sin cos cos sinx x x x x x x x
Câu 25.
3 3
sin cos sin cos 1 sin cosx x x x x x
Câu 26.
2
tan cot
sin 2
x x
x
Câu 27.
3 2 3 2 3 3
cos 2 cos 1 sin 2 sin 1 cos 2 cos sin 0
x x x x x x x
Câu 28. Chia hai vế cho
2
cos x
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V¬ng - 0946798489
Trang
58
Câu 29.
2
2
8 8 4 4 4 4 2 4
1 1
sin cos sin cos 2sin cos 1 sin 2 sin 2
2 8
x x x x x x x x
Đặt
2
sin 2t x
Câu 30. Đặt
cos 2t x
Câu 31.
3
sin 3 sin 3 sin sin 3
cos sin 2 ,2 sin
2 2
x x x x
x x x
Câu 32. Dùng công thức hạ bậc đưa về hàm
cos
Câu 37.
2 2 2
2 1 sin 2 2 cos 2 3 4 .
2 1 2 3 4
ycbt
y x y x y
y y y
Câu 39. Giống câu 37.
Câu 40. Đặt
3 sin 4 cos , 5;5
t x x t
. Khi đó
2
3 4 1
y t t f t
với
5;5 .
t
Lập bảng biến thiên cho hàm
f t
suy ra đáp án.
| 1/59

Tài liệu khác của Toán 11

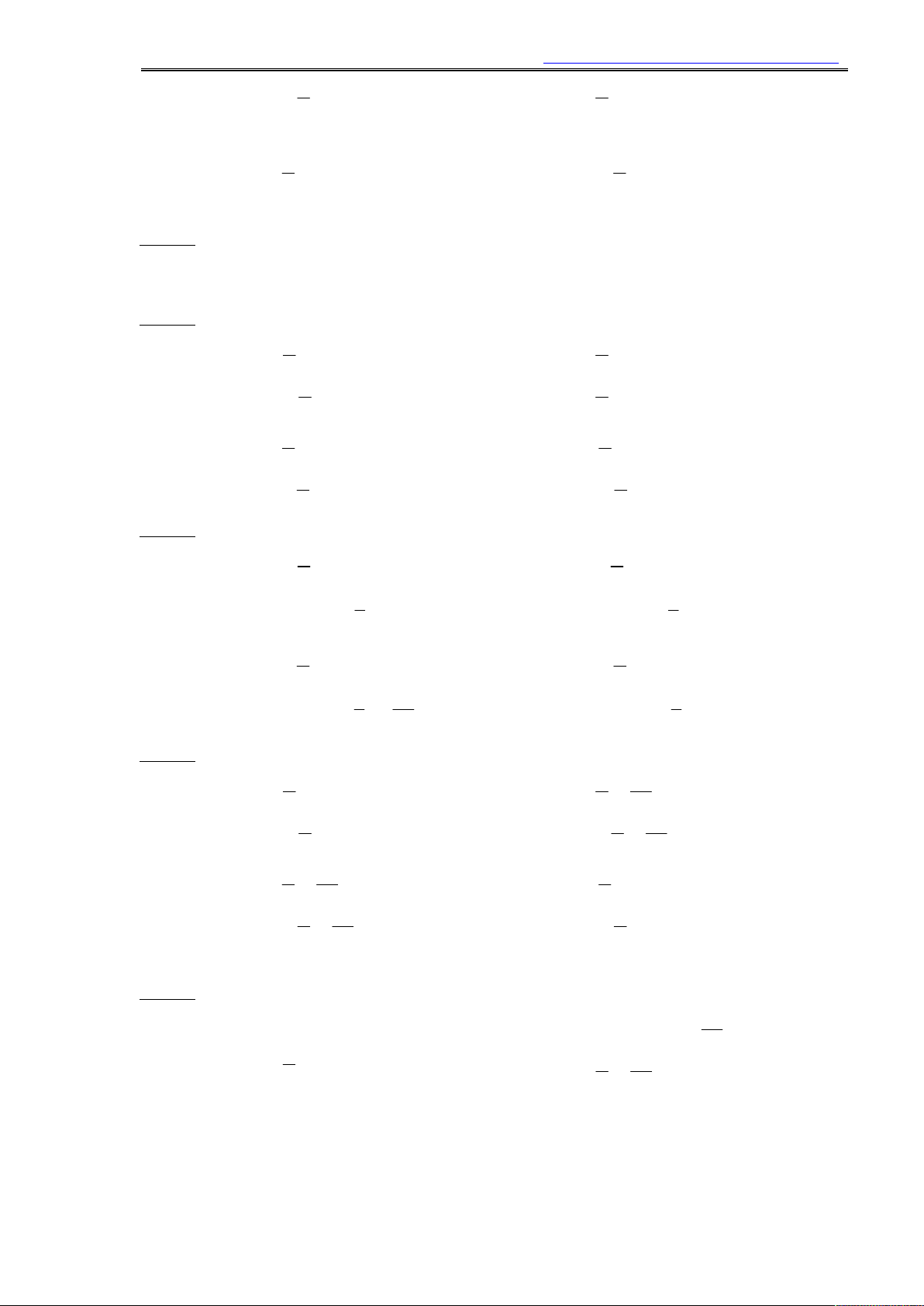
Preview text:

Ch­¬ng i. hµm sè l­îng gi¸c vµ ph­¬ng tr×nh l­îng gi¸c. NguyÔn b¶o v­¬ng
TµI LIÖU Cã §¸P ¸N Vµ Hdg
C¸c em häc sinh theo dâi facebook: https://www.facebook.com/phong.baovuong
®Ó nhËn ®­îc nhiÒu tµi liÖu hay h¬n.
Gi¸o viªn muèn mua file word liªn hÖ 0946798489 ®Ó biÕt thªm chi tiÕt. Năm học: 2017-2018
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong BµI 1. HµM Sè L­îng gi¸c a. kiÕn thøc cÇn nhí.
 Hàm số sin: y  sin x Tính chất: •Tập xác định  .
•Tập giá trị:  1;1  
 ,có nghĩa là 1  sin x  1, x   .
•Hàm số tuần hoàn với chu kì 2, có nghĩa sin x k2  sin x với k   .    
•Hàm số đồng biến trên mỗi khoảng    k2 ; k2 
và nghịch biến trên mỗi  2 2   3    khoảng   k2 ; k2  ,k   .  2 2 
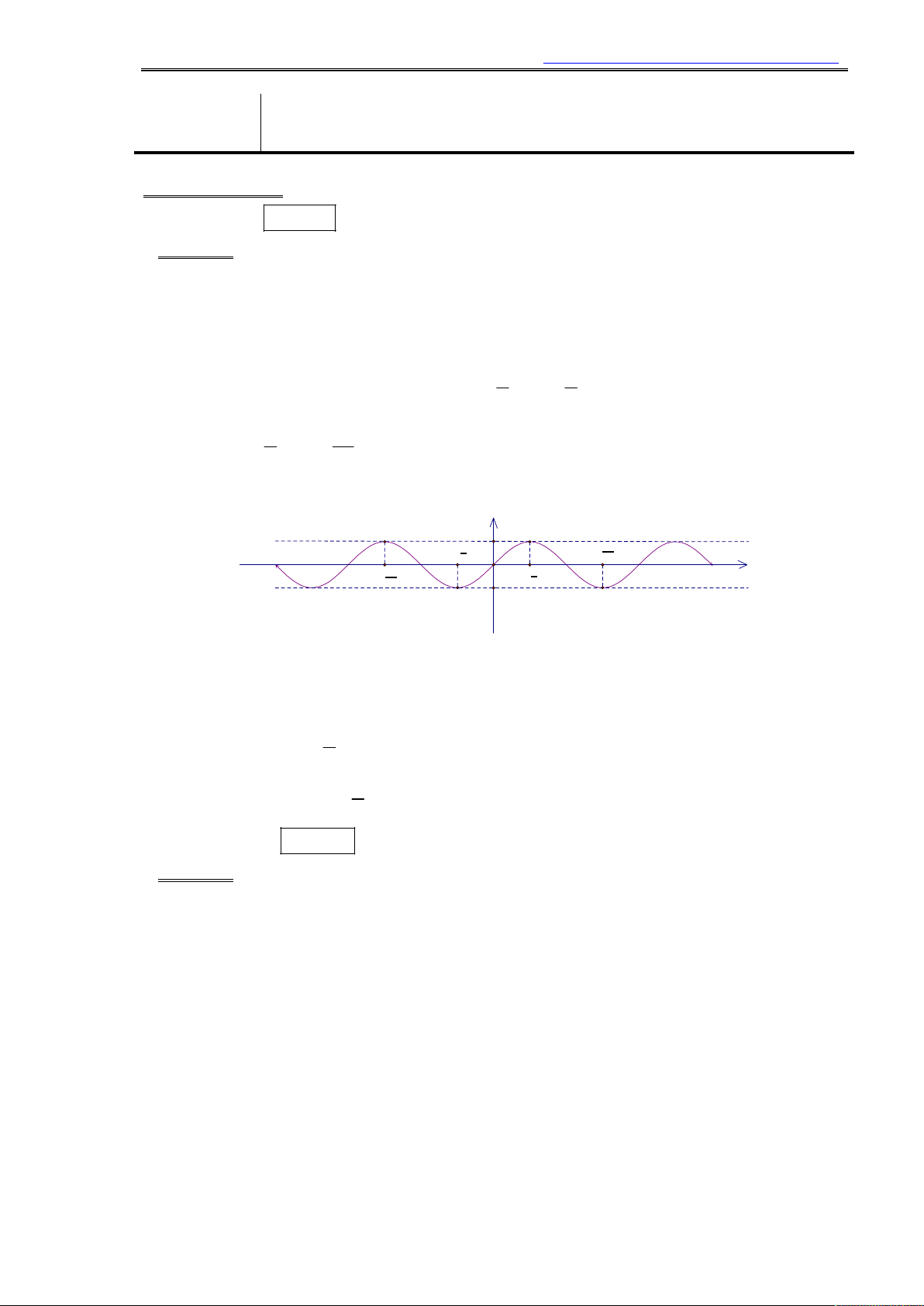
•y  sin x là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng (Hình 1). y
f(x) = sin(x) 1 π 3π - -3π -2π -π 2 π 2 2π 3π 3π O π x - 2 2 -1 Hình 1.
•Một số giá trị đặc biệt:
sin x  0  x k , (k  )
sin x  1  x   k2 , (k  )  2
sin x  1  x    k2 , (k  )  2
 Hàm số côsin: y  cos x Tính chất: •Tập xác định  .
•Tập giá trị:  1;1  
 ,có nghĩa là 1  cos x  1, x   .
•Hàm số tuần hoàn với chu kì 2, có nghĩa cos x k2  cos x với k   .
•Hàm số đồng biến trên mỗi khoảng    k2 ;
 k2 và nghịch biến trên mỗi khoảng
k2 ; k2,k  .
•y  cos x là hàm số chẵn, đồ thị hàm số nhận Oy làm trục đối xứng (Hình 2).
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 1
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong y 1 f x ( ) = cos x ( ) -3π -π π 3π -2π π O 3π π 3π 2π x - - 2 2 2 2 -1 Hình 2.
•Một số giá trị đặc biệt:
cos x  0  x   k , (k  )  2
cos x  1  x k2 ,
(k  ).
cos x  1  x k2 ,
(k  ) . sin x
 Hàm số tang: y  tan x  cos xTính chất:    
•Tập xác định:  \   k k     2    •Tâp giá trị là  .
•Hàm số tuần hoàn với chu kì , có nghĩa tan x k  tan x,(k  )  .    
•Hàm số đồng biến trên mỗi khoảng    k ; k,   k    .  2 2 
•y  tan x là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng và nhận
mỗi đường thẳng x   k ,
 k   làm đường tiệm cận.(Hình 3) 2 y
f(x) = tan(x) -2π 3π -π π π π 3π 2π - 2 - O x 2 2 2 Hình 3.
•Một số giá trị đặc biệt :
tan x  0  x k ,  k  
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 2
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
tan x  1  x   k ,  k   . 4
tan x  1  x    k ,  k   . 4 cos x
 Hàm số cotang: y  cotx  . sin xTính chất:
•Tập xác định:  \ k k  . •Tập giá trị:  .
•Hàm số tuần hoàn với chu kì , có nghĩa cotx k  cotx,(k  )  .
•Hàm số nghịch biến trên mỗi khoảng k ;
  k,k   .
•y  cot x là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng và nhận
mỗi đường thẳng x k ,
 k   làm đường tiệm cận (Hình 4). y f(x)=cotan(x) 3π π π 3π -2π - -π - π 2π 2 2 O 2 2 x Hình 4
•Một số giá trị đặc biệt :
cotx  0  x   k ,  k   . 2
cotx  1  x   k ,  k   . 4
cotx  1  x    k ,  k   . 4
ii. c¸c d¹ng to¸n th­êng gÆp vµ ph­¬ng ph¸p gi¶i.
Daïng toaùn 1: Tìm taäp xaùc ñònh cuûa haøm soá. 
Phương pháp giải:
Khi tìm tập xác định của hàm số, ta cần chú ý:
• Các hàm số y  sin x,y  cos x xác định trên . 
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 3
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong P x • Hàm số y
xác định khi Q x   0. Từ đó suy ra: Q x
- Hàm số y  tan x xác định khi cos x  0.
- Hàm số y  cot x xác định khi sin x  0. • Hàm số y
f x xác định khi f x  0. sin x  2
Ví dụ 1. Tìm tập xác định D của hàm số y  2 sin x.cos x k        A. D   \  ,k    .
D     k k    B. \ , . 2    2       
C. D   \   k2 ,  k    . D   \ k ,  k   .  D.   2    2 cos x  3
Ví dụ 2. Tìm tập xác định của hàm số y  . sin x  1         A. D   \    k ,  k    . D      k  k    B. \ 2 , . 2     2        C. D  . 
D. D   \   k2 ,  k    .  2   
Áp dụng làm các bài tập sau: cos x Câu 1. Hàm số y  có tập xác định là: 2 sin x  3         A.  \   k2 ,  k    .
   k k    B. \ , . 3    6     5     2    C.  \   k2 , k2 ,  k    .  \   k2 , k2 ,  k    .  D. 6 6    3 3    x   
Câu 2. Hàm số y  tan    có tập xác định là: 2 4          A.  \   k2 ,  k    .
   k k    B. \ , . 2    2    3    C.  \   k2 ,  k    .  D. .  2       
Câu 3. Tập xác định của hàm số y  cot 2  x    2  là:  3          A.  \   k ,  k    .
   k  k    B. \ 2 , . 6    6    5 k     k    C.  \   ,k    .    k    C. \ , . 12 2    6 2   
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 4
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 1  cos x Câu 4. Hàm số y  có tập xác định là: 1  sin x     A.  \ k ,  k  . B.  \   k ,  k    .  2        k    C.  \   k2 ,  k    .   k    D. \ , . 2     2    sin x
Câu 5. Cho hàm số y  và k  .
 Khoảng nào dưới đây không nằm trong tập xác 1  tan x định của hàm số?      3    A.    k2 ; k2.  k2 ; k2.  B.  2 2   2  3 3     3    C.   k2 ; k2.    k2 ; k2.  D.  4 2  2 4  cos x  1 Câu 6. Hàm số y  có tập xác định là: 3  sin x A. . B.  \ k2 ,
 k  . C. k2 ,  k  . D. .   Đáp án: 1D 2C 3D 4C 5A 6C
Daïng toaùn 2: Xaùc ñònh tính chaün, leû cuûa haøm soá. 
Phương pháp giải:
Khi xác định tính chẵn, lẻ của hàm số y f x  ta thực hiện các bước sau:
Bước 1. Tìm tập xác định D của hàm số.
• Nếu D không là tập đối xứng, nghĩa là x D sao cho x
  D thì ta kết luận ngay hàm số
y f x không, chẵn, không lẻ.
• Nếu D là tập đối xứng ta thực hiện bước 2. Bước 2.
• Nếu f x
   f x với mọi x D thì hàm số y f x là hàm số chẵn.
• Nếu f x
   f x với mọi x D thì hàm số y f x là hàm số lẻ.
• Nếu x D mà f x
   f x hoặc f x
   f x thì hàm số y f x là hàm số không chẵn (không lẻ).
Chú ý: Khi xác định tính chẵn, lẻ của hàm số lượng giác ta cần lưu ý: • x   ,  sin x    sinx. • x  ,  cos x    cosx.    
• x   \   k ,  k    , tan x    tanx.
x   \ k ,
 k   , cot x    cotx.  •     2   
Ví dụ 3. Hàm số nào sau đây không phải là hàm số lẻ? A. y  sin x. B. y  cos x. C. y  tan x. D. y  cotx.
Ví dụ 4. Hàm số y  sin x. cos x là:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 5
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
A. Hàm số không có tính chẵn, lẻ. B. Hàm chẵn.
C. Hàm có giá trị lớn nhất bằng 1. D. Hàm lẻ.
Áp dụng làm các bài tập sau:
Câu 7. Hàm số y  sin x. cos 2x là: A. Hàm chẵn.
B. Hàm không có tính chẵn, lẻ.
C. Hàm không có tính tuần hoàn. D. Hàm lẻ. tan 3x Câu 8. Hàm số y
thỏa mãn tính chất nào sau đây? 3 sin x A. Hàm chẵn.
B. Hàm không có tính chẵn , lẻ. C. Xác định trên .  D. Hàm lẻ.
Câu 9. Trong các hàm số sau, hàm số nào là hàm số lẻ? tan x cos x A. 2 y  sin x. B. 2
y  sin x.cos x. C. y  . D. y  . cos x sin x
Câu 10. Trong các hàm số sau, hàm số nào là hàm số chẵn? tan 2x A. y
. B. y  sin x.cos 2x. C. y cos x sin  x. D. 3
y  cos x sin x. 2 tan x  1
Câu 11. Trong các hàm số sau, hàm số nào không là hàm chẵn và cũng không là hàm lẻ? 1    
A. y  tan x  . B.y  2 sin x   . sin x  4 
C. y  sin x  tan x. D. 4 4
y  sin x  cos x.  Đáp án 7D 8A 9C 10C 11B
Daïng toaùn 3: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá. 
Phương pháp giải:
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số lượng giác, ta biến đổi hàm số đã cho
về dạng y a b sin t hoặc y a b cos t. Và sử dụng kết quả: 1
  sint  1, 1  cost  1.
Ví dụ 5. Hàm số y  2 sin x cos x  cos 2x có giá trị lớn nhất là: A. 3. B. 2 2. C. 2. D. 2.
Ví dụ 6. Hàm số y   x x 2 sin cos
 cos2x có giá trị nhỏ nhất là: A. 1. B. 1  2. C. 0. D. 1  2.
Áp dụng làm các bài tập sau:
Câu 12. Hàm số y   x x2 sin cos
 cos2x có giá trị lớn nhất là: A. 1  2. B. 3. C. 5. D. 2.
Câu 13. Hàm số y  3 sin x  cos x có giá trị nhỏ nhất là: A. 1  3. B.  3. C.2. D.1  3. cos x  1
Câu 14. Cho hàm số y
. Mệnh đề nào trong số các mệnh đề sau là sai? cos x  2
A. Tập xác định của hàm số là . 
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 6
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
B. Hàm số có giá trị lớn nhất bằng 0.
C. Hàm số có giá trị nhỏ nhất bằng 2.
D. Hàm số tuần hoàn với chu kì T  2.
Câu 15. Hàm số nào sau đây có giá trị lớn nhất bằng 2.
A. y  tan x  cot x.
B. y  2 tan x.    
C. y  2 cos x  sin x. D. y  sin 2  x  .   4 
Câu 16. Giá trị nhỏ nhất của hàm số 2 2
y  3  4 sin x cos x là: A. 1. B. 2. C.1. D. 3.  Đáp án 12A 13C 14D 15C 16B
Daïng toaùn 4: Tìm chu kì cuûa haøm soá löôïng giaùc. 
Phương pháp giải:
Khi tìm chu kì của hàm số lượng giác ta cần lưu ý rằng:
• Hàm số y  sin x,y  cos x có chu kì T  2 .
• Hàm số y  tan x,y  cot x có chu kì T  . 2
• Hàm số y  sinax b,y  cosax b,a  0 có chu kì T  . a
• Hàm số y  tanax b,y  tanax b,a  0 có chu kì T  . a
• Nếu hàm số f có chu kì là T , f có chu kì là T thì hàm số f f f có chu kì T với T là 1 1 2 2 1 2 số nhỏ nhất sao cho *
T kT lT : k,l   . 1 2 Ví dụ 7. Hàm số 2
y  2 cos x  1 là hàm tuần hoàn với chu kì: A. T  . B.T  2 . C. 2 T . D. T  . 2     x
Ví dụ 8. Hàm số y  sin  x  cos 
là hàm tuần hoàn với chu kì:  2  3 A. T  . B.T  2 . C. T  3 . D. T  6 .
Áp dụng làm các bài tập sau:
Câu 17. Hàm số y  1  cos 2x có chu kì là: A. T  2 . B.T  2. C. T  . D. T .
Câu 18. Hai hàm số nào sau đây có chu kì khác nhau? x x x A. cos
và sin . B. sin x và tan x. C. cos x và cot . D. tan 2x và cot2x. 2 2 2        
Câu 19. Chu kì của hàm số y  2 sin 2
x    3 cos 2  x    là:  3     4  A. T  2 . B.T  . C. T  . D. T  4 . 2
Câu 20. Chu kì hàm số y  sin 2x  2 cos 3x là:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 7
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 2 A. T  2 . B.T  . C. T  . D. T  . 3 3  Đáp án 17C 18B 19B 20A
Daïng toaùn 5: Xaùc ñònh haøm soá coù ñoà thò cho tröôùc. 
Phương pháp giải:
Khi xác định hàm số lượng giác có đồ thị cho trước, ta cần chú ý đến các yếu tố sau:
• Các điểm đặc biệt mà đồ thị đi qua;
• Xác định chu kì của đồ thị hàm số thông qua đồ thị.
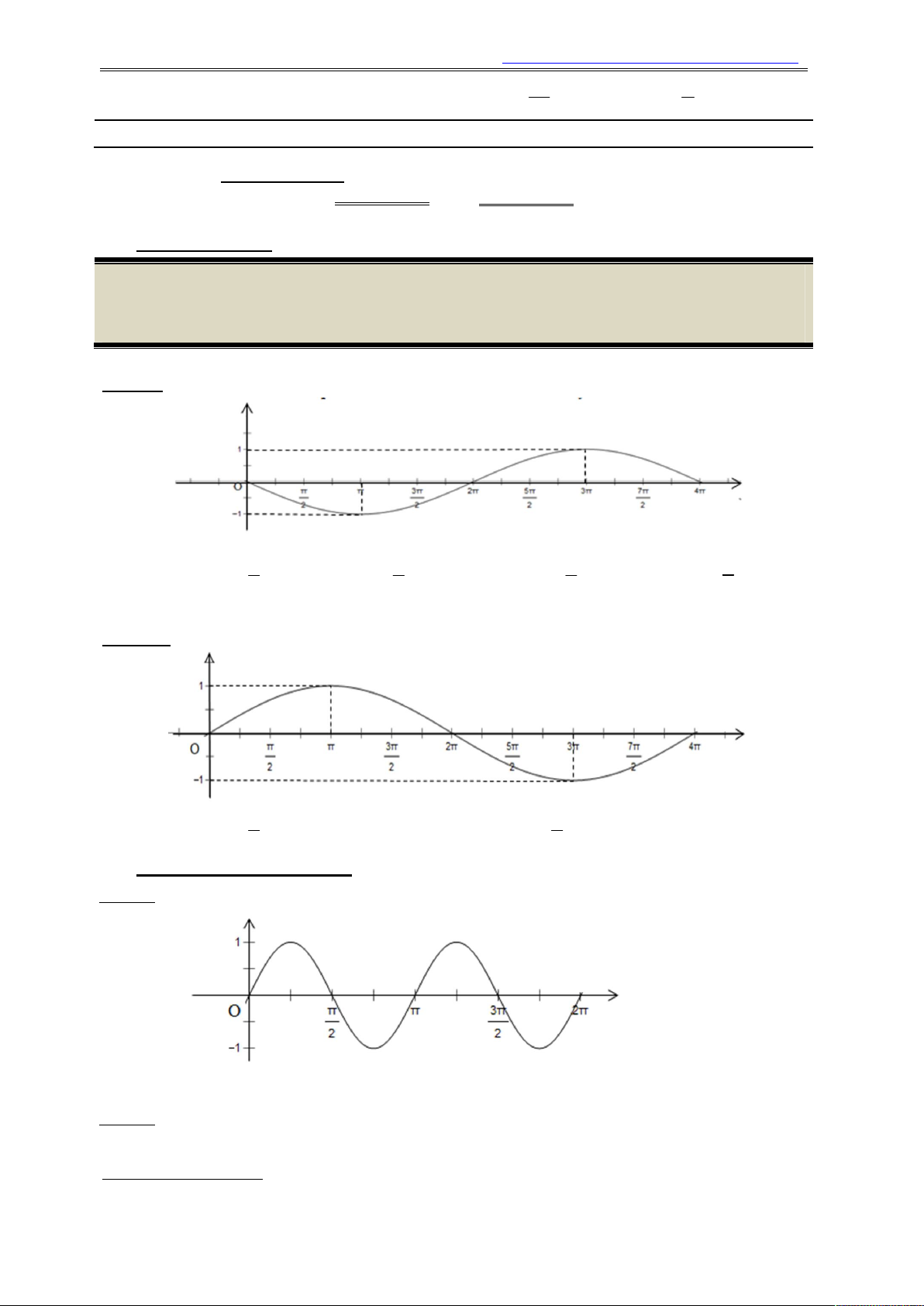
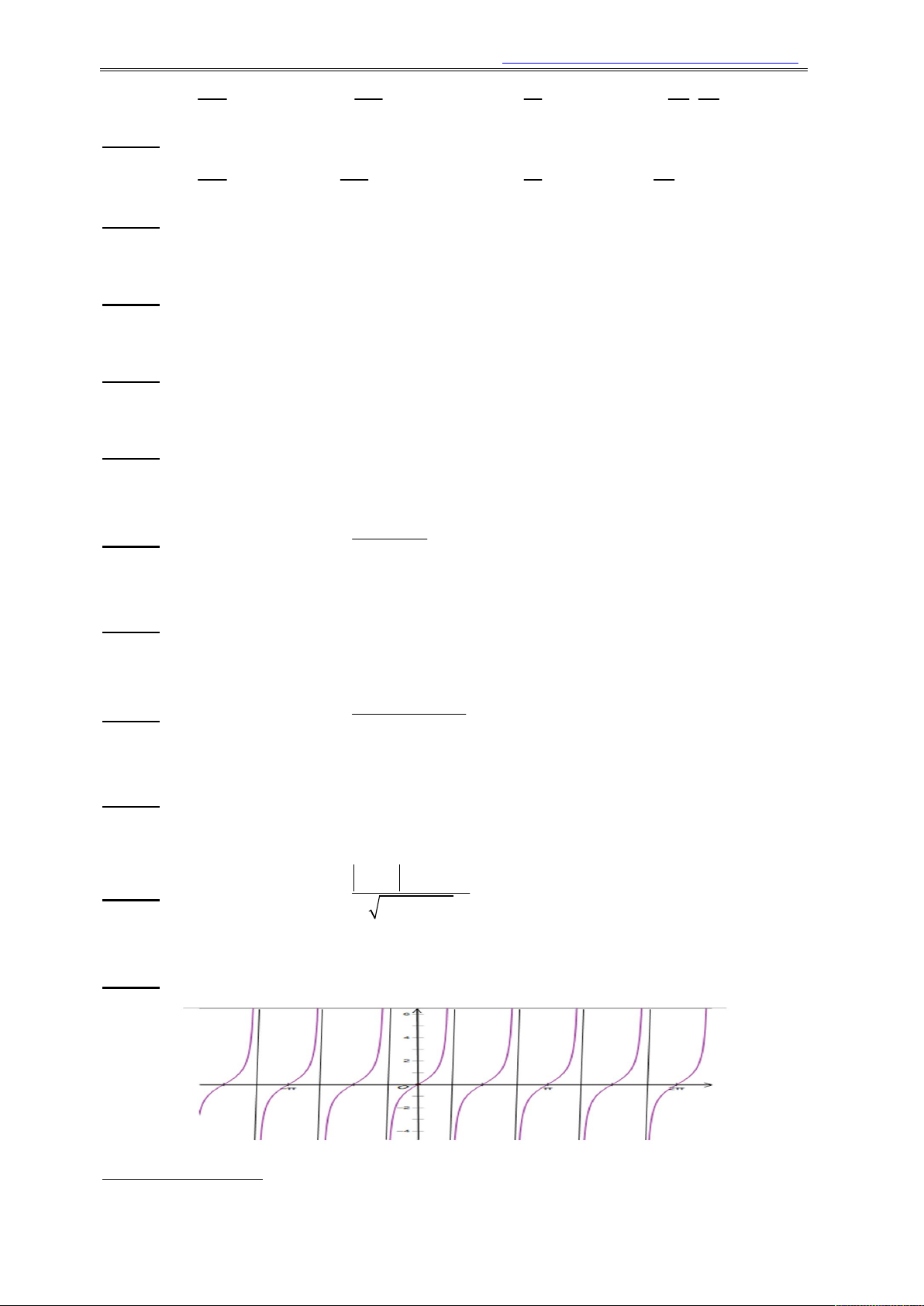
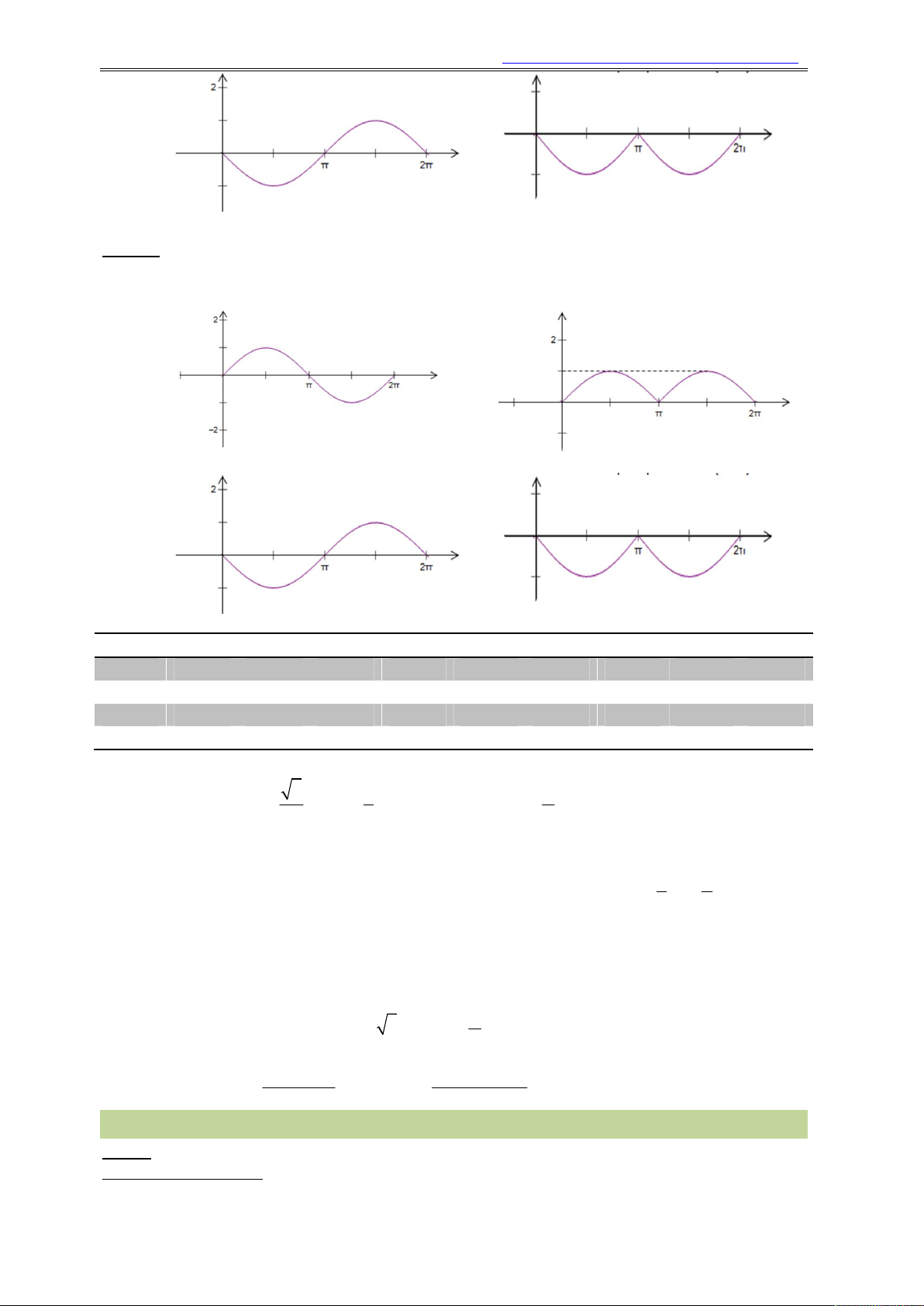
Ví dụ 9. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây: x x xx    A. y  sin . B. y  cos . C. y  cos . D. y  sin   . 2 2 4  2
Ví dụ 10. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây: x x A. y  sin . B. y  sin x. C. y  cos . D. y  cos x. 2 2
Áp dụng làm các bài tập sau:
Câu 21. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây:
A. y  sin 2x.
B. y  sin 3x. C. y  cos x.
D. y  cos 2x.
Câu 22. Hình vẽ sau là một phần đồ thị của hàm số nào sau đây:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 8
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong x
A. y  tan 2x.
B. y  cot 3x. C. y  tan .
D. y  cot 2x. 2  Đáp án 21A 22A
Ph­¬ng ph¸p sö dông casio ®Ó gi¶I quyÕt d¹ng to¸n t×m tËp x¸c ®Þnh.
Bước 1. Chọn đơn vị sử dụng
Bước 2. Nhập biểu thức vào máy tính
Bước 3. Thử các giá trị tường minh. 1
Ví dụ 11. Cho hàm số y
. Tập xác định của hàm số là: 2 cos x  1         A. D   \    k2 ,  k    . D      k  k    B. \ 2 , . 6     4            C. D   \    k2 ,  k    .
D     k k    D. \ , . 3    2   
Sử dụng máy tính CASIO fx – 570MS, bằng cách thực hiện theo thứ tự:
• Chọn đơn vị là radial ta ấn: wwww2
• Nhập biểu thức 2 cos x  1 ta ấn: 2kQ[)p1
• Ta lần lượt thử với các giá trị x  ,x  ,x  qr… 6 4 3 Dễ thấy x
thì kết quả máy tính bằng 0 . Nên chọn C. 3
Ngoài ra, phương pháp này có thể áp dụng cho các bài toán phương trình lượng giác, vấn đề này sẽ nói sau.
iii. bµi tËp tr¾c nghiÖm tù luyÖn (cã ®¸p ¸n). Câu 1.
Tập xác định của hàm số y  1  sin x là: A. D  1;1   .     B. D   0;1   C. D  . D. D  1;  1 . Câu 2.
Tập xác định của hàm số 2
y  1  cos x là: A. D  1;1   .   B. D  0;  1 . C. D  . D. D   \   1 . Câu 3.
Tập xác định của hàm số y  tan x  cot x là:         A. x    | x   k ,  k    . x
   x k k    B. | , . 2     2   
C. x   | x k ,  k  .
D. x   | x k2 ,  k  .
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 9
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 1 Câu 4.
Tập xác định của hàm số y  cotx  là: 2 cos x         A. x
   | x k ,k    . x
   x k k    B. | , . 2     3     k     k    C. x    | x  ,k    . x    x k    D. | , . 5     7    Câu 5.
Tập xác định của hàm số y  1  cos x là: A. D  1;1   .   B. D  .  C. D  1;  1 . D. D  .  Câu 6.
Trong các hàm số sau đây, hàm số nào là hàm số lẻ? A. 2
y  cos x  sin x.
B. y  sin x  cos x.
C. y   cos x.
D. y  sin x. cos 3x. Câu 7.
Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A. y   sin x.
B. y   sin x  cos x. C. 2
y   cos x  sin x.
D. y  sin x. cos x.
cos x  2 sin x  3 Câu 8.
Giá trị lớn nhất của hàm số y  là:
2 cos x  sin x  4 2  2 A. . B. 4 8. C. 2. D.1. 4
cos x  2 sin x  3 Câu 9.
Giá trị bé nhất của hàm số y  là:
2 cos x  sin x  4 2 1 A. . B. 0. C. . D. 1. 11 2
Câu 10. Giá trị lớn nhất của hàm số y
cos x  sin x là: 2  2 A. . B. 4 8. C. 2. D.1. 4
Câu 11. Giá trị lớn nhất của hàm số sau đây bằng bao nhiêu y  sin x  cos x. A. 2. B. 2. C.1. D. 0.
Câu 12. Hàm số nào sau đây đồng biến trên khoảng 0; ? A. y  sin x. B.y  cos x. C.y  tan x. D. 2 y x .
Câu 13. Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
A. y  2x  3 sin x.
B.y  sin x  cos x x. C. 2 y  sin x. D. 2
y x sin x.
Câu 14. Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn? A. 2
y x cos x. B. 2 y  cos x. C. 2 2
y x  cos x. D. 2 y x .
Câu 15. Chu kì của hàm số 2
y  sin x là: A. T  . B. T  2 . C. 2 T . D. T  4 .
Câu 16. Chu kì của hàm số y  sin 2x  cos 3x. là: A. T  . B. T  3 . C. T  . D. T  2 . 6
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 10
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong x x
Câu 17. Chu kì của hàm số f x  cotx  cot  cot . là: 2 3 A. T  . B. T  2 . C. T  3 . D. T  6 . x
Câu 18. Chu kì của hàm số y  cos x  tan . là: A. T  . B. T  2. C. 2 T . D. Không có chu kì.
Câu 19. Tập giá trị của hàm số 2
y  sin x  2 sin x  5 là: A. T 4;8  .      B. T   0;1 .   C.T   3;5 .   D.T  . 
Câu 20. Tập giá trị của hàm số 2
y  cos x  cos x  1là:  3  A. T  3;3   .         B. T ; 3 .  C.T  1; 4 . T   4    D. .  
Câu 21. Cho hàm số f x   sin 2x  2 cos 3x . Chu kì tuần hoàn của hàm số bằng: 2 A. T  . B. T  . C. T  2 . D. T  4 . 3
Câu 22. Giá trị lớn nhất của biểu thức 4 4
sin x  cos x là: 1 A. 0. B.1. C. 2. D. . 2
Câu 23. Giá trị nhỏ nhất của hàm số y  cos 2x  4 cos x là: A. 5. B.3. C. 0. D.1.
Câu 24. Tập giá trị của hàm số y  2 sin 2x  3 là: A. T 0;1  .        B. T   2; 3 .   C.T   2; 3 .   D.T  1; 5 .   x x
Câu 25. Cho hàm số f x   2 tan  3 tan . Chu kì tuần hoàn của hàm số là: 2 3 A. T  12 . B. T  6 . C. T  3 . D. T  .
Câu 26. Giá trị bé nhất của biểu thức 2
cos x  sin x bằng: 3 A. 2. B. . C.1. D. 0. 2
Câu 27. Giá trị lớn nhất của biểu thức 2
cos x  sin x bằng: 5 A. 2. B. 0. C. . D.1. 4
Câu 28. Tập giá trị của hàm số y  1  2 sin 3x là: A. T  1;1   .       B. T   0;1 .   C.T   1; 0 .   D.T   1; 3 .   Đáp án. 1C 2C 3B 4A 5B 6D 7C 8C 9A 10B 11B 12D 13C 14B 15A 16D 17C 18D 19A 20B 21C 22B 23B 24D 25B 26C 27C 28A
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 11
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong BµI 2.
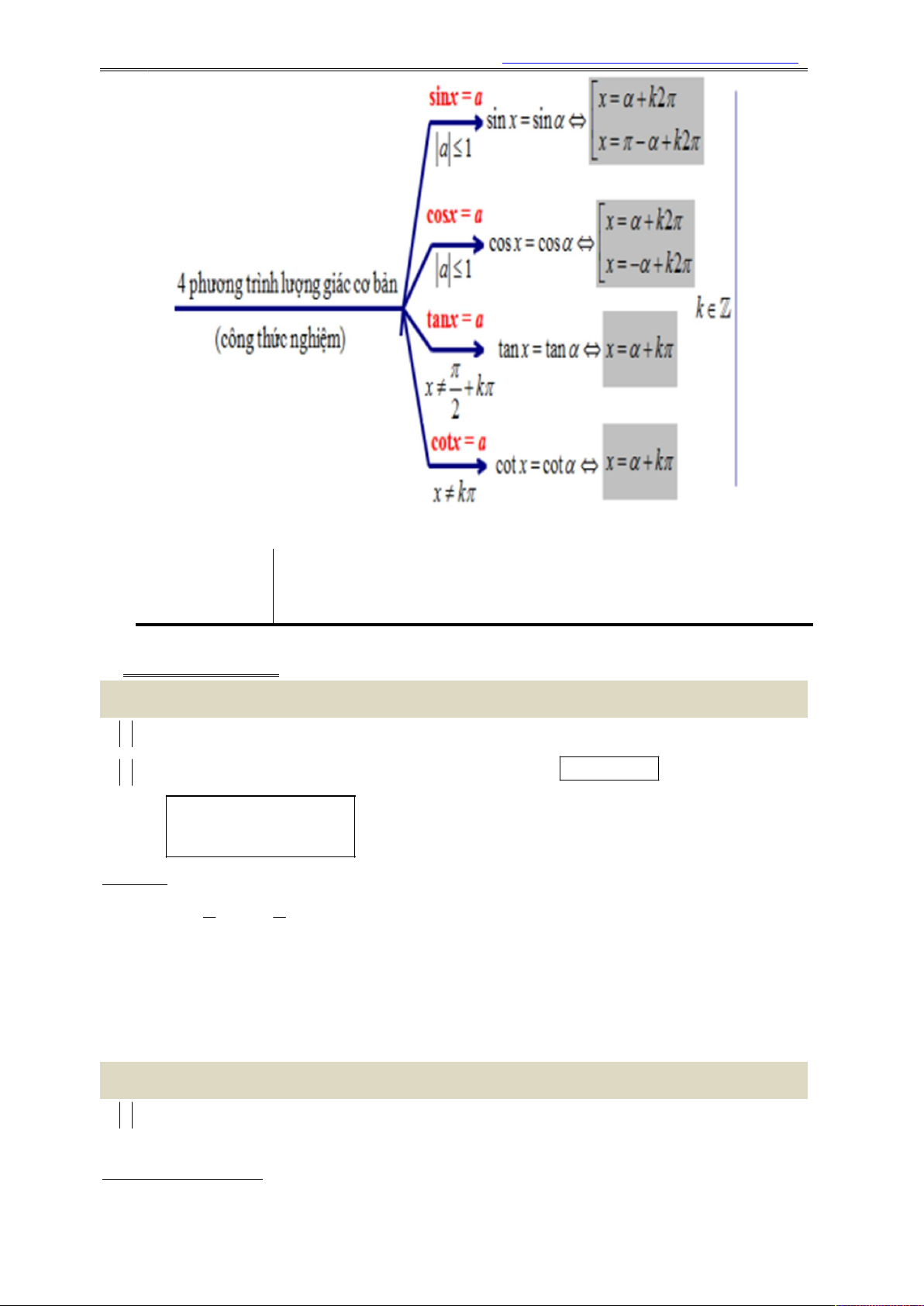
PH¦¥NG TR×NH L­îng gi¸c c¬ b¶n I. kiÕn thøc cÇn nhí.
 Phương trình sin x a  1
• a  1 : Phương trình   1 vô nghiệm.
• a  1 : Gọi là một cung sao cho sin  . a Khi đó  
1  sin x  sin và   1 có các
x k2 ,  k    nghiệm . 
x k2 ,  k     Chú ý: - Khi 
 và sin a thì ta viết  arcsina. 2 2
x   k360,k   
- Phương trình sin x  sin  có các nghiệm: . 
x  180    k360,k   
- Trong một công thức nghiệm của phương trình lượng giác, không được đồng thời
dùng hai đơn vị độ và radian.
 Phương trình cos x a   2
• a  1 : Phương trình 2 vô nghiệm.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 12
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
• a  1 : Gọi là một cung sao cho sin  .
a Khi đó 2  cosx  cos và   2 có các
x k2 ,  k    nghiệm .  x   k2 ,  k     Chú ý:
- Khi 0  và cos a thì ta viết  arccos a. x
    k360,k   
- Phương trình cos x  cos  có các nghiệm: . x  
   k360,k   
 Phương trình tan x a 3 • `Phương trình  
3 xác định khi x   k ,  k  .  2 • a
   , tồn tại cung sao cho tana , Khi đó 3  tanx  tan và   3 có nghiệm
x k ,  k  .   Chú ý: - Khi  
và tan a thì ta viết  arctan . a 2 2
- Phương trình tan x  tan  có các nghiệm: x   k180,k  . 
 Phương trình cotx a 4
• `Phương trình 4 xác định khi x k ,  k  .  • a
   , tồn tại cung sao cho tana , Khi đó 4  cotx  cot và 4 có nghiệm
x k ,  k  .   Chú ý: - Khi
  và cota thì ta viết  arccot . a
- Phương trình cotx  cot  có các nghiệm: x   k180,k  . 
Ph­¬ng ph¸p casio ®Ó gi¶I to¸n tr¾c nghiÖm ph­¬ng tr×nh l­îng gi¸c
Với mục đích là kiểm tra nghiệm của phương trình lượng giác.
Dạng 1. Nghiệm phương trình lượng giác F sin;cos; tan;co 
t  0 . Để kiểm tra nghiệm
ta dùng chức năng tính bảng giá trị (Table).
Khi làm việc với hàm lượng giác, máy tính phải đưa về chế độ RAD ® : Shift >Mode>4. Phương pháp:
Nhập hàm, chuyển tất cả phương trình về 1 vế trái, vế phải luôn bằng 0.
Nhận xét trước các phương án để chọn khoảng xét:
+ Nếu các nghiệm đều dương thì chọn khoảng xét là 0;2   .
+ Nếu có nghiệm âm thì chọn  ;      .    
+ Chọn 1 vòng đường tròn lượng giác là để xét  k
 2 hay  k hay k     .  2 
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 13
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Xét các giá trị nghiệm chọn bước nhảy thích hợp. Sau khi có bảng, thì nếu cột
F X  0  X là nghiệm.
Ví dụ: giải phương trình sin 3x  sin x  cos 3x  cos x có nghiệm là: A.  k2 ; k B.  k ; k 2 4 2 4 C.  k ; k D. k ;
k k   . 2 8 2 8
Ấn mode 7. Nhập hàm sin 3X  sin X  cos 3X  cos X Start?: 0 End? 2 Step: 8
Nhìn vào cột F(X) nhanh chóng chọn đáp án
k và là nghiệm chọn C. 8 2 2 II. Mét sè vÝ dô.
Ví dụ 1. Phương trình sin x  cos x có số nghiệm thuộc đoạn 0;    là: A. 1. B. 4. C. 5. D. 2.
Ví dụ 2. Phương trình sin 2x  1 có nghiệm là: A. x   k 4 ,  k  .  B. x   k ,  k  .  2 2 C. x   k2 ,  k  .  D. x   k ,  k  .  4 4 x Ví dụ 3. Phương trình 2 sin  1 có nghiệm là: 3 3 A. x   k2 ,  k  .  B. x   k2 ,  k  .  2 2 3 C. x   k3 ,  k  .  D. x k ,  k  .  2
Ví dụ 4. Phương trình 2 cos x  3  0 có tập nghiệm trong khoảng 0;2 :
11  
24  
5  
57   A.  ; .  ; .  ; .  ; .  B. C. D. 6 6     3 3     3 3     6 6   
Ví dụ 5. Phương trình sin cos 2x   1 có nghiệm là: A. x k ,  k  . 
B. x k2 ,  k  .  C. x   k ,  k  .  D. x    k ,  k  .  2 6
IIi. Bµi tËp tr¾c nghiÖm (cã ®¸p ¸n). x Câu 29. Phương trình cos  1  có nghiệm là: 2
A. x  2k 4 ,  k  .  B. x k2 ,  k  . 
C. x k2 ,  k  . 
D. x  2k ,  k  . 
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 14
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong Câu 30. Phương trình 2
cos 3x  1 có nghiệm là: k A. x k ,  k  .  B. x  ,k  .  2 k k C. x  ,k  .  D. x  ,k  .  3 4    
Câu 31. Phương trình tan x     0  có nghiệm là:  4  3 A. x   k ,  k  .  B. x   k ,  k  .  4 4 C. x k ,  k  .  D. x k2 ,  k  .     
Câu 32. Phương trình cot x     0  có nghiệm là:  4  A. x    k ,  k  .  B. x   k ,  k  .  4 4 C. x    k2 ,  k  .  D. x   k2 ,  k  .  4 4
Câu 33. Trong 0;    , phương trình 2
sin x  1  cos x có tập nghiệm là:   
3       A.  .  ; . 0; .   B. C.   D. 0; ; . 2    2 2     2   
Câu 34. Trong 0;2 
 , phương trình cos2x  sinx  0 có tập nghiệm là:
711  
711  
57  
75   A.  ; .  ; ; .  ; .  ; ; .  B. C. D. 6 6    2 6 6     6 6     6 6 6   
Câu 35. Trong 0;2   
, phương trình sin 2x  sin x  0 có số nghiệm là: A.1. B. 2. C. 3. D. 4.
Câu 36. Phương trình sin x  3 cos x  1 có số nghiệm thuộc 0; 3 là: A. 2. B. 3. C. 4. D. 6.    
Câu 37. Số nghiệm của phương trình 2 cos x     1    thuộc 0;2  3    là: A. 0. B. 2. C. 1. D. 3.    
Câu 38. Số nghiệm của phương trình sin x     1    thuộc 0; 3  4    là: A.1. B. 0. C. 2. D. 3.
Câu 39. Trong các phương trình sau, phương trình nào có nghiệm? 1 1 A. 3 sin x  2. B. cos 4x  . 4 2
C. 2 sin x  3 cos x  1. D. 2
cot x  cot x  5  0.
Câu 40. Trong các phương trình sau, phương trình nào vô nghiệm?
A. sin 2x  cos 2x  1.
B. sin 2x  cos x  0.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 15
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 2 C. sin x  .
D. sin x  3 cos x  0. 5 x
Câu 41. Tập nghiệm của phương trình 3 tan
 3 trong khoảng 0;2   4  là: 2   3  
2  
3   A.  .  .  ; .  ; .  B. C. D. 3     2     3 3    2 2   
Câu 42. Tập nghiệm của phương trình 2
cos x  cos 2x  0 trong khoảng 0;2    là:    
3    3   A. 0; . B. 0  ; .  ; . 0  ; .  C. D. 2    2 2     2   
Câu 43. Phương trình cossin x   1 có nghiệm là: A. x k ,  k  . 
B. x k2 ,  k  .  C. x   k ,  k  .  D. x   k ,  k  .  2 4
Câu 44. Phương trình coscos 3x   1 có nghiệm là: A. x   k ,k  .  B. x   k ,k  .  8 4 4 2 C. x   k ,k  .  D. x   k ,  k  .  6 3 2 sin x  1 Câu 45. Phương trình có tập nghiệm là: tan x  1         A.   k ,  k    .   k  k    B. 2 , . 2    2        C. .  D.    k2 ,  k    .  2   
sin 2x  2 cos x  sin x  1 Câu 46. Phương trình  0 có tập nghiệm là: tan x  3         A.   k2 ,  k    .    k  k    B. 2 , . 3     3            C.    k2 ,   k2 ,  k    .    k  k    D. 2 , . 3 2     2   
Câu 47. Phương trình sin 3x  cos 2x  sin x  0 có tập nghiệm trong 0;  là:
3      3  
  3   A.  ; .  .  ; ; .  B. . C. D. 4 4    4    4    6 4 4    Câu 48. Phương trình 2
cos 2x  2 cos x  1  0 có tập nghiệm là:         A.   k ,  k    .   k k    B. , . 4    4 2        C.   k2 ,  k    . k ,  k   .  D.   4   
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 16
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong x Câu 49. Phương trình 2 cos  3  0 có nghiệm là: 2 5 5 A. x    k4 ,  k  .  B. x    k2 ,  k  .  3 6 5 5 C. x    k4 ,  k  .  D. x    k ,  k  .  6 3
Câu 50. Phương trình 3 tan x  3  0 có nghiệm là: A. x   k ,  k  .  B. x    k2 ,  k  .  3 3 C. x   k ,  k  .  D. x    k ,  k  .  6 3
Câu 51. Mệnh đề nào sau đây sai?
A. sin x  1  x    k2 ,  k  .  2
B. sin x  0  x k ,  k  . 
C. sin x  0  x k2 ,  k  . 
D. sin x  1  x   k2 ,  k  .  2
Câu 52. Nghiệm của phương trình sin x 2 cosx  3  0 là: x k   x k  A.  ,k  .   k    B. , . x    k2   x    k  6  6
x k2 C.  ,k  . x    k  k    D. 2 , . x    k2  6  3
Câu 53. Nghiệm của phương trình 2
cos x  cos x  0 thuộc 0; là: A. x  . B. x  0. C. x . D. x   . 2 2
Câu 54. Phương trình cos 2x  0 có nghiệm là:  x
   k2 A. 6  ,k  .  B. x   k ,k  .   5 4 2 x   k2   6 2 C. x    k2 ,  k  .  D. x   k ,  k  .  3 4 2
Câu 55. Phương trình sin 3x  có nghiệm là: 2 k A. x  ,k  .  B. x k ,  k  .  4 k2 k2 k C. x   ;x   ,k  .  D. x   ,k  .  12 3 4 3 6 2
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 17
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 1
Câu 56. Nghiệm phương trình cos x   0 là: 2 5 A. x   k2 ,  k  .  B. x   k ,  k  .  6 6 2 C. x    k2 ,  k  .  D. x    k2 ,  k  .  3 3
Câu 57. Nghiệm phương trình tan x  1  0 là: A. x   k ,  k  .  B. x   k ,  k  .  2 4 3 C. x    k ,  k  .  D. x   k2 ,  k  .  4 4
Câu 58. Nghiệm phương trình 3 tan x  3  0 là: A. x   k2 ,  k  .  B. x    k ,  k  .  3 6 C. x   k ,  k  .  D. x    k ,  k  .  6 3 1
Câu 59. Nghiệm phương trình cot2x  là: 3 A. x k ,k  .  B. x k ,  k  .  4 k2 k2 k C. x   ;x   ,k  .  D. x   ,k  .  12 3 4 3 6 2 19
Câu 60. Nghiệm phương trình sin 9x   là: 18 A. x k ,k  .  B. x k ,  k  .  4 k  C. x   ,k  .  D. Vô nghiệm. 6 2
Câu 61. Phương trình tan 4x  0 có nghiệm là: A. x k ,k  .  B. x k ,  k  .  4 k2 k2 k C. x   ;x   ,k  .  D. x   ,k  .  12 3 4 3 6 2 Câu 62. Phương trình  x   3 sin 4 1  có nghiệm là: 2 1 k 1 k A. x    ;x    ,k  .  4 12 2 4 6 2 B. x    k2 ;
 x k2 ,  k  .  2 1 k C. x   ,k  .  24 12
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 18
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 165  115 D. x
k180 ;x  
k180,k  .  2 2 Câu 63. Phương trình  x   2 cos 2 30   có nghiệm là: 2 1 k 1 k A. x    ;x    ,k  .  4 12 2 4 6 2 B. x    k2 ;
 x k2 ,  k  .  2 1 k C. x   ,k  .  24 12 165  115 D. x
k180 ;x  
k180,k  .  2 2 1
Câu 64. Các giá trị nào sau đây là nghiệm của phương trình sin x  ? 2 A. x   k2 ,  k  .  B. x   k ,  k  .  3 6 5 C. x   k2 ,  k  .  D. x    k2 ,  k  .  6 6 3
Câu 65. Nghiệm của phương trình sin x   là: 2 n A. x   n ,  n  .  B. x    1 1  n ,  n  .  3 3 n  n  C. x    1  n ,  n  .  D. x    1  n ,  n  .  4 3 2
Câu 66. Nghiệm của phương trình sin x  là: 2 n A. x    1 1  n ,  n  .  B. x   k ,  k  .  4 8 n  2 C. x    1  n ,  n  .  D. x  . 4 2 1
Câu 67. Nghiệm của phương trình cos x   là: 2 A. x    k ,  k  .  B. x    k2 ,  k  .  6 6 2 C. x    k ,  k  .  D. x    k2 ,  k  .  3 3 3
Câu 68. Nghiệm của phương trình cos x   là: 2 A. x    k ,  k  .  B. x    k2 ,  k  .  6 6
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 19
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 5 5 C. x    k ,  k  .  D. x    k2 ,  k  .  6 6
Câu 69. Phương trình tan x  1 có nghiệm là: 5 k A. x   k2 ;  x   k2 ,  k  .  B. x   ,k  .  6 6 4 2 C. x   k ,  k  .  D. x    k ,  k  .  4 6
Câu 70. Phương trình cot x   3 có nghiệm là: 5 k A. x   k2 ;  x   k2 ,  k  .  B. x   ,k  .  6 6 4 2 C. x   k ,  k  .  D. x    k ,  k  .  4 6 3 Câu 71. Phương trình 2 sin 3x  có nghiệm là: 4 k 1 k A. x    ,k  .  B. x   ,k  .  6 2 10 5 2 k k C. x    ,k  .  D. x    ,k  .  9 3 12 4 Câu 72. Phương trình 2
tan 2x  3 có nghiệm là: k 1 k A. x    ,k  .  B. x   ,k  .  6 2 10 5 2 k k C. x    ,k  .  D. x    ,k  .  9 3 12 4 1 Câu 73. Phương trình 2 cot 4x  có nghiệm là: 3 k 1 k A. x    ,k  .  B. x   ,k  .  6 2 10 5 2 k k C. x    ,k  .  D. x    ,k  .  9 3 12 4 1
Câu 74. Cho hàm số y
. Tập xác định của hàm số là: 2 cos x  1         A. D   \    k2 ,  k    . D      k  k    B. \ 2 , . 6     4            C. D   \    k2 ,  k    . D      k k    D. \ , . 3     2    x   
Câu 75. Số nghiệm của phương trình cos    0       thuộc đoạn 2 ; 4 2 4    là: A.1. B. 2. C. 3 . D. 4.
Câu 76. Phương trình cos x  sin x có số nghiệm thuộc đoạn  ;     là: A. 2. B. 4. C. 5. D. 6.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 20
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong    
Câu 77. Số nghiệm của phương trình sin x     1       thuộc đoạn ;2  4    là: A.1. B. 2. C. 3 . D. 0.
Câu 78. Giải phương trình 2 2
sin 2x  cos (x  ) 4  x    k   x   2k  A. 4  ,k  .  B. 4  ,k  .   k k x    x     2 3  12 3  x     k   x   k  C. 4  ,k  .  D. 4  ,k  .   k k x    x     12 3  12 3 ĐÁP ÁN 1A 2C 3A 4B 5D 6B 7D 8B 9B 10C 11C 12C 13A 14A 15A 16C 17C 18A 19A 20B 21A 22D 23C 24A 25A 26B 27C 28C 29B 30B 31D 32D 33A 34A 35D 36C 37B 38C 39D 40D 41C 42D 43C 44A 45D 46C 47A 48A 49D 50D BµI 3.
MéT Sè PH¦¥NG TR×NH L­îng gi¸c th­êng gÆp i. kiÕn thøc cÇn nhí.
Tài liệu chỉ nhắc đến các dạng toán thường gặp.
ii.c¸c d¹ng to¸n th­êng gÆp vµ ph­¬ng ph¸p gi¶i.
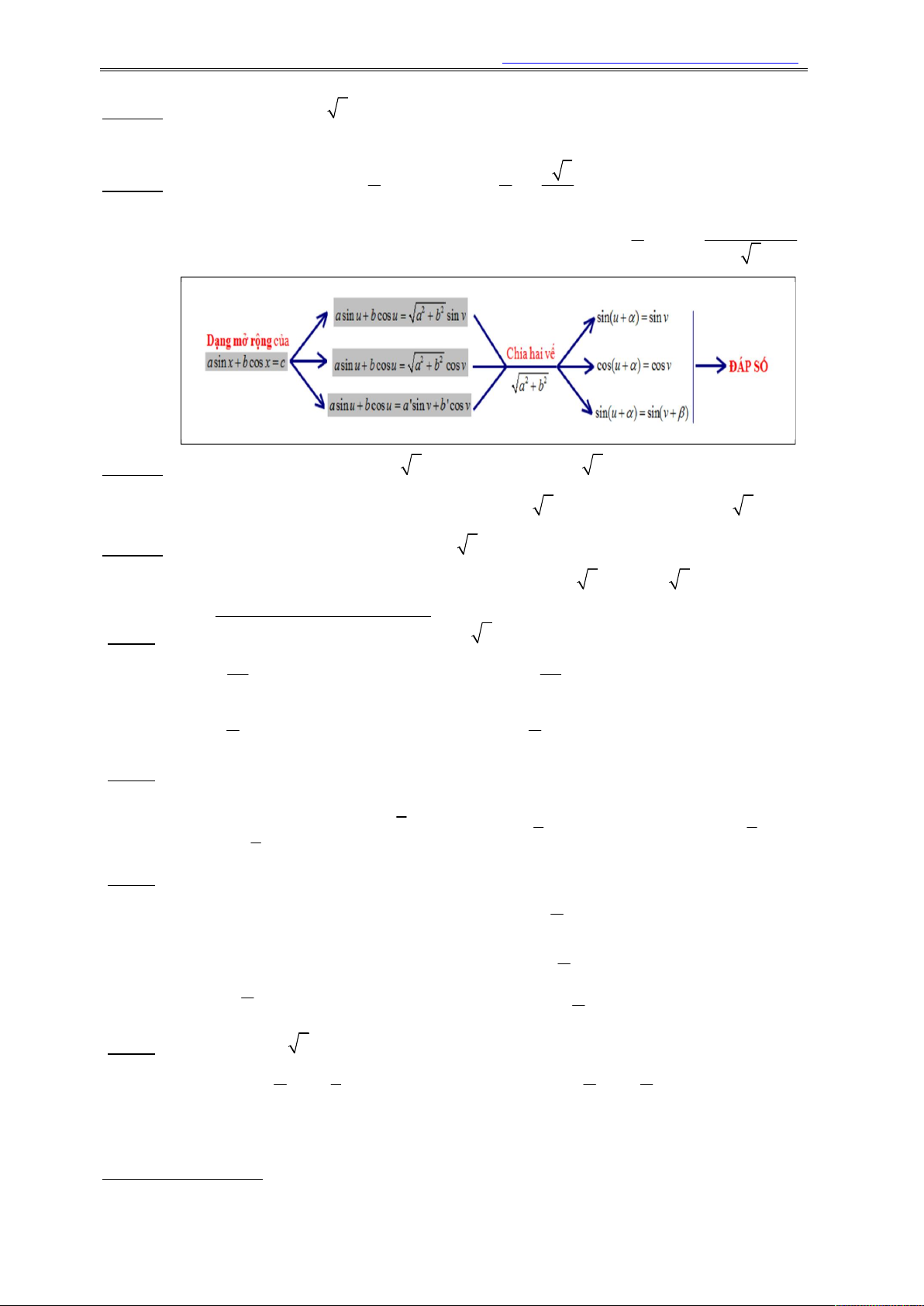
Daïng toaùn 1: Phöông trình baäc nhaát ñoái vôùi sinx vaø cosx
a sin x b cos x c  0 . 
Phương pháp giải: chia 2 a b c
a sin x b cos ve
x c   sin x  cos x  2 2 a b  2 2 2 2 2 2 a b a b a b a cos  2 2 c a b  
 sin x  Dap An b   DK 2 2 2 sin 2 2 a bc a b   2 2 a b
Ví dụ 1. Giải phương trình: 3 sin 2x  cos 2x  1.
Hướng dẫn: Chia hai vế cho 2.
Ví dụ 2. Giải phương trình: 5 sin 2x  12 cos 2x  13
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 21
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Hướng dẫn: Chia hai vế cho 13.
Ví dụ 3. Giải phương trình: 3 sin 2x  cos 2x  2 cos x  1. Hướng dẫn: 2
sin 2x  2 sin x cos x, cos 2x  2 cos x  1.        3 2
Ví dụ 4. Giải phương trình: 2 sin   x   sin x     .   4     4  2     sin x  cos x Hướng dẫn: sin   x  .   4  2
Ví dụ 5. Giải phương trình: 2cos x  3 sin xcosx  cos x  3 sin x  1. Hướng dẫn: x x  2 2 cos 3 sin
cos x  2 cos x  3 sin 2x.
Ví dụ 6. Giải phương trình: sin 8x  cos 6x  3 sin 6x  cos 8x
Hướng dẫn: sin 8x  3 cos 8x
3 sin 6x  cos 6x.
Áp dụng làm các bài tập sau: Câu 1.
Tập nghiệm của phương trình: sin x  3 cos x  2 là:  5     5    A.    k ,  k    .    k2 ,  k    .  B. 6     6            C.    k ,  k    .   k  k    D. 2 , . 2    6    Câu 2.
Phương trình 2  asin x  1  2acos x  3a  1 có nghiệm khi: a   2   1 a   1 1 A.  . 1 B.  2 . C.   a  2. D. 2  a  . a         2 2  2 a 2  Câu 3.
Nghiệm của phương trình sin x  cos x  1 là: A. x k2 ,  k  .  B. x   k2 ,  k  .  4  
x k2 x
   k2  C.  ,k  .  4  ,k  .   D. x   k2  2
x    k2   4 Câu 4.
Phương trình 3 sin 3x  cos 3x  1 tương đương với phương trình nào sau đây?     1    
A. sin 3x     .   x      B. sin 3 .  6  2  6  6
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 22
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong     1     1
C. sin 3x     .  sin3x    .  D.  6  2  6  2 Câu 5.
Điều kiện để phương trình 3 sin x m cos x  5 vô nghiệm là: m   4  A. . B.m  4. C.m  4  . D. 4   m  4. m   4  Câu 6.
Tổng các nghiệm của phương trình cos 2x  sin 2x  1 trong khoảng 0;2 là: 7 14 15 13 A. . B. . C. . D. . 4 4 8 4 Câu 7.
Nghiệm của phương trình 2 sin x cos x   1  3 cos 2x là:  x
   k2   x   k  A. 3  ,k  .  B. 3  ,k  .   4 2  4 x   kx   k   9 3  9 3  x
    k2  
x    k  C. 3  ,k  .  D. 3  ,k  .   2 2  2 x   kx   k   9 3  9 3 Câu 8.
Tổng các nghiệm của phương trình cos 2x  3 sin 2x  1 trong khoảng 0;  là: 2 A. 0. B. . C. 2 . D. . 3
2 sin x  cos x  1 Câu 9. Phương trình
m có nghiệm khi:
sin x  2 cos x  3 m   2  1 1 1 A.  . 1 B.2  m  . C.  m  2. D.  m  2. m     2 2 2  2 Câu 10.
Phương trình m  2sin x  2m cos x  2m   1 có nghiệm khi: m   4   m  0  A. . B. . C. 4   m  0. D. 0  m  4. m   0      m 4  Câu 11.
Giải phương trình 3 sin x  cos x  1  0. x   k   x k  A.  ,k  .  B.  ,k  . x    k   x  2  k2  3  3 x   2k   x k  C.  ,k  . 4  D.  ,k  . 2x    k2   x   k  3  3 Câu 12.
Giải phương trình 3 sin 2x  cos 2x  2.  7  7 x    k   x   k2  A. 24  ,k  .  B. 24  ,k  .   x   kx   k2   24  24
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 23
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  7 k  5 x      x   k  C. 24 2  ,k  .  D. 24  ,k  .   k x    x   k   24 2  24 Câu 13.
Giải phương trình sin 3x  3 cos 3x  2 cos 5x  5 k  5 k x      x    A. 48 5  ,k  .  B. 48 4  ,k  .   5  5 x    kx    k2   12  12  5 k  5 k x      x    C. 48 4  ,k  .  D. 48 4  ,k  .   5  5 x    kx    k   12 2  12 Câu 14.
Giải phương trình 3 sin 2x  cos 7x   sin 7x  cos 2x k2 k3 x       x    A. 10 5  ,k  .  B. 10 5  ,k  .   7 2  7 x   kx   k   54 9  54 3  k k2 x      x    C. 10 5  ,k  .  D. 10 5  ,k  .   7 2  7 2 x   kx   k   54 9  54 9 Câu 15. Giải phương trình  4 4
4 sin x  cos x  3 sin 4x  2.  k k x      x    A. 4 7  ,k  .  B. 4 5  ,k  .   x    kx    k   12 7  12 5  k k x      x    C. 4 3  ,k  .  D. 4 2  ,k  .   x    kx    k   12 3  12 2 Câu 16.
Tìm tất cả các giá trị của tham số m để phương trình 2 sin x m 3 cos x  2m có nghiệm. A. 2  m  2. B. 1  m  1. C. m  2. D. 2  m. Câu 17.
Tìm tất cả các giá trị của tham số m để phương trình 2
sin x m sin 2x  1 có nghiệm. A. m  0. B. m  1. C. m  2. D. m   .  Câu 18.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y  3 sin x  4 cos x  5 .
A. min y  0, max y  12.
B. min y  0, max y  10.
C. min y  0, max y  5.
D. min y  2, max y  5.
sin x  2 cos x  1 Câu 19.
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y  .
sin x  cos x  2
A. min y  2, max y  1.
B. min y  1, max y  1.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 24
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
C. min y  1, max y  2.
D. min y  2, max y  2. Đ/a 1B 2C 3C 4C 5D 6B 7A 8D 9C 10A 11C 12A 13D 14D 15D 16D 17D 18B 19A
Daïng toaùn 2: Phöông trình baäc hai ñoái vôùi moät haøm soá löôïng giaùc. 
Phương pháp giải: 2
a sin u b sin u c  0a  0. Đặt t  sinu ,điều kiện 1   t  1 . 2
a cos u b cos u c  0a  0. Đặt t  cosu ,điều kiện 1   t  1 . 2
a tan u b tan u c  0a  0. Đặt t  tanu , điều kiện cosu  0 . 2
a cot u b cotu c  0a  0. Đặt t  cotu ,điều kiện sinu  0 .
Ví dụ 7. Giải phương trình sau: 2
2 cos x  3 cosx  1  0
Hướng dẫn: t  cos x
Ví dụ 8. Giải phương trình sau: 2
4 sin x  4 sin x  3  0 .
Hướng dẫn: t  sin x.
Ví dụ 9. Giải phương trình sau: 2 tan x   3   1 tan x  3  0 .
Hướng dẫn: tan x t.
Ví dụ 10. Giải phương trình sau: 2
cot x  4 cotx  3  0 .
Hướng dẫn: cot x t.
Ví dụ 11. Giải phương trình sau: 3 2
sin x  3 sin x  2 sin x  0 .
Hướng dẫn: t  sin x. 3
Ví dụ 12. Giải phương trình sau: tan x  cotx  . 2 1
Hướng dẫn: cotx  .t  tan x tan x
Áp dụng làm các bài tập sau:   Câu 20.
Nghiệm của phương trình 2
2 cos x  3 sin x  3  0 thuộc 0;   là:  2  5 A. x  . B. x  . C. x  . D. x  . 3 4 6 6   3      Câu 21.
Tổng các nghiệm của phương trình 2 sin 2
x    3 cos  2x  2  0  trong  4     4 
khoảng 0;2 là: 7 3 7 A. . B. . C. x  . D. x  . 8 8 4 Câu 22.
Nghiệm bé nhất của phương trình 2
2 sin x  5 sin x  3  0 thuộc 0;2   là: A. 1. B. 2. C. 3. D. 4. Câu 23.
Số nghiệm của phương trình 2
cos 2x  sin x  2 cosx  1  0 thuộc 0;4   là:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 25
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong A. 1. B. 2. C. 4. D. 6. Câu 24.
Nghiệm của phương trình 2
2 sin x  5 sin x  3  0 là: A. x    k2 ,  k  .  B. x    k ,  k  .  2 2 C. x   k ,  k  . 
D. x k2 ,  k  .  2 Câu 25.
Phương trình cos 2x  2 cos x  11  0 có tập nghiệm là: A. k2 ,  k  . B. k ,  k  .     C.  k2 ,  k    .  D. .  2    Câu 26. Giải phương trình 2
2 sin x  5 sin x  3  0. A. x    k ,  k  .  B. x    k ,k  .  2 2 2 C. x    k3 ,  k  .  D. x    k2 ,  k  .  2 2 Câu 27.
Giải phương trình cos 2x  5 sin x  3  0.  x     k  
x    k3  A. 6  ,k  .  B. 6  ,k  .   7  7 x   kx   k3   6  6  x
    k4  
x    k2  C. 6  ,k  .  D. 6  ,k  .   7  7 x   k4x   k2   6  6 x Câu 28. Giải phương trình 2
cos 2x  3 cos x  4 cos . 2 2 2 2 A. x    k ,  k  .  B. x    k ,  k  .  3 3 3 2 2 C. x    k4 ,  k  .  D. x    k2 ,  k  .  3 3
Hướng dẫn: Đưa về cùng cung x . Câu 29.
Giải phương trình cos 3x  cos 2x  cos x  1  0. 2 2 A. x k ,  k  .  B. x    k ,  k  .  3 3  2 2 2 x     k ,  k   C. x    k2 ,  k  .  D.  3 3 . 3
x  k ,k   
Hướng dẫn: Đưa về cùng cung x . 1 Câu 30. Giải phương trình
 3 cotx  1  0. 2 sin x x     k   x    k  A. 4 2  ,k  .  B. 4 3  ,k  .   kk
x  arccot2  
x  arccot2    2  3
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 26
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  x     k x    k C.  4 ,k  .     D. 4 ,k .   x   arccot 2    k x
  arccot2  k  1 Hướng dẫn: 2
 1  cot x. 2 sin x Câu 31. Giải phương trình 2
1  5 sin 2 cos x  0.  x
   k2   x   k2  A. 6  ,k  .  B. 6  ,k  .   5 x   k2
x    k2   6  6  x
   k2   x   k2  C. 3  ,k  .  D. 3  ,k  .   2 x   k2
x    k2   3  3 1 Câu 32. Giải phương trình sau
 1  3 tan x  1  3  0. 2   cos x x    k   x    k2  A. 3  ,k  .  B. 3  ,k  .  
x    kx    k2   3  4  x    k   x   k  C. 3  ,k  .  D. 4  ,k  .    3 x   kx   k   4  4 1 Hướng dẫn: 2
 1  tan x. 2 cos x 1  1    Câu 33. Giải phương trình 2 cos x   2cosx    2  0. 2   cos x  cos x  A. x k2 ,  k  .  B. x   k2 ,  k  .  2 C. x   k ,  k  . 
D. x k2 ,  k  .  2 2 1  1    Hướng dẫn: 2 cos x   2  cosx   2   cos x  cos x  Câu 34.
Giải phương trình 1  tan x 1  sin 2x   1  tan x. x
  k2  
x k2  A.  ,k  .  B.  ,k  . x
    k2   x   k2  4  4 x   k2   x k  C.  ,k  .  D.  ,k  . x
   k2  
x    k2  2  4
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 27
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 2t
Hướng dẫn: Đặt t  tan x  sin 2x 2 1  t Câu 35. Giải phương trình x x  2 cos 2 cos 2 tan x   1  2. x   k2  
x k2  A.  ,k  .  B.  ,k  . x
   k2  
x    k2  3  3 x
  k  
x k2  C.  ,k  .  D.  ,k  . x
    k2  
x    k2  3  3 sin x
Hướng dẫn: tan x cos x Câu 36. Giải phương trình 2
tan x  tan x tan 3x  2. k A. x    ,k  .  B. x   k ,  k  .  4 2 3 k C. x   ,k  .  D. x   k2 ,  k  .  4 2 4 sin x
Hướng dẫn: tan x cos x 1 1 Câu 37. Giải phương trình 2 2 sin x   sin x  2 2 sin x sin x A. x k2 ,  k  . 
B. x k2 ,  k  .  C. x    k2 ,  k  .  D. x   k2 ,  k  .  2 2
Hướng dẫn: Đặt t  sin x 1 Câu 38.
Giải phương trình 2 tan x  cotx  2 sin 2x  sin 2x x     k   x    k  A. 6  ,k  .  B. 3  ,k  .   x   kx   k   4 2  4 2  x
    k2   x    k2  C. 3  ,k  .  D. 3  ,k  .   x    kx   k   4  2 sin x cos x
Hướng dẫn: tan x  , cotx cos x sin x 11 Câu 39. Giải phương trình 4 4
sin x  cos x   sin 2x 8  x    k   x   k  A. 6  ,k  .  B. 12  ,k  .   5  5 x   kx   k   6  12
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 28
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  x    k2   x   k2  C. 12  ,k  .  D. 6  ,k  .   5  5 x   k2x   k2   12  6 1 Hướng dẫn: 4 4 2
sin x  cos x  1  sin 2x 2 Câu 40. Giải phương trình 5 5 4
4 sin x cos x  4 cos x sin x  sin 4x x   k   x    k A.  ,k  .  B.  2 ,k  .  x
    k2        2 x k2   kk x     x   C. 4  ,k  .  D. 4  ,k  .   k k x     x      8 2  4 2 Hướng dẫn: 5 5 x x x x x x  2 2 x x 2 2 4 sin cos 4 cos sin 4 sin cos sin cos
sin x  cos x         Câu 41. Giải phương trình cos 2  x    cos 2
x    4 sin x  2  2       1 sinx  4   4   x
   k2   x   k2  A. 6  ,k  .  B. 3  ,k  .    2
x    k2x   k2   6  3  x
   k2   x   k2  C. 6  ,k  .  D. 3  ,k  .   5 x   k2
x    k2   6  3         Hướng dẫn: cos 2  x    cos 2
x    2 cos2x cos   4     4  4 Đáp án 20C 21D 22A 23B 24A 25D 26A 27A 28D 29D 30C 31A 32C 33C 34D 35B 36C 37D 38A 39B 40C 41C
Daïng toaùn 3: Phöông trình thuaàn nhaát ( ñaúng caáp) ñoái vôùi sin vaø cos 2 2
a sin x b sin x cos x c cos x d   1 . 
Phương pháp giải: 2 2
a sin x b sin x cos x c cos x d   1
Cách giải.Xét 2 trường hợp :
 Trường hợp 1 :Xét cosx  0  sin x  1
 .Thay vào (1) xem thoả hay không thoả.Kết luận
 Trường hợp 2:Xét cos x  0. Chia hai vế của (1) cho 2
cos x ,rồi đưa về phương trình bậc hai
theo tan x ,giải bình thường.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 29
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
   a d 2 1
tan x b tan x c d  0. Sơ đồ tư duy:
Ví dụ 13. Giải phương trình: 2 x x x     2 3 sin 6 sin cos 3 2 3 cos x   3 .
Hướng dẫn: Chia hai vế cho 2 cos x.
Ví dụ 14. Giải phương trình: 2 2
2 sin x  3 3 sin cos x  cos x  4 .
Hướng dẫn: Chia hai vế cho 2 cos x. 1
Ví dụ 15. Giải phương trình: 2 2
sin x  sin 2x  2 cos x  . 2
Hướng dẫn: Chia hai vế cho 2 cos x.
Ví dụ 16. Giải phương trình: 4 2 2 4
3 cos x  4 sin x cos x  sin x  0 .
Hướng dẫn: Chia hai vế cho 4 cos x.
Ví dụ 17. Giải phương trình:  x x x x  
  x  x2 2 sin sin sin 2 cos 3 1 sin 1 sin .
Hướng dẫn:   x   x  x x 
  x  x2 1 sin 1 sin sin 2 cos 3 1 sin 1 sin
Áp dụng làm các bài tập sau: Câu 42.
Tập nghiệm của phương trình: 2 2
3 sin x  2 3 sin x cos x  3 cos x  0 là:         A.    k , k ,  k    .    k k  k    B. 2 , 2 , . 6 3     6 3        5 C.    k ,  k    . x  .  D. 6    6 Câu 43. Phương trình 2 2
3 sin x m sin 2x  4 cos x  0 có nghiệm khi: A. m  4. B.m  4. C.m  4. D.m  .  Câu 44.
Nghiệm của phương trình 2
sin x  sin x cos x  1 là:    x    k   x   k  A. 4  ,k  .  B. 4  ,k  .   x   kx   k   2  2   
x    k2   x   k2  C. 4  ,k  .  D. 4  ,k  .   x   k2x   k2   2  2 Câu 45.
Nghiệm của phương trình 2 2
cos x  3 sin 2x  1  sin x là:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 30
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  x
    k2 x    k A.  3 ,k  .   k    B. 3 , .  x   k   x k   x
   k2 x     k C.  3 ,k  .   k    D. 3 , .  x   k   x k  Câu 46.
Số nghiệm của phương trình 2 2
sin x  2 sin x cos x  3 cos x  3 thuộc khoảng 0;2 là: A. 1. B. 2. C. 3. D. 4. Câu 47.
Nghiệm của phương trình: 3 2 2 2
sin x  3 cos x  3 sin x cos x  sin x cos x  0 là:  x    k   x   k  A. 4  ,k  .  B. 4  ,k  .   x    kx   k   3  3  x    k   x   k2  C. 4  ,k  .  D. 4  ,k  .  
x    kx    k2   3  3 Câu 48. Giải phương trình 2 2
2 cos x  6 sin x cos x  6 sin x  1  x
    k2  
x    k2 4  4 A.  ,k  .    ,k  .  1  B.  1  x     arctan      k2  x  arctan     k   5      5    
x    k  
x    k 4  4 C.  ,k  .    ,k  .  1  D.   k  1    x  arctan      x  arctan     k   5 2      5  Câu 49. Giải phương trình 3 2 2
4 sin x  3 cos x  3 sin x  sin x cosx  0  k x
   k2   x    A. 4  ,k  .  B. 4 2  ,k  .   k x    k2x      3  3 2  k x      x   k  C. 4 3  ,k  .  D. 4  ,k  .   k x     x    k   3 3  3
Hướng dẫn: Chia 2 vế cho 3 cos x Câu 50. Giải phương trình 3
2 cos x  sin 3x x   arctan k   2
   k2 x   arctan2   A.  ,k  .  B. 2  ,k  .  x
   k2 k  4 x     4 2
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 31
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  k x   arctan2  x   arctan   2    k  C. 3  ,k  .  D.  ,k  .   kx   x   k    4 3  4 Hướng dẫn: 3
sin 3x  3 sinx  4 sin x Câu 51. Giải phương trình 2 2
2 sin x  3 sin x cos x  3 cos x  2   1 x
   k2    
x  arctan   k 2  3 A.  ,k  .    ,k  .  1  B.  x   arctan     k    3 x   k   2   x k 1    C. x  arctan     k ,  k  .      k    D. 1 , .  3 x   arctan      k2     3  Câu 52.
Giải phương trình sin 2x  2 tan x  3 x   k  
x k2  A.  ,k  .  B.  ,k  . x     k  
x    k  3  4 x   k  C. x   k ,  k  .  D.  ,k  .  4 x     k  4
Hướng dẫn: Chia hai vế cho 2 cos x Câu 53. Giải phương trình sau
2 x     x x     2 2 sin 3 3 sin cos 3 1 cos x  1 A. x    k ;
 x    k ,  k  .  B. x   k2 ;  x   k ,  k  .  4 6 4 6 C. x    k ;  x   k ,  k  .  D. x   k ;
 x    k ,  k  .  4 2 2 6 Câu 54. Giải phương trình 2 2
2 sin x  sin x cos x  3 cos x  0  3   A. x   k2 ;  x  arctan     k ,  k  .  2  2 B. x   k ;  x  arctan 3    k ,  k  .  4  3   C. x   k ;  x  arctan     k ,  k  .  4  2 D. x k ;
 x  arctan3  k2 ,  k  .  Câu 55. Giải phương trình 2 2
2 cos x  6 3 sin x cos x  4 sin x  4 A. x   k ;  x   k ,  k  .  B. x   k2 ;  x   k ,  k  .  2 6 2 6 C. x    k2 ;
 x    k ,  k  .  D. x   k ;
 x    k ,  k  .  2 6 2 6 Câu 56. Giải phương trình 2 2
cos x  3 sin 2x  1  sin x A. x k ;
 x    k ,  k  .  B. x   k2 ;  x   k ,  k  .  3 2 3
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 32
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong C. x k ;  x   k ,  k  .  D. x    k ,  k  .  3 3 Câu 57. Giải phương trình 3 3 2
cos x  4 sin x  3 cos x sin x  sin x  0 A. x   k ;
 x    k ,  k  .  B. x    k ;  x   k ,  k  .  4 3 4 6 C. x k ;  x   k ,  k  .  D. x    k ;
 x    k ,  k  .  3 4 6 Câu 58. Giải phương trình 2 2
3 sin x  4 sin x cos x  5 cos x  2. A. x   k ;
 x  arctan 3  k ,  k  .  4 B. x   k ;
 x  arctan  3  k ,  k  .  4  3   C. x   k ;  x  arctan     k ,  k  .  4  2 D. x k ;
 x  arctan3  k2 ,  k  .  1 Câu 59. Giải phương trình 2 2
sin x  sin 2x  2 cos x  . 2 A. x   k ;
 x  arctan 3  k ,  k  .  4 B. x   k ;
 x  arctan5  k ,  k  .  4  5   C. x   k ;  x  arctan     k ,  k  .  4  2 D. x k ;
 x  arctan 5  k2 ,  k  .  Câu 60. Giải phương trình 4 2 2 4
3 cos x  4 sin x cos x  sin x  0 A. x   k ;  x   k ,  k  .  B. x   k ;
 x    k2 ,  k  .  4 3 4 4 C. x    k ;
 x    k ,  k  .  D. x    k ,  k  .  4 3 3 Câu 61. Giải phương trình 2
sin x sin 2x  sin 3x  6 cos x A. x k ;  x   k ,  k  .  3 B. x   k ;
 x  arctan 2  k2 ,  k  .  3 C. x    k ;
 x    k ,  k  .  4 3 D. x    k ;
 x  arctan 2  k ,  k  .  3 cos 2x 1 Câu 62. Giải phương trình 2 cotx  1 
 sin x  sin 2x 1  tan x 2 A. x k ;  x   k ,  k  .  B. x   k ;  x   k2 ,  k  .  4 3 4 C. x   k ,  k  .  D. x    k ,  k  .  4 4
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 33
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong Câu 63.
Giải phương trình sin 3x  cos 3x  2 cos x  0 A. x k ;  x   k ,  k  .  B. x    k ;  x   k2 ,  k  .  4 3 4 C. x   k ;  x   k ,  k  .  D. x    k ;
 x    k ,  k  .  3 4 4 3 Câu 64. Giải phương trình 3
sin x  4 sin x  cos x  0 A. x   k ,  k  .  B. x   k2 ;  x   k ,  k  .  4 4 3 C. x k ;  x   k ,  k  .  D. x    k ,  k  .  4 4 Câu 65. Giải phương trình 2 2
tan x sin x  2 sin x  3cos2x  sin x cosx A. x k ;  x   k ,  k  .  B. x    k ;
 x    k ,  k  .  4 3 4 C. x   k ;  x   k ,  k  .  D. x    k ;  x   k2 ,  k  .  3 4 3 4 Câu 66. Giải phương trình 3 2
cos x  sin x  3 sin x cos x  0 A. x   k ,  x  arctan 2    k ,  k  .  4 B. x    k ,  k  .  4  1   C. x   k ,  x  arctan     k ,  k  .  4  2 D. x    k ,  k  .  4 Câu 67. Giải phương trình 2
sin x tan x  
1  3 sin x cosx  sin x   3 A. x    k ;
 x    k ,  k  .  B. x k ;  x   k ,  k  .  4 3 4 C. x   k ;  x   k ,  k  .  D. x   k2 ;
 x    k ,  k  .  4 3 4 3 Đáp án 42A 43D 44A 45D 46C 47A 48D 49D 50D 51B 52C 53A 54C 55A 56A 57D 58A 59B 60C 61D 62C 63D 64A 65B 66C 67A
Daïng toaùn 4: Phöông trình ñoái xöùng
a sin x  cosx  b sin x cos x c  0  1 . 
Phương pháp giải:
a sin x  cosx  b sin x cos x c  0  1 Cách giải.Đặt :
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 34
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 2 t  1
t  sin x  cos x  sin x cos x   2 t  2 2 2 1  t
t  sin x  cos x  sin x cos x   2 t  2 2 2 1  t
t  cos x  sin x  sin x cos x   2 t  2 2
Thay vào (1) rồi giải phuong trình bậc 2 theo t. Sơ đồ tư duy:
Ví dụ 18. Giải phương trình sin x  cos x  sin x cos x  1  0. 2 t  1
Hướng dẫn: t  sin x  cos x  sin x cos x   2 t  2 2
Ví dụ 19. Giải phương trình tan x  1  2 2 sin x . sin x
Hướng dẫn: tan x cos x
Ví dụ 20. Giải phương trình 2 sin 2x  3 3 sin x  cos x  5  0 . 2 t  1
Hướng dẫn: t  sin x  cos x  sin x cos x   2 t  2 2
Ví dụ 21. Giải phương trình 2 sin 2x  3 6 sin x  cos x  8  0.
Hướng dẫn: Đặt t  sin x  cos x ( Đk : 0  t  2 ) 2 2
t  (sin x  cos x) 2
 sin2x t 1   
Ví dụ 22. Giải phương trình sin 2x  2 sin x     1.   4 
Hướng dẫn: sin 2x  (sin x  cos x )  1
Daïng toaùn 5: Phöông trình ñoái xöùng. a  2 2
tan x  cot x btanx  cotx  c  0  1 . 
Ví dụ 23. Giải phương trình lượng giác 2 tan x  5tan x  2 cotx  5cotx  8  0 .
Hướng dẫn:     2 2 1
tan x  cot x  5tanx  cotx  8  0.
Ví dụ 24. Giải phương trình lượng giác 2 2
3 tan x  8 cotx  8 tan x  3 cot x  2 3 .
Hướng dẫn:     2 2 1
3 tan x  cot x  8tan x  cotx  2 3  0.
Áp dụng làm các bài tập sau:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 35
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong Câu 68.
Giải phương trình sin 2x  4sin x  cos x   4.   2  x    k x   k   A.  2 ,k  .  2 3    B. ,k .  x  2
  k
x k    3  1 x    k x
   k2 C. 2 2  ,k  .  C.  2 ,k  .   1 
x k x
  k2  2      Câu 69.
Giải phương trình sin 2x  2 sin x     1.   4  A. x   k ;  x   k ;
 x k2 ,  k  .  4 2 1 1 1 B. x   k ;  x   k ;
 x k ,  k  .  4 2 2 2 2 2 2 C. x   k ;  x   k ;
 x k2 ,  k  .  4 3 2 3 D. x   k ;  x   k2 ;
 x k2 ,  k  .  4 2 Câu 70.
Giải phương trình cos x  sin x  2 sin 2x  1 1 A. x k ,  k  .  B. x k ,  k  .  2 C. x k2 ,  k  .  D. x   k ,  k  .  2 Câu 71.
Giải phương trình cos x  sin x  3 sin 2x  1 1 A. x k ,  k  .  B. x k ,  k  .  2 C. x k2 ,  k  .  D. x   k ,  k  .  2 Câu 72.
Giải phương trình 2sin x  cos x   3 sin 2x  2 A. x k2 ;  x   k2 ,  k  .  B. x k ;  x   k ,  k  .  2 2 C. x k2 ;
 x k2 ,  k  .  D. x k ;  x   k2 ,  k  .  3 3 Câu 73. Giải phương trình 3 3
1  sin 2x  cos 2x  sin 4x 2 A. x   k ;  x   k2 ,  k  .  B. x    k ;  x   k ,  k  .  4 2 4 2 C. x k2 ;
 x k2 ,  k  .  D. x k ;  x   k2 ,  k  .  3
Hướng dẫn: Dùng hằng đẳng thức 3 3      2 2 a b a
b a ab b phân tích 3 3
sin 2x  cos 2x và chuyển sin 4x  2 sin 2x cos 2x. Câu 74.
Giải phương trình 6sin x  cos x   sin x cos x  6  0
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 36
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong A. x k ,  x   k2 ,  k  .  B. x k2 ,  x   k2 ,  k  .  2 2 3 C. x k2 ,  x   k2 ,  k  .  D. x k2 ,  x   k2 ,  k  .  2 3 Câu 75.
Giải phương trình cos 2x  5  22  cos x sin x  cos x A. x k ,  x   k2 ,  k  .  B. x k2 ,  x   k2 ,  k  .  2 2 3 C. x k2 ,  x   k2 ,  k  .  D. x   k2 ,
 x k2 ,  k  .  2 2 Hướng dẫn: 2 2
cos 2x  cos x  sin x  cosx  sin xcos x  sin x 3 Câu 76.
Giải phương trình sin x  cos x   2 sin 2x  
1  sin x  cos x  2 A. x k ,
 x    k2 ,  k  .  B. x    k2 ,  k  .  4 4 C. x k2 ,  x   k2 ,  k  . 
D. x k2 ,  x   k ,  k  .  4 2 Hướng dẫn: x    x x 2 sin 2 1 sin cos
,t  sin x  cos x Câu 77. Giải phương trình 3 3 x x   2 2 tan cot
3 tan x  cot x  3tan x  cotx  10  0 k 1 1   k A. x   
,x  arctan   ,k  .  8 2 2 2 2 B. x   k2 ,
 x    k2 ,  k  .  8 4 7 C. x   k ,  x   k ,  k  .  4 8 D. x   k ,
 x k2 ,  k  .  2 Hướng dẫn:  2 2 2 t
 an x  cot x t  2  t tan x cotx,  
tan x cot x  tanx cotx3 3 3
 3 tan x cotx tanx  cotx 3  t  3t  Câu 78.
Giải phương trình 3  cos 4x sin x  cos x   2 k A. x   
,x    k2 ,  k  .  B. x   k2 ,
 x    k2 ,  k  .  8 2 4 8 4 7 C. x   k ,  x   k ,  k  .  D. x   k2 ,
 x k2 ,  k  .  4 8 2 3 Câu 79. Giải phương trình 2
 3 cot x  4 tan x  cotx  1  0 2   cos x A. x    k ,  k  .  B. x    k2 ,  k  .  4 4 7 C. x   k ,  k  .  D. x   k ,  k  .  12 2
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 37
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 2 Câu 80. Giải phương trình 2
 2 tan x  5 tan x  cotx  4  0 2   sin x A. x   k ,  k  .  B. x    k2 ,  k  .  12 4 C. x    k ,  k  .  D. x   k2 ,  k  .  4 2   4 4 1
sin x  cos x Câu 81. Giải phương trình  cosx sin x A. x   k2 ;
 x    k ,  k  .  B. x    k2 ,  k  .  2 4 4 C. x    k ,  k  .  D. x   k ;  x   k ,  k  .  4 2 4 Câu 82. Giải phương trình 3
2 cos x  cos 2x  sin x  0 A. x   k2 ;
 x    k ,  k  .  B. x   k ;  x   k ,  k  .  2 4 2 4 C. x    k ,  k  .  D. x   k2 ,  k  .  4 2 Câu 83.
Giải phương trình tan x  3 cotx  4sinx  3 cosx 4 k2 A. x    k ;  x   ,k  .
 B. x    k ;
 x    k ,  k  .  3 9 3 3 4 k2 C. x   k2 ;
 x    k ,  k  .  D. x   k ;  x   ,k  .  3 4 3 9 3 Câu 84. Giải phương trình 3 3
sin x  cos x  sin x  cos x A. x   k2 ,  k  .  B. x    k ,  k  .  3 3 C. x    k ,  k  .  D. x   k ,  k  .  4 2 Câu 85.
Giải phương trình 2 cos x  
1 sin x  cos x  1 k2 A. x k2 ;  x   ,k  .  B. x k2 ;
 x    k ,  k  .  6 3 3 C. x k ;
 x    k ,  k  .  D. x k ;  x   k ,  k  .  4 2 Câu 86.
Giải phương trình 2 cos 2x  6 cos x  sin x k2 A. x   k2 ;  x   ,k  .  B. x   k2 ;
 x    k ,  k  .  12 6 3 12 3 5 C. x   k2 ;  x   k2 ,  k  .  D. x   k2 ;  x   k ,  k  .  12 12 6 2 Đáp án 68D 69D 70B 71B 72A 73B 74C 75D 76B 77A 78D 79A 80C 81D 82A 83A 84D 85A 86C `
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 38
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong ÔN TẬP CHƯƠNG I.
PhÇn 1. Hµm sè l­îng gi¸c. 1  sin 2x
Câu 1. Tìm tập xác định của hàm số y  . cos 3x  1 k2    k    A. D   \  ,k    . D    k    B. \ , . 3     6    k    k    C. D   \  ,k    . D    k    D. \ , . 3     2    1  cos 3x
Câu 2. Tìm tập xác định của hàm số y  1  sin 4x   k     3 k    A. D   \    ,k    . D   \    ,k    .  B. 8 2     8 2      k      k    C. D   \    ,k    . D      k    D. \ , . 4 2     6 2    tan 2x
Câu 3. Tìm tập xác định của hàm số y
3 sin 2x  cos 2x  k  t    A. D   \   ,  ;k,t    .  4 2 12 2     k  t    B. D   \   ,  ;k,t    .  3 2 5 2     k  t    C. D   \   ,  ;k,t    .  4 2 3 2     k  t    D. D   \   ,  ;k,t    .  3 2 12 2       
Câu 4. Tìm tập xác định của hàm số sau y  tan 2  x     3   k     k    A. D   \   ,k    . D     k    B. \ , . 3 2    4 2     k     k    C. D   \   ,k    . D     k    D. \ , . 12 2    8 2   
Câu 5. Tìm tập xác định của hàm số sau y  tan 3x. cot 5x  k n     k n    A. D   \   , ;k,n    . D     k n    B. \ , ; , . 6 3 5     5 3 5     k n     k n    C. D   \   , ;k,n    . D     k n    D. \ , ; , . 6 4 5    4 3 5           
Câu 6. Tìm tập xác định của hàm số sau y  tan x   .cot x      4     3  3    3    A. D   \   k , k ;  k    . D   \   k , k ;  k    .  B. 4 3     4 5   
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 39
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong     3   
C. D   \   k , k ;  k    . D   \   k , k ;  k    .  D. 4 3     5 6   
Câu 7. Hàm số f x   sin x tuần hoàn với chu kì: A. T  2 . B. T  . C. T  . D. T  . 2 4
Câu 8. Hàm số f x   tan 2x tuần hoàn với chu kì: A. T  . B. T  2 . C. T  . D. T  . 2 4
Câu 9. Hàm số f x   sin 2x  sin x tuần hoàn với chu kì: A. T  2 . B. T  . C. T  . D. T  . 2 4
Câu 10. Hàm số f x   tan x. tan 3x tuần hoàn với chu kì: A. T  . B. T  2 . C. T  . D. T  . 4 2
Câu 11. Hàm số f x   sin 3x  2 cos 2x tuần hoàn với chu kì: A. T  2 . B. T  . C. T  . D. T  . 2 4
Câu 12. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2  3 sin 3x
A. min y  2; max y  5.
B. min y  1; max y  4.
C. min y  1; max y  5.
D. min y  5; max y  5.
Câu 13. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  1  4 sin 2x
A. min y  2; max y  1.
B. min y  3; max y  5.
C. min y  5; max y  1.
D. min y  3; max y  1.
Câu 14. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 sin x  3
A. min y  1; max y  5.
B. min y  5; max y  2 5.
C. min y  2; max y  5.
D. min y  5; max y  3.
Câu 15. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  3  2 2  sin 4x
A. min y  3  2 2; max y  3  2 3. B. min y  2  2 2; max y  3  2 3.
C. min y  3  2 2; max y  3  2 3. D. min y  3  2 2; max y  3  3 3.
Câu 16. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
3 cos x  sin x  4
A. min y  2; max y  4.
B. min y  2; max y  6.
C. min y  4; max y  6.
D. min y  2; max y  8.
Câu 17. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  1  2 cos x  1
A. min y  1  3; max y  1.
B. min y  1  3; max y  3.
C. min y  1  3; max y  2.
D. min y  1  3; max y  0.
Câu 18. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2
y  3  2 cos 3x
A. min y  1; max y  2.
B. min y  1; max y  3.
C. min y  2; max y  3.
D. min y  1; max y  3.
Câu 19. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  1  2  sin 2x
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 40
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
A. min y  2; max y  1  3.
B. min y  2; max y  2  3.
C. min y  1; max y  1  3.
D. min y  1; max y  2. 4
Câu 20. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  2 1  2 sin x 4 4 A. min y  ;max y  4. B. min y  ;max y  3. 3 3 4 1 C. min y  ; max y  2. D. min y  ; max y  4. 3 2
Câu 21. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2
y  2 sin x  cos 2x 3 A. min y  ;max y  4.
B. min y  2; max y  3. 4 3
C. min y  2; max y  4. D. min y  ;max y  3. 4
Câu 22. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  3 sin x  4 cos x  1
A. min y  6; max y  4.
B. min y  6; max y  5.
C. min y  3; max y  4.
D. min y  6; max y  6.
Câu 23. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2
y  2 sin x  3 sin 2x  4 cos x A. min y  3 
2  1; max y  3 2  1. B. min y  3 2  1; max y  3 2  1. C. min y  3
 2;max y  3 2  1.
D. min y  3 2  2; max y  3 2  1.
Câu 24. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2
y  sin x  3 sin 2x  3 cos x
A. min y  2  10; max y  2  10. B. min y  2  5; max y  2  5.
C. min y  2  2; max y  2  2.
D. min y  2  7; max y  2  7.    
Câu 25. Khi x thay đổi trong nửa khoảng   ;   y x  thì
cos lấy mọi giá trị thuộc:  3 3  1   1 1    1 1   1 A.  ;1 .         B. ; . C. ; . D. 1; . 2           2 2  2 2 2   57  
Câu 26. Khi x thay đổi trong khoảng  ;   y x  thì
sin lấy mọi giá trị thuộc:  4 4   2        2   2   A.  ;1 .   B. 1;  . C.  ;0 . D.  1;1  . 2            2    2    
Câu 27. Tập giá trị của hàm số y  4 cos 2x  3 sin 2x  6 là: A. 3;10 .          B. 6;10 .   C. 1;13 .   D. 1;11 .  
Câu 28. Trong các mệnh đề sau, mệnh đề nào sai?
A. y  2 sin x là hàm số lẻ.
B. y   tan x  sin x là hàm số lẻ.
C. y  tan x  cos x là hàm số lẻ.
D. y  sin x x là hàm số lẻ.
Câu 29. Trong các mệnh đề sau, mệnh đề nào sai?
A. Tổng của hai hàm số chẵn là một hàm số chẵn.
B. Tích của hai hàm số lẻ là một hàm số chẵn.
C. Tổng của hai hàm lẻ là một hàm số lẻ.
D. Tổng của hai hàm số chẵn là một hàm số lẻ.
Câu 30. Hàm số y  sin x nghịch biến trên khoảng:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 41
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 19     11     15     35   A.  ;10.    ;5. 7  ; .   ; .  B. C. D.  2   2   2   2 2 
Câu 31. Hàm số y  cos x nghịch biến trên khoảng: 19    11     15    5    A.  ;10.   ;6. 7  ; .  ;6.  B. C. D.  2   2   2   2 
Câu 32. Cho hàm số y  sin x. cos 3x . Chọn mệnh đề đúng?
A. y là hàm số chẵn.
B. y là hàm số lẻ.
C. y là hàm số không chẵn, không lẻ.
D. y là hàm số vừa chẵn, vừa lẻ.
Câu 33. Cho hàm số y f x  2n 1  *  cos
x,n   . Hàm số f x  là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 34. Cho hàm số y f x  2
 sin x . Hàm số f x là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 35. Cho hàm số y f x  2
 sin x cos x . Hàm số f x là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn. 2 tan x
Câu 36. Cho hàm số y f x  
. Hàm số f x  là: 2 1  tan x
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 37. Cho hàm số y f x   cos x  sin x . Hàm số f x  là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
tan x  3 cos x
Câu 38. Cho hàm số y f x  2 
. Hàm số f x  là: 2 x  2
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
Câu 39. Cho hàm số y f x   tan x  cos x . Hàm số f x  là:
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
sin 2x  3 cos x
Câu 40. Cho hàm số y f x  
. Hàm số f x  là: 2 cos x  3
A. Hàm số vừa chẵn, vừa lẻ. B. Hàm số lẻ.
C. Hàm số không có tính chẵn, lẻ. D. Hàm số chẵn.
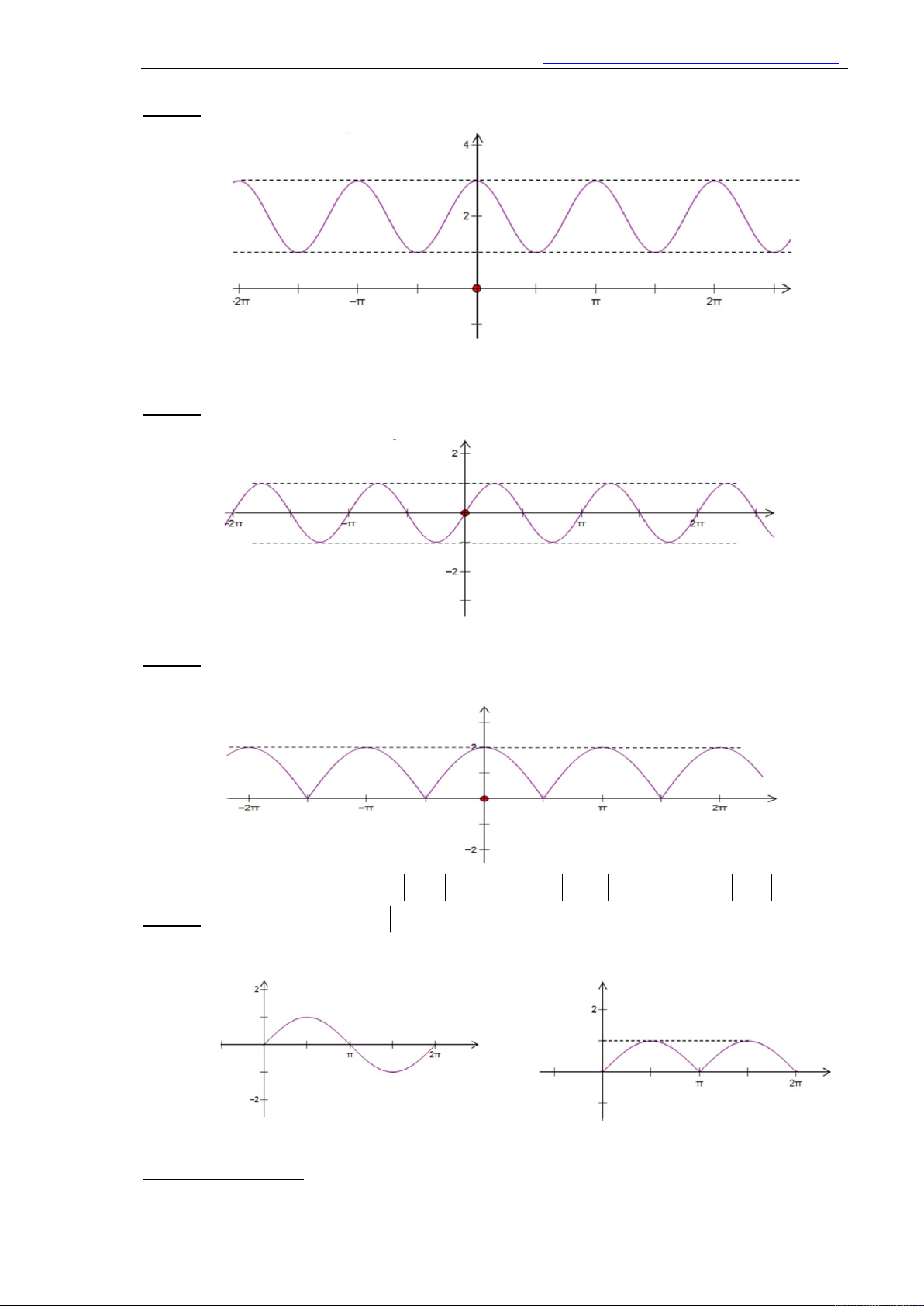
Câu 41. Hình vẽ dưới đây là đồ thị của hàm số nào?
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 42
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
A. y  tan 2x. B. y  tan x.
C.y  2 tan x. D.y  cotx.
Câu 42. Hình vẽ dưới đây là đồ thị của hàm số nào?
A. y  tan 2x. B. 2
y  1  2 cos x. C.y  2 tan x. D.y  cotx.
Câu 43. Hình vẽ dưới đây là đồ thị của hàm số nào?
A. y  cos 2x. B.y  tan x. C.y  sin 2x. D.y  cos x.
Câu 44. Hình vẽ dưới đây là đồ thị của hàm số nào?
A. y  cos 2x. B.y  tan x .
C.y  sin 2x .
D.y  2 cos x .
Câu 45. Đồ thị hàm số y  sin x trên đoạn 0;2   là: A. B. C. D.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 43
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Câu 46. Đồ thị hàm số y   sin x trên đoạn 0;2   là: A. B. C. D. ĐÁP ÁN. 1A 2A 3A 4C 5A 6A 7A 8A 9A 10A 11A 12C 13D 14A 15A 16B 17D 18B 19A 20A 21D 22A 23B 24A 25A 26B 27D 28C 29D 30C 31D 32B 33D 34D 35D 36B 37C 38D 39C 40D 41A 42B 43C 44D 45B 46C Hướng dẫn giải:  3 1          Câu 16. y 2 cos x  sin x    4  2 sin x     4.   2 2       3  Câu 21. Đặt 2  1   3 2 2
t  sin x, 0  t  1  cos 2x  1  2t y  4t  2t  1  2  t      2 4
Câu 22. y  5 sin x   1 Câu 23.
y  1  cos 2x  3 sin 2x  21  cos2x 
 3 sin 2x  3 cos 2x  1  3 2 sin 2  x     1  4  3  1 cos2 1 cos 2 x x  Câu 24. y   3 sin 2x
 3 sin 2x  cos 2x  2 2 2
PhÇn 2. Ph­¬ng tr×nh l­îng gi¸c c¬ b¶n.
Câu 1. Trong các mệnh đề sau, mệnh đề nào sai?
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 44
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
A. sin x  1  x    k2 ,  k  .
 B. sin x  0  x k ,  k  .  2
C. sin x  0  x k2 ,  k  . 
D. sin x  1  x   k2 ,  k  .  2 1
Câu 2. Giải phương trình: sin x  . 2  x
   k2   x   k  A. 6  ,k  .  B. 6  ,k  .   5 x   k2
x    k   6  6  x   k  C. x    k ,  k  .  D. 3  ,k  .  6 
x    k   3 2x   
Câu 3. Giải phương trình sin     0.   3 3  k2 A. x    ,k  .  B. x k ,  k  .  3 3 k2 C. x   k ,  k  .  D. x   ,k  .  2 2 3
Câu 4. Giải phương trình 1  2 cos 2x  0. A. x    k ,  k  .  B. x    h2 ,  k  .  3 3 C. x   k ,  k  .  D. x   k ,  k  .  3 3
Câu 5. Giải phương trình cos 3x  cos . 15 k2 A. x    k2 ,  k  .  B. x    ,k  .  15 45 3 k2 k2 C. x    ,k  .  D. x   ,k  .  45 3 45 3 3
Câu 6. Giải phương trình sin 2x   . 2  x     k   x   k  A. 6  ,k  .  B. 6  ,k  .   2 x   k
x    k   3  6  x   k  C. x    k ,  k  .  D. 3  ,k  .  6 
x    k   3 x
Câu 7. Giải phương trình 2 cos  3  0. 2 5 5 A. x    k2 ,  k  .  B. x    k2 ,  k  .  3 6
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 45
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 5 5 C. x    k4 ,  k  .  D. x    k4 ,  k  .  6 3
Câu 8. Giải phương trình sin x  cos x.  k x     A. 8 2  ,k  .  B. x   k ,  k  .   8 x   k   4  x   k2  C. x   k ,  k  .  D. 4  ,k  .  4  x   k   8
Câu 9. Giải phương trình lượng giác: 3 tan x  3  0. A. x   k ,  k  .  B. x    k2 ,  k  .  3 3 C. x   k ,  k  .  D. x    k ,  k  .  6 3
Câu 10. Giải phương trình: 2 tan x  3. A. x    k ,  k  .  B. x    k ,  k  .  6 3 C. Vô nghiệm. D. x   k ,  k  .  6
Câu 11. Giải phương trình cos2x  60  cosx  30.
A. x  90  k 360,k  . 
B. x  10  k120,k  .   x
  90  k360 x
   k2   C. ,k  .  D. 2  ,k  .  x   10  k120    2x   k   18 3    
Câu 12. Hàm số y  tan 3x và y  tan   2x  
có giá trị bằng nhau khi:  3  A. x   k ,  k  .  B. x   k2 ,  k  .  15 15 C. x   k ,k  .  D. x   k ,k  .  15 5 15 2
Câu 13. Giải phương trình 2 2
sin 2x  cos 2x  cos 3x 2 x
   k2 x    k A.  7 ,k  .   7 7 ,k  .   B.  x     k2     x k2  C. x   k2 ,  k  .  D. x   k2 ,  k  .  7
Câu 14. Giải phương trình 6 sin 4x  5 sin 8x  0.  kk x     x  4  4 A.  ,k  .   ,k  .  1  3  B.   k 1  3    k x   arccos     x    arccos      4  5 2     3  5 2 
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 46
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  kk x   1    x  4  4 C.  ,k  .   ,k  .  1  3  D.   k 1  3    k x    arccos     x    arccos      4  5 2     4  5 2 
Câu 15. Nghiệm của phương trình sin x 2 cos x  3  0 là: x   k   x k  A.  ,k  .  B.  ,k  . x
    k2   x    k  6  6 x   k2 C.  ,k  .  D. x    k2 ,  k  .  x
    k2  6  3
Câu 16. Phương trình sin x. cos x. cos 2x  0 có nghiệm là: A. x k ,k  .
 B. x k ,k  .
 C. x k ,k  .
 D. x k ,k  .  16 2 4 8
Câu 17. Giải phương trình cot 2x. sin 3x  0.  x    k  4 2   x    k  2  A. x   k,k  .   B. 4 2  ,k  .   3  2 x   kx    k  3  3   x    k   x   k  C. 4 2  ,k  .  D. 4 2  ,k  .   x   kx k   3  3
Câu 18. Giải phương trình cot x. cot 2x  1. A. x   k ,k  .  B. x   k ,k  .  6 3 3 3 C. x    k ,  k  .  D. x   k ,  k  .  6 3
Câu 19. Giải phương trình tan 3x  tan 4x . A. x   k ,  k  . 
B. x  2  k ,  k  .  2 C. x k2 ,  k  .  D. x k ,  k  .  sin x
Câu 20. Giải phương trình  0 có nghiệm. 1  cos x A. x k ,  k  . 
B. x  2k   1 ,  k  .  C. x k2 ,  k  . 
D. x  2k   1 ,k  .  2
cos x  3 sin x
Câu 21. Giải phương trình  0 . 1 sin x  2
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 47
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong A. x   k2 ,  k  .  B. Vô nghiệm. 6 7 C. x   k ,  k  .  D. x   k2 ,  k  .  6 6
Câu 22. Giải phương trình  x   2 3 tan 1 sin x   1  0 có nghiệm là: A. x   k2 ,  k  .  B. x    k2 ,  k  .  3 6 C. x   k ,  k  .  D. x    k ,  k  .  6 3         Câu 23. Phương trình cos 2  x    cos 2  x   
có nghiệm dương nhỏ nhất là:  3     3  3 A. x  . B. x  . C. x  2 . D. x  . 2 2  3  
Câu 24. Nghiệm dương nhỏ nhất của phương trình cot x     1  là:  2  3 7 A. x  . B. x  . C. x  . D. x  . 4 4 4 2 2 2  
Câu 25. Giải phương trình cos sin x    1  .  3 3  2 A. x   k ,  k  .  B. x   k ,k  .  2 2 3 C. x   k2 ,  k  .  D. x   k2 ,  k  .  2 3    
Câu 26. Giải phương trình cot cos x   1   1   .  4  A. x   k2 ,  k  .  B. x   k ,k  .  2 2 2 C. x   k ,k  .  D. x   k ,  k  .  2 3 2
Câu 27. Phương trình sin x  cos x có nghiệm thuộc đoạn  ;      là: A. 2. B. 4. C. 5. D. 6. cos 4x   Câu 28. Phương trình
 tan 2x có số nghiệm thuộc khoảng 0;  là: cos 2x  2 A. 2. B. 3. C. 4. D. 5.
Câu 29. Giải phương trình 2 sin 2x  1 với điều kiện cos x  0.  x     k   x   k  A. 12  ,k  .  B. 12  ,k  .   5  5 x    k2x    k2   12  12  x     k   x   k  C. 12  ,k  .  D. 12  ,k  .   5  5 x   k2x   k2   12  12
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 48
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Câu 30. Giải phương trình 3 cot 2x   3 với điều kiện cos x  0.  x
    k2  
x    k2  A. 6  ,k  .  B. 6  ,k  .   x   k2
x    k2   3  3  x
   k2   x   k2  C. 6  ,k  .  D. 6  ,k  .   x   k2
x    k2   3  3 2 sin x  3
Câu 31. Giải phương trình  0 . cos x x
   k2  
x    k2  A. 3  ,k  .  B. 3  ,k  .   2  2 x   k2x   k2   3  3  x
   k2   x   k2  C. 3  ,k  .  D. 6  ,k  .   2 x    k2
x    k2   3  3 2 cos x  2
Câu 32. Giải phương trình  0. 2 sin x  1 3 3 A. x   k ,  k  .  B. x   k2 ,  k  .  4 4 3 C. x    k ,  k  .  D. x   k2 ,  k  .  4 4
Câu 33. Phương trình cos x m  0 vô nghiệm khi và chỉ khi: m   1  A. . B. m  1. C.1  m  1. D.m  1  . m   1  1
Câu 34. Phương trình sin 2x   có bao nhiêu nghiệm thỏa 0  x  . 2 A.1. B. 3. C. 2. D. 4. 1
Câu 35. Phương trình sin x  có nghiệm thỏa   x  là: 2 2 2 A. x   . B. x  . C. x  . D. x   . 6 6 3 3    
Câu 36. Số nghiệm của phương trình sin x     1 
x  với 3 là:  4  A.1. B. 0. C. 2. D. 3.
Câu 37. Nghiệm của phương trình lượng giác: 2
cos x  cos x  0 thỏa điều kiện 0  x là: A. x  . B. x  0. C. x  . D. x  . 2 4    
Câu 38. Số nghiệm của phương trình 2 cos x     1   x  với 0 2 là:  3  A. 0. B. 2. C.1. D. 3.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 49
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Câu 39. Giải phương trình  x   2 sin 2 15  , với 1
 20  x  90 . 2
A. x  30;x  75;x  105 . 
B. x  30;x  105 . 
C. x  60;x  90;x  105 . 
D. x  30;x  75;x  45 .         
Câu 40. Phương trình sin x     sin x     0  0; 4
có tổng các nghiệm thuộc khoảng    4     4  bằng: A. 10 . B. 9 . C. 6 . D. 2 . ĐÁP ÁN: 1C 2A 3D 4A 5B 6A 7D 8C 9D 10B 11C 12C 13B 14D 15A 16C 17A 18A 19D 20C 21C 22B 23D 24D 25C 26D 27A 28A 29A 30A 31A 32B 33A 34C 35B 36A 37A 38B 39A 40C
PhÇn 3.Mét sè ph­¬ng tr×nh l­îng gi¸c th­êng gÆp.
Câu 1. Giải phương trình 2
2 sin x  3 sin x  1  0.  x
   k2   x   k2 2   2   2 A. x
k ,k  .   B. x
k  ,k  .    6  6 3  5  5 2 x    k x    k   6   6 3   x
   k2   x   k2 2   2   1  C. x
k  ,k  .   D. x
k2,k  .    6 2  6  5 1  5 x    k  x    k2  6 2   6 
Câu 2. Giải phương trình 2 cos 2x  3 sin x  1  0.    1 x    k x    k   2  2 2   1       1    1 A. x  arcsin     k ,k  .    x  arcsin     k  ,k  .   B.  4      4 2    1   1    1 x
   arcsin      k  
x  arcsin     k   4      4 2    2  x    k  x    k2  2 3   2  2   1    C. x
k  ,k  .   D. x  arcsin     k2 ,k  .      6 3  4   5 2 x    k    1     6 3
x  arcsin     k2    4 
Câu 3. Giải phương trình cos 2x  cos x  1  0.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 50
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 2 A. x   k2 ,  x    k ,  k  .  2 3 2 B. x   k ,  x   k ,  k  .  2 3 2 7 C. x   k3 ,  x    k ,  k  .  2 3 2 2 D. x   k ,  x    k2 ,  k  .  2 3
Câu 4. Giải phương trình 2 2
6 sin x  2 sin 2x  5. 2 A. x   k ,k  .  B. x   k ,k  .  4 3 4 3 C. x   k ,k  .  D. x   k ,k  .  4 4 4 2
Câu 5. Giải phương trình 4 4
2 sin x  2 cos x  2 sin 2x  1. 2 A. x   k2 ,  k  .  B. x   k ,k  .  4 4 3 C. x   k ,k  .  D. x   k ,  k  .  4 2 4
Câu 6. Giải phương trình   x  4 4 5 1 cos
 2  sin x  cos x. 2 2 k A. x    k ,  k  .  B. x    ,k  .  3 3 2 2 C. x    k2 ,  k  .  D. x    k2 ,  k  .  3 3
Câu 7. Giải phương trình 3 tan x  cotx  3  1  0.  x    k   x   k2  A. 4  ,k  .  B. 4  ,k  .   x   kx   k2   6 2  6  x
   k3   x   k  C. 4  ,k  .  D. 4  ,k  .   x   k3x   k   6  6 Câu 8. Giải phương trình 2
3 cos 4x  sin 2x  cos 2x  2  0.  x    k   x   k2  A. 2  ,k  .  B. 2  ,k  .   6  6
x   arccos  k2
x   arccos  k2   7  7  x    k   x   k  C. 3  ,k  .  D. 2  ,k  .   6  6
x  arccos  k2
x  arccos  k   7  7
Câu 9. Giải phương trình 4 cos x cos 2x  1  0.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 51
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  x
    k2   x    k2 3  3 A.  ,k  .  B.  ,k  .   1  5  1  5 x    arccos  k2 x    arccos  k2  8  8  x
   k2  
x    k2 3  3 C.  ,k  .  D.  ,k  .   1   5  1  5 x    arccos  k2 x    arccos  k2  8  8 3
Câu 10. Giải phương trình 2 2 tan x  3  . cos x 2 A. x k2 ,  k  .  B. x k ,  k  .  C. x k . D. x k . 3 3 4
Câu 11. Giải phương trình 9  13 cos x   0. 2 1  tan x 2 A. x k2 ,  k  .  B. x k ,  k  .  C. x k ,k  .  D.x k ,k  .  2 3  5  7    
Câu 12. Giải phương trình sin 2  x    3 cos x     1  2 sin x  .  2     2    x   k2 x   k   2    A. x
   k2,k  .   B. x
k ,k  .   6   6  5  5 x   kx    k2  6  6    x   k  
x k2   C. x
   k2,k  .    D. x
k2,k  .  6   6   5  5 x   k2x   k2   6  6
Câu 13. Giải phương trình 2
cos x  3 sin x cos x  1  0.  x   k2 x   k  A.  ,k  .  B. 2  ,k  .  x
   k2  3 x   k   3 2  x   k x   k   C. 3  ,k  .  D.  ,k  .   x   k x   k    3 3  3
Câu 14. Giải phương trình 2 2
cos x  3 sin 2x  1  sin x. x   k   x k  A.  ,k  .  B.  ,k  . x    k  
x    k2  3  3
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 52
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  x   k x   k   C. 2  ,k  .  D.  ,k  .   x   k x   k2    3  3
cos x  2 sin x.cos x
Câu 15. Giải phương trình  3. 2
2 cos x  sin x  1 5 2 A. x   k ,k  .  B. x    k ,k  .  18 3 18 3 5 5 C. x    k ,  k  .  D. x   k ,k  .  18 18 3
Câu 16. Giải phương trình 2 2
cos x  sin x.cos x  2 sin x  1  0.  x   k2 x   k  3 A.   1 ,k  .  B.  ,k  .  x   arctan      k2       1          3 x arctan k     3 3   x   k x   k  2  C.  ,k  .      k   1  D. 1 , .      x x  arctan     k   arctan     k         3 2   3  
Câu 17. Giải phương trình 2
cos 4x  cos 3x. x   k2   x k  A.  ,k  . 3  B.  ,k  . 3x     k   x    k  12 2  12 2 x   k2   x k  C.  ,k  .  D.  ,k  . x     k   x    k  12 2  12 2 2 tan x
Câu 18. Giải phương trình  5. 2 1  tan x 1  26 1   26 A. x  arctan  k2 ,  k  .  B. x  arctan  k ,k  .  5 5 2 1  26 1  26 C. x  arctan  k ,  k  .  D. x  arctan  k ,  k  .  5 5
Câu 19. Giải phương trình sin x  cos x  1.  x
   k2   x   k  A. 4  ,k  .  B. 4  ,k  .  
x    k2
x    k   4  4 x   k2  
x k2  C.  ,k  .  D.  ,k  . x
   k2  
x    k2  2  4
Câu 20. Phương trình sin x  cos x  1
 chỉ có các nghiệm là:
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 53
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  x
   k2   x   k  A. 4  ,k  .  B. 4  ,k  .  
x    k2
x    k   4  4 x   k2   x  2k   1 C.  ,k  .  D.  ,k  . x
   k2  
x    k2  4  2
Câu 21. Giải phương trình sin 2x  12sin x  cos x   12  0. 2 A. x   k ,  x   k2 ,  k  .  B. x   k2 ,  x   k ,  k  .  2 2 3 2 C. x
k ,x   k ,  k  .  D. x   k2 ,  x   k2 ,  k  .  2 3 3 2
Câu 22. Giải phương trình 1  tan x  2 2 sin x. A. x   k ,  k  .  B. x   k2 ,  k  .  4 4 2 C. x   k ,  k  .  D. x   k ,k  .  4 3 4 3
Câu 23. Giải phương trình cos x  sin x  2 sin 2x  1. k A. x  ,k  .  B. x k ,  k  .  2 k C. x   k ,  k  .  D. x  ,k  .  2 4
Câu 24. Giải phương trình 3 3
cos x  sin x  cos 2x. A. x    k2 ,
 x    k ,  x k ,  k  .  4 2 2 B. x    k ,
 x    k ,  x k ,  k  .  4 3 2 1 2 C. x    k ,
 x    k ,  x k2 ,  k  .  4 3 2 3 D. x    k ,
 x    k2 ,  x k2 ,  k  .  4 2
Câu 25. Giải phương trình 3 3
cos x  sin x  2 sin 2x  sin x  cos x. k A. x  ,k  .  B. x k ,  k  .  2 k C. x   k ,  k  .  D. x  ,k  .  2 4
Câu 26. Giải phương trình tan x  cot x  2sin 2x  cos 2x .  x    k   x   k  A. 4 3  ,k  .  B. 4  ,k  .   x   kx   k   8 3  8
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 54
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong  x     k   x   k  C. 4  ,k  .  D. 4 2  ,k  .   x   kx   k   8 2  8 2
Câu 27. Giải phương trình 3 3 x x   5 5 cos sin
2 cos x  sin x . A. x    k2 ,  k  .  B. x    k ,  k  .  4 4 C. x    k ,k  .  D. x    k ,k  .  4 3 4 2
Câu 28. Giải phương trình 2
sin x  3 tan x  cos x 4 sin x  cosx. A. x   k2 ,  x  arctan 1   2  k2 ,  k  .  4 B. x
k ,x  arctan 1
  2 k ,k  .  4 2 2 2 2 C. x   k ,  x  arctan 1   2  k ,  k  .  4 3 3 D. x   k ,
 x  arctan1  2  k ,  k  .  4
Câu 29. Giải phương trình  8 8 x x 2 16 sin cos  17 cos 2x. 7 A. x   k ,k  .  B. x   k ,k  .  8 4 8 4 9 5 C. x   k ,k  .  D. x   k ,k  .  8 4 8 4
Câu 30. Giải phương trình 4 6
cos x  cos 2x  2 sin x  0. 2 A. x k2 ,  k  .
 B. x k ,k  .  C. x k ,  k  .  D. x k ,  k  .  2 3
Câu 31. Giải phương trình x x x x   3 sin cos sin 2 3 cos 3
2 cos 4x  sin x .  x
    k2  
x    k2  A. 6  ,k  .  B. 6  ,k  .   2 x   kx    k2   42 7  42  x    k  
x    k2  C. 6  ,k  .  D. 6  ,k  .   2 x    kx    k   42 7  42
Câu 32. Giải phương trình 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x.  x    k   x   k  A. 2  ,k  .  B. 2  ,k  .   kk2 x   x    9  9  k x     x   k  C. 2  ,k  .  D. 2  ,k  .   k k x   x     9  9 9
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 55
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong
Câu 33. Phương trình 3 sin x  m  
1 cos x m  2 (với m là tham số) có nghiệm khi: A. m  1. B. m  1. C.m  1. D.m  1.
Câu 34. Phương trình m sin x  3 cos x  2m có nghiệm khi: A. m  3. B. m   3. C. m  3. D. m  3.
Câu 35. Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y  3 cos x  sin x  2.
A. min y  2  5; max y  2  5. B. min y  2  7; max y  2  7. C. min y  2   3;max y  2
  3. D. miny  2  10;max y  2   10.
Câu 36. Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y  4 sin 3x  3 cos 3x  1.
A. min y  3; max y  6.
B. min y  4; max y  6.
C. min y  4; max y  4.
D. min y  2; max y  6.
sin 2x  2 cos 2x  3
Câu 37. Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y  .
2 sin 2x  cos 2x  4 2 2 A. min y   ; max y  2. B. min y  ;max y  3. 11 11 2 2 C. min y  ; max y  4. D. min y  ;max y  2. 11 11 2
2 sin 3x  4 sin 3x cos 3x  1
Câu 38. Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y  .
sin 6x  4 cos 6x  10 11  9 7 11  9 7 A. min y  ; max y  . 83 83 22  9 7 22  9 7 B. min y  ; max y  . 11 11 33  9 7 33  9 7 C. min y  ; max y  . 83 83 22  9 7 22  9 7 D. min y  ; max y  . 83 83 2
sin 2x  3 sin 4x
Câu 39. Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y  . 2
2 cos 2x  sin 4x  2 5  2 22 5   2 22 A. min y  ; max y  . 7 7 5  2 22 5  2 22 B. min y  ; max y  . 7 7 5  97 5  97 C. min y  ; max y  . 8 8 7  97 7  97 D. min y  ; max y  . 8 8
Câu 40. Tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số y   x x2 3 3 sin 4 cos
 43sinx  4 cosx  1. 1 1 A. min y  ;max y  96.
B. min y   ; max y  6. 3 3
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 56
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong 1
C. min y   ; max y  96.
D. min y  2; max y  6. 3 ĐÁP ÁN: 1D 2D 3D 4D 5D 6C 7D 8A 9B 10A 11A 12C 13D 14B 15B 16D 17D 18D 19C 20D 21D 22C 23A 24D 25A 26D 27B 28D 29A 30D 31A 32C 33B 34C 35D 36B 37D 38D 39B 40C Hướng dẫn giải:
Câu 2. Dùng công thức nhân đôi 2
cos 2x  1  2 sin x
Câu 3. Dùng công thức nhân đôi 2
cos 2x  2 cos x  1. 1  cos 2x
Câu 4. Dùng công thức hạ bậc 2 sin x  và 2 2
sin 2x  1  cos 2x. 2
Câu 5. Áp dụnga b  a b 2 4 4 2 2 2 2  2a b . Câu 6. Áp dụng 4 4 a b   2 2 a b  2 2 a b . 1 Câu 7. cotx  . tan x Câu 8. 2 2 2
cos 4x  2 cos 2x  1, sin 2x  1  cos 2x. Câu 9. 2
cos 2x  2 cos x  1 1 Câu 10. 2 tan x   1 2 cos x 1 Câu 11. 2 tan x  1  2 cos x   Câu 12. 2 sin 2
x    cos 2x, cos2x  1  2 sin x.   2  Câu 13. 2 2
cos x  1   sin x. Câu 14. 2 2
cos x  sin x  cos 2x Câu 15. 2
2 cos x  1  cos 2x, 2 sin x cos x  sin 2x.
Câu 16.  sin x 3 sin x  cos x Câu 17. 3 2
 2 cos 4x  1  cos 6x  4 cos 2x  4 cos 2x  3 cos 2x  3  0.     Câu 23. 2
t  sin x  cos x  2 cos x
    sin 2x  1  t   4 
Câu 24.  sin x  cos x 1  sin x cos x   sin x  cos x cos x  sin x  Câu 25. 3 3
sin x  cos x  sin x  cosx1  sin x cos x 2
Câu 26. tan x  cotx  sin 2x Câu 27. 3  x  2 x   3  x  2 x    x  3 3 cos 2 cos 1 sin 2 sin 1
cos 2 cos x  sin x  0 Câu 28. Chia hai vế cho 2 cos x
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 57
Tt GIA SÖ CHö seâ- 094.6798.489
ÑEÀ CÖÔNG HOÏC TAÄP LÔÙP 11
Soá 17. Hoaøng Vaên Thuï. TT. Chö Seâ. Gia Lai
https://www.facebook.com/phong.baovuong Câu 29. 2  
sin x  cos x  sin x  cos x2 1   1 8 8 4 4 4 4 2 4
 2 sin x cos x  1
  sin 2x  sin 2x  Đặt  2  8 2 t  sin 2x
Câu 30. Đặt t  cos 2x sin 3x  sin x
3 sin x  sin 3x Câu 31. 3 cos x sin 2x  ,2 sin x  2 2
Câu 32. Dùng công thức hạ bậc đưa về hàm cos Câu 37.  2y  
1 sin 2x  y  2cos 2x  3  4y. ycbt
2y  2
1  y  22  3  4y2 Câu 39. Giống câu 37. Câu 40. Đặt t 3 sin x 4 cos x,t  5;5     2 
 . Khi đó y  3t  4t  1  f t với t  5;5   .  
Lập bảng biến thiên cho hàm f t suy ra đáp án.
Biªn so¹n vµ gi¶ng d¹y: NguyÔn B¶o V­¬ng - 0946798489 Trang 58
Document Outline

  • Daïng toaùn 1: Tìm taäp xaùc ñònh cuûa haøm soá.
  • Daïng toaùn 2: Xaùc ñònh tính chaün, leû cuûa haøm soá.
  • Daïng toaùn 3: Tìm giaù trò lôùn nhaát, giaù trò nhoû nhaát cuûa haøm soá.
  • Daïng toaùn 4: Tìm chu kì cuûa haøm soá löôïng giaùc.
  • Daïng toaùn 5: Xaùc ñònh haøm soá coù ñoà thò cho tröôùc.
  • Daïng toaùn 1: Phöông trình baäc nhaát ñoái vôùi sinx vaø cosx .
  • Daïng toaùn 2: Phöông trình baäc hai ñoái vôùi moät haøm soá löôïng giaùc.
  • Daïng toaùn 3: Phöông trình thuaàn nhaát ( ñaúng caáp) ñoái vôùi sin vaø cos
  • .
  • Daïng toaùn 4: Phöông trình ñoái xöùng
  • .
  • Daïng toaùn 5: Phöông trình ñoái xöùng.
  • .