

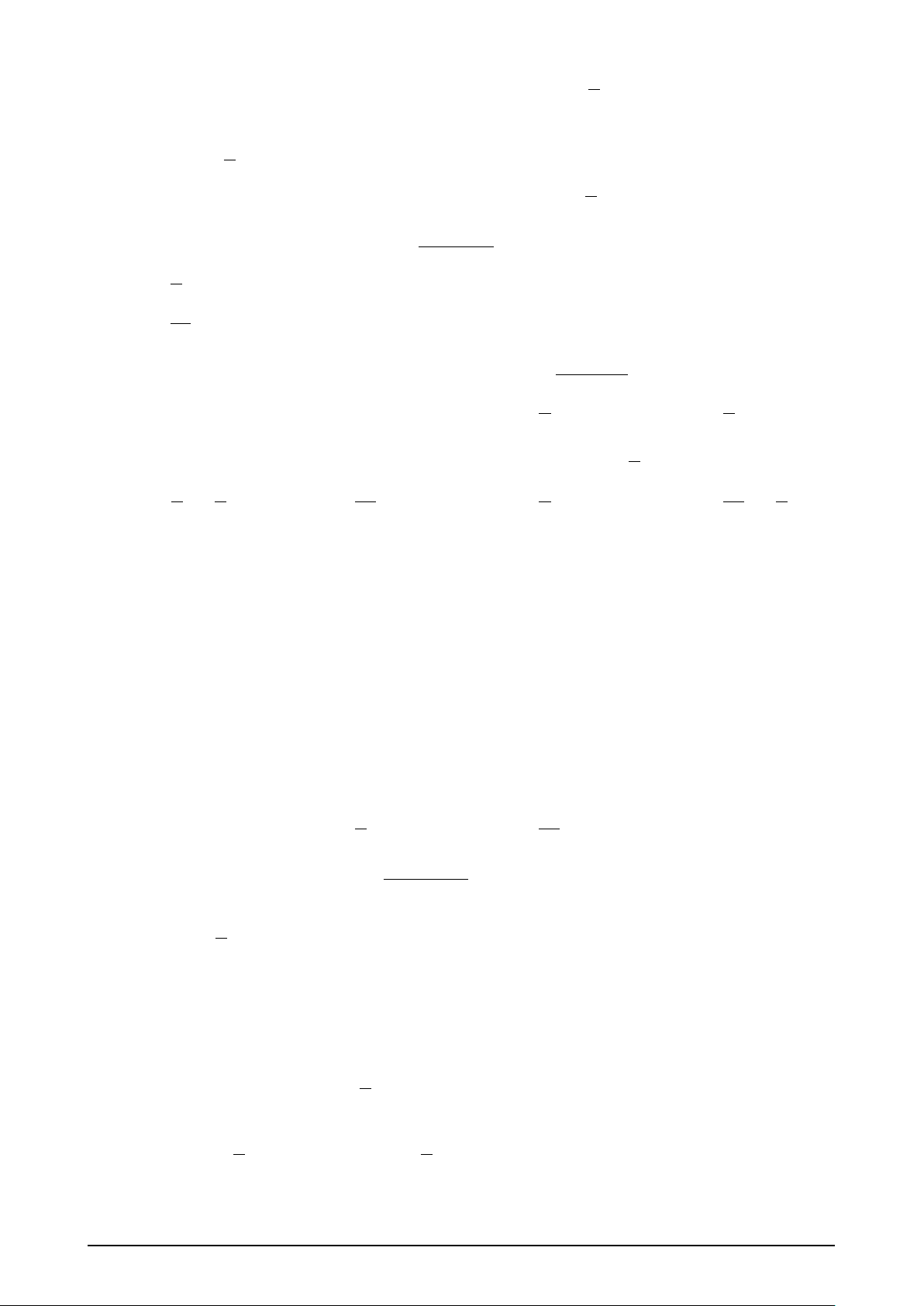















Preview text:
MỤC LỤC MỤC LỤC CHƯƠNG 1
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 1 1.
HÀM SỐ LƯỢNG GIÁC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 A
KIẾN THỨC CẦN NHỚ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 B
PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Dạng 1. Tìm tập xác định của hàm số lượng giác . . . . . . . . . . . . . . . . . . . . . . . 2
Dạng 2. Tính chẵn lẻ của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Dạng 3. Tìm giá trị lớn nhất - giá trị nhỏ nhất . . . . . . . . . . . . . . . . . . . . . . . . . 4 C
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 2.
PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 A
KIẾN THỨC CẦN NHỚ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 B
PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
Dạng 1. Giải các phương trình lượng giác cơ bản . . . . . . . . . . . . . . . . . . . . . . . 10
Dạng 2. Giải các phương trình lượng giác dạng mở rộng . . . . . . . . . . . . . . . . 11
Dạng 3. Giải các phương trình lượng giác có điều kiện xác định . . . . . . . . . . 11
Dạng 4. Giải các phương trình lượng giác trên khoảng (a; b) cho trước . . . 11 C
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 3.
MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP . . . . . . . . . . . . . . . . . . . . . . . 15 A
KIẾN THỨC CẦN NHỚ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 B
PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
Dạng 1. Giải phương trình bậc nhất đối với một hàm số lượng giác . . . . . . 16
Dạng 2. Giải phương trình bậc hai đối với một hàm số lượng giác . . . . . . . . 17
Dạng 3. Giải phương trình bậc nhất đối với sinx và cosx . . . . . . . . . . . . . . . . . 17
Dạng 4. Phương trình đẳng cấp bậc hai đối với sinx và cosx . . . . . . . . . . . . . 18
Dạng 5. Phương trình chứa sin x ± cos x và sin x · cos x . . . . . . . . . . . . . . . . . . . 19 C
BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 4.
MỘT SỐ PHƯƠNG PHÁP GIẢI PT LƯỢNG GIÁC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 A
PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Dạng 1. Biến đổi đưa phương trình về dạng phương trình bậc hai (ba) đối
với một hàm số lượng giác . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Dạng 2. Biến đổi asinx + bcosx . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Dạng 3. Biến đổi đưa về phương trình tích . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Dạng 4. Một số bài toán biện luận theo tham số . . . . . . . . . . . . . . . . . . . . . . . 25 B
BÀI TẬP TỰ LUYỆN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 5.
ĐỀ ÔN TẬP CUỐI CHƯƠNG . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 A
Đề số 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 B
Đề số 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 6.
ĐÁP ÁN TRẮC NGHIỆM CÁC CHỦ ĐỀ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 Trang i
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC CHƯƠNG
1 HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§ 1. HÀM SỐ LƯỢNG GIÁC
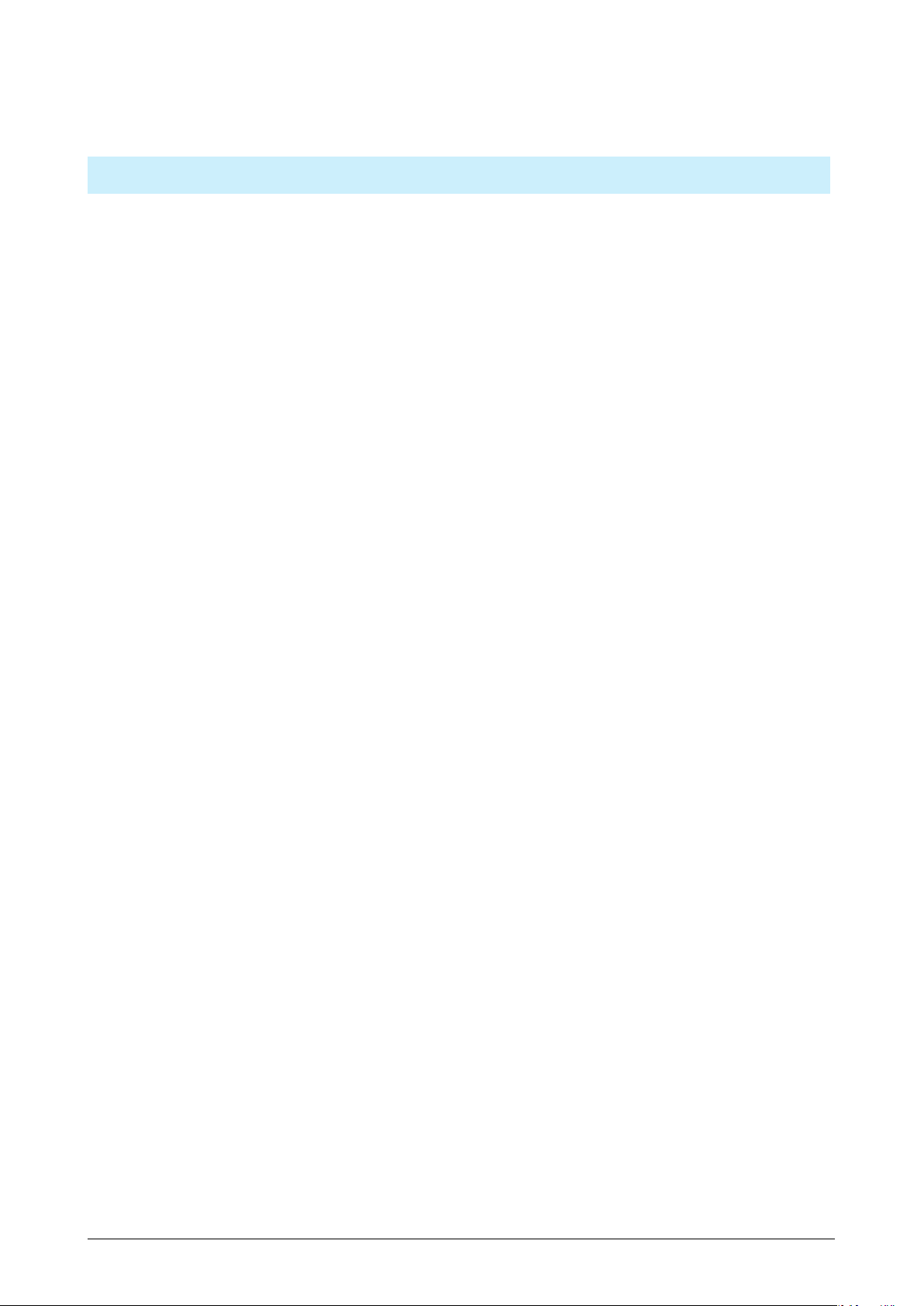
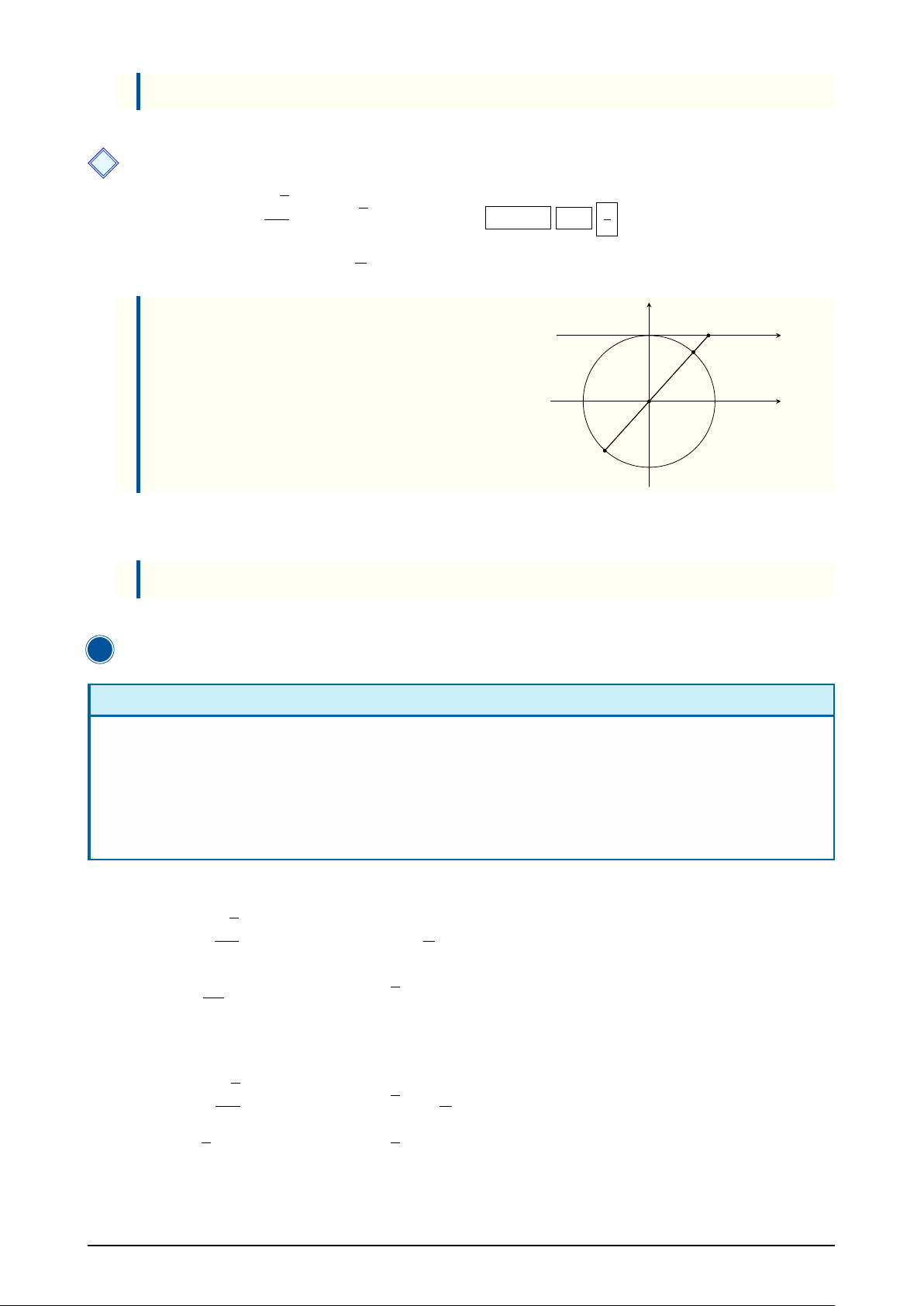
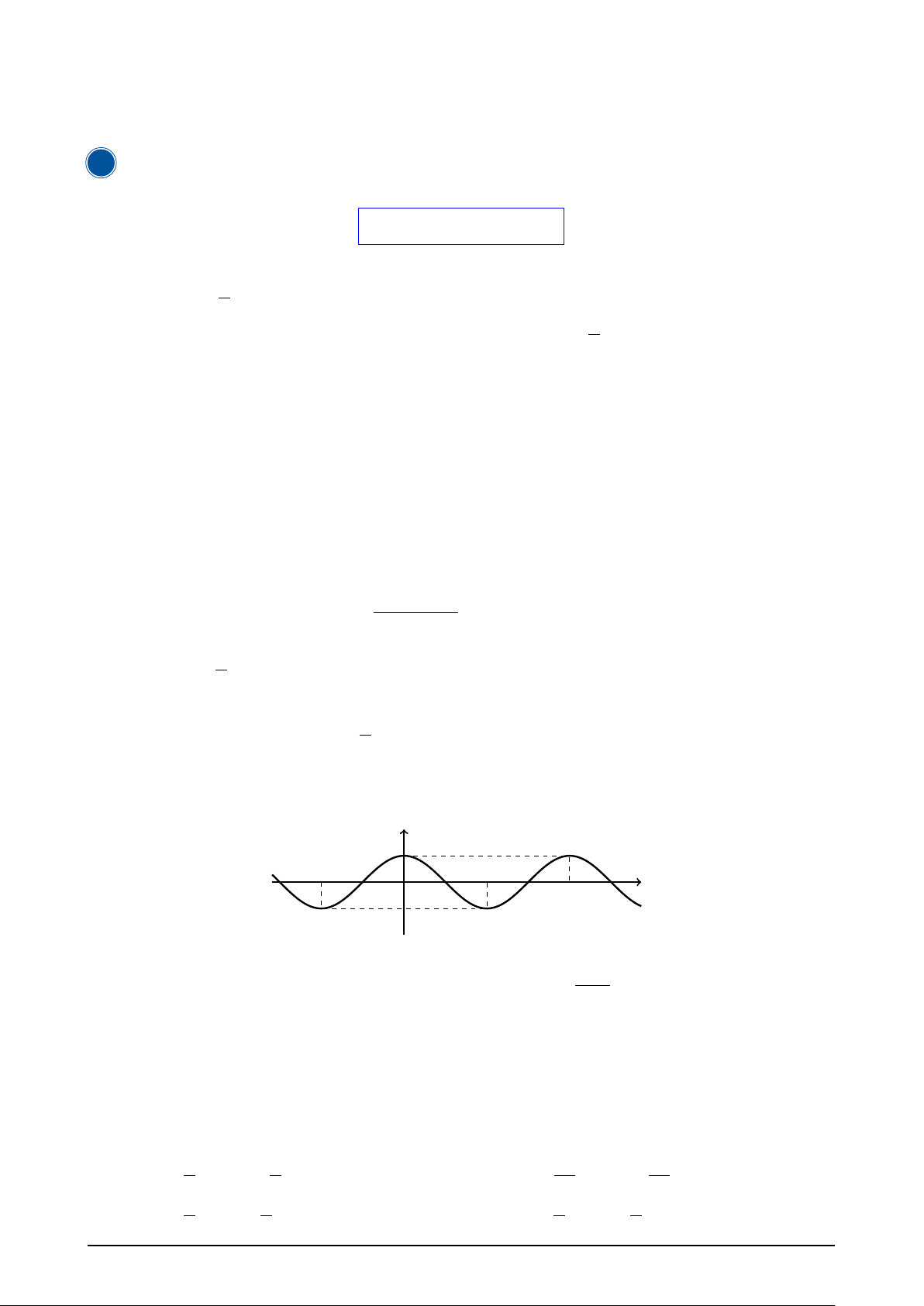
A KIẾN THỨC CẦN NHỚ 1 Hàm số y = sin x • Tập xác định: D = R. y
• Tập giác trị: [−1; 1], tức là −1 ≤ sin x ≤ 1, − π ∀ 2 x ∈ R. x −π π π
• Hàm số y = sin x là hàm số lẻ nên đồ thị hàm 2
số nhận gốc tọa độ O làm tâm đối xứng.
Đồ thị hàm số y = sin x
• Hàm số y = sin x tuần hoàn với chu kì T =
2π, nghĩa là sin(x + k2π) = sin x, với k ∈ Z. 2 Hàm số y = cos x • Tập xác định: D = R. y
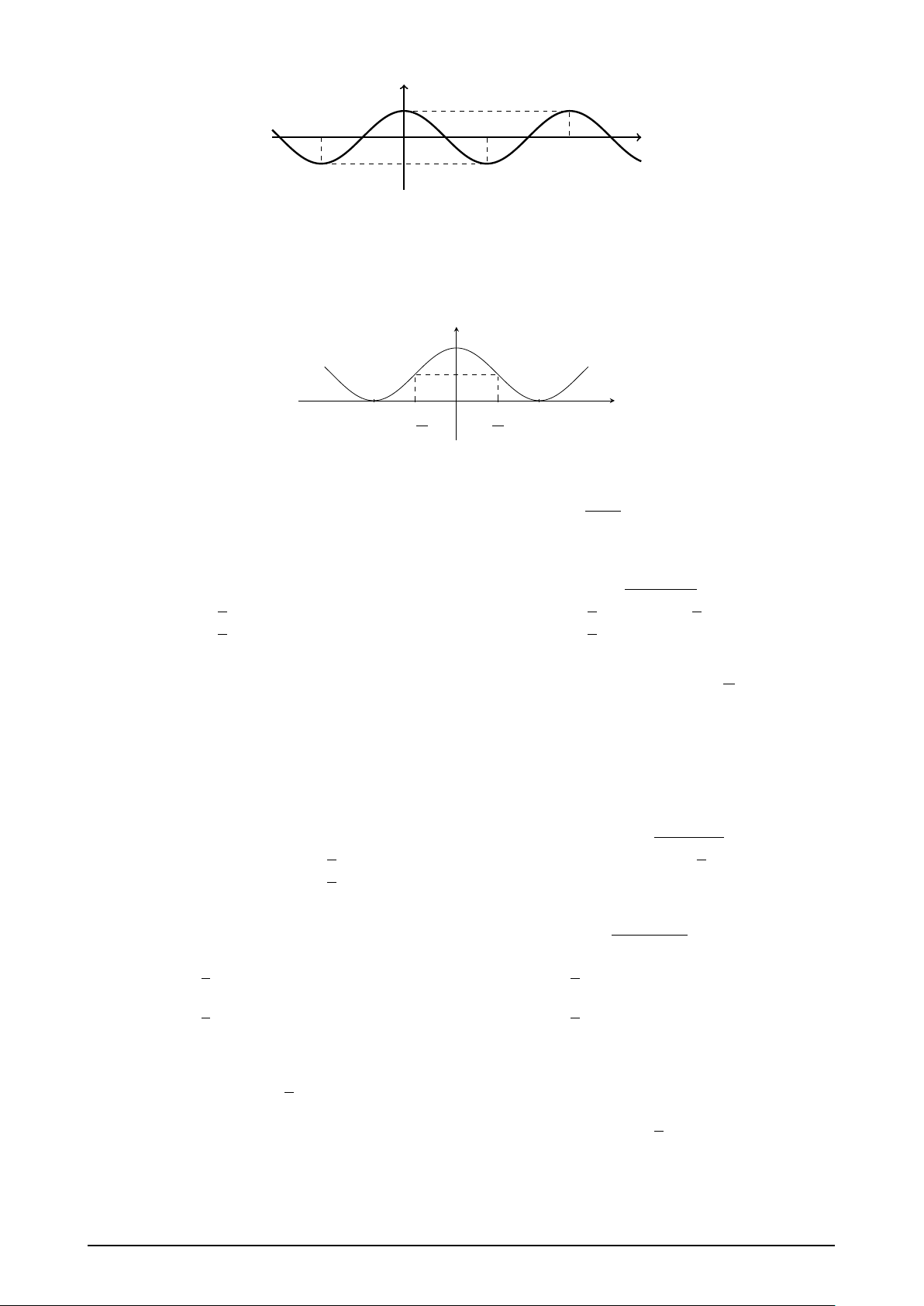
• Tập giác trị: [−1; 1], tức là −1 ≤ cos x ≤ 1, − − π π ∀ 2 π x ∈ R. x π
• Hàm số y = cos x là hàm số chẵn nên đồ thị 2
hàm số nhận trục Oy làm trục đối xứng.
Đồ thị hàm số y = cos x
• Hàm số y = cos x là hàm số tuần hoàn với chu
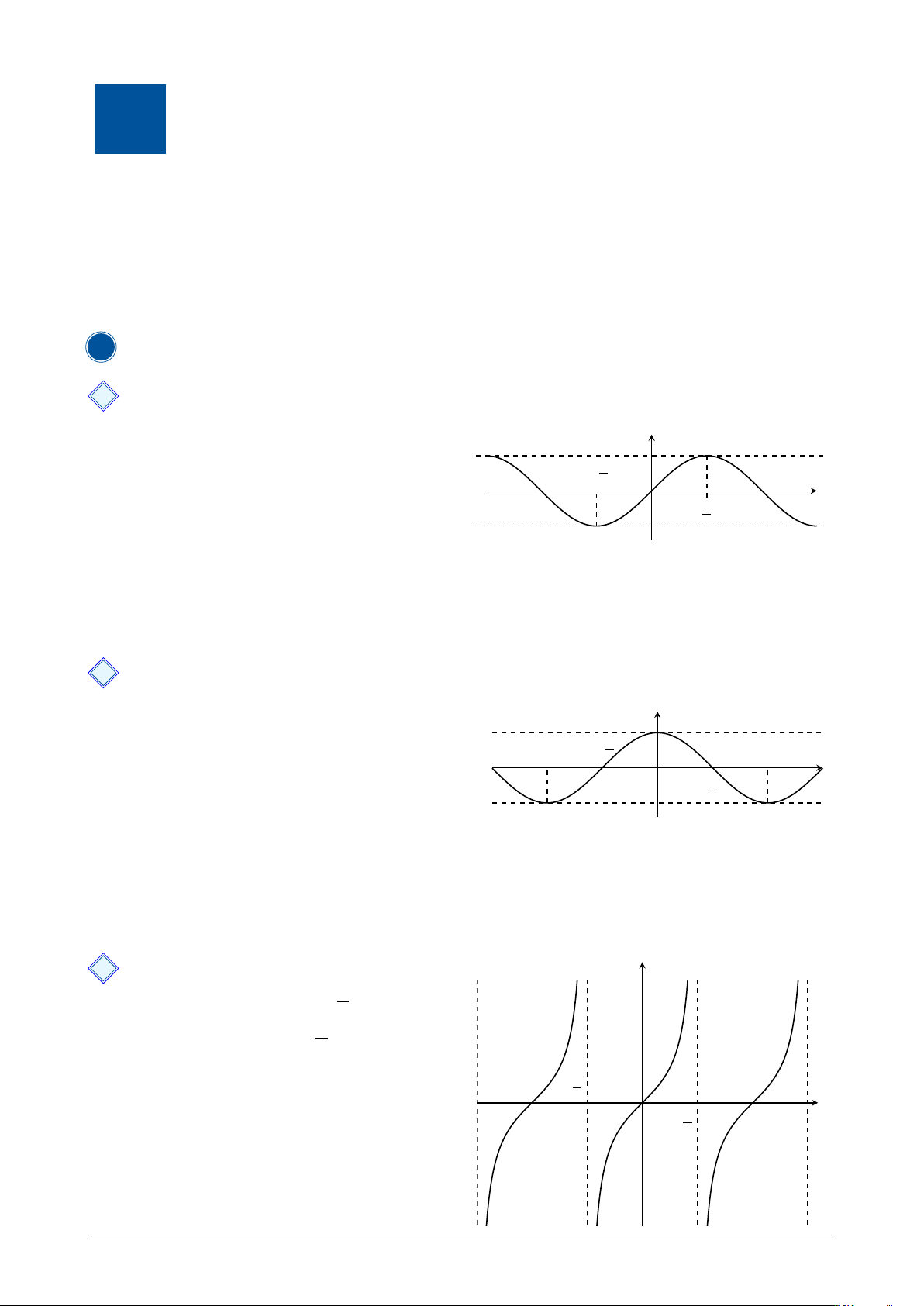
kì T = 2π, nghĩa là cos(x + k2π) = cos x, với k ∈ Z. y 3 Hàm số y = tan x π
• Điều kiện cos x 6= 0 ⇔ x 6= + kπ, k ∈ Z. 2 n π o Tập xác định: D = R\ + kπ, k ∈ Z . 2 • Tập giá trị: R. −π − π2 • Là hàm số lẻ. x O π π 2
• Là hàm số tuần hoàn với chu kì T = π, nghĩa
là tan(x + kπ) = tan x, với k ∈ Z. Trang 1
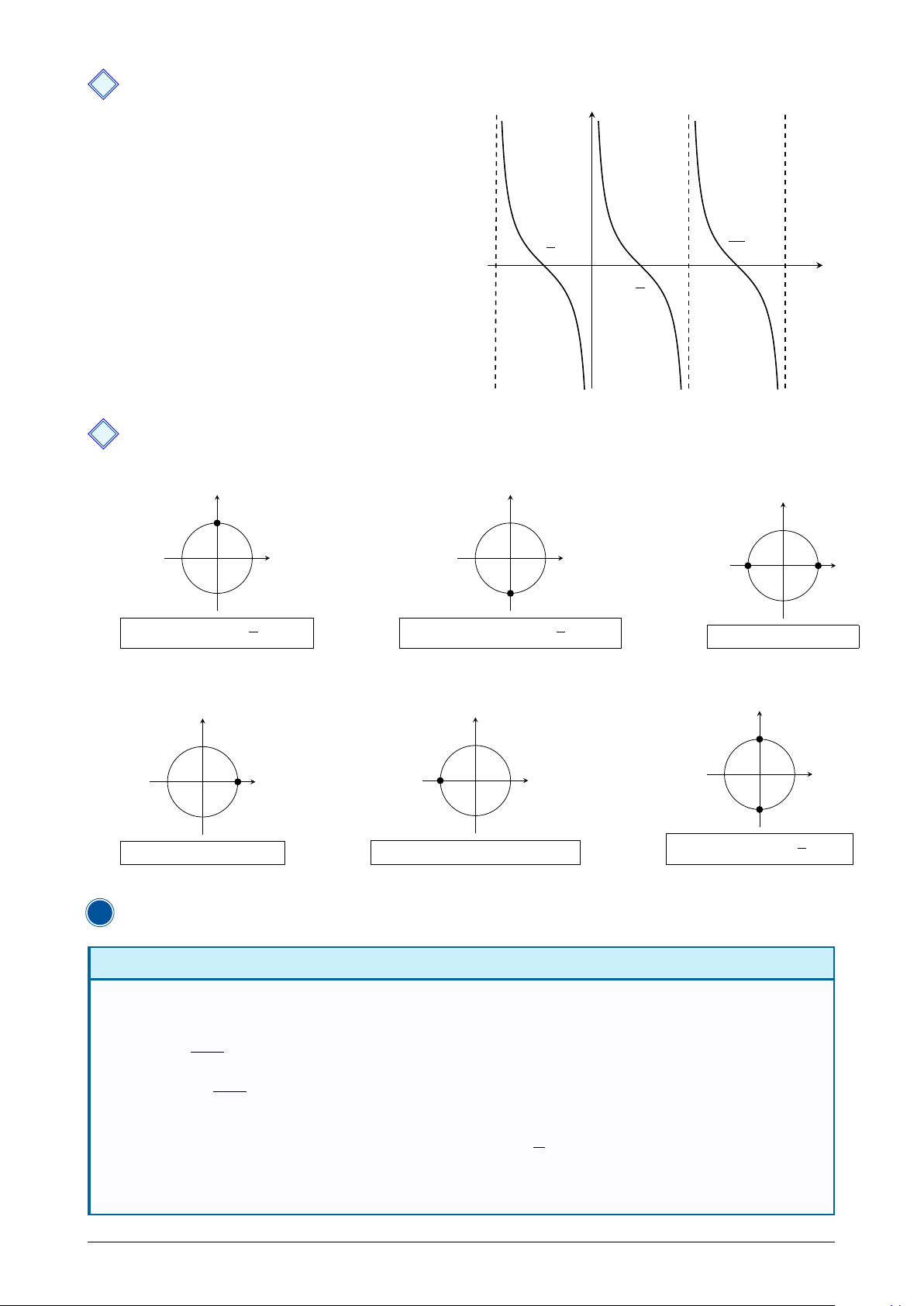
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 4 Hàm số y = cot x y
• Điều kiện sin x 6= 0 ⇔ x 6= kπ, k ∈ Z.
Tập xác định: D = R \ {kπ, k ∈ Z} . • Tập giá trị: R. • Là hàm số lẻ. 3 • π
Là hàm số tuần hoàn với chu kì T = π, − − π π 2 2
nghĩa là cot(x + kπ) = cot x, với k ∈ Z. π x O π 2
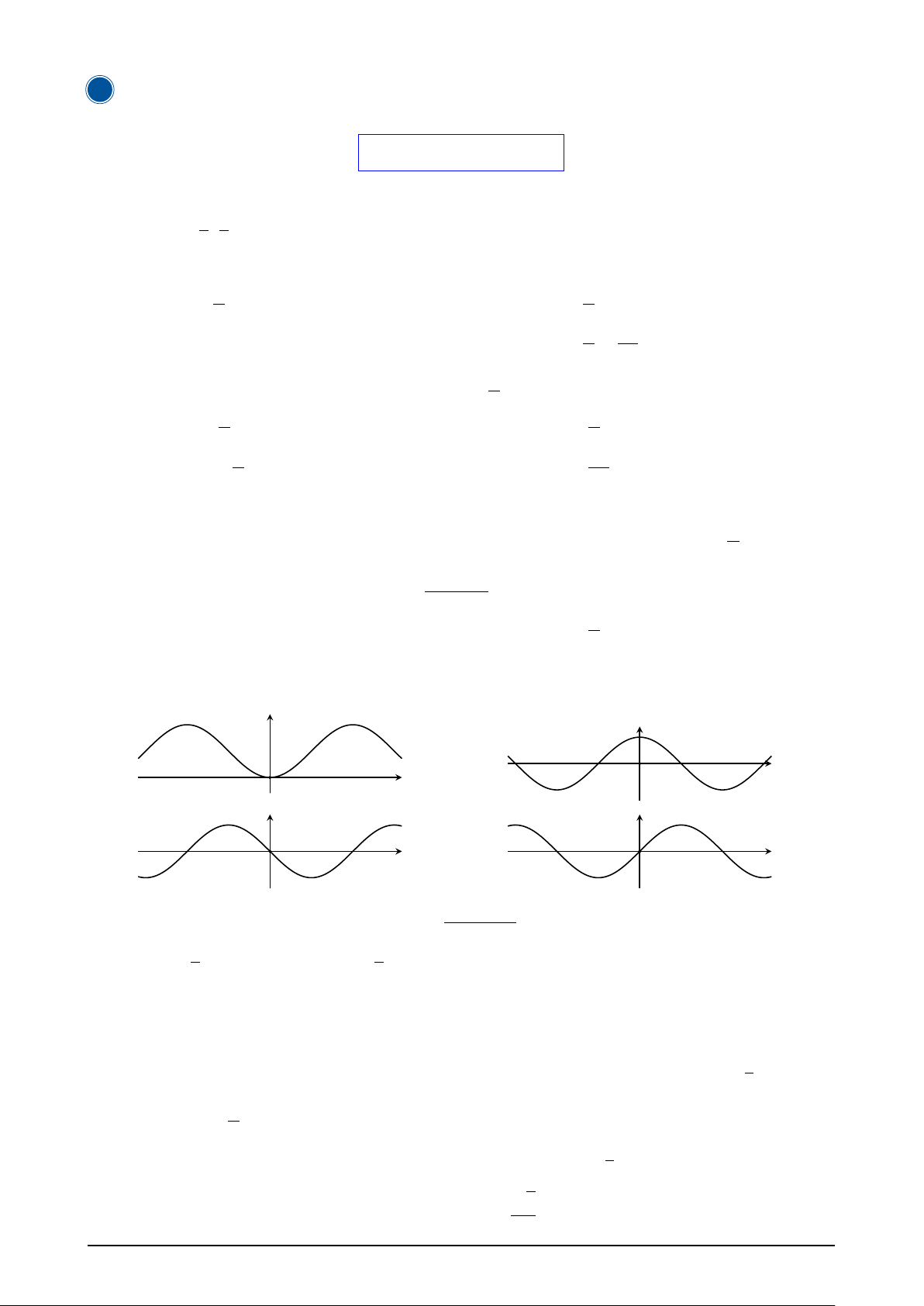
5 Một số trường hợp đặc biệt
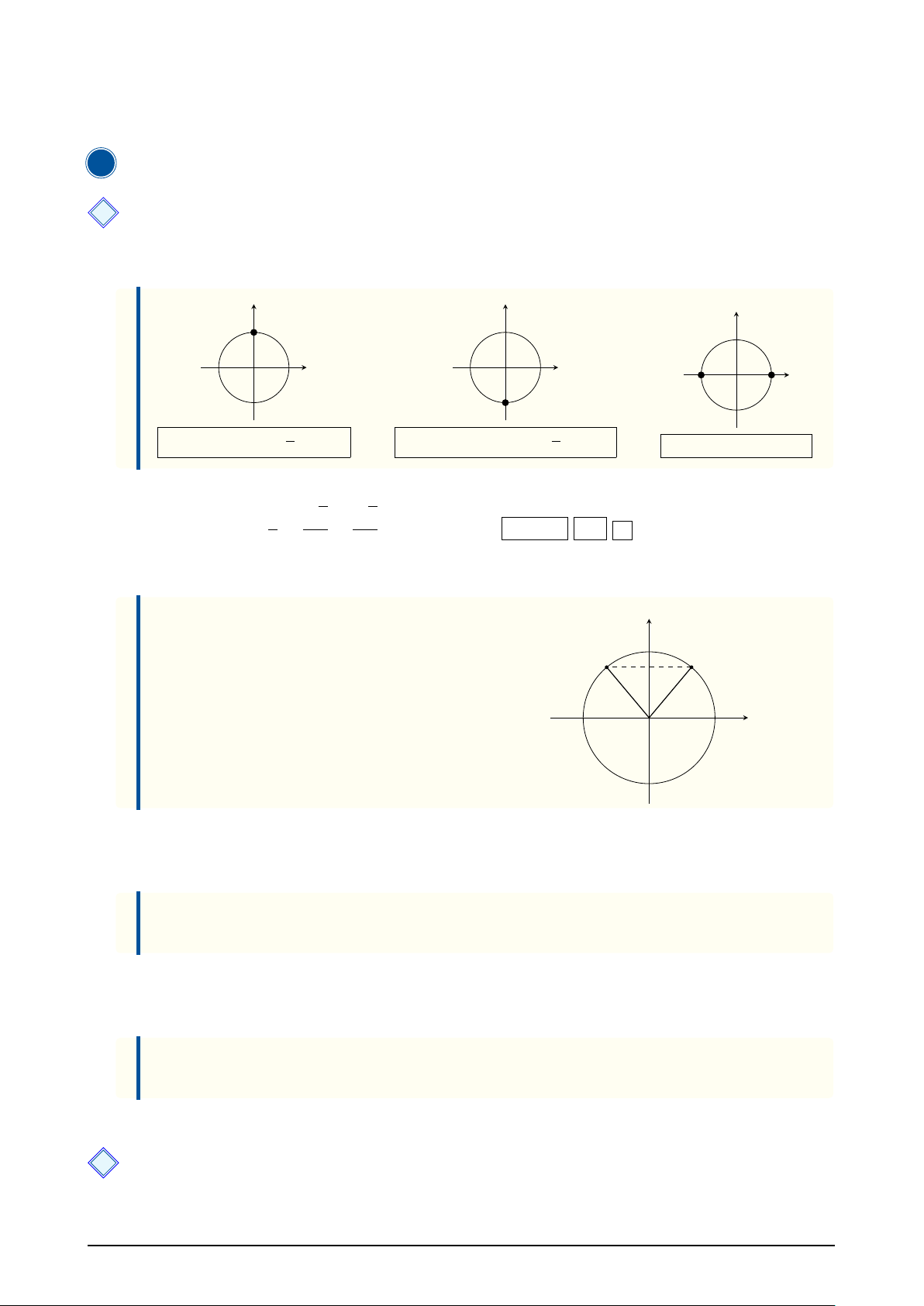
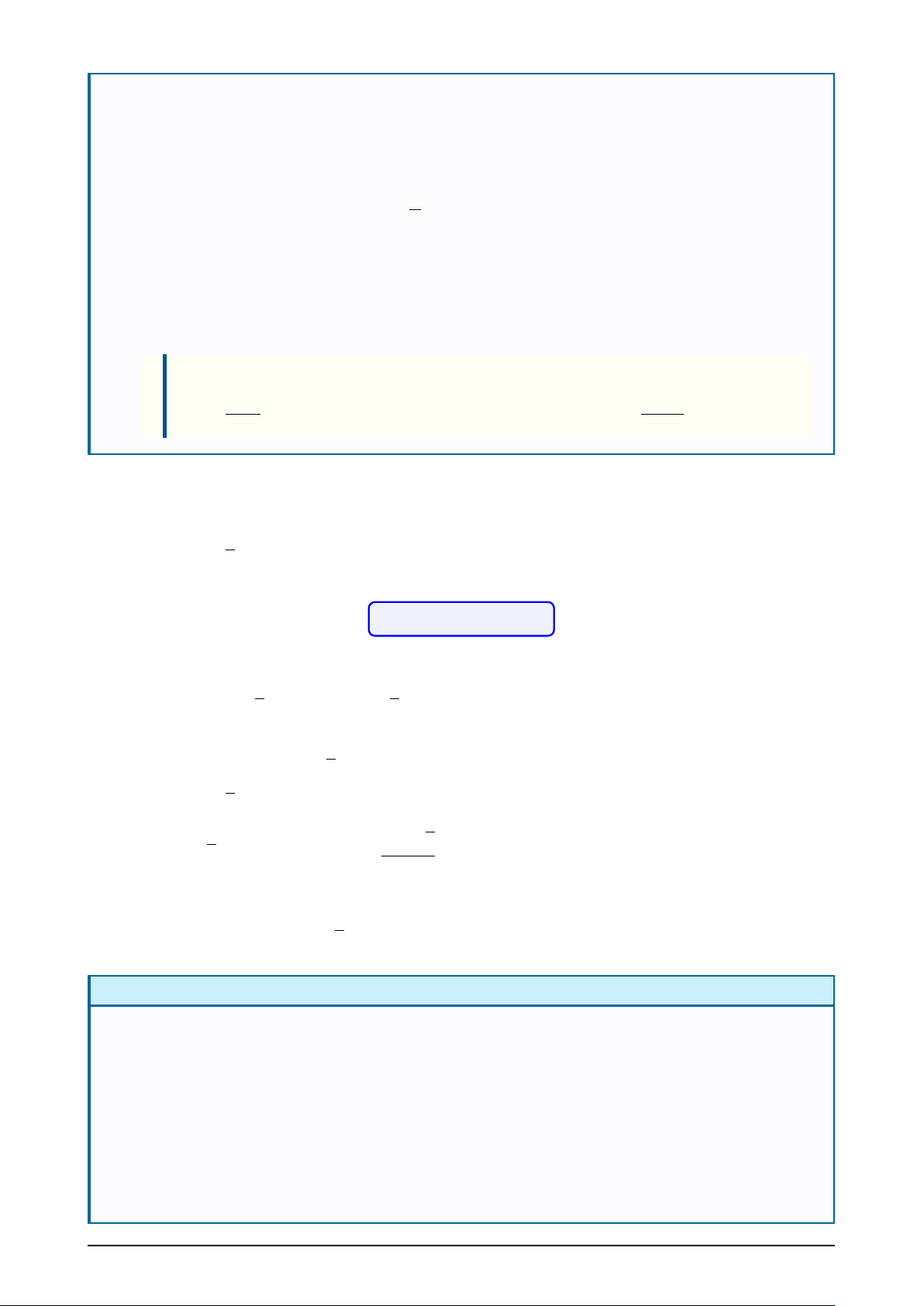
Các trường hợp đặc biệt cho hàm y = sin x sin sin sin B A0 A cos O cos O cos O B0 sin x = 1 ⇔ x = π + k2
sin x = −1 ⇔ x = − π + k2 2 π 2 π sin x = 0 ⇔ x = kπ
Các trường hợp đặc biệt cho hàm y = cos x sin sin sin B A A0 cos cos O O cos O B0 cos x = 1 ⇔ x = k2 cos x = 0 ⇔ x = π + k π cos x = −1 ⇔ x = π + k2π 2 π
B PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
{ DẠNG 1. Tìm tập xác định của hàm số lượng giác
Phương pháp giải. Ta chú ý một số điều kiện sau: f (x) 1. y = xác định ⇔ g(x) 6= 0. g(x) 2. y = 2n
p f (x) xác định ⇔ f (x) > 0, trong đó n ∈ ∗ N . π
3. y = tan [u(x)] xác định ⇔ u(x) xác định và u(x) 6= + kπ, k ∈ Z. 2
4. y = cot [u(x)] xác định ⇔ u(x) xác định và u(x) 6= kπ, k ∈ Z. Trang 2
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
# Ví dụ 1. Tìm tập xác định của các hàm số sau đây: 2 sin x + 3 1 + cos x 2 + 3 cos 2x a) y = b) y = c) y = cos x 1 − cos x sin x 1 + cos x sin x − 3 2 sin x + 3 d) y = e) y = f) y = 1 + sin x cos x + 1 cos x + 2 2 sin x + 3 2 sin x − 3 x − 1 g) y = h) y = i) y = sin . sin x − 1 2 sin x + 3 x + 2 √ √ cos x − 2 … 1 + cos x j) y = 3 − 2 cos x. k) y = l) y = 1 + cos x 1 − cos x
# Ví dụ 2. Tìm tập xác định của các hàm số sau đây: π a) y = 2 tan x + 3 b) y = 2 tan 2x − 4 sin x c) y = cot x + + 1 4
# Ví dụ 3. Tìm tất cả các giá trị của m để hàm số sau có tập xác định R. √ √ sin x − 1 a) y = m − cos x b) y = 2 sin x − m c) y = cosx+m
# Ví dụ 4. Tìm tất cả các giá trị của m để hàm số y = pcos2 x − (2 + m)cosx + 2m có tập xác định R.
{ DẠNG 2. Tính chẵn lẻ của hàm số
Phương pháp giải. Ta thực hiện các bước sau:
1. Tìm tập xác định D của hàm số – Tập D phải đối xứng.
2. Tính f (−x) (chỗ nào có biến x, ta thay bởi −x) và thu gọn kết quả. Khi đó
• Nếu f (−x) = f (x): hàm số đã cho là hàm chẵn.
• Nếu f (−x) = − f (x): hàm số đã cho là hàm lẻ.
• Nếu không rơi vào 2 trường hợp trên, ta kết luận hàm số không chẵn, không lẻ. CHÚ Ý
¬ Hàm số y = sin x là hàm số lẻ.
Hàm số y = cos x là hàm số chẵn.
® Hàm số y = tan x là hàm số lẻ.
¯ Hàm số y = cot x là hàm số lẻ.
# Ví dụ 5. Xét tinh chẵn lẻ của hàm số Å 9π ã a) y = f (x) = sin 2x + ; b) y = f (x) = tan x + cot x. 2
# Ví dụ 6. Xét tính chẵn lẻ của hàm số y = tan7 2x · sin5x. Trang 3
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
{ DẠNG 3. Tìm giá trị lớn nhất - giá trị nhỏ nhất
Phương pháp giải. Ta thường dùng một trong 3 phương pháp sau:
Sử dụng các bất đẳng thức cơ bản
¬ −1 ≤ sin x ≤ 1, ∀x ∈ R;
−1 ≤ cos x ≤ 1, ∀x ∈ R;
® 0 ≤ sin2 x, cos2 x ≤ 1, ∀x ∈ R;
¯ 0 ≤ | sin x|, | cos x| ≤ 1, ∀x ∈ R. ° Cô – si: ± Bunhiacopxki: √
a + b ≥ 2 ab, với mọi a, b ≥ 0
(ab + cd)2 ≤ (a2 + c2)(b2 + d2) a c
Dấu bằng xảy ra khi a = b. Dấu bằng xảy ra khi = . b d
Sử dụng điều kiện có nghiệm
¬ sin x = f (m) có nghiệm khi −1 ≤ f (m) ≤ 1.
cos x = f (m) có nghiệm khi −1 ≤ f (m) ≤ 1.
® sin x + b cos x = c có nghiệm khi a2 + b2 ≥ c2.
Sử dụng bảng biến thiên: Lập bảng biến thiên của hàm số, từ đó, kết luận.
# Ví dụ 7. Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau 1 − 2sin2x √ a) y = 2 sin x + 3 b) y = c) y = 2 + cos x − 1 3 d) y = 4 sin x cos x + 1; e) y = 4 − 3 sin2 2x. f) y = (3 − sin x)2 + 1 g) y = sin4x + cos4x h) y = sin6x + cos6x
# Ví dụ 8. Tìm x để hàm số y = (sinx + 3)2 − 1 đạt giá trị nhỏ nhất. √
# Ví dụ 9. Tìm x để hàm số y = 1 − 3 1 − cos2x đạt giá trị nhỏ nhất.
# Ví dụ 10. Tìm giá trị lớn nhất và nhỏ nhất của hàm số sau √ a) y = 3 sin x + cos x b) y = sin 2x − cos 2x c) y = 3 sin x + 4 cos x
# Ví dụ 11. Tìm giá trị lớn nhất và nhỏ nhất của hàm số sau a) y = 2sin2x − 3 sin x + 1 b) y = 2cos2x + 3 cos x − 2 c) y = cos 2x − sin x + 3 √
# Ví dụ 12. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2cos2 x − 2 3sinx cosx + 1. sin x + 3 cos x + 1
# Ví dụ 13. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = . sin x − cos x + 2
C BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm tập xác định D của hàm số y = − tan x. n π o A. D = R \ + kπ, k ∈ Z .
B. D = R \ {kπ, k ∈ Z}. 2 Trang 4
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC n π o
C. D = R \ {k2π, k ∈ Z}. D. D = R \ + k2π, k ∈ Z . 2
Câu 2. Tìm tập xác định của hàm số y = cot x. n π o A. D = R\ k |k ∈ Z . B. D = R\{kπ|k ∈ Z}. 2 n π o
C. D = R\{k2π|k ∈ Z}. D. D = R\ + kπ|k ∈ Z . 2 1 − 3 cos x
Câu 3. Điều kiện xác định của hàm số y = là sin x π A. x 6= + kπ, k ∈ Z. B. x 6= k2π, k ∈ Z. 2 kπ C. x 6= , k ∈ Z. D. x 6= kπ, k ∈ Z. 2 2 sin x + 1
Câu 4. Với ký hiệu k ∈ Z, điều kiện xác định của hàm số y = là 1 − cos x π π A. x 6= k2π. B. x 6= kπ. C. x 6= + kπ. D. x 6= + k2π. 2 2 π
Câu 5. Với ký hiệu k ∈ Z, điều kiện xác định của hàm số y = tan 2x − là 3 π π 5π π 5π π A. x 6= + k . B. x 6= + kπ. C. x 6= + kπ. D. x 6= + k . 6 2 12 2 12 2
Câu 6. Tập giá trị của hàm số y = cos x là tập hợp nào sau đây? A. R. B. (−∞; 0]. C. [0; +∞]. D. [−1; 1].
Câu 7. Tập giá trị của hàm số y = sin 2x là A. [−2; 2]. B. [0; 2]. C. [−1; 1]. D. [0; 1].
Câu 8. Mệnh đề nào dưới đây đúng?
A. Hàm số y = sin x là hàm số chẵn.
B. Hàm số y = cos x là hàm số chẵn.
C. Hàm số y = tan x là hàm số chẵn.
D. Hàm số y = cot x là hàm số chẵn.
Câu 9. Tìm hàm số lẻ trong các hàm số sau: A. y = sin2 x. B. y = x cos 2x. C. y = x sin x. D. y = cos x.
Câu 10. Tìm điều kiện xác định của hàm số y = tan x + cot x. π kπ A. x 6= kπ, k ∈ Z. B. x 6= + kπ, k ∈ Z. C. x 6= , k ∈ Z. D. x ∈ R. 2 2 2 cos 3x − 1
Câu 11. Tập xác định của hàm số y = là cos x + 1
A. D = R \ {π + kπ; k ∈ Z}.
B. D = R \ {k2π; k ∈ Z}. π
C. D = R \ { + kπ; k ∈ Z}.
D. D = R \ {π + k2π; k ∈ Z}. 2
Câu 12. Mệnh đề nào dưới đây sai?
A. Hàm số y = tan x tuần hoàn với chu kì π.
B. Hàm số y = cos x tuần hoàn với chu kì π.
C. Hàm số y = cot x tuần hoàn với chu kì π.
D. Hàm số y = sin 2x tuần hoàn với chu kì π.
Câu 13. Hàm số y = sin 2x có chu kỳ là π A. T = 2π. B. T = . C. T = π. D. T = 4π. 2
Câu 14. Hàm số nào là hàm số chẵn? π π A. y = sin x + . B. y = cos x + . C. y = sin 2x.
D. y = tan x − sin 2x. 2 2
Câu 15. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A,B,C,D. Hỏi hàm số đó là hàm số nào? Trang 5
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC y 1 −π π O x 2π −1 A. y = 1 + sin x. B. y = 1 − sin x. C. y = sin x. D. y = cos x.
Câu 16. Đường cong trong hình vẽ bên dưới là đồ thị của một trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D. Hỏi đó là hàm số nào? y 2 1 x −π π O π π − 2 2 A. y = cos x + 1. B. y = 2 − sin x. C. y = 2 cos x. D. y = cos2 x + 1. √
Câu 17. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = cos x + 2.
A. max y = 3 và min y = 1.
B. max y = 3 và min y = 2.
C. max y = 3 và min y = −2.
D. max y = 3 và min y = −1. √
Câu 18. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 2 sin x + 3. √ √ √ A. max y = 5, min y = 1. B. max y = 5, min y = 2 5. √ √ C. max y = 5, min y = 2. D. max y = 5, min y = 3. π
Câu 19. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 1 + 3 sin 2x − . 4
A. min y = −2, max y = 4.
B. min y = 2, max y = 4.
C. min y = −2, max y = 3.
D. min y = −1, max y = 4.
Câu 20. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 − 2 cos2 3x.
A. min y = 1, max y = 2.
B. min y = 1, max y = 3.
C. min y = 2, max y = 3.
D. min y = −1, max y = 3. √
Câu 21. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 1 + 2 + sin 2x. √ √
A. min y = 2, max y = 1 + 3.
B. min y = 2, max y = 2 + 3. √
C. min y = 1, max y = 1 + 3.
D. min y = 1, max y = 2. 4
Câu 22. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = . 1 + 2sin2x 4 4 A. min y = , max y = 4. B. min y = , max y = 3. 3 3 4 1 C. min y = , max y = 2. D. min y = , max y = 4. 3 2
Câu 23. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 2 sin2 x + cos2 2x. 3 A. max y = 4, min y = .
B. max y = 3, min y = 2. 4 3
C. max y = 4, min y = 2. D. max y = 3, min y = . 4
Câu 24. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 sin x + 4 cos x + 1.
A. max y = 6, min y = −2.
B. max y = 4, min y = −4.
C. max y = 6, min y = −4.
D. max y = 6, min y = −1. Trang 6
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 25. Tìm tập giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 3 sin x + 4 cos x − 1.
A. min y = −6; max y = 4.
B. min y = −6; max y = 5.
C. min y = −3; max y = 4.
D. min y = −6; max y = 6.
Câu 26. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 sin x + 4 cos x − 1.
A. max y = 4, min y = −6.
B. max y = 6, min y = −8.
C. max y = 6, min y = −4.
D. max y = 8, min y = −6. 1 3
Câu 27. Gọi T là tập giá trị của hàm số y = sin2 x −
cos 2x + 3. Tìm tổng các giá trị nguyên của 2 4 T . A. 4. B. 6. C. 7. D. 3.
Câu 28. Hàm số y = cos2x + sin x + 1 có giá trị lớn nhất và giá trị nhỏ nhất lần lượt bằng 9 9 A. 3; 1. B. 1; −1. C. ; 0. D. ; 2. 4 4
Câu 29. Giá trị lớn nhất của hàm số y = 2 cos2 x − sin 2x + 5 là √ √ √ √ A. 6 + 2. B. 6 − 2. C. 2. D. − 2. sin x + 2 cos x + 1
Câu 30. Tìm giá trị lớn nhất M của hàm số y = . sin x + cos x + 2 A. M = −2. B. M = −3. C. M = 3. D. M = 1. —HẾT— Trang 7
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§ 2. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
A KIẾN THỨC CẦN NHỚ 1 Phương trình sin x = a.
Trường hợp a ∈ {−1; 0; 1}. sin sin sin B A0 A cos O cos O cos O B0 sin x = 1 ⇔ x = π + k2
sin x = −1 ⇔ x = − π + k2 2 π 2 π sin x = 0 ⇔ x = kπ √ √ ® ´ 1 2 3 Trường hợp a ∈ ± ; ± ; ±
. Ta bấm máy SHIFT sin a để đổi số a về góc α hoặc 2 2 2 ◦ β tương ứng.
¬ Công thức theo đơn vị rad: sin ñx = α + k2π sin x = a ⇔ , k ∈ Z N M x = π − α + k2π a
Công thức theo đơn vị độ: O ñx = ◦ β + k360◦
sin x = a ⇔ x = 180◦ − ◦ β + k360◦ , k ∈ Z
Trường hợp a ∈ [−1; 1] nhưng khác các số ở trên. ñx = arcsin a + k2π sin x = a ⇔ , k ∈ Z x = π − arcsin a + k2π
Công thức mở rộng cho hai hàm f (x) và g(x) ñ f (x) = g(x) + k2π sin[ f (x)] = sin[g(x)] ⇔ , k ∈ Z f (x) = π − g(x) + k2π 2 Phương trình cos x = a.
Trường hợp a ∈ {−1; 0; 1}. Trang 8
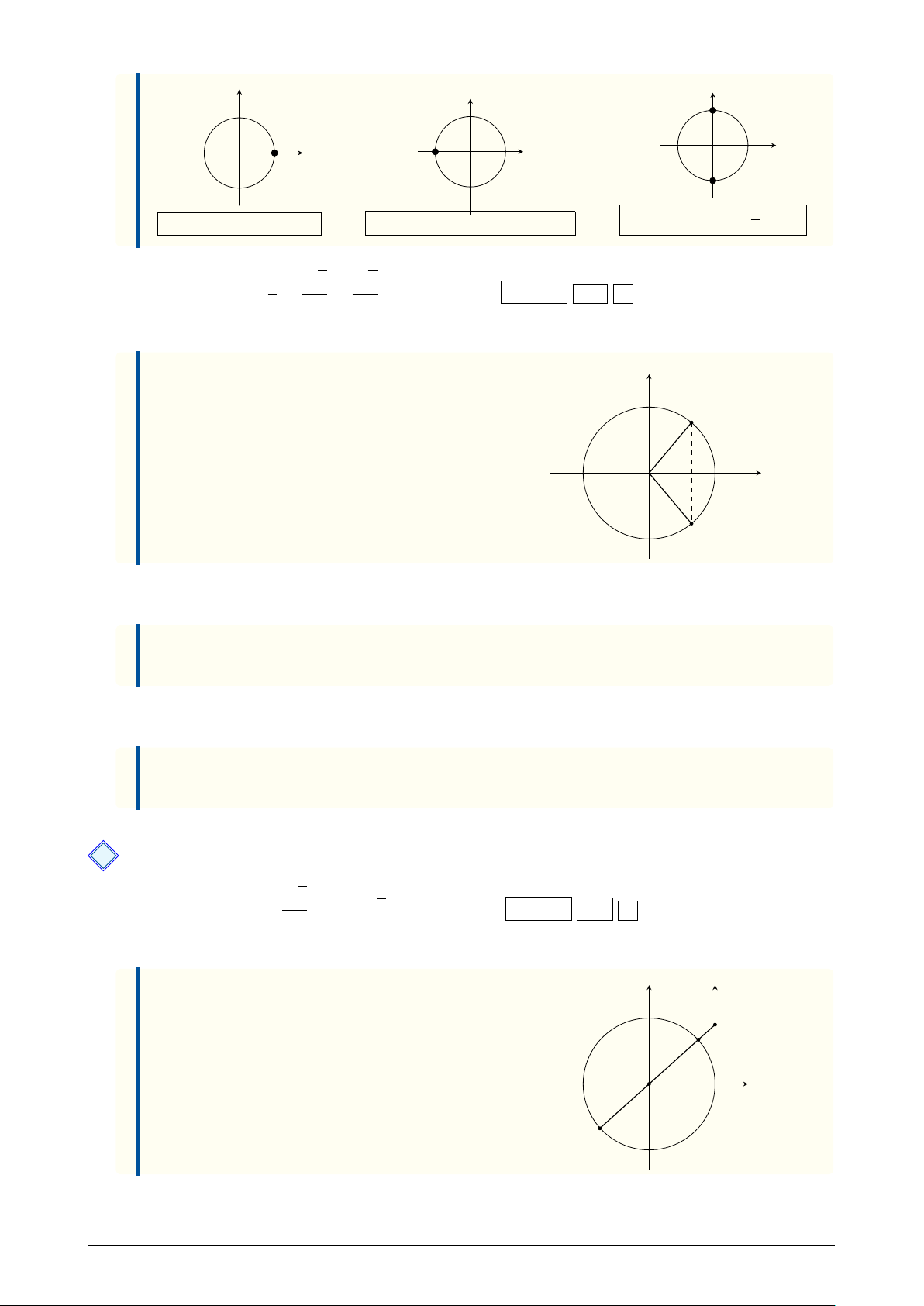
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC sin sin B A cos cos O O cos O A0 B0 cos x = 1 ⇔ x = k2 cos x = 0 ⇔ x = π + k π cos x = −1 ⇔ x = π + k2π 2 π √ √ ® ´ 1 2 3 Trường hợp a ∈ ± ; ± ; ±
. Ta bấm máy SHIFT cos a để đổi số a về góc α hoặc 2 2 2 ◦ β tương ứng.
¬ Công thức theo đơn vị rad: ñx = α + k2π cos x = a ⇔ , k ∈ M Z x = −α + k2π cos
Công thức theo đơn vị độ: O a ñx = ◦ β + k360◦ cos x = a ⇔ N x = − ◦ β + k360◦ , k ∈ Z
Trường hợp a ∈ [−1; 1] nhưng khác các số ở trên. ñx = arccos a + k2π cos x = a ⇔ , k ∈ Z x = − arccos a + k2π
Công thức mở rộng cho hai hàm f (x) và g(x) ñ f (x) = g(x) + k2π cos[ f (x)] = cos[g(x)] ⇔ , k ∈ Z f (x) = −g(x) + k2π 3 Phương trình tan x = a. √ ® ´ 3 √ Trường hợp a ∈ 0; ±
; ±1; ± 3 . Ta bấm máy SHIFT tan a để đổi số a về góc α hoặc 3 ◦ β tương ứng. tang
¬ Công thức theo đơn vị rad: N a
tan x = a ⇔ x = α + kπ, k ∈ Z O
Công thức theo đơn vị độ: M tan x = a ⇔ x = ◦ β + k180◦, k ∈ Z
Trường hợp a khác các số ở trên thì Trang 9
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
tan x = a ⇔ x = arctan a + kπ, k ∈ Z. 4 Phương trình cot x = a. √ ® ´ 3 √ Trường hợp a ∈ ±
; ±1; ± 3 . Ta bấm máy SHIFT tan
1 để đổi số a về góc ◦ α hoặc β 3 a π
tương ứng. Riêng a = 0 thì α = 2 cotang a
¬ Công thức theo đơn vị rad: N
cot x = a ⇔ x = α + kπ, k ∈ Z O
Công thức theo đơn vị độ: M cot x = a ⇔ x = ◦ β + k180◦, k ∈ Z
Trường hợp a khác các số ở trên thì
cot x = a ⇔ x = arccot a + kπ, k ∈ Z.
B PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
{ DẠNG 1. Giải các phương trình lượng giác cơ bản Phương pháp giải.
• Nhận dạng (biến đổi) về đúng loại phương trình cơ bản, xem số a quy đổi về góc "đẹp" hay xấu;
• Chọn và ráp công thức nghiệm.
# Ví dụ 1. Giải các phương trình sau: √3 π a) sin 3x = − b) 2 sin − x = 1
c) 2 sin (x − 45◦) − 1 = 0 2 5 Å 2π ã √ d) cos x − = 1 e) 2 cos 2x − 1 = 0 f) 3 cos x − 1 = 0. 3
# Ví dụ 2. Giải các phương trình sau: √3 √ π a) tan 3x = − b) 3 tan − x = 1 c) tan (x − 45◦) − 1 = 0 3 6 √ √ d) sin x − 3 cos x = 0 e) 3 cot x − 1 = 0
f) (tan x − 2)(cot x + 1) = 0.
# Ví dụ 3. (A.2014). Giải phương trình sinx + 4cosx = 2 + sin2x Trang 10
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
{ DẠNG 2. Giải các phương trình lượng giác dạng mở rộng Phương pháp giải.
• Biến đổi về một trong các cấu trúc sau ¬ sin u = sin v cos u = cos v ® tan u = tan v ¯ cot u = cot v
• Chú ý các công thức biến đổi lượng giác sau: ¬ − sin x = sin(−x). − cos x = cos (π − x). π π ® sin x = cos − x . ¯ cos x = sin − x . 2 2
# Ví dụ 4. Giải các phương trình sau: a) sin 3x = sin 2x b) sin 2x − sin x = 0 c) sin 5x + sin x = 0 d) cos 2x − cos x = 0 e) cos 8x + cos x = 0 f) cos 4x − sin x = 0
# Ví dụ 5. (B.2013). Giải phương trình sin5x + 2cos2 x = 1
{ DẠNG 3. Giải các phương trình lượng giác có điều kiện xác định Phương pháp giải.
# Ví dụ 6. Giải các phương trình sau: cos x cos2 x − sin2 x a) = 0 b) √ = 0 c) tan x(1 − 2 sin2 x) = 0 1 − sin x 2 − sin x π π
# Ví dụ 7. Giải phương trình tan 2x + + tan − x = 0. 6 3 −π • Đáp số x = + kπ, k ∈ Z. 2 x x
# Ví dụ 8. Giải phương trình cot − 1 cot + 1 = 0. 3 2 3π π • Đáp số x = + k3π, x = − + k2π, (k ∈ Z). 4 2
sin 2x + 2 cos x − sin x − 1
# Ví dụ 9. Giải phương trình √ = 0 3 + tan x π • Đáp số x = + k2π. 3
{ DẠNG 4. Giải các phương trình lượng giác trên khoảng (a;b) cho trước Phương pháp giải.
¬ Giải phương trình, tìm các họ nghiệm x = α + kπ
Vì x ∈ (a; b) nên a < α + kπ < b, chuyển vế tìm khoảng "dao động" của k.
® Kết hợp với k ∈ Z, ta chọn các giá trị k nguyên nằm trong khoảng vừa tìm được.
¯ Với mỗi giá trị k, ta thay vào tìm nghiệm tương ứng. Trang 11
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
# Ví dụ 10. Tìm nghiệm của các phương trình lượng giác sau trên khoảng cho trước √ √ a) 3 tan x − 3 = 0 trên (0, 3 π ). b)
2 sin(x − 1) = −1 trên − 7π , π . 2 2 π √ c) 2 cos 3x − − 1 = 0 trên (− π , π ). d) tan(3x + 2) − 3 = 0 trên − π , π . 3 2 2 √ π −π 2π
# Ví dụ 11. Giải phương trình 3 − 3tan 2x − = 0 với < x < . 3 4 3
# Ví dụ 12. Giải phương trình tan(x + 30◦) + 1 = 0 với −90◦ < x < 360◦. π π
# Ví dụ 13. Tìm x ∈ (−π;π) sao cho sin x − + 2 cos x + = 0. 3 6
C BÀI TẬP TRẮC NGHIỆM √
Câu 1. Với k ∈ Z thì phương trình 2 sin(x + 60◦) = 3 có nghiệm là
A. x = k.1800; x = 600 + k.1800.
B. x = k.3600; x = −1200 + k.3600.
C. x = k.3600; x = 600 + k.3600.
D. x = −300 + k.3600; x = 900 + k.3600.
Câu 2. Phương trình nào dưới đây có tập nghiệm trùng với tập nghiệm của phương trình sin x = 0? A. tan x = 0. B. cos x = −1. C. cot x = 1. D. cos x = 1.
Câu 3. Tìm m để phương trình cos 2x = 1 − m có nghiệm. A. −1 6 m 6 3. B. 0 6 m 6 2. C. m 6 2. D. m > 0.
Câu 4. Phương trình nào sau đây vô nghiệm? 1 √ 1 A. sin x = . B. tan x = 3. C. sin x = 3. D. cos x = − . 2 2
Câu 5. Phương trình sin x = m vô nghiệm khi và chỉ khi ñm < −1 A. m > 1. B. m < −1. C. −1 ≤ m ≤ 1. D. m > 1.
Câu 6. Nghiệm của phương trình sin x = −1 là π A. x = − + kπ, k ∈ Z. B. x = kπ, k ∈ Z. 2 3π π C. x = + kπ, k ∈ Z. D. x = − + k2π, k ∈ Z. 2 2 √ π 3
Câu 7. Tìm nghiệm của phương trình cot x − = . 3 3 π 2π A. x = + kπ, k ∈ Z. B. x = + kπ, k ∈ Z. 3 3 π C. x = + k2π, k ∈ Z. D. x = kπ, k ∈ Z. 3 √3
Câu 8. Phương trình cos x = − có tập nghiệm là 2 ß 5π ™ n π o A. x = ± + k2π; k ∈ Z . B. x = ± + kπ; k ∈ Z . 6 3 n π o n π o C. x = ± + k2π; k ∈ Z . D. x = ± + kπ; k ∈ Z . 3 6 √3
Câu 9. Tìm tất cả các nghiệm của phương trình sin 3x = . 2 Trang 12
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC π k2π π x = + , k ∈ Z x = + k2π, k ∈ Z 9 A. 9 3 . B. . 2π k2π 2π x = + , k ∈ Z x = + k2π, k ∈ Z 9 3 9 π kπ π k2π x = + , k ∈ Z x = + , k ∈ Z C. 9 3 3 3 . D. . 2π kπ 2π k2π x = + , k ∈ Z x = + , k ∈ Z 9 3 3 3
Câu 10. Nghiệm của phương trình 2 sin x + 1 = 0 là 11π −π π −7π A. x = + k2π và x = + k2π. B. x = + k2π và x = + k2π. 6 6 6 6 −π 7π −π 7π C. x = + kπ và x = + kπ. D. x = + k2π và x = + k2π. 6 6 6 6
Câu 11. Phương trình sin x − cos x = 1 có một nghiệm là π π 2π A. − . B. . C. . D. π. 2 4 3
Câu 12. Tập nghiệm của phương trình sin 2x = 1 là n π o n π o A. + 2kπ, k ∈ Z . B. + kπ, k ∈ Z . 4 4 n π o C. {kπ, k ∈ Z}. D. + 2kπ, k ∈ Z . 2 2
Câu 13. Phương trình sin x =
có số nghiệm thuộc (−π; π) 3 A. 1. B. 3. C. 2. D. 4. √3
Câu 14. Cho phương trình sin 2x =
. Gọi n là số các nghiệm của phương trình trong đoạn [0; 3π] 2 thì giá trị của n là A. n = 8. B. n = 5. C. n = 6. D. n = 2.
Câu 15. Tìm tất cả các nghiệm của phương trình sin x − cos x = 0. π π 5π A. x = ± + k2π (k ∈ Z). B. x = + k2π; x = + k2π (k ∈ Z). 4 4 4 π 5π C. x = + k2π (k ∈ Z). D. x = + k2π (k ∈ Z). 4 4
Câu 16. Tìm số đo ba góc của một tam giác cân biết rằng số đo của một góc là nghiệm của phương 1 trình cos 2x = − . 2 ß ™ n π π π o n π π π o n π π π o 2π π π A. , , ; , , . B. , , ; , , . 3 3 3 4 4 2 3 3 3 3 6 6 ß 2π π π ™ n π π π o C. , , . D. , , . 3 6 6 3 3 3 m
Câu 17. Tìm tất cả các giá trị m để phương trình sau có nghiệm: cos 2x = . 2 A. m ≤ 1. B. −1 ≤ m ≤ 1. C. −2 ≤ m ≤ 2.
D. m ≤ −1 hoặc m ≥ 1. π
Câu 18. Số nghiệm của phương trình 2 cos x − = 1 trong khoảng (0; π) là 2 A. 4. B. 1. C. 2. D. 3.
Câu 19. Phương trình 2 cos x − 1 = 0 có nghiệm là π π A. x = ± + k2π, k ∈ Z. B. x = ± + kπ, k ∈ Z. 6 3 π π C. x = ± + 2π, k ∈ Z. D. x = ± + k2π, k ∈ Z. 6 3 Trang 13
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 20. Tập nghiệm của phương trình cos 2x = −1 là n π o A. −kπ, k ∈ Z. B. − + kπ, k ∈ Z . 4 n π o C. − + k2π, k ∈ Z .
D. {90◦ + k180◦, k ∈ Z}. 2 π 1
Câu 21. Số điểm biểu diễn các nghiệm của phương trình sin 2x + = trên đường tròn lượng 3 2 giác là A. 4. B. 6. C. 1. D. 2. x Câu 22. Phương trình cos = −1 có tập nghiệm là 2
A. {2π + k4π|k ∈ Z}. B. {π + k2π|k ∈ Z}. C. {k4π|k ∈ Z}. D. {k2π|k ∈ Z}.
Câu 23. Nghiệm của phương trình sin4 x − cos4 x = 0 là π π π A. x = π + k2π. B. x = kπ. C. x = + kπ. D. x = + k . 2 4 2
Câu 24. Tìm tất cả nghiệm của phương trình sin x. cos x. cos 2x = 0. π π π A. k (k ∈ Z). B. kπ (k ∈ Z). C. k (k ∈ Z). D. k (k ∈ Z). 2 4 8
Câu 25. Tính tổng các nghiệm x ∈ [0; 2018π] của phương trình sin 2x = 1. 4071315π 4071315π 8141621π 8141621π A. S = . B. S = . C. S = . D. S = . 2 4 2 4
Câu 26. Tìm số nghiệm thuộc khoảng (−π; π) của phương trình cos x + sin 2x = 0 A. 1. B. 4. C. 2. D. 3.
Câu 27. Phương trình sin 5x − sin x = 0 có bao nhiêu nghiệm thuộc đoạn [−2018π; 2018π]? A. 16145. B. 20181. C. 20179. D. 16144.
Câu 28. Tìm tất cả các giá trị nguyên của tham số m để phương trình cos2 πx = m2 −9 có nghiệm. A. 5. B. 2. C. 1 . D. 3 . —HẾT— Trang 14
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§ 3. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
A KIẾN THỨC CẦN NHỚ
1 Phương trình bậc nhất đối với một hàm số lượng giác L Dạng phương trình ¬ a · sin x + b = 0 a · cos x + b = 0 ® a · tan x + b = 0 ¯ a · cot x + b = 0
L Phương pháp giải: Chuyển vế, biến đổi về phương trình cơ bản. b b
¬ a · sin x + b = 0 ⇔ sin x = −
a · cos x + b = 0 ⇔ cos x = − a a b b
® a · tan x + b = 0 ⇔ tan x = −
¯ a · cot x + b = 0 ⇔ cot x = − a a
2 Phương trình bậc nhất đối với sinx và cosx L Dạng phương trình • a sin x ± b cos x = c (1).
• Điều kiện có nghiệm a2 + b2 ≥ c2. √
L Phương pháp giải: Chia 2 vế phương trình cho a2 + b2. Khi đó a b c (1) ⇔ √ sin x ± √ cos x = √ a2 + b2 a2 + b2 a2 + b2 c
⇔ cos φ · sin x ± sin φ · cos x = √a2 +b2 c a b ⇔ sin (x ± φ ) = √ (2), với cos φ = √ và sin φ = √ . a2 + b2 a2 + b2 a2 + b2
Phương trình (2) là phương trình cơ bản đã xét ở bài trước. Chú ý hai công thức sau:
• sin a cos b ± cos a sin b = sin(a ± b).
• cos a cos b ± sin a sin b = cos(a ∓ b).
3 Phương trình bậc hai đối với một hàm số lượng giác L Dạng phương trình
¬ a · sin2 x + b · sin x + c = 0
a · cos2 x + b · cos x + c = 0
® a · tan2 x + b · tan x + c = 0
¯ a · cot2 x + b · cot x + c = 0 Trang 15
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC L Phương pháp giải
• Đặt ẩn phụ t, chuyển phương trình về ẩn t.
• Bấm máy, tìm nghiệm t. Sau đó, giải tìm x.
• Chú ý với phương trình số ¬ và thì −1 ≤ t ≤ 1.
B PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
{ DẠNG 1. Giải phương trình bậc nhất đối với một hàm số lượng giác Phương pháp giải.
# Ví dụ 1. Giải các phương trình sau: √ a) 2 sin x + 1 = 0; b) 2 cos x − 1 = 0; √ √ c) tan x + 3 = 0; d) 3 cot x − 1 = 0.
# Ví dụ 2. Giải các phương trình sau: π √ π a) 2 sin x − + 1 = 0. b) 2 cos 3x − − 1 = 0. 6 4 π √ √ π c) tan − x + 3 = 0. d) 3 cot x + + 3 = 0. 3 6
# Ví dụ 3. Tìm tất cả các nghiệm của phương trình 2sin2x − 1 = 0 trong đoạn [−2π;2π].
# Ví dụ 4. Giải phương trình (2cosx − 1)(sinx + cosx) = sin2x − sinx. BÀI TẬP TỰ LUYỆN
c Bài 1. Giải các phương trình sau √ a) 2 cos 2x + 3 = 0. b) 2 sin 3x + 1 = 0 √ √ π c) 2 cos 2x − 2 = 0. d) 3 − 2 3 cos x + = 0. 4 Å ã π √ 2π √ e) 2 cos x − + 1 = 0. f) 2 2 sin x + = 6. 6 5 √ π g) 3 sin(x − 1) + 2 = 0. h) 3 tan − 2x + 1 = 0. 6 √ √ π i) (cos 2x + 2)(cot 3x − 1) = 0. j) 2 − 2 3 tan x + = 0. 3
c Bài 2. Tìm nghiệm của các phương trình lượng giác sau trên khoảng cho trước √ √ Å 7π π ã a)
3 tan x − 3 = 0 trên (0, 3π). b) 2 sin(x − 1) = −1 trên − , . 2 2
c Bài 3. Giải phương trình 2 sin2 2x + sin 7x − 1 = sin x.
c Bài 4. Giải phương trình (cos x − sin x) sin x cos x = cos x cos 2x.
c Bài 5. Giải phương trình (2 sin x − cos x)(1 + cos x) = sin2 x. Trang 16
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
{ DẠNG 2. Giải phương trình bậc hai đối với một hàm số lượng giác Phương pháp giải.
# Ví dụ 5. Giải các phương trình sau
a) 3 sin2 x − 5 sin x + 2 = 0;
b) 4 cos2 x − 4 cos x − 3 = 0. √ √
c) 3 sin2 2x + 7 cos 2x − 3 = 0; d) 3 tan2 x − 2 tan x + 3 = 0.
# Ví dụ 6. Giải các phương trình sau a) cos 2x + cos x + 1 = 0; b) 6 sin2 3x + cos 12x = 14; c) cos 4x + 6 = 7 cos 2x; d) 7 tan x − 4 cot x = 12.
# Ví dụ 7. Giải các phương trình sau √ √ Ä ä 2 2 5 a) 1 − 2 + 2 sin x + = 0; b) tan2 x − + 7 = 0. 1 + cot2 x cos x
# Ví dụ 8. Giải các phương trình sau cos 2x + 3 cot x + sin 4x
4 sin2 2x + 6 sin2 x − 9 − 3 cos 2x a) = 2; b) = 0. cot 2x − cos 2x cos x BÀI TẬP TỰ LUYỆN
c Bài 6. Giải các phương trình sau a) cos2 x + cos x − 2 = 0;
b) 2 sin2 x − 5 sin x + 2 = 0; √
c) 6 cos2 x + 5 sin x − 7 = 0;
d) 3 tan2 x − 2 3 tan x + 1 = 0.
c Bài 7. Giải các phương trình sau: a) 2 tan x + cot x − 3 = 0
b) 5 sin x − 2 = 3(1 − sin x) tan2 x ; x
c) 2 cos 2x. cos x = 1 + cos 2x + cos 3x; d) cos 2x + cos x = 4 sin2 − 1 2
c Bài 8. Tìm nghiệm x ∈ (0; 10π) của phương trình √3 √ x
− tan x − 2 3 = sin x 1 + tan x. tan . cos2 x 2
{ DẠNG 3. Giải phương trình bậc nhất đối với sinx và cosx Phương pháp giải.
# Ví dụ 9. Giải các phương trình sau: √ √ a) sin x + 3 cos x = 1; b) 3 sin 2x − cos 2x = 2; √ c) sin 2x − 3 cos 2x = 2; d) 3 sin x + cos x = 2. Trang 17
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC Å 2π 6π ã √ √
# Ví dụ 10. Tìm các nghiệm x ∈ ;
của phương trình cos 7x − 3 sin 7x = − 2. 5 7 x x 2 √
# Ví dụ 11. (D.2007). Giải phương trình sin + cos + 3 cos x = 2. 2 2 (1 − 2 sin x) cos x √
# Ví dụ 12. Giải phương trình = 3. (1 + 2 sin x)(1 − sin x) BÀI TẬP TỰ LUYỆN
c Bài 9. Giải các phương trình sau: √ √ √ a) cos x − 3 sin x = 1 b) 3 sin x + cos x = 2 √ √ c) 3 cos x − sin x = 0 d) sin 3x − 3 cos 3x = 2 sin 4x
c Bài 10. Giải các phương trình sau π √ a) cos(π − 2x) − cos 2x + = 2; 2 √ π √ b)
3 cos 2x + sin 2x + 2 sin 2x − = 2 2; 6 √ √ √ c) sin x − 2 cos 3x = 3 cos x + 2 sin 3x; √ d) cos 7x cos 5x − 3 sin 2x = − sin 5x sin 7x.
c Bài 11. Giải các phương trình sau: √ a) sin x − 3 cos x = 2 sin 5x √ b) 3 sin 2x + 2sin2x = 2 √ c)
3 cos 5x − 2 sin 3x cos 2x − sin x = 0 √ d) cos 7x cos 5x − 3 sin 2x = 1 − sin 7x sin 5x √ sin x + cos x sin 2x + 3 cos 3x = 2 cos 4x + sin3x e) √ Ä ä
f) tan x − 3 cot x = 4 sin x + 3 cos x π
c Bài 12. Giải phương trình 2 sin(x + ) + sin x + 2 cos x = 3. 6
c Bài 13. Giải phương trình (sin 2x + cos 2x) cos x + 2 cos 2x − sin x = 0.
c Bài 14. Giải phương trình sin 2x − cos 2x + 3 sin x − cos x − 1 = 0.
{ DẠNG 4. Phương trình đẳng cấp bậc hai đối với sinx và cosx Phương pháp giải. L Dạng phương trình
• a sin2 x + b sin x cos x + c cos2 x = 0 Trang 18
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
• Tổng quát: a sin2 x + b sin x cos x + c cos2 x = d L Phương pháp giải
• Trường hợp 1. Xét cos x = 0, khi đó sin x = ±1. Ta thay trực tiếp vào phương trình π Nếu thỏa mãn, suy ra x =
+ kπ là nghiệm và xét tiếp Trường hợp 2. 2
Nếu không thỏa mãn, ta bỏ qua và xét tiếp Trường hợp 2.
• Trường hợp 2. Xét cos x 6= 0, chia 2 vế phương trình cho cos2 x ta đưa phương trình
đang xét về dạng phương trình bậc hai theo tan x.
• Tổng hợp nghiệm ở 2 trường hợp. Chú ý công thức sin x 1 ¬ = tan x. sin 2x = 2 sin x cos x ® = tan2 x + 1 cos x cos2 x
# Ví dụ 13. Giải các phương trình sau:
a) 2cos2x − 3 sin x. cos x + sin2x = 0
b) sin2x − sin 2x − 3cos2x + 2 = 0 √
c) 4sin2x + 3 3 sin 2x − 2cos2x = 4 d) 4cos2x + sin 2x − 3 = 0 BÀI TẬP TỰ LUYỆN
c Bài 15. Giải các phương trình sau: √ √ Ä ä Ä ä a) 2sin2x + 3 + 3 sin x cos x + 3 − 1 cos2x = −1 1
b) sin2x + sin 2x − 2cos2x = 2 √
c) 4sin2x + 3 3 sin 2x − 2cos2x = 4 √ √ 3 + 2 d) sin2x + 3 sin x cos x + 2cos2x = 2
e) 2sin2x − 5 sin x cos x − cos2x = −2 √ Ä ä
f) 3sin2x + 8 sin x cos x + 8 3 − 9 cos2x = 0
{ DẠNG 5. Phương trình chứa sinx ± cosx và sinx · cosx Phương pháp giải. L Dạng phương trình
• a (sin x + cos x) + b sin x cos x + c = 0.
• a (sin x − cos x) + b sin x cos x + c = 0. L Phương pháp giải: • Đặt t = sin x ± cos x Trang 19
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
• Tính t2 = (sin x ± cos x)2 = 1 ± 2 sin x · cos x. Từ đây ta tính được sin x · cos x.
• Thay trở lại phương trình, chuyển phương trình về ẩn t. Giải tìm t, sau đó tìm x. Chú ý √ √ √ π
¬ Điều kiện của t là − 2 ≤ t ≤ 2. sin x ± cos x = 2 sin x ± . 4
# Ví dụ 14. Giải các phương trình
a) sin x cos x + 2 (sin x + cos x) = 2
b) sin x − cos x + 4 sin x cos x + 1 = 0 √ √ π
c) 4 2 (sin x + cos x) + 3 sin 2x − 11 = 0 d) sin 2x + 2 sin x − = 1 4 BÀI TẬP TỰ LUYỆN
c Bài 16. Giải các phương trình
a) sin x − cos x + 7 sin 2x = 1
b) cot x − tan x = sin x + cos x 1 1 10 3 c) sin x + cos x + + = d) 1 + sin3x + cos3x = sin 2x sin x cos x 3 2
C BÀI TẬP TRẮC NGHIỆM √
Câu 1. Phương trình 2 sin x − 3 = 0 có các nghiệm là π π x = + k2π x = + k2π 3 A. 3 , k ∈ Z. B. , k ∈ Z. π 2π x = − + k2π x = + k2π 3 3 π π x = + k2π x = + kπ 3 C. 3 , k ∈ Z. D. , k ∈ Z. π 2π x = − + k2π x = + kπ 3 3
Câu 2. Cho phương trình sin x − (m + 1) cos x = 2. Tìm m để phương trình có nghiệm. √ √ Ä ó î ä A. m ∈ [0; −2].
B. m ∈ −∞; −1 − 3 ∪ −1 + 3; +∞ . √ √ î ó
C. m ∈ (−∞; −2] ∪ [0; +∞). D. m ∈ −1 − 3; −1 + 3 .
Câu 3. Giải phương trình 2 cos x − 1 = 0. π π A. x = ± + k2π, k ∈ Z. B. x = ± + k2π, k ∈ Z. 3 6 π π C. x = + k2π, k ∈ Z. D. x = ± + 2π, k ∈ Z. 3 3
Câu 4. Nghiệm của phương trình cot 3x = −1 là π π A. x = + kπ với k ∈ Z. B. x = − + kπ với k ∈ Z. 12 12 π π π π C. x = + k với k ∈ Z. D. x = − + k với k ∈ Z. 12 3 12 3
Câu 5. Nghiệm của phương trình sin 2x = 1 là π π kπ π A. x = + k2π. B. x = + kπ. C. x = . D. x = + k2π. 4 4 2 2 Trang 20
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 6. Điều kiện cần và đủ để phương trình m sin x − 3 cos x = 5 có nghiệm là m ∈ (−∞; a] ∪ [b; +∞) với a, b ∈ Z. Tính a + b. A. −4. B. 4. C. 0. D. 8.
Câu 7. Giải phương trình sin 2x = 1. kπ π A. x = , với k ∈ Z. B. x = + k2π, với k ∈ Z. 2 2 π π C. x = + kπ, với k ∈ Z. D. x = + k2π, với k ∈ Z. 4 4
Câu 8. Trong các phương trình sau phương trình nào vô nghiệm? π 2017 A. tan x = π. B. sin x = . C. sin x + cos x = 2. D. cos x = . 4 2018
Câu 9. Nghiệm của phương trình sin 3x = cos x là π π kπ π A. x = ± + k2π; k ∈ Z. B. x = + , x = + kπ; k ∈ Z. 4 8 2 4 π π C. x = − kπ; k ∈ Z. D. x = + kπ; k ∈ Z. 4 8
Câu 10. Tìm số điểm phân biệt biểu diễn các nghiệm của phương trình sin 2x − cos x = 0 trên đường tròn lượng giác. A. 1. B. 4. C. 3. D. 2.
Câu 11. Gọi x0 là nghiệm dương nhỏ nhất của phương trình 3 sin2 x + 2 sin x cos x − cos2 x = 0. Chọn khẳng định đúng. Å ã Å ã π 3π π 3π A. x0 ∈ 0; . B. x0 ∈ ; 2π . C. x0 ∈ ; π . D. x0 ∈ π; . 2 2 2 2 π
Câu 12. Nghiệm của phương trình 2 sin 4x − − 1 = 0 là 3 x = k2π ñx = kπ A. π (k ∈ Z). B. (k ∈ Z). x = + k2π x = π + k2π 2 π π x = π + k2π x = + k 8 2 C. π (k ∈ Z). D. (k ∈ Z). x = k 7π π 2 x = + k 24 2
Câu 13. Phương trình 2 sin x − 1 = 0 có bao nhiêu nghiệm x ∈ (0; 2π)? A. 1 nghiệm. B. 4 nghiệm. C. Vô số nghiệm. D. 2 nghiệm.
Câu 14. Giải phương trình cos 2x + 5 sin x − 4 = 0. π π π A. x = + kπ. B. x = k2π. C. x = + kπ. D. x = + k2π. 2 2 2 1 π Câu 15. Cho sin x + cos x = và 0 < x < . Tính giá tri của sin x. √ 2 2 √ √ √ 1 − 7 1 + 7 1 − 7 1 + 7 A. sin x = . B. sin x = . C. sin x = . D. sin x = . 4 4 6 6
Câu 16. Cho x0 là nghiệm của phương trình sin x cos x + 2(sin x + cos x) = 2. Khi đó, giá trị của P = 3 + sin 2x0 là √2 A. P = 3 + . B. P = 2. C. P = 0. D. P = 3. 2 √
Câu 17. Giải phương trình sin 3x + cos 3x = 2. π 2π π π A. x = + k , k ∈ Z. B. x = + k , k ∈ Z. 9 3 6 3 π π 2π C. x = + kπ, k ∈ Z. D. x = + k , k ∈ Z. 3 12 3 Trang 21
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC √ π
Câu 18. Số nghiệm của phương trình 2 cos x + = 1 với 0 ≤ x ≤ 2π. 3 A. 4. B. 3. C. 1. D. 2.
Câu 19. Phương trình cos x = 0 có bao nhiêu nghiệm thuộc khoảng (−π; π)? A. 3. B. 1. C. 2. D. 4. 1
Câu 20. Tổng 2 nghiệm dương liên tiếp nhỏ nhất của phương trình cos 4x + = 0 là 2 5π π π 7π A. . B. . C. . D. . 6 6 2 6
Câu 21. Cho phương trình cos 2x +cos x = 2. Khi đặt t = cos x, phương trình đã cho trở thành phương trình nào dưới đây? A. 2t2 + t − 3 = 0. B. 2t2 − t − 1 = 0. C. 2t2 − t − 3 = 0. D. 2t2 + t − 1 = 0. sin 3x
Câu 22. Số nghiệm phương trình
= 0 thuộc đoạn [2π; 4π] là cos x + 1 A. 6. B. 2. C. 4. D. 5.
Câu 23. Tìm tất cả các giá trị của tham số m để phương trình cos2 x = m − 1 có nghiệm. A. 1 ≤ m ≤ 2. B. m ≤ 2. C. 1 < m < 2. D. m ≥ 1. √
Câu 24. Điều kiện của tham số thực m để phương trình sin x + (m + 1) cos x = 2 vô nghiệm là ñm ≥ 0 A. m > 0. B. −2 < m < 0. C. . D. m < −2. m ≤ −2
Câu 25. Có bao nhiêu giá trị nguyên dương của m để phương trình m sin 2x − 3 cos 2x = 2m + 1 có nghiệm? A. 4. B. 2. C. 1. D. 10.
Câu 26. Tìm số đo góc của một tam giác cân biết rằng có số đo của một góc là nghiệm của phương 1 trình cos 2x = − . 2 n π π π o n π π π o n π π π o A. ; ; , ; ; . B. ; ; . 3 3 3 2 4 4 3 3 3 ß ™ ß ™ n π π π o 2π π π 2π π π C. ; ; , ; ; . D. ; ; . 3 3 3 3 6 6 3 6 6 π √ π √ π Câu 27. Cho 0 < α < thỏa mãn sin α + 2 sin − α = 2. Tính tan α + . √ 2 √ 2 √ 4 √ 9 + 4 2 −9 + 4 2 9 − 4 2 9 + 4 2 A. − . B. . C. . D. . 7 7 7 7
Câu 28. Tính tổng tất cả T các nghiệm thuộc đoạn [0; 200π] của phương trình cos 2x − 3 cos x − 4 = 0. A. T = 10000π. B. T = 5100π. C. T = 5151π. D. T = 10100π. √ π
Câu 29. Số nghiệm của phương trình cos2 x − sin 2x = 2 + cos2
+ x trên khoảng (0; 3π) bằng 2 A. 4. B. 1. C. 3. D. 2.
Câu 30. Số các giá trị thực của tham số m để phương trình (sin x −1)(2 cos2 x −(2m +1) cos x +m) =
0 có đúng 4 nghiệm thực thuộc đoạn [0; 2π] là A. 1. B. 2. C. 3. D. Vô số. —HẾT— Trang 22
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§ 4. MỘT SỐ PHƯƠNG PHÁP GIẢI PT LƯỢNG GIÁC
A PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
{ DẠNG 1. Biến đổi đưa phương trình về dạng phương trình bậc hai (ba) đối
với một hàm số lượng giác Phương pháp giải.
# Ví dụ 1. Giải các phương trình sau x
4 sin2 2x + 6 sin2 x − 9 − 3 cos 2x a) cos 2x + 2 cos x = 2 sin2 b) √ = 0. 2 Ç å 3 cos x sin x − 2 c) 2 tan2 x + cos 4x = 1
d) 2 sin3 x + 4 cos3 x = 3 sin x. Đáp số: π π 4π π a) x = + k2π; x = − + k2π. b) x = + k2π; x = − + k2π. 3 3 3 3 π kπ π c) x = + ; x = kπ. d) + kπ. 4 2 4
# Ví dụ 2. Cho phương trình cos5x cosx = cos4x cos2x + 3cos2x + 1. Tìm các nghiệm của
phương trình thuộc (−π; π) Đáp số: π π 5π • Nghiệm x = ± + kπ.
• Do x ∈ (−π; π) nên x = ± ; x = ± . 6 6 6 Å 9π ã Å 15π ã
# Ví dụ 3. Phương trình sin 2x + − 3 cos x −
= 1 + 2 sin x có tất cả bao nhiêu 2 2 ï π 5π ò nghiệm thuộc đoạn ; ? 6 6 Đáp số: π 5π ï π 5π ò π 5π • x = kπ; x = + k2π; x = + k2π. • Do x ∈ ; nên x = ; x = . 6 6 6 6 6 6
# Ví dụ 4. (A-2002). Tìm nghiệm thuộc khoảng (0;2π) của phương trình Å cos 3x + sin 3x ã 5 sin x + = cos 2x + 3. 1 + 2 sin 2x Đáp số: π 5π
• Biến đổi phương trình về 5 cos x = • Nghiệm x = ; x = . 3 3 2 cos 2x + 3. Trang 23
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
{ DẠNG 2. Biến đổi asinx + bcosx Phương pháp giải.
# Ví dụ 5. Giải các phương trình sau √ π √ a) cos x − 3 sin x = 2 cos 2x − . b)
3 cos 5x − 2 sin 3x cos 2x − sin x = 0. 6 (1 − 2 sin x) cos x √ √ c) = 3 d) sin x + cos x. sin 2x + 3 cos 3x = (1 + 2 sin x)(1 − sin x) 2 cos 4x + sin3x. Đáp số: π π k2π π π π π a) x = + k2π; x = − + . b) x = + k ; x = − + k . 2 18 3 18 3 6 2 π 2π π π 2π c) x = − + k . d) x = − + k2π; x = + k . 18 3 6 42 7
# Ví dụ 6. (DB1-2008) Tìm nghiệm trên khoảng (0;π) của phương trình x √ Å 3π ã 4sin2 − 3 cos 2x = 1 + 2cos2 x − 2 4 Đáp số: 5π 2π 7π • Nghiệm x = + k ; x = − + k2π 18 3 6 5π 17π 5π • Do x ∈ (0; π) nên x = ; x = ; x = . 18 18 6
{ DẠNG 3. Biến đổi đưa về phương trình tích Phương pháp giải.
# Ví dụ 7. Giải các phương trình sau 3
a) 2 sin2 2x + sin 7x − 1 = sin x
b) cos2 x + cos2 2x + cos2 3x = . 2
c) sin x + sin 2x + 4 sin 3x + sin 4x + sin 5x = 0
d) sin2 3x − cos2 4x = sin2 5x − cos2 6x Đáp số: ß π π π 2π 5π 2π ™ π kπ π a) + k , + k , + k , k ∈ Z b) + ; ± + kπ (k ∈ Z) 8 4 18 3 18 3 8 4 3 kπ π π c) x = d) x = k , x = k 3 9 2
# Ví dụ 8. Giải các phương trình sau
a) (2 sin x − cos x)(1 + cos x) = sin2x
b) 2 cos x − sin 2x = 1 + cos 2x
c) (2 cos x − 1)(2 sin x + cos x) = sin 2x − sin x
d) (2 sin x − 1) (2 sin 2x + 1) = 3 − 4 cos2 x. Đáp số: Trang 24
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC π 5π π a) x = π +k2π; x = + k2π; x = + k2π. b) x = + kπ; x = k2π. 6 6 2 π π π π c) x = ± + k2π; x = − + kπ. d) x = kπ, x = ± + k2π, x = + k2π, x = 3 4 3 6 5π +k2π. 6
# Ví dụ 9. Giải các phương trình sau 1 1 Å 7π ã 1 1 a) + = 4 sin − x . b) sin 2x + sin x − − = 2 cot 2x sin x Å 3π ã 4 2 sin x sin 2x sin x − 2
c) (sin 2x + cos 2x) cos x + 2 cos 2x − sin x = 0
d) sin 2x − cos 2x + 3 sin x − cos x − 1 = 0 Đáp số: π π 5π π π a) x = − + kπ; x = − + kπ; x = + b) x = + k . 4 8 8 4 2 kπ. π π π 5π c) x = + k . d) x = + k2π; x = + k2π 4 2 6 6
{ DẠNG 4. Một số bài toán biện luận theo tham số Phương pháp giải.
# Ví dụ 10. Cho phương trình cos2x + 5cosx + 5 − m = 0. Xác định tất cả các giá trị của m để h π i
phương trình có nghiệm x ∈ ; π . 2 Đáp số:
• Biến đổi cos 2x = 2 cos2 x − 1. • Kết quả m > 1. √ √
# Ví dụ 11. Biết rằng phương trình 2 sin x +
2 cos x + m2 − m = 0 (với m là tham số) có
nghiệm khi m ∈ [a; b]. Tính giá trị biểu thức P = a2 + b2. Đáp số:
• Sử dụng điều kiện có nghiệm.
• Kết quả m ∈ [−1; 2]. Vậy P = 5.
# Ví dụ 12. Cho phương trình (sinx + 1)(sin2x − msinx) = mcos2 x. Tìm tập tất cả các giá trị π
thực của tham số m để phương trình có nghiệm trên khoảng 0; . 6 Đáp số: • Phân tích nhân tử; √3 • Kết quả 0 < m < . 2 Trang 25
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
# Ví dụ 13. Tìm tập các giá trị thực của tham số m để phương trình msin2 x − 3sinx cosx − m − Å 3π ã
1 = 0 có đúng ba nghiệm thuộc khoảng 0; . 2 Đáp số: • Chia hai vế cho cos2 x.
• Kết quả m ∈ (−∞; −1).
# Ví dụ 14. Số các giá trị nguyên của m để phương trình (cosx + 1)(4cos2x − mcosx) = ï 2π ò
m sin2 x có đúng 2 nghiệm x ∈ 0; là 3 Đáp số: • Phân tích nhân tử.
• Kết quả: m ∈ Z nên m ∈ {−3; −2}
# Ví dụ 15. Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ. Số y
nghiệm thuộc đoạn [0; 5π] của phương trình f (cos x) = 1. 4 Đáp số: 2
• Giao của đồ thị với đường nằm ngang. • Kết quả 5 nghiệm. O x −1 1
B BÀI TẬP TỰ LUYỆN
c Bài 1. Tìm x thuộc đoạn [0; 14] nghiệm đúng phương trình cos 3x − 4 cos 2x + 3 cos x − 4 = 0 π 3π 5π 7π Đáp số: x = ; x = ; x = ; x = 2 2 2 2 x
c Bài 2. Giải phương trình tan x + cos x − cos2x = sin x 1 + tan x. tan . 2 Đáp số: x = k2π 2 − sin22x sin 3x
c Bài 3. Giải phương trình tan4x + 1 = cos4x π 2π 5π 2π Đáp số: x = + k ; x = + k 18 3 18 3 sin4x + cos4x 1 1
c Bài 4. Giải phương trình = cot 2x − . 5 sin 2x 2 8 sin 2x π Đáp số: x = ± + kπ. 6 x π x
c Bài 5. Giải phương trình sin2 − tan2x − cos2 = 0. 2 4 2 π
Đáp số: x = π + k2π; x = − + kπ. 4
c Bài 6. Giải phương trình cos 2x + cos x 2tan2x − 1 = 2 π
Đáp số: x = (2k + 1)π, x = ± + k2π 3
c Bài 7. Giải phương trình 3 − tan x (tan x + 2 sin x) + 6 cos x = 0 π Đáp số: x = ± + kπ 3 Trang 26
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
c Bài 8. 3 cos 4x − 8cos6x + 2cos2x + 3 = 0. π π Đáp số: x = + k , x = kπ. 4 2 √ Ä ä x π 2 − 3 cos x − 2sin2 −
c Bài 9. Giải phương trình 2 4 = 1. 2 cos x − 1 π Đáp số: x = + (2k + 1)π. 3 cos2x (cos x − 1)
c Bài 10. Giải phương trình = 2(1 + sin x). sin x + cos x π Đáp số: x = − + kπ, x = π + k2π. 2 2 cos 4x
c Bài 11. Giải phương trình cot x = tan x + sin2xπ Đáp số: x = ± + kπ. 3
c Bài 12. Giải phương trình cos23x. cos 2x − cos2x = 0. π Đáp số: x = k 2
c Bài 13. Giải phương trình 1 + sin x + cos x + sin 2x + cos 2x = 0. π 2π Đáp số: x = − + kπ; x = ± + k2π, 4 3√ 2 + 3 2
c Bài 14. Giải phương trình cos 3x. cos3 x − sin 3x. sin3 x = . 8 π π Đáp số: x = ± + k 16 2
c Bài 15. Giải phương trình: (1 tan x)(1 + sin 2x) = 1 + tan x. π Đáp số: x = − + kπ; x = kπ. 4 2
c Bài 16. cot x − tan x + 4 sin 2x = . sin 2x π Đáp số: x = ± + kπ. 3 cos 2x 1
c Bài 17. Giải phương trình cot x − 1 = + sin2x − sin 2x. 1 + tan x 2 π Đáp số: x = + kπ. 4 √ √
c Bài 18. Giải phương trình 2cos2x + 2 3 sin x cos x + 1 = 3(sin x + 3 cos x). 2π Đáp số: x = + kπ. 3 sin 2x cos 2x
c Bài 19. Giải phương trình + = tan x − cot x. cos x sin x π Đáp số: x = ± + k2π. 3
c Bài 20. Xác định m để phương trình 2 sin4x + cos4x + cos 4x + 2 sin 2x − m = 0(*) có ít nhất h π i
một nghiệm thuộc đoạn 0; . 2 10 Đáp số: − ≤ m ≤ −2. 3 Trang 27
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§ 5. ĐỀ ÔN TẬP CUỐI CHƯƠNG A ĐỀ SỐ 1
BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm tập xác định D của hàm số y = − tan x. n π o A. D = R \ + kπ, k ∈ Z .
B. D = R \ {kπ, k ∈ Z}. 2 n π o
C. D = R \ {k2π, k ∈ Z}. D. D = R \ + k2π, k ∈ Z . 2
Câu 2. Tập giá trị của hàm số y = cos x là tập hợp nào sau đây? A. R. B. (−∞; 0]. C. [0; +∞]. D. [−1; 1].
Câu 3. Tập giá trị của hàm số y = sin 2x là A. [−2; 2]. B. [0; 2]. C. [−1; 1]. D. [0; 1].
Câu 4. Mệnh đề nào dưới đây đúng?
A. Hàm số y = sin x là hàm số chẵn.
B. Hàm số y = cos x là hàm số chẵn.
C. Hàm số y = tan x là hàm số chẵn.
D. Hàm số y = cot x là hàm số chẵn.
Câu 5. Tìm hàm số lẻ trong các hàm số sau: A. y = sin2 x. B. y = x cos 2x. C. y = x sin x. D. y = cos x. 2 cos 3x − 1
Câu 6. Tập xác định của hàm số y = là cos x + 1
A. D = R \ {π + kπ; k ∈ Z}.
B. D = R \ {k2π; k ∈ Z}. π
C. D = R \ { + kπ; k ∈ Z}.
D. D = R \ {π + k2π; k ∈ Z}. 2
Câu 7. Hàm số y = sin 2x có chu kỳ là π A. T = 2π. B. T = . C. T = π. D. T = 4π. 2
Câu 8. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở
bốn phương án A,B,C,D. Hỏi hàm số đó là hàm số nào? y 1 −π π O x 2π −1 A. y = 1 + sin x. B. y = 1 − sin x. C. y = sin x. D. y = cos x. √
Câu 9. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = cos x + 2.
A. max y = 3 và min y = 1.
B. max y = 3 và min y = 2.
C. max y = 3 và min y = −2.
D. max y = 3 và min y = −1.
Câu 10. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 sin x + 4 cos x − 1.
A. max y = 4, min y = −6.
B. max y = 6, min y = −8.
C. max y = 6, min y = −4.
D. max y = 8, min y = −6.
Câu 11. Tập nghiệm của phương trình 2 cos 2x + 1 = 0 là ß ™ n π π o 2π 2π A. S = + k2π, − + k2π, k ∈ Z . B. S = + k2π, − + k2π, k ∈ Z . 3 3 3 3 n π π o n π π o C. S = + kπ, − + kπ, k ∈ Z . D. S = + kπ, − + kπ, k ∈ Z . 3 3 6 6 Trang 28
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC π
Câu 12. Phương trình sin x − = 1 có nghiệm là 3 x 5π 5π π A. x = + kπ. B. x = + k2π. C. x = + kπ. D. x = + k2π. 3 6 6 3 √3
Câu 13. Nghiệm của phương trình tan x = − được biểu diễn trên y 3
đường tròn lượng giác ở hình bên là những điểm nào? B
A. Điểm F, điểm D. D C
B. Điểm C, điểm F.
C. Điểm C, điểm D, điểm E, điểm F. x
D. Điểm E, điểm F. A0 O A E F B0
Câu 14. Gọi S là tổng các nghiệm thuộc khoảng (0; 2π) của phương trình 3 cos x − 1 = 0. Tính S. A. S = 0. B. S = 4π. C. S = 3π. D. S = 2π. 1
Câu 15. Số nghiệm của phương trình cos x =
thuộc đoạn [−2π; 2π] là 2 A. 4. B. 2. C. 3. D. 1. ï 3π ò
Câu 16. Số nghiệm thực của phương trình sin 2x + 1 = 0 trên đoạn − ; 10π là 2 A. 12. B. 11. C. 20. D. 21. √
Câu 17. Cho phương trình 2 sin x −
3 = 0. Tổng các nghiệm thuộc [0; π] của phương trình đã cho là π 2π 4π A. π. B. . C. . D. . 3 3 3
Câu 18. Phương trình sin x = cos x có bao nhiêu nghiệm thuộc đoạn [−π; π]? A. 0. B. 1. C. 3. D. 2.
Câu 19. Phương trình cos2 x + cos x − 2 = 0 có bao nhiêu nghiệm trong đoạn [0; 2π]. A. 4. B. 3. C. 2. D. 1. √
Câu 20. Phương trình sin x −
3 cos x = 1 có tập nghiệm là n π π o n π π o A. − + k2π; + k2π , với k ∈ Z. B. − + k2π; − + k2π , với k ∈ Z. 6 2 6 2 ß 7π π ™ n π π o C. + k2π; + k2π , với k ∈ Z. D. − + kπ; − + kπ , với k ∈ Z. 6 2 6 2
Câu 21. Tìm tất cả các giá trị của tham số m để phương trình cos2 x = m − 1 có nghiệm. A. m ≤ 2. B. 1 < m < 2. C. m ≥ 1. D. 1 ≤ m ≤ 2. √
Câu 22. Điều kiện của tham số thực m để phương trình sin x + (m + 1) cos x = 2 vô nghiệm là ñm ≥ 0 A. . B. m < −2. C. −2 < m < 0. D. m > 0. m ≤ −2
Câu 23. Số các giá trị thực của tham số m để phương trình (sin x −1)(2 cos2 x −(2m +1) cos x +m) =
0 có đúng 4 nghiệm thực thuộc đoạn [0; 2π] là A. 1. B. 2. C. 3. D. Vô số.
Câu 24. Giả sử A, B là các điểm lần lượt nằm trên y
các đồ thị hàm số y = sin x và y = cos x sao cho tam √ A Ç å π 2 giác OAB nhận điểm G ; làm trọng tâm. O y = cos x π 3 3 x
Tính diện tích S của tam giác OAB, biết xA ∈ [0; 2π]. B y = sin x Trang 29
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC √ √ √ √ π 3 π 2 π 2 π 3 A. S = . B. S = . C. S = . D. S = . 6 8 6 8
Câu 25. Cho hai điểm A, B thuộc đồ thị hàm số y = sin x y
trên đoạn [0; π], các điểm C, D thuộc trục Ox thỏa mãn A B 2π
ABCD là hình chữ nhật và CD = . Tính độ dài đoạn O π x 3 D C BC. √ √ 2 1 3 y = sin x A. . B. . C. 1. D. . 2 2 2 BÀI TẬP TỰ LUẬN
c Bài 1. Giải phương trình a) 2 sin x − 1 = 0
b) 2 cos2 x − 3 sin x − 3 = 0 √ c) sin x + cos x = 2 cos 5x d) cos 3x + cos x + sin 2x = 0
c Bài 2. Giải phương trình
4 sin4 x + cos4 x − 2 sin2 x − 1
a) 4 sin x cos x − 3 = 3(sin x + cos x) b) = 0 1 − cos 4x —HẾT— Trang 30
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC B ĐỀ SỐ 2
BÀI TẬP TRẮC NGHIỆM
Câu 1. Tìm tập giá trị T của hàm số y = sin 2x. ï 1 1 ò A. T = − ; . B. T = [−2; 2]. C. T = R. D. T = [−1; 1]. 2 2
Câu 2. Tìm tập xác định D của hàm số y = tan 2x. n π o n π o A. D = R\ + kπ, k ∈ Z . B. D = R\ + kπ, k ∈ Z . 2 4 n π kπ o C. D = R\kπ, k ∈ Z . D. D = R\ + , k ∈ Z . 4 2 π
Câu 3. Tìm tập xác định D của hàm số y = cot x − . 3 n π o n π o A. D = R \ + k2π, k ∈ Z . B. D = R \ + kπ, k ∈ Z . 3 3 ß ™ n π o 5π
C. D = R \ − + k2π, k ∈ Z . D. D = R \ + kπ, k ∈ Z . 3 6
Câu 4. Chu kì tuần hoàn T của hàm số y = cos x là bao nhiêu? π A. T = 2π. B. T = π. C. T = 3π. D. T = . 2 sin x
Câu 5. Tìm tập xác định D của hàm số y = . 1 − cos x n π o A. D = R. B. D = R \ + kπ, k ∈ Z . 2
C. D = R \ {kπ, k ∈ Z}.
D. D = R \ {k2π, k ∈ Z}.
Câu 6. Hình nào dưới đây là đồ thị của hàm số y = sin x? y y x O x A. O B. y y O x O x C. D. 2 sin x − 1
Câu 7. Tìm giá trị nhỏ nhất m của hàm số y = . 3 1 2 A. m = − . B. m = − . C. m = −3. D. m = −1. 3 3
Câu 8. Tìm giá trị lớn nhất M của hàm số y = 2 − | cos x|. A. M = 1. B. M = 3. C. M = 0. D. M = 2.
Câu 9. Tìm giá trị lớn nhất M của hàm số y = sin x − cos x. √ A. M = 0. B. M = 1. C. M = 2. D. M = 2. π Câu 10. Hỏi x =
là nghiệm của phương trình nào sau đây? 4 1 A. sin x = 1. B. cos x = 1. C. sin x. cos x = . D. sin 2x = 0. 2 √3
Câu 11. Tìm tập nghiệm S của phương trình sin 2x = − . 2 Trang 31
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC ß π 2π ™ ß π 4π ™ A. S = − + kπ, + kπ, k ∈ Z . B. S = − + k2π, + k2π, k ∈ Z . 6 3 3 3 ß π 5π ™ ß π 5π ™ C. S = + k2π, + k2π, k ∈ Z . D. S = + k2π, + k2π, k ∈ Z . 6 6 12 12 π
Câu 12. Tìm tập nghiệm S của phương trình sin x. cos x − = 0. 4 ß 3π ™ A. S = {kπ, k ∈ Z}. B. S = + kπ, k ∈ Z . 4 ß ™ n π o 3π C. S = − + kπ, k ∈ Z . D. S = kπ; + kπ, k ∈ Z . 4 4 √
Câu 13. Tìm tập nghiệm S của phương trình cos 2x = 2. A. S = R. ß 1 √ 1 √ ™ B. S = − arccos 2 + kπ; arccos 2 + kπ, k ∈ Z . 2 2 C. S = ∅. n π π o D. S = − + k2π; + k2π . 4 4
Câu 14. Tìm tất cả các giá trị của số thực a để phương trình cos x = a2 có nghiệm. A. a ∈ R. B. a ∈ R \ {0}. C. a ∈ [0; 1]. D. a ∈ [−1; 1].
Câu 15. Phương trình tan 2x = 1 có họ nghiệm là π kπ π A. x = + , k ∈ Z. B. x = + kπ, k ∈ Z. 8 2 4 π π C. x = + k2π, k ∈ Z. D. x = + k2π, k ∈ Z. 4 4 √
Câu 16. Họ nghiệm của phương trình cot x + 3 = 0 là π π A. x = − + kπ, k ∈ Z. B. x = − + kπ, k ∈ Z. 3 6 π π C. x = + k2π, k ∈ Z. D. x = + kπ, k ∈ Z. 3 6
Câu 17. Phương trình tan (2x + 12◦) = 0 có họ nghiệm là
A. x = −6◦ + k180◦, k ∈ Z.
B. x = −6◦ + k360◦, k ∈ Z.
C. x = −12◦ + k90◦, k ∈ Z.
D. x = −6◦ + k90◦, k ∈ Z.
Câu 18. Cho phương trình a sin x + cos x = b. Tìm tất cả các giá trị thực của a, b để phương trình có nghiệm. A. b2 − a2 ≤ 1. B. b2 − a2 < 1. C. b2 + a2 ≤ 1. D. b2 + a2 ≥ 1. √
Câu 19. Tìm tập nghiệm của phương trình sin x + 3 cos x = −2. ß 5π ™ A. S = ∅. B. S = − + k2π k ∈ Z . 6 ß ™ n π o 5π C. S = + k2 π k ∈ Z . D. S = − + kπ k ∈ Z . 6 6
Câu 20. Tìm số nghiệm thuộc khoảng (−π; π) của phương trình sin x + sin 2x = 0. A. 3. B. 1. C. 2. D. 4.
Câu 21. Giải phương trình 2 sin2 x + 5 sin x + 3 = 0. π π A. x = − + kπ, k ∈ Z. B. x = − + k3π, k ∈ Z. 2 2 π π kπ C. x = − + k2π, k ∈ Z. D. x = − + , k ∈ Z. 2 2 2
Câu 22. Giải phương trình cos 2x − 5 sin x − 3 = 0. π 7π π 7π A. x = − + kπ, x = + kπ, k ∈ Z. B. x = − + k3π, x = + k3π, k ∈ Z. 6 6 6 6 π 7π π 7π C. x = − + k4π, x = + k4π, k ∈ Z. D. x = − + k2π, x = + k2π, k ∈ Z. 6 6 6 6 Trang 32
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Câu 23. Giải phương trình tan x + 2 cot x − 3 = 0. π π A. x = ± + k2π, k ∈ Z. B. x = ± + kπ, k ∈ Z. 4 4 π π C. x =
+ kπ, x = arctan 2 + kπ, k ∈ Z. D. x = ±
+ kπ, x = ± arctan 2 + kπ, k ∈ Z. 4 4
Câu 24. Tìm tất cả các giá trị thực của tham số m để phương trình m cos x + sin x = 1 − m có nghiệm. A. m ≤ 0. B. m < 0. C. m ≥ 0. D. m < 1.
Câu 25. Có bao nhiêu giá trị nguyên của m để phương trình cos 2x − cos x + m = 0 có nghiệm? A. 4. B. 3. C. 2. D. 1. BÀI TẬP TỰ LUẬN
c Bài 1. Giải các phương trình sau: π a) 2 cos x − = 0; b) sin 3x − cos 3x = −1; 4 √ π c) 3 tan − x = 1;
d) sin x + cos x − sin x cos x = 1. 3
c Bài 2. Tính tổng các nghiệm x ∈ 0; 100 của phương trình
cos3 x − cos2 x + 1 = cos2x+tan2x. cos2 x —HẾT— Trang 33
Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§ 6. ĐÁP ÁN TRẮC NGHIỆM CÁC CHỦ ĐỀ
ĐÁP ÁN TRẮC NGHIỆM BÀI 1 1. A 2. B 3. D 4. A 5. D 6. D 7. C 8. B 9. B 10. C 11. D 12. B 13. C 14. A 15. D 16. A 17. B 18. A 19. A 20. B 21. A 22. A 23. D 24. C 25. A 26. A 27. C 28. C 29. A 30. D
ĐÁP ÁN TRẮC NGHIỆM BÀI 2 1. C 2. A 3. B 4. C 5. D 6. D 7. B 8. A 9. A 10. D 11. D 12. B 13. C 14. C 15. B 16. B 17. C 18. C 19. D 20. D 21. A 22. A 23. D 24. C 25. A 26. B 27. A 28. B
ĐÁP ÁN TRẮC NGHIỆM BÀI 3 1. B 2. B 3. A 4. D 5. B 6. C 7. C 8. C 9. B 10. B 11. A 12. D 13. D 14. D 15. B 16. D 17. D 18. D 19. C 20. C 21. A 22. A 23. A 24. B 25. C 26. C 27. A 28. A 29. C 30. B
ĐÁP ÁN TRẮC NGHIỆM ĐỀ SỐ 1 1. A 2. D 3. C 4. B 5. B 6. D 7. C 8. D 9. B 10. A 11. C 12. B 13. A 14. D 15. A 16. A 17. A 18. D 19. C 20. C 21. D 22. C 23. B 24. B 25. B
ĐÁP ÁN TRẮC NGHIỆM ĐỀ SỐ 2 1. D 2. D 3. B 4. A 5. D 6. D 7. D 8. D 9. D 10. C 11. A 12. D 13. C 14. D 15. A 16. B 17. D 18. A 19. B 20. A 21. C 22. D 23. C 24. C 25. A Trang 34
Document Outline
- HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
- HÀM SỐ LƯỢNG GIÁC
- KIẾN THỨC CẦN NHỚ
- PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
- blackDạng 1. Tìm tập xác định của hàm số lượng giác
- blackDạng 2. Tính chẵn lẻ của hàm số
- blackDạng 3. Tìm giá trị lớn nhất - giá trị nhỏ nhất
- BÀI TẬP TRẮC NGHIỆM
- PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
- KIẾN THỨC CẦN NHỚ
- PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
- blackDạng 1. Giải các phương trình lượng giác cơ bản
- blackDạng 2. Giải các phương trình lượng giác dạng mở rộng
- blackDạng 3. Giải các phương trình lượng giác có điều kiện xác định
- blackDạng 4. Giải các phương trình lượng giác trên khoảng (a;b) cho trước
- BÀI TẬP TRẮC NGHIỆM
- MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP
- KIẾN THỨC CẦN NHỚ
- PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
- blackDạng 1. Giải phương trình bậc nhất đối với một hàm số lượng giác
- blackDạng 2. Giải phương trình bậc hai đối với một hàm số lượng giác
- blackDạng 3. Giải phương trình bậc nhất đối với sinx và cosx
- blackDạng 4. Phương trình đẳng cấp bậc hai đối với sinx và cosx
- blackDạng 5. Phương trình chứa sinx cosx và sinx cosx
- BÀI TẬP TRẮC NGHIỆM
- MỘT SỐ PHƯƠNG PHÁP GIẢI PT LƯỢNG GIÁC
- PHÂN LOẠI, PHƯƠNG PHÁP GIẢI TOÁN
- blackDạng 1. Biến đổi đưa phương trình về dạng phương trình bậc hai (ba) đối với một hàm số lượng giác
- blackDạng 2. Biến đổi asinx + bcosx
- blackDạng 3. Biến đổi đưa về phương trình tích
- blackDạng 4. Một số bài toán biện luận theo tham số
- BÀI TẬP TỰ LUYỆN
- ĐỀ ÔN TẬP CUỐI CHƯƠNG
- Đề số 1
- Đề số 2
- ĐÁP ÁN TRẮC NGHIỆM CÁC CHỦ ĐỀ
- HÀM SỐ LƯỢNG GIÁC




