CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 1. GÓC LƯỢNG GIÁC
1. GÓC LƯỢNG GIÁC
a. Khái niệm góc lượng giác và số đo của góc lượng giác
Trong mặt phẳng cho hai tia
, Oa Ob
. Xét tia
Om
cùng nằm trong mặt phẳng này. Nếu tia
Om
quay quanh gốc
O
, theo một chiều nhất định từ vị trí tia
Oa
và dừng tại vị trí tia
Ob
, thì ta nói
nó quét một góc lượng giác có tia đầu
Oa
, tia cuối
Ob
và kí hiệu là
( )
,.Oa Ob
Góc lượng giác
(
)
,.
Oa Ob
chỉ được xác định khi ta biết được chiều chuyển động quay của tia
Om
từ tia đầu
Oa
đến tia cuối
Ob
. Ta quy ước: chiều quay ngược với chiều quay của kim đồng
hồ là chiều dương, chiều quay cùng với chiều quay của kim đồng hồ là chiều âm.
Khi tia
Om
quay góc
α
thì ta nói góc lượng giác mà tia đó quét nên có số đo
α
. Số đo của góc
lượng giác với tia đầu
Oa
, tia cuối
Ob
được
kí hiệu là
( )
,.sd Oa Ob
α
=
Chú ý: Với hai tia
, Oa Ob
cho trước, có vô số góc lượng giác có tia đầu
Oa
, tia cuối
Ob
.
Ta
dùng chung kí hiệu là
( )
, Ou Ov
cho tất cả các góc lượng giác này.
Nhận xét: Số đo của các góc lượng giác có cùng tia đầu
Oa
và tia cuối
Ob
sai khác nhau một
bội nguyên của
360°
nên có công thức tổng quát là:
(
) ( )
, .360 sd Oa Ob k k
α
= °+ ° ∈
thường
viết là
( )
, .360Oa Ob k
α
= °+ °
b. Hệ thức Chasles: với 3 tia
, , Oa Ob Oc
bất kì ta có:
(
) ( ) ( )
( )
, , , .360 Oa Ob Ob Oc Oa Oc k k+ = + °∈
2. ĐƠN VỊ RADIAN
Trên một đường tròn bán kính
R
tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng bán kính
được gọi là một góc có số đo bằng
1 radian
( đọc là ra-di-an, viết tắt là
1 rad
)
Quan hệ giữa độ và radian
1 rad rad
180 180
a
a
ππ
°= ⇒ °=
và
180 .180
1rad rad
α
α
ππ
°°
= ⇒=
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUY
Ế
T.
I
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
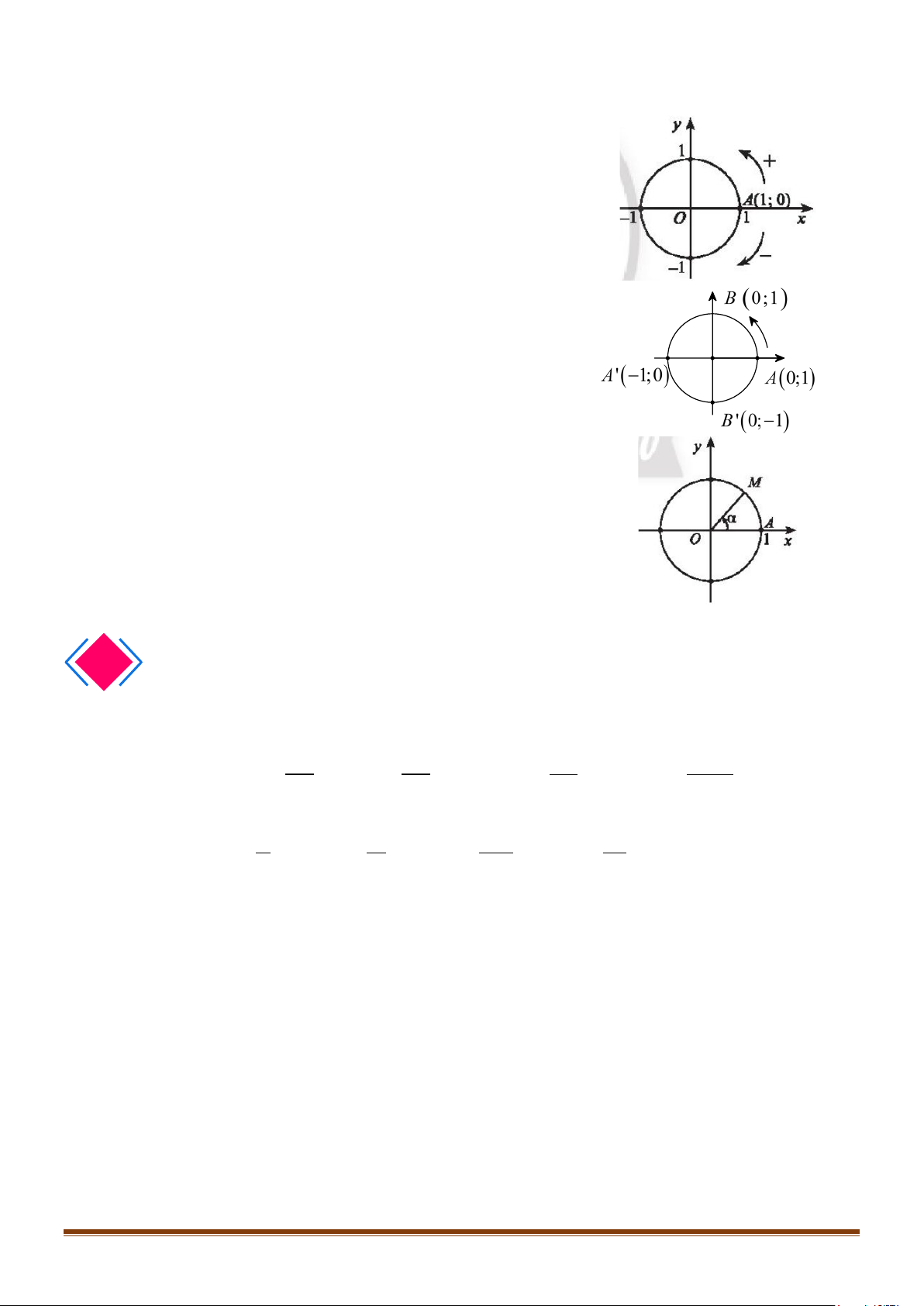
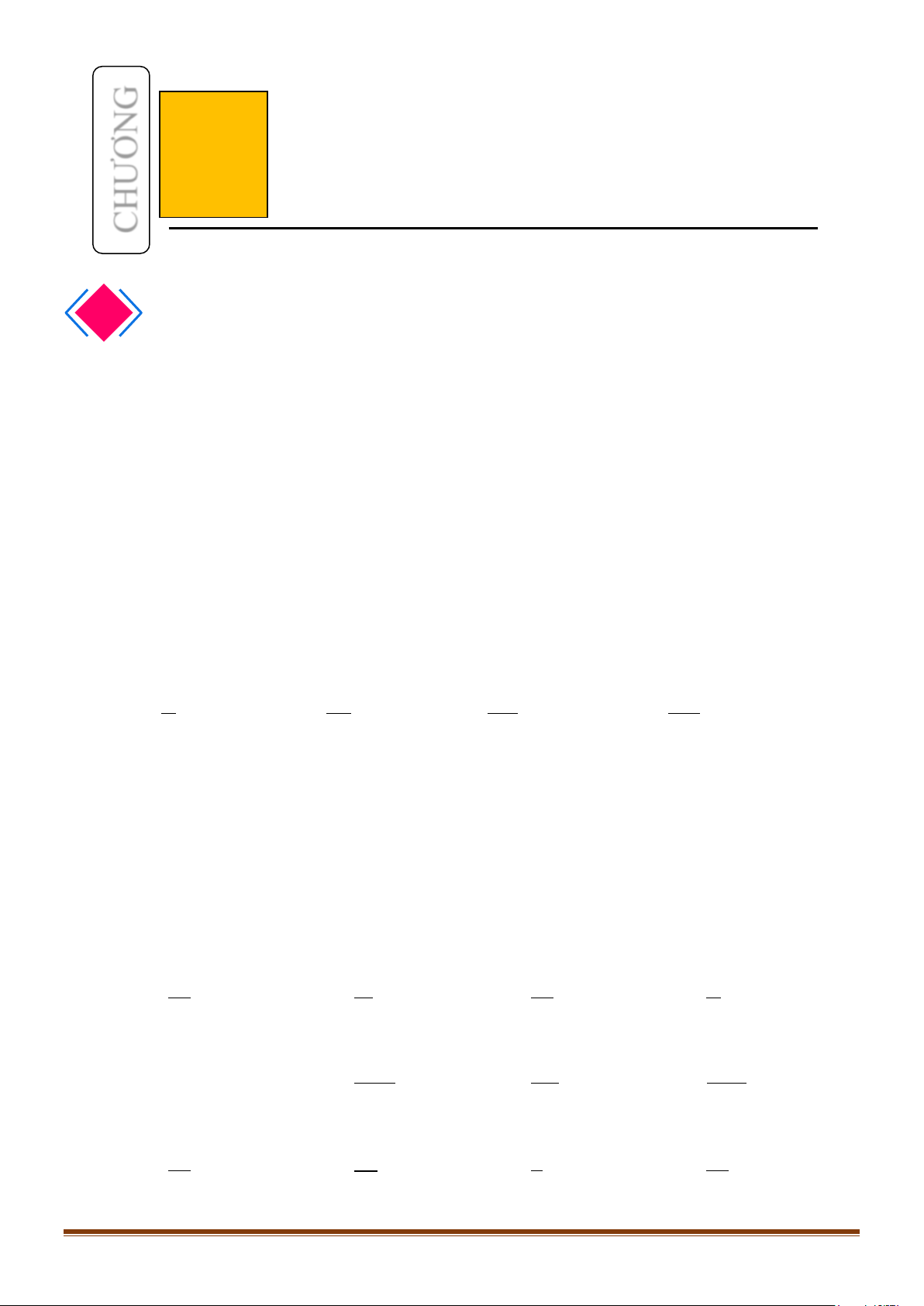
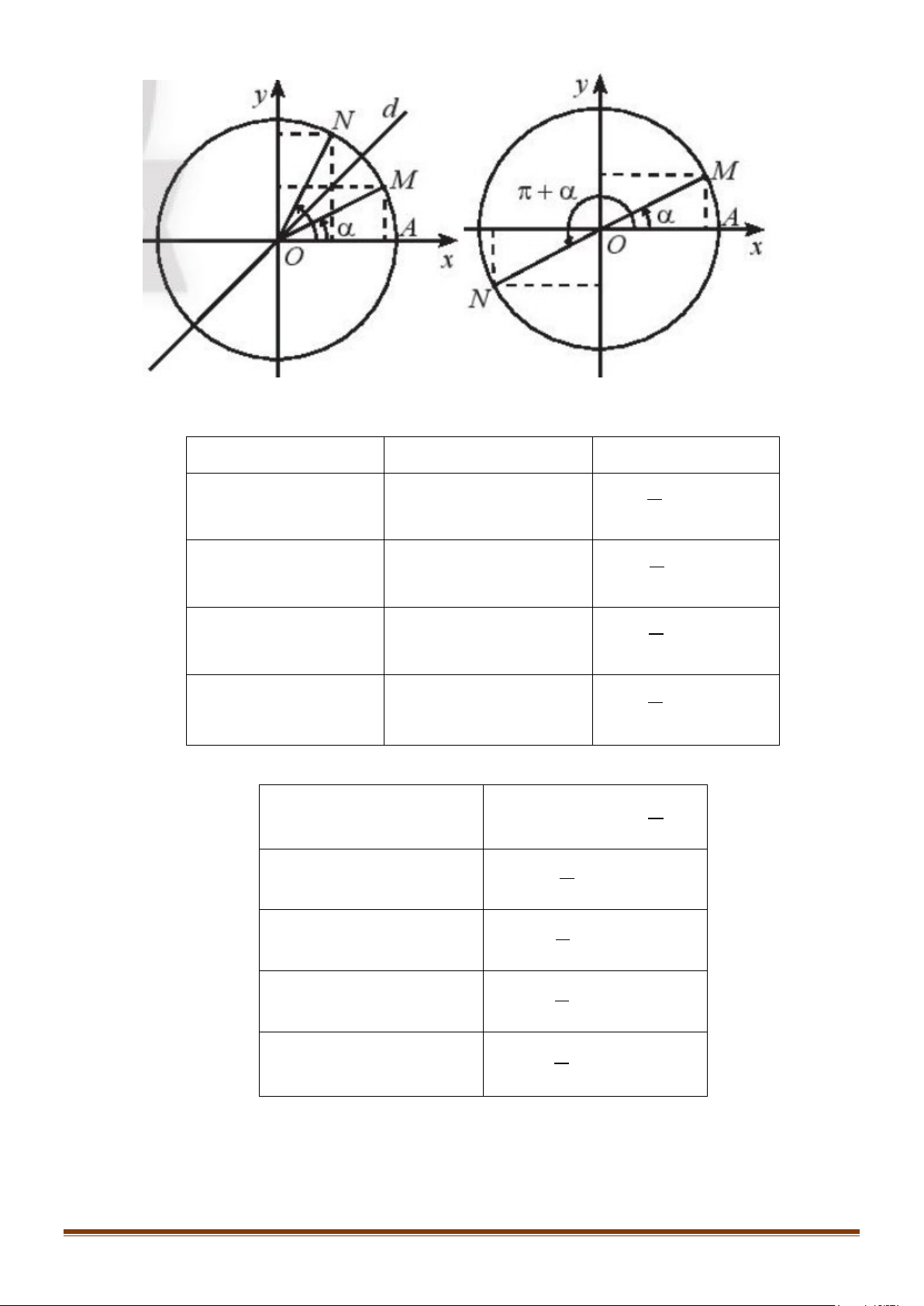
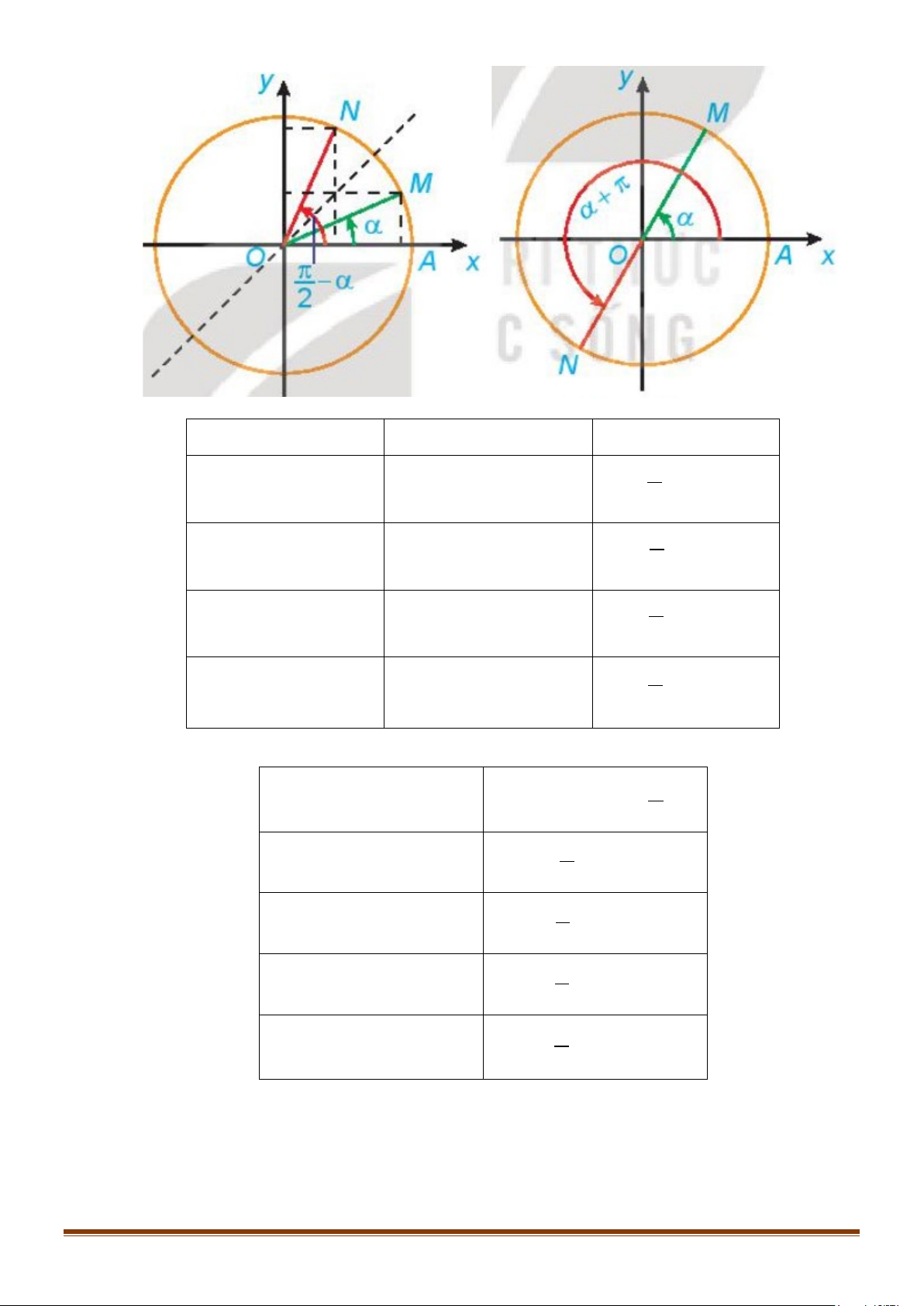
3. ĐƯỜNG TRÒN LƯỢNG GIÁC
Trên mặt phẳng tọa độ
Oxy
, cho đường tròn tâm
O
bán
kính bằng 1. TRên đường tròn này, chọn điểm
( )
1; 0A
làm
gốc, chiều dương là chiều ngược với chiều kim đồng hồ và
chiều âm là chiều cùng chiều kim đồng hồ. Đường tròn cùng
với gốc và chiều như trên được gọi là đường tròn lượng
giác.
Đường tròn này cắt hai trục tọa độ tại bốn điểm
(
)
1; 0A
( )
' 1; 0 ,A −
( )
0;1 ,
B
( )
' 0; 1 .B −
Cho số đo góc
α
bất kì. Trên đường tròn lượng giác ta xác
định được duy nhất một điểm
M
sao cho số đo góc lượng
giác
( )
, .
OA OM
α
=
Khi đó điểm
M
được gọi là điểm biểu
diễn của góc có số đo
α
trên đường tròn lượng giác.
DẠNG: ĐỔI ĐƠN VỊ ĐO
1 rad rad
180 180
a
a
ππ
°= ⇒ °=
và
180 .180
1rad rad
α
α
ππ
°°
= ⇒=
Câu 1. Đổi số đo radian sang số đo độ
a)
()rad
π
b)
()
3
rad
π
c)
()
10
rad
π
d)
22
()
3
rad
π
e)
5
()
9
rad
π
−
.
Câu 2. Đổi số đo độ của cung tròn sang radian
a)
170°
b)
1000°
c)
3100°
d)
90
−°
e)
240−°
Câu 3. Trên đồng hồ tại thời điểm đang xét kim giờ OG chỉ số 3, kim phút OP chỉ số 12. Đến khi kim phút
và kim giờ gặp nhau lần đầu tiên, tính số đo góc lượng giác mà kim phút quét được
+
O
HỆ THỐNG BÀI TẬP TỰ LUẬN
.
II
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 1. GÓC LƯỢNG GIÁC
1. GÓC LƯỢNG GIÁC
a. Khái niệm góc lượng giác và số đo của góc lượng giác
Trong mặt phẳng cho hai tia
, Oa Ob
. Xét tia
Om
cùng nằm trong mặt phẳng này. Nếu tia
Om
quay quanh gốc
O
, theo một chiều nhất định từ vị trí tia
Oa
và dừng tại vị trí tia
Ob
, thì ta nói
nó quét một góc lượng giác có tia đầu
Oa
, tia cuối
Ob
và kí hiệu là
( )
,.Oa Ob
Góc lượng giác
(
)
,.
Oa Ob
chỉ được xác định khi ta biết được chiều chuyển động quay của tia
Om
từ tia đầu
Oa
đến tia cuối
Ob
. Ta quy ước: chiều quay ngược với chiều quay của kim đồng
hồ là chiều dương, chiều quay cùng với chiều quay của kim đồng hồ là chiều âm.
Khi tia
Om
quay góc
α
thì ta nói góc lượng giác mà tia đó quét nên có số đo
α
. Số đo của góc
lượng giác với tia đầu
Oa
, tia cuối
Ob
được
kí hiệu là
( )
,.sd Oa Ob
α
=
Chú ý: Với hai tia
, Oa Ob
cho trước, có vô số góc lượng giác có tia đầu
Oa
, tia cuối
Ob
.
Ta
dùng chung kí hiệu là
( )
, Ou Ov
cho tất cả các góc lượng giác này.
Nhận xét: Số đo của các góc lượng giác có cùng tia đầu
Oa
và tia cuối
Ob
sai khác nhau một
bội nguyên của
360°
nên có công thức tổng quát là:
(
) ( )
, .360 sd Oa Ob k k
α
= °+ ° ∈
thường
viết là
( )
, .360Oa Ob k
α
= °+ °
b. Hệ thức Chasles: với 3 tia
, , Oa Ob Oc
bất kì ta có:
(
) ( ) ( )
( )
, , , .360 Oa Ob Ob Oc Oa Oc k k+ = + °∈
2. ĐƠN VỊ RADIAN
Trên một đường tròn bán kính
R
tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng bán kính
được gọi là một góc có số đo bằng
1 radian
( đọc là ra-di-an, viết tắt là
1 rad
)
Quan hệ giữa độ và radian
1 rad rad
180 180
a
a
ππ
°= ⇒ °=
và
180 .180
1rad rad
α
α
ππ
°°
= ⇒=
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUY
Ế
T.
I
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
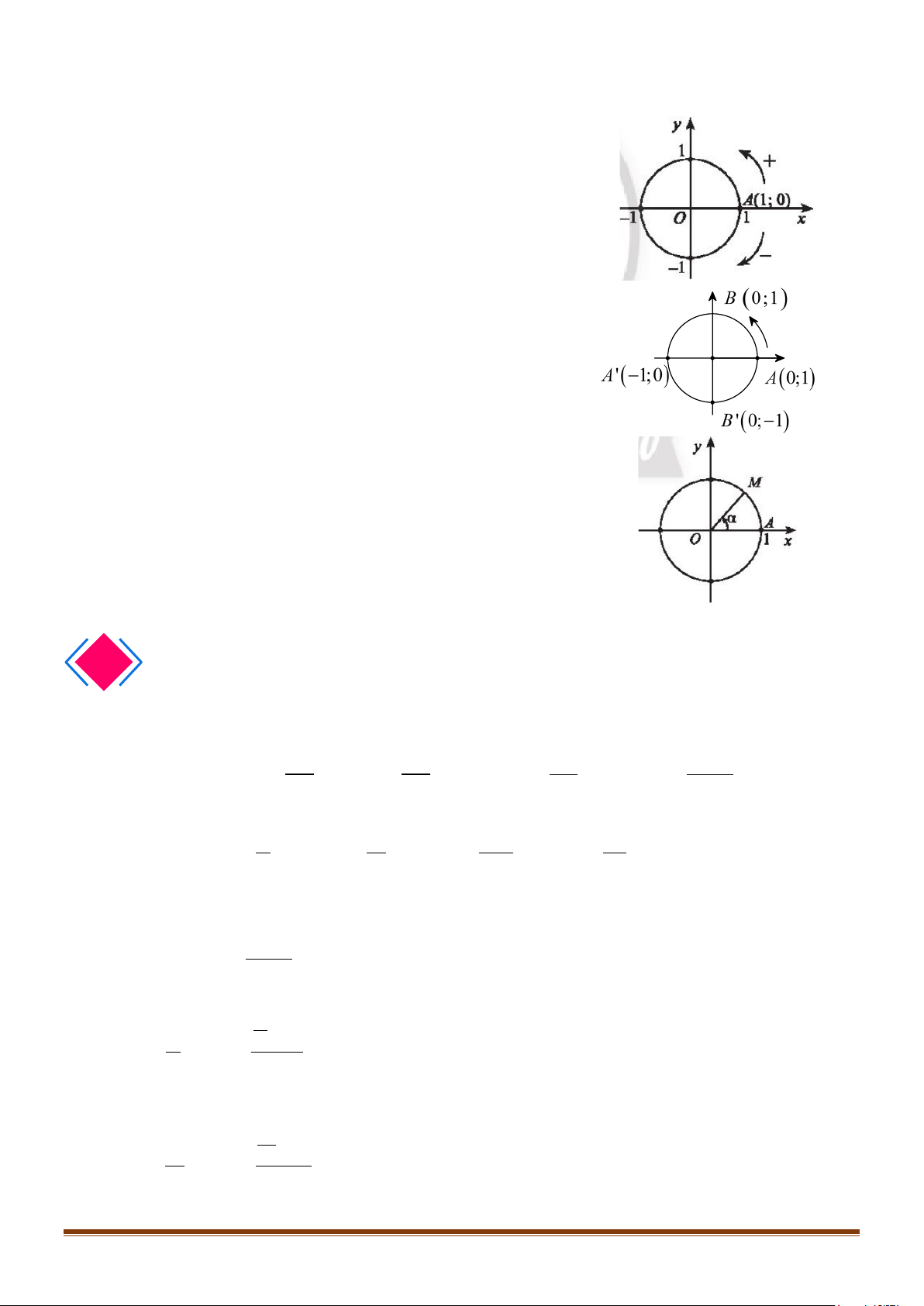
3. ĐƯỜNG TRÒN LƯỢNG GIÁC
Trên mặt phẳng tọa độ
Oxy
, cho đường tròn tâm
O
bán
kính bằng 1. TRên đường tròn này, chọn điểm
( )
1; 0A
làm
gốc, chiều dương là chiều ngược với chiều kim đồng hồ và
chiều âm là chiều cùng chiều kim đồng hồ. Đường tròn cùng
với gốc và chiều như trên được gọi là đường tròn lượng
giác.
Đường tròn này cắt hai trục tọa độ tại bốn điểm
(
)
1; 0A
( )
' 1; 0 ,A −
( )
0;1 ,
B
( )
' 0; 1 .B −
Cho số đo góc
α
bất kì. Trên đường tròn lượng giác ta xác
định được duy nhất một điểm
M
sao cho số đo góc lượng
giác
( )
, .
OA OM
α
=
Khi đó điểm
M
được gọi là điểm biểu
diễn của góc có số đo
α
trên đường tròn lượng giác.
DẠNG: ĐỔI ĐƠN VỊ ĐO
1 rad rad
180 180
a
a
ππ
°= ⇒ °=
và
180 .180
1rad rad
α
α
ππ
°°
= ⇒=
Câu 1. Đổi số đo radian sang số đo độ
a)
()rad
π
b)
()
3
rad
π
c)
()
10
rad
π
d)
22
()
3
rad
π
e)
5
()
9
rad
π
−
.
a)
.180
( ) 180rad
π
π
π
°
= = °
b)
.180
3
( ) 60
3
rad
π
π
π
°
= = °
c)
.180
10
( ) 18
10
rad
π
π
π
°
= = °
+
O
HỆ THỐNG BÀI TẬP TỰ LUẬN
.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
d)
22
.180
22
3
( ) 1320
3
rad
π
π
π
°
= = °
e)
5
.180
5
9
( ) 100
9
rad
π
π
π
°
−
− = =−°
.
Câu 2. Đổi số đo độ của cung tròn sang radian
a)
170°
b)
1000°
c)
3100°
d)
90−°
e)
240
−°
a)
.170 17
170 rad ( )
180 18
rad
ππ
°= =
b)
.1000 50
1000 rad ( )
180 9
rad
ππ
°= =
c)
.3100 155
3100 rad ( )
180 9
rad
ππ
°= =
d)
( )
90
90 rad ( )
180 2
rad
π
π
−
− °= =−
e)
( )
240
4
240 rad ( )
180 3
rad
π
π
−
− °= =−
Câu 3. Trên đồng hồ tại thời điểm đang xét kim giờ OG chỉ số 3, kim phút OP chỉ số 12. Đến khi kim phút
và kim giờ gặp nhau lần đầu tiên, tính số đo góc lượng giác mà kim phút quét được
Khi kim phút chỉ số 12, kim giờ chỉ số 3 thì sđ
(,)OG OP
là
2
2
k
π
π
+
Trong 1 giờ, kim phút quét được một góc lượng giác
2
π
−
, kim giờ quét được góc
6
π
−
Thời gian từ lúc 3h đến lúc hai kim trùng nhau lần đầu tiên là
3
:2
2 6 11
ππ
π
− −− =
(giờ)
Kim phút đã quét được một góc có số đo là
36
2.
11 11
π
π
−
−=
Vậy số đo góc lượng giác mà kim phút quét được là
6
2
11
k
π
π
−
+
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
BÀI 1. GÓC LƯỢNG GIÁC
DẠNG 1. CÂU HỎI LÝ THUYẾT
Câu 1: Trong hệ trục tọa độ
Oxy
, cho là hai điểm
M
và
N
thuộc đường tròn lượng giác. Hai góc lượng
giác
( )
,Ox OM
và
( )
,Ox ON
lệch nhau
0
180
. Chọn nhận xét đúng
A.
,
MN
có tung độ và hoành độ đều bằng nhau.
B.
,MN
có tung độ và hoành độ đều đối nhau.
C.
,MN
có tung độ bằng nhau và hoành độ đối nhau.
D.
,MN
có hoành độ bằng nhau và tung độ đối nhau.
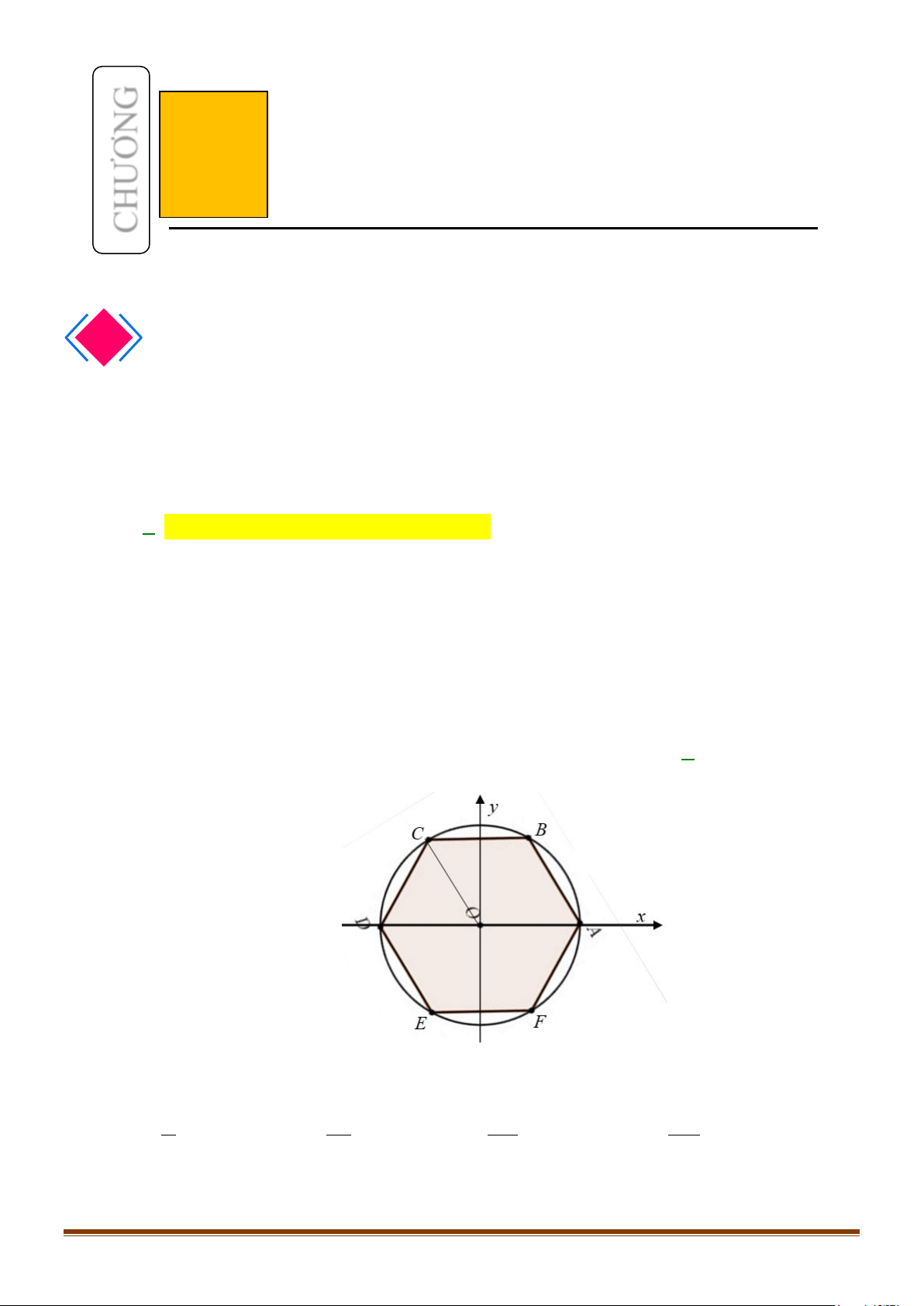
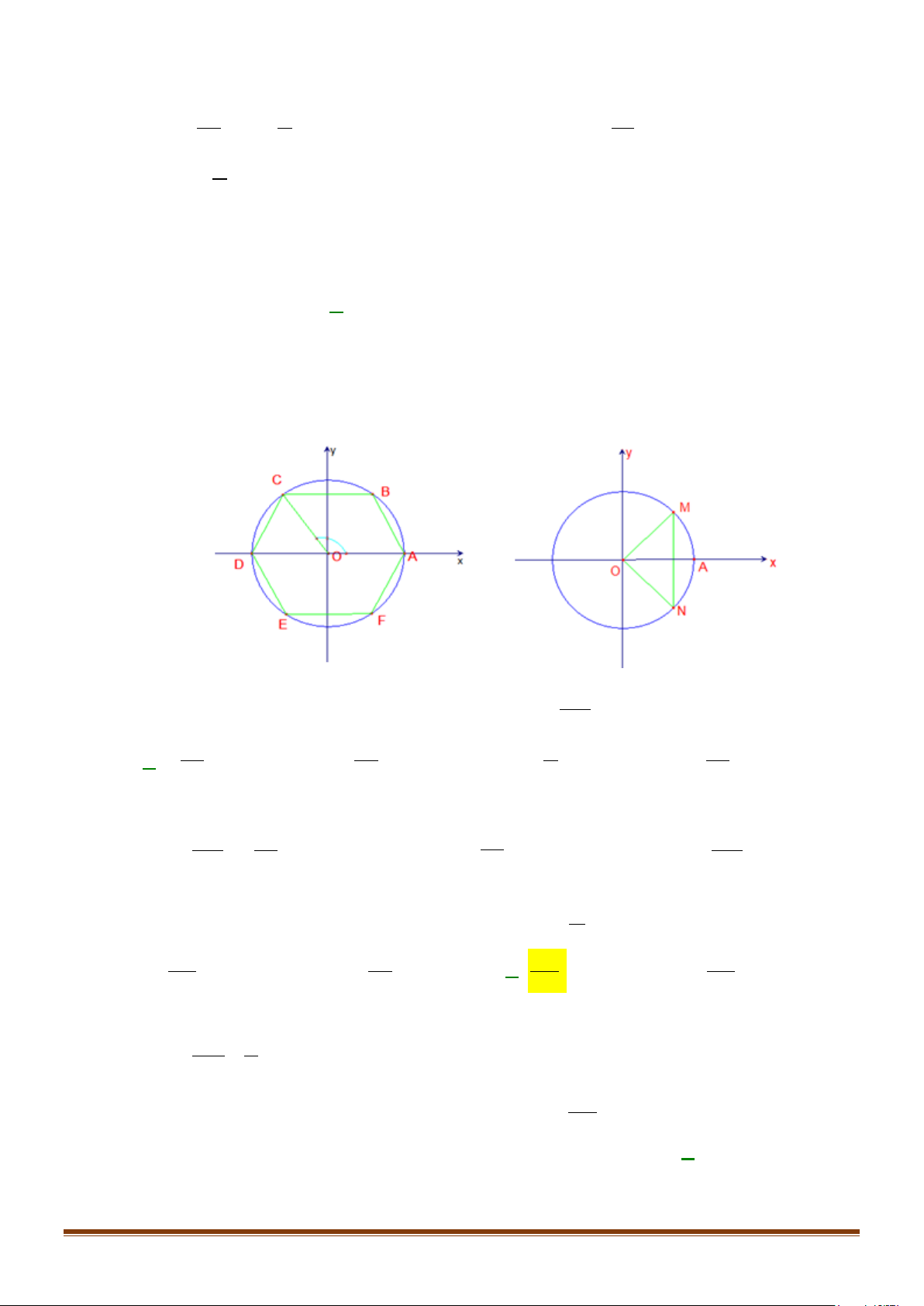
Câu 2: Cho lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo thứ tự
đó và các điểm
,BC
có tung độ dương. Khi đó góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng
A.
240 360 ,k
k°+ ° ∈
. B.
120°
. C.
240−°
. D.
120 360 ,k
k°+ ° ∈
.
Câu 3: Trên đường tròn lượng giác gốc
(1; 0)A
, cho các cung có số đo:
I.
.
4
π
II.
7
.
4
−
π
III.
13
.
4
π
IV.
71
.
4
−
π
Hỏi các cung nào có điểm cuối trùng nhau?
A. Chỉ I, II và IV. B. Chỉ I, II và III. C. Chỉ II, III và IV. D. Chỉ I và II.
Câu 4: Trên đường tròn định hướng gốc
(
)
1; 0
A
có bao nhiêu điểm
M
thỏa mãn
( )
; 30 45OA OM k= °+ °
,
k ∈
?
A.
10
. B.
6
. C.
4
. D.
8
.
DẠNG 2. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ
Câu 5: Góc có số đo
108
đổi ra rađian là:
A.
3
5
π
. B.
10
π
. C.
3
2
π
. D.
4
π
.
Câu 6: Nếu một cung tròn có số đo là
°a
thì số đo radian của nó là:
A.
180 a
π
. B.
180
a
π
. C.
180
a
π
. D.
180a
π
.
Câu 7: Cho góc có số đo
405
, khi đổi góc này sang đơn vị rađian ta được
A.
8
9
. B.
9
4
. C.
9
4
. D.
9
8
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Câu 8: Đổi số đo của góc
10 rad
sang đơn vị độ, phút, giây ta được
A.
572 57 28
′
°
. B.
1800
°
. C.
18
π
. D.
527 57 28
′
°
.
Câu 9: Góc có số đo
7
4
π
−
thì góc đó có số đo là
A.
o
315−
. B.
o
630
−
. C.
o
1 45
′
−
. D.
o
135−
.
Câu 10: Số đo theo đơn vị rađian của góc
405°
là:
A.
9
.
4
π
B.
7
.
4
π
C.
5
.
4
π
D.
4
.
7
π
Câu 11: Góc
0
70
có số đo bằng radian là:
A.
18
7
π
. B.
7
18
π
. C.
9
7
π
. D.
7
9
π
.
Câu 12: Góc có số đo
120°
đổi sang radian là
A.
3
2
π
. B.
2
3
π
. C.
4
π
. D.
10
π
.
Câu 13: Số đo theo đơn vị rađian của góc
315°
là
A.
7
2
π
. B.
7
4
π
. C.
2
7
π
. D.
4
7
π
.
Câu 14: Cung tròn có số đo là
5
4
π
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.
A.
5°
. B.
15
°
. C.
172°
. D.
225°
.
Câu 15: Cung tròn có số đo là
π
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.
A.
30°
. B.
45°
. C.
90°
. D.
180°
.
Câu 16: Góc
63 48
′
°
bằng
A.
1,113rad
. B.
1,108rad
. C.
1,107 rad
. D.
1,114 rad
.
Câu 17: Góc có số đo
2
5
π
đổi sang độ là:
A.
135 .°
B.
72 .°
C.
270 .°
D.
240 .°
Câu 18: Góc có số đo
108°
đổi ra rađian là:
A.
3
5
π
. B.
10
π
. C.
3
2
π
. D.
4
π
.
Câu 19: Góc có số đo
9
π
đổi sang độ là:
A.
25 .
°
B.
15 .°
C.
18 .
°
D.
20 .°
Câu 20: Cho
2
2
ak
π
π
= +
. Tìm
k
để
10 11
a
ππ
<<
A.
7k =
. B.
5k =
. C.
4k =
. D.
6k
=
.
Câu 21: Một bánh xe có
72
răng. Số đo góc mà bánh xe đã quay được khi di chuyển
10
răng là:
A.
0
60
. B.
0
30
. C.
0
40
. D.
0
50
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
Câu 22: Đổi số đo góc
0
105
sang rađian.
A.
7
12
π
. B.
9
12
π
. C.
5
8
π
. D.
5
12
π
.
Câu 23: Số đo góc
22 30
′
°
đổi sang rađian là:
A.
5
π
. B.
8
π
. C.
7
12
π
. D.
6
π
.
Câu 24: Một cung tròn có số đo là
45
°
. Hãy chọn số đo radian của cung tròn đó trong các cung tròn sau
đây.
A.
2
π
B.
π
C.
4
π
D.
3
π
Câu 25: Góc có số đo
24
π
đổi sang độ là:
A.
7
.°
B.
7 30 .
′
°
C.
8 .°
D.
8 30 .
′
°
Câu 26: Góc có số đo
120°
đổi sang rađian là:
A.
2
3
π
. B.
3
2
π
. C.
4
π
. D.
10
π
.
DẠNG 3. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN
Câu 27: Trên đường tròn lượng giác
Số đo của góc lượng giác
( )
,OA OB
′
là
A.
4
π
−
. B.
2
π
−
. C.
4
π
. D.
2
π
.
Câu 28: Trên đường tròn lượng giác, góc có số đo
( )
42
k
k
ππ
+∈
được biểu diễn bởi bao nhiêu điểm?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 29: Góc lượng giác nào sau đây có cùng điểm cuối với góc
7
4
π
?
A.
4
π
−
. B.
4
π
. C.
3
4
π
. D.
3
4
π
−
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
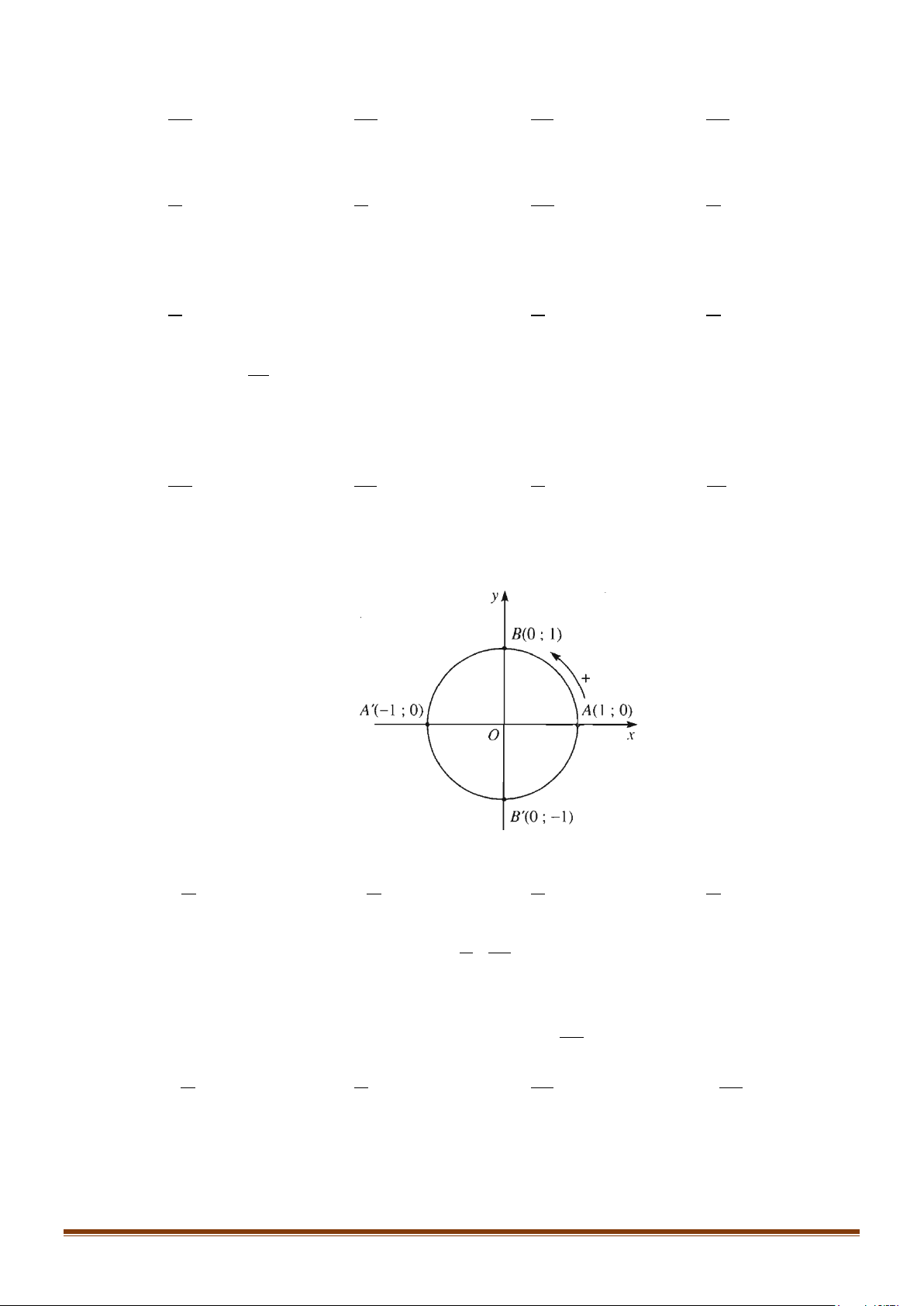
Câu 30: Cho đường tròn lượng giác gốc
A
như hình vẽ.
Điểm biểu diễn của điểm cuối góc lượng giác có số đo
5
2
π
là điểm nào trong các điểm sau?
A. Điểm
E
. B. Điểm
F
. C. Điểm
B
. D. Điểm
B
′
.
Câu 31: Lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo thứ tự đó
và các điểm
B
,
C
có tung độ dương. Khi đó góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng
A.
240 360 ,kk+∈
. B.
120
.
C.
240−
. D.
120 360 ,kk+∈
.
Câu 32: Góc lượng giác nào sau đây có cùng điểm cuối với góc
13
4
π
?
A.
3
4
π
−
. B.
3
4
π
. C.
4
π
−
. D.
3
2
π
.
Câu 33: Khi biểu diễn trên đường tròn lượng giác góc lượng giác nào trong các góc lượng giác có số đo
dưới đây có cùng điểm cuối với góc lượng giác có số đo
4
π
?
A.
10
3
π
. B.
5
4
π
−
. C.
25
4
π
. D.
7
4
π
.
Câu 34: Trên đường tròn lượng giác, điểm cuối của góc có số đo
26
3
π
nằm ở góc phần tư thứ mấy?
A.
IV
. B.
III
. C.
I
. D.
II
.
Câu 35: Trên đường tròn lượng giác gốc
A
, cho góc lượng giác
( )
;OA OM
có số đo
( )
4
2
3
kk
π
απ
=+∈
. Điểm cuối
M
nằm ở góc phần tư nào trong các phần tư sau?
A. thứ tư
( )
IV
. B. thứ hai
( )
II
. C. thứ ba
( )
III
. D. thứ nhất
( )
I
.
Câu 36: Trên đường tròn lượng giác gốc
A
, biết gốc lương giác
( )
,OA OM
có số đo bằng
0
4100
, điểm
M
nằm ở gốc phần tư thứ mấy?
A.
I
. B.
IV
. C.
III
. D.
II
.
Câu 37: Trên đường tròn lượng giác, có bao nhiêu điểm
M
thỏa mãn
; 30 45 ,OA OM k k
?
A.
6
. B.
4
. C.
8
. D.
10
.
Câu 38: Trên đường tròn lượng giác góc
A
, biết góc lượng giác
( )
,OA OM
có số đo
4100
, điểm
M
nằm
ở góc phần tư thứ mấy?
A.
I
. B.
IV
. C.
III
. D.
II
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
Câu 39: Trên đường tròn lượng giác gốc
A
, cho cung lượng giác
AM
có số đo là
( )
4
2
3
kk
π
απ
=+∈
. Điểm cuối
M
nằm ở góc phần tư:
A. thứ tư
( )
IV
. B. thứ hai
(
)
II
. C. thứ ba
( )
III
. D. thứ nhất
( )
I
.
Câu 40: Trên đường tròn lượng giác gốc
A
, có bao nhiêu điểm M thỏa mãn số đo góc lượng giác
( )
;OA OM
bằng
65
k
ππ
+
, với
k
là số nguyên.
A.
12
. B.
10
. C. 5. D. 6.
Câu 41: Trong hệ trục tọa độ
Oxy
, cho
M
là điểm nằm trên đường tròn lượng giác. Điểm
M
có tung độ
và hoành độ đều âm, góc
(
)
,Ox OM
có thể là:
A.
90−°
. B.
200°
. C.
60−°
. D.
180
−°
.
Câu 42: Trên đường tròn lượng giác gốc
A
, biết góc lượng giác
( )
,OA OM
có số đo bằng
0
410
, điểm
M
nằm ở góc phần tư thứ mấy?
A.
II
. B.
IV
. C.
I
. D.
III
.
Câu 43: Cho góc lượng giác có số đo
( )
59
,
2
Ox Oy
π
= −
. Khi đó hai tia
Ox
,
Oy
.
A. Tạo với nhau một góc
3
4
π
. B. Vuông góc.
C. Trùng nhau. D. Đối nhau.
Câu 44: Cho góc lượng giác
( )
,OA OB
có số đo bằng
3
π
. Trong các số sau, số nào là số đo của một góc
lượng giác có cùng tia đầu
OA
và tia cuối
OB
?
A.
5
3
π
. B.
11
3
π
−
. C.
10
3
π
. D.
3
π
−
.
Câu 45: Cho hai góc lượng giác có sđ
( )
5
, 2,
2
Ox Ou m m
π
π
=−+ ∈
và sđ
(
)
, 2, .
2
Ox Ov n n
π
π
=−+ ∈
Khẳng định nào sau đây đúng?
A.
Ou
và
Ov
trùng nhau. B.
Ou
và
Ov
đối nhau.
C.
Ou
và
Ov
vuông góc. D. Tạo với nhau một góc
4
π
.
Câu 46: Trên đường tròn lượng giác gốc
A
cho các góc lượng giác có số đo:
I.
4
π
. II.
7
4
π
−
. III.
13
4
π
. IV.
71
4
π
−
.
Hỏi các góc lượng giác nào có điểm cuối trùng nhau?
A. Chỉ I, II và IV. B. Chỉ II, III và IV. C. Chỉ I, II và III. D. Chỉ I và II.
Câu 47: Cho hai góc lượng giác có sđ
( )
oo
, 45 360 ,Ox Ou m m=+∈
và sđ
(
)
oo
, 135 360 ,Ox Ov n n=−+ ∈
. Ta có hai tia
Ou
và
Ov
A. Tạo với nhau góc
o
45
. B. Trùng nhau.
C. Đối nhau. D. Vuông góc.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 1. GÓC LƯỢNG GIÁC
DẠNG 1. CÂU HỎI LÝ THUYẾT
Câu 1: Trong hệ trục tọa độ
Oxy
, cho là hai điểm
M
và
N
thuộc đường tròn lượng giác. Hai góc lượng
giác
(
)
,Ox OM
và
( )
,Ox ON
lệch nhau
0
180
. Chọn nhận xét đúng
A.
,MN
có tung độ và hoành độ đều bằng nhau.
B.
,MN
có tung độ và hoành độ đều đối nhau.
C.
,MN
có tung độ bằng nhau và hoành độ đối nhau.
D.
,
MN
có hoành độ bằng nhau và tung độ đối nhau.
Lời giải
Vì hai góc lượng giác
( )
,
Ox OM
và
(
)
,Ox ON
lệch nhau
0
180
nên
M
và
N
đối xứng với nhau
qua gốc tọa độ
O
nên có tung độ và hoành độ đều đối nhau.
Câu 2: Cho lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo thứ tự
đó và các điểm
,BC
có tung độ dương. Khi đó góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng
A.
240 360 , kk
°+ ° ∈
. B.
120°
. C.
240−°
. D.
120 360 , kk
°+ ° ∈
.
Lời giải
Theo giả thiết ta có hình vẽ như trên. Khi đó
( )
, 120 360 ,OA OC k k= °+ ° ∈
.
Câu 3: Trên đường tròn lượng giác gốc
(1; 0)A
, cho các cung có số đo:
I.
.
4
π
II.
7
.
4
−
π
III.
13
.
4
π
IV.
71
.
4
−
π
Hỏi các cung nào có điểm cuối trùng nhau?
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
A. Chỉ I, II và IV. B. Chỉ I, II và III. C. Chỉ II, III và IV. D. Chỉ I và II.
Lời giải.
Xét: II.
78
2.
4 44 4
− =− +=−+
π ππ π
π
trùng với điểm
.
4
π
III.
13 12
3.
4 44 4
= += +
π ππ π
π
IV.
71 72
8.
4 44 4
− =− +=−+
π ππ π
π
trùng với điểm
.
4
π
Vậy Chỉ I, II và IV có điểm cuối trùng nhau.
Câu 4: Trên đường tròn định hướng gốc
( )
1; 0A
có bao nhiêu điểm
M
thỏa mãn
( )
; 30 45OA OM k= °+ °
,
k ∈
?
A.
10
. B.
6
. C.
4
. D.
8
.
Lời giải
Vẽ đường tròn lượng giác và biểu diễn các góc có số đo
30 45k°+ °
, trong khoảng từ
0°
đến
360°
. Có
8
điểm
M
biểu diễn.
DẠNG 2. MỐI LIÊN HỆ GIỮA RADIAN VÀ ĐỘ
Câu 5: Góc có số đo
108
đổi ra rađian là:
A.
3
5
π
. B.
10
π
. C.
3
2
π
. D.
4
π
.
Lời giải
Ta có:
108 . 3
108 .
180 5
ππ
= =
Câu 6: Nếu một cung tròn có số đo là
°a
thì số đo radian của nó là:
A.
180 a
π
. B.
180
a
π
. C.
180
a
π
. D.
180a
π
.
Lời giải
Số đo radian của một cung tròn có số đo
°a
là
180
π
a
.
x
y
A
M
30
°
O

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
Câu 7: Cho góc có số đo
405
, khi đổi góc này sang đơn vị rađian ta được
A.
8
9
. B.
9
4
. C.
9
4
. D.
9
8
.
Lời giải
Khi đổi góc
405
sang đơn vị rađian ta được
ππ
9
405
180 4
.
Câu 8: Đổi số đo của góc
10 rad
sang đơn vị độ, phút, giây ta được
A.
572 57 28
′
°
. B.
1800°
. C.
18
π
. D.
527 57 28
′
°
.
Lời giải
Tính được:
10
10rad .180 572 57 28
π
′
= °°
.
Câu 9: Góc có số đo
7
4
π
−
thì góc đó có số đo là
A.
o
315−
. B.
o
630
−
. C.
o
1 45
′
−
. D.
o
135−
.
Lời giải
Góc có số đo
7
4
π
−
thì góc đó có số đo là:
o
o
7.180
315
4
−
= −
.
Câu 10: Số đo theo đơn vị rađian của góc
405
°
là:
A.
9
.
4
π
B.
7
.
4
π
C.
5
.
4
π
D.
4
.
7
π
Lời giải
Ta có:
405 9
.
108 4
°
=
°
Vậy
405°
tương ứng với
9
( ).
4
rad
π
Câu 11: Góc
0
70
có số đo bằng radian là:
A.
18
7
π
. B.
7
18
π
. C.
9
7
π
. D.
7
9
π
.
Lời giải
Góc
0
a
có số đo bằng radian là
.
180
a
π
Suy ra góc
0
70
có số đo bằng radian là
( )
.70 7
180 18
rad
ππ
=
Câu 12: Góc có số đo
120°
đổi sang radian là
A.
3
2
π
. B.
2
3
π
. C.
4
π
. D.
10
π
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Ta có
120°
đổi sang radian là:
2
120
180 3
ππ
⋅=
ra D.
Câu 13: Số đo theo đơn vị rađian của góc
315°
là
A.
7
2
π
. B.
7
4
π
. C.
2
7
π
. D.
4
7
π
.
Lời giải
Ta có
315 7
315 .
180 4
π
π
°= =
.
Câu 14: Cung tròn có số đo là
5
4
π
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.
A.
5°
. B.
15
°
. C.
172°
. D.
225°
.
Lời giải
Ta có:
5
4
.180 .180 225a
π
α
ππ
°= °= °= °
.
Câu 15: Cung tròn có số đo là
π
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây.
A.
30°
. B.
45°
. C.
90°
. D.
180°
.
Lời giải
Ta có:
.180 180a
α
π
°= °= °
.
Câu 16: Góc
63 48
′
°
bằng
A.
1,113rad
. B.
1,108rad
. C.
1,107 rad
. D.
1,114 rad
.
Lời giải
Ta có
0
63,8 3,1416
63 48 63,8 1,114
180
rad
°×
′
° = °= ≈
Câu 17: Góc có số đo
2
5
π
đổi sang độ là:
A.
135 .°
B.
72 .°
C.
270 .°
D.
240 .°
Lời giải
Ta có:
2 2.180
72 .
55
π
=
°
°=
Câu 18: Góc có số đo
108°
đổi ra rađian là:
A.
3
5
π
. B.
10
π
. C.
3
2
π
. D.
4
π
.
Lời giải
Chọn A
Ta có:
108. 3
108 .
180 5
ππ
=° =

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
Câu 19: Góc có số đo
9
π
đổi sang độ là:
A.
25 .°
B.
15 .°
C.
18 .
°
D.
20
.
°
Lời giải
Ta có:
180
20 .
99
π
= =
°
°
Câu 20: Cho
2
2
ak
π
π
= +
. Tìm
k
để
10 11a
ππ
<<
A.
7k =
. B.
5k =
. C.
4k =
. D.
6
k =
.
Lời giải
+ Để
10 11a
ππ
<<
thì
19 21
25
22
kk
ππ
π
< < ⇒=
Câu 21: Một bánh xe có
72
răng. Số đo góc mà bánh xe đã quay được khi di chuyển
10
răng là:
A.
0
60
. B.
0
30
. C.
0
40
. D.
0
50
.
Lời giải
+ 1 bánh răng tương ứng với
0
0
360
5
72
=
10⇒
bánh răng là
0
50
.
Câu 22: Đổi số đo góc
0
105
sang rađian.
A.
7
12
π
. B.
9
12
π
. C.
5
8
π
. D.
5
12
π
.
Lời giải
0
0
0
105 . 7
105
180 12
ππ
= =
.
Câu 23: Số đo góc
22 30
′
°
đổi sang rađian là:
A.
5
π
. B.
8
π
. C.
7
12
π
. D.
6
π
.
Lời giải
22,5..
22 30 22,5
180 8
ππ
°
′
= = =°
.
Câu 24: Một cung tròn có số đo là
45°
. Hãy chọn số đo radian của cung tròn đó trong các cung tròn sau
đây.
A.
2
π
B.
π
C.
4
π
D.
3
π
Lời giải
Chọn C
Ta có:
.
180 4
a
ππ
α
°
= =
°
.
Câu 25: Góc có số đo
24
π
đổi sang độ là:
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
A.
7
.
°
B.
7 30 .
′
°
C.
8 .°
D.
8 30 .
′
°
Lời giải
Ta có:
180
7 30 .
24 24
π
=
°
°
′
=
Câu 26: Góc có số đo
120
°
đổi sang rađian là:
A.
2
3
π
. B.
3
2
π
. C.
4
π
. D.
10
π
.
Lời giải
Ta có:
0
120. 2
120
180 3
ππ
= =
.
DẠNG 3. ĐƯỜNG TRÒN LƯỢNG GIÁC VÀ CÁC BÀI TOÁN LIÊN QUAN
Câu 27: Trên đường tròn lượng giác
Số đo của góc lượng giác
(
)
,OA OB
′
là
A.
4
π
−
. B.
2
π
−
. C.
4
π
. D.
2
π
.
Lời giải
Từ hình vẽ ta có
( )
,
2
OA OB
π
′
= −
.
Câu 28: Trên đường tròn lượng giác, góc có số đo
( )
42
k
k
ππ
+∈
được biểu diễn bởi bao nhiêu điểm?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
Cách 1: Trên đường tròn lượng giác, xét theo chiều dương với
0,1, 2,3,4k =
ta thấy góc có số
đo
( )
42
k
k
ππ
+∈
được biểu diễn bởi
4
điểm.
Cách 2: Góc có số đo
( )
*
2
,
k
kn
n
π
α
+ ∈∈
được biểu diễn bởi
n
điểm trên đường tròn
lượng giác. Do đó, góc
( )
2
424 4
kk
k
π ππ π
+=+ ∈
nên được biểu diễn bởi
4
điểm trên đường
tròn lượng giác.
Câu 29: Góc lượng giác nào sau đây có cùng điểm cuối với góc
7
4
π
?
A.
4
π
−
. B.
4
π
. C.
3
4
π
. D.
3
4
π
−
.
Lời giải
Ta có
7
2
44
ππ
π
= −
.
Góc lượng giác có cùng điểm cuối với góc
7
4
π
là
4
π
−
.
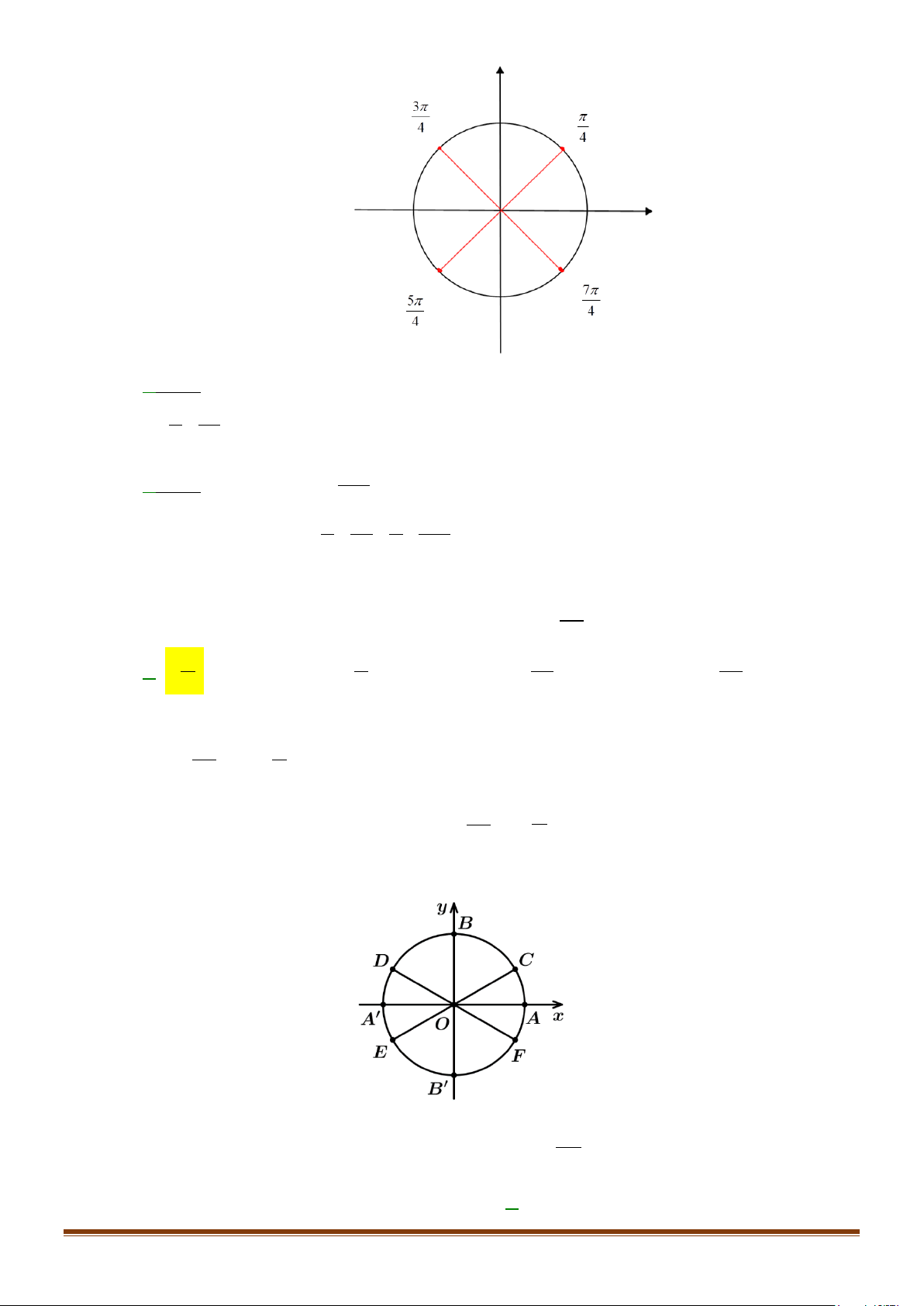
Câu 30: Cho đường tròn lượng giác gốc
A
như hình vẽ.
Điểm biểu diễn của điểm cuối góc lượng giác có số đo
5
2
π
là điểm nào trong các điểm sau?
A. Điểm
E
. B. Điểm
F
. C. Điểm
B
. D. Điểm
B
′
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Lời giải
Ta có:
5
2.
22
ππ
π
= +
Do đó, điểm biểu diễn của cung có số đo
5
2
π
là điểm biểu diễn của cung
có số đo
,
2
π
đó là điểm
B
.
Câu 31: Lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo thứ tự đó
và các điểm
B
,
C
có tung độ dương. Khi đó góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng
A.
240 360 ,kk
+∈
. B.
120
.
C.
240−
. D.
120 360 ,kk
+∈
.
Lời giải
Theo bài ra ta có
0
120AOC =
nên góc lượng giác có tia đầu
OA
, tia cuối
OC
có số đo bằng
00
120 360 ,kk
+∈
.
Câu 32: Góc lượng giác nào sau đây có cùng điểm cuối với góc
13
4
π
?
A.
3
4
π
−
. B.
3
4
π
. C.
4
π
−
. D.
3
2
π
.
Lời giải
Ta có
13 3
4
44
ππ
π
=−+
nên góc lượng giác
3
4
π
−
có cùng điểm cuối với góc
13
4
π
.
Câu 33: Khi biểu diễn trên đường tròn lượng giác góc lượng giác nào trong các góc lượng giác có số đo
dưới đây có cùng điểm cuối với góc lượng giác có số đo
4
π
?
A.
10
3
π
. B.
5
4
π
−
. C.
25
4
π
. D.
7
4
π
.
Lời giải
Ta có
25
3.2
44
ππ
π
= +
Câu 34: Trên đường tròn lượng giác, điểm cuối của góc có số đo
26
3
π
nằm ở góc phần tư thứ mấy?
A.
IV
. B.
III
. C.
I
. D.
II
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
Ta có:
26 2
4.2
33
ππ
π
= +
.
Vậy điểm cuối của cung có số đo
26
3
π
nằm ở góc phần tư thứ II.
Câu 35: Trên đường tròn lượng giác gốc
A
, cho góc lượng giác
(
)
;OA OM
có số đo
( )
4
2
3
kk
π
απ
=+∈
. Điểm cuối
M
nằm ở góc phần tư nào trong các phần tư sau?
A. thứ tư
( )
IV
. B. thứ hai
( )
II
. C. thứ ba
( )
III
. D. thứ nhất
( )
I
.
Lời giải
Theo định nghĩa ta có số đo cung lượng giác
AM
bằng số đo góc
α
nên điểm cuối
M
nằm ở góc
phần tư thứ ba
( )
III
.
Câu 36: Trên đường tròn lượng giác gốc
A
, biết gốc lương giác
( )
,OA OM
có số đo bằng
0
4100
, điểm
M
nằm ở gốc phần tư thứ mấy?
A.
I
. B.
IV
. C.
III
. D.
II
.
Lời giải
Ta có Sđ
( )
00 0
,OM 4100 140 11.360OA = = +
.
Vậy điểm
M
nằm góc phần tư thứ
II
.
Câu 37: Trên đường tròn lượng giác, có bao nhiêu điểm
M
thỏa mãn
; 30 45 ,OA OM k k
?
A.
6
. B.
4
. C.
8
. D.
10
.
Lời giải
; 30 45 30 360 .
8
k
OA OM k
Số dư của
k
chia cho
8
là
0, 1, 2,...,7
. Vậy số các điểm
trên đường tròn lượng giác là
8
.
Câu 38: Trên đường tròn lượng giác góc
A
, biết góc lượng giác
(
)
,OA OM
có số đo
4100
, điểm
M
nằm
ở góc phần tư thứ mấy?
A.
I
. B.
IV
. C.
III
. D.
II
.
Lời giải
Ta có:
4100 652 2 0,22ππ
≈ × ++
, với
π
0 0, 22
2
<<
nên
M
nằm ở góc phần tư thứ
III
.
Câu 39: Trên đường tròn lượng giác gốc
A
, cho cung lượng giác
AM
có số đo là
( )
4
2
3
kk
π
απ
=+∈
. Điểm cuối
M
nằm ở góc phần tư:
A. thứ tư
( )
IV
. B. thứ hai
( )
II
. C. thứ ba
( )
III
. D. thứ nhất
( )
I
.
Lời giải
Ta có
43
;
32
ππ
π
∈
, do đó điểm cuối
M
nằm ở góc phần tư thứ ba
( )
III
.
Câu 40: Trên đường tròn lượng giác gốc
A
, có bao nhiêu điểm M thỏa mãn số đo góc lượng giác
( )
;OA OM
bằng
65
k
ππ
+
, với
k
là số nguyên.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
A.
12
. B.
10
. C. 5. D. 6.
Lời giải
Ta có số đo 1 vòng đường tròn lượng giác là
2
π
nên
0 2 0 10
5
kk
π
π
≤ ≤ ⇒≤≤
.
k
nguyên nên
có 10 giá trị cho
k
.
Câu 41: Trong hệ trục tọa độ
Oxy
, cho
M
là điểm nằm trên đường tròn lượng giác. Điểm
M
có tung độ
và hoành độ đều âm, góc
( )
,Ox OM
có thể là:
A.
90−°
. B.
200°
. C.
60−°
. D.
180−°
.
Lời giải
Điểm
M
có tung độ và hoành độ đều âm nên điểm
M
nằm trong góc phần tư thứ ba.
Do đó góc
( )
,
Ox OM
có thể là
200°
.
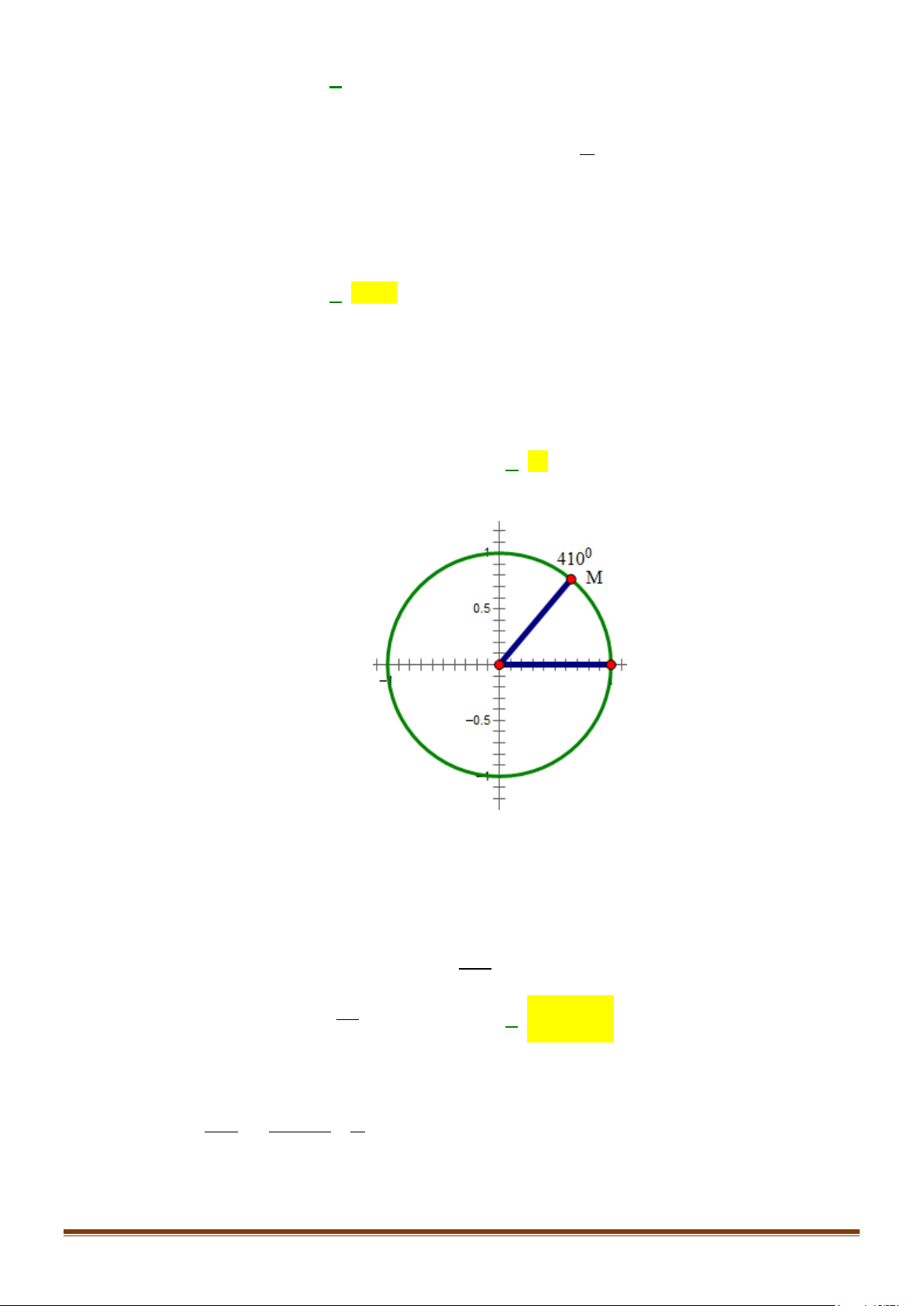
Câu 42: Trên đường tròn lượng giác gốc
A
, biết góc lượng giác
( )
,OA OM
có số đo bằng
0
410
, điểm
M
nằm ở góc phần tư thứ mấy?
A.
II
. B.
IV
. C.
I
. D.
III
.
Lời giải
Ta có biểu diễn góc lượng giác
( )
,OA OM
có số đo bằng
0
410
như trên hình. Vậy điểm
M
nằm
ở góc phần tư thứ
I
.
Cách khác: Ta có
410 360 50
o oo
= +
. Suy ra góc lượng giác
( )
, 410
o
OA OM =
nằm ở góc phần
tư thứ nhất.
Câu 43: Cho góc lượng giác có số đo
( )
59
,
2
Ox Oy
π
= −
. Khi đó hai tia
Ox
,
Oy
.
A. Tạo với nhau một góc
3
4
π
. B. Vuông góc.
C. Trùng nhau. D. Đối nhau.
Lời giải
Ta có
59 60
22
π ππ
−
−=−
30
2
π
π
= −
suy ra hai tia
Ox
,
Oy
vuông góc với nhau.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Câu 44: Cho góc lượng giác
( )
,OA OB
có số đo bằng
3
π
. Trong các số sau, số nào là số đo của một góc
lượng giác có cùng tia đầu
OA
và tia cuối
OB
?
A.
5
3
π
. B.
11
3
π
−
. C.
10
3
π
. D.
3
π
−
.
Lời giải
Ta có:
11
4
33
ππ
π
−=−
Câu 45: Cho hai góc lượng giác có sđ
( )
5
, 2,
2
Ox Ou m m
π
π
=−+ ∈
và sđ
( )
, 2, .
2
Ox Ov n n
π
π
=−+ ∈
Khẳng định nào sau đây đúng?
A.
Ou
và
Ov
trùng nhau. B.
Ou
và
Ov
đối nhau.
C.
Ou
và
Ov
vuông góc. D. Tạo với nhau một góc
4
π
.
Lời giải
Tia cuối của góc lượng giác có sđ
( )
5
, 2,
2
Ox Ou m m
π
π
=−+ ∈
trùng với tia
OB
′
.
Tia cuối của góc lượng giác có sđ
( )
, 2 ,n
2
Ox Ov n
π
π
=−+ ∈
trùng với tia
OB
′
.
Do đó hai tia
Ou
và
Ov
trùng nhau.
Câu 46: Trên đường tròn lượng giác gốc
A
cho các góc lượng giác có số đo:
I.
4
π
. II.
7
4
π
−
. III.
13
4
π
. IV.
71
4
π
−
.
Hỏi các góc lượng giác nào có điểm cuối trùng nhau?
A. Chỉ I, II và IV. B. Chỉ II, III và IV. C. Chỉ I, II và III. D. Chỉ I và II.
Lời giải
Có
7
2
44
ππ
π
−
−=
và
71
18 9.2
44
ππ
ππ
−
−==
nên
4
π
,
7
4
π
−
và
71
4
π
−
là các cung có điểm
cuối trùng nhau.
13
3
44
ππ
π
−=
nên
13
4
π
là cung có điểm cuối không trùng với điểm cuối của các cung còn lại.
Câu 47: Cho hai góc lượng giác có sđ
( )
oo
, 45 360 ,Ox Ou m m=+∈
và sđ
( )
oo
, 135 360 ,Ox Ov n n=−+ ∈
. Ta có hai tia
Ou
và
Ov
A. Tạo với nhau góc
o
45
. B. Trùng nhau.
C. Đối nhau. D. Vuông góc.
Lời giải
sđ
( )
oooo00o
, 135 360 225 360 45 180 360 ,Ox Ov n n n n=−+=+=++ ∈
.
Mà sđ
( )
oo
, 45 360 ,Ox Ou m m=+∈
nên hai tia
Ou
và
Ov
đối nhau.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
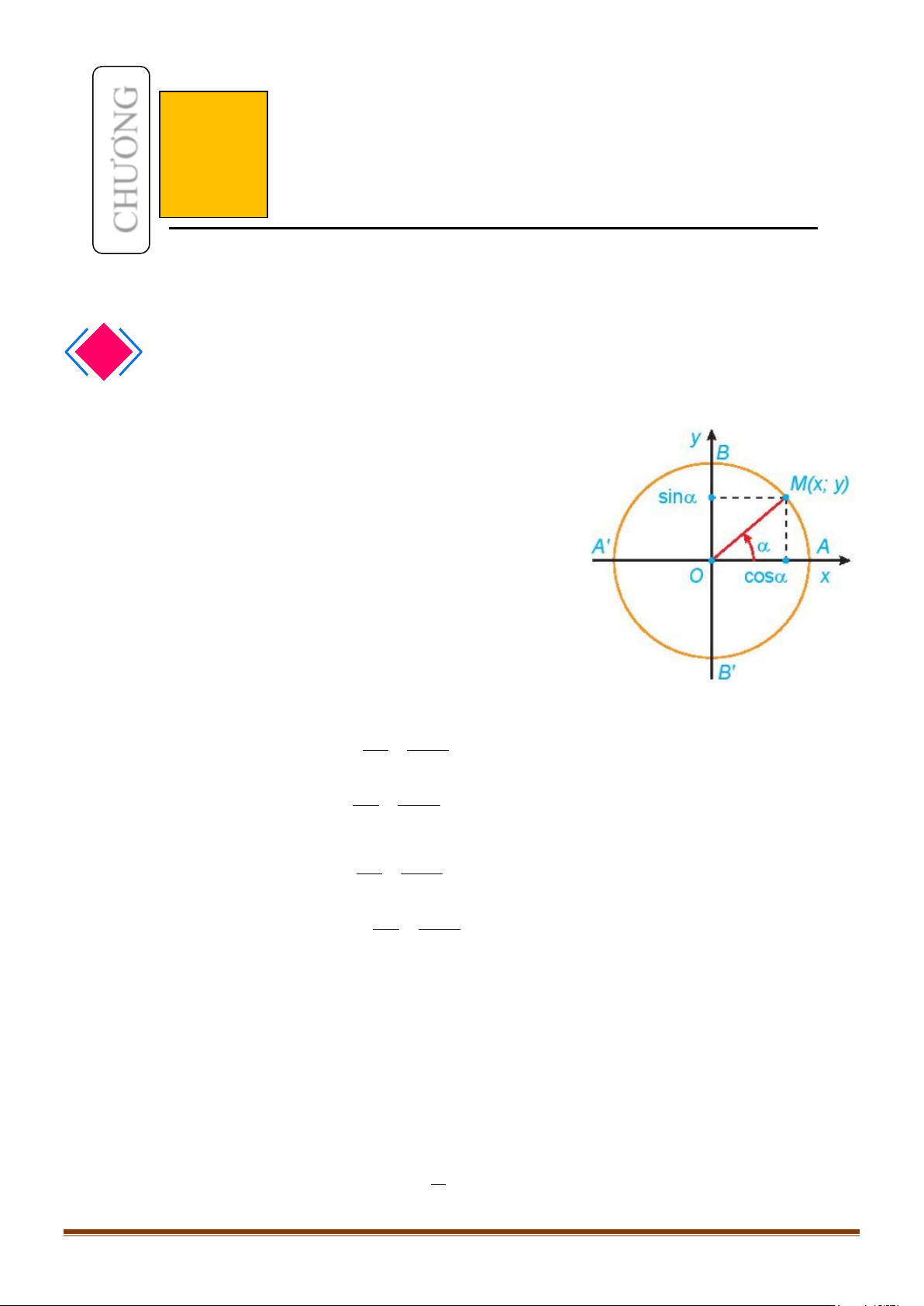
BÀI 2. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
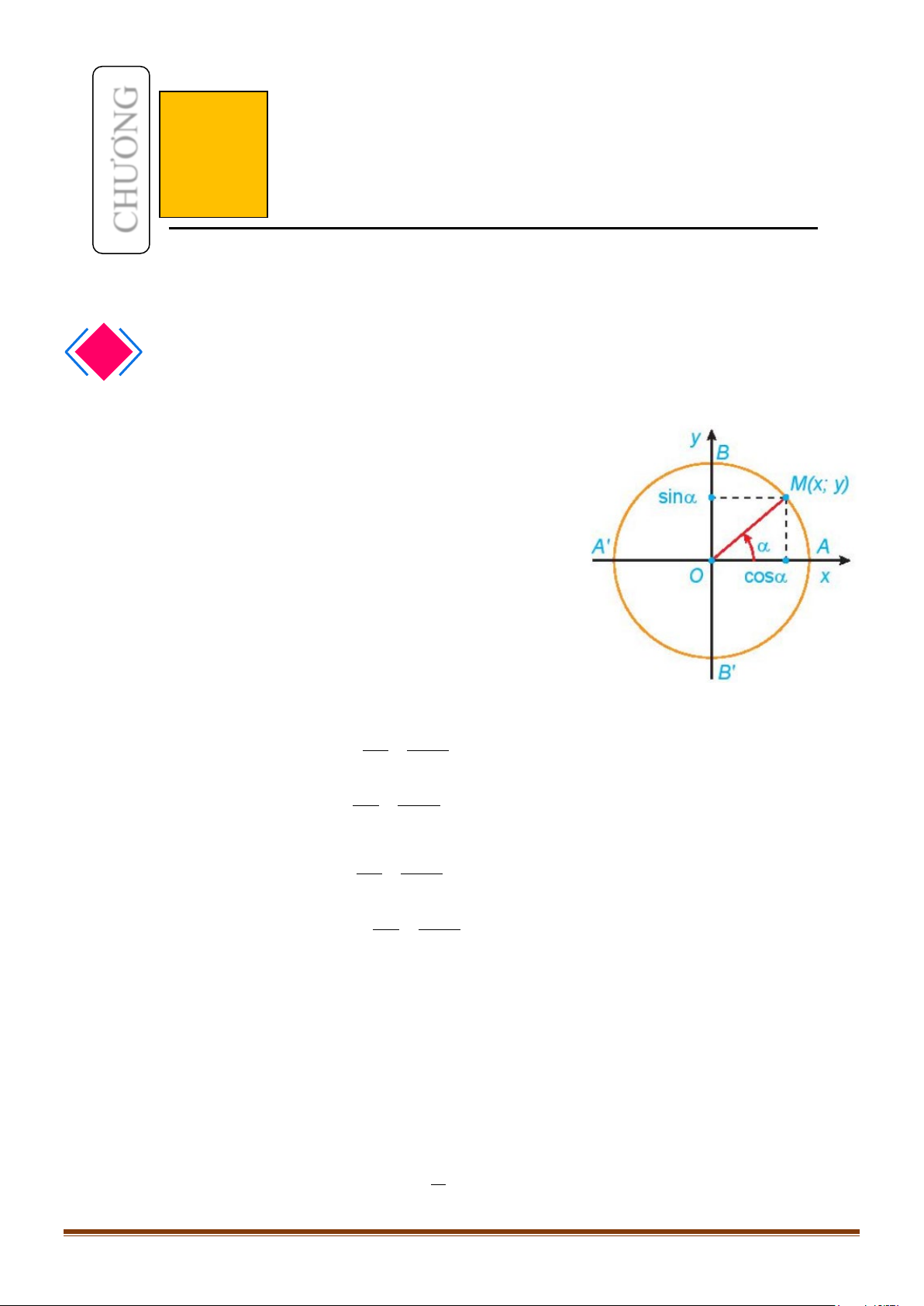
1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
Trên đường tròn lượng giác, gọi
( )
;
MM
Mx y
là điểm biểu
diễn góc lượng giác có số đo
α
. Khi đó:
•
Tung độ
M
y
của điểm
M
gọi là sin của
α
và kí hiệu là
sin .
α
sin
M
y
α
=
•
Hoành độ
M
x
của điểm
M
gọi là côsin của
α
và kí hiệu
là
cos .
α
cos
M
x
α
=
•
Nếu
cos 0,
M
x
α
= ≠
tỉ số
sin
cos
M
M
y
x
α
α
=
gọi là tang của
α
và kí hiệu là
tan
α
(người ta còn
dùng kí hiệu
tg
α
):
sin
tan .
cos
M
M
y
x
α
α
α
= =
•
Nếu
sin 0,
M
y
α
= ≠
tỉ số
cos
sin
M
M
x
y
α
α
=
gọi là côtang của
α
và kí hiệu là
cot
α
(người ta còn
dùng kí hiệu
cotg
α
) :
cos
cot .
sin
M
M
x
y
α
α
α
= =
Các giá trị
sin , cos , tan , cot
αααα
được gọi là các giá trị lượng giác của góc
.
α
Chú ý:
a) Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin
b) Từ định nghĩa ta suy ra:
1)
sin
α
và
cos
α
xác định với mọi
.
α
∈
2)
tan
α
xác định với mọi
( )
.
2
kk
π
απ
≠+ ∈
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUY
Ế
T.
I
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
3)
cot
α
xác định với mọi
( )
.kk
απ
≠∈
c) Với mọi góc lượng giác
α
, ta có
( )
( )
sin 2 sin , ;
cos 2 cos , .
kk
kk
απ α
απ α
+ = ∀∈
+ = ∀∈
1 sin 1
1 cos 1.
α
α
−≤ ≤
−≤ ≤
( )
( )
tan tan , , ;
2
cot cot , , .
k kk
k kk
π
α π αα π
α π αα π
+ = ≠ + ∀∈
+ = ≠ ∀∈
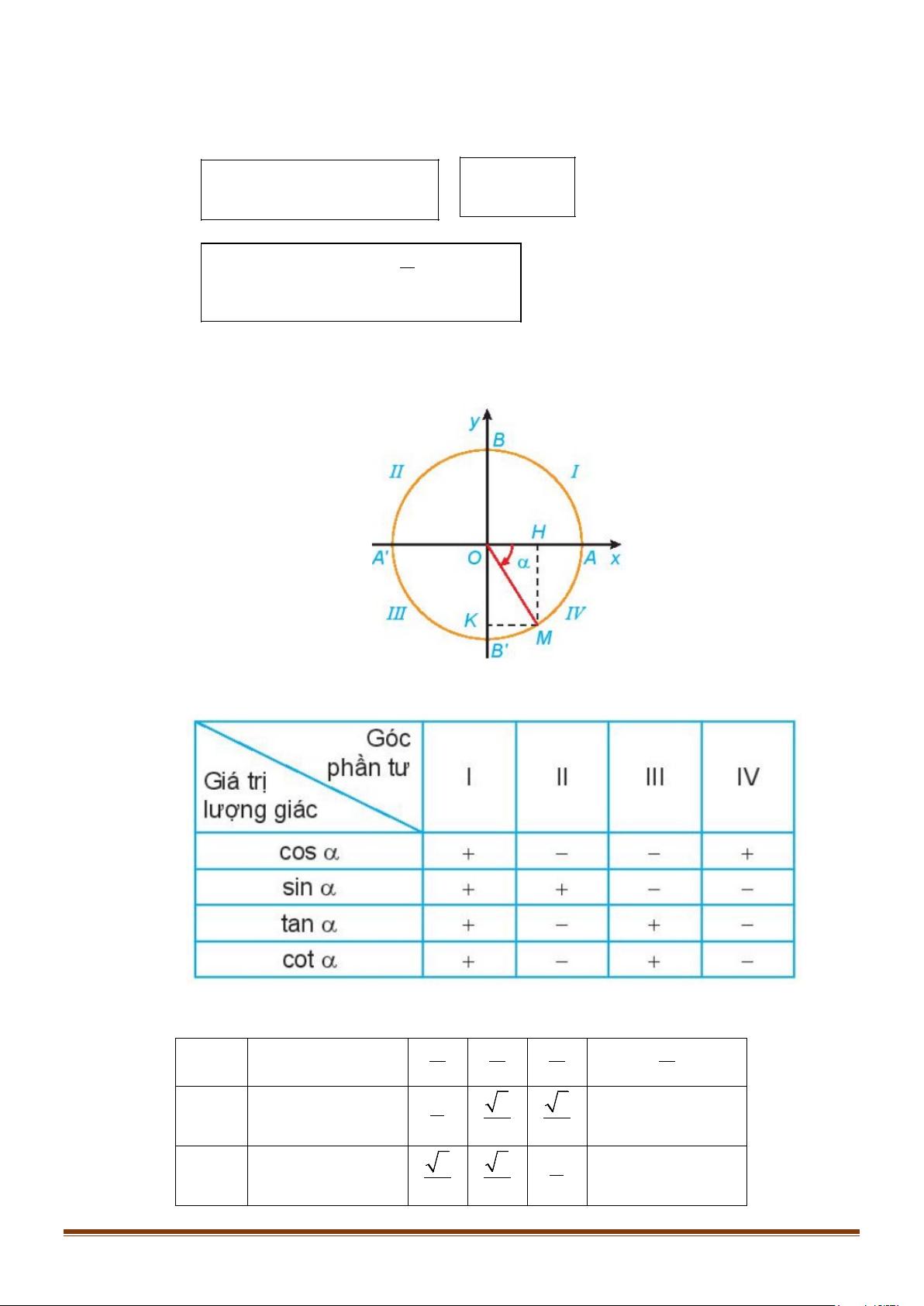
d) Dấu của các giá trị lượng giác của góc
α
phụ thuộc vào vị trí điểm biểu diễn
M
trên đường
tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
e. Giá trị lượng giác của các cung đặc biệt
α
0
6
π
4
π
3
π
2
π
sin
α
0
1
2
2
2
3
2
1
cos
α
1
3
2
2
2
1
2
0

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
tan
α
0
1
3
1
3
Không xác định
cot
α
Không xác định
3
1
1
3
0
2. TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẰNG MÁY TÍNH CẦM TAY
3. HỆ THỨC CƠ BẢN GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau
22
sin cos 1
αα
+=
2
2
1
1 tan ,
cos
α
α
+=
,
2
kk
π
απ
≠+ ∈
2
2
1
1 cot ,
sin
α
α
+=
, kk
απ
≠∈
tan .cot 1,
αα
=
,
2
k
k
π
α
≠∈
4. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC CÓ LIÊN QUAN ĐẶC BIỆT
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Góc đối nhau
Góc bù nhau
Góc phụ nhau
cos( ) cos
αα
−=
sin( ) sin
πα α
−=
sin cos
2
π
αα
−=
sin( ) sin
αα
−=−
cos( ) cos
πα α
−=−
cos sin
2
π
αα
−=
tan( ) tan
αα
−=−
tan( ) tan
πα α
−=−
tan cot
2
π
αα
−=
cot( ) cot
αα
−=−
cot( ) cot
πα α
−=−
cot t an
2
π
αα
−=
Góc hơn kém
π
Góc hơn kém
2
π
sin( ) sin
πα α
+=−
sin cos
2
π
αα
+=
cos( ) cos
πα α
+=−
cos sin
2
π
αα
+=−
tan( ) tan
πα α
+=
tan cot
2
π
αα
+=−
cot( ) cot
πα α
+=
cot tan
2
π
αα
+=−

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
DẠNG 1: TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC HOẶC MỘT BIỂU THỨC
Sử dụng công thức lượng giác cơ bản trong các bài toán:
1)
22
sin cos 1
αα
+=
2)
2
2
1
1 tan ,
cos
α
α
+=
,
2
kk
π
απ
≠+ ∈
3)
2
2
1
1 cot ,
sin
α
α
+=
, kk
απ
≠∈
4)
tan .cot 1,
αα
=
,
2
k
k
π
α
≠∈
5)
sin
tan .
cos
α
α
α
=
6)
cos
cot .
sin
α
α
α
=
Câu 1: Cho
2
cos 0
2
5
xx
π
= − <<
. Tính giá trị của các giá trị lượng giác còn lại.
Câu 2: Cho
3
sin
52
xx
π
π
= <<
. Tính giá trị của các giá trị lượng giác còn lại.
Câu 3: Cho
3
tan
42
xx
π
π
= − < <−
. Tính giá trị của các giá trị lượng giác còn lại.
Câu 4: Cho
33
cot
42
xx
π
π
= <<
. Tính giá trị của các giá trị lượng giác còn lại.
Câu 5: Biết
tan 2
α
=
và
00
180 270
α
<<
. Tính giá trị của biểu thức:
sin osc
αα
+
Câu 6: Cho
tan 2
α
=
. Tính giá trị của biểu thức:
3sin cos
sin cos
A
αα
αα
+
=
−
Câu 7: Cho
tan 3x =
. Tính
2sin cos
sin cos
xx
P
xx
−
=
+
.
Câu 8: Cho
1
sin
3
a
=
. Giá trị của biểu thức
cot tan
tan 2co t
aa
A
aa
−
=
+
bằng
Câu 9: Cho
tan 4.x = −
Giá trị của biểu thức
2sin 5cos
3cos sin
xx
A
xx
−
=
+
là
Câu 10: Cho
tan 3
α
=
, khi đó giá trị của biểu thức
2sin cos
3sin 5cos
P
αα
αα
−
=
−
là
Câu 11: Cho góc
α
thỏa mãn
0
2
π
α
−<<
và
1
cos
2
α
=
. Giá trị của biểu thức
1
sin
cos
P
α
α
= +
bằng
Câu 12: Cho
tan 2
α
=
. Tính giá trị của biểu thức
43 2
2 22 2
sin 3sin cos cos
sin sin cos 2cos
P
.
HỆ THỐNG BÀI TẬP TỰ LUẬN
.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
Câu 13: Cho
2 tan cot 1aa−=
với
0
2
π
α
−<<
. Tính giá trị biểu thức
( ) ( )
tan 8 2cot
3
3tan
2
aa
P
a
ππ
π
−+ +
=
+
Câu 14: Cho
sin cos
x xm
+=
. Tính giá trị của biểu thức:
sin cosM xx= −
Câu 15: Cho
44
sin cos 1
a b ab
αα
+=
+
Tính giá trị của biểu thức:
88
33
sin cos
A
ab
αα
= +
DẠNG 2: GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC CÓ LIÊN QUAN ĐẶC BIỆT
Câu 16: Tính giá trị của biểu thức:
2 22
3 sin 90 2cos 60 3tan 45S
= − °+ °− °
Câu 17: Rút gọn biểu thức
( ) ( )
5
sin cos 13 3sin 5
2
D
π
α πα α π
= −+ +− −
.
Câu 18: Tính giá trị của biểu thức:
202020 2020
sin 10 sin 20 sin 30 ... sin 70 sin 80+ + ++ +
Câu 19: Tính giá trị của biểu thức:
2020202020202020
cos 10 cos 20 cos 30 cos 40 cos 50 cos 60 cos 70 cos 80M =++++++++
.
20 20 20 20 20 20 20 20
cos 90 cos 100 cos 110 cos 120 cos 130 cos 140 cos 15
0 cos 160+++++++++
20 20
cos 170 cos 180++
DẠNG 3: RÚT GỌN BIỂU THỨC LƯỢNG GIÁC. ĐẲNG THỨC LƯỢNG GIÁC
Câu 20: Rút gọn biểu thức
( ) ( )
22 2
1– sin .cot 1– cotA xx x= +
Câu 21: Rút gọn biểu thức
( ) ( )
22
sin cos sin cosM xx xx=+ +−
.
Câu 22: Rút gọn biểu thức
( ) ( )
2
4 4 22 8 8
C 2 cos sin cos sin cos sin = ++ − +x x xx x x
Câu 23: Đơn giản biểu thức
( )
2
sin cos 1
tan sin .cos
xx
A
x xx
−−
=
−
Câu 24: Tính giá trị của biểu thức
6 6 22
sin cos 3sin cosA
=++
α α αα
.
Câu 25: Cho
0
2
π
α
<<
. Tính
1 sin 1 sin
1 sin 1 sin
αα
αα
+−
+
−+
DẠNG 4: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC LƯỢNG GIÁC
Câu 26: Giá trị lớn nhất của
66
sin cosQxx
bằng:
Câu 27: Giá trị lớn nhất của biểu thức
22
7cos 2sinM xx= −
là.
Câu 28: Tìm giá trị nhỏ nhất của biểu thức
4 4 22
cot cot 2 tan .tan 2P a b ab
=++ +
Câu 29: Tính giá trị lượng giác còn lại của góc
x
biết:
a.
3
sin
5
x
với
3
2
x
. b.
1
cos
4
x
với
0
2
x
.
c.
3
cos
5
x
với
0
0 90x
. d.
5
cos
13
x
với
00
180 270x
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
Câu 30: Tính giá trị lượng giác còn lại của góc
x
biết
a)
2
cos
5
x
với
0
2
x
. b)
4
cos
5
x
với
270 360 x
.
c)
5
sin
13
x
với
2
x
d)
1
sin
3
x
với
180 270 x
.
Câu 31: Tính giá trị lượng giác còn lại của góc
x
biết
a)
tan 3x
với
3
2
x
. b)
tan 2x
với
2
x
.
c)
1
tan
2
x
với
2
x
d)
cot 3x
với
3
2
x
.
Câu 32: Tính giá trị lượng giác của các biểu thức sau:
a) Cho
tan 2.x
Tính:
12
5cot 4tan 2sin cos
,.
5cot 4 tan cos 3sin
x x xx
AA
x x xx
b) Cho
cot 2.x
Tính:
12
3sin cos sin 3cos
,.
sin cos sin 3cos
xx x x
BB
xx x x
c) Cho
cot 2.x
Tính:
12
2
2sin 3cos 2
,.
3sin 2cos cos sin cos
xx
CC
x x x xx
d) Cho
3
sin ,0 .
52
xx
Tính:
cot tan
.
cot tan
xx
E
xx
e) Cho
00
1
sin ,90 180 .
5
xx
Tính:
2
8tan 3cot 1
.
tan cot
xx
F
xx
Câu 33: Chứng minh các đẳng thức sau:
a)
22 2
cos sin 1 2sin xx x
. b)
22
2cos 1 1 2sinxx
c)
22
3 4sin 4cos 1 xx
d)
sin cot cos tan sin cos xxxxxx
Câu 34: Chứng minh các đẳng thức sau:
a.
4 4 22
sin cos 1 2sin .cos
x x xx
b.
44 22
cos sin cos sin xx xx
c.
2
4cos 3 1 2sin 1 2sin x xx
d.
2 22
1 cos sin cos cos sin xxx x x
Câu 35: Chứng minh các đẳng thức sau:
a.
44 2 2
sin cos 1 2cos 2sin 1 xx x x
b.
33
sin .cos sin .cos sin .cos
xx x x xx
c.
2 2 22
tan sin tan .sinx x xx
d.
2 2 22
cot cos cot .cosx x xx
Câu 36: Chứng minh các đẳng thức sau:
a.
1
tan cot
sin .cos
xx
xx
b.
1 cos sin
sin 1 cos
xx
xx
c.
11
1
1 tan 1 cot
xx
d.
2
11
1 1 tan 0
cos cos
x
xx

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
Câu 37: Chứng minh các đẳng thức sau không phụ thuộc vào biến
x
:
a)
44 2
A sin cos 2sin
xx x
.
b)
4222
B sin cos sin cos
xxxx
.
c)
4 22 2
B cos cos sin sin
x xx x
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 2. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
Trên đường tròn lượng giác, gọi
( )
;
MM
Mx y
là điểm biểu
diễn góc lượng giác có số đo
α
. Khi đó:
•
Tung độ
M
y
của điểm
M
gọi là sin của
α
và kí hiệu là
sin .
α
sin
M
y
α
=
•
Hoành độ
M
x
của điểm
M
gọi là côsin của
α
và kí hiệu
là
cos .
α
cos
M
x
α
=
•
Nếu
cos 0,
M
x
α
= ≠
tỉ số
sin
cos
M
M
y
x
α
α
=
gọi là tang của
α
và kí hiệu là
tan
α
(người ta còn
dùng kí hiệu
tg
α
):
sin
tan .
cos
M
M
y
x
α
α
α
= =
•
Nếu
sin 0,
M
y
α
= ≠
tỉ số
cos
sin
M
M
x
y
α
α
=
gọi là côtang của
α
và kí hiệu là
cot
α
(người ta còn
dùng kí hiệu
cotg
α
) :
cos
cot .
sin
M
M
x
y
α
α
α
= =
Các giá trị
sin , cos , tan , cot
αααα
được gọi là các giá trị lượng giác của góc
.
α
Chú ý:
a) Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin
b) Từ định nghĩa ta suy ra:
1)
sin
α
và
cos
α
xác định với mọi
.
α
∈
2)
tan
α
xác định với mọi
( )
.
2
kk
π
απ
≠+ ∈
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUY
Ế
T.
I
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
3)
cot
α
xác định với mọi
( )
.kk
απ
≠∈
c) Với mọi góc lượng giác
α
, ta có
( )
( )
sin 2 sin , ;
cos 2 cos , .
kk
kk
απ α
απ α
+ = ∀∈
+ = ∀∈
1 sin 1
1 cos 1.
α
α
−≤ ≤
−≤ ≤
( )
( )
tan tan , , ;
2
cot cot , , .
k kk
k kk
π
α π αα π
α π αα π
+ = ≠ + ∀∈
+ = ≠ ∀∈
d) Dấu của các giá trị lượng giác của góc
α
phụ thuộc vào vị trí điểm biểu diễn
M
trên đường
tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
e. Giá trị lượng giác của các cung đặc biệt
α
0
6
π
4
π
3
π
2
π
sin
α
0
1
2
2
2
3
2
1
cos
α
1
3
2
2
2
1
2
0
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
tan
α
0
1
3
1
3
Không xác định
cot
α
Không xác định
3
1
1
3
0
2. TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẰNG MÁY TÍNH CẦM TAY
3. HỆ THỨC CƠ BẢN GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau
22
sin cos 1
αα
+=
2
2
1
1 tan ,
cos
α
α
+=
,
2
kk
π
απ
≠+ ∈
2
2
1
1 cot ,
sin
α
α
+=
, kk
απ
≠∈
tan .cot 1,
αα
=
,
2
k
k
π
α
≠∈
4. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC CÓ LIÊN QUAN ĐẶC BIỆT
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Góc đối nhau
Góc bù nhau
Góc phụ nhau
cos( ) cos
αα
−=
sin( ) sin
πα α
−=
sin cos
2
π
αα
−=
sin( ) sin
αα
−=−
cos( ) cos
πα α
−=−
cos sin
2
π
αα
−=
tan( ) tan
αα
−=−
tan( ) tan
πα α
−=−
tan cot
2
π
αα
−=
cot( ) cot
αα
−=−
cot( ) cot
πα α
−=−
cot t an
2
π
αα
−=
Góc hơn kém
π
Góc hơn kém
2
π
sin( ) sin
πα α
+=−
sin cos
2
π
αα
+=
cos( ) cos
πα α
+=−
cos sin
2
π
αα
+=−
tan( ) tan
πα α
+=
tan cot
2
π
αα
+=−
cot( ) cot
πα α
+=
cot tan
2
π
αα
+=−
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
DẠNG 1: TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC HOẶC MỘT BIỂU THỨC
Sử dụng công thức lượng giác cơ bản trong các bài toán:
1)
22
sin cos 1
αα
+=
2)
2
2
1
1 tan ,
cos
α
α
+=
,
2
kk
π
απ
≠+ ∈
3)
2
2
1
1 cot ,
sin
α
α
+=
, kk
απ
≠∈
4)
tan .cot 1,
αα
=
,
2
k
k
π
α
≠∈
5)
sin
tan .
cos
α
α
α
=
6)
cos
cot .
sin
α
α
α
=
Câu 1: Cho
2
cos 0
2
5
xx
π
= − <<
. Tính giá trị của các giá trị lượng giác còn lại.
Lời giải
Vì
0 sin 0
2
xx
π
− <<⇒ <
Ta có
22
sin cos 1
xx+=
22
sin 1 cosxx⇒=−
2
2
1
5
= −
1
5
=
Vậy
1
sin
5
x = −
.
12
sin 1 cos
55
tan ; cot 2
21
cos 2 sin
55
xx
xx
xx
−
===−===−
−
Câu 2: Cho
3
sin
52
xx
π
π
= <<
. Tính giá trị của các giá trị lượng giác còn lại.
Lời giải
Vì
cos 0
2
xx
π
π
<<⇒ <
Ta có
22
sin cos 1xx+=
2
22
3 16
cos 1 sin 1
5 25
xx
⇒ =− =−=
HỆ THỐNG BÀI TẬP TỰ LUẬN
.
II
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
Vậy
4
cos
5
x
= −
.
34
sin 3 cos 4
55
tan ; cot
43
cos 4 sin 3
55
xx
xx
xx
−
===−===−
−
Câu 3: Cho
3
tan
42
xx
π
π
= − < <−
. Tính giá trị của các giá trị lượng giác còn lại.
Lời giải
Vì
cos 0
2
xx
π
π
− < <− ⇒ <
1 14
tan .cot 1 cot
3
tan 3
4
xx x
x
=⇒= ==
Ta có
2
22
2
1 3 25 16
1 tan 1 cos
cos 4 16 25
xx
x
=+ =+=⇒ =
Vậy
4
cos
5
x = −
.
sin 3 4 3
tan sin tan .cos .
cos 4 5 5
x
x x xx
x
= ⇒ = = −=−
Câu 4: Cho
33
cot
42
xx
π
π
= <<
. Tính giá trị của các giá trị lượng giác còn lại.
Lời giải
Vì
3
sin 0
2
xx
π
π
<< ⇒ <
1 14
tan .cot 1 tan
3
cot 3
4
xx x
x
=⇒===
Ta có
2
22
2
1 3 25 16
1 cot 1 sin
sin 4 16 25
xx
x
=+ =+=⇒ =
Vậy
4
sin
5
x = −
.
cos 3 4 3
cot cos cot .sin .
sin 4 5 5
x
x x xx
x
= ⇒ = = −=−
Câu 5: Biết
tan 2
α
=
và
00
180 270
α
<<
. Tính giá trị của biểu thức:
sin osc
αα
+
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
2
2
11 1
cos cos
5
1 tan
5
= =⇒=±
+
αα
α
.
Do
00
180 270<<
α
nên
0<cos
α
. Suy ra,
1
cos
5
= −
α
.
2
sin tan .cos
5
= = −
α αα
.
Do đó,
35
sin os
5
+=−c
αα
.
Câu 6: Cho
tan 2
α
=
. Tính giá trị của biểu thức:
3sin cos
sin cos
A
αα
αα
+
=
−
Lời giải
3sin cos 3tan 1
7
sin cos tan 1
A
αα α
αα α
++
= = =
−−
.
Câu 7: Cho
tan 3
x
=
. Tính
2sin cos
sin cos
xx
P
xx
−
=
+
.
Lời giải
Ta có
sin
tan 3 3 sin 3cos .
cos
x
x xx
x
=⇒ =⇒=
Khi đó
2.3cos cos 5cos 5
3cos cos 4cos 4
xx x
P
xx x
−
= = =
+
.
Câu 8: Cho
1
sin
3
a =
. Giá trị của biểu thức
cot tan
tan 2co t
aa
A
aa
−
=
+
bằng
Lời giải
Ta có
22
22
cos sin
cot tan cos sin
sin cos
tan 2cot sin cos
sin 2cos
2
cos sin
aa
aa a a
aa
A
a aa a
aa
aa
−
−−
= = =
+
+
+
( )
(
)
22
2
2
22
1 sin sin
1 2sin 7
17
2 sin
sin 2 1 sin
aa
a
a
aa
−−
−
= = =
−
+−
Câu 9: Cho
tan 4.x
= −
Giá trị của biểu thức
2sin 5cos
3cos sin
xx
A
xx
−
=
+
là
Lời giải
Ta có:
( )
( )
sin cos
25
2. 4 5
2sin 5cos 2 tan 5
cos cos
13
cos sin
3cos sin 3 tan 3 4
3
cos cos
xx
xx x
xx
A
xx
xx x
xx
−
−−
−−
= = = = =
+ + +−
+
.
Câu 10: Cho
tan 3
α
=
, khi đó giá trị của biểu thức
2sin cos
3sin 5cos
P
αα
αα
−
=
−
là
Lời giải
Chia cả tử và mẫu của
P
cho
cos 0
α
≠
ta được:
2sin cos 2 tan 1 5
3sin 5cos 3tan 5 4
P
αα α
αα α
−−
= = =
−−
.
cos 0
α
<

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Câu 11: Cho góc
α
thỏa mãn
0
2
π
α
−<<
và
1
cos
2
α
=
. Giá trị của biểu thức
1
sin
cos
P
α
α
= +
bằng
Lời giải
Cách 1: Ta có:
22 2 2
sin cos 1 sin 1 cos
αα α α
+=⇔=−
Với
1
cos
2
α
=
2
2
13
sin 1 sin
22
3
4
αα
⇒ =−= =
±⇔
Vì
0
2
π
α
−<<
nên
3
sin 0 sin .
2
αα
<⇒ =−
Vậy:
1 31 3 4 3
sin 2 .
1
cos 2 2 2
2
P
α
α
−
= + =−+=−+=
Cách 2: Theo giả thiết:
1
cos
2
.
3
0
2
α
π
α
π
α
=
⇒=−
− <<
Vậy
1 1 3 43
sin sin 2 .
cos 3 2 2
cos
3
P
π
α
π
α
−
= + = − + =− +=
−
Câu 12: Cho
tan 2
α
=
. Tính giá trị của biểu thức
43 2
2 22 2
sin 3sin cos cos
sin sin cos 2cos
P
.
Lời giải
Do
tan 2
α
=
nên
cos 0
α
≠
. Chia cả tử và mẫu của biểu thức
P
cho
4
cos
α
ta được:
43 2
4 44
2 22 2
44 4
sin sin cos cos
3.
cos cos cos
sin sin cos cos
2.
cos cos cos
P
α αα α
α αα
α αα α
αα α
−+
=
++
43
2
22
22
1
tan 3tan
cos
11
tan . tan 2.
cos cos
αα
α
αα
αα
−+
=
++
( )
( ) ( )
4 32
22 2 2
tan 3tan tan 1
tan . tan 1 tan 2. tan 1
ααα
αα α α
−++
=
++ + +
4 32
42
tan 3tan tan 1
tan 4 tan 2
α αα
αα
− ++
=
++
4 32
42
2 3.2 2 1 3
2 4.2 2 34
− ++
= = −
++
.
Vậy
3
34
P = −
.
Câu 13: Cho
2 tan cot 1aa−=
với
0
2
π
α
−<<
. Tính giá trị biểu thức
( ) ( )
tan 8 2cot
3
3tan
2
aa
P
a
ππ
π
−+ +
=
+
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
tan 1
1
2 tan cot 1 2 tan 1
1
tan
tan
2
a
aa a
a
a
=
−=⇔ − =⇔
= −
.
Vì
0
2
π
α
−<<
nên
tan 0
a <
, suy ra
1
tan
2
a = −
,
cot 2
a = −
Ta có:
( )
tan 8 tanaa
π
−=−
;
( )
cot cotaa
π
+=
;
3
tan cot
2
aa
π
+=−
.
( ) (
)
1
4
tan 8 2cot
tan 2cot 7
2
3
3cot 6 12
3tan
2
aa
aa
P
a
a
ππ
π
−
−+ +
−+ −
= = = =
−
+
.
Câu 14: Cho
sin cosx xm
+=
. Tính giá trị của biểu thức:
sin cosM xx= −
Lời giải
Ta có:
( )
2
2 22
sin cos sin 2sin .cos cos 1 2sin .cosM x x x xx x xx=− =− +=−
.
Mặt khác:
( ) ( )
22
22
sin cos sin cos 4sin .cos 4sin .cosM x x x x xxm xx=−=+− =−
.
Suy ra:
2
2
1
1 2sin .cos 4sin .cos sin .cos
2
m
xxm xx xx
−
−=−⇔=
.
Do đó:
22 2
22
M mM m=−⇒=−
.
Câu 15: Cho
44
sin cos 1
a b ab
αα
+=
+
Tính giá trị của biểu thức:
88
33
sin cos
A
ab
αα
= +
Lời giải
Đặt
( )
2
2
2
1
1
cos
t
t
t
a b ab
α
−
=⇒ +=
+
(
)
2
2
1
ab
b t at
ab
⇔ −+ =
+
22
2
ab
at bt bt b
ab
⇔ + − +=
+
( )
2
2
ab
a b t bt b
ab
⇔ + − +=
+
( ) (
)
2
22
20abt babtb⇔+ − + +=
b
t
ab
⇔=
+
Suy ra
22
cos ;sin
ba
ab ab
αα
= =
++
Vậy:
( ) ( ) ( )
88
44 3
33
sin cos 1
.
ab
ab
ab ab ab
αα
+= + =
+++
DẠNG 2: GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC CÓ LIÊN QUAN ĐẶC BIỆT
Câu 16: Tính giá trị của biểu thức:
2 22
3 sin 90 2cos 60 3tan 45S = − °+ °− °
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
Ta có
2 22
3 sin 90 2cos 60 3tan 45S
° °°
=−+ −
2
22
1
3 1 2. 3.1
2
=−+ −
1
2
= −
.
Câu 17: Rút gọn biểu thức
( ) ( )
5
sin cos 13 3sin 5
2
D
π
α πα α π
= −+ +− −
.
Lời giải
Ta có
( ) ( )
5
sin cos 13 3sin 5
2
D
π
α πα α π
= −+ +− −
(
)
( )
sin cos 3sin
2
π
α πα πα
= −+ ++ −
cos cos 3sin
αα α
=−+
3sin
α
=
.
Câu 18: Tính giá trị của biểu thức:
202020 2020
sin 10 sin 20 sin 30 ... sin 70 sin 80+ + ++ +
Lời giải
202020 2020
sin 10 sin 20 sin 30 ... sin 70 sin 80+ + ++ +
20 2 0 2 0 2 2 0 20
sin 10 sin 20 sin 30 ...cos 30 cos 20 cos 10
+++ + +
Câu 19: Tính giá trị của biểu thức:
2020202020202020
cos 10 cos 20 cos 30 cos 40 cos 50 cos 60 cos 70 cos 80
M =++++++++
.
20 20 20 20 20 20 20 20
cos 90 cos 100 cos 110 cos 120 cos 130 cos 140 cos 150 cos 160+++++++++
20 20
cos 170 cos 180++
Lời giải
Áp dụng công thức
( )
0
cos cos 180
αα
= −
,
22
cos sin 1
αα
+=
ta có:
202020 2020
cos 10 cos 20 cos 30 ... cos 170 cos 180M = + + ++ +
2020 202020 202020
cos 10 cos 20 ... cos 80 cos 90 cos 80 ... cos 20 cos 10 cos 90= + ++ + + +++ + +
( )
202020 2020
2 cos 10 cos 20 cos 30 ... cos 80 cos 90= + + ++ +
( )
20 20 20 20 20
2 sin 80 ... sin 50 cos 50 ... cos 80 cos 90 8= ++ + ++ + =
DẠNG 3: RÚT GỌN BIỂU THỨC LƯỢNG GIÁC. ĐẲNG THỨC LƯỢNG GIÁC
Câu 20: Rút gọn biểu thức
( ) ( )
22 2
1– sin .cot 1– cot
A xx x= +
Lời giải
( ) ( )
22 2
1– sin .cot 1– cotA xx x= +
22 2
cot cos 1 cotxx x= − +−
2
sin x=
.
Câu 21: Rút gọn biểu thức
( ) ( )
22
sin cos sin cosM xx xx=+ +−
.
Lời giải
( ) ( )
22
sin cos sin cos 1 2sin cos 1 2sin cos 2M x x x x xx xx= + + − =+ +− =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Câu 22: Rút gọn biểu thức
( ) (
)
2
4 4 22 8 8
C 2 cos sin cos sin cos sin = ++ − +x x xx x x
Lời giải
Ta có :
( )
2
8 8 2 2 22 22
cos sin cos sin 2cos sin 1 2cos sin +=+− =−x x x x xx xx
( )
2
4 4 44
cos sin 2cos sin= +−x x xx
22 44
1 4cos sin 2cos sin=−+xx xx
( )
2
22 44
1 2cos sin 2cos sin =−−xx xx
22 44
1 4cos sin 2cos sin=−+xx xx
.
Suy ra :
( ) ( )
2
22 22 44
2 1 cos sin 1 4cos sin 2cos sin = − −− +C xx xx xx
.
( ) ( )
22 44 22 44
2 1 2cos sin cos sin 1 4cos sin 2cos sin =1=−+−−+C xx xx xx xx
.
Câu 23: Đơn giản biểu thức
( )
2
sin cos 1
tan sin .cos
xx
A
x xx
−−
=
−
Lời giải
Ta có:
( )
( )
2
2
2
2
2
sin cos 1
2cos .sin 2cos .sin cos 2cos
2cot
sin
tan sin .cos sin
sin 1 cos
sin .cos
cos
xx
xx xxx x
Ax
x
x xx x
xx
xx
x
−−
−− −
= = = = = −
−
−
−
Câu 24: Tính giá trị của biểu thức
6 6 22
sin cos 3sin cos
A =++
α α αα
.
Lời giải
Ta có:
( ) ( )
2
6 6 2 2 22 2 2 22
sin cos sin cos 3sin cos sin cos 1 3sin cos+= + − + =−
α α α α αα α α αα
.
Suy ra:
22 22
1 3sin cos 3sin cos 1A =−+=
αα αα
.
Câu 25: Cho
0
2
π
α
<<
. Tính
1 sin 1 sin
1 sin 1 sin
αα
αα
+−
+
−+
Lời giải
Đặt
1 sin 1 sin
1 sin 1 sin
A
αα
αα
+−
= +
−+
Khi đó
2
2
1 sin 1 sin
1 sin 1 sin
A
αα
αα
+−
= +
−+
2
4
cos
α
=
Vì
0
2
π
α
<<
nên
cos 0
α
>
do đó
2
cos
A
α
=
DẠNG 4: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC LƯỢNG GIÁC
Câu 26: Giá trị lớn nhất của
66
sin cosQxx
bằng:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
Lời giải
Ta có
66 2
3
sin cos 1 sin 2
4
Qxx x
.
Vì
222
33 1 3
0 sin 2 1 sin 2 0 1 sin 2 1
44 4 4
xxx
.
Nên giá trị lớn nhất là
1.
.
Câu 27: Giá trị lớn nhất của biểu thức
22
7cos 2sinM xx= −
là.
Lời giải
( )
22 2
7 1 sin 2sin 7 9sin
M xx x=−− =−
.
Ta có:
22 2
0 sin 1, 0 9sin 9, 7 7 2sin 2,xx xx xx≤ ≤ ∀ ∈ ⇔ ≥− ≥− ∀ ∈ ⇔ ≥ − ≥− ∀ ∈
.
Gía trị lớn nhất là
7
.
Câu 28: Tìm giá trị nhỏ nhất của biểu thức
4 4 22
cot cot 2 tan .tan 2
P a b ab
=++ +
Lời giải
(
)
(
) (
)
(
)
( )
(
)
(
)
2
2 2 22 22
2
22 2222
2
22 2222
2
2
22
cot cot 2cot .cot 2 tan .tan 2
cot cot 2 cot .cot tan .tan 2 6
cot cot 2 cot .cot tan .tan 2cot .cotb.tan .tan 6
cot cot 2 cot .cot tan .tan 6 6
P a b ab ab
a b ab ab
a b a b a b a ab
a b ab ab
=−+ + +
= − + + −+
=−+ + − +
= − + − +≥
Dấu bằng xảy ra khi
2
22
2
cot 1
cot cot
cot .cot tan .tan
cot 1
a
ab
ab ab
b
=
=
⇔
=
=
,( )
42
k
ab k
ππ
⇔== + ∈
.
Câu 29: Tính giá trị lượng giác còn lại của góc
x
biết:
a.
3
sin
5
x
với
3
2
x
. b.
1
cos
4
x
với
0
2
x
.
c.
3
cos
5
x
với
0
0 90x
. d.
5
cos
13
x
với
00
180 270
x
.
Lời giải
a. Do
sin 0
cos 0
3
tan 0
2
cot 0
x
x
x
x
x
.
Từ đó với
2
sin 3
tan
34
cos 4
sin cos 1 sin
cos 4
55
cot
sin 3
x
x
x
xx x
x
x
x
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
b. Do
sin 0
cos 0
0
tan 0
2
cot 0
x
x
x
x
x
.
Từ đó với
2
sin
tan 15
1 15
cos
cos sin 1 cos
cos 1
44
cot
sin
15
x
x
x
xx x
x
x
x
.
c. Do
0
sin 0
cos 0
0 90
tan 0
cot 0
x
x
x
x
x
.
Từ đó với
2
sin 4
tan
34
cos 3
cos sin 1 cos
cos 3
55
cot
sin 4
x
x
x
xx x
x
x
x
.
d. Do
00
sin 0
cos 0
180 270
tan 0
cot 0
x
x
x
x
x
.
Từ đó với
2
sin 12
tan
5 12
cos 5
cos sin 1 cos
cos 5
13 13
cot
sin 12
x
x
x
xxx
x
x
x
.
Câu 30: Tính giá trị lượng giác còn lại của góc
x
biết
a)
2
cos
5
x
với
0
2
x
. b)
4
cos
5
x
với
270 360 x
.
c)
5
sin
13
x
với
2
x
d)
1
sin
3
x
với
180 270 x
.
Lời giải
a) Do
0
2
x
sin 0
cos 0
tan 0
cot 0
x
x
x
x
.
Từ đó với
2
cos
5
x
2
5
sin 1 cos
5
xx
sin 1
tan
cos 2
1
cot 2
tan
x
x
x
x
x
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
b) Do
270 360 x
sin 0
cos 0
tan 0
cot 0
x
x
x
x
.
Từ đó với
4
cos
5
x
2
3
sin 1 cos
5
xx
sin 3
tan
cos 4
14
cot
tan 3
x
x
x
x
x
.
c) Do
2
x
sin 0
cos 0
tan 0
cot 0
x
x
x
x
.
Từ đó với
5
sin
13
x
2
12
cos 1 sin
13
xx
sin 5
tan
cos 12
1 12
cot
tan 5
x
x
x
x
x
.
d) Do
180 270 x
sin 0
cos 0
tan 0
cot 0
x
x
x
x
.
Từ đó với
1
sin
3
x
2
22
cos 1 sin
3
xx
sin 2
tan
cos 4
1
cot 2 2
tan
x
x
x
x
x
.
Câu 31: Tính giá trị lượng giác còn lại của góc
x
biết
a)
tan 3x
với
3
2
x
. b)
tan 2x
với
2
x
.
c)
1
tan
2
x
với
2
x
d)
cot 3x
với
3
2
x
.
Lời giải
a)
tan 3x
1
cot
3
x
tan 3x
sin
3
cos
x
x
22
sin 9cosxx
22
sin 9 1 sin 0 xx
2
9
sin
10
x
.
Vì
3
2
x
sin 0
cos 0
x
x
Do đó
3 10
sin
10
x
;
10
cos
10
x
.
b)
tan 2x
1
cot
2
x

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
tan 2
x
sin
2
cos
x
x
22
sin 4cosxx
22
sin 4 1 sin 0
xx
2
4
sin
5
x
.
Vì
2
x
sin 0
cos 0
x
x
Do đó
25
sin
5
x
;
5
cos
5
x
.
c)
1
tan
2
x
cot 2 x
1
tan
2
x
sin 1
cos 2
x
x
22
4sin cosxx
22
4sin 1 1 sin 0 xx
2
1
sin
5
x
.
Vì
2
x
sin 0
cos 0
x
x
Do đó
5
sin
5
x
;
25
cos
5
x
.
d)
cot 3x
1
tan
3
x
1
tan
3
x
sin 1
cos 3
x
x
22
9sin cos
xx
22
9sin 1 sin 0 xx
2
1
sin
10
x
.
Vì
3
2
x
sin 0
cos 0
x
x
Do đó
10
sin
10
x
;
3 10
cos
10
x
.
Câu 32: Tính giá trị lượng giác của các biểu thức sau:
a) Cho
tan 2.x
Tính:
12
5cot 4 tan 2sin cos
,.
5cot 4 tan cos 3sin
x x xx
AA
x x xx
b) Cho
cot 2.
x
Tính:
12
3sin cos sin 3cos
,.
sin cos sin 3cos
xx x x
BB
xx x x
c) Cho
cot 2.x
Tính:
12
2
2sin 3cos 2
,.
3sin 2cos cos sin cos
xx
CC
x x x xx
d) Cho
3
sin ,0 .
52
xx
Tính:
cot tan
.
cot tan
xx
E
xx
e) Cho
00
1
sin ,90 180 .
5
xx
Tính:
2
8tan 3cot 1
.
tan cot
xx
F
xx
Lời giải
a)
11
5
4. 2
1 5cot 4 tan 21
2
tan 2 cot
5
2 5cot 4 tan 11
4. 2
2
xx
x x AA
xx
2 22 2 2
sin 4
tan 2 2 sin 4cos sin 4 1 sin 0 sin
cos 5
x
x x xx x x
x
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
+) TH1:
sin 0
21
0 sin ;cos
cos >0
2
55
x
x xx
x
2
21
2.
2sin cos 5
55
1
12
cos 3sin
5
3.
55
xx
A
xx
+) TH2:
sin 0
21
sin ;cos
cos <0
2
55
x
x xx
x
2
21
2.
2sin cos 3
55
.
12
cos 3sin 7
3.
55
xx
A
xx
b)
222 2 2
cos 2
cot 2 2 cos 2sin cos 2 1 cos cos
sin 3
x
x x xx x x
x
+) TH1:
sin 0
21
0 cos ;sin
cos >0
23
3
x
x xx
x
1
2
12
3.
3sin cos 3 2
33
5 42
sin cos
1 212
3
3
12
3.
sin 3cos 1 3 2 19 6 2
3
3
sin 3cos 17
1 2 1 32
3.
3
3
xx
B
xx
xx
B
xx
+) TH2:
sin 0
21
cos ;sin
cos <0
23
3
x
x xx
x
1
2
12
3.
3sin cos 3 2
33
1 22
sin cos
1 2 12
3
3
12
3.
sin 3cos 1 3 2 19 6 2
3
3
sin 3cos 17
1 2 1 32
3.
3
3
xx
B
xx
xx
B
xx
c)
2 22 2 2
cos 4
cot 2 2 cos 4sin cos 4 1 cos cos
sin 5
x
x x xx x x
x
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
+) TH1:
sin 0
21
0 cos ;sin
cos >0
2
55
x
x xx
x
1
2
2
12
2. 3.
2sin 3cos 2 3.2
55
8
12
3sin 2cos 3 2.2
3. 2.
55
2 22
5
4 12 2
cos sin cos
.
55
55
xx
C
xx
C
x xx
+) TH2:
sin 0
21
cos ;sin
cos <0
2
55
x
x xx
x
1
2
2
12
2. 3.
2sin 3cos 2 3.2 4
55
12
3sin 2cos 3 2.2 7
3. 2.
55
2 2 25
4 12 6
cos sin cos 3
.
55
55
xx
C
xx
C
x xx
d)
sin 0
0
cos 0
2
x
x
x
2
34
cos 1
55
x
sin 3
tan
cos 4
x
x
x
;
4
cot
3
x
.
43
cot tan 25
34
43
cot tan 7
34
xx
E
xx
.
e) Ta có
sin 0
90 180
cos 0
oo
x
x
x
2
1 22
cos 1
33
x
sin 1
tan
cos
22
x
x
x
;
cot 2 2x
.
Do đó
2
2
1
8. 3.2 2 1
8tan 3cot 1 8
22
1
tan cot 3
22
22
xx
F
xx
.
Câu 33: Chứng minh các đẳng thức sau:
a)
22 2
cos sin 1 2sin xx x
. b)
22
2cos 1 1 2sinxx
c)
22
3 4sin 4cos 1 xx
d)
sin cot cos tan sin cos xxxxxx
Lời giải
a) Ta có
22 2 2 2
cos sin 1 sin cos 1 2sin
xx x x x
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
b) Ta có
222
2cos 1 2 1 sin 1 1 2sin
xxx
.
c) Có
2 22
3 4sin 3 4 1 cos 4cos 1 x xx
.
d) Ta có
cos sin
sin cot cos tan sin . cos . sin cos
sin cos
xx
xxxxx x xx
xx
.
Câu 34: Chứng minh các đẳng thức sau:
a.
4 4 22
sin cos 1 2sin .cos
x x xx
b.
44 22
cos sin cos sin
xx xx
c.
2
4cos 3 1 2sin 1 2sin x xx
d.
2 22
1 cos sin cos cos sin
xxx x x
Lời giải
a.
2
4 4 2 2 22 22
sin cos sin cos 2sin .cos 1 2sin .cos x x x x xx xx
b.
44 222 2 22
cos sin cos sin cos sin cos sin xx xxxx xx
c.
2 22
1 2sin 1 2sin 1 4sin 1 4 1 cos 4cos 3 xx x xx
d.
2 2 22
1 cos sin cos cos 1 cos 1 cos 1 cos sin xxx x x x x x
Câu 35: Chứng minh các đẳng thức sau:
a.
44 2 2
sin cos 1 2cos 2sin 1
xx x x
b.
33
sin .cos sin .cos sin .cosxx x x xx
c.
2 2 22
tan sin tan .sinx x xx
d.
2 2 22
cot cos cot .cosx x xx
Lời giải
a.
44
sin cosxx
2 22 2
sin cos cos sin x xx x
22
cos sin
xx
22
1 sin sin xx
2
2sin 1x
2
2 1 cos 1 x
2
1 2cos x
b.
3 3 22
sin .cos sin .cos sin .cos sin cos sin .cos xx x x xx x x xx
c.
22
2 2 2 2 2 22
2 22
sin 1 1 cos
tan sin sin sin 1 sin . tan .sin
cos cos cos
xx
x x x x x xx
x xx
d.
22
2 2 2 2 2 22
2 22
cos 1 1 sin
cot cos cos cos 1 cos . cot .cos
sin
xx
x x x x x xx
sin x sin x x
Câu 36: Chứng minh các đẳng thức sau:
a.
1
tan cot
sin .cos
xx
xx
b.
1 cos sin
sin 1 cos
xx
xx
c.
11
1
1 tan 1 cot
xx
d.
2
11
1 1 tan 0
cos cos
x
xx
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
a.
22
sin cos sin cos 1
tan cot
cos sin sin .cos sin .cos
xx x x
xx
x x xx xx
b.
2 22 22
1 cos sin
1 cos 1 cos sin 1 cos sin sin cos 1
sin 1 cos
xx
x x x xx xx
xx
c.
1 1 1 1 1 tan
1
1
1 tan 1 cot 1 tan 1 tan 1 tan
1
tan
x
xx x xx
x
d.
2 22
2
22 2
1 1 1 sin sin cos 1
1 1 tan 1 0
cos cos cos cos cos
x xx
x
x x xx x
Câu 37: Chứng minh các đẳng thức sau không phụ thuộc vào biến
x
:
a)
44 2
A sin cos 2sin xx x
.
b)
4222
B sin cos sin cos xxxx
.
c)
4 22 2
B cos cos sin sin
x xx x
Lời giải
a) Ta có
44 2 2222 2
sin cos 2sin sin cos sin cos 2sin xx x xxxx x
22
sin cos 1.
xx
b) Ta có
4222222 2
B sin cos sin cos sin sin cos cos
xxxxxxx x
22
1. sin cos 1. xx
c) Ta có
4 222 222 2
B cos cos sin sin cos cos sin sin x xxx xxx x
22
cos .1 sin 1 xx
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
BÀI 2. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
DẠNG 1: XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC
Câu 1: Cho góc
α
thoả mãn
90 180
α
°< < °
. Trong các khẳng định sau, khẳng định nào đúng?
A.
sin 0
α
<
. B.
cos 0
α
≥
. C.
tan 0
α
<
. D.
cot 0
α
>
.
Câu 2: Cho
5
2
2
π
πα
<<
. Chọn mệnh đề đúng.
A.
tan 0
α
>
. B.
cot 0
α
<
. C.
sin 0
α
<
. D.
cos 0
α
<
.
Câu 3: Cho
3
2
π
πα
<<
, tìm phát biểu đúng trong các phát biểu sau:
A.
sin 0.x >
B.
cos 0.x >
C.
tan 0.
x >
D.
cot 0.x <
Câu 4: Cho góc
α
thỏa
3
2
π
απ
− < <−
. Tìm mệnh đề đúng trong các mệnh đề sau.
A.
cos 0
α
>
. B.
cot 0
α
>
. C.
sin 0
α
>
. D.
tan 0
α
>
.
Câu 5: Cho
2021 2023
44
x
ππ
<<
. Khẳng định nào sau đây đúng?
A.
sin 0,cos 2 0xx>>
. B.
sin 0, cos 2 0xx<>
. C.
sin 0,cos 2 0xx><
. D.
sin 0, cos 2 0xx<<
.
Câu 6: Ở góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau
đây.
A.
sin 0
α
>
. B.
cos 0
α
<
. C.
tan 0
α
<
. D.
cot 0
α
<
.
Câu 7: Cho
5
2
2
<<
π
πα
. Kết quả đúng là:
A.
tan 0;cot 0>>
αα
. B.
tan 0;cot 0<<
αα
. C.
tan 0;cot 0><
αα
. D.
tan 0;cot 0<>
αα
.
Câu 8: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
sin , cos
αα
cùng dấu?
A. Thứ
II.
B. Thứ
IV.
C. Thứ
II
hoặc
IV.
D. Thứ
I
hoặc
III.
Câu 9: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
2
cos 1 sin .
αα
= −
A. Thứ
II.
B. Thứ
I
hoặc
II.
C. Thứ
II
hoặc
III.
D. Thứ
I
hoặc
IV.
Câu 10: Cho
2
<<
π
απ
. Kết quả đúng là:
A.
sin 0;cos 0>>
αα
. B.
sin 0; cos 0<<
αα
. C.
sin 0;cos 0><
αα
. D.
sin 0; cos 0<>
αα
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
Câu 11: Ở góc phần tư thứ tư của đường tròn lượng giác. hãy chọn kết quả đúng trong các kết quả sau
đây.
A.
tan 0
α
>
. B.
sin 0
α
>
. C.
cos 0
α
>
. D.
cot 0
α
>
.
Câu 12: Cho
α
thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các
kết quả sau đây.
A.
sin 0.
α
>
B.
cos 0.
α
<
C.
tan 0.
α
<
D.
cot 0.
α
<
Câu 13: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
sin , tan
αα
trái dấu?
A. Thứ
I.
B. Thứ
II
hoặc
IV.
C. Thứ
II
hoặc
III.
D. Thứ
I
hoặc
IV.
Câu 14: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
2
sin sin .
αα
=
A. Thứ
III.
B. Thứ
I
hoặc
III.
C. Thứ
I
hoặc
II.
D. Thứ
III
hoặc
IV.
Câu 15: Cho
0
1500
a
=
.Xét câu nào sau đây đúng?
I.
3
sin
2
α
=
. II.
1
cos
2
α
=
. III.
tan 3
α
=
.
A. Chỉ I và II. B. Chỉ II và III. C. Cả I, II và III. D. Chỉ I và III.
Câu 16: Cho
10
3
3
π
πα
<<
.Xét câu nào sau đây đúng?
A.
cos 0
α
>
. B.
sin 0
α
<
. C.
tan 0
α
<
. D.
cot 0
α
<
.
Câu 17: Cho
7
2
4
π
απ
<<
. Khẳng định nào sau đây đúng?
A.
cos 0
α
>
. B.
sin 0
α
>
. C.
tan 0
α
>
. D.
cot 0
α
>
.
Câu 18: Cho
2
π
απ
<<
. Xét các mệnh đề sau:
I.
cos 0
2
π
α
−>
. II.
sin 0
2
π
α
−>
. III.
tan 0
2
π
α
−>
.
Mệnh đề nào sai?
A. Chỉ I. B. Chỉ II. C. Chỉ II và III. D. Cả I, II và III.
Câu 19: Cho
2
π
απ
<<
. Xét các mệnh đề sau đây:
I.
cos 0
2
π
α
+<
. II.
sin 0
2
π
α
+<
. III.
cot 0
2
π
α
+>
.
Mệnh đề nào đúng?
A. Chỉ I. B. Chỉ I và II. C. Chỉ II và III. D. Cả I, II và III.
Câu 20: Bất đẳng thức nào dưới đây là đúng?
A.
sin 90 sin150°< °
. B.
sin 90 15' sin 90 30'°< °
.
C.
cos90 30' cos100°> °
. D.
cos150 cos120°> °
.
Câu 21: Cho hai góc nhọn
α
và
β
phụ nhau. Hệ thức nào sau đây là sai?
A.
sin cos
αβ
= −
. B.
cos sin
αβ
=
. C.
cos sin
βα
=
. D.
cot tan
αβ
=
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Câu 22: Cho
0.
2
π
α
<<
Khẳng định nào sau đây đúng?
A.
( )
sin 0.
απ
−≥
B.
( )
sin 0.
απ
−≤
C.
( )
sin 0.
απ
−>
D.
( )
sin 0.
απ
−<
Câu 23: Cho
0.
2
π
α
<<
Khẳng định nào sau đây đúng?
A.
cot 0.
2
π
α
+>
B.
cot 0.
2
π
α
+≥
C.
( )
tan 0.
απ
+<
D.
( )
tan 0.
απ
+>
Câu 24: Cho
.
2
π
απ
<<
Giá trị lượng giác nào sau đây luôn dương?
A.
( )
sin .
πα
+
B.
cos .
2
π
α
−
C.
( )
cos .
α
−
D.
( )
tan .
πα
+
Câu 25: Cho
3
.
2
π
πα
<<
Khẳng định nào sau đây đúng?
A.
3
tan 0.
2
π
α
−<
B.
3
tan 0.
2
π
α
−>
C.
3
tan 0.
2
π
α
−≤
D.
3
tan 0.
2
π
α
−≥
Câu 26: Cho
.
2
π
απ
<<
Xác định dấu của biểu thức
( )
cos .tan .
2
M
π
α πα
= −+ −
A.
0.M ≥
B.
0.M >
C.
0.M ≤
D.
0.
M <
Câu 27: Cho
3
2
π
πα
<<
. Xác định dấu của biểu thức
( )
sin .cot .
2
M
π
α πα
=−+
A.
0.M ≥
B.
0.M >
C.
0.M ≤
D.
0.M <
DẠNG 2: TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
Câu 28: Cho
1
cos = ;
62
π
α πα
−−
−< <
. Tính
sin
α
.
A.
35
sin
6
α
−
=
. B.
35
sin
36
α
=
. C.
5
sin
6
α
=
. D.
35
sin
6
α
=
.
Câu 29: Tính
sin
α
, biết
5
cos
3
α
=
và
3
2
2
π
απ
<<
.
A.
1
3
. B.
1
3
−
. C.
2
3
. D.
2
3
−
.
Câu 30: Cho
2
cos 0
2
5
xx
π
= − <<
thì
sin x
có giá trị bằng
A.
3
5
. B.
3
5
−
. C.
1
5
−
. D.
1
5
Câu 31: Cho
1
sin
4
α
=
biết
00
0 90
α
<<
. Tính
cos ; tan
αα
A.
15 15
cos ;tan
4 15
αα
=−=
. B.
15 15
cos ;tan
4 15
αα
=−=−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
C.
15 15
cos ; tan
4 15
αα
= = −
. D.
15 15
cos ; tan
4 15
αα
= =
.
Câu 32: Cho
2
cos
5
= −
α
( )
oo
90 180<<
α
, khi đó
tan
α
bằng:
A.
21
5
. B.
21
2
−
. C.
21
5
−
. D.
21
3
.
Câu 33: Cho
3
sin
5
α
=
và
2
π
απ
<<
. Giá trị của
cos
α
là:
A.
4
5
. B.
4
5
−
. C.
4
5
±
. D.
16
25
.
Câu 34: Cho
3
sin
5
α
= −
và
3
2
π
πα
<<
. Khi đó giá trị của
cos
α
và
tan
α
lần lượt là
A.
43
;
54
−
. B.
43
;
54
−−
. C.
43
;
54
−
. D.
34
;
45
−
.
Câu 35: Cho
cos
4
5
α
= −
với
2
π
απ
< <
. Tính giá trị của biểu thức
10si csn 5oM
αα
+=
.
A.
10−
. B.
2
. C.
1
. D.
1
4
.
Câu 36: Cho
cos
1
3
α
=
và
7
4
2
π
απ
<
<
. Khẳng định nào sau đây đúng?
A.
22
sin
3
α
= −
. B.
22
sin
3
α
=
. C.
2
sin
3
α
=
. D.
2
sin
3
α
= −
.
Câu 37: Cho góc
α
thỏa mãn
0
2
π
α
−<<
và
1
cos
2
α
=
. Giá trị của biểu thức
1
sin
cos
P
α
α
= +
bằng
A.
43
2
+
. B.
43
2
−
. C.
13
2
−
. D.
13
2
+
.
Câu 38: Nếu
3
tan
4
α
=
thì
2
sin
α
bằng
A.
16
25
. B.
9
25
. C.
25
16
. D.
25
9
.
Câu 39: Cho
tan 3
x =
. Tính
2sin cos
sin cos
xx
P
xx
−
=
+
.
A.
3
2
P =
. B.
5
4
P =
. C.
3P
=
. D.
2
5
P =
.
Câu 40: Cho
1
sin
3
a =
. Giá trị của biểu thức
cot tan
tan 2co t
aa
A
aa
−
=
+
bằng
A.
1
9
. B.
7
9
. C.
17
81
. D.
7
17
.
Câu 41: Cho
tan 4.x = −
Giá trị của biểu thức
2sin 5cos
3cos sin
xx
A
xx
−
=
+
là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
A.
13
. B.
13
−
. C.
13
11
. D.
5
.
Câu 42: Cho
tan 3
α
=
, khi đó giá trị của biểu thức
2sin cos
3sin 5cos
P
αα
αα
−
=
−
là
A.
5
2
P = −
. B.
5
4
P =
. C.
1P
=
. D.
3P
= −
.
Câu 43: Cho
cot 3= −
α
. Giá trị của biểu thức
3cos 4sin
2sin cos
P
−
=
+
αα
αα
bằng
A.
13
−
. B.
13
. C.
3−
. D.
3
.
Câu 44: Cho
cot 4 tan
αα
=
và
;
2
π
απ
∈
. Khi đó
sin
α
bằng
A.
5
5
−
. B.
1
2
. C.
25
5
. D.
5
5
.
Câu 45: Nếu
tan cot 2
αα
+=
thì
22
tan cot
αα
+
bằng bao nhiêu?
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 46: Biết
2
sin cos
2
+=
αα
. Trong các kết quả sau, kết quả nào sai?
A.
1
sin cos
4
= −
αα
. B.
6
sin cos
2
−=±
αα
.
C.
44
7
sin cos
8
+=
αα
. D.
22
tan cot 12
+=
αα
.
Câu 47: Nếu
(
)
( ) (
)
22
cot tan sin 1445 cos 1085
2
oo
xx
π
π
+− − = − +
thì
sin
x
bằng.
A.
1
5
±
. B.
2
5
±
. C.
1
5
±
. D.
2
5
±
.
Câu 48: Cho biết
1
sin cos
2
aa−=
. Kết quả nào sau đây đúng?
A.
3
sin .cos
8
aa=
. B.
7
sin cos
4
aa+=
.
C.
44
21
sin cos
32
aa
+=
. D.
22
14
tan cot
3
aa+=
.
Câu 49: Biết
1
tan
2
x =
, giá trị của biểu thức
22
22
2sin 3sin .cos 4cos
5cos sin
x xx x
M
xx
+−
=
−
bằng:
A.
8
13
−
. B.
2
19
. C.
2
19
−
. D.
8
19
−
.
Câu 50: Nếu
( )
( )
cot1, 25.tan 4 1, 25 sin .cos 6 0
2
xx
π
ππ
+ − + −=
thì
tan x
bằng
A.
1
. B.
1−
. C.
0
. D. Giá trị khác.
Câu 51: Biết
2
tan
b
x
ac
=
−
. Giá trị của biểu thức
22
cos 2 sin . sinA a x b x cosx c x=++
bằng

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
A.
–a
. B.
a
. C.
–b
. D.
b
.
Câu 52: Nếu biết
44
sin s 1x co x
a b ab
+=
+
thì biểu thức
33
33
sin sx co x
ab
+
bằng:
A.
( )
2
1
ab+
. B.
22
1
ab+
. C.
( )
3
1
ab+
. D.
33
1
ab+
.
Câu 53: Nếu biết
44
98
3sin 2cos
81
xx+=
thì giá trị biểu thức
44
2sin 3cosAxx= +
bằng
A.
101
81
hay
601
504
. B.
103
81
hay
603
405
. C.
105
81
hay
605
504
. D.
107
81
hay
607
405
.
Câu 54: Nếu
44
sin cos 1
a b ab
αα
+=
+
thì biểu thức
10 10
44
sin cos
M
ab
αα
= +
bằng.
A.
55
11
ab
+
. B.
( )
5
1
ab+
. C.
44
11
ab
+
. D.
( )
4
1
ab+
.
Câu 55: Nếu biết thì biểu thức bằng:
A. . B. . C. . D. .
Câu 56: Nếu
3cos 2sin 2xx+=
và
sin 0x <
thì giá trị đúng của
sin x
là:
A.
5
13
−
. B.
7
13
−
. C.
9
13
−
. D.
12
13
−
.
Câu 57: Nếu thì bằng:
A. hay . B. hay .
C. hay . D. hay .
DẠNG 3: GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC CÓ LIÊN QUAN ĐẶC BIỆT
Câu 58: Tính
000
tan 20 tan 45 tan 70L =
A.
0
. B.
1
. C.
1−
. D.
2
.
Câu 59: Tính
22 2 2
25
cos cos ... cos cos
66 6
G
ππ π
π
= + ++ +
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 60: Tính
000
sin 390 2sin1140 3cos1845A =−+
A.
( )
1
132 23
2
+−
. B.
( )
1
132 23
2
−−
. C.
( )
1
1 23 32
2
+−
. D.
( )
1
1 23 32
2
++
.
Câu 61: Giá trị đúng của biểu thức
tan 225 cot81 .cot 69
cot 261 tan 201
° °°
°°
−
+
bằng:
44
sin cos 1
a b ab
αα
+=
+
88
33
sin cos
A
ab
αα
= +
2
1
()
ab+
22
1
ab+
3
1
()ab+
33
1
ab+
sin co
1
2
sxx+=
3sin 2cosxx+
57
4
−
57
4
+
55
7
−
55
4
+
23
5
−
23
5
+
32
5
−
32
5
+

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
A.
1
3
. B.
1
3
−
. C.
3
. D.
3−
.
Câu 62: Với mọi góc
α
, biểu thức
29
cos cos cos ... cos
55 5
ππ π
αα α α
+++++++
nhận giá trị
bằng
A.
10
. B.
10
−
. C.
1
. D.
0
.
Câu 63: Tính
22 2 2
25
sin sin ... sin sin
66 6
F
ππ π
π
= + ++ +
.
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 64: Đơn giản biểu thức
( ) ( )
5
sin cos 13 3sin 5
2
D
π
α πα α π
= −+ +− −
.
A.
3sin 2cos
αα
−
. B.
3sin
α
. C.
3sin
α
−
. D.
2cos 3sin
αα
+
.
Câu 65: Giả sử
tan tan tan
33
Ax x x
ππ
= −+
được rút gọn thành
tanA nx=
khi đó
n
bằng
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 66: Nếu
sin 3cos
xx=
thì
sin cosxx
bằng
A.
3
10
. B.
2
9
. C.
1
4
. D.
1
6
.
Câu 67: Với mọi
α
thì
3
sin
2
π
α
+
bằng
A.
sin
α
−
. B.
cos
α
−
. C.
cos
α
. D.
sin
α
.
Câu 68: Giá trị
89
cot
6
π
bằng
A.
3
. B.
3−
. C.
3
3
. D.
3
3
−
.
Câu 69: Đơn giản biểu thức
cos
2
A
π
α
= −
, ta được:
A.
cos
α
. B.
sin
α
. C.
– cos
α
. D.
sin
α
−
.
Câu 70: Nếu
2
1
sin
3
α
=
thì
2
1 tan
α
+
bằng
A.
9
8
. B.
4
. C.
3
2
. D.
8
9
.
Câu 71: Tính
cot1 .cot 2 .cot 3 ...cot89P =°°° °
.
A.
0
. B.
1
. C.
3
. D.
4
.
Câu 72: Giá trị của biểu thức
tan110 tan 340 sin160 cos110 sin 250 cos340
° °+ ° °+ ° °
bằng
A.
0
. B.
1
. C.
1−
. D.
2
.
Câu 73: Rút gọn biểu thức
( )
00
0
00
sin 234 cos 216
A .tan 36
sin144 cos126
−−
=
−
, ta được

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
A.
A2=
. B.
A2= −
. C.
A1=
. D.
A1= −
.
Câu 74: Giá trị của biểu thức A =
( )
00
0 00
2sin 2550 .cos 188
1
tan 368 2cos638 cos98
−
+
+
bằng:
A.
1
. B.
2
. C.
1−
. D.
0
.
Câu 75: Với mọi α, biểu thức:
9
cos +cos ... cos
55
A
ππ
αα α
= + ++ +
nhận giá trị bằng:
A.
–10
. B.
10
. C.
0
. D.
5
.
Câu 76: Biểu thức
(
)
(
) (
)
( )
00 0 0
0
0
sin 328 .sin 958 cos 508 .cos 1022
cot 572
tan 212
A
− −−
= −
−
rút gọn bằng:
A.
1−
. B.
1
. C.
0
. D.
2
.
DẠNG 4: RÚT GỌN BIỂU THỨC LƯỢNG GIÁC. ĐẲNG THỨC LƯỢNG GIÁC
Câu 77: Biểu thức
22 2 2 2
cos cot 3cos cot 2sinD xx x x x
= + −+
không phụ thuộc
x
và bằng:
A.
2
. B.
2−
. C.
3
. D.
3
−
.
Câu 78: Đơn giản biểu thức
(
)
( )
5
sin cos 13 3sin 5
2
D a aa
π
ππ
= −+ +− −
A.
2cos 3sinaa+
. B.
3sin 2cos
aa−
. C.
3sin a−
. D.
4cos sinaa−
.
Câu 79: Đơn giản biểu thức
33 77
cos sin cos sin
22 22
C a aa a
ππ ππ
= −− −+ − − −
A.
2sin a
. B.
2sin a−
. C.
2cos a
. D.
2cos a−
.
Câu 80: Biểu thức
22
22
22
sin
cot cot
sin sin
−
= −
cos x y
B xy
xy
không phụ thuộc vào
,xy
và bằng
A.
2
. B.
2
−
. C.
1
. D.
1−
.
Câu 81: Rút gọn biểu thức
2
2cos 1
sin cos
x
A
xx
−
=
+
, ta được kết quả
A.
sin cosAxx= +
. B.
cos sinA xx= −
. C.
cos 2 sin 2A xx= −
. D.
cos 2 sin 2A xx= +
.
Câu 82: Biểu thức rút gọn của A =
22
22
tan sin
cot cos
aa
aa
−
−
bằng:
A.
6
tan
a
. B.
6
cos a
. C.
4
tan a
. D.
6
sin a
.
Câu 83: Hệ thức nào sai trong bốn hệ thức sau:
A.
tan tan
tan .tan
cot cot
xy
xy
xy
+
=
+
. B.
2
2
1 sin 1 sin
4 tan
1 sin 1 sin
aa
a
aa
+−
−=
−+
.
C.
2
2
sin cos 1 cot
cos sin cos sin 1 cot
αα α
αα αα α
+
−=
+ −−
. D.
sin cos 2cos
1 cos sin cos 1
αα α
α αα
+
=
− −+
.
Câu 84: Biết
tan 3x =
và
22
22
2sin 3sin .cos 4cos
5tan 6cot
x xx x
M
xx
++
= ⋅
+
Giá trị của
M
bằng.
A.
31
47
M = ⋅
B.
93
137
M = ⋅
C.
93
1370
M = ⋅
D.
31
51
M = ⋅

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
Câu 85: Giả sử
44
1
3sin cos
2
xx−=
thì
44
sin 3cosxx+
có giá trị bằng
A.
1
. B.
2
. C.
3
. D.
4
Câu 86: Rút gọn biểu thức
(
) (
)
22
85 5
sin cos 2017 sin 33 sin
22
Ax x x x
ππ
ππ
= + + ++ ++ −
ta được:
A.
sin
Ax=
. B.
1A =
. C.
2A =
. D.
0A =
.
Câu 87: Có bao nhiêu đẳng thức đúng trong các đẳng thức sau đây?
i)
2
2
1
cos
tan 1
α
α
=
+
. iii)
2 cos cos sin
4
π
α αα
+= +
.
ii)
sin cos
2
π
αα
−=−
. iv)
2
cot 2 2cot 1
αα
= −
.
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 88: Biểu thức
( )
2
2
2 22
1 tan
1
4 tan 4sin cos
x
A
x xx
−
= −
không phụ thuộc vào
x
và bằng
A.
1
. B.
1−
. C.
1
4
. D.
1
4
−
.
Câu 89: Biểu thức
( )
2
2
2 22
1 tan
1
4 tan 4sin cos
x
x xx
A
−
−=
không phụ thuộc vào
x
và bằng
A.
1
. B.
–1
. C.
1
4
. D.
1
4
−
.
Câu 90: Biểu thức
( )
( )
0 0 00
0 0 00
sin 515 .cos 475 cot 222 .cot 408
cot 415 .cot 505 tan197 .tan 73
A
−+
=
−+
có kết quả rút gọn bằng
A.
20
1
sin 25
2
. B.
20
1
cos 55
2
. C.
20
1
cos 25
2
. D.
20
1
sin 65
2
.
Câu 91: Biểu thức:
( ) ( )
( ) ( )
2003
cos 26 2sin 7 cos1,5 cos cos 1,5 .cot 8
2
A
π
α π απ π α α π απ
= + − −− − + + − −
có
kết quả thu gọn bằng:
A.
sin
α
−
. B.
sin
α
. C.
cos
α
−
. D.
cos
α
.
Câu 92: Biểu thức
( )
( )
( )
2
2
3 1 31
tan .tan . cos . sin 2
3
2 2 sin
cos
2
xx x x
x
x
ππ
ππ
π
π
− + −+ −
−
−
có
kết quả rút gọn bằng:
A.
2
sin
x
. B.
2
cos x
. C.
2
tan x
. D.
2
cot x
.
Câu 93: Cho
20 0 0 2
20 20
cos 696 tan( 260 ).tan530 cos 156
tan 252 cot 342
o
B
+− −
=
+
. Biểu thức thu gọn nhất của
B
là:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
A.
20
1
tan 24
2
. B.
20
1
cot 24
2
. C.
20
1
tan 18
2
. D.
20
1
cot 18
2
.
Câu 94: Cho
(
)
(
)
0 0 00
0 0 00
sin 515 .cos 475 cot 222 .cot 408
cot 415 .cot 505 tan197 .tan 73
A
−+
=
−+
. Biểu thức rút gọn của
A
bằng:
A.
20
1
cos 25
2
. B.
20
1
cos 25
2
−
. C.
20
1
sin 25
2
. D.
20
1
sin 25
2
−
.
Câu 95: Cho biểu thức
3
3
1 tan
,( , , )
(1 tan ) 4 2
x
M x kx kk
x
ππ
ππ
+
= ≠− + ≠ + ∈
+
, mệnh đề nào trong các mệnh
đề sau đúng?
A.
1
M <
. B.
1M ≤
. C.
1
4
M ≥
. D.
1
1
4
M≤≤
.
Câu 96: Hệ thức nào sai trong bốn hệ thức sau:
A.
tan tan
tan tan
cot cot
xy
xy
xy
+
= +
+
. B.
2
2
1 sin 1 sin
4 tan
1 sin 1 sin
+−
−=
−+
αα
α
αα
.
C.
2
sin sin 2
cos sin cos sin 1 cot
−=
+ −−
αα
αα αα α
. D.
sin cos 2cos
1 cos sin cos 1
+
=
− −+
αα α
α αα
.
Câu 97: Tính
( )
( )
sin cos 3 2 cot
2
P
π
α π α πα
= ++ − + −
, biết
1
sin
2
α
= −
và
0
2
π
α
−<<
.
A.
33 1
2
−
. B.
33 3
2
−
. C.
33 3
2
+
. D.
33 1
2
+
.
DẠNG 5: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC LƯỢNG GIÁC
Câu 98: Giá trị nhỏ nhất của
66
sin cos
Mxx= +
là.
A.
0
. B.
1
4
. C.
1
2
. D.
1
.
Câu 99: Giá trị nhỏ nhất của
44
sin cosMxx= +
là.
A.
0
. B.
1
4
. C.
1
2
. D.
1
.
Câu 100: Giá trị lớn nhất của
44
sin cosNxx
bằng:
A.
0.
B.
1.
C.
2.
D.
3.
Câu 101: Giá trị lớn nhất của
44
sin cosM xx
bằng:
A.
1.
B.
2.
C.
3.
D.
4.
Câu 102: Cho
22
6cos 5sinM xx
= +
. Khi đó giá trị lớn nhất của
M
là.
A.
1
. B.
5
. C.
6
. D.
11
.
Câu 103: Giá trị lớn nhất của biểu thức
22
7cos 2sinM xx= −
là.
A.
2−
. B.
5
. C.
7
. D.
16
.
Câu 104: Cho
2
5 2sinMx= −
. Khi đó giá trị lớn nhất của
M
là.
A.
3
. B.
5
. C.
6
. D.
7
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
Câu 105: Tính giá trị nhỏ nhất của
2
cos 2sin 2F aa=++
A.
1−
. B.
0
. C.
1
. D.
2
.
Câu 106: Tính giá trị lớn nhất của
2
2sin sin 3E
αα
= −+
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 107: Giá trị lớn nhất của
66
sin cos
M xx
bằng:
A.
0.
B.
1.
C.
2.
D.
3.
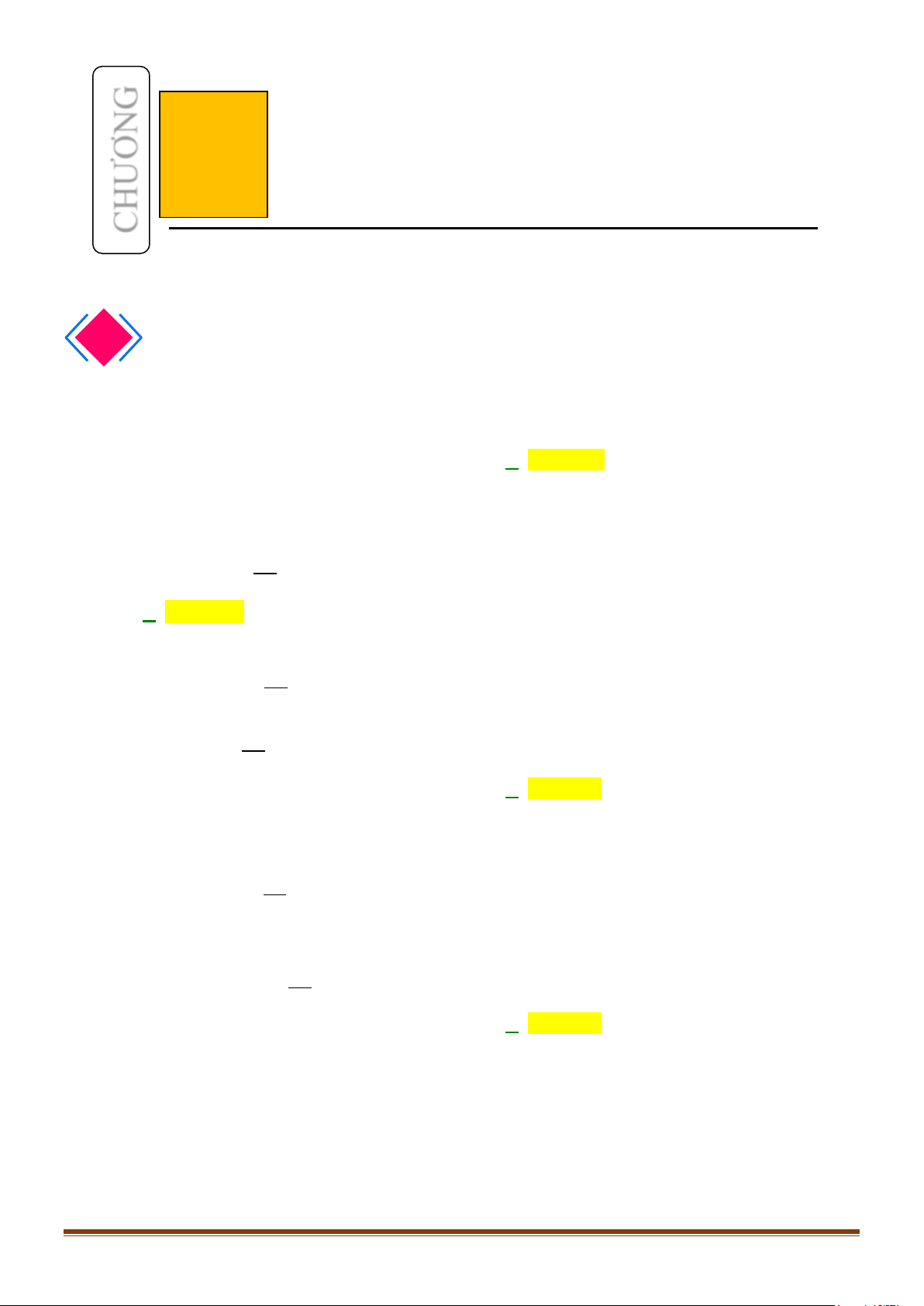
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 1. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
DẠNG 1: XÉT DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC
Câu 1: Cho góc
α
thoả mãn
90 180
α
°< < °
. Trong các khẳng định sau, khẳng định nào đúng?
A.
sin 0
α
<
. B.
cos 0
α
≥
. C.
tan 0
α
<
. D.
cot 0
α
>
.
Lời giải
Khẳng định đúng là
tan 0
α
<
.
Câu 2: Cho
5
2
2
π
πα
<<
. Chọn mệnh đề đúng.
A.
tan 0
α
>
. B.
cot 0
α
<
. C.
sin 0
α
<
. D.
cos 0
α
<
.
Lời giải
Ta có
5
2
2
π
πα
<<
nên
tan 0
α
>
.
Câu 3: Cho
3
2
π
πα
<<
, tìm phát biểu đúng trong các phát biểu sau:
A.
sin 0.x
>
B.
cos 0.x >
C.
tan 0.x >
D.
cot 0.x <
Lời giải
Ta có :
sin 0
cos 0
3
.
tan 0
2
cot 0
x
x
x
x
π
πα
<
<
<< ⇒
>
>
Câu 4: Cho góc
α
thỏa
3
2
π
απ
− < <−
. Tìm mệnh đề đúng trong các mệnh đề sau.
A.
cos 0
α
>
. B.
cot 0
α
>
. C.
sin 0
α
>
. D.
tan 0
α
>
.
Lời giải
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
II
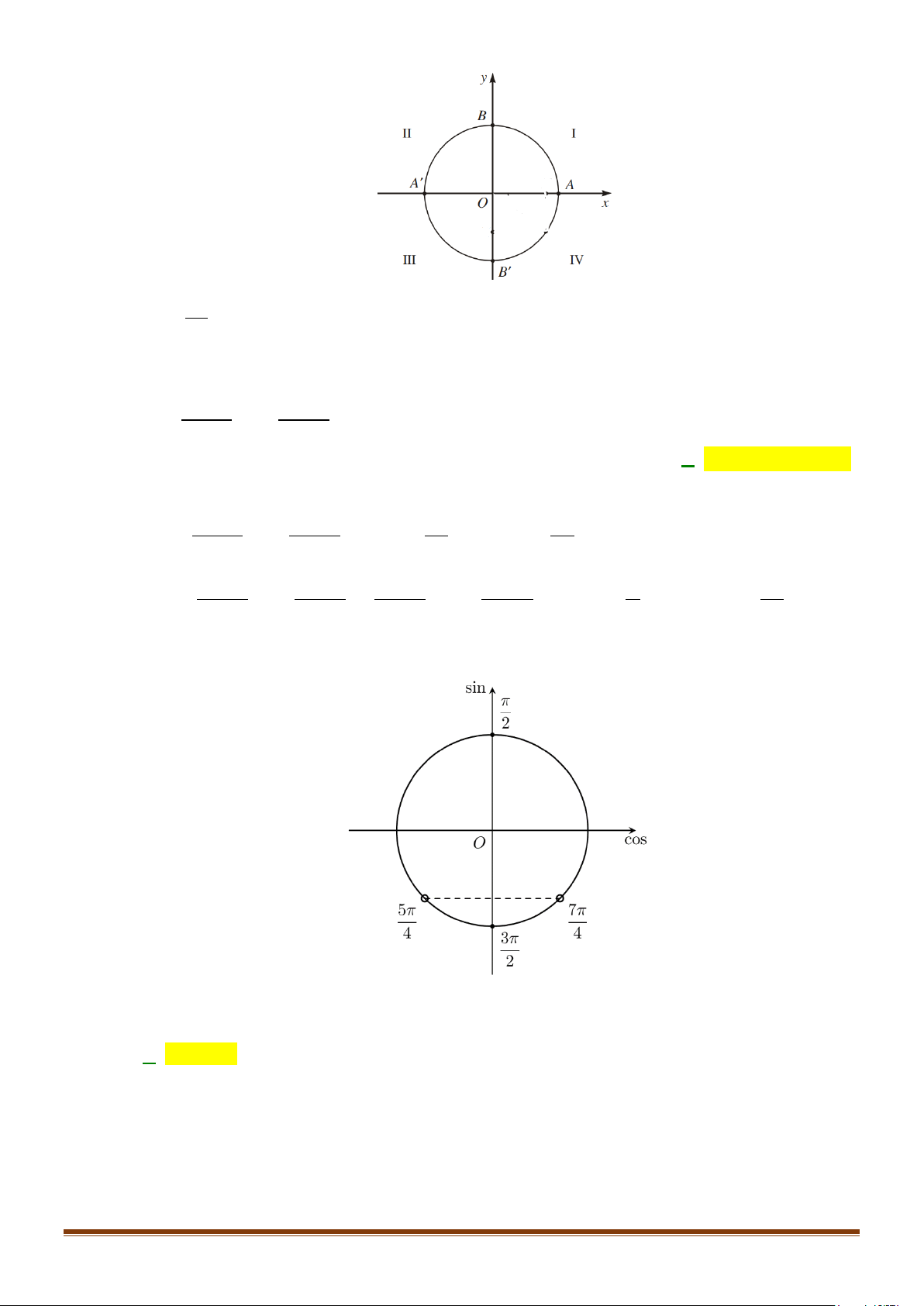
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
Do
3
2
π
απ
− < <−
nên điểm
M
biểu diễn cung
AM
có số
α
thuộc góc phần tư số II. Do đó
sin 0, cos 0, tan 0, cot 0
αααα
><<<
.
Câu 5: Cho
2021 2023
44
x
ππ
<<
. Khẳng định nào sau đây đúng?
A.
sin 0,cos 2 0xx>>
. B.
sin 0, cos 2 0xx
<>
. C.
sin 0,cos 2 0xx><
. D.
sin 0, cos 2 0xx<<
.
Lời giải
Ta có
2021 2023 5 7
504 504
44 4 4
xx
ππ π π
ππ
<< ⇔ + << +
nên
sin 0
x
<
.
Lại có
2021 2023 2021 2023 3
2 1010 2 1010
4 42 2 2 2
xx x
π ππ π π π
ππ
<< ⇔ << ⇔ +<< +
nên
cos 2 0
x <
.
Câu 6: Ở góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau
đây.
A.
sin 0
α
>
. B.
cos 0
α
<
. C.
tan 0
α
<
. D.
cot 0
α
<
.
Lời giải
Nhìn vào đường tròn lượng giác:
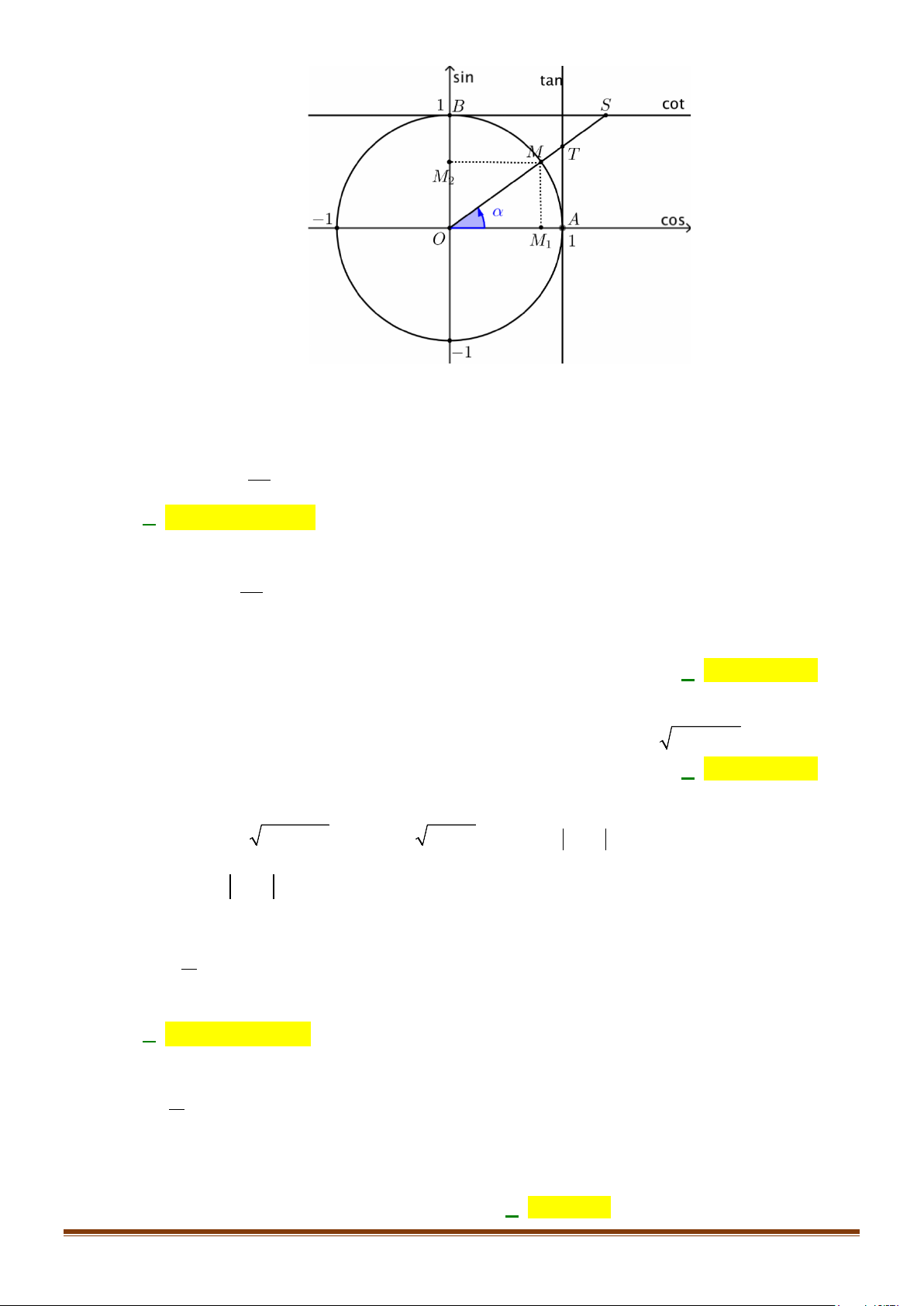
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
-Ta thấy ở góc phần tư thứ nhất thì:
sin 0;cos 0; tan 0;cot 0
αααα
>>>>
=> chỉ có Câu A thỏa mãn.
Câu 7: Cho
5
2
2
<<
π
πα
. Kết quả đúng là:
A.
tan 0;cot 0
>>
αα
. B.
tan 0;cot 0<<
αα
. C.
tan 0;cot 0
><
αα
. D.
tan 0;cot 0<>
αα
.
Lời giải
Vì
5
2
2
<<
π
πα
nên
tan 0;cot 0
>>
αα
Câu 8: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
sin , cos
αα
cùng dấu?
A. Thứ
II.
B. Thứ
IV.
C. Thứ
II
hoặc
IV.
D. Thứ
I
hoặc
III.
Lời giải
Câu 9: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
2
cos 1 sin .
αα
= −
A. Thứ
II.
B. Thứ
I
hoặc
II.
C. Thứ
II
hoặc
III.
D. Thứ
I
hoặc
IV.
Lời giải
Ta có
22
cos 1 sin cos cos cos cos cos .
α αα αααα
=− ⇔= ⇔= ⇔
Đẳng thức
cos cos cos 0
α αα
⇔ → ≥→
điểm cuối của góc lượng giác
ở góc phần tư thứ
I
hoặc
IV.
Câu 10: Cho
2
<<
π
απ
. Kết quả đúng là:
A.
sin 0;cos 0>>
αα
. B.
sin 0; cos 0<<
αα
.
C.
sin 0;cos 0
><
αα
. D.
sin 0; cos 0<>
αα
.
Lời giải
Vì
2
<<
π
απ
nên
tan 0;cot 0<<
αα
.
Câu 11: Ở góc phần tư thứ tư của đường tròn lượng giác. hãy chọn kết quả đúng trong các kết quả sau
đây.
A.
tan 0
α
>
. B.
sin 0
α
>
. C.
cos 0
α
>
. D.
cot 0
α
>
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Lời giải
- Ở góc phần tư thứ tư thì:
sin 0; cos 0; tan 0; cot 0
αααα
<><<
.
⇒
chỉ có C thỏa mãn.
Câu 12: Cho
α
thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các
kết quả sau đây.
A.
sin 0.
α
>
B.
cos 0.
α
<
C.
tan 0.
α
<
D.
cot 0.
α
<
Lời giải
thuộc góc phần tư thứ nhất
sin 0
cos 0
tan 0
cot 0
α
α
α
α
>
>
→
>
>
Câu 13: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
sin , tan
αα
trái dấu?
A. Thứ
I.
B. Thứ
II
hoặc
IV.
C. Thứ
II
hoặc
III.
D. Thứ
I
hoặc
IV.
Lời giải
Câu 14: Điểm cuối của góc lượng giác
α
ở góc phần tư thứ mấy nếu
2
sin sin .
αα
=
A. Thứ
III.
B. Thứ
I
hoặc
III.
C. Thứ
I
hoặc
II.
D. Thứ
III
hoặc
IV.
Lời giải
Ta có
2
sin sin sin sin .
α α αα
⇔⇔ =
Đẳng thức
sin sin sin 0
αα α
= → ≥→
điểm cuối của góc lượng giác
ở góc phần tư thứ
I
hoặc
II.
Câu 15: Cho
0
1500a =
.Xét câu nào sau đây đúng?
I.
3
sin
2
α
=
. II.
1
cos
2
α
=
. III.
tan 3
α
=
.
A. Chỉ I và II. B. Chỉ II và III. C. Cả I, II và III. D. Chỉ I và III.
Lời giải
Bấm máy ta được:
31
sin ; cos = ; tan 3.
22
α αα
= =
=>Cả I, II, III đều đúng.
Câu 16: Cho
10
3
3
π
πα
<<
.Xét câu nào sau đây đúng?
A.
cos 0
α
>
. B.
sin 0
α
<
. C.
tan 0
α
<
. D.
cot 0
α
<
.
Lời giải
10
3 22
33
ππ
πα ππα ππ
<< ⇔ +<< ++
nên α thuộc cung phần tư thứ III vì vậy đáp án đúng là
B

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
Câu 17: Cho
7
2
4
π
απ
<<
. Khẳng định nào sau đây đúng?
A.
cos 0
α
>
. B.
sin 0
α
>
. C.
tan 0
α
>
. D.
cot 0
α
>
.
Lời giải
73
22
4 24
π ππ
απ απ
<< ⇔ +<<
nên α thuộc cung phần tư thứ IV vì vậy đáp án đúng là A
Câu 18: Cho
2
π
απ
<<
. Xét các mệnh đề sau:
I.
cos 0
2
π
α
−>
. II.
sin 0
2
π
α
−>
. III.
tan 0
2
π
α
−>
.
Mệnh đề nào sai?
A. Chỉ I. B. Chỉ II. C. Chỉ II và III. D. Cả I, II và III.
Lời giải
0
22
ππ
απ α
<<⇒−<<
nên α thuộc cung phần tư thứ IV nên chỉ II, II sai.
Câu 19: Cho
2
π
απ
<<
. Xét các mệnh đề sau đây:
I.
cos 0
2
π
α
+<
. II.
sin 0
2
π
α
+<
. III.
cot 0
2
π
α
+>
.
Mệnh đề nào đúng?
A. Chỉ I. B. Chỉ I và II. C. Chỉ II và III. D. Cả I, II và III.
Lời giải
3
2 22
π ππ
απ π α
<<⇒< + <
nên đáp án là D
Câu 20: Bất đẳng thức nào dưới đây là đúng?
A.
sin 90 sin150°< °
. B.
sin 90 15' sin 90 30'
°< °
.
C.
cos90 30' cos100°> °
. D.
cos150 cos120°> °
.
Lời giải
Các góc trong đề bài đều là góc tù, chú ý rằng các góc tù thì nghịch biến với cả hàm
sin
và
cos
Từ đó dễ nhận thấy phương án đúng là phương án C.
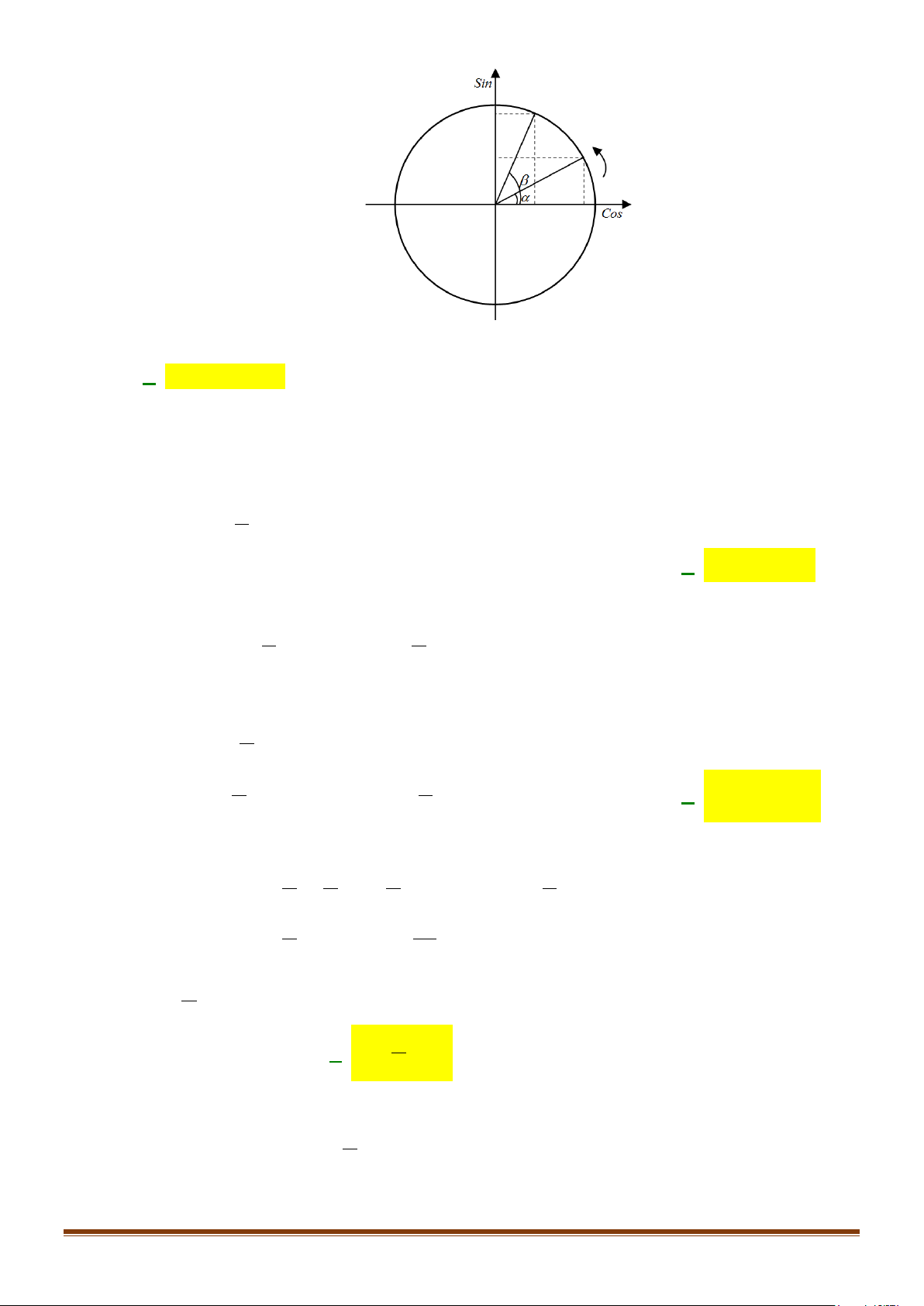
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
Câu 21: Cho hai góc nhọn
α
và
β
phụ nhau. Hệ thức nào sau đây là sai?
A.
sin cos
αβ
= −
. B.
cos sin
αβ
=
. C.
cos sin
βα
=
. D.
cot tan
αβ
=
.
Lời giải
Thường nhớ: các góc phụ nhau có các giá trị lượng giác bằng chéo nhau
Nghĩa là
cos sin
αβ
=
;
cot tan
αβ
=
và ngược lại.
Câu 22: Cho
0.
2
π
α
<<
Khẳng định nào sau đây đúng?
A.
( )
sin 0.
απ
−≥
B.
( )
sin 0.
απ
−≤
C.
( )
sin 0.
απ
−>
D.
( )
sin 0.
απ
−<
Lời giải
Ta có
0
22
ππ
α παπ
→< < →− < − <−
điểm cuối cung
απ
−
thuộc góc phần tư thứ
( )
III sin 0.
απ
→ −<
Câu 23: Cho
0.
2
π
α
<<
Khẳng định nào sau đây đúng?
A.
cot 0.
2
π
α
+>
B.
cot 0.
2
π
α
+≥
C.
( )
tan 0.
απ
+<
D.
( )
tan 0.
απ
+>
Lời giải
Ta có
( )
0 cot 0
22 2 2
.
3
0 tan 0
22
ππ π π
α απ α
ππ
α παπ απ
<< → <+ <→ + <
< < → < + < → + >
Câu 24: Cho
.
2
π
απ
<<
Giá trị lượng giác nào sau đây luôn dương?
A.
( )
sin .
πα
+
B.
cos .
2
π
α
−
C.
( )
cos .
α
−
D.
( )
tan .
πα
+
Lời giải
( )
sin sin ;
πα α
+=−
cos sin ;
2
π
αα
−=
(
)
cos cos ;
αα
−=
( )
tan tan .
πα α
+=

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
Do
sin 0
cos 0
2
tan 0
α
π
απ α
α
>
<<→ <
<
Câu 25: Cho
3
.
2
π
πα
<<
Khẳng định nào sau đây đúng?
A.
3
tan 0.
2
π
α
−<
B.
3
tan 0.
2
π
α
−>
C.
3
tan 0.
2
π
α
−≤
D.
3
tan 0.
2
π
α
−≥
Lời giải
Ta có
3
sin 0
2
33 3
0 tan 0.
2 22 2
3
cos 0
2
π
α
π ππ π
πα α α
π
α
−>
< < → < − < → → − >
−>
Câu 26: Cho
.
2
π
απ
<<
Xác định dấu của biểu thức
(
)
cos .tan .
2
M
π
α πα
= −+ −
A.
0.M ≥
B.
0.M
>
C.
0.M ≤
D.
0.M <
Lời giải
Ta có
( )
0 cos 0
2 22 2
0 tan 0
22
π ππ π
απ α α
ππ
απ πα πα
<<→<−+< → −+ >
< < → < − < → − >
0.M
→
>
Câu 27: Cho
3
2
π
πα
<<
. Xác định dấu của biểu thức
( )
sin .cot .
2
M
π
α πα
=−+
A.
0.
M ≥
B.
0.M >
C.
0.M
≤
D.
0.
M <
Lời giải
Ta có
( )
33
sin 0
22 2 2 2
35
2 cot 0
22
ππ π π π
πα α π π α α
ππ
πα ππα πα
< < →− <− <− →− < − <− → − <
<<→<+<→ +>
0M → <
.
DẠNG 2: TINH GIA TRỊ LƯỢNG GIAC CỦA MỘT CUNG
Câu 28: Cho
1
cos = ;
62
π
α πα
−−
−< <
. Tính
sin
α
.
A.
35
sin
6
α
−
=
. B.
35
sin
36
α
=
. C.
5
sin
6
α
=
. D.
35
sin
6
α
=
.
Lời giải
Ta có
sin 0
2
π
πα α
−
−< < ⇒ <
. Nên
2
2
1 35
sin 1 os 1
66
c
αα
−
=−− =−− =−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Câu 29: Tính
sin
α
, biết
5
cos
3
α
=
và
3
2
2
π
απ
<<
.
A.
1
3
. B.
1
3
−
. C.
2
3
. D.
2
3
−
.
Lời giải
Ta có:
22
54
sin 1 cos 1
99
αα
=− =−=
2
sin
3
α
⇔=±
.
Do
3
2
2
π
απ
<<
nên
sin 0
α
<
. Vậy
2
sin
3
α
= −
.
Câu 30: Cho
2
cos 0
2
5
xx
π
= − <<
thì
sin x
có giá trị bằng
A.
3
5
. B.
3
5
−
. C.
1
5
−
. D.
1
5
Lời giải
Vì
0 sin 0
2
xx
π
− <<⇒ <
Ta có
22
sin cos 1
xx
+=
22
sin 1 cosxx⇒=−
2
2
1
5
= −
1
5
=
Vậy
1
sin
5
x = −
.
Câu 31: Cho
1
sin
4
α
=
biết
00
0 90
α
<<
. Tính
cos ; tan
αα
A.
15 15
cos ;tan
4 15
αα
=−=
. B.
15 15
cos ;tan
4 15
αα
=−=−
.
C.
15 15
cos ; tan
4 15
αα
= = −
. D.
15 15
cos ; tan
4 15
αα
= =
.
Lời giải
Ta có
22
1
sin
15
4
cos
15
4
cos 1 sin
16
α
α
αα
=
⇒=±
=−=
; với
00
0 90
α
<<
nên
15
cos
4
α
=
.
Và
1
sin
4
α
=
nên
sin 1 15
tan
cos 15
15
α
α
α
= = =
.
Câu 32: Cho
2
cos
5
= −
α
( )
oo
90 180<<
α
, khi đó
tan
α
bằng:
A.
21
5
. B.
21
2
−
. C.
21
5
−
. D.
21
3
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
Ta có:
22
4 21
sin 1 cos 1
25 25
=− =−=
αα
21
sin
5
⇒=
α
.
Vậy,
sin 21
tan
cos 2
= = −
α
α
α
.
Câu 33: Cho
3
sin
5
α
=
và
2
π
απ
<<
. Giá trị của
cos
α
là:
A.
4
5
. B.
4
5
−
. C.
4
5
±
. D.
16
25
.
Lời giải
Ta có:
22
sin cos 1
αα
+=
22
9 16
cos =1 sin 1
25 25
αα
⇒ − =−=
4
cos
5
4
cos
5
α
α
=
⇔
= −
.
Vì
2
π
απ
<<
4
cos
5
α
⇒=−
.
Câu 34: Cho
3
sin
5
α
= −
và
3
2
π
πα
<<
. Khi đó giá trị của
cos
α
và
tan
α
lần lượt là
A.
43
;
54
−
. B.
43
;
54
−−
. C.
43
;
54
−
. D.
34
;
45
−
.
Lời giải
Áp dụng hệ thức
22
sin cos 1
αα
+=
ta có:
2
2 22
9 16 4
cos
α 1 sin cos 1
25 25 5
αα
=− ⇔ =−==
.
Do
34
cos 0 cos
25
π
πα α α
<< ⇒ <⇒ =−
3
sin 3
5
tan
4
cos 4
5
α
α
α
−
= = =
−
.
Vậy
43
cos ; tan
54
αα
=−=
.
Câu 35: Cho
cos
4
5
α
= −
với
2
π
απ
< <
. Tính giá trị của biểu thức
10si csn 5oM
αα
+=
.
A.
10−
. B.
2
. C.
1
. D.
1
4
.
Lời giải
cos
4
5
α
= −
2
2
sin 1 cos
αα
⇒=−
2
49
1
5 25
=−− =
3
sin
5
α
⇒=±
Vì
2
π
απ
< <
nên
3
sin
5
α
=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
10si csn 5o
M
αα
+=
34
10. 5. 2
55
= +−=
.
Câu 36: Cho
cos
1
3
α
=
và
7
4
2
π
απ
<
<
. Khẳng định nào sau đây đúng?
A.
22
sin
3
α
= −
. B.
22
sin
3
α
=
. C.
2
sin
3
α
=
. D.
2
sin
3
α
= −
.
Lời giải
cos
1
3
α
=
2
2
sin 1 cos
αα
⇒=−
2
18
1
39
=−=
22
sin
3
α
⇒=±
Vì
7
4
2
π
απ
< <
nên
22
sin
3
α
= −
.
Câu 37: Cho góc
α
thỏa mãn
0
2
π
α
−<<
và
1
cos
2
α
=
. Giá trị của biểu thức
1
sin
cos
P
α
α
= +
bằng
A.
43
2
+
. B.
43
2
−
. C.
13
2
−
. D.
13
2
+
.
Lời giải
Cách 1: Ta có:
22 2 2
sin cos 1 sin 1 cos
αα α α
+=⇔=−
Với
1
cos
2
α
=
2
2
13
sin 1 sin
22
3
4
αα
⇒ =−= =
±⇔
Vì
0
2
π
α
−<<
nên
3
sin 0 sin .
2
αα
<⇒ =−
Vậy:
1 31 3 4 3
sin 2 .
1
cos 2 2 2
2
P
α
α
−
= + =−+=−+=
Cách 2: Theo giả thiết:
1
cos
2
.
3
0
2
α
π
α
π
α
=
⇒=−
− <<
Vậy
1 1 3 43
sin sin 2 .
cos 3 2 2
cos
3
P
π
α
π
α
−
= + = − + =− +=
−
Câu 38: Nếu
3
tan
4
α
=
thì
2
sin
α
bằng
A.
16
25
. B.
9
25
. C.
25
16
. D.
25
9
.
Lời giải
Ta có
2
2
2
1 3 25
1 tan 1
cos 4 16
α
α
=+ =+=
2
16
cos
25
α
⇒=
22
16 9
sin 1 cos 1
25 25
αα
⇒ =− =−=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Câu 39: Cho
tan 3x
=
. Tính
2sin cos
sin cos
xx
P
xx
−
=
+
.
A.
3
2
P =
. B.
5
4
P
=
. C.
3P
=
. D.
2
5
P
=
.
Lời giải
Ta có
sin
tan 3 3 sin 3cos .
cos
x
x xx
x
=⇒ =⇒=
Khi đó
2.3cos cos 5cos 5
3cos cos 4cos 4
xx x
P
xx x
−
= = =
+
.
Câu 40: Cho
1
sin
3
a =
. Giá trị của biểu thức
cot tan
tan 2co t
aa
A
aa
−
=
+
bằng
A.
1
9
. B.
7
9
. C.
17
81
. D.
7
17
.
Lời giải
Ta có
22
22
cos sin
cot tan co s sin
sin cos
tan 2cot sin co s
sin 2cos
2
cos sin
aa
aa a a
aa
A
a aa a
aa
aa
−
−−
= = =
+
+
+
( )
( )
22
2
2
22
1 sin sin
1 2sin 7
17
2 sin
sin 2 1 sin
aa
a
a
aa
−−
−
= = =
−
+−
Câu 41: Cho
tan 4.x
= −
Giá trị của biểu thức
2sin 5cos
3cos sin
xx
A
xx
−
=
+
là
A.
13
. B.
13−
. C.
13
11
. D.
5
.
Lời giải
Ta có:
( )
(
)
sin cos
25
2. 4 5
2sin 5cos 2 tan 5
cos cos
13
cos sin
3cos sin 3 tan 3 4
3
cos cos
xx
xx x
xx
A
xx
xx x
xx
−
−−
−−
= = = = =
+ + +−
+
.
Câu 42: Cho
tan 3
α
=
, khi đó giá trị của biểu thức
2sin cos
3sin 5cos
P
αα
αα
−
=
−
là
A.
5
2
P = −
. B.
5
4
P =
. C.
1P =
. D.
3P = −
.
Lời giải
Chia cả tử và mẫu của
P
cho
cos 0
α
≠
ta được:
2sin cos 2 tan 1 5
3sin 5cos 3tan 5 4
P
αα α
αα α
−−
= = =
−−
.
Câu 43: Cho
cot 3= −
α
. Giá trị của biểu thức
3cos 4sin
2sin cos
P
−
=
+
αα
αα
bằng
A.
13−
. B.
13
. C.
3−
. D.
3
.
Lời giải
Chia cả tử và mẫu của biểu thức
P
cho
sin
α
, ta có:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
( )
3. 3 4
3cos 4sin 3cot 4
13
2sin cos 2 cot 2 3
P
−−
−−
= = = =
++ −
αα α
αα α
.
Câu 44: Cho
cot 4 tan
αα
=
và
;
2
π
απ
∈
. Khi đó
sin
α
bằng
A.
5
5
−
. B.
1
2
. C.
25
5
. D.
5
5
.
Lời giải
Ta có
cot 4 tan
αα
=
22
cot
4 cot 4 1 cot 5
tan
α
αα
α
⇔ = ⇔ = ⇔+ =
2
2
1 15
5 sin sin
sin 5 5
αα
α
⇔ =⇔ =⇔=±
.
Vì
;
2
π
απ
∈
nên
5
sin
5
α
=
.
Câu 45: Nếu
tan cot 2
αα
+=
thì
22
tan cot
αα
+
bằng bao nhiêu?
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Ta có
tan cot 2
αα
+=
( )
2
tan cot 4
αα
⇒+ =
⇒
22
tan cot 2tan .cot 4
α α αα
++ =
22
tan cot 2
αα
⇒+=
.
Câu 46: Biết
2
sin cos
2
+=
αα
. Trong các kết quả sau, kết quả nào sai?
A.
1
sin cos
4
= −
αα
. B.
6
sin cos
2
−=±
αα
.
C.
44
7
sin cos
8
+=
αα
. D.
22
tan cot 12+=
αα
.
Lời giải
( )
2
2 11
sin os sin os sin os
2 24
+=⇒ + =⇒ =−c cc
αα αα αα
Suy ra, đáp án A đúng.
( )
2
22
sin os 1 sin os 2sin os 1
+=⇔− + =
c cc
α α α α αα
.
( )
2
13
sin os 1 2
42
⇔ − =−− =
c
αα
.
Suy ra,
36
sin cos
22
− =±=±
αα
. Suy ra, đáp án B đúng.
( )
2
44 22 22
17
sin cos sin cos 2sin cos 1 2
48
+ = + − =−− =
αα αα αα
Suy ra, C đúng.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
44
22
22
7
sin cos
8
tan cot 14
1
sin cos
4
+
+= ==
−
αα
αα
αα
.Suy ra,
22
tan cot 12+=
αα
sai.
Câu 47: Nếu
( )
( ) ( )
22
cot tan sin 1445 cos 1085
2
oo
xx
π
π
+− − = − +
thì
sin x
bằng.
A.
1
5
±
. B.
2
5
±
. C.
1
5
±
. D.
2
5
±
.
Lời giải
(
)
( ) ( )
22
cot tan sin 1445 cos 1085
2
oo
xx
π
π
+− − = − +
.
2
1 12
cot cot 1 cot tan 2 sin
2
5
1 cot
xx x x
α
α
⇔− − = ⇔ =− ⇔ =− ⇒ =± =±
+
.
Câu 48: Cho biết
1
sin cos
2
aa−=
. Kết quả nào sau đây đúng?
A.
3
sin .cos
8
aa
=
. B.
7
sin cos
4
aa+=
.
C.
44
21
sin cos
32
aa+=
. D.
22
14
tan cot
3
aa
+=
.
Lời giải
Ta có
( )
2
1 sin cos
3
sin cos
28
αα
αα
−−
= =
.
( )
2
2
44 22 22
3 23
sin cos sin cos 2sin cos 1 2.
8 32
αα αα αα
+= + − =− =
.
Câu 49: Biết
1
tan
2
x
=
, giá trị của biểu thức
22
22
2sin 3sin .cos 4cos
5cos sin
x xx x
M
xx
+−
=
−
bằng:
A.
8
13
−
. B.
2
19
. C.
2
19
−
. D.
8
19
−
.
Lời giải
Cách 1:
Chia cả tử và mẫu của
M
cho
2
cos x
ta có:
2
22
2
2
sin sin .cos
11
23 4
2. 3. 4
8
cos cos
42
1
sin
19
5
5
4
cos
x xx
xx
M
x
x
+−
+−
= = = −
−
−
.
Cách 2: Ta có:
1 sin 1
tan cos 2sin
2 cos 2
x
x xx
x
=⇔ =⇔=
, thay
cos 2sinxx=
vào
M
:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
( )
( )
2
2
2
2
2
2
2sin 3sin .2sin 4. 2sin
8sin 8
19sin 19
5. 2sin sin
x xx x
x
M
x
xx
+−
−
= = = −
−
.
Câu 50: Nếu
( ) ( )
cot1, 25.tan 4 1, 25 sin .cos 6 0
2
xx
π
ππ
+ − + −=
thì
tan
x
bằng
A.
1
. B.
1
−
. C.
0
. D. Giá trị khác.
Lời giải
( )
( )
cot1, 25.tan 4 1, 25 sin .cos 6 0
2
xx
π
ππ
+ − + −=
.
cot1, 25.tan1,25 cos .cos 0
xx−=
.
22
1 cos 0 sin 0 sin 0 tan 0x xxx− =⇔ =⇔=⇔=
.
Câu 51: Biết
2
tan
b
x
ac
=
−
. Giá trị của biểu thức
22
cos 2 sin .cos sin
Aa x b x xc x=++
bằng
A.
a
. B.
a
. C.
b
. D.
b
.
Lời giải
22
cos 2 sin .cos sinAa x b x xc x=++
2
2
2 tan tan
cos
A
a b xc x
x
⇔=+ +
( )
22
1 tan 2 tan tanA x a b xc x
⇔+ =+ +
22
2 22
12
b bb
A ab c
ac ac ac
⇔+ =+ +
− −−
( ) ( )
( )
( ) ( )
( )
22 2
22
22
2 44ac b aac bac cb
A
ac ac
−+ −+ −+
⇔=
−−
Câu 52: Nếu biết
44
sin s 1x co x
a b ab
+=
+
thì biểu thức
33
33
sin sx co x
ab
+
bằng:
A.
( )
2
1
ab+
. B.
22
1
ab+
. C.
( )
3
1
ab+
. D.
33
1
ab+
.
Lời giải
Đặt
( )
2
sin x u, 0 u 1= ≤≤
2
cos x 1 u⇒=−
.
Từ
44
sin x co s x 1
a b ab
+=
+
ta suy ra
( )
( )
22
2
2
1u bu a1u
u1 1
a b ab ab ab
− +−
+=⇒ =
++
.
( )
2
a b u 2au a
1
ab a b
+ −+
=
+
( ) ( ) ( )
2
2
abu 2aabuaab ab⇒+ − + + +=
.
( ) ( )
2
22
abu 2aabua 0⇒+ − + +=
(
)
2
a
a bu a 0 u
ab
⇒ + − =⇒=
+
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
Suy ra
2
2
a
sin x
ab
b
cos x
ab
=
+
=
+
.
Do đó
( )
44
33
33 3 3 2
ab
ab ab
sin x co s x 1
A
ab a b
ab
++
=+= + =
+
Câu 53: Nếu biết
44
98
3sin 2cos
81
xx+=
thì giá trị biểu thức
44
2sin 3cosAxx= +
bằng
A.
101
81
hay
601
504
. B.
103
81
hay
603
405
. C.
105
81
hay
605
504
. D.
107
81
hay
607
405
.
Lời giải
Ta có
44
98
sin cos
81
xx A−=−
98
cos 2
81
xA⇔=−
( )
44
98
5 sin cos
81
xx A+=+
2
1 1 98
1 sin 2
2 5 81
xA
⇔− = +
2
1 1 1 98
cos 2
2 2 5 81
xA
⇔+ = +
2
98 2 98 2 98 392
81 5 81 5 81 405
A AA
⇔1+ − = + = − +
Đặt
98
81
At
−=
2
2 13
0
5 405
tt⇒− + =
13
45
1
9
t
t
=
⇔
=
+)
13 607
45 405
tA= ⇒=
+)
1 107
.
9 81
tA=⇒=
Câu 54: Nếu
44
sin cos 1
a b ab
αα
+=
+
thì biểu thức
10 10
44
sin cos
M
ab
αα
= +
bằng.
A.
55
11
ab
+
. B.
( )
5
1
ab+
. C.
44
11
ab
+
. D.
( )
4
1
ab+
.
Lời giải
44 4422
sin cos 1 sin cos sin cos
a b ab a b ab ab
αα αααα
+=⇔+=+
+ ++
.
22
22
sin 1 cos 1
sin cos 0
a ab b ab
αα
αα
⇔ −+ −=
++
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
( )
( )
2 2 22
22
sin cos cos sin
sin cos 0
ba a b
aab bab
α α αα
αα
−−
⇔+=
++
.
24 2 2 2 4
sin 2 sin cos cos 0b ab a
α αα α
⇔− + =
.
( )
22
2
22
sin cos 1
sin cos 0ba
a b ab
αα
αα
⇔ − =⇔==
+
.
Do đó
( )
( ) ( )
2
44 4
2
11 1
cos
sin
M
ab ab ab
α
α
=+=
++ +
.
Câu 55: Nếu biết thì biểu thức bằng:
A. . B. . C. . D. .
Lời giải
Đặt
Từ ta suy ra
Suy ra
Do đó
Câu 56: Nếu
3cos 2sin 2xx+=
và
sin 0x <
thì giá trị đúng của
sin x
là:
A.
5
13
−
. B.
7
13
−
. C.
9
13
−
. D.
12
13
−
.
Lời giải
ta có:
( )
2
3cos 2sin 2 3cos 2sin 4xx xx+=⇔ + =
.
( )
22
2
9cos 12cos .sin 4sin 4
cos 0
5cos 12cos .sin 0 cos 5cos 12sin 0
5cos 12sin 0
x xx x
x
x xx x x x
xx
⇔+ + =
=
⇔+ =⇔ + =⇔
+=
.
Với
cos 0x =
sin 1x⇒=
loại vì
sin 0x <
.
44
sin cos 1
a b ab
αα
+=
+
88
33
sin cos
A
ab
αα
= +
2
1
()
ab+
22
1
ab+
3
1
()ab+
33
1
ab+
( )
2
sin , 0 1uu
α
= ≤≤
2
cos 1 .u
α
⇒=−
44
sin cos 1
a b ab
αα
+=
+
( )
( )
22
2
2
11
11
u bu a u
u
a b ab ab ab
− +−
+=⇒ =
++
( )
2
2
1
a b u au a
ab a b
+ −+
⇒=
+
( ) ( ) ( )
2
2
2abu aabuaab ab⇒+ − + + +=
( ) ( )
2
22
20abu aabua⇒+ − + +=
( )
2
0
a
a bu a u
ab
⇒ + − =⇒=
+
2
2
sin
cos
a
ab
b
ab
α
α
=
+
=
+
( )
44
88
3
33 3 3
sin cos 1
ab
ab ab
A
ab a b
ab
αα
++
=+= + =
+

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
Với
5cos 12sin 0xx+=
, ta có hệ phương trình:
5
sin
5cos 12sin 0
13
3cos 2sin 2 12
cos
13
x
xx
xx
x
= −
+=
⇔
+=
=
.
Câu 57: Nếu thì bằng:
A. hay . B. hay .
C. hay . D. hay .
Lời giải
Ta biến đổi: .
Từ
Khi đó là nghiệm của phương trình
Với suy ra
Với suy ra
DẠNG 3: GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG CÓ LIÊN QUAN ĐẶC BIỆT
Câu 58: Tính
000
tan 20 tan 45 tan 70L =
A.
0
. B.
1
. C.
1−
. D.
2
.
Lời giải
Chọn B
( )
000 00 0
tan 20 tan 45 tan 70 tan 20 tan 70 tan 45= =L
( )
00 0
tan 20 cot 20 tan 45 1= =
Câu 59: Tính
22 2 2
25
cos cos ... cos cos
66 6
G
ππ π
π
= + ++ +
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
sin co
1
2
sxx+=
3sin 2cosxx+
57
4
−
57
4
+
55
7
−
55
4
+
23
5
−
23
5
+
32
5
−
32
5
+
( ) ( )
3sin 2cos 2 sin cos sin 1 sinx x xx x x+ = + +=+
sin co
1
2
sxx+=⇒
3
sin .cos
8
xx= −
sin , cosxx
2
13
0
28
XX− −=
22
17
13
4
0 8 4 30
28
17
4
X
X X XX
X
+
=
− − =⇔ − −=⇔
−
=
17
sin
4
x
+
=
( )
1 75 7
3sin 2cos 1
44
xx
++
+ =+=
17
sin
4
x
−
=
( )
1 75 7
3sin 2cos 1
44
xx
−−
+ =+=

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
22 2 2
25
cos cos ... cos cos
66 6
G
ππ π
π
= + ++ +
2222 2 2
25
cos cos cos cos cos cos
632 3 6
πππ π π
π
=+++ + +
G
2222 2 2
22
cos sin cos cos sin cos
66 2 3 3
πππ π π
π
= +++ + +
Câu 60: Tính
000
sin 390 2sin1140 3cos1845
A =−+
A.
( )
1
132 23
2
+−
. B.
( )
1
132 23
2
−−
. C.
( )
1
1 23 32
2
+−
. D.
( )
1
1 23 32
2
++
.
Lời giải
000
sin 390 2sin1140 3cos1845=−+A
( )
( ) ( )
00 00 00
sin 2.180 30 2sin 6.180 60 3cos 10.180 45= +− ++ +
( )
00 0
1 3 21
sin 30 2sin 60 3cos45 2. 3. . 1 2 3 3 2 .
2 2 22
= − + =− + =−+
Câu 61: Giá trị đúng của biểu thức
tan 225 cot81 .cot 69
cot 261 tan 201
° °°
°°
−
+
bằng:
A.
1
3
. B.
1
3
−
. C.
3
. D.
3−
.
Lời giải
(
)
( ) ( )
( )
tan 180 45 tan 9 .cot 69
tan 225 cot81 .cot 69
cot 261 tan 201 cot 180 81 tan 180 21
1 tan 9 .tan 21 1 1
3
tan 9 tan 21 tan 9 21 tan 30
°+ ° − ° °
°− ° °
=
°+ ° °+ ° + °+ °
−° °
= = = =
°+ ° °+ ° °
1011 3=+ ++=
Câu 62: Với mọi góc
α
, biểu thức
29
cos cos cos ... cos
55 5
ππ π
αα α α
+++++++
nhận giá trị
bằng
A.
10
. B.
10−
. C.
1
. D.
0
.
Lời giải
Ta có
5
cos cos
5
π
αα
=−+
;
6
cos cos
55
ππ
αα
+=− +
;
27
cos cos
55
ππ
αα
+=− +
;
38
cos cos
55
ππ
αα
+=− +
;
49
cos cos
55
ππ
αα
+=− +
.
Do đó
29
cos cos cos ... cos 0
55 5
ππ π
αα α α
+++++++=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
Câu 63: Tính
22 2 2
25
sin sin ... sin sin
66 6
F
ππ π
π
= + ++ +
.
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Ta có
22 2 2
25
sin sin ... sin sin
66 6
F
ππ π
π
= + ++ +
2222 2 2
25
sin sin sin sin sin sin
632 3 6
πππ π π
π
=+++ + +
22
2 sin cos 1 0
63
ππ
= + ++
3=
.
Câu 64: Đơn giản biểu thức
( ) (
)
5
sin cos 13 3sin 5
2
D
π
α πα α π
= −+ +− −
.
A.
3sin 2cos
αα
−
. B.
3sin
α
. C.
3sin
α
−
. D.
2cos 3sin
αα
+
.
Lời giải
Ta có
( ) ( )
5
sin cos 13 3sin 5
2
D
π
α πα α π
= −+ +− −
( ) (
)
sin cos 3sin
2
π
α πα πα
= −+ ++ −
cos cos 3sin
αα α
=−+
3sin
α
=
.
Câu 65: Giả sử
tan tan tan
33
Ax x x
ππ
= −+
được rút gọn thành
tanA nx=
khi đó
n
bằng
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Ta có
tan tan tan
33
Ax x x
ππ
= −+
3 tan 3 tan
tan . .
1 3 tan 1 3 tan
xx
x
xx
−+
=
+−
2
2
3 tan
tan .
1 3tan
x
x
x
−
=
−
3
2
3tan tan
1 3tan
xx
x
−
=
−
tan 3x=
.
Câu 66: Nếu
sin 3cosxx=
thì
sin cosxx
bằng
A.
3
10
. B.
2
9
. C.
1
4
. D.
1
6
.
Lời giải
Ta có

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 20
Sưu tầm và biên soạn
22 2
1
cos
10
1
cos
3
sin
10
sin cos 1 10cos 1 10
1
cos
sin 3cos sin 3cos
1
cos
10
10
sin 3cos
3
sin
10
x
x
x
xx x
x
xx xx
x
xx
x
−
=
= −
−
=
+= =
⇔⇔ ⇔
=
= =
=
=
=
Suy ra
3
sin cos
10
xx=
.
Câu 67: Với mọi
α
thì
3
sin
2
π
α
+
bằng
A.
sin
α
−
. B.
cos
α
−
. C.
cos
α
. D.
sin
α
.
Lời giải
Cách 1: Ta có
3
sin sin 2 sin sin cos
2 2 22
π π ππ
α πα α α α
+= +−= −=− −=−
.
Cách 2: Ta có
( )
(
)
33 3
sin sin cos sin cos 1 cos sin . 0 cos
22 2
ππ π
α αα αα α
+= + =− + =−
.
Câu 68: Giá trị
89
cot
6
π
bằng
A.
3
. B.
3−
. C.
3
3
. D.
3
3
−
.
Lời giải
Ta có:
89
cot
6
π
5
cot 14
6
π
π
= +
5
cot
6
π
=
3= −
.
Câu 69: Đơn giản biểu thức
cos
2
A
π
α
= −
, ta được:
A.
cos
α
. B.
sin
α
. C.
– cos
α
. D.
sin
α
−
.
Lời giải
Ta có:
cos
2
A
π
α
= −
cos
2
π
α
= −
sin
α
=
.
Câu 70: Nếu
2
1
sin
3
α
=
thì
2
1 tan
α
+
bằng
A.
9
8
. B.
4
. C.
3
2
. D.
8
9
.
Lời giải
Ta có:
22
2
cos 1 sin
3
αα
=−=
mà
2
2
1
1 tan
cos
α
α
+=
⇒
2
3
1 tan
2
α
+=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 21
Sưu tầm và biên soạn
Câu 71: Tính
cot1 .cot 2 .cot 3 ...cot89P
°°° °
=
.
A.
0
. B.
1
. C.
3
. D.
4
.
Lời giải
Ta có:
cot 89 tan1°= °
cot1 cot89 cot1 tan1 1.⇒ ° °= ° °=
cot 88 tan 2°= °
cot 2 cot82 cot 2 tan 2 1.⇒ ° °= ° °=
.....
cot 46 tan 44°= °
cot 44 cot 46 cot 44 tan 44 1.⇒ ° °= ° °=
Vậy
cot1 cot 2 cot 3 ...cot 89P =°°° °
cot 45 1= °=
.
Câu 72: Giá trị của biểu thức
tan110 tan 340 sin160 cos110 sin 250 cos340
° °+ ° °+ ° °
bằng
A.
0
. B.
1
. C.
1−
. D.
2
.
Lời giải
tan110 tan 340 sin160 cos110 sin 250 cos340
A
= ° °+ ° °+ ° °
( ) ( ) ( ) ( )
( ) ( )
tan 90 20 tan 360 20 sin 180 20 cos 90 20
sin 360 110 cos 360 20
A = °+ ° °− ° + °− ° °+ ° +
+ °− ° °− °
cot 20 tan 20 sin 20 sin 20 sin110 cos 20A = ° °− ° °− ° °
( )
2
1 sin 20 sin 90 20 cos 20A
= − °− °+ ° °
22
1 sin 20 cos 20A = − °− °
( )
22
1 sin cos 0A xx=−+ =
.
Câu 73: Rút gọn biểu thức
( )
00
0
00
sin 234 cos 216
A .tan 36
sin144 cos126
−−
=
−
, ta được
A.
A2=
. B.
A2= −
. C.
A1=
. D.
A1= −
.
Lời giải
Cách 1: Sử dụng mối quan hệ của các cung có liên quan đặc biệt
( ) ( )
( ) ( )
00 000
0
00 00
sin 180 54 cos 180 36 16
A .tan 36
sin 180 36 cos 900 36
− +− +
=
−− +
.
00
0 00
00
sin 54 cos 36
A .tan 36 2cot 36 .tan 36 2
sin 36 sin 36
+
= = =
+
.
Cách 2: Sử dụng máy tính cầm tay, nhập biểu thức đã cho vào máy và bấm =, được kết quả
bằng
1
.
Câu 74: Giá trị của biểu thức A =
( )
00
0 00
2sin 2550 .cos 188
1
tan 368 2cos638 cos98
−
+
+
bằng:
A.
1
. B.
2
. C.
1−
. D.
0
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 22
Sưu tầm và biên soạn
( )
00
0 00
2sin 2550 .cos 188
1
tan 368 2cos638 cos98
A
−
= +
+
( )
(
) (
)
( )
(
)
0 0 00
0 0 0 0 00
2sin 30 7.360 .cos 8 180
1
tan 8 360 2cos 82 2.360 cos 90 8
A
++
⇔= +
+ −+ + +
00
0 00
1 2sin 30 .cos8
tan 8 2cos82 sin8
A
−
⇔= +
−
( )
00
0
00 0
1 2sin 30 .cos8
tan 8
2cos 90 8 sin 8
A
⇔= −
−−
00
0 00
1 2sin 30 .cos8
tan8 2sin8 sin8
A⇔= −
−
0
0 00
0
1.cos8
cot 8 cot 8 cot 8 0
sin8
A⇔= − = − =
.
Câu 75: Với mọi α, biểu thức:
9
cos +cos ... cos
55
A
ππ
αα α
= + ++ +
nhận giá trị bằng:
A.
–10
. B.
10
. C.
0
. D.
5
.
Lời giải
9
cos +cos ... cos
55
A
ππ
αα α
= + ++ +
9 45
cos cos ... cos cos
5 55
A
π ππ
αα α α
=++++ +++
99 97 9
2cos cos 2cos cos ... 2cos cos
10 10 10 10 10 10
A
π π π π ππ
αα α
=+ ++ +++
9 9753
2cos cos cos cos cos cos
10 10 10 10 10 10
A
π π π π ππ
α
= + ++++
92
2cos 2cos cos 2cos cos cos
10 2 5 2 5 2
A
π π π ππ π
α
=+ ++
9
2cos .0 0.
10
A
π
α
⇔= + =
Câu 76: Biểu thức
( ) ( ) ( )
( )
00 0 0
0
0
sin 328 .sin 958 cos 508 .cos 1022
cot 572
tan 212
A
− −−
= −
−
rút gọn bằng:
A.
1−
. B.
1
. C.
0
. D.
2
.
Lời giải
( ) ( )
( )
( )
00 0 0
0
0
sin 328 .sin 958 cos 508 .cos 1022
cot 572
tan 212
A
− −−
= −
−
00 0 0
00
sin 32 .sin 58 cos32 .cos58
cot 32 tan 32
A⇔=− −
0 0 00
20 20
00
sin 32 .cos32 cos32 .sin 32
sin 32 cos 32 1
cot 32 tan 32
A =− − =−− =−
.
DẠNG 4: RÚT GỌN BIỂU THỨC LƯỢNG GIÁC. ĐẲNG THỨC LƯỢNG GIÁC
Câu 77: Biểu thức
22 2 2 2
cos cot 3cos cot 2sinD xx x x x= + −+
không phụ thuộc
x
và bằng:
A.
2
. B.
2−
. C.
3
. D.
3−
.
Lời giải
Ta biến đổi:
22 2 2 2
cos cot 3cos cot 2sinD xx x x x= + −+
( ) ( )
22 2 2 2 2 2
cot cos 1 2 sin cos cos cos 2 cos 2xx x x x x x= −+ + +=−++=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 23
Sưu tầm và biên soạn
Câu 78: Đơn giản biểu thức
( ) ( )
5
sin cos 13 3sin 5
2
D a aa
π
ππ
= −+ +− −
A.
2cos 3sin
aa
+
. B.
3sin 2cosaa−
. C.
3sin a
−
. D.
4cos sin
aa
−
.
Lời giải
( ) ( )
sin 2 cos 12 3sin 6
2
D a aa
π
π ππ π π
= + − + ++ − +−
( ) ( )
sin cos 3sin
2
D a aa
π
ππ
= −+ +− +
cos sin 3cosD aa a= −+
4cos sinD aa= −
Câu 79: Đơn giản biểu thức
33 77
cos sin cos sin
22 22
C a aa a
ππ ππ
= −− −+ − − −
A.
2sin
a
. B.
2sin a−
. C.
2cos a
. D.
2cos a−
.
Lời giải
cos 2 sin 2 cos 4 sin 4
22 22
C a aa a
ππ ππ
ππ ππ
= −− − −− + − + − − +
cos sin cos sin
2 2 22
C a aa a
π π ππ
= + − −− + + − +
sin cos sin cos
C a aa a=−+ −−
2sinCa= −
Câu 80: Biểu thức
22
22
22
sin
cot cot
sin sin
−
= −
cos x y
B xy
xy
không phụ thuộc vào
,xy
và bằng
A.
2
. B.
2−
. C.
1
. D.
1−
.
Lời giải
( )
2 22
2 2 22
22 22
cos 1 cos sin
cos sin cos cos
sin sin sin sin
x yy
x y xy
B
xy xy
−−
−−
= =
.
( )
22
22 2 22
22 22 22
sin cos 1
cos sin sin sin sin
1
sin sin sin sin sin sin
yx
xy y xy
B
xy xy xy
−
−−
= = = = −
.
Câu 81: Rút gọn biểu thức
2
2cos 1
sin cos
x
A
xx
−
=
+
, ta được kết quả
A.
sin cosAxx= +
. B.
cos sinA xx= −
.
C.
cos 2 sin 2A xx= −
. D.
cos 2 sin 2A xx= +
.
Lời giải
( )
2 22
22
2cos sin cos
cos sin
cos sin
sin cos sin cos
x xx
xx
A xx
xx xx
−+
−
= = = −
++
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 24
Sưu tầm và biên soạn
Câu 82: Biểu thức rút gọn của A =
22
22
tan sin
cot cos
aa
aa
−
−
bằng:
A.
6
tan
a
. B.
6
cos a
. C.
4
tan a
. D.
6
sin a
.
Lời giải
22
22
tan sin
cot cos
aa
A
aa
−
=
−
2
22
2
6
2
2
2
1
sin 1
tan .tan
cos
tan
1
cot
cos 1
sin
a
aa
a
Aa
a
a
−
⇔= = =
−
.
Câu 83: Hệ thức nào sai trong bốn hệ thức sau:
A.
tan tan
tan .tan
cot cot
xy
xy
xy
+
=
+
. B.
2
2
1 sin 1 sin
4 tan
1 sin 1 sin
aa
a
aa
+−
−=
−+
.
C.
2
2
sin cos 1 cot
cos sin cos sin 1 cot
αα α
αα αα α
+
−=
+ −−
. D.
sin cos 2cos
1 cos sin cos 1
αα α
α αα
+
=
− −+
.
Lời giải
A đúng vì
tan tan
tan .tan
11
tan tany
xy
VT x y VP
x
+
= = =
+
B đúng vì
( ) ( )
22
2
2
22
1 sin 1 sin
1 sin 1 sin 2 2sin
2 2 2 4 tan
1 sin 1 sin 1 sin cos
aa
aa a
VT a VP
aa a a
+ +−
+− +
= + −= −= −= =
−+ −
C đúng vì
22 22 2
22 2 2 2
sin cos sin cos 1 cot
cos sin sin cos 1 cot
VT VP
αααα α
αα α α α
−− + +
= = = =
− −−
.
Câu 84: Biết
tan 3x =
và
22
22
2sin 3sin .cos 4cos
5tan 6cot
x xx x
M
xx
++
= ⋅
+
Giá trị của
M
bằng.
A.
31
47
M = ⋅
B.
93
137
M = ⋅
C.
93
1370
M = ⋅
D.
31
51
M = ⋅
Lời giải
Ta có:
sin
tan sin tan .cos
cos
x
x x xx
x
= ⇒=
;
2
2
1
cos
tan 1
x
x
=
+
và
1
cot
tan
x
x
= ⋅
.
Suy ra:
( )
22
2
2
2 tan 3tan 4 cos
93
6
1370
5tan
tan
xx x
M
x
x
++
= = ⋅
+
.
Câu 85: Giả sử
44
1
3sin cos
2
xx−=
thì
44
sin 3cosxx+
có giá trị bằng
A.
1
. B.
2
. C.
3
. D.
4
Lời giải
Ta có
22
sin cos 1xx+=
22
cos 1 sinxx⇒=−

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 25
Sưu tầm và biên soạn
Vậy
44
1
3sin cos
2
xx
−=
( )
2
42
1
3sin 1 sin
2
xx⇔ −− =
1
sin
2
x⇔=±
Vậy
44
sin 3cosxx+
( )
2
42
sin 3 1 sin
xx= +−
2
11
31
42
=+−
13
44
= +
1=
.
Câu 86: Rút gọn biểu thức
( ) ( )
22
85 5
sin cos 2017 sin 33 sin
22
Ax x x x
ππ
ππ
= + + ++ ++ −
ta được:
A.
sinAx=
. B.
1A =
. C.
2A =
. D.
0A =
.
Lời giải
( ) (
)
22
85 5
sin cos 2017 sin 33 sin
22
Ax x x x
ππ
ππ
= + + ++ ++ −
.
( ) ( )
22
sin 42 cos 2016 sin 32 sin 2
22
x x xx
ππ
π ππ ππ π
= + + + ++ + ++ + − −
.
( )
( )
22
sin cos sin sin
22
x x xx
ππ
ππ
= + + ++ ++ −
.
(
) (
)
22
cos cos sin cos 1xx x x= − +− +− =
.
Câu 87: Có bao nhiêu đẳng thức đúng trong các đẳng thức sau đây?
i)
2
2
1
cos
tan 1
α
α
=
+
. iii)
2 cos cos sin
4
π
α αα
+= +
.
ii)
sin cos
2
π
αα
−=−
. iv)
2
cot 2 2cot 1
αα
= −
.
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Ta có:
22
22
11
1 tan cos
cos 1 tan
αα
αα
=+⇔=
+
. Vậy i) đúng.
Và:
sin sin cos
22
ππ
α αα
−=− −=−
. Vậy ii) đúng.
Và:
2 cos 2 cos cos sin sin cos sin
4 44
π ππ
α α α αα
+= − = −
. Vậy iii) sai.
Với
2
22
2
2cos
cos 0 sin 1 2cot 1 1 1
sin
α
αα α
α
= ⇔ =⇒ −= −=−
.
Mà:
cos 2 cos 2
cot 2
sin 2 2sin cos
αα
α
α αα
= =
không xác định khi
cos 0
α
=
.
Suy ra iv) không đúng với mọi
α
. Vậy iv) sai.
Vậy có
2
đẳng thức đúng.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 26
Sưu tầm và biên soạn
Câu 88: Biểu thức
( )
2
2
2 22
1 tan
1
4 tan 4sin cos
x
A
x xx
−
= −
không phụ thuộc vào
x
và bằng
A.
1
. B.
1−
. C.
1
4
. D.
1
4
−
.
Lời giải
( )
2
2
2
22
2
2 22 22 22
sin
1
cos sin
cos
11
4 tan 4sin cos 4sin cos 4sin cos
x
xx
x
A
x xx xx xx
−
−
=−= −
.
( )
( )
( )
22 22 2 2
22 22
cos sin 1 cos sin 1 2cos . 2sin
1
4sin cos 4sin cos
−+ −− −
= = = −
xx xx x x
A
xx xx
.
Câu 89: Biểu thức
( )
2
2
2 22
1 tan
1
4 tan 4sin cos
x
x xx
A
−
−
=
không phụ thuộc vào
x
và bằng
A.
1
. B.
–1
. C.
1
4
. D.
1
4
−
.
Lời giải
Ta có
( )
(
)
22
22
2
2 22 2 2 2
1 tan 1 tan
1 11
4 tan 4sin cos 4 tan 4 tan cos
xx
x xx x x x
A
−−
− −⋅
=
=
( ) ( ) (
) ( )
2 2 22
2 2 22
22 2
1 tan 1 tan 1 tan 1 tan
4 tan 4 tan 4 tan
x x xx
xx x
− + − −+
−= =
2
2
4 tan
1
4 tan
x
x
−
= = −
.
Câu 90: Biểu thức
( )
( )
0 0 00
0 0 00
sin 515 .cos 475 cot 222 .cot 408
cot 415 .cot 505 tan197 .tan 73
A
−+
=
−+
có kết quả rút gọn bằng
A.
20
1
sin 25
2
. B.
20
1
cos 55
2
. C.
20
1
cos 25
2
. D.
20
1
sin 65
2
.
Lời giải
( )
0 0 00
0 0 00
sin155 .cos115 cot 42 .cot 48
cot 55 .cot 145 tan17 .cot17
A
+
=
−+
( )
0 0 00
00
sin 25 . sin 25 cot 42 .tan 42
cot 55 .tan 55 1
A
−+
⇔=
+
20
sin 25 1
2
A
−+
⇔=
20
cos 25
2
A⇔=
.
Câu 91: Biểu thức:
( ) ( ) ( ) ( )
2003
cos 26 2sin 7 cos1,5 cos cos 1,5 .cot 8
2
A
π
α π απ π α α π απ
= + − −− − + + − −
có
kết quả thu gọn bằng:
A.
sin
α
−
. B.
sin
α
. C.
cos
α
−
. D.
cos
α
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 27
Sưu tầm và biên soạn
(
)
( ) ( ) ( )
( )
cos 26 2sin 7 cos 1,5 cos 2003 cos 1,5 .cot 8
2
A
π
α π απ π α α π απ
= + − −− − + + − −
( )
cos 2sin cos cos( cos .cot
2 22
A
π ππ
α απ α α α
= − −− − − + +
cos 2sin 0 sin sin .cot cos sin cos sin .A
α α α αα α α α α
= + −− − = + − =
Câu 92: Biểu thức
( )
( )
( )
2
2
3 1 31
tan .tan . cos . sin 2
3
2 2 sin
cos
2
xx x x
x
x
ππ
ππ
π
π
− + −+ −
−
−
có
kết quả rút gọn bằng:
A.
2
sin
x
. B.
2
cos x
. C.
2
tan x
. D.
2
cot x
.
Lời giải
(
)
( )
(
)
2
2
3 1 31
tan .tan cos . sin 2
3
2 2 sin
cos
2
xx x x
x
x
ππ
ππ
π
π
− + −+ −
−
−
.
( )
2
2
2
2
11
t anx.tan . cos sin
2 2 sinx
cos
2
1 sinx
tan . cot . .sin
sin sinx
x xx
x
xx x
x
ππ
ππ
π
π
=− ++ − ++
+−
=−− −
.
2 22 2
2
1
1 .sin cot .sin cos .
sin
x xx x
x
=−= =
Câu 93: Cho
20 0 0 2
20 20
cos 696 tan( 260 ).tan530 cos 156
tan 252 cot 342
o
B
+− −
=
+
. Biểu thức thu gọn nhất của
B
là:
A.
20
1
tan 24
2
. B.
20
1
cot 24
2
. C.
20
1
tan 18
2
. D.
20
1
cot 18
2
.
Lời giải
Ta có:
200 0 0 0 0 2 0
20 0 200
cos (720 24 ) tan(360 100 ).tan(360 170 ) cos (180 24 )
tan (360 108 ) cot (360 18 )
o
B
−− − + − −
=
−+ −
.
20 0 0 0 0 2
2 0 0 20
cos 24 tan(90 10 ).tan(180 10 ) cos 24
tan (90 18 ) cot 18
o
+ + −−
=
++
00
20
20 20 20
cot10 .( tan10 ) 1 1
tan 18
cot 18 cot 18 2cot 18 2
−−
= = =
+
.
Câu 94: Cho
( )
( )
0 0 00
0 0 00
sin 515 .cos 475 cot 222 .cot 408
cot 415 .cot 505 tan197 .tan 73
A
−+
=
−+
. Biểu thức rút gọn của
A
bằng:
A.
20
1
cos 25
2
. B.
20
1
cos 25
2
−
. C.
20
1
sin 25
2
. D.
20
1
sin 25
2
−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 28
Sưu tầm và biên soạn
Lời giải
( )
0 0 00 0
sin 515 sin155 sin 180 25 sin 25= = −=
(
)
( ) ( )
0 0 00 0
cos 475 cos 115 cos 90 25 sin 25−=−=−−=−
.
00
cot 222 cot 42=
00
cot 408 cot 48
=
;
00
cot 415 cot 55=
( )
00
cot 505 cot 35−=
.
00
tan197 tan17=
.
0000 2000
00 00 00 00
sin 25 .sin 25 cot 42 .cot 48 sin 25 cot 42 .tan 42
cot 55 .cot 35 tan17 .tan 73 cot 55 .tan55 tan17 .cot17
A
− + −+
= =
++
20
20
1 sin 25 1
cos 25
22
−
= =
.
Câu 95: Cho biểu thức
3
3
1 tan
,( , , )
(1 tan ) 4 2
x
M x kx kk
x
ππ
ππ
+
= ≠− + ≠ + ∈
+
, mệnh đề nào trong các mệnh
đề sau đúng?
A.
1M <
. B.
1
M
≤
. C.
1
4
M ≥
. D.
1
1
4
M≤≤
.
Hướng dẫn giải
Đặt
{ }
tan , \ 1t xt= ∈−
.
Ta có:
32
32
11
(1 ) 2 1
t tt
M
ttt
+ −+
= =
+ ++
2
( 1) (2 1) 1 0M t M tM⇒ − + + + −=
.
Với
1M =
thì có nghiệm
0.t =
.
Với
1M ≠
để có nghiệm khác
1−
thì.
22
1
0 (2 1) 4(M 1) 0 12 3 0 .
4
∆≥⇔ − − − ≥⇔ −≥ ≥
M MM
.
Và
2
( 1)( 1) (2 1)( 1) ( 1) 1 0 4.
− − + + −+−−≠⇔ ≠−MM M
Câu 96: Hệ thức nào sai trong bốn hệ thức sau:
A.
tan tan
tan tan
cot cot
xy
xy
xy
+
= +
+
. B.
2
2
1 sin 1 sin
4 tan
1 sin 1 sin
+−
−=
−+
αα
α
αα
.
C.
2
sin sin 2
cos sin cos sin 1 cot
−=
+ −−
αα
αα αα α
. D.
sin cos 2cos
1 cos sin cos 1
+
=
− −+
αα α
α αα
.
Lời giải
+)
sin sin sin cos sin cos
tan tan sin sin
cos cos cos cos
tan tan
cos cos sin cos sin cos
cot cot cos cos
sin sin sin sin
x y xy yx
x y xy
x y xy
xy
x y yx xy
x y xy
x y xy
+
+
+
= = = =
+
+
+
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 29
Sưu tầm và biên soạn
+)
( )( ) ( )( )
2
2
22
1 sin 1 sin 1 sin 1 sin
1 sin 1 sin
1 sin 1 sin cos cos
++ −−
+−
−= −
−+
αα αα
αα
αα α α
( )
( )
( )
2
22
22
2
1 sin 1 sin
1 sin 1 sin
cos co
1
s cos
+−
= − +−
= −
αα
αα
α αα
( )
2
2
2
22
sin
1 sin 1
1
sin
cos cos
4
4 tan=
+−
−==
α
αα
αα
α
.
+)
2
22 2
sin sin 2sin 2
cos sin cos sin cos sin 1 cot
−= =
+ − −−
αα α
αα αα α α α
.
cos sin 2cos
1 cos sin cos 1
VT VP
+
−= −
− −+
αα α
α αα
( )
( )( )
22 2
sin cos cos sin 2cos 2cos
1 cos sin cos 1
− ++− +
=
− −+
α α αα α α
ααα
( )
( )
( )( )
22
sin cos sin cos
1
0
1 cos sin cos 1 1 cos
+ +−
= = ≠
− −+ −
α α αα
ααα α
.
Câu 97: Tính
(
) ( )
sin cos 3 2 cot
2
P
π
α π α πα
= ++ − + −
, biết
1
sin
2
α
= −
và
0
2
π
α
−<<
.
A.
33 1
2
−
. B.
33 3
2
−
. C.
33 3
2
+
. D.
33 1
2
+
.
Lời giải
Ta có:
(
) ( ) (
) (
) ( )
sin cos 3 2 cot cos cos 2 cot
2
P
π
α π α πα α α α
= + + − + − = −− − + −
(
)
2
cos cos 2 cot cos 2cos 1 cot
α αα α α α
= − − = − −−
.
Mặt khác
2
22
13
cos 1 sin 1
24
αα
=− =−− =
mà
0
2
π
α
−<<
nên
3
cos
2
α
=
.
Suy ra
cos
cot 3
sin
α
α
α
= = −
.
Do đó
( )
2
3 3 33 1
cos 2cos 1 cot 2. 1 3
24 2
P
ααα
−
= − −− = − −+ =
nên A đúng.
Cách khác:
Vì
1
sin
2
α
= −
và
0
2
π
α
−<<
nên
6
π
α
= −
. Thế vào
P
ta được:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 30
Sưu tầm và biên soạn
33 1
sin cos 3 2. cot sin cos cot
62 6 6 3 3 6 2
P
ππ π π π π π
ππ
−
= −+ + + + + = − − =
.
DẠNG 5: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA BIỂU THỨC LƯỢNG GIÁC
Câu 98: Giá trị nhỏ nhất của
66
sin cosMxx= +
là.
A.
0
. B.
1
4
. C.
1
2
. D.
1
.
Lời giải
66 2
3 31
sin cos 1 sin 2 1 .
4 44
= + =− ≥− =Mxx x
.
Dấu bằng xảy ra khi
,.
42
x kk
ππ
=+∈
.
Câu 99: Giá trị nhỏ nhất của
44
sin cosMxx
= +
là.
A.
0
. B.
1
4
. C.
1
2
. D.
1
.
Lời giải
44 2
1 11
sin cos 1 sin 2 1 .
2 22
= + =− ≥− =M xx x
.
Dấu bằng xảy ra khi
,.
42
x kk
ππ
=+∈
.
Câu 100: Giá trị lớn nhất của
44
sin cosNxx
bằng:
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Ta có
4422
sin cos sin cos cos 2Nxxxx x
.
Vì
1 cos 2 1 1 cos 2 1xx
.
Nên giá trị lớn nhất là
1.
.
Câu 101: Giá trị lớn nhất của
44
sin cosM xx
bằng:
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Ta có
44 2
1
sin cos 1 sin 2
2
M xx x
.
Vì
222
11 1 1
0 sin 2 1 sin 2 0 1 sin 2 1
22 2 2
xxx
.
Nên giá trị lớn nhất là
1.
.
Câu 102: Cho
22
6cos 5sinM xx= +
. Khi đó giá trị lớn nhất của
M
là.
A.
1
. B.
5
. C.
6
. D.
11
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 31
Sưu tầm và biên soạn
(
)
22 2 2 2
6cos 5sin 6 1 sin 5sin 6 sinM xx x x x= +=−+=−
.
Ta có:
22 2
0 sin 1, 0 sin 1, 6 6 sin 5,
xx x x x x≤ ≤ ∀∈ ⇔ ≥− ≥− ∀∈ ⇔ ≥ − ≥ ∀∈
.
Gía trị lớn nhất là
6
.
Câu 103: Giá trị lớn nhất của biểu thức
22
7cos 2sinM xx
= −
là.
A.
2
−
. B.
5
. C.
7
. D.
16
.
Lời giải
(
)
22 2
7 1 sin 2sin 7 9sin
M xx x=−− =−
.
Ta có:
22 2
0 sin 1, 0 9sin 9, 7 7 2sin 2,xx xx xx
≤ ≤ ∀ ∈ ⇔ ≥− ≥− ∀ ∈ ⇔ ≥ − ≥− ∀ ∈
.
Gía trị lớn nhất là
7
.
Câu 104: Cho
2
5 2sinMx= −
. Khi đó giá trị lớn nhất của
M
là.
A.
3
. B.
5
. C.
6
. D.
7
.
Lời giải
Ta có:
22 2
0 sin 1, 0 2sin 2, 5 5 2sin 3,xx x x x x≤ ≤ ∀∈ ⇔ ≥− ≥− ∀∈ ⇔ ≥ − ≥ ∀∈
.
Gía trị lớn nhất là
5
.
Câu 105: Tính giá trị nhỏ nhất của
2
cos 2sin 2Faa=++
A.
1−
. B.
0
. C.
1
. D.
2
.
Lời giải
2
cos 2sin 2F aa
=++
2
sin 2sin 3aa=−+ +
( )
2
sin 1 4a=− −+
1 sin 1 2 sin 1 0
αα
− ≤ ≤ ⇒− ≤ − ≤
( )
2
0 sin 1 4
α
⇒≤ − ≤
( )
2
4 sin 1 0 0 4F
α
− ≤− − ≤ ⇒ ≤ ≤
Câu 106: Tính giá trị lớn nhất của
2
2sin sin 3E
αα
= −+
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
( )
2
2
2sin sin 3 sin 1 4E
αα α
= − +=− − +
Ta có
1 sin 1 2 sin 1 0
αα
− ≤ ≤ ⇒− ≤ − ≤
( )
2
0 sin 1 4
α
⇒≤ − ≤
( )
2
4 sin 1 0 0 4E
α
− ≤− − ≤ ⇒ ≤ ≤
Câu 107: Giá trị lớn nhất của
66
sin cosM xx
bằng:
A.
0.
B.
1.
C.
2.
D.
3.
Lời giải
Ta có.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 32
Sưu tầm và biên soạn
6 6 2 2 4 22 4
22 2
22
sin cos (sin cos )(sin sin cos cos )
1
cos 2 (1 sin .cos ) cos 2 (1 sin 2 )
4
31 31 31
cos 2 cos 2 cos 2 1( cos 2 1)
44 44 44
M x x x x x xx x
x xx x x
x x x do x
.
Nên giá trị lớn nhất là
1.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 33
Sưu tầm và biên soạn
BẢNG ĐÁP ÁN
1.A
2.C
3.B
4.A
5.A
6.A
7.B
8.B
9.B
10.B
11.C
12.B
13.B
14.C
15.C
16.C
17.B
18.C
19.A
20.C
21.A
22.A
23.A
24.D
25.A
26.A
27.A
28.C
29.C
30.A
31.D
32.D
33.D
34.D
35.A
36.D
37.A
38.D
39.B
40.D
41.D
42.D
43.A
44.B
45.C
46.A
47.A
48.B
49.B
50.C
51.D
52.B
53.A
54.A
55.A
56.A
57.A
58.A
59.C
60.A
61.C
62.C
63.D
64.A
65.A
66.D
67.D
68.C
69.C
70.A
71.C
72.C
73.C
74.B
75.A
76.C
77.D
78.C
79.A
80.D
81.D
82.B
83.B
84.B
85.D
86.A
87.D
88.C
89.D
90.B
91.B
92.A
93.B
94.A
95.B
96.B
97.B
98.D
99.A
100.B
101.B
102.D
103.C
104.D
105.D
106.A
107.D
108.C
109.B
110.C
111.D
112.D
113.C
114.A
115.A
116.B
117.D
118.A
119.C
120.B
121.A
122.B
123.D
124.A
125.B
126.B
127.B
128.C
129.B
130.A
131.A
132.D
133.C
134.A
135.A
136.D
137.B
138.D
139.B
140.A
141.D
142.C
143.A
144.B
145.B
146.B
147.B
148.C
149.B
150.B
151.C
152.A
153.C
154.D
155.A
156.B
157.C
158.B
159.A
160.C
161.C
162.B
163.B
164.C
165.B
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 27
Sưu tầm và biên soạn
BÀI 3. CÔNG THỨC LƯỢNG GIÁC
1. CÔNG THỨC CỘNG
( )
( )
( )
( )
( )
( )
cos cos cos sin sin
cos cos cos sin sin
sin sin cos cos sin
sin sin cos cos sin
tan tan
tan
1 tan tan
tan tan
tan .
1 tan tan
ab a b a b
ab a b a b
ab a b a b
ab a b a b
ab
ab
ab
ab
ab
ab
−= +
+= −
−= −
+= +
−
−=
+
+
+=
−
2. CÔNG THỨC NHÂN ĐÔI
1. Công thức nhân đôi
22 2 2
2
sin 2 2sin cos
cos 2 cos sin 2cos 1 1 2sin
2 tan
tan 2 .
1 tan
a aa
a aa a a
a
a
a
=
= − = −=−
=
−
2. Công thức hạ bậc
2
2
2
1 cos 2
cos
2
1 cos 2
sin
2
1 cos 2
tan
1 cos 2
a
a
a
a
a
a
a
+
=
−
=
−
=
+
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUYẾT.
I
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 28
Sưu tầm và biên soạn
3. CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG
( ) ( )
( ) ( )
( ) ( )
1
cos cos cos cos
2
1
sin sin cos cos
2
1
sin cos sin sin .
2
a b ab ab
a b ab ab
a b ab ab
= −+ +
= −− +
= −+ +
4. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH
cos cos 2cos cos
22
cos cos 2sin sin
22
sin sin 2sin cos
22
sin sin 2cos sin
22
uv uv
uv
uv uv
uv
uv uv
uv
uv uv
uv
+−
+=
+−
−=−
+−
+=
+−
−=
Câu 1: Rút gọn các biểu thức sau:
a.
( ) ( )
cos cos 2 cos 3
2
Ax x x
π
ππ
= ++ −+ +
b.
( )
73
2cox 3cos 5sin cos
22
B x xx
ππ
π
= − −+ −+ −
.
c.
(
)
3
2sin sin 5 sin cos
2 22
C xx xx
π ππ
π
= ++ −+ ++ +
d.
( ) ( )
33
cos 5 sin tan cot 3
22
Dx x x x
ππ
ππ
= −− ++ −+ −
Câu 2: Rút gọn biểu thức sau:
a.
( )
3 11
cos 15 sin tan cot
22 2
G xx x x
ππ π
π
= −+ − − + −
b.
( ) ( )
3
sin cos cot 2 tan
22
Hx x x x
ππ
ππ
= +− −+ −+ −
c.
( ) ( )
33
cos 5 sin tan cot 3
22
Ix x x x
ππ
ππ
= −− ++ −+ −
HỆ THỐNG BÀI TẬP TỰ LUẬN
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 29
Sưu tầm và biên soạn
Câu 3: Rút gọn biểu thức sau:
a.
(
) ( )
( )
66 4 4 2
3
sin cos 2sin 2 sin cos
22
N xx x x x
ππ
π ππ
= ++ −− + − − + −
b.
(
)
( )
( )
19
tan cos 36 sin 5
2
9
sin cos 99
2
x xx
O
xx
π
ππ
π
π
− −−
=
−−
c.
(
)
( )
22
85 3
sin cos 207 sin 33 sin
22
Px x x x
ππ
ππ
= + + ++ ++ −
Câu 4: Rút gọn và tính giá trị biểu thức sau:
a.
(
)
00
cos 315 .sin 765A = −
b.
00 00
sin 32 sin148 sin 302 sin122B
= −
c.
0 0 00
sin810 cos540 tan135 cot 585
C = +
d.
(
) ( )
00 0 0
sin825 cot 15 cos75 sin 555D = −+ −
Câu 5: Rút gọn và tính giá trị biểu thức sau:
a.
2 tan540 2 os1170 4sin990Ec= °+ °+ °
b.
( )
sin 234 cos 216
.tan 36
sin144 os126
F
c
− °− °
= °
°− °
c.
( )
cos 234 os666
.cot 36
sin1206 cos36
c
G
− °− °
= °
°+ °
d.
( ) ( ) (
)
(
)
sin 328 .sin 958 cos 508 .cos 1022
cot 572 tan 212
H
−° ° −° − °
= −
° −°
Câu 6: Rút gọn và tính giá trị biểu thức sau:
a.
( )
( )
00
0
00
cos 288 .cot 72
tan18
tan 142 .sin108
I
−
= −
−
.
b.
(
) ( ) ( ) ( )
0 0 00
2sin 790 cos 1260 tan 630 .tan 1260J x x xx= ++ −+ + −
.
c.
( )
00
0 00
2sin 2550 .cos 188
1
tan 368 2cos638 cos98
K
−
= +
+
.
Câu 7: Rút gọn và tính giá trị biểu thức sau:
a.
( )
0 00
00
0
cos44 tan 226 cos406
cos72 .cot18
cos316
L
+
= −
.
b.
( )
00 0
00
0
tan 46 .sin 44 cot 136 .sin 404
tan 36 .tan 54
cos316
o
M
+−
= −
.
c.
( ) ( ) ( )
( )
00 0 0
0
0
sin 328 .sin958 cos 508 .cos 1022
cos572
tan 212
N
− −−
= −
−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 30
Sưu tầm và biên soạn
Câu 8: Tính
23
cos cos cos
77 7
D
πππ
=−+
Câu 9: Tính giá trị của biểu thức
tan 9 tan 27 tan 63 tan81
°− °− °+ °
Câu 10: Tính giá trị
cos15 cos 45 cos75°°°
bằng
Câu 11: Tính giá trị của biểu thức
cot 30 cot 40 cot 50 cot 60°+ °+ °+ °
Câu 12: Tính giá trị của
cos75 sin105
A = °+ °
.
Câu 13: Tính giá trị của
5
sin sin
99
5
cos cos
99
F
ππ
ππ
+
=
+
.
Câu 14: Cho
12
sin
13
a
= −
;
3
2
2
a
π
π
<<
. Tính
cos
3
a
π
−
.
Câu 15: Biểu thức
sin sin3 sin 5
cos cos3 cos5
xxx
A
xxx
++
=
++
được rút gọn thành:
Câu 16: Tính
cos68 cos78 cos22 cos12 cos10B
= ° °+ ° °− °
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 3. CÔNG THỨC LƯỢNG GIÁC
1. CÔNG THỨC CỘNG
( )
( )
( )
( )
( )
( )
cos cos cos sin sin
cos cos cos sin sin
sin sin cos cos sin
sin sin cos cos sin
tan tan
tan
1 tan tan
tan tan
tan .
1 tan tan
ab a b a b
ab a b a b
ab a b a b
ab a b a b
ab
ab
ab
ab
ab
ab
−= +
+= −
−= −
+= +
−
−=
+
+
+=
−
2. CÔNG THỨC NHÂN ĐÔI
1. Công thức nhân đôi
22 2 2
2
sin 2 2sin cos
cos 2 cos sin 2cos 1 1 2sin
2 tan
tan 2 .
1 tan
a aa
a aa a a
a
a
a
=
= − = −=−
=
−
2. Công thức hạ bậc
2
2
2
1 cos 2
cos
2
1 cos 2
sin
2
1 cos 2
tan
1 cos 2
a
a
a
a
a
a
a
+
=
−
=
−
=
+
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUYẾT.
I
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
3. CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG
( ) ( )
( ) ( )
( ) ( )
1
cos cos cos cos
2
1
sin sin cos cos
2
1
sin cos sin sin .
2
a b ab ab
a b ab ab
a b ab ab
= −+ +
= −− +
= −+ +
4. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH
cos cos 2cos cos
22
cos cos 2sin sin
22
sin sin 2sin cos
22
sin sin 2cos sin
22
uv uv
uv
uv uv
uv
uv uv
uv
uv uv
uv
+−
+=
+−
−=−
+−
+=
+−
−=
Câu 1: Rút gọn các biểu thức sau:
a.
( ) ( )
cos cos 2 cos 3
2
Ax x x
π
ππ
= ++ −+ +
b.
( )
73
2cox 3cos 5sin cos
22
B x xx
ππ
π
= − −+ −+ −
.
c.
(
)
3
2sin sin 5 sin cos
2 22
C xx xx
π ππ
π
= ++ −+ ++ +
d.
( ) ( )
33
cos 5 sin tan cot 3
22
Dx x x x
ππ
ππ
= −− ++ −+ −
Lời giải
a.
( ) (
)
cos cos 2 cos 3
2
Ax x x
π
ππ
= ++ −+ +
sin cos cos sinxxx x=−+ − =−
b.
( )
73
2cos 3cos 5sin cos
22
Bx x x x
ππ
π
= − −+ −+ −
.
2cos 3cos 5sin cos
22
xx x x
ππ
−−
= + + −+ −
5cos 5sin cos
22
xxx
ππ
= − ++ +
5cos 5cos sin sinx xx x= − −=−
c.
( )
3
2sin sin 5 sin cos
2 22
C xx xx
π ππ
π
= ++ −+ ++ +
2cos sin sin sin
2
xx x x
π
−
= + + +−
2cos cosxx= −
cos x=
HỆ THỐNG BÀI TẬP TỰ LUẬN
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
d.
(
)
( )
33
cos 5 sin tan cot 3
22
Dx x x x
ππ
ππ
= −− ++ −+ −
cos sin tan cot
22
x x xx
ππ
−−
=− − ++ −−
cos cos cot cotxxxx
=−++−
0
=
.
Câu 2: Rút gọn biểu thức sau:
a.
(
)
3 11
cos 15 sin tan cot
22 2
G xx x x
ππ π
π
= −+ − − + −
b.
( ) ( )
3
sin cos cot 2 tan
22
Hx x x x
ππ
ππ
= +− −+ −+ −
c.
( ) ( )
33
cos 5 sin tan cot 3
22
Ix x x x
ππ
ππ
= −− ++ −+ −
Lời giải
a.
( )
3 11
cos 15 sin tan cot
22 2
G xx x x
ππ π
π
= −+ − − + −
cos sin cot cot
22
xx x x
ππ
−
=− + ++ −
cos cos cot tanx x xx
=−++
1
=
b.
(
) (
)
3
sin cos cot 2 tan
22
Hx x x x
ππ
ππ
= +− −+ −+ −
sin sin cot tan
2
xxx x
π
−
=−−−+ −
2sin cot cotxxx=− −+
2sin x= −
c.
( ) ( )
33
cos 5 sin tan cot 3
22
Ix x x x
ππ
ππ
= −− ++ −+ −
cos sin tan cot
22
x x xx
ππ
−−
= − ++ −−
cos cos cot cotxxxx=++−
2cos x=
Câu 3: Rút gọn biểu thức sau:
a.
( ) (
) ( )
66 4 4 2
3
sin cos 2sin 2 sin cos
22
N xx x x x
ππ
π ππ
= ++ −− + − − + −
b.
( ) ( )
( )
19
tan cos 36 sin 5
2
9
sin cos 99
2
x xx
O
xx
π
ππ
π
π
− −−
=
−−
c.
( ) ( )
22
85 3
sin cos 207 sin 33 sin
22
Px x x x
ππ
ππ
= + + ++ ++ −
Lời giải
a.
( ) ( ) ( )
66 4 4 2
3
sin cos 2sin 2 sin cos
22
N xx x x x
ππ
π ππ
= ++ −− + − − + −
6 6 4 42
sin cos 2sin cos sinx x x xx=+− −+
4 22 2
sin sin cos sinx xx x=−− +
( )
42 2
sin sin 1 cosxx x=−+ −
0=

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
b.
(
) (
)
(
)
19
tan cos 36 sin 5
2
9
sin cos 99
2
x xx
O
xx
π
ππ
π
π
− −−
=
−−
(
)
(
)
tan cos sin
2
sin cos
2
xx x
xx
π
π
π
−
−−
=
−+
cot cos sin
1
cos cos
x xx
xx
−
= =
−
c.
(
) ( )
22
85 3
sin cos 207 sin 33 sin
22
Px x x x
ππ
ππ
= + + ++ ++ −
(
)
22
sin cos sin cos
2
x x xx
π
= + +− + +
cos cos 1xx=−+
1=
Câu 4: Rút gọn và tính giá trị biểu thức sau:
a.
( )
00
cos 315 .sin 765
A
= −
b.
00 00
sin 32 sin148 sin 302 sin122B = −
c.
0 0 00
sin810 cos540 tan135 cot 585C = +
d.
( )
( )
00 0 0
sin825 cot 15 cos75 sin 555
D
= −+ −
Lời giải
a.
( )
(
)
0 0 0 00
cos 315 sin 765 cos315 sin 720 45
A =−= +
( )
( )
00 00
cos 360 45 sin 720 45=−+
00
cos45 sin 45=
1
2
=
b.
00 00
sin 32 sin148 sin 302 sin122B
= −
( )
( ) (
)
0 00 00 00
sin 32 sin 180 32 sin 360 58 sin 180 58
= −− − −
20 20
sin 32 sin 58= +
20 20
sin 32 cos 32
= +
1=
c.
0 0 00
sin810 cos540 tan135 cot 585C = +
( )
( ) ( ) (
)
00 0 0 0 0 0
sin 720 90 cos 720 180 tan 180 45 cot 720 135= + −+ − −
( )
0 0 00
sin 90 cos 180 tan 45 cot135= −+
( )
11=−+−
2= −
d.
( )
( )
00 0 0
sin825 cos 15 cos75 sin 555D = −+ −
( ) ( ) ( )
0 00 0 00 0 00
sin 720 90 15 cos15 cos 90 15 sin 720 180 15= ++ + − − +
( ) ( ) ( )
00 0 00 00
sin 90 15 cos15 cos 90 15 sin 180 15= + + − −+
( )
00 0 0
cos15 cos15 sin15 sin15= +−
20 20
cos 15 sin 15= −
0
cos30=
3
2
=
.
Câu 5: Rút gọn và tính giá trị biểu thức sau:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
a.
2 tan540 2 os1170 4sin990
Ec= °+ °+ °
b.
( )
sin 234 cos 216
.tan 36
sin144 os126
F
c
− °− °
= °
°− °
c.
( )
cos 234 os666
.cot 36
sin1206 cos36
c
G
− °− °
= °
°+ °
d.
(
)
( )
(
)
(
)
sin 328 .sin 958 cos 508 .cos 1022
cot 572 tan 212
H
−° ° −° − °
= −
° −°
Lời giải.
a.
2 tan540 2 os1170 4sin 990Ec= °+ °+ °
( ) ( ) ( )
2 tan 3.180 2cos 90 3.360 4sin 90 3.360= ° + °+ ° + − °+ °
4=
b.
( )
sin 234 cos 216
.tan 36
sin144 os126
F
c
− °− °
= °
°− °
( )
( )
os 90 234 os216
.tan 36
os 90 144 os126
cc
cc
°+ ° − °
= °
°− ° − °
( )
os324 os216
.tan 36
os 54 os126
cc
cc
°− °
= °
− °− °
( )
2sin 270 .sin 54 sin 36
.
2sin 90 .sin 36 os36c
− °° °
=
− ° −° °
( ) ( )
( )
2. 1 . os 90 54
sin 36
.
2.1. sin 36 os36
c
c
− − °− °
°
=
−− ° °
1=
c.
( )
cos 234 os666
.cot 36
sin1206 cos36
c
G
− °− °
= °
°+ °
( ) (
)
( )
cos 126 360 os -54 +2.360
.cot 36
sin 126 3.360 os36
c
c
°− ° − ° °
= °
°+ ° + °
( )
cos126 os 54
.cot 36
sin126 os36
c
c
°− − °
= °
°+ °
( ) ( )
( )
sin 90 126 sin 90 54
os36
.
os 90 126 os36 sin 36
c
cc
°− ° − °− °
°
=
°− ° + ° °
( )
( )
sin 36 sin 36
os36
.
os 36 os36 sin 36
c
cc
− °− °
°
=
− °+ ° °
2sin36 cos36
.
2cos36 sin 36
−°°
=
°°
1= −
d.
( ) ( ) ( )
( )
sin 328 .sin 958 cos 508 .cos 1022
cot 572 tan 212
H
−° ° −° − °
= −
° −°
( ) ( )
( )
( ) ( )
( )
sin 32 360 .sin 238 2.360 cos 148 360 .cos 58 3.360
cot 32 3.180 tan 32 180
°− ° °+ ° − °− ° °− °
= −
°+ ° − °− °
sin 32 .sin 238 cos148 .cos58
cot 32 tan 32
° ° °°
= −
° −°
( ) ( ) ( )
sin 32 .sin 180 238 .tan32 sin 90 148 .sin 90 58 .cot32= ° °− ° °+ °− ° °− ° °
( ) ( )
sin 32 os32
sin 32 .sin 58 . sin 58 .sin 32 .
os32 sin 32
c
c
°°
= ° −° + −° °
°°

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
( )
( )
2
sin 32 . os32 os 90 58 .sin32 . os32
os32 sin 32
cc c
c
° − ° °− ° ° °
= −
°°
22
sin 32 os 32c
=−−°
1= −
.
Câu 6: Rút gọn và tính giá trị biểu thức sau:
a.
( )
( )
00
0
00
cos 288 .cot 72
tan18
tan 142 .sin108
I
−
= −
−
.
b.
( )
( )
( ) ( )
0 0 00
2sin 790 cos 1260 tan 630 .tan 1260J x x xx= ++ −+ + −
.
c.
( )
00
0 00
2sin 2550 .cos 188
1
tan 368 2cos638 cos98
K
−
= +
+
.
Lời giải.
a.
( )
(
)
00
0
00
cos 288 .cot 72
tan18
tan 162 .sin108
I
−
= −
−
.
( )
( ) ( )
00 0
0
0 0 00
cos 72 360 .cot 72
tan18
tan 18 180 .sin 90 18
I
−
= −
−+
00
0
00
cos72 .cot 72
tan18
tan18 .cos18
= −
00
0
00
sin18 .tan18
tan18
tan18 .cos18
= −
00
tan18 tan18 0=−=
.
b.
( ) ( ) ( ) ( )
0 0 00
2sin 790 cos 1260 tan 630 .tan 1260J x xxx= ++ −+ + −
(
) ( )
( ) ( )
00 00 00 00
2sin 360 .2 70 cos 360 .3 180 tan 360 .2 90 .tan 360 .3 180
J x xxx= +++ +−+ −+ +−
(
)
0
2sin 70 cos cot .tanx x xx= +− −
( )
0
2sin 70 cos 1xx= +− −
.
c.
( )
00
0 00
2sin 2550 .cos 188
1
tan 368 2cos638 cos98
K
−
= +
+
.
( )
( ) ( )
( ) ( )
0 0 00
00 0 00 00
2sin 360 .7 30 .cos 180 8
1
tan 360 8 2cos 360 .2 90 8 cos 90 8
K
+ −−
= +
+ −++ +
00
0 00
1 2sin 30 .cos8
tan8 2sin8 sin8
−
= +
−
0
0
0
cos8
cot 8
sin8
= −
0=
.
Câu 7: Rút gọn và tính giá trị biểu thức sau:
a.
(
)
0 00
00
0
cos44 tan 226 cos406
cos72 .cot18
cos316
L
+
= −
.
b.
( )
00 0
00
0
tan 46 .sin 44 cot 136 .sin 404
tan 36 .tan 54
cos316
o
M
+−
= −
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
c.
( ) ( ) ( )
( )
00 0 0
0
0
sin 328 .sin958 cos 508 .cos 1022
cos572
tan 212
N
− −−
= −
−
.
Lời giải.
a.
( )
0 00
00
0
cos44 tan 226 cos406
cos72 .cot18
cos316
L
+
= −
.
( )
( )
( )
( )
( )
0 000 000
00 0
00
cos44 tan 180 90 44 cos 360 90 44
cos 90 18 .cot18
cos 360 44
L
+ +− +−
= −−
−
( )
0 00
00
0
cos44 cot 44 sin 44
sin18 .cot18
cos44
+
= −
00
sin 44 1 cos18= +−
.
b.
( )
00 0
00
0
tan 46 .sin 44 cot 136 .sin 404
tan 36 .tan 54
cos316
o
M
+−
= −
.
( ) ( ) ( )
( )
( )
0 00 00 00
00 0
000
tan 46 .sin 90 46 cot 90 46 .sin 360 90 46
tan 90 54 .tan54
cos 360 90 46
o
M
− + −− + −
= −−
+−
00 00
00
0
tan 46 .cos 46 tan 46 .cos46
cot 54 .tan54
sin 46
+
= −
00
00
0
sin 46 sin 46
cot 54 .tan54
sin 46
+
= −
211= −=
.
c.
( ) ( ) ( )
( )
00 0 0
0
0
sin 328 .sin958 cos 508 .cos 1022
cos572
tan 212
N
− −−
= −
−
.
( ) ( )
( )
( ) ( )
( )
0 0 0 00 0 0 00 0
0 0 00
sin 32 360 .sin 180 .5 90 32 cos 32 180 .3 .cos 32 90 180 .5
cos 180 .3 32 tan 180 32
N
− + − − −− −
= −
+ −−
0 0 00
00
sin 32 .cos32 cos32 .sin 32
cos32 tan 32
−
= −
−
02
sin 32 cos 32
= −
.
Câu 8: Tính
23
cos cos cos
77 7
D
πππ
=−+
Lời giải
Ta có:
( )
2sin cos cos3 cos5 sin 2 sin 2 sin 4 sin 4 sin 6 sin 6xxx x xxxxxx++ =−+−+=
Do vậy, với
sin 0
x ≠
, ta được:
sin 6
cos cos3 cos5
2sin
x
xxx
x
++=
Từ đó, với
7
x
π
=
, ta có:
6
sin
sin
35 1
7
7
cos cos cos .
77 7 2
2sin 2sin
77
π
π
π
πππ
ππ
−
++= = =
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Mặt khác:
52
cos cos
77
ππ
= −
. Vậy
2 31
cos cos cos .
7 7 72
D
πππ
=−+=
Câu 9: Tính giá trị của biểu thức
tan 9 tan 27 tan 63 tan81°− °− °+ °
Lời giải
Ta có
tan 9 tan 27 tan 63 tan81°− °− °+ °
tan 9 cot 9 tan 27 cot 27= °+ °− °− °
tan 9 tan 27 cot 9 cot 27= °− °+ °− °
sin18 sin18
cos9 cos 27 sin 9 sin 27
−° °
= +
°° °°
cos36
sin18
sin 9 sin 27 .cos9 cos 27
°
= °
° °° °
sin18 .sin54
4
1
sin18 .sin54
4
°°
= =
°°
.
Câu 10: Tính giá trị
cos15 cos 45 cos75°°°
bằng
Lời giải
Ta có
cos15 cos 45 cos75°°°
( )
21
. cos90 cos60
22
= °+ °
21 2
.
42 8
= =
.
Câu 11: Tính giá trị của biểu thức
cot 30 cot 40 cot 50 cot 60°+ °+ °+ °
Lời giải
Ta có
cot 30 cot 40 cot 50 cot 60°+ °+ °+ °
sin 90 sin 90
sin 30 .sin 60 sin 40 .sin50
°°
= +
°° °°
22
cos30 cos10
= +
°°
2cos 20 .cos10
2
cos30 .cos10
°°
=
°°
8cos20
3
°
=
.
Câu 12: Tính giá trị của
cos75 sin105A = °+ °
.
Lời giải
Ta có
cos75 sin105A = °+ °
cos75 sin 75 cos75 cos15
= °+ °= °+ °
2cos 45 .cos30
= °°
23
2. .
22
=
6
2
=
.
Câu 13: Tính giá trị của
5
sin sin
99
5
cos cos
99
F
ππ
ππ
+
=
+
.
Lời giải
Ta có
5
sin sin
99
5
cos cos
99
F
ππ
ππ
+
=
+
2
2sin .cos
39
2
2.cos .cos
39
ππ
ππ
=
tan 3
3
π
= =
.
Câu 14: Cho
12
sin
13
a = −
;
3
2
2
a
π
π
<<
. Tính
cos
3
a
π
−
.
Lời giải
Ta có
22
25
cos 1 sin
169
αα
=−=
mà
3
2
2
a
π
π
<<
5
cos 0 cos
13
αα
⇒ <⇒ =−
.
Suy ra
1 3 5 12 3
cos sin
2 2 26
P
αα
+
=+=−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
Câu 15: Biểu thức
sin sin3 sin 5
cos cos3 cos5
xxx
A
xxx
++
=
++
được rút gọn thành:
Lời giải
Ta có
sin sin3 sin 5
cos cos3 cos5
xxx
A
xxx
++
=
++
sin sin5 sin 3
cos cos5 cos3
xxx
xxx
++
=
++
2sin3 2 sin3
2cos 3 .cos 2 cos3
xco x x
xx x
+
=
+
sin 3
cos3
x
x
=
tan 3
x=
.
Câu 16: Tính
cos68 cos78 cos22 cos12 cos10
B = ° °+ ° °− °
.
Lời giải
Ta có
cos68 cos78 cos22 cos12 cos10
B = ° °+ ° °− °
cos68 cos78 sin 68 sin 78 cos10= ° °+ ° °− °
( )
cos 10 cos10= − °− °
cos10 cos10 0
= °− °=
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 31
Sưu tầm và biên soạn
BÀI 3. CÔNG THỨC LƯỢNG GIÁC
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG
Câu 1: Trong các công thức sau, công thức nào đúng?
A.
( )
sin – sin .cos cos .sin .ab a b a b= −
B.
( )
cos – cos .cos sin .sin .ab a b a b= −
C.
( )
sin sin .cos cos .sin .ab a b a b+= −
D.
( )
cos cos .cos sin .sin .ab a b a b+= +
Câu 2: Mệnh đề nào sau đây đúng?
A.
( )
tan tan
tan
tan tan
xy
xy
xy
+
−=
. B.
( )
tan tan
tan
1 tan tan
xy
xy
xy
−
−=
+
.
C.
( )
tan tan
tan
1 tan tan
xy
xy
xy
−
−=
−
. D.
( )
tan tan
tan
tan tan
xy
xy
xy
−
−=
.
Câu 3: Trong các công thức sau, công thức nào đúng?
A.
( )
sin sin .cos cos .sin
ab a b a b+= −
. B.
( )
cos cos .cos sin .sinab a b a b
+= +
.
C.
( )
sin sin .cos cos .sinab a b a b−= +
. D.
( )
cos cos .cos sin .sinab a b a b−= +
.
Câu 4: Phát biểu nào sau đây đúng?
A.
( )
tan tan
tan
1 tan .tan
αβ
αβ
αβ
−
+=
+
. B.
( )
1 tan .tan
tan
tan tan
αβ
αβ
αβ
+
+=
−
.
C.
( )
tan tan
tan
1 tan .tan
αβ
αβ
αβ
−
−=
+
. D.
( )
1 tan .tan
tan
tan tan
αβ
αβ
αβ
−
−=
+
.
Câu 5: Biểu thức
sin cos cos sinx y xy−
bằng
A.
( )
cos xy−
. B.
( )
cos xy+
. C.
( )
sin xy−
. D.
( )
sin
yx
−
.
Câu 6: Chọn khẳng định sai trong các khẳng định sau:
A.
cos( ) cos cos sin sinab a b a b+= +
. B.
sin( ) sin cos cos sinab a b a b+= +
.
C.
sin( ) sin cos cos sinab a b a b−= −
. D.
2
cos 2 1 2sinaa= −
.
Câu 7: Trong các khẳng định sau, khẳng định nào sai?
A.
sin sin 2cos sin
22
+−
−=
ab ab
ab
. B.
( )
cos cos cos sin sin−= −ab a b a b
.
C.
( )
sin sin cos cos sin
−= −ab a b a b
. D.
( ) ( )
2cos cos cos cos= −+ +a b ab ab
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 32
Sưu tầm và biên soạn
Câu 8: Biểu thức
( )
( )
sin
sin
ab
ab
+
−
bằng biểu thức nào sau đây?
A.
( )
( )
sin
sin sin
.
sin sin sin
ab
ab
ab a b
+
+
=
−−
B.
( )
( )
sin
sin sin
.
sin sin sin
ab
ab
ab a b
+
−
=
−+
C.
( )
(
)
sin
tan tan
.
sin tan tan
ab
ab
ab a b
+
+
=
−−
D.
( )
( )
sin
cot cot
.
sin cot cot
ab
ab
ab a b
+
+
=
−−
Câu 9: Cho
tan 2
α
=
. Tính
tan
4
π
α
−
.
A.
1
3
−
. B.
1
. C.
2
3
. D.
1
3
.
Câu 10: Cho hai góc
,
αβ
thỏa mãn
5
sin
13
α
=
,
2
π
απ
<<
và
3
cos
5
β
=
,
0
2
π
β
<<
. Tính giá trị
đúng của
( )
cos
αβ
−
.
A.
16
65
. B.
18
65
−
. C.
18
65
. D.
16
65
−
.
Câu 11: Cho góc lượng giác
α
2
π
απ
<<
. Xét dấu
sin
2
π
α
+
và
( )
tan
α
−
. Chọn kết quả đúng.
A.
( )
sin 0
2
tan 0
π
α
α
+<
−<
. B.
( )
sin 0
2
tan 0
π
α
α
+>
−<
. C.
( )
sin 0
2
tan 0
π
α
α
+<
−>
. D.
( )
sin 0
2
tan 0
π
α
α
+>
−>
.
Câu 12: Rút gọn biểu thức:
( ) ( ) ( ) ( )
sin –17 .cos 13 – sin 13 .cos –17aa aa° °°+° +
, ta được:
A.
sin 2a
. B.
cos 2a
. C.
1
2
−
. D.
1
2
.
Câu 13: Cho hai góc
α
và
β
thỏa mãn
3
sin
5
α
=
,
2
π
απ
<<
và
12
cos
13
β
=
,
0
2
π
β
<<
. Giá trị của
( )
sin
αβ
−
là
A.
56
65
−
. B.
56
65
. C.
16
65
. D.
16
65
−
.
Câu 14: Tính giá trị
cos
6
π
α
−
biết
1
sin , .
32
π
α απ
= <<
A.
22
3
−
. B.
126
6
+
−
. C.
126
6
−
. D.
126
6
+
.
Câu 15: Cho
sin
25
5
α
=
với
0
2
π
α
<
<
. Biết giá trị của
5 15
cos
103
ab
π
α
−
=
+
với
,ab∈
và
( )
,1ab =
. Tính
ab+
.
A.
4
. B.
10
. C.
7
. D.
3
.
Câu 16: Với
α
là số thực bất kỳ, rút gọn biểu thức
( )
cos sin
2
A
π
α απ
= −+ −
.
A.
2sinA
α
=
. B.
2cosA
α
=
. C.
1A =
. D.
0A =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 33
Sưu tầm và biên soạn
Câu 17: Cho
, xy
là các góc nhọn,
4
cot
3
x =
,
cot 7y
=
. Tổng
xy+
bằng
A.
.
3
π
B.
.
4
π
C.
.
6
π
D.
2
.
3
π
Câu 18: Cho hai góc nhọn
a
và
b
với
sin
1
3
a =
,
sin
3
2
=b
. Giá trị của
( )
sin 2 ab+
là
A.
73 42
18
−
. B.
73 42
18
+
. C.
73 22
18
−
. D.
73 22
18
+
.
Câu 19: Biết
5
sin
13
a =
,
3
cos
5
b =
,
,0
22
ab
ππ
π
<< <<
. Hãy tính
( )
sin ab+
.
A.
33
65
−
. B.
63
65
. C.
56
65
. D.
0
.
Câu 20: Cho
3
sin ,
52
π
α απ
= <<
. Tính
tan
3
π
α
+
.
A.
48 25 3
11
+
. B.
8 53
11
−
. C.
83
11
−
. D.
48 25 3
11
−
.
Câu 21: Rút gọn biểu thức:
( ) ( )
( ) (
)
sin –17 .cos 13 – sin 13 .cos –17aa aa
+°°°+ °
, ta được:
A.
sin 2 .a
B.
cos 2 .
a
C.
1
.
2
−
D.
1
.
2
Câu 22: Giá trị của biểu thức
37
cos
12
π
bằng
A.
62
.
4
+
B.
62
.
4
−
C. –
62
.
4
+
D.
26
.
4
−
Câu 23: Đẳng thức nào sau đây là đúng.
A.
1
cos cos
32
π
αα
+= +
. B.
13
cos sin cos
32 2
π
α αα
+= −
.
C.
31
cos sin cos
32 2
π
α αα
+= −
. D.
13
cos cos sin
32 2
π
α αα
+= −
.
Câu 24: Cho
tan 2
α
=
. Tính
tan
4
π
α
−
.
A.
1
3
−
. B.
1
. C.
2
3
. D.
1
3
.
Câu 25: Kết quả nào sau đây sai?
A.
π
+= +
sin cos 2 sin
4
xx x
. B.
π
−=− +
sin cos 2 cos
4
xx x
.
C.
π
+= −
sin 2 cos 2 2 sin 2
4
xx x
. D.
π
+= −
sin 2 cos 2 2 cos 2
4
xx x
.
Câu 26: Cho
3
sin
5
x =
với
2
x
π
π
<<
khi đó
tan
4
x
π
+
bằng.
A.
2
7
. B.
1
7
. C.
2
7
. D.
1
7
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 34
Sưu tầm và biên soạn
Câu 27: Cho
sin
1
3
α
=
với
0
2
π
α
< <
. Giá trị của
3
cos
π
α
+
bằng
A.
26
26
−
. B.
63−
. C.
11
2
6
−
. D.
1
6
2
−
.
Câu 28: Cho hai góc
,
αβ
thỏa mãn
5
sin
13
α
=
,
2
π
απ
<<
và
3
cos
5
β
=
,
0
2
π
β
<<
. Tính giá trị
đúng của
(
)
cos
αβ
−
.
A.
16
65
. B.
18
65
. C.
18
65
. D.
16
65
.
Câu 29: Cho
33
sin , ;
5 22
ππ
αα
= ∈
. Tính giá trị
21
cos
4
π
α
−
?
A.
2
10
. B.
72
10
−
. C.
2
10
−
. D.
72
10
.
Câu 30: Biểu thức
(
)
( )
cos –53 .sin –337 sin 307 .sin113M = °+ °° °
có giá trị bằng:
A.
1
.
2
−
B.
1
.
2
C.
3
.
2
−
D.
3
.
2
Câu 31: Rút gọn biểu thức:
cos54 .cos 4 – cos36 .cos86°° ° °
, ta được:
A.
cos50
.°
B.
cos58 .°
C.
sin 50
.°
D.
sin 58 .°
Câu 32: Cho hai góc nhọn
a
và
b
với
tan
1
7
a =
và
tan
3
4
b =
. Tính
ab+
.
A.
.
3
π
B.
.
4
π
C.
.
6
π
D.
2
.
3
π
Câu 33: Cho
, xy
là các góc nhọn,
cot
3
4
x =
,
1
cot
7
y =
. Tổng
xy+
bằng:
A.
.
4
π
B.
3
.
4
π
C.
.
3
π
D.
.
π
Câu 34: Biểu thức
22 2
cos cos cos
33
xx
A x
ππ
+++−
=
không phụ thuộc
x
và bằng:
A.
3
.
4
B.
4
.
3
C.
3
.
2
D.
2
.
3
Câu 35: Biết
sin
4
5
β
=
,
0
2
π
β
<<
và
k
απ
≠
. Giá trị của biểu thức:
( )
( )
4cos
3 sin
3
sin
A
αβ
αβ
α
+
+
=
−
không phụ thuộc vào
α
và bằng
A.
5
.
3
B.
5
.
3
C.
3
.
5
D.
3
.
5
Câu 36: Nếu
tan 4 tan
22
βα
=
thì
tan
2
βα
−
bằng:
A.
3sin
.
5 3cos
α
α
−
B.
3sin
.
5 3cos
α
α
+
C.
3cos
.
5 3cos
α
α
−
D.
3cos
.
5 3cos
α
α
+

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 35
Sưu tầm và biên soạn
Câu 37: Cho
3
cos
4
a =
;
sin 0a >
;
3
sin
5
b =
;
cos 0b
<
. Giá trị của
( )
cos .ab+
bằng:
A.
37
1.
54
+
B.
37
1.
54
−+
C.
37
1.
54
−
D.
37
1.
54
−−
Câu 38: Biết
1
cos
22
b
a
−=
và
sin 0
2
b
a
−>
;
3
sin
25
a
b
−=
và
cos 0
2
a
b
−>
. Giá trị
( )
cos ab+
bằng:
A.
24 3 7
.
50
−
B.
7 24 3
.
50
−
C.
22 3 7
.
50
−
D.
7 22 3
.
50
−
Câu 39: Rút gọn biểu thức:
(
)
( )
cos 120 – cos 120 – cos
x xx
° + °+
ta được kết quả là
A.
0.
B.
– cos .x
C.
–2cos .x
D.
sin – cos .xx
Câu 40: Cho
3
sin
5
a =
;
cos 0a <
;
3
cos
4
b
=
;
sin 0b >
. Giá trị
( )
sin ab−
bằng:
A.
19
7.
54
−+
B.
19
7.
54
−−
C.
19
7.
54
+
D.
19
7.
54
−
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC
Câu 41: Biết
2
αβ
π
γ
++=
và
cot , cot , cot
αβγ
theo thứ tự lập thành một cấp số cộng. Tích số
cot .cot
αγ
bằng:
A.
2.
B.
–2.
C.
3.
D.
–3.
Câu 42: Đẳng thức nào không đúng với mọi
x
?
A.
2
1 cos 6
cos 3
2
x
x
+
=
. B.
2
cos 2 1 2sin
xx
= −
. C.
sin 2 2sin cosx xx=
. D.
2
1 cos 4
sin 2
2
x
x
+
=
.
Câu 43: Trong các công thức sau, công thức nào sai?
A.
2
cot 1
cot 2
2cot
x
x
x
−
=
. B.
2
2 tan
tan 2
1 tan
x
x
x
=
+
.
C.
3
cos3 4cos 3cosx xx= −
. D.
3
sin 3 3sin 4sin
xx x= −
Câu 44: Trong các công thức sau, công thức nào sai?
A.
22
cos 2 cos – sin .a aa=
B.
22
cos 2 cos sin .a aa= +
C.
2
cos2 2cos –1.aa=
D.
2
cos 2 1– 2sin .aa=
Câu 45: Mệnh đề nào sau đây đúng?
A.
22
cos 2 cos sina aa= −
. B.
22
cos 2 cos sina aa= +
.
C.
2
cos 2 2 cos 1aa= +
. D.
2
cos 2 2sin 1aa= −
.
Câu 46: Cho góc lượng giác
.a
Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
2
cos 2 1 2sinaa= −
. B.
22
cos 2 cos sin
a aa= −
.
C.
2
cos 2 1 2cos
aa= −
. D.
2
cos 2 2cos 1
aa= −
.
Câu 47: Khẳng định nào dưới đây SAI?
A.
2
2sin 1 cos 2aa= −
. B.
cos 2 2cos 1aa= −
.
C.
sin 2 2sin cosa aa
=
. D.
( )
sin sin cos sin .cosab a b b a+= +
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 36
Sưu tầm và biên soạn
Câu 48: Chọn đáo án đúng.
A.
sin 2 2sin cosx xx=
. B.
sin 2 sin cos
x xx
=
. C.
sin 2 2cos
xx
=
. D.
sin 2 2sinxx=
.
Câu 49: Cho
4
cos , ;0
52
xx
π
= ∈−
. Giá trị của
sin 2x
là
A.
24
25
. B.
24
25
−
. C.
1
5
−
. D.
1
5
.
Câu 50: Cho
2
cos
3
α
= −
,
cos 2
α
nhận giá trị nào trong các giá trị sau
A.
1
9
−
. B.
4
3
−
. C.
4
3
. D.
2
3
−
.
Câu 51: Biết
(
)
cos cos .cos sin .sinab a b a b−= +
. Với
ab= −
thì
cos 2a
bằng
A.
22
cos sinaa+
. B.
22
cos sinaa−−
. C.
22
cos sinaa−
. D.
22
sin cosaa−
.
Câu 52: Với
α
là số thực bất kỳ, trong các mệnh đề sau, mệnh đề nào sai?
A.
sin 2 2sin .cos
α αα
=
. B.
2
cos 2 2cos 1
αα
= −
.
C.
2
cos 2 2sin 1
αα
=−+
. D.
22
cos 2 sin cos
ααα
= −
.
Câu 53: Biết rằng
5
sin18
ab
c
+
°=
, với
,,abc
∈
,
0c ≠
và
,
ab
cc
là các phân số tối giản. Giá trị của
biểu thức
S abc=++
là
A.
2S =
. B.
4S =
. C.
3S =
. D.
1S =
.
Câu 54: Cho
4
sin 2
5
α
= −
và
3
4
π
απ
<<
. Giá trị của
sin
α
là
A.
2
5
. B.
1
5
. C.
25
5
. D.
5
5
Câu 55: Cho
3
cos ;
52
π
α απ
=− <<
thì
sin 2
α
bằng
A.
24
25
−
. B.
24
25
. C.
4
5
. D.
4
5
−
.
Câu 56: Trong các khẳng định sau, khẳng định nào sai?
A.
cos3 cos 2cos 2 .cosx x xx+=
. B.
cos3 cos 2sin 2 .sinx x xx−=
.
C.
sin 3 sin 2cos 2 .sinx x xx−=
. D.
sin 3 sin 2sin 2 .cosx x xx+=
.
Câu 57: Với
α
là số thực bất kỳ, mệnh đề nào sau đây là mệnh đề đúng?
A.
cos 2 cos 4 2cos 2 .cos 6a
α αα
+=
. B.
sin 2 sin 4 2sin .cos3a
α αα
+=
.
C.
cos 2 cos 4 2sin 3 .sina
α αα
−=−
. D.
sin 2 sin 4 2cos3 .sin
a
α αα
−=−
.
Câu 58: Số khẳng định đúng trong các khẳng định sau:
( ) ( ) ( )
1
cos cos cos cos
2
I a b ab ab= −+ +
.
( ) ( ) ( )
1
sin sin cos cos
2
II a b a b a b= −− +
.
( )
cos cos 2cos cos
22
ab ab
III a b
+−
+=
.
( )
sin sin 2cos cos
22
ab ab
VI a b
+−
−=
.
A.
0
. B.
1
. C.
2
. D.
3
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 37
Sưu tầm và biên soạn
Câu 59: Nếu
1
sinx cos
2
x
+=
thì sin2x bằng
A.
3
4
. B.
3
8
. C.
2
2
. D.
3
4
−
.
Câu 60: Biết rằng
66 2
sin cos sin 2
x x ab x+=+
, với
,
ab
là các số thực. Tính
34Tab= +
.
A.
7T = −
. B.
1T =
. C.
0T =
. D.
7T =
.
Câu 61: Cho
3
sin 2 .
4
α
=
Tính giá trị biểu thức
tan cotA
αα
= +
A.
4
3
A =
. B.
2
3
A =
. C.
8
3
A =
. D.
16
3
A =
.
Câu 62: Cho
,
ab
là hai góc nhọn. Biết
11
cos ,cos
34
ab= =
. Giá trị của biểu thức
( ) ( )
cos cosab ab+−
bằng
A.
119
144
−
. B.
115
144
−
. C.
113
144
−
. D.
117
144
−
.
Câu 63: Cho số thực
α
thỏa mãn
1
sin
4
α
=
. Tính
( )
sin 4 2sin 2 cos
α αα
+
A.
25
128
. B.
1
16
. C.
255
128
. D.
225
128
.
Câu 64: Cho
cot 15a =
, giá trị
sin 2a
có thể nhận giá trị nào dưới đây:
A.
11
.
113
B.
13
.
113
C.
15
.
113
D.
17
.
113
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH TÍCH
Câu 65: Mệnh đề nào sau đây sai?
A.
( )
(
)
1
cos cos cos cos
2
a b ab ab= −+ +
. B.
( ) ( )
1
sin cos sin cos
2
a b ab ab= −− +
.
C.
( ) ( )
1
sin sin cos cos
2
a b ab ab= −− +
. D.
( ) ( )
1
sin cos sin sin
2
a b ab ab= −+ +
.
Câu 66: Trong các đẳng thức sau, đẳng thức nào sai?
A.
( ) cos .cos sin .sincos a b a b a b−= +
. B.
[
]
1
cos .cos ( ) ( )
2
a b cos a b cos a b= ++ −
.
C.
sin( ) sin .cos sin .cosab a b b a−= −
. D.
cos cos 2 ( ). ( )a b cos a b cos a b+= + −
.
Câu 67: Công thức nào sau đây là sai?
A.
cos cos 2cos .cos
22
ab ab
ab
+−
+=
. B.
cos cos 2sin .sin
22
ab ab
ab
+−
−=−
.
C.
sin sin 2sin .cos
22
ab ab
ab
+−
+=
. D.
sin sin 2sin .cos
22
ab ab
ab
+−
−=
.
Câu 68: Rút gọn biểu thức
( )
sin 3 cos 2 sin
sin 2 0;2 sin 1 0
cos sin 2 cos 3
x xx
A xx
xxx
+−
= ≠ +≠
+−
ta được:
A.
cot 6Ax=
. B.
cot 3Ax=
.
C.
cot 2Ax
=
. D.
tan tan 2 tan 3
Ax x x=++
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 38
Sưu tầm và biên soạn
Câu 69: Rút gọn biểu thức
sin sin
44
Pa a
ππ
=+−
.
A.
3
cos 2
2
a
−
. B.
1
cos 2
2
a
. C.
2
cos 2
3
a−
. D.
1
cos 2
2
a
−
.
Câu 70: Biến đổi biểu thức
sin 1
α
−
thành tích.
A.
sin 1 2sin cos
22
ππ
α αα
−= − +
. B.
sin 1 2sin cos
24 24
απ απ
α
−= − +
.
C.
sin 1 2sin cos
22
ππ
α αα
−= + −
. D.
sin 1 2sin cos
24 24
απ απ
α
−= + −
.
Câu 71: Rút gọn biểu thức
cos 2 cos 3 cos 5
sin 2sin 3 sin 5
a aa
P
a aa
++
=
++
.
A.
tan
Pa
=
. B.
cot
Pa
=
. C.
cot 3Pa
=
. D.
tan 3Pa=
.
Câu 72: Tính giá trị biểu thức
sin 30 .cos60 sin 60 .cos30
oo oo
P = +
.
A.
1P =
. B.
0P =
. C.
3P =
. D.
3P
= −
.
Câu 73: Giá trị đúng của
246
cos cos cos
777
πππ
++
bằng:
A.
1
.
2
B.
1
.
2
−
C.
1
.
4
D.
1
.
4
−
Câu 74: Giá trị đúng của
7
tan tan
24 24
ππ
+
bằng:
A.
( )
2 6 3.−
B.
( )
2 6 3.+
C.
( )
2 3 2.
−
D.
( )
2 3 2.+
Câu 75: Biểu thức
0
0
1
2sin 70
2sin10
A
−=
có giá trị đúng bằng:
A.
1.
B.
–1.
C.
2.
D.
–2.
Câu 76: Tích số
cos10 .cos30 .cos50 .cos70°°°°
bằng:
A.
1
.
16
B.
1
.
8
C.
3
.
16
D.
1
.
4
Câu 77: Tích số
45
cos .cos .cos
77 7
πππ
bằng:
A.
1
.
8
B.
1
.
8
−
C.
1
.
4
D.
1
.
4
−
Câu 78: Giá trị đúng của biểu thức
tan 30 tan 40 tan 50 tan 60
cos20
A
°+ °+ °
=
°+
°
bằng:
A.
2
.
3
B.
4
.
3
C.
6
.
3
D.
8
.
3
Câu 79: Cho hai góc nhọn
a
và
b
. Biết
cos
1
3
a =
,
cos
1
4
b =
. Giá trị
( ) ( )
cos .cosab ab+−
bằng:
A.
113
.
144
−
B.
115
.
144
−
C.
117
.
144
−
D.
119
.
144
−
Câu 80: Rút gọn biểu thức
sin sin 2 sin 3
cos cos 2 cos3
xxx
A
xxx
++
=
++
A.
tan 6 .Ax=
B.
tan 3 .Ax=
C.
tan 2 .Ax=
D.
tan tan 2 tan 3 .Ax x x=++

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 39
Sưu tầm và biên soạn
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC
Câu 81: Biến đổi biểu thức
sin 1
a
+
thành tích.
A.
sin 1 2sin cos .
24 24
aa
a
ππ
+= + −
B.
sin 1 2cos sin .
24 24
aa
a
ππ
+= + −
C.
sin 1 2sin cos .
22
a aa
ππ
+= + −
D.
sin 1 2cos sin .
22
a aa
ππ
+= + −
Câu 82: Cho góc
α
thỏa mãn
2
π
απ
<<
và
2
sin
2
5
α
=
.Tính giá trị của biểu thức
tan
24
απ
= −
A
.
A.
1
3
A =
. B.
1
3
A = −
. C.
3
A
=
. D.
3A = −
.
Câu 83: Cho
1
cos 0
32
xx
π
= − <<
. Giá trị của
tan 2x
là
A.
5
2
. B.
42
7
. C.
5
2
−
. D.
42
7
−
.
Câu 84: Cho
cos 0x
=
. Tính
22
sin sin
66
Ax x
ππ
= −+ +
.
A.
3
2
. B. 2. C. 1. D.
1
4
.
Câu 85: Cho biết
2
os
3
c
α
= −
. Giá trị của biểu thức
cot 3tan
2cot tan
P
αα
αα
+
=
+
bằng bao nhiêu?
A.
19
.
13
P =
B.
25
.
13
P =
C.
25
.
13
P = −
D.
19
.
13
P = −
Câu 86: Cho
( )
sin .cos sin
α αβ β
+=
với
2
k
π
αβ π
+≠+
,
2
l
π
απ
≠+
,
( )
,kl∈
. Ta có
A.
( )
tan 2cot
αβ α
+=
. B.
( )
tan 2cot
αβ β
+=
.
C.
( )
tan 2 tan
αβ β
+=
. D.
( )
tan 2 tan
αβ α
+=
.
Câu 87: Biết rằng
( )
( )
( )
22 2
cos
1 2.tan
,
cos sin 1 tan sin
ax
x
ab
x x x b ax
+= ∈
−− −
. Tính giá trị của biểu thức
P ab
.
A.
4P =
. B.
1P =
. C.
2P =
. D.
3P =
.
Câu 88: Cho
2
cos 2
3
α
=
. Tính giá trị của biểu thức
cos .cos3P
αα
=
.
A.
7
18
P =
. B.
7
9
P =
. C.
5
9
P =
. D.
5
18
.
Câu 89: Cho
tan 2x =
3
2
x
π
π
<<
. Giá trị của
sin
3
x
π
+
là
A.
23
25
−
. B.
23
25
+
−
. C.
23
25
+
. D.
23
25
−+
.
Câu 90: Tổng
tan 9 cot 9 tan15 cot15 tan 27 cot 27A
° ° ° °°°
=++ +
bằng:
A.
4.
B.
–4.
C.
8.
D.
–8.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 40
Sưu tầm và biên soạn
Câu 91: Cho hai góc nhọn
a
và
b
với
sin
1
3
a =
,
sin
1
2
b =
. Giá trị của
(
)
sin 2 ab+
là:
A.
22 73
.
18
+
B.
32 73
.
18
+
C.
42 73
.
18
+
D.
52 73
.
18
+
Câu 92: Biểu thức
2
2
2cos 2 3 sin 4 1
2sin 2 3 sin 4 1
A
αα
αα
=
+−
+−
có kết quả rút gọn là:
A.
( )
( )
cos 4 30
.
cos 4 30
α
α
+°
−°
B.
( )
( )
cos 4 30
.
cos 4 30
α
α
−°
+°
C.
( )
( )
sin 4 30
.
sin 4 30
α
α
+°
−°
D.
( )
( )
sin 4 30
.
sin 4 30
α
α
−°
+°
Câu 93: Kết quả nào sau đây SAI?
A.
sin 33 cos 60 co .s3°+=°°
B.
sin 9 sin12
.
sin 48 sin 81
°°
=
°°
C.
2
cos20 2sin 55 1 2 sin 65 .°°
= + °+
D.
1 14
.
cos290
3 sin 250 3
+=
°
°
Câu 94: Nếu
( )
5sin 3sin 2
α αβ
= +
thì:
A.
( )
tan 2 tan .
αβ β
+=
B.
( )
tan 3tan .
αβ β
+=
C.
( )
tan 4 tan .
αβ β
+=
D.
( )
tan 5 tan .
αβ β
+=
Câu 95: Cho biểu thức
( )
2 22
sin – sin – si .nA ab a b= +
Hãy chọn kết quả đúng:
A.
( )
2cos .sin .sin .A a b ab= +
B.
( )
2sin .cos .cos .A a b ab= +
C.
( )
2cos .cos .cos .A a b ab= +
D.
( )
2sin .sin .cos .A a b ab= +
Câu 96: Xác định hệ thức SAI trong các hệ thức sau ?
A.
( )
cos 40
cos40 tan .sin 40 .
cos
α
α
α
°−
°+ °=
B.
6
sin15 tan 30 .cos15 .
3
°+ ° °=
C.
( )
( )
2 22
cos – 2cos .cos .cos cos sin .x a x ax ax a++ +=
D.
( ) ( )
2 22
sin 2sin – .sin .cos sin s .– cox ax x a a ax+ +=
Câu 97: Cho
,
αβ
thoả mãn
2
sin sin
2
α+ β=
và
6
cos cos
2
α+ β=
. Tính
( ) ( )
cos sin
αβ αβ
−+ +
.
A.
12 3
6
+
. B.
4 33
2
+
. C.
3
2
−
. D.
3
2
.
Câu 98: Cho tam giác
ABC
. Tính giá trị của biểu thức
222
sin sin sin 2cos cos cosA A B C ABC=++−
.
A. 1. B. 3. C. 2. D. 0.
Câu 99: Cho
7
sin cos
5
xx+=
. Giá trị của biểu thức
2
2
2
2 sin
cos 4 sin
3tan 2
x
A xx
x
+
= −−
+
bằng.
A.
1152
625
−
. B.
8
25
−
. C.
98
625
. D.
98
625
−
.
Câu 100: Biểu thức
2
4cos sin sin
63
mn
ππ
αα α
− −=+
, với
,mn∈
. Khi đó
22
mn−
bằng
A.
7
. B.
15
. C.
7−
. D.
15−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 41
Sưu tầm và biên soạn
DẠNG 5. MIN-MAX
Câu 101: Giá trị nhỏ nhất của
66
sin cos
xx
+
là
A. 0. B.
1
2
. C.
1
4
. D.
1
8
.
Câu 102: Giá trị lớn nhất của
44
sin cosMxx= +
bằng:
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 103: Cho
3sin 4cosxMx= +
. Chọn khẳng định đúng.
A.
55M−≤ ≤
. B.
5M >
. C.
5M ≥
. D.
5M
≤
.
Câu 104: Giá trị lớn nhất của
66
sin cosM xx= −
bằng:
A.
2
. B.
3
C.
0
. D.
1
.
Câu 105: Cho biểu thức
(
)
3
3
1 tan
1 tan
x
M
x
+
=
+
,
,,
42
x kx kk
ππ
ππ
≠− + ≠ + ∈
, mệnh đề nào trong các mệnh
đề sau đúng?
A.
1M ≤
. B.
1
4
M
≥
. C.
1
1
4
M≤≤
. D.
1M <
.
Câu 106: Cho
22
6cos 5sin
M xx= +
. Khi đó giá trị lớn nhất của
M
là
A.
11
. B.
1
. C.
5
. D.
6
.
Câu 107: Giá trị lớn nhất của biểu thức
22
7cos 2sinM xx= −
là
A.
2−
. B.
5
. C.
7
. D.
16
.
DẠNG 5. NHẬN DẠNG TAM GIÁC
Câu 108: Cho
,,
ABC
là các góc của tam giác
ABC
thì.
A.
sin 2 sin 2 2sin
AB C+>
. B.
sin 2 sin 2 2sinAB C
+≤
.
C.
sin 2 sin 2 2sin
AB C+≥
. D.
sin 2 sin 2 2sinAB C+=
.
Câu 109: Một tam giác
ABC
có các góc
,,ABC
thỏa mãn
33
sin cos sin cos 0
22 22
AB BA
−=
thì tam giác đó
có gì đặc biệt?
A. Tam giác đó vuông. B. Tam giác đó đều.
C. Tam giác đó cân. D. Không có gì đặc biệt.
Câu 110: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì
cot .cot cot .cot cot .cotAB BC C A++
bằng :
A.
( )
2
cot .cot .cotABC
. B. Một kết quả khác các kết quả đã nêu trên.
C.
1
. D.
1−
.
Câu 111: Cho
A
,
B
,
C
là ba là các góc nhọn và
1
tan
2
A =
;
1
tan
5
B =
,
1
tan
8
C =
. Tổng
ABC++
bằng
A.
5
π
. B.
4
π
. C.
3
π
. D.
6
π
.
Câu 112: Biết
,,ABC
là các góc của tam giác
,ABC
khi đó.
A.
cot cot .
22
AB C+
=
B.
cos cos .
22
AB C+
=
C.
cos cos .
22
AB C+
= −
D.
tan cot .
22
AB C+
=
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 42
Sưu tầm và biên soạn
Câu 113:
,A
,B
,C
là ba góc của một tam giác. Hãy tìm hệ thức sai:
A.
( )
sin sin 2A ABC=− ++
.
B.
3
sin cos
2
ABC
A
++
= −
.
C.
3
cos sin
2
AB C
C
++
=
. D.
( )
sin sin 2C AB C= ++
.
Câu 114: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì:
A.
tan tan tan tan .tan .tan++=A B C ABC
. B.
tan tan tan tan .tan .tan
222
++=−
ABC
ABC
.
C.
tan tan tan tan .tan .tan++=−A B C ABC
. D.
tan tan tan tan .tan .tan
222
++=
ABC
ABC
.
Câu 115: Biết
,,ABC
là các góc của tam giác
,
ABC
khi đó.
A.
sin cos .
22
AB C+
=
B.
sin cos .
22
AB C+
= −
C.
sin sin .
22
AB C+
=
D.
sin sin .
22
AB C+
= −
Câu 116: Nếu
2ab=
và
abc
π
++=
. Hãy chọn kết quả đúng.
A.
( )
sin sin sin sin 2bb c a
+=
. B.
(
)
2
sin sin sin sin
bb c a+=
.
C.
( )
2
sin sin sin cosbb c a+=
. D.
( )
sin sin sin cos2bb c a+=
.
Câu 117: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì:
A.
sin 2 sin 2 sin 2 4sin .sin .sin++=A B C ABC
.
B.
sin 2 sin 2 sin 2 4cos .cos .cos++=A B C ABC
.
C.
sin 2 sin 2 sin 2 4cos .cos .cos++=−A B C ABC
.
D.
sin 2 sin 2 sin 2 4sin .sin .sin++=A B C ABC
.
Câu 118:
,A
,B
,C
là ba góc của một tam giác. Hãy chỉ hệ thức sai:
A.
43
cot tan
22
ABC A
++
= −
. B.
2
cos sin
2
A BC
B
−+
= −
.
C.
3
sin cos 2
2
AB C
C
+−
=
. D.
65
tan cot
22
AB C C++
= −
.
Câu 119: Biết
,,ABC
là các góc của tam giác
ABC
khi đó.
A.
( )
cos cosC AB= +
. B.
( )
tan tan
C AB= +
.
C.
( )
cot cotC AB=−+
. D.
( )
sin sinC AB=−+
.
Câu 120: Cho
,,ABC
là các góc của tam giác
ABC
thì
cot .cot cot .cot cot .cotAB BC C A++
bằng
A. Một kết quả khác các kết quả đã nêu trên. B.
1
.
C.
1
−
. D.
( )
2
cot .cot .cotABC
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 43
Sưu tầm và biên soạn
Câu 121: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì:
A.
cot cot cot cot .cot .cot
2 2 2 222
++=
A B C ABC
.
B.
cot cot cot cot .cot .cot
2 2 2 222
++=−
A B C ABC
.
C.
cot cot cot cot .cot .cot
222
++=
ABC
ABC
.
D.
cot cot cot cot .cot .cot
222
++=−
ABC
ABC
.
Câu 122: Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chọn hệ thức đúng trong các hệ thức sau.
A.
222
cos cos cos 1 cos .cos .cos .A B C ABC++=+
B.
222
cos cos cos 1– cos .cos .cos .A B C ABC++=
C.
222
cos cos cos 1 2cos .cos .cos .A B C ABC++=+
D.
222
cos cos cos 1– 2cos .cos .cos .A B C ABC++=
Câu 123: Hãy chỉ ra công thức sai, nếu
,,ABC
là ba góc của một tam giác.
A.
cos cos sin sin sin
2 2 22 2
B C BC A
−=
. B.
cos .cos sin .sin cos 0B C BC A− +=
.
C.
sin cos sin cos cos
22 22 2
BC CC A
+=
. D.
222
cos cos cos 2cos cos cos 1A B C ABC++− =
.
Câu 124: Cho tam giác
ABC
có
sin sinC
sin
cos cos
B
A
BC
+
=
+
. Khẳng định nào dưới đây đúng?
A. Tam giác
ABC
vuông tại
A
. B. Tam giác
ABC
cân tại
A
.
C. Tam giác
ABC
đều. D. Tam giác
ABC
là tam giác tù.
Câu 125: Cho bất đẳng thức
( )
4
1 13
2 2cos 2 4sin 0
64cos 4
cos A B B
A
+ − + +≤
với
,,ABC
là ba góc của
tam giác
ABC
.Khẳng định đúng là:
A.
120
o
BC
+=
. B.
130
o
BC+=
. C.
120
o
AB+=
. D.
140
o
AC+=
.
Câu 126: Cho
A
,
B
,
C
là các góc nhọn và
tan
1
2
A =
,
1
tan
5
B =
,
tan
1
8
C =
. Tổng
ABC++
bằng:
A.
.
6
π
B.
.
5
π
C.
.
4
π
D.
.
3
π
Câu 127: Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A.
3
sin cos .
2
AB C
C
++
=
B.
( )
cos – – cos 2 .ABC C+=
C.
23
tan cot .
22
AB C C+−
=
D.
2
cot tan .
22
AB C C++
=
Câu 128: Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A.
cos sin .
22
AB C+
=
B.
(
)
cos 2 – cos .AB C C++ =
C.
( )
sin – sin .AC B+=
D.
( )
cos – cos .AB C+=

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 44
Sưu tầm và biên soạn
Câu 129: Cho
A
,
B
,
C
là ba góc của một tam giác không vuông. Hệ thức nào sau đây SAI?
A.
cos cos sin sin sin .
2 2 22 2
B C BC A
−=
B.
tan tan tan tan .tan .tan .A B C ABC++=
C.
cot cot cot cot .cot .cot .
A B C ABC
++=
D.
tan .tan tan .tan tan .tan 1.
22 22 22
AB BC C A
++=
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 3. CÔNG THỨC LƯỢNG GIÁC
DẠNG 1. ÁP DỤNG CÔNG THỨC CỘNG
Câu 1: Trong các công thức sau, công thức nào đúng?
A.
( )
sin – sin .cos cos .sin .ab a b a b= −
B.
( )
cos – cos .cos sin .sin .
ab a b a b
= −
C.
( )
sin sin .cos cos .sin .ab a b a b
+= −
D.
( )
cos cos .cos sin .sin .ab a b a b+= +
Lời giải
Công thức cộng:
( )
sin – sin .cos cos .sin .ab a b a b= −
Câu 2: Mệnh đề nào sau đây đúng?
A.
( )
tan tan
tan
tan tan
xy
xy
xy
+
−=
. B.
( )
tan tan
tan
1 tan tan
xy
xy
xy
−
−=
+
.
C.
( )
tan tan
tan
1 tan tan
xy
xy
xy
−
−=
−
. D.
( )
tan tan
tan
tan tan
xy
xy
xy
−
−=
.
Lời giải
Ta có
( )
tan tan
tan
1 tan tan
xy
xy
xy
−
−=
+
.
Câu 3: Trong các công thức sau, công thức nào đúng?
A.
( )
sin sin .cos cos .sinab a b a b+= −
. B.
(
)
cos cos .cos sin .sinab a b a b
+= +
.
C.
( )
sin sin .cos cos .sin
ab a b a b−= +
. D.
( )
cos cos .cos sin .sinab a b a b−= +
.
Lời giải
Theo công thức cộng ta có:
+)
( )
cos cos .cos sin .sinab a b a b±=
.
+)
( )
sin sin .cos cos .sinab a b a b±= ±
.
Câu 4: Phát biểu nào sau đây đúng?
A.
(
)
tan tan
tan
1 tan .tan
αβ
αβ
αβ
−
+=
+
. B.
( )
1 tan .tan
tan
tan tan
αβ
αβ
αβ
+
+=
−
.
C.
( )
tan tan
tan
1 tan .tan
αβ
αβ
αβ
−
−=
+
. D.
( )
1 tan .tan
tan
tan tan
αβ
αβ
αβ
−
−=
+
.
Lời giải
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
Theo công thức cộng ta có:
(
)
tan tan
tan
1 tan .tan
αβ
αβ
αβ
±
±=
.
Câu 5: Biểu thức
sin cos cos sinx y xy−
bằng
A.
(
)
cos xy−
. B.
( )
cos xy+
. C.
( )
sin xy−
. D.
( )
sin yx−
.
Lời giải
Áp dụng công thức cộng lượng giác ta có đáp án.
C.
Câu 6: Chọn khẳng định sai trong các khẳng định sau:
A.
cos( ) cos cos sin sinab a b a b+= +
. B.
sin( ) sin cos cos sinab a b a b+= +
.
C.
sin( ) sin cos cos sinab a b a b−= −
. D.
2
cos 2 1 2sinaa= −
.
Lời giải
Ta có công thức đúng là:
cos( ) cos cos sin sin
ab a b a b+= −
.
Câu 7: Trong các khẳng định sau, khẳng định nào sai?
A.
sin sin 2cos sin
22
+−
−=
ab ab
ab
. B.
( )
cos cos cos sin sin−= −ab a b a b
.
C.
( )
sin sin cos cos sin−= −ab a b a b
. D.
( ) ( )
2cos cos cos cos= −+ +a b ab ab
.
Lời giải
Câu A, D là công thức biến đổi đúng
Câu C là công thức cộng đúng
Câu B sai vì
( )
cos cos cos sin sin−= +ab a b a b
.
Câu 8: Biểu thức
( )
( )
sin
sin
ab
ab
+
−
bằng biểu thức nào sau đây?
A.
( )
( )
sin
sin sin
.
sin sin sin
ab
ab
ab a b
+
+
=
−−
B.
( )
( )
sin
sin sin
.
sin sin sin
ab
ab
ab a b
+
−
=
−+
C.
( )
(
)
sin
tan tan
.
sin tan tan
ab
ab
ab a b
+
+
=
−−
D.
( )
(
)
sin
cot cot
.
sin cot cot
ab
ab
ab a b
+
+
=
−−
Lời giải.
Ta có :
( )
(
)
sin
sin cos cos sin
sin sin cos cos sin
ab
a b ab
ab a b a b
+
+
=
−−
tan tan
tan tan
ab
ab
+
=
−
.
Câu 9: Cho
tan 2
α
=
. Tính
tan
4
π
α
−
.
A.
1
3
−
. B.
1
. C.
2
3
. D.
1
3
.
Lời giải
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
Ta có
tan tan
21 1
4
tan
4 12 3
1 tan tan
4
π
α
π
α
π
α
−
−
−= = =
+
+
.
Câu 10: Cho hai góc
,
αβ
thỏa mãn
5
sin
13
α
=
,
2
π
απ
<<
và
3
cos
5
β
=
,
0
2
π
β
<<
. Tính giá trị
đúng của
( )
cos
αβ
−
.
A.
16
65
. B.
18
65
−
. C.
18
65
. D.
16
65
−
.
Lời giải
Ta có:
5
sin
13
α
=
,
2
π
απ
<<
nên
2
5 12
cos 1
13 13
α
=−− =−
.
3
cos
5
β
=
,
0
2
π
β
<<
nên
2
34
sin 1
55
β
=−=
.
( )
cos cos cos sin sin
αβ α β α β
−= +
12 3 5 4 16
..
13 5 13 5 65
=−+=−
.
Câu 11: Cho góc lượng giác
α
2
π
απ
<<
. Xét dấu
sin
2
π
α
+
và
( )
tan
α
−
. Chọn kết quả đúng.
A.
( )
sin 0
2
tan 0
π
α
α
+<
−<
. B.
( )
sin 0
2
tan 0
π
α
α
+>
−<
. C.
( )
sin 0
2
tan 0
π
α
α
+<
−>
. D.
( )
sin 0
2
tan 0
π
α
α
+>
−>
.
Lời giải
Ta có
(
)
3
sin 0
22
2
2
tan 0
2
ππ
π
πα
α
π
απ
π
πα
α
<+<
+<
<<⇒ ⇒
− <− <−
−>
.
Câu 12: Rút gọn biểu thức:
( ) ( ) ( ) ( )
sin –17 .cos 13 – sin 13 .cos –17aa aa° °°+° +
, ta được:
A.
sin 2a
. B.
cos 2
a
. C.
1
2
−
. D.
1
2
.
Lời giải
Ta có:
( ) ( ) ( ) ( ) ( ) ( )
sin –17 .cos 13 – sin 13 .cos –17 sin 17 13aa aa aa+°
°°+ =−+° °− °
( )
1
sin 30 .
2
= − °=−
Câu 13: Cho hai góc
α
và
β
thỏa mãn
3
sin
5
α
=
,
2
π
απ
<<
và
12
cos
13
β
=
,
0
2
π
β
<<
. Giá trị của
( )
sin
αβ
−
là
A.
56
65
−
. B.
56
65
. C.
16
65
. D.
16
65
−
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Lời giải
Ta có:
2
π
απ
<<
nên
cos 0
α
<
2
4
cos 1 sin
5
αα
⇒ =−− =−
.
Lại có:
0
2
π
β
<<
nên
sin 0
β
>
2
5
sin 1 cos
13
βα
⇒=− =
.
Vậy
( )
3 12 4 5 56
sin sin cos cos sin . .
5 13 5 13 65
αβ α β α β
−
−= − = − =
.
Câu 14: Tính giá trị
cos
6
π
α
−
biết
1
sin , .
32
π
α απ
= <<
A.
22
3
−
. B.
126
6
+
−
. C.
126
6
−
. D.
126
6
+
.
Lời giải
Vì
1
sin ,
32
π
α απ
= <<
nên
22
cos
3
α
= −
.
Do đó
2 2 3 11 1 2 6
cos cos .cos sin .sin . .
6 6 6 3 2 32 6
π ππ
ααα
−
−= + =− + =
.
Câu 15: Cho
sin
25
5
α
=
với
0
2
π
α
< <
. Biết giá trị của
5 15
cos
103
ab
π
α
−
=
+
với
,ab∈
và
( )
,1ab =
. Tính
ab+
.
A.
4
. B.
10
. C.
7
. D.
3
.
Lời giải
Ta có:
2 22
15
cos 1 cos cos
55
sin
αα α α
+ =⇔ =⇔=
.
Ta có:
3 1 5 3 2 5 5 2 15 5 2 15
sin
3 2 2 5 2 5 10 10 10
1
cos cos
2
π
α αα
=
−
+ − = ⋅= =
⋅− −
.
Suy ra
1, 2 3a b ab= =⇒+=
.
Câu 16: Với
α
là số thực bất kỳ, rút gọn biểu thức
( )
cos sin
2
A
π
α απ
= −+ −
.
A.
2sinA
α
=
. B.
2cosA
α
=
. C.
1A =
. D.
0A =
.
Lời giải
Ta có:
cos cos sin
22
ππ
α αα
−= −=
;
( )
sin sin .
απ α
−=−
Do đó
0.A =
Câu 17: Cho
, xy
là các góc nhọn,
4
cot
3
x =
,
cot 7y =
. Tổng
xy+
bằng

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
A.
.
3
π
B.
.
4
π
C.
.
6
π
D.
2
.
3
π
Lời giải
Ta có:
4
c tot
43
an
3
= ⇔=x x
;
1
cot 7 tan
7
=⇔=yy
.
( )
tan tan
tan 1
1 tan .tan
+
+= =
−
xy
xy
xy
, suy ra
4
π
+=xy
.
Câu 18: Cho hai góc nhọn
a
và
b
với
sin
1
3
a
=
,
sin
3
2
=b
. Giá trị của
(
)
sin 2
ab
+
là
A.
73 42
18
−
. B.
73 42
18
+
. C.
73 22
18
−
. D.
73 22
18
+
.
Lời giải
Ta có:
0
22
2
cos
1
3
sin
3
π
<<
⇒=
=
a
a
a
;
0
1
2
cos
2
sin
3
2
π
<<
⇒=
=
b
b
b
.
( ) (
) ( )
sin 2 2sin .cosab ab ab
+= + +
( )( )
2 sin .cos sin .cos cos .cos sin .sin=+−ab ba ab ab
73 42
18
−
=
.
Câu 19: Biết
5
sin
13
a =
,
3
cos
5
b =
,
,0
22
ab
ππ
π
<< <<
. Hãy tính
( )
sin ab
+
.
A.
33
65
−
. B.
63
65
. C.
56
65
. D.
0
.
Lời giải
Ta có:
2
cos 1 sinaa=±−
Do
cos 0
2
aa
π
π
<<⇒ <
2
5 12
cos 1
13 13
a
⇒ =−− =−
.
Ta có:
2
sin 1 cosbb=±−
Do
0 sin 0
2
bb
π
<< ⇒ >
2
34
sin 1
55
b
⇒=− =
.
Vậy
( )
5 3 12 4 33
sin sin cos cos sin
13 5 13 5 65
ab a b a b
−
+ = + = ⋅+ ⋅=−
.
Câu 20: Cho
3
sin ,
52
π
α απ
= <<
. Tính
tan
3
π
α
+
.
A.
48 25 3
11
+
. B.
8 53
11
−
. C.
83
11
−
. D.
48 25 3
11
−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
Lời giải
Ta có
tan tan
tan 3
3
tan
3
1 3 tan
1 tan .tan
3
π
α
πα
α
π
α
α
+
+
+= =
−
−
Mà
2
3 94
sin cos 1 sin 1
5 25 5
αα α
=⇒ =−− =−− =−
,
3
tan
4
α
⇒=−
.
Vậy
3
3
tan 3 3 4 3 48 25 3
4
tan
3
3 11
1 3 tan 4 3 3
1 3.
4
πα
α
α
−+
+ −+ −
+= = = =
−+
+
.
Câu 21: Rút gọn biểu thức:
(
) (
) ( ) ( )
sin –17 .cos 13 – sin 13 .cos –17aa aa+°°°+ °
, ta được:
A.
sin 2 .a
B.
cos 2 .a
C.
1
.
2
−
D.
1
.
2
Lời giải.
Ta có:
( )
( ) ( )
( ) ( ) ( )
sin –17 .cos 13 – sin 13 .cos –17 sin 17 13
aa aa aa+° + = −° °− + °
°°
(
)
1
sin 30 .
2
= − °=−
Câu 22: Giá trị của biểu thức
37
cos
12
π
bằng
A.
62
.
4
+
B.
62
.
4
−
C. –
62
.
4
+
D.
26
.
4
−
Lời giải.
37
cos
12
π
cos 2
12
π
ππ
= ++
cos
12
π
π
= +
cos
12
π
= −
cos
34
ππ
=−−
cos .cos sin .sin
3 4 34
ππ ππ
=−+
62
4
+
= −
.
Câu 23: Đẳng thức nào sau đây là đúng.
A.
1
cos cos
32
π
αα
+= +
. B.
13
cos sin cos
32 2
π
α αα
+= −
.
C.
31
cos sin cos
32 2
π
α αα
+= −
. D.
13
cos cos sin
32 2
π
α αα
+= −
.
Lời giải
Ta có
13
cos cos .cos sin .sin cos sin
3 3 32 2
π ππ
α α α αα
+= − = −
.
Câu 24: Cho
tan 2
α
=
. Tính
tan
4
π
α
−
.
A.
1
3
−
. B.
1
. C.
2
3
. D.
1
3
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
Lời giải
Ta có
tan tan
21 1
4
tan
4 12 3
1 tan tan
4
π
α
π
α
π
α
−
−
−= = =
+
+
.
Câu 25: Kết quả nào sau đây sai?
A.
π
+= +
sin cos 2 sin
4
xx x
. B.
π
−=− +
sin cos 2 cos
4
xx x
.
C.
π
+= −
sin 2 cos 2 2 sin 2
4
xx x
. D.
π
+= −
sin 2 cos 2 2 cos 2
4
xx x
.
Lời giải
Ta có
+= +
11
sin 2 cos 2 2 sin 2 cos 2
22
xx x x
ππ
= +
2 cos sin 2 sin cos 2
44
xx
ππ
= +≠ −
2 sin 2 2 sin 2
44
xx
Câu 26: Cho
3
sin
5
x =
với
2
x
π
π
<<
khi đó
tan
4
x
π
+
bằng.
A.
2
7
. B.
1
7
. C.
2
7
. D.
1
7
.
Lời giải
Từ
22 2
94
sin cos 1 cos 1 sin 1
25 5
xx x x+ =⇒ =±− =±− =±
.
Vì
2
x
π
π
<<
nên
4
cos
5
x = −
do đó
sin 3
tan
cos 4
x
x
x
= = −
.
Ta có:
3
tan tan 1
1
44
tan
3
47
1 tan .tan 1
44
x
x
x
π
π
π
+ −+
+= = =
−+
.
Câu 27: Cho
sin
1
3
α
=
với
0
2
π
α
< <
. Giá trị của
3
cos
π
α
+
bằng
A.
26
26
−
. B.
63−
. C.
11
2
6
−
. D.
1
6
2
−
.
Lời giải
Ta có:
2 22
26
cos 1 cos cos
33
sin
αα α α
+ =⇔ =⇔=
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Ta có:
3 1 6 31 1 1 2 6
sin
3 2 23 2 2
3 6 26
1
cos cos
2
π
α αα
−
+− ⋅
=⋅ − = −==
.
Câu 28: Cho hai góc
,
αβ
thỏa mãn
5
sin
13
α
=
,
2
π
απ
<<
và
3
cos
5
β
=
,
0
2
π
β
<<
. Tính giá trị
đúng của
( )
cos
αβ
−
.
A.
16
65
. B.
18
65
. C.
18
65
. D.
16
65
.
Lời giải
5
sin
13
α
=
,
2
π
απ
<<
nên
2
5 12
cos 1
13 13
α
=−− =−
.
3
cos
5
β
=
,
0
2
π
β
<<
nên
2
34
sin 1
55
β
=−=
.
( )
cos cos cos sin sin
αβ α β α β
−= +
12 3 5 4 16
..
13 5 13 5 65
=−+=−
.
Câu 29: Cho
33
sin , ;
5 22
ππ
αα
= ∈
. Tính giá trị
21
cos
4
π
α
−
?
A.
2
10
. B.
72
10
−
. C.
2
10
−
. D.
72
10
.
Lời giải
Ta có:
22
16 4
cos 1 sin cos
25 5
αα α
=− =⇔=±
.Do
3
; cos 0
22
ππ
αα
∈ ⇒<
nên
4
cos
5
α
−
=
.
Vậy:
21 21 21 4 2 3 2 2
cos cos cos sin sin
4 4 4 5 2 5 2 10
π ππ
ααα
−− −
−= + = + =
.
Câu 30: Biểu thức
( ) ( )
cos –53 .sin –337 sin 307 .sin113M = °+ °° °
có giá trị bằng:
A.
1
.
2
−
B.
1
.
2
C.
3
.
2
−
D.
3
.
2
Lời giải.
( ) ( )
cos –53 .sin –337 sin 307 .sin113
M = °+ °° °
( ) ( ) ( ) ( )
cos –53 .sin 23 – 360 sin 53 360 .sin 90 23°= ° ° + − °+ ° °+ °
( ) ( )
cos –53 .sin 23 sin 53 .cos 23
= °+ − °° °
( )
sin 23 53= °− °
1
sin 30
2
=− °=−
.
Câu 31: Rút gọn biểu thức:
cos54 .cos 4 – cos36 .cos86°° ° °
, ta được:
A.
cos50 .°
B.
cos58 .°
C.
sin 50 .°
D.
sin 58 .°
Lời giải.
Ta có:
cos54 .cos 4 – cos36 .cos86 cos54 .cos 4 – sin54 .sin 4 cos58 .° ° ° °= ° ° ° °= °
Câu 32: Cho hai góc nhọn
a
và
b
với
tan
1
7
a =
và
tan
3
4
b =
. Tính
ab+
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
A.
.
3
π
B.
.
4
π
C.
.
6
π
D.
2
.
3
π
Lời giải.
( )
tan tan
tan 1
1 tan .tan
ab
ab
ab
+
+= =
−
, suy ra
4
ab
π
+=
Câu 33: Cho
, xy
là các góc nhọn,
cot
3
4
x
=
,
1
cot
7
y =
. Tổng
xy+
bằng:
A.
.
4
π
B.
3
.
4
π
C.
.
3
π
D.
.
π
Lời giải.
Ta có :
( )
4
7
tan tan
3
tan 1
4
1 tan .tan
1 .7
3
xy
xy
xy
+
+
+= = =−
−
−
, suy ra
3
4
xy
π
+=
.
Câu 34: Biểu thức
22 2
cos cos cos
33
xx
A x
ππ
+++−
=
không phụ thuộc
x
và bằng:
A.
3
.
4
B.
4
.
3
C.
3
.
2
D.
2
.
3
Lời giải.
Ta có :
2
22 2
cos cos cos
33
A xx x
ππ
+++−
=
2
2
31 31
cos cos sin cos sin
22 22
x xx xx
=+−++
3
2
=
.
Câu 35: Biết
sin
4
5
β
=
,
0
2
π
β
<<
và
k
απ
≠
. Giá trị của biểu thức:
( )
( )
4cos
3 sin
3
sin
A
αβ
αβ
α
+
+
=
−
không phụ thuộc vào
α
và bằng
A.
5
.
3
B.
5
.
3
C.
3
.
5
D.
3
.
5
Lời giải.
Ta có
2
4
5
0
3
cos
5
sin
β
β
β
π
<<
⇒=
=
, thay vào biểu thức
( )
( )
4cos
3 sin
5
3
sin
3
A
αβ
αβ
α
−
=
+
+
=
.
Câu 36: Nếu
tan 4 tan
22
βα
=
thì
tan
2
βα
−
bằng:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
A.
3sin
.
5 3cos
α
α
−
B.
3sin
.
5 3cos
α
α
+
C.
3cos
.
5 3cos
α
α
−
D.
3cos
.
5 3cos
α
α
+
Lời giải.
Ta có:
22
tan tan 3tan 3sin .cos
3sin
2 2 2 22
tan .
2 5 3cos
1 tan .tan 1 4 tan 1 3sin
22 2 2
β α α αα
βα α
βα α α
α
−
−
= = = =
−
+ ++
Câu 37: Cho
3
cos
4
a
=
;
sin 0a >
;
3
sin
5
b
=
;
cos 0
b <
. Giá trị của
( )
cos .ab+
bằng:
A.
37
1.
54
+
B.
37
1.
54
−+
C.
37
1.
54
−
D.
37
1.
54
−−
Lời giải.
Ta có :
2
3
cos
7
sin 1 cos
4
4
sin 0
a
aa
a
=
⇒=− =
>
.
2
3
sin
4
cos 1 sin .
5
5
cos 0
b
bb
b
=
⇒ =−− =−
<
( )
3 4 73 3 7
cos cos cos sin sin . . 1 .
4 5 45 5 4
ab a b a b
+= − = − − =− +
Câu 38: Biết
1
cos
22
b
a
−=
và
sin 0
2
b
a
−>
;
3
sin
25
a
b
−=
và
cos 0
2
a
b
−>
. Giá trị
( )
cos ab+
bằng:
A.
24 3 7
.
50
−
B.
7 24 3
.
50
−
C.
22 3 7
.
50
−
D.
7 22 3
.
50
−
Lời giải.
Chọn A
Ta có :
1
cos
22
sin 0
2
b
a
b
a
−=
−>
2
3
sin 1 cos
2 22
bb
aa
⇒ −=− −=
.
3
sin
25
cos
2
a
b
a
b
−=
−
2
4
cos 1 sin
2 25
aa
bb
⇒ −=− −=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
cos cos cos sin sin
2 2 2 22
ab b a b a
a ba b
+
= − −+ − −
14 3 3 33 4
.. .
2 5 5 2 10
+
=+=
( )
2
24 3 7
cos 2cos 1 .
2 50
ab
ab
+−
+ = −=
Câu 39: Rút gọn biểu thức:
( ) ( )
cos 120 – cos 120 – cos
x xx
° + °+
ta được kết quả là
A.
0.
B.
– cos .x
C.
–2cos .x
D.
sin – cos .xx
Lời giải.
Chọn C
( ) (
)
cos 120 – cos 120 – cosx xx° + °+
1313
cos sin cos sin cos
2222
xxx xx=−+−+−
2cos x= −
Câu 40: Cho
3
sin
5
a =
;
cos 0a <
;
3
cos
4
b =
;
sin 0b >
. Giá trị
( )
sin ab−
bằng:
A.
19
7.
54
−+
B.
19
7.
54
−−
C.
19
7.
54
+
D.
19
7.
54
−
Lời giải.
Chọn A
Ta có :
3
sin
5
cos 0
a
a
=
<
2
4
cos 1 sin
5
aa⇒ =−− =−
.
3
cos
4
sin 0
b
b
=
>
2
7
sin 1 cos
4
bb⇒=− =
.
( )
33 4 7 1 9
sin sin cos cos sin . . 7
54 5 4 5 4
ab a b a b
− = − = −− = +
.
Câu 41: Biết
2
αβ
π
γ
++=
và
cot , cot , cot
αβγ
theo thứ tự lập thành một cấp số cộng. Tích số
cot .cot
αγ
bằng:
A.
2.
B.
–2.
C.
3.
D.
–3.
Lời giải.
Chọn C
Ta có :
2
αβ
π
γ
++=
, suy ra
( )
tan tan
cot tan
1 tan tan
αγ
β αγ
αγ
+
= +=
−
cot cot 2cot
cot cot 1 cot cot 1
αγ β
αγ αγ
+
= =
−−
cot cot 3.
αγ
⇒=

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
DẠNG 2. ÁP DỤNG CÔNG THỨC NHÂN ĐÔI – HẠ BẬC
Câu 42: Đẳng thức nào không đúng với mọi
x
?
A.
2
1 cos 6
cos 3
2
x
x
+
=
. B.
2
cos 2 1 2sinxx= −
.
C.
sin 2 2sin cos
x xx
=
. D.
2
1 cos 4
sin 2
2
x
x
+
=
.
Lời giải
Chọn D
Ta có
2
1 cos 4
sin 2
2
x
x
−
=
.
Câu 43: Trong các công thức sau, công thức nào sai?
A.
2
cot 1
cot 2
2cot
x
x
x
−
=
. B.
2
2 tan
tan 2
1 tan
x
x
x
=
+
.
C.
3
cos3 4cos 3cosx xx= −
. D.
3
sin 3 3sin 4sin
xx x= −
Lời giải.
Chọn B
Công thức đúng là
2
2 tan
tan 2
1 tan
x
x
x
=
−
.
Câu 44: Trong các công thức sau, công thức nào sai?
A.
22
cos 2 cos – sin .
a aa=
B.
22
cos 2 cos sin .a aa
= +
C.
2
cos2 2cos –1.aa
=
D.
2
cos 2 1– 2sin .aa=
Lời giải.
Chọn B
Ta có
22 2 2
cos 2 cos – sin 2cos 1 1 2sin .a aa a a= = −=−
Câu 45: Mệnh đề nào sau đây đúng?
A.
22
cos 2 cos sina aa= −
. B.
22
cos 2 cos sina aa= +
.
C.
2
cos 2 2 cos 1aa= +
. D.
2
cos 2 2sin 1aa= −
.
Lời giải
Chọn A
Câu 46: Cho góc lượng giác
.a
Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A.
2
cos 2 1 2sin
aa= −
. B.
22
cos 2 cos sina aa
= −
.
C.
2
cos 2 1 2cosaa= −
. D.
2
cos 2 2cos 1aa= −
.
Lờigiải
Chọn C
Ta có:
22 2 2
cos 2 cos sin 1 2sin 2cos 1
a aa a a=−=− = −
.
Câu 47: Khẳng định nào dưới đây SAI?
A.
2
2sin 1 cos 2aa= −
. B.
cos 2 2cos 1aa= −
.
C.
sin 2 2sin cosa aa=
. D.
( )
sin sin cos sin .cosab a b b a+= +
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
Chọn B
Có
2
cos 2 2cos 1aa= −
nên đáp án B sai.
Câu 48: Chọn đáo án đúng.
A.
sin 2 2sin cos
x xx=
. B.
sin 2 sin cosx xx=
. C.
sin 2 2cosxx=
. D.
sin 2 2sin
xx=
.
Lời giải
Chọn A
Câu 49: Cho
4
cos , ;0
52
xx
π
= ∈−
. Giá trị của
sin 2
x
là
A.
24
25
. B.
24
25
−
. C.
1
5
−
. D.
1
5
.
Lời giải
Chọn B
Ta có
22
16 9
sin 1 cos 1
25 25
xx=− =−=
3
sin
5
x⇒=−
vì
;0 sin 0
2
xx
π
∈− ⇒ <
.
Vậy
4 3 24
sin 2 2sin .cos 2. .
5 5 25
x xx
= = −=−
.
Câu 50: Cho
2
cos
3
α
= −
,
cos 2
α
nhận giá trị nào trong các giá trị sau
A.
1
9
−
. B.
4
3
−
. C.
4
3
. D.
2
3
−
.
Lời giải
Ta có:
2
2
21
cos2 2cos 1 2. 1
39
αα
−
= −= − −=
.
Câu 51: Biết
( )
cos cos .cos sin .sinab a b a b−= +
. Với
ab= −
thì
cos 2a
bằng
A.
22
cos sinaa+
. B.
22
cos sin
aa−−
. C.
22
cos sinaa−
. D.
22
sin cosaa−
.
Lời giải
Khi
22
cos 2 cos sinab a a a
=−⇒ = −
.
Câu 52: Với
α
là số thực bất kỳ, trong các mệnh đề sau, mệnh đề nào sai?
A.
sin 2 2sin .cos
α αα
=
. B.
2
cos 2 2cos 1
αα
= −
.
C.
2
cos 2 2sin 1
αα
=−+
. D.
22
cos 2 sin cos
ααα
= −
.
Lời giải
Ta có:
sin 2 2sin .cos
α αα
=
;
22 2 2
cos 2 cos sin 2cos 1 1 2sin
α αα α α
= − = −=−
.
Do đó A, B, C đúng; D sai.
Câu 53: Biết rằng
5
sin18
ab
c
+
°=
, với
,,abc∈
,
0c ≠
và
,
ab
cc
là các phân số tối giản. Giá trị của
biểu thức
S abc=++
là
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
A.
2S =
. B.
4
S =
. C.
3S =
. D.
1S =
.
Lời giải
Ta có
23
cos36 sin 54 1 2sin 18 3sin18 4sin 18
°= °⇔ − °= °− °
.
32
4sin 18 2sin 18 3sin18 1 0⇔ °− °− °+ =
(
)
( )
2
sin18 1 4sin 18 2sin18 1 0
⇔ °− °+ °− =
sin18 1
15
sin18
2
°=
⇔
−±
°=
Vì
0 18 90°< °< °
nên
0 sin18 1< °<
, do đó
15
sin18
2
−+
°=
.
Suy ra
1, 1, 2a bc=−==
. Vậy
2S abc=++=
.
Câu 54: Cho
4
sin 2
5
α
= −
và
3
4
π
απ
<<
. Giá trị của
sin
α
là
A.
2
5
. B.
1
5
. C.
25
5
. D.
5
5
Lời giải
Ta có:
3
sin 0
4
π
απ α
<<⇒ >
.
3
22 cos20
2
π
απ α
<<⇒ >
.
2
22
49 3
cos 2 1 sin 2 1 cos 2
5 25 5
αα α
=− =−− = ⇒ =
.
2
3
1
1 cos 2 1 5
5
sin sin
2 25 5
α
αα
−
−
= ==⇒=
.
Câu 55: Cho
3
cos ;
52
π
α απ
=− <<
thì
sin 2
α
bằng
A.
24
25
−
. B.
24
25
. C.
4
5
. D.
4
5
−
.
Lời giải
Vì
2
π
απ
<<
nên
sin 0>
α
;
3
cos
5
−
=
α
.
Ta có
22
sin cos 1
αα
+=⇒
4
sin
5
=
α
.
4 3 24
sin 2 2sin cos 2. . .
5 5 25
α αα
−−
= = =
Câu 56: Trong các khẳng định sau, khẳng định nào sai?
A.
cos3 cos 2cos 2 .cosx x xx
+=
. B.
cos3 cos 2sin 2 .sinx x xx−=
.
C.
sin 3 sin 2cos 2 .sinx x xx−=
. D.
sin 3 sin 2sin 2 .cosx x xx+=
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
cos3 cos 2sin 2 .sinx x xx−=−
Câu 57: Với
α
là số thực bất kỳ, mệnh đề nào sau đây là mệnh đề đúng?
A.
cos 2 cos 4 2cos 2 .cos 6a
α αα
+=
. B.
sin 2 sin 4 2sin .cos3
a
α αα
+=
.
C.
cos 2 cos 4 2sin 3 .sina
α αα
−=−
. D.
sin 2 sin 4 2cos3 .sina
α αα
−=−
.
Lời giải
Ta có:
24 24
cos 2 cos 4 2cos cos 2cos3 cos
22
a
αα αα
α αα
+−
+= =
. Do đó A sai.
24 24
sin 2 sin 4 2sin .cos 2sin 3 .cos
22
a
αα αα
α αα
+−
+= =
. Do đó B sai.
24 24
cos2 cos4 2sin .sin 2sin3 .sin
22
a
αα αα
α αα
+−
−=− =
. Do đó C sai.
24 24
sin 2 sin 4 2cos .sin 2cos3 .sin
22
a
αα αα
α αα
+−
−= =−
. Do đó D đúng.
Câu 58: Số khẳng định đúng trong các khẳng định sau:
(
) ( ) ( )
1
cos cos cos cos
2
I a b ab ab= −+ +
.
(
)
( ) ( )
1
sin sin cos cos
2
II a b a b a b= −− +
.
( )
cos cos 2cos cos
22
ab ab
III a b
+−
+=
.
( )
sin sin 2cos cos
22
ab ab
VI a b
+−
−=
.
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Khẳng định
( )
VI
sai nên có 3 khẳng định đúng.
Câu 59: Nếu
1
sinx cos
2
x+=
thì sin2x bằng
A.
3
4
. B.
3
8
. C.
2
2
. D.
3
4
−
.
Lời giải
Chọn D
Ta có
1
sinx cos
2
x+=
22
1
sin 2sin cos cos
4
x xx x⇔+ +=
3
sin 2
4
x
−
⇔=
Câu 60: Biết rằng
66 2
sin cos sin 2x x ab x+=+
, với
,ab
là các số thực. Tính
34Tab= +
.
A.
7T = −
. B.
1T =
. C.
0T =
. D.
7T =
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
Chọn C
Ta có
( )
( )
3
66 22 2222
sin cos sin cos 3sin .cos sin cosxx xx xxxx+= + − +
22 2
3
1 3sin .cos 1 sin 2
4
xx x=−=−
.
Vậy
3
1,
4
ab= = −
. Do đó
34 0Tab
=+=
.
Câu 61: Cho
3
sin 2 .
4
α
=
Tính giá trị biểu thức
tan cotA
αα
= +
A.
4
3
A =
. B.
2
3
A =
. C.
8
3
A =
. D.
16
3
A =
.
Lời giải
Chọn C
tan cotA
αα
= +
22
sin cos sin cos
cos sin sin cos
αα α α
α α αα
+
=+=
1 18
1 13
3
sin 2 .
2 24
α
= = =
.
Câu 62: Cho
,ab
là hai góc nhọn. Biết
11
cos ,cos
34
ab
= =
. Giá trị của biểu thức
( ) ( )
cos cosab ab+−
bằng
A.
119
144
−
. B.
115
144
−
. C.
113
144
−
. D.
117
144
−
.
Lời giải
Chọn A
Từ
2
17
cos cos 2 2cos 1
39
a aa= ⇒ = −=−
2
17
cos cos 2 2cos 1
48
b bb
= ⇒ = −=−
Ta có
( ) ( ) ( )
1 1 7 7 119
cos cos cos 2 cos 2
2 2 9 8 144
ab ab a b
+ − = + = −− =−
.
Câu 63: Cho số thực
α
thỏa mãn
1
sin
4
α
=
. Tính
( )
sin 4 2sin 2 cos
α αα
+
A.
25
128
. B.
1
16
. C.
255
128
. D.
225
128
.
Lời giải
Ta có
( )
sin 4 2sin 2 cos
α αα
+
( )
2sin 2 cos 2 1 cos
αα α
= +
( )
2
4sin cos 1 2sin 1 cos
αα α α
= −+
( )( )
22
4sin 1 sin 2 2sin
αα α
=−−
( )
2
2
8 1 sin sin
αα
= −
2
11
81 .
16 4
= −
225
128
=
.
Câu 64: Cho
cot 15a =
, giá trị
sin 2a
có thể nhận giá trị nào dưới đây:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
A.
11
.
113
B.
13
.
113
C.
15
.
113
D.
17
.
113
Lời giải.
Chọn C
cot 15a =
2
1
226
sin a
⇒=
2
2
1
sin
226
225
cos
226
a
a
=
⇒
=
15
sin 2
113
a⇒=±
.
DẠNG 3. ÁP DỤNG CÔNG THỨC BIẾN ĐỔI TÍCH THÀNH TỔNG, TỔNG THÀNH
TÍCH
Câu 65: Mệnh đề nào sau đây sai?
A.
( ) ( )
1
cos cos cos cos
2
a b ab ab= −+ +
. B.
( ) ( )
1
sin cos sin cos
2
a b ab ab= −− +
.
C.
(
) ( )
1
sin sin cos cos
2
a b ab ab
= −− +
. D.
( ) ( )
1
sin cos sin sin
2
a b ab ab= −+ +
.
Lời giải
Chọn B
Ta có
( ) ( )
1
sin cos sin sin
2
a b ab ab= ++ −
.
Câu 66: Trong các đẳng thức sau, đẳng thức nào sai?
A.
( ) cos .cos sin .sin
cos a b a b a b−= +
. B.
[ ]
1
cos .cos ( ) ( )
2
a b cos a b cos a b= ++ −
.
C.
sin( ) sin .cos sin .cosab a b b a−= −
. D.
cos cos 2 ( ). ( )
a b cos a b cos a b+= + −
.
Lời giải
Chọn D
Ta có:
cos cos 2 . .
22
ab ab
a b cos cos
+−
+=
Câu 67: Công thức nào sau đây là sai?
A.
cos cos 2cos .cos
22
ab ab
ab
+−
+=
. B.
cos cos 2sin .sin
22
ab ab
ab
+−
−=−
.
C.
sin sin 2sin .cos
22
ab ab
ab
+−
+=
. D.
sin sin 2sin .cos
22
ab ab
ab
+−
−=
.
Lời giải
Chọn D
Ta có
sin sin 2cos .sin
22
ab ab
ab
+−
−=
.
Câu 68: Rút gọn biểu thức
( )
sin 3 cos 2 sin
sin 2 0;2 sin 1 0
cos sin 2 cos 3
x xx
A xx
xxx
+−
= ≠ +≠
+−
ta được:
A.
cot 6Ax=
. B.
cot 3Ax=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
C.
cot 2Ax=
. D.
tan tan 2 tan 3Ax x x=++
.
Lời giải
Chọn C
sin 3 cos 2 sin
cos sin 2 cos 3
x xx
A
xxx
+−
=
+−
2 cos 2 sin cos 2
2sin 2 sin sin 2
xx x
xx x
+
=
+
cos 2 (1 2 sin )
cot 2
sin 2 (1 2sin )
xx
x
xx
+
= =
+
.
Câu 69: Rút gọn biểu thức
sin sin
44
Pa a
ππ
=+−
.
A.
3
cos 2
2
a−
. B.
1
cos 2
2
a
. C.
2
cos 2
3
a
−
. D.
1
cos 2
2
a−
.
Lời giải
Chọn D
Ta có:
11
sin sin cos cos 2 cos 2
4 42 2 2
aa a a
ππ π
+ −= − =−
.
Câu 70: Biến đổi biểu thức
sin 1
α
−
thành tích.
A.
sin 1 2sin cos
22
ππ
α αα
−= − +
. B.
sin 1 2sin cos
24 24
απ απ
α
−= − +
.
C.
sin 1 2sin cos
22
ππ
α αα
−= + −
. D.
sin 1 2sin cos
24 24
απ απ
α
−= + −
.
Lời giải
Chọn B
22
sin 1 sin sin 2cos sin 2cos sin .
2 2 2 24 24
ππ
αα
π απ απ
αα
+−
−= − = = + −
Câu 71: Rút gọn biểu thức
cos 2 cos 3 cos 5
sin 2sin 3 sin 5
a aa
P
a aa
++
=
++
.
A.
tanPa=
. B.
cotPa=
. C.
cot 3Pa=
. D.
tan 3Pa=
.
Lời giải
Chọn C
cos 2cos 3 cos5
sin 2sin3 sin 5
a aa
P
a aa
++
=
++
2cos3 cos 2cos3
2sin3 cos 2sin3
aa a
aa a
+
=
+
( )
( )
2cos3 cos 1
2sin 3 cos 1
aa
aa
+
=
+
cos3
cot 3
sin 3
a
a
a
= =
.
Câu 72: Tính giá trị biểu thức
sin 30 .cos60 sin 60 .cos30
oo oo
P = +
.
A.
1P =
. B.
0P =
. C.
3P =
. D.
3P = −
.
Lời giải
Chọn A
Ta có
( )
sin 30 60 sin 90 1
oo o
P = += =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
Câu 73: Giá trị đúng của
246
cos cos cos
777
πππ
++
bằng:
A.
1
.
2
B.
1
.
2
−
C.
1
.
4
D.
1
.
4
−
Lời giải.
Chọn B
Ta có
246
cos cos cos
777
πππ
++
246
sin cos cos cos
77 7 7
sin
7
ππ π π
π
++
=
3 53 5
sin sin sin sin sin sin
7 77 7 7
2sin
7
π ππ π π
π
π
+−+ +−+ +−
=
sin
1
7
2
2sin
7
π
π
−
= = −
.
Câu 74: Giá trị đúng của
7
tan tan
24 24
ππ
+
bằng:
A.
( )
2 6 3.−
B.
( )
2 6 3.+
C.
( )
2 3 2.
−
D.
( )
2 3 2.+
Lời giải.
Chọn A
( )
sin
73
3
tan tan 2 6 3
7
24 24
cos .cos cos cos
24 24 3 4
π
ππ
π π ππ
+= = =−
+
.
Câu 75: Biểu thức
0
0
1
2sin 70
2sin10
A −=
có giá trị đúng bằng:
A.
1.
B.
–1.
C.
2.
D.
–2.
Lời giải.
Chọn A
00 0 0
0
0 0 00
1 1 4sin10 .sin 70 2sin80 2sin10
2sin 70 1
2sin10 2sin10 2sin10 2sin10
A
−
−= = ===
.
Câu 76: Tích số
cos10 .cos30 .cos50 .cos70°°°°
bằng:
A.
1
.
16
B.
1
.
8
C.
3
.
16
D.
1
.
4
Lời giải.
Chọn C
( )
oo
1
cos10 .cos30 .cos50 .cos70 cos10 .cos30 . cos120 cos20
2
° +° ° °= ° °
3 cos10 cos30 cos10
42 2
° °+ °
=−+
31 3
.
4 4 16
= =
.
Câu 77: Tích số
45
cos .cos .cos
77 7
πππ
bằng:
A.
1
.
8
B.
1
.
8
−
C.
1
.
4
D.
1
.
4
−

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 20
Sưu tầm và biên soạn
Lời giải.
Chọn A
45
cos .cos .cos
77 7
πππ
245
sin .cos .cos
777
2sin
7
πππ
π
=
224
sin .cos .cos
777
2sin
7
πππ
π
= −
44
sin .cos
77
4sin
7
ππ
π
= −
8
sin
1
7
8
8sin
7
π
π
=−=
.
Câu 78: Giá trị đúng của biểu thức
tan 30 tan 40 tan 50 tan 60
cos20
A
°+ °+ °
=
°+
°
bằng:
A.
2
.
3
B.
4
.
3
C.
6
.
3
D.
8
.
3
Lời giải.
Chọn D
tan 30 tan 40 tan 50 tan 60
cos20
A
°+ °+ °
=
°+
°
sin 70 sin110
cos30 .cos 40 cos50 .cos60
cos20
°°
+
°° °°
=
°
11
cos30 .cos 40 cos50 .cos60
= +
°° °°
22
cos50
3 cos 40
= +
°
°
cos50 3 cos 40
2
3 cos 40 .cos50
°+ °
=
°°
sin 40 3 cos 40
2
3 cos 40 .cos50
°+ °
=
°°
( )
sin100
4
3
cos10 cos90
2
°
=
°+ °
8cos10 8
3 cos10 3
°
= =
°
.
Câu 79: Cho hai góc nhọn
a
và
b
. Biết
cos
1
3
a =
,
cos
1
4
b =
. Giá trị
( ) ( )
cos .cos
ab ab+−
bằng:
A.
113
.
144
−
B.
115
.
144
−
C.
117
.
144
−
D.
119
.
144
−
Lời giải.
Chọn D
Ta có :
( ) ( ) ( )
22
22
1 1 1 119
cos .cos cos 2 cos 2 cos cos 1 1 .
2 3 4 144
ab ab a b a b
+ − = + = + −= + −=−
Câu 80: Rút gọn biểu thức
sin sin 2 sin 3
cos cos 2 cos3
xxx
A
xxx
++
=
++
A.
tan 6 .Ax=
B.
tan 3 .
Ax=
C.
tan 2 .Ax
=
D.
tan tan 2 tan 3 .Ax x x=++
Lời giải.
Chọn C
Ta có :

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 21
Sưu tầm và biên soạn
sin sin 2 sin 3
cos cos 2 cos3
xxx
A
xxx
++
=
++
2sin 2 .cos sin 2
2cos 2 .cos cos 2
xx x
xx x
+
=
+
( )
( )
sin 2 2cos 1
tan 2 .
cos 2 2cos 1
xx
x
xx
+
= =
+
Câu 81: Biến đổi biểu thức
sin 1a +
thành tích.
A.
sin 1 2sin cos .
24 24
aa
a
ππ
+= + −
B.
sin 1 2cos sin .
24 24
aa
a
ππ
+= + −
C.
sin 1 2sin cos .
22
a aa
ππ
+= + −
D.
sin 1 2cos sin .
22
a aa
ππ
+= + −
Lời giải.
Chọn D
Ta có
sin 1a +
22
2sin cos sin cos
22 2 2
aa a a
= ++
2
sin cos
22
aa
= +
2
2sin
24
a
π
= +
2sin cos
24 42
aa
ππ
=+−
2sin cos .
24 24
aa
ππ
=+−
DẠNG 4. KẾT HỢP CÁC CÔNG THỨC LƯỢNG GIÁC
Câu 82: Cho góc
α
thỏa mãn
2
π
απ
<<
và
2
sin
2
5
α
=
.Tính giá trị của biểu thức
tan
24
απ
= −
A
.
A.
1
3
A =
. B.
1
3
A = −
. C.
3A =
. D.
3A = −
.
Lời giải
Chọn A
Vì góc
α
thỏa mãn
2
π
απ
<<
nên
422
παπ
<<
suy ra
cos 0
2
α
>
.
Do
2
sin
2
5
α
=
nên
2
1
cos 1 sin
22
5
αα
=−=
.
Biểu thức
tan 1
2
tan
24
tan 1
2
α
απ
α
−
= −=
+
A
.
Do đó
tan 2
2
α
=
.
Vậy biểu thức
21 1
21 3
−
= =
+
A
.
Câu 83: Cho
1
cos 0
32
xx
π
= − <<
. Giá trị của
tan 2x
là
A.
5
2
. B.
42
7
. C.
5
2
−
. D.
42
7
−
.
Lời giải
Chọn B

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 22
Sưu tầm và biên soạn
22
18
sin 1 cos 1
99
xx
=− =−=
22
sin
3
x
⇒=−
.
tan 2 2
x⇒=−
2
2tan 42 42
tan 2 .
1 tan 7 7
x
x
x
−
⇒= ==
−−
Câu 84: Cho
cos 0x =
. Tính
22
sin sin
66
Ax x
ππ
= −+ +
.
A.
3
2
. B. 2. C. 1. D.
1
4
.
Lời giải
Chọn A
Ta có
2
cos 2 2cos 1 1xx= −=−
. Sử dụng công thức hạ bậc và công thức biến đổi tổng thành
tích ta được:
1 cos 2 1 cos 2
13
33
1 cos 2 cos 1
2 3 22
xx
Ax
ππ
π
−−+−+
= =− =+=
Câu 85: Cho biết
2
os
3
c
α
= −
. Giá trị của biểu thức
cot 3tan
2cot tan
P
αα
αα
+
=
+
bằng bao nhiêu?
A.
19
.
13
P
=
B.
25
.
13
P =
C.
25
.
13
P = −
D.
19
.
13
P = −
Lời giải
Chọn A
Ta có:
2
2
2
2 1 15
cos tan 1 1
3 cos 4
2
3
αα
α
=− ⇒ = −= −=
−
2
2
2
2
1 1 3tan
5
3tan
1 3.
cot 3tan 1 3tan 19
tan tan
4
25
2 tan
2cot tan 2 tan 13
tan 2
tan 4
tan
P
α
α
αα α
αα
α
αα α
α
α
α
+
+
+
++
= = = = = =
+
++
++
Câu 86: Cho
( )
sin .cos sin
α αβ β
+=
với
2
k
π
αβ π
+≠+
,
2
l
π
απ
≠+
,
( )
,kl∈
. Ta có
A.
( )
tan 2cot
αβ α
+=
. B.
( )
tan 2cot
αβ β
+=
.
C.
( )
tan 2 tan
αβ β
+=
. D.
( )
tan 2 tan
αβ α
+=
.
Lời giải
Chọn D
Ta có
( )
( )
1
sin .cos sin sin 2 sin sin
2
α αβ β αβ β β
+= ⇔ +− =
( )
sin 3sin
αβ α β
⇔ ++=
( ) ( )
sin cos sin cos 3sin
αβ α α αβ β
⇔ + + +=

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 23
Sưu tầm và biên soạn
(
)
(
) ( )
sin
3sin
cos sin
cos cos
αβ
β
αα
αβ αβ
+
⇔ +=
++
( )
( )
( )
( )
sin
3sin sin
*
cos cos cos cos
αβ
βα
αβ α αβ α
+
⇔= −
++
Mà
( )
sin
sin
cos
β
α
αβ
=
+
, suy ra
( ) ( )
3sin sin
* tan 2 tan
cos cos
αα
αβ α
αα
⇔ += − =
Vậy
( )
tan 2 tan
αβ α
+=
.
Câu 87: Biết rằng
(
)
(
)
(
)
22 2
cos
1 2.tan
,
cos sin 1 tan sin
ax
x
ab
x x x b ax
+= ∈
−− −
. Tính giá trị của biểu thức
P ab
.
A.
4
P =
. B.
1P =
. C.
2P =
. D.
3P =
.
Lời giải
Chọn D
Ta có:
2
22 2
2
2sin
1 2.tan 1
cos
sin
cos sin 1 tan cos 2
1
cos
x
x
x
x
xx x x
x
+=+
−−
−
22
1 2sin .cos
cos 2 cos sin
xx
x xx
= +
−
( )
2
1 sin 2 cos 2
1 sin 2 1 sin 2
cos 2 cos 2 cos 2 cos 2
xx
xx
xx x x
+
+
=+= =
( )
2
1 sin 2 cos 2
1 sin 2
xx
x
+
=
−
cos 2
1 sin 2
x
x
=
−
. Vậy
2, 1ab
. Suy ra
3P ab
.
Câu 88: Cho
2
cos 2
3
α
=
. Tính giá trị của biểu thức
cos .cos3
P
αα
=
.
A.
7
18
P =
. B.
7
9
P =
. C.
5
9
P =
. D.
5
18
.
Lời giải
Chọn D
Ta có
( )
( )
2
2
1 1 122 5
cos .cos3 cos 2 cos 4 2cos 2 cos 2 1 2 1
2 2 2 3 3 18
P
αα αα αα
= = + = + −= +− =
.
Câu 89: Cho
tan 2x =
3
2
x
π
π
<<
. Giá trị của
sin
3
x
π
+
là
A.
23
25
−
. B.
23
25
+
−
. C.
23
25
+
. D.
23
25
−+
.
Lời giải
Chọn B

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 24
Sưu tầm và biên soạn
3
2
x
π
π
<<
suy ra
sin 0, cos 0
xx<<
.
Ta có:
2
2
1
1 tan
cos
x
x
+=
2
2
1
cos
1 tan
x
x
⇔=
+
2
1
cos
5
x
⇔=
1
cos
5
x⇔=±
Do
cos 0
x <
nên nhận
1
cos
5
x = −
.
sin 2
tan sin tan .cos
cos
5
x
x x xx
x
= ⇒= =−
21 1 3 2 3
sin sin .cos cos .sin . .
3 332 2
5 5 25
xx x
π ππ
+
+ = + =− +− =−
Câu 90: Tổng
tan 9 cot 9 tan15 cot15 tan 27 cot 27A
° ° ° °°°
=++ +
bằng:
A.
4.
B.
–4.
C.
8.
D.
–8.
Lời giải.
Chọn C
tan 9 cot 9 tan15 cot15 – tan 27 – cot 27A = °+ °+ °+ ° ° °
tan 9 cot 9 – tan 27 – cot 27 tan15 cot15= °+ ° ° °+ °+ °
tan 9 tan 81 – tan 27 – tan 63 tan15 cot15= °+ ° ° °+ °+ °
.
Ta có
sin18 sin18
tan 9 – tan 27 tan81 – tan 63
cos9 .cos 27 cos81 .cos63
−° °
° °+ ° °= +
°° °°
cos9 .cos 27 cos81 .cos 63
sin18
cos81 .cos 63 .cos9 .cos27
° °− ° °
= °
° °° °
( )
sin18 cos9 .cos 27 sin 9 .sin 27
cos81 .cos63 .cos9 .cos 27
° ° °− ° °
=
° °° °
( )(
)
4sin18 .cos36
cos72 cos90 cos36 cos90
°°
=
°+ ° °+ °
4sin18
4
cos72
°
= =
°
.
22
sin 15 cos 15 2
tan15 cot15 4
sin15 .cos15 sin 30
°+ °
°+ °= = =
°° °
.
Vậy
8
A =
.
Câu 91: Cho hai góc nhọn
a
và
b
với
sin
1
3
a =
,
sin
1
2
b =
. Giá trị của
( )
sin 2
ab+
là:
A.
22 73
.
18
+
B.
32 73
.
18
+
C.
42 73
.
18
+
D.
52 73
.
18
+
Lời giải.
Ta có
0
22
2
cos
1
3
3
sin a
a
a
π
<<
⇒=
=
;
0
3
2
cos
1
sn
2
2
i b
b
b
π
<<
⇒=
=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 25
Sưu tầm và biên soạn
( ) (
) (
)
sin 2 2sin .cosab ab ab+= + +
( )( )
2 sin .cos sin .cos cos .cos sin .sinab ba ab ab=++
42 73
18
+
=
.
Câu 92: Biểu thức
2
2
2cos 2 3 sin 4 1
2sin 2 3 sin 4 1
A
αα
αα
=
+−
+−
có kết quả rút gọn là:
A.
( )
( )
cos 4 30
.
cos 4 30
α
α
+°
−°
B.
( )
( )
cos 4 30
.
cos 4 30
α
α
−°
+°
C.
( )
( )
sin 4 30
.
sin 4 30
α
α
+°
−°
D.
( )
( )
sin 4 30
.
sin 4 30
α
α
−°
+°
Lời giải.
Ta có :
2
2
2cos 2 3 sin 4 1
2sin 2 3 sin 4 1
A
αα
αα
=
+−
+−
cos 4 3 sin 4
3 sin 4 cos 4
αα
αα
+
=
−
( )
( )
sin 4 30
sin 4 30
α
α
+°
=
−°
.
Câu 93: Kết quả nào sau đây SAI?
A.
sin 33 cos60 co .
s3°
+=°°
B.
sin 9 sin12
.
sin 48 sin 81
°°
=
°°
C.
2
cos20 2sin 55 1 2 sin 65 .
°°= + °
+
D.
1 14
.
cos290
3 sin 250 3
+=
°
°
Lời giải.
Ta có :
sin 9 sin12
sin 48 sin 81
°°
=
°°
sin 9 .sin81 sin12 .sin 48 0⇔ ° °− ° °=
( ) ( )
11
cos72 cos90 cos36 cos60 0
22
⇔ °− ° − °− ° =
2cos72 2cos36 1 0⇔ °− °+ =
2
4cos 36 2cos36 1 0⇔ °− °− =
. Suy ra B đúng.
Tương tự, ta cũng chứng minh được các biểu thức ở C và D đúng.
Biểu thức ở đáp án A sai.
Câu 94: Nếu
(
)
5sin 3sin 2
α αβ
= +
thì:
A.
( )
tan 2 tan .
αβ β
+=
B.
( )
tan 3tan .
αβ β
+=
C.
(
)
tan 4 tan .
αβ β
+=
D.
(
)
tan 5 tan .
αβ β
+=
Lời giải.
Ta có :
( )
5sin 3sin 2
α αβ
= +
( ) ( )
5sin 3sin
αβ β αβ β
⇔ +−= ++
( ) ( ) ( ) ( )
5sin cos 5cos sin 3sin cos 3cos sin
αβ β αβ β αβ β αβ β
⇔+ −+ =+ ++
( ) ( )
2sin cos 8cos sin
αβ β αβ β
⇔+ =+
( )
( )
sin
sin
4
cos cos
αβ
β
αβ β
+
⇔=
+
( )
tan 4 tan
αβ β
⇔ +=
.
Câu 95: Cho biểu thức
( )
2 22
sin – sin – si .nA ab a b= +
Hãy chọn kết quả đúng:
A.
( )
2cos .sin .sin .A a b ab= +
B.
( )
2sin .cos .cos .A a b ab= +
C.
( )
2cos .cos .cos .A a b ab= +
D.
( )
2sin .sin .cos .A a b ab= +
Lời giải.
Ta có :

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 26
Sưu tầm và biên soạn
( )
2 22
sin – sin – sinA ab a b= +
( )
2
1 cos 2 1 cos 2
sin
22
ab
ab
−−
= +− −
( ) (
)
2
1
sin 1 cos 2 cos 2
2
ab a b= + −+ +
( ) ( ) (
)
2
cos cos cosab ab ab=− ++ + −
( )
( ) ( )
cos cos cosab ab ab= + −− +
( )
2sin sin cos .a b ab= +
Câu 96: Xác định hệ thức SAI trong các hệ thức sau ?
A.
( )
cos 40
cos40 tan .sin 40 .
cos
α
α
α
°−
°+ °=
B.
6
sin15 tan 30 .cos15 .
3
°+ ° °=
C.
( )
(
)
2 22
cos – 2cos .cos .cos cos sin .x a x ax ax a++ +=
D.
(
) ( )
2 22
sin 2sin – .sin .cos sin s .– cox ax x a a ax+ +=
Lời giải.
Ta có :
sin
cos40 tan .sin 40 cos 40 .sin 40
cos
α
α
α
°+ °= °+ °
( )
cos 40
cos40 cos sin 40 sin
.
cos cos
α
αα
αα
°−
°+°
= =
A đúng.
sin15 .cos30 sin 30 .cos15 sin 45 6
sin15 tan 30 .cos15 .
cos30 cos30 3
° °+ ° ° °
°+ ° °= = =
°°
B đúng.
( ) ( )
22
cos – 2cos .cos .cos cosx a x ax ax++ +
( ) ( )
2
cos cos 2cos cos cosx ax a x ax=++− ++
( ) ( )
2
cos cos cosx ax ax
=−+ −
( )
2 222 2
1
cos cos 2 cos 2 cos cos cos 1 sin .
2
x a x xax a= − + = − − +=
C đúng.
( ) (
)
22
sin 2sin – .sin .cos sin –
x ax x a ax++
( ) ( )
( )
2
sin sin 2sin cos sinx ax x a ax
=+− +−
( ) ( )
2
sin sin sinx ax ax=+− +
( )
2
1
sin cos 2 cos 2
2
x xa=+−
2 22 2
sin cos sin 1 sinxax a= − − +=
. D sai.
Câu 97: Cho
,
αβ
thoả mãn
2
sin sin
2
α+ β=
và
6
cos cos
2
α+ β=
. Tính
( ) ( )
cos sin
αβ αβ
−+ +
.
A.
12 3
6
+
. B.
4 33
2
+
. C.
3
2
−
. D.
3
2
.
Lời giải
Ta có:
22
21
sin sin sin sin 2sin sin
22
α β α β αβ
+=⇔ + + =
( )
1

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 27
Sưu tầm và biên soạn
22
63
cos cos cos cos 2cos cos
22
α β α β αβ
+=⇔ + + =
(
)
2
Cộng vế theo vế
( )
1
với
( )
2
ta được
( ) ( ) ( )
22 2 2
sin sin cos cos 2sin sin 2cos cos 2
2 2 sin sin cos cos 2 2cos 0 cos 0.
α β α β αβ α β
α β α β αβ αβ
+++ + + =
⇔+ + =⇔ −=⇔ −=
Từ giả thiết ta lại có:
( )( )
26
sin sin cos cos .
22
αβα β
+ +=
3
sin cos sin cos sin cos sin cos
2
αα αβ βα ββ
⇔+++=
( )
(
)
13
sin 2 sin 2 sin .
22
α β αβ
⇔ + + +=
Mặt khác
( ) (
)
sin 2 sin 2 2sin cos 0
α β αβ αβ
+ = + −=
.
Suy ra
( )
3
sin
2
αβ
+=
.
Vậy
(
) (
)
3
cos sin
2
αβ αβ
−+ +=
.
Câu 98: Cho tam giác
ABC
. Tính giá trị của biểu thức
222
sin sin sin 2cos cos cosA A B C ABC=++−
.
A. 1. B. 3. C. 2. D. 0.
Lời giải
222 2 2
1 cos 2 1 cos 2 cos 2 cos 2
sin sin sin 1 cos 2 cos
22 2
A B AB
ABC C C
−− +
+ + = + +− = − −
( ) ( )
2
2 cos cos cosAB AB C=− + −−
( ) ( ) ( )
2
2 cos cos 2 cos cos cosC AB C AB C
π
=− − −=+ −−
(
) ( )
(
)
( )
( )
2cos cos cos cos cos cos cos cos cos
A B C AB AB C C AB C= ++− =−+−
(
) ( )
22
2 cos cos cos cos cos cos 2A C AB C C C AB=+ −− + − −=
Câu 99: Cho
7
sin cos
5
xx
+=
. Giá trị của biểu thức
2
2
2
2 sin
cos 4 sin
3tan 2
x
A xx
x
+
= −−
+
bằng.
A.
1152
625
−
. B.
8
25
−
. C.
98
625
. D.
98
625
−
.
Lời giải
Ta có:
7
sin cos
5
xx+=
22
49 49 24
sin 2sin cos cos 1 sin 2 sin 2
25 25 25
x xx x x x⇒ + + = ⇒+ = ⇒ =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 28
Sưu tầm và biên soạn
2
2
2
2 sin
cos 4 sin
3tan 2
x
A xx
x
+
= −−
+
2
2
2
21cos
cos 4 sin
3tan 3 1
x
xx
x
+−
= −−
+−
(
)
2
2
2
3 cos
cos 4 sin
3 tan 1 1
x
xx
x
−
= −−
+−
2
2
2
3 cos
cos 4 sin
3
1
cos
x
xx
x
−
= −−
−
( )
22
2
2
3 cos cos
cos 4 sin
3 cos
xx
xx
x
−
= −−
−
22
cos 4 sin cos
xx x= −−
2
1 2sin 2 1x=−−
2
2sin 2
x= −
2
24
2
25
= −
1152
625
= −
.
Câu 100: Biểu thức
2
4cos sin sin
63
mn
ππ
αα α
− −=+
, với
,mn∈
. Khi đó
22
mn−
bằng
A.
7
. B.
15
. C.
7−
. D.
15−
.
Lời giải
Ta có
3
π
α
−
và
6
π
α
+
phụ nhau nên
sin cos
36
ππ
αα
−= +
.
Suy ra
4cos sin 4cos cos
63 6 6
ππ ππ
αα α α
− −= − +
1
4 cos cos
266 6 6
ππ π π
αα α α
=⋅ −+ + + − − +
( )
2 cos cos 2 2 cos 2 cos2
33
ππ
αα
=⋅ + − =⋅ +⋅
( )
2 22
1
2 2. 1 2sin 1 2 4sin 3 4sin
2
α αα
=⋅+ − =+− =−
.
DẠNG 5. MIN-MAX
Câu 101: Giá trị nhỏ nhất của
66
sin cosxx+
là
A. 0. B.
1
2
. C.
1
4
. D.
1
8
.
Lời giải
Ta có
( )
3
66 22 2222 2
3 31
sin cos sin cos 3sin cos (sin cos ) 1 sin 2 1 .
4 44
xx xx xxxx x+ = + − + =− ≥− =
Dấu “=” xảy ra khi và chỉ khi
( )
2
sin21cos202 .
2 42
x x xkxkk
π ππ
π
=⇔ =⇔ = + ⇔= + ∈
Câu 102: Giá trị lớn nhất của
44
sin cosMxx
= +
bằng:
A.
4
. B.
1
. C.
2
. D.
3
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 29
Sưu tầm và biên soạn
Lời giải
Ta có
2
1
1 sin 2
2
Mx
= −
Vì
2
0 sin 1
x
≤≤
2
11
sin 2 0
22
x
⇔− ≤− ≤
2
11
1 sin 2 1
22
x⇔ ≤− ≤
.
Nên giá trị lớn nhất là
1
.
Câu 103: Cho
3sin 4cosxMx= +
. Chọn khẳng định đúng.
A.
55M−≤ ≤
. B.
5M >
. C.
5M ≥
. D.
5M ≤
.
Lời giải
( )
34
5 sin cosx 5sin
55
M x xa
= +=+
với
34
cos ;sin
55
aa= =
.
Ta có:
(
)
1 sin 1xa
−≤ + ≤
( )
5 5sin 5xa⇔− ≤ + ≤
.
Câu 104: Giá trị lớn nhất của
66
sin cos
M xx= −
bằng:
A.
2
. B.
3
C.
0
. D.
1
.
Lời giải
Ta có.
(
)
( )
2 2 4 22 4
sin cos sin sin cos cosM x x x xx x=− ++
(
)
22
cos 2 1 sin cos
x xx=−−
2
1
cos 2 1 sin 2
4
xx
=−−
22
31 31 31
cos 2 cos 2 cos 2 1
44 44 44
xx x
=− + ≤+ ≤+=
( )
cos 2 1do x ≤
.
Nên giá trị lớn nhất là
1
.
Câu 105: Cho biểu thức
( )
3
3
1 tan
1 tan
x
M
x
+
=
+
,
,,
42
x kx kk
ππ
ππ
≠− + ≠ + ∈
, mệnh đề nào trong các mệnh
đề sau đúng?
A.
1M
≤
. B.
1
4
M ≥
. C.
1
1
4
M≤≤
. D.
1M <
.
Lời giải
Đặt
{ }
tan , \ 1t xt= ∈−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 30
Sưu tầm và biên soạn
Ta có:
( )
32
3
2
11
21
1
t tt
M
tt
t
+ −+
= =
++
+
(
) (
)
2
1 2 1 10M t M tM⇒ − + + + −=
.
Với
1
M
=
thì có nghiệm
0t =
.
Với
1M ≠
để có nghiệm khác
1−
thì.
( ) (
)
22
1
0 2 1 4 1 0 12 3 0
4
MM M M
∆≥⇔ + − − ≥⇔ −≥⇔ ≥
.
Và
( )( ) ( )( ) ( )
2
11 2 11 110 4MM M− − + + −+−−≠⇔ ≠
.
Câu 106: Cho
22
6cos 5sinM xx= +
. Khi đó giá trị lớn nhất của
M
là
A.
11
. B.
1
. C.
5
. D.
6
.
Lời giải
( )
22 2
6 1 sin 5sin 6 sinM xx x=−+ =−
Ta có:
2
0 sin 1x≤≤
,
xR∀∈
2
0 sin 1,x xR⇔ ≥− ≥− ∀ ∈
2
6 6 sin 5x⇔≥− ≥
,
xR∀∈
.
Gía trị lớn nhất là
6
.
Câu 107: Giá trị lớn nhất của biểu thức
22
7cos 2sinM xx= −
là
A.
2−
. B.
5
. C.
7
. D.
16
.
Lời giải
( )
22
7 1 sin 2sinM xx=−−
2
7 9sin x= −
Ta có:
2
0 sin 1
x≤≤
2
0 9sin 9,x xR⇔ ≥− ≥− ∀ ∈
2
7 7 2sin 2x⇔ ≥ − ≥−
.
Gía trị lớn nhất là
7
.
DẠNG 5. NHẬN DẠNG TAM GIÁC
Câu 108: Cho
,,ABC
là các góc của tam giác
ABC
thì.
A.
sin 2 sin 2 2sinAB C+>
. B.
sin 2 sin 2 2sinAB C+≤
.
C.
sin 2 sin 2 2sinAB C+≥
. D.
sin 2 sin 2 2sinAB C+=
.
Lời giải
Ta có:
( ) ( )
( ) ( )
sin 2 sin 2 2sin .cos 2sin .cos
A B AB AB C AB
π
+ = + −= − −
( )
2sin .cos 2sin .C AB C= −≤
Dấu đẳng thức xảy ra khi
( )
cos 1AB A B− =⇔=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 31
Sưu tầm và biên soạn
Câu 109: Một tam giác
ABC
có các góc
,,ABC
thỏa mãn
33
sin cos sin cos 0
22 22
AB BA
−=
thì tam giác đó
có gì đặc biệt?
A. Tam giác đó vuông. B. Tam giác đó đều.
C. Tam giác đó cân. D. Không có gì đặc biệt.
Lời giải
Chọn C
Ta có
33
23
sin sin
22
sin cos sin cos 0
22 22
cos cos
22
AB
AB BA
AB
− =⇔=
.
22
tan 1 tan tan 1 tan tan tan
22222222
AABBABAB
AB
⇔+=+⇔=⇔=⇔=
.
Câu 110: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì
cot .cot cot .cot cot .cotAB BC C A++
bằng :
A.
(
)
2
cot .cot .cotABC
. B. Một kết quả khác các kết quả đã nêu trên.
C.
1
. D.
1−
.
Lời giải
Chọn C
Ta có
cot .cot cot .cot cot .cotAB BC C A++
1 1 1 tan tan tan
tan .tan tan .tan tan .tan tan .tan .tan
ABC
AB BC C A ABC
++
=++=
.
Mặt khác
tan tan tanABC++
( )( )
tan 1 tan .tan tanAB A B C= +− +
( )( )
tan 1 tan .tan tanC AB C
π
= −− +
(
)(
)
tan 1 tan .tan tan
C AB C
=−− +
tan .tan .tanC AB=
.
Nên
cot .cot cot .cot cot .cot 1AB BC C A++=
.
Câu 111: Cho
A
,
B
,
C
là ba là các góc nhọn và
1
tan
2
A =
;
1
tan
5
B =
,
1
tan
8
C =
. Tổng
ABC++
bằng
A.
5
π
. B.
4
π
. C.
3
π
. D.
6
π
.
Lời giải
Ta có
( )
11
tan tan 7
25
tan
11
1 tan .tan 9
1.
25
AB
AB
AB
+
+
+= = =
−
−
.
Suy ra
( ) ( )
( )
( )
71
tan tan
98
tan tan 1
71
1 tan .tan
1.
98
AB C
ABC AB C
AB C
+
++
++ = + + = = =
−+
−
Vậy
4
ABC
π
++=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 32
Sưu tầm và biên soạn
Câu 112: Biết
,,ABC
là các góc của tam giác
,ABC
khi đó.
A.
cot cot .
22
AB C+
=
B.
cos cos .
22
AB C
+
=
C.
cos cos .
22
AB C
+
= −
D.
tan cot .
22
AB C+
=
Lời giải
Vì
,,ABC
là các góc của tam giác
ABC
nên
(
)
180 180
oo
ABC C AB++= ⇒ = − +
.
90 .
22
o
C AB+
⇒= −
Do đó
2
C
và
2
AB+
là 2 góc phụ nhau.
sin cos ; cos sin ; tan cot ; cot tan .
2 22 22 22 2
C AB C AB C AB C AB++++
⇒= = = =
Câu 113:
,
A
,
B
,
C
là ba góc của một tam giác. Hãy tìm hệ thức sai:
A.
(
)
sin sin 2A ABC
=− ++
.
B.
3
sin cos
2
ABC
A
++
= −
.
C.
3
cos sin
2
AB C
C
++
=
. D.
( )
sin sin 2C AB C= ++
.
Lời giải
( )
( ) (
)
00
sin 2 sin 180 2 sin 180 sin
AB C C C C C++ = −+ = + =−
.
Câu 114: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì:
A.
tan tan tan tan .tan .tan++=A B C ABC
. B.
tan tan tan tan .tan .tan
222
++=−
ABC
ABC
.
C.
tan tan tan tan .tan .tan++=−
A B C ABC
. D.
tan tan tan tan .tan .tan
222
++=
ABC
ABC
.
Lời giải
Ta có:
tan tan tan++ABC
( )
tan tan tan=++AB C
( )
sin
sin
cos .cos cos
+
= +
AB
C
AB C
.
( )
cos cos .cos
sin .
cos .cos .cos
− ++
=
AB A B
C
ABC
sin .sin .sin
cos .cos .cos
=
ABC
ABC
tan .tan .tan= ABC
.
Câu 115: Biết
,,ABC
là các góc của tam giác
,ABC
khi đó.
A.
sin cos .
22
AB C+
=
B.
sin cos .
22
AB C+
= −
C.
sin sin .
22
AB C+
=
D.
sin sin .
22
AB C+
= −
Lời giải
Vì
,,ABC
là các góc của tam giác
ABC
nên
( )
180 180
oo
ABC C AB++= ⇒= − +
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 33
Sưu tầm và biên soạn
90 .
22
o
C AB
+
⇒= −
Do đó
2
C
và
2
AB+
là 2 góc phụ nhau.
sin cos ; cos sin ; tan cot ; cot tan .
2 22 22 22 2
C AB C AB C AB C AB
++++
⇒= = = =
Câu 116: Nếu
2ab=
và
abc
π
++=
. Hãy chọn kết quả đúng.
A.
(
)
sin sin sin sin 2
bb c a
+=
. B.
( )
2
sin sin sin sinbb c a+=
.
C.
(
)
2
sin sin sin cosbb c a
+=
. D.
( )
sin sin sin cos 2bb c a+=
.
Lời giải
( )
2
3
,2 ;
22
1 cos 2 cos(b c) cos(b c)
sin sin sin sin sin .sin =
22
aa
abc a b b c
b
b b c b bc
ππ
++= = ⇒= = −
− −− +
+=+ +
( ) ( )
2
1 cos cos cos 2
1 cos 2
= sin
22
a aa
a
a
ππ
− − −+ −
−
= =
.
Câu 117: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì:
A.
sin 2 sin 2 sin 2 4sin .sin .sin++=A B C ABC
.
B.
sin 2 sin 2 sin 2 4cos .cos .cos
++=A B C ABC
.
C.
sin 2 sin 2 sin 2 4cos .cos .cos
++=−A B C ABC
.
D.
sin 2 sin 2 sin 2 4sin .sin .sin++=A B C ABC
.
Lời giải
Ta có:
sin 2 sin 2 sin 2++ABC
( )
sin 2 sin 2 sin 2AB C=++
( )
(
)
2sin .cos 2sin .cosC= + −+AB AB C
(
)
2sin .cos 2sin .cosC= −+C AB C
( )
( )
2sin . cos cosC= −+C AB
(
)
( )
4sin .cos .cos= −− −+
C ABC ABC
4sin .cos .cos
22
−− −+
=
ABC ABC
C
4sin .cos .cos
22
ππ
= −−
CA B
4sin .sin .sin
= C AB
.
Câu 118:
,A
,B
,C
là ba góc của một tam giác. Hãy chỉ hệ thức sai:
A.
43
cot tan
22
ABC A++
= −
. B.
2
cos sin
2
A BC
B
−+
= −
.
C.
3
sin cos 2
2
AB C
C
+−
=
. D.
65
tan cot
22
AB C C++
= −
.
Lời giải
0
0
2 180 2 3 3
cos cos cos 90 sin
2 2 22
A BC B B B B− + −−
= = −=
.
Câu 119: Biết
,,ABC
là các góc của tam giác
ABC
khi đó.
A.
( )
cos cosC AB= +
. B.
( )
tan tanC AB= +
.
C.
( )
cot cotC AB=−+
. D.
(
)
sin sinC AB=−+
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 34
Sưu tầm và biên soạn
Vì
,,ABC
là các góc của tam giác
ABC
nên
( )
180 180ABC C AB+ + = °⇒ = °− +
.
Do đó
( )
AB+
và
C
là 2 góc bù nhau.
( ) ( )
sin sin ;cos cos=+ =−+C AB C AB
.
( ) ( )
tan tan ;cot cot=−+ =+C AB C AB
Câu 120: Cho
,,ABC
là các góc của tam giác
ABC
thì
cot .cot cot .cot cot .cotAB BC C A++
bằng
A. Một kết quả khác các kết quả đã nêu trên. B.
1
.
C.
1−
. D.
( )
2
cot .cot .cot
ABC
.
Lời giải
Ta có :
cot .cot cot .cot cot .cotAB BC C A++
.
111
tan .tan tan .tan tan .tanAB BC C A
=++
tan tan tan
tan .tan .tan
ABC
ABC
++
=
.
Mặt khác :
( )( )
tan tan tan tan 1 tan .tan tan
A B C AB A B C+ + = +− +
.
( )( )
tan 1 tan .tan tanC AB C
π
= −− +
.
( )
tan 1 tan .tan tanC AB C=−− +
tan tan .tan
CAB=
.
Nên
cot .cot cot .cot cot .cot 1AB BC C A++=
.
Câu 121: Cho
A
,
B
,
C
là các góc của tam giác
ABC
thì:
A.
cot cot cot cot .cot .cot
2 2 2 222
++=
A B C ABC
.
B.
cot cot cot cot .cot .cot
2 2 2 222
++=−
A B C ABC
.
C.
cot cot cot cot .cot .cot
222
++=
ABC
ABC
.
D.
cot cot cot cot .cot .cot
222
++=−
ABC
ABC
.
Lời giải
Ta có:
cot cot cot
222
++
ABC
cot cot cot
22 2
=++
AB C
sin
cos
22
2
sin .sin sin
22 2
+
= +
AB
C
AB C
.
sin sin .sin
2 22
cos .
2
sin .sin .sin
222
+
=
C AB
C
C AB
cos sin .sin
22 2 2
cos .
2
sin .sin .sin
222
++
=
AB A B
C
C AB
cos .cos .cos
222
sin .sin .sin
222
=
CBA
C AB
cot .cot .cot
222
=
ABC
.
Câu 122: Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chọn hệ thức đúng trong các hệ thức sau.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 35
Sưu tầm và biên soạn
A.
222
cos cos cos 1 cos .cos .cos .A B C ABC++=+
B.
222
cos cos cos 1– cos .cos .cos .
A B C ABC
++=
C.
222
cos cos cos 1 2cos .cos .cos .
A B C ABC++=+
D.
222
cos cos cos 1– 2cos .cos .cos .A B C ABC++=
Lời giải
Ta có :
222
cos cos cosABC++
2
1 cos 2 A 1 cos 2
cos
22
B
C
++
= ++
( )
( )
2
1 cos cos cosAB AB C
=+ + −+
(
) (
)
1 cos cos cos cosCAB CAB=−−−+
( ) ( )
1 cos cos cosC AB AB=− −+ +
1 2cos cos cos .ABC= +
Câu 123: Hãy chỉ ra công thức sai, nếu
,,ABC
là ba góc của một tam giác.
A.
cos cos sin sin sin
2 2 22 2
B C BC A
−=
. B.
cos .cos sin .sin cos 0B C BC A− +=
.
C.
sin cos sin cos cos
22 22 2
BC CC A
+=
. D.
222
cos cos cos 2cos cos cos 1A B C ABC++− =
.
Lời giải
( )
( )( )
2 2 2 22 2 2
2 2 22
222
cos cos cos .cos cos sin .sin
cos .cos 2cos .cos .cos cos sin .sin 1 cos 1 cos
1 cos cos cos .cos
cos cos cos 2cos .cos .cos 1
AB C A B C A B
A B ABC C A B A B
A B AB
A B C ABC
+=− ⇒ + =
⇒ + += =− −
=−−+
⇒+++ =
Câu 124: Cho tam giác
ABC
có
sin sinC
sin
cos cos
B
A
BC
+
=
+
. Khẳng định nào dưới đây đúng?
A. Tam giác
ABC
vuông tại
A
. B. Tam giác
ABC
cân tại
A
.
C. Tam giác
ABC
đều. D. Tam giác
ABC
là tam giác tù.
Lời giải
Ta có
2sin cos cos
sin sinC
22 2
sin sin sin
cos cos
2cos cos sin
22 2
BC BC A
B
AA A
BC BC A
BC
+−
+
= ⇔= ⇔=
+−
+
2
cos
2
2sin cos 2sin 1
22 2
sin
2
A
AA A
A
⇔ =⇔=
cos 0 90AA⇔ =⇒=°
suy ra tam giác ABC vuông tại
A
.
Câu 125: Cho bất đẳng thức
( )
4
1 13
2 2cos 2 4sin 0
64cos 4
cos A B B
A
+ − + +≤
với
,,ABC
là ba góc của
tam giác
ABC
.Khẳng định đúng là:
A.
120
o
BC+=
. B.
130
o
BC+=
. C.
120
o
AB+=
. D.
140
o
AC+=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 36
Sưu tầm và biên soạn
Lời giải
Từ giả thiết suy ra:
(
)
22
4
1 13
2cos 2 4sin 4sin 0
64cos 4
A BB
A
+ −− + + ≤
( )
22 2
4
13
cos cos 4sin 4sin 1 *
64cos 4
AA BB
A
⇔ + + + − +≤
AD BĐT Cauchy thì
22
4
13
cos cos (1)
64cos 4
AA
A
++ ≥
Mặt khác
( ) ( )
2
2
4sin 4sin 1 2sin 1 0 2BB B− += − ≥
Từ, và suy ra bđt thỏa mãn khi và chỉ khi dấu bằng ở và xảy ra
2
4
1
64
1
sin
2
cos A
cos A
B
=
⇔
=
1
60
2
30 .
1
sin
90
2
o
o
o
A
cosA
B
B
C
=
=
⇔ ⇔=
=
=
Nên
120
o
BC
+=
Chọn A
Câu 126: Cho
A
,
B
,
C
là các góc nhọn và
tan
1
2
A =
,
1
tan
5
B =
,
tan
1
8
C =
. Tổng
ABC++
bằng:
A.
.
6
π
B.
.
5
π
C.
.
4
π
D.
.
3
π
Lời giải
( )
( )
( )
tan tan
tan
tan tan
1 tan .tan
tan 1
tan tan
1 tan .tan
.tan
1 tan .tan
AB
C
AB C
AB
ABC
AB
AB C
C
AB
+
+
++
−
++ = = =
+
−+
−
suy ra
4
ABC
π
++=
.
Câu 127: Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A.
3
sin cos .
2
AB C
C
++
=
B.
( )
cos – – cos 2 .ABC C+=
C.
23
tan cot .
22
AB C C+−
=
D.
2
cot tan .
22
AB C C++
=
Lời giải
Ta có:
ABC
π
++=
3
22
AB C
C
π
++
⇒=+
3
sin sin cos .
22
AB C
CC
π
++
⇒ = +=
A đúng.
2ABC C
π
+−=−
( )
( )
cos – cos 2 cos 2 .ABC C C
π
⇒ + = −=−
B đúng.
23
2 22
AB C C
π
+−
= −
2 33
tan tan cot .
2 22 2
AB C C C
π
+−
⇒ = −=
C đúng.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 37
Sưu tầm và biên soạn
2
2 22
AB C C
π
++
= +
2
cot cot tan .
2 22 2
AB C C C
π
++
⇒ = +=−
D sai.
Câu 128: Cho
A
,
B
,
C
là ba góc của một tam giác. Hãy chỉ ra hệ thức SAI.
A.
cos sin .
22
AB C+
=
B.
(
)
cos 2 – cos .AB C C
++ =
C.
( )
sin –sin .AC B+=
D.
( )
cos – cos .
AB C+=
Lời giải
Ta có:
2 22
AB C
π
+
= −
cos cos sin .
2 22 2
AB C C
π
+
⇒ = −=
A đúng.
2AB C C
π
++ =+
( ) ( )
cos 2 cos cos .AB C C C
π
⇒ ++ = + =−
B đúng.
AC B
π
+=−
(
) ( )
sin sin sin .AC B B
π
⇒ += −=
C sai.
AB C
π
+=−
(
) (
)
cos cos cos .AB C C
π
⇒ += −=−
D đúng.
Câu 129: Cho
A
,
B
,
C
là ba góc của một tam giác không vuông. Hệ thức nào sau đây SAI?
A.
cos cos sin sin sin .
2 2 22 2
B C BC A
−=
B.
tan tan tan tan .tan .tan .
A B C ABC
++=
C.
cot cot cot cot .cot .cot .A B C ABC++=
D.
tan .tan tan .tan tan .tan 1.
22 22 22
AB BC C A
++=
Lời giải
Ta có :
+
cos cos sin sin cos cos sin .
2 2 2 2 22 22 2
B C B C BC A A
π
− = += −=
A đúng.
+
tan tan tan tan .tan .tanA B C ABC++=
( )
tan 1 tan tan tan tanA BC B C⇔− − = +
tan tan
tan
1 tan tan
BC
A
BC
+
⇔=−
−
( )
tan tanA BC⇔=− +
. B đúng.
+
cot cot cot cot .cot .cotA B C ABC
++=
( )
cot cot cot 1 cot cot
A BC B C⇔ −= +
1 cot cot 1
cot cot cot
BC
A BC
−
⇔=
+
( )
tan cot .A BC
⇔= +
C sai.
+
tan .tan tan .tan tan .tan 1
22 22 22
AB BC C A
++=
tan . tan tan 1 tan .tan
2 2 2 22
A B C BC
⇔ +=−
tan tan
1
22
tan 1 tan .tan
2 22
BC
A BC
+
⇔=
−
cot tan
2 22
A BC
⇔= +
. D đúng.
BẢNG ĐÁP ÁN
1.A
2.B
3.D
4.C
5.C
6.A
7.B
8.C
9.D
10.D
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 38
Sưu tầm và biên soạn
11.C
12.C
13.B
15.C
16.D
17.D
18.B
19.A
20.A
21.D
22.C
23.C
24.D
25.D
26.C
27.D
28.A
29.D
30.A
31.A
32.D
33.B
34.C
35.C
36.B
37.A
38.A
39.A
40.C
41.A
42.C
43.D
44.B
45.B
46.A
47.C
48.B
49.A
50.B
51.A
52.C
53.D
54.A
55.D
56.A
57.B
58.D
59.D
60.D
61.C
62.C
63.A
64.D
65.C
66.B
67.D
68.D
69.C
70.D
71.B
72.C
73.A
74.B
75.A
76.A
77.C
78.A
79.D
80.D
81.C
82.D
83.A
84.B
85.A
86.A
87.D
88.D
89.D
90.B
91.C
92.C
93.C
94.A
95.C
96.D
97.D
98.D
99.C
100.A
101.C
102.C
103.B
104.A
105.D
106.B
107.D
108.C
109.B
110.C
111.C
112.B
113.D
114.D
115.A
116.A
117.B
118.D
119.B
120.C
121.B
122.A
123.C
124.C
125.A
126.A
127.C
128.D
129.C
130.C

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 45
Sưu tầm và biên soạn
BÀI 4: HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
1. Định nghĩa hàm số lượng giác
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
a) Hàm số chẵn, hàm số lẻ
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUYẾT.
I

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 46
Sưu tầm và biên soạn
b) Hàm số tuần hoàn
3. Đồ thị và tính chất của hàm số
sinyx=
Hàm số
sin
yx=
xác định trên
, nhận giá trị trên đoạn
[
]
1;1−
và
Là hàm số lẻ vì:
( )
sin sin ,
x xx− =− ∀∈
.
Là hàm số tuần hoàn với chu kỳ
2
π
.
Hàm số
sinyx=
nhận các giá trị đặc biệt:
sin 0 ,
x xkk
π
=⇔= ∈
.
sin 1 2 ,
2
x x kk
π
π
=⇔= + ∈
.
sin 1 2 ,
2
x x kk
π
π
=−⇔ =− + ∈
Đồ thị hàm số
sinyx=
:
4. Đồ thị và tính chất của hàm số
cosyx=
Hàm số
cosyx
=
xác định trên
, nhận giá trị trên đoạn
[ ]
1;1−
và
Là hàm số chẳn vì:
( )
cos cos ,x xx
− = ∀∈
.
Là hàm số tuần hoàn với chu kỳ
2
π
.
Hàm số
cosyx=
nhận các giá trị đặc biệt:
cos 0 ,
2
x x kk
π
π
=⇔= + ∈
.
cos 1 2 ,x xk k
π
=⇔= ∈
.
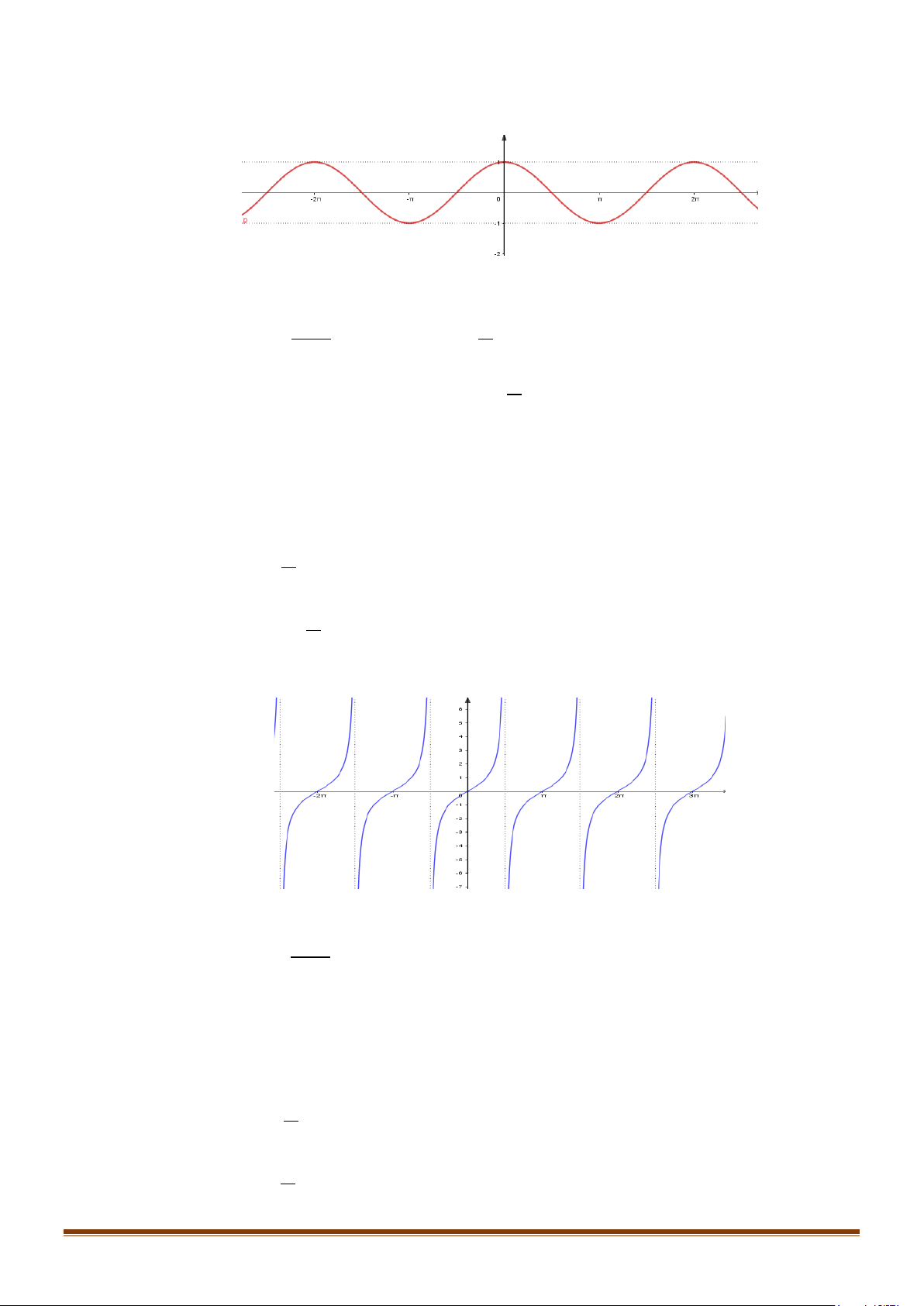
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 47
Sưu tầm và biên soạn
cos 1 2 ,x x kk
ππ
=−⇔ = + ∈
Đồ thị hàm số
cosyx=
:
5. Đồ thị và tính chất của hàm số
tanyx=
Hàm số
sin
tan
cos
x
yx
x
= =
xác định trên
\,
2
kk
π
π
+∈
, nhận giá trị trên
và
Là hàm số chẳn vì:
( )
tan tan , \ ,
2
x xx kk
π
π
− = ∀∈ + ∈
.
Là hàm số tuần hoàn với chu kỳ
π
.
Hàm số
tanyx
=
nhận các giá trị đặc biệt:
tan 0 ,x xkk
π
=⇔= ∈
.
tan 1 ,
4
x x kk
π
π
=⇔= + ∈
.
tan 1 ,
4
x x kk
π
π
=−⇔ =− + ∈
Đồ thị hàm số
tanyx
=
:
6. Đồ thị và tính chất của hàm số
cotyx=
Hàm số
cos
cot
sin
x
yx
x
= =
xác định trên
{ }
\,kk
π
∈
, nhận giá trị trên
và
Là hàm số lẻ vì:
( ) { }
cot cot , \ ;x xx kk
π
− =− ∀∈ ∈
.
Là hàm số tuần hoàn với chu kỳ
π
.
Hàm số
cotyx=
nhận các giá trị đặc biệt:
cot 0 ,
2
x x kk
π
π
=⇔= + ∈
.
cot 1 ,
4
x x kk
π
π
=⇔= + ∈
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 48
Sưu tầm và biên soạn
cot 1 ,
4
x x kk
π
π
=−⇔ =− + ∈
Đồ thị hàm số
cot
yx=
:
DẠNG 1. TẬP XÁC ĐỊNH CỦA HÀM SỐ
TẬP XÁC ĐỊNH CỦA HÀM SỐ LƯỢNG GIÁC CƠ BẢN.
Hàm số
xyxy cos;sin ==
có tập xác định là
.
Hàm số
tanyx=
có tập xác định là
\,
2
kk
π
π
+∈
.
Hàm số
cotyx=
có tập xác định là
{ }
\,kk
π
∈
.
PHƯƠNG PHÁP
+ Tìm điều kiện để hàm số có nghĩa
+ Giải ra điều kiện
+ Suy ra tập xác định của hàm số
Chú ý: Cho hàm số
( )
y fx=
xác định bởi:
+
( )
( )
( )
Px
y fx
Qx
= =
lưu ý
( )
0Qx≠
.
+
( ) ( )
2n
y f x Qx= =
thì
( )
y fx=
có nghĩa khi
( )
0Qx≥
.
+
( )
( )
( )
2n
Px
y fx
Qx
= =
lưu ý
( )
0
Qx>
.
+
( )
( )
tany ux=
xác định
( )
;
2
ux k k
π
⇔ ≠ +π ∈
.
+
( )
( )
coty ux=
xác định
( )
; ux k k⇔ ≠π ∈
.
HỆ THỐNG BÀI TẬP TỰ LUẬN
II
KIẾN THỨC CẦN THIẾT.
1
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 49
Sưu tầm và biên soạn
Câu 1: Tìm tập xác định của hàm số
tan( )
6
yx
π
= −
Câu 2: Tìm tập xác định của hàm số
2
2
cot ( 3 )
3
yx
π
= −
Câu 3: Tìm tập xác định của hàm số
tan 2
cot(3 )
sin 1 6
x
yx
x
π
= ++
+
Câu 4: Tìm tập xác định của hàm số
tan 5
sin 4 cos3
x
y
xx
=
−
Câu 5: Tìm tập xác định của hàm số
3 2cos
yx
= +
Câu 6: Tìm tập xác định của hàm số
2
sin
21
y
x
π
=
−
Câu 7: Tìm tập xác định của hàm số
( )
3cot 2 3yx= +
Câu 8: Tìm tập xác định của hàm số
22
sin
sin cos
x
y
xx
=
−
Câu 9: Tìm tập xác định của các hàm số sau
a)
sin cosyxx= +
b).
sin 4yx= +
c)
1 tan
sin
x
y
x
+
=
d).
tan
4
yx
π
= +
e)
cot
2
yx
π
= +
f).
3 2cosyx= −
g)
1 sin
cos
x
y
x
+
=
h)
22
sin
sin cos
x
y
xx
=
−
i)
tan 2
cot 3
6 sin 1
x
yx
x
π
= ++
+
j)
2
5 2cot sin cot
2
y xx x
π
=+ −+ +
Câu 10: Tìm
m
để hàm số sau xác định trên
.
a)
2 3cosym x
= −
b)
2
2
sin 2sin 1
y
x xm
=
− +−
Câu 11: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
5 sin 1 cosy m xm x=− −+
xác định
trên
.
BÀI T
Ậ
P.
2

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 50
Sưu tầm và biên soạn
DẠNG 2. XÉT TÍNH CHẴN LẺ CỦA CÁC HÀM SỐ LƯỢNG GIÁC CƠ BẢN
Định nghĩa: Cho hàm số
( )
y fx=
xác định trên
D
- Hàm số
f
được gọi là hàm số chẵn nếu với mọi
x
thuộc
D
, ta có
x−
cũng thuộc
D
và
( ) ( )
.f x fx−=
- Hàm số
f
được gọi là hàm số lẻ nếu với mọi
x
thuộc
D
, ta có
x−
cũng thuộc
D
và
( ) ( )
.f x fx−=−
Phương pháp giải
Ta thực hiện theo các bước sau:
Bước 1: Tìm tập xác định của hàm số, khi đó:
Nếu
D
là tập đối xứng (tức là
xD xD∀ ∈ ⇒− ∈
), ta thực hiện tiếp bước 2.
Nếu
D
không phải là tập đối xứng (tức là
xD∃∈
mà ), ta kết luận hàm số không chẵn
cũng không lẻ.
Bước 2: Xác định
( )
fx−
, khi đó:
Nếu
( ) ( )
f x fx−=
kết luận hàm số là hàm chẵn.
Nếu
( ) ( )
f x fx−=−
kết luận hàm số là hàm lẻ.
Ngoài ra kết luận hàm số không chẵn cũng không lẻ.
Chú ý: Với các hàm số lượng giác cơ bản, ta có:
1. Hàm số
sinyx=
là hàm số lẻ.
2. Hàm số là hàm số chẵn
3. Hàm số
tanyx=
là hàm số lẻ.
4. Hàm số
cotyx=
là hàm số lẻ.
* Lưu ý: Một số công thức liên quan đến việc xử lí dấu “
−
’’
1. Công thức hai cung đối nhau:
( ) ( ) ( ) ( )
sin sin ; cos cos ; tan tan ; cot cotx x xxx xx x−=− −= −=− −=−
2.
xx−=
3.
( )
n
n
xx−=
khi
n
chẵn và
( )
n
n
xx−=−
khi
n
lẻ.
D
xD−∉
cosyx=
KIẾN THỨC CẦN THIẾT.
1

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 51
Sưu tầm và biên soạn
Câu 12: Xét tính chẵn lẻ của các hàm số sau
a)
2 sin
yxx=
b)
cos sin 2 .
yx x= +
c)
cos 2
.
x
y
x
=
d)
7
tan 2 .sin5 .y xx
=
Câu 13: Xét tính chẵn lẻ của các hàm số sau
a)
tan coty xx
= +
b)
9
sin 2
2
yx
π
= +
c)
( )
(
)
2020
sin 2020
,
cos
n
x
yn
x
+
= ∈
Câu 14: Xác định tất cả các giá trị của tham số
m
để hàm số
( )
3 sin 4 cos 2fx m x x= +
là hàm chẵn.
DẠNG 3: TÍNH TUẦN HOÀN CỦA HÀM SỐ
Định nghĩa: Hàm số
( )
y fx=
có tập xác định là
D
được gọi là hàm số tuần hoàn, nếu tồn tại
một số
0T ≠
sao cho với mọi
xD∈
ta có:
xT D−∈
và
xT D+∈
.
( )
( )
fxT fx+=
.
Số dương
T
nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì hàm số tuần hoàn đó.
Người ta chứng minh được rằng hàm số
sinyx
=
tuần hoàn với chu kì
2T
π
=
; hàm số
cosyx=
tuần hoàn với chu kì
2
T
π
=
; hàm số
tanyx
=
tuần hoàn với chu kì
T
π
=
; Hàm số
cotyx=
tuần hoàn với chu kì
T
π
=
.
Chú ý:
Sử dụng định nghĩa hàm số tuần hoàn và tìm chu kì của nó.
Sử dụng các kết quả sau:
- Hàm số
.sin( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
2
a
π
Τ=
- Hàm số
.cos( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
2
a
π
Τ=
- Hàm số
.tan( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
a
π
Τ=
- Hàm số
.cot( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
a
π
Τ=
- Nếu hàm số
( )
y fx=
chỉ chứa các hàm số lượng giác có chu kì lần lượt là
12
, ,...,
n
ΤΤ Τ
thì
hàm số
f
có chu kì
Τ
là bội chung nhỏ nhất của
12
, ,...,
n
ΤΤ Τ
.
2 sin .
yxx=
BÀI T
Ậ
P.
2
KIẾN THỨC CẦN THIẾT.
1

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 52
Sưu tầm và biên soạn
- Nếu hàm số
( )
y fx=
tuần hoàn với chu kì T thì hàm số
( )
y fx c= +
(c là hằng số) cũng là
hàm số tuần hoàn với chu kì T.
Một số dấu hiệu nhận biết hàm số
( )
y fx=
không phải là hàm tuần hoàn
Hàm số
( )
y fx=
không phải là hàm tuần hoàn khi một trong các điều kiện sau bị vi phạm:
+ Tập xác định của hàm số là tập hữu hạn.
+ Tồn tại số a sao cho hàm số không xác định với
xa>
hoặc
xa<
.
+ Phương trình
( )
fx k=
có nghiệm nhưng số nghiệm hữu hạn.
+ Phương trình
( )
fx k=
có vô số nghiệm sắp thứ tự:
1
... ...
nn
xx
+
<< <
mà
1
0
nn
xx
+
−→
hay
∞
.
Câu 15: Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau:
2
cos 1yx= −
.
Câu 16: Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau:
22
sin .cos
55
yxx
=
.
Câu 17: Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau:
( )
cos cos 3.yx x= +
Câu 18: Chứng minh rằng hàm số sau là hàm số tuần hoàn và tìm chu kì của nó:
1
sin
y
x
=
.
Câu 19: Cho
,,,abcd
là các số thực khác 0. Chứng minh rằng hàm số
( ) sin cosf x a cx b dx= +
là hàm
số tuần hoàn khi và chỉ khi
c
d
là số hữu tỉ.
Câu 20: Cho hàm số
()y fx=
và
()y gx=
là hai hàm số tuần hoàn với chu kỳ lần lượt là
12
,TT
. Chứng
minh rằng nếu
1
2
T
T
là số hữu tỉ thì các hàm số
() (); ().()f x gx f x gx±
là những hàm số tuần hoàn.
Câu 21: Tìm chu kì (nếu có) của các hàm số sau:
a) b) .
b) c) . d)
Câu 22: Tìm chu kỳ của hàm số:
( )
sin 3 3cos 2fx x x= +
.
1 sin 5 .yx= −
2
cos 1
yx
= −
22
sin .cos
55
yxx
=
( )
cos cos 3.yx x= +
BÀI T
Ậ
P.
2

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 53
Sưu tầm và biên soạn
DẠNG 4: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC
PHƯƠNG PHÁP GIẢI TOÁN
1)
1 sin 1
1 cos 1
x
x
−≤ ≤
−≤ ≤
2)
0 sin 1
0 cos 1
x
x
≤ ≤
≤≤
3)
2
2
0 sin 1
0 cos 1
x
x
≤≤
≤≤
4)
0 sin 1
0 cos 1
x
x
≤≤
≤≤
Câu 23: Tìm GTLN - GTNN của các hàm số sau:
a. . b. .
c. . d. .
e. . f. với .
g. với .
Câu 24: Tìm GTLN – GTNN của các hàm số sau:
a.
b.
c.
d.
e. trên đoạn
f. trên đoạn .
g. trên đoạn .
h. .
i. Tìm min của hàm số: với .
2 3cosyx= +
3sin 2
6
yx
π
= −−
2
4cos 2 1yx= +
3 2 sinyx= −
( )
44
2 sin cos 3y xx= ++
3sin 2 12yx= −
3
;
88
x
ππ
∈−
2
4cos 7
2 12
x
y
π
= −−
[ ]
0;x
π
∈
2
2sin 3sin 1y xx=− +−
2
cos 2sinx 2yx= ++
cos 2cos 2yx x= +
( )
2
22
1 cos 2cos 1
y xx=− −+
2
2sin sin 2y xx= −+
[ ]
0;
π
2cos cos 2 8y xx= +−
;
24
ππ
−
2
tan tan 1
y xx= −+
;
44
ππ
−
sin cos 4sin cos 7y x x xx=++ +
2
2
11
sin sin
sin sin
yx x
xx
= + −−
0 x
π
<<
KIẾN THỨC CẦN THIẾT.
1
BÀI T
Ậ
P.
2

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 4: HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
1. Định nghĩa hàm số lượng giác
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
a) Hàm số chẵn, hàm số lẻ
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUYẾT.
I

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
b) Hàm số tuần hoàn
3. Đồ thị và tính chất của hàm số
sinyx=
Hàm số
sin
yx=
xác định trên
, nhận giá trị trên đoạn
[
]
1;1−
và
Là hàm số lẻ vì:
( )
sin sin ,
x xx− =− ∀∈
.
Là hàm số tuần hoàn với chu kỳ
2
π
.
Hàm số
sinyx=
nhận các giá trị đặc biệt:
sin 0 ,
x xkk
π
=⇔= ∈
.
sin 1 2 ,
2
x x kk
π
π
=⇔= + ∈
.
sin 1 2 ,
2
x x kk
π
π
=−⇔ =− + ∈
Đồ thị hàm số
sinyx=
:
4. Đồ thị và tính chất của hàm số
cosyx=
Hàm số
cosyx
=
xác định trên
, nhận giá trị trên đoạn
[ ]
1;1−
và
Là hàm số chẳn vì:
( )
cos cos ,x xx
− = ∀∈
.
Là hàm số tuần hoàn với chu kỳ
2
π
.
Hàm số
cosyx=
nhận các giá trị đặc biệt:
cos 0 ,
2
x x kk
π
π
=⇔= + ∈
.
cos 1 2 ,x xk k
π
=⇔= ∈
.
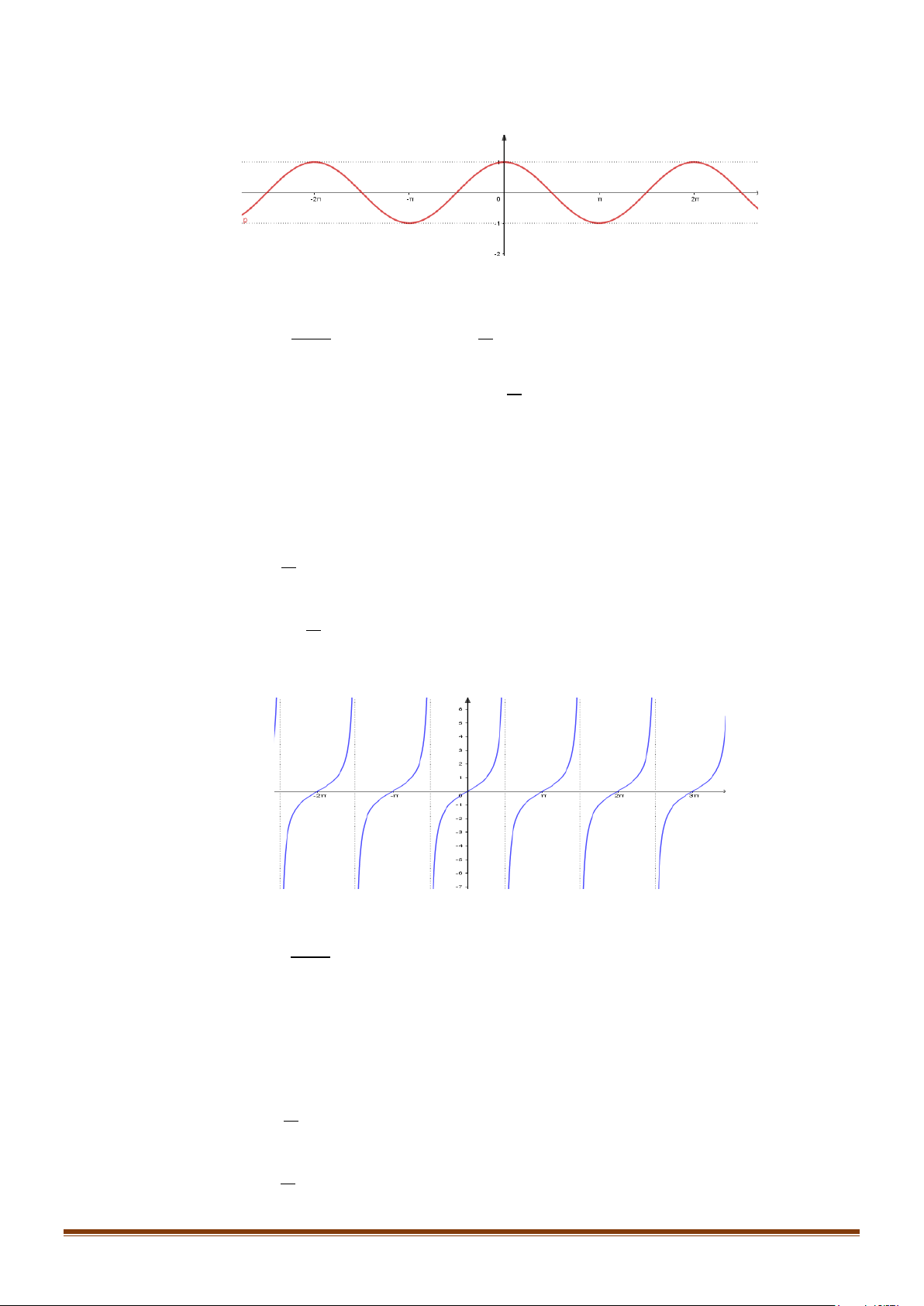
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
cos 1 2 ,x x kk
ππ
=−⇔ = + ∈
Đồ thị hàm số
cosyx=
:
5. Đồ thị và tính chất của hàm số
tanyx=
Hàm số
sin
tan
cos
x
yx
x
= =
xác định trên
\,
2
kk
π
π
+∈
, nhận giá trị trên
và
Là hàm số chẳn vì:
( )
tan tan , \ ,
2
x xx kk
π
π
− = ∀∈ + ∈
.
Là hàm số tuần hoàn với chu kỳ
π
.
Hàm số
tanyx
=
nhận các giá trị đặc biệt:
tan 0 ,x xkk
π
=⇔= ∈
.
tan 1 ,
4
x x kk
π
π
=⇔= + ∈
.
tan 1 ,
4
x x kk
π
π
=−⇔ =− + ∈
Đồ thị hàm số
tanyx
=
:
6. Đồ thị và tính chất của hàm số
cotyx=
Hàm số
cos
cot
sin
x
yx
x
= =
xác định trên
{ }
\,kk
π
∈
, nhận giá trị trên
và
Là hàm số lẻ vì:
( ) { }
cot cot , \ ;x xx kk
π
− =− ∀∈ ∈
.
Là hàm số tuần hoàn với chu kỳ
π
.
Hàm số
cotyx=
nhận các giá trị đặc biệt:
cot 0 ,
2
x x kk
π
π
=⇔= + ∈
.
cot 1 ,
4
x x kk
π
π
=⇔= + ∈
.
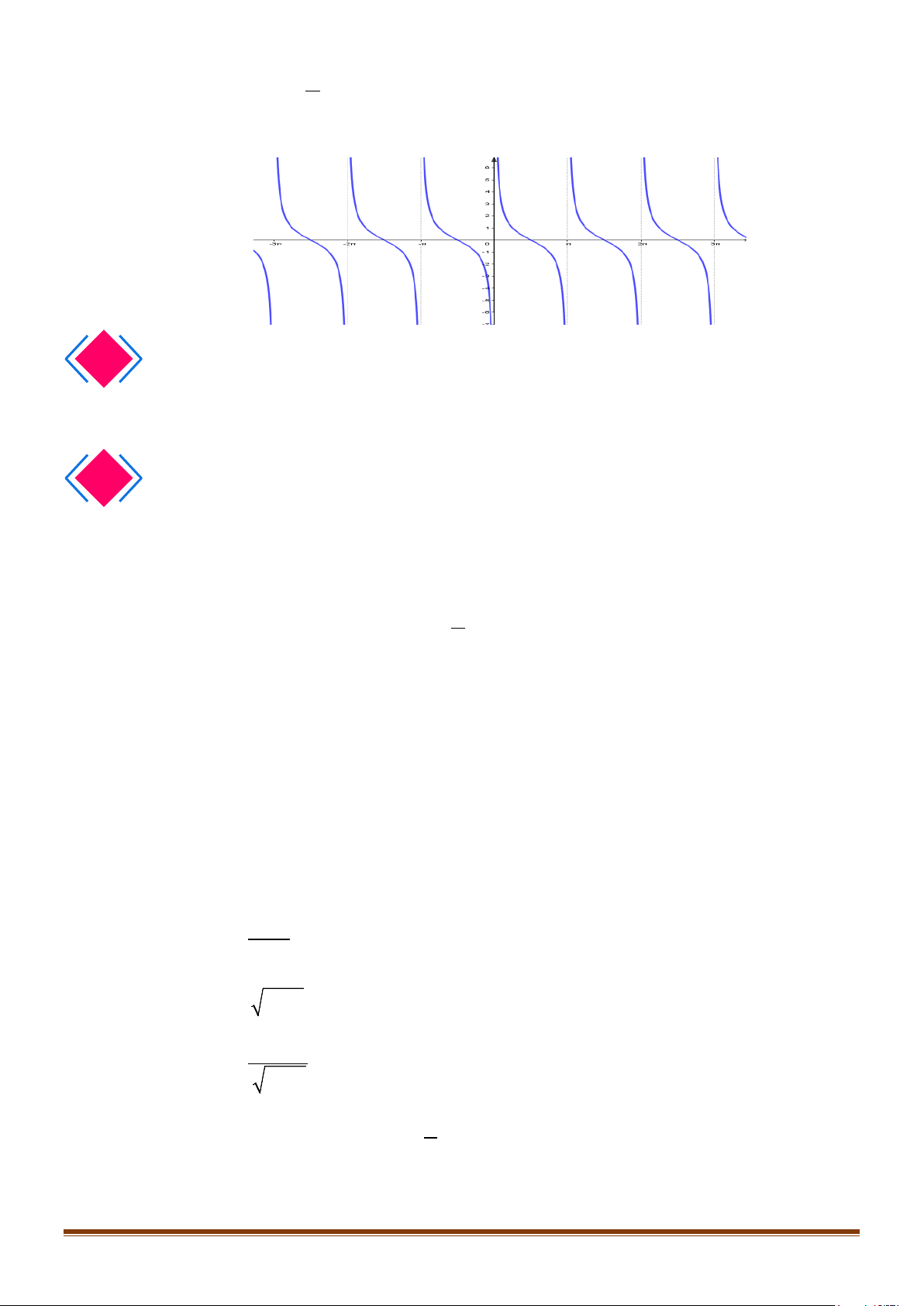
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
cot 1 ,
4
x x kk
π
π
=−⇔ =− + ∈
Đồ thị hàm số
cot
yx=
:
DẠNG 1. TẬP XÁC ĐỊNH CỦA HÀM SỐ
TẬP XÁC ĐỊNH CỦA HÀM SỐ LƯỢNG GIÁC CƠ BẢN.
Hàm số
xyxy cos;sin ==
có tập xác định là
.
Hàm số
tanyx=
có tập xác định là
\,
2
kk
π
π
+∈
.
Hàm số
cotyx=
có tập xác định là
{ }
\,kk
π
∈
.
PHƯƠNG PHÁP
+ Tìm điều kiện để hàm số có nghĩa
+ Giải ra điều kiện
+ Suy ra tập xác định của hàm số
Chú ý: Cho hàm số
( )
y fx=
xác định bởi:
+
( )
( )
( )
Px
y fx
Qx
= =
lưu ý
( )
0Qx≠
.
+
( ) ( )
2n
y f x Qx= =
thì
( )
y fx=
có nghĩa khi
( )
0Qx≥
.
+
( )
( )
( )
2n
Px
y fx
Qx
= =
lưu ý
( )
0
Qx>
.
+
( )
( )
tany ux=
xác định
( )
;
2
ux k k
π
⇔ ≠ +π ∈
.
+
( )
( )
coty ux=
xác định
( )
; ux k k⇔ ≠π ∈
.
HỆ THỐNG BÀI TẬP TỰ LUẬN
II
KIẾN THỨC CẦN THIẾT.
1
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
Câu 1: Tìm tập xác định của hàm số
tan( )
6
yx
π
= −
Lời giải
Điều kiện:
2
cos( ) 0
6 62 3
x x kx k
π ππ π
ππ
− ≠⇔− ≠ + ⇔≠ +
TXĐ:
2
\ ,
3
D kk
π
π
= +∈
.
Câu 2: Tìm tập xác định của hàm số
2
2
cot ( 3 )
3
yx
π
= −
Lời giải
Điều kiện:
22 2
sin( 3 ) 0 3
3 3 93
x xk x k
π π ππ
π
− ≠⇔ − ≠ ⇔≠ −
TXĐ:
2
\ ,
93
D kk
ππ
= +∈
.
Câu 3: Tìm tập xác định của hàm số
tan 2
cot(3 )
sin 1 6
x
yx
x
π
= ++
+
Lời giải.
Điều kiện:
sin 1
2
2
sin(3 ) 0
6
18 3
x
xk
k
x
x
π
π
π
ππ
≠−
≠− +
⇔
+≠
≠− +
Vậy TXĐ:
\ 2, ;
2 18 3
k
Dk k
π ππ
π
= −+ − + ∈
Câu 4: Tìm tập xác định của hàm số
tan 5
sin 4 cos3
x
y
xx
=
−
Lời giải.
Ta có:
sin 4 cos3 sin 4 sin 3
2
xxx x
π
−=−−
7
2cos sin
24 2 4
xx
ππ
=+−
BÀI T
Ậ
P.
2

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
Điều kiện:
cos5 0
10 5
cos 0 2
24 2
2
7
sin 0
14 7
24
xk
x
x
xk
k
x
x
ππ
ππ
π
ππ
π
≠+
≠
+ ≠⇔ ≠+
≠− +
+≠
Vậy TXĐ:
2
\ ; 2,
10 5 2 14 7
kk
Dk
π ππ π π
π
= + + −+
.
Câu 5: Tìm tập xác định của hàm số
3 2cos
yx= +
Lời giải
hàm số xác định khi
3
3 2cos 0 cos
2
xx
+ ≥ ⇔ ≥−
(đúng
x∀∈
), vì
1 cos 1,xx−≤ ≤ ∀∈
.
Suy ra tập xác định là
D =
.
Câu 6: Tìm tập xác định của hàm số
2
sin
21
y
x
π
=
−
Lời giải
hàm số xác định
2
21x
π
⇔
−
xác định
1
2 10
2
xx⇔ −≠ ⇔ ≠
.Tập xác định của hàm số
1
\
2
D
=
Câu 7: Tìm tập xác định của hàm số
( )
3cot 2 3yx= +
Lời giải
( )
(
)
( )
3cos 2 3
3cot 2 3
sin 2 3
x
yx
x
+
= +=
+
hàm số xác định
( )
sin 2 3 0x⇔ +≠
23xk
π
⇔ +≠
3
,( )
22
k
xk
π
⇔ ≠− + ∈
.
Tập xác định của hàm số
3
\
22
k
Dk
π
= −+ ∈
.
Câu 8: Tìm tập xác định của hàm số
22
sin
sin cos
x
y
xx
=
−
Lời giải
22
sin sin sinx
sin cos cos 2 cos 2
xx
y
xxxx
= = = −
−−
hàm số xác định
cos 2 0x⇔≠
2
2
xk
π
π
⇔ ≠+
,
42
k
xk
ππ
⇔≠ + ∈
. Tập xác định của hàm số
\
42
k
Dk
ππ
= +∈
.
Câu 9: Tìm tập xác định của các hàm số sau

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
a)
sin cosyxx= +
b).
sin 4yx= +
c)
1 tan
sin
x
y
x
+
=
d).
tan
4
yx
π
= +
e)
cot
2
yx
π
= +
f).
3 2cosyx= −
g)
1 sin
cos
x
y
x
+
=
h)
22
sin
sin cos
x
y
xx
=
−
i)
tan 2
cot 3
6 sin 1
x
yx
x
π
= ++
+
j)
2
5 2cot sin cot
2
y xx x
π
=+ −+ +
Lời giải
a) Ta có hàm số
x
yx
y cos
;
sin
=
=
có tập xác định là
nên hàm số
xx
y cossin
+
=
có tập
xác định là
.
b) Điều kiện xác định của hàm số là
4
04 −≥⇔≥+ xx
. Vậy
[
)
∞+−= ;4D
.
c) Điều kiện xác định của hàm số là
sin 0
sin 2 0 2 ,
cos 0
2
x
k
x xk x k
x
π
π
≠
⇔ ≠⇔ ≠ ⇔≠ ∈
≠
Vậy tập xác định của hàm số là
\;
2
k
Dk
π
= ∈
.
d) Điều kiện xác định của hàm số là
cos 0 ; .
4 42 4
x x k x kk
π ππ π
ππ
+ ≠⇔+≠+ ⇔≠+ ∈
Vậy tập xác định của hàm số là
\;
4
D kk
π
π
= +∈
.
e) Điều kiện xác định của hàm số là
∈+−≠⇔≠+⇔≠
+ kkxkxx ;
22
0
2
sin
π
π
π
ππ
ℤ.
Vậy tập xác định của hàm số là
\;
2
D kk
π
π
= −+ ∈
.
f) Điều kiện xác định của hàm số là
3
3 2cos 0 2cos 3 cos
2
x x xx
− ≥ ⇔ ≤ ⇔ ≤ ∀∈
. Vậy tập xác định của hàm số là
.D =
g) Điều kiện xác định của hàm số là
cos 0 2 ; 2 ;
22
x x k kk
ππ
ππ
−
>⇔∈ + + ∈
.
Vậy
2; 2 ;
22
D k kk
ππ
ππ
−
=++ ∈
.
h) Điều kiện xác định của hàm số là
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
22
sin cos 0 cos 2 0 2 ;
2 42
k
x x x x kx k
π ππ
π
− ≠⇔− ≠⇔ ≠ + ⇔≠ + ∈
.
Vậy tập xác định của hàm số là
\;
42
k
Dk
ππ
= +∈
.
i) Điều kiện xác định của hàm số là
3
sin 3 0
6 18 3
6
cos 2 0 2 ;
2 42
sinx 1
22
22
k
xk x
x
k
x xk x k
xkxk
π ππ
π
π
π ππ
π
ππ
ππ
−
+≠ ≠ +
+≠
≠ ⇔ ≠+ ⇔ ≠+ ∈
≠−
−−
≠+ ≠+
.
Vậy tập xác định của hàm số là
\ ; 2; ;
18 3 2 4 2
kk
D kk
πππ ππ
π
−−
= + + +∈
.
j) Ta có điều kiện xác định của hàm số là
( )
( )
2
5 2cot sinx 0 1
sin 0 2
2
x
x
π
+ −≥
+≠
Ta có
( )
( )
( )
22
2
2
5 2cot sinx 3 sinx 2 1 cot 3 sinx 0
sin
x xx
x
+ −=−++ =−+ >∀∈
.
(
)
2;
22
x k x kk
ππ
ππ
−
⇔+ ≠ ⇔≠ + ∈
.
Vậy tập xác định của hàm số là
\;
2
D kk
π
π
= −+ ∈
.
Câu 10: Tìm
m
để hàm số sau xác định trên
.
a)
2 3cos
ym x= −
b)
2
2
sin 2sin 1
y
x xm
=
− +−
Lời giải
a) Hàm số xác định trên
khi chỉ khi:
2 3cos 0, 3cos 2 ,m x x x mx− ≥ ∀∈ ⇔ ≤ ∀∈
2
cos
3
m
xx⇔ ≤ ∀∈
.
2
3
1
3
2
≥⇔≥⇔
m
m
.
b) Hàm số xác định trên
khi chỉ khi:
2
sin 2sin 1 0 ,x xm x− + − > ∀∈
( )
2
2
sin 2sin 1 2 sin 1 ,m xx x x⇔ >− + + = − − ∀ ∈
( )
( )
2
;
max sin 2sin 1 2 2m xx m
−∞ +∞
⇔> − + +=⇔>
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
Câu 11: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
5 sin 1 cosy m xm x=− −+
xác định
trên
.
Lời giải
Hàm số xác định trên
khi chỉ khi:
( ) ( )
5 sin 1 cos 0, sin 1 cos 5,mxm x x mxm x x− − + ≥ ∀∈ ⇔ + + ≤ ∀∈
.
( )
( )
( )
22 2
22 2
15
sin cos ,
11 1
mm
x xx
mm mm mm
+
⇔ + ≤ ∀∈
++ ++ ++
.
( )
( )
2
22
2
55
sin , 1 2 2 1 5.
2 21
1
x x mm
mm
mm
α
⇔ + ≤ ∀∈ ⇔ ≥ ⇔ + + ≤
++
++
2
2 2 24 0 4 3mm m⇔ + − ≤ ⇔− ≤ ≤
. Mà
m ∈
{ }
4; 3; 2; 1;0;1; 2;3m⇒ ∈− − − −
.
DẠNG 2. XÉT TÍNH CHẴN LẺ CỦA CÁC HÀM SỐ LƯỢNG GIÁC CƠ BẢN
Định nghĩa: Cho hàm số
( )
y fx=
xác định trên
D
- Hàm số
f
được gọi là hàm số chẵn nếu với mọi
x
thuộc
D
, ta có
x−
cũng thuộc
D
và
( ) ( )
.f x fx−=
- Hàm số
f
được gọi là hàm số lẻ nếu với mọi
x
thuộc
D
, ta có
x−
cũng thuộc
D
và
( ) ( )
.f x fx−=−
Phương pháp giải
Ta thực hiện theo các bước sau:
Bước 1: Tìm tập xác định của hàm số, khi đó:
Nếu
D
là tập đối xứng (tức là
xD xD∀ ∈ ⇒− ∈
), ta thực hiện tiếp bước 2.
Nếu
D
không phải là tập đối xứng (tức là
xD∃∈
mà ), ta kết luận hàm số không chẵn
cũng không lẻ.
Bước 2: Xác định
( )
fx−
, khi đó:
Nếu
( ) ( )
f x fx−=
kết luận hàm số là hàm chẵn.
Nếu
( ) ( )
f x fx−=−
kết luận hàm số là hàm lẻ.
Ngoài ra kết luận hàm số không chẵn cũng không lẻ.
Chú ý: Với các hàm số lượng giác cơ bản, ta có:
1. Hàm số
sinyx=
là hàm số lẻ.
D
xD−∉
KIẾN THỨC CẦN THIẾT.
1

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
2. Hàm số là hàm số chẵn
3. Hàm số
tanyx=
là hàm số lẻ.
4. Hàm số
cotyx=
là hàm số lẻ.
* Lưu ý: Một số công thức liên quan đến việc xử lí dấu “
−
’’
1. Công thức hai cung đối nhau:
( ) ( ) ( ) ( )
sin sin ; cos cos ; tan tan ; cot cotx x xxx xx x−=− −= −=− −=−
2.
xx−=
3.
( )
n
n
xx−=
khi
n
chẵn và
( )
n
n
xx−=−
khi
n
lẻ.
Câu 12: Xét tính chẵn lẻ của các hàm số sau
a)
2 sinyxx=
b)
cos sin 2 .yx x= +
c)
cos 2
.
x
y
x
=
d)
7
tan 2 .sin5 .y xx=
Lời giải
a) Tập xác định:
D =
là tập đối xứng do đó
( )
1.xD xD∀ ∈ ⇒− ∈
Đặt
( )
2 sin .y fx x x= =
NX:
xD∀∈
,
( ) ( ) ( ) ( ) ( )
2 sin 2 sin 2 .f x x x x x fx−=− −= =
Từ
( )
1
và
( )
2
ta kết luận hàm số đã cho là hàm số chẵn.
b) Tập xác định:
D =
là tập đối xứng do đó
.xD xD∀ ∈ ⇒− ∈
Đặt
( )
cos sin 2 .y fx x x= = +
Xét
33
x Dx D
ππ
= ∈ ⇒− =− ∈
.
213
os sin
3 3 322
fc
π ππ
=+=+
;
2 13
os sin
3 3 3 22
fc
ππ π
−= −+ − =−
.
Ta thấy
33
ff
ππ
≠−
nên hàm số đã cho không là hàm số chẵn
Và
33
ff
ππ
− ≠−
nên hàm số đã cho không là hàm số lẻ.
c) Tập xác định:
{ }
\0D =
là tập đối xứng do đó
.xD xD∀ ∈ ⇒− ∈
Đặt
( )
cos 2
.
x
y fx
x
= =
Ta có
xD∀∈
:
( )
( )
( )
( )
cos 2 cos 2
.
xx
f x f
x
xx
−
−= =− =−
−
Do đó hàm số đã cho là hàm số lẻ.
cosyx=
2 sin .yxx=
BÀI TẬP.
2

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
d) Tập xác định:
\|
42
k
Dk
ππ
= +∈
là tập đối xứng do đó
.xD xD∀ ∈ ⇒− ∈
Đặt
( )
7
tan 2 .sin5 .y fx x x= =
Ta có
xD∀∈
:
( ) ( ) ( ) ( ) ( ) ( )
77
tan 2 sin 5 tan 2 sin 5 .f x x x x x fx−= − − = =
Do đó hàm số đã cho là hàm số chẵn.
Chú ý: Đôi khi người ta còn phát biểu bài toán dưới dạng:
Với câu a) Chứng minh đồ thị hàm số
2 sinyxx=
nhận trục tung làm trục đối xứng.
Với câu c) Chứng minh đồ thị hàm số nhận gốc tọa độ làm tâm đối xứng.
Câu 13: Xét tính chẵn lẻ của các hàm số sau
a)
tan coty xx= +
b)
9
sin 2
2
yx
π
= +
c)
( )
( )
2020
sin 2020
,
cos
n
x
yn
x
+
= ∈
Lời giải
a) Tập xác định:
\|
2
k
Dk
π
= ∈
là tập đối xứng do đó
.xD xD∀ ∈ ⇒− ∈
Ta có
xD∀∈
:
( ) ( ) ( ) ( ) ( )
tan cot tan cot tan cotfx x xxxxxfx−= −+ −=− − =− + −
Do đó hàm số đã cho là hàm số lẻ.
b) Tập xác định:
D =
là tập đối xứng do đó
.xD xD∀ ∈ ⇒− ∈
NX:
( ) ( )
9
sin 2 sin 2 os 2 .
22
fx x x c x
ππ
= + = +=
Ta có
xD∀∈
:
( ) ( ) ( ) ( )
os 2 cos 2 .f x c x x fx−= − = =
Do đó hàm số đã cho là hàm số chẵn.
c) Tập xác định:
\|
2
D kk
π
π
= +∈
là tập đối xứng do đó
.xD xD∀ ∈ ⇒− ∈
+ NX:
( ) ( ) ( ) { }
2020
2020 2020
sin sin sin , \ 0
n
nn
x x xn− =− = ∀∈
Do đó
xD∀∈
:
( )
( )
( )
( )
( )
( )
2020 2020
sin 2020 sin 2020
.
cos c
os
nn
xx
f x f
x
xx
−+ +
−= = =
−
Suy ra hàm số là hàm số chẵn
{ }
\0n∀∈
.
+ Với
0n =
thì
( )
2020
sin 1
n
x =
. Do đó
xD∀∈
:
( )
( )
( )
( )
2021 2021
.
cos cos
f x fx
xx
−= = =
−
Suy ra hàm số là hàm số chẵn với
0n =
.
Vậy hàm số đã cho là hàm số chẵn
n∀∈
.
Câu 14: Xác định tất cả các giá trị của tham số
m
để hàm số
( )
3 sin 4 cos 2fx m x x= +
là hàm chẵn.
Lời giải
- Tập xác định:
D =
là tập đối xứng do đó
.xD xD∀ ∈ ⇒− ∈
cos 2
=
x
y
x

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
- Để hàm số đã cho là hàm số chẵn thì
( ) ( )
,.f x fx x D− = ∀∈
( ) ( )
3 sin 4 cos 2 3 sin 4 cos 2 ,m x x m x x xD⇔ − + − = + ∀∈
( ) ( )
3 sin 4 cos 2 3 sin 4 cos 2 ,m x x m x x xD⇔− + = + ∀ ∈
( )
6 sin 4 0,m x xD⇔ = ∀∈
`
0.m
⇔=
DẠNG 3: TÍNH TUẦN HOÀN CỦA HÀM SỐ
Định nghĩa: Hàm số
( )
y fx=
có tập xác định là
D
được gọi là hàm số tuần hoàn, nếu tồn tại
một số
0T ≠
sao cho với mọi
xD∈
ta có:
xT D
−∈
và
xT D+∈
.
( )
( )
fxT fx+=
.
Số dương
T
nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì hàm số tuần hoàn đó.
Người ta chứng minh được rằng hàm số
sin
yx=
tuần hoàn với chu kì
2T
π
=
; hàm số
cosyx=
tuần hoàn với chu kì
2T
π
=
; hàm số
tan
yx
=
tuần hoàn với chu kì
T
π
=
; Hàm số
cotyx=
tuần hoàn với chu kì
T
π
=
.
Chú ý:
Sử dụng định nghĩa hàm số tuần hoàn và tìm chu kì của nó.
Sử dụng các kết quả sau:
- Hàm số
.sin( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
2
a
π
Τ=
- Hàm số
.cos( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
2
a
π
Τ=
- Hàm số
.tan( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
a
π
Τ=
- Hàm số
.cot( ) ( . 0)y ax b a=Α + Α≠
là một hàm số tuần hoàn với chu kì
a
π
Τ=
- Nếu hàm số
( )
y fx=
chỉ chứa các hàm số lượng giác có chu kì lần lượt là
12
, ,...,
n
ΤΤ Τ
thì
hàm số
f
có chu kì
Τ
là bội chung nhỏ nhất của
12
, ,...,
n
ΤΤ Τ
.
- Nếu hàm số
( )
y fx=
tuần hoàn với chu kì T thì hàm số
( )
y fx c= +
(c là hằng số) cũng là
hàm số tuần hoàn với chu kì T.
Một số dấu hiệu nhận biết hàm số
( )
y fx=
không phải là hàm tuần hoàn
Hàm số
( )
y fx=
không phải là hàm tuần hoàn khi một trong các điều kiện sau bị vi phạm:
KIẾN THỨC CẦN THIẾT.
1

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
+ Tập xác định của hàm số là tập hữu hạn.
+ Tồn tại số a sao cho hàm số không xác định với
xa>
hoặc
xa<
.
+ Phương trình
( )
fx k
=
có nghiệm nhưng số nghiệm hữu hạn.
+ Phương trình
(
)
fx k
=
có vô số nghiệm sắp thứ tự:
1
... ...
nn
xx
+
<< <
mà
1
0
nn
xx
+
−→
hay
∞
.
Câu 15: Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau:
2
cos 1yx= −
.
Lời giải
Ta biến đổi:
2
1 cos 2 1 1
cos 1 1 cos 2 .
2 22
x
yx x
+
= −= −= −
Do đó
f
là hàm số tuần hoàn với chu kì
2
2
π
π
Τ= =
.
Câu 16: Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau:
22
sin .cos
55
yxx
=
.
Lời giải
Ta biến đổi:
2 2 14
sin .cos sin
5 5 25
yxx x
= =
.
Do đó
f
là hàm số tuần hoàn với chu kì
25
4
2
5
ππ
Τ= =
.
Câu 17: Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số sau:
( )
cos cos 3.
yx x= +
Lời giải
Giả sử hàm số đã cho tuần hoàn
⇒
có số thực dương
Τ
thỏa :
(
) (
) ( )
( )
cos cos 3 cos cos 3
fx fx x x x x+Τ = ⇔ +Τ + +Τ = +
cos 1 2
0 cos cos 3 2 3
cos 3 1 3 2
n
m
x
n
m
π
π
Τ= Τ=
= ⇒ Τ+ Τ= ⇔ ⇒ ⇒ =
Τ= Τ=
vô lí, do
,
m
mn
n
∈⇒
là số hữu tỉ. Vậy hàm số đã cho không tuần hoàn.
Câu 18: Chứng minh rằng hàm số sau là hàm số tuần hoàn và tìm chu kì của nó:
1
sin
y
x
=
.
Lời giải
Tập xác định:
{ }
D \,kk
π
∈=
.
BÀI TẬP.
2

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
Ta xét đẳng thức
(
)
( )
( )
( )
11
sin sin .
sin sin
fx fx x x
xx
+Τ = ⇔ = ⇔ +Τ =
+Τ
Chọn
2
x
π
=
thì
sin 1x =
và do đó
sin 1 2 , .
2 22
kk
π ππ
π
+Τ = ⇔ +Τ= + ∈
Số dương nhỏ nhất trong các số T là
2
π
.
Rõ ràng
D, 2 D, 2 Dx xk xk
ππ
∀∈+∈+∈
và
( )
( )
( )
11
2
sin 2 sin
fx k fx
xk x
π
π
+= ==
+
Vậy
f
là hàm số tần hoàn với chu kì
2
π
Τ=
.
Câu 19: Cho
,,,
abcd
là các số thực khác 0. Chứng minh rằng hàm số
( ) sin cosf x a cx b dx= +
là hàm
số tuần hoàn khi và chỉ khi
c
d
là số hữu tỉ.
Lời giải
* Giả sử
()
fx
là hàm số tuần hoàn
0: ( ) ( ) T fx T fx x⇒∃ > + = ∀
Cho
sin cos cos 1
0,
sin cos sin 0
a cT b dT b dT
x xT
a cT b dT b cT
+= =
= =−⇒ ⇒
−+ = =
2
2
dT n
cm
cT m
dn
π
π
=
⇒ ⇒= ∈
=
.
* Giả sử
, :
c ck
kl
d dl
∈ ⇒∃ ∈ =
. Đặt
22kl
T
cd
ππ
= =
Ta có:
( ) ( ) fx T fx x
+ = ∀∈
()fx⇒
là hàm số tuần hoàn với chu kì
22kl
T
cd
ππ
= =
.
Câu 20: Cho hàm số
()y fx=
và
()y gx
=
là hai hàm số tuần hoàn với chu kỳ lần lượt là
12
,TT
. Chứng
minh rằng nếu
1
2
T
T
là số hữu tỉ thì các hàm số
() (); ().()f x gx f xgx±
là những hàm số tuần hoàn.
Lời giải
Vì
1
2
T
T
là số hữu tỉ nên tồn tại hai số nguyên
,; 0mnn≠
sao cho
1
12
2
T
m
nT mT T
Tn
=⇒= =
Khi đó
1
( )( )()fx T fx nT fx+= + =
và
2
( )( )()gx T gx mT gx+= + =
Suy ra
( ) ( ) () ()f x T gx T f x gx+± += ±
và
( ). ( ) ( ). ( )
f x T gx T f xgx+ +=
,
( ) ()
( ) ()
fx T fx
gx T gx
+
=
+
.
Từ đó ta có điều phải chứng minh.
Câu 21: Tìm chu kì (nếu có) của các hàm số sau:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
a) b) .
b) c) . d)
Lời giải
Ta có hàm số
( )
y sink ax b c= ++
;
( )
y cosk ax b c= ++
là hàm số tuần hoàn và có chu kỳ
2
T
a
π
=
a. Hàm số
y 1 sin 5x= −
tuần hoàn và có chu kỳ
1
2
5
T
π
=
.
b. Hàm số
2
cos 2 1
cos 1
2
x
yx
−
= −=
tuần hoàn và có chu kỳ
2
T
π
=
.
c. Hàm số
2 2 14
sin .cos sin
5 5 25
yxx x
= =
tuần hoàn và có chu kỳ
2
5
2
T
π
=
.
d. Hàm số
( )
cos cos 3.yx x= +
không tuần hoàn
Vì ta có hàm số
y cos x=
có chu kỳ
1
2T
π
=
và hàm số
( )
y cos 3.x=
có chu kỳ
2
2
3
T
π
=
nhưng không tồn tại bội số chung nhỏ nhất của
1
2T
π
=
và
2
2
3
T
π
=
Câu 22: Tìm chu kỳ của hàm số:
( )
sin 3 3cos 2fx x x= +
.
Lời giải
Ta có hàm số
y sin3x=
có chu kỳ
1
2
3
T
π
=
và hàm số
y cos 2x=
có chu kỳ
2
T
π
=
⇒
chu kỳ
T
của hàm số
sin 3 3cos 2yx x= +
là bội chung nhỏ nhất của
1
2
3
T
π
=
và
2
T
π
=
⇒
2T
π
=
.
DẠNG 4: GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ LƯỢNG GIÁC
PHƯƠNG PHÁP GIẢI TOÁN
1)
1 sin 1
1 cos 1
x
x
−≤ ≤
−≤ ≤
2)
0 sin 1
0 cos 1
x
x
≤ ≤
≤≤
3)
2
2
0 sin 1
0 cos 1
x
x
≤≤
≤≤
4)
0 sin 1
0 cos 1
x
x
≤≤
≤≤
1 sin 5 .yx= −
2
cos 1
yx
= −
22
sin .cos
55
yxx
=
( )
cos cos 3.yx x= +
KIẾN THỨC CẦN THIẾT.
1

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
Câu 23: Tìm GTLN - GTNN của các hàm số sau:
a. . b. .
c. . d. .
e. . f. với .
g. với .
Lời giải
a. Tập xác định:
D =
.
Ta có:
1 cos 1x−≤ ≤
3 3cos 3x⇔− ≤ ≤
1 2 3cos 5x⇔− ≤ + ≤
15y⇒− ≤ ≤
.
Vậy giá trị lớn nhất của hàm số là
5
cos 1x⇔=
2,xk k
π
⇔= ∈
.
Giá trị nhỏ nhất của hàm số là
1−
cos 1x⇔=−
2,x kk
ππ
⇔=+ ∈
.
b. Tập xác định:
D =
.
Ta có:
1 sin 1
6
x
π
−≤ − ≤
3 3sin 3
6
x
π
⇔− ≤ − ≤
5 3sin 2 1
6
x
π
⇔− ≤ − − ≤
51y⇒− ≤ ≤
.
Vậy giá trị lớn nhất của hàm số là
1
2
sin 1 2 ,
63
x x kk
ππ
π
⇔ − =⇔= + ∈
.
Giá trị nhỏ nhất của hàm số là
5−
sin 1 2 ,
63
x x kk
ππ
π
⇔ − =−⇔ =− + ∈
.
c. Tập xác định:
D =
.
Ta có:
2
0 cos 2 1x≤≤
2
1 4cos 2 1 5x⇔≤ +≤
15y⇒≤ ≤
.
Vậy giá trị lớn nhất của hàm số là
5
2
cos 2 1 sin 2 0 ,
2
k
x x xk
π
⇔ =⇔ =⇔= ∈
.
Giá trị nhỏ nhất của hàm số là
1
2
cos 2 0 cos 2 0 ,
42
k
x xx k
ππ
⇔ =⇔ =⇔= + ∈
.
d. Tập xác định:
D =
.
Ta có:
0 sin 1x≤≤
0 2 sin 2x⇔ ≥− ≥−
31y⇔≥≥
.
Vậy giá trị lớn nhất của hàm số là
3
sin 0 sin 0 ,x x xkk
π
⇔ =⇔ =⇔= ∈
.
2 3cosyx= +
3sin 2
6
yx
π
= −−
2
4cos 2 1yx= +
3 2 sinyx= −
( )
44
2 sin cos 3y xx= ++
3sin 2 12yx= −
3
;
88
x
ππ
∈−
2
4cos 7
2 12
x
y
π
= −−
[ ]
0;x
π
∈
BÀI T
Ậ
P.
2
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
Giá trị nhỏ nhất của hàm số là
1
sin 1 cos 0 ,
2
x x x kk
π
π
⇔ =⇔ =⇔= + ∈
.
e. Tập xác định:
D =
.
( ) ( )
4 4 22 2
2 sin cos 3 2 1 2sin .cos 3 5 sin 2
y x x xx x
= + += − +=−
Ta có:
2
0 sin 2 1x
≤≤
2
4 5 sin 2 5x
⇔≤− ≤
45y⇔≤≤
.
Vậy giá trị lớn nhất của hàm số là
5
sin 2 0 ,
2
k
x xk
π
⇔ =⇔= ∈
.
Giá trị nhỏ nhất của hàm số là
4
2
sin21cos20 ,
42
k
x xx k
ππ
⇔ =⇔ =⇔= + ∈
.
f. Với
3
;
88
x
ππ
∈−
3
2;
44
x
ππ
⇒ ∈−
2
sin 2 1
2
x
⇒− ≤ ≤
32
12 9
2
y⇔− − ≤ ≤−
.
Vậy giá trị lớn nhất của hàm số với
3
;
88
x
ππ
∈−
là
9−
sin 2 1 .
4
xx
π
⇔ =⇔=
Giá trị nhỏ nhất của hàm số với
3
;
88
x
ππ
∈−
là
32
12
2
−−
2
sin 2
28
xx
π
⇔ =− ⇔=−
.
g. Ta có
2
4cos 7 2cos 5
2 12 6
x
yx
ππ
= − −= − −
Với
[ ]
0;x
π
∈
5
;
6 66
x
π ππ
⇒ − ∈−
3
cos 1
26
x
π
⇒− ≤ − ≤
35 3y⇔− − ≤ ≤−
.
Vậy giá trị lớn nhất của hàm số với
[ ]
0;x
π
∈
là
3
−
cos 1
66
xx
ππ
⇔ − =⇔=
.
Giá trị nhỏ nhất của hàm số với
[
]
0;x
π
∈
là
35−−
3
cos
62
xx
π
π
⇔ − =− ⇔=
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
Ví dụ: Tìm GTLN – GTNN của các hàm số sau:
a.
b.
c.
d.
e. trên đoạn
f. trên đoạn .
g. trên đoạn .
h. .
i. Tìm min của hàm số: với .
Lời giải
a.Đặt
sinx t=
( )
1t ≤
, hàm số có dạng:
2
2 31y tt=− +−
.
Xét hàm số
2
2 31y tt=− +−
trên
[ ]
1;1−
, hàm số có BBT như sau:
Nhìn vào BBT ta thấy:
Giá trị nhỏ nhất của hàm số bằng
6−
khi và chỉ khi
1t = −
tức là
sinx 1= −
( )
2
2
x kk
π
π
⇔=−+ ∈
.
Giá trị lớn nhất của hàm số bằng
1
8
khi và chỉ khi
3
4
t =
tức là
3
sinx
4
=
⇔
3
arcsin 2
4
xk
π
= +
hoặc
( )
3
arcsin 2
4
x kk
ππ
=− +∈
.
b.Hàm số được viết lại thành
22
1 sin 2sin 2 sin 2sinx 3y xx x=− + +=− + +
Đặt
( )
sinx 1tt= ≤
, xét hàm số
2
23yt t=−+ +
trên
[ ]
1;1−
có BBT như sau:
2
2sin 3sin 1
y xx=− +−
2
cos 2sinx 2yx
= ++
cos 2cos 2yx x= +
( )
2
22
1 cos 2cos 1
y xx=− −+
2
2sin sin 2y xx= −+
[ ]
0;
π
2cos cos 2 8y xx= +−
;
24
ππ
−
2
tan tan 1
y xx= −+
;
44
ππ
−
sin cos 4sin cos 7y x x xx=++ +
2
2
11
sin sin
sin sin
yx x
xx
= + −−
0 x
π
<<
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
Nhìn vào BBT ta thấy:
Giá trị nhỏ nhất của hàm số bằng
0
khi và chỉ khi
1
t = −
tức
sinx 1
= −
(
)
2
2
x kk
π
π
⇔=−+ ∈
.
Giá trị lớn nhất của hàm số bằng
4
khi và chỉ khi
1t
=
tức là
sinx 1=
⇔
( )
2
2
x kk
π
π
⇔= + ∈
.
c.Ta có
22
cos 2.(2cos 1) 4cos cos 2y x x xx= + −= + −
Đặt
cosx t=
( )
1t ≤
, hàm số có dạng:
2
42y tt= +−
.
Xét hàm số
2
42
y tt= +−
trên
[ ]
1;1−
có BBT như sau:
Giá trị nhỏ nhất của hàm số bằng
33
16
−
khi và chỉ khi
1
8
t = −
tức
1
cosx
8
= −
⇔
1
arccos 2
8
xk
π
=± −+
( )
k ∈
.
Giá trị lớn nhất của hàm số bằng
3
khi và chỉ khi
1t =
tức là
cos 1x =
⇔
2xk
π
=
( )
k ∈
.
d.Hàm số được viết lại thành
( )
( )
2
2 2 24 2 4 2
1 cos 2cos 1 1 2cos cos 2cos 1 cos 4cos 2y x x xx x x x=− −+=−+−+=−+
Đặt
[ ]
2
cos x, t 0;1t = ∈
, xét hàm số
2
42yt t=−+
trên
[ ]
0;1
có BBT như sau:
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 20
Sưu tầm và biên soạn
Nhìn vào BBT ta thấy:
Giá trị nhỏ nhất của hàm số bằng
1−
khi và chỉ khi
1t =
tức
2
cos x 1 sinx 0
=⇔=
( )
kk
π
⇔∈
.
Giá trị lớn nhất của hàm số bằng
2
khi và chỉ khi
0t =
tức là
2
cos x 0 cosx 0=⇔=
⇔
2
xk
π
π
= +
,
k
∈
e.Đặt
sinx t=
với
[ ]
0;x
π
∈
thì
[ ]
0;1t ∈
, hàm số có dạng:
2
22y tt= −+
.
Xét hàm số
2
22y tt= −+
trên
[ ]
0;1
, hàm số có BBT như sau:
Nhìn vào BBT ta thấy:
Giá trị nhỏ nhất của hàm số bằng
15
8
khi và chỉ khi
1
4
t =
tức là
1
sinx
4
=
⇔
1
arcsin 2
4
xk
π
= +
hoặc
1
arcsin 2
4
xk
ππ
=−+
,
k ∈
.
Giá trị lớn nhất của hàm số bằng
3
khi và chỉ khi
1t =
tức là
sinx 1=
⇔
2
2
xk
π
π
= +
,
k ∈
.
f.Hàm số được viết lại thành
22
2cos 2cos 1 8 2cos 2cos 9y x x xx= + −− = + −
Đặt
cosx t=
, với
;
24
x
ππ
∈−
thì
[ ]
0;1t ∈
, hàm số có dạng:
2
2 29yt t= +−
.
Xét hàm số
2
2 29yt t= +−
trên
[ ]
0;1
có BBT như sau:
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 21
Sưu tầm và biên soạn
Giá trị nhỏ nhất của hàm số bằng
9−
khi và chỉ khi
0t =
tức
cos x 0=
⇔
2
xk
π
π
= +
,
k ∈
.
Giá trị lớn nhất của hàm số bằng
5−
khi và chỉ khi
1t =
tức là
cosx 1
=
⇔
2xk
π
=
,
k ∈
.
g.Đặt
tanx t=
,
[ ]
1;1t
∈−
, hàm số có dạng:
2
1yt t= −+
.
Xét hàm số
2
1yt t= −+
trên
[ ]
1;1−
có BBT như sau:
Giá trị nhỏ nhất của hàm số bằng
3
4
khi và chỉ khi
1
2
t =
tức
1
tanx
2
=
⇔
1
arctan
2
xk
π
= +
,
k ∈
.
Giá trị lớn nhất của hàm số bằng
3
khi và chỉ khi
1t = −
tức là
tanx 1= −
⇔
4
xk
π
π
=−+
,
k ∈
.
h. Đặt
( )
sinx cos 2 sin 2
4
t x xt
π
=+= + ≤
2
2sinx cosx t 1⇒=−
, hàm số trở thành:
22
2( 1) 7 2 5yt t t t=+ − + = ++
.
Xét hàm số
2
25
y tt= ++
trên
2; 2
−
có BBT như sau:
Giá trị nhỏ nhất của hàm số bằng
39
8
.
Giá trị lớn nhất của hàm số bằng
92+
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 22
Sưu tầm và biên soạn
i.Đặt
1
sinx
sinx
t = +
, với
0 x
π
<<
thì
2t ≥
22
2
1
sin t 2
sin
x
x
⇒+ =−
, hàm số trở thành:
2
2yt t= −−
.
Xét hàm số
2
2yt t= −−
trên
[
)
2;+∞
có BBT như sau:
Vậy giá trị nhỏ nhất của hàm số bằng
0
1
sinx 2 sinx 1 2
sinx 2
xk
π
π
⇔ + =⇔ =⇔= +
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 54
Sưu tầm và biên soạn
BÀI 4: HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
DẠNG 1. TẬP XÁC ĐỊNH
Câu 1: Tập xác định của hàm số
sin
yx
=
là
A.
[ ]
1;1−
. B.
( )
1;1−
. C.
( )
0; +∞
. D.
.
Câu 2: Tập xác định của hàm số
1
sin
y
x
=
là
A.
{ }
D \0.=
B.
{ }
D \ 2, .kk
π
= ∈
C.
{ }
D \, .kk
π
= ∈
D.
{ }
D \ 0; .
π
=
Câu 3: Tập xác định của hàm số
tan 2yx=
là
A.
\
42
D kk
ππ
= +∈
∣
. B.
\
42
D kk
ππ
= +∈
∣
.
C.
\2
2
D kk
π
π
=+∈
∣
. D.
\
2
D kk
π
π
= +∈
∣
.
Câu 4: Tập xác định của hàm số
1 sin
cos
x
y
x
+
=
là
A.
{ }
\,D kk
π
= ∈
. B.
\,
2
D kk
π
π
= +∈
.
C.
{
}
\ 2,
D kk
π
= ∈
. D.
\ 2,
2
D kk
π
π
= +∈
.
Câu 5: Điều kiện xác định của hàm số
2021 cos
sin
x
y
x
−
=
là
A.
,
2
x kk
π
π
≠+ ∈
. B.
,xkk
π
≠∈
. C.
2,x kk
π
≠∈
. D.
,
2
k
xk
π
≠∈
.
Câu 6: Tập xác định của hàm số
tanyx=
là
A.
{ }
D \ 2, .kk
π
= ∈
B.
D \ 2, .
2
kk
π
π
= +∈
C.
D\ , .
2
kk
π
π
= +∈
D.
{ }
D \, .kk
π
= ∈
Câu 7: Tập xác định của hàm số
2
1
cos
x
y
x
+
=
là
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
III
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 55
Sưu tầm và biên soạn
A.
D
=
. B.
2
\,D kk
π
π
= +∈
.
C.
{ }
\,D kk
π
= ∈
. D.
2
\,
k
Dk
π
= ∈
.
Câu 8: Tập xác định
D
của hàm số
5sin
cos 3
x
y
x
=
−
là
A.
( )
3;D = +∞
. B.
{ }
\3= D
. C.
( )
;3= −∞D
. D.
D =
.
Câu 9: Tập xác định của hàm số
1 sin
cos
x
y
x
là
A.
{ }
\;D xkk
π
= ≠∈
. B.
{ }
\ 2;D xk k
π
=≠∈
.
C.
\;
2
D x kk
π
π
= ≠+ ∈
. D.
\ 2;
2
D x kk
π
π
= ≠− + ∈
.
Câu 10: Tập xác định của hàm số
tan 2
3
yx
là
A.
\;
62
k
Dx k
ππ
= ≠+ ∈
. B.
5
\;
12
D x kk
π
π
= ≠+ ∈
.
C.
\;
2
D x kk
π
π
= ≠+ ∈
. D.
5
\;
12 2
k
Dx k
.
Câu 11: Tập xác định của hàm số
cotyx=
là
A.
{ }
\ kk
π
∈
. B.
\2
2
kk
π
π
+∈
.
C.
\
2
kk
π
π
+∈
. D.
{ }
\2kk
π
∈
.
Câu 12: Tập xác định của hàm số
1 cos
sin
x
y
x
−
=
là
A.
{ }
\|
D kk= ∈
π
. B.
\|
2
D kk
= +∈
π
π
.
C.
{ }
\ 2|D kk= ∈
π
. D.
\ 2|
2
D kk
=+∈
π
π
.
Câu 13: Tập xác định của hàm số
2 3tanyx
là
A.
\
3
Dk
. B.
\
6
Dk
. C.
\
2
Dk
. D.
\
4
Dk
.
Câu 14: Tập xác định của hàm số
1
2sin 1
y
x
=
−
là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 56
Sưu tầm và biên soạn
A.
\ 2,
6
D kk
π
π
= ±+ ∈
. B.
\ 2,
3
D kk
π
π
= ±+ ∈
.
C.
5
\ 2; 2,
66
D k kk
ππ
ππ
= + +∈
. D.
2
\ 2; 2,
33
D k kk
ππ
ππ
= + +∈
.
Câu 15: Tìm tập xác định
D
của hàm số
1 sin
1 cos
x
y
x
−
=
+
.
A.
\ 2; 2,
22
D k kk
= −+ + ∈
ππ
ππ
. B.
{ }
\,D kk=−∈
π
.
C.
{ }
\ 2,D kk=+∈
ππ
. D.
\ 2,
2
D kk
= +∈
π
π
.
Câu 16: Tập xác định của hàm số
1
sin 2 1
y
x
=
+
là
A.
\,
2
D kk
π
π
= −+ ∈
. B.
\ 2,
2
D kk
π
π
= −+ ∈
.
C.
\,
4
D kk
π
π
= −+ ∈
. D.
\ 2,
4
D kk
π
π
= −+ ∈
.
Câu 17: Tập xác định của hàm số
sin
2 2cos
x
y
x
=
−
là
A.
D
=
. B.
\
2
D kk
π
= ∈
.
C.
\
2
D kk
π
π
= +∈
. D.
{ }
\2D kk
π
= ∈
.
Câu 18: Tập xác định của hàm số
2021
1 cos
y
x
=
−
là
A.
\, .
2
k
Dk
π
= ∈
B.
{
}
\ 2, .
D kk
π
= ∈
C.
\ ,.
2
D kk
π
π
= +∈
D.
{ }
\, .D kk
π
= ∈
Câu 19: Tập xác định của hàm số
2sin 1
1 cos
x
y
x
là
A.
{
}
\ 2;
D xk k
π
=≠∈
. B.
{ }
\ 2;D x kk
ππ
= ≠+ ∈
.
C.
\;
2
D x kk
π
π
= ≠+ ∈
D.
\ 2;
2
D x kk
π
π
= ≠+ ∈
.
Câu 20: Tập xác định của hàm số
1
sin cos
y
xx
là
A.
{ }
\;D xkk
π
= ≠∈
. B.
{ }
\ 2;D xk k
π
=≠∈
C.
\;
2
D x kk
π
π
= ≠+ ∈
. D.
\;
4
D x kk
.
Câu 21: Tập xác định của hàm số
2020
tan( 2019 )
y
x
π
=
+
là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 57
Sưu tầm và biên soạn
A.
\,
2
D kk
π
= ∈
. B.
{ }
\,D kk
π
= ∈
.
C.
\,
2
D kk
π
π
= +∈
. D.
{ }
\ 2,D kk
π
= ∈
.
Câu 22: Tìm tập xác định của hàm số
s
1 2cos
=
−
y
x
inx
.
A.
\2
3
π
π
±+ ∈
kk
. B.
1
\
2
.
C.
. D.
\2
3
π
π
+∈
kk
.
Câu 23: Tập xác định của hàm số
3 sin
cos 1
x
y
x
+
=
−
là
A.
{ }
\,
D kk
π
= ∈
. B.
\,
2
D kk
π
π
= +∈
.
C.
\ 2,
2
D kk
π
π
= +∈
. D.
{ }
\ 2,D kk
π
= ∈
.
Câu 24: Tập xác định của hàm số
2sin 1
cos
x
y
x
−
=
là
A.
\,
2
D kk
π
π
= +∈
. B.
{ }
\,D kk
π
= ∈
.
C.
\,
2
D kk
π
= ∈
.
D.
{ }
\ 2,D kk
π
= ∈
.
Câu 25: Tập xác định của hàm số
tan
cos 1
x
y
x
=
+
là
A.
{ }
\ 2,kk
ππ
+∈
. B.
\ ;2,
2
kk k
π
ππ
+∈
.
C.
\ ; 2,
2
k kk
π
ππ π
++ ∈
. D.
\,
2
k
k
π
∈
.
Câu 26: Tìm tập xác định
D
của hàm số
tan
4
yx
π
= −
.
A.
,
2
D x x kk
π
π
= ∈ ≠+ ∈
. B.
,
4
D x x kk
π
π
= ∈ ≠+ ∈
.
C.
3
,
2
D x x kk
π
π
=∈ ≠+ ∈
. D.
3
,
4
D x x kk
π
π
=∈ ≠+ ∈
.
Câu 27: Tìm tập xác định của hàm số
2021cot 2 2022yx= +
.
A.
\
2
Dk
π
π
= +
. B.
\
2
Dk
π
=
. C.
\
42
Dk
ππ
= +
. D.
D
=
.
Câu 28: Tập xác định của hàm số
cotyx=
là
A.
{ }
\Dk
π
=
. B.
{ }
\,D kk
π
= ∈
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 58
Sưu tầm và biên soạn
C.
\,
2
D kk
π
π
= +∈
. D.
D
=
.
Câu 29: Tập xác định của hàm số:
tan 2
6
yx
π
= +
?
A.
\,
2
kk
π
π
+∈
. B.
\,
62
k
k
ππ
−
+∈
.
C.
\,
6
kk
π
π
+∈
. D.
\,
62
k
k
ππ
+∈
.
Câu 30: Tập xác định của hàm số
1
sin
y
x
=
là:
A.
{ }
,\D kk
π
= ∈
. B.
{ }
2,\
D kk
π
= ∈
.
C.
{ }
\ 0;
D
π
=
. D.
{ }
0\D =
.
Câu 31: Điều kiện xác định của hàm số
tan 2yx=
là
A.
4
xk
π
π
≠− +
. B.
2
xk
π
π
≠+
. C.
42
k
x
ππ
≠+
. D.
4
xk
π
π
≠+
Câu 32: Tập xác định của hàm số
2cos 1
sin 2
−
=
x
y
x
là:
A.
\,
2
π
= ∈
k
Dk
. B.
\ 2; ,
32
ππ
π
= ±+ ∈
k
D kk
.
C.
\ 2,
3
π
π
= +∈
D kk
. D.
{ }
\,
π
= ∈D kk
.
Câu 33: Tìm tập xác định của hàm số
tan
yx=
.
A.
\|
2
kk
π
π
+∈
. B.
{ }
\|kk
π
∈
.
C.
\ 2|
2
kk
π
π
+∈
. D.
{ }
\ 2|kk
π
∈
.
Câu 34: Tập xác định của hàm số
1
1 cos
y
x
=
−
là
A.
{ }
\ 2,D kk
π
= ∈
. B.
{ }
\ 2,D kk
ππ
=+∈
.
C.
\ 2,
2
D kk
π
π
= +∈
. D.
\ 2,
2
D kk
π
π
= −+ ∈
.
Câu 35: Tập xác định của hàm số
tan
1 tan
x
y
x
là
A.
\ 2; 2,
24
ππ
ππ
D k kk
= + +∈
. B.
\ 2; 2,
24
ππ
ππ
D k kk
= −+ −+ ∈
.
C.
\ ;,
24
ππ
ππ
D k kk
= + +∈
. D.
\ ; 2,
24
ππ
ππ
D k kk
= ++ ∈
.
Câu 36: Tập xác định của hàm số
tan coty xx= +
là
A.
\;
2
kk
π
π
+∈
. B.
\;
2
kk
π
∈
. C.
{ }
\;kk
π
∈
. D.
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 59
Sưu tầm và biên soạn
Câu 37: Tập xác định của hàm số
cot
2
x
y =
là
A.
{
}
\,D kk
π
= ∈
. B.
{ }
\ 2,D kk
ππ
=+∈
.
C.
\,
2
k
Dk
π
= ∈
. D.
{ }
\ 2,D kk
π
= ∈
.
Câu 38: Tìm tập xác định
D
của hàm số
−
= −
2cos 1
3tan
sin
x
yx
x
.
A.
\; ,
2
D k kk
π
= π +π ∈
. B.
{ }
\,D kk= π∈
.
C.
\,
2
D kk
π
= +π ∈
. D.
\ ; 2,
2
D k kk
π
= π + π∈
.
Câu 39: Tập xác định của hàm số
2 sin
tan
−
=
x
y
x
.
A.
\,
2
π
π
= +∈
D kk
. B.
{
}
\,
π
= ∈DRkk
.
C.
\,
2
π
= ∈
k
Dk
. D.
{ }
\ 2,
π
= ∈
D kk
.
Câu 40: Tìm tập xác định của hàm số
tan 3
6
π
= −
yx
.
A.
\,
33
ππ
= +∈
k
Dk
. B.
\,
93
ππ
= +∈
k
Dk
.
C.
4
\,
93
ππ
= +∈
k
Dk
. D.
2
\,
93
ππ
= +∈
k
Dk
.
Câu 41: Hàm số
1 3sin
cos 2
x
y
x
−
=
xác định khi
A.
,
42
x kk
ππ
≠+ ∈
. B.
,
2
x kk
π
π
≠+ ∈
. C.
,
4
x kk
π
π
≠+ ∈
. D.
2,xk k
π
≠∈
.
Câu 42: Tập xác định của hàm số
1
sin 2 1
y
x
=
+
là:
A.
\ 2|
2
D kk
π
π
= −+ ∈
. B.
\ 2|
4
D kk
π
π
= −+ ∈
.
C.
\|
4
D kk
π
π
= −+ ∈
. D.
D =
.
Câu 43: Tập xác định của hàm số
2
tan 2022
sin 1
x
y
x
+
=
+
A.
\ 2,
2
kk
+∈
π
π
. B.
\,
2
kk
+∈
π
π
.
C.
. D.
{ }
\,kk∈
π
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 60
Sưu tầm và biên soạn
Câu 44:
Tìm tập xác định
D
của hàm số
1
.
1 sin
y
x
=
−
A.
{ }
D \, .kk
π
= ∈
B.
D\ , .
2
kk
π
π
= +∈
C.
D \ 2, .
2
kk
π
π
= +∈
D.
D.= ∅
Câu 45: Tìm tập xác định
D
của hàm số
2
5 2cot sin cot .
2
y xx x
π
=+ −+ +
A.
D\ , .
2
k
k
π
= ∈
B.
D\ , .
2
kk
π
π
= −+ ∈
C.
D.=
D.
{ }
D \, .kk
π
= ∈
Câu 46: Tìm tập xác định
D
của hàm số
tan cos .
2
yx
π
=
A.
D\ ,
2
kk
π
π
= +∈
. B.
D \ 2,
2
kk
π
π
= +∈
.
C.
D =
. D.
{ }
D \,kk
π
= ∈
.
Câu 47: Tập xác định của hàm số
1
tan
y
x
=
là
A.
,
2
Dkk
π
= ∈
. B.
\,
2
D kk
π
= ∈
.
C.
{ }
\,D kk
π
= ∈
. D.
{
}
,D kk
π
= ∈
.
Câu 48: Tìm tập xác định của hàm số
3sin
2cos 1
x
y
x
=
+
.
A.
4
\ 2, 2
33
D k kk
= −+ + ∈
ππ
ππ
. B.
2
\2
3
D kk
= ±+ ∈
π
π
.
C.
5
\2
6
D kk
= ±+ ∈
π
π
. D.
\2
3
D kk
= ±+ ∈
π
π
.
Câu 49: Hàm số
2
sin
1 2sin
x
y
x
=
−
có tập xác định là
A.
\
4
D kk
π
π
= +∈
. B.
\
2
D kk
π
π
= +∈
.
C.
\
42
k
Dk
ππ
= +∈
. D.
\2
4
D kk
π
π
= ±+ ∈
.
Câu 50: Hàm số
1
sin 2 cos 2
y
xx
=
có tập xác định là
A.
\|
42
k
Dk
ππ
= +∈
. B.
\|
4
k
Dk
π
= ∈
.
C.
{ }
\|D kk
π
= ∈
. D.
\|
2
k
Dk
π
= ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 61
Sưu tầm và biên soạn
Câu 51: Hàm số
sin 2
cot 3
x
y
x
=
−
có tập xác định là
A.
\|
6
D kk
π
π
= +∈
. B.
{ }
\|D kk
π
= ∈
.
C.
\; |
6
D k kk
π
ππ
= +∈
. D.
\ ;|
26
D k kk
ππ
ππ
= ++∈
.
Câu 52: Tập xác định của hàm số
2cot 5
cos 1
x
y
x
+
=
−
là
A.
\
2
k
π
π
+
. B.
{
}
\2
k
π
. C.
{ }
\ k
π
. D.
\2
2
k
π
π
+
.
Câu 53: Tìm tập xác định của hàm số
1
sin 2 1
y
x
=
−
.
A.
\,
4
D kk
π
π
= +∈
. B.
\,
2
D kk
π
π
= +∈
.
C.
{ }
\ 2,D kk
π
= ∈
. D.
{ }
\,D kk
π
= ∈
.
Câu 54: Hàm số
tan
1 tan
x
y
x
=
+
không xác định tại các điểm
A. chỉ
2
xk
π
π
= +
( )
k
∈
. B. chỉ
4
xk
π
π
= +
(
)
k ∈
.
C. chỉ
4
xk
π
π
=−+
( )
k ∈
. D.
4
xk
π
π
=−+
và
2
xk
π
π
= +
( )
k ∈
.
Câu 55: Tập xác định của hàm số
2020
1
y
tanx
=
−
A.
\,
4
kk
π
π
+∈
. B.
\,
2
kk
π
π
+∈
.
C.
\ 2,
4
kk
π
π
+∈
. D.
\ ;,
24
k kk
ππ
ππ
+ +∈
.
Câu 56: Tìm tập xác định của hàm số
cot 2 tan
2
yx x
π
=+−
.
A.
{ }
\;D k kZ
π
= ∈
. B.
\;
2
D k kZ
π
π
= +∈
.
C.
\;
3
k
D kZ
π
= ∈
. D.
\;
2
k
D kZ
π
= ∈
.
Câu 57: Tìm tập xác định
D
của hàm số
tan 1
cos
sin 3
x
yx
x
π
−
= ++
.
A.
{ }
\,D kk
π
= ∈
. B.
\,
2
k
Dk
π
= ∈
.
C.
\,
2
D kk
π
π
= +∈
. D.
D =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 62
Sưu tầm và biên soạn
Câu 58: Tập xác định của hàm số
3cot
2sin 4
x
y
x
=
−
là
A.
{ }
\ arcsin 2 2 , arcsin 2 2 ,
R k k kZ
ππ π
+ − +∈
B.
.R
C.
{
}
\ arcsin 2 2 ,R k kZ
π
± +∈
. D.
{ }
\, .RkkZ
π
∈
Câu 59: Tập xác định của hàm số
2020
tan 1
y
x
=
−
là
A.
\
4
k
π
π
+
. B.
\
2
k
π
π
+
.
C.
\2
4
k
π
π
+
. D.
\;
24
kk
ππ
ππ
++
.
Câu 60: Tìm tập xác định của hàm số
1 cos coty xx
=−+
?
A.
{
}
\;π∈kk
. B.
(
]
;1
−∞
. C.
\;
2
π
+π ∈
kk
. D.
[ ]
{ }
1;1 \ 0−
.
Câu 61: Tập xác định
D
của hàm số
2sin 3
tan 1
x
y
x
+
=
−
.
A.
\,
2
D kk
π
π
= +∈
. B.
{ }
\1D =
.
C.
\,
4
D kk
π
π
= +∈
. D.
\ ;,
24
D k kk
ππ
ππ
= + +∈
.
Câu 62: Tìm tập xác định
D
của hàm số
1
1 sin
y
x
=
+
.
A.
{ }
\ 2,D kk
π
= ∈
. B.
{ }
\ 2,D kk
ππ
=+∈
.
C.
\ 2,
2
D kk
π
π
= +∈
. D.
\ 2,
2
D kk
π
π
−
= +∈
.
Câu 63: Hàm số
11
tan cot
sin cos
y xx
xx
=+++
không xác định trong khoảng nào trong các khoảng sau
đây?
A.
2; 2
2
kk
π
ππ
+
với
k ∈
. B.
3
2; 2
2
kk
π
ππ π
++
với
k ∈
.
C.
2; 2
2
kk
π
ππ π
++
với
k ∈
. D.
( )
2 ;2 2kk
ππππ
++
với
k ∈
.
Câu 64: Tập xác định của hàm số
tan 3yx
=
là.
A.
\ ,k R
63
DR k
ππ
= +∈
B.
\ ,k R
2
DR k
π
π
= +∈
C.
{ }
\ ,k RDR k
ππ
= +∈
D.
2
\ ,k R
3
DR k
π
= ∈
Câu 65: Tìm
m
để hàm số
5sin 4 6cos 4 2 1y x xm= − +−
xác định với mọi
x

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 63
Sưu tầm và biên soạn
A.
61 1
2
+
≥m
. B.
1
≥m
. C.
61 1
2
−
≥m
. D.
61 1
2
+
<m
.
Câu 66: Có bao nhiêu số nguyên
m
sao cho hàm số
sin 3y mx
= +
có tập xác định là
?
A.
7
. B.
6
. C.
3
. D.
4
.
Câu 67: Hàm số
3 sin 2
cos 1
x
y
mx
+
=
+
có tập xác định là
khi
A.
0m >
. B.
01m≤<
. C.
11m−< <
. D.
1m ≠−
.
Câu 68: Cho hàm số
44
sin cos sin .cos
y x xm x x= +−
. Tìm
m
để hàm số xác định với mọi
x
.
A.
11
;
22
m
∈−
. B.
( )
1;1m∈−
. C.
(
]
;1m∈ −∞
. D.
[
]
1;1
m ∈−
.
DẠNG 2. TÍNH CHẴN LẺ
Câu 69: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx=
B.
cos .yx=
C.
tan .yx=
D.
cot .yx=
Câu 70: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx= −
B.
cos sin .
y xx= −
C.
2
cos sin .yx x= +
D.
cos sin .
y xx=
Câu 71: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin 2 .yx=
B.
cos .yx x=
C.
cos .cot .y xx
=
D.
tan
.
sin
x
y
x
=
Câu 72: Hàm số nào sau đây là hàm số lẻ?
A.
2 cos
yx x
= +
. B.
cos3yx
=
. C.
(
)
2
sin 3yx x= +
. D.
3
cos
x
y
x
=
.
Câu 73: Mệnh đề nào dưới đây đúng?
A. Hàm số
cot
yx=
là hàm số chẵn. B. Hàm số
sin
yx
=
là hàm số chẵn.
C. Hàm số
tanyx=
là hàm số chẵn. D. Hàm số
cosyx=
là hàm số chẵn.
Câu 74: Trong các khẳng định sau đây, khẳng định nào đúng?
A. Hàm số
sinyx=
là hàm số chẵn. B. Hàm số
cosyx=
là hàm số lẻ.
C. Hàm số
tanyx=
là hàm số lẻ. D. Hàm số
cotyx
=
là hàm số chẵn.
Câu 75: Chọn phát biểu đúng:
A. Các hàm số
sinyx=
,
cosyx=
,
cot
yx=
đều là hàm số chẵn.
B. Các hàm số
sinyx
=
,
cosyx=
,
cotyx=
đều là hàm số lẻ.
C. Các hàm số
sin
yx=
,
cotyx=
,
tan
yx=
đều là hàm số chẵn.
D. Các hàm số
sinyx=
,
cotyx=
,
tanyx
=
đều là hàm số lẻ.
Câu 76: Hàm số nào sau đây là hàm số chẵn ?
A.
( ) sinfx x=
. B.
( ) sin 2fx x=
. C.
( ) sinfx x=
. D.
2
( ) sinfx x x=
.
Câu 77: Hàm số nào dưới đây là hàm số lẻ?
A.
cosyx=
. B.
2
sinyx=
. C.
2
cotyx=
. D.
tanyx=
.
Câu 78: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin 3 .yx=
B.
tan .
2
x
y =
C.
sin .cos .y xx=
D.
2
sin .cos .y xx=
Câu 79: Trong các hàm số sau đây, hàm số nào là hàm số chẵn?

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 64
Sưu tầm và biên soạn
A.
tan 4yx=
. B.
cos3yx=
. C.
cot 5yx=
. D.
sin 2yx=
.
Câu 80: Hàm số nào sau đây là hàm số chẵn
A.
3
3sin 4siny xx= +
. B.
3sin 4cosyxx= +
.
C.
2
4cos sin
y xx= −
. D.
2
4sin cos
y xx= −
.
Câu 81: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
3
cos .siny xx=
. B.
sin .cos 2
yxx
=
.
C.
2019cos 2020yx= +
. D.
2
tan
tan 1
x
y
x
=
+
.
Câu 82: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
sin 3
yx= +
. B.
2
2cos
sin 2
x
y
x
=
+
. C.
2
sinyx x=
. D.
2cos sin 2y xx= −
.
Câu 83: Trong các hàm số sau, hàm số nào là hàm số chẵn.
A.
sin 2021 cos2022
yxx
= +
. B.
cot 2021 2022sinyxx
= −
.
C.
tan 2021 cot 2022yxx
= +
. D.
2021cos 2022sin
y xx= +
.
Câu 84: Có bao nhiêu hàm số chẵn trong các hàm số sau:
sinyx=
,
cos3yx=
,
tan 2yx
=
và
cotyx=
?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 85: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx=
. B.
2
sin .
yx x=
C.
.
cos
x
y
x
=
D.
sin .yx x= +
Câu 86: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A.
sin cos 2 .y xx=
B.
3
sin .cos .
2
y xx
π
= −
C.
2
tan
.
tan 1
x
y
x
=
+
D.
3
cos sin .y xx=
Câu 87: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
cos sin .yx x= +
B.
sin cos .
yxx= +
C.
cos .
yx= −
D.
sin .cos3 .y xx=
Câu 88: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
cot 4 .yx=
B.
sin 1
.
cos
x
y
x
+
=
C.
2
tan .yx=
D.
cot .yx=
Câu 89: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
sin .
2
yx
π
= −
B.
2
sin .yx=
C.
cot
.
cos
x
y
x
=
D.
tan
.
sin
x
y
x
=
Câu 90: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
1 sin .yx= −
B.
2
cot .sin .y xx=
C.
2
tan 2 cot .yx x x= −
D.
1 cot tan .y xx=++

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 65
Sưu tầm và biên soạn
Câu 91: Cho hàm số
( )
sin 2fx x=
và
(
)
2
tan .gx x=
Chọn mệnh đề đúng
A.
( )
fx
là hàm số chẵn,
( )
gx
là hàm số lẻ. B.
( )
fx
là hàm số lẻ,
( )
gx
là hàm số chẵn.
C.
( )
fx
là hàm số chẵn,
( )
gx
là hàm số chẵn. D.
( )
fx
và
( )
gx
đều là hàm số lẻ.
Câu 92: Cho hai hàm số
( )
2
cos 2
1 sin 3
x
fx
x
=
+
và
( )
2
sin 2 cos3
2 tan
xx
gx
x
−
=
+
. Mệnh đề nào sau đây là đúng?
A.
( )
fx
lẻ và
(
)
gx
chẵn. B.
( )
fx
và
( )
gx
chẵn.
C.
( )
fx
chẵn,
( )
gx
lẻ. D.
( )
fx
và
( )
gx
lẻ.
Câu 93: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
3
1
.
sin
y
x
=
B.
sin .
4
yx
π
= +
C.
2 cos .
4
yx
π
= −
D.
sin 2 .yx
=
Câu 94: Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số
sinyx=
đối xứng qua gốc tọa độ
.O
B. Đồ thị hàm số
cosyx=
đối xứng qua trục
.Oy
C. Đồ thị hàm số
tan
yx=
đối xứng qua trục
.Oy
D. Đồ thị hàm số
tanyx
=
đối xứng qua gốc tọa độ
.O
Câu 95: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
( )
2cos sin 2 .
2
yx x
π
π
= ++ −
B.
sin sin .
44
yx x
ππ
= −+ +
C.
2 sin sin .
4
yx x
π
= +−
D.
sin cos .yxx= +
Câu 96: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
4
cos .
3
yx x
π
=+−
B.
2017
cos .
2
yx x
π
=+−
C.
2018
2015 cos sin .
y xx=++
D.
2017 2018
tan sin .y xx= +
Câu 97: Trong các hàm số sau sau. Hàm số nào có đồ thị nhận trục tung làm trục đối xứng?
A.
tanyx=
. B.
sinyx=
. C.
cot
yx=
. D.
cosyx=
.
Câu 98: Hàm số nào là hàm số chẵn trong các hàm số sau?
A.
sin .cosy xx=
. B.
tanyx=
. C.
cotyx=
. D.
2
sin .cosy xx=
.
Câu 99: Hàm số nào sau đây là hàm số chẵn?
A.
sin 4yx
=
. B.
cos5yx
=
. C.
tan 4
yx=
. D.
cot10yx=
.
Câu 100: Trong các hàm số sau hàm số nào là hàm số chẵn?
A.
2cosyx=
. B.
2 tanyx
=
. C.
2sinyx=
. D.
( )
2cos 1yx= −
.
Câu 101: Hàm số nào sau đây là hàm số chẵn trên
?
A.
.cos2yx x=
. B.
( )
2
1 .sinyx x= +
. C.
2
cos
1
x
y
x
=
+
. D.
2
tan
1
x
y
x
=
+
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 66
Sưu tầm và biên soạn
Câu 102: Trong các hàm số sau, hàm số nào là hàm số chẵn trên
?
A.
sin
2
yx
π
= −
. B.
tanyx=
. C.
sinyx=
. D.
sin
6
yx
π
= +
.
Câu 103: Trong các hàm số sau, hàm số nào có đồ thị nhận gốc tọa độ làm tâm đối xứng?
A.
sin
yx x
=
. B.
cosyx=
. C.
1 sin
yx
= −
. D.
sin cosy xx=
.
Câu 104: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin 2022 cos 2021yxx
= +
. B.
2021cos 2023siny xx= +
.
C.
cot 2021 2022sinyxx
= −
. D.
tan 2021 cot 2022yxx= +
.
Câu 105: Hàm số nào sau đâu có đồ thị nhận trục tung làm trục đối xứng?
A.
| sin |yx=
. B.
cotyx=
. C.
tan
yx=
. D.
sin
yx= −
.
Câu 106: Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A.
sin
yx
=
. B.
sin
yx x= +
. C.
cosyx x=
. D.
sin x
y
x
=
.
Câu 107: Hàm số nào sau đây là hàm số chẵn
A.
sin
yx=
. B.
tanyx=
. C.
( )
cot 2yx=
. D.
sin
yx=
.
Câu 108: Trong các hàm số:
2sinyx=
;
sin 3yx= +
;
5
sin 2019
2
yx
π
= −
, có bao nhiêu hàm lẻ?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 109: Cho hai hàm số
( )
sin 2fx x=
và
( )
cos3gx x=
. Chọn mệnh đề đúng
A.
f
là hàm số chẵn và
g
là hàm số lẻ. B.
f
và
g
là hai hàm số chẵn.
C.
f
và
g
là hai hàm số lẻ. D.
f
là hàm số lẻ và
g
là hàm số chẵn.
Câu 110: Trong các hàm số sau có bao nhiêu hàm số là hàm số chẵn trên tập xác định của nó?
tan 2yx=
,
2018
sinyx=
,
( )
3yc x
π
= +os
,
cotyx=
.
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 111: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
cot 4yx=
. B.
sin 1
cos
x
y
x
+
=
. C.
2
tanyx=
. D.
cotyx
=
.
Câu 112: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A.
sin .cos 2yxx=
. B.
3
sin .cos
2
y xx
π
= −
.
C.
2
tan
tan 1
x
y
x
=
+
. D.
3
cos .siny xx=
.
Câu 113: Cho hàm số
( )
sin 2fx x=
và
( )
2
tangx x=
. Chọn mệnh đề đúng?
A.
( )
fx
là hàm số chẵn,
( )
gx
là hàm số lẻ.
B.
( )
fx
là hàm số lẻ,
( )
gx
là hàm số chẵn.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 67
Sưu tầm và biên soạn
C.
( )
fx
là hàm số chẵn,
( )
gx
là hàm số chẵn.
D.
( )
fx
và
( )
gx
đều là hàm số lẻ.
Câu 114: Trong các hàm số:
2sinyx=
;
sin 3
yx= +
;
5
sin 2021
2
yx
π
= −
, có bao nhiêu hàm lẻ?
A.
3
. B.
0
. C.
1
. D.
2
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 4: HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
DẠNG 1. TẬP XÁC ĐỊNH
Câu 1: Tập xác định của hàm số
sinyx=
là
A.
[ ]
1;1−
. B.
( )
1;1−
. C.
(
)
0; +∞
. D.
.
Lời giải
Câu 2: Tập xác định của hàm số
1
sin
y
x
=
là
A.
{ }
D \0.=
B.
{ }
D \ 2, .kk
π
= ∈
C.
{
}
D \, .kk
π
= ∈
D.
{ }
D \ 0; .
π
=
Lời giải
Hàm số
1
sin
y
x
=
xác định khi và chỉ khi
sin 0x ≠
,.
xkk
π
⇔≠ ∈
Câu 3: Tập xác định của hàm số
tan 2yx=
là
A.
\
42
D kk
ππ
= +∈
∣
. B.
\
42
D kk
ππ
= +∈
∣
.
C.
\2
2
D kk
π
π
=+∈
∣
. D.
\
2
D kk
π
π
= +∈
∣
.
Lời giải
Điều kiện xác định của hàm số
cos 2 0 2 ( )
2 42
x xkxkk
π ππ
π
≠⇔ ≠+ ⇔≠+ ∈
.
Vậy tập xác định của hàm số
\
42
D kk
ππ
= +∈
∣
Câu 4: Tập xác định của hàm số
1 sin
cos
x
y
x
+
=
là
A.
{ }
\,D kk
π
= ∈
. B.
\,
2
D kk
π
π
= +∈
.
C.
{ }
\ 2,D kk
π
= ∈
. D.
\ 2,
2
D kk
π
π
= +∈
.
Lời giải
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
III

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
Điều kiện xác định
cos 0
2
x xk
π
π
≠⇔≠ +
.
Câu 5: Điều kiện xác định của hàm số
2021 cos
sin
x
y
x
−
=
là
A.
,
2
x kk
π
π
≠+ ∈
. B.
,xkk
π
≠∈
. C.
2,x kk
π
≠∈
. D.
,
2
k
xk
π
≠∈
.
Lời giải
Hàm số đã cho xác định khi:
sin 0
x ≠
xk
π
⇔≠
,
k ∈
.
Câu 6: Tập xác định của hàm số
tan
yx
=
là
A.
{ }
D \ 2, .kk
π
= ∈
B.
D \ 2, .
2
kk
π
π
= +∈
C.
D\ , .
2
kk
π
π
= +∈
D.
{
}
D \, .kk
π
= ∈
Lời giải
Hàm số
tanyx
=
xác định khi và chỉ khi
cos 0x ≠
,.
2
x kk
π
π
⇔≠ + ∈
Vậy TXĐ là:
D\ , .
2
kk
π
π
= +∈
Câu 7: Tập xác định của hàm số
2
1
cos
x
y
x
+
=
là
A.
D =
. B.
2
\,D kk
π
π
= +∈
.
C.
{ }
\,D kk
π
= ∈
. D.
2
\,
k
Dk
π
= ∈
.
Lời giải
Điều kiện:
0
2
cos ,x x kk
π
π
≠⇔≠ + ∈
.
Vậy tập xác định của hàm số là
2
\,
D kk
π
π
= +∈
.
Câu 8: Tập xác định
D
của hàm số
5sin
cos 3
x
y
x
=
−
là
A.
( )
3;D = +∞
. B.
{ }
\3= D
. C.
(
)
;3= −∞
D
. D.
D =
.
Lời giải
Ta có
1 cos 1,xx−≤ ≤ ∀∈
. Do đó
cos 3 0,xx− ≠ ∀∈
.
Vậy tập xác định của hàm số là
D =
.
Câu 9: Tập xác định của hàm số
1 sin
cos
x
y
x
là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
A.
{
}
\;D xkk
π
= ≠∈
. B.
{ }
\ 2;D xk k
π
=≠∈
.
C.
\;
2
D x kk
π
π
= ≠+ ∈
. D.
\ 2;
2
D x kk
π
π
= ≠− + ∈
.
Lời giải
Hàm số xác định khi
cos 0
2
x xk
,
k
.
Câu 10: Tập xác định của hàm số
tan 2
3
yx
là
A.
\;
62
k
Dx k
ππ
= ≠+ ∈
. B.
5
\;
12
D x kk
π
π
= ≠+ ∈
.
C.
\;
2
D x kk
π
π
= ≠+ ∈
. D.
5
\;
12 2
k
Dx k
.
Lời giải
Hàm số xác định khi
5
cos 2 0 2
3 3 2 12 2
k
x x kx
,
k
.
Câu 11: Tập xác định của hàm số
cot
yx=
là
A.
{ }
\ kk
π
∈
. B.
\2
2
kk
π
π
+∈
.
C.
\
2
kk
π
π
+∈
. D.
{ }
\2kk
π
∈
.
Lời giải
Hàm số
cotyx=
xác định khi và chỉ khi:
sin 0x xk
π
≠⇔≠
với
k ∈
. Do đó tập xác định của
hàm số
cotyx=
là
{
}
\D kk
π
= ∈
.
Câu 12: Tập xác định của hàm số
1 cos
sin
x
y
x
−
=
là
A.
{ }
\|D kk= ∈
π
. B.
\|
2
D kk
= +∈
π
π
.
C.
{ }
\ 2|D kk= ∈
π
. D.
\ 2|
2
D kk
=+∈
π
π
.
Lời giải
Điều kiện
sin 0 ,x xk k≠⇔≠ ∈
π
.
Tập xác định
{ }
\|D kk= ∈
π
.
Câu 13: Tập xác định của hàm số
2 3tanyx
là
A.
\
3
Dk
. B.
\
6
Dk
. C.
\
2
Dk
. D.
\
4
Dk
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Chọn C
ĐKXĐ
cos 0
2
x xk
. Do đó tập xác định của hàm số là
\
2
Dk
.
Câu 14: Tập xác định của hàm số
1
2sin 1
y
x
=
−
là
A.
\ 2,
6
D kk
π
π
= ±+ ∈
. B.
\ 2,
3
D kk
π
π
= ±+ ∈
.
C.
5
\ 2; 2,
66
D k kk
ππ
ππ
= + +∈
. D.
2
\ 2; 2,
33
D k kk
ππ
ππ
= + +∈
.
Lời giải
Chọn C
Hàm số xác định khi
2
1
6
sin ,
5
2
2
6
xk
xk
xk
π
π
π
π
≠+
≠⇔ ∈
≠+
.
Vậy
5
\ 2; 2,
66
D k kk
ππ
ππ
= + +∈
.
Câu 15: Tìm tập xác định
D
của hàm số
1 sin
1 cos
x
y
x
−
=
+
.
A.
\ 2; 2,
22
D k kk
= −+ + ∈
ππ
ππ
. B.
{
}
\,D kk=−∈
π
.
C.
{ }
\ 2,D kk=+∈
ππ
. D.
\ 2,
2
D kk
= +∈
π
π
.
Lời giải
Chọn C
Điều kiện xác định của hàm số:
cos 1 2x xk≠− ⇔ ≠π+ π
.
Câu 16: Tập xác định của hàm số
1
sin 2 1
y
x
=
+
là
A.
\,
2
D kk
π
π
= −+ ∈
. B.
\ 2,
2
D kk
π
π
= −+ ∈
.
C.
\,
4
D kk
π
π
= −+ ∈
. D.
\ 2,
4
D kk
π
π
= −+ ∈
.
Lời giải
ĐKXĐ của hàm số là
sin 2 1 2 2 ,
24
x xkxkk
ππ
ππ
≠− ⇔ ≠− + ⇔ ≠− + ∈
.
Vậy TXĐ:
\,
4
D kk
π
π
= −+ ∈
.
Câu 17: Tập xác định của hàm số
sin
2 2cos
x
y
x
=
−
là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
A.
D =
. B.
\
2
D kk
π
= ∈
.
C.
\
2
D kk
π
π
= +∈
. D.
{ }
\2D kk
π
= ∈
.
Lời giải
Hàm số xác định
⇔
2 2cos 0 cos 1 2 ,
x x xk k
π
− ≠ ⇔ ≠⇔ ≠ ∈
.
Vậy tập xác định của hàm số là
{
}
\2
D kk
π
= ∈
.
Câu 18: Tập xác định của hàm số
2021
1 cos
y
x
=
−
là
A.
\, .
2
k
Dk
π
= ∈
B.
{ }
\ 2, .D kk
π
= ∈
C.
\ ,.
2
D kk
π
π
= +∈
D.
{ }
\, .D kk
π
= ∈
Lời giải
Hàm số xác định khi
cos 1 2x xk
π
≠⇔ ≠
Câu 19: Tập xác định của hàm số
2sin 1
1 cos
x
y
x
là
A.
{ }
\ 2;D xk k
π
=≠∈
. B.
{
}
\ 2;D x kk
ππ
= ≠+ ∈
.
C.
\;
2
D x kk
π
π
= ≠+ ∈
D.
\ 2;
2
D x kk
π
π
= ≠+ ∈
.
Lời giải
Hàm số xác định khi
1 cos 0 cos 1 2
x x xk
,
k
.
Câu 20: Tập xác định của hàm số
1
sin cos
y
xx
là
A.
{ }
\;D xkk
π
= ≠∈
. B.
{ }
\ 2;D xk k
π
=≠∈
C.
\;
2
D x kk
π
π
= ≠+ ∈
. D.
\;
4
D x kk
.
Lời giải
Hàm số xác định khi
sin cos 0 sin 0
44
xx x x k
,
k
.
Câu 21: Tập xác định của hàm số
2020
tan( 2019 )
y
x
π
=
+
là
A.
\,
2
D kk
π
= ∈
. B.
{ }
\,D kk
π
= ∈
.
C.
\,
2
D kk
π
π
= +∈
. D.
{ }
\ 2,
D kk
π
= ∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
Chọn A
Ta có
tan( 2019 ) tan
xx
π
+=
Hàm số xác định khi và chỉ khi
tan 0 ,
2
x xk k
π
≠⇔≠ ∈
.
Câu 22: Tìm tập xác định của hàm số
s
1 2cos
=
−
y
x
inx
.
A.
\2
3
π
π
±+ ∈
kk
. B.
1
\
2
.
C.
. D.
\2
3
π
π
+∈
kk
.
Lời giải
Chọn A
Ta có
1
1 2cos 0 cos 2
23
π
π
− ≠ ⇔ ≠ ⇔ ≠± +x xx k
.
Câu 23: Tập xác định của hàm số
3 sin
cos 1
x
y
x
+
=
−
là
A.
{
}
\,D kk
π
= ∈
. B.
\,
2
D kk
π
π
= +∈
.
C.
\ 2,
2
D kk
π
π
= +∈
. D.
{ }
\ 2,
D kk
π
= ∈
.
Lời giải
Chọn D
Điều kiện
cos 1 0 cos 1 2 ,
x x xk k
π
−≠ ⇔ ≠⇔ ≠ ∈
.
Vậy
{
}
\ 2,
D kk
π
= ∈
.
Câu 24: Tập xác định của hàm số
2sin 1
cos
x
y
x
−
=
là
A.
\,
2
D kk
π
π
= +∈
. B.
{ }
\,
D kk
π
= ∈
.
C.
\,
2
D kk
π
= ∈
.
D.
{ }
\ 2,D kk
π
= ∈
.
Lời giải
Chọn A
Hàm số
2sin 1
cos
x
y
x
−
=
xác định khi
cos 0 ,
2
x x kk
π
π
≠⇔≠ + ∈
.
Tập xác định của hàm số là
\;
2
D kk
π
π
= +∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
Câu 25: Tập xác định của hàm số
tan
cos 1
x
y
x
=
+
là
A.
{ }
\ 2,kk
ππ
+∈
. B.
\ ;2,
2
kk k
π
ππ
+∈
.
C.
\ ; 2,
2
k kk
π
ππ π
++ ∈
. D.
\,
2
k
k
π
∈
.
Lời giải
Chọn C
Điều kiện xác định:
( )
cos 0
,
2
cos 1
2
x
xk
k
x
xk
π
π
ππ
≠
≠+
⇔∈
≠−
≠+
.
Câu 26: Tìm tập xác định
D
của hàm số
tan
4
yx
π
= −
.
A.
,
2
D x x kk
π
π
= ∈ ≠+ ∈
. B.
,
4
D x x kk
π
π
= ∈ ≠+ ∈
.
C.
3
,
2
D x x kk
π
π
=∈ ≠+ ∈
. D.
3
,
4
D x x kk
π
π
=∈ ≠+ ∈
.
Lời giải
Chọn D
Hàm số
tan
4
yx
π
= −
xác định
cos 0
4
x
π
⇔ −≠
3
42 4
x kx k
ππ π
ππ
⇔− ≠ + ⇔≠ +
( )
k ∈
.
Câu 27: Tìm tập xác định của hàm số
2021cot 2 2022
yx= +
.
A.
\
2
Dk
π
π
= +
. B.
\
2
Dk
π
=
. C.
\
42
Dk
ππ
= +
. D.
D =
.
Lời giải
Chọn B
Điều kiện xác định
sin 2 0 2 ,
2
k
x xk x k
π
π
≠⇔ ≠ ⇔≠ ∈
.
Tập xác định
\;
2
D kk
π
= ∈
.
Câu 28: Tập xác định của hàm số
cotyx=
là
A.
{ }
\Dk
π
=
. B.
{ }
\,D kk
π
= ∈
.
C.
\,
2
D kk
π
π
= +∈
. D.
D =
.
Lời giải
Chọn B

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Ta có
cos
cot
sin
x
x
x
=
.
Điều kiện xác định của hàm số là:
sin 0 ,x xkk
π
≠⇔≠ ∈
.
Vậy tập xác định của hàm số
cotyx=
là:
{ }
\,D kk
π
= ∈
.
Câu 29: Tập xác định của hàm số:
tan 2
6
yx
π
= +
?
A.
\,
2
kk
π
π
+∈
. B.
\,
62
k
k
ππ
−
+∈
.
C.
\,
6
kk
π
π
+∈
. D.
\,
62
k
k
ππ
+∈
.
Lời giải
Chọn D
Điều kiện:
cos 2 0 2 ,
6 62 6 2
k
x x kx k
π ππ π π
π
+ ≠⇔ +≠+ ⇔≠+ ∈
.
Do đó tập xác định
\,
62
k
Dk
ππ
= +∈
.
Câu 30: Tập xác định của hàm số
1
sin
y
x
=
là:
A.
{ }
,\D kk
π
= ∈
. B.
{
}
2,\
D kk
π
= ∈
.
C.
{ }
\ 0;D
π
=
. D.
{ }
0\D =
.
Lời giải
Chọn A
Hàm số đã cho xác định khi và chỉ khi
sin 0
x xk
π
≠⇔≠
( )
k ∈
.
Vậy tập xác định của hàm số là:
{ }
,\D kk
π
= ∈
.
Câu 31: Điều kiện xác định của hàm số
tan 2yx=
là
A.
4
xk
π
π
≠− +
. B.
2
xk
π
π
≠+
. C.
42
k
x
ππ
≠+
. D.
4
xk
π
π
≠+
Lời giải
Chọn C
Điều kiện để hàm số
tan 2yx=
xác định là
cos 2 0 2
2 42
k
x x kx
π ππ
π
≠⇔ ≠+ ⇔≠+
,
k ∈
.
Câu 32: Tập xác định của hàm số
2cos 1
sin 2
−
=
x
y
x
là:
A.
\,
2
π
= ∈
k
Dk
. B.
\ 2; ,
32
ππ
π
= ±+ ∈
k
D kk
.
C.
\ 2,
3
π
π
= +∈
D kk
. D.
{ }
\,
π
= ∈D kk
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
Lời giải
Chọn A
Hàm số xác định
sin 2 0 ,
2
π
⇔ ≠⇔≠ ∈
k
x xk
. Tập xác định
\,
2
π
= ∈
k
Dk
.
Câu 33: Tìm tập xác định của hàm số
tanyx
=
.
A.
\|
2
kk
π
π
+∈
. B.
{ }
\|kk
π
∈
.
C.
\ 2|
2
kk
π
π
+∈
. D.
{ }
\ 2|kk
π
∈
.
Lời giải
Chọn A
Hàm số xác định khi và chỉ khi
cos 0
2
x xk
π
π
≠⇔≠ +
,
( )
k ∈
.
Câu 34: Tập xác định của hàm số
1
1 cos
y
x
=
−
là
A.
{ }
\ 2,D kk
π
= ∈
. B.
{ }
\ 2,D kk
ππ
=+∈
.
C.
\ 2,
2
D kk
π
π
= +∈
. D.
\ 2,
2
D kk
π
π
= −+ ∈
.
Lời giải
Chọn A
Hàm số xác định
1 cos 0 cos 1 cos 1 2 .x x x xk
π
⇔− > ⇔ <⇔ ≠⇔ ≠
Tìm tập xác định của hàm số
sin 2
2cos 3
x
y
x
=
+
A.
\2
6
Dk
π
π
= ±+
. B.
\
6
Dk
π
π
= ±+
.
C.
5
\2
6
Dk
π
π
= ±+
. D.
5
\
6
Dk
π
π
= ±+
.
Lời giải
Hàm số có nghĩa khi :
35
2cos 3 0 cos 2
26
x x xk
π
π
+ ≠ ⇔ ≠− ⇔ ≠± +
Vậy tập xác định của hàm số là :
5
\2
6
Dk
π
π
= ±+
.
Câu 35: Tập xác định của hàm số
tan
1 tan
x
y
x
là
A.
\ 2; 2,
24
ππ
ππ
D k kk
= + +∈
. B.
\ 2; 2,
24
ππ
ππ
D k kk
= −+ −+ ∈
.
C.
\ ;,
24
ππ
ππ
D k kk
= + +∈
. D.
\ ; 2,
24
ππ
ππ
D k kk
= ++ ∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
Hàm số xác định khi
cos 0
2
1 tan 0
4
xk
x
x
xk
,
k
.
Vậy tập xác định của hàm số là
\ ;,
24
ππ
ππ
D k kk
= + +∈
.
Câu 36: Tập xác định của hàm số
tan coty xx= +
là
A.
\;
2
kk
π
π
+∈
. B.
\;
2
kk
π
∈
. C.
{ }
\;kk
π
∈
. D.
.
Lời giải
Điều kiện
sin 0
sin 2 0
cos 0
x
x
x
≠
⇔≠
≠
2,
2
xk xk k
π
π
⇔ ≠ ⇔≠ ∈
.
Câu 37: Tập xác định của hàm số
cot
2
x
y =
là
A.
{ }
\,D kk
π
= ∈
. B.
{ }
\ 2,D kk
ππ
=+∈
.
C.
\,
2
k
Dk
π
= ∈
. D.
{ }
\ 2,D kk
π
= ∈
.
Lời giải
Hàm số xác định khi:
sin 0 2 ,
22
xx
k xk k
ππ
≠⇔ ≠ ⇔≠ ∈
.
Câu 38: Tìm tập xác định
D
của hàm số
−
= −
2cos 1
3tan
sin
x
yx
x
.
A.
\; ,
2
D k kk
π
= π +π ∈
. B.
{ }
\,D kk
= π∈
.
C.
\,
2
D kk
π
= +π ∈
. D.
\ ; 2,
2
D k kk
π
= π + π∈
.
Lời giải
Điều kiện:
( )
≠
≠
⇔∈
≠
≠+
π
π
π
sin 0
,
cos 0
2
xk
x
k
x
xk
.
Tập xác định:
\; ,
2
D k kk
π
= π +π ∈
.
Câu 39: Tập xác định của hàm số
2 sin
tan
−
=
x
y
x
.
A.
\,
2
π
π
= +∈
D kk
. B.
{ }
\,
π
= ∈
DRkk
.
C.
\,
2
π
= ∈
k
Dk
. D.
{ }
\ 2,
π
= ∈D kk
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Lời giải
ĐK:
( )
2 sin 0 luon dung
cos 0
cos 0
sin 0
tan 0
−≥
≠
≠⇔
≠
≠
x
x
x
x
x
(
)
sin 2 0 2
2
π
π
⇔ ≠⇔ ≠ ⇔≠ ∈
k
x xk x k
.
Tập xác định của hàm số:
\,
2
π
= ∈
k
Dk
.
Câu 40: Tìm tập xác định của hàm số
tan 3
6
π
= −
yx
.
A.
\,
33
ππ
= +∈
k
Dk
. B.
\,
93
ππ
= +∈
k
Dk
.
C.
4
\,
93
ππ
= +∈
k
Dk
. D.
2
\,
93
ππ
= +∈
k
Dk
.
Lời giải
Điều kiện:
22
cos 3 0 3 3 ,
6 62 3 9 3
π ππ π π π
ππ
−≠⇔−≠+⇔≠ +⇔≠ + ∈
k
x x k x kx k
.
Vậy tập xác định của hàm số trên là
2
\,
93
ππ
= +∈
k
Dk
.
Câu 41: Hàm số
1 3sin
cos 2
x
y
x
−
=
xác định khi
A.
,
42
x kk
ππ
≠+ ∈
. B.
,
2
x kk
π
π
≠+ ∈
. C.
,
4
x kk
π
π
≠+ ∈
. D.
2,xk k
π
≠∈
.
Lời giải
Hàm số xác định khi
cos 2 0 2 ,
2 42
x xkxkk
π ππ
π
≠⇔ ≠+ ⇔≠+ ∈
.
Câu 42: Tập xác định của hàm số
1
sin 2 1
y
x
=
+
là:
A.
\ 2|
2
D kk
π
π
= −+ ∈
. B.
\ 2|
4
D kk
π
π
= −+ ∈
.
C.
\|
4
D kk
π
π
= −+ ∈
. D.
D =
.
Lời giải
Hàm số
1
sin 2 1
y
x
=
+
xác định khi và chỉ khi
sin 2 1 0 sin 2 1 sin 2 1x xx+>⇔>−⇔≠−
.
Do đó
( ) ( )
22
24
xkk xkk
ππ
ππ
≠− + ∈ ⇔ ≠− + ∈
.
Câu 43: Tập xác định của hàm số
2
tan 2022
sin 1
x
y
x
+
=
+

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
A.
\ 2,
2
kk
+∈
π
π
. B.
\,
2
kk
+∈
π
π
.
C.
. D.
{ }
\,kk∈
π
.
Lời giải
Hàm số xác định
cos 0x⇔≠
,
2
x kkZ
π
π
⇔≠ + ∈
Câu 44:
Tìm tập xác định
D
của hàm số
1
.
1 sin
y
x
=
−
A.
{ }
D \, .kk
π
= ∈
B.
D\ , .
2
kk
π
π
= +∈
C.
D \ 2, .
2
kk
π
π
= +∈
D.
D.= ∅
Lời giải
Chọn C
Hàm số xác định khi và chỉ khi
1 sin 0 sin 1.xx− >⇔ <
( )
*
Mà
1 sin 1x−≤ ≤
nên
( )
* sin 1 2 , .
2
x x kk
π
π
⇔ ≠⇔ ≠ + ∈
Vậy tập xác định
D \ 2, .
2
kk
π
π
= +∈
Câu 45: Tìm tập xác định
D
của hàm số
2
5 2cot sin cot .
2
y xx x
π
=+ −+ +
A.
D\ , .
2
k
k
π
= ∈
B.
D\ , .
2
kk
π
π
= −+ ∈
C.
D.=
D.
{ }
D \, .kk
π
= ∈
Lời giải
Chọn A
Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời
2
5 2cot sin 0xx+ −≥
,
cot
2
x
π
+
xác định và
cot x
xác định.
Ta có
2
2
2cot 0
5 2cot sin 0, .
1 sin 1 5 sin 0
x
xx x
xx
≥
⇒ + − ≥ ∀∈
−≤ ≤⇒ − ≥
cot
2
x
π
+
xác định
sin 0 , .
22 2
x xk x k k
ππ π
ππ
⇔ + ≠ ⇔ + ≠ ⇔ ≠− + ∈
cot x
xác định
sin 0 , .x xk k
π
⇔ ≠⇔≠ ∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
Do đó hàm số xác định
,.
2
2
xk
k
xk
xk
π
π
π
π
≠− +
⇔ ⇔≠ ∈
≠
Vậy tập xác định
D\ , .
2
k
k
π
= ∈
Câu 46: Tìm tập xác định
D
của hàm số
tan cos .
2
yx
π
=
A.
D\ ,
2
kk
π
π
= +∈
. B.
D \ 2,
2
kk
π
π
= +∈
.
C.
D =
. D.
{ }
D \,kk
π
= ∈
.
Lời giải
Chọn D
Hàm số xác định khi và chỉ khi
.cos cos 1 2
22
xk xk
ππ
π
≠ + ⇔ ≠+
.
( )
*
Do
k ∈
nên
( )
* cos 1 sin 0 , .
x x xkk
π
⇔ ≠± ⇔ ≠ ⇔ ≠ ∈
Vậy tập xác định
{ }
D \, .kk
π
= ∈
Câu 47: Tập xác định của hàm số
1
tan
y
x
=
là
A.
,
2
Dkk
π
= ∈
. B.
\,
2
D kk
π
= ∈
.
C.
{ }
\,D kk
π
= ∈
. D.
{ }
,
D kk
π
= ∈
.
Lời giải
Chọn B
Điều kiện xác định:
cos 0
tan 0
x
x
≠
≠
cos 0
sin 0
x
x
≠
⇔
≠
sin 2 0x
⇔≠
2xk
π
⇔≠
,
2
xk k
π
⇔≠ ∈
.
Vậy tập xác định của hàm số đã cho là
\,
2
D kk
π
= ∈
.
Câu 48: Tìm tập xác định của hàm số
3sin
2cos 1
x
y
x
=
+
.
A.
4
\ 2, 2
33
D k kk
= −+ + ∈
ππ
ππ
. B.
2
\2
3
D kk
= ±+ ∈
π
π
.
C.
5
\2
6
D kk
= ±+ ∈
π
π
. D.
\2
3
D kk
= ±+ ∈
π
π
.
Lời giải
Chọn B

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
Điều kiện:
2cos 1 0
x +≠
⇔
1
cos
2
x ≠−
⇔
2
2
3
π
xk
π≠± +
.
Tập xác định:
2
\2
3
D kk
= ±+ ∈
π
π
.
Câu 49: Hàm số
2
sin
1 2sin
x
y
x
=
−
có tập xác định là
A.
\
4
D kk
π
π
= +∈
. B.
\
2
D kk
π
π
= +∈
.
C.
\
42
k
Dk
ππ
= +∈
. D.
\2
4
D kk
π
π
= ±+ ∈
.
Lời giải
Chọn C
Điều kiện:
2
1 2sin 0−≠x
2
sin
2
2
sin
2
≠
⇔
≠−
x
x
(
)
42
ππ
⇔≠ + ∈
x kk
.
Vậy tập xác định là
\
42
k
Dk
ππ
= +∈
.
Câu 50: Hàm số
1
sin 2 cos 2
y
xx
=
có tập xác định là
A.
\|
42
k
Dk
ππ
= +∈
. B.
\|
4
k
Dk
π
= ∈
.
C.
{ }
\|D kk
π
= ∈
. D.
\|
2
k
Dk
π
= ∈
.
Lời giải
Chọn B
Điều kiện xác đinh của hàm số là:
sin 2 cos 2 0
xx
≠
sin 4 0x⇔≠
4xk
π
⇔≠
4
k
x
π
⇔≠
( )
k ∈
.
Vậy tập xác định
\|
4
k
Dk
π
= ∈
.
Câu 51: Hàm số
sin 2
cot 3
x
y
x
=
−
có tập xác định là
A.
\|
6
D kk
π
π
= +∈
. B.
{ }
\|D kk
π
= ∈
.
C.
\; |
6
D k kk
π
ππ
= +∈
. D.
\ ;|
26
D k kk
ππ
ππ
= ++∈
.
Lời giải
Chọn C

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
Điều kiện xác định của hàm số là:
( )
cot 3
6
sin 0
xk
x
k
x
xk
π
π
π
≠+
≠
⇔∈
≠
≠
.
Câu 52: Tập xác định của hàm số
2cot 5
cos 1
x
y
x
+
=
−
là
A.
\
2
k
π
π
+
. B.
{
}
\2k
π
. C.
{ }
\ k
π
. D.
\2
2
k
π
π
+
.
Lời giải
Chọn C
Hàm số xác định
cos 1 0
sin 0
x
x
−≠
⇔
≠
sin 0x⇔≠
xk
π
⇔≠
.
Vậy tập xác định là
{ }
\Dk
π
=
.
Câu 53: Tìm tập xác định của hàm số
1
sin 2 1
y
x
=
−
.
A.
\,
4
D kk
π
π
= +∈
. B.
\,
2
D kk
π
π
= +∈
.
C.
{ }
\ 2,D kk
π
= ∈
. D.
{ }
\,D kk
π
= ∈
.
Lời giải
Chọn A
Ta có:
sin 2 1 0 sin 2 1 2 2 , .
24
x x xkxkk
ππ
ππ
−≠⇔ ≠⇔ ≠+ ⇔≠+ ∈
Câu 54: Hàm số
tan
1 tan
x
y
x
=
+
không xác định tại các điểm
A. chỉ
2
xk
π
π
= +
( )
k ∈
. B. chỉ
4
xk
π
π
= +
( )
k ∈
.
C. chỉ
4
xk
π
π
=−+
( )
k ∈
. D.
4
xk
π
π
=−+
và
2
xk
π
π
= +
( )
k ∈
.
Lời giải
Chọn D
Hàm số không xác định khi
( )
1 tan 0
4
cos 0
2
xk
x
k
x
xk
π
π
π
π
=−+
+=
⇔∈
=
= +
.
Câu 55: Tập xác định của hàm số
2020
1
y
tanx
=
−
A.
\,
4
kk
π
π
+∈
. B.
\,
2
kk
π
π
+∈
.
C.
\ 2,
4
kk
π
π
+∈
. D.
\ ;,
24
k kk
ππ
ππ
+ +∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
Chọn D
Điều kiện
( )
cos 0
2
1
4
xk
x
k
tanx
xk
π
π
π
π
≠+
≠
⇔∈
≠
≠+
.
Vậy tập xác định của hàm số là:
\ ;,
24
D k kk
ππ
ππ
= + +∈
.
Câu 56: Tìm tập xác định của hàm số
cot 2 tan
2
yx x
π
=+−
.
A.
{ }
\;D kkZ
π
= ∈
. B.
\;
2
D k kZ
π
π
= +∈
.
C.
\;
3
k
D kZ
π
= ∈
. D.
\;
2
k
D kZ
π
= ∈
.
Lời giải
Chọn D
Điều kiện xác định
sin 2 0
2.sin .cos 0
2.sin .cos 0
cos 0
sin 0
2
x
xx
xx
x
x
π
≠
≠
⇔ ⇔≠
−≠
≠
sin 2 0 ;
2
k
x x kZ
π
⇔ ≠⇔ ≠ ∈
Tập xác định
\;
2
k
D kZ
π
= ∈
.
Câu 57: Tìm tập xác định
D
của hàm số
tan 1
cos
sin 3
x
yx
x
π
−
= ++
.
A.
{ }
\,D kk
π
= ∈
. B.
\,
2
k
Dk
π
= ∈
.
C.
\,
2
D kk
π
π
= +∈
. D.
D =
.
Lời giải
Chọn B
Hàm số
tan 1
cos
sin 3
x
yx
x
π
−
= ++
xác định khi:
sin 0
sin 2 0 2
cos 0
2
x
k
x xk x
x
π
π
≠
⇔ ≠⇔ ≠ ⇔≠
≠
()k
∈
.
Câu 58: Tập xác định của hàm số
3cot
2sin 4
x
y
x
=
−
là
A.
{ }
\ arcsin 2 2 , arcsin 2 2 ,R k k kZ
ππ π
+ − +∈
B.
.R
C.
{ }
\ arcsin 2 2 ,R k kZ
π
± +∈
. D.
{ }
\, .RkkZ
π
∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
Lời giải.
Chọn D
Ta có
2sinx 4 0, xR
− ≠ ∀∈
,
Nên hàm số xác định khi
cot x
xác định
⇔
sinx 0 ,xkkZ
π
≠⇔≠ ∈
Vậy tập xác định của hàm số là
{ }
\,RkkZ
π
∈
.
Câu 59: Tập xác định của hàm số
2020
tan 1
y
x
=
−
là
A.
\
4
k
π
π
+
. B.
\
2
k
π
π
+
.
C.
\2
4
k
π
π
+
. D.
\;
24
kk
ππ
ππ
++
.
Lời giải
Điều kiện xác định
2
2
tan 1 0
4
xk
xk
x
xk
π
π
π
π
π
π
≠+
≠+
⇔
−≠
≠+
.
Câu 60: Tìm tập xác định của hàm số
1 cos coty xx=−+
?
A.
{ }
\;π∈kk
. B.
(
]
;1−∞
. C.
\;
2
π
+π ∈
kk
. D.
[ ]
{ }
1;1 \ 0−
.
Lời giải
ĐKXĐ:
( )
1 cos 0
;
sin 0
xx
x kk
x
− ≥∀
⇔ ≠π ∈
≠
Lời giải
Hàm số xác định
1 cos 0 cos 1
,
sin 0
xx
xk k
x xk
π
π
−≥ ≤
⇔ ⇔ ⇔≠ ∈
≠≠
.
Tập xác định của hàm số
{
}
\,D kk
π
= ∈
.
Câu 61: Tập xác định
D
của hàm số
2sin 3
tan 1
x
y
x
+
=
−
.
A.
\,
2
D kk
π
π
= +∈
. B.
{ }
\1D =
.
C.
\,
4
D kk
π
π
= +∈
. D.
\ ;,
24
D k kk
ππ
ππ
= + +∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
ĐK:
cos 0
tan 1
x
x
≠
≠
(
)
2
,
4
xk
k
xk
π
π
π
π
≠+
⇔∈
≠+
. Vậy TXĐ:
\ ;,
24
D k kk
ππ
ππ
= + +∈
.
Câu 62: Tìm tập xác định
D
của hàm số
1
1 sin
y
x
=
+
.
A.
{ }
\ 2,D kk
π
= ∈
. B.
{ }
\ 2,
D kk
ππ
=+∈
.
C.
\ 2,
2
D kk
π
π
= +∈
. D.
\ 2,
2
D kk
π
π
−
= +∈
.
Lời giải
Điều kiện xác định của hàm số là
10sin x
Mà
10sin ,xx
Nên
10 1 2
2
sin sin ,x x x kk
.
Câu 63: Hàm số
11
tan cot
sin cos
y xx
xx
=+++
không xác định trong khoảng nào trong các khoảng sau
đây?
A.
2; 2
2
kk
π
ππ
+
với
k ∈
. B.
3
2; 2
2
kk
π
ππ π
++
với
k ∈
.
C.
2; 2
2
kk
π
ππ π
++
với
k ∈
. D.
( )
2 ;2 2
kk
ππππ
++
với
k
∈
.
Lời giải
Điều kiện xác định của hàm số là
sin 0
,
cos 0
2
xk
x
k
x
xk
π
π
π
≠
≠
⇔∈
≠
≠+
Khi đó, hàm số không xác định tại
3
2
2
xk
π
π
= +
với
k ∈
.
Suy ra, hàm số không xác định trên khoảng
( )
2 ;2 2kk
ππππ
++
với
k ∈
.
Câu 64: Tập xác định của hàm số
tan 3yx=
là.
A.
\ ,k R
63
DR k
ππ
= +∈
B.
\ ,k R
2
DR k
π
π
= +∈
C.
{ }
\ ,k RDR k
ππ
= +∈
D.
2
\ ,k R
3
DR k
π
= ∈
Lời giải
Điều kiện
cos3 0 3
2 63
k
x x kx
π ππ
π
≠⇔ ≠+ ⇔≠+
Tập xác định:
\ ,k R
63
DR k
ππ
= +∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
Câu 65: Tìm
m
để hàm số
5sin 4 6cos 4 2 1y x xm= − +−
xác định với mọi
x
A.
61 1
2
+
≥m
. B.
1≥m
. C.
61 1
2
−
≥m
. D.
61 1
2
+
<m
.
Lời giải
Hàm số xác định với mọi
x
5sin 4 6cos 4 1 2 ⇔ − ≥− ∀x x mx
.
Ta có
( )
2
2
5sin 4 6cos4 5 6 61− ≤ +− =xx
, do đó
( )
min 5sin 4 6cos 4 61−=−xx
.
61 1 2⇒− ≥ − m
61 1
2
+
⇔≥m
.
Câu 66: Có bao nhiêu số nguyên
m
sao cho hàm số
sin 3y mx= +
có tập xác định là
?
A.
7
. B.
6
. C.
3
. D.
4
.
Lời giải
Ta có
s
,sin . inm xm xmx≤= ∀∈
nên
3 sin 3 3,m mx
x
m− +≤ + +
∀≤
∈
.
Do đó, hàm số
sin 3y mx= +
có tập xác định là
30 3 3 3
mm m⇔− + ≥ ⇔ ≤ ⇔− ≤ ≤
.
Mà
m ∈
nên
{ }
3; 2; 1;0;1;2;3
m ∈− − −
.
Vậy ta có
7
giá trị nguyên của
m
thỏa mãn bài toán.
Câu 67: Hàm số
3 sin 2
cos 1
x
y
mx
+
=
+
có tập xác định là
khi
A.
0m >
. B.
01m≤<
. C.
11m−< <
. D.
1m ≠−
.
Lời giải
Hàm số
3 sin 2
cos 1
x
y
mx
+
=
+
có tập xác định là
cos 1 0mx⇔ +>
+
0 10 0m xm
= ⇒ > ∀∈ ⇒ =
thỏa ycbt.
+
0m >
Ta có
1 cos 1x−≤ ≤⇒
cos 1 cos 1 1mmxm m mx m− ≤ ≤ ⇒− +< +< +
⇒
GTNN của
cos 1mx
+
là
1m−+
10 0 1mm⇒− + > ⇒ < <
.
+
0m <
Ta có
1 cos 1x−≤ ≤⇒
cos 1 cos 1 1mmxm m mx m− ≥ ≥ ⇒− +≥ +≥ +
⇒
GTNN của
cos 1mx+
là
1m +
10 1 0mm⇒ + > ⇒− < <
.
Suy ra:
11m−< <
.
Câu 68: Cho hàm số
44
sin cos sin .cosy x xm x x= +−
. Tìm
m
để hàm số xác định với mọi
x
.
A.
11
;
22
m
∈−
. B.
( )
1;1m ∈−
. C.
(
]
;1m ∈ −∞
. D.
[ ]
1;1m ∈−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 20
Sưu tầm và biên soạn
Lời giải
2 22 2 2
(sin cos ) 2sin .cos sin .cos
y x x x xm x x
= +− −
22 2
11
2sin .cos sin .cos 1 sin 2 sin 2 1
22
x xm x x x m x=− − +=− − +
Đặt
sin 2 , 1 1
t xt
= −≤≤
ta có hàm số
2
11
1
22
y t mt=−− +
Hàm số
44
sin cos sin .cosy x xm x x= +−
xác định với mọi
x
khi và chỉ khi hàm số
2
11
1
22
y t mt=−− +
xác định với mọi
11
t−≤≤
2
11
10 :1 1
22
t mt t t⇔− − + ≥ ∀ − ≤ ≤
2
20 :1 1t mt t t⇔− − + ≥ ∀ − ≤ ≤
Ta có
2
8 0, .mm∆= + > ∀
Bảng xét dấu
( )
2
2f t t mt=−− +
Từ BXD, ta suy ra
2
12
2 0 :1 1 11t mt t t t t− − + ≥∀ −≤≤⇔ ≤−<≤
2
2
22
8
1
8 2 (1)
2
8 8 2 (2)
1
2
mm
mm
mm m m
−− +
≤−
+≥−
⇔⇔
−+ + +≥ +
≥
22
20
2
20
(1) 1
2
1
8 44
m
m
m
m
m
m
m mm
−<
>
−≥
⇔ ⇔ ⇔ ≥−
≤
≥−
+≥ − +
22
20
2
20
(2) 1
2
1
8 44
m
m
m
m
m
m
m mm
+<
<−
+≥
⇔ ⇔ ⇔≤
≥−
≤
+≥ + +
Vậy
[ ]
1;1m ∈−
.
DẠNG 2. TÍNH CHẴN LẺ
Câu 69: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx=
B.
cos .yx=
C.
tan .yx=
D.
cot .yx=
Lời giải
Nhắc lại kiến thức cơ bản:
Hàm số
sinyx=
là hàm số lẻ.
Hàm số
cosyx=
là hàm số chẵn.
Hàm số
tanyx=
là hàm số lẻ.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 21
Sưu tầm và biên soạn
Hàm số
cot
yx
=
là hàm số lẻ.
Vậy B là đáp án đúng.
Câu 70: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx
= −
B.
cos sin .
y xx
= −
C.
2
cos sin .yx x= +
D.
cos sin .y xx=
Lời giải
Tất các các hàm số đều có TXĐ:
D =
. Do đó
D D.xx
∀ ∈ ⇒− ∈
Bây giờ ta kiểm tra
( ) ( )
f x fx−=
hoặc
(
)
(
)
.f x fx−=−
Với
( )
siny fx x= = −
. Ta có
(
) (
)
( )
sin sin sin
fx x x x
−=− −= =−−
( ) ( )
f x fx → − = −
. Suy ra hàm số
sinyx= −
là hàm số lẻ.
Với
(
)
cos sin .y fx x x= = −
Ta có
( ) ( ) ( )
cos sin cos sinfx x x x x−= −− −= +
( ) ( ) ( )
{ }
,f x fx fx → − ≠ −
. Suy ra hàm số
cos siny xx= −
không chẵn không lẻ.
Với
( )
2
cos siny fx x x= = +
. Ta có
( )
( ) ( )
2
cos sin
fx x x−= −+ −
(
) ( )
[ ]
2
2
2
cos sin cos sin cos sin
x x x x xx= − + − = +− = +
( ) ( )
f x fx → − =
. Suy ra hàm số
2
cos sinyx x= +
là hàm số chẵn.
Với
( )
cos sin .y fx x x= =
Ta có
( ) ( ) ( )
cos .sin cos sinfx x x xx−= − −=−
(
)
( )
f x fx → − = −
. Suy ra hàm số
cos siny xx
=
là hàm số lẻ.
Câu 71: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin 2 .yx
=
B.
cos .yx x=
C.
cos .cot .y xx
=
D.
tan
.
sin
x
y
x
=
Lời giải
Xét hàm số
(
)
sin 2 .y fx x= =
TXĐ:
D =
. Do đó
D D.xx∀ ∈ ⇒− ∈
Ta có
( ) (
) ( )
sin 2 sin 2f x x x fx−= − =− =−
( )
fx →
là hàm số lẻ.
Xét hàm số
( )
cos .y fx x x= =
TXĐ:
D =
. Do đó
D D.xx∀ ∈ ⇒− ∈
Ta có
( ) ( ) ( ) ( )
.cos cosf x x x x x fx−=− −=− =−
( )
fx →
là hàm số lẻ.
Xét hàm số
( )
cos cot .y fx x x= =

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 22
Sưu tầm và biên soạn
TXĐ:
( )
{ }
D \ .kk
π
= ∈
Do đó
D D.xx∀ ∈ ⇒− ∈
Ta có
( ) ( ) ( ) ( )
cos .cot cos cotf x x x x x fx−= − −=− =−
( )
fx →
là hàm số lẻ.
Xét hàm số
(
)
tan
.
sin
x
y fx
x
= =
TXĐ:
( )
D\ .
2
kk
π
= ∈
Do đó
D D.xx∀ ∈ ⇒− ∈
Ta có
( )
( )
( )
( )
tan
tan tan
sin sin sin
x
xx
f x fx
x xx
−
−
−= = = =
−−
( )
fx →
là hàm số chẵn.
Câu 72: Hàm số nào sau đây là hàm số lẻ?
A.
2 cos
yx x= +
. B.
cos3
yx
=
. C.
( )
2
sin 3yx x= +
. D.
3
cos x
y
x
=
.
Lời giải
Xét hàm số
( )
3
cos x
y fx
x
= =
. Tập xác định
\ {0}D =
là tập đối xứng.
( )
( )
( )
( )
33
cos cos
.
xx
f x fx
xx
−
−= =− =−
−
Do đó hàm số
3
cos x
y
x
=
là hàm số lẻ.
Câu 73: Mệnh đề nào dưới đây đúng?
A. Hàm số
cotyx
=
là hàm số chẵn. B. Hàm số
sinyx=
là hàm số chẵn.
C. Hàm số
tanyx=
là hàm số chẵn. D. Hàm số
cos
yx
=
là hàm số chẵn.
Lời giải
Xét hàm số
cosyx=
có tập xác định
D =
.
Với mọi
xD xD∈ ⇔− ∈
và
(
)
cos cos
xx= −
. Do đó hàm số
cosyx=
là hàm số chẵn.
Câu 74: Trong các khẳng định sau đây, khẳng định nào đúng?
A. Hàm số
sinyx=
là hàm số chẵn. B. Hàm số
cosyx=
là hàm số lẻ.
C. Hàm số
tanyx=
là hàm số lẻ. D. Hàm số
cotyx=
là hàm số chẵn.
Lời giải
Câu 75: Chọn phát biểu đúng:
A. Các hàm số
sinyx=
,
cosyx=
,
cotyx=
đều là hàm số chẵn.
B. Các hàm số
sinyx=
,
cosyx=
,
cotyx=
đều là hàm số lẻ.
C. Các hàm số
sinyx=
,
cot
yx=
,
tanyx
=
đều là hàm số chẵn.
D. Các hàm số
sinyx=
,
cotyx=
,
tanyx=
đều là hàm số lẻ.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 23
Sưu tầm và biên soạn
Ta có, các hàm số
sinyx=
,
cotyx
=
,
tanyx
=
là các hàm số lẻ, hàm số
cosyx=
là hàm số
chẵn.
Câu 76: Hàm số nào sau đây là hàm số chẵn ?
A.
( ) sinfx x=
. B.
( ) sin 2
fx x
=
. C.
( ) sinfx x=
. D.
2
( ) sinfx x x
=
.
Lời giải
Xét hàm số
( ) sin
fx x=
. Tập xác định
D =
. Với mọi
x D xD∈ ⇒− ∈
.
( ) sin( ) sin ( )f x x x fx
−= −=− ≠
. Hàm số đã cho không phải hàm chẵn.
Xét hàm số
( ) sin 2
fx x
=
. Tập xác định
D =
. Với mọi
x D xD∈ ⇒− ∈
.
( ) sin( 2 ) sin 2 ( )f x x x fx−= − =− ≠
. Hàm số đã cho không phải hàm chẵn.
Xét hàm số
( ) sinfx x=
. Tập xác định
D =
. Với mọi
x D xD∈ ⇒− ∈
.
( ) sin( ) sin sin ( ), xDf x x x x fx
−= − − =
∀= ∈=
. Hàm số đã cho là hàm chẵn.
Xét hàm số
2
( ) sinfx x x=
. Tập xác định
D =
. Với mọi
x D xD∈ ⇒− ∈
.
( ) ( )
2
2
( ) sin sin ( )f x x x x x fx−=− − =− ≠
. Hàm số đã cho không phải hàm chẵn.
Câu 77: Hàm số nào dưới đây là hàm số lẻ?
A.
cosyx
=
. B.
2
sin
yx=
. C.
2
cotyx
=
. D.
tanyx=
.
Lời giải
Hàm số
tanyx
=
là hàm số lẻ.
Câu 78: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin 3 .yx
=
B.
tan .
2
x
y =
C.
sin .cos .y xx=
D.
2
sin .cos .y xx=
Lời giải
Hàm số
( )
2
sin .cos
y fx x x
= =
có tập xác định
D =
, thỏa mãn 2 điều kiện
( ) ( )
( )
( ) (
)
2
2
sin .cos sin .cos .
xD xD
f x x x x x fx
∀ ∈ ⇒− ∈
−= − −= =
Nên là hàm số chẵn.
Câu 79: Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A.
tan 4yx=
. B.
cos3yx=
. C.
cot 5yx=
. D.
sin 2yx=
.
Lời giải
Hàm số
cos3yx=
là hàm số chẵn do có tập xác định là
D =
,
,xDxD∀∈ −∈
ta có:
cos3( ) cos( 3 ) cos3x xx
−= − =
.
Câu 80: Hàm số nào sau đây là hàm số chẵn
A.
3
3sin 4siny xx= +
. B.
3sin 4cosyxx= +
.
C.
2
4cos siny xx= −
. D.
2
4sin cosy xx= −
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 24
Sưu tầm và biên soạn
Hàm số
2
4sin cosy xx= −
có tập xác định
D =
.
Suy ra
,
xD xD
∀∈ − ∈
.
( )
2
4sin cosfx x x= −
.
( )
( ) (
)
( )
22
4sin cos 4sin cosf x x x x x fx−= −− −= − =
.
Vậy suy ra hàm số
2
4sin cos
y xx
= −
là hàm số chẵn.
Câu 81: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
3
cos .sin
y xx=
. B.
sin .cos 2yxx=
.
C.
2019cos 2020
yx= +
. D.
2
tan
tan 1
x
y
x
=
+
.
Lời giải
Xét hàm số
( )
2019cos 2020y fx x= = +
TXĐ:
D =
.
xx∀ ∈ ⇒− ∈
.
( ) (
) ( )
2019cos 2020 2019cos 2020f x x x fx−= −+= +=
.
Kết luận: Hàm số
2019cos 2020yx= +
là hàm số chẵn.
Câu 82: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
sin 3yx= +
. B.
2
2cos
sin 2
x
y
x
=
+
. C.
2
sinyx x=
. D.
2cos sin 2y xx= −
.
Lời giải
Xét các đáp án ta thấy ở phương án C hàm số
( )
2
siny fx x x= =
có
Tập xác định
D =
thỏa mãn:
1)
.xD xD∀ ∈ ⇒− ∈
2)
( ) ( ) (
)
2
2
sin sin , .
f x x x x x fx xD− =− − =− =− ∀∈
Do đó hàm số
2
sinyx x=
là hàm số lẻ.
Các hàm số ở các đáp án còn lại không thỏa mãn định nghĩa hàm số lẻ.
Câu 83: Trong các hàm số sau, hàm số nào là hàm số chẵn.
A.
sin 2021 cos2022yxx= +
. B.
cot 2021 2022sinyxx= −
.
C.
tan 2021 cot 2022yxx= +
. D.
2021cos 2022siny xx= +
.
Lời giải
Xét hàm
( )
sin 2021 cos2022 1yxx= +
ta có
TXĐ
D =
.
xD xD∀ ∈ ⇒− ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 25
Sưu tầm và biên soạn
Có
( )
( ) ( ) ( )
sin 2021 cos 2022 sin 2021 cos2022y x x x x x yx−= − + − = + =
nên là hàm chẵn.
Câu 84: Có bao nhiêu hàm số chẵn trong các hàm số sau:
sinyx=
,
cos3yx=
,
tan 2yx=
và
cot
yx=
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Vì hàm số
sin
yx
=
có tập xác định
D =
và
sin sinxx
−=
nên
sinyx=
là hàm số chẵn.
Vì hàm số
cos3yx=
có tập xác định
D =
và
(
)
(
)
( )
cos 3 cos 3 cos3x xx−= −=
nên
cos3
yx=
là hàm số chẵn.
Câu 85: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .
yx=
. B.
2
sin .yx x=
C.
.
cos
x
y
x
=
D.
sin .yx x= +
Lời giải
Ta kiểm tra được A là hàm số chẵn, các đáp án B, C, D là hàm số lẻ.
Câu 86: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A.
sin cos 2 .y xx=
B.
3
sin .cos .
2
y xx
π
= −
C.
2
tan
.
tan 1
x
y
x
=
+
D.
3
cos sin .y xx=
Lời giải
Ta dễ dàng kiểm tra được A, C, D là các hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ
O
.
Xét đáp án B, ta có
( )
3 34
sin .cos sin .sin sin
2
y fx x x x x x
π
= = −= =
. Kiểm tra được đây là
hàm số chẵn nên có đồ thị đối xứng qua trục tung.
Câu 87: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
cos sin .yx x= +
B.
sin cos .yxx
= +
C.
cos .yx= −
D.
sin .cos3 .y xx=
Lời giải
Ta kiểm tra được đáp án A và C là các hàm số chẵn. Đáp án B là hàm số không chẵn, không lẻ.
Đáp án D là hàm số lẻ.
Câu 88: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
cot 4 .yx=
B.
sin 1
.
cos
x
y
x
+
=
C.
2
tan .yx=
D.
cot .yx=
Lời giải
Ta kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Đáp án B là hàm số không chẵn, không lẻ. Đáp án C và D là các hàm số chẵn.
Câu 89: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
sin .
2
yx
π
= −
B.
2
sin .yx=
C.
cot
.
cos
x
y
x
=
D.
tan
.
sin
x
y
x
=
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 26
Sưu tầm và biên soạn
Lời giải
Viết lại đáp án A là
sin cos .
2
y xx
π
= −=
Ta kiểm tra được đáp án A, B và D là các hàm số chẵn. Đáp án C là hàm số lẻ.
Câu 90: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
1 sin .yx= −
B.
2
cot .sin .y xx=
C.
2
tan 2 cot .yx x x
= −
D.
1 cot tan .y xx=++
Lời giải
Chọn C
Ta kiểm tra được đáp án A, B và D là các hàm số chẵn. Đáp án C là hàm số lẻ.
Câu 91: Cho hàm số
( )
sin 2fx x=
và
( )
2
tan .gx x=
Chọn mệnh đề đúng
A.
( )
fx
là hàm số chẵn,
( )
gx
là hàm số lẻ. B.
( )
fx
là hàm số lẻ,
(
)
gx
là hàm số chẵn.
C.
( )
fx
là hàm số chẵn,
( )
gx
là hàm số chẵn. D.
(
)
fx
và
( )
gx
đều là hàm số lẻ.
Lời giải
Chọn B
Xét hàm số
( )
sin 2 .fx x=
TXĐ:
D =
. Do đó
D D.xx∀ ∈ ⇒− ∈
Ta có
( ) ( ) ( )
sin 2 sin 2f x x x fx−= − =− =−
( )
fx →
là hàm số lẻ.
Xét hàm số
( )
2
tan .gx x=
TXĐ:
( )
D\ .
2
kk
π
π
= +∈
Do đó
D D.
xx
∀ ∈ ⇒− ∈
Ta có
( ) ( ) ( ) ( )
2
2
2
tan tan tang x x x x gx−= − =− = =
( )
fx →
là hàm số chẵn.
Câu 92: Cho hai hàm số
( )
2
cos 2
1 sin 3
x
fx
x
=
+
và
( )
2
sin 2 cos3
2 tan
xx
gx
x
−
=
+
. Mệnh đề nào sau đây là đúng?
A.
( )
fx
lẻ và
( )
gx
chẵn. B.
( )
fx
và
( )
gx
chẵn.
C.
( )
fx
chẵn,
( )
gx
lẻ. D.
( )
fx
và
( )
gx
lẻ.
Lời giải
Xét hàm số
( )
2
cos 2
.
1 sin 3
x
fx
x
=
+
TXĐ:
D =
. Do đó
D D.xx∀ ∈ ⇒− ∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 27
Sưu tầm và biên soạn
Ta có
( )
( )
(
)
( )
22
cos 2
cos 2
1 sin 3 1 sin 3
x
x
f x fx
xx
−
−= = =
+− +
( )
fx →
là hàm số chẵn.
Xét hàm số
( )
2
sin 2 cos3
.
2 tan
xx
gx
x
−
=
+
TXĐ:
( )
D\
2
kk
π
π
= +∈
. Do đó
D D.xx∀ ∈ ⇒− ∈
Ta có
( )
(
) ( )
( )
( )
22
sin 2 cos 3
sin 2 cos3
2 tan 2 tan
xx
xx
g x gx
xx
−− −
−
−= = =
+− +
( )
gx →
là hàm số chẵn.
Vậy
( )
fx
và
( )
gx
chẵn.
Câu 93: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
3
1
.
sin
y
x
=
B.
sin .
4
yx
π
= +
C.
2 cos .
4
yx
π
= −
D.
sin 2 .yx=
Lời giải
Viết lại đáp án B là
( )
1
sin sin cos .
4
2
y x xx
π
= += +
Viết lại đáp án C là
2 cos sin cos .
4
y x xx
π
= −= +
Kiểm tra được đáp án A là hàm số lẻ nên có đồ thị đối xứng qua gốc tọa độ.
Ta kiểm tra được đáp án B và C là các hàm số không chẵn, không lẻ.
Xét đáp án D.
Hàm số xác định
[ ]
sin 2 0 2 2 ; 2 ;
2
x xk k x k k
π
ππ π π π
⇔ ≥⇔ ∈ + ⇔∈ +
( )
; .
2
Dk k k
π
ππ
→ = + ∈
Chọn
D
4
x
π
= ∈
nhưng
D.
4
x
π
−=− ∉
Vậy
sin 2yx=
không chẵn, không lẻ.
Câu 94: Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số
sinyx=
đối xứng qua gốc tọa độ
.O
B. Đồ thị hàm số
cosyx=
đối xứng qua trục
.Oy
C. Đồ thị hàm số
tanyx=
đối xứng qua trục
.
Oy
D. Đồ thị hàm số
tanyx=
đối xứng qua gốc tọa độ
.O
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 28
Sưu tầm và biên soạn
Ta kiểm tra được hàm số
sinyx
=
là hàm số chẵn nên có đồ thị đối xứng qua trục
Oy
. Do đó
đáp án A sai.
Câu 95: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
( )
2cos sin 2 .
2
yx x
π
π
= ++ −
B.
sin sin .
44
yx x
ππ
= −+ +
C.
2 sin sin .
4
yx x
π
= +−
D.
sin cos .yxx= +
Lời giải
Viết lại đáp án A là
( )
2cos sin 2 2sin sin 2 .
2
y x x xx
π
π
= ++ − =− +
Viết lại đáp án B là
sin sin 2sin .cos 2 sin .
44 4
yx x x x
ππ π
= −+ += =
Viết lại đáp án C là
2 sin sin sin cos sin cos .
4
y x x x xx x
π
= +−=+−=
Ta kiểm tra được đáp án A và B là các hàm số lẻ. Đáp án C là hàm số chẵn.
Xét đáp án D.
Hàm số xác định
( )
sin 0
D 2; 2 .
cos 0
2
x
k kk
x
π
ππ
≥
⇔ → = + ∈
≥
Chọn
D
4
x
π
= ∈
nhưng
D.
4
x
π
−=− ∉
Vậy
sin cosyxx
= +
không chẵn, không lẻ.
Câu 96: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
4
cos .
3
yx x
π
=+−
B.
2017
cos .
2
yx x
π
=+−
C.
2018
2015 cos sin .y xx=++
D.
2017 2018
tan sin .y xx= +
Lời giải
Viết lại đáp án B là
2017 2017
cos sin .
2
yx x yx x
π
= + −== +
Ta kiểm tra được đáp án A và D không chẵn, không lẻ. Đáp án B là hàm số lẻ. Đáp án C là hàm
số chẵn.
Câu 97: Trong các hàm số sau sau. Hàm số nào có đồ thị nhận trục tung làm trục đối xứng?
A.
tanyx=
. B.
sinyx
=
. C.
cotyx=
. D.
cosyx=
.
Lời giải
Xét hàm số
cosyx=
.
Tập xác định
D
=
là tập đối xứng và
( )
cos cosxx−=
nên
cosyx=
là hàm số chẵn.
Câu 98: Hàm số nào là hàm số chẵn trong các hàm số sau?

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 29
Sưu tầm và biên soạn
A.
sin .cos
y xx
=
. B.
tanyx=
. C.
cotyx=
. D.
2
sin .cosy xx=
.
Lời giải
Hàm số
2
sin .cosy xx=
thỏa mãn tính chất của hàm số chẵn:
(
) ( )
2
sin .cos
yx x x−= −
(
)
2
sin .cosx x yx= =
,
x∀∈
.
Câu 99: Hàm số nào sau đây là hàm số chẵn?
A.
sin 4
yx=
. B.
cos5
yx=
. C.
tan 4yx=
. D.
cot10
yx=
.
Lời giải
Hàm số
cos 2yx=
có tập xác định
D =
.
Với mọi
xD∈
ta có
xD−∈
và
( ) ( )
cos 2 cos 2xx−=
nên hàm số
cos 2yx=
là hàm số chẵn.
Câu 100: Trong các hàm số sau hàm số nào là hàm số chẵn?
A.
2cosyx=
. B.
2 tanyx=
. C.
2sinyx=
. D.
(
)
2cos 1yx= −
.
Lời giải
Hàm số
2 tanyx=
và
2sinyx=
là hàm số lẻ.
Hàm số
( )
2cos 1yx= −
không thỏa
( ) ( )
y x yx−=
nên là hàm số không chẵn.
Hàm số
2cosyx=
là hàm số chẵn vì TXĐ:
D =
và
( )
2cos 2cosxx= −
.
Câu 101: Hàm số nào sau đây là hàm số chẵn trên
?
A.
.cos2yx x
=
. B.
(
)
2
1 .sinyx x= +
. C.
2
cos
1
x
y
x
=
+
. D.
2
tan
1
x
y
x
=
+
.
Lời giải
Xét hàm số
( )
2
cos
1
x
y fx
x
= =
+
có tập xác định
D =
xD xD∀ ∈ ⇒− ∈
xD∀∈
:
( )
( )
( )
( )
2
2
cos
cos
1
1
x
x
f x fx
x
x
−
−= = =
+
+−
Vậy hàm số
f
là hàm chẵn.
Câu 102: Trong các hàm số sau, hàm số nào là hàm số chẵn trên
?
A.
sin
2
yx
π
= −
. B.
tanyx=
. C.
sinyx=
. D.
sin
6
yx
π
= +
.
Lời giải
Ta có
sin cos
2
y xx
π
= −=
là hàm số chẵn trên
.
Câu 103: Trong các hàm số sau, hàm số nào có đồ thị nhận gốc tọa độ làm tâm đối xứng?

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 30
Sưu tầm và biên soạn
A.
sin
yx x
=
. B.
cosyx=
. C.
1 sinyx= −
. D.
sin cosy xx=
.
Lời giải
Đồ thị nhận gốc tọa độ làm tâm đối xứng là đồ thị của hàm số lẻ.
A:. Hàm số
( ) sin
y fx x x
= =
:
Tập xác định:
D
=
.
Ta có:
:
xD xD∀∈ −∈
và
()()sin() sin ().f x x x x x fx−=− −= =
Do đó hàm số
sinyx x=
là hàm số chẵn.
B:. Hàm số
cosyx=
là hàm số chẵn trên
.
C:. Hàm số
( ) 1 siny fx x= = −
:
Ta có:
0; 2
22
ff
ππ
= −=
.
Lúc đó:
22
ff
ππ
≠−
và
22
ff
ππ
≠− −
Do đó, hàm số
1 sin
yx= −
không phải là hàm số chẵn và không phải hàm số lẻ.
D:. Hàm số
( ) cos siny fx x x= =
:
Tập xác định:
D =
.
Ta có:
:xD xD
∀∈ −∈
và
( ) cos( )sin( ) cos sin ( ).f x x x x x fx−= − −=− =−
Do đó hàm số
( ) cos sin
y fx x x= =
là hàm số lẻ.
Vậy đồ thị nhận gốc tọa độ làm tâm đối xứng là đồ thị của hàm số
( ) cos sin .y fx x x= =
Câu 104: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin 2022 cos 2021yxx= +
. B.
2021cos 2023sin
y xx= +
.
C.
cot 2021 2022siny xx
= −
. D.
tan 2021 cot 2022yxx= +
.
Lời giải
Xét hàm số
( )
sin 2016 cos 2017y fx x x= = +
. Tập xác định.
D =
.
Với mọi
xD∈
, ta có
xD−∈
.
Ta có
( )
( ) ( )
sin 2016 cos 2017 sin 2016 cos 2017f x x x x x fx−= − + − = + =
.
Vậy
( )
fx
là hàm số chẵn.
Câu 105: Hàm số nào sau đâu có đồ thị nhận trục tung làm trục đối xứng?
A.
| sin |yx=
. B.
cot
yx=
. C.
tanyx=
. D.
sinyx= −
.
Lời giải
Vì
| sin( ) | | sin |xx−=
với mọi
x ∈
nên hàm số
| sin |yx=
là hàm số chẵn, nên đồ thị sẽ đối xứng
qua trục tung.
Câu 106: Trong các hàm số sau đây, hàm số nào là hàm số chẵn?
A.
sinyx=
. B.
sinyx x= +
. C.
cosyx x=
. D.
sin x
y
x
=
.
Lời giải
Xét hàm số
sinyx=
Tập xác định
D =
nên
xx∀ ∈ ⇒− ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 31
Sưu tầm và biên soạn
( ) ( ) ( )
sin siny x x x yx
−= −=− =−
.
⇒
Hàm lẻ.
Xét hàm số
sinyx x= +
, tập xác định
D =
nên:
xx∀ ∈ ⇒− ∈
.
( ) ( ) ( ) (
) (
)
sin siny x x x x x yx−=−+ −=−+ =−
.
⇒
Hàm lẻ.
Xét hàm số
cos
yx x=
có tập xác định
D =
nên:
xx∀ ∈ ⇒− ∈
.
(
) ( ) ( ) ( ) ( )
cos cosy x x x x x yx
−=− −=− =−
.
⇒
Hàm lẻ.
Xét hàm số
sin x
y
x
=
tập xác định
{ }
\0D =
nên:
xD xD∀ ∈ ⇒− ∈
.
(
)
( )
( )
sin
sin
x
y x x yx
x
−
−= = = ⇒
−
Hàm chẵn.
Câu 107: Hàm số nào sau đây là hàm số chẵn
A.
sin
yx=
. B.
tanyx=
. C.
( )
cot 2
yx=
. D.
sin
yx=
.
Lời giải
Ta có hàm số
sinyx=
có tập xác định
D =
Và
( )
( )
sin siny x x x yx− = −= =
Vậy hàm số
sinyx=
là hàm số chẵn.
Câu 108: Trong các hàm số:
2sinyx=
;
sin 3yx= +
;
5
sin 2019
2
yx
π
= −
, có bao nhiêu hàm lẻ?
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
* Xét
2sinyx
=
Tập xác định:
D =
.
Với
xD xD∀ ∈ ⇔− ∈
và
( ) ( ) ( )
2sin 2siny x x x yx−= −=− =−
nên
2sinyx=
là hàm lẻ
* Xét
sin 3yx= +
Tập xác định:
D =
.
Với
xD xD∀ ∈ ⇔− ∈
và
( ) ( ) (
)
sin 3 sin 3y x x x yx−= −+=− +≠−
nên
sin 3yx= +
không
là hàm lẻ

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 32
Sưu tầm và biên soạn
* Xét
5
sin 2019 sin 2019 cos 2019
22
y x xx
ππ
=−=−=
Tập xác định:
D =
.
Với
xD xD∀ ∈ ⇔− ∈
và
( ) ( ) ( ) (
)
cos 2019 cos 2019 cos 2019y x x x x yx−= − = − = =
nên
5
sin 2019
2
yx
π
= −
là hàm chẵn.
Câu 109: Cho hai hàm số
( )
sin 2fx x=
và
( )
cos3gx x=
. Chọn mệnh đề đúng
A.
f
là hàm số chẵn và
g
là hàm số lẻ. B.
f
và
g
là hai hàm số chẵn.
C.
f
và
g
là hai hàm số lẻ. D.
f
là hàm số lẻ và
g
là hàm số chẵn.
Lời giải
Tập xác định của hai hàm số là:
D =
.
Ta có:
( ) ( ) ( )
sin 2 sin 2f x x x fx−= − =− =− ⇒
f
là hàm số lẻ.
( ) ( ) ( )
cos 3 cos3
g x x x gx−= − = =
g⇒
là hàm số chẵn.
Câu 110: Trong các hàm số sau có bao nhiêu hàm số là hàm số chẵn trên tập xác định của nó?
tan 2yx=
,
2018
sinyx=
,
( )
3yc x
π
= +os
,
cot
yx
=
.
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Hàm số
tan 2yx=
có
Tập xác định:
\ ,.
42
D kk
ππ
= +∈
Ta có:
xD xD∀ ∈ ⇒− ∈
và
( ) (
) ( )
tan 2 tan 2f x x x fx−= − =− =−
.
Vậy hàm số
tan 2yx=
là hàm số lẻ.
Hàm số
( )
cos 3 cosyx x
π
= +=−
là hàm số chẵn.
Tương tự, kiểm tra được các hàm số
2018
sin ; coty xy x= =
là các hàm số chẵn trên tập xác
định của nó.
Câu 111: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua gốc tọa độ?
A.
cot 4yx=
. B.
sin 1
cos
x
y
x
+
=
. C.
2
tanyx=
. D.
cot
yx=
.
Lời giải
Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Trong các hàm số trên, chỉ có hàm số
cot 4yx=
là hàm số lẻ.
Vậy, hàm số nào có đồ thị đối xứng qua gốc tọa độ là
cot 4yx=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 33
Sưu tầm và biên soạn
Câu 112: Trong các hàm số sau, hàm số nào có đồ thị đối xứng qua trục tung?
A.
sin .cos 2yxx
=
. B.
3
sin .cos
2
y xx
π
= −
.
C.
2
tan
tan 1
x
y
x
=
+
. D.
3
cos .siny xx=
.
Lời giải
Xét hàm số
( )
34
sin .cos sin
2
y fx x x x
π
= = −=
có tập xác định
D =
xD xD
∀ ∈ ⇒− ∈
.
( ) ( )
( )
( )
4
4
: sin sinx Df x x x fx∀∈ − = − = =
Vậy hàm số
f
là hàm số chẵn
⇒
Đồ thị của hàm số nhận trục tung làm trục đối xứng.
Câu 113: Cho hàm số
( )
sin 2fx x
=
và
(
)
2
tan
gx x=
. Chọn mệnh đề đúng?
A.
( )
fx
là hàm số chẵn,
(
)
gx
là hàm số lẻ.
B.
( )
fx
là hàm số lẻ,
(
)
gx
là hàm số chẵn.
C.
( )
fx
là hàm số chẵn,
( )
gx
là hàm số chẵn.
D.
( )
fx
và
( )
gx
đều là hàm số lẻ.
Lời giải
Hàm số
(
)
fx
có TXĐ là
D =
xD
⇒∀ ∈
thì
xD−∈
.
( ) (
) (
)
: sin 2 sin 2
x Df x x x fx
∀∈−=−=−=−
⇒
hàm số
( )
fx
là hàm số lẻ.
Hàm số
( )
gx
có TXĐ là
\,
2
D kk
π
π
= +∈
xD⇒∀ ∈
thì
xD−∈
.
( ) ( ) ( )
22
: g tan tanx D x x x gx∀∈ −= −= =
⇒
hàm số
( )
gx
là hàm số chẵn.
Câu 114: Trong các hàm số:
2sinyx
=
;
sin 3
yx= +
;
5
sin 2021
2
yx
π
= −
, có bao nhiêu hàm lẻ?
A.
3
. B.
0
. C.
1
. D.
2
.
Lời giải
* Xét
2sinyx=
Tập xác định:
D =
.
Với
xD xD∀ ∈ ⇔− ∈
và
( ) ( ) ( )
2sin 2siny x x x yx−= −=− =−
nên
2sinyx=
là hàm lẻ
* Xét
sin 3yx= +
Tập xác định:
D =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 34
Sưu tầm và biên soạn
Với
xD xD∀ ∈ ⇔− ∈
và
( ) ( ) ( )
sin 3 sin 3y x x x yx−= −+=− +≠−
nên
sin 3
yx= +
không là
hàm lẻ
* Xét
5
sin 2019 sin 2019 cos 2019
22
y x xx
ππ
=−=−=
Tập xác định:
D
=
.
Với
xD xD∀ ∈ ⇔− ∈
và
( ) ( ) ( ) ( )
cos 2019 cos 2019 cos 2019y x x x x yx−= − = − = =
nên
5
sin 2019
2
yx
π
= −
là hàm chẵn.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 68
Sưu tầm và biên soạn
BÀI 4: HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
DẠNG 3. TẬP GIÁ TRỊ - GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Câu 115: Tập giá trị của hàm số
sin 2yx=
là:
A.
[ ]
2;2−
. B.
[ ]
0;2
. C.
[ ]
1;1−
. D.
[ ]
0;1
.
Câu 116: Giá trị lớn nhất của hàm số
sin 2yx
=
bằng
A.
2
. B.
0
. C.
1
. D.
1−
.
Câu 117: Tập giá trị của hàm số
sinyx=
là
A.
11;T = −
. B.
11
( ;)T = −
. C.
10;T = −
. D.
01;T =
.
Câu 118: Giá trị lớn nhất của hàm số
3sinyx=
trên tập xác định
là?
A.
1
. B.
2
. C.
3
. D.
3−
.
Câu 119: Giá trị nhỏ nhất của hàm số
cos
yx=
là
A.
1
. B.
0
. C.
1
−
. D. 2.
Câu 120: Giá trị lớn nhất của hàm số
2 sin 1 3yx= +−
là
A.
23 2+
. B.
23 2
−
. C.
23 3
−
. D.
32
.
Câu 121: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3sin 1
4
yx
lần lượt là:
A.
4; 2−
. B.
2; 4
. C.
1; 1
. D.
3; 3
.
Câu 122: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
cos 6 5yx= +
lần lượt là
A.
4
và
6
. B.
0
và
4
. C.
1−
và
11
. D.
6
và
4
.
Câu 123: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
8sin 2 5yx= −
.
A.
max 11; min 21yy= = −
. B.
max 8; min 8yy= = −
.
C.
max 4; min 6yy
=−=−
. D.
max 3; min 13yy= = −
.
Câu 124: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
4sin cos 1y xx= +
. Tính
Mm+
A.
2
. B.
4
. C.
3
. D.
1−
.
Câu 125: Tập giá trị của hàm số
3sin3 2yx= +
là
A.
. B.
( )
0; +∞
. C.
[ ]
1; 5
−
. D.
[ ]
7;11−
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
III

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 69
Sưu tầm và biên soạn
Câu 126: Giá trị lớn nhất và nhỏ nhất của hàm số
3sin 2 5yx= −
lần lượt là:
A.
8; 2
. B.
2; 8−−
. C.
2; 5−
. D.
3; 5−
.
Câu 127: Giá trị lớn nhất và nhỏ nhất của hàm số là
2 sin
= −
yx
là
A.
1
và
3
. B.
4
và
4−
. C.
2
và
4
. D.
3
và
1
.
Câu 128: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
6cos 2 7yx
= −
trên đoạn
;
36
ππ
−
. Tính
.Mm+
A.
14.−
B.
3.
C.
11.−
D.
10.−
Câu 129: Tập giá trị của hàm số
sin 4 3
= −yx
là:
A.
[ ]
4; 2−−
. B.
[ ]
3;1−
. C.
[ ]
2; 2−
. D.
[ ]
4; 2−
.
Câu 130: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
22
2sin 3sin 2 4cosyxxx=+−
.
A.
min 3 2 1; max 3 2 1.yy=−− = +
B.
min 3 2 2; max 3 2 1.yy=−− = −
C.
min 3 2; max 3 2 1.yy=−=−
D.
min 3 2 1; max 3 2 1.yy=−− = −
Câu 131: Tập giá trị của hàm số
sin 4 3= −yx
là:
A.
[ ]
4; 2−−
. B.
[
]
3;1
−
. C.
[ ]
2; 2
−
. D.
[ ]
4; 2
−
.
Câu 132: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3sin 4 cos 1yx x
=+−
.
A.
max 4,min 6yy
= = −
. B.
max 8,min 6yy= = −
.
C.
max 6,min 4yy= = −
. D.
max 6,min 8
yy= = −
.
Câu 133: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2cos 2 3 sin .cos 1y x xx=−+
.
A.
min 1 3;max 3 3yy=−+ = +
. B.
min 0;max 4yy= =
.
C.
min 4;max 0
yy=−=
. D.
min 1 3; max 3 3yy=−=+
.
Câu 134: Tập giá trị
T
của hàm số
cos 2 cos 2
3
yx x
π
= +−
là
A.
3; 3T
= −
. B.
2; 2T
= −
. C.
[ ]
1;1T = −
. D.
[ ]
2; 2T = −
.
Câu 135: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
24
2sin 2sin 2sin 2 1
y xxx=−−+
là
A. 4. B.
5
2
. C.
3
2
−
. D. 3.
Câu 136: Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos 2 4cos 1y xx=++
. Khi
đó
Mm−
bằng
A.
2
. B.
8
. C.
4
. D.
8
−
.
Câu 137: Giá trị lớn nhất của hàm số
2
cos sin 9y xx= ++
trên đoạn
[ ]
0;
π
bằng
A.
41
4
. B.
10
. C.
21
2
. D.
39
4
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 70
Sưu tầm và biên soạn
Câu 138: Gọi
m
là giá trị nhỏ nhất của hàm số
4cos 2 1
yx= −
trên đoạn
;
36
ππ
−
. Tìm
.
m
A.
5.−
B.
3.
C.
1.
−
D.
3.
−
Câu 139: Tìm giá trị lớn nhất của hàm số
2
sin cos 2y xx= −+
A.
3
. B.
13
4
. C.
7
4
. D.
1
.
Câu 140: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2cos sin 3.y xx= −+
A.
[ ]
1;1
min 4y
−
=
;
[ ]
1;1
41
max .
8
y
−
=
B.
[ ]
1;1
min 2y
−
=
;
[ ]
1;1
max 4y
−
=
.
C.
[ ]
1;1
41
min
8
y
−
= −
;
[ ]
1;1
max 2
y
−
=
. D.
[ ]
1;1
min 2y
−
=
;
[ ]
1;1
41
max .
8
y
−
=
Câu 141: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin 2021 3cos2021yx x= +
.
Tích
.Mm
bằng
A.
4
−
. B.
2
−
. C.
9−
. D.
1−
.
Câu 142: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2cos 5sin 1y xx= ++
trên
5
;
36
ππ
. Khi đó
Mm−
bằng bao nhiêu?
A.
1Mm−=
. B.
11Mm
−=
. C.
1
2
Mm−=
. D.
6Mm−=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 4: HÀM SỐ LƯỢNG GIÁC VÀ DỒ THỊ
DẠNG 3. TẬP GIÁ TRỊ - GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Câu 115: Tập giá trị của hàm số
sin 2yx=
là:
A.
[ ]
2;2−
. B.
[ ]
0;2
. C.
[ ]
1;1−
. D.
[ ]
0;1
.
Lời giải
Ta có
1 sin 2 1x−≤ ≤
,
x∀∈
.
Vậy tập giá trị của hàm số đã cho là
[ ]
1;1
−
.
Câu 116: Giá trị lớn nhất của hàm số
sin 2yx=
bằng
A.
2
. B.
0
. C.
1
. D.
1
−
.
Lời giải
Ta có
1 sin 2 1x−≤ ≤
x∀∈
.
sin 2 1x =
22
2
xk
π
π
⇔=+
4
xk
π
π
⇔= +
(
k ∈
).
Vậy giá trị lớn nhất của hàm số
sin 2yx=
bằng
1
khi
4
xk
π
π
= +
(
k ∈
).
Câu 117: Tập giá trị của hàm số
sin
yx=
là
A.
11;T
= −
. B.
11( ;)T = −
. C.
10;T = −
. D.
01;T =
.
Lời giải
Dựa vào tính chất hàm số
sin
yx=
.
Câu 118: Giá trị lớn nhất của hàm số
3sinyx=
trên tập xác định
là?
A.
1
. B.
2
. C.
3
. D.
3−
.
Lời giải
Hàm số
sinyx=
có tập giá trị là
[ ]
1;1−
. Do đó
3 3sin 3x−≤ ≤
,
x∀∈
.
Vậy giá trị lớn nhất của hàm số
3sinyx=
trên tập xác định
là 3, xảy ra khi
sin 1 2
2
x xk
π
π
=⇔= +
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM
III

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
Câu 119: Giá trị nhỏ nhất của hàm số
cosyx
=
là
A.
1
. B.
0
. C.
1
−
. D. 2.
Lời giải
Ta có:
1 cos 1,
−≤ ≤ ∀∈
xx
nên giá trị nhỏ nhất của hàm số
cosyx
=
là
1
−
khi
2xk
ππ
= +
.
Câu 120: Giá trị lớn nhất của hàm số
2 sin 1 3yx= +−
là
A.
23 2+
. B.
23 2−
. C.
23 3−
. D.
32
.
Lời giải
Vì
1 sin 1x−≤ ≤
0 sin 1 2x⇔ ≤ +≤
0 sin 1 2x⇔ ≤ +≤
02sin 122x⇔ ≤ +≤
3 22 3y⇔− ≤ ≤ −
.
Vậy
max 2 2 3y = −
khi
(
)
sin 1 2
2
x x kk
π
π
=⇔= + ∈
.
Câu 121: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
3sin 1
4
yx
lần lượt là:
A.
4; 2−
. B.
2; 4
. C.
1; 1
. D.
3; 3
.
Lời giải
Tập xác định:
D
=
.
+)
x∀∈
ta có:
3
1 sin 1
4
x
π
−≤ + ≤
3
3 3sin 3
4
x
π
⇔− ≤ + ≤
3
4 3sin 1 2
4
x
π
⇔− ≤ + − ≤
42y⇒− ≤ ≤
.
Vậy giá trị lớn nhất của hàm số
3
3sin 1
4
yx
là
2
khi
4
x
π
= −
.
Giá trị nhỏ nhất của hàm số
3
3sin 1
4
yx
là
4−
khi
3
4
x
π
=
.
Câu 122: Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
cos6 5yx= +
lần lượt là
A.
4
và
6
. B.
0
và
4
. C.
1−
và
11
. D.
6
và
4
.
Lời giải
Ta có :
1 cos 6 1 4 cos6 5 6 4 6x xy−≤ ≤⇔≤ +≤⇔≤≤
.
Câu 123: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
8sin 2 5yx= −
.
A.
max 11; min 21yy= = −
. B.
max 8; min 8yy= = −
.
C.
max 4; min 6
yy=−=−
. D.
max 3; min 13yy
= = −
.
Lời giải
Ta có
1 sin 2 1 8 8sin 2 8 13 8sin 2 5 3xx x− ≤ ≤ ⇔− ≤ ≤ ⇔− ≤ − ≤
Vậy
max 3;min 13yy
= = −
Câu 124: Gọi
M
là giá trị lớn nhất,
m
là giá trị nhỏ nhất của hàm số
4sin cos 1y xx= +
. Tính
Mm+
A.
2
. B.
4
. C.
3
. D.
1−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
Lời giải
Ta có
2sin 2 1
yx= +
.
Do
1 sin 2 1 2 2sin 2 2 1 2sin 2 1 3xxx− ≤ ≤ ⇒− ≤ ≤ ⇒− ≤ + ≤
.
13
y⇒− ≤ ≤
.
*
1 sin 2 1 2 2
24
y x xkxk
ππ
ππ
=−⇔ =−⇔ =− + ⇔ =− +
.
*
3 sin 2 1
4
y x xk
π
π
=⇔ =⇔= +
.
Vậy giá trị lớn nhất của hàm số bằng
3M =
, giá trị nhỏ nhất bằng
1m = −
.
Suy ra:
2Mm+=
.
Câu 125: Tập giá trị của hàm số
3sin3 2yx
= +
là
A.
. B.
( )
0; +∞
. C.
[ ]
1; 5−
. D.
[ ]
7;11−
.
Lời giải
Tập xác định:
D =
x∀∈
, ta có:
[ ]
1 sin3 1 1 3sin3 2 5 1 5 1; 5x x yy−≤ ≤ ⇔−≤ + ≤ ⇔−≤ ≤ ⇔ ∈−
Câu 126: Giá trị lớn nhất và nhỏ nhất của hàm số
3sin 2 5yx= −
lần lượt là:
A.
8; 2
. B.
2; 8−−
. C.
2; 5
−
. D.
3; 5−
.
Lời giải
Ta có:
1 sin 2 1x−≤ ≤
3 3sin 2 3x⇔− ≤ ≤
8 3sin 2 5 2x⇔− ≤ − ≤−
Vậy giá trị lớn nhất và nhỏ nhất của hàm số lần lượt là
2−
và
8−
.
Câu 127: Giá trị lớn nhất và nhỏ nhất của hàm số là
2 sin= −yx
là
A.
1
và
3
. B.
4
và
4−
. C.
2
và
4
. D.
3
và
1
.
Lời giải
Ta có
1 sin 1 1 2 sin 3 1 3−≤− ≤⇔≤− ≤⇔≤ ≤x xy
.
Suy ra,
Max 3y =
khi
sin -1 2 , .
2
= ⇔=−+ ∈x x kk
π
π
Min 1y =
khi
sin = 1 2 , .
2
⇔= + ∈x x kk
π
π
Câu 128: Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
6cos 2 7yx= −
trên đoạn
;
36
ππ
−
. Tính
.Mm+
A.
14.−
B.
3.
C.
11.−
D.
10.−
Lời giải
Ta có:
36
x
ππ
− ≤≤
2
2
33
x
ππ
⇔− ≤ ≤
1
cos2 1 10 6cos 2 7 1
2
xx⇔− ≤ ≤ ⇔− ≤ − ≤−
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Suy ra
1, 10.
Mm
=−=−
Vậy
11.Mm+=−
Câu 129: Tập giá trị của hàm số
sin 4 3= −
yx
là:
A.
[ ]
4; 2−−
. B.
[ ]
3;1−
. C.
[ ]
2; 2−
. D.
[ ]
4; 2−
.
Lời giải
Do
1 sin 4 1, −≤ ≤ ∀∈xx
nên
4 sin 4 3 2, − ≤ − ≤− ∀ ∈xx
.
Vậy tập giá trị của hàm số là
[
]
4; 2−−
.
Câu 130: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
22
2sin 3sin 2 4cos
yxxx=+−
.
A.
min 3 2 1; max 3 2 1.yy=−− = +
B.
min 3 2 2; max 3 2 1.yy=−− = −
C.
min 3 2; max 3 2 1.yy=−=−
D.
min 3 2 1; max 3 2 1.
yy=−− = −
Lời giải
Ta có:
1 cos 2 3sin 2 2(1 cos2 )y xx x
=− + −+
3sin 2 3cos2 1 3 2 sin 2 1
4
xx x
π
= − −= − −
.
32 1 32 1y⇒− − ≤ ≤ −
x∀∈
.
Vậy
min 3 2 1; max 3 2 1yy=−− = −
.
Câu 131: Tập giá trị của hàm số
sin 4 3= −
yx
là:
A.
[ ]
4; 2−−
. B.
[ ]
3;1−
. C.
[
]
2; 2
−
. D.
[
]
4; 2−
.
Lời giải
Do
1 sin 4 1, −≤ ≤ ∀∈xx
nên
4 sin 4 3 2, − ≤ − ≤− ∀ ∈xx
.
Vậy tập giá trị của hàm số là
[ ]
4; 2−−
.
Câu 132: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3sin 4c os 1yx x=+−
.
A.
max 4,min 6
yy= = −
. B.
max 8,min 6yy= = −
.
C.
max 6,min 4yy= = −
. D.
max 6,min 8yy= = −
.
Lời giải
Ta có:
( )
34
5 sin cos 1 5sin 1
55
y xx x
α
= + −= + −
.
Trong đó
α
thỏa mãn
34
cos , sin
55
αα
= =
.
Khi đó, do
( )
α
−≤ + ≤
1 sin 1x
, nên
( )
α
−≤ + −≤ ⇔−≤ ≤6 5sin 1 4 6 4xy
.
Vậy
max 4,min 6yy= = −
.
Câu 133: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2cos 2 3 sin .cos 1y x xx=−+
.
A.
min 1 3; max 3 3yy=−+ = +
. B.
min 0;max 4yy= =
.
C.
min 4;max 0yy=−=
. D.
min 1 3; max 3 3yy=−=+
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
2
2cos 2 3 sin .cos 1 cos 2 3 sin 2 2 2sin 2 2
6
yxxx xx x
π
= − += − + = − +
Ta có:
02sin 2 24 0 4
6
xy
π
≤ − +≤⇔≤≤
min 0y =
khi
sin 2 1 2 2 ,
6 62 3
x x k x kk
π ππ π
ππ
− =−⇔ − =− + ⇔ = − ∈
;
max 4y =
khi
sin 2 1 2 2 ,
6 62 6
x x k x kk
π ππ π
ππ
− =⇔ − = + ⇔=−− ∈
.
Vậy
min 0;max 4yy= =
.
Câu 134: Tập giá trị
T
của hàm số
cos 2 cos 2
3
yx x
π
= +−
là
A.
3; 3T
= −
. B.
2; 2T
= −
. C.
[ ]
1;1T = −
. D.
[
]
2; 2T = −
.
Lời giải
Ta có
cos 2 cos 2 2sin 2 .sin sin 2
3 66 6
yx x x x
π ππ π
= +− =− + =− +
. Do đó
[ ]
1;1T
= −
.
Câu 135: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
24
2sin 2sin 2sin 2 1
y xxx=−−+
là
A. 4. B.
5
2
. C.
3
2
−
. D. 3.
Lời giải
24
2sin 2sin 2sin 2 1y xxx=−−+
.
( )
22
2sin 1 sin 2sin 2 1xx x= −− +
22
2sin .cos 2sin 2 1xx x= −+
2
sin 2
2sin 2 1
2
x
x=−+
Đặt
( )
2
sin 2 , 1 1 2 1
2
t
txt y t= −≤≤ ⇒ = − +
.
Xét hàm số:
( )
2
2 1, 1 1
2
t
yt t= − + −≤≤
có đồ thị là một phần của Parabol, đỉnh
( )
I 2; 1−
.
Ta có bảng biến thiên sau:
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
Vậy
17
min ;max min max 3
22
y y yy=− =⇒+ =
.
Câu 136: Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
cos 2 4cos 1y xx=++
. Khi
đó
Mm−
bằng
A.
2
. B.
8
. C.
4
. D.
8
−
.
Lời giải
Ta có:
cos 2 4cos 1yxx
=++
2
2cos 1 4cos 1xx= −+ +
( )
2
2 cos 2cosxx= +
(
)
2
2 cos 1 2x
= +−
( ) (
)
22
1 cos 1 0 cos 1 2 0 cos 1 4 0 2 cos 1 8
xx x x−≤ ≤⇔≤ +≤⇒≤ + ≤⇔≤ + ≤
( )
2
2 2 cos 1 2 6x⇔− ≤ + − ≤
Suy ra:
6; 2Mm= = −
nên
8Mm−=
Câu 137: Giá trị lớn nhất của hàm số
2
cos sin 9y xx= ++
trên đoạn
[ ]
0;
π
bằng
A.
41
4
. B.
10
. C.
21
2
. D.
39
4
.
Lời giải
Ta có
2 22
cos sin 9 1 sin sin 9 sin sin 10y xx y xx y xx
= ++⇔=− ++⇔=− ++
.
Đặt
sintx=
, khi đó với
[ ] [ ]
0; 0;1
xt
π
∀∈ ⇒∈
.
Xét hàm số
( )
[ ]
2
10, 0;1ft t t t=− ++ ∈
, đồ thị hàm số là Parabol có tọa độ đỉnh
1 41
;
24
I
.
Ta có bảng biến thiên của hàm số trên
[ ]
0;1
.
Vậy
[ ] [ ]
( )
0; 0;1
41
max max
4
y ft
π
= =
.
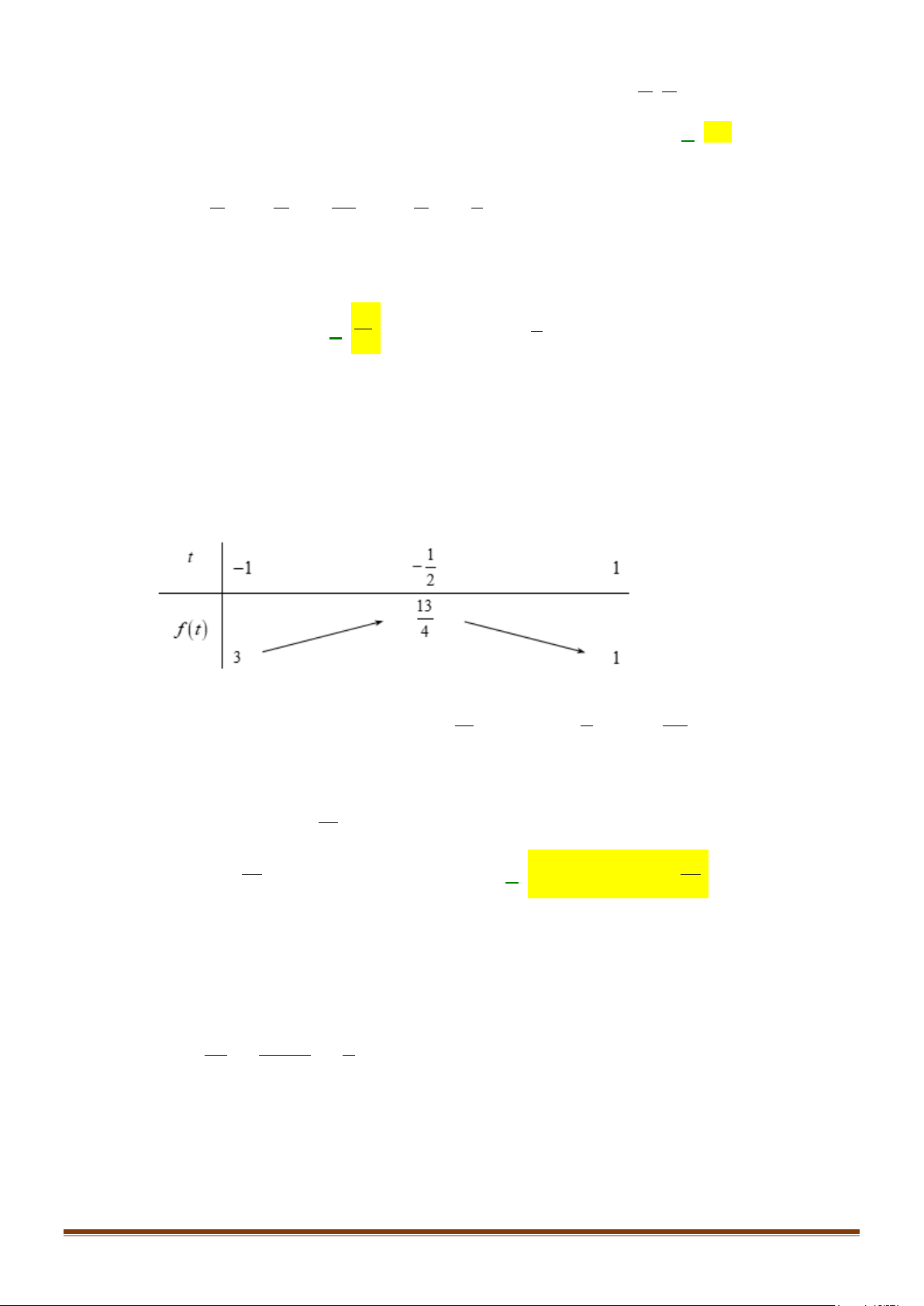
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
Câu 138: Gọi
m
là giá trị nhỏ nhất của hàm số
4cos 2 1
yx= −
trên đoạn
;
36
ππ
−
. Tìm
.
m
A.
5.−
B.
3.
C.
1.
−
D.
3.
−
Lời giải
Ta có:
36
x
ππ
− ≤≤
2
2
33
x
ππ
⇔− ≤ ≤
1
cos 2 1 3 4cos 2 1 3
2
xx⇔− ≤ ≤ ⇔− ≤ − ≤
.
Vậy
3.m = −
Câu 139: Tìm giá trị lớn nhất của hàm số
2
sin cos 2y xx= −+
A.
3
. B.
13
4
. C.
7
4
. D.
1
.
Lời giải
Ta có:
22
sin cos 2 cos cos 3
y xx xx= −+=− −+
Đặt
costx=
,
[ ]
1;1t ∈−
. Khi đó
( )
2
3y ft t t= =− −+
.
Bảng biến thiên hàm số
( )
ft
trên
[ ]
1;1
−
:
Vậy giá trị lớn nhất của hàm số đã cho là
13
4
khi
12
cos 2
23
xxk
π
π
=−⇔=± +
.
Câu 140: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2cos sin 3.y xx= −+
A.
[ ]
1;1
min 4y
−
=
;
[ ]
1;1
41
max .
8
y
−
=
B.
[ ]
1;1
min 2y
−
=
;
[
]
1;1
max 4y
−
=
.
C.
[ ]
1;1
41
min
8
y
−
= −
;
[ ]
1;1
max 2y
−
=
. D.
[ ]
1;1
min 2y
−
=
;
[ ]
1;1
41
max .
8
y
−
=
Lời giải
Ta có
2 22
2cos sin 3 2 2sin sin 3 2sin sin 5y xx y xx y xx= −+⇔=− −+⇔=− −+
Đặt
sin
tx=
, ĐK:
[ ]
1;1t ∈−
, khi đó hàm số có dạng
2
25y tt=− −+
, với
[ ]
1;1t ∈−
Ta có
( )
11
2 2. 2 4
b
a
−
− =− =−⇒
−
bảng biến thiên sau
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Từ bảng biến thiên suy ra
[ ]
1;1
min 2 sin 1yx
−
=⇔=
và
[ ]
1;1
41 1
max sin
84
yx
−
−
=⇔=
Câu 141: Gọi
,Mm
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
sin 2021 3cos2021yx x
= +
.
Tích
.Mm
bằng
A.
4−
. B.
2−
. C.
9−
. D.
1−
.
Lời giải
Ta có
( )
(
)
( )
2
2 22 2
2
sin 2021 3cos2021 1 3 sin 2021 cos 2021
42 2
min 2 , m ax 2 . 4
y x x xx
yy
y m y M Mm
= + ≤+ +
⇒ ≤ ⇔− ≤ ≤
⇒ =−= = = ⇒ =−
Câu 142: Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2cos 5sin 1y xx= ++
trên
5
;
36
ππ
. Khi đó
Mm−
bằng bao nhiêu?
A.
1Mm−=
. B.
11Mm
−=
. C.
1
2
Mm−=
. D.
6
Mm−=
.
Lời giải
Ta có
( )
2 22
2cos 5sin 1 2 1 sin 5sin 1 2sin 5sin 3
y xx x x xx= ++=− ++=− ++
Ta được
2
2sin 5sin 3y xx=− ++
.
Đặt
sintx=
. Với
5
36
x
ππ
≤≤
ta có
1
1
2
t
≤≤
.
Khi đó ta có
( )
2
2 53y ft t t= =− ++
,
1
1
2
t≤≤
.
Ta có bảng biến thiên:
Từ bảng biến thiên ta có:
Giá trị lớn nhất của hàm số đã cho trên
5
;
36
ππ
là
6M =
khi
1t =
hay
2
x
π
=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
Giá trị nhỏ nhất của hàm số đã cho trên
5
;
36
ππ
là
5m =
khi
1
2
t =
hay
5
6
x
π
=
.
Vậy
1
Mm−=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 71
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
1. KHÁI NIỆM PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG
2. PHƯƠNG TRÌNH
sin xm=
( )
1
.
+ Trường hợp
1m >
, phương trình vô nghiệm.
+ Trường hợp
1m ≤
, tồn tại duy nhất một số
;
22
ππ
α
∈−
thỏa mãn
sin m
α
=
. Ta có
sin sinx
α
=
( )
2
,
2
xk
k
xk
α
απ
ππ
= +
⇔∈
=−+
.
Nếu số thực
α
thỏa mãn:
22
sin m
ππ
α
α
−≤≤
=
thì ta viết
arcsin m
α
=
. Ta có
sin xm=
( )
rcsin
arcsin 2
,
a2
x mk
k
x mk
π
ππ
= +
⇔∈
=−+
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUYẾT.
I

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 72
Sưu tầm và biên soạn
Chú ý:
+ Một số trường hợp đặc biệt
(
)
sin 0 ,x xk k
π
=⇔= ∈
(
)
sin 1 2 ,
2
x x kk
π
π
=⇔= + ∈
( )
sin 1 2 ,
2
x x kk
π
π
=−⇔ =− + ∈
+ Phương trình
sin sinx
β
= °
( )
.360
,
180 .360
xk
k
xk
β
β
= °+ °
⇔∈
= °− °+ °
.
+
sin sinuv=
( )
2
,
2u v
u vk
k
k
π
ππ
= +
⇔∈
= −+
.
Trong một công thức về nghiệm của phương trình lượng giác, không được dùng đồng thời hai
đơn vị độ và radian.
3. PHƯƠNG TRÌNH
cos xm=
.
+ Trường hợp
1m >
phương trình vô nghiệm.
+ Trường hợp
1m ≤
, khi đó: Tồn tại duy nhất một số thực
;
22
ππ
α∈ −
sao cho
cos m
α
=
.
Ta có
( )
2
cos cos ,
2
xk
xk
xk
απ
α
απ
= +
=⇔∈
=−+
.
.Nếu số thực
α
thỏa mãn:
0
cos a
απ
α
≤≤
=
thì ta viết
arccos a
α
=
. Ta có:
cos xa
= ⇔
( )
arccos 2 ,
x ak k
π
=±+∈
.
Chú ý:
+ Một số trường hợp đặc biệt
( )
( )
( )
( )
cos 0
2
cos 1 2
cos 1 2 1
;
;
;
x xk
x xk
x xk
k
k
k
π
π
π
π
= ⇔= +
= ⇔=
=−⇔ = +
∈
∈
∈
.
+ Phương trình
( )
.360
cos cos ,
.360
xk
xk
xk
β
β
β
= °+ °
= °⇔ ∈
=− °+ °
.
+
( )
2
cos cos ,
2
u vk
uv k
u vk
π
π
= +
=⇔∈
=−+
( )
1
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 73
Sưu tầm và biên soạn
Trong một công thức nghiệm về nghiệm của phương trình lượng giác, không được dùng đồng
thời hai đơn vị độ và radian.
4. PHƯƠNG TRÌNH
tan xm=
( )
1
VÀ
cot
xm=
( )
2
.
( )
tan 1xm=
( )
cot 2xm=
Điều kiện
xk
2
π
≠ +π
với
k ∈
xk≠π
với
k ∈
Tổng quát
Tồn tại một số
α
sao cho
tanm
α
=
( )
( )
1 tan x tan x k k⇔ = α⇔ =α+ π ∈
Tồn tại một số
α
sao cho
cotm
α
=
( )
( )
cot x2 cot x k
k= α⇔ =α+ π⇔
∈
Chú ý 1:
Đặc biệt:
( )
( )
( )
4
4
tan 0 ;
tan 1 ;
tan 1 ;
k
x xk k
x x kk
xx k
π
π
π
π
π
+
+
=⇔= ∈
=⇔= ∈
=−⇔ =− ∈
( )
( )
( )
2
4
4
cot 0 ;
cot 1 ;
cot 1 ;
k
x x kk
x x kk
xx k
π
π
π
π
π
π
+
+
+
=⇔= ∈
=⇔= ∈
=−⇔ =− ∈
Chú ý 2:
Số thực
α
thỏa mãn:
22
tan m
ππ
α
α
−<<
=
ta viết
arctan m
α
=
.
(
)
1 arctan ,x mk k
π
⇔= + ∈
Số thực
α
thỏa mãn:
0
cot m
απ
α
<<
=
ta viết
arccot m
α
=
.
( )
2 arccot ,x mk k
π
⇔= + ∈
Chú ý 3:
tan x tan
= β°
(
)
x k.180
k
⇔ = β° + °
∈
cot x cot= β°
( )
x k.180
k
⇔ = β° + °
∈
Chú ý 4 : Trong một công thức nghiệm về phương trình lượng giác, không được dùng đồng thời
hai đơn vị độ và radian.
DẠNG 1: PHƯƠNG TRÌNH
sin xm
=
Câu 1: Giải các phương trình sau
a.
3
sin
2
x
= −
b.
1
sin
4
x =
. c.
( )
sin 60x −°
.
d.
sin 1x =
.
e.
4
in 3
3
x = −
. f.
( )
sin 2019 2020 2x +=
.
g.
1
sin 3
2
x =
. h.
3
sin
23 2
x
π
+=−
. i.
( )
2sin 3 1 1x +=
.
LÝ THUYẾT.
I
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 74
Sưu tầm và biên soạn
j.
sin sin 0
3
x
π
+=
. k.
sin 2 sin
23
xx
ππ
+= −
.
l.
2
3
sin 3
4
x
=
. m.
sin 2 cos 0xx−=
.
n.
sin 3 sin 0
xx
+=
. o.
sin cos 2 + 0
3
xx
π
+=
.
Câu 2: Tìm nghiệm của phương trình
1
sin
2
x
= −
trên khoảng .
Câu 3: Tìm nghiệm của phương trình
( )
2sin 40 3
x + °=
trên khoảng
( )
180 ;180−° °
.
Câu 4: Tìm nghiệm của phương trình
sin 3
0
cos 1
x
x
=
+
trên đoạn
[ ]
2 ;4
ππ
.
DẠNG 2: PHƯƠNG TRÌNH
cos
xm=
.
Câu 5: Giải các phương trình sau
a.
2
cos 3
62
x
π
−=−
. b.
( )
2
cos 2
5
x −=
.
c.
(
)
1
cos 2 50
2
x
+ °=
. d.
(1 2cos )(3 cos ) 0xx+ −=
.
e.
cos 3 1
6
x
π
−=
. f.
2cos 1x = −
.
g.
( )
2019.cos 30 2020x + °=
. h.
( )
cos 3 10 1x + °=−
.
i.
sin 3 cos 2 0xx
−=
. j.
(
)
( )
cos cos 2 1x +=
.
Câu 6: Phương trình
2 cos 1
2
x
π
+=
có bao nhiêu nghiệm thỏa mãn
02
x≤ ≤π
?
DẠNG 3. PHƯƠNG TRÌNH
tan
xm=
( )
1
VÀ
cot xm=
( )
2
.
Câu 7: Giải các phương trình sau
a.
2
tan 2 tan
7
x
π
=
. b.
tan 3
2
x
=
.
c.
( )
3
tan 3 30
3
x − °=−
. d.
2
tan 1x
=
.
e.
tan 2 0x =
.
f.
cot 4 3
6
x
π
−=
.
g.
cot 1 cot 1 0
22
xx
− +=
.
h.
tan 2 tan 1
22
xx
ππ
−+ + =
.
i.
( ) ( )
tan 30 .cos 2 150 0xx−° − =
.
j.
( )
( )
3tan 3 2sin 1 0xx+ −=
.
( )
0;
π
( )
1

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 75
Sưu tầm và biên soạn
k.
tan .tan 2 1xx= −
.
l.
tan 4 .cot 2 1xx=
.
m.
sin 2 .cot 0xx=
.
Câu 8: Tìm số nghiệm của phương trình
3
tan tan
11
x
π
=
trên khoảng
;2
4
π
π
.
Câu 9: Giải phương trình
tan x
+=
3
3
Câu 10: Giải phương trình
( )
tan x −=−
0
3
3 30
3
Câu 11: Giải phương trình
tan tanxx
+ + −=
20
63
Câu 12: Giải phương trình
tan cotxx
− − +=
0
63
Câu 13: Giải phương trình
tan x
− −=
33 2 0
3
với
x
−
<<
2
43
Câu 14: Giải phương trình
tan tanxx
++ + =
20
36
.
Câu 15: Giải phương trình
cot cot
xx
− +=
1 10
32
(1)
Câu 16: Giải phương trình
( ) ( )
tan cosxx− −=
00
30 2 150 0
(1)
Câu 17: Giải phương trình
( )
( )
3tan 3 2sin 1 0xx
+ −=
(1).
Câu 18: Giải phương trình
cos cotxx
−=
20
4
(1)
Câu 19:
sin
cos sin
x
xx
+= +
11
2
4
(*) (CĐ CNTP khối A_2007)
Câu 20:
s n2 2cos sin 1
0
tan 3
ix x x
x
+ −−
=
+
(ĐH D-2011)
Câu 21:
( sin ) cos
( sin )( sin )
xx
xx
−
=
+−
12
3
12 1
(*) (ĐH A-2009)
BÀI TẬP TỰ LUẬN TỔNG HỢP.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
1. KHÁI NIỆM PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG
2. PHƯƠNG TRÌNH
sin xm=
( )
1
.
+ Trường hợp
1m >
, phương trình vô nghiệm.
+ Trường hợp
1m ≤
, tồn tại duy nhất một số
;
22
ππ
α
∈−
thỏa mãn
sin m
α
=
. Ta có
sin sinx
α
=
( )
2
,
2
xk
k
xk
α
απ
ππ
= +
⇔∈
=−+
.
Nếu số thực
α
thỏa mãn:
22
sin m
ππ
α
α
−≤≤
=
thì ta viết
arcsin m
α
=
. Ta có
sin xm=
( )
rcsin
arcsin 2
,
a2
x mk
k
x mk
π
ππ
= +
⇔∈
=−+
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
LÝ THUYẾT.
I

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
Chú ý:
+ Một số trường hợp đặc biệt
(
)
sin 0 ,x xk k
π
=⇔= ∈
(
)
sin 1 2 ,
2
x x kk
π
π
=⇔= + ∈
( )
sin 1 2 ,
2
x x kk
π
π
=−⇔ =− + ∈
+ Phương trình
sin sinx
β
= °
( )
.360
,
180 .360
xk
k
xk
β
β
= °+ °
⇔∈
= °− °+ °
.
+
sin sinuv=
( )
2
,
2u v
u vk
k
k
π
ππ
= +
⇔∈
= −+
.
Trong một công thức về nghiệm của phương trình lượng giác, không được dùng đồng thời hai
đơn vị độ và radian.
3. PHƯƠNG TRÌNH
cos xm=
.
+ Trường hợp
1m >
phương trình vô nghiệm.
+ Trường hợp
1m ≤
, khi đó: Tồn tại duy nhất một số thực
;
22
ππ
α∈ −
sao cho
cos m
α
=
.
Ta có
( )
2
cos cos ,
2
xk
xk
xk
απ
α
απ
= +
=⇔∈
=−+
.
.Nếu số thực
α
thỏa mãn:
0
cos a
απ
α
≤≤
=
thì ta viết
arccos a
α
=
. Ta có:
cos xa
= ⇔
( )
arccos 2 ,
x ak k
π
=±+∈
.
Chú ý:
+ Một số trường hợp đặc biệt
( )
( )
( )
( )
cos 0
2
cos 1 2
cos 1 2 1
;
;
;
x xk
x xk
x xk
k
k
k
π
π
π
π
= ⇔= +
= ⇔=
=−⇔ = +
∈
∈
∈
.
+ Phương trình
( )
.360
cos cos ,
.360
xk
xk
xk
β
β
β
= °+ °
= °⇔ ∈
=− °+ °
.
+
( )
2
cos cos ,
2
u vk
uv k
u vk
π
π
= +
=⇔∈
=−+
( )
1
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
Trong một công thức nghiệm về nghiệm của phương trình lượng giác, không được dùng đồng
thời hai đơn vị độ và radian.
4. PHƯƠNG TRÌNH
tan xm=
( )
1
VÀ
cot
xm=
( )
2
.
( )
tan 1xm=
( )
cot 2xm=
Điều kiện
xk
2
π
≠ +π
với
k ∈
xk≠π
với
k ∈
Tổng quát
Tồn tại một số
α
sao cho
tanm
α
=
( )
( )
1 tan x tan x k k⇔ = α⇔ =α+ π ∈
Tồn tại một số
α
sao cho
cotm
α
=
( )
( )
cot x2 cot x k
k= α⇔ =α+ π⇔
∈
Chú ý 1:
Đặc biệt:
( )
( )
( )
4
4
tan 0 ;
tan 1 ;
tan 1 ;
k
x xk k
x x kk
xx k
π
π
π
π
π
+
+
=⇔= ∈
=⇔= ∈
=−⇔ =− ∈
( )
( )
( )
2
4
4
cot 0 ;
cot 1 ;
cot 1 ;
k
x x kk
x x kk
xx k
π
π
π
π
π
π
+
+
+
=⇔= ∈
=⇔= ∈
=−⇔ =− ∈
Chú ý 2:
Số thực
α
thỏa mãn:
22
tan m
ππ
α
α
−<<
=
ta viết
arctan m
α
=
.
(
)
1 arctan ,x mk k
π
⇔= + ∈
Số thực
α
thỏa mãn:
0
cot m
απ
α
<<
=
ta viết
arccot m
α
=
.
( )
2 arccot ,x mk k
π
⇔= + ∈
Chú ý 3:
tan x tan
= β°
(
)
x k.180
k
⇔ = β° + °
∈
cot x cot= β°
( )
x k.180
k
⇔ = β° + °
∈
Chú ý 4 : Trong một công thức nghiệm về phương trình lượng giác, không được dùng đồng thời
hai đơn vị độ và radian.
DẠNG 1: PHƯƠNG TRÌNH
sin xm
=
Câu 1: Giải các phương trình sau
a.
3
sin
2
x
= −
b.
1
sin
4
x =
. c.
( )
sin 60x −°
.
d.
sin 1x =
.
e.
4
in 3
3
x = −
. f.
( )
sin 2019 2020 2x +=
.
g.
1
sin 3
2
x =
. h.
3
sin
23 2
x
π
+=−
. i.
( )
2sin 3 1 1x +=
.
LÝ THUYẾT.
I
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
j.
sin sin 0
3
x
π
+=
. k.
sin 2 sin
23
xx
ππ
+= −
.
l.
2
3
sin 3
4
x
=
. m.
sin 2 cos 0xx−=
.
n.
sin 3 sin 0
xx
+=
. o.
sin cos 2 + 0
3
xx
π
+=
.
Lời giải
a.
( )
2
3
3
sin sin sin
4
23
2
3
xk
xx k
xk
π
π
π
π
π
=−+
=−⇔ = −⇔ ∈
= +
.
b.
( )
1
sin 2
4
1
sin
4
1
sin 2
4
x arc k
xk
x arc k
π
ππ
= +
=⇔∈
=−+
.
c.
(
) (
)
sin
1
sin 60
2
60 sin30xx − °= ⇔ − °= °
( ) ( )
60 30 360 90 360
60 150 360 210 360
x k xk
kk
x k xk
− °= °+ ° = °+ °
⇔ ∈⇔ ∈
− °= °+ ° = °+ °
.
d.
(
)
sin 1 2
2
x x kk
π
π
=⇔= + ∈
.
e. Ta có
[ ]
4
sin3 1;1 sin 3
3
xx∈− ⇒ =−
vô nghiệm.
f. Ta có:
( )
[ ]
( )
sin 2019 2020 1;1 sin 2019 2020 2xx+ ∈− ⇒ + =
vô nghiệm
g.
( )
2
32
1
6 18 3
sin 3
5 52
2
32
sin 3 si
6 83
6
1
n
k
xk x
x x k
k
xkx
π ππ
π
ππ
π
π
π
=+=+
=⇔⇔ ⇔ ∈
=+=+
=
.
h.
( )
2
3
23 3
sin sin sin
4
23 2 23 3
2
23 3
x
k
xx
k
x
k
ππ
π
π ππ
ππ
π
+=−+
+=−⇔ += −⇔ ∈
+= +
.
( ) ( )
2
4
2
4
23
3
24
2
2
x
k
xk
kk
x
xk
k
π
π
π
π
ππ
ππ
=−+
=−+
⇔ ∈⇔ ∈
= +
= +
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
i.
( ) ( )
( ) ( )
31 2
1
2sin 3 1 1 sin 3 1 sin 3 1 sin
5
26
31
6
2
6
xk
xx x k
xk
π
π
π
π
π
+= +
+=⇔ +=⇔ += ⇔ ∈
+= +
.
( )
(
)
12
3 12
6 18 3 3
5 512
3 12
6 18 3 3
k
xk x
kk
k
xk x
π ππ
π
π ππ
π
= −+ = − +
⇔ ∈⇔ ∈
= −+ = − +
.
j.
( )
sin sin 0 sin
33
x x kk
ππ
π
+ =⇔ += ∈
.
Vì
[ ]
sin 1;1
3
x
π
+ ∈−
và
k ∈
nên ta có
0k =
.
( ) ( )
sin 0
33 3
x x kk x kk
ππ π
ππ
+ =⇔+ = ∈ ⇔=− + ∈
⇒
.
k. Ta có
sin 2 sin
23
xx
ππ
+= −
( )
22
23
22
23
x xk
k
x xk
ππ
π
ππ
ππ
+=−+
⇔∈
+=−− +
( )
5
2
6
52
18 3
xk
k
k
x
π
π
ππ
=−+
⇔∈
= +
.
l. Ta có
2
3
sin 3
4
x =
3
sin 3
2
3
sin 3
2
x
x
=
⇔
= −
( )
32
3
2
32
3
32
3
4
32
3
xk
xk
k
xk
xk
π
π
π
π
π
π
π
π
= +
= +
⇔∈
=−+
= +
(
)
2
93
22
93
2
93
42
93
xk
xk
k
xk
xk
ππ
ππ
ππ
ππ
= +
= +
⇔∈
=−+
= +
m. Ta có
sin 2 cos 0xx−=
sin 2 cosxx⇔=
sin 2 sin
2
xx
π
⇔= −

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
( )
22
2
22
2
x xk
k
x xk
π
π
π
π
= −+
⇔∈
= ++
( )
2
63
2
2
xk
k
xk
ππ
π
π
= +
⇔∈
= +
.
n. Ta có
sin 3 sin 0xx+=
sin 3 sinxx⇔=−
( )
sin 3 sinxx⇔=−
( )
32
32
x xk
k
x xk
π
ππ
=−+
⇔∈
= ++
( )
2
2
xk
k
xk
π
π
π
=
⇔∈
= +
( )
2
xk k
π
⇔= ∈
o. Ta có
sin cos 2 + 0
3
xx
π
+=
sin cos 2 +
3
xx
π
⇔=−
sin sin 2
6
xx
π
⇔= −
( )
22
6
7
22
6
xx k
k
x xk
π
π
π
π
= −+
⇔∈
= −+
( )
2
6
72
18 3
xk
k
xk
π
π
ππ
= −
⇔∈
= +
.
Câu 2: Tìm nghiệm của phương trình
1
sin
2
x = −
trên khoảng .
Lời giải
Ta có
( )
2
1
6
sin
7
2
2
6
xk
xk
xk
π
π
π
π
=−+
=−⇔ ∈
= +
.
Theo đề bài:
17
02
6 12 12
kk
π
ππ
<−+ <⇔ << ⇒
không tồn tại
k
.
7 71
02
6 12 12
kk
π
ππ
< + < ⇔− < <− ⇒
không tồn tại
k
.
Vậy phương trình đã cho vô nghiệm.
Câu 3: Tìm nghiệm của phương trình
( )
2sin 40 3x + °=
trên khoảng
( )
180 ;180−° °
.
Lời giải
Ta có
( )
2sin 40 3x + °=
( )
3
sin 40
2
x⇔ + °=
( )
0;
π

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
(
)
40 60 360
40 120 360
xk
k
xk
+ °= °+ °
⇔∈
+ °= °+ °
(
)
20 360
80 360
xk
k
xk
= °+ °
⇔∈
= °+ °
Theo đề bài:
54
180 20 360 180 0
99
k kk
− °< °+ °< °⇔− < < ⇒ =
.
13 5
180 80 360 180 0
18 18
k kk− °< °+ °< °⇔− < < ⇒ =
.
Vậy phương trình có hai nghiệm
20x = °
và
80x = °
.
Câu 4: Tìm nghiệm của phương trình
sin 3
0
cos 1
x
x
=
+
trên đoạn
[ ]
2 ;4
ππ
.
Lời giải
Điều kiện:
( )
cos 1 2x x ll
ππ
≠− ⇔ ≠ + ∈
Khi đó
( ) ( )
sin 3
0sin303
cos 1 3
x
x xk k xk k
x
π
π
=⇔ =⇔ = ∈ ⇔= ∈
+
Kết hợp điều kiện ta được:
(
)
2
3
2
3
xm
x mm
xm
π
π
π
π
π
=
=+∈
= +
.
Vì
[ ]
2 ;4x
ππ
∈
nên
7 8 10 11
2; ; ; ;
33 3 3
x
ππ π π
π
∈
.
DẠNG 2: PHƯƠNG TRÌNH
cos
xm=
.
Câu 5: Giải các phương trình sau
a.
2
cos 3
62
x
π
−=−
. b.
( )
2
cos 2
5
x −=
.
c.
( )
1
cos 2 50
2
x
+ °=
. d.
(1 2cos )(3 cos ) 0
xx+ −=
.
e.
cos 3 1
6
x
π
−=
. f.
2cos 1x = −
.
g.
( )
2019.cos 30 2020x + °=
. h.
( )
cos 3 10 1x + °=−
.
i.
sin 3 cos 2 0xx−=
. j.
(
)
( )
cos cos 2 1
x +=
.
Lời giải
( )
1
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
a. Ta có
2
cos 3
62
x
π
−=−
3
cos 3 cos
64
x
ππ
−=
⇔
(
)
3
32
64
3
32
64
k
k
k
x
x
ππ
π
ππ
π
⇔∈
−= +
−=− +
( )
11 2
36 3
72
36 3
k
x
x
k
k
ππ
ππ
⇔∈
= +
−
= +
.
b. Ta có
( )
2
cos 2
5
x −=
2
arc
2 cos 2
5
kx
π
⇔
=±+
−
( )
2
arccos 2 2
5
kkx
π
=± ++ ∈
⇔
.
c. Ta có
( )
1
cos 2x 50
2
+ °=
(
)
cos 2 50 cos60
x⇔
+ °= °
( )
2 50 60 .360
2 50 60 .360
xk
k
xk
+ °= °+ °
⇔∈
+ °=− °+ °
( )
5 .180
55 .180
xk
k
xk
= °+ °
⇔∈
=− °+ °
.
d. Ta có
( )( )
1 2cos 3 co 0sxx+−=
1 2cos 0
3 cos 0
x
x
+=
⇔
−=
( )
12
cos 2
23
xxkk
π
π
=−⇔=± +⇔ ∈
.
e. Ta có
cos
3
1
6
x
π
−=
(
)
( )
2
2
6 18
3
3
k
kk x
x k
π ππ
π
⇔ − = ∈ ⇔= + ∈
f. Ta có
2cos 1x = −
( )
12
cos 2
23
xxkk
π
π
=−⇔=± +⇔ ∈
.
g. Ta có
( )
2019.cos 30 2020x +=°
⇔
( )
2020
cos 30 1
2019
x += >°
( vô nghiệm).
h. Ta có
( )
cos 3 10 1x + ° = −
⇔
( )
.36
170
3 10 180 0
12
3
0.kx k
x
k
°
°= °+ °⇔ = + °
+ ∈
.
i. Ta có
sin 3 cos 2 0xx
−=
sin 3 sin 2
2
xx
π
⇔= −
( ) ( )
2
3 22
10 5
2
3 22
2
2
2
k
x
x xk
kk
x xk
xk
ππ
π
π
π
π
π
π
= +
=−+
⇔ ∈⇔ ∈
=++
= +
.
j. Ta có
( )
cos cos x 2 1+=
( ) ( )
cos 2 2x kk
π
⇔ += ∈
Vì:
( )
1 cos 2 1x−≤ + ≤
nên
0k =
.
Khi đó:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
( )
( )
cos 2 0 2 2 , .
22
x x m x mm
ππ
ππ
+ =⇔+= + ⇔ = −+ ∈
Câu 6: Phương trình
2 cos 1
2
x
π
+=
có bao nhiêu nghiệm thỏa mãn
02x≤ ≤π
?
Lời giải
Ta có
2 cos 1
3
x
π
+=
1
cos
3
2
x
π
⇔ +=
( ) ( )
2
2
34
12
7
22
3 4 12
xk
xk
kk
x k xk
ππ
π
π
π
ππ π
ππ
+=+
=−+
⇔ ∈⇔ ∈
+=−+ =− +
Với
02x
π
≤≤
ta có
1 25
0 22
1
12 24 24
kk
k
kk
π
ππ
≤− + ≤ ≤ ≤
⇔ ⇔=
∈∈
nghiệm là
23
12
x
π
=
.
7 7 31
0 22
1
12 24 24
kk
k
kk
π
ππ
≤− + ≤ ≤ ≤
⇔ ⇔=
∈∈
17
12
x
π
⇒=
.
Vậy phương trình đã cho có hai nghiệm thỏa mãn
02x
π
≤≤
.
DẠNG 3. PHƯƠNG TRÌNH
tan xm=
( )
1
VÀ
cot xm=
( )
2
.
Câu 7: Giải các phương trình sau
a.
2
tan 2 tan
7
x
π
=
. b.
tan 3
2
x
=
.
c.
(
)
3
tan 3 30
3
x − °=−
. d.
2
tan 1
x
=
.
e.
tan 2 0x =
.
f.
cot 4 3
6
x
π
−=
.
g.
cot 1 cot 1 0
22
xx
− +=
.
h.
tan 2 tan 1
22
xx
ππ
−+ + =
.
i.
(
) ( )
tan 30 .cos 2 150 0xx−° − =
.
j.
( )
( )
3tan 3 2sin 1 0xx+ −=
.
k.
tan .tan 2 1xx= −
.
l.
tan 4 .cot 2 1
xx
=
.
m.
sin 2 .cot 0xx=
.
Lời giải
a. Ta có
2
tan 2 tan
7
x
π
=
2
2
7
xk
π
π
⇔= +
,
72
x kk
ππ
⇔= + ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
b. Ta có
tan 3
2
x
=
tan tan
23
x
π
⇔=
23
x
k
π
π
⇔=+
2
2,
3
x kk
π
π
⇔= + ∈
.
c. Ta có
( )
3
tan 3 30
3
x − °=−
( ) ( )
tan 3 30 tan 30
x
⇔ − °= − °
3 30 30 180xk⇔ − °=− °+ °
60 ,xk k⇔= °∈
.
d. Ta có
2
tan 1
x
=
tan 1x⇔=±
,
4
x kk
π
π
⇔=±+ ∈
,
42
x kk
ππ
⇔= + ∈
.
e. Ta có
tan 2 0x =
2xk
π
⇔=
,
2
xk k
π
⇔= ∈
.
f. Ta có
cot 4 3
6
x
π
−=
cot 4 cot
66
x
ππ
⇔ −=
4
66
xk
ππ
π
⇔ −=+
,
12 4
x kk
ππ
⇔= + ∈
.
g. Điều kiện:
sin 0 2 ,
22
xx
l xl l
ππ
≠⇔ ≠ ⇔≠ ∈
.
Ta có
cot 1 cot 1 0
22
xx
− +=
cot 1
2
cot 1
2
x
x
=
⇔
= −
24
24
x
k
x
k
π
π
π
π
= +
⇔
=−+
( )
2
2
,
2
2
xk
k TM
xk
π
π
π
π
= +
⇔∈
=−+
.
h. Ta có
tan 2 tan 1
22
xx
ππ
−+ + =
cot 2cot 1
xx⇔− =
cot 1x⇔=−
4
xk
π
π
⇔=−+
,
k ∈
.
Vậy phương trình đã cho có tập nghiệm
,
4
S kk
π
π
=−+ ∈
.
i. Điều kiện
( )
cos 30 0 120 180x xl− ≠⇔≠ +
,
l
∈
.
Với điều kiện trên, phương trình đã cho tương đương với
( ) ( )
tan 30 cos 2 150 0xx°−−° =
( )
( )
tan 30 0
cos 2 150 0
x
x
°
⇔
°
−=
−=
30 180
2 150 90 180
xk
xk
°−=
⇔
°
°−=+°°
30 180
120 90
xk
xk
= +
⇔
= +
°
°°
°
,
k ∈
.
So sánh với điều kiện, phương trình đã cho có tập nghiệm
{ }
30 180 ,S kk°°=+∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
j. Điều kiện
cos 0
2
x xl
π
π
≠⇔≠ +
,
l
∈
.
Với điều kiện trên, phương trình đã cho tương đương với
3tan 3 0
2sin 1 0
x
x
+=
−=
3
tan
3
1
sin
2
x
x
= −
⇔
=
6
2
6
5
2
6
xk
xk
xk
π
π
π
π
π
π
=−+
⇔=+
= +
6
2
6
xk
xk
π
π
π
π
=−+
⇔
= +
,
k ∈
.
So sánh với điều kiện, phương trình đã cho có tập nghiệm
; 2,
66
S k kk
ππ
ππ
=−+ + ∈
.
k. Điều kiện
cos 0
2
cos 2 0
42
xl
x
x
xl
π
π
ππ
≠+
≠
⇔
≠
≠+
,
l ∈
.
Với điều kiện trên, phương trình đã cho tương đương với
1
tan 2
tan
x
x
= −
tan 2 cot
xx⇔=−
tan 2 tan
2
xx
π
⇔= +
2
2
x xk
π
π
⇔ = ++
2
xk
π
π
⇔ = +
,
k ∈
.
So sánh với điều kiện, phương trình đã cho vô nghiệm.
l. Điều kiện
sin 2 0
2
cos 4 0
84
xl
x
x
xl
π
ππ
≠
≠
⇔
≠
≠+
,
l
∈
.
Với điều kiện trên, phương trình đã cho tương đương với
1
tan 4
cot 2
x
x
=
42
x xk
π
⇔=+
2
xk
π
⇔=
,
k ∈
.
So sánh với điều kiện, phương trình đã cho vô nghiệm.
m. Điều kiện:
sin 0 ,x xl l
π
≠⇔≠ ∈
.
Với điều kiện trên, phương trình đã cho tương đương với
2
cos
2sin cos 0
si
cos 0 c 0
n
os
x
x xxx
x
= ⇔ =⇔=
2
xk
π
π
⇔= +
,
k ∈
.
So sánh với điều kiện, phương trình đã cho có tập nghiệm
,
2
S kk
π
π
=+∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
Câu 8: Tìm số nghiệm của phương trình
3
tan tan
11
x
π
=
trên khoảng
;2
4
π
π
.
Lời giải
Ta có
3
tan tan
11
x
π
=
3
11
xk
π
π
⇔= +
,
k
∈
.
Với
;2
4
x
π
π
∈
, ta có
3 1 19
2
4 11 44 11
kk
ππ
ππ
< + < ⇔− < <
suy ra
{ }
0;1k ∈
.
Vậy trên khoảng
;2
4
π
π
, phương trình đã cho có hai nghiệm.
Câu 9: Giải phương trình
tan
x
+=
3
3
Giải:
Ta có:
tan x
+=
3
3
⇔
tan tanx
+=
33
⇔
xk+=+
33
⇔
,.xkk= ∈
Vậy phương trình có một họ nghiệm
,.
xkk= ∈
Câu 10: Giải phương trình
( )
tan x −=−
0
3
3 30
3
Giải:
Ta có
( )
tan x −=−
0
3
3 30
3
⇔
( )
( )
tan tanx −=−
00
3 30 30
⇔
,.xk k= ∈
0
60
Vậy phương trình có một họ nghiệm
,.
xk k
= ∈
0
60
Câu 11: Giải phương trình
tan tanxx
+ + −=
20
63
Giải:
Điều kiện
,.
m
x mx
m
xm x m
+≠+ ≠+
⇔∈
− ≠ + ≠− −
2
62 6 2
32 6
PT
tan tan tan tan , .x x x x x kk
−
⇔ +=− −⇔ += −+⇔=+ ∈
22
63 63 2
Kết hợp với điều kiện ta suy ra phương trình có một họ nghiệm
,.x kk
−
=+∈
2
Câu 12: Giải phương trình
tan cotxx
− − +=
0
63
BÀI TẬP TỰ LUẬN TỔNG HỢP.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
Giải:
Điều kiện
,.
x mx m
x mm
xm x m
−≠+ ≠ +
⇔ ⇔≠ + ∈
+ ≠ ≠− +
2
2
62 3
3
33
PT
tan cot tan tan , .
k
x x x xx k
⇔ −= +⇔ −= −⇔=+ ∈
6 3 6 6 62
Kết hợp với điều kiện ta được
,x kk=+∈
6
.
Câu 13: Giải phương trình
tan
x
− −=
33 2 0
3
với
x
−
<<
2
43
Giải:
Phương trình tương đương với
tan , .
k
x xk
− = ⇔= + ∈
23
3 32
kk
xVì
k
−− − −
<<⇔<+<⇔ <<⇔<<
2 2 7 72
4 3 4 3 2 3 12 2 3 6 3
Do
k ∈
nên
{ }
;k
∈−10
.
Với
k = −1
thì
x
−
=
6
, với
k = 0
thì
x =
3
.
Vậy
x
−
=
6
và
x =
3
thỏa mãn yêu cầu bài toán.
Câu 14: Giải phương trình
tan tanxx
++ + =
20
36
.
Đáp số
,.
k
xk
−
=+∈
63
Câu 15: Giải phương trình
cot cot
xx
− +=
1 10
32
(1)
Điều kiện:
( )
sin
,
sin
xx
k
xk
k
x x xk
k
≠≠
≠
⇔⇔ ∈
≠
≠≠
0
3
33
2
0
22
( ) ( )
cot cot
,
cot cot
x xx
k xk
k
x xx
kx k
−= = = + = +
⇔ ⇔⇔ ⇔ ∈
+= =− =−+ =−+
3
10 1 3
3 3 34 4
1
10 1 2
2 2 24 2
So với điều kiện các nghiệm này thỏa.
Vậy phương trình có nghiệm:
( )
,,x kx k k
= + =−+ ∈
3
32
42
.
Câu 16: Giải phương trình
( ) ( )
tan cosxx− −=
00
30 2 150 0
(1)
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
Điều kiện:
( )
( )
cos ,x x k x kk− ≠⇔−≠+ ⇔≠ + ∈
0 000 00
30 0 30 90 180 120 180
.
(
)
(
)
(
)
(
)
tan
,
cos
xk xk
x
x k x kk
x
x k xk
−= =+
−=
⇔ ⇔ − = + ⇔= + ∈
−=
− =−+ = +
0 0 00
0
00 0 0 0
0
00 0 0 0
30 180 30 180
30 0
1 2 150 90 360 120 180
2 150 0
2 150 90 360 30 180
So với điều kiện nghiệm
xk= +
00
120 180
loại.
Vậy phương trình có nghiệm:
( )
,x kk=+∈
00
30 180
Câu 17: Giải phương trình
( )
( )
3tan 3 2sin 1 0xx+ −=
(1).
Điều kiện
( )
cos ,x x kk≠⇔≠ + ∈
0
2
.
( ) ( )
tan
tan
,
sin
sin
xk
x
x
x kk
x
x
xk
= +
= −
+=
⇔ ⇔ ⇔=+ ∈
−=
=
= +
5
6
3
3 30
3
12
6
2 10 1
5
2
2
6
So với điều kiện các nghiệm này thỏa.
Vì tập các giá trị
,x kk
=+∈
5
2
6
là tập con của tập các giá trị
,x kk
=+∈
5
6
.
Vậy phương trình có các nghiệm:
( )
,,
x kx k k=+=+ ∈
5
2
66
Câu 18: Giải phương trình
cos cotxx
−=
20
4
(1)
Điều kiện
( )
sin ,x x k x kk
− ≠⇔− ≠ ⇔≠ + ∈
0
44 4
( )
cos
cot
k
x
xk x
x
x kx k
=
=+=+
⇔⇔⇔
−=
−=+ = +
20
2
2 42
1
0
3
4
42 4
Câu 19:
sin
cos sin
x
xx
+= +
11
2
4
(*) (CĐ CNTP khối A_2007)
Điều kiện:
cos , sinxx≠≠00
Với điều kiện trên,
(*) (sin cos ) sin (cos sin )x x xx x⇔ += +22
(sin cos )( sin )xx x⇔+ − =1 20
sin cos tanxx x⇔+ =⇔ =−01

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
,.x kkZ
⇔=−+ ∈
4
.
So với điều kiện, nghiệm của phương trình là:
,.
x kkZ=−+ ∈
4
Câu 20:
s n2 2cos sin 1
0
tan 3
ix x x
x
+ −−
=
+
(ĐH D-2011)
Điều kiện:
tan
cos
x
x
≠−
≠
3
0
Với điều kiện trên, phương trình
s n2 cos sinix x x⇔ + − −=
2 10
sin cos cos (sin )
xx x x⇔ + − +=
2 2 10
(
)
cos sin (sin )xx x⇔ +− +=2 1 10
( )
sin ( cos )xx⇔ + −=12 1 0
cos
sin
xk
x
x
xk
=±+
=
⇔⇔
= −
=−+
1
2
3
2
1
2
2
So với điều kiện, nghiệm của phương trình là
()
x kk=+∈
2
3
Câu 21:
( sin ) cos
( sin )( sin )
xx
xx
−
=
+−
12
3
12 1
(*) (ĐH A-2009)
Điều kiện:
sin
sin
x
x
+≠
−≠
12 0
10
(1)
Với điều kiện trên,
(*) ( sin )cos ( sin )( sin )
xx x x⇔− = + −1 2 31 2 1
cos sin sin cos
x xx x⇔− = +3 2 32
cos cosxx
⇔ += −
2
36
,.
x xk x k
kZ
x xk x k
+= −+ =+
⇔ ⇔∈
+=−++ =− +
22 2
36 2
2
22
3 6 18 3
Kết hợp với điều kiện (1), nghiệm phương trình là
xk
=−+
2
18 3
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 76
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
DẠNG 1. PHƯƠNG TRÌNH
sin
xm
=
Câu 1: Phương trình
2.sin 1 0x −=
có tập nghiệm là
A.
5
2; 2,
66
S k kk
ππ
ππ
=+ +∈
. B.
2
2; 2,
33
S k kk
ππ
ππ
=+ −+ ∈
.
C.
2; 2,
66
S k kk
ππ
ππ
= + −+ ∈
. D.
1
2,
6
S kk
π
=+∈
.
Câu 2: Tất cả các nghiệm của phương trình
sin sin
3
x
π
=
là
A.
( )
2
3
2
3
xk
k
xk
π
π
π
π
= +
∈
=−+
. B.
( )
2
3
2
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
.
C.
( )
3
x kk
π
π
=+∈
. D.
( )
3
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
.
Câu 3: Nghiệm của phương trình
2sin 1 0x +=
là
A.
7
2; 2.
66
x kx k
ππ
ππ
=+=+
B.
7
2; 2.
66
x kx k
ππ
ππ
=−+ = +
C.
2; 2.
8
x kx k
π
ππ π
=+=+
D.
5
2; 2.
66
x kx k
ππ
ππ
=−+ = +
Câu 4: Nghiệm của phương trình
sin 1 0
3
x
π
− +=
là
A.
7
2
6
xk
π
π
= +
,
k ∈
. B.
5
6
xk
π
π
= +
,
k ∈
.
C.
7
6
xk
π
π
=−+
,
k ∈
. D.
5
2
6
xk
π
π
= +
,
k ∈
.
Câu 5: Phương trình
2
0
33
sin
x
π
−=
có nghiệm là
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TRẮC NGHIỆM.
II
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 77
Sưu tầm và biên soạn
A.
( )
3
.
x kk
π
π
=+∈
B.
( )
.xk k
π
= ∈
C.
(
)
23
32
.
k
xk
ππ
=+∈
D.
( )
3
22
.
k
xk
ππ
=+∈
Câu 6: Nghiệm của phương trình
( )
sin sin 2
x
= −
là:
A.
22
22
xk
xk
π
π
=−+
= +
,
k ∈
. B.
22
22
xk
xk
π
ππ
=−+
= −+
,
k
∈
.
C.
2
2
xk
xk
π
ππ
=−+
= −+
,
k ∈
. D.
22
22
xk
xk
π
ππ
=−+
= ++
,
k ∈
.
Câu 7: Họ nghiệm của phương trình
sin sin
5
=
x
π
là
A.
5
,,
4
5
= +
∈
= +
xk
kl
xl
π
π
π
π
. B.
2
5
,,
4
2
5
= +
∈
= +
xk
kl
xl
π
π
π
π
.
C.
2
5
,,
2
5
= +
∈
=−+
xk
kl
xl
π
π
π
π
. D.
5
,,
5
= +
∈
=−+
xk
kl
xl
π
π
π
π
.
Câu 8: Phương trình
sin 2 0
3
x
π
−=
có nghiệm là
A.
,
π
= ∈xkk
. B.
,
62
ππ
=+∈
k
xk
. C.
,
2
π
π
=+∈x kk
. D.
,
3
π
π
=+∈x kk
.
Câu 9: Tập nghiệm của phương trình
5
sin sin
3
x
π
=
là
A.
52
2; 2;
33
S k kk
ππ
ππ
−
=+ +∈
B.
57
2; 2;
33
S k kk
ππ
ππ
=+ +∈
.
C.
55
2; 2;
33
S k kk
ππ
ππ
−
=+ +∈
. D.
52
;;
33
S k kk
ππ
ππ
−
=+ +∈
.
Câu 10: Phương trình
sin sin80x = °
có tập nghiệm là
A.
{ }
80 360 ,100 360 ,= °+ ° °+ ° ∈S k kk
. B.
{ }
80 360 , 80 360 ,= °+ ° − °+ ° ∈S k kk
.
C.
{ }
40 360 ,140 360 ,= °+ ° °+ ° ∈S k kk
. D.
{ }
80 180 ,100 180 ,= °+ ° °+ ° ∈S k kk
.
Câu 11: Tập nghiệm của phương trình
sin 2 1x = −
là
A.
2,
4
S kk
π
π
=−+ ∈
. B.
,
2
S kk
π
π
=−+ ∈
.
C.
,
4
S kk
π
π
=+∈
. D.
,
4
S kk
π
π
=−+ ∈
.
Câu 12: Họ nghiệm của phương trình
1
sin
2
x =
là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 78
Sưu tầm và biên soạn
A.
2
3
,
2
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
. B.
2
6
,
5
2
6
xk
k
xk
π
π
π
π
= +
∈
= +
.
C.
,xkk
π
= ∈
. D.
1
2
2
,
1
2
2
xk
k
xk
π
ππ
= +
∈
=−+
.
Câu 13: Nghiệm của phương trình
sin 1
2
x
=
là
A.
4,x kk
ππ
=+∈
. B.
2,xk k
π
= ∈
. C.
2,x kk
ππ
=+∈
. D.
2,
2
x kk
π
π
=+∈
.
Câu 14: Phương trình
sin 1
3
x
π
−=
có nghiệm là
A.
2
3
xk
π
π
= +
. B.
5
6
xk
π
π
= +
. C.
5
2
6
xk
π
π
= +
. D.
2
3
x
π
π
= +
.
Câu 15: Tìm nghiệm của phương trình
sin 2 1x =
.
A.
2
2
xk
π
π
= +
. B.
4
xk
π
π
= +
. C.
2
4
xk
π
π
= +
. D.
2
k
x
π
=
.
Câu 16: Tìm nghiệm của phương trình
2sin 3 0x −=
.
A.
x ∈∅
. B.
(
)
3
arcsin 2
2
3
arcsin 2
2
xk
k
xk
π
ππ
= +
∈
=−+
.
C.
( )
3
arcsin 2
2
3
arcsin 2
2
xk
k
xk
π
π
= +
∈
=−+
. D.
x ∈
.
Câu 17: Phương trình
3
sin
2
x =
có nghiệm là:
A.
2
3
xk
π
π
=±+
. B.
3
xk
π
π
= +
. C.
6
5
6
xk
xk
π
π
π
π
= +
= +
. D.
2
3
2
2
3
xk
xk
π
π
π
π
= +
= +
.
Câu 18: Tập nghiệm của phương trình
sin sin 30x = °
là
A.
{ }
30 2 |S kk
π
= °+ ∈
∪
{ }
150 2 |kk
π
°+ ∈
.
B.
{ }
30 2 |S kk
π
= ± °+ ∈
.
C.
{ }
30 360 |S kk= ± °+ ° ∈
.
D.
{ }
30 360 |Sk= °+ ° ∈
∪
{ }
150 360 | k°+ ° ∈
.
Câu 19: Tìm tất cả các nghiệm của phương trình
sin 1
6
x
π
+=
.
A.
3
xk
π
π
= +
( )
k ∈
. B.
2
6
xk
π
π
=−+
( )
k ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 79
Sưu tầm và biên soạn
C.
2
3
xk
π
π
= +
( )
k ∈
. D.
5
2
6
xk
π
π
= +
( )
k ∈
.
Câu 20: Phương trình
2sin 1 0x −=
có tập nghiệm là:
A.
5
2; 2,
66
S k kk
ππ
ππ
=+ +∈
. B.
2
2; 2,
33
S k kk
ππ
ππ
=+ −+ ∈
.
C.
2; 2,
66
S k kk
ππ
ππ
= + −+ ∈
. D.
1
2,
2
S kk
π
=+∈
.
Câu 21: Phương trình
2sin 1 0
x +=
có nghiệm là:
A.
2
6
7
2
6
xk
xk
π
=−+ π
π
=− +π
B.
2
6
7
2
6
xk
xk
π
=−+ π
π
= +π
C.
2
6
5
2
6
xk
xk
π
=+π
π
= +π
D.
6
7
6
xk
xk
π
= +π
π
=− +π
Câu 22: Phương trình
2sin 3 0x
−=
có tập nghiệm là:
A.
2,
6
kk
π
π
±+ ∈
. B.
2,
3
kk
π
π
±+ ∈
.
C.
5
2, 2,
66
k kk
ππ
ππ
+ +∈
. D.
2
2, 2,
33
k kk
ππ
ππ
+ +∈
.
Câu 23: Tổng các nghiệm của phương trình
( )
2sin 40 3
x
+ °=
trên khoảng
( )
180 ;180−° °
là
A.
20°
. B.
100°
. C.
80°
. D.
120°
.
Câu 24: Tìm tổng các nghiệm của phương trình
cos 5 cos 2
63
xx
ππ
−= −
trên
[
]
0;
π
.
A.
47
18
π
. B.
4
18
π
. C.
45
18
π
. D.
7
18
π
.
Câu 25: Số nghiệm phương trình
sin 3
0
cos 1
x
x
=
+
thuộc đoạn
[ ]
2 ;4
ππ
là
A.
7
. B.
6
. C.
4
. D.
5
.
Câu 26: Phương trình
2sin 3 0x +=
có tổng nghiệm dương nhỏ nhất và nghiệm âm lớn nhất bằng
A.
4
3
π
. B.
2
π
. C.
3
π
. D.
π
.
Câu 27: Với những giá trị nào của
x
thì giá trị của các hàm số
3sinyx=
và
sin
yx=
bằng nhau?
A.
( )
2
2
4
xk
k
xk
π
π
π
=
∈
= +
. B.
( )
4
xk k
π
= ∈
.
C.
( )
2
xk k
π
= ∈
. D.
( )
42
.
xk
k
xk
π
ππ
=
∈
= +
Câu 28: Số nghiệm của phương trình
sin 0x =
trên đoạn
[ ]
0;
π
là
A.
1
. B.
2
. C.
0
. D. Vô số.
Câu 29: Tập nghiệm của phương trình
2sin 2 1 0x +=
là
A.
7
,,
12 12
S k kk
ππ
ππ
=−+ + ∈
. B.
7
2, 2,
6 12
S k kk
ππ
ππ
=−+ + ∈
.
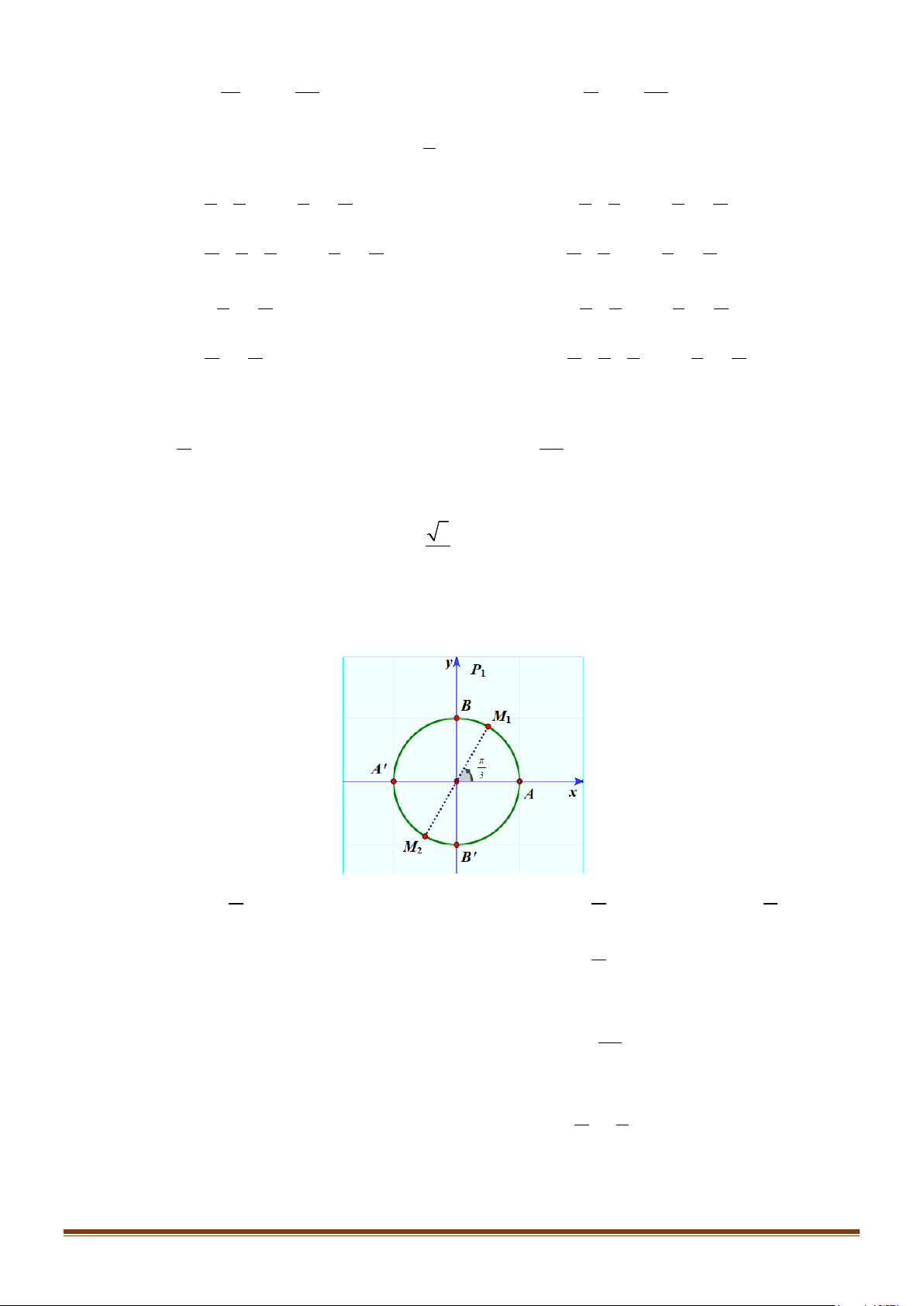
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 80
Sưu tầm và biên soạn
C.
7
2, 2,
12 12
S k kk
ππ
ππ
=−+ + ∈
. D.
7
,,
6 12
S k kk
ππ
ππ
=−+ + ∈
.
Câu 30: Nghiệm của phương trình
1
3 sin 4 1 0
2
x
+ −=
là:
A.
11 1
arcsin
84 3 2
,
11 1
arcsin
484 3 2
xk
k
xk
π
ππ
=−+
∈
= −− +
. B.
11 1
arcsin
84 3 2
,
11
arcsin
44 3 2
xk
k
xk
π
ππ
=−− +
∈
=−+
.
C.
1
82
,
42
xk
k
xk
π
ππ
=−+
∈
= +
. D.
11 1
arcsin
84 3 2
,
11 1
arcsin
484 3 2
xk
k
xk
π
ππ
=−+ +
∈
= −− +
.
Câu 31: Tập nghiệm của phương trình
( )
0
sin sin 60xx= −
là
B.
,
3
kk
π
π
+∈
. B.
2
;
3
kk
π
π
+∈
.
C.
{ }
00
120 180 ,kk+∈
. D.
{ }
00
60 180 ,kk+∈
Câu 32: Số nghiệm của phương trình
3
sin 2
2
=x
trong khoảng
( )
0; 3
π
là
A.
2
. B.
1
. C.
4
. D.
6
.
Câu 33: Cung lượng giác có điểm biểu diễn là
12
,
MM
như hình vẽ là nghiệm của phương trình lượng
giác nào sau đây?
A.
sin 0
3
x
π
−=
. B.
sin 0x =
. C.
cos 0
3
x
π
−=
. D.
sin 0
3
x
π
+=
.
Câu 34: Số nghiệm thuộc khoảng
( )
0; 2
π
của phương trình
sin sin 2 0
3
xx
π
++ =
là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 35: Số nghiệm thực của phương trình
2sin 1 0x −=
trên đoạn
3
; 10
2
π
π
−
là:
A.
11
. B.
9
. C.
20
. D.
21
.
Câu 36: Số vị trí biểu diễn các nghiệm của phương trình
1
sin 2
32
x
π
+=
trên đường tròn lượng giác là
A.
4
. B.
3
. C.
6
. D.
1
.
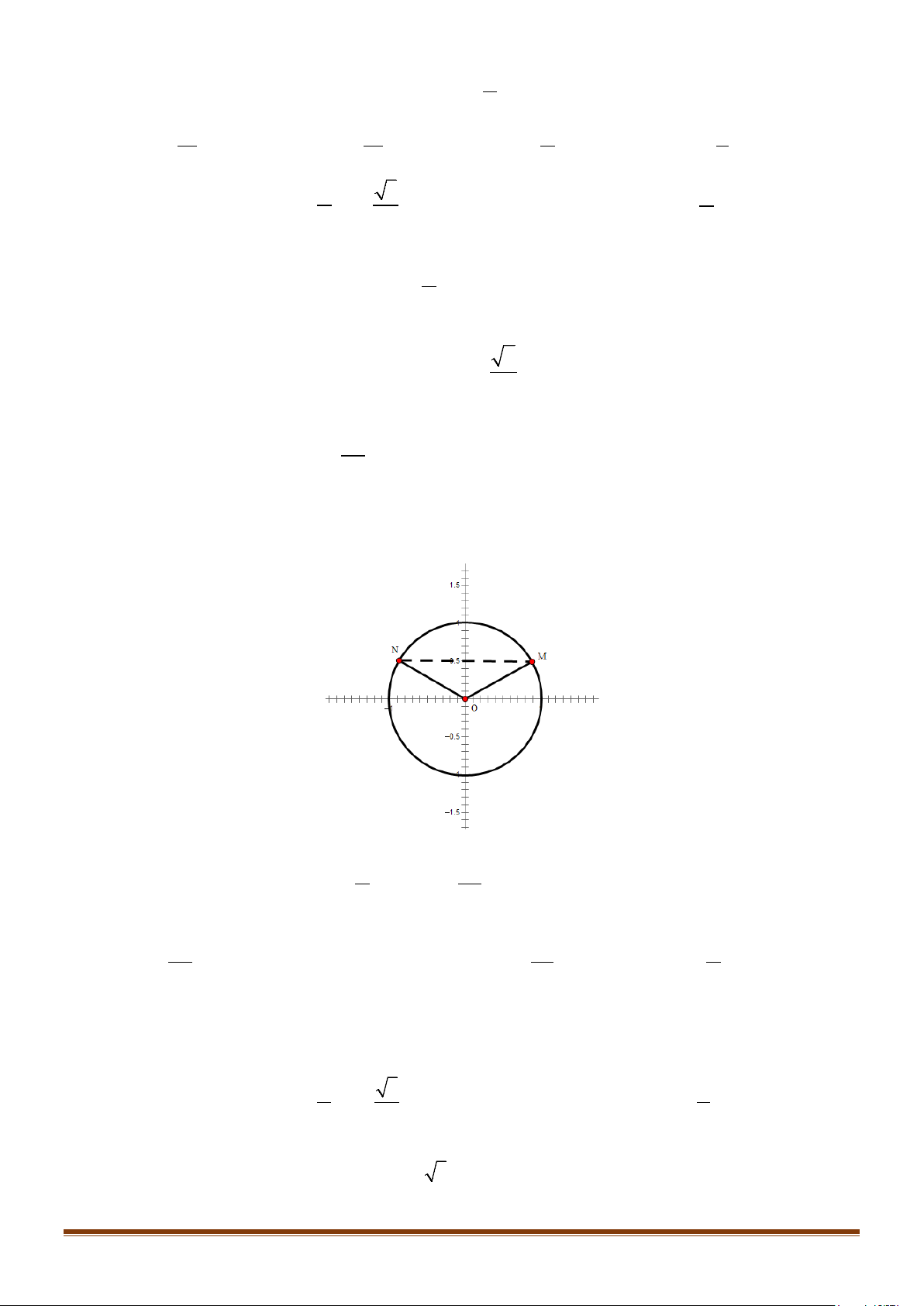
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 81
Sưu tầm và biên soạn
Câu 37: Tập nghiệm của phương trình
sin cos
3
xx
là:
A.
,
12
kk
π
π
+∈
. B.
1
,
12
kk
+∈
. C.
,
2
kk
π
π
+∈
. D.
1
,
2
kk
π
+∈
.
Câu 38: Phương trình
3
sin 3
32
x
π
+=−
có bao nhiêu nghiệm thuộc khoảng
0;
2
π
?
A. 2. B. 3. C. 4. D. 5.
Câu 39: Số nghiệm của phương trình
sin 1
4
x
π
+=
với
5x
ππ
≤≤
là
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 40: Có bao nhiêu nghiệm phương trình
2
sin 2
2
x = −
trong khoảng
(
)
0;
π
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 41: Số nghiệm thuộc đoạn
5
0;
2
π
của phương trình
2sin 1x =
là
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 42: Phương trình nào dưới đây có tập nghiệm biểu diễn trên đường tròn lượng giác là 2 điểm
,MN
?
A.
2sin 2 1x =
. B.
2cos 2 1x =
. C.
2sin 1x =
. D.
2cos 1x =
.
Câu 43: Cho phương trình
3
sin 2 sin
44
xx
ππ
−= +
. Tính tổng các nghiệm thuộc khoảng
( )
0;
π
của
phương trình trên.
A.
7
2
π
. B.
π
. C.
3
2
π
. D.
4
π
.
Câu 44: Tìm số nghiệm của phương trình
( )
sin cos 2 0x =
trên
[ ]
0; 2 .
π
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 45: Phương trình
3
sin 3
32
x
có bao nhiêu nghiệm thuộc khoảng
0;
2
?
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 46: Số nghiệm của phương trình
2sin 3 0x −=
trên đoạn đoạn
[ ]
0; 2
π
.
A. 3. B. 1. C. 4. D. 2.
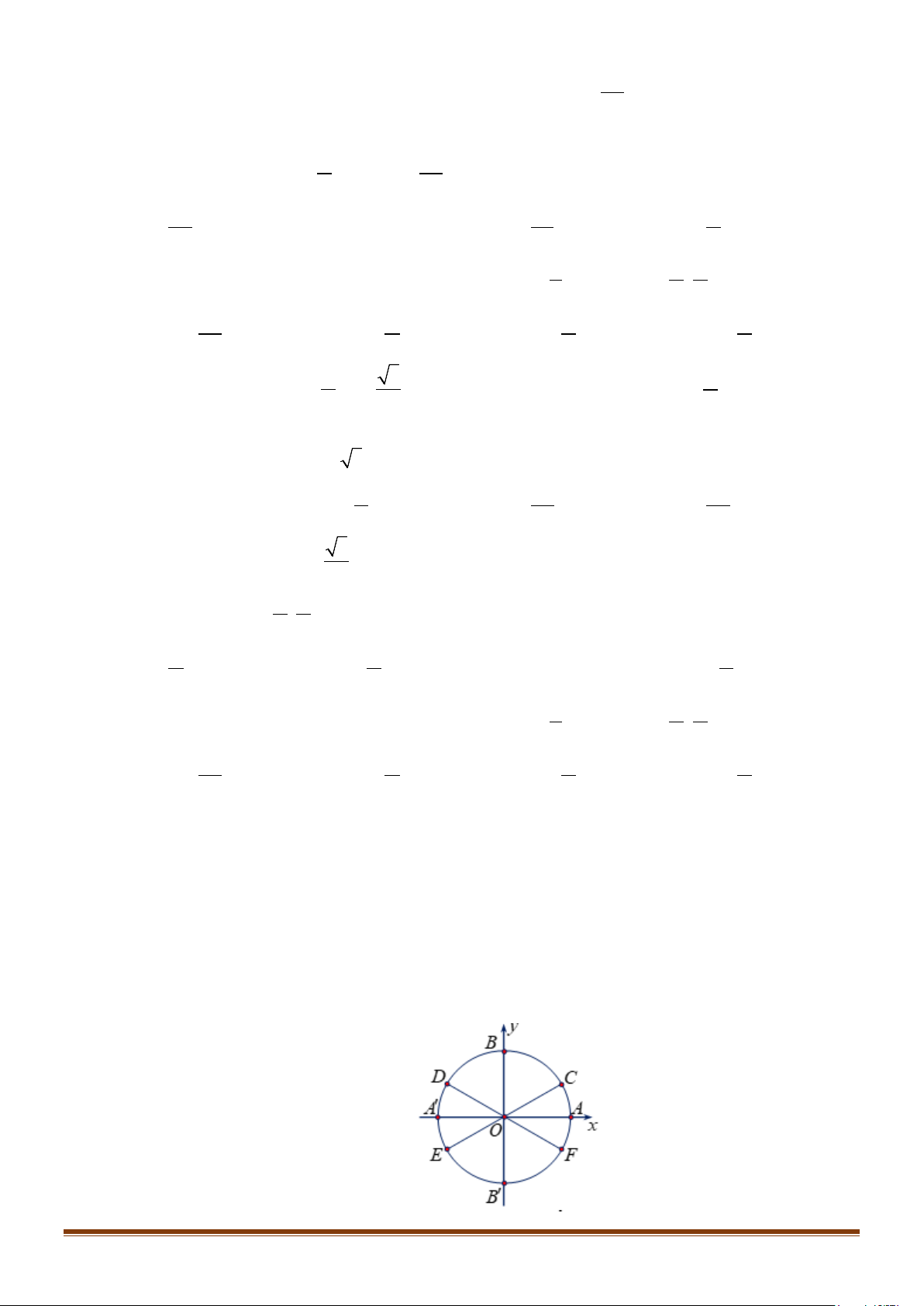
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 82
Sưu tầm và biên soạn
Câu 47: Số nghiệm thực của phương trình
2sin 1 0x +=
trên đoạn
3
;10
2
π
π
−
là:
A.
12
. B.
11
. C.
20
. D.
21
.
Câu 48: Phương trình
3
sin 2 sin
44
xx
ππ
−= +
có tổng các nghiệm thuộc khoảng
( )
0;
π
bằng
A.
7
2
π
. B.
π
. C.
3
2
π
. D.
4
π
.
Câu 49: Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x
=
trên đoạn
;
22
ππ
−
.
A.
5
6
S
π
=
. B.
3
S
π
=
. C.
2
S
π
=
. D.
6
S
π
=
.
Câu 50: Phương trình
3
sin 3
32
x
π
+=−
có bao nhiêu nghiệm thuộc khoảng
0;
2
π
?
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 51: Cho phương trình
2sin 3 0x −=
. Tổng các nghiệm thuộc
[ ]
0;
π
của phương trình là:
A.
π
. B.
3
π
. C.
2
3
π
. D.
4
3
π
.
Câu 52: Phương trình
3
sin 2
2
x = −
có hai công thức nghiệm dạng
k
απ
+
,
k
βπ
+
(
)
k ∈
với
α
,
β
thuộc khoảng
;
22
ππ
−
. Khi đó,
αβ
+
bằng
A.
2
π
. B.
2
π
−
. C.
π
. D.
3
π
−
.
Câu 53: Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x =
trên đoạn
;
22
ππ
−
.
A.
5
6
S
π
=
. B.
3
S
π
=
. C.
2
S
π
=
. D.
6
S
π
=
.
Câu 54: Nghiệm của phương trình
2sin 1 0x +=
được biểu diễn trên đường tròn lượng giác ở hình bên là
những điểm nào?

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 83
Sưu tầm và biên soạn
A. Điểm
D
, điểm
C
. B. Điểm
E
, điểm
F
. C. Điểm
C
, điểm
F
. D. Điểm
E
, điểm
D
.
Câu 55: Số nghiệm của phương trình
sin 1
4
x
π
+=
thuộc đoạn
[ ]
;2
ππ
là:
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 56: Phương trình
2sin 1 0x −=
có bao nhiêu nghiệm
( )
0; 2x
π
∈
?
A. 2 nghiệm. B. 1 nghiệm. C. 4 nghiệm. D. Vô số nghiệm.
Câu 57: Phương trình
sin 5 sin 0xx−=
có bao nhiêu nghiệm thuộc đoạn
[ ]
2018 ;2018
ππ
−
?
A.
20179
.
B.
20181
. C.
16144
. D.
16145
.
Câu 58: Số nghiệm thuộc đoạn
5
0;
2
của phương trình
2sin 1 0x
là:
A.
3
. B.
1
. C.
4
. D.
2
.
Câu 59: Cho phương trình
2sin 3 0
x −=
. Tổng các nghiệm thuộc
[ ]
0;
π
của phương trình là:
A.
4
3
π
. B.
π
. C.
3
π
. D.
2
3
π
.
Câu 60: Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x =
trên đoạn
;
22
ππ
−
.
A.
6
S
π
=
. B.
3
S
π
=
. C.
2
S
π
=
. D.
5
6
S
π
=
.
Câu 61: Số nghiệm thực của phương trình
2sin 1 0x +=
trên đoạn
3
;10
2
π
π
−
là:
A.
12
. B.
11
. C.
20
. D.
21
.
Câu 62: Phương trình:
2sin 2 3 0
3
x
π
−−=
có mấy nghiệm thuộc khoảng
( )
0;3
π
.
A.
8
. B.
6
. C.
2
. D.
4
.
Câu 63: Nghiệm của phương trình
sin 2 sinxx=
là
A.
2
,
3
2
4
xk
k
xk
π
π
π
=
∈
= +
. B.
,
2
2
3
xk
k
xk
π
π
π
=
∈
= +
C.
2
,
2
3
xk
k
xk
ππ
π
π
= +
∈
= +
. D.
2
,
2
33
xk
k
k
x
π
ππ
=
∈
= +
.
DẠNG 2. PHƯƠNG TRÌNH
cos xm=
Câu 64: Nghiệm của phương trình
1
cos
2
x =
là
A.
2
2
xk
π
π
=±+
. B.
2
3
xk
π
π
=±+
. C.
2
4
xk
π
π
=±+
. D.
2
6
xk
π
π
=±+
.
Câu 65: Nghiệm của phương trình
( )
2cos 15 1 0x − °− =
là
A.
75 360
135 360
xk
xk
= °+ °
= °+ °
,
k ∈
. B.
60 360
60 360
xk
xk
= °+ °
=− °+ °
,
k ∈
.
C.
45 360
45 360
xk
xk
= °+ °
=− °+ °
,
k ∈
. D.
75 360
45 360
xk
xk
= °+ °
=− °+ °
,
k ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 84
Sưu tầm và biên soạn
Câu 66: Giải phương trình
3
cos
2
x =
A.
( )
3
2
2
x kk
π
=±+ ∈
. B.
(
)
6
x kk
π
π
=±+ ∈
.
C.
( )
2
6
x kk
π
π
=±+ ∈
. D.
( )
2
3
x kk
π
π
=±+ ∈
.
Câu 67: Nghiệm của phương trình
cos cos
12
x
π
=
là
A.
( )
2
12
,
11
2
12
xk
kl
xl
π
π
π
π
= +
∈
= +
. B.
(
)
2
12
,
2
12
xk
kl
xl
π
π
π
π
= +
∈
=−+
.
C.
(
)
2
12
x kk
π
π
=+∈
. D.
( )
11
2
12
x kk
π
π
=+∈
.
Câu 68: Nghiệm của phương trình
cos 2 0x =
là
A.
( )
xk k
π
= ∈
. B.
( )
42
x kk
ππ
=+∈
.
C.
( )
2
x kk
π
π
=+∈
. D.
( )
2
xk k
π
= ∈
.
Câu 69: Phương trình
3
cos
2
x = −
có tập nghiệm là :
A.
;
3
x kk
π
π
=±+ ∈
. B.
;
6
x kk
π
π
=±+ ∈
.
C.
5
2;
6
x kk
π
π
=±+ ∈
. D.
2;
3
x kk
π
π
=±+ ∈
.
Câu 70: Phương trình
1
cos
2
x
= −
có các nghiệm là
A.
2
2
3
xk=±+
π
π
,
k ∈
. B.
6
xk
=±+
π
π
,
k ∈
.
C.
2
3
xk=±+
π
π
,
k ∈
. D.
2
6
xk
=±+
π
π
,
k ∈
.
Câu 71: Tập nghiệm của phương trình
2
cos3 sin 0
3
x
π
+=
là
A.
52
,
16 3
k
k
ππ
±+ ∈
. B.
22
,
93
k
k
ππ
±+ ∈
.
C.
52
,
93
k
k
ππ
±+ ∈
. D.
52
,
12 3
k
k
ππ
±+ ∈
.
Câu 72: Trong các phương trình sau, phương trình nào có nghiệm?
A.
cos 3x
. B.
sin 2 2x
.
C.
cos 2 1
3
x
. D.
( )
7
cos 2 1
2
x −=
.
Câu 73: Phương trình nào sau đây có nghiệm?
A.
sin 2021 2 0x −=
. B.
( )
cos 2 2021 3x +=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 85
Sưu tầm và biên soạn
C.
2
sin 1 0x +=
. D.
(
)
cos 2 2021 1x +=−
.
Câu 74: Nghiệm của phương trình
2
cos
42
π
+=
x
là:
A.
( )
2
2
π
π
π
=
∈
=−+
xk
kZ
xk
B.
()
2
π
π
π
=
∈
=−+
xk
kZ
xk
C.
()
2
2
π
π
π
=
∈
=−+
xk
kZ
xk
D.
2
()
2
2
π
π
π
=
∈
=−+
xk
kZ
xk
Câu 75: Nghiệm của phương trình
1
cos
2
x
là
A.
2
2
3
xk
B.
6
xk
C.
2
3
xk
D.
2
6
xk
Câu 76: Giải phương trình
cos 1x
.
A.
2
k
x
,
k
. B.
xk
,
k
.
C.
2
2
xk
,
k
. D.
2xk
,
k
.
Câu 77: Phương trình
cos cos
3
x
π
=
có tất cả các nghiệm là:
A.
( )
2
2
3
x kk
π
π
=+∈
B.
( )
3
x kk
π
π
=±+ ∈
C.
( )
2
3
x kk
π
π
=±+ ∈
D.
( )
2
3
x kk
π
π
=+∈
Câu 78: Phương trình
cos 0x =
có nghiệm là:
A.
(
)
2
x kk
π
π
=+∈
. B.
( )
2 xk k
π
= ∈
.
C.
( )
2
2
x kk
π
π
=+∈
. D.
( )
xk k
π
= ∈
.
Câu 79: Nghiệm của phương trình
2
cos
42
x
π
+=
là
A.
( )
2
2
xk
k
xk
π
π
π
=
∈
=−+
. B.
( )
2
xk
k
xk
π
π
π
=
∈
=−+
.
C.
( )
2
2
xk
k
xk
π
π
π
=
∈
=−+
. D.
( )
2
2
2
xk
k
xk
π
π
π
=
∈
=−+
.
Câu 80: Tìm tất cả các nghiệm của phương trình
cos 0.
3
x
=
A.
,.xk k
π
= ∈
B.
,.
2
x kk
π
π
=+∈
C.
3
6, .
2
x kk
π
π
=+∈
D.
3
3, .
2
x kk
π
π
=+∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 86
Sưu tầm và biên soạn
Câu 81: Phương trình
2cos 1 0
x −=
có nghiệm là:
A.
2
6
xk
π
π
=±+
,
k ∈
. B.
2
3
xk
π
π
=±+
,
k ∈
.
C.
2
6
x
π
π
=±+
,
k ∈
. D.
3
xk
π
π
=±+
,
k ∈
.
Câu 82: Phương trình
2cos 2 0
x −=
có tất cả các nghiệm là
A.
3
2
4
,
3
2
4
xk
k
xk
π
π
π
π
= +
∈
=−+
. B.
2
4
,
2
4
xk
k
xk
π
π
π
π
= +
∈
=−+
.
C.
2
4
,
3
2
4
xk
k
xk
π
π
π
π
= +
∈
= +
. D.
7
2
4
,
7
2
4
xk
k
xk
π
π
π
π
= +
∈
=−+
.
Câu 83: Giải phương trình
2cos 1 0x −=
A.
3
,xkk
π
±+π=
∈
. B.
2
3
,
2
2
3
xk
xk
k
= +
= +
π
π
π
π
∈
.
C.
3
,2xk
k+
π
± π=
∈
. D.
3
,
2
3
x
k
k
k
x
= +
= +
π
π
π
π
∈
.
Câu 84: Nghiệm của phương trình
cos 1
x = −
là:
A.
2
xk
π
π
= +
,
k
∈
. B.
2xk
π
=
,
k
∈
.
C.
2xk
ππ
= +
,
k ∈
. D.
xk
π
=
,
k ∈
.
Câu 85: Phương trình
2
cos
2
x
= −
có tập nghiệm là
A.
2;
3
x kk
π
π
=±+ ∈
. B.
;
4
x kk
π
π
=±+ ∈
.
C.
3
2;
4
x kk
π
π
=±+ ∈
. D.
;
3
x kk
π
π
=±+ ∈
.
Câu 86: Khẳng định nào sau đây là khẳng định sai?
A.
cos 1 2x xk
ππ
=−⇔ = +
. B.
cos 0
2
x xk
π
π
=⇔= +
.
C.
cos 1 2x xk
π
=⇔=
. D.
cos 0 2
2
x xk
π
π
=⇔= +
.
Câu 87: Phương trình lượng giác:
2cos 2 0x +=
có nghiệm là
A.
2
4
2
4
xk
xk
π
π
π
π
= +
=−+
. B.
3
2
4
3
2
4
xk
xk
π
π
π
π
= +
=−+
. C.
2
4
3
2
4
xk
xk
π
π
π
π
= +
= +
. D.
7
2
4
7
2
4
xk
xk
π
π
π
π
= +
=−+
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 87
Sưu tầm và biên soạn
Câu 88: Tìm công thức nghiệm của phương trình
( )
2cos 1x
α
+=
.
A.
(
)
2
3
2
2
3
xk
k
xk
π
απ
π
απ
=−+ +
∈
=−+ +
. B.
( )
2
3
2
xk
k
xk
π
απ
απ
=−+ +
∈
=−+
.
C.
( )
2
3
2
3
xk
k
xk
π
απ
π
απ
=−+ +
∈
=−+
D.
( )
2
3
2
3
xk
k
xk
π
απ
π
απ
=−+ +
∈
=−− +
.
Câu 89: Tìm tổng các nghiệm của phương trình
cos 5 cos 2
63
xx
ππ
−= −
trên
[ ]
0;
π
.
A.
47
18
π
. B.
4
18
π
. C.
45
18
π
. D.
7
18
π
.
Câu 90: Phương trình
22
8sin cos 1 0
22
xx
−=
tương đương với phương trình nào sau đây?
A.
2
sin
2
x =
. B.
cos 2 0x =
. C.
2
cos
2
x =
. D.
2
sin
2
x = −
.
Câu 91: Họ các nghiệm của phương trình
1
cos3
2
x =
là
A.
2
,
93
k
xk
ππ
=±+ ∈
. B.
2,
9
x kk
π
π
=±+ ∈
.
C.
2
,
33
k
xk
ππ
=±+ ∈
. D.
2,
3
x kk
π
π
=±+ ∈
.
Câu 92: Tổng các nghiệm của phương trình
2
cos
52
π
+=−
x
trong khoảng
3
;
32
ππ
−
là
A.
21
20
π
. B.
2
π
. C.
8
5
π
. D.
13
20
π
.
Câu 93: Tập nghiệm của phương trình
( )
( )
2
1 2 cos 2022 sin 0xx− +=
là
A.
;
44
k kk
ππ
ππ
+ −+ ∈
. B.
2; 2
44
k kk
ππ
ππ
+ −+ ∈
.
C.
4
kk
π
π
+∈
. D.
4
kk
π
π
−+ ∈
.
Câu 94: Phương trình lượng giác:
2cos 2 0x +=
có nghiệm là:
A.
2
4
3
2
4
xk
xk
π
π
π
π
= +
= +
. B.
3
2
4
3
2
4
xk
xk
π
π
π
π
= +
−
= +
. C.
5
2
4
5
2
4
xk
xk
π
π
π
π
= +
−
= +
. D.
x2
4
2
4
k
xk
π
π
π
π
= +
−
= +
.
Câu 95: Tất cả nghiệm của phương trình
2cos 1x = −
là
A.
( )
2
3
x kk
π
π
=±+ ∈
. B.
( )
2
3
x kk
π
π
=±+ ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 88
Sưu tầm và biên soạn
C.
(
)
2
2
3
x kk
π
π
=±+ ∈
. D.
( )
2
6
x kk
π
π
=±+ ∈
.
Câu 96: Tổng các nghiệm thuộc khoảng
;
22
ππ
−
của phương trình
2
4sin 2 1 0
x −=
bằng:
A.
.
π
B.
.
3
π
C.
0
. D.
.
6
π
Câu 97: Phương trình
2c
os 1
3
x
π
+=
có số nghiệm thuộc đoạn
[ ]
0; 2
π
là
A.
1
B.
2
C.
0
D.
3
Câu 98: Biết các nghiệm của phương trình
1
cos 2
2
x = −
có dạng
xk
m
π
π
= +
và
xk
n
π
π
=−+
,
k ∈
; với
,mn
là các số nguyên dương. Khi đó
mn
+
bằng
A. 4. B. 3. C. 5. D. 6.
Câu 99: Phương trình
2c
os 1
3
x
π
+=
có số nghiệm thuộc đoạn
[ ]
0; 2
π
là
A.
1
B.
2
C.
0
D.
3
Câu 100: Nghiệm lớn nhất của phương trình
2cos 2 1 0x −=
trong đoạn
[ ]
0;
π
là:
A.
x
π
=
. B.
11
12
x
π
=
. C.
2
3
x
π
=
. D.
5
6
x
π
=
.
Câu 101: Cho hai phương trình
cos3 1 0x −=
;
1
cos 2
2
x
= −
. Tập các nghiệm của phương trình đồng thời
là nghiệm của phương trình là
A.
2
3
xk
π
π
= +
,
k
∈
. B.
2xk
π
=
,
k ∈
.
C.
2
3
xk
π
π
=±+
,
k
∈
D.
2
2
3
xk
π
π
=±+
,
k ∈
.
Câu 102: Số nghiệm của phương trình
2cos 3x =
trên đoạn
5
0;
2
π
là
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 103: Số nghiệm của phương trình
1
cos
2
x =
thuộc đoạn
[ ]
2 ;2
ππ
−
là?
A.
4
. B.
2
. C.
3
. D.
1
.
Câu 104: Phương trình
cos 2 cos 0xx+=
có bao nhiêu nghiệm thuộc khoảng
( )
;
ππ
−
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 105: Tổng tất cả các nghiệm của phương trình
cos 2 cos 0xx−=
trên khoảng
( )
0; 2
π
bằng
T
. Khi đó
T
có giá trị là:
A.
7
6
T
π
=
. B.
2
T
π
=
. C.
4
3
T
π
=
. D.
T
π
=
.
Câu 106: Số nghiệm của phương trình
2cos 3
x =
trên đoạn
5
0;
2
π
là
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 107: Tìm tập nghiệm
S
của phương trình
cos .sin 2 0
3
xx
π
−=
.
A.
;,
2 62
k
Sk k
π ππ
π
=++∈
. B.
{ }
180 ;75 90 ,Sk k k= ° °+ ° ∈
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 89
Sưu tầm và biên soạn
C.
5
;,
12 2
k
Sk k
ππ
π
= +∈
. D.
{ }
100 180 ;30 90 ,S k kk= °+ ° °+ ° ∈
.
Câu 108: Giải phương trình
2
3cos 5cosxx=
A.
2
xk
π
π
= +
(
)
k
∈
. B.
2
2
xk
π
π
= +
(
)
k
∈
.
C.
2xk
ππ
= +
( )
k ∈
. D.
xk
π
=
(
)
k ∈
.
Câu 109: Giải phương trình
5sin sin 2 0xx−=
A.
2xk
π
=
( )
k ∈
. B.
2
xk
π
π
= +
(
)
k
∈
.
C.
xk
π
=
(
)
k
∈
. D. Phương trình vô nghiệm.
Câu 110: Giải phương trình
( )
sin cos 2 0
2
xx
−− − =
π
π
A.
{
}
2|
Sk k= ∈
π
. B.
2
2, |
33
k
Sk k
= +∈
ππ
π
.
C.
2
,|
33
k
Sk k
=+∈
ππ
π
. D.
2
|
33
k
Sk
=+∈
ππ
Câu 111: Nghiệm âm lớn nhất của phương trình
22
cos 4 sin cos
6
x xx
π
−+ =
A.
35
36
π
−
. B.
11
36
π
−
. C.
11
12
π
−
. D.
12
π
−
.
Câu 112: Trên khoảng
;2
2
π
π
, phương trình
cos 2 sin
6
xx
π
−=
có bao nhiêu nghiệm?
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 113: Số điểm biểu diễn nghiệm của phương trình
( )
sin4 2cos 2 0xx−=
trên đường tròn lượng giác
là
A.
4
. B.
6
. C.
8
. D.
10
.
Câu 114: Các họ nghiệm của phương trình
sin 2 3 sin 0xx−=
là:
A.
6
xk
xk
π
π
π
=
=±+
. B.
6
xk
π
π
=±+
. C.
2
6
xk
xk
π
π
π
=
=±+
. D.
2
2
3
xk
xk
π
π
π
=
=±+
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
DẠNG 1. PHƯƠNG TRÌNH
sin xm
=
Câu 1: Phương trình
2.sin 1 0x −=
có tập nghiệm là
A.
5
2; 2,
66
S k kk
ππ
ππ
=+ +∈
. B.
2
2; 2,
33
S k kk
ππ
ππ
=+ −+ ∈
.
C.
2; 2,
66
S k kk
ππ
ππ
= + −+ ∈
. D.
1
2,
6
S kk
π
=+∈
.
Lời giải
Ta có:
( )
2
1
6
2.sin 1 0 sin sin si n
5
26
2
6
xk
x xx k
xk
π
π
π
π
π
= +
−=⇔=⇔= ⇔ ∈
= +
Câu 2: Tất cả các nghiệm của phương trình
sin sin
3
x
π
=
là
A.
( )
2
3
2
3
xk
k
xk
π
π
π
π
= +
∈
=−+
. B.
(
)
2
3
2
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
.
C.
( )
3
x kk
π
π
=+∈
. D.
( )
3
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
.
Lời giải
Áp dụng công thức:
( )
2
sin sin
2
xak
xa k
x ak
π
ππ
= +
=⇔∈
= −+
.
Câu 3: Nghiệm của phương trình
2sin 1 0x +=
là
A.
7
2; 2.
66
x kx k
ππ
ππ
=+=+
B.
7
2; 2.
66
x kx k
ππ
ππ
=−+ = +
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TRẮC NGHIỆM.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
C.
2; 2.
8
x kx k
π
ππ π
=+=+
D.
5
2; 2.
66
x kx k
ππ
ππ
=−+ = +
Lời giải
Ta có:
1
2sin 1 0 si n
2
xx
−
+= ⇔ =
22
66
()
7
22
66
xk xk
k
x kxk
ππ
ππ
ππ
ππ π
=−+ =−+
⇔⇔ ∈
=++ = +
Vậy phương trình có nghiệm là
7
2; 2.
66
x kx k
ππ
ππ
=−+ = +
Câu 4: Nghiệm của phương trình
sin 1 0
3
x
π
− +=
là
A.
7
2
6
xk
π
π
= +
,
k ∈
. B.
5
6
xk
π
π
= +
,
k
∈
.
C.
7
6
xk
π
π
=−+
,
k ∈
. D.
5
2
6
xk
π
π
= +
,
k ∈
.
Lời giải
sin 1 0 sin 1
33
xx
ππ
− += ⇔ − =−
5
22
32 6
x kx k
ππ π
ππ
⇔ −=− + ⇔= −
,
k ∈
.
Với
k ∈
,
5
2
6
xk
π
π
= +
cũng là nghiệm của phương trình.
Câu 5: Phương trình
2
0
33
sin
x
π
−=
có nghiệm là
A.
(
)
3
.
x kk
π
π
=+∈
B.
( )
.xk k
π
= ∈
C.
( )
23
32
.
k
xk
ππ
=+∈
D.
( )
3
22
.
k
xk
ππ
=+∈
Lời giải
Phương trình
22
0
33 33
sin
xx
k
ππ
π
− =⇔ −=
( )
23
33 2 2
.
xk
kx k
π ππ
π
⇔ = + ⇔= + ∈
Câu 6: Nghiệm của phương trình
( )
sin sin 2x = −
là:
A.
22
22
xk
xk
π
π
=−+
= +
,
k ∈
. B.
22
22
xk
xk
π
ππ
=−+
= −+
,
k ∈
.
C.
2
2
xk
xk
π
ππ
=−+
= −+
,
k ∈
. D.
22
22
xk
xk
π
ππ
=−+
= ++
,
k ∈
.
Lời giải
( )
22
sin sin 2
22
xk
x
xk
π
ππ
=−+
= −⇔
= ++
với
k ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
Câu 7: Họ nghiệm của phương trình
sin sin
5
=
x
π
là
A.
5
,,
4
5
= +
∈
= +
xk
kl
xl
π
π
π
π
. B.
2
5
,,
4
2
5
= +
∈
= +
xk
kl
xl
π
π
π
π
.
C.
2
5
,,
2
5
= +
∈
=−+
xk
kl
xl
π
π
π
π
. D.
5
,,
5
= +
∈
=−+
xk
kl
xl
π
π
π
π
.
Lời giải
Áp dụng công thức nghiệm của phương trình
2
sin sin , ,
2
= +
=⇔∈
=−+
xk
x kl
xl
απ
α
πα π
.
Ta có
sin sin
5
=x
π
2
5
,,
4
2
5
= +
⇔∈
= +
xk
kl
xl
π
π
π
π
.
Câu 8: Phương trình
sin 2 0
3
x
π
−=
có nghiệm là
A.
,
π
= ∈xkk
. B.
,
62
ππ
=+∈
k
xk
. C.
,
2
π
π
=+∈x kk
. D.
,
3
π
π
=+∈x kk
.
Lời giải
Ta có
π
−=⇔
sin 2 0
3
x
π
π
−= ∈2,
3
x kk
ππ
⇔= + ∈,
62
k
xk
.
Câu 9: Tập nghiệm của phương trình
5
sin sin
3
x
π
=
là
A.
52
2; 2;
33
S k kk
ππ
ππ
−
=+ +∈
B.
57
2; 2;
33
S k kk
ππ
ππ
=+ +∈
.
C.
55
2; 2;
33
S k kk
ππ
ππ
−
=+ +∈
. D.
52
;;
33
S k kk
ππ
ππ
−
=+ +∈
.
Lời giải
Áp dụng công thức nghiệm, ta có
(
)
55
22
5
33
sin sin
52
3
22
33
xk xk
xk
x kx k
ππ
ππ
π
ππ
ππ π
=+=+
=⇔⇔∈
−
=−+ = +
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Câu 10: Phương trình
sin sin 80x = °
có tập nghiệm là
A.
{ }
80 360 ,100 360 ,= °+ ° °+ ° ∈S k kk
. B.
{ }
80 360 , 80 360 ,= °+ ° − °+ ° ∈S k kk
.
C.
{ }
40 360 ,140 360 ,= °+ ° °+ ° ∈S k kk
. D.
{ }
80 180 ,100 180 ,= °+ ° °+ ° ∈S k kk
.
Lời giải
Ta có
80 360 80 360
sin sin80
180 80 360 100 360
xk xk
x
x k xk
= °+ ° = °+ °
= °⇔ ⇔
= °− °+ ° = °+ °
với
k ∈
.
Câu 11: Tập nghiệm của phương trình
sin 2 1
x = −
là
A.
2,
4
S kk
π
π
=−+ ∈
. B.
,
2
S kk
π
π
=−+ ∈
.
C.
,
4
S kk
π
π
=+∈
. D.
,
4
S kk
π
π
=−+ ∈
.
Lời giải
Ta có
sin 2 1 2 2
24
x xkxk
ππ
ππ
=−⇔ =−+ ⇔=−+
,
k ∈
.
Câu 12: Họ nghiệm của phương trình
1
sin
2
x
=
là
A.
2
3
,
2
2
3
xk
k
xk
π
π
π
π
= +
∈
= +
. B.
2
6
,
5
2
6
xk
k
xk
π
π
π
π
= +
∈
= +
.
C.
,xkk
π
= ∈
. D.
1
2
2
,
1
2
2
xk
k
xk
π
ππ
= +
∈
=−+
.
Lời giải
22
1
66
sin sin sin ,
5
26
22
66
xk xk
xx k
x kxk
ππ
ππ
π
ππ
ππ π
=+=+
=⇔= ⇔ ⇔ ∈
=−+ = +
Câu 13: Nghiệm của phương trình
sin 1
2
x
=
là
A.
4,
x kk
ππ
=+∈
. B.
2,xk k
π
= ∈
. C.
2,x kk
ππ
=+∈
. D.
2,
2
x kk
π
π
=+∈
.
Lời giải
Phương trình tương đương
sin 1 2 4 ,
2 22
xx
k x kk
π
π ππ
=⇔ = + ⇔=+ ∈
Câu 14: Phương trình
sin 1
3
x
π
−=
có nghiệm là
A.
2
3
xk
π
π
= +
. B.
5
6
xk
π
π
= +
. C.
5
2
6
xk
π
π
= +
. D.
2
3
x
π
π
= +
.
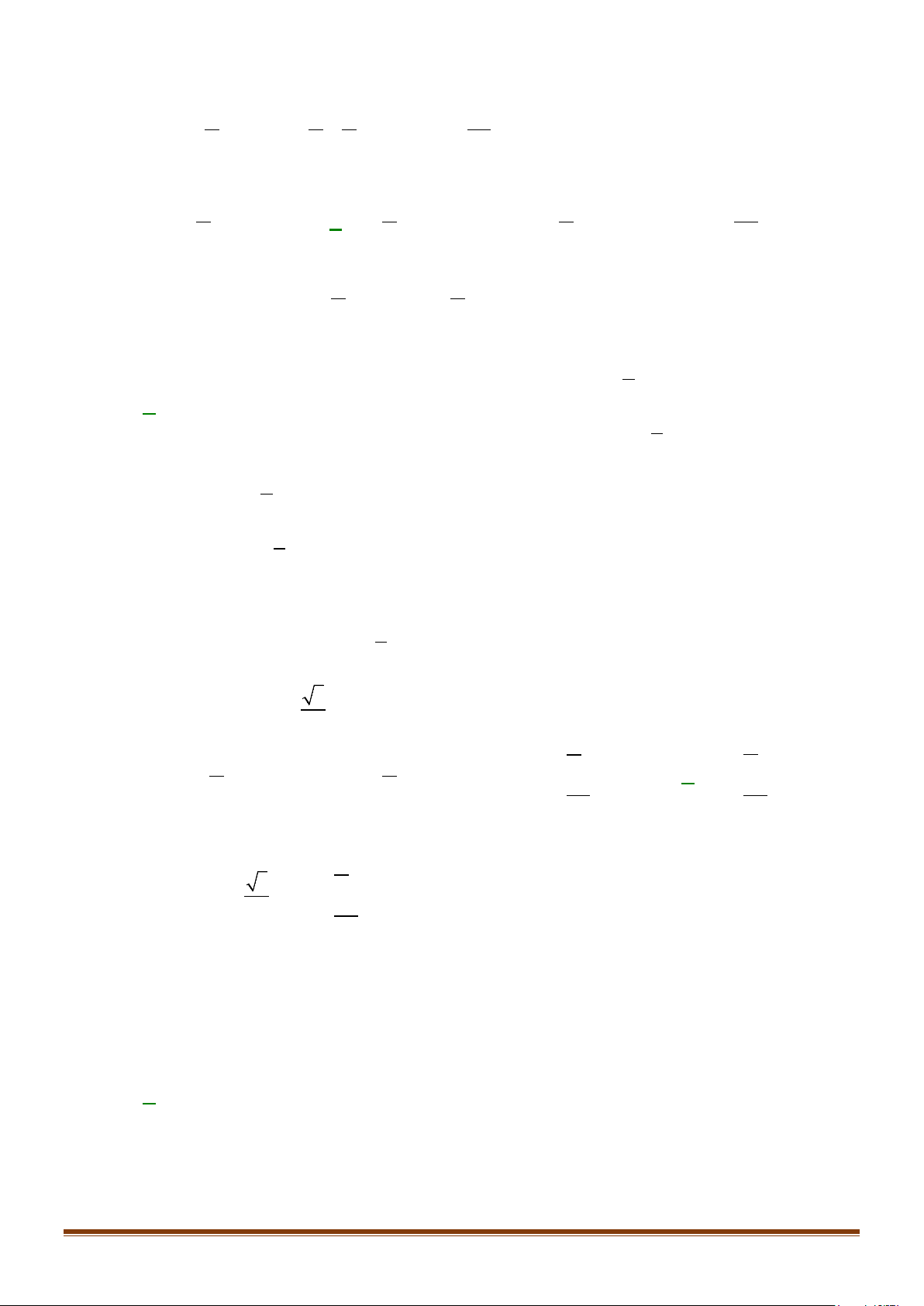
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
Lời giải
sin 1
3
x
π
−=
2
32
xk
ππ
π
⇔− = +
5
2
6
xk
π
π
⇔= +
( )
k ∈
.
Câu 15: Tìm nghiệm của phương trình
sin 2 1x =
.
A.
2
2
xk
π
π
= +
. B.
4
xk
π
π
= +
. C.
2
4
xk
π
π
= +
. D.
2
k
x
π
=
.
Lời giải
Ta có:
sin 2 1 2 2
24
x xkxk
ππ
ππ
=⇔ = + ⇔= +
.
Câu 16: Tìm nghiệm của phương trình
2sin 3 0x −=
.
A.
x ∈∅
. B.
( )
3
arcsin 2
2
3
arcsin 2
2
xk
k
xk
π
ππ
= +
∈
=−+
.
C.
( )
3
arcsin 2
2
3
arcsin 2
2
xk
k
xk
π
π
= +
∈
=−+
. D.
x ∈
.
Lời giải
Ta có:
3
2sin 3 0 sin 1
2
xx−=⇔ = >
nên phương trình vô nghiệm.
Câu 17: Phương trình
3
sin
2
x =
có nghiệm là:
A.
2
3
xk
π
π
=±+
. B.
3
xk
π
π
= +
. C.
6
5
6
xk
xk
π
π
π
π
= +
= +
. D.
2
3
2
2
3
xk
xk
π
π
π
π
= +
= +
.
Lời giải
Ta có
2
3
3
sin
2
2
2
3
xk
x
xk
π
π
π
π
= +
= ⇔
= +
, với
k ∈
.
Câu 18: Tập nghiệm của phương trình
sin sin 30x
= °
là
A.
{ }
30 2 |S kk
π
= °+ ∈
∪
{ }
150 2 |kk
π
°+ ∈
.
B.
{ }
30 2 |
S kk
π
= ± °+ ∈
.
C.
{ }
30 360 |S kk= ± °+ ° ∈
.
D.
{ }
30 360 |Sk= °+ ° ∈
∪
{
}
150 360 | k°+ ° ∈
.
Lời giải
Ta có
sin sin 30x = °
⇔
30 360
180 30 360
xk
xk
= °+ °
= °− °+ °
30 360
150 360
xk
xk
= °+ °
⇔
= °+ °
( )
k ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
Câu 19: Tìm tất cả các nghiệm của phương trình
sin 1
6
x
π
+=
.
A.
3
xk
π
π
= +
(
)
k ∈
. B.
2
6
xk
π
π
=−+
( )
k ∈
.
C.
2
3
xk
π
π
= +
( )
k
∈
. D.
5
2
6
xk
π
π
= +
( )
k ∈
.
Lời giải
Ta có
sin 1
6
x
π
+=
2
62
xk
ππ
π
⇔+ = +
2
3
xk
π
π
⇔= +
( )
k ∈
.
Câu 20: Phương trình
2sin 1 0x −=
có tập nghiệm là:
A.
5
2; 2,
66
S k kk
ππ
ππ
=+ +∈
. B.
2
2; 2,
33
S k kk
ππ
ππ
=+ −+ ∈
.
C.
2; 2,
66
S k kk
ππ
ππ
= + −+ ∈
. D.
1
2,
2
S kk
π
=+∈
.
Lời giải
Ta có:
2
1
6
2sin 1 0 sin sin sin
5
26
2
6
xk
x xx k
xk
π
π
π
π
π
= +
−=⇔=⇔= ⇔ ∈
= +
.
Câu 21: Phương trình
2sin 1 0x +=
có nghiệm là:
A.
2
6
7
2
6
xk
xk
π
=−+ π
π
=− +π
B.
2
6
7
2
6
xk
xk
π
=−+ π
π
= +π
C.
2
6
5
2
6
xk
xk
π
=+π
π
= +π
D.
6
7
6
xk
xk
π
= +π
π
=− +π
Lời giải
Chọn B
Ta có:
1
2sin 1 0 sin sin
26
xx
π
+= ⇔ =− = −
( )
2
6
7
2
6
xk
k
xk
π
=−+ π
⇔∈
π
= +π
Câu 22: Phương trình
2sin 3 0x −=
có tập nghiệm là:
A.
2,
6
kk
π
π
±+ ∈
. B.
2,
3
kk
π
π
±+ ∈
.
C.
5
2, 2,
66
k kk
ππ
ππ
+ +∈
. D.
2
2, 2,
33
k kk
ππ
ππ
+ +∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
( )
2
3
3
2sin 3 0 sin .
2
2
2
3
xk
xx k
xk
π
π
π
π
= +
−=⇔ = ⇔ ∈
= +
Vậy tập nghiệm của phương trình là:
2
2, 2,
33
S k kk
ππ
ππ
=+ +∈
Câu 23: Tổng các nghiệm của phương trình
( )
2sin 40 3x + °=
trên khoảng
( )
180 ;180−° °
là
A.
20°
. B.
100°
. C.
80
°
. D.
120°
.
Lời giải
Ta có:
( )
2sin 40 3x + °=
( )
3
sin 40
2
x⇔ + °=
( )
40 60 360
40 120 360
xk
k
xk
+ °= °+ °
⇔∈
+ °= °+ °
( )
20 360
80 360
xk
k
xk
= °+ °
⇔∈
= °+ °
Theo đề bài:
54
180 20 360 180 0 20
99
k kkx− °< °+ °< °⇔− < < ⇒ = ⇒ = °
.
13 5
180 80 360 180 0 80
18 18
k k kx− °< °+ °< °⇔− < < ⇒ = ⇒ = °
.
Vậy tổng các nghiệm của phương trình là
20 80 100°+ °= °
.
Câu 24: Tìm tổng các nghiệm của phương trình
cos 5 cos 2
63
xx
ππ
−= −
trên
[ ]
0;
π
.
A.
47
18
π
. B.
4
18
π
. C.
45
18
π
. D.
7
18
π
.
Lời giải
Ta có:
cos 5 cos 2
63
xx
ππ
−= −
52 2
63
,
522
63
x xk
k
x xk
ππ
π
ππ
π
−= −+
⇔∈
−=−++
2
18 3
,
2
14 7
k
x
k
k
x
ππ
ππ
=−+
⇔∈
= +
.
Vì
[ ]
0;x
π
∈
nên ta có :
+) Với
2 2 1 19
0
18 3 18 3 12 12
kk
xk
ππ ππ
π
=−+ ⇒≤−+ ≤⇔ ≤≤
, do
1kk∈⇒=
nên
11
18
x
π
=
.
+) Với
2 2 1 13
0
14 7 14 7 4 4
kk
xk
ππ ππ
π
−
= + ⇒≤ + ≤ ⇔ ≤≤
, do
{ }
0;1; 2;3kk∈⇒∈
nên
5 9 13
;;;
14 14 14 14
x
πππ π
∈
.
Tổng tất cả các nghiệm là:
11 5 9 13 47
18 14 14 14 14 18
ππ π π π π
++ + + =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Câu 25: Số nghiệm phương trình
sin 3
0
cos 1
x
x
=
+
thuộc đoạn
[ ]
2 ;4
ππ
là
A.
7
. B.
6
. C.
4
. D.
5
.
Lời giải
Điều kiện:
cos 1 0 2
x xk
ππ
+≠ ⇔ ≠ +
.
Ta có
( )
sin 3
0 sin 3 0 .
cos 1 3
xk
x xk
x
π
=⇒ =⇔= ∈
+
So với điều kiện nghiệm của phương trình là
3
k
x
π
=
với
( )
, 32 1
kk l
∈≠+
Vì
2 4 2 4 6 12
3
k
xk
π
π ππ π
≤≤⇔≤≤⇔≤≤
nên ta chọn
{
}
6,7,8,10,11,12
k ∈
.
Câu 26: Phương trình
2sin 3 0
x +=
có tổng nghiệm dương nhỏ nhất và nghiệm âm lớn nhất bằng
A.
4
3
π
. B.
2
π
. C.
3
π
. D.
π
.
Lời giải
* Ta có:
2
3
3
2sin 3 0 sin sin ,
4
23
2
3
xk
xx k
xk
π
π
π
π
π
=−+
+=⇔ =−= −⇔ ∈
= +
.
* Xét
2
3
xk
π
π
=−+
,
k ∈
ta được nghiệm dương nhỏ nhất là
1
5
3
x
π
=
và nghiệm âm lớn nhất
là
2
3
x
π
= −
.
* Xét
4
2
3
xk
π
π
= +
,
k ∈
ta được nghiệm dương nhỏ nhất là
3
4
3
x
π
=
và nghiệm âm lớn nhất
là
4
2
3
x
π
= −
.
* So sánh
1
x
và
3
x
ta suy ra nghiệm dương nhỏ nhất của phương trình đã cho là
3
4
3
x
π
=
.
So sánh
2
x
và
4
x
ta suy ra nghiệm âm lớn nhất của phương trình đã cho là
2
3
x
π
= −
.
* Ta có
23
4
33
xx
ππ
π
+ =−+ =
.
Câu 27: Với những giá trị nào của
x
thì giá trị của các hàm số
3sinyx=
và
sinyx=
bằng nhau?
A.
( )
2
2
4
xk
k
xk
π
π
π
=
∈
= +
. B.
( )
4
xk k
π
= ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
C.
(
)
2
xk k
π
= ∈
. D.
( )
42
.
xk
k
xk
π
ππ
=
∈
= +
Lời giải
Xét phương trình hoành độ giao điểm:
3sin sinxx=
( )
32
32
42
.
xk
xxk
k
x xk
xk
π
π
ππ
ππ
=
=+
⇔ ⇔∈
= −+
= +
Câu 28: Số nghiệm của phương trình
sin 0x =
trên đoạn
[ ]
0;
π
là
A.
1
. B.
2
. C.
0
. D. Vô số.
Lời giải
Ta có
sin 0x xk
π
=⇔=
,
k ∈
.
[ ]
0; 0 0 1x kk
π ππ
∈ ⇔≤ ≤⇔≤≤
mà
k ∈
nên
0
k =
;
1k =
. Suy ra
0
x =
;
x
π
=
.
Vậy phương trình
sin 0
x
=
có 2 nghiệm trên đoạn
[ ]
0;
π
.
Câu 29: Tập nghiệm của phương trình
2sin 2 1 0x +=
là
A.
7
,,
12 12
S k kk
ππ
ππ
=−+ + ∈
. B.
7
2, 2,
6 12
S k kk
ππ
ππ
=−+ + ∈
.
C.
7
2, 2,
12 12
S k kk
ππ
ππ
=−+ + ∈
. D.
7
,,
6 12
S k kk
ππ
ππ
=−+ + ∈
.
Lời giải
Ta có:
2sin 2 1 0x +=
1
sin 2
2
x⇔=−
sin 2 sin
6
x
π
⇔=−
22
6
,
7
22
6
xk
k
xk
π
π
π
π
=−+
⇔∈
= +
12
,
7
12
xk
k
xk
π
π
π
π
=−+
⇔∈
= +
.
Vậy tập nghiệm của phương trình là
7
,,
12 12
S k kk
ππ
ππ
=−+ + ∈
.
Câu 30: Nghiệm của phương trình
1
3 sin 4 1 0
2
x
+ −=
là:
A.
11 1
arcsin
84 3 2
,
11 1
arcsin
484 3 2
xk
k
xk
π
ππ
=−+
∈
= −− +
. B.
11 1
arcsin
84 3 2
,
11
arcsin
44 3 2
xk
k
xk
π
ππ
=−− +
∈
=−+
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
C.
1
82
,
42
xk
k
xk
π
ππ
=−+
∈
= +
. D.
11 1
arcsin
84 3 2
,
11 1
arcsin
484 3 2
xk
k
xk
π
ππ
=−+ +
∈
= −− +
.
Lời giải
11
4 arcsin 2
1 11
23
3 sin 4 1 0 sin 4 ,
11
2 23
4 arcsin 2
23
xk
xx k
xk
π
ππ
+= +
+ −= ⇔ + = ⇔ ∈
+=− +
11 1
arcsin
84 3 2
,
11 1
arcsin
484 3 2
xk
k
xk
π
ππ
=−+ +
⇔∈
= −− +
Câu 31: Tập nghiệm của phương trình
( )
0
sin sin 60
xx
= −
là
B.
,
3
kk
π
π
+∈
. B.
2
;
3
kk
π
π
+∈
.
C.
{ }
00
120 180 ,kk+∈
. D.
{ }
00
60 180 ,
kk+∈
Lời giải
( )
( )
( )
00
0 00
0 00
60 360
sinx sin 60 120 180
180 60 360
xx k
x x kk
x xk
=−+
= − ⇔ ⇔= + ∈
= −− +
Câu 32: Số nghiệm của phương trình
3
sin 2
2
=x
trong khoảng
( )
0; 3
π
là
A.
2
. B.
1
. C.
4
. D.
6
.
Lời giải
Ta có
22
3
36
sin 2 sin 2 sin
2
23
22
33
xk xk
xx k k
x k xk
ππ
ππ
π
ππ
ππ
=+=+
= ⇔ = ⇔ ∈⇔ ∈
=+=+
Xét
(
)
6
x kk
π
π
=+∈
:
1 17
0 30 3
6 66
x kk
π
π ππ
−
<<⇔<+<⇔<<
.
Mà
k ∈
nên
0
6
7
1
6
13
2
6
kx
kx
kx
π
π
π
=⇒=
=⇒=
=⇒=
Xét
( )
3
x kk
π
π
=+∈
:
18
0 30 3
3 33
x kk
π
π ππ
−
<<⇔<+<⇔<<
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Mà
k
∈
nên
0
3
4
1
3
7
2
3
kx
kx
kx
π
π
π
=⇒=
=⇒=
=⇒=
Vậy phương trình
3
sin 2
2
=
x
có 6 nghiệm trong khoảng
(
)
0; 3
π
.
Câu 33: Cung lượng giác có điểm biểu diễn là
12
,MM
như hình vẽ là nghiệm của phương trình lượng
giác nào sau đây?
A.
sin 0
3
x
π
−=
. B.
sin 0x =
. C.
cos 0
3
x
π
−=
. D.
sin 0
3
x
π
+=
.
Lời giải
Cung lượng giác có điểm biểu diễn là
12
,
MM
có số đo là:
( )
3
kk
π
π
+∈
.
Và phương trình
( )
sin 0
33 3
x x k x kk
ππ π
ππ
− =⇔− = ⇔= + ∈
.
Câu 34: Số nghiệm thuộc khoảng
( )
0; 2
π
của phương trình
sin sin 2 0
3
xx
π
++ =
là
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
( )
sin sin 2 0 sin sin 2 sin sin 2
3 33
x x x xx x
π ππ
++ =⇔ +=− ⇔ += −
2
22
3 93
2
22 2
33
x xk x k
x xk x k
π ππ
π
ππ
ππ π
+=−+ =−+
⇔⇔
+=+ + =− −
.
Các nghiệm thuộc khoảng
( )
0; 2
π
của phương trình là:
22
; 2. ; 2 ;
93 9 3 9
π ππ ππ
π
−+ −+ −+
2
2
3
π
π
−+
hay
5
9
π
;
11
9
π
;
17
9
π
;
4
3
π
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
Vậy có 4 nghiệm thỏa yêu cầu bài toán.
Câu 35: Số nghiệm thực của phương trình
2sin 1 0x −=
trên đoạn
3
; 10
2
π
π
−
là:
A.
11
. B.
9
. C.
20
. D.
21
.
Lời giải
Phương trình tương đương:
1
sin
2
x =
2
6
5
2
6
xk
xk
π
π
π
π
= +
⇔
= +
,
+ Với
2
6
xk
π
π
= +
,
k
∈
ta có
3
2 10
26
k
ππ
ππ
− ≤+ ≤
,
k ∈
5 59
6 12
k⇔− ≤ ≤
,
k ∈
04
k⇒≤≤
,
k ∈
. Do đó phương trình có
5
nghiệm.
+ Với
5
2
6
xk
π
π
= +
,
k ∈
ta có
35
2 10
26
k
ππ
ππ
−≤+ ≤
,
k ∈
7 55
6 12
k⇔− ≤ ≤
,
k ∈
14k⇒− ≤ ≤
,
k ∈
. Do đó, phương trình có
6
nghiệm.
+ Rõ ràng các nghiệm này khác nhau từng đôi một, vì nếu
51
22
66 3
k k kk
ππ
ππ
′′
+ = + ⇔− =
.
Vậy phương trình có
11
nghiệm trên đoạn
3
; 10
2
π
π
−
.
Câu 36: Số vị trí biểu diễn các nghiệm của phương trình
1
sin 2
32
x
π
+=
trên đường tròn lượng giác là
A.
4
. B.
3
. C.
6
. D.
1
.
Lời giải
Phương trình
22
36
sin 2 sin ,
36
22
36
xk
xk
xk
ππ
π
ππ
ππ
ππ
+=+
⇔ += ⇔ ∈
+=−+
12
,
4
xk
k
xk
π
π
π
π
=−+
⇔∈
= +
Biểu diễn nghiệm
12
xk
π
π
=−+
trên đường tròn lượng giác ta được 2 vị trí.
Biểu diễn nghiệm
4
xk
π
π
= +
trên đường tròn lượng giác ta được 2 vị trí.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
Vậy có tất cả 4 vị trí biểu diễn các nghiệm các nghiệm của phương trình.
Câu 37: Tập nghiệm của phương trình
sin cos
3
xx
là:
A.
,
12
kk
π
π
+∈
. B.
1
,
12
kk
+∈
. C.
,
2
kk
π
π
+∈
. D.
1
,
2
kk
π
+∈
.
Lời giải
Ta có:
sin cos
3
xx
sin sin
23
xx
sin sin
6
xx
2
1
6
,
12
2
6
x xk
x kk
x x k VL
.
Câu 38: Phương trình
3
sin 3
32
x
π
+=−
có bao nhiêu nghiệm thuộc khoảng
0;
2
π
?
A. 2. B. 3. C. 4. D. 5.
Lời giải
Ta có
( )
32
3
33
sin 3 si n 3 sin
32 3 3
32
33
xk
xx k
xk
ππ
π
π ππ
ππ
ππ
+=−+
+=−⇔ += −⇔ ∈
+=++
( )
22
93
2
33
xk
k
xk
ππ
ππ
=−+
⇔∈
= +
.
TH1:
22 22 1 13
0; 0
93 2 9323 12
xk k k
ππ π πππ
=−+ ∈ ⇔<−+ <⇔<<
. Do
1kk∈⇒=
.
Suy ra trường hợp này có nghiệm
4
9
x
π
=
thỏa mãn.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
TH2:
2 2 11
0; 0
33 2 332 2 4
xk k k
ππ π πππ
= + ∈ ⇔ < + < ⇔− < <
. Do
0kk∈⇒=
.
Suy ra trường hợp này có nghiệm
3
x
π
=
thỏa mãn.
Vậy phương trình chỉ có
2
nghiệm thuộc khoảng
0;
2
π
.
Câu 39: Số nghiệm của phương trình
sin 1
4
x
π
+=
với
5x
ππ
≤≤
là
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Ta có
sin 1
4
x
π
+=
2
42
xk
ππ
π
⇔+ = +
2,
4
x kk
π
π
⇔= + ∈
Nên
3 19
5 25
4 88
x kk
π
π ππ ππ
≤≤⇔≤+ ≤⇔≤≤
Vì
k ∈
nên
{ }
1; 2; 3k ∈
.
Câu 40: Có bao nhiêu nghiệm phương trình
2
sin 2
2
x = −
trong khoảng
( )
0;
π
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
22
2
8
4
sin 2
55
2
22
48
xk
xk
x
xk xk
π
π
π
π
ππ
ππ
−
−
= +
= +
=−⇔ ⇔
=+=+
Vì
19 7
00 1
8 88 8
x k k kx
ππ
π ππ
−
<<⇔< + < ⇔<<→=→=
Vì
5 53 5
00 0
8 88 8
x k kkx
ππ
π ππ
−
<<⇔< + < ⇔ <<→=→=
Câu 41: Số nghiệm thuộc đoạn
5
0;
2
π
của phương trình
2sin 1x
=
là
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Phương trình
.2
1
6
2sin 1 sin ( , )
5
2
.2
6
xk
x x kl Z
xl
π
π
π
π
= +
=⇔=⇔ ∈
= +
Vì
5
0; 0, 1 0.
2
x nên k k và l
π
∈===
Câu 42: Phương trình nào dưới đây có tập nghiệm biểu diễn trên đường tròn lượng giác là 2 điểm
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
,
MN
?
A.
2sin 2 1x =
. B.
2cos 2 1x =
. C.
2sin 1x =
. D.
2cos 1x =
.
Lời giải
Chọn C
Ta thấy 2 điểm M và N là các giao điểm của đường thẳng vuông góc với trục tung tại điểm
1
2
với đường tròn lượng giác ⇒ M và N là các điểm biểu diễn tập nghiệm của phương trình lượng
giác cơ bản:
1
si n 2 si n 1
2
xx=⇔=
⇒ Đáp án. C.
Câu 43: Cho phương trình
3
sin 2 sin
44
xx
ππ
−= +
. Tính tổng các nghiệm thuộc khoảng
( )
0;
π
của
phương trình trên.
A.
7
2
π
. B.
π
. C.
3
2
π
. D.
4
π
.
Lời giải
Chọn B
Ta có:
3
2
22
3
44
sin 2 sin
2
3
44
22
63
44
xk
xx k
xx
xk
x xk
ππ
ππ
π
ππ
ππ
ππ
ππ
= +
−=+ +
−= + ⇔ ⇔
= +
− = −− +
( )
k ∈
.
+ Xét
2xk
ππ
= +
(
)
k ∈
.
Do
1
0 02 0
2
xk k
π π ππ
<<⇔<+ <⇔−<<
. Vì
k ∈
nên không có giá trị
k
.
+ Xét
2
63
xk
ππ
= +
( )
k ∈
.
Do
2 15
00
63 4 4
xk k
ππ
ππ
<<⇔<+ <⇔−<<
. Vì
k ∈
nên có hai giá trị
k
là:
0; 1kk= =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
•
Với
0
6
kx
π
=⇒=
.
•
Với
5
1
6
kx
π
=⇒=
.
Do đó trên khoảng
( )
0;
π
phương trình đã cho có hai nghiệm
6
x
π
=
và
5
6
x
π
=
.
Vậy tổng các nghiệm của phương trình đã cho trong khoảng
( )
0;
π
là:
5
66
ππ
π
+=
.
Câu 44: Tìm số nghiệm của phương trình
(
)
sin cos 2 0
x
=
trên
[ ]
0; 2 .
π
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Ta có
(
)
sin 2 0 2
cos x cos x k
π
=⇔=
( )
k ∈
Vì
[ ]
( )
1 11
2 1;1 0 202 .
2 42
cos x k cos x x k x k k
π ππ
π
∈− ⇒ = ⇒ = ⇔ = + ⇔ = + ∈
[ ]
{
}
1
0; 2 0;1; 2;3 .
xk
π
∈ ⇒∈
Vậy phương trình có
4
nghiệm trên
[ ]
0; 2 .
π
Câu 45: Phương trình
3
sin 3
32
x
có bao nhiêu nghiệm thuộc khoảng
0;
2
?
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Ta có
32
3
33
sin 3 sin 3 sin
32 3 3
32
33
xk
xx k
xk
( )
22
93
2
33
xk
k
xk
=−+
⇔∈
= +
ππ
ππ
.
+) TH1:
22 22 1 13
0; 0
93 2 9323 12
xk k k
=−+ ∈ ⇔<−+ <⇔<<
ππ π πππ
. Do
1kk
.
Suy ra trường hợp này có nghiệm
4
9
x
=
π
thỏa mãn.
+) TH2:
2 2 11
0; 0
33 2 332 2 4
xk k k
= + ∈ ⇔ < + < ⇔− < <
ππ π πππ
. Do
0kk
. Suy ra
trường hợp này có nghiệm
3
x =
π
thỏa mãn.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
Vậy phương trình chỉ có
2
nghiệm thuộc khoảng
0;
2
.
Câu 46: Số nghiệm của phương trình
2sin 3 0x −=
trên đoạn đoạn
[ ]
0; 2
π
.
A. 3. B. 1. C. 4. D. 2.
Lời giải
Chọn D
Tự luận
22
3
33
2sin 3 0 sin sin sin ,
2
23
22
33
xk xk
x xx k
x kxk
ππ
ππ
π
ππ
ππ π
=+=+
−=⇔=⇔= ⇔ ⇔ ∈
=−+ = +
- Xét
2
3
xk
π
π
= +
5 15
0 2 0 22 2 0
3 3 366
x k k kk
π ππ
π ππ π
≤ ≤ ⇔ ≤ + ≤ ⇔− ≤ ≤ ⇔− ≤ ≤ ⇒ =
Chỉ có một nghiệm
[ ]
0; 2
3
x
π
π
= ∈
- Xét
2
2
3
xk
π
π
= +
2 2 4 12
0 2 0 22 2 0
3 3 333
x k k kk
π ππ
π ππ π
≤ ≤ ⇔ ≤ + ≤ ⇔− ≤ ≤ ⇔− ≤ ≤ ⇒ =
Chỉ có một nghiệm
[ ]
2
0; 2
3
x
π
π
= ∈
Vậy phương trình có 2 nghiệm thuộc đoạn
[ ]
0; 2
π
.
Câu 47: Số nghiệm thực của phương trình
2sin 1 0x +=
trên đoạn
3
;10
2
π
π
−
là:
A.
12
. B.
11
. C.
20
. D.
21
.
Lời giải
Phương trình tương đương:
1
sin
2
x = −
2
6
7
2
6
xk
xk
π
π
π
π
−
= +
⇔
= +
, (
k ∈
)
+ Với
2
6
xk
π
π
=−+
,
k ∈
ta có
3
2 10
26
k
ππ
ππ
− ≤− + ≤
,
k ∈
2 61
3 12
k
−
⇔ ≤≤
,
k ∈
05k⇒≤≤
,
k ∈
. Do đó phương trình có
6
nghiệm.
+ Với
7
2
6
xk
π
π
= +
,
k ∈
ta có
37
2 10
26
k
ππ
ππ
−≤+ ≤
,
k ∈
4 53
3 12
k
−
⇔ ≤≤
,
k ∈
14k⇒− ≤ ≤
,
k ∈
. Do đó, phương trình có
6
nghiệm.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
+ Rõ ràng các nghiệm này khác nhau từng đôi một, vì nếu
72
22
66 3
k k kk
ππ
ππ
′′
− + = + ⇔− =
.
Vậy phương trình có
12
nghiệm trên đoạn
3
;10
2
π
π
−
.
Câu 48: Phương trình
3
sin 2 sin
44
xx
ππ
−= +
có tổng các nghiệm thuộc khoảng
( )
0;
π
bằng
A.
7
2
π
. B.
π
. C.
3
2
π
. D.
4
π
.
Lời giải
Ta có
3
sin 2 sin
44
xx
ππ
−= +
3
22
44
22
44
xx k
x xl
ππ
π
ππ
π
−=+ +
⇔
− = −+
( )
2
,
2
63
xk
kl
xl
ππ
ππ
= +
⇔∈
= +
.
Họ nghiệm
2xk
ππ
= +
không có nghiệm nào thuộc khoảng
( )
0;
π
.
( )
2
0;
63
xl
ππ
π
=+∈
2
0
63
l
ππ
π
⇒< + <
{ }
0; 1l⇔∈
.
Vậy phương trình có hai nghiệm thuộc khoảng
( )
0;
π
là
6
x
π
=
và
5
6
x
π
=
. Từ đó suy ra tổng
các nghiệm thuộc khoảng
(
)
0;
π
của phương trình này bằng
π
.
Câu 49: Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x =
trên đoạn
;
22
ππ
−
.
A.
5
6
S
π
=
. B.
3
S
π
=
. C.
2
S
π
=
. D.
6
S
π
=
.
Lời giải
Ta có:
2
1
6
sin
5
2
2
6
xk
x
xk
π
π
π
π
= +
= ⇔
= +
( )
k ∈
.
Vì
;
22
x
ππ
∈−
nên
66
xS
ππ
= ⇒=
.
Câu 50: Phương trình
3
sin 3
32
x
π
+=−
có bao nhiêu nghiệm thuộc khoảng
0;
2
π
?
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Ta có:
3
sin 3
32
x
π
+=−
32
33
4
32
33
xk
xk
ππ
π
ππ
π
+=−+
⇔
+= +
( )
k ∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
2
32
3
32
xk
xk
π
π
ππ
=−+
⇔
= +
( )
k ∈
22
93
2
33
xk
xk
ππ
ππ
=−+
⇔
= +
( )
k ∈
.
Vì
0;
2
x
π
∈
nên
3
x
π
=
,
4
9
x
π
=
.
Vậy phương trình đã cho có hai nghiệm thuộc khoảng
0;
2
π
.
Câu 51: Cho phương trình
2sin 3 0x −=
. Tổng các nghiệm thuộc
[ ]
0;
π
của phương trình là:
A.
π
. B.
3
π
. C.
2
3
π
. D.
4
3
π
.
Lời giải
2sin 3 0x −=
⇔
3
sin sin
23
x
π
= =
⇔
2
2
2
3
3
xk
xk
π
π
π
π
= +
= +
.
Các nghiệm của phương trình trong đoạn
[ ]
0;
π
là
3
π
;
2
3
π
nên có tổng là
2
33
ππ
π
+=
.
Câu 52: Phương trình
3
sin 2
2
x = −
có hai công thức nghiệm dạng
k
απ
+
,
k
βπ
+
( )
k ∈
với
α
,
β
thuộc khoảng
;
22
ππ
−
. Khi đó,
αβ
+
bằng
A.
2
π
. B.
2
π
−
. C.
π
. D.
3
π
−
.
Lời giải
Ta có:
3
sin 2 sin
23
x
π
=−= −
22
3
4
22
3
xk
xk
π
π
π
π
=−+
⇔
= +
6
2
3
xk
xk
π
π
π
π
=−+
⇔
= +
6
3
xk
xk
π
π
π
π
=−+
⇔
=−+
.
Vậy
6
π
α
= −
và
3
π
β
= −
. Khi đó
2
π
αβ
+=−
.
Câu 53: Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x =
trên đoạn
;
22
ππ
−
.
A.
5
6
S
π
=
. B.
3
S
π
=
. C.
2
S
π
=
. D.
6
S
π
=
.
Lời giải
Ta có:
2
1
6
sin
5
2
2
6
xk
x
xk
π
π
π
π
= +
= ⇔
= +
( )
k ∈
.
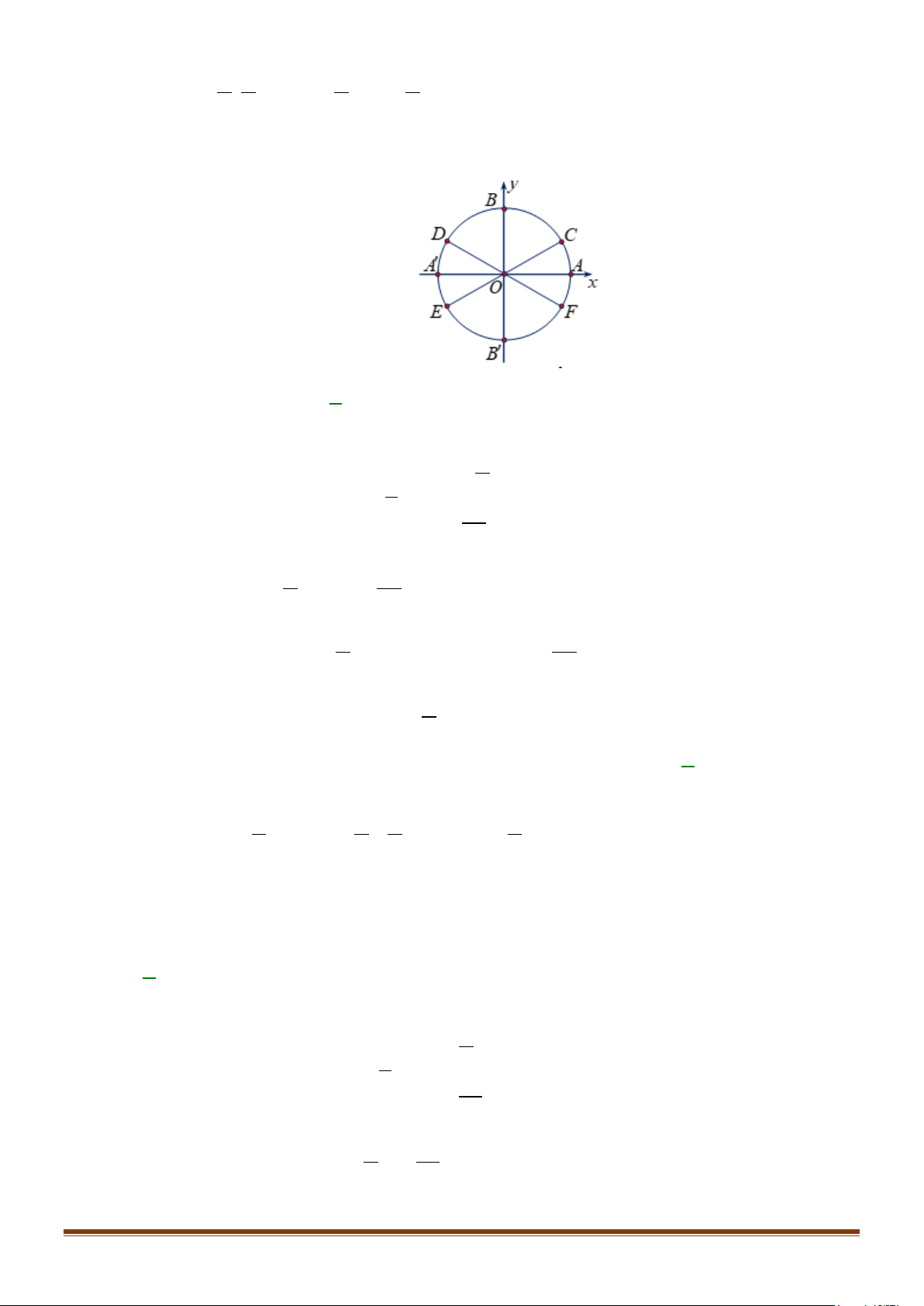
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 20
Sưu tầm và biên soạn
Vì
;
22
x
ππ
∈−
nên
66
xS
ππ
= ⇒=
.
Câu 54: Nghiệm của phương trình
2sin 1 0x +=
được biểu diễn trên đường tròn lượng giác ở hình bên là
những điểm nào?
A. Điểm
D
, điểm
C
. B. Điểm
E
, điểm
F
. C. Điểm
C
, điểm
F
. D. Điểm
E
, điểm
D
.
Lời giải
Ta có
2sin 1 0x +=
⇔
2
1
6
sin
7
2
2
6
xk
x
xk
π
π
π
π
=−+
=−⇔
= +
( )
k ∈
Với
0
6
kx
π
=⇒=−
hoặc
7
6
x
π
=
.
Điểm biểu diễn của
6
x
π
= −
là
F
, điểm biểu diễn
7
6
x
π
=
là
E
.
Câu 55: Số nghiệm của phương trình
sin 1
4
x
π
+=
thuộc đoạn
[ ]
;2
ππ
là:
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Ta có
sin 1 2 2
4 42 4
x x k xk
π ππ π
ππ
+ =⇔+ = + ⇔= +
,
k
∈
.
Suy ra số nghiệm thuộc
[ ]
;2
ππ
của phương trình là
1
.
Câu 56: Phương trình
2sin 1 0x −=
có bao nhiêu nghiệm
( )
0; 2x
π
∈
?
A. 2 nghiệm. B. 1 nghiệm. C. 4 nghiệm. D. Vô số nghiệm.
Lời giải
Ta có:
2sin 1 0x −=
1
sin
2
x⇔=
2
6
5
2
6
xk
xk
π
π
π
π
= +
⇔
= +
( )
k ∈
.
Do
( )
0; 2x
π
∈
nên ta có
5
;
66
xx
ππ
= =
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 21
Sưu tầm và biên soạn
Câu 57: Phương trình
sin 5 sin 0xx−=
có bao nhiêu nghiệm thuộc đoạn
[ ]
2018 ;2018
ππ
−
?
A.
20179
.
B.
20181
. C.
16144
. D.
16145
.
Lời giải
Ta có
sin 5 si n 0xx−=
sin 5 sinxx⇔=
52
52
x xk
x xk
π
ππ
= +
⇔
= −+
2
63
xk
xk
π
ππ
=
⇔
= +
(
)
(
)
( )
2
5
6
6
xk k
x mm
xn n
π
π
π
π
π
= ∈
⇔= + ∈
=+∈
.
Vì
[ ]
2018 ;2018x
ππ
∈−
nên
2018 2018
2
5
2018 2018
6
2018 2018
6
k
m
n
π
ππ
π
π ππ
π
π ππ
− ≤≤
− ≤+≤
− ≤+ ≤
4036 4036
12113 12103
66
12109 12107
66
k
m
n
− ≤≤
⇔− ≤ ≤
− ≤≤
.
Do đó có
8073
giá trị
k
,
4036
giá trị
m
,
4036
giá trị
n
, suy ra số nghiêm cần tìm là
16145
.
nghiệm.
Câu 58: Số nghiệm thuộc đoạn
5
0;
2
của phương trình
2sin 1 0x
là:
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn A
+ Phương trình tương đương
1
sin
2
x
sin sin
6
x
2
6
5
2
6
xk
xk
,
k
.
+ Với
2
6
xk
,
k
.
Vì
5
0;
2
x
nên
5
02
62
k
,
k
17
12 6
k
,
k
0;1k
.
Suy ra:
3
;
66
x
.
+ Với
5
2
6
xk
,
k
.
Vì
5
0;
2
x
nên
55
02
62
k
,
k
55
12 6
k
,
k
0k
.
(*)

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 22
Sưu tầm và biên soạn
Suy ra:
5
6
x
.
Do đó
53
;;
66 6
x
.
Vậy số nghiệm của phương trình là
3
.
Câu 59: Cho phương trình
2sin 3 0x −=
. Tổng các nghiệm thuộc
[ ]
0;
π
của phương trình là:
A.
4
3
π
. B.
π
. C.
3
π
. D.
2
3
π
.
Lời giải
Chọn B
2sin 3 0x −=
⇔
3
sin sin
23
x
π
= =
⇔
2
2
2
3
3
xk
xk
π
π
π
π
= +
= +
.
Các nghiệm của phương trình trong đoạn
[ ]
0;
π
là
3
π
;
2
3
π
nên có tổng là
2
33
ππ
π
+=
.
Câu 60: Tính tổng
S
của các nghiệm của phương trình
1
sin
2
x =
trên đoạn
;
22
ππ
−
.
A.
6
S
π
=
. B.
3
S
π
=
. C.
2
S
π
=
. D.
5
6
S
π
=
.
Lời giải
Chọn A
Ta có:
2
1
6
sin
5
2
2
6
xk
x
xk
π
π
π
π
= +
= ⇔
= +
( )
k ∈
.
Vì
;
22
x
ππ
∈−
nên
66
xS
ππ
= ⇒=
.
Câu 61: Số nghiệm thực của phương trình
2sin 1 0x +=
trên đoạn
3
;10
2
π
π
−
là:
A.
12
. B.
11
. C.
20
. D.
21
.
Lời giải
Chọn A
Phương trình tương đương:
1
sin
2
x = −
2
6
7
2
6
xk
xk
π
π
π
π
−
= +
⇔
= +
, (
k ∈
)
+ Với
2
6
xk
π
π
=−+
,
k ∈
ta có
3
2 10
26
k
ππ
ππ
− ≤− + ≤
,
k ∈
2 61
3 12
k
−
⇔ ≤≤
,
k ∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 23
Sưu tầm và biên soạn
05
k⇒≤≤
,
k
∈
. Do đó phương trình có
6
nghiệm.
+ Với
7
2
6
xk
π
π
= +
,
k ∈
ta có
37
2 10
26
k
ππ
ππ
−≤+ ≤
,
k ∈
4 53
3 12
k
−
⇔ ≤≤
,
k ∈
14k⇒− ≤ ≤
,
k ∈
. Do đó, phương trình có
6
nghiệm.
+ Rõ ràng các nghiệm này khác nhau từng đôi một, vì nếu
72
22
66 3
k k kk
ππ
ππ
′′
− + = + ⇔− =
.
Vậy phương trình có
12
nghiệm trên đoạn
3
;10
2
π
π
−
.
Câu 62: Phương trình:
2sin 2 3 0
3
x
π
−−=
có mấy nghiệm thuộc khoảng
( )
0;3
π
.
A.
8
. B.
6
. C.
2
. D.
4
.
Lời giải
Chọn B
Ta có
2sin 2 3 0
3
x
π
−−=
3
2sin 2
32
x
π
⇔ −=
22
33
22
33
xk
xk
ππ
π
ππ
ππ
−=+
⇔
−=−+
3
,
2
xk
k
xk
π
π
π
π
= +
⇔∈
= +
. Vì
( )
0;3x
π
∈
nên
47 35
;;;;;
33 322 2
x
ππππππ
∈
.
Câu 63: Nghiệm của phương trình
sin 2 sin
xx
=
là
A.
2
,
3
2
4
xk
k
xk
π
π
π
=
∈
= +
. B.
,
2
2
3
xk
k
xk
π
π
π
=
∈
= +
C.
2
,
2
3
xk
k
xk
ππ
π
π
= +
∈
= +
. D.
2
,
2
33
xk
k
k
x
π
ππ
=
∈
= +
.
Lời giải
Ta có
2
22
sin 2 sin ,
2
22
33
xk
x xk
xx k
k
x xk
x
π
π
ππ
ππ
=
= +
=⇔ ⇔∈
= −+
= +
.
DẠNG 2. PHƯƠNG TRÌNH
cos xm=
Câu 64: Nghiệm của phương trình
1
cos
2
x =
là
A.
2
2
xk
π
π
=±+
. B.
2
3
xk
π
π
=±+
. C.
2
4
xk
π
π
=±+
. D.
2
6
xk
π
π
=±+
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 24
Sưu tầm và biên soạn
Ta có
( )
2
3
cos cos
3
2
3
xk
xk
xk
π
π
π
π
π
= +
=⇔∈
=−+
.
Câu 65: Nghiệm của phương trình
( )
2cos 15 1 0x − °− =
là
A.
75 360
135 360
xk
xk
= °+ °
= °+ °
,
k
∈
. B.
60 360
60 360
xk
xk
= °+ °
=− °+ °
,
k
∈
.
C.
45 360
45 360
xk
xk
= °+ °
=− °+ °
,
k ∈
. D.
75 360
45 360
xk
xk
= °+ °
=− °+ °
,
k ∈
.
Lời giải
(
)
( ) ( )
1
2cos 15 1 0 cos 15 cos 15 cos60
2
x xx−°−=⇔ −°=⇔ −°= °
15 60 360 75 360
15 60 360 45 360
x k xk
x k xk
− °= °+ ° = °+ °
⇔⇔
− °=− °+ ° =− °+ °
,
k ∈
.
Câu 66: Giải phương trình
3
cos
2
x =
A.
( )
3
2
2
x kk
π
=±+ ∈
. B.
( )
6
x kk
π
π
=±+ ∈
.
C.
( )
2
6
x kk
π
π
=±+ ∈
. D.
( )
2
3
x kk
π
π
=±+ ∈
.
Lời giải
Ta có:
( )
3
cos cos cos 2
2 66
x x x kk
ππ
π
= ⇔ = ⇔=±+ ∈
.
Câu 67: Nghiệm của phương trình
cos cos
12
x
π
=
là
A.
( )
2
12
,
11
2
12
xk
kl
xl
π
π
π
π
= +
∈
= +
. B.
( )
2
12
,
2
12
xk
kl
xl
π
π
π
π
= +
∈
=−+
.
C.
( )
2
12
x kk
π
π
=+∈
. D.
( )
11
2
12
x kk
π
π
=+∈
.
Lời giải
Ta có
( )
2
12
cos cos ,
12
2
12
xk
x kl
xl
π
π
π
π
π
= +
=⇔∈
=−+
.
Câu 68: Nghiệm của phương trình
cos 2 0x =
là
A.
( )
xk k
π
= ∈
. B.
( )
42
x kk
ππ
=+∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 25
Sưu tầm và biên soạn
C.
( )
2
x kk
π
π
=+∈
. D.
(
)
2
xk k
π
= ∈
.
Lời giải
Ta có:
cos 2 0x
=
2
2
xk
π
π
⇔=+
( )
42
x kk
ππ
⇔= + ∈
.
Câu 69: Phương trình
3
cos
2
x = −
có tập nghiệm là :
A.
;
3
x kk
π
π
=±+ ∈
. B.
;
6
x kk
π
π
=±+ ∈
.
C.
5
2;
6
x kk
π
π
=±+ ∈
. D.
2;
3
x kk
π
π
=±+ ∈
.
Lời giải
3 55
cos cos cos 2 ,
2 66
x x x kk
ππ
π
=− ⇔ = ⇔=± + ∈
Câu 70: Phương trình
1
cos
2
x = −
có các nghiệm là
A.
2
2
3
xk=±+
π
π
,
k
∈
. B.
6
xk=±+
π
π
,
k ∈
.
C.
2
3
xk
=±+
π
π
,
k ∈
. D.
2
6
xk=±+
π
π
,
k ∈
.
Lờigiải
12
cos cos co
2
2 33
2s
x xk
x=−⇔ = ⇔
=±+
ππ
π
,
k ∈
.
Câu 71: Tập nghiệm của phương trình
2
cos3 sin 0
3
x
π
+=
là
A.
52
,
16 3
k
k
ππ
±+ ∈
. B.
22
,
93
k
k
ππ
±+ ∈
.
C.
52
,
93
k
k
ππ
±+ ∈
. D.
52
,
12 3
k
k
ππ
±+ ∈
.
Lời giải
Phương trình
( )
2
cos3 sin 0, 1
3
x
π
+=
có tập xác định
D
=
( )
25
1 cos3 sin cos3 cos
36
xx
ππ
⇔=−⇔=
5
3 .2 ,
6
x kk
π
π
⇔=± + ∈
52
,
18 3
k
xk
ππ
=±+ ∈
.
Câu 72: Trong các phương trình sau, phương trình nào có nghiệm?

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 26
Sưu tầm và biên soạn
A.
cos 3
x
. B.
sin 2 2x
.
C.
cos 2 1
3
x
. D.
( )
7
cos 2 1
2
x −=
.
Lời giải
Phương trình lượng giác cơ bản dạng
sin u
,
cosua=
có nghiệm khi và chỉ khi
1
a
≤
. Nên
ta chọn đáp án C.
Câu 73: Phương trình nào sau đây có nghiệm?
A.
sin 2021 2 0x −=
. B.
( )
cos 2 2021 3
x
+=
.
C.
2
sin 1 0x +=
. D.
(
)
cos 2 2021 1
x
+=−
.
Lời giải
Phương trình
sin xa=
và
cos xa=
có nghiệm khi và chỉ khi
1a ≤
.
Đối chiếu các đáp án ta thấy chỉ có đáp án D là phương trình có nghiệm.
Câu 74: Nghiệm của phương trình
2
cos
42
π
+=
x
là:
A.
( )
2
2
π
π
π
=
∈
=−+
xk
kZ
xk
B.
()
2
π
π
π
=
∈
=−+
xk
kZ
xk
C.
()
2
2
π
π
π
=
∈
=−+
xk
kZ
xk
D.
2
()
2
2
π
π
π
=
∈
=−+
xk
kZ
xk
Lời giải
Chọn D
Phương trình
2
2
cos cos cos ( )
42 4 4
2
2
π
π ππ
π
π
=
+= ⇔ += ⇔ ∈
=−+
xk
x x kZ
xk
.
Câu 75: Nghiệm của phương trình
1
cos
2
x
là
A.
2
2
3
xk
B.
6
xk
C.
2
3
xk
D.
2
6
xk
Lời giải
Chọn A
Ta có:
1 22
cos cos cos 2
2 33
x x x kk
.
Câu 76: Giải phương trình
cos 1x
.
A.
2
k
x
,
k
. B.
xk
,
k
.
C.
2
2
xk
,
k
. D.
2xk
,
k
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 27
Sưu tầm và biên soạn
Chọn D
Ta có
cos 1x
2xk
,
k
.
Câu 77: Phương trình
cos cos
3
x
π
=
có tất cả các nghiệm là:
A.
( )
2
2
3
x kk
π
π
=+∈
B.
( )
3
x kk
π
π
=±+ ∈
C.
(
)
2
3
x kk
π
π
=±+ ∈
D.
(
)
2
3
x kk
π
π
=+∈
Lời giải
Chọn C
Phương trình
( )
cos cos 2
33
x x kk
ππ
π
= ⇔=±+ ∈
Câu 78: Phương trình
cos 0x
=
có nghiệm là:
A.
( )
2
x kk
π
π
=+∈
. B.
( )
2 xk k
π
= ∈
.
C.
(
)
2
2
x kk
π
π
=+∈
. D.
( )
xk k
π
= ∈
.
Lời giải
Chọn A
Theo công thức nghiệm đặc biệt thì
(
)
cos 0
2
x kkx
π
π
= += ⇔ ∈
. Do đó Chọn A
Câu 79: Nghiệm của phương trình
2
cos
42
x
π
+=
là
A.
( )
2
2
xk
k
xk
π
π
π
=
∈
=−+
. B.
( )
2
xk
k
xk
π
π
π
=
∈
=−+
.
C.
( )
2
2
xk
k
xk
π
π
π
=
∈
=−+
. D.
( )
2
2
2
xk
k
xk
π
π
π
=
∈
=−+
.
Lời giải
Phương trình
( )
2
2
cos cos cos
42 4 4
2
2
xk
xx k
xk
π
π ππ
π
π
=
+= ⇔ += ⇒ ∈
=−+
.
Câu 80: Tìm tất cả các nghiệm của phương trình
cos 0.
3
x
=
A.
,.xk k
π
= ∈
B.
,.
2
x kk
π
π
=+∈
C.
3
6, .
2
x kk
π
π
=+∈
D.
3
3, .
2
x kk
π
π
=+∈
Lời giải
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 28
Sưu tầm và biên soạn
cos 0
3
x
=
32
x
k
π
π
⇔=+
3
3
2
xk
π
π
⇔= +
,
.
k ∈
Câu 81: Phương trình
2cos 1 0x −=
có nghiệm là:
A.
2
6
xk
π
π
=±+
,
k ∈
. B.
2
3
xk
π
π
=±+
,
k ∈
.
C.
2
6
x
π
π
=±+
,
k ∈
. D.
3
xk
π
π
=±+
,
k ∈
.
Lời giải
Phương trình
2cos 1 0
x −=
1
cos
2
x⇔=
2
3
xk
π
π
⇔=±+
,
k ∈
.
Câu 82: Phương trình
2cos 2 0x −=
có tất cả các nghiệm là
A.
3
2
4
,
3
2
4
xk
k
xk
π
π
π
π
= +
∈
=−+
. B.
2
4
,
2
4
xk
k
xk
π
π
π
π
= +
∈
=−+
.
C.
2
4
,
3
2
4
xk
k
xk
π
π
π
π
= +
∈
= +
. D.
7
2
4
,
7
2
4
xk
k
xk
π
π
π
π
= +
∈
=−+
.
Lời giải
2cos 2 0x
−=
2
cos
2
x⇔=
2
4
,
2
4
xk
k
xk
π
π
π
π
= +
⇔∈
=−+
.
Câu 83: Giải phương trình
2cos 1 0x −=
A.
3
,xkk
π
±+π= ∈
. B.
2
3
,
2
2
3
xk
xk
k
= +
= +
π
π
π
π
∈
.
C.
3
,2xkk+
π
±
π= ∈
. D.
3
,
2
3
x
k
k
k
x
= +
= +
π
π
π
π
∈
.
Lời giải
TXĐ:
D =
. Ta có
2cos 1 0x −=
1
cos
2
x⇔=
2
3
xk
π
π
⇔=±+
,
k ∈
.
Câu 84: Nghiệm của phương trình
cos 1x = −
là:
A.
2
xk
π
π
= +
,
k ∈
. B.
2xk
π
=
,
k ∈
.
C.
2xk
ππ
= +
,
k ∈
. D.
xk
π
=
,
k ∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 29
Sưu tầm và biên soạn
Phương trình
cos 1x
= −
2xk
ππ
⇔=+
,
k ∈
.
Câu 85: Phương trình
2
cos
2
x = −
có tập nghiệm là
A.
2;
3
x kk
π
π
=±+ ∈
. B.
;
4
x kk
π
π
=±+ ∈
.
C.
3
2;
4
x kk
π
π
=±+ ∈
. D.
;
3
x kk
π
π
=±+ ∈
.
Lời giải
2
cos
2
x = −
3
cos cos
4
x
π
⇔=
3
2,
4
x kk
π
π
⇔=± + ∈
.
Vậy tập nghiệm của phương trình là
3
2;
4
Sx kk
π
π
==±+ ∈
.
Câu 86: Khẳng định nào sau đây là khẳng định sai?
A.
cos 1 2x xk
ππ
=−⇔ = +
. B.
cos 0
2
x xk
π
π
=⇔= +
.
C.
cos 1 2x xk
π
=⇔=
. D.
cos 0 2
2
x xk
π
π
=⇔= +
.
Lời giải
Ta có:
cos 1 2x xk
ππ
=−⇔ = +
( )
k ∈
.
cos 0
2
x xk
π
π
=⇔= +
( )
k ∈
.
cos 1 2x xk
π
=⇔=
( )
k ∈
.
Câu 87: Phương trình lượng giác:
2cos 2 0
x +=
có nghiệm là
A.
2
4
2
4
xk
xk
π
π
π
π
= +
=−+
. B.
3
2
4
3
2
4
xk
xk
π
π
π
π
= +
=−+
. C.
2
4
3
2
4
xk
xk
π
π
π
π
= +
= +
. D.
7
2
4
7
2
4
xk
xk
π
π
π
π
= +
=−+
.
Lời giải
Phương trình tương đương với
23 3
cos cos 2
24 4
x xk
ππ
π
=− = ⇒=± +
Câu 88: Tìm công thức nghiệm của phương trình
( )
2cos 1x
α
+=
.
A.
( )
2
3
2
2
3
xk
k
xk
π
απ
π
απ
=−+ +
∈
=−+ +
. B.
( )
2
3
2
xk
k
xk
π
απ
απ
=−+ +
∈
=−+
.
C.
( )
2
3
2
3
xk
k
xk
π
απ
π
απ
=−+ +
∈
=−+
D.
( )
2
3
2
3
xk
k
xk
π
απ
π
απ
=−+ +
∈
=−− +
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 30
Sưu tầm và biên soạn
( ) (
)
1
2cos 1 cos
2
xx
αα
+=⇔ +=
2
3
xk
π
απ
⇔+ =± +
( )
2
3
2
3
xk
k
xk
π
απ
π
απ
=−+ +
⇔∈
=−− +
.
Câu 89: Tìm tổng các nghiệm của phương trình
cos 5 cos 2
63
xx
ππ
−= −
trên
[
]
0;
π
.
A.
47
18
π
. B.
4
18
π
. C.
45
18
π
. D.
7
18
π
.
Lời giải
Ta có:
cos 5 cos 2
63
xx
ππ
−= −
52 2
63
,
522
63
x xk
k
x xk
ππ
π
ππ
π
−= −+
⇔∈
−=−++
2
18 3
,
2
14 7
k
x
k
k
x
ππ
ππ
=−+
⇔∈
= +
.
Vì
[ ]
0;x
π
∈
nên ta có :
+) Với
2 2 1 19
0
18 3 18 3 12 12
kk
xk
ππ ππ
π
=−+ ⇒≤−+ ≤⇔ ≤≤
, do
1kk∈⇒=
nên
11
18
x
π
=
.
+) Với
2 2 1 13
0
14 7 14 7 4 4
kk
xk
ππ ππ
π
−
= + ⇒≤ + ≤ ⇔ ≤≤
, do
{ }
0;1; 2;3kk
∈⇒∈
nên
5 9 13
;;;
14 14 14 14
x
πππ π
∈
.
Tổng tất cả các nghiệm là:
11 5 9 13 47
18 14 14 14 14 18
ππ π π π π
++ + + =
.
Câu 90: Phương trình
22
8sin cos 1 0
22
xx
−=
tương đương với phương trình nào sau đây?
A.
2
sin
2
x =
. B.
cos 2 0x =
. C.
2
cos
2
x =
. D.
2
sin
2
x = −
.
Lời giải
Ta có:
2
22 2
8sin cos 1 0 2. 2sin cos 1 0 2sin 1 0
2 2 22
x x xx
x
−= ⇔ −= ⇔ −=
2
1 2sin 0 cos 2 0xx⇔− = ⇔ =
.
Câu 91: Họ các nghiệm của phương trình
1
cos3
2
x =
là
A.
2
,
93
k
xk
ππ
=±+ ∈
. B.
2,
9
x kk
π
π
=±+ ∈
.
C.
2
,
33
k
xk
ππ
=±+ ∈
. D.
2,
3
x kk
π
π
=±+ ∈
.
Lời giải
Ta có
12
cos3 3 2 ,
2 3 93
k
x x kx k
π ππ
π
=⇔ =±+ ⇔=±+ ∈
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 31
Sưu tầm và biên soạn
Câu 92: Tổng các nghiệm của phương trình
2
cos
52
π
+=−
x
trong khoảng
3
;
32
ππ
−
là
A.
21
20
π
. B.
2
π
. C.
8
5
π
. D.
13
20
π
.
Lời giải
Ta có phương trình
( )
3 11
22
23
5 4 20
cos cos cos .
3 19
52 5 4
22
5 4 20
x k xk
xx k
x kx k
ππ π
ππ
π ππ
ππ π
ππ
+= + = +
−
+= ⇔ += ⇔ ⇔ ∈
−−
+= + = +
Với
1
11 3 53 19 11
2, ; ; 0 .
20 3 2 120 40 20
π ππ π
π
= + ∈ − ⇒− < < ∈ ⇒ = ⇒ =
x kx k k k x
Với
2
19 3 37 49 21
2, ; ; 1 .
20 3 2 120 40 20
π ππ π
π
=− + ∈− ⇒ < < ∈ ⇒ =⇒ =
x kx k k k x
Vậy tổng các nghiệm là
12
11 21 8
.
20 20 5
xx
π ππ
+= + =
Câu 93: Tập nghiệm của phương trình
( )
( )
2
1 2 cos 2022 sin 0xx− +=
là
A.
;
44
k kk
ππ
ππ
+ −+ ∈
. B.
2; 2
44
k kk
ππ
ππ
+ −+ ∈
.
C.
4
kk
π
π
+∈
. D.
4
kk
π
π
−+ ∈
.
Lời giải
( )
( )
2
1 2 cos 2022 sin 0xx− +=
( )
2
1 2 cos 0
1
cos
2
2022 sin 0 VN
x
x
x
−=
⇔ ⇔=
+=
cos cos 2 ,
44
x x kk
ππ
π
⇔ = ⇔=±+ ∈
.
Vậy tập nghiệm của phương trình đã cho là
2; 2
44
k kk
ππ
ππ
+ −+ ∈
.
Câu 94: Phương trình lượng giác:
2cos 2 0x +=
có nghiệm là:
A.
2
4
3
2
4
xk
xk
π
π
π
π
= +
= +
. B.
3
2
4
3
2
4
xk
xk
π
π
π
π
= +
−
= +
. C.
5
2
4
5
2
4
xk
xk
π
π
π
π
= +
−
= +
. D.
x2
4
2
4
k
xk
π
π
π
π
= +
−
= +
.
Lời giải
Ta có
3
2
2
4
2cos 2 0 cos
3
2
2
4
xk
xx
xk
π
π
π
π
= +
+=⇔ =−⇔
−
= +
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 32
Sưu tầm và biên soạn
Câu 95: Tất cả nghiệm của phương trình
2cos 1
x
= −
là
A.
( )
2
3
x kk
π
π
=±+ ∈
. B.
( )
2
3
x kk
π
π
=±+ ∈
.
C.
(
)
2
2
3
x kk
π
π
=±+ ∈
. D.
( )
2
6
x kk
π
π
=±+ ∈
.
Lời giải
( )
1 22
2cos 1 cos cos cos 2
2 33
x x x x kk
ππ
π
=−⇔ =− ⇔ = ⇔ =± + ∈
.
Câu 96: Tổng các nghiệm thuộc khoảng
;
22
ππ
−
của phương trình
2
4sin 2 1 0x −=
bằng:
A.
.
π
B.
.
3
π
C.
0
. D.
.
6
π
Lời giải
Ta có:
(
) (
)
2
1
4sin 2 1 0 2 1 cos 4 1 0 cos 4
2 12 2
x x x x kk
ππ
−= ⇔ − −= ⇔ = ⇔ =± + ∈
.
Do
;
12 2 2 2
xk
π π ππ
=± + ∈−
1
2
3
4
12
12
5
12
5
12
x
x
x
x
π
π
π
π
=
= −
⇒
= −
=
1234
0xxxx⇒+++=
.
Câu 97: Phương trình
2cos 1
3
x
π
+=
có số nghiệm thuộc đoạn
[ ]
0; 2
π
là
A.
1
B.
2
C.
0
D.
3
Lời giải
Phương trình:
2c c
2
os 1 os
3 32
xx
ππ
+=⇔ +=
( )
2
32
2
32
xk
k
xk
ππ
π
ππ
π
+=+
⇔∈
+=−+
( )
2
6
5
2
6
xk
k
xk
π
π
π
π
= +
⇔∈
=−+
Vì
[ ]
0; 2x
π
∈
nên
7
,
66
x
ππ
∈
. Vậy số nghiệm phương trình là 2
Câu 98: Biết các nghiệm của phương trình
1
cos 2
2
x = −
có dạng
xk
m
π
π
= +
và
xk
n
π
π
=−+
,
k ∈
; với
,mn
là các số nguyên dương. Khi đó
mn+
bằng
A. 4. B. 3. C. 5. D. 6.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 33
Sưu tầm và biên soạn
Chọn D
1
cos 2
2
x = −
( )
2
22
2
33
cos 2 cos
2
3
22
33
x k xk
xk
x kx k
ππ
ππ
π
ππ
ππ
=+=+
⇔= ⇔ ⇔ ∈
=− + =−+
336mn⇒ +=+=
.
Câu 99: Phương trình
2cos 1
3
x
π
+=
có số nghiệm thuộc đoạn
[ ]
0; 2
π
là
A.
1
B.
2
C.
0
D.
3
Lời giải
Chọn B
Phương trình:
2c c
2
os 1 os
3 32
xx
ππ
+=⇔ +=
( )
2
32
2
32
xk
k
xk
ππ
π
ππ
π
+=+
⇔∈
+=−+
( )
2
6
5
2
6
xk
k
xk
π
π
π
π
= +
⇔∈
=−+
Vì
[
]
0; 2
x
π
∈
nên
7
,
66
x
ππ
∈
. Vậy số nghiệm phương trình là 2
Câu 100: Nghiệm lớn nhất của phương trình
2cos 2 1 0x
−=
trong đoạn
[ ]
0;
π
là:
A.
x
π
=
. B.
11
12
x
π
=
. C.
2
3
x
π
=
. D.
5
6
x
π
=
.
Lời giải
Phương trình
2cos 2 1 0
x −=
1
cos 2
2
x⇔=
22
3
22
3
xk
xk
π
π
π
π
= +
⇔
=−+
6
6
xk
xk
π
π
π
π
= +
⇔
=−+
.
Xét
[ ]
0;x
π
∈
0
6
0
6
k
k
π
ππ
π
ππ
≤+ ≤
⇔
≤− + ≤
15
66
17
66
k
k
−
≤≤
⇔
≤≤
mà
k ∈
suy ra
0
1
k
k
=
=
6
5
6
x
x
π
π
=
⇔
=
.
Vậy nghiệm lớn nhất của phương trình
2cos 2 1 0x −=
trong đoạn
[ ]
0;
π
là
5
6
x
π
=
.
Câu 101: Cho hai phương trình
cos3 1 0x −=
;
1
cos 2
2
x = −
. Tập các nghiệm của phương trình đồng thời
là nghiệm của phương trình là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 34
Sưu tầm và biên soạn
A.
2
3
xk
π
π
= +
,
k ∈
. B.
2
xk
π
=
,
k ∈
.
C.
2
3
xk
π
π
=±+
,
k
∈
D.
2
2
3
xk
π
π
=±+
,
k ∈
.
Lời giải
Ta có
cos3 1 0
x −=
cos3 1
x⇔=
2
3
xk
π
⇔=
,
k ∈
.
1
cos 2
2
x = −
2
22
3
xk
π
π
⇔=±+
3
xk
π
π
⇔=±+
,
k ∈
.
Biểu diễn các nghiệm trên đường tròn lượng giác ta có tập các nghiệm của phương trình đồng
thời là nghiệm của phương trình là
2
3
xk
π
π
=±+
,
k ∈
.
Câu 102: Số nghiệm của phương trình
2cos 3x =
trên đoạn
5
0;
2
π
là
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
2cos 3x =
3
cos
2
x⇔=
2,
6
x kk
π
π
⇔=±+ ∈
.
Mà
5
0;
2
x
π
∈
và
k
∈
nên
11 13
;;
66 6
x
πππ
∈
.
Câu 103: Số nghiệm của phương trình
1
cos
2
x =
thuộc đoạn
[ ]
2 ;2
ππ
−
là?
A.
4
. B.
2
. C.
3
. D.
1
.
Lời giải
Ta có
1
cos
2
x =
⇔
2
3
2
3
xk
xk
π
π
π
π
= +
=−+
,
k ∈
.
Xét
2
3
xk
π
π
= +
, do
[ ]
2 ;2x
ππ
∈−
và
k ∈
nên
2 22
3
k
π
π ππ
− ≤+ ≤
1k⇒=−
;
0k =
.
Xét
2
3
xk
π
π
=−+
, do
[ ]
2 ;2x
ππ
∈−
và
k ∈
nên
2 22
3
k
π
π ππ
− ≤− + ≤
1
k⇒=
;
0k =
.
Vậy phương trình có
4
nghiệm trên đoạn
[ ]
2 ;2
ππ
−
.
Câu 104: Phương trình
cos 2 cos 0xx+=
có bao nhiêu nghiệm thuộc khoảng
( )
;
ππ
−
?
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Ta có
( ) ( )
2
cos 2 cos 0 cos 2 cos
2
33
xk
xx x x k
xk
ππ
π
ππ
= +
+ =⇔ = +⇔ ∈
=−+

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 35
Sưu tầm và biên soạn
Vì
3
3
x
x
x
π
ππ
π
= −
−<< ⇒
=
.
Câu 105: Tổng tất cả các nghiệm của phương trình
cos 2 cos 0
xx−=
trên khoảng
( )
0; 2
π
bằng
T
. Khi đó
T
có giá trị là:
A.
7
6
T
π
=
. B.
2T
π
=
. C.
4
3
T
π
=
. D.
T
π
=
.
Lời giải
Ta có:
cos 2 cos 0
xx
−=
cos 2 cosxx⇔=
22
22
x xk
x xk
π
π
= +
⇔
=−+
2
2
3
xk
k
x
π
π
=
⇔
=
( )
2
;
3
k
xk
π
⇔= ∈
.
Vì
( )
0; 2x
π
∈
nên
2
02
3
k
π
π
<<
03k⇔<<
.
Do
k
∈
nên
{ }
1; 2k ∈
2
3
x
π
⇒=
;
4
3
x
π
=
.
Vậy
24
2
33
T
ππ
π
=+=
.
Câu 106: Số nghiệm của phương trình
2cos 3x =
trên đoạn
5
0;
2
π
là
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải
Chọn D
2cos 3x =
3
cos
2
x⇔=
2,
6
x kk
π
π
⇔=±+ ∈
.
Mà
5
0;
2
x
π
∈
và
k ∈
nên
11 13
;;
66 6
x
πππ
∈
.
Câu 107: Tìm tập nghiệm
S
của phương trình
cos .sin 2 0
3
xx
π
−=
.
A.
;,
2 62
k
Sk k
π ππ
π
=++∈
. B.
{ }
180 ;75 90 ,Sk k k= ° °+ ° ∈
.
C.
5
;,
12 2
k
Sk k
ππ
π
= +∈
. D.
{ }
100 180 ;30 90 ,S k kk= °+ ° °+ ° ∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 36
Sưu tầm và biên soạn
Ta có:
cos 0
22
cos .sin 2 0 , .
sin 2 0
3
2
3
3 62
x
xk xk
xx k
x
k
xkx
ππ
ππ
π
π
π ππ
π
=
=+=+
−=⇔ ⇔ ⇔ ∈
−=
−= =+
Vậy tập nghiệm của phương trình đã cho là:
;,
2 62
k
Sk k
π ππ
π
=++∈
.
Câu 108: Giải phương trình
2
3cos 5cosxx=
A.
2
xk
π
π
= +
( )
k ∈
. B.
2
2
xk
π
π
= +
( )
k ∈
.
C.
2
xk
ππ
= +
( )
k
∈
. D.
xk
π
=
(
)
k ∈
.
Lời giải
2
cos 0
3cos 5cos
5
cos
3
x
xx
x
=
= ⇔
=
+)
( )
cos 0
2
x xk k
π
π
=⇔= + ∈
+)
5
cos
3
x
=
Câu 109: Giải phương trình
5sin sin 2 0xx−=
A.
2
xk
π
=
( )
k ∈
. B.
2
xk
π
π
= +
( )
k ∈
.
C.
xk
π
=
( )
k ∈
. D. Phương trình vô nghiệm.
Lời giải
5sin sin 2 0xx−=
5sin 2sin .cos 0x xx⇔− =
( )
sin 5 2cos 0
xx⇔− =
sin 0
5 2cos 0
x
x
=
⇔
−=
+)
(
)
sin 0x xk k
π
=⇔= ∈
+)
5
5 2cos 0 cos
2
xx− =⇔=
Câu 110: Giải phương trình
(
)
sin cos 2 0
2
xx
−− − =
π
π
A.
{ }
2|Sk k= ∈
π
. B.
2
2, |
33
k
Sk k
= +∈
ππ
π
.
C.
2
,|
33
k
Sk k
=+∈
ππ
π
. D.
2
|
33
k
Sk
=+∈
ππ
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 37
Sưu tầm và biên soạn
(
)
sin cos 2 0
2
xx
π
π
−− − =
sin sin 2 0xx⇔− =
sin 2 sinxx⇔=
22
22
x xk
x xk
π
ππ
= +
⇔
= −+
( )
2
2
33
xk
k
k
x
π
ππ
=
⇔∈
= +
.
Câu 111: Nghiệm âm lớn nhất của phương trình
22
cos 4 sin cos
6
x xx
π
−+ =
A.
35
36
π
−
. B.
11
36
π
−
. C.
11
12
π
−
. D.
12
π
−
.
Lời giải
22
cos 4 sin cos
6
x xx
π
−+ =
22
cos 4 cos sin
6
x xx
π
⇔ −= −
( )
cos 4 cos 2
6
4 22
6
12
4 22
36 3
6
xx
x xk
xk
k
xk
x xk
π
π
π
π
π
ππ
π
π
⇔ −=
−= +
= +
⇔ ⇔∈
= +
−=−+
Ta có mỗi họ nghiệm lần lượt có các nghiệm âm lớn nhất là:
12
11 11
;
12 12 36 3 36
xx
π π ππ π
π
= −=− = − =−
Vậy nghiệm âm lớn nhất của phương trình là
11
36
x
π
= −
.
Câu 112: Trên khoảng
;2
2
π
π
, phương trình
cos 2 sin
6
xx
π
−=
có bao nhiêu nghiệm?
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải
Ta có
cos 2 sin
6
xx
π
−=
cos 2 cos
62
xx
ππ
⇔ −= −
2
62
22
62
x xk
x xk
ππ
π
ππ
π
− = −+2
⇔
− =− ++
2
3
,
2
93
xk
k
k
x
π
π
ππ
=−−
⇔∈
2
= −
.
8 14
;2 ; ;
2 39 9
xx
π ππ π
π
5
∈ ⇒∈
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 38
Sưu tầm và biên soạn
Vậy phương trình đã cho có 3 nghiệm trên khoảng
;2
2
π
π
.
Câu 113: Số điểm biểu diễn nghiệm của phương trình
(
)
sin4 2cos 2 0
xx−=
trên đường tròn lượng giác
là
A.
4
. B.
6
. C.
8
. D.
10
.
Lời giải
( )
sin4 2cos 2 0xx−=
⇔
sin4 0
2cos 2 0
x
x
=
−=
⇔
4
2
cos
2
xk
x
π
=
=
⇔
( )
4
2
4
2
4
k
x
xkk
xk
π
π
π
π
π
=
=+∈
=−+
.
Vậy có
8
điểm biểu diễn nghiệm của phương trình trên trên đường tròn lượng giác.
Câu 114: Các họ nghiệm của phương trình
sin 2 3 sin 0xx−=
là:
A.
6
xk
xk
π
π
π
=
=±+
. B.
6
xk
π
π
=±+
. C.
2
6
xk
xk
π
π
π
=
=±+
. D.
2
2
3
xk
xk
π
π
π
=
=±+
.
Lời giải
Ta có
( )
sin 2 3 sin 0 sin 2cos 3 0x x xx− =⇔ −=
sin 0
3
2
cos
6
2
x
xk
xk
x
π
π
π
=
=
⇔⇔
=±+
=
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 91
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
DẠNG 3. PHƯƠNG TRÌNH
tan xm=
Câu 115: Tìm tất cả các nghiệm của phương trình
tan xm=
,
( )
m ∈
.
A.
arctanx mk
π
= +
hoặc
arctanx mk
ππ
=−+
,
( )
k ∈
.
B.
arctanx mk
π
=±+
,
( )
k ∈
.
C.
arctan 2x mk
π
= +
,
( )
k ∈
.
D.
arctanx mk
π
= +
,
( )
k ∈
.
Câu 116: Phương trình
tan 3x =
có tập nghiệm là
A.
2,
3
kk
π
π
+∈
. B.
∅
. C.
,
3
kk
π
π
+∈
. D.
,
6
kk
π
π
+∈
.
Câu 117: Số điểm biểu diễn nghiệm của phương trình
tan 2 1x =
trên đường tròn lượng giác là
A.
6
. B.
2
. C.
8
. D.
4
.
Câu 118: Nghiệm của phương trình
( )
tan 1 1x +=
là
A.
( )
1 x kk
π
=+∈
. B.
( )
1
4
x kk
π
π
=−+ + ∈
.
C.
( )
xk k
π
= ∈
. D.
( )
1 .180
4
x kk
π
=−+ + ° ∈
.
Câu 119: Nghiệm của phương trình
tan 3 tanxx=
là
A.
,.
2
k
xk
π
= ∈
B.
,xk k
π
= ∈
. C.
2, .xk k
π
= ∈
D.
,.
6
k
xk
π
= ∈
Câu 120: Phương trình có các nghiệm là:
A. . B. . C. . D. .
Câu 121: Phương trình lượng giác:
3.tan 3 0x +=
có nghiệm là:
A.
x
3
k
π
π
= +
. B.
x2
3
k
π
π
=−+
. C.
x
6
k
π
π
= +
. D.
x
3
k
π
π
=−+
.
Câu 122: Giải phương trình:
2
tan 3x =
có nghiệm là:
( )
tan 3 15 3x − °=
60 180xk= °+ °
75 180xk= °+ °
75 60xk= °+ °
25 60xk= °+ °
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TRẮC NGHIỆM.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 92
Sưu tầm và biên soạn
A.
x
3
k
π
π
= +
. B.
x
3
k
π
π
=−+
. C.
x
3
k
π
π
=±+
. D. vô nghiệm.
Câu 123: Nghiệm của phương trình
3 3tan 0x+=
là:
A.
6
xk
π
π
=−+
. B.
2
xk
π
π
= +
. C.
3
xk
π
π
= +
. D.
2
2
xk
π
π
= +
.
Câu 124: Giải phương trình
3 tan 2 3 0x −=
.
A.
( )
6
x kk
π
π
=+∈
. B.
( )
32
x kk
ππ
=+∈
.
C.
( )
3
x kk
π
π
=+∈
. D.
( )
62
x kk
ππ
=+∈
.
Câu 125: Họ nghiệm của phương trình:
tan 1 0
4
x
π
− −=
là
A.
,
2
x kk
π
π
=+∈
. B.
,xk k
π
= ∈
.
C.
2,
2
x kk
π
π
=+∈
. D.
,
4
x kk
π
π
=+∈
.
Câu 126: Tổng các nghiệm phương trình
( )
0
tan 2 15 1x −=
trên khoảng
( )
00
90 ;90−
bằng
A.
0
30
. B.
0
60−
. C.
0
0
. D.
0
30−
.
Câu 127: Số nghiệm của phương trình
tan 3 tan 0−=xx
trên nửa khoảng
[
)
0; 2
π
bằng:
A. 1. B. 2. C. 3. D. 4.
Câu 128: Phương trình
tan 1 0x +=
có nghiệm là
A.
( )
4
x kk
π
π
=+∈
. B.
( )
2
x kk
π
π
=−+ ∈
.
C.
( )
4
x kk
π
π
=−+ ∈
. D.
( )
,
44
x kx kk
ππ
ππ
=+ =−+ ∈
.
Câu 129: Tính tổng các nghiệm trong đoạn
[ ]
0;30
của phương trình:
tan tan 3xx=
A.
55 .
π
B.
171
.
2
π
C.
45 .
π
D.
190
.
2
π
Câu 130: Trong các nghiệm dương bé nhất của các phương trình sau, phương trình nào có nghiệm dương
nhỏ nhất?
A. . B. . C. . D. .
Câu 131: Nghiệm của phương trình
3
tan
3
x
−
=
được biểu diễn trên đường tròn lượng giác ở hình bên là
những điểm nào?
tan 2 1x =
tan 3
4
x
π
−=
cot 0x =
cot 3x = −
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 93
Sưu tầm và biên soạn
A. Điểm
F
, điểm
D
. B. Điểm
C
, điểm
F
.
C. Điểm
C
, điểm
D
, điểm
E
, điểm
F
. D. Điểm
E
, điểm
F
.
Câu 132: Số nghiệm của phương trình
3
tan tan
11
x
π
=
trên khoảng
;2
4
π
π
là?
A.
4.
B.
1.
C.
2.
D.
3.
Câu 133: Tổng các nghiệm của phương trình
tan 5 tan 0
xx−=
trên nửa khoảng
[
)
0;
π
bằng:
A.
5
2
π
. B.
π
. C.
3
2
π
. D.
2
π
.
Câu 134: Tính tổng các nghiệm của phương trình
( )
0
tan 2 15 1x −=
trên khoảng
(
)
00
90 ;90
−
bằng.
A.
0
0.
B.
0
30 .−
C.
0
30 .
D.
0
60 .−
DẠNG 4. PHƯƠNG TRÌNH
cot xm=
Câu 135: Giải phương trình
co t 3.
x
=
A.
x ∈∅
. B.
(
)
3 x kk
π
=+∈
.
C.
( )
arccot 3 x kk
π
= +∈
. D.
( )
arccot 3 2 x kk
π
=+∈
.
Câu 136: Nghiệm của phương trình
( )
cot 2 1
x +=
là:
A.
22
4
xk
π
π
=++
,
k ∈
. B.
2
4
xk
π
π
=−+ +
,
k ∈
.
C.
2
4
xk
π
π
=−− +
,
k ∈
. D.
2
4
xk
π
π
=++
,
k ∈
.
Câu 137: Tập nghiệm của phương trình
cot 3=x
A.
5
;
6
π
π
−
+∈
kk
. B.
;
6
π
π
±+ ∈
kk
.
y
x
B'
A'
B
D
F
O
A
C
E

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 94
Sưu tầm và biên soạn
C.
;
3
π
π
+∈
kk
. D.
2;
6
π
π
+∈
kk
.
Câu 138: Giải phương trình
( )
cot 3 1 3x
−=−
A.
1
,
36
x kk
π
π
=−+ ∈
. B.
5
,
83
k
xk
ππ
=+∈
.
C.
1
,
3 18 3
k
xk
ππ
=++ ∈
. D.
15
,
3 18 3
k
xk
ππ
=++ ∈
.
Câu 139: Giải phương trình
2
cot 3
3
x
=
.
A.
()
4
x kk
π
π
=+∈
. B.
2
()
43
k
xk
ππ
=+∈
.
C.
3
()
42
k
xk
ππ
=+∈
. D.
3
()
22
k
xk
ππ
=+∈
.
Câu 140: Tổng tất cả các nghiệm của phương trình
cot 3x =
trên đoạn
[ ]
0;2
π
bằng.
A.
6
π
. B.
7
6
π
. C.
5
6
π
. D.
4
3
π
.
Câu 141: Phương trình lượng giác
3cot 3 0x −=
có nghiệm là:
A.
x2
3
k
π
π
= +
. B. Vô nghiệm. C.
6
xk
π
π
= +
. D.
x
3
k
π
π
= +
.
Câu 142: Phương trình
2cot 3 0x −=
cónghiệmlà
A.
( )
2
6
2
6
xk
kZ
xk
π
π
π
π
= +
∈
=−+
. B.
(
)
2
3
x k kZ
π
π
=+∈
C.
(
)
3
arccot
2
x k kZ
π
= +∈
. D.
( )
6
x k kZ
π
π
=+∈
.
Câu 143: Giải phương trình
( )
cot 3 1 3.x −=−
A.
( )
15
.
3 18 3
x k kZ
ππ
=++ ∈
B.
( )
1
.
3 18 3
x k kZ
ππ
=++ ∈
C.
( )
5
.
18 3
x k kZ
ππ
=+∈
D.
( )
1
.
36
x k kZ
π
π
=−+ ∈
Câu 144: Số nghiệm của phương trình
3cot3 3 0x −=
trên khoảng
2
;
99
ππ
−
là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 145: Nghiệm của phương trình
cot 3
3
x
π
+=
có dạng
k
x
mn
ππ
=−+
, với
k ∈
và
m
,
*
n ∈
.
Khi đó
mn−
bằng
A.
5−
. B.
5
. C.
3
. D.
3−
.
Câu 146: Số nghiệm của phương trình
cot 20 1x =
trên đoạn
[ ]
50 ;0
π
−
là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 95
Sưu tầm và biên soạn
A.
980
. B.
1001
. C.
1000
. D.
981
.
Câu 147: Hỏi trên đoạn
[
]
0;2018
π
, phương trình
3 cot 3 0x −=
có bao nhiêu nghiệm?
A. 2018. B. 6340. C. 6339. D. 2017.
Câu 148: Phương trình
cot 3 cot
xx=
có các nghiệm là:
A.
2,
2
x kk
π
π
=+∈
. B.
,xkk
π
= ∈
.
C.
,
3
k
xk
π
= ∈
. D.
,
2
x kk
π
π
=+∈
.
DẠNG 5. MỘT SỐ BÀI TOÁN TỔNG HỢP
Câu 149: Trong các phương trình sau, phương trình nào vô nghiệm?
A.
tan 99x
. B.
2
cos 2
23
x
. C.
cot 2018 2017x
. D.
3
sin 2
4
x
.
Câu 150: Phương trình
sin cosxx
=
có số nghiệm thuộc đoạn
[ ]
;−π π
là:
A.
3
B.
5
C.
2
D.
4
Câu 151: Giải phương trình
2cos 1 sin 2 0
22
xx
− +=
A.
( )
2
2,
3
x kk
π
π
=±+ ∈
B.
(
)
2,
3
x kk
π
π
=±+ ∈
C.
( )
4,
3
x kk
π
π
=±+ ∈
D.
( )
2
4,
3
x kk
π
π
=±+ ∈
Câu 152: Phương trình
8.cos2 .sin 2 .cos 4 2xx x= −
có nghiệm là
A.
( )
32 4
5
32 4
xk
k
xk
ππ
ππ
−
= +
∈
= +
. B.
( )
16 8
3
16 8
xk
k
xk
ππ
ππ
= +
∈
= +
.
C.
( )
88
3
88
xk
k
xk
ππ
ππ
= +
∈
= +
. D.
( )
32 4
3
32 4
xk
k
xk
ππ
ππ
= +
∈
= +
.
Câu 153: Tìm số nghiệm của phương trình
( )
sin cos 2 0
x =
trên
[ ]
0; 2 .
π
A.
2
. B.
1
. C.
4
. D.
3
.
Câu 154: Trong khoảng
(
)
0;
π
, phương trình
cos 4 sin 0xx+=
có tập nghiệm là
S
. Hãy xác định
S
.
A.
237
;;;
3 3 10 10
S
ππππ
=
. B.
3
;
6 10
S
ππ
=
.
C.
7
;;
6 10 10
S
ππ π
=
. D.
537
;;;
6 6 10 10
S
ππππ
=
.
Câu 155: Phương trình
sin 2 cosxx=
có nghiệm là

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 96
Sưu tầm và biên soạn
A.
( )
63
2
2
k
x
k
xk
ππ
π
π
= +
∈
= +
. B.
( )
63
2
3
k
x
k
xk
ππ
π
π
= +
∈
= +
.
C.
( )
2
6
2
2
xk
k
xk
π
π
π
π
= +
∈
= +
. D.
( )
2
63
2
2
k
x
k
xk
ππ
π
π
= +
∈
= +
.
Câu 156: Phương trình
sin cosxx=
có bao nhiêu nghiệm
( )
0;5x
π
∈
?
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 157: Nghiệm của phương trình
sin 3 cosxx
=
là
A.
xk
π
=
;
2
xk
π
=
. B.
82
xk
ππ
= +
;
4
xk
π
π
= +
.
C.
2xk
π
=
;
2
2
xk
π
π
= +
. D.
xk
π
=
;
4
xk
π
π
= +
.
Câu 158: Phương trình
sin 2 cos 0xx+=
có tổng các nghiệm trong khoảng
( )
0; 2
π
bằng
A.
2
π
. B.
3
π
. C.
5
π
. D.
6
π
.
Câu 159: Số nghiệm chung của hai phương trình
2
4cos 3 0x −=
và
2sin 1 0x +=
trên khoảng
3
;
22
ππ
−
bằng
A.
2
. B.
4
. C.
3
. D.
1
.
Câu 160: Giải phương trình
sin sin 7 sin 3 sin 5xx xx=
.
A.
,xkk
π
= ∈
. B.
,
6
k
xk
π
= ∈
. C.
,
4
k
xk
π
= ∈
. D.
,
2
k
xk
π
= ∈
.
Câu 161: Tìm số nghiệm của phương trình
sin cos 2xx=
thuộc đoạn
[ ]
0; 20
π
.
A.
20
. B.
40
. C.
30
. D.
60
.
Câu 162: Số vị trí biểu diễn các nghiệm của phương trình
tan 3 cot 0
2
xx
π
+ −=
trên đường tròn lượng
giác là?
A.
4
. B.
2
. C.
0
. D.
1
.
Câu 163: Phương trình
sin cos 0
4
xx
π
++ =
có tập nghiệm được biểu diễn bởi bao nhiêu điểm trên đường
tròn lượng giác?
A.
1
. B.
2
. C.
4
. D.
3
.
Câu 164: Tìm tập nghiệm
S
của phương trình
cos .sin 2 0
3
xx
π
−=
.
A.
;,
2 62
k
Sk k
π ππ
π
=++∈
. B.
{
}
180 ;75 90 ,Sk k k= ° °+ ° ∈
.
C.
5
;,
12 2
k
Sk k
ππ
π
= +∈
. D.
{ }
100 180 ;30 90 ,S k kk= °+ ° °+ ° ∈
.
Câu 165: Giải phương trình
5sin sin2 0xx−=

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 97
Sưu tầm và biên soạn
A.
2xk
π
=
(
)
k
∈
. B.
2
xk
π
π
= +
( )
k ∈
.
C.
xk
π
=
( )
k ∈
. D. Phương trình vô nghiệm.
Câu 166: Giải phương trình
( )
sin cos 2 0
2
xx
−− − =
π
π
A.
{
}
2|Sk k
= ∈
π
. B.
2
2, |
33
k
Sk k
= +∈
ππ
π
.
C.
2
,|
33
k
Sk k
=+∈
ππ
π
. D.
2
|
33
k
Sk
=+∈
ππ
Câu 167: Nghiệm âm lớn nhất của phương trình
22
cos 4 sin cos
6
x xx
π
−+ =
A.
35
36
π
−
. B.
11
36
π
−
. C.
11
12
π
−
. D.
12
π
−
.
Câu 168: Các họ nghiệm của phương trình
sin 2 3 sin 0xx−=
là:
A.
6
xk
xk
π
π
π
=
=±+
. B.
6
xk
π
π
=±+
. C.
2
6
xk
xk
π
π
π
=
=±+
. D.
2
2
3
xk
xk
π
π
π
=
=±+
.
Câu 169: Giải phương trình
cot sin 1 tan .tan 4
2
x
xx x
++ =
Câu 170: Số điểm phân biệt biểu diễn các nghiệm phương trình
sin 2 sin 0−=xx
trên đường tròn lượng
giác là
A. 4 B. 1. C. 2. D. 3.
Câu 171: Số nghiệm phương trình
sin 3
0
cos 1
x
x
=
+
thuộc đoạn
[ ]
2 ;4
ππ
là
A.
7
. B.
6
. C.
4
. D.
5
.
Câu 172: Giải phương trình sau:
3 2 3sin3
4sin
cos sin 2
x
x
xx
= −
Câu 173: Cho phương trình:
( )
( )( )
1 2sinx cos
3
1 2sinx 1 sinx
x−
=
+−
. Phương trình có bao nhiêu nghiệm trên khoảng
( )
2021 ;2021
ππ
−
?

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
DẠNG 3. PHƯƠNG TRÌNH
tan xm=
Câu 115: Tìm tất cả các nghiệm của phương trình
tan xm=
,
( )
m ∈
.
A.
arctanx mk
π
= +
hoặc
arctan
x mk
ππ
=−+
,
( )
k ∈
.
B.
arctanx mk
π
=±+
,
( )
k ∈
.
C.
arctan 2x mk
π
= +
,
( )
k ∈
.
D.
arctan
x mk
π
= +
,
( )
k ∈
.
Lời giải
Ta có:
tan arctanx m x mk
π
= ⇔= +
,
(
)
k ∈
.
Câu 116: Phương trình
tan 3x =
có tập nghiệm là
A.
2,
3
kk
π
π
+∈
. B.
∅
. C.
,
3
kk
π
π
+∈
. D.
,
6
kk
π
π
+∈
.
Lời giải
Ta có
tan 3x =
tan tan
3
x
π
⇔=
3
xk
π
π
⇔= +
,
k ∈
.
Câu 117: Số điểm biểu diễn nghiệm của phương trình
tan 2 1x =
trên đường tròn lượng giác là
A.
6
. B.
2
. C.
8
. D.
4
.
Lời giải
Ta có
( )
tan 2 1 2
4 82
k
x x kx k
π ππ
π
=⇔ = + ⇔= + ∈
.
Biểu diễn trên đường tròn lượng giác ta được
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TRẮC NGHIỆM.
II
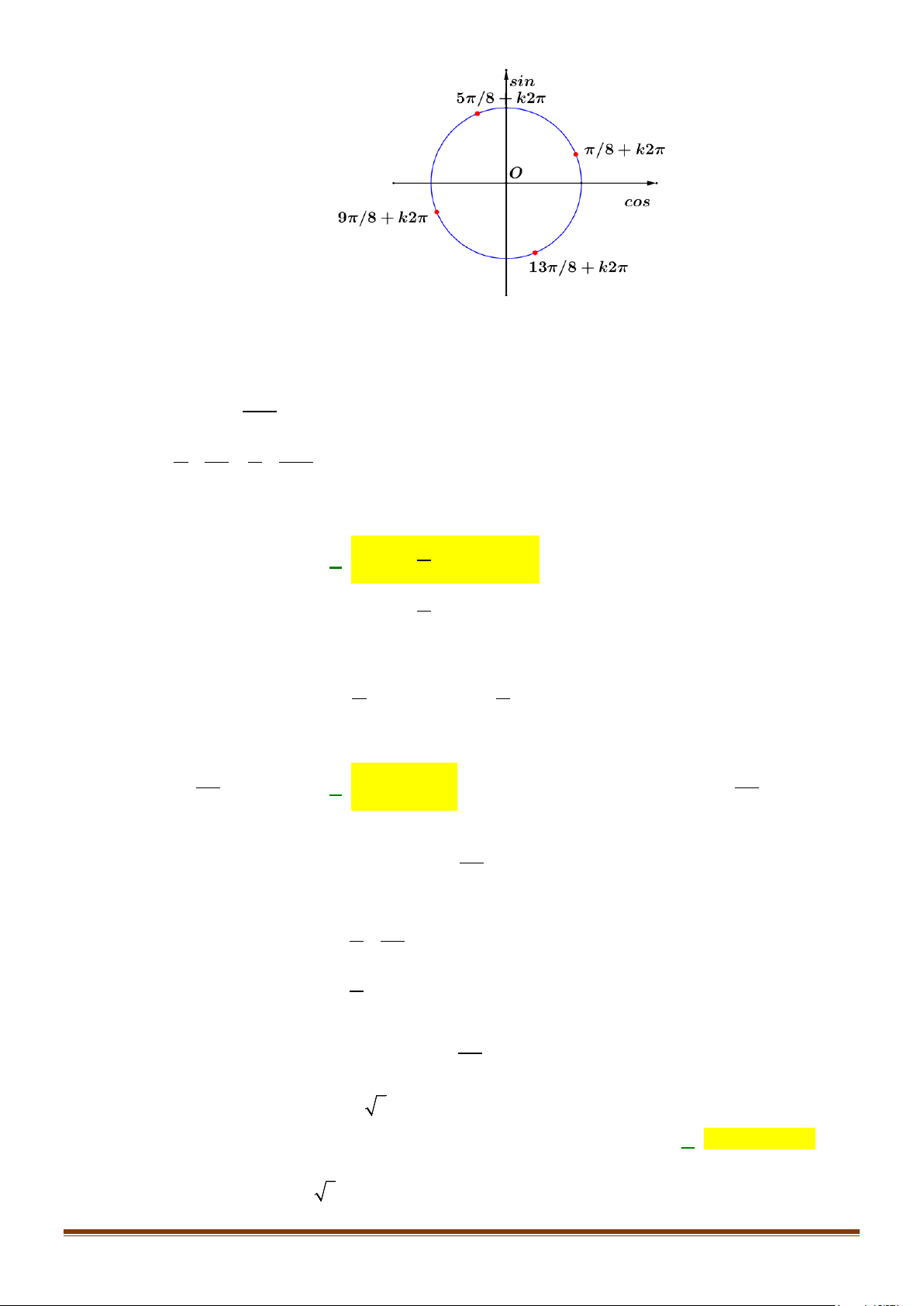
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
Vậy số điểm biểu diễn nghiệm của phương trình
tan 2 1x =
là
4
.
Cách khác
Họ cung
( )
2
,
k
kn
n
π
α
+∈
có
n
điểm biểu diễn trên đường tròn lượng giác nên
( )
2
828 4
kk
xk
π ππ π
=+=+ ∈
có 4 điểm biểu diễn trên đường tròn lượng giá C.
Câu 118: Nghiệm của phương trình
( )
tan 1 1x +=
là
A.
( )
1 x kk
π
=+∈
. B.
( )
1
4
x kk
π
π
=−+ + ∈
.
C.
( )
xk k
π
= ∈
. D.
( )
1 .180
4
x kk
π
=−+ + ° ∈
.
Lời giải
Ta có:
( ) ( )
tan 1 1 1 1 .
44
x x k x kk
ππ
ππ
+ = ⇔ + = + ⇔ =−+ + ∈
Câu 119: Nghiệm của phương trình
tan 3 tanxx=
là
A.
,.
2
k
xk
π
= ∈
B.
,xk k
π
= ∈
. C.
2, .xk k
π
= ∈
D.
,.
6
k
xk
π
= ∈
Lời giải
Ta có
tan 3 tan 3 , .
2
k
x x x xk x k
π
π
= ⇔ =+ ⇔= ∈
Trình bày lại
ĐK:
cos3x 0
63
cosx 0
2
k
x
xk
ππ
π
π
≠+
≠
⇔⇔
≠
≠+
( )
*
Ta có
tan 3 tan 3 , .
2
k
x x x xk x k
π
π
= ⇔ =+ ⇔= ∈
Kết hợp điều kiện
( )
*
suy ra
,xk k
π
= ∈
Câu 120: Phương trình có các nghiệm là:
A. . B. . C. . D. .
Lời giải
Ta có:
( )
tan 3 15 3x − °=
60 180xk= °+ °
75 180xk= °+ °
75 60xk= °+ °
25 60xk= °+ °
( ) ( )
tan 3 15 3 tan 3 15 tan 60 3 15 60 180x x xk−°= ⇔ −°= °⇔ −°= °+ °

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
.
Câu 121: Phương trình lượng giác:
3.tan 3 0x +=
có nghiệm là:
A.
x
3
k
π
π
= +
. B.
x2
3
k
π
π
=−+
. C.
x
6
k
π
π
= +
. D.
x
3
k
π
π
=−+
.
Lời giải
3.tan 3 0 3 .
3
x tanx x k
π
π
+=⇔ =− ⇔ =− +
Câu 122: Giải phương trình:
2
tan 3x =
có nghiệm là:
A.
x
3
k
π
π
= +
. B.
x
3
k
π
π
=−+
. C.
x
3
k
π
π
=±+
. D. vô nghiệm.
Lời giải
2
33 ,
3
tan x tanx x k k
π
π
=⇔ =± ⇔=±+ ∈
.
Câu 123: Nghiệm của phương trình
3 3tan 0x+=
là:
A.
6
xk
π
π
=−+
. B.
2
xk
π
π
= +
. C.
3
xk
π
π
= +
. D.
2
2
xk
π
π
= +
.
Lời giải
( )
3
3 3tan 0 tan
36
x x xkk
π
π
+ =⇔ =− ⇔=−+ ∈
.
Câu 124: Giải phương trình
3 tan 2 3 0x −=
.
A.
( )
6
x kk
π
π
=+∈
. B.
( )
32
x kk
ππ
=+∈
.
C.
( )
3
x kk
π
π
=+∈
. D.
( )
62
x kk
ππ
=+∈
.
Lời giải
3 tan 2 3 0 tan 2 3xx−=⇔ =
2
3
xk
π
π
⇔=+
( )
62
x kk
ππ
⇔= + ∈
.
Câu 125: Họ nghiệm của phương trình:
tan 1 0
4
x
π
− −=
là
A.
,
2
x kk
π
π
=+∈
. B.
,xk k
π
= ∈
.
C.
2,
2
x kk
π
π
=+∈
. D.
,
4
x kk
π
π
=+∈
.
Lời giải
Ta có
tan 1 0 tan 1
4 4 44 2
x x x kx k
π π ππ π
ππ
− −= ⇔ − =⇔ − = + ⇔ = +
.
Vậy nghiệm của phương trình là
,
2
x kk
π
π
=+∈
.
( )
25 60x kk⇔ = °+ ° ∈

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Câu 126: Tổng các nghiệm phương trình
( )
0
tan 2 15 1
x −=
trên khoảng
( )
00
90 ;90−
bằng
A.
0
30
. B.
0
60
−
. C.
0
0
. D.
0
30−
.
Lời giải
Ta có phương trình
( )
0 00 0 0 0
tan 2 15 1 2 15 45 180 30 90x x k xk− =⇔ − = + ⇔= +
với
k ∈
.
Xét:
0
1
00 00
0
2
60
1
42
90 30 90 90
0
33
30
x
k
kk
k
x
= −
= −
− < + < ⇔− < < ⇒ ⇒
=
=
.
Vậy
0
12
30xx+=−
.
Câu 127: Số nghiệm của phương trình
tan 3 tan 0−=xx
trên nửa khoảng
[
)
0; 2
π
bằng:
A. 1. B. 2. C. 3. D. 4.
Lời giải
Điều kiện:
( )
cos3 0
63
cos 0
2
≠+
≠
⇔∈
≠
≠+
k
x
x
k
x
xk
ππ
π
π
( )
*
Ta có:
tan 3 tan 0 tan 3 tan 3 , .
2
− =⇔ = ⇔ =+ ⇔= ∈
k
x x x x x xk x m
π
π
Vì
0 20 20 4
2
≤< ⇔≤ < ⇔≤ <
k
xm
π
ππ
. Mà
m ∈
nên
{ }
0;1; 2;3 .
m =
Khi đó nghiệm
x
nhận giá trị tương ứng trên nửa khoảng
[
)
0;
π
là:
3
0; ; ; .
22
=
x
ππ
π
Vậy số nghiệm cần tìm là 4.
Câu 128: Phương trình
tan 1 0x +=
có nghiệm là
A.
( )
4
x kk
π
π
=+∈
. B.
( )
2
x kk
π
π
=−+ ∈
.
C.
(
)
4
x kk
π
π
=−+ ∈
. D.
( )
,
44
x kx kk
ππ
ππ
=+ =−+ ∈
.
Lời giải
Ta có
( )
tan 1 0 tan 1 tan tan
44
x x x x kk
ππ
π
+=⇔=−⇔=−⇔=−+ ∈
.
Câu 129: Tính tổng các nghiệm trong đoạn
[ ]
0;30
của phương trình:
tan tan 3xx=
A.
55 .
π
B.
171
.
2
π
C.
45 .
π
D.
190
.
2
π
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
Điều kiện để phương trình có nghĩa
( )
cos 0
2
*
cos3 0
63
xk
x
k
x
x
π
π
ππ
≠+
≠
⇔
≠
≠+
Khi đó, phương trình
3
2
k
x xk x
π
π
=+ ⇔=
so sánh với đk
[ ]
{ } { }
2
, 0;30 0;...;4 0; ;2 ;....;9
2
xk
xk x
xk
π
ππ π
ππ
=
=∈ ⇒= ⇒∈
= +
Vậy, tổng các nghiệm trong đoạn
[ ]
0;30
của phương trình là:
45
π
.
Câu 130: Trong các nghiệm dương bé nhất của các phương trình sau, phương trình nào có nghiệm dương
nhỏ nhất?
A. . B. . C. . D. .
Lời giải
A. .
B. .
Nghiệm dương bé nhất là .
C. Nghiệm dương bé nhất là .
D. .
Chọn Nghiệm dương bé nhất là .
Vậy giá trị nhỏ nhất là nên ta chọn đáp án A.
Câu 131: Nghiệm của phương trình
3
tan
3
x
−
=
được biểu diễn trên đường tròn lượng giác ở hình bên là
những điểm nào?
tan 2 1x =
tan 3
4
x
π
−=
cot 0x =
cot 3x
= −
( )
tan 2 1 tan 2 tan 2
4 4 82
x x xkxkk
π π ππ
π
=⇔ = ⇔ = + ⇔= + ∈
( )
7
tan 3
4 4 3 12
x x k x kk
π ππ π
ππ
− = ⇔− = + ⇔= + ∈
⇒
7
12
x
π
=
( )
cot 0 cos 0
2
x x x kk
π
π
=⇔ =⇔= + ∈ ⇒
2
x
π
=
( )
cot 3 cot cot
66
x x x kk
ππ
π
=− ⇔ = − ⇔=−+ ∈
1k = ⇒
5
6
x
π
=
8
x
π
=
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
A. Điểm
F
, điểm
D
. B. Điểm
C
, điểm
F
.
C. Điểm
C
, điểm
D
, điểm
E
, điểm
F
. D. Điểm
E
, điểm
F
.
Lời giải
3
tan ,
33
x x kk
π
π
−
= ⇔=−+ ∈
.
Với
02
3
xx
π
π
<< ⇒=−
hoặc
2
3
x
π
=
.
Câu 132: Số nghiệm của phương trình
3
tan tan
11
x
π
=
trên khoảng
;2
4
π
π
là?
A.
4.
B.
1.
C.
2.
D.
3.
Lời giải.
Ta có
(
)
33
tan tan .
11 11
x x k kZ
ππ
π
= ⇔= + ∈
Do
{ }
3
;2 2 0,027 0;1 .
4 4 11
CASIO k Z
xapxi
xk k
π ππ
π ππ
∈
∈ → < + < →− → ∈
Câu 133: Tổng các nghiệm của phương trình
tan 5 tan 0xx−=
trên nửa khoảng
[
)
0;
π
bằng:
A.
5
2
π
. B.
π
. C.
3
2
π
. D.
2
π
.
Lời giải:
Ta có:
tan 5 tan 0xx−=
tan 5 tanxx⇔=
( )
5
4
k
x xk x k
π
π
⇔ =+ ⇔= ∈
Vì
[
)
0;x
π
∈
, suy ra
{ }
0 0 4 0;1; 2;3
4
k
k
kk
π
π
∈
≤ < ⇔ ≤ < → =
Suy ra các nghiệm của phương trình trên
[
)
0;
π
là
3
0;;;
42 4
ππ π
Suy ra
33
0
42 4 2
ππ π π
+++ =
y
x
B'
A'
B
D
F
O
A
C
E

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 7
Sưu tầm và biên soạn
Câu 134: Tính tổng các nghiệm của phương trình
( )
0
tan 2 15 1x −=
trên khoảng
( )
00
90 ;90−
bằng.
A.
0
0.
B.
0
30 .−
C.
0
30 .
D.
0
60 .−
Lời giải.
Ta có
( )
( )
0 00 0 0 0
tan 2 15 1 2 15 45 180 30 90 .x x k x k kZ− =⇔ − = + ⇔= + ∈
Do
( )
00 00 00
42
90 ;90 90 30 90 90
33
x kk∈ − →− < + < ⇔− < <
0
00 0
0
1 60
60 30 30 .
0 30
kZ
kx
kx
∈
=−→ =−
→ → − + = −
=→=
DẠNG 4. PHƯƠNG TRÌNH
cot xm=
Câu 135: Giải phương trình
co t 3.
x =
A.
x ∈∅
. B.
( )
3 x kk
π
=+∈
.
C.
( )
arccot 3 x kk
π
= +∈
. D.
( )
arccot 3 2 x kk
π
=+∈
.
Lời giải
Ta có:
( )
co t 3 arccot 3 x x kk
π
=⇔= + ∈
.
Câu 136: Nghiệm của phương trình
( )
cot 2 1x
+=
là:
A.
22
4
xk
π
π
=++
,
k
∈
. B.
2
4
xk
π
π
=−+ +
,
k
∈
.
C.
2
4
xk
π
π
=−− +
,
k ∈
. D.
2
4
xk
π
π
=++
,
k ∈
.
Lời giải
( ) ( )
cot 2 1 cot 2 cot 2
44
x x xk
ππ
π
+=⇔ += ⇔=−++
với
k ∈
.
Câu 137: Tập nghiệm của phương trình
cot 3=x
A.
5
;
6
π
π
−
+∈
kk
. B.
;
6
π
π
±+ ∈
kk
.
C.
;
3
π
π
+∈
kk
. D.
2;
6
π
π
+∈
kk
.
Lời giải
Ta có:
cot 3=x
cot cot
6
π
⇔=x
( )
6
π
π
⇔= + ∈x kk
(
)
5
6
x kk
π
π
−
⇔= + ∈
.
Câu 138: Giải phương trình
( )
cot 3 1 3
x −=−
A.
1
,
36
x kk
π
π
=−+ ∈
. B.
5
,
83
k
xk
ππ
=+∈
.
C.
1
,
3 18 3
k
xk
ππ
=++ ∈
. D.
15
,
3 18 3
k
xk
ππ
=++ ∈
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 8
Sưu tầm và biên soạn
Ta có
(
)
5 15
cot31 3 31 ,
6 3 18 3
k
x x kx k
π ππ
π
− =− ⇔ −= + ⇔ = + + ∈
.
Câu 139: Giải phương trình
2
cot 3
3
x
=
.
A.
()
4
x kk
π
π
=+∈
. B.
2
()
43
k
xk
ππ
=+∈
.
C.
3
()
42
k
xk
ππ
=+∈
. D.
3
()
22
k
xk
ππ
=+∈
.
Lời giải
Ta có:
2 22 3
cot 3 cot cot ( )
3 3 6 36 4 2
x xx k
kx k
π π ππ
π
= ⇔ = ⇔ = + ⇔= + ∈
.
Câu 140: Tổng tất cả các nghiệm của phương trình
cot 3x =
trên đoạn
[
]
0;2
π
bằng.
A.
6
π
. B.
7
6
π
. C.
5
6
π
. D.
4
3
π
.
Lờigiải
Ta có
cot 3 , ( ).
6
x x kk
π
π
= ⇔= + ∈
Mà
[ ]
0;2x
π
∈
nên phương trình có các nghiệm thỏa mãn là
7
,
66
xx
ππ
= =
.
Vậy tổng các nghiệm là
4
3
π
.
Câu 141: Phương trình lượng giác
3cot 3 0x −=
có nghiệm là:
A.
x2
3
k
π
π
= +
. B. Vô nghiệm. C.
6
xk
π
π
= +
. D.
x
3
k
π
π
= +
.
Lời giải
Ta có
3
3cot 3 0 cot cot cot ,
3 33
x x x xk
ππ
π
−=⇔=⇔= ⇔=+
( )
.k ∈
Câu 142: Phương trình
2cot 3 0
x
−=
cónghiệmlà
A.
( )
2
6
2
6
xk
kZ
xk
π
π
π
π
= +
∈
=−+
. B.
( )
2
3
x k kZ
π
π
=+∈
C.
( )
3
arccot
2
x k kZ
π
= +∈
. D.
( )
6
x k kZ
π
π
=+∈
.
Lời giải
Ta có
3
2cot 3 0 cot
2
xx−=⇔ =
( )
3
arccot
2
kx kZ
π
⇔ += ∈
Câu 143: Giải phương trình
( )
cot 3 1 3.x −=−

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 9
Sưu tầm và biên soạn
A.
(
)
15
.
3 18 3
x k kZ
ππ
=++ ∈
B.
(
)
1
.
3 18 3
x k kZ
ππ
=++ ∈
C.
(
)
5
.
18 3
x k kZ
ππ
=+∈
D.
( )
1
.
36
x k kZ
π
π
=−+ ∈
Lời giải.
Ta có
(
) ( )
cot 3 1 3 cot 3 1 cot
6
xx
π
−=− ⇔ −= −
.
1
11
31 .
6 3 18 3 3 18
k
x kx k x
π ππ π
π
=
−
⇔ − = + ⇔ = − + → = +
Câu 144: Số nghiệm của phương trình
3cot3 3 0x −=
trên khoảng
2
;
99
ππ
−
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
+) Ta có
3
tan 3 3 , ,
3 3 93
k
x x kk x k
π ππ
π
= ⇔ = + ∈⇔= + ∈
.
+)
22
;
99 9 9 3 9
k
x
ππ ππ ππ
∈ − ⇔− < + <
01 0
33
k
k
ππ
⇔− < < ⇔− < <
.
Vì
k ∈
nên không có giá trị nào của k thỏa mãn.
Vậy phương trình đã cho không có nghiệm nào trên khoảng
2
;
99
ππ
−
.
Câu 145: Nghiệm của phương trình
cot 3
3
x
π
+=
có dạng
k
x
mn
ππ
=−+
, với
k ∈
và
m
,
*
n ∈
.
Khi đó
mn−
bằng
A.
5−
. B.
5
. C.
3
. D.
3−
.
Lời giải
Ta có
cot 3
3
x
π
+=
cot cot
36
x
ππ
⇔ +=
36
xk
ππ
π
⇔+ = +
6
xk
π
π
⇔=−+
,
( )
k ∈
.
Vậy
6
1
m
n
=
=
5mn⇒ −=
.
Câu 146: Số nghiệm của phương trình
cot 20 1x =
trên đoạn
[ ]
50 ;0
π
−
là
A.
980
. B.
1001
. C.
1000
. D.
981
.
Lời giải
Ta có
cot 20 1 20 ,
4 80 20
x x k x kk
π ππ
π
=⇔ = + ⇔= + ∈
.
Với
80 20
xk
ππ
= +
,
50 0x
π
− ≤≤
suy ra
50 0 50
80 20 80 20 80
kk
ππ πππ
ππ
− ≤ + ≤ ⇔− − ≤ ≤−
11
1000 ,
44
kk⇔− − ≤ ≤− ∈
. Do đó
{ }
1000, 999,..., 1k ∈− − −
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 10
Sưu tầm và biên soạn
Vậy phương trình đã cho có nghiệm trên
[
]
50 ;0
π
−
.
Câu 147: Hỏi trên đoạn
[
]
0;2018
π
, phương trình
3 cot 3 0x −=
có bao nhiêu nghiệm?
A. 2018. B. 6340. C. 6339. D. 2017.
Lời giải
Ta có:
( )
3 cot 3 0 cot 3
6
x x x kk
π
π
−=⇔ = ⇔ = + ∈
.
Vì
[ ]
0;2018x
π
∈
nên ta có:
11
0 2018 2018
6 66
kk
π
ππ
≤ + ≤ ⇔− ≤ ≤− +
.
Vì
k ∈
nên
{ }
0;1;2;...;2017k ∈
.
Vậy phương trình đã cho có 2018 nghiệm.
Câu 148: Phương trình
cot 3 cotxx=
có các nghiệm là:
A.
2,
2
x kk
π
π
=+∈
. B.
,
xkk
π
= ∈
.
C.
,
3
k
xk
π
= ∈
. D.
,
2
x kk
π
π
=+∈
.
Lời giải
ĐKXĐ:
sin3 0
3
sinx 0
x
xk
xk
π
π
≠
≠
⇔
≠
≠
Phương trình tương đương:
cos 3 cos
sin cos3 cos sin 3 0
sin3 sin
xx
x x xx
xx
=⇔−=
sin 2 0
2
x xk
π
⇔ =⇔=
Kết hợp điều kiện ta được các nghiệm của phương trình:
2
xk
π
π
= +
DẠNG 5. MỘT SỐ BÀI TOÁN TỔNG HỢP
Câu 149: Trong các phương trình sau, phương trình nào vô nghiệm?
A.
tan 99x
. B.
2
cos 2
23
x
. C.
cot 2018 2017x
. D.
3
sin 2
4
x
.
Lời giải
Chọn B
Vì
2
1
3
là nên phương trình
2
cos 2
23
x
vô nghiệm.
Câu 150: Phương trình
sin cosxx=
có số nghiệm thuộc đoạn
[ ]
;−π π
là:
A.
3
B.
5
C.
2
D.
4
Lời giải
Chọn C
1000

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 11
Sưu tầm và biên soạn
Ta có
(
)
sin cos 2 sin 0
44 4
x x x x k x kk
ππ π
= ⇔ − = ⇔ − = π⇔ = + π ∈
Trong
[ ]
;−π π
phương trình có hai nghiệm
Câu 151: Giải phương trình
2cos 1 sin 2 0
22
xx
− +=
A.
( )
2
2,
3
x kk
π
π
=±+ ∈
B.
( )
2,
3
x kk
π
π
=±+ ∈
C.
( )
4,
3
x kk
π
π
=±+ ∈
D.
( )
2
4,
3
x kk
π
π
=±+ ∈
Lời giải
Chọn D
Vì
1 sin 1, sin 2 0
22
xx
x−≤ ≤ ∀∈ ⇒ + >
Vậy phương trình tương đương
(
)
1
2cos 1 0 cos 2
2 22 2 3
2
4,
3
x xx
k
x kk
π
π
π
π
−= ⇔ = ⇔ =± +
⇔=± + ∈
Câu 152: Phương trình
8.cos2 .sin 2 .cos 4 2xx x= −
có nghiệm là
A.
( )
32 4
5
32 4
xk
k
xk
ππ
ππ
−
= +
∈
= +
. B.
( )
16 8
3
16 8
xk
k
xk
ππ
ππ
= +
∈
= +
.
C.
( )
88
3
88
xk
k
xk
ππ
ππ
= +
∈
= +
. D.
( )
32 4
3
32 4
xk
k
xk
ππ
ππ
= +
∈
= +
.
Lời giải
Ta có:
8.cos2 .sin 2 .cos 4 2xx x= −
4.sin 4 .cos 4 2xx⇔=−
2.sin8 2x⇔=−
2
sin8
2
x⇔=−
sin8 sin
4
x
π
⇔=−
( )
32 4
5
32 4
xk
k
xk
ππ
ππ
=−+
⇔∈
= +
.
Vậy phương trình có nghiệm
( )
32 4
5
32 4
xk
k
xk
ππ
ππ
−
= +
∈
= +
.
Câu 153: Tìm số nghiệm của phương trình
( )
sin cos 2 0x =
trên
[ ]
0; 2 .
π
A.
2
. B.
1
. C.
4
. D.
3
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 12
Sưu tầm và biên soạn
Ta có
( )
sin 2 0 2cos x cos x k
π
=⇔=
( )
k ∈
Vì
[
]
( )
1 11
2 1;1 0 202 .
2 42
cos x k cos x x k x k k
π ππ
π
∈− ⇒ = ⇒ = ⇔ = + ⇔ = + ∈
[ ]
{ }
1
0; 2 0;1; 2;3 .xk
π
∈ ⇒∈
Vậy phương trình có
4
nghiệm trên
[ ]
0; 2 .
π
Câu 154: Trong khoảng
(
)
0;
π
, phương trình
cos 4 sin 0xx+=
có tập nghiệm là
S
. Hãy xác định
S
.
A.
237
;;;
3 3 10 10
S
ππππ
=
. B.
3
;
6 10
S
ππ
=
.
C.
7
;;
6 10 10
S
ππ π
=
. D.
537
;;;
6 6 10 10
S
ππππ
=
.
Lời giải
Ta có
( )
cos 4 sin 0 cos4 sin cos4 sin cos4 cos
2
xx x x x x x x
π
+=⇔=−⇔=−⇔= +
2
42
63
2
2
42
2 10 5
xk
x xk
x xk x k
ππ
π
π
π ππ
π
= +
= ++
⇔⇔
=− −+ =− +
,
k ∈
.
Vì
( )
0;
x
π
∈
nên
537
;;;
6 6 10 10
S
ππππ
=
.
Câu 155: Phương trình
sin 2 cosxx=
có nghiệm là
A.
( )
63
2
2
k
x
k
xk
ππ
π
π
= +
∈
= +
. B.
( )
63
2
3
k
x
k
xk
ππ
π
π
= +
∈
= +
.
C.
( )
2
6
2
2
xk
k
xk
π
π
π
π
= +
∈
= +
. D.
( )
2
63
2
2
k
x
k
xk
ππ
π
π
= +
∈
= +
.
Lời giải
( )
63
sin 2 cos sin 2 sin
2
2
2
k
x
xx x x k
xk
ππ
π
π
π
= +
= ⇔ = −⇔ ∈
= +
.
Câu 156: Phương trình
sin cosxx=
có bao nhiêu nghiệm
( )
0;5x
π
∈
?
A.
3
. B.
4
. C.
5
. D.
6
.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 13
Sưu tầm và biên soạn
Ta có
sin cosxx=
tan 1x⇔=
4
xk
π
π
⇔= +
,
k ∈
.
Vì
( )
0;5x
π
∈
nên ta có
0 5,
4
kk
π
ππ
<+ < ∈
1 19
,
44
kk⇔− < < ∈
.
Do đó,
{ }
0, 1, 2, 3, 4k ∈
.
Suy ra phương trình có
5
nghiệm thuộc
( )
0;5
π
là
4
π
,
5
4
π
,
9
4
π
,
13
4
π
,
17
4
π
.
Câu 157: Nghiệm của phương trình
sin 3 cos
xx=
là
A.
xk
π
=
;
2
xk
π
=
. B.
82
xk
ππ
= +
;
4
xk
π
π
= +
.
C.
2xk
π
=
;
2
2
xk
π
π
= +
. D.
xk
π
=
;
4
xk
π
π
= +
.
Lời giải
sin 3 cosxx
=
sin 3 sin
2
xx
π
⇔= −
32
2
32
2
x xk
x xk
π
π
π
ππ
= −+
⇔
= − ++
82
4
xk
xk
ππ
π
π
= +
⇔
= +
.
Câu 158: Phương trình
sin 2 cos 0xx+=
có tổng các nghiệm trong khoảng
( )
0; 2
π
bằng
A.
2
π
. B.
3
π
. C.
5
π
. D.
6
π
.
Lời giải
( )
2
cos 0
sin 2 cos 0 2sin cos cos 0 2 ,
2sin 1 0
6
7
2
6
xk
x
xx xxx x kk
x
xk
π
π
π
π
π
π
= +
=
+=⇔ +=⇔ ⇔=−+ ∈
+=
= +
( )
3 11 7
0; 2 ; ; ;
22 6 6
xx
ππ ππ
π
∈ ⇒=
5S
π
⇒=
.
Câu 159: Số nghiệm chung của hai phương trình
2
4cos 3 0x −=
và
2sin 1 0x +=
trên khoảng
3
;
22
ππ
−
bằng
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Trên khoảng
3
;
22
ππ
−
phương trình
1
2sin 1 0 sin
2
xx+= ⇔ =−
có hai nghiệm là
6
π
−
và
7
6
π
.
Cả hai nghiệm này đều thỏa phương trình
2
4cos 3 0x −=
.
Vậy hai phương trình có
2
nghiệm chung.
Câu 160: Giải phương trình
sin sin 7 sin 3 sin 5xx xx=
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 14
Sưu tầm và biên soạn
A.
,xkk
π
= ∈
. B.
,
6
k
xk
π
= ∈
. C.
,
4
k
xk
π
= ∈
. D.
,
2
k
xk
π
= ∈
.
Lời giải
Ta có:
sin sin 7 sin 3 sin 5xx xx=
cos6 cos8 cos 2 cos8xx xx⇔−=−
.
cos6 cos 2
xx
⇔=
62 2
622
x xk
x xk
π
π
= +
⇔
=−+
2
4
k
x
k
x
π
π
=
⇔
=
,
4
k
xk
π
⇔= ∈
.
Câu 161: Tìm số nghiệm của phương trình
sin cos 2xx=
thuộc đoạn
[ ]
0; 20
π
.
A.
20
. B.
40
. C.
30
. D.
60
.
Lời giải
Chọn C
Ta có
sin cos 2xx=
2
sin 1 2sinxx⇔=−
1
sin
2
sin 1
x
x
=
⇔
= −
.
1
sin
2
x =
2
6
5
2
6
xk
xk
π
π
π
π
= +
⇔
= +
( )
k ∈
.
sin 1x = −
2
2
xk
π
π
⇔=−+
( )
k ∈
Xét
[ ]
0; 20
x
π
∈
:
Với
2
6
xk
π
π
= +
, ta có
0 2 20
6
k
π
ππ
≤+ ≤
1 119
12 12
k⇔− ≤ ≤
, do
k ∈
nên.
Với
5
2
6
xk
π
π
= +
, ta có
5
0 2 20
6
k
π
ππ
≤+ ≤
5 115
12 12
k⇔− ≤ ≤
, do
k ∈
nên.
Với
2
2
xk
π
π
=−+
, ta có
0 2 20
2
k
π
ππ
≤− + ≤
1 41
44
k⇔ ≤≤
, do
k ∈
nên.
Vậy phương trình đã cho có
30
nghiệm thuộc đoạn
[ ]
0; 20
π
.
Câu 162: Số vị trí biểu diễn các nghiệm của phương trình
tan 3 cot 0
2
xx
π
+ −=
trên đường tròn lượng
giác là?
A.
4
. B.
2
. C.
0
. D.
1
.
Lời giải
ĐK:
cos3x 0
63
sin 0
2
2
k
x
x
xk
ππ
π
π
π
≠
≠+
⇔
−≠
≠+
( )
*

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 15
Sưu tầm và biên soạn
Ta có
tan 3 cot
2
xx
π
=−−
( )
tan 3 tan
tan 3 tan
3 ,.
2
xx
xx
k
x xk x k
π
π
⇔ =−−
⇔=
⇔ =+ ⇔= ∈
Kết hợp điều kiện
( )
*
suy ra
,xk k
π
= ∈
nghĩa là có 2 điểm biểu diễn trên đường tròn lượng
giá C.
Câu 163: Phương trình
sin cos 0
4
xx
π
++ =
có tập nghiệm được biểu diễn bởi bao nhiêu điểm trên đường
tròn lượng giác?
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
sin cos 0
4
xx
π
++ =
sin sin
42
xx
ππ
⇔ += −
4
x
π
⇔+
2
2
xk
π
ππ
= −+ +
5
22
4
xk
π
π
⇔= +
5
8
xk
π
π
⇔= +
.
Cung
5
8
xk
π
π
= +
biểu diễn được hai điểm trên đường tròn lương giác.
Câu 164: Tìm tập nghiệm
S
của phương trình
cos .sin 2 0
3
xx
π
−=
.
A.
;,
2 62
k
Sk k
π ππ
π
=++∈
. B.
{
}
180 ;75 90 ,
Sk k k= ° °+ ° ∈
.
C.
5
;,
12 2
k
Sk k
ππ
π
= +∈
. D.
{ }
100 180 ;30 90 ,S k kk= °+ ° °+ ° ∈
.
Lời giải
Ta có:
cos 0
22
cos .sin 2 0 , .
sin 2 0
3
2
3
3 62
x
xk xk
xx k
x
k
xkx
ππ
ππ
π
π
π ππ
π
=
=+=+
−=⇔ ⇔ ⇔ ∈
−=
−= =+
Vậy tập nghiệm của phương trình đã cho là:
;,
2 62
k
Sk k
π ππ
π
=++∈
.
Câu 165: Giải phương trình
5sin sin2 0
xx−=
A.
2xk
π
=
( )
k ∈
. B.
2
xk
π
π
= +
( )
k ∈
.
C.
xk
π
=
( )
k ∈
. D. Phương trình vô nghiệm.
Lời giải

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 16
Sưu tầm và biên soạn
5sin sin 2 0xx−=
5sin 2sin .cos 0x xx⇔− =
( )
sin 5 2cos 0
xx
⇔− =
sin 0
5 2cos 0
x
x
=
⇔
−=
+)
(
)
sin 0x xk k
π
=⇔= ∈
+)
5
5 2cos 0 cos
2
xx− =⇔=
Câu 166: Giải phương trình
( )
sin cos 2 0
2
xx
−− − =
π
π
A.
{ }
2|
Sk k
= ∈
π
. B.
2
2, |
33
k
Sk k
= +∈
ππ
π
.
C.
2
,|
33
k
Sk k
=+∈
ππ
π
. D.
2
|
33
k
Sk
=+∈
ππ
Lời giải
( )
sin cos 2 0
2
xx
π
π
−− − =
sin sin 2 0xx⇔− =
sin 2 sinxx⇔=
22
22
x xk
x xk
π
ππ
= +
⇔
= −+
( )
2
2
33
xk
k
k
x
π
ππ
=
⇔∈
= +
.
Câu 167: Nghiệm âm lớn nhất của phương trình
22
cos 4 sin cos
6
x xx
π
−+ =
A.
35
36
π
−
. B.
11
36
π
−
. C.
11
12
π
−
. D.
12
π
−
.
Lời giải
22
cos 4 sin cos
6
x xx
π
−+ =
22
cos 4 cos sin
6
x xx
π
⇔ −= −
( )
cos 4 cos 2
6
4 22
6
12
4 22
36 3
6
xx
x xk
xk
k
xk
x xk
π
π
π
π
π
ππ
π
π
⇔ −=
−= +
= +
⇔ ⇔∈
= +
−=−+
Ta có mỗi họ nghiệm lần lượt có các nghiệm âm lớn nhất là:
12
11 11
;
12 12 36 3 36
xx
π π ππ π
π
= −=− = − =−
Vậy nghiệm âm lớn nhất của phương trình là
11
36
x
π
= −
.
Câu 168: Các họ nghiệm của phương trình
sin 2 3 sin 0xx−=
là:

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 17
Sưu tầm và biên soạn
A.
6
xk
xk
π
π
π
=
=±+
. B.
6
xk
π
π
=±+
. C.
2
6
xk
xk
π
π
π
=
=±+
. D.
2
2
3
xk
xk
π
π
π
=
=±+
.
Lời giải
Ta có
( )
sin 2 3 sin 0 sin 2cos 3 0x x xx− =⇔ −=
sin 0
3
2
cos
6
2
x
xk
xk
x
π
π
π
=
=
⇔⇔
=±+
=
.
Câu 169: Giải phương trình
cot sin 1 tan .tan 4
2
x
xx x
++ =
Lời giải
ĐK:
sin 0
cos 0
2
cos 0
x
x
x
≠
≠
≠
( )
sin 2 0
,
2
cos 0
2
x
k
xk
x
π
≠
⇔ ⇔≠ ∈
≠
cot sin 1 tan .tan 4
2
x
xx x
++ =
sin
cos sin
2
sin 1 . 4
sin cos
cos
2
x
xx
x
x
xx
⇔+ + =
cos .cos sin .sin
cos
22
sin 4
sin
cos .cos
2
xx
xx
x
x
x
x
x
+
⇔+ =
cos
cos
2
sin 4
sin
cos .cos
2
x
x
x
x
x
x
x
−
⇔+ =
cos sin
4
sin cos
xx
xx
⇔+=
4sin cos 1xx⇔=
1
sin 2
2
x⇔=
( )
12
,
5
12
xk
k
xk
π
π
π
π
= +
⇔∈
= +
Thỏa mãn điều kiện
Vậy, nghiệm của phương trình là
12
xk
π
π
= +
;
5
12
xk
π
π
= +
( )
k ∈
Câu 170: Số điểm phân biệt biểu diễn các nghiệm phương trình
sin 2 sin 0−=xx
trên đường tròn lượng
giác là
A. 4 B. 1. C. 2. D. 3.
Lời giải
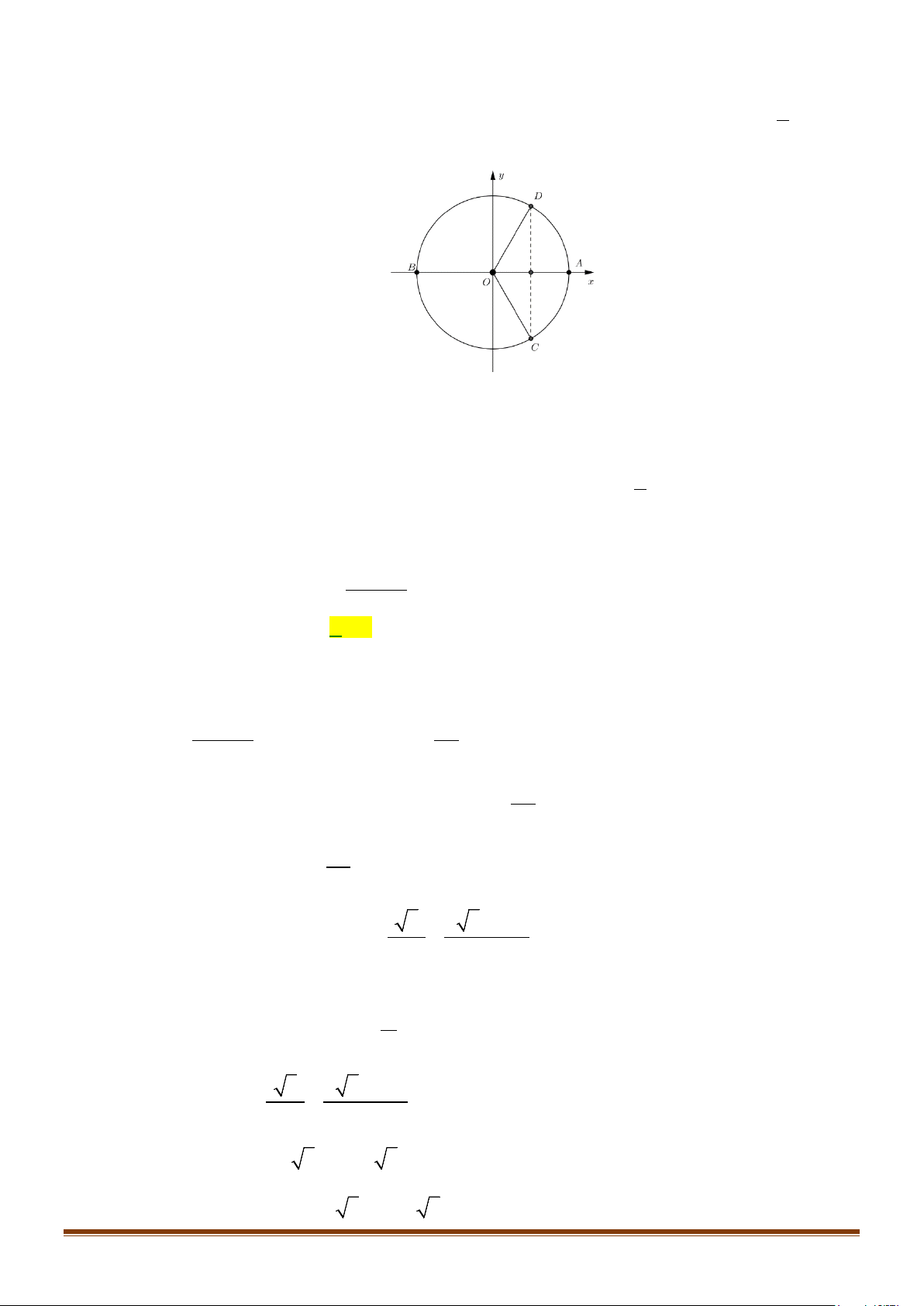
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 18
Sưu tầm và biên soạn
Ta có:
( )
sin 0
sin 2 sin 0 2sin cos sin 0 sin 2cos 1 0
1
cos
2
=
−=⇔ −=⇔ −=⇔
=
x
xx xxx x x
x
.
Các điểm biểu diễn tập nghiệm trên đường tròn lượng giác như sau:
+ Các điểm
,
AB
biểu diễn cho nghiệm của phương trình
sin 0=x
.
+ Các điểm
,CD
biểu diễn cho nghiệm của phương trình
1
cos
2
=
x
.
Vậy có tất cả 4 điểm biểu diễn nghiệm của phương trình.
Câu 171: Số nghiệm phương trình
sin 3
0
cos 1
x
x
=
+
thuộc đoạn
[ ]
2 ;4
ππ
là
A.
7
. B.
6
. C.
4
. D.
5
.
Lời giải
Điều kiện:
cos 1 0 2x xk
ππ
+≠ ⇔ ≠ +
.
Ta có
( )
sin 3
0 sin 3 0 .
cos 1 3
xk
x xk
x
π
=⇒ =⇔= ∈
+
So với điều kiện nghiệm của phương trình là
3
k
x
π
=
với
( )
, 32 1kk l∈≠+
Vì
2 4 2 4 6 12
3
k
xk
π
π ππ π
≤≤⇔≤ ≤⇔≤≤
nên ta chọn
{ }
6,7,8,10,11,12k ∈
.
Câu 172: Giải phương trình sau:
3 2 3sin3
4sin
cos sin 2
x
x
xx
= −
Lời giải
Điều kiện:
( )
sin 2 0
2
x xk k
π
≠⇔≠ ∈
.
Ta có:
3 2 3sin3
4sin
cos sin 2
x
x
xx
= −
2
4sin cos 3sin 3sin 3xx x x⇔=−
( )
2 1 cos2 cos 3 sin 3sin 3xx x x⇔− = −

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 19
Sưu tầm và biên soạn
2cos 2cos2 cos 3sin 3sin 3x xx x x⇔− = −
( )
2cos cos3 cos 3sin 3sin 3x xx x x⇔ − += −
3sin3 cos3 3 sin cos
x x xx
⇔ −= −
sin 3 sin
66
xx
ππ
⇔ −= −
( )
32
xk
k
xk
π
ππ
=
⇔∈
= +
.
So với điều kiện, suy ra phương trình có 1 họ nghiệm:
( )
32
x kk
ππ
=+∈
.
Câu 173: Cho phương trình:
( )
( )( )
1 2sinx cos
3
1 2sinx 1 sinx
x−
=
+−
. Phương trình có bao nhiêu nghiệm trên khoảng
( )
2021 ;2021
ππ
−
?
Lời giải
ĐK:
sin 1
1
sinx
2
x ≠
≠−
( )
( )( )
1 2sinx cos
3
1 2sinx 1 sinx
x−
=
+−
2
cos sin 2 x 3 3sinx 2 3 sinx 2 3 sin x
x
⇒− =− + −
cos sin 2x 3 sinx 3cos2xx⇔− = +
cos 3 sinx sin 2x 3cos2
xx
⇔− = +
sin x sin 2x
63
ππ
⇔ −= +
2
18 3
2
2
k
x
xk
ππ
π
π
=−+
⇔
= +
Kết hợp với điều kiện ta có
2
18 3
k
x
ππ
=−+
( )
2021 ;2021x
ππ
∈−
nên
2
2021 2021
18 3
k
ππ
ππ
− <− + <
12
2021 2021
18 3
k
⇔− <− + <
.
3031, 42 3031,58k⇒− < <
. Do
k ∈
{ }
3031; 3028;......;3031k⇒ ∈− −
{ }
3031; 3030;......;3031k
⇒ ∈− −

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 20
Sưu tầm và biên soạn
Vậy có
( )
3031 3031 1 6063
−− + =
nghiệm thỏa mãn.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 98
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
Câu 1: Tìm tất cả các giá trị thực của tham số m để phương trình:
sin 1
xm= +
có nghiệm?
A.
1 m≤
. B.
01m≤≤
. C.
0m ≤
. D.
20m−≤ ≤
.
Câu 2: Tìm tất cả các giá trị thực của tham số
m
để phương trình
sin xm=
có nghiệm thực.
A.
0m ≥
. B.
0m <
. C.
11m−< <
. D.
11
m
−≤ ≤
.
Câu 3: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3sin 2 5 0xm− +=
có nghiệm?
A.
6.
B.
2.
C.
1.
D.
7.
Câu 4: Có bao nhiêu giá trị nguyên của m để phương trình:
3sin 1 0xm
có nghiệm?
A. 7 B. 6 C. 3 D. 5
Câu 5: Tìm tất cả các giá trị thực của tham số
m
để phương trình
cos 0xm−=
vô nghiệm.
A.
( ) (
)
; 1 1;m ∈ −∞ − ∪ +∞
B.
( ; 1] [1; )m ∈ −∞ − ∪ +∞
C.
( )
1;m∈ +∞
D.
( ; 1)m ∈ −∞ −
Câu 6: Cho phương trình
cos 2 2
3
xm
π
− −=
. Tìm
m
để phương trình có nghiệm?
A. Không tồn tại
m
. B.
[ ]
1; 3m ∈−
. C.
[ ]
3; 1m ∈− −
. D.
m ∈
.
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
cos 1xm= +
có nghiệm?
A. Vô số. B.
1.
C.
2.
D.
3.
Câu 8: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[ ]
2018;2018−
để phương trình
cos 1 0mx+=
có nghiệm?
A.
4036
. B.
4037
. C.
2018
. D.
2019
.
Câu 9: Tìm
m
để phương trình
sin 3 6 5 0xm−− =
có nghiệm.
A.
7
1
5
m− ≤ ≤−
. B.
7
1
5
m− < <−
. C.
1
7
5
m
m
≥−
≤−
. D.
1
7
5
m
m
>−
<−
.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TRẮC NGHIỆM.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 99
Sưu tầm và biên soạn
Câu 10: Tìm
m
để phương trình
( )
1 sin 2 1 2 sin 2
m xmx+ =−−
có đúng
2
nghiệm thuộc
2
;
12 3
ππ
.
Câu 11: Cho phương trình
cos5 3 5xm= −
. Gọi đoạn
[ ]
;ab
là tập hợp tất cả các giá trị của
m
để phương
trình có nghiệm. Tính
3ab
+
.
A.
5
. B.
2
−
. C.
19
3
. D.
6
.
Câu 12: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
cos 2 2
3
xm
π
− −=
có nghiệm. Tính tổng
T
của các phần tử trong
.S
A.
6.
T =
B.
3.T =
C.
2.T = −
D.
6.T = −
Câu 13: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
3 cos 1 0xm
+ −=
có
nghiệm?
A.
1.
B.
2.
C.
3.
D. Vô số.
Câu 14: Tìm giá trị thực của tham số
m
để phương trình
( )
2 sin 2 1m xm−=+
nhận
12
x
π
=
làm nghiệm.
A.
2.m ≠
B.
( )
2 31
.
32
m
+
=
−
C.
4.m = −
D.
1.m = −
Câu 15: Tìm tất cả các giá trị của tham số
m
để phương trình
( )
1 sin 2 0m xm+ +− =
có nghiệm.
A.
1.m ≤−
B.
1
.
2
m ≥
C.
1
1.
2
m−< ≤
D.
1.m
>−
Câu 16: Phương trình
sin 5x m=
có nghiệm khi
A.
5m ≤
. B.
5m ≤
. C.
1m ≤
. D.
1m ≤
.
Câu 17: Tìm tất cả các giá trị của tham số m để phương trình
2
cos 1xm= −
có nghiệm.
A.
2m ≤
. B.
12m<<
. C.
1
m ≥
. D.
12m≤≤
.
Câu 18: Tìm
m
để phương trình
cos 2 1 0xm− +=
có nghiệm.
A.
1
2
m >−
. B.
01m<<
. C.
01m≤≤
. D.
1
2
m ≥−
.
Câu 19: Phương trình
.cos 1 0mx−=
có nghiệm khi
m
thỏa mãn điều kiện
A.
1
1
m
m
≥−
≤
. B.
1
1
m
m
≤−
≥
. C.
1m ≥−
D.
1m ≥
.
Câu 20: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2sin 2 7 0xm+− =
có nghiệm?
A.
4
. B.
5
. C.
6
. D. Vô số.
Câu 21: Tìm
m
để phương trình
cos 2 1xm
= −
có nghiệm.
A.
0 2.m≤≤
B.
1 1.m−≤ ≤
C.
2 2.m−≤ ≤
D.
0 1.m≤≤
Câu 22: Tìm tất cả các giá trị thực của tham số m để phương trình
2
cos ( )
22
x
m
π
−=
có nghiệm.
A.
11m−≤ ≤
B.
1m ≤
. C.
0m ≥
. D.
01m≤≤
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 100
Sưu tầm và biên soạn
Câu 23: Có bao nhiêu số nguyên
m
để phương trình
3cos 5 0
6
xm
π
+ − +=
có nghiệm?
A.
5
. B.
7
. C.
6
. D.
9
.
Câu 24: Tìm m để phương trình
2 sin
4
xm
π
+=
có nghiệm
0;
2
x
π
∈
.
A.
1
2
m
m
>
≤
. B.
12m≤≤
. C.
12m≤<
. D.
12m<≤
.
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 1
Sưu tầm và biên soạn
BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
Câu 1: Tìm tất cả các giá trị thực của tham số m để phương trình:
sin 1
xm= +
có nghiệm?
A.
1 m≤
. B.
01m≤≤
. C.
0m ≤
. D.
20m−≤ ≤
.
Lời giải
Phương trình:
sin 1xm= +
có nghiệm
1 11 2 0
mm
⇔− ≤ + ≤ ⇔− ≤ ≤
.
Câu 2: Tìm tất cả các giá trị thực của tham số
m
để phương trình
sin xm=
có nghiệm thực.
A.
0m ≥
. B.
0m <
. C.
11m−< <
. D.
11m−≤ ≤
.
Lời giải
Do
1 sin 1, xx−≤ ≤ ∀∈
nên phương trình
sin
xm=
có nghiệm khi và chỉ khi
11m
−≤ ≤
.
Câu 3: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3sin 2 5 0xm− +=
có nghiệm?
A.
6.
B.
2.
C.
1.
D.
7.
Lời giải
Chọn B
Phương trình đã cho tương đương với phương trình
2
5
sin 2
3
m
x
−
=
Vì
[ ]
sin 2 1;1x ∈−
nên
[ ] [ ]
2
2
22 2
5
1;1 2; 8
3
2 22
m
m
m
m
− ≤ ≤−
−
∈− ⇔ ∈ ⇔
≤≤
Vậy có 2 giá trị.
Câu 4: Có bao nhiêu giá trị nguyên của m để phương trình:
3sin 1 0xm
có nghiệm?
A. 7 B. 6 C. 3 D. 5
Lời giải
3sin 1 0xm
1
sin
3
m
x
, để có nghiệm ta có
1
11
3
m
24m
Nên có 7 giá trị nguyên từ
2;
đến
4
.
Câu 5: Tìm tất cả các giá trị thực của tham số
m
để phương trình
cos 0xm−=
vô nghiệm.
CHƯƠNG
I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
HỆ THỐNG BÀI TRẮC NGHIỆM.
II

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 2
Sưu tầm và biên soạn
A.
(
)
( )
; 1 1;
m
∈ −∞ − ∪ +∞
B.
( ; 1] [1; )m∈ −∞ − ∪ +∞
C.
( )
1;m∈ +∞
D.
( ; 1)m ∈ −∞ −
Lời giải
Chọn A
Do
cos 1x ≤
,
x∀∈
nên phương trình:
cos 0 cosxm x m−=⇔ =
có nghiệm khi
1m ≤
và vô nghiệm khi
1m >
.
Câu 6: Cho phương trình
cos 2 2
3
xm
π
− −=
. Tìm
m
để phương trình có nghiệm?
A. Không tồn tại
m
. B.
[ ]
1; 3m ∈−
. C.
[ ]
3; 1m ∈− −
. D.
m ∈
.
Lời giải
Ta có:
cos 2 2
3
xm
π
− −=
⇔
cos 2 2.
3
xm
π
−=+
1 cos 2 1
3
x
π
−≤ − ≤⇒
phương trình có nghiệm khi
1 21
m−≤ + ≤
3 1.m⇔− ≤ ≤−
Câu 7: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
cos 1xm= +
có nghiệm?
A. Vô số. B.
1.
C.
2.
D.
3.
Lời giải
Phương trình
cos 1xm
= +
có nghiệm
1 1 1 2 0.mm⇔− ≤ + ≤ ⇔− ≤ ≤
Mà
{ }
2; 1; 0 .mm∈ ⇒ ∈− −
Câu 8: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
[ ]
2018;2018−
để phương trình
cos 1 0mx+=
có nghiệm?
A.
4036
. B.
4037
. C.
2018
. D.
2019
.
Lời giải
TH1: Nếu
0
m =
thì phương trình đã cho vô nghiệm.
TH2: Nếu
0
m ≠
thì phương trình
1
cos 1 0 cosmx x
m
+= ⇔ =−
.
Phương trình đã cho có nghiệm
1
11
m
⇔− ≤− ≤
1
1
m
m
≥
⇔
≤−
Kết hợp với điều kiện
m
nguyên và
m
thuộc đoạn
[ ]
2018;2018−
suy ra
{ }
1;2;3;...;2018m∈
hoặc
{ }
2018;...; 3; 2; 1m ∈− − − −
.
Vậy có
4036
giá trị của tham số
m
thỏa mãn đề bài.
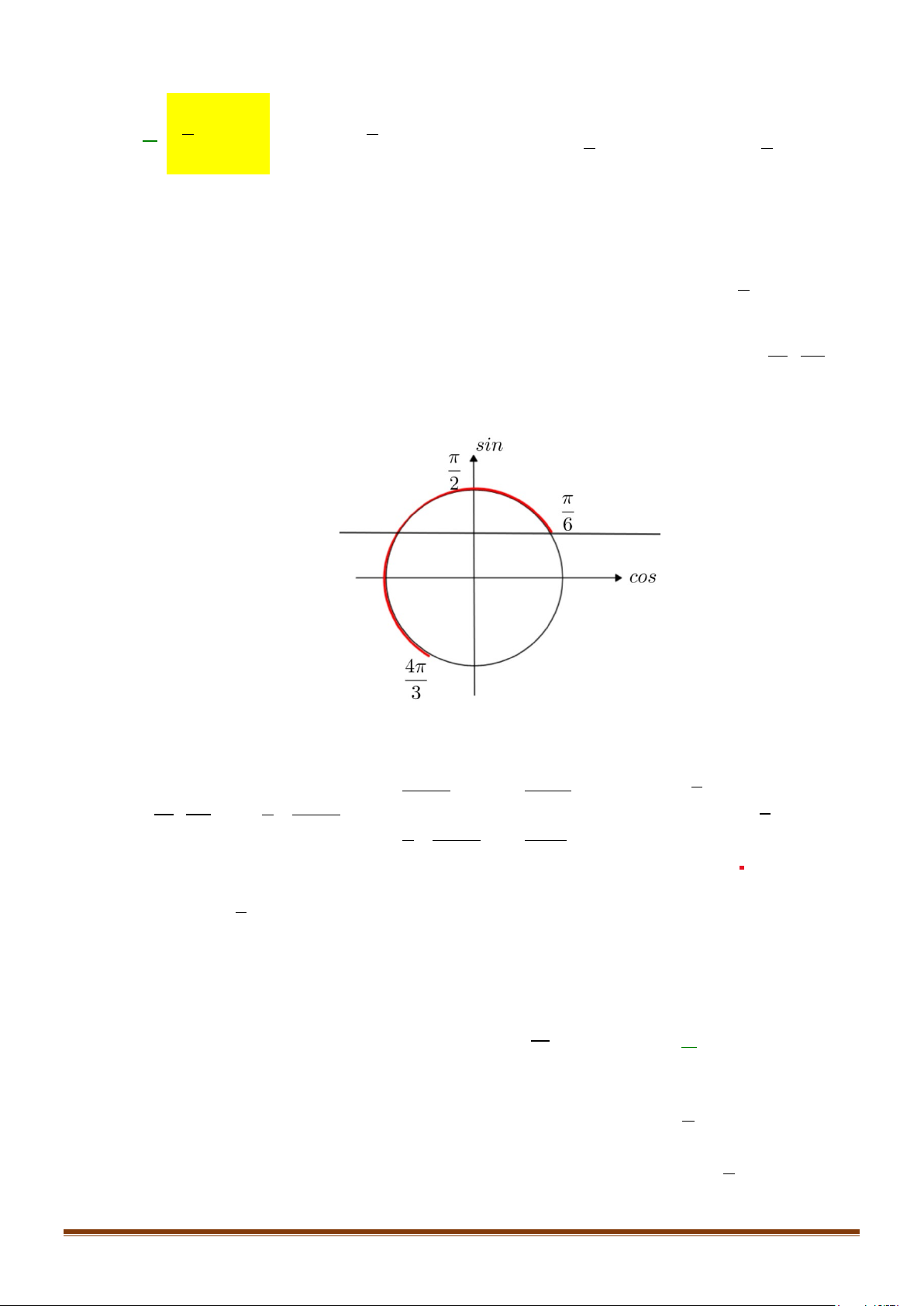
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 3
Sưu tầm và biên soạn
Câu 9: Tìm
m
để phương trình
sin 3 6 5 0xm−− =
có nghiệm.
A.
7
1
5
m− ≤ ≤−
. B.
7
1
5
m− < <−
. C.
1
7
5
m
m
≥−
≤−
. D.
1
7
5
m
m
>−
<−
.
Lời giải
Ta có:
( )
sin 3 6 5 0 sin 3 6 5 1xm x m−− =⇔ =+
.
Phương trình đã cho có nghiệm
⇔
( )
1
có nghiệm
165 1m⇔− ≤ + ≤
7
1
5
m
⇔− ≤ ≤−
.
Câu 10: Tìm
m
để phương trình
(
)
1 sin 2 1 2 sin 2
m xmx
+ =−−
có đúng
2
nghiệm thuộc
2
;
12 3
ππ
.
Lời giải
Dựa vào đường tròn lượng giác ta thấy phương trình đã cho có đúng
2
nghiệm thuộc
2
;
12 3
ππ
khi
12
1
1 12
2
1
1 12
22
22
m
m
m
m
m
m
−
<
−
+
≤ <⇔
−
+
≤
+
13
0
2
5
0
2
m
m
m
m
+
>
+
⇔
≤
+
1
3
2
20
m
m
m
>−
⇔
<−
−< ≤
1
0
3
m⇔− < ≤
.
Vậy
1
;0
3
m
∈−
thỏa mãn yêu cầu bài toán.
Câu 11: Cho phương trình
cos5 3 5xm= −
. Gọi đoạn
[ ]
;ab
là tập hợp tất cả các giá trị của
m
để phương
trình có nghiệm. Tính
3ab+
.
A.
5
. B.
2−
. C.
19
3
. D.
6
.
Lời giải
Phương trình đã cho có nghiệm khi
4
13 51 43 6 2
3
m mm−≤ − ≤ ⇔ ≤ ≤ ⇔ ≤ ≤
.
Khi đó tập hợp tất cả các giá trị của
m
để phương trình có nghiệm là
4
;2
3
.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 4
Sưu tầm và biên soạn
Ta được
4
3
a
=
;
2
b
=
. Suy ra
36
ab
+=
.
Câu 12: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để phương trình
cos 2 2
3
xm
π
− −=
có nghiệm. Tính tổng
T
của các phần tử trong
.S
A.
6.T =
B.
3.T =
C.
2.T = −
D.
6.T = −
Lời giải
Phương trình
cos 2 2 cos 2 2.
33
xm x m
ππ
− −=⇔ − =+
Phương trình có nghiệm
1 21 3 1mm⇔− ≤ + ≤ ⇔− ≤ ≤−
{ } ( ) ( ) ( )
3;2;1 3 2 1 6.
m
ST
∈
→ = − − − → = − + − + − = −
Câu 13: Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
3 cos 1 0xm+ −=
có
nghiệm?
A.
1.
B.
2.
C.
3.
D. Vô số.
Lời giải
Ta có
1
3 cos 1 0 cos
3
m
xm x
−
+ −= ⇔ =
.
Phương trình có nghiệm
{ }
1
1 1 1 3 1 3 0;1; 2 .
3
m
m
mm
∈
−
⇔−≤ ≤⇔−≤≤+→∈
Vậy có tất cả 3 giá trị nguyên của tham số
m
.
Câu 14: Tìm giá trị thực của tham số
m
để phương trình
( )
2 sin 2 1m xm−=+
nhận
12
x
π
=
làm nghiệm.
A.
2.m
≠
B.
( )
2 31
.
32
m
+
=
−
C.
4.
m
= −
D.
1.m = −
Lời giải
Vì
12
x
π
=
là một nghiệm của phương trình
( )
2 sin 2 1m xm−=+
nên ta có:
(
)
22
2 .sin 1 1 2 2 2 4
12 2
m
m m mm m m
π
−
− = +⇔ = +⇔ − = + ⇔ =−
.
Vậy
4m
= −
là giá trị cần tìm.
Câu 15: Tìm tất cả các giá trị của tham số
m
để phương trình
( )
1 sin 2 0m xm+ +− =
có nghiệm.
A.
1.m ≤−
B.
1
.
2
m ≥
C.
1
1.
2
m−< ≤
D.
1.m >−
Lời giải
Phương trình
( ) ( )
2
1 sin 2 0 1 sin 2 sin .
1
m
mxm mxm x
m
−
+ +− =⇔ + = −⇔ =
+
Để phương trình có nghiệm
2
11
1
m
m
−
⇔− ≤ ≤
+

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 5
Sưu tầm và biên soạn
1
2 21
01 0
2
1
11
1
23
2
10 0
11
1
mm
m
mm
m
m
m
mm
m
−−
≥
≤+ ≥
++
⇔ ⇔ ⇔ ⇔≥
<−
−
−≤ − ≤
++
>−
là giá trị cần tìm.
Câu 16: Phương trình
sin 5x m=
có nghiệm khi
A.
5m
≤
. B.
5m ≤
. C.
1m ≤
. D.
1m ≤
.
Lời giải
Ta có
1 sin 5x 1 1 1 1mm
−≤ ≤ ⇔−≤ ≤⇔ ≤
.
Câu 17: Tìm tất cả các giá trị của tham số m để phương trình
2
cos 1xm= −
có nghiệm.
A.
2m ≤
. B.
12
m
<<
. C.
1m ≥
. D.
12
m≤≤
.
Lời giải
Do
2
0 cos 1x
≤≤
với
x∀∈
nên phương trình có nghiệm khi
0 11 1 2
mm
≤ −≤⇔≤ ≤
.
Câu 18: Tìm
m
để phương trình
cos 2 1 0
xm− +=
có nghiệm.
A.
1
2
m
>−
. B.
01m
<<
. C.
01m≤≤
. D.
1
2
m
≥−
.
Lời giải
Ta có
cos 2 1 0xm− +=
cos 2 1xm⇔=−
có nghiệm khi và chỉ khi
12 11m−≤ −≤ ⇔
02 2m
≤≤
01m⇔≤ ≤
.
Câu 19: Phương trình
.cos 1 0mx−=
có nghiệm khi
m
thỏa mãn điều kiện
A.
1
1
m
m
≥−
≤
. B.
1
1
m
m
≤−
≥
. C.
1m ≥−
D.
1m ≥
.
Lời giải
Dễ thấy với
0m =
thì phương trình đã cho vô nghiệm.
Với
0m ≠
, ta có:
( )
1
.cos 1 0 cos 1mx x
m
−= ⇔ =
.
Phương trình đã cho có nghiệm
⇔
phương trình
( )
1
có nghiệm
⇔
1
11
1 11
1
m
m
m
mm
≥
≤⇔ ≤⇔ ≥⇔
≤−
.
Câu 20: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2sin 2 7 0
xm+− =
có nghiệm?
A.
4
. B.
5
. C.
6
. D. Vô số.
Lời giải
7
2sin 2 7 0 sin 2
2
m
xm x
−
+− =⇔ =
Do đó phương trình có nghiệm
7
1 15 9
2
m
m
−
⇔− ≤ ≤ ⇔ ≤ ≤
{ }
5, 6, 7,8,9m⇒∈
.
Câu 21: Tìm
m
để phương trình
cos 2 1xm= −
có nghiệm.

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Page 6
Sưu tầm và biên soạn
A.
0 2.m≤≤
B.
1 1.m−≤ ≤
C.
2 2.m−≤ ≤
D.
0 1.m≤≤
Lời giải
Phương trình
cos 2 1xm= −
có nghiệm khi và chỉ khi
1 1 1.
m
−≤ −≤
22m⇔− ≤ ≤
Câu 22: Tìm tất cả các giá trị thực của tham số m để phương trình
2
cos ( )
22
x
m
π
−=
có nghiệm.
A.
11m−≤ ≤
B.
1m ≤
. C.
0m ≥
. D.
01
m
≤≤
.
Lời giải
Ta có:
2
0 cos ( ) 1
22
x
π
≤ −≤
. Để phương trình có nghiệm thì
01m≤≤
.
Câu 23: Có bao nhiêu số nguyên
m
để phương trình
3cos 5 0
6
xm
π
+ − +=
có nghiệm?
A.
5
. B.
7
. C.
6
. D.
9
.
Lời giải
Ta có:
5
3cos 5 0 cos
6 63
m
xm x
ππ
−
+ − +=⇔ + =
Điều kiện để phương trình có nghiệm:
5
1 12 8
3
m
m
−
−≤ ≤ ⇔ ≤ ≤
Do
m
nguyên nên
{ }
2;3;4;5;6;7;8m =
, Vậy có 7 số nguyên
m
.
Câu 24: Tìm m để phương trình
2 sin
4
xm
π
+=
có nghiệm
0;
2
x
π
∈
.
A.
1
2
m
m
>
≤
. B.
12m≤≤
. C.
12m≤<
. D.
12m<≤
.
Lời giải
Vì
3
0
2 4 44
xx
ππ ππ
<< ⇒ <+ <
2
sin 1
24
x
π
⇒ < +≤
Phương trình đã cho có nghiệm
0;
2
x
π
∈
khi
2
1
2
2
m
<≤
12m⇔< ≤
.
Bấm Tải xuống để xem toàn bộ.




