Chuyên đề hàm số lượng giác và phương trình lượng giác – Trần Văn Tài

Tài liệu gồm 137 trang với nội dung gồm các phần:

1. Phương trình lượng giác đưa về bậc hai và bậc cao cùng 1 hàm lượng giác
2. Phương trình lượng giác bậc nhất đối với sin và cosin (phương trình cổ điển)

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

137 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 1 | THBTN
1. Phöông trình löôïng giaùc ñöa veà baäc hai vaø baäc cao cuøng 1 haøm löôïng giaùc
Quan sát và dùng các công thức biến đổi để đưa phương trình về cùng một hàm lượng giác (cùng sin
hoặc cùng cos hoặc cùng tan hoặc cùng cot) với cung góc giống nhau, chẳng hạn:
Dạng Đặt ẩn phụ Điều kiện
2
sin sin 0a X b X c
sintX
11t
2
cos cos 0a X b X c
costX
11t
2
tan tan 0a X b X c
tantX
2
cot cot 0a X b X c
cottX
Xk
Nếu đặt
22
sin , cost X X
hoặc
sin , cost X X
thì điều kiện là
01t
.
Ví d 1. Giải phương trình:
2
4cos 4sin 1 0.xx
Gii:
22
pt 4 1 sin sin 1 0 4sin sin 3 0x x x x
sin 1
3
sin
4
x
x

Với
sin 1 2 ,
2
x x k k
Với
3
arcsin 2
4
3
sin ,
4
3
arcsin 2
4
xk
xk
xk








Ví d 2. Giải phương trình:
cos2 3cos 2 0.xx
Gii:
2
2
cos 1
pt 2cos 3cos 1 0 ,
1
2
cos
3
2
xk
x
x x k
xk
x
Ví d 3. Giải phương trình:
3cos2 7sin 2 0.xx
Gii:
CHUYÊN ĐỀ 1: PHƯƠNG TRÌNH LƯỢNG GIÁC
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
2 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
22
pt 3 1 2sin 7sin 2 0 6sin 7sin 5 0x x x x
5
sin
3
1
sin
2
x
x

Với
5
sin
3
x
thì pt vô nghiệm vì
sin [ 1;1]x
Với
2
1
6
sin ,
7
2
2
6
xk
xk
xk

Ví dụ 4. Giải phương trình:
42
4sin 5cos 4 0.xx
Giải:
4 2 4 2
pt 4sin 5 1 sin 4 0 4sin 5sin 1 0x x x x
2
2
sin 1
1
sin
4
x
x
Với
22
sin 1 cos 0 cos 0 ,
2
x x x x k k
Với
2
1 1 cos2 1 1
sin cos 2 ,
4 2 4 2 6
x
x x x k k
Ví dụ 5. Giải phương trình:
2
cos4 12sin 1 0.xx
Giải:
22
pt 2cos 2 1 6 1 cos2 1 0 2cos 2 6cos 2 4 0x x x x
cos2 1
cos2 2
x
x
Với
cos2 1 ,x x k k
Với
cos2 2x
thì phương trình vô nghiệm
Ví dụ 6. Giải phương trình:
2
1 2 5
tan 0.
2 cos 2
x
x
Giải:
Điều kiện
cos 0x
2
1 1 2 5
pt 1 0
2 cos cos 2xx



2
1 1 1
. 2. 2 0
2 cos cosxx
11
2 cos 2 ,
cos 2 3
x x k k
x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 3 | THBTN

BT 1. [1D1-2]Giải các phương trình lượng giác sau:
a)
2
2sin sin 1 0.xx
b)
2
4sin 12sin 7 0.xx
c)
2
2 2 sin (2 2)sin 1 0.xx
d)
32
2sin sin 2sin 1 0.x x x
e)
2
2cos 3cos 1 0.xx
f)
2
2cos 3cos 2 0.xx
g)
2
2cos ( 2 2)cos 2.xx
h)
2
4cos 2( 3 2)cos 6.xx
i)
2
tan 2 3 tan 3 0.xx
j)
2
2tan 2 3 tan 3 0.xx
k)
2
tan (1 3)tan 3 0.xx
l)
2
3cot 2 3cot 1 0.xx
m)
2
3cot (1 3)cot 1 0.xx
n)
2
3cot (1 3)cot 1 0.xx
Lời giải
a) [1D1-2]
2
2sin sin 1 0xx
2
2
sin 1
2,
1
6
sin
2
7
2
6
xk
x
x k k
x
xk



.
b) [1D1-2]
2
4sin 12sin 7 0.xx
7
2
sin
6
2
,
15
sin 2
26
xk
x
k
x x k

.
c)
2
2 2 sin (2 2)sin 1 0xx
2
sin 2
6
,
1
5
sin
2
2
6
xk
x
k
x
xk


.
d) [1D1-2]
32
2sin sin 2sin 1 0x x x
2
2
sin 1
2
1
6
sin ,
5
2
2
sin 1
6
2
2
xk
x
xk
xk
xk
x
xk




e)
2
2cos 3cos 1 0xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
4 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
cos 1
,
1
2
cos
3
2
xk
x
k
xk
x
f) [1D1-2]
2
2cos 3cos 2 0xx
cos 2
2,
1
3
cos
2
x
x k k
x

.
g) [1D1-2]
2
2cos ( 2 2)cos 2xx
cos 1
2
,
3
2
2
cos
4
2
x
xk
k
xk
x

.
h) [1D1-2]
2
4cos 2( 3 2)cos 6.xx
5
3
2
cos
6
2
,
3
2
2
cos
4
2
xk
x
k
xk
x



.
i) [1D1-2]
2
tan 2 3 tan 3 0xx
2
tan 3 0 tan 3 , .
3
x x x k k
j) [1D1-2]
2
2tan 2 3 tan 3 0xx
3 3 3 3
tan arctan ,
22
x x k k





.
k) [1D1-2]
2
tan (1 3)tan 3 0xx
tan 1
4
,,
tan 3
3
xk
x
kl
x
xl


.
l) [1D1-2]
2
3cot 2 3cot 1 0xx
2
1
3cot 1 0 cot ,
3
3
x x x k k
.
m) [1D1-2]
2
3cot (1 3)cot 1 0xx
cot 1
4
,,
3
cot
3
3
x
xk
kl
x
xl


.
n) [1D1-2]
2
3cot (1 3)cot 1 0xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 5 | THBTN
cot 1
4
,,
3
cot
3
3
x
xk
kl
x
xl


BT 2. [1D1-2] Giải các phương trình lượng giác sau:
a)
2
6cos 5sin 2 0.xx
b)
2
2cos 5sin 4 0.xx
c)
2
3 4cos sin (2sin 1).x x x
d)
2
sin 3cos 3 0.xx
e)
2
2sin 3cos 3 0.xx
f)
2
2cos 2 5sin2 1 0.xx
g)
24
3sin 2cos 2 0.xx
h)
42
4sin 12cos 7.xx
i)
42
4cos 4sin 1.xx
j)
42
4sin 5cos 4 0.xx
Li gii
a)
22
6cos 5sin 2 0 6 1 sin 5sin 2 0x x x x
2
1
sin
2
6sin 5sin 4 0
4
sin
3
x
xx
x

Với
2
1
6
sin sin sin ,
7
26
2
6
xk
x x k
xk




Với
4
sin
3
x 
Phương trình vô nghiệm.
b)
22
2cos 5sin 4 0 2 1 sin 5sin 4 0x x x x
2
1
sin
2sin 5sin 2 0
2
sin 2
x
xx
x
Với
2
1
6
sin sin sin ,
5
26
2
6
xk
x x k
xk


Với
sin 2x 
Phương trình vô nghiệm.
c)
2 2 2
3 4cos sin (2sin 1) 3 4 1 sin 2sin sinx x x x x x
2
sin 1
2sin sin 1 0
1
sin
2
x
xx
x

.
Với
sin 1 2 ,
2
x x k k
.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
6 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Với
2
1
6
sin sin sin ,
7
26
2
6
xk
x x k
xk




.
d)
22
sin 3cos 3 0 1 cos 3cos 3 0x x x x
2
cos 1
cos 3cos 2 0
cos 2
x
xx
x
.
Với
cos 1 2 ,x x k k
.
Với
cos 2x 
Phương trình vô nghiệm.
e)
22
2sin 3cos 3 0. 2 1 cos 3cos 3 0x x x x
2
cos 1
2cos 3cos 1 0
1
cos
2
x
xx
x
.
Với
cos 1 2 ,x x k k
.
Với
1
cos cos cos 2 ,
2 3 3
x x x k k

.
f)
22
2cos 2 5sin2 1 0 2 1 sin 2 5sin2 1 0x x x x
2
sin 2 1
2sin 2 5sin 2 3 0
3
sin 2
2
x
xx
x
.
Với
sin 2 1 2 2 k ,
24
x x k x k


.
Với
3
sin
2
x 
Phương trình vô nghiệm.
g)
2 4 2 4
3sin 2cos 2 0 3 1 cos 2cos 2 0x x x x
2
42
2
2
1 cos2
cos 1
1
cos2 1
2cos 3cos 1 0
2
1
cos2 0
cos
2cos 1 0
2
x
x
x
xx
x
x
x






Với
cos2 1 2 2 k ,x x k x k

.
Với
cos2 0 2 k ,
2 4 2
x x k x k
.
h)
4 2 4 2
4sin 12cos 7 4sin 12 1 sin 7 0x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 7 | THBTN
2
42
2
2
5
1 cos2 5
sin
cos2 4
2
4sin 12sin 5 0
22
1 cos2 0
sin
1 2sin 0
2
x
x
x
xx
x
x
x


.
Với
cos2 4x
Phương trình vô nghiệm.
Với
cos2 0 2 ,
2 4 2
x x k x k k
.
i)
4 2 4 2
4cos 4sin 1 4cos 4 1 cos 1x x x x
2
42
2
2
1
cos2 0
cos
2
4cos 4cos 3 0
3
3
cos
cos
2
2
x
x
xx
x
x


.
Với
2
3
cos
2
x
Phương trình vô nghiệm.
Với
cos2 0 2 k ,
2 4 2
x x k x k
.
j)
4 2 4 2
4sin 5cos 4 0 4sin 5 1 sin 4 0x x x x
22
42
2
cos 0
sin 1 1 sin 0
4sin 5sin 1 0
1
1 1 cos2 1
cos2
sin
2
4 2 4
x
xx
xx
x
x
x






Với
cos 0 ,
2
x x k k
.
Với
1
cos2 cos2 cos 2 2 k ,
2 3 3 6
x x x k x k

.
BT 3. [1D1-3] Giải các phương trình lượng giác sau:
a)
2cos2 8cos 5 0.xx
b)
1 cos2 2cos .xx
c)
9sin cos2 8.xx
d)
2 cos2 5sin 0.xx
e)
3sin cos2 2.xx
f)
2cos2 8sin 5 0.xx
g)
2cos2 3sin 1 0.xx
h)
5cos 2sin 7 0.
2
x
x
i)
2
sin cos2 cos 2.x x x
j)
2
cos2 cos sin 2 0.x x x
Li gii
a) [1D1-3]
2cos2 8cos 5 0.xx
Ta có:
2
2cos2 8cos 5 0 2 2cos 1 8cos 5 0x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
8 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
3
cos
2
4cos 8cos 3 0
1
cos
2
xl
xx
x
Với
1
cos 2 .
23
x x k k
b)[1D1-3]
1 cos2 2cos .xx
Ta có:
2
1 cos2 2cos 2cos 2cos 0 2cos cos 1 0x x x x x x
cos 0
,
2
cos 1
2
x
xk
k
x
xk

.
c) [1D1-3]
9sin cos2 8.xx
Ta có:
2
9sin cos2 8 1 2sin 9sin 8x x x x
2
2sin 9sin 7 0xx
sin 1
7
sin
2
x
xl
Với
sin 1 2 ,
2
x x k k
.
d) [1D1-3]
2 cos2 5sin 0.xx
Ta có:
2
2 cos2 5sin 0 2 1 2sin 5sin 0x x x x
2
sin 3
2sin 5sin 3 0
1
sin
2
xl
xx
x

Với
2
1
6
sin ,
7
2
2
6
xk
xk
xk

.
e)[1D1-3]
3sin cos2 2xx
Ta có:
2
3sin cos2 2 3sin 1 2sin 2 0x x x x
2
sin 1
2sin 3sin 1 0
1
sin
2
x
xx
x
Với
sin 1 2 , .
2
x x k k
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 9 | THBTN
Với
2
1
6
sin , .
5
2
2
6
xk
xk
xk


f) [1D1-3]
2cos2 8sin 5 0.xx
Ta có:
2
2cos2 8sin 5 0 2 1 2sin 8sin 5 0x x x x
2
3
sin
2
4sin 8sin 3 0
1
sin
2
xl
xx
x
Với
2
1
6
sin , .
5
2
2
6
xk
xk
xk


g) [1D1-3]
2cos2 3sin 1 0.xx
Ta có:
22
sin 1
2cos2 3sin 1 0 2 1 2sin 3sin 1 0 4sin 3sin 1 0
1
sin
4
x
x x x x x x
x

Với
sin 1 2 , .
2
x x k k
1
arcsin 2
4
1
sin ,
4
1
arcsin 2
4
xk
xk
xk







.
h) [1D1-3]
5cos 2sin 7 0.
2
x
x
Ta có:
2
5cos 2sin 7 0 5 1 2sin 2sin 7 0
2 2 2
x x x
x



2
sin 1
2
10sin 2sin 12 0
6
22
sin
25
x
xx
x
l

Với
sin 1 2 4 , .
2 2 2
xx
k x k k
i) [1D1-3]
2
sin cos2 cos 2.x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
10 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Ta có:
2 2 2
sin cos2 cos 2 1 cos 2cos 1 cos 2 0x x x x x x
2
cos 1
cos cos 2 0
cos 2
x
xx
xl

Với
cos 1 2 , .x x k k
j) [1D1-3]
2
cos2 cos sin 2 0.x x x
Ta có:
2 2 2
cos2 cos sin 2 0 1 2sin 1 sin sin 2 0x x x x x x
2
sin 1
3sin sin 4 0
4
sin
3
x
xx
xl

Với
sin 1 2 , .
2
x x k k
BT 4. [1D1-3] Giải các phương trình lượng giác sau:
a)
2
3cos 2cos2 3sin 1.x x x
b)
2
cos4 12sin 1 0.xx
c)
2
cos4 2cos 1 0.xx
d)
2
16sin cos2 15.
2
x
x
e)
2
cos 2 2cos 2sin
2
x
xx
f)
2
cos 2 3cos 4cos
2
x
xx
g)
2
1 cos4 2sin 0.xx
h)
2
8cos cos4 1.xx
i)
2
6sin 3 cos12 4.xx
j)
44
5(1 cos ) 2 sin cos .x x x
k)
44
cos sin cos4 0.x x x
l)
44
4(sin cos ) cos4 sin 2 0.x x x x
Li gii
a. [1D1-3]
2
3cos 2cos2 3sin 1x x x
22
3 1 sin 2 1 2sin 3sin 1x x x
2
sin 3sin 2 0xx
sin 1x
hay
sin 2x
(loại)
sin 1x
2
2
x k k
.
b. [1D1-3]
2
cos4 12sin 1 0xx
2
2cos 2 1 6 1 cos2 1 0xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 11 | THBTN
2
2cos 2 6cos2 4 0xx
cos2 1x
hay
cos2 2x 
(loại)
2
x k k
.
c. [1D1-3]
2
cos4 2cos 1 0.xx
2
2cos 2 1 1 cos2 1 0xx
2
2cos 2 cos2 1 0xx
cos2 1x
hay
1
cos2
2
x 
x k k
hay
3
x k k
.
d. [1D1-3]
2
16sin cos2 15.
2
x
x
2
8 1 cos 2cos 1 15xx
2
2cos 8cos 6 0xx
cos 1x
hay
cos 3x 
(loại)
2x k k

.
e. [1D1-3]
2
cos 2 2cos 2sin
2
x
xx
2
2cos 1 2cos 1 cosx x x
2
2cos 3cos 2 0xx
cos 2x
(loại) hay
1
cos
2
x
2
3
x k k
.
f. [1D1-3]
2
cos 2 3cos 4cos
2
x
xx
2
2cos 1 3cos 2 1 cosx x x
2
2cos 5cos 3 0xx
cos 3x
(loại) hay
1
cos
2
x 
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
12 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2
3
x k k
.
g. [1D1-3]
2
1 cos4 2sin 0xx
2
1 2cos 2 1 cos2 0xx
2
2cos 2 cos2 0xx
cos2 0x
hay
1
cos2
2
x
42
x k k

hay
6
x k k
.
h. [1D1-3]
2
8cos cos4 1xx
2
4 1 cos2 2cos 2 1 1xx
2
2cos 2 4cos2 4 0xx
cos2 1 3x
(loại) hay
cos2 1 3x 
1
arccos 1 3
2
x k k
.
i. [1D1-3]
2
6sin 3 cos12 4xx
2
3 1 cos6 2cos 6 1 4xx
2
2cos 6 3cos6 0xx
cos6 0x
hay
3
cos6
2
x 
(loại)
12 6
x k k

.
j. [1D1-3]
44
5(1 cos ) 2 sin cosx x x
2 2 2 2
5 1 cos 2 sin cos sin cosx x x x x
22
5 5cos 2 1 cos cosx x x
2
2cos 5cos 2 0xx
cos 2x
(loại) hay
1
cos
2
x 
2
2
3
x k k
.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 13 | THBTN
k. [1D1-3]
44
cos sin cos4 0x x x
2 2 2 2 2
cos sin cos sin 2cos 2 1 0x x x x x
2
2cos 2 cos2 1 0xx
cos2 1x
hay
1
cos2
2
x
42
x k k

hay
6
x k k
.
l. [1D1-3]
44
4(sin cos ) cos4 sin 2 0x x x x
2 2 2
4 1 2sin cos 1 2sin 2 sin 2 0x x x x
22
4 2sin 2 1 2sin 2 sin2 0x x x
2
4sin 2 sin2 5 0xx
sin 2 1x
hay
5
sin 2
4
x
(loại).
4
x k k
.
BT 5. [1D1-3] Giải các phương trình lượng giác sau:
a)
2
cos 2 3cos 1 0.
33
xx
b)
2
cos 4cos 4.
36
xx

c)
22
4cos (6 2) 16cos (1 3 ) 13.xx
d)
5
5cos 2 4sin 9.
36
xx

e)
57
sin 2 3cos 1 2sin .
22
x x x

f)
cos2 3sin 2 3sin 4 cos .x x x x
g)
3sin2 3sin cos2 cos 2.x x x x
h)
2
2
42
2 cos 9 cos 1.
cos cos
xx
xx
i)
2
2
11
4 sin 4 sin 7.
sin sin
xx
xx
j)
2
2
11
cos 2 2 cos
cos cos
xx
xx



Li gii
a)
2
cos 2 3cos 1 0.
33
xx

Xét phương trình
2
cos 2 3cos 1 0.
33
xx

cos 2 3cos 1 0
33
xx




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
14 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2cos 3cos 0 cos 2cos 3 0
3 3 3 3
x x x x



cos 0
3
3
cos
32
x
xl








Xét
cos 0 ,
3 3 2 6
x x k x k k




.
Vậy tập nghiệm của phương trình là
,
6
S k k

.
b)
2
cos 4cos 4.
36
xx

Li gii
Xét phương trình
2
cos 4cos 4.
36
xx

.
22
sin 4cos 4 1 cos 4cos 4
6 6 6 6
x x x x
2
cos 4cos 3 0 cos 1
6 6 6
x x x
hoặc
cos 3
6
x




(loại)
Với
cos 1 cos 1 2 2 ,
6 6 6 6
x x x k x k k

.
Vậy tập nghiệm của phương trình
2,
6
S x k k

.
c)
22
4cos (6 2) 16cos (1 3 ) 13.xx
Li gii
Xét phương trình
22
4cos (6 2) 16cos (1 3 ) 13.xx
.
2 2 2
4cos 6 2 8.2cos 1 3 13 4cos 6 2 8. cos2 1 3 1 13x x x x


22
4cos 6 2 8cos 6 2 8 13 4cos 6 2 8cos 6 2 5 0x x x x
1
cos 6 2
2
x
hoặc
5
cos 6 2
2
x
(loại).
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 15 | THBTN
Với
1
cos 6 2 cos 6 2 cos
23
xx
1
6 2 2 6 2 2
3 3 18 3 3
,
1
6 2 2 6 2 2
3 3 18 3 3
k
x k x k x
k
k
x k x k x


.
Vậy tập nghiệm của phương trình là
1
,.
18 3 3
k
Sk



d)
5
5cos 2 4sin 9.
36
xx

Li gii
Xét phương trình
5
5cos 2 4sin 9.
36
xx

5cos 2 4sin 9 5cos 2 4sin 9
6 6 6 6
x x x x
22
5 1 2sin 4sin 9 10sin 4sin 14 0
6 6 6 6
x x x x



sin 1
6
x



hoặc
7
sin
65
x



(loại).
Với
sin 1 2 2 ,
6 6 2 3
x x k x k k

.
Vậy tập nghiệm của phương trình là
2,
3
S k k

.
e)
57
sin 2 3cos 1 2sin .
22
x x x

Li gii
Ta có:
5
sin 2 sin 2x 2 cos2x,
22
x




7
cos cos 3 cos sinx
2 2 2
x x x
Phương trình đã cho trở thành
cos2 3sin 1 2sinx x x
2
1 cos2 sin 0 2sin sin 0 sin 2sin 1 0x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
16 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
sin 0
2,
1
6
sin sin
sin
6
2
5
2
6
xk
xk
x
x k k
x
x
xk

.
Vậy tập nghiệm của phương trình
5
; 2 ; 2 ,
66
S k k k k



.
f)
cos2 3sin 2 3sin 4 cos .x x x x
Li gii
Xét phương trình
cos2 3sin 2 3sin 4 cos .x x x x
cos 2 3sin 2 cos 3sin 4 cos 2 cos 2
33
x x x x x x

cos 2 cos 2 cos 2 sin 2
3 3 6 2 3
x x x x
2
cos 2 sin 2 2sin sin 3 0
6 6 6 6
x x x x



sin 1
6
x



hoặc
3
sin
62
x



(loại).
Với
sin 1 2 2 ,
6 6 2 3
x x k x k k

.
Vậy tập nghiệm của phương trình là
2,
3
S k k

.
g)
3sin2 3sin cos2 cos 2.x x x x
Li gii
Xét phương trình
3sin2 3sin cos2 cos 2.x x x x
biến đổi tương tự như câu f ta được:
cos 2 cos 1 cos 2 1 sin 0
3 3 6 6
x x x x



2
2sin sin 0 sin 2sin 1 0
6 6 6 6
x x x x



TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 17 | THBTN
66
sin 0
6
2 2 ,
6 6 3
1
sin sin
52
6 2 6
2
66
x k x k
x
x k x k k
x
xk
xk





















.
Vậy tập nghiệm của phương trình
; 2 ; 2 ,
63
S k k k k


.
h)
2
2
42
2 cos 9 cos 1.
cos cos
xx
xx
Li gii
Xét phương trình
2
2
42
2 cos 9 cos 1.
cos cos
xx
xx
ĐKXĐ.
,
2
x k k
.
Đặt
2 2 2 2
22
2 4 4
cos cos 4 4 cos
cos cos cos
t x t x t x
x x x
Khi đó phương trình đã cho trở thành:
22
2 4 9 1 2 9 7 0t t t t
1
7
2
t
t


Khi
2
2
1 cos 1 cos cos 2 0
cos
t x x x
x
cos 1x
hoặc
cos 2x 
(loại).
Với
cos 1 2x x k
(TM)
Khi
2
7 2 7
cos 2cos 7cos 4 0
2 cos 2
t x x x
x
1
cos
2
x
hoặc
cos 4x
(loại)
Với
1 2 2
cos cos 2 ,
2 3 3
x x k k

.
Vậy tập nghiệm của phương trình
2
2 ; 2 ,
3
S k k k



.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
18 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
i)
2
2
11
4 sin 4 sin 7.
sin sin
xx
xx
Li gii
Xét phương trình
2
2
11
4 sin 4 sin 7.
sin sin
xx
xx
ĐKXĐ.
,x k k

.
Đặt
2 2 2 2
22
1 1 1
sin sin 2 2 sin
sin sin sin
t x t x t x
x x x
.
Phương trình đã cho trở thành:
22
3
2
4 2 4 7 4 4 15 0
5
2
t
t t t t
t

.
Khi
2
3 1 3
sin 2sin 3sin 2 0
2 sin 2
t x x x VN
x
Khi
5 1 5
sin
2 sin 2
tx
x
.
2
1
2sin 5sin 2 0 sin
2
x x x
hoặc
sin 2x 
(loại).
Với
1
sin sin
26
x



2
6
,
7
2
6
xk
k
xk


.
Vậy tập nghiệm của phương trình là:
7
2 ; 2 ,
66
S k k k




.
j)
2
2
11
cos 2 2 cos
cos cos
xx
xx



Li gii
Xét phương trình
2
2
11
cos 2 2 cos
cos cos
xx
xx



. ĐKXĐ
,
2
x k k
Đặt
22
2
11
cos cos 2
cos cos
t x t x
xx



.
Phương trình đã cho trở thành:
2
0
2
2
t
tt
t


.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 19 | THBTN
Khi
1
0 cos 0
cos
t x VN
x
Khi
2
1
2 cos 2 cos 2cos 1 0 cos 1 2
cos
t x x x x x k
x
(TMĐK) .
Vậy tập nghiệm của phương trình:
2,S k k

.
BT 6. [1D1-2] Giải các phương trình lượng giác sau:
a)
2
2
3
3 2tan .
cos
x
x

b)
2
2
1
3cot 5.
cos
x
x

c)
2
3
3cot 3.
sin
x
x

d)
2
4
9 13cos 0.
1 tan
x
x
e)
2
3
2tan 3
cos
x
x
f)
2
1 2 5
tan 0.
2 cos 2
x
x
g)
1
3sin cos
cos
xx
x
g)
22
2sin tan 2.xx
a)
2
2
3
3 2tan .
cos
x
x

Li gii
Điều kiện:
2
xk

.
2 2 2
2
3
3 2tan 3 1 tan 3 2tan .
cos
x x x
x
tan 0 .x x k k
b)
2
2
1
3cot 5.
cos
x
x

Li gii
Điều kiện
2
k
x
.
22
22
13
3cot 5 1 tan 5.
cos tan
xx
xx
Đặt
2
tan ( 0)t x t
, ta có phương trình:
2
1
4 3 0 .
3
t
tt
t
tan 1
4
.
tan 3
3
xk
x
k
x
xk


c)
2
3
3cot 3.
sin
x
x

Li gii
Điều kiện:
xk
.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
20 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2
3
3cot 3 3 1 cot 3cot 3.
sin
x x x
x
2
cot 0
2
3 cot 3cot 0 .
cot 3
6
xk
x
xx
x
xk


d)
2
4
9 13cos 0.
1 tan
x
x
Li gii
Điều kiện:
2
xk

.
2
2
4
9 13cos 0 9 13cos 4cos 0.
1 tan
x x x
x
9
cos ko tm
2.
4
cos 1
x
xk
x
e)
2
3
2tan 3
cos
x
x
Li gii
Điều kiện:
2
xk

.
2
2
3 1 3
2tan 3 2 1 3 .
cos cos cos
x
x x x



Đặt
1
1
cos
tt
x

, ta có phương trình
2
1
2 3 1 0
1
ko tm
2
t
tt
t
.
cos 1 2 . .x x k k
f)
2
1 2 5
tan 0.
2 cos 2
x
x
Li gii
Điều kiện:
2
xk

.
2
2
1 2 5 1 1 2 5
tan 0 1 0.
2 cos 2 2 cos cos 2
x
x x x



Đặt
1
1
cos
tt
x

, ta có phương trình
2
1
4 4 0 2 cos 2 .
23
t t t x x k
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 21 | THBTN
g)
1
3sin cos
cos
xx
x
Li gii
Điều kiện:
2
xk

.
Chia cả 2 vế cho
cos x
ta được:
2
2
2
1
3 tan 1 3 tan 1 1 tan .
cos
tan 0
tan 3 tan 0 .
tan 3
3
x x x
x
xk
x
x x k
xk
x

g)
22
2sin tan 2.xx
Li gii
Điều kiện:
2
xk

.
2 2 2
2
1
2sin tan 2 2 1 cos 1 2.
cos
x x x
x



Đặt
2
cos 0 1t x t
. Ta có phương trình
2
1
2 1 0 .
1
2
t loai
tt
t

Vậy
1
cos
2
2
4
.
13
42
cos 2
4
2
x
xk
k
x
x x k


BT 7. [1D1-3] Giải các phương trình lượng giác sau:
a)
8sin cos cos4 3 0.x x x
b)
2
2sin 8 6sin4 cos4 5.x x x
c)
cos
1 sin .
1 sin
x
x
x

d)
1 cos (2cos 1) 2.sin
1.
1 cos
x x x
x
e)
3sin 2 2sin
2.
sin 2 cos
xx
xx
f)
2
2
2sin 3 2 sin sin 2 1
1.
(sin cos )
x x x
xx

g)
1
2cos 2 8cos 7
cos
xx
x
g)
2
3 4 2sin 2
2 3 2(cot 1).
cos sin2
x
x
xx
h)
26
3cos4 2cos 3 8cos .x x x
k)
2
3cos 2 3(1 cos ).cot .x x x
l)
sin3 cos2 1 2sin cos2 .x x x x
m)
2cos5 .cos3 sin cos8 .x x x x
n)
66
4(sin cos ) 4sin2 .x x x
o)
sin4 2 cos3 4sin cos .x x x x
Li gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
22 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
a)
8sin cos cos4 3 0.x x x
Li gii
Ta có:
2
8sin cos cos4 3 0 4sin 2 2sin 2 2 0 sin 2 1x x x x x x
4
x k k
.
b)
2
2sin 8 6sin 4 cos4 5.x x x
Li gii
Ta có:
22
sin8 1
2sin 8 6sin 4 cos4 5 2sin 8 3sin8 5 0
5
sin8
2
xN
x x x x x
xL

82
2 16 4
k
x k x k
.
c)
cos
1 sin .
1 sin
x
x
x

Li gii
Điều kiện:
sin 1 2
2
x x k k
.
PT
2
cos 0
cos
1 sin . cos cos
2
cos 1
1 sin
2
x
xk
x
x x x k
x
x
xk

.
Kết hợp điều kiện, phương trình có hai họ nghiệm là:
2
2
2
xk
k
xk

.
d)
1 cos (2cos 1) 2.sin
1.
1 cos
x x x
x
Li gii
Điều kiện:
2x k k

.
Ta có:
2
1 cos (2cos 1) 2.sin
1 1 2cos cos 2 sin 1 cos
1 cos
x x x
x x x x
x
2
sin 2
2
4
2 1 sin sin 0
2
5
sin sin
2
24
4
xL
xk
x x k
x
xk




.
e)
3sin 2 2sin
2.
sin 2 cos
xx
xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 23 | THBTN
Li gii
Điều kiện:
sin 2 0
2
x x k k
.
2sin 3cos 1
12
2sin cos cos
xx
xxx

.
2
3cos 1 2cosxx
.
2
2cos 3cos 1 0xx
.
cos 1
1
cos
2
x
x
.
2
2
3
x k l
xk
.
Kết hợp điều kiện, phương trình có nghiệm:
2
3
x k k
.
3sin2 2sin
21
sin2 cos
xx
xx
ĐK:
sin2 0
2
x x k
f)
2
2
2sin 3 2 sin sin 2 1
1
(sin cos )
x x x
xx

.
Li gii
Điều kiện:
sin cos 0 sin 0
44
x x x x k k




.
Ta có:
2
2
2
2sin 3 2 sin sin 2 1
1 2sin 3 2 sin sin 2 1 1 sin 2
(sin cos )
x x x
x x x x
xx
2
sin 2
2
4
2sin 3 2 sin 2 0
2
5
sin sin
2
24
4
x VN
xk
x x k
x
xk





.
Kết hợp với điều kiện, suy ra phương trình có nghiệm:
5
2
4
x k k
.
g)
1
2cos 2 8cos 7
cos
xx
x
.
Li gii
Điều kiện:
cos 0
2
x x k k
.
PT
2
2cos2 .cos 8cos 7cos 1 0x x x x
2 2 3 2
2cos 2cos 1 8cos 7cos 1 0 4cos 8cos 5cos 1 0x x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
24 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2
cos 1
cos 1 4cos 4cos 1 0
1
2
cos
3
2
xk
x
x x x k
xk
x
.
Vậy, phương trình có nghiệm:
2
2
3
xk
k
xk
.
h)
2
3 4 2sin 2
2 3 2 cot 1
cos sin2
x
x
xx
.
Li gii
Điều kiện:
sin 2 0
2
k
x x k
.
PT
2
2
1 tan
3 1 tan 4 2 2 3 2 cot 1
2tan
x
xx
x



3 2 3 2
3 tan 2 1 tan 3 tan 2 0 3 tan 2tan 3 tan 0x x x x x x
tan 0
3
tan
36
tan 3
3
x
xk
x x k k
x
xk

. Kết hợp điều kiện suy ra phương trình có nghiệm:
6
3
xk
k
xk

.
i)
26
3cos4 2cos 3 8cos .x x x
Li gii
Ta có:
26
3cos4 2cos 3 8cosx x x
3
2
3 2cos 2 1 1 cos2 3 1 cos2x x x
2 2 3
6cos 2 1 cos2 1 3cos2 3cos 2 cos 2x x x x x
32
cos2 0
cos 2 3cos 2 2cos2 0 cos2 1
42
cos2 2
x
k
x
x x x x k
xk
x VN


.
k)
2
3cos 2 3(1 cos ).cot .x x x
Li gii
Điều kiện:
sin 0x x k k
.
PT
2 2 2
3cos .sin 2sin 3 1 cos cos 0x x x x x
2 2 2
3cos . 1 cos 2 1 cos 3 1 cos cos 0x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 25 | THBTN
32
2
cos
3
6cos 5cos 3cos 2 0 cos 1
1
cos
2
x
x x x x
x

2
cos 2
3
2
2
3
x arc k
x k k
xk



.
Kết hợp điều kiện, suy ra phương trình có nghiệm:
2
cos 2
3
2
3
x arc k
k
xk




.
l)
sin3 cos2 1 2sin cos2 .x x x x
Li gii
PT
2
sin 0
sin3 cos2 1 sin sin3 1 2sin 1 sin
1
sin
2
x
x x x x x x
x
2
6
5
2
6
xk
x k k
xk

.
m)
2cos5 .cos3 sin cos8 .x x x x
Li gii
Ta có:
2cos5 .cos3 sin cos8 cos2 cos8 sin cos8x x x x x x x x
2
1 2sin sin 0
2
2
sin 1
2
1
6
sin
2
7
2
6
xx
xk
x
x k k
x
xk



2
.
63
k
x

n)
66
4(sin cos ) 4sin2 .x x x
Li gii
Ta có:
6 6 2 2
4(sin cos ) 4sin2 1 3sin cos sin 2x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
26 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2
2 sin 2
2
sin 2
3
3
3
1 sin 2 sin 2
4
2
sin 2 2
2 sin 2
3
x arc k
x
xx
x vn
x arc k









12
arcsin
23
12
arcsin
2 2 3
xk
k
xk








.
o)
sin4 2 cos3 4sin cos .x x x x
Li gii
PT
sin4 2 cos3 4sin cos .x x x x
2sin 2 .cos2 2 2cos2 .cos 4sin 2sin .cos .cos2 1 cos2 .cos 2sinx x x x x x x x x x x
cos2 .cos 2sin 1 1 2sin 0 2sin 1 cos2 .cos 1 0x x x x x x x
2
1
1
sin
sin
2
2
2cos 1 .cos 1 0
cos2 .cos 1 0
x
x
xx
xx


3
1
sin
2
2cos cos 1 0
x
xx
3
2
6
1
1
sin
sin
5
2
2
2
6
cos 1
2cos cos 1 0
2
xk
x
x
x k k
x
xx
xk

.
BT 8. [1D1-3] Giải các phương trình lượng giác sau:
a)
23
2
2
cos cos 1
cos2 tan
cos
xx
xx
x

b)
2
3 2tan 2
3tan 2 4cos 2.
cos 2 1 tan
x
xx
xx
c)
2
(2tan 1)cos 2 cos2 .x x x
d)
2
2cos 3cos 2cos3 4sin sin2 .x x x x x
e)
2
4sin 3 2(1 sin )tan .x x x
f)
32
2sin 3 (3sin 2sin 3)tan .x x x x
g)
2
5sin 3(1 cos )cot 2.
2
x x x



h)
2
3
3sin 2sin 3
3 2sin .
cot
xx
x
x


i)
cos3 sin3
5sin 3 cos2 .
1 2sin 2
xx
xx
x
k)
2
3
tan 2 3 sin 1 tan tan
cos 2
x
x x x
x



Li gii
a)
23
2
2
cos cos 1
cos2 tan
cos
xx
xx
x

Li gii
Điều kiện:
2
,xkk

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 27 | THBTN
23
2
2
cos cos 1
cos2 tan
cos
xx
xx
x


(1). Điều kiện:
cos 0
2
x x k
.
Khi đó pt (1)
2 2 2 2 3
2cos 1 cos sin cos cos 1x x x x x
432
2cos cos cos 0x x x
2
2cos cos 1 0xx
cos 1
12
cos cos
23
x
x
2
2
2
3
xk
k
xk

2
3
k
xk
.
Vậy phương trình (1) có các nghiệm:
2
3
k
xk

.
b)
2
3 2tan 2
3tan 2 4cos 2.
cos 2 1 tan
x
xx
xx
Li gii
Điều kiện:
cos2 0
cos 0
x
x
2
3 2tan 2
3tan 2 4cos 2
cos 2 1 tan
x
xx
xx
(1).
Điều kiện:
cos2 0
cos 0
tan 1
x
x
x

42
2
4
xk
xk
xk


42
2
xk
xk



.
Khi đó pt (1)
2 sin cos
3sin 2 3
2cos 2 0
cos 2 x cos2 sin cos
xx
x
x
x x x
2
2
3sin2 3 2 sin cos 2cos 2 0x x x x
2
3sin2 3 2 2sin2 2cos 2 0x x x
2
2sin 2 5sin2 3 0xx
sin 2 1
3
sin 2
2
x
x VN
4
x k k
.
Vậy phương trình (1) vô nghiệm.
c)
2
(2tan 1)cos 2 cos2 .x x x
Li gii
Điều kiện:
2
xk

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
28 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
(2tan 1)cos 2 cos2x x x
22
(2tan 1)cos 3 2cosx x x
(1).
Khi đó pt(1)
2 2 3
2sin cos 3cos 2cosx x x x
32
2cos 3cos 3cos 2 0x x x
cos 1
cos 2
1
cos cos
23
x
x VN
x



2
2
3
xk
k
xk



.
Vậy phương trình (1) có các nghiệm:
2xk


và
2
3
xk
.
d)
2
2cos 3cos 2cos3 4sin sin2 .x x x x x
Li gii
2
2cos 3cos 2cos3 4sin sin2x x x x x
2
2cos 3cos 2 cos2 cos sin2 sin 4sin sin2x x x x x x x x
2
2cos 3cos 2 cos2 cos sin2 sin 0x x x x x x
2
2cos 3cos 2cos 0x x x
cos 0
12
cos cos
23
x
x
2
2
2
3
xk
k
xk


.
Vậy phương trình có các nghiệm
2
xk

và
2
2
3
xk
.
e)
2
4sin 3 2(1 sin )tan .x x x
Li gii
2
4sin 3 2(1 sin )tanx x x
2
2
sin
4sin 3 2(1 sin )
1 sin
x
xx
x
(1).
Điều kiện:
2
xk

.
Khi đó phương trình (1)
2
4sin 3 1 sin 2sinx x x
2
2sin 7sin 3 0xx
1
sin sin
26
sin 3
x
x VN




2
6
7
2
6
xk
xk

k
.
Vậy phương trình có các nghiệm:
2
6
xk
và
7
2
6
xk

.
f)
32
2sin 3 (3sin 2sin 3) tan .x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 29 | THBTN
Li gii
Ta có:
32
sin
2sin 2sin 3cos
os
3
c
x
x x
x
x 
3 2 2
cos 3c2s os 2sin 3cos siin nx x x x x x
2
2sin sin cos 1 3cos sin cos 1x x x x xx
2
sin cos 1 0
2sin 3cos
x
xx
x


2
sin 2 2
2cos 3cos 2 0xx
x
sin 2 2
cos 2
1
cos
2
x
x
x


2
2
3
xk
.
g)
2
5sin 3(1 cos )cot 2.
2
x x x



Li gii
Điều kiện:
,x kk
2
5sin 3(1 cos )cot 2
2
x x x



2
2
cos
5cos 3 1 cos 2
1 cos
x
x
x
x
2
5cos 1 cos 3 2cos 1 cosxx x x
2
3co2co s 2 0s xx
1
cos
2
cos 2
x
x

2
3
xk
.
h)
2
3
3sin 2sin 3
3 2sin .
cot
xx
x
x


Li gii
Điều kiện:
,
2
k
xk

2
3
3sin 2sin 3
3 2sin
cot
xx
x
x


32
sin
2sin 2sin 3cos
cos
3 x x
x
x
x

3 2 2
cos 3c2s os 2sin 3cos siin nx x x x x x
2
2sin sin cos 1 3cos sin cos 1x x x x xx
2
sin cos 1 0
2sin 3cos
x
xx
x


2
sin 2 2
2cos 3cos 2 0xx
x
sin 2 2
cos 2
1
cos
2
x
x
x


2
2
3
xk
.
i)
cos3 sin3
5 sin 3 cos2 .
1 2sin 2
xx
xx
x



Li gii
Điều kiện:
1 sin2 0x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
30 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
33
cos3 sin3 4cos 3cos 3sin 4sin
1 2sin 2 1 4sin cos
x x x x x x
x x x

4 cos sin 1 sin cos 3 cos sin
1 4sin cos
x x x x x x
xx
cos sin 1 4sin cos
1 4sin cos
x x x x
xx

cos sinxx
Ta có:
cos3 sin3
5 sin 3 cos2
1 2sin 2
xx
xx
x



5cos 3 cos2xx
2
cos 2
2cos 5cos 2 0
1
cos
2
xl
xx
x
+ Với
1
cos 2 ,
23
x x k k
. (thỏa mãn điều kiện).
k)
2
3
tan 2 3 sin 1 tan tan
cos 2
x
x x x
x



Li gii
Điều kiện:
cos 0;cos 0
2
x
x 
2
3
tan 2 3 sin 1 tan tan
cos 2
x
x x x
x



2
cos cos sin sin
22
3 1 tan tan 2 3 sin
cos cos
2
xx
xx
xx
x
x
x





2
3 1 tan tan 2 3 tanxxx
2
2ta3 ta 3 0nn xx
tan 3
3
tan
3
x
x

3
6
xk
xk

.
2. Phöông trình löôïng giaùc baäc nhaát ñoái vôùi sin vaø cosin (phöông trình coå ñieån)
Dng tng quát:
sin cos ( ) , , \ 0a x b x c a b
Điều kiện có nghiệm của phương trình:
2 2 2
,a b c
(kiểm tra trước khi giải)
i:
Chia 2 vế
22
0,ab
thì
2 2 2 2 2 2
( ) sin cos
a b c
xx
a b a b a b
()
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 31 | THBTN
Giả sử:
2 2 2 2
cos , sin , 0;2
ab
a b a b

thì:
2 2 2 2
( ) sin cos cos sin sin( ) :
cc
x x x
a b a b


dạng cơ bản.
. Hai công thức sử dụng nhiều nhất là:
sin cos cos sin sin( )
cos cos sin sin cos( )
a b a b a b
a b a b a b
Các dng có cách gi:
22
22
22
22
2 2 2 2
cos
.sin .cos , ( 0)
Chia : .
sin
.sin .cos .sin .cos , ( )
PP
a b nx
a mx b mx a b
ab
a b nx
a mx b mx c nx d nx a b c d

Ví d 1. Giải phương trình:
sin 3cos 3.xx
Gii:
Vì
22
2
1 3 3
nên phương trình luôn có nghiệm
Khi đó:
1 3 3 3
pt sin cos sin
2 2 2 3 2
x x x



2
,
5
2
3
xk
k
xk


Ví d 2. Giải phương trình:
cos2 3 sin 2 2cos
3
x x x



Gii:
13
pt cos2 sin 2 cos cos 2 cos
2 2 3 3 3
x x x x x
2
22
3 3 3
,
2
2 2 2
3 3 3
x x k x k
k
x x k x k







Ví d 3. Giải phương trình:
cos4 sin 3(cos sin 4 ).x x x x
Gii:
1 3 3 1
pt cos 4 3sin4 3 cos sin cos4 sin 4 cos sin
2 2 2 2
x x x x x x x x
cos 4 cos
36
xx

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
32 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
42
3 6 18 3
,
2
42
3 6 10 5
x x k x k
k
x x k x k






BÀI TP ÁP DNG 2
BT 9. Giải các phương trình lượng giác sau:
a)
sin 3cos 1xx
Li gii
Phương trình tương đương với:
1 3 1
sin cos
2 2 2
xx
1
cos sin sin cos
3 3 2
xx

2
1
36
sin
32
2
36
xk
x
xk






2
6
2
2
xk
k
xk


b)
3sin cos 1.xx
Li gii
Phương trình tương đương với:
3 1 1
sin cos
2 2 2
xx
1
cos sin sin cos
6 6 2
xx

1
sin
62
x



sin sin
66
x

2
66
7
2
66
xk
xk


2
3
2
xk
k
xk



c)
3cos sin 2xx
Li gii
Phương trình tương đương với:
3 1 2
cos sin
2 2 2
xx
2
sin cos cos sin
3 3 2
xx

2
sin
32
x



2
34
2
34
xk
xk



2
12
5
2
12
xk
k
xk


.
d)
sin 3cos 2.xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 33 | THBTN
Li gii
Phương trình tương đương với:
cos sin sin cos 1
33
xx

sin 1
3
x



2 2 ,
3 2 6
x k x k k

e)
3sin3 cos3 2.xx
Li gii
Phương trình tương đương với:
3 1 2
sin3 cos3
2 2 2
xx
2
cos sin3 sin cos3
6 6 2
xx

2
sin 3
62
x



52
32
6 4 36 3
,
11 2
32
6 4 36 3
x k x k
k
x k x k







.
f)
cos7 3sin7 2.xx
Li gii
Phương trình tương đương với:
1 3 2
cos7 sin 7
2 2 2
xx
3
cos .cos7 sin .sin7 cos
3 3 4
xx
3
cos 7 cos
34
x

3
72
34
3
72
34
xk
xk


5
72
12
13
72
12
xk
xk

52
84 7
,
13 2
84 7
k
x
k
k
x




.
g)
3sin sin 2.
2
xx



Li gii
Phương trình tương đương với:
3cos sin 2xx
31
cos sin 1
22
xx
cos .cos sin .sin 1
66
xx

cos 1
6
x



2
6
xk
2,
6
x k k
g)
sin 2 3sin( 2 ) 1.
2
xx



Li gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
34 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Phương trình tương đương với:
cos2 3sin 2 1xx
1 3 1
cos2 sin 2
2 2 2
xx
1
cos .cos2 sin .sin 2
3 3 2
xx

cos 2 cos
33
x

22
33
22
33
xk
xk


22
2
22
3
xk
xk
,
2
xk
k
xk

h)
3sin sin 2.
44
xx

Li gii
Phương trình tương đương với:
3sin sin 2
4 2 4
xx



3sin cos 2
44
xx

3 1 2
sin cos
2 4 2 4 2
xx

2
cos .sin sin .cos
6 4 6 4 2
xx
5
sin sin
12 4
x




5
2
12 4
53
2
12 3
xk
xk


2
6
,
2
3
xk
k
xk



.
k)
4sin 2cos 3 2
44
xx

4 sin cos cos sin 2 cos cos sin sin 3 2
4 4 4 4
x x x x
2 2sin 2 2 cos 2 cos 2sin 3 2x x x x
2
sin cos 1 2 sin 1 sin sin sin
4 4 2 4 4
x x x x x
2
2
44
,
2
2
2
44
xk
xk
k
xk
xk




.
l)
2
22
sin cos 3 cos 2 sin 2sin cos cos 3 cos 2
2 2 2 2 2 2
x x x x x x
xx



1 3 1 1
sin 3 cos 1 sin cos sin cos cos sin
2 2 2 3 3 2
x x x x x x

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 35 | THBTN
2
2
36
6
sin sin ,
36
2
2
36
2
xk
xk
xk
xk
xk








.
m)
2
1 1 cos2 1
3sin sin 2 3 3 sin 2 3
2 2 2
x
x x x
1 3 3 3
sin 2 cos2 sin 2 cos cos2 sin
2 2 2 6 6 2
x x x x

22
63
4
sin 2 sin ,
5
63
22
6 3 12
xk
xk
xk
x k x k







n)
22
sin (sin 1) cos (1 cos ) sin sin cos cosx x x x x x x x
2
sin cos 1 2sin 1 sin
4 4 2
x x x x

2
2
44
sin sin ,
44
2
2
2
44
xk
xk
xk
xk
xk








.
o)
22
sin ( 3 sin ) cos (1 cos ) 3sin sin cos cosx x x x x x x x
3 1 1 1
3sin cos 1 sin cos sin cos cos sin
2 2 2 6 6 2
x x x x x x

2
66
sin sin ,
3
66
2
2
66
xk
xk
xk
xk
xk











.
p)
2
2sin 3sin 2 2 0 1 cos2 3sin2 2 0x x x x
3 1 1 1
3sin2 cos2 1 sin 2 cos2 sin 2 cos cos2 sin
2 2 2 6 6 2
x x x x x x

2
66
6
sin 2 sin ,
66
22
66
2
xk
xk
xk
xk
xk










.
q)
cos7 cos5 3sin2 1 sin7 sin5x x x x x
Li gii
Phương trình tương đương với:
11
cos12 cos2 3sin 2 1 cos12 cos2
22
x x x x x
1
cos 2 3sin 2 1 cos 2
32
x x x



TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
36 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
22
33
22
3
33
xk
xk
k
xk
xk


r)
cos sin3 3cos2 3 cos3 sinx x x x x
Li gii
Phương trình tương đương với:
11
sin 4 sin 2 3 cos2 3 sin 4 sin 2
22
x x x x x
3
sin 2 3cos2 3 sin 2
32
x x x



22
33
3
2
22
33
2
xk
xk
k
xk
xk





s)
44
2(cos sin ) 1 3cos sinx x x x
Li gii
Phương trình tương đương với:
2 2 2 2
2 cos sin cos sin 1 3 cos sinx x x x x x
22
3cos sin 3cos sinx x x x
3cos sin 3 cos sin 1 0x x x x
3 cos sin 0
3 cos sin 1
xx
xx


cos 0
6
1
cos
62
x
x








2
3
2,
2
2
6
xk
x k k
xk


.
t)
3sin2 cos2 2cos 1x x x
Li gii
Phương trình tương đương với:
2
2 3sin cos 2cos 1 2cos 1x x x x
cos 3sin cos 1 0x x x
cos 0
3sin cos 1
x
xx

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 37 | THBTN
2
1
sin
62
xk
x





2
2,
2
2
3
xk
x k k
xk


u)
2
2sin sin 2 3sin cos 2x x x x
Li gii
Phương trình tương đương với:
2
2sin 3sin 2 2sin cos cos 0x x x x x
sin 2 2sin 1 cos 2sin 1 0x x x x
2sin 1 sin cos 2 0x x x
1
sin
2
2sin 1 0
2
6
,
sin cos 2 0 7
2 sin 2 VN
2
4
6
x
xk
x
k
xx
x
xk







v)
2sin 2 4sin 1
6
xx



Li gii
Phương trình tương đương với:
2 sin 2 cos cos2 sin 4sin 1
66
x x x




3sin2 cos2 4sin 1x x x
2
2 3sin cos 1 2sin 4sin 1x x x x
sin 2 3 cos 2sin 4 0x x x
sin 0
2 3 cos 2sin 4 0
x
xx
sin 0x x k k
31
2 3 cos 2sin 4 0 cos sin 1
22
x x x x
5
cos 1 2 2
6 6 6
x x k x k k



Vậy phương trình có 2 họ nghiệm
xk
và
5
2
6
x k k
x)
5
cos 2cos2 2sin cos 2
6
x x x x



Li gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
38 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Phương trình tương đương với:
31
cos 2cos2 2sin cos2 sin 2
22
x x x x x




cos 2cos2 3sin cos2 sin sin 2 0x x x x x x
2
cos 2cos2 3sin cos2 2sin cos 0x x x x x x
2
cos 1 2sin 2cos2 3sin cos2 0x x x x x
cos2 cos 2 3sin 0x x x
2
cos2 0
2
42
cos 2 3sin 0
cos 1
2
3
3
xk
xk
x
k
xx
x
xk








BT 10. Giải các phương trình lượng giác sau:
a)
3sin cos 2sin
12
xx

Phương trình tương đương với:
31
sin cos sin sin sin
2 2 12 6 12
x x x



2
2
6 12
12
,
3
22
6 12 4
xk
xk
k
x k x k

b)
cos 2 sin2 sin .x x x
Phương trình tương đương với:
sin cos 2 sin 2x x x
2 sin 2 sin 2
4
xx



2 sin 2 sin 2 sin sin 2
44
x x x x

2
22
4
4
.
2
22
43
4
xk
x x k
k
k
x
x x k




c)
sin3 3 cos3 2sin 2 .x x x
Phương trình tương đương với:
13
sin3 cos3 sin 2
22
x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 39 | THBTN
sin 3 sin 2
3
xx



3 2 2 2
33
42
3 2 2
3 15 5
x x k x k
k
k
x x k x









.
d)
sin cos 2 2 sin cos .x x x x
Phương trình tương đương với:
2 sin 2 sin 2 sin sin 2
44
x x x x

2
22
4
4
.
2
22
43
4
xk
x x k
k
k
x
xxk




e)
2cos3 3sin cos 0.x x x
Phương trình tương đương với:
13
cos sin cos3 cos cos 3
2 2 3
x x x x x



f)
2
(sin cos ) 3 cos2 1 2cos .x x x x
Phương trình tương đương với:
1 sin2 3cos2 1 2cosx x x
13
sin 2 cos2 x cosx
22
x
cos 2 cos
3
xx



22
3
22
3
x k x
x k x
2
93
,( )
2
3
xk
k
xk




g)
2 cos2 sin cos 0.x x x
Phương trình đã cho tương đương với:
2 cos2 cos sin 2 cos2 x 2 cos
4
x x x x



cos2x cos
4
x



22
4
22
4
x x k
x x k
2
4
,
2
12 3
xk
k
xk



g)
sin3 3cos3 2sin 0.x x x
Phương trình đã cho tương đương với:
13
sin3 3 cos3 2sin sin3 cos3 sin
22
x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
40 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
sin 3 sin
3
xx



32
3
32
3
x x k
x x k

6
,
62
xk
k
xk



Vậy nghiệm phương trình là
, ( )
6 6 2
x k x k k
h)
cos 3sin 2cos
3
x x x



Phương trình tương đương với :
13
cos sin cos
2 2 3
x x x



cos cos
33
xx

2
33
,
2 ( )
33
x x k
x k k
x x k VN


k)
2
2cos 3sin 1 2sin3 .
2
x
xx
Phương trình tương đương với :
1 cos 3sin 1 2sin3x x x
31
sin cos sin3
22
x x x
sin sin3
6
xx



32
6
5
32
6
x x k
x x k
12
,
5
24 2
xk
k
xk




l)
2
sin 3cos 2 4cosx x x
Phương trình tương đương với :
2
sin 3cos 4cos 2x x x
2
sin 3cos 2 2cos 1x x x
13
sin cos cos2
22
x x x
sin cos2
3
xx



5
cos cos2
6
xx



5
22
6
5
22
6
x x k
x x k



5
12
,
5
2
6
xk
k
xk


m)
2
4sin sin 2 3 cosx x x
Phương trình tương đương với :
2
sin 3 cos 2 4sinx x x
2
sin 3 cos 2 1 2sinx x x
sin 3cos 2cos2x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 41 | THBTN
13
sin cos cos2
22
x x x
cos cos2
6
xx



22
6
22
6
x x k
x x k
n)
2cos 3sin cos 1 1x x x
Phương trình tương đương với :
2
2 3sin cos 2cos 2cos 1x x x x
3sin2 cos2 1 2cos 1x x x
3sin2 cos2 2cosx x x
cos 2 cos
3
xx



22
3
22
3
x x k
x x k
2
3
,
2
93
xk
k
k
x




o)
2
3sin2 2sin 4sin3 .cos 2x x x x
Phương trình tương đương với :
2
3sin 2 2 1 sin 4sin3 .cosx x x x
2
3sin2 2cos 4sin3 .cosx x x x
2
2 3sin cos 2cos 4sin3 .cos 0x x x x x
2cos 3sin cos 2sin3 0x x x x
cos 0
3sin cos 2sin3 0
x
x x x
Xét TH 1:
cos 0x
,
2
x k k
Xét TH 2:
3sin cos 2sin3 0x x x
3sin cos 2sin3x x x
sin sin3
6
xx



32
6
7
32
6
x x k
x x k
12
,
7
24 2
xk
k
k
x



Vậy phương trình có 3 họ nghiệm là:
2
,
12
7
24 2
xk
x k k
k
x



p)
3cos5 2sin3 .cos2 sinx x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
42 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Phương trình tương đương với :
3cos5 sin5 sin sinx x x x
3cos5 sin5 2sinx x x
31
cos5 sin5 sin
22
x x x
sin 5 sin
3
xx



52
3
2
52
3
x x k
x x k
18 3
,
62
k
x
k
k
x




.
q)
2(cos6 cos4 ) 3(1 cos2 ) sin 2 .x x x x
Li gii
Phương trình tương đương với:
2
4cos5 cos 2 3cos 2sin cosx x x x x
2cos 2cos5 3 cos sin 0x x x x
cos 0 (1)
3 cos sin 2sin5 (2)
x
x x x

1
2
xk
52
3
12 2
2 sin sin5 .
3
52
93
3
k
x x k
x
x x k
k
x
xxk








Vậy, nghiệm của phương trình là
,
2
xk

12 2
.
93
k
x
k
k
x




r)
3sin7 2sin4 sin3 cos .x x x x
Li gii
Phương trình tương đương với:
3sin7 cos7 cos cosx x x x
3sin7 cos7 2cos cos 7 cos
3
x x x x x



72
3
18 3
.
72
3
24 4
k
x x k
x
k
k
x x k
x




s)
22
2sin (cos sin ) sin 3cos3 .x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 43 | THBTN
Li gii
Phương trình tương đương với:
2
2sin (1 2sin ) sin 3cos3 .x x x x
2
2sin (1 2sin ) sin 3 cos3 .x x x x
t)
2
sin 2
sin 2 sin sin 3
24
x
x x x



Li gii
Phương trình tương đương với:
2
sin 2
sin 2 sin sin 3
24
x
x x x



2
sin sin cos 2 sin sin 3
4
x x x x x



sin 0
sin cos 2 sin 3
4
x
x x x



sin sin 3
4
xk
xx




.
8
3
16 2
xk
x k k
k
x

u)
22
3 cos2 3
cos sin
2 2 4
xx
x



Phương trình tương đương với:
22
3 cos2 3
2cos 1 sin
2 2 4
xx
x



2
3
4cos 3 cos2 2 cos 2
22
x
xx



2
4cos 3 cos2 2 sin 2
2
x
xx
3cos2 sin2 2cosx x x
cos 2 cos
6
xx



52
18 3
.
7
2
6
k
x
k
xk




v)
2
2 3cos2 sin2 4cos 3 .x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
44 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Phương trình tương đương với:
2
sin 2 3 cos2 2 2cos 3 1x x x
sin 2 cos6 sin 2 sin 6
3 3 2
x x x x
5
2 6 2
32
48 4
.
5
2 6 2
32
24 2
x x k
xk
k
x x k
xk





x)
2
3sin2 2cos 2 2 2cos2 .x x x
Phương trình tương đương với:
2
2 3sin cos 2cos 2 2(1 cos2 )x x x x
22
2 3sin cos 2cos 2 4cosx x x x
2
2 3sin cos 2cos 4 cos *x x x x
Trường hợp 1:
cos 0x
* cos 2 3sin 2cos 4 0x x x
cos 0
cos 0
22
sin 1
2
3sin cos 2
22
6
6 2 3
x
x k x k
x
x
xx
x k x k














Vì
cos 0x
nên loại nghiệm:
2
2.
3
x k k
Trường hợp 2:
cos 0x
* cos 2 3 sin 2cos 4 0
3sin cos 2 sin 1 2 2
6 6 2 3
x x x
x x x x k x k




Vì:
cos 0x
nên loại nghiệm
2
3
xk
Kết luận: Phương trình có nghiệm:
.
2
x k k
BT 11. Giải các phương trình lượng giác sau:
a)
sin2 cos cos2 sin .x x x x
Li gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 45 | THBTN
Cách 1:
sin2 cos cos2 sinx x x x
sin2 cos2 sin cosx x x x
2 sin 2 2 sin
44
xx

sin 2 sin
44
xx

22
44
22
44
x x k
x x k






2
3
2
k
x
k
xk



.
Cách 2:
sin2 cos cos2 sinx x x x
2
2sin cos cos 2cos 1 sinx x x x x
2
2sin cos sin 2cos cos 1x x x x x
sin 2cos 1 cos 1 2cos 1x x x x
2cos 1 sin cos 1 0x x x
2cos 1 0
sin cos 1
x
xx

1
cos
2
2
sin
42
x
xx




2
2
3
2
44
2
44
xk
xk
xk



2
2
3
2
3
2
2
xk
xk
xk


k
.
b)
cos2 3sin 2 3sin cos .x x x x
Li gii
Cách 1:
cos2 3sin 2 3sin cosx x x x
1 3 3 1
cos 2 sin 2 sin cos
2 2 2 2
x x x x
cos 2 cos sin 2 sin cos cos sin sin
3 3 3 3
x x x x
cos 2 cos
33
xx

22
33
22
33
x x k
x x k


TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
46 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2
3
2
3
xk
k
x
2
3
k
x

k
.
Cách 2:
cos2 3sin 2 3sin cosx x x x
cos2 cos 3sin 2 3sinx x x x
Li gii
2
2cos cos 1 2 3sin cos 3sinx x x x x
cos 1 2cos 1 3sin 2cos 1x x x x
2cos 1 cos 3sin 1 0x x x
1
cos
2
cos 3 sin 1
x
xx


2
2
3
cos cos
33
xk
x





2
2
3
2
33
2
33
xk
xk
xk


2
2
3
2
xk
xk
k
.
c)
3(cos2 sin3 ) sin2 cos3 .x x x x
Li gii
cos3 3sin3 3cos2 sin2x x x x
1 3 3 1
cos3 sin3 cos 2 sin 2
2 2 2 2
x x x x
cos3 cos sin3 sin cos2 cos sin 2 sin
3 3 6 6
x x x x
cos 3 cos 2
36
xx

3 2 2
36
3 2 2
36
x x k
x x k


2
6
52
2
xk
xk
2
6
10 5
xk
k
x

k
.
d)
cos7 sin5 3(cos5 sin7 ).x x x x
Li gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 47 | THBTN
cos7 3sin7 3cos5 sin5x x x x
1 3 3 1
cos7 sin 7 cos5 sin5
2 2 2 2
x x x x
cos7 cos sin7 sin cos5 cos sin5 sin
3 3 6 6
x x x x
cos 7 cos 5
36
xx

7 5 2
36
7 5 2
36
x x k
x x k


22
6
12 2
2
xk
xk


12
24 6
xk
k
x



k
.
e)
2
sin 2 2cos sin cos 1.x x x x
Li gii
2
sin 2 2cos sin cos 1x x x x
2
sin 2 2cos 1 cos sinx x x x
sin2 cos2 cos sinx x x x
sin 2 sin
44
xx

22
44
22
44
x x k
x x k






2
3
.
2
2
k
x
k
xk


f)
2
4sin tan 2(1 tan )sin3 1.x x x x
Điều kiện
cos 0x
.
2
4sin tan 2 1 tan sin3 1.x x x x
2
2 2sin 1 tan 1 2 1 tan sin3 0x x x x
sin cos
2 sin cos sin cos 1 2 sin3 0
cos
xx
x x x x x
x



sin cos 2cos sin cos 1 2 sin3 0x x x x x x


sin cos 0 1
2cos sin cos 1 2 sin3 0 2
xx
x x x x

(thoả điều kiện)
2 sin2 cos2 2 sin3x x x
1 sin 0
44
x x k k




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
48 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
sin 2 sin 3
4
xx



2 3 2
4
2 3 2
4
x x k
x x k

2
20 5
.
5
2
4
k
x
k
xk



(thoả điều kiện)
g)
sin sin 2
3.
cos cos2
xx
xx
Điều kiện
cos 1
cos cos2 0
1
cos
2
x
xx
x

sin sin 2
3.
cos cos2
xx
xx
3
2cos sin
22
3
3
2sin sin
22
xx
xx

3
cot 3
2
x
3
26
x
k
2
.
93
k
x

(thoả điều kiện)
g)
1 2sin 1 sin
1 2sin
3 cos
xx
x
x


Điều kiện
1 2sin 0
cos 0
x
x

.
Với điều kiện trên phuowg trình trở thành.
3cos 1 2sin 1 sin 1 2sinx x x x
2
3cos 3sin2 1 sin 2sinx x x x
sin 3cos 3sin2 cos2x x x x
sin sin 2
36
xx

22
36
22
36
x x k
x x k






So với điều kiện phương trình có nghiệm
2
18 3
k
xk

.
h)
2
cos sin 2
3.
2cos sin 1
xx
xx

Li gii
2
18 3
2
2
k
x
xk



TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 49 | THBTN
Điều kiện
22
1
sin
2cos sin 1 0 2sin sin 1 0
2
sin 1
x
x x x x
x

.
Với điều kiện trên phương trình trở thành:
2
cos sin 2 3 2cos sin 1x x x x
cos 1 2sin 3 1 2sin sin 1x x x x
cos 3 sin 1xx
(do
1
sin
2
x
)
3sin cos 3xx
3
sin
62
x



2
2
63
6
3
2
2
63
2
xk
xk
k
xk
xk




.
So với điều kiện phương trình có nghiệm là
2
6
x k k
.
k)
sin sin3
3.
cos cos3
xx
xx
Li gii
Điều kiện
cos cos3 0 sin2 .sin 0 sin2 0x x x x x
.
Với điều kiện trên phương trình trở thành
2sin .cos2
3 cot 2 3
2sin 2 .sin 12 2
xx
x x k k
xx

.
So với điều kiện phương trình có nghiệm
12 2
x k k

.
l)
(1 2sin )cos
3.
(1 2sin )(1 sin )
xx
xx

Li gii
Điều kiện:
sin 1
(1 2sin )(1 sin ) 0
1
sin
2
x
xx
x

Với điều kiện trên phương trình trở thành
cos 2sin cos 3 1 2sin 1 sinx x x x x
2
cos 2sin cos 3 2sin sin 1x x x x x
3sin cos sin 2 3cos2x x x x
sin sin 2
63
xx

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
50 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
22
63
18 3
22
2
63
2
x x k
xk
k
x x k
xk








.
So với điều kiện phương trình có nghiệm
2
18 3
x k k

.
m)
2
4sin 4cos2 cos 2 1.
63
x x x

2
4sin 4cos 2 cos 2 1.
63
x x x

2 1 cos 2 2 cos cos 4 1
3 3 3
xx
2
2 2cos 2 cos 4 2
33
xx

2
2cos 2 2cos 2 1 0
33
xx

13
cos 2
32
13
cos 2
32
xl
xn








13
2 cos 2
32
13
2 cos 2
32
x arc k
x arc k
Vậy phương trình có nghiệm:
1 1 3
cos
6 2 2
1 1 3
cos
6 2 2
x arc k
k
x arc k

n)
22
3cos 2sin cos 3sin 1.x x x x
Li gii
* 3 cos2 sin2 -1 0xx
3 1 1 1
cos 2 sin 2 cos2 cos sin2 sin
2 2 2 6 6 2
x x x x

22
63
os 2 os
63
22
63
22
2
4
22
6
12
xk
c x c
xk
xk
xk
k
xk
xk









o)
2(cos 3sin )cos cos 3sin 1.x x x x x
Li gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 51 | THBTN
2
* 2cos 2 3 sin cos cos 3 sin 1 cos2 3 sin 2 cos 3 sin
1 3 1 3
cos2 sin 2 cos sin cos 2 cos
2 2 2 2 3 3
2
2
2 2 2
2
2
3 3 3
3
2
3
32
22
3 3 3
x x x x x x x x x
x x x x x x
x x k x k
xk
xk
xk
x x k x k









k
p)
3(cos2 sin ) cos (2sin 1) 0.x x x x
Li gii
* 3 cos2 3sin 2sin .cos cos 0
3 1 3 1
3 cos2 sin 2 3 sin cos cos2 sin 2 sin cos
2 2 2 2
x x x x x
x x x x x x x x
22
36
sin 2 sin
36
22
36
22
22
5 5 2
32
6 18 3
x x k
xx
x x k
x k x k
k
x k x k












q)
cos 2 1 tan tan tan 2sin 1.
2
x
x x x x



Li gii
Điều kiện:
2
2
2
22
xk
xk
k
x
xk
k









sin
sin sin
2
* cos2 1 tan tan tan 2sin 1 cos2 1 . 2sin 1
2 cos cos
cos
2
x
x x x
x x x x x x
x
xx








2
sin
sin sin
2
cos2 cos2 . . 2sin 1 cos2 .cos 2cos2 .sin sin 2sin .cos cos
cos cos 2
cos
2
x
x x x
x x x x x x x x x x
x
xx
1 cos
cos 2 .cos 2cos2 . sin 2sin .cos cos
2
x
x x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
52 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
cos2 sin2 cos sinx x x x
2
22
44
2 cos 2 2 cos ,
2
44
22
63
44
xk
x x k
x x k
xk
x x k




Kết hợp điều kiện, ta được
7
2 , 2 , 2 ,
66
x k x k x k k

BT 12. Giải các phương trình lượng giác sau:
a)
2
sin 2 2 3cos 2cos .x x x
22
2sin cos 2 3cos 2cos 2 3 cos 2sin cos 2cos 0x x x x x x x
2cos 3cos sin 1 0x x x
Với
cos 0 , .
2
x x k k
Với
3cos sin 1 0xx
3 1 1 2 2
cos sin cos cos sin sin cos cos cos
2 2 2 6 6 3 6 3
x x x x x
2
2,
2
63
2
,
5
2
2
2,
6
63
x k k
xk
k
xk
x k k



Vậy phương trình có hai họ nghiệm là
2
2
,
5
2
6
xk
k
xk


.
b)
3sin2 1 cos2 2cos .x x x
22
2 3sin cos 1 2cos 1 2cos 2cos 2 3sin cos 2cos 0x x x x x x x x
cos 0
2cos cos 3sin 1 0
cos 3 sin 1 0
x
x x x
xx
Với
cos 0 , .
2
x x k k
Với
cos 3sin 1 0xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 53 | THBTN
1 3 1
cos sin cos cos sin sin cos
2 2 2 3 3 3
x x x x
cos cos cos cos
3 3 3 3
xx
2
2,
2
33
,
3
2
2,
33
x k k
xk
k
xk
x k k



Vậy phương trình có các nghiệm
2
2
2,
3
2
xk
x k k
xk

c)
sin2 cos sin 1.x x x
1 sin 2 sin cosx x x
Đặt
2 2 2
t sin cos sin cos 2sin cos 1 sin2x x t x x x x x
Vậy ta có
2
0
1
t
tt
t

Với
0 1 sin 2 0 sin 2 1 2 2 , .
24
t x x x k x k k


Với
1 1 sin 2 1 sin 2 0 2 , .
2
t x x x k x k k
Vậy phương trình có nghiệm
4
,
2
xk
k
xk

.
d)
cos2 2sin 1 3sin 2 .x x x
22
1 2sin 2sin 1 2 3sin cos 2sin 2 3sin cos 2sin 0x x x x x x x x
sin 0
2sin sin 3 cos 1 0
sin 3 cos 1 0
x
x x x
xx
Với
sin 0 , .x x k k
Với
sin 3cos 1 0xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
54 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
1 3 1
sin cos cos sin sin cos sin sin sin
2 2 2 3 3 6 3 6
x x x x x



2
2,
36
6
2
2,
36
2
xk
x k k
xk
x k k




e)
3sin2 cos2 4sin 1.x x x
Phương trình tương đương với :
2
3sin2 1 2sin 4sin 1x x x
2
3sin2 2sin 4sin 0x x x
sin 0
2sin 3cos sin 2 0
3cos sin 2
x
x x x
xx

sin 0
sin 0
13
sin 1
sin cos 1
3
22
x
x
x
xx






,
22
3 2 6
x k x k
k
x k x k







Vậy nghiệm phương trình là
, 2 ,
6
x k x k k

f)
2sin6 2sin4 3cos2 3 sin2 .x x x x
2
4cos5 sin 3 1 2sin 3 2sin cosx x x x x
2sin 2cos5 3sin cos 0x x x x
sin 0
sin 0
31
2cos5 3sin cos
sin cos cos5
22
x
x
x x x
x x x



sin 0
cos cos5
3
x
xx




5 2 ,
3 12 2
52
18 3
3
x k x k
x x k x k k
xk
x x k




Vậy nghiệm phương trình là
, ,x ,
12 2 18 3
x k x k k k
g)
2
tan sin 2cos 2.
72
x
x
phương trình tương đương với :
tan sin 1 cos 2 tan sin cos 1
77
x x x x

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 55 | THBTN
sin sin cos cos cos
7 7 7
xx
2
77
cos cos
77
2
77
xk
x
xk







2
2
,
7
2
xk
k
xk


Vậy nghiệm phương trình là
2
2 , 2 ,
7
x k x k k

g)
cos cos3 1 2 sin 2
4
x x x



Li gii
2cos2 .cos 1 sin cos2x x x x
2
2cos2 .cos 2sin cos 2cosx x x x x
cos (cos2 sin cos ) 0x x x x
22
cos cos sin sin cos 0x x x x x


cos sin cos cos sin 1 0x x x x x
cos 0
sin cos 0
sin cos 1
x
xx
xx

cos 0
tan 1
1
sin
4
2
x
x
x




2
4
2
3
2
2
xk
xk
xk
xk


2
4
2
xk
xk
xk

h)
31
8sin
cos sin
x
xx
Li gii
Điều kiện xác định:
sin cos 0xx
2
k
x
Cách 1:
2
8sin cos 3sin cosx x x x
4 1 cos2 cos 3sin cosx x x x
4cos 4cos2 cos 3sin cosx x x x x
4cos 2 cos3 cos 3sin cosx x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
56 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
cos 3sin 2cos3x x x
cos cos3
3
xx




6
12 2
xk
k
x


(thỏa điều kiện)
Cách 2: Nhân 2 vế (h) cho
sin x
ta được:
2
2
tan
8. 3 tanx 1
1 tan
x
x

( đưa về phương trình bậc 3 theo
tantx
)
k)
3 cos2 sin 2 2sin(2 ) 2 2.
6
x x x
Li gii
cos 2 sin 2 2
66
xx

sin 2 1
64
x




22
12 2
xk

7
24
xk

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 57 | THBTN
3. Phöông trình löôïng giaùc ñaúng caáp (baäc 2, baäc 3, baäc 4)
Dng tng quát:
22
.sin .sin cos .cos (1) , , , .a X b X X c X d a b c d
Du hiu nhn dng: Đ ng bậc hoặc lệch nhau hai bậc của hàm sin hoặc cosin (tan
và cotan được xem là bậc 0).
i:
Bước 1. Kiểm tra
2
cos 0
2
sin 1
X
Xk
X
có phải là nghiệm hay không ?
Bước 2. Khi
2
cos 0
, ( )
2
sin 1
X
X k k
X
. Chia hai vế (1) cho
2
cos X
:
22
2 2 2 2
sin sin cos cos
(1)
cos cos cos cos
X X X X d
a b c
X X X X
22
tan tan (1 tan )a X b X c d X
Bước 3. Đặt
tantX
để đưa về phương trình bậc hai theo ẩn
.tx
. Giải tương tự đối với phương trình đẳng cấp bậc ba và bậc bốn.
Ví d 1. Giải phương trình:
22
2cos 2sin2 4sin 1.x x x
Gii:
22
pt 2cos 4sin cos 4sin 1x x x x
Xét
cos 0x
thì
2
sin 1x
, phương trình trở thành
4.1 1
(vô lí)
Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
22
2 4tan 4tan 1 tanx x x
2
5tan 4tan 1 0xx
tan 1
4
,
1
1
tan
arctan
5
5
xk
x
k
x
xk





Ví d 2. Giải phương trình:
3 3 2
4sin 3(cos sin ) sin cos .x x x x x
Gii:
3 2 3
pt 4sin sin cos 3sin 3cos 0x x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
4.1 3.1 0
(vô lí); hoặc
3
4.( 1) 3.( 1) 0
(vô lí)
Suy ra
cos 0x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
58 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
3 2 2
4tan tan 3tan 1 tan 3 0x x x x
32
tan tan 3tan 3 0x x x
tan 1
4
,
tan 3
3
xk
x
k
x
xk


Ví d 3. Giải phương trình:
2
sin (tan 1) 3sin (cos sin ) 3.x x x x x
Gii:
Điều kiện
cos 0x
Dễ thấy
sin 0x
không là nghiệm của phương trình
Chia hai vế phương trình cho
2
sin x
ta được
2
1 tan 3 cot 1 3 1 cot 0x x x
2
3cot cot 1 3cot 1 cot cot 1x x x x x
3 2 2
3cot 3cot cot 1 0 cot 1 3cot 1 0x x x x x
cot 1
4
,
1
cot
3
3
x
xk
k
x
xk



BT 13. Giải các phương trình lượng giác sau:
a)
22
2sin 3 3sin cos cos 2.x x x x
b)
22
sin sin cos 2cos 0.x x x x
c)
22
cos 3sin2 1 sin .x x x
d)
22
2cos 3 3sin2 4 4sin .x x x
e)
22
3sin (1 3)sin cos cos 1 3.x x x x
f)
22
2sin (3 3)sin cos ( 3 1)cos 1 0.x x x x
g)
22
4sin 5sin cos 6cos 0.x x x x
h)
22
9
cos (3 2 ) 3 cos 4 1 sin 2 .
2
x x x



BT 14. Giải các phương trình lượng giác sau:
a)
3
sin 2cos .xx
b)
33
cos sin sin cos .x x x x
c)
3
sin 4sin cos 0.x x x
d)
33
4(sin cos ) cos 3sin .x x x x
e)
3
6sin 2cos 5sin 2 cos .x x x x
f)
3 3 2
cos 4sin sin 3cos sin .x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 59 | THBTN
g)
4 4 2 2
3cos sin 4sin cos .x x x x
h)
3 3 2
4sin 3(cos sin ) sin cos .x x x x x
i)
3
2 2 cos 3cos sin .
4
x x x



j)
2
2
(1 cos2 )
sin 2cos2 .
2sin 2
x
xx
x

k)
22
cos tan 4 1 sin2 0.x x x
l)
22
tan sin 2sin 3(cos2 sin cos ).x x x x x x
m)
3 3 2 2
sin 3cos sin cos 3sin cos .x x x x x x
n)
4 4 2
4sin 4cos 5sin2 cos2 cos 2 6.x x x x x
o)
22
3cot 2 2 sin (2 3 2)cos .x x x
GII BÀI TP VN DNG 3
BT 13.
a)
22
2sin 3 3sin cos cos 2.x x x x
Xét
cos 0x
thì
2
sin 1x
, phương trình trở thành
22
(đúng)
Suy ra
2
xk

là nghiệm phương trình.
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
22
2tan 3 3 tan 1 2 1 tanx x x
1
tan ,
6
3
x x k k
Vậy, nghiệm phương trình là
2
xk

;
,
6
x k k
.
b)
22
sin sin cos 2cos 0.x x x x
Xét
cos 0x
thì
2
sin 1x
, phương trình trở thành
10
(vô lí)
Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
2
tan tan 2 0xx
tan 1
4
,
tan 2
arctan 2
xk
x
k
x
xk


.
c)
22
cos 3sin2 1 sin .x x x
22
pt cos 2 3sin cos sin 1x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
11
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
60 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
22
1 2 3 tan tan 1 tanx x x
2
2tan 2 3 tan 0xx
tan 0
,
tan 3
3
xk
x
k
xk
x

.
d)
22
2cos 3 3sin2 4 4sin .x x x
22
cos 3 3sin cos 2sin 2.x x x x
Xét
cos 0x
thì
2
sin 1x
, phương trình trở thành
22
(đúng)
Suy ra
cos 0
2
x x k
là nghiệm phương trình.
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
22
1 3 3 tan 2tan 2 1 tanx x x
1
tan
3
x
,
6
x k k
.
e)
22
3sin (1 3)sin cos cos 1 3.x x x x
22
3sin (1 3)sin cos cos 1 3.x x x x
Xét
cos 0x
thì
2
sin 1x
, phương trình trở thành
3 1 3
(vô lý)
Suy ra
cos 0x
.
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
22
3 tan 1 3 tan 1 1 3 1 tanx x x
2
tan 1 3 tan 3 0xx
tan 1
4
,
tan 3
tan
3
xk
x
k
x
xk


.
f)
22
2sin (3 3)sin cos ( 3 1)cos 1.x x x x
Xét
cos 0x
thì
2
sin 1x
, phương trình trở thành
21
(vô lý)
Suy ra
cos 0x
.
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
22
2tan 3 3 tan 3 1 1 tanx x x
2
3tan 3 3 tan 3 0xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 61 | THBTN
tan 1
4
,
3
tan
tan
3
6
x
xk
k
x
xk


.
g)
22
4sin 5sin cos 6cos 0.x x x x
Xét
cos 0x
thì
2
sin 1x
, phương trình trở thành
40
(vô lý)
Suy ra
cos 0x
.
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
2
4tan 5tan 6 0xx
arctan 2
tan 2
,
3
3
arctan
tan
4
4
xk
x
k
xk
x





.
h)
22
9
cos (3 2 ) 3 cos 4 1 sin 2 .
2
x x x



22
pt cos 2 3sin4 sin 2 1x x x
22
cos 2 2 3sin2 cos2 sin 2 1x x x x
Xét
cos2 0x
thì
2
sin 2 1 sin2 1xx
, phương trình trở thành
11
(vô lí); Suy ra
cos2 0x
Xét
cos2 0x
, chia hai vế phương trình cho
2
cos 2x
ta được
22
1 2 3 tan 2 tan 2 1 tan 2x x x
2
2tan 2 2 3 tan 2 0xx
tan 2 0
2
,
tan 2 3
62
xk
x
k
x
xk


.
BT 14.
a)
3
sin 2cos .xx
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
10
(vô lý)
Suy ra
cos 0x
.
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
2
tan 1 tan 2xx
tan 1 ,
4
x x k k
.
b)
33
cos sin sin cos .x x x x
3 3 2 2 2 2
pt cos sin sin sin cos cos sin cosx x x x x x x x
2 2 3
sin .cos cos .sin 2cos 0x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
62 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
22
cos sin .cos sin 2cos 0x x x x x
22
cos 0 (1)
sin .cos sin 2cos 0 (2)
x
x x x x
(1)
2
xk
,
k
.
(2)
2
tan tan 2 0xx
(vô nghiệm)
Vậy,
2
xk

,
k
.
c)
3
sin 4sin cos 0.x x x
2 2 3 2 2
pt sin sin cos 4sin cos sin cos 0x x x x x x x
3 2 2 3
3sin sin .cos cos .sin cos 0x x x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
30
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
32
3tan tan tan 1 0x x x
tan 1 ,
4
x x k k
.
d)
33
4(sin cos ) cos 3sin .x x x x
3 3 2 2 2 2
pt 4 sin cos cos sin cos 3sin sin cosx x x x x x x x
3 2 2 3
sin sin .cos 3sin .cos 3cos 0x x x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
10
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
32
tan tan 3tan 3 0x x x
tan 1
4
tan 3 ,
tan 3
3
x
xk
xk
xk
x


.
e)
3
6sin 2cos 5sin 2 cos .x x x x
2 2 3 2
pt 6sin sin cos 2cos 10sin .cos 0x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 63 | THBTN
3 2 3
6sin 4sin .cos 2cos 0x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
60
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
3
6tan 4tan 2 0xx
tan 1 ,
4
x x k k
.
f)
3 3 2
cos 4sin sin 3cos sin .x x x x x
3 3 2 2 2
pt cos 4sin sin sin cos 3cos .sin 0x x x x x x x
3 2 2 3
3sin 3sin .cos sin cos cos 0x x x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
30
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
32
3tan 3tan tan 1 0x x x
tan 1
3
4
tan ,
3
6
3
tan
3
x
xk
xk
xk
x

.
g)
4 4 2 2
3cos sin 4sin cos .x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
10
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
4
cos x
ta được
42
tan 4tan 3 0xx
tan 1
4
,
tan 3
3
xk
x
k
x
xk


.
h)
3 3 2
4sin 3(cos sin ) sin cos .x x x x x
3 2 2 3
pt sin 3sin cos sin cos 3cos 0x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
64 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
10
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
32
tan tan 3tan 3 0x x x
tan 1
4
,
tan 3
3
xk
x
k
x
xk


.
i)
3
2 2 cos 3cos sin .
4
x x x



3
pt cos sin 3cos sin 0x x x x
23
2sin cos 2cos 0x x x
Xét
cos 0x
thì phương trình đúng
Suy ra
2
xk

là nghiệm.
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
2tan 2 0x 
tan 1 ,
4
x x k k
.
(Lưu ý: bài này cũng có thể đặt
2
cos x
làm nhân tử chung)
j)
2
2
(1 cos2 )
sin 2cos2 .
2sin 2
x
xx
x

Đk :
sin 2 0 ,
2
k
x x k
3
22
cos
pt sin 2 2cos 1 0
sin
x
xx
x
3 3 2 2 2
sin cos 4sin cos 2sin sin cos 0x x x x x x x
3 3 2
3sin cos 2sin cos 0x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
30
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
3
3tan 2tan 1 0xx
tan 1 ,
4
x x k k
. So với đk, ta nhận nghiệm
,
4
x k k
.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 65 | THBTN
k)
22
cos tan 4 1 sin2 0.x x x
Đk:
cos4 0x
Xét
cos 0x
thì phương trình trở thành
10
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
2
cos x
ta được
2
2
pt tan 4 tan 1 0xx
tan 1
tan 4 0
x
x

4
,
4
xk
k
k
x

,
4
x k k
. So với đk, ta nhận nghiệm
,
4
x k k
.
l)
22
tan sin 2sin 3(cos2 sin cos ).x x x x x x
Đk :
cos 0x
3 2 3 2
pt sin 2sin cos 6cos 3cos 3sin cos 0x x x x x x x
3 2 3 2
sin sin cos 3cos 3sin cos 0x x x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
10
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
32
tan tan 3tan 3 0x x x
tan 1
4
,
tan 3
3
xk
x
k
x
xk


. So với đk, ta nhận tất cả nghiệm.
m)
3 3 2 2
sin 3cos sin cos 3sin cos .x x x x x x
Xét
cos 0x
thì
2
sin 1 sin 1xx
, phương trình trở thành
10
(vô lí); Suy ra
cos 0x
Xét
cos 0x
, chia hai vế phương trình cho
3
cos x
ta được
32
tan 3 tan tan 3 0x x x
tan 1
4
,
tan 3
3
xk
x
k
x
xk


.
n)
4 4 2
4sin 4cos 5sin2 cos2 cos 2 6.x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
66 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
22
pt 2sin 2 5sin2 cos2 cos 2 2x x x x
Xét
cos2 0x
thì
2
sin 2 1 sin 2 1xx
, phương trình trở thành
22
(vô lí); Suy ra
cos2 0x
Xét
cos2 0x
, chia hai vế phương trình cho
2
cos 2x
ta được
22
2tan 2 5tan 2 1 2 1 tan 2x x x
2
4tan 2 5tan2 1 0xx
tan 1
4
,
1
1
tan
arctan
4
4
x
xk
k
x
xk


.
o)
22
3cot 2 2 sin (2 3 2)cos .x x x
Đk:
sin 0x
2 4 2
pt 3cos 2 2 sin 2 3 2 cos .sin 0x x x x
2 2 2
3cos cos 2 sin 2sin 2 sin cos 0x x x x x x
2
2
cos 2 sin 0
3cos 2sin 0
xx
xx


2
2
cos 2 2 cos 0
3cos 2 2cos 0
xx
xx
2
cos
2
1
cos
2
x
x
2
4
,
2
3
xk
k
xk

. So với đk, ta nhận tất cả nghiệm.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 67 | THBTN
4. Phöông trình löôïng giaùc ñoái xöùng
Dng 1.
(sin cos ) sin cos 0a x x b x x c
(dng tng/hiu tích)
PP
Đặt
2
sin cos , 2t x x t t
và viết
sin cosxx
theo
.t
Lưu ý, khi đặt
sin cost x x
thì điều kiện là:
02t
.
Dng 2.
22
(tan cot ) (tan cot ) 0a x x b x x c
PP
Đặt
2
tan cot , 2t x x t t
và biểu diễn
22
tan cotxx
theo
t
và
lúc này thường sử dụng:
2
tan cot 1, tan cot
sin 2
x x x x
x
Ví d 1. Giải phương trình:
sin2 (2 2)(sin cos ) 1 2 2 0.x x x
Gii:
Đặt
sin cos 2 sin
4
t x x x



;
2t
Ta có:
2
22
sin cos sin 2 1t x x x t
Phương trình trở thành:
22
1 2 2 1 2 2 0 2 2 2 2 0t t t t
2
2
t
t

Với
2t
thì
sin 1 2 ,
44
x x k k




Với
2t 
thì
22
vô lí
Ví d 2. Giải phương trình:
22
2tan 2cot (4 2)(tan cot ) 4 2 2 0.x x x x
Gii:
Điều kiện
sin 2 0x
Đặt
tan cott x x
Ta có:
2
2 2 2 2
tan cot tan cot 2t x x x x t
Phương trình trở thành:
22
2 2 4 2 4 2 2 0 2 4 2 2 2 0t t t t
Phương trình vô nghiệm

BT 15. Ging giác:
a)
sin 2 2 2 sin cos 5x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
68 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 sin 2 sin2 1t x x x x t
Phương trình trở thành :
22
2
1 2 2 5 2 2 6 0
3 2(L)
t
t t t t
t

Với
2t 
:
3
2 sin 2 sin 1 2 2 , .
4 4 4 2 4
x x x k x k k

b)
2 sin cos 6sin cos 2.x x x x
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos 2sin cos 1t x x x x x x t
Phương trình trở thành :
22
1
2 3 1 2 3 2 5 0
5
(L)
3
t
t t t t
t
Với
1t
:
2
2
1
44
2 sin 1 sin , .
3
44
2
2
2
2
44
xk
xk
x x k
xk
xk




c)
sin cos sin cos 1.x x x x
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
2
2
1
sin cos 1 2sin cos sin cos .
2
t
t x x x x x x
Phương trình trở thành :
22
1
1
1 1 2 3 0
3 (L)
2
t
t t t t
t

Với
1t
2
2
1
44
2 sin 1 sin , .
3
44
2
2
2
2
44
xk
xk
x x k
xk
xk




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 69 | THBTN
d)
1 2 sin cos 2sin cos 1 2.x x x x
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos 2sin cos 1 .t x x x x x x t
Phương trình trở thành :
22
1
1 2 1 1 2 1 2 2 0
2
t
t t t t
t
Với
1t
2
2
1
44
2 sin 1 sin , .
2
3
44
2
2
2
44
xk
xk
x x k
xk
xk







Với
2t
:
3
2 sin 2 sin 1 2 2 , .
4 4 4 2 4
x x x k x k k

e)
2 2 sin cos 3 sin 2 .x x x
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos sin2 1 .t x x x x x t
Phương trình trở thành :
22
2 2 3 1 2 2 2 0 2t t t t t
Với
2t
:
3
2 sin 2 sin 1 2 2 , .
4 4 4 2 4
x x x k x k k

f)
1 2 1 sin cos sin 2 .x x x
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos sin2 1 .t x x x x x t
Phương trình trở thành :
22
2
1 2 1 2 1 1 2 2 0
1
t
t t t t
t

Với
2t
:
3
2 sin 2 sin 1 2 2 , .
4 4 4 2 4
x x x k x k k

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
70 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Với
1t 
2
2
1
44
2 sin 1 sin sin , .
3
5
4 4 4
2
2
2
2
44
xk
xk
x x k
xk
xk





g)
2 2 sin cos 2sin2 1x x x
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos sin2 1 .t x x x x x t
Phương trình trở thành :
22
2
2
2 2 2 1 1 2 2 2 3 0
32
(L)
2
t
t t t t
t
Với
2
2
t
:
5
2
2
21
46
12
2 sin sin , .
5 13
4 2 4 2
22
4 6 12
xk
xk
x x k
x k x k





h)
sin cos 2 2 sin cosx x x x
Gii:
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos 2sin cos 1 .t x x x x x x t
Phương trình trở thành :
22
2
2 1 0 2 2 0
2
2
t
t t t t
t

Với
2
2
t
:
5
2
2
21
46
12
2 sin sin , .
5 13
4 2 4 2
22
4 6 12
xk
xk
x x k
x k x k





TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 71 | THBTN
Với
2t 
:
2 sin 2 sin 1 2 2 , .
4 4 4 2 4
x x x k x k k


i)
sin 2 2 sin 1.
4
xx



2
2 sin 1 sin 2 0 2 sin 2 sin 0
4 4 4
2 sin . 1 2 sin 0
44
4
2 sin 0 sin 0
44
2
44
1
2 sin 1 sin
44
2
x x x x
xx
xk
xx
xk
xx

















4
2 , .
2
32
2
44
xk
x k k
xk
xk











j)
11
2 2.
sin cosxx

Điều kiện:
sin 2 0.x
Ta có:
sin cos
2 2 sin cos 2 2 sin .cos
sin .cos
xx
x x x x
xx
. (1)
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos 2sin cos 1t x x x x x x t
Phương trình (1) trở thành :
22
2
2 1 2 2 0
2
2
t
t t t t
t
Với
2t
2 sin 2 sin 1 2 2 , .
4 4 4 2 4
x x x k x k k

(t/m)
Với
2
2
t
:
5
2
2
21
46
12
2 sin sin , .
7 11
4 2 4 2
22
4 6 12
xk
xk
x x k
x k x k





(t/m)
k)
11
2 2 cos
cos sin 4
x
xx



Điều kiện:
sin 2 0.x
sin cos
2 2 cos
sin .cos 4
xx
x
xx




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
72 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Đặt
sin cos 2 cos , 2
4
t x x x t



Ta có
2
22
1
sin cos 1 2sin cos sin cos 1 .
2
t x x x x x x t
Phương trình trở thành :
2
22
2
2 . 2 0
21
2 2 . 1 0 0
11
1
2
t t t
t
tt
tt
t
t






Với
2 2 cos( ) 2 cos( ) 1 2 2 , .
4 4 4 4
t x x x k x k k

(Đ)
Với
3
2 2 cos( ) 2 cos( ) 1 2 2 , .
4 4 4 4
t x x x k x k k
(Đ)
Với
0 2 cos( ) 0 cos( ) 0 2 , .
4 4 4 2 4
t x x x k x k k

(Đ)
l)
2sin 2 8 3 6 sin cos .x x x
Giải:
Đặt
sin cost x x
điều kiện
02t
Ta có :
2
22
sin cos 1 sin 2 sin2 1t x x x x t
Phương trình trở thành:
22
6
2 1 8 3 6 2 3 6 6 0
2
6(L)
t
t t t t
t
Với
6
2
t
thì
6 6 3
sin cos 2 cos cos cos
2 4 2 4 2 6
t x x x x
cos cos
2
46
64
,.
5
5
2
cos cos cos
64
4 6 6
x
xk
k
xk
x










m)
sin cos 4sin2 1.x x x
Giải
Đặt
sin cos 2 cos
4
t x x x



điều kiện
02t
Ta có :
2
22
sin cos 1 sin2 sin 2 1t x x x x t
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 73 | THBTN
Phương trình trở thành:
22
1
4 1 1 4 3 0
3
4
t
t t t t
tL
Với
1t
thì
2
22
1
4 4 2
2 cos 1 cos .
32
44
2
2
2
44
2
2
xk
xk
x k x k
x x k
xk
xk
xk
xk




n)
cos sin cos sin 1.x x x x
Gii:
Đặt
sin cost x x
điều kiện
02t
Ta có :
2
22
1
sin cos 1 sin 2 sin .cos 1
2
t x x x x x t
Phương trình trở thành:
22
1
1
1 1 2 3 0
3(L)
2
t
t t t t
t

Với
1t
thì
11
sin cos 1 2 cos 1 cos cos
4 4 4
22
x x x x x
2
22
4 4 2
32
2
2
44
2
2
xk
xk
x k x k
k
xk
xk
xk
xk




BT 16. Ging giác:
a)
22
3tan 4tan 4cot 3cot 2 0.x x x x
Điều kiện
sin 2 0.x
22
3 tan cot 4 tan cot 2 0x x x x
Đặt
tan cott x x
,
2
2
sin 2
t
x

Ta có:
2
2 2 2 2
tan cot tan cot 2t x x x x t
Phương trình trở thành:
22
2
3 2 4 2 0 3 4 4 0
2
(L)
3
t
t t t t
t

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
74 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Với
2
2 2 sin 2 1 2 2 , .
sin 2 2 4
t x x k x k k
x



(t/m)
b)
2
2
2
2tan 5tan 5cot 4 0.
sin
x x x
x
Điều kiện
sin 2 0.x
22
22
2 1 cot 2tan 5tan 5cot 4 0
2 tan cot 5 tan cot 6 0
x x x x
x x x x
Đặt
tan cott x x
,
2
2
sin 2
t
x

Ta có:
2
2 2 2 2
tan cot tan cot 2t x x x x t
Phương trình trở thành:
22
2
2 2 5 6 0 2 5 2 0
1
(L)
2
t
t t t t
t

Với
2
2 2 sin 2 1 2 2 , .
sin 2 2 4
t x x k x k k
x



(t/m)
c)
tan 3cot 4(sin 3cos ).x x x x
Điều kiện
sin 2 0.x
22
sin 3cos
4 sin 3cos
sin .cos
sin 3 cos
sin 3 cos . 4 0
sin .cos
2sin 2sin 2
3
2cos . 0
6 sin .cos
62
cos 0
6
22
3
sin sin 2
3
22
3
xx
xx
xx
xx
xx
xx
xx
x
xx
xk
x
x x k
xx
x x k





















2
3
2 , (t/ m).
3
42
93
xk
x k k
k
x












d)
3
2sin cos2 cos 0.x x x
22
22
2sin .sin 2cos cos 1 0
2sin . 1 cos 2cos cos 1 0
2.sin . 1 cos 1 cos 1 cos 2cos 1 0
1 cos . 2sin . 1 cos 2cos 1 0
1 cos . 2sin .cos 2 sin cos 1 0
cos 1
2sin .cos 2 sin cos 1 0
x x x x
x x x x
x x x x x
x x x x
x x x x x
x
x x x x




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 75 | THBTN
Với
cos 1 2x x k
Với
2sin .cos 2 sin cos 1 0x x x x
Đặt
sin cos 2 cos , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos 2sin cos 1 .t x x x x x x t
Phương trình trở thành :
22
0
1 2 1 0 2 0
2(L)
t
t t t t
t

Với
0t
thì
3
cos 0 2 2 , .
4 4 2 4
x x k x k k




e)
3
2cos cos2 sin 0.x x x
22
22
2cos .cos 1 2sin sin 0
2cos . 1 sin 2sin sin 1 0
2.cos . 1 sin 1 sin 1 sin 2sin 1 0
1 sin . 2cos . 1 sin 2sin 1 0
1 sin . 2sin .cos 2 sin cos 1 0
sin 1
2sin .cos 2 sin cos 1 0
x x x x
x x x x
x x x x x
x x x x
x x x x x
x
x x x x




Với
sin 1 2
2
x x k
Với
2sin .cos 2 sin cos 1 0x x x x
Đặt
sin cos 2 cos , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos 2sin cos 1 .t x x x x x x t
Phương trình trở thành :
22
0
1 2 1 0 2 0
2(L)
t
t t t t
t

Với
0t
thì
3
cos 0 2 2 , .
4 4 2 4
x x k x k k




f)
33
2sin sin 2cos cos cos2 .x x x x x
3 2 3 2
33
2sin sin sin 2cos cos cos
2 sin cos sin cos 1 0
2 sin cos 1 sin .cos sin cos 1 0(*)
x x x x x x
x x x x
x x x x x x
Đặt
sin cos 2 cos , 2
4
t x x x t



TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
76 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Ta có
2
22
1
sin cos 1 2sin cos sin cos 1 .
2
t x x x x x x t
Phương trình (*) trở thành:
23
1
1 1 5
2 . 1 1 1 0 2 1 0
22
15
(L)
2
t
t t t t t t
t




Với
1
1 cos 2 2 ; 2 .
4 4 4 2
2
t x x k x k x k



Với
15
2
t
10 2 10 2
cos arccos 2 arccos 2 ,cos , .
4 4 4 4 4
x x k x k k




g)
33
sin cos 1 sin2 .x x x
2
sin cos . 1 sin .cos sin cos
sin cos . 1 sin .cos sin cos 0
x x x x x x
x x x x x x
Đặt
sin cos 2 cos , 2
4
t x x x t



Ta có
2
22
1
sin cos 1 2sin cos sin cos 1 .
2
t x x x x x x t
Phương trình trở thành:
22
0
1
. 1 1 0 . 2 3 0 1
2
3(L)
t
t t t t t t t
t




Với
0 cos 0 2 2 .
4 2 4 4
t x x k x k




Với
13
1 cos 2 2 ; 2 .
4 4 4 2
2
t x x k x k x k



h)
cos2 5 2(2 cos )(sin cos ).x x x x
2
22
2cos 1 5 2.(2 cos )(sin cos ).
cos 2 2sin 2cos cos .sin cos
2 sin cos cos .sin 2 0
x x x x
x x x x x x
x x x x
Đặt
sin cos 2 cos , 2
4
t x x x t



TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 77 | THBTN
Ta có
2
22
1
sin cos 1 2sin cos sin cos 1 .
2
t x x x x x x t
Phương trình trở thành:
22
1
1 1 5
2 1 2 0 2 0
5(L)
2 2 2
t
t t t t
t

Với
13
1 cos 2 2 ; 2 .
4 4 4 2
2
t x x k x k x k



i)
(3 cos4 )(sin cos ) 2.x x x
2
2
22
22
3 2cos 2 1 . sin cos 2
2 cos sin . sin cos 1
2 cos sin . cos sin . sin cos 1
x x x
x x x x
x x x x x x







Đặt
sin cos 2 cos , 2
4
t x x x t



Ta có
2
22
sin cos 1 2sin cos 2sin cos 1 .t x x x x x x t
Khi đó:
2
22
sin cos 1 1 2x x t t
Phương trình trở thành :
53
2 2 1 0t t t
có nghiệm
1t
j)
2 3 3
tan . 1 sin cos 1x x x
Điều kiện :
2
xk

.
2
33
2
1 cos
. 1 sin 1 cos
1 sin
x
xx
x
23
2
3
2
2
2
2
1 cos 1 cos
1 sin
1 sin
1 cos 1 cos 1 cos cos
.0
1 sin 1 sin 1 sin sin
1 cos
0
1 sin
1 cos 1 cos cos
0
1 sin 1 sin sin
xx
x
x
x x x x
x x x x
x
x
x x x
x x x






22
2 2 2 2
cos 1
1 cos . 1 sin sin 1 sin . 1 cos cos
cos 1
sin cos .sin cos sin .cos
x
x x x x x x
x
x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
78 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TH 1:
cos 1 2x x k
TH 2:
2 2 2 2
sin cos .sin cos sin .cosx x x x x x
sin cos . sin cos sin .cos 0
sin cos 0
sin cos sin .cos 0
x x x x x x
xx
x x x x

Với:
sin cos 0 cos 0
4 4 2 4
x x x x k x k




Với :
sin cos sin cos 0.x x x x
Đặt
sin cos 2 sin , 2
4
t x x x t



Ta có
2
2
2
1
sin cos 1 2sin cos sin cos .
2
t
t x x x x x x
Phương trình trở thành :
22
13
1
1 0 2 2 0
2
1 3 (L)
t
t t t t
t
Với
13t
arcsin 2
62
4
2 sin 1 3 sin
4 4 2
arcsin 2
4
arcsin 2
4
3
arcsin 2
4
xk
xx
xk
xk
xk



,.k
Với
62
sin
2




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 79 | THBTN
5. Moät soá phöông trình löôïng giaùc daïng khaùc
Dng 1.
.sin2 .cos2 .sin .cos 0m x n x p x q x r
Ta luôn viết
sin2 2sin cos ,x x x
còn:
22
2
2
cos sin
cos2 2cos 1
1 2sin
xx
xx
x


(1)
(2)
(3)
Nếu thiếu
sin2x
, ta sẽ biến đổi
cos2x
theo
(1)
và lúc này thường sẽ đưa được về
dạng:
22
( )( ) 0.A B A B A B
Nếu theo
(2)
được:
2
()
sin .(2 .cos ) (2 .cos .cos ) 0
i
x m x p n x q x r n
và theo
(3)
được:
2
()
cos (2 .sin ) ( 2 .sin .sin ) 0.
ii
x m x q n x p x r n
Ta sẽ phân tích
( ), ( )i ii
thành nhân tử dựa vào:
2
12
( )( )at bt c a t t t t
với
12
, tt
là hai
nghiệm của
2
0at bt c
để xác định lượng nhân tử chung.
Ví d 1. Giải phương trình:
cos2 cos 3sin 2 0.x x x
Gii:
22
pt cos sin cos 3sin 2 0x x x x
22
13
cos sin
22
xx
13
cos sin
22
13
cos sin
22
xx
xx
cos sin 2
cos sin 1
xx
xx

Với
cos sin 2 cos 2 1
4
x x x



phương trình vô nghiệm
Với
2
1
cos sin 1 sin ,
2
4
2
2
xk
x x x k
xk





Ví d 2. Giải phương trình:
2sin 2 cos2 7sin 2cos 4.x x x x
Gii:
2
pt 4sin cos 1 2sin 7sin 2cos 4 0x x x x x
2
2sin 7sin 3 4sin cos 2cos 0x x x x x
2sin 1 sin 3 2cos 2sin 1 0x x x x
2sin 1 sin 2cos 3 0x x x
1
2sin 1 0
sin
2
sin 2cos 3 0
sin 2cos 3
x
x
xx
xx



TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
80 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Với
sin 2cos 3xx
thì phương trình vô nghiệm vì
2 2 2
1 2 3
Với
2
1
6
sin ,
5
2
2
6
xk
xk
xk



BT 17. Giải các phương trình lượng giác sau:
a)
cos2 3cos 2 sin .x x x
b)
5 cos2
2cos .
3 2tan
x
x
x
c)
3sin cos 2 cos2 sin2 .x x x x
d)
5cos sin 3 2 sin 2
4
x x x



e)
sin2 cos2 sin cos 1.x x x x
f)
2 sin 2 3sin cos 2.
4
x x x



g)
cos sin sin2 cos2 1.x x x x
h)
2
sin 2 cos 2sin cos2 3sin .x x x x x
i)
2
sin 2 2cos 3sin cos .x x x x
j)
2 2sin 2 cos2 7sin 4 2 2 cos .x x x x
k)
sin2 cos2 3sin cos 1.x x x x
l)
sin2 cos2 3cos 2 sin .x x x x
m)
sin2 2cos2 1 sin 4cos .x x x x
n)
2sin 2 cos2 7sin 2cos 4.x x x x
o)
1
2sin sin 2
3 6 2
xx

p)
2 sin 2 sin 3cos 2.
4
x x x



q)
2 tan 1 tan
2 sin
cos 5
4
xx
x
x





r)
2
3(sin2 3sin ) 2cos 3cos 5.x x x x
Giải
a)
cos2 3cos 2 sinx x x
cos sin cos sin 2 cos sin cos sin 2 0
cos sin cos sin 2 cos sin 2 0
cos sin 1 cos sin 2 0
cos sin 1 0
cos sin 2 0
x x x x x x x x
x x x x x x
x x x x
xx
xx
2
1
cos sin 1 0 sin cos 1 sin
2
4
2
2
xk
x x x x x k
xk






cos sin 2 0 PTVNxx
Vậy phương trình đã cho có nghiệm là:
2 , 2
2
x k x k k
b)
5 cos2
2cos .
3 2tan
x
x
x
Điều kiện:
3
tan ,cos 0
2
xx
.
5 cos2
2cos
3 2tan
x
x
x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 81 | THBTN
22
5 cos sin 6cos 4sinx x x x
22
cos 3 sin 2xx
2
1
cos 3 sin 2 sin cos 1 sin
4
2
2
2
xk
x x x x x k
x k l




Vậy phương trình đã cho có nghiệm là:
2x k k

c)
3sin cos 2 cos2 sin2 .x x x x
2
2sin 3sin 1 2sin cos cos
sin 1 2sin 1 cos 2sin 1
x x x x x
x x x x
2sin 1 sin cos 1 0x x x
2sin 1 0
sin cos 1 0
x
xx

2sin 1 0x
1
sin
2
x
2
6
7
2
6
xk
k
xk


2
2
sin cos 1 0 sin
3
42
2
2
xk
x x x k
xk




Vậy phương trình đã cho có các nghiệm là
7
2 , 2
66
x k x k


,
3
2 , 2
2
x k x k

k
d)
5cos sin 3 2 sin 2
4
x x x



2
2
5cos sin 3 sin 2 cos2
5cos sin 3 2sin cos 2cos 1
2cos 5cos 2 2sin cos sin 0
cos 2 2cos 1 sin 2cos 1 0
2cos 1 sin cos 2 0
2cos 1 0
sin cos 2 0
x x x x
x x x x x
x x x x x
x x x x
x x x
x
xx

1
2cos 1 0 cos 2
23
x x x k k
sin cos 2 0 sin cos 2x x x x
(PTVN)
Vậy phương trình đã cho có các nghiệm là
2
3
xk
k
e)
sin2 cos2 sin cos 1x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
82 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2sin cos 2cos sin cos 0
2cos sin cos sin cos 0
sin cos 2cos 1 0
tan 1
sin cos 0
4
1
2
2cos 1 0
cos
2
2
3
x x x x x
x x x x x
x x x
x
xk
xx
k
x
x
xk




Vậy phương trình đã cho có các nghiệm là
2
,2
43
x k x k


k
f)
2 sin 2 3sin cos 2
4
x x x



2
sin 2 cos2 3sin cos 2
2sin cos 3sin 2cos cos 3 0
sin 2cos 3 cos 1 2cos 3 0
2cos 3 sin cos 1 0
2cos 3 0 PTVN
2
1
sin cos 1 sin
2
4
2
2
x x x x
x x x x x
x x x x
x x x
x
xk
x x x k
xk






Vậy phương trình đã cho có các nghiệm là
2 , 2
2
x k x k
k
g)
cos sin sin 2 cos2 1.x x x x
2
cos sin 2sin cos 2cos 0
cos sin 2cos sin cos 0
cos sin 1 2cos 0
tan 1
cos sin 0
4
1
1 2cos 0
cos
2
2
3
x x x x x
x x x x x
x x x
x
xk
xx
k
x
x
xk



Vậy phương trình đã cho có các nghiệm là
,2
43
x k x k


k
h)
2
sin 2 cos 2sin cos2 3sinx x x x x
22
2
2
2sin cos cos 2sin 2cos 1 3 1 cos
2sin cos cos 2sin cos 2
2sin cos 2sin cos cos 2 0
2sin cos 1 cos 1 cos 2 0
cos 1 2sin cos 2 0
cos 1 0 cos 1
2sin cos 2 0 2sin cos 2
x x x x x x
x x x x x
x x x x x
x x x x
x x x
xx
x x x x




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 83 | THBTN
cos 1 2x x k k

2sin cos 2xx
2 1 2 2
sin cos sin cos sin cos
5 5 5 5
x x x x

2
ar sin 2
5
2
sin
5
2
ar sin 2
5
x c k
xk
x c k







Vậy phương trình đã cho có các nghiệm là
2
2 , ar sin 2 ,
5
x k x c k



2
ar sin 2
5
x c k



k
i)
2
sin2 2cos 3sin cos .x x x x
2
sin2 1 cos2 3sin cos
2sin cos cos 2sin 3sin 2 0
x x x x
x x x x x
cos 2sin 1 sin 2 2sin 1 0
2sin 1 sin cos 2 0
x x x x
x x x
2
1
6
2sin 1 0 sin
7
2
2
6
sin cos 2 0 PTVN
xk
x x k
xk
xx

Vậy phương trình đã cho có các nghiệm là
7
2 , 2
6
6
x k x k


k
i)
2 2sin2 cos2 7sin 4 2 2cos 1x x x x
Li gii
2 2sin2 cos2 7sin 4 2 2cosx x x x
2
2 2 sin 2 2 2 cos os2 7sin 4 0
2 2 cos 2sin 1 2sin 7sin 3 0
2 2 cos 2sin 1 sinx 3 2sin 1 0
2sin 1 2 2 cos sinx 3 0
x x c x x
x x x x
x x x
xx
2sin 0
2 2 cos sin 3
x
xx

Với
2
6
2sin 1
5
2
6
xk
xk
xk


TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
84 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Với
2 2 cos sinx 3 os 1 2 ,x c x x k k
với
2 2 1
cos sin
33
và






Vậy phương trình có nghiệm:
5
2 , 2 , 2 ,
66
x k x k x k k

k)
sin2 cos2 3sin cos 1.x x x x
Li gii
2
2
sin2 cos2 3sin cos 1
2sin .cos cos 1 2sin 3sin 1 0
cos 2sin 1 2sin 3sin 2 0
cos 2sin 1 2sin 1 sin 2 0
x x x x
x x x x x
x x x x
x x x x
2sin 1 0
2sin 1 cos sin 2 0
cos sin 2 0
x
x x x
xx

Với
2
1
6
2sin 1 0 sinx ,
5
2
2
6
xk
xk
xk


Với
cos sin 2 0 sin 2
4
x x x



(vô nghiệm)
Vậy phương trình có nghiệm:
5
2 , 2 ,
66
x k x k k


.
l)
sin2 cos2 3cos 2 sin .x x x x
Li gii
2
sin2 cos2 3cos 2 sin
sin2 sinx 2cos 3cos 1 0
sinx 2cos 1 2cos 1 cos 1 0
x x x x
x x x
x x x
1
cos
2cos 1 sinx cos 1 0
2
sinx cos 1 0
x
xx
x
Với
2
sinx cos 1 0 2 sin 1 ,
4
2
2
xk
x x k
xk




Vậy phương trình có nghiệm:
2 , 2 , 2 ,
32
x k x k x k k

m)
sin2 2cos2 1 sin 4cos .x x x x
Li gii
sin2 2cos2 1 sin 4cos
sin2 sin 2cos2 4cos 1 0
sin 2cos 1 2cos 3 2cos 1 0
x x x x
x x x x
x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 85 | THBTN
2cos 1
2cos 1 sin 2cos 3 0
sin 2cos 3 0
x
x x x
xx
2cos 1 2 ,
3
x x k k
sin 2cos 3 0xx
(vô nghiệm vì
2 2 2
1 2 3
)
Vậy phương trình có nghiệm:
2,
3
x k k
n)
2sin2 cos2 7sin 2cos 4.x x x x
Li gii
2
2sin 2 cos2 7sin 2cos 4
2sin 2 2cos cos2 7sin 4 0
2cos 2sin 1 2sin 7sin 3 0
2cos 2sin 1 2sin 1 sin 3 0
x x x x
x x x x
x x x x
x x x x
2sin 1 2cos sinx 3 0xx
1
sin
2
2cos sin 3 0
x
xx
Với
2
1
6
sinx ,
5
2
2
6
xk
k
xk



Với
2cos sin 3 0xx
(vô nghiệm vì
2 2 2
1 2 3
)
Vậy phương trình có nghiệm:
5
2 , 2 ,
66
x k x k k


.
o)
1
2sin sin 2
3 6 2
xx

Li gii.
1 3 1 1
2sin sin 2 sin 3cos - sin2 cos2
3 6 2 2 2 2
x x x x x x

2
sin 1
2
2sin 1 sin 2 3cos 1 sin 0
tan 3
3
xk
x
x x x x
x
xk


p)
2sin 2 sin 3cos 2.
4
x x x



Li gii.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
86 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2sin 2 sin 3cos 2 sin 2 cos2 sin 3cos 2
4
2cos 1 sin 2cos 3cos 1 0 2cos 1 sin cos 1 0
2
1
cos
3
2
2
1
sin
4
2
2
2
x x x x x x x
x x x x x x x
xk
x
xk
x
xk








q)
2 tan 1 tan
2sin
cos 5
4
xx
x
x





Li gii.
ĐK:
cos 5 0
4
sin2x 0
x




2 tan 1 tan 2cos sin cos sin
2sin 2 cos2 1 cos6 sin 4
cos5 sin5 2sin
2 sin
cos 5
4
2sin 2 sin 4 1 cos6 cos2 2sin 2 sin 4 1 2sin 4 sin 2
82
sin 4 1
1
12
sin 2
2
7
12
x x x x x x
x x x x
x x x
x
x
x x x x x x x x
k
x
x
xk
x
xk







r)
2
3(sin2 2sin ) 2cos 3cos 5.x x x x
Li gii.
2
3(sin2 2sin ) 2cos 3cos 5 2 3sin cos 1 cos 1 2cos 5
2
cos 1 0
2 3sin 2cos 5
2 3sin 2cos 5
x x x x x x x x
xk
x
x x VN
xx




Dng 2: Phương trình có chứa
(...,tan ,cot ,sin2 ,cos2 ,tan2 ,...),R X X X X X
sao cho cung của
sin, cos gấp đôi cung của tan hoặc cotan. Lúc đó đặt
tantX
và sẽ biến đổi:
2
22
sin 2tan 2
sin2 2sin cos 2 cos
cos 1 tan 1
X X t
X X X X
X X t

22
2
2 2 2
1 1 tan 1
cos2 2cos 1 2 1
1 tan 1 tan 1
Xt
XX
X X t

2
sin2 2
tan2
cos2 1
Xt
X
Xt

và
2
1
cot 2
2
t
X
t

Từ đó thu được phương trình bậc 2 hoặc bậc cao theo
,t
giải ra sẽ tìm được
.tx
Ví d. Giải phương trình:
sin2 2tan 3.xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 87 | THBTN
Gii:
Điều kiện
cos 0x
pt 2sin cos 2tan 3x x x
2
2tan
2tan 3
1 tan
x
x
x
32
2tan 3tan 4tan 3 0x x x
2
2
1 23
tan 1 2tan tan 3 0 tan 1 2 tan 0
48
x x x x x







tan 1x
,
4
x k k

BT 18. Giải các phương trình lượng giác sau:
a)
1 3tan 2sin2 .xx
b)
cos2 tan 1.xx
c)
sin2 2tan 3.xx
d)
(1 tan )(1 sin2 ) 1 tan .x x x
e)
1 tan
1 cot
2 1 sin2
x
x
x



f)
sin2 cos2
cot , ;0
2 sin2 2
xx
xx
x



g)
2
cot tan 4sin2
sin2
x x x
x
h)
2
cos2 1
cot 1 sin sin2 .
1 tan 2
x
x x x
x
Li gii
a)
1 3tan 2sin2 .xx
Điều kiện
cos 0.x
Pt
32
2
4tan
1 3tan 3tan tan tan 1 0.
1 tan
x
x x x x
x
2
tan 1 3tan 2tan 1 0.x x x
2
tan 1 0
3tan 2tan 1 0 « nghiÖm
x
x x v

.
tan 1 , .
4
x x k k
b)
cos2 tan 1.xx
Điều kiện
cos 0.x
Pt
2
32
2
1 tan
tan 1 tan 2tan tan 0.
1 tan
x
x x x x
x
2
tan tan 1 0.xx
tan 0
,.
tan 1
4
xk
x
k
x
xk

c)
sin2 2tan 3.xx
Điều kiện
cos 0.x
Pt
32
2
2tan
2tan 3 2tan 3tan 4tan 3 0.
1 tan
x
x x x x
x
2
tan 1 2tan tan 3 0.x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
88 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
tan 1 0
2tan tan 3 0 « nghiÖm
x
x x v

.
tan 1 , .
4
x x k k
d)
(1 tan )(1 sin2 ) 1 tan .x x x
Điều kiện
cos 0.x
Pt
2
2tan
1 tan 1 1 tan
1 tan
x
xx
x



2
2
1 tan tan 1 1 tan 1 tan .x x x x
2
2tan tan 1 0.xx
tan 0
,.
tan 1
4
xk
x
k
x
xk

e)
1 tan
1 cot
2 1 sin2
x
x
x



1 tan
1 tan .
1 sin2
x
pt x
x
Điều kiện
cos 0
.
sin2 1
x
x

Điều kiện
cos 0.x
Pt
2
2tan
1 tan 1 1 tan
1 tan
x
xx
x



2
2
1 tan tan 1 1 tan 1 tan .x x x x
2
2tan tan 1 0.xx
tan 0
tan 1
lo¹i
4
xk
x
x
xk


,.x k k
f)
sin2 cos2
cot , ;0
2 sin2 2
xx
xx
x



Điều kiện
sin 0.x
Pt
2
2
22
2
2
2tan 1 tan
1 1 tan 2tan 1
1 tan 1 tan
.
2tan
tan tan 2tan 2tan 2
2
1 tan
xx
xx
xx
x
x x x x
x



2
3
tan 3tan 2 0 tan 2 tan 1 0.x x x x
acrtan2
tan 2
,.
tan 1
4
xk
x
k
x
xk


g)
2
cot tan 4sin2
sin2
x x x
x
Điều kiện
sin2 0.x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 89 | THBTN
Pt
2
2
1 8tan 1 tan
tan
tan 1 tan tan
xx
x
x x x
2
2 2 2 2 2
1 tan tan 1 tan 8tan 1 tanx x x x x
.
4 2 2 2
2tan 6tan 0 2tan tan 3 0x x x x
.
tan 0
3
tan 3 , .
tan 3
3
x loai
xk
xk
xk
x


h)
2
cos2 1
cot 1 sin sin2 .
1 tan 2
x
x x x
x
Điều kiện
sin 0
tan 1
x
x

.
Pt
2
2
2
22
1 tan
1 tan tan
1 tan
1.
tan 1 tan 1 tan 1 tan
x
xx
x
x x x x
2
2 2 2
1 1 tan tan tan
1.
tan 1 tan 1 tan 1 tan
x x x
x x x x
22
1 tan 1 tan tan tan 2tan 1 .x x x x x
2
2
2
tan tan 1 tan 1 1 tan 0.
tan 1 2tan tan 1 0.
x x x x
x x x
2
tan 1
2tan tan 1 0 « nghiÖm
x
x x v
.
,.
4
x k k
Dng 3: Áp dụng
tan( )tan( ) 1 khi
2
cot( )cot( ) 1 khi
2
x a b x a b k
x a b x a b k
hay
tan tan
tan( )
1 tan .tan
ab
ab
ab
Ví d. Giải phương trình:
33
sin cos cos2 tan tan
44
x x x x x

Gii:
Điều kiện
cos 0
4
x




và
cos 0
4
x




Ta có
tan 1 tan 1
tan .tan . 1
4 4 1 tan 1 tan
xx
xx
xx



Khi đó
pt sin cos 1 sin cos cos sin cos sinx x x x x x x x
pt sin cos 1 sin cos cos sin 0x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
90 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
sin cos 1 cos sin cos sin 0x x x x x x


sin cos 1 cos 1 sin 0x x x x
tan 1
4
cos 1 2 ,
sin 1
2
2
xk
x
x x k k
x
xk


So sánh điều kiện, phương trình có nghiệm
2
,
2
2
xk
k
xk


BT 19. Giải các phương trình lượng giác sau:
a)
sin cos3 2cos2 cos
sin2
2
tan tan
2 4 4
x x x x
x
xx




b)
33
sin sin3 cos cos3 1
8
tan tan
63
x x x x
xx

c)
44
4
sin 2 cos 2
cos 4 .
tan tan
44
xx
x
xx


d)
44
7
sin cos cot cot
8 3 6
x x x x

e)
tan tan sin3 sin sin2 .
36
x x x x x

ng dn gii.
a) Điều kiện:
cos 0
4
cos 0 .
4
tan tan 0
44
x
x
xx









Phương trình đã cho tương đương
sin cos3 2cos2 cos
sin2
2
tan cot
2 4 4
x x x x
x
xx



2
sin cos3 2cos2 cos sin2
2
x x x x x
2
sin cos3 cos cos3 sin2
2
x x x x x
2
sin cos sin2
2
x x x
Đặt
sin cos , 2t x x t
, suy ra
2
sin2 1xt
Phương trình trở thành:
2 2 2
2 2 6
1 1 2 2 1 0
22
t t t t t t t
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 91 | THBTN
Với
26
2
t
suy ra
2 6 2 6 1 3
sin cos 2sin sin
2 4 2 4 2
x x x x

(loại)
Với
26
2
t
suy ra
2 6 2 6 1 3
sin cos 2sin sin
2 4 2 4 2
x x x x

13
arcsin 2
42
13
arcsin 2
42
xk
xk

b) Điều kiện:
cos 0
6
cos 0 .
3
tan tan 0
63
x
x
xx









Phương trình đã cho tương đương
33
sin sin3 cos cos3 1
8
tan tan
63
x x x x
xx


33
sin sin3 cos cos3 1
8
tan cot
66
x x x x
xx


33
1
sin sin3 cos cos3
8
x x x x
3sin sin3 3cos cos3 1
.sin3 .cos3
4 4 8
x x x x
xx

22
1
3sin sin3 sin 3 3cos .cos3 cos 3
2
x x x x x x
22
1
3 sin sin3 cos .cos3 cos 3 sin 3
2
x x x x x x
22
1
3 cos .cos3 sin sin3 cos 3 sin 3
2
x x x x x x
1
3cos2 cos6
2
xx
3
1
3cos2 4cos 2 3cos2
2
x x x
3
1
cos 2
8
x 
1
cos2
2
x 
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
92 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
22
3
xk
,.
3
x k k
Đối chiếu với điều kiện nghiệm của phương trình là
,.
3
x k k
c) Điều kiện:
cos 0
4
cos 0 .
4
tan tan 0
44
x
x
xx









Phương trình đã cho tương đương
44
4
sin 2 cos 2
cos 4
tan cot
44
xx
x
xx


4 4 4
sin 2 cos 2 cos 4x x x
2
2 2 2 2 4
sin 2 cos 2 2sin 2 cos 2 cos 4x x x x x
2
4
1 2 sin2 cos2 cos 4x x x
2
4
1
1 2 sin4 cos 4
2
xx




24
1
1 1 cos 4 cos 4
2
xx
42
2cos 4 cos 4 1 0 1xx
Đặt
2
cos 4 0xt
Phương trình (1) trở thành:
2
2 1 0tt
1
1
2
t
tl

2
1 cos 4 1tx
cos4 1x 
4xk
,.
4
k
xk

Đối chiếu với điều kiện nghiệm của pt là
xk
và
,.
2
x k k
d) Điều kiện:
sin 0
3
.
sin 0
6
x
x







Phương trình đã cho tương đương
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 93 | THBTN
44
7
sin cos cot tan
8 3 3
x x x x

44
7
sin cos
8
xx
2
2 2 2 2
7
sin cos 2sin cos
8
x x x x
2
7
1 2 sin cos
8
xx
2
17
1 2 sin 2
28
x




1 1 cos4 7
1
2 2 8
x




1
cos4
2
x
42
3
xk
,.
12 2
x k k

Đối chiếu với điều kiện nghiệm của pt là
,.
12 2
x k k

e) Điều kiện:
cos 0
3
.
cos 0
6
x
x







Phương trình đã cho tương đương
tan cot sin3 sin sin 2
33
x x x x x

sin3 sin sin2x x x
3 3 3
2sin cos 2sin cos
2 2 2 2
x x x x
33
sin cos cos 0
2 2 2
x x x




3
sin 0
2
3
cos cos
22
x
xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
94 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
3
2
3
2
22
3
2
22
x
k
xx
k
xx
k

2
3
2
k
x
xk
xk
2
,.
3
k
x
k
xk
Đối chiếu với điều kiện nghiệm của pt là
xk
và
2
2 , .
3
x k k
BT 20. Giải các phương trình lượng giác sau (đặt ẩn phụ
t
bởi cung phức tạp):
a)
2
4
cos cos .
3
x
x
b)
3
tan tan 1.
4
xx



c)
3 1 3
sin sin
10 2 2 10 2
xx

d)
sin 3 sin 2 sin
44
x x x

e)
3
8cos cos3 .
3
xx




f)
3
2 sin 2sin .
4
xx




g)
3
sin 2 sin .
4
xx




h)
cos 2cos3 1 3sin .x x x
Lời giải
a) Đặt
23
32
x
t x t
Khi đó phương trình trở thành:
1 cos3
cos 2 2cos 2 1 cos3 cos2 cos3 1 cos2
2
t
t t t t t t
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 95 | THBTN
2
55
2sin sin 2sin 2sin sin sin 0
2 2 2 2 2 2
sin 0
2
2
2
3 3 2
4sin cos sin 0 cos 0
33
2 2 2 3 3
sint 0
2
.
3
2
2
t t t t t t
t
tk
t k k
t t t
t t k
tk
tk
xk
x k k
xk



.
b) ĐK:
2
.
3
4
xk
k
xk


3
3
3
tan tan
tan 1
4
tan tan 1 tan tan 1
4 1 tan
1 tan tan
4
1 tan 1 tan 0 .
x
x
x x x x
x
x
x x x k k





c) Đặt
33
2.
10 2 5
x
t x t
Khi đó phương trình trở thành:
3
11
sin sin 3 sin sin3 2sin sin3 2sin 3sin 4sin
22
t t t t t t t t t
32
2
sin 0
6
4sin sin 0 sin 4sin 1 0
5
1
2
sin
6
2
7
2
6
.
6
tk
tk
t
t t t t
tk
t
tk
tk
k
tk




1
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
96 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
3
2
5
4
2.
15
14
2
15
xk
x k k
xk


d) Đặt
.
44
x t x t

Khi đó phương trình trở thành:
sin 3 sin 2 sin sin 3 sin 2 sin sin3 cos2 sin
22
t t t t t t t t t


sin 2 cos2 sin sin 2 cos cos2 sin cos2 sin sin 2 cos 0t t t t t t t t t t t t
2
sin 2 0
2
.
cos 0
2
2
2
x.
42
tk
tk
t
t k k
t
tk
tk
kk



e) Đặt
.
33
x t x t

Khi đó phương trình trở thành:
333
3 3 3 2
8cos cos 3 8cos cos 3 8cos cos3t
8cos 4cos 3cos 0 12cos 3cos 0 cos 4cos 1 0
2
cos 0
2.
1
3
cos
2
2
2
3
t t t t t
t t t t t t t
tk
t
t k k
t
tk



6
2
.
3
2
2
3
2
xk
xk
k
xk
xk



f) Đặt
.
44
x t x t

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 97 | THBTN
Khi đó phương trình trở thành:
33
2 sin 2sin 2 sin 2 sin cos cos sin
4 4 4
t t t t t
3 3 2
2 sin 2 sin cos sin sin cos 0 sin sin 1 cos 0t t t t t t t t t
2
1
sin cos cos 0 cos 1 sin cos 0 cos 1 sin 2 0
2
cos 0
.
sin 2 2
2
t t t t t t t t
t
t k k
tL



.
4
x k k
f) Đặt
.
44
x t x t

Khi đó phương trình trở thành:
33
sin 2 sin sin sin cos
4
t t t t t



32
sin sin cos 0 sin sin 1 cos 0t t t t t t
2
1
sin cos cos 0 cos 1 sin cos 0 cos 1 sin 2 0
2
cos 0
.
sin 2 2
2
t t t t t t t t
t
t k k
tL




3
.
4
x k k
h)
cos 2cos3 1 3sin cos 3 sin 2cos3 1 0
2 cos cos sin sin 2cos3 1 0
33
2cos 2cos3 1 0
3
x x x x x x
x x x
xx







Đặt
.
33
x t x t

Khi đó phương trình trở thành:
2cos 2cos 3 1 0 2cos 2cos 3 1 0t t t t

3
2cos 2cos3 1 0 2cos 2 4cos 3cos 1 0t t t t t
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
98 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
32
8cos 4cos 1 0 2cost 1 4cos 2cost 1 0t t t
2
1
t2
cost
3
2
15
15
cost
t arccos
4
4
k



2
3
2
15
arccos
43
xk
xk
x


.
Dng 4. Phương trình lượng giác có cách giải đặc biệt
Tổng các số không âm:
22
0
0
0
A
AB
B
Đối lập:
AB
mà chứng minh được
A M A M
B M B M






Hoặc:
A B M N
mà chứng minh được:
A M A M
B N B N






Một số trường hợp đặc biệt:
sin 1
sin sin 2
sin 1
u
uv
v

sin 1
sin sin 2
sin 1
u
uv
v


cos 1
cos cos 2
cos 1
u
uv
v

cos 1
cos cos 2
cos 1
u
uv
v


sin 1
sin 1
sin .sin 1
sin 1
sin 1
u
v
uv
u
v



sin 1
sin 1
sin .sin 1
sin 1
sin 1
u
v
uv
u
v

cos 1
cos 1
cos .cos 1
cos 1
cos 1
u
v
uv
u
v



cos 1
cos 1
cos .cos 1
cos 1
cos 1
u
v
uv
u
v


BT 21. Giải các phương trình lượng giác sau:
a)
22
4cos 3tan 4 3cos 2 3 tan 4 0.x x x x
b)
22
4cos 4cos 3tan 2 3 tan 2 0.x x x x
c)
22
2sin 3tan 6tan 2 2sin 4 0.x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 99 | THBTN
d)
3 2 2
8sin sin 2 6sin cos 1 0.x x x x
e)
22
cos tan 4 1 sin2 0.x x x
f)
2 2 2
4sin sin 3 4sin sin 3 .x x x x
g)
22
5sin 3cos 3sin 2 2 3cos 2sin 2 0.x x x x x
h)
2
2
1
sin 2 2sin 2 2tan 1 0.
cos
x x x
x
i)
22
4cos 3tan 2 3 tan 4sin 6.x x x x
j)
2
8cos4 cos 2 1 cos3 1 0.x x x
k)
2
2 3 3 2
sin 3
sin cos3 sin sin3 cos sin sin 3 .
3sin 4
x
x x x x x x x
x
ng dn gii
a.
22
4cos 3tan 4 3 cos 2 3 tan 4 0.x x x x
ĐK
:
cosx 0
22
22
4cos 3tan 4 3 cos 2 3 tan 4 0.
2cos 3 3 tan 1 0
2
2cos 3 0
6
2
6
3 tan 1 0
6
x x x x
xx
xk
x
x k k
x
xk




b.
22
4cos 4cos 3tan 2 3 tan 2 0.x x x x
ĐK
:
cosx 0
22
2
2
4cos 4cos 3tan 2 3 tan 2 0.
2cos 1 3 tan 1 0
2
2cos 1 0
3
3 tan 1 0
6
x x x x
xx
xk
x
k
x
xk





Vậy phương trình vô nghiệm
c.
22
2sin 3tan 6tan 2 2sin 4 0.x x x x
ĐK
:
cosx 0
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
100 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
22
2
2
2sin 3tan 6 tan 2 2 sin 4 0.
2 sin 1 3 tanx 1 0
2
4
1
sinx
3
2
2
2
4
4
tan 1
2
4
x x x x
x
xk
x k k
xk
x
xk






d.
22
cos tan 4 1 sin2 0.x x x
ĐK
:
cosx 0
22
2
22
cos tan 4 1 sin 2 0.
cos tan 4 sinx cos 0
2
cos 0
tan 4 0
4
4
sinx cos 0
4
x x x
x x x
xk
x
k
x k k
x
x
x
xk







e.
2 2 2
4sin sin 3 4sin sin 3 .x x x x
2 2 2
2
2 2 4
2
2 2 2
4sin sin 3 4sin sin 3 0
2sinx sin 3 sin 3 sin 3 0
2sinx sin 3 sin 3 .cos 3 0
x x x x
x x x
x x x
2
22
sin 0
2sinx sin 3 0
1
6
sin
sin 3 .cos 3 0
2
5
6
xk
x
x
x k k
x
xx
xk



f.
2
2
1
sin 2 2sin 2 2tan 1 0.
cos
x x x
x
ĐK
:
cosx 0
2
2
22
22
1
sin 2 2sin 2 2 tan 1 0
cos
sin 2 2sin 2 1 tan 2tan 1 0
sin 2 1 tan 1 0
sin 2 1
tan 1
4
x x x
x
x x x x
xx
x
x k k
x


TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 101 | THBTN
l)
22
4cos 3tan 2 3 tan 4sin 6.x x x x
Điều kiện
cosx 0
22
22
2
2
4cos 3tan 2 3 tan 4sin 6
4sin 4sin 1 3tan 2 3 tan 1 0
2sin 1 3 tan 1 0
2
1
6
sin
5
2
5
2
2
1
6
6
tan
3
6
x x x x
x x x x
xx
xk
x
x k k
xk
x
xk







m)
2
8cos4 cos 2 1 cos3 1 0.x x x
22
42
2
2
2
8 2cos 2 1 cos 2 1 cos3 1 0.
16cos 2 8cos 2 1 1 cos3 0
4cos 2 1 1 cos3 0
1
2cos 4 1 0
4cos 2 1 0
cos4
2
1 cos3 0
1 cos3 0
cos3 1
62
2
2
6
63
x x x
x x x
xx
x
x
x
x
x
x
k
x
x k k
k
x







n)
2
2 3 3 2
sin 3
sin cos3 sin sin3 cos sin sin 3 .
3sin 4
x
x x x x x x x
x
Điều kiện
sin 4 0x
2
2 3 3 2
2
22
2 2 2
2
2 2 4
2
2 2 2
2
22
sin 3
sin cos3 sin sin3 cos sin sin 3
3sin 4
sin 3
sin sin sin 3
4
4sin sin 3 4sin sin 3 0
2sinx sin 3 sin 3 sin 3 0
2sinx sin 3 sin 3 .cos 3 0
2sinx sin 3 0
sin 3 .cos 3 0
x
x x x x x x x
x
x
x x x
x x x x
x x x
x x x
x
xx


sin 0
1
6
sin
2
5
6
xk
x
x k k
x
xk




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
102 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
BT 22. Giải các phương trình lượng giác sau:
a)
cos cos2 1.xx
b)
sin 2 cos4 1.xx
c)
sin sin3 1.xx
d)
cos2 cos6 1.xx
e)
22
(cos sin )sin5 1 0.x x x
f)
(cos sin )(sin2 cos2 ) 2 0.x x x x
g)
sin7 sin 2.xx
g)
cos4 cos6 2.xx
i)
33
sin cos 1.xx
j)
53
sin cos 1.xx
ng dn gii
a)
cos cos2 1.xx
2
2
cos 1
cos 1
cos2 1 2cos 2
cos 1 2
cos 1
cos 1
cos2 1
2cos 0
x
x
xx
x x k k
x
x
x
x







b)
sin 2 cos4 1.xx
2
2
sin 2 1
sin 2 1
cos4 1 1 2sin 2 1
sin 2 1
4
sin 2 1
sin 2 1
cos4 1
1 2sin 2 1
x
x
xx
x x k k
x
x
x
x






c)
sin sin3 1.xx
3
3
sin 1
sin 1
sin3 1 3sin 4sin 1
sin 1
2
sin 1
sin 1
sin3 1
3sin 4sin 1
x
x
x x x
x x k k
x
x
x
xx






d)
cos2 cos6 1.xx
3
3
cos2 1
cos2 1
cos6 1 4cos 2 x 3cos2 x 1
cos2 1
2
cos2 1
cos2 1
cos6 1
4cos 2 x 3cos2 x 1
x
x
x
k
x x k
x
x
x






e)
22
(cos sin )sin5 1 0.x x x
2
cos2x 1
2
sin5 1
10 5
cos2x.sin 5 1
2
cos2x 1
sin5 1
2
10 5
xk
k
x
x
x x k k
xk
x
k
x






TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 103 | THBTN
f)
(cos sin )(sin2 cos2 ) 2 0.x x x x
sin 1
3
4
2
4
sin 2 1
3
4
sin sin 2 1
8
44
sin 1
2
4
4
sin 2 1
4
x
xk
x
xk
x x k
x
xk
xk
x















Phương trình vô nghiệm
g)
sin7 sin 2.xx
2cos 4 3 2
cos4 sin 3 1
2
cos4 1
2
sin 3 1
63
cos4 1
42
sin 3 1
2
63
xsin x
xx
k
x
x
k
x
x
k
xk
x
x
k
x













Phương trình vô nghiệm
g)
cos4 cos6 2.xx
2
2
sin 1
2
2
sin5 1
10 5
2
sinx.sin 5 1
sin 1
2
2
2
2
sin5 1
2
10 5
xk
x
k
x
xk
x
xk
x
xk
xk
x
k
x












i)
33
sin cos 1.xx
33
3 3 2 2
sin cos 1.
VT sin cos sin cos 1
sinx 0
2
cos 1
2
sinx 1
2
cos 0
xx
x x x x VP
xk
x
VT VP k
xk
x



j)
53
sin cos 1.xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
104 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
52
53
32
sin sin
sin cos 1
cos cos
sin 0
2
cos 1
2
sin 1
2
cos 0
xx
xx
xx
x
xk
x
VT VP k
xk
x
x






BT 23. Giải các phương trình lượng giác sau:
a)
2 2 5
tan cot 2sin
4
x x x



b)
2cos 2 sin10 3 2 2cos28 sin .x x x x
c)
2
2sin5 cos4 3 cot .x x x
d)
1
tan 2 tan3
sin cos2 cos3
xx
x x x
e)
2
(cos2 cos4 ) 6 2sin3 .x x x
f)
44
sin cos sin cos .x x x x
g)
22
cos 3 cos2 cos 0.x x x
g)
3
cos 2 cos 2 0.
4
x
x
i)
cos2 cos4 cos6 cos cos2 cos3 2.x x x x x x
ng dn gii
a)
2 2 5
tan cot 2sin
4
x x x



Ta có
2 2 2 2
5
5
tan cot 2 tan .cot 2
2sin 2 2
4
tan cot 1
2
2
4
2
sin 1
2
4
2
4
4
x x x x VT
x VP
xx
xk
VP
VP VP x k k
x
Vp
xk










c)
2
2sin5 cos4 3 cot .x x x
Ta có:
2
VT 2sin 5 cos4 3
3 cot . 3
sin5 1
3
cos4 1
3
2
cot 0
xx
VP x
x
VP
VT VP x x k k
VT
x

d)
1
tan 2 tan3
sin cos2 cos3
xx
x x x
Điều kiện xác định:
sin cos2 cos3 0x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 105 | THBTN
sin 5 1
cos2 cos3 sin cos2 cos3
2
2
sin 1
2
sin 5 1
10 5
sinx.sin 5 1
sin 1
2
2
sin 5 1
2
10 5
x
x x x x x
xk
x
k
x
x
xk
x
xk
x
k
x











Phương trình vô nghiệm
e)
2
(cos2 cos4 ) 6 2sin3 .x x x
22
22
22
4sin 3 .sin 2sin3 6
4sin 3 .sin 2sin3 6
sin 3 .sin 1
2
sin3 1
x x x
VT x x x VP
xx
VP VP x k k
x

f)
44
sin cos sin cos .x x x x
4
4
sin sin
cos cos
sin 1
cos 0
2
xx
VT VP
xx
x
VT VP x k k
x


g)
22
cos 3 cos2 cos 0.x x x
3
3
1 cos6 cos2 1 cos2 0.
cos6 .cos2x 1
cos2 x 1
cos2 x 1
cos6 1 4cos 2 3cos2 1
cos2 x 1
cos2 x 1
2
cos2 x 1
cos2 x 1
cos6 1
4cos 2 3cos2 1
x x x
x
x x x
k
xk
x
xx








g)
3
cos 2 cos 2 0.
4
x
x
3
cos2 cos 2
4
cos2 1
2
8
3
cos 1
3
4
x
x
xk
x
x k k
k
x
x
i)
cos2 cos4 cos6 cos cos2 cos3 2.x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
106 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
cos2 cos6 cos4 cos cos2 cos3 2.
2cos 4 .cos2 2cos 2 1 cos cos 2 cos3 2
2cos 2 cos 4 cos 2 1 cos cos2 cos3 2
4cos cos 2 cos3 cos cos2 cos3 3
cos cos 2 cos3 3
cos 1
cos2 cos3 1
cos 1
cos2 cos
x x x x x x
x x x x x x
x x x x x x
x x x x x x
x x x
x
xx
x
x


23
23
cos 1
2cos 1 4cos 3cos 1
cos 1
cos 1
cos 1
31
2cos 1 4cos 3cos 1
x
x x x
x
x k k
x
x
x
x x x





BT 24. Tìm tham số
m
để các phương trình sau đây có nghiệm:
a)
02
cos(2 15 ) 2 .x m m
b)
cos 1 3cos 2 .m x x m
c)
(4 1)sin 2 sin 3.m x m x
d)
2 2 2
( )cos2 3 cos2 .m m x m m m x
e)
sin 2cos 1.m x x
f)
cos2 ( 1)sin2 2.m x m x m
g)
2
sin cos sin .m x x x m
g)
sin 5 cos 1 (2 sin ).x x m x
i)
sin2 4(cos sin ) .x x x m
j)
2(sin cos ) sin2 1.x x x m
k)
sin 2 2 2 (sin cos ) 1 4 .x m x x m
l)
22
3sin sin2 4cos 0.x m x x
m)
22
( 2)cos sin2 ( 1)sin 2.m x m x m x m
n)
22
sin (2 2)sin cos (1 )cos .x m x x m x m
ng dn gii
a)
02
cos(2 15 ) 2 .x m m
Ta có :
02
1 cos(2 15 ) 1 1 2 1x m m
22
22
2 1 2 1 0.
1
1
2
2 1 2 1 0
m m m m m
m
m m m m





Vậy
1
1
2
m
thì phương trình có nghiệm
b)
cos 1 3cos 2 .m x x m
3 cos 1 2 (*)m x m
Th1:
3 (*) 0 7m
vô lý. Phương trình vô nghiệm
Th2:
12
3 * cos
3
m
mx
m

Ta có
43
12
1
1 2 4
4
3
1 cos 1 1 1 4
12
33
3
1
3
3
m
m
m
m
xm
m
m
m
m
m








TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 107 | THBTN
Vậy
4
4
3
m
thì phương trình có nghiệm
c)
(4 1)sin 2 sin 3.m x m x
(3 1)sin 5(*).mx
Th1:
1
(*) 0 5
3
m
( vô lý). Vậy phương trình vô nghiệm
Th2:
15
(*) sin
3 3 1
mx
m
Có
1
3
5
4
2
1
5
31
1 sin 1 1 1
3
4
5
31
1
2
3
31
1
3
m
m
m
m
x
m
m
m
m
m






Vậy
2
4
3
m
m

thì phương trình có nghiệm.
d)
2 2 2
( )cos2 3 cos2 .m m x m m m x
2
cos2 3(*)m x m m
Th1:
0 (*) 0 3m
vô lý. Vậy phương trình vô nghiệm
Th2:
2
3
0 (*) cos2
mm
mx
m

Có
2
3
1 cos2 1 1 1
mm
x
m

2
2
3
1
3;0 3;
1;0 3;
3
1;0 3;
1
mm
m
m
m
mm
m
m











Vậy
1;0 3;m 
thì phương trình có nghiệm.
e)
sin 2cos 1.m x x
Để phương trình có nghiệm
22
4 1 3.m m m
Vậy phương trình có nghiệm với mọi giá trị
m
f)
cos2 ( 1)sin2 2.m x m x m
Để phương trình có nghiệm
2
2 2 2
3
( 1) 2 2 3 0
1
m
m m m m m
m

g)
2
sin cos sin .m x x x m
sin2 cos2 2 1m x x m
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
108 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Để phương trình có nghiệm
2
22
4
1 2 1 3 4 0 0
3
m m m m m
Vậy
4
0
3
m
thì phương trình có nghiệm.
g)
sin 5 cos 1 (2 sin ).x x m x
1 sin 5 cos 1 2m x x m
Để phương trình có nghiệm
22
2
1 5 1 2 3 2 5 0m m m m
5
1
3
m
Vậy
5
1
3
m
thì phương trình có nghiệm
i)
sin 2 4(cos sin ) .(*)x x x m
Đặt
cos sinx ; 2t x t
22
sin2 1 (*) 1 4x t t t m
Đặt
2
1 4 ; 2y t t t
.
Ta có bảng biến thiên:
Từ bảng biến thiên ta có để phương trình có nghiệm :
4 2 1 4 2 1m
j)
2(sin cos ) sin 2 1.(*)x x x m
Đặt
cos sinx ; 2t x t
22
sin2 1 (*) 2 2x t t t m
2
2 ; 2y t t t
Ta có bảng biến thiên
Từ bảng biến thiên ta có để phương trình có nghiệm:
1 2 2 2 2 3mm
Vậy
23m
thì phương trình có nghiệm
k)
sin 2 2 2 (sin cos ) 1 4 .x m x x m
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 109 | THBTN
Đặt
sin cos ; 2t x x t
2
sin2 1xt
2
(*) 1 2 2 1 4
2 2 2 2 0
2
2 2 2
t mt m
t t m
t
tm

Vậy phương trình luôn có nghiệm với mọi giá trị m
l)
22
3sin sin2 4cos 0.x m x x
1 cos2 1 cos2
3 sin 2 4 0
22
3 3cos2 2 sin 2 4 4cos2 0
2 sin 2 cos2 1
xx
mx
x m x x
m x x

Để phương trình có nghiệm
22
4 1 1 4 0.m m m
Vậy phương trình có nghiệm
m
m)
22
( 2)cos sin2 ( 1)sin 2.m x m x m x m
1 cos2 1 cos2
( 2) sin 2 ( 1) 2
22
( 2) ( 2)cos2 2 sin 2 ( 1) ( 1)cos2 2 4
cos2 2 sin 2 7
xx
m m x m m
m m x m x m m x m
x m x

Để phương trình có nghiệm
22
4
1 4 49 16
4
m
mm
m

Vậy
4
4
m
m

thì phương trình có nghiệm.
n)
22
sin (2 2)sin cos (1 )cos .x m x x m x m
1 cos2 1 cos2
( 1)sin 2 (1 )
22
1 cos2 2( 1)sin 2 (1 ) (1 )cos2 2
cos2 2( 1)sin 2 3
xx
m x m m
x m x m m x m
m x m x m

Để phương trình có nghiệm
2 2 2 2
2
4( 1) 9 4 8 4 0
2 2 0 1 3 1 3
m m m m m
m m m
Vậy
1 3 1 3m
thì phương trình có nghiệm.
BT 25. Cho phương trình:
cos2 (2 1)cos 1 0.x m x m
a) Giải phương trình khi
3
2
m 
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
110 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
b) Tìm tham số
m
để phương trình có nghiệm nằm trong khoảng
3
;
22




?
ng dn gii
Có
cos2 (2 1)cos 1 0x m x m
2
2
2cos (2 1)cos 0
2cos 1 cos 0
2cos (2 1)cos 0
2cos 1 cos 0
1
cos
2
cos
x m x m
x x m
x m x m
x x m
x
xm
c) Giải phương trình khi
3
2
m 
1
cos
2
2
3
3
cos ( )
2
x
xk
xL
d) Tìm tham số
m
để phương trình có nghiệm nằm trong khoảng
3
;
22




?
Có
1
cos 2
23
x x k
không có nghiệm thuộc
3
;
22




Phương trình có nghiệm nằm trong khoảng
3
;
22




cosxm
có nghiệm nằm trong khoảng
3
;
22




10m
Vậy
10m
thì phương trình có nghiệm nằm trong khoảng
3
;
22




BT 26. Cho phương trình:
cos4 6sin cos .x x x m
a) Giải phương trình khi
1.m
b) Tìm tham số
m
để phương trình có hai nghiệm phân biệt trên đoạn
0;
4



ng dn gii:
Có:
cos4 6sin cos .x x x m
2
1 2sin 2x 3sin 2 (*)xm
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 111 | THBTN
Đặt
sin 2tx
với
1t
2
(*) 2 3 1t t m
(**)
c) Giải phương trình khi
1.m
Với
1m
. Đặt
sin 2tx
với
1t
2
2
2 3 1 1
0
2 3 0 sin 2 0
3
2
()
2
tt
t
k
t t x x
tL
d) Tìm tham số
m
để phương trình có hai nghiệm phân biệt trên đoạn
0;
4



Phương trình (*) có nghiệm
0;
4



Phương trinh (**) có nghiệm
0;1
Đặt
2
2 3 1y t t
Ta có bảng biến thiên
Từ bảng biến thiên ta có để phương trình có 2 nghiêm phân biệt :
17
2
8
m
Vậy
17
2
8
m
thì phương trình có 2 nghiệm phân biệt trên đoạn
0;
4



BT 27. Tìm tham số
m
để phương trình
2
cos cos 1x x m
có nghiệm
0;
2
x



ng dn gii
Đặt
costx
Ta có
0; 0;1
2
xt



Phương trình trở thành:
2
1t t m
Đặt
2
1y t t
Ta có bẳng biến thiên
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
112 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Từ bảng biến thiên ta có để phương trình có nghiệm:
3
1
4
m
Vậy
3
1
4
m
thì phương trình có nghiệm
0;
2
x



BT 28. Tìm tham số
m
để
2cos2 ( 4)sin 2x m x m
có
2
nghiệm
;
22
x




ng dn gii
2
2
2cos2 ( 4)sin 2
1 2sin ( 4)sin 2
2sin ( 4)sin 1 0
x m x m
x m x m
x m x m
Đặt
sinxt
Có
; 1;1
22
xt




Phương trình trở thành
2
2t 4 1 0m t m
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 113 | THBTN
Giải các phương trình lượng giác sau:
a)
cos 3 sin 3
5 sin cos2 3, (0; 2 ).
1 2 sin2
xx
x x x
x

b)
2 2 2 2
sin 3 cos 4 sin 5 cos 6 .x x x x

c)
cos 3 4 cos2 3cos 4 0, 0; 14 .x x x x

BT 29. Giải các phương trình lượng giác sau:
a)
2
cos 2 1
cot 1 sin sin2 .
1 tan 2
x
x x x
x

b)
2
cot tan 4 sin2
sin2
x x x
x

c)
2 2 2
sin tan cos 0.
2 4 2
xx
x

BT 30. Giải các phương trình lượng giác sau:
a)
2
5sin 2 3(1 sin )tan .x x x

b)
(2cos 1)(2 sin cos ) sin2 sin .x x x x x

BT 31. Giải các phương trình lượng giác sau:
a)
22
cos 3 cos2 cos 0.x x x

b)
1 sin cos sin2 cos2 0.x x x x

c)
44
3
cos sin cos sin 3 0.
4 4 2
x x x x

BT 32. Giải các phương trình lượng giác sau:
a)
66
2(cos sin ) sin cos
0.
2 2sin
x x x x
x

b)
cot sin 1 tan tan 4.
2
x
x x x

c)
cos3 cos2 cos 1 0.x x x

BT 33. Giải các phương trình lượng giác sau:
a)
22
(1 sin )cos (1 cos )sin 1 sin2 .x x x x x

b)
2
2sin 2 sin7 1 sin .x x x
i B 
c)
2
sin cos 3 cos 2.
22
xx
x

BT 34. Giải các phương trình lượng giác sau:
a)
1 1 7
4 sin
sin 4
3
sin
2
x
x
x

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
114 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
b)
3 3 2 2
sin 3 cos sin cos 3 sin cos .x x x x x x

c)
2sin (1 cos2 ) sin2 1 2cos .x x x x

BT 35. Giải các phương trình lượng giác sau:
a)
(1 2sin )cos
3.
(1 2 sin )(1 sin )
xx
xx

b)
3
sin cos sin2 3 cos 3 2(cos4 sin ).x x x x x x

c)
3 cos5 2sin3 cos2 sin 0.x x x x

BT 36. Giải các phương trình lượng giác sau:
a)
(1 sin cos2 )sin
4
1
cos .
1 tan
2
x x x
x
x

b)
(sin2 cos2 )cos 2cos2 sin 0.x x x x x

c)
sin2 cos2 3sin cos 1 0.x x x x

BT 37. Giải các phương trình lượng giác sau:
a)
2
1 sin2 cos2
2 sin sin2 .
1 cot
xx
xx
x

b)
sin2 cos sin cos cos2 sin cos .x x x x x x x

c)
sin2 2 cos sin 1
0.
tan 3
x x x
x
 kh
BT 38. Giải các phương trình lượng giác sau:
a)
3 sin2 cos2 2cos 1.x x x

b)
2(cos 3 sin )cos cos 3 sin 1.x x x x x

c)
sin 3 cos 3 sin cos 2 cos2 .x x x x x

BT 39. Giải các phương trình lượng giác sau:
a)
1 tan 2 2 sin
4
xx

b)
2
sin5 2cos 1.xx

c)
sin3 cos2 sin 0.x x x

BT 40. Giải các phương trình lượng giác sau:
a)
sin 4cos 2 sin2 .x x x

b)
2(sin 2cos ) 2 sin2 .x x x
14)
BT 41. Giải phương trình:
2
2sin 7 sin 4 0.xx

BT 42. Giải các phương trình lượng giác sau:
a)
cos cos3 sin2 sin6 sin4 sin6 0.x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 115 | THBTN
b)
1
cos cos2 cos 3 sin sin2 sin 3
2
x x x x x x
c)
cot cos2 sin sin2 cot cos cot .x x x x x x x
d)
sin2 cos sin cos cos2 sin cos .x x x x x x x
e)
3 2 6
4 3sin sin 3cos cos .x x x x
f)
g)
2cos cos2 cos3 5 7cos2 .x x x x
h)
22
sin (4cos 1) cos (sin cos sin3 ).x x x x x x
i)
2
cos 3(sin2 sin ) 4 cos2 cos 2cos 2 0.x x x x x x
j)
22
2
(sin cos ) 2 sin 2
sin sin 3
2 4 4
1 cot
x x x
xx
x
k)
2 2 2
1 1 15 cos 4
2 cot 1 2 tan 1 8 sin 2
x
x x x
l)
2 sin
4
cos3 2 sin 2 1.
tan 1 4
x
xx
x
m)
2 2 2 2
3
3 sin cos sin cos sin cos 3 sin cos .
22
x x x x x x x x
n)
(2sin 1)(cos2 sin ) 2 sin 3 6 sin 1
2cos 3 0.
2cos 3
x x x x x
x
x
o)
2
3 3 1
cos cos2 2.
4 4 2
xx
r)
sin2 3 cos2 3(sin 3) 7 cos .x x x x
s)
66
8(sin cos ) 3 3 cos2 11 3 3 sin4 9 sin2 .x x x x x
t)
sin5 2sin3 2 cos3
5.
sin sin cos
x x x
x x x
u)
22
2cos2 sin cos sin cos 2(sin cos ).x x x x x x x
v)
2 3 4 2 3 4
sin sin sin sin cos cos cos cos .x x x x x x x x
w)
33
sin cos
1 cos2 2 cos .
1 cos 1 sin
xx
xx
xx
x)
(2 cos2 1)cos sin 2(sin cos )sin 3 .x x x x x x
p)
(tanx 1)sin
2
x cos2x 2 3(cosx sinx)sinx.
q)
sin
3
x cos
3
x 3sin
2
x 4sinx cosx 2 0.
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
116 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
p ôn cu
BT 31. Giải các phương trình lượng giác sau:
a)
cos 3 sin 3
5 sin cos2 3, (0; 2 ).
1 2 sin2
xx
x x x
x

b)
2 2 2 2
sin 3 cos 4 sin 5 cos 6 .x x x x

c)
cos 3 4 cos2 3cos 4 0, 0; 14 .x x x x

ng dn gii:
a) Điều kiện:
1
1 sin2 0 sin2
2
xx
Ta có:
cos 3 sin 3
5 sin cos2 3
1 2 sin2
xx
xx
x
sin 2sin sin2 cos 3 sin 3
5( ) cos2 3
1 2 sin2
x x x x x
x
x
sin cos - cos 3 cos3 sin 3
5( ) cos2 3
1 2 sin2
x x x x x
x
x
(sin2 1)cos
5( ) cos2 3
1 2 sin2
xx
x
x
2
5cos cos2 3 2cos 5cos 2 0x x x x
cos 2
2 ( )
1
3
cos
2
x
x k k
x
Do
(0; 2 )x
nên lấy
1
3
x
và
2
5
3
x
. Ta thấy
12
,xx
thỏa điều kiện. Vậy nghiệm của
phương trình là
1
3
x
và
2
5
3
x
.
b) Ta có:
2 2 2 2
sin 3 cos 4 sin 5 cos 6x x x x
1 cos6 1 cos8 1 cos10 1 cos12
2 2 2 2
x x x x
(cos12 cos10 ) (cos8 cos6 ) 0x x x x
cos (cos11 cos7 ) 0x x x
cos sin9 sin2 0x x x
9
sin 9 sin2 0 ( )
2
k
x
x x k
k
x
c) Ta có:
cos3 4 cos2 3cos 4 0x x x
cos3 3cos 4(cos2 1) 0x x x
32
4cos 8cos 0.xx
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 117 | THBTN
2
4 cos (cos 2) 0xx
cos 0 ,x x k k
Do
[0; 14]x
nên lấy
0 1 2 3k k k k
Vậy nghiệm phương trình là
357
: : :
2 2 2 2
x x x x
BT 32. Giải các phương trình lượng giác sau:
a)
2
cos 2 1
cot 1 sin sin2 .
1 tan 2
x
x x x
x

b)
2
cot tan 4 sin2
sin2
x x x
x

c)
2 2 2
sin tan cos 0.
2 4 2
xx
x
03)
ng dn gii:
a) Điều kiện:
2
()
4
xk
kZ
xk
Ta có:
2
cos 2 1
cot 1 sin sin2
1 tan 2
x
x x x
x
22
cos cos sin
1 sin (sin cos )
sin sin
1
cos
x x x
x x x
xx
x
cos sin
cos (cos sin ) sin (sin cos )
sin
xx
x x x x x x
x
2
(cos sin )(1 sin cos sin ) 0x x x x x
TH1:
cos sin 0 ( )
4
x x x k k
thỏa mãn điều kiện
TH2:
22
1
1 sin cos sin 0 1 sin2 sin 0
2
x x x x x
Vô nghiệm
Vậy nghiệm của phương trình là
()
4
x k k
.
b) Điều kiện:
()
2
xk
k
xk
2
cot tan 4 sin2
sin2
x x x
x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
118 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
cos sin 2
4 sin2
sin cos sin2
xx
x
x x x
22
cos sin 2
4 sin2
sin cos sin2
xx
x
x x x
22
2cos2 4sin 2 2 2cos 2 cos2 1 0x x x x
cos2 1
()
1
cos2
23
x x k
k
x x k
Kết hợp điều kiện nghiệm của phương trình là:
()
3
x k k
.
c) Điều kiện:
()
2
x k k
Ta có:
2 2 2
sin tan cos 0
2 4 2
xx
x
2
2
1 sin 1
(1 cos( )) (1 cos )
2 2 2
cos
x
xx
x
22
(1 sin )sin (1 cos )cosx x x x
(1 sin )(1 cosx)(1 cosx) (1 cos )(1 sin )(1 sin )x x x x
(1 sinx)(1 cosx)(sinx cosx) 0
2
sin 1
2
cos 1 2 ( )
tan 1
4
xk
x
x x k k
x
xk
Kết hợp điều kiện nghiệm của phương trình là:
2
()
4
xk
k
xk
BT 33. Giải các phương trình lượng giác sau:
a)
2
5sin 2 3(1 sin )tan .x x x

b)
(2cos 1)(2sin cos ) sin2 sin .x x x x x

ng dn gii:
a) Điều kiện:
()
2
x k k
Ta có:
2
5sin 2 3(1 sin )tanx x x
2
2
sin
5 sin 2 3(1 sin )
cos
x
xx
x
2 2 3
(5sin 2)(1 sin ) 3(sin sin )x x x x
32
2sin sin 5sin 2 0x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 119 | THBTN
2
2
sin 1
sin 2 2 ( )
6
1
5
sin
2
2
6
xk
x
x x k k
x
xk
Kết hợp điều kiện nghiệm của phương trình là
2
6
()
5
2
6
xk
k
xk
.
b) Ta có:
(2cos 1)(2sin cos ) sin2 sinx x x x x
(2cos 1)(2sin cos ) sin (2cos 1) 0x x x x x
(2cos 1)(sin cos ) 0x x x
1
cos
6
()
2
s inx cos 0
4
xk
x
k
x
xk
Vậy nghiệm của phương trình là:
6
()
4
xk
k
xk
.
BT 34. Giải các phương trình lượng giác sau:
a)
22
cos 3 cos2 cos 0.x x x

ng dn gii
22
cos 3 cos2 cos 0 1 cos6 cos2 (1 cos2 ) 0 cos6 cos2 1 0x x x x x x x x
2
cos8 cos4 2 0 2cos 4 cos4 3 0x x x x
cos 4 1
3
2
cos 4 ( )
2
x
k
xk
xl
b)
1 sin cos sin2 cos2 0.x x x x

ng dn gii
1 sin cos sin2 cos2 0 sin cos 2cos sin cos 0x x x x x x x x x
tan 1 0
sin cos 0
4
sin cos 2 cos 1 0
1
2 cos 1 0 2
cos
2
2
3
x
xk
xx
x x x
x
x
xk
c)
44
3
cos sin cos sin 3 0.
4 4 2
x x x x

ng dn gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
120 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Phương trình
22
13
1 2 sin cos sin 4 sin2 0
2 2 2
x x x x
2 2 2
2 sin 2 cos 4 sin2 3 0 sin 2 1 2 sin 2 sin2 1 0x x x x x x
2
sin2 1
sin 2 sin2 2 0 2 2
sin2 2 ( )
24
x
x x x k x k
xl
BT 35. Giải các phương trình lượng giác sau:
a)
66
2(cos sin ) sin cos
0.
2 2sin
x x x x
x

ng dn gii
ĐK:
2
2
4
sin
3
2
2
4
xk
x
xk
Phương trình
6 6 2
31
2 sin cos sin cos 0 2 1 sin 2 sin2 0
42
x x x x x x
2
sin2 1
3 sin 2 sin2 4 0 2 2
4
24
sin2 ( )
3
x
x x x k x k
xl
Đối chiếu ĐK suy ra phương trình có nghiệm
5
2
4
xk
b)
cot sin 1 tan tan 4.
2
x
x x x

ng dn gii
ĐK:
sin 0
cos 0
2
cos 0
2
x
k
xx
x
PT
cos cos sin sin
cos
22
sin 4
sin
cos cos
2
xx
xx
x
x
x
x
x
cos sin 1 1
12
4 4 sin 2
5
sin cos sin cos 2
12
xk
xx
x
x x x x
xk
(thỏa ĐK)
c)
cos3 cos2 cos 1 0.x x x

ng dn gii
PT
22
2sin2 sin 2sin 0 sin sin2 sin 0 sin 2cos 1 0x x x x x x x x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 121 | THBTN
sin 0
12
cos 2
23
x x k
x x k
BT 36. Giải các phương trình lượng giác sau:
a)
22
(1 sin )cos (1 cos )sin 1 sin2 .x x x x x

ng dn gii
PT
2
sin cos 1 sin cos sin cos sin cos 1 sin 1 cos 0x x x x x x x x x x
, 2 , 2
42
x k x k x k
b)
2
2sin 2 sin 7 1 sin .x x x

ng dn gii
PT
2
cos 4 0
sin7 sin 2 sin 2 1 0 cos4 2 sin 3 1 0
1
sin 3
2
x
x x x x x
x
84
2 5 2
,
18 3 18 3
k
x
kk
xx
c)
2
sin cos 3 cos 2.
22
xx
x

ng dn gii
PT
1
1 sin 3 cos 2 cos
62
x x x
2 , 2
26
x k x k
BT 37. Giải các phương trình lượng giác sau:
a)
1 1 7
4sin .
3
sin 4
sin
2
x
x
x







b)
3 3 2 2
sin 3cos sin cos 3sin cos .x x x x x x

c)
2sin 1 cos2 sin2 1 2cos .x x x x

Li gii
a) Điều kiện
sin 0
3
sin 0
2
x
x




.
Ta có
1 1 7 1 1
4sin 4sin
3
sin 4 sin cos 4
sin
2
xx
x x x
x




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
122 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
cos sin 2 2 sin cos cos sin cos sin 1 2 sin2 0x x x x x x x x x
cos sin 0 1
.
1 2 sin 2 0 2
xx
x


1 tan 1
4
x x k k
(thỏa điều kiện).
22
2
8
4
2 sin 2
55
2
22
48
xk
xk
x k k
x k x k


(thỏa điều kiện).
Vậy phương trình có nghiệm
5
, , .
4 8 8
x k x k x k k
b) Ta có
3 3 2 2
sin 3cos sin cos 3sin cosx x x x x x
2 2 2 2
sin cos sin 3 cos cos sin
cos2 sin 3 cos 0
cos2 0 1
.
sin 3 cos 0 2
x x x x x x
x x x
x
xx

1 2 .
2 4 2
k
x k x k
2 sin 0 .
3 3 3
x x k x k k




Vậy nghiệm của phương trình
,.
4 2 3
k
x x k k
c) Ta có
2sin 1 cos2 sin2 1 2cosx x x x
2
4sin cos 2sin cos 1 2cos
2sin cos 2cos 1 1 2cos
2cos 1 sin 2 1 0
2cos 1 0 1
.
sin 2 1 0 2
x x x x x
x x x x
xx
x
x


12
1 cos 2 .
23
x x k k
2 sin 2 1 2 2 .
24
x x k x k k


Vậy phương trình có nghiệm
2
2 , .
34
x k x k k


BT 38. Giải các phương trình lượng giác sau
a)
(1 2sin )cos
3.
(1 2sin )(1 sin )
xx
xx


b)
3
sin cos sin2 3 cos3 2(cos4 sin ).x x x x x x

c)
3cos5 2sin3 cos2 sin 0.x x x x

Li gii
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 123 | THBTN
a) Điều kiện
sin 1
.
1
sin
2
x
x

Ta có
(1 2sin )cos
3 1 2sin cos 3 1 2sin 1 sin
(1 2sin )(1 sin )
xx
x x x x
xx

2
cos sin2 3 1 sin 2sin cos sin 2 3 sin cos2x x x x x x x x
11
cos 3sin sin 2 3 cos2 cos cos 2
2 3 2 6
x x x x x x

22
2
36
2
.
2
22
18 3
36
x x k
xk
k
k
x
x x k




Đối chiếu điều kiện ta có nghiệm
2
2
xk

không thỏa mãn.
Vậy phương trình có nghiệm
2
.
18 3
k
xk

b) Ta có
3
sin cos sin2 3cos3 2(cos4 sin )x x x x x x
3
sin 2sin cos sin 2 3 cos3 2cos4
sin cos2 cos sin 2 3 cos3 2cos4
sin3 3cos3 2cos4
x x x x x x
x x x x x x
x x x
cos 3 cos4
6
xx



4 3 2
6
4 3 2
6
2
6
.
2
42 7
x x k
k
x x k
xk
k
k
x




Vậy phương trình có nghiệm
2
6
xk
,
2
42 7
k
x


k
.
d) Ta có
3cos5 2sin3 cos2 sin 0x x x x
52
3
52
3
18 3
.
62
x x k
k
x x k
k
x
k
k
x






TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
124 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
3 cos5 sin 5 sin sin 0
3 cos5 sin 5 2sin
sin 5 sin
3
x x x x
x x x
xx



Vậy phương trình có nghiệm
18 3
k
x


,
62
k
x

k
.
BT 39. Giải các phương trình lượng giác sau :
a)
(1 sin cos2 )sin
1
4
cos .
1 tan
2
x x x
x
x




b)
(sin 2 cos2 )cos 2cos2 sin 0.x x x x x

c)
sin2 cos2 3sin cos 1 0.x x x x

Li gii
a) Điều kiện
cos 0
.
tan 1
x
x

Ta có
(1 sin cos2 )sin
1
4
cos
1 tan
2
x x x
x
x



2(1 sin cos 2 )sin 1 tan cos
4
x x x x x



cos sin
1 sin cos2 sin cos cos
cos
xx
x x x x x
x
sin cos sin cos 2 0x x x x
sin cos 0 1
sin cos2 0 2
xx
xx


1 tan 1x
(loại).
2
sin 1
2
6
2 sin 1 2sin 0 .
1
7
sin
2
2
6
xL
xk
x x k
x
xk


Đối chiếu điều kiện, phương trình có nghiệm
2
6
xk
,
7
2
6
xk

k
.
b) Ta có
(sin 2 cos2 )cos 2cos2 sin 0x x x x x
2
2
2sin cos cos2 cos 2cos 2 sin 0
2sin cos cos2 cos 2cos2 sin 0
sin 2cos 1 cos2 cos 2 0
cos2 sin cos 2 0
x x x x x x
x x x x x x
x x x x
x x x
sin cos 2 0
2.
2 4 2
cos2 0
x x VN
k
x k x k
x
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 125 | THBTN
Vậy phương trình có nghiệm
.
42
k
xk

c) Ta có
sin2 cos2 3sin cos 1 0x x x x
2
2
2sin cos 1 2sin 3sin cos 1 0
cos 2sin 1 2sin sin 1 2sin 1 0
cos 2sin 1 sin 1 2sin 1 2sin 1 0
2sin 1 cos sin 2 0
cos sin 2 0
2
6
.
1
5
sin
2
2
6
x x x x x
x x x x x
x x x x x
x x x
x x VN
xk
k
x
xk


Vậy phương trình có nghiệm
2
6
xk

,
5
2
6
xk

k
.
BT 40. Giải các phương trình lượng giác sau:
a)
2
1 sin 2 cos2
2 sin sin 2 .
1 cot
xx
xx
x


b)
sin2 cos sin cos cos2 sin cos .x x x x x x x

c)
sin 2 2cos sin 1
0.
tan 3
x x x
x

ng dn gii
a)
2
1 sin2 cos2
2 sin sin2 . 1
1 cot
xx
xx
x


o Điều kiện:
sin 0x
2
1 sin 1 sin 2 cos 2 2 sin sin2x x x x x
2 2 2
sin 2cos 2sin cos 2 2 sin cosx x x x x x
2
cos 0
2sin cos cos sin 2 0
cos sin 2
x
x x x x
xx

cos 0 ;
2
x x k k
cos sin 2 cos 1 2 ;
44
x x x x k k




b)
sin2 cos sin cos cos2 sin cos .x x x x x x x

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
126 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2
2
2sin cos sin cos 2cos –1 sin cos
sin cos 2cos 1 cos 2cos 1 –1 sin
cos 2cos 1 si
2
2
2cos cos -1 0
2
2
n –1 – sin 1 0
sin 1
cos 2cos 1 –1 0
2
cos 1
1
cos
2
x x x x x x x
x x x x x x
x x x x
xk
xx
x k x k
x
x
x
x
x




2
2
2
3
xk
xk


c)
sin 2 2cos sin 1
0.
tan 3
x x x
x

Điều kiện:
tan 3;cos 0xx
Pt sin 2 2cos sin 1 0 2sin cos 2cos sin 1 0
2cos sin 1 sin 1 0 2cos 1 sin 1 0
x x x x x x x
x x x x x
1
2
cos
3
2
sin 1
2
2
xk
x
x
xk


.
Kiểm tra điều kiện, phương trình có nghiệm
2 ( )
3
x k k
BT 41. Giải các phương trình lượng giác sau:
b)
3sin2 cos2 2cos 1.x x x

c)
2(cos 3sin )cos cos 3sin 1.x x x x x

d)
sin3 cos3 sin cos 2cos2 .x x x x x

ng dn gii
a)
3sin2 cos2 2cos 1.x x x

2
2 3sin cos 2cos 2cos cos 3 sin cos 1 0
2
cos 0
2
3sin cos 1
2
2
3
x x x x x x x
xk
x
x k k
xx
xk



b)
2(cos 3sin )cos cos 3sin 1.x x x x x

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 127 | THBTN
(2cos 1)(cos 1) 3 sin (2cos 1) 0
1
cos
2
2cos 1 0
2
2
3
1
cos 3 sin 1
cos
2
32
x x x x
x
x
xk
xx
x
xk







c)
sin3 cos3 sin cos 2cos2x x x x x

sin 3 sin cos3 cos 2 cos2 0
2cos 2 sin 2cos 2 .cos 2 cos2 0
cos2 2cos 2sin 2 0
42
cos2 0
7
2.
12
2cos 2sin 2
2
12
x x x x x
x x x x x
x x x
xk
x
x k k
xx
xk



BT 42. Giải các phương trình lượng giác sau:
b)
1 tan 2 2 sin
4
xx




c)
2
sin5 2cos 1.xx

d)
sin3 cos2 sin 0.x x x

ng dn gii
a)
1 tan 2 2 sin
4
xx




DK : cos 0x
1 tan 2 sin cos cos sin 2cos sin cos
sin cos 2cos 1 0
sin cos 0
4
.
1
cos
2
2
3
x x x x x x x x
x x x
xx
xk
k
x
xk

b)
2
sin5 2cos 1.xx

2
sin5 1 2cos sin5 cos2 sin5 sin 2
2
x x x x x x



2
5 2 2
63
2
.
32
5 2 2
2 14 7
k
x
x x k
k
k
x x k x


c)
sin3 cos2 sin 0.x x x

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
128 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2cos2 sin cos2 0 cos2 2sin 1 0x x x x x
cos2 0x
hay
1
sin
2
x 
42
xk

hay
2
6
xk
hay
7
2
6
xk

(
kZ
)
BT 43. Giải các phương trình lượng giác sau:
a)
sin 4cos 2 sin2 .x x x

Li gii
Phương trình trên tương đương với
sin 4cos 2 sin 2 0
sin 2 2cos sin 2 0
sin 2 1 2cos 0
sin 2
1 2cos 0.
x x x
x x x
xx
x
x

Trường hợp 1.
sin x 2
(Vô nghiệm).
Trường hợp 2.
2
1
3
1 2cos 0 cos cos
23
2
3
xk
xx
xk

.k
Vậy phương trình đã cho có hai họ nghiệm là
2
3
.
2
3
xk
k
xk

b)
2(sin 2cos ) 2 sin2 .x x x

Li gii
Phương trình trên tương đương với
2(sin 2 cos ) 2 sin 2 0
2 sin 2 2 cos sin 2 0
sin 2 2 2 cos 0
sin 2
2 2 cos 0
x x x
x x x
xx
x
x
Trường hợp 1.
sin x 2
(Vô nghiệm).
Trường hợp 2.
3
2
23
4
2 2cos 0 cos cos
3
24
2
4
xk
xx
xk

.k
Vậy phương trình đã cho có hai họ nghiệm là
3
2
4
3
2
4
xk
xk

.k
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 129 | THBTN
BT 44. Giải phương trình:
2
2sin 7 sin 4 0.xx

Li gii
Phương trình đã cho tương đương với
2
2sin sin 8sin 4 0
sin 2sin 1 4 2sin 1 0
sin 4 0
sin 4 2sin 1 0
2sin 1 0
x x x
x x x
x
xx
x


Trường hợp 1.
sin 4 0 sin 4xx
(Vô nghiệm).
Trường hợp 2.
2
1
6
2sin 1 0 sin sin
5
26
2
6
xk
xx
xk


.k
BT 45. Giải các phương trình lượng giác sau:
a)
cos cos3 sin2 sin6 sin4 sin6 0.x x x x x x
Li gii
Phương trình đã cho tương đương với
2
cos cos 3 sin2 sin 6 sin 4 sin 6 0
cos cos 3 sin 6 sin 2 sin 4 0
cos cos 3 sin 6 .2.sin 3 .cos
cos cos 3 2 sin 6 sin 3 0
cos cos 3 1 4 sin 3 0
cos cos 3 2 cos 6 1 0
2
cos 0
cos 3 0
2 cos 6 1 0
x x x x x x
x x x x x
x x x x x
x x x x
x x x
x x x
xk
x
x
x
x
63
.
18 3
18 3
k
k
xk
xk
b)
1
cos cos2 cos3 sin sin2 sin 3
2
x x x x x x
Li gii
Phương trình đã cho tương đương với
0
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
130 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
2
2
1
cos cos2 cos 3 sin sin 2 sin 3
2
1 1 1
cos2 cos 2 cos 4 sin 2 cos2 cos 4
2 2 2
cos 2 cos 2 cos 4 sin2 cos2 sin 2 cos 4 1
cos2 cos 4 sin 2 sin 2 cos2 sin 2 cos 4 0
cos 4 cos2 sin 2 sin 2 cos 2 sin2 0
cos 4
x x x x x x
x x x x x x
x x x x x x x
x x x x x x x
x x x x x x
x sin 2 cos 2 sin 2 0
cos 4 sin 2 0
cos2 sin 2 0
x x x
xx
xx
2
4
sin 2 1
cos4 sin 2 0 1 2sin 2 sin 2 0 .
1
12
sin 2
2
5
12
xk
x
x x x x x k k
x
xk


sin 2 cos 2 0 2 sin 2 0 sin 2 0 .
4 4 8 2
x x x x x k k
c)
cot cos2 sin sin2 cot cos cot .x x x x x x x
Li gii
Điều kiện:
sin 0 .x x k k
Phương trình đã cho tương đương với
2 2 2
2 2 2
cot cos2 sin sin 2 cot cos cot
cos cos 2 sin sin 2sin cos cos
2 sin cos cos2 sin cos sin cos 0
sin cos sin cos sin cos 0
sin cos 1 sin cos 0
sin cos 0
1 sin cos 0
x x x x x x x
x x x x x x x
x x x x x x x
x x x x x x
x x x x
xx
xx
sin cos 0 2 sin 0 .
44
x x x x k k




1 sin cos 0
2 sin 1
4
1
sin sin
44
2
2
2
44
.
3
2
2
2
44
xx
x
x
x k L
xk
k
xk
xk










d)
sin2 cos sin cos cos2 sin cos .x x x x x x x
Li gii
Phương trình đã cho tương đương với
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 131 | THBTN
2
2
2
sin 2 cos sin cos cos 2 sin cos
2 sin cos sin cos cos 2 sin cos 0
sin 2cos 1 cos cos2 cos 0
sin 1 cos2 cos 0
sin 1 0
sin 1 0
cos2 cos 0
2 cos cos 1 0
sin 1
cos 1
1
cos
2
x x x x x x x
x x x x x x x
x x x x x
x x x
x
x
xx
xx
x
x
x
2
2
2.
2
3
xk
x k k
xk
e)
3 2 6
4 3sin sin 3cos cos .x x x x
Li gii
Phương trình đã cho tương đương với
3 2 6
24
2 4 4
2 3 2
33
3
4 3 sin sin 3 cos cos
sin 1 sin sin 4 1 sin 1 sin 3 cos
sin 1 sin sin 4 3 cos 3 sin sin cos 0
sin 1 sin 1 1 sin 1 sin 0
sin 1 0
sin 1 1 1 sin 0
1
x x x x
x x x x x x
x x x x x x x
x x x x
x
xx
x
sin 1
2
.
2
sin 0
x
xk
k
x
xk
f)
Li gii
Phương trình đã cho tương đương với
3
32
2
2 sin cos2 cos 0
2 sin 1 2 sin cos 0
2 sin sin 1 1 cos 0
2 1 cos 1 cos sin 1 1 cos 0
1 cos 2 1 cos sin 1 1 0
1 cos 0 1
2 1 cos sin 1 1 0 2
x x x
x x x
x x x
x x x x
x x x
x
xx
Giải (1):
1 cos 0 cos 1 2 .x x x k k

Giải (2): Đặt
sin cos 2 2 .t x x t
Khi đó, phương trình (2) trở thành
2
2
0
1
2 1 0 2 0 .
2
2
t
t
t t t
t loai



2sin
3
x cos2x cosx 0.
1 sin
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
132 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
0 sin cos 0 2 sin 0 .
44
t x x x x k k




g)
2cos cos2 cos3 5 7 cos2 .x x x x
Lời giải
2cos cos2 cos 3 5 7 cos2x x x x
2cos cos3 cos2 5 7 cos2x x x x
(cos4 cos2 )cos2 5 7 cos2x x x x
2
(2 cos 2 1 cos2 )cos2 5 7 cos2 0x x x x
32
2cos 2 cos 2 8cos2 5 0x x x
cos2 1
22
5
cos2 ( )
2
x
x k x k
x VN
Vậy nghiệm của phương trình đã cho là
xk
()k
.
h)
22
sin (4cos 1) cos (sin cos sin3 ).x x x x x x
Lời giải
22
2 2 2 2
2 2 2 2
2
sin (4 cos 1) cos (sin cos sin 3 )
4 sin cos sin sin cos cos sin 3 cos
4 sin cos (sin cos ) sin cos sin 3 cos 0
11
sin 2 1 sin 2 (sin 4 sin 2 ) 0
22
1 cos 4 1
1 sin 4 0
22
sin 4 cos 4 1
2s
x x x x x x
x x x x x x x x
x x x x x x x x
x x x x
x
x
xx
in 4 1
4
42
44
3
42
44
82
( )
42
x
xk
xk
k
x
k
k
x
Vậy nghiệm của phương trình đã cho là
82
( )
42
k
x
k
k
x
.
i)
2
cos 3(sin2 sin ) 4cos2 cos 2 cos 2 0.x x x x x x
Lời giải
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 133 | THBTN
2
22
32
2
2
cos 3(sin 2 sin ) 4 cos2 cos 2 cos 2 0.
cos 3(sin 2 sin ) 4(2 cos 1)cos 2 cos 2 0
3 sin (2 cos 1) 8 cos 2 cos 5 cos 2 0
3 sin (2 cos 1) (2 cos 1)(4 cos cos 2) 0
(2 cos 1)( 3 sin cos 4 cos 2)
x x x x x x
x x x x x x
x x x x x
x x x x x
x x x x
2
2
0
2 cos 1 0
3 sin cos 4 cos 2 0
2 cos 1 0
3 sin cos 2(2 cos 1)
2 cos 1 0
31
2 sin cos 2 cos2
22
2 cos 1 0
cos cos sin sin cos 2
33
1
cos
2
cos
3
x
x x x
x
x x x
x
x x x
x
x x x
x
x
22
22
33
2 2 2 ( ).
33
cos2
2
22
93
3
x k x k
x x k x k k
x
k
x
x x k
j)
22
2
(sin cos ) 2 sin 2
sin sin 3
2 4 4
1 cot
x x x
xx
x
Lời giải
ĐK:
sin 0x x k
22
2
22
2
2 2 2 2
2
(sin cos ) 2 sin 2
sin sin 3
2 4 4
1 cot
(sin cos ) 2 sin
2 cos 2 sin
4
1 cot
sin (sin 2 sin cos cos 2 sin ) (sin 2 cos 2 )sin
sin (sin 2
x x x
xx
x
x x x
xx
x
x x x x x x x x x
xx
22
2 2 2
2
cos sin ) (sin 2 cos2 )sin
sin (sin 2 cos sin ) (sin 2 cos2 )sin 0
sin (sin 2 cos2 ) (sin 2 cos2 )sin 0
sin (sin 2 cos 2 )(sin 1) 0
sin 0( )
tan 2 1
sin 2 cos2 0
sin 1
sin 1
2
x x x x x
x x x x x x x
x x x x x x
x x x x
xL
x
xx
x
x
4 8 2
( ).
22
22
k
x k x
k
x k x k
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
134 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
Đối chiếu điều kiện, nghiệm của phương trình đã cho là
82
()
2
2
k
x
k
xk
k)
2 2 2
1 1 15cos 4
2cot 1 2 tan 1 8 sin 2
x
x x x
Lời giải
ĐK:
sinx 0
()
cos 0
2
xk
k
x
xk



2 2 2
2 2 2
22
2 2 2
2 2 2 2
2 2 2
22
1 1 15 cos 4
2 cot 1 2 tan 1 8 sin 2
1 1 15 cos 4
2(cot 1) 1 2(tan 1) 1 8 sin 2
sin cos 15 cos 4
2 sin 2 cos 8 sin 2
sin (2 cos ) cos (2 sin ) 15 cos 4
(2 sin )(2 cos ) 8 sin 2
2(sin cos )
x
x x x
x
x x x
x x x
x x x
x x x x x
x x x
xx
22
2 2 2 2 2
2
2 2 2
2
22
2 sin cos 15 cos 4
4 2(sin cos ) sin cos 8 sin 2
1
2 sin 2
15 cos 4
2
2 sin cos 8 sin 2
8 2 sin 2 15 cos 4
8 sin 2 8 sin 2
7 cos 4 15 cos 4
1
cos 4 4 2 ( ).
2 3 12 2
x x x
x x x x x
x
x
x x x
xx
xx
xx
k
x x k x k
Vậy nghiệm của phương trình đã cho là
( ).
12 2
k
xk
l)
2 sin
4
cos 3 2 sin 2 1.
tan 1 4
x
xx
x
Lời giải
ĐK:
cosx 0
2
()
tan 1
4
xk
k
x
xk




TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 135 | THBTN
2
2 sin
4
cos 3 2 sin 2 1.
tan 1 4
sin cos
cos 3 sin 2 cos2 1
sin
1
cos
cos cos 3 sin2 cos2 1
2 cos 2 cos sin 2 cos2 1 0
2 cos 2 cos 2 sin cos 2 cos 0
2 cos (cos 2 sin cos
x
xx
x
xx
x x x
x
x
x x x x
x x x x
x x x x x
x x x
22
)0
2 cos cos sin (cos sin ) 0
2 cos (cos sin )(cos sin 1) 0
cos 0 ( )
cos sin 0
cos sin 1
42
2 cos 0
4
2
44
2 sin 1
5
4
44
x
x x x x x
x x x x x
xL
xx
xx
xk
x
xk
x
x
2
( ).
2
2
2
xk
k
xk
k
Kết hợp với điều kiện, nghiệm của phương trình đã cho là
2 ( ).x k k

m)
2 2 2 2
3
3 sin cos sin cos sin cos 3sin cos .
22
x x x x x x x x
Lời giải
2 2 2 2
2 2 2 2
22
22
2
3
3 sin cos sin cos sin cos 3 sin cos .
22
3 sin sin cos cos sin cos 3 sin cos
3 sin (sin cos ) cos (cos sin ) 0
(sin cos )(3 sin cos ) 0
sin cos 0
3 sin c
x x x x x x x x
x x x x x x x x
x x x x x x
x x x x
xx
x
2
2
2 sin 0
4
os 0
1
tan
3
2 sin 0
4
44
1
tan
66
3
x
x
x
x
x k x k
x k x k
x
Vậy nghiệm của phương trình đã cho là
4
( ).
6
xk
k
xk
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
136 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
n)
(2 sin 1)(cos2 sin ) 2 sin3 6 sin 1
2cos 3 0.
2cos 3
x x x x x
x
x
Lời giải
ĐK:
3
2cos 3 0 cos 2 .
26
x x x k
32
(2 sin 1)(cos2 sin ) 2 sin 3 6 sin 1
2 cos 3 0
2 cos 3
(2 sin 1)(cos2 sin ) 2 sin 3 6 sin 1 (2 cos 3)(2 cos 3)
0
2 cos 3
(2 sin 1)(cos2 sin ) 2(3 sin 4 sin ) 6 sin 1 4 cos 3 0
(2 sin 1)(cos2 sin ) 8 s
x x x x x
x
x
x x x x x x x
x
x x x x x x x
x x x
32
32
2
22
2
2
in 1 4(1 sin ) 3 0
(2 sin 1)(cos2 sin ) 8 sin 4 sin 2 0
(2 sin 1)(cos2 sin ) 2(2 sin 1)(2 sin 2 sin 1) 0
(2 sin 1)(1 2 sin sin 4 sin 4 sin 2) 0
(2 sin 1)(2 sin 3 sin 3) 0
2 sin 1 0
2 sin 3
xx
x x x x x
x x x x x x
x x x x x
x x x
x
x sin 3 0( )
2
1
6
sin ( ).
7
2
2
6
x VN
xk
xk
xk
Vậy nghiệm của phương trình
2
6
( ).
7
2
6
xk
k
xk
o)
2
3 3 1
cos cos 2 2.
4 4 2
xx
2
22
22
2 2 2 2 2 2
22
22
3 3 1
cos cos2 2.
4 4 2
3 3 1
cos (1 2 sin ) 2.
4 4 2
31
cos sin 2
44
3 1 3 1
1. cos 1. sin 1 1 . cos sin 2
4 4 4 4
31
2 cos sin
44
31
cos sin
44
12
cos2 2 2
2 3 3
xx
xx
xx
VT x x x x
VT x x
xx
x x k x k
Vậy nghiệm của phương trình đã cho là
( ).
3
x k k
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017 BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
ADMIN TRN & THY CÔ THÀNH VIÊN TOÁN HC BC–TRUNG–NAM 137 | THBTN
NG BÀI TN HÌNH VÀ GII CHI TIT - HY VNG
LÀ TÀI LIU B ÍCH GIÚP CÁC THY CÔ TRONG QUÁ TRÌNH BIÊN SON 
GING DC SINH CÓ TÀI LIU THAM KHO T
HC
THI GIAN BIÊN TP NGC CÒN HN CH, CHC CHN
KHÔNG TH C NHNG SAI SÓT, MONG BC THÔNG CM
 B TÀI LIT CHNG T
CHÚC CÁC BN CÓ MT CH THÀNH CÔNG!
LƯU Ý: BỘ TÀI LIỆU CÒN 500 CÂU TRẮC NGHIỆM - FULL GIẢI DO BAN BIÊN TẬP
BTN SOẠN GIẢI - CÁC THẦY CÔ CÙNG CÁC EM TÌM ĐỌC NHÉ !
THY TRN TÀI - 0977.413.341
THÂN TNG
| 1/137
| | Tải xuống

Có thể bạn quan tâm:

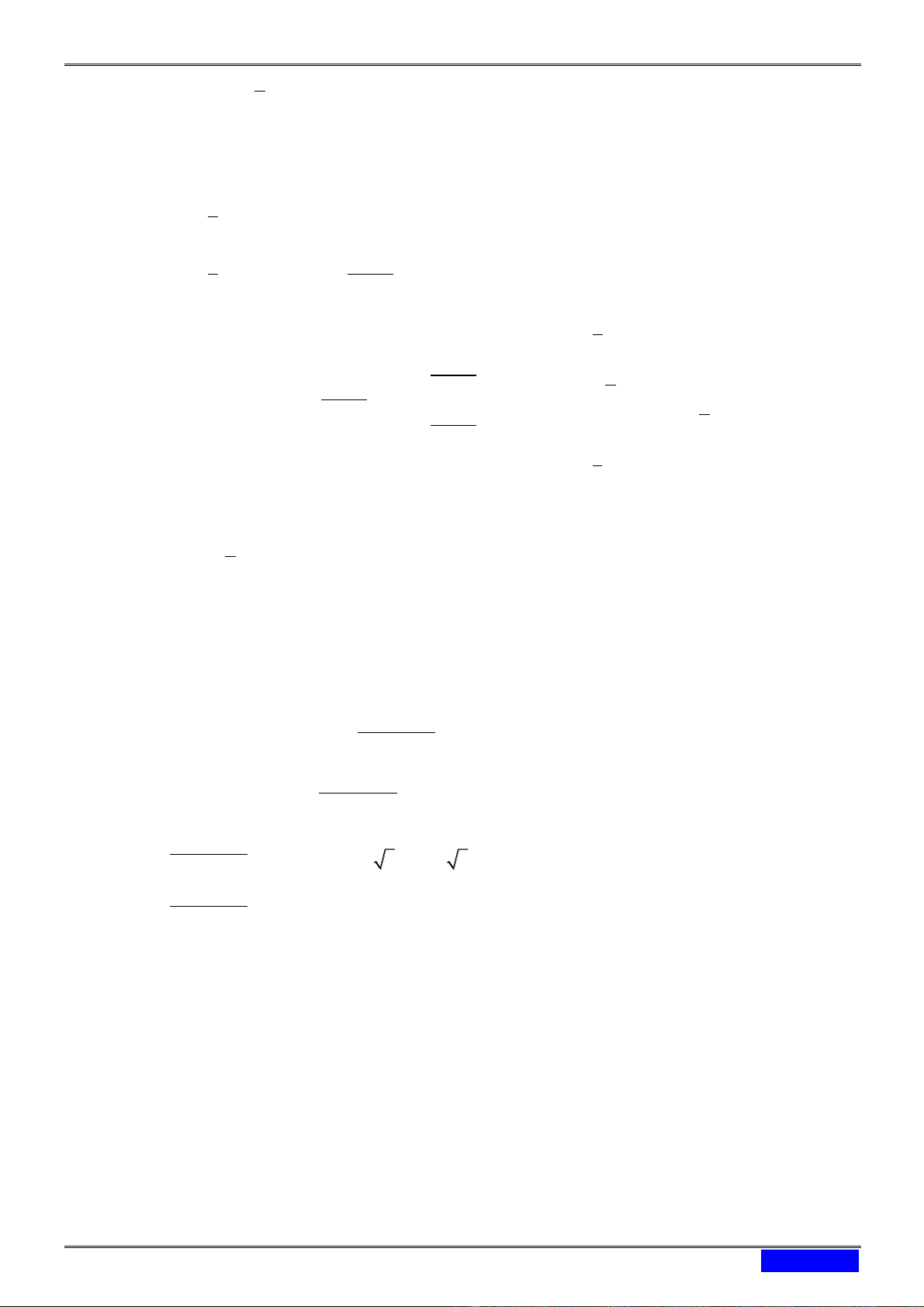
Preview text:

TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
CHUYÊN ĐỀ 1: PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Phöông trình löôïng giaùc ñöa veà baäc hai vaø baäc cao cuøng 1 haøm löôïng giaùc
Quan sát và dùng các công thức biến đổi để đưa phương trình về cùng một hàm lượng giác (cùng sin
hoặc cùng cos hoặc cùng tan hoặc cùng cot) với cung góc giống nhau, chẳng hạn: Dạng Đặt ẩn phụ Điều kiện 2
a sin X bsin X c  0 t  sin X 1   t 1 2
a cos X b cos X c  0 t  cos X 1   t 1  2
a tan X b tan X c  0 t  tan X X    2 k 2
a cot X b cot X c  0 t  cot X X k Nếu đặt 2 2
t  sin X , cos X hoặc t  sin X , cos X thì điều kiện là 0  t 1.
Ví dụ 1. Giải phương trình: 2
4cos x  4sin x 1 0. Giải:   2  x 2 pt 4 1 sin
sin x 1 0  4sin x  sin x 3  0 sin x  1    3 sin x   4   Với sin x  1
  x    k 2,  2 k   3  x   arcsin    2 k  3  4 
 Với sin x    ,  4 k   3  x    arcsin     2    4 k
Ví dụ 2. Giải phương trình: cos 2x 3cos x  2  0. Giải: cos x 1 x k2 2 pt  2cos  
x  3cos x 1  0  1   ,  cos x
x    k2 k   2  3
Ví dụ 3. Giải phương trình: 3cos 2x  7sin x  2  0. Giải:
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 1 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  5 sin x     2  3 x 2 pt 3 1 2sin
 7sin x  2  0  6
 sin x  7sin x 5  0   1 sin x    2  Với 5
sin x  thì pt vô nghiệm vì sin x[ 1;1] 3   x    k2 1   Với 6 sin x     ,  2  7 kx   k2  6
Ví dụ 4. Giải phương trình: 4 2
4sin x 5cos x  4  0. Giải: 2 sin x 1 4   x   2  x 4 2 pt 4sin 5 1 sin
 4  0  4sin x 5sin x 1 0   2 1 sin x   4   Với 2 2
sin x 1 cos x  0  cos x  0  x   k,  2 k    Với 2 1 1 cos2 x 1 1 sin x  
  cos2 x  x   k,  4 2 4 2 6 k
Ví dụ 5. Giải phương trình: 2
cos4x 12sin x 1 0. Giải: cos 2x 1   2 x      x 2 pt
2cos 2 1 6 1 cos2 1 0  2cos 2x 6cos2x  4  0  cos2x 2  Với cos2 x 1
  x k ,  k
 Với cos2 x 2 thì phương trình vô nghiệm 1 2 5
Ví dụ 6. Giải phương trình: 2  tan x    0. 2 cos x 2 Giải:
Điều kiện cosx  0 1  1  2 5 pt   1    1 1 1   0   .  2.  2  0 2 2  cos x  cos x 2 2 2 cos x cos x 1 1  
 2  cos x   x    k2,  cos 2 3 k x 2 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC ÀI T V N ỤN BT 1.
[1D1-2]Giải các phương trình lượng giác sau: a) 2
2sin x sin x 1 0. b) 2
4sin x 12sin x 7  0. c) 2
2 2 sin x (2 2)sin x 1 0. d) 3 2 2
 sin x sin x  2sin x 1 0. e) 2
2cos x 3cos x 1 0. f) 2
2cos x 3cos x  2  0. g) 2
2cos x  ( 2  2)cos x  2. h) 2
4cos x  2( 3  2)cos x  6. i) 2
tan x  2 3 tan x 3  0. j) 2
2tan x  2 3 tan x 3  0. k) 2
tan x  (1 3)tan x  3  0. l) 2
3cot x  2 3cot x 1 0. m) 2
3cot x (1 3)cot x 1 0. n) 2
3cot x  (1 3)cot x 1 0. Lời giải a) [1D1-2] 2
2sin x sin x 1  0   x   k2  2 sinx 1     1 
x    k2 ,k  . sin x    6  2  7 x   k2  6 b) [1D1-2] 2
4sin x 12sinx  7 0.  7   sinx x   k2  2  6     ,  .  1  5 k  sin x x   k2  2  6 c) 2
2 2 sin x (2 2)sin x 1 0   sinx  2 x   k2   6    ,  1 k  . sin x   5  x   k  2 2   6 d) [1D1-2] 3 2 2
 sin x sin x  2sin x 1 0   x   k2  2 sin  x  1    x   k2 1  6
 sin x    ,   2 5 k  x   k2 sinx  1    6  
x    k2  2 e) 2
2cos x 3cos x 1 0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 3 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC cos x 1 x k2   1    ,  cos x
x    k2 k   2  3 f) [1D1-2] 2
2cos x 3cos x 2  0 cos x  2    
1  x    k2,   . cos  3 k x  2 g) [1D1-2] 2
2cos x  ( 2 2)cosx  2 cos x 1 x k2  2    3 ,k   . cos x    x    k2  2  4 h) [1D1-2] 2
4cos x  2( 3 2)cosx  6.  3  5 cos x   x   k 2 2  6     ,k  .  2  3 cos   x    k x 2  2  4 i) [1D1-2] 2
tan x 2 3 tan x 3  0    x  2 tan
3  0  tan x   3  x    k, k  . 3 j) [1D1-2] 2
2tan x 2 3 tan x 3  0  3  3  3 3  tan x   x  arctan 
  k ,k   2  2  .   k) [1D1-2] 2
tan x  (1 3) tanx  3 0   tan  1 x       4 k x    
, k,l   . tan x  3  x     3 l l) [1D1-2] 2
3cot x 2 3cot x 1  0     x  2 1 3 cot
1  0  cot x  
x    k,k   . 3 3 m) [1D1-2] 2
3 cot x  (1 3)cotx  1 0 cot   x  1 x      4 k    ,k,  3 l   . cot x     3 x     3 l n) [1D1-2] 2
3cot x (1  3)cot x 1  0  4 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC cot   x  1 x      4 k    ,k,  3 l   cot x      3 x      3 l BT 2.
[1D1-2] Giải các phương trình lượng giác sau: a) 2
6cos x 5sin x  2  0. b) 2
2cos x 5sin x  4  0. c) 2
3 4cos x  sin x(2sin x 1). d) 2
sin x 3cos x 3  0. e) 2 2
 sin x 3cos x 3  0. f) 2
2cos 2x 5sin 2x 1 0. g) 2 4
3sin x  2cos x  2  0. h) 4 2
4sin x 12cos x  7. i) 4 2
4cos x  4sin x 1. j) 4 2
4sin x 5cos x  4  0. Lời giải a) 2 x x     2 6cos 5sin 2 0
6 1sin x5sin x 2  0  1 sin x    2 2
 6sin x 5sin x  4  0   4 sin x   3   x    k2 1      Với 6
sin x   sin x sin       ,  2  6   7 kx   k2  6  Với 4
sin x   Phương trình vô nghiệm. 3 b) 2 x x     2 2cos 5sin 4 0
2 1sin x5sin x 4  0  1 sin  2 2sin 5sin 2 0 x x x       2  sin x  2   x   k2 1    Với 6
sin x  sin x sin    ,  2 6  5 kx   k2  6
 Với sin x 2  Phương trình vô nghiệm. c) 2  x x x     2  x 2 3 4cos sin (2sin 1) 3 4 1 sin
 2sin x sin x sin x 1 2 2sin x sin x 1 0       1 . sin x    2   Với sin x 1
  x   k 2,  . 2 k
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 5 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   x    k2 1      Với 6
sin x   sin x sin       ,  . 2  6   7 kx   k2  6 d) 2  x x     2 sin 3cos 3 0
1cos x3cos x 3  0 cos x 1 2
cos x 3cos x  2  0   . cos x  2  Với cosx 1
  x k2 ,  k  .
 Với cosx 2  Phương trình vô nghiệm. e) 2  x x      2 2sin 3cos 3 0.
2 1cos x3cos x 3  0 cos x 1 2
2cos x 3cos x 1 0       1 . cos x   2  Với cosx 1
  x k2 ,  k  .    Với 1
cosx  cos x c  os
x   k 2,  . 2 3 3 k f) 2 x x     2 2cos 2 5sin 2 1 0
2 1sin 2x5sin2x 1 0 sin 2x 1 2
2sin 2x 5sin 2x 3 0      3 . sin 2x   2    Với sin2 x 1  2 x   2 k   x   k,  . 2 4 k  Với 3
sin x   Phương trình vô nghiệm. 2 g) 2 4 x x     2  x 4 3sin 2cos 2 0 3 1 cos  2cos x  2  0 2 cos x 1
1 cos2x 1 cos2x 1 4 2 2cos   
x  3cos x 1  0  1  2  2 cos   x   2 cos2x  0  2 2cos x 1 0  Với cos2 x 1  2 x  2 k   x k  , k  .   
 Với cos2 x 0 2 x   k  x   k ,  . 2 4 2 k h) 4 2 4 x x   x   2 4sin 12cos 7 4sin 12 1 s  in x 7  0 6 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  2 5 sin x  1 cos2x 5  2  cos2x  4  4 2 4sin 
x 12sin x  5  0    2 2    .  2 1 2 cos2x  0 sin x  1   2sin x  0  2  Với cos2 x  4
  Phương trình vô nghiệm.   
 Với cos2 x 0 2 x   k  x   k ,  . 2 4 2 k i) 4 2 4 x x   x   2 4cos 4sin 1 4cos 4 1cos x1  2 1 cos x  cos2x  0  4 2 2
4cos x 4cos x 3 0         . 2 3   2 3 cos cos x   x    2  2  Với 2 3
cos x    Phương trình vô nghiệm. 2   
 Với cos2 x 0 2 x   k  x   k ,  . 2 4 2 k j) 4 2 4 x x    x   2 4sin 5cos 4 0 4sin
5 1sin x4  0 2 2 sin x 1 1  sin x  0 cos x  0 4 2 4sin   x 5sin x 1 0 1 1 cos2       x 1  1  2 sin x    cos2x   4  2 4  2 
 Với cosx 0  x   k ,  . 2 k     Với 1
cos2 x  cos2 x c  os 2
x    2k   x    k,  . 2 3 3 6 k BT 3.
[1D1-3] Giải các phương trình lượng giác sau:
a) 2cos2x 8cos x 5  0.
b) 1 cos2x  2cos . x
c) 9sin x cos2x  8.
d) 2cos2x 5sin x  0.
e) 3sin x cos2x  2.
f) 2cos2x 8sin x 5  0. g) 2cos2 x
x  3sin x 1  0.
h) 5cos x  2sin  7  0. 2 i) 2
sin x  cos2x  cos x  2. j) 2
cos2x  cos x sin x  2  0. Lời giải
a) [1D1-3] 2cos2x 8cos x 5  0. Ta có: x x     2 2cos2 8cos 5 0 2 2cos x   1 8cos x 5  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 7 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  3
cos x  l  2 2
 4cos x 8cos x  3  0    1 cos x   2 1 
 Với cos x   x    k2 k  . 2 3
b)[1D1-3] 1 cos2x  2cos . x Ta có: 2
1 cos2x  2cos x  2cos x  2cos x  0  2cos xcos x   1  0 cos   x  0    x    2 k ,   . cos 1 k x  x k2
c) [1D1-3] 9sin x cos2x  8. Ta có: 2
9sin x  cos2x  8 1 2sin x 9sin x  8 sin x 1 2  2
 sin x 9sin x 7 0   7
sin x  l  2   Với sin x 1
  x   k2 ,   . 2 k
d) [1D1-3] 2cos2x 5sin x  0. Ta có: 2
2 cos2x 5sin x  0  21 2sin x 5sin x  0
sin x  3 l 2 2sin   
x  5sin x  3  0   1 sin x    2   x    k2 1   Với 6 sin x     ,  . 2  7 kx   k2  6
e)[1D1-3] 3sin x cos2x  2 Ta có: 2
3sin x  cos2x  2  3sin x 12sin x 2  0 sin x 1 2
2sin x 3sin x 1 0        1 sin x   2   Với sin x 1
  x   k 2,k  . 2
8 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   x   k2 1   Với 6 sin x    ,k  . 2  5 x   k2  6
f) [1D1-3] 2cos2x 8sin x 5  0. Ta có: x x     2 2cos2 8sin 5 0
2 1 2sin x8sin x 5  0  3
sin x  l  2 2  4
 sin x  8sin x 3  0   1 sin x   2   x   k2 1   Với 6 sin x    ,k  . 2  5 x   k2  6
g) [1D1-3] 2cos2x 3sin x 1 0. Ta có: sin x 1
2cos2x 3sin x 1 0 2 2 1 2sin x 2 3sin x 1 0
4sin x 3sin x 1 0                1 sin x    4   Với sin x 1
  x   k 2,k  . 2   1  x   arcsin   k   2 1  4 
 sin x     ,  . 4 k   1  x     arcsin   k   2   4  h) [1D1-3] 5cos 2sin x x   7  0. 2 Ta có: x  2 5cos 2sin 7 0 5 1 2sin x        2sin x x  7    0 2  2  2 sin x 1  2 x x 2  1  0sin  2sin 12  0   2 2 x  6 sin   l  2 5   Với sin x 1 x
    k2  x    k4, k  . 2 2 2 i) [1D1-3] 2
sin x  cos2x  cos x  2.
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 9 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Ta có: 2 2 2
sin x  cos2x  cos x  2 1cos x  2cos x 1 cos x  2  0 cos x 1 2
 cos x  cos x  2  0  cosx  2   l  Với cos x 1
  x k2 ,  k  . j) [1D1-3] 2
cos2x  cos x sin x  2  0. Ta có: 2 2 2
cos2x  cos x sin x  2  0 1 2sin x 1sin x sin x  2  0 sin x 1 2 3sin   
x  sin x  4  0  4
sin x   l  3   Với sin x 1
  x   k 2,k  . 2 BT 4.
[1D1-3] Giải các phương trình lượng giác sau: a) 2
3cos x  2cos2x  3sin x 1. b) 2
cos4x 12sin x 1 0. c) 2 cos4 x
x  2cos x 1  0. d) 2 16sin  cos 2x 15. 2 e) 2
cos2  2cos  2sin x x x x  f) 2
cos2x 3cos x  4cos  2 2 g) 2
1 cos4x  2sin x  0. h) 2
8cos x cos4x 1. i) 2
6sin 3x cos12x  4. j) 4 4
5(1 cos x)  2sin x cos . x k) 4 4
cos x sin x  cos4x  0. l) 4 4 4(sin x  cos )
x  cos 4x  sin 2x  0. Lời giải a. [1D1-3] 2
3cos x  2cos2x  3sin x 1   2  x   2 3 1 sin
2 1 2sin x  3sin x 1 2
 sin x 3sin x  2  0
 sin x 1 hay sin x  2 (loại)  sin x 1 
x   k2 k   . 2 b. [1D1-3] 2
cos4x 12sin x 1 0 2
 2cos 2x 1 61 cos2x 1 0 10 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2
 2cos 2x  6cos2x  4  0  cos2x  1  hay cos2x  2  (loại) 
x   k k   . 2 c. [1D1-3] 2
cos4x 2cos x 1  0. 2
 2cos 2x 11 cos2x 1 0 2
 2cos 2x cos2x 1 0  cos2x 1 hay 1 cos 2x   2 
x k k   hay x    k k   . 3 d. [1D1-3] 2
16sin x  cos 2x  15. 2    x   2 8 1 cos 2cos x   1 15 2
 2cos x 8cos x  6  0  cos x  1
 hay cosx  3(loại)
x    k2 k   . e. [1D1-3] 2 cos2 2cos 2sin x x x 2 2
 2cos x 1 2cos x 1cos x 2
 2cos x 3cos x  2  0  cos x  2  (loại) hay 1 cos x  2 
x    k2 k   . 3 f. [1D1-3] 2 cos2 3cos 4cos x x x 2 2
 2cos x 13cos x  21 cos x 2
 2cos x 5cos x 3  0
 cos x  3(loại) hay 1 cos x   2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 11 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2  x  
k2 k   . 3 g. [1D1-3] 2
1 cos4x  2sin x  0 2
1 2cos 2x 1cos2x  0 2
 2cos 2x  cos2x  0  cos2x  0 hay 1 cos 2x  2   
x   k k   hay x    k k   . 4 2 6 h. [1D1-3] 2
8cos x cos4x 1    x 2
4 1 cos2  2cos 2x 11 2
 2cos 2x  4cos2x  4  0
 cos2x 1 3 (loại) hay cos2x 1 3 1
x   arccos1 3 k k   . 2 i. [1D1-3] 2
6sin 3x cos12 x 4     x 2
3 1 cos6  2cos 6x 1 4 2
 2cos 6x 3cos6x  0  cos6x  0 hay 3 cos6x   (loại) 2    x
k k   . 12 6 j. [1D1-3] 4 4
5(1 cos x)  2sin x cos x    x    2 2 x x 2 2 5 1 cos 2 sin cos
sin x cos x 2 2
 55cos x  21cos x cos x 2
 2cos x 5cos x  2  0  cos x  2  (loại) hay 1 cos x   2 2  x  
k2 k   . 3 12 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC k. [1D1-3] 4 4
cos x sin x  cos4x  0   2 2 x x 2 2 x x 2 cos sin cos sin  2cos 2x 1 0 2
 2cos 2x  cos2x 1 0  cos2x  1  hay 1 cos 2x  2   
x   k k   hay x    k k   . 4 2 6 l. [1D1-3] 4 4 4(sin x  cos )
x  cos 4x  sin 2x  0   2 2  x x 2 4 1 2sin cos
1 2sin 2x sin 2x  0 2 2
 4 2sin 2x 1 2sin 2x sin 2x  0 2
 4sin 2x sin 2x 5  0  sin 2x  1  hay 5 sin 2x  (loại). 4 
x    k k   . 4 BT 5.
[1D1-3] Giải các phương trình lượng giác sau:          a) 2 cos 2    x   3cos x  1     0. b) 2 cos  x  4cos  x      4.  3   3   3   6       c) 2 2 4cos (6 
x  2) 16cos (1 3 ) x 13. d) 5 5cos 2x   4sin  x      9.  3   6       e) 5 7 sin 2  x   3cos x  1     2sin .
f) cos 2x  3 sin 2x  3 sinx  4 cosx .  2   2 x  g) 3sin 2  4   2 
x  3 sin x  cos 2x  cos x  2. h) 2 2 cos x   9  cos x      1. 2  cos x   cos x  i)  2 1   1 4 sin  1  1  x   4 sin x       7. j) 2 cos x   2  2cos   2 x   sin x   sin x  2 cos x  cos x Lời giải      a) 2 cos 2  x   3cos x  1     0.  3   3       Xét phương trình 2 cos 2  x   3cos x  1     0.  3   3        cos 2   x    3cos x  1      0   3   3 
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 13 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC             2  2cos   x   3cos x   0  cos x  2cos x   3           0  3   3   3    3       cos  x     0  3       3 cos  x      l   3  2       Xét cos x  
 0  x    k  x   k ,   .  3  3 2 6 k 
Vậy tập nghiệm của phương trình là 
S    k ,  . 6 k         b) 2 cos   x  4cos  x      4.  3   6  Lời giải      Xét phương trình 2 cos   x  4cos  x      4. .  3   6  2       2      sin    x  4cos  x  4 1 cos  x  4cos  x          4  6   6   6   6  2           cos     x  4cos
x  3  0  cos  x        1 hoặc cos     3(loại)  6   6   6   6 x           Với cos  x 1  cos x    1   x   k  
2  x  k 2,   .  6   6   6  6 k  
Vậy tập nghiệm của phương trình  S  x   k2,  . 6 k    c) 2 2
4cos (6x  2) 16cos (13 ) x 13. Lời giải Xét phương trình 2 2
4cos (6x  2) 16cos (13 ) x 13. . 2   x   2    x 2 4cos 6
2 8.2cos 1 3 13  4cos 6x  28.cos2 
13x1 13  2   x   x  2 4cos 6 2 8cos 6
2 8 13  4cos 6x  28cos6x  25  0   x   1 cos 6 2  hoặc  x   5 cos 6 2   (loại). 2 2 14 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  Với  x   1
cos 6 2  cos 6 x 2   c  os 2 3       1  6  2   k2
6x   2  k2 k x      3  3 x  18 3 3       ,  .       1 k
6  2    k2
6x    2  k2 k x       3  3 x  18 3 3   
Vậy tập nghiệm của phương trình là 1 kS     ,k  .  18 3 3       d) 5 5cos 2  x   4sin  x      9.  3   6  Lời giải      Xét phương trình 5 5cos 2  x   4sin  x      9.  3   6                5cos 2   x    4sin    x  
 9  5cos 2 x    4sin  x          9   6    6    6   6              2 2 51 2sin    x    4sin x   9 10sin x   4sin x  14          0   6   6   6   6      sin    x     1 hoặc 7 sin x      (loại).  6   6  5         Với sin x   1   x    k  
2  x  k 2,   .  6   6  2 3 k 
Vậy tập nghiệm của phương trình là 
S    k2 ,  . 3 k         e) 5 7 sin 2  x   3cos x  1     2sin .  2   2 xLời giải        Ta có: 5 sin 2x   sin  2x   2       cos 2x,  2   2    7       cos  x
 cos x  3  cos x          sinx  2   2   2 
Phương trình đã cho trở thành cos2x 3sin x 1 2sinx 2
1cos2x sin x  0  2sin x sin x  0  sin x2sinx   1  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 15 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   x k sin x  0  x k    1     
x   k2 ,  . sin x  sin x  sin  6 k  2  6  5 x   k2  6   
Vậy tập nghiệm của phương trình 5 
S  k ;  k2 ;  k2,  . 6 6 k   
f) cos2x  3sin 2x  3sin x  4  cos . x Lời giải
Xét phương trình cos2x  3sin 2x  3sin x  4  cos . x       cos2  
x  3 sin 2x cos x  3sin x  4   cos 2x    cos x     2    3   3                cos 2  x    cos x     2   cos 2 x     sin  x      2    3   3    6   2  3              2 cos 2   x    sin x   2   2sin x   sin x   3          0   6   6   6   6      sin    x     1 hoặc 3 sin x      (loại).  6   6  2         Với sin x   1   x    k  
2  x  k 2,   .  6   6  2 3 k 
Vậy tập nghiệm của phương trình là 
S    k2 ,  . 3 k    g)
3sin 2x  3sin x cos2x cos x  2. Lời giải
Xét phương trình 3sin 2x  3sin x  cos2x cos x  2. biến đổi tương tự như câu f ta được:             cos 2  x   cos x  1 cos 2 x    1 sin x           0  3   3    6   6              2  2  sin   x   sin x   0  sin x   2  sin x  1           0  6   6   6    6   16 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC     x            6 k x  6 k  sin x     0  6          
x    k2  x   k2 ,k  .     1   6 6  3 sin x      sin     6  2 6  5
x    k 2 x    k2   6 6   
Vậy tập nghiệm của phương trình 
S    k ;  k2 ;  k2 ,  . 6 3 k    h)  2 4   2 2 cos  x   9  cos x      1. 2  cos x   cos xLời giải  Xét phương trình  2 4   2 2 cos  x   9  cos x    
 1. ĐKXĐ. x   k ,  . 2 k  cos x   cos x  2 Đặt  2  2 4 2 2  4 2  t
 cos x t
 cos x  4  t  4      cos 2 2 cos  cos  cos x   x x x
Khi đó phương trình đã cho trở thành:  2t   2 2
4 9t 1 2t 9t  7  0 t  1    7 t    2 Khi 2 2 t  1
 cos x 1 cos x  cos x  2  0 cos x
 cos x 1 hoặc cos x  2  (loại). Với cos x 1
  x k2 (TM) Khi 7 2 7 2 t   
 cos x    2cos x  7cos x  4  0 2 cos x 2 1
 cos x   hoặc cos x  4 (loại) 2   Với 1 2 2 cos x   cos  x    k 2,  . 2 3 3 k  
Vậy tập nghiệm của phương trình 2 
S  k2 ;  k2,  . 3 k   
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 17 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC i)  2 1   1 4 sin  x   4 sin x       7. 2  sin x   sin x Lời giải Xét phương trình  2 1   1 4 sin  x   4 sin x     
 7. ĐKXĐ. x k,  . 2 k  sin x   sin x  Đặt  1  2 2 1   t x   t x     2t   2 1 sin sin 2 2  sin    . 2 x 2 sin   x  sin x  sin x   3 t  
Phương trình đã cho trở thành:  2t   2 2 4
2  4t  7  4t  4t 15  0   .  5 t    2 Khi 3 1 3 2 t   sin x
  2sin x 3sin x  2  0VN  2 sin x 2 Khi 5 1 5 t    sin    . 2 x sin x 2 2 1
 2sin x  5sin x  2  0  sin x   hoặc sin x  2  (loại). 2   Với 1 sin  x   sin  2  6      x    k2  6   ,  .  7 kx   k2  6   
Vậy tập nghiệm của phương trình là: 7  S    k2;  k2,  . 6 6 k    j) 2 1  1 cos  x   2  2cos   2 cos xx  cos x Lời giải  Xét phương trình 2 1  1 cos  x   2  2cos 
. ĐKXĐ x   k,  2 cos xk x  cos x  2 Đặt  1  2 2 1 t  cos x
t  cos x     2. 2  cos x  cos xt  0
Phương trình đã cho trở thành: 2t  2t   . t  2  18 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Khi 1
t  0  cos x   0VN  cos x Khi 1 2 t  2   cos x   2
  cos x  2cos x 1 0  cos x 1 x k2 (TMĐK) . cos x
Vậy tập nghiệm của phương trình: S k2,k  . BT 6.
[1D1-2] Giải các phương trình lượng giác sau: a) 3 2  3 2tan . b) 1 2  3cot  5. 2 cos x x 2 cos x x c) 3 4  3cot  3. d) 9 13cos x   0. 2 sin x x 2 1 tan x e) 2 3 2tan 1 2 5 x  3   f) 2  tan x    0. cos x 2 cos x 2 g) 1
3sin x  cos x   g) 2 2
2sin x  tan x  2. cos x a) 3 2  3 2tan . 2 cos x x Lời giải
Điều kiện: x    . 2 k 3 2  3 2tan  3 2 1 tan  2  3 2tan . 2 cos x x x x
 tan x  0  x k k  . b) 1 2  3cot  5. 2 cos x x Lời giải  Điều kiện k x  . 2 1 2  x    2 3 3cot 5 1 tan x   5. 2  2 cos x tan xt 1 Đặt 2
t  tan x (t  0) , ta có phương trình: 2
t  4t  3  0   . t  3   tan  1 x       4 k x     k  . tan x   3  x      3 k c) 3  3cot  3. 2 sin x x Lời giải
Điều kiện: x k .
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 19 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 3 3cot  3  3 2 1 cot  3cot  3. 2  sin x x x x   cot  0 x   kx  2 2
 3 cot x 3cot x  0     . cot x  3  x     6 k d) 4 9 13cos x   0. 2 1 tan x Lời giải
Điều kiện: x    . 2 k 4 2 9 13cos x
 0  9 13cos x  4cos x  0. 2 1 tan x  9 cos x  ko tm   4
x k2.  cos x 1 e) 2 3 2tan x  3   cos x Lời giải
Điều kiện: x    . 2 k 2 3  1  3 2tan x  3   2 1  3    . 2 cos x  cos x  cos xt 1 Đặt 1 t   t   1 , ta có phương trình 2 2t 3t 1 0      . cos 1 xt  ko tm  2
 cos x 1 x k2. k  . f) 1 2 2 5  tan x    0. 2 cos x 2 Lời giải
Điều kiện: x    . 2 k 1 2 2 5 1  1  2 5  tan x    0   1      0. 2 2 cos x 2
2  cos x  cos x 2 Đặt 1 t   t   1 , ta có phương trình cos x 2 1 
t  4t  4  0  t  2  cos x
x    k2. 2 3
20 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC g) 1
3sin x  cos x   cos x Lời giải
Điều kiện: x    . 2 k Chia cả 2 vế cho cos x ta được: 1 2 3 tan x 1 
 3 tan x 1 1 tan . 2 cos x x tan  0 x kx 2 tan  
x  3 tan x  0     k  . tan x  3 x     3 k g) 2 2
2sin x  tan x  2. Lời giải
Điều kiện: x    . 2 k 2 2   x x    2  x 1 2sin tan 2 2 1 cos  1    2. 2  cos x  t  1  loai Đặt 2  t  cos x 0  t   1 . Ta có phương trình 2 2
t t 1  0  .  1 t   2  1 cos   x x    k  2    Vậy 2 4 k     x   .  1  3 4 2 cos x   x    k2  2  4 BT 7.
[1D1-3] Giải các phương trình lượng giác sau:
a) 8sin xcos x cos4x 3  0. b) 2
2sin 8x  6sin 4xcos4x  5. c) cos x    1sin .
d) 1 cos x(2cos x 1) 2.sin x 1. 1 sin x x 1 cos x  2   
e) 3sin 2x 2sin x  2.
f) 2sin x 3 2 sin x sin 2x 1  1.  sin 2xcos x 2
(sin x  cos x) g) 1 2cos2 3 4  2sin 2x
x  8cos x  7   g) 
 2 3  2(cot x 1). cos x 2 cos x sin 2x h) 2 6
3cos4x  2cos x 3  8cos . x k) 2 3cos x  2  3  (1cos x).cot . x
l) sin3x cos2x 1 2sin xcos2 . x m) 2cos5 .
x cos3x  sin x  cos8 . x n) 6 6
4(sin x  cos x)  4sin 2 .x
o) sin 4x  2  cos3x  4sin x cos . x Lời giải
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 21 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
a) 8sin xcos x cos4x 3  0. Lời giải Ta có: 2
8sin xcos x cos4x 3  0  4sin 2x  2sin 2x  2  0  sin 2x  1  
x    k k  . 4 b) 2
2sin 8x  6sin 4xcos4x  5. Lời giải
sin8x 1N  Ta có: 2 2 2sin 8 
x  6sin 4x cos 4x  5  2sin 8x  3sin 8x  5  0   5
sin8x   L  2     8   2 k x k   x   k   2 16 4 . c) cos x 1sin . 1 sin x x Lời giải
Điều kiện: sin x  1
  x    k2 k   . 2   cos x cos x  0    PT 2 1 sin . x cos x cos x x        2 k k    . 1 sin x cos x 1  x k2   x   k2
Kết hợp điều kiện, phương trình có hai họ nghiệm là:  2 k  .  x k2
d) 1 cos x(2cos x 1)  2.sin x 1. 1 cos x Lời giải
Điều kiện: x k2 k  .   
Ta có: 1 cos x(2cos x 1) 2.sin x 2
11 2cos x  cos x  2 sin x 1 cos 1 cos x x sin   x  2  Lx    k2     2  x 4 2 1 sin  sin x  0       k   2 . sin  x    sin     5 x   k2  2  4    4 
e) 3sin 2x 2sin x  2. sin 2xcos x 22 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Lời giải
Điều kiện: sin 2x  0  x k k  . 2
  2sin x3cos x   1 1   2.
2sin xcos xcos x 2
 3cos x 1 2cos x . 2
 2cos x 3cos x 1 0 . cos x 1   1 . cos x   2
x k2 l     . x    k2  3 
Kết hợp điều kiện, phương trình có nghiệm: x    k2 k   . 3
3sin2x  2sin x   2  
1 ĐK: sin2x  0   sin2 x k x cos x 2 2
f) 2sin x  3 2 sin x sin 2x 1  1  . 2
(sin x  cos x) Lời giải    
Điều kiện: sin x  cos x  0  sin x
 0  x    k k     .  4  4 2
Ta có: 2sin x  3 2 sin x sin 2x 1 2  1
  2sin x  3 2 sin x sin 2x 1 1  sin 2 2 (sin  cos ) x x x sin  
x   2 VN x    k2   2 4
 2sin x  3 2 sin x  2  0      k   2 . sin  x    sin     5 x   k2  2  4    4 
Kết hợp với điều kiện, suy ra phương trình có nghiệm: 5 x
k2 k   . 4 g) 1
2cos2x 8cos x  7  . cos x Lời giải
Điều kiện: cos x  0  x   k k   . 2 PT 2  2cos2 .
x cos x  8cos x  7 cos x 1 0  x  2 x   2 3 2 2cos 2cos
1 8cos x  7cos x 1 0  4cos x 8cos x 5cos x 1 0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 23 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC cos x 1 x k2  cos   x   1  2
4cos x  4cos x   1  0  1   k  . cos x
x    k2  2  3 x k2
Vậy, phương trình có nghiệm:   k   .
x    k2  3 h) 3 4  2sin 2x
 2 3  2 cot x 1 . 2   cos x sin 2x Lời giải  Điều kiện: sin 2  0 k xx  k   . 2 2    PT   2   1 tan 3 1 tan  4 x x
  2  2 3  2cot x   1  2 tan x  3  x   2  x 3 2 3 tan 2 1 tan
 3 tan x  2  0  3 tan x  2tan x  3 tan x  0  tan x  0 x k   3   tan x   
x   k k   
. Kết hợp điều kiện suy ra phương trình có nghiệm: 3  6  tan  x   3  x      3 k   x     6 k  k  .  x      3 k i) 2 6
3cos4x  2cos x 3  8cos . x Lời giải Ta có: 2 6
3cos4x  2cos x 3  8cos x   2 3 2cos 2x  
1 1 cos2x 3  1 cos2x3 2 2 3
 6cos 2x 1 cos2x 13cos2x 3cos 2x cos 2x cos2x  0   k    3 2 cos 2 3cos 2 2cos 2 0 cos 2 1 x x x x x         4 2 k    .  cos2  2 
  x k x VN  k) 2 3cos x  2  3  (1cos x).cot . x Lời giải
Điều kiện: sin x  0  x k k   . PT 2 2  x x x    x 2 3cos .sin 2sin 3 1 cos cos x  0  x  2  x   2  x    x 2 3cos . 1 cos 2 1 cos 3 1 cos cos x  0 24 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  2 cos x    3  3 2
 6cos x  5cos x  3cos x  2  0  cos x   1  1 cos x   2   2  x  arc  cos   k   2  3  
 x k2 k   .  
x    k2  3   2  x  arc  cos   k   2
Kết hợp điều kiện, suy ra phương trình có nghiệm:  3    k   .   x    k  2  3
l) sin3x cos2x 1 2sin xcos2 . x Lời giải sin x  0 PT 2
sin3x cos2x 1 sin x sin3x 1 2sin x 1 sin x            1 sin x   2  x k   
x   k2 k   .  6  5 x   k2  6 m) 2cos5 .
x cos3x  sin x  cos8 . x Lời giải
Ta có: 2cos5 .xcos3xsin x  cos8x  cos2xcos8xsin x  cos8x 2
 1 2sin x  sin x  0   x   k2  2 sin x 1   k2    x    .  1 
x    k2 k   6 3 sin x    6  2  7 x   k2  6 n) 6 6
4(sin x  cos x)  4sin 2 .x Lời giải Ta có: 6 6 2 2
4(sin x  cos x)  4sin 2x 13sin xcos x  sin 2x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 25 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   2  2 2  x arc sin  k   2 3 sin 2x    3 2  1 sin 2  x  sin 2x  3   4      x    vn 2 sin 2 2
2x    arcsin  k   2   3   1  2  x   arcsin   2   3 k     k   .   1  2  x   arcsin     2 2  3 k   
o) sin 4x  2  cos3x  4sin x cos . x Lời giải PT
sin 4x  2  cos3x  4sin x cos . x  2sin 2 .
x cos 2x  2  2cos 2 .
x cos x  4sin x  2sin . x cos .
x cos 2x 1  cos 2 .
x cos x  2sin x  cos2 .
x cos x2sin x  
1 1 2sin x  0  2sin x  
1 cos2 .xcos x   1  0  1  1 sin  1  sin x x   sin   x 2   2     2  cos 2 .
x cos x 1  0  3  2 2cos x   1 .cos x 1  0
2cos x  cos x 1 0   x   k2  6  1  1 sin  x  sin x     5  2  2  x
k2 k    .   3 6
2cos x  cos x 1 0 cos x 1 x k2   BT 8.
[1D1-3] Giải các phương trình lượng giác sau: 2 3  a) 2
cos x  cos x 1 cos2 3 2tan x 2 x  tan x   b) 2 3tan 2x    4cos x  2. 2 cos x cos2x 1 tan x c) 2
(2tan x 1)cos x  2cos2 .x d) 2
2cos x 3cos x 2cos3x  4sin xsin 2 . x e) 2
4sin x 3  2(1sin x)tan .x f) 3 2
2sin x 3  (3sin x  2sin x 3)tan .x   2 g)  2 5sin    3(1 cos )cot  3sin x 2sin x 3   2. h) 3  3  2sin . x  2 x x x  cot x  i) cos3x sin3 5sin x 3  x x   3 cos2 . k)
 tan x  2 3  sin x1 tan x tan  1 2sin 2 xx 2 cos x  2  Lời giải 2 3   a) 2 cos x cos x 1
cos2x  tan x   2 cos x Lời giải
Điều kiện: x   k,  2 k 26 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 3  2
cos x  cos x 1
cos2x  tan x
(1). Điều kiện: cos x  0     . 2 cos x k x 2 Khi đó pt (1)   2 x   2 2 2 3 2cos
1 cos x sin x  cos x  cos x 1 4 3 2
 2cos x cos x cos x  0 2
 2cos x cos x 1 0 cos x 1 x k2  k 2  1 2   2
k    x  k  .
cos x    cos x    k2 3  2 3  3 
Vậy phương trình (1) có các nghiệm: k 2 x  k   . 3 b) 3 2tan x  2 2 3tan 2x    4cos x  2. cos2x 1 tan x Lời giải cos 2x  0
Điều kiện: cosx  0 3 2tan x 2 2 3tan 2x    4cos x  2 (1). cos2x 1tan x    x   k  cos 2 4 2    x  0  x   k  Điều kiện:     4 2
cos x  0  x   k   .  2  tan   x  1        x  2 k x      4 k 3sin 2x 3
2sin x cos x Khi đó pt (1)     2cos2x  0 cos2x cos2x sin x  cos xx    x x2 2 3sin 2 3 2 sin cos  2cos 2x  0 2
 3sin 2x 3 2 2sin 2x  2cos 2x  0 sin 2x 1  2  2
 sin 2x 5sin 2x 3  0   3
x   k k   .
sin 2x  VN  4  2
Vậy phương trình (1) vô nghiệm. c) 2
(2tan x 1)cos x  2cos2 .x Lời giải
Điều kiện: x    2 k
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 27 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2
(2tan x 1)cos x  2cos2x 2 2
 (2tan x 1)cos x  3 2cos x (1). Khi đó pt(1) 2 2 3
 2sin x cos x  3cos x 2cos x 3 2
 2cos x 3cos x 3cos x  2  0  cos x  1  
x    k2
 cos x  2VN     k  . 
x    k2 1  cos  3 x   cos  2 3 
Vậy phương trình (1) có các nghiệm: x    k2 và x    k2 . 3 d) 2
2cos x 3cos x 2cos3x  4sin xsin 2 . x Lời giải 2
2cos x 3cos x  2cos3x  4sin xsin 2x 2
 2cos x 3cos x  2cos2xcos x sin 2xsin x  4sin xsin 2x 2
 2cos x 3cos x  2cos2xcos x sin 2xsin x  0   cos x  0 x   k  2  2cos 2
x  3cos x  2cos x  0   1 2   k   .
cos x    cos  2  2 3 x    k2  3  
Vậy phương trình có các nghiệm x    và 2 x    k2 . 2 k 3 e) 2
4sin x 3  2(1sin x)tan . x Lời giải 2 2 4sin sin x x 3  2(1 sin )
x tan x  4sin x 3  2(1 sin ) x (1). 2 1sin x
Điều kiện: x    . 2 k
Khi đó phương trình (1)   x    x 2 4sin 3 1 sin  2sin x 2
 2sin x  7sin x 3  0  1     x    k2 sin  x    sin    2   6  6    k   .    7 sin x  3   VNx   k2  6  
Vậy phương trình có các nghiệm: x    k2 và 7 x   k2 . 6 6 f) 3 2
2sin x 3  (3sin x  2sin x 3)tan .x 28 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Lời giải Ta có: 3 x 3   2   sin 2sin 2sin 3cos x x x os c x 3 2 2
 2sin xcos x 3cos x  2sin x 3cos xsin x 2
 2sin xsin xcos x   1  3
 cos xsin xcos x   1  sin 2x  2
sin x cos x 1  0 sin 2x  2    2    cos x   2  x    k2 . 2  2sin x  3  cos x 2
2cos x  3cos x  2  0  3 1 cos x    2   g)  2 5sin  3(1 cos )cot    2.  2 x x xLời giải
Điều kiện: x k,k     2 2 5sin  3(1 cos )cot  cos x  
2  5cos x 31cos x  2  2 x x x  2 1 cos xx   x 2
5cos 1 cos 3cos x  21cos x 2
 2cos x 3cos x  2  0  1 cos x    
2  x    k2 .  3 cos x  2  2
h) 3sin x  2sin x 3 3  3  2sin . cot x x Lời giải  Điều kiện: k x  ,  2 k 2
3sin x  2sin x 3 3  3  2sin 3 xx  3   2 x x sin 2sin 2sin 3cos cot x x cos x 3 2 2
 2sin xcos x 3cos x  2sin x 3cos xsin x 2
 2sin xsin xcos x   1  3
 cos xsin xcos x   1  sin 2x  2
sin x cos x 1  0 sin 2x  2    2    cos x   2  x    k2 . 2  2sin x  3  cos x 2
2cos x  3cos x  2  0  3 1 cos x    2   i) cos3x sin3 5 sin x x   3   cos2 .  1 2sin 2 x x Lời giải
Điều kiện: 1sin 2x  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 29 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 3 3
cos3x  sin3x 4cos x 3cos x 3sin x  4sin x  1 2sin 2x 1 4sin xcos x
4cos x sin x1sin xcos x 3cos x sin x  1 4sin xcos x
cos x sin x1 4sin xcos x   cos x sin 1 x  4sin xcos x Ta có:  cos3x sin3 5 sin x x   3  
cos2  5cos x  3cos2x  1 2sin 2 x x
cos x  2 l 2 2cos  
x  5cos x  2  0   1 cos x   2  + Với 1
cos x   x    k2,k   . (thỏa mãn điều kiện). 2 3 k) 3 tan   
x  2 3  sin x 1 tan x tan x  2 cos  x  2  Lời giải Điều kiện: cos 0;cos x x   0 2 3 tan   
x  2 3  sin x 1  tan x tan x 2 cos  x  2   cos 
x cos x  sin x sin x     2  x 2 2 3 1 tan
 tan x  2 3  sin x   cos x x cos   2  tan x  3   2 3 1 tan 2 
x  tan x  2 3  tan x  3 tan x  2tan x  3  0   3 tan x    3   x     3 k   .  x      6 k
2. Phöông trình löôïng giaùc baäc nhaát ñoái vôùi sin vaø cosin (phöông trình coå ñieån)
Dạng tổng quát: a sin x b cos x c ( )  ,  , a b  \  0 
Điều kiện có nghiệm của phương trình: 2 2 2
a b c , (kiểm tra trước khi giải) hƣơng pháp giải:  Chia 2 vế 2 2 a b c
a b  0, thì ( )   sin x  cos x  ( )  2 2 2 2 2 2 a b a b a b 30 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  Giả sử: cos a   , sin b  
,  0;2  thì: 2 2 2 2 a b a b ( )   sin cos  cos sin c    sin( ) c x x x  : dạng cơ bản. 2 2 2 2 a b a b s
 in a cosb  cosasinb  sin(a  ) b
Lƣu ý. Hai công thức sử dụng nhiều nhất là:  
cosa cosb  sin asinb  cos(a b)
Các dạng có cách giải tƣơng tự:   2 2
a b cos nx 2 2  . a sin mx  . b cos mx  
, (a b  0) PP 2 2  2 2    
Chia : a b . a b sin nx  2 2 2 2
 .asin mx  .bcosmx  .csin nx d.cosn ,x (a b c d )
Ví dụ 1. Giải phương trình: sin x  3 cos x   3. Giải:
Vì   2   2 2 1 3
3 nên phương trình luôn có nghiệm x k2   Khi đó: 1 3 3  3 pt  sin x  cos x    sin      5 ,  2 2 2 x  3  k   2 x   k2  3   
Ví dụ 2. Giải phương trình: cos 2x  3 sin 2x  2cos    3 x   Giải: 1 3         pt cos2   x  sin 2x  cos  x    cos2x    cos  2 2 3 3  3 x           2
2x    x k2   3 3 x k  3     ,      2 k
2x     x k2 x    k2  3 3  3
Ví dụ 3. Giải phương trình: cos 4x  sin x  3(cos x  sin 4x). Giải: 1 3 3 1
pt  cos4x  3sin 4x  3 cos x  sin x  cos4x  sin 4x  cos x  sin 2 2 2 2 x      cos 4   x    cos   3 x  6     
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 31 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC      2
4x   x   k2    3 6 x  18 k 3     ,       2 k
4x   x   k2    3 6 x  10 k 5 BÀI T P ÁP DỤNG 2 BT 9.
Giải các phương trình lượng giác sau:
a) sin x  3 cos x 1 Lời giải  
Phương trình tương đương với: 1 3 1 sin 1 x
cos   cos sin x  sin cos  2 2 x 2 3 3 x 2      x    k2      1  x k 2   3 6   sin 6 x         k    3  2      x      k2  x   k2  3 6  2
b) 3sin x  cos x  1  . Lời giải  
Phương trình tương đương với: 3 1 1 1  sin x  cos  
 cos sin x  sin cos   2 2 x 2 6 6 x 2    x     k2    1        sin  6 6 x      sin x     sin    6      2  6   6    7 x    k2  6 6   x    k2   3 k   
x    k2
c) 3cos x sin x  2 Lời giải  
Phương trình tương đương với: 3 1 2  cos x  sin  2
 sin cos x  cos sin  2 2 x 2 3 3 x 2     
x   k2 x   k2    2    sin   3 4 12      k   . 3 x   2       5 x     k2  x    k2  3 4  12
d) sin x  3cos x  2. 32 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Lời giải    
Phương trình tương đương với:  cos sin  x  sin
cos x 1  sin x     1 3 3  3    
x    k2  x   k2,k   3 2 6
e) 3sin3x cos3x  2. Lời giải  
Phương trình tương đương với: 3 1 2  sin3x  cos3  2
 cos sin3x sin cos3  2 2 x 2 6 6 x 2     5 2
3x    k2      2 x k    sin 3 6 4 36 3 x        ,k  . 6    2     11 2
3x      k2    6 4 x  36 k 3
f) cos7x  3sin7 x   2. Lời giải
Phương trình tương đương với: 1 3 2 cos7x  sin 7   2 2 x 2   3       cos .cos7 3  x  sin .sin 7x  cos  cos 7x     cos 3 3 4 3  4        3    7  5 5 k 2 x    k2  7x   k2   3 4  x    12   84 7   ,k    .  3    7  13  13 k 2 x     k2  7x    k2 x     3 4  12  84 7   g) 3sin    sin    2.  2 x xLời giải
Phương trình tương đương với: 3cos 3 1
x  sin x  2 
cos x  sin x 1 2 2        cos .cos  x  sin
.sin x 1  cos x   
 1  x   k2  x    k2 ,k   6 6  6  6 6   g) sin 2    3sin(  2 )    1.  2 x xLời giải
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 33 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Phương trình tương đương với: cos2 1 3 1
x  3 sin 2x  1  cos 2x  sin 2  2 2 x 2   1       cos .cos2  x  sin .sin 2   cos 2x     cos 3 3 x 2 3  3        
2x    k2  2x k2    3 3 x k        ,k     2    2 2x    k2 x    kx     k2  3 3  3  2      h) 3sin  x   sin  x      2.  4   4  Lời giải      
Phương trình tương đương với:  3sin  x   sin  x        2  4   2  4            3sin   3 1  2 x   cos x       2  sin x   cos x        4   4  2  4  2  4  2         2      cos .sin 5 x     sin .cos    sin x     sin 6 4 6 x  4      2  12  4  5     x    k2  x   k2 12 4    6   ,k   .  5 3   x    k2     x k 2  12 3  3      k) 4sin  x   2cos x       3 2  4   4         4 sin c   x os  cos xsin  2 cos c x os  sin xsin      3 2  4 4   4 4 
 2 2 sin x  2 2 cos x  2 cos x  2 sin x  3 2       2    
 sin x  cos x 1 2 sin x  1 sin x    sin x         sin  4   4  2  4  4    x    k2 x k2  4 4      ,  .     x   k2 kx      k2  2  4 4 2 l)  x x  2 x x x 2 sin  cos  3 cos  2  sin  2sin cos  cos x x  3 cos x    2  2 2  2 2 2 2 1 3 1   1
 sin x  3 cos x 1 sin x  cos x   sin c x os  cos xsin  2 2 2 3 3 2 34 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC      x    k2 x    k2    3 6    6  sin x     sin     ,  .  3  6 k      x      k2 x   k2  3 6  2 m) 2 1 1 cos2x 1
3sin x  sin 2x  3  3  sin 2x  3 2 2 2 1 3 3   3 sin 2x  cos2x   sin 2 c x os  cos2xsin  2 2 2 6 6 2    2   x    k2       6 3 x    4 k sin2x    sin     ,   6  3     5 k
2x      k2     6 3 x  12 k n) 2 2
sin x(sin x 1)  cos ( x 1 cos )
x  sin x  sin x  cos x  cos x       2
 sin x  cos x 1 2 sin x    1  sin    4 x  4      2    x    k2 x k2      4 4 sin x   sin         ,  .  4  4     x   k2 kx      k2  2  4 4 o) 2 2 sin x( 3 sin ) x  cos ( x 1 cos )
x  3 sin x  sin x  cos x  cos x 3 1 1   1
 3sin x  cos x 1
sin x  cos x   sin c x os  cos xsin  2 2 2 6 6 2    x            6 6 k x   k2 sin   x     sin    3 ,  .  6  6 k   
x      k2 x  k2  6 6 p) 2
2sin x  3sin 2x  2  0 1cos2x  3sin 2x  2  0 3 1 1   1
 3sin 2x  cos2x 1
sin 2x  cos2x   sin 2 c x os  cos2xsin  2 2 2 6 6 2    2   x           6 6 k x    6 k  sin2x    sin     ,  .  6  6 k   2   x      k2     6 6 x  2 k
q) cos7xcos5x  3sin 2x 1sin7xsin5x Lời giải
Phương trình tương đương với: 1  x x 1 cos12
cos2  3sin 2x 1 cos12x cos2x 2 2    1
 cos 2x  3sin 2x 1  cos  2   3 x   2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 35 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  
 2x   k2 x k  3 3      k        2     x    k2 x   3 k  3 3
r) cos xsin3x  3cos2 x  3 c  os3 s x in x Lời giải
Phương trình tương đương với: 1  x x 1 sin 4
sin 2  3 cos2x  3  sin 4x sin 2x 2 2    3
 sin 2x  3 cos 2x  3  sin 2x    3    2    2   x    k2     3 3 x  3 k     k     2 2   x    k2     3 3 x  2 k s) 4 4
2(cos x sin x) 1 3cos x sin x Lời giải
Phương trình tương đương với:  2 2 x x 2 2 2 cos sin
cos x  sin x1 3cosx  sin x 2 2
 3cos x sin x  3cos x sin x   3cos x sin x 3cos x sin x   1  0  2        x  3 k  cos x     0 3 cos 
x  sin x  0  6       
x    k2 ,k  .  
 3 cos x  sin x 1     1 2 cos x       6    2 
x   k2  6
t) 3sin 2x  cos2x  2cos x 1 Lời giải
Phương trình tương đương với: 2
2 3sin xcos x  2cos x 1 2cos x 1 cos x  0
 cos x 3sin x cos x  
1  0   3sinxcosx 1 36 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC     x   kx      2 k 2     x k2 ,k        1 sin x     2  6     2 x   k2  3 u) 2
2sin x sin 2x 3sin x cos x  2 Lời giải
Phương trình tương đương với: 2
2sin x 3sin x  2 2sin xcos x  cos x  0
 sin x  22sin x  
1  cos x2sin x  
1  0  2sin x  
1 sin x cos x 2  0  1 sin   x   x    k  2 2sin  x 1  0 2  6       ,k  
sin x  cos x  2  0       x       7 2 sin 2 VN x   k2   4    6   v) 2sin 2  x   4sin x    1  6  Lời giải   
Phương trình tương đương với: 2 sin 2  x cos  cos 2xsin  4sin x    1  6 6 
 3sin 2x  cos2x  4sin x 1 2
 2 3sin xcos x 1 2sin x  4sin x 1 sin x  0
 sin x2 3cos x 2sin x  4  0  2 3cosx2sinx40
 sin x  0  x k k   3 1
 2 3 cos x  2sin x  4  0 
cos x  sin x  1  2 2     5  cos  x  1
   x    k2  x
k2 k      6  6 6 
Vậy phương trình có 2 họ nghiệm 5
x k và x
k2 k   6   x) 5 cos 
x  2cos 2x  2sin x cos 2x   6    Lời giải
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 37 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  
Phương trình tương đương với: 3 1
cos x  2cos 2x  2sin x cos 2x  sin 2 2 2 x     
 cos x  2cos2x  3sin xcos2x sin xsin 2x  0 2
 cos x  2cos2x  3sin xcos2x  2sin xcos x  0  x  2
cos 1 2sin x2cos2x  3sin xcos2x  0
 cos2xcos x 2 3sin x  0   2    cos 2  0 x       2 k x  4 k x 2       k  
cos x  2  3 sin x  0    cos    x     1 x   k2   3   3
BT 10. Giải các phương trình lượng giác sau: 
a) 3sin x  cos x  2sin 12     
Phương trình tương đương với: 3 1
sin x  cos x  sin  sin x     sin 2 2 12  6  12      x    k2 x    k2  6 12  12     ,k       3 x      k2 x   k2  6 12  4
b) cos x  2 sin 2x sin . x  
Phương trình tương đương với: sin 
x  cos x  2 sin 2x  2 sin x     2 sin 2  4 x       2 sin   x
 2 sin 2x  sin x       sin 2  4   4 x      x   2x k2 x   k2  4  4     k  .   k   2 x
   2x k2    4 x  4 3
c) sin3x  3cos3x  2sin 2 . x
Phương trình tương đương với: 1 3 sin3x  cos3x  sin 2 2 2 x 38 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC    
3x   2x k2 x   k2     sin 3   3 3 x     sin 2     k   .  3 x     4 k2
3x     2x k2    3 x  15 5
d) sin x  cos x  2 2 sin xcos . x     
Phương trình tương đương với: 2 sin  x
 2 sin 2x  sin x       sin 2  4   4 x     
2x x   k2 x   k2  4  4     k  .   k   2
2x    x   k2    4 x  4 3
e) 2cos3x  3sin x  cos x  0.  
Phương trình tương đương với: 1 3 cos  x
sin x  cos3x  cos x   cos    3x 2 2  3  f) 2 (sin x cos ) x  3cos2 x 1  2cos .x
Phương trình tương đương với: 1sin 2x  3cos2x 1 2cos x 1 3    sin 2  x  cos2x  cosx  cos  2    cos 2 2  3 x x       2 2 x k 2     3 x x k    9 3   ,(k  )     2 
x k 2    x   k2  3 x  3
g) 2 cos2x sin x cos x  0.  
Phương trình đã cho tương đương với: 2 cos2 
x  cos x  sin x  2 cos 2 x  2 cos x   4       
2x x   k2 x   k2     cos2x cos    4 4 x       ,k   4        2  2 x  x   k2     x k  4  12 3
g) sin3x  3cos3x  2sin x  0.
Phương trình đã cho tương đương với: 1 3
sin3x  3 cos3x  2sin x  sin3x  cos3x  sin 2 2 x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 39 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC    
3x   x k2        x k  sin 3   3 6 x     sin     ,k    3 x      3  x
   x k2  x   k  3  6 2   
Vậy nghiệm phương trình là x    k, x   k (k  ) 6 6 2   h) cos 
x  3 sin x  2cos     3 x  
Phương trình tương đương với : 1 3 cos  x  sin x  cos  2 2  3 x      x
  x k2       cos   3 3 x    cos    
x k ,k   3  3 x      
x     x k2(VN)  3 3 k) 2
2cos x  3sin x 1 2sin3 . 2 x
Phương trình tương đương với : 1 cos 3 1
x  3 sin x 1 2sin 3x
sin x  cos x  sin3 2 2 x   3   x x   k2       x k  sin   6 12 x     sin 3     ,k    6 x   5   3  5 x   x k2  x   k  6  24 2 l) 2
sin x  3cos x  2  4cos x
Phương trình tương đương với : 2
sin x  3cos x  4cos x  2 1 3     x x   2 sin 3 cos 2 2cos x   1  sin x
cos x  cos2  sin x     cos 2 2 2 x  3 x   5 2  5 x   x k2     5  x k  cos     6 12   cos 2     ,k    6 x x    5 2   5 x    x k    2 x    k2   6   6 m) 2
4sin x sin x  2  3cos x
Phương trình tương đương với : 2
sin x  3cos x  2  4sin xx x   2 sin 3cos
2 1 2sin x  sin x  3cos x  2cos2x 40 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC       1 3 2x x k 2     sin  6 x
cos x  cos2  cos x     cos 2   2 2 x  6 x  
2x  x   k2  6
n) 2cos x 3sin x cos x  1 1
Phương trình tương đương với : 2
2 3sin xcos x  2cos x  2cos x 1    3sin 2 
x  cos 2x 1 2cos x 1  3 sin 2x  cos 2x  2cos x  cos 2x     cos  3 x     
2x   x k2  x   k2 3    3   ,k       2 k  2 x
 x k2  x    3  9 3 o) 2
3sin 2x  2sin x  4sin3x .cosx 2
Phương trình tương đương với :  x   2 3sin 2
2 1sin x  4sin3 .xcos x 2
 3sin 2x  2cos x  4sin3 . x cos x 2
 2 3sin xcos x  2cos x  4sin3 . x cos x  0 cos x  0
 2cos x 3sin x cos x 2sin3x  0   3sinxcosx2sin3x 0 
Xét TH 1: cos x  0  x   k,k   2
Xét TH 2: 3sin x cos x  2sin3x  0    3sin 
x  cos x  2sin 3x  sin x     sin 3  6 x    3   x x   k2      6 x k    12   ,k    7   3  7 k x  x   k2  x    6  24 2   x     2 k  
Vậy phương trình có 3 họ nghiệm là: x    k ,k    12  7 k x    24 2 p) 3cos5x  2sin3 .
x cos 2x  sin x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 41 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Phương trình tương đương với : 3cos5x sin5x sin x  sin x  3cos5x sin5x  2sin x 3 1    cos5  x  sin5x  sin  sin 5    sin 2 2 x  3 x x      kx   5x k2    3 x    18 3   ,k   .  2  k  x   5x k2  x     3  6 2 q) 2(cos6x  cos4 ) x  3(1 cos 2 ) x  sin 2 . x Lời giải
Phương trình tương đương với: 2
4cos5xcos x 2 3cos x  2sin xcos x
 2cos x2cos5x  3cos x sin x  0 cos x  0 (1)
  3cosxsinx 2sin5x (2)    1  x    2 k   5    2   kx x k x          3 12 2 2  sin x     sin 5x     k  .  3     5 
x    x   k2 k     3 x  9 3   k  x   
Vậy, nghiệm của phương trình là 12 2 x   k ,  k  . 2  k x    9 3 r)
3sin7x  2sin 4xsin3x  cos .x Lời giải
Phương trình tương đương với: 3sin7x cos7x cos x  cos x   3sin 7  
x  cos 7x  2cos x  cos 7x     cos  3 x    7      x k2 k x     3 x  18 3     k  .  7   
  x k2 k x     3 x  24 4 s) 2 2
2sin x(cos x sin )
x  sin x  3 cos3 . x 42 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Lời giải
Phương trình tương đương với: 2
2sin x(1 2sin x)  sin x  3cos3 .x 2  2sin x(1 2sin )
x  sin x  3 cos3 . x   t) 2 sin 2 sin xx   2 sin xsin 3   2 x 4    Lời giải  
Phương trình tương đương với: 2 sin 2 sin xx   2 sin xsin 3  2 x 4    2   sin  
x  sin x cos x  2 sin x sin 3x   4        sin x k x  0 x k              x
k k  . sin   
x  cos x  2 sin 3x  
sin x  sin 3x     8  4       4   3 k x     16 2   u) 2 x 3 cos2x 2 3 cos sin      2 2 x  4     
Phương trình tương đương với: 2 x 3 cos2x 2 3 2cos 1 sin      2 2 x  4    2 x  3 4cos 3 cos2   
x  2  cos 2  2 x 2    2
 4cos x  3 cos2x  2  sin 2 2 x
 3cos2x sin 2x  2  cosx   cos2   x    cos  x  6   5 k2 x    18 3   k  .  7   x   k2  6 v) 2
2 3cos2x sin 2x  4cos 3 .x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 43 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Phương trình tương đương với: x x   2 sin 2 3cos2 2 2cos 3x   1         sin 2   x
 cos6x  sin 2x   sin       6 3 3 2 x            5 2   x
  6x k2    3 2 x  48 k 4     k  .     5 2   x
  6x k2     3 2 x  24 k 2 x) 2
3sin 2x  2cos x  2 2  2cos2x.
Phương trình tương đương với: 2
2 3sin xcos x  2cos x  2 2(1 cos2 ) x 2 2
 2 3sin xcos x  2cos x  2 4cos x 2
 2 3sin xcos x  2cos x  4 cos x   *
Trường hợp 1: cos x  0  
*  cos x2 3sin x 2cos x 4  0 cos     x  0 cos  0 x         2 k x  2 k x            3 sin 
x  cos x  2 sin x     1     2   6 x    k  2 x   k2  6 2  3  Vì cos 2
x  0 nên loại nghiệm: x
k2 k  . 3
Trường hợp 2: cos x  0  
*  cos x2 3sin x  2cos x  4  0      
 3 sin x  cos x  2   sin x     1
  x     k2  x    k2  6  6 2 3 
Vì: cos x  0 nên loại nghiệm x    k2 3 
Kết luận: Phương trình có nghiệm: x   k k  . 2
BT 11. Giải các phương trình lượng giác sau:
a) sin 2x cos x  cos2x sin . x Lời giải 44 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Cách 1:
sin 2x cos x  cos2x sin x  sin 2x cos2x  sin x cos x           2 sin 2    x     2 sin    sin2x    sin   4 x  4  x        4   4    
2x   x   k2   k 2 4 4    x   3 k  .      2  x     x   k   2 
x    k2  4  4  Cách 2:
sin 2x cos x  cos2x sin x 2
 2sin xcos x  cos x  2cos x 1sin x 2
 2sin xcos x sin x  2cos x cos x 1
 sin x2cos x   1  cos x   1 2cos x   1  2cos x  
1 sin x cos x   1  0  1 cos x   2cos  x 1  0 2    
sin x  cos x  1      2 sin x x        4  2  2 x    k2   2 3 x    k2     3  
x     k2    k    x k  2 . 4 4     3  x   k2 x      k2   2  4 4
b) cos2x  3sin 2x  3sin x  cos . x Lời giải Cách 1: cos2 1 3 3 1
x  3 sin 2x  3 sin x  cos x  cos 2x  sin 2x  sin x  cos 2 2 2 2 x    
 cos2xcos sin 2xsin  cos xcos sin xsin 3 3 3 3   
2x   x   k2       cos 2   3 3 x    cos     3 x  3       
2x   x   k2  3 3
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 45 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  2 x    k2  3 k 2    x  k   . k  2 3 x   3 Cách 2:
cos2x  3sin 2x  3sin x  cos x cos2x cos x  3sin 2x  3sin x Lời giải 2
 2cos x cos x 1 2 3sin xcos x  3sin x  cos x   1 2cos x  
1  3sin x2cos x   1  2cos x  
1 cos x  3sin x   1  0  2  1 cos x    k2 x      2 3       
cos x  3sin x 1 cos x      cos   3  3  2 x    k2  3   2    x    k2   x    k2 k     3 . 3 3   x k2  
x     k2  3 3 c) 3(cos2x sin3 )
x  sin 2x  cos3 . x Lời giải  cos3 1 3 3 1
x  3 sin 3x  3 cos 2x  sin 2x  cos3x  sin3x  cos2x  sin 2 2 2 2 2 x           cos3  x cos
sin3xsin  cos2xcos sin 2xsin  cos3x    cos 2  3 3 6 6 3 x 6           3   x
 2x   k2  x    k2 x    k2 3 6     6   6   k   .      3   kx   2
x   k2 
5x    k2 x     3 6  2  10 5
d) cos7x sin5x  3(cos5x sin7 ) x . Lời giải 46 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  cos7 1 3 3 1
x  3 sin 7x  3 cos5x  sin 5x  cos 7x  sin 7x  cos5x  sin5 2 2 2 2 x           cos7  x cos
 sin 7xsin  cos5xcos sin5xsin  cos7x    cos5  3 3 6 6 3 x 6         7     x
 5x   k2  2x   k2    3 6  x k    6   12   k   .      7   kx   5
x   k2 
12x   k2 x    3 6  2  24 6 e) 2
sin 2x  2cos x sin x cos x 1. Lời giải 2
sin 2x  2cos x sin x cos x 1 2
 sin 2x  2cos x 1 cos x sin x       sin 2 
x  cos 2x  cos x  sin x  sin 2x    sin   4  4 x        2  k 2 x
  x k2   4 4 x    3   k  .     2    x      x k   2  x   k2  4  4   2 f) 2
4sin x  tan x  2(1 tan ) x sin 3x 1.
Điều kiện cosx  0. 2
4sin x  tan x  2 1 tan xsin3x 1.   2 2 2sin x   1 tan x  
1  2 1 tan xsin3x  0       sin x cos 2 sin cos sin cos x   x x x x  1 2sin3x   0  cos x
 sin x  cos x2cos xsin x cos x  
1 2sin3x 0 
sin x  cos x  0   1
 2cosxsinxcosx 
1 2sin3x0 2       1  sin x
 0  x    k k     (thoả điều kiện)  4  4
2  sin2xcos2x   2sin3x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 47 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   2x   3  x k2    sin 4  2   x    sin  3  x    4  
2x   3x k2  4   k 2 x    20 5  
k  .(thoả điều kiện)  5 x    k2  4
g) sin x sin 2x  3. cos x  cos2x cos x  1 Điều kiện cos 
x  cos 2x  0  1 cos x   2 3x x sin 2cos sin
x  sin 2x  3. 2 2   3 3 cot x    3 cos x  cos2x 3 2  sin x sin x 2 2 2 3x         k 2  x    . (thoả điều kiện) 2 6 k 9 3  
g) 1 2sin x 1 sin x   1 2sin x 3 cos x 1   2sin x  0 Điều kiện  . cos x  0
Với điều kiện trên phuowg trình trở thành.
3cos x1 2sin x  1sin x1 2sin x 2
 3cos x  3sin 2x 1sin x  2sin x  sin x  3cos x  3sin 2x  cos2x      k2 x  2x   k2         x  sin    3 6 18 3 x   sin  2       3 x 6             x      2x   k  2 x   k2  3  6   2  
So với điều kiện phương trình có nghiệm k 2 x   k  . 18 3  h)
cos x sin 2x  3. 2
2cos x sin x 1 Lời giải 48 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  1   Điều kiện sin 2 2 2cos sin 1 0  2  sin sin 1  0 x x x x x   2 . s  in x  1 
Với điều kiện trên phương trình trở thành: x x   2 cos sin 2
3 2cos x sin x  
1  cos x1 2sin x  312sin xsin x   1    3
 cos x  3sin x   1 (do 1
sin x  )  3sin x cos x   3  sin    2 x  6    2      x     k2 x    k2  6 3  6     k  .     3 x      k2 x   k2  6 3  2 
So với điều kiện phương trình có nghiệm là x    k2 k   . 6
k) sin x sin3x  3. cos x  cos3x Lời giải
Điều kiện cosx  cos3x  0 sin 2x .sinx  0 sin 2x 0.
Với điều kiện trên phương trình trở thành 2sin .xcos2x  
 3  cot 2x   3  x    kk   . 2  sin 2 . x sin x 12 2  
So với điều kiện phương trình có nghiệm x    k k   . 12 2  l)
(1 2sin x)cos x  3.
(1 2sin x)(1sin x) Lời giải s  inx  1 Điều kiện: (1 2 sin  
x )(1 sinx ) 0 1 sinx    2
Với điều kiện trên phương trình trở thành
cos x  2sin xcos x  31 2sin x1sin x  x x x   2 cos 2sin cos 3 2
 sin x sin x   1        3sin 
x  cos x  sin 2x  3 cos 2x  sin  x   sin  2   6 x 3     
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 49 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC     2
x  2x   k2     6 3 x  18 k 3     k   .        x      2x   k  2 x   k2  6  3    2  
So với điều kiện phương trình có nghiệm 2 x    kk  . 18 3      m) 2 4sin  x
 4cos 2xcos 2x       1.  6   3  2              4sin   x
 4cos 2xcos 2x     
 1.  21 cos 2x  
 2cos  cos 4x       1  6   3    3   3  3      2      2 2cos 2     x   cos 4x       2 2  2cos 2x   2cos 2x  1      0  3   3   3   3      1 3   1 3 cos 2x    l
2x   arc cos  k2  3  2   3 2       1 3   cos 2 1 3 x     n
2x   arc cos  k2   3  2  3 2   1 1 3
x    arc cos  k
Vậy phương trình có nghiệm: 6 2 2   k     1 1 3
x    arc cos    6 2 2 k n) 2 2
3cos x  2sin xcos x  3sin x 1. Lời giải  
*  3cos2x sin 2x -1 0 3 1 1   1 
cos2x  sin 2x   cos2xcos sin 2xsin  2 2 2 6 6 2   
2x    k2      6 3  os c  2x    os    6 c  3  
2x     k2  6 3   2   x   k2     2 x  4 k     k    2   x    k2      6 x  12 k
o) 2(cos x  3sin x)cos x  cos x  3sin x 1. Lời giải 50 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   2
*  2cos x  2 3 sin xcos x  cos x  3 sin x 1 cos 2x  3 sin 2x  cos x  3 sin x 1 3 1 3      cos 2   x
sin 2x  cos x
sin x  cos2x    cos  2 2 2 2 3 x  3          2
2x   x   k2  2 x   k2  3 3 x   k2   3 2    3     k        2 x k  3
2x   x   k2 3x k2   3 3 x k  3 p) 3(cos2x sin ) x  cos (
x 2sin x 1)  0. Lời giải  
*  3 cos 2x  3sin x  2sin .xcos x  cos x  0 3 1 3 1
 3 cos 2x  sin 2x  3 sin x  cos x
cos 2x  sin 2x  sin x  cos 2 2 2 2 x  
 2x x   k2        3 6  sin   2x   sin       3 x   6   
  2x    x   k2  3 6     x    k2 x    k2  2  2     k    5  5 2 3x   k2    6 x  18 k 3
q) cos2 1 tan tan x x x
 tan x  2sin x    1.  2  Lời giải   x   k        Điều kiện: 2 x    2 k k   x     k
x    k2 2 2  sin x       * x sin x 2 sin  cos 2 1 tan tan 
 tan  2sin 1  cos 2 1 . x x x x x x    2sin x 1  2  cosx x cos  cos x   2  sin x sin x 2 sin x 2  cos 2  cos 2 . . 
 2sin 1 cos 2 .cos  2cos 2 .sin x x x x x x x  sin x  2sin . x cosx  cos cosx x cosx 2 x cos 2 1 cos  cos2 .cos  2cos2 . x x x x  sin x  2sin . x cosx  cos 2 x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 51 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 cos2x sin 2x  cosx sin x   
2x   x   k2 x k2        4 4 2 cos2   x    2 cos x        2 ,k    4   4     2      2 x      6 k x x k 3  4 4   
Kết hợp điều kiện, ta được 7
x k 2 , x   k2, x
k2,k   6 6
BT 12. Giải các phương trình lượng giác sau: a) 2
sin 2x  2 3cos x  2cos .x 2 2
 2sin xcos 2 3cos x  2cos x  2 3cos x  2sin xcos x  2cos x  0
 2cos x 3cos x sin x   1  0 
 Với cos x 0  x   k ,k  . 2  Với 3cos x s  in x 1  0  3 1 1    2      2 cos   x
sin x    cos cos x sin sin x  cos  cos  x      cos 2 2 2 6 6 3 6  3         2    x   k2 ,k x   k2  6 3  2     ,k     2  5  x    k2,k x    k2  6 3  6   x   k2 
Vậy phương trình có hai họ nghiệm là 2   ,k   .  5 x    k2  6
b) 3sin 2x 1 cos2x  2cos . x 2 2
 2 3sin xcos x 1 2cos x 1 2cos x  2cos x  2 3sin xcos x  2cos x  0    x x x   cos x 0 2cos cos 3sin
1  0  cosx 3sinx10 
 Với cos x 0  x   k ,k  . 2
 Với cos x  3sin x 1  0  52 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 1 3 1     cos x
sin x   cos cos x  sin sin x  cos 2 2 2 3 3 3          cos
x  cos  cos x       cos  3  3  3  3    x
  k2,k   2  3 3 x   k2     3 ,k     
x     k2,k  x k2  3 3   x     2 k
Vậy phương trình có các nghiệm  2 x
k2 ,k    3 x k2  
c) sin 2x cos x sin x 1.
1sin 2x  sin x cos x Đặt 2 2 2
t  sin x cos x t  sin x  cos x  2sin xcos x 1sin 2xt  0
Vậy ta có 2t t  t 1  
 Với t  0 1 sin 2x  0  sin 2x 1  2x   k2  x   k,k  . 2 4 
 Với t 11 sin 2x 1  sin 2x  0  2x k  x k ,k  . 2   x   k 
Vậy phương trình có nghiệm 4  ,k  .  x k  2
d) cos2x  2sin x 1 3sin 2 . x 2 2
1 2sin x  2sin x 1 2 3sin xcos x  2sin x  2 3sin xcos x  2sin x  0    x x x   sin x 0 2sin sin 3 cos
1  0  sinx 3cosx10
 Với sin x 0  x k ,  k  .
 Với sin x  3cos x 1  0 
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 53 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 1 3 1         sin x
cos x   cos sin x  sin cos x  sin  sin  x    sin 2 2 2 3 3 6  3  6    
x   k2 x    k2 ,   3 6  6 k         
x     k2 x   k2 ,   3 6  2 k
e) 3sin 2x cos2x  4sin x 1.
Phương trình tương đương với : x   2 3sin2
1 2sin x  4sinx 1  x  2
 3sin2x  2sin x  4sinx  0  x x x   sin 0 2sin
3cos sin 2  0   3cosxsinx2 sinx  0 sinx  0 x k x k      1 3          ,k  sin  x  cosx 1 sin x     1
x    k2
x   k2 2 2   3   3 2  6 
Vậy nghiệm phương trình là x k, x   k2,k   6
f) 2sin6x  2sin 4x  3cos2x  3 sin 2 .x x x   2 4cos5 sin
3 1 2sin x  3  2sin c x osx sinx  0 sinx  0  2sin 
x 2cos5x  3sinx cosx  0     3 1
2cos5x  3sinx  cosx
sinx  cosx  cos5  2 2 x         sin x k x k x  0          x 5x k2       x    k ,  cos   k x     cos5  3  12 2   3 x       x   5  x k2     3 x  18 k 3    
Vậy nghiệm phương trình là x k, x    k ,x   k ,  12 2 18 3 k  g) 2 tan sin  2cos x x  2. 7 2  
phương trình tương đương với : tan sin x 1  c  os x 2  t an sin x co  s x 1 7 7 54 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC       x    k2       sin s 7 7 x in  cos c x os  cos  cos x     cos   7 7 7  7  7  
x     k2  7 7  2 x   k2   7 ,k   x k2 
Vậy nghiệm phương trình là 2 x
k2, x k2,k   7   g) cos 
x  cos 3x  1 2 sin 2x    4    Lời giải  2cos2 .
x cos x 1 sin x  cos 2x  2 2cos2 .
x cos x  2sin x cos x  2cos x
 cos x(cos2x sin x cos x)  0  2 2
cos x cos x sin x sin x  cos x  0  
 cos xsin x  cos xcos x sin x   1  0    x       2 k x   k  cos   2 x  0 cos x  0           sin x k
x  cos x  0   tan x  1    4  x      4 k sin  
x  cos x  1      1    x k 2  sin  x     x k 2   4     2  3 x   k  2   2 h) 3 1 8sin x    cos x sin x Lời giải
Điều kiện xác định: sin k
x cos x  0  x  2 Cách 1:  2
8sin xcos x  3sin x  cos x
 41cos2xcos x  3sin x  cos x
 4cos x  4cos2xcos x  3sin x  cos x
 4cos x  2cos3x  cos x  3sin x  cos x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 55 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 cos x  3sin x  2cos3x    cos  x     cos3  3 x    x   k   6  (thỏa điều kiện)  k x     12 2
Cách 2: Nhân 2 vế (h) cho sin x ta được: 2  tan 8. x
 3 t anx 1 ( đưa về phương trình bậc 3 theo t  tan ) 2 1 x  tan x
k) 3 cos2x  sin 2x  2sin(2x  )  2 2. 6 Lời giải       cos 2  x   sin 2x       2  6   6      sin 2  x      1  6 4      2x    k2  7    12 2 x 24 k 56 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
3. Phöông trình löôïng giaùc ñaúng caáp (baäc 2, baäc 3, baäc 4) Dạng tổng quát: 2 2 . a sin X  .
b sin X cos X  .
c cos X d (1)  , a , b , c d  .
Dấu hiệu nhận dạng: Đ ng bậc hoặc lệch nhau hai bậc của hàm sin hoặc cosin (tan
và cotan được xem là bậc 0). hƣơng pháp giải:  cos X  0
 Bước 1. Kiểm tra X   k  
có phải là nghiệm hay không ? 2 2 s  in X 1  cos X  0
 Bước 2. Khi X   k, (k  )   . Chia hai vế (1) cho 2 cos X : 2 2 s  in X  1 2 2 sin X sin X cos X cos (1) X da    2 b 2 c 2 2 cos X cos X cos X cos X 2 2
a tan X btan X c d(1 tan X )
 Bước 3. Đặt t  tan X để đưa về phương trình bậc hai theo ẩn t  . x
Lƣu ý. Giải tương tự đối với phương trình đẳng cấp bậc ba và bậc bốn.
Ví dụ 1. Giải phương trình: 2 2
2cos x  2sin 2x  4sin x 1. Giải: 2 2
pt  2cos x  4sin xcos x 4sin x 1
 Xét cos x  0 thì 2
sin x 1, phương trình trở thành 4  .11 (vô lí) Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được 2 2
2 4tan x  4tan x 1 tan x 2
 5tan x  4tan x 1 0   tan x 1 x     4 k   1   ,  tan     1 k x   5 x  arctan      5 k    
Ví dụ 2. Giải phương trình: 3 3 2
4sin x 3(cos x sin x)  sin xcos .x Giải: 3 2 3
pt  4sin x sin xcos x 3sin x 3cos x  0
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành
4.13.1 0 (vô lí); hoặc 3 4.( 1  ) 3.( 1  )  0 (vô lí) Suy ra cos x  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 57 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3 2 x x x  2 4tan tan
3tan 1 tan x3  0 3 2
 tan x  tan x 3tan x 3  0   tan 1 x     4 k x     ,k  tan x   3  x      3 k
Ví dụ 3. Giải phương trình: 2
sin x(tan x 1)  3sin (
x cos x  sin ) x  3. Giải:
Điều kiện cosx  0
 Dễ thấy sin x  0 không là nghiệm của phương trình
 Chia hai vế phương trình cho 2 sin x ta được  x   x     2 1 tan 3 cot
1 3 1 cot x  0  x x    x  2 3cot cot
1 3cot 1 cot x  cot x 1 3 2  x x   x      x   2 3cot 3cot cot 1 0 cot 1 3cot x   1  0 cot   x  1  x       4 k  1   ,  cot k x     3 x      3 k ÀI T V N ỤN
BT 13. Giải các phương trình lượng giác sau: a) 2 2
2sin x 3 3sin xcos x cos x  2. b) 2 2
sin x sin xcos x  2cos x  0. c) 2 2
cos x  3sin 2x 1sin . x d) 2 2
2cos x 3 3sin 2x  4  4sin .x e) 2 2
3sin x  (1 3)sin xcos x cos x 1 3. f) 2 2
2sin x  (3 3)sin xcos x  ( 3 1)cos x 1 0. g) 2 2
4sin x 5sin xcos x 6cos x  0.   h) 9  2 2
cos (3  2x)  3 cos 4x  1   sin 2 .  2 x
BT 14. Giải các phương trình lượng giác sau: a) 3 sin x  2cos . x b) 3 3
cos x sin x  sin x cos . x c) 3
sin x  4sin x  cos x  0. d) 3 3
4(sin x  cos x)  cos x 3sin . x e) 3
6sin x  2cos x  5sin 2xcos . x f) 3 3 2
cos x  4sin x sin x  3cos xsin . x 58 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC g) 4 4 2 2
3cos x sin x  4sin xcos . x h) 3 3 2
4sin x 3(cos x sin x)  sin xcos .x   2 i) 3 2 2 cos   x x   3cos x    sin . j) 2 (1 cos2 ) sin x   2cos 2 . x  4 x  2sin 2x k) 2 2
cos x tan 4x 1sin 2x  0. l) 2 2
tan xsin x  2sin x  3(cos2x sin xcos x). m) 3 3 2 2
sin x  3cos x  sin xcos x  3sin xcos .x n) 4 4 2
4sin x  4cos x 5sin 2xcos2x cos 2x  6. o) 2 2
3cot x  2 2 sin x  (2 3 2)cos .x
GIẢI BÀI T P V N DỤNG 3 BT 13. a) 2 2
2sin x 3 3sin xcos x cos x  2.
 Xét cos x  0 thì 2
sin x 1, phương trình trở thành 2  2 (đúng) 
Suy ra x    là nghiệm phương trình. 2 k
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được  2 1 x x    2 2tan 3 3 tan
1 2 1 tan x  tan x
x   k ,k  3 6  
Vậy, nghiệm phương trình là x    ; x   k,  . 2 k 6 k b) 2 2
sin x sin xcos x 2cos x  0.
 Xét cos x  0 thì 2
sin x 1, phương trình trở thành 1 0 (vô lí) Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được 2
tan x  tan x  2  0   tan x 1 x       4 k ,   . tan  2 k x   x  arctan   2    k c) 2 2
cos x  3sin 2x 1sin . x 2 2
pt  cos x  2 3sin xcos x sin x 1
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 1
 1 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 59 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 2
1 2 3 tan x  tan x 1 tan x 2
 2tan x  2 3 tan x  0 tan  0 x kx      ,k  . tan x   3 x      3 k d) 2 2
2cos x 3 3sin 2x  4  4sin .x 2 2
 cos x 3 3sin xcos x  2sin x  2  .
 Xét cos x  0 thì 2
sin x 1, phương trình trở thành 2   2  (đúng) 
Suy ra cos x  0  x    là nghiệm phương trình. 2 k
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được 2 1  x x    2 1 3 3 tan 2tan
2 1 tan x  tan x  3 
x   k ,  . 6 k e) 2 2
3sin x  (1 3)sin xcos x cos x 1 3. 2 2
 3sin x  (1 3)sin xcos x cos x  1   3.
 Xét cos x  0 thì 2
sin x 1, phương trình trở thành 3  1   3 (vô lý) Suy ra cos x  0.
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được
2 x     x     2 3 tan 1 3 tan 1 1 3 1 tan x 2
 tan x  1 3tan x  3  0   tan  1 x       4 k x     ,k  . tan x  3  tan x     3 k f) 2 2
2sin x  (3 3)sin xcos x  ( 3 1)cos x  1  .
 Xét cos x  0 thì 2
sin x 1, phương trình trở thành 2  1  (vô lý) Suy ra cos x  0.
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được
2 x     x      2 2tan 3 3 tan 3 1 1 tan x 2
 3tan x  3 3tan x  3  0 60 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC tan   x  1  x       4 k    ,  3 k  . tan x      tan 3 x      6 k g) 2 2
4sin x 5sin xcos x 6cos x  0.
 Xét cos x  0 thì 2
sin x 1, phương trình trở thành 4  0 (vô lý) Suy ra cos x  0.
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được tan x  2
x  arctan 2  k 2 4tan  
x  5tan x  6  0  3   3  ,k  . tan x    x  arctan   k  4    4      h) 9  2 2
cos (3  2x)  3 cos 4x  1   sin 2 .  2 x  2 2
pt  cos 2x  3sin 4x sin 2x 1 2 2
 cos 2x  2 3sin 2xcos2x sin 2x 1
 Xét cos 2x  0 thì 2
sin 2x 1 sin 2x  1
 , phương trình trở thành 1
 1 (vô lí); Suy ra cos2x  0
 Xét cos 2x  0 , chia hai vế phương trình cho 2 cos 2x ta được 2  2 x x   2 1 2 3 tan 2 tan 2
1 tan 2x  2tan 2x  2 3 tan2x  0   tan 2  0 x k x  2     ,k  . tan 2x   3   x     6 k 2 BT 14. a) 3 sin x  2cos . x
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 1   0 (vô lý) Suy ra cos x  0.
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được  x  2
tan 1 tan x  2  tan x 1 x   k,  . 4 k b) 3 3
cos x sin x  sin x cos . x 3 3  x x x  2 2 x x  x  2 2 pt cos sin sin sin cos
cos sin x  cos x 2 2 3  sin .
x cos x  cos .
x sin x  2cos x  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 61 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC x  2 2 cos sin .
x cos x  sin x  2cos x  0 cos x  0 (1)   2 2 sin .
x cos x  sin x  2cos x  0 (2) 
(1)  x    , 2 k k  . (2)  2
 tan x  tan x  2  0 (vô nghiệm)  Vậy, x    , 2 k k  . c) 3
sin x  4sin x  cos x  0.  x  2 2 x x 3  x x  2 2 pt sin sin cos 4sin
cos sin x  cos x  0 3 2 2 3  3  sin x sin .
x cos x  cos .
x sin x  cos x  0
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 3
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3 2 3
 tan x  tan x  tan x 1 0 
 tan x 1 x   k,  . 4 k d) 3 3
4(sin x  cos x)  cos x 3sin . x   3 3 x x  x  2 2 x x  x  2 2 pt 4 sin cos cos sin cos
3sin sin x  cos x 3 2 2 3  sin x sin .
x cos x  3sin .
x cos x  3cos x  0
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 1
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3 2
tan x  tan x 3tan x 3  0 tan x 1   x      4 k
 tan x  3   ,k  .    tan    3 x      3 k x e) 3
6sin x  2cos x  5sin 2xcos . xx  2 2 x x 3 2 pt 6sin sin cos  2cos x 10sin . x cos x  0 62 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 3 2 3  6sin x  4sin .
x cos x  2cos x  0
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 6
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3
6tan x  4tan x  2  0   tan x  1
  x    k,  . 4 k f) 3 3 2
cos x  4sin x sin x  3cos xsin . x 3 3  x x x  2 2 x x 2 pt cos 4sin sin sin cos 3cos . x sin x  0 3 2 2 3  3  sin x 3sin .
x cos x  sin x cos x  cos x  0
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 3
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3 2 3
 tan x 3tan x  tan x 1 0  tan x  1         3 x   4 k  tan x    ,   . 3 k    x    k   3  6 tan x   3 g) 4 4 2 2
3cos x sin x  4sin xcos . x
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành
1 0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 4 cos x ta được 4 2
tan x  4tan x 3  0   tan  1 x       4 k x     ,k  . tan x   3  x      3 k h) 3 3 2
4sin x 3(cos x sin x)  sin xcos .x 3 2 2 3
pt  sin x 3sin xcos x sin xcos x 3cos x  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 63 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 1
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3 2
tan x  tan x 3tan x 3  0   tan 1 x     4 k x     ,k  . tan x   3  x      3 k   i)  3 2 2 cos x   3cos x    sin .  4 x    x x3 pt cos sin
3cos x sin x  0 2 3
 2sin xcos x  2cos x  0
 Xét cos x  0 thì phương trình đúng 
Suy ra x    là nghiệm. 2 k
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 
2tan x  2  0  tan x 1 x   k,  . 4 k
(Lưu ý: bài này cũng có thể đặt 2
cos x làm nhân tử chung) 2 j)  x 2 (1 cos2 ) sin x   2cos 2 . 2sin 2 x x  Đk : sin 2  0 k xx  ,  2 k 3 2 cos pt  sin x x   2 2 2cos x   1  0 sin x 3 3 2  x x x x x  2 2 sin cos 4sin cos
2sin sin x  cos x  0 3 3 2
 3sin x  cos x  2sin xcos x  0
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 3
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3
3tan x  2tan x 1 0    tan x  1
  x    k,  . So với đk, ta nhận nghiệm x    k,  . 4 k 4 k 64 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC k) 2 2
cos x tan 4x 1sin 2x  0. Đk: cos4x  0
 Xét cos x  0 thì phương trình trở thành
1 0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 2 cos x ta được tan x  1  2
pt  tan 4x tan x  2
1  0  tan4x 0   x      4 k    
,k   x    k,k  . So với đk, ta nhận nghiệm x    k, k  . k  4 4 x   4 l) 2 2
tan xsin x  2sin x  3(cos2x sin xcos x). Đk : cos x 0 3 2 3 2
pt  sin x  2sin xcos x 6cos x 3cos x 3sin xcos x  0 3 2 3 2
 sin x sin xcos x 3cos x 3sin xcos x  0
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 1
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3 2
tan x  tan x 3tan x 3  0   tan  1 x       4 k x    
,k  . So với đk, ta nhận tất cả nghiệm. tan x   3  x      3 k m) 3 3 2 2
sin x  3cos x  sin xcos x  3sin xcos .x
 Xét cos x  0 thì 2
sin x 1 sin x  1
 , phương trình trở thành 1
  0 (vô lí); Suy ra cos x  0
 Xét cos x  0, chia hai vế phương trình cho 3 cos x ta được 3 2
tan x  3 tan x  tan x  3  0   tan  1 x       4 k x     ,k  . tan x   3  x      3 k n) 4 4 2
4sin x  4cos x 5sin 2xcos2x cos 2x  6.
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 65 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 2 pt  2
 sin 2x 5sin 2xcos2x  cos 2x  2
 Xét cos 2x  0 thì 2
sin 2x 1 sin 2x  1
 , phương trình trở thành 2
  2 (vô lí); Suy ra cos2x  0
 Xét cos 2x  0 , chia hai vế phương trình cho 2 cos 2x ta được 2  x x    2 2tan 2
5tan 2 1 2 1 tan 2x 2  4
 tan 2x 5tan 2x 1 0 tan   x  1 x      4 k  1   ,  . tan   1 k x  4 x  arctan    4 k o) 2 2
3cot x  2 2 sin x  (2 3 2)cos .x Đk: sin x  0 2 4  x x     2 pt 3cos 2 2 sin 2 3 2 cos . x sin x  0  x  2 x x 2  x  2 3cos cos 2 sin 2sin
2 sin x cos x  0  2 2 cos cos x
x  2 sin x  0 2
cos x  2  2 cos x  0     2   2
3cos x  2sin x  0 2
3cos x  2  2cos x  0  1 cos x   2   x    k2  4  
,k  . So với đk, ta nhận tất cả nghiệm. 
x    k2  3 66 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
4. Phöông trình löôïng giaùc ñoái xöùng
Dạng 1. a (sin x  cos x)  bsin xcos x c  0 (dạng tổng/hiệu – tích) PP  Đặt 2
t  sin x  cos ,
x t  2  t   và viết sin x cos x theo t.
Lưu ý, khi đặt t  sin x  cos x thì điều kiện là: 0  t  2 .  Dạng 2. 2 2
a  (tan x  cot x)  b (tan x  cot x)  c  0 PP  Đặt 2
t  tan x  cot ,
x t  2  t   và biểu diễn 2 2
tan x  cot x theo t và
lúc này thường sử dụng: 2
tan xcot x 1, tan x  cot x   sin 2x
Ví dụ 1. Giải phương trình: sin 2x  (2  2)(sin x  cos ) x 1 2 2  0. Giải:   Đặt 
t  sin x  cos x  2 sin x   ; t  2 4    Ta có: 2t   x x2 2 sin cos
 sin 2x t 1 
Phương trình trở thành: 2 t  2 t      2 1 2
2 t 1 2 2  0  t  2 2t 2 2  0  t  2    
 Với t  2 thì sin x  
 1  x   k2,    4  4 k  Với t  2  thì 2   2 vô lí
Ví dụ 2. Giải phương trình: 2 2
2tan x  2cot x (4 2)(tan x  cot ) x  4  2 2  0. Giải:
Điều kiện sin 2x  0
Đặt t  tan x  cot x Ta có: 2t   x x2 2 2 2 tan cot
 tan x  cot x t  2
Phương trình trở thành:  2t     2 2 2 4
2 t  4  2 2  0  2t 4 2t  2 2  0 Phương trình vô nghiệm ÀI T V N ỤN
BT 15. Giải các phƣơng trình lƣợng giác:
a) sin 2x  2 2 sin x  cos x  5
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 67 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  Ta có 2t   x x2 2 sin cos
1sin 2x  sin 2x t 1 t   2
Phương trình trở thành : 2 2
t 1 2 2t  5  t  2 2t  6  0  t 3 2(L) Với t   2 :         3    2 sin x    2  sin x   1
  x     k2  x   k2,k      .  4   4  4 2 4
b) 2sin x  cos x 6sin xcos x  2. Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  Ta có 2t   x x2 2 sin cos
1 2sin xcos x  2sin xcos x t 1 t 1
Phương trình trở thành : 2  t  3 2 t   2
1  2  3t  2t 5  0  5  t  (L)  3    x    k2 x k2  Với       1 4 4 t  1: 2 sin x   1 sin x              ,k  .  4   4  2   3
x   k2 x    k2  2  4 4
c) sin x  cos x sin xcos x 1. Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  2  Ta có 2t   x x2 t 1 sin cos
1 2sin xcos x  sin xcos x  . 2 1 t 1
Phương trình trở thành : t   2t   2
1 1 t  2t 3  0  2  t  3  (L)    x    k2 x k2       Với  1 4 4 t  1 2 sin x   1 sin x              ,k  .  4   4  2   3
x   k2 x    k2  2  4 4 68 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
d) 1 2sin xcos x2sin xcos x 1 2. Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  Ta có 2t   x x2 2 sin cos
1 2sin xcos x  2sin xcos x 1t . t 1
Phương trình trở thành : 1 2t  2 1t  2
1 2  t  1 2t  2  0  t  2    x    k2         1  4 4 x   k2 Với t 1 2 sin x   1 sin x             2 ,k  .  4   4  2   3  x    k2
x    k2  4 4          Với t  2 : 3  2 sin x   2  sin x
 1 x    k2  x   k2,k      .  4   4  4 2 4
e) 2 2 sin x cos x  3sin 2 .x Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  Ta có 2t   x x2 2 sin cos
1 2sin xcos x  sin 2x 1t .
Phương trình trở thành : t    2 t  2 2 2 3 1
t  2 2t  2  0  t  2          Với t  2 : 3  2 sin x   2  sin x
 1 x    k2  x   k2,k      .  4   4  4 2 4
f) 1 21sin x cos x  sin2 .x Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  Ta có 2t   x x2 2 sin cos
1 2sin xcos x  sin 2x 1t . 
Phương trình trở thành :         t   2  t  2  t     t 2 1 2 1 2 1 1
2 t  2  0  t  1          Với t  2 : 3  2 sin x   2  sin x
 1 x    k2  x   k2,k      .  4   4  4 2 4
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 69 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Với t  1      x    k2 x k2       1     4 4 2 sin x   1 sin x   sin             3 ,k  .  4   4  2 4   5
x    k2 x    k2  2  4 4
g) 2 2 sin x cos x  2sin 2x 1 Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  Ta có 2t   x x2 2 sin cos
1 2sin xcos x  sin 2x 1t .  2 t
Phương trình trở thành : t   2  t  2 2 2 2 2 1
1  2t  2 2t 3  0   3 2 t  (L)  2 Với 2 t  : 2     5 x    k2 x   k2  2  1  4 6      12  2 sin x      sin x         ,k  .  4  2  4  2   5  13 x    k2 x   k2  4 6  12
h) sin x  cos x  2 2 sin x cos x Giải:   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  Ta có 2t   x x2 2 sin cos
1 2sin xcos x  2sin xcos x 1t .  2  
Phương trình trở thành :  2  2 1  2  0  2   2  0 t t t t t  2  t   2 Với 2 t  : 2     5 x    k2 x   k2  2  1  4 6      12  2 sin x      sin x         ,k  .  4  2  4  2   5  13 x    k2 x   k2  4 6  12 70 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Với t   2 :            2 sin  x    2  sin x   1   x  
k2  x   k2,k      .  4   4  4 2 4   i) sin 2 
x  2 sin x     1.  4  2           2 sin  x
 1sin 2 x 0  2 sin x    2 sin x         0  4   4    4         2 sin  x  . 1  2 sin x       0  4    4      x                4 k x  4 k  2 sin x   0 sin x       0    4   4            x
  k2  x   k2 ,k  .         1  4 4  2 2 sin x     1 sin       4 x   4      2  3
x    k 2 x    k2   4 4  j) 1 1   2 2.
Điều kiện: sin 2x  0. sin x cos x
Ta có: sin x  cos x  2 2  sin x  cos x  2 2 sin . x cos . (1) sin .cos x x x   Đặt 
t  sin x  cosx  2 sin x ,t    2  4  Ta có 2t   x x2 2 sin cos
1 2sin xcos x  2sin xcos x t 1 t  2
Phương trình (1) trở thành :  t  2  2 t   2
1  2t t  2  0    2 t   2         
Với t  2  2sin x   2 sin x  1
  x   k 2  x  k 2,k      . (t/m)  4   4  4 2 4 Với  2 t  : 2      5   x    k2 x   k2     2    1   4 6  12  2 sin x      sin x         ,k  .(t/m)  4  2  4  2   7  11 x    k2 x   k2  4 6  12   k) 1 1    2 2 cos  
Điều kiện: sin 2x  0. cos sin x   x x  4    
 sin x cos x 2 2 cos    sin .cos x   x x  4 
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 71 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   Đặt 
t  sin x  cos x   2 cos x  , t    2  4  Ta có 2t   x x2 1 sin cos
1 2sin xcos x  sin xcos x   2 1t . 2 2  1  2t. 2 2 t  t t  0
Phương trình trở thành :   2  t  2t.   1   0   0  2  1t  2 2 1 t  1tt   2     Với 
t   2   2 cos( x  )   2 c  os( x  ) 1
  x   2k   x
k 2,k  . (Đ) 4 4 4 4     Với 3
t  2   2 cos( x )  2 cos( x )  1
  x   k 2 x
k 2,k . (Đ) 4 4 4 4     
Với t  0   2cos( x  ) 0  c  os( x  ) 0
  x   k  x  k 2,k  . (Đ) 4 4 4 2 4
l) 2sin 2x 8  3 6 sin x  cos x . Giải:
Đặt t  sin x  cos x điều kiện 0  t  2 Ta có : 2t   x x2 2 sin cos
1sin 2x  sin 2x t 1  6  
Phương trình trở thành: 2 2   2
1 8  3 6  2 3 6  6  0 t t t t t  2  t  6(L)        Với 6 t  thì 6 6 3
t  sin x  cos x   2 cos x    cos x        cos 2 2  4  2  4  2 6      cos    x     cos x     k2 4 6       6 4   ,k  .      5  5  cos x   cos     cos x     k2   4  6 6  6 4
m) sin x cos x  4sin 2x 1. Giải   Đặt 
t  sin x  cos x  2 cos x  
điều kiện 0  t  2 4    Ta có : 2t   x x2 2 sin cos
1sin 2x  sin 2x 1t 72 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC t 1
Phương trình trở thành: t 4 2 1 t  2 1 4t t 3 0          3  t  L  4 Với t  1 thì x k2       x     k2 x   k2      1 x k      4 4  2 2 cos x   1 cos x               k  .  4   4  2   3 x     k2         k2 x    2 k x  4 4    x   k2  2
n) cos xsin x  cos x sin x 1. Giải:
Đặt t  sin x  cos x điều kiện 0  t  2 Ta có : 2t   x x2 1 sin cos
1 sin 2x  sin .
x cos x   2 t   1 2 1 t 1
Phương trình trở thành:  2t   2
1  t 1 t  2t 3  0  2  t  3  (L)         Với  t  1 thì 1 1
sin x  cos x 1 2 cos x    1  cos x      cos     4 4 x 2  4        2 x k2      x     k2
x   k2 x k  4 4  2        3   
x    k2 k          k2 x    2 k x  4 4    x   k2  2
BT 16. Giải các phƣơng trình lƣợng giác: a) 2 2
3tan x  4tan x  4cot x 3cot x  2  0.
Điều kiện sin 2x  0.   2 2
3 tan x  cot x 4tan x cot x 2  0
Đặt t  tan x  cot x , 2 t   2 sin 2x Ta có: 2t   x x2 2 2 2 tan cot
 tan x  cot x t  2 t  2 
Phương trình trở thành: 3 2  t  2 2
 4t  2  0  3t  4t  4  0  2 t  (L)  3
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 73 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC    Với 2  t  2    2   sin2 x  1  2  x   2 k   x
k ,k  . (t/m) sin2 x 2 4 b) 2 2
 2tan  5tan  5cot  4  0.
Điều kiện sin 2x  0. 2 sin x x x x  2 2 1 cot x 2
 2tan x  5tan x  5cot x  4  0  2 2 2
tan x  cot x5tan x  cot x 6  0
Đặt t  tan x  cot x , 2 t   2 sin 2x Ta có: 2t   x x2 2 2 2 tan cot
 tan x  cot x t  2 t  2 
Phương trình trở thành: 2 2t 2 2 5t 6 0 2t 5t 2 0           1  t  (L)  2    Với 2  t  2    2   sin2 x  1  2  x   2 k   x
k ,k  . (t/m) sin2 x 2 4
c) tan x 3cot x  4(sin x  3cos x).
Điều kiện sin 2x  0. 2 2 sin x  3cos x
 4sin x  3cos x sin .xcos x   x x  sin x 3 cos x sin 3 cos  . 4     0  sin .xcos x    2sin    x     2sin 2     3 x 2cos   x  .    0  6  sin .xcos x     2 x             6 2 k x  3 k cos x     0    6          x   2x k2  x
k2 ,k  (t/ m).      3  3 sin x      sin 2     3 x   4 k2
x     2x k2     3 x  9 3 d) 3
2sin x cos2x  cos x  0. 2 2  2sin .
x sin x  2 cos x  cos x 1  0  2sin . x  2 1 cos x 2
 2cos x  cos x 1  0  2.sin .
x 1 cos x1 cos x  1 cos x2 cos x   1  0
 1 cos x.2sin .x
1cos x2cos x   1   0 
 1 cos x.2sin .xcos x  2 
sin x cos x1  0  cos x 1
 2sin .xcosx2 
sin x  cos x1 0 74 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  Với cos x 1
  x k2  Với 2sin .
x cos x  2sin x  cos x 1  0   Đặt 
t  sin x  cos x  2 cos x  , t    2  4  Ta có 2t   x x2   x x x x   2 sin cos 1 2sin cos 2sin cos t   1 . t  0
Phương trình trở thành : 2 2
t 1 2t 1  0  t  2t  0  t  2  (L)       Với t  0 thì 3 cos x
 0  x    k2  x   k2,k    .  4  4 2 4 e) 3
2cos x  cos2x sin x  0. 2 2  2cos .
x cos x 1 2sin x  sin x  0  2cos . x  2 1sin x 2
 2sin x  sin x 1  0  2.cos .
x 1 sin x1 sin x  1 sin x2sin x   1  0
 1sin x.2cos .x
1sin x2sin x   1   0 
 1sin x.2sin .xcos x  2 
sin x cos x1  0  sin x 1
 2sin .xcosx2 
sin x cos x1 0   Với sin x 1
  x   k 2 2  Với 2sin .
x cos x  2sin x  cos x 1  0   Đặt 
t  sin x  cosx  2 cos x ,t    2  4  Ta có 2t   x x2   x x x x   2 sin cos 1 2sin cos 2sin cos t   1 . t  0
Phương trình trở thành : 2 2
t 1 2t 1  0  t  2t  0  t  2  (L)       Với t  0 thì 3 cos x
 0  x    k2  x   k2,k    .  4  4 2 4 f) 3 3
2sin x sin x  2cos x cos x cos2 . x 3 2 3 2
 2sin x  sin x sin x  2cos x  cos x  cos x  2 3 3
sin x  cos x sin x cos x 1 0
 2sin x  cos x1 sin .xcos x sin x  cos x 1 0(*)   Đặt 
t  sin x  cos x   2 cos x  , t    2  4 
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 75 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Ta có 2t   x x2 1 sin cos
1 2sin xcos x  sin xcos x   2 1t . 2  t  1  
Phương trình (*) trở thành:  1    t   2  t  3 1 5 2 . 1 1
t 1  0  t
  2t 1  0    2 t     2   1 5 t  (L)  2       Với 1  t  1   cos x  
x     k 2  x k 2;x k    2 .   4  2 4 4 2 Với 1 5 t  2    10  2   10  2  cos x  
x    arccos  k2  x    arccos  k2,cos  ,k    .  4  4 4 4 4 g) 3 3
sin x cos x 1sin 2 . x   x x   x x   x x2 sin cos . 1 sin .cos sin cos
 sin x  cos x.1sin .xcos x sin x cos x  0   Đặt 
t  sin x  cos x   2 cos x  , t    2  4  Ta có 2t   x x2 1 sin cos
1 2sin xcos x  sin xcos x   2 1t . 2 t  0
Phương trình trở thành:  1   t. 1  2
1t t  0  t. 2t
  2t  3  0  t    1 2    t  3   (L)      
Với t  0  cos x   
 0  x    k 2  x  k 2.  4  2 4 4        Với 1 3
t  1 cos x    x     k   2  x  
  k2; x   k2.  4  2 4 4 2
h) cos2x 5  2(2cos )
x (sin x  cos ) x . 2
 2cos x 1 5  2.(2  cos x)(sin x  cos x). 2  cos x  2   2
2sin x  2cos x  cos .xsin x  cos x
 2sin x  cos x  cos .xsin x  2  0   Đặt 
t  sin x  cos x   2 cos x  , t    2  4  76 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Ta có 2t   x x2 1 sin cos
1 2sin xcos x  sin xcos x   2 1t . 2 1 1 5 t 1
Phương trình trở thành: 2t   2 1t  2
 2  0  t  2t   0  2 2 2  t  5  (L)        Với 1 3
t  1 cos x    x     k   2  x  
  k2; x   k2.  4  2 4 4 2 i) (3cos4 )
x (sin x  cos ) x  2.  3   2 2cos 2x  
1 .sin x  cos x  2  2 cos    x  sin x2 2 2
.sin x  cos x 1  
 2  cos x sin x2 .cos x  sin x2 .sin x  cos x 1     Đặt 
t  sin x  cos x   2 cos x  , t    2  4  Ta có 2t   x x2   x x x x   2 sin cos 1 2sin cos 2sin cos 1t . Khi đó:  x x2 2 2 sin cos
11t  2 t
Phương trình trở thành : 5 3
t  2t  2t 1  0 có nghiệm t  1  j) 2 x  3  x 3 tan . 1 sin  cos x 1
Điều kiện : x    . 2 k 2 1 cos x  . 3 1sin x 3 1 cos 2 1sin x x 2 3 1 cos x 1 cos x   2 1 sin x  3 1 sin x 2
1 cos x 1 cos x 1 cos x  cos   . x     0 2
1 sin x  1sin x 1sin x sin x  1 cos x  0 1sin x   2
1 cos x 1 cos x  cos x   0  2
1 sin x 1 sin x  sin x cos x 1  1cosx.   2
1 sin x  sin x  1sin x. 2 1 cos x   cos x cos x 1   2 2 2 2 sin x  cos .
x sin x  cos x  sin . x cos x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 77 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
TH 1: cos x 1 x k2 TH 2: 2 2 2 2 sin x  cos .
x sin x  cos x  sin . x cos x
 sin x  cos x.sin x  cos x  sin .xcos x  0
sin x  cos x  0
 sinxcosxsin .xcosx 0      
Với: sin x  cos x  0  cos x   
 0           4 x  4 2 k x 4 k
Với : sin x  cos x sin xcos x  0.   Đặt 
t  sin x  cos x  2 sin x  , t    2  4  2 Ta có 2  t   x x2 t 1 sin cos
1 2sin xcos x  sin xcos x  . 2 1 t  1   3
Phương trình trở thành : t   2t   2
1  0  t  2t  2  0   2 t  1   3 (L) Với t  1   3   x   arcsin  k2       6 2   4  2 sin x     1   3  sin        4 x   4  2 
x    arcsin  k2  4    x   arcsin  k2  4   ,k  .  3 x   arcsin  k2  4    Với 6 2 sin  2      78 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
5. Moät soá phöông trình löôïng giaùc daïng khaùc Dạng 1. . m sin 2x  . n cos 2x  . p sin x  .
q cos x r  0 2 2
 cos x sin x (1) 
Ta luôn viết sin 2x  2sin xcos , x còn: 2
cos 2x   2cos x   1 (2)  2 1 2sin x  (3)
Nếu thiếu sin 2x , ta sẽ biến đổi cos2x theo (1) và lúc này thường sẽ đưa được về dạng: 2 2
A B  (A B)(A B)  0. Nếu theo (2) được: 2 sin . x (2 .
m cos x p)  (2 . n cos x  .
q cos x r  ) n  0 và theo (i) (3) được: 2 cos x(2 .
m sin x q)  ( 2  . n sin x  .
p sin x r  )
n  0. Ta sẽ phân tích (ii)
(i), (ii) thành nhân tử dựa vào: 2
at bt c a(t t )(t t ) với t , 1 2 1 t là hai 2 nghiệm của 2
at bt c  0 để xác định lượng nhân tử chung.
Ví dụ 1. Giải phương trình: cos 2x  cos x  3sin x  2  0. Giải: 2 2 2 2 pt  cos  1   3 
x  sin x  cos x  3sin x  2  0  cos x    sin   2 x 2       1 3 cos x   sin   2 x 2
cos x  sin x  2      1 3     cos cos x sin x 1 x   sin   2 x 2   
 Với cos x sin x 2  c  os x    2 1    phương trình vô nghiệm  4       1 x    k2
 Với cos x sin x 1 sin x           2 ,    4 k  2 
x    k2
Ví dụ 2. Giải phương trình: 2sin 2x  cos 2x  7sin x  2cos x  4. Giải: 2
pt  4sin xcos x 1 2sin x 7sin x 2cos x  4  0   2
2sin x 7sin x 34sin xcos x 2cos x  0  2sin x  
1 sin x 3  2cos x2sin x   1  0  2sin x  
1 sin x  2cos x 3  0  1 2sin x 1  0 sin x      2
sin x  2cos x  3  0 
sin x  2cos x  3
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 79 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 Với sin x 2cos x 3
 thì phương trình vô nghiệm vì 2 2 2 1  2  3   x   k2 1   Với 6 sin x    ,  2  5 kx   k2  6 ÀI T V N ỤN
BT 17. Giải các phương trình lượng giác sau: a) cos2  x
x  3cos x  2  sin . x b) 5 cos2  2cos . 3 2tan x x   c) 3sin 
x  cos x  2  cos 2x  sin 2 . x
d) 5cos x  sin x 3  2 sin 2x    4      e) sin 2 
x  cos 2x  sin x  cos x 1. f) 2 sin 2x
 3sin x  cos x    2.  4 
g) cos x sin x sin 2x cos2x 1. h) 2
sin 2x cos x  2sin x  cos2x 3sin . x i) 2
sin 2x  2cos x  3sin x cos . x
j) 2 2 sin 2x cos2x 7sin x  4  2 2 cos . x
k) sin 2x cos2x 3sin x cos x 1.
l) sin 2x cos2x 3cos x  2  sin . x
m) sin 2x  2cos2x 1sin x 4cos . x
n) 2sin 2x cos2x  7sin x  2cos x 4.        o)  1 2sin  x    sin  2     p) 2 sin 2x
 sin x  3cos x    2. 3 x 6      2  4  q) 2  tan x 1 tan x   r) 2 3(sin 2x 3sin )
x  2cos x  3cos x  5.    2 sin cos 5 x x   4    Giải
a) cos2x 3cos x  2  sin x
 cos x sin xcos x  sin x  2cos x  sin x  cos x  sin x  2  0
 cos x sin xcos x  sin x  2  cos x  sin x  2  0
 cos x sin x  
1 cos x  sin x  2  0
cos x  sin x 1  0
 cosxsinx20      1 x   k2
 cos x sin x 1 0 sin x cos x 1 sin x            2 k      4  2 
x    k2 
cos x sin x  2  0 PTVN 
Vậy phương trình đã cho có nghiệm là: x   k2, x    k2 k   2  b) 5 cos2x  2cos . 3 2tan x x Điều kiện: 3
tanx   , cosx  0. 2 5 cos2x  2cos 3 2tan x x 80 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 2
 5 cos x sin x  6cos x  4sin x   x  2   x  2 cos 3 sin 2 x k2    1 cos x 3 sin x 2 sin x cos x 1 sin x               k      4  2
x   k2 l  2
Vậy phương trình đã cho có nghiệm là: x k2 k  
c) 3sin x cos x  2cos2x  sin 2 . x 2
 2sin x  3sin x 1  2sin xcos x  cos x
 sin x   1 2sin x  
1  cos x2sin x   1 2sin x 1  0  2sin x  
1 sin x cos x  
1  0  sinxcosx10   x    k2   2sin 1 6
x 1  0  sin x     k   2  7 x   k2  6 x k2     2 sin x cos x 1 0 sin x          3 k      4  2 x   k2  2   
Vậy phương trình đã cho có các nghiệm là 7 x    k2, x   k2 , 3
x k 2 , x   k2 6 6 2 k     d) 5cos 
x  sin x  3  2 sin 2x   4   
 5cos x  sin x  3  sin 2x  cos 2x 2
 5cos x  sin x  3  2sin xcos x  2cos x 1 2
 2cos x  5cos x  2  2sin xcos x sin x  0
 cos x  22cos x  
1  sin x2cos x   1  0  2cos x  
1 sin x  cos x  2  0 2cos x 1  0
 sinxcosx20 1 
 2cos x 1 0  cos x   x    k2 k   2 3 
sin x cos x 2  0  sin x cos x  2 (PTVN) 
Vậy phương trình đã cho có các nghiệm là x    k2 k   3
e) sin 2x cos2x sin x cos x 1
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 81 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2
 2sin xcos x  2cos x  sin x  cos x  0
 2cos xsin x  cos x  sin x  cos x  0
 sin x  cos x2cos x   1  0 tan   x  1 sin  cos  0 x      4 k x x    1   k   2cos x 1  0 cos x    2  2 x    k2  3  
Vậy phương trình đã cho có các nghiệm là 2 x
k , x  
k2 k   4 3   f) 2 sin 2  x
 3sin x  cos x    2  4 
 sin 2x  cos 2x  3sin x  cos x  2 2
 2sin x cos x  3sin x  2cos x  cos x  3  0
 sin x2cos x 3  cos x  
1 2cos x 3  0
 2cos x  3sin x  cos x   1  0
2cos x  3  0 PTVN         1 x    k2
sin x  cos x 1 sin x      2 k       4  2  
x    k2 
Vậy phương trình đã cho có các nghiệm là x    k2, x    k2 k   2
g) cos x sin x sin 2x cos2x 1. 2
 cos x  sin x  2sin xcos x  2cos x  0
 cos x  sin x  2cos xsin x  cos x  0
 cos x  sin x1 2cos x  0 tan   x  1 cos  sin  0  x       4 k x x    1   k   1   2cos x  0 cos x    2
x    k2  3  
Vậy phương trình đã cho có các nghiệm là x    k, x    k2 k   4 3 h) 2
sin2x cos x 2sin x cos2 x 3  sin x 2
 2sin x cos x  cos x  2sin x  2cos x 1 3 2 1 cos x 2
 2sin x cos x  cos x  2sin x  cos x  2 2
 2sin x cos x  2sin x  cos x  cos x  2  0
 2sin xcos x   1  cos x  
1 cos x  2  0  cos x  
1 2sin x  cos x  2  0 cos x 1  0 cos x  1     2sin 
x  cos x  2  0
2sin x  cos x  2
82 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  cos x  1
  x    k2 k   
2sin x  cos x  2 2 1 2 2  sin x  cos x
 sin xcos  sin cos x  5 5 5 5   2  x  ar sin c   k2        sin x   2 5   k   5   2  x    ar sin c   k2     5 
Vậy phương trình đã cho có các nghiệm là  2 
x    k 2 , x  ar s c in   k2,    5   2  x    ar s c in   k2   k    5  i) 2
sin 2x  2cos x  3sin x  cos . x
 sin 2x 1 cos 2x  3sin x  cos x 2
 2sin xcos x  cos x  2sin x 3sin x  2  0
 cos x2sin x  
1  sin x  22sin x   1  0  2sin x  
1 sin x  cos x  2  0    x    k2  1  6
2sin x 1  0  sin x     k     2 7 x   k2   6 
sin x  cos x  2  0  PTVN  
Vậy phương trình đã cho có các nghiệm là 7 x  
k2 , x
k2 k   6 6
i) 2 2 sin 2x cos2x 7sin x 4 2 2 cos x 1  Lời giải
2 2 sin 2x  cos 2x  7sin x  4  2 2 cos x
 2 2 sin 2x  2 2 cos x o
c s2x  7 sin x  4  0
 2 2 cos x2sin x   1   2
2sin x  7 sin x  3  0
 2 2 cos x2sin x  
1  s inx  32sin x   1  0  2sin x  
1 2 2 cos x  sinx  3  0 2sin x  0
 2 2cosxsinx 3   x   k2   Với 6 2sin x 1    k   5 x   k2  6
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 83 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  Với 2 2 cos x s  inx 3
  ocs x  1   x  2 k ,  k với  2 2 1    cos và  sin    3 3    5
Vậy phương trình có nghiệm: x   k2, x
k2, x    k2,k  6 6
k) sin 2x cos2x 3sin x cos x 1. Lời giải
sin 2x  cos 2x  3sin x  cos x  1  2sin .
x cos x  cos x   2
1 2sin x  3sin x 1  0
 cos x2sin x   1   2
2sin x  3sin x  2  0
 cos x2sin x   1  2sin x  
1 sin x  2  0      x   x x   2sin x 1 0 2sin 1 cos sin
2  0  cosxsin x2  0   x   k2  Với 1 6 2sin x 1  0 s  inx    , k  2 5 x   k2  6   Với  cos x sin x 2  0  s  in x    2   (vô nghiệm)  4   5
Vậy phương trình có nghiệm: x   k2, x
k2,k  . 6 6
l) sin2x cos2x 3cos x 2 sin .x Lời giải
sin 2x  cos 2x  3cos x  2  sin x
 sin 2x sinx   2
2 cos x  3cos x   1  0
 sinx 2cos x   1  2cos x   1 cos x   1  0  1   x  x  cos x 2 cos 1 s inx cos 1 0       2 
sinx  cos x 1  0 x k2   Với  sinx cos x 1 0 2 sin x 1          , k     4 
x   k2  2  
Vậy phương trình có nghiệm: x    k2, x k2, x   k2,k  3 2
m) sin 2x  2cos2x 1sin x 4cos . x Lời giải
sin 2x  2 cos 2x  1 sin x  4 cos x
 sin 2x sin x  2cos 2x  4cos x   1  0
 sin x2cos x  
1  2cos x  32cos x   1  0 84 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC     x   x x   2 cos x 1 2 cos 1 sin 2 cos
3  0  sin x2cosx3 0  
2 cos x  1  x    k2,k  3
 sin x  2cos x 3  0(vô nghiệm vì 2 2 2 1  2  3 ) 
Vậy phương trình có nghiệm: x    k2,k  3
n) 2sin 2x cos2x  7sin x  2cos x 4. Lời giải
2sin 2x  cos 2x  7 sin x  2 cos x  4
 2sin 2x  2cos x  cos 2x  7sin x  4  0
 2cos x2sin x   1   2
2sin x  7 sin x  3  0
 2cos x2sin x   1  2sin x  
1 sin x  3  0  2sin x  
1 2cos x  sinx 3  0  1 sin x    2 
2cos x  sin x  3  0   x   k2  Với 1 6 sinx    , k  2 5 x   k2  6 Với 2cos x s  in x 3  0  (vô nghiệm vì 2 2 2 1  2  3 )  5
Vậy phương trình có nghiệm: x   k2, x
k2,k  . 6 6      o)  1 2sin x   sin 2x         3   6  2 Lời giải.       1 3 1 1 2sin x   sin 2x
  sin x  3 cos x - sin 2x  cos 2x       3   6  2 2 2 2   x   k2     x   x  x   x sin x 1 2 2sin 1 sin 2 3 cos 1 sin  0     tan x  3 
x   k  3   p)  2 sin 2x
 sin x  3cos x  2.    4  Lời giải.
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 85 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC    2 sin 2x
 sin x  3cos x  2  sin 2x  cos 2x  sin x  3cos x  2    4   2cos x   2
1 sin x  2 cos x  3cos x 1  0  2 cos x  
1 sin x  cos x   1  0    1 x    k2 cos x   3  2     x k2      1 sin x         4  2
x   k2  2 q) 2  tan x 1 tan x      2 sin x cos 5x     4  Lời giải.        ĐK: cos 5x 0     4  sin  2x  0 2  tan x 1 tan x
2 cos x  sin x cos x  sin x   
 2sin 2x  cos 2x 1  cos 6x  sin 4x    2 sin x
cos 5x  sin 5x 2 sin x cos 5x     4 
 2sin 2x  sin 4x 1  cos 6x  cos 2x  2sin 2x  sin 4x 1  2  sin 4xsin 2x   kx     8 2 sin 4x  1       1  x    k sin 2x    12  2  7 x   k  12 r) 2 3(sin 2x  2sin )
x  2cos x  3cos x  5. Lời giải. 2
3(sin 2x  2sin x)  2 cos x  3cos x  5  2 3 sin x cos x   1  cos x   1 2cos x  5 cos x 1  0 x k2    
2 3 sin x  2cos x  5
2 3 sin x  2cos x  5  VN
Dạng 2: Phương trình có chứa (
R ..., tan X , cot X ,sin 2X , cos 2X , tan 2X ,...), sao cho cung của
sin, cos gấp đôi cung của tan hoặc cotan. Lúc đó đặt t  tan X và sẽ biến đổi:  sin X 2 tan X 2t 2
sin 2X  2sin X cos X  2  cos X    2 2 cos X 1 tan X 1 t 2 2    1 1 tan X 1 t 2
cos 2X  2 cos X 1  2  1    2 2 2 1 tan X 1 tan X 1 t 2   sin 2X 2t 1 t tan 2X   và cot 2X   2 cos 2X 1 t 2t
Từ đó thu được phương trình bậc 2 hoặc bậc cao theo t, giải ra sẽ tìm được t  . x
Ví dụ. Giải phương trình: sin 2x  2 tan x  3. 86 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Giải:
Điều kiện cosx  0 2 tan x
pt  2sin x cos x  2 tan x  3   2 tan x  3 3 2
 2tan x 3tan x  4tan x 3  0 2 1 tan x 2       tan x   1  1 23 2
2 tan x  tan x  3  0  tan x   1 2 tan x       0   4  8   
 tan x 1  x   k ,k  4 ÀI T V N ỤN
BT 18. Giải các phương trình lượng giác sau:
a) 13tan x  2sin 2 . x
b) cos2x  tan x 1.
c) sin 2x  2tan x  3. d) (1 tan ) x (1 sin 2 ) x  1 tan . x      e)  1 tan x x x  1 cot x      f) sin 2 cos 2 cot x  , x    ;0     2  1 sin 2x 2  sin 2x  2  g) 2 cos 2x 1
cot x  tan x  4sin 2x   h) 2 cot x 1   sin x  sin 2 . x sin 2x 1 tan x 2 Lời giải
a) 13tan x  2sin 2 . x
Điều kiện cosx  0. Pt 4 tan x 3 2 1 3tan x
 3tan x  tan x  tan x 1  0. 2 1 tan x   x   2 tan
1 3tan x  2 tan x   1  0. tan x 1  0   . 2
3tan x  2 tan x 1  0  v« nghiÖm   tan x  1
  x    k, k  . 4
b) cos2x  tan x 1.
Điều kiện cosx  0. 2  Pt 1 tan x 3 2 
 tan x 1  tan x  2 tan x  tan x  0. 2 1 tan xx x  2 tan tan 1  0. x k tan x  0      , k  . tan x 1
x   k  4
c) sin 2x  2tan x  3.
Điều kiện cosx  0. Pt 2 tan x 3 2 
 2 tan x  3  2 tan x 3tan x  4 tan x 3  0. 2 1 tan x   x   2 tan
1 2 tan x  tan x  3  0.
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 87 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC tan x 1  0   . 2
2 tan x  tan x  3  0  v« nghiÖm 
 tan x 1  x   k, k  . 4 d) (1 tan ) x (1 sin 2 ) x  1 tan . x
Điều kiện cosx  0. Pt      2 x 2 tan x 1 tan 1 1 tan x      x x      x 2 1 tan tan 1 1 tan 1 tan x. 2  1 tan x  2
 2tan xtan x   1  0. x k tan x  0      , k  . tan x  1 
x    k  4   e)  1 tan x 1 cot x       2  1 sin 2x 1 tan x
pt  1 tan x  . 1 sin 2x   Điều kiện cos x 0  . s  in 2x  1
Điều kiện cosx  0. Pt      2 x 2 tan x 1 tan 1 1 tan x      x x      x 2 1 tan tan 1 1 tan 1 tan x. 2  1 tan x  2
 2tan xtan x   1  0. x k tan x  0     
x k, k  . tan x  1 
x    k lo¹i  4    f) sin 2x cos 2x  cot x  , x    ;0    2  sin 2x  2 
Điều kiện sin x  0. 2 2 tan x 1 tan x  2 Pt 2 2 1   1
tan x  2 tan x 1 1 tan x 1 tan x     . 2 tan x 2 tan x tan x
2 tan x  2 tan x  2 2  2 1 tan xx x     x   x  2 3 tan 3tan 2 0 tan 2 tan 1  0.
x  acrtan2  k tan x  2      , k  . tan x  1 
x    k  4 g) 2
cot x  tan x  4sin 2x   sin 2x
Điều kiện sin 2x  0. 88 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 Pt 1 8 tan x 1 tan x   tan x   2 tan x 1 tan x tan x   x x   x  x    x2 2 2 2 2 2 1 tan tan 1 tan 8 tan 1 tan . 4 2 2  x x   x  2 2 tan 6 tan 0 2 tan tan x  3  0 .
tan x  0loai   x   k   3  tan x  3   , k  .        tan   3 x k x   3 h) cos 2x 1 2 cot x 1   sin x  sin 2 . x 1 tan x 2   Điều kiện sin x 0  . tan x  1 2 1 tan x 2 Pt 2 1  tan x tan 1 tan x  1 x    . 2 2 tan x 1 tan x 1 tan x 1 tan x 2 1 1 tan x tan x tan x  1    . 2 2 2 tan x 1 tan x 1 tan x 1 tan x    x 2  x  x  2 1 tan 1 tan tan
tan x  2 tan x   1 .
 tan xtan x  2 1  tan x   1  2 1 tan x  0.  tan x   1  2
2 tan x  tan x   1  0. tan x 1   . 2
2 tan x  tan x 1  0  v« nghiÖm 
x   k , k  . 4  
tan(x a) tan(b x)  1 khi a b   k  2 tan a  tan b
Dạng 3: Áp dụng     
hay tan(a b)  1 tan . a tan b
cot(x a) cot(b x)  1 khi a b   k  2      
Ví dụ. Giải phương trình: 3 3
sin x  cos x  cos 2x tan x  tan x        4   4  Giải:     Điều kiện   cos x   0   và cos x   0    4   4          Ta có tan x 1 tan x 1 tan x  .tan x   .  1       4  
4  1 tan x 1 tan x
Khi đó pt  sin x cos x1sin xcos x  cos x sin xcos x sin x
pt  sin x  cos x1 sin x cos x  cos x  sin x  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 89 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 sin x cos x   1 cos x
sin xcos x sin x  0 
 sin x cos x1cos x1sin x  0   x   k tan x 1  4  
 cos x 1  x k2 , k    sin x 1   
x   k2  2 x k2
So sánh điều kiện, phương trình có nghiệm   , k
x   k2  2 ÀI T V N ỤN
BT 19. Giải các phương trình lượng giác sau: 3 3 a)
sin x  cos 3x  2 cos 2x cos x
sin x sin 3x  cos x cos 3x 1 sin 2x   b)    2             8 tan  x tan  x     tan x   tan x      2  4   4   6   3  4 4      c)
sin 2x  cos 2x 7  4  cos 4 . x d) 4 4
sin x  cos x  cot x  cot  x            8  3   6  tan  x tan  x      4   4       e)  tan x  tan x
sin 3x  sin x  sin 2 . x      3   6  Hƣớng dẫn giải.     cos  x  0     4      a) Điều kiện:  cos  x  0 .     4         tan  x tan  x  0       4   4 
Phương trình đã cho tương đương
sin x  cos 3x  2 cos 2x cos x sin 2x   2
sin x  cos 3x  2 cos 2x cos x  sin 2x 2       2 tan  x cot  x     2  4   4   2
sin x  cos 3x  cos x  cos 3x  sin 2x  2
sin x  cos x  sin 2x 2 2
Đặt t  sin x  cos , x t  2 , suy ra 2
sin 2x t 1  Phương trình trở thành: 2 t   2 6 2 t   2 2
1  t 1  2t t  2t 1  0  t  2 2 90 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Với 2  6 t  suy ra 2 2  6    2  6    1 3
sin x  cos x   2 sin x    sin x       (loại) 2  4  2  4  2 Với 2  6 t  suy ra 2 2  6    2  6    1 3
sin x  cos x   2 sin x    sin x       2  4  2  4  2   1 3 x    arcsin  k2 4 2    1 3
x     arcsin  k2  4 2     cos x   0     6      b) Điều kiện:  cos x   0 .     3         tan x  tan x   0       6   3 
Phương trình đã cho tương đương 3 3
sin x sin 3x  cos x cos 3x 1 3 3 
   sin xsin 3x cos x cos3x 1         8       8 tan x   tan x      tan x  cot x       6   3   6   6   1 3 3
sin x sin 3x  cos x cos 3x   8  
 3sin x sin 3x 3cos x cos 3x 1 .sin 3x  .cos 3x   4 4 8  1 2 2
3sin x sin 3x  sin 3x  3cos .
x cos 3x  cos 3x   2
 3sin xsin3x  cos .xcos3x   1 2 2
cos 3x  sin 3x   2
 3cos .xcos3x sin xsin3x   1 2 2
cos 3x  sin 3x   2  1
3cos 2x  cos 6x   2  1 3
3cos 2x  4 cos 2x  3cos 2x   2  1 3 cos 2x   8  1 cos 2x   2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 91 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC   2 2x    k2 3 
x    k ,k  . 3 
Đối chiếu với điều kiện nghiệm của phương trình là x   k,k  . 3     cos  x  0     4      c) Điều kiện:  cos  x  0 .     4         tan  x tan  x  0       4   4 
Phương trình đã cho tương đương 4 4
sin 2x  cos 2x 4  cos 4x  4 4 4
sin 2x  cos 2x  cos 4x       tan  x cot  x      4   4    x x2 2 2 2 2 4 sin 2 cos 2
 2sin 2xcos 2x  cos 4x    x x2 4 1 2 sin 2 cos 2  cos 4x 2   1  4 1 2 sin 4x  cos 4x    2   1 1  2 1 cos 4x 4  cos 4 x 2  4 2
2cos 4x  cos 4x 1  0   1 Đặt 2
cos 4x t  0 t  1 2
2t t 1  0   1
t   l  2
Phương trình (1) trở thành: k 2
t  1 cos 4x  1  cos 4x  1
  4x k  x  , k  . 4  x kx
k , k  . 2
Đối chiếu với điều kiện nghiệm của pt là và     sin x   0    d) Điều kiện:   3   .     sin  x  0     6 
Phương trình đã cho tương đương 92 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 4 4 7      sin 
x  cos x  cot x    tan  8 3 x  3       4 4 7
sin x  cos x  8   x x2 2 2 2 2 7 sin cos
 2sin xcos x  8    x x2 7 1 2 sin cos  8 2   1  7 1 2 sin 2   2 x    8    1 1 cos4x  7 1  2  2    8  1 cos 4x  2 
 4x    k2 3    x    k ,k  . 12 2   x    k ,k  . 12 2
Đối chiếu với điều kiện nghiệm của pt là    cos  x     0   3 e) Điều kiện:   .    cos  x     0   6 
Phương trình đã cho tương đương      tan  x  cot x
sin3x  sin x      sin 2  3   3 x
 sin3x  sin x sin 2x x x  3 3 3 2sin cos 2sin x cos x  2 2 2 2  3x  3 sin cos x cos x      0 2  2 2   3 sin x  0   2   3 cos x  cos x  2 2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 93 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 3x    2 k   3x x   k2  2 2 3x x     k2  2 2  k 2 x   3   x k  2 x k    k 2   x  3 ,k  .  x k 2 x kx  
k2,k  . 3
Đối chiếu với điều kiện nghiệm của pt là và
BT 20. Giải các phương trình lượng giác sau (đặt ẩn phụ t bởi cung phức tạp):   a) 4x 2 cos  cos . b) 3 tan  x   tan x    1. 3 x  4            c) 3 x 1 3 sin   sin x       d) sin3x    sin 2xsin   10 2 2 10 2  x        4   4      e) 3 8cos   x     cos3 . f) 3 2 sin x     2sin . x  3 x   4    g) 3 sin  x     2 sin .
h) cos x  2cos3x 1 3sin . x  4 x  Lời giải a) Đặt 2x 3    3 t x 2 t
Khi đó phương trình trở thành: 1 cos3 cos2 t t
 2cos2t 1 cos3t  cos2t cos3t 1cos2 2 t 94 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC t  5t 2 t t t 5 2sin sin 2sin 2sin sin sin t           0 2 2 2 2  2 2      sin t  0  2 t k2     2 t 3t 3t  2 t
k k     4sin cos sin       t 0 cos 0 t   k  3 3 2 2  2  3 3       sint  0 t k t k      x     . 2 k   
x k k  .  3 2 x    2 k   x   k  b) ĐK:  2  k  . 3 x     4 k 3  tan   x  tan 3     3  4  tan x 1 tan  x     tan x 1     tan x  1    tan x 1  4   1 tan 1 tan tan x   x   4   1
  tan x 1  tan x  0  x k k  .  c) Đặt 3 x 3
  t x    2t. 10 2 5
Khi đó phương trình trở thành: 1
sint  sin 3t 1 3
 sint  sin3t  2sint  sin3t  2sint  3sint  4sin 2 2 tt k  
t    k2 sin  t  0  6 3
 4sin t  sin t  0  sin t  2 4sin t   1  0   1   5 sint   t   k2  2  6  7 t   k2  6 t k    k  . t      6 k
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 95 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC  3 x   k2  5   4  x
k2 k  .  15  14 x   k2  15  
d) Đặt x   t x t  . 4 4
Khi đó phương trình trở thành:      sin3 
t     sin 2t
sint  sin 3t  sin
 2t sint  sin3t      cos2t sin  2   2 t
 sin2t t  cos2t sint  sin 2t cost  cos2t sint  cos2t sint  sin 2t cost  0 2   sin 2  0 t kt k t   2       
t k k  . cost  0
t   k   2  2 t     2 k  
 x    k k  . 4 2  
e) Đặt x   t x t  . 3 3
Khi đó phương trình trở thành: 3
8cos t  cos3t   3
 8cos t  cos 3t 3  8cos t  cos3t 3 3 3
 8cos t  4cos t  3cost  0  12cos t  3cost  0  cost  2 4cos t   1  0   t     2 k cost  0     1 
t    k2  k  . cost    3  2  2 t    k2  3   x     6 k  
x   k2   3  k  .  2 x    k2  3 x     k2  
f) Đặt x   t x t  . 4 4 96 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Khi đó phương trình trở thành: 3    3    2 sin  t  2sin t
 2 sin t  2 sint cos     cost sin 4 4 4      3  t   t t 3  t t t   t  2 2 sin 2 sin cos sin sin cos 0 sin sin t   1  cost  0 2     t t t   t   t t  1 sin cos cos 0
cos 1 sin cos  0  cost 1 sin 2t    0  2  cost  0         t   Lt k k . sin 2 2 2 
x   k k  . 4  
f) Đặt x   t x t  . 4 4
Khi đó phương trình trở thành: 3    3
sin t  2 sin t
 sin t  sint    cos  4 t  3  t t t   t  2 sin sin cos 0 sin sin t   1 cost  0 2     t t t   t   t t  1 sin cos cos 0
cos 1 sin cos  0  cost 1 sin 2t    0  2  cost  0         t    Lt k k . sin 2 2 2 3  x
k k  . 4 h)
cos x  2cos3x 1 3 sin x  cos x  3sin x 2cos3x 1 0    2 cos cos   x  sin
sin x  2cos3x 1   0  3 3    2cos  
x  2cos3x 1    0  3   
Đặt  x t x t  . 3 3
Khi đó phương trình trở thành:
2cost  2cos3t  1 0  2cost  2cos 3t1 0  t t    t   3 2cos 2cos3 1 0
2cos 2 4cos t 3cost1 0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 97 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 3  t t       2 8cos 4cos 1 0
2cost 1 4cos t  2cost  1  0  1  2 cost   t    k2  2  3      1 5  1 5 cost  t  arccos  4  4  
x   k2 3   x     k2 .  1  5  x   arccos   4 3
Dạng 4. Phương trình lượng giác có cách giải đặc biệt A  0
Tổng các số không âm: 2 2
A B  0    B  0    
Đối lập: A B mà chứng minh được A M A M     B MB M    
Hoặc: AB M N mà chứng minh được: A M A M     B NB N
Một số trường hợp đặc biệt: s  in u 1 s  in u  1 
sinu  sin v  2  
 sin u  sin v  2     s  in v  1  s  in v  1  cosu 1 cosu  1 
cosu  cosv  2  
 cosu  cosv  2     cosv  1  cosv  1   sin  u  1  sin  u  1   sin    v  1 sin  v  1 sin .
u sin v  1    sin . u sin v  1    sin  u  1   sin  u  1    sin   v  1   sin  v  1  cosu 1 cosu  1    cosv 1 cos v 1 cos .
u cos v  1    cos . u cos v  1    cosu  1  cosu 1   cosv  1  cosv  1  ÀI T V N ỤN
BT 21. Giải các phương trình lượng giác sau: a) 2 2
4cos x 3tan x  4 3cos x  2 3 tan x  4  0. b) 2 2
4cos x  4cos x 3tan x 2 3 tan x  2  0. c) 2 2
2sin x 3tan x 6tan x  2 2 sin x  4  0.
98 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC d) 3 2 2
8sin x sin 2x 6sin x cos x 1 0. e) 2 2
cos x tan 4x 1sin 2x  0. f) 2 2 2
4sin x sin 3x  4sin xsin 3 . x g) 2 2
5sin x 3cos x  3sin 2x  2 3cos x  2sin x  2  0. h) 2 1
sin 2x  2sin 2x   2tan x 1 0. 2 cos x i) 2 2 4
 cos x 3tan x  2 3 tan x  4sin x 6. j) 2
8cos4xcos 2x  1cos3x 1 0. 2 k) 2 sin 3 sin x x   3 3
cos3xsin x  sin3xcos x 2  sin xsin 3 . 3sin 4 x x Hƣớng dẫn giải a. 2 2
4cos x 3tan x  4 3cos x  2 3 tan x  4  0. ĐK : cosx  0 2 2
 4cos x  3tan x  4 3 cos x  2 3 tan x  4  0.
 2cos x  32  3 tan x  2 1  0   x    k2 2cos  x  3  0  6     
x    2k k  
 3 tan x 1  0  6 x      6 k b. 2 2
4cos x  4cos x 3tan x 2 3 tan x  2  0. ĐK : cosx  0 2 2
 4cos x  4cos x  3tan x  2 3 tan x  2  0.  2cos x  
1   3 tan x  2 2 1  0   x    k2 2cos  x 1  0  3     k  
 3 tan x 1  0  x     6 k
Vậy phương trình vô nghiệm c. 2 2
2sin x 3tan x 6tan x  2 2 sin x  4  0. ĐK : cosx  0
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 99 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 2
 2sin x  3tan x  6 tan x  2 2 sin x  4  0.
  2 sin x  2 1  3tanx 2 1  0   x   k  2  4  1 s  inx    3    2   x
k2  x   k2 k      4 4 tan x 1  
x   k2  4 d. 2 2
cos x tan 4x 1sin 2x  0. ĐK : cosx  0 2 2
 cos x tan 4x 1 sin 2x  0. 2 2
 cos x tan 4x  sinx  cos x2  0   x     2 k cos x  0      tan 4    x  0 k   x   x
k k      4 4 s  inx  cos x  0    x     4 k e. 2 2 2
4sin x sin 3x  4sin xsin 3 . x 2 2 2
 4sin x  sin 3x  4sin xsin 3x  0
 2sinx sin 3x2 2 2 4
 sin 3x  sin 3x  0
 2sinx sin 3x2 2 2 2  sin 3 . x cos 3x  0  x k 2 sin  x  0 2sinx sin 3    x  0       
1  x   k k   2 2 sin  3 .xcos 3x  0 sin x  6  2    5 x     6 k f. 1 2
sin 2x  2sin 2x   2tan x 1 0. 2 cos x ĐK : cosx  0 2 1
 sin 2x  2sin 2x   2 tan x 1  0 2 cos x 2 2
 sin 2x  2sin 2x 1 tan x  2 tan x 1  0  sin 2x  2 1  tan x  2 1  0 sin  2x  1       x
k k   tan x  1  4 100 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC l) 2 2 4
 cos x 3tan x  2 3 tan x  4sin x 6. Điều kiện cosx  0 2 2  4
 cos x  3tan x  2 3 tan x  4sin x  6 2 2
 4sin x  4sin x 1 3tan x  2 3 tan x 1  0  2sin x  
1   3 tan x  2 2 1  0   x   k  2 1   6 sin x    2  5 5     x
k2  x
k2 k   1      6 6 tan x  3    x     6 k m) 2
8cos4xcos 2x  1cos3x 1 0.  8 2 2cos 2x   2
1 cos 2x  1 cos3x 1  0. 4 2
 16cos 2x 8cos 2x 1 1 cos3x  0  4cos 2x  2 2 1  1 cos3x  0 2  1 4cos 2  x 1  0 2cos4x 1  0 cos 4x        2  1 cos3x  0  1 cos3x  0 cos3x 1   kx     6 2   
x    k2 k    2k 6 x    6 3 2 n) sin 3x 2 sin x   3 3
cos3xsin x  sin3xcos x 2  sin xsin 3 . 3sin 4 x x
Điều kiện sin 4x  0 2 2 sin 3  sin x x   3 3
cos3xsin x  sin 3xcos x 2  sin xsin 3 3sin 4 x x 2 2 sin 3x 2  sin x   sin xsin 3 4 x 2 2 2
 4sin x  sin 3x  4sin xsin 3x  0
 2sinx sin 3x2 2 2 4
 sin 3x  sin 3x  0
 2sinx sin 3x2 2 2 2  sin 3 . x cos 3x  0  x k 2  si  n x  0 
2sinx  sin 3x  0       
1  x   k k   2 2 si
 n 3 .xcos 3x  0 si  n x  6 2    5 x     6 k
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 101 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
BT 22. Giải các phương trình lượng giác sau:
a) cos xcos2x 1.
b) sin 2xcos4x 1.
c) sin xsin3x  1  .
d) cos2xcos6x 1. e) 2 2
(cos x sin x)sin5x 1 0. f) (cos x sin )
x (sin 2x  cos 2 ) x  2  0.
g) sin7x sin x  2.
g) cos4x cos6x  2. i) 3 3
sin x  cos x 1. j) 5 3
sin x cos x 1. Hƣớng dẫn giải
a) cos xcos2x 1. cos x 1 cos x 1   2 cos 2x 1 2cos x  2  
 cos x 1  x k2 k   cos  x  1  cos x  1      2 cos2x  1  2cos x  0
b) sin 2xcos4x 1.  sin  2x 1  sin  2x 1   2 cos 4x 1  1   2sin 2x 1     sin 2  x  1   x
k k    sin  2  x  1  sin  2x  1  4     2 cos4x  1   1   2sin 2x  1 
c) sin xsin3x  1  .  sin  x  1  sin  x  1   3 sin  3x  1   3
 sin x  4sin x  1      sin x  1
  x   k k    sin   x  1  sin  x  1  2     3  sin  3x 1  3
 sin x  4sin x 1
d) cos2xcos6x 1. cos 2x 1 cos 2x 1   3 cos6x 1
4cos 2 x 3cos 2 x 1     cos 2  1 k x   x  k   cos2  x  1  cos 2x  1  2     3 cos6x  1 
4cos 2x3cos2x  1  e) 2 2
(cos x sin x)sin5x 1 0.   x     2 k cos 2 x  1      k 2 sin  5  x  1      cos 2 x.sin 5  1 x x      10
5  x   k k   cos2x 1  2  x k  sin  5x  1      k 2  x     10 5 102 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC f) (cos x sin )
x (sin 2x  cos 2 ) x  2  0.    sin  x    1      3   4    x    k  2   4     sin  2   x    1  3          4       sin  sin 2   1 x         8 k x xk    4   4       sin   x      1     4
x   k2   4      sin 2     1   x kx    4  Phương trình vô nghiệm
g) sin7x sin x  2.  2cos 4xsi 3 n x  2
 cos 4xsin 3x 1  kx   2 cos 4  x 1      k2   si  n 3 1 x   x  6 3    k   cos4x  1    k  x    si   n 3  x  1   4 2    k 2 x    6 3 Phương trình vô nghiệm
g) cos4x cos6x  2.   x    2   2 k sin   x 1      2k     x   x   2 sin  5 1   10 5  2 k x
 sinx.sin 5x 1      k    sin  x  1         x    2kx   2k  sin  5      x 1 2  2    2k x    10 5 i) 3 3
sin x  cos x 1. 3 3
sin x  cos x 1. 3 3 2 2
VT  sin x  cos x  sin x  cos x 1  VP  s  inx  0  x k2 cos  x  1 VT VP       k    s  inx 1
x   k2   2 cos x  0 j) 5 3
sin x cos x 1.
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 103 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 5 2 sin  x  sin x 5 3 
 sin x  cos x 1 3 2
cos x  cos x  sin  x  0 
x    k2 cos  x  1  VT VP       k    sin  x  1
x   k2   2 cos x  0
BT 23. Giải các phương trình lượng giác sau:   a) 2 2 5 tan 
x  cot x  2sin x   
b) 2cos x  2 sin10x  3 2  2cos28xsin . 4  x   c) 2 
2sin5x  cos4x  3cot . x d) 1
tan 2x  tan3x  
sin xcos2xcos3x e) 2
(cos2x cos4x)  6 2sin3 .x f) 4 4
sin x cos x  sin x  cos x . g) 2 2 cos 3 x
x cos 2x  cos x  0. g) 3 cos2x  cos  2  0. 4
i) cos2x cos4x cos6x  cos xcos2xcos3x  2. Hƣớng dẫn giải   a) 2 2 5 tan 
x  cot x  2sin x    4    Ta có 2 2 2 2
tan x  cot x  2 tan .
x cot x VT  2 5   2sin  x   2  VP    2  4  tan  
x  cot x  1  x    k2 VP   2    4 
VP VP         
x   k2  5 kVp   2 sin x      1  4   4 x   k  2  4 c) 2
2sin5x  cos4x  3cot . x Ta có:
VT  2sin5x  cos 4x  3 2 VP  3  cot .x  3 sin  5x 1 VP   3  
VT VP  
 cos4x 1 x   k k   VT   3 2 cot x   0  d) 1
tan 2x  tan3x  
sin xcos2xcos3x
sin xcos2xcos3x  0 Điều kiện xác định: 104 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC sin 5x 1   
cos 2xcos3x sin xcos 2xcos3x   x    2   2 k si  n  x 1       2k   si  n 5  1 x   x   10 5  sinx.sin 5x  1     k    si  n x  1      x    2k  si  n 5  x  1  2   2k x    10 5 Phương trình vô nghiệm e) 2
(cos2x cos4x)  6 2sin3 .x 2 2  4sin 3 .
x sin x  2sin 3x  6 2 2 VT  4sin 3 .
x sin x  2sin 3x  6  VP 2 2 sin  3 .xsin x 1 
VP VP  
x   k k   sin  3x  1  2 f) 4 4
sin x cos x  sin x  cos x . 4 sin  x   sin x    VT VP 4
cos x  cos x  sin  x  1  
VT VP  
x   k k   cos x  0 2 g) 2 2
cos 3xcos2x cos x  0.
 1 cos6xcos 2x 1 cos 2x  0.  cos6 . x cos 2 x  1 cos 2 x 1 cos 2 x 1   3 cos6x 1
4cos 2x  3cos 2x 1 cos 2 x 1 k     x  k      cos 2 x  1  cos 2 x  1  cos 2 x  1  2     3 cos6x  1 
4cos 2x 3cos2x  1  g) 3 cos2 cos x x   2  0. 4 3  cos 2  cos x x  2 4 cos 2x 1 x k   3   x
8k  x k2 k   cos   1    4 x  3
i) cos2x cos4x cos6x  cos xcos2xcos3x  2.
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 105 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 cos 2x  cos6x  cos 4x  cos xcos 2xcos3x  2. 2  2cos 4 .
x cos 2x  2 cos 2x 1  cos x cos 2x cos 3x  2
 2cos 2xcos 4x  cos 2x 1  cos xcos 2xcos3x  2
 4cos x cos 2x cos3x  cos x cos 2x cos3x  3
 cos x cos 2x cos3x  3 cos cos x 1 x  1     2 3 cos 2    2cos x  
14cos x3cosxx cos 3x  1 1 cos x 1      x k  k   cos x  1  cos x  1   cos x  1   cos2  x cos 3x  1    2  2cos x   1 3
4cos x  3cos x  1 
BT 24. Tìm tham số m để các phương trình sau đây có nghiệm: a) 0 2
cos(2x 15 )  2m  . m
b) mcos x 1 3cos x 2 . m
c) (4m1)sin x  2  msin x 3. d) 2 2 2 (m  )
m cos 2x m m  3 m cos 2 . x
e) msin x  2cos x 1.
f) mcos2x  (m1)sin 2x m 2. g) 2
msin x cos x  sin x  . m
g) sin x  5 cos x 1 ( m 2  sin ) x .
i) sin 2x  4(cos x sin x)  . m
j) 2(sin x  cos x) sin 2x m 1. k) sin 2x  2 2 (
m sin x  cos ) x 1  4 . m l) 2 2
3sin x msin 2x  4cos x  0. m) 2 2
(m 2)cos x msin 2x  (m1)sin x m 2. n) 2 2
sin x  (2m 2)sin xcos x (1 ) m cos x  . m Hƣớng dẫn giải a) 0 2
cos(2x 15 )  2m  . m 0 2 Ta có : 1
  cos(2x 15 ) 1 1
  2m m 1 2 2
2m m  1 
2m m 1 0. m  1      1   m  2 2
2m m 1
2m m 1 0 2 1 Vậy 1   m
thì phương trình có nghiệm 2
b) mcos x 1 3cos x 2 . m
 m 3cos x  1   2 ( m *)
Th1: m  3 (*)  0  7
 vô lý. Phương trình vô nghiệm   Th2:     1 2 3 *  cos m m x m3  1   2  4   m m  3  1  1   2   mm  3  4 4 Ta có 1   cos x 1 1   1    m    4      m  3 1   2 m m   3 3 1   m 3 m  3 106 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Vậy 4 4
  m   thì phương trình có nghiệm 3
c) (4m1)sin x  2  msin x 3.
 (3m1)sin x  5  (*). 1
Th1: m   (*)  0  5
 ( vô lý). Vậy phương trình vô nghiệm 3 Th2: 1 5  m   (*)  sin  3 x 3m 1  1 m   3  5    1  4 m  2        Có 5 3 1 1   sin 1  1    1 m m      x  3  4 3m 1 5   1   2 m       m  3 3m 1   1 m   3 m  2 Vậy 
4 thì phương trình có nghiệm.  m    3 d) 2 2 2 (m  )
m cos 2x m m  3 m cos 2 . x 2
mcos2x m m 3(*)
Th1: m  0  (*)  0  3
 vô lý. Vậy phương trình vô nghiệm 2 Th2:   3  0  (*)  cos 2 m m m x m 2 m m  3 Có 1
  cos 2x 11 1 m 2
m m  3   1  m  3;0     m   3;        m 1  ;03; 2 m m  3 m    1  ;0 3; 1  m Vậy m 1  ;  0 3; 
 thì phương trình có nghiệm.
e) msin x  2cos x 1.
Để phương trình có nghiệm 2 2
m  4 1  m  3  . m
Vậy phương trình có nghiệm với mọi giá trị m
f) mcos2x  (m1)sin 2x m 2. m  3 2 2 2
Để phương trình có nghiệm  m  (m 1) m  2
2  m 2m 3  0 m 1 g) 2
msin x cos x  sin x  . m
msin 2x cos2x  2m1
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 107 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 2 4
Để phương trình có nghiệm  m 1 2m  2
1  3m  4m  0  0  m  3 4
Vậy 0  m  thì phương trình có nghiệm. 3
g) sin x  5 cos x 1 ( m 2  sin ) x .  m  
1 sin x  5 cos x 1 2m 2 2
Để phương trình có nghiệm  m       m 2 1 5 1 2
 3m  2m 5  0 5  1   m  3 Vậy 5 1
  m  thì phương trình có nghiệm 3
i) sin 2x  4(cos x sin x)  . m (*)
Đặt t  cos x sinx; t  2 2 2
 sin 2x 1t  (*) 1t  4t m Đặt 2
y  1 t  4t; t  2 . Ta có bảng biến thiên:
Từ bảng biến thiên ta có để phương trình có nghiệm : 4
 2 1 m  4 2 1 j) 2(sin x  cos )
x  sin 2x m 1.(*)
Đặt t  cos x sinx; t  2 2 2
 sin 2x t 1 (*)  t  2t  2 m 2
y t  2t; t  2 Ta có bảng biến thiên
Từ bảng biến thiên ta có để phương trình có nghiệm: 1
  2 m  2 2  2  m  3
Vậy 2  m  3 thì phương trình có nghiệm k) sin 2x  2 2 (
m sin x  cos ) x 1  4 . m 108 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Đặt t  sin x  cos ; x t  2 2
 sin 2x 1t 2
 (*)  1 t  2 2mt 1  4m
 t  2t  2 2m  2  0 t  2
 t 2 2m2
Vậy phương trình luôn có nghiệm với mọi giá trị m l) 2 2
3sin x msin 2x  4cos x  0. 1 cos 2x 1 cos 2  3  sin 2  4 x m x  0 2 2
 33cos 2x  2msin 2x  4  4cos 2x  0
 2msin 2x  cos 2x 1
Để phương trình có nghiệm 2 2
4m 11 4m  0. m
Vậy phương trình có nghiệm m  m) 2 2
(m 2)cos x msin 2x  (m1)sin x m 2. 1 cos 2x 1 cos 2  (  2)  sin 2  ( 1) x m m x mm  2 2 2
 (m  2)  (m  2)cos 2x  2msin 2x  (m 1)  (m 1)cos 2x  2m  4
 cos 2x  2msin 2x  7  m  4 2 2
Để phương trình có nghiệm 1 4m  49  m 16  m  4  m  4 Vậy 
thì phương trình có nghiệm. m  4  n) 2 2
sin x  (2m 2)sin xcos x (1 ) m cos x  . m 1 cos 2x 1 cos 2 
 (m 1)sin 2x  (1 ) x  2 m 2 m
 1 cos 2x  2(m 1)sin 2x  (1 ) m  (1 )
m cos 2x  2m
mcos 2x  2(m 1)sin 2x  3m
Để phương trình có nghiệm 2 2 2 2
m  4(m 1)  9m  4m 8m  4  0 2
m  2m  2  0  1   3  m  1   3 Vậy 1   3  m  1
  3 thì phương trình có nghiệm.
BT 25. Cho phương trình: cos 2x  (2m 1)cos x m 1  0. a) Giải phương trình khi 3 m   2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 109 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC b)    
Tìm tham số m để phương trình có nghiệm nằm trong khoảng 3  ; ? 2 2    Hƣớng dẫn giải
Có cos2x (2m1)cos x m1 0 2
 2cos x  (2m 1)cos x m  0  2cos x  
1 cos x m  0 2
 2cos x  (2m 1)cos x m  0  2cos x  
1 cos x m  0  1 cos x    2  cos x m c) Giải phương trình khi 3 m   2  1 cos x   2   
x    k2  3 3 cos x  (L)  2    d) 
Tìm tham số m để phương trình có nghiệm nằm trong khoảng 3  ; ? 2 2        Có 1 cos  x
x    k2 không có nghiệm thuộc 3  ; 2 3 2 2      
Phương trình có nghiệm nằm trong khoảng 3 ;   2 2        cos 
x m có nghiệm nằm trong khoảng 3  ; 2 2     1   m  0    Vậy 1   
m  0 thì phương trình có nghiệm nằm trong khoảng 3  ; 2 2   
BT 26. Cho phương trình: cos 4x  6sin x cos x  . m
a) Giải phương trình khi m 1.   b) 
Tìm tham số m để phương trình có hai nghiệm phân biệt trên đoạn 0;   4    Hƣớng dẫn giải:
Có: cos4x 6sin xcos x  . m 2
1 2sin 2x3sin 2x  ( m *)
110 | THBTN – CA BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Đặt t  sin 2x với t 1 2  (*)  2
t  3t 1 m (**)
c) Giải phương trình khi m 1.
Với m 1. Đặt t  sin 2x với t 1 2  2
t  3t 11 t  0 2  2 3 0 k t t       3
 sin 2x  0  x  t  (L) 2  2   d) Tìm tham số 
m để phương trình có hai nghiệm phân biệt trên đoạn 0;   4      0;    
Phương trình (*) có nghiệm  4  0  ;1
Phương trinh (**) có nghiệm Đặt 2 y  2
t  3t 1 Ta có bảng biến thiên
Từ bảng biến thiên ta có để phương trình có 2 nghiêm phân biệt : 17 2  m  8   Vậy 17 2   m
thì phương trình có 2 nghiệm phân biệt trên đoạn 0;  8  4      
BT 27. Tìm tham số m để phương trình 2
cos x cos x 1 m có nghiệm x   0;   2    Hƣớng dẫn giải t  cos x Đặt    x  0;  t 0  ;1   Ta có  2 
Phương trình trở thành: 2t t 1 m Đặt 2
y t t 1 Ta có bẳng biến thiên
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 111 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Từ bảng biến thiên ta có để phương trình có nghiệm: 3  1 4 m  
Vậy 3  1 thì phương trình có nghiệm  x   0;  4 m  2       
BT 28. Tìm tham số m để 2cos 2x  (m  4)sin x m  2 có 2 nghiệm x   ;   2 2    Hƣớng dẫn giải
2cos 2x  (m  4)sin x m  2 2
 1 2sin x  (m  4)sin x m  2 2
 2sin x  (m  4)sin x m 1  0 Đặt t  sinx     Có x  ;  t  1   ;1  2 2    2
2t m 4t m1 0 Phương trình trở thành 112 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Giải các phương trình lượng giác sau: a) cos 3x sin 3x 5 sin x cos2x 3, x
(0; 2 ). (ĐH khối A năm 2002) 1 2 sin 2x b) 2 2 2 2 sin 3x cos 4x sin 5x cos 6x. (ĐH khối năm 2002)
c) cos3x 4cos2x 3cosx 4 0, x 0; 14 . (ĐH khối năm 2002)
BT 29. Giải các phương trình lượng giác sau: a) cos2x 2 1 cotx 1 sin x sin 2x.
(ĐH khối A năm 200 ) 1 tan x 2 b) 2 cotx tan x 4 sin 2x (ĐH khối năm 200 ) sin 2x c) x x 2 2 2 sin tan x cos 0. (ĐH khối năm 200 ) 2 4 2
BT 30. Giải các phương trình lượng giác sau: a) 2 5 sinx 2 3(1 sinx)tan x. (ĐH khối năm 200 )
b) (2cosx 1)(2sinx cosx) sin2x sinx. (ĐH khối năm 200 )
BT 31. Giải các phương trình lượng giác sau: a) 2 2 cos 3x cos2x cos x 0.
(ĐH khối A năm 200 )
b) 1 sinx cosx sin2x cos2x 0. (ĐH khối năm 200 ) c) 4 4 3 cos x sin x cos x sin 3x 0. (ĐH khối năm 200 ) 4 4 2
BT 32. Giải các phương trình lượng giác sau: 6 6
a) 2(cos x sin x) sinx cosx 0.
(ĐH khối A năm 200 ) 2 2 sin x b) x cotx sin x 1 tan x tan 4. (ĐH khối năm 200 ) 2
c) cos3x cos2x cosx 1 0. (ĐH khối năm 200 )
BT 33. Giải các phương trình lượng giác sau: a) 2 2 (1 sin x)cosx (1 cos x)sinx 1 sin2x.
(ĐH khối A năm 200 ) b) 2 2sin 2x sin7x 1 sinx.
(ĐH khối B năm 200 ) 2 c) x x sin cos 3 cos x 2. (ĐH khối năm 200 ) 2 2
BT 34. Giải các phương trình lượng giác sau: a) 1 1 7 4 sin x
(ĐH khối A năm 200 ) sin x 3 4 sin x 2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 113 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC b) 3 3 2 2 sin x 3 cos x sinx cos x 3 sin x cosx. (ĐH khối năm 200 )
c) 2sinx(1 cos2x) sin2x 1 2cosx. (ĐH khối năm 200 )
BT 35. Giải các phương trình lượng giác sau: a) (1 2 sin x)cos x 3.
(ĐH khối A năm 2009)
(1 2 sin x)(1 sin x) b) 3 sinx cosx sin2x 3 cos 3x 2(cos 4x sin x). (ĐH khối năm 2009) c) 3 cos 5x 2 sin 3x cos2x sinx 0. (ĐH khối năm 2009)
BT 36. Giải các phương trình lượng giác sau: (1 sin x cos 2x)sin x a) 4 1 cosx.
(ĐH khối A năm 20 0) 1 tan x 2
b) (sin2x cos2x)cosx 2cos2x sinx 0. (ĐH khối năm 20 0)
c) sin2x cos2x 3sinx cosx 1 0. (ĐH khối năm 20 0)
BT 37. Giải các phương trình lượng giác sau: a) 1 sin2x cos2x 2 sin x sin 2x. (ĐH khối A năm 20 ) 2 1 cot x
b) sin2x cosx sinx cosx cos2x sinx cosx. (ĐH khối năm 20 )
c) sin2x 2cosx sinx 1 0. (ĐH khối năm 20 ) tan x 3
BT 38. Giải các phương trình lượng giác sau: a) 3 sin2x cos2x 2 cosx 1.
(ĐH khối A năm 20 2) b) 2(cosx 3 sinx)cosx cosx 3 sin x 1. (ĐH khối năm 20 2)
c) sin 3x cos3x sinx cosx 2 cos2x. (ĐH khối năm 20 2)
BT 39. Giải các phương trình lượng giác sau: a) 1 tanx 2 2 sin x (ĐH khối A năm 20 ) 4 b) 2 sin 5x 2cos x 1. (ĐH khối năm 20 )
c) sin3x cos2x sinx 0. (ĐH khối năm 20 )
BT 40. Giải các phương trình lượng giác sau:
a) sinx 4cosx 2 sin2x. (ĐH khối A năm 20 ) b) 2(sinx 2 cosx) 2 sin2x. (ĐH khối năm 2014)
BT 41. Giải phương trình: 2 2sin x 7 sinx 4 0. (TN TH T Q năm 20 )
BT 42. Giải các phương trình lượng giác sau:
a) cosx cos3x sin2x sin6x sin4x sin6x 0. 114 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC b) 1
cosx cos2x cos 3x
sin x sin 2x sin 3x 2
c) cotx cos2x sinx sin2x cotx cosx cotx.
d) sin2x cosx sinx cosx cos2x sinx cosx. e) 3 2 6 4 3sinx sin x 3cos x cos x. f)
g) 2cosx cos2x cos3x 5 7 cos2x. h) 2 2 sin x(4 cos x 1) cosx(sinx cosx sin 3x). i) 2 cosx 3(sin2x
sinx) 4 cos2x cosx 2 cos x 2 0. 2 2 j) (sinx cosx) 2 sin x 2 sin x sin 3x 2 1 cot x 2 4 4 k) 1 1 15 cos 4x 2 2 2 2 cot x 1 2 tan x 1 8 sin 2x 2 sin x l) 4 cos 3x 2 sin 2x 1. tan x 1 4 m) 2 3 2 2 2 3 sin x cos x sin x cosx sin x cos x 3 sin x cosx. 2 2
n) (2sinx 1)(cos2x sinx) 2sin 3x 6sinx 1 2cosx 3 0. 2 cosx 3 o) 3 2 3 1 cos x cos2x 2. 4 4 2
p) (tanx 1)sin2 x cos2x 2 3(cosx sinx)sinx.
q) sin3 x cos3 x 3sin2 x 4sinx cosx 2 0. r) sin2x 3 cos2x 3(sinx 3) 7 cosx. s) 6 6 8(sin x cos x) 3 3 cos2x 11 3 3 sin 4x 9sin2x. t) sin 5x 2 sin 3x 2 cos 3x 5. sin x sin x cosx u) 2 2 2 cos2x sin x cosx sinx cos x 2(sinx cosx). v) 2 3 4 2 3 4 sinx sin x sin x sin x cosx cos x cos x cos x. 3 3 w) sin x cos x 1 cos2x 2 cos x. 1 cos x 1 sin x x) (2cos2x 1)cosx sinx 2(sinx cosx)sin 3x.
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 115 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Đáp án bài tập ôn cuối chƣơng
BT 31. Giải các phương trình lượng giác sau: a) cos 3x sin 3x 5 sin x cos2x 3, x
(0; 2 ). (ĐH khối A năm 2002) 1 2 sin 2x b) 2 2 2 2 sin 3x cos 4x sin 5x cos 6x. (ĐH khối năm 2002)
c) cos3x 4cos2x 3cosx 4 0, x 0; 14 . (ĐH khối năm 2002) Hƣớng dẫn giải: a) Điều kiện: 1 1 sin 2x 0 sin 2x 2 Ta có: cos 3x sin 3x 5 sin x cos2x 3 1 2 sin 2x sin x 2 sin x sin 2x cos 3x sin 3x 5( ) cos2x 3 1 2 sin 2x sin x cosx - cos 3x cos 3x sin 3x 5( ) cos2x 3 1 2 sin 2x (sin 2x 1)cos x 5( ) cos2x 3 1 2 sin 2x 2 5cosx cos2x 3 2cos x 5cosx 2 0 cos x 2 x k2 (k ) 1 cos x 3 2 Do 5 x (0; 2 ) nên lấy x và x
. Ta thấy x ,x thỏa điều kiện. Vậy nghiệm của 1 3 2 3 1 2 phương trình là 5 x và x . 1 3 2 3 b) Ta có: 2 2 2 2 sin 3x cos 4x sin 5x cos 6x 1 cos 6x 1 cos 8x 1 cos10x 1 cos12x 2 2 2 2 (cos12x cos10x) (cos 8x cos 6x) 0 cosx(cos11x cos 7x) 0
cosx sin9x sin2x 0 k x 9 sin 9x sin 2x 0 (k ) k x 2 c) Ta có: cos 3x 4 cos2x 3cosx 4 0 cos 3x 3 cosx 4(cos2x 1) 0 3 2 4 cos x 8 cos x 0. 116 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 4 cos x(cosx 2) 0 cosx 0 x k , k
Do x [0; 14] nên lấy k 0 k 1 k 2 k 3
Vậy nghiệm phương trình là 3 5 7 x : x : x : x 2 2 2 2
BT 32. Giải các phương trình lượng giác sau: a) cos2x 2 1 cotx 1 sin x sin 2x.
(ĐH khối A năm 200 ) 1 tan x 2 b) 2 cotx tan x 4 sin 2x (ĐH khối năm 200 ) sin 2x c) x x 2 2 2 sin tan x cos 0. (ĐH khối năm 2003) 2 4 2 Hƣớng dẫn giải: x k a) Điều kiện: 2 (k Z) x k 4 Ta có: cos2x 2 1 cotx 1 sin x sin 2x 1 tan x 2 2 2 cos x cos x sin x 1 sin x(sin x cos x) sin x sin x 1 cos x cosx sin x cosx(cosx sin x) sin x(sin x cos x) sin x 2 (cosx
sinx)(1 sinx cosx sin x) 0 TH1: cosx sinx 0 x k (k ) thỏa mãn điều kiện 4 TH2: 2 1 2 1 sin x cosx sin x 0 1 sin 2x sin x 0 Vô nghiệm 2
Vậy nghiệm của phương trình là x k (k ). 4 b) Điều kiện: x k 2 (k ) x k 2 cotx tan x 4 sin 2x sin 2x
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 117 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC cosx sin x 2 4 sin 2x sin x cos x sin 2x 2 2 cos x sin x 2 4 sin 2x sin x cos x sin 2x 2 2 2cos2x 4 sin 2x 2 2cos 2x cos2x 1 0 cos 2x 1 x k (k ) 1 cos 2x x k 2 3
Kết hợp điều kiện nghiệm của phương trình là:x k (k ). 3 c) Điều kiện: x k (k ) 2 Ta có: x x 2 2 2 sin tan x cos 0 2 4 2 2 1 sin x 1 (1 cos(x )) (1 cos x) 2 2 2 cos x 2 2 2 (1 sinx)sin x (1 cosx)cos x (1 sinx)(1 cosx)(1 cosx)
(1 cosx)(1 sinx)(1 sinx) (1 sinx)(1 cosx)(sinx cosx) 0 x k2 sin x 1 2 cos x 1 x k2 (k ) tan x 1 x k 4 x k2
Kết hợp điều kiện nghiệm của phương trình là: (k ) x k 4
BT 33. Giải các phương trình lượng giác sau: a) 2 5 sinx 2 3(1 sin x)tan x. (ĐH khối năm 200 )
b) (2cosx 1)(2sinx cosx) sin2x sinx. (ĐH khối năm 200 ) Hƣớng dẫn giải: a) Điều kiện: x k (k ) 2 Ta có: 2 5 sinx 2 3(1 sin x)tan x 2 sin x 5 sin x 2 3(1 sin x) 2 cos x 2 2 3 (5 sinx 2)(1 sin x) 3(sin x sin x) 3 2 2sin x sin x 5sinx 2 0 118 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC x k2 sin x 1 2 sin x 2 x k2 (k ) 6 1 5 sin x x k2 2 6 x k2
Kết hợp điều kiện nghiệm của phương trình là 6 (k ) . 5 x k2 6 b) Ta có: (2 cosx 1)(2 sinx cosx) sin2x sinx (2cosx 1)(2sinx
cosx) sinx(2cosx 1) 0 (2 cosx 1)(sinx cosx) 0 1 cos x k x 6 2 (k ) s inx cos x 0 x k 4 x k
Vậy nghiệm của phương trình là: 6 (k ). x k 4
BT 34. Giải các phương trình lượng giác sau: a) 2 2 cos 3x cos2x cos x 0.
(ĐH khối A năm 200 ) Hƣớng dẫn giải 2 2 cos 3x cos2x cos x 0 1 cos 6x cos2x (1 cos2x) 0 cos 6x cos2x 1 0 2 cos 8x cos 4x 2 0 2cos 4x cos 4x 3 0 cos 4x 1 k 3 x k cos 4x (l) 2 2
b) 1 sinx cosx sin2x cos2x 0. (ĐH khối năm 200 ) Hƣớng dẫn giải 1 sinx cosx sin2x cos2x 0 sinx cosx 2 cosx sinx cosx 0 tan x 1 0 sin cos 0 x k x x 4 sin x cosx 2 cosx 1 0 1 2 cos x 1 0 cosx 2 x k2 2 3 c) 4 4 3 cos x sin x cos x sin 3x 0. (ĐH khối năm 200 ) 4 4 2 Hƣớng dẫn giải
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 119 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC Phương trình 2 2 1 3 1 2 sin x cos x sin 4x sin 2x 0 2 2 2 2 2 2 2 sin 2x cos 4x sin2x 3 0 sin 2x 1 2 sin 2x sin2x 1 0 sin 2x 1 2 sin 2x sin 2x 2 0 2x k2 x k sin 2x 2 (l) 2 4
BT 35. Giải các phương trình lượng giác sau: 6 6
a) 2(cos x sin x) sinx cosx 0.
(ĐH khối A năm 200 ) 2 2 sin x Hƣớng dẫn giải x k2 ĐK: 2 4 sin x 2 3 x k2 4 Phương trình 6 6 3 2 1 2 sin x cos x sin x cosx 0 2 1 sin 2x sin 2x 0 4 2 sin 2x 1 2 3 sin 2x sin 2x 4 0 2x k2 4 x k sin 2x (l) 2 4 3
Đối chiếu ĐK suy ra phương trình có nghiệm 5 x k2 4 b) x cotx sin x 1 tan x tan 4. (ĐH khối năm 200 ) 2 Hƣớng dẫn giải sin x 0 ĐK: k cos x 0 x 2 x cos 0 2 x x cos x cos sin x sin PT cos x 2 2 sin x 4 sin x x cos x cos 2 cos sin 1 1 x k x x 12 4 4 sin 2x (thỏa ĐK) sin x cosx sin x cosx 2 5 x k 12
c) cos3x cos2x cosx 1 0. (ĐH khối năm 200 ) Hƣớng dẫn giải PT 2 2 2 sin2x sinx 2 sin x 0 sinx sin2x sinx 0 sin x 2 cosx 1 0 120 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC sin x 0 x k 1 2 cosx x k2 2 3
BT 36. Giải các phương trình lượng giác sau: a) 2 2 (1 sin x)cosx (1 cos x)sinx 1 sin2x.
(ĐH khối A năm 200 ) Hƣớng dẫn giải PT 2 sinx
cosx 1 sinx cosx sinx cosx sinx
cosx 1 sinx 1 cosx 0 x k ,x k2 ,x k2 4 2 b) 2 2sin 2x sin7x 1 sinx. (ĐH khối năm 200 ) Hƣớng dẫn giải cos 4x 0 PT 2 sin 7x sin x 2 sin 2x 1 0
cos 4x 2 sin 3x 1 0 1 sin 3x 2 k x 8 4 k2 5 k2 x ,x 18 3 18 3 2 c) x x sin cos 3 cos x 2. (ĐH khối năm 200 ) 2 2 Hƣớng dẫn giải PT 1 1 sin x 3 cos x 2 cos x 6 2 x k2 ,x k2 2 6
BT 37. Giải các phương trình lượng giác sau:   a) 1 1 7 4sin     x  .
(ĐH khối A năm 200 ) sin x  3   4 sin  x   2    b) 3 3 2 2
sin x  3cos x  sin xcos x  3sin xcos .x (ĐH khối năm 200 )
c) 2sin x1 cos2x sin 2x 1 2cos .x (ĐH khối năm 200 ) Lời giải sin  x  0 a) Điều kiện   3 . sin  x      0   2       Ta có 1 1 7 1 1 4sin     x      4  sin  sin 3 4 sin       x cos x  4 x x sin  x   2   
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 121 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 cos x  sin x  2
 2 sin xcos xcos x sin x  cos x sin x1 2sin2x  0
cos x  sin x  0   1    x    . 1 2 sin 2 0 2    1  tan x  1
  x    k k   (thỏa điều kiện). 4    
2x    k2 x    k     2 4 2  sin 2x     k   8  
k   (thỏa điều kiện). 2  5  5 2x   k2     4 x  8 k
Vậy phương trình có nghiệm   5 x  
k , x    k, x
k  k  . 4 8 8 b) Ta có 3 3 2 2
sin x  3cos x  sin xcos x  3sin xcos xx  2 2 x x  x  2 2 sin cos sin
3 cos cos x sin x
 cos 2xsin x  3cos x  0 cos 2x  0   1   xx    . sin 3 cos 0 2      1  2 k x
k  x   k  . 2 4 2       2  sin x
 0  x   k  x    k k    .  3  3 3
Vậy nghiệm của phương trình  k  x  
, x    k k  . 4 2 3
c) Ta có 2sin x1 cos2x sin 2x 1 2cos x 2
 4sin xcos x  2sin xcos x 1 2cos x
 2sin xcos x2cos x   1 1 2cos x  2cos x   1 sin 2x   1  0
2cos x 1  0  1   x     . sin 2 1 0 2   1 2
1  cos x    x  
k2 k  . 2 3   
2  sin 2x 1 2x   k2  x   k k  . 2 4  
Vậy phương trình có nghiệm 2 x  
k2, x   k k  . 3 4
BT 38. Giải các phương trình lượng giác sau
a) (1 2sin x)cos x  3.
(ĐH khối A năm 2009) (1
 2sin x)(1sin x) b) 3
sin x  cos xsin 2x  3cos3x  2(cos4x sin ) x . (ĐH khối năm 2009)
c) 3cos5x  2sin3xcos2x sin x  0. (ĐH khối năm 2009) Lời giải 122 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC sin  x  1 a) Điều kiện  1 . sin x    2
Ta có (1 2sin x)cos x  3  1 2sin xcos x  31 2sin x1sin x
(1 2sin x)(1sin x)  x x   2 cos sin 2
3 1sin x  2sin x  cos x sin 2x  3sin x  cos2x 1    1   cos  
x  3 sin x  sin 2x  3 cos 2x  cos x     cos2  2 3 2 x 6           x
 2x   k2 x   k2  3 6  2     k  .    k   2 x   2
x   k2     3 6 x  18 3
Đối chiếu điều kiện ta có nghiệm  x
k2 không thỏa mãn. 2
Vậy phương trình có nghiệm  k 2 x    k  . 18 3 b) Ta có 3
sin x  cos xsin 2x  3cos3x  2(cos4x sin ) x 3
 sin x  2sin x  cos xsin 2x  3 cos3x  2cos 4x
 sin xcos 2x  cos xsin 2x  3 cos3x  2cos 4x
 sin3x  3 cos3x  2cos 4x   cos 3   x     cos 4  6 x   
4x  3x   k2  6   k    4x  3
x   k2  6   x    k2  6   k  .  k  2 x    42 7
Vậy phương trình có nghiệm   k x    k2 , 2   k   . 6 x 42 7
d) Ta có 3cos5x  2sin3xcos2x sin x  0
 5x xk2  3   k   
 5x    x k2  3   kx    18 3   k  .  k x     6 2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 123 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 3 cos5x  sin5x  sin x sin x  0
 3 cos5x sin 5x  2sin x   sin 5    x    sin  3 x
Vậy phương trình có nghiệm  k  kx   ,    k   . 18 3 x 6 2
BT 39. Giải các phương trình lượng giác sau : (1 sin    
x  cos 2x)sin x    a)  4  1  cos .
(ĐH khối A năm 20 0) 1 tan x x 2 b) (sin 2x  cos2 )
x cos x  2cos 2x  sin x  0. (ĐH khối năm 20 0)
c) sin 2x cos2x 3sin x cos x 1 0. (ĐH khối năm 20 0) Lời giải cos x  0 a) Điều kiện  . tan x  1 (1 sin    
x  cos 2x)sin x    Ta có  4  1  cos 1 tan x x 2   2(1 sin   
x  cos 2x)sin x   1   tan xcos  4 x         cos x sin 1 sin cos2 sin cos x x x x x  cos cos x x
 sin x  cos xsin x  cos2x  0
sin x  cos x  0   1
 sinxcos2x 0  2   1  tan x  1  (loại). sin   x  1 Lx    k2    2  6
2  sin x 1 2sin x  0   1   k  . sin x    7  x   k  2 2   6
Đối chiếu điều kiện, phương trình có nghiệm   x    k2 , 7 x
k2 k   . 6 6
b) Ta có (sin 2x  cos2 )
x cos x  2cos 2x sin x  0
 2sin xcos x  cos 2xcos x  2cos 2x sin x  0 2
 2sin xcos x  cos 2xcos x  2cos 2x sin x  0  sin x 2
2cos x  1cos2xcos x  2  0
 cos 2xsin x  cos x  2  0
sin x  cos x  2  0VN        2 k x
k  x   k  . cos 2x  0 2 4 2 124 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Vậy phương trình có nghiệm  kx   k  . 4 2
c) Ta có sin 2x cos2x 3sin x cos x 1 0
 2sin xcos x   2
1 2sin x3sin x cos x 1 0
 cos x2sin x   1   2
2sin x  sin x  12sin x  1  0
 cos x2sin x   1  sin x   1 2sin x   1  2sin x   1  0  2sin x  
1 cos x  sin x  2  0 cos  
x  sin x  2  0VN x   k2   6   1   k  . sin x   5  x   k  2 2   6
Vậy phương trình có nghiệm   x   k2 , 5 x
k2 k   . 6 6
BT 40. Giải các phương trình lượng giác sau:
a) 1 sin 2x  cos2x  2 sin xsin 2 . (ĐH khối A năm 20 ) 2 1 cot x x
b) sin 2xcos x sin xcos x  cos2x sin x cos . x (ĐH khối năm 20 )
c) sin 2x  2cos x sin x 1  0. (ĐH khối năm 20 ) tan x  3 Hƣớng dẫn giải
a) 1 sin 2x  cos2x  2 sin xsin 2 .x 1 (ĐH khối A năm 20 ) 2   1 cot x
o Điều kiện: sin x  0   2
1  sin x1sin 2x cos2x  2 sin xsin 2x 2  x  2 x x x 2 sin 2cos 2sin cos 2 2 sin c x os x cos x  0 2
 2sin xcos xcos x sin x  2  0  cosxsin x  2  
cos x  0  x   k;  2 k     
cos x  sin x  2  cos x  
 1  x   k2;    4  4 k
b) sin 2xcos x sin xcos x  cos2x sin x cos . x (ĐH khối năm 20 )
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 125 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 2
 2sin xcos x  sin xcos x  2cos x –1 sin x  cos x
  sin xcos x2cos x  
1  cos x2cos x   1 –1 sin x
 cos x2cos x   1 sin x –  1 – sin x 1  0 sin   x  1 x   k2    
cos x2cos x   2 1 –1  0   2
2cos x  cos x -1  0     x   k2    2 2 x  2 k    cos x  1 
x    k  2  1   cos x
x    k2  2  3
c) sin 2x  2cos x sin x 1  0. (ĐH khối năm 20 ) tan x  3
 Điều kiện: tan x   3;cos x  0
Pt  sin 2x  2cos x sin x 1 0  2sin xcos x  2cos x sin x   1  0
 2cos xsin x   1 sin x  
1  0  2cos x   1 sin x   1  0  1   x    k2 cos  x    3  2   .  sin   x  1  x    k2  2
Kiểm tra điều kiện, phương trình có nghiệm  x
k2 (k  ) 3
BT 41. Giải các phương trình lượng giác sau: b)
3sin 2x  cos2x  2cos x 1.
(ĐH khối A năm 20 2)
c) 2(cos x  3sin x)cos x  cos x  3sin x 1. (ĐH khối năm 20 2)
d) sin3x  cos3x sin x cos x  2 cos2 . x (ĐH khối năm 20 2) Hƣớng dẫn giải
a) 3sin 2x  cos2x  2cos x 1.
(ĐH khối A năm 20 2) 2
 2 3 sin xcos x  2cos x  2cos x  cos x 3sin x  cos x   1  0   x     2 k cos x  0     x k  2 k  
 3 sin x  cos x 1  2 x   k2  3
b) 2(cos x  3sin x)cos x  cos x  3sin x 1. (ĐH khối năm 20 2) 126 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 (2cos x 1)(cos x 1)  3 sin x(2cos x 1)  0  1 cos x        2 2cos  x 1 0 2 x    k2       3
cos x  3 sin x 1     1  cos x     x k2   3  2
c) sin3x  cos3x sin x cos x  2 cos2x (ĐH khối năm 20 2)
 sin 3x sin x  cos3x  cos x  2 cos 2x  0
 2cos 2xsin x  2cos 2 .
x cos x  2 cos 2x  0
 cos 2x2cos x  2sin x  2  0    x    4 k 2 cos 2  x  0  7    x   k2 k  . 2cos x 2sin x 2    12  
x    k2  12
BT 42. Giải các phương trình lượng giác sau:   b) 
1 tan x  2 2 sin x    (ĐH khối A năm 20 ) 4    c) 2
sin5x  2cos x 1. (ĐH khối năm 20 )
d) sin3x cos2x sin x  0. (ĐH khối năm 20 ) Hƣớng dẫn giải   a) 1 tan  
x  2 2 sin x    (ĐH khối A năm 20 ) 4    DK :cos x  0  1 tan x
2 sin x  cos x  cos x  sin x  2cos xsin x  cos x
 sin x  cos x2cos x   1  0 sin  
x  cos x  0 x       4 k  1   k  . cos x    2
x    k2  3 b) 2
sin5x  2cos x 1. (ĐH khối năm 20 ) 2   sin5  
x  1 2cos x  sin 5x   cos 2x  sin 5x  sin 2x   2        k2
5x  2x   k2     2 x  6 3     k  .    3 k2
5x    2x   k2    2 x  14 7
c) sin3x cos2x sin x  0. (ĐH khối năm 20 )
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 127 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
 2cos2xsin x  cos2x  0  cos2x2sin x   1  0  cos2x  0 hay 1 sin x   2      x  
hay x    k2 hay 7 x
k2 ( k Z ) 4 k 2 6 6
BT 43. Giải các phương trình lượng giác sau:
a) sinx 4cosx 2 sin2x. (ĐH khối A năm 20 ) Lời giải
Phương trình trên tương đương với
sin x  4cos x  2 sin 2x  0
 sin x  2  2cos xsin x  2  0
 sin x  21 2cos x  0 sin x  2
 12cosx 0.
Trường hợp 1. sin x  2 (Vô nghiệm).   x   k2  Trường hợp 2. 1  3
1 2cos x  0  cos x   cos   k  . 2 3 
x    k2  3   x   k2 
Vậy phương trình đã cho có hai họ nghiệm là 3  k  . 
x    k2  3 b) 2(sinx 2 cosx) 2 sin2x. (ĐH khối năm 20 ) Lời giải
Phương trình trên tương đương với 2(sin x 2 cos x) 2 sin 2x 0 2 sin x 2 2 cos x sin x 2 0 sin x 2 2 2 cos x 0 sin x 2 2 2 cos x 0
Trường hợp 1. sin x  2 (Vô nghiệm).  3 x   k2   Trường hợp 2. 2 3 4
2  2cos x  0  cos x    cos   k  . 2 4  3 x    k2  4  3 x   k2 
Vậy phương trình đã cho có hai họ nghiệm là 4  k  .  3 x    k2  4 128 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
BT 44. Giải phương trình: 2 2sin x 7 sinx 4 0. (TN TH T Q năm 20 ) Lời giải
Phương trình đã cho tương đương với 2
2sin x sin x 8sin x  4  0
 sin x2sin x  
1  42sin x   1  0      x   x   sin x 4 0 sin 4 2sin
1  0  2sinx10
Trường hợp 1. sin x  4  0  sin x  4  (Vô nghiệm).   x   k2  Trường hợp 2. 1  6
2sin x 1  0  sin x   sin   k  . 2 6  5 x   k2  6
BT 45. Giải các phương trình lượng giác sau:
a) cosx cos3x sin2x sin6x sin4x sin6x 0. Lời giải
Phương trình đã cho tương đương với cos x cos 3x sin 2x sin 6x sin 4x sin 6x 0 cos x cos 3x sin 6x sin 2x sin 4x 0 cos x cos 3x
sin 6x.2.sin 3x.cos x 0 cos x cos 3x 2 sin 6x sin 3x 0 2
cos x cos 3x 1 4 sin 3x 0
cos x cos 3x 2 cos 6x 1 0 x k 2 cos x 0 x k cos 3x 0 6 3 k . 2 cos 6x 1 0 x k 18 3 x k 18 3 b) 1
cos x cos2x cos 3x
sin x sin 2x sin 3x 2 Lời giải
Phương trình đã cho tương đương với
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 129 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 1
cos x cos 2x cos 3x
sin x sin 2x sin 3x 2 1 1 1 cos 2x cos 2x cos 4x sin 2x cos 2x cos 4x 2 2 2 2 cos 2x cos 2x cos 4x sin 2x cos 2x sin 2x cos 4x 1 2 cos 2x cos 4x sin 2x sin 2x cos 2x sin 2x cos 4x 0 cos 4x cos 2x sin 2x sin 2x cos 2x sin 2x 0 cos 4x sin 2x cos 2x sin 2x 0 cos 4x sin 2x 0 cos 2x sin 2x 0   x      4 k sin 2x  1   2  cos 4  
x  sin 2x  0  1 2sin 2x  sin 2x  0  1  x
k k  . sin 2x   12  2  5 x     12 k        
sin 2x  cos2x  0  2 sin 2x   0  sin 2x
 0  x    k k      .  4   4  8 2
c) cotx cos2x sinx sin2x cotx cosx cotx. Lời giải
Điều kiện: sin x  0  x k k  .
Phương trình đã cho tương đương với cotx cos 2x sin x sin 2x cotx cos x cotx 2 2 2 cos x cos 2x sin x sin x 2 sin x cos x cos x 2 2 2 2 sin x cos x cos 2x sin x cos x sin x cos x 0 sin x cosx sin x cosx sin x cosx 0 sin x cosx 1 sin x cos x 0 sin x cos x 0 1 sin x cos x 0    
sin x  cos x  0  2 sin x
 0  x   k k    .  4  4 1
  sin x  cos x  0   2 sin   x     1  4     1   sin x      sin  4  2 4    x    k2
x k2 L  4 4      k  .   3
x   k2 x    k2   2  4 4
d) sin2x cosx sinx cosx cos2x sinx cosx. Lời giải
Phương trình đã cho tương đương với 130 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC sin 2x cos x sin x cos x cos 2x sin x cos x 2 2 sin x cos x sin x cos x cos 2x sin x cos x 0 2 sin x 2 cos x 1 cos x cos 2x cos x 0 sin x 1 cos 2x cos x 0 sin x 1 0 sin x 1 0 2 cos 2x cos x 0 2 cos x cos x 1 0 sin x 1 x k2 2 cos x 1 x k2 k . 1 cos x x k2 2 3 e) 3 2 6 4 3sinx sin x 3cos x cos x. Lời giải
Phương trình đã cho tương đương với 3 2 6 4 3 sin x sin x 3 cos x cos x 2 4 sin x 1 sin x sin x 4 1 sin x 1 sin x 3 cos x 2 4 4 sin x 1 sin x sin x 4 3 cos x 3 sin x sin x cos x 0 2 3 2 sin x 1 sin x 1 1 sin x 1 sin x 0 sin x 1 0 3 3 sin x 1 1 1 sin x 0 3 1 sin x 1 sin x 1 x k2 2 k . sin x 0 x k f) 2sin3 x cos2x cosx 0. Lời giải
Phương trình đã cho tương đương với 3 2 sin x cos 2x cos x 0 3 2 2 sin x 1 2 sin x cos x 0 2 2 sin x sin x 1 1 cos x 0 2 1 cos x 1 cos x sin x 1 1 cos x 0 1
cos x 2 1 cos x sin x 1 1 0 1 cos x 0 1 2 1 cos x sin x 1 1 0 2
Giải (1): 1 cos x  0  cos x  1
  x    k2 k  .
Giải (2): Đặt t  sin x  cos x 2  t  2. Khi đó, phương trình (2) trở thành 2  1 t t  0 2 2t
 1  0  2t t  0  2 t     loai. 2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 131 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC     t
  0  sin x  cos x  0  2 sin x
 0  x    k k    .  4  4 g)
2cosx cos2x cos 3x 5 7 cos2x. Lời giải
2cosx cos2x cos 3x 5 7 cos2x
2cosx cos 3x cos2x 5 7 cos2x (cos 4x cos2x)cos2x 5 7 cos2x 2 (2 cos 2x 1 cos2x)cos2x 5 7 cos2x 0 3 2 2cos 2x cos 2x 8 cos2x 5 0 cos2x 1 2x k2 x 5 k cos2x (VN ) 2
Vậy nghiệm của phương trình đã cho là x k (k ) . h) 2 2 sin x(4 cos x 1) cosx(sinx cosx sin 3x). Lời giải 2 2 sin x(4 cos x 1) cos x(sin x cos x sin 3x) 2 2 2 2 4 sin x cos x sin x sin x cos x cos x sin 3x cos x 2 2 2 2 4 sin x cos x (sin x
cos x) sin x cos x sin 3x cos x 0 2 1 1 sin 2x 1 sin 2x (sin 4x sin 2x) 0 2 2 1 cos 4x 1 1 sin 4x 0 2 2 sin 4x cos 4x 1 2 sin 4x 1 4 4x k2 4 43 4x k2 4 4 k x 8 2 (k ) k x 4 2 k x
Vậy nghiệm của phương trình đã cho là 8 2 (k ). k x 4 2 i) 2 cosx 3(sin2x
sinx) 4 cos2x cosx 2 cos x 2 0. Lời giải 132 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 cos x 3(sin 2x
sin x) 4 cos 2x cos x 2 cos x 2 0. 2 2 cos x 3(sin 2x sin x) 4(2 cos x 1)cos x 2 cos x 2 0 3 2 3 sin x(2 cos x 1) 8 cos x 2 cos x 5 cos x 2 0 2 3 sin x(2 cos x 1) (2 cos x 1)(4 cos x cos x 2) 0 2 (2 cos x 1)( 3 sin x cos x 4 cos x 2) 0 2 cos x 1 0 2 3 sin x cos x 4 cos x 2 0 2 cos x 1 0 2 3 sin x cos x 2(2 cos x 1) 2 cos x 1 0 3 1 2 sin x cos x 2 cos 2x 2 2 2 cos x 1 0 cos cos x sin sin x cos 2x 3 3 2 2 1 x k2 x k2 cos x 3 3 2 2x x k2 x k2 (k ). cos x 3 3 cos 2x 3 k2 2x x k2 x 3 9 3 2 2 j) (sinx cosx) 2 sin x 2 sin x sin 3x 2 1 cot x 2 4 4 Lời giải
ĐK: sin x  0  x k 2 2 (sin x cos x) 2 sin x 2 sin x sin 3x 2 1 cot x 2 4 4 2 2 (sin x cos x) 2 sin x 2 cos 2x sin x 2 1 cot x 4 2 2 2 2 sin x(sin x 2 sin x cos x cos x 2 sin x) (sin 2x cos 2x)sin x 2 sin x(sin 2x 2 2 cos x sin x) (sin 2x cos 2x)sin x 2 2 2 sin x(sin 2x cos x sin x) (sin 2x cos 2x)sin x 0 2 sin x(sin 2x cos 2x) (sin 2x cos 2x)sin x 0 sin x(sin 2x cos 2x)(sin x 1) 0 sin x 0(L) tan 2x 1 sin 2x cos 2x 0 sin x 1 sin x 1 k 2x k x 4 8 2 (k ). x k2 x k2 2 2
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 133 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
Đối chiếu điều kiện, nghiệm của phương trình đã cho là k x 8 2 (k ) x k2 2 k) 1 1 15 cos 4x 2 2 2 2 cot x 1 2 tan x 1 8 sin 2x Lời giải x k   ĐK: sinx 0      (k  ) cos x  0 x     2 k 1 1 15 cos 4x 2 2 2 2 cot x 1 2 tan x 1 8 sin 2x 1 1 15 cos 4x 2 2 2 2(cot x 1) 1 2(tan x 1) 1 8 sin 2x 2 2 sin x cos x 15 cos 4x 2 2 2 2 sin x 2 cos x 8 sin 2x 2 2 2 2 sin x(2 cos x) cos x(2 sin x) 15 cos 4x 2 2 2 (2 sin x)(2 cos x) 8 sin 2x 2 2 2(sin x cos x) 2 2 2 sin x cos x 15 cos 4x 2 2 2 2 2 4 2(sin x cos x) sin x cos x 8 sin 2x 1 2 2 sin 2x 15 cos 4 2 x 2 2 2 2 sin x cos x 8 sin 2x 2 8 2 sin 2x 15 cos 4x 2 2 8 sin 2x 8 sin 2x 7 cos 4x 15 cos 4x 1 k cos 4x 4x k2 x (k ). 2 3 12 2
Vậy nghiệm của phương trình đã cho là k x (k ). 12 2 2 sin x l) 4 cos 3x 2 sin 2x 1. tan x 1 4 Lời giải   cos x  0 x   k  ĐK:  2    (k  ) tan x  1  x     4 k 134 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC 2 sin x 4 cos 3x 2 sin 2x 1. tan x 1 4 sin x cos x cos 3x sin 2x cos 2x 1 sin x 1 cos x cos x cos 3x sin 2x cos 2x 1 2 cos 2x cos x sin 2x cos 2x 1 0 2 2 cos 2x cos x 2 sin x cos x 2 cos x 0 2 cos x(cos 2x sin x cos x) 0 2 2 2 cos x cos x sin x (cos x sin x) 0 2 cos x(cos x sin x)(cos x sin x 1) 0 cos x 0 (L) cos x sin x 0 cos x sin x 1 x k 2 cos x 0 4 2 4 x k2 x k2 2 (k ). 4 4 2 sin x 1 x k2 5 4 x k2 4 4
Kết hợp với điều kiện, nghiệm của phương trình đã cho là x    k2(k  ). m) 2 3 2 2 2 3 sin x cos x sin x cosx sinx cos x 3 sin x cosx. 2 2 Lời giải 2 3 2 2 2 3 sin x cos x sin x cos x sin x cos x 3 sin x cos x. 2 2 2 2 2 2 3 sin x sin x cos x cos x sin x cos x 3 sin x cos x 2 2 3 sin x(sin x
cos x) cos x(cos x sin x) 0 2 2 (sin x cos x)(3 sin x cos x) 0 sin x cos x 0 2 sin x 0 4 2 3 sin x c 2 os x 0 2 1 tan x 3 2 sin x 0 4 x k x k 4 4 1 tan x x k x k 6 6 3 x k
Vậy nghiệm của phương trình đã cho là 4 (k ). x k 6
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 135 | THBTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
n) (2sinx 1)(cos2x sinx) 2sin 3x 6sinx 1 2cosx 3 0. 2 cosx 3 Lời giải ĐK: 3 
2cos x  3  0  cos x
x    k2. 2 6 (2 sin x 1)(cos 2x sin x) 2 sin 3x 6 sin x 1 2 cos x 3 0 2 cos x 3 (2 sin x 1)(cos 2x sin x) 2 sin 3x 6 sin x 1 (2 cos x 3)(2 cos x 3) 0 2 cos x 33 2 (2 sin x 1)(cos 2x sin x) 2(3 sin x 4 sin x) 6 sin x 1 4 cos x 3 0 (2 sin x 1)(cos 2x sin x) 8 s 3 2 in x 1 4(1 sin x) 3 0 3 2 (2 sin x 1)(cos 2x sin x) 8 sin x 4 sin x 2 0 2 (2 sin x 1)(cos 2x sin x) 2(2 sin x 1)(2 sin x 2 sin x 1) 0 2 2 (2 sin x 1)(1 2 sin x sin x 4 sin x 4 sin x 2) 0 2 (2 sin x 1)(2 sin x 3 sin x 3) 0 2 sin x 1 0 2 2 sin x 3 sin x 3 0(VN ) x k2 1 6 sin x (k ). 2 7 x k2 6 x k2
Vậy nghiệm của phương trình 6 (k ). 7 x k2 6 o) 3 2 3 1 cos x cos2x 2. 4 4 2 3 2 3 1 cos x cos 2x 2. 4 4 2 3 2 3 1 2 cos x (1 2 sin x) 2. 4 4 2 3 2 1 2 cos x sin x 2 4 4 3 2 1 2 2 2 3 2 1 2 VT 1. cos x 1. sin x 1 1 . cos x sin x 2 4 4 4 4 3 2 1 2 VT 2 cos x sin x 4 4 3 2 1 2 cos x sin x 4 4 1 2 cos 2x 2x k2 x k 2 3 3
Vậy nghiệm của phương trình đã cho là x k (k ). 3 136 | THBTN – CA
BIÊN SOẠN THẦY TÀI + THẦY CÔ BTN
TÀI LIỆU HỌC TẬP CHẤT LƯỢNG CAO – 2017
BÀI GIẢNG: CHUYÊN ĐỀ HÀM SỐ - PT LƯỢNG GIÁC
TRÊN ĐÂY LÀ CÁC ẠNG BÀI T ĐIỂN HÌNH VÀ GIẢI CHI TIẾT - HY VỌNG
LÀ TÀI LIỆU BỔ ÍCH GIÚP CÁC THẦY CÔ TRONG QUÁ TRÌNH BIÊN SOẠN ĐỂ
GIẢNG DẠY CŨN NHƢ CÁC EM HỌC SINH CÓ TÀI LIỆU THAM KHẢO TỰ HỌC
THỜI GIAN BIÊN T P NGẮN + NĂN LỰC CÒN HẠN CHẾ, CHẮC CHẮN
KHÔNG THỂ TRÁNH ĐƢỢC NHỮNG SAI SÓT, MONG BẠN ĐỌC THÔNG CẢM
VÀ Ó Ý ĐỂ BỘ TÀI LIỆU ĐẠT CHẤT LƢỢNG TỐT HƠN!
CHÚC CÁC BẠN CÓ MỘT CHUYÊN ĐỀ THÀNH CÔNG!
 LƯU Ý: BỘ TÀI LIỆU CÒN 500 CÂU TRẮC NGHIỆM - FULL GIẢI DO BAN BIÊN TẬP
BTN SOẠN GIẢI - CÁC THẦY CÔ CÙNG CÁC EM TÌM ĐỌC NHÉ !
THẦY TRẦN TÀI - 0977.413.341 THÂN TẶNG
ADMIN TRẦN VĂN TÀI & THẦY CÔ THÀNH VIÊN TOÁN HỌC BẮC–TRUNG–NAM 137 | THBTN