








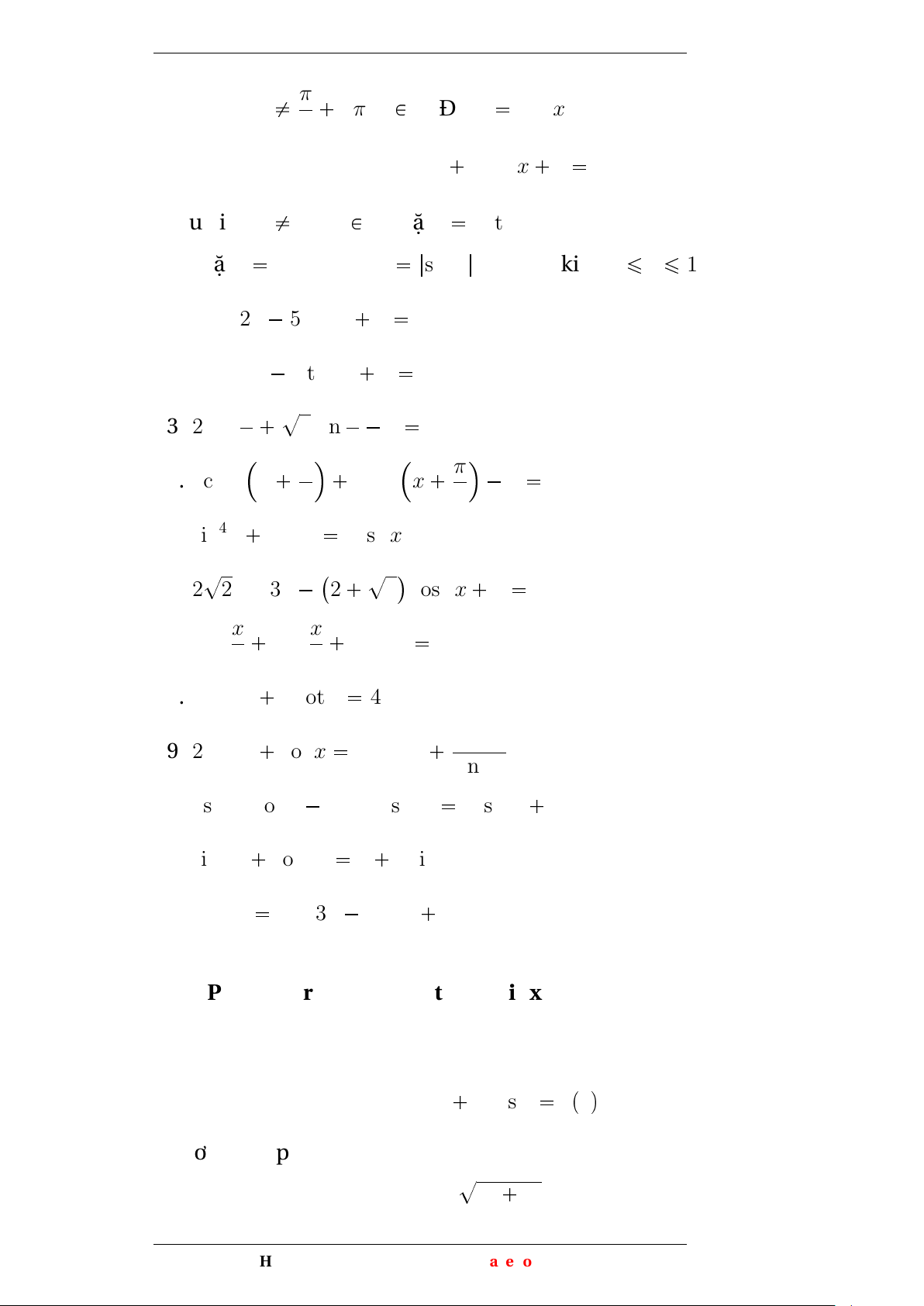





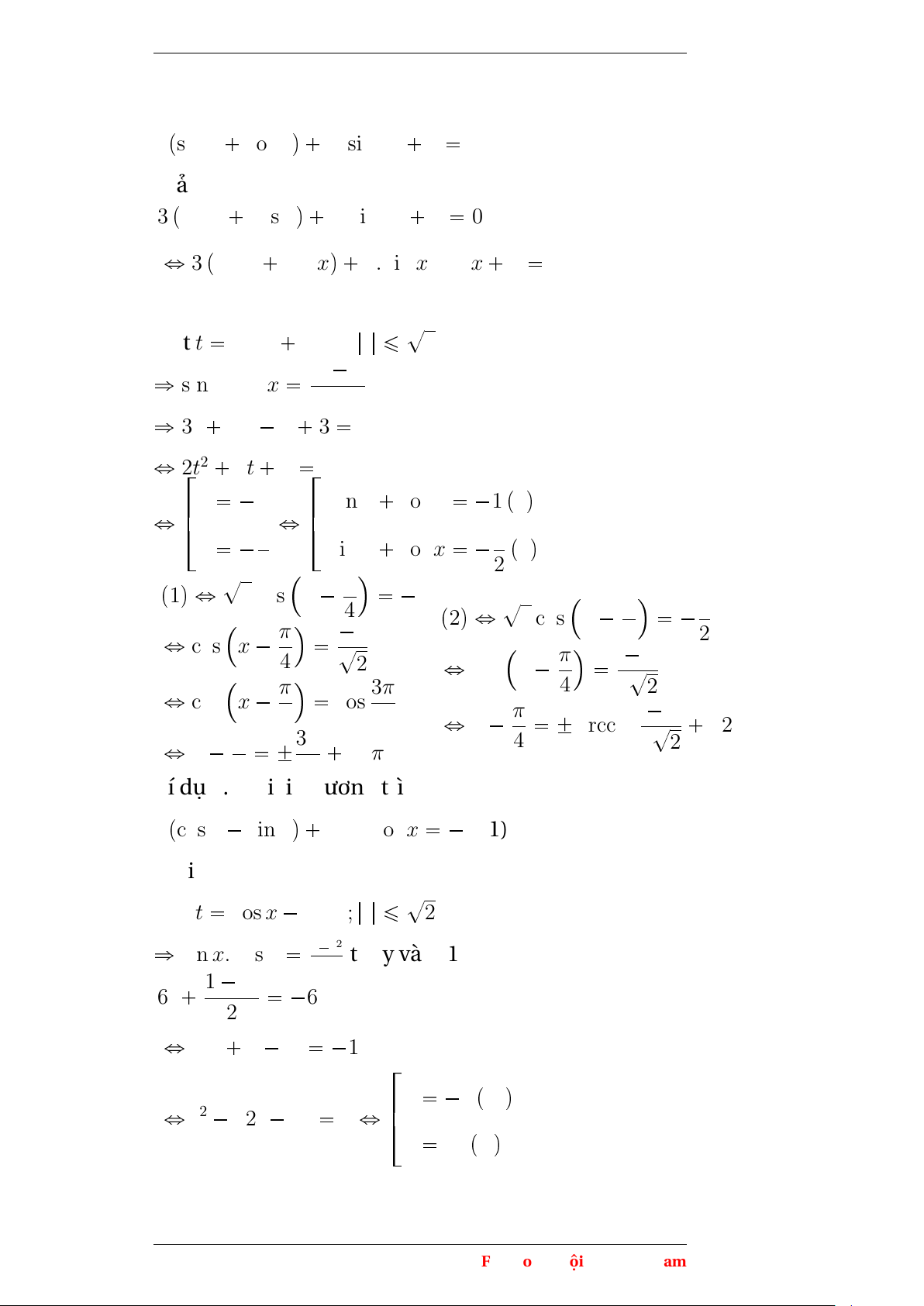


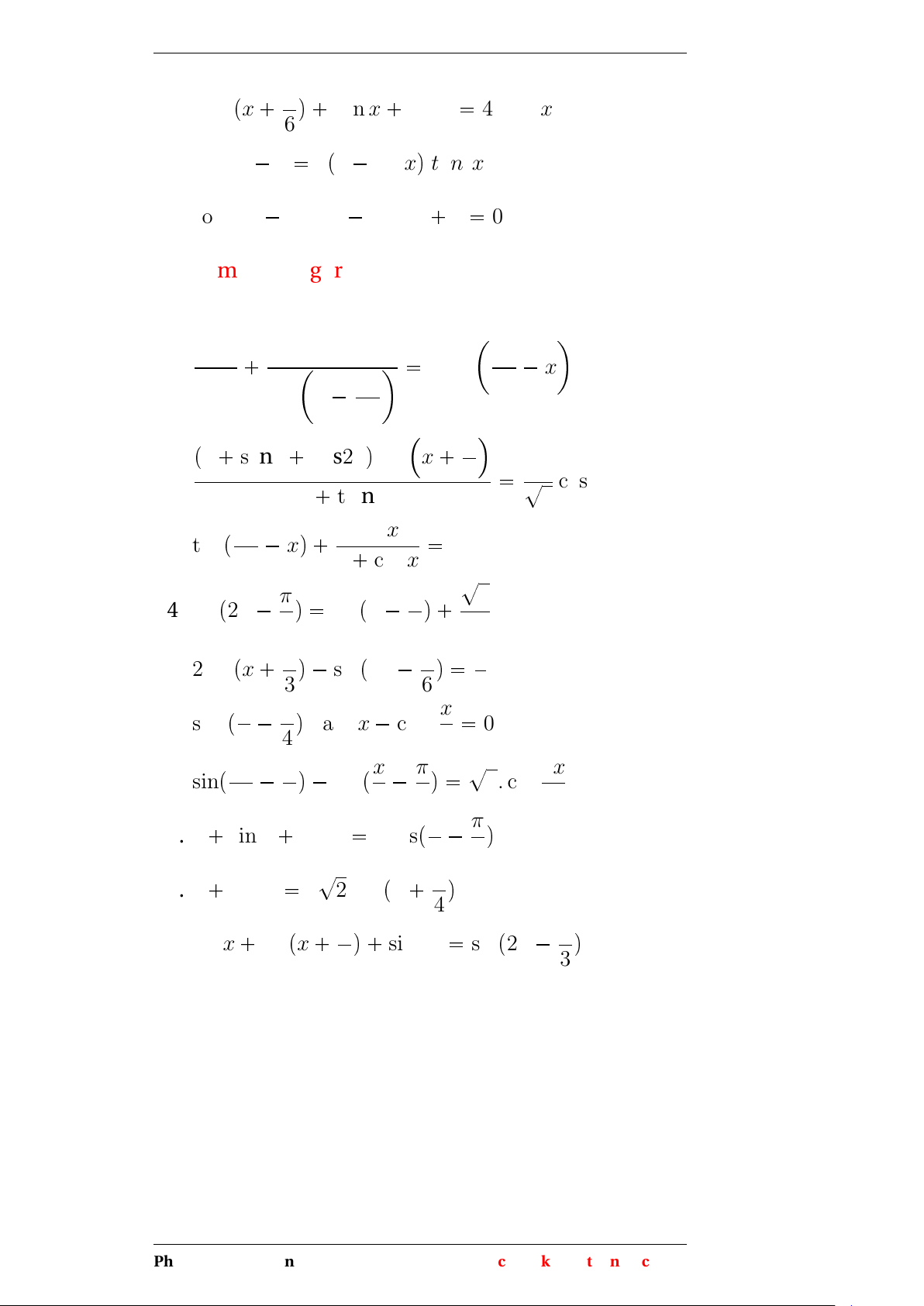








Preview text:
HỘI TOÁN BẮC NAM
THÁNG MỘT CHỦ ĐỀ
CHUYÊN ĐỀ LƯỢNG GIÁC
BUÔN MA THUỘT, 12/2016
Chuyên đề lượng giác MỞ ĐẦU
Lượng giác đóng vai trò quan trọng và xuyên suốt trong chương
trình toán phổ thông và được ứng dụng khá nhiều trong thực tế,
đặc biệt là trong lĩnh vực nghiên cứu thiên văn. Đây sẽ là một trong
những vấn đề quan trọng trong kì thi THPT quốc gia 2018, khi chương
trình 10 và 11 được đưa vào trong đề thi.
Trong chủ đề tháng 12/2016 của Hội Toán Bắc Nam tôi xin trình bày
một số vấn đề về lượng giác.
Chủ đề lượng giác được chia làm ba phần:
Phần 1: Cơ sở lí thuyết như cung liên kết, công thức lượng giác, hằng
đẳng thức lượng giác, hàm số lượng giác.
Phần 2: Các dạng phương trình lượng giác thường gặp.
Phần 3: Một số bài toán lượng giác điển hình có liên quan.
Chuyên đề chủ yếu xoay quanh các bài toán THPT, hi vọng sẽ giúp
ích được phần nào cho bạn đọc, đặc biệt là các bạn học sinh THPT.
Sẽ không tránh khỏi thiếu sót khi biên tập, rất mong nhận được sự
đóng góp từ quý bạn đọc để chuyên đề ngày một hoàn thiện hơn.
Mọi ý kiến đóng góp, quý bạn đọc vui lòng gửi về địa chỉ
email: phamthithuhien117@gmail.com hoặc gửi trực tiếp cho Hội Toán Bắc Nam.
Buôn Ma Thuột, ngày 15 tháng 12 năm 2016 Phạm Thị Thu Hiền 2
Facebook: Hội toán Bắc Nam Mục lục Mở đầu 2 1 CƠ SỞ LÝ THUYẾT 2
1.1 Cung liên kết . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Công thức lượng giác . . . . . . . . . . . . . . . . . . . . 2
1.3 Hằng đẳng thức thường dùng . . . . . . . . . . . . . . . 4
1.4 Hàm số lượng giác . . . . . . . . . . . . . . . . . . . . . . 4
2 PHƯƠNG TRÌNH LƯỢNG GIÁC 5
2.1 Phương trình lượng giác cơ bản . . . . . . . . . . . . . . 5
2.2 Phương trình bậc hai đối với một hàm số lượng giác . . 8
2.3 Phương trình bậc nhất theo sinx và cosx . . . . . . . . . 9
2.4 Phương trình thuần nhất . . . . . . . . . . . . . . . . . . 11
2.5 Phương trình đối xứng . . . . . . . . . . . . . . . . . . . 14
2.6 Phương trình không mẫu mực . . . . . . . . . . . . . . . 16
3 MỘT SỐ VẤN ĐỀ KHÁC 19
3.1 GTLN-GTNN . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.2 NHẬN DẠNG TAM GIÁC . . . . . . . . . . . . . . . . . . 21
3.3 ĐÁNH GIÁ HAI VẾ . . . . . . . . . . . . . . . . . . . . . . 23
3.4 PHƯƠNG TRÌNH LƯỢNG GIÁC CHỨA THAM SỐ . . . 26 1 Chương 1 CƠ SỞ LÝ THUYẾT 1.1 Cung liên kết Cung đối: cos pxq cos x; sin pxq sin x; tan pxq tan x; cot pxq cot x. Cung bù:
cos pπ xq cos x; sin pπ xq sin x;
tan pπ xq tan x; cot pπ xq cot x. Cung phụ: π π cos x sin x; sin x cos x; 2 2 π tanpπ xq cot x; cot x tan x. 2 2 Cung hơn kém nhau π: cos pπ xq cos x; sin pπ xq sin x; tan pπ xq tan x; cot pπ xq cot x. 1.2
Công thức lượng giác 1. Công thức cộng cos pa bq cos a cos b sin a sin b 2
Chuyên đề lượng giác sinpa bq sin a cos b cos a sin b tanpa bq tan a tan b 1 tan a tan b cotpa bq cot a cot b 1 cot a cot b 2. Công thức nhân đôi sin 2a 2 sin a. cos a cos 2a cos2a sin2a 2cos2a 1 1 2sin2a tan 2a 2 tan a 1 tan2a 3. Công thức nhân ba sin 3a 3 sin a 4sin3a cos 3a 4cos3a 3 cos a 4. Công thức hạ bậc sin2a 1 cos 2a; cos2a 1 cos 2a 2 2
sin3a 3 sin a sin 3a; cos3a 3 cos a cos 3a 4 4
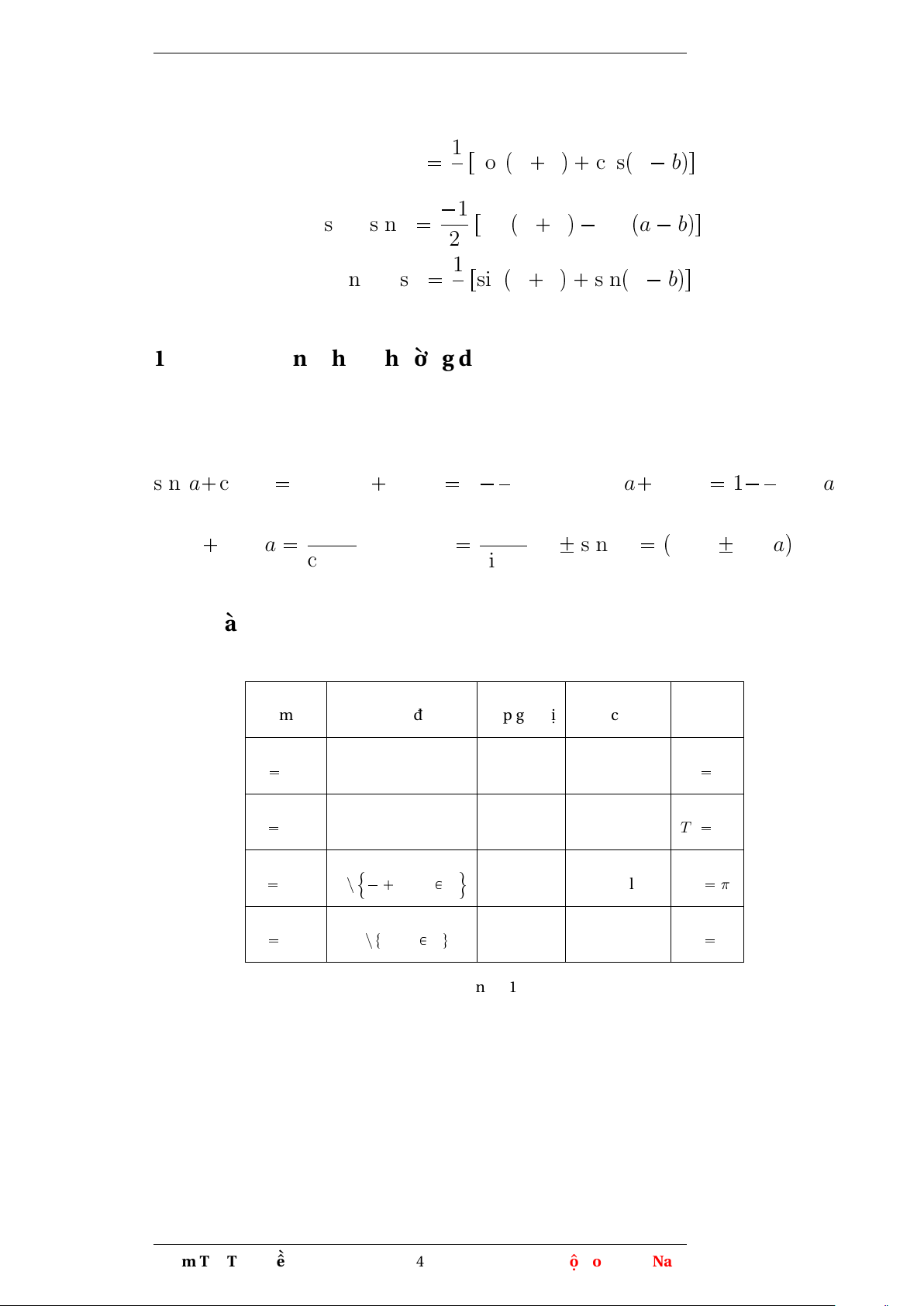
5. Công thức tổng thành tích a b a b cos a cos b 2 cos cos 2 2 a b a b cos a cos b 2 sin sin 2 2 a b a b sin a sin b 2 sin cos 2 2 a b a b sin a sin b 2 cos sin 2 2 Phạm Thị Thu Hiền 3
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác
6. Công thức tích thành tổng cos a cos b 1 rcospa bq cospa bqs 2 1 sin a sin b rcospa bq cospa bqs 2 sin a cos b 1 rsinpa bq sinpa bqs 2 1.3
Hằng đẳng thức thường dùng
sin2a cos2a 1; sin4a cos4a 1 1sin22a ; sin6a cos6a 1 3sin22a 2 4 1 tan2a 1 ; 1+cot2a 1 ; 1 sin2a psina cosaq2 cos2a sin2a 1.4
Hàm số lượng giác Hàm số Tập xác định Tập giá trị Tính chẵn lẻ Chu kỳ y sin x D=R T=[-1,1] hàm lẻ T0 2π y cos x D=R T=[-1,1] hàm chẵn T0 2π ! ) π y tan x Rz kπ, k P Z T=R hàm lẻ T0 π 2 y cot x Rz tkπ, k P Zu T=R hàm lẻ T0 π Bảng 1.1: * Phạm Thị Thu Hiền 4
Facebook: Hội toán Bắc Nam Chương 2
PHƯƠNG TRÌNH LƯỢNG GIÁC 2.1
Phương trình lượng giác cơ bản 1. Phương trình sin x a
• Nếu |a| > 1 : Phương trình vô nghiệm
• Nếu |a| ¤ 1 : Phương trình có nghiệm là x α k2π và x π α k2π với sin α a
Các trường hợp đặc biệt: sin x 0 ô x kπpk P Zq sin x 1 ô x π k2πpk P Zq 2 sin x 1 ô x π k2πpk P Zq 2
sin x 1 ô sin2 x 1 ô cos2 x 0 ô cos x 0 ô x π kπpk P 2 Zq 2. Phương trình cos x a
• Nếu |a| > 1 : Phương trình vô nghiệm
• Nếu |a| ¤ 1 : Phương trình có nghiệm là x α k2π và x α k2π với cos α a
Các trường hợp đặc biệt: cos x 0 ô x π kπpk P Zq 2 cos x 1 ô x k2πpk P Zq cos x 1 ô x π k2πpk P Zq 5
Chuyên đề lượng giác
cos x 1 ô cos2 x 1 ô sin2 x 0 ô sin x 0 ô x kπpk P Zq 3. Phương trình tan x a
Điều kiện cos x 0 hay x π kπ, k P Z 2
Nghiệm của phương trình x α kπ, k P Z với tan α a
Các trường hợp đặc biệt:
tan x 0 ô x kπpk P Zq tan x 1 ô x π kπpk P Zq 4 4. Phương trình cot x a
Điều kiện sin x 0 hay x kπ, k P Z
Nghiệm của phương trình x α kπ, k P Z với cot α a
Các trường hợp đặc biệt: cot x 0 ô x π kπpk P Zq cot x 1 ô x π kπpk P Zq 2 4 BÀI TẬP
Bài 1: Giải các phương trình sau: π 1. sin x sin 5 2. sin x 12 3. sin 2x 54 π ? 4. 2 sin x 3 0 4 π ? 5. 2 sin x 3 0 4 6. 2 sin 900 2x 1 0 7. sin x 13 8. 4sin2 x 400 1 0 9. sin 3x cos 2x 0 10. sin 4x cos 5x 0 Phạm Thị Thu Hiền 6
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác
Bài 2: Giải các phương trình sau 1. cos x 12 2. cosp3x 1q cospx 2q 3. sinpx 1200q cos 2x 0 4. cos 3x cos 4x 0 5. cos 2x sin 3x 0 6. 3 cosp2x 1q 4 0 π 7. cosp2x 1q cospx q 0 3 8. 3 cospx π q 1 0 4 9. 2 cos2 x cos x 0 10. cos 2x cos 4x cos 6x 0
Bài 3: Giải các phương trình sau 1. tan 7x cot 9x 0 2. tan2px π q 3 4 3. tan 3x cot x 0 4. 3 tanp2x π q 5 0 4 5. |cos x| 12 6. cos 3x. tan 5x sin 7x 7. tan 5x. tan 2x 1 8. |sin x| cos 3x 0 π 9. cotp2x π q cotpx q 4 3 Phạm Thị Thu Hiền 7
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác ?3 10. cotp3x 100q 3?2 11. cospx 450q 2 12. sin2px π q cos2 x 4
Bài 4: Giải các phương trình sau ? 1.
3 tanpx 500q 1 0 với x P r1800, 2700s ? 2. cotpx π q 3 0, x P rπ ; 2πs 3 2 3. sin2 x cos2 3x 1 4. cos 2x cos 4x cos 6x 0 5. cos x cos 2x cos 3x cos 4x 0
6. cos x. cos 7x cos 3x. cos 5x 7. sin2 x sin2 2x sin2 3x sin2 4x
8. cos 5x. sin 4x cos 3x. sin 2x 9. cos2 x cos2 2x cos2 3x 32 10. sinpcospx π qq 1 4 2 2.2
Phương trình bậc hai đối với một hàm số lượng giác Dạng asin2x b sin x c 0
Đặt t sin x điều kiên 1 ¤ t ¤ 1. acos2x b cos x c 0
Đặt t cos x điều kiên 1 ¤ t ¤ 1. atan2x b tan x c 0 Phạm Thị Thu Hiền 8
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác Điều kiện x π kπ, k P Z. Đặt t tan x. 2 acot2x b cot x c 0
Điều kiện x kπ, k P Z. Đặt t cot x.
Nếu đặt t sin2x hoặc t |sin x| thì điều kiện 0 ¤ t ¤ 1 Bài tập 1. 3 cos 2x 5 cos x 2 0 2. 3 tan 2x 2 tan x 3 0 x ? x 3. 2sin2 2 sin 2 0 2 2 π π 4. 2cos2 x 5 sin x 4 0 3 3 5. sin4x cos4x cos 2x ? ? 6. 2 2cos23x 2 2 cos 3x 1 0 x x 7. cos4 sin4 2 sin x 1 2 2 8. 2 tan x 3 cot x 4 1 9. 2 tan x cot x 2 sin 2x sin 2x
10. 4sin5x cos x 4cos5x sin x cos24x 1 11. sin 3x cos 2x 1 2 sin x cos 2x 12. cos 4x cos23x cos2x 1 2.3
Phương trình bậc nhất theo sinx và cosx Dạng a sin x b cos x cp1q Phương pháp: ?
Chia cả 2 vế phương trình cho a2 b2 ta được: Phạm Thị Thu Hiền 9
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác p b 1q ô a ? s inx +? cos x c ? a2 b2 a2 b2 a2 b2 Đặt sin α a ? , cos α b ? , pα P r0, 2πsq a2 b2 a2 b2 (1) trở thành sin α. s inx cos α. cos x c ?a2 b2 ô cos px αq c ? cos β (2) a2 b2
Điều kiện để phương trình (2) có nghiệm là: c ? ¤ 1 ô a2 b2 ¥ c2. a2 b2 p2q ô x α β k2π pk P Zq Bài tập
Giải các phương trình sau ? ? 1. 3 sin x cos x 2 0 2. 3 sin 2x 2 cos 2x 3 3. 4 cos 3x 3 sin 3x 5 0 ? 4. 2 sin 3x 3 cos 7x sin 7x 0 ? 5. cos 5x sin 3x 3 pcos 3x sin 5xq ? 6. 3 sin x 1 4sin3x 3 cos 3x ? 7. cos x 3 sin x 32 8. p2 sin x cos xq p1 cos xq sin2x 9. sin x cos x sin2x cos 2x ? 10. 3 sin x cos x 2 cos x π 2 3 Phạm Thị Thu Hiền 10
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác 2.4
Phương trình thuần nhất
1. Phương trình thuần nhất bậc 2 Dạng: asin2x b sin x. cos x ccos2x =d p1q
Phương pháp: Xét cos x 0 ô x π
kπ, k P Zcó thỏa mãn không? 2
Xét cos x 0, chia cả 2 vế của (1) cho cos2x
Ví dụ 2.1. Giải phương trình
2sin2x 5 sin x. cos x cos2x 2(1) Giải Ta thấy cos x 0 ô x π
kπ, k P Z không thỏa mãn (1) 2
Xét cos x 0, chia cả 2 vế của (1) cho cos2x: ô 2sin2x 5 sin x 1 2 cos2x cos x cos2x ô 2tan2x 5 tan x 1 2p1 tan2xq ô 4tan2x 5 tan x 1 0 tan x 1 x π kπ ô ô 4 k P 1 Z tan x 1 x arctan kπ 4 4
Ví dụ 2.2. Giải phương trình sin2x sin 2x 2cos2x 12 Giải sin2x sin 2x 2cos2x 12
ô sin2x 2 sin x. cos x 2cos2x 1p1q 2 Ta thấy cos x 0 ô x π
kπ, k P Z không thỏa mãn (1) 2
Xét cos x 0, chia cả 2 vế của (1) cho cos2x: Phạm Thị Thu Hiền 11
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác
p1q ô tan2x 2 tan x 2 1 1 tan2x 2 ô 1tan2x 2 tan x 5 0 2 2 ô tan2x 4 tan x 5 0 tan x 1 x π kπ ô ô 4 tan x 5 x arctanp5q kπ
Ví dụ 2.3. Giải phương trình sin x cos x 1 (1) sin x Giải
Điều kiện sin x 0 ô x kπ p cos x 1q ô sin x 1 sin x sin x sin2x ô 1 cot x 1 cot2x cot x 0 x π kπ ô ô 2 cot x 1 x π kπ 4
2. Phương trình thuần nhất bậc 3 Dạng: asin3x bsin2x. cos x c sin xcos2x +dcos3x=... p1q
Phương pháp: Xét cos x 0 ô x π
kπ, k P Zcó thỏa mãn không? 2
Xét cos x 0, chia cả 2 vế của (1) cho cos3x
Ví dụ 2.4. Giải phương trình cos3x 3cos2x sin x 2sin3x 0p1q Giải Xét cos x 0 ô x π
kπ, k P Zcó thỏa mãn không? 2
Xét cos x 0, chia cả 2 vế của (1) cho cos3x Phạm Thị Thu Hiền 12
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác p1q ô 1 3 tan x 2tan3x 0 ô 2tan3x 3 tan x 1 0
ô ptan x 1q 2tan2x 2 tan x 1 0 x π kπ tan x 1 4 ? ? 1 3 ô 1 3 ô x arctan kπ tan x 2 2 ? ? 1 3 1 3 tan x x arctan kπ 2 2
Ví dụ 2.5. Giải phương trình
6 sin x 2cos3x 5 sin 2x cos xp1q Giải Xét cos x 0 ô x π
kπ, k P Zcó thỏa mãn không? 2
Xét cos x 0, chia cả 2 vế của (1) cho cos3x p1q ô 6 sin x 2 10 sin x cos3x cos x ô 1 6 tan x 2 10 tan x cos2x ô 6 tan x 1 tan2x 2 10 tan x ô 6tan3x 4 tan x 2 0
ô ptan x 1qp6tan2x 6 tan x 2q 0 tan x 1 0 ô 6tan2x 6 tan x 2 0pV Nq ô tan x 1 ô x π kπ 4 Bài tập
Giải các phương trình sau Phạm Thị Thu Hiền 13
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác 1. 2 sin 2x 3cos2x 5 sin x cos x 2 0 2. 2sin2x sin x cos x 3cos2x 0 ? 3. 3sin2x 4 sin 2x 8 3 9 cos2x 0 ? 4. 3cos3x 5sin3x 7 sin x 8 ? cos x 0 3
5. 6 sin x 2cos3x 5 sin 4x cos x 2 cos 2x 6. 3sin2x 2 sin 2x cos2x 0 7. 4 cos3 x 2 sin3 x 3 sin x 0 8. 3 cos3 x
4 sin3 x 3 sin x sin2 x. cos x 0 9. 3pcos3 x sin3 xq p4 sin 2xq cos x 10. 4pcos3 x sin3 xq sin x 3 cos x 2.5
Phương trình đối xứng Dạng 1: a psin x cos xq b. sin x. cos x c 0 ? π ? Đặt t sin x cos x 2. sin x ; |t| ¤ 2 4
ñ t2 1 2 sin x. cos x ñ sin x. cos x t2 1 2
Thay vào phương trình đã cho ta được phương trình bậc hai theo t. ?
Giải phương trình này tìm t thỏa điều kiện |t| ¤ 2 từ đó suy ra x. Pt a psin x cos xq b. sin x. cos x c 0 tương tự. Dạng 2: a |sin x cos x| b. sin x. cos x c 0 ? π ? t |sin x cos x| 2. sin x ; 0 ¤ t ¤ 2 4 ñ sin x. cos x t2 1 2 Pt a |sin x cos x| b. sin x. cos x c 0 tương tự.
Dạng 3 : Phương trình đối xứng theo tan và cot. π Đặt t tan x cot x; x k , |t| ¥ 2 2 Phạm Thị Thu Hiền 14
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác
Ví dụ 2.6. Giải phương trình 3 psin x cos xq 2. sin 2x 3 0 Giải 3 psin x cos xq 2. sin 2x 3 0
ô 3 psin x cos xq 4. sin x. cos x 3 0 ? Đặt t sin x cos x; |t| ¤ 2 ñ sin x. cos x t2 1 2 ñ 3t 2t2 2 3 0 ô 2t2 3t 1 0 t 1 sin x cos x 1 p1q ô ô t 1 sin x cos x 1 p2q 2 2 ? p1q ô 2 cos x π 1 ? 4 p2q ô 2 cos x π 1 ô 1 4 2 cos x π ? 4 2 1 ô cos x π ? 4 2 2 ô 3π cos x π cos 4 4 ô 1 x π arccos ? k2π ô 4 2 2 x π 3π k2π 4 4
Ví dụ 2.7. Giải phương trình 6 pcos x sin xq sin x cos x 6 (1) Giải ? Đặt t cos x sin x; |t| ¤ 2
ñ sin x. cos x 1t2 thay vào (1) 2 1 t2 6t 6 2 ô 12t 1 t2 12 t 1 pN q ô t2 12t 13 0 ô t 13 pLq Phạm Thị Thu Hiền 15
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác ? π t 1 ô 2 cos x 1 4 ô π cos x 1 ? 4 2 π x 3π k2π x π k2π ô 4 4 ô 2 π x 3π k2π x π k2π 4 4 Bài tập:
Bài 1: Giải các phương trình sau: 1. 2 psin x cos xq sin 2x 1 0
2. sin x cos x 6 psin x cos x 1q ? 3. sin 2x 2 sin x π 1 4 ? 4. tan x 2 2 sin x 1 5. sin3x cos3x 1 6. cos3x sin3x cos 2x 7. sin3x cos3x 2 psin x cos xq 3 sin 2x 0 π 8. 2 sin x tan x cot x 4 9. psin x cos xq4 3 sin 2x 1 0 1 1 10. sin x cos x 2 tan x cot x 0 sin x cos x 1 1 11. sin x cos x 2 tan x cot x 0 sin x cos x 12. 9ptan x cot xq4 48 tan2x cot2x 96 13. 3 ptan x cot xq tan2x cot2x 6 1 1 14. sin x cos x 2 tan x cot x 0 sin x cos x 15. 3ptan x cot xq4 8 tan2x cot2x 21 2.6
Phương trình không mẫu mực
A. Phương pháp đưa về phương trình tích
Mình hay nói vui là phương pháp chia để trị. Phạm Thị Thu Hiền 16
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác Dạng: A 0 A.B 0 ô B 0
Ví dụ 2.8. Giải phương trình 2 sin xp1 cos 2xq sin 2x 1 2 cos x Giải 2 sin xp1 cos 2xq sin 2x 1 2 cos x
ô 2 sin xp1 2 cos2 x 1q 2 sin x cos x 1 2 cos x
ô 4 sin x cos2 x 2 sin x cos x 1 2 cos x ô sin 2xp1 2 cos xq 1 2 cos x ô p1 2 cos xqpsin 2x 1q 0 1 2 cos x 0 ô sin 2x 1 0 Bài tập
Giải các phương trình lượng giác sau 1. p2 cos x 1qp2 sin x cos xq sin 2x sin x 2. 2 cos3 x cos 2x sin x 0 3. 2 sin x cos 3x sin 2x 1 sin 4x 4. p1 cot xq sin3 x
pcos x sin xq cos2 x cos x sin x 5. p1 cos xq cot x cos 2x sin x sin 2x 6. 1 sin x 2 cos x p1 cos xq cot x 7. p2 sin x 1qp3 cos 4x 2 sin x 4q 4 cos2 x 3 8. cos 3x cos 2x cos x 1 0 9. sin 3x cos x. cos 2xptan2 x tan 2xq Phạm Thị Thu Hiền 17
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác π 10. 8 sinpx q tan x cot x 4 cot 2x 6 11. 5 sin x 2 3p1 sin xq.tan2x 12. cos 10x cos 8x cos 6x 1 0
B.Nhóm phương trình lượng giác có cung phức tạp 1 1 7π 1. 4 sin x . sin x 4 sin x 3π 2 p π 1 s inx cos2xq sin x 2. 4 1 ? cos x. 1 t anx 2 3. tanp3π xq sin x 2 2 1 cos x ?2 4. sinp2x π q sinpx π q 4 4 2 π 5. 2 sinpx q sinp2x πq 1 3 6 2 x 6. sin2px π q. tan2 x cos2 0 2 4 2 ? 3x 7. sinp5x π q cospx π q 2. cos 2 4 2 4 2 8. 1 sin x cos x 2 cospx π q 2 4 ? π 9. 1 tan x 2 2. sinpx q 4 π 10. sin x sinpx q sin 4x sinp2x πq 3 3 Phạm Thị Thu Hiền 18
Facebook: Hội toán Bắc Nam Chương 3
MỘT SỐ VẤN ĐỀ KHÁC 3.1 GTLN-GTNN Những điểm cần chú ý: 1. Phương trình a sin x b cos x c có nghiệm ô a2 b2 ¥ c2 a 2. BĐT Bunhiacopxki |a.x b.y| ¤ pa2 b2q px2 y2q
Ví dụ 3.1. Tìm GTLN, GTNN của hàm số y cos2 x cos x 3 Đặt t cos x, y t2 t 3 BBT t 1 1 1 2 5 3 y & 11 % 4
M axy 5 khi t 1 ô cos x 1 ô x π k2π
M iny 11 khi t 1 ô cos x 1 ô x π k2π 4 2 2 3
Ví dụ 3.2. Tìm GTLN-GTNN của hàm số ?3cosx y (1) 2 sin x Giải TXĐ: D R 19
Chuyên đề lượng giác ? (1)ô 2y y sin x 3 cos x ?3cosx ysinx 2y(2)
Phương trình (2) có nghiệm ô 3 pyq2 ¥ p2yq2 ô 3 y2 ¥ 4y2 ô 3 ¥ 3y2 ô y2 ¤ 1 ô 1 ¤ y ¤ 1 Vậy M axy 1 M iny 1 Bài tập:
Bài 1 Tìm GTLN-GTNN của mỗi hàm số sau: 1. y cos 2x 4 sin x 1 2. y p4 cos xqp4 sin xq 3. y sin x cos x sin 2x 2 4. y cos x sin x 1 sin x 2 cos x 4 5. y cos 3x sin 3x 1 cos 3x 2 6. y 1 3 sin x 2 cos x 2 sin x cos x 7. y sin x cos x cos2x sin x cos x 1 1 8. y 5 cos x s sin x 2 c 9. y 3 cos 2x π 2 4 Phạm Thị Thu Hiền 20
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác 3.2 NHẬN DẠNG TAM GIÁC Những điểm cần lưu ý 1. sin pA Bq sin C 2. cos pA Bq cos C A B C 3. sin cos 2 2 A B C 4. cos sin 2 2 5. Định lí côsin a2 b2 c2 2bc. cos A ñ cos A b2 c2 a2 2bc a 6. Định lí sin: b c 2R sin A sin B sin C sin A
Ví dụ 3.3. Tam giác ABC có tính chất gì nếu: 2(1) sin B. sin C p1q ô sin A 2 sin B. sin C ô sin pB Cq 2 sin B. cos C
ô sin B. cos C cos B sin C 2 sin B. cos C ô sin B. cos C cos B sin C 0 ô sin pB Cq 0 ô B C kπ
Vì B, C là 2 góc của tam giác nên k 0 ô B C. Vậy tam giác ABC cân ở A.
Ví dụ 3.4. Chứng minh rằng nếu cos A. cos B. cos C 1 thì tam giác 8 ABC đều. Chứng minh Phạm Thị Thu Hiền 21
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác p1q ô 8 cos A. cos B. cos C 1 ô 1 8 cos A. rcos pB Cq cos pB Cqs 1 2
ô 4 cos A. r cos A cos pB Cqs 1 ô 4cos2A 4 cos A. cos pB Cq 1
ô 4cos2A 4 cos A. cos pB Cq 1 0
ô 4cos2A 4 cos A. cos pB Cq cos2 pB Cq sin2 pB Cq 0
ô r2 cos A cos pB Cqs2 sin2 pB Cq 0 $ ' & 2 cos A cos pB Cq 0 ô '% sinpB Cq 0 $ $ $ ' & ' ' 2 cos A cos pB Cq & 2 cos A 1 & cos A 1 ô 2 ' ô ô % ' ' B C kπ % B C % B C $ $ ' & ' A π k2π & A π ô 3 3 ' ô ô A B C π % ' 3 B C % B C
Vậy tam giác ABC là tam giác đều. Bài tập
Bài 1: Chứng mình tam giác ABC vuông biết: a) cos2A cos2B cos2C 1 A B C A B C b) cos cos cos sin sin sin 1 2 2 2 2 2 2 2 sin A cos B c) tan A sin B cos A sin B sin C d) sin A cos B cos C e) cos B cos C b c a B f ) cot a c 2 b g) sin 2A sin 2B 4 sin A. sin B Phạm Thị Thu Hiền 22
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác
Bài 2:Chứng mình tam giác ABC cân biết: sin C a) 2 cos A sin B sin A sin B sin C A C b) cot cot sin A sin B sin C 2 2 C c) tan A tan B 2 cot 2 b c B C d) tan b c 2 A B e) a tan A b tan B pa bq tan 2 1 cos B f ) 2a c ? sin B 4a2 c2
Bài 3:Chứng mình tam giác ABC đều biết: A B C a) cot A cot B cot C tan tan tan 2 2 2 A B C b) cos A cos B cos C sin sin sin 2 2 2 c) sin2A sin2B sin2C 94 A B C d) sin sin sin 1 2 2 2 8 $ ' & sin A sin C 2 sin B e) ' % A B tan tan 2 ? 2 2 3 3.3 ĐÁNH GIÁ HAI VẾ Những điểm cần lưu ý i) 1 $ ¤ sin x ¤ 1; 1 ¤ cos x $
¤ 1; 0 ¤ sin2 x ¤ 1; 0 ¤ cos2 x ¤ 1 ' & ' A ¥ 0; B ¥ 0 & A 0 ii) ' ô % ' A B 0 % B 0 $ ' & A 0 iii) A2 B2 0 ô ' % B 0 Phạm Thị Thu Hiền 23
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác $ $ ' & | ' A| ¤ 1, |B| ¤ 1 & A 1 ' ô % ' A B 2 % B 1 $ ' ' ' ' A ¥ M & iv) 'B ¤ M ô A B M ' ' ' % A B Ví dụ 3.5. cos x cos 2x cos 4x 3 (1)
Ta có 1 ¤ cos x ¤ 1; 1 ¤ cos 2x ¤ 1; 1 ¤ cos 4x ¤ 1 với mọi x $ $ $ ' ' ' ' ' ' cos x 1 ' x k2π ' x k2π & ' ' & ' ' &
Do đó p1q ô ' cos2x 1 ô 2x k2π ô x kπ ô x k2π ' ' ' ' ' ' ' % ' ' ' ' cos 4x 1 % 4x k2π % x kπ2 Ví dụ 3.6. sin x. sin 5x 1
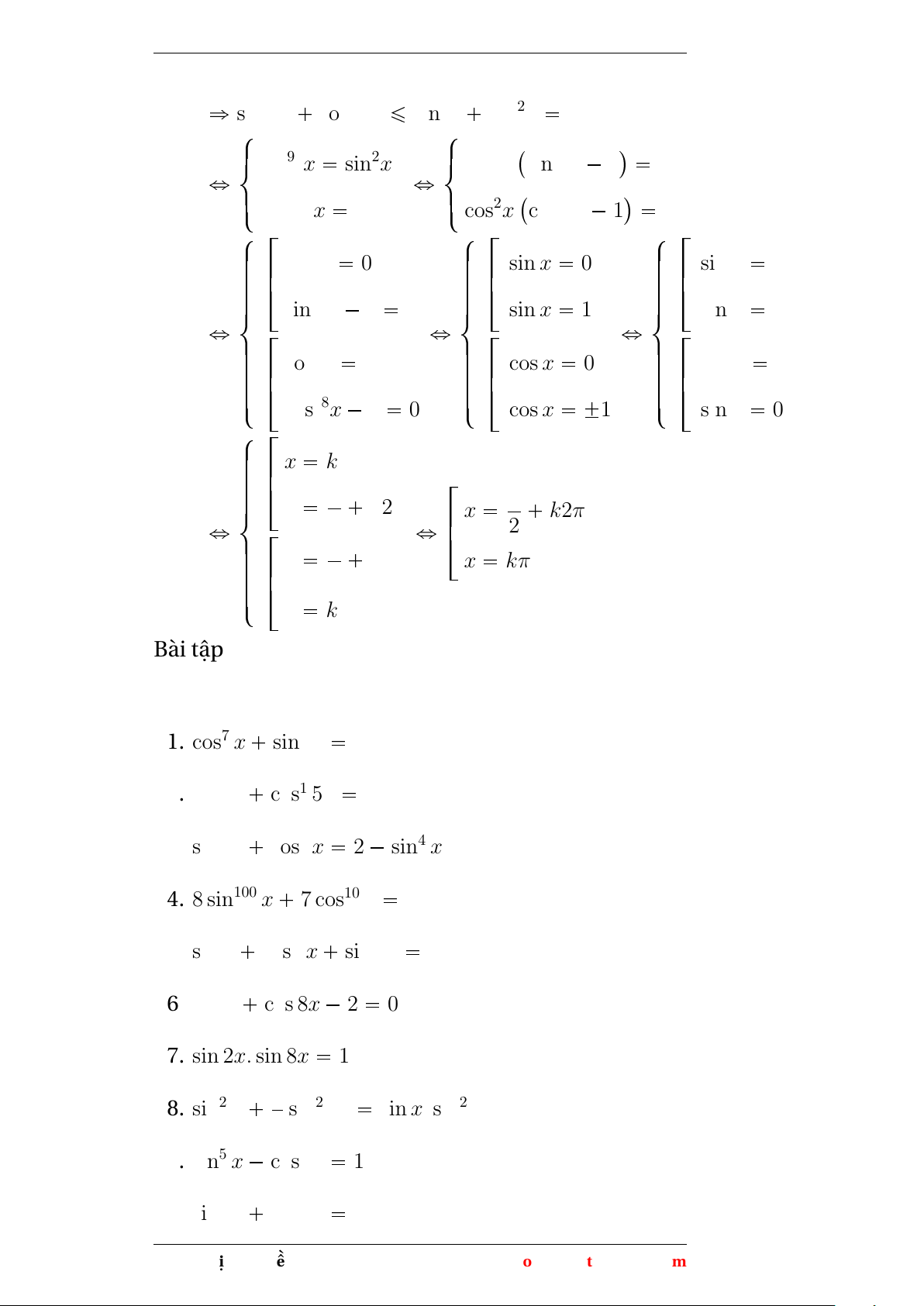
Ta có 1 ¤ sin x ¤ 1; 1 ¤ sin 5x ¤ 1 với mọi x Do đó $ $ $ ' & ' & ' x π k2π & x π k2π sin x 1 2 2 ' ' ' k2π % sin 5x 1 % 5x π k2π % x π p 1q ô 2 10 5 $ ô $ ô $ ' ' ' & sin x 1 & x π k2π & x π k2π 2 2 ' % ' ' k2π sin 5x 1 % 5x π k2π % x π 2 10 5 x π k2π ô 2 ô x x π kπ 2 x π k2π 2 Ví dụ 3.7. sin99 x cos100 x 1
Ta có 1 ¤ sin x ¤ 1; 1 ¤ cos x ¤ 1 Suy ra $ ' & sin99x ¤ sin2x ' % cos100x ¤ cos2x Phạm Thị Thu Hiền 24
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác
ñ sin99x cos100x ¤ sin2x cos2x 1 $ $ ' & ' sin99x sin2x & sin2x sin97x 1 0 ô ' ô % ' cos100x cos2x % cos2x cos98x 1 0 $ $ $ ' ' ' ' ' ' sin2x 0 ' sin x 0 ' sin x 0 ' ' ' ' ' ' ' ' ' ' ' ' & ' ' sin97x 1 0 ' & sin x 1 ' & sin x 1 ô ' ô ô ' ' ' ' ' ' ' ' cos2x 0 ' cos x 0 ' cos x 0 ' ' ' ' ' ' ' ' ' % ' ' ' ' cos98x 1 0 % cos x 1 % sin x 0 $ ' ' ' ' x kπ ' ' ' ' & x π k2π x π k2π ô 2 2 ' ô ' ' ' ' x π kπ x kπ ' ' 2 ' % x kπ Bài tập 1. cos7 x sin4 x 1 2. sin4 x cos1 5x 1 3. sin3 x cos3 x 2 sin4 x 4. 8 sin100 x 7 cos10 x 8 5. sin x cos 4x sin 5x 3 6. cos x cos 8x 2 0 7. sin 2x. sin 8x 1 1 8. sin2 x sin2 3x sin x. sin2 3x 4 9. sin5 x cos2 x 1 10. sin3 x cos3 x 1 Phạm Thị Thu Hiền 25
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác ? 11. sin x cos x 2p2 sin 3xq 3.4
PHƯƠNG TRÌNH LƯỢNG GIÁC CHỨA THAM SỐ
Ví dụ 3.8. Tìm m để phương trình sau có nghiệm sin2 xsin xm 3 0(1) Đặt t sin x, t P r1; 1s
Khi đó (1) trở thành t2 t m 3 0 ô t2 t 3 m Xét hàm số y t2 t 3 BBT t 1 1 1 2 5 3 y & 11 % 4 11
Dựa vào BBT, phương trình có nghiệm khi và chỉ khi ¤ m ¤ 5 4 Bài tập
Bài 1: Tìm m để phương trình sau đây có nghiệm 1. cos 2x cos x m 1 0 2. p2 sin xqp2 cos xq m HD đặt t sin x cos x 3. sin x. cos x 6psin x cos x mq 4. tan2 x cot2 x mptan x cot xq ? 1 5. 3 sin2 x m 2 6. pm 1q sin x cos x 2 7. 2 sin 2x p2m 1q sinx m 0
Bài 2: Giải và biện luận các phương trình 1. pm 1q cos x m 0 Phạm Thị Thu Hiền 26
Facebook: Hội toán Bắc Nam
Chuyên đề lượng giác ? 2. m tan x m 1 0 3. sin m. cos 2x 1 Phạm Thị Thu Hiền 27
Facebook: Hội toán Bắc Nam
Document Outline
- Mở đầu
- CƠ SỞ LÝ THUYẾT
- Cung liên kết
- Công thức lượng giác
- Hằng đẳng thức thường dùng
- Hàm số lượng giác
- PHƯƠNG TRÌNH LƯỢNG GIÁC
- Phương trình lượng giác cơ bản
- Phương trình bậc hai đối với một hàm số lượng giác
- Phương trình bậc nhất theo sinx và cosx
- Phương trình thuần nhất
- Phương trình đối xứng
- Phương trình không mẫu mực
- MỘT SỐ VẤN ĐỀ KHÁC
- GTLN-GTNN
- NHẬN DẠNG TAM GIÁC
- ĐÁNH GIÁ HAI VẾ
- PHƯƠNG TRÌNH LƯỢNG GIÁC CHỨA THAM SỐ




