Chuyên đề phương trình lượng giác – Lưu Huy Thưởng

Tài liệu gồm 18 trang trình bày công thức lượng giác thường sử dụng, các dạng toán phương trình lượng giác và phương pháp giải, ví dụ mẫu và bài tập có đáp số.

31 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

18 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC
2013 - 2014
PHƯƠNG TRÌNH LƯỢNG GIÁC
BIÊN SOẠN: LƯU HUY THƯỞNG
HÀ NỘI, 8/2013
HỌ VÀ TÊN: …………………………………………………………………
LỚP :………………………………………………………………….
TRƯỜNG :…………………………………………………………………
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 1
ỨI BÊ
CHUYÊN ĐỀ 2: CHUYÊN ĐỀ LƯỢNG GIÁC
KIẾN THỨC CẦN NHỚ
Giá trị lượng giác của góc (cung) lượng giác
1. Định nghĩa các giá trị lượng giác
Cho
( , )
OA OM
. Giả sử
M x y
.
cos
sin
sin
tan
cos 2
cos
cot
sin
x OH
y OK
AT k
BS k
Nhận xét:
, 1 cos 1; 1 sin 1
tan xác định khi ,
2
k k Z
cot xác định khi
,
k k Z
sin( 2 ) sin
k
tan( ) tan
k
cos( 2 ) cos
k
cot( ) cot
k
2. Dấu của các giá trị lượng giác
3. Giá trị lượng giác của các góc đặc biệt
4. Hệ thức cơ bản:
2 2
sin cos 1
;
tan cot 1
.
;
2 2
2 2
1 1
1 tan ; 1 cot
cos sin
Phần tư
Giá trị lượng giác
I II III IV
cos
+
–
–
+
sin
+
+
–
–
tan
+
–
+
–
cot
+
–
+
–
0
0
0
30
0
45
0
60
0
90
0
120
0
135
0
150
0
180
0
270
0
360
0
sin 0
1
0 –1 0
cos 1
0
–1 0 1
tan 0
1
–1
0
0
cot
1
0
–1
0
cosin
O
cotang
sin
tang
H
A
M
K
B S
T
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 2
ỨI BÊ
5. Giá trị lượng giác của các góc có liên quan đặc biệt
II. Công thức lượng giác
1. Công thức cộng
2. Công thức nhân đôi
sin 2 2 sin .cos
2 2 2 2
cos 2 cos sin 2 cos 1 1 2 sin
Góc đ
ố
i nhau
Góc bù nhau
Góc ph
ụ
nhau
Góc hơn kém
Góc hơn kém
Hệ quả:
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 3
ỨI BÊ
3. Công thức biến đổi tổng thành tích
4. Công thức biến đổi tích thành tổng
III. Phương trình lượng giác cơ bản (Các trường hợp đặc biệt)
1.Phương trình sinx = sin
a)
2
sin sin ( )
2
x k
x k Z
x k
b)
sin . ( 1 1)
arcsin 2
sin ( )
arcsin 2
x a a
x a k
x a k Z
x a k
c)
sin sin sin sin( )
u v u v
d) sin cos sin sin
2
u v u v
e) sin cos sin sin
2
u v u v
Công thức hạ bậc
Công thức nhân ba (*)
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 4
ỨI BÊ
Các trường hợp đặc biệt:
sin 0 ( )
x x k k Z
sin 1 2 ( )
2
x x k k Z
sin 1 2 ( )
2
x x k k Z
2 2
sin 1 sin 1 cos 0 cos 0 ( )
2
x x x x x k k Z
2. Phương trình cosx = cos
a)
cos cos 2 ( )
x x k k Z
b)
cos . ( 1 1)
cos arccos 2 ( )
x a a
x a x a k k Z
c)
cos cos cos cos( )
u v u v
d) cos sin cos cos
2
u v u v
e) cos sin cos cos
2
u v u v
Các trường hợp đặc biệt:
cos 0 ( )
2
x x k k Z
cos 1 2 ( )
x x k k Z
cos 1 2 ( )
x x k k Z
2 2
cos 1 cos 1 sin 0 sin 0 ( )
x x x x x k k Z
3. Phương trình tanx = tan
a)
tan tan ( )
x x k k Z
b)
tan arctan ( )
x a x a k k Z
c)
tan tan tan tan( )
u v u v
d) tan cot tan tan
2
u v u v
e) tan cot tan tan
2
u v u v
Các trường hợp đặc biệt:
tan 0 ( )
x x k k Z
tan 1 ( )
4
x x k k Z
4. Phương trình cotx = cot
cot cot ( )
x x k k Z
cot arccot ( )
x a x a k k Z
Các trường hợp đặc biệt:
cot 0 ( )
2
x x k k Z
cot 1 ( )
4
x x k k Z
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 5
ỨI BÊ
5. Một số điều cần chú ý:
a) Khi giải phương trình có chứa các hàm số tang, cotang, có mẫu số hoặc chứa căn bậc chẵn, thì nhất thiết phải
đặt điều kiện để phương trình xác định.
* Phương trình chứa tanx thì điều kiện:
( ).
2
x k k Z
* Phương trình chứa cotx thì điều kiện:
( )
x k k Z
* Phương trình chứa cả tanx và cotx thì điều kiện
( )
2
x k k Z
* Phương trình có mẫu số:
sin 0 ( )
x x k k Z
cos 0 ( )
2
x x k k Z
tan 0 ( )
2
x x k k Z
cot 0 ( )
2
x x k k Z
b) Khi tìm được nghiệm phải kiểm tra điều kiện. Ta thường dùng một trong các cách sau để kiểm tra điều kiện:
1. Kiểm tra trực tiếp bằng cách thay giá trị của x vào biểu thức điều kiện.
2. Dùng đường tròn lượng giác.
3. Giải các phương trình vô định.
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 6
ỨI BÊ
CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
HT 1: Giải các phương trình sau:
1.
1
sin
6 2
x
4.
1
cos(2 )
3 2
x
2.
2 sin(2 ) 2
3
x 5.
2 cos( ) 1
6
x
3.
3 sin( ) 1
4
x 6.
4 cos( ) 3
3
x
HT 2: Giải các phương trình sau:
) sin 3 1 sin 2
a x x
) cos cos 2
3 6
b x x
) cos 3 sin 2
c x x
) cos 2 cos 0
3 3
d x x
) sin 3 sin 0
4 2
x
e x
) tan 3 tan
4 6
f x x
) cot 2 cot
4 3
g x x
) tan 2 1 cot 0
h x x
HT 3: Giải các phương trình sau (Đưa về phương trình bậc hai)
1.
2
sin 3 sin 2 0
x x
2.
2
3 cos 2 4 cos 2 1 0
x x
3.
2
tan 5 tan 6 0
x x
4.
2
cot 3 cot 4 0
x x
5.
2
4 sin 2 3 1 sin 3 0
x x
6.
2
cos 2 3 sin 2 3 0
x x
7.
2
cos 3 5 sin 3 5 0
x x
8.
2
sin 7 cos 7 0
x x
9.
2
cos 2 6 sin cos 3 0
x x x
10.
cos 4 5 sin 2 2 0
x x
11.
3 cos 2 4 cos 7 0
x x
12.
3
4 cos 3 2 sin 2 8 cos
x x x
13.
5 5 2
4 cos . sin 4 sin . cos sin 4
x x x x
14.
2
tan 1 3 tan 3 0
x x
15.
2 tan 2 cot 3
x x
16.
2 2
tan cot 2
x x
17.
2
8 cot 2 4 cot 2 3 0
x x
18.
2 2
cos 2 2(sin cos ) 3 sin 2 3 0
x x x x
19. os
2
2 3 cos 4 cos
2
x
c x x
20.
9 13 cos
x
2
4
1 tan
x
= 0
HT 4: Giải các phương trình sau
( sin cos 0)
a x b x c
1.
sin 3 cos 1
x x
2.
2(sin 2 cos 2 ) 2
x x
3.
sin 2 3 cos 2 1
x x
4.
3 cos 3 sin 3 2
x x
5.
cos 2 2 3 sin cos 2 sin 3
x x x x
6.
3 cos 4 2 sin 2 cos 2 2 cos
x x x x
7.
3 sin 5 2 cos cos 5 0
x x x
8.
3 sin 2 sin 2 1
2
x x
9.
2
2 sin 3 sin 2 3
x x
10.
sin cos 2 sin 5
x x x
11.
2(sin 2 cos 2 ) 2 cos( )
2
x x x
12.
6
3 cos 4 sin 6
3 cos 4 sin 1
x x
x x
13. cos 3 sin 2 cos
3
x x x
14.
3 1
8 cos
sin cos
x
x x
HT 5: Giải các phương trình sau
( sin cos 0)
a x b x c
(Nâng cao)
1.
2
sin cos 3 cos 2 2
x x x
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 7
ỨI BÊ
2.
4 4
4(sin cos ) 3 sin 2 2
x x x
3.
2 2
cos 3 2 sin 6 1 sin 3
x x x
4.
3
2 sin 4 3 cos 2 16 sin cos 5 0
x x x x
5.
2(cos 2 3 sin 2 )cos 2 cos 2 3 sin 2 1
x x x x x
6.
3
sin cos sin 2 3 cos 3 2(cos 4 sin )
x x x x x
7.
2
1 2(cos 2 tan sin 2 )cos cos 2
x x x x x
8.
3 3
4 sin cos 3 4 cos sin 3 3 3 cos 4 3
x x x x x
HT 6: Giải các phương trình sau (Đẳng cấp bậc hai
2 2
sin sin cos cos 0
a x b x x c x d
)
1.
2 2
3 sin 4 sin cos cos 0
x x x x
2.
2 2
2 sin 3 cos 5 sin cos 2 0
x x x
3.
2
sin 4 2 sin 2 2 cos 4 0
x x x
4.
2 2
sin 2 2 sin 2 cos 2 3 cos 2
x x x x
5.
3
2 cos 4 sin
cos
x x
x
6.
3 3
2 cos 3 sin 4 sin
x x x
7.
sin cos 2 6 cos (1 2 cos 2 )
x x x x
8.
2 2
2 sin 1 3 sin .cos 1 3 cos 1
x x x x
9.
2 2
3 sin 8 sin . cos 8 3 9 cos 0
x x x x
10.
2 2
4 sin 3 3 sin . cos 2 cos 4
x x x x
11.
4 2 2 4
3 cos 4 sin cos sin 0
x x x x
12.
2 2
3 1 sin 2 3 sin . cos 3 1 cos 0
x x x x
13.
3 3 2
4 sin 3 cos 3 sin sin cos 0
x x x x x
14.
3 3 2 2
sin 3 cos sin cos 3 sin cos
x x x x x x
15.
3 1
2 sin 2 3 cos
cos sin
x x
x x
16.
2
2 1
3 sin . cos sin
2
x x x
HT 7: Giải các phương trình sau (Đối xứng
(sin cos ) sin cos 0
a x x b x x c
)
1.
3(sin cos ) 2 sin cos 3 0
x x x x
2.
sin 2 cos 2 7 sin 4 1
x x x
3.
2 sin sin 2 2 cos 2 0
x x x
4.
3 cos 2 sin 4 6 sin cos 3
x x x x
5.
3 3
3
1 sin cos sin 2
2
x x x
6.
3 3
1
sin 2 cos 2 sin 4 1
2
x x x
7.
2 sin 2 3 3 sin cos 8 0
x x x
8.
2 sin cos 3 sin 2 2
x x x
9.
3 sin cos 2 sin 2 3
x x x
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 8
ỨI BÊ
10.
1 2 1 sin cos sin 2
x x x
11.
sin 2 2 sin 1
4
x x
12.
os
3 3
sin 1 2 2 sin cos
x c x x x
HT 8: Giải các phương trình sau (Tổng hiệu thành tích)
1.
sin sin 2 sin 3 0
x x x
2.
cos cos 2 cos 3 0
x x x
3.
cos cos 2 cos 3 1 0
x x x
4.
2
sin 4 sin 2 2 cos 0
x x x
5.
2
sin sin 5 1 2 cos 0
x x x
6.
2
2 sin 2 sin 6 1 sin 2
x x x
7.
2
sin 2 sin 6 2 sin 1 0
x x x
8.
sin sin 2 sin 3 1 cos cos 2
x x x x x
9.
cos 3 sin 3 cos sin 2 cos 2
x x x x x
10.
sin sin 2 sin 3 cos cos 2 cos 3
x x x x x x
HT 9: Giải các phương trình sau (Tích về tổng hiệu)
1.
cos 3 . cos cos 2
x x x
2.
sin . sin5 sin2 .sin 3
x x x x
3.
cos cos 3 sin 2 . sin6 sin 4 .sin 6 0
x x x x x x
4.
3 cos 6 2 sin 4 . cos 2 sin 2 0
x x x x
5.
5 3
4 cos cos 2(8 sin 1) cos 5
2 2
x x
x x
HT 10: Giải các phương trình sau (Hạ bậc)
1.
2 2 2
3
sin sin 2 sin 3
2
x x x
2.
os os os
2 2 2
2 3 1
c x c x c x
3.
2 2
17
sin 2 sin 8 sin 10
2
x x x
4.
2 2
1 sin sin cos sin 2 cos
2 2 4 2
x x x
x x
HT 11: Giải các phương trình sau (Dạng khác)
1. os
6 6
1
sin
4
x c x
2.
os os
3 3
sin 2
x c x c x
3.
os
sin 2 1 2 cos 2
x x c x
4.
2
(2 sin 1)(2 cos 2 2 sin 1) 3 4 cos
x x x x
5.
2
(sin sin 2 )(sin sin 2 ) sin 3
x x x x x
6.
os os
sin sin 2 sin 3 2(cos 2 3 )
x x x x c x c x
7.
2
(1 2 sin ) cos 1 sin cos
x x x x
8.
2
sin (2 cos ) (1 cos ) (1 cos )
x x x x
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 9
ỨI BÊ
9.
cos 2 (1 2 cos )(sin cos ) 0
x x x x
10.
cos 2 5 2(2 cos )(sin cos )
x x x x
11.
4 sin 2 3 cos 2 3(4 sin 1)
x x x
12.
os os os
2
5 . cos 4 . 2 3 cos 1
c x x c x c x x
13.
os
2 2
sin 7 2 sin 2 sin
x c x x x
14.
os
3 3
1
sin sin 2 . sin cos sin 3
4
2
x c x x x x x
15.
os
1 sin 2 2 cos 3 (sin cos ) 2 sin 2 cos 3 2 )
x x x x x x c x
16.
cos sin(2 ) sin(2 ) 1 3(1 2 cos )
6 6
x x x x
HT 12: Giải các phương trình sau:
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 10
ỨI BÊ
ÔN TẬP
Giải các phương trình sau:
HT 1.
2 sin 5 3 cos 3 sin 3 0
x x x
Đ/s:
2
;
24 4 3
k
x x k
HT 2.
2 2
cos 3 sin 2 1 sin
x x x
Đ/s: ;
3
x k x k
HT 3.
4 2 2 4
3 cos 4 sin . cos sin 0
x x x x
Đ/s: ;
4 3
x k x k
HT 4.
sin 2 2 sin 1
4
x x
Đ/s:
2 ; 2 ; 2
4 2
x k x k x k
HT 5. 4sin
3
1 3 sin 3 cos 3
x x x
Đ/s:
2 2
;
18 3 2 3
k k
x x
HT 6.
3 3 2
4 sin 3 cos 3 sin sin cos 0
x x x x x
Đ/s: ;
4 3
x k x k
HT 7.
3
2 sin 4 3 cos 2 16 sin cos 5 0
x x x x
Đ/s:
3 4
;( ); cos ; sin
2 5 5
x k k
HT 8.
3
sin 4 sin cos 0
x x x
Đ/s:
4
x k
HT 9.
2 2
tan sin 2 sin 3(cos 2 sin cos )
x x x x x x
Đ/s: ;
4 3
x k x k
HT 10.
cos 2 5 2(2 cos )(sin cos )
x x x x
Đ/s:
2 ; 2
2
x k x k
HT 11.
1
2 cos 2 8 cos 7
cos
x x
x
Đ/s:
2 ; 2
3
x k x k
HT 12.
2 2
4 cos 3 tan 4 3 cos 2 3 tan 4 0
x x x x
Đ/s:
2
6
x k k
HT 13.
3 3
sin cos cos 2 . tan . tan
4 4
x x x x x
Đ/s:
; 2 ; 2
4 2
x k x k x k
HT 14.
2 2
2 1
cos cos (sin 1)
3 3 2
x x x
Đ/s:
5
2 ; 2 ; 2
6 6
x k x k x k
HT 15.
2 2
2 sin 1 4 cos
2 4 3 6
x x
. Đ/s:
3 ; 6 ( )
2
x k x k k
HT 16.
2 cos sin
1
tan cot2 cot 1
x x
x x x
Đ/s:
2
4
x k k
HT 17.
4 4
sin cos 1
tan cot
sin 2 2
x x
x x
x
Đ/s: Vô nghiệm
HT 18.
2 cos 1 sin cos 1
x x x Đ/s:
2
2 ;
6 3
k
x k x
HT 19.
2 2
2 sin ( ) 2 sin tan
4
x x x
Đ/s:
;
4
x k
HT 20.
1 1
sin 2 sin 2 cot 2
2 sin sin 2
x x x
x x
Đ/s:
4 2
x k
HT 21.
os os inx
3
sin 2 cos 3 2 3 3 3 2 8 3 cos s 3 3 0
x x c x c x x
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 11
ỨI BÊ
Đ/s: ; 2 ,
3
x k x k k
HT 22.
5 3
sin cos 2 cos
2 4 2 4 2
x x x
Đ/s:
2
2 2
3 3 2
x k v x k v x k
HT 23.
2 2 sin cos 1
12
x x
Đ/s:
4 3
x k hay x k k Z
HT 24.
2
2 co 2 3 sin cos 1 3(sin 3 cos )
s x x x x x
Đ/s:
2
3
x k
HT 25.
sin 2 cos 2
tan cot
cos sin
x x
x x
x x
Đ/s:
2
3
x k
HT 26.
(1 tan )(1 sin 2 ) 1 tan
x x x
Đ/s:
;
4
x k x k
HT 27.
2 2
2 sin 1 4 cos
2 4 3 6
x x
Đ/s:
3 ; 6 ( )
2
x k x k k
HT 28.
os
2 sin 6 2 sin 4 3 2 3 sin 2
x x c x x
Đ/s:
;
12 2 18 3
k k
x x
HT 29.
cos 2 cos 4 cos 6 cos .cos 2 . cos 3 2
x x x x x x
Đ/s:
x k
HT 30.
2
2
cot cot
2 cos
4
cot 1
x x
x
x
Đ/s:
4
x k
HT 31.
3 2
cos cos
2 1 sin .
sin cos
x x
x
x x
Đ/s:
2 ; 2
2
x k x m
HT 32.
2 2
4 sin 3 cos 2 3 2 cos
2 4
x
x x
Đ/s:
5 2 7
; 2
18 3 6
k
x x k k
HT 33.
inx+cosx)=5
sin 2 2 2(sx Đ/s:
5
2
4
x k
HT 34.
os os
2 4 2
3
sin 4 . sin 1
2
x x c x c x
Đ/s: Vô nghiệm
HT 35.
1 5 sin 2
tan 2 cos
2 sin cos
2
x
x x
x x
Đ/s:
5 2
; 2 ;
4 12 3
k
x k x k x
HT 36.
9 sin 6 cos 3 sin 2 cos 2 8
x x x x
Đ/s:
2
2
x k
HT 37.
cos cos
2
4 sin . sin .sin 4 3. cos . . 2
3 3 3 3
x x x x x x
Đ/s:
Z
2
,
18 3
x k k
HT 38.
2
9 6
2 cos cos 1
10 5
x x
Đ/s:
5 10
,
3 3
k
x k
HT 39.
2
2 cos (2 ) cot tan 2
4
x x x Đ/s: ,
8 2
l
x l
HT 40.
2 2
4
4
(2 sin 2 )(2 cos cos )
cot 1
2 sin
x x x
x
x
Đ/s:
2
2 ,
3
x l l
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 12
ỨI BÊ
HT 41.
anx
2 2
2 sin 2 sin t
4
x x
Đ/s:
4 2
x k
HT 42.
2 cos 6 2 cos 4 3 cos 2 sin 2 3
x x x x
Đ/s:
2
; ;
2 24 2 42 7
k k
x k x x
HT 43.
2
2 cos 3 . cos 3(1 sin 2 ) 2 3 cos (2 )
4
x x x x Đ/s:
2
x k
và
18 3
x k
.
HT 44.
1 2(cos sin )
tan cot2 cot 1
x x
x x x
Đ/s:
2
4
x k
HT 45.
os
os
4 4
4
sin 2 2
4
tan( ). tan( )
4 4
x c x
c x
x x
Đ/s: ,
2
x k k Z
HT 46.
cotg
2
3 4 2 sin 2
2 3 2( 1)
sin 2
cos
x
x
x
x
Đ/s:
6 2
x k
HT 47.
3 sin 2 . 2 cos 1 2 cos 3 cos 2 3 cos .
x x x x x
Đ/s:
2
2
3
x k
;
2
2
3
x k
và
6
x k
(k
)
HT 48.
6 6
8 sin 3 3 sin 4 3 3 2 9 sin 2 11
x cos x x cos x x
Đ/s:
5 7
; ; ;
12 12 12 4
x k x k x k x k
HT 49. an2x
os
2
1 sin 2
1 t
2
x
c x
Đ/s:
, ;( , )
2
x k x l k l Z
HT 50.
2
cos . cos 1
2 1 sin .
sin cos
x x
x
x x
Đ/s:
2
2
x k
và
2
x m
HT 51. in
2
17
sin(2 ) 16 2 3.s cos 20 sin ( )
2 2 12
x
x x x Đ/s:
2
2
x k
5
2
6
x k
HT 52.
2 3 4 2 3 4
sin sin sin sin cos cos cos cos
x x x x x x x x
Đ/s:
; 2 ; 2
4 2
x k x m x m
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 13
ỨI BÊ
TUYỂN TẬP ĐỀ THI ĐẠI HỌC CÁC NĂM 2002 – 2013
HT 1. (ĐH 2002A) Tìm nghiệm thuộc khoảng (0;
2
) của phương trình:
cos 3 sin 3
5 sin cos 2 3
1 2 sin 2
x x
x x
x
Đ/S:
5
;
3 3
x x .
HT 2. (ĐH 2002B)
2 2 2 2
sin 3 cos 4 sin 5 cos 6
x x x x
Đ/S: ;
9 2
x k x k
.
HT 3. (ĐH 2002D) Tìm x thuộc đoạn [0; 14] nghiệm đúng phương trình:
cos 3 4 cos 2 3 cos 4 0
x x x
Đ/S:
3 5 7
; ; ;
2 2 2 2
x x x x .
HT 4. (ĐH 2003A) Giải phương trình:
2
cos 2 1
cot 1 sin sin 2
1 tan 2
x
x x x
x
.Đ/S:
4
x k
.
HT 5. (ĐH 2003B) Giải phương trình:
2
cot tan 4 sin 2
sin 2
x x x
x
. Đ/S:
3
x k
.
HT 6. (ĐH 2003D) Giải phương trình:
2 2 2
sin tan cos 0
2 4 2
x x
x
.
Đ/S: 2 ;
4
x k x k
.
HT 7. (ĐH 2004B) Giải phương trình:
2
5 sin 2 3(1 sin ) tan
x x x
.
Đ/S:
5
2 ; 2
6 6
x k x k
.
HT 8. (ĐH 2004D) Giải phương trình:
(2 cos 1)(2 sin cos ) sin 2 sin
x x x x x
.
Đ/S: 2 ;
3 4
x k x k
.
HT 9. (ĐH 2005A) Giải phương trình:
2 2
cos 3 . cos 2 cos 0
x x x
. Đ/S:
2
x k
.
HT 10. (ĐH 2005B) Giải phương trình:
1 sin cos sin 2 cos 2 0
x x x x
.
Đ/S:
2
; 2
4 3
x k x k
.
HT 11. (ĐH 2005D) Giải phương trình:
4 4
3
cos sin cos sin 3 0
4 4 2
x x x x . Đ/S:
4
x k
.
HT 12. (ĐH 2006A) Giải phương trình:
6 6
2 cos sin sin . cos
0
2 2 sin
x x x x
x
. Đ/S:
5
2
4
x m
.
HT 13. (ĐH 2006B) Giải phương trình:
cot sin 1 tan . tan 4
2
x
x x x .
Đ/S:
5
;
12 12
x k x k
.
HT 14. (ĐH 2006D) Giải phương trình:
cos 3 cos 2 cos 1 0
x x x
. Đ/S
2
; 2
3
x k x k
.
HT 15. (ĐH 2007A) Giải phương trình:
2 2
1 sin cos 1 cos sin 1 sin 2
x x x x x
Đ/S:
; 2 ; 2
4 2
x k x k x k
.
HT 16. (ĐH 2007B) Giải phương trình:
2
2 sin 2 sin 7 1 sin
x x x
.
Đ/S:
2 5 2
; ;
8 4 18 3 18 3
x k x k x k .
HT 17. (ĐH 2007D) Giải phương trình:
2
sin cos 3 cos 2
2 2
x x
x . Đ/S
2 ; 2
2 6
x k x k
HT 18. (ĐH 2008A) Giải phương trình:
1 1 7
4 sin
sin 4
3
sin
2
x
x
x
.
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 14
ỨI BÊ
Đ/S:
5
; ;
4 8 8
x k x k x k
HT 19. (ĐH 2008B) Giải phương trình:
3 3 2 2
sin 3 cos sin cos 3 sin cos
x x x x x x
.
Đ/S: ;
4 2 3
x k x k
.
HT 20. (ĐH 2008D) Giải phương trình:
2 sin (1 cos 2 ) sin 2 1 2 cos
x x x x
.
Đ/S:
2
2 ;
3 4
x k x k
.
HT 21. (ĐH 2009A) Giải phương trình:
(1 2 sin ) cos
3
(1 2 sin )(1 sin )
x x
x x
. Đ/S:
2
18 3
x k .
HT 22. (ĐH 2009B) Giải phương trình:
3
sin cos .sin 2 3 cos 3 2 cos 4 sin
x x x x x x
.
Đ/S:
2
2 ;
6 42 7
x k x k
.
HT 23. (ĐH 2009D) Giải phương trình:
3 cos 5 2 sin 3 cos 2 sin 0
x x x x
.
Đ/S: ;
18 3 6 2
x k x k
.
HT 24. (ĐH 2010A) Giải phương trình:
(1 sin cos 2 ) sin
1
4
1 tan
2
x x x
x
x
Đ/S:
7
2 ; 2
6 6
x k x k
.
HT 25. (ĐH 2010B) Giải phương trình:
(sin 2 cos 2 ) cos 2 cos 2 sin 0
x x x x x
. Đ/S:
4 2
x k
.
HT 26. (ĐH 2010D) Giải phương trình:
sin 2 cos 2 3 sin cos 1 0
x x x x
.
Đ/S:
5
2 ; 2
6 6
x k x k
.
HT 27. (ĐH 2011A) Giải phương trình:
os
x
2
1 sin 2 2
2 sin sin 2
1 cot
x c x
x
x
Đ/S
; 2 ( )
2 4
x k x k k
HT 28. (ĐH 2011B) Giải phương trình:
x os inx
sin 2 cos sin cos 2 s cos
x x x c x x
Đ/S:
2
2 ; ( )
2 3 3
x k x k k
HT 29. (ĐH 2011D) Giải phương trình:
inx
anx
sin 2 2 cos s 1
0
t 3
x x
Đ/S:
2 ( )
3
x k k
HT 30. (ĐH 2012A+A1)
3 sin 2 cos 2 2 cos 1
x x x
Đ/s:
2
; 2 ; 2
2 3
x k x k x k
HT 31. (ĐH 2012B)
2(cos 3 sin )cos cos 3 sin 1
x x x x x Đ/s:
2 2
2 ;
3 3
x k x k
HT 32. (ĐH 2012D)
sin 3 cos 3 sin cos 2 cos 2
x x x x x
Đ/s:
7
; 2 ; 2
4 2 12 12
k
x x k x k
HT 33. (ĐH 2013A+A1)
1 tan 2 2 sin
4
x x
Đ/s:
; 2 ( )
4 3
x k x k k
HT 34. (ĐH 2013B)
2
sin 5 2 cos 1
x x
Đ/s:
2 2
; ( )
6 3 14 7
x k x k k
HT 35. (ĐH 2013D)
sin 3 cos 2 sin 0
x x x
Đ/s:
7
; 2 ; 2 ( )
4 2 6 6
x k x k x k k
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 15
ỨI BÊ
TUYỂN TẬP ĐỀ THI DỰ BỊ CÁC NĂM
HT 1. (ĐH 2002A–db2) Giải phương trình:
2
tan cos cos sin 1 tan .tan
2
x
x x x x x .
Đ/S:
2
x k
.
HT 2. (ĐH 2002B–db1) Giải phương trình:
2
4
4
2 sin 2 sin 3
tan 1
cos
x x
x
x
.
Đ/S:
2 5 2
;
18 3 18 3
x k x k .
HT 3. (ĐH 2002B–db2) Giải phương trình:
4 4
sin cos 1 1
cot 2
5 sin 2 2 8 sin 2
x x
x
x x
.
Đ/S:
6
x k
.
HT 4. (ĐH 2003A–db1) Giải phương trình:
2
cos 2 cos 2 tan 1 2
x x x
.
Đ/S:
(2 1) , 2
3
x k x k
HT 5. (ĐH 2003A–db2) Giải phương trình:
3 tan tan 2 sin 6 cos 0
x x x x
.
Đ/S:
3
x k
HT 6. (ĐH 2003B–db1) Giải phương trình:
6 2
3 cos 4 8 cos 2 cos 3 0
x x x
.
Đ/S ,
4 2
x k x k
HT 7. (ĐH 2003B–db2) Giải phương trình:
2
2 3 cos 2 sin
2 4
1
2 cos 1
x
x
x
.
Đ/S:
(2 1)
3
x k
HT 8. (ĐH 2003D–db1) Giải phương trình:
2
cos cos 1
2(1 sin )
sin cos
x x
x
x x
.
Đ/S:
, 2
2
x k x k
HT 9. (ĐH 2003D–db2) Giải phương trình:
2 cos 4
cot tan
sin 2
x
x x
x
. Đ/S
3
x k
.
HT 10. (ĐH 2004A–db1) Giải phương trình:
3 3
4 sin cos cos 3 sin
x x x x
.
Đ/S: ;
4 3
x k x k
HT 11. (ĐH 2004B–db1) Giải phương trình:
1 1
2 2 cos
4 sin cos
x
x x
. Đ/S:
4 2
k
x
HT 12. (ĐH 2004B–db2) Giải phương trình:
sin 4 .sin 7 cos 3 . cos 6
x x x x
.
Đ/S: ;
2 20 10
k
x k x
HT 13. (ĐH 2004D–db1) Giải phương trình:
2 sin . cos 2 sin 2 . cos sin 4 . cos
x x x x x x
.
Đ/S: ;
3 4
k
x x k
HT 14. (ĐH 2004D–db2) Giải phương trình:
sin sin 2 3(cos cos 2 )
x x x x
.
Đ/S:
2 2
; 2
9 3
k
x x k
HT 15. (ĐH 2005A–db1) Tìm
(0; )
x
của pt:
2 2
3
4 sin 3 cos 2 1 2 cos
2 4
x
x x .
Đ/S:
5 17 5
; ;
18 18 6
x x x .
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 16
ỨI BÊ
HT 16. (ĐH 2005A–db2) Giải phương trình:
3
2 2 cos 3 cos sin 0
4
x x x .
Đ/S: PT có nghiệm:
2
x k
hoặc
4
x k
.
HT 17. (ĐH 2005B–db1) Giải phương trình :
2 2 3
sin . cos 2 cos tan 1 2 sin 0
x x x x x
.
Đ/S:
5
2 ; 2
6 6
x k x k
.
HT 18. (ĐH 2005B–db2) Giải phương trình :
2
2
cos 2 1
tan 3 tan
2
cos
x
x x
x
Đ/S:
4
x k
.
HT 19. (ĐH 2005D–db1) Giải phương trình:
3 sin
tan 2
2 1 cos
x
x
x
.
Đ/S:
5
2 ; 2
6 6
x k x k
.
HT 20. (ĐH 2005D–db2) Giải phương trình:
sin 2 cos 2 3 sin cos 2 0
x x x x
.
Đ/S:
5
2 ; 2 ; 2 ; 2
6 6 2
x k x k x k x k
.
HT 21. (ĐH 2006A–db1) Giải phương trình:
3 3
2 3 2
cos 3 . cos sin 3 . sin
8
x x x x .
Đ/S:
16 2
x k
.
HT 22. (ĐH 2006A–db2) Giải phương trình:
2 sin 2 4 sin 1 0
6
x x .
Đ/S:
7
; 2
6
x k x k
.
HT 23. (ĐH 2006B–db1) Giải phương trình:
2 2 2
2 sin 1 tan 2 3 2 cos 1 0
x x x
.
Đ/S
6 2
x k
.
HT 24. (ĐH 2006B–db2) Giải phương trình:
cos 2 (1 2 cos )(sin cos ) 0
x x x x
.
Đ/S:
; 2 ; 2
4 2
x k x k x k
.
HT 25. (ĐH 2006D–db1) Giải phương trình:
3 3 2
cos sin 2 sin 1
x x x
.
Đ/S:
; 2 ; 2
4 2
x k x k x k
.
HT 26. (ĐH 2006D–db2) Giải phương trình:
3 2
4 sin 4 sin 3 sin 2 6 cos 0
x x x x
.
Đ/S
2
2 ; 2
2 3
x k x k
.
HT 27. (ĐH 2007A–db1) Giải phương trình:
1 1
sin 2 sin 2 cot2
2 sin sin 2
x x x
x x
.
Đ/S:
4 2
x k
.
HT 28. (ĐH 2007A–db2) Giải phương trình:
2
2 cos 2 3 sin cos 1 3(sin 3 cos )
x x x x x
.
Đ/S:
2
3
x k
.
HT 29. (ĐH 2007B–db1) Giải phương trình:
5 3
sin cos 2 cos
2 4 2 4 2
x x x
Đ/S:
2
; 2 ; 2
3 3 2
x k x k x k .
HT 30. (ĐH 2007B–db2) Giải phương trình:
sin 2 cos 2
tan cot
cos sin
x x
x x
x x
. Đ/S:
2
3
x k
.
GV.Lưu Huy Thưởng 0968.393.899
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 17
ỨI BÊ
HT 31. (ĐH 2007D–db1) Giải phương trình:
2 2 sin cos 1
12
x x
Đ/S:
4 3
x k hay x k
.
HT 32. (ĐH 2007D–db2) Giải phương trình:
(1 – tan )(1 sin 2 ) 1 tan
x x x
.
Đ/S: ;
4
x k x k
.
HT 33. (ĐH 2008A–db1) Tìm
(0; )
x
của phương trình:
2 2
3
4 sin 3 cos 2 1 2 cos
2 4
x
x x .
Đ/S:
5 17 5
; ;
18 18 6
x x x .
HT 34. (ĐH 2008A–db2) Giải phương trình:
3
2 2 cos 3 cos sin 0
4
x x x .
Đ/S:
2
x k
hoặc
4
x k
.
HT 35. (ĐH 2008B–db1) Giải phương trình:
2 2 3
sin cos 2 cos tan 1 2 sin 0
x x x x x
.
Đ/S:
5
2 ; 2
6 6
x k x k
.
HT 36. (ĐH 2008B–db2) Giải phương trình:
2
2
cos 2 1
tan 3 tan
2
cos
x
x x
x
.
Đ/S:
4
x k
.
HT 37. (ĐH 2008D–db1) Giải phương trình:
3 sin
tan 2
2 1 cos
x
x
x
.
Đ/S:
5
2 ; 2
6 6
x k x k
.
HT 38. (ĐH 2008D–db2) Giải phương trình:
sin 2 cos 2 3 sin cos 2 0
x x x x
Đ/S:
5
2 ; 2 ; 2 ; 2
6 6 2
x k x k x k x k
.
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC 2013 - 2014
PHƯƠNG TRÌNH LƯỢNG GIÁC
BIÊN SOẠN: LƯU HUY THƯỞNG
HỌ VÀ TÊN: ………………………………………………………………… LỚP
:………………………………………………………………….
TRƯỜNG :………………………………………………………………… HÀ NỘI, 8/2013
GV.Lưu Huy Thưởng 0968.393.899
CHUYÊN ĐỀ 2: CHUYÊN ĐỀ LƯỢNG GIÁC
KIẾN THỨC CẦN NHỚ
Giá trị lượng giác của góc (cung) lượng giác
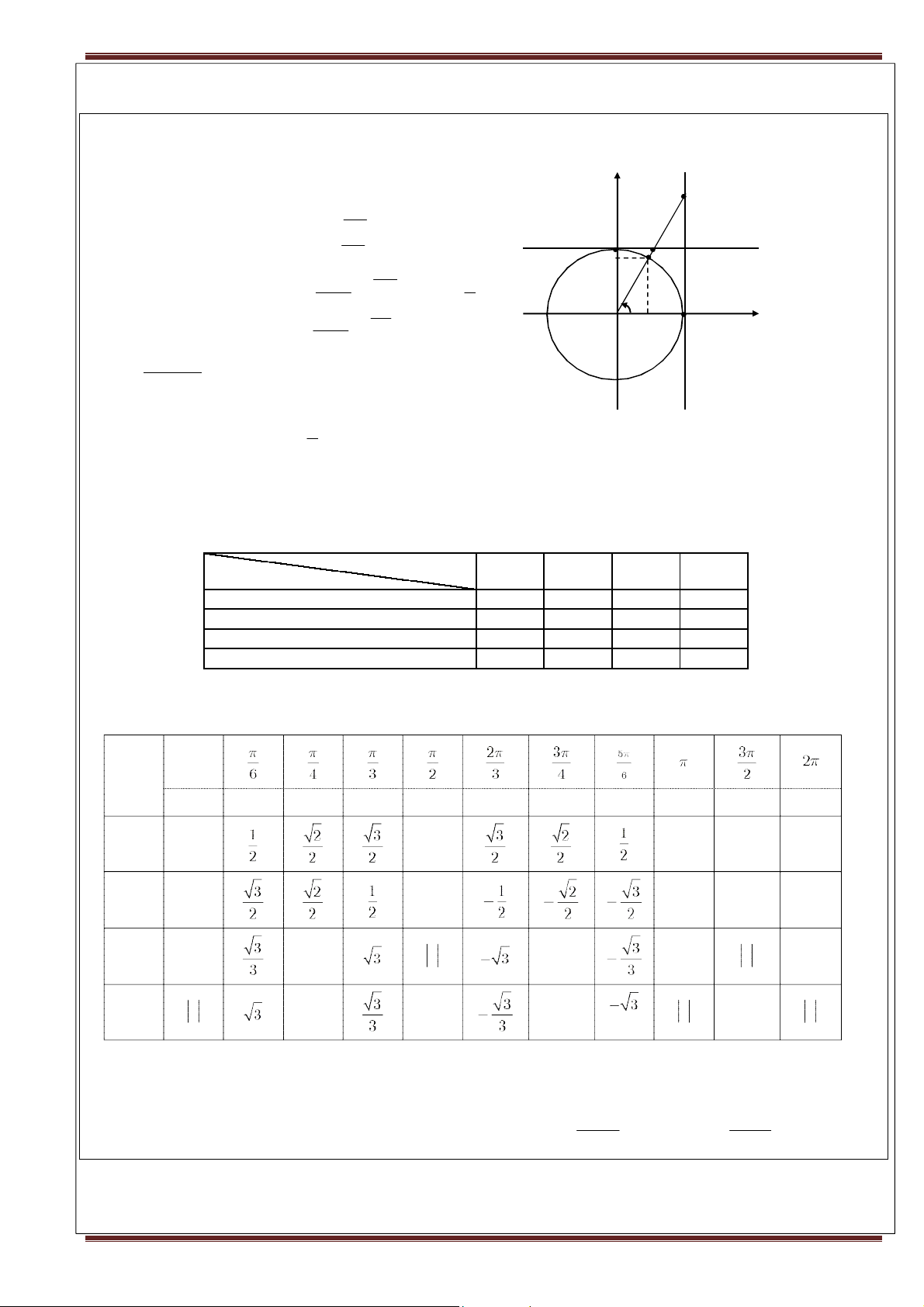
1. Định nghĩa các giá trị lượng giác g T Cho (O ,
A OM)  . Giả sử M(x;y) . tan sin
cos x OH B S cotang
sin y OK K M sin  tan   AT
   k cos  2  cosin cos O H A cot   BS
k sin Nhận xét:   ,
 1  cos  1;  1  sin  1
 tan xác định khi   k ,
 k Z  cot xác định khi k ,  k Z 2
 sin(k2)  sin
 tan(k )  tan
cos(k2)  cos
cot(k)  cot
2. Dấu của các giá trị lượng giác Phần tư I II III IV Giá trị lượng giác cos + – – + sin + + – – tan ỨI BÊ + – + – cot + – + –
3. Giá trị lượng giác của các góc đặc biệt 0 00 300 450 600 900 1200 1350 1500 1800 2700 3600 sin 0 1 0 –1 0 cos 1 0 –1 0 1 tan 0 1 –1 0 0 cot 1 0 –1 0
4. Hệ thức cơ bản: 2 2 1 1
sin  cos  1 ; tan c .
ot 1; 2 2 1  tan  ; 1  cot 2 2 cos sin
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 1
GV.Lưu Huy Thưởng 0968.393.899
5. Giá trị lượng giác của các góc có liên quan đặc biệt Góc đối nhau Góc bù nhau Góc phụ nhau Góc hơn kém Góc hơn kém ỨI BÊ
II. Công thức lượng giác 1. Công thức cộng
2. Công thức nhân đôi sin 2 2 sin . cos Hệ quả: 2 2 2 2
cos 2 cos  sin  2 cos  1  1  2 sin
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 2
GV.Lưu Huy Thưởng 0968.393.899
Công thức hạ bậc
Công thức nhân ba (*)
3. Công thức biến đổi tổng thành tích ỨI BÊ
4. Công thức biến đổi tích thành tổng
III. Phương trình lượng giác cơ bản (Các trường hợp đặc biệt)
1.Phương trình sinx = sin
x k2 a) sin x sin    (k Z) 
x k2 
sin x a. (1  a  1) b)
x  arcsina k2 sin  x a  (k Z)
x  arcsina k2 
c) sin u   sin v  sin u  sin(v) 
d) sin u  cos v  sin u  sin     v  2  
e) sin u   cos v  sin u  sin   v    2 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 3
GV.Lưu Huy Thưởng 0968.393.899
Các trường hợp đặc biệt:
sin x  0  x k  (k Z )
sin x  1  x
k2(k Z) 2
sin x  1  x  
k2(k Z) 2 2 2
sin x   1  sin x  1  cos x  0  cos x  0  x
k (k Z) 2 2.
Phương trình cosx = cos
a) cos x  cos x   k2(k Z ) cos x a. ( 1   a  1)
b) cosx a x   arccosa k2(k Z)
c) cos u   cos v  cos u  cos(v) 
d) cos u  sin v  cos u  cos     v  2  
e) cos u   sin v  cos u  cos     v  2 
Các trường hợp đặc biệt:
cos x  0  x
k  (k Z) 2
cos x  1  x k2(k Z ) ỨI BÊ
cos x   1  x k2(k Z ) 2 2
cos x   1  cos x  1  sin x  0  sin x  0  x k  (k Z ) 3.
Phương trình tanx = tan
a) tan x  tan x k (k Z )
b) tan x a x  arctan a k  (k Z )
c) tan u   tan v  tan u  tan(v) 
d) tan u  cot v  tan u  tan     v  2  
e) tan u   cot v  tan u  tan     v  2 
Các trường hợp đặc biệt:
tan x  0  x k  (k Z )
tan x   1  x  
k (k Z) 4 4.
Phương trình cotx = cot
cot x  cot x k  (k Z )
cot x a x  arccota k (k Z )
Các trường hợp đặc biệt:
cot x  0  x   k (k Z)
cot x   1  x  
k (k Z) 2 4
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 4
GV.Lưu Huy Thưởng 0968.393.899 5.
Một số điều cần chú ý:
a) Khi giải phương trình có chứa các hàm số tang, cotang, có mẫu số hoặc chứa căn bậc chẵn, thì nhất thiết phải
đặt điều kiện để phương trình xác định.
* Phương trình chứa tanx thì điều kiện: x
k (k Z). 2
* Phương trình chứa cotx thì điều kiện: x k (k Z )
* Phương trình chứa cả tanx và cotx thì điều kiện x k (k Z) 2
* Phương trình có mẫu số: 
sin x  0  x k (k Z )
cos x  0  x
k (k Z) 2
tan x  0  x k (k Z) 2
cot x  0  x k (k Z) 2
b) Khi tìm được nghiệm phải kiểm tra điều kiện. Ta thường dùng một trong các cách sau để kiểm tra điều kiện:
1. Kiểm tra trực tiếp bằng cách thay giá trị của x vào biểu thức điều kiện.
2. Dùng đường tròn lượng giác.
3. Giải các phương trình vô định. ỨI BÊ
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 5
GV.Lưu Huy Thưởng 0968.393.899
CÁC DẠNG PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
HT 1: Giải các phương trình sau:   1 1
1. sin x      cos(2x  )    4.  6  2 3 2
2. 2 sin(2x  )   2 5. 2 cos(x  )  1  3 6 3. 3 sin(x  )  1
6. 4 cos(x  )  3 4 3
HT 2: Giải các phương trình sau:   
a) sin 3x   1  sin x 2
b) cosx    cos 2      x        3   6      
c) cos 3x  sin 2x   d) cos 2  x    cos   x    0   3     3  x   
e) sin 3x  sin       0    f ) tan 3  x    tan   x        4 2  4   6       g) cot 2
x    cot    x  
h) tan 2x   1  cot x  0  4     3 
HT 3: Giải các phương trình sau (Đưa về phương trình bậc hai) 1. 2
sin x  3 sin x  2  0 12. 3
4 cos x  3 2 sin 2x  8 cos x 2. 2
3 cos 2x  4 cos 2x  1  0 13. 5 5 2
4 cos x. sin x  4 sin . cos x  sin 4x 3. 2
tan x  5 tan x  6  0 14. 2
tan x  1  3 tan x  3  0 4. 2
cot x  3 cot x  4  0
15. 2 tan x  2 cot x  3 ỨI BÊ 5. 2
4 sin x  2 3   1 sin x  3  0 16. 2 2
tan x  cot x  2 x x   6. 17. 2 8 cot 2 4 cot 2 3 0 2
cos 2x  3 sin 2x  3  0 x x xx   7. 2
cos 3x  5 sin 3x  5  0 18. 2 2 cos 2 2(sin cos ) 3 sin 2 3 0 8. x 2
sin x  7 cos x  7  0 19. cos 2
2x  3 cos x  4 cos 2 9. 2
cos 2x  6 sin x cos x  3  0 4
10. cos 4x  5 sin 2x  2  0 20. 9 13 cos x  = 0 2 11. 1  tan x
3 cos 2x  4 cos x  7  0
HT 4: Giải các phương trình sau (a sin x b cos x c  0)
1. sin x  3 cos x  1  9. 2
2 sin x  3 sin 2x  3 2.
2(sin 2x  cos 2x)  2 
10. sin x  cos x  2 sin 5x 3.
sin 2x  3 cos 2x  1 11.
2(sin 2x  cos 2x)  2 cos(x  ) 2 4.
3 cos 3x  sin 3x  2 6
3 cos x  4 sin x   6 5. 12.
cos 2x  2 3 sin x cos x  2 sin 3x
3 cos x  4 sin x  1 6.
3 cos 4x  2 sin 2x cos 2x  2 cos x  13.  
cos x  3 sin x  2 cos   x    7.  
3 sin 5x  2 cos x  cos 5x  0 3   3 1 8.  
3 sin 2x  sin   2x  1  14. 8 cos x    2  sin x cos x
HT 5: Giải các phương trình sau (a sin x b cos x c  0) (Nâng cao) 1. x x2 sin cos
 3 cos 2x  2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 6
GV.Lưu Huy Thưởng 0968.393.899 2. 4 4
4(sin x  cos x)  3 sin 2x  2 3. 2 2
cos 3x  2 sin 6x  1  sin 3x 4. 3
2 sin 4x  3 cos 2x  16 sin x cos x  5  0
5. 2(cos 2x  3 sin 2x) cos 2x  cos 2x  3 sin 2x  1 6. 3
sin x  cos x sin 2x  3 cos 3x  2(cos 4x  sin ) 7. 2
1  2(cos 2x tan x  sin 2x) cos x  cos 2x 8. 3 3
4 sin x cos 3x  4 cos x sin 3x  3 3 cos 4x  3
HT 6: Giải các phương trình sau (Đẳng cấp bậc hai 2 2
a sin x b sin x cos x c cos x d  0 ) 1. 2 2
3 sin x  4 sin x cos x  cos x  0 2. 2 2
2 sin x  3 cos  5 sin x cos x  2  0 3. 2
sin 4x  2 sin 2x  2 cos 4x  0 4. 2 2
sin 2x  2 sin 2x cos 2x  3 cos 2x 3 5.
2 cos x  4 sin x  cos x 6. 3 3
2 cos x  3 sin x  4 sin x 7.
sin x cos 2x  6 cos x(1  2 cos 2x) 2 2 ỨI BÊ 8.
2 sin x  1  3 sin x.cos x  1  3 cos x  1 9. 2 x x x     2 3 sin 8 sin . cos 8 3 9 cos x  0 10. 2 2
4 sin x  3 3 sin x. cos x  2 cos x  4 11. 4 2 2 4
3 cos x  4 sin x cos x  sin x  0 12.    2 x x x     2 3 1 sin 2 3 sin . cos 3 1 cos x  0 13. 3 3 2
4 sin x  3 cos x  3 sin x  sin x cos x  0 14. 3 3 2 2
sin x  3 cos x  sin x cos x  3 sin x cos x 3 1
15. 2 sin x  2 3 cos x   cos x sin x16. 2 2 1
3 sin x. cos x  sin x 2
HT 7: Giải các phương trình sau (Đối xứng a(sin x  cos x)  b sin x cos x c  0 )
1. 3(sin x  cos x)  2 sin x cos x  3  0
2. sin 2x  cos 2x  7 sin 4x  1
3. 2 sin x  sin 2x  2 cos x  2  0
4. 3 cos 2x  sin 4x  6 sin x cos x  3 5. 3 3 3
1  sin x  cos x  sin 2x 2 6. 3 3 1
sin 2x  cos 2x  sin 4x  1 2
7. 2 sin 2x  3 3 sin x  cos x  8  0
8. 2sin x  cos x   3 sin 2x  2
9. 3sin x  cos x  2 sin 2x  3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 7
GV.Lưu Huy Thưởng 0968.393.899
10. 1  21  sin x  cos x   sin 2x  11.  
sin 2x  2 sin x    1  4  12. 3 x cos3 sin
x  1   2  2sin x cos x
HT 8: Giải các phương trình sau (Tổng hiệu thành tích)
1. sin x  sin 2x  sin 3x  0
2. cos x  cos 2x  cos 3x  0
3. cos x  cos 2x  cos 3x  1  0 4. 2
sin 4x  sin 2x  2 cos x  0 5. 2
sin x  sin 5x  1  2 cos x  0 6. 2
2 sin 2x  sin 6x  1  sin 2x 7. 2
sin 2x  sin 6x  2 sin x  1  0
8. sin x  sin 2x  sin 3x  1  cos x  cos 2x
9. cos 3x  sin 3x  cos x  sin x  2 cos 2x
10. sin x  sin 2x  sin 3x  cos x  cos 2x  cos 3x
HT 9: Giải các phương trình sau (Tích về tổng hiệu)
1. cos 3x. cos x  cos 2x
2. sin x. sin 5x  sin 2x. sin 3x
3. cos x cos 3x  sin 2x. sin 6x  sin 4x. sin 6x  0
4. 3 cos 6x  2 sin 4x. cos 2x  sin 2x  0 ỨI BÊ 5x 3x 5. 4 cos cos
 2(8 sin x  1) cos x  5 2 2
HT 10: Giải các phương trình sau (Hạ bậc) 1. 2 2 2 3
sin x  sin 2x  sin 3x  2
2. cos2x cos2 x cos2 2 3x  1     3. 2 2 17
sin 2x  sin 8x  sin   10x   2   x x   x  4. 2 2 1  sin
sin x  cos sin x  2 cos    2 2 4 2
HT 11: Giải các phương trình sau (Dạng khác) 1. 6 6 1
sin x cos x  4 2. 3 x cos3 sin
x cos2x
3. sin 2x  1  2 cos x cos2x 4. 2
(2 sin x  1)(2 cos 2x  2 sin x  1)  3  4 cos x 5. 2
(sin x  sin 2x)(sin x  sin 2x)  sin 3x
6. sin x  sin 2x  sin 3x  2(cos x cos2x cos3x) 7. 2
(1  2 sin x) cos x  1  sin x  cos x 8. 2
sin x(2  cos x)  (1  cos x) (1  cos x)
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 8
GV.Lưu Huy Thưởng 0968.393.899
9. cos 2x  (1  2 cos x)(sin x  cos x)  0
10. cos 2x  5  2(2  cos x)(sin x  cos x)
11. 4 sin 2x  3 cos 2x  3(4 sin x  1) 12. cos x
x cos x cos 2 5 . cos 4 .
2x  3 cos x  1 13. x cos2 2 sin 7
2x  sin 2x  sin x    14. 3 3 1
sin x cos x
sin 2x. sin x    cos x  sin 3  x   4  2 
15. 1  sin 2x  2 cos 3x(sin x  cos x)  2 sin x  2 cos 3x cos2x)
16. cos x  sin(2x  )  sin(2x  )  1  3(1  2 cos x) 6 6
HT 12: Giải các phương trình sau: ỨI BÊ
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 9
GV.Lưu Huy Thưởng 0968.393.899 ÔN TẬP
Giải các phương trình sau: k 2 HT 1.
2 sin 5x  3 cos 3x  sin 3x  0 Đ/s: x    ;x   k  24 4 3 HT 2. 2 2
cos x  3 sin 2x  1  sin x
Đ/s: x k ;
 x    k 3 HT 3. 4 2 2 4
3 cos x  4 sin x. cos x  sin x  0 Đ/s: x    k ;
 x    k 4 3     HT 4.
sin 2x  2 sin x    1  x   k  x
k  x k  Đ/s: 2 ; 2 ; 2  4  4 2 k2 k2 HT 5.
4sin3x  1  3 sin x  3 cos 3x Đ/s: x   ;x   18 3 2 3 HT 6. 3 3 2
4 sin x  3 cos x  3 sin x  sin x cos x  0 Đ/s: x   k ;
 x    k  4 3 3 4 HT 7. 3
2 sin 4x  3 cos 2x  16 sin x cos x  5  0 Đ/s: x   k ; (k  )
 ; cos  ; sin  2 5 5 HT 8. 3
sin x  4 sin x  cos x  0 Đ/s: x   k  4 HT 9. 2 2
tan x sin x  2 sin x  3(cos 2x  sin x cos x) Đ/s: x    k ;
 x    k 4 3
HT 10. cos 2x  5  2(2  cos x)(sin x  cos x) Đ/s: x   k2 ;
 x k2 2 ỨI BÊ 1
HT 11. 2 cos 2x  8 cos x  7 
Đ/s: x k2 ;
 x    k2 cos x 3 HT 12. 2 2
4 cos x  3 tan x  4 3 cos x  2 3 tan x  4  0 Đ/s: x  
k2k   6     3 3    
HT 13. sin x  cos x  cos 2x. tan x  . tan   x   x
k x    k  x k  Đ/s: ; 2 ; 2  4     4  4 2     2   2 2   1 5
HT 14. cos x    cos   x    (sin x  1) x k2 ;  x   k2 ;  x   k2 Đ/s:  3     3  2 6 6     2 x   2 x   HT 15. 2 sin     1  4 cos     
x k  x   k  k    . Đ/s: 3 ; 6 ( ) 2 4    3 6  2 2 cos x  sin 1 x HT 16. Đ/s: x  
k2k   tan x  cot2x cot x 1 4 4 4 sin x  cos x 1 HT 17.
tan x  cotx
Đ/s: Vô nghiệm sin 2x 2 k2
HT 18. 2 cos x  
1 sin x  cos x  1
Đ/s: x k2 ;  x   6 3 2 2
HT 19. 2 sin (x
)  2 sin x  tan x Đ/s: x   k ; 4 4 1 1
HT 20. sin 2x  sin x    2 cot 2x Đ/s: x   k 2 sin x sin 2x 4 2 3
HT 21. sin 2x cos x  
3  2 3cos x  3 3cos2x  8  3 cos x  s inx 3 3  0
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 10
GV.Lưu Huy Thưởng 0968.393.899 Đ/s: x   k ;  x k2 ,  k   3 5x  x      3x 2 HT 22. sin     cos       2 cos x   k v x
k2 v x k2Đ/s:  2 4    2 4  2 3 3 2    
HT 23. 2 2 sin x   cos x  1   x   k hay x   k k ZĐ/s:    12 4 3 2 HT 24. 2
2 co s x  2 3 sin x cos x  1  3(sin x  3 cos x) Đ/s: x   k 3 sin 2x cos 2x HT 25.
 tan x  cot x
Đ/s:x    k2 cos x sin x 3
HT 26. (1  tan x)(1  sin 2x)  1  tan x x k ;
 x    k Đ/s: 4     2 x   2 x   HT 27. 2 sin     1  4 cos     
x k3 ;  x   k6 (k  )   2 4    3 6  2 Đ/s: k k
HT 28. 2 sin 6x  2 sin 4x
3cos2x  3  sin 2x Đ/s: x    ;x   12 2 18 3
HT 29. cos 2x  cos 4x  cos 6x  cos x. cos 2x. cos 3x  2 Đ/s: x k 2 cot x cot  x     HT 30.  2 cosx   x   k 2  x   4  cot 1  4 Đ/s: 3 2 cos x  cos x HT 31.
 21  sin x. ỨI BÊ
Đ/ s: x    k2 ;
 x m2 sin x  cos x 2   2 x 2   5 k2 7 HT 32. 4 sin
 3 cos 2x  3  2 cos   xĐ/s: x   ;x  
k2k  2 4  18 3 6 5
HT 33. sin 2x  2 2(s inx+cosx)=5 Đ/s: x   k2 4 2 3 4 2
HT 34. sin 4x. sin
x cos x 1  cos x Đ/s: Vô nghiệm 2 1  5   sin 2x 5 k2 HT 35.
tan x  2 cos x      x k ;
 x    k2 ;  x    Đ/s:  2  sin x  cos 2 x 4 12 3
HT 36. 9 sin x  6 cos x  3 sin 2x  cos 2x  8 Đ/s: x   k2 2        2         2
HT 37. 4 sin x. sin   x. sin  
  x 4 3. cos x c . os x x x   k , k         c . os Đ/s: Z           2 3  3   3     3  18 3 2 9x 6x 5 k10 HT 38. 2 cos  cos 1 Đ/s: x   ,k   10 5 3 3 2 l
HT 39. 2 cos (2x
)  cot x  tan x  2 Đ/s: x   , l   4 8 2 2 2 4
(2  sin 2x)(2 cos x  cos x) 2
HT 40. cot x  1  Đ/s: x    l2 ,  l   4 2 sin x 3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 11
GV.Lưu Huy Thưởng 0968.393.899   2   2
HT 41. 2 sin x
  2 sin x  t anx  x   kĐ/s:  4  4 2 k k2
HT 42. 2 cos 6x  2 cos 4x  3 cos 2x  sin 2x  3 Đ/s: x   k ;  x    ; x   2 24 2 42 7 2
HT 43. 2 cos 3x. cos x  3(1  sin 2x)  2 3 cos (2x  ) Đ/s: x
k  và x    k . 4 2 18 3 1
2(cos x  sin x) HT 44. Đ/s: x    k2 tan x  cot 2x cot x 1 4 4
sin 2x cos42x 4 HT 45. cos 4x
Đ/s: x k ,k Z 2
tan(  x). tan(  x) 4 4 3 4  2 sin 2x HT 46.   2 3  2 c ( otg x  1) Đ/s: x   k 2 sin 2 cos x x 6 2 HT 47.
3 sin 2x.2 cos x  
1  2  cos 3x  cos 2x  3 cos x. 2 2 Đ/s: x
k2; x  
k2 và x    k (k  ) 3 3 6 6 6
HT 48. 8 sin x cos x  3 3 sin 4x  3 3cos2x  9 sin 2x  11 5 7 Đ/s: x   k ;  x   k ;  x   k ;  x   k 12 12 12 4 ỨI BÊ 1  sin 2x HT 49. 1  t an2x 
Đ/s: x k ,x l ;
(k,l Z) cos22x 2 2
cos x.cos x   1 HT 50.
 21  sin x. Đ/s: x  
k2 và x m2 sin x  cos x 2 17 x 5
HT 51. sin(2x  )  16  2 3. s in 2
x cos x  20 sin (  ) Đ/s: x
k2 x    k2 2 2 12 2 6 HT 52. 2 3 4 2 3 4
sin x  sin x  sin x  sin x  cos x  cos x  cos x  cos x Đ/s: x   k ;
 x m2 ;
 x    m2 4 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 12
GV.Lưu Huy Thưởng 0968.393.899
TUYỂN TẬP ĐỀ THI ĐẠI HỌC CÁC NĂM 2002 – 2013
HT 1. (ĐH 2002A) Tìm nghiệm thuộc khoảng (0; 2) của phương trình:  cos 3x sin 3    x 5 5 s  in x    cos 2x  3  x  ;x   Đ/S: .  1  2 sin 2  x  3 3
HT 2. (ĐH 2002B) 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x Đ/S: x k ;x k . 9 2
HT 3. (ĐH 2002D) Tìm x thuộc đoạn [0; 14] nghiệm đúng phương trình:
cos 3x  4 cos 2x  3 cos x  4  0 3 5 7 Đ/S: x  ;x  ; x  ; x . 2 2 2 2 cos 2x 1
HT 4. (ĐH 2003A) Giải phương trình: 2 cot x  1 
 sin x  sin 2x .Đ/S: x   k  . 1  tan x 2 4 2
HT 5. (ĐH 2003B) Giải phương trình: cot x  tan x  4 sin 2x
. Đ/S: x    k . sin 2x 3 x    x
HT 6. (ĐH 2003D) Giải phương trình: 2 2 2
sin    tan x  cos  0  . 2 4  2
Đ/S: x k2 ;
 x    k . 4
HT 7. (ĐH 2004B) Giải phương trình: 2
5 sin x  2  3(1  sin x) tan x . 5 Đ/S: x   k2 ;  x   k2 . 6 6
HT 8. (ĐH 2004D) Giải phương trình: (2 cos x  1)(2 sin x  cos x)  sin 2x  sin x . Đ/S: x    k2 ;
 x    k . 3 4
HT 9. (ĐH 2005A) Giải phương trình: 2 2
cos 3x. cos 2x Ứ  c I oBÊ s x  0 . Đ/S: x k . 2
HT 10. (ĐH 2005B) Giải phương trình: 1  sin x  cos x  sin 2x  cos 2x  0 . 2 Đ/S: x    k ;  x    k2 . 4 3        
HT 11. (ĐH 2005D) Giải phương trình: 4 4 3
cos x  sin x  cosx   sin   3x    0 x   k   . Đ/S: . 4   4  2 4  6 6
2 cos x  sin x   sin x. cos x 5
HT 12. (ĐH 2006A) Giải phương trình:
 0 . Đ/S: x   2m . 2  2 sin x 4    x
HT 13. (ĐH 2006B) Giải phương trình: cot x  sin x 1
  tan x. tan   4  . 2 5 Đ/S: x   k ;  x   k . 12 12 2
HT 14. (ĐH 2006D) Giải phương trình: cos 3x  cos 2x  cos x  1  0 . Đ/S x k ;  x    k2 . 3 2 2
HT 15. (ĐH 2007A) Giải phương trình: 1  sin x  cos x  1  cos x  sin x  1  sin 2x Đ/S: x    k ;  x   k2 ;
 x k2 . 4 2
HT 16. (ĐH 2007B) Giải phương trình: 2
2 sin 2x  sin 7x  1  sin x . 2 5 2 Đ/S: x   k ;x   k ;x   k . 8 4 18 3 18 3 2    x x
HT 17. (ĐH 2007D) Giải phương trình: sin
 cos   3 cos x  2  x
k  x    k   . Đ/S 2 ; 2 2 2 2 6 1 1 7   
HT 18. (ĐH 2008A) Giải phương trình:   4 sin   x . sin x     3  4  sin   x    2 
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 13
GV.Lưu Huy Thưởng 0968.393.899 5 Đ/S: x    k ;
 x    k ;  x   k  4 8 8
HT 19. (ĐH 2008B) Giải phương trình: 3 3 2 2
sin x  3 cos x  sin x cos x  3 sin x cos x . Đ/S: x
k ; x    k . 4 2 3
HT 20. (ĐH 2008D) Giải phương trình: 2 sin x(1  cos 2x)  sin 2x  1  2 cos x . 2 Đ/S: x    k2 ;  x   k . 3 4
(1  2 sin x) cos x 2
HT 21. (ĐH 2009A) Giải phương trình:  3 . Đ/S: x    k .
(1  2 sin x)(1  sin x) 18 3 3
HT 22. (ĐH 2009B) Giải phương trình: sin x  cos x. sin 2x  3 cos 3x  2 cos 4x  sin x  . 2 Đ/S: x    k2 ;  x   k . 6 42 7
HT 23. (ĐH 2009D) Giải phương trình: 3 cos 5x  2 sin 3x cos 2x  sin x  0 . Đ/S: x
k ;x    k . 18 3 6 2 
(1  sin x  cos 2x) sin   x    4  1
HT 24. (ĐH 2010A) Giải phương trình:  cos x 1  tan x 2 7 Đ/S: x    k2 ;  x   k2 . 6 6
HT 25. (ĐH 2010B) Giải phương trình: (sin 2x  cos 2x) cos x  2 cos 2x  sin x  0 . Đ/S: x   k . 4 2
HT 26. (ĐH 2010D) Giải phương trình: sin 2x  cos 2x  3 sin x  cos x  1  0 . 5 Đ/S: x   k2 ;  x   k2 . ỨI BÊ 6 6
1  sin 2x cos2x
HT 27. (ĐH 2011A) Giải phương trình:  2 sin x sin 2x 2 1  cot x Đ/S x   k ;  x
k2(k ) 2 4
HT 28. (ĐH 2011B) Giải phương trình: sin 2x cos x  sin x cos x cos2x  s inx  cos x 2 Đ/S: x   k2 ;  x   k
(k ) 2 3 3
sin 2x  2 cos x  s inx 1
HT 29. (ĐH 2011D) Giải phương trình:
 0 Đ/S: x
k2(k  ) t anx  3 3 2
HT 30. (ĐH 2012A+A1) 3 sin 2x  cos 2x  2 cos x  1 Đ/s: x   k ;  x k2 ;  x   k2 2 3 2 2
HT 31. (ĐH 2012B) 2(cos x  3 sin x) cos x  cos x  3 sin x  1 Đ/s: x   k2 ;  x k 3 3
HT 32. (ĐH 2012D) sin 3x  cos 3x  sin x  cos x  2 cos 2x k  7 Đ/s: x   ;x   k2 ;  x    k2 4 2 12 12    
HT 33. (ĐH 2013A+A1) 1  tan x  2 2 sin x    
Đ/s: x    k ;
 x    k2(k  )   4  4 3 2 2
HT 34. (ĐH 2013B) 2
sin 5x  2 cos x  1 Đ/s: x    k ;x    k (k  ) 6 3 14 7
HT 35. (ĐH 2013D) sin 3x  cos 2x  sin x  0 7 Đ/s: x   k ;x    k2 ;  x
k2(k  )  4 2 6 6
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 14
GV.Lưu Huy Thưởng 0968.393.899
TUYỂN TẬP ĐỀ THI DỰ BỊ CÁC NĂM    x
HT 1. (ĐH 2002A–db2) Giải phương trình: 2
tan x  cos x  cos x  sin x 1   tan x. tan   . 2
Đ/S: x k2 .  2 2  sin 2x  4 sin 3x
HT 2. (ĐH 2002B–db1) Giải phương trình: tan x  1  . 4 cos x 2 5 2 Đ/S: x   k ; x   k . 18 3 18 3 4 4 sin x  cos x 1 1
HT 3. (ĐH 2002B–db2) Giải phương trình:  cot 2x  . 5 sin 2x 2 8 sin 2x Đ/S: x    k . 6 2
HT 4. (ĐH 2003A–db1) Giải phương trình: cos 2x  cos x 2 tan x   1  2 .
Đ/S: x  (2k  1) ,
 x    k2 3
HT 5. (ĐH 2003A–db2) Giải phương trình: 3  tan x tan x  2 sin x  6 cos x  0 . Đ/S: x    k 3
HT 6. (ĐH 2003B–db1) Giải phương trình: 6 2
3 cos 4x  8 cos x  2 cos x  3  0 . Đ/S x
k , x k  4 2  x     2 2 3 cos x  2 sin      2 4
HT 7. (ĐH 2003B–db2) Giải phương trình:  1 . 2 cos x  1 ỨI BÊ Đ/S: x
 (2k  1) 3 2
cos x cos x   1
HT 8. (ĐH 2003D–db1) Giải phương trình:  2(1  sin x). sin x  cos x Đ/S: x    k ,
 x k2 2 2 cos 4x
HT 9. (ĐH 2003D–db2) Giải phương trình: cot x  tan x  . Đ/S x    k . sin 2x 3 3 3
HT 10. (ĐH 2004A–db1) Giải phương trình: 4 sin x  cos x   cos x  3 sin x . Đ/S: x   k ;
 x    k  4 3     1 1 k 
HT 11. (ĐH 2004B–db1) Giải phương trình: 2 2 cos x      x    . Đ/S: 4  sin x cos x 4 2
HT 12. (ĐH 2004B–db2) Giải phương trình: sin 4x. sin 7x  cos 3x. cos 6x . k  Đ/S: x   k ;  x    2 20 10
HT 13. (ĐH 2004D–db1) Giải phương trình: 2 sin x. cos 2x  sin 2x. cos x  sin 4x. cos x . k Đ/S: x  ;x   k  3 4
HT 14. (ĐH 2004D–db2) Giải phương trình: sin x  sin 2x
3(cos x  cos 2x) . 2 k2 Đ/S: x   ;x   k2 9 3  x   
HT 15. (ĐH 2005A–db1) Tìm x  (0; ) của pt: 2 2 3 4 sin
 3 cos 2x  1  2 cos x   . 2  4  5 17 5 Đ/S: x  ; x  ; x . 18 18 6
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 15
GV.Lưu Huy Thưởng 0968.393.899  
HT 16. (ĐH 2005A–db2) Giải phương trình: 3
2 2 cos x    3 cos x  sin x  0  . 4 
Đ/S: PT có nghiệm: x   k hoặc x   k . 2 4 2 2 3
HT 17. (ĐH 2005B–db1) Giải phương trình : sin x. cos 2x  cos x tan x   1  2 sin x  0 . 5 Đ/S: x   k2 ;  x   k2 . 6 6     cos 2x 1
HT 18. (ĐH 2005B–db2) Giải phương trình : 2
tan   x  3 tan x      2 2 cos x Đ/S: x    k . 4 3    sin x
HT 19. (ĐH 2005D–db1) Giải phương trình: tan   x   2  . 2  1  cosx 5 Đ/S: x   k2 ;  x   k2 . 6 6
HT 20. (ĐH 2005D–db2) Giải phương trình: sin 2x  cos 2x  3 sin x  cos x  2  0 . 5 Đ/S: x   k2 ;  x   k2 ;  x   k2 ;
 x k2 . 6 6 2 
HT 21. (ĐH 2006A–db1) Giải phương trình: 3 3 2 3 2
cos 3x. cos x  sin 3x. sin x  . 8 Đ/S: x    k . 16 2    
HT 22. (ĐH 2006A–db2) Giải phương trình: 2 sin 2
x    4 sin x  1  0  . 6  7
Đ/S: x k ;  x   k2 . ỨI BÊ 6 2 2 2
HT 23. (ĐH 2006B–db1) Giải phương trình: 2 sin x  
1 tan 2x  3 2 cos x   1  0 . Đ/S x    k . 6 2
HT 24. (ĐH 2006B–db2) Giải phương trình: cos 2x  (1  2 cos x)(sin x  cos x)  0 . Đ/S: x   k ;  x   k2 ;
 x k2 . 4 2
HT 25. (ĐH 2006D–db1) Giải phương trình: 3 3 2
cos x  sin x  2 sin x  1 . Đ/S: x    k ;  x k2 ;
 x    k2 . 4 2
HT 26. (ĐH 2006D–db2) Giải phương trình: 3 2
4 sin x  4 sin x  3 sin 2x  6 cos x  0 . 2 Đ/S x    k2 ;  x    k2 . 2 3 1 1
HT 27. (ĐH 2007A–db1) Giải phương trình: sin 2x  sin x    2 cot2x . 2 sin x sin 2x Đ/S: x   k . 4 2
HT 28. (ĐH 2007A–db2) Giải phương trình: 2
2 cos x  2 3 sin x cos x  1  3(sin x  3 cos x) . 2 Đ/S: x   k . 3 5x  x      3x
HT 29. (ĐH 2007B–db1) Giải phương trình: sin 
   cos    2 cos   2 4    2 4  2 2 Đ/S: x   k ; x   k2 ;
 x k2. 3 3 2 sin 2x cos 2x
HT 30. (ĐH 2007B–db2) Giải phương trình: 
 tan x  cotx . Đ/S: x  
k2. cos x sin x 3
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 16
GV.Lưu Huy Thưởng 0968.393.899  
HT 31. (ĐH 2007D–db1) Giải phương trình: 2 2 sin x   cos x  1   12 Đ/S: x   k hay x   k . 4 3
HT 32. (ĐH 2007D–db2) Giải phương trình: (1 – tan x)(1  sin 2x)  1  tan x . Đ/S: x    k ;
 x k . 4  x   
HT 33. (ĐH 2008A–db1) Tìm x  (0; ) của phương trình: 2 2 3 4 sin
 3 cos 2x  1  2 cos x   . 2  4  5 17 5 Đ/S: x  ; x  ; x  . 18 18 6    
HT 34. (ĐH 2008A–db2) Giải phương trình: 3
2 2 cos x    3 cos x  sin x  0  . 4  Đ/S: x   k hoặc x   k . 2 4 2 2 3
HT 35. (ĐH 2008B–db1) Giải phương trình: sin x cos 2x  cos x tan x   1  2 sin x  0 . 5 Đ/S: x   k2 ;  x   k2. 6 6     cos 2x 1
HT 36. (ĐH 2008B–db2) Giải phương trình: 2
tan   x  3 tan x      . 2 2 cos x Đ/S: x    k . 4 3    sin x
HT 37. (ĐH 2008D–db1) Giải phương trình: tan   x   2  . 2  1  cosx 5 Đ/S: x   k2 ;  x
k2. ỨI BÊ 6 6
HT 38. (ĐH 2008D–db2) Giải phương trình: sin 2x  cos 2x  3 sin x  cos x  2  0 5 Đ/S: x   k2 ;  x   k2 ;  x   k2 ;
 x k2 . 6 6 2
BỂ HỌC VÔ BỜ - CHUYÊN CẦN SẼ TỚI BẾN Page 17