







Preview text:
Chuyên đề bồi dưỡng học sinh giỏi toán 8
CHUYÊN ĐỀ: TAM GIÁC ĐỒNG DẠNG, TA-LÉT VÀ LIÊN QUAN MỤC LỤC
Chủ đề 1: ĐỊNH LÝ TALET TRONG TAM GIÁC ....................................................................................... 2
Chủ đề 2. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC ............................................................ 16
Chủ đề 3. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC ............................................................. 26
Chủ đề 4. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VUÔNG ............................................. 42
Chủ đề 5. ĐỊNH LÝ MENELAUS, ĐỊNH LÝ CE-VA, ĐỊNH LÝ VAN-OBEN ........................................ 53
A. Kiến thức cần nhớ ................................................................................................................................. 53
B. Bài tập vận dụng ................................................................................................................................... 57
PHẦN II. TỔNG HỢP VÀ MỞ RỘNG ....................................................................................................... 70 I.
Kiến thức mở rộng ............................................................................................................................. 70
II. Một số ví dụ ....................................................................................................................................... 70
BÀI TẬP TỔNG HỢP .................................................................................................................................. 75
Biên soạn: Trần Đình Hoàng 0814000158 1
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Chủ đề 1: ĐỊNH LÝ TALET TRONG TAM GIÁC
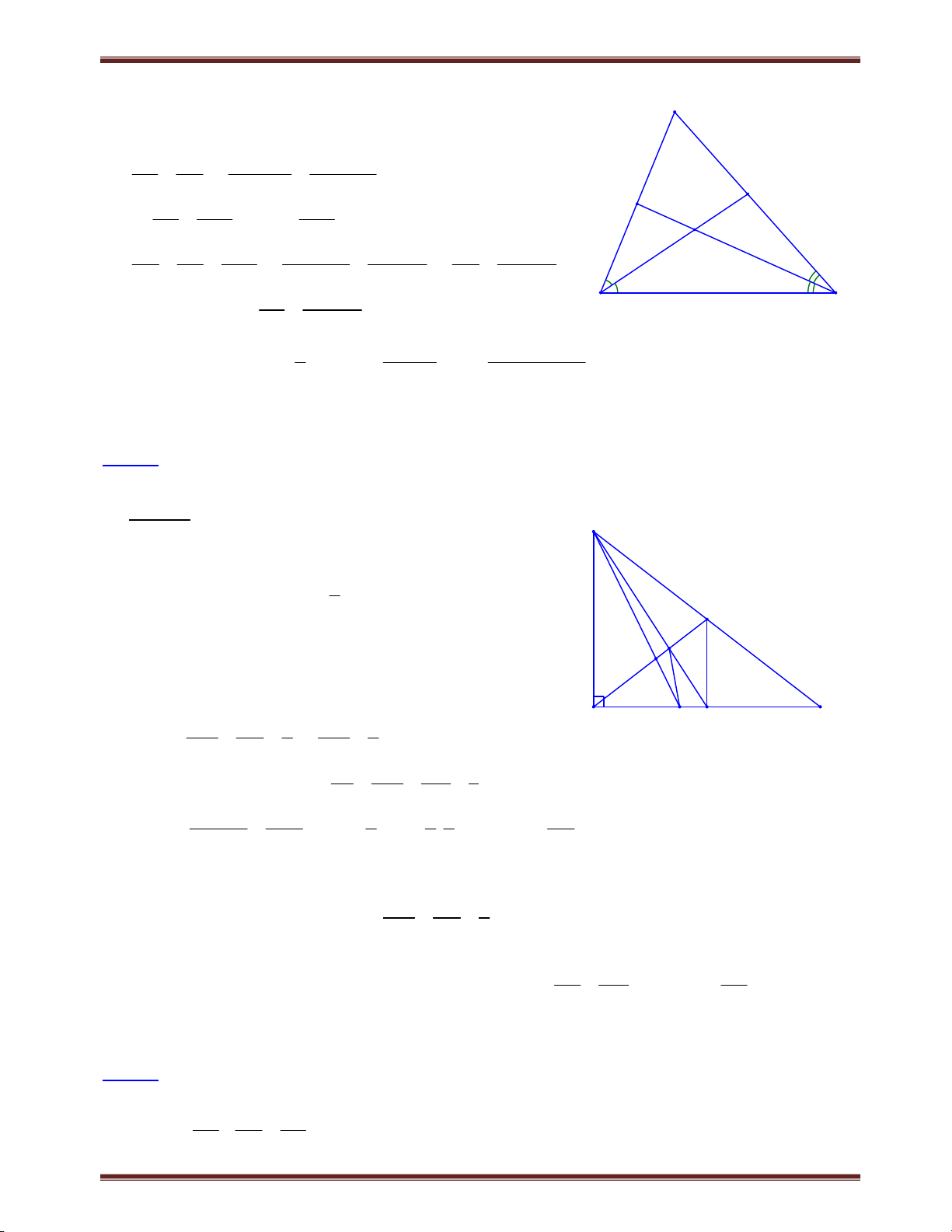
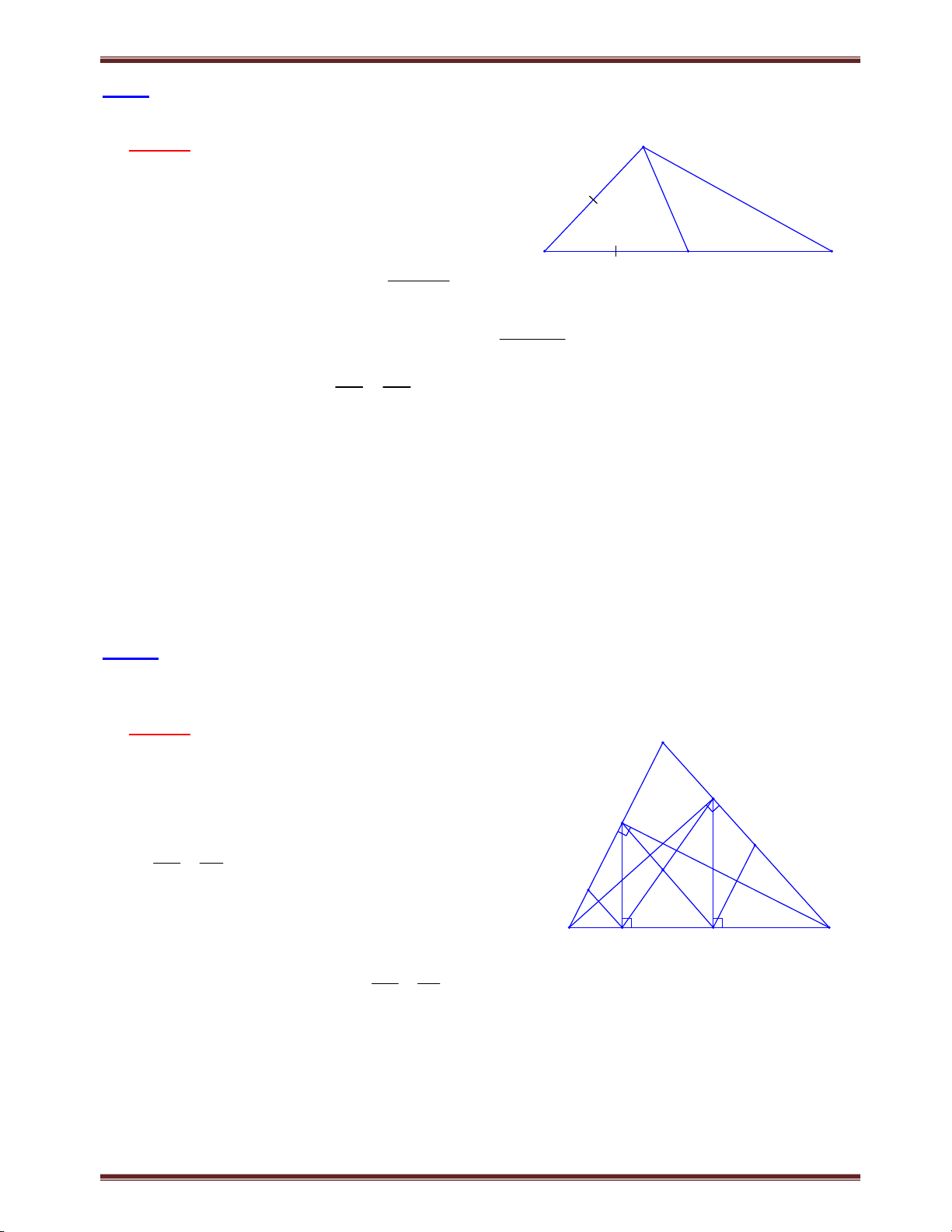
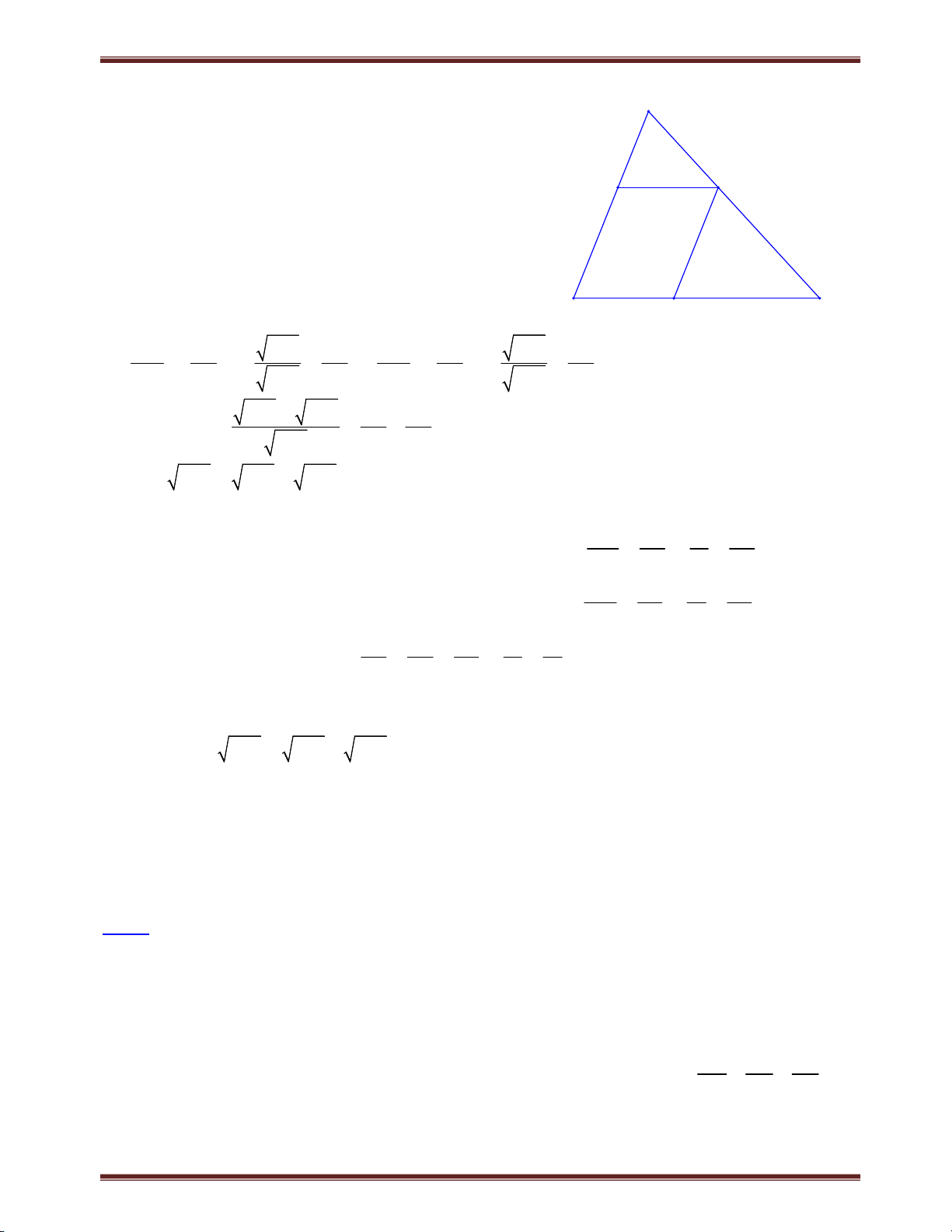
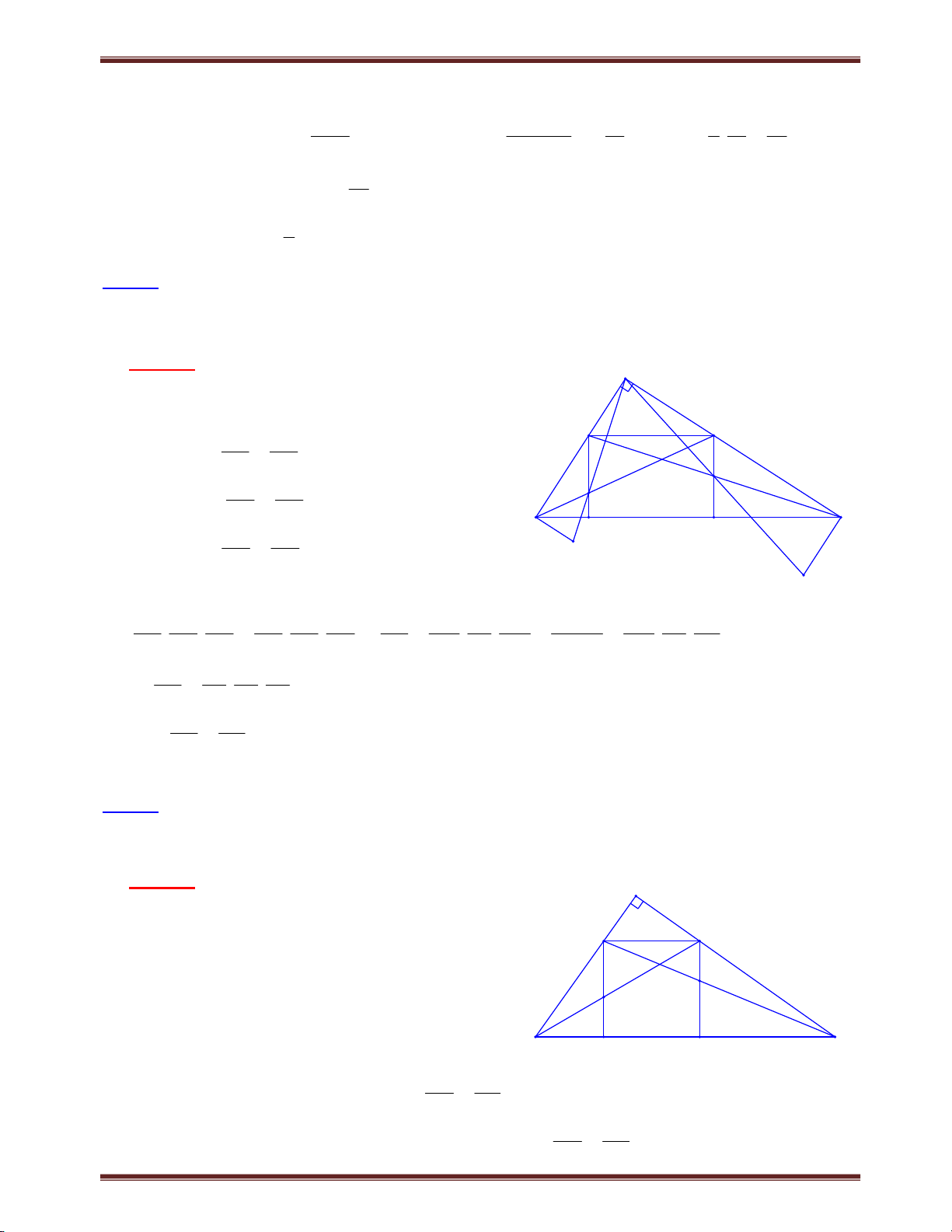
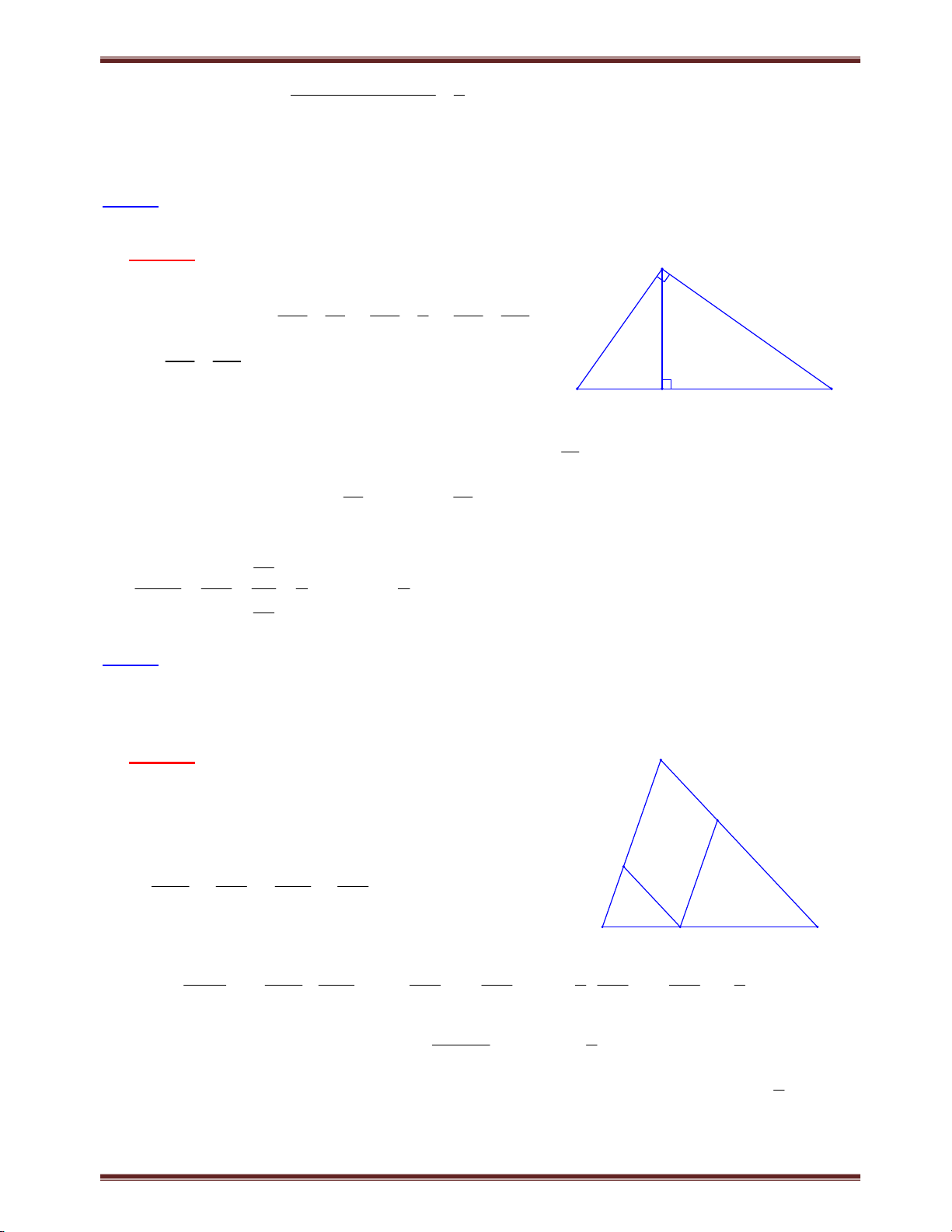
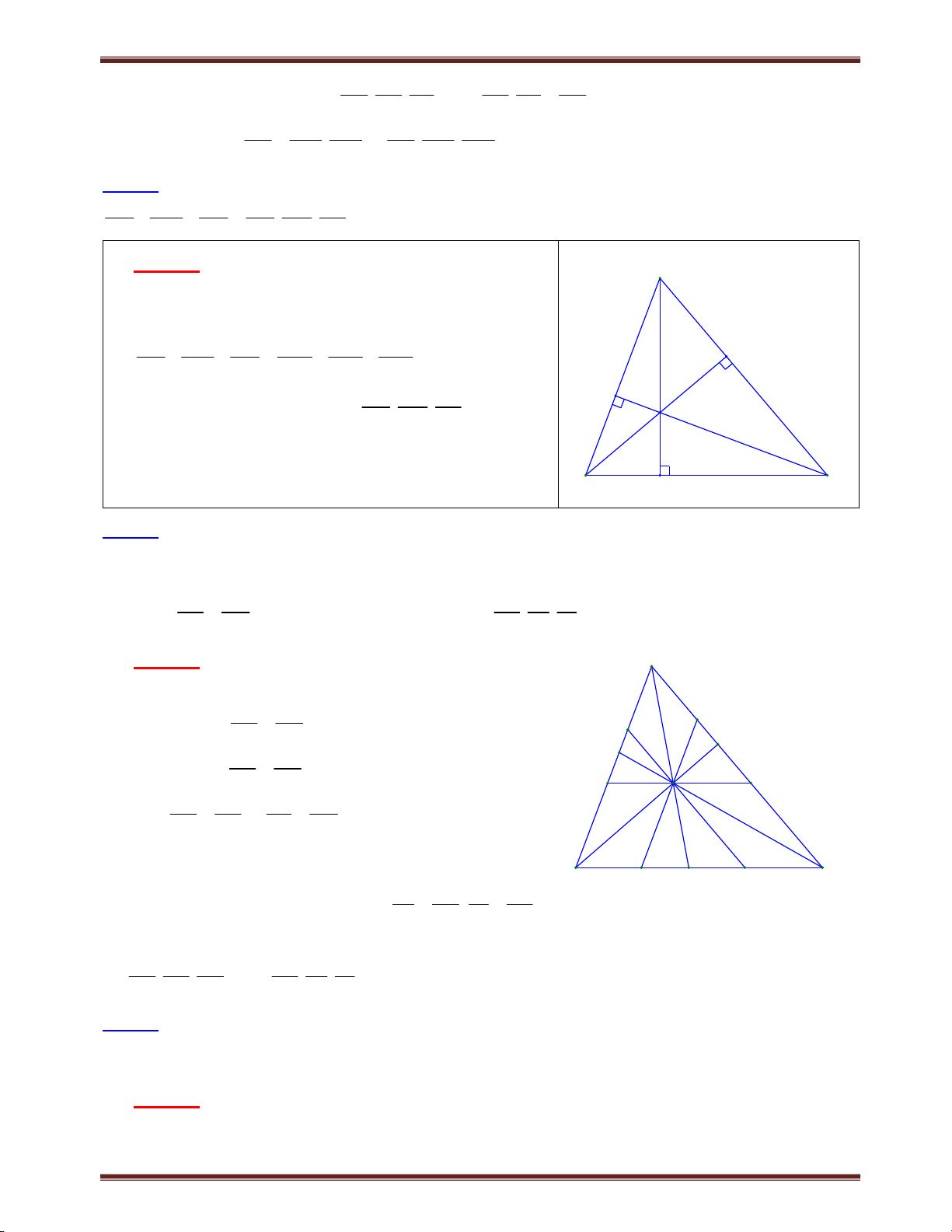
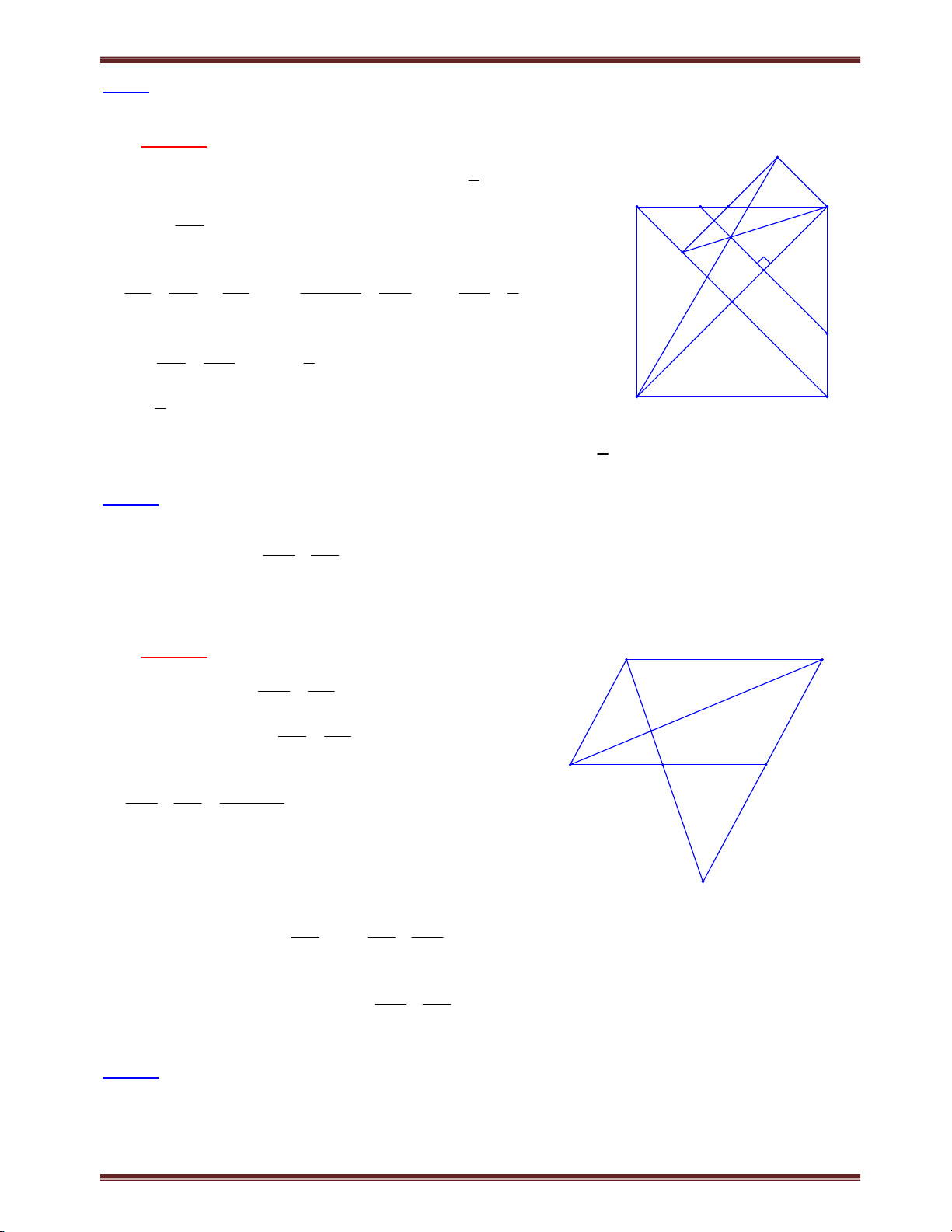
Bài 1. Cho tam giác ABC có trung tuyến AM. Từ một điểm E trên cạnh BC ta kẻ đường thẳng Ex
song song với AM và cắt tia CA, BA lần lượt tại F và G. Chứng minh: EF EG 2.AM . Tìm cách giải.
- Để chứng minh EF EG 2.AM , suy luận thông thường là dựng đoạn thẳng trên tia EF, EG
bằng đoạn thẳng AM, rồi biến đổi cộng trừ đoạn thẳng. Chẳng hạn trong ví dụ này, qua A kẻ
đường thẳng song song với BC, cắt EF tại I. Dễ dàng nhận thấy EI = AM, do vậy chỉ cần
chứng minh GI = IF là xong. Tuy nhiên để chứng minh GI = IF bằng cách ghép vào hai tam
giác bằng nhau là khó khăn, chính vì vậy chúng ta chứng minh tỉ số bằng nhau có cùng mẫu
số. Quan sát kỹ nhận thấy GI và IF có thể đặt trên mẫu số là IE! Từ đó vận dụng định lý và hệ
quả Ta-let để chứng minh FI IG là xong. IE IE
- Ngoài cách trên, chúng ta có thể biến đổi kết luận thành tổng tỉ số và chứng minh FF EG
2 là xong. Do đó vận dụng định lý Ta-lét và biến đổi linh hoạt tỷ lệ thức là yêu AM AM
cầu tất yếu trong dạng toán này. Trình bày lời giải F
Cách 1. Giả sử E thuộc đoạn BM.
Qua A kẻ đường thẳng song song với BC cắt EF tại
I. Ta có AMEI là hình bình hành, suy ra EI = AM. A I
Áp dụng định lý Ta-lét, xét ΔEFC có AI // CE, IF FA EM AM//EF 1 IE AC MC G Xét G EB có AI // BE, AM // GE IG AG EM 2 IE AB BM
Từ (1) và (2), kết hợp với BM = MC B E M C Suy ra IG = IF.
Ta có: EF EG EI IF+EI - IG=2.EI=2.AM F
Cách 2. Giả sử E thuộc đoạn BM.
Theo hệ quả định lý Ta-lét: Xét EF EC ΔEFC có EF//AM 3 A AM CM Xét EG BE ΔABM có EG//AM 4 AM BM G
Cộng vế theo vế (3) và (4) ta có: EF EG EC BE hay EF EG BC 2. AM AM CM BM AM BM Suy ra EF EG 2.AM . B E M C
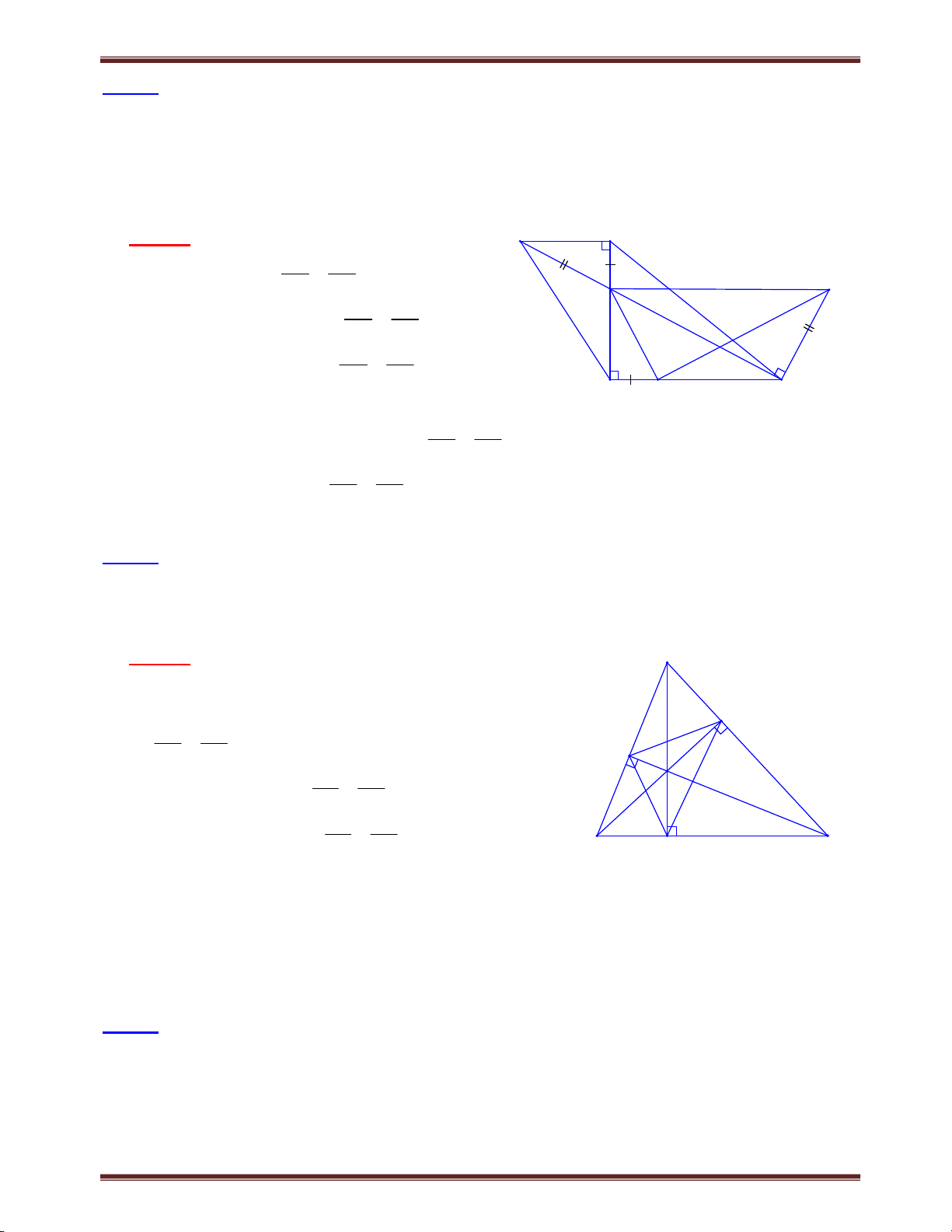
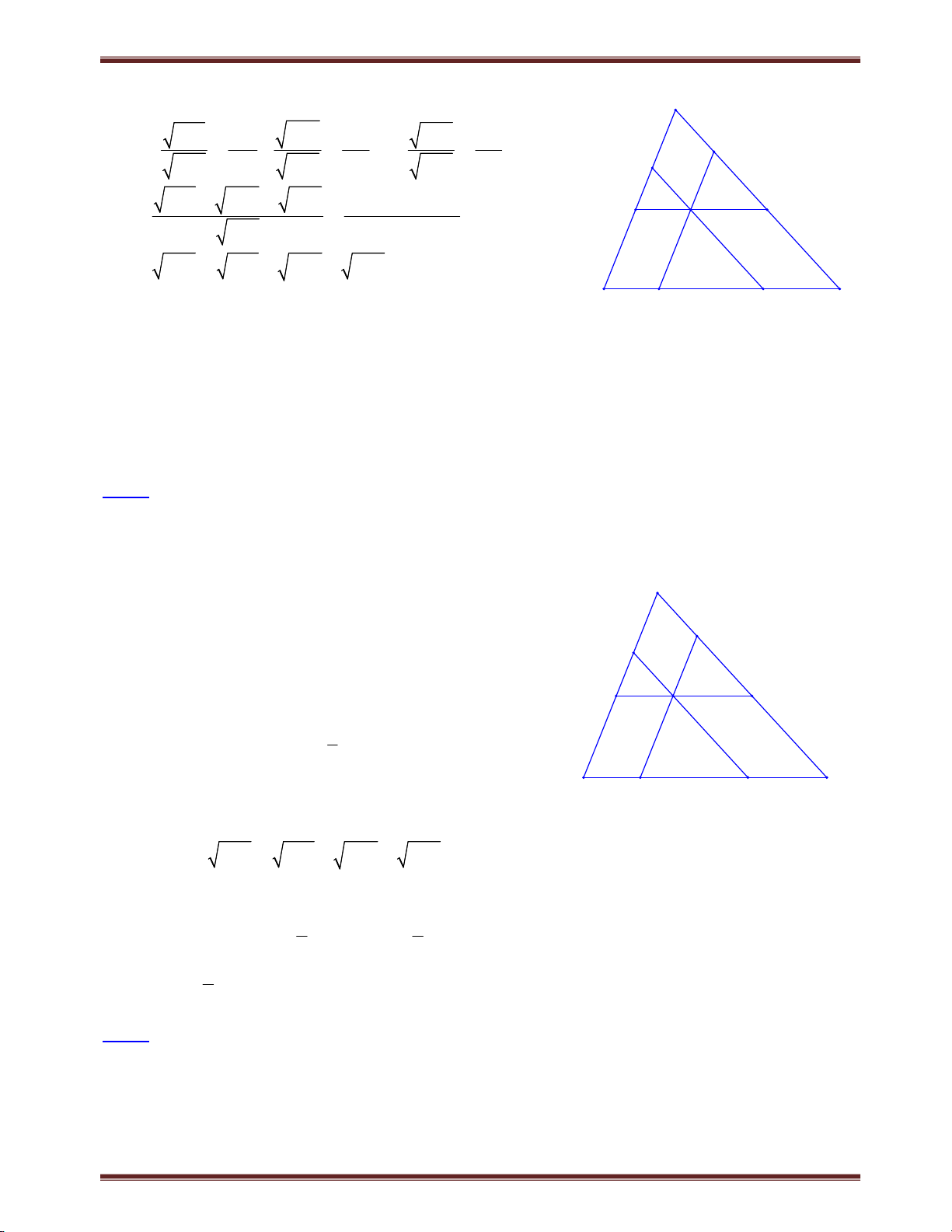
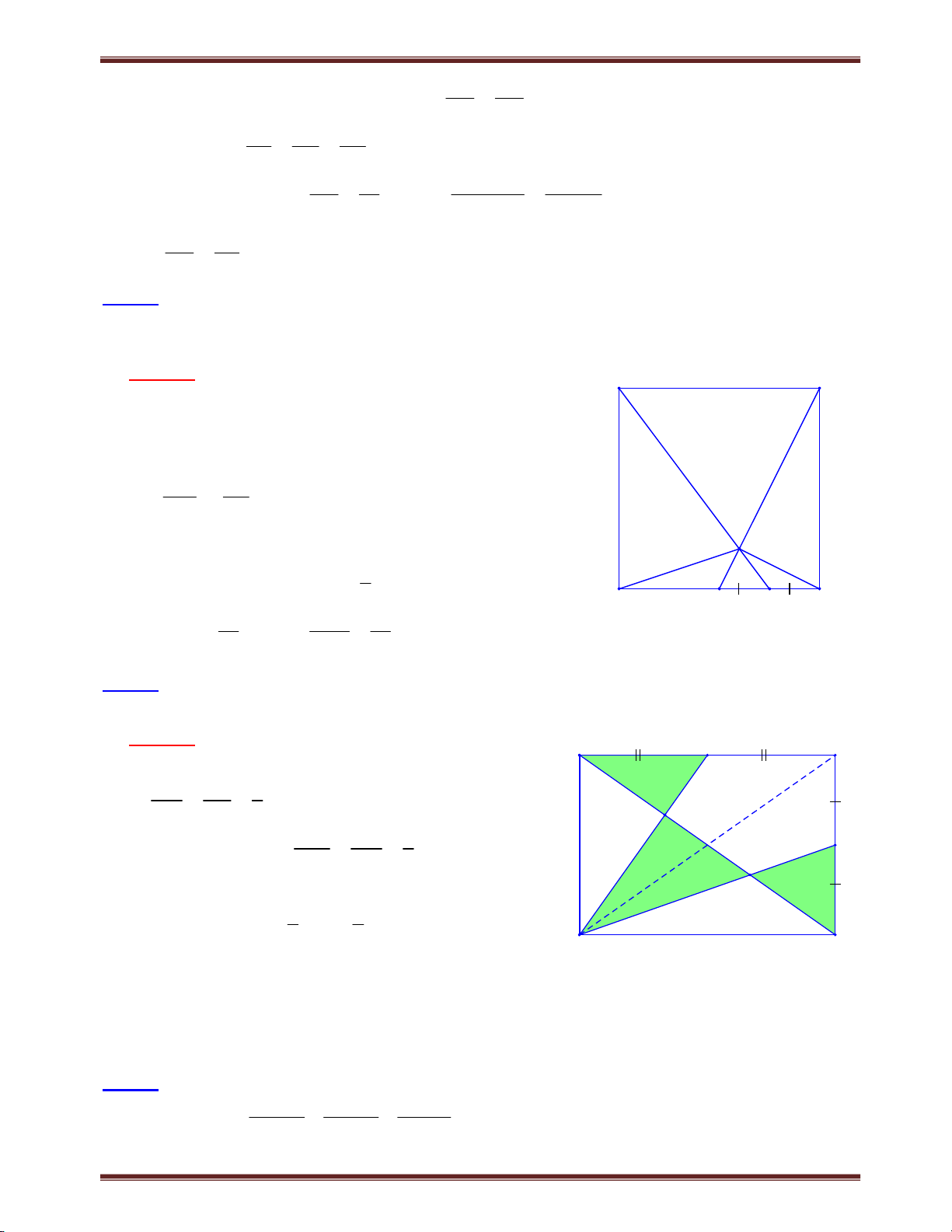
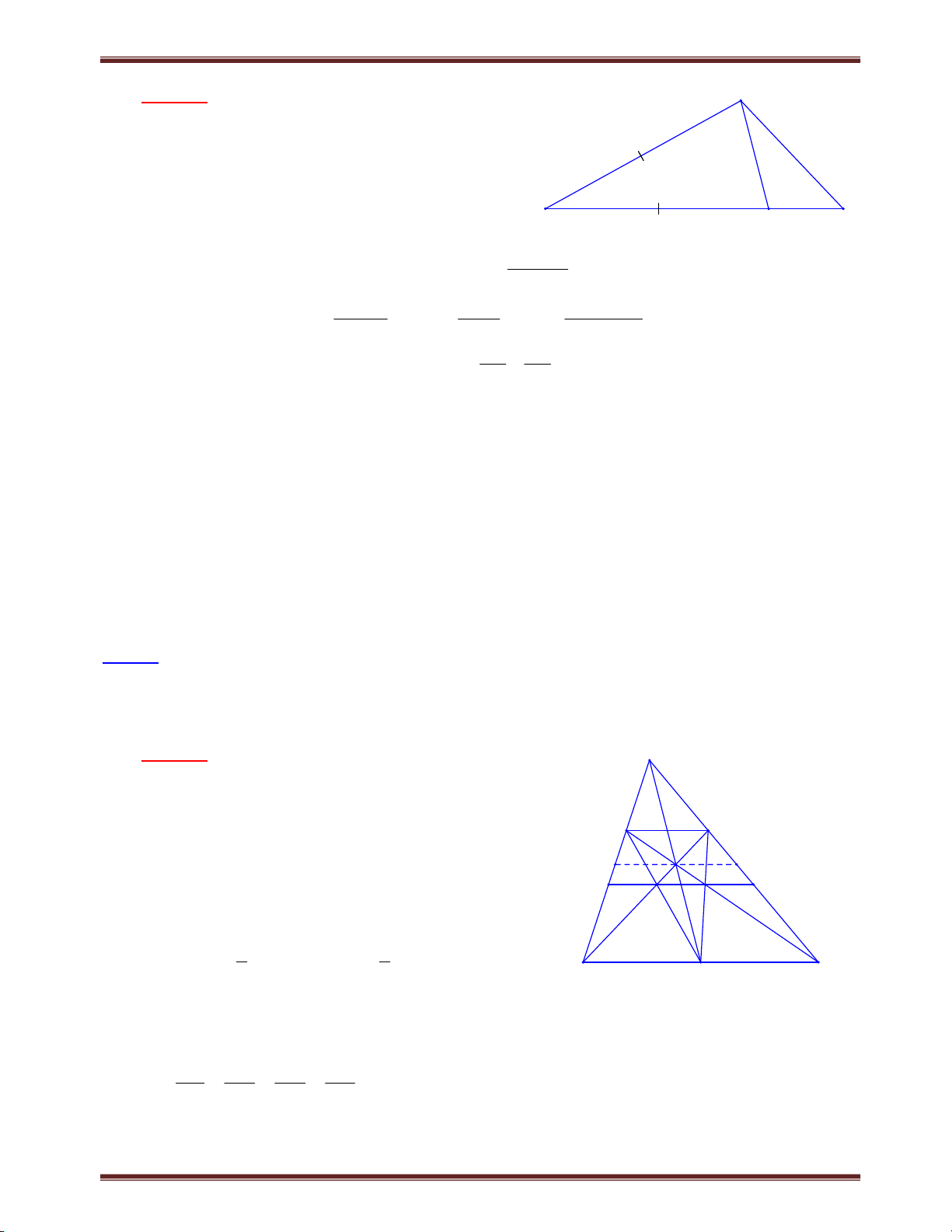
Bài 2. Cho hình thang ABCD (AB//CD). Trên tia đối của tia BA lấy điểm E sao cho BE = CD.
Gọi giao điểm của AC với DB và DE theo thứ tự là I và K. Chứng minh hệ thức AK AC . KC CI
Biên soạn: Trần Đình Hoàng 0814000158 2
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Tìm cách giải. A B
Nhận thấy rằng: chúng ta không thể chứng minh E trực tiếp AK AC
, do vậy nên sử dụng tỉ số KC CI I
trung gian. Khai thác BE = CD và AB//CD rất tự K
nhiên chúng ta vận dụng hệ quả định lý Ta-lét. Trình bày lời giải D C
Đặt AB = a, BE = CD = b. Theo hệ quả định lý Ta-lét Ta có: AK AE a b AE//CD 1 KC CD b AI AB a AI CI a b AC a b AB//CD 2 CI CD b CI b CI b Từ (1) và (2) suy ra: AK AC . KC CI
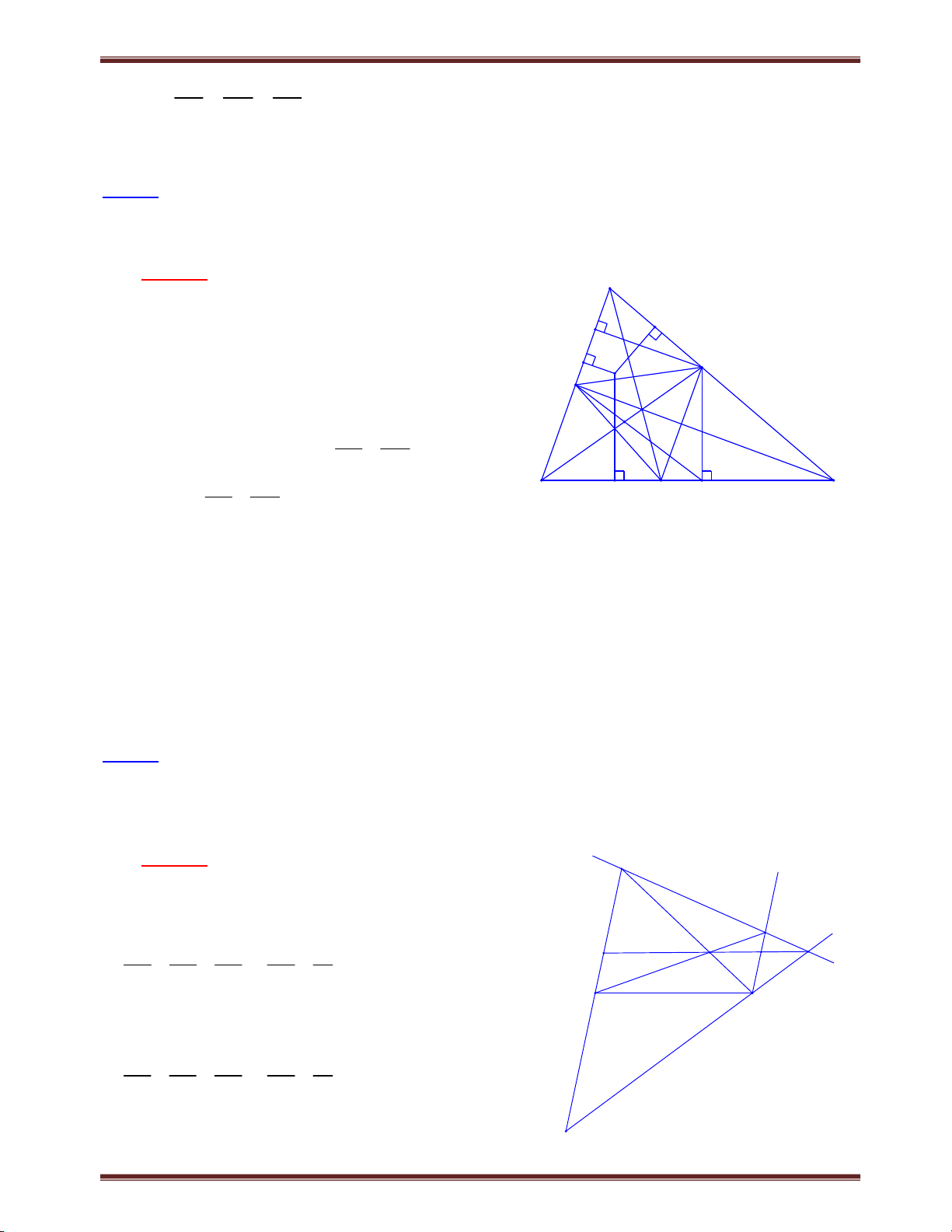
Bài 3. Cho tam giác ABC có A 120 , AD là đường phân giác. Chứng minh rằng: 1 1 1 . AB AC AD Lời giải Kẻ DE // AB, ta có: B D A 60 ;
A 60 nên tam giác ADE đều. Suy 1 1 2 D ra AD = AE = DE. 1
Áp dụng hệ quả định lý Ta-lét: DE CE hay AB AC 1 2 AD CE C . A E AB AC Mặt khác AD AE nên AD AD CE AE AC 1. AC AC AB AC AC AC AC Suy ra 1 1 1 . AB AC AD
Nhận xét. Những bài toán chứng minh đẳng thức có nghịch đảo độ dài đoạn thẳng, bạn nên
biến đổi và chứng minh hệ thức tương đương có tỉ số của hai đoạn thẳng.
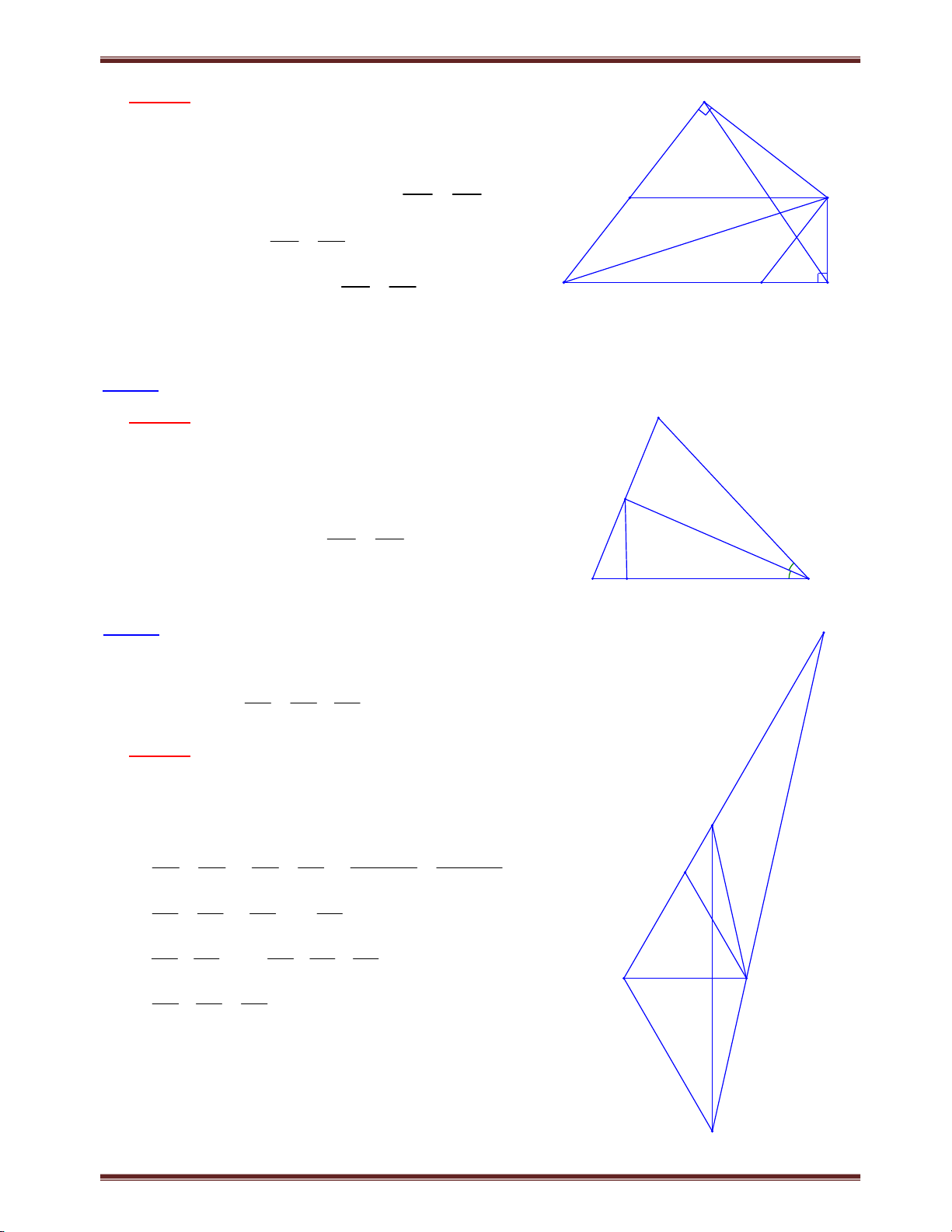
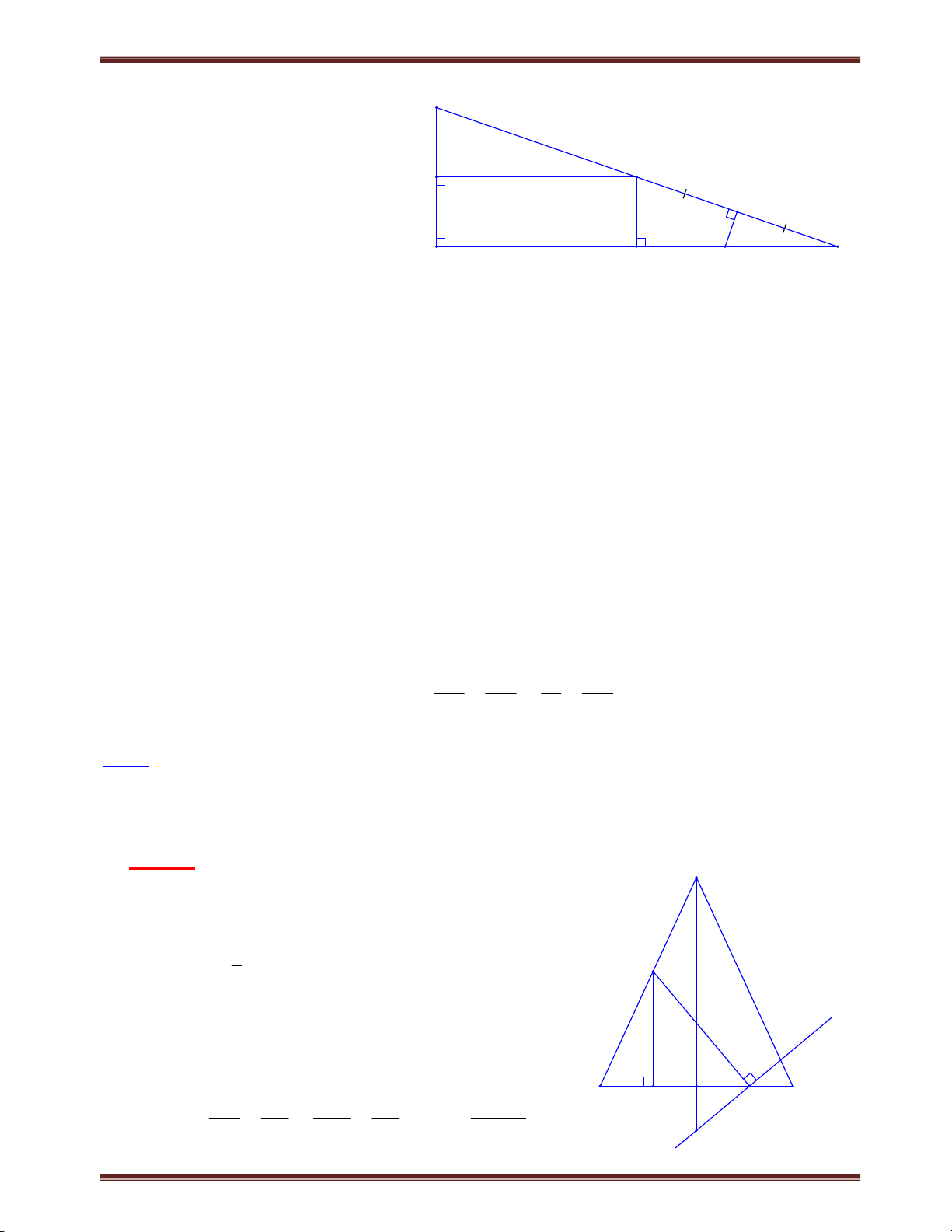
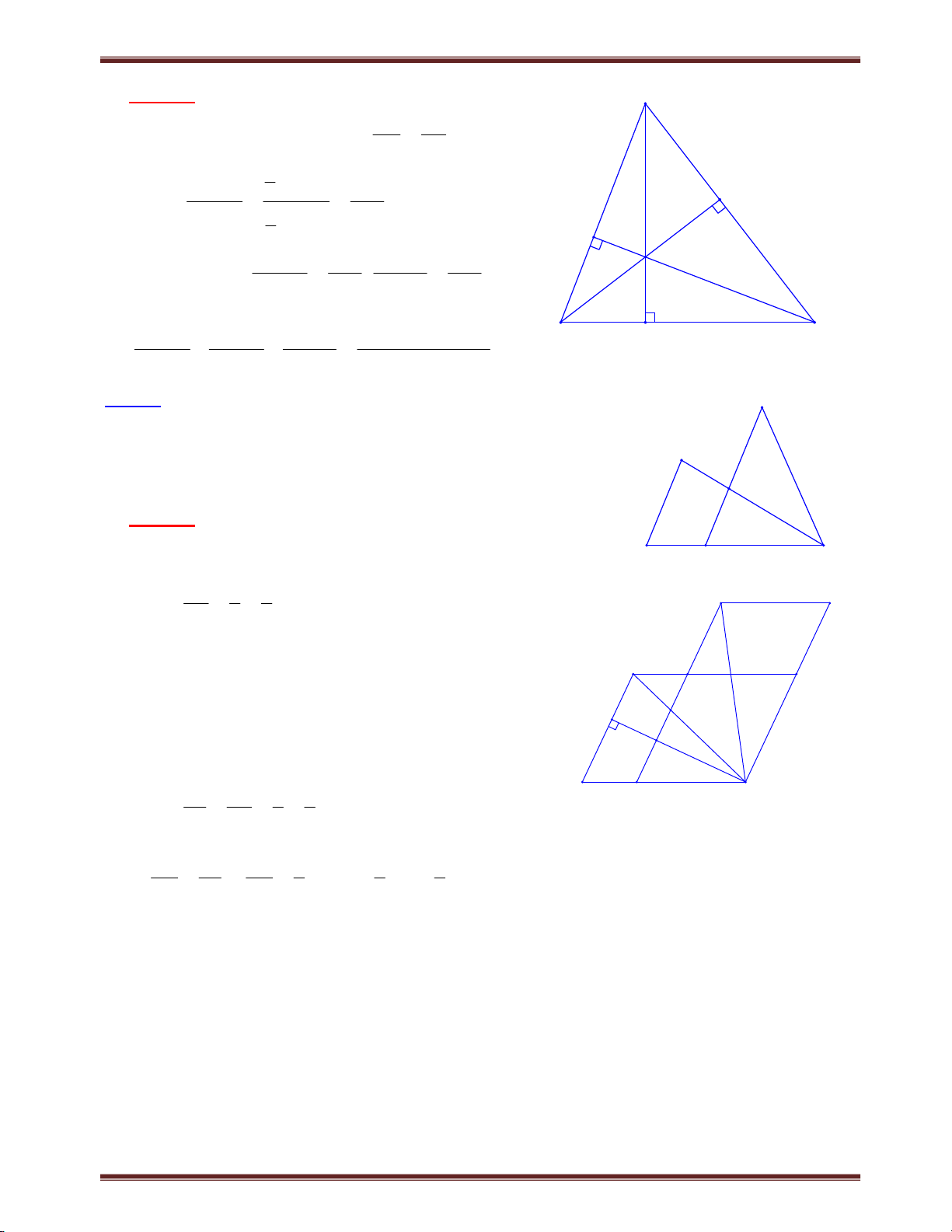
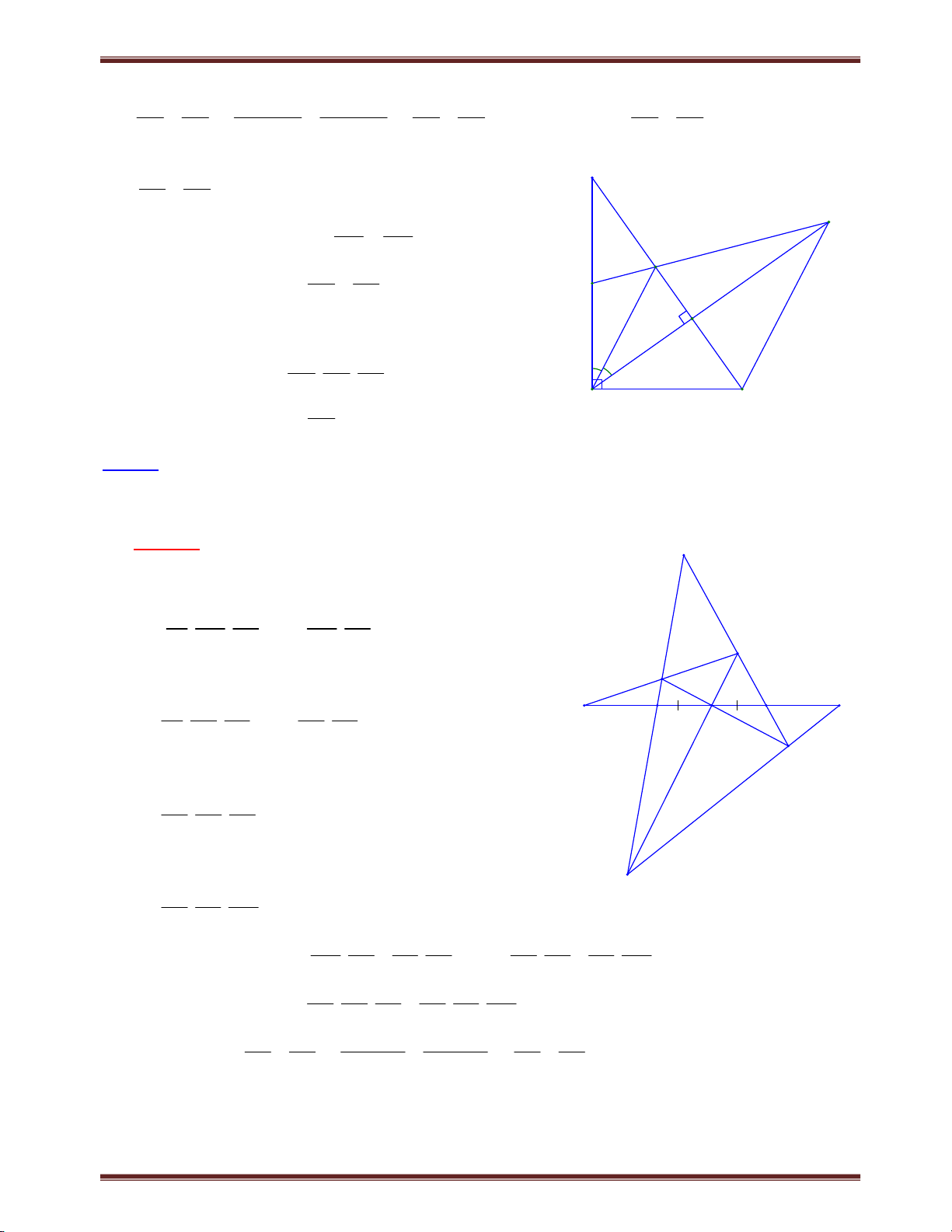
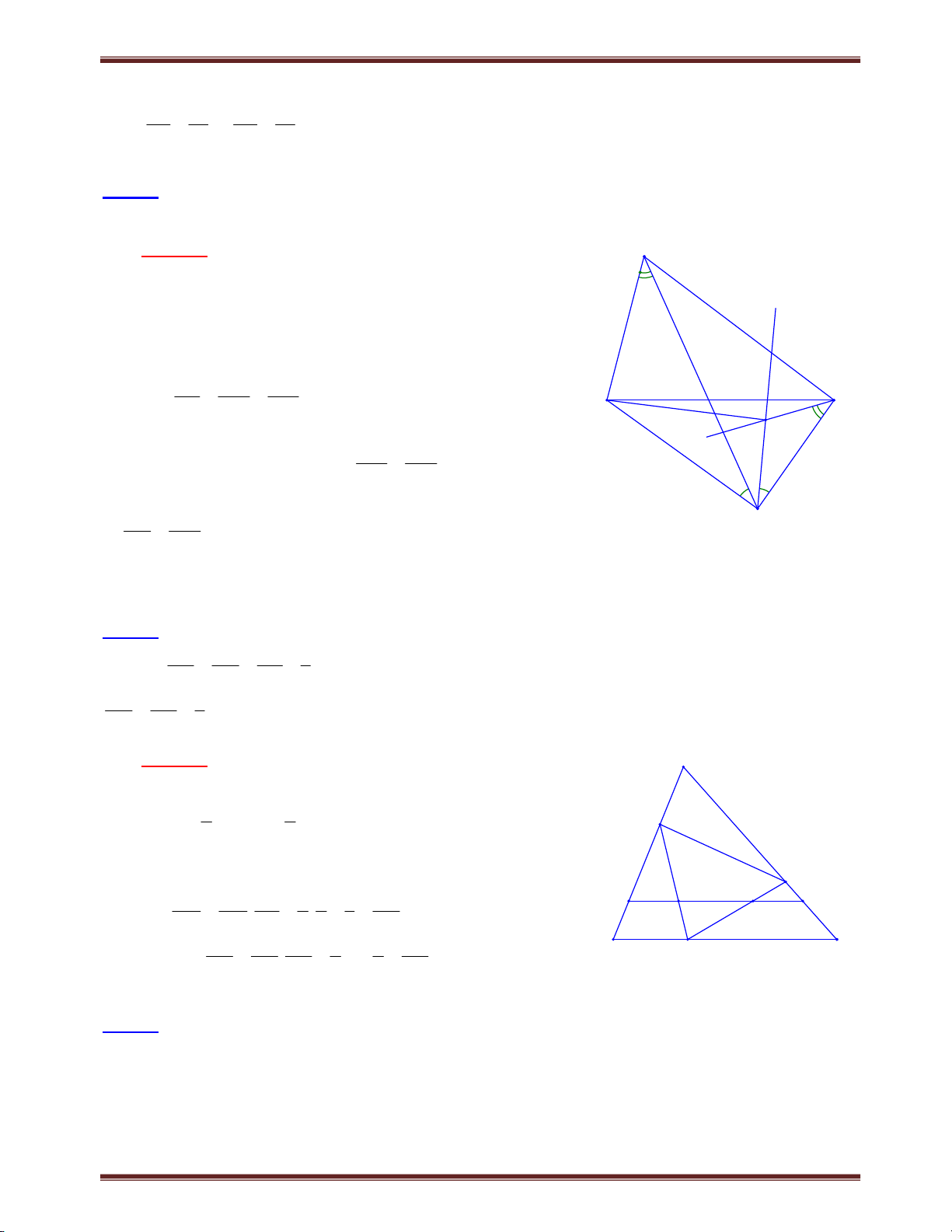
Bài 4. Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại M và N. Chứng minh rằng: a) AB AC 3; b) BM CN 1. AM AN AM AN Tìm cách giải. A Để tạo ra tỉ số AB AC ;
chúng ta cần vận dụng định AM AN
lý Ta-let, mà hình vẽ chưa có yếu tố song song do
vậy chúng ta cần kẻ thêm yếu tố song song. Kẻ N
đường thẳng song song với MN từ B và C vừa khai G
thác được yếu tố trọng tâm, vừa tạo ra được tỉ số M I yêu cầu. Trình bày lời giải B D C
Trường hợp 1. Nếu MN // BC, thì lời giải giản đơn K
Trường hợp 2. Xét MN không song song với BC.
Biên soạn: Trần Đình Hoàng 0814000158 3
Chuyên đề bồi dưỡng học sinh giỏi toán 8
a) Gọi giao điểm của AG và BC là D BD CD.
Kẻ BI // CK // MN I ,K AD Xét BDI và C DK có BD CD; IBD KCD; IDB KDC nên B DI C DK g.cg DI DK .
Áp dụng định lý Ta-lét, ta có AB AI (vì MG // BI); AM AG AC AK (vì GN // CK). AN AG Suy ra AB AC 2.AD 3 (1) (vì 3 AD .AG ). AM AN AG 2 b) Xét BM GI CN KG ; hay BM CN GI GK 2.GD 1, suy ra BM CN 1. AM AG AN AG AM AN AG AG AM AN
Nhận xét. Từ kết quả (1), chúng ta thấy rằng bởi G là trọng tâm nên 2AD 3 . AG
Vậy nếu G không phải là trọng tâm thì ta có bài toán sau:
- Một đường bất kỳ cắt cạnh AB, AC và đường trung tuyến AD của tam giác ABC lần lượt
tại M, N và G. Chứng minh rằng: AB AC AD 2. . AM AN AG
- Nếu thay yếu tố trung tuyến bằng hình bình hành, ta có bài toán sau: Cho hình bình hành
ABCD. Một đường thẳng bất kỳ cắt AB, AD và AC lần lượt tại M, N và G. Chứng minh rằng: AB AD AC . AM AN AG
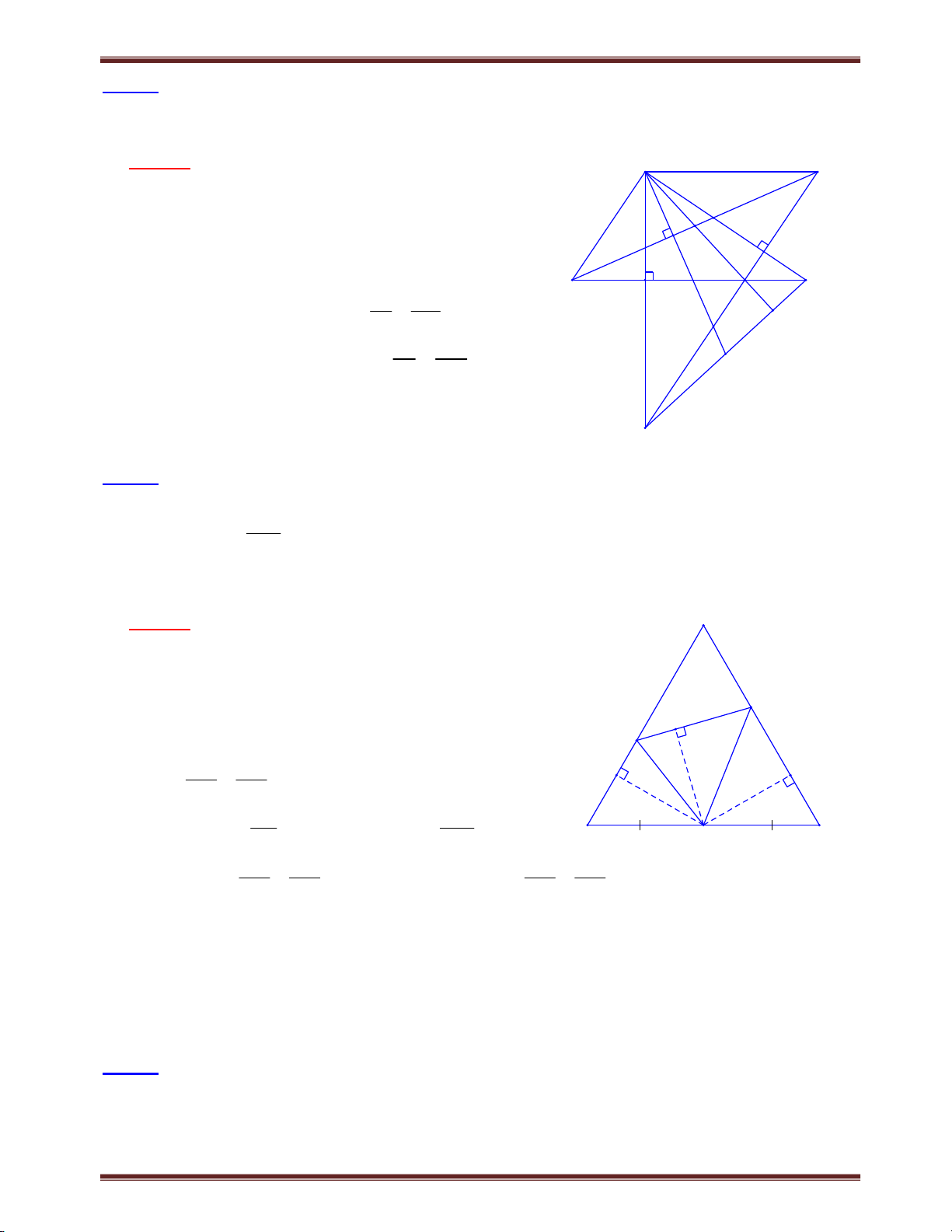
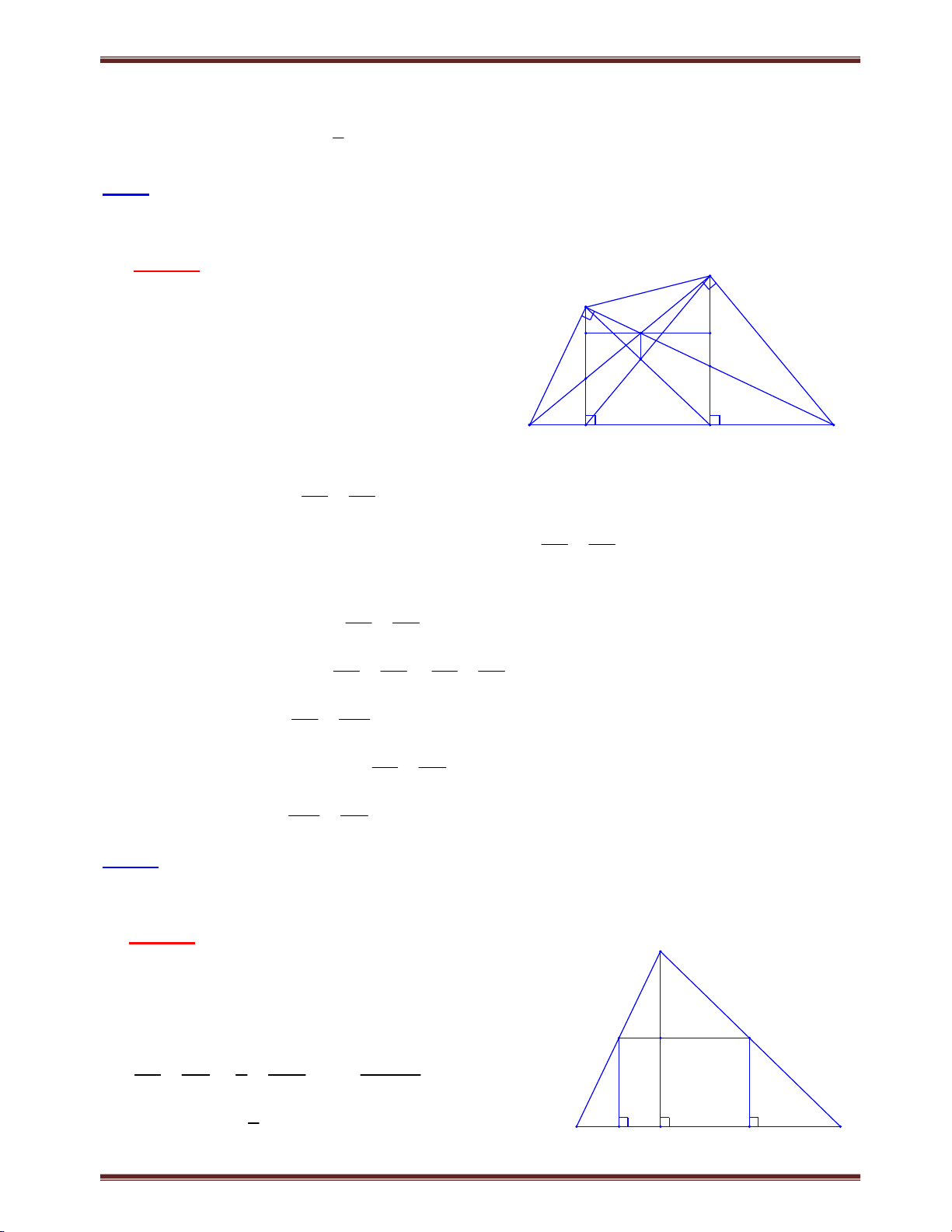
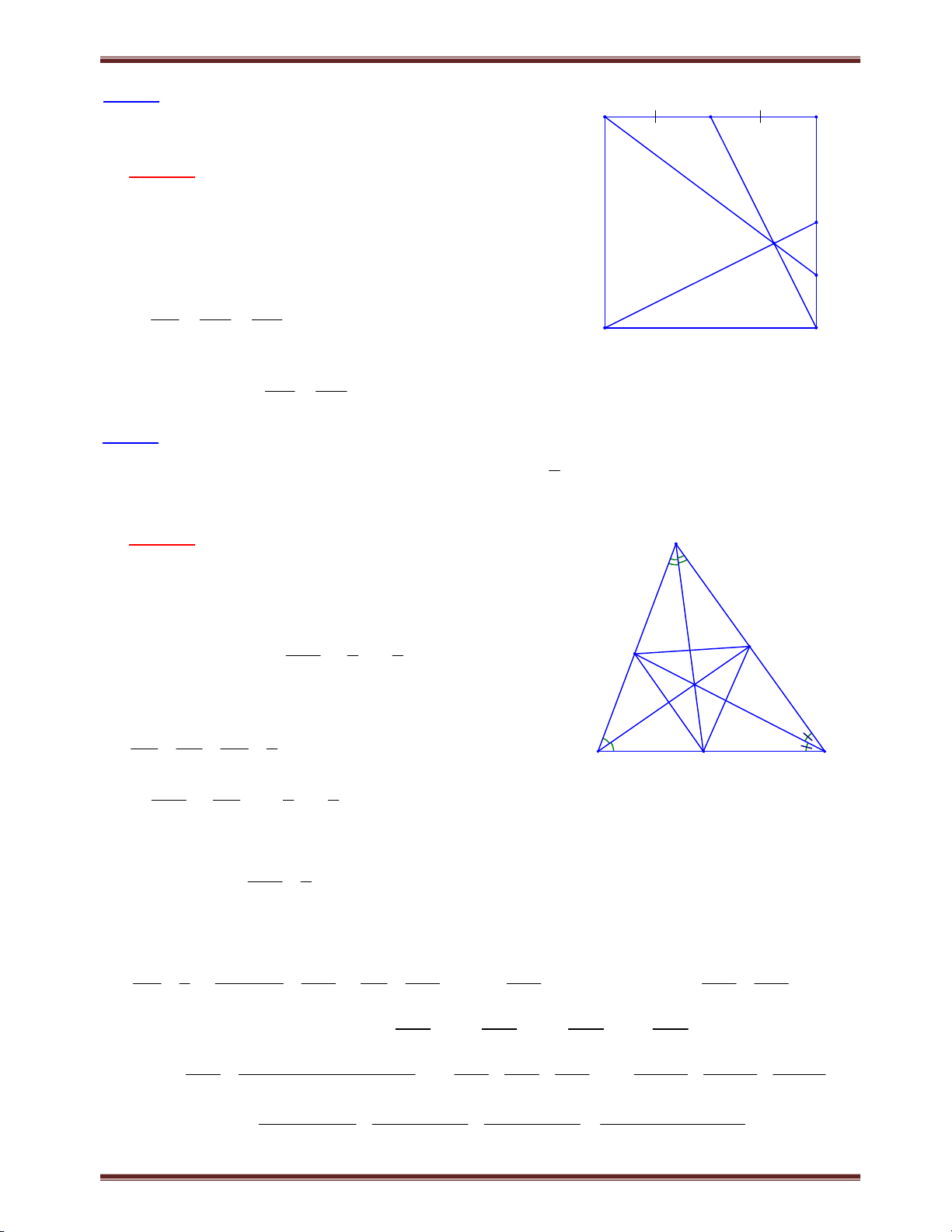
Bài 5. Một đường thẳng đi qua trọng tâm G của tam giác ABC cắt cạnh AB, AC lần lượt tại P, Q. Chứng minh rằng: PB QC 1 . PA QA 4 Tìm cách giải. A
Vẽ hình xong và quan sát, chúng ta nhận thấy tỉ số PB QC ;
đã có ở câu b, bài 1.4 và có kết quả là PA QA PB QC Q
1. Do vậy khai thác yếu tố này, kết hợp với PA QA G P
bất đẳng thức đại số cho lời giải đẹp. Trình bày lời giải B M C
Dựa vào ví dụ 4, ta có: BP CQ 1 AP AQ
Áp dụng bất đẳng thức 2 x y 4xy; 2 Ta có: BP CQ BP QC 1 4. . hay BP QC 1 . . AP AQ PA QA PA QA 4
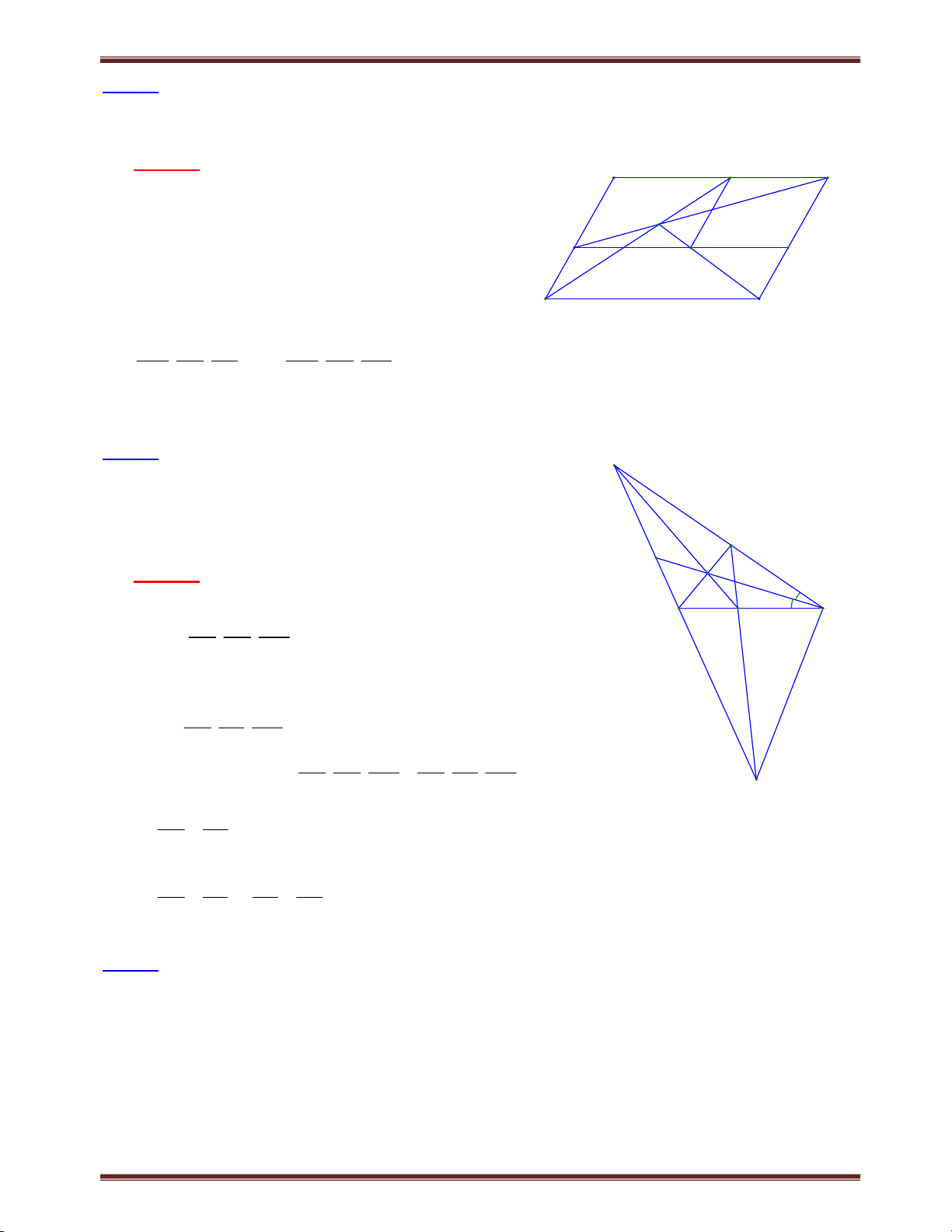
Bài 6. Cho ABCD là hình bình hành có tâm O. Gọi M, N là trung điểm BO; AO. Lấy F trên cạnh
AB sao cho FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K. Chứng minh rằng: a) BA BC 4; b) BE AK BC. BF BE Tìm cách giải.
Với phân tích và suy luận như câu a, bài 1.4 thì ta có:
Biên soạn: Trần Đình Hoàng 0814000158 4
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Tương tự câu a, chúng ta có kết quả: AD AB 4 A F AK AF B N và suy ra AD AB AB BC
8 để liên kết được I M AK AF BF BE K
BE + AK với nhau, mà với suy luận trên thì BE, O
AK cùng nằm ở mẫu số, do đó chúng ta liên tưởng H E
tới bất đẳng thức đại số 1 1 4 sẽ cho D x y x y C
chúng ta yêu cầu. Với suy luận đó, chúng ta có lời giải sau: Trình bày lời giải
a) Kẻ CI //AH // EF (với I ,H BD ) Xét A OH và C OI có AOH
COI (đối đỉnh); OA = OB; HAO ICO (so le trong)
AOH COI (c.g.c) IO OH . Áp dụng định lý Ta-lét, ta có: BA BC BH BI BH BI BO OH BO OI 2.BO 4. BF BE BM BM BM BM BM b) Tương tự ta có: AD AB AD AB AB BC 4 8 1 1 1 1 BC. AB 8 (1) AK AF AK AF BF BE AK BE AF BF
Áp dụng bất đẳng thức 1 1 4 (với x; y 0 ) x y x y Ta có: 1 1 4 4 1 1 AB 4 (2) AF BF AF BF AB AF BF Từ (1) và (2) suy ra: 1 1 BC. 4 AK BE Mà 1 1 4 1 1 4BC BC 4BC 4 AK BE BC. AK BE AK BE AK BE AK BE AK BE
Bài 7. Cho tam giác ABC nhọn có AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho EDC
FDB 90 . Chứng minh rằng: EF//BC .
(Thi học sinh giỏi Toán 9, tỉnh Quảng Ngãi, năm học 2011-2012) Tìm cách giải. A
Để chứng minh EF//BC , suy luận một cách tự nhiên
chúng ta cần vận dụng định lý Ta-let đảo.
Do vậy cần chứng minh tỉ lệ thức AB AC . Nhận AE AF D
thấy để định hướng tỉ lệ thức ấy cũng như khai thác được EDC
FDB 90 chúng ta cần kẻ BO CD ; E O F M
CM DB, để có các đường thẳng song song rồi vận
dụng định lý Ta-let. Từ đó chúng ta có lời giải sau: I Trình bày lời giải.
Kẻ BO CD;CM DB , BO và CM cắt nhau tại I D là trực tâm của B
IC DI BC I, D, A thẳng B H C hàng. AI AB DE//BI AI AC . IC//FD suy ra AB AC EF//BC AD AE AD AF AE AF (Định lý Ta-let đảo).
Biên soạn: Trần Đình Hoàng 0814000158 5
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 8. Cho tam giác ABC vuông cân tại A có BM là đường trung tuyến. Lấy điểm F trên cạnh BC
sao cho FB=2.FC . Chứng minh AF BM . Tìm cách giải. C
Nhận thấy từ FB=2.FC suy ra: BF 2 mang tính chất CF
trọng tâm tam giác. Do vậy nếu gọi G là trọng tâm tam
giác, AH là đường trung tuyến thì dễ dàng nhận được GF
// AC và AH BC nên G là trực tâm tam giác ABF. Do H đó ta có lời giải sau: G F Trình bày lời giải.
Gọi G là trọng tâm tam giác ABC và AG kéo dài cắt BC
tại H AH là đường trung tuyến của tam giác ABC. B Mặt khác, A
BC vuông cân tại A nên AH BC A M
Ta có: BG 2 (vì G là trọng tâm); Và BF 2 (giả thiết) GM FC BG BF
FG//AC (theo định lý Ta-let đảo) GM FC
FG AB nên G là trực tâm A
BF BG AF hay BM AF .
Bài 9. Cho tam giác ABC. Biết tồn tại điểm M, N lần lượt trên cạnh AB, BC sao cho BM BN 2. và BNM
ANC . Chứng minh tam giác ABC vuông. AM CN Lời giải A
Cách 1. Gọi P là trung điểm của AM, Q là giao P điểm của AN với CP Ta có: BM BM BN 2. MN //CP (định lý Ta- M PM AM CN Q let đảo). QCN MNB ANC QC N cân tại Q. Mặt khác: C B N
PA PM ,PQ //MN QA QN nên QA QC QN C AN vuông tại C A BC vuông tại C. A
Cách 2. Dựng D là điểm đối xứng của N qua C ND CN CD 2.CN Ta có: MB BN MB BN BN 2 MA CN MA 2.CN DN M
MN//AD (định lý Ta-let đảo). D =N
=N AND cân. Do đó đường trung 1 2
tuyến AC cũng là đường cao. 1 1 2 B Vậy AC CB A BC vuông tại C. D C N
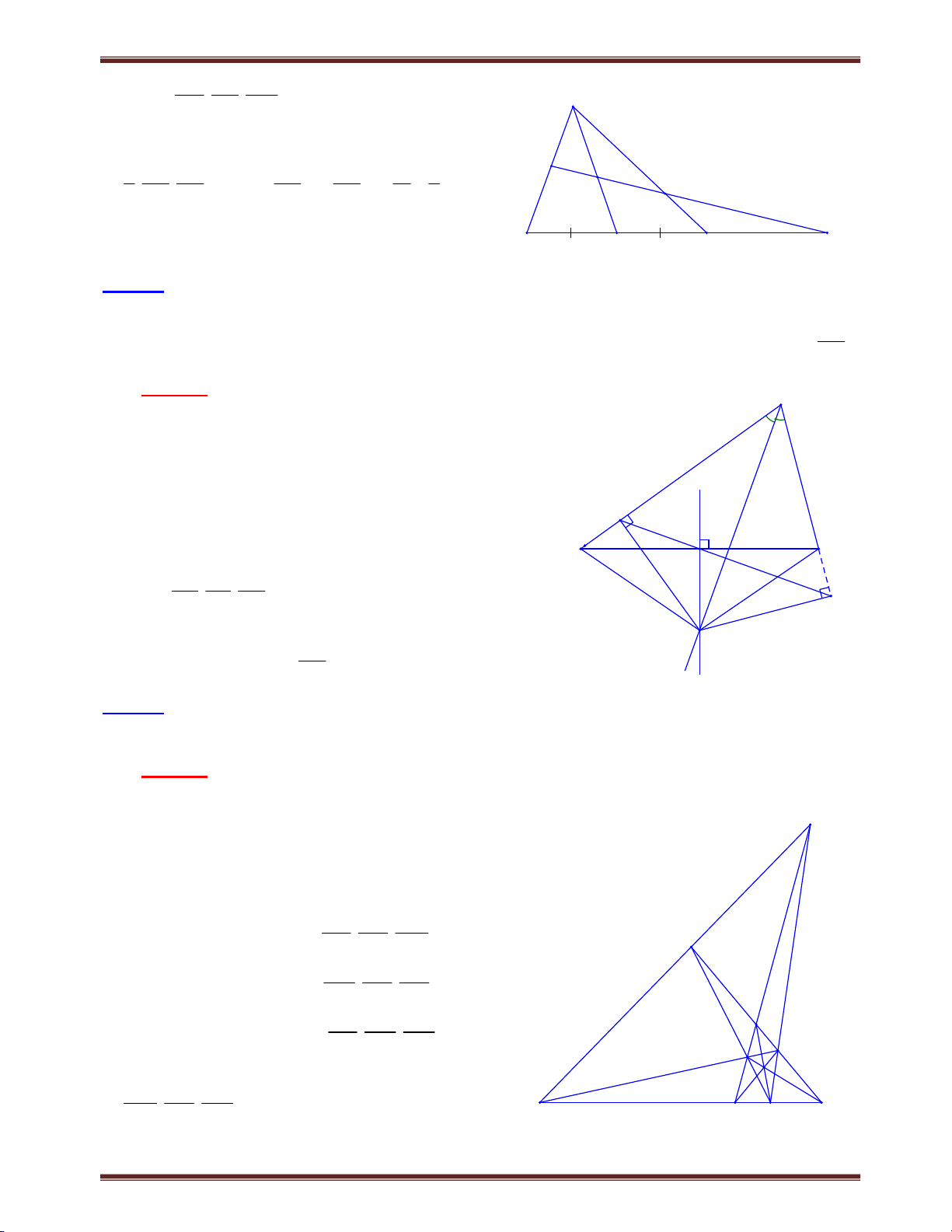
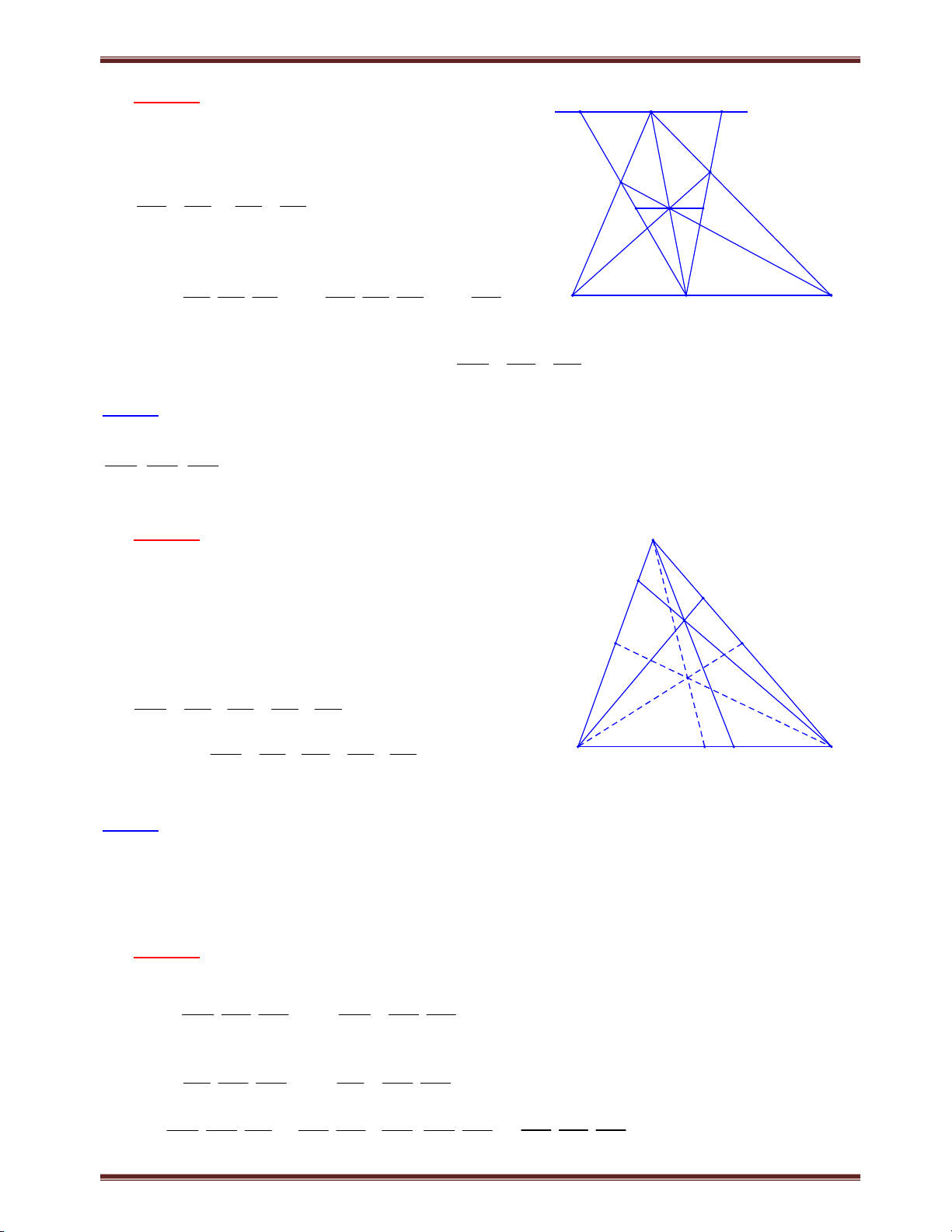
Bài 10. Cho tam giác ABC có AD là đường trung tuyến. Gọi M là điểm tùy ý thuộc khoảng BD.
Lấy E thuộc AB và F thuộc AC sao cho ME // AC; MF // AB. Gọi H là giao điểm MF và AD.
Đường thẳng qua B song song với EH cắt MF tại K. Đường thẳng AK cắt BC tại I. Tính tỉ số IB ? ID
Biên soạn: Trần Đình Hoàng 0814000158 6
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải A
Qua D kẻ đường thẳng song song với AB, cắt tia AI
tại P. Áp dụng định lý Ta-let, cho các đoạn thẳng F song song ta có: IB AB AB HK DP//AB . (1). ID DP HK DP H AB AB BC ME//AC (2). E HK BE BM K HK//DP và HK AH BM MH//AB (3). DP AD BD B M I D C Từ (1), (2) và (3) suy ra: IB BC BM BC . 2 . Vậy IB 2. ID BM BD BD ID P Bài 11. Cho A
BC nhọn. Hình chữ nhật MNPQ thay đổi thỏa mãn M thuộc cạnh AB, N thuộc
cạnh AC và P, Q thuộc cạnh BC. Gọi giao điểm của BN với CM là X của QN với PM là Y. Gọi H
là giao điểm của XY với BC. Chứng minh rằng đường thẳng AH vuông góc với BC. Tìm cách giải. A
Bài toán có nhiều yếu tố song song, do vậy để
chứng minh đường thẳng AH vuông góc với BC,
chúng ta nên chứng minh AH song song với NP
hoặc MQ. Với định hướng ấy chúng ta tìm cách vận Z M N
dụng định lý Ta-let đảo. Chẳng hạn nếu chứng minh X
AH song song với NP, chúng ta cần chứng minh HP AN
. Bằng cách vận dụng định lý Ta-lét cùng Y HC AC
hệ quả và biến đổi khéo léo các dãy tỉ số bằng nhau, B C
chúng ta sẽ có lời giải đẹp. Q H P Trình bày lời giải.
Gọi Z là giao điểm của XY với MN vì tứ giác MNPQ là hình chữ nhật, HP = ZM và MN // BC nên: HP ZM XM MN AN HC HC XC CB AC
Do đó AH // NP (định lý Ta-let đảo) mà NP BC nên AH BC .
Bài 12. Cho hình bình hành ABCD có I; E là trung điểm của BC; AD. Qua điểm M tùy ý trên AB
kẻ đường thẳng MI cắt đường thẳng AC tại K. Đường thẳng KE cắt CD tại N. Chứng minh rằng: AD = MN. Lời giải Q A M B
Gọi P là giao điểm của đường thẳng MI và CD
Gọi Q là giao điểm của đường thẳng KN và AB. E I Nhận thấy: IB M I CP (g.c.g) nên BM = CP.
Ta có theo định lý Ta-lét AM//CP nên P D C AM AM KA N (1) MB CP KC
Nhận thấy EAQ EDN (g.c.g) nên DN = AQ. K
Biên soạn: Trần Đình Hoàng 0814000158 7
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Theo định lý Ta-lét, ta có: AQ // CN nên DN AQ KA (2) NC NC KC Từ (1) và (2) suy ra: AM DN AM DN AM DN MB NC AM MB DN NC AB DC
Suy ra AM = DN. Do đó ADNM là hình bình hành suy ra AD = MN.
Bài 13. Cho tam giác ABC vuông tại A, đường cao AH. Gọi I là trung điểm của AH. Đường
vuông góc với BC tại C cắt đường thẳng BI tại D. Chứng minh DA = DC. Lời giải D
Gọi M là trung điểm của AC, N là giao điểm của MI và
AB. Tam giác AHC có MI là đường trung bình nên MI // HC, tức là MN // BC. A Theo định lý Ta-lét: Do AH // CD nên IB HB 1 ID HC N M I Do MN // BC nên IN AI IM , HB AH HC Tức là IN HB B C 2 H IM HC Từ (1) và (2) suy ra: IB IN
, do đó BN // DM (định lý Ta-let đảo). ID IM
Ta lại có: BN AC nên DM AC . Vậy DM là đường trung trực của AC, suy ra DA = DC.
Bài 14. Cho hình bình hành ABCD. Trên đường chéo AC lấy một điểm I. Tia DI cắt đường thẳng
AB tại M, cắt đường thẳng BC tại N. Chứng minh rằng: a) AM DM CB ; b) 2 ID IM .IN . AB DN CN Lời giải M
a) Áp dụng hệ quả định lý Ta-lét vào tam giác BMN với BM // CD, ta có: MN BN MN ND BN NC (tính chất tỉ lệ ND NC ND NC B N thức) C MD BC 1 I ND NC
Áp dụng hệ quả định lý Ta-lét vào tam giác MAD với BN // AD ta có: AM DM 2 A D AB DN Từ (1) và (2) suy ra: AM DM CB . AB DN CN
b) Áp dụng hệ quả định lý Ta-lét vào tam giác ADI với AD // NC, ta có: ID IA 3 IN IC
Áp dụng hệ quả định lý Ta-lét vào tam giác DIC với DC // AM, ta có: IM IA 4 ID IC Từ (3) và (4) suy ra: ID IM hay 2 ID IM .IN . IN ID
Biên soạn: Trần Đình Hoàng 0814000158 8
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 15. Cho tam giác ABC vuông tại A. Vẽ về phía ngoài hai tam giác ABD và ACE vuông cân
tại B và E. Gọi H là giao điểm của AB và CD; K là giao điểm của AC và BE. Chứng minh rằng: a) AH = AK b) 2 AH BH .CK . Lời giải E a) BD//AC AB A AH AC AH AC D K BH BD AH BH BD AC H AH AC AB BD AC B C Mà BD = AB nên AB.AC AH 1 AB AC AB//CE( AK AB AK AB AK AB AC) KC CE AK KC BD EC AC BD EC Mà CE = AC nên AB.AC AK 2 AB AC
Từ (1) và (2) suy ra: AH = AK. b) AH AC CK CE BD//AC 3;CE//AB 4 BH BD AK AB Mà AC = CE, BD = AB.
Kết hợp với (3) và (4) ta có AH CK , suy ra 2 AH BH .CK . BH AK
Bài 16. Cho hình vuông ABCD, điểm E thuộc cạnh BC. Gọi F là giao điểm của AE và CD, G là giao điểm của DE và BF.
a) Gọi I và K theo thứ tự là giao điểm của AB và CG và DG. Chứng minh rằng IE song song với BD.
b) Chứng minh rằng AE vuông góc với CG. Lời giải B A I K a) Ta sẽ chứng minh IK KE . Do BK // DF nên IB ED G
theo định lý Ta-lét, ta có: IK IG IB CD GC CF E suy ra IK CD 1 IB CF F D C
Cũng theo định lý Ta-lét với AK // DF, ta có: KE BE AB 2 ED EC CF
Ta lại có: AB = CD nên từ (1) và (2) suy ra: IK KE . IB ED
Theo định lý đảo Ta-lét ta có: IE // BD.
b) Ta có: BD AC và IE // BD nên IE AC .
Tam giác ACI có CB AI ,IE AC nên E là trực tâm của tam giác ACI. Suy ra AE CG .
Biên soạn: Trần Đình Hoàng 0814000158 9
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 17. Cho tam giác ABC và D là một điểm tùy ý trên A
AC. Gọi G là trọng tâm ABD . Gọi E là giao điểm của CG và BD. Tính EB CA . ED CD F Lời giải G
Gọi F là giao điểm BG với AC thì AF = FD. D E
Lấy M thuộc CG sao cho DM // BG.
Ta có: CA CD CF FA CF FD hay M
CA CD 2.CF CA 2.CF CA 2.CF CD
Vì G là trọng tâm ABD nên GB 2.GF B C Vì EB CA GB 2.CF CD 2.GF 2.CF MD//BG 1 1 ED CD MD CD MD CD Mà GF // MD nên GF CF
do vậy, từ (1) suy ra: EB CA 1. MD CD ED CD
Bài 18. Cho hình bình hành ABCD, điểm E thuộc cạnh AB, điểm F thuộc cạnh BC. Gọi I là giao
điểm của CE và AD, gọi K là giao điểm của AF và DC. Chứng minh rằng EF song song với IK. Lời giải I
Gọi O là giao điểm của AF và CE. Theo định lý Ta-let: OE OA A E AE//CK . B OC OK OC OF DI//CF . O OI OA Ta có: OE OE OC OA OF OF . . . F OI OC OI OK OA OK OE OF K D C
EF//IK (theo định lý Ta-let đảo). OI OK
Bài 19. Cho tam giác ABC cân tại A. Trên cạnh BC kéo dài về phái C lấy điểm M. Một đường
thẳng đi qua M cắt các cạnh CA, AB lần lượt tại N và P. Chứng minh rằng BM CM không BP CN
đổi khi M và thay đổi. Lời giải A
Kẻ NH // AB (Với H BC ) suy ra: BM CM MH CM MH CM CH BP CN NH CN CN CN CN Mặt khác NH //AB CH CN CH BC P . BC AC CN AC N Vậy BM CM BC
không đổi khi M và thay BP CN AC đổi. B H C M
Bài 20. Giả sử O là giao điểm của hai đường chéo AC và BD của tứ giác lồi ABCD. Gọi E, F, H
lần lượt là chân các đường vuông góc kẻ từ B, C và O đến AD. Chứng minh rằng:
AD.BE.CF AC.BD.OH . Đẳng thức xảy ra khi nào?
Biên soạn: Trần Đình Hoàng 0814000158 10
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải C
Kẻ AT BDT BD , thì AT AO
Nên AD.BE BD.AT 2.S B ABD T Suy ra AD.BE BD.AO O AO AD.BE AC.BD 1 AC
Mặt khác, OH // CF nên AO OH 2 AC CF A E H F D Từ (1) và (2) suy ra: OH AD.BE AC.BD. AD.BE.CF AC.BD.OH . CF
Đẳng thức xảy ra khi T trùng với O hay AC vuông góc với BD.
Bài 21. Cho tam giác ABC vuông tại A. Các tứ giác MNPQ và AXYZ là các hình vuông sao cho
M AB;Q,P BC; N AC; X, Y, Z tương ứng thuộc AB, BC, AC. Chứng minh MN AX .
11. Đặt x; y là cạnh hình vuông MNPQ; AXYZ; và a, b, c là độ dài BC, AC, AB. Kẻ AH BC ;
đặt AH = h. Từ đó suy ra: a.h b.c 2.S và 2 2 2 a b c . ABC Lời giải A Ta có N 2 2 2 2 2 2 a h a h 2ah b c 2bc b c M Z a h b c X a h b c 1 1 1 1 1 ah bc a h b c
Theo định lý Ta-let, ta có: B Q H Y C P x x MN MQ AM MB 1 a h BC AH AB AB y y XY ZY BY CY 1 1 1 1 1 x y 2 b c AC AB BC BC a h b c
Từ (1) và (2) suy ra: x y hay MN AX .
Bài 22. Gọi M là điểm bất kì trên đường trung tuyến trên đường trung tuyến AD của tam giác
ABC. Gọi P là giao điểm của BM và AC, gọi Q là giao điểm của CM và AB. Chứng minh PQ // BC. Lời giải A F E
Qua A kẻ đường thẳng song song với BC, lần lượt
cắt BP và CQ kéo dài tại E và F.
Áp dụng hệ quả định lý Ta-let, ta có: AF AM AE P Q CD MD BD M Mà CD = BD nên AF = AE.
Áp dụng hệ quả định lý Ta-let, ta có: AF AQ AE AP C ; B D BC QB BC PC Suy ra: AP AQ
PQ//BC (định lý đảo Ta-let). PC QB
Biên soạn: Trần Đình Hoàng 0814000158 11
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 23. Cho tam giác ABC có ABthuộc AC). Đường thẳng vuông góc với BE qua C cắt BE, BD lần lượt tại F, G. Chứng minh rằng
đường thẳng DF chia đôi đoạn thẳng GE. Lời giải B
Gọi giao điểm của CG và AB là K và giao điểm của DF và BC là M. M Ta có B
CK cân (vì có BF vừa là đường phân giác, vừa
là đường cao) F là trung điểm của CK. A
CK có FK = FC, AD = CD suy ra DF là đường trung D A C bình FD//AK . E B
CK có FK = FC, FM // BK suy ra M là trung điểm O G của BC. F
Xét tam giác DBC có trung tuyến DM, ta có GE//BC, suy ra OE OG
. Mà BM = MC, do đó OE = OF hay K BM MC
DF chia đôi đoạn thẳng GE.
Bài 24. Cho tam giác ABC. Lấy điểm O nằm trong tam giác, các tia BO và CO cắt AC và AB lần
lượt tại M và N. Vẽ hình bình hành BOCF. Qua N kẻ đường thẳng song song với BM cắt AF tại E. Chứng minh rằng: a) MONE là hình bình hành b) AE AM .AN OM .ON . AF AB.AC OB.OC Lời giải A
a) Gọi G là giao điểm của NE và AC, H là giao điểm G CF và AB. E
Theo định lý Ta-let, ta có: N GE CF M NE//CH EN FH GM NB NO O NE//BM//CH . MC BH OC B CF BN C CN//BF . FH BH Suy ra GE GM ME//NC EN MC F
MONE là hình bình hành.
b) Ta có BM // HC và NE // HF, theo định lý Ta-lét, ta có: AM .AN AM AN AB AN AN AE . . 1 H AB.AC AC AB AH AB AH AF
Ta có: OM // NG; OB // CH. Theo định lý Ta-lét, ta có:
OM.ON OM ON NG NC NG . OB OC OC OB NC HC HC Mà NG AN NG//HC HC AH AN AE OM .ON AE NE//HF 2 AH AF OB.OC AF
Từ (1) và (2) suy ra điều phải chứng minh.
Biên soạn: Trần Đình Hoàng 0814000158 12
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 25. Cho hình thang ABCD có đáy lớn CD. Qua A kẻ đường thẳng song song với BC cắt
đường chéo BD tại M và cắt CD tại I. Qua B kẻ đường thẳng song song với AD cắt cạnh CD tại K.
Qua K kẻ đường thẳng song song với BD cắt BC tại P. Chứng minh rằng: MP//DC. Lời giải A B
Tứ giác ABKD có AB // DK; BK //AD nên ABKD là
hình bình hành, suy ra: DK = AB (1) P
Tứ giác ABCI có AB // CI, AI // BC nên ABCI là M
hình bình hành, suy ra: CI=AB (2)
Từ (1) và (2) ta có: DK CI DI KC
Áp dụng định lý Ta-lét vào ABM với AB // DI, ta D C có: BM AB K I . MD DI
Áp dụng định lý Ta-lét vào C
BD với KP // BD, ta có: BP DK hay BP AB . PC KC PC KC Mà AB AB BM BP DI KC
, do đó MP //CD (định lý Ta-lét đảo). DI KC MD PC
Bài 26. Cho tam giác ABC có CM là trung tuyến. Qua điểm Q trên AB vẽ đường thẳng d song
song với CM. Đường thẳng d cắt AC, BC lần lượt tại P, R. Chứng minh rằng nếu QA.QB = QP.QR
thì tam giác ABC vuông tại C. Lời giải A Trong tam giác BQR có CM//QR CM MB Nên
(hệ quả định lý Ta-let) QR QB QR QA CM .MB .MB QB QP M QR QA (do QA.QB QP.QR ). QB QP Q
Mặt khác, trong tam giác ACM có PQ // CM C Nên: QA AM K B QP CM QA Vì CM .MB nên AM CM .MB QP CM 2 2
CM MA.MB AM (vì MA = MB) P CM AM BM . Vậy A BC vuông tại C.
Bài 27. Cho tam giác ABC có trọng tâm G. Một điểm P thuộc cạnh BC. Các đường thẳng qua P
theo thứ tự song song với CG và BG cắt AB, AC lần lượt tại E và F. Gọi giao điểm của BG và CG
với EF lần lượt là I, J. Chứng minh rằng: a) EI = IJ = JF;
b) PG đi qua trung điểm của EF. Lời giải
a) Gọi BM và CN là các đường trung tuyến của tam giác ABC. Gọi giao điểm của BG và EP là H, của CG và FP là T.
Từ HI // PF, EP // CN, theo định lý Ta-let, ta có: EI EH NG 1 EF EP NC 3
Biên soạn: Trần Đình Hoàng 0814000158 13
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Suy ra 1 EI EF A 3 Tương tự ta có: 1 FJ EF. 3 Do đó: 1 EI IJ FJ EF. 3 O M
b) Từ PE // CN, theo định lý Ta-let, ta có: PH CG 2 G . E PE CN 3 I J F
Từ PF // BM, theo định lý Ta-let, ta có: K H O PT BG 2 PH PT T , do đó TH // EF PF BM 3 PE PF B C P (định lý Ta-let đảo).
Gọi O, K là giao điểm của PG với HT và EF. Ta có PHGT là hình bình hành OH OT .
Theo hệ quả định lý Ta-lét, ta có: HO PO OT
. Từ đó suy ra KE = KF, điều phải chứng EK PK KF minh.
Bài 28. Cho hình thang ABCD ( ADđường thẳng d đi qua trung điểm E của CD cắt BD và BC tại M; N. Gọi P; Q là giao điểm của AM; AN với CD. Chứng minh MAD =QAC. Lời giải N
Gọi I là giao điểm của đường thẳng d và AB.
Áp dụng định lý Ta-lét, ta có: DP DE EC NC QC AB//CD AB BI AI NB AB
Do đó DP = QC theo giả thiết AC = AD A DC cân tại A A I B ADP
ACQ ADP ACQ c.g.c Suy ra MAD QAC M D Q E P C
Bài 29. Cho tam giác ABC. M là điểm thuộc BC. Chứng minh rằng: MA.MB MC.AB MB.AC. Lời giải A
Kẻ MN // AB (hình vẽ). Ta có: MN MC MC MN AB. . AB BC BC N NA MB MB NA AC. . AC BC BC
Mà AM MN NA (bất đẳng thức tam giác), Hay MC MB AM AB. AC. BC BC B C
Vậy AM .BC MC.AB MB.AC. M
Biên soạn: Trần Đình Hoàng 0814000158 14
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 30. Cho tam giác nhọn ABC có A 45 , các đường cao BD và CE cắt nhau ở H. Đường
vuông góc với AB tại B cắt AC ở I. Đường vuông góc với AC tại C cắt AB ở K. Gọi F là giao
điểm của BI và CK, G là giao điểm của FH và EI. Chứng minh rằng G là trọng tâm của tam giác AIK. Lời giải A
Tam giác vuông ACK có A 45 nên là tam giác
vuông cân, CE là đường cao nên AE = EK, IE là 45°
đường trung tuyến của A IK.
Ta sẽ chứng minh IG = 2.GE (bằng cách chứng minh FI = 2EH). Ta có: FI CF 2 (vì C IF vuông cân), D
CF = BH (vì BFCH là hình bình hành). E H
BH EH 2 (vì BEH vuông cân) nên FI = 2EH. Do G
EH // FI nên theo định lý Ta-let, ta có: B C IG FI 2 suy ra IG = 2GE. GE EH F
Vậy G là trọng tâm của A IK. I K
Bài 31. Đường thẳng d đi qua trọng tâm G của tam giác ABC cắt cạnh AB tại M, cạnh AC tại N 2 2 2 AB AC BC
và tia CB tại P. Chứng minh rằng: 9 AM .BM AN .CN BP.CP Lời giải A'
Qua A và C kẻ đường thẳng song song với
đường thẳng d, cắt đường thẳng BG lần lượt tại A’ và C’. A Áp dụng ví dụ 4, ta có: AB AC AC BC 3; 3 1 AM AN CN CP N
Vì MN cắt tia CB tại P nên tương tự cách chứng M G minh ví dụ 4, ta có: P C BA BA' BA BC' BA BC B ; 3 2. BM BG BP BG BM BP Từ (1) và (2) suy ra: AB AC AC BC AB BC 9 C' AM AN CN CP BM BP
AB AM MB AC AN NC BC CP BP 2 2 2 AB AC BC 9 9 (đpcm). AM .BM AN .CN BP.CP AM .BM AN .CN BP.CP
Nhận xét. Dựa trên bài toán trên, chúng ta giải được bài toán sau: Đường thẳng d đi qua trọng
tâm G của tam giác đều ABC, cạnh a, cắt cạnh AB tại M, cạnh AC tại N và tia CB tại P. Chứng minh rằng: 1 1 1 9 . 2 AM .BM AN .CN BP.CP a
Bài 32. Cho tam giác ABC với điểm M thuộc miền trong tam giác. Gọi I, J, K thứ tự là giao điểm
của các tia AM, BM, CM với các cạnh BC, CA, AB. Đường thẳng qua M và song song với BC cắt
IK, IJ tại E,F. Chứng minh: ME = MF.
Biên soạn: Trần Đình Hoàng 0814000158 15
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải A
Gọi EF cắt AB, AC tại P, Q. Theo định lý Ta-lét, ta có: MP IB 1 MQ IC J K ME IC M 2 P Q MP BC E F MQ BC 3 MF BI
Từ (1), (2) và (3) nhân vế với vế ta được: B D C MP ME MQ IB IC BC . . . . MQ MP MF IC BC IB ME 1 hay ME = MF. MF
Chủ đề 2. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC
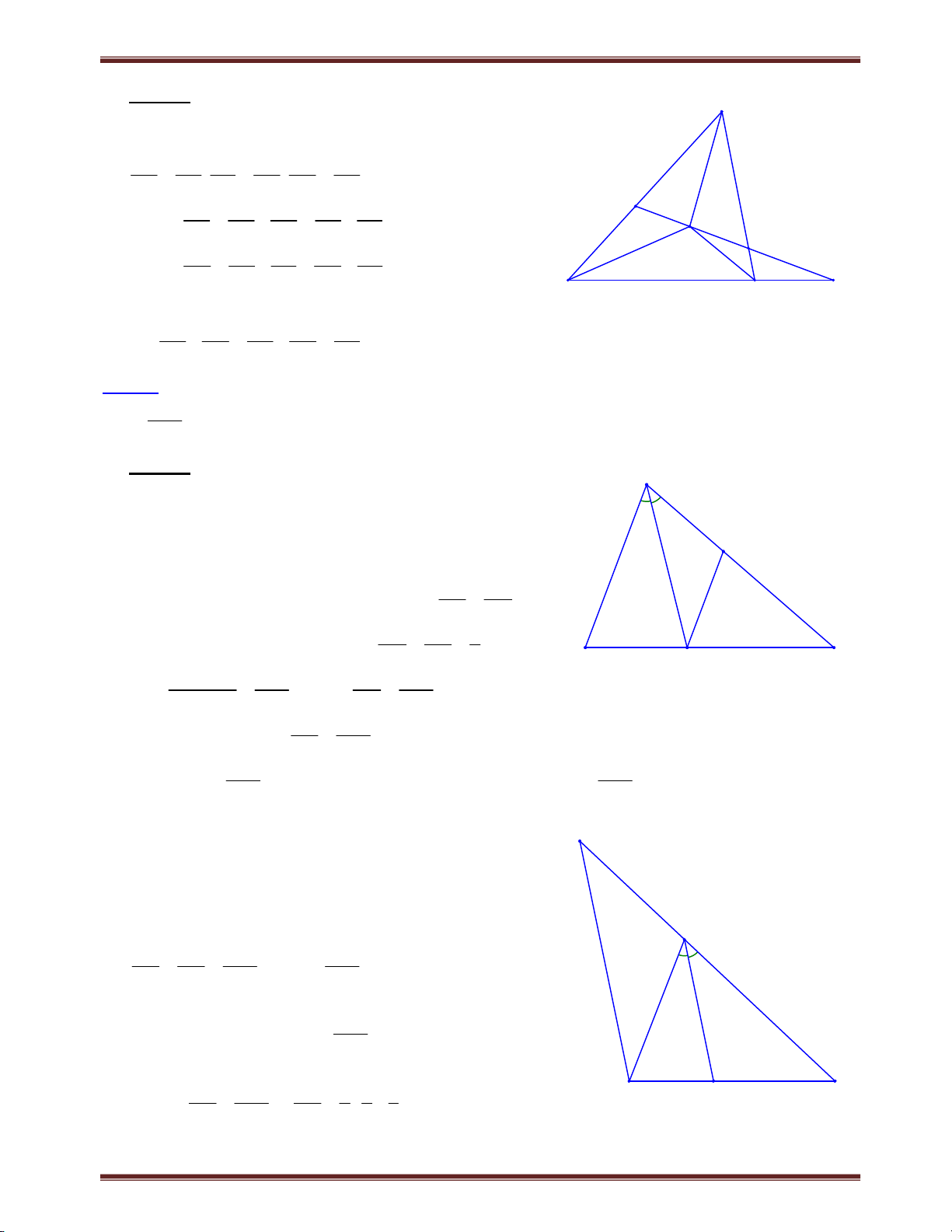
Bài 2.1 Cho tam giác ABC , trung tuyến BM cắt phân giác CD tại P . Chứng minh rằng: PC AC 1. PD BC Lời giải A PC AC PC AC
Dựa vào định ý Ta-lét: 1 1. PD BC PD BC K
CD là phân giác của ABC nên D M DA AC DA AC AB AC 1 1 1 DB BC DB BC DB BC P
Vì vậy chỉ cần chứng minh: PC AB . PD DB B C
Cách 1. Vẽ DK // BM ( K thuộc AM ), theo định lý A Ta-lét, ta có: PC MC MA AB . PD MK MK DB Cách 2.
Vẽ DI // AC ( I thuộc BM ), D M
Theo định lý Ta-lét, ta có: P PC MC MA AB . I PD DI DI DB B C Cách 3.
Vẽ AN // BM ( N thuộc tia CD ) A Do MA MC suy ra PC PN PC PN PD PD N M Mặt khác ND DA (do AN // BP ), D PD DB P Suy ra PN ND DA AB 1 1 PC AB PD PD DB DB PD DB B C
Biên soạn: Trần Đình Hoàng 0814000158 16
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Cách 4.
Vẽ AH // CD ( H thuộc tia BM ), A E Ta có: A MH C MP .cg.c PC AH Suy ra M PC AH . D PD PD
Mặt khác, do PD // AH nên theo hệ quả định lý P AH AB PC AB Ta-lét, ta có: . B C PD DB PD DB Cách 5.
Trên tia đối cỉa tia MB , lấy điểm E sao cho A
MB ME . Suy ra ABCE là hình bình hành.
Suy ra AB // CE và AB CE . H
Theo hệ quả của định lý Ta-lét, ta có: D M PC CE AB . PD BP DB P B C
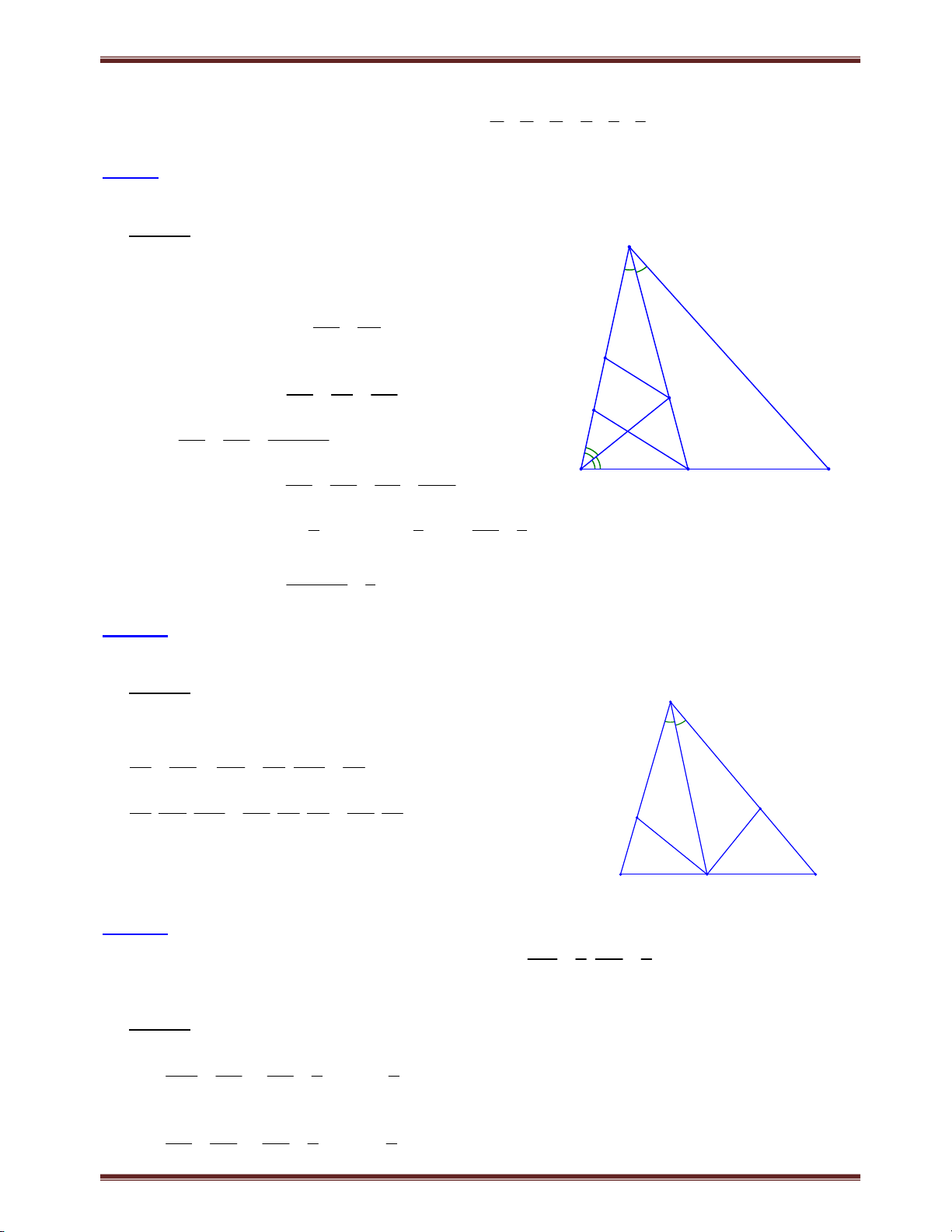
Bài 2.2 Cho ABC cân tại A và A 36 . Chứng minh rằng: 2 2 AB A . B BC BC Lời giải A
Tìm cách giải. Phân tích đề bài, chúng ta thu được
B C 72 , nhận thấy 72 2.36 do đó chúng ta nên kẻ
phân giác góc B (hoặc góc C ) là suy luận tự nhiên. Từ đó
vận dụng tính chất dường phân giác trong tam giác và biển
đổi linh hoạt tỉ lệ thức ta được lời giải hay. Trình bày lời giải. Kẻ phân giác BD của
ABC D AC , khi đó B B 36 1 2 D
ABD cân tại D và BCD cân tại B AD BC B . D
Theo tính chất đường phân giác trong tam giác ABC , ta có: BA AD BA BC BC CD BC AC AD BA BC 1 Mà AB AC; AD BC nên 2 BC BA BC B C 2 BA BA BC BC 2 2 2 2 BA B . A BC BC AB A . B BC BC .
Nhận xét. Tương tự chúng ta giải được bày toán sau: Cho ABC cân tại A và A 108 . Chứng minh rằng: 2 2 AB BC A . B BC..
Bài 2.3 Cho tam giác ABC có trọng tâm G và I là giao điểm của ba đường phân giác trong. Biết
rằng IG // BC . Chứng minh rằng: AB AC 2.BC. Lời giải
Tìm cách giải. Nhận thấy để khai thác IG // BC chúng ta nên kẻ đường phân giác góc A và
trung tuyến ứng với cạnh BC thì sẽ vận dụng được giả thiết đó.
Từ suy luận đó chúng ta có kết quả AI 2 . Mặt khác, tỉ số AI , kết hợp với I là giao điểm ID ID
Biên soạn: Trần Đình Hoàng 0814000158 17
Chuyên đề bồi dưỡng học sinh giỏi toán 8
của ba đường phân giác trong cho phép chúng ta liên tưởng tới khả năng vận dụng tính chất
đường phân giác trong tam giác ABD, ACD . Từ đó chúng ta có lời giải sau: Trình bày lời giải A
Gọi D, M lần lượt là giao điểm của AI, AG với BC .
Theo tính chất đường phân giác trong tam giác ABD, ACD , ta có: IA AB CA AB AC AB AC ID BD CD BD CD BC IA GA AB AC IG // BC 2 2 I G ID GM BC Hay AB AC 2BC .
Nhận xét. Với kỹ thuật và lối tư duy trên, chúng ta B D M C
có thể giải được bài toán đảo: Cho tam giác ABC có
trọng tâm G và I là giao điểm ba đường phân giác
trong. Biết rằng AB AC 2.BC . Chứng minh rằng: IG // BC .
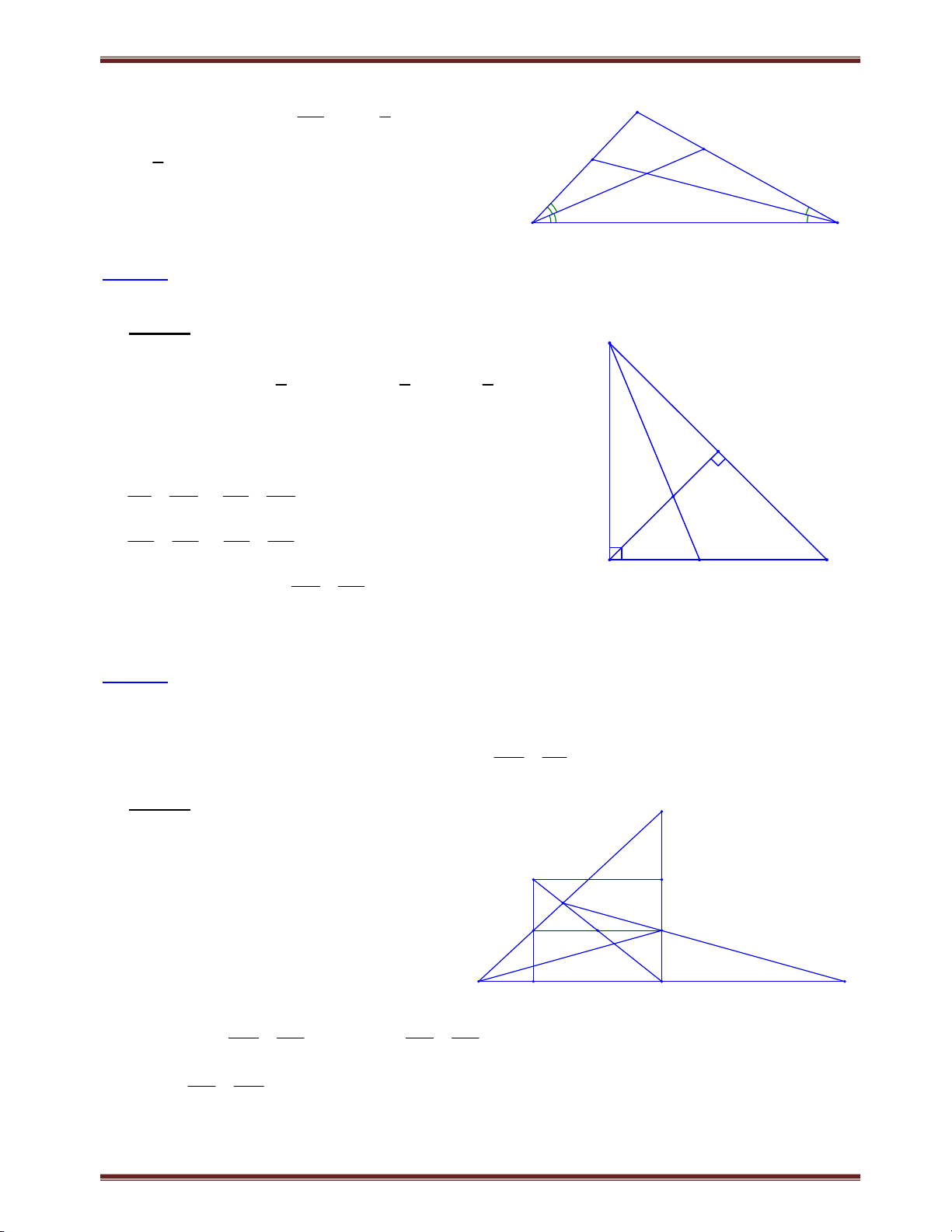
Bài 2.4 Cho tam giác ABC có tỉ số giữa hai cạnh chung đỉnh A là 3:2. Vẽ đường trung tuyến AM
và đường phân giác AK . Tính tỉ số diện tích của hai tam giác AKM và AKB . Lời giải A
Trường hợp 1. Xét AB 3 . AC 2 Chú ý rẳng: KB KC KM và KC AC 2 KB AB S KM KB KC 1 KC Ta có: AKM 1 S KB 2KB 2 KB AKB C K M B 1 AC 1 2 1 1 1 2 AB 2 3 6
Trường hợp 2. Xét AC 3 . A AB 2 Chú ý rẳng KC KB KM và KC AC 2 KB AB S KM KC KB 1 KC Ta có: AKM 1 S KB 2KB 2 KB AKB 1 AC 1 2 1 1 1 B K M C 2 AB 2 3 4
Nhận xét. Bài này dễ bỏ sót trường hợp.
Bài 2.5 Cho tam giác ABC có BE và CF là hai đường phân giác cắt nhau tại O . Chứng minh rằng nếu 1 .
OB OC BE.CF thì ABC vuông tại A . 2
Tìm cách giải. Với giả thiết 1 .
OB OC BE.CF và chứng minh ABC vuông tại A , dễ dàng 2
nhận thấy từ mối quan hệ về độ dài mà chứng minh tam giác vuông, tất yếu chúng ta nghĩ tới
định lý Py-ta-go đảo. Do đó chúng ta cần biểu diễn 1 .
OB OC BE.CF thông qua các cạnh của 2
tam giác ABC . Định hướng cuối cùng là 2 2 2 a b c .
Biên soạn: Trần Đình Hoàng 0814000158 18
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Trình bày lời giải. A
Đặt BC a, AC b, AB . c
Theo tính chất đường phân giác, ta có: BF BC BF BC FA AC BF FA BC AC E BF a ac F BF . c a b a b O OF BF c OF OC a b c CF a b c . OC BC a b OC a b OC a b Tương tự, ta có: BE a b c . B C OB a c 1 BE.CF a b c2 Từ giả thiết O . B OC BE.CF 2 OB OC a ca b 2 2 . 2 2 2 2
a b c 2ab 2ac 2bc 2a 2ab 2ac 2bc 2 2 2 a b c
suy ra ABC vuông tại A .
Bài 2.6 Cho tam giác ABC vuông tại A có G là trọng tâm, BM là đường phân giác. Biết rằng
GM AC . Chứng minh rằng BM vuông góc với trung tuyến AD . Lời giải B
Cách 1. (Không dùng tính chất đường phân giác). Gọi
I là giao điểm của BM và AD, H là trung điểm 1
AC DH // AB và DH AB (vì DH là đường trung 2 D bình ABC ). G
Lại có GM // AB (cùng vuông góc với AC ) I
GM // DH . Áp dụng hệ quả định lý ta-lét: Xét A DH có GM // DH A M H C GM AG 2 GM 2 . DH AD 3 DH 3 Xét GI GM GH ABI có 1 GM // AB AI AB BH 3 GI AI A 3 3 3 2 AD
AI .AG . .AD AI
I là trung điểm của AD . AI 3 4 4 3 2
ABD có BI vừa là đường phân giác, vừa là đường trung tuyến, suy ra A BD cân tại B nên
BI vừa là đường cao vừa là đường phân giác. Do đó BM AD . Cách 2. AM AG ADH có 2 GM // DH
3.AM 2.AH AC AM MC AH AD 3 hay MC 2.AM .
Áp dụng tính chất đường phân giác trong BC MC BC ABC , ta có: 2 AB B . D AB MA 2
Vậy ABD cân tại B nên BI vừa là phân giác vừa là đường cao. Do đó BM AD
Bài 2.7 Cho tam giác ABC có I là giao điểm của ba đường phân giác. Đường thẳng qua I cắt các đường thẳng BC,C ,
A AB lần lượt tại D, E, F sao cho D, E nằm cùng phía đối với điểm I . Chứng minh rằng: BC AC AB . ID IE IF
Biên soạn: Trần Đình Hoàng 0814000158 19
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải A
Áp dụng tính chất đường phân giác trong và ngoài của tam giác, ta có: BD BF CE CD AF AE ; ; ID IF IE ID IF IE F Ta có: BC BD CD BF CE (1) ID ID ID IF IE I E AC AE CE AF CE Ta có: (2) IE IE IE IF IE B
Từ (1) và (2) cộng vế với vế, suy ra: C D BC AC BF AF AB . ID IE IF IF IF
Bài 2.8 Cho tam giác ABC , đường phân giác AD . Đặt AC b, AB c . Chứng minh rằng 2bc AD . b c Lời giải A
Cách 1. Qua D kẻ đường thẳng song song với AB , cắt AC ở E . 2 1 Ta có : D A A nên AE DE . 1 1 2 E Ta tính DE theo b và c .
Do DE // AB nên theo định lý Ta-lét thì DE DC (1). AB BC 1
Theo tính chất đường phân giác DC AC b DB AB c B C D Nên DC b tức là: DC b (2) DC DB b c BC b c Từ (1) và (2) suy ra: DE b . c b c Do đó bc bc DE . Tam giác ADE có 2 AD AE DE 2DE . b c b c
Cách 2. (không dùng tính chất đường phân giác).
Qua B kẻ đường thẳng song song với AD , cắt đường K thẳng AC ở K . Ta có: K A ; B A K B 1 2 1 2 1 1
ABK cân tại K , nên AK AB . c
Do BK // AD nên theo định lý Ta-lét thì A AD AC b b AD .BK (1) 1 2 BK KC b c b c
Tam giác ABK có BK AB AK 2c (2) Từ (1) và (2) suy ra: 2bc AD . b c 1
Nhận xét. Từ kết luận bài toàn, suy ra: 1 b c 1 1 1 1 B C . D AD 2bc AD 2 b c
Tương tự như vậy đối với đường phân giác góc B và góc C , thì chúng ta giải được bài toán
Biên soạn: Trần Đình Hoàng 0814000158 20
Chuyên đề bồi dưỡng học sinh giỏi toán 8
hay và khó sau: Cho tam giác ABC . Gọi l ,l ,l là độ dài đường phân giác góc , A B,C . a b c
Đặt BC a, AC b , AB c . Chứng minh rằng: 1 1 1 1 1 1 . l l l a b c a b c
Bài 2.9 Cho ABC có AD là đường phân giác, I là giao điểm của ba đường phân giác và K là
trung điểm của AB . Biết rằng
KIB 90 . Chứng minh rằng: AB AC 3BC. Lời giải A
Trên BA lấy điểm E sao cho BE BD
Ta có: BDE cân tại B có BI là đường phân giác nên BI BE do đó KE DI DE // KI BI (1) KA AI
Áp dụng tính chất đường phân giác trong K A
BD, ACD ta có : BD ID CD (2) I BA IA CA E Do đó BD CD BC (3) BA CA BA CA Từ (1) và (2) suy ra: KE BD BE BE B D C KA BA BA 2.KA Hay BD 2KE 2 1 1
BE BE BK BD BA (4) 3 3 BA 3 Từ (3) và (4) suy ra: BC 1 AB AC 3.BC. BA CA 3
Bài 2.10 Gọi AI là đường phân giác của tam giác ABC; IM , IN thứ tự là các đường phân giác của
góc AIC và góc AIB . Chứng minh rằng: AN.BI.CM BN.IC.AM Lời giải A
Áp dụng tính chất đường phân giác vào các tam giác ABC, ABI, AIC : BI AB AN AI CM IC ; ; IC AC NB BI MA AI BI AN CM AB AI IC AB IC M . . . . . 1 N IC NB MA AC BI AI AC BI BI.AN.CM BN.IC.AM B D C
Bài 2.11 Cho tam giác ABC có chu vi bằng 18cm . Đường phân giác của góc B cắt AC tại M ,
đường phân giác của góc MA NA
C cắt AB tại N . Biết rẳng: 1 3 ;
. Tính độ dài các cạnh của MC 2 NC 4 tam giác ABC . Lời giải
Xét ABC có BC là đường phân giác của ABC nên: AM AB AB 1 1 AB BC. MC BC BC 2 2
Gọi CN là đường phân giác của ACB , suy ra: NA AC AC 3 3 AC .BC NB BC BC 4 4
Biên soạn: Trần Đình Hoàng 0814000158 21
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Ta có: BC 3 A AB BC AC 18 BC BC 18 2 4 9 M
.BC 18 BC 8cm N 4
Từ đó ta tính được AB 4cm; AC 6cm B C
Bài 2.12 Cho ABC vuông cân tại A . Đường cao AH và đường phân giác BE cắt nhau tại I .
Chứng minh rằng: CE 2.HI Lời giải B Ta có: AIE BAH 1 ABI A B 1 1 45 B 45 C AEI 2 2 2
Suy ra AIE cân tại A AI AE (1).
Áp dụng tính chất đường phân giác của ABH và BAC , H ta có: IH BH AB BH (2) IA BA AI IH I EC BC AB BC (3) EA BA AE EC BH BC A C Từ (2) và (3) suy ra : (4) E IH EC
Vì ABC vuông cân tại v nên BC 2.BH .
Từ đó kết hợp với (4), suy ra EC 2.IH .
Bài 2.13 Cho hình chữ nhật ABCD . Gọi M là trung điểm AD, N là trung điểm BC . Trên tia đối
của tia DC lấy điểm P , đường thẳng PM cắt AC tại Q và cắt BC tại S . Đường thẳng QN cắt
DC tại R . Chứng minh rằng: MQ SQ a) NPR là tam giác cân. b) . MP SP Lời giải S
a) Ta có: CN // DM ;CN DM và
NCD 90 nên CDMN là hình chữ nhật A MN // CD B
Gọi O là giao điểm của AC và MN . Q AOM và CON có: M N AM CN; AMO CNO 90 ; MAO NCO O A MO C
NO .cg.c MO ON.
Áp dụng hệ quả định lý Ta-lét, ta có: P D C R MO QO NO QO MO // CP , NO // CR CP QC CR QC Suy ra NO MO
mà MO NO suy ra CR CP . CR CP
NRP có NC PR,CR CP nên NRP cân. b) MN // RP nên QNM NRP, MNP NPR
Biên soạn: Trần Đình Hoàng 0814000158 22
Chuyên đề bồi dưỡng học sinh giỏi toán 8 mà NRP NPR QNM
MNP NM là tia phân giác QNP .
Ta có: NS MN nên NS là tia phân giác góc ngoài đỉnh N của PNQ .
Áp dụng tính chất đường phân giác trong và ngoài của NPQ , MQ NQ SQ NQ MQ SQ ta có: ; . MP NP SP NP MP SP
Bài 2.14 Cho ABC có AM .BN.CP là các đường phân giác. Đặt BC a; AC ; b AB c . Chứng S 2abc minh rằng: MNP S a b b c c a ABC . Lời giải A
Theo tính chất đường phân giác của ABC , ta có: AN AB AN AB NC BC NC AN BC AB AN c bc N AN . P b c a c a Tương tự, ta có: bc AP . b a S AN.AP bc Mặt khác: ANP (1) S A . B AC a b a c B M C ABC S ac Tương tự: BMP (2) S a b b c ABC S ab và CMN (3) S a c b c ABC S S S S
Từ (1), (2) và (3) ta có: MNP 1 ANP BMP CMN S S S S ABC ABC ABC ABC bc ac ab 1
a ba c a bb c a cb c
a ba cb c bcb c aca c aba b S 2abc MNP .
a ba cb c S a b a c b c ABC Bài 2.15 Cho A BC có AB 4c ; m BC 6c ;
m CA 8cm . Gọi I là giao điểm ba đường phân giác
của tam giác ABC và G là trọng tâm. Tính độ dài đoạn thẳng IG . Lời giải A
Gọi D, M lần lượt là giao điểm của AI, AG với BC .
Áp dụng tính chất đường phân giác trong tam giác ABD , ta có: BD AB BD AB . I G CD AC BD CD AB AC BD 4 6.4 BD 2c . m 6 4 8 12 D M C B ID BD ID 2 1 . IA AB IA 4 2
Biên soạn: Trần Đình Hoàng 0814000158 23
Chuyên đề bồi dưỡng học sinh giỏi toán 8 GM 1
Mặt khác G là trọng tâm A BC . AG 2 ID GM 1 IG // DM
(theo định lý Ta-lét đảo) IA GA 2 IG AG IG 2 2 2 2 2
IG DM . IG .BM BD .3 2 cm . DM AM DM 3 3 3 3 3
Bài 2.16 Cho hình bình hành ABCD AD AB các điểm M , N lần lượt thuộc AB, AD sao cho
BM DN . Gọi O là giao điểm của BN và DM . Đường thẳng CO cắt đường thẳng AB và AD
theo thứ tự là I và K . Chứng minh rằng: CD DK; BI BC Lời giải K
Gọi E là giao điểm của đường thẳng BN và CD BM BO BM // DE nên I M A B ED OE mà BM DN nên BO DN (1) O OE ED N DN BC Ta có DN // BC nên (2) ED CE E D C Từ (1) và (2) suy ra BO BC OE CE
CO là đường phân giác BCD DKC DCK BCK C
DK cân tại D CD DK BIC DCI ICD B
CI cân tại B BI BC.
Bài 2.17 Cho tam giác ABC vuông tại A . Có đường cao B
AH , đường trung tuyến BM và đường phân giác CD đồng BC BH
quy tại O . Chứng minh rằng: . AC CH Lời giải
Kẻ MI HC vì AH HC nên MI // AH .
Mặt khác MA MC nên HI CI 2.HI CH . H
Áp dụng tính chất đường phân giác và định lý ta-lét, ta có: D BH BH BO BC BC . I CH 2.HI 2.OM 2.CM AC O A M C
Bài 2.18 Cho tam giác ABC vuông tại A . Hai đường phân giác BD và CE cắt nhau ở O . Biết số
đo diện tích tam giác BOC bằng a . Tính tích B . D CE theo a . Lời giải Đặt BC ; x CA y; AB z .
Theo tính chất đường phân giác của ABC , ta có: DA AB z DA z yz DA (1) DC BC x DA DC z x z x AO là phân giác BAD nên
Biên soạn: Trần Đình Hoàng 0814000158 24
Chuyên đề bồi dưỡng học sinh giỏi toán 8 OB AB OB AB (2) OD DA OB OD AB DA B Từ (1) và (2) suy ra: OB x z BD x y z OC x y Tương tự . Từ đó CE x y z O . B OC x yx z 2 O . B OC x xy xz yz 1 H B . D CE x y z2 B . D CE 2 2 x xy yz zx 2 E O 2 O . B OC x xy xz yz 1 Vì 2 2 2 y z x nên B . D CE 2 2 x xy yz zx 2 hay C B . D CE 2.O . B OC (3) A D
Để ý rằng nếu kẻ BH OC , mặt khác dễ thấy
BOC 135 , nên BHO vuông cân tại H . 1 2 Do đó S BH.OC O . B OC , suy ra . OB OC 2a 2 (4) BOC 2 4 Từ (3) và (4) suy ra: . B . D CE 4a 2
Bài 2.19 Cho tam giác ABC có BAC 3
ACB . Các điểm D , E thuộc cạnh BC sao cho BAD DAE
EAC . Gọi M là điểm thuộc cạnh AB, MC cắt AE tại L ; gọi K là giao điểm ME và
AD . Chứng minh rằng KL // BC. Lời giải A
Trên AE lấy điểm N sao cho MN // BC . Từ giả thiết EAC ECA EAC cân tại E M N AE = EC (1) L Cũng theo giả thiết K AEB EAC ECA 2. ECA EAB B AE B D E C
cân tại B MAN cân tại M (vì MN // BE ) AM NM (2) Vậy ta có LM NM (vì MN // EC ) AM (theo (1) và (2)) KM (theo tính chất đường LC EC AE KE phân giác)
Suy ra KL // BC (định lý Ta-lét đảo)
Bài 2.20 Cho tam giác ABC với đường trung tuyến CM . Điểm D thuộc đoạn BM sao cho
BD 2.MD . Biết rằng MCD
BCD . Chứng minh rằng: ACD là tam giác vuông. Lời giải P A
BCM có CD là đường phân giác nên BC BD 2 BC 2.CM CM MD M
Trên tia đối của tia MC lấy điểm P sao cho D MC MP suy ra CP 2.CM CP BC C BP cân tại C ,
mà CD là phân giác nên CD BP (1) B C Mặt khác: CMA P MB .cg.c.
Biên soạn: Trần Đình Hoàng 0814000158 25
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Do đó CAM PBM suy ra AC // BP (2)
Từ (1) và (2), ta có: CD AC hay ACD vuông tại C .
Chủ đề 3. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC
Bài 1. Cho tứ giác lồi ABCD có BAC CAD và ABC
ACD . Hai tia AD và BC cắt nhau tại E. Chứng minh rằng A . B DE BC.CE . Tìm cách giải. B
Để chứng minh đẳng thức tích, thông thường chúng ta
biến đổi chúng dưới dạng tỉ lệ thức và chứng minh tỉ lệ
thức ấy. Vậy để chứng minh A . B DE BC.CE chúng ta C cần chứng minh AB CE
. Nhận thấy tỉ số AB có thể BC DE BC
vận dụng được tính chất đường phân giác và ta có AB AE
. Do vậy chúng ta cần chứng minh CE AE . BC CE DE CE A D E
Từ đó chúng ta tìm cách chứng minh CDE ” ECA , vậy chỉ cần chứng minh ECD BAC là xong. Trình bày lới giải Vì BAC CBA
ECA (góc ngoài tam giác) và ABC ACD nên ECD BAC
Do đó CDE ” ECA , suy ra CE AE (1) DE CE AE AB
Trong ABE có AC là đường phân giác suy ra (2) CE BC Từ (1) và (2) suy ra AB CE A . B DE BC.CE BC DE
Bài 2. Cho tam giác ABC vuông tại A có điểm D nằm giữa A và C. Qua C dựng CE vuông góc với
đường thẳng BD tại E. Chứng minh: a) ADE ” BDA b) A . B CE AE.BC AC.BE Tìm cách giải. M ADE và BDA có ADE
BDC ; để tìm một cặp góc nữa
bằng nhau thật khó khăn. Do đó chúng ta tìm cách chứng
minh cặp góc trên tỉ lệ thông qua hai tam giác khác. Chẳng DA DE hạn cần có chúng ta nên chứng minh A DB DC E ABD ” E CD - Để chứng minh A .
B CE AE.BC AC.BE , ta có vế trái là D
một tổng nên vế phải ta cần tách thành một tổng: F
AC.BE AC.x AC.y với x y BE . Do vậy ta chọn B C
điểm F thuộc BD khi đó x BF , y FE và chứng minh A . B CD AC.BF , A .
D BC AC.FE . Từ đó chúng ta chỉ cần chọn điểm F sao cho ABF ” A CE, A FE ” A BC , là xong. Trình bày lời giải
Biên soạn: Trần Đình Hoàng 0814000158 26
Chuyên đề bồi dưỡng học sinh giỏi toán 8
a) Xét ABDvà ECD có ADB EDC ; BAD CED 90 (gt) DA DE Do đó: A BD ” E CD DB DC DA DE Xét ADE và BDA có ADE BDC ;
. Do đó ADE BDA (c.g.c) DB DC
b) Cách 1. Gọi M là giao điểm AB và CE. Xét M BE và M CA, ta có M chung; MEB MAC 0 90 Do đó M BE M CA (g.g) MB MC ME MA Xét M AE và M CB có MB MC , M chung M AE M CB (c.g.c) MEA MBC ME MA
Lấy F BE sao cho AF AE . Xét A BF và ACE có: BAF CAE 90 DAF ; ABF ACE 90 M AB BF Do đó: A BF ACE A . B CE A . C BF (1) AC CE Xét AFE và ABC có: EAF BAC 90 ; AEF
ACB (cùng phụ với hai góc bằng nhau) AE EF
Do đó: AFE ABC AE.BC A . C EF (2) AC BC
Từ (1) và (2) cộng vế với vế ta được: A .
B CE AE.BC AC BF EF AC.BE
Cách 2. Gọi J là điểm trên cạnh AC sao cho A ABJ EBC . E Xét ABJ và EBC có: J BAC BEC 90 ; ABJ EBC D
Do đó: ABJ EBC (g.g) AB AJ A . B CE BE.AJ (3) B C BE CE Xét A BE và JBC có: ABE JBC ; AEB JCB AE BE Do đó: A BE JBC AE.BC BE.JC (4) JC BC
Từ (3) và (4) cộng vế với vế ta được: A .
B CE AE.BC BE AJ JC BE.AC
Bài 3. Cho tam giác ABC có AB 2 cm; AC 3 cm; BC 4 cm. Chứng minh rằng BAC ABC 2. ACB Tìm cách giải. A
Về mặt suy luận, muốn chứng minh một góc BAC
thành tổng các góc như đề bài. Ta có hai cách suy nghĩ: Cách 1: trong góc BAC dựng một góc BAD hoặc C DAC bằng góc
ABC và chứng minh phần còn lại B D bằng 2.
ACB . Tuy nhiên cách này vẫn gặp khó khăn bởi còn hệ số 2.
Biên soạn: Trần Đình Hoàng 0814000158 27
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Cách 2: trong góc BAC dựng một góc BAD bằng góc
ACB và chứng minh phần còn lại bằng DAC ABC
ACB . Cách này có tính khả thi. Thật vậy, ta viết BAC ABC ACB ACB nên
nếu lấy điểm D trên cạnh BC sao cho BAD
ACB , thì dễ dàng nhận thấy ADC ACB ABC
nên chúng ta chỉ cần chứng minh tam giác ACD cân tại C là xong.
Với suy luận như trên, chúng ta có hai cách trình bày sau: Trình bày lời giải
Cách 1. Trên đoạn thẳng BC lấy điểm D sao cho BAD ACB suy ra ABD ” C BA (g.g) BD AB BD 2 Suy ra
BD 1 cm CD BC BD 3 cm BA CB 2 4
CD AC nên ACD cân tại C, do vậy DAC ADC . Mà ADC ABC
BAD (tính chất góc ngoài tam giác). Suy ra: BAC BAD DAC ACB ADC ACB ABC BAD Do đó BAC ACB 2. ACB .
Cách 2. Trên đoạn thẳng BC lấy điểm D sao cho BD 1cm
CD BC BD 3 cm CD AC nên ACD cân tại C Do vậy DAC ADC (1) Xét A BD và BD AB CBA có ABD chung và 1 . BA CB 2
Suy ra ABD CBA (c.g.c) BAD BCA (2) Từ (1) và (2) ta có: BAC BAD DAC ACB ADC ACB ABC BAD Do đó BAC ABC 2. ACB .
Bài 4. Cho tam giác ABC ( AB AC ) có góc ở đỉnh bằng 20o; cạnh đáy BC a ; cạnh bên AB b . Chứng minh rằng 3 3 2 a b 3ab . Lời giải A
Cách 1. Dựng tia Bx ở nửa mặt phẳng bờ BC có chứa điểm A sao cho
CBx 20 ; tia Bx cắt AC ở D; kẻ AH Bx . Tam
giác ABC cân tại A, ta có: 20°
A 20 B C 80 ABH ABC
CBx 80 20 60 AB b Suy ra ABH có ABH 60 ; AHB 90 BH . 2 2 Ta có: 2 2 2
AH AB BH (định lý Py-ta-go) 2 2 b 3b 2 2 AH b 4 4 BDC có BCD 80 ; CBD 20 BDC 80
BCDcân tại B BD BC a , x Do đó b DH BH BD a . H 2 D BC AC Nhận thấy: A BC ” BDC (g.g) CD BC B C 2 2 BC a a CD
, mà AD AC CD b AC b b 2 2 Và 3b b 2 2 2 2 2 AD AH DH a b ab a . 4 2
Biên soạn: Trần Đình Hoàng 0814000158 28
Chuyên đề bồi dưỡng học sinh giỏi toán 8 2 2 Vậy a 2 2 4 4 2 2 4 3 2 2 b
b ab a b a 2a b b ab a b b a 3 3 a b 2 2 3 3 2 3a b a b 3ab Cách 2. A
Dựng tam giác ABE đều sao cho E và C nằm cùng phía so với AB.
Dựng ACD cân tại A sao cho D; E nằm cùng phía với AC 20° và 0 CAD 20 A BC A CD A DE ( . c g.c)
Gọi F và G là giao điểm của BE với AD AC. Khi đó BG EF a . Vì ABE 60 nên CBG BAC CBE 20 và CBG cân tại B. BA C ” C BG (g.g) E F 2 BC CG a CG a hay CG G D AC GB b A b 2 a B C
Ta có: AG AC CG b b
Ta có: FG / /CD nên theo định lý Ta-lét, ta có: 2 a b 2 3 GF AG GF b ab a GF 2 CD AC a b b 2 3 ab a Mà BE BG GF FE 3 2 2 3 b 2a b 2ab ab a 3 3 2 a b 3ab 2 b
Bài 5. Cho hình thoi ABCD có A 60 . Gọi M là một cạnh thuộc cạnh AD. Đường thẳng CM cắt đường thẳng AB tại N. a) Chứng minh 2 AB DM .BN ;
b) BM cắt DN tại P. Tính góc BPD . Lời giải B C
a) Ta có: AM / /BC (do AD / /BC ), NA NB suy ra: N AM ” N BC AM BC hay NA NB (1) (vì BC AB ). AM AB A
Ta có: NA / / DC (do AB/ / DC ), D M NA CD suy ra N AM ” C DM AM DM P Hay NA AB (2) (vì CD AB ). AM DM N Từ (1) và (2) suy ra: NA AB hay 2 AB DM .BN . AB DM b) Từ NB AB NB BD AB DM BD DM Xét BN D và DB M có NB BD và NBD BDM 60 BD DM Suy ra BN D DB M (c.g.c) MBD BND MBD MBN BND MBN 60
Biên soạn: Trần Đình Hoàng 0814000158 29
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Mà BPD BND MBN nên BPD 60
Nhận xét. Với kỹ thuật như trên, bạn có thể giải bài toán sau. Cho hình thoi ABCD có
A 60 vẽ đường thẳng qua C cắt tia đối của tia BA tại M và cắt tia đối của tia DA tại N. Gọi
K là giao điểm của DM và BN. Tính số đo MKB .
Bài 6. Cho ABC cân tại A. Lấy M tùy ý thuộc BC, kẻ MN song song với AB (với N AC ), kẻ
MP song song với AC (với P AB ). Gọi O là giao điểm của BN và CP. Chứng minh rằng OMP AMN . Tìm cách giải. A Nhận thấy BPM MNC QPM ANM Do đó OMP AMN Q PM ” A NM
Mặt khác chúng ta thấy QPM và A NM khó có thể tìm
thêm được một cặp góc nữa bằng nhau. Do vậy chúng ta Q N
nên tìm cách biến đổi thêm hai cặp cạnh kề với hai góc OMP ; AMN tỉ lệ là xong. P Trình bày lời giải O
Giả sử MB MC . Gọi Q là giao điểm MO và AB; K là R giao điểm CP và MN.
Vì MNAP là hình bình hành nên QPM ANM (1)
Vì ABC cân tại A nên suy ra P BM cân tại P và B C M NCM cân tại N.
Do đó PB PM AN và NC NM AP kết hợp với MN / / AP suy ra: PQ PQ KM PB NA (2) PM PB KN PA NM
Từ (1) và (2) suy ra: QPM ” ANM ( . c g.c) QMP AMN hay OMP AMN (đpcm)
Bài 7. Cho tam giác ABC có AB 2 cm, AC 3 cm và BC 2,5 cm. Chứng minh rằng B 2. C . Tìm cách giải. A
Để chứng minh B 2.
C , chúng ta cũng có hai hướng sau:
- Cách 1. Dựng phân giác BD và chứng tỏ ABD C .
- Cách 2. Từ đỉnh C dựng thêm một góc bằng góc B và D
chứng minh cặp góc bằng nhau.
Vì bài toán biết khá nhiều độ dài đoạn thẳng nên chúng ta
chứng minh cặp góc bằng nhau bằng cách chứng minh hai
tam giác đồng dạng theo trường hợp cạnh-góc-cạnh. B C Trình bày lời giải Cách 1. AB 2 3 AC 3 AC AB Ta có: , suy ra . AD 4 2 AB 2 AB AD 3
Biên soạn: Trần Đình Hoàng 0814000158 30
Chuyên đề bồi dưỡng học sinh giỏi toán 8 AC AB
Xét ABC và ADB có A chung, A AB AD Do đó ABC A DB (c.g.c) Do đó: ACB ABD , vậy ABC 2. C . Cách 2.
Trên tia đối tia BA lấy điểm E sao cho BE BC suy ra: ABC 2. BEC 2. BCE B C Ta có AB 2 ; AC 3 2 suy ra AC AB . AC 3 AE 2 2,5 3 AE AC AC AB
Xét ABC và ACE có A chung, AE AC
Do đó: ABC ACE (c.g.c) do đó ACE ABC suy ra ACE 2. BCE ACB BCE Hay ABC 2. ACB . E
Bài 8. Cho tam giác ABC có A 90 và B 20 . Các điểm E và F lần lượt nằm trên các cạnh AC và AB sao cho ABE 10 và ACF 30 . Tính CFE .
(Thi Olympic Toán quốc tế Đài Loan TAIMC, năm 2012) Tìm cách giải. A
Những bài toán tính số đo góc thường khó, F G
trước hết chúng ta nên vẽ hình chính xác, E
sau đó phân tích giả thiết để dự đoán kỹ
thuật kẻ thêm yếu tố phụ. Trong giả thiết 300 chúng ta nhận thấy
ACF 30 FC 2.AF . B D C Từ B 20 C 70 , khi đó
BCF 40 , chúng ta có liên tưởng gì góc 40o này với góc 20o
và 30o ở đề bài không? Với suy nghĩ ấy, chúng ta lấy điểm G trên AB sao cho BCG 20 khi
đó bài toàn tạo nên những yếu tố mới: CF là phân giác góc ACG, tam giác BCG cân tại G. Với
hình vẽ chính xác, chúng ta hoàn toàn có thể dự đoán được CG song song với FE. Từ đó định
hướng để chứng minh dự đoán ấy bằng định lý Ta-lét đảo. Trình bày lời giải
Xét ABC có A 90 và B 20 C 70
ACF có A 90 và
ACF 30 FC 2.AF .
Gọi D là trung điểm của BC và G là điểm trên AB sao cho GD vuông góc với BC. BD BA Do đó ABC ” DBG ; GCB GBC 20 GCF 20 BG BC
Mặt khác CG và BE lần lượt là tia phân giác của BCF và ABC nên FC BC ; BA AE FG BG BC EC 1 1 FC BC AF BD BA AE AF AE Do đó: 2 2 FG FG BG BG BC EC FG EC
Từ đó ta có: CD / /EF (định lý Ta-lét đảo) CFE GCF 20 .
Biên soạn: Trần Đình Hoàng 0814000158 31
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 9. Cho tam giác ABC có 3A 2B 180 . Tính số đo các cạnh của tam giác biết số đo ấy là ba
số tự nhiên liên tiếp. Lời giải C
Vì 3A 2B 180 A B C C 2.A B C A và C B AB BC và AB AC
Trên AB lấy điểm D sao cho AD AC D nằm giữa A và B. B A D Ta có: A
CD cân tại A nên 180 A ADC 2 2 A B
Mà 3A 2B 180 180 A 2 A B ADC A B CDB 180 ADC C 2 AB BC Vậy 2 A BC ” C BD (g.g)
BC AB.BD AB AB AC (*) BC BD
Do AB, BC, AC là ba số nguyên liên tiếp và AB maxAB, BC,A C nên AB BC 1 hoặc AB BC 2 .
Trường hợp 1. Nếu AB BC 1 thì AC BC 1 thay vào (*), ta có: 2
BC 2.BC 2 0 , không tồn tại BC là số nguyên.
Trường hợp 2. Nếu AB BC 2 thì AC BC 1 thay vào (*), ta có: 2
BC BC 2 0 BC 2BC
1 0 BC 2 (vì BC 0 ).
Vậy BC 2 ; AC 3 và AB 4 .
Nhận xét. Vận dụng kỹ thuật trên, bạn có thể làm được bài toán đảo: Cho tam giác MNP thỏa mãn 2 2 PN .
MP MN MN 0 . Chứng minh rằng: 3. M 2. N 180.
Bài 10. Cho tam giác ABC nhọn có hai đường cao BE và CF. Kẻ FI và EJ cùng vuông góc với BC
(I; J thuộc BC). Các điểm K, L lần lượt thuộc AB, AC sao cho KI / / AC , LJ / / AB . Chứng mình
rằng ba đường thẳng EI, FJ và KL đồng quy. Lời giải A
Gọi O là giao điểm của EI và FJ. Ta có: KFI FCB 90 ABC 90 LJC EJL (1) E Lại có: IKF ELJ (cùng bù với BAC ) (2)
Từ (1) và (2) suy ra: KFI ” L JE (g.g) F L KF FI (3) LJ EJ K O Xét FOI và JOE có: FOI JOE (đối đỉnh) B C IFO EJO (so le trong) I J
Do đó: FOI JOE suy ra FO FI (4) OJ JE Lại có: KFO LJO (so le trong) (5)
Từ (3), (4), (5) suy ra KFO ” LJ O (c.g.c). Do đó FOK
JOL , mà hai góc ở vị trí đối đỉnh.
Suy ra K, O, L thẳng hàng, tức là FJ, EI, KL đồng quy.
Biên soạn: Trần Đình Hoàng 0814000158 32
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 11. (Đề thi HSG lớp 9) Cho hình thang ABCD CD AB với AB / /CD và AB BD . Hai
đường chéo AC và BD cắt nhau tại G. Trên đường thẳng vuông góc với AC tại C lấy điểm E sao
cho CE AG và đoạn thẳng GE không cắt đường thẳng CD. Trên đoạn thẳng DC lấy điểm F sao cho DF GB . a) Chứng minh FDG ” E CG b) Chứng minh GF EF . Lời giải A B BG GD a) Ta có: AB / /CD . AG GC E G 2 Mà AG CE ; DF GD BG DF . 1 CE GC DF GD Xét FDG và ECG có: ; CE CG D F C GDF GCE nên FDG ” E CG (c.g.c) b) Ta có: FDG ” E CG G G ; GD GC 2 2 GF GE GD GC Xét GDC và GFE có ; DGC FGE (vì G G ) GF GE 1 2
Do đó: GDC GFE GFE 0
GDC 90 . Do đó GF FE .
Bài 12. Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh rằng: AE.AC AF.AB ;
b) Chứng minh rằng: AEF ” A BC ;
c) Chứng minh rằng H là giao điểm ba đường phân giác trong của DEF . Lời giải A a) Xét A BE và ACF có AEB AFC 90 ; BAC chung Do A BE ACF (g.g) E AB AE AE.AC AF.AB AC AF F AE AF b) Từ AE.AC AF.AB . AB AC Xét A EF và ABC có AE AF ; BAC chung AB AC B D C Do đó: AEF ” A BC (c.g.c)
c) Chứng minh tương tự, ta có: A EF ” A BC AEF ABC
Chứng minh tương tự, ta được: CAB ” CDE (g.g) ABC CED Từ đó suy ra AEF
CED EB là tia phân giác DEF .
Chứng minh tương tự, ta có DA là tia phân giác
EDF . Từ đó suy ra điều phải chứng minh.
Bài 13. Cho hình hình hành ABCD có đường chéo AC lớn hơn DB. Gọi H, K là hình chiếu của C
trên đường thẳng AB, AD. Chứng minh rằng CHK ” BCA.
Biên soạn: Trần Đình Hoàng 0814000158 33
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải H Xét CBH và CDK có: CHB CKD 90. HBC KDC BCD CH CK
Do đó: CBH và CDK (g.g) B C CB CD CH CK Mà CD AB nên . CB AB Xét CHK và BCA có: CH CK CB AB A K D và ABC HCK (cùng bù với BAD )
Do đó: CHK ” BCA (c.g.c).
Bài 14. Cho tam giác ABC, đường phân giác CD. Chứng minh rằng 2 CD C . A CB . Lời giải A Ta có
CDB A (tính chất góc ngoài), do đó trên cạnh BC lấy E sao cho CDE A . Xét A CD và DC E có C C ; A CDE D 1 2 AC CD ACD ” DCE (g.g) CD CE 1 2 CD AC.CE AC.BC 2 B E C
Bài 15. Cho tam giác đều ABC. Trên tia BA lấy điểm E (A F
nằm giữa B và E). Gọi D là điểm đối xứng với E qua đường
thẳng BC. Gọi F là giao điểm của đường thẳng CD và AB. Chứng minh rằng 1 1 1 . BC BD BF Lời giải Ta có AEC BDC và DBC EBC 60 Vì DBC ACB 60 nên AC / / BD . E Suy ra: ACF BDC AEC A EC ” A CF (g.g) AC AE AB AE AB AE A AF AC AF AB AB AF AB AE AB AE AB AB 1 BF BE BF BE AB AB 1 1 1 1 BF BE BF BE AB B 1 1 1 C
. Điều phải chứng minh. BD BF BC D
Biên soạn: Trần Đình Hoàng 0814000158 34
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 16. Cho hình bình hành ABCD có góc A tù. Từ A, vẽ các đường thẳng vuông góc với BC, CD
cắt CD, BC tương ứng tại E và F. Đường thẳng qua A vuông góc với BD, cắt EF tại M. Chứng minh ME MF . Lời giải A B
Từ giả thiết suy ra C là trực tâm A EF nên AC EF .
Kết hợp với BD AM và ED AF I
theo tính chất góc có cạnh tương ứng vuông góc ta có: ICD MFA; CDI MAF E D C Do đó: ICD ” MFA (g.g) IC MF (1) ID MA IC ME Tương tự IC B ” M EA(g.g) (2) IB MA M
Từ (1) và (2) kết hợp với giả thiết IB ID suy ra ME MF . F
Bài 17. Cho tam giác đều ABC, gọi M là trung điểm của BC. Một góc xMy bằng 60o quay quanh
điểm M sao cho 2 cạnh Mx, My luôn cắt cạnh AB và AC lần lượt tại D và E. Chứng minh: 2 BC a) a) B . D CE 4
b) DM; EM lần lượt là tia phân giác của các góc BDE và CED;
c) Chu vi tam giác ADE không đổi. Lời giải A
a) Trong tam giác BDM ta có D 120 M 1 1 Vì M 60 nên ta có: M 120 M 2 3 1 E Suy ra D M mà B C 60 1 3 I 1 Do đó BMD ” CEM (1) D 2 3 BD CM Suy ra , từ đó: B . D CE BM .CM H K BM CE 2 BC Vì BC BM CM , nên ta có: B . D CE 2 4 B M C b) Từ (1) suy ra BD MD mà BM CM nên ta có: BD MD CM EM BM EM
Do đó BMD ” MED. Từ đó suy ra:
D D , do đó DM là tia phân giác của góc BDE. 1 2
Chứng minh tương tự ta có EM là tia phân giác của góc CED.
c) Gọi H, I, K là hình chiếu của M trên AB, DE, AC.
Theo tính chất đường phân giác, ta có: DH DI, EI EK AH AK .
Từ đó suy ra chu vi tam giác ADE bằng:
AD DE EA AD DH EK EA 2AH . Vậy chu vi tam giác ADE không đổi.
Bài 18. Cho hình vuông ABCD. Trên cạnh AB lấy điểm M. Vẽ BH vuông góc với CM. Nối DM.
Gọi HN vuông góc với DH (N thuộc BC).
a) Chứng minh rằng tam giác DHC đồng dạng với tam giác NHB;
b) Chứng minh rằng AM .NB NC.MB
Biên soạn: Trần Đình Hoàng 0814000158 35
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải A M B
a) Xét DHC và NHB có: DHC NHB 90 CHN ; HCD HBC 90 BCH H Suy ra: DH C NHB (g.g) b) Xét MBH và BCH có: N MHB BHC 90; MBH HCB 90 CBH MB HB
Suy ra MBH ” BCH (g.g) (1) D C BC HC Mà DHC ” NHB (g.g) NB HB (2) và BC CD DC HC
nên từ (1) và (2), suy ra: MB NB AM CN , suy ra AM .NB NC.MB .
Bài 19. Cho tam giác ABC thỏa mãn AB 2.AC và A 2.B . D
Chứng minh rằng ABC là tam giác vuông. Lời giải
Trên tia đối của tia AC lấy điểm D sao cho AD AB .
Từ đó suy ra DC 3.AC và BAC 2 BDA nên BDC ABC . AC BC Từ đó ABC ” B DC 2 BC . DC AC BC DC 2 2 2 2 2
BC 3.AC BC AC 4.AC = 2 (2AC) A hay 2 2 2
AB BC AC . Vậy ABC là tam giác vuông tại C. B C
Bài 20. Cho ABC nhọn có AH là đường cao lấy điểm M thuộc đoạn BC, kẻ MK vuông góc với
AB và ML vuông góc với AC. Đường thẳng qua A vuông góc với AM cắt MK, ML tại E và F. Từ
B kẻ đường thẳng vuông góc với CE cắt AH tại I. Chứng minh rằng: a) AIB ” MCE b) EM ML và BM AI ; FM KM FM AC c) AH, BF, CE đồng qui. Lời giải I F a) Ta có: BIA MCE 90 IBH (1). Lại có: IAB BAH 180 ; CME EMB 180 ; A và BAH EMB 90 ABC IAB CME (2) E
Từ (1) và (2) suy ra: IAB ” MCE (g.g) K
b) Xét MAK và MEA có: L MKA MAE 90, AME chung B H C M MA MK 2
MAK ” MEA (g.g) MA ME.MK (3) ME MA
Biên soạn: Trần Đình Hoàng 0814000158 36
Chuyên đề bồi dưỡng học sinh giỏi toán 8 MA ML Tương tự: MAL ” M FA (g.g) 2 MA MF.ML (4) MF MA EM ML
Từ (3) và (4) suy ra: ME.MK MF.ML . FM KM MB S A . B MK Ta có: AMB . Mặt khác EM ML MK MF MC S AC.ML FM MK ML ME AMC Suy ra MB A . B MF MB A . B MC (5) MC AC.ME MF AC.ME
Mặt khác AIB ” MCE , suy ra MC AI (6) ME AB Từ (4) và (5) suy ra: MB A . B AI AI MF AC.AB AC
c) Xét MBF và AIC có MB MF và IAC BMF AI AC Do đó M
BF AIC (c.g.c) AIC MBF mà AIC
ICB 90 AI BC MBF
ICB 90 hay BF vuông góc với CI.
Tam giác IBC có IH, BF, CE là đường cao, suy ra điều phải chứng minh.
Bài 21. Cho ABC . Gọi P là giao điểm của ba đường phân giác trong của tam giác. Một đường
thẳng đi qua P vuông góc với CP, cắt AC và BC lần lượt tại M và N. Chứng minh rằng: 2 2 a) AM AP AM BN CP b) 1. BN BP AC BC AC.BC Lời giải A a) Ta có: A B
APB 180 A B 180 1 2 1 1 2 2 360 A B 180 C 180 C M C 90 . 1 2 2 2 2 Xét CMP có: C P M MPC MCP M 90 APB M . 1 1 1 2 Xét APB và AMP có: 1 APB M ; A
A . Dp đó: APB AMP (g.g) 2 1 1 2 B C AM AP N 2 AM .AB AP (1) AP AB BN BP
Tương tự, ta có: APB ” PNB (g.g) 2 BN.AB BP (2) BP AB 2 Từ (1) và (2) suy ra: AM AP
, điều phải chứng minh. BN BP
b) Ta có: AMP ” APB (chứng minh trên); APB ” PNB (chứng minh trên). AM MP AMP ” PNB AM .BN . MP PN hay 2 AM .BN MP PN BN
CMN có CP là phân giác, CP là đường cao nên CMN cân tại C CM CN; MP PN . Xét 2 2 2
AM .BC BN.AC CP AM .BC BN.AC CM MP
Biên soạn: Trần Đình Hoàng 0814000158 37
Chuyên đề bồi dưỡng học sinh giỏi toán 8 2
AM .BC BN.AC CM AM .BN AM BC BN 2 . BN.AC CM
CM. AM CM BN.AC
CM.AC BN.AC AC.CM BN AC.BC Do đó: 2
AM .BC BN.AC CP AC.BC . 2 AM BN CP Suy ra
1, điều phải chứng minh. AC BC AC.BC
Bài 22. Cho tam giác ABC vuông tại A AC AB , đường cao AH H BC . Trên tia HC lấy
điểm D sao cho HD HA . Đường vuông góc với BC tại D cắt AC tại E.
a) Chứng minh rằng hai tam giác BEC và ADC đồng dạng. Tính độ dài đoạn BE theo m AB .
b) Gọi M là trung điểm của đoạn BE. Chứng minh rằng hai tam giác BHM và BEC đồng dạng. Tính số đo của góc AHM
c) Tia AM cắt BC tại G. Chứng minh: GB HD . BC AH HC Lời giải A a) Xét CDE và CAB có: CDE CAB 90 E DCE chung, M CD CA
suy ra CDE CAB (g.g) CE CB B H G C Xét ADC và BEC có: D ACB chung, CD CA (chứng minh trên) CE CB
Do đó ADC BEC (c.g.c) Suy ra: BEC
ADC 135 (vì tam giác AHD vuông cân tại H theo giả thiết). Nên
AEB 45 do đó tam giác ABE vuông cân tại A. Suy ra: BE AB 2 m 2 b) Ta có BM 1 BE 1 AD . . (do ADC BEC ) BC 2 BC 2 AC
mà AD AH 2 (tam giác AHD vuông cân tại H) nên BM 1 AD 1 AH 2 BH BH . . (do ABH ” CBA ). BC 2 AC 2 AC AB 2 BE Xét BHM và BEC có BM BH và CBE chung BC BE
Do đó BHM BEC , suy ra BHM BEC 135 AHM 45 .
c) Ta có AG còn là phân giác góc GB AB BAC . GC AC AB ED AH HD ABC DEC (g.g) (do ED / / AH ) AC DC HD HC GB HD GB HD GB HD . GC HC GB GC HD HC BC AH HC
Bài 23. Trong tam giác ABC, các điểm D, E, F tương ứng nằm trên các cạnh BC, CA, AB sao cho: AFE BFD , BDF CDE , CED AEF .
Biên soạn: Trần Đình Hoàng 0814000158 38
Chuyên đề bồi dưỡng học sinh giỏi toán 8 a) Chứng minh rằng: BDF BAC
b) Cho AB 5 , BC 8 , CA 7 . Tính độ dài đoạn BD. Lời giải A a) Đặt AFE BFD , BDF CDE , CED AEF . Ta có:
BAC 180 (*) E
Gọi O là giao điểm ba đường phân giác của tam giác
DEF. Suy ra OD, OE, OF lần lượt vuông góc với BC, F AC, AB. O OFD OED ODF 90 (1) Ta có: OFD OED ODF 270 (2)
(1) và (2) 180 (**) (*) và (**) BAC BDF . D C B
b) Chứng minh tương tự câu a), ta có:
B , C AEF ” DB F ” DE C ” A BC Suy ra BD BA 5 5BF 5BF 5BF BD BD BD BF BC 8 8 8 8 CD CA 7 7CE 7CE 7CE C D C D C D CE CB 8 8 8 8 AE AB 5 7AE 5AF
77 CE 55 BF 7CE 5BF 24 AF AC 7 CD BD 3 (3)
Ta lại có: CD BD 8 (4)
Từ (3) và (4) BD 2,5 .
Bài 24. Cho ABCD là hình bình hành. Giả sử MAB MCB . Chứng minh rằng MBC MDC . Lời giải A G B
Kẻ từ M các đường thẳng song song với các cạnh
AB, BC cắt các cạnh tại E, F, G, H (hình vẽ) M E Ta có: AGM CFM ABC F Mặt khác MAB MCB do đó A GM ” C FM AG MG . D H C CF MF
Mặt khác, AG DH;CF MH;MG FB nên DH BF (1) MH MF Ta lại có: DHM BFM BCD (2)
Từ (1) và (2) suy ra: DHM ” B FM MDC MBC
Bài 25. Giả sử D là một điểm nằm trong tam giác nhọn ABC sao cho ADB ACB 90 và AB CD AC.DB A . D BC . Chứng minh . 2 . A . D BC
Biên soạn: Trần Đình Hoàng 0814000158 39
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải A
Về phía ngoài ABC vẽ BCE vuông cân tại C 2 1 ADB ACE ACB90 AD BD Mà (vì AC.BD A . D BC ) AC BC D AD BD do đó A BD ” A CE ( . c g.c) (1) AC CE B C A A BAE DAC 1 2 Từ (1) AB AE do đó A BE ” A DC ( . c g.c) AD AC AB BE A . B CD A . D BE . AD DC
Mặt khác, ABE vuông cân nên BE 2.BC Do đó AB CD A . B CD 2.A . D BC hay . 2 . A . D BC E
Bài 26. Cho tam giác ABC cân tại A. Từ điểm M thuộc cạnh BC vẽ MB AB ; MQ AC ; P A ;
B Q AC . Vẽ PE PQ ; QE PQ E; F BC . Chứng minh rằng: BE CF Lời giải A
Lấy N trên PQ sao cho MN BC . Ta có: PBE PMN (cùng phụ với PMB ) BPE MPN (cùng phụ với EPM ) P nên P BE ” P MN (g.g) N Q BE BP BP BE MN. (1) MN MP MP Tương tự, ta có: CQ CF MN. (2) B E M F C MQ BP CQ Mặt khác: B PM ” CQM (g.g) (3) MP MQ
Từ (1), (2) và (3) suy ra: BE CF .
Bài 27. Cho tam giác ABC nhọn có đường cao BE, CF. Qua A vẽ các đường thẳng song song với
BE, CF lần lượt cắt các đường thẳng CF, BE tại P và Q. Chứng minh rằng: PQ vuông góc với trung tuyến AM. Lời giải A
Gọi H là giao điểm của BE và CF. Gọi I là giao điểm của AH và PQ. Q Ta có: ABQ ACP 90 BAC ; BAQ PAC K suy ra A BQ ” A CP (g.g) I E P AQ AB AQ AP . F AP AC AB AC H
Mặt khác APHQ là hình bình hành nên AQ HQ AP HQ . AB AC B M C
Biên soạn: Trần Đình Hoàng 0814000158 40
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Ta lại có: BAC AQH 180 PAQ suy ra A BC ” G HA ( . c g.c) AB BC BM ABC QAH ;
(vì BC 2.BM .AH 2.AI ). QA AH AI Do đó: ABM ” QAI ( . c g.c) BAM AQI QAM AQI 180 AM PQ
Bài 28. Cho tam giác BAC cân tại A có góc BAC 20 . Dựng tam giác đều BDC sao cho D, A
cùng phía so với BC. Dựng tam giác DEB cân tại D có góc EDB 80 và C, E khác phía so với
DB. Chứng minh tam giác AEC cân tại E. Lời giải A
Gọi P là giao điểm của AB và DE;
Q là giao điểm của BD và CE. DE
C có DC DE DB và
EDC 60 80 140 20° nên DEC 1 DCE 180 EDC 20. 2 Ta có: ABD DBC ABC nên ABD 20 . B DP và EDQ có DEQ DBP 20 ; BD E ; D EDB chung B DP EDQ (g. . c g) EQ BP; PD DQ E Xét B PD và ABC có: P D PDB 0 ABC DBA 0 80 ; BAC 20 800 Do đó: B PD ” A BC (g.g) AB BC BD ED Q hay AB ED AE / /BD (định lý BP PD PD PD BP PD Pa-lét đảo) B C EAP PBD (so le trong) EAP 20 EAC 40. Mặt khác ACE ACD DCE 40 EAC ACE A CE cân tại E.
Bài 29. Cho tam giác ABC có A 90 . Lấy điểm D thuộc đoạn thẳng AC sao cho CD 2.AD . Gọi
E là điểm thuộc đoạn thẳng BD sao cho CED
ABC . Gọi F là điểm đối xứng với C qua A. Chứng minh rằng DEF 2. ABC . Lời giải F K
Gọi K là điểm đối xứng với B qua A.
Gọi M là giao điểm của BD và CK.
BCK có CA là đường trung tuyến AB AK , A
mà CD 2.AD nên D là trọng tâm tam giác M MC MK . D
BCK có AK AB, MC MK nên AM là đường E
trung bình AM / /BC AMB EBC B C mà ABC DEC ABM ABC MBC DEC EBC ECB BC BE AMB và EBC có AMB EBC, ABM ECB AMB ” E BC (g.g) MB AM
Ta có: AB AK, AC AF và BK CF nên BCKF là hình thoi BC CK AM MC .
Biên soạn: Trần Đình Hoàng 0814000158 41
Chuyên đề bồi dưỡng học sinh giỏi toán 8 BF BC BE BE BF BE MB MB AM MC MB MC mà EBF CMB E BF ” C MB ( . c g.c) BEF MCB
kết hợp với BCKF là hình thoi nên: DEF 180 BEF 180 MCB FBC 2. ABC hay DEF 2. ABC .
Chủ đề 4. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VUÔNG
Bài 1. Cho tam giác nhọn ABC có đường cao CK. Dựng ra phía ngoài tam giác ABC hai tam giác
ACE và CBF tương ứng vuông góc tại E; F và thỏa mãn ACE CB ; A BCF CAB . Chứng minh rằng: 2 CK AE.BF . Tìm cách giải. F Để chứng minh 2
CK AE.BF chúng ta không thể C
vận dụng định lý Ta-lét hay xét một cặp tam giác
đồng dạng là xong ngay được. Do vậy, chúng ta suy luận để tạo ra 2
CK , chúng ta cần ghép CK vào E
hai cặp tam giác đồng dạng. Mỗi cặp tam giác
đồng dạng đó đều biểu thị CK dưới dạng biểu thức
(chứa AE hoặc BF). Dễ dạng nhận thấy có hai cặp
tam giác đồng dạng thỏa mãn điều kiện trên. A K B Trình bày lời giải
ACK và CBF có :
CKA BFC 90 ; CAK BCF CK BF
∆ACK ∆CBF (g.g) (1). CA BC CK AE
Tương tự, ta có: ∆BCK ∆CAE (g.g) (2) CB AC CK CK BF AE
Nhân từng vế của (1) và (2) ta được: 2 . . CK AE.BF . CA CB BC AC
Bài 2. Cho hình bình hành ABDC (AC > BD) vẽ CE vuông góc với AB tại E, vẽ CF vuông góc
với AD tại F. Chứng minh rằng: 2 A . B AE AD.A F AC . Tìm cách giải. E Để chứng minh 2 A .
B AE AD.A F AC , ta có vế
trái là một tổng nên vế phải cần tách ra một tổng: .
AB AE AD.EF AC.x AC.y với x y AC . Do
vậy ta chọn điểm H thuộc AC khi đó B C
x AH,y HC và chứng minh .
AB AE AC.AH, AD.EF AC.CH . Từ đó chúng ta
chỉ cần chọn điểm H sao cho ∆ABH ∆ACE là H
xong. Nhận thấy tam giác ACE vuông tại E, nên tất
yếu cần kẻ BH vuông góc với AC. A D F Trình bày lời giải Vẽ BH ACH AC
Biên soạn: Trần Đình Hoàng 0814000158 42
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Xét AB H và ACE có
ABH AEC 90 ; BAC chung. AB AH
Suy ra ABH ACE (g.g) AB.AE AC.AH . (1) AC AE
Xét CHB và CAF có
BCH CAF (so le trong); CHB CFA 90 BC CH
Suy ra CHB CAF (g.g) BC.A F AC.CH (2) AC AF
Cộng vế theo vế (1) và (2) ta được:
AB AE BC F AC AH AC CH AB AE AD F ACAH CH 2 . .A . . . .A AC .
Bài 3. Cho tam giác ABC vuông tại A. Lấy một điểm M bất kỳ trên cạnh AC. Từ C vẽ một đường
thẳng vuông góc với tia BM, đường thẳng này cắt tia BM tại D, cắt tia BA tại E. a) Chứng minh: E . A EB ED.EC .
b) Chứng minh rằng khi điểm M di chuyển trên cạnh AC thì tổng BM.BD CM.CA có giá trị không đổi.
c) Kẻ DH BC, H BC. Gọi P, Q lần lượt là trung điểm của các đoạn thẳng BH, DH. Chứng minh CQ PD . Lời giải E a) Chứng minh E . A EB ED.EC Xét EBD và ECA có:
ADB EAC 90 ,BEC chung nên E BD ECA (g-g) D EB ED A Từ đó suy ra . EA EB ED.EC EC EA M Q
b) Kẻ MI vuông góc với BC I BC. Ta có: B IM và BDC có:
BIM BDC 90 , MBC chung B P H C BM BI Do đó: B IM BDC (g-g) BM.BD BC.BI . (1) BC BD CM CI
Tương tự: ACB ICM (g-g) CM.CA BC.CI (2) BC CA
Từ (1) và (2) cộng vế với vế, suy ra:
BM BD CM CA BC BI BC CI BCBI CI 2 . . . . BC (không đổi) BH HD 2.HP HD HP HD
c) Xét BHD DHC (g-g) DH HC 2.HQ HC HQ HC
HPD HQC (c-g-c) PDH QCH Mà
HDP DPC 90 HCQ DPC 90 CQ PD
Bài 4. Cho tam giác ABC. Lấy điểm E, F, P lần lượt thuộc AB, AC, BC sao cho BEFP là hình bình
hành. Biết rằng diện tích AE
F và CFP lần lượt là 2 16cm ; 2
25cm . Tính diện tích ABC . Tìm cách giải.
Khi vẽ hình xong, chúng ta có hai hướng suy luận:
Vì tam giác AEF, FPC cùng đồng dạng với tam giác ABC nên chúng ta tìm mối liên hệ giữa
Biên soạn: Trần Đình Hoàng 0814000158 43
Chuyên đề bồi dưỡng học sinh giỏi toán 8
tỷ số hai tam giác đồng dạng. A
Hướng thứ hai, để tính diện tích tam giác ABC,
chúng ra tìm cách tính diện tích hình bình hành.
Nhận thấy tam giác BEF và BPF có diện tích bằng
nhau, mặt khác tam giác AEF và BEF có chung E F
đường cao kẻ từ F; tam giác BPF và CPF có chung
đường cao kẻ từ F. sử dụng tính chất đó, kết hợp với
định lý Ta-lét, chúng ta có lời giải hay. Trình bày lời giải
Cách 1. Ta có: AEF ABC ; FPC ABC nên: B C P 2 S EF S EF 2 S CP S CP AEF AEF ; FPC FPC S BC S BC S BC S BC ABC ABC ABC ABC S S EF CP Từ đó suy ra AEF FPC 1 S BC BC ABC Hay 2 2 S S S
45 S 9 81cm . ABC AEF FPC ABC Cách 2. Đặt 2 S S x cm . BFE BFP S AE 16 AE
Tam giác AEF và BEF có chung đường cao kẻ từ F, suy ra: FEA ; S BE x BE FEB S BP x BP
Tam giác BPF và CPF có chung đường cao kẻ từ F, suy ra: FBP . S CP 25 CP FPC AE AF BP 16 25
Áp dụng định lý Ta-let, ta có: 2 x 400 x 20 . BE FC CP x x Vậy 2 S
16202025 81 cm . ABC Nhận xét. Từ kết quả S S S
S ab2 S a 2 2 2 b a b 2ab ABC AEF FPC ABC BEFP
Từ đó ta có thể giải được bài toán sau:
Cho tam giác ABC. Lấy điểm E, F, P lần lượt thuộc AB, AC, BC sao cho BEFP là hình bình hành. Đặt 2 2 S a ; S b (với ; a b 0 ). AEF CFP
a) Tính diện tích hình bình hành BEFP.
b) Xác định vị trí điểm E, F, P trên AB, AC, BC để diện tích hình bình hành BEFP đại giá trị lớn nhất.
Bài 5. Cho tam giác ABC. Qua điểm F nằm trong tam giác kẻ MN //BC, PQ // AB, IK // AC. ( I, M ;
AB N,P AC; Q,K BC ). Biết rằng: 2 2 2 S 9cm ;S 16cm ;S 25cm . Tính diện tích IMF PFN FQK ABC . Tìm cách giải.
Với lối tư duy như ví dụ trên, chúng ta hoàn toàn nghĩ tới hai cách giải. Song trong ví dụ này MF QK FN
sẽ trình bày một cách giải, mà bản chất của bài toán là vận dụng kết quả 1 BC BC BC
kết hợp với tỷ số diện tích của hai tam giác đồng dạng, Trình bày lời giải
Biên soạn: Trần Đình Hoàng 0814000158 44
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Nhận thấy BMFQ, CNFK là các hình bình hành.
Ta có: ∆FQK ∆ABC; ∆IMF ∆ABC; ∆PFN ∆ABC A S MF S QK S FN Thì IMF ; PQK ; và PFN ; P S BC S BC S BC I ABC ABC ABC S S S IMF PQK PFN MF QK FN F 1 N M S BC ABC S S S S 354 12 ABC IMF PQK PFN 2 S 144cm . C ABC B Q K
Nhận xét: Như vậy, với các giải trên, chúng ta hoàn toàn làm được bài toán tổng quát sau:
Cho tam giác ABC. Qua điểm F nằm trong tam giác kẻ MN / /BC; PQ / / ; AB IK / / AC I,M ; AB N,P AC;Q,K BC. Đặt 2 2 2 S a ;S b ; S c ;a ;bc 0 IMF PFN FQK Chứng minh rằng: S abc2 . ABC
Bài 6. Cho tam giác ABC. Qua điểm F nằm trong tam giác kẻ MN // BC, PQ // AB, IK // AC
( I, M AB , N,P AC; Q,K BC ). Đặt diện tích tam giác ABC là S. Tìm vị trí điểm F để tổng T S S S
đạt giá trị lớn nhất. APFI MBQF CNFK Tìm cách giải. A
Tương tự ví dụ trên, chúng ta đặt: 2 2 2 S a ;S b ; S c ;a ;bc 0 P IMF PFN FQK
Chúng ta hoàn toàn biểu thị tổng I T S S S
theo a, b, c. Vậy hiển nhiên APFI MBQF CNFK F N M
để tìm giá trị lớn nhất chúng ta dùng cực trị đại số với 1
chú ý rằng ab bc ca abc2 . 3 Trình bày lời giải Q C B K Đặt 2 2 2 S a ;S b ; S c ;a ;bc 0 IMF PFN FQK Ta có: S S S S Hay S a b c ABC 2. ABC IMF FQK PFN S S S S S S S
2 2 2 2 T a b c a b c APFI MBQF CNFK ABC IMF PFN FQK T abbcca 2 abc2 2 2 S 3 3 2
Vậy T S khi a b c hay F là trọng tâm của tam giác ABC 3
Bài 7. Cho tấm bìa hình thang ABCD có
A D 90 , AD 4c ;
m AB 32cm, CD 64cm . Gấp tấm
bìa lại để cho hai điểm C và B trùng nhau. Tính độ dài của nếp gấp. Tìm cách giải.
Trước hết chúng ta hãy vẽ và xác định đường nếp gấp: Gọi M là trung điểm của BC, qua M kẻ
đường thẳng vuông góc với BC, cắt CD tại N. Độ dài nếp gấp cần tính chính là độ dài đoạn
Biên soạn: Trần Đình Hoàng 0814000158 45
Chuyên đề bồi dưỡng học sinh giỏi toán 8 thẳng MN. E Từ đề bài A D 90 ; AD 4 ; cm AB 32cm, CD 64cm
, dễ dàng tính được độ dài BC A B
bằng định lý Py-ta-go. Từ đó tính M
được độ dài CM. Do vậy để tính
được CM trong tam giác vuông D C F N
CMN, chúng ta chỉ cần tính được
độ dài hai cạnh của một tam giác vuông đồng dạng với tam giác vuông CMN là xong. Từ đó,
chúng ta có hai cách vẽ thêm đường phụ: Cách 1. Vì
A D 90 nên chỉ cần gọi giao điểm DA và CB là E. Sau đó tính độ dài cạnh của tam giác vuông CDE.
Cách 2. Kẻ BF vuông góc với CD, khi đó ∆MCN ∆FCB. Bài toán cũng được giải. Trình bày lời giải
Gọi M là trung điểm của BC, qua M kẻ đường thẳng vuông góc với BC, cắt CD tại N. Độ dài
nếp gấp cần tính chính là độ dài đoạn thẳng MN.
Cách 1. Gọi E là giao điểm của AD và BC; F là chân đường vuông góc kẻ từ B tới CD. Dễ
thấy F là trung điểm của CD, từ đó: 2 2 2 2 2
BC BF FC 24 32 1600 . Suy ra BC 40cm MC 20 cm
Cũng từ F là trung điểm của CD, Suy ra B và A lần lượt là trung điểm của CE và DE, Suy ra DE 2AD 48cm . MC MN 20 MN
Ta nhận thấy ∆MCN ∆DCE nên MN 15cm DC DE 64 48
Vậy độ dài nếp gấp là 15cm. MC MN 20 MN
Cách 2. Ta có ∆MCN ∆FCB suy ra: MN 15cm CF BF 32 32
Vậy độ dài nếp gấp là 15cm.
Bài 8. Cho tam giác ABC cân tại A. Trên AB lấy điểm D và trên BC lấy điểm E sao cho hình 1
chiếu của DE lên BC bằng BC . Chứng minh rằng đường vuông góc với DE tại E luôn đi qua một 2 điểm cố định. Lời giải. A
Gọi M, H lần lượt là hình chiếu vuông góc của D và A
trên BC. Giả sử đường thẳng qua E vuông góc với DE
cắt đường thẳng AH tại N. 1
Ta có: BH BC BM HE . 2 D Mặt khác ta có:
HNE MED (cùng phụ với HEN );
DME NHE , nên ∆HNE ∆MED HN HE 2HN HE 2HN BM ME DM BC DM BC DM C BM BH 2HN BH BH.BC B M H E Mặt khác HN DM HA BC HA 2.HA
Vậy N là điểm cố định N
Biên soạn: Trần Đình Hoàng 0814000158 46
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Nhận xét: Điểm mấu chốt của bài là khai thác điều kiện 1
“Hình chiếu của DE bằng BC ” để từ đó xác định việc kẻ thêm đường phụ. 2
Bài 9. Cho tứ giác ABCD có
ABD ACD 90 . Gọi I, K thứ tự là hình chiếu của B, C trên cạnh
AD. Gọi M là giao điểm của CI và BK, O là giao điểm của AC và BD. Chứng minh rằng OM AD . Lời giải. C Kẻ HI BC tại I. B BIH và DBC có BIH BDC 90 mà O DBC F
chung do 4.4. Qua O kẻ đường thẳng E
song song với AD, cắt đường thẳng BI, CK lần N M
lượt tại E, F OE BI, OF CK .
Xét BEO và AIB có: BEO AIB ; A D
ABI BOE90OBI I K BO EO BEO AIB (g.g) (1) AB IB CO OF
Chứng minh tương tự, ta có: ∆CFO ∆DKC (g.g) (2) CD CK Xét AOB và D OC có: AOB DOC; ABO DCO BO OC ∆AOB ∆DOC(g.g) (3) AB CD EO OF OE IB
Từ 91), (2), và (3) suy ra: (4) IB CK OF CK IB BM Ta có: BI / /CK nên . (5) CK MK OE BO
Ta có: ∆BEO ∆NFO (g.g) (5) OF ON BM BO Từ (5) và (6) suy ra
, do đó OM / / NK (định lý Ta-lét đảo) hay OM AD . MK ON Bài 10. Cho AB
C cố định có các góc B, C nhọn và hình chữ nhật MNPG thay đổi nhưng luôn có
M, N trên cạnh BC còn P, Q lần lượt trên cạnh AC và AB. Xác định vị trí của các điểm P, Q sao
cho hình chữ nhật MNPQ có diện tích lớn nhất. Lời giải. A
Gọi AH là đường cao của ABC, AH cắt PQ tại I. Đặt BA ; a AH ; h PQ x; MQ y Ta có: AI h y Vì ∆APQ ∆ACB nên Q I P PQ AI x hy ahy x BC AH a h h a S xy h y y MNPQ h B M H N C
Biên soạn: Trần Đình Hoàng 0814000158 47
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Vì a, h là các hằng số dương nên S lớn nhất khi hyy lớn nhất. 2 ab 2 2 2 hy y h a h ah Áp dụng hệ thức: ab , ta có: hyy S . . 2 2 4 MNPQ h 4 4 ah
Vậy giá trị lớn nhất của S là 4 h
Khi hy y y tức P, Q lần lượt là trung điểm của AC, AB. 2
Bài 11. Cho tam giác ABC vuông tại A. Hình chữ nhật MNPQ thay đổi thỏa mãn M thuộc cạnh
AB, N thuộc cạnh AC và P, Q thuộc cạnh BC. Gọi giao điểm của BN với MQ là K, của CM và NQ là L. Chứng minh rằng KAB LAC . Lời giải. A
Lấy U, V theo thứ tự thuộc AK, AL sao cho
ABU ACV 90 , Ta có: BU BK N M NA / /BU (1) NA NK L K / / NA BK MN BC (2) MA NK MA ML B Q P C MA / /VC (3) CV CL U Từ (1), (2) và (3) suy ra: V BU . NA .MA BK . BK . ML BU BQ CA MN B . . . Q CA BQ .CA . NP (vì MQ NP ) NA MA CV NK NK CL CV NM BA CP B . A CP MQ BA CP BU BA CA BA . .
(Vì ∆BMQ ∆BCA; ∆CNP ∆CBA) CV CA BA CA BU AB Hay và
ABU ACV 90 do đó ∆ABU ∆ACV (c.g.c) CV AC Vậy KAB LAC
Bài 12. Cho tam giác ABC vuông tại A. Một hình vuông nối tiếp tam giác ABC với D thuộc cạnh
AB, E thuộc AC và F, G thuộc cạnh BC. Gọi H là giao điểm của BE và DG, I là giao điểm của CD
và EF. Chứng minh rằng IE = HG. Lời giải. A Ta có:
ADE EDG BDG 180 , mà EDG 90 Nên ADE BDG 90 . E D Mặt khác, ta lại có: ADE AED 90 I nên BDG AED . H
∆BGD ∆DAE (g.g) (1)
Chứng minh TT, ta có ∆EFC ∆DAE (g.g) (2) B G F C BG EF
Từ (1) và (2) suy ra: ∆BGD ∆EFC (3) DG FC HG BG
Sử dụng định lý Ta-lét trong BHG , ta có: DE / /BG HD DE
Biên soạn: Trần Đình Hoàng 0814000158 48
Chuyên đề bồi dưỡng học sinh giỏi toán 8 HG BG
Mà DE DG (tính chất hình vuông) nên (4) HD DG IE DE EF Tườn tự, ta có: (5) EF FC FC HG IE HG IE Từ (3), (4) và (5) ta có: , suy ra: HD IF HG HD IE IF HG IE Hay
. Mà DG EF nên ta có HG IE DG EF
Bài 13. Cho hình vuông ABCD, F là trung điểm của AD và E là trung điểm của FD, Các đường
thẳng BE và CF cắt nhau tại G. Tính tỉ số diện tích của tam giác EFG với diện tích hình vuông ABCD. Lời giải. B C Vì ED EF nên S S mà AF 2.E F GED EFG nên S 2.S . GAF EFG Ta lại có GBC GEF 2 S BC nên GBC S 16S GBC EFG S EF EFG Do đó S
S S 11216.S 20.S EFG GED GBC EFG EFG G 1 Mà S S S S .S EFG GED GAF GBC 2 ABCD A F E D 1 SEFG 1 Vậy S .S EFG 40 ABCD S 40 ABCD
Bài 14. Cho hình chữ nhật ABCD có diện tích 2
150cm (như hình vẽ). Gọi E, F là trung điểm của
AB và BC. Gọi M, N là giao điểm của DE. DF với AC. Tính tổng diện tích phần tô đậm. Lời giải. A E B Ta có: ∆AME ∆CMD EM AE 1 DM 2.EM DM DC 2 M S EM 1 Đặt S x . Ta có: AEM S 2x . AEM F S DM 2 ADM ADM Ta có: N 1 1 2 S S S S S x 2x 37,5cm AEM ADM ADE 2 ABD 4 ABCD D C 2 2 x 12,5cm S 25cm . AMD Tương tự, ta có: 2 2 S 12,5cm ; S 25cm . CNE CND 2 S S S S 752525 25cm DMN ACD AMD CND
diện tích phần tô đậm là: 2 12,512,525 50cm
Bài 15. Cho tam giác nhọn ABC có AD, BE, CF là đường cao cắt nhau tại H. . HB HC HC.HA H . A HB Chứng minh rằng: 1. . AB AC BC.BA C . A CB
Biên soạn: Trần Đình Hoàng 0814000158 49
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. A CH CE
Dễ thấy ∆CHE ∆CAF (g.g) . CA CF 1 H . H . B CE B HC S Do đó: 2 HBC E . AB AC 1 AB. SABC CF 2 F HC.HA S H . A HB S Tương tự ta có: HAC ; HAC . H BC.BA S C . A CB S ABC ABC Từ đó suy ra: H . B HC HC.HA HB.HA S S S B D C HBC HCA HBC 1 . AB AC BC.BA C . A CB SABC
Bài 16. Trong hình vẽ dưới đây các tam giác ABC và CDE có D
diện tích bằng nhau và F là giao điểm của CA và DE. Biết AB
song song với DE. AB = 9cm và EF = 6cm. Tính độ dài theo cm A của DE
(Olympic Toán học trẻ quốc tế Bulgaria (BICMC) F Lời giải.
Cách 1. Vẽ hai hình bình hành DECG và ABCH, do đó điểm H C
thuộc đoạn GC. Gọi K là giao điểm của AH và DF. B E AB 9 3 Ta có: và CE 2.BE . D G EF 6 2
Vì hai tam giác ABC và CDE có diện tích bằng nhau
nên hai hình bình hành ABCH và DECG có diện tích A K bằng nhau. H Do đó CH 2.HG . Suy ra: F
DE GC 94,513,5cm và I
DF DE EF 13,56 7,5cm J
Cách 2. Kẻ đường cao CI của ABC , CI cắt EF tại J. CJ EF 6 2 B E C Ta có: . CI AB 9 3
Hai tam giác ABC và CDE có diện tích bằng nhau nên . AB CI DE.CJ AB CJ AB 2 2 3
DE .AB .9 13,5cm DE CI DE 3 3 2
Suy ra: DF DE EF 13,56 7,5cm
Biên soạn: Trần Đình Hoàng 0814000158 50
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 17. Cho hình vuông ABCD. Gọi Q, E lần lượt là trung Q
điểm của AB, BC. Gọi M là giao điểm của DE và CQ; gọi I A B
là giao điểm của AM và BC. Chứng minh rằng AM = 4.MI. Lời giải.
Ta có CBQ DCE (c.g.c) BCQ CDE Mà
CDE CED 90 nên BCQ CED 90 M E Do đó: EMC 90
Vậy tam giác vuông DCE, DMC, CME đồng dạng I DC DM MC mà DC 2.CE CE MC ME D C
DM 2.MC; MC 2.ME DM 4.ME AM DM Mà EI / / AD nên 4 AM 4.MI MI ME
Bài 18. Giả sử AD, BE và CF là các đường phân giác của tam giác ABC. Chứng minh rằng tam 1
giác ABC đều khi và chỉ khi diện tích tam giác DEF bằng diện tích tam giác ABC. 4
(Tuyển sinh lớp 10, THPT chuyên, tỉnh Hòa Bình, năm học 2013 – 2014) Lời giải. A
Chứng minh điều kiện cần. Cho tam giác ABC đều, AD,
BE và CF là các đường phân giác trong của tam giác ABC ta cần chứng minh: 2 S 1 1 E DEF F S 2 4 ABC
Do tam giác ABC đều và AD, BE, CF là các đường
phân giác của tam giác nên ta có: DE EF DF 1 ∆DEF ∆ABC AB BC AC 2 B D C 2 2 S DE 1 1 DEF S AB 2 4 ABC
Chứng minh điều kiện đủ. Cho tam giác ABC, AD, BE và CF là các đường phân giác của tam S giác, thỏa mãn 1
DEF , ta cần chứng minh : ABC là tam giác đều. S 4 ABC
Đặt BC = a, AC = b; AB = c (a, b, c >0)
Vì AD là đường phân giác BAC nên ta có: DB c DB c DB c ac ac ab DB DC a DB a DC b DB DC c b a c b c b c b c b
Chứng minh tương tự, ta có: ab bc bc ca EC ; EA ; FA ; FB . a c a c a b a b S S S S S S S S Ta có: AF AE BF BD CE CD DEF ABC AEF BDF CDE 1 AEF BDF CDE . . . 1 S S S S S A . B AC B . A BC C . A CB ABC ABC ABC ABC ABC bc ab ac 2abc 1
a ba c a cb c a cb c a bb cc a
Biên soạn: Trần Đình Hoàng 0814000158 51
Chuyên đề bồi dưỡng học sinh giỏi toán 8 2abc 1 Theo giả thiết ta có:
a bb cc a 4
a bb cc a abc ab c2 bc a2 cb a2 8 0 a b c A BC là tam giác đều.
Bài 19. Cho tam giác ABC vuông tại A có AH là đường cao. Biết rằng chu vi tam giác ABH, ACH
lần lượt là 30cm, 40cm. tính chu vi tam giác ABC. Lời giải. A Ta có: A
BH ” CAH nên tỉ số chu vi bằng tỉ số đồng dạng, suy ra: AH 30 AH 3 AH HC . HC 40 HC 4 3 4 Đặt AH HC
k k 0 AH 3k, HC 4k 3 4
Áp dụng định lý Py-ta-go, ta có: B H C 2 2 2
AH HC AC AC 5k . Mà chu vi 10
CAH là 40 (cm) nên 3k 4k 5k 40 k cm. 3 Suy ra AH cm 40 50 10 , HC (cm), AC (cm) . 3 3
Ta có ∆ABC ∆HAC nên tỉ số chu vi bằng tỉ số đồng dạng, suy ra: 50 2P AC 5 5 ABC 3 2P 40 50 (cm) 2P HC 40 4 ABC 4 HAC 3
Bài 20. Qua điểm M thuộc cạnh BC của tam giác ABC kẻ các đường thẳng song song với các cạnh
AB và AC, chúng tạo thành với hai cạnh ấy một hình bình hành. Tìm vị trí của điểm M để hình
bình hành đó có diện tích lớn nhất.
(Thi học sinh giỏi lớp 9, TP. Hồ Chí Minh, năm học 2014 – 2015 Lời giải. A
Qua điểm M trên cạnh BC vẽ đường thẳng song song
với AB cắt AC tại E, vẽ đường thẳng song song với AC E cắt AB tại D.
Ta có ∆DBM ∆ABC ∆EMC 2 2 D S BM S CM DBM ; EMC S BC S BC ABC ABC B C F 2 2 2 2 S S S Ta có: BM CM 1 BM CM 1 MDAE 1 DBM EMC 1 1 S S S BC BC 2 BC BC 2 ABC ABC ABC x y 2 2 2
(áp dụng bất đẳng thức đại số: x y ) 1 S .S 2 MDAE 2 ABC 1
Vậy khi M là trung điểm của BC thì hình bình hành AEMD có diện tích lớn nhất là: .S 2 ABC
Biên soạn: Trần Đình Hoàng 0814000158 52
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Chủ đề 5. ĐỊNH LÝ MENELAUS, ĐỊNH LÝ CE-VA, ĐỊNH LÝ VAN-OBEN A. Kiến thức cần nhớ 1. Định lý Menelaus
Menelaus sinh ra khoảng năm 70 và mất khoảng năm 130 , những gì được biết về cuộc đời
ông rất ít, thông qua một số tác phẩm khoa học của những người sau. Chỉ biết chung chung rằng
ông có một thời là sinh viên trường đại học Alexandrie cổ đại, rồi làm cán bộ giảng dạy cũng ở đó
và về sau thành nhà thiên văn học ở La Mã. Trong hình học ông có một định lý nổi tiếng mang tên ông: định lý Menelaus.
Định lý: Cho tam giác ABC và ba điểm A,B,C (không trùng với các đỉnh của tam giác)
lần lượt trên các đường thẳng BC,CA và AB sao cho cả ba điểm A,B,C đều nằm trên phần kéo
dài của ba cạnh, hoặc một trong ba điểm nằm trên phần kéo dài một cạnh và hai điểm còn lại nằm A B B C C A
trên hai cạnh của tam giác. Điều kiện cần và đủ để A,B,C thẳng hàng là: . . 1. AC B A C B Chứng minh M A
Trường hợp 1. Nếu trong ba điểm A,B,C có
đúng hai điểm thuộc cạnh của tam giác ABC , C'
chẳng hạn là điểm B và C . B'
Nếu A,B,C thẳng hàng.
Qua A kẻ đường thẳng song song với BC cắt B C
tại M , ta có: C A AM B C A C ; . A'' C B AB B A AM B C A' A B B C C A AM AC AB Vậy: . . . 1. AC B A C B AB AM AC
Ngược lại, nếu A B B C C A . . 1. AC B A C B
Gọi A là giao điểm của B C với BC .
Theo phần thuận: A B B C C A . . 1. Suy ra: A B A B . A C B A C B A C A C
Do B,C lần lượt thuộc cạnh CA, AB nên A nằm ngoài cạnh BC . Vậy A B A B
và A , A cùng nằm ngoài đoạn BC . A C A C
Suy ra A A . Vậy ba điểm A,B,C thẳng hàng.
Trường hợp 2. Trong ba điểm A,B,C không có điểm nào thuộc cạnh của tam giác được chứng minh tương tự.
Ví dụ 1. Trong tam giác ABC , gọi M là trung điểm của cạnh BC , cho AB 12 và AC 16.
Điểm E và F lấy lần lượt trên hai cạnh AC và AB sao cho AE 2AF . Các đường EF và AM EG
cắt nhau tại G . Hãy tính tỉ số GF Lời giải.
Kéo dài BC và FE cắt nhau tại H .
Áp dụng Định lí Menelaus vào GH AF MB FBH với 3 điểm G, , A M : . . 1 (1) GF AB MH
Áp dụng Định lí Menelaus vào E CH với 3 điểm G, , A M :
Biên soạn: Trần Đình Hoàng 0814000158 53
Chuyên đề bồi dưỡng học sinh giỏi toán 8 ta có : GH AE MC . . 1 (2) A GE AC MH
Vì MB MC và EA 2FA nên chia vế theo vế của (1) cho (2) ta đươc: 1 GE AC GE AB F . . 1, hay 12 3 2. 2. . G E 2 GF AB GF AC 16 2 B M C H
Ví dụ 2. Cho tam giác ABC với AB AC . Gọi P là giao điểm của đường trung trực của BC và
đường phân giác trong của góc A . Dựng các điểm X trên AB và Y trên AC sao cho PX vuông góc BZ
với AB và PY vuông góc với AC . Gọi Z là giao điểm của XY và BC . Xác định giá trị tỉ số ZC Lời giải. A Vì PAX PAY và PXA
PYA 90 nên các tam giác
PAX và PAY bằng nhau, suy ra AX AY và PX PY .
Do P nằm trên trung trực của BC , a có PC PB Như thế, P
YC và PXB là hai tam giác vuông bằng X nhau, suy ra CY BX . Vì C
X ,Y , Z thẳng hàng, áp dụng Định lí Menelaus ta B Z được: AY CZ BX . . 1. YC ZB XA Y
Nhưng AX AY và CY BX nên đẳng thức này cho ta: BZ P
BZ ZC 1. Vậy tỉ số bằng 1. ZC
Ví dụ 3. Cho tam giác ABC và ba điểm A , B ,C tương ứng nằm trên ba cạnh BC,C , A AB sao cho 1 1 1
các đường thẳng AA , BB cắt nhau tại O . 1 1 Lời giải.
Giả sử ba cặp đường thẳng AB và A B , BC và 1 1 C
B C , CA và C A lần lượt cắt nhau tại ba điểm 2 1 1 1 1
C , A , B . Chứng minh rằng C , A , B thẳng hàng. 2 2 2 2 2 2
Giải. Áp dụng Định lí Menelaus vào các tam giác và các điểm: AA OB BC OAB và A , B ,C , ta có: 1 1 2 . . 1; (1) 1 1 2 B OA BB AC 2 1 1 2 OBC và OC BB CA B ,C , A , ta có: 1 1 2 . . 1; (2) 1 1 2 CC OB BA 1 1 2 A OAC và OA CC AB A ,C , B , ta có: 1 1 2 . . 1; (3) 1 1 2 AA OC CB C B 1 1 2 1 1
Nhân (1), (2) và (3) vế theo vế ta được: O BC CA AB 2 2 2 . . 1. AC BA CB A A C B 2 2 2 2 1
Áp dụng Định lí Menelaus (phần đảo) ta suy ra điều phải chứng minh.
Biên soạn: Trần Đình Hoàng 0814000158 54
Chuyên đề bồi dưỡng học sinh giỏi toán 8 2. Định lý Ce-va.
Ce-va là kỹ sư người Ý, nhưng yêu thích Toán học. Ông sinh năm 1648 , mất năm 1734 . Thời
thanh niên Ce-va theo học ở Đại học Pise rồi giúp việc cho Quận công vùng Mantoue. Công trình
nghiên cứu của ông là về Cơ học và Hình học. Đời sau biết đến ông thông qua một định lý hình
học mang tên ông: định lý Ce-va.
Định lý: Cho ba điểm D,E,F nằm trên ba cạnh tương ứng BC,CA, AB của tam giác ABC
(không trùng với ba đỉnh của tam giác) khi đó ba đường thẳng AD,BE,CF đồng quy khi và chỉ khi DB EC FA . . 1. DC EA FB Chứng minh P A Q
Xét đường thẳng AD,BE,CF đồng quy
Qua A kẻ đường thẳng song song với BC , đường E
thẳng này cắt đường thẳng BE,CF lần lượt tại Q F M và P .
Áp dụng định lý Ta-lét, ta có: FA AP EC BC ; FB BC EA AQ B D C AP AQ AM AP CD . CD BD MD AQ BD Từ đó suy ra: DB EC FA AQ BC AP . . . . 1. DC EA FB AP AQ BC Ngược lại, nếu DB EC FA . . 1. DC EA FB
Gọi M là giao điểm của BE và CF . Gọi D là giao điểm của AM và BC .
Theo phần thuận, ta có: D B EC FA D B DB D B DB . . 1 D C EA FB D C DC D B D C DB DC D B DB
BD BD D D . BC BC Vậy AD,BE,CF đồng quy.
Ví dụ. Cho hình thang ABCD với AB CD ; E là giao điểm hai cạnh bên AD và BC ; F là trung điểm AB .
a) Chứng minh AC, BD, EF đồng quy.
b) Biết diện tích hình thang bằng 1. Đường chéo hình thang có thể lấy giá trị bé nhất bằng bao nhiêu? Lời giải
a) Theo Định lí Céva, xét tam giác ABE , ba đường thẳng EF, BD và AC đồng quy khi và chỉ khi FA CB DE CB DE . . 1 . 1 (do FA FB ). FB CE DA CE DA
Điều này hiển nhiên đúng do AB // CD .
b) Gọi D ,C lần lượt là hình chiếu của D và C lên AB 1 1
Đặt d BD,d AC, p BD , p AC ,CC , h AB a,CD . b 1 2 1 1 2 1 1
Không mất tính tổng quát, có thể giả sử d d , khi đó, p p . 1 2 1 2
Biên soạn: Trần Đình Hoàng 0814000158 55
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Dễ thấy p p a b . 1 2 E Ta có a b S 1 1 ABCD 2 2 2 2 p d p h h 2 , 1 1 1 2 2 h h h
dấu bằng xảy ra khi p p h . 1 2
Lúc đó, d 2 .Vậy đường chéo hình thang có thể lấy D C 1 giá trị bé nhất là 2 . A D C B 1 F 1 3. Định lý Van Oben.
Van Oben (Van Aubel) sinh ngày 20.11 18
. 30 tại Maastricht (Hà Lan), mất ngày 03 0 . 2.1906
tại Anlwerpen (Bỉ). Ông nghiên cứu và dạy Toán cho các lớp dự bị đại học ở Atheneum,
Maastricht (Hà Lan) và đại học Gent (Bỉ). Trong quá trình nghiên cứu, ông công bố nhiều tính
chất, định lý hình học đặc sắc mang tên ông
Định lý: Cho M là một điểm nằm trong tam giác ABC . Gọi D,E,F thứ tự là giao điểm của AM AE AF
AM ,BM ,CM với các cạnh BC, AC, AB . Khi đó thì: . MD EC FB Chứng minh P A Q
Cách 1. Qua A kẻ đường thẳng song song với BC
cắt đường thẳng CM và BM lần lượt tại P và Q E
Áp dụng định lý Ta-lét, ta có: F AF AQ M AQ//BC . FB BC AE AP AP//BC . EC BC B D C AF AE AQ AP PQ . FB EC BC BC Mặt khác PQ PM AM PQ//BC từ đó suy ra AM AF AE . BC MB MD MD FB EC
Cách 2. Áp dụng định lý Menelaus cho ABD và ba điểm F ,M ,C thẳng hàng ta có: AF BC MD AF CD AM . . 1 . 1. FB CD AM FB BC MD
Áp dụng định lý Menelaus cho A
CD và ba điểm E,M ,B thẳng hàng ta có: AE BC MD AE BD MA . . 1 . 2 EC BD AM EC BC MD Từ 1 và 2 suy ra: AF AE AM CD BD AM . . FB EC MD BC BC MD
Biên soạn: Trần Đình Hoàng 0814000158 56
Chuyên đề bồi dưỡng học sinh giỏi toán 8 B. Bài tập vận dụng
Bài 1. (Mở rộng Van-Oben) Cho tam giác ABC . Trên tia đối của tia BA lấy điểm K , trên tia đối
của tia CA lấy điểm N . Gọi E là giao điểm CK và BN ; gọi M là giao điểm của AE và BC . AE AK AN Chứng minh rằng: . EM KB NC Tìm cách giải. P A Q
Với cách suy luận như định lý Van-Oben, chúng ta
cũng có thể chứng minh bằng hai cách. Trình bày lời giải M
Cách 1. Qua A kẻ đường thẳng song song với B C
BC cắt đường thẳng BN và BK lần lượt tại P và Q . E
Áp dụng định lý Ta-lét, ta có: AK AQ K AQ//BC . KB BC N AN AP AP//BC AK AN AQ AP PQ . NC BC KB NC BC BC PQ PE AE AE AK AN Mặt khác PQ//BC từ đó suy ra: . BC BE ME EM KB NC
Cách 2. Áp dụng định lý Menelaus cho ABM và ba điểm K ,E,C thẳng hàng ta có: AK BC ME AK CM AE . . 1 . 1. KB CM AE KB BC ME
Áp dụng định lý Menelaus cho ACM và ba điểm E,N ,B thẳng hàng, ta có: AN BC ME AN BM EA . . 1 . 2 NC BM EA NC BC ME AK AN AE CM BM AE Từ 1 và 2 suy ra: . . KB NC ME BC BC ME Bài 2. Cho tam giác BD
ABC . Trên cạnh BC lần lượt lấy điểm D sao cho 1 . Lấy điểm O trên DC 2 AO AE đoạn thẳng AD sao cho
4 . Gọi E là giao của hai đường thẳng AC và BO . Tính tỷ số . OD EC Lời giải. A Từ BD 1 suy ra BC 3 . DC 2 BD
Áp dụng định lý Menelaus cho ADC với
ba điểm B,O,E thẳng hàng, ta có: E AE BC OD AE 1 AE 4 . . 1 .3. 1 . O EC BD OA EC 4 EC 3
Nhận xét. Ngoài cách vận dụng định lý, chúng ta có thể kẻ B D C
thêm đường thẳng song song để vận dụng định lý ta-lét.
Bài 3. (Định lý Menelaus trong tứ giác) Cho tứ giác ABCD . Đường thẳng d cắt AB,BC,CD,DA tại MA NB PC QD
M ,N ,P,Q . Chứng minh rằng . . . 1. MB NC PD QA
Biên soạn: Trần Đình Hoàng 0814000158 57
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Tìm cách giải. N
Tương tự như chúng ta chứng minh định lý Menelaus
trong tam giác, chúng ta có nhiều cách chứng minh. Sau đây là một cách. Q Trình bày lời giải
Từ A,B vẽ AE//BF //CD E;F d A E
Theo hệ quả của định lý Ta-lét: M MA AE NB BE QD DP B ; ; F MB BF NC CP QA AE MA NB PC QD AE BE PC DP Suy ra: . . . . . . 1. MB NC PD QA BF CP PD AE D C P
Bài 4. Cho tam giác ABC nhọn có BD;CE là đường cao, H là trực tâm. Qua H kẻ đường thẳng 2 cắt cạnh HM BM .EM
AB, AC tại M ,N . Chứng minh rằng: HN DN .CN Lời giải. A
Áp dụng định lý Menelaus cho B,H ,D thẳng hàng đối với HM DN AB AMN , ta có: . . 1 1 HN DA BM D
Áp dụng định lý Menelaus cho C,H ,E thẳng hàng N E đối với HM CN AE AMN , ta có: . . 1 2 HN CA EM H Từ 1 , 2 nhân vế ta có: M 2 HM DN CN AB AE . . . . 1 3 2 HN DA CA BM EM B C Mặt khác AEC A DB g.g AB AD AB.AE AC.AD . AC AE 2 HM DN.CN 2 Thay vào HM BM .EM 3 suy ra: . 1 hay
(điều phải chứng minh). 2 HN BM .EM HN DN .CN
Bài 5. Cho tam giác ABC vuông tại A có đường cao AH , trung tuyến BM , phân giác CD cắt
nhau tại điểm O . Chứng minh rằng BH AC Tìm cách giải.
Để chứng minh BH AC bằng cách ghép vào hai tam giác là không khả thi bởi không khai
thác được tính đồng quy của giả thiết. Để khai thác được tính đồng quy của giả thiết này,
chúng ta liên tưởng tới định lý Ce-va. Vận dụng định lý Ce-va, chúng ta suy ra được BH DA .
1. Đã xuất hiện BH song chưa có AC . Để xuất hiện AC , chúng ta vận dụng tiếp HC DB
yếu tố giả thiết CD là phân giác. Từ đó chúng ta suy ra được: BH .AC HC.BC . Để có
BH AC , phần cuối cùng là chứng minh 2 HC.BC AC .
Biên soạn: Trần Đình Hoàng 0814000158 58
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Trình bày lời giải A Theo định lý Ce-va ta có: BH MC DA . . 1 HC MA DB D M BH DA O mà MA MC nên . 1 1 HC DB Vì DA AC CD là phân giác nên 2 DB BC B H C Từ BH AC 1 và 2 ta có: .
1 BH .AC HC.BC 3 HC BC HC AC
Nhận thấy ABC HAC g.g 2 AC HC.BC 4 AC BC
Từ 3 và 4 suy ra 2 BH .AC AC hay BH AC .
Bài 6. Cho tam giác ABC có điểm M nằm trong tam giác các tia AM ,BM ,CM cắt các cạnh
BC,CA, AB tương ứng tại D,E,F . Gọi H là giao điểm của DF và BM . Gọi K là giao điểm của
CM và DE . Chứng minh AD,BK ,CH đồng quy. Tìm cách giải. A
Để chứng minh AD,BK ,CH đồng quy, dễ dàng nghĩ tới
việc vận dụng định lý Ce-va đảo trong tam giác MBC .
Để vận dụng định lý Ce-va, chúng ta cần chứng minh E F KM BH CD M . .
1. Muốn xuất hiện tỉ số KM BH CD ; ; KC HM BD KC HM BD K H
chúng ta cần linh hoạt trong các tam giac để vận dụng
định lý Menelaus hoặc Ce-va. Trình bày lời giải B C D
Áp dụng định lý Menelaus trong tam giác AMC; AMB Ta có: KM EC DA BH DM FA . . 1; . . 1 KC EA DM HM DA FB KM EA DM BH FB DA Suy ra . ; . 1 KC EC DA HM FA DM
Áp dụng định lý Ce-va trong tam giác ABC , ta có: CD BF AE CD EC FA . . 1 . 2 BD FA EC BD AE BF Từ
1 và 2 nhân vế với vế ta được: KM BH CD EA DM FB DA EC FA KM BH CD . . . . . . . . . 1. KC HM BD EC DA FA DM AE BF KC HM BD
Theo định lý Ce-va đảo ta có AD,BK ,CH đồng qui.
Bài 7. Cho tam giác ABC nhọn có AH là đường cao. Lấy điểm O tùy ý thuộc đoạn AH ( O khác
A; H ). Các tia BO và CO cắt AC; AB tương ứng tại M ,N . Chứng minh rằng HA là tia phân giác của MHN . Lời giải
Cách 1. Qua A kẻ đường thẳng xy song song với BC . Gọi I ;K lần lượt là giao điểm của các
tia HN; HM với đường thẳng xy .
Biên soạn: Trần Đình Hoàng 0814000158 59
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Theo hệ quả định lý Ta-lét, ta có: AI AN AK AM I A K ; . BH BN CH MC
Áp dụng định lý Ce-va trong tam giác ABC đối M
với ba đường thẳng đồng qui AH ,BM ,CN ta có: N AN BH CM AI BH CH O . . 1 . . 1 BN CH MA BH CH AK AI 1 AI AK . AK
Xét HKI có HA IK; AI AK B H C
HIK cân tại H HA là đường phân giác MHN .
Cách 2. Xét trường hợp ABC AC AB . A
Dựng ABP cân tại A có AH là đường cao. AP cắt
HM tại Q . Gọi N là điểm đối xứng với Q qua AH .
Vì A,Q,P thẳng hàng suy ra A,N ,B thẳng hàng. Khi M QA N A N'
đó HA là đường phân giác của QHN và . Q N QP N B O
Áp dụng định lý Menelaus cho ACP với ba điểm thẳng hàng H ,Q,M ta có: HP MC QA HB MC N A . . 1 . . 1, theo định lý đảo HC MA QP HC MA N B B H P C
của Ce-va thì AH ,BM ,CN đồng quy.
Theo giả thiết AH ,BM ,CN đồng quy N N. Vậy HA là đường phân giác MHN
Xét trường hợp ABC AC AB . Chứng minh tương tự như trên.
Xét trường hợp ABC AC AB . Chứng minh tương tự
Bài 8. Giả sử O là điểm bất kì nằm trong tam giác ABC các tia AO,BO,CO lần lượt cắt
BC, AC, AB tại M ,N ,P . Chứng minh rằng: AO.AP BO.BM CO.CN . .
không phụ thuộc vào vị trí OP OM ON điểm O . Tìm cách giải. A
Nhận thấy phần kết luận của chúng ta là một tích các tỉ
số nên chúng ta liên tưởng tới hai định lý có thể dùng là N
Menelaus hoặc Ce-va. Nhận thấy nếu muốn có AO.AP P OP O
thì AO hay AP không thể xuất hiện được nếu vận OP OP
dụng định lý trên (bởi cả hai định lý đều không xuất
hiện tỉ số trên). Song nếu đảo mẫu số, tức là AO.AP thì OM B C M
tỉ số AO có thể xuất hiện được nhờ vận dụng định lý OM
Menelaus trong tam giác AMC hoặc AMB . Nhận thấy ý tưởng đó khả thi. Tiếp tục biểu diễn
các tỉ số BO ; CO một cách tương tự, chúng ta có một lời giải hay. ON OP Trình bày lời giải.
Biên soạn: Trần Đình Hoàng 0814000158 60
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Áp dụng định lý Menelaus trong: AO BM CN AO BC AN
AMC với ba điểm B,O,N thẳng hàng ta có: . . 1 . 1 OM BC NA OM BM CN BO AN CM BO AC BM
BCN với ba điểm A,O,M thẳng hàng, ta có: . . . 2 ON AC MB ON AN CM Xét CO BP AN CO AB NC A
CP với ba điểm B,O,N thẳng hàng ta có: . . 1 . 3 OP BA NC OP BP AN AO.AP BO.BM CO.CN AO BO CO Từ
1 ,2 và 3 ta có: . . . . .AP.BM .CN OP OM ON OM ON OP BC AN AC BM AB CN BM .AP.CN . . . . . .AP.BM .CN BC.AC.AB. 4 BM CN AN CM BP AN CM .BP.NA
Mặt khác, áp dụng định lý Ce-va đối với ABC có ba đường thẳng AM ,BN ,CP đồng quy ta BM CN AP có: . . 1 5 CM AN BP
Từ 4 và 5 suy ra: AO.AP BO.BM CO.CN . . BC.AC.AB . OP OM ON
Không phụ thuộc vào vị trí điểm O
Bài 9. Trên ba cạnh BC,CA, AB của tam giác ABC lần lượt lấy ba điểm H ,M ,N sao cho
AH ,BM ,CN đồng quy tại G . Gọi P,Q lần lượt là giao điểm của HN và BM ; HM và CN . Tia AP và tia AP AQ AN AM
AQ cắt BC lần lượt tại E và F . Chứng minh rằng: 3. PE QF NB MC Tìm cách giải. A
Định hướng và sự lựa chọn định lý để vận dụng vấn
đề quan trọng, nó quyết định sự thành công của bài
toán. Trong bài toán này, nhận thấy có nhiều đường
đồng quy, mặt khác phần kết luận lại xuất hiện tổng M
các tỉ số nên việc vận dụng định lý Van-Oben là điều N
chúng ta nên nghĩ tới. Để xuất hiện AP nên vận G PE Q P
dụng định lý Van-Oben trong tam giác ABH đối với
AE,BG và HN đồng quy. Để xuất hiện AQ nên vận QF B E F C H
dụng định lý Van-Oben trong tam giác ACH đối với
AF,CG và HM đồng quy. Sau đó, vì vế phải chỉ xuất hiện AN AM , chúng ta nên vận dụng NB MC
định lý Van-Oben trong tam giác ABC đối với AH ,CN và BM đồng quy. Từ đó chúng ta có lời giải hay. Trình bày lời giải.
Áp dụng định lý Van-Oben cho ABH với AE,BG,HN đồng quy tại P , ta có: AP AN AG 1 PE NB GH
Áp dụng định lý Van-Oben cho ACH Với AQ AM AG
AF,CG,HM đồng quy tại Q , ta có: 2 QF MC GH Từ AP AQ AN AM AG
1 và 2 cộng vế với vế, ta được: 2. 3 PE QF NB MC GH
Biên soạn: Trần Đình Hoàng 0814000158 61
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Áp dụng định lý Van-Oben cho ABC đối với AH ,BM ,CN đồng quy tại G , ta có: AG AN AM 4 GH NB MC AP AQ AN AM Từ 3 và 4 suy ra: 3.
(Điều phải chứng minh). PE QF NB MC
Nhận xét. Từ kết luận của bài toán, chúng ta nhận thấy:
- Áp dụng định lý Van-Oben cho ABC đối với AH ,BM ,CN đồng quy tại G , ta có AN AM AG
do đó chúng ta giải được bài toán: Trên ba cạnh BC,CA, AB của tam giác NB MC GH
ABC lần lượt lấy ba điểm H ,M ,N sao cho AH ,BM ,CN đồng quy tại G . Gọi P,Q lần lượt là
giao điểm của HN và BM ; HM và CN . Tia AP và tia AQ cắt BC lần lượt tại E và F . AP AQ AG Chứng minh rằng: 3. . PE QF GH
- Trường hợp H là trung điểm của BC thì MN //BC . Ta có kết quả sau: AN AM do đó ta NB MC
giải được bài toán sau: Trên ba cạnh BC,CA, AB của tam giác ABC lần lượt lấy ba điểm
H ,M ,N sao cho AH ,BM ,CN đồng quy tại G . Gọi P,Q lần lượt là giao điểm của HN và
BM ; HM và CN . Tia AP và tia AQ cắt BC lần lượt tại E và F . Chứng minh rằng: AP AQ AN 6. . PE QF NB AN AM
- Trường hợp G là trung điểm của AH thì
1. Do đó ta giải được bài toán sau: NB MC
Trên ba cạnh BC,CA, AB của tam giác ABC lần lượt lấy ba điểm H ,M ,N sao cho
AH ,BM ,CN đồng quy tại G . Gọi P,Q lần lượt là giao điểm của HN và BM ; HM và CN . Tia AP AQ
AP và tia AQ cắt BC lần lượt tại E và F . Chứng minh rằng: 3 . PE QF Bài 10. Cho tam giác BD CA
ABC . Trên cạnh BC,CA lần lượt lấy điểm D và E thỏa mãn 1 . DC EA 2
Gọi O là giao điểm của AD và BE . Tính tỷ số AO và BO . OD OE Lời giải. A Từ BD CE 1 suy ra BD 1 CD AE 2 ; 2; . DC EA 2 BC 3 DB AC 3
Áp dụng định lý Menelaus trong ADC với ba
điểm B,O,E thẳng hàng, ta có: AO BD CE AO 1 1 AO E . . 1 . . 1 6 . OD BC EA OD 3 2 OD
Áp dụng định lý Menelaus trong BEC với ba O
điểm A,O,D thẳng hàng, ta có: BO AE CD BO 2 2 BO 3 C . . 1 . . 1 . B D OE AC DB OE 3 1 OE 4
Bài 11. Cho tam giác ABC vuông tại A . Có đường cao AH , đường trung tuyến BM và phân giác BC BH
CD đồng quy tại O . Chứng minh rằng: AC CH
Biên soạn: Trần Đình Hoàng 0814000158 62
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. A
Trong tam giác ABC có AH ,CD,BM đồng quy tại O . D
Theo định lý Ce-va, ta có: BH CM AD . . 1 M O HC MA DB CM BD BC mà 1 và MA AD AC
(Tính chất đường phân giác) C H B BH AC BC BH suy ra .1. 1 . HC BC AC CH
Bài 12. Cho tam giác ABC có đường cao AH , đường trung tuyến BM và phân giác CD đồng
quy. Đặt a,b,c lần lượt là độ dài ba cạnh BC,CA, AB . Chứng minh rằng: a b 2 2 2 a b c 2 2a b . Lời giải. A
Áp dụng định lý Ce-va cho ba đường thẳng đồng quy AD BH CM AH ,BM ,CD , ta có: . . 1 mà AM CM BD CH AM D M nên AD BH AD CH . 1 . O BD CH BD BH
Mặt khác, CD là đường phân giác nên AD AC b CH b suy ra hay a.CH b.BH 1 B C BD BC a BH a G
Áp dụng định lý Py-ta-go cho tam giác vuông, ta có: 2 2 2 2
a BC HB HC 2.HB.HC 2 2 2 2 b AC HA HC 2 2 2 2 c AB HA HB Từ đó: a b 2 2 2
a b c a b2a.CH 2a.a.HC b.HC
2a.b.BH b.HC ( theo (1) 2 2a.ab 2a b .
Bài 13. Cho tam giác ABC AB AC , M là trung điểm của BC . Một đường thẳng qua M và
song song với đường phân giác AD của góc BAC cắt AC, AB lần lượt ở E và F . Chứng minh rằng CE BF Lời giải. F
Cách 1. (không dùng Menelaus)
Ta giải vắn tắt như sau: Từ AD//FM và ME//AD A
Áp dụng định lý Ta-lét, ta có: E BA BF CE CA 1 và 2 BD BM CM CD
Mặt khác, theo tính chất đường phân giác ta có: BA CA 3 BD CD B D M C Từ
1 ,2 và 3 suy ra: BF CE . BM CM
Do đó BF CE (do BM CM ).
Biên soạn: Trần Đình Hoàng 0814000158 63
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Cách 2. (dùng Menelaus) Xét tam giác EA MC FB
ABC với ba điểm F ,E,M thẳng hàng, ta có: . . 1 4 EC MB FA Do BAC AEF AFE nên A
EF cân ở A . Suy ra AE AF 5 2
Từ 4 và 5 suy ra BF CE . Điều phải chứng minh.
Bài 14. Cho tam giác ABC lấy điểm E thuộc cạnh AB và điểm F thuộc cạnh AC . Gọi AM là
đường trung tuyến của tam giác ABC . Chứng minh rằng điều kiện cần và đủ để EF song song với
BC là AM ,BF và CE đồng qui. Lời giải. A AE BM CF AE CF Xét . . . 1 EB MC FA EB FA
Nếu AM ,BF,CE đồng qui thì theo định AE BM CF E F lý Ce-va: . . 1. EB MC FA Từ AE CF AE AF 1 suy ra: . 1 EB FA EB CF
EF //BC (định lý Ta-lét đảo). Nếu AE AF EF //BC . Từ 1 suy ra: B D C BE CF AE BM CF AE CF . . .
1 AM ,BF ,CE đồng qui (theo đinh lý Ce-va đảo). EB MC FA EB FA Bài 15. Cho tam giác AK
ABC có trung tuyến AD . Trên AD lấy điểm K sao cho 3. Hỏi đường KD
thẳng BK chia tam giác ABC theo tỉ số nào? Lời giải. A
Gọi E là giao điểm của đường thẳng
BK và AC . Áp dụng định lý Menelaus
trong ACD đối với ba điểm B,K ,E thẳng hàng, ta có: AK BD CE . . 1 KD BC EA E 1 CE CE 2 K 3. . . 2 EA EA 3
Mặt khác ABE và BCE có chung C S AE S B D
đường cao kẻ từ B , suy ra: 3 ABE ABE . S CE S 2 BCE BCE
Bài 16. Cho tứ giác ABCD . Cạnh AB cắt CD kéo dài tại E , cạnh BC cắt AD kéo dài tại I .
Đường chéo AC cắt BD và EI lần lượt tại M ,N . Chứng minh rằng MA NA . MC NC
Biên soạn: Trần Đình Hoàng 0814000158 64
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. M
Áp dụng định lý Menelaus trong AEC với ba điểm MA DC BE M ,D,B thẳng hàng, ta có: . . 1. MC DE BA
Áp dụng định lý Menelaus trong ABC với ba điểm NA IC EB
N ,I ,E thẳng hàng, ta có: . . 1 I NC IB EA MA DC BE NA IC EB Suy ra . . . . MC DE BA NC IB EA A do đó MA NA IC DE AB B . . . 1 MC NC IB DC AE M
Áp dụng định lý Menelaus trong BEC với ba
điểm I ,D,A thẳng hàng, nên IC AB DE . . 1 2 D IB AE DC C E MA NA Từ 1 và 2 suy ra . MC NC
Bài 17. Cho tam giác ABC . Lấy K thuộc cạnh AB và T thuộc tia đối tia BC . Gọi F là giao điểm
của TK với AC;O là giao điểm của BF và CK . Gọi E là giao điểm của AO và BC . Chứng minh TB EB rằng: . TC EC Lời giải. A
Áp dụng định lý Ce-va trong
ABC với 3 đường thẳng đồng F quy EB FC KA AE,BF ,CK , ta có: . . 1 1 EC FA KB
Áp dụng định lý Menelaus trong K ABC O
với ba điểm T ,K ,F thẳng hàng, ta có: TC KB FA . . 1 2 TB KA FC K B E C Từ
1 và 2 nhân vế với vế ta được: TB EB . TC EC
Bài 18. Cho tam giác ABC có D là điểm bất kỳ nằm trong tam giác. Lấy điểm M tùy ý thuộc
AD . Gọi giao điểm của BM và AC là E ; gọi giao điểm CM và AB là F . Các tia DE và CM
giao nhau tại K ; các tia DF và BM tại H . Chứng minh rằng CH ; AD; BK đồng quy. Lời giải. A
Gọi BC giao với AD tại G .
Áp dụng định lý Menelaus trong A BM , A MC ta E được: DM FA HB . . 1 1 F DA FB HM M DM EA KC K . . 1 2 H DA EC KM D Chia EC FA KC HM 1 cho 2 , ta được: . . 3 EA FB KM HB B G C
Biên soạn: Trần Đình Hoàng 0814000158 65
Chuyên đề bồi dưỡng học sinh giỏi toán 8 GB EC FA EC FA GC Vì AG,BE,CF đồng quy . . 1 . 4 GC EA FB EA FB GA Từ GC KC HM GB KC HM 3 và 4 : . . .
1 (điều phải chứng minh) GB KM HB GC KM HB
Bài 19. Cho tam giác nhọn ABC có ba đường cao AD,BM ,CN cắt nhau tại H . Chứng minh rằng: HD HM HN DB MC NA . . . AD BM CN DC MA NB Lời giải. A
Áp dụng tỉ số diện tích hai tam giác có chung cạnh đáy, ta có: HD HM HN S S S HBC HCA HAB 1. M AD BM CN S S S ABC ABC ABC N
Áp dụng định lý Ce-va, ta có: DB MC NA . . 1. DC MA NB H
Từ đó suy ra điều phải chứng minh. B D C
Bài 20. Từ điểm I thuộc miền trong tam giác ABC , kẻ AI cắt BC tại D . Qua I kẻ MN ,PQ và
RS lần lượt song song với BC, AB, AC ( M ,S thuộc AB;Q,R thuộc BC; N ,P thuộc AC ) Chứng minh rằng: a) IM DB ; b) IM IP IR . . 1. IN DC IN IQ IS Lời giải. A
a) Áp dụng hệ quả định lý ta-lét, ta có: MI AI P MI //BD S BD AD E IN AI F IN //CD I CD AD N M MI IN MI DB . BD CD NI DC
b) Gọi E là giao điểm của giao điểm của đường thẳng
BI và AC; F là giao điểm của đường thẳng CI và AB Q R C B D
Chứng minh tương tự câu a, ta có: IP AF IR CE ; IQ BF IS AE
Áp dụng định lý Ce-va trong ABC đối với AD,BE,CF đồng quy, ta có: BD CE AF IM IP IR . . 1 . .
1. Điều phải chứng minh. CD AE BF IN IQ IS
Bài 21. Cho tam giác ABC vuông tại C có đường cao CK . Vẽ đường phân giác CE của tam giác
ACK . Đường thẳng qua B song song với CE cắt đường thẳng CK tại F . Chứng minh rằng
đường thẳng EF chia đoạn thẳng AC thành hai phần bằng nhau. Lời giải. Ta có: BEC A ACE KCB KCE BCE
Do đó BCE cân tại B nên BE BC .
Biên soạn: Trần Đình Hoàng 0814000158 66
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Mặt khác BF //CE nên theo định lý Ta-lét, ta có: CK EK CK FK EK BK CF BE mà CF BC BC BE nên 1 FK BK FK BK FK BK FK BK
Vì CE là đường phân giác của góc ACK nên: A AE AC 2 KE CK BC AE F A BC ” CKB (g.g) (3) BK CK E Từ CF AE 2 và 3 suy ra: 4 D FK KE K
Giả sử đường thẳng EF cắt AC tại D . Áp dụng định
lý Mennenlaus vào tam giác ACK bị cát tuyến DEF AD CF KE cắt các cạnh, ta có: . . 1 5 CD KF AE C B Từ AD 4 và 5 suy ra: 1 hay ta có: AD CD . CD
Bài 22. Cho tam giác ABC . Gọi I là trung điểm của cạnh BC . Lấy M thuộc tia đối của tia CA .
Tia MI cắt đường thẳng AB tại N . Trên tia đối của tia BC lấy điểm E , tia EN cắt tia AC tại P .
Tia PI cắt đường thẳng AB tại Q . Gọi F là giao điểm của QM và IC . Chứng minh IE IF . Lời giải. A
Áp dụng định lý Menelaus trong ABC với ba điểm M ,N ,I thẳng hàng, ta có: IB MC NA MC NA . . 1 . 1 1 IC MA NB MA NB P
Áp dụng định lý Menelaus trong ABC với ba điểm N Q,P,I thẳng hàng, ta có: C IC PA QB PA QB F . . 1 . 1 2 E B I IB PC QA PC QA
Áp dụng định lý Menelaus trong ABC với ba điểm M N ,E,P thẳng hàng, ta có: EB PC NA . . 1 3 EC PA NB
Áp dụng định lý Menelaus trong ABC với ba điểm Q,M ,F thẳng hàng, ta có: Q FC QB MA . . 1 4 FB QA MC MC NA QB PA PC NA QB MA Từ 1 và 2 suy ra : . . do đó . . . MA NB QA PC PA NB QA MC
Từ 3 và 4 suy ra: EB PC NA FC QB MA . . . . EC PA NB FB QA MC EB FC EB FC EB FC Từ đó suy ra: BE FC IE IF . EC FB EB EC FB FC BC BC
Biên soạn: Trần Đình Hoàng 0814000158 67
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 23. Cho hình bình hành ABCD . Trên cạnh AB lấy điểm K . Qua K kẻ đường thẳng song song
với AD . Trên đường thẳng đó lấy điềm L bên trong hình bình hành, trên cạnh AD lấy điểm M
sao cho AM KL . Chứng minh rằng ba đường thẳng CL,DK và BM đồng quy. Lời giải. A K B
Gọi N là giao điểm của hai đường thẳng BM và
CL . Tứ giác MLKA là hình bình hành. Giả sử N
đường thẳng ML cắt cạnh BC tại P . Khi đó, ta M
có: LP KP;MD CP . Ta sẽ chứng minh P L D,N ,K thẳng hàng.
Áp dụng định lý Mennenlaus vào tam giác BMP D C
bị cắt bởi cát tuyến CLN cắt các cạnh, ta có: BN ML PC BN AK MD . . 1 . . 1 NM LP CB NM KB AD
Suy ra ba điểm K ,N ,D thẳng hàng (theo định lý Menelaus đảo vào ABM )
Vậy ba đường thẳng CL,DK và BM đồng quy.
Bài 24. Cho ABC không cân có CD là đường phân giác. A
Lấy điểm O thuộc đường thẳng CD ( O khác C và D ). Gọi
M ,N lần lượt là giao điểm của đường thẳng AO,BO với BC
và AC . Gọi P là giao điểm của đường thẳng MN và AB .
Chứng minh rằng CD vuông góc với CP . N D O Lời giải.
Áp dụng định lý Ce-va vào tam giác ABC , ta có: B C CN AD BM M . . 1 1 NA DB MC
Áp dụng định lý Menelaus vào tam giác
ABC với ba điểm N ,M ,P thẳng hàng, ta có: CN AP BM . . 1 2 NA PB MC Từ 1 và 2 suy ra CN AD BM CN AP BM . . . . NA DB MC NA PB MC P AD AP 3 DB PB
Từ giả thiết CD là đường phân giác của ABC AD CA AP CA
CP là đường phângiác ngoài của tam giác ABC . DB CB PB CD Từ đó suy ra CD CP .
Bài 25. Cho tam giác ABC có điểm O nằm trong tam giác. Các đường thẳng AO,BO,CO cắt các
cạnh BC,CA, AB lần lượt tại D,E,F . Qua O kẻ đường thẳng song song với BC , cắt DF ,DE lần
lượt tại M và N . Chứng minh rằng: OM ON .
Biên soạn: Trần Đình Hoàng 0814000158 68
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. H A I
Qua A kẻ đường thẳng xy song song với BC cắt
DM ,DN lần lượt tại H và I .
Theo hệ quả định lý Ta-lét, ta có: E AH AF AI AE F O ; BD BF CD EC N M
Áp dụng định lý Ce-va trong tam giác
ABC với ba đường AD,BE,CF đồng quy tại O , AF BD CE AH BD CD AH ta có: . . 1 . . 1 1 BF CD EA BD CD AI AI B D C hay AH AI OM DO ON
MN //HI theo hệ quả định lý Ta-lét, ta có: . Mà AH AI nên OM ON AH DA AI
Bài 26. Cho tam giác ABC có điểm M nằm trong tam giác. Gọi D,E,F thứ tự là giao điểm của
đường thẳng AM ,BM ,CM với các cạnh BC, AC, AB . Chứng minh rằng trong các tỉ số AM BM CM ; ;
có ít nhất một tỉ số không lớn hơn 2 và ít nhất một tỉ số không nhỏ hơn 2 . MD ME MF
(Thi vô địch Toán Quốc tế, IMO ) Lời giải. A
Kẻ ba đường trung tuyến AI ,BK ,CP của tam giác
ABC có trọng tâm G chia tam giác thành 6 tam giác F E
BGI ,BGP,CGK , AGK , AGP, CGI . Do đó điểm M nằm trong một trong M
6 tam giác đó kể cả trên cạnh. P K
Giải sử M nằm trong hoặc trên cạnh của AGK .
Theo định lý Van-Oben, ta có: AM AF AE AF AE G 2 . MD FB EC PB KC BM BF BD BF BD Mặt khác 2 . B D C ME FA DC PA IC I
Dấu bằng xảy ra khi M trùng với G . Suy ra điều phải chứng minh.
Bài 27. Cho tam giác ABC , trên ba cạnh BC,CA, AB lần lượt lấy ba điểm A ,B ,C sao cho
AA,BB,CC đồng quy tại K . Gọi M ,N lần lượt là giao điểm của AC và BB ; A B và CC . Tia
AM , tia AN lần lượt cắt BC tại E,F . Chứng minh rằng:
a) EN ,FM , AA đồng quy tại I b) IA.KA 3.IA .KA. Lời giải.
a) Áp dụng định lý Menelaus cho tam giác ABE với 3 điểm thẳng hàng A,M ,C , ta có: AM EA BC AM C A A B . . 1 . ME A B C A ME BC EA
Áp dụng định lý Menelaus cho tam giác AFC với 3 điểm thẳng hàng A,N ,B , ta có: FN AB CA FN A F B C . . 1 . NA B C A F NA CA AB Xét AM EA FN C A A B EA A F B C C A A B B C . . . . . . . 1 ME A F
NA BC EA AF CA AB BC CA AB
Biên soạn: Trần Đình Hoàng 0814000158 69
Chuyên đề bồi dưỡng học sinh giỏi toán 8
(Do AA,BB,CC đồng quy tại K - định lý Ce-va) A
Cũng theo định lý Ce-va ta có AA,EN và FM đồng quy tại I .
b) Áp dụng định lý Van-Oben cho tam giác ABA ; ACA ; AEF , ta có: B' AM AK AC C' 1 ; K ME KA C B N AN AK AB M 2 ; I NF KA B C AM AN AI 3 ME NF IA B E A' F C Thay AK AC AB AI
1 ,2 vào 3 ta được: 2. 4 KA C B B C IA AC AB AK
Áp dụng định lý Van- Oben cho tam giác ABC , ta có: C B B C KA Thay vào AK AI 4 , ta được: 3. 3.IA.AK KA.AI . KA IA
PHẦN II. TỔNG HỢP VÀ MỞ RỘNG I. Kiến thức mở rộng
1. Một số hệ thức trong tam giác vuông suy từ các tam giác đồng dạng a) Hệ thức 1
Cho tam giác ABC vuông tại A có đường cao AH . Khi đó: 2 AB BH.BC; (1) 2 AC CH.C . B (2) b) Hệ thức 2
Cho tam giác ABC vuông tại A có đường cao AH . Khi đó: 2 AH BH.HC. II. Một số ví dụ
Ví dụ 4. Giả sử H là trực tâm của tam giác nhọn ABC . Trên đoạn HB và HC lấy hai điểm M ,
N sao cho các góc AMC và ANB đều vuông. Chứng minh rằng AN AM . Lời giải. A
Vì tam giác ANB vuông tại N với đường cao NF nên 2 AN AF.AB (1)
Do tam giác AMC vuông tại M với đường cao ME nên E 2 AM AE.AC (2) F
Các tam giác AEB và AFC đồng dạng cho ta AE AF AE.AC AF.AB (3) H N M AB AC
Từ (1), (2) và (3) ta suy ra AM AN . B C
2. Áp dụng Định lí Thales và tam giác đồng dạng trong việc tính diện tích và chứng minh các hệ thức hình học
Biên soạn: Trần Đình Hoàng 0814000158 70
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Ví dụ 5. Cho hình vuông ABCD ; M là trung điểm của AB ; N là trung điểm của BC ; AN và CM
cắt nhau tại O . Tính tỉ số diện tích của tứ giác AOCD và diện tích của ABCD . Lời giải. D C
Gọi s là diện tích hình vuông. Vì O là giao điểm hai trung tuyến
của tam giác ABC nên O là trọng tâm tam giác ABC , suy ra BO
đi qua trung điểm của AC và do đó qua D . N
Theo định lí Thales: ta có : OH AH . O NB AB
Mà AB 2NB nên AH 2OH 2HB . Suy ra 1 HB AB . Ta có: 3 A M H B 1 s S .S
(chung đáy AB , đường cao 1 OH BC ) 1 1 . .s . AOB 3 ABC 3 3 2 6 Tương tự: s s s s S . Vậy: 2 S s
. Do đó tỉ số cần tính là 2 . BOC 6 AOCD 6 6 3 3
Ví dụ 6. Qua điểm O bất kì trong tam giác ABC , dựng các đường thẳng DE , FK , MN lần lượt
song song với AB , AC , BC sao cho F , M ở trên AB ; E , K ở trên BC và N , D ở trên AC . Chứng minh rằng: AF BE CN 1. AB BC CA Lời giải. A Ta có S S S S S ABC ABO BCO CAO (1) F
Gọi I , J , H lần lượt là hình chiếu của O lên các D
cạnh BC , CA , AB . Khi đó, (1) tương đương với J H
2S OI.BC OJ.CA OH.AB M N (2) O Mặt khác, tam giác C
MOF đồng dạng với tam giác 1
BCA (do có hai cặp cạnh song song và cặp cạnh còn
lại nằm trên cùng một đường thẳng) nên tỉ số hai
đường cao bằng tỉ số đồng dạng; ngoài ra, MOEB là B E I K C
hình bình hành nên OM BE . Do đó, gọi CC là 1 1 OH.AB BE đường cao kẻ từ OH OM BE
C của tam giác ABC , ta có Suy ra 2 (3) CC BC BC 1 BC 1 CC .AB 1 2
Tương tự, gọi BB và AA tương ứng là các đường cao kẻ từ B và A của tam giác ABC , ta 1 1 1 1 OI.BC CN OJ.CA AF cũng có 2 (4) ; 2 (5) 1 1 .BC CA AA . AB BB CA 1 2 1 2
Cộng vế theo vế của (3), (4), (5) và để ý (2), suy ra điểu phải chứng minh.
3. Tam giác đồng dạng và mối liên hệ với các biến đổi đại số
Ví dụ 7. Trung điểm cạnh AB của hình chữ nhật ABCD là F . Gọi P là điểm nằm trên đường
phân giác của góc C . Hạ PQ BC Q BC.Chứng minh rằng nếu: PF DQ thì AP BC .
Biên soạn: Trần Đình Hoàng 0814000158 71
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. D 2b C
Gọi R là điểm trên đường thẳng AB sao cho
PR AB , kí hiệu a , b , x lần lượt là độ dài các đoạn x thẳng CB , BF , CQ .
Giả sử PF vuông góc DQ , khi đó tam giác DCQ P a Q
đồng dạng với tam giác PRF . Suy ra CQ RF , hay, x b x , CD RP 2b a x R do đó 2 2 ax x 2b 2bx . A F B b
Biến đổi hệ thức trên ta được: b x2 a x2 2 2 a 0
Do đó, AP AR RP b x2 a x2 2 2 2 2 2 2
a BC , suy ra AP BC
Chú ý. Dùng các hệ thức trên, dễ dàng chứng minh được điều ngược lại cũng đúng, với điều kiện P F .
Ví dụ 8. Tam giác vuông ABC có các cạnh góc vuông AC b, AB c và độ dài đường phân giác AD d .Chứng minh: 1 1 2 . b c d Lời giải. C Hạ DE AB .
Tam giác AED vuông cân tại E , D do đó: d AD AE 2 .
Đặt EA ED x thì d x 2 .
Vì DE // AC nên theo định lí Thales ta có: DE BE hay x c x x c x c bc x . AC BA b c b c b c b c A E B Từ đó ta có: bc 2 d x 2 bd dc bc 2. b c
Chia cả hai vế của đẳng thức trên cho dbc 0 ta được: 1 1 2 . b c d
Ví dụ 9. Trong tất cả các hình chữ nhật nội tiếp tam giác cho trước, tìm hình chữ nhật có diện tích lớn nhất. Lời giải. A
Giả sử hình tam giác cho trước có cạnh BC a không
đổi và đường cao AD h không đổi.
Gọi các cạnh của hình chữ nhật là MN y, MQ x , thì
AD AD DD h . x Q D' P
Diện tích hình chữ nhật MNPQ là S x . y
Dễ thấy AQP ” ABC (g.g) cho tỉ lệ: PQ AD , hay y h x a y h x. BC AD a h h B M D N C Do đó: ax a S h x 2 x hx , hay h h
Biên soạn: Trần Đình Hoàng 0814000158 72
Chuyên đề bồi dưỡng học sinh giỏi toán 8 2 2 2 2 a h h h a h h 2 2 a h h ah 2 2 S x 2 .x x xh x . h 2 4 4 h 4 4 h 2 4 4
Vậy diện tích hình chữ nhật lớn nhất bằng ah , khi h x . 4 2
Kết luận: Trong tất cả các hình chữ nhật nội tiếp A
BC cho trước thì hình có một cạnh bằng
nửa đường cao tam giác ( h ), cạnh kia bằng nửa cạnh đáy tam giác ( a h a y h ), thì 2 h 2 2
hình chữ nhật đó có diện tích lớn nhất.
Ví dụ 10. Cho tam giác cân ABC có góc BAC 20, A AB AC b, BC . a Chứng minh rằng 3 3 2 a b 3ab . Lời giải.
Lấy điểm E trên cạnh AC sao cho góc ABE 60 . 20° Dựng AD BE , suy ra 1 1 BD AB b . Ta có 2 2 2 2 2 2 2 2
AE ED AD , AB BD AD , do đó 2 2 2 2 AB BD EA DE . (*)
Tam giác ABC đồng dạng với tam giác BCE (hai tam giác
cân có góc ở đỉnh bằng 20 và góc đáy bằng 80 ) nên CE BC 2 a
, và BE BC a nên suy ra CE . BC AB b Thay vào (*) ta được: 2 2 2 b a b 2 4 2 b a b D 2 b b a 2 2 2 b 2a a ab E 4 b 2 2 4 b 4 60° 20° 80° 4 4 4 2 2 3 3 3 2
b b a 3a b ab a b 3ab (đpcm). B C
Ví dụ 11. Cho a,b,c và a ,b ,c là các độ dài các cạnh tương ứng của hai tam giác ABC và A B C
. Chứng minh rằng điều kiện cần và đủ để hai tam giác này đồng dạng là:
aa bb cc a b ca b c . Lời giải.
Cả hai vế đẳng thức đã cho đều dương, do đó đẳng thức đã cho tương đương với bình phương
hai vế: aa bb cc 2 aa bb
2 aa cc 2 bb c
c a b ca b c. 2 2 2
Biến đổi, đẳng thức trên tương đương với: ab a b ac a c bc b c 0 a b ab a b 0 a b ab a b a c a b c ac a c
0 ac a c A BC đồng dạng với A B C . a c a b c 0 bc b c bc b c b c b c
4. Tam giác đồng dạng và bài toán quỹ tích
Biên soạn: Trần Đình Hoàng 0814000158 73
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Ví dụ 12. Cho tứ giác ABCD . Điểm M di động trên đường chéo BD . Qua M vẽ đường thẳng song
song BC cắt AB ở E . Qua M vẽ đường thẳng song song CD cắt AD ở F . Vẽ hình bình hành
MEKF . Tìm tập hợp các điểm K . Lời giải.
a) Phần thuận: Vẽ BP // CDP AD , vẽ CQ // BC Q AB. P , Q cố định. BDQ có
EM // QD nên theo Định lí Thales ta có: QE DM . QB DB BPD có MF // PB nên: MF DM . BP DB
MF EK (tứ giác MEKF là hình bình hành). QE EK A Do đó: . QB BP Xét QEK và QBP có QEK QBP EK // BP , Q K QE EK . P E QB BP
Vậy QEK đồng dạng với QPB , suy ra F EQK
BQP , do đó P , K , Q thẳng hàng. Vậy K
thuộc đường thẳng cố định PQ . B D M b) Giới hạn:
* Khi M B thì E B, F P ta có K P .
* Khi M D thì E Q, F D ta có K Q . C
Vậy K di động trên đoạn thẳng PQ . c) Phần đảo:
Lấy điểm K bất kì trên đoạn thẳng PQ .
Vẽ KE // CDE AB , EM // BC M BD , MF // CDF AD .
Ta sẽ chứng minh tứ giác MEKF là hình bình hành.
Ta có KE // CD , MF // CD , suy ra KE // MF . (1)
BDQ có EM // QD nên theo Định lí Thales ta có: QE DM (2) QB DB DF DM
BPD có MF // BP (vì MF // CD, BP // CD MF // BP ) nên . (3) DP DB QK QE
QBP có KE // BP (vì KE // CD, BP // CD KE // BP ) , do đó . (4) QP QB
Từ (2), (3) và (4) ta có QK DF
. Theo Định lí Thales đảo, KF // QD . Mà EM // QD nên QP DP
KF // EM . Kết hợp với (1), ta có MEKF là hình bình hành.
Ví dụ 13. Cho tứ giác lồi ABCD . Tìm trong tứ giác đó tập hợp các điểm O sao cho diện tích các tứ
giác OBCD và OBAD bằng nhau. Lời giải.
a) Phần thuận: Qua O kẻ các đường thẳng d song song với BD ; d cắt AB, AD lần lượt tại
B , D . Gọi h là khoảng cách từ A đến B D ; h là khoảng cách giữa hai đường thẳng song 1 1 a 1 1 o
song B D và BD ; h là khoảng cách từ C đến BD . 1 1 c
Biên soạn: Trần Đình Hoàng 0814000158 74
Chuyên đề bồi dưỡng học sinh giỏi toán 8 B D h
ABD có B D // BD , suy ra: 1 1 a . 1 1 BD h h B a o S B D h h OBAD 1 1 a o 1 S BD h h C OBCD c o 1 B1 h h h ho a . a o 1 h h h a c o O h h h h hc a o c o h
Do đó, B D đi qua trung điểm của AC . Vậy O thuộc a 1 1 M
đường thẳng d song song với BD và đi qua trung điểm M của AC . A D1 D
b) Giới hạn: Điểm O nằm trong tứ giác ABCD nên M chuyển động trên đoạn thẳng B D . 1 1
c) Phần đảo: Lấy điểm D bất kì thuộc đường thẳng B D , Gọi h là khoảng cách từ A đến B D ; 1 1 a 1 1
h là khoảng cách từ C đến BD ; h là khoảng cách giữa hai đường thẳng song song BD và c o
B D . M là trung điểm AC nên h h h . 1 1 a o c S B D h h h h h OBAD 1 1 a o Ta có: B D h 1 1 a B D // BD , a . a o 1 S S . 1 1 BD h h S BD h h h h h h OBCD c o OBAD OBCD a o a o c o
d) Kết luận: Tập hợp các điểm O là đoạn thẳng B D song song với BD và đi qua trung điểm 1 1 của AC . BÀI TẬP TỔNG HỢP
Bài 1. Cho tam giác cân ABC đỉnh A , O là trung điểm BC . Hai điểm M , N chạy trên hai cạnh BA , CA thỏa mãn 2 2
BM .CN OB OC .Chứng minh ba tam giác MON, MBO,OCN đồng dạng. Lời giải. A BM OB BM OC Từ giả thiết ta có: OB CN OB CN
(do OB OC ). Kết hợp với hai góc đáy bằng nhau của tam
giác cân, dễ dàng suy ra MBO đồng dạng OCN . Suy ra N OM ON OM OC . M OB NC ON NC
Mặt khác, dễ dàng chứng minh MON C . Do đó OCN đồng
dạng với MON , suy ra điều phải chứng minh. B O C
Bài 2. Cho tam giác cân ABC AB AC , có góc BAC bằng . Gọi D và E theo thứ tự là trung
điểm các cạnh AB và AC . Trên tia đối của tia DE , lấy một điểm M tùy ý không trùng với D . Trên tia đối
của tia ED , lấy một điểm N sao cho góc MAN bằng 1
90 . Hai đường thẳng MB và NC cắt 2
nhau tại P . Tính góc BPC .
Biên soạn: Trần Đình Hoàng 0814000158 75
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. A
Mặt khác, trong tam giác AMD ta có 1 2 A M 180 D 90 . 1 1 1 2 2 1 D E 1 M N Từ (1) và (2) suy ra 2 2 M A . (3) 1 2
Vì tam giác ABC cân và DE là đường trung bình nên MDA AEN. B C
Kết hợp điều này với (3), hai tam giác MDA và AEN đồng dạng, từ đó MD AE MD EC , DA EN DB EN
suy ra hai tam giác MDB và CEN đồng dạng (có hai góc P
D và E bằng nhau xen giữa hai cặp cạnh tương ứng tỉ lệ). Từ đó: N MBD , suy ra M N BMD MBD 180 D . 2 1 2 2
Mặt khác, trong tam giác MNP ta lại có M N 180 MPN. Vì vậy, BPC MPN D 90 . 2 2 1 2
Bài 3. Chứng minh rằng trong một tứ giác bất kì, các đoạn thẳng nối đỉnh tứ giác với trọng tâm
tam giác tạo bởi ba đỉnh còn lại đồng quy. Lời giải. B
Gọi A , B ,C , D lần lượt là trọng tâm các tam giác 1 1 1 1
BCD, CDA, DAB, ACB. Các đường thẳng BA , AB 1 1
cùng đi qua trung điểm I của CD và ta có A C1 D1 IB IA 1 1 1 A B //AB, 1 1 IA IB 3 A B 1 OA OB 1 A1 1 1 1 1 . AB 3 OA OB 3 B Vậy 1
BB cắt AA tại O, điểm chia AA theo tỉ lệ 3 :1. 1 1 1
Tương tự, CC và DD cũng cắt AA tại điểm chia D I C 1 1 1
AA theo tỉ lệ 3 :1, suy ra điều phải chứng minh. 1
Bài 4. Đường cao của một hình thang cân bằng h và diện tích bằng 2
h . Hỏi góc tạo bởi hai đường
chéo của nó bằng bao nhiêu? Lời giải. D N C
Theo đề bài: MN h . Theo tính chất hình thang cân; hai
đường chéo bằng nhau, cắt nhau tạo thành hai tam giác O
cân AOB và COD. Qua O kẻ MN vuông góc với hai
đáy,theo tính chất hình bình hành thì MN là trục đối xứng
của hình thang cân nên M, N là trung điểm của AB và CD. Ta có: 1 S (AB CD)MN . Thay 2 S h và MN h , ta có A M B 2 1 1 1 2
h (AB CD) h h AB CD h AM N . D 2 2 2
Từ đó, kết hợp với hai tam giác OMA và OND đồng dạng, cho ta: OM ON OM ON 1. AM DN AM DN
Biên soạn: Trần Đình Hoàng 0814000158 76
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Suy ra AM MO và DN NO , nghĩa là các tam giác MAO và DON là các tam giác vuông cân.
Từ đó ta có các đường chéo vuông góc với nhau.
Bài 5. Một hình chữ nhật được gọi là nối tiếp một tam giác khi hình chữ nhật có một cạnh trùng
với một cạnh của tam giác, hai đỉnh còn lại của hình chữ nhật thuộc hai cạnh kia của tam giác. Tìm
điều kiện của tam giác để hai hình chữ nhật nội tiếp tam giác có chu vi bằng nhau. Lời giải. A
Trước hết, ta dựng hình chữ nhật PQRS nội tiếp
ABC .RS cắt đường cao AH tại D. K L
Qua D kẻ DK //AC . Qua K kẻ KL//BC và ta dựng được
hình chữ nhật KLMN như hình vẽ. Q
Ta sẽ tìm điều kiện để hai hình chữ nhật này có chu vi D S R bằng nhau. I
Giả sử hai hình chữ nhật này có chu vi bằng nhau, ta phải có SP RS KN KL (1) B P N H M Q C
Nhưng KLRD là hình bình hành (theo cách dựng) nên KL DR RS SD .
Ta có KN KI IN và SP IN . Thay chúng vào (1), ta có IN RS KI IN RS SD,
hay KI SD . Mặt khác, dễ thấy SKD B AC(g g) cho tỉ lệ: BC AH
, nên phải có BC AH . Đó chính là điều kiện cần tìm. SD KI
(Đảo lại, nếu BC AH , đi ngược lại lí luận trên, ta cũng dễ dàng chứng minh được rằng hai
hình chữ nhật nội tiếp nói trên có chu vi bằng nhau).
Tóm lại, để hai hình chữ nhật nội tiếp tam giác có chu vi bằng nhau, ta phải có một đường cao
bằng cạnh đáy tương ứng. Bài 6. Cho tam giác S
ABC . Tìm tập hợp các điểm M sao cho MAB a ( a 0 , a cho trước) SMAC Lời giải. A
Phần thuận: Gọi D là giao điểm AM và BC.
Vẽ BH AM , CK AM (H , K AM ) , ta có DB BH M BH //CK . DC CK H S S Mặt khác BH MAB , mà MAB a , do đó: S CK S MAC MAC DB DB a B D C a , DC DB DC a 1 K hay DB a a DB
BC , suy ra D cố định. Vậy M thuộc đường thẳng cố định AD. BC a 1 a 1 S
Giới hạn: MAB a (a 0) nên suy ra M không nằm trên các đường thẳng AB, AC, do đó M SMAC
không trùng A. Vậy M chuyển động trên đường thẳng cố định AD (trừ điểm A).
Phần đảo: Lấy điểm M bất kì thuộc đường thẳng AD (trừ A). Vẽ BH DB
BH AB , CK AD ,với H , K AD, ta có: BH //CK . a CK DC
Biên soạn: Trần Đình Hoàng 0814000158 77
Chuyên đề bồi dưỡng học sinh giỏi toán 8 S Do đó BH MAB . a S CK MAC a
Kết luận: Tập hợp các điểm M là đường thẳng AD (trừ điểm A) (với DB BC, D BC ). a 1
Bài 7. Cho tam giác ABC . Các điểm M , N , P lần lượt thuộc các cạnh BC,C , A AB sao cho 1 1 1 BM BC,CN C ,
A AP AB .Gọi A , B ,C là các giao điểm của BN và CP , CP và AM , AM 3 3 3
và BN tương ứng. Tính tỉ số diện tích của các tam giác A B C và ABC . Lời giải. A
Qua A, kẻ đường thẳng song song với BC, đường thẳng này cắt CP ở D. P Khi đó AB AD 3AD 3 AP 3 AB . , suy ra 3 . (1) B' B M MC 2BC 2 PB 4 AM 4
Qua N, kẻ đường thẳng song song BC, cắt AM tại Q, ta có N MC BM 3BC 3 MC , do đó 3 , C' A' C Q QN 3.2MC 4 MQ 4 MC 1 suy ra . (2) B M C AM 7
Từ (1) và (2) ta được B C 3 , do đó AB B C
. Tương tự, ta có CA A B . AM 7 3 3 1 Từ đó suy ra S 3 1 4 1 . S . s . . S S A B C 4 A B M 4 2 CB M 4 2 7 CAM 2 ABC
Bài 8. Cho tam giác ABC vuông ở A , có góc B 20; vẽ phân giác trong BI , vẽ góc ACH 30
về phía trong tam giác H AB . Tính góc CHI . Lời giải. B
Vẽ phân giác CK của góc HCB.ta có: AH 1 BC . HK 2 BK
Vẽ KM vuông góc với BC tại M, vì tam giác KCB cân tại K nên
BC 2BM . Do BMK đồng dạng BAC (hai tam giác vuông có
góc nhọn chung) nên suy ra AH BM AB . (1) HK BK BC
Lại do BI là phân giác của góc ABC nên IA AB . (2) IC BC AH AI Từ (1) và (2) ta có: CK IH CHI 0 / / HCK 20 M HK IC K Vậy 0 CHI 20 H A I C
Biên soạn: Trần Đình Hoàng 0814000158 78
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bài 9. Cho hình vuông ABCD tâm O , điểm M di động trên đường chéo AC . Vẽ hình chữ nhật
MOBE . DE cắt MB tại I . Chứng minh I luôn nằm trên một đường thẳng cố định. Lời giải. E 1
Vẽ IH BD K BD.Ta có ME OB , OB BD , 2 I1 A B suy ra BD 2. ME Xét IB D có ME//BD nên I M H BI BD BI BI 2 BI 2 , hay 2 . IM ME IM BI IM 2 1 BM 3 G
OBM có IH //OM ( vì IH BD,OM BD suy ra IH //OM ) I2 nên BH BI 2 BH O . B OB BM 3 2
Mà OB không đổi, đường thẳng AC cố định. Vậy I thuộc D C 3
đường thẳng song song với AC và cách AC một khoảng bằng 2 OB 3
Bài 10. Cho hình bình hành ABCD . Qua A vẽ một đường thẳng sao cho đường thẳng này cắt
đường chéo BD ở P và cắt DC, BC lần lượt ở M , N . a) Chứng minh: AP AP 1 (*) AM AN
b) Có hay không hệ thức (*) khi đường thẳng vẽ qua A cắt các tia CD,CB, DB lần lượt ở M , N, P ? Vì sao? Lời giải. A B a) Vì AP BP DB//AB nên . AM BD AP DP P Từ AD//BN , suy ra . AN BD
Cộng từ vế của (1) và (2) ta có: D M C AP AP BP DP 1. AM AN BD
b) Trường hợp thứ nhất: Điểm B nằm giữa D và P. Ta có: DBA CBA nên ABP ABN , suy ra N nằm giữa A và P. N Khi đó AP AP AP AP AN nên 1 1. AN AN AM
*Trường hợp thứ hai: Điểm D nằm giữa B và P. Tương tự ta có: AP AP AP AM suy ra 1. AM AN
Tóm lại, không có hệ thức (*) khi đường thẳng vẽ qua A cắt tia CD, CB, DB ở M, N, Bài 11. 1) Cho tam giác ABC có. ˆ
3A 2B 180 . Chứng minh rằng: 2 BC AB AB AC.
2) Biết rằng số đo độ dài các cạnh của tam giác là ba số tự nhiên liên tiếp, hãy tìm độ dài các cạnh của tam giác.
Biên soạn: Trần Đình Hoàng 0814000158 79
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. C
1) Theo giả thiết, 3A 2B 180 mà
A B C 180, nên 3A 2B A B C , do đó
C 2A B , suy ra C A, C B, vì thế, trong
tam giác ABC ta có AB AC, AB BC.
Trên cạnh AB ta lấy điểm D sao cho AD AC . A D B
Tam giác ACD cân tại đỉnh A nên 180 A ADC ACD . Ta có: 2 A B C B 2A B CDB 180 180 ADC 180 180 180 180 A B ACB . 2 2 2
Vậy ABC đồng dạng với CBD (g g) , nên BC DB , suy ra 2 CB A . B DB , nhưng AB CB
BD AB AD AB AC , do đó: 2 BC AB AB AC. (1)
2) Vì số đo độ dài các cạnh của tam giác ABC là ba số tự nhiên liên tiếp, nên dĩ nhiên chúng là
ba số nguyên dương liên tiếp. Hơn nữa, do góc C lớn nhất nên AB là cạnh có độ dài lớn nhất
trong tam giác, suy ra rằng AB BC 1 hoặc AB BC 2.
Nếu AB BC 1 thì AB BC 1, còn AC BC 1, từ đó (1) cho ta: 2
BC 2BC 2 BC BC 2 2, dễ thấy phương trình này không có nghiệm nguyên.
Nếu AB BC 2 thì AB BC 2 , còn AC BC 1 , từ đó, thay vào (1) ta được: 2 2
BC BC 2 BC BC 2 0 BC 1 BC 2 0,
Nhưng BC 1 0 nên ta suy ra BC 2 0 , tức là BC 2.
Vậy độ dài các cạnh của tam giác ABC là BC 2, AC 3, AB 4.
Bài 12. Cho hình thang có hai cạnh bên không song song nhau. Hãy dựng hai đường thẳng song
song hai đáy sao cho đoạn thẳng nằm giữa hai cạnh bên của mỗi đường thẳng này được chia làm
ba phần bằng nhau bởi hai đường chéo của hình thang (không cần chứng minh rằng chỉ có hai
đường thẳng dựng được thỏa mãn tính chất đó). Lời giải. E
Xét hình thang ABCD có đáy lớn AB, đáy nhỏ CD.
Gọi E là giao điểm AD và BC ; F là giao điểm của hai
đường chéo AC, BD. Qua F, vẽ đường song song hai D C
đáy, cắt hai cạnh bên AD, BC lần lượt tại A và B. Ta F A' B'
có S AFD S ABD S AFB T S
S ABC S AFB S BFC. P Q
Từ đó, kí hiệu m là đường cao hình thang ABCD ta 1 1 có : S AFD . m A F , S BFC . m FB , 2 2 A G B
suy ra AF FB. Tiếp theo, giả sử G là giao điểm EF và AB, từ Định lí Thales, suy ra G là trung điểm AB.
Gọi P, Q lần lượt là giao điểm của DG và CG với các đường chéo AC và BD. AP AG GB BQ Ta có PC DC DC QD
Do đó, nếu gọi S,T lần lượt là giao điểm của đường thẳng PQ với AD, BC, thì Định lí Thales
Biên soạn: Trần Đình Hoàng 0814000158 80
Chuyên đề bồi dưỡng học sinh giỏi toán 8 SP AG PQ cho ta 1 hay SP PQ QT. PQ GB QT
Từ phân tích trên, các bạn dễ dàng suy ra cách dựng ST, đường thẳng này thỏa mãn tính chất đề bài.
Bài 13. Cho tam giác ABC , M là điểm nằm trong tam giác. Gọi MI, MK, ML lần lượt là khoảng
cách từ M đến các cạnh BC,C ,
A AB . Chứng minh rằng nếu MI, MK , ML là ba cạnh của một tam
giác thì nằm trong tam giác DEF . Lời giải. A
Giả sử AD, BE, CF là ba đường phân giác của tam giác ABC. P K
Ta khẳng định rằng nếu M EF thì có L MI MK M . L M E
Thật vậy, vẽ EP AB, EQ BC. Ta có F O EP E .
Q FQ cắt BE tại J. EFQ có MJ //EQ MJ MF J (MJ BC, EQ BC) suy ra . EQ EF Tương tự: ML MF . Do đó MJ M . L B C R D Q EP EF
Lập luận tương tự, ta cũng có MK JI . Vậy MI MJ JI MK M . L
Từ khẳng định trên, ta suy ra:
Nếu MI MK ML thì M nằm trong tứ giác BFEC.
Tương tự: Nếu MK MI ML thì M nằm trong tứ giác ACDF.
Nếu ML MI MK thì M nằm trong tứ giác AEDB. MI MK ML
Do đó nếu MI, MK, ML là ba cạnh của một tam giác thì MK MI ML ML MI MK
Vậy M nằm trong tam giác DEF.
Bài 14. Cho tam giác ABC . Gọi Cx,Cy là các tia trên nửa mặt phẳng bờ AC có chứa điểm B sao
cho tia Cx nằm giữa hai tia CB,Cy và Cx // AB . Một đường thẳng bất kì qua B cắt Cx,Cy tại D, E .
Gọi F là giao điểm AD với BC . Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định. Lời giải. B x
Gọi I, K lần lượt là giao điểm của đường thẳng EF và
AB, Cx. Hai tam giác IFA và KFD đồng dạng, FKC
và FIB đồng dạng, từ đó D y E KD FK KC KD IA I . (1) F K IA FI IB KC IB
Gọi J là giao điểm của đường thẳng CE và đường A C
thẳng AB. Hiển nhiên A nằm giữa B và J và J là điểm
cố định. Định lí Thales cho ta: KC EK KD KD IB . (2) IJ IE IB KC IJ Từ (1) và (2) ta được 2 IB . IA IJ , do đó
JB JI 2 JI JA.JI J
Biên soạn: Trần Đình Hoàng 0814000158 81
Chuyên đề bồi dưỡng học sinh giỏi toán 8 2 2 2 JB 2J . B JI JI JI J .
A JI JB JB JI JI JB JA J . B IB JI.BA BA IB BA IA (để ý (1) và (2)). BJ IJ BJ IB
Vậy điểm I cố định, do A, B, J cố định.
Bài 15. Cho tam giác ABC . Xét điểm M sao cho tứ giác ABMC có AM.BC A . B CM AC.BM . Chứng minh BAM BCM . Lời giải. B Vẽ tia Mx trong góc BMC sao cho CMx AMB ,vẽ Cy sao cho MCy BAM ,Mx cắt Cy tại I. x Xét BAM ICM có BAM ICM , BMA IMC . Do đó
BAM đồng dạng ICM , AB AM BM suy ra A . B CM AM .IC. IC CM MI A C
Xét BMI và AMC , ta có: I BM AM y BMI AMC BMA IMC ; . MI CM
Do đó BMI đồng dạng AMC suy ra BI BM AC.BM AM.BI. M AC AM Ta có A .
B CM AC.BM AM . IC AM . BI , suy ra AM.BC AM IC BI hay BC IC BI,
suy ra B, I, C thẳng hàng. Do đó BAM BCM
Bài 16. Cho 3 điểm P,Q, R lần lượt nằm trên các cạnh BC,C ,
A AB tương ứng của tam giác ABC sao cho PB CQ RA 1
.Các điểm X ,Y tương ứng nằm trên RP và PQ sao cho BC AC AB 3 PX QY 1
. Chứng minh rằng XY // BC . PR QP 3 Lời giải. A
Gọi U, V tương ứng là các điểm nằm trên AB và AC sao cho 2 2 BU B , A CV C . A R 9 9
Như thế, ta có UV //BC . Để chứng minh XY //BC , ta sẽ
chứng minh X,Y nằm trên UV. Q X Ta có BU BU BA 2 3 1 PX U V . . , do đó UX //B . P Y BR BA BR 9 2 3 PR Tương tự: CV CV CA 2 2 PY . .3 , suy ra YV //PC. B P C CQ CA CQ 9 3 PQ
Vậy X, Y nằm trên UV, ta có điều phải chứng minh.
Bài 17. Trong tam giác ABC , các điểm U và V chia cạnh BC thành 3 phần bằng nhau; W và X
chia cạnh AC thành 3 phần bằng nhau; Y và Z chia cạnh AB thành 3 phần bằng nhau. AU và
BX cắt nhau tại R , BW và CZ cắt nhau tại P , AV và CY cắt nhau tại Q .
Chứng minh rằng các cạnh của tam giác PQR song song với các cạnh của tam giác ABC .
Biên soạn: Trần Đình Hoàng 0814000158 82
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Lời giải. A ZW AZ AW 2 Dễ dàng chứng minh: , BC AB AC 3 Y X Suy ra ZW ZP PW 2 . BC PC PC 3 Q R
Tương tự như vậy ta được XR 2 , QY 2 . Z W RB 3 QC 3
Từ đó, sử dụng Định lí Thales đảo để đi đến điều phải P chứng minh. B U V C
Bài 18. Cho hình vuông ABCD , I là điểm di động nằm trên cạnh AB . Tia DI cắt tia CB tại E .
Đường thẳng CI cắt AE tại M . Đường thẳng DE cắt đường thẳng BM tại S . Chứng minh ta luôn có DSB 90 . Lời giải. E
Trên tia đối của tia AB lấy N sao cho AN BE . AE cắt NC,
DN lần lượt tại K, L. DE cắt NC tại H. Xét B
EA và AND , ta có: BE AN , ABE 0 DAN ( 90 ) M và AB A . D S
Do đó BEA AND (c.g.c) , suy ra BAE ADN . A I Ta có: BAE 0 0 0 LAN 180 90 90 B ADL 0 LAD 0 90 ALD 90 AL DN
Tương tự: BCN CDE nên CN DE.
EDN có EL và NH là hai đường cao, suy ra K là trực tâm
EDN . Do đó DK NE . CEN có NB và EH là hai đường
cao, suy ra I là trực tâm CEN , do đó CI NE.
Hơn nữa: DK NE , CI NE DK //CI; EI EM EKD có IM //DK ; ED EK D C EI EB EM EB EI EDC có IB//DC ; EKC có BM //CK; ED EC EK EC ED
BM / /CK, DE CK BM DE. Vậy DSB 90 .
Bài 19. Trên hình vẽ bên, hình vuông PQRS nội tiếp trong tam giác ABC . Chứng minh rằng
AB 3QR . Khi nào dấu đẳng thức xảy ra? Lời giải. C Cách 1. Vì A CPS RSB, B CSP QPA và AQP C
SRB 90 nên 2 tam giác ABC, SRB P S đồng dạng nhau.
Cho AQ 1 và x PQ PS QR RS, ta có: AQ PQ 1 x 2 BR x RS BR x BR A Q R B 2
AB BR QR AQ x x 1.
Biên soạn: Trần Đình Hoàng 0814000158 83
Chuyên đề bồi dưỡng học sinh giỏi toán 8
Bất đẳng thức AB 3QR đúng vì nó tương đương với x x x x 2 2 1 3 1 0.
Đẳng thức xảy ra khi QR AQ 1, khi đó, tam giác ABC vuông cân.
Cách 2. Từ các tỉ lệ đồng dạng ta có: AQ AQ AC RB RB BC , . QR PQ BC QR RS AC
Áp dụng bất đẳng thức Cauchy cho 2 số dương a b 2 ab ta được: AC BC AC BC
AB QR AQ RB QR 1 QR 1 2 . 3QR , BC AC BC AC AC BC Dấu bằng xảy ra khi
AC BC . Khi đó , tam giác ABC vuông cân. BC AC
Bài 20. Trong tam giác ABC , như hình bên, các đoạn PQ , RS , TU tương ứng song song với các
cạnh AB , BC , CA ; chúng giao nhau tại X , Y, Z . Hãy xác định diện tích tam giác ABC nếu mỗi
một trong các cạnh PQ, RS và TU chia tam giác ABC thành hai phần có diện tích bằng nhau và nếu
diện tích tam giác XYZ bằng 1. Hãy viết đáp số của bạn dưới dạng a b 2 , với a,b là các số nguyên dương. Lời giải. C
Đặt AB x . Vì PQ chia tam giác ABC thành 2 phần S 2 T
có diện tích bằng nhau nên PQ 1 , AB 2 Z suy ra x 2 PQ . 2 P Q
Vì các tam giác PCQ, UTB và ASR đồng dạng nhau, X Y
hơn nữa, lại có cùng diện tích, nên chúng bằng nhau. A U R B Từ đó: 2x x 2 PX YQ , 2 x 2 4x 2x 2 3x 2 4x XY . 2 2 2 dt XYZ 2 2
Hai tam giác XYZ và ABC đồng dạng nên: XY 3 2 4 17 12 2 dt ABC . AB 2 2
Mà dt XYZ 1 nên ta có: dt ABC 2 34 24 2. 17 12 2
Bài 21. Cho hình thang cân ABCD có đáy lớn BC . Giả sử đường cao AH thỏa mãn 2 AH AD.BC . Gọi 1 AD BC
P là hình chiếu của H lên AB . Chứng minh rằng: AB CD AD BC , 2 . AP 2 BC AD Lời giải. A D
Từ Định lí Pythagore ta có 2 2 2 AB BH CH , (1)
và do ABCD là hình thang cân nên 2BH BC A . D (2) Giả thiết cho ta: 2 AH A . D BC. P BC AD 2 2 Từ (2) ta được: BH . 4 B H C
Thay (4) và (3) vào (1), biến đổi và cuối cùng ta có:
Biên soạn: Trần Đình Hoàng 0814000158 84
Chuyên đề bồi dưỡng học sinh giỏi toán 8 BC AD2 BC AD 2 AB AB . 4 2 AP AH
Từ các tam giác đồng dạng ta có: 2 AH A . P A . B (5) AH AB
Kết hợp (3) và (5) ta suy ra: 2A . D BC AP . BC AD
Bài 22. Cho hình thang ABCD có AB // CD và AD a ; DC b ; A và B là hai điểm cố định. AC
cắt BD tại O . C và D di động .
a) Chứng minh rằng O cách một điểm cố định một đoạn không đổi.
b) Chứng minh rằng O cách một điểm cố định một đoạn không đổi. Lời giải. D b C
a) Trên tia AB lấy điểm E sao cho AE b E cố định, O
Tứ giác AECD có AE//DC, AE DC( b) nên là hình a
bình hành, từ đó, EC AD a , Do đó C thuộc đường tròn tâm E bán kính a.
b) Vẽ OF //CE (F thuộc AB) vì AD//EC nên OF //A . D Đặt AB c , OA B có AB//CD, suy ra A F B OA AB c OA c OA c E . OC DC b OA OC c b AC b c c AF OA OF bc ac ACE có OF //CE nên AF ,OF F cố định. AE AE CE b c b c
Bài 23. Tứ giác lồi ABCD có BC // AD . Gọi M , P,Q lần lượt là trung điểm các cạnh CD , MA và
MB . Các đường thẳng DP và CQ gặp nhau tại N . Chứng minh rằng N không nằm ngoài tam giác ABM . Lời giải. B C
Gọi L là trung điểm AB. Nếu AD BC , ta có N trùng
L, tức N nằm trên cạnh của tam giác ABM. Do đó, có Q
thể giả sử AD BC . Gọi X, Y tương ứng là đỉnh thứ
tư của 2 hình bình hành MDAX và MCBY. Khi đó, Y X L M
nằm giữa L và M, và L nằm giữa X và M. Chú ý rằng Y
N nằm trên các đường thẳng DX và CY, hai đường N
này tương ứng cắt AB tại H và K. K P
Hai tam giác HAD và HLX đồng dạng nên ta có: HL : HX HA : . HD A D HL HA LA KB KB KL
Tương tự, KL : LY KB : BC, từ đó suy ra: , do đó HL HK. LX AD AD AD BC LY
Điều này chứng tỏ N không nằm ngòai tam giác ABM.
Bài 24. Cho ABC là tam giác nhọn. Đường phân giác của
ACB cắt AB tại điểm L . Gọi M , N
tương ứng là chân các đường vuông góc hạ từ L xuống AC và BC . Giả sử P là giao điểm của
AN và BM . Chứng minh rằng CP AB . Lời giải.
Gọi (d) là đường thẳng qua C song song với AB. Cho F và E lần lượt là các giao điểm của AN
và BM với (d). Kí hiệu D là giao điểm của CP và AB.
Biên soạn: Trần Đình Hoàng 0814000158 85
Chuyên đề bồi dưỡng học sinh giỏi toán 8 AD PD BD AD CF Ta có , suy ra . E CF PC CE BD CE Mặt khác, AM AB AM .CE CM CM CE AB A BN AB BN.CF và CN . CN CF AB Mà CM CN nên AM CF . L M BN CE D Do đó, AD AM AM BN , suy ra . (1) P BD BN AD BD
Ngoài ra, nếu CH AB(H AB) thì B N C
ALM đồng dạng AHC , suy ra AL AM . Tuơng tự, ta cũng có BL BN . AC AH BC BH AL BL Vì CL là phân giác nên .Từ đó, ta AC BC được AM BN
. Kết hợp đẳng thức (1) ta có hai AH BH
điểm D, H trùng nhau và do đó CP A . B F
Bài 25. Cho tứ giác lồi ABCD có hai đường chéo cắt nhau tại một điểm K . Gọi I là trung điểm
của đoạn thẳng nối hai trung điểm các đường chéo; gọi O là điểm đối xứng của K qua I . Chứng
minh rằng bốn đoạn thẳng nối O với trung điểm các cạnh tứ giác thì chia tứ giác thành 4 đa giác có diện tích bằng nhau. Lời giải. C
Gọi M, N, P, Q lần lượt là các trung điểm của AB, N B
BC, CA, AD; E và F lần lựơt là trung điểm hai đường chéo AC và BD. Dễ thấy K OE//BD//QM , suy ra S S và do đó P E MOQ MEQ M F I S S S S S S . AMOQ AMQ MEQ AMEQ AME AEQ O S AM .AE 1 S AE AQ AME EAQ . 1 Mà , S A . B AC 4 S AC.AD 4 ABC ACD A Q D 1 1 nên S S S S S S AMOQ AME AEQ ABC ACD . 4 4 ABCD Tương tự ta cũng có 1 S S S S
, điều phải chứng minh. BNOM CPON DQOP 4 ABCD
Bài 26. Gọi M là điểm bất kì trong tam giác ABC . Qua M kẻ các đường thẳng AM , BM ,CM cắt
các cạnh tương ứng tại các điểm AM BM CM
A , B ,C . Chứng minh rằng: 6 . 1 1 1 A M B M C M 1 1 1 Lời giải.
Gọi diện tích các tam giác MAB, MBC, MCA lần lượt là a, b, c; A, A tương ứng là hình chiếu của A, M xuống cạnh BC.
Biên soạn: Trần Đình Hoàng 0814000158 86
Chuyên đề bồi dưỡng học sinh giỏi toán 8 Vì MA //AAnên 1 A AA .BC AA AA a b c AA 1 2 1 . MA MA b 1 MA 1 1 MA.BC 2 C1 B1 AM AA MA M Từ đó, a c a c 1 1 . MA MA b b b 1 1 Tương tự, ta có BM a b CM b c , . B M c c C M a a 1 1 B C A1 Như vậy, AM BM CM a b b c c a
6. A M B M C M b a c b a c 1 1 1
Bài 27. Cho hai đường thẳng cố định a và b , hai đường thẳng di động c , d sao cho chúng luôn
song song với nhau và theo thứ tự qua hai điểm ,
A B nằm trên a,C là giao điểm của c và b, D là
gia điểm của d và b . Qua giao điểm M của AD và BC dựng đường thẳng song song với c , cắt a
ở E và b ở F . Chứng tỏ M thuộc một đường thẳng cố định. Lời giải. d
Xét hai trường hợp: a cắt b và a// . b a B
Trường hợp 1. a cắt b tại I. Do AC//BD nên MA EA AC IA không đổi. MD EB BD IB ME MA FC MF c Mà nên suy ra ME MF . BD AD CD BD E
Vậy M là trung điểm của EF. A
Vẽ MM b, EE b, (M , Eb) , ta có M 1
MM //EE , MM EE . 2 1 I C F M' E' D b
Do đó MM EE ; EE không đổi. 2
Vậy M thuộc đường thẳng song song với đường thẳng b và cách b một khoảng bằng nữa
khoảng cách từ E đến b. Trường hợp 2. a // . b
Tứ giác ABCD là hình bình hành. M là giao điểm a B
hai đường chéo AD và BC, suy ra M là trung điểm E
của AD và BC. ABC có ME//AC , M là trung điểm A
BC, do đó E là trung điểm AB, suy ra E cố định. Ta có: 1 ME MF AC . M 2
Tương tự như trường hợp (1), ta có M thuộc đường
thẳng song song với đường thẳng b và cách b một b D
khoảng bằng nửa khoảng cách từ trung điểm E của F C d AB đến b. c
Biên soạn: Trần Đình Hoàng 0814000158 87




