





























Preview text:
Giáo Viên Trườ ng THPT Tuy Phong HÌNH HOÏC 10 CHƯƠNG II TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG LỜI NÓI ĐẦU
Quý đọc giả, quý thầy cô và các em học sinh thân mến!
Nhằm giúp các em học sinh có tài liệu tự học môn Toán,
tôi biên soạn cuốn giải toán trọng tâm của lớp 10.
Nội dung của cuốn tài liệu bám sát chương trình chuẩn và
chương trình nâng cao về môn Toán đã được Bộ Giáo
dục và Đào tạo quy định. Nội dung gồm 3 phần
Phần 1. Kiến thức cần nắm
Phần 2. Dạng bài tập có hướng dẫn giải và bài tập làm tương tự.
Phần 3. Phần câu hỏi trắc nghiệm.
Cuốn tài liệu được xây dựng sẽ còn có những khiếm
khuyết. Rất mong nhận được sự góp ý, đóng góp của quý
đồng nghiệp và các em học sinh.
Mọi góp ý xin gọi về số 0355.334.679 – 0916.620.899 Email: lsp02071980@gmail.com Chân thành cảm ơn. Lư Sĩ Pháp MỤC LỤC CHƯƠNG II
TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
§1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KÌ TỪ o 0 ĐẾN o 180 ------ 1 – 7
§2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ -------------------------------------------- 8 – 19
§3. CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC --- 20 – 29
ÔN TẬP CHƯƠNG II -------------------------------------------------------------------- 29 – 38 Toán 10 I Love Math GV. Lư Sĩ Pháp CHƯƠNG II
TÍCH VÔ HƯỚNG CỦA HAI VÉCTƠ VÀ ỨNG DỤNG ---o0o--
§1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC BẤT KÌ TỪ o 0 ĐẾN o 180
KIẾN THỨC CẦN NẮM
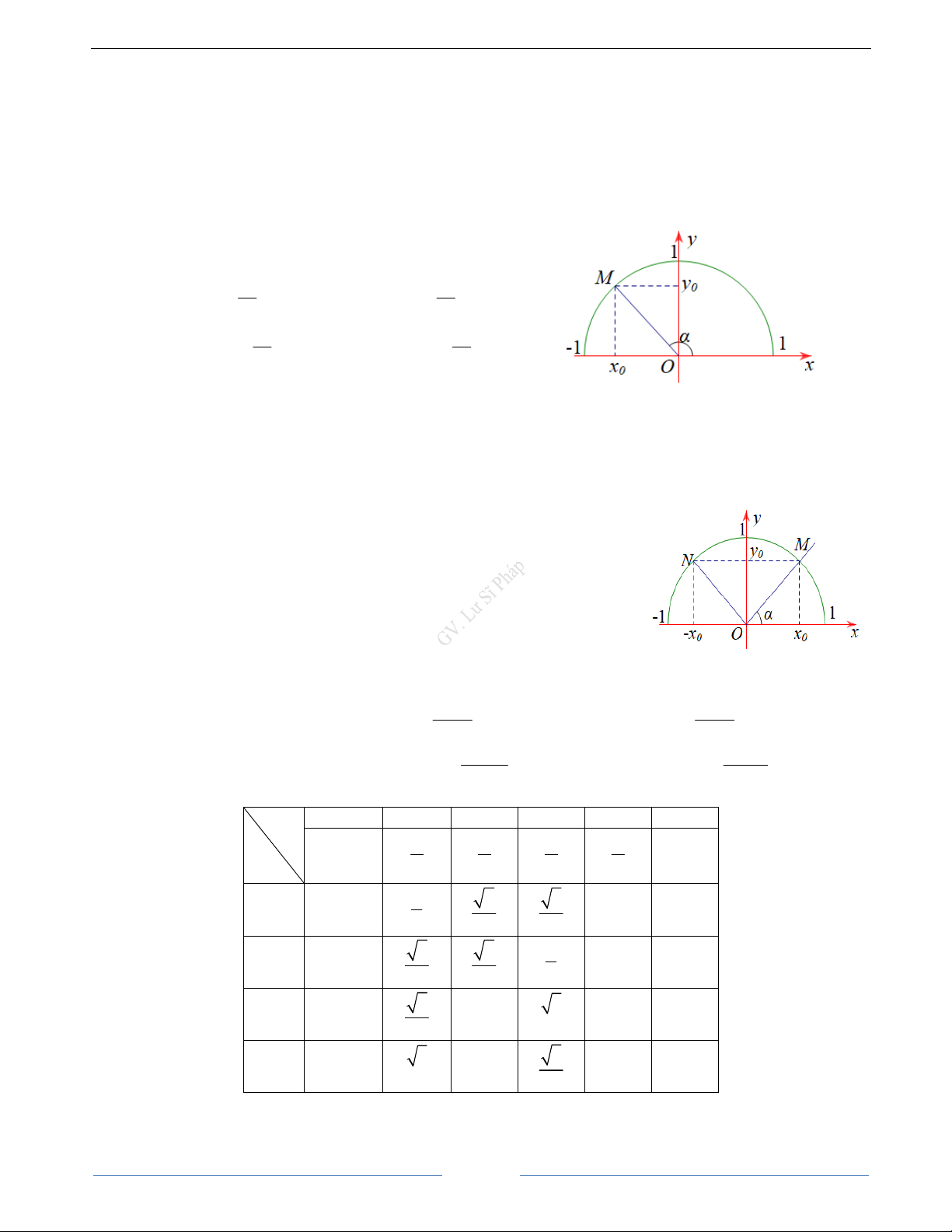
1. Định nghĩa: Với mỗi góc 0 0
(0 180 ) ta xác định một điểm M trên nữa đường tròn đơn vị sao cho
xOM và giả sử điểm M có tọa độ M x ; y . Khi đó ta định nghĩa: 0 0
sin của góc là y , kí hiệu sin y 0 0
côsin của góc là x , kí hiệu cos x 0 0 y y
tan của góc là 0 (x 0) , kí hiệu 0 tan 0 x x 0 0 x x
côtan của góc là 0 ( y 0) , kí hiệu 0 cot 0 y y 0 0
Các số sin , cos , tan , cot được gọi là các giá trị lượng giác của góc .
Chú ý: Nếu là góc tù thì cos 0, tan 0, cot 0
tan chỉ xác định khi 0
90 , cot chỉ xác định khi 0 0 hoặc 0 180
2. Các hệ thức lượng giác
a. Giá trị lượng giác của hai góc bù nhau 0
sin 180 sin 0
cos 180 cos 0
tan 180 tan 0
cot 180 cot
Lưu ý: Hai góc bù nhau có sin bằng nhau và côsin, tang, cotang đối nhau.
b. Các hệ thức lượng giác cơ bản
Từ định nghĩa giá trị lượng giác của một góc ta suy ra các hệ thức: sin cos 2 2 sin cos 1 0 tan ( 90 ) 0 0 cot ( 0 ;180 ) cos sin 1 1 tan.cot 1 2 1 tan 2 1 cot 2 cos 2 sin
3. Giá trị lượng giác của các góc đặt biệt 00 300 450 600 900 1800 0 6 4 3 2 HSLG sin 1 3 0 2 2 1 0 2 2 cos 3 2 1 1 0 1 2 2 2 tan 3 3 0 1 || 0 3 cot 3 3 || 1 0 || 3 || : Không xác định 1
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
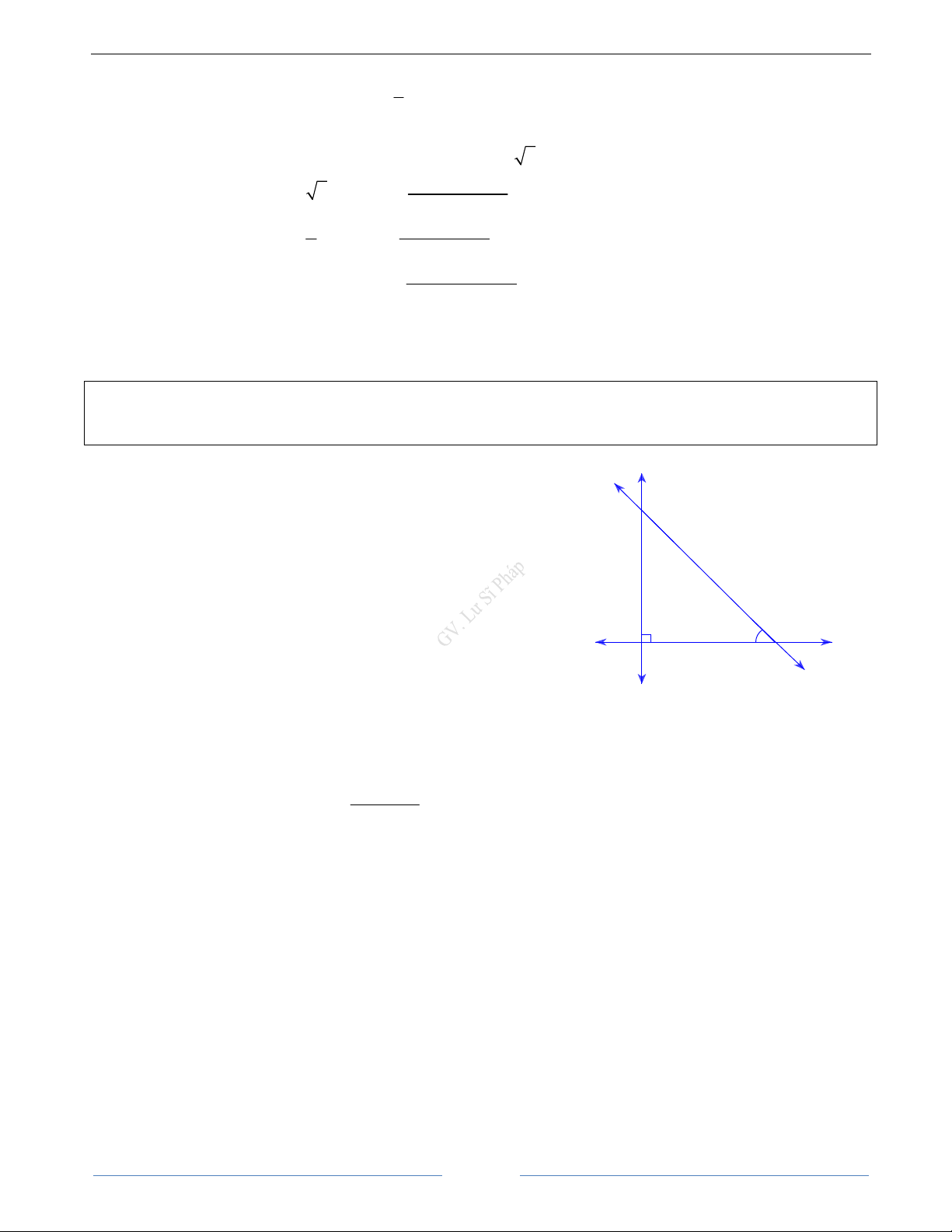
4. Góc giữa hai vectơ
Cho hai vectơ a, b đều khác 0 . Từ một điểm O bất A a
kì, ta vẽ OA a và OB b . Khi đó góc AOB với B số đo từ 0 0 đến 0
180 được gọi là góc giữa hai vcetơ
a và b . Kí hiệu a,b O b Lưu ý:
a,b , b a 0 a b 0 0 , 180 a b 0 ,
90 a b
CÁC DẠNG TOÁN CƠ BẢN
ấn đề 1. Tính giá trị lượng giác của một số góc đặt biệt
VPhương pháp: Áp dụng định nghĩa và các hệ thức lượng giác Bài 1. Cho góc 0
135 . Tính sin , cos , tan và cot HD Giải 2 Ta có: 0 sin135 sin 0 0 180 135 0 sin 45 2 2 0 cos135 cos 0 0 180 135 0 cos 45 2 sin 0 0 0 0 tan135 tan 180 135 tan 45 1 hay tan 1 cos 1 0 0 0 0 cot135 co 180 135
co 45 1 hay cot 1 tan Bài tập tương tự: Bài 2. a). Cho góc 0
120 . Tính sin , cos , tan và cot b) Cho góc 0
150 . Tính sin , cos , tan và cot
Bài 3. Cho tam giác cân ABC có 0
B C 15 . Hãy tính giá trị lượng giác của góc . A HD Giải 0 0
Ta có: A B C A
B C 0 0 0 180 180 180 30 150 1
Vậy: sin A sin 0 0 180 150 0 s in30 2 3
cos A cos 0 0 180 150 0 cos 30 2 sin 3 1 tan và cot 3 cos 3 tan Bài tập tương tự:
Bài 4. Tính giá trị của biểu thức a) 0 0 0
A 2 sin 30 3cos 45 sin 60 b) 0 0 0
B 2 cos 30 3sin 45 cos 60 c) 0 0 0
C sin120 2 cos180 tan 60 d) 0 0 2 0 2 0
D cot 60 . tan 60 cos 30 sin 30 2
Bài 5.Tính giá trị các biểu thức lượng giác sau: 1 a) 0
A cos 2 2 sin
tan( 15 ) 2 cos 6 biết 0 30 b) 0 0 0
B 2 sin 60 3cos 30 tan 45 2 2 0 2 sin 30 c) 0 0 0
C cot 30 2 sin 60 2 cos 30 d) D 2 0 1 2 cos 30 e) 0 0 0 0
E 3sin 90 2 cos 0 3 cos 60 10 cos180
ấn đề 2. Chứng minh các hệ thức về giá trị lượng giác VPhương pháp:
Dựa vào định nghĩa giá trị lượng giác của một góc 0 0 (0 180 ) 2
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Dựa vào tính chất tổng ba góc trong một tam giác bằng 0 180
Sửa dụng 6 công thức lượng giác cơ bản
Bài 6. Cho góc bất kì. Chứng minh rằng 4 4 2
sin cos 2 sin 1 HD Giải 2 2 Ta có: 4 4 4 2 4 2 4 2 4 2 sin cos sin (cos ) sin 1 sin
sin 1 2 sin sin 2sin 1 Cách khác: 4 4 2 2 2 2 2 2 2 sin cos sin cos sin cos
sin (1 sin ) 2 sin 1
Bài tập tương tự: 1 1
Bài 7. Chứng minh rằng: a) 2 0 1 tan , 90 b) 2 0 0 1 cot , 0 ;180 2 cos 2 sin
Bài 8. Cho tam giác ABC. Chứng minh rằng A B C
a) sin A sin(B C) b) cos sin
c) tan A tan(B C) 2 2
Bài 9. Chứng minh rằng với mọi 0 0
0 x 180 ta có: a) 2
(sin x cos x) 1 2sin x cos x b) 2
(sin x cos x) 1 2 sin x cos x c) 4 4 2 2
sin x cos x 1 2 sin x cos x c) 6 6 2 2
sin x cos x 1 3sin x cos x
Bài 10. Chứng minh biểu thức sau đây không phụ thuộc vào : 2 2
a) A sin cos sin cos b) 4 4 2
B sin cos 2 sin 1
ấn đề 3. Cho biết một giá trị lượng giác của góc , tìm các giá trị lượng giác còn lại của
VPhương pháp: Áp dụng định nghĩa giá trị lượng giác của góc và các 6 công thức lượng giác cơ bản Với 0 0 0 180 suy ra: sin 0 0 0
cos 0 khi 0 90 và 0 0
cos 0 khi 90 180 0 0
tan 0 khi 0 90 và 0 0
tan 0 khi 90 180 0 0
cot 0 khi 0 90 và 0 0
cot 0 khi 90 180 1
Bài 11. Cho góc x , với cos x . Tính 2 2
P 3sin x cos x 3 HD Giải 2 1 25 Ta có: 2 2
P 3sin x cos x 3 2 1 cos x 2 2
cos x 3 2 cos x 3 2 3 9 2
Bài 12. Cho cos . Tính sin , tan và cot 3 HD Giải Vì cos 0 nên 0 0
90 180 , suy ra sin 0, tan 0, cot 0. 2 2 5 5 Ta có: 2 2 2 2
sin cos 1 sin 1 cos 1 sin 3 9 3 sin 5 1 2 tan và cot cos 2 tan 5
Bài 13. Cho góc biết 0 0
0 90 và tan 2 . Tính sin và cos HD Giải Vì 0 0
0 90 , suy ra sin 0, cos 0. sin Ta có: tan
2 sin 2 cos cos 1 1 Mặt khác: 2 2 2 2
sin cos 1 5 cos 1 cos cos 5 5 1 2 Như vậy: cos , sin 2 cos 5 5 3
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Bài tập tương tự: 3 Bài 14.
a) Cho góc biết cos
. Hãy tính sin , tan , cot 5
b) Cho góc biết tan 2
. Hãy tính sin , tan , cot c) Cho góc biết 0 0
0 90 và tan 2 2 . Hãy tính sin , tan , cot 3sin cos Bài 15.
a) Biết tan 2. Tính A sin cos 2 cot tan b) Biết sin . Tính B 3 cot tan 3cos 4sin c) Biết tan 2 . Tính C sin cos
ấn đề 4. Xác định góc giữa hai vectơ
VPhương pháp: Áp dụng định nghĩa góc giữa hai vectơ
Lưu ý: 0 a b 0 0 ,
180 a b 0 ,
90 a b
Bài 16. Cho tam giác ABC vuông tại A và có góc 0 ˆ
B 50 . Xác định góc giữa các cặp vectơ a) B ,
A BC b) AB, BC c) ,
CA CB d) AC, BC e) AC,CB f) AC, BA HD Giải Ta có: a) BA BC 0 , 50 b) AB BC 0 , 130 C c) CA CB 0 , 40 d) AC BC 0 , 40 e) AC CB 0 , 140 f) AC BA 0 , 90 50o A B
Bài tập tương tự:
Bài 17. Cho hình vuông AB .
CD Tính cos AC, BA,sin AC, BD,cos AB,CD
Bài 18. Cho tam giác ABC vuông tại A và có góc 0 ˆ
B 30 . Tính giá trị các biểu thức sau AC,CB
a) cos AB, BC sin B , A BC tan 2
b) sin AB, AC cosBC, BA cosC , A BA
Bài 19. Cho tam giác ABC. Tổng AB, BC BC,CA ,
CA AB có thể nhận giá trị nào trong các giá trị sau: 0 0 0 0 90 , 180 , 270 , 360 . 4
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
CÂU HỎI TRẮC NGHIỆM
Câu 1. Khẳng định nào sau đây đúng?
A. cos145 cos125 .
B. sin 90 sin100 .
C. cos 95 cos100 .
D. tan 85 tan125 .
Câu 2. Cho hình vuông ABCD tâm .
O Tính tổng AB, DC AD,CB CO, DC. A. 0 225 . B. 0 405 . C. 0 315 . D. 0 45 .
Câu 3. Trong các đẳng thức sau đây đẳng thức nào là đúng? 1 3 3 A. O tan150 . B. O cot150 3. C. O sin150 . D. O cos150 . 3 2 2
Câu 4. Cho tam giác đều ABC. Tính P cos AB, BC cosBC,CA cos , CA AB. 3 3 3 3 3 3
A. P . B. P . C. P . D. P . 2 2 2 2
Câu 5. Cho là góc tù. Khẳng định nào sau đây là đúng?
A. cot 0.
B. sin 0.
C. cos 0.
D. tan 0.
Câu 6. Cho hai góc và với 90 . Tính giá trị của biểu thức P sin cos sin cos .
A. P 2.
B. P 1.
C. P 1 .
D. P 0.
Câu 7. Giá trị của 0 0
tan 30 cot 30 bằng bao nhiêu? 2 4 1 3 A. . B. 2. C. . D. . 3 3 3
Câu 8. Cho hai góc và với 90 . Tính giá trị của biểu thức P cos cos sin sin .
A. P 1 .
B. P 2.
C. P 0.
D. P 1.
Câu 9. Khẳng định nào sau đây sai?
A. cos 75 cos 50 .
B. sin 80 sin 50 .
C. tan 45 tan 60 .
D. cos 30 sin 60 .
Câu 10. Cho tam giác ABC . Tính P sin .
A cos B C cos .
A sin B C .
A. P 2.
B. P 1.
C. P 1 .
D. P 0.
Câu 11. Tam giác ABC có góc A bằng 100 và có trực tâm H. Tính tổng ,
HA HB HB, HC HC, HA. A. 80 . B. 160 . C. 360 . D. 180 .
Câu 12. Tam giác đều ABC có đường cao AH . Khẳng định nào sau đây là đúng? 1 A. 1 sin AHC . B. 3 sin BAH . C. cos BAH . D. 3 sin ABC . 2 2 3 2
Câu 13. Trong các khẳng định sau đây, khẳng định nào sai? A. O O cos 30 sin120 . B. O O sin 60 cos120 . C. O O cos 45 sin 45 . D. O O cos 45 sin135 .
Câu 14. Cho tam giác ABC với
A 60 . Tính tổng AB, BC BC,CA. A. 120 . B. 360 . C. 270 . D. 240 . 2 cot 3 tan
Câu 15. Cho biết cos . Giá trị của P bằng bao nhiêu ? 3 2 cot tan 25 19 19 25 A. P . B. P . C. P . D. P . 13 13 13 13 6 sin 7 cos
Câu 16. Cho biết tan 3
. Giá trị của P bằng bao nhiêu ? 6 cos 7 sin 4 5 4 5
A. P .
B. P . C. P .
D. P . 3 3 3 3
Câu 17. Cho tam giác ABC . Tính tổng AB, BC BC,CA , CA AB. A. 120 . B. 180 . C. 360 . D. 270 . 5
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 18. Cho O là tâm đường tròn ngoại tiếp tam giác đều MN .
P Góc nào sau đây bằng O 120 ?
A. MN, NP
B. MO,ON .
C. MN,OP.
D. MN, MP.
Câu 19. Cho hai góc nhọn và trong đó . Khẳng định nào sau đây là sai?
A. tan tan 0.
B. sin sin .
C. cot cot .
D. cos cos .
Câu 20. Tam giác ABC vuông ở A và có góc 0
B 50 . Hệ thức nào sau đây sai? A. AC CB 0 , 40 . B. AB BC 0 , 130 . C. BC AC 0 , 40 . D. AB CB 0 , 50 .
Câu 21. Cho biết 2 cos 2 sin 2 , 0 0
0 90 . Tính giá trị của cot . 2 3 2 5 A. cot . B. cot . C. cot . D. cot . 2 4 4 4
Câu 22. Trong các đẳng thức sau, đẳng thức nào đúng?
A. sin 180 cos.
B. sin 180 sin.
C. sin 180 sin.
D. sin 180 cos.
Câu 23. Cho hình vuông ABCD . Tính cos AC, BA.
A. cos AC, BA 0.
B. cos AC, BA 1. C. AC BA 2 cos , . D. AC BA 2 cos , . 2 2
Câu 24. Cho hai góc nhọn và phụ nhau. Hệ thức nào sau đây là sai?
A. cot tan .
B. sin cos .
C. cos sin .
D. tan cot .
Câu 25. Chọn hệ thức đúng được suy ra từ hệ thức 2 2
cos sin 1? 1 A. 2 2 5 cos sin 5. B. 2 2 cos sin . 5 5 3 3 3 1 1 C. 2 2 cos sin . D. 2 2 cos sin . 4 4 4 2 2 2
Câu 26. Tính giá trị biểu thức P sin 30 cos15 sin150 cos165 . 3 1
A. P .
B. P 0.
C. P .
D. P 1. 4 2 1
Câu 27. Cho biết cos sin . Giá trị của 2 2
P tan cot bằng bao nhiêu ? 3 11 7 9 5 A. P . B. P . C. P . D. P . 4 4 4 4 1
Câu 28. Cho biết sin cos . Giá trị của 4 4
P sin cos bằng bao nhiêu ? 5 15 17 19 21 A. P . B. P . C. P . D. P . 5 5 5 5
Câu 29. Tính giá trị biểu thức 2 2 2 2
S sin 15 cos 20 sin 75 cos 110 .
A. S 4.
B. S 0.
C. S 1.
D. S 2.
Câu 30. Trong các đẳng thức sau, đẳng thức nào sai? A. O O
sin120 cos 30 0. B. O O
sin 45 cos 45 2. C. O O
sin 30 cos 60 1. D. O O
sin 60 cos150 0. Câu 31. Giá trị 0 0
cos 45 sin 45 bằng bao nhiêu? A. 1. B. 2. C. 3. D. 0.
Câu 32. Tính giá trị biểu thức P sin 30 cos 60 sin 60 cos 30 .
A. P 3.
B. P 3.
C. P 1.
D. P 0. 6
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 33. Cho biết sin cos .
a Tính giá trị của sin cos. 2 a 1 2 a 11 A. sin cos . B. sin cos . 2 2 C. 2
sin cos a .
D. sin cos 2 . a
Câu 34. Cho tam giác đều ABC có đường cao AH. Tính AH, BA. A. 0 150 . B. 0 60 . C. 0 120 . D. 0 30 .
Câu 35. Cho biết cot 5. Giá trị của 2
P 2 cos 5sin cos 1 bằng bao nhiêu ? 101 100 50 10 A. P . B. P . C. P . D. P . 26 26 26 26 3 Câu 36. Cho biết sin . Giá trị của 2 2 P 3sin 5 cos bằng bao nhiêu ? 3 5 3 3 111 105 107 109 A. P . B. P . C. P . D. P . 25 25 25 25
Câu 37. Tính giá trị biểu thức P cos 30 cos 60 sin 30 sin 60 . 3
A. P 3. B. P .
C. P 1.
D. P 0. 2
Câu 38. Cho và là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào sai?
A. sin sin .
B. cos cos .
C. tan tan .
D. cot cot .
Câu 39. Khẳng định nào sau đây đúng?
A. sin 90 sin150 . B. sin 90 1 5 sin 90 3 0 . C. cos 90 3 0 cos100 .
D. cos150 cos120 .
Câu 40. Tam giác ABC vuông ở A và có BC 2AC. Tính cos AC,CB. A. AC CB 3 cos , . B. AC CB 3 cos , . 2 2 C. AC CB 1 cos , . D. AC CB 1 cos , . 2 2
Câu 41. Tam giác ABC vuông ở A có góc 0
B 30 . Khẳng định nào sau đây là sai? 1 3 1 1 A. sin B . B. sin C . C. cos C . D. cos B . 2 2 2 3
Câu 42. Trong các đẳng thức sau, đẳng thức nào sai? A. O O
sin 0 cos 0 0. B. O O
sin 90 cos 90 1. 3 1 C. O O sin180 cos180 1. D. O O sin 60 cos 60 . 2
Câu 43. Cho hai góc và với 180 . Tính giá trị của biểu thức P cos cos sin sin .
A. P 0.
B. P 1.
C. P 1 .
D. P 2.
Câu 44. Cho biết 3cos sin 1, 0 0
0 90 . Giá trị của tan bằng 4 3 4 5 A. tan . B. tan . C. tan . D. tan . 3 4 5 4
Câu 45. Cho tam giác ABC . Tính P cos .
A cos B C sin .
A sin B C .
A. P 2.
B. P 0.
C. P 1.
D. P 1 . ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 7
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
§2. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
KIẾN THỨC CẦN NẮM 1. Định nghĩa
Cho hai vectơ a và b đều khác vectơ 0. Tích vô hướng của a và b là một số, kí hiệu là .
a b, được xác định bởi công thức sau: .
a b a . b cos a,b.
Trường hợp ít nhất một trong hai vectơ a và b bằng vectơ 0 ta quy ước . a b 0. Chú ý
Với a và b khác vectơ 0 ta có .
a b 0 a . b
Khi a b tích vô hướng .
a a được kí hiệu là 2
a và số này được gọi là bình phương vô hướng của vectơ . a 2 2 Ta có: 0
a a . a .cos 0 a .
2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:
Với ba vectơ a, b, c bất kì và mọi số k ta có: . a b .
b a (tính chất giao hoán);
a b c . a b .
a c (tính chất phân phối);
ka.b k . a b . a kb; 2 2
a 0, a 0 a 0.
Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
a b2 2 2 a 2 . a b b ;
a b2 2 2 a 2 . a b b ;
a ba b 2 2 a b .
3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ ;
O i; j , cho hai vectơ a a ;a , b b ;b . Khi đó tích vô hướng . a b là: 1 2 1 2 .
a b a b a b . 1 1 2 2
Nhận xét. Hai vectơ a a ;a , b b ;b đều khác vectơ 0 vuông góc với nhau khi và chỉ khi 1 2 1 2
a b a b 0. 1 1 2 2 4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ a a ; a được tính theo công thức: 2 2
a a a . 1 2 1 2
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu a a ; a và b b ;b đều khác 0 thì ta có 1 2 1 2 a b a b a b cos a,b . 1 1 2 2 . 2 2 2 2 a . b
a a . b b 1 2 1 2 8
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A x ; y
và B x ; y được tính theo công thức: B B A A
AB x x 2 y y 2 . B A B A BÀI TẬP
ấn đề 1. Tính tích vô hướng của hai vectơ
VPhương pháp: Áp dụng công thức của định nghĩa: .ab a.b cosa,b
Xác định đúng góc giữa hai vectơ
Dùng tính chất phân phối: a b c . a b . a c
Bài 1. Cho hình vuông ABCD cạnh a . Tính a) A . B AD b) A . B AC HD Giải Ta có: a A
a) AB AD AB AD AB AD 0 . . cos , . a a cos 90 0 B
b) AB AC AB AC AB AC 0 2 . . cos , .
a a 2 cos 45 a a D C
Bài 2. Cho tam giác ABC vuông tại C có AC 9, CB 5 . Tính A . B AC HD Giải Ta có: A .
B AC AB . AC cos AB, AC B AC Mặt khác: AB AC ˆ cos , cos A AB 5 9 AC Vậy: 2 . AB AC . AB AC. AC 81 AB C A
Bài tập tương tự 0
Bài 3. Cho tam giác ABC có 0
A 90 , B 60 và AB a . Tính a) A . B AC b) . CA CB c) AC.CB
Bài 4. Cho tam giác ABC vuông cân tại A có AB AC a . Tính a) A . B AC b) B . A BC c) A . B BC
Bài 5. Cho tam giác ABC đều cạnh a và trọng tâm G . Tính a) A . B AC b) AC.CB c) A . G AB a) G . B GC b) B . G GA c) G . A BC
ấn đề 2. Chứng minh các đẳng thức về vectơ có liên quan đến tích có hướng
VPhương pháp: Sử dụng các tính chất phân phối của tích có hướng đối với phép cộng các vectơ
Dùng quy tắc ba điểm: AC AB BC ; AC BC BA
Dùng quy tắc trung điểm: I là trung điểm của AB , ta có: IA IB 0 và 1 MI
MA MB , với M tùy ý 2
Sử dụng tính chất của tích vô hướng: a b a.b 0
Bài 6. Cho tam giác ABC . Chứng minh rằng với điểm M tùy ý, ta có: M . A BC M .
B CA MC.AB 0 9
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp HD Giải
Ta có: M . A BC M .
A MC MB M . A MC M . A MB (1)
M . B CA M .
B MA MC M . B MA M . B MC (2)
MC.AB MC.MB MA MC.MB MC.MA (3)
Cộng vế theo vế (1), (2) và (3), ta được: M . A BC M .
B CA MC.AB 0 (đpcm)
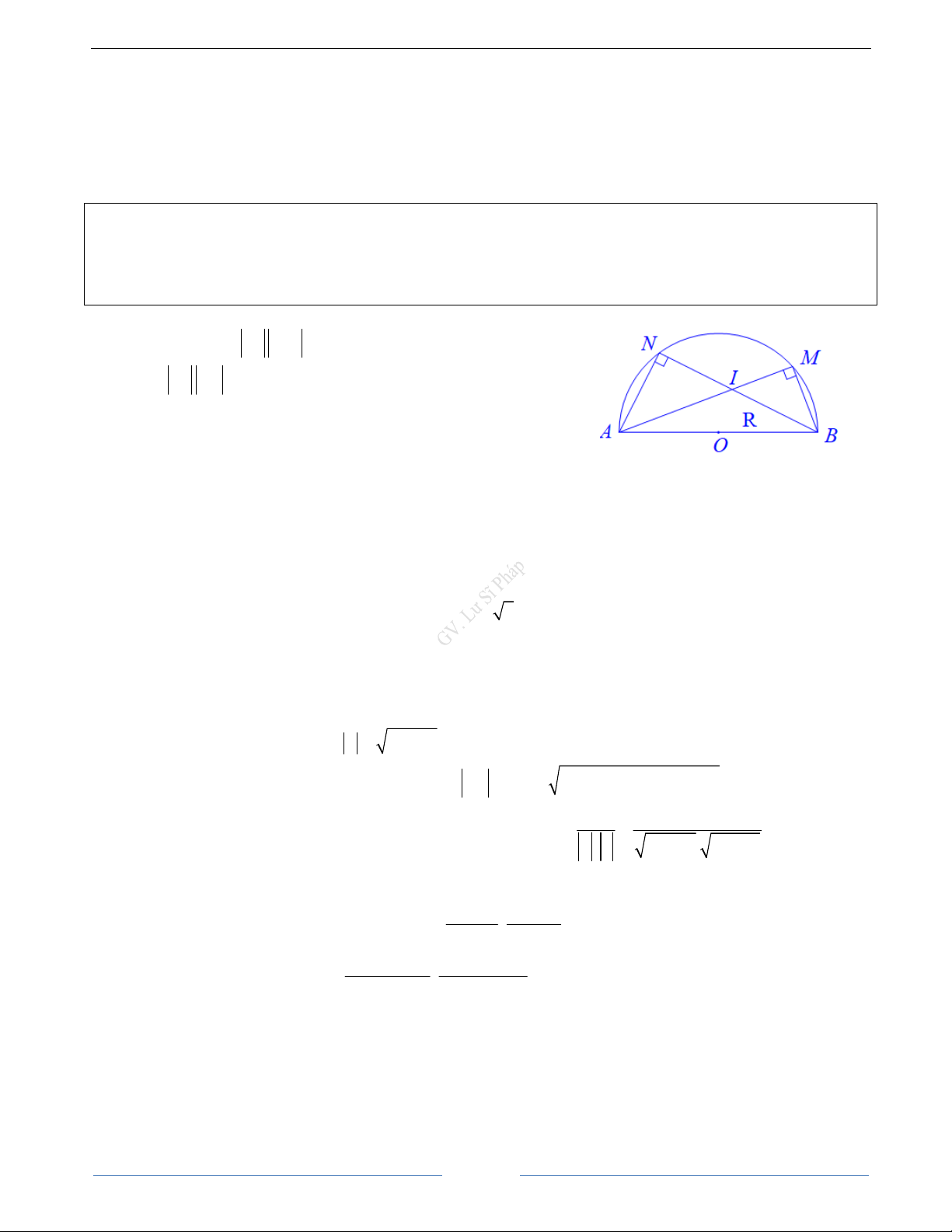
Bài 7. Cho nữa đường tròn tâm O có đường kính AB 2R . Gọi M , N là hai điểm thuộc nữa đường tròn sao
cho hai dây cung AM , BN cắt nhau tại I .
a) Chứng minh rằng: AI.AM AI.AB và BI.BN BI.BA
b) Hãy dùng kết quả câu a) tính AI.AM BI.BN theo R HD Giải
a) Ta có: AI.AM AI AM cos AI, AM AI.AM (1)
AI.AB AI AB cos AI, AB
AI.AB cos IAB AI.AM (2)
Từ (1) và (2), suy ra AI.AM AI.AB
Chứng minh tương tự cho BI.BN BI.BA
b) Ta có: AI.AM BI.BN AI.AB BI.BA AI.AB I . B AB
AB AI IB 2 2 2
AB AB 4R
Bài tập tương tự
Bài 8. Gọi O là trung điểm của AB và M là điểm tùy ý. Chứng minh rằng: 2 2 M .
A MB OM OA
Bài 9. Cho tam giác ABC có góc A nhọn. Vẽ bên ngoài tam giác ABC các tam giác vuông cân đỉnh A là
ABD và ACE . Gọi M là trung điểm của BC . Chứng mính rằng AM vuông góc với DE .
Bài 10. Cho hình chữ nhật ABCD có AB a và AD a 2 . Gọi K là trung điểm của cạnh A . D Chứng minh
rằng BK vuông góc với AC .
ấn đề 3. Biểu thức tọa độ của tích vô hướng và các ứng dụng của tích vô hướng
VPhương pháp: Áp dụng:
Cho hai vectơ a a ; a , b b ;b .Ta có: .
a b a b a b . 1 2 1 2 1 1 2 2
Cho vectơ u (u ;u ). Ta có: 2 2
u u u 1 2 1 2 2 2
Cho hai điểm A x ; y và B x ; y . Ta có: AB AB x x y y B A B A B B A A . a b a b a b
Tính góc giữa hai vectơ a a ; a và b b ;b : cosa,b 1 1 2 2 1 2 1 2 2 2 2 2 a . b
a a . b b 1 2 1 2
Cho tam giác ABC với ba đỉnh có tọa độ xác định A x ; y , B x ; y , C x ; y A A B B C C x x y y
Trung điểm I của đoạn AB , tọa độ điểm A B I ; A B 2 2
x x x
y y y
Trọng tâm G , tọa độ điểm A B C G ; A B C 3 3 . HA BC 0
Trực tâm H , có điều kiện là . HB CA 0 2 2 AE BE
Tâm đường tròn ngoại tiếp I tam giác, có điều kiện là IA IB IC 2 2 AE CE 10
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp AH.BC 0
Chân đường cao H hạ từ đỉnh A , có điều kiện là BH k BC AB
Chân đường phân giác trong góc A là điểm D , có điều kiện là DB .DC AC
Chu vi: P AB BC CA. 1 1 Diện tích: 2 S A . B AC.sin A .
AB AC. 1 cos A . 2 2
Góc A : cos A cos AB, AC . . AB AC 0
Tam giác ABC vuông cân tại A , có điều kiện là AB AC 3
Bài 11. Trong mặt phẳng Oxy , cho điểm A4; 6, B 1; 4,C 7; 2
a) Chứng minh rằng tam giác ABC vuông tại A
b) Tính độ dài các cạnh AB, AC và BC của tam giác đó. HD Giải 9 9 a) Ta có: AB 3
; 2, AC 3; , Xét .
AB AC (3).3 (2)
0 AB AC hay AB AC 2 2
Vậy tam giác ABC vuông tại A 81 117
b) Ta có: AB AB 9 4 13 ;
AC AC 9 4 2 5 25 13
Ta lại có: BC 6;
BC BC 36 2 4 2
Bài 12. Tính góc giữa hai vectơ a, b với a (1; 2), b (1; 3) . HD Giải . a b a b a b 1.(1) ( 2) ( 3 ) 2
Ta có: cos a,b 1 1 2 2 a,b 0 45 2 2 2 2 a . b
a a . b b 1 4. 1 9 2 1 2 1 2
Bài 13. Trong mặt phẳng Oxy , cho hai điểm (
A 2; 4), B(1;1). Tìm tọa độ điểm C sao cho tam giác ABC là
tam giác vuông cân tại B . HD Giải . BA BC 0 Gọi C( ;
x y). Theo giả thiết: tam giác ABC là tam giác vuông cân tại B (1) BA BC
Ta có: BA (1;3) và BC x 1; y 1 1
(x 1) 3( y 1) 0
x 3 4 y x 4 x 2 Từ (1) hoặc 2 3 2 2 2
1 3 (x 1) ( y 1)
10 y 20 y 0 y 0 y 2
Vậy có hai điểm C thỏa mãn YCBT là (4; 0), ( 2 ; 2) .
Bài tập tương tự
Bài 14. Tính góc giữa hai vectơ a, b trong các trường hợp sau:
a) a (3; 4), b (4;3)
b) a (2;5), b (3; 7)
c) a (2; 3), b (6; 4)
d) a (3; 2), b (5; 1 ) e) a ( 2 ; 2 3), b (3; 3)
Bài 15. Trong mặt phẳng Oxy , cho hai điểm (
A 1;3), B(4; 2).
a) Tìm tọa độ điểm D nằm trên Ox sao cho DA DB 11
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
b) Tính chu vi tam giác OAB
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OA . B
Bài 16. Trong mặt phẳng Oxy , cho bốn điểm (
A 7; 3), B(8; 4), C(1;5), D(0; 2). Chứng minh rằng tứ giác
ABCD là hình vuông.
Bài 17. Trong mặt phẳng Oxy , cho điểm (
A 2;1). Gọi B là điểm đối xứng với điểm A qua gốc tọa độ O .
Tìm tọa độ điểm C có tung độ bằng 2 sao cho tam giác ABC vuông tại C .
Bài 18. Trong mặt phẳng Oxy , cho tam giác ABC với ( A 2; 4), B( 3 ;1), C(3; 1 ).
a) Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành
b) Tìm tọa độ điểm A là chân đường cao vẽ từ A
Bài 19. Trong mặt phẳng Oxy , cho cho tam giác ABC với (
A 1;1), B(1;3), C(1; 1).
a) Chứng minh tam giác ABC vuông cân tại . A
b) Tính diện tích tam giác ABC và góc . B
Bài 20. Trong mặt phẳng Oxy , cho bốn điểm (
A 1;1), B(0; 2), C(3;1), D(0; 2) . Chứng minh tứ giác ABCD là hình thang cân.
Bài 21. Trong mặt phẳng Oxy , cho ba điểm (
A 1; 1), B(3;1), C(6, 0). a) Chứng minh ba điểm ,
A B, C không thằng hàng
b) Tính góc B, C của tam giác ABC.
Bài 22. Trong mặt phẳng Oxy , cho bốn điểm (
A 3; 4), B(4;1), C(2; 3), D(1; 6) . Chứng minh rằng tứ giác
ABCD nội tiếp được trong một đường tròn.
Bài 23. Trong mặt phẳng Oxy , cho hai điểm (5
A ;3), B(3; 2). Một điểm M di động trên trục Ox . Tìm giá trị
nhỏ nhất của MA MB 1
Bài 24. Trong mặt phẳng Oxy , cho u
i 5 j, v ki 4 j. 2
a) Tìm các giá trị của k để u v
b) Tìm các giá trị của k để u v
Bài 25. Trong mặt phẳng Oxy , cho tam giác ABC với (
A 4;1), B(2; 4), C(2; 2).
a) Tính chu vi và diện tích của tam giác đó
b) Tìm tọa độ trọng tâm G , trực tâm H và tâm I của đường tròn ngoại tiếp tam giác ABC. Từ đó kiểm tra
tính chất thẳng hàng của ba điểm G, H , I.
Bài 26. Cho các vectơ a ( 2 ;3), b (4;1).
a) Tính côsin của góc giữa mỗi cặp vectơ sau: a và b ; a và i ; j và b ; a b và a b .
b) Tìm các số k và l sao cho c ka lb vuông góc với vectơ a b
c) Tìm vectơ d biết .
a d 4 và b.d 2 .
Bài 27. Trong mặt phẳng Oxy , cho hai điểm (
A 3; 2), B(4;3).Tìm tọa độ của
a) điểm M trên trục Ox sao cho tam giác MAB vuông tại M .
b) điểm N trên trục Oy sao cho NA N . B
Bài 28. Trong mặt phẳng Oxy , cho hai điểm (
A 1; 1), B(3, 0) là hai đỉnh của hình vuông ABCD . Tìm tọa độ đỉnh C, . D 12
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho hai vectơ a và b khác 0 . Xác định góc giữa hai vectơ a và b khi .
a b a . b . A. 0 45 . B. 0 0 . C. 0 90 . D. 0 180 .
Câu 2. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng A . B BC. 2 a 3 2 a 2 a A. 2 A .
B BC a . B. . AB BC . C. . AB BC . D. A . B BC . 2 2 2
Câu 3. Cho hai vectơ a và b thỏa mãn a 3, b 2 và a.b 3
. Xác định góc giữa hai vectơ a và . b A. 0 60 . B. 0 120 . C. 0 30 . D. 0 45 .
Câu 4. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A1; 4, B 3; 2, C 5; 4 . Tính chu vi P của tam giác đã cho.
A. P 4 2 2.
B. P 4 4 2.
C. P 8 8 2.
D. P 2 2 2.
Câu 5. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A1;
1 và B 3;0. Tìm tọa độ điểm D , biết
D có tung độ âm. A. D 2 ; 3 .
B. D 0; 1 . C. D 2; 3 . D. D 2; 3 , D 0; 1 .
Câu 6. Cho hình vuông ABCD cạnh a . Gọi E là điểm đối xứng của D qua C. Tính AE.A . B A. 2 A .
E AB 5a . B. 2
AE.AB 3a . C. 2
AE.AB 5a . D. 2 A .
E AB 2a .
Câu 7. Cho tam giác đều ABC có cạnh bằng .
a Tính tích vô hướng . AB AC. 2 a 2 a 3 A. . AB AC . B. . AB AC . 2 2 2 a C. . AB AC . D. 2 .
AB AC 2a . 2 AC
Câu 8. Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AM . Gọi N 4
là trung điểm của đoạn thẳng DC. Tính M . B MN. A. M . B MN 4. B. M . B MN 16. C. M . B MN 4 . D. M . B MN 0.
Câu 9. Cho tam giác ABC vuông tại A và có AB c, AC . b Tính . BA BC. A. 2 .
BA BC b . B. 2 .
BA BC c . C. 2 2 .
BA BC b c . D. 2 2 .
BA BC b c .
Câu 10. Trong mặt phẳng tọa độ Oxy, cho tam giác OAB với A1;3 và B 4; 2 . Tìm tọa độ điểm E là chân
đường phân giác trong góc O của tam giác OA . B 5 5 A. E 2
3 2; 4 2 . B. E ; . 2 2 3 1 C. E ; . D. E 2
3 2; 4 2 . 2 2
Câu 11. Trong mặt phẳng tọa độ Oxy, cho ba điểm A1; 2, B 1 ; 1 và C 5;
1 . Tính cosin của góc giữa hai
vectơ AB và AC. A. AB AC 5 cos , . B. AB AC 1 cos , . 5 2 C. AB AC 3 cos , . D. AB AC 2 cos , . 2 5
Câu 12. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A4;3, B 2;7 và C 3;8. Tìm toạ độ chân
đường cao A ' kẻ từ đỉnh A xuống cạnh B . C 13
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
A. A'1; 4.
B. A'1;4.
C. A'1;4. D. A'4; 1 .
Câu 13. Trong mặt phẳng tọa độ Oxy, cho ba vectơ a 1; 2, b 4;3 và c 2;3. Tính P .
a b c.
A. P 20.
B. P 28.
C. P 0.
D. P 18.
Câu 14. Trong mặt phẳng tọa độ Oxy, cho hai điểm M –2; 2 và N 1
;1 . Tìm tọa độ điểm P thuộc trục hoành
sao cho ba điểm M , N , P thẳng hàng.
A. P 0;4.
B. P 0; –4.
C. P –4;0.
D. P 4;0. 1
Câu 15. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u
i 5 j và v ki 4 j. Tìm k để vectơ u vuông góc 2 với . v
A. k 40. B. k 2 0. C. k 4 0.
D. k 20.
Câu 16. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A2; 4, B 3 ;1 , C 3; 1 . Tìm tọa độ chân
đường cao A ' vẽ từ đỉnh A của tam giác đã cho. 3 1 3 1 3 1 3 1 A. A ' ; . B. A ' ; . C. A ' ; . D. A ' ; . 5 5 5 5 5 5 5 5 3 4
Câu 17. Trong hệ tọa độ ;
O i ; j , cho vectơ a i
j . Độ dài của vectơ a bằng 5 5 6 7 1 A. . B. . C. . D. 1. 5 5 5
Câu 18. Cho tam giác ABC có BC a, CA b, AB .
c Gọi M là trung điểm cạnh B .
C Tính AM .BC. 2 2 2
c b a 2 2
b c
A. AM .BC .
B. AM .BC . 2 2 2 2 c b 2 2 2
c b a
C. AM .BC .
D. AM .BC . 2 3
Câu 19. Cho hình vuông ABCD cạnh a . Tính P AC.CD CA. A. 2
P 2a . B. P 1 . C. 2
P 3a . D. 2
P 3a . 3
Câu 20. Trong mặt phẳng tọa độ Oxy, cho các điểm A1; 2, B 2; 4, C 0; 1 và D 1; . Mệnh đề nào 2 sau đây đúng ?
A. AB C . D
B. AB cùng phương với C . D
C. AB CD .
D. AB C . D
Câu 21. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A6;0, B 3; 1 và C 1 ; 1 . Tính số đo góc
B của tam giác đã cho. A. O 120 . B. O 135 . C. O 15 . D. O 60 .
Câu 22. Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M 1; 2 và N 3; 4.
A. MN 3 6.
B. MN 2 13.
C. MN 4.
D. MN 6.
Câu 23. Cho tam giác ABC vuông cân tại A và có AB AC . a Tính A . B BC. 2 a 2 A. A . B BC . B. 2 A .
B BC a . 2 2 a 2 C. 2 A .
B BC a . D. . AB BC . 2
Câu 24. Trong mặt phẳng tọa độ Oxy, cho hai điểm A1;3 và B 4; 2. Tìm tọa độ điểm C thuộc trục hoành
sao cho C cách đều hai điểm A và . B 14
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp 3 5 5 3 A. C ; 0 . B. C ; 0 . C. C ; 0 . D. C ; 0 . 5 3 3 5
Câu 25. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 2; 1 và b 4; 3
. Tính cosin của góc giữa hai
vectơ a và b. A. a b 5 cos , . B. a b 2 5 cos , . C. a b 3 cos , . D. a b 1 cos , . 5 5 2 2
Câu 26. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 4i 6 j và b 3i 7 j. Tính tích vô hướng . a . b A. . a b 43. B. . a b 3. C. . a b 30. D. . a b 3 0.
Câu 27. Trong mặt phẳng tọa độ Oxy, cho hai điểm A 2
; 4 và B 8; 4. Tìm tọa độ điểm C thuộc trục hoành
sao cho tam giác ABC vuông tại C.
A. C 6;0.
B. C 0;0, C 6;0.
C. C 0;0. D. C 1 ;0.
Câu 28. Trong mặt phẳng tọa độ Oxy, cho ba điểm A2;0, B 0; 2 và C 0;7. Tìm tọa độ đỉnh thứ tư D
của hình thang cân AB . CD
A. D 9;2.
B. D 7;0.
C. D 7;0, D 2;9.
D. D 0;7, D 9; 2.
Câu 29. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A 2 ; 1 , B 1; 1 và C 2 ; 2 . Khẳng định nào sau đây là đúng?
A. Tam giác ABC vuông cân tại C .
B. Tam giác ABC đều.
C. Tam giác ABC vuông cân tại A .
D. Tam giác ABC vuông tại B .
Câu 30. Cho hình bình hành ABCD có AB 8 cm, AD 12 cm , góc
ABC nhọn và diện tích bằng 2 54 cm .
Tính cos AB, BC. A. AB BC 2 7 cos , . B. AB BC 2 7 cos , . 16 16 C. AB BC 5 7 cos , . D. AB BC 5 7 cos , . 16 16
Câu 31. Trong mặt phẳng tọa độ Oxy, cho hai điểm A3;
1 và B 2;10. Tính tích vô hướng A . O O . B A. A . O OB 4. B. A . O OB 16. C. A . O OB 4 . D. A . O OB 0.
Câu 32. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A 3
;0, B 3;0 và C 2;6. Gọi H ; a b là
tọa độ trực tâm của tam giác đã cho. Tính a 6 . b
A. a 6b 8.
B. a 6b 6.
C. a 6b 7.
D. a 6b 5.
Câu 33. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u 3; 4 và v 8;6 . Khẳng định nào sau đây đúng?
A. u vuông góc với v .
B. u v. 1
C. u v . D. M 0; .
và v cùng phương. 2
Câu 34. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A1; 2, B 1;3, C 2;
1 và D 0; 2. Mệnh đề nào sau đây đúng ?
A. ABCD là hình bình hành.
B. ABCD là hình chữ nhật.
C. ABCD là hình thoi.
D. ABCD là hình vuông.
Câu 35. Trong mặt phẳng tọa độ Oxy, cho ba điểm A3;
1 , B 2;10, C 4
; 2. Tính tích vô hướng A . B AC. A. A . B AC 40. B. A . B AC 4 0. C. A . B AC 26. D. A . B AC 2 6.
Câu 36. Cho M , N , P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
A. MN NP PQ MN.NP MN.PQ . B. M .
P MN MN.MP .
C. MN.PQ P . Q MN . D. 2 2 MN PQ MN
PQ MN PQ . 15
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 37. Cho tam giác ABC có AB 2 cm, BC 3 cm, CA 5 cm. Tính . CA C . B A. C . A CB 19. B. C . A CB 15. C. C . A CB 17. D. C . A CB 13.
Câu 38. Cho hình chữ nhật ABCD có AB a và AD a 2 . Gọi K là trung điểm của cạnh A . D Tính BK.AC. A. 2
BK.AC 2a .
B. BK.AC 0. C. 2
BK.AC a 2. D. 2
BK.AC a 2.
Câu 39. Trong mặt phẳng tọa độ Oxy, cho hai điểm A2; 4 và B 1;
1 . Tìm tọa độ điểm C sao cho tam giác
ABC vuông cân tại . B
A. C 4;0, C 2 ; 2.
B. C 2;0.
C. C 4;0. D. C 2 ; 2.
Câu 40. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A 8
;0, B 0; 4, C 2;0 và D 3 ; 5 . Khẳng định
nào sau đây là đúng?
A. Hai góc BAD và
BCD phụ nhau. B. Góc
BCD là góc nhọn.
C. cos AB, AD cosCB,CD.
D. Hai góc BAD và BCD bù nhau.
Câu 41. Cho tam giác ABC có BC a, CA b, AB .
c Tính P AB AC .BC. 2 2 2
c b a 2 2 c b 2 2 2
c b a
A. P . B. 2 2
P b c .
C. P .
D. P . 2 2 3
Câu 42. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A 4 ;
1 , B 2; 4, C 2; 2
. Tìm tọa độ tâm I
của đường tròn ngoại tiếp tam giác đã cho. 1 1 1 1 A. I ;1 . B. I ;1 . C. I 1; . D. I 1; . 4 4 4 4
Câu 43. Trong mặt phẳng tọa độ Oxy, cho ba vectơ a 2
;3, b 4
;1 và c k a mb với k, m . Biết
rằng vectơ c vuông góc với vectơ a b . Khẳng định nào sau đây đúng?
A. 2k 3m 0.
B. 3k 2m 0. C. 2k 2 . m D. 3k 2 . m
Câu 44. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u 4;
1 và v 1; 4. Tìm m để vectơ a .
m u v tạo
với vectơ b i j một góc 0 45 . 1 1 1
A. m . B. m .
C. m 4.
D. m . 4 2 2
Câu 45. Cho ba điểm O, ,
A B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng OA OB.AB 0 là
A. tam giác OAB đều.
B. tam giác OAB cân tại . O
C. tam giác OAB vuông tại . O
D. tam giác OAB vuông cân tại . O
Câu 46. Trong mặt phẳng tọa độ Oxy, cho hai vectơ x 1; 2 và y 3 ;
1 . Tính góc giữa hai vectơ x và . y A. O 135 . B. O 60 . C. O 90 . D. O 45 . 2
Câu 47. Cho hai vectơ a và b thỏa mãn a b 1 và hai vectơ u
a 3b và v a b vuông góc với nhau. 5
Xác định góc giữa hai vectơ a và . b A. 0 45 . B. 0 90 . C. 0 180 . D. 0 60 .
Câu 48. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A 1 ;
1 , B 1;3 và C 1; 1 . Khẳng định nào sau đây là đúng ?
A. Tam giác ABC đều.
B. Tam giác ABC có ba góc đều nhọn.
C. Tam giác ABC cân tại B .
D. Tam giác ABC vuông cân tại A . 16
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 49. Trong mặt phẳng tọa độ Oxy, cho ba điểm A –4;0, B –5;0 và C 3;0. Tìm điểm M thuộc trục
hoành sao cho MA MB MC 0.
A. M –5;0.
B. M –2;0.
C. M 2;0.
D. M –4;0.
Câu 50. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A10;5, B 3; 2 và C 6; 5
. Khẳng định nào sau đây là đúng?
A. Tam giác ABC đều.
B. Tam giác ABC vuông cân tại A .
C. Tam giác ABC vuông cân tại B .
D. Tam giác ABC có góc A tù.
Câu 51. Trong mặt phẳng tọa độ Oxy, cho vectơ a 9;3 . Vectơ nào sau đây không vuông góc với vectơ a ?
A. v 1;3 .
B. v 1;3 . C. v 1; 3 . D. v 2; 6 . 2 1 4 3
Câu 52. Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a . Mệnh đề nào sau đây là sai? 1 1 2 a 1 A. 2 . AB AC a . B. 2 AC.CB a . C. . GA GB . D. 2 . AB AG a . 2 2 6 2
Câu 53. Cho tam giác đều ABC có cạnh bằng a và chiều cao AH . Mệnh đề nào sau đây là sai? 2 a 2 a
A. AC.CB .
B. AH.BC 0. C. AB HA 0 , 150 . D. A . B AC . 2 2
Câu 54. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 2;5 và b 3; 7
. Tính góc giữa hai vectơ a và b. A. O 135 . B. O 45 . C. O 60 . D. O 30 .
Câu 55. Trong mặt phẳng tọa độ Oxy , cho ba điểm A 3 ; 2
, B 3;6 và C 11;0. Tìm tọa độ điểm D để tứ
giác ABCD là hình vuông.
A. D 5; 8.
B. D 8;5.
C. D 5;8.
D. D 8;5.
Câu 56. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A7; 3
, B 8;4, C 1;5 và D 0; 2
. Khẳng định nào sau đây đúng?
A. Tứ giác ABCD không nội tiếp đường tròn.
B. AC C . B
C. Tam giác ABC đều.
D. Tứ giác ABCD là hình vuông.
Câu 57. Cho hình thoi ABCD có AC 8 và BD 6. Tính A . B AC. A. A . B AC 32. B. A . B AC 26. C. A . B AC 28. D. A . B AC 24.
Câu 58. Cho a và b là hai vectơ cùng hướng và đều khác vectơ 0 . Mệnh đề nào sau đây đúng? A. . a b 1 . B. .
a b a . b . C. .
a b a . b . D. . a b 0 .
Câu 59. Cho hình vuông ABCD cạnh .
a Tính P AB AC.BC BD BA. A. 2
P 2a . B. P 2 2 . a C. 2
P 2a . D. 2
P a .
Câu 60. Cho hai vectơ a và b . Đẳng thức nào sau đây sai? 2 2 1 2 2 2 1 2
A. a.b
a b a b .
B. a.b
a b a b 2 . 2 2 2 1 2 2 1
C. a.b
a b a b .
D. a.b
a b a b 4 . 2
Câu 61. Trong mặt phẳng tọa độ Oxy, cho hai điểm A2; 2, B 5; 2. Tìm điểm M thuộc trục hoàng sao cho 0 AMB 90 ?
A. M 1;6.
B. M 0;6. C. M 0 ;1 .
D. M 6;0.
Câu 62. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 3; 2 và b 1 ; 7
. Tìm tọa độ vectơ c biết . c a 9 và . c b 20 .
A. c 1;3.
B. c 1; 3. C. c 1 ;3. D. c 1; 3 . 17
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp 1
Câu 63. Trong mặt phẳng tọa độ Oxy, cho hai vectơ u
i 5 j và v ki 4 j. Tìm k để vectơ u và vectơ 2
v có độ dài bằng nhau. 5 37 37 37
A. k . B. k . C. k . D. k . 8 2 2 4
Câu 64. Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD biết A 2
;0, B 2;5, C 6; 2. Tìm tọa độ điểm . D A. D 2 ; 3 . B. D 2 ;3. C. D 2; 3 .
D. D 2;3.
Câu 65. Cho hình chữ nhật ABCD có AB 8, AD 5. Tích A . B B . D A. A . B BD 6 4. B. A . B BD 64. C. A . B BD 6 2. D. A . B BD 62.
Câu 66. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A1;3, B 2
; 4, C 5;3. Tìm tọa độ trọng tâm
G của tam giác đã cho. 4 10 8 10 10 A. G ; . B. G ; .
C. G 2;5. D. G 2; . 3 3 3 3 3
Câu 67. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 4;3 và b 1;7 . Tính góc giữa hai vectơ a và b. A. O 30 . B. O 60 . C. O 45 . D. O 90 .
Câu 68. Cho hình vuông ABCD cạnh . a Tính A . B AC. 1 2 A. 2 . AB AC a . B. 2 A . B AC a 2. C. 2 . AB AC a . D. 2 A .
B AC a . 2 2
Câu 69. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 2;3 và b 4;
1 . Tìm vectơ d biết . a d 4 và . b d 2 . 5 6 5 6 5 6 5 6
A. d ; . B. d ; . C. d ; . D. d ; . 7 7 7 7 7 7 7 7
Câu 70. Trong mặt phẳng tọa độ Oxy, cho hai điểm A1;2 và B 3
;1 . Tìm tọa độ điểm C thuộc trục tung
sao cho tam giác ABC vuông tại . A
A. C 0;6.
B. C 5;0. C. C 3; 1 . D. C 0; 6 .
Câu 71. Trong mặt phẳng tọa độ Oxy, cho ba vectơ u 4;
1 , v 1; 4 và a u .
m v với m . Tìm m để
a vuông góc với trục hoành. A. m 2 .
B. m 2.
C. m 4. D. m 4 .
Câu 72. Trong mặt phẳng tọa độ Oxy, cho hai vectơ a 1
;1 và b 2;0 . Tính cosin của góc giữa hai vectơ
a và b. A. a b 1 cos , . B. a b 1 cos , . 2 2 2 C. a b 1 cos , . D. a b 2 cos , . 2 2
Câu 73. Trong mặt phẳng tọa độ Oxy, cho bốn điểm A 1 ;
1 , B 0; 2, C 3; 1 và D 0; 2 . Khẳng định nào sau đây là đúng?
A. Tứ giác ABCD là hình thang cân.
B. Tứ giác ABCD không nội tiếp được đường tròn.
C. Tứ giác ABCD là hình bình hành.
D. Tứ giác ABCD là hình thoi. 18
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 74. Trong mặt phẳng tọa độ Oxy, cho hai điểm A1;
1 và B 3; 2. Tìm M thuộc trục tung sao cho 2 2
MA MB nhỏ nhất. 1 1 A. M 0; .
B. M 0; 1 . C. M 0; . D. M 0 ;1 . 2 2
Câu 75. Trong mặt phẳng tọa độ Oxy, tìm điểm M thuộc trục hoành để khoảng cách từ đó đến điểm N 1; 4 bằng 2 5.
A. M 1;0, M 3;0.
B. M 1;0, M 3 ;0.
C. M 3;0. D. M 1;0. ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 19
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
§3. CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC VÀ GIẢI TAM GIÁC
KIẾN THỨC CẦN NẮM 1. Định lí côsin
Cho tam giác ABC có BC a, AC b và AB c . A Ta có 2 2 2
a b c 2 . bc cos ; A c b 2 2 2
b c a 2c .
a cos B; 2 2 2 a C B
c a b 2 . ab cos C. Hệ quả 2 2 2 2 2 2 2 2 2
b c a
c a b
a b c cos A ; cos B ; cos C . 2bc 2ca 2ab 2. Định lí sin
Cho tam giác ABC có BC a, AC b , AB c và R là bán kính A
đường tròn ngoại tiếp. a b c c Ta có : b 2R sin A sin B sin C I B a C
3. Độ dài đường trung tuyến
Cho tam giác ABC có m , m , m lần lượt là các trung tuyến a b c A kẻ từ ,
A B, C . Ta có m c a b 2 2 2 2 2 2 2 2 2 b c a a c b a b c 2 2 2 m ; m ; m . mb a m 2 4 b 2 4 c 2 4 c M a C B
4. Công thức tính diện tích tam giác Cho tam giác ABC có
● h , h , h là độ dài đường cao lần lượt tương ứng với các cạnh BC, C , A AB ; a b c
● R là bán kính đường tròn ngoại tiếp tam giác;
● r là bán kính đường tròn nội tiếp tam giác;
a b c ● p là nửa chu vi tam giác; 2
● S là diện tích tam giác, được tính bởi các công thức sau 1 1 1 S ah bh ch 2 a 2 b 2 c 1 1 1
S bc sin A ca sin B ab sin C 2 2 2 abc S 4R S pr S
p p a p b p c (Công thức Hê-rông) 20
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp BÀI TẬP
ấn đề 1. Tính một số yếu tố trong tam giác theo một số yếu tố ch trước
VPhương pháp: Trong các yếu cho biết phải có ít nhất một cạnh
Sử dụng trực tiếp định lí côsin và định lí sin.
Chọn các hệ thức lượng thích hợp đối với tam giác để tính một số yếu tố trung gian cần thiết để việc giải toán thuận lợi hơn. 3
Bài 1. Cho tam giác ABC có b 7 cm, c 5 cm và cos A 5
a) Tính cạnh a, sin A và diện tích S của tam giác ABC
b) Tính chiều cao h xuất phát từ đỉnh A và bán kính R của đường tròn ngoại tiếp tam giác AB . C a HD Giải 3
a) Theo định lí côsin, ta có: 2 2 2 2 2
a b c 2bc cos A 7 5 2.7.5.
32 a 4 2 cm 5 2 3 16 4 Ta lại có: 2 2
sin A 1 cos A 1 sin A (do sin A 0) 5 25 5 1 1 4 2 S bc sin A 7.5. 14 cm 2 2 5 1 2S 28 7 2 b) Ta có: S ah h cm 2 a a a 4 2 2 a a 4 2 5 2 Theo định lí sin, ta có: 2R R cm sin A 2 sin A 4 2 2. 5
Bài 2. Cho tam giác ABC có AC 10 cm, BC 16 cm và góc 0
C 110 . Tính cạnh AB và góc , A B của tam giác đó. HD Giải
Theo định lí côsin, ta có: C 2 2 2 2 2 0
c a b 2ab cos C 16 10 2.16.10sin110
465, 44 . Vậy c 21, 6 cm 1100
Theo hệ quả định lí côsin, ta có b a 2 2 2 2 2 2
b c a 10 (21, 6) 16 cos A 0, 7188 2bc 2.10.21, 6 c B A Suy ra: 0 0 0 A 44 2 ,
B 180 ( A C) 25 58
Bài 3. Cho tam giác ABC có 0 0
B 20 , C 31 và cạnh b 210 cm . Tính góc ,
A các cạnh còn lại và bán kính
R của đường tròn ngoại tiếp tam giác đó. HD Giải Ta có: 0 0
A 180 (B C) 129 C a b c Theo định lí sin: 2R 310 sin A sin B sin C a 0 . b sin A 210.sin129 Suy ra: a 477, 2 cm 210 0 sin B sin 20 0 . b sin C 210.sin 31 200 c 316, 2 cm B 0 A c sin B sin 20 a 477, 2 R 309, 02 cm 0 2sin A 2sin129
Bài 4. Cho tam giác ABC có 0
A 60 , b 8 c , m c 5 c .
m Tính đường cao h và bán kính R của đường tròn a
ngoại tiếp tam giác ABC . 21
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp HD Giải Ta có: 2 2 2 2 2 0
a b c 2bc cos A 8 5 2.8.5.cos 60 49 a 7 cm 1 1 0 2 S bc sin A
8.3.sin 60 10 3 cm 2 2 1 2S 20 3 Ta lại có: S ah h cm 2 a a a 7 abc abc 7.8.5 7 3 S R cm 4R 4S 40 3 3
Bài 5. Cho tam giác ABC có AB 5 c , m BC 7 c , m CA 8 c . m Tính a) . AB AC b) Góc . A HD Giải 2 2 2 2 2 2 2 1 1
Ta có: BC AC AB AC AB 2 . AB AC . AB AC
AC AB BC 2 2 2 5 8 7 20 2 2 . AB AC 20 1 Theo định nghĩa, ta có: 0 .
AB AC AB . AC cos A cos A A 60 . AB . AC 5.8 2 Bài tập tương tự
Bài 6. Cho tam giác ABC biết a 21c , m b 17 c , m c 10 . cm a) Tính các góc , A B,C .
b) Tính diện tích S của tam giác ABC và các chiều cao h , h , h . a b c
c) Tính bán kính nội, ngoại tiếp của tam giác ABC
d) Tính độ dài các đường trung tuyến m , m , m . a b c
Bài 7. Cho tam giác ABC biết a 6 cm, b 2 c ,
m c (1 3) c . m Tính các góc ,
A B, C , chiều cao h , độ a
dài đường trung tuyến m và bán kính đường tròn ngoại tiếp R của tam giác ABC . a
ấn đề 2. Chứng minh các hệ thức về mối quan hệ giữa các yếu tố của một tam giác
VPhương pháp: Dùng các hệ thức cơ bản biến đổi vế này thành về kia hoặc chứng minh cả hai vế cùng
bằng một biểu thức nào đó hoặc chứng minh hệ thức cần chứng minh tương đương với một hệ thức đã biết là
đúng. Khi chứng minh cần khai thác các giả thiết và kết luận để tìm được các hệ thức thích hợp làm trung gian
trong quá trình biến đổi.
Bài 8. Cho tam giác ABC có BC a,CA , b AB .
c Chứng minh rằng a b cos C c cos B HD Giải 2 2 2
a c b
Theo định lí côsin, ta có: 2 2 2
b a c 2ac cos B c cos B 2a 2 2 2
a b c
Tương tự: b cos C 2a 2 2 2 2 2 2 2
a c b
a b c 2a
Khi đó: b cos C c cos B a (đpcm) 2a 2a 2a
Bài 9. Cho tam giác ABC có BC a, CA ,
b AB c và đường trung tuyến AM AB c Chứng minh rằng: a) 2 a 2 2 2 b c b) 2 A 2 2 sin
2 sin B sin C HD Giải 2 2 2 2 2 2 b c a a b c a) Ta có: 2 2 m c A a 2 4 4 2 2 2 2 a b c c 2 a 2 2
2 b c (đpcm) b c 4 2 ma a b c
b) Theo định lí sin ta có: 2R . / / C B sin A sin B sin C a M 22
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp 2 2 2 2 2 a b c b c Suy ra: . Từ câu a) ta có: 2 2 2 2 2 sin A sin B sin C sin B sin C 2 2 2 b c 2 2 b c 2 1 2 A 2 2 sin
2 sin B sin C (đpcm) 2 2 2 2 2 2 sin A sin B sin C sin A sin B sin C Bài tập tương tự
Bài 10. Cho tam giác ABC có BC a,CA ,
b AB c và G là trọng tâm của tam giác. 1 Chứng minh rằng: 2 2 2
GA GB GC 2 2 2
a b c 3
Bài 11. Cho tam giác ABC vuông tại A có các cạnh góc vuông là b và c . Lấy điểm M trên cạnh BC và cho bc
BAM . Chứng minh rằng AM
b cos c sin
Bài 12. Cho hình bình hành ABCD có AB a, BC ,
b BD m và AC n . Chứng minh rằng: 2 2
m n 2 2 2 a b
Bài 13. Cho tam giác ABC có b c 2 .
a Chứng minh rằng: 2 1 1
a) 2 sin A sin B sin C b) h h h a b c
Bài 14. Cho tam giác ABC có 2 .
b c a . Chứng minh rằng: a) 2 sin A sin . B sin C b) 2
h h .h a b c
Bài 15. Chứng minh rằng trong tam giác ABC ta có các hệ thức:
a) sin A sin B cos C sin C cos B
b) h 2R sin B sin C a
ấn đề 3. Giải tam giác
VPhương pháp: Một tam giác thường được xác định khi biết ba yếu tố. Trong các bài toán giải tam giác,
thường cho tam giác với ba yếu tố như sau:
Biết một cạnh và hai góc kề cạnh đó (g, c, g)
Biết một góc và hai cạnh kề góc đó (c, g, c)
Biết ba cạnh (c, c, c)
Để tìm các yếu tố còn lại của tam giác người ta thường sử dụng các định lí côsin, định lí sin, định lí tổng ba
góc của một tam giác bằng 0
180 và đặc biệt có thể sử dụng các hệ thức lượng trong tam giác vuông.
Bài 16. Giải tam giác ABC biết 0
b 14, c 10, A 145 . HD Giải Ta có: 2 2 2 2 2 0
a b c 2bc cos A 14 10 2.14.10.cos145 525,35 a 23. 0 a b . b sin A 14.sin145 0 sin B
0,34913 B 20 26 ' sin A sin B a 23 0 0 0 0 0
C 180 ( A B) 180 (145 20 26 ') 14 34 '
Bài tập tương tự
Bài 17. Giải tam giác ABC biết 0 a 17, 4 , m B 44 30 ' và 0 C 64 .
Bài 18. Giải tam giác ABC biết a 49, 4 m, b 26, 4 m và 0 C 27 20 ' .
Bài 19. Giải tam giác ABC biết a 4, b 5, c 7 .
Bài 20. Cho tam giác ABC biết a 24 ,
cm b 13cm và c 15 cm . Tính diện tích S của tam giác và bán kính
đường tròn nội ngoại tiếp tam giác ABC .
Bài 21. Cho tam giác ABC biết 0 a 137,5c , m B 83 và 0
C 57 . Tính góc A , cạnh b, c bán kính R diện
tích S của tam giác.
Bài 22. Cho tam giác ABC vuông tại A , 0
B 58 và a 72 cm . Tính góc C , cạnh b, c , đường cao h , h và a b
đường trung tuyến m , m , m . a b c
Bài 23. Cho tam giác ABC có 0
A 120 , b 8c ,
m c 5cm . Tính
a, B, C, h , m , S, R, r. a c 23
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Bài 24. Tính S, R, r, ,
A B, C của tam giác ABC có số đo các cạnh lần lượt là 7, 9, 12 . Bài 25. Cho A BC . 0 a) Biết 0
A 90 , B 58 , a 72cm . Tính
C , cạnh b, cạnh c và đường cao h a b) Biết a 52,1 ,
cm b 85 cm và c 54cm . Tính các góc , A B, C
c) Biết a 3, b 4, c 6 . Tính diện tích của A BC
d) Biết a 8, b 10, c 13 . Tam giác có góc tù không? Và tính m của A BC . a
Bài 26. Cho tam giác đều ABC có cạnh bằng 6cm . Một điểm M nằm trên cạnh BC sao cho BM 2c . m
a) Tính độ dài của đoạn thẳng AM và tính cosin của góc BAM
b) Tính bán kính đường tròn ngoại tiếp tam giác ABM
c) Tính độ dài trung tuyến vẽ từ đỉnh C của tam giác ACM
d) Tính diện tích tam giác ABM
Bài 27. Cho tam giác ABC có 0
A 60 , a 30 , bán kính đường tròn nội tiếp r 5 3 .
a) Tính bán kính đường tròn ngoại tiếp R
b) Tính độ dài các cạnh , b c Bài 28. Cho A
BC có AB = 10, AC = 4 và 0 A 60 .
a) Tính chu vi của và tanC của A BC
b) Trên tia đối của AB lấy điểm D sao cho AD 6 , trên tia AC lấy điểm E sao cho AE x . Tìm x để BE là
tiếp tuyến của đường tròn ADE .
ấn đề 4. Ứng dụng vào việc đo đạc
VPhương pháp: Vận dụng linh hoạt các hệ thức lượng.
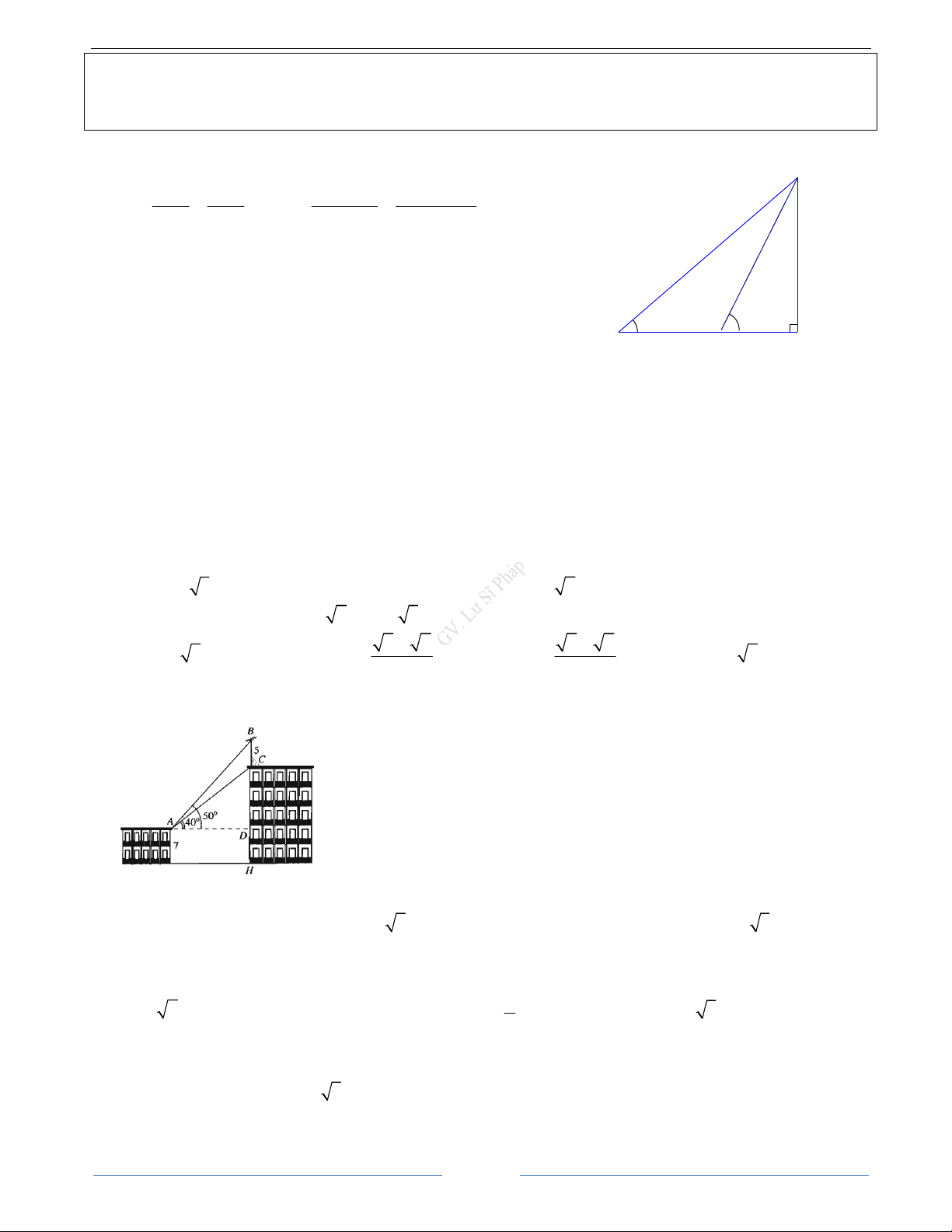
Bài 29. Giả sử CD h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm ,
A B trên mặt đất sao 0 cho ba điểm ,
A B và C thẳng hàng. Ta đo được AB 24 m , 0
CAD 63 , CBD 48 . Tính chiều cao h của tháp. HD Giải AD AB
Trong tam giác ABD , ta có: sin sin D 0 . AB sin . AB sin 24.sin 48 AD 68, 91 sin D sin 0 sin15
Bài 30. Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một
điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Giả sử ta đo được khoảng cách
AB 40 m , 0 CAB 45 và 0
CBA 70 . Như vậy khoảng cách từ một điểm A trên bờ sông đến gốc cây C bao nhiêu? HD Giải AC AB
Trong tam giác ABC, ta có: sin B sin C 0 AB sin B AB sin 40.sin 70 AC 41, 47 m 0 sin C sin( ) sin115 24
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Bài 31. Hai chiếc tàu thủy P và Q cách nhau 300 m . Từ P và Q thẳng hàng với chân A của tháp hải đăng
AB ở trên bờ biển, người ta nhìn chiều cao AB của tháp dưới một góc 0 BPA 35 và 0
BQA 48 . Tính chiều cao của tháp. HD Giải Ta có: 0 0 0
PBQ 48 35 13 . Xét tam giác BPQ : B 0 BQ PQ P . Q sin P 300.sin 35 Ta có: BQ 764,935 m 0 sin P sin B sin B sin13
Xét tam giác ABQ , ta có: h p 0 0 AB .
BQ sin 48 764,935.sin 48 568, 457 m 350 480 300 m P b A Q Bài tập tương tự
Bài 32. Giả sử ta cần đo chiều cao CD của một tháp với C là chân tháp, D là đỉnh tháp. Vì không thể đến
chân tháp được nên từ hai điểm ,
A B có khoảng cách AB 30 m sao cho ba điểm ,
A B, C thẳng hàng người ta 0 đo được các góc 0
CAD 43 ,CBD 67 . Hãy tính chiều cao CD của tháp.
Bài 33. Trên ngọn đồi có một cái tháp cao 100 m . Đỉnh tháp B và chân tháp C nhìn điểm A ở chân đồi dưới
một góc tương ứng bằng 0 30 và 0
60 so với phương thẳng đứng. Xác định chiều cao HA của ngọn đồi.
CÂU HỎI TRẮC NGHIỆM
Câu 1. Tam giác ABC có AB 2, AC 1 và
A 60 . Độ dài cạnh BC là
A. BC 3.
B. BC 2.
C. BC 2.
D. BC 1.
Câu 2. Tam giác ABC có AB 2, AC 3 và
C 45 . Độ dài cạnh BC là 6 2 6 2
A. BC 5. B. BC . C. BC .
D. BC 6. 2 2
Câu 3. Trên nóc một tòa nhà có một cột ăng-ten cao 5 m . Từ vị trí quan sát A cao 7 m so với mặt đất, có thể
nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 0 50 và 0
40 so với phương nằm ngang.
Chiều cao của tòa nhà gần nhất với giá trị nào dưới đây?
A. 12 m .
B. 19 m . C. 24 m . D. 29 m .
Câu 4. Tam giác ABC có AC 4, BAC 30 ,
ACB 75 . Diện tích tam giác ABC là A. S 8 . B. S 4 3 . C. S 4 . D. S 8 3 . AB C ABC ABC A BC
Câu 5. Cho góc xOy 30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB 1. Độ dài
lớn nhất của đoạn OB bằng 3 A. 2 2. B. 2. C. . D. 3. 2
Câu 6. Tam giác ABC có AB 6cm, AC 8cm và BC 10cm . Độ dài đường trung tuyến xuất phát từ đỉnh
A của tam giác bằng A. 5cm . B. 3cm . C. 7cm . D. 4cm . 25
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 7. Giả sử CD h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm ,
A B trên mặt đất sao 0 cho ba điểm ,
A B và C thẳng hàng. Ta đo được AB 24 m , 0
CAD 63 , CBD 48 .
Chiều cao h của tháp gần với giá trị nào dưới đây? A. 60m . B. 60, 5m . C. 18m . D. 18, 5m .
Câu 8. Tam giác ABC vuông tại A , đường cao AH 32 cm . Hai cạnh AB và AC tỉ lệ với 3 và 4 . Cạnh
nhỏ nhất của tam giác này có độ dài bằng bao nhiêu? A. 38 . cm B. 40 . cm C. 42 . cm D. 45 . cm
Câu 9. Tam giác ABC vuông tại A và có AB AC a . Độ dài đường trung tuyến BM của tam giác đã cho là a 5 A. BM . B. BM 1, 5 . a
C. BM a 2.
D. BM a 3. 2
Câu 10. Cho tam giác ABC có AB 3 3, BC 6 3 và CA 9 . Gọi D là trung điểm BC . Bán kính R của
đường tròn ngoại tiếp tam giác ABD là 9 9 A. R . B. R .
C. R 3 .
D. R 3 3 . 2 6
Câu 11. Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết 0 AH 4 , m HB 20 , m BAC 45 .
Chiều cao của cây gần nhất với giá trị nào dưới đây?
A. 16, 5 m .
B. 16 m .
C. 17, 5 m . D. 17 m .
Câu 12. Cho góc xOy 30 . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB 1. Khi
OB có độ dài lớn nhất thì độ dài của đoạn OA bằng 3 A. . B. 3. C. 2 2. D. 2. 2
Câu 13. Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một
điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta đo được khoảng cách AB 40m , 0 CAB 45 và 0 CBA 70 .
Vậy sau khi đo đạc và tính toán được khoảng cách AC gần
nhất với giá trị nào dưới đây? A. 41 m .
B. 30 m .
C. 41, 5 m . D. 53 m .
Câu 14. Tam giác ABC có AB 4, BC 6, AC 2 7 . Điểm M thuộc đoạn BC sao cho MC 2MB . Độ
dài cạnh AM là
A. AM 4 2.
B. AM 3.
C. AM 2 3.
D. AM 3 2.
Câu 15. Tam giác ABC có BC 21 ,
cm CA 17 cm, AB 10 cm . Bán kính R của đường tròn ngoại tiếp tam giác ABC là 26
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp 7 85 7 85 A. R cm . B. R cm . C. R cm . D. R cm . 2 2 4 8
Câu 16. Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân
tháp một khoảng CD 60 m , giả sử chiều cao của giác kế là OC 1m . Quay thanh giác kế sao cho khi ngắm
theo thanh ta nhình thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc 0 AOB 60 .
Chiều cao của ngọn tháp gần với giá trị nào ? A. 105 m .
B. 110 m . C. 40 m . D. 114 m .
Câu 17. Tam giác ABC có BC 10 và O
A 30 . Bán kính R của đường tròn ngoại tiếp tam giác ABC là 10
A. R 10 3 .
B. R 10 . C. R .
D. R 5 . 3
Câu 18. Tam giác ABC có AB c, BC a, CA b . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức 2 2 2 2 b b a
c a c . Khi đó góc BAC bằng A. 90 . B. 45 . C. 60 . D. 30 .
Câu 19. Tam giác ABC vuông tại A có AB 6 cm , BC 10 cm . Bán kính r của đường tròn nội tiếp tam giác đã cho là
A. r 3 cm . B. r 2 cm .
C. r 2 cm .
D. r 1cm .
Câu 20. Tam giác ABC có B 60 ,
C 45 và AB 5 . Độ dài cạnh AC là 5 6
A. AC 5 2.
B. AC 10. C. AC .
D. AC 5 3. 2
Câu 21. Tam giác ABC có AB 9 cm , AC 12 cm và BC 15 cm . Độ dài đường trung tuyến AM của tam giác đã cho là 13 15 A. AM cm .
B. AM 10 cm .
C. AM 9 cm . D. AM cm . 2 2 6 2
Câu 22. Tam giác ABC có AB
, BC 3, CA
2 . Gọi D là chân đường phân giác trong góc A 2
. Khi đó góc ADB bằng A. 45 . B. 60 . C. 75 . D. 90 .
Câu 23. Bán kính r của đường tròn nội tiếp tam giác đều cạnh a là a 3 a 5 a 3 a 2 A. r . B. r . C. r . D. r . 6 7 4 5
Câu 24. Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R . Khi đó bán kính R bằng a 3 a 2 a 3 a 3 A. R . B. R . C. R . D. R . 2 3 3 4
Câu 25. Tam giác ABC có a 21, b 17, c 10 . Diện tích của tam giác ABC bằng A. S 84 . B. S 48 . C. S 24 . D. S 16 . AB C ABC ABC AB C 15
Câu 26. Tam giác ABC cân tại C , có AB 9 cm và AC
cm . Gọi D là điểm đối xứng của B qua C . Độ 2
dài cạnh AD là
A. AD 12 2 cm .
B. AD 6 cm .
C. AD 9 cm .
D. AD 12 cm . 27
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 27. Tam giác A1;3, B 5;
1 có AB 3, AC 6, BAC 60 . Độ dài đường cao h của tam giác là a 3
A. h 3. B. h .
C. h 3 3 .
D. h 3 . a a 2 a a
Câu 28. Tam giác ABC có AB 8 cm, AC 18 cm và có diện tích bằng 64 2
cm . Giá trị sin A bằng 3 3 4 8 A. sin A . B. sin A . C. sin A . D. sin A . 2 8 5 9
Câu 29. Tam giác A1;3, B 5;
1 có AB 3, AC 6, BAC 60 . Diện tích tam giác ABC là 9 9 3 A. S . B. S 9 3 . C. S . D. S 9 . AB C 2 ABC ABC 2 AB C
Câu 30. Tam giác ABC có AB 5, AC 8 và 0
BAC 60 . Bán kính r của đường tròn nội tiếp tam giác đã cho là
A. r 1.
B. r 2 .
C. r 3 .
D. r 2 3 .
Câu 31. Tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ
bằng nhau. Đặt MP q, PQ m, PE x, PF y . Trong các hệ thức dưới đây, hệ thức nào đúng?
A. ME EF . FQ B. 2 2 2
ME q x x . q C. 2 2 2
MF q y y . q D. 2 2 2
MQ q m 2 . qm
Câu 32. Hai chiếc tàu thủy cùng xuất phát từ một vị trí A , đi thẳng theo hai hướng tạo với nhau góc 0 60 . Tàu
B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Kết quả gần nhất với số nào dưới đây? A. 21 hải lí.
B. 18 hải lí. C. 61 hải lí. D. 36 hải lí.
Câu 33. Tam giác ABC có a 21, b 17, c 10 . Gọi B ' là hình chiếu vuông góc của B trên cạnh AC . Độ dài BB ' là 168 84 84 A. BB ' . B. BB ' .
C. BB ' 8 . D. BB ' . 17 17 5
Câu 34. Tam giác ABC có a 21, b 17, c 10 . Bán kính r của đường tròn nội tiếp tam giác đã cho là 7
A. r 8 .
B. r 16 .
C. r 7 . D. r . 2
Câu 35. Tam giác ABC có AB 3, AC 6 và
A 60 . Bán kính R của đường tròn ngoại tiếp tam giác ABC là
A. R 6 .
B. R 3 3 .
C. R 3 .
D. R 3 .
Câu 36. Cho hình thoi ABCD cạnh bằng 1 cm và có
BAD 60 . Độ dài cạnh AC là
A. AC 2. B. AC 2.
C. AC 2 3.
D. AC 3.
Câu 37. Tam giác ABC vuông tại A , có AB c, AC b . Gọi là độ dài đoạn phân giác trong góc BAC . a
Tính theo b và c . a 2bc 2 b c 2bc 2 b c A. . B. . C. . D. . a b c a bc a b c a bc
Câu 38. Tam giác ABC có AC 4, ACB 60 . Độ dài đường cao h xuất phát từ đỉnh A của tam giác là
A. h 2 .
B. h 4 .
C. h 2 3 .
D. h 4 3 .
Câu 39. Hình bình hành ABCD có AB a, BC a 2 và 0
BAD 45 . Khi đó hình bình hành có diện tích bằng 28
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp A. 2 a 3 . B. 2 2a . C. 2 a 2 . D. 2 a .
Câu 40. Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3 , cạnh AB 9 và ACB 60 .
Độ dài cạnh cạnh BC là 3 3 33 A. BC .
B. BC 3 3 6.
C. BC 3 6 3.
D. BC 3 7. 2 12 AB 3
Câu 41. Tam giác ABC vuông tại A có đường cao AH cm và
. Bán kính R của đường tròn 5 AC 4
ngoại tiếp tam giác ABC bằng
A. R 3, 5 cm .
B. R 2, 5 cm .
C. R 1, 5 cm .
D. R 2 cm .
Câu 42. Tam giác ABC có AB 5, BC 7, CA 8 . Số đo góc A bằng A. 90 . B. 30 . C. 45 . D. 60 .
Câu 43. Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao
AB 70m , phương nhìn AC tạo với phương nằm ngang góc 0
30 , phương nhìn BC tạo với phương nằm ngang góc 0 15 30 ' .
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây? A. 195 m .
B. 234 m . C. 165 m . D. 135 m .
Câu 44. Tam giác ABC có AB 3, BC 8 . Gọi M là trung điểm của BC . Biết 5 13 cos AMB và AM 3 26
. Độ dài cạnh AC là
A. AC 7 .
B. AC 13 .
C. AC 7 . D. AC 13 . ĐÁP ÁN 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19 20 21 22
23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 29
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp ÔN TẬP CHƯƠNG II
TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG
KIẾN THỨC CẦN NẮM
1. Định nghĩa: Với mỗi góc 0 0
(0 180 ) ta xác định một điểm M trên nữa đường tròn đơn vị sao cho
xOM và giả sử điểm M có tọa độ M x ; y . Khi đó ta định nghĩa: 0 0
sin của góc là y , kí hiệu sin y 0 0
côsin của góc là x , kí hiệu cos x 0 0 y y
tan của góc là 0 (x 0) , kí hiệu 0 tan 0 x x 0 0 x x
côtan của góc là 0 ( y 0) , kí hiệu 0 cot 0 y y 0 0
Các số sin , cos , tan , cot được gọi là các giá trị lượng giác của góc .
Chú ý: Nếu là góc tù thì cos 0, tan 0, cot 0
tan chỉ xác định khi 0
90 , cot chỉ xác định khi 0 0 hoặc 0 180
2. Các hệ thức lượng giác a. Tính chất 0
sin 180 sin 0
cos 180 cos 0
tan 180 tan 0
cot 180 cot
Lưu ý: Hai góc bù nhau có sin bằng nhau và côsin, tang, cotang đối nhau.
b. Các hệ thức lượng giác cơ bản
Từ định nghĩa giá trị lượng giác của một góc ta suy ra các hệ thức: sin cos 2 2 sin cos 1 0 tan ( 90 ) 0 0 cot ( 0 ;180 ) cos sin 1 1 tan.cot 1 2 1 tan 2 1 cot 2 cos 2 sin
3. Các giá trị lượng giác của các góc đặt biệt 00 300 450 600 900 1800 0 6 4 3 2 HSLG sin 1 3 0 2 2 1 0 2 2 cos 3 2 1 1 0 1 2 2 2 tan 3 3 0 1 || 0 3 cot 3 3 || 1 0 || 3 || : Không xác định 30
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
4. Góc giữa hai vectơ
Cho hai vectơ a, b đều khác 0 . Từ một điểm O bất A a
kì, ta vẽ OA a và OB b . Khi đó góc AOB với B số đo từ 0 0 đến 0
180 được gọi là góc giữa hai vcetơ
a và b . Kí hiệu a,b O b
Lưu ý: a,b , b a 0 a b 0 0 , 180 a b 0 ,
90 a b
5. Tích vô hướng của hai vectơ
a. Định nghĩa: Cho hai vectơ a và b đều khác vectơ 0. Tích vô hướng của a và b là một số, kí hiệu là . a b,
được xác định bởi công thức sau: .
a b a . b cos a,b.
Trường hợp ít nhất một trong hai vectơ a và b bằng vectơ 0 ta quy ước . a b 0. Chú ý
Với a và b khác vectơ 0 ta có .
a b 0 a . b
Khi a b tích vô hướng .
a a được kí hiệu là 2
a và số này được gọi là bình phương vô hướng của vectơ . a 2 2 Ta có: 0
a a . a .cos 0 a .
b. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:
Với ba vectơ a, b, c bất kì và mọi số k ta có: . a b .
b a (tính chất giao hoán);
a b c . a b .
a c (tính chất phân phối);
ka.b k . a b . a kb; 2 2
a 0, a 0 a 0.
Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
a b2 2 2 a 2 . a b b ;
a b2 2 2 a 2 . a b b ;
a ba b 2 2 a b .
c. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ ;
O i; j , cho hai vectơ a a ;a , b b ;b . Khi đó tích vô hướng . a b là: 1 2 1 2 .
a b a b a b . 1 1 2 2
Nhận xét. Hai vectơ a a ; a , b b ;b đều khác vectơ 0 vuông góc với nhau khi và chỉ khi 1 2 1 2
a b a b 0. 1 1 2 2 d. Ứng dụng
i) Độ dài của vectơ 31
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Độ dài của vectơ a a ; a được tính theo công thức: 2 2
a a a . 1 2 1 2
ii) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu a a ; a và b b ;b đều khác 0 thì ta có 1 2 1 2 a b a b a b cos a,b . 1 1 2 2 . 2 2 2 2 a . b
a a . b b 1 2 1 2
iii) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A x ; y
và B x ; y được tính theo công thức: B B A A
AB x x 2 y y 2 . B A B A
6. Các hệ thức lượng trong tam giác a. Định lí côsin
Cho tam giác ABC có BC a, AC b và AB c . A Ta có 2 2 2
a b c 2 . bc cos ; A c b 2 2 2
b c a 2c . a cos ; B 2 2 2 a C B
c a b 2a . b cos C. Hệ quả 2 2 2 2 2 2 2 2 2
b c a
c a b
a b c cos A ; cos B ; cos C . 2bc 2ca 2ab b. Định lí sin
Cho tam giác ABC có BC a, AC b , AB c và R là bán kính A
đường tròn ngoại tiếp. a b c Ta có : c 2R b sin A sin B sin C I B a C
c. Độ dài đường trung tuyến
Cho tam giác ABC có m , m , m lần lượt là các trung tuyến a b c A kẻ từ ,
A B, C . Ta có m c a b 2 2 2 2 2 2 2 2 2 b c a a c b a b c 2 2 2 m ; m ; m . mb a m 2 4 b 2 4 c 2 4 c M a C B
d. Công thức tính diện tích tam giác Cho tam giác ABC có
● h , h , h là độ dài đường cao lần lượt tương ứng với các cạnh BC, C , A AB ; a b c
● R là bán kính đường tròn ngoại tiếp tam giác;
● r là bán kính đường tròn nội tiếp tam giác;
a b c ● p là nửa chu vi tam giác; 2
● S là diện tích tam giác, được tính bởi các công thức sau 32
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp 1 1 1 S ah bh ch 2 a 2 b 2 c 1 1 1
S bc sin A ca sin B ab sin C 2 2 2 abc S 4R S pr S
p p a p b p c (Công thức Hê-rông) BÀI TẬP
Bài 1. Cho tam giác ABC có 0
A 60 , cạnh CA 8 c , m AB 5 c . m
a) Tính cạnh và các góc còn lại.
b) Tính diện tích tam giác ABC
c) Tính độ dài các đường cao trong tam giác ABC d) Tính bán kính R, r của tam giác ABC .
Bài 2. Cho tam giác ABC có a 13cm , b 14 cm, c 15cm .
a) Tính diện tích tam giác ABC
b) Góc B nhọn hay tù? Tính góc B
c) Tính bán kính R, r của tam giác ABC
d) Tính h , h ; m , m a b b c
Bài 3. Chứng minh rằng diện tích hình bình hành bằng tích hai cạnh liên tiếp với sin của góc xen giữa chúng.
Bài 4. Cho bốn điểm A 8
; 0, B 0;4,C 2;0, D 3 , 5
.CMR tứ giác ABCD nội tiếp được trong một đường tròn
Bài 5. Cho tam giác đều ABC có cạnh bằng 6cm . Một điểm M nằm trên cạnh BC sao cho BM 2cm .
a) Tính độ dài của đoạn thẳng AM và tính cosin của góc BAM
b) Tính bán kính đường tròn ngoại tiếp tam giác ABM
c) Tính độ dài trung tuyến vẽ từ đỉnh C của tam giác ACM
d) Tính diện tích tam giác ABM Bài 6. Cho A
BC có AB = 10, AC = 4 và 0 A 60 .
a) Tính chu vi của và tan C của A BC
b) Trên tia đối của AB lấy điểm D sao cho AD 6 , trên tia AC lấy điểm E sao cho AE x . Tìm x để BE là
tiếp tuyến của đường tròn ADE
Bài 7. Cho tam giác ABC có 0
A 60 , a 30 , bán kính đường tròn nội tiếp r 5 3 .
a) Tính bán kính đường tròn ngoại tiếp R
b) Tính độ dài các cạnh , b c Bài 8. Cho A
BC có trọng tâm G . Chứng các hệ thức sau : 3 2 2 2
a b c a) 2 2 2
m m m
a b c b) 2 2 2
GA GB GC a b c 2 2 2 4 3
c) h 2R sin . B sin C
d) sin A sin B cos C cos B sin C a
Bài 9. Chứng minh rằng tam giác ABC vuông ở A khi và chỉ khi 2 2 2
m m 5m . b c a Bài 10. Cho A
BC thoả hệ thức 2
bc cos A ac cos B ab cos C a . CMR: A BC vuông.
Bài 11. Chứng minh rằng: Nếu ABC thoả hệ thức sinA = 2sinBcosC thì A BC cân.
Bài 12. CMR trong tam giác ABC , ta có: a) 2 2
b c a b cos C c cos B b) 2 2
b c cos A a c cosC b cos B Bài 13. Cho A
BC có BC 12, CA 13, trung tuyến AM 8 . Tính diện tích và góc B của A BC . Bài 14. Trong A BC . Tính ,
A B,C, R và m trong các trường hợp sau: a a) 0
A 60 ,b 8, c 5
b) a 21,b 17, c 10
c) a 6, b 2, c 1 3
d) a 2 3, b 2 2, c 6
Bài 15. Tính giá trị của mỗi biểu thức sau: 0 0 0
A 2 sin 30 3cos 45 – sin 60 0 0 0
B 2 cos 45 3sin 60 cos 60 0 0 0 0 0
C tan 5 . tan10 .tan15 ... tan 80 . tan 85 0 0 0 0
D 3sin 90 2 cos 0 3cos 60 10 cos180 33
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp 0 0 0 0 0 0 0
E cos 0 cos 20 cos 40 cos 60 ... c 140 os cos160 cos180
Bài 16. Tính giá trị các biểu thức lượng giác sau: 1
a) A sin x cos x tan x , biết cos x
b) B sin x cos xsin x – cos x , biết tan x 2 2 cot x 3 1 tan a 3 c) C , biết 0 0 sin x
, (0 x 90 ) d) D , biết 0 0
cos a , (90 a 180 ) cot x tan x 5 1 tan a 5 1 1 e) E , biết tan x 2 2
sin x sin x cos x cos x 4 1 f) 0
F cos 2 2sin
tan( 15 ) 2 cos 6 biết 0 30 2
Bài 17. Cho tam giác ABC có các cạnh BC a, AB c, AC b . 2 2 2
b c a a) Chứng minh: . AB AC 2
b) Cho AB 5, BC 7, AC 8 . Tính A .
B AC , suy ra giá trị của góc A .
Bài 18. Cho tam giác ABC có AB a, AC 2a và BC a 7 . Tính A . B AC , rối suy ra BAC
Bài 19. Cho tam giác ABC có AB 4, BC 8, CA 6 .
a) Tính cos A , góc A nhọn hay tù ?
b) Gọi G là trọng tâm tam giác. Tính AG .
Bài 20. Cho các điểm A2;3, B 9; 4, M 5; y và P ; x 2
a) Tìm y để tam giác AMB vuông tại M
b) Tìm x sao cho ba điểm ,
A P và B thẳng hàng
Bài 21. Trong mp Oxy cho điểm A 2 ;
1 . Gọi B là điểm đối xứng với điểm A qua gốc toạ độ . O
Tìm toạ độ điểm C có tung độ bằng 2 sao cho A
BC vuông ở C .
Bài 22. Trong mp Oxy cho hai điểm A3; 2 vàB 4;3 . Tìm toạ độ của :
a) Điểm M trên trục Ox sao cho tam giác MAB vuông tại M
b) Điểm N trên trục Oy sao cho NA NB .
Bài 23. Trong mp Oxy cho hai điểm A1;
1 và B 3;0 là hai đỉnh của hình vuông ABCD .
Tìm toạ độ của đỉnh C và D . 2 Bài 24. Cho A
BC vuông cân tại A , trung điểm của BC là M 1; 1 và trọng tâm G ; 0 . 3
Tìm toạ độ các đỉnh ,
A B,C của A BC
Bài 25. Cho tam giác ABC có A 1
; 2, B 2;0 và C 3 ;
1 .Xác định tâm I đường tròn ngoại tiếp A BC
Bài 26. Cho tam giác ABC có C 2 ; 4
và trọng tâm G 0; 4 biết M 2;0 là trung điểm của BC . Hãy tìm toạ độ của ,
A B và xác định tâm đường tròn ngoại tiếp của A BC
Bài 27. Trong mp Oxy cho A1; 2
và B 3;3.Tìm điểm C ;
x x 2 để A
BC vuông tại C .
Bài 28. Cho tam giác ABC biết 0 0 c 35c ,
m A 40 , C 120 . Tính a, , b C .
Bài 29. Cho tam giác ABC biết 0 a 7 c , m b 23c , m C 130 . Tính , c , A B
Bài 30. Cho tam giác ABC biết a 14 cm, b 18 cm, c 20 c . m . Tính , A , B C.
CÂU HỎI TRẮC NGHIỆM
Câu 1. Cho tam giác đều cạnh bằng 3a . Gọi H là trung điểm BC, M là điểm trên đoạn BC và
BM a . Giá trị AB AC AM bằng 2 27a 2 3a 2 9a A. 2 9a . B. . C. . D. . 2 2 2
Câu 2. Trong tam giác ABC , cho a (3; 4), b (4; 3) . Kết luận nào sau đây là Sai ? 34
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp A. . a b 0. B. a . b C. . a b 0.
D. a . b 0.
Câu 3. Cho tam giác ABC có A10;5, B 3; 2 vàC 6; 5
. Khẳng định nào sau đây là Đúng ? A. A
BC là tam giác đều. B. A
BC là tam giác vuông cân tại B . C. A
BC là tam giác vuông cân tại A . D. A
BC là tam giác có góc tù tại A .
Câu 4. Tìm khẳng định Sai trong các khẳng định sau: A. 0 . 0 cos35 > cos10 B. 0 . 0 sin60 < sin80 C. 0 . 0 tan45 < tan 60 D. 0 0 cos 45 sin 45 .
Câu 5. Tam giác ABC vuông ở A và có góc 0
B 30 . Khẳng định nào sau đây là Sai ? 1 1 1 3 A. cos C . B. sin B . C. cos B . D. sin C . 2 2 3 2
Câu 6. Cho tam giác ABC có AB 8cm, AC 18cm và có diện tích bằng 2
64cm . Giá trị sin A bằng 8 3 4 3 A. . B. . C. . D. . 9 8 5 2
Câu 7. Cho và là hai góc khác nhau và bù nhau. Trong các đẳng thức sau đây, đẳng thức nào Sai?
A. tan tan .
B. cot cot .
C. sin sin .
D. cos cos .
Câu 8. Cho tam giác ABC có AB 2, AC 3, BC 4. Trong các đáp số sau, đáp số nào Sai ? 3 15 10
A. Đường cao AH .
B. Trung tuyến AM . 16 2 1 3 15
C. cos A . D. S . 4 AB C 4
Câu 9. Cho hình vuông ABCD cạnh a , có tâm O . Giá trị của A . O AB bằng 2 a 2 a 2 a 2 a A. . B. . C. . D. . 4 2 2 4 Câu 10. Cho A
BC thoả b c 2a . Khẳng định nào sau đây là Đúng ? 1
A. sin B sin C sin . A
B. sin B cos C 2 sin . A 2
C. sin B sin C 2 sin . A
D. cos B cos C 2 cos . A
Câu 11. Cho tam giác ABC có AB 4c , m BC 7c , m CA 9c .
m Giá trị cos A bằng 1 2 1 2 A. . B. . C. . D. . 2 3 3 3 Câu 12. Giá trị 0 0 cos 45 sin 45 bằng A. 1. B. 2. C. 3. D. 2 2.
Câu 13. Gọi O là tâm đường tròn ngoại tiếp tam giác đều MNP . Góc giữa hai vectơ nào sau đây bằng 0 120 ?
A. MN, MP.
B. MN, NP.
C. MO,ON .
D. MN,OP.
Câu 14. Cho tam giác ABC vuông cân tại A có AB AC 30cm . Hai đường trung tuyến BF và CE cắt nhau
tại G . Diện tích GFC bằng A. 2 15 105 cm . B. 2 50 2 cm . C. 2 75 cm . D. 2 50 cm .
Câu 15. Cho hai góc nhọn và phụ nhau. Hệ thức nào sau đây là Sai ? A. tan = cot B. cos = sin C. cot = tan D. sin = - cos
Câu 16. Trong tam giác ABC . Giá trị cos B bằng 2 2 2
b c a 2 2 2
a c b A. . B. 2 1 sin B.
C. cos A C . D. . 2bc 2ac
Câu 17. Cho M , N, P, Q là bốn điểm tuỳ ý. Trong các hệ thức sau, hệ thức nào Sai ?
A. MN PQMN PQ 2 2
MN PQ . B. M .
P MN MN.M . P
C. MN.PQ P . Q MN.
D. MN. NP PQ MN.NP MN. . PQ 35
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp
Câu 18. Cho tam giác ABC , có các cạnh BC a, CA b, AB c . Khi đó, khẳng định Đúng là: A. 2 2 2
a b c bc cos . A B. 2 2 2
a b c 2bc cos . A C. 2 2 2
a b c 2bc cos . A D. 2 2 2
a b c bc cos . A Câu 19. Cho góc 0
xOy 30 hai điểm ,
A B di động lần lượt trên Ox và Oy sao cho AB 1. Độ dài lớn nhất của đoạn OB bằng A. 2. B. 1,5. C. 3. D. 2 2.
Câu 20. Cho tam giác DEF có DE DF 10cm và EF 12cm . Gọi I là trung điểm của cạnh EF . Đoạn thẳng
DI có độ dài bằng A. 6, 5 c . m B. 7 c . m C. 8 c . m D. 4 c . m
Câu 21. Tam giác có ba cạnh là 6, 10, và 8 . Bán kính đường tròn nội tiếp tam giác đó bằng: A. 1. B. 4. C. 2. D. 3.
Câu 22. Tam giác đều ABC có đường cao AH . Khẳng định nào sau đây là Đúng ? 3 3 A. 1 sin AHC . B. sin BAH . C. 3 cos BAH . D. sin ABC . 2 2 2 2
Câu 23. Trong tam giác ABC . Độ dài đường trung tuyến mc là: 1 2 2 2
b a c A. 2 2 2
2(b a ) c . B. . 2 4 2 2 2 b a c 2 2 2 b a c C. . D. . 2 4 2 4
Câu 24. Cho và là hai góc nhọn trong đó < . Khẳng định nào sau đây là Sai?
A. tan + tan > 0.
B. cos < cos .
C. sin < sin . D. 0
sin cos 90 .
Câu 25. Cho là góc tù. Khẳng định nào sau đây là Đúng ?
A. tan < 0
B. cot > 0
C. sin < 0 D. cos > 0
Câu 26. Cho tam giác ABC có A 1 ;
1 , B 1;3 vàC 1;
1 . Trong các khẳng định nào dưới đây đúng? A. A
BC có ba cạnh bằng nhau. B. A
BC có ba góc đều nhọn C. A
BC cân tại B . D. A
BC vuông cân tại A .
Câu 27. Trong các đẳng thức sau, đẳng thức nào Đúng ? A. 0
sin 90 cos. B. 0 sin 90 sin. C. 0
sin 90 cos. D. 0
cos 90 sin.
Câu 28. Cho tam giác ABC có BC 10 , 0
A 60 . Bán kính đường tròn ngoại tiếp A BC bằng 10 3 A. . B. 10 3. C. 5. D. 10. 3
Câu 29. Cho hình bình hành ABCD có AB a , BC = a 2 và 0
BAD 45 . Diện tích của hbh ABCD bằng A. 2
2a đvdt . B. 2 a 2 (đvdt). C. 2
a đvdt . D. 2 a 3 (đvdt).
Câu 30. Cho tam giác đều ABC nội tiếp đường tròn bán kính R 8. Diện tích của A BC là:
A. 24 3 (đvdt). B. 30(đvdt). C. 26(đvdt). D. 26 2 (đvdt).
Câu 31. Trong các hệ thức sau, hệ thức nào không Đúng ? A. 4 4 2 2
cos sin cos sin . B. 4 4 cos sin 1. C. 2 sin cos
1 2 sin cos. D. 2 sin cos 1 2 sin cos. Câu 32. Cho A
BC vuông tại A . Hệ thức liên hệ giữa ba đường trung tuyến AD, BE và CF là : A. 2 2 2
2BE 3CF 5AD . B. 2 2 2
3BE 2CF 5AD . C. 2 2 2
BE CF 5AD . D. 2 2 2
BE CF 3AD .
Câu 33. Trong các khẳng định sau, khẳng định nào Đúng ? A. 0 0 sin 90 sin150 . B. 0 0 sin 90 15 ' sin 90 30 '. 36
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp C. 0 0
cos 90 30 ' cos100 . D. 0 0 cos150 cos120 .
Câu 34. Cho tam giác ABC có 0 0
B 60 , C 45 và AB 5 . Độ dài cạnh AC là: 5 6 A. 10. B. 5 3 . C. 5 2 . D. . 2
Câu 35. Cho hai điểm M 1;2 và N ( ;
3 4 ). Khoảng cách giữa hai điểm M và N là bằng A. 2 13 . B. 6. C. 3 6 . D. 4.
Câu 36. Trong các khẳng định sau, Khẳng định nào sau đây là Đúng ? A. 0 tan tan 180 . B. 0 cot cot 180 . C. 0 sin sin 180 . D. 0 cos cos 180 .
Câu 37. Cho tam giác ABC , có các cạnh BC a, CA b, AB c . Mệnh đề nào sau đây là Đúng ? A. Nếu 2 2 2
b c a < 0 thì góc 0 A 90 . B. Nếu 2 2 2
b c a > 0 thì góc A tù. C. Nếu 2 2 2
b c a < 0 thì góc A nhọn. D. Nếu 2 2 2
b c a > 0 thì góc A nhọn.
Câu 38. Trong các khẳng định sau, khẳng định nào Sai? A. 0 0 sin 60 cos120 . B. 0 0 cos 45 sin135 . C. 0 0 cos 30 sin120 . D. 0 0 cos 45 sin 45 .
Câu 39. Gọi S là diện tích tam giác ABC. Khẳng định nào sau đây là Đúng ? 1 abc
A. S ab sin C . B. S
ab cos C . C. S .
D. S ah . 2 4R a
Câu 40. Cho tam giác có độ dài ba cạnh lần lượt là 5, 12 và 13. Diện tích của tam giác ABC là: A. 30(đvdt).
B. 20 2 (đvdt).
C. 10 3 (đvdt). D. 20(đvdt). 2
Câu 41. Cho hai điểm A1; 2 và B 3; 4.Giá trị của AB bằng A. 6 2 . B. 8. C. 4. D. 4 2 .
Câu 42. Trong các khẳng định sau, khẳng định nào là Sai ? 3 1 A. 0 0
sin180 cos180 1 . B. 0 0 sin 60 cos 60 . 2 C. 0 0
sin 0 cos 0 0 . D. 0 0 sin 90 cos 90 1 .
Câu 43. Nếu tam giác MNP có MP 5, PN 8 và 0
MPN 120 thì độ dài cạnh MN ( làm tròn đến chữ số thập phân thứ nhất ) là : A. 12,0. B. 11,4. C. 12,4. D. 7,0.
Câu 44. Cho hai vectơ a, b cùng hướng và đều khác vectơ_không. Trong các khẳng định sau, khẳng định nào là đúng ? A. .
a b a . b . B. .
a b a . b . C. . a b 0 . D. . a b 1 .
Câu 45. Cho hai vectơ a (4;3), b (1; 7) . Góc giữa hai vectơ a và b bằng A. 0 30 . B. 0 60 . C. 0 45 . D. 0 90
Câu 46. Trong các hệ thức sau, hệ thức nào Đúng ? 2 2
A. a a .
B. a a .
C. a a . D. .
a b a . b .
Câu 47. Cho tam giác đều ABC cạnh 2a, nội tiếp đường tròn bán kính . R Khi đó R là: 2a 2 2a 3 a 3
A. R a 3 . B. R . C. R . D. R . 3 3 2
Câu 48. Trong mp Oxy cho a (1; 2), b (3; 0) và c ( ; ) . Nếu c a, . b c 3 thì : 1 1 1 1
A. 1; . B. 1 ; . C. 1; . D. 1 ; . 2 2 2 2
Câu 49. Tam giác ABC vuông ở A có góc 0
B 50 . Khẳng định nào sau đây là Sai ? 37
Chương 2. Tích vô hương của hai vectơ 0916620899 Toán 10 I Love Math GV. Lư Sĩ Pháp A. AB BC 0 , 130 . B. BC AC 0 , 40 . C. AB CB 0 , 50 . D. AC CB 0 , 120 .
Câu 50. Trong các đẳng thức sau đây, đẳng thức nào Đúng ? 3 3 3 A. 0 sin150 . B. 0 cos150 . C. 0 tan150 . D. 0 cot150 3 . 2 2 3
Câu 51. Cho tam giác ABC có AB 9cm, BC 15cm, CA 12cm . Khi đó đường trung tuyến AM của tam giác có độ dài là : A. 7, 5c . m B. 10c . m C. 9c . m D. 8 . cm
Câu 52. Trong mp Oxy cho a 9;3 . Vectơ nào dưới đây không vuông góc với vectơ a ?
A. t 1;3 . B. s 1 ;3 . C. u 1; 3 .
D. v 2; 6 .
Câu 53. Cho tam giác ABC vuông cân tại ,
A AB 2a . Đường trung tuyến BM có độ dài bằng
A. 2a 3 .
B. a 5 . C. 3a . D. 2a 2 . ĐÁP ÁN 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 38
Chương 2. Tích vô hương của hai vectơ 0916620899




