Chuyên đề trắc nghiệm hàm số lượng giác và phương trình lượng giác – Nguyễn Đại Dương

Tài liệu gồm 24 với nội dung gồm:

+ Tóm tắt lý thuyết, công thức lượng giác và cách giải các phương trình lượng giác cơ bản

+ Bài tập ôn luyện

42 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hàm số lượng giác và phương trình lượng giác (KNTT)

Môn: Toán 11

Thông tin:

24 trang 9 tháng trước

Tác giả:

Profile Kim Oanh
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
1

Năm học: 2016-2017
Giáo viên: Nguyễn Đại Dƣơng
Chuyên Luyện Thi THPT QG 10 – 11 – 12
Chuyên Luyện Thi Trắc Nghiệm
Địa chỉ: 76/5 Phan Thanh – 135 Nguyễn Chí Thanh
Hotline: 0932589246
CHINH PHỤC
GIẢI TÍCH 11

L
TÀI LIỆU LƢU HÀNH NỘI BỘ
(KHÔNG SAO CHÉP DƢỚI MỌI HÌNH THỨC)
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
2
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
3

 
2
π
0
O
-1
-1
1
1
3
π
2
π
π
2
cosx
(IV)
(III)
(II)
(I)
 
tan .cot 1
22
sin cos 1
2
2
1
1 tan
cos
2
2
1
1 cot
sin
 



cos( ) cosaa
sin( ) sinaa
sin cos
2
aa



sin( ) sinaa
cos( ) cosaa
cos sin
2
aa



tan( ) tanaa
tan( ) tanaa
tan cot
2
aa



cot( ) cotaa
cot( ) cotaa
cot tan
2
aa





2
sin( ) sinaa
sin cos
2
aa



cos( ) cosaa
cos sin
2
aa


tan( ) tanaa
tan cot
2
aa


cot( ) cotaa
cot tan
2
aa


 
sin( ) sin cos cos sina b a b a b
cos( ) cos cos sin sina b a b a b
tan tan
tan( )
1 tan .tan
ab
ab
ab

tan tan
tan( )
1 tan .tan
ab
ab
ab

:
1 tan 1 tan
tan , tan
4 1 tan 4 1 tan
xx
xx
xx

 
Cung 


I
II
III
IV
sin
+
+
cos
+
+
tan
+
+
cot
+
+
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
4
N

sin2 2sin cos
2
1 cos2
sin
2


22
22
cos sin
cos2
2cos 1 1 2sin

2
1 cos2
cos
2


2
2tan
tan2
1 tan


2
1 cos2
tan
1 cos2




3
3
sin3 3sin 4sin
cos3 4cos 3cos
3
2
3tan tan
tan3
1 3tan


6. 
cos cos 2cos cos
22
a b a b
ab


cos cos 2sin sin
22
a b a b
ab

sin sin 2sin cos
22
a b a b
ab


sin sin 2cos sin
22
a b a b
ab


sin( )
tan tan
cos cos
ab
ab
ab

sin( )
tan tan
cos cos
ab
ab
ab

sin( )
cot cot
sin sin
ab
ab
ab

sin( )
cot cot
sin sin
ba
ab
ab


sin cos 2 sin 2 cos
44
x x x x
sin cos 2 sin 2 cos
44
x x x x
 
1
cos .cos cos( ) cos( )
2
a b a b a b

1
sin .sin cos( ) cos( )
2
a b a b a b

1
sin .cos sin( ) sin( )
2
a b a b a b

-
3
-1
-
3
/3
(Ñieåm goác)
t
t'
y
y'
x
x'
u
u'
-
3
-1
-
3
/3
1
1
-1
-1
-
/2
5
/6
3
/4
2
/3
-
/6
-
/4
-
/3
-1/2
-
2
/2
-
3
/2
-1/2
-
2
/2
-
3
/2
3
/2
2
/2
1/2
3
/2
2
/2
1/2
A
/3
/4
/6
3
/3
3
B
/2
3
/3
1
3
O
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
5
t
0
0
30
0
45
0
60
0
90
0
120
0
135
0
150
0
180
0
360
0
0
6
4
3
2
2
3
3
4
5
6
2
sin
0
1
2
2
2
3
2
1
3
2
2
2
1
2
0
0
cos
1
3
2
2
2
1
2
0
1
2
2
2
3
2
1
1
tan
0
3
3
1
3

3
1
3
3
0
0
cot

3
1
3
3
0
3
3
1
3





sin , cosy x y x
2
tan , coty x y x

LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
6


2
sin sin
2
a b k
ab
a b k
()k
sin 0
sin 1 2
2
sin 1 2
2
x x k
x x k
x x k
()k
2
cos cos
2
a b k
ab
a b k
()k
cos 1 2
cos 0
2
cos 1 2
x x k
x x k
x x k
()k
tan tana b a b k
()k
tan 0
tan 1
4
x x k
x x k
()k
cot cota b a b k
()k
cot 0
2
cot 1
4
x x k
x x k
()k
MỘT SỐ KỸ NĂNG GIẢI PHƢƠNG TRÌNH LƢỢNG GIÁC
a. Sử dụng thành thạo công thức cung liên kết
b. Ghép cung thích hợp và sử dụng công thức biến tổng thành tích
cos cos 2cos cos
22
a b a b
ab
cos cos 2sin sin
22
a b a b
ab
sin sin 2sin cos
22
a b a b
ab
sin sin 2cos sin
22
a b a b
ab
sin( )
tan tan
cos cos
ab
ab
ab
sin( )
tan tan
cos cos
ab
ab
ab
sin( )
cot cot
sin sin
ab
ab
ab
sin( )
cot cot
sin sin
ba
ab
ab
   

;
22
a b a b



c. Hạ bậc khi gặp bậc chẵn của sin và cos
2
1 cos2
sin
2
2
1 cos2
cos
2
2
1 cos2
tan
1 cos2
2
1 cos2
cot
1 cos2
:
i ln h bc xut hin hng s
1
2


LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
7


d.Xác định nhân tử chung để nhóm đưa về tích số.
a s thi thng pha v. Do 
           

u thc c nhn t 
cos sinxx

3 3 4 4
1 sin2 ; cos2 ; 1 tan ; 1 cot ; sin3 cos3 ; cos sin ; cos sin ;x x x x x x x x x x
u thc c nhn t chung vi
cos sinxx

3 3 4 4
1 sin2 ; cos2 ; 1 tan ; 1 cot ; sin3 cos3 ; cos sin ;cos sin ;x x x x x x x x x x
T
22
sin cos 1xx

3,

+
22
sin ; tanxx

2
(1 cos )(1 cos ) 1 cos .x x x
+
22
cos ; cotxx

2
(1 sin )(1 sin ) 1 sin .x x x

2
12
( ) .( ) ( )f X aX bX c a X X X X

X
 
sin ,cos ,xx


12
,XX

( ) 0.fX
2.Phƣơng trình lƣợng giác đƣa về phƣơng trình bậc 2, bậc cao của cùng 1 cung.






2
sin sin 0a x b x c
sintx
11t
2
cos cos 0a x b x c
costx
11t
2
tan tan 0a x b x c
tantx
2
xk
2
cot cot 0a x b x c
cottx
xk

22
sin , cost x t x

sin , cost x t x

01t
.
3.Phƣơng trình lƣợng giác bậc nhất theo sin và cos (cùng một cung)
:
sin cos ( ) , , \ 0a x b x c a b

2 2 2
,a b c

:

22
0,ab

2 2 2 2 2 2
( ) sin cos
a b c
xx
a b a b a b
()

2 2 2 2
cos , sin , 0;2
ab
a b a b

2 2 2 2
( ) sin cos cos sin sin( ) :
cc
x x a b
a b a b


sin cos cos sin sin( )
cos cos sin sin cos( )
a b a b a b
a b a b a b
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
8
:
22
22
22
22
2 2 2 2
cos
.sin .cos , ( 0)
Chia : .
sin
.sin .cos .sin .cos , ( )
PP
a b nx
a mx b mx a b
ab
a b nx
a mx b mx c nx d nx a b c d
4.Phƣơng trình lƣợng giác đẳng cấp (bậc 2, bậc 3, bậc 4)
:
22
.sin .sin cos .cos (1) , , , a X b X X c X d a b c d


:
Bc 1
2
cos 0
, ( )
2
sin 1
X
X k k
x

Bc 2. Khi
2
cos 0
, ( )
2
sin 1
X
X k k
X

2
cos X
:
22
22
2 2 2 2
sin sin cos cos
(1) tan tan (1 tan )
cos cos cos cos
X X X X d
a b c a X b X c d X
X X X X
Bc 3
tantX

. G
3 2 2 3
4 3 2 2 3 4
sin sin cos sin cos cos 0
sin sin cos sin cos sin cos cos 0
a X b X X c X X d X
a X b X X c X X d X X e X
PP
Ki cho
34
cos 0 (hay cos ).XX
5.Phƣơng trình lƣơng giác đối xứng
Dng 1.
(sin cos ) sin cos 0a x x b x x c
(dng tng/hiu 
PP

sin cos , 2t x x t
 suy ra:
sin cosxx
theo
.t
t
sin cost x x
u ki 
02t
.
Dng 2.
22
(tan cot ) (tan cot ) 0a x x b x x c
PP
t
tan cot , 2t x x t
   suy ra:
22
tan cotxx
  
ng s dng:
2
tan .cot 1; tan cot
sin2
x x x x
x
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
9

HÀM SỐ LƢỢNG GIÁC
 
sinyx
. 
A.
Tnh c 
B.
T c 
C.
 .
D.
 tu
2
.
 
cosyx
. 
A.
Tnh c 
B.
T c 
1,1


.
C.
 .
D.
 tu
2
.
 
tanyx
. 
A.
Tnh c 
B.
T c 
C.
 .
D.
 tu
.
 
cotyx
. 
A.

\|R k k Z


.
B.
 
C.
 n.
D.
 tu
.
 
A.

sinyx

B.

cosyx
 
C.

sinyx

cosyx

2
.
D.

tanyx

cotyx

2
.
 Tnh c
3 cosyx
 ?
A.
,3

B.
,3
C.
3,

D.
R
 Tnh c
1 sin
cos
x
y
x
 ?
A.
\|
2
R k k Z




B.
\2Rk
C.
\Rk
D.
\ 2 |
2
R k k Z




 Tp nh c
tan 2
3
yx




 ?
A.
\0R
B.
\|
2
R k k Z




C.
5
\|
12 2
R k k Z





D.
\|
62
R k k Z





   l?
A.
2
sin 2yx
B.
2
cos 2yx
C.
sin2yx
D.
cos2yx
   l?
A.
3
sin 3yx
B.
3
cos 3yx
C.
sin3 1yx
D.
cos3 1yx
   chn?
A.
sin cosy x x
B.
sin cosy x x
C.
siny x x
D.
2
sin cosy x x
   chn?
A.
sin
3
yx




B.
3
siny x x
C.
tan 3yx
D.
3
sin tan3y x x x
 
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
10

A.
sinyx
B.
cosyx
C.
tanyx
D.
cotyx
 

A.
sinyx
B.
sin 2yx
C.
cosyx
D.
cos 2yx
  th 
cos 2yx

Hình 1
Hình 2
Hình 3
Hình 4
A.

B.

C.

D.

LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
11
 
 

A.
2sin
6
yx




B.
2sin
3
yx




C.
2sin
6
yx




D.
2sin
3
yx




 
sin cos cos2y x x x
 ?
A.
2
B.
4
C.
D.

 
2
cos 2 cos8y x x
 ?
A.
2
B.
2
C.
4
D.

 
2
sin 3 3
3
y x x



 ?
A.
2
B.
3
C.
2
3
D.

 
.siny f x A ax b

,,A a b

,0Aa
. 

A.

2
.
B.

2A
.
C.

2
a
.
D.

2
A
a
.
PHƢƠNG TRÌNH LƢỢNG GIÁC
 17. Cho
3
2



4
sin
5
   
1 cot
1 cot
A

A.
7
B.
1
7
C.
7
D.
1
7
 Cho
tan 2.

3
3
sin 2cos
cos 2sin
A



A.
7
4
B.
4
7
C.
5
21
D.
12
13
 
(1 3cos2 )(2 3cos2 ),P


2
sin
3

LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
12
A.
14
9
B.
22
9
C.
8
9
D.
20
9
 Cho
cot 2


2sin 3cos
5cos 6sin
A



A.
1
17
B.
1
4
C.
1
17
D.
1
4
 
2 cos 2 1
3
x





A.
24
xk

7
24
xl

B.
24
xk


7
24
xl

C.
24
xk

7
24
xl
D.
24
xk


7
24
xl
 
2
2cos cos5 1
2
x
x
  
A.
63
k
x



42
l
x

B.
6
xk


42
l
x

C.
62
k
x



43
l
x

D.
6
xk


4
xl
 
cos sin2 0
2
xx





A.
xk
B.
2
3
xk
C.
xk


D.
xk

2
3
xl
 
2 cos2 5sinxx

A.
2
2
3
xk


2
3
xl

B.
2
3
xk


3
xl
C.
2
2
3
xk

2
3
xl
D.
2
3
xk

3
xl

 
2
cos4 12sin 1 0xx
   

A.
2xk
B.
2xk


C.
2
xk

D.
xk
 
tan cot 2xx

A.
2
4
xk

B.
2
4
xk
C.
4
xk

D.
4
xk
 
22
2sin tan 2xx
  
A.
2
4
xk
B.
4
xk
C.
2xk
D.
xk
 
3 sin cos 2xx
  
A.
2
6
xk

B.
2
3
xk

LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
13
C.
2
2
3
xk

D.
2
2
xk

   
2
1
3 sin sin2 3
2
xx
      

A.
3
xk


2
xl
B.
3
xk

2
xl

C.
3
xk

2
xl
D.
3
xk


2
xl

 
cos 2 sin2 sinx x x
   

A.
2
43
k
x


B.
2
43
k
x

C.
2
4
xk

D.
2
4
xk
   
cos2 3 sin2 3 sin cosx x x x
     

A.
2
3
xk

B.
2
3
k
x
C.
2
3
xk
D.
2
3
xk

 
3
cos 2sinxx
  
A.
2
4
xk

B.
4
xk
C.
4
xk
D.
4
xk

   
22
2sin 3 3 sin cos cos 2x x x x
     

A.
2
2
xk


2
6
xl
B.
2
xk


6
xl

C.
2
2
xk

2
6
xl
D.
2
xk


5
6
xl

 Gii 
2 2(sin cos ) 3 sin2x x x
vi
3x

.
A.
37
,
44
xx



11
4
x
B.
3
4
x

11
4
x
C.
3
,
44
xx


11
4
x
D.
4
x


7
4
x
 
sin2 2 sin 1
4
xx




0,2

A.
2
B.
4
C.
3
D.
5
 
sin3
0
cos 1
x
x

2 ,4




A.
2
B.
4
C.
5
D.
6
     
22
tan tan co t cot 2
0
sin2 1
x x x x
x
 
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
14
,3


A.
0
B.
1
C.
2
D.
4
BIẾN ĐỔI LƢỢNG GIÁC
 Cho
2



3
sin
5


2
tan
1 tan
A

A.
12
25
B.
12
25
C.
15
34
D.
15
34
 
44
sin cos ,A



2
sin2
3

A.
1
9
B.
7
9
C.
5
9
D.
7
9
 Cho
0
2

1
sin
3
. 
cos
3
A




.
A.
63
6
B.
36
6
C.
63
6
D.
36
6
 Cho
2



1
sin( )
3


7
tan
2
A



A.
2
B.
2
C.
22
D.
22
 Cho
2



4
cos
5

sin
cot
1 cos
A
A.
9
4
B.
5
3
C.
9
4
D.
5
3
 Cho
4
cos
5


3
2


tan
4
A



A.
1
7
B.
1
7
C.
7
D.
7
 Cho
0
2

4
cos
5


sin cos
44
A


A.
49
50
B.
1
50
C.
49
50
D.
1
50
 Cho
1
cos4
3


66
1
cos sin
4
A

A.
1
B.
1
2
C.
1
D.
1
2
 Cho
tan 2.

33
sin
sin 3cos
A


A.
11
10
B.
10
11
C.
10
11
D.
11
10
 Cho
tan 3.

33
3sin 2cos
5sin 4cos
A



A.
70
139
B.
10
19
C.
70
139
D.
10
19
 Cho
5
sin cos
2



0
4

sin cos .A


LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
15
A.
3
2
B.
3
2
C.
1
2
D.
1
2
 n biu thc
22
1
, 0
2
sin cot cos
Px
x x x




A.
sin
cos2
x
P
x
B.
sin2
cos
x
P
x
C.
sin
cos2
x
P
x

D.
sin2
cos
x
P
x

 n biu thc
73
2cos 3cos( ) sin tan
22
P x x x x

A.
tanPx
B.
cotPx
C.
0P
D.
cosPx
 n biu thc
3 11
cos(15 ) sin tan cot
2 2 2
P x x x x
A.
0P
B.
1P
C.
sinPx
D.
cosPx
 
sin cos sin cos
3 4 4 3
P x x x x
A.
0P
B.
1P
C.
sin2Px
D.
cos2Px
   a mng th  ng thc sai ?
A.
sin sin sin 4cos cos cos
2 2 2
A B C
A B C
B.
sin2 sin2 sin2 4sin sin sin .A B C A B C
C.
sin sin sin sin sin cos
2 2 2
A B C
A B C
D.
cos cos cos 1 4sin sin sin
2 2 2
A B C
A B C
PHƢƠN TRÌNH LƢỢNG GIÁC CƠ BẢN
 Gi
sin 1
3
x




.
A.
2
xk

B.
2
2
xk

C.
5
2
6
xk

D.
2
6
xk

 Gi
cos 1
3
x




.
A.
2
3
xk

B.
3
xk

C.
2
3
xk
D.
3
xk
 Gi
sin 2 0
3
x




.
A.
2
3
xk

B.
3
xk

C.
2
6
xk

D.
6
xk

 Gi
cos 0
6
x




.
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
16
A.
2
2
3
xk

B.
2
3
xk

C.
2
6
xk

D.
6
xk

 Gi
2cos 1
6
x




.
A.
6
xk

B.
2
xk
C.
6
xk


'
2
xk
D.
2
6
xk


'2
2
xk
 Gi
2
2cos 1 0x
.
A.
4
xk

B.
4
xk
C.
2
4
xk
D.
42
xk


 Gi
cos cos
3
xx



.
A.
2
2
3
xk

B.
2
2
3
xk
C.
3
xk

D.
3
xk
 Gi
sin sin
3
xx



.
A.
2
3
xk

B.
2
3
xk
C.
6
xk

D.
6
xk
 Gi
sin cos
3
xx




.
A.
5
2
6
xk

B.
2
6
xk

C.
5
12
xk

D.
12
xk

 Gi
tan2 cot .xx
A.
2xk
B.
2xk


C.
2
xk

D.
2
xk
PHƢƠNG TRÌNH ĐẶT ẨN PHỤ
 Gi
2
tan 2 3 tan 3 0.xx
A.
3
xk
B.
3
xk

C.
6
xk
D.
6
xk

 Gi
2cos2 8cos 5 0.xx
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
17
A.
2
6
xk
B.
2
3
xk
C.
2
3
xk

D.
2
3
xk
 Gi
2
cos4 12sin 1 0.xx
A.
2xk
B.
xk
C.
2
xk

D.
2
xk
 Gi
2
cos4 2cos 1 0.xx
A.
2xk
B.
6
xk
C.
xk

'
3
xk
D.
xk

'
6
xk
 Gi
2
3
2tan 3
cos
x
x
A.
2
3
xk
B.
2
6
xk
C.
3
xk
D.
6
xk
 Gi
cos
1 sin .
1 sin
x
x
x

A.
xk
B.
2
2
xk
C.
2xk

'2
2
xk
D.
2xk

'2
2
xk

 Gi
2
3cos 2cos2 3sin 1.x x x
A.
xk
B.
2
2
xk
C.
2
2
xk

D.
2
2
xk
 Gii 
22
2sin 3 3 sin cos cos 2.x x x x
A.
2
2
xk
B.
6
xk
C.
2
xk


'
6
xk

D.
2
xk


'
6
xk
 Gi
4 2 2 4
3cos 4sin cos sin 0.x x x x
A.
4
xk
B.
3
xk
C.
4
xk

'
3
xk
D.
2
4
xk

'2
3
xk
 Gi
3 3 2
cos 4sin 3cos sin sin 0x x x x x
A.
4
xk

'
3
xk
B.
4
xk

'
6
xk
C.
4
xk


'
6
xk
D.
4
xk

'
6
xk
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
18
PHƢƠNG TRÌNH BẬC NHẤT
 Gi
sin 3 cos 2.xx
A.
2
6
xk

B.
5
2
6
xk

C.
2
3
xk

D.
2
2
3
xk

 Gi
sin 3 cos 1.xx
A.
7
2
6
xk


'2
2
xk

B.
2
6
xk

'2
2
xk

C.
2xk

2
'2
3
xk

D.
2
3
xk


'2xk


 Gi
3 sin cos 2.xx
A.
2
3
xk
B.
2
6
xk
C.
2
2
3
xk
D.
5
2
6
xk
 Gi
3 cos sin 2.xx
A.
7
2
12
xk

11
'2
12
xk

B.
5
2
12
xk

11
'2
12
xk
C.
2
12
xk

7
'2
12
xk
D.
2
12
xk


5
'2
12
xk

 Gi
sin cos( ) 1.xx
A.
2
2
xk


'2xk


B.
2xk

'2
2
xk
C.
2xk
D.
2
2
xk
 Gi
3 sin sin 2.
2
xx
A.
5
2
6
xk
B.
2
6
xk
C.
2
2
3
xk
D.
2
3
xk
 Gi
1 sin2 cos2 .xx
A.
2xk

'2
2
xk
B.
2xk

'2
2
xk

C.
xk

'
4
xk
D.
xk

'
4
xk

 Gi
2
1
3 sin sin2 3.
2
xx
A.
2xk

'2
3
xk

B.
2
2
3
xk


'2xk


C.
xk

'
6
xk

D.
3
xk


'
2
xk

 Gi
sin cos 2 sin
3
x x x
A.
5
24
xk

B.
5
2
12
xk

LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
19
C.
11
24
xk

D.
11
12
xk

 Gi
sin cos 2 sin2x x x
A.
2
4
xk

5
'2
3
xk

B.
2
4
xk

52
'
12 3
xk


C.
2
4
xk


'2xk


D.
2
4
xk


2
'
33
xk


 Gi
sin 3 cos 2sin 2x x x
A.
2
3
xk

2
'2
3
xk
B.
2
3
xk


2
'2
3
xk

C.
2
3
xk

42
'
93
xk


D.
2
3
xk


22
'
93
xk


 Gi
sin 3 cos 2sin 3x x x
A.
6
xk


2
'
63
xk


B.
2
3
xk


2
'2
3
xk

C.
2
3
xk

4
'2
3
xk

D.
6
xk

'
32
xk


PHƢƠNG TRÌNH ĐỐI XỨNG
 Gi
sin 2 2 2.(sin cos ) 5.x x x
A.
5
2
12
xk

11
'2
12
xk

B.
2
12
xk


7
'2
12
xk
C.
2
12
xk

7
'2
12
xk

D.
5
2
12
xk


11
'2
12
xk
 Gi
sin cos sin cos 1 0.x x x x
A.
2xk



'2
2
xk

B.
2xk

'2
2
xk

C.
2xk



'2xk
D.
2
2
xk
 Gi
2(sin cos ) 6sin cos 2 0.x x x
A.
2xk



2xk
B.
'2
2
xk
C.
2xk

'2
2
xk

D.
2xk



'2
2
xk

 Gi
2 2(sin cos ) 3 sin2 .x x x
A.
2
4
xk

B.
2
4
xk
C.
2xk
D.
3
2
4
xk

 Gi
sin cos 4sin2 1.x x x
A.
2
2
xk


'2xk


B.
3
2
4
xk

C.
2
xk
D.
2xk

'2
2
xk

LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
20
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
  ln nht ca biu thc
1 2sinAx
A.
max 1A 
B.
max 1A
C.
max 2A
D.
max 3A
  ln nht ca biu thc
22
1 2sin cosA x x
A.
max 1A
B.
max 2A
C.
max 3A
D.
max 4A
  ln nht ca biu thc
44
sin cosA x x
A.
max 1A 
B.
max 0A
C.
max 1A
D.
max 2A
  ln nht ca biu thc
44
sin cosA x x
A.
max 0A
B.
1
max
2
A
C.
max 1A
D.
3
max
2
A
  nh nht ca biu thc
sin cosA x x
A.
min 2A 
B.
min 2A 
C.
min 1A 
D.
13
min
2
A

  nh nht ca biu thc
sin cos 1A x x
A.
min 1A 
B.
min 2 1A
C.
min 0A
D.
13
min
2
A
  nh nht ca biu thc
sin 3 cos 2A x x
A.
min 3 3A
B.
min 4A 
C.
min 2 3A
D.
min 3A 
  nh nht ca biu thc
3 sin cos 2A x x
A.
min 1 3A 
B.
min 2 3A 
C.
min 0A
D.
min 1A
  nh nht ca biu thc
2
2sin sin2A x x
A.
min 1A
B.
min 2A
C.
min 1A 
D.
min 1 2A 
  nh nht ca biu thc
2
sin2 2cos 2A x x
A.
min 1A
B.
min 2A
C.
min 3 2A 
D.
min 3 2A 
  ln nht ca biu thc
sin cos
sin 3
xx
A
x
A.
1 17
max
8
A

B.
1
max
2
A
C.
1
max
4
A
D.
23
max
8
A
  nh nht ca biu thc
2sin cos
sin 2
xx
A
x
A.
min 1A 
B.
5
min
3
A 
C.
min 3A 
D.
min 2A 
 G ln nh nh nht ca biu thc
sin 2cos 1
2sin cos 3
xx
A
xx




Mm
.
A.
0Mm
B.
1
2
Mm
C.
1
2
Mm
D.
17
2
Mm
 G ln nh nh nht ca biu thc
sin 1
cos 2
x
A
x

 
Mm
.
A.
0Mm
B.
4
3
Mm
C.
4
3
Mm
D.
1Mm
 G ln nh nh nht ca biu thc
2cos 1
sin 2
x
A
x

 
.Mm
.
A.
.1Mm
B.
.0Mm
C.
1
.
3
Mm
D.
13
.
3
Mm
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
21
 
tanyx
A.
\,
2
kk



B.
\,
22
kk




C.
\,
4
kk



D.
\ 2 ,
2
kk



  
sin 1
sin
x
y
x

A.
\,
2
kk



B.
\ 2 ,
2
kk



C.
\,kk
D.
\ 2 ,kk
 
sinyx

A.1 B.0 C.
1
D.
3
 
2cos 2yx

A.
2
B.
22

22
C.
42

42
D.
2

22
 
tan 3x

A.
2
x k k
B.
2
2
x k k
C.
4
x k k
D.
2
4
x k k
 
1
sin
2
x 

A.
2
4
xk


5
2
4
xk

(
k
) B.
2
4
xk

5
2
4
xk
(
k
)
C.
2
4
xk

3
2
4
xk
(
k
) D.
2
4
xk


5
2
4
xk
(
k
)
 
3
cos
2
x 

A.
2
3
xk


2
2
3
xk

(
k
) B.
2
6
xk


5
2
6
xk

(
k
)
C.
5
2
6
xk


5
2
6
xk
(
k
) D.
2
3
xk


2
3
xk
(
k
)
 
3
tan
3
x 

A.
6
xk

(
k
). B.
6
xk
(
k
).
C.
3
xk

(
k
). D.
3
xk
(
k
).
 
12
cot
2
x 

A.
6
xk

(
k
). B.
6
xk
(
k
).
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
22
C.
3
xk

(
k
). D.
3
xk
(
k
).
 m 
sin2xm

A.
1m
B.
11m
C.
0m
D.
1m
 D 
tan 2
8
yx





A.
3
\,
42
D k k




B.
3
\,
16 2
D l l




C.
3
\,
2
D k k



D.
3
\,
2
D k k



 
sin cosxx
A.
4
xk

(
k
). B.
2
4
xk

(
k
).
C.
4
xk


4
xk
(
k
). D.
2
4
xk


2
4
xk
(
k
).
 
2
4sin 3x
A.
2
3
xk


2
3
xk
(
k
). B.
3
xk


3
xk
(
k
).
C.
6
xk


6
xk
(
k
). D.
2
6
xk


2
6
xk
(
k
)
 
2
tan 3x

A.
2
3
xk


2
3
xk
(
k
). B.
3
xk


3
xk
(
k
).
C.
6
xk


6
xk
(
k
). D.
2
6
xk


2
6
xk
(
k
).
 
sin cos 1xx

A.
2
4
()
2
4
xk
k
xk

. B.
4
()
4
xk
k
xk

.
C.
2
()
2
4
xk
k
xk

. D.
21
()
2
2
xk
k
xk

.
 
0;2x

2cos 3 0x 

A.
57
;
66

. B.
5
;
33

. C.
11
;
66

. D.
7 11
;
66

.
 
0;2x

3cot 3 0
4
x


A.
2
3



. B.
10
3



. C.
4



. D.
5
;
44




.
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246
23

Bài 1. 
a)
2
2sin 5cos 1 0.xx
b)
22
3 4cos 2sin sin .x x x
c)
42
2cos 3sin 2 0.xx
d)
42
4sin 12cos 7 0.xx
e)
5cos2 22sin 17 0.xx
f)
cos10 4 2 cos5 4.xx
g)
2
cos4 2cos 1 0.xx
h)
2
6sin 3 cos12 4 0.xx
i)
2
cos2 2cos 2sin
2
x
xx
j)
2
cos2 3cos 4cos
2
x
xx
k)
3tan 6cot 2 3 3 0.xx
l)
5tan 2cot 3 0.xx
m)
2
1 2 5
tan 0.
2 cos 2
x
x
n)
1
3sin cos
cos
xx
x
Bài 2. 
a)
sin 3cos 1.xx
b)
3cos3 sin3 2.xx
c)
sin3 cos 3cos2 2 sin cos3 .x x x x x
d)
cos6 cos 3sin5 1 sin6 sin .x x x x x
e)
sin3 3cos3 2sin .x x x
f)
3cos sin 4sin cos .x x x x
g)
2
(sin cos ) 3cos2 1 2cos .x x x x
h)
3cos5 2sin3 cos2 sin .x x x x
i)
cos7 sin5 3(cos5 sin7 ).x x x x
j)
3(cos2 sin3 ) sin2 cos3 .x x x x
Bài 3. 
a)
22
6sin 7 3sin2 8cos 6.x x x
b)
22
2cos 2sin2 4sin 1.x x x
c)
3
sin 4sin cos 0.x x x
e)
2
sin (tan 1) 3sin (cos sin ) 3.x x x x x
Bài 4. 
a)
1 sin cos2 sin3 0.x x x
b)
cos2 cos6 cos4 1.x x x
c)
2sin cos2 sin2 cos2 sin4 cos .x x x x x x
d)
cos cos3 sin2 sin6 sin4 sin6 .x x x x x x
e)
2 2 2 2
sin 4 sin 3 sin 2 sin .x x x x
f)
22
2sin 2 sin6 2cos .x x x
Bài 5. 
a)
cos2 cos 3sin 2 0.x x x
b)
cos2 3cos 2 sin .x x x
c)
sin2 2cos2 1 sin 4cos .x x x x
d)
2sin2 cos2 7sin 2cos 4.x x x x
e)
2
(2sin 1)(2cos2 2sin 3) 1 4sin .x x x x
f)
2
(2sin 3)(sin cos 3) 1 4cos .x x x x
g)
cos2 (1 2cos )(sin cos ) 0.x x x x
h)
(sin cos 1)(2sin cos ) sin2 .x x x x x
i)
44
2(cos sin ) 1 3cos sin .x x x x
j)
3
2sin cos2 cos 0.x x x
k)
2
cos sin cos sin 1 2cos .x x x x x
l)
2
4sin 4sin 2sin2 1 2cos .x x x x
m)
sin2 sin 1 0.xx
n)
3 2 6
4 3sin sin 3cos cos .x x x x
o)
tan sin2 2cot2 .x x x
p)
3sin3 2 sin (3 8cos ) 3cos .x x x x
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
24

Thƣờng xuyên mở các lớp 10-11-12 theo yêu cầu (5-10 học sinh)
Thƣờng xuyên mở các lớp luyện thi Trắc Nghiệm 12 theo cấu trúc
2017.
Mở các lớp luyện đề Trắc Nghiệm Môn Toán theo cấu trúc của Bộ
Giáo Dục và Đào Tạo.
Mọi chi tiết xin liên hệ:
Hotline: 0932589246.
Facebook: https://www.facebook.com/ThayNguyenDaiDuong
Website: http://www.toanmath.com/
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
LUYỆN THI TRẮC NGHIỆM TOÁN
Năm học: 2016-2017 CHINH PHỤC GIẢI TÍCH 11 TRẮC NGHIỆM LƢỢNG GIÁC
TÀI LIỆU LƢU HÀNH NỘI BỘ
(KHÔNG SAO CHÉP DƢỚI MỌI HÌNH THỨC)
Giáo viên: Nguyễn Đại Dƣơng
Chuyên Luyện Thi THPT QG 10 – 11 – 12
Chuyên Luyện Thi Trắc Nghiệm
Địa chỉ: 76/5 Phan Thanh – 135 Nguyễn Chí Thanh
Hotline: 0932589246
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 1
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG 2
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
ÔN TẬP BIẾN ĐỔI LƢỢNG GIÁC
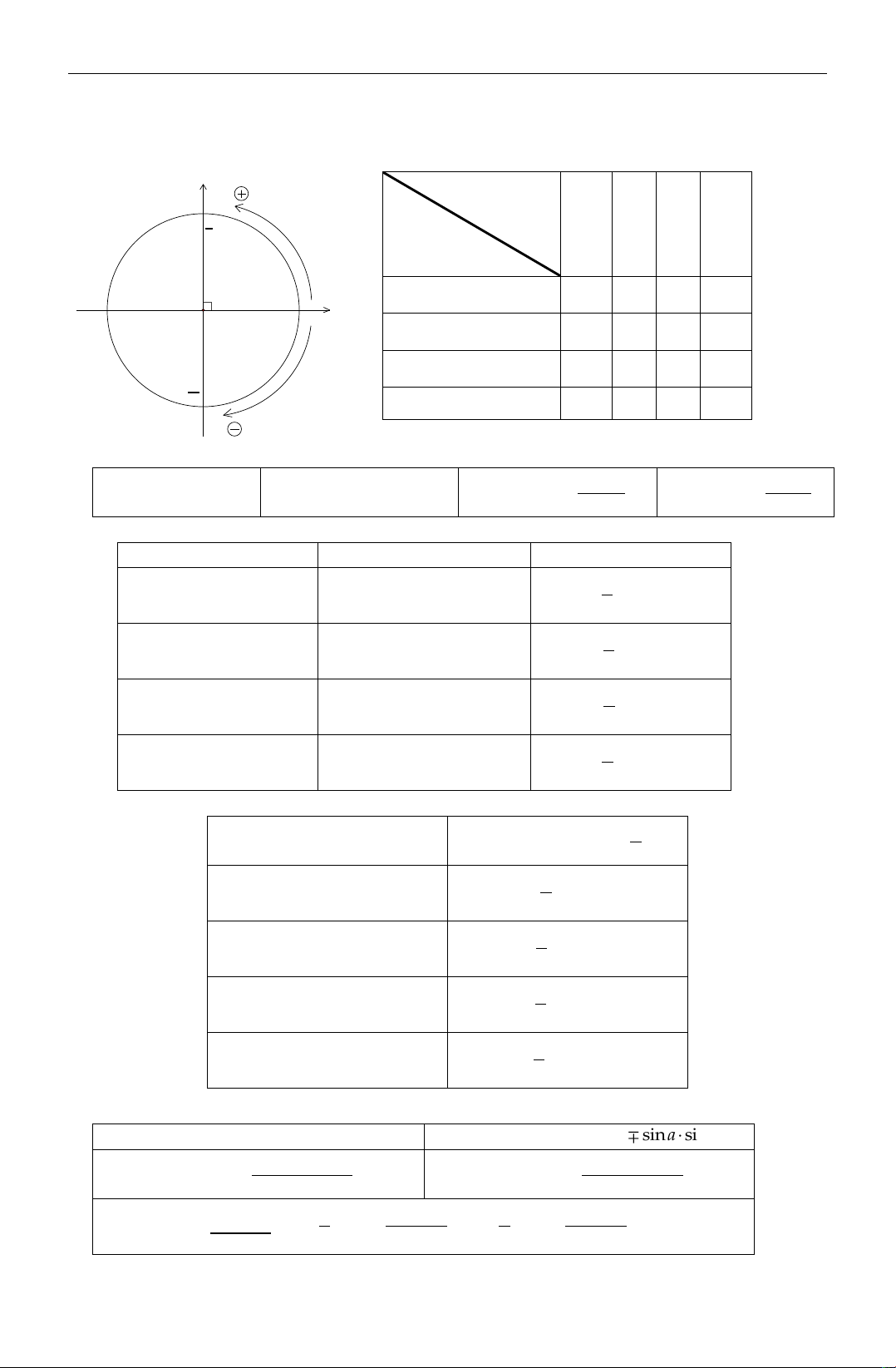
1. Đƣờng tròn lƣợng giác và dấu của các giá trị lƣợng giác sinx Cung phần 1 I II III IV π tư 2 Giá trị LG (II) (I) sin  + + – – π 0 1 cosx -1 2π O cos + – – + (III) (IV) tan  + – + – 3π 2 cot  + – + – -1
2. Công thức lƣợng giác cơ bản 2 1 1 1  tan   2 1  cot   tan .  cot  1 2 2 sin   cos   1 2 cos  2 sin  3. Cung liên kết Cung đối nhau Cung bù nhau Cung phụ nhau    cos( ) a  cos a sin(  ) a  sin a sin  a    cos a  2     sin( ) a   sin a cos(  ) a   cos a cos  a    sin a  2     tan( ) a   tan a tan(  ) a   tan a tan  a    cot a  2     cot( ) a   cot a cot(  ) a   cot a cot  a    tan a  2   Cung hơn kém  Cung hơn kém 2    sin(  ) a   sin a sin  a    cos a  2     cos(  ) a  cos a cos  a     sin a  2     tan(  ) a  tan a tan  a     cot a  2     cot(  ) a  cot a cot  a     tan a  2 
4. Công thức cộng cung sin(a  )
b  sin a  cosb  cos a  sinb cos(a  )
b  cos a  cosb sin a  sinb tan a  tan b tan a  tan b tan(a  ) b  tan(a  ) b  1  tan . a tan b 1  tan . a tan b    1 tan x    1 tan x Hệ quả: tan  x  , tan  x        4  1  tan x  4  1  tan x
5. Công thức nhân đôi và hạ bậc
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 3
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG Nhân đôi Hạ bậc  
sin 2  2sin  cos 2 1 cos 2 sin   2 2 2 cos   sin    cos 2   2 1 cos 2   2 2  cos
2cos   1  1  2sin  2 2 tan    tan 2  2 1 cos 2 tan   2 1  tan  1  cos 2 Nhân ba 3
sin3  3sin  4sin   3 3 tan   tan    3
cos3  4cos   3cos tan 3 2 1  3 tan 
6. Công thức biến đổi tổng thành tích a b a b a b a b
cos a  cos b  2 cos cos
cos a  cos b  2  sin sin 2 2 2 2 a b a b a b a b
sin a  sin b  2sin cos
sin a  sin b  2cos sin 2 2 2 2 sin(a  ) b sin(a  ) b
tan a  tan b
tan a  tan b  cos a  cos b cos a  cos b sin(a  ) b sin(b  ) a
cot a  cot b
cot a  cot b  sin a  sin b sin a  sin b Đặc biệt            
sin x  cos x  2 sin x   2 cos x     
sin x  cos x  2 sin x    2 cos x       4   4   4   4 
7. Công thức biến đổi tích thành tổng 1 1 cos . a cos b  cos(a  )
b  cos(a  ) b    sin . a sin b  cos(a  )
b  cos(a  ) b    2 2 1 sin . a cosb  sin(a  )
b  sin(a  ) b    2 y t 3 - 3 -1 - 3 /3 B /2 3 /3 1 3 u' 1 /3 u 2/3 3 /2 /4 3/4 2 /2 /6 5/6 3 /3 1/2 x'  - 3/2 - 2/2 -1/2 1/2 2 /2
3 /2 1 A (Ñieåm goác) x -1 O -1/2 - 3 /3 -/6 - 2 /2 - 3 /2 -/4 -1 -/3 -1 -/2 - 3 y' t' 4
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
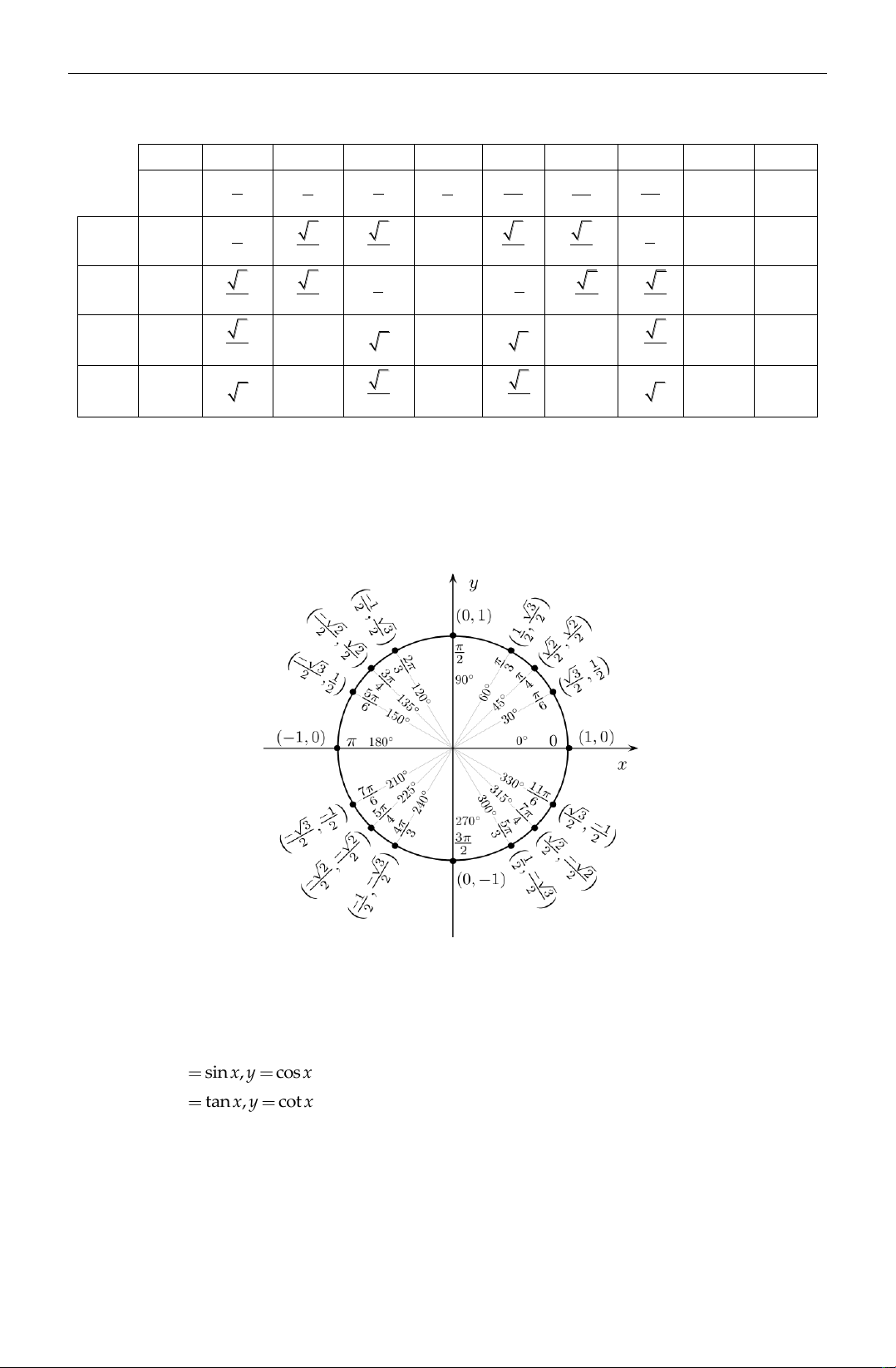
Bảng lƣợng giác của một s g c đặc biệt 00 300 450 600 900 1200 1350 1500 1800 3600     2 3 5 0  2 6 4 3 2 3 4 6 1 1 sin  2 3 3 2 0 1 0 0 2 2 2 2 2 2 cos  3 2 1 1 1 0  2  3  1  1 2 2 2 2 2 2 tan  3 0 1 3 kxđ  3 1  3  0 0 3 3 cot  3 3 kxđ 3 1 0  1   3 kxđ kxđ 3 3
Một đi m M thuộc đƣờng tròn lƣợng giác s c t a độ M cosα, sinα)
II.Hàm s lƣợng giác.
1.Hàm s y sin x, y cos x 2.Hàm s y tan x, y cot x
3.Tính chẵn l , chu kì của hàm s lƣợng giác.
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 5
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
III.Phƣơng trình lƣợng giác.
1.Phƣơng trình lƣơng giác cơ bản: sin x 0 x ka b k2 sin a sin b (k  ) sin x 1 x k2 (k  ) a b k2 2 sin x 1 x k2 2 cos x 1 x k2  a b k2 cos a cos b (k  ) cos x 0 x k (k  ) a b k2 2 cos x 1 x k2 tan x 0 x k  tana tanb a b k (k  ) (k  ) tan x 1 x k 4 cot x 0 x k  cot a cotb a b k (k  ) 2 (k ) cot x 1 x k 4
MỘT SỐ KỸ NĂNG GIẢI PHƢƠNG TRÌNH LƢỢNG GIÁC
a. Sử dụng thành thạo công thức cung liên kết
b. Ghép cung thích hợp và sử dụng công thức biến tổng thành tích a b a b a b a b cos a cos b 2 cos cos
cos a cosb 2sin sin 2 2 2 2 a b a b a b a b sin a sin b 2 sin cos
sin a sin b 2 cos sin 2 2 2 2 sin(a ) b sin(a ) b tan a tan b
tan a tan b cos a cos b cos a cos b sin(a ) b sin(b ) a cot a cot b
cot a cot b sin a sin b sin a sin b
Khi áp dụng tổng thành tích đối với 2 hàm sin và cosin thì được hai cung a b a b mới: ;
Do đó khi sử dụng nên nhẩm hai cung mới này trước để 2 2
nhóm hạng tử thích hợp sao cho xuất hiện nhân tử chung (cùng cung) với
hạng tử còn lại hoặc cụm ghép khác.
c. Hạ bậc khi gặp bậc chẵn của sin và cos 2 1 cos 2 sin 2 1 cos 2 cos 2 2 2 1 cos 2 tan 2 1 cos 2 cot 1 cos 2 1 cos 2
Lƣu ý đ i với công thức hạ bậc của sin và cosin: 1
― Mỗi lần hạ bậc xuất hiện hằng số và cung góc tăng gấp đôi. 2
― Mục đích của việc hạ bậc: hạ bậc để triệt tiêu hằng số không mong muốn và 6
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
nhóm hạng tử thích hợp để sau khi áp dụng công th c (tổng thành tích sau
khi hạ bậc) s xuất hiện nhân tử chung hoặc làm bài toán đơn gi n hơn.
d.Xác định nhân tử chung để nhóm đưa về tích số.
Đa số đ thi thư ng là nh ng phương trình đưa v tích số. Do đó trước khi gi i
ta ph i quan sát xem ch ng có nh ng lượng nhân tử chung nào sau đó định
hướng để tách ghép nhóm phù hợp. M t số lượng nhân tử thư ng gặp:
– Các biểu th c có nhân tử chung với cos x
sin x thư ng gặp là: 3 3 4 4 1 sin 2 ; x cos 2 ; x 1 tan ; x 1 cot ;
x sin 3x cos 3 ; x cos x sin ; x cos x sin ; x …
– Các biểu th c có nhân tử chung với cos x sin x thư ng gặp là: 3 3 4 4 1 sin 2 ; x cos 2 ; x 1 tan ; x 1 cot ; x sin 3x cos 3 ; x cos x sin ; x cos x sin ; x … – Từ 2 2 sin x cos x
1 và nhìn nhận với góc đ hằng đẳng th c số 3, ta có: + 2 2 sin ;
x tan x có nhân tử chung là: 2 (1 cos ) x (1 cos ) x 1 cos . x + 2 2 cos ;
x cot x có nhân tử chung là: 2 (1 sin ) x (1 sin ) x 1 sin . x – Phân tích 2 f (X) aX bX c . a (X X ) (X
X ) với X có thể là sin x,cos x, … 1 2
và X ,X là 2 nghiệm của f (X) 0. 1 2
2.Phƣơng trình lƣợng giác đƣa về phƣơng trình bậc 2, bậc cao của cùng 1 cung.
Quan sát và dùng các công th c biến đổi để đưa phương trình v cùng m t hàm lượng
giác với cung góc giống nhau chẳng hạn: Dạng Đặt ẩn Đi u kiện phụ 2 asin x bsin x c 0 t sin x 1 t 1 2 acos x bcos x c 0 t cos x 1 t 1 2 atan x btan x c 0 t tan x x k 2 2 acot x bcot x c 0 t cot x x k Nếu đặt 2 2 t sin x, t cos x hoặc t sin x , t
cos x thì đi u kiện l c này là 0 t 1.
3.Phƣơng trình lƣợng giác bậc nhất theo sin và cos (cùng một cung)
Dạng tổng quát: asin x bcos x
c ( ) , a,b \ 0
Đi u kiện có nghiệm của phương trình: 2 2 2 a b
c , (kiểm tra trước khi gi i) Phƣơng pháp giải: a b c Chia hai vế cho 2 2 a b 0, thì ( ) sin x cos x ( ) 2 2 2 2 2 2 a b a b a b a b Gi sử: cos , sin , 0; 2 thì: 2 2 2 2 a b a b c c ( ) sin xcos cos xsin sin(a ) b : dạng cơ b n. 2 2 2 2 a b a b sin a cos b cos a sin b sin(a ) b
Lƣu ý. Hai công th c sử dụng nhi u nhất là: cosa cosb sina sinb cos(a )b
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 7
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Các dạng c cách giải tƣơng tự: 2 2 a b cos nx 2 2 . a sin mx . b cos mx , (a b 0) PP 2 2 2 2 Chia : a b . a b sin nx 2 2 2 2 . a sin mx . b cos mx . c sin nx .
d cos nx, (a b c d )
4.Phƣơng trình lƣợng giác đẳng cấp (bậc 2, bậc 3, bậc 4) Dạng tổng quát: 2 2 . a sin X .
b sin X cos X . c cos X
d (1) a, b, c, d
Dấu hiệu nhận dạng: Đ ng bậc hoặc lệch nhau hai bậc của hàm sin hoặc cosin (tan và cotan được xem là bậc 0). Phƣơng pháp giải: cos X 0
Bước 1. Kiểm tra xem X k , (k )
có ph i là nghiệm hay không ? 2 2 sin x 1 cos X 0 Bước 2. Khi X k , (k ) . Chia hai vế (1) cho 2 cos X : 2 2 sin X 1 2 2 sin X sin X cos X cos X d 2 2 (1) a b c a tan X b tan X c ( d 1 tan X) 2 2 2 2 cos X cos X cos X cos X Bước 3. Đặt t
tan X để đưa v phương trình bậc hai mà biết cách gi i.
Lƣu ý. Gi i tương tự đối với phương trình đẳng cấp bậc ba và bậc bốn: 3 2 2 3 asin X
bsin X cos X
c sin X cos X dcos X 0 4 3 2 2 3 4 asin X
bsin X cos X
c sin X cos X
dsin X cos X e cos X 0 PP
Kiểm tra và chia hai vế cho 3 4 cos X 0 (hay cos X).
5.Phƣơng trình lƣơng giác đối xứng
Dạng 1. a (sin x cos ) x
b sin xcos x c
0 (dạng tổng/hiệu – tích PP Đăt t sin x cos x, t
2 và bình phương để suy ra: sin xcos x theo t. Lưu ý khi đặt t sin x
cos x thì đi u kiện là: 0 t 2 .  Dạng 2. 2 2 a (tan x cot ) x b (tan x cot ) x c 0 PP Đặt t tan x cot x, t
2 và bình phương để suy ra: 2 2 tan x cot x và l c này 2 thư ng sử dụng: tan . x cot x 1; tan x cot x sin 2x 8
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
BÀI TẬP TRẮC NGHIỆM KHÁCH QUAN.
HÀM SỐ LƢỢNG GIÁC
Câu 1. Cho hàm số y  sin x . Phát biểu nào sau đây không đ ng? A.
Tập xác định của hàm số là R. B.
Tập giá trị của hàm số là R. C. Hàm số là hàm lẻ.
D. Hàm số tuần hoàn với chu kì 2 .
Câu 2. Cho hàm số y  cos x . Phát biểu nào sau đây không đ ng? A.
Tập xác định của hàm số là R. B.
Tập giá trị của hàm số là  1  ,1   . C. Hàm số là hàm lẻ.
D. Hàm số tuần hoàn với chu kì 2 .
Câu 3. Cho hàm số y  tan x . Phát biểu nào sau đây không đ ng? A.
Tập xác định của hàm số là R. B.
Tập giá trị của hàm số là R. C. Hàm số là hàm lẻ.
D. Hàm số tuần hoàn với chu kì  .
Câu 4. Cho hàm số y  cot x . Phát biểu nào sau đây không đ ng? A.
Có tập xác định là R
\   k |k   Z . B. Có tập giá trị là R. C. Hàm số là hàm chẵn.
D. Hàm số tuần hoàn với chu kì  .
Câu 5. Phát biểu nào sau đây đ ng? A.
Hàm số y  sin x là hàm số chẵn nên nhận trục Oy làm trục đối x ng. B.
Hàm số y  cos x là hàm số lẻ nên nhận gốc tọa đ O làm tâm đối x ng. C.
Hàm số y  sin x và y  cos x tuần hoàn với chu kì 2 . D.
Hàm số y  tan x và y  cot x tuần hoàn với chu kì 2 .
Câu 6. Tập xác định của hàm số y  3  cos x là tập nào dưới đây ? A. ,3 B. ,3 C. 3,   D. R 1  sin x
Câu 7. Tập xác định của hàm số y
là tập nào dưới đây ? cos x     A.
R\  k |k ZB. R  \ k2 C. R  \ k D.
R\  k2 |k Z  2   2    
Câu 8. Tập xác định của hàm số y  tan 2x  
 là tập nào dưới đây ?  3    A. R  \  0 B.
R\  k |k Z  2  5      C. R\
k |k ZD.
R\  k |k Z  12 2   6 2 
Câu 9. Hàm số nào sau đây là hàm số lẻ? A. 2 y  sin 2x B. 2 y  cos 2x C. y  sin 2x D. y  cos2x
Câu 10. Hàm số nào sau đây là hàm số lẻ? A. 3 y  sin 3x B. 3 y  cos 3x C.
y  sin 3x  1 D.
y  cos3x  1
Câu 11. Hàm số nào sau đây là hàm số chẵn? 2 A.
y  sin x  cos x B.
y  sin x  cos x C.
y  sin x x D.
y  sinx   cosx
Câu 12. Hàm số nào sau đây là hàm số chẵn?    A. y  sin x    B. 3
y  sin x x  3  3 C.
y  tan3xD.
y  sinx x tan3x
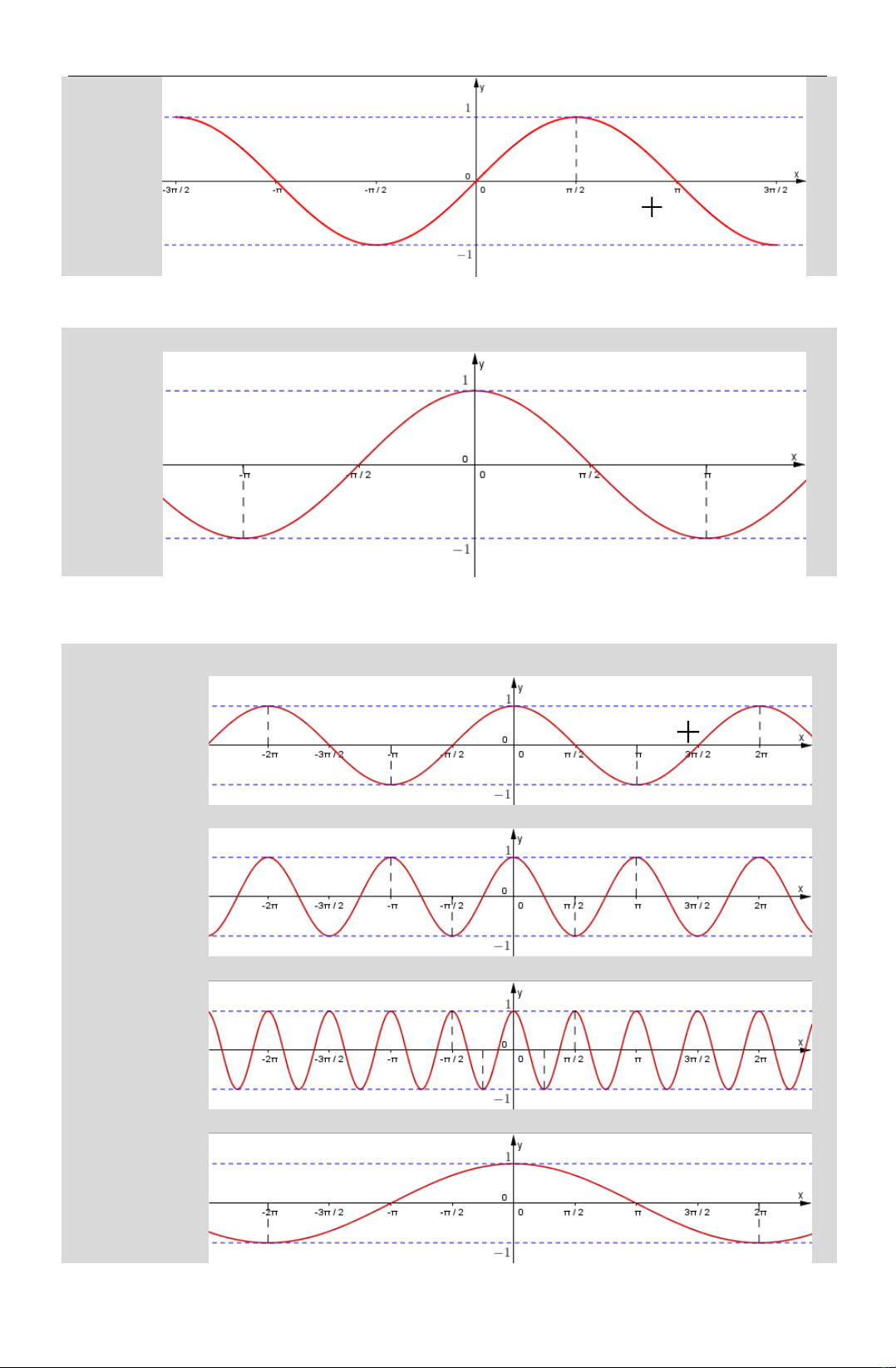
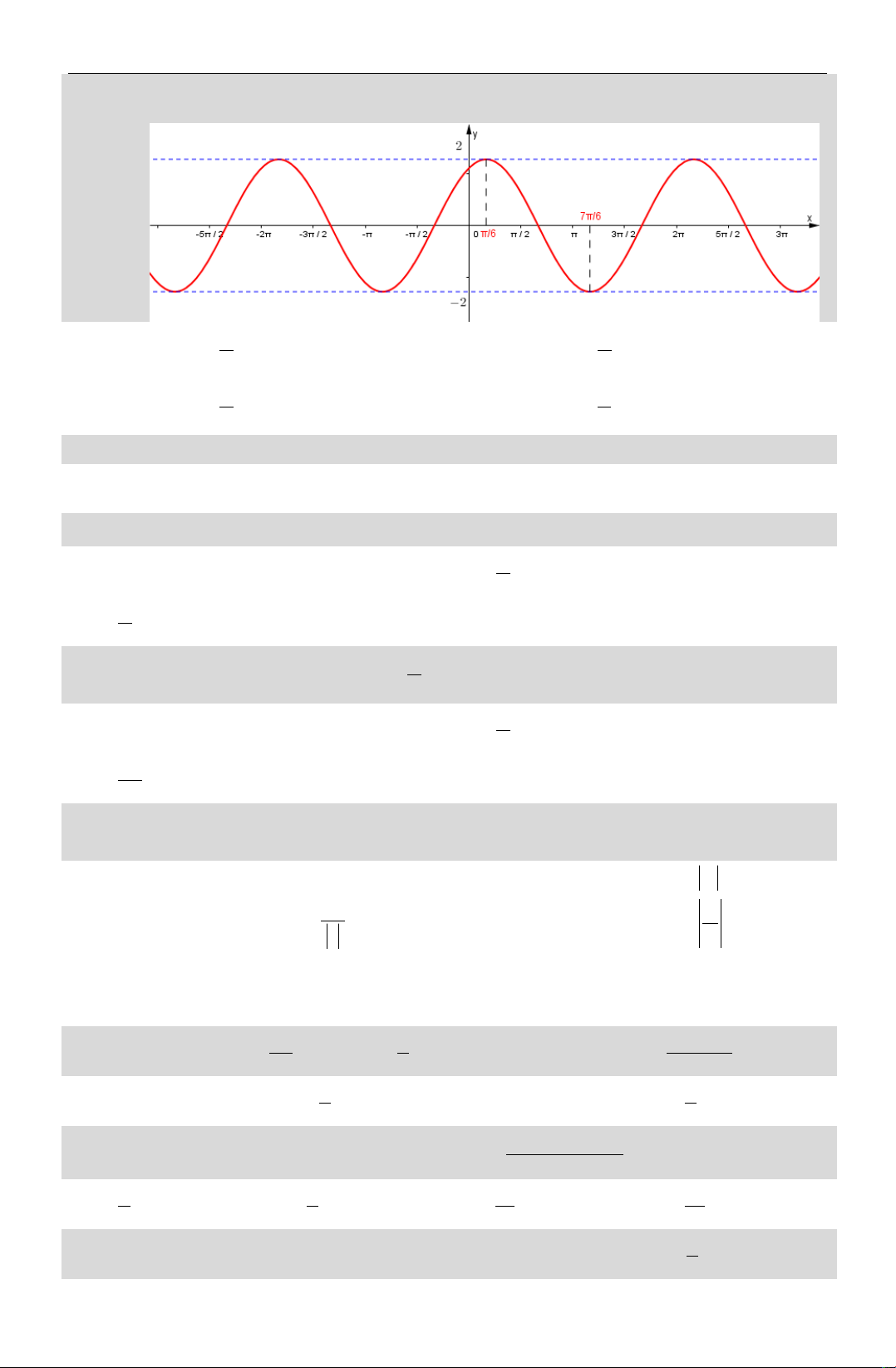
Câu 13. Hàm số nào sau đây có đ thị như hình đã cho?
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 9
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG Câu 14. A. y  sin x B. y  cos x C. y  tan x D. y  cot x
Câu 15. Hàm số nào sau đây có đ thị như hình đã cho? Câu 16. A. y  sin x B.
y  sin2xC.
y  cosx
D. y  cos2x
Câu 17. Đ thị hàm số y  cos2x là đ thị nào dưới đây? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 10
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Câu 18. Đư ng cong bên dưới là đ thị của m t hàm số được liệt kê trong các đáp án A B C
D. Hàm số đó là hàm số nào? Câu 19.       A. y  2sin x    B. y  2sin x     6   3        C. y  2sin x    D. y  2sin x     6   3 
Câu 20. Chu kì của hàm số y  sin xcos x  cos2x là ? A. 2 B. 4 C.
D. Không có chu kì.
Câu 21. Chu kì của hàm số 2
y  cos 2x  cos8x là ?  A. 2 B. 2  C.
D. Không có chu kì. 4   
Câu 22. Chu kì của hàm số 2 y  sin 3x     3x là ?  3   A. 2 B. 3 2 C.
D. Không có chu kì. 3
Câu 23. Cho hàm số y f x  .
A sinax b với A,a,b là các hằng số A,a  0 . Phát biểu nào sau đây đ ng? A.
Hàm số đã cho có chu kì 2 . B.
Hàm số đã cho có chu kì A 2 . 2 A C. Hàm số đã cho có chu kì .
D. Hàm số đã cho có chu kì 2 . a a
PHƢƠNG TRÌNH LƢỢNG GIÁC 3 4 1  cot
Câu 24. 17. Cho    
và sin    Tính giá trị của biểu th c A   2 5 1  cot 1 1 A. 7  B. C. 7 D. 7 7 3 sin  2cos 
Câu 25. Cho tan  2. Tính giá trị của biểu th c A   3 cos  2sin  7 4 5 12 A. B. C. D. 4 7 21 13 2
Câu 26. Tính giá trị của biểu th c P  (1 3cos2)(2  3cos2), biết sin   3
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 11
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG 14 22 8 20 A. B. C. D. 9 9 9 9 2sin  3cos
Câu 27. Cho cot  2
 . Tính giá trị của biểu th c A   5cos  6sin 1 1 1 1 A. B. C. D. 17 4 17 4   
Câu 28. Cho phương trình 2 cos 2x   
 1. Các nghiệm lượng giác của phương trình là?  3   7  7 A. x  
k và x   lB. x
k và x   l 24 24 24 24  7  7 C. x  
k và x    lD. x
k và x    l 24 24 24 24 x
Câu 29. Cho phương trình 2 2cos
 cos5x  1. Các nghiệm lượng giác của phương trình là? 2  k  l   lA. x   và x    B. x
k và x    6 3 4 2 6 4 2  k  l   C. x   và x    D. x
k và x    l 6 2 4 3 6 4   
Câu 30. Cho phương trình cos
x  sin2x   
0 . Các nghiệm lượng giác của phương trình  2  là? 2 A. x kB. x    k 3 2 C.
x    kD.
x k và x    l 3
Câu 31. Cho phương trình 2  cos2x  5
 sinx . Các nghiệm lượng giác của phương trình là? 2  2  A. x
k2 và x   l2 B. x
k và x    l 3 3 3 3 2  2  C. x  
k2 và x    l2 D. x  
k và x   l 3 3 3 3
Câu 32. Cho phương trình 2
cos4x  12sin x  1  0 . Các nghiệm lượng giác của phương trình là? A. x k2 B.
x    k2  C. x   kD. x k 2
Câu 33. Cho phương trình tan x  cot x  2 . Các nghiệm lượng giác của phương trình là?   A. x   k2 B. x    k2 4 4   C. x   kD. x    k 4 4
Câu 34. Cho phương trình 2 2
2sin x  tan x  2 . Các nghiệm lượng giác của phương trình là?   A. x    k2 B. x    k 4 4 C. x k2 D. x k
Câu 35. Cho phương trình 3 sin x  cos x  2 . Các nghiệm lượng giác của phương trình là?   A. x   k2 B. x   k2 6 3 12
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG 2  C. x   k2 D. x   k2 3 2
Câu 36. Cho phương trình 2 1
3 sin x  sin 2x  3 . Các nghiệm lượng giác của phương 2 trình là?     A. x
k và x    lB. x  
k và x   l 3 2 3 2     C. x  
k và x    lD. x
k và x   l 3 2 3 2
Câu 37. Cho phương trình cos x  2 sin 2x  sin x . Các nghiệm lượng giác của phương trình là?  k2  k2 A. x   B. x    4 3 4 3   C. x   k2 D. x    k2 4 4
Câu 38. Cho phương trình cos2x  3 sin 2x  3 sin x  cos x . Các nghiệm lượng giác của phương trình là?  k2 A. x   k2 B. x  3 3  2 C. x    k2 D. x   k 3 3
Câu 39. Cho phương trình 3
cos x  2sin x . Các nghiệm lượng giác của phương trình là?   A. x   k2 B. x    k 4 4   C. x    kD. x   k 4 4
Câu 40. Cho phương trình 2 2
2sin x  3 3 sin xcos x  cos x  2 . Các nghiệm lượng giác của phương trình là?     A. x
k2 và x    l2 B. x
k và x   l 2 6 2 6    5 C. x  
k2 và x    l2 D. x
k và x   l 2 6 2 6
Câu 41. Gi i phương trình 2 2(sin x  cos )
x  3  sin 2x với    x  3 . 3 7 11 3 11 A. x  , x  và x B. x  và x  4 4 4 4 4  3 11  7 C. x   , x  và x D. x   và x  4 4 4 4 4   
Câu 42. Số nghiệm của phương trình sin 2x  2 sin x   
 1 thu c kho ng 0,2  là?  4  A. 2 B. 4 C. 3 D. 5 sin 3x
Câu 43. Số nghiệm của phương trình
 0 thu c đoạn 2 ,4    là? cos x  1 A. 2 B. 4 C. 5 D. 6 2 2
tan x  tan x  co t x  cot x  2
Câu 44. Số nghiệm của phương trình  0 thu c kho ng sin 2x  1
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 13
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG ,3  là? A. 0 B. 1 C. 2 D. 4
BIẾN ĐỔI LƢỢNG GIÁC  3 tan Câu 45. Cho
    và sin   Tính A   2 5 2 1  tan  12 12 15 15 A. B. C. D.  25 25 34 34 2 Câu 46. Tính 4 4
A  sin   cos  , biết sin 2   3 1 7 5 7 A. B. C. D.  9 9 9 9  1   
Câu 47. Cho 0     và sin 
. Tính A  cos     . 2 3  3  6  3 3  6 6  3 3  6 A. B. C. D.  6 6 6 6  1  7  Câu 48. Cho
    và sin(   )    Tính A  tan     2 3  2  A. 2 B.  2 C. 2 2 D. 2  2  4 sin Câu 49. Cho
    và cos    Tính A  cot   2 5 1  cos 9 5 9 5 A. B. C. D. 4 3 4 3 4 3   
Câu 50. Cho cos   và    
 Tính A  tan      5 2  4  1 1 A. B. C. 7 D. 7  7 7  4       Câu 51. Cho 
   0 và cos   Tính A  sin   cos        2 5  4   4  49 1 49 1 A. B. C. D. 50 50 50 50 1
Câu 52. Cho cos 4   Tính 6 6 1
A  cos   sin    3 4 1 1 A. 1 B. C. 1  D.  2 2 sin
Câu 53. Cho tan  2. Tính A   3 3 sin   3cos  11 10 10 11 A. B. C. D.  10 11 11 10 3sin  2cos
Câu 54. Cho tan  3. Tính A   3 3 5sin   4cos  70 10 70 10 A. B. C. D. 139 19 139 19 5 
Câu 55. Cho sin  cos  và 0   
 Tính A  sin  cos. 2 4 14
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG 3 3 1 1 A. B. C. D.  2 2 2 2 1   
Câu 56. R t gọn biểu th c P  , 0  x     2 2    2 sin x cot x cos x  sin x sin 2x sin x sin 2x A. P B. P C. P   D. P   cos 2x cos x cos 2x cos x 7 3
Câu 57. R t gọn biểu th c P 2cos x 3cos(        x)  sin  x  tan  x       2   2  A. P  tan x B. P  cot x C. P  0 D. P  cos x 3  11
Câu 58. R t gọn biểu th c P cos(15       
x)  sin x   tan  x cot  x         2   2   2  A. P  0 B. P  1 C. P  sin x D. P  cos x            
Câu 59. R t họn biểu th c P  sin x  cos  x  sin  x cos x            3   4   4   3  A. P  0 B. P  1
C. P  sin2x
D. P  cos2x
Câu 60. Cho A B C là 3 góc của m t tam giác. Đẳng th c nào dau đây là đẳng th c sai ? A B C A.
sin A  sin B  sinC  4cos cos cos  2 2 2 B.
sin2A  sin2B  sin2C  4sin Asin Bsin . C A B C C.
sin A  sin B  sinC  sin sin cos  2 2 2 A B C D.
cos A  cos B  cosC  1  4sin sin sin  2 2 2
PHƢƠN TRÌNH LƢỢNG GIÁC CƠ BẢN   
Câu 61. Gi i phương trình sin x     1.  3    A. x   kB. x   k2 2 2 5  C. x   k2 D. x   k2 6 6   
Câu 62. Gi i phương trình cos x     1 .  3    A. x   k2 B. x   k 3 3   C. x    k2 D. x    k 3 3   
Câu 63. Gi i phương trình sin 2x     0 .  3    A. x   k2 B. x   k 3 3   C. x   k2 D. x   k 6 6   
Câu 64. Gi i phương trình cos x     0 .  6 
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 15
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG 2 2 A. x   k2 B. x   k 3 3   C. x   k2 D. x   k 6 6   
Câu 65. Gi i phương trình 2cos x     1 .  6    A. x   kB. x    k 6 2     C. x
k và x    k' D. x
k2 và x    k'2 6 2 6 2
Câu 66. Gi i phương trình 2
2cos x   1  0 .   A. x   kB. x    k 4 4    C. x    k2 D. x   k 4 4 2   
Câu 67. Gi i phương trình cos x  cos x    .  3  2 2 A. x   k2 B. x    k2 3 3   C. x   kD. x    k 3 3   
Câu 68. Gi i phương trình sin x  sin x    .  3    A. x   k2 B. x    k2 3 3   C. x   kD. x    k 6 6   
Câu 69. Gi i phương trình sin x  cos x    .  3  5  A. x   k2 B. x   k2 6 6 5  C. x   kD. x   k 12 12
Câu 70. Gi i phương trình tan2x  cot . x A. x k2 B.
x    k2   C. x   kD. x    k 2 2
PHƢƠNG TRÌNH ĐẶT ẨN PHỤ
Câu 71. Gi i phương trình 2
tan x  2 3 tan x  3  0.   A. x    kB. x   k 3 3   C. x    kD. x   k 6 6
Câu 72. Gi i phương trình 2cos2x  8cos x  5  0. 16
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG   A. x    k2 B. x    k2 6 3 2 2 C. x   kD. x    k 3 3
Câu 73. Gi i phương trình 2
cos4x  12sin x  1  0. A. x k2 B. x k   C. x   kD. x    k 2 2
Câu 74. Gi i phương trình 2
cos4x  2cos x  1  0.  A. x k2 B. x    k 6   C.
x k và x    k' D.
x k và x    k' 3 6
Câu 75. Gi i phương trình 2 3 2 tan x  3   cos x   A. x    k2 B. x    k2 3 6   C. x    kD. x    k 3 6 cos x
Câu 76. Gi i phương trình  1 sin . x 1  sin xA. x kB. x    k2 2   C.
x k2 và x    k'2
D. x k2 và x   k'2 2 2
Câu 77. Gi i phương trình 2
3cos x  2cos2x  3sin x  1.  A. x kB. x    k2 2   C. x   k2 D. x    k2 2 2
Câu 78. Gi i phương trình 2 2
2sin x  3 3 sin xcos x  cos x  2.   A. x    k2 B. x    k 2 6     C. x
k và x   k' D. x
k và x    k' 2 6 2 6
Câu 79. Gi i phương trình 4 2 2 4
3cos x  4sin xcos x  sin x  0.   A. x    kB. x    k 4 3     C. x  
k và x    k' D. x  
k2 và x    k'2 4 3 4 3
Câu 80. Gi i phương trình 3 3 2
cos x  4sin x  3cos xsin x  sin x  0     A. x  
k và x    k' B. x  
k và x    k' 4 3 4 6     C. x
k và x    k' D. x  
k và x    k' 4 6 4 6
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 17
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
PHƢƠNG TRÌNH BẬC NHẤT
Câu 81. Gi i phương trình sin x 3 cos x 2.  5 A. x   k2 B. x   k2 6 6  2 C. x   k2 D. x   k2 3 3
Câu 82. Gi i phương trình sin x 3 cos x 1. 7    A. x
k2 hoặc x   k'2 B. x  
k2 hoặc x   k'2 6 2 6 2 2  C.
x k2 hoặc x   k'2 D. x
k2 hoặc x   k'2 3 3
Câu 83. Gi i phương trình 3 sin x cos x 2.   A. x    k2 B. x    k2 3 6 2 5 C. x    k2 D. x    k2 3 6
Câu 84. Gi i phương trình 3 cos x sin x 2. 7 11 5 11 A. x  
k2 hoặc x   k'2 B. x  
k2 hoặc x    k'2 12 12 12 12  7  5 C. x  
k2 hoặc x    k'2 D. x
k2 hoặc x   k'2 12 12 12 12
Câu 85. Gi i phương trình sin x cos( ) x 1.   A. x
k2 hoặc x   k'2 B.
x k2 hoặc x    k'2 2 2  C. x k2 D. x    k2 2
Câu 86. Gi i phương trình 3 sin x sin x 2. 2 5  A. x    k2 B. x    k2 6 6 2  C. x    k2 D. x    k2 3 3
Câu 87. Gi i phương trình 1 sin2x cos2 . x   A.
x k2 hoặc x    k'2 B.
x k2 hoặc x   k'2 2 2   C.
x k hoặc x    k' D.
x k hoặc x   k' 4 4
Câu 88. Gi i phương trình 2 1 3 sin x sin 2x 3. 2  2 A.
x k2 hoặc x   k'2 B. x
k2 hoặc x   k'2 3 3    C.
x k hoặc x   k' D. x
k hoặc x   k' 6 3 2
Câu 89. Gi i phương trình sin x cos x 2 sin x 3 5 5 A. x   kB. x   k2 24 12 18
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG 11 11 C. x   kD. x   k 24 12
Câu 90. Gi i phương trình sin x cos x 2 sin 2x  5  5 2 A. x  
k2 hoặc x   k'2 B. x  
k2 hoặc x   k' 4 3 4 12 3    2 C. x
k2 hoặc x   k'2 D. x
k2 hoặc x   k' 4 4 3 3
Câu 91. Gi i phương trình sin x 3 cos x 2sin 2x  2  2 A. x  
k2 hoặc x    k'2 B. x
k2 hoặc x   k'2 3 3 3 3  4 2  2 2 C. x  
k2 hoặc x   k' D. x
k2 hoặc x   k' 3 9 3 3 9 3
Câu 92. Gi i phương trình sin x 3 cos x 2sin 3x   2  2 A. x
k hoặc x   k' B. x
k2 hoặc x   k'2 6 6 3 3 3  4    C. x  
k2 hoặc x   k'2 D. x  
k hoặc x   k' 3 3 6 3 2
PHƢƠNG TRÌNH ĐỐI XỨNG
Câu 93. Gi i phương trình sin 2x 2 2.(sin x cos ) x 5. 5 11  7 A. x  
k2 hoặc x   k'2 B. x
k2 hoặc x    k'2 12 12 12 12  7 5 11 C. x  
k2 hoặc x   k'2 D. x
k2 hoặc x    k'2 12 12 12 12
Câu 94. Gi i phương trình sin x cos x sin xcos x 1 0.   A.
x    k2 hoặc x   k'2 B.
x k2 hoặc x   k'2 2 2  C.
x    k2 hoặc x k'2 D. x    k2 2
Câu 95. Gi i phương trình 2(sin x cos ) x 6sin xcos 2 0.  A.
x    k2 hoặc x k2 B. x    k'2 2   C.
x k2 hoặc x   k'2
D. x    k2 hoặc x   k'2 2 2
Câu 96. Gi i phương trình 2 2(sin x cos ) x 3 sin 2 . x   A. x   k2 B. x    k2 4 4 3 C. x k2 D. x   k2 4
Câu 97. Gi i phương trình sin x cos x 4sin 2x 1.  3 A. x
k2 hoặc x   k'2 B. x   k2 2 4   C. x k D.
x k2 hoặc x   k'2 2 2
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 19
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT
Câu 98. Tìm giá trị lớn nhất của biểu th c A  1 2sin x A. max A  1 
B. max A  1 C. max A  2 D. max A  3
Câu 99. Tìm giá trị lớn nhất của biểu th c 2 2
A  1 2sin x  cos x A. max A  1
B. max A  2 C. max A  3 D. max A  4
Câu 100. Tìm giá trị lớn nhất của biểu th c 4 4
A  sin x  cos x A. max A  1 
B. max A  0 C. max A  1 D. max A  2
Câu 101. Tìm giá trị lớn nhất của biểu th c 4 4
A  sin x  cos x 1 3 A. max A  0
B. max A C. max A  1
D. max A  2 2
Câu 102. Tìm giá trị nhỏ nhất của biểu th c A  sin x  cos x 1   3 A. min A  2  B. min A   2 C. min A  1 
D. min A  2
Câu 103. Tìm giá trị nhỏ nhất của biểu th c A  sin x  cos x  1 1  3 A. min A  1  B. min A   2  1
C. min A  0
D. min A  2
Câu 104. Tìm giá trị nhỏ nhất của biểu th c A  sin x  3 cos x  2 A. min A  3   3
B. min A  4  C. min A  2   3
D. min A  3 
Câu 105. Tìm giá trị nhỏ nhất của biểu th c A  3 sin x  cos x  2 A. min A  1  3 B. min A  2  3 C. min A  0 D. min A  1
Câu 106. Tìm giá trị nhỏ nhất của biểu th c 2
A  2sin x  sin 2x A. min A  1
B. min A  2 C. min A  1  D. min A  1  2
Câu 107. Tìm giá trị nhỏ nhất của biểu th c 2
A  sin 2x  2cos x  2 A. min A  1 B. min A  2 C. min A  3  2 D. min A  3  2 sin x  cos x
Câu 108. Tìm giá trị lớn nhất của biểu th c A  sin x  3 1   17 1 1 2  3 A. max A
B. max A
C. max A
D. max A  8 2 4 8 2sin x  cos x
Câu 109. Tìm giá trị nhỏ nhất của biểu th c A  sin x  2 5 A. min A  1 
B. min A   C. min A  3  D. min A  2  3
sin x  2cos x  1
Câu 110. Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu th c A  lần lượt là
2sin x  cos x  3
M và m. Tính gía trị M m . 1 1 17 A. M m  0
B. M m
C. M m  
D. M m  2 2 2 sin x  1
Câu 111. Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu th c A  lần lượt là M và cos x  2
m. Tính gía trị M m . 4 4 A. M m  0
B. M m
C. M m   D. M m  1 3 3 2cos x  1
Câu 112. Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu th c A  lần lượt là M và sin x  2 m. Tính gía trị . M m . 1 13 A. . M m  1  B. . M m  0
C. M.m
D. M.m  3 3 20
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
Câu 113. Tập xác định của hàm số y  tan x là      A.
\   k , k   B. \   k , k    2   2 2      C.
\   k , k   D.
\   k2 , k    4   2  sin x 1
Câu 114. Tập xác định của hàm số y  là sin x     A.
\   k , k   B.
\   k2 , k    2   2  C.
\   k , k   D.
\ k2 , k  
Câu 115. Giá trị lớn nhất của hàm số y  sin x là A.1 B.0 C. 1  D. 3
Câu 116. Giá trị bé nhất và giá trị lớn nhất của hàm số y  2cos x  2 theo th tự là: A.0 và 2 B. 2   2 và 2  2 C. 4   2 và 4  2 D. 2 và 2  2
Câu 117. Đi u kiện xác định của phương trình tan x  3 là   A. x
k k   B. x
k2 k   2 2   C. x
k k   D. x  
k2 k   4 4 1
Câu 118. Tất c các nghiệm của phương trình sin x   là 2  5  5 A. x
k2 và x
k2 ( k  ) B. x  
k2 và x  
k2 ( k  ) 4 4 4 4  3  5 C. x  
k2 và x  
k2 ( k  ) D. x   k2 và x  
k2 ( k  ) 4 4 4 4 3
Câu 119. Tất c các nghiệm của phương trình cos x   là 2  2  5 A. x
k2 và x
k2 ( k  ) B. x
k2 và x
k2 ( k  ) 3 3 6 6 5 5   C. x
k2 và x  
k2 ( k  ) D. x   k2 và x    k2 ( k  ) 6 6 3 3 3
Câu 120. Tất c các nghiệm của phương trình tan x   là 3   A. x
k ( k  ). B. x  
k ( k  ). 6 6   C. x
k ( k  ). D. x  
k ( k  ). 3 3 12
Câu 121. Tất c các nghiệm của phương trình cot x   là 2   A. x
k ( k  ). B. x  
k ( k  ). 6 6
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 21
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG   C. x
k ( k  ). D. x  
k ( k  ). 3 3
Câu 122. Tìm tất c giá trị của m để phương trình sin 2x m có nghiệm? A. m  1 B. 1   m 1 C. m  0 D. m  1   
Câu 123. Tập xác định D của hàm số y  tan  2x   là  8   3    3   A. D  \   k ,k   B. D  \ 
l , l    4 2   16 2   3   3  C. D  \ 
k ,k   D. D  \ 
k ,k    2   2 
Câu 124. Tất c các nghiệm của phương trình sin x  cos x là   A. x
k ( k  ). B. x
k2 ( k  ). 4 4     C. x
k và x    k (k  ). D. x
k2 và x    k2 (k  ). 4 4 4 4
Câu 125. Tất c các nghiệm của phương trình 2 4sin x  3 là     A. x
k2 và x    k2 ( k  ). B. x
k và x    k ( k  ). 3 3 3 3     C. x
k và x    k (k  ). D. x
k2 và x    k2 (k  ) 6 6 6 6
Câu 126. Tất c các nghiệm của phương trình 2 tan x  3 là     A. x
k2 và x    k2 ( k  ). B. x
k và x    k ( k  ). 3 3 3 3     C. x
k và x    k (k  ). D. x
k2 và x    k2 (k  ). 6 6 6 6
Câu 127. Tất c các nghiệm của phương trình sin x  cos x  1  là     x   k2  x   k  4 4 A.  (k  )    . B. (k ) .    x    k2      x k  4  4 x k2
x  2k   1    C.  (k  )   . D. (k )  . x   k2       x k 2 4  2
Câu 128. Tất c các nghiệm x 0;2  của phương trình 2cos x  3  0 là 5 7  5  11 7 11 A. ; . B. ; . C. ; . D. ; . 6 6 3 3 6 6 6 6 x
Câu 129. Tất c các nghiệm x 0;2  của phương trình 3 cot  3  0 là 4 2  10       5  A.   . B.   . C.   . D.  ;  .  3   3   4   4 4  22
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG TỰ LUẬN Bài 1.
Gi i các phương trình lượng giác sau: a) 2
2sin x  5cos x 1  0. b) 2 2
3  4cos x  2sin x  sin . x c) 4 2
2cos x  3sin x  2  0. d) 4 2
4sin x 12cos x  7  0.
e) 5cos 2x  22sin x 17  0.
f) cos10x  4 2 cos5x  4. g) 2
cos 4x  2cos x 1  0. h) 2
6sin 3x  cos12x  4  0. x x i) 2
cos 2x  2 cos x  2sin  j) 2
cos 2x  3cos x  4 cos  2 2 k)
3 tan x  6cot x  2 3  3  0.
l) 5 tan x  2cot x  3  0. 1 2 5 1 m) 2  tan x    0. n)
3 sin x  cos x   2 cos x 2 cos x Bài 2.
Gi i các phương trình lượng giác sau:
a) sin x  3 cos x  1. b)
3 cos 3x  sin 3x  2.
c) sin 3x cos x  3 cos 2x  2  sin x cos3 . x
d) cos 6x cos x  3 sin 5x 1 sin 6xsin . x
e) sin 3x  3 cos3x  2sin . x f)
3 cos x  sin x  4sin x cos . x g) 2 (sin x  cos ) x
 3 cos 2x 1 2cos . x h)
3 cos 5x  2sin 3x cos 2x  sin . x
i) cos 7x  sin 5x  3(cos5x  sin 7 ) x . j) 3(cos 2x  sin 3 )
x  sin 2x  cos 3 . x Bài 3.
Gi i các phương trình lượng giác sau: a) 2 2
6sin x  7 3 sin 2x  8cos x  6. b) 2 2
2cos x  2sin 2x  4sin x 1. c) 3
sin x  4sin x  cos x  0. e) 2
sin x(tan x 1)  3sin (
x cos x  sin ) x  3. Bài 4.
Gi i các phương trình lượng giác sau:
a) 1 sin x  cos 2x  sin 3x  0.
b) cos 2x  cos 6x  cos 4x 1.
c) 2sin x cos 2x  sin 2x cos 2x  sin 4x cos . x
d) cos x cos3x  sin 2xsin 6x  sin 4xsin 6 . x e) 2 2 2 2
sin 4x  sin 3x  sin 2x  sin . x f) 2 2
2sin 2x  sin 6x  2cos . x Bài 5.
Gi i các phương trình lượng giác sau:
a) cos 2x  cos x  3sin x  2  0.
b) cos 2x  3cos x  2  sin . x
c) sin 2x  2cos 2x 1 sin x  4cos . x
d) 2sin 2x  cos 2x  7sin x  2cos x  4. e) 2
(2sin x 1)(2cos 2x  2sin x  3) 1  4sin . x f) 2
(2sin x  3)(sin x cos x  3) 1 4cos . x
g) cos 2x  (1 2cos )
x (sin x  cos ) x  0.
h) (sin x  cos x 1)(2sin x  cos ) x  sin 2 . x i) 4 4
2(cos x  sin x) 1  3 cos x  sin . x j) 3
2sin x  cos 2x  cos x  0. k) 2
cos x  sin x cos x  sin x 1  2cos . x l) 2
4sin x  4sin x  2sin 2x 1  2cos . x
m) sin 2x  sin x 1  0. n) 3 2 6
4  3sin x  sin x  3cos x  cos . x
o) tan x  sin 2x  2cot 2 . x
p) 3sin3x  2  sin ( x 3 8cos ) x  3cos . x
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt: 0932589246 23
LUYỆN THI TRẮC NGHIỆM MÔN TOÁN 2017
LỚP TOÁN THẦY DƢƠNG 76/5 PHAN THANH – 135 NGUYỄN CHÍ THANH ĐÀ NẴNG
LỚP TOÁN THẦY DƢƠNG
Thƣờng xuyên mở các lớp 10-11-12 theo yêu cầu (5-10 học sinh)
Thƣờng xuyên mở các lớp luyện thi Trắc Nghiệm 12 theo cấu trúc 2017.
Mở các lớp luyện đề Trắc Nghiệm Môn Toán theo cấu trúc của Bộ
Giáo Dục và Đào Tạo.
Mọi chi tiết xin liên hệ: Hotline: 0932589246.
Facebook: https://www.facebook.com/ThayNguyenDaiDuong
Website: http://www.toanmath.com/ 24
Fb: https://www.facebook.com/ThayNguyenDaiDuong – Sdt 0932589246