







Preview text:
Phần 1:
NHIỆT ĐỘNG HÓA HỌC ÔN TẬP: CƠ SỞ CỦA
NHIỆT ĐỘNG HÓA HỌC
I. Ý NGHĨA CỦA NHIỆT ĐỘNG HỌC TRONG CÔNG NGHỆ VÀ KĨ THUẬT HOÁ HỌC
Ø Không thể có động cơ vĩnh cửu loại 1
Ø Không thể có động cơ vĩnh cửu loại 2
II. NHẮC LẠI CÁC NGUYÊN LÝ CƠ BẢN CỦA NHIỆT ĐỘNG HỌC 1. Nguyên lý I
vNội dung: Trong 1 quá trình bất kỳ, nhiệt mà hệ nhận dùng để
sinh công và biến thiên nội năng
vBiểu thức: Q = A + ∆U hay dQ = dA + dU
Vậy: ∆U = U2 – U1 = Q1 – A1 = Q2 – A2 = … 1 2
•Lưu ý: Nếu hệ chỉ sinh công giãn nở thuận nghịch: dA = pdV.
Vậy: dU = dQ – pdV Hay: ∆ U = Q - ∫PdV
II. NHẮC LẠI CÁC NGUYÊN LÝ CƠ BẢN CỦA NHIỆT ĐỘNG HỌC 2. Nguyên lý II
vNội dung: Nhiệt không tự ý truyền từ nơi có nhiệt độ
thấp về nơi có nhiệt độ cao
vVới quá trình nhiệt động thực tế xảy ra trong một hệ cô
lập, entropy của hệ luôn luôn tăng
v Biểu thức toán học Q d dS ³ T
a. Entropi là một hàm trạng thái
b. Entropi có tính chất cộng tính
c. Kết hợp nguyên lý I và II ta có: dA + dU ≤ TdS
III. BIỂU THỨC KẾT HỢP HAI NGUYÊN LÝ
1. Thế nhiệt động
Có: dQ = dU + dA mà dA = dA’ + PdV và dQ ≤ TdS
Vậy: dU ≤ TdS – PdV - dA’
Tùy theo cách chọn điều kiện quá trình, công có ích cực đại
bằng độ giảm của hàm trạng thái:
Nếu T, V = const: dA’max = -dFT,V hay A’max = -∆FT,V
Nếu T, P = const: dA’max = -dGT,P hay A’max = -∆GT,P
2. Phương trình tổng quát của nhiệt động học:
dF = -SdT - PdV – dA’max
dG = -SdT + VdP – dA’max
III. BIỂU THỨC KẾT HỢP HAI NGUYÊN LÝ
3. Dùng thế nhiệt động để xét chiều tự diễn biến của các quá trình trong hệ
a. Xét chiều của quá trình trong hệ đẳng nhiệt đẳng áp:
Ta có: dG ≤ -SdT + VdP – dA’. Khi T, P = const: dG≤ - dA’
Nếu dG < 0 (hay ∆G < 0): quá trình tự xảy ra
Nếu dG = 0 (hay ∆G = 0) và d2G > 0 (Gmin): cân bằng
b. Xét chiều trong hệ đẳng nhiệt đẳng tích:
Ta có: dF ≤ -SdT - PdV – dA’. Khi T, V = const: dF ≤ - dA’
Nếu dF < 0 (hay ∆F < 0): quá trình tự xảy ra
Nếu dF = 0 (hay ∆F = 0) và d2F > 0 (Fmin): cân bằng
III. BIỂU THỨC KẾT HỢP HAI NGUYÊN LÝ
4. Sự phụ thuộc của G vào T và P
a. Phương trình Gibbs – Helmholtz viết cho thế đẳng áp G: G D H D d = - dT + J ò ò T T 2
b. Xét quá trình thuận nghịch không sinh công có ích: dG = - SdT + VdP Ta có: æ G ¶ ö æ G D ¶ ö ç ÷ = V ç ÷ = V D è P ¶ ø è P ¶ ø T T P P Vậy: G VdP VdP P = G0 + và ∆G ò P = ∆G0 +ò D 1 1
Nếu hệ khí lý tưởng: G = Go + RTlnPi
IV. ĐẠI LƯỢNG MOL RIÊNG PHẦN VÀ THẾ HOÁ HỌC
1. Đại lượng mol riêng phần
X = X(T, P, n1, n2, …, ni) æ X ¶ ö æ X ¶ ö æ X ¶ ö æ X ¶ ö dX = ç ÷ dP + ç ÷ dT + dn + ... + ç ÷ dn çç ÷÷ 1 j è P ¶ ø , , ,..., è T ¶ ø n ç ¶ n ÷ ¶ T n n n
P,n ,n ,...,n 1 2 1 2 è 1 ø , , ¹ 1 è j ø i i T P n n i
T ,P,n ¹n i j Đặt
là đại lượng mol riêng phần của cấu tử i
Ý nghĩa: đại lượng mol riêng phần là số đo sự thay đổi dung
độ chung của hệ khi thay đổi số mol 1 cấu tử i của hệ
VD: Hệ gồm 2 cấu tử là CH3OH (1) và C2H5OH (2) ! 𝑉
Tốc độ tăng thể tích của dung dịch != "# "$! $
theo số mol chất (1) thêm vào ",&,'
Thể tích dung dịch: V = n ! !𝑉! + n(𝑉(
IV. ĐẠI LƯỢNG MOL RIÊNG PHẦN VÀ THẾ HOÁ HỌC
1. Đại lượng mol riêng phần
Tính chất của đại lượng mol riêng phần:
- Tính chất 1: những phương trình viết cho các đại lượng
mol (hệ 1 cấu tử) đều có thể chuyển thành những phương
trình có dạng tương tự viết cho đại lượng mol riêng phần (hệ nhiều cấu tử) VD: G = H – TS →
-Tính chất 2: trong điều kiện T,P = const, đại lượng dung
độ X bằng tổng dung độ riêng phần của các cấu tử X = ån X i i
(hệ thức Gibbs – Duhem I)
- Tính chất 3: Trong điều kiện T, P = const, tổng vi phân
các đại lượng mol riêng phần của hệ bằng 0
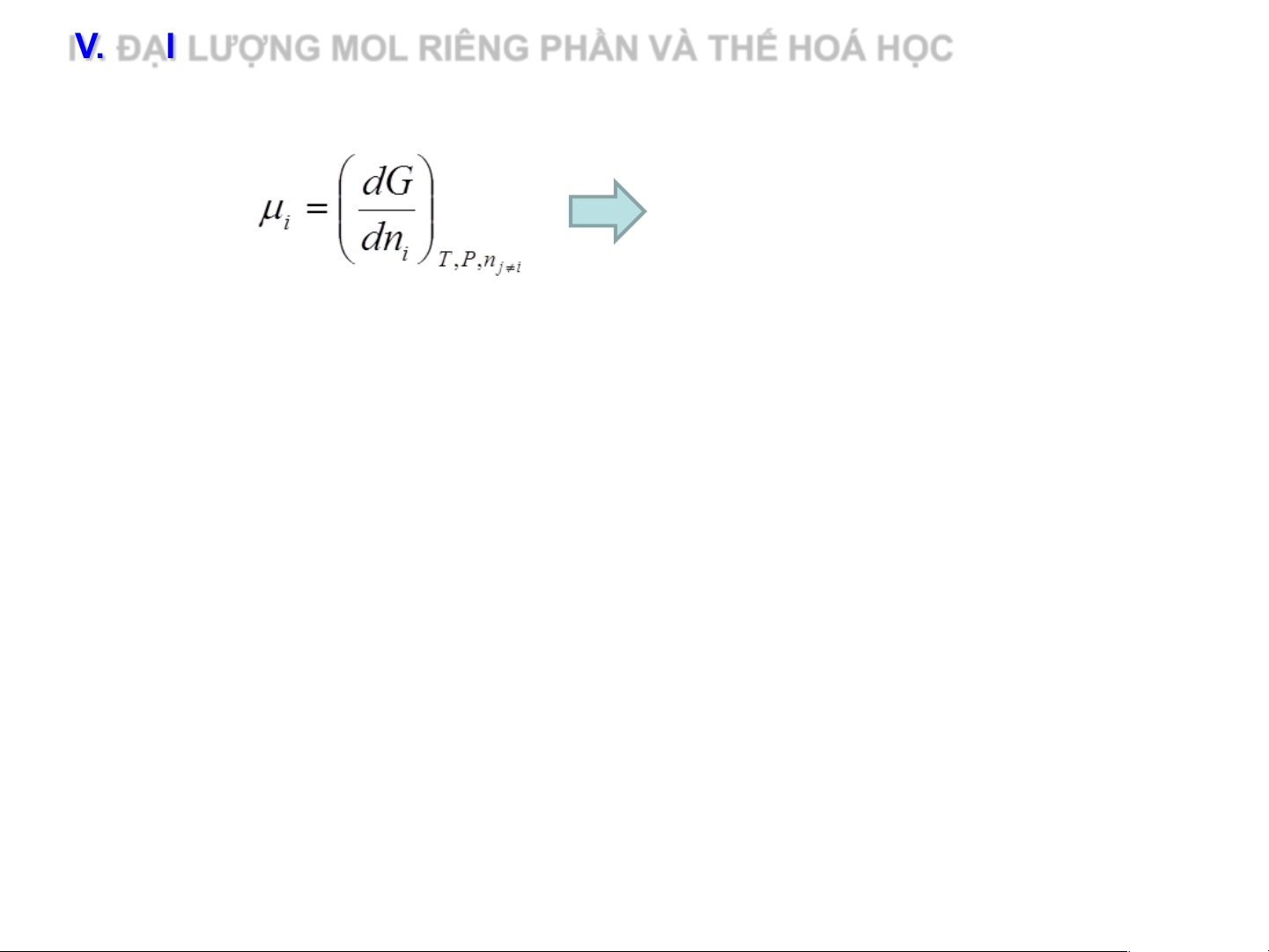
IV. ĐẠI LƯỢNG MOL RIÊNG PHẦN VÀ THẾ HOÁ HỌC 2. Thế hóa học
Tốc độ tăng thế đẳng áp của hệ
theo số mol cấu tử i thêm vào
Tính chất của thế hóa học: G = μini μi = μoi + RTlnPi Ý nghĩa:
- Thế hóa học của chất i là số đo ảnh hưởng sự thay đổi thế
đẳng áp chung của cả hệ khi thay đổi số mol cấu tử i, các
cấu tử khác được giữ không đổi
- Đặc trưng cho khả năng sinh công có ích của hệ
- Chất sẽ chuyển từ pha I sang pha II nếu thế hóa của nó ở
pha I lớn hơn pha II và sẽ đạt trạng thái cân bằng khi thế hóa
của chúng ở hai pha như nhau.




