Cơ Sở Vật Lý Điện (Từ) – Quang 1: Tóm Tắt Chương 1 Và Định Luật Coulomb môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

CƠ SỞ VẬT LÝ ĐIỆN (TỪ) – QUANG
Chương 1: Điện tích và điện trường
1. Điện tích - Định luật Coulomb. Điện - Điện tích
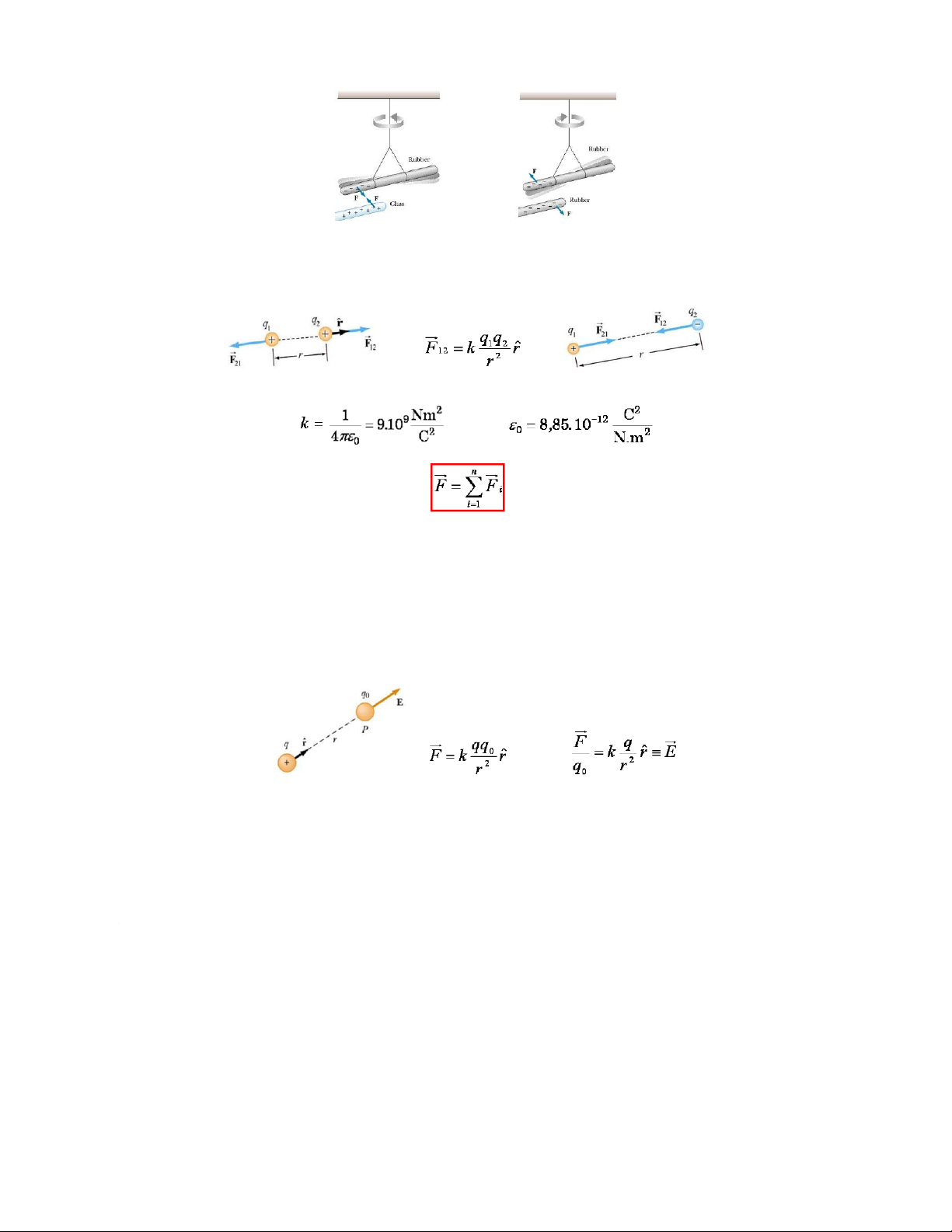
Cọ xát ↔ hút các vật nhẹ - nhiễm điện
Thực nghiệm ↔ 2 loại : điện dương và điện âm.
Quy ước: Điện dương ↔ Thuỷ tinh # Lụa. Điện â m ↔ Ebônit # Len, Dạ.
Điện tích là một thuộc tính cơ bản của vật chất.
Tồn tại điện tích tự do nhỏ nhất trong vũ trụ: Điện tích nguyên tố e = 1,6.10-19 C
Độ lớn điện tích của điện tử
Điện tích luôn luôn được bảo toàn. Sự nhiễm điện
Nhiễm điện do cảm ứng (hưởng ứng)
Nhiễm điện do tiếp xúc
Vật dẫn điện & Vật cách điện
• Vật dẫn điện (kim loại) :
điện tử có thể tự do chuyển động trong toàn bộ thể tích của vật.
• Vật cách điện (điện môi) :
điện tích bị định xứ tại các liên kết hóa học giữa các nguyên tử; chỉ có thể
được giải phóng khi vật nhận năng lượng từ bên ngoài (nhiệt, bức xạ).
Tương tác giữa các vật nhiễm điện
Các vật tích điện khác dấu hút nhau
Các vật tích điện cùng dấu đẩy nhau
Tương tác giữa các điện tích đứng yên: tương tác tĩnh điện (tương tác Coulomb). 1 Định luật Coulomb
Lực tương tác tĩnh điện giữa hai điện tích điểm có phương nằm trên đường thẳng
nối hai điện tích, có độ lớn tỷ lệ thuận với tích độ lớn của hai điện tích và tỷ lệ
nghịch với bình phương khoảng cách giữa chúng. Trong hệ SI Nguyên lý chồng chất 2. Điện trường
Điện tích gây ra một điện trường trong không gian xung quanh nó.
Điện trường - dạng vật chất đặc biệt - làm nhân tố trung gian, truyền tương tác tĩnh
điện giữa các điện tích với một vận tốc hữu hạn (c).
Tính chất cơ bản của điện trường là tác dụng một lực tĩnh điện lên bất kỳ một điện
tích nào đặt trong điện trường đó.
Cường độ điện trường
Điện trường gây bởi điện tích điểm q tại điểm P được xác định nhờ tương tác giữa
nó với một điện tích thử dương q0 đủ nhỏ đặt tại P.
Vectơ cường độ điện trường tại một điểm bằng lực tác dụng của điện trường lên
một đơn vị điện tích dương đặt tại điểm đó.
Đơn vị SI của cường độ điện trường là N/C. 2
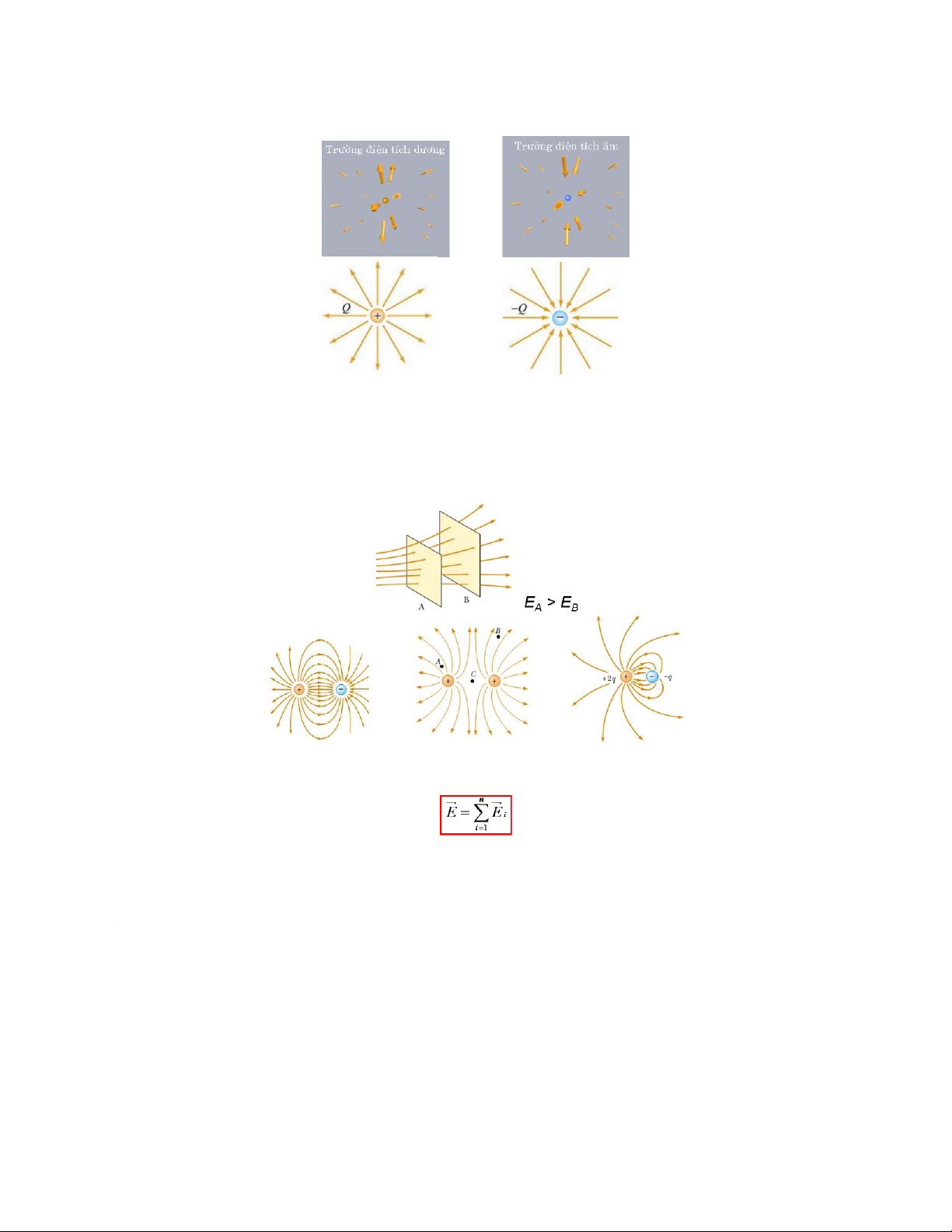
Đường sức điện trường
biểu diễn đơn giản, trực quan bức tranh không gian của điện trường
Tiếp tuyến tại mỗi điểm của đường sức điện trường trùng với phương của vectơ
cường độ điện trường tại điểm đó.
Chiều đường sức là chiều vectơ cường độ điện trường.
Quy ước: Số đường sức điện trường đi qua một đơn vị diện tích đặt vuông góc với
đường sức tại mỗi điểm tỷ lệ với độ lớn của cường độ điện trường tại điểm đó.
Độ lớn của cường độ điện trường tại mỗi điểm tỷ lệ với mật độ đường sức tại điểm đó.
Tìm cường độ điện trường tại một điểm
+ Hệ điện tích điểm phân bố rời rạc 3
+ Vật có điện tích phân bố liên tục
Mật độ điện tích dài
Mật độ điện tích mặt
Mật độ điện tích khối
3. Thông lượng điện trường
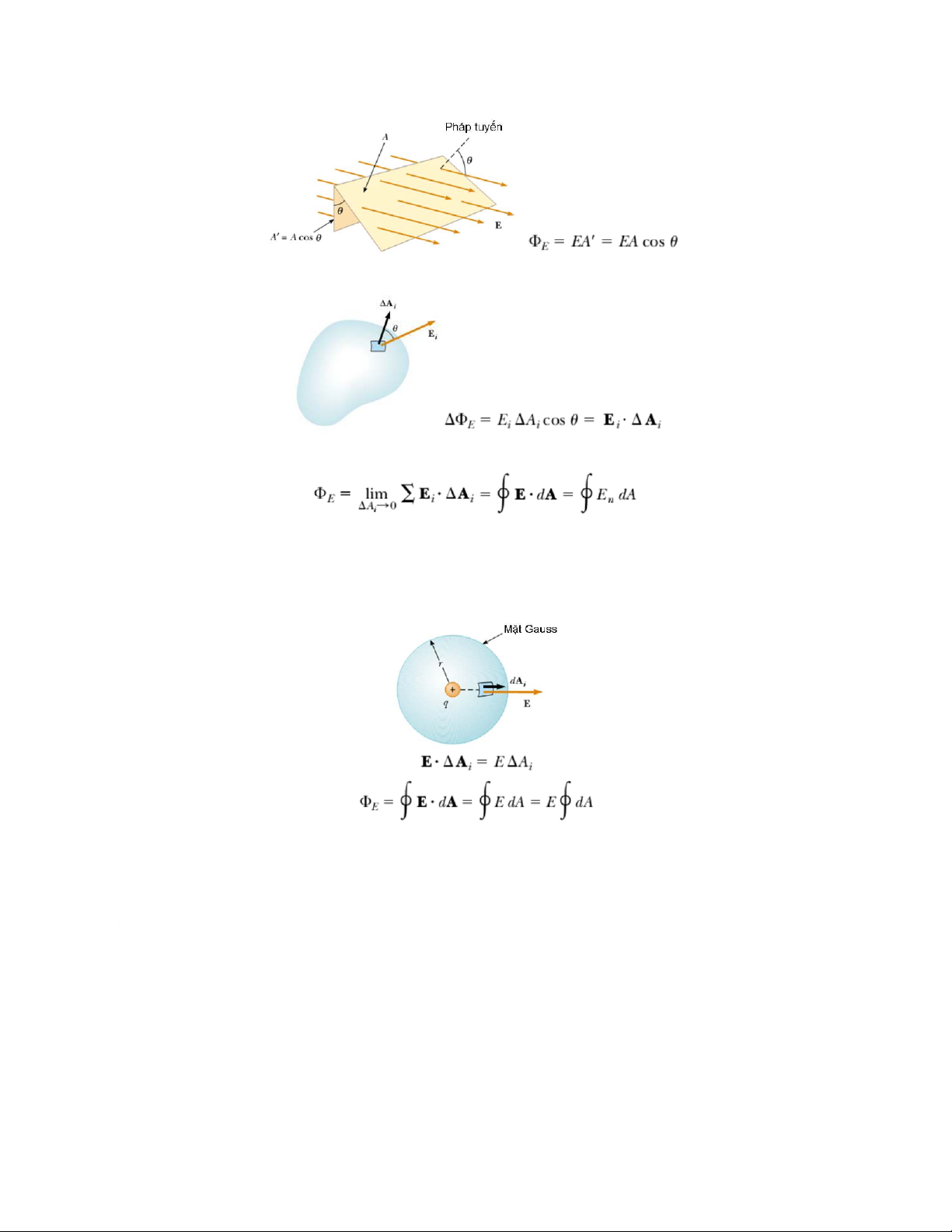
+ Thông lượng điện trường qua mặt phẳng thẳng góc
Thông lượng điện trường tỷ lệ với số đường sức đi qua mặt A! 4
+ Thông lượng điện trường qua mặt phẳng xiên
Số đường sức đi qua mặt A = Số đường sức đi qua mặt A’ !
+ Thông lượng điện trường qua một mặt kín bất kỳ
Vector diện tích Ai có độ lớn bằng diện tích mặt Ai hướng theo pháp tuyến ngoài n của mặt Ai . 4. Định lý Gauss
liên hệ thông lượng điện trường qua một mặt kín(mặt Gauss) với tổng điện tích chứa trong mặt kín đó.
Xét một điện tích điểm +q nằm ở tâm một mặt cầu bán kính r (mặt Gauss).
Tại mỗi điểm trên mặt cầu, vector E luôn song song với vector Ai 5
Thông lượng điện trường qua mặt cầu không phụ thuộc bán kính r và tỷ lệ với điện
tích chứa trong mặt cầu đó.
Thông lượng điện trường toàn phần đi qua một mặt kín bất kỳ bao quanh một điện tích điểm q bằng q/ε0.
Thông lượng điện trường toàn phần qua một mặt kín bất kỳ không chứa điện tích phải bằng 0.
Nếu trong mặt kín có chứa hệ điện tích điểm và/hoặc vật có điện tích phân bố liên
tục, ta áp dụng nguyên lý chồng chất để tính thông lượng điện trường toàn phần:
Định lý Gauss: Trong chân không, thông lượng điện trường toàn phần qua
một mặt kín bất kỳ bằng tổng điện tích qin chứa trong mặt kín đó chia cho ε0.
LƯU Ý: Mặt Gauss chỉ là một thủ thuật toán học. Nếu biết cách chọn mặt Gauss,
ta có thể dễ dàng tính tích phân thông lượng điện trường ФE. 6
Định lý Gauss được dùng để tính cường độ điện trường trong các trường hợp
phân bố điện tích có tính đối xứng cầu, trụ hoặc đối xứng qua mặt phẳng. Áp dụng định lý Gauss
1. Xác định miền cần tính cường độ điện trường E.
2. Chọn mặt kín Gauss sao cho tại mỗi điểm trên mặt đó:
hoặc E song song với dA và E = const → dФE = + EdA hoặc dФE = – EdA;
hoặc E vuông góc với dA → dФE = 0. 3. Tính tích phân ФE.
4. Tính tổng điện tích qin chứa trong mặt Gauss.
5. Tính độ lớn cường độ điện trường E từ định lý Gauss.
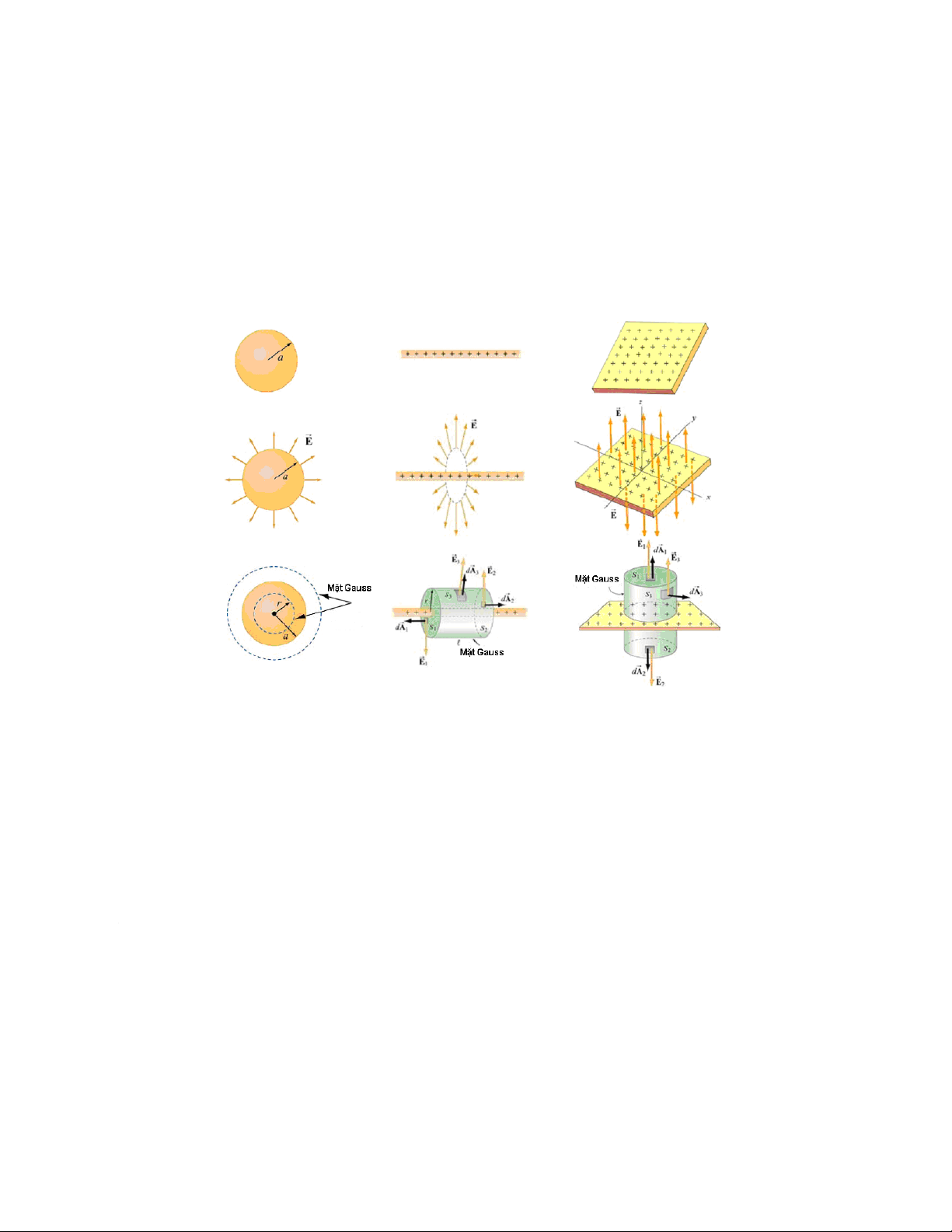
Quả cầu tích điện đều Dây thẳng dài vô hạn tích điện đều Mặt phẳng vô hạn tích điện đều 7 8