PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN
CÔNG THỨC VẬT LÝ ĐẠI CƯƠNG II (PH1120)
CHƯƠNG I. TRƯỜNG TĨNH ĐIỆN | q || q |
k | q || q |
1. Lực tương tác Coulomb giữa 2 điện tích: 1 2 1 2 F   . với 2 2 4π 0 ε εr εr 2 2 C   1 Nm 12 7 9 ε  8,86.10 ; μ  4π.10 H / ; m k   9.10 0 2 0 2 Nm 4πε0 C
2. Điện trường: Vector cường độ điện trường:
▪ Cường độ điện trườ
ng tại 1điểm cách điện tích điểm (cầu rỗng) mang điện: • M | q | k | q | • N r E   E   . q 2 2 4πε εr εr 0 R
▪ Cường độ điện trường gây
bởi 1 sợi dây thẳng (trụ rỗng)
dài vô hạn mang điện đều tại 1 điểm cách dây khoảng r: λ 2kλ E   . với λ : m
ật độ điện dài của dây. A • 2πεε r εr q A 0 r A r
▪ Cường độ điện trường gây
bởi 1 mặt phẳng mang điện
đều tại mọi điểm xung quanh mặt đề ằ u b ng: σ E  . σ : m
ật độ điện tích mặt. 2ε ε 0
▪ Cường độ điện trườ ng t m
ại điể nằm trên trục mặt phẳng đĩa tròn bán kính R n
mang điệ q cách tâm đĩa     h σ 1
khoảng h: E     A 1 . 2 • A   • B 2 ε ε 0 R  1  2  h h 
▪ Cường độ điện trườ ng t m
ại điể nằm trên trục vòng dây tròn R R q qh tích điện bán kính q
R, cách tâm vòng khoảng h: E  . B 4πε . ε R  h 3 2 2 2 0
▪ Cường độ điện trườ
ng tại điểm M nằm trong quả cầu đặc bán kính R cách tâm khoả qr E  . r  R • N ng r: ( ) M 3 • M r 4πε εR 0 R
▪ Cường độ điện trườ
ng tại điểm N nằm ngoài quả cầu đặc bán kính R cách tâm khoả q ng r: E  . (r  R) N 2 4πε εr 0
▪ Cường độ điện trườ
ng tại điểm M nằm trong ng t ố r
ụ đặc bán kính R λr R
cách trục khoảng r: E  . (r  R) M 2 2πε εR 0 r
▪ Cường độ điện trườ ng tại điểm N n ng t ằm ngoài ố r
ụ đặc bán kính R M • • N λ
cách tâm khoảng r: E  . (r  R) N 2πε εr 0
 Tổng quát cho trường hợp quả cầu r ng hay tr ỗ
ụ rỗng tương tự như quả c c ầu đặ hay tr ụ đặc .Chỉ khác
điện trường bên trong chúng bằng 0. ▪ Trường hợp 2 mặt c t
ầu đồng tâm (2 mặ trụ ng t song song đồ
rục)  xem xét vị trí điểm: ✓ Điểm n t
ằm ngoài mặ cầu (trụ) trong, nằm trong mặt cầu (trụ) ngoài  Chỉ mặt cầu trong gây ra E. 1 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN
✓ Điểm nằm trong cả 2 mặt  E = 0. ✓ Điểm n 2 m ằm ngoài cả
ặt  Cả 2 mặt đều gây ra E  Áp dụng nguyên lý chồng chất E.
3. Điện thế. Hi n
ệu điệ thế:  • A V  Er r  Quy t c
ắ chung: dV  Edr . (Điện trường đều). q •  rB U  Edr AB r   A q •
▪ Điện thế do điện tích điểm q t gây ra ại A: V   Er A  . • N M r 4 π 0ε εr R
▪ Điện thế do mặt cầu rỗng bán kính R gây ra tại điểm: q
✓ Bên trong mặt cầu (M): VM = 0. q
✓ Bên ngoài mặt cầu (N) , cách tâm mặt cầu đoạn r: V 
 Er (coi như điện tích điểm). N  . 4πε εr 0 q
✓ Sát mặt cầu (do không xác đinh được trên mặt cầu): V    Er. 4π 0 ε εr
Q (R  R )
▪ Hiệu điện thế giữa hai mặt cầu đồng tâm, mang điệ ằng nhau, trái dấ n b u: 2 1
U  V V  . 1 2 4π 0 ε ε 1 R 2 R λ R
▪ Hiệu điện thế giữa hai mặt trụ đồng trục, mang điệ ằng nhau, trái dấ n b u: 2
U  V V  ln . 1 2 2πε ε R 0 1  Chủ y ếu dùng để
liên hệ giữa U và , q , λ σ, . ρ
4. Công. Năng lượng.  A   qU  Quy t c ắ chung: dA 
 q.dU  qEdr  r2 • A  A  q Edr r rA  1
▪ Công mà lực điện trường thực hiện khi điện tích q di chuyển trong nó: r B r λ r • B B
✓ Dây dẫn thẳng: A  q Edr  q ln B .  A r 2πε ε r 0 A • A r A r • Q   B qQ 1 1
✓ Điện tích điểm: A  q Edr   .    r r B A 4πε ε  r r 0 A B  • A • A   Qr h  
✓ Trên trục vòng dây: A q Edr q dr.   h h 4πε ε R  r 0  3 2 2 2 R Q
5.Dạng bài tập hai quả cầu giống nhau treo trong chất điện môi: α
Khối lượng riêng của mỗi quả cầu để góc lệch trong điệ môi và không khí là như nhau là: n ερ 1 ρ 
. Trong đó: ρ là khối lượng riêng của điện môi, ε là hằng số điện môi. 1 ε  1
6. Dạng toán hạt mang điện rơi tự do:
Hạt mang điện rơi tự do trong không khí với vận tốc v , khi có điện trường rơi với vận tốc v 1 2 • q • q   mg v
Khi đó điện tích q của hạt: 2 q  1  . E v  1 
7. Một số công thức dạng bài tập khác: 2 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN qQ
▪ Lực gây ra tại tâm nửa vòng xuyế mang điện tích n
Q bán kính R: F  . 2 2 R 2π ε εR 0 • q σ Q
▪ Điện trường trên trục đĩa tròn bán kính R bị khoét 1 lỗ bán kính r: E  . 2 r 2ε ε 1 0 2 R
▪ Điện trường cách thanh kim loại (dây) dài hữ ạn trên trung trự u h
c của thanh (dây), cách thanh (dây) đoạ q
n h, cách đầu mút của thanh (dây) đoạn R: E  . • A • A 4πε0εhR h R R  h
CHƯƠNG II. VẬT DẪN – TỤ ĐIỆN
1. Điện dung: q Công thứ Q c chung: C  . U ε εS ▪ Tụ ẳ ph ng: 0 C  . với :
S diện tích mỗi bản tụ, :
d khoảng cách giữa hai bản tụ. d c u: R ▪ Tụ ầ
✓ Tụ cầu 1 mặt: C  4πε .
εR với R: bán kính mặt cầu. 0 R R ✓ Tụ cầu 2 mặt: 2 1 C  4πε ε . với R 0
1,R2: bán kính hai mặt cầu. R2 R  R 2 1 R1 2πε εh C  ớ ề ụ ụ h tr : 0
. v i h: chi u cao t , R1,R2: Bán kính hai mặt tr . ▪ Tụ ụ R 1  R  2 ln  R  1 
2. Mắc ghép tụ điện: n 1 1 1 1 1 C1 C C C1 2 n ▪ Mắc nối tiếp:    ...  .  C C C C  C 1 2 n i 1 i C 2 n
▪ Mắc song song: C  C  C  ... C   C n . i . 1 2 i 1 C n
3. Các công thức liên quan tới tụ điện: W σ q 1
▪ Lực tương tác giữa hai bản tụ: F  .
Điện trường trong tụ: E   . . d ε ε S ε ε 0 0
4. Dạng e
bài tập tính công lectron chuy n
ển độ g trong tụ c u
ầ (trụ) : ▪ Xét tụ điện có R , R a
là các bán kính củ hai mặt, hiệu điện thế U. electron chuyển động t ừ hai điểm 1 2 trong t
ụ A tới B có khoảng cách so với tâm (trục) c a ủ t
ụ tương ứng là r r r  r A, B ( B A ) ➢ Tụ trụ:  r   r  eU ln A   2eU ln A   r   r  Công của electron B A  , vận t c ố của electron: B v  . ,  R   R  2 ln   2 m ln  R   R 1  1  h R rA 1  9 3  1 • A rB e  1,6.10
C,m  9,1.10 kg • B Chứng minh: λ 2πε εl q λl 2πε εU
dA  q Edx  eEdx   e dx Mà 0 0 C     λ  e 2πε εx  R  U U   0 R 2 2 ln  ln  R R  1   1  3 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN  r   r  eU ln A   2eU ln A 2   r r U  r B B mv  r B    A  dA   e dx  .   Lại có B A   v  . r r       A A R R 2 R 2 2 xln   ln   2 m ln   R   R 1 1   1 R  ➢ Tụ cầu:
eUR R (r r )
2eUR R (r r ) Công của electron 1 2 A B A 
, vận tốc của electron: 1 2 A B v  ,
(R  R )r r
m(R R )r r 2 1 A B 2 1 A B 1  9 3  1   R e 1,6.10
C,m 9,1.10 kg 2 R Chứng minh: • A 1 q 4πε εR R q 4πε εR R U rB
dA  q Edx  eEdx   e dx Mà 0 1 2 0 1 2 C    q  e 2 • B 4πε εx R  R U R  R 0 2 1 2 1 2 r r  mv
2eUR R ( r  r ) B B R R U eUR R (r r A B ) 1 2 1 2  A  dA   e dx  .   Lại có 1 2 A B A   v  . 2 r r  A A
(R  R )x
(R  R )r r 2 m(R R )r r 2 1 2 1 A B 2 1 A B
5. Dạng toán năng lượng: 2 ε εE ED ▪ M
ật độ năng lượng điện trường: 0 w   . 2 2 2 2 2 2 ε εE ε εSU ε εE Sd σ Sd ▪ ng c Năng lượ a ủ t ụ điện phẳng: 0 0 0 W  . wV  S w .D  dV    .  2 2d 2 2ε ε V 0
(còn gọi là công cần thiết dịch chuyển 2 bản tụ lại gần nhau). 2 2 QU CU Q ▪ ng c Năng lượ a ủ t
ụ điện (dùng chung mọi t ) ụ : W    . 2 2 2C 2 2 QV CV Q ▪ ng v Năng lượ ật dẫn: W    . 2 2 2C 2 Q
▪ Năng lượng điện trường bên trong quả cầu điện môi ε tích điện Q, bán kính R: W  40πε εR 0 Chứng minh: R  1 2 2 W  ε εE dV ;dV   4πr dr  0 R 2 4 2 2  2 Q r Q Q 0   W  dr   . k .  6  1 Qr 8πε εR 40 πε εR 10 εR 0 0 0 E  3  4πε ε R 0 2 Q
▪ Năng lượng điện trường bên ngoài quả cầu điện môi ε tích điện Q, bán kính R: W  8πε εR 0 Chứng minh:   1 2 2 W   ε εE d ; V dV  4 πr dr  0  2 2 2  2 Q Q Q R   W  dr   k. .  2 1 Q 8πε εr 8πε εR 2εR R  0 0 E  2  4πε ε r  0
6. Dạng toán tụ điện m t
ộ nửa chứa điện môi, nửa còn lại không: 2πε (ε  1)R R 1 ▪ Tụ cầu: 0 2 1 C   C (ε  1). 0 R  R 2 2 1 4 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN Trong đó C n dung c là điệ a ủ t
ụ điện bình thường với kích thước tương đương và không chứa điện 0 môi. πε ( ε 1) l 1 ▪ Tụ trụ: 0 C   C (ε 1). 0  R  2 2 ln   R  1  Trong đó C n dung c là điệ a ủ t
ụ điện bình thường với kích thước tương đương và không chứa điện 0
môi, l là chiều cao của tụ.
CHƯƠNG III. ĐIỆN MÔI
1. Liên hệ giữa vector cường độ điện trường và vector điệ
n cảm: | | q Vector cảm n c ứng điện (điệ
ảm): D  ε εE  D  . 0 2 4πr
2. Định lý Ostrogradski – Gauss trong điện môi, vector phân cực điện môi: n
▪ Công thức OG: Φ   e i S 1 
▪ Vector phân cực điện môi: P  χε E ; D  ε E  P với ε 1 χ ,
ệ ố phân cực điện môi. 0 0 χ : h s
3. Mật độ điện tích liên kết: U
σ ' P  χε E  ε  ε E  ε  ε n n ( 1) ( 1) . 0 0 0 d
Trong đó: P E là hình chiếu của vector phân cực điện môi và vector cường độ điện trường lên n , n
phương pháp tuyến ngoài của mặt có điện tích xuất hiện. d
4. Dạng toán đặt tấm điện môi vào giữa tụ điện phẳng điện dung C: ε εS 0 C '   C S εd  (1 ε )d '
Trong đó: d: khoảng cách giữa hai bản tụ điện, :
d’ bề dày tấm điện môi.
CHƯƠNG IV. TỪ TRƯỜNG d’
1. Dạng bài tập tìm cảm ứng từ B, cường độ
từ trường H:
▪ Tại điểm A cách dây dẫn thẳng dài đoạn r:  μ . μ I(cos θ  cos θ ) 0 1 2 B   4πr θ   0 μ . μ I I  .  Dây dài vô hạn: 1 0  B   H   . B I (cosθ  cosθ )  1 2  θ π 2πr 2πr H    2. • A  μ μ  4πr 0 r I
▪ Vòng dây tròn bán kính R:
Tại điểm A là tâm của vòng dây: • M  μ . μ I  1 μ . μ I 0 B  0 B'  B  h  2  R  2 4 R  . ửa vòng dây:  . R  N B I  1 B ' I  H   H  H   A • ' • A I  μ μ 2 R  2 μ μ 4 R I  0 0
Tại điểm M nằm trên trục của dây dẫn: 2  μ μ.IR 2  1 μ μ .IR 0 0 R B   B'  B   3  2 2 2 2 2  R h  3 2 2 2  4  R  h  • B • A  .  Nửa vòng dây:  . 2 B IR  2  1 B ' IR H       H ' H 3 μ μ  2 2 μ μ  R  h 3 2 2 2 0 2 2 2  0 4  R  h  
▪ Dây dẫn điện đặc dạng hình trụ bán kính R. 5 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN μ μIr
▪ Tại điểm A nằm bên trong dây dẫn: (r  R 0 B  A . A ) 2 2πR μ μI
▪ Tại điểm B nằm bên ngoài dây dẫn: (r  R) 0 B  A . B 2πr
2. Dạng toán hạt mang điện chuyển động trong từ trường B:
▪ Lực Lorentz: F  qv  B  F  qv B  q . vB sin α , L n
▪ Vận tốc: v  v sin α n
Nếu là electron: F  ev .B  ev .
B sin α . Trong đó v: vận tốc chuyển động của hạt, α  ( ; v B) là góc n
hợp bởi phương bay của h ng c ạt và hướ ủa từ trường. ▪ Bán kính quỹ đạo: π mv ➢ Dạng chuy ng s
ển động tròn đều: Khi điện tích bay vuông góc với đườ ức từ ( α  ): R  2 qB mv sin α ➢ Dạng xoắn p v
ốc: Khi điện tích bay phương hợ
ới đường sức từ góc α : R  qB Bướ 2πmv 2πmv cosα h 2πm π πR c xoắn c ố : 1 h  v T   Chu kỳ: T   hoặ 2 2 c: T   1 qB qB v qB ω v E
▪ Liên hệ g ữa B và E khi electron không lệ i
ch khỏi quỹ đạo: B  . v a
3. Từ thông, khung dây, vòng dây: r
▪ Từ thông: Φ  BS  BdS  I a S b
▪ Từ thông dây dẫn mang điện I1 gây ra cho khung dây a b đặt cách dây đoạn r: r a  μ μI bdx μ μI b r a  0 1 0 1 Φ   Φ  ln .    r 2πx 2π  r 
▪ Trường hợp thanh kim loại có chiều dài quét trong từ a
trường do dây dẫn mang điện gây ra thì ta coi
vùng mà thanh quét được là một khung hình chữ nhật (cùng hình minh họa trên), khi đó: r a  μ μI bdx μ μI b r a  0 1 0 1 Φ   Φ  ln .    Trong đó: : là b d
độ ời của thanh sau khi thanh quét r 2πx 2π  r  được.
▪ Công của lực từ khi cho khung dây
a bquay: Khi đó trong khung dây cần xuất hiện dòng điện (I ) 2 μ μI I b  r  a 
A  I .ΔΦ  I Φ Φ   0 1 2  A  ln . 2 2 2 1   π  r 
4. Dạng toán vòng xuyến đặt trong từ trường:
Vòng xuyến bán kính R, mang dòng điện có cường độ I. Lực từ tác dụ BIl
ng: F  BIR 
, Trong đó l  πR là độ dài vòng xuyến. π 6 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN
CHƯƠNG V. CẢM ỨNG ĐIỆ N TỪ
1. Biểu thức của suất điện động cảm ứng và suất điện động tự cảm: Φ d dI Φ E   ; E  L ; Trong đó: L 
được gọi là độ tự cảm hay hệ s t ố ự cảm. c tc dt dt I
2. Cuộn dây tự cảm: dI
▪ Suất điện động tự cảm: E  L . ; tc dt
▪ Từ thông gửi qua cuộn dây: Φ  . L I 1
▪ Năng lượng từ trường trong lòng c ộn dâ u y: 2 W  LI . 2 2 W 1 B
▪ Mật độ năng lượng từ trường: w   . V 2 μ μ 0 Chứng minh: 2 1  N S  2 2  1  N S  μ μ I 2 1 2  0  2 W   LI  μ μ I   W 2 l   1 N Ta có: 0 2  2 2 l  w    μ μ I   0 2 V lS 2 l V  lS 2 1 B Mà: N B   w  . ống dây: 0 μ μ I (Trong B = constain) . l 2 μ μ 0 1
▪ Năng lượng từ trường trong không gian: W  BHdV  2 V Chứng minh: Ta chia nh
ỏ không gian V càn tính thành các thể
tích vô cùng nhỏ dV, trong mỗi dV thì B = constain. 2 2 1 B 1 B  W d  wdV  dV  W  W d  dV    2 V μ μ 2 μ μ  0 V V 0 1   W  BHdV . V  B 2  V H  μ μ  0 
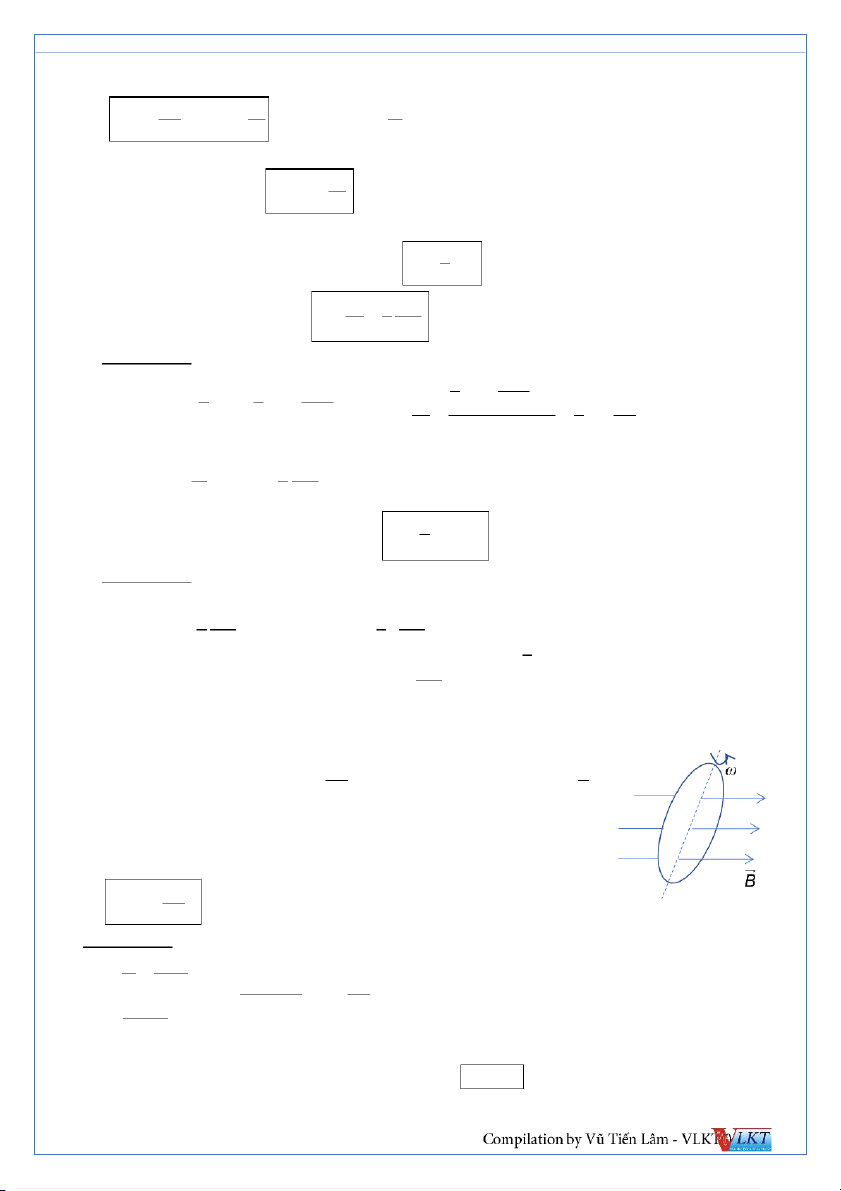
3. Ống dây quay trong từ trường: Φ   B c S os ωt  
Các đai lượng biến thiên: Φ d  π .  E    BSωsin  ωt   BSωcos ωt    dt   2 
▪ Từ thông cực đại: Φ  BS. 0
▪ Suất điện động cảm ứng cực đại: E  BS . ω 0 S
4. Hệ số tự cảm của ống dây: 2 N L  μ μ
S ; Trong đó: N là số vòng dây, l là chiều dài ống, S là tiết diện ngang của ng. ố 0 l Chứng minh:  Φ NBS L   2 2  I I μ μN IS N 0   L   μ μ . S 0 μ μNI  0 lI l B   l
5. Bài toán thanh dẫn chuyển động vuông góc trong từ trường:
Khi đó: suất điện động cảm ứng xuất hiện trong thanh: E  Blv c
Trong đó: l là chiều dài củ
a thanh, v là tốc độ
chuyển động của thanh trong từ trường B. 7 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN
6. Mạch tự cảm:
Ban đầu mạch ổn định, xuất hiện dòng điện I chạy trong mạch. Khi ngắt khóa K của mạch 0  R r    t  
▪ Dòng điện I còn lạ i sau thời gian t:  L I I e   . 0 t
▪ Nhiệt lượng tỏa ra trên điện trở: 2 Q  RI dt .  0 
▪ Toàn bộ nhiệt lượng: 2 Q  RI dt.  0
CHƯƠNG VI TRƯỜNG ĐIỆ . N TỪ
1. Hệ phương trình Maxwell:
▪ Phương trình Maxwell – Faraday: 
Nội dung: Từ trường bi
ến thiên theo thời gian sinh ra điện trường xoáy. Bd S  dt  (C) S  .  B rot E    t 
▪ Phương trình Maxwell – Ampère:  
Nội dung: Điện trường biến thiên theo thời gian sinh ra từ trường.  d  S  t  (C) S    .
rotH  j   t 
▪ Phương trình Ostrogradski – Gauss đố i với điện trường: 
Nội dung: Điện thông gửi qua một mặt kín bất kỳ bằng tổng số điện tích  trong đó. S V  .
Trong đó: ρ là mật độ điện khối. di  vD  ρ
▪ Phương trình Ostrogradski – Gauss đố i với từ trường: 
Nội dung: Đường sức từ a t
là đường khép kín (tính bảo toàn củ ừ thông).  S  . divB   0
▪ Nếu môi trường đồng chất và đẳng hướng thì trường điện từ còn nêu lên tính chất điện và từ:  D  ε εE
Nội dung: Các tính chất điện và từ củ trường điệ a n từ. 0  Trong đó: σ n d là điệ
ẫn suất của môi trường (ph t
ụ huộc vào bản chất vật B  μ μH. 0 dẫn).  j  σE 
2. Liên hệ giữa mật độ dòng điệ
n dịch ( j ) và mật độ dòng điện dẫn ( j ) : d
▪ Dòng điện dịch: I  j S d d .
▪ Dòng điện dẫn: I  j.S , Trong đó: S a
là diện tích củ bản t . ụ
3. Vector mật độ dòng điện tích: E
Trong lòng tụ có điện trườ
ng E  E(t):  Vector m
ật độ dòng điện dịch: j   ε ε . d 0 t t E
Vector mật độ dòng điện toàn phần: j  j  j  σ E  ε ε tp d . 0 t 
4. Trường điện từ và năng lượng điệ
n từ:
▪ Mật độ năng lượng trường điện từ bằng tổng mật độ năng lượ
ng của điên trường và từ trường: 1 w  w   ε εE  μ μH  DE  B H e w m  1 2 2 . 0 0    2 2 8 PH1120
VIỆN VẬT LÝ KỸ THUẬT - ĐHBKHN
▪ Năng lượng trường điên từ: 1 W  wdV    1 2 ε εE  μ μH  2 dV  DE  BH dV. 0 0    2 2 V V V
CHƯƠNG VII. DAO ĐỘNG VÀ SÓNG ĐIỆN TỪ
1. Mạch dao động:  Q  Q cos ωt 0     Q
▪ Các đại lượng biến thiên: U   C   dQ  π  I    Q ωcos ωt   I  I  Q ω  0   max 0 0  dt  2  1 2π
▪ Tần số góc cộng hưởng: ω  , chu kỳ: T   2π LC. 0 LC ω0
2. Năng lượng: 1
▪ Năng lượng từ trường trong ống dây: 2 W  LI B 2 2 1 1 1 Q
▪ Năng lượng điện trường trong tụ điện: 2
W  CU  QU  . E 2 2 2 C
▪ Năng lượng điện từ toàn phầ n: W  W  W . B E
3. Dao động điện từ tắt dần:
▪ Phương trình dao động điện từ tắt dần: βt I  I e cos ωt  φ . 0   Trong đó: R β  được g s ọi là hệ t
ố ắt dần của dao động. 2L 2 1  R  2π 2π ▪ Tần số góc: 2 2 ω  ω  β   . Chu kỳ: T   . 0   LC  2L  2 ω 1  R     LC  2L 
▪ Giảm lượng loga: δ  βT.  γ  ln   100 
▪ Thời gian để biên độ g ảm còn lạ i iγ(%) : t  . 2  β
4. Dao động điện từ cưỡng bức:
▪ Phương trình dao động điện từ cưỡng bức: I  I cos Ωt  φ . 0   1 ΩL ξ Trong đó: 0 I 
. φ là pha ban đầu của dao động, với Ω cot C φ  . 0 2   R 2 1 R  ΩL   Ω   C  1
▪ Tần số góc cộng hưởng: Ω  ω  . ch 0 LC 9