ĐẠO HÀM CỦA MỘT SỐ HÀM SỐ THƯỜNG GẶP
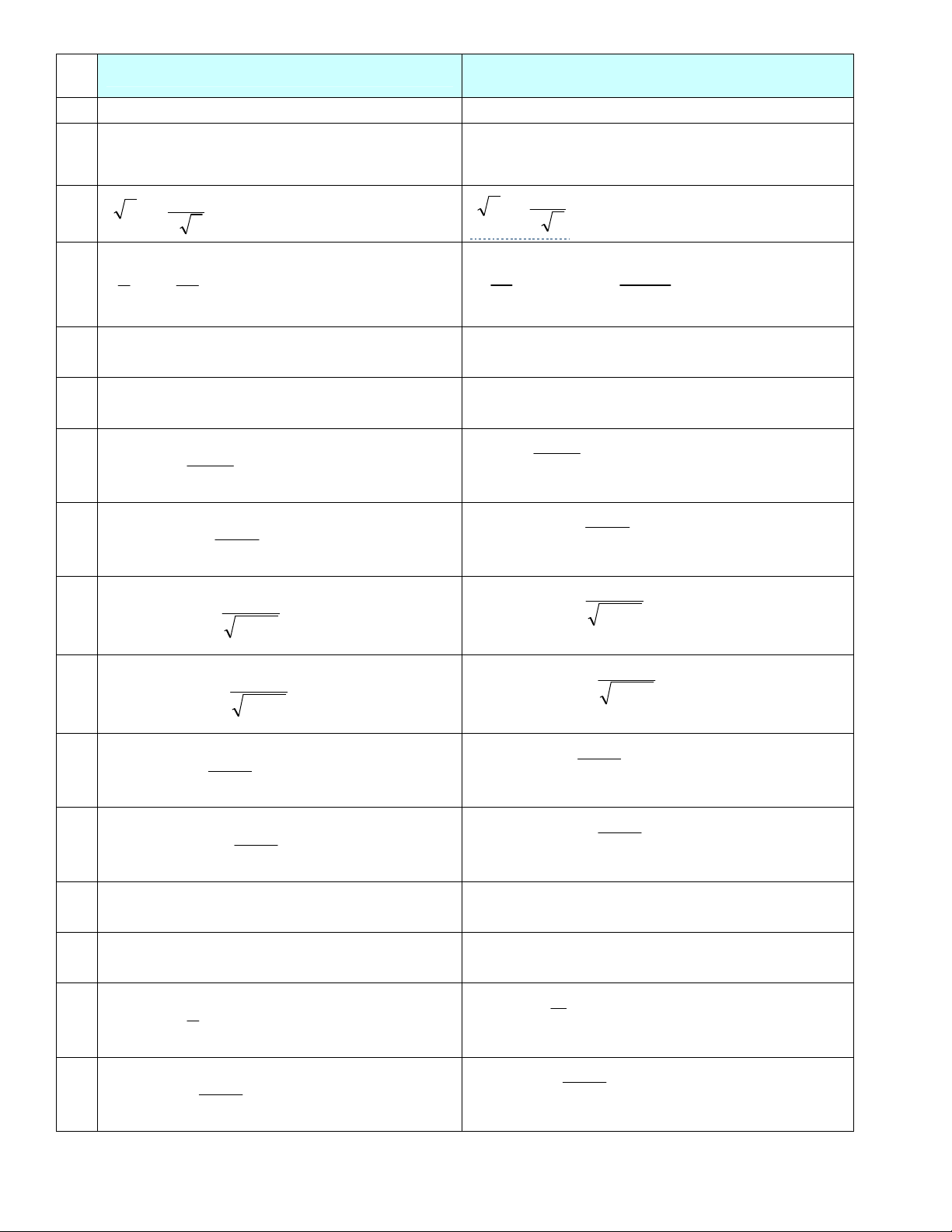
Đạo hàm của hàm hợp
Đạo hàm theo biến x 1
C = 0 (C là hằng số) 2    x = α.xα -1    u = α.uα -1.u’  1  u' 3  x   u  2 x 2 u   u   1  1 4 1        u   x  x2 2 u (sin u)’ = cos u. u’ 5 (sin x)’ = cos x (cos u)’ = - sin u. u’ 6 (cos x)’ = - sin x  u 1 tgu  7 (tg x)’ = 2 cos u 2 cos x u 1 (cotg u)’ =  8 (cotg x)’ = - 2 sin u 2 sin x u 1 (arcsin u)’ = 9 (arcsin x)’ = 2 1  u 2 1  x u 1 (arccosu)’ =  10 (arcos x)’ =  2 1  u 2 1  x u 1 (arctg u)’ = 11 (arctg x)’= 2 1  u 2 1  x  u  1 (arccotg u)’ = 12 (arccotg x)’ = 2 1  u 2 1  x (ex)’ = ex 13 (eu)’ = u’.eu 14 (ax)’ = lna. ax
(au)’ = u’. lna. au (điều kiện: a>0) (điều kiện: a>0) u 1 (ln u)’ = (điều kiện: u >0) 15 (ln x)’ = (điều kiện x>0) u x u 1 (logau)’ =
(điều kiện a>0, u>0) 16 (logax)’ =
(điều kiện x>0, a>0) u.ln a x.ln a
XQ- caohockinhte.vn 24/6/2010
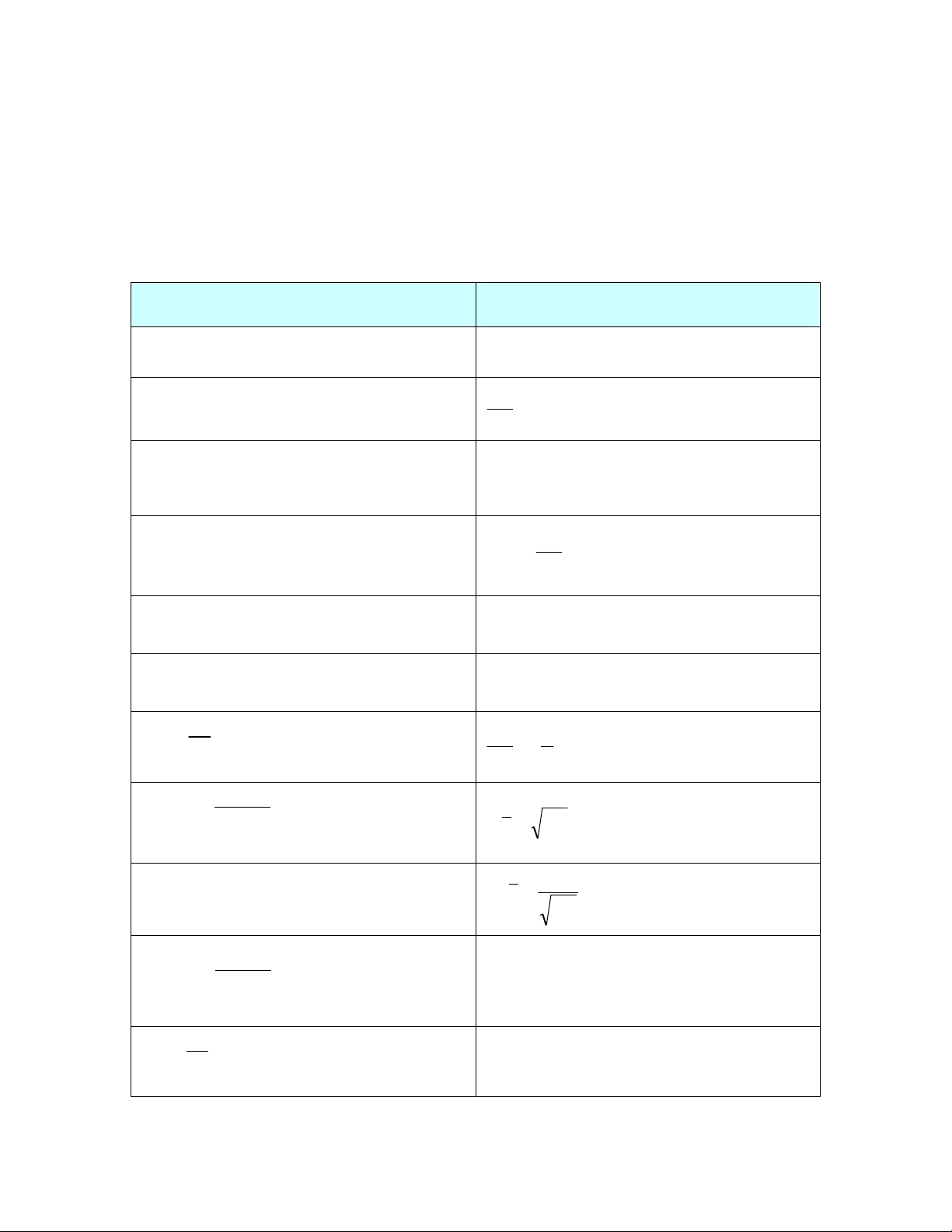
HÀM SỐ MŨ VÀ LOGARIT * Định nghĩa:
M = logax  aM = x (điều kiện: x>0, a>0)
Hàm mũ y = ax và hàm logarit y = logax là 2 hàm ngược nhau. * Lưu ý:
Hàm y = logax thì điều kiện là a>0, x>0;
Hàm y= ax thì điều kiện là a> 0, a  1; * Tính chất: Hàm mũ Hàm logarit logaa = 1 am. an = am+n am m n log  a1 = 0 n a a logaaM = M n  m.n
am  a M  m 1 a log  a = M (a mũ logaM) a am  M log = M  log a  a0 = 1 MN  M  N log log log a a a am.an = (ab)m M m log m  M N log  log  a a  a N a a    m  b  b log 1 b  m a log a n m n a  a b log m ab.logbc = logac  1 n  a n m a log c c log = a b log b a
log 1  log M a M a
XQ- caohockinhte.vn 24/6/2010