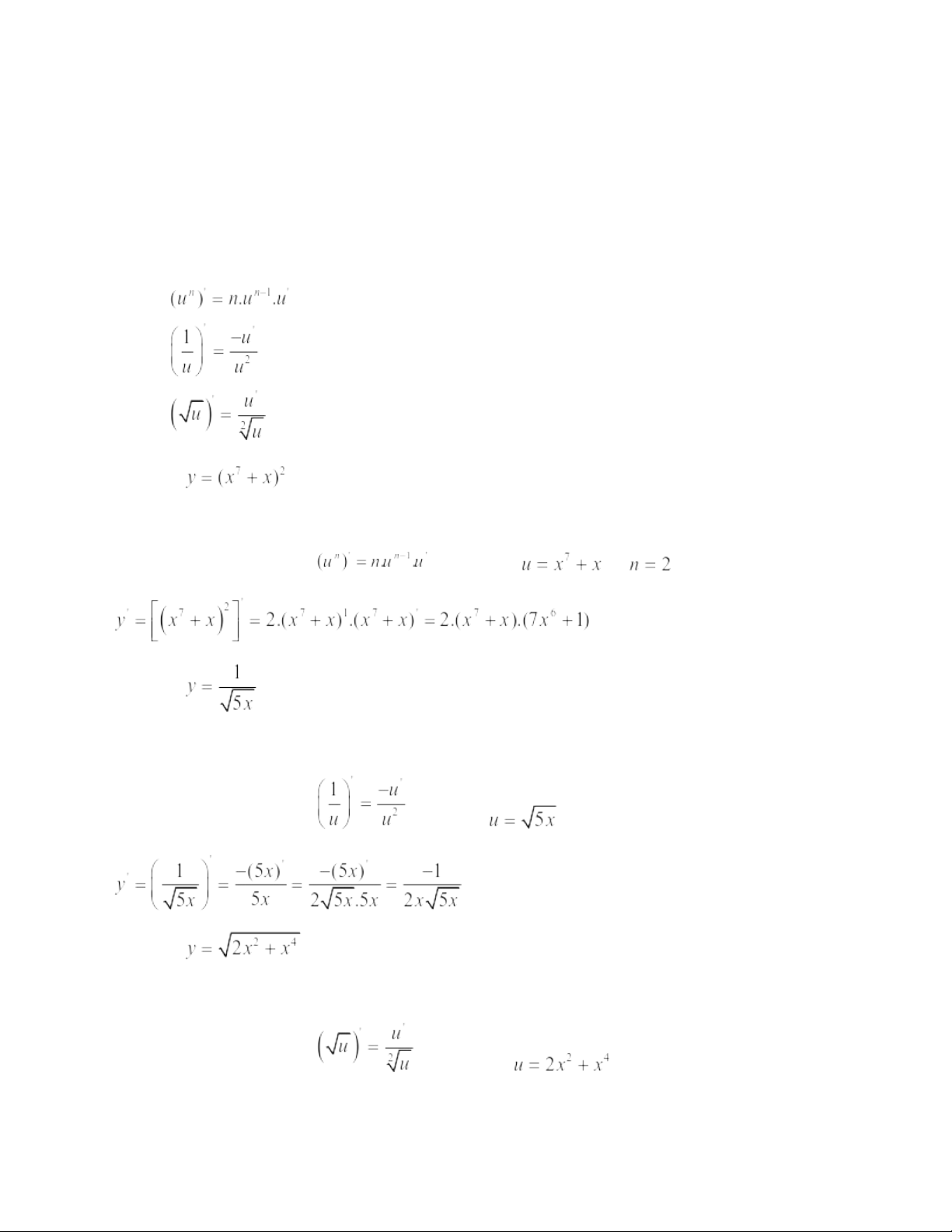

Preview text:
2.2. 111Equation Chapter 1 Section 1ĐẠO HÀM HÀM HỢP VÀ HÀM NGƯỢC
2.2.1. Đạo hàm của hàm số hợp:
- Nếu hàm số u = u(x) có đạo hàm theo x, hàm y = f(u) có đạo hàm tương ứng u = u(x) thì
hàm số hợp f(u) có đạo hàm theo x và y’(x) = y’(u).u’(x).
2.2.1.1. Một số công thức áp dụng tính đạo hàm của hàm số hợp: 1. 2. 3. Ví dụ 1: Hướng dẫn giải
Áp dụng công thức số 1. . Trong đó và Ta có: Ví dụ 2: Hướng dẫn giải
Áp dụng công thức số 2. . Trong đó Ta có: Ví dụ 3: Hướng dẫn giải
Áp dụng công thức số 3. . Trong đó Ta có:
2.2.2. Đạo hàm của hàm số ngược:
2.2.2.1. Nếu hàm số y = f(x) có đạo hàm tại x, f’(x) ≠ 0 và có hàm số ngược x = f-1(y) thì
hàm số x = f-1(y) có đạo hàm tại y = f(x): Ta thường viết:
Một số công thức tính đạo hàm của hàm số ngược: Hàm f(x) Hàm ngược f-1(y) Điều kiện ax + b (y – )/ba a ≠0 1/x 1/y x, y ≠0 xa ya x, y ≥ 0, p ∈ Z+ 2x lby y > 0 ex lny y > 0 10x logy y > 0 ax logay y > 0 và a > 0 xex W(y) x ≥- 1 và y ≥ -1/e sin(x) arcsin(y) -π/2 ≤ y ≤ π/2 cos(x) arccos(y) 0 ≤ y ≤ π tan(x) arctan(y) -π/2 < y < π/2 cot(x) arccot(y) 0 < y < π
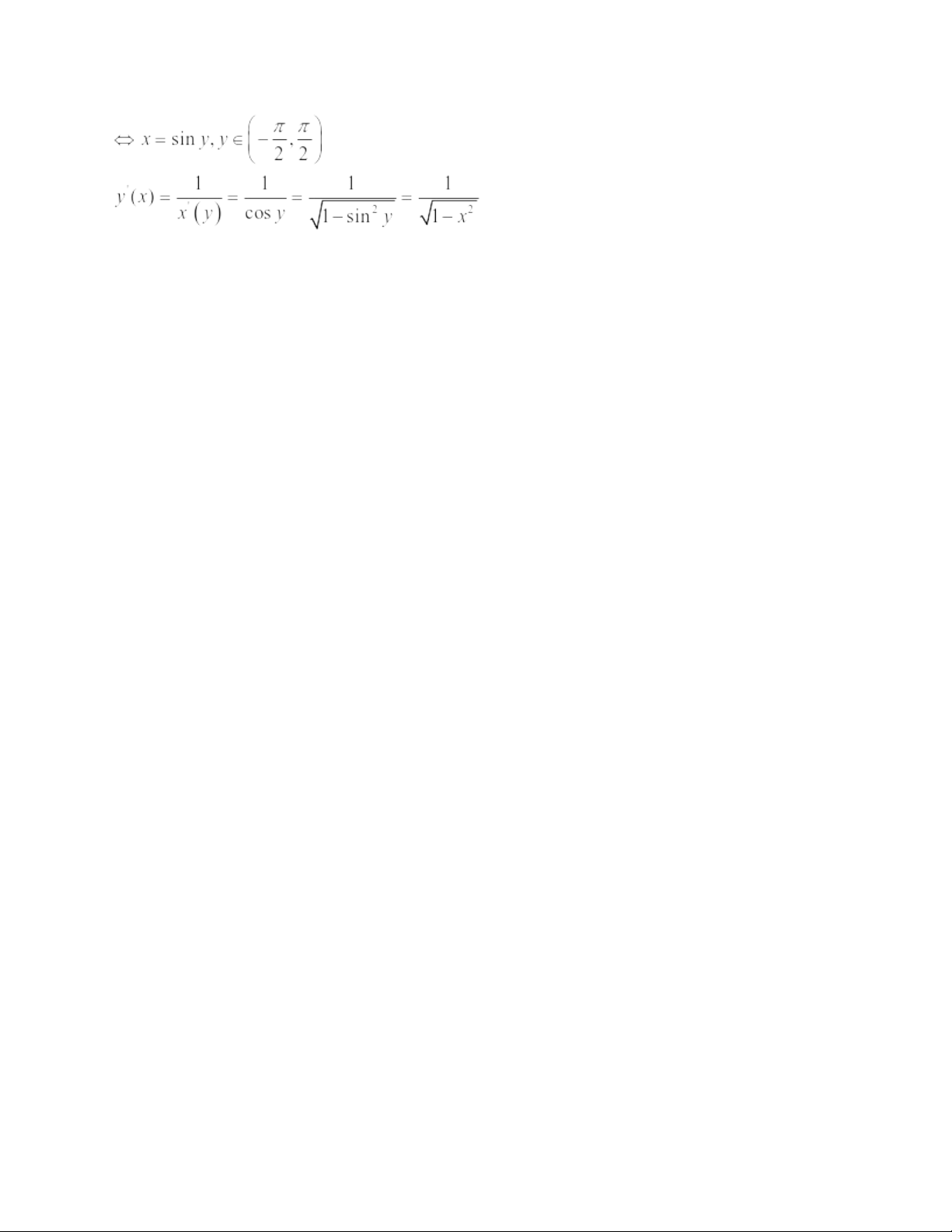
Ví dụ 4: Tìm đạo hàm của hàm số:
Ví dụ 5: Cho f(x) = (3x + 2)/(x+1). Hãy tìm hàm nghịch đảo của hàm trên Hướng dẫn giải: Điều kiện x ≠ -1 Ta có: (3x + 2)/(x+1) = y ⇔ 3x + 2 = y (x + 1) ⇔ 3x + 2 = yx + y ⇔ 3x – yx = y – 2 ⇔ x (3 – y) = y – 2 ⇔ x = (y – 2)/(3-y)
Vậy hàm nghịch đảo của hàm f(x) đã cho là f-1 = (y – 2)/(3-y).
Document Outline
- 2.2. 111Equation Chapter 1 Section 1ĐẠO HÀM HÀM HỢP VÀ HÀM NGƯỢC
- 2.2.1. Đạo hàm của hàm số hợp:




