Đạo Hàm Và Vi Phân Hàm Hợp - Hàm Ẩn | Đại học Bách Khoa Hà Nội

ĐẠO HÀM VÀ VI PHÂN Nội dung
1. Đạo hàm và vi phân hàm hợp.
2. Đạo hàm và vi phân hàm ẩn.
ĐẠO HÀM VÀ VI PHÂN HÀM HỢP VÍ DỤ
A heath store caries two kinds of vitamin water, brand A and
brand B. Sales figures indicate that if brand A is sold for x
dollars per bottle and brand B for y dollars per bottle, the demand for A will be Q ( x y) 2 ,
= 300 − 20x + 30y (bottle per month)
It is estimated that t months from now the price of brand A will be x = 2 + 0.0
5t (USD/ bottle) and the price of brand B will be y = 2 + 0.1 t (USD/bottle).
At what rate will be the demand for brand A be changing
with respect to time 4 months from now?
ĐẠO HÀM VÀ VI PHÂN CỦA HÀM HỢP
Trường hợp cơ bản: hợp của hàm 2 biến và hàm 2 biến
Cho z = f(x, y) và x = x(u, v), y = y(u, v). Nếu z, x, y khả vi:
dz = f dx + f dy x y
= f (x du + x dv) + f (y du + y dv) x u v y u v
= ( f x + f y du + f x + f y dv x u y u ) ( x v y v)
z u v = f x + f y u ( , ) x u y u
z u v = f x + f y v ( , ) x v y v
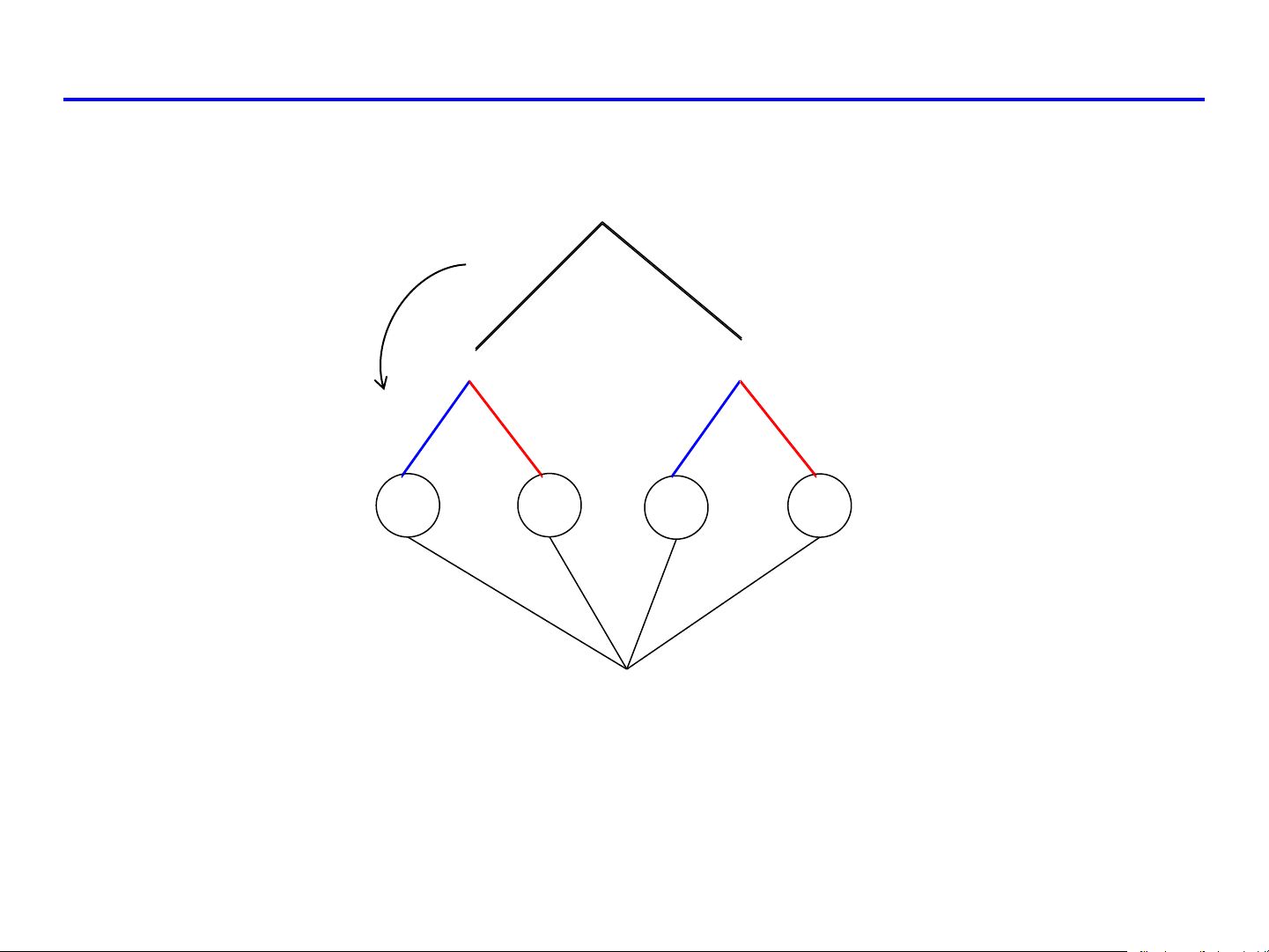
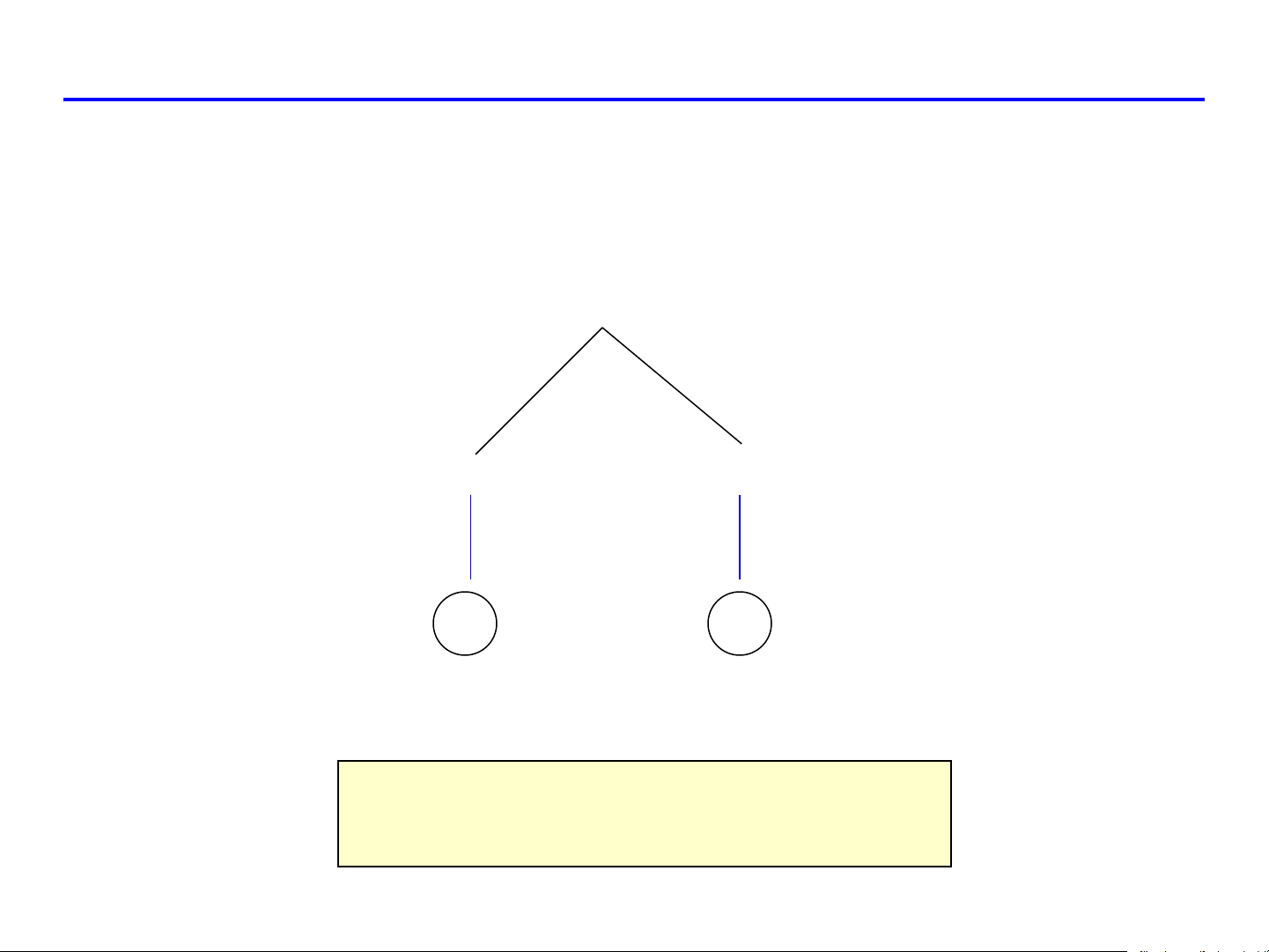
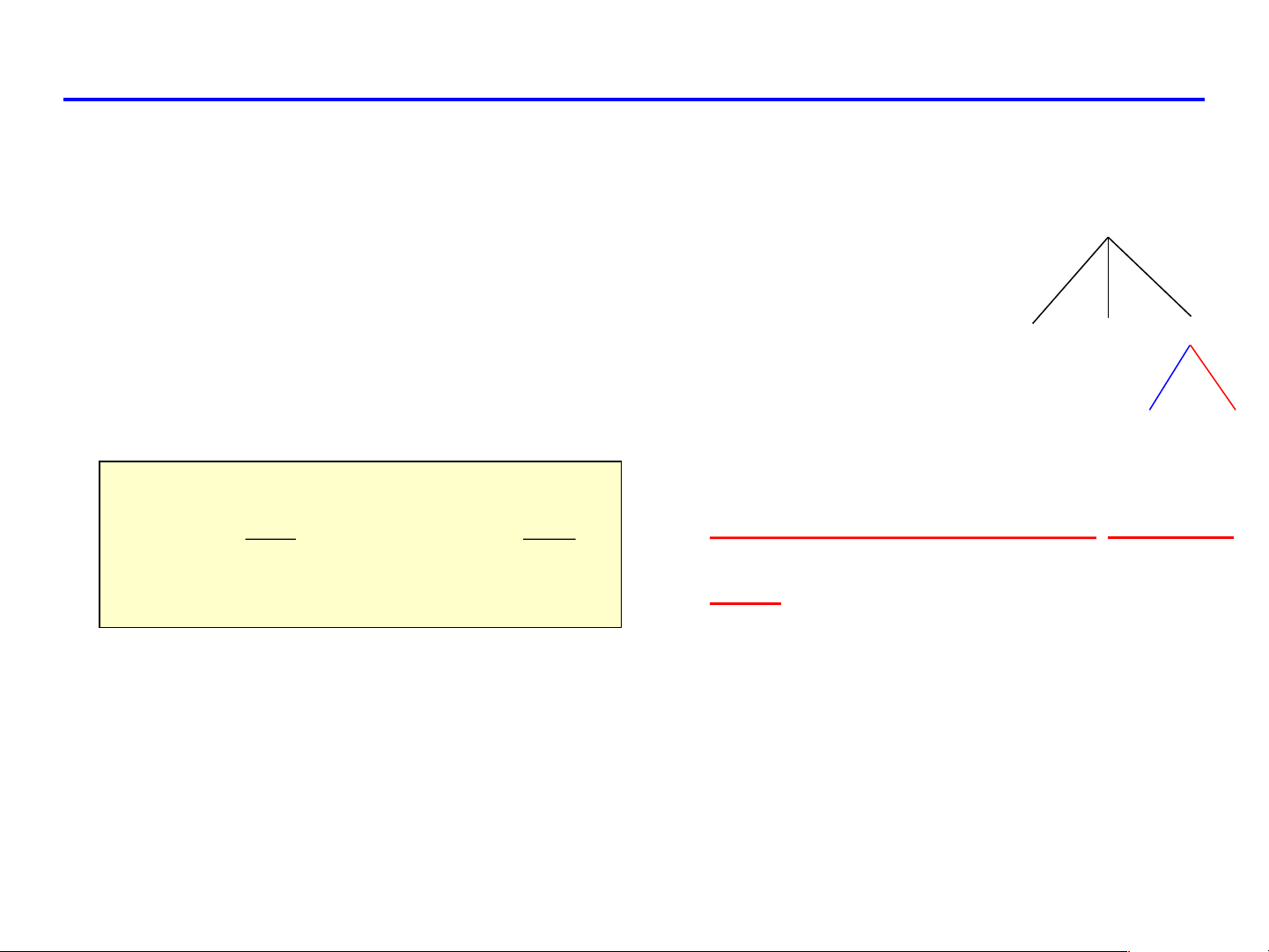
SƠ ĐỒ ĐẠO HÀM HÀM HỢP
z = f ( x, y) f f x y   x y xu y x y u v v u v u v Biến độc lập
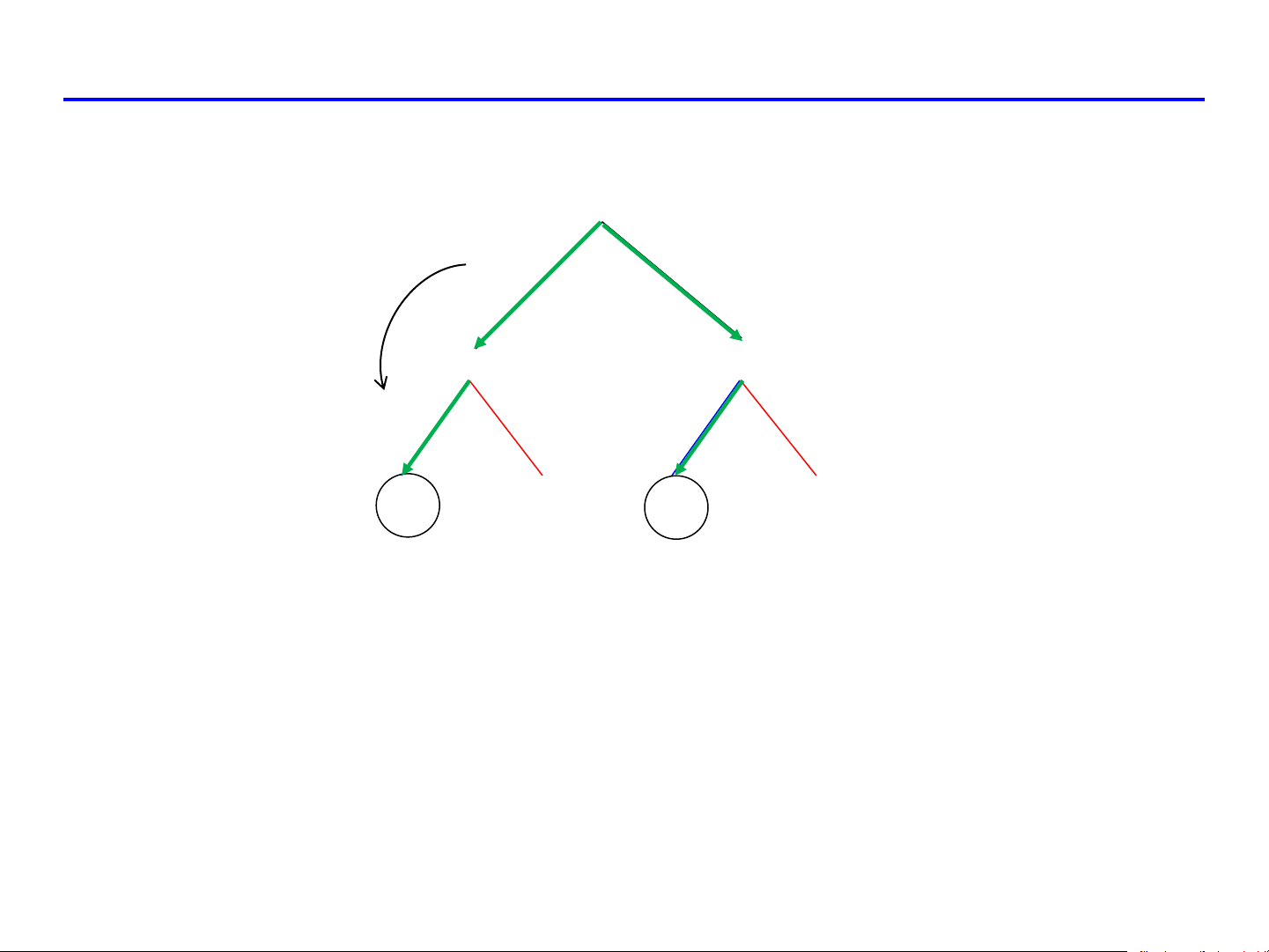
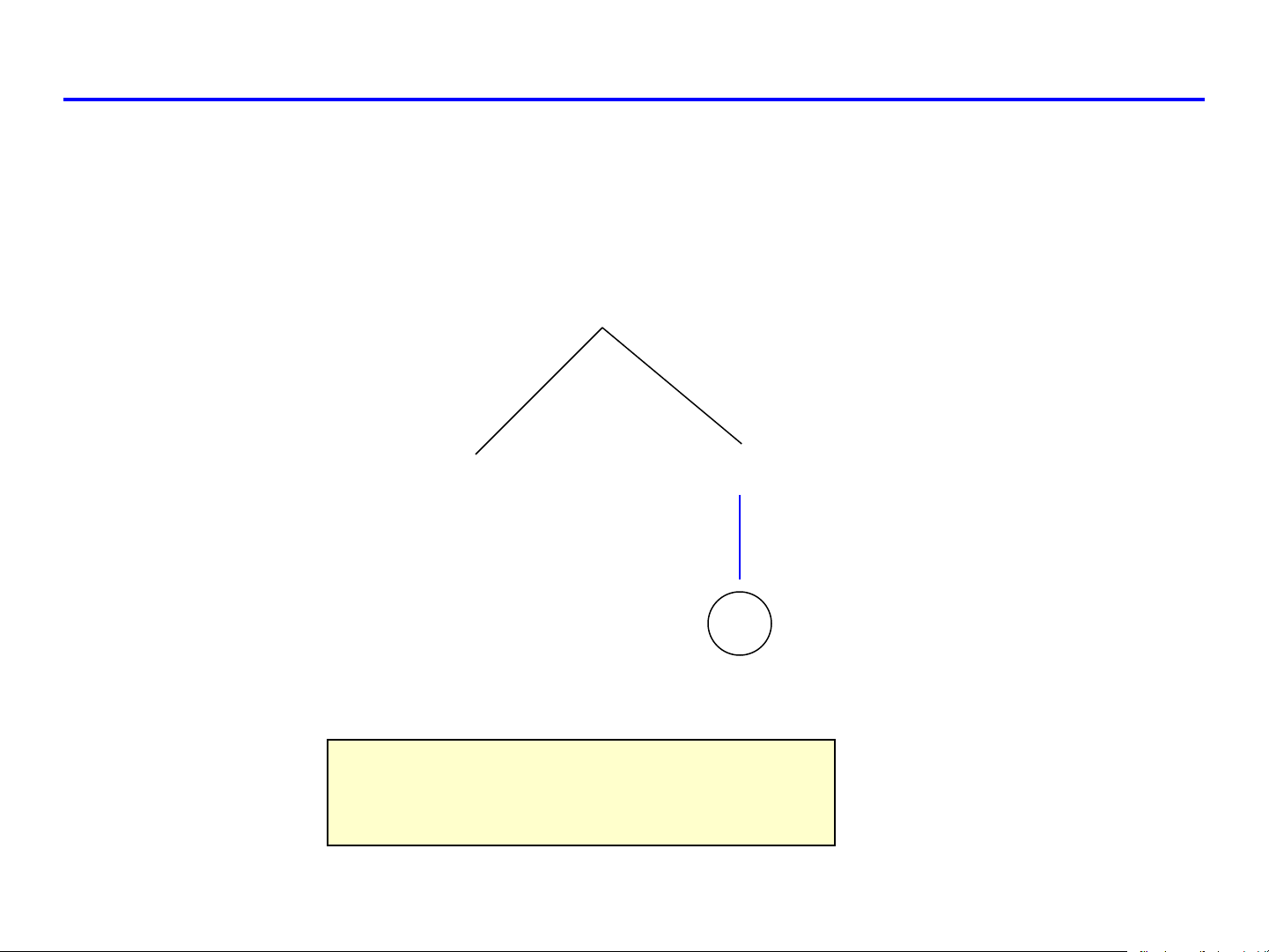
SƠ ĐỒ ĐẠO HÀM HÀM HỢP
z = f ( x, y) f f x y   x y x y y u x u v v u v u v z = f .x f .y  u x u y u
z = f .x + f .y , v x v y v
ĐẠO HÀM VÀ VI PHÂN CỦA HÀM HỢP Lưu ý khi tính vi phân:
Cho z = f(x, y) và x = x(u, v), y = y(u, v). Nếu z, x, y khả vi:
dz = z du + z dv
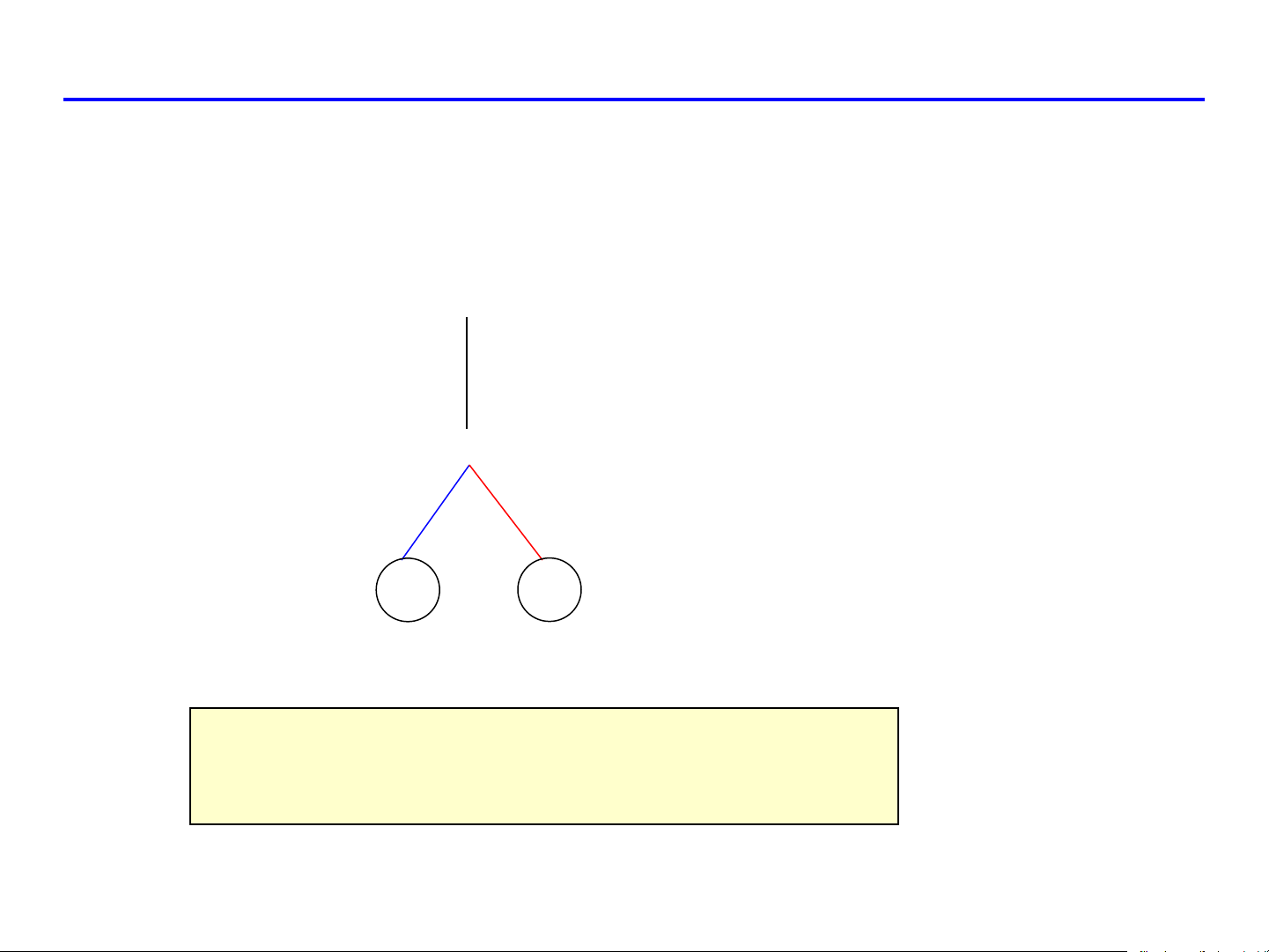
(liên kết z và các biến ĐỘC LẬP) u v Trường hợp riêng 1
Cho z = f(x) và x = x(u, v) (hợp của 1 biến và 2 biến)
z = f ( x) x xu xv u v z = f (
 x) .x , z = f (x).x u u v v Trường hợp riêng 2
z = f(x,y) và x = x(t), y = y(t). (hợp 2 biến và 1 biến)
z = f ( x, y) x y t t z (
 t) = f .x (t) + f .y (t) x y Trường hợp riêng 3
z = f(x, y) và y = y(x)(hợp 2 biến và 1 biến)
z = f ( x, y) x y x
z(x) = f + f .y (  x) x y VÍ DỤ 1 Cho: xy 2
z = f (x, y) = e , x = u , y = u + v
z = f ( x, y)
tìm z , z , dz tại (u, v)= (1, 1). u v x y
(u, v)= (1, 1)  (x, y) = (1, 2) u u v z (u,v = xy ye .2u xy +xe 2 2 2 u ) .1
z (1,1) = 2.e .2 +1.e .1 = 5e u   xy 2  =
z (u,v = xe .1 z (1,1) e v v ) 2 2
dz(1,1) = z (1,1)du + z (1,1)dv = 5e du + e dv u v VÍ DỤ 2  u  z = f ( , x y ) Cho: 2
z = f (x) = sin(x + x ), x = arctan    v 
Tính z , z tại (0, 1). x u v u v x(0, 1) = 0 1 1 z (u,v) 2
= (1+ 2x)cos(x + x )   u 2 v u 1+ 2 v u − 1 z (u,v) 2
= (1+ 2x)cos(x + x )   v 2 2 v u 1+ z (0,1) =1 2 v u  z (0,1) = 0 v VÍ DỤ 3
z = f ( x, y)
z = f (x, y) = sin(xy), Cho: x = arctan  (t), t y = e x y
Tính dz(t) tại t = 0. t t
dz = z(t )dt với z(t ) = f .x(t ) + f .y t x y ( ) 1 t z (
 t) = ycos(xy)
+xcos(xy) e 2 1 + t
t = 0  x = 0, y = 1
 z(0) =1  dz(0) = dt VÍ DỤ 4 2 ln( y +1)
z = f ( x, y) Cho:
z = f (x, y) = . 2 x x y a/ Tính z tại (1,0). x x
b/ Nếu y = ex, tính z′(x) tại x = 1 2 +
a z ( x y) = f ( x y) ln( y 1) / , , = 2 − ln(1)  z (1,0) = 2 − = 0 x x 3 x x 1 2 ln( y + 1)
b / z ( x) = f + f .y x x y ( ) = 2 y 2 − + x e 3 x 2 2 ( y + 1)x 2 2 2e
x = 1  y = e  z (
 0) = −2ln(e +1) + 2 e +1 Ví dụ
Một thiết bị dò tìm cảm ứng nhiệt đang di chuyển trên con đường có dạng ( ) t
x t = 1 + t , y (t ) = 2 +
x(cm), y(cm),t(s) 3
Nhiệt độ sinh ra trên con đường chuyển động của thiết bị là T = T x y ( 0 ( , ) C ).
Biết T (2,3) = 4, T (2,3) =
3, hỏi nhiệt độ thay đổi thế nào x y
sau 3 giây trên đường thiết bị này di chuyển. Ví dụ
Với 1 mol khi lý tưởng, pt trạng thái là: PV = 8.3T, với
P(Kpascal), T(0K), V(lit).
Tại thời điểm T = 3000K, V = 100l, nhiệt độ đang tăng với tốc
độ 0.1K/s, thể tích đang tăng với tốc độ 0.2l/s, tính tốc độ thay
đổi của áp suất theo thời gian tại thời điểm này. Ví dụ
Nhu cầu thị trường của một sản phẩm A được cho bởi
trong đó x là giá của một đơn vị sản phẩm A và y là giá một
đơn vị sản phẩm cạnh tranh B.
Sau t tháng kể từ thời điểm hiện tại, giá của 2 loại sản
phẩm này thay đổi theo mô hình
Xác định tốc độ thay đổi lượng cầu của sản phẩm A theo
thời gian tại thời điểm 4 tháng tính từ thời điểm hiện tại. Đạo hàm hàm hợp
Hàm sản xuất hàng ngày của một nhà máy cho bởi mô hình
Trong đó K là chi phí (vốn) hàng ngày (tính theo ngàn
USD) và L là số giờ công lao động. Hiện tại nhà máy đang
chi $400,000 mỗi ngày và dự kiến chi phí đó sẽ tăng thêm
với tốc độ 9,000 USD/ngày. Số giờ công hiện tại là 1,000
giờ và dự kiến giảm với tốc độ 4h/ngày. Tính tốc độ thay
đổi lượng sản phẩm theo thời gian ở ngày thứ 5 tính từ thời điểm hiện tại. VÍ DỤ 5
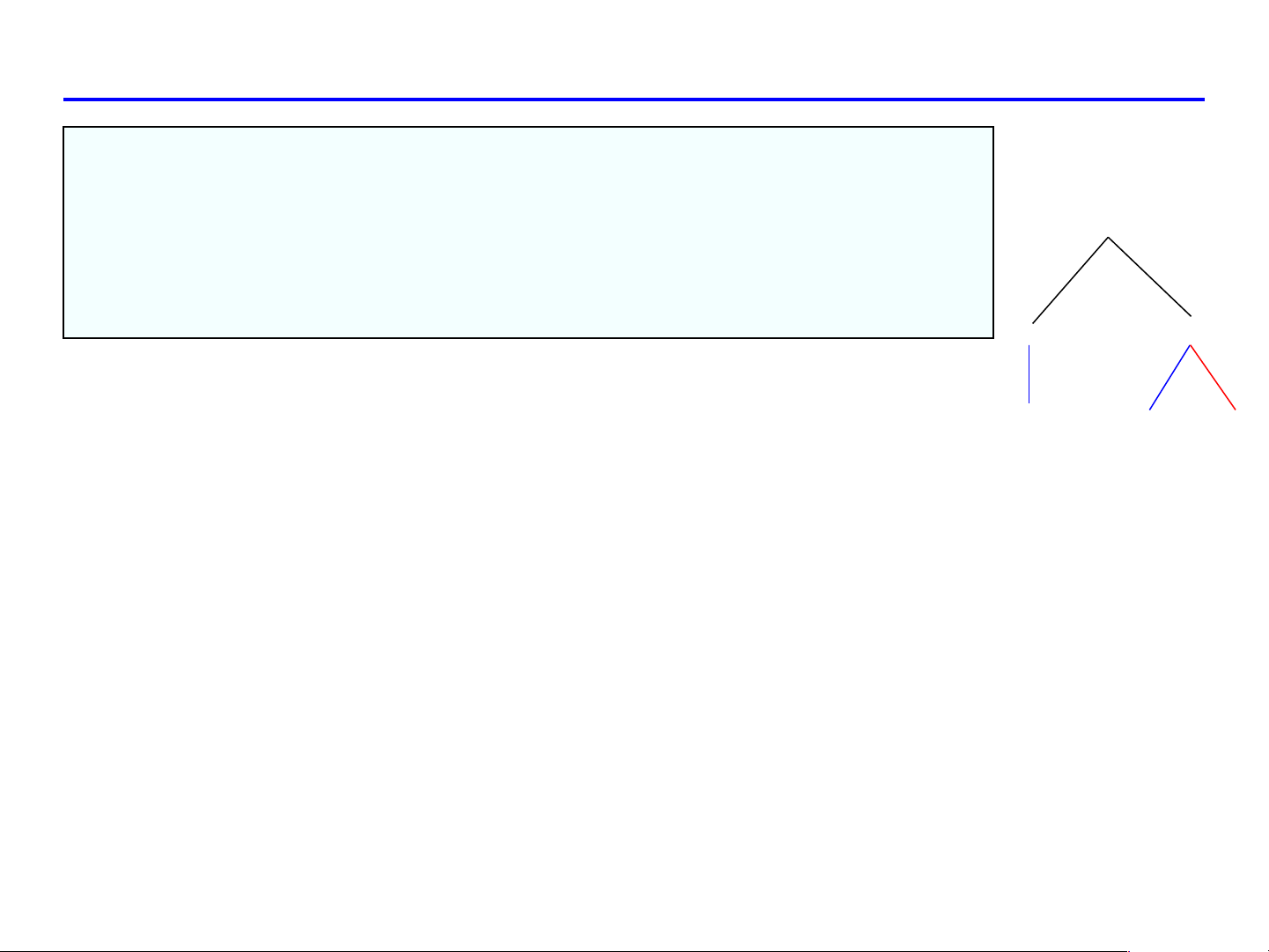
Đặt: u = x – y , v = xy  z = f(u, v)
(u, v là biến chính của f)
z = f .u + f .  v x u x v x
= f .1+ f y u v
z = f .u + f .  v = f .( 1 − ) + f x  y u y v y u v VÍ DỤ 6  x  Cho: z = xf 
 với f là hàm khả vi tại mọi điểm. 2  y 
Chứng minh đẳng thức: 2xz + yz = 2z x y x Đặt : u =  2 z = x.f(u) y
z = f (u) + x  . f (u) z = x  . f (u) y  x x y 2 − x = =  =  f (u) + . x f (  u).u xf (u).u . x f (u). x y 3 y 1 = f (u) + . x f (  u). 2 y VÍ DỤ 7 Đặt: 2 2
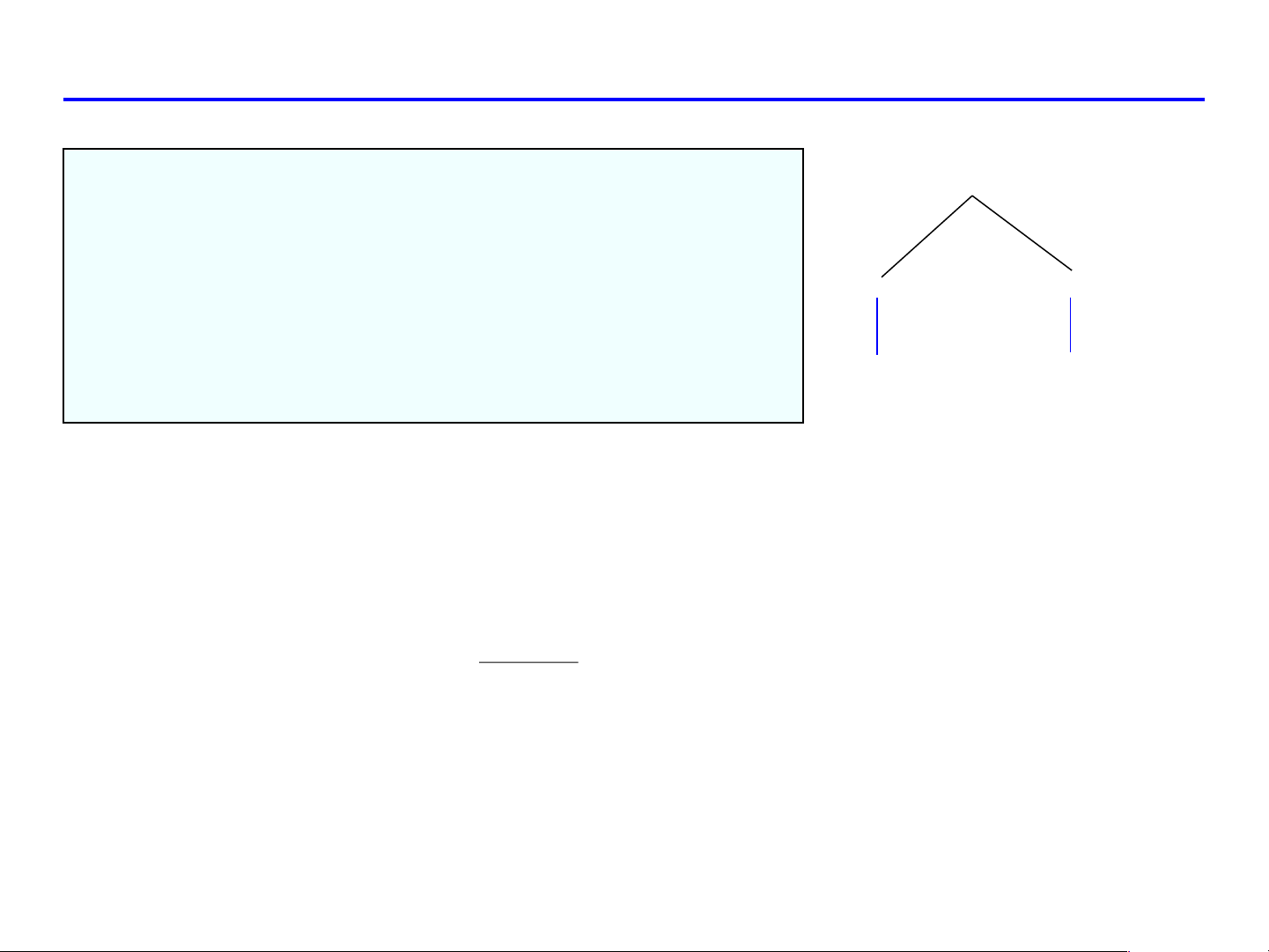
u = x − y,v = xy  z = f (u,v)
z = f .u + f .  v 2 =  +  x u x v x f .2x f .y u v
z = f .u + f .
 v = f .( 1 − ) + f .2  xy y u y v y u v
dz = z dx + z dy x y
Chứng minh cách tính đạo hàm theo hướng
z (t ) = f (M + te = f x, y 0 ) ( )
với x = x(t) = x + te , y = y t = y + te 0 1 ( ) 0 2
z(t ) = f ( x, y) x(t ) + f ( x, y y t x y ) ( )
= f (x, y)e + f x, y e x 1 y ( ) 2
z(0) = f ( x , y e + f x , y e x 0 0 ) 1 y ( 0 0 ) 2 = f  (x , y e 0 0 ) f  (M = f  x , y e 0 ) ( 0 0) e 
ĐẠO HÀM VÀ VI PHÂN HÀM ẨN
Đạo hàm riêng hàm ẩn 1 biến
Hàm ẩn y = y(x) xác định bởi phương trình F(x, y) = 0. Để tính
y’(x), lấy đạo hàm phương trình F = 0 theo x và giải tìm y’(x).
G = F ( x, y) F y (  x) x = − Fy x y x
Xem x, y là 2 biến độc lập khi lấy đh của F.
Đạo hàm riêng hàm ẩn 1 biến
Hàm ẩn y = y(x) xác định bởi phương trình F(x, y) = 0. Để tính
y’(x), lấy đạo hàm phương trình F = 0 theo x và giải tìm y’(x).
G = F ( x, y) Lưu ý:
Sử dụng đạo hàm hàm hợp ta có:
G(x) = F(x, y) = 0, với y = y(x) x y  x
G′(x) = F + F .y’(x) = 0 x y F y (  x) x = −
Xem x, y là 2 biến độc lập F khi lấy đh của F. y
Đạo hàm riêng hàm ẩn 2 biến
Hàm ẩn 2 biến : z = z(x, y) xác định từ pt :
G = F ( x, y, z)
F(x, y, z) = 0 (1). x z y x y F F z = − , y x z = −
x, y, z là các biến độc lập khi x y F F z z tính F ,F ,F . x y z VÍ DỤ 1 y
Cho y = y(x) xác định từ pt: e + xy − e = 0 (1) Tìm y′(0). ( , ) y
F x y = e + xy − e = 0
(1)  F(x, y) = 0 F y y (  x) x = − = − F y + y e x
x = 0, (1)  y (0) = 1, 1 1 −  y (0) = − = −e e + 0 VÍ DỤ 2
2. Tìm đạo hàm tại x = 1 của hàm ẩn y = y(x) xác định bởi pt: 3 2
y + x y − x +1 = 0 (1) VÍ DỤ 3
Cho z = z(x, y), thỏa pt: x/ ( , , ) z
F x y z = z − ye = 0 (1)
Tìm dz tại (x, y) = (0, 1).
từ (1) ta có: (x, y) = (0, 1)  z = 1 y x/z − F e − x z = − 1 z = −  z (0,1) = − = 1 x F x yx x/z 1+ 0 z 1 + e 2 z x/ z F − y e − z = − = − 1  = − = y z (0,1) 1 F yx y x/ 1 z + z + e 1 0 2 z
dz (1,0) = z (1,0) dx + z (1,0 dy = dx + dy x y ) VÍ DỤ 4
Cho z = z(x, y), thỏa pt: F ( ,
x y, z) = xy − sinh(x + y − z) = 0 (1) Tìm dz(1, 0). ( ,
x y) = (1,0)  z = 1 VÍ DỤ 5
Cho mặt cong z = f(x, y), thỏa pt: 3 2
F (x, y, z) = z − 4xz + y − 4 = 0 (1)
Nếu z(1, −2) = 2 , viết phương trình tiếp diện tại (1, −2,2).
Dùng xấp xỉ tuyến tính tại (1,-2) để tính gần đúng z(1.03, − 2.11) .
Phương trình tiếp diện tại (1, −2,2) có dạng z = z (1, 2 − ) + z (1, 2 − )(x − ) 1 + z (1, 2 − )( y + 2 x y ) Trong đó z − = z − = x ( ) y ( ) 1 1, 2 1, 1, 2 2 VÍ DỤ 6
Cho z = z(x, y), thỏa pt:
F = f (x + z, y) = 0 với f là hàm khả vi. Tìm z , z x y
Đặt u = x + z, v = y  F(x, y, z) = f(u, v) = 0
F = f .u + f .v = f ,
F = f .u + f .v = f x u x v x u y u y v y v
F = f .u + f .v = f z u z v z u F f F f z = − = − = 1 − , y x u v z = − = − , x y F f F f z u z u
Pháp vector và tiếp diện của mặt cong
Giả sử L  S có pt: x = x(t), y = y(t),z = z(t)
M ( x(t ), y(t ), z(t )  S 0 0 0 )
Vector chỉ phương của tiếp tuyến tại M là :
u = (x (t ), y (t ),z (t ) 0 0 0 )
M S: F(x,y,z) = 0, ta có: F (M )x (
 t ) + F (M )y (t ) + F (M )z (t ) = 0 x 0 y 0 z 0  u ⊥ F
 (M )  F(M) là pháp vector của S tại M.
Pháp vector và tiếp diện của mặt cong
Pháp vector của (C): F (x, y) = 0 tại (x , y ) là 0 0 n = k F
 (x , y , k  0 0 0 )
Phương trình tiếp tuyến của (C) tại (x , y ) 0 0 F ( x , y x − x + F x , y y − y = 0 x 0 0 ) ( 0 ) y ( 0 0 ) ( 0 )
Pháp vector của (S): F (x, y, z) =
0 tại (x , y , z ) là 0 0 0 n = k F
 (x , y , z , k  0 0 0 0 )
Phương trình tiếp diện của (S) tại (x , y ,z ) 0 0 0
F ( x , y , z
x − x + F x , y , z
y − y + F x , y , z z − z = 0 x 0 0 0 ) ( 0 ) y ( 0 0 0 ) ( 0 ) z ( 0 0 0 ) ( 0 ) VÍ DỤ
Tìm một pháp vector của mặt cong 3 2
F (x, y, z) = z − 4xz + y − 4 = 0
tại (1, −2,2), biết rằng pvt hợp với chiều dương trục Oz một góc tù.
ĐẠO HÀM THEO HƯỚNG VECTOR GRADIENT Đạo hàm theo hướng Định nghĩa:
Cho hàm f xác định trong lân cận M và một hướng cho bởi 0 vector đơn vị e .
Đạo hàm của f theo hướng e tại M : 0 ( f  M
f M + te − f M D f M = = lim e 0 ) ( 0) ( 0 ) ( 0) →0 e t  t f
 (M0 ) chỉ tốc độ thay đổi của f theo hướng e. e 
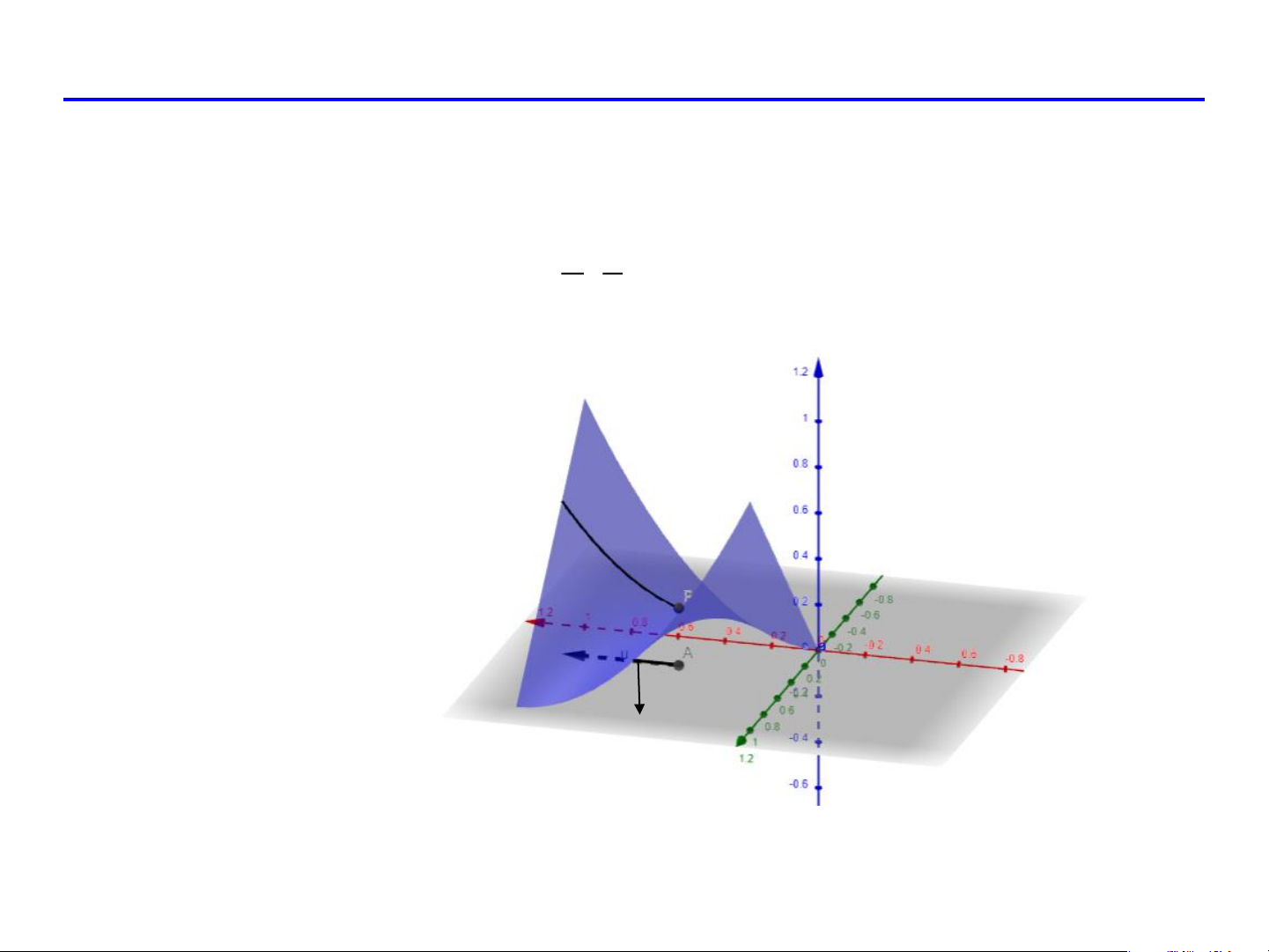
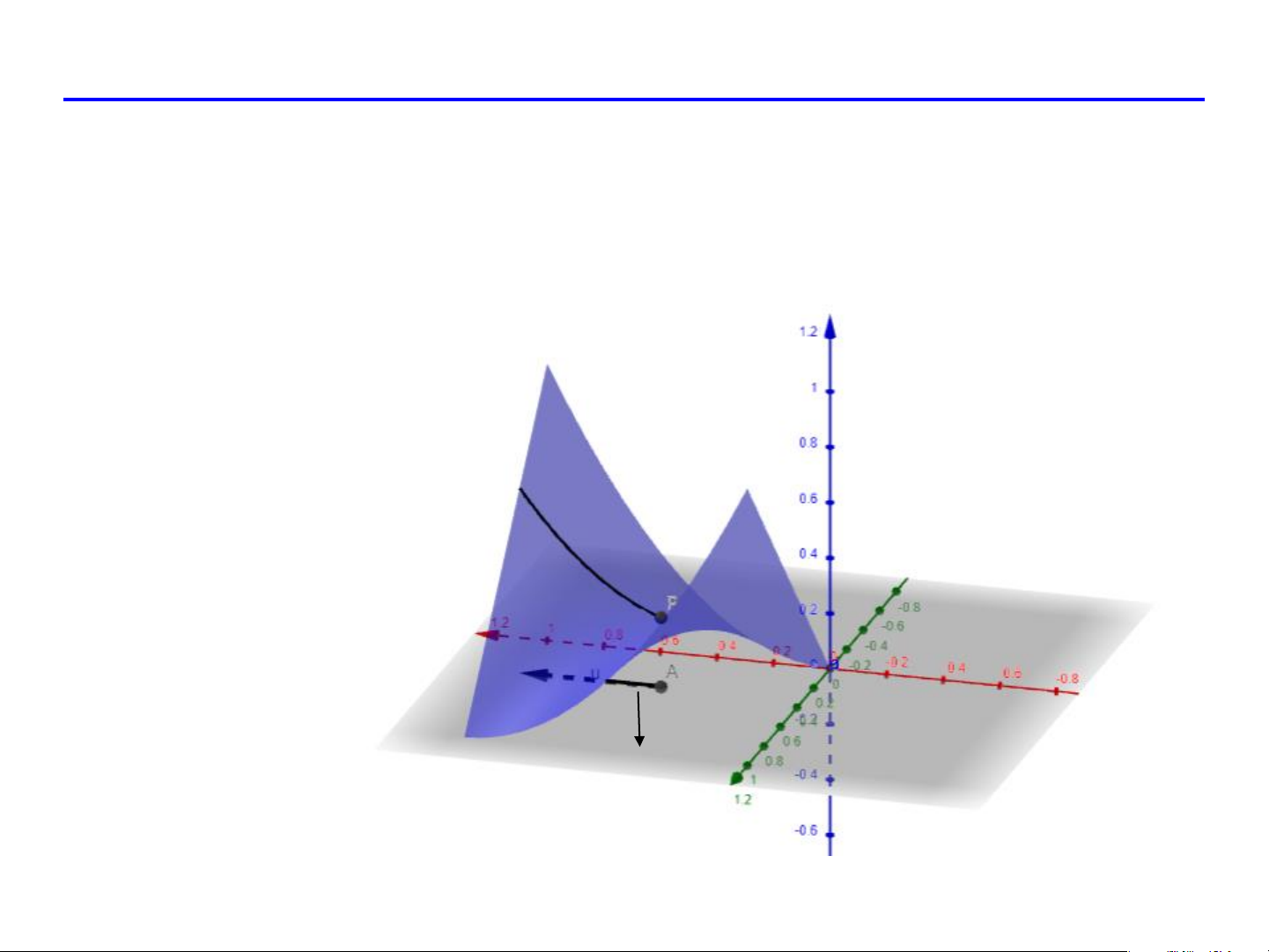
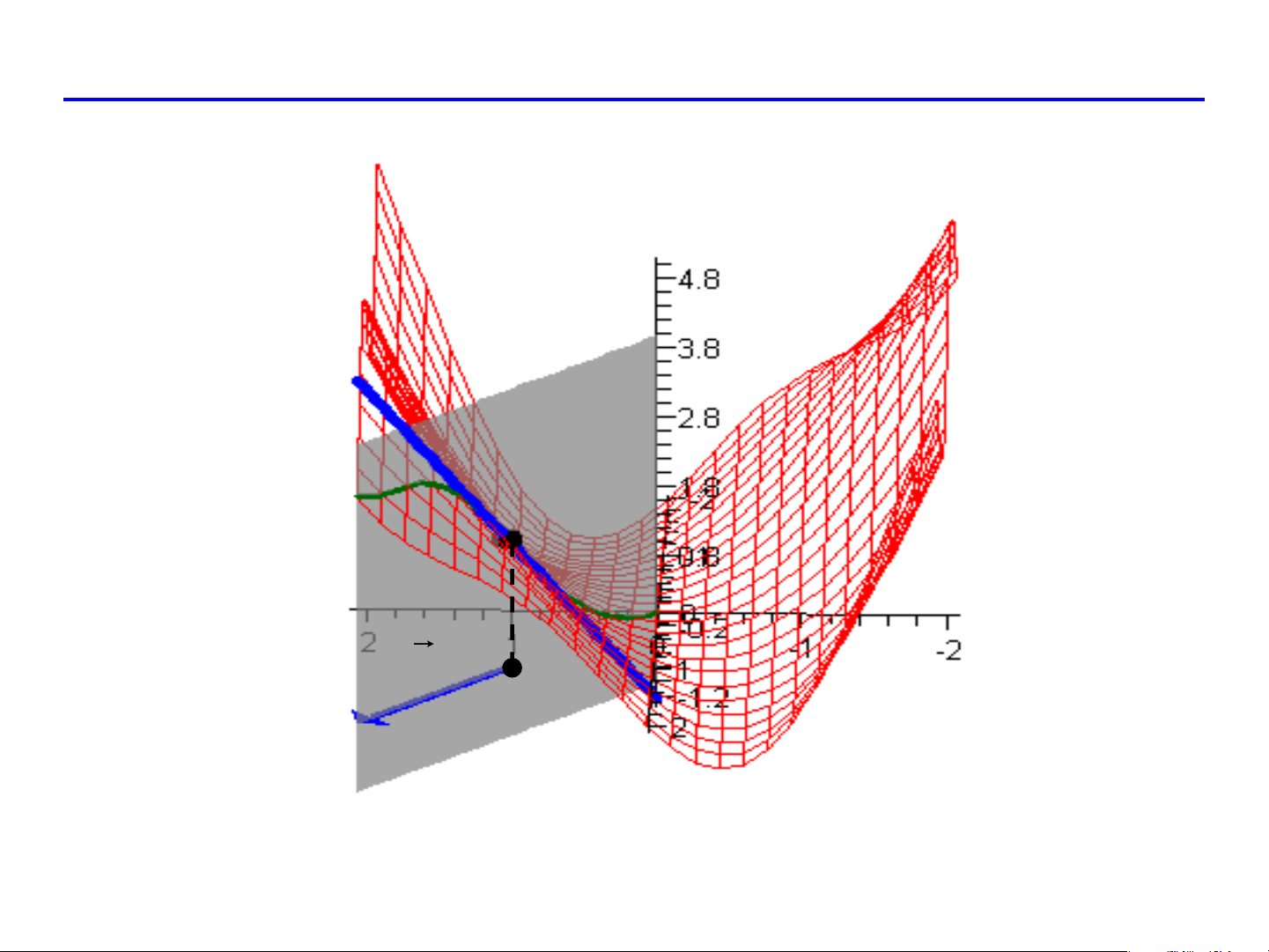
Ý nghĩa của đạo hàm theo hướng
Xét đường cong L : z(t) = f (M + te 0 ) f  (M
f M + t.e − f M z t − z 0 0 ) ( 0 ) ( 0) ( ) ( ) = lim = lim →0 →0 e t t  t t f  (M0 )  = z(0) e 
là hệ số góc tiếp tuyến của đường cong L tại M . 0
Hướng của gradient là hướng tăng nhanh nhất của f f ( x y) 2 ,
= x − 2xy + y  1 1  M ,    2 3 
Sự thay đổi của độ cao z
khi (x, y) đi qua M theo hướng grad. M f (M ) Vector Gradient
Gọi i, j (k) là các vector đơn vị trên các trục tọa độ,
f có các đạo hàm riêng tại M x , y 0 ( . 0 0 )
Gradient của f tại M là: 0
f (M = grad M = f M , f M 0 ) ( 0) x ( 0 ) y ( 0 )
M  R , f x, y, z 0 3 ( )
f (M = grad M = f M , f M , f M 0 ) ( 0) x ( 0 ) y ( 0 ) z ( 0 )
Định lý (cách tính đạo hàm theo hướng)
Nếu hàm f khả vi tại M , e =
e , e là vector đơn vị, khi đó 0 1 2
đạo hàm theo hướng e tại M tồn tại và: 0 f
 (M0 ) = f (M .e 0 ) e  u là vector tùy ý: f  (M u 0 ) = f (M . 0 ) u  u
Hàm 3 biến cũng được tính tương tự. Chứng minh định lý
z (t ) = f (M + te = f x + te , y + te 0 ) ( 0 1 0 2 )
z (t ) = f ( x, y) x(t ) + f ( x, y y t x y ) ( )
= f (x, y)e + f x, y e x 1 y ( ) 2
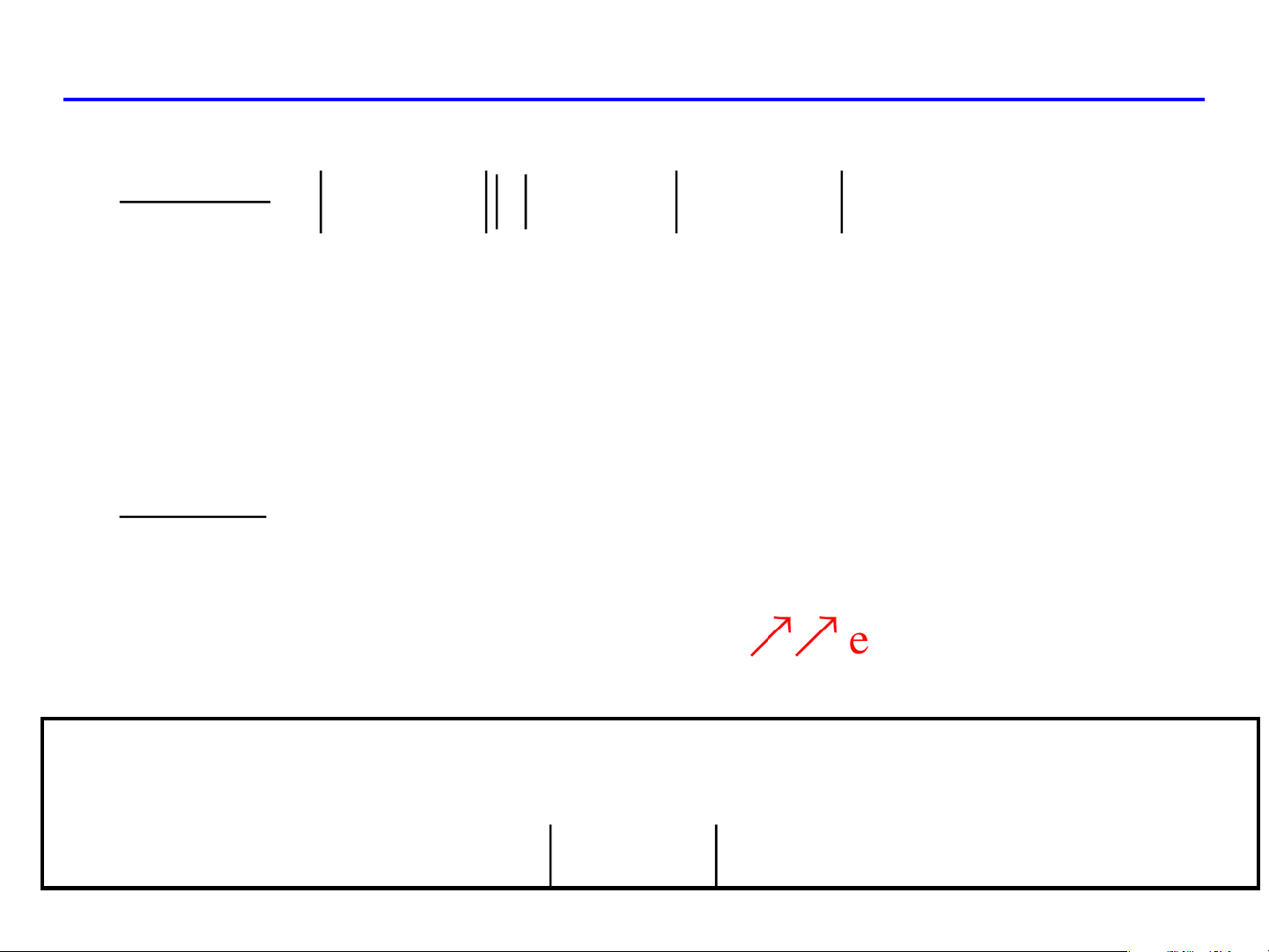
z (0) = f ( x , y e + f x , y e x 0 0 ) 1 y ( 0 0 ) 2 = f  (x , y e 0 0 ) f  (M = f  x , y  e 0 ) ( 0 0) e  Lưu ý f  (M0 ) = f
 (M e cos = f  M cos 0 ) ( 0) e   là góc giữa f  (M & e 0 ) f
 (M0 ) đạt giá trị lớn nhất khi và chỉ khi: e 
cos = 1   = 0  f  (M e 0 )
Hướng của vector gradient là hướng mà hàm f tăng nhanh nhất,
gtln của đh theo hướng là f (M0 )
Hướng của gradient là hướng tăng nhanh nhất của f f ( x y) 2 ,
= x − 2xy + y M (1/ 2,1/ 3)
Sự thay đổi của độ cao z khi
(x, y) đi qua M theo hướng grad. M f (M ) Ví dụ
Tìm đạo hàm theo hướng u = −1,2 tại điểm (− 2,1) của hàm số 2 2 f ( ,
x y) = xy − 2x y Giải: 1 − ,2
Vector đơn vị theo hướng của u = −1,2 là e = 5 f  ( 2 − , ) 1 = f (−2, )1.e e  1 − ,2 = 9, 1 − 34 2 = − 5 5 Ví dụ
Tìm đạo hàm theo hướng u = 1,1, t 1 − ại M = ( 2, 1, 2 ) của f ( x y z) 2 2 3 , ,
= x + 2xz − 3y z u 1,1, 1 − = u 3 f
 (M ) = f (M ) u . u  u 1,1, 1 − 8 − = 8, 4 − 8, 3 − 2 . = 3 3 Ví dụ Cho ( , , ) = . yz f x y z x e , u = 2, 3 − ,0 ,M (2, 3 − ,0).
Biết i, j, k là vector đơn vị trên các trục Ox, Oy, Oz. f  f  1. Tìm (M ), M i  (−k) ( ) f 
2. Với v =  f (2, − 3 , 0) , tìm (M ) v 
3. Xác định giá trị lớn nhất của đạo hàm theo hướng tại M. f  4. Tìm (M ) u  Ví dụ Cho f (x y) 2 = x + 3 , 2xy − 7 y, M ( 2 − ,3 ). Đi theo hướng
nào dưới đây khi qua M thì f tăng nhanh nhất. u = 2 − ,3 u = 10, 23 − 1 2 u = 12 − ,7 u = 17, 22 3 4 Ví dụ
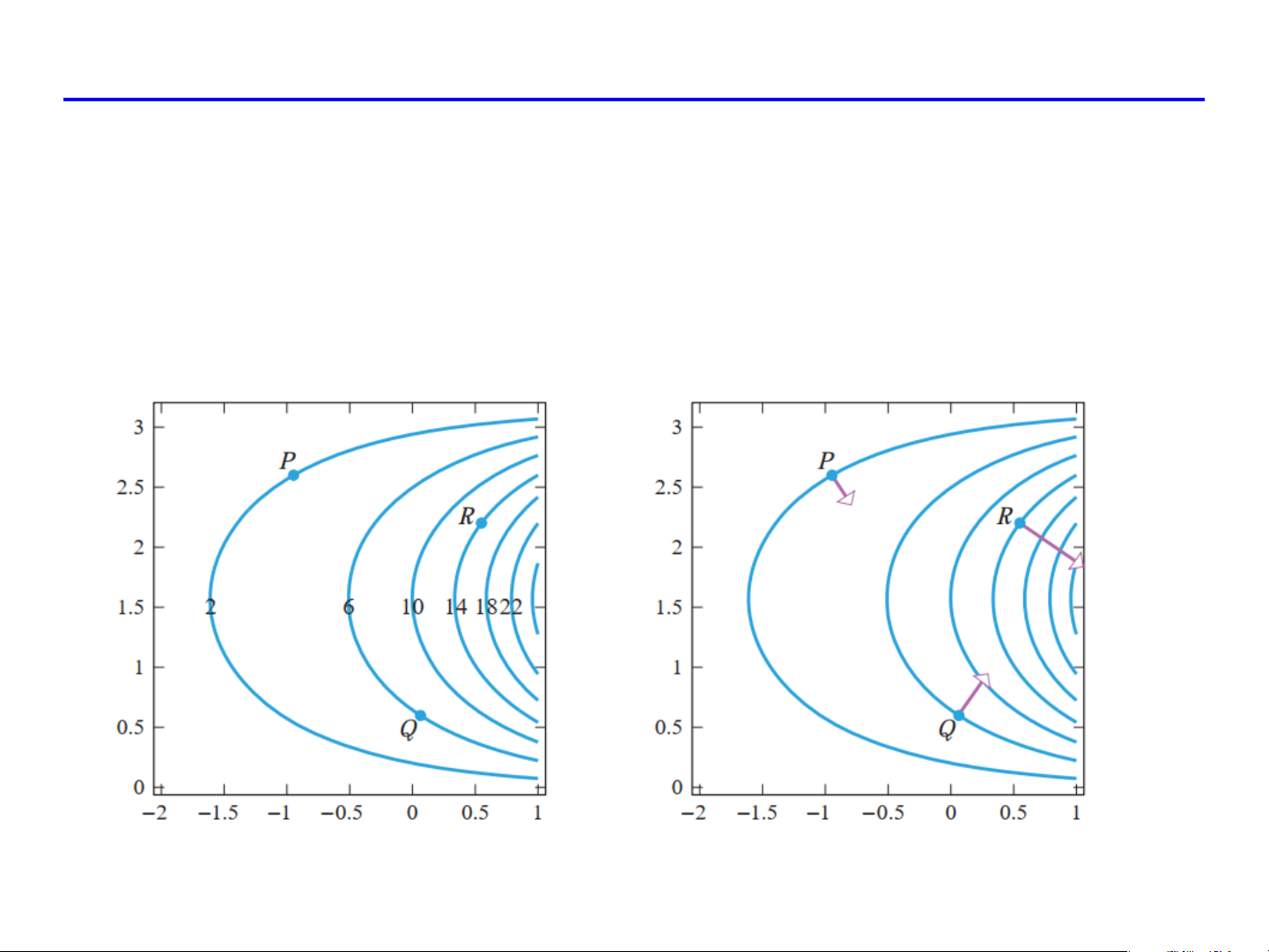
Hàm số z = f (x, y) có bản đồ mức như hình vẽ. Các vector tại
P, Q, R lần lượt là vector gradient của f tại các điểm tương
ứng. Giải thích về độ dài của 3 vector này. Ví dụ
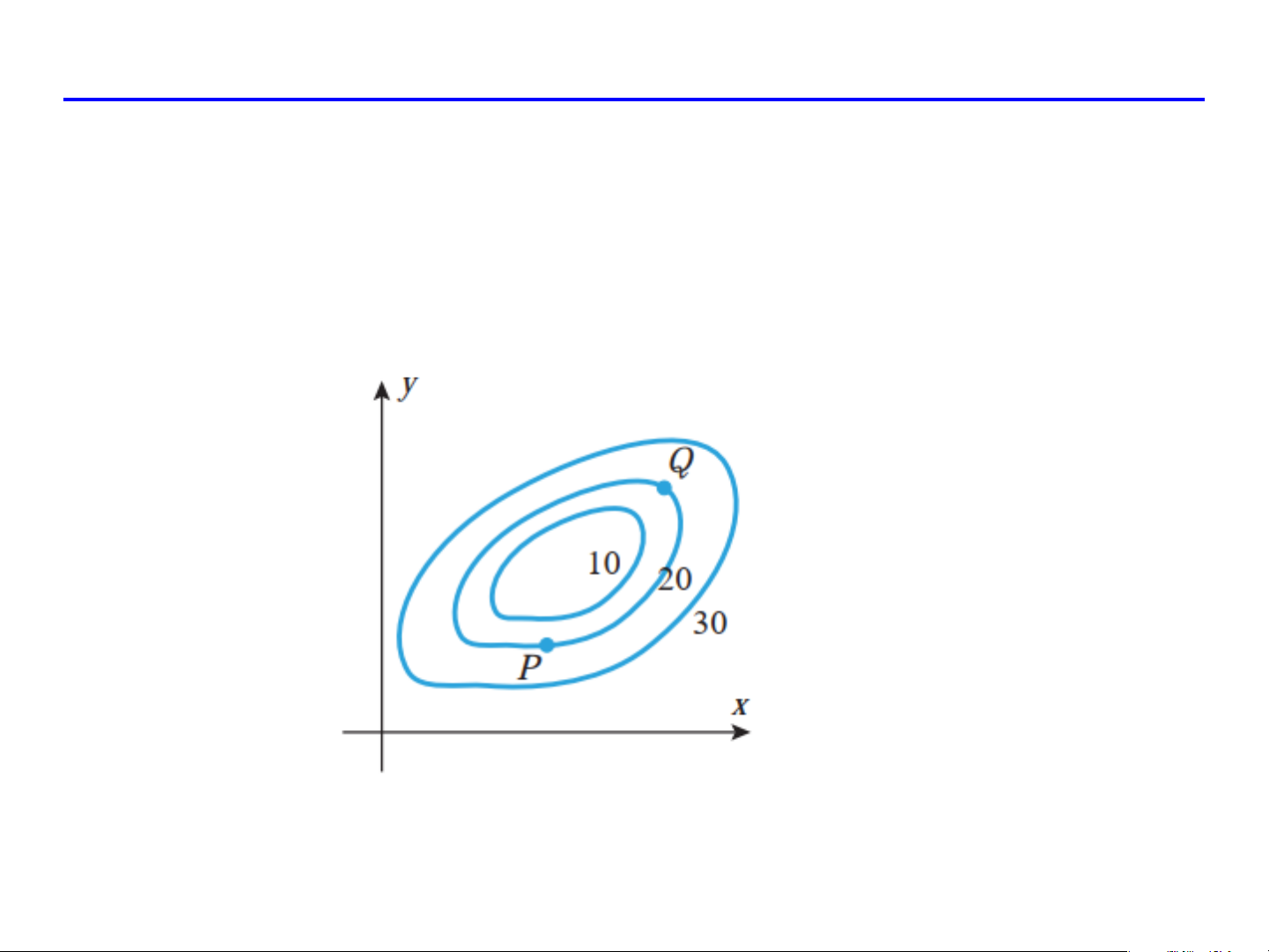
Hàm số z = f (x, y) có bản đồ mức như hình vẽ. Theo bạn,
vector gradient của f tại P có dài hơn tại Q hay không, tại sao? BÀI TOÁN ÁP DỤNG
Một ngọn đồi có hình dạng bề mặt mô tả bởi pt 2 2
z = 1000 − 0.005x − 0.01y
Trong đó z là chiều cao và x, y, z tính bằng mét. Giả sử phía
dương Ox là hướng đông, phía dương Oy là hướng bắc.
Một người đang đứng ở tọa độ (60,40,966), hỏi
1. Nếu đi theo hướng nam là đi lên hay đi xuống.
2. Đi theo hướng tây bắc là đi lên hay đi xuống.
3. Đi theo hướng nào chiều cao bề mặt ngọn đồi tăng nhanh
nhất, độ dốc theo hướng này là bao nhiêu?
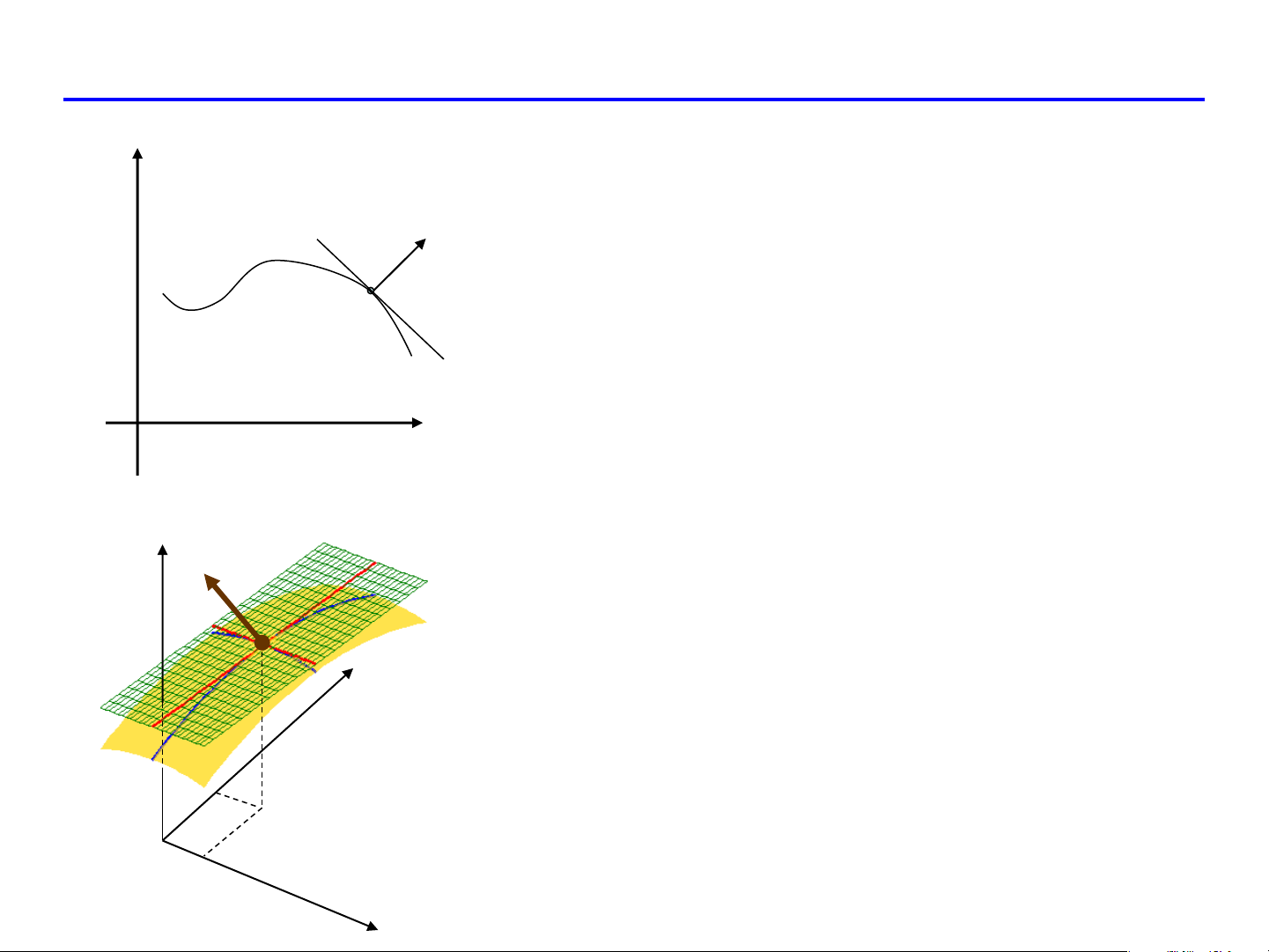
Ý nghĩa hình học của đạo hàm theo hướng u M x , y 0 ( 0 0 )
Ý nghĩa phương của vector Gradient
Với đường cong f ( x, y) = 0 n phương của  f ( là M ) pvt của M đường cong tại M. n
Với mặt cong F (x, y, z ) = 0 P phương của  F là (P) pvt của mặt cong tại P. (x , y 0 0 ) Ví dụ
2/ Tìm phương trình tiếp diện của mặt cầu: 2 2 2
x + y + z = 4 . a M = (0,0,2) . b M = (1, 3,0) F ( x y z) 2 2 2 , ,
= x + y + z − 4 = 0
gradF ( x, y, z) = (2x,2 y,2z)
a. gradF (0,0,2) = (0,0,4)
(T ): (x − 0).0 + ( y − 0).0 + (z − 2).4 = 0  z = 2
b. gradF (1, 3,0) = (2,2 3,0) (T ): (x − )
1 .2 + ( y − 3).2 3 + ( z − 0).0 = 0
 x + y 3 − 4 = 0
Document Outline

• Slide 1: ĐẠO HÀM VÀ VI PHÂN
• Slide 2: Nội dung
• Slide 3: ĐẠO HÀM VÀ VI PHÂN HÀM HỢP
• Slide 4: VÍ DỤ
• Slide 5: ĐẠO HÀM VÀ VI PHÂN CỦA HÀM HỢP
• Slide 6: SƠ ĐỒ ĐẠO HÀM HÀM HỢP
• Slide 7: SƠ ĐỒ ĐẠO HÀM HÀM HỢP
• Slide 8: ĐẠO HÀM VÀ VI PHÂN CỦA HÀM HỢP
• Slide 9: Trường hợp riêng 1
• Slide 10: Trường hợp riêng 2
• Slide 11: Trường hợp riêng 3
• Slide 12: VÍ DỤ 1
• Slide 13: VÍ DỤ 2
• Slide 14: VÍ DỤ 3
• Slide 15: VÍ DỤ 4
• Slide 16: Ví dụ
• Slide 17: Ví dụ
• Slide 18: Ví dụ
• Slide 19: Đạo hàm hàm hợp
• Slide 20: VÍ DỤ 5
• Slide 21: VÍ DỤ 6
• Slide 22: VÍ DỤ 7
• Slide 23: Chứng minh cách tính đạo hàm theo hướng
• Slide 24: ĐẠO HÀM VÀ VI PHÂN HÀM ẨN
• Slide 25: Đạo hàm riêng hàm ẩn 1 biến
• Slide 26: Đạo hàm riêng hàm ẩn 1 biến
• Slide 27: Đạo hàm riêng hàm ẩn 2 biến
• Slide 28: VÍ DỤ 1
• Slide 29: VÍ DỤ 2
• Slide 30: VÍ DỤ 3
• Slide 31: VÍ DỤ 4
• Slide 32: VÍ DỤ 5
• Slide 33: VÍ DỤ 6
• Slide 34: Pháp vector và tiếp diện của mặt cong
• Slide 35: Pháp vector và tiếp diện của mặt cong
• Slide 36: VÍ DỤ
• Slide 37: ĐẠO HÀM THEO HƯỚNG VECTOR GRADIENT
• Slide 38: Đạo hàm theo hướng
• Slide 39: Ý nghĩa của đạo hàm theo hướng
• Slide 40: Hướng của gradient là hướng tăng nhanh nhất của f
• Slide 41: Vector Gradient
• Slide 42: Định lý (cách tính đạo hàm theo hướng)
• Slide 43: Chứng minh định lý
• Slide 44: Lưu ý
• Slide 45: Hướng của gradient là hướng tăng nhanh nhất của f
• Slide 46: Ví dụ
• Slide 47: Ví dụ
• Slide 48: Ví dụ
• Slide 49: Ví dụ
• Slide 50: Ví dụ
• Slide 51: Ví dụ
• Slide 52: BÀI TOÁN ÁP DỤNG
• Slide 53: Ý nghĩa hình học của đạo hàm theo hướng
• Slide 54: Ý nghĩa phương của vector Gradient
• Slide 55: Ví dụ
• Slide 56
• Slide 57