Đáp án đề thi | Môn Tối ưu hóa - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58794847
TRƯỜNG ĐẠI HỌC SPKT TPHCM
Đáp án môn: Tối ưu hóa HK1 NH 2021-2022 KHOA KINH TẾ Mã môn học: MAOP230706 Bài 1 (4đ):
a) Lập bài toán đối ngẫu (D) : G(y) = 6y1 + 9y2 + 10y3 max y1 + 2y2 + 3y3 ≤ 5 4y1 + 2y3 ≤ 10 y1 + y2 ≤ 7 2y1 + 4y2 + y3 ≤ 3 y1 ≤ 0, y2 k.h.c, y3 ≥ 0
b) Giải bài toán (P). Suy ra kết quả bài toán (D).
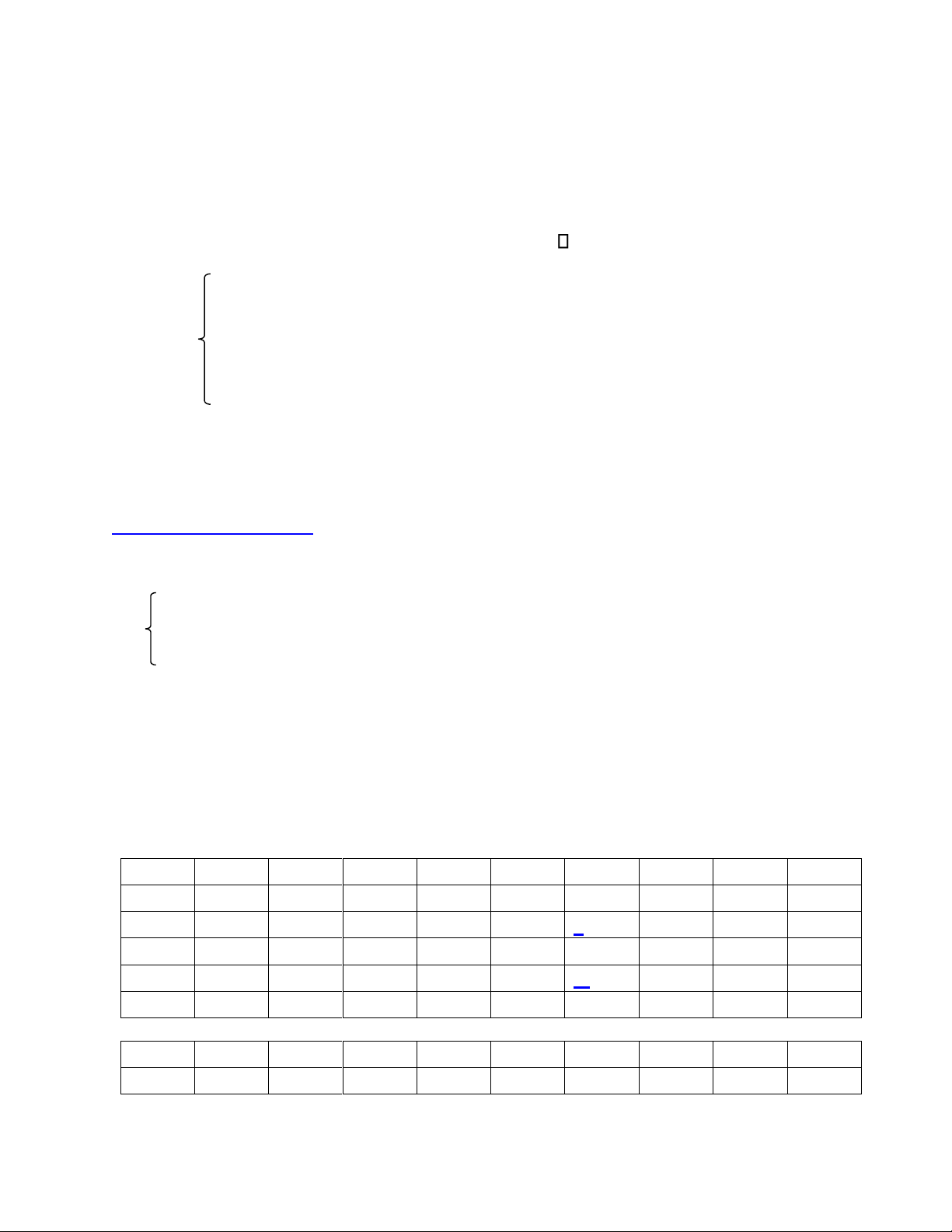
Bài toán ở dạng chuẩn: F(x) =
5x1 + 10x2 + 7x3 + 3x4 + Mx7 + Mx8 => MIN
x1 + 4x2 + x3 + 2x4 + x5 = 6 2x1 + x3 + 4x4 + x7 = 9 3x1 + 2x2 + x4 - x6 + x8 = 10 Xj >=0, j=̅1̅,̅8̅ Ci Xi Yi X1 X2 X3 X4 X5 X6 Lamda 0 X5 6 1 4 1 2 1 0 3 M X7 9 2 0 1 4 0 0 9/4 M X8 10 3 2 0 1 0 -1 10 F(x) 0 -5 -10 -7 -3 0 0 M 19 5 2 1 5 0 -1 Ci Xi Yi X1 X2 X3 X4 X5 X6 Lamda 0 X5 3/2 0 4 1/2 0 1 0 - lOMoAR cPSD| 58794847 3 X4 9/4 1/2 0 1/4 1 0 0 9/2 M X8 31/4 5/2 2 -1/4 0 0 -1 31/10 F(x) 27/4 -7/2 -10 -25/4 0 0 0 M 31/4 5/2 2 -1/4 0 0 -1 Ci Xi Yi X1 X2 X3 X4 X5 X6 Lamda 0 X5 3/2 0 4 1/2 0 1 0 - 3 X4 7/10 0 -2/5 3/10 1 0 1/5 - 5 X1 31/10 1 4/5 -1/10 0 0 -2/5 - F(x) 88/5 0 -36/5 -33/5 0 0 -7/5 M 0 0 0 0 0 0 0
Tại Bảng 3: Ta có ij 0
ô i j( , ) nên PA đang xét là
PATƯ của bài toán dạng chuẩn:
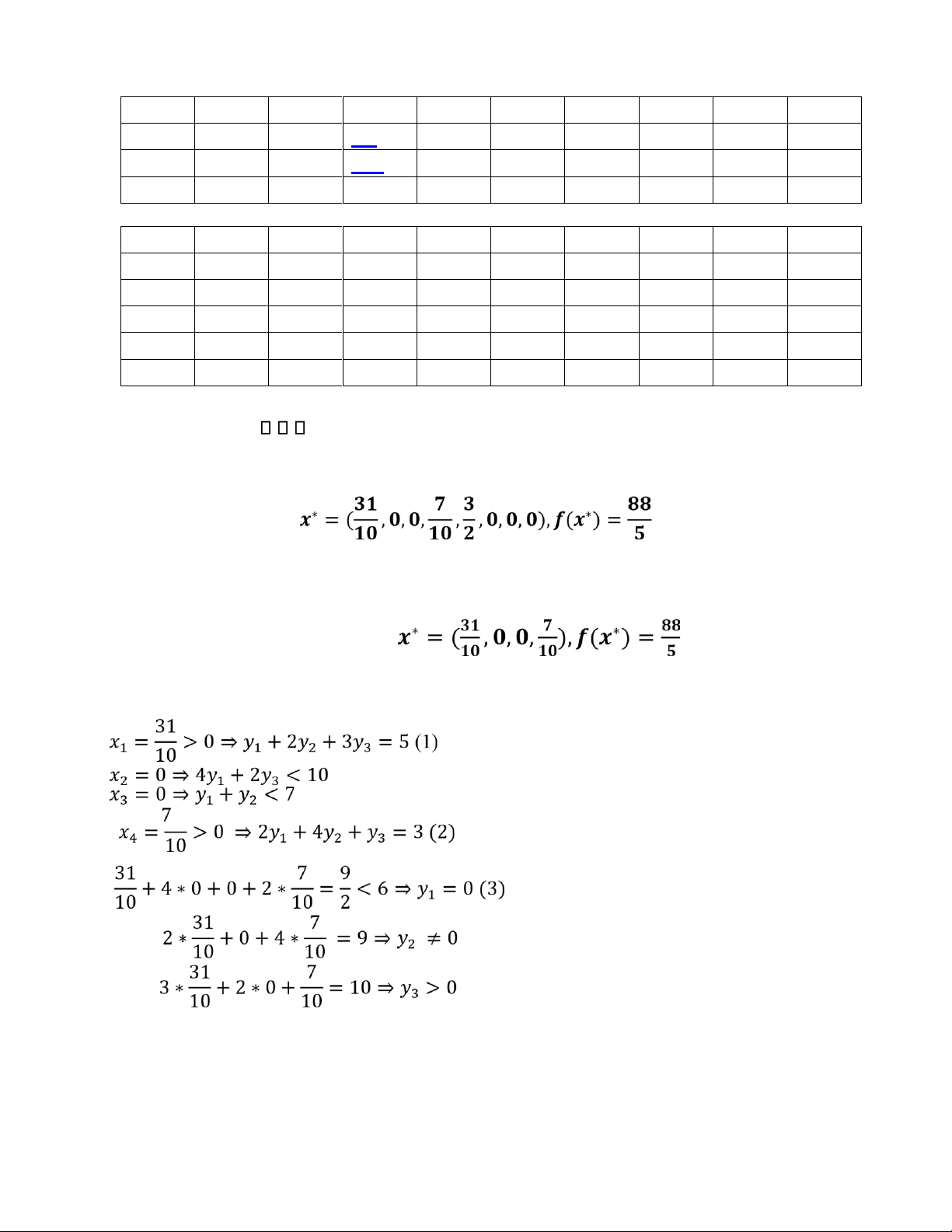
Vì ẩn giả x7 = 0, x8 = 0 => Bài toán dạng tổng quát có PATU
PATU của bài toán dạng tổng quát:
Áp dụng định lý đối ngẫu 2 (định lý độ lệch bù yếu)
Giải (1); (2); (3) ta được: lOMoAR cPSD| 58794847 Bài 2 (3đ):
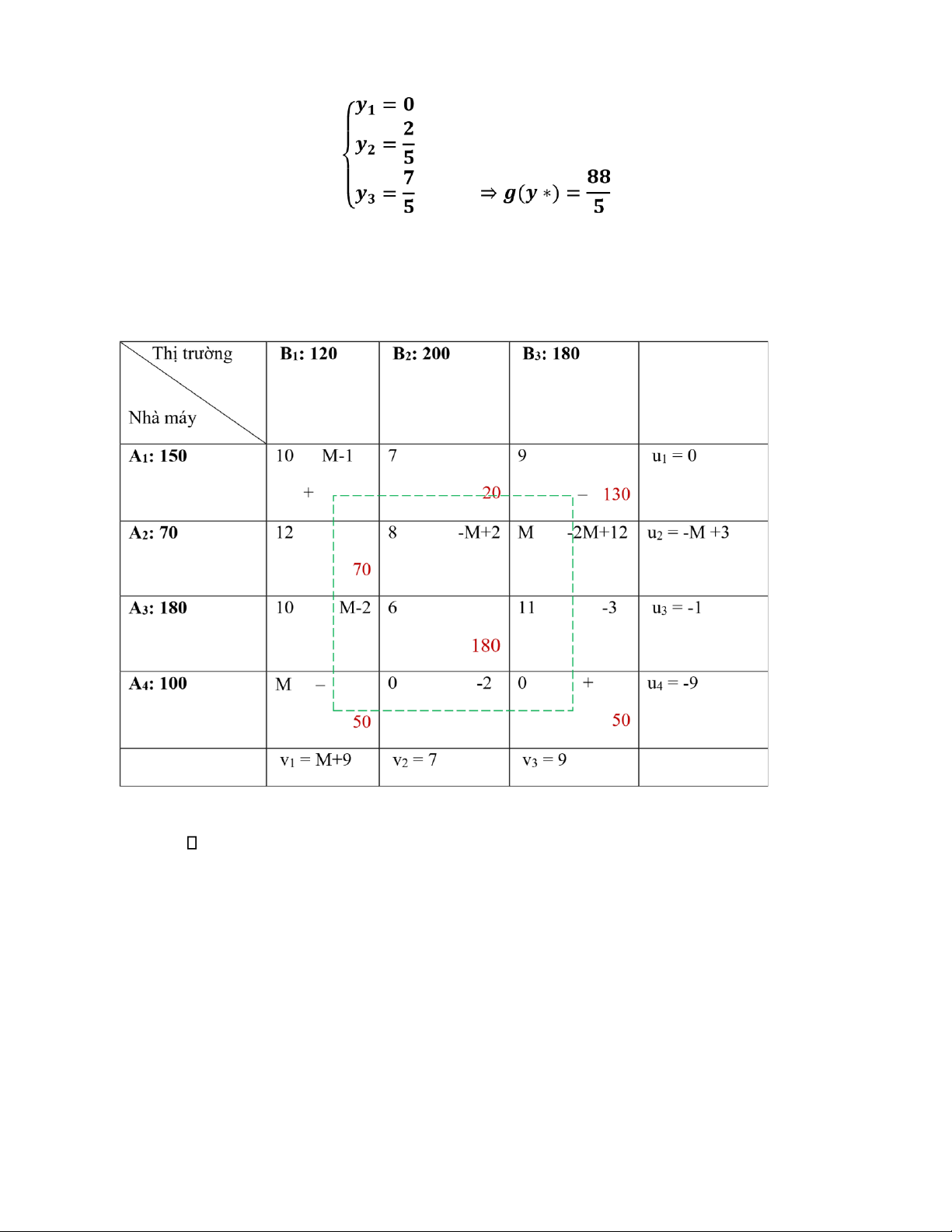
Ta có: ⅀A= 400, ⅀B= 500, vì vậy ⅀A < ⅀B => thêm A4 = 100
Do điều kiện thi trường B1 phải tiêu thụ hết sản phẩm và tuyến đường A2 đến B3 bị cấm nên C41 =
M; C23 = M (M > 0, rất lớn)
Vì tồn tại ij > 0 => Phương án này không tối ưu
Ô đưa vào (1,1); ô đưa ra (4,1); d = 50 lOMoAR cPSD| 58794847
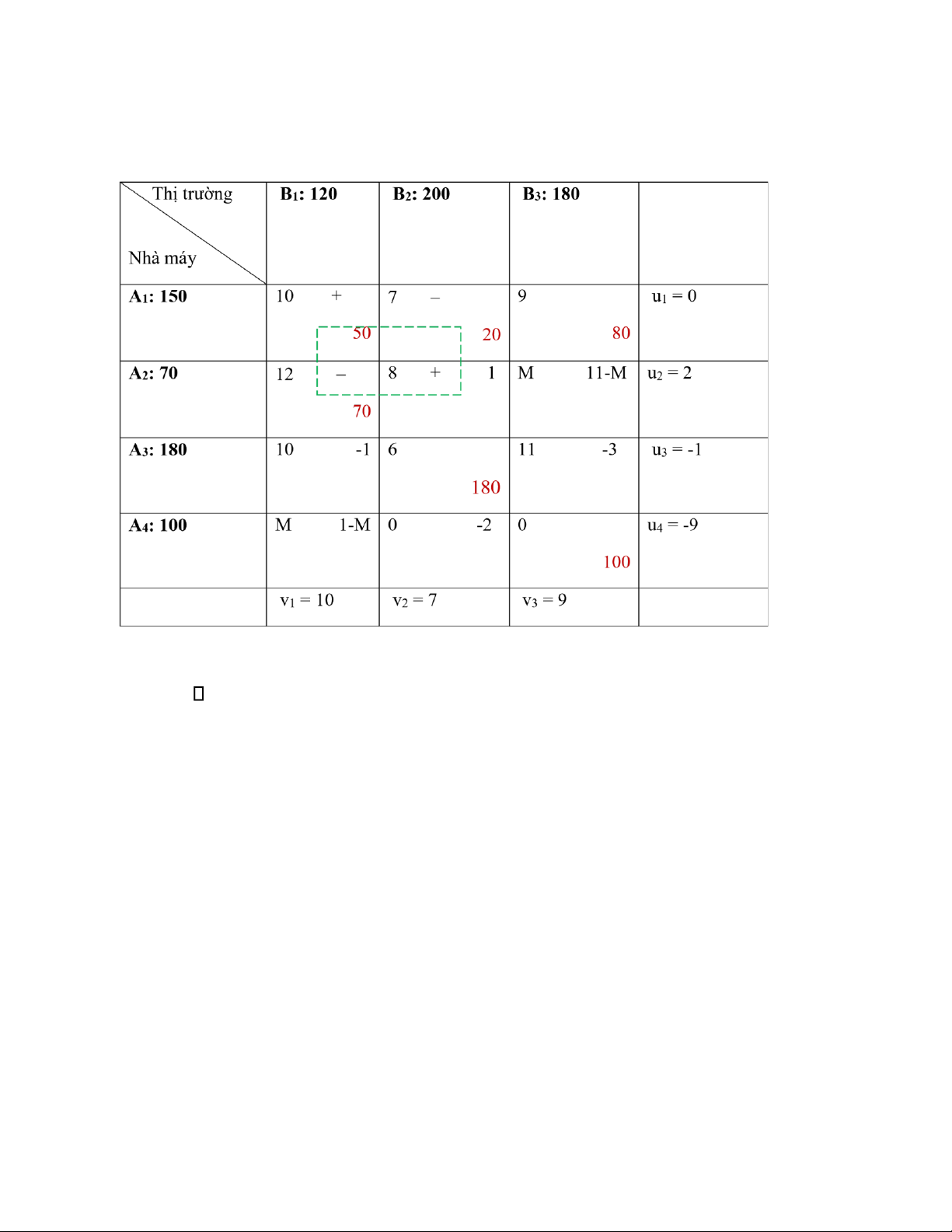
Vì tồn tại ij > 0 => Phương án này không tối ưu
Ô đưa vào (2,2); ô đưa ra (1,2); d = 20 lOMoAR cPSD| 58794847
Vì ij ≤ 0 với mọi ô (i,j)
=> Phương án tối ưu của BT CBTP có ô cấm
Vì các ô cấm có lượng phân phối bằng 0 nên PATƯ trên cũng là PATƯ của bài toán ban đầu Bài 3 (2đ): TH1: M/C C1: 1 C2: 1 C3: 1 U i lOMoAR cPSD| 58794847 M1: 1 180* 200 150 345 M2: 1 160* 220 160 306,67 M3: 1 120* 230* 120* 230 + Vj 1,92 1 1,92 + + Giá trị Z = Giải hệ phương trình: Ma trận phương án: 1 0 0 1 0 0 -1,31 0,79 1,52
Phương án tìm được chưa phải là tối ưu vì còn tồn tại giá trị x < 0 là: X31 = -1,31
Vì vậy ta cần điều chỉnh hệ thống nhân tử và ô chọn Ô đưa ra là: (3,1) Hệ số Lamda = min ( Ô đưa vào là: (2,3)
Hệ thống nhân tử và ô chọn: M/C C1: 1 C2: 1 C3: 1 U i M1: 1 180* 200 150 345 M2: 1 160* 220 160* 306,67 M3: 1 120 230* 120* 230 Vj 1,92 1 1,92 lOMoAR cPSD| 58794847 Giá trị Z = Giải hệ phương trình: Ma trận phương án: 1 0 0 0,015 0 0,985 0 0,79 0,21
Do mọi giá trị x đều >= 0 nên phương án tìm được là tối ưu.
Phương án tối ưu của bài toán là: M/C C1: 1 C2: 1 C3: 1 M1: 1 1 0 0 M2: 1 0,015 0 0,985 M3: 1 0 0,79 0,21 TH2:
Chỉnh sửa hệ thống nhân tử và ô chọn: M/C C1: 1 C2: 1 C3: 1 U i M1: 1 180* 200 150 345 M2: 1 160* 220 160* 306,67 M3: 1 120 230* 120* 230 Vj 1,92 1 1,92 Giá trị Z = Giải hệ phương trình: lOMoAR cPSD| 58794847 Ma trận phương án: 1 0 0 0,015 0 0,985 0 0,79 0,21
Do mọi giá trị Xij đều >= 0 nên phương án tìm được là tối ưu.
Phương án tối ưu của bài toán là: M/C C1: 1 C2: 1 C3: 1 M1: 1 1 0 0 M2: 1 0,015 0 0,985 M3: 1 0 0,79 0,21 TH3:
Chỉnh sửa hệ thống nhân tử và ô chọn: M/C C1: 1 C2: 1 C3: 1 U i M1: 1 180* 200 150 345 M2: 1 160 220 160* 306,67 M3: 1 120* 230* 120* 230 Vj 1,92 1 1,92
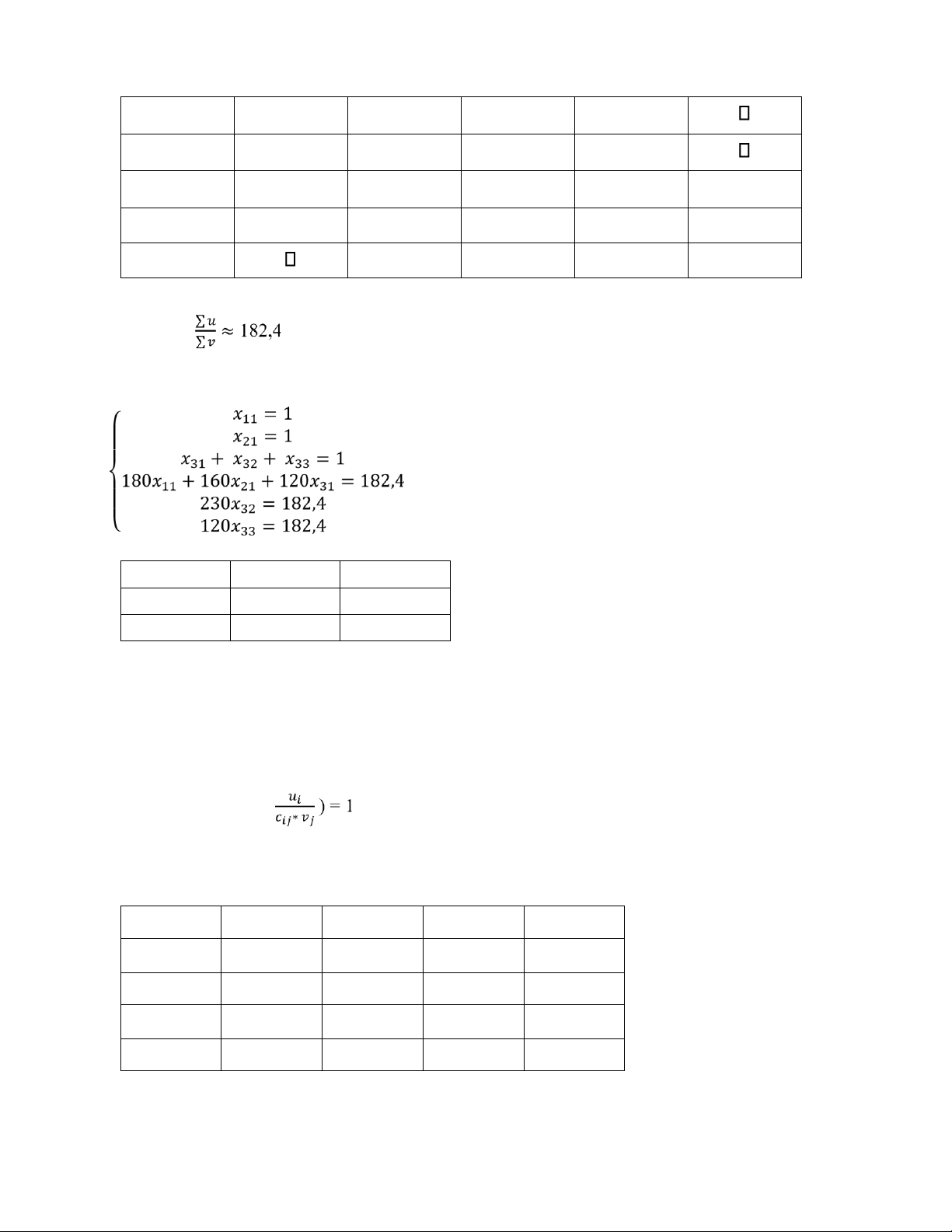
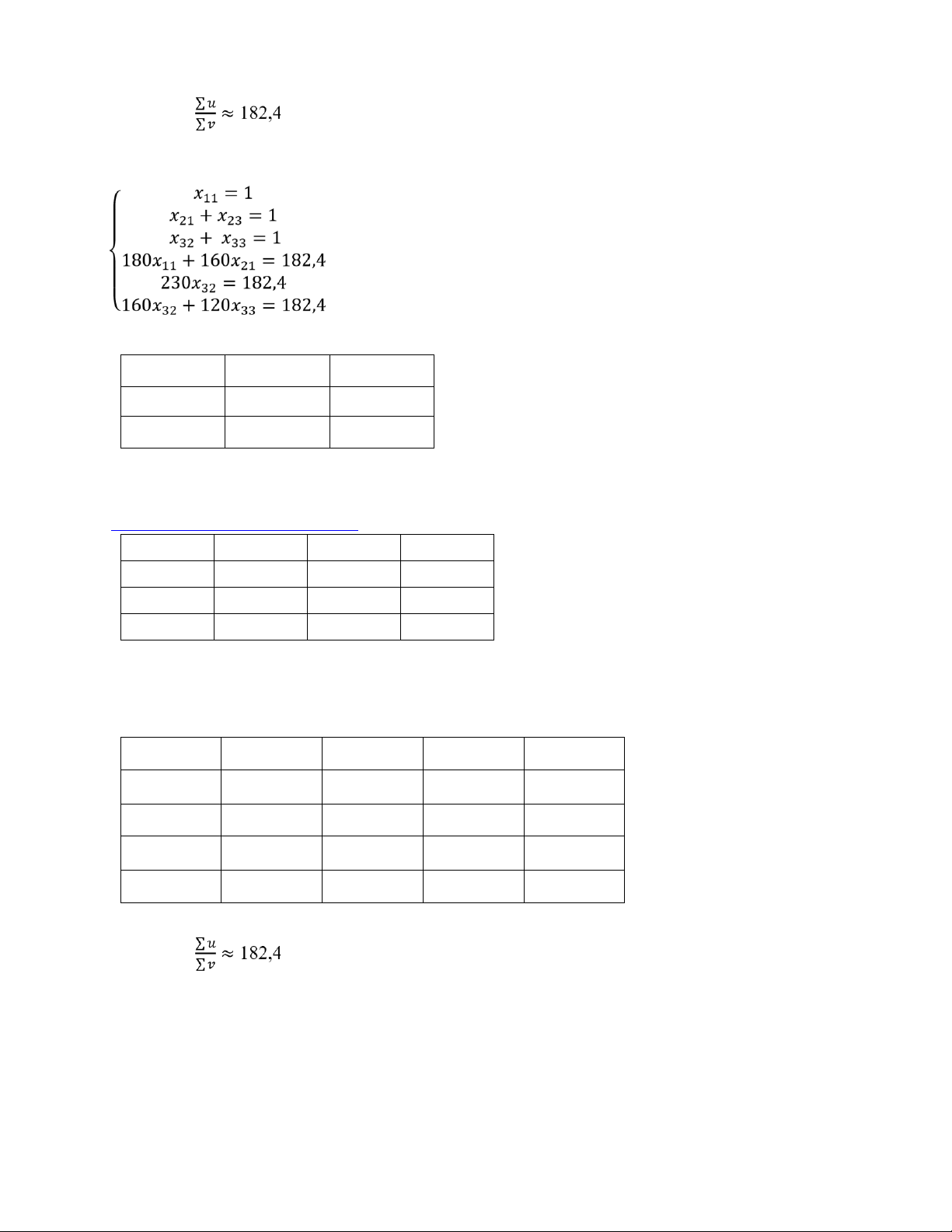
Giá trị Z = ∑ 𝑢 ≈ 182,4 ∑ 𝑣 Giải hệ phương trình: Ma trận phương án: lOMoAR cPSD| 58794847 1 0 0 0 0 1 0,02 0,79 0,19
Do mọi giá trị x đều >= 0 nên phương án tìm được là tối ưu.
Phương án tối ưu của bài toán là: M/C C1: 1 C2: 1 C3: 1 M1: 1 1 0 0 M2: 1 0 0 1 M3: 1 0,02 0,79 0,19 Với giá trị Z = 182,4
Thời gian trung bình hoàn thành hợp đồng là:
c. Hỏi phải phân công trình tự sản xuất quần, áo, găng tay cho các xí nghiệp như thế nào
để hoàn thành hợp đồng sớm nhất? TH1 và TH2: M/C C1: 1 C2: 1 C3: 1 M1: 1 1 0 0 M2: 1 0,015 0 0,985 M3: 1 0 0,79 0,21
XN 1: dành toàn bộ thời gian để sản xuất quần (198 ngày)
XN 2: sản xuất quần trước (khoảng 2,97 ngày), xong quần thì chuyển sang sản xuất găng tay (khoảng 195,03 ngày)
XN 3: sản xuất áo trước (khoảng 156,42 ngày), xong áo thì chuyển sang sản xuất găng
tay (khoảng 41,58 ngày) TH3: M/C C1: 1 C2: 1 C3: 1 M1: 1 1 0 0 M2: 1 0 0 1 M3: 1 0,02 0,79 0,19 lOMoAR cPSD| 58794847
XN 1: dành toàn bộ thời gian để sản xuất quần (198 ngày)
XN 2: dành toàn bộ thời gian để sản xuất găng tay (198 ngày)
XN 3: sản xuất áo (khoảng 156,42 ngày) trước, sau đó chuyển sang sản xuất quần
(khoảng 3,96 ngày) và cuối cùng là sản xuất găng tay (khoảng 37,62 ngày).