Đề 2 - Ôn tập full lớp 12 môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 ĐỀ SỐ 58
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
Câu 1. Gọi M m, lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y x= − +3 3x2 2 trên đoạn −1;1
.Tính M + m. A. 1. B. 0. C. 2.
D. 3.
Câu 2. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng đi qua điểm M (2;0;−1) và có vectơ chỉ
phương a = (4; 6;− 2) . Phương trình tham số của là
x =− +2 4t x =− +2 2t x = +4 2t x = +2 2t A.
y =−6t . B.
y =−3t . C. y =− − 6 3t . D. y =−3t . z = +12t z = +1 t z = +2 t z =− +1 t
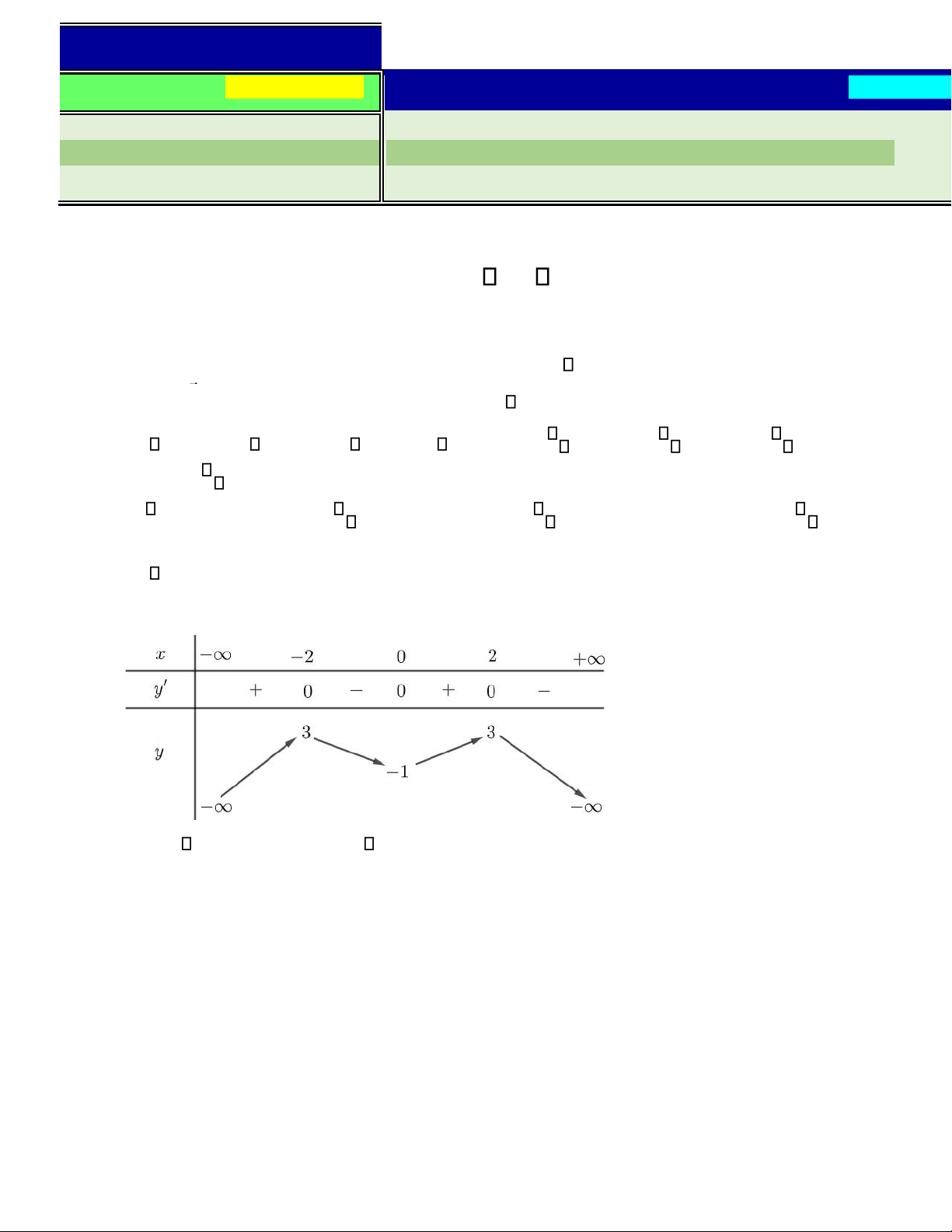
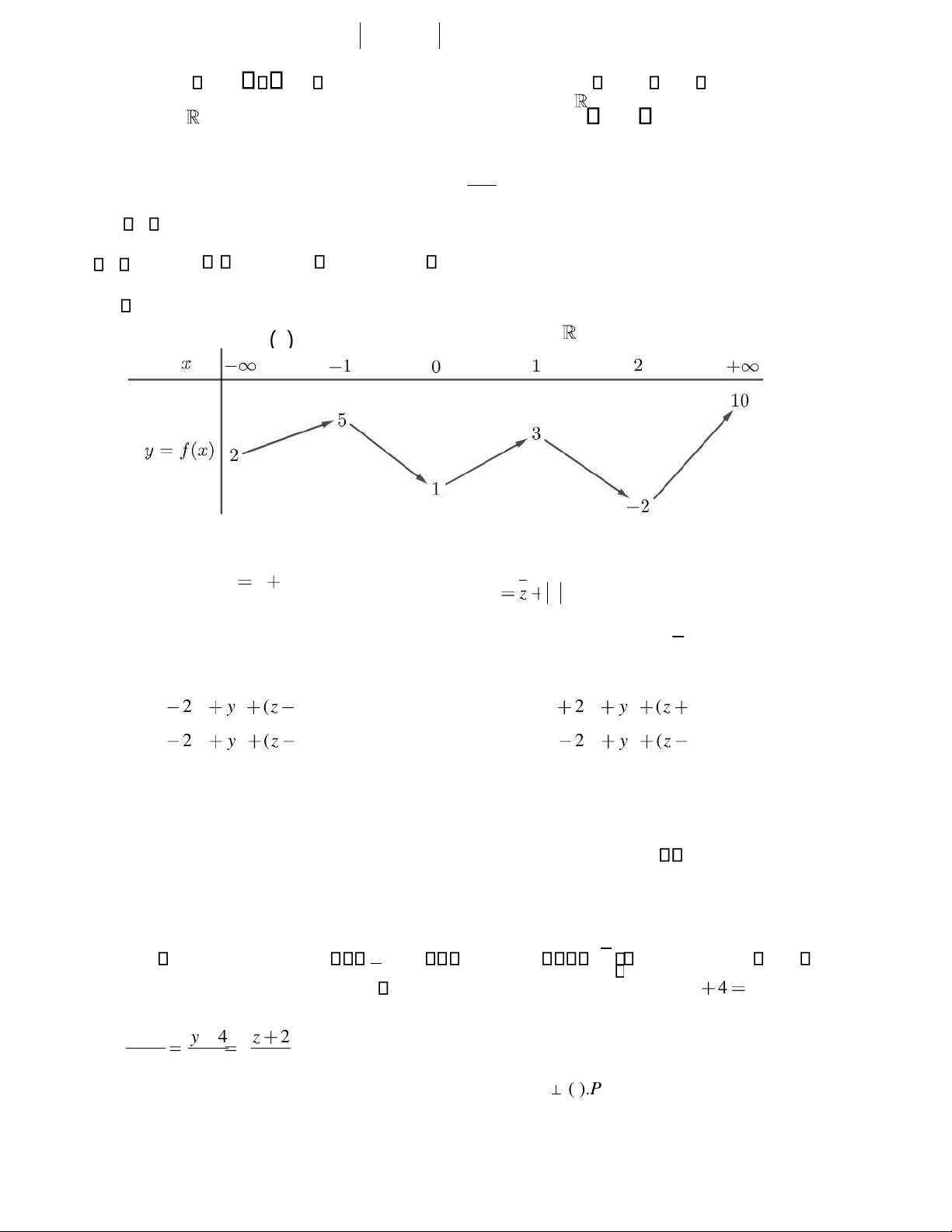
Câu 3. Cho hàm số y = f x( ) có bảng biến thiên như hình vẽ. Hàm số y = f x( ) nghịch biến trên khoảng nào dưới đây? A.(0;+ ). B. (− ;−2). C. (0;2). D. (2;4) . + ax b lOMoAR cPSD| 22014077
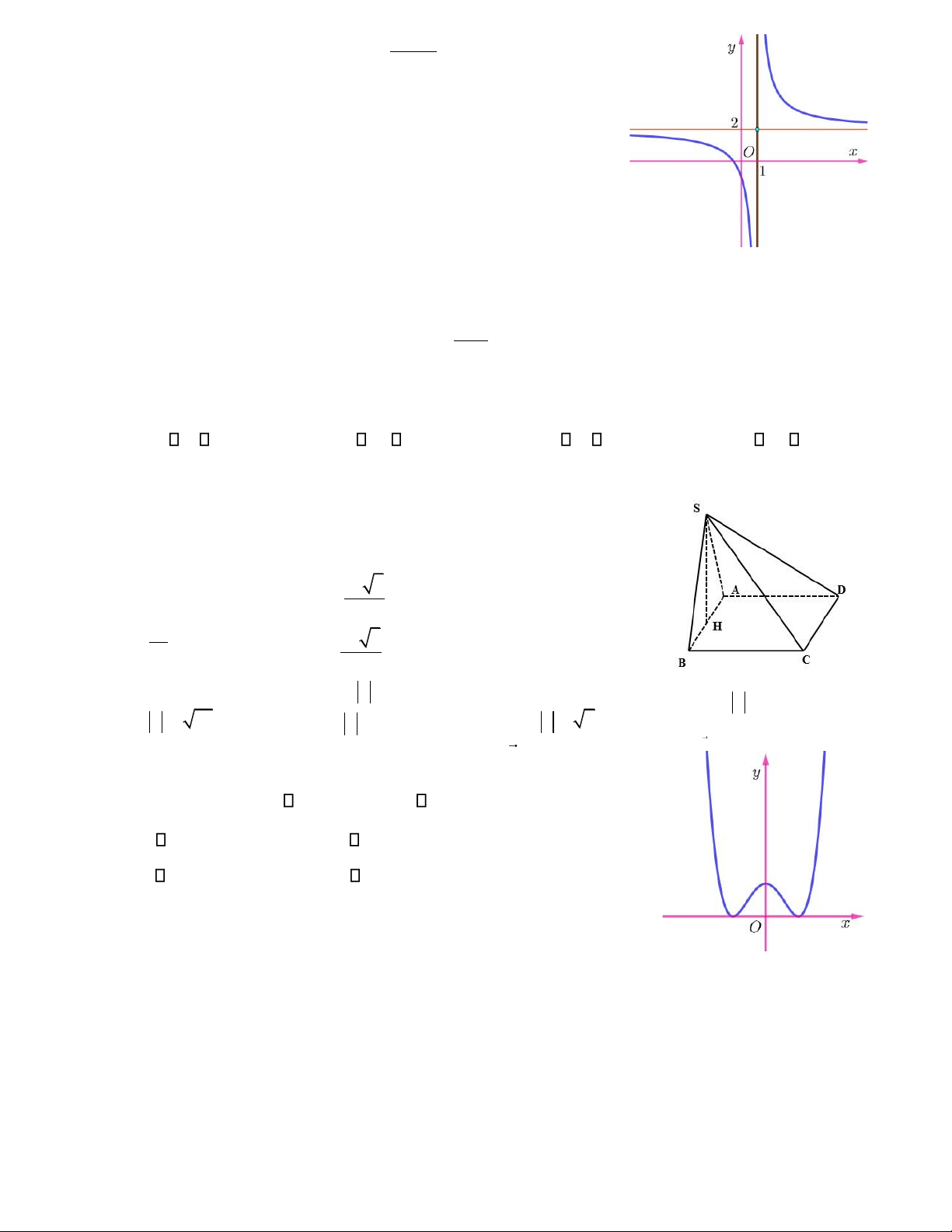
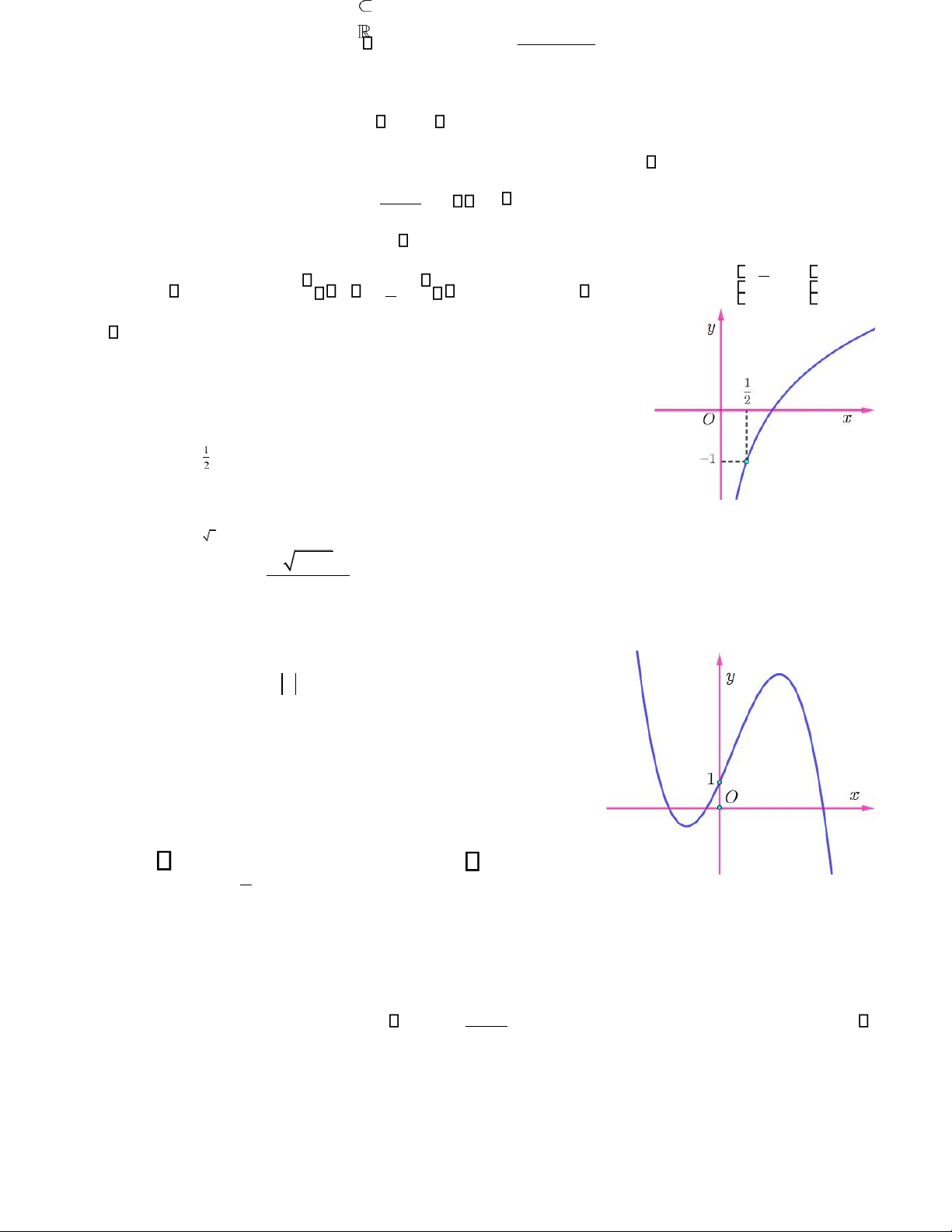
Câu 4. Hình vẽ bên là đồ thị của hàm số y=
. Đường tiệm cận đứng cx d+
của đồ thị hàm số có phương trình là A. x =1. B. x = 2 . C. y =1. D. y = 2
Câu 5. Cho f x( )= 5x thì f x( + −2) f x( ) bằng. A. 25 . B. 24. C. 25 f x( ). D. 24 f x( ). Câu 6. 1
Biết F x( ) là một nguyên hàm của f x( ) =
và F (0) = 2 thì F (1) bằng. x +1 A. ln2. B. 2+ln2. C. 3 . D. 4.
Câu 7. Tất cả các giá trị của tham số m để hàm số y x= −4 2x m2 + cắt trục hoành tại 4 điểm là A. −1 m 0 . B. 0 m 1. C. −1 m 0 . D. 0 m 1.
Câu 8. Cho hình chóp S ABCD. có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều cạnh a và nằm
trong mặt phẳng vuông góc với mặt phẳng (ABCD) . Tính thể tích khối chóp S ABCD. . 3 . B. a3 3 . A. a 6 a3 a3 3 C. . D. . 3 2
Câu 9. Cho số phức z = − +1 3i . Tính z . D. z 10 = . A. z = 10 . B. z = 2. C. z = 2. v
Câu 10. Trong mặt phẳng Oxy, cho điểm A(3;0) và vectơ v = (1;2) . Phép tịnh
tiến T biến A thành A . Tọa độ điểm A là A. A (4;2) . B. A (2;−2) . C. A (−2;2) . D. A (2;−1) .
Câu 11. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây ?
A. y = x4 −2x2 +1. B. y = x4 −2x2 .
C. y=− −x4 2x2 −1.
D. y = x3 −2x2 +1.
Câu 12. Tổng tất cả các nghiệm của phương trình log ( (
2 x−1) +log2 x = +1 log2 3x−5) bằng A. 7 . B. 6 . C. 5 . D. 4 .
Câu 13. Hàm số nào sau đây đồng biến trên khoảng (−1;1) ? lOMoAR cPSD| 22014077
A. y = 1− x2 .
B. y = x2. C. y = x +1.
D. y =− +x3 3x . x
Câu 14. Cho khối nón đỉnh S có độ dài đường sinh là a, góc giữa đường sinh và mặt đáy là 60 . Thể tích khối nón là 3 a3 a3 3 a3 a3 3 A. V = . B. V = . C. V = . D. V = . 8 8 8 24
Câu 15. Cho a b c, , là các số dương và a 1. Mệnh đề nào sau đây sai? 1 A. log =− ( a b loga b.
B. loga b+ =c) loga b.loga c. C. log ( a
bc = loga b−loga c. D. loga bc) = loga b +loga c.
Câu 16. Cho số phức z = −1 2i thì số phức liên hợp z có
A. phần thực bằng 1 và phần ảo bằng −2.
B. phần thực bằng −2 và phần ảo bằng 1.
C. phần thực bằng 1 và phần ảo bằng 2.
D. phần thực bằng 2 và phần ảo bằng 1. 42 là Câu 17. Cho log 2 = = 15 5
a, log 35 b. Khi đó giá trị của log5 A. . B. . . D. .
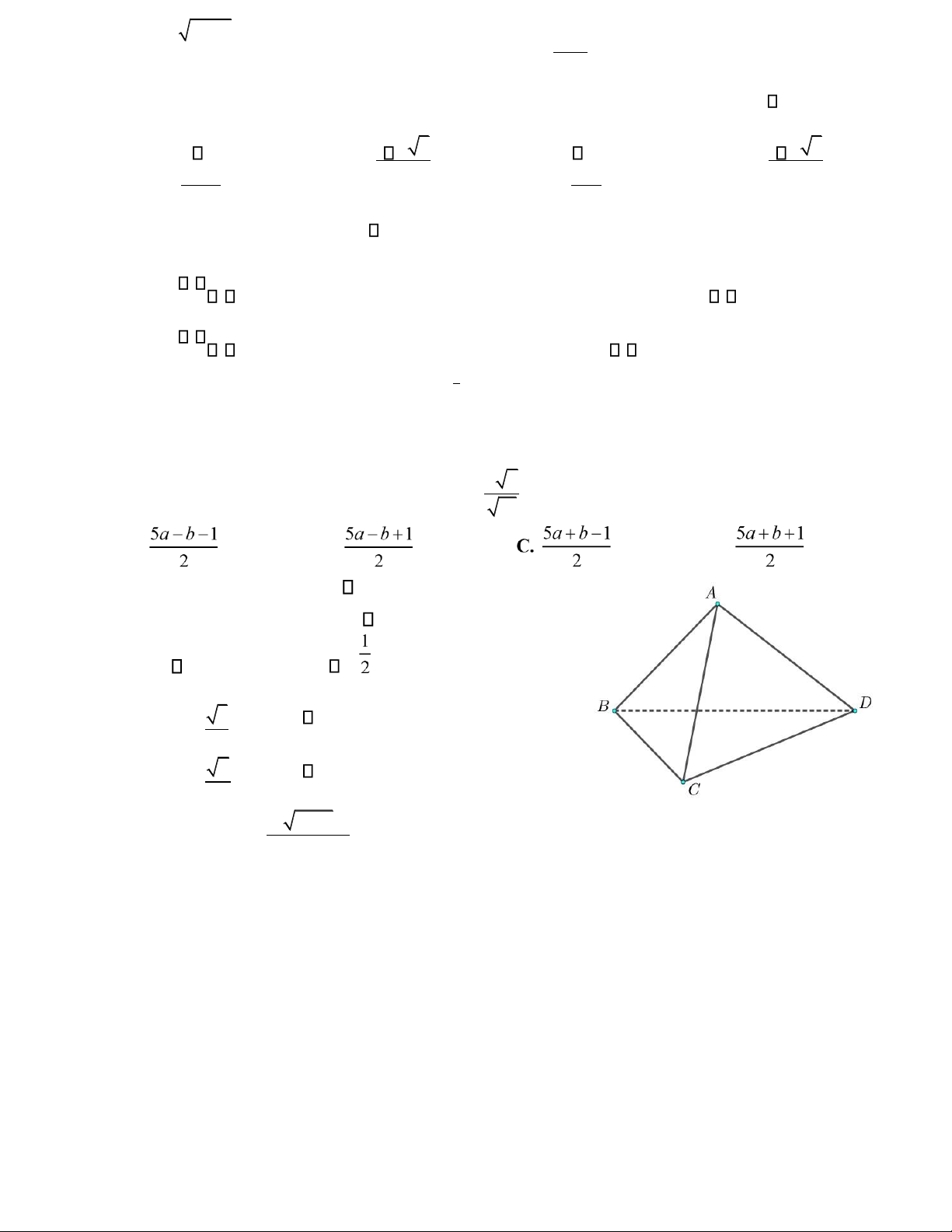
Câu 18. Cho tứ diện đều ABCD. Gọi là góc giữa đường thẳng AB
và mặt phẳng (BCD) . Tính cos . A. cos = 0 . B. cos = . 3 C. cos =. 3 2 D. cos =. 3
Câu 19. Đồ thị hàm số y = x 2 − x 2 4x +3 có bao nhiêu đường tiệm cận? − A. 1. B. 3 . C. 4 . D. 2 .
Câu 20. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S): x2 + + −y2 z2
2(x+ +2y 3z)= 0 . Gọi A, B ,
C lần lượt là giao điểm (khác gốc tọa độ O) của mặt cầu (S) và các trục tọa độ Ox , Oy , Oz . Phương
trình mặt phẳng (ABC) là:
A. 6x−3y−2z +12 = 0.
B. 6x−3y+2z −12 = 0.
C. 6x+3y+2z −12 = 0.
D. 6x−3y−2z −12 = 0. lOMoAR cPSD| 22014077
Câu 21. Cho hình chóp tứ giác S ABCD. có đáy ABCD là hình vuông cạnh bằng a, SA ⊥(ABC), SA= 3a. Thể
tích của khối chóp S ABCD. là
A. V = 6a3.
B. V = a3.
C. V =3a3.
D. V = 2a3.
Câu 22. Cho hàm số f x( ) thỏa mãn f '(x) = x2 (x −1), x R. Mệnh đề nào sau đây là mệnh đề đúng?
A. f x( ) đạt cực tiểu tại x=1.
B. f x( ) không có cực trị.
C. f x( ) đạt cực tiểu tại x=0.
D. f x( ) có hai điểm cực trị.
Câu 23. Cho hàm số y = f x( ) có bảng biến thiên như sau: 1
Hàm số g x( ) = đồng biến trên khoảng nào dưới đây? f x( ) A. (−2;0) . B. (3;+ ). C. (1;2) . D. (− ; 1− ).
Câu 24. Hàm số y x e= 2 x nghịch biến trên khoảng nào? A. (−2;0 .) B. (− ; 2 .− ) C. (− ;1 .) D. (1;+ ).
Câu 25. Đường thẳng d y: = +x 1 và đường cong (C): y = − − +x3 x2
x 1 có bao nhiêu điểm chung? A. 2. B. 3. C. 1. D. 0.
Câu 26. Phương trình 2sinx− =3 0 có các họ nghiệm là A. = 3 + k2 ,k . B. x = 3 + k ,k . x x = − + k2 x = − + k 3 3 = + k2 x 3 C. x ,k . D. = 3 + k ,k . x = 2 + k2 x = 2 + k 3 3 lOMoAR cPSD| 22014077
Câu 27. Tập xác định của hàm số y = ln x2 + 2x −3 là:
A. D = −( ; 3− 1;+ )
B. D = −( ; 3− ) (1;+ ) C. D=
D. D = \ −3;1 .
Câu 28. Tất cả các giá trị của tham số m để hàm số y =
−x3 +mx2 −2mx+1 có hai điểm cực trị là 3 m 2
A. m 0. B. 0 m 2. C. m 2.
D. m 0.
Câu 29. Cho hàm số y ( fx =
) liên tục và có bảng biến thiên trên như hình vẽ bên dưới
Tìm giá trị lớn nhất của hàm số y = f (cos x) A. 5. B. 3. C. 10. D. 1. z
Câu 30. Cho số phức z
3 4 .i Phần thực của số phức w z là A. 3. B. 8. C. 4 . D.5.
Câu 31. Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;2;4),B(3; 2;2), mặt cầu đường kính AB có phương trình là 2 2 2 2 A. 2 y ( z 3)
36. xB. x 2 2 2 y ( z 3) 6. 2 2 2 2 C. 2 y ( z 3) 6. xD. x 2 2 2 y ( z 3) 24.
Câu 32. Cho khối chóp S ABCD.
có đáy là hình chữ nhật và thể tích bằng 8.Thể tích của khối chóp S BCD. bằng. A.2 . B. 4 . C.6 . D.3 .
Câu 33. Cho hàm số f x( )= −x2 2xln .x Kí hiệu x0 là nghiệm của phương trình f
(x) = 0, mệnh đề nào dưới đây đúng? . 0 A. x −( 0 2;0 .) B. x0 23;2 . C. x0 0 2 ; 3 D. x (2;+ ).
x 2 y z 4
Câu 34. Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( ):3P 0 và đường thẳng d : x 2 y 4 z 2 4 3 1
. Trong các mệnh đề sau, mệnh đề nào đúng?
A. d cắt ( )P . B. d P( ). C.d ( ).P
D. d//( ).P lOMoAR cPSD| 22014077
Câu 35. Cho số phức z = a +bi (a b,
). Biết z+ + = −2z
i2 5 i . Giá trị a b+ là A. 7 . B. 5. C. 1. D. 3. Câu 36. 1 2 1x+
Tập nghiệm của bất phương trình 1 +a2
1 (với a là tham số) là A. (− ;0). B. − ;− 12 . C. (0;+ ). D. − 12;+ .
Câu 37. Đường cong trong hình bên là đồ thị của một trong bốn hàm số được
liệt kê ở bốn phương án A B C D, , , dưới đây. Hỏi hàm số đó là hàm số nào? A. y = log ( 2 2x) .
B. y=log2 x . C. y= logx .
D. y = log2 x .
Câu 38. Đồ thị hàm số y = x2 4x +3 có bao nhiêu đường tiệm cận? x 2 − − A. 1. B. 3 . C. 4 . D. 2 .
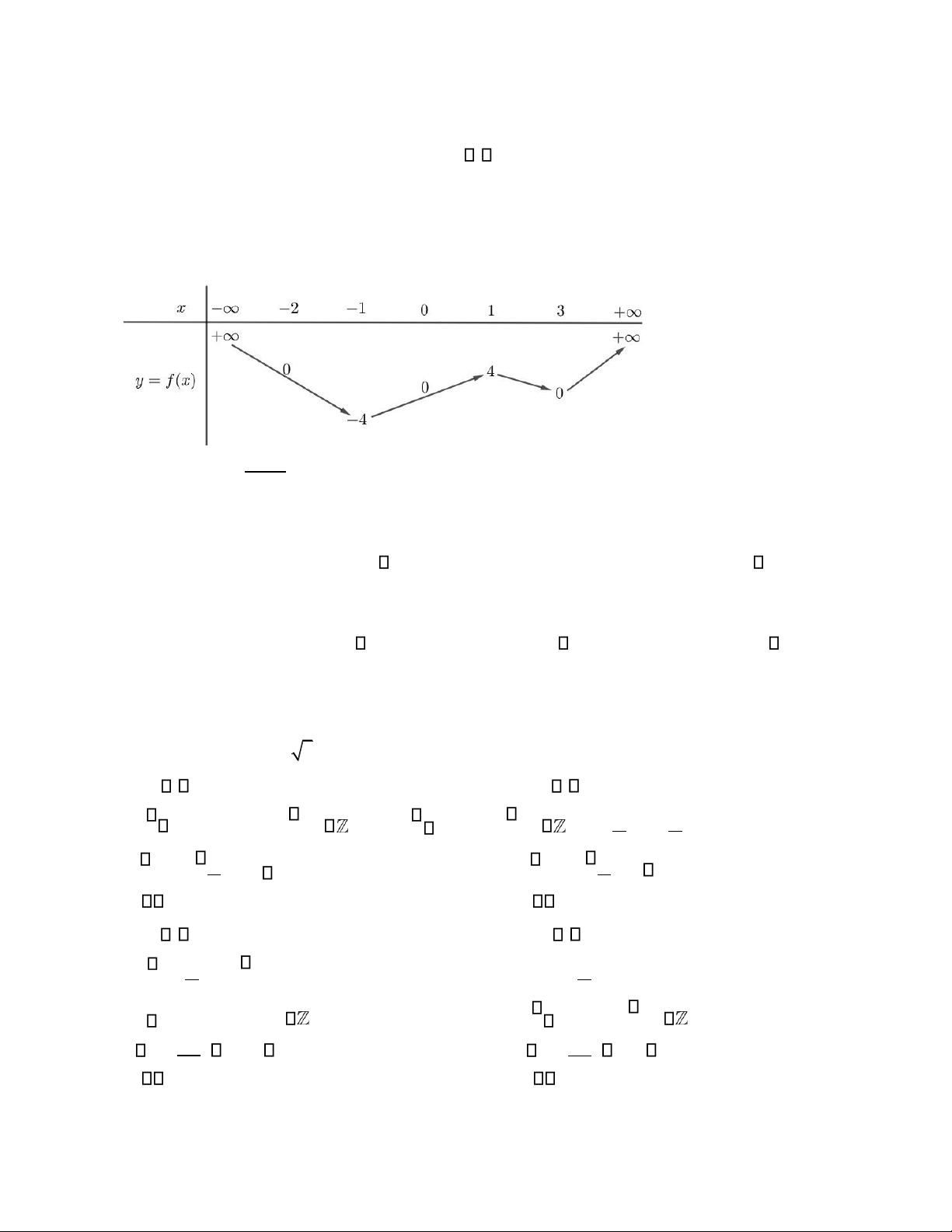
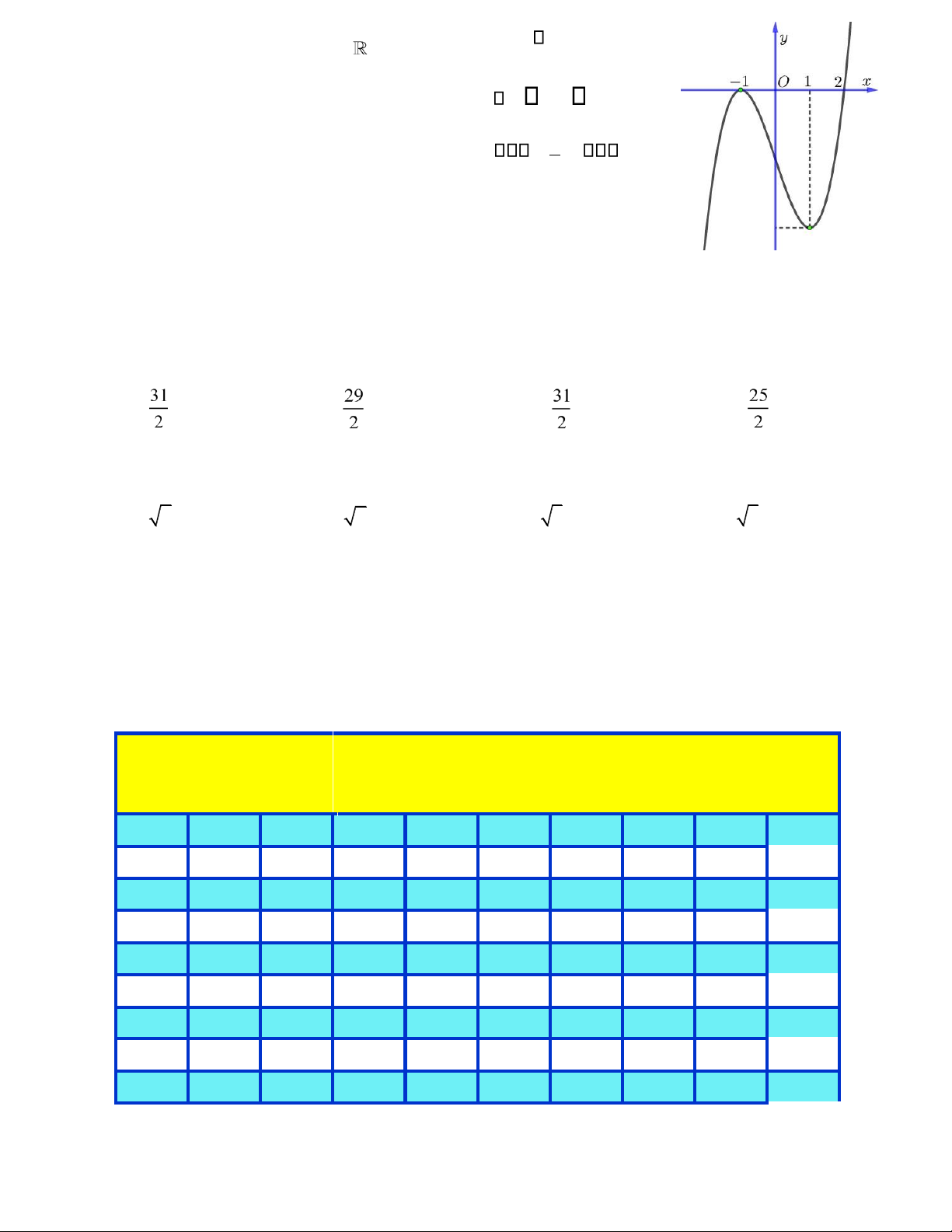
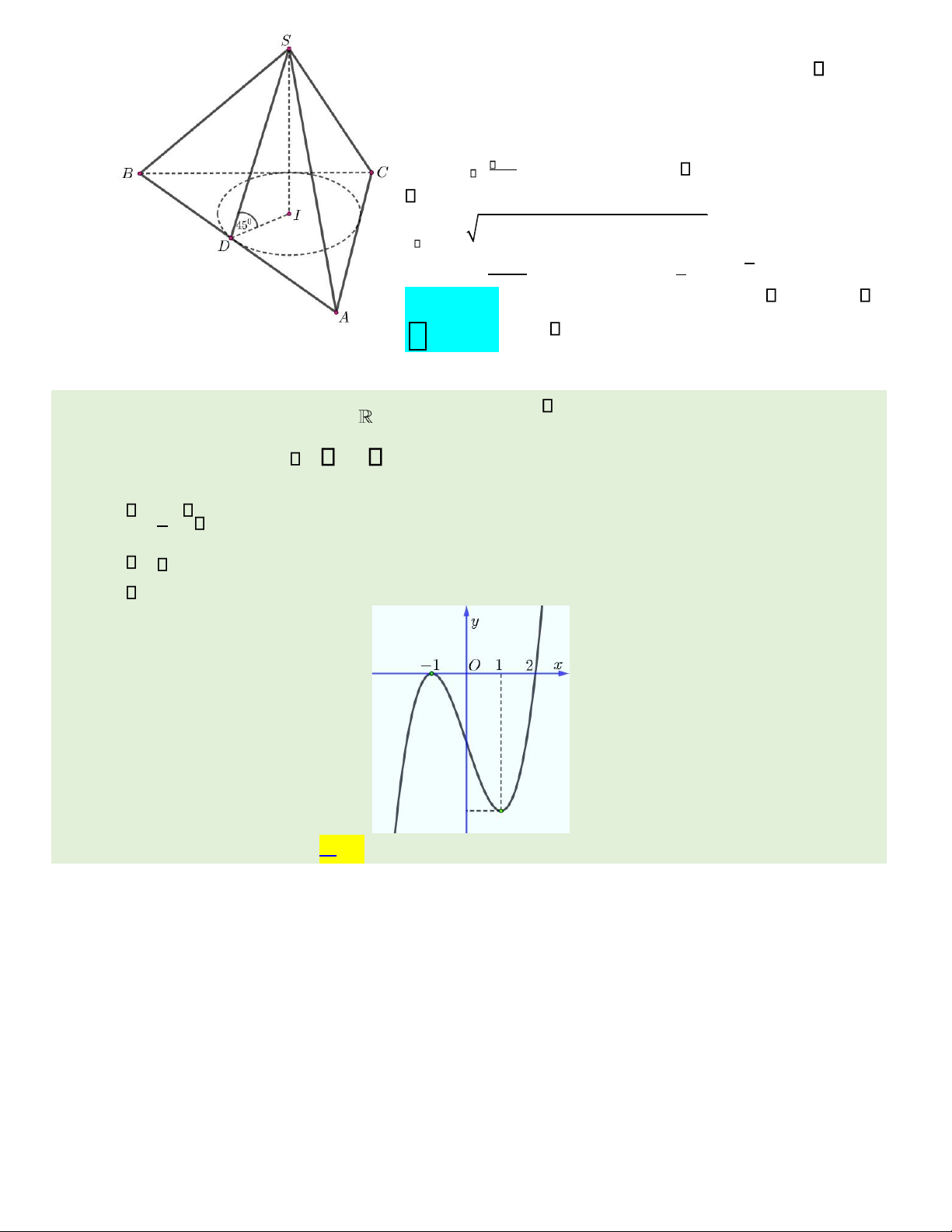
Câu 39. Cho hàm số bậc ba y = f x( ) có đồ thị như hình vẽ. Số nghiệm
của phương trình f ( x )+ =1 0 là A. 4. B. 3. C. 2. D. 1. e4 4 1 Câu 40. Biết
f (ln x) x dx = 4. Tính tích phân I = 1 f x( )dx . e A. I =8. B. I =16. C. I = 2. D. I = 4. x
Câu 41. Cho hàm số y = f x( ) có đạo hàm f (x) = − x2
1 . Với a và b là các số dương thỏa mãn a b, giá + lOMoAR cPSD| 22014077
trị nhỏ nhất của hàm số f x( ) trên đoạn a b; bằng: f b( ) .
B. f a( ).
C. f a( )+2 f b( ) . b D. f a+2 . A. −2
Câu 42. Cho hàm số y = 3x
có đồ thị (C). Có tất cả bao nhiêu đường thẳng cắt (C) tại hai điểm phân biệt x
mà hoành độ và tung độ của hai giao điểm này đều là các số nguyên? A. 10 . B. 4. C. 6. D. 2.
Câu 43. Cho một hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng a. Gọi AB và CD là hai đường
kính tương ứng của hai đáy. Biết góc giữa hai đường thẳng AB và CD bằng 300. Tính thể tích khối tứ diện ABCD. a3 a3 3 a3 a3 3 A. . B. . C. . D. . 12 6 6 12 +log 5
Câu 44. Cho các số nguyên a, b, c thỏa mãn a+ b 2 = log 45 . Tổng 6
a+b+c bằng: c+log 32 A. 1. B. 4 . C. 2 . D. 0 .
Câu 45. Cho khối lăng trụ tam giác ABC ABC. mà mặt bên ABBA có diện tích bằng 4. Khoảng cách
giữa cạnh CC và AB bằng 7. Thể tích khối lăng trụ bằng: A. 10. B. 16. C. 12. D. 14.
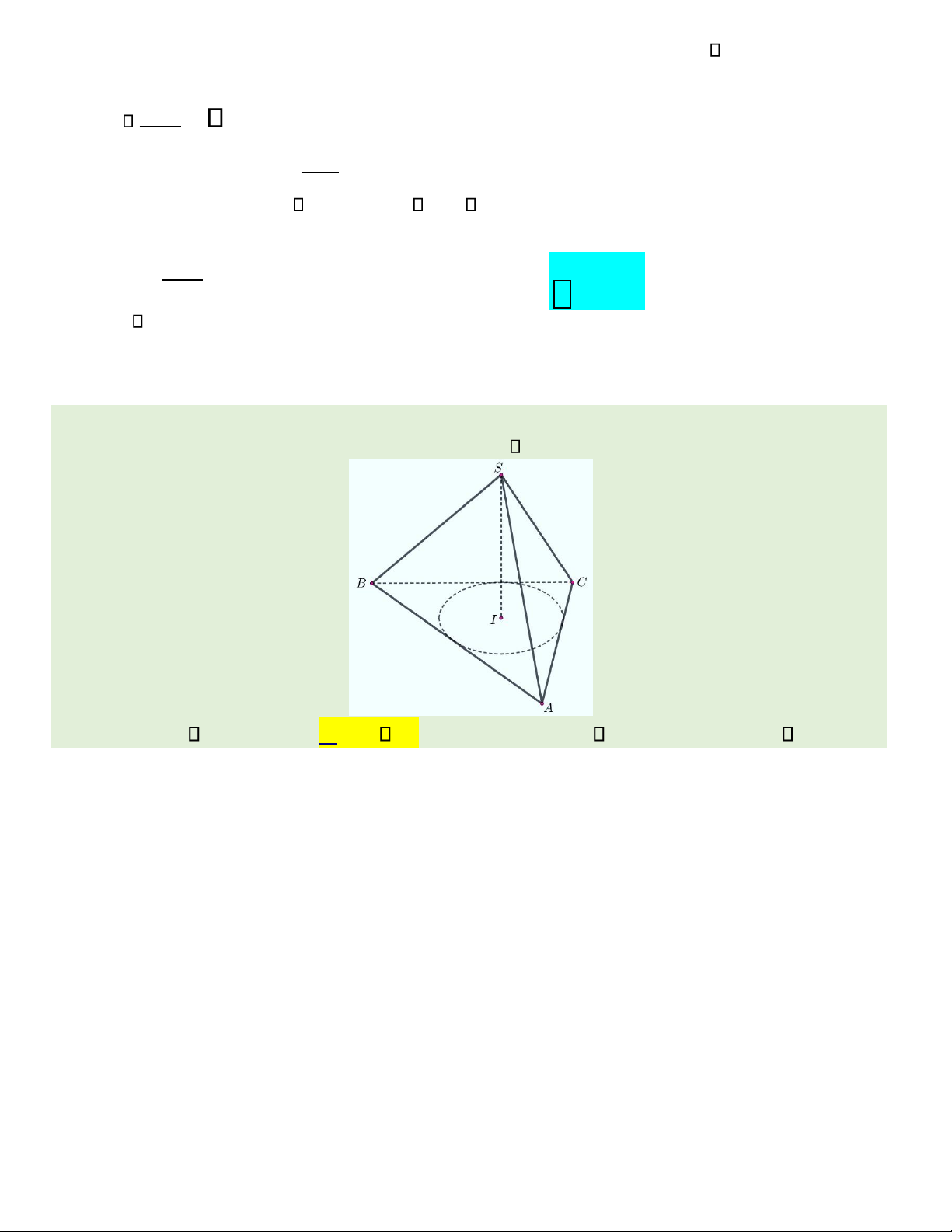
Câu 46. Cho hàm số y = f x( ) có đạo hàm liên tục trên 1;2 , thỏa mãn f x( ) = x f. (x)− x2 . Biết f (1) = 3, tính f (2) . A. 16. B. 2. C. 8. D. 4.
Câu 47. Cho hình nón đỉnh S , đáy là đường tròn nội tiếp tam giác ABC .
Biết rằng AB = BC =10a, AC =12a, góc tạo bởi hai mặt phẳng
(SAB) và (ABC) bằng 45 . Tính thể tích V của khối nón đã cho.
A. V =3 a3. B. V =9 a3. C. V = 27 a3.
D. V =12 a3. lOMoAR cPSD| 22014077
Câu 48. Cho hàm số f x( ) liên tục trên và có đồ thị hàm số f (x) như hình vẽ.
Gọi S là tập hợp các giá trị nguyên của tham số m − 5;5 để hàm số y = f x( − + 2
2mx + m2 1) nghịch biến trên khoảng 0; 12 . Tổng giá
trị các phần tử của S bằng A. 10. B. 14. C. −12. D. 15.
Câu 49. Giả sử a b, là các số thực sao cho x3 + y3 = a.103z +b.102z đúng với mọi số thực dương x y z, , thỏa mãn
log(x+ y) = z và log(x2 + y2 ) = z +1. Giá trị của a+b bằng: A. . B. . C. − . D. − .
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(3;0;0 ,) B(−3;0;0) và C(0;5;1). Gọi M là một
điểm nằm trên mặt phẳng tọa độ (Oxy) sao cho MA MB+ =10, giá trị nhỏ nhất của MC là A. 6. B. 2. C. 3. D. 5.
________________HẾT________________ ÑAÙP AÙN ÑEÀ SOÁ 58 1 2 3 4 5 6 7 8 9 10 B D D A D B D B A A 11 12 13 14 15 16 17 18 19 20 A A D D B C A C D C 21 22 23 24 25 26 27 28 29 30 B A C A B C D A A B 31 32 33 34 35 36 37 38 39 40 C B C A D B B D C D 41 42 43 44 45 46 47 48 49 50 lOMoAR cPSD| 22014077 A C A A D C B B B B
Lôøi giaûi caâu hoûi vaän duïng cao ñeà soá 58 −2
Câu 42. Cho hàm số y =
có đồ thị (C). Có tất cả bao nhiêu đường thẳng cắt (C) tại hai điểm phân biệt 3x x
mà hoành độ và tung độ của hai giao điểm này đều là các số nguyên? A. 10 . B. 4. C. 6 . D. 2. Hướng dẫn giải: −2 3x
Trước hết, ta tìm các điểm có tọa độ nguyên thuộc đồ thị hàm số y = (C). x 2 2 − Ta có: y 3 = = − (x 0 . Gi xy C , suy ra )
ả s ử ( 0 ; 0 là đi ể m có t ọ a đ ộ nguyên thu ộ c ( x x ) ) x 0 x 0 2 2 x ; 1 2 . 0 3 − x x 0 0 3x
Do đó, các điểm cần tìm là: A(1;1 ,) B(−1;5 ,) C(2;2 ,) D(−2;4).
Số đường thẳng đi qua hai trong bốn điểm A, B, C, D là C 2 = 4
6. ⎯⎯⎯→Choïn C
 Kỹ thuật máy tính bỏ túi:
Trong bài này, khi tìm điểm có tọa độ nguyên của đồ thị hàm số, ta sử dụng máy tính bỏ túi như
sau. Dưới đây là các lệnh của dòng máy VINACAL 680EX PLUS:
MODE ⎯⎯→next 8 ⎯⎯→next F X( ) = 3X −2 ⎯⎯→next START : 10− ⎯⎯→next END:10 X ⎯⎯→ =
next STEP:1 ⎯⎯→next
Đến đây, các bạn học sinh chỉ cần quan sát xem dòng nào có cặp (X;F(X)) nguyên thì ta chọn làm điểm cần tìm.
 Lưu ý rằng: Với dòng máy VINACAL cũ hơn, ta khởi động bằng lệnh MODE ⎯⎯→next 7
mọi dòng máy, khi dùng ; với chức năng Table, màn hình thường có thêm dòng G X( ) , khi ấy dấu = để bỏ ta nhấn qua hàm này.
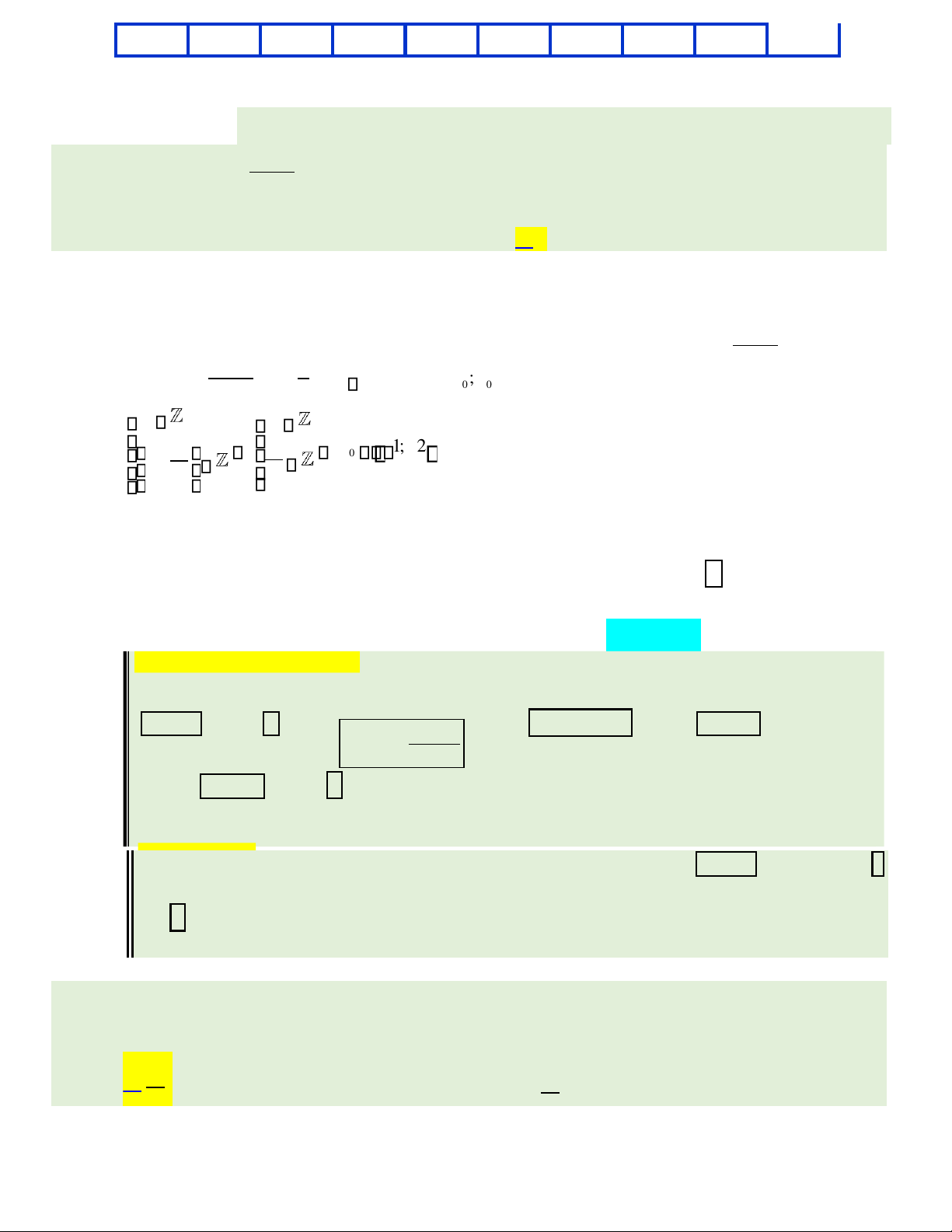
Câu 43. Cho một hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng a. Gọi AB và CD là hai đường
kính tương ứng của hai đáy. Biết góc giữa hai đường thẳng AB và CD bằng 300. Tính thể tích khối tứ diện ABCD. a3 a3 3 a3 a3 3 A. . B. . C. . D. . lOMoAR cPSD| 22014077 12 6 6 12 Hướng dẫn giải:
Xét đường tròn (O) có đường kính AB, đường tròn (O ) có đường
kính CD. Ta vẽ thêm các đường kính EF của (O) và GH của (O ) sao
cho EF CD GH AB// , // . Khi đó góc (AB EF,
) = (AB CD, ) = 300, đồng thời ABHG
là thiết diện qua trục của hình trụ nên ABHG là hình vuông cạnh a, suy ra
AB = AG = a. Thể 3 1 a 0
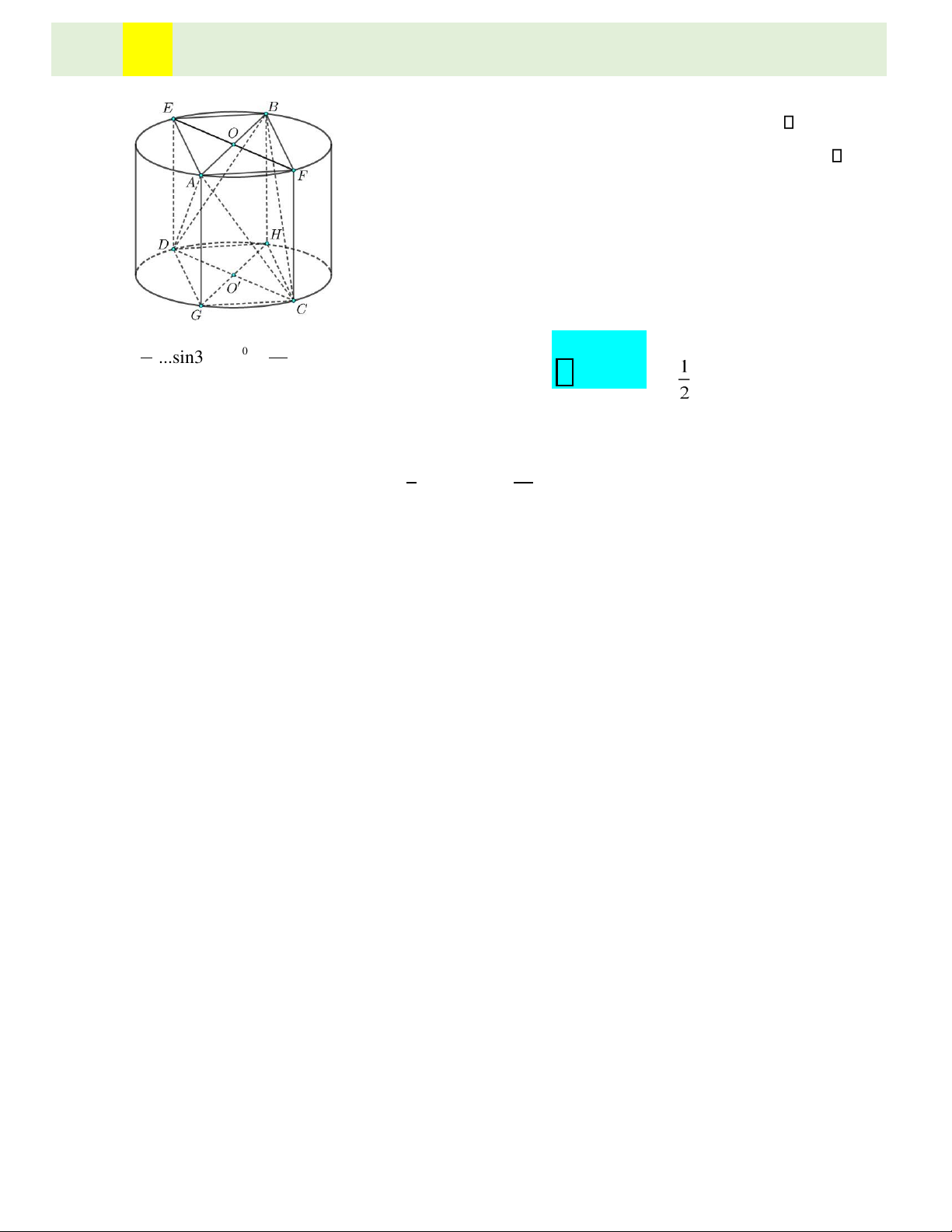
tích khối lăng trụ AEBF ⎯⎯⎯→Choïn GDHC. là: ....sin30 aaa 2 A V = = AEBFGDHC. AG S. AEBF AG. AB EF. .sin(AB EF, ) 1 a3 = = . Suy ra V = = A CDB VAEBF G. DHC . 4 3 12 lOMoAR cPSD| 22014077  Lưu ý: Học sinh có th
ể dùng công thức nhanh để tìm thể tích tứ diện như sau: ABCDd AB CD. . ( ,
. Ta có thể chứng minh công V = ABCD thức này dựa vào ).sin(AB CD, ) hình vẽ
Từ tứ diện bên dưới. Xét trường hợp tổng quát AEBF không chắc là hình bình hành.
Chứng minh: ABCD, ta dựng hình lăng trụ AEBF.GDHC như hình vẽ. Xét tứ giác Khi đó: S
AEBF với lưu ý: sin(OA OE, ) = sin(OE OB,) = sin(OB OF,) = sin(OA OF, ) = . = = S + S + S + S AEBF OAE OAF OBF OBE = 1 1 1 1
OAOE. .sin + OAOF. .sin + OBOE. .sin + OBOF. .sin = 2 2 2 2 1 1
Vậy SAEBF Ta OA OE( +OF)sin + OB OE( +OF)sin 2 2 có: V 1 1 1 1
OAEF. .sin + OB EF. .sin = EF OA OB( + )sin =AB EF. = d 1 1 .sin . AB CD( 2 2 2 2
= AB EF. .sin = ABCD. .sin(AB CD, ) 2 2 V = ABCD . 1 1 ABCDd AB CD. . ( , ).sin(AB CD, ) = = ABCD VAEBFGDHC. . .h SAEBF 3 3 ,).
ABCD..sin(AB CD, ) . b +log 5
Câu 44. Cho các số nguyên a, b, c thỏa mãn a+ 2 = log 45 . Tổng 6
a+b+c bằng: c+log 32 A. 1 . B. 4 . C. 2 . D. 0 . Hướng dẫn giải: lOMoAR cPSD| 22014077
Ta có: a+b+log 52 = log 456 +a b+log 52 = log 452 c+log 32 c+log 32 log 62 ) ( a + +log 52 = log2 3 .52
a+ b+log 52 = 2log2 3+log 52 b c+log 3 ( 2 log2 2.3) c+log 32 1+log 32
+a b+log 52 = 2+ 2log2 3− +2 log 52 +a b+log 52 = +2 − +2 log 52 c+log 32
1+log 32 c+log 32 1+log 32
Đồng nhất hệ số hai vế, ta có a = 2, b =−2, c =1.Vậy a+ + = + − + =bc 2 ⎯⎯⎯→Choïn ( 2) 1 1. A
Câu 45. Cho khối lăng trụ tam giác ABC ABC. mà mặt bên ABBA có diện tích bằng 4. Khoảng cách
giữa cạnh CC và AB bằng 7. Thể tích khối lăng trụ bằng: A. 10. B. 16. C. 12. D. 14 . Hướng dẫn giải:
Ta có: CC //AA nên CC //(ABB A ) AB . Do đó d
CC AB( , ) = d CC( ,(ABB A )) = d C( ,(ABB A )) = 7. 1 1 28 Khi đó ta có: VC ABBA .
= d C( ,(ABB A )).SABBA = .7.4 = . ⎯⎯⎯→ 3 3 3 Choïn 2 3 3 28 D Ta lại có: VC ABBA .
= VABCABC. VABCABC. = VC ABBA . = . =14 . 3 2 2 3
Câu 46. Cho hàm số y = f x( ) có đạo hàm liên tục trên 1;2 , thỏa mãn f x( ) = x f. (x)− x2 . Biết f (1) = 3, tính f (2) . A. 16. B. 2. C. 8 . D. 4. Hướng dẫn giải:
2 x f. (x)− f x( ) = x2 x f.
(x)x−2 x f x . ( ) =1 f x(x )
=1 Ta có: f x( ) = x f. (x)− x lOMoAR cPSD| 22014077 f x( ) x =
dx = +x C (với C là hằng số). Mặt khác:
f (1)= 3 f (1) = +1 C = + 3 1 C C = 2. 1
⎯⎯⎯→Choïn
f x( ) 2 2x. Khi đó: f (2)= 8. Vậy = +x C 2 f x( )= +x x
Câu 47. Cho hình nón đỉnh S , đáy là đường tròn nội tiếp tam giác ABC . Biết rằng AB = BC =10a, AC =12a ,
góc tạo bởi hai mặt phẳng (SAB) và (ABC) bằng 45 . Tính thể tích V của khối nón đã cho.
A. V =3 a3.
B. V =9 a3.
C. V = 27 a3.
D. V =12 a3. Hướng dẫn giải: lOMoAR cPSD| 22014077
Trong mặt phẳng (ABC), dựng ID⊥ AB tại D, khi đó góc tạo
bởi hai mặt phẳng (SAB) và (ABC) chính là SDI = 45 nên
ID = SI = r = h (với r, h lần lượt là bán kính đáy và đường cao của hình nón đã cho).
S ABC (với p là nửa chu vi ABC). Ta có: S = ABC pr.
=r p Ta có: p =16a , S = ABC
p p( −10a)(p−10a)(p−12a) = 48a2 .
Suy ra r= 48a = = = 2
3a h . Vậy V =1 2 1 3a)3 9 a3
⎯⎯⎯→Choïn . r h= ( B 16a 3 3
Câu 48. Cho hàm số f x( ) liên tục trên và có đồ thị hàm số f (x) như hình vẽ. Gọi S là tập hợp các giá trị
nguyên của tham số m − 5;5 để hàm số y = f x( 2 −2mx + m2 +1) nghịch biến trên khoảng 0; 1
. Tổng giá trị các phần tử của S bằng 2 A. 10. B. 14. C. −12. D. 15. lOMoAR cPSD| 22014077
Hướng dẫn giải: Dựa vào đồ thị của hàm f (x) ta thấy: f ( = − x) = 0 xx = 21 (1) và
f (x) 0 x 2 (2).
Ta có: y = (2 2x− m f) (x2 −2mx+m2 +1 2) = (x−m f) ((x−m)2 + ) 1 ; x = m x −m = 0 (1) 2 y = 0 ( 2
x−m) + = −1 1 (x ). ( ) f (x −m) +1 = 0 (x −m) + = + = 2 1
2 Ta có: (x −m)2 1 2 (x −m) = 2 1
xx −−mm = −=11 xx == mm+−11. ( ) − Xét f (x −m)2 +1 0 ( −m
2) (x −m)2 +1 2 (x −m)2 1 xx m − 11 xx m + 1 m − 1 . lOMoAR cPSD| 22014077 Bảng biến thiên: 1 m 1 − 3 2 m 2 0 .
Từ đây ta có: Hàm y = f x( − + 2
2mx + m2 1) nghịch biến trên 0; 12 m 1 − 1 m 0 m+1 2 2
Vì m nguyên và m − 5;5 m S = 0;2;3;4;5 .
Tổng các phần tử của S là: 0 + 2 + +3 4 + 5 =14 ⎯⎯⎯→Choïn . B
Câu 49. Giả sử a b, là các số thực sao cho x3 + y3 = a.103z +b.102z đúng với mọi số thực dương x y z, , thỏa mãn
log(x+ y) = z và log(x2 + y2 ) = z +1. Giá trị của a+b bằng: A. . B. . C. − . D. − . Hướng dẫn giải:
log(x + y) = z
x+ y =10z 2 2 Ta có: 2 2 2 2 z+1
z . Suy ra x + y =10(x+ y) (*).
log(x + y ) = z +1 x + y =10 =10.10
Khi đó: x3 + y3 = a.103z +b.102z (x+ y)(x2 − xy + y2 ) = a(10 )z 3 +b(10 )z 2 x 0, y 0
(x y x xy y+ )( 2 − + 2 )=a x y( + )3 +b x y( + )2 x xy y2 −+ 2 =a x y( + )2 +b x y( + ) b 2 2 (*) 2 2 b 2 2 x ( 2 + y2 −xy= a+10 x2 + y2 x xy y a x− + = ( +2xy y+ )+ (x + y ) ) (**) +2axy 10 lOMoAR cPSD| 22014077
Đồng nhất hệ số hai vế của (**), ta được: a+10 b =1
a=− 12 . Vậy a +b = 29 .
⎯⎯⎯→Choïn B 2 2a=−1 b=15
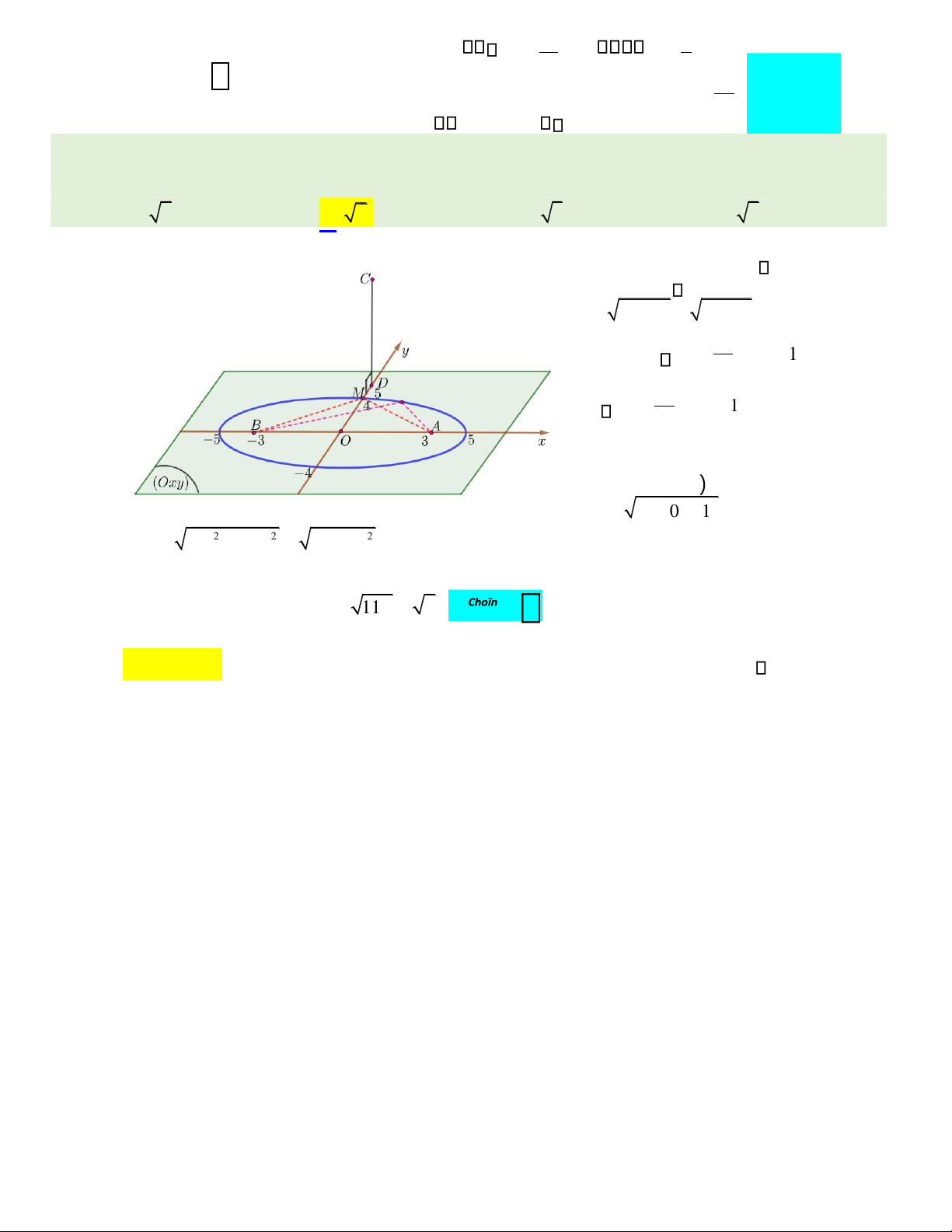
Câu 50. Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(3;0;0 ,) B(−3;0;0) và C(0;5;1). Gọi M là một
điểm nằm trên mặt phẳng tọa độ (Oxy) sao cho MA MB+ =10, giá trị nhỏ nhất của MC là A. 6. B. 2. C. 3. D. 5.
Đặt MA MB 2 a 10 a 5 + = = = , AB 2 c 6 c 3 = = = , 2 2 2 2 b a c 5 3 4 = − = − = . 2 x Do vậy M (E : hay ) 2 1 += a 2 2 x y M (E : 1 . ) += 25 16 Gọi D ( 0 ;5;0
) là hình chiếu của C trên mặt phẳng (Oxy ) . Khi đó ta có: 2 2 2 CD 0 0 1 = ++= 2 2 2 MC CDDM 1 DM = + = + (* . Do vậy )
MC bé nhất khi và chỉ khi DM bé nhất.
Theo hình vẽ, ta thấy khi M trùng với đỉnh elip ( E ) thuộc tia Oy thì DM bé nhất , hay M (0 ;4; 0 . ) Suy ra DM 1 = , khi đó MC 11 2 =+= . ⎯⎯⎯→ B Hướng dẫn giải:
 Nhận xét: Hai điểm A B,
cùng thuộc mặt phẳng (Oxy) và MA+MB =10 6 = AB. Do
vậy, tập hợp điểm M là một elip thuộc mặt phẳng (Oxy) với hai tiểu điểm là A và B. y2 b2 1 và