Đề 3 - Ôn tập full lớp 12 môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 ĐỀ SỐ 3
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
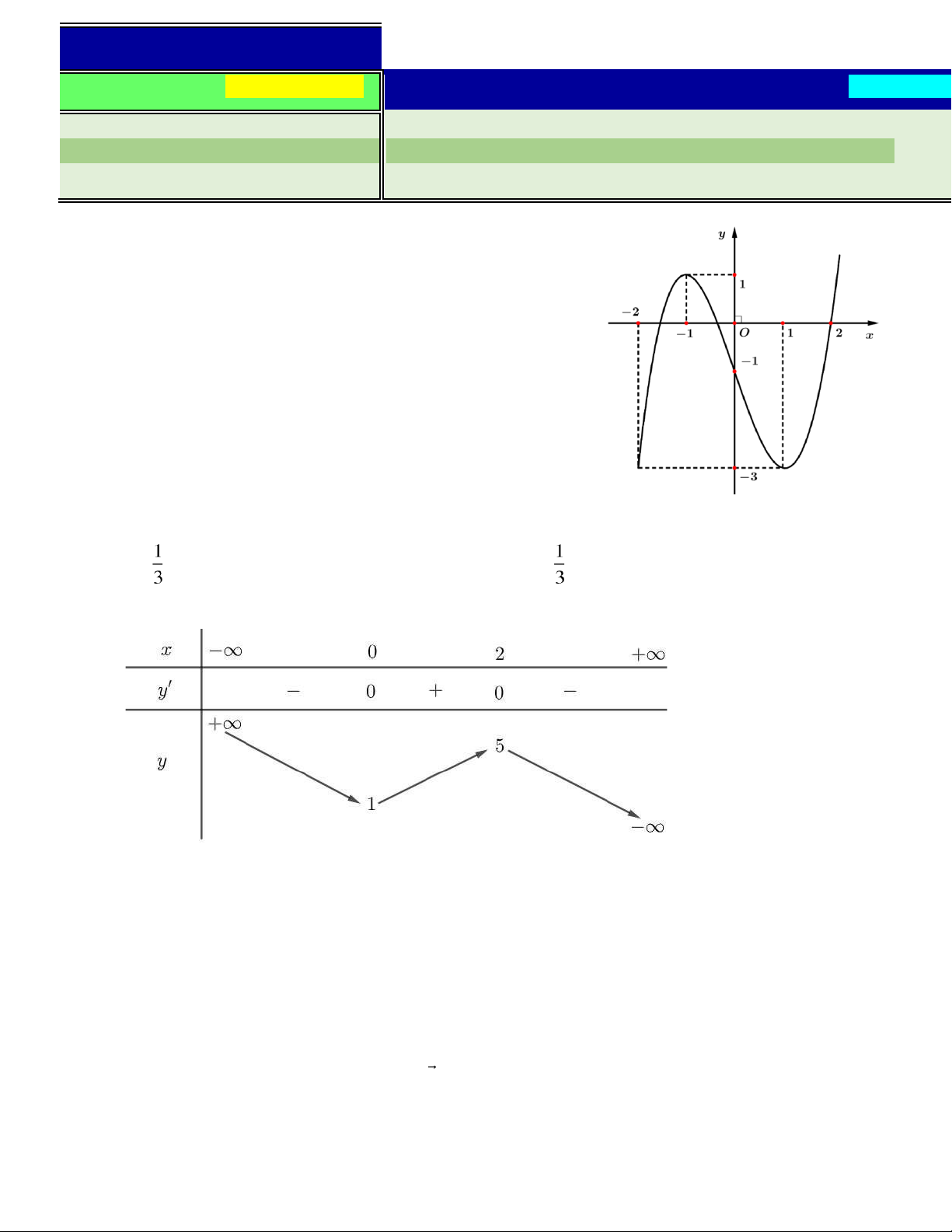
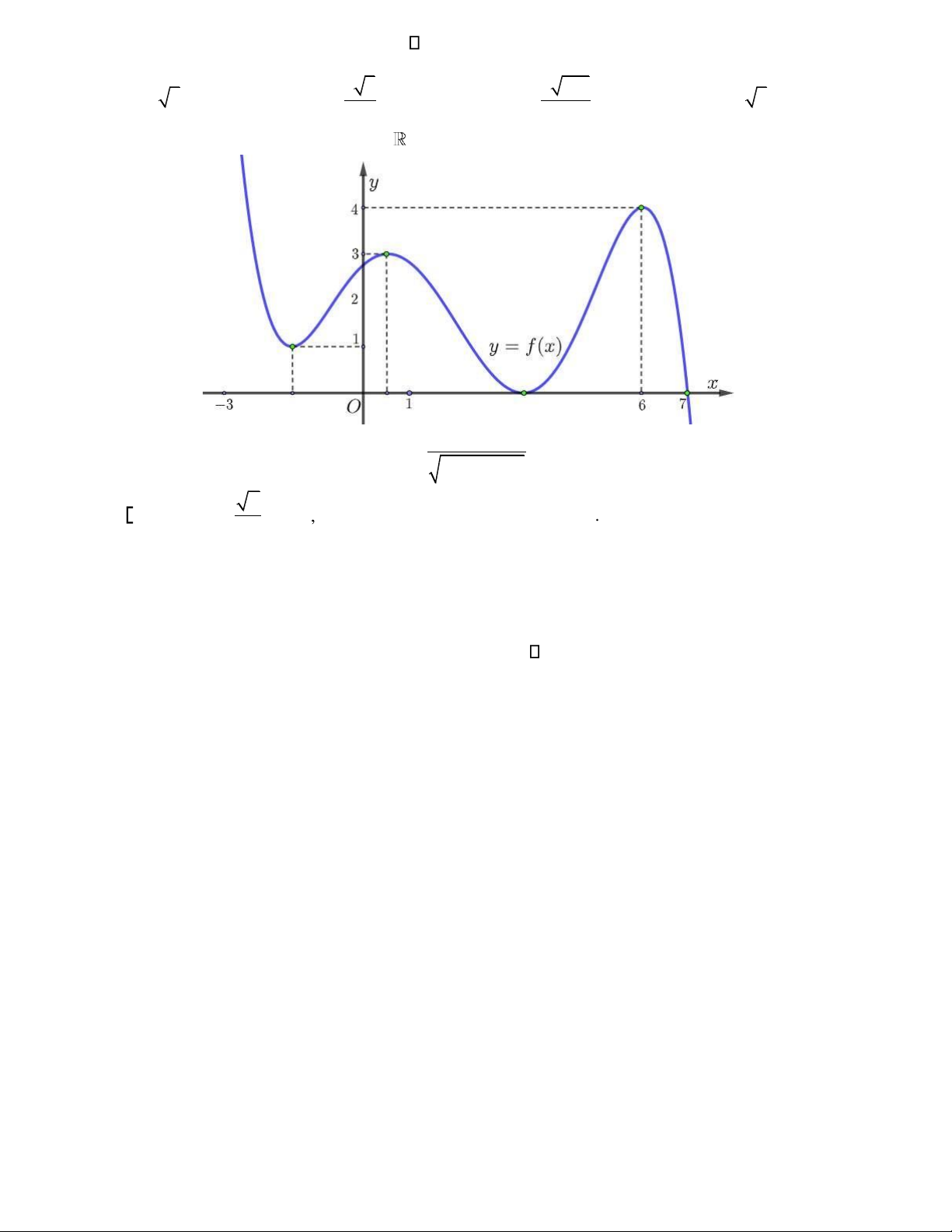
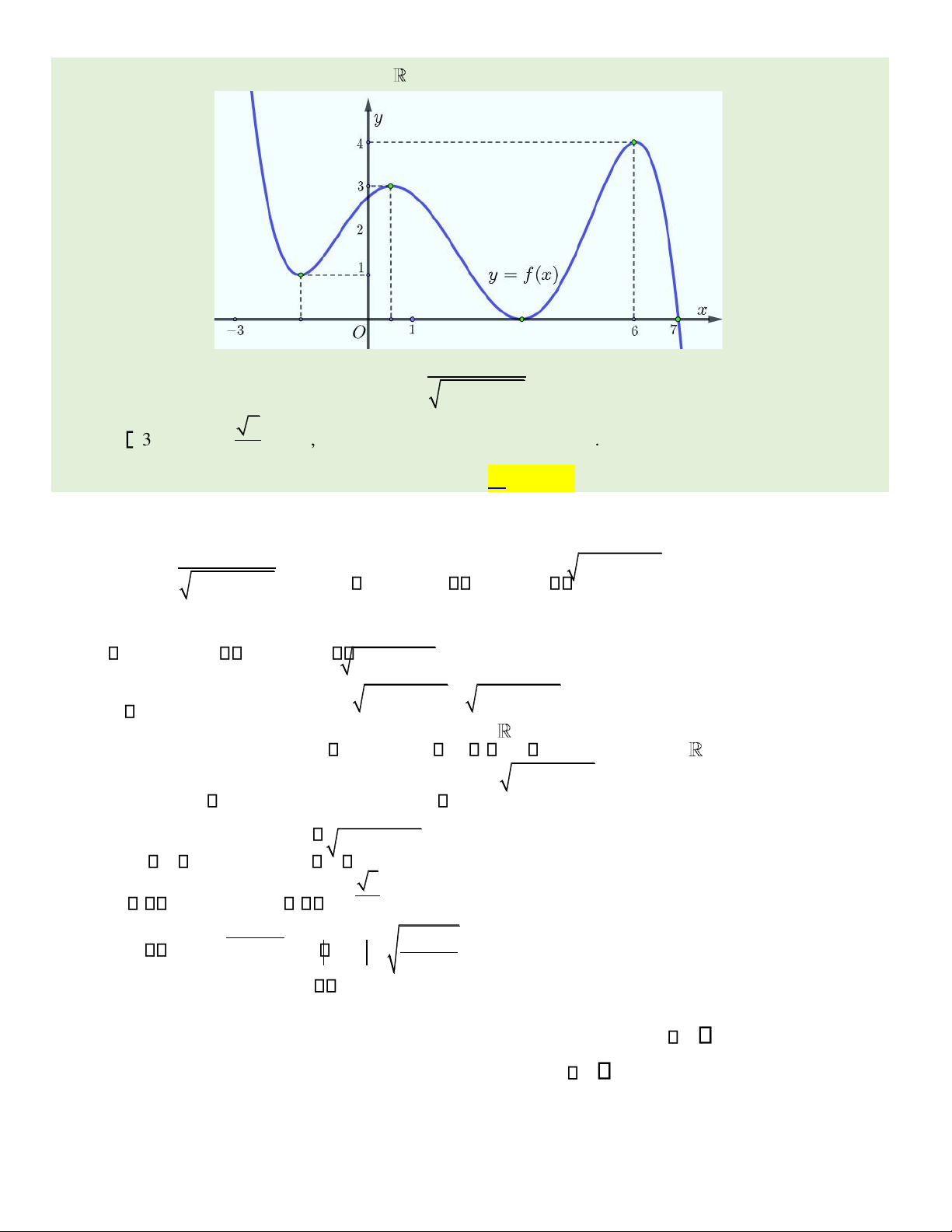
Câu 1. Hàm số y = f x( ) có ồ thị như hình vẽ bên. Hàm số y = f x( )
ồng biến trên khoảng nào dưới ây? A. (−1;2).
B. (−2;1) . C. (−2;−1). D. (−1;1) .
Câu 2. Số iểm cực trị của ồ thị hàm số y=− −x4 1 là A. 2 . B. 0 . C. 1. D. 3.
Câu 3. Nguyên hàm của hàm số f x( ) = sin3x là:
A. cos3x+C .
B. cos3x+C .
C. − cos3x +C .
D. −cos3x C+ .
Câu 4. Cho hàm số y = f x( ) có bảng biến thiên như sau
Hàm số ạt cực ại tại iểm. A. x = 0. B. x =1. C. x =5. D. x = 2.
Câu 5. Cho số phức z = 3+2i. Tìm phần thực của số phức z2 A. 9. B. 5. C. 12. D.13.
Câu 6. Trong không gian Oxyz , phương trình mặt cầu ( )S có tâm I (1;0;−1)và qua iểm A(2;2;−3) là
A. (x −1)2 + y2 +(z +1)2 = 3.
B. (x +1)2 + y2 +(z −1)2 = 9.
C. (x +1)2 + y2 +(z −1)2 = 3.
D. (x −1)2 + y2 +(z +1)2 = 9. Câu 7. 2 3
Trong mặt phẳng tọa ộ Oxy, cho vectơ v = (1; ) . Tìm ảnh của iểm A(−2; ) qua phép tịnh tiến theo lOMoAR cPSD| 22014077 vectơ v. A. A (5;−1). B. A (−1;5). C. A (3;−1). D. A (−3;1).
Câu 8. Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20cm. Thể tích khối trụ tương ứng bằng A. 800 cm .3 B. 8000 cm3. C. 400 cm3. D. 2000 cm3.
Câu 9. Số ỉnh của một hình bát diện ều là: A. 6 . B. 8. C. 12. D. 4 .
Câu 10. Chọn khẳng ịnh sai.
A. Hàm số y = ln x không có cực trị trên (0;+ ).
B. Hàm số y = ln x có ồ thị nhận trục tung làm ường tiệm cận ứng.
C. Hàm số y = ln x luôn ồng biến trên (0;+ ).
D. Hàm số y = ln x có giá trị nhỏ nhất trên (0;+ ) bằng 0. Câu 11. Tập xác ịnh của hàm số
y = log(4010−2005x) là A. − ; 12 . B. (− ;2 . C. (2;+ ) . D. (− ;2) .
Câu 12. Cho số phức z = 2−i. Trên mặt phẳng tọa ộ, tìm iểm biểu diễn số phức w iz= . A. P(2;1) . B. Q(1;2). C. N (2;−1). D. M (−1;2) .
Câu 13. Cho logabb=3 ( với a 0, b 0, ab 1). Tính log ab a2 . b A. 5. B. −4. C. −10. D. −16.
Câu 14. Khối nón có bán kính áy bằng a và ộ dài ường sinh bằng 2a có thể tích bằng 3 a 2 a A. 2 a3. B. 3 a3. C. 3 . D. 3 . 3 3
Câu 15. Giá trị lớn nhất của hàm số y= 2x4 − −3x2 5 trên oạn −1;1 là A. 0 . B. −5. C. −1. D. 1.
Câu 16. Cho khối lập phương ABCD ABCD. có thể tích bằng 8a3. Tính ộ dài cạnh của hình lập phương ó. A. a. B. 2a. C. a 2 . D. 2 2a .
Câu 17. Tập nghiệm của bất phương trình 32 1x− 27 là: A. 12;+ . B. (3;+ ). C. 13;+ . D. (2;+ ) . lOMoAR cPSD| 22014077
Câu 18. Trong không gian Oxyz , cho mặt phẳng ( )P :2x y− + =1 0. Véctơ nào dưới ây là một véc-tơ pháp tuyến của ( )P ? A. n =( = ( =( =( 4 2; 1;− 1). B. n1 2;0;−1). C. n2 2;1;−1) . D. n3 2; 1;− 0) .
Câu 19. Nếu có một khối chóp có thể tích và diện tích áy lần lượt bằng a3 và a2 thì chiều cao của nó bằng a a A. . B. 3a . C. a. D. .
3 Câu 20. Tìm nguyên hàm của hàm 6 = số ln x f ( )x . x B.
f ( )x dx = 1 ln2 x +C . A.
f x( )dx = ln2 x +C. 2 C.
f x( )dx = ln x+C . D.
f x( )dx = ex +C .
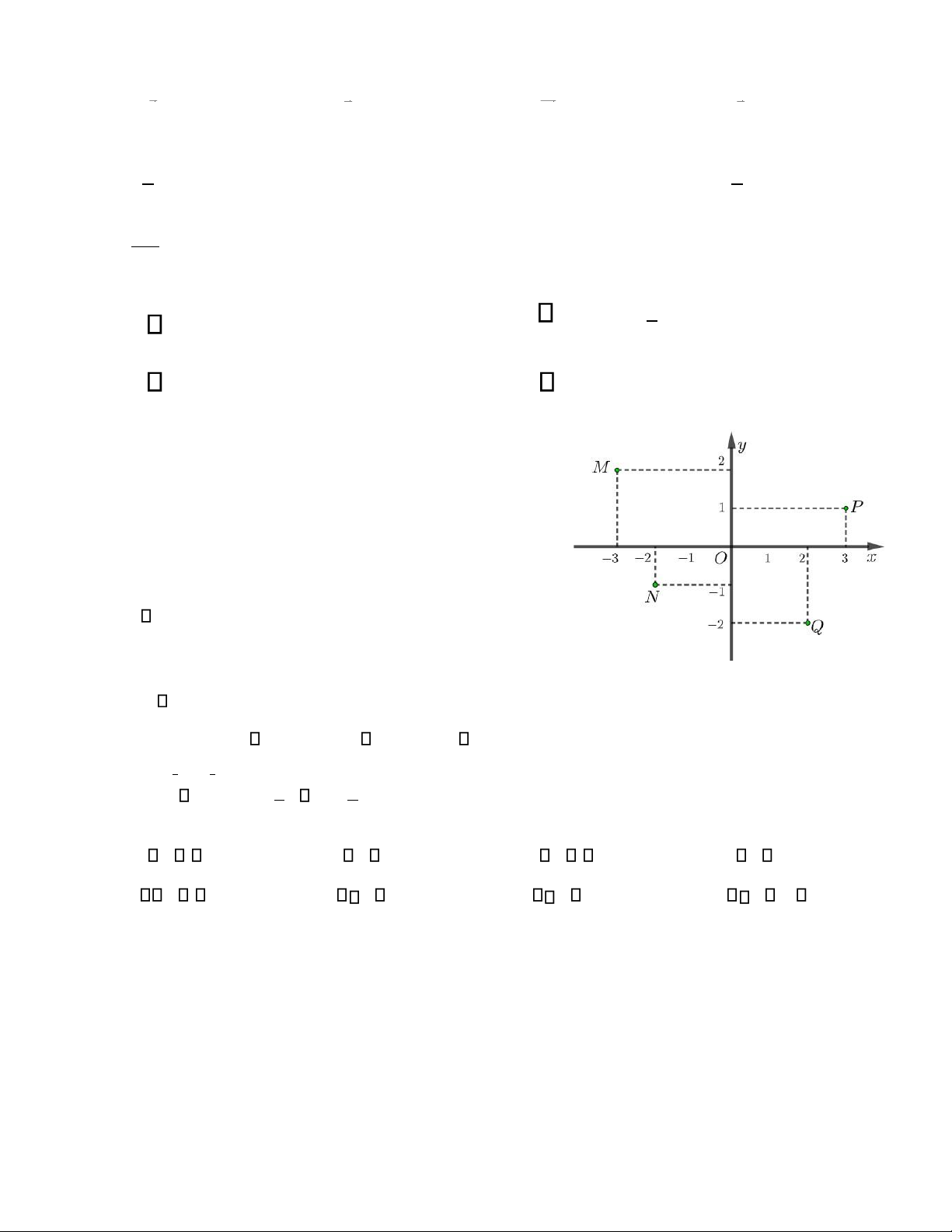
Câu 21. Các iểm M N P Q, , , trong hình vẽ bên là iểm bểu diễn lần lượt của các số phức z z z z1 2 3 4, , , . Khi ó
w= + + +3z z1 2 z3 z4 bằng
A. w = 6+4i .
B. w= − +6 4i . C. w= 4−3i .
D. w=3−4i . Câu 22. Cho hàm số f x( ) có ạo hàm là
f ( )x = x2003 (x −1)2006 (x + 2)2005 . Khoảng nghịch biến của hàm số là
A.(− ;− 2) (; 0;1) . B.(−2;0) .
C.(−2;0 ; 1;) ( + ) .
D.(− ;−2) (; 0;+ ). 1 1
Câu 23. Nếu a15 a13 và log b logb thì 3 2 0 a 1 a 1 0 a 1 a 1 A. 0 b1. B. b 1. C. b 1 . D. 0 b 1. lOMoAR cPSD| 22014077
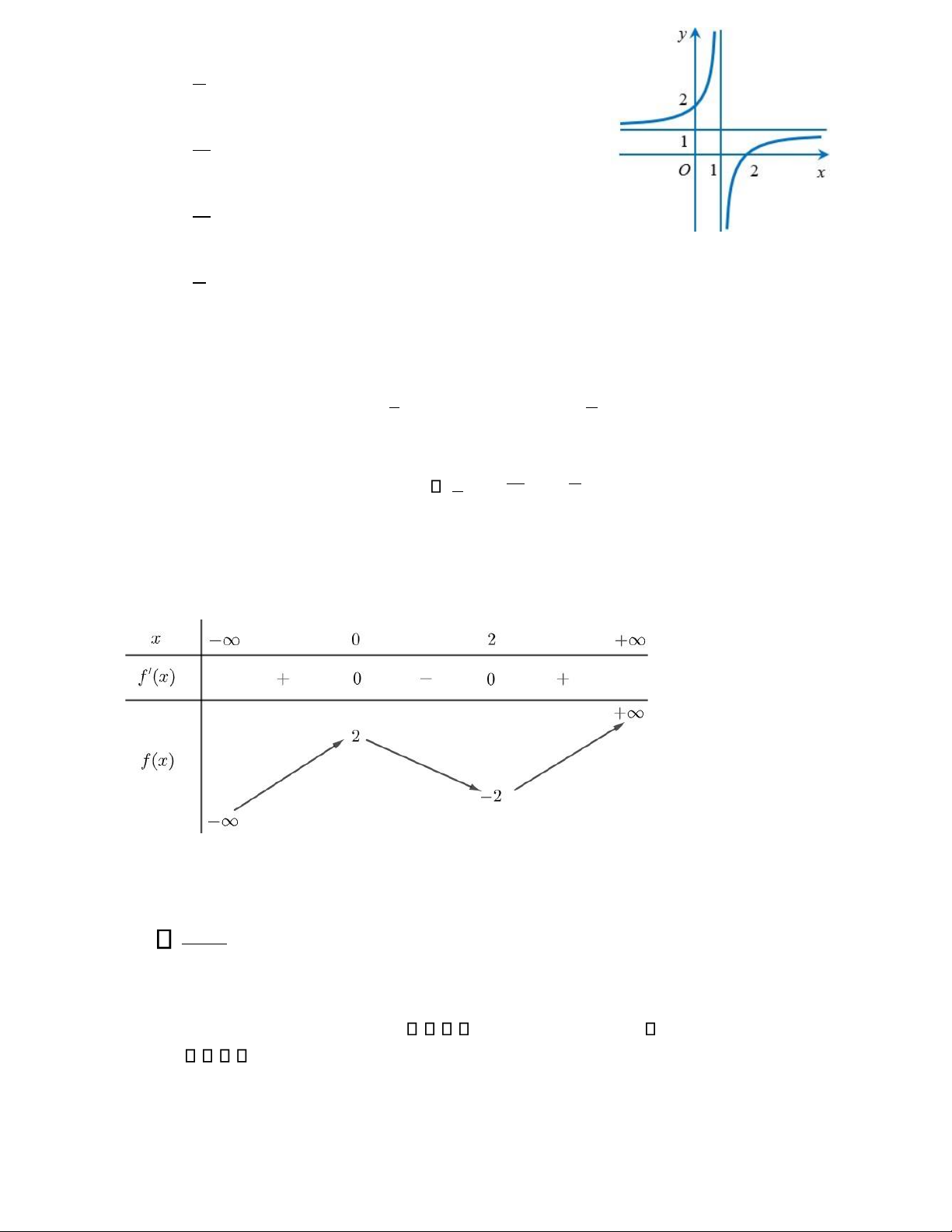
Câu 24. Đường cong trong hình vẽ là ồ thị của hàm số nào dưới ây?
A. y = x −2 . x −1
B. y = x + 2 . x +1
C. y = x + 2 . x −1
D. y = x −2 . x +1
Câu 25. Biết phương trình log2 (
2 x −2log2 2x)− =1 0 có hai nghiệm x x1 2, . Tính xx1 2 . = 1 = 1 A. xx = =− 1 2 4. B. x x1 2 . C. x x1 2 . D. xx1 2 3. 8 2
x = y + 2 = z −1
Câu 26. Trong không gian Oxyz , cho ường thẳng :
i qua iểm M(2;m n; ). Giá trị m+n 1 −1 3 bằng A. 7 . B. 3. C. −1. D. 1.
Câu 27. Cho hàm số y = f x( ) có bảng biến thiên như sau.
Số nghiệm thực của phương trình f x( ) = f ( )2 là A. 0 . B. 2 . C. 1. D. 3. 2x Câu 28. Cho 2 2
dx = aln2+bln5 với a b, là các số hữu tỉ. Tính S = a b+ . 1 x + 4 A. S = −2. B. S = −1. C. S = 3. D. S = 2.
Câu 29. Cho hình hộp chữ nhật ABCD ABCD. có AB =1, AD = 2, AA =3. Thể tích của khối chóp D ABCD. là A. V = 2. B. V =1. C. V = 6 . D. V = 3. lOMoAR cPSD| 22014077
Câu 30. Viết công thức tính diện tích hình phẳng ược giới hạn bởi ồ thị hàm số y = f x( ), trục Ox và các ường
thẳng x = a x, = b a( b). b b b b A. ( ) ( ) ( f x dx . B. f 2( )x dx. C. f x dx . D. f x dx ) . a a a a
Câu 31. Một hộp có 5 bi en, 4 bi trắng. Chọn ngẫu nhiên 2 bi. Xác suất 2 bi ược chọn cùng màu là: A. . B. . C. . D. .
Câu 32. Ông A vay ngân hàng 96 triệu ồng với lãi suất 1% tháng theo hình thức mỗi tháng trả góp số tiền giống
nhau sao cho sau úng 2 năm thì hết nợ. Hỏi số tiền ông phải trả hàng tháng là bao nhiêu? (làm tròn ến
hai chữ số sau dấu phẩy) A. 4,53 triệu ồng.
B. 4,54 triệu ồng. C. 4,51 triệu ồng. D. 4,52 triệu ồng.
Câu 33. Cho hình chóp . SABC có , , SAABBC
ôi mộ t vuông góc v ớ i nhau. Tính th ể tích kh ố i chóp . SABC , bi ế t = 3 , SA a AB = BC = a . 3 3 3 3 3 3 3 3 A. a a a a V = . B. V = . C. V = . D. V = . 9 2 6 3
Câu 34. Trong không gian v ớ i h ệ t ọa ộ Oxyz , cho vectơ a (
=− 1 ;−2 ;3 ) . Tìm t ọa ộ c ủa véctơ =( 2 ;; b yz ) ,
bi ế t r ằng vectơ b cùng phương với vectơ a . A. ( 2 ;4; 6) b = − . B. b =( ; 2 − ; 4 6 ) . C. b =( ;4; 2 6 ) .
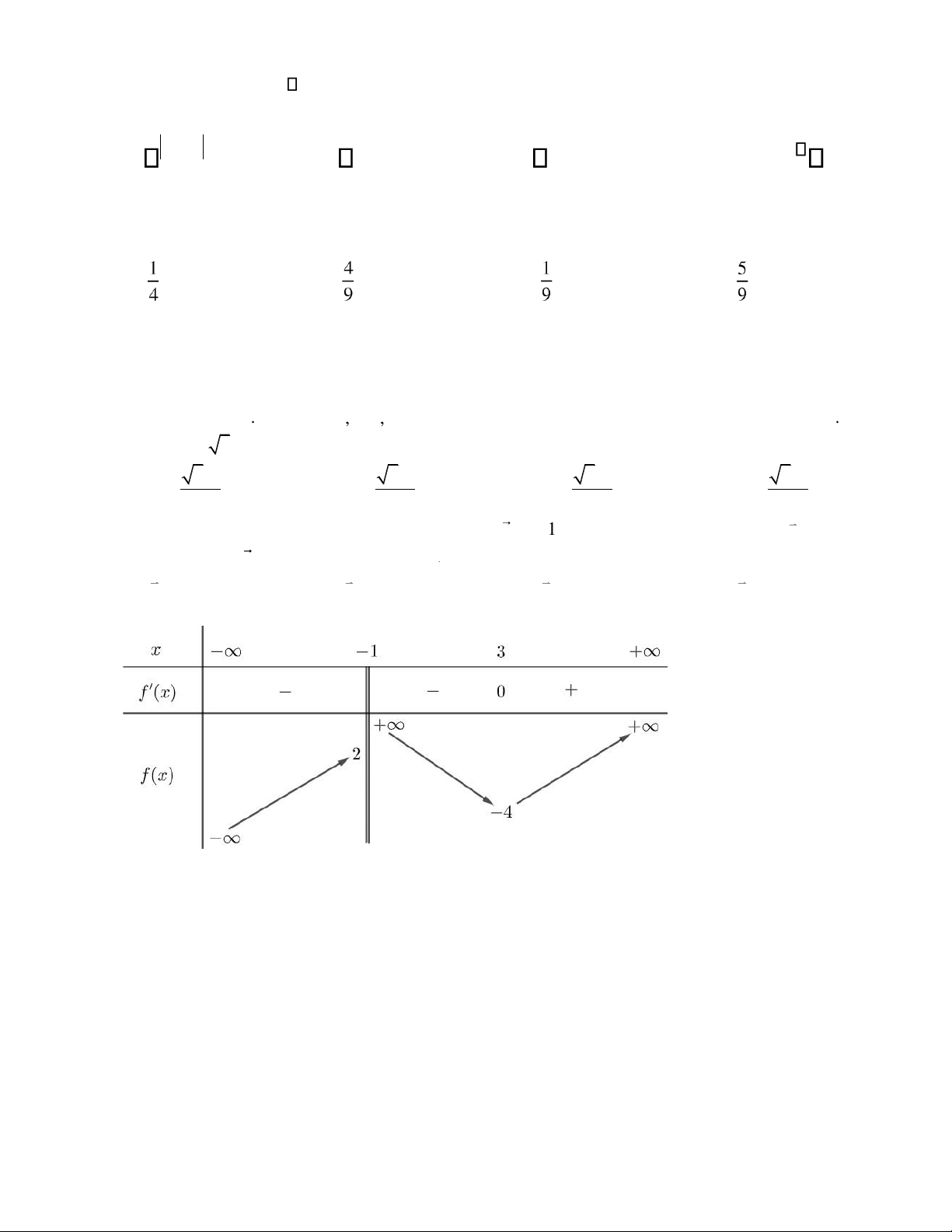
Câu 35. Cho hàm s ố có b ả ng bi ến thiên như sau
D. b = (2;−3;3). lOMoAR cPSD| 22014077
Tổng các giá trị nguyên của m ể ường thẳng y = m cắt ồ thị hàm số tại ba iểm phân biệt bẳng
A. −3 . B. −5. C.0 . D. −1. 3 2 3
Câu 36. Trong không gian với hệ tọa ộ Oxyz , cho ba iểm A(1;1; ) , B(−1;3; ), C(−1;2; ). Tính khoảng cách
h từ gốc tọa ộ O ến mặt phẳng ( ) ABC . = 3 A. h =. B. h . C. h= 3. D. h =3. 2
Câu 37. Biết rằng a b, là những số thực ể phương trình 9x −a.3x +b = 0 luôn có 2 nghiệm thực phân biệt x x1, 2. Khi ó tổng x + 1 x2 bằng A. log3b. B. log3 a . C. b . D. a.
Câu 38. Cho hình thang cân ABCD, AB CD// , AB = 2, CD = 4. Khi quay hình thang quanh trục CD thu ược
một khối tròn xoay có thể tích bằng 6 . Diện tích hình thang ABCD bằng: A. . B. . C. 6 . D. 3.
Câu 39. Giá trị cực tiểu của hàm số y e x= x ( 2 −3) là: 6 6 3 A. . B. . e C. −3e.
D. −2e . e 2
Câu 40. Có bao nhiêu số phức z thỏa mãn z + z 2 = 50 và z + =z 8? A. 4. B.1. C. 2. D. 3.
Câu 41. Tìm tổng tất cả các giá trị của tham số thực m ể ồ thị hàm số y = x −1 có hai ường tiệm cận tạo x −m
với hai trục tọa ộ một hình chữ nhật có diện tích bằng 5. A. 0. B. 5. C. 4. D. 2.
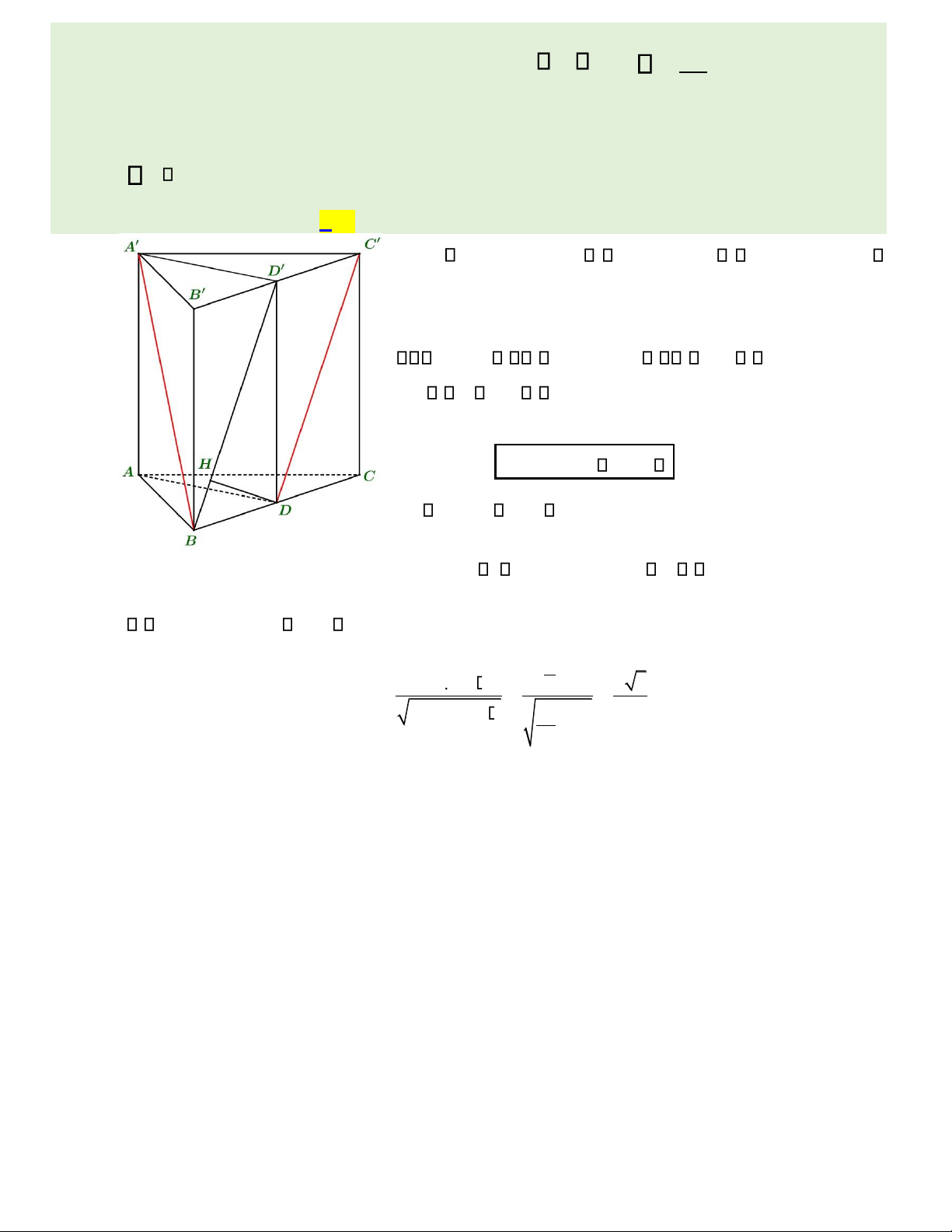
Câu 42. Cho hình lăng trụ ABCABC. có các mặt bên ều là hình vuông cạnh a. Gọi D là trung iểm của
cạnh BC . Tính khoảng cách giữa hai ường thẳng AB và DC . a 3 a 2 a 5 a 3 A. . B. . C. . D. . 6 6 5 4 f x
Câu 43. Cho hàm số f x( ) có ạo hàm liên tục và có ạo hàm trên 1;e . Biết e ( ) dx =1, f e( ) = 2. Tính 1 x lOMoAR cPSD| 22014077
e f ( )x ln xdx . 1 A. 2. B. 1. C. 0. D. 3 .
Câu 44. Cho hình hộp chữ nhật ABCD ABCD. có diện tích các mặt ABCD ABBA ADDA, , lần lượt bằng 30cm , 40cm , 48cm .2 2
2 Bán kính mặt cầu ngoại tiếp hình hộp bằng 5 5 2 5 A. 3 10cm. B. 5 10cm. C. cm. D. cm. 2 5
Câu 45. Có bao nhiêu giá trị nguyên của tham số m ể hàm y =
5−msin x−(m+1)cosx xác ịnh trên ? A. 6 . B. 8. C. 7 . D. 5.
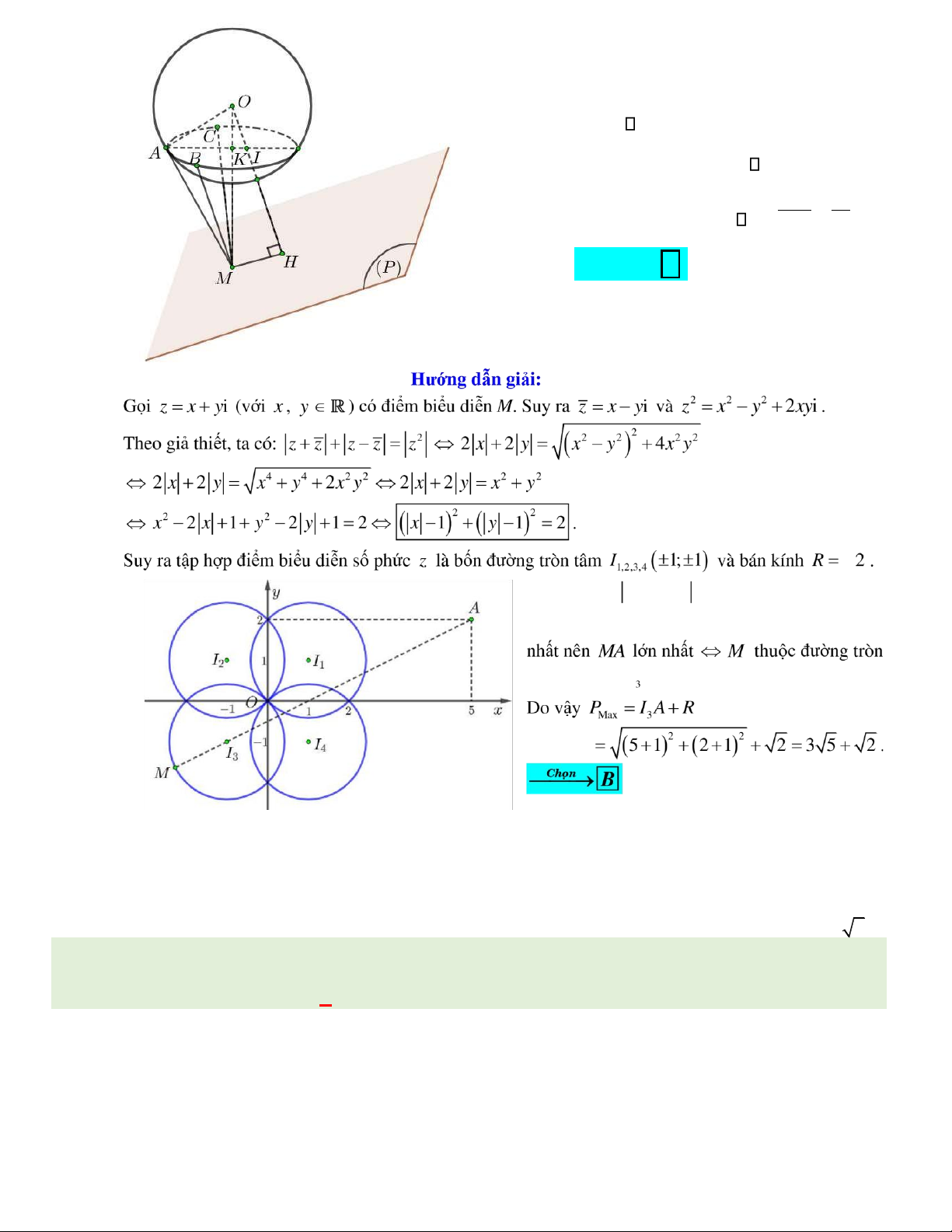
Câu 46. Cho mặt cầu ( )S tâm O, bán kính bằng 2 và mặt phẳng ( )P . Khoảng cách từ O ến ( )P bằng 4 . Từ
iểm M thay ổi trên ( )P kẻ các tiếp tuyến MA, MB , MC tới ( )S với A, B , C là các tiếp iểm. Biết mặt phẳng ( )
ABC luôn i qua một iểm I cố ịnh. Tính ộ dài OI . 3 B. . A. 3 . 2 C. . D. 1. 2
Câu 47. Cho số phức z thỏa mãn
z + z + z − z = z. Giá trị lớn nhất của biểu thức P = z
−5− 2i bằng: B. 2 35 + . A. 2 +5 3. C. 5+2 3. D. 5+3 2 . 1
Câu 48. Trong không gian Oxyz cho mặt phẳng ( ) : x − z −3 = 0 và iểm M (1;1; ). Gọi A là iểm thuộc tia lOMoAR cPSD| 22014077
Oz , gọi B là hình chiếu của A lên ( ) . Biết rằng tam giác MAB cân tại M . Diện tích của tam giác 33 3123 A. 63 . B. . C. . D. 33 . 2 2
Câu 49. Cho hàm số y = ()
fx liên tục trên , có ồ thị như hình vẽ. 3 + Giá trị 4 của tham số m m 2 m ể phương trình = f () +3 x
có hai nghiệm phân biệt trên oạn 2 2 f () +5 x − ; 3 7 ) = = là a m với ,
ab là hai số nguyên tố. Tính + . T ab b MABbằng
A. T = 43.
B. T =35.
C. T =39.
D. T = 45.
Câu 50. Có tất cả bao nhiêu giá trị nguyên của y sao cho ứng với mỗi y luôn tồn tại không quá 63 số nguyên x thỏa mãn iều kiện log ( ( (
2024 x+ y2)+log2025 y2 + +y 64) log4 x− y) ? A. 301. B. 302. C. 604. D. 603.
________________HẾT________________ lOMoAR cPSD| 22014077 AP AN E SO` 60 1 2 3 4 5 6 7 8 9 10 C C C D B D B D A D 11 12 13 14 15 16 17 18 19 20 D B D C B B D D B B 21 22 23 24 25 26 27 28 29 30 B B C A A B B D A A 31 32 33 34 35 36 37 38 39 40 B D C A B D A A D C 41 42 43 44 45 46 47 48 49 50 A C B C B D B B C C
Lłi giaßi cau hoßi van dung cao æe soÆ 60
Câu 42. Cho hình lăng trụ ABCABC. có các mặt bên ều là hình vuông cạnh a. Gọi D là trung iểm của
cạnh BC . Tính khoảng cách giữa hai ường thẳng AB và DC . a 5 a 3 a 2 a 3 C. . A. . B. . D. . 5 6 64 Hướng dẫn giải: Vậy d DC AB DH(
⎯Choïn⎯⎯→C , ) = = a 5 . 5 lOMoAR cPSD| 22014077 f x
Câu 43. Cho hàm số f x( ) có ạo hàm liên tục và có ạo hàm trên 1;e . Biết e ( ) dx =1, f e( ) = 2. Tính 1 x
e f ( )x ln xdx . 1 A. 2. B. 1 . C. 0. D. 3 .
Gọi D là trung iểm BC ; trong (BBCC ), vẽ DH ⊥ BD tại H (1). Ta có:
A DA D ⊥⊥ B CBB A D ⊥ (BB
C C ) A D ⊥ DH (2) . Từ (1)
và (2) suy ra DH ⊥ (A BD ) (3). Ta có: DC //(A BD ) suy ra:
d DC AB( , ) = d DC ABD( ,( )) = d D ABD( ,(
)) (3)= DH . Xét BDD vuông tại D có: a . . a 5 BDDD 2 a = = 2 2 2 + 5 BD DD a 2 +a DH = 4 . Hướng dẫn giải: lOMoAR cPSD| 22014077
Vì m nguyên nên m − 4; 3;...;−3 . Vậy có 8 giá trị nguyên của m thỏa mãn ề bài. ⎯Choïn⎯⎯→B
Câu 46. Cho mặt cầu ( )S tâm O, bán kính bằng 2 và mặt phẳng ( )P . Khoảng cách từ O ến ( )P bằng 4 . Từ
iểm M thay ổi trên ( )P kẻ các tiếp tuyến MA, MB , MC tới ( )S với A, B , C là các tiếp iểm. Biết mặt phẳng ( )
ABC luôn i qua một iểm I cố ịnh. Tính ộ dài OI 1 . 3 2 A. 3 . B. . C. . D. 1. 2 Hướng dẫn giải: lOMoAR cPSD| 22014077
Gọi K là giao của mặt phẳng ( )
ABC và OM . Gọi H là
hình chiếu của O trên ( )P . Trong mặt phẳng ( ) OMH
kẻ KI ⊥OM tại K ( )
I OH) . Ta có (ABC là mặt phẳng
qua K và vuông góc với OM nên KI (ABC). Ta có OA2 =OK OM. =OI OH.
OI = OA2 = 22 =1. OH 4
Mặt khác I ⎯Choïn⎯⎯→ D thuộc oạn thẳng OH nên I cố ịnh. Vậy OI =1.
Câu 47. Cho số phức z thỏa mãn z + z + z − z = z2 . Giá trị lớn nhất của biểu thức P = z −5− 2i bằng: A. 2 +5 3. B. 2 +3 5 . C. 5+2 3. D. 5+3 2 .
Khi ó, P = z −5− 2i = MA, với A(5;2). 2
Mặt khác, vì A(5; ) thuộc góc phần tư thứ lOMoAR cPSD| 22014077 (C )
3 có tâm I (−1;−1) và bán kính R = 2 . 1
Câu 48. Trong không gian Oxyz cho mặt phẳng ( ) : x z−
−3 = 0 và iểm M (1;1; ). Gọi A là iểm thuộc tia
Oz , gọi B là hình chiếu của A lên ( ) . Biết rằng tam giác MAB cân tại M . Diện tích của tam giác MABbằng 3 3 3 123 A. 6 3 . B. .
C. . D. 3 3. 2 2 Hướng dẫn giải: x = t
Gọi A(0;0;a). Đường thẳng ABqua A và vuông góc với ( ) có phương trình y = 0 ;
z = a −t x = t y; =
; z = a −t
B là hình chiếu của A lên ( ) nên tọa ộ B thỏa mãn hệ x − z −3 =00
tx =t y; = 0; z = −at
x = a+2+33; y = 0; z = −a a2+3 = a2−3 hay a+3 . B 2 ;0; a −3 2
−(a− − =t) 3 0 t = a 2
Tam giác MAB cân tại M nên MA = + + − = + + 2 MB2 1 1 (1 a)2 a2+1 2 1 a2−5 2 aa =−=33 .  3 0 MA
Nếu a =3 thì A(0;0; ), B(3;0; ); ta có: = − −(( 1; 1;2)) MA MB, =(3;3;3). MB = 2; 1;− −1
⎯Choïn⎯⎯→B
Diện tích tam giác MAB: S = 1 MAB 2 MA MB, = 3 32 . lOMoAR cPSD| 22014077
 Nếu a = −3 thì tọa ộ A(0;0;−3) và B(0;0;−3); trường hợp này bị loại do A, B trùng nhau.
Câu 49. Cho hàm số y = ()
fx liên tục trên , có ồ thị như hình vẽ. 3 4 + Giá trị của tham số m m 2 m ể phương trình = f () +3 x
có hai nghiệm phân biệt trên oạn 2 2 f () +5 x 3 − ; 7) = = là a m với ,
ab là hai số nguyên tố. Tính + . T ab b
A. T = 43.
B. T =35.
C. T =39.
D. T = 45. Hướng dẫn giải: 4m 3 +m ( ) Ta có: 2f ( ) 2
x +5 = f 2 x +3 4m3 + =m
f 2( )x +3 2f 2( )x +5 8m3 + 2m = 2 f 2 ( )x +6 2 f 2 ( )x +5
(2m)3 +2m = (2 f 2 ( )x +5) 2 f 2 ( )x +5 + 2 f 2 ( )x +5 * .( )
Xét hàm số: f t( ) = t3 +t f; ( )t = 3t2 +1 0, t
f t( ) ồng biến trên . ( )
Do ó: ( )* f (2m) = f 2 f 2( )x +5
2m = 2 f 2( )x +5 5 m 0 m − 2 4m2 5 2 2 . f ( )x = ( ) = 4m −5 2 f x 2 7
Ta thấy toàn bộ ồ thị hàm số y = f x( ) ều nằm phía trên trục hoành với x − 3; ), vì vậy hàm số y = 7
f x( ) có ồ thị trùng với ồ thị hàm số y = f x( ) với mọi x − 3; ). lOMoAR cPSD| 22014077
Do vậy f x( ) = 4m − − 5 2 5 x −
3;7) f x( ) = 4m2 5 với m (*). 2 2 2 5 m 2 2 4 5 − m m = 37 = 2 a .
Dựa vào ồ thị hàm số ã cho, ta thấy (*) tương ương = 4 2 b
Vậy a =37, b = 2 T a b=
⎯Choïn⎯⎯→C + =39.
Câu 50. Có tất cả bao nhiêu giá trị nguyên của y sao cho ứng với mỗi y luôn tồn tại không quá 63 số nguyên x thỏa mãn iều kiện log ( ( (
2024 x+ y2)+log2025 y2 + +y 64) log4 x− y) ? A. 301 B. 302 C. 604 D. 603 Hướng dẫn giải:
Bất phương trình ã cho trở thành: log ( ( (
2024 x + y2 )+log2025 y2 + y +64)−log4 x − y) 0. Đặt f x( ) = log ( ( (
2024 x + y2 )+log2025 y2 + y +64)−log4 x − y) (ta xem y là tham số). x + y2 0 0
Điều kiện xác ịnh của f x( ) là: y2 + y +64 0 x + y2
x y −y2 (do x y, nguyên). x − y 0 x − y 0
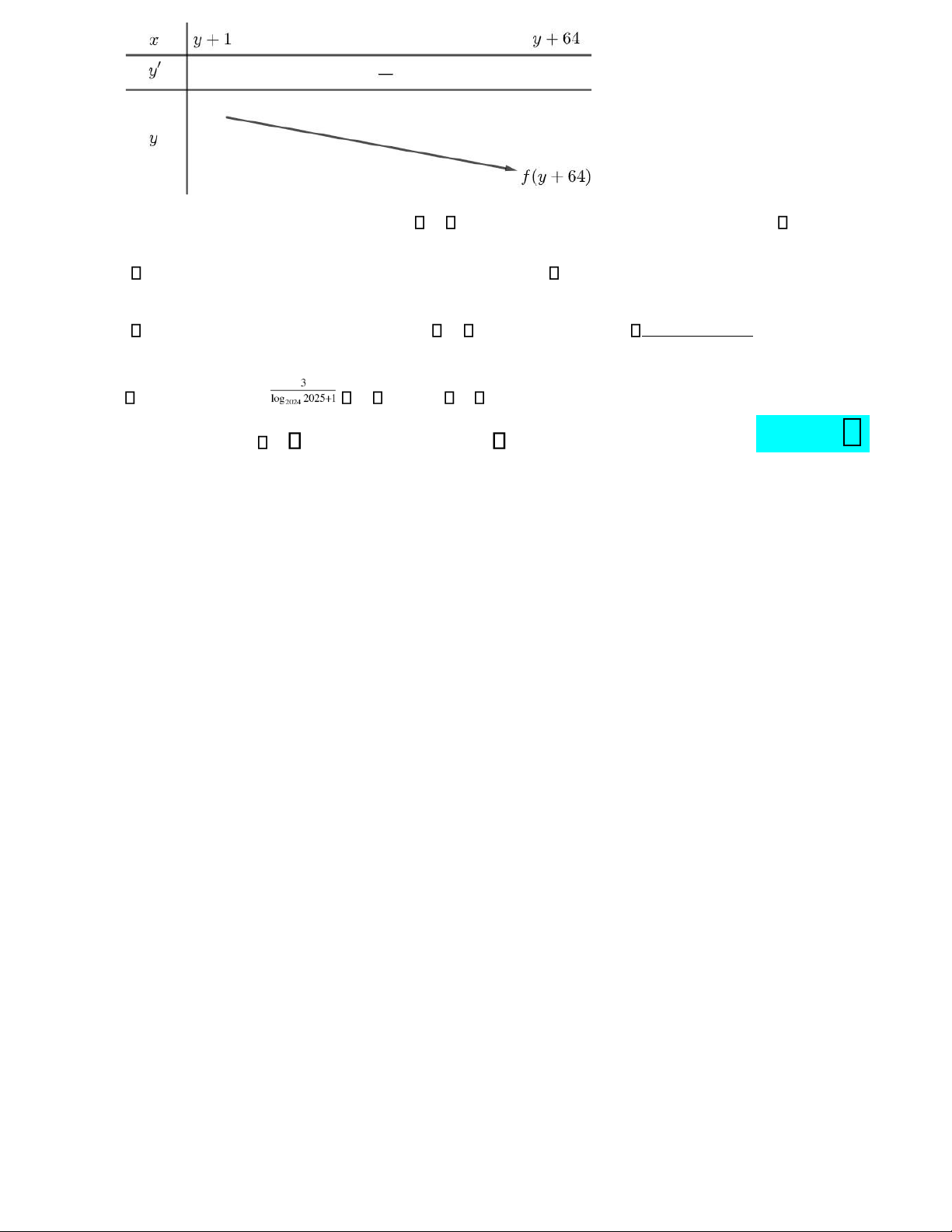
Với x y, nguyên thì ta chỉ xét f x( ) trên nửa khoảng y +1;+ ). Ta có:
f ( )x = (x+ y21)ln2024 − (x− y)1ln2025 − (x− y1)ln4 0, xy +1 1
(vì x+ y2 x− y 0, ln2024 ln4 ( ) 1 2 ). x+ y
ln2024 (x− y)ln4
Ta có bảng biển thiên của hàm số f x( ): lOMoAR cPSD| 22014077
Yêu cầu bài toán trở thành: ( (
f (y +64) 0 log2024 y2 + +y 64)+log2025 y2 + +y 64) log 644 log ( (
2024 2025.log2025 y2 + y +64)+log2025 y2 + y +64) log 644 log ( (
2025 y2 + y +64). log( 2024 2025+1) 3
log2025 y2 + y +64) 3 log2024 2025+1
y2 + y +64−2025 0 −302,2 y 301,2.
⎯Choïn⎯⎯→C
Vì y nguyên nên y − 302; 301;...;300;301 .−
Vậy có 604 giá trị của y thỏa mãn.