Đề 4 - Ôn tập full lớp 12 môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 ĐỀ SỐ 4
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
Câu 1. Cho hai số phức z = = − − 1 2+3i và z2
1 i . Mô un của số phức 2 3z1 z2 bằng A. A. 58. B. 113 . C. 82 . D. 137 . 3+a . B. . Câu 2. + 4
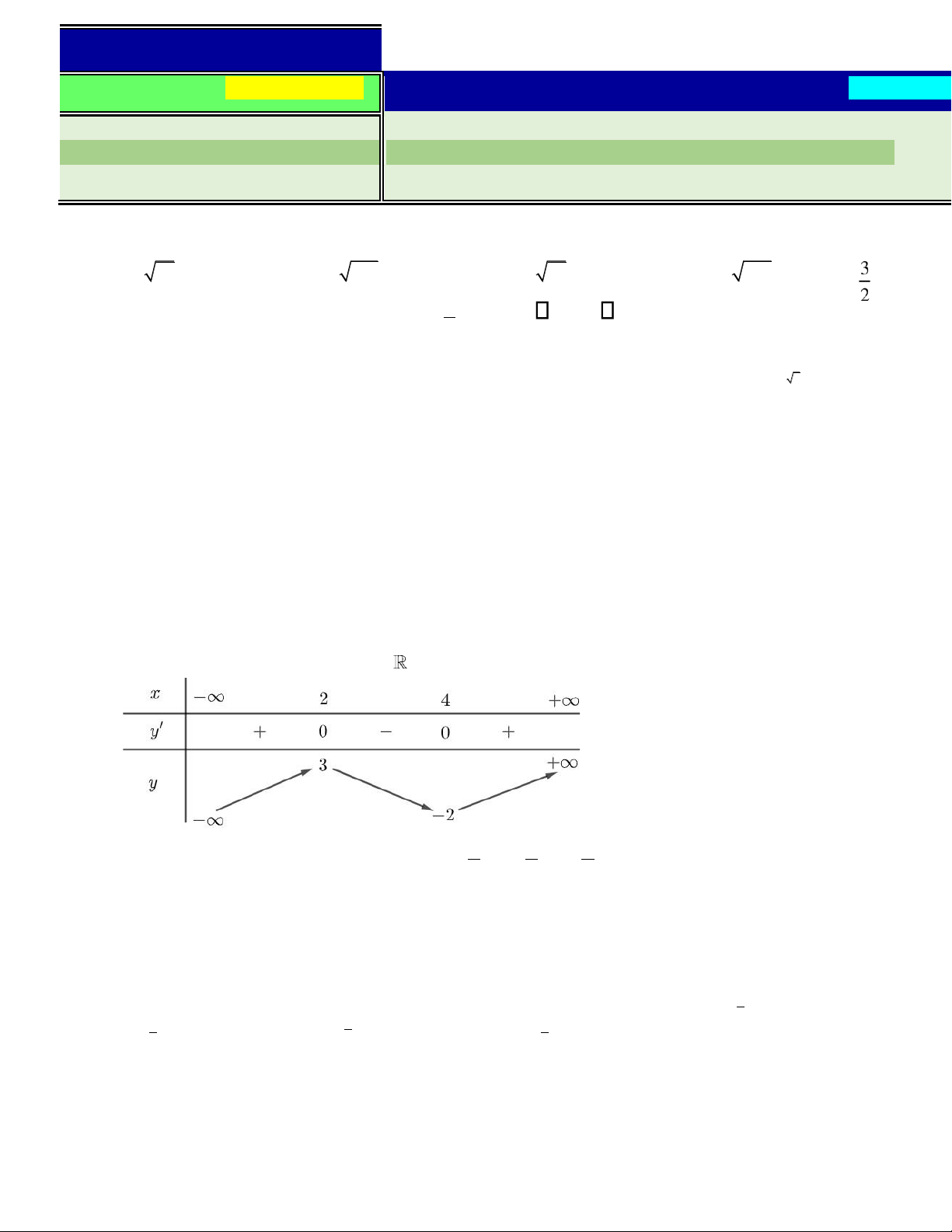
Giá trị nhỏ nhất của hàm số y = +1 x trên oạn −3;−1 C. 6 . bằng x D. 3 . A. 5. B. −4. C. −6. D. −5. a
Câu 3. Cho a là số thực dương và khác 1. Giá trị của biểu thức T = log (a3) bằng
, có b ả ng bi ến thiên như sau: Câu 4. x−3 = y −2
Trong không gian Oxyz , cho ường thẳng d :
= z +1. Điểm nào sau ây không thuộc d ? −1 3 −2
A. Q(−3; 2;− 1) .
B. M (4; 1;− 1) .
C. N (2;5;−3) . D. P(3;2;−1).
Câu 5. Số phức liên hợp của số phức z = i(3−4i) là
A. z = +4 3i .
B. z =− −4 3i.
C. z = −4 3i .
D. z =− +4 3i .
Câu 6. Cho hàm số y = f x( ) liên tục trên lOMoAR cPSD| 22014077
Hàm số ã cho ạt cực tiểu tại A. x = 4. B. x = 2. C. x = 3. D. x = −2.
Câu 7. Cho hình hộp ứng ABCD ABCD. có cạnh bên AA = h và diện tích tam giác ABC bằng S . Thể
tích của khối hộp ABCD ABCD. bằng:
A. V = Sh . B. V = Sh .
C. V = Sh. D. V = 2Sh. log ( 2 x − ) 1 1 . 2
Câu 8. Tìm tập xác ịnh của hàm số y = 1 = = A. D = (1;+ ) . B. D ;1 . C. D = 1;+ ). D. D 12;1 . 2
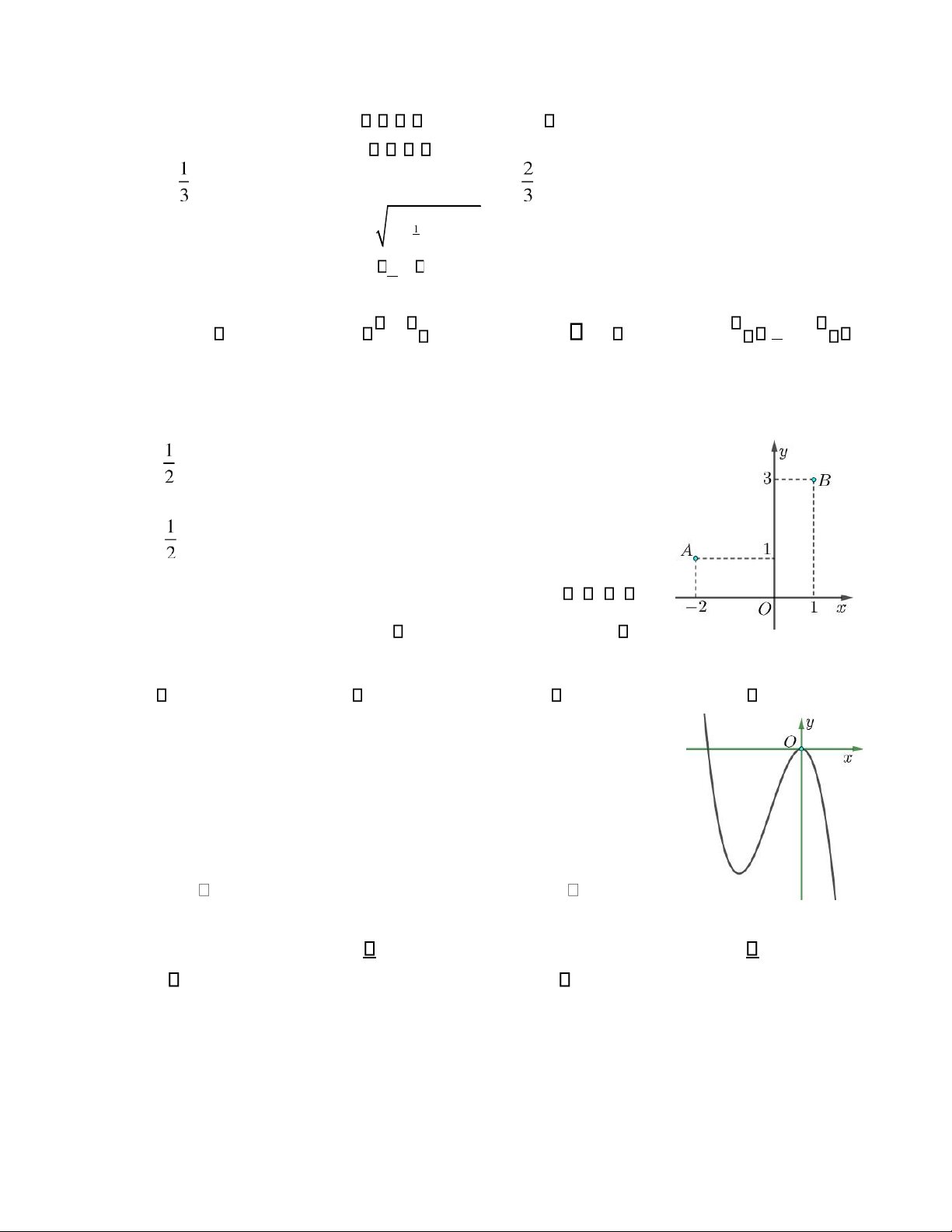
Câu 9. Trong mặt phẳng Oxy, cho các iểm A B, như hình vẽ bên. Trung iểm của oạn thẳng AB là iểm biểu diễn
của số phức nào sau ây? A. − + 2i. B. − +1 2i . C. 2−i . D.2− i .
Câu 10. Trong không gian Oxyz , cho hình hộp ABCD ABCD. có
A(1;0;1), B(2;1;2), D(1; 1;− 1), C (4;5;−5) . Tính tọa ộ ỉnh A của hình hộp.
A. A (4;6;−5) . B. A (2;0;2) .
C. A (3;5;−6).
D. A (3;4;−6).
Câu 11. Đồ thị của hàm số nào dưới ây có dạng là ường cong trong hình bên ?
A. y = −x3 +3x .
B. y = −x4 + x2.
C. y = −x3 −3x2 .
D. y = x4 + x2.
Câu 12. Cho mặt c u có ường k椃Ānh bằng 4a. Thể t椃Āch khối c u tương ứng bằng 3 32 a3 3 8 a3 A. 32 a . B. . C. 16 a . D. . 3 3
Câu 13. Trong không gian Oxyz , cho ba iểm M (2;0;0) , N (0;1;0) và P(0;0;2) . Mặt phẳng (MNP) có phương trình là lOMoAR cPSD| 22014077 x x x x
A. + y + z = −1
B. + y + z =1.
C. + y + z =1.
D. + y + z = −1. 2 1 2 1 2 2 2 1 2 2 2 1
Câu 14. Cho hàm số y = f x( ) có ồ thị như hình vẽ bên. Mệnh ề nào sau ây úng về hàm số ó? Tính S = + + + 1 z z2 z3 z4 . A. S = ( S = ( S =23 . B. 22 − 3) . C. S =22 . D. 22 + 3) . 3 Câu 16. x 1 + d x 2 Cho e = .e a + .e b +c = + + +
. V ớ i a , b , c là các s ố nguyên. Tính S a b c . 0 x 1
A. Đồng biến trên khoảng (0;2).
B. Nghịch biến trên khoảng (−3;0).
C. Đồng biến trên khoảng (−1;0).
D. Nghịch biến trên khoảng (0;3).
Câu 15. Kí hiệu z1, z2 , z3, z4 là bốn nghiệm của phương trình z4 + z2 −6 = 0. A. S =1. B. S = 2. C. S = 0. D. S = 4.
Câu 17. Tìm tập nghiệm S của phương trình log ( (
3 x2 −2x +3)−log3 x +1) =1.
A. S = 0;5 . B. S = 5 .
C. S = 0 . D. S = 1;5 .
Câu 18. Cho hình chóp S ABCD. . Gọi M , N , P , Q theo thứ tự là trung iểm của SA, SB , SC , SD . Tính tỉ số
thể tích của hai khối chóp S MNPQ. và S ABCD. bằng A. . B. . C. . D. . = x 7x
Câu 19. Tìm số tiệm cận của ồ thị hàm số y 2 − +6 2 . x −1 lOMoAR cPSD| 22014077 A. 1. B. 2 . C. 3. D. 0 . dx Câu 20. Tích phân 1 bằng 0 3x+1 A. . B. . C. . D. .
Câu 21. Bất phương trình log ( ( 4 x +7)
log2 x +1) có tập nghiệm là. A. (5;+ ). B. (−1;2). C. (2;4). D. (−3;2).
Câu 22. Trong không gian Oxyz , cho mặt phẳng ( ) :3x −2y + z +6 = 0 . Hình chiếu vuông góc của iểm A(2;
1;− 0) lên mặt phẳng ( ) có tọa ộ là A. (1;0;3). B. (2; 2;− 3). C. (1;1;−1) . D. (−1;1;−1) .
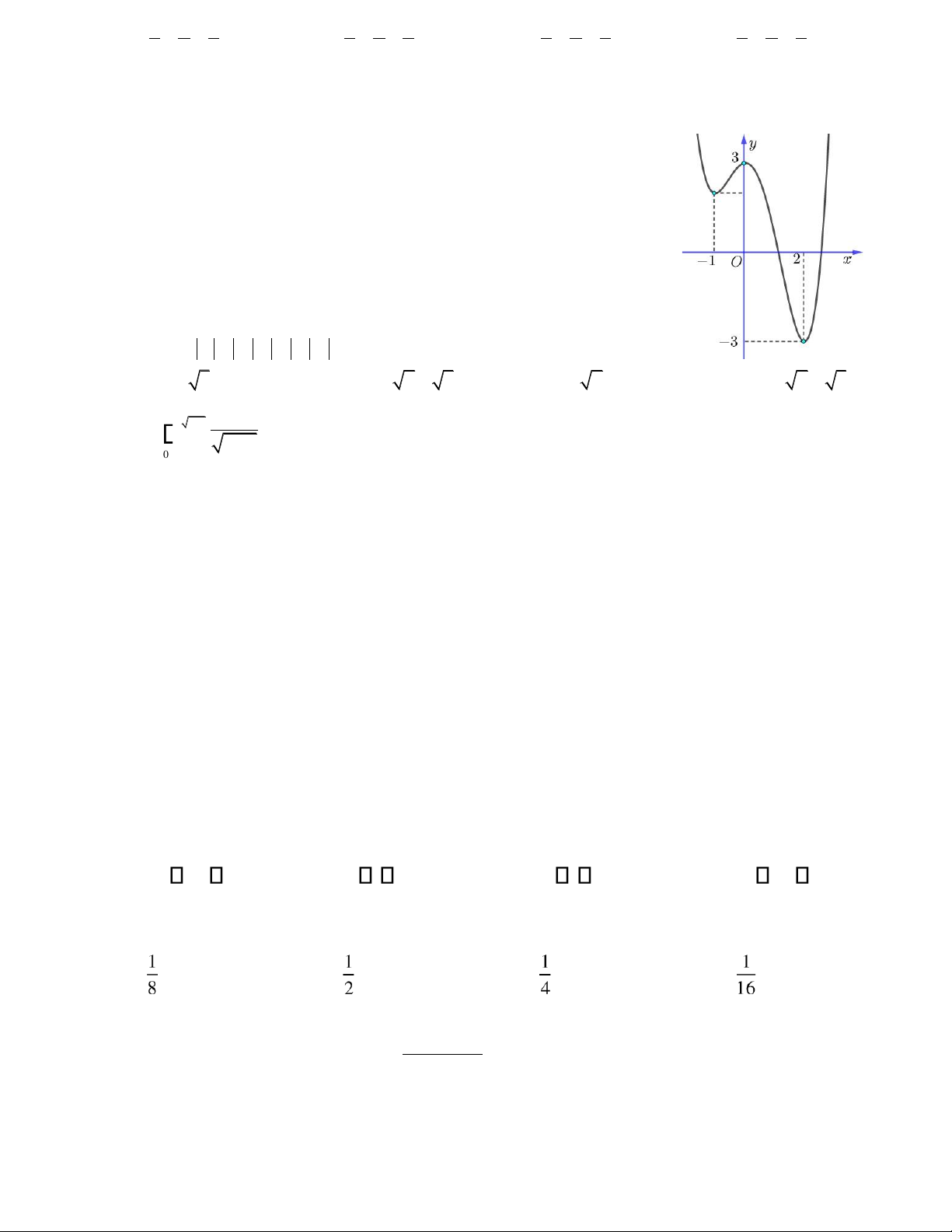
Câu 23. Cho hàm số bậc bốn y = f x( ) có ồ thị như hình bên dưới, số nghiệm
của phương trình 2 f x( )+ =1 0 là A. 2. B. 4. C. 3. D. 1.
Câu 24. Cho hàm số y = f x( ) thỏa mãn 2 sin .x f x( )dx = f ( )0 =1. Tính 0 = I
2 cos .x f ( )x dx . 0 A. I =1. B. I = 0. C. I = 2. D. I = −1. mx+1
Câu 25. Tìm tất cả các giá trị của m ể hàm số y = 2x m+ nghịch biến trên 1;+ . 2 lOMoAR cPSD| 22014077 1
A. m −( 1;1). B. m 12;1 . C. m 2;1 . D. m − 12;1 .
Câu 26. Cho hai số thực a b, thoả mãn 2a b 0 và 2log (
3 2a −b) = log3 a +log3b. Giá trị của biểu thức
T = b bằng a A. 1. B. 4. C. 3. D. 2.
Câu 27. Cho hình chóp tứ giác ều S ABCD. có tất cả các cạnh ều bằng a, M là trung iểm cạnh SD . Giá trị tang
của góc giữa ường thẳng BM và mặt phẳng (ABCD) bằng A. . B. 2 . C. 3 . D. . 2 3
Câu 28. Thể tích khối lập phương ABCD ABCD. có ường chéo D. 162 . AC = 2 6 bằng A.24 3. B.48 6 . C. 6 6 .
Câu 29. Cho hàm số f x( ), biết f ( )x có ồ thị như hình bên. Số iểm cực
trị của hàm số f x( ) là A. 2 . B. 1. C. 3. D. 0 .
Câu 30. Trong không gian Oxyz , cho iểm M (1;0;−1). Mặt phẳng ( ) i
qua M và chứa trục Ox có phương trình là A. y= 0.
B. x+ z = 0.
C. y+ z + =1 0.
D. x+ y+ z = 0.
Câu 31. Giá trị của biểu thức A=log 3.log 4.log 5...log 6423 4 63 bằng A. 7. B. 6. C. 8. D. 10.
Câu 32. Cho số phức z thỏa mãn: z(1−2i)+ zi. =15+i . Tìm mô- un của số phức z ? A. z = 5. B. z = 4. C. z = 2 5 . D. z = 2 3 .
Câu 33. Khi quay một tam giác ều cạnh bằng a (bao gồm cả iểm trong tam giác) quanh một cạnh của nó ta ược
một khối tròn xoay. Tính thể tích V của khối tròn xoay ó theo a. a 3 3a3 3 a3 3a3 A. . B. . C. . D. . lOMoAR cPSD| 22014077 4 8 4 24
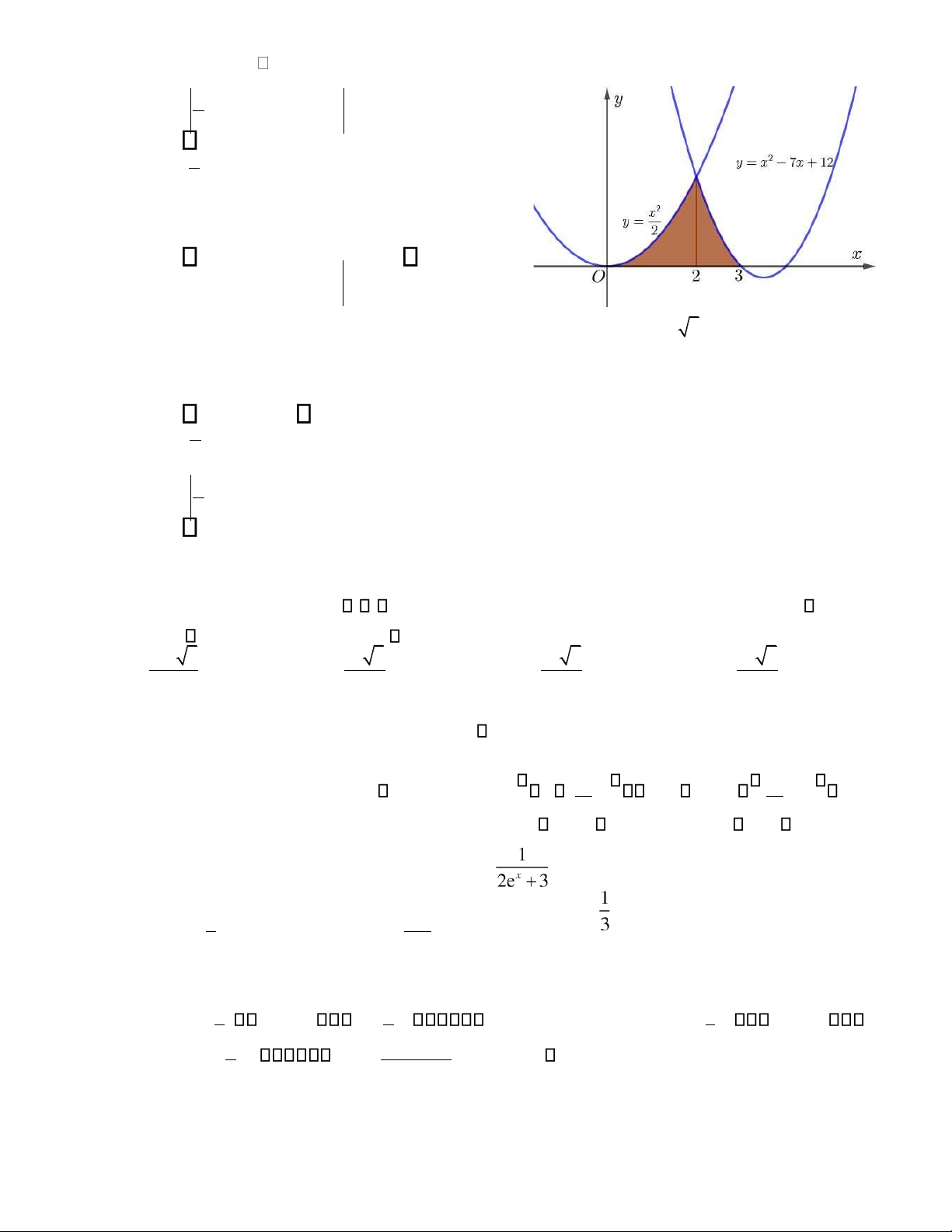
Câu 34. Diện tích S của ph n hình phẳng ược gạch chéo trong hình bên bằng 1 A. S = 3 x2 +(x2 −7x+12)dx. 0 2 1 B. S = 2 x dx2 − 3(x2 −7x+12)dx . 0 2 2 1 C. S = 2 x dx2
+ 3(x2 −7x+12)dx . 0 2 2 1 D. S = 3
x2 −(x2 −7x+12)dx . 0 2
Câu 35. Cho khối lăng trụ ABC ABC. có áy ABC là tam giác ều cạnh bằng a 3 , cạnh bên AA = a, góc
giữa AA và mặt phẳng áy bằng 30 . Tính thể tích khối lăng trụ ã cho theo a. A. 3a3 3 . B. a3 3 . C. a3 3 . D. a3 3 . 8 3 4 2
Câu 36. Tập nghiệm của bất phương trình ln2 x+2ln x−3 0 là 1 1 A. (e e; 3). B. (e;+ ). C. − ; ( 3 e;+ ) . D. 3 ;e . e e
Câu 37. Cho F x( ) là một nguyên hàm của hàm số f x( ) = thỏa
mãn F ( )0 =10. Tìm F x( ) .
A. F x( ) = 1(x −ln 2e(x +3))+10+
ln5 . B. F x( ) = (x +10−ln 2e( x +3)). 3 3 3 C. F x( ) = 1 x −ln e x + 2
+10+ln5−ln2 . D. F x( ) = 13 x −ln e x + 3 ln2 2 +10− ln5−3 . 3
Câu 38. Tìm giá trị thực của tham số m ể ường thẳng d y:
= (3m+1)x +3+ m vuông góc với ường thẳng lOMoAR cPSD| 22014077
i qua hai iểm cực trị của ồ thị hàm số y x= 3 −3x2 −1. A. m = . B. − . C. . D. − . = mx
Câu 39. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (−10;10) ể hàm số y +10 nghịch
2x+m biến trên khoảng (0;2). A. 5. B. 8. C. 6 . D. 7 .
Câu 40. Cho s ố ph ứ c z th ỏ a mãn z − z =
2 . Biết rằng ph n thực của z 2
bằng a. Tính z theo a − + 2 + + A. 1 a a 1 a a 4 z = . B. z = D. z = 1 −a 2 a + a2 +1 7 3 x m = m . C. d x z = . . v ớ i 3 2 + n n 0 1 x 2 2 Câu 41. Cho biết
là một phân số tối giản. Tính m−7n. A. 0 . B. 1. C. 2 . D. 91.
Câu 42. Cho hình chóp S ABCD. có áy ABCD là hình vuông cạnh a. Hình chiếu của S lên mặt phẳng áy trùng
với trọng tâm của tam giác ABD. Cạnh SD tạo với áy một góc 60 . Tính thể tích của khối chópS ABCD. . A. a3 15 . B. a3 15 . C. a3 15 . D. a3 . 3 27 9 3
Câu 43. Một nhóm các chuyên gia y tế ang nghiên cứu và thử nghiệm ộ chính xác của một bộ xét nghiệm
COVID−19. Giả sử cứ sau n l n thử nghiệm và iều chỉnh bộ xét nghiệm thì tỷ lệ chính xác của bộ
xét nghiệm ó tuân theo công thức S n( ) = + 2020.101
− 0,01n . Hỏi phải tiến hành ít nhất bao nhiêu l n 1
thử nghiệm và iều chỉnh bộ xét nghiệm ể ảm bảo tỉ lệ chính xác của bộ xét nghiệm ó ạt trên 90%? A. 426. B. 425. C. 428. D. 427.
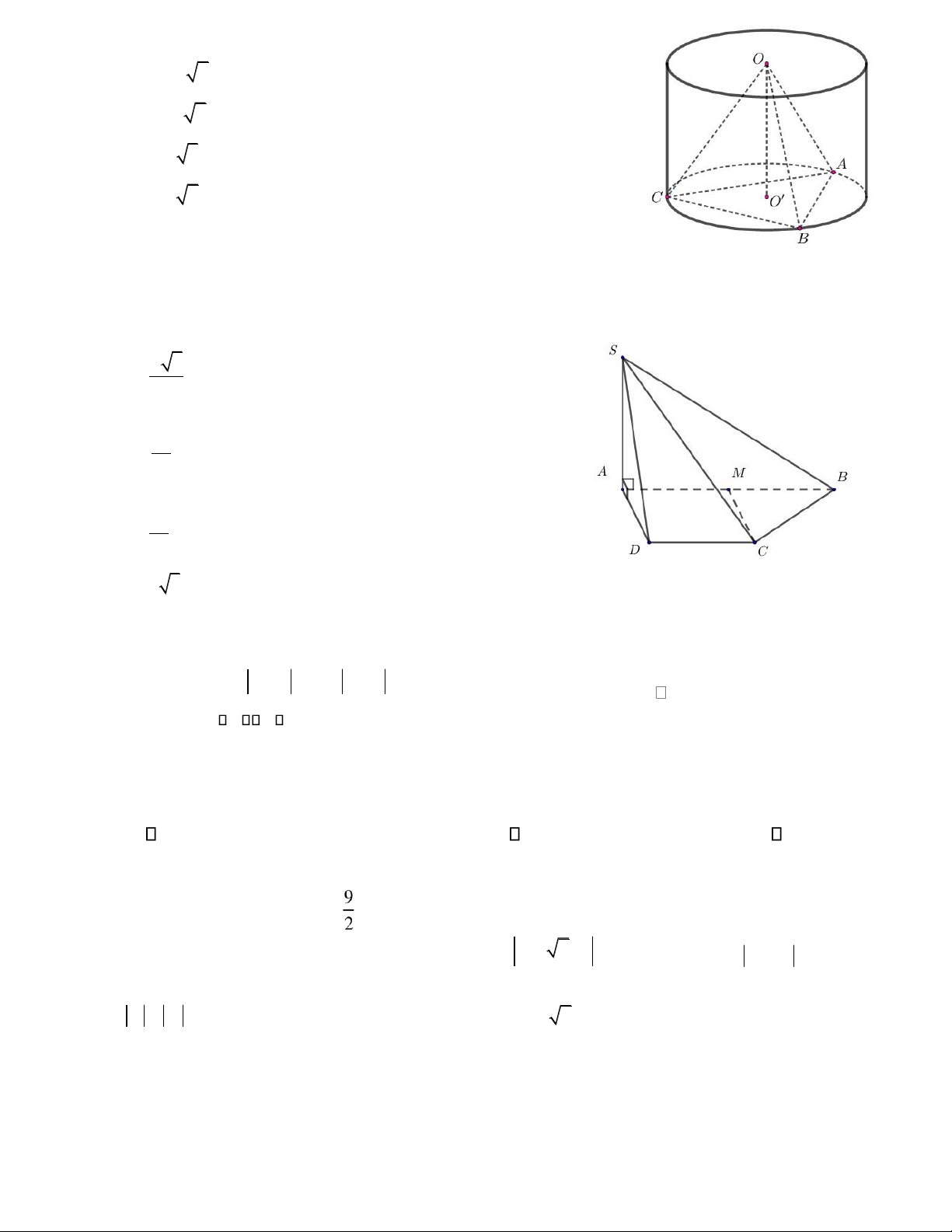
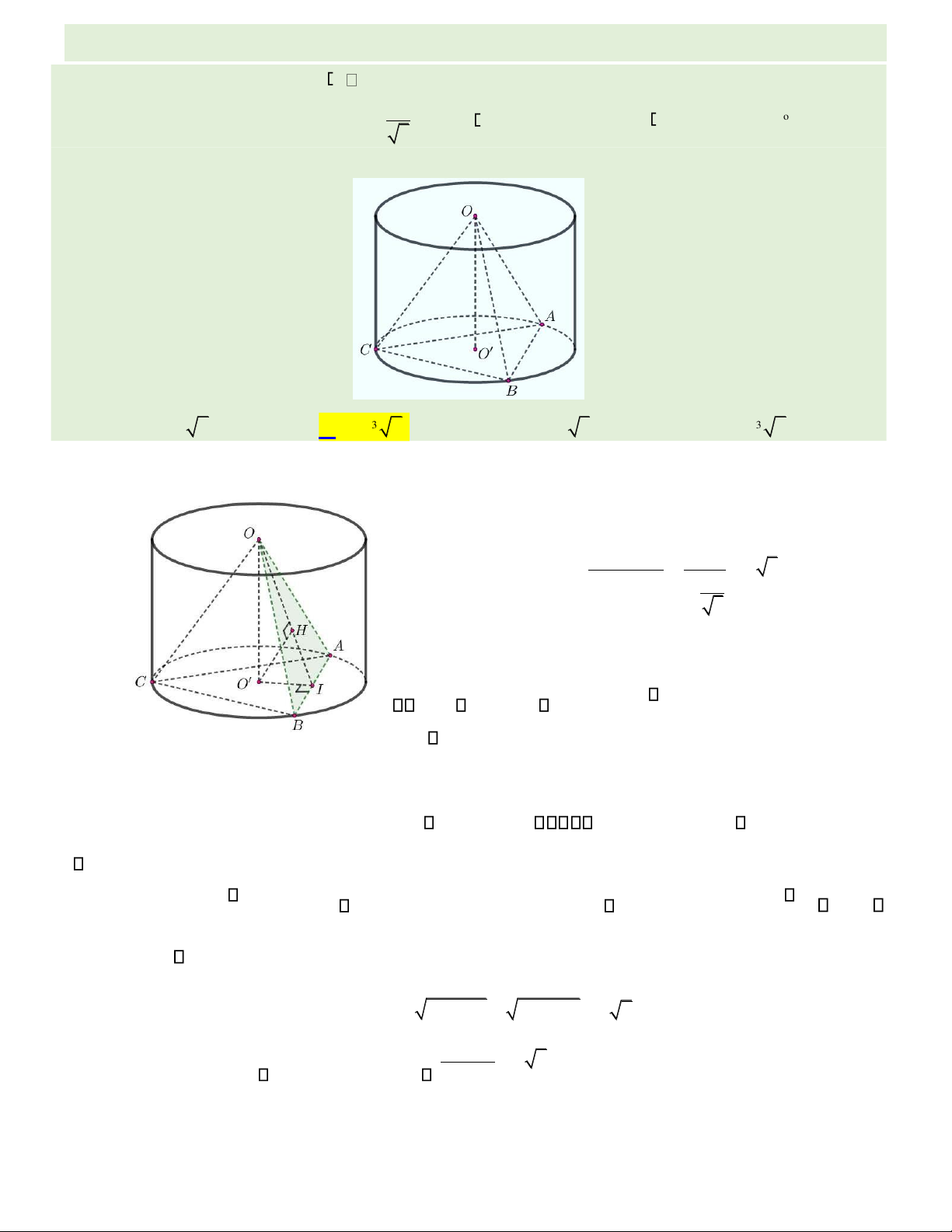
Câu 44. Cho hình trụ ( )T có O, O l n lượt là tâm hai ường tròn áy. Tam giác ABC nội tiếp trong ường 1
tròn tâm O, AB = 2a, sin ACB = 3 và OO tạo với mặt phẳng (OAB ) một góc 30o (tham khảo lOMoAR cPSD| 22014077
hình bên dưới). Thể tích khối trụ ( )T bằng A. 2πa3 6.
B. 3π 6a3. C. πa3 3. D. π 6a3.
Câu 45. Số 7100000 có bao nhiêu chữ số? A. 84510. B. 194591. C. 194592. D. 84509.
Câu 46. Cho hình chóp S ABCD. có áy là hình thang AB = 2a AD, = DC =CB = a và SA vuông góc với mặt
phẳng áy (minh họa như hình vẽ dưới ây). Gọi M là trung iểm của cạnh AB . Khoảng cách giữa hai
ường thẳng CM và SD bằng A. a 3 . 2 B. 3a . 4 C. 3a . 2 D. a 3 .
Câu 47. Cho hàm số f x( ) = log32 x −log2 x3 + m (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của
m sao cho max f x( ) +min f x( ) = 6. Tổng bình phương tất cả các ph n tử của S bằng 1;4 1;4 A. 13. B. 18. C. 5. D. 8. Câu 48. Trong không gian Oxyz , cho hai
iểm A(10;6;−2), B(5;10;−9) và mặt phẳng
( ) :2x + 2y + z −12 = 0 . Điểm M di ộng trên ( ) sao cho MA, MB luôn tạo với ( ) các góc bằng
nhau. Biết rằng M luôn thuộc một ường tròn ( )C cố ịnh. Hoành ộ của tâm ường tròn ( )C bằng A. −4. B. . C. 2 . D. 10.
Câu 49. Giả sử z1, z2 là hai trong số các số phức z thỏa mãn
iz + 2 −i =1 và z − = 1 z2 2. Giá trị lớn nhất của z + C. 1 z2 bằng 32 . A. 4 . B. 2 3. D. 3. lOMoAR cPSD| 22014077 + −
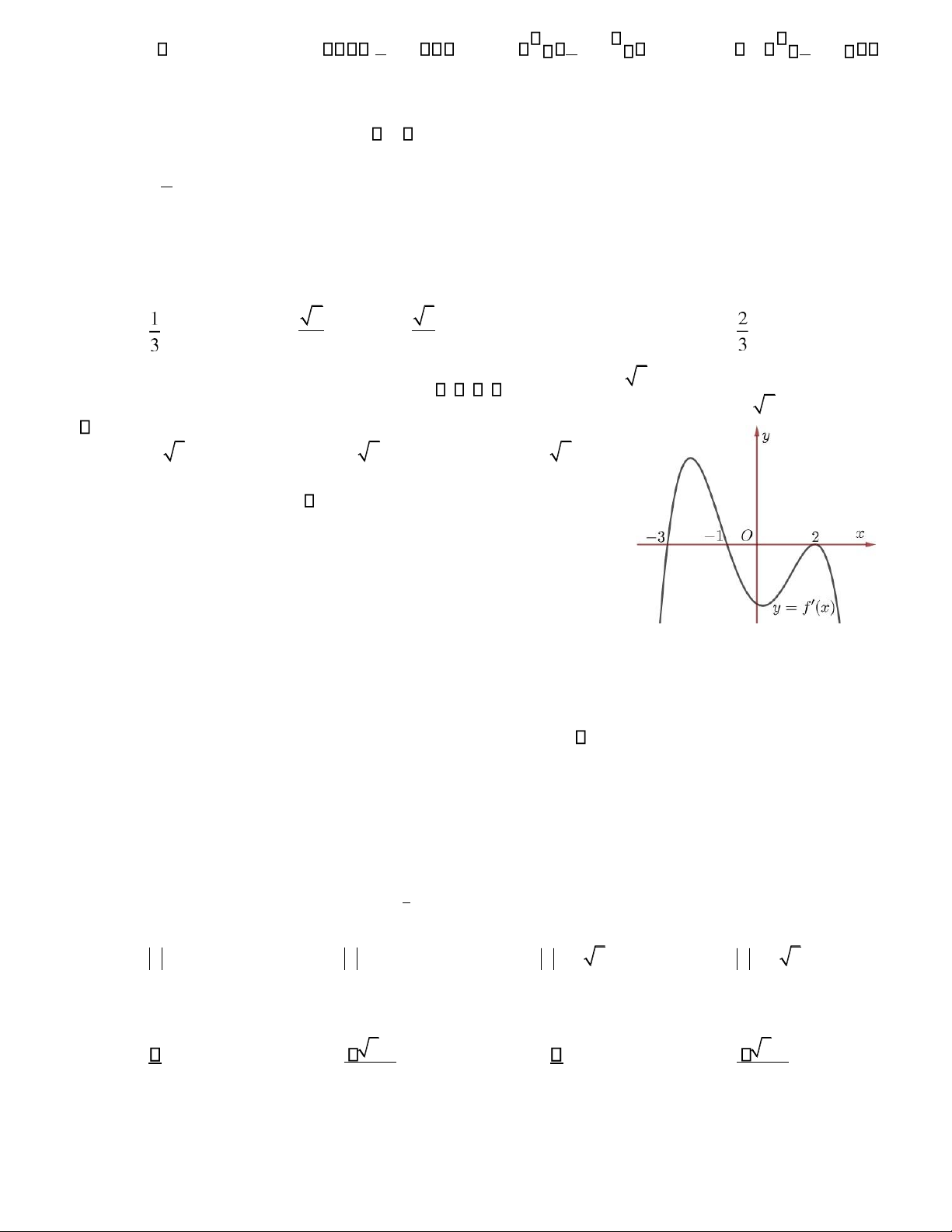
Câu 50. Cho hàm số f x( )=(m2024 +1)x4
( 2m2024 −22024m2 −3)x2 +m2024 +2024 , với m là tham số. Số cực
trị của hàm số y = f x( )−2023 . A. 3. B. 5. C. 6 . D. 7 .
________________HẾT________________ AP AN E SO` 55 1 2 3 4 5 6 7 8 9 10 C B C A C A D B A C 11 12 13 14 15 16 17 18 19 20 C B C C D C A A B D 21 22 23 24 25 26 27 28 29 30 B D B B D A A D A A 31 32 33 34 35 36 37 38 39 40 B A A C A D A D C D 41 42 43 44 45 46 47 48 49 50 B C A B A A B C A D lOMoAR cPSD| 22014077
Lłi giaßi cau hoßi van dung cao æe soÆ 55
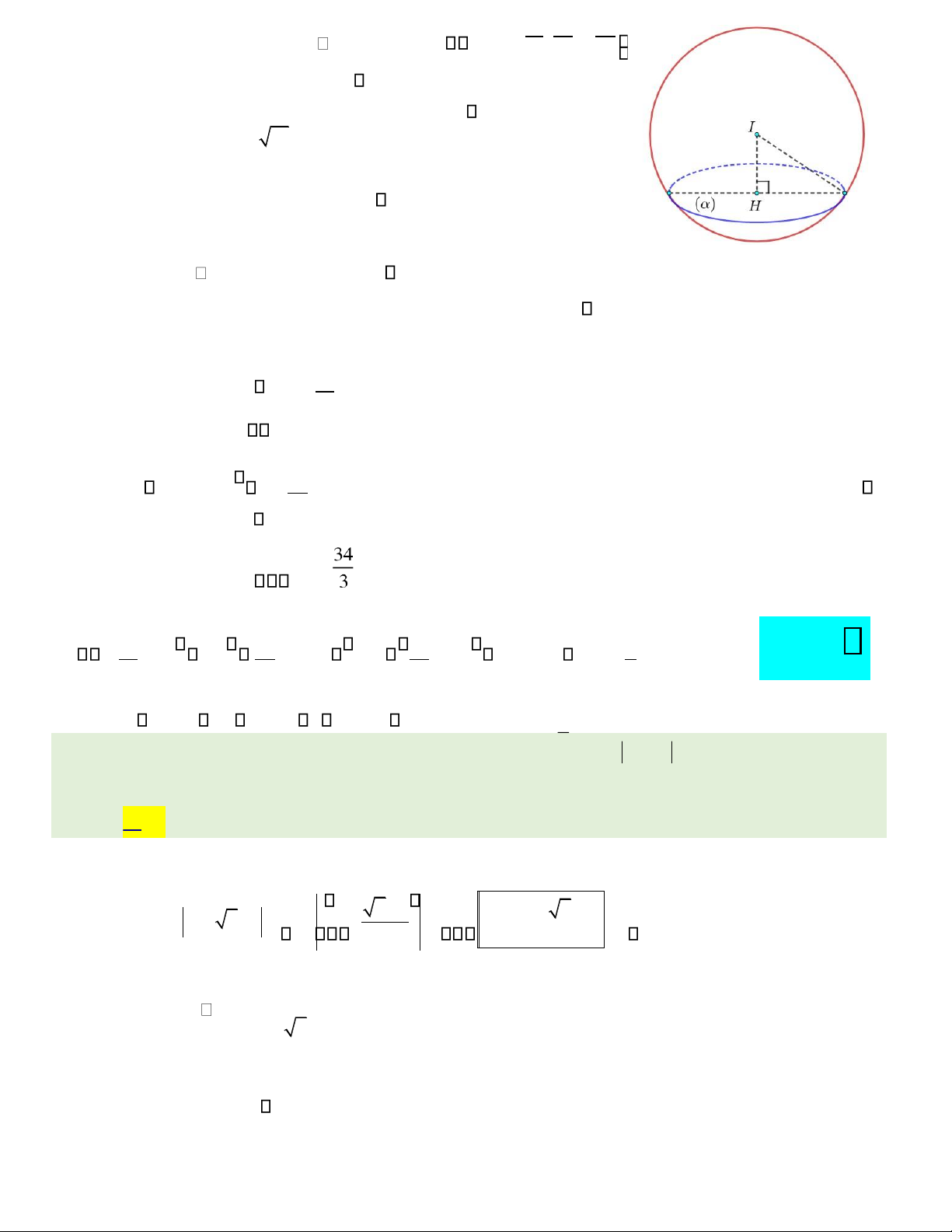
Câu 44. Cho hình tr ụ ()
T có O , O
l n lượt là tâm hai ường tròn áy. Tam giác ABC n ộ i ti ếp trong ườ ng 1
tròn tâm O , AB = 2 a , sin ACB = và OO
t ạ o v ớ i m ặ t ph ẳ ng ( OAB ) m ộ t góc o 30 (tham kh ả o 3
hình bên dướ i). Th ể tích kh ố i tr ụ () T b ằ ng 3 A. 3 3 2 π 6 a . B. 3 π6 a . C. π 3 a . D. 3 π6 a . Hướng dẫn giải:
Gọi r là bán k椃Ānh áy của hình trụ. Tam giác ABC nội tiếp trong AB 2 a = 1 2 sin ACB 2.
ường tròn tâm O nên r = 3
=a 3. Gọi I là
trung iểm của oạn thẳng AB , ta có: OI ⊥ ⊥AB
AB AB ⊥ (O OI
). Kẻ ường cao OH của tam giác OO OOI , ta có:
OHOH ⊥⊥ O IAB (do AB ⊥ (O OI )), suy ra OH ⊥ (O AB
). Do ó: OH là hình chiếu vuông góc của OO lên mặt phẳng (O AB ) OOH =OOI =30o.
Xét tam giác OAI vuông tại I có: OI = r2 − IA2 =
3a2 − a2 = a 2 .
Xét tam giác OOI vuông tại O có: OO = OI = 0
a 6 = h với h là chiều cao của khối trụ ( )T . Thể tan30 lOMoAR cPSD| 22014077
⎯Choïn⎯⎯→B
tích khối trụ ( )T bằng V = r h2 =3 a3 6.
Câu 45. Số 7100000 có bao nhiêu chữ số? A. 84510. B. 194591. C. 194592. D. 84509.
Hướng dẫn giải:
Ta có: log7100 000 =100 000.log7 84 509,804 84 509;84 510 .
Do ó: log1084509 log7100000 log1084510, suy
ra số 7100000 có 椃Āt hơn 1084 510 một chữ số
⎯Choïn⎯⎯→
mà 1084 510 có 84 511 chữ số nên 7100000 có 84510 chữ số. A
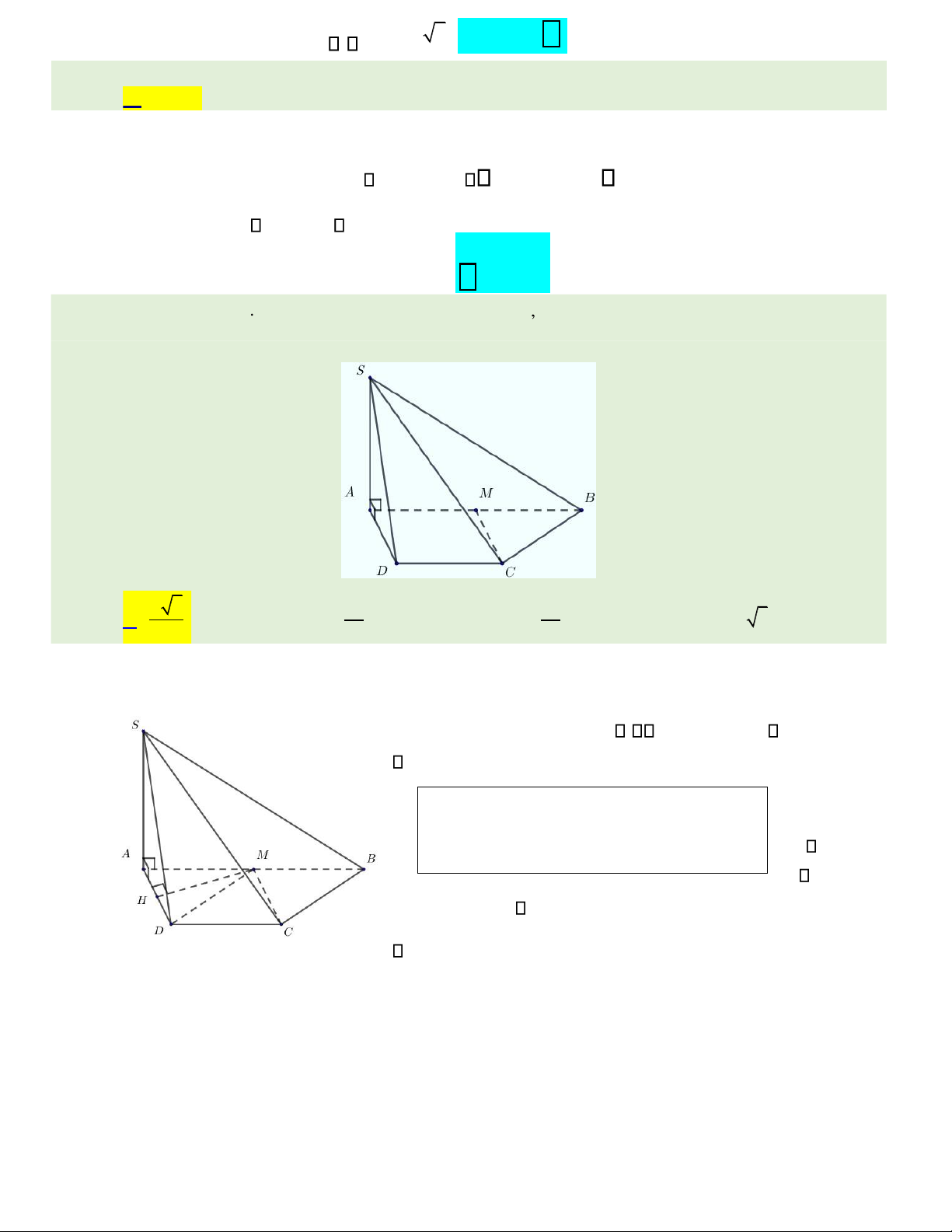
Câu 46. Cho hình chóp .
S ABCD có áy là hình thang AB = 2 , a AD = DC =CB = a
và SA vuông góc v ớ i m ặ t
ph ẳng áy (minh họa như hình vẽ dưới ây). Gọ i M là trung iể m c ủ a c ạ nh AB . Kho ả ng cách gi ữ a
hai ườ ng th ẳ ng CM và SD b ằ ng A . a 3 a a . B. 3 . C. 3 . D. a 3 . 2 4 2
Hướng dẫn giải :
Ta có M là trung iểm của AD
AM = a = CD AMCD là AM //CD hình bình d CM SD( ,
) = d CM( ,(SAD)) = hành CM // d M(,(SAD)) AD CM
//(SAD), mà SD (SAD) ( )1 .
Dễ thấy MBCD cũng là hình bình hành suy ra DM = BC = a .
Ta thấy: AD = AM = DM = a nên tam giác ADM ều cạnh a. lOMoAR cPSD| 22014077 = a 3
Gọi H là trung iểm của AD MH ⊥ AD (1) và MH . 2 lOMoAR cPSD| 22014077
Ta lại có: MH ⊥ SA (2) (do SA ⊥ (ABCD)). Từ (1) và (2) suy ra MH ⊥ ( ) SAD .
⎯Choïn⎯⎯→ Do ó: d M SAD(
,( ))=MH = a 3 . Vậy d A CM SD( , )= a 3 . 2 2
Câu 47. Cho hàm số f x( ) = log32 x −log2 x3 + m (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của
m sao cho max f x( ) +min f x( ) = 6. Tổng bình phương tất cả các ph n tử của S bằng 1;4 1;4 A. 13. B. 18. C. 5. D. 8.
Hướng dẫn giải:
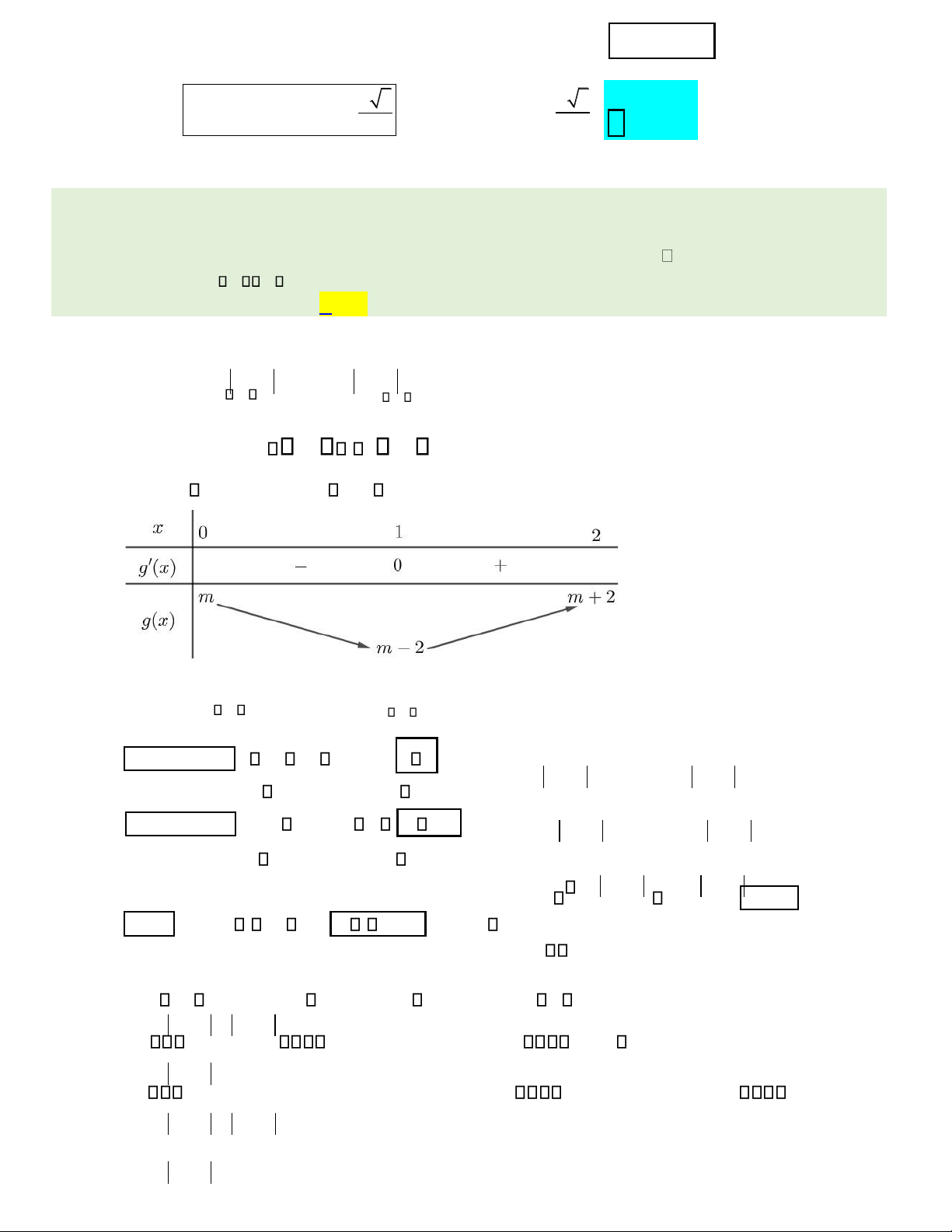
Đặt M = max 1;4 f x( ) , N = min 1;4 f x( ) .
Đặt t = log2 x ; vì x 1;4
t 0;2 . Hàm số ã cho trở thành: g t( ) = t3 −3t + m .
Ta có g t ( ) = 3t2 −3 = 0 t = 1. Bảng biến thiên của g t( ) :
Suy ra: max 0;2 g t( )= +m 2, min 0;2 g t( )= −m 2.
Trường hợp 1: 0 − + m 2 m 2 m 2 . Ta có M = m+ 2 = m+ 2, N = m−2 = m− 2 .
Khi ó: M + N = 6 m+2+m−2 = 6 m = 3 (nhận).
Trường hợp 2: m−2 m+ 2 0
m −2 . Ta có: M = m−2 = 2−m N, = m+ 2 = −m− 2 .
Khi ó: M +m = 6 2−m−m−2 = 6 m = −3 (nhận).
M m= +2 M m= −2 Trường
hợp 3: m−2 0 + m 2 − 2 m 2 . Ta có: . N = 0 m + m 2 −2
m2 + 4m+ 4 m2 −4m+ 4 m 0 Xét M m+ =2 6
m= 4 m= 4 (loại). m + + = M 2 0N 6 m+ =−2 6 m=−8 lOMoAR cPSD| 22014077 m + m 2 −2
m2 + 4m+ 4 m2 −4m+ 4 m 0 Xét M m− =2 6
m= 8 m=−4 (loại). m − + = M 2 0N 6 m− =−2 6 m=−4
⎯Choïn⎯⎯→B
Vậy S = − 3;3 . Suy ra tổng bình phương tất cả các ph n tử của S bằng 18. Câu 48. Trong không gian Oxyz , cho hai
iểm A(10;6;−2), B(5;10;−9) và mặt phẳng
( ) :2x + 2y + z −12 = 0 . Điểm M di ộng trên ( ) sao cho MA, MB luôn tạo với ( ) các góc bằng
nhau. Biết rằng M luôn thuộc một ường tròn ( )C cố ịnh. Hoành ộ của tâm ường tròn ( )C bằng HO NG XU´N NH N 585 C. 2 . D. 10. A. −4. B. .
Hướng dẫn giải:
Gọi H K, l n lượt là hình chiếu vuông góc của A B, trên mặt phẳng ( ) , khi ó:
(( ) )= 2.10+2.62 + − −2( 2 ) 2 12 = 6 ; AH d A= ; 2 +2 +1 )
BK d B= ( ;( ) )= 2.5+ 2.10+ − −( 9 212 = 3. 22 + 22 +1
Vì MA, MB tạo với ( ) các góc bằng nhau nên AMH = BMK mà AH=2BK suy ra MA=2MB.
Gọi M x y z( ; ; ), ta có:MA=2MB MA2 = 4MB2
(x−10)2 +(y −6)2 +(z +2)2 = 4 (x−5)2 +(y −10)2 +(z +9)2 x + + − 2 y2 z2
20 x− 68 y + 68 z +228 =
3x2 +3y2 +3z2 −20x−68y+68z+684=0 . 0 3 3 3 lOMoAR cPSD| 22014077 10 34 −
Như vậy, iểm M nằm trên mặt c u ( )S có tâm I ; ; 3 3 3 34
và bán kính R = 2 10 .
Mặt khác ta có M di ộng trên ( ) , vì vậy tập hợp
iểm M chính là ường tròn giao tuyến ( )C ược tạo
bởi mặt c u ( )S và mặt phẳng ( ) . Gọi H là tâm của ường tròn (
)C , khi ó H là hình chiếu vuông góc của I trên mặt phẳng ( ) .
Phương trình ường thẳng d i qua I và vuông góc với mặt phẳng x = 10 + 2t 3 = 34 ( ) là: d : y
+ 2t . Thay phương trình tham số của d vào ( ) : 3 z = − +t
⎯Choïn⎯⎯→C 2 10 + 2t + 2 34 + 2t + −
34 +t −12 = 0 t = − 2 , từ ó suy ra H (2;10;−12). 3 3 3 3
Câu 49. Giả sử z − =
1, z2 là hai trong số các số phức z thỏa mãn iz + −2 i =1 và z1 z2
2. Giá trị lớn nhất của z + 1 z2 bằng A. 4 . B. 2 3. C. 3 2 . D. 3.
Hướng dẫn giải: 2 −i ) =1
Ta có : iz + 2 −i =1 i z + i z −(1+i 2 =1 (*) .
Gọi A, B l n lượt là các iểm biểu diễn của z1, z2 . Khi ó A B, thỏa (*) nên A B, di ộng trên ường tròn ( ) ( )
C có tâm I 1; 2 , bán kính R=1. Ta có : z − = 1 z2
2 AB = 2 = 2R , suy ra AB là ường kính của ( )C hay I là trung iểm của AB . lOMoAR cPSD| 22014077 Khi ó : z + = 1 z2 OA OB+ 2(OA2 +OB2) = 2 2 OI2 + AB2 =
4OI2 + AB2 = 16 = 4. 2 Cauchy Sch arz− w
⎯Choïn⎯⎯→
Dấu bằng khi OA = OB. A + −
Câu 50. Cho hàm số f x( ) = (m2024 +1)x4
( 2m2024 −22024m2 −3)x2 +m2024 + 2024 , với m là tham số. Số cực
trị của hàm số y = f x( )−2023 . A. 3. B. 5. C. 6 . D. 7 .
Hướng dẫn giải:
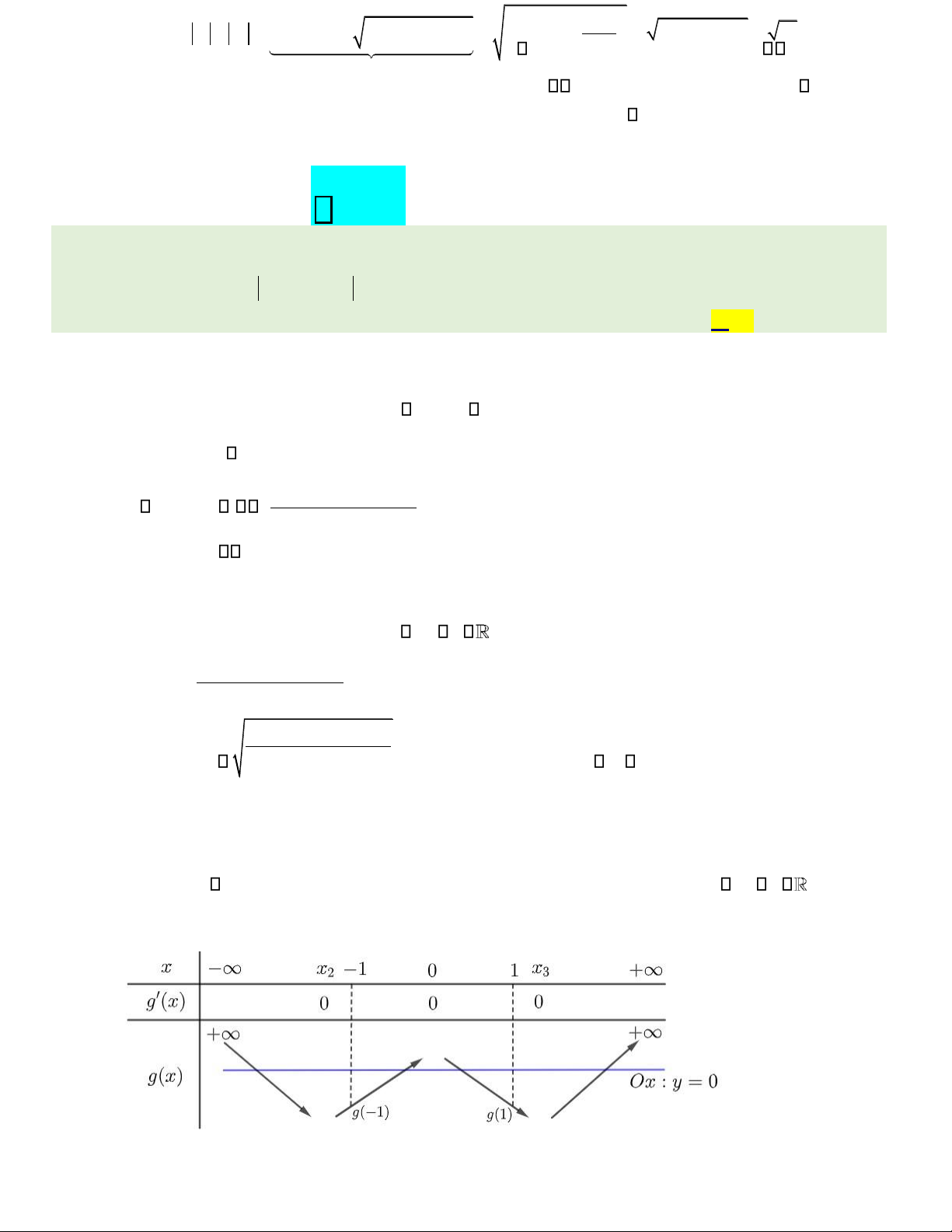
Đặt g x( ) = f x( )− 2023. Ta có: g x ( ) = f ( )x = 4(m + + − − 2024
1)x3 2(−2m2024 22024m2 3)x ; x = 0 f ( )x = 0 x = + 2
2m2024 22024 2m +3 2(m + 2024 1) 2m 2 Ta thấy 2024( + 2024 2+m) +3 2024 0, m
nên hàm số g x( ) = f x( )− 2023 luôn có 3 cực trị gồm 2 m 1 x = = (+ + = + 1 0, x2,3 2m2024
202422024 m)2 3 . Ta lại có: ag
m2024 1 0 Đồ thị hàm g x( ) có nhánh phải 2 m +1 hướng lên trên.
Mặt khác: g( 1) = (m + − − + = − − 2024
1) (+ −2m2024 22024m2 3)+ m2024 122024m2 1 0, m .
Ta có bảng biến thiên hàm g x( ) = f x( )− 2023 như sau: lOMoAR cPSD| 22014077
Từ bảng biến thiên, ta thấy ồ thị hàm số g x( ) luôn có ba iểm cực trị, trong ó có hai iểm cực tiểu nằm
bên dưới trục Ox . Vì vậy số cực trị của hàm số y = f x( )−2023 là m+n = 3+4 = 7; trong ó m =3 là y =
số cực trị của hàm g x( ), n = 4 là số giao iểm của hai ồ thị hàm số g x( ) . y = 0 (Ox) ⎯ ⎯⎯→ Choïn D