Đề 5 - Ôn tập full lớp 12 môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 ĐỀ SỐ 5
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
Câu 1. Họ nguyên hàm của hàm số −
y =e2x −e x là A. e − + + + − + + + 2x e−x C .
B. 2e2x e−x C .
C. 2e2x e−x C .
D. e2x e−x C .
Câu 2. Tập nghiệm của phương trình : log5 x2 = 2là : A. B. C. 5 . 5 . −5 . D. .
Trên mặt phẳng tọa ộ, cho iểm M (5;1) biểu diễn số ph
ức z . Phần ảo của số ph ức z là Câu 3. A. 5. B. i . C. 1. D. 5i .
Câu 4. Cho (u ) =
n là một cấp số cộng có u1
3 và công sai d = 2. Tìm u20 . A. 39. B. 43. C. 41. D.45.
Câu 5. Trong không gian với hệ tọa ộ Oxyz , phương trình nào dưới ây là phương trình mặt phẳng ( ) Oyz ?
A. y + z = 0. B. x =0.
C. y = 0. D. z =0.
Câu 6. Cho khối nón có diện tích áy bằng a2 và ường sinh l = 5 .a Tính thể tích khối nón ó. A. V = a3. B. V = a3.
C. V = 2 a3. D. V = a3. lOMoAR cPSD| 22014077 Câu 7. 1 =
Cho hàm số F x( ) là một nguyên hàm của f x( ). Biết F ( )1 =−3, F (− =2) 12 . Tính I ( f x x )d ? −2 A. I =15. B. I = −36. C. I = −15. D. I =9.
Câu 8. Tập xác ịnh của hàm số − y = x 5 là A. (− ;0). B. \ 0 . C. (− ;0 . D. 0;+ ) .
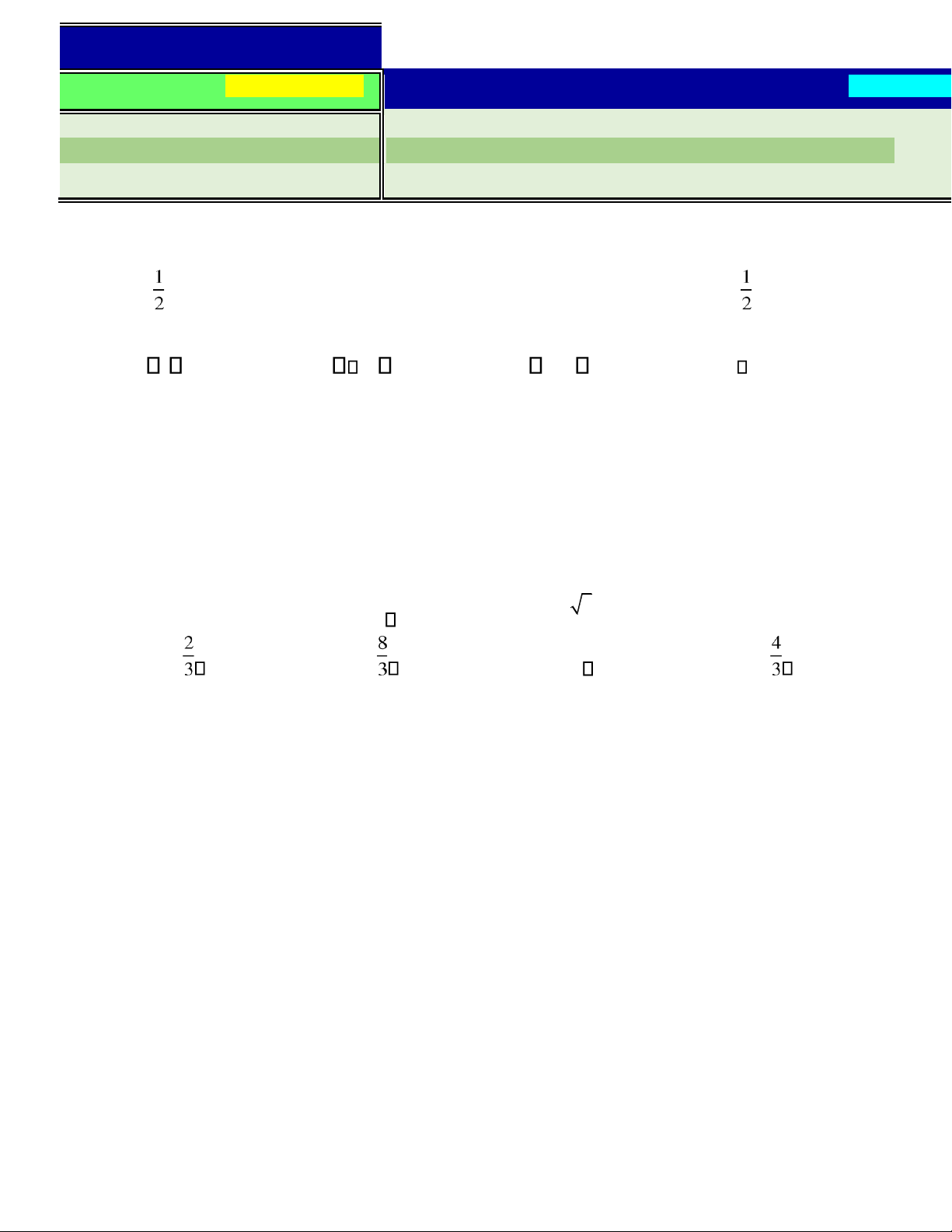
Câu 9. Cho hàm số y =ax4 + +bx2
c có ồ thị như hình vẽ bên dưới. Số
nghiệm thực của phương trình f x( )= f ( )0 là A. 3. B. 0 . C. 4 . D. 2 .
Câu 10. Trong không gian với hệ tọa ộ Oxyz , hình chiếu của iểm M (1;2;3) lên trục Oy là iểm A. R(1;0;0).
B. P(1;0;3) . C. Q(0;2;0).
D. S (0;0;3).
Câu 11. Trong không gian Oxyz , cho mặt cầu ( ) (S : x−2)2 + + + − =(y 3)2 (z 1)2
49. Tìm tọa ộ tâm I và tính
bán kính R của ( )S .
A. I (2; 3;1 ,− ) R = 49. B. (
I 2; 3;1 ,− ) R= 7 . C. I (−2;3; 1 ,− ) R = 7. D. I (2; 3;1 ,− ) R = 7.
Câu 12. Cho hàm số f x( ) = m x3 −2mx2 +(m−9)x+ 2021 2022 . Có bao nhiêu giá trị nguyên của tham số 3
m ể hàm số ã cho nghịch biến trên ? A. 4 . B. 3. C. 2 . D. Vô số.
Câu 13. Cho tứ diện ều ABCD. Gọi M là trung iểm của BC , cosin góc giữa AB và DM bằng A. 2 . B. 3 . C. 3 . D. 3 . 2 3 6 x
Câu 14. Trong không gian Oxyz , cho iểm A(1;2;3) và ường thẳng d : −3 = y −1 = z +7 . Đường thẳng 2 1 −2
i qua A và song song với d có phương trình là x = +1 3t x = +3 t x = +1 2t x = +2 t
A. y = +2 t . B. y = +1 2t . C. y = +2 t . D. y = +1 2t . lOMoAR cPSD| 22014077 z = −3 7t z =− +7 3t z = −3 2t z =− +2 3t Câu 15. Cho log 2 = = = + + 5
a và log 35 b. Biểu diễn log 3605 dưới dạng log 3605
ma nb p, với mn p, , là các
số nguyên. Tính A= m+n+2p. A. A=9. B. A=7 . C. A=8. D. A=10.
Câu 16. Trong không gian, cho tam giác ABC vuông tại A, AB = 2a và AC a= . Khi quay tam giác ABC xung
quanh cạnh góc vuông AB thì ường gấp khúc ACB tạo thành một hình nón. Diện tích xung quanh của hình nón ó bằng A. 5 a2. B. 5 a2.
C. 20 a2 . D. 2 5 a2 .
Câu 17. Tập nghiệm của bất phương trình 4x −6.2x +8 0 là A. B. C. D. (2;4). (0;2). (− + ;1) (2; ). (1;2) . = 1
Câu 18. Tổng số tiệm cận ứng và ngang của ồ thị hàm số y 4 2 bằng: x + x −2 A. 5. B. 3. C. 4 . D. 1.
Câu 19. Trong không gian Oxyz , cho mặt cầu ( )S : x2 + − + + =(y 1)2 (z 1)2
4 và mặt phẳng ( )P :
2x+ y −2z + =1 0. Khoảng cách từ tâm I của ( )S ến ( )P bằng A. . B. 2. C. 1. D. .
Câu 20. Thể tích của vật thể tròn xoay sinh bởi hình phẳng giới hạn bởi ồ thị hàm số y = − −x2 x 6 và trục hoành
quay quanh trục hoành ược tính theo công thức A. 1( ( 0
x2 − −x6)dx . B.
32 x4 −2x3 −11x2 +12x+36)dx . − C. 3 ( 1(
2 x2 − −x 6)dx. D. 0
x4 −2x3 −11x2 +12x+36)dx. − = x
Câu 21. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
3 + 2x2 +3x−4 trên oạn −4;0 lần lượt là 3 M
và m. Giá trị của tổng M +m bằng bao nhiêu?
A. M + m = − .
B. M + m = .
C. M + m = − . D. M m+ = −4.
Câu 22. Cho hình chóp S ABC.
có áy là tam giác ều cạnh a. Biết SA vuông góc với mặt phẳng áy và
SBA=30 . Thể tích khối chóp S ABC. bằng: a3 a3 a3 a3 A. . B. . C. . D. . 2 4 6 12 lOMoAR cPSD| 22014077 Câu 23. Xét e
ln x dx , nếu ặt u = ln x thì e ln x dx bằng 2x 1 2x 1 1 1 A. 2 1u ud . B. 1u ud . C. e u ud . D. e u ud . 0 2 0 1 2 1
Câu 24. Tập nghiệm của bất phương trình log ( (
1 2x+ +3) log2 3x+1) 0 là 2 A. − x 2. B. − x 2 . C. x 2. D. x 2.
Câu 25. Cho khối lăng trụ ều ABC ABC. có AB = 2a, M là trung iểm BC và AM =3a. Thể tích của
khối lăng trụ ã cho bằng A. 18a3 2 . B. 3a3 2 . C. a3 2 . D. 9a3 2 . 2 = Câu 26. Xét I ( ) f x
cos dx x . Nếu ặt u = f x( ) và dv = cos dx x thì 0 2 2 ) +
A. I = ( f x( )sin x 2 0
f ( )x sin dx x . B. I = ( f x( )sin x)− f ( )x sin dx x . 00 2 0 2 2 ) ) − +
C. I = −( f x( )sin x 2 2 0
f ( )x sin dx x. D. I = −( f x( )sin x0
f ( )x sin dx x. 0 0 x Câu 27. Trong không gian Oxyz , cho
ường thẳng : +1 = y + 2 = z và mặt phẳng 2 1 1
( ) (P : 2m+1)x−(5m−1) y − +(m 1)z − =50 . Tìm m ể song song với ( )P . A.m =−1. B.m=−3. C.m =1.
D. Không tồn tạim.
Câu 28. Gọi S là tập hợp tất cả các giá trị của tham số m ể hàm số y x= −4 2mx2 + +m 1 có giá trị cực tiểu bằng
−1. Tổng các phần tử thuộc S là A.−2. B.0 . C.1. D.−1. lOMoAR cPSD| 22014077
Câu 29. Trong không gian Oxyz , cho ba iểm A(2;0;0 ,) B(0; 3;0 ,− ) C(0;0;6) . Tọa ộ một vectơ pháp tuyến
của mặt phẳng (ABC) là
A. n= −(2; 3;6).
B. n= −(1; 2;3).
C. n= −(3; 2;1). D. n=(3;2;1).
Câu 30. Ký hiệu z0 là nghiệm phức có phần ảo âm của phương trình z2 −4z +13= 0. Trên mặt phẳng toạ ộ, iểm
nào dưới ây là iểm biểu diễn của số phức iz0? A. M1(3;2). B. M2(2;3). C. M3(2; 3).− D. M4( 3;2).−
Câu 31. Cho hình lăng trụ ứng ABCABC. có áy ABC là tam giác vuông cân tại B có AB = a AA, = a 2
. Góc giữa ường thẳng A C với mặt phẳng (AA B B ) bằng: A. 60 . B. 30 . C. 45 . D. 90 . 1 1
Câu 32. Cho hàm số f x( ) có ạo hàm liên tục trên . Biết x f. ( ) ( )
x dx =10 và f ( )1 = 3, tính f x dx . 0 0 A. 30. B. 7 . C. 13. D. −7.
Câu 33. Số phức nào sau ây không phải số thuần ảo? )
A. z =i 3.
B. z = +(i 1)i.
C. z = 0.
D. z = −(1 2 i .
Câu 34. Trong không gian Oxyz cho hai iểm A(1;2;3) và B(3;3;4) và mặt phẳng ( )P : x+ − =2y z 0. Gọi A B ,
lần lượt là hình chiếu vuông góc của A và B lên mặt phẳng ( )P . Tính ộ dài oạn thẳng AB . A. 6 . B. 3 . C. 6 . D. 3 . 2 2
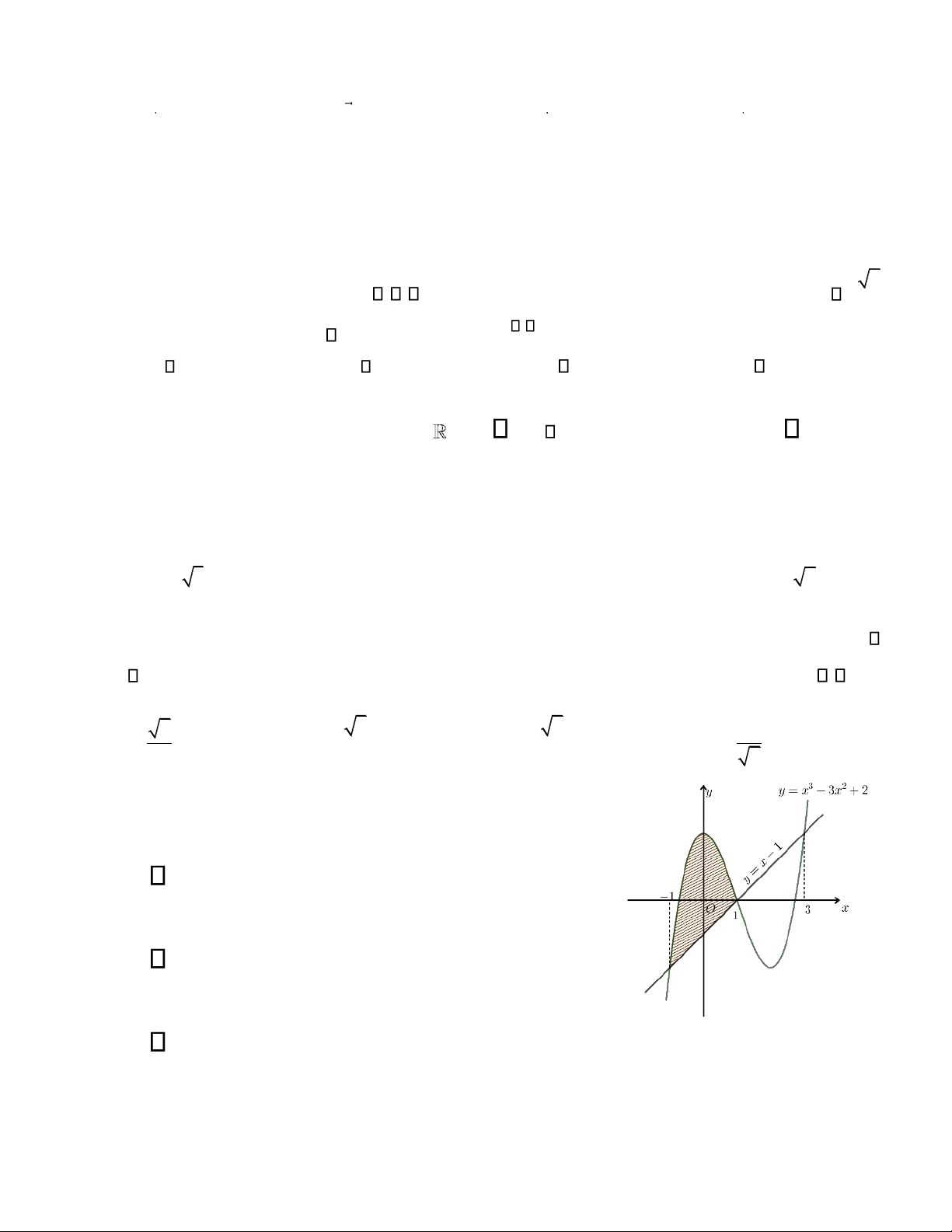
Câu 35. Diện tích hình phẳng gạch chéo trong hình vẽ bên ược tính theo
công thức nào dưới ây? 1 A.
(−x3 +3x2 + x −3)dx. −1 1 B.
(x3 −3x2 − x +3)dx. −1 1 C.
(x3 −3x2 + x +3)dx. −1 3 lOMoAR cPSD| 22014077 D.
(x3 −3x2 − x +3)dx. −1
Câu 36. Cường ộ trận ộng ất M (Richter) ược cho bởi công thức M =log A−log A0, với A là biên ộ
rung chấn tối a và A0 là một biên ộ chuẩn (hằng số). Đầu thế kỷ 20, một trận ộng ất ở San Francisco có
cường ộ 8,3 ộ Richter. Cũng trong cùng năm ó, một trận ộng ất khác ở Nam Mỹ có cường ộ 9,3 ộ
Richter. Hỏi trận ộng ất ở Nam Mỹ có biên ộ rung chấn tối a gấp mấy lần biên ộ trận ộng ất ở San Francisco? A. 20. B. 10. C. 2 . D. 100.
Câu 37. Có tất cả bao nhiêu giá trị thực của tham số m ể ường thẳng y = mx−m+1 cắt ồ thị hàm số y = − + +x3 3x2 x 2 tại ba iểm A B, và C(1;1)
phân biệt sao cho (y − )2 = A yB 4 . A. 1. B. 3. C. 2 . D. 0 .
Câu 38. Cho hình chóp S ABCD. có áy ABCD là hình chữ nhật cạnh AB = 2AD = 2a . Tam giác SAB ều nằm
trong mặt phẳng vuông góc với mặt áy. Khoảng cách từ A ến mặt phẳng (SBD) bằng A. a. B. a 3 . C. a . D. a 3 . 4 2 2 x x
Câu 39. Trong không gian Oxyz , cho hai ường thẳng d = y = z −1 −3 = y = z ) 1 : ,d2 : . Gọi M a b c( , , 2 −1 1 1 1 −2 * )
là giao iểm của d1 và d2. Tính a+2b+3c. A.2 . B. 5. C. 6 . D. 3. dx Câu 40. Cho 1 = a b − 8
a + 2 (a b, . Tính a+2b. 0 x+2 + x+1 3 3
A. a+2b = −1.
B. a+2b =8.
C. a+2b = 7 .
D. a+2b =5.
x−1 = y −2 = z
Câu 41. Trong không gian Oxyz , cho ương thẳng :
và mặt phẳng ( )P : x+ + − =2y2z 6 0. 1 1 −1
Phương trình ường thẳng d nằm trong ( )P sao cho d cắt, ồng thời vuông góc với là x = 2+ 4t x = 2+ 4t x = 2+ 4t x = 2+ 4t lOMoAR cPSD| 22014077 B. C. D. A.
y = 3+3t .
y = 3−3t .
y = 3+3t .
y = 3−3t . z = +1 t z = +1 t z = − +1 t z = − +1 t
Câu 42. Cho hình trụ có bán kính áy bằng 3 2a. Biết rằng khi cắt hình trụ ã cho bởi một mặt phẳng song song
với trục và cách trục một khoảng bằng 3a , thiết diện thu ược là một hình vuông. Thể tích của khối trụ
ược giới hạn bởi hình trụ ã cho bằng A. a3. B. 54 a3. C. 216 a3. D. 108 a3.
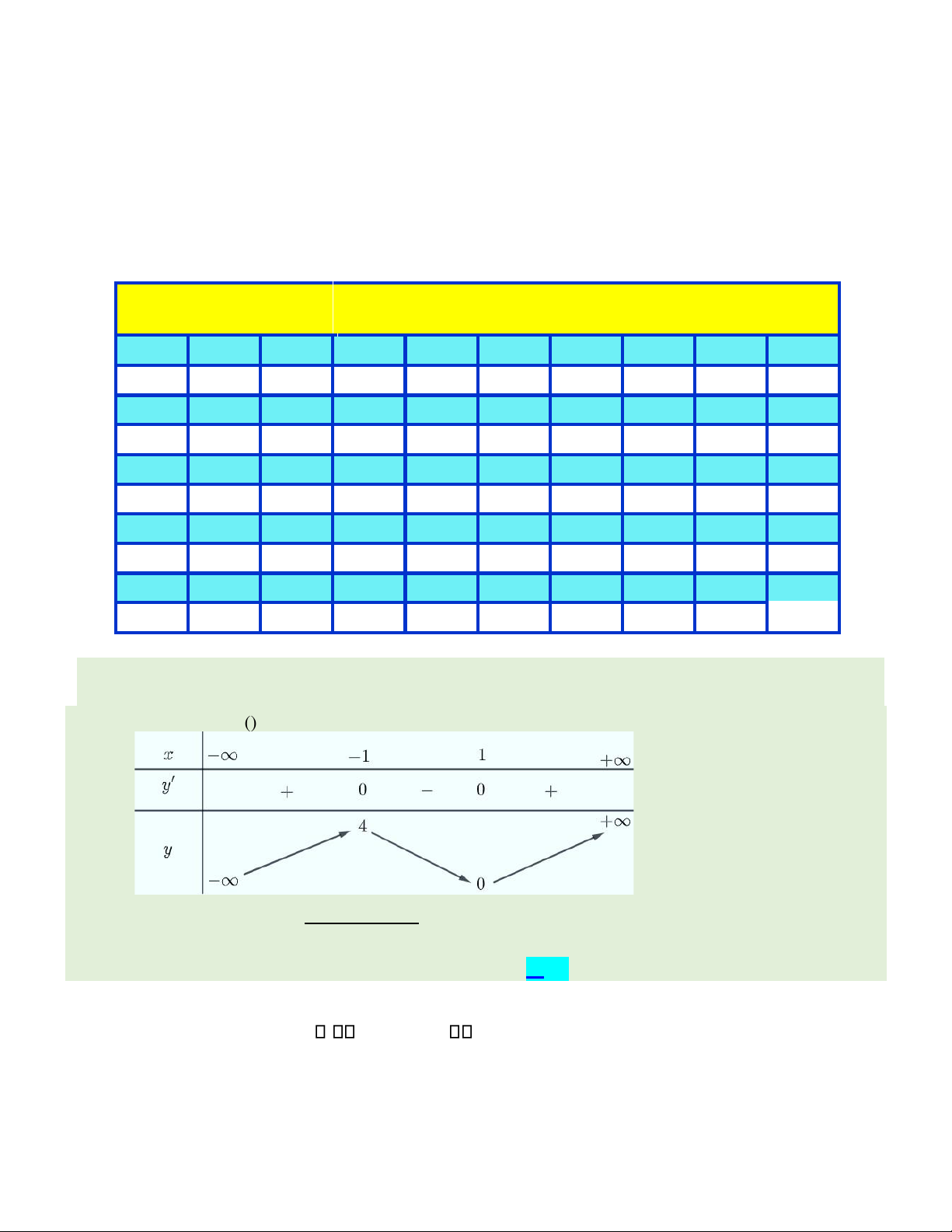
Câu 43. Cho hàm s ố ()
fx có b ả ng bi ến thiên như sau. 4 − Đồ x 1 th ị hàm s ố () gx =
có t ấ t c ả bao nhiêu ườ ng ti ệ m c ận ứ ng 2 () x −4 () fx f A. 2 . B. 5. C. 4 . D. 3.
Câu 44. Cho hình chóp S ABC. có áy ABC là tam giác ều cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong
mặt phẳng vuông góc với áy. Biết rằng góc giữa (SBC) và (ABC) bằng 60 . Tính thể tích khối chóp S ABC. . 3 a 3 a3 3a3 3 3a3 3 . A.. B. C. . D. . 16 48 16 10 = z
Câu 45. Cho số phức z thỏa mãn (1 3 2+ i z) −2+i. z 2 . D. z ; .
Khẳng ịnh nào sau ây là úng? 2 A. z 1 . B. C. z 2. 1 3 22 2
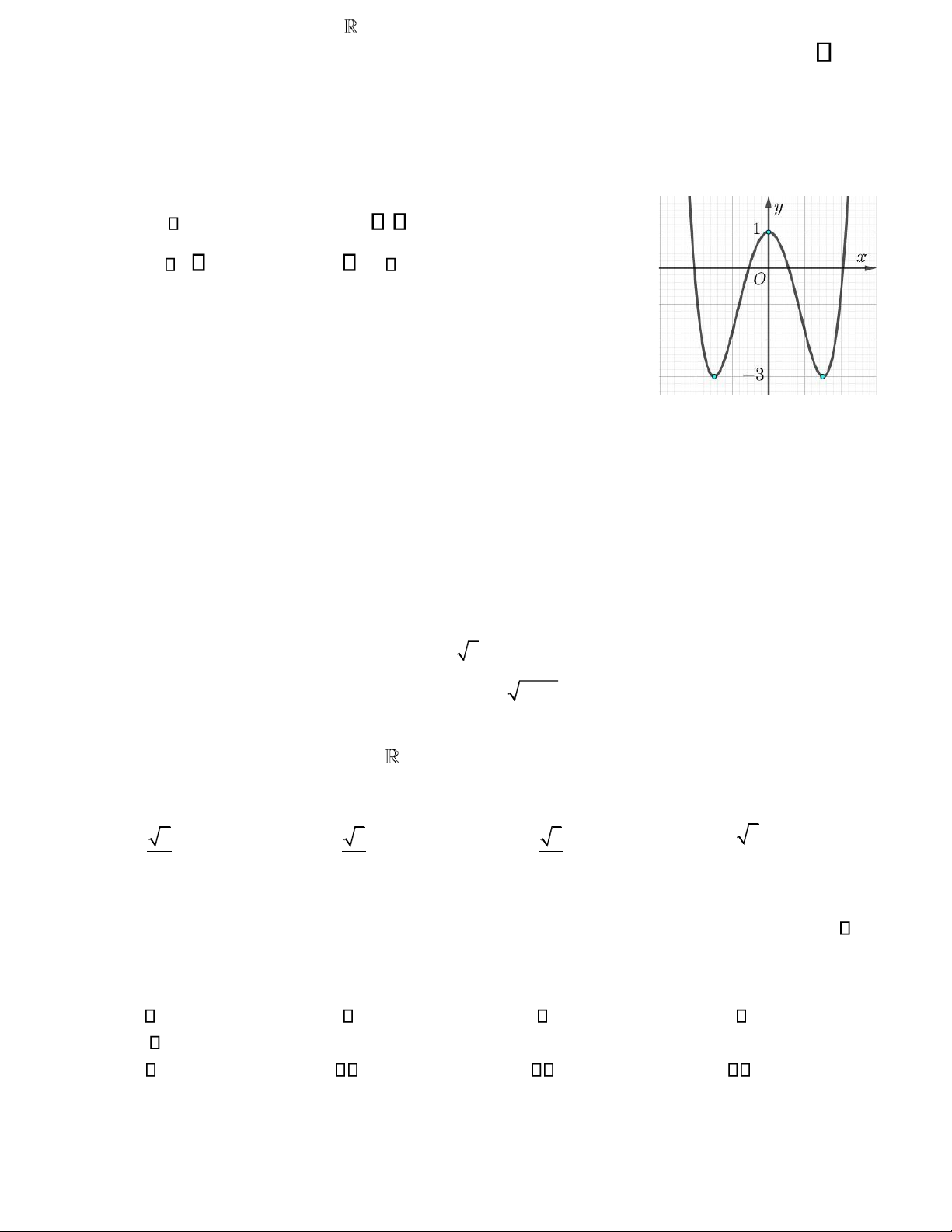
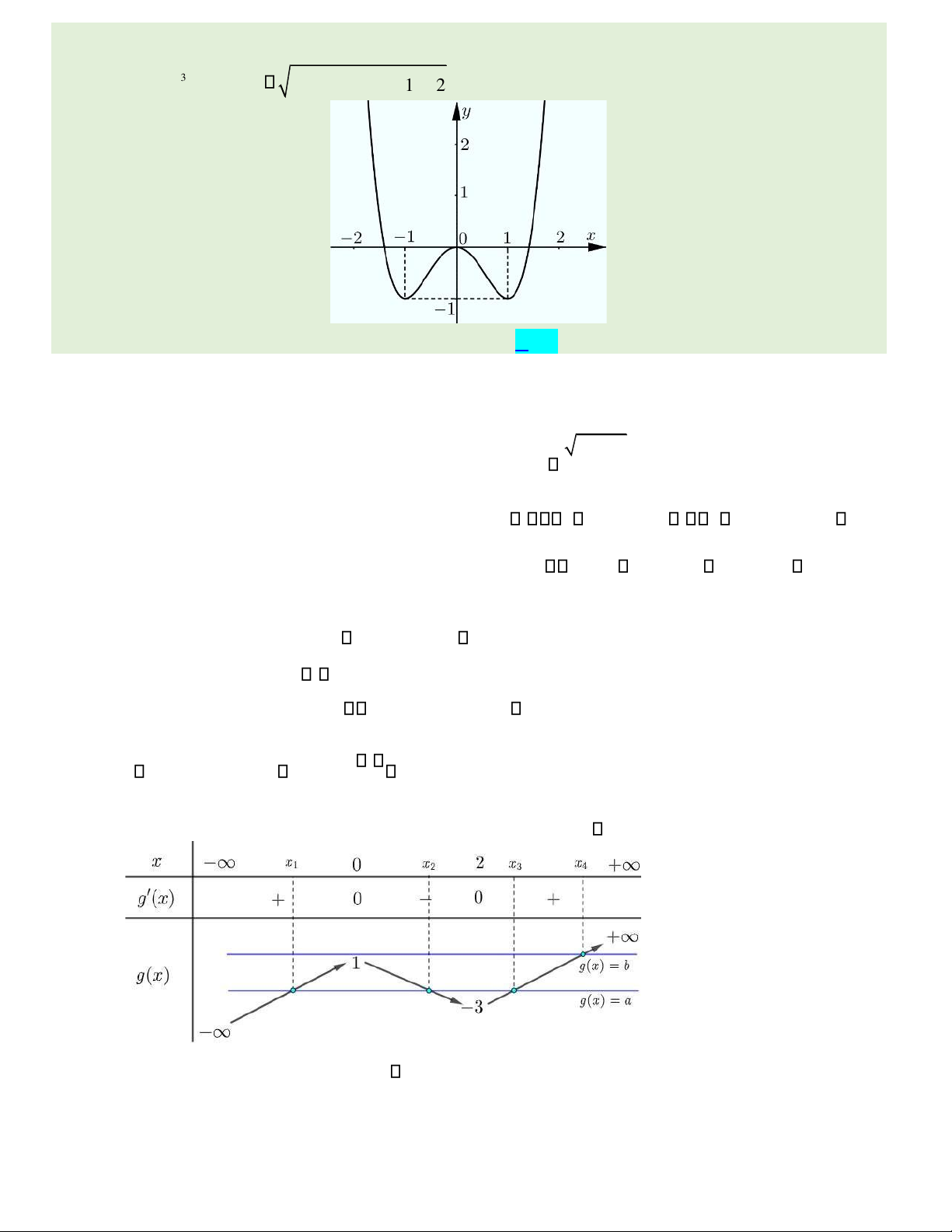
Câu 46. Cho hàm số y = f x( ) có ồ thị như hình vẽ bên. Số nghiệm thực của bất phương trình
1+ f x( 3 −3x2 +1) 2 f 2(x3 −3x2 + +1) 2 là
A. 3. B. 5. C. 4 . D. 2 . lOMoAR cPSD| 22014077
Câu 47. Gọi S là tập hợp tất cả các số tự nhiên có 7 chữ số. Lấy ngẫu nhiên một số từ tập S . Xác suất ể số lấy
ược có tận cùng là 3 và chia hết cho 7 (làm tròn ến chữ số phần nghìn) có dạng 0,abc. Tính a + + 2 b2 c2. A. 15. B. 10. C. 17 . D. 16. c c
Câu 48. Cho các số thực dương a b c; ; khác 1 và thỏa mãn iều kiện log2 2 =
a b+logb c+ 2logb loga 3 . Gọi b a b
M m, lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = loga ab−logb bc. Tìm giá trị của biểu
thức S = 2m2 +9M2. A. S = 28. B. S = 25. C. S = 26. D. S = 27.
Câu 49. Cho mặt cầu ( ):S
x2 + + − − − =y2 z2 2x 2y
2z0 . Điểm A(2;2;0) . Viết phương trình mặt phẳng
(OAB) biết iểm B là một iểm thuộc mặt cầu ( )S , có hoành ộ dương và tam giác OAB ều.
A. x− + =y 2z 0.
B. x− − =y 2z 0.
C. x− − =y z 0.
D. 2− + =y z 0 . 20
Câu 50. Cho hàm số f x( )= − +x3 3x
m . Có tất cả bao nhiêu số nguyên m thuộc khoảng (−20; ) ể với −
mọi bộ ba số thực a b c , ,
2;1 thì f a( ), f b( ), f c( ) là ộ dài ba cạnh của tam giác ? A. 24. B. 26. C. 28. D. 30.
________________HẾT________________ lOMoAR cPSD| 22014077 AP AN E SO` 54 1 2 3 4 5 6 7 8 9 10 D B C C B A C B A C 11 12 13 14 15 16 17 18 19 20 D A C C B B D B D B 21 22 23 24 25 26 27 28 29 30 C D B D B B C B C A 31 32 33 34 35 36 37 38 39 40 B D B D B B B D C B 41 42 43 44 45 46 47 48 49 50 D D C B D C C D C B
L łi giaßi cau hoßi van dung cao æe soÆ 54
Câu 43. Cho hàm s ố ()
fx có b ả ng bi ến thiên như sau. 4 x 1 − Đồ th ị hàm s ố () gx =
có t ấ t c ả bao nhiêu ườ ng ti ệ m c ận ứ ng 2 () () f x −4 f x A. 2 . B. 5. C. 4 . D. 3. Hướng dẫn giải: Xét f ( ) 2
x −4 f x( ) = 0
f x( ) = 0 . f x( ) = 4 lOMoAR cPSD| 22014077 x f x( )= 0
x ==1x1 (trong ó x =1 là nghiệm kép, x = x1 là là nghiệm ơn). Không làm mất tính
tổng quát, ta biểu diễn f x( )= a ( )
1 x−1) (2 x− x1 , a1 0. x =− 1 f x( )= 4
= x2 (trong ó x = −1 là nghiệm kép, x = x2 là là nghiệm ơn). Không làm mất tính x
tổng quát, ta biểu diễn f x( )− =4 a ( )
2 x+1) (2 x− x2 , a2 0. (x2 − )( ) 1 x2 +1
Ta viết lại hàm số ban ầu: g x( ) = f x( ) ( ) f x −4 = ( + ) = +
2x−1)(x+1)(x2 12 x2 1 . a x ( − ) ( ) ( )( ) 1
1) (x− x a1 2 x+1) (x− x2
a a1 2 x−1)(x+1)(x− x1 x− x2
⎯Choïn⎯⎯→
Ta thấy ồ thị hàm số y = g x( ) có bốn ường tiệm cận ứng: x = 1, x = x1, x = x2 .
Câu 44. Cho hình chóp S ABC. có áy ABC là tam giác ều cạnh a, mặt bên SAB nằm trong mặt C và ể
là tam giác cân tại S
phẳng vuông góc với áy. Biết rằng góc giữa (SBC) và (ABC) bằ tích khối chóp S ng 60 . Tính th ABC. . a 3 3a3 33a3 3 A. B. . a C. 3 . 3 D. . 48 16 . 16 Hướng dẫn giải: lOMoAR cPSD| 22014077
Gọi H là trung iểm của AB SH ⊥ AB. Ta có (SAB)⊥(ABC)
suy ra SH ⊥(ABC).
Gọi M là trung iểm của BC và I là trung iểm của BM . Khi ó:
AM ⊥ BC mà HI AM// (tính chất ường trung bình), suy ra HI ⊥ BC . Vì
BCBC ⊥⊥ SHHI BC ⊥ (SHI) BC ⊥ SI .
(SBC) (ABC)=BC Ta có: lOMoAR cPSD| 22014077 HI BC SI BC⊥ , ⊥ ( )) )
(SBC) (, ABC =(HI SI, = SIH = 60 . lOMoAR cPSD| 22014077
Câu 46. Cho hàm số y = f x( ) có
ồ thị như hình vẽ bên. Số nghiệm thực của bất phương trình 1 + ( 3 2 2 3 2 fx −3 x + ) 1 2 f ( x −3 x )1 ++ 2 là A. 3. B. 5. C. 4 . D. 2 .
Hướng dẫn giải:
Đặt t = f x( 3 −3x2 +1). Bất phương trình trở thành: 1+t 2t2 + 2 t −1 2 2 t −2 1 t =1. (1+t) 2t +2 −t +2t −1 0 ( ) 3 2
x3 −3x2 + =1a −( 2;−1)
Ta có: f x −3x +1 =1 . x3 −3x2 + =1
b (1;2) Xét hàm số g x( ) = x3 −3x2 +1, x
g ( )x = 3x2 −6x g, ( )x = 0
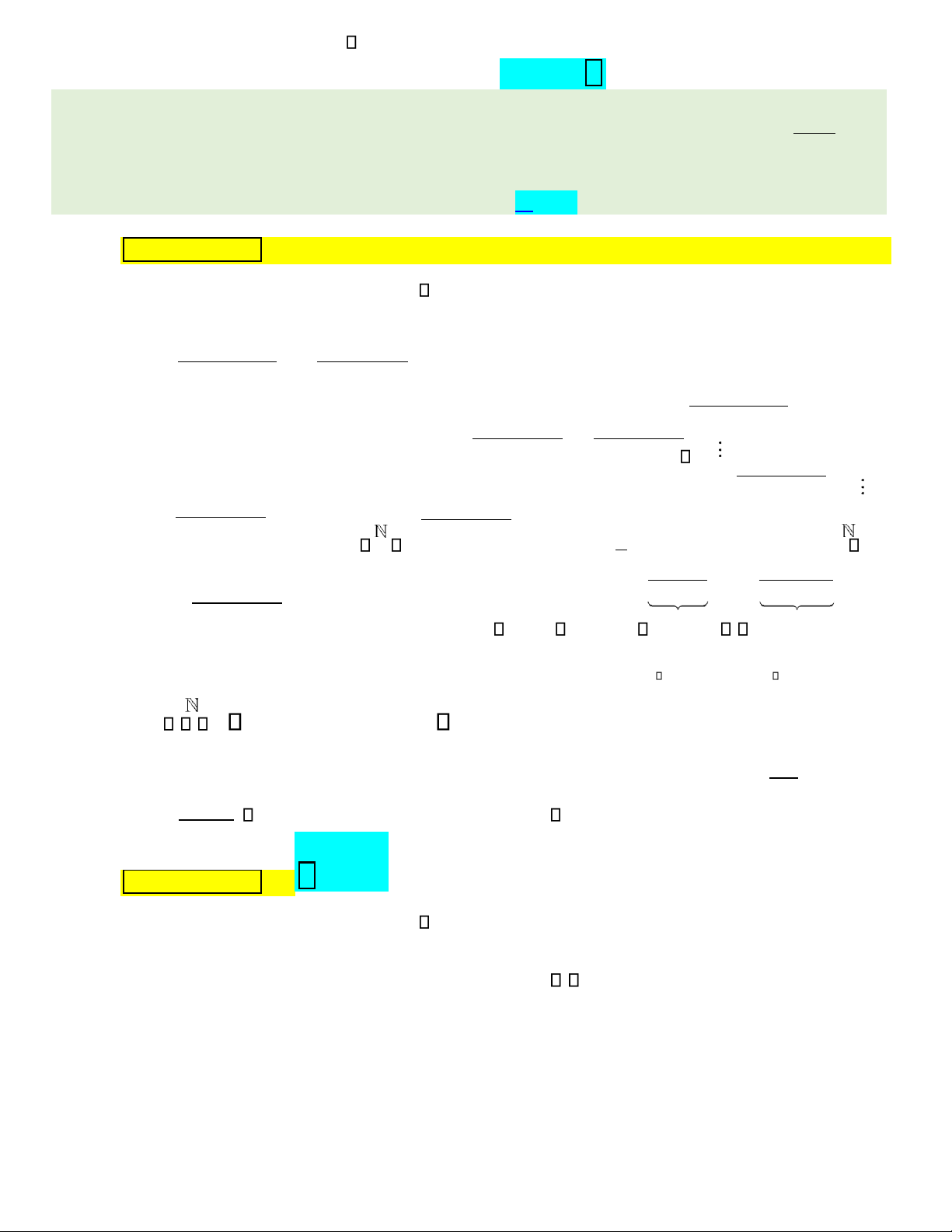
x == 02 . Bảng biến thiên g x( ):
Ta có: Phương trình x3 −3x2 + =1 a (− −2; 1) có ba nghiệm phân biệt x x1, 2, x3 . lOMoAR cPSD| 22014077
Phương trình x3 −3x2 + =1 b (1;2) có một nghiệm x4 khác x x1, 2, x3 .
Vậy bất phương trình ã cho có bốn nghiệm thực. ⎯Choïn⎯⎯→C
Câu 47. Gọi S là tập hợp tất cả các số tự nhiên có 7 chữ số. Lấy ngẫu nhiên một số từ tập S . Xác suất ể số
lấy ược có tận cùng là 3 và chia hết cho 7 (làm tròn ến chữ số phần nghìn) có dạng 0,abc. Tính a + 2 b2 +c2. A. 15. B. 10. C. 17 . D. 16.
Hướng dẫn giải: ☺ Cách giải 1:
Số phần tử của không gian mẫu là: n( ) = 9.106 .
Gọi A là biến cố: “Số lấy ược có tận cùng là 3 và chia hết cho 7”.
Gọi số tự nhiên có 7 chữ số chia hết cho 7 và có chữ số tận cùng bằng 3 là: a a a a a a1 2 3 4 5 63 . ( ) Ta có: a a a a a a + = + +
1 2 3 4 5 63 =10.a a a a a a1 2 3 4 5 6
3 3.a a a a a a1 2 3 4 5 6 7.a a a a a a1 2 3 4 5 6 3 7 ( ) 3.a a a a a a + 1 2 3 4 5 6 3 7 . k m Đặt: 3.a a a a a a + = (m ) 1 2 3 4 5 6
3 = 7k (k ) a a a a a a1 2 3 4 5 6 2k − +1
là số nguyên nên k = 3 . 3 1 000 000 Khi ó : a a a a a a = 1 2 3 4 5 6
7m−1. Do ó: 100 000 7m−1 999 999 100 001 m . 7 7 14 285,8 142 857,1
Do m m 14 286;14 287;...;142 857 . Vì vậy có 142857 14286 1 128572− + = giá n A
trị của m thỏa mãn. Suy ra
( ) =128 572 . Xác suất của biến cố A là: P A( ) = n A( ) = 128572 6
0,014. Suy ra: a = 0, b =1, c = 4. n( ) 9.10
⎯Choïn⎯⎯→
Vây a2 +b2 +c2 =17. ☺ Cách giải 2: C
Số phần tử của không gian mẫu là: n( ) = 9.106 .
Gọi A là biến cố: “Số tự nhiên lấy ược có tận cùng là 3 và chia hết cho 7”.
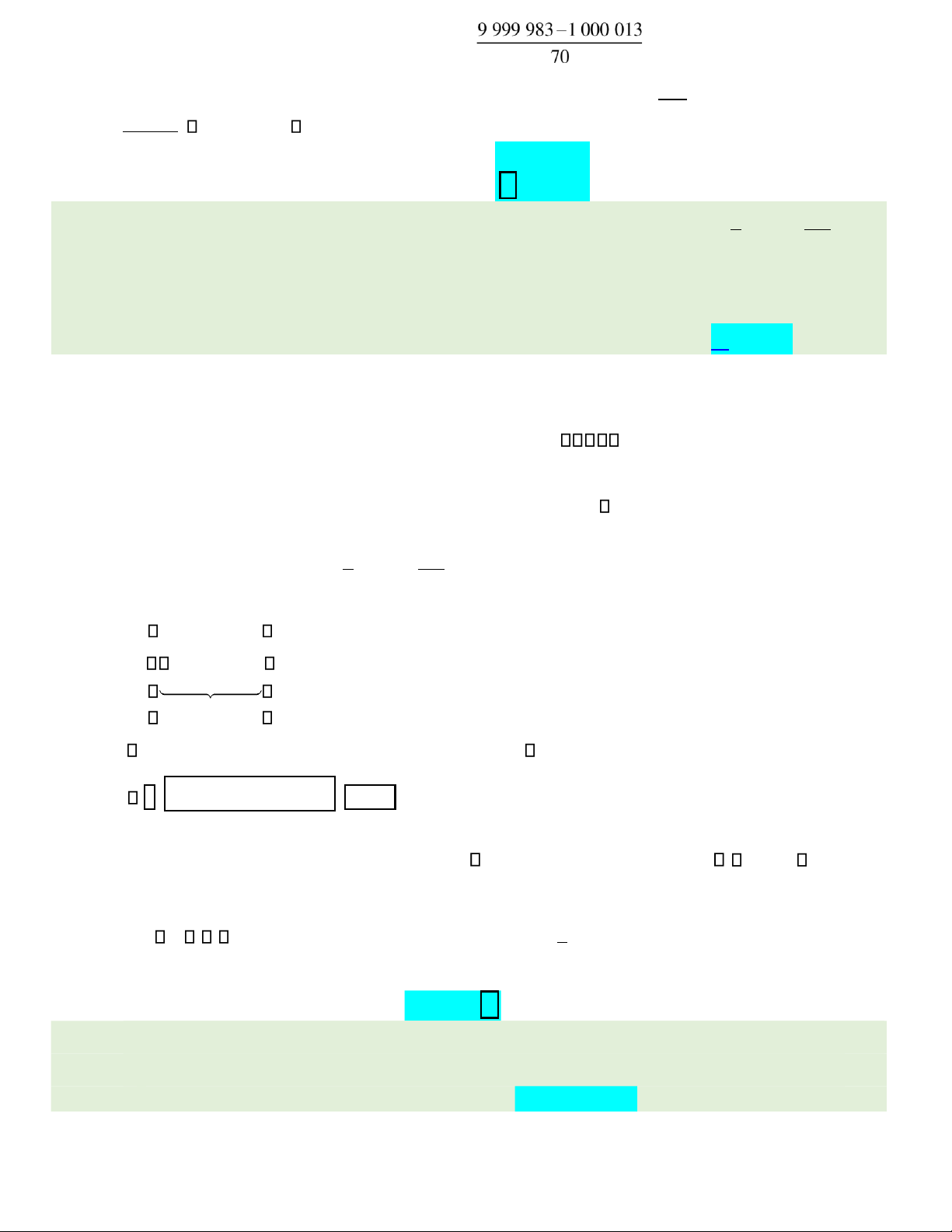
Gọi số tự nhiên thỏa mãn biến cố A là X, ta có: 1000 013 X 9999983.
Ta thấy số nhỏ nhất mà X có thể nhận ược là 1 000 013, số lớn nhất mà X có thể nhận là 9 999 983.
Chênh lệch giữa hai số liên tiếp thỏa mãn ề bài là 70 ơn vị. Vì vậy ta có thể thấy tập hợp các số tự
nhiên X sẽ lập nên một cấp số cộng có số hạng ầu là u = 1
1 000 013, công sai d = 70, số hạng cuối là 9 999 983. lOMoAR cPSD| 22014077
Do vậy số các số tự nhiên mà X có thể nhận là: + =1 128 572
(số). Suy ra n A( ) =128 572 . Xác suất của biến cố A là: P A( ) = n A( ) = 128572 6 0,014. n( ) 9.10
Suy ra: a = 0, b =1, c = 4. Vây a2 +b2 +c2 =17. ⎯Choïn⎯⎯→ C c c
Câu 48. Cho các số thực dương a b c; ; khác 1 và thỏa mãn iều kiện log2 2 =
a b+logb c+ 2logb loga 3 . Gọi b a b
M m, lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = loga ab−logb bc. Tìm giá trị của biểu
thức S = 2m2 +9M2. A. S = 28. B. S = 25. C. S = 26. D. S = 27.
Hướng dẫn giải:
Ta có: P =loga ab−logbbc =loga b−logb c . Đặt loga b = x
logba c = −= logx aPb.logb c = x x( −P). log c Ta có: log2 2
a b+logb c+ 2logb c = loga c 3 b a b 2
loga b−logb c +2loga b.logb c+2logb c− =2
loga c− −3 loga b = P =x x P− x P− x x P( − ) x
+P2 2x x( − +P) 2(x− − =P) 2 x x( − − −P) 3 x +P2 2x2 −2Px+ − − = − − −2x 2P 2 x2 Px 3 x
x2 + −(3 P x) + − + =P2 2P 1 0 (*). Do phương trình
( )* luôn có nghiệm x nên = −(3 P)2 −4(P P2 − +2 1 0) − + + 3P2 2P 5 0 5 = 5 − =−1 P m 1, M . 3 3
Thay vào ta có S = 2m2 +9M2 = 27. ⎯Choïn⎯⎯→ D
Câu 49. Cho mặt cầu ( ):S
x2 + + − − − =y2 z2 2x 2y
2z0 . Điểm A(2;2;0) . Viết phương trình mặt phẳng lOMoAR cPSD| 22014077
(OAB) biết iểm B là một iểm thuộc mặt cầu ( )S , có hoành ộ dương và tam giác OAB ều.
A. x y− + =2z 0.
B. x y− − =2z 0.
C. x y z− − = 0.
D. 2− + =y z 0 .
Hướng dẫn giải:
Gọi B x y z( ; ; ) với x 0 và H trung iểm OA H (1;1;0).
Gọi ( )P là mặt phẳng trung trực oạn OA, do ó ( )P i qua trung iểm H (1;1;0) của oạn OA và nhận
OA=(2;2;0) làm vectơ pháp tuyến. Suy ra ( )P :2.(x −1)+ 2.(y −1) = 0 x y+ − =2 0 . B OB = AB ( )P x+ y −2 = 0 Theo giả thiết: OB =OA OB = + + = 2 OA2 x2 y2 z2 8 B ( )S B ( )S x + + − 2 y2
z2 2x−2y −2z = 0 x+ y = 2 x+ y = 2 x+ =y 2 x+ =y 2 x + + = + = 2 y2 z2 8 x2 y2 4
(x+ y)2 −2xy = 4 xy = 0
2x+2y +2z =8 z = 2 z = 2 z = 2 x = 2 Suy ra:
y = 0 B(2;0;2) , (do x 0). z = 2
Ta có : OA=(2;2;0 ,) OB =(2;0;2) OA OB,
=(4; 4;− − =4) 4 1( ; 1;− −1) .
Mặt phẳng (OAB) i qua O, nhận n= − −(1; 1; 1) là một vectơ pháp tuyến. ậy phương trình
⎯Choïn⎯⎯→ V
(OAB) là: x− − =y z 0. C 20
Câu 50. Cho hàm số f x( )= − +x3 3x
m . Có tất cả bao nhiêu số nguyên m thuộc khoảng (−20; ) ể với −
mọi bộ ba số thực a b c , ,
2;1 thì f a( ), f b( ), f c( ) là ộ dài ba cạnh của tam giác ? A. 24. B. 26. C. 28. D. 30.
Hướng dẫn giải: Xét
g x( ) = x3 −3x + m , g ( )x = 3x2 −3 = 0 x = 1.
Ta có: g(−2) = m− 2 ; g(−1) = m + 2; g( )1 = m−2 . Suy ra: m−2 f x( ) +m 2 , −x 2;1 . lOMoAR cPSD| 22014077 Ta có: .
Min f x( ) f a( ), f b( ), f c( ) Max f x( ) Không −2;1 −2;1
mất tính tổng quát, giả sử f a( ) f b( ) f c( ).
Điều kiện cần và ủ ể f a( ), f b( ), f c( ) là ộ dài ba cạnh của tam giác là:
f a( )+ f b( ) f c( ) f a( )+ f b( )− f c( ) 0 .
Yêu cầu bài toán cho ta iều kiện: f a( )+ f b( )− f c( ) 2Min f x( )−Max f x( ) 0 (1) . −2;1 −2;1
Trường hợp m+2 − m 2 0 m 2 . Khi ó 1: Max −2;1 f x( )= Max
m−2 ; m+ = + = +2 m 2 m 2 ; Min −2;1 f x( )= Min
m−2 ; m+ = − = −2 m+ 2 m 2 . + 20
Thay vào (1): 2(m−2) (− m+2) 0 m−6 0 m 6 . Vì m nguyên thuộc khoảng (−20; ) m 19 nên 7;8;...;
, ta tìm ược 13 giá trị m thỏa mãn.
Trường hợp m−2 + m 2 0 m −2 . Khi ó: 2: Max −2;1 f x( )= Max
m−2 ; m+ = − =− +2 m− 2 m 2; Min −2;1 f x( )= Min
m−2 ; m+ = + =− −2 m+ 2 m 2 .
Thay vào (1): 2(− − − − +m 2) ( m 2) 0
m −6 . Vì m nguyên
thuộc khoảng (−20;20) nên
m − 19;−18;...−7 , ta tìm ược 13 giá trị m thỏa mãn.
m−2 Trường hợp 0 m+2 − 2 m 2 . 3: Khi ó: Max f x( )= Max m−2 ; m+ =2
(m− + + + − − +2) (m 2)(m 2) (m 2) = +m 2; −2;1 2 − Min (
−2;1 f x( )=0. Do vậy (1) trở thành: 2.0
m +2) 0 − m −2 0 (vô lí). lOMoAR cPSD| 22014077
⎯Choïn⎯⎯→
Vậy số giá trị m thỏa mãn ề bài là: 13 13+ = 26. B