Đề 6 - Ôn tập full lớp 12 môn Toán ứng dụng | Trường Đại học Sư phạm Thành phố Hồ Chí Minh

lOMoAR cPSD| 22014077 ĐỀ SỐ 6
ĐỀ RÈN LUYỆN MÔN TOÁN 12
HƯỚNG ĐẾN KÌ THI THPT QUỐC GIA
Trắc nghiệm: 50 câu Nội dung:
Thời gian: 90 phút
FULL KIẾN THỨC TOÁN 12+
Câu 1. Đẳng thức nào sau ây úng với mọi số dương x ? A. (log x) = x .
B. (log x) = ln10 . C. (log x) = 1 . x D. 3 là:
(logx) = xln10. ln10xln10
Câu 2. Thể tích hình lập phương cạnh A. 3 . B. 3. C. 6 3 . D. 3 3.
Câu 3. Trong các hàm số sau,hàm số nào ồng biến trên tập xác ịnh của nó? y
A. y=lnx. B. y = log = 0,99 x . C. 34 x.
D. y = x−3.
Câu 4. Trong không gian với hệ tọa ộ Oxyz , khoảng cách từ A(−2;1;−6) ến mặt phẳng (Oxy) là 7 A. 6 . B. 2 . C. 1. D. 41 .
Câu 5. Bất phương trình (3x −1)(x2 +3x −4) 0 có bao nhiêu nghiệm nguyên nhỏ hơn 6? A. 9. B. 5. C. 7 . D. Vô số.
Câu 6. Tập xác ịnh D của hàm số 2022 y=log (2x−1) là . A. D = (0;+ ). B. D= D. 1 C. D= 1;+ . ;+ . 2 2
Câu 7. Kí hiệu z0 là nghiệm phức có phần ảo dương của phương trình 4z2 − + =16z 17 0. Trên mặt phẳng toạ
ộ, iểm nào dưới dây là iểm biểu diễn của số phức w=iz0. 1 A. M − 1 1 − 1 2 ;2 . B. M4 ;1 . C. M1 ;2 . D. M3 ;1 . 2 4 2 4
Câu 8. Xét hình trụ T có thiết diện qua trục của hình trụ là hình vuông cạnh bằng a. Tính diện tích toàn phần S của hình trụ. 2 2 a2 3 a2
A. S = 4 a .
B. S= a . C. S = . D. S = . 2 2
Câu 9. Cho x y, là hai số thực thỏa mãn x2 − + =− +1 yi 1
2i . Giá trị của 2x y+ là A. 5. B. 4 . C. 2 . D. 2 . lOMoAR cPSD| 22014077
Câu 10. Cho z =3+5i. Tính z . A. 8 . B. 8. C. 34. D. 34 .
Câu 11. Tâm ối xứng của ồ thị hàm số nào sau ây cách gốc tọa ộ một khoảng lớn nhất ? A. y =
2x−1. B. y = 1− x . C. y = 2x3 −3x2 −2. D. y =− + −x3 3x 2. x+3 1+ x
Câu 12. Trong không gian với hệ trục tọa ộ Oxyz , xác ịnh tọa ộ tâm I của mặt cầu ( )S :x2 + + − + − =y2 z2 4x 2y 8z 0 .
A. I (−2;1;− 4) .
B. I (−4;2;−8).
C. I (2; 1;− 4).
D. I (4;− 2;8) .
Câu 13. Họ nguyên hàm của hàm số −
y =e2x −e x là
A. e2x −e−x +C .
B. 2e2x + + − e x C . C. 2e − + + + 2x e−x C .
D. e2x e−x C .
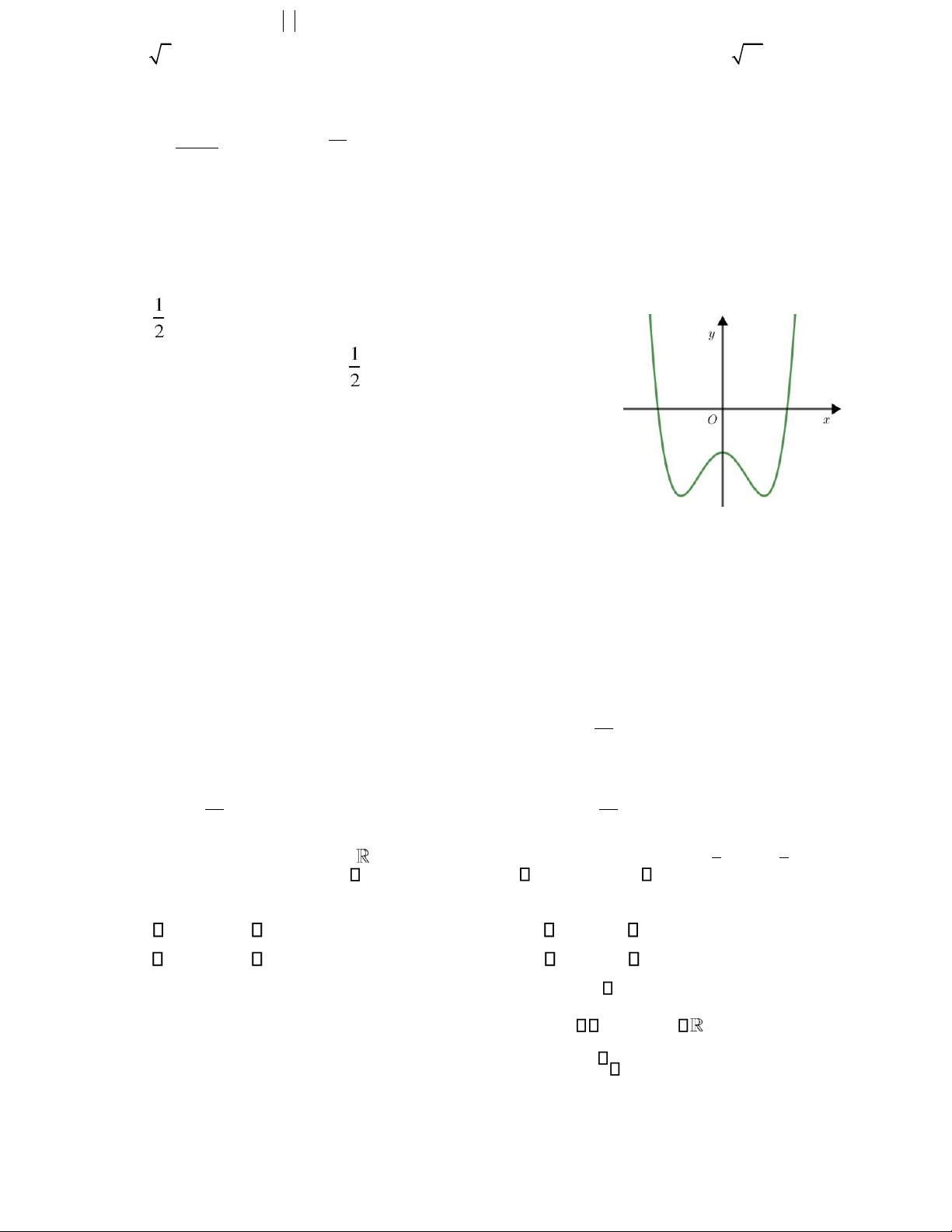
Câu 14. Hàm số nào dưới ây có ồ thị như trong hình bên ?
A. y =− + −x3 3x 1.
B. y =− +x4 2x2 −1.
C. y x= 4 −2x2 −1.
D. y = − −x3 3x 1.
Câu 15. Cho hình chóp S ABCD. có áy ABCD là hình chữ nhật, AB= 2, AD= 4; SA vuông góc với mặt phẳng
áy và SA=6. Tính thể tích của khối chóp. A. 8. B. 16. C. 24. D. 48.
Câu 16. Cho hàm số f x( ) = x2 +sin x +1. Biết F x( ) là một nguyên hàm của f x( ) và F ( )0 =1. Tìm F x( ) .
A. F x( )= −x3 cos x+ +x 2. B. F x( )=
x3 +cosx+ x . 3 C. F x( )=
x3 −cosx+ +x 2. D. F x( )= x3 −cosx+2. 3 3
Câu 17. Cho số phức z = a bi+ (a b, ) và xét hai số phức = z2 +( ) )
z 2 và = 2 .z z + −i z( z . Trong các
khẳng ịnh dưới ây, khẳng ịnh nào úng?
A. là số thực, là số thực.
B. là số ảo, là số thực.
C. là số thực, là số ảo.
D. là số ảo, là số ảo. x = +12t
Câu 18. Trong không gian với hệ trục tọa ộ Oxyz , cho ường thẳng d :
y = −1 t ;t
. Đường thẳng d có z = +53t
một vec tơ chỉ phương là lOMoAR cPSD| 22014077 A. u = (2;1;3).
B. u = (2; 1;−3). C. u = (1;1;5).
D. u = −( 2; 1;−3) .
Câu 19. Cho a, b , c là các số thực dương thỏa mãn alog 52 = 4, blog 64 =16, clog 37 = 49. Tính giá trị T =a + + log 52 b 3c 2 . 2 log 624 log 37 A.
D. T = −3 2 3. T =126. B. T =5+2 3 . C. T =88. 2 4 1 = Câu 20. Cho
f x x( )d =1, f t( )dt = −4. Tính I
f (2y)dy . −2 −2 2 A. I = 2,5. B. I = −5. C. I = −3. D. I =3.
Câu 21. Trong không gian với hệ trục tọa ộ Oxyz, mặt phẳng ( )P : x+ ( )S : x2 + 2y− + =z 3
y2 + z2 = 5 theo giao tuyến là một ường tròn có diện tích là: 0 cắt mặt cầu A. 11 . B. 9 . C. 15 . D. 7 . 4 4 4 4
Câu 22. Cho hàm s ố y = ()
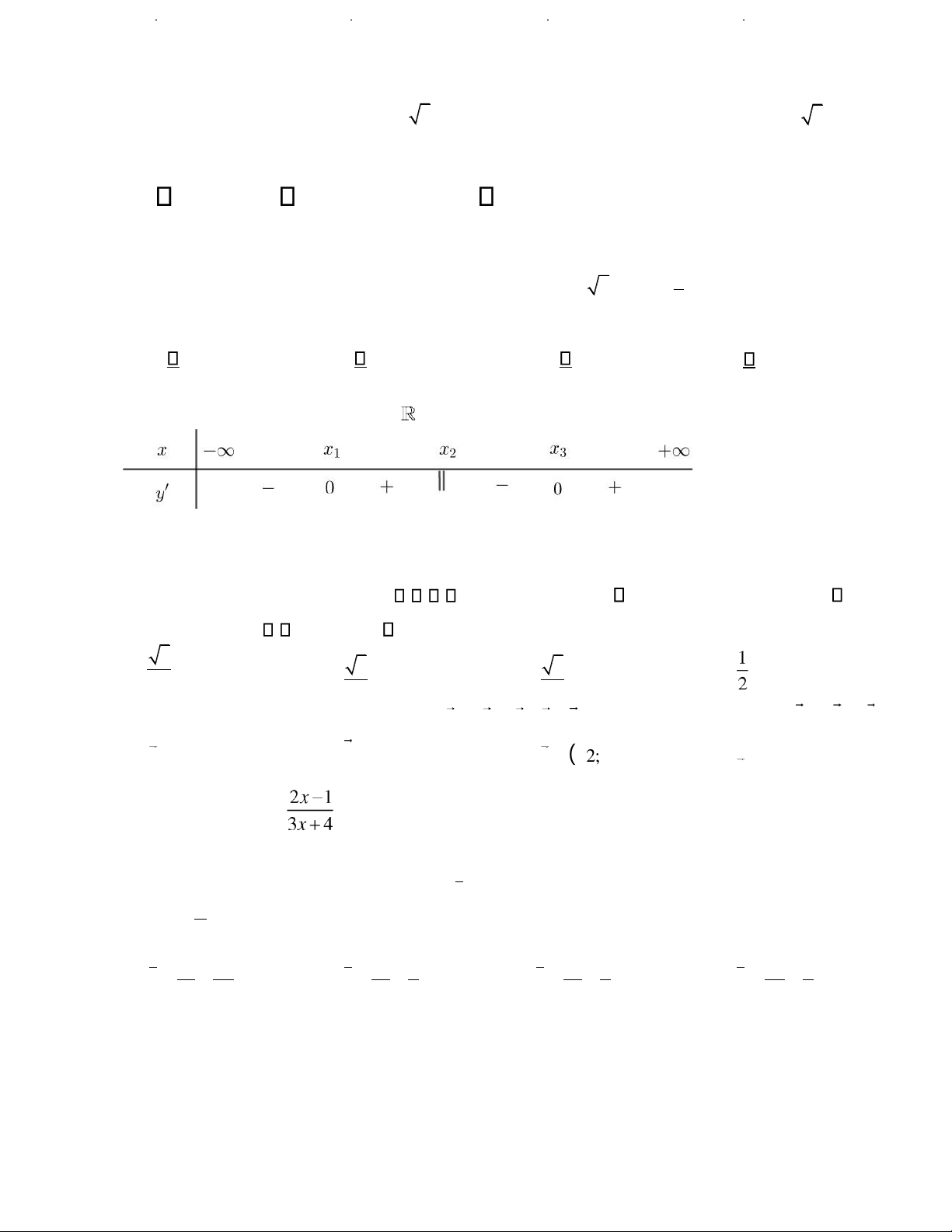
fx xác ị nh trên và có b ả ng xét d ấ u c ủa ạo hàm như sau.
Khi ó số cực trị của hàm số y = f x( ) là A. 3. B. 2 . C. 4 . D. 1.
Câu 23. Cho hình lập phương ABCD ABCD. có cạnh bằng a, gọi là góc giữa ường thẳng AB và
mặt phẳng (BB D D ) . Tính sin . A. 3 . B. 3 3 D. . . C. . 4 2 5 (
Câu 24. Trong không gian với hệ tọa ộ Oxyz cho a = 2i +3j −k , b = 2;3;−7) . Tìm tọa ộ của x = 2a −3b C. x ( 2 =−− ;
A. x =(2; −1;19).
B. x = −( 2; 3;19) . 3; 19).
D. x = − −( 2;1;19) .
Câu 25. Trên ồ thị hàm số y =
có bao nhiêu iểm có tọa ộ nguyên? A. 1. B. 2. C. 0. D. 4. = 2 Câu 26. Cho z
+3i . Xác ịnh số phức liên hợp z của z . 4+ 2i
A. z = 2 + 8 i .
B. z = 7 − 2i.
C. z = 1 + 2i .
D. z = 14 + 2 i . 10 20 10 5 10 5 20 5
Câu 27. Cho khối chóp S ABC.
có thể tích V , nếu giữ nguyên chiều cao và tăng các cạnh áy lên 3 lần thì
thể tích khối chóp thu ược là A. 3V . B. 6V . C. 9V . D. 12V . lOMoAR cPSD| 22014077
Câu 28. Số phức z = (2+3i)(1−i) có phần ảo bằng: A. 0 .
B. 1. C. 2 . D. 5.
Câu 29. Tập tất cả các giá trị của tham số m ể hàm số y = (m−1)x3 −6mx2 −6x +5 nghịch biến trên là oạn
a b; . Khi ó a b+ bằng A.1. B.− . C. . D.2 .
Câu 30. Trong không gian Oxyz , ường thẳng i qua M (−1;2;1) ồng thời vuông góc với mặt phẳng ( )P : x + y
− z + =1 0 có phương trình là
A. x+1 = y −2 = z −1.
B. x −1 = y + 2 = z +1 . 1 1 −1 1 1 −1
C. x +1 = y +1 = z −1.
D. x −1 = y −1 = z +1. −1 2 1 −1 2 1
Câu 31. Cho lăng trụ tam giác ABC ABC. có áy là tam giác ABC ều cạnh bằng a. Hình chiếu vuông góc
của A trên mặt phẳng (ABC) trùng với trung iểm H của cạnh AB. Góc giữa cạnh bên của lăng trụ và
mặt phẳng áy bằng 30o . Tính thể tích của khối lăng trụ ã cho theo a. 3a3 a3 a3 a3 A. . B. . C. . D. . 4 4 24 8 − 5 + 481
Câu 32. Cho hàm số y = x3 x2 −6x
. Tìm số các tiếp tuyến của ồ thị hàm số song song với ường 2 27
thẳng y = 2x − . A. 3. B. 2 . C. 1. D. 0 .
Câu 33. Trong không gian Oxyz , cho iểm A(1;2;−1). Mặt phẳng i qua A và chứa trục Oy là A. y = 2.
B. x+ z = 0.
C. x− z = 0.
D. x−2z = 0.
Câu 34. Cho ABCD ABCD.
là hình lập phương cạnh 2a. Bán kính mặt cầu tiếp xúc với tất cả các cạnh
của hình lập phương bằng A. 2a 2 . B. a 2 . C. a 3 . D. a 2 . 2
Câu 35. Cho một hình nón ỉnh S có chiều cao bằng 8cm, bán kính áy bằng 6cm . Cắt hình nón ã cho bởi
một mặt phẳng song song với mặt phẳng chứa áy ược một hình nón (N ) ỉnh S có ường sinh bằng
4cm. Tính thể tích của khối nón (N ). lOMoAR cPSD| 22014077 A. V = cm3. B. V = cm3. C. V = cm3 . D. V = cm3.
Câu 36. Tập nghiệm của bất phương trình 15.25x −34.15x +15.9x 0 là A. (− ; 1− 1; ). B. 5 33 5; . C. −1;1 . D. − ;53 53; . = x
Câu 37. Cho hàm số y
+1 có ồ thị ( )C và ường thẳng d y: = −2x m+ −1 (m là tham số thực). Gọi k1, x + 2
k2 là hệ số góc của tiếp tuyến tại giao iểm của d và ( )C . Khi ó k k1. 2 bằng A. 3. B. 4 . C. . D. 2 .
Câu 38. Trong không gian với hệ tọa ộ Oxyz , biết mặt phẳng ( )P :ax +by +cz + d = 0 với c 0 i qua hai
iểm A(0;1;0), B(1;0;0) và tạo với mặt phẳng (yOz) một góc 60 . Khi ó giá trị a b c+ + thuộc khoảng nào dưới ây? A. B. C. D. (0;3). (3;5). (5;8). (8;11)
Tìm tập nghiệm của bất phương trình log12 log2 4 x 1 x −+1 −1 Câu 39. A. \ 1 . B. (1;+ ). C. . D. − ;− 3 (1;+ ) . 2
Câu 40. Trong không gian Oxyz , cho iểm M (1;3;−1) và mặt phẳng ( )P : x − 2y + 2z =1. Gọi N là hình chiếu
vuông góc của M trên ( )P . Viết phương trình mặt phẳng trung trực của oạn MN .
A. x−2y+2z +3= 0.
B. x−2y+2z + =1 0.
C. x−2y+2z −3= 0.
D. x−2y+2z +2 = 0. = 1
Câu 41. Giả sử giá trị nhỏ nhất của hàm số y
(m+1)x+2 trên oạn 1;3 bằng , mệnh ề nào dưới ây − +x m 2 úng? − 1
A. m −( 5;−3). B.m (2;4).
C. m −( 9;−6) . D.m 1; . lOMoAR cPSD| 22014077 2
Câu 42. Cho tích phân
0 cos2 cos4 dx x x a b= + 3 , trong ó a b, là các hằng số hữu tỉ. Tính ea + log2 b . −3 A. −2. B. −3. C. . D. 0 .
Câu 43. Cho hình chóp S ABC. có SA vuông góc với mặt phẳng (ABC) . Tam giác ABC ều cạnh bằng a 3 , tam
giác SAC cân. Tính khoảng cách h từ A ến (SBC) .
A. h = 3a .
B. h= a 3 . C. a .
D. h= a 3 . 7 4 7 7 Câu 44. Cho hàm số f x( ) liên tục tập số thực thỏa mãn trên 1
f x( ) (+ 5x −2) f (5x2 −4x) = 50x3 −60x2 + 23x −1, x . Hãy tính ( ) f x x d . 0 A. 2 . B. 1. C. 3. D. 6 .
Câu 45. Tính thể tích V của khối chóp tứ giác ều có chiều cao là h và bán kính mặt cầu nội tiếp là r (h 2r 0) .
A. V = 4r h2 2 .
B. V = 4r h2 2 .
C. V = 4r h2 2 .
D. V = 3r h2 2 . 3(h+2r) (h+2r) 3(h−2r) 4(h−2r)
Câu 46. Gọi S là tập tất cả các giá trị thực của tham số m sao cho ường thẳng d y mx m: = − −3 cắt ồ thị
( )C : y = 2x3 −3x2 −2 tại ba iểm phân biệt A, B , I (1;−3) mà tiếp tuyến của ( )C tại A và tại B vuông
góc với nhau. Tính tổng các phần tử của S . A. −1. B. 1. C. 2 . D. 5.
Câu 47. Cho ường thẳng y = x và parabol y = x2 + a (a là tham số thực dương). Gọi S S1, 2 lần lượt là
diện tích của hai hình phẳng ược gạch chéo trong hình vẽ bên. Khi S = 1
S2 thì a thuộc khoảng nào dưới ây? 9 A. 1 ; . 4 32 1 B. 7 ; . 32 4 lOMoAR cPSD| 22014077 7 C. 3 ; . 16 32 3 D. 0; . 16 + +
Câu 48. Có bao nhiêu giá trị của m ể hàm số y = mx9 (m2 −3m+ 2)x6 (2m3 −m2 −m x) 4 + m2024 −m2025 ồng biến trên . A. Vô số. B. 1. C. 3 . D. 2 .
Câu 49. Trong không gian Oxyz , cho mặt cầu ( )S : x2 + + − + + =y2 z2 2x 2z 1 0 và ường thẳng = y −2 = z d : x
. Hai mặt phẳng ( )P , ( ) P
chứa d và tiếp xúc với ( )S tại T và T . Tìm tọa ộ 1 1 −1
trung iểm H của TT . A. H
5 1; ; − 5 . B. H 5 2; ; − 7 . C. H − 5 1 5; ; . D. H − 7 1 7; ; . 6 3 6 6 3 6 6 3 6 6 3 6
Câu 50. Cho hệ bất phương trình 3 − ) + 22x+ +(x 1
32 + +x 1 22024x−2024 0 (m là tham số). Gọi S là tập tất cả các
x − m+2 x m− +3 0
giá trị nguyên của tham số m ể hệ bất phương trình ã cho có nghiệm. Tính tổng các phần tử của S . A. 10. B. 15. C. 6 . D. 3.
________________HẾT________________ AP AN E SO` 57 1 2 3 4 5 6 7 8 9 10 C D A A C C A D D D 11 12 13 14 15 16 17 18 19 20 A C D C B C A B C A 21 22 23 24 25 26 27 28 29 30 A A D C B B C B B A 31 32 33 34 35 36 37 38 39 40 D C B D A A B A B A 41 42 43 44 45 46 47 48 49 50 lOMoAR cPSD| 22014077 C A A A C A C B A D
Lłi giaßi cau hoßi van dung cao æe soÆ 57 thỏa mãn Câu 44. Cho hàm số f x( ) liên tục trên tập số thực 1
f x( ) (+ 5x −2) f (5x2 −4x) = 50x3 −60x2 + 23x −1, x . Hãy tính ( ) f x x d . 0 A. 2 . B. 1. C. 3. D. 6 .
Hướng dẫn giải:
Theo giả thiết: f x( ) (+ 5x −2) f (5x2 −4x) = 50x3 −60x2 + 23x −1, x (*) . 1 + =
Lấy tích phân hai vế của (*): ( 1( 1 f x( )dx
5x−2) f (5x2 −4x x)d
50x3 −60x2 +23x−1)dx 0 0 0 1 + Suy ra ( 1 f x( )dx
5x−2) f (5x2 −4x)dx =3 (**). 0 0 I J 1 = Xét J
(5x−2) f (5x2 −4x)dx. Đặt t = 5x2 −4x dt = (10x−4)dx dt = (5x −2)dx. 0 = = 1 1 Đổ x 0 t 0 1 1 1 i c ậ n:
. Khi ó: J = ft() . d t = ()
fx d x = I . 2 2 2 0 0 1 Thay vào (**), ta ượ 1 c: I + I =3 I =2. V ậ y ( ) d ⎯ . ⎯ ⎯ → A 2 f x x 0
Câu 45. Tính th ể tích V c ủ a kh ố i chóp t ứ giác ề u có chi ề u cao là h và bán kính m ặ t c ầ u n ộ i ti ế p là r ( h 2 r 0 ) . 2 2 2 2 2 2 2 2 A. 4 r h 4 r h 4 r h 3 r h V = . B. V = . C. V = . D. V = . 3( h +2 r ) ( h +2 r) 3( h −2 r ) 4 ( h −2 r )
Hướng dẫn giải : x =1 t =1 lOMoAR cPSD| 22014077
Xét hình chóp t ứ giác ề u S.ABCD v ớ i M , N l ầ n
lượt là trung iể m c ủ a CD , AB .
G ọ i I là giao iểm ba ườ ng phân giác trong c ủ a tam giác SM
N , suy ra I là tâm ườ ng tròn n ộ i ti ế p tam giác SM
N . M ặ t khác, do . SABCD là
hình chóp t ứ giác ề u nên I là tâm m ặ t c ầ u n ộ i ti ế p
hình chóp này, bán kính m ặ t c ầ u là r = IO . Xét SM
O có MI là ườ ng phân giác ta có: 2 2 SM SI + − = h x hr = (v ớ i x = MO ). MO IO x r ( ) 2 2 2 2 2 2 2 2 2 2 2 hr2 BC x=2 ABCD 2 hr2
r x +h =x h r( − ) x r
−(h r− ) =−r h x =
h−2r S = BC =4 h−2r . 1 4h r2 2
⎯Choïn⎯⎯→C V =
Vậy thể tích khối chóp S.ABCD là = hS. ( ) ABCD . 3 3 h−2r
Câu 46. Gọi S là tập tất cả các giá trị thực của tham số m sao cho ường thẳng d y mx m: = − −3 cắt ồ thị
( )C : y = 2x3 −3x2 −2 tại ba iểm phân biệt A, B , I (1;−3) mà tiếp tuyến của ( )C tại A và tại B vuông
góc với nhau. Tính tổng các phần tử của S . A. −1. B. 1. C. 2 . D. 5.
Hướng dẫn giải:
Phương trình hoành ộ giao iểm của ( )C và ( )d : 2 ( 2 ) 3 x=1 1 2
2x −3x −2 = mx m−
−3 −(x ) x x m− − − =1 0 ( )=2 − − − = 2 1 0 (*) g x x x m
Phương trình (*) có ba nghiệm phân biệt g x( ) = 0 có hai nghiệm phân biệt x 1 = + + g1 8m2 8 0 m −89 .
g( )1 = 2.1 − − −1 m 1 0 m 0
Do hai tiếp tuyến của ( )C tại A và B vuông góc nhau nên k k = − 1. 2
1 trong ó k k1, 2 lần lượt là hệ số
góc tiếp tuyến của ( )C tại A và B. = = Ta có : ( ) ( )
y =6x2 −6x k 2 − 2 − 1 6x1 6x1 , k2 6x2 6x2 . lOMoAR cPSD| 22014077 ) ( ) Do k k = − 2 −
)( 2 − ) = − 36(x x 2 −36x x x + +x 36x x + 1. 2 1 nên (6x1 6x1 6x2 6x2 1 1 2 1 2 1 2 1 2 (*) . =1 0
ịnh lí Vi-ét, ta có : x + = 1 x2 12+1 . Theo x x =− 1 2 m 2 Do ó ( )* 36 − m+1 − + 2 36 − m+1 1 +36 − m+1
+ =10 9m2 9m+ =1 0 . 2 2 2 2
⎯Choïn⎯⎯→A
Tổng các phần tử của S là: m + = − = − 1 m2 1.
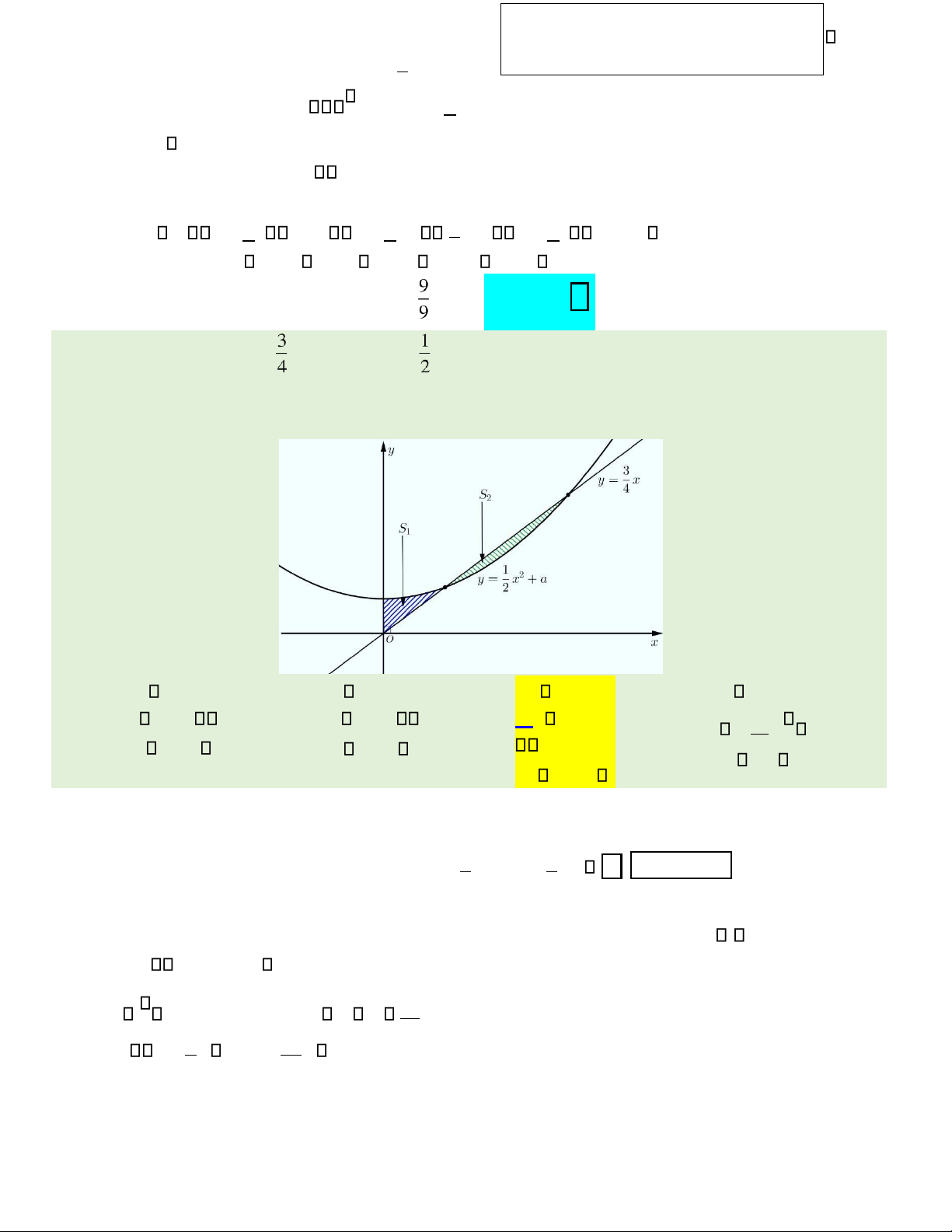
Câu 47. Cho ường thẳng y = x và parabol y = x2 + a (a là tham số thực dương). Gọi S S1, 2 lần lượt là
diện tích của hai hình phẳng ược gạch chéo trong hình vẽ bên. Khi S = 1
S2 thì a thuộc khoảng nào dưới ây? A. 1 ; 9 . B. 7 ; 1 . C. 3 ; 7 3 D. 0; . 4 32 32 4 . 16 16 32
Hướng dẫn giải:
Xét phương trình hoành ộ 1 giao iểm hai ồ thị:
x2 +a = 3 x 2x2 −3x+ 4a = 0 ( )1 . 2 4
Dựa vào ồ thị, ta thấy rằng phương trình ( )1 có hai nghiệm dương phân biệt 0 x1 x2 = 9 32− a 0 3 4a 0 a 9 . S = 2 0; P = 2 0 32 lOMoAR cPSD| 22014077 Ta có: S = + − = − 1 x 01 12 x2 a 43 x dx ; S2 xx 12
43 x− 12 x2 a dx = −xx 12 12 x + 2 a− 43 x dx . S = − = 1 S2 S1 S2 0 x 1
1 x2 +a− 3 x dx+ x 2
1 x2 +a− 3 x dx = 0 0 2 4 x1 2 4 + − + = x 2 1 x2 a 3 x x d = 0
x3 ax− 3 x2 x2 0 0 2 4 6 8 0 1 x 3 + − 3 2 = 2 + = 2 + = 2 ax2 x 0 1 x a − 3 x 0 4x 24a −9x 0 (2). 2 2 2 2 2 6 8 6 8 Hơn nữa, x 2 − +
2 cũng thỏa mãn (1), tức là: 2x2 3x2 4 0a= (3). x2 4a=−(2x − ) 22 3x2 0 (loaïi) a
Thay (3) vào (2): 4x 2 − 2 − )− = 2 + = 2 6 2( x2 3x2 9x2 0 −8x2 9x2 0 x 9 (nhaän) (do 0). 2 8
⎯Choïn⎯⎯→ 9 ( ) C Với x = = 2 3 a27 3 ; 7 . 8 128 16 32 + +
Câu 48. Có bao nhiêu giá trị của m ể hàm số y = mx9 (m2 −3m+ 2)x6 (2m3 −m2 −m x) 4 + m2024 −m2025 ồng biến trên . A. Vô số. B. 1 . C. 3 . D. 2 .
Hướng dẫn giải:
Tập xác ịnh hàm số: D= . Ta có: y = 9mx8 +6(m2 −3m+ 2)x5 + 4 2( m3 −m2 −m x) 3; y = x3
9mx5 +6(m2 −3m+2)x2 +4 2( m3 −m2 −m) = 0 x 0 (nghieäm boäi . leû) g x( ) 9mx5 6(m2
3m 2)x2 4 2( m3 m2 m) 0
Điều kiện cần: Hàm số ã cho ồng biến trên
x =0 là nghiệm bội chẵn của phương trình
y = 0 x = 0 là nghiệm bội lẻ của phương trình g x( ) = 0 . m=1 lOMoAR cPSD| 22014077
Do ó: g( )0 0 2= m3 −m2 − =m 0 m=− 1 . 2 m=0
Điều kiện ủ: Thử lại các giá trị m vừa tìm ược.
Với m =0, ta có y =12x5 (không thỏa mãn y 0, x ).
Với m=1, ta có y =9x8 0, x (thỏa mãn).
Với m = − 1 , ta có y = − 9 x8 + 45 x5 = − 9 x x5( 3 −5) = 0
x = 03 (không thỏa mãn 2 2 2 2 x = 5 y 0, x ).
Vậy có duy nhất 1 giá trị của m thỏa mãn yêu cầu bài toán là m=1. ⎯Choïn⎯⎯→B
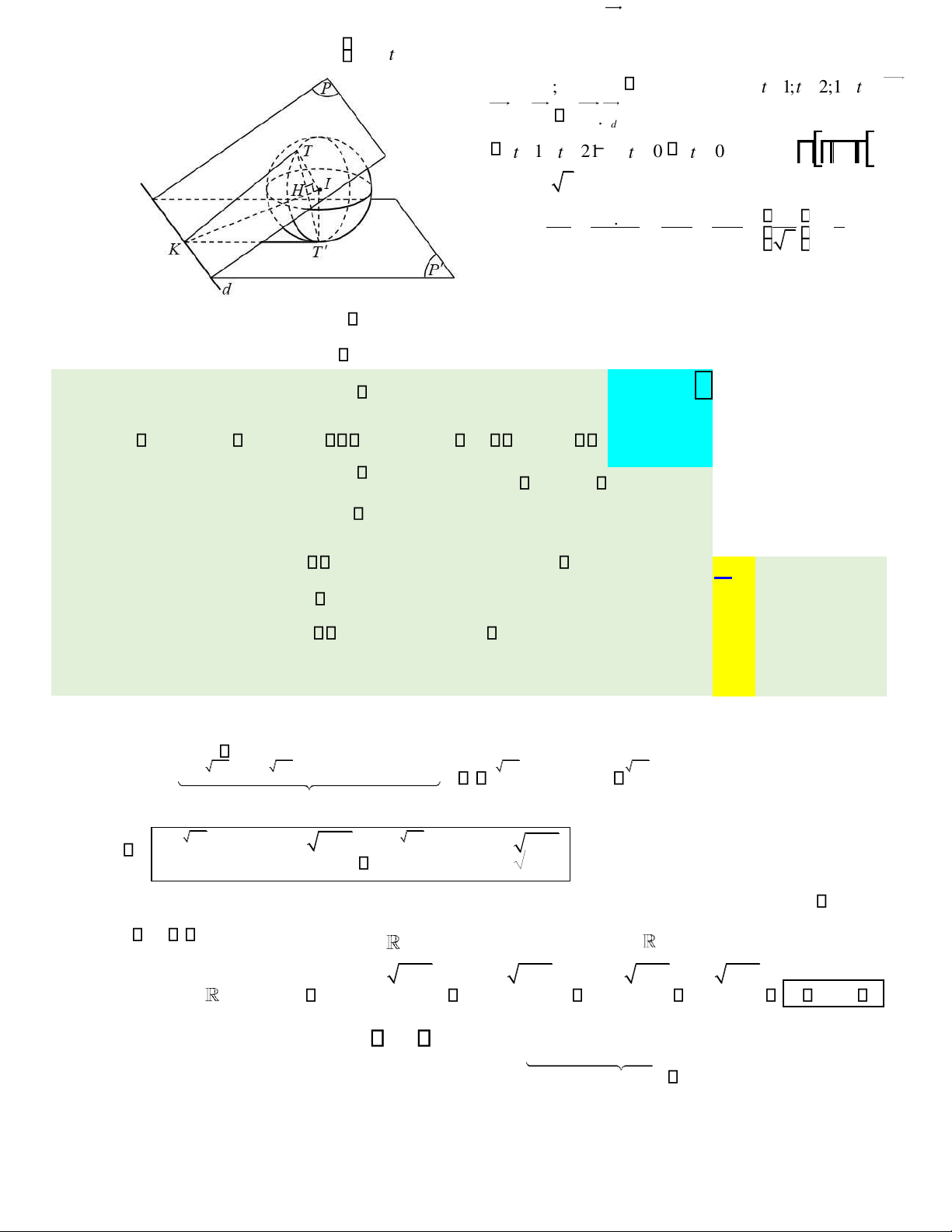
Câu 49. Trong không gian Oxyz , cho mặt cầu ( )S : x2 + y2 + z2 − 2x + 2z + =1 0 và ường thẳng = y −2 = z d : x
. Hai mặt phẳng ( )P , ( ) P
chứa d và tiếp xúc với ( )S tại T và T . Tìm tọa ộ 1 1 −1
trung iểm H của TT . A. H 5 1; ; − 5 . B. H 5 2; ; − 7 . C. H − 5 1 5; ; . D. H − 7 1 7; ; . 6 3 6 6 3 6 6 3 6 6 3 6
Hướng dẫn giải:
Mặt cầu ( )S có tâm I (1; 0; −1) , bán kính R =1. Gọi K = d (ITT ) . Ta có
dd ⊥⊥ ITIT d ⊥ (ITT ) nên K là hình chiếu vuông góc của I trên d . x =t lOMoAR cPSD| 22014077 z t =− G ọ i (
Kt ;2 +t ; t
− ) d , suy ra IK =( t− + 1− ;t 2 ;1 t) ; IK ⊥u = d I . Ku d 0 t 1 −++ t 21 − t += 0 t
= 0 . Suy ra K ( 0 ;2; 0) và IK = 6 . 2 2 2 IH IH. IK IT R 1 1 Ta có : = = = = = . 2 2 2 IK IK IK IK 6 6
= +2 t với vectơ chỉ phương là u =( d 1;1;−1).
Phương trình tham số của d: y
⎯Choïn⎯⎯→ 6(x − =− A H 1)1 = 1 5 1 IH
IK 6IH = IK 6y = H 2 H ; ;−5 . 6 (x + = H 1) 1 6 3 6 6
. Gọi S là tập tất cả các
ổng các phần tử của S .
Câu 50. Cho hệ bất phương trình 3 − + là tham số) 2x+ +x 1
32+ +x 1 2024x−2024 0 (m D. 3 . 2 2 m. Tính t
x −(m+2)x m− +3 0
giá trị nguyên của tham số m ể hệ bất phương trình ã cho có nghiệ A. 10. B. 15. C. 6 .
Hướng dẫn giải:
Điều kiện: x −1. Ta có: 3 − + + + 2x+ +x 1
32+ +x 1 2024 2024 0 3x− 2x+ +x 1 2024 3x 2+ +x 1 2024 ( )1 (2). ( ) ( ) 3 + + + 2x+ +x 1 1012 2 x+ x+1 32+ +x 1 1012 2 x+1
t( ) = 3t +1012t trên
; f ( )t = 3t Xét hàm số f
ln3+1012 0, t, suy ra f t( ) là hàm số ồng Do ó ( ) ( ) biến trên .
( )2 f 2x+ x+1 f 2+ x+1
2x+ x+1 2+ x+1 − 1 x 1 . = −
Vậy tập nghiệm của (1) là S 1 1;1 .
Hệ bất phương trình ã cho có nghiệm khi và chỉ khi x2 −(m+2)x m− 2 +3 0 có tập nghiệm S2 ( )3 lOMoAR cPSD| 22014077 thỏa S S 2
1 tức là (3) có ít nhất một nghiệm thuộc −1;1 . Đặt g x m( )
, = x 2 −(m+2)x m− 2 +3 với = (m+ 2)2 + 4m2 −12 = 5m2 + 4m−8. 2 −− 211 2 − + 211 Trường hợp 1: 0 m
. Khi ó g x m( , ) 0, x nên 5 5 1 − , 73 0 ,93 2 −− 211 2 − + 211
g x m( , ) 0, −x 1;1 m
. Vì vậy thỏa mãn yêu cầu của bài 5 5 toán. 1 − ,73 0 ,93 2 − + 211 m 5 0 , 93 2 −− 211 m Trường hợp 2: 0 . Khi ó g x m 5 ( , ) = 0 có hai nghiệm x 1 − , 73 1 x2 . Ta cần g x m( ) ,
0 có nghiệm thuộc oạn −1;1 . Tuy nhiên, ta xét trường hợp phủ ịnh với nó là:
g x m( , ) 0 không có nghiệm thuộc oạn −1;1 , khi ó: g(−1) 0 1+ + −m 2 m + 22 3 0 g( )1 0
1− − −m 2 m +3 0 m 3 2
m − − 22 m 1
mm − 3 (*). Lấy phủ ịnh lại kết quả của (*), ta có: −2 m 3. m −
Hợp kết quả của hai trường hợp trên, ta có m
2;3 mà m nguyên nên S = − 2;
⎯Choïn⎯⎯→D 1;0;1;2;− 3 .
Tổng các phần tử của S bằng 3.