Đề chọn đội tuyển HSG Toán 12 năm 2019 – 2020 trường Lê Quý Đôn – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ KHẢO SÁT CHỌN ĐỘI TUYỂN HSG 12
TRƯỜNG THPT LÊ QUÝ ĐÔN - ĐỐNG ĐA MÔN: TOÁN (Đề gồm 01 trang) NĂM HỌC: 2019 - 2020
Thời gian làm bài 180 phút Câu 1 (4 điểm).
Tìm m để đồ thị hàm số 3 2
y  x  3x  mx  2  m cắt trục hoành tại 3 điểm phân biệt ,
A B, C sao cho tổng hệ số góc của các tiếp tuyến với đồ thị hàm số tại các điểm ,
A B, C bằng 3. Câu 2 (6 điểm).
a. Giải phương trình: 2 sin 2x  cos 2x  2  2 sin 2 .
x cos x  sin x  2 cos x. 3 x    y  2 2 x  2xy  1
b. Giải hệ phương trình:  . 2
x  3x  y  2  0  Câu 3 (4 điểm).  2020 u  
Cho dãy số u xác định bởi 1 *  2019 , n   . n  2 2u  u  2u  n 1  n n 1 1 1 Đặt S    ...  . Tính lim S . n u  2 u  2 u  2 n 1 2 n Câu 4 (4 điểm).
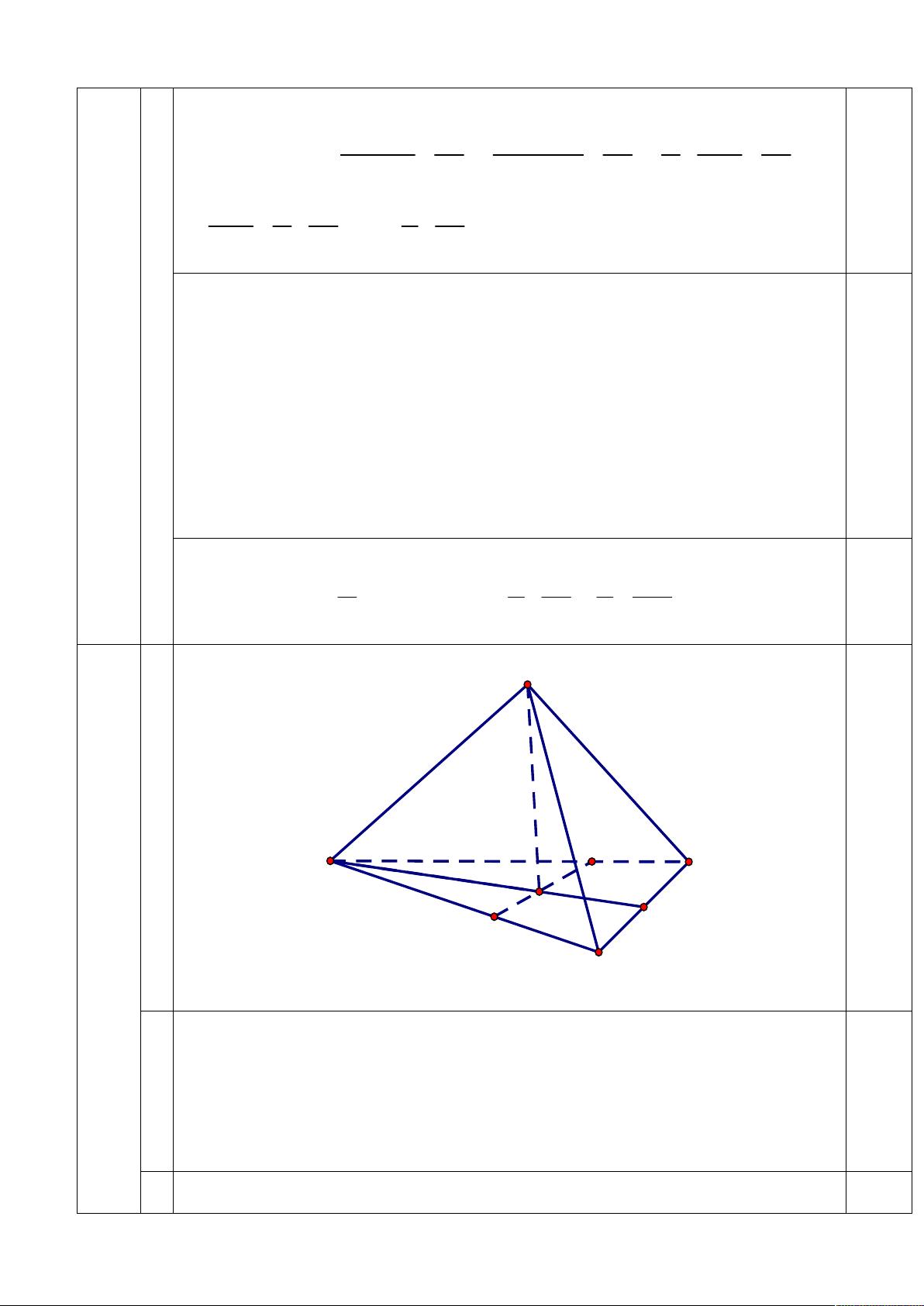
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 1. Gọi M , N là hai điểm thay
đổi lần lượt thuộc các cạnh AB , AC SMN sao cho mặt phẳng   luôn vuông góc với
mặt phẳng  ABC  . Đặt AM  x, AN  . y
a. Chứng minh rằng x  y  3x . y
b. Tìm x , y để S
 MN có diện tích bé nhất, lớn nhất. Câu 5 (2 điểm).
Cho a, b, c là các số thực dương thoả mãn a  b  c  3 . Tìm giá trị lớn nhất của biểu thức. 2 abc abc P    3 .
3  ab  bc  ca 6
1 a1 b1 c
----------------------- HẾT -----------------------
Thí sinh không sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
ĐÁP ÁN ĐỀ KHẢO SÁT CHỌN ĐỘI TUYỂN HỌC SINH GIỎI 12 CÂU Ý NỘI DUNG ĐIỂM
Tìm m để đồ thị hàm số 3 2
y  x  3x  mx  2  m cắt trục hoành tại 3 điểm phân biệt ,
A B,C sao cho tổng hệ số góc của các tiếp tuyến với đồ thị hàm số tại các điểm 4 , A B,C bằng 3.
Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt khi và chỉ khi phương trình 3 2
x  3x  mx  2  m  0
(1) có 3 nghiệm phân biệt. 1,0 3 2 2
x  3x  mx  2  m  0  (x 1)(x  2x  m  2)  0
Phương trình (1) có 3 nghiệm phân biệt 2
 x  2x  m  2  0 (2) có hai nghiệm phân
 '  3  m  0 biệt khác 1 (*)    m  3 . 1,0 1
1 2  m  2  0 
Gọi x , x là nghiệm của phương trình (2), suy ra tổng hệ số góc tiếp tuyến của đồ thị 1 2 hàm số tại giao điểm , A B, C là: 1,5 2
y '(1)  y '(x )  y '(x )  3(x  x )  6x x  6(x  x )  3m  3  9  3m 1 2 1 2 1 2 1 2
Tổng HSG của các tiếp tuyến bằng 3  9  3m  3  m  2 (t/m đk (*)). 0.5 ĐS: m  2
Giải phương trình: 2 sin 2x  cos 2x  2  2 sin 2 .
x cos x  sin x  2 cos x a 1,0  os2x = c
 2 sin 2x.cosx - sin2x 2 sin x - sin2x2 2cosx - 2 2  2 os c
x 1  sin 2x  2 osx - c 1 2 sinx 2 os c x -  1  2  2 osx - c 1 1,0 2   2 osx + c 1 2 osx - c 1   2 osx - c 1sin 2x - 2 sinx +2    1 0.5 osx = c   1   2 
 2 sinx + cosx  2sinx.cosx - 1 = 0 2   + (1)  x    k 2 4 0.5   + (2)  x  
 k  x   k 2 , 4 4
Kết luận phương trình có 3 họ nghiệm : ……….. 3 x    y  2 2 x  2xy  1
Giải hệ phương trình:  . 2 b
x  3x  y  2  3  2  x  2x 
x  y 1 Viết lại hệ:  2
x  2x  x  y  2  1,0 Đặt 2
u  x  2x, v  x  y . Dễ có: u  1  . 0.5  . u v  1 Hệ trở thành:  u  v  2  u   1  Suy ra:  v  1  0.5 2
x  2x  1  Ta có  x  y  1   0.5 x  1   y  0  0.5  2020 u  
Cho dãy số u xác định bởi: 1 *  2019 , n   n  2 2u  u  2u  n 1  n n 4 1 1 1 Đặt S    ...  . Tính: lim S . n u  2 u  2 u  2 n 1 2 n Ta chứng minh * u  1, n
   (1) bằng phương pháp qui nạp toán học. n 3 2020 1,0
Với n  1, u 
 1  (1) đúng với n  1 . 1 2019
Giả sử (1) đúng với n  k (k  1) ta có u  1 gtqn . Ta phải chứng minh (1) đúng với k  
n  k 1 tức là phải chứng minh u  1 . k 1  2 2 2 u  2u u  2(u 1) u 1 Thật vậy u 1 k k  1 k k k     0  u 1  0  u  1. k 1  k 1  k 1 2 2 2 2 
Theo nguyên lý qui nạp toán học ta có * u  1, n    n Mặt khác 2 * u
 u  u  u  0, n
   vì dãy số u  1 nên dãy số u là dãy số n  n 1  n n n n tăng.
Với mọi k  N*, ta có : 2 1 (u  2)  u 1 1 1 1 2u  u (u  2) k k        k 1  k k u (u  2) u u (u  2) u u u  2 u k k k 1  k k k 1  k k k 1  1,0 1 1 1 1 1     S   u  2 n u u u u k k k 1  1 n 1 
Ta chứng minh dãy số u là dãy số không bị chặn. n 
Giả sử phản chứng dãy số (un) bị chặn . Do dãy số u là dãy tăng (cmt) nên ta có dãy n 
u tăng và bị chặn thì dãy số u có giới hạn hữu hạn. Giả sử limu  a . Vì u  1 n  n  n  n 1,0
Nên ta có a  1 . Từ định nghĩa 2 2u
 u  2u . Chuyển qua giới hạn ta có: n 1  n n
 2a = a2 + 2a  a = 0. Mâu thuẫn với a ≥1.
Vậy giả sử sai, suy ra dãy u không bị chặn trên . do u là dãy tăng nên n  n  1 1 1 1 2019 lim u      S     1,0 n  lim 0 lim lim ( ) n u u u u 2020 n 1 n 1  1 S 4 M A B O H N C
Chứng minh x  y  3xy
Kẻ SO  MN ,O  MN do SMN    ABC   SO   ABC  1,0
a. Do hình chóp S.ABC là hình chóp đều nên O là tâm đương tròn ngoại tiếp tam giác ABC .
Gọi H là trung điểm của BC .Và O là trọng tâm của tam giác ABC .    AB  AC   1  1  3 
Ta có AB  AC  2.AH  AM  AN  2AH  .AM  AN  2 AO . AM AN x y 2 4
Vì M  AB, N  AC  1,0    . x AM  . y AN  3x . y AO .
Do M , N , O thẳng hàng nên x  y  3x . y (đpcm). 1 1 S  . SO MN  S
nhỏ nhất khi MN nhỏ nhất và S  . SO MN  S SMN  2 SMN  SMN  2 SMN 
lớn nhất khi MN lớn nhất 2 2 Ta có 2 2 2 0 2 2
MN  x  y  2 . xy os
c 60  x  y  xy   x  y  3xy  9 xy  3xy 1,0
Từ giả thiết ta có 0  ; x y  1 4
Từ (1) ta có 3xy  x  y  2 xy  xy  9 0.5 1  x   1  y  
1  0  xy 1  x  y  xy 1  3xy  xy  2  4 1  Đặt t = xy, 2 2 t  ;
 MN  9t  3t  9 2     4 1 
Lập bảng biến thiên của hàm số f t  2
 9t  3t; t  ;  ta được 9 2    4 2
MN nhỏ nhất khi t  khi x  y  9 3 x  1  1 1  x 
MN lớn nhất khi t  khi  1 hoặc  2 0,5 2 y     2 y  1 
Cho a, b, c là các số thực dương thoả mãn a  b  c  3 . Chứng minh rằng: 2 abc abc   3  1
3  ab  bc  ca 6
1 a1 b1 c 2 2 abc abc Đặt : P    3
3  ab  bc  ca 6
1 a1 b1 c 0.5 2
Áp dụng bất đẳng thức:  x  y  z   3 xy  yz  zx x
 , y, z   0.5
Với a, b, c  0 ta có: 5
ab  bc  ca2  3abc a  b  c  9abc  0  ab  bc  ca  3 abc
Ta có:   a  b  c    abc 3 3 1 1 1 1 a
 , b, c  0. Thật vậy:
1 a1 b1 c  1 a  b  c  ab  bc  ca  abc 3
 1 3 abc  3 abc  abc  1 abc 3 2 3 3 3 2 abc abc Khi đó: P    31 abc  3 1 abc 6 0.5 Đặt: 6 3 2 3
abc  t  abc  t , abc  t . 3
 a  b  c 
Vì a, b, c  0 nên 0  abc   1  0  t  1    3  2 2 t 1 Xét hàm số 3 f (t)   
t , t  0; 1 3 2 
31 t  1 t 6 2 2 2 2  t 2t t  t 1  t 0.5 f '(t)     2t.   3 2 2 2  3 2 2 2  (1 t ) (1 t ) 2 (1 t ) (1 t ) 2   5 2
(1 t)(1 t ) t  2t.   0, t   (0;1] 2 2 3 2
(1 t ) .(1 t ) 2
Suy ra f (t) đồng biến trên f (t) trên (0;1] ta có f (t)  f (1)  1, t   (0;1] . 2 abc abc    3  1
3  ab  bc  ca 6
1 a1 b1 c 0.5
Dấu ‘=’ xảy ra khi a  b  c  1.
Vậy MaxP  1 khi a  b  c  1
Lưu ý: Học sinh giải cách khác mà đúng vẫn cho điểm tối đa